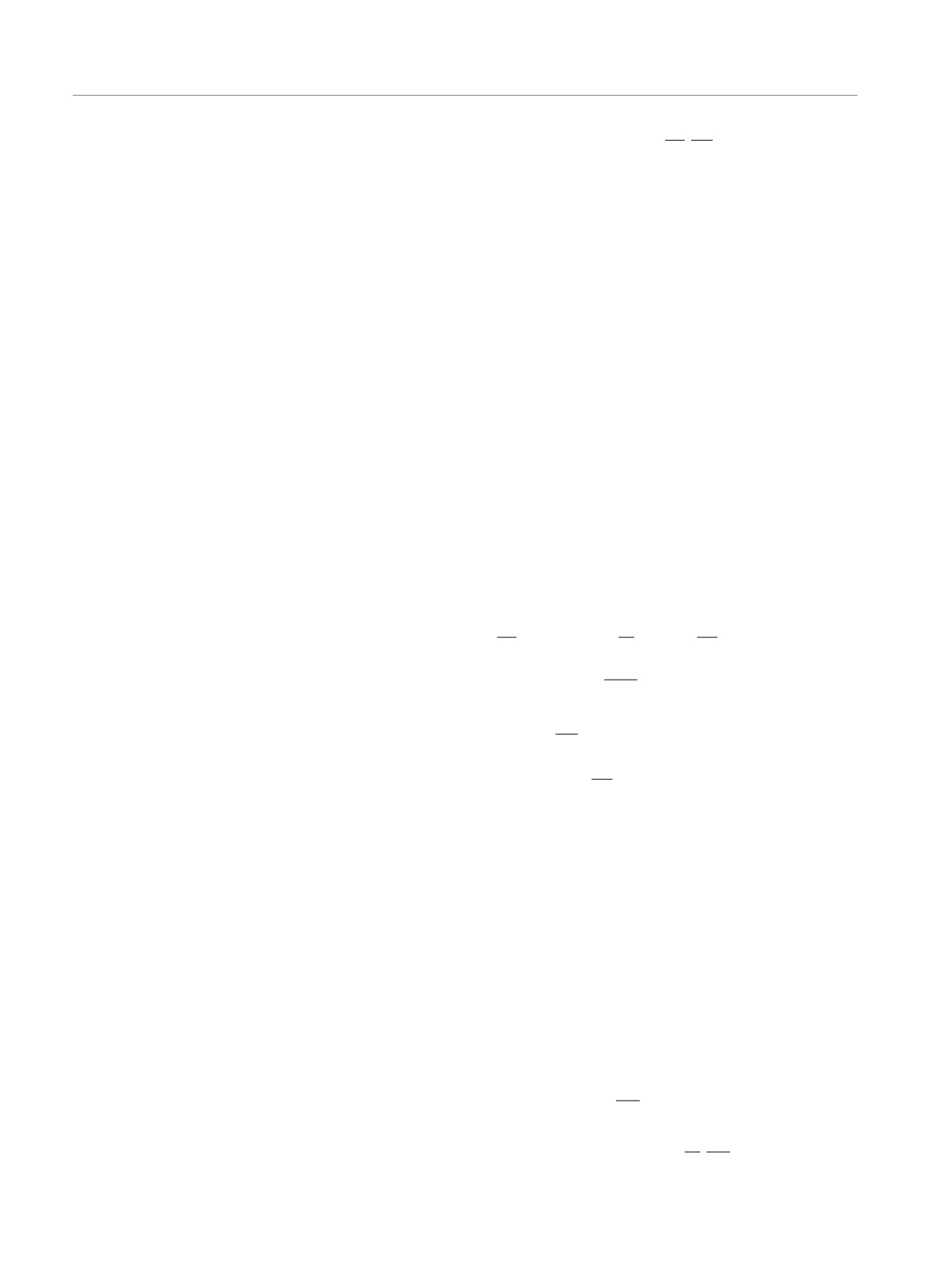ЖЭТФ, 2020, том 157, вып. 5, стр. 901-927
© 2020
МАГНИТНАЯ КОНВЕКЦИЯ В НЕОДНОРОДНО
ВРАЩАЮЩЕЙСЯ ЭЛЕКТРОПРОВОДЯЩЕЙ СРЕДЕ ПОД
ДЕЙСТВИЕМ МОДУЛЯЦИИ ВНЕШНЕГО МАГНИТНОГО ПОЛЯ
М. И. Коппa, А. В. Турc*, В. В. Яновскийa,b**
a Институт монокристаллов Национальной академии наук Украины
61001, Харьков, Украина
b Харьковский национальный университет им. В. Н. Каразина
61000, Харьков, Украина
c Université de Toulouse [UPS], CNRS, Institut de Recherche en Astrophysique et Planétologie
BP 44346, 31028 Toulouse Cedex 4, France
Поступила в редакцию 1 октября 2019 г.,
после переработки 27 ноября 2019 г.
Принята к публикации 28 ноября 2019 г.
Исследуется колебательный режим магнитной конвекции (задача Рэлея - Бенара) в неоднородно враща-
ющейся электропроводящей жидкости во внешнем периодическом магнитном поле. В линейной теории
колебательной конвекции получено критическое значение числа Рэлея Rac в зависимости от профиля
неоднородного вращения (числа Россби Ro). Показано, что кеплеровский профиль вращения с числом
Россби Ro = -3/4 оказывает дестабилизирующий эффект. С помощью метода теории возмущений по
малому параметру надкритичности числа Рэлея получено нелинейное комплексное уравнение Гинзбур-
га - Ландау. Численные решения этого уравнения позволили определить теплоперенос (по числу Нус-
сельта Nu) в слое жидкости для разных значений амплитуд δ и частот модуляции ωB. С помощью
метода Галеркина получена нелинейная динамическая система неавтономных уравнений типа Лоренца.
Численный анализ этих уравнений показал возможность управления хаотическим поведением конвектив-
ных течений в неоднородно вращающейся (Ro = -3/4) жидкости при помощи изменения параметров
модуляции внешнего магнитного поля.
DOI: 10.31857/S0044451020050132
клонения осей вращения и магнитного поля от вер-
тикальной оси (поля тяжести) развита в работе [12].
1. ВВЕДЕНИЕ
Очевидно, что линейная теория дает информа-
цию о начале конвекции и не дает информации
В последнее время свободная конвекция в сло-
о конечной амплитуде конвекции. Эта амплитуда
ях жидкости (конвекция Рэлея - Бенара) [1-3] ин-
возникает, когда происходит взаимодействие между
тенсивно исследуется при решении ряда инженер-
несколькими модами возмущений. Поэтому важно
но-технических, астро- и геофизических задач. Осо-
понять физический механизм нелинейных эффек-
бый интерес вызывают задачи, связанные с влияни-
тов и количественно оценить тепло- и массоперенос
ем вращения и магнитного поля на конвекцию Рэ-
в терминах конечных амплитуд. В настоящее время
лея - Бенара, например, из-за их приложений к тео-
для построения нелинейной теории конвекции ши-
рии вихревого и магнитного динамо [4-6]. Линей-
роко используется метод возмущений, разработан-
ная теория конвективной неустойчивости достаточ-
ный в работе [13]. В ней показано, что первоначаль-
но хорошо изложена в монографиях [1-3, 7] и час-
ный перенос тепла конвекцией линейно зависит от
тично в обзорах [8-11]. Линейная теория вращаю-
числа Рэлея, а затем, при больших числах Рэлея,
щейся магнитной конвекции для произвольного от-
перенос тепла немного отличается от линейного слу-
* E-mail: Anatoly.Tour@irap.omp.eu
чая. Авторы работы [13] называли этот процесс сла-
** E-mail: yanovsky@isc.kharkov.ua
бонелинейным.
901
М. И. Копп, А. В. Тур, В. В. Яновский
ЖЭТФ, том 157, вып. 5, 2020
Дальнейшее развитие слабонелинейная теория
редь, вызывает уменьшение переноса тепловой энер-
конвекции получила в работах [14-17]. В них слабо-
гии в этих областях [37]. Поскольку вращение сол-
нелинейный режим конвекции описывался автоном-
нечной плазмы в однородном (крупномасштабном)
ным уравнением Гинзбурга - Ландау для конечной
магнитном поле приводит к возбуждению различ-
амплитуды. Следующий этап развития слабонели-
ных спектров волн [38], они могут модулировать
нейной теории конвекции включал в себя учет мо-
однородное магнитное поле. Как было показано в
дуляции параметров, управляющих процессом кон-
работах [28, 39], модуляция магнитного поля может
векции, что очень важно для решения многих тех-
приводить как к увеличению, так и к уменьшению
нологических проблем. Различные типы модуляции
теплопереноса в конвективной среде. Таким обра-
внешних полей, такие как вращение [18-21], грави-
зом, время жизни и появление солнечных пятен мо-
тация [22-24], температура [25-27], магнитное по-
жет быть связано с влиянием осциллирующего маг-
ле [28, 29], исследовались для стационарной слабо-
нитного поля на конвекцию. В работах [28, 39] ис-
нелинейной конвекции в различных средах: в пори-
следовался стационарный и колебательный режимы
стых средах, наножидкостях и т.д. В работах [18-29]
нелинейной магнитоконвекции под влиянием маг-
выяснено влияние модуляции параметров (враще-
нитного поля, зависящего от времени. Магнитное
ния, гравитации, температуры, магнитного поля) на
поле в работах [28, 39] было представлено в виде
тепло- массоперенос в конвективных средах.
суммы постоянной (стационарной) и осциллирую-
В отличие от работ [18-29], существует большое
щей частей. Причем осциллирующая часть имеет
количество работ (см., например, [30-36]), посвя-
второй порядок малости по параметру разложения
щенных исследованию параметрического возбужде-
(параметру надкритичности числа Рэлея). В рабо-
ния конвекции в различных конвективных средах
тах [28,39] также был проведен анализ ковективной
под действием внешних периодических полей произ-
неустойчивости для стационарного и колебательно-
вольной амплитуды и частоты. Поиск границ линей-
го режимов численным методом решения неавто-
ной конвективной неустойчивости и анализ отклика
номного уравнения Гинзбурга - Ландау.
системы в этих работах проводились с помощью тео-
Однако в этих работах [28, 39] не учитывалось
рии Флоке. Согласно этой теории, в параметриче-
вращательное движение среды. Кроме того, влия-
ски возбуждаемых конвективных средах могут на-
ние неоднородного (или дифференциального) вра-
растать возмущения синхронного, субгармоническо-
щения на конвективные процессы еще мало изуче-
го или квазипериодического отклика. Нелинейные
но. Интерес к этим исследованиям вызван преж-
волновые режимы конвекции в горизонтальном слое
де всего различными астрофизическими проблема-
несжимаемой бинарной смеси с аномальной термо-
ми. Известно, что большинство различных косми-
диффузией под воздействием модулированного по-
ческих объектов, состоящих из плотных газов или
ля тяжести изучались в работах [33, 34, 36], а под
жидкости (Юпитер, Сатурн, Солнце и т. д.), враща-
действием вибраций теплового поля — в [35]. В этих
ется неоднородно, т. е. разные части объекта враща-
работах были установлены нелинейные режимы, со-
ются вокруг общей оси вращения с различной уг-
ответствующие стоячим волнам (режим субгармо-
ловой скоростью. Дифференциальное вращение на-
нического отклика), модулированным бегущим вол-
блюдается также в галактиках, аккреционных дис-
нам (режим квазипериодического отклика), режи-
ках и кольцах планет. Крупномасштабные вихревые
му модулированной конвекции (режим синхронного
структуры, такие как тайфуны, циклоны и антицик-
отклика). Вибрации поля тяжести, модуляции тем-
лоны, также вращаются неоднородно. Устойчивость
пературы, переменные электрические и магнитные
неоднородного вращения идеально проводящей сре-
поля могут эффективно использоваться для управ-
ды в магнитном поле была впервые рассмотрена в
ления тепло- массопереносом в различных техноло-
работах [40, 41]. Там же показано, что слабое осе-
гических процессах.
вое магнитное поле дестабилизирует азимутальное
Кроме технологических задач учет модуляции,
дифференциальное вращение плазмы, и при выпол-
например магнитного поля, играет важную роль в
нении условия dΩ2/dR < 0 в бездиссипативной плаз-
моделировании конвективных процессов, происхо-
ме возникает магнитовращательная неустойчивость
дящих на Солнце. Известно, что солнечные пят-
(МВН) или стандартная МВН. Поскольку это усло-
на являются областями выхода в фотосферу силь-
вие выполняется и для кеплеровских течений Ω ∼
ных магнитных полей, и потемнение фотосферы в
∼ R-3/2, МВН является наиболее вероятным ис-
пятнах обусловлено подавлением магнитным полем
точником турбулентности в аккреционных дисках.
конвективных движений вещества. Это, в свою оче-
Открытие МВН послужило толчком к многочислен-
902
ЖЭТФ, том 157, вып. 5, 2020 Магнитная конвекция в неоднородно вращающейся электропроводящей среде. . .
ным теоретическим исследованиям.
0
Первые теоретические исследования, которые
а
касались проблемы аккреционных течений, прово-
дились в приближении бездиссипативной плазмы с
учетом радиальной тепловой стратификации [42], а
U0(X)
Z
также замагниченности тепловых потоков [43]. В ра-
Y
боте [44] рассматривалась устойчивость дифферен-
циально-вращающейся плазмы в аксиальном маг-
нитном поле с одновременным учетом как дисси-
X
пативных эффектов (вязкость и омическая дисси-
пация), так и тепловой радиальной стратификации
Z
0
плазмы. МВН в спиральном магнитном поле или с
б
B0
нетривиальной топологией B0rotB0 = 0 изучалась
в работах [45, 46]. При исследовании МВН диффе-
ренциальное вращение среды моделируется течени-
ем Куэтта, заключенным между двумя вращающи-
T2
мися с разными угловыми скоростями цилиндрами,
что оказывается удобным для реализации лабора-
торных экспериментов [47].
Y
В работах [48,49] была совместно рассмотрена за-
U0
дача об устойчивости электропроводящей жидкос-
T1
ти между двумя вращающимися цилиндрами (те-
g
чение Куэтта) и задача Рэлея - Бенара во внешнем
X
постоянном магнитном поле. Там же было прове-
дено исследование хаотического режима на основе
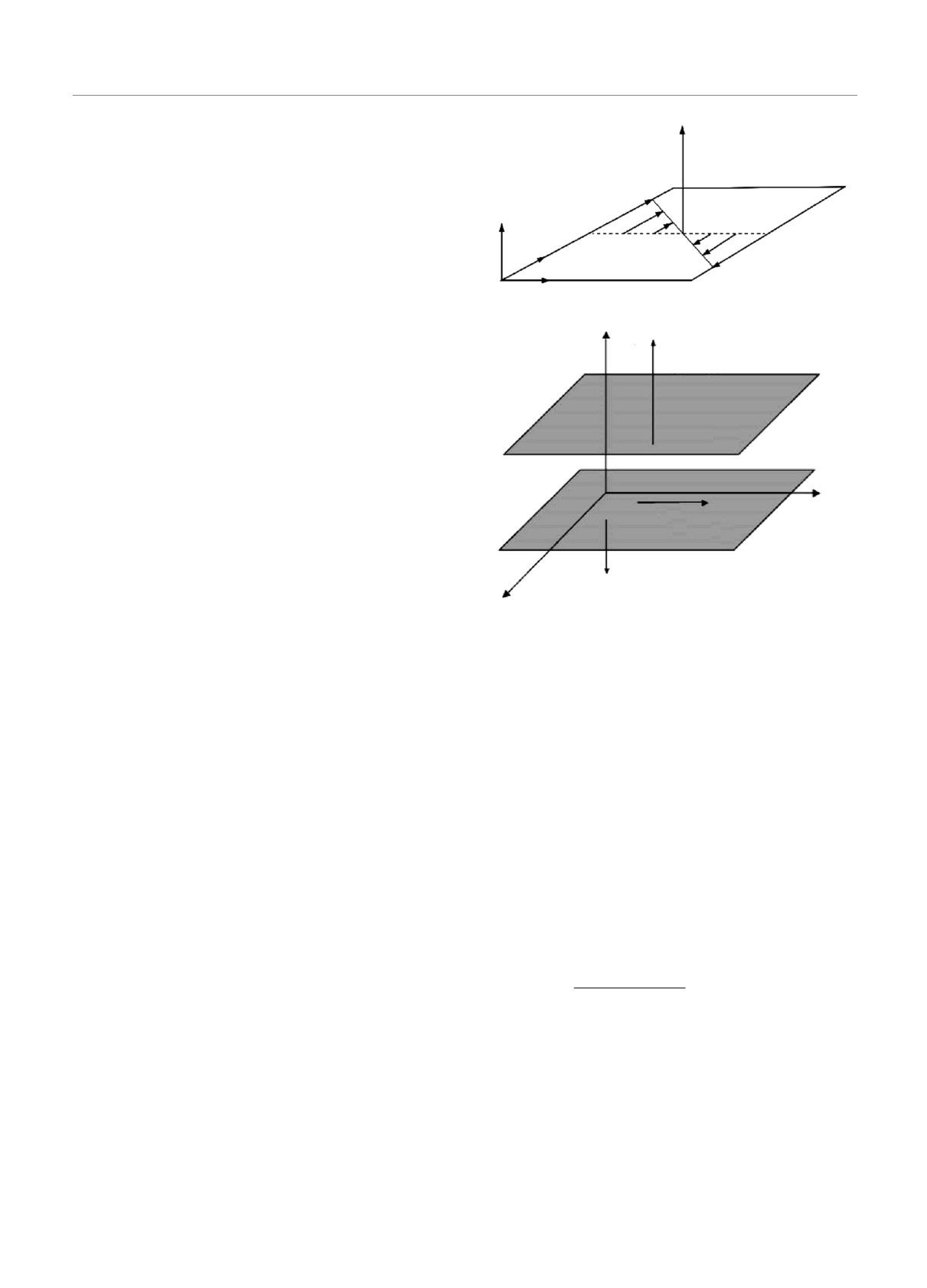
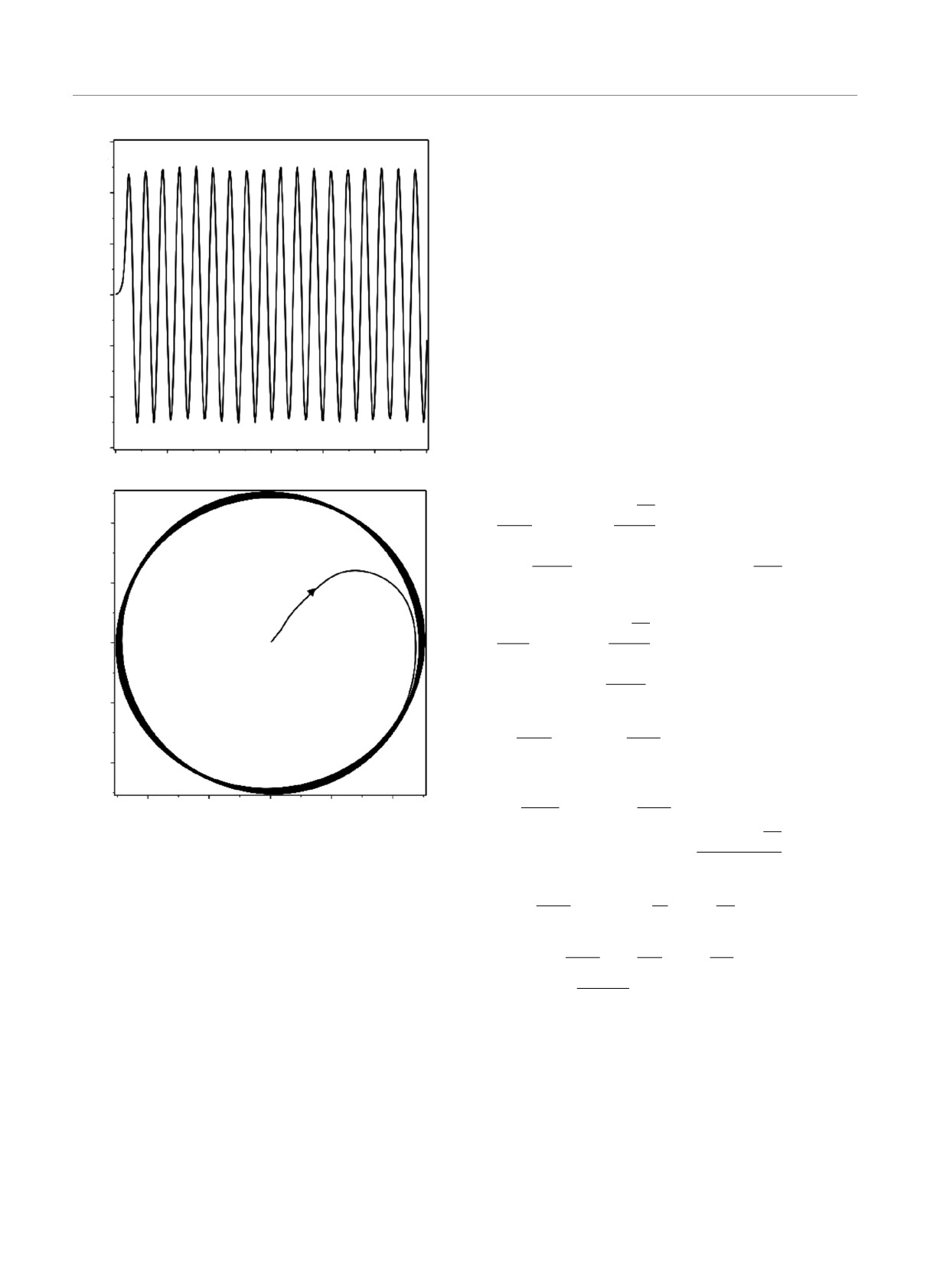
Рис. 1. a) Схема сдвигового течения во вращающихся по-
уравнений нелинейной динамики шестимерного фа-
токах. В локальной декартовой системе координат этот
зового пространства. Анализ этих уравнений пока-
поток аппроксимируется как линейный сдвиг со скоро-
зал существование сложной хаотической структу-
стью U0(x). б) Декартова аппроксимация задачи для неод-
ры — странного аттрактора. Кроме того, был най-
нородно вращающейся магнитоконвекции. Неоднородное
ден режим конвекции, при котором возникает хао-
вращение в локальной декартовой системе координат со-
тическое изменение направления (инверсии) и ам-
стоит из вращения с постоянной угловой скоростью Ω0 и
плитуды возмущенного магнитного поля с учетом
сдвиговой скорости U0, направленной вдоль оси y
неоднородного вращения среды. Ранее слабонели-
нейная стадия для вращающейся магнитоконвекции
(при Ω = const), в которой возникает хаотический
режим, исследовалась во вращающихся слоях жид-
кости [50, 51], в проводящих средах с однородным
сывают неоднородно вращающуюся конвекцию во
магнитным полем [52-55], а также во вращающихся
внешнем осциллирующем магнитном поле. В разд. 3
с магнитным полем проводящих средах [56]. Однако
мы исследуем слабонелинейную стадию колебатель-
в этих работах не рассматривалась сама динамика
ной конвекции в неоднородно вращающемся слое
магнитного поля, что соответствует безындукцион-
электропроводящей жидкости в модулированном
ному приближению. Такое приближение допустимо
магнитном поле. Применяя метод теории возмуще-
для некоторых технологических приложений: роста
ний по малому параметру надкритичности числа
√
кристаллов, химических процессов затвердевания и
Рэлея, ϵ =
(Ra - Rac)/Rac, мы получили нелиней-
центробежного литья металлов и т. д.
ное комплексное уравнение Гинзбурга - Ландау с пе-
В отличие от работ [48,49], здесь мы исследуем
риодическими коэффициентами. Идентичное урав-
колебательную магнитную конвекцию для неодно-
нение Гинзбурга - Ландау (см. Приложение B) полу-
родно вращающегося слоя электропроводящей сре-
чается из шестимерной модели уравнений Лоренца с
ды (плазмы) во внешнем осциллирующем магнит-
периодическими коэффициентами, которое было по-
ном поле (рис. 1). Настоящая работа состоит из
лучено при исследовании слабонелинейного режима
следующих разделов. В разд. 2 получены основные
конвекции с помощью галеркинской аппроксимации
уравнения в приближении Буссинеска, которые опи-
минимального порядка.
903
М. И. Копп, А. В. Тур, В. В. Яновский
ЖЭТФ, том 157, вып. 5, 2020
R ∂Ω
В разд.
4
приведены результаты численных
Ro =
решений неавтономного комплексного уравнения
2Ω ∂R
Гинзбурга - Ландау, показывающих зависимость ве-
соотношением q = -2Ro. Отметим, что для твер-
личины теплопереноса (числа Нуссельта Nu) от ам-
дотельного вращения параметр Россби равен нулю
плитуды δ, частоты ωB модуляции и от профи-
Ro = 0, в случае кеплеровского вращения Ro =
ля неоднородного вращения (числа Россби Ro). В
= - 3/4, для рэлеевского профиля угловой скорости
разд. 5 проведен бифуркационный анализ получен-
Ω(R) ∝ R-2 соответственно Ro = -1.
ного в разд. 3 комплексного уравнения Гинзбур-
Полагаем, что направление внешнего магнитно-
га - Ландау в двух случаях: когда нет внешней моду-
го поля B0 совпадает с осью вращения жидкости
ляции магнитного поля, δ = 0, и когда она присут-
Ω0 ∥ eZ. Кроме того, внешнее магнитное поле B0
ствует, δ = 0. В разд. 6, применяя метод Галеркина
изменяется со временем по гармоническому закону:
к нелинейной системе уравнений для неоднородно
B0 = B00(1 + δϵ2 cos ωBt)eZ,
вращающейся магнитоконвекции, мы получили ди-
намическую систему уравнений Лоренца (6D) с пе-
где ϵ — малый возмущающий параметр, δ — малая
риодическими коэффициентами. Численный анализ
амплитуда магнитной модуляции, B00 = const, ωB —
этой системы уравнений проведен в разд. 7.
частота модуляции магнитного поля, eZ — единич-
Полученные в работе результаты могут найти
ный вектор, направленный вертикально вверх по
применение в различных астрофизических задачах,
оси Z. Конвективные течения, вызванные градиен-
рассматривающих магнитную конвекцию во враща-
том температуры, в вязкой несжимаемой электро-
ющихся слоях Солнца, горячих галактических кла-
проводящей жидкости (плазме) с внешним магнит-
стерах, аккреционных дисках и других объектах.
ным полем описываются известными уравнениями
магнитной гидродинамики в приближении Бусси-
неска [1, 2]:
2. ПОСТАНОВКА ЗАДАЧИ И ОСНОВНЫЕ
УРАВНЕНИЯ
(
)
∂v
1
B2
+ (v∇)v = -
∇ P +
+
Рассмотрим неоднородно вращающийся поток
∂t
ρ0
8π
электропроводящей жидкости, находящейся между
1
+
(B∇)B + gβT eZ + ν∇2v,
(1)
двумя горизонтальными плоскостями, z = 0 и z = h.
0
4πρ
Жидкость нагревается снизу (T1 > T2) при посто-
янном градиенте температуры A = (T1 - T2)/h =
∂B
+ (v∇)B - (B∇)v = η∇2B,
(2)
= ΔT/h = const. Для описания нелинейных конвек-
∂t
тивных явлений в неоднородно вращающемся слое
∂T
+ (v∇)T = χ∇2T,
(3)
электропроводящей жидкости удобно перейти от ци-
∂t
линдрической системы координат (R, ϕ, z) к локаль-
div B = 0, div v = 0,
(4)
ной декартовой (X, Y, Z). Если рассмотреть фикси-
рованную область слоя жидкости радиусом R0 с уг-
где β — коэффициент теплового расширения, ρ0 =
ловой скоростью вращения Ω0 = Ω(R0), то коорди-
= const — плотность среды, ν — коэффициент ки-
наты X = R - R0 соответствуют радиальному на-
нематической вязкости, η = c2/4πσ — коэффициент
правлению, Y = R0(ϕ - ϕ0) — азимутальному и Z =
магнитной вязкости, σ — коэффициент электропро-
= z — вертикальному (рис. 1). В этом случае неод-
водности, χ — коэффициент теплопроводности сре-
нородное вращение слоя жидкости локально мож-
ды.
но представить в виде вращения с постоянной угло-
Представим все величины в уравнениях (1)-(4) в
вой скоростью Ω0 и азимутальным сдвигом (a linear
виде суммы основного и возмущенного состояний:
shear flow) [57], профиль скорости которого локаль-
но линеен:
v = U0+u, B = B0+b, P = p0+p, T = Tb+θ.
U0 = -qΩ0XeY ,
Уравнения для основного состояния имеют вид
где q ≡ -d ln Ω/d ln R — безразмерный шировой па-
dp0
раметр, определяемый из профиля угловой скорости
=ρ0g0βTb,
(5)
dZ
вращения Ω(R) = Ω0(R/R0)-q. Сдвиговый (широ-
вый) параметр q связан с гидродинамическим чис-
1
dp0
-2qΩ20X =
,
(6)
лом Россби
ρ0 dX
904
ЖЭТФ, том 157, вып. 5, 2020 Магнитная конвекция в неоднородно вращающейся электропроводящей среде. . .
)
d2Tb
(∂
1
∂p
= 0.
(7)
-ν∇2
w + (u∇)w = -
+ gβθ +
dZ2
∂t
ρ0 ∂Z
1
B00fm ∂
w
Выражения (5), (6) показывают, что в радиальном
+
(b∇)w+
,
(12)
направлении устанавливается центробежное равно-
4πρ0
4πρ0
∂Z
)
весие, а в вертикальном - гидростатическое. Вычи-
(∂
∂u
тая из (1)-(4) уравнения для основного состояния
-η∇2
u-B00fm
+ (u∇)u-(b∇)u = 0, (13)
∂t
∂Z
(5)-(7), находим уравнения эволюции возмущений:
)
∂u
∂u
(∂
∂v
- qΩ0X
+ (u∇)U0 + 2Ω0 × u +
- η∇2
v-B00fm
+ qΩ0u+
∂t
∂Y
∂t
∂Z
1
1
+ (u∇)v - (b∇)v = 0,
(14)
+ (u∇)u = -
∇p+
((B0∇)b +
ρ0
4πρ0
+ (b∇)b) + gβθeZ + ν∇2u,
)
(∂
∂w
∂b
∂b
(8)
- η∇2
w-B00fm
+
- qΩ0X
- (B0∇)u - (b∇)U0 +
∂t
∂Z
∂t
∂Y
+ (u∇)w - (b∇)w = 0,
(15)
+ (u∇)b - (b∇)u = η∇2b,
)
∂θ
∂θ
(∂
- qΩ0x
+ (u∇)Tb + (u∇)θ = χ∇2θ,
- χ∇2
θ - Aw + (u∇)θ = 0,
(16)
∂t
∂y
∂t
div b = 0, div u = 0.
где fm = 1 + δϵ2 cos ωBt. В уравнениях (10)-(16) дей-
ствие операторов набла определяется как
Здесь давление p = p + pm включает в себя возму-
щенное магнитное давление pm = b2/8π + bB0/4π.
∂
∂
∂2
∂2
(a · ∇) = aX
+aZ
,
∇2 =
+
Рассмотрим динамику осесимметричных возмуще-
∂X
∂Z
∂X2
∂Z2
ний, тогда все возмущенные величины в уравне-
Чтобы исключить давление p в уравнениях (10) и
ниях (8) будут зависеть только от двух перемен-
(12), продифференцируем уравнение (10) по Z, а
ных (X, Z):
уравнение (12) по X, а затем, вычитая одно из дру-
гого, получим уравнение для Y -компоненты вихря
u = (u(X,Z),v(X,Z),w(X,Z)),
rotu = eY ω:
)
(
)
b=(u(X,Z),v(X,Z),
w(X, Z)),
(∂
∂
∂u
∂u
-ν∇2
ω+
u
+w
-
∂t
∂Z
∂X
∂Z
p= p(X,Z), θ = θ(X,Z).
(
)
∂
∂w
∂w
B00fm ∂I
1
u
+w
=
+
×
Уравнения соленоидальности для осесимметричных
- ∂X
∂X
∂Z
4πρ0
∂Z
4πρ0
(
(
)
(
))
возмущений скорости и магнитного поля примут
∂
∂u
∂u
∂
w
w
×
u
w
-
u
w
+
вид
∂Z
∂X
∂Z
∂X
∂X
∂Z
∂u
∂w
∂u
w
+
= 0,
+
= 0.
(9)
∂v
∂θ
∂X
∂Z
∂X
∂Z
+ 2Ω0
- gβ
,
(17)
∂Z
∂X
Остальные уравнения в координатном представле-
где ω = ∂u/∂Z -∂w/∂X — Y -компонента вихря, I =
нии принимают следующий вид:
=∂u/∂Z-
w/∂X — Y -компонента тока I = rotb =
)
=IeY.
(∂
1
∂p
-ν∇2
u + (u∇)u = -
+ 2Ω0v +
Согласно уравнениям (9), удобно ввести функ-
∂t
ρ0 ∂X
цию тока ψ, через которую выражаются компонен-
1
B00fm ∂u
+
(b∇)u +
,
(10)
ты возмущенной скорости:
4πρ0
4πρ0
∂Z
∂ψ
∂ψ
u=-
,
w=
∂Z
∂X
)
(
(∂
q)
Аналогично можем ввести функцию тока φ для воз-
−ν∇2
v + (u∇)v = -2Ω0u
1-
+
∂t
2
мущений магнитного поля:
1
B00fm ∂v
+
(b∇)v +
,
(11)
∂φ
∂φ
4πρ0
4πρ0
∂Z
u=-
,
w=
∂Z
∂X
905
М. И. Копп, А. В. Тур, В. В. Яновский
ЖЭТФ, том 157, вып. 5, 2020
В результате уравнения (17) и (11) приобретают бо-
описывают неоднородно вращающуюся конвекцию
лее компактный вид:
во внешнем осциллирующем магнитном поле. Для
)
ее исследования удобно привести эти уравнения к
(∂
∂v
B00fm
∂
безразмерному виду, вводя безразмерные величины,
-ν∇2
∇2ψ + 2Ω0
-
∇2φ-
∂t
∂Z
4πρ0
∂Z
которые отметим «звездочкой»:
∂θ
1
− gβ
=
J (φ, ∇2φ) - J(ψ, ∇2ψ),
(18)
h2
∂X
4πρ0
(X, Z) = h(x∗, z∗), t =
t∗, ψ = χψ∗,
ν
)
χ
(∂
∂ψ
B00fm ∂v
φ = hB00φ∗, v =
v∗,
v = B00v∗, θ = Ahθ∗.
-ν∇2
v - 2Ω0(1+Ro)
-
=
h
∂t
∂Z
4πρ0
∂Z
1
Опуская «звездочку», получим следующую систему
=
J (φ, v) - J(ψ, v).
(19)
безразмерных уравнений:
4πρ0
)
Здесь для оператора якобиана или скобки Пуассона
(∂
√
∂v
-∇2
∇2ψ +
Ta
-
J (a, b) ≡ {a, b} введено обозначение
∂t
∂z
∂a
∂b
∂a
∂b
∂
∂θ
J (a, b) =
-
− PrPm-1
Qfm
∇2φ - Ra
=
∂X ∂Z
∂Z ∂X
∂z
∂x
Далее, дифференцируя уравнение (13) по Z, а
= PrPm-1Q · J(φ, ∇2φ)-Pr-1 · J(ψ, ∇2ψ),
уравнение (15) по X и вычитая одно из другого, на-
)
ходим уравнение для тока I:
(∂
√
∂ψ
-∇2
v-
Ta(1 + Ro)
-
)
(
)
∂t
∂z
(∂
∂
∂u
∂u
∂u
∂u
-η∇2
I+
u
+w
-u
w
-
∂t
∂Z
∂X
∂Z
∂X
∂Z
∂v
(
)
− PrPm-1Qfm
= PrPm-1Q · J(φ, v)-
∂z
∂
w
w
∂w
∂w
-
u
+w
-u
-
w
=
∂X
∂X
∂Z
∂X
∂Z
- Pr-1 · J(ψ, v),
(25)
∂ω
)
=B00fm
(20)
(∂
∂ψ
∂Z
- Pm-1∇2
φ - Pr-1
=
∂t
fm ∂z
Уравнения (20) и (14) также можно записать в ком-
пактном виде, используя определения функций тока
= -Pr-1J(ψ, φ)),
ψ и φ:
)
)
(∂
∂v
(∂
∂ψ
- Pm-1∇2
v- Pr-1
- η∇2
φ-B00fm
= -J(ψ, φ),
(21)
∂t
fm ∂z+
∂t
∂Z
√
∂φ
+ Ro
Ta
= Pr-1(J(φ, v) - J(ψ, v)),
)
∂z
(∂
∂v
∂φ
- η∇2
v-B00fm
+ 2Ω0Ro
=
(
)
∂t
∂Z
∂Z
∂
∂ψ
Pr
−∇2
θ-
= -J(ψ, θ).
∂t
∂x
= J(φ,v) - J(ψ,v).
(22)
Подобным образом упрощается вид уравнения (16)
Здесь безразмерные параметры: Pr = ν/χ — чис-
для температурных возмущений:
ло Прандтля, Pm
= ν/η — магнитное число
)
Прандтля, числа Ta = 4Ω20h4/ν2 — Тейлора, Q =
(∂
∂ψ
- χ∇2
θ-A
= -J(ψ, θ).
(23)
= B200h2/4πρ0νη — Чандрасекара, Ra = gβAh4/νχ —
∂t
∂X
Рэлея на масштабе h.
Уравнения (18), (19), (21)-(23) совместно с гра-
При Ra = 0 и fm = 1 система уравнений (25) при-
ничными условиями
менялась для исследования нелинейного механизма
насыщения МВН [58]. В случае, когда Ra = 0 и мо-
ψ|Z=0,h = ∇2ψ|Z=0,h =
дуляция магнитного поля отсутствует, δ = 0, систе-
dv
ма уравнений (25) применялась для исследования
=
= v|Z=0,h = 0,
dZ
(24)
слабонелинейного и хаотического режимов конвек-
Z=0,h
ции в неоднородно вращающейся плазме в аксиаль-
dφ
= θ|Z=0,h = 0
ном магнитном поле [48, 49, 59].
dZ
Z=0,h
906
ЖЭТФ, том 157, вып. 5, 2020 Магнитная конвекция в неоднородно вращающейся электропроводящей среде. . .
3. СЛАБОНЕЛИНЕЙНЫЙ АНАЛИЗ
Здесь U† — нетривиальное решение линейной само-
КОНВЕКЦИИ С МОДУЛЯЦИЕЙ ВНЕШНЕГО
сопряженной задачи L†U† = 0, где L† — самосопря-
МАГНИТНОГО ПОЛЯ
женный (self-adjoint) оператор, который определя-
ется из следующего соотношения:
В слабонелинейной теории конвективной неус-
1
2
1
2
тойчивости взаимодействие малых амлитуд конвек-
U†, LU
≡
L†U†, U
,
(27)
тивных ячеек можно описать следующим образом.
где 〈. . . , . . .〉
— внутреннее произведение (inner
Пусть малая амплитуда конвективных ячеек имеет
product), которое здесь имеет следующее определе-
порядок O(ϵ1), тогда взаимодействие ячеек друг с
ние:
другом приводит ко второй гармонике и нелиней-
1
∫
∫
ности порядка O(ϵ2), а затем к нелинейности O(ϵ3)
〈f, g〉 =
f · gdxdz,
и т. д. При этом нелинейные члены в уравнениях
z=0 x=0
(25) рассматриваются как возмущенный отклик для
R.H. — правые части возмущенных уравнений с
задачи линейной конвекции. В этом случае пара-
нелинейными членами. Применим эти общие прин-
метр Рэлея Ra, контролирующий конвекцию, бли-
ципы разрешения нелинейных уравнений к нашей
зок к критическому значению Rac. Будем считать,
задаче. Для простоты будем учитывать нелинейные
что амплитуда осциллирующего внешнего магнит-
члены в (25) только в уравнении теплового балан-
ного поля ϵ2 · δB00 имеет второй порядок малости
са. Как будет показано ниже (см. Приложение B),
O(ϵ2), тогда его влияние на нелинейное взаимодей-
это приближение равносильно применению галер-
ствие конвективных ячеек следует ожидать уже в
кинской аппроксимации минимального порядка.
третьем порядке O(ϵ3). Так как влияние неустойчи-
Далее, представим все переменные в уравнениях
вых мод мало, наша задача состоит в том, чтобы
(25) в виде асимптотического разложения:
получить уравнения, описывающие взаимодействия
этих мод. Общая схема построения слабонелиней-
Ra = Rac + ϵ2R2 + ϵ4R4 + . . . ,
ной теории состоит в следующем. Поскольку малым
ψ = ϵψ1 + ϵ2ψ2 + ϵ3ψ3 + ...,
параметром нашей задачи является относительное
v = ϵv1 + ϵ2v2 + ϵ3v3 + ...,
отклонение числа Рэлея Ra от критического значе-
(28)
φ = ϵφ1 + ϵ2φ2 + ϵ3φ3 + ...,
ния Rac,
Ra - Rac
v=ϵv1 +ϵ2v2 +ϵ3v3 +...,
ϵ2 =
≪ 1,
Rac
θ = ϵθ1 + ϵ2θ2 + ϵ3θ3 + ...
все возмущенные величины U в уравнениях типа
Здесь Rac — критическое значение числа Рэлея для
конвекции без модуляции. Для исследования перио-
LU = -N(U|U) (N(. . .)-нелинейные члены)
дических по времени конвективных явлений введем
представляются в виде ряда теории возмущений
«быстрые» (t0) и «медленные» (τ) временные мас-
штабы. Тогда производную по времени в уравнениях
U → ϵU(1) + ϵ2U(2) + ϵ3U(3) + ...
(25) можно представить в виде [61]:
∂
∂
∂
Уравнения для возмущений в разных порядках по ϵ
→
+ϵ2
(29)
∂t
∂t0
∂τ
принимают вид
Подставляя (28), (29) в систему (25), будем решать
ϵ1 : L(0)U(1) = 0,
ее для разных порядков по ϵ. В самом низком по-
рядке получим уравнение
ϵ2 : L(0)U(2) = -N(U(1)|U(1)),
̂M1 = 0,
(30)
где
ϵ3 : L(0)U(3) = -L(2)U(0) - N(U(1)|U(2))-
⎡
⎤
ψ1
- N(U(2)|U(1)).
⎢
⎥
⎢θ
1
⎥
⎢
⎥
⎢
⎥
M1 =
φ1
,
Условие разрешимости этой цепочки нелинейных
⎢
⎥
⎢
⎥
уравнений известно как альтернатива Фредгольма
⎣v1
⎦
(Fredholm’s alternative) [60]:
v
1
1
2
U†, R.H.
= 0.
(26)
L— матричный оператор, имеющий вид
907
М. И. Копп, А. В. Тур, В. В. Яновский
ЖЭТФ, том 157, вып. 5, 2020
⎡
(
)
⎤
∂
∂
√
∂
-∇2
∇2
-Rac
-Q∂
∇2
Ta
0
⎢
∂t0
∂x
∂z
∂z
⎥
⎢
⎥
⎢
∂
∂
⎥
⎢
− Pr-1
- Pr-1 ∇2
0
0
0
⎥
⎢
∂x
∂t0
⎥
⎢
⎥
⎢
∂
∂
⎥
L=
⎢
− Pr-1
0
- Pm-1∇2
0
0
⎥,
⎢
∂z
∂t0
⎥
⎢
⎥
⎢
√
∂
∂
⎥
⎢−
Ta(1 + Ro)
0
0
-∇2
-Q∂
⎥
⎢
∂z
∂t0
∂z
⎥
⎣
⎦
√
∂
∂
∂
0
0
Ro
Ta
- Pr-1
- Pm-1∇2
∂z
∂z
∂t0
где введено обозначение
Q= PrPm-1Q. Общие ре-
Предельный случай ω = 0 в выражении (32) соот-
шения уравнений (30), с учетом граничных усло-
ветствует критическому значению числа Рэлея для
вий (24), выражаются через неизвестные функции
стационарной конвекции [48]:
от медленного времени:
(π2 + k2)3
π2(π2 + k2)Q
(
)
Rast =
+
+
ψ1 =
A(τ)eiωt0 + A∗(τ)e-iωt0
sinkxsinπz,
k2
k2
(
)
v1 =
V (τ)eiωt0 + V ∗(τ)e-iωt0
sinkxcosπz,
π2(π2 + k2)2Ta
(
)
+
+
k2((π2 + k2)2π2Q)
φ1 =
Φ(τ)eiωt0 + Φ∗(τ)e-iωt0
sinkxcosπz,
(31)
(
)
π2TaRo((π2 + k2)2 + π2QPm)
v1 =
V (τ)eiωt0 +
V ∗(τ)e-iωt0 sinkxsinπz,
+
(33)
k2((π2 + k2)2 + π2Q)
(
)
θ1 =
Θ(τ)eiωt0 + Θ∗(τ)e-iωt0
coskxsinπz,
Здесь минимальное значение критического числа
Рэлея находится из условия ∂Rast/∂k = 0 и соответ-
где A∗, V∗, Φ∗,
V ∗, Θ∗ — комплексно-сопряженные
ствует волновым числам k = kc, удовлетворяющим
амплитуды колебаний. Подставляя решения (31) в
следующему уравнению:
уравнения (30), получим следующие соотношения
между амплитудами колебаний:
2k2c - π2
π4Q
2π2kcTa(1 + Ro)
-
+
-
kA(τ)
πPmA(τ)
kc
kca4c
a2c (a4c
+ π2Q)
Θ(τ) =
,
Φ(τ) =
,
Γχ
PrΓη
π2Ta(a4c + π2Q + 2k2ca2c)
−
-
kc(a4c + π2Q)2
√
(
)
π
Ta
(1 + Ro)Γ2
η
+ π2RoPmQ
π2TaRo(a4c + π2QPm)(a4c + π2Q + 2k2ca2c)
V (τ) =
A(τ),
−
= 0,
ΓηΓ2
kca4c(a4c + π2Q)2
A
(
(
))
√
Pm(iω+a2)
2
a2c = π2 + k2c.
π
Ta
1+Ro
1-
Pm
Γη
V (τ) = -
A(τ),
Для колебательного режима конвекции критическое
PrΓ2
A
число Рэлея имеет вид [48]
где введены следующие обозначения:
Raosc =
Γ2A = (iω + a2)Γη + π2Q, Γχ = iω Pr+a2,
a2
[
]
=
ζ(a4+ω2Pm Pr)-ω2a4(1+Pm)(Pr -Pm)
+
k2ξ
Γη = iωPm + a2, a2 = π2 + k2.
Ta(1 + Ro) ×
+π2
Амплитуда A(τ) остается пока неизвестной. Из пер-
(a4 - ω2Pm Pr)ζ + ω2a4(1 + Pm)(Pm + Pr)
вого уравнения системы (25) нетрудно найти выра-
×
+
k2(ζ2 + ω2a4(1 + Pm)2)
жение для критического числа Рэлея Rac, которое
+ π4QTaRoPm×
совпадает с дисперсионным уравнением для линей-
ной конвективной неустойчивости из работы [48]:
(a4 + ω2Pm Pr)ζ + ω2a4(1 + Pm)(Pr -Pm)
×
,
(34)
k2ξ(ζ2 + ω2a4(1 + Pm)2)
Rac =
где введены обозначения
+π4QTaRoPm)
Γχ(a2Γ4A+π2Ta(1+Ro)Γ2η
=
(32)
k2Γη
Γ2
ξ = a4 + ω2Pm2, ζ = a4 + π2Q - ω2Pm.
A
908
ЖЭТФ, том 157, вып. 5, 2020 Магнитная конвекция в неоднородно вращающейся электропроводящей среде. . .
Raosc
Частота нейтральных колебаний удовлетворяет сле-
дующему уравнению:
30000
K0ω6 + K1ω4 + K2ω2 + K3 = 0,
а
25000
где
K0 = Pm2(1 + Pr)Pm2,
20000
K1 = (a4(1 + Pm) + (Pr-Pm)(a4 + π2Q))Pm2 +
+ Pm2(1 + Pr)(a4(1 + Pm)2 - 2Pm(a4 + π2Q)) +
2
15000
π
+
Ta(1 + Ro)Pm3(Pr -1),
a2
n
Rami
10000
K2 = (a4(1+Pm)+(Pr-Pm)(a4+π2Q))(a4(1+Pm)2 -
- 2Pm(a4 + π2Q)) + Pm2(1 + Pr)(a4 + π2Q)2 +
0
1
2
3
4
5
2
k
π
+
Ta(1 + Ro) ×
a2
(
×
a4Pm2(Pr -1) + (a4 + π2Q)(Pr +Pm)Pm -
б
)
4
π
18.8
- a4(1 + Pm)Pm
-
QTaRoPm ×
a2
(
)
×
2Pm Pr +Pm2(Pr -1)
,
18.6
K3 = (a4(1 + Pm) + (Pr-Pm)(a4 + π2Q))×
18.4
2
π
× (a4 + π2Q)2 +
Ta(1 + Ro)a4 ×
a2
(
)
×
(Pr +Pm)(a4 + π2Q) - a4(1 + Pm)
+
18.2
4
π
+
QTaRoPm ×
a2
(
)
18.0
×
(Pr -Pm)(a4 + π2Q) - a4(1 + Pm)
0
0.5
1.0
1.5
На рис. 2 показаны зависимости критического
k
числа Рэлея Raosc и частоты ω колебательного ре-
Рис. 2. a) Зависимости критического числа Рэлея Raosc
жима конвекции от волновых чисел k для однород-
от волнового числа k для однородного Ro = 0 (штрихо-
ного Ro = 0 и кеплеровского Ro = -3/4 профилей
вая линия) и кеплеровского Ro = -3/4 (сплошная линия)
вращения. Из графиков рис. 2 видно, что при от-
профилей вращения. б) Зависимости частоты ω от волно-
рицательных числах Россби Ro = -3/4 пороговое
вого числа k для однородного Ro = 0 (штриховая линия)
число Рэлея Raminosc и частота ω(0) уменьшаются.
и кеплеровского Ro = -3/4 (сплошная линия) профилей
вращения. Графики построены для постоянных значений
Для второго порядка по ϵ имеем следующее урав-
параметров Q = 50, Ta = 100, Pm = 1, Pr = 9
нение:
LM2 = N2,
(35)
]
где
[∂ψ1 ∂θ1
∂θ1 ∂ψ1
⎡
⎤
⎡
⎤
N22 = -Pr-1
-
ψ2
N21
∂x
∂z
∂x
∂z
⎢
⎥
⎢
⎥
⎢θ2⎥
⎢N22⎥
⎢
⎥
⎢
⎥
⎢
⎥
⎢
⎥
Используя решения (31) и граничные условия (24),
M2 =
φ2
,
N2 =
N23
,
⎢
⎥
⎢
⎥
⎢
⎥
⎢
⎥
найдем решения уравнений (35):
⎣v2⎦
⎣N24⎦
v2
N25
ψ2 = 0, v2 = 0,
v2 = 0, φ2 = 0,
[
]
(36)
N21 = N23 = N24 = N25 = 0,
θ2 =
θ20 + θ22e2iωt0 + θ∗22e-2iωt0
sin2πz,
909
М. И. Копп, А. В. Тур, В. В. Яновский
ЖЭТФ, том 157, вып. 5, 2020
∂θ1
где введены обозначения
N32 = -
-
∂τ
]
2
k2a2|A(τ)|
[∂ψ1 ∂θ2
∂θ2 ∂ψ1
∂ψ2 ∂θ1
∂θ1 ∂ψ2
θ20 = -
,
− Pr-1
-
+
-
=
∂x
∂z
∂x
∂z
∂x
∂z
∂x
∂z
4π(ω2 Pr2 +a4)
[
k
∂A(τ)
= -eiωt0
coskxsinπz +
Γχ
∂τ
πk2A2(τ)
θ22 = -
]
4(iω Pr +2π2)(iω Pr +a2)
k3(3a2π2+iωk2 Pr)|A(τ)|2A(τ)
+
coskxsinπz cos2πz
+
2 Pr(iω Pr+2π2)(iω Pr+a2)
Решения второго порядка для возмущений темпе-
π2k3A3(τ)
ратуры θ2 включают в себя слагаемые, зависящие
+
×
2 Pr(iω Pr+2π2)(iω Pr+a2)
только от медленного времени τ, и слагаемые, про-
× e3iωt0 coskxsinπz cos2πz + c.c.,
порциональные частоте 2ω. Для анализа интенсив-
ности теплопереноса вводится усредненный по гори-
зонтали теплопоток на границе слоя электропрово-
∂φ1
∂ψ1
дящей жидкости (число Нуссельта):
N33 = -
+ δ cos(ωBτ)Pr-1
=
∂τ
∂z
[
]
⎡
⎤
πPm ∂A(τ)
πA(τ)
= -
+ δcos(ωBτ)
×
∫
PrΓη
∂τ
Pr
⎢
kc
(∂θ2)
⎥
⎣
dx⎦
2π
∂z
× eiωt0 sinkxcosπz + c.c.,
0
z=0
Nu = 1 +
⎡
⎤
∫
⎢
kc
(∂T0)
⎥
∂v1
⎣
dx⎦
N34 = -
+ δ cos(ωBτ)Q ∂v1
=
2π
∂z
∂τ
∂z
[
√
(
)
0
z=0
π
Ta
(1 + Ro)Γ2η + π2RoPmQ
∂A(τ)
= -
-
ΓηΓ2
∂τ
Подставляя в это выражение значение θ2 и усредняя
A
√
по быстрому времени t0, находим
π3Q
TaA(τ)
− δ cos(ωBτ)
×
Γ2A
k2a2|A(τ)|
2
(
(
))]
Nu(τ) = 1 +
(37)
Pm(iω + a2)
2(a4 + ω2 Pr2)
×
1 + Ro
1-
×
η
Γ
× eiωt0 sinkxcosπz + c.c.,
Из формулы (37) видно, что число Нуссельта зави-
сит от амплитуды A(τ), которая будет определена
ниже.
∂v
1
∂v1
N35 = -
+ δ cos(ωBτ)Pr-1
=
Для третьего порядка по ϵ находим
∂τ
∂z
⎡
(
(
))
√
Pm(iω+a2)
π2
Ta
1+Ro
1-
Pm
LM3 = N3,
(38)
⎢
Γ
η
∂A(τ)
=
⎢
-
⎣
PrΓ2
∂τ
A
где
⎡
⎤
⎡
⎤
√
(
)
]
ψ3
N31
π2
Ta
(1+Ro)Γ2η+π2RoPmQ
⎢
⎥
⎢
⎥
− δ cos(ωBτ)
A(τ)
×
⎢
θ3⎥
⎢N32⎥
2
PrΓηΓ
⎢
⎥
⎢
⎥
A
M3 =
⎢
φ3⎥,
N3 =
⎢N33⎥,
⎢
⎥
⎢
⎥
× eiωt0 sinkxsinπz + c.c.,
⎢
⎥
⎢
⎥
⎣v3⎦
⎣N34⎦
здесь ωB = ωB/ϵ2. Условие разрешимости (альтер-
v3
N35
натива Фредгольма) для уравнений третьего поряд-
ка O(ϵ3) находится из формулы (26):
∂
∂θ1
N31 = -
∇2ψ1+Ra2
+δ cos(ωBτ)Q∂
∇2φ1 =
∫
1
∫
[
∂τ
∂x
∂z
[
]
Pψ†1 ·R31 +Rac
Pθ†1 ·R32 +
∂A(τ)
k2Ra2A(τ)
π2a2QA(τ)
= a2
-
+ δ cos(ωBτ)
×
z=0 x=0
∂τ
Γχ
Γη
]
+ QPr2Pm-1P∇2φ†1 · R33+v†
·R34 dx dz = 0,
(39)
× eiωt0 sinkxsinπz + c.c.,
1
910
ЖЭТФ, том 157, вып. 5, 2020 Магнитная конвекция в неоднородно вращающейся электропроводящей среде. . .
(
)
где введены обозначения
kA(τ)
θ†1 =
-
eiωt0 + c.c. coskxsinπz,
Γχ
(
)
∂
∂2
(
)
P = (1 + Ro) Pm
-∇2
- RoPmQ
,
A(τ)πPm
∂t0
∂z2
φ†1 =
-
eiωt0 + c.c. sinkcxcosπz,
Γη
Pr
R31 = N31, R32 = N32, R33 = N33,
(
√
A(τ)π
Ta
(
)
(
)
v†1 =
-
(1 + Ro)Γ2η + π2QPmRo
×
∂
ΓηΓ2
A
R34
= - Pm
-∇2
×
)
∂t0
((
)
)
∂
∂N35
× eiωt0 + c.c. sinkxcosπz.
× Pm
-∇2
N34 + QPr
+
∂t0
∂z
√
∂2N33
Матрица M†1 имеет вид
+
Ta Ro Pm PrQ
∂z2
†
M1
= (ψ†1, θ†1, φ†1, v†1)Tr,
Выражения для ψ†1, θ†1, φ†1, v†1 определяются из реше-
ния линейной самосопряженной задачи
L†M†1 = 0:
а L† — самосопряженный (self-adjoint) матричный
(
)
оператор,
ψ†1 =
A(τ)eiωt0 + c.c.
sinkxsinπz,
⎡(
)
⎤
∂
∂
∂
√
∂
∇2 - ∇4
P
Rac
P
P
∇2
-
T
P
⎢
∂t0
∂x
∂z
∂z⎥
⎢
(
)
⎥
⎢
∂
∂
⎥
2
⎢
Rac
P
-Rac
P
-∇
0
0
⎥
⎢
∂x
∂t0
⎥
L† =
⎢
(
)
⎥,
(40)
⎢
∂
∂
⎥
⎢
P
∇2
0
QPrP
- Pm-1∇2
∇2
0
⎥
⎢
∂z
∂t0
⎥
⎣
⎦
√
∂
−
T
P
0
0
-Q
∂z
√
здесь
k2 Pr
π2a2
π
Ta
s=a2+Ra
-QPm
-
Λ1,
2
c Γ2
Γ2η
ΓηΓ
A
χ
k2 Pr
π2a2
F (τ) = Ra2
- 2Q
δ cos(ωBτ)+
((
)(
)
)
Γχ
Γη
∂
∂
∂2
Q=
√
-∇2
Pm
-∇2
-Q
×
∂t0
∂t0
∂z2
π
Ta
(
)
+
Λ2δ cos(ωBτ),
∂
ΓηΓ2
A
× Pm
-∇2
(
∂t0
k4a2
π2k4
R = Ra
c
+
+
4(ω2Pr2+a4)Γ
4(iωPr+2π2)Γ2
χ
χ
)
π2k4
+
=
4(iωPr + 2π2)(ω2Pr2 + a4)
(42)
Выполняя интегрирование в (39) и усредняя по
k4(π2(1 + Γ∗2χ)Γχ + a2(iωPr + 2π2))
= Rac
,
быстрому времени t0, получим нелинейное уравне-
4(iωPr + 2π2)Γ2χΓ∗
χ
ние для комплексной амплитуды A(τ):
√
π
Ta
π3 √
Λ1 =
Ξ1 +
TaRoQPm2,
Γ2A
Γη
(
)
Ξ1 = (1+Ro)Γ3η+π2QPm
RoPm(iω+a2)-Γη
,
∂A(τ)
[
]
- s-1F(τ)A(τ) + s-1R|A(τ)|2A(τ) = 0, (41)
√
Γη
∂τ
Λ2 = π3
TaQ
Ξ2 - RoPm ,
Γ2
A
(
)
π2Q
Ξ2 = 2(1+Ro)Γη+RoPm
-(iω+a2)
где коэффициенты имеют следующий вид:
Γη
911
М. И. Копп, А. В. Тур, В. В. Яновский
ЖЭТФ, том 157, вып. 5, 2020
Выражение (41) соответствует комплексному урав-
Nu
нению Гинзбурга - Ландау с периодическим коэф-
3.2
фициентом F (τ). В предельном случае, когда нет
вращения (Ta = 0, Ro = 0), уравнение (41) совпада-
3.0
ет с результатом работы [39]. Запишем коэффициен-
ты в уравнении (41) в виде суммы действительной
2.8
и мнимой частей:
2.6
s-1F(τ) = f(1)r - δ cos(ωBτ)f(2)r +
2.4
+ i(f(1)i + δ cos(ωBτ)f(2)i), s-1R = lr + ili.
2.2
В результате уравнение (41) примет следующий вид:
2.0
0
1
2
3
4
5
∂A(τ)
- (f(1)r - δ cos(ωB τ) f(2)r)A(τ) -
∂τ
Рис. 3. Зависимости числа Нуссельта Nu от времени τ
(
)
для чисел Россби Ro = 2 (сплошная линия) и Ro = -3/4
- i f(1)i + δ cos(ωBτ)f(2)
A(τ) + (lr + ili) ×
i
(штриховая линия) во внешнем осциллирующем с часто-
× |A(τ)|2A(τ) = 0.
(43)
той ωB = 10 и амплитудой δ = 0.3 магнитном поле
Явный вид коэффициентов
r
,
r
, f(1)i, f(2)i, lr,
li имеет очень громоздкий вид, который приведен
Nu
в Приложении A. Уравнение вида (41) (или (43))
2.8
= 10
было получено во многих работах, где исследовался
а
B
= 25
B
2.7
слабонелинейный режим колебательной конвекции
(см., например, [39,62-66]). В отличие от этих работ,
2.6
в нашем результате (41) учитывается неоднородное
вращение (Ro = 0) электропроводящей жидкости.
2.5
Далее приведем результаты численных исследова-
ний уравнения (41).
2.4
2.3
= 100
B
= 50
B
4. ТЕПЛОПЕРЕНОС ПОД ВОЗДЕЙСТВИЕМ
2.2
ОСЦИЛЛЯЦИЙ МАГНИТНОГО ПОЛЯ
0
0.5
1.0
1.5
2.0
2.5
3.0
Nu
При выполнении численных расчетов комплекс-
ного уравнения Гинзбурга - Ландау с периодически-
2.54
= 10
= 25
б
B
B
ми коэффициентами будем считать Ra2 ≈ Rac, так
2.52
как нелинейность рассматривается вблизи крити-
ческого состояния конвекции. Согласно разложе-
2.50
нию (28), число Рэлея в этой системе равно Ra ≈
2.48
≈ Rac(1+ϵ2). С помощью численного решения урав-
= 100
= 50
B
2.46
B
нения (41) и формулы (37) мы можем определить
изменение величины теплопереноса (числа Нуссель-
2.44
та Nu) от времени τ. Параметры конвективной сре-
2.42
ды и начальную амплитуду выберем следующими:
Q/π2 = Q1 = 80, Ta/π4 = T1 = 105, Rac/π4 = R1 =
2.40
0
0.5
1.0
1.5
2.0
2.5
3.0
= 9500, Pm = 1, Pr = 10, A0 = 0.5. Результаты
численного анализа уравнения (41) представлены на
Рис. 4. Эффект влияния частоты модуляции ωB на тепло-
рис. 3-5.
перенос (Nu) в неоднородно вращающейся плазме с чис-
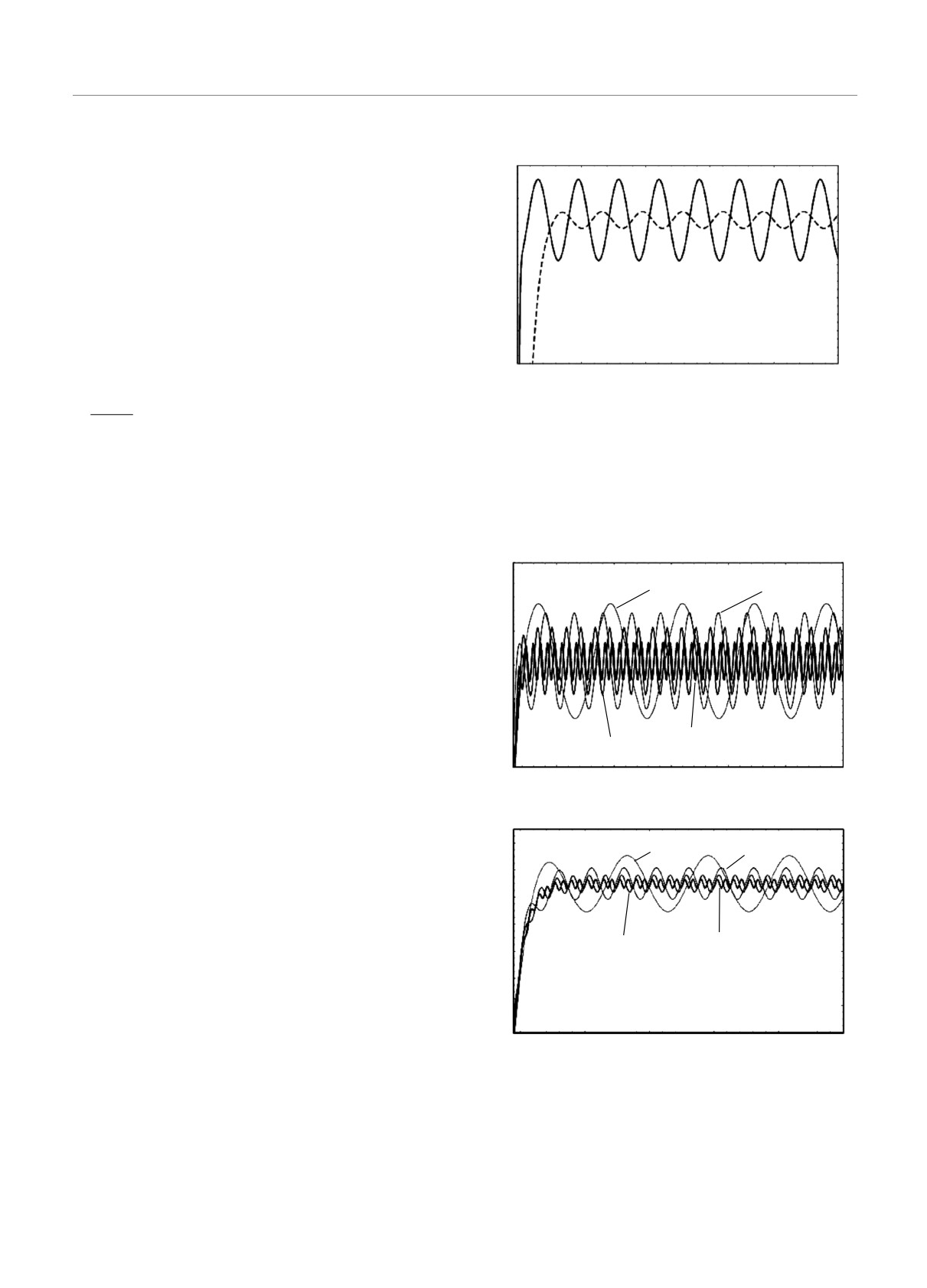
На рис. 3 показана зависимость числа Нуссель-
лами Россби Ro = 2 (а) и Ro = -3/4 (б)
та Nu от времени τ для положительного (Ro = 2)
и отрицательного (Ro = -3/4) профилей вращения
912
ЖЭТФ, том 157, вып. 5, 2020 Магнитная конвекция в неоднородно вращающейся электропроводящей среде. . .
Nu
что модуляция магнитного поля приводит к пери-
3.2
одическому изменению теплопотока, т. е. величина
числа Nu изменяется периодически во времени τ,
3.0
причем ΔNu|δ=0.3 > ΔNu|δ=0.
Проведенный выше численный анализ неавто-
2.8
номного комплексного уравнения Гинзбурга - Лан-
2.6
дау (41) показал, что с помощью регулирования па-
раметров модуляции (амплитуды δ и частоты ωB)
2.4
внешнего магнитного поля можно управлять теп-
2.2
лопереносом в магнитной конвекции в неоднород-
но вращающейся среде. Для исследования динами-
2.0
ческих свойств уравнения (41) (или (43)), описыва-
0
0.5
1.0
1.5
2.0
2.5
3.0
ющего эволюцию конечной амплитуды A(τ), необ-
ходимо провести качественный (бифуркационный)
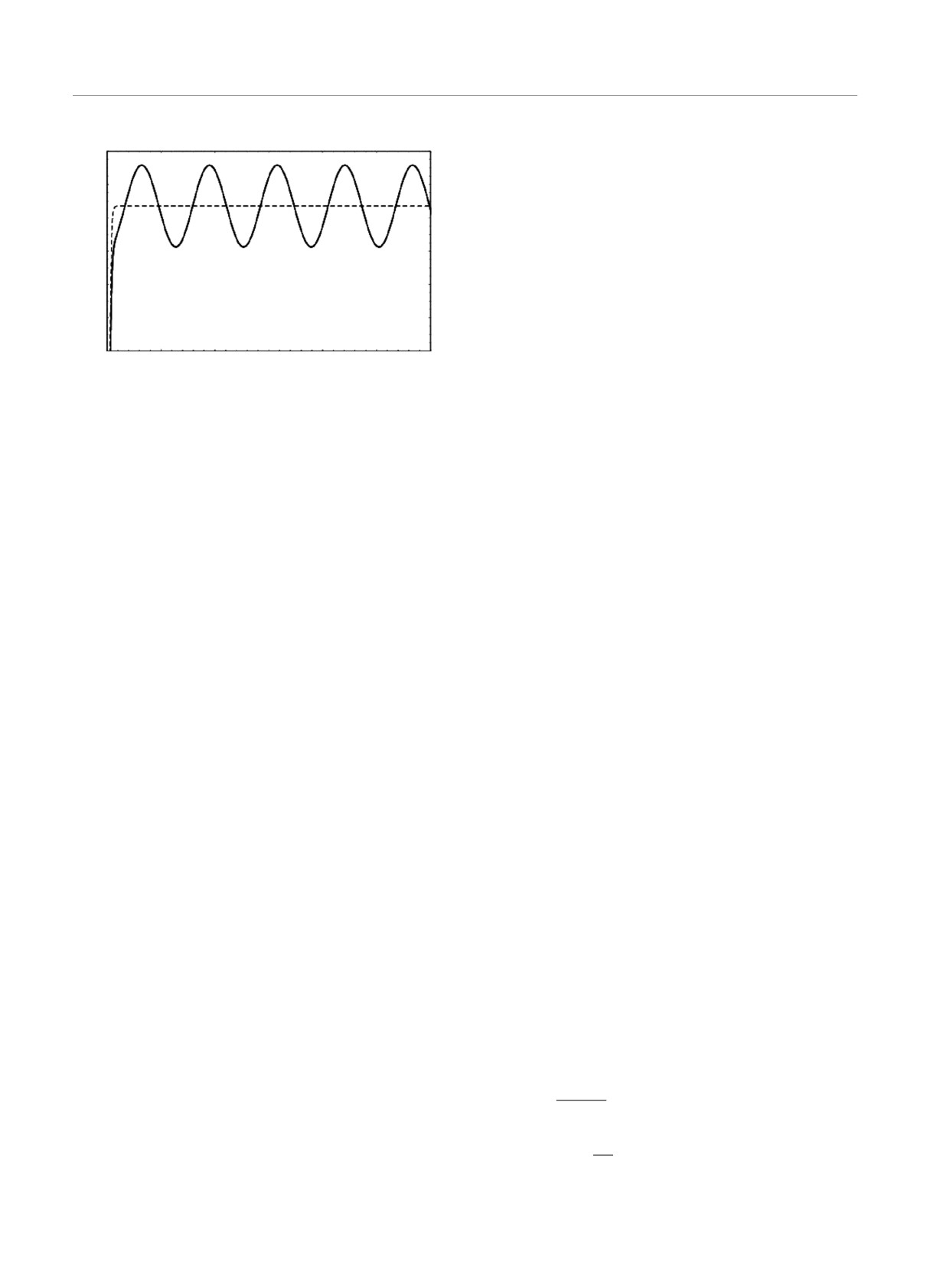
Рис. 5. Вариации числа Нуссельта (Nu) в отсутствие (δ =
анализ этого уравнения.
= 0, штриховая линия) и при наличии (δ = 0.3, ωB = 10,
сплошная линия) модуляции магнитного поля
5. БИФУРКАЦИОННЫЙ АНАЛИЗ
электропроводящей среды (плазмы) во внешнем ос-
В этом разделе мы исследуем динамическое по-
циллирующем магнитном поле с частотой ωB = 10
ведение комплексного уравнения Гинзбурга - Лан-
и амплитудой δ = 0.3. Видно, что при неоднородном
дау (43) в двух случаях: когда нет внешней моду-
вращении с положительным числом Россби (Ro > 0)
ляции магнитного поля (δ = 0) и когда она при-
теплоперенос в плазме увеличивается:
сутствует (δ = 0). Коэффициенты
r
,
r
, f(1)i,
ΔNu|Ro=-3/4 < ΔNu|Ro=2.
f(2)i, lr, li, входящие в уравнение (43) имеют доста-
точно сложную зависимость от параметров задачи
Также представляет интерес вопрос о влиянии час-
Pm, Q, Pr, Ta, Ra, k. Поэтому здесь мы рассмотрим
тоты модуляции магнитного поля на величину теп-
модельную задачу, в которой значения параметров
лопереноса. На рис. 4а приведены графики Nu(τ)
r
,
r
, f(1)i, f(2)i, lr, li изменяются независимо.
для разных частот модуляции (ωB = 10, 25, 50, 100)
в случае вращения плазмы с числом Россби Ro = 2.
5.1. Анализ комплексного уравнения
Здесь мы видим, что увеличение частоты модуляции
Гинзбурга - Ландау при δ = 0
ωB приводит к подавлению теплопереноса, т. е. вари-
ации числа Nu уменьшаются. Аналогичную картину
Рассмотрим случай, когда модуляции внешнего
мы наблюдаем и для случая кеплеровского профиля
магнитного поля нет (δ = 0). Тогда комплексное
вращения (Ro = -3/4), рис. 4б:
уравнение Гинзбурга - Ландау (43) будет иметь по-
стоянные коэффициенты. Это уравнение описыва-
ΔNu|ωB=10 > ΔNu|ωB=25 > ΔNu|ωB=50 >
ет слабонелинейную стадию (с конечной амплитудой
A(τ)) нестационарной магнитной конвекции в неод-
> ΔNu|ωB=100.
нородно вращающейся электропроводящей жидкос-
Сравнение величины теплопереноса в отсутствие
ти. Представим комплексную амплитуду A(τ) в амп-
(δ = 0) и при наличии (δ = 0.3, ωB = 10) модуляции
литудно-фазовом виде, т. е.
магнитного поля можно провести на графике рис. 5.
Здесь штриховой линией показан режим установле-
A(τ) = |A(τ)|eiΦ(τ).
(44)
ния конечного значения Nu(τ) для случая δ = 0.
Очевидно, что превышение числа Nu над единицей
Затем, подставляя выражение (44) в (43), при усло-
вии δ = 0 получим уравнения для амплитуды |A(τ)|:
обусловлено возникновением конвекции. В работе
[59] был проведен анализ интенсивности теплопере-
d|A(τ)|
носа для случая δ = 0 при различных профилях
= f(1)r|A(τ)| - lr|A(τ)|3,
(45)
dτ
вращения среды и было установлено, что интенсив-
ность теплопереноса увеличивается в сторону поло-
dΦ
жительных чисел Россби (Ro > 0). На рис. 5 видно,
= f(1)i - li|A(τ)|2.
(46)
dτ
913
10
ЖЭТФ, вып. 5
М. И. Копп, А. В. Тур, В. В. Яновский
ЖЭТФ, том 157, вып. 5, 2020
|A|
амплитуду как A(τ) = X(τ) + iY (τ), запишем урав-
1.0
нение (43) в виде автономной системы нелинейных
дифференциальных уравнений:
dX(τ)
= f(1)rX(τ) - f(1)iY (τ)-
0.8
dτ
- (lrX(τ) - liY (τ))(X2(τ) + Y 2(τ)),
(48)
dY (τ)
= f(1)iX(τ) + f(1)rY (τ)-
0.6
dτ
- (liX(τ) + lrY (τ))(X2(τ) + Y 2(τ)).
Качественный анализ положений равновесия сис-
0.4
темы (48) показал наличие единственной неподвиж-
ной точки в начале координат. В зависимости от
знака действительной части собственных значений
0.2
(λ1,2) линеаризованной системы (48) эта точка клас-
5
10
15
20
сифицируется как устойчивый (Re λ1,2
< 0) или
неустойчивый (Re λ1,2 > 0) фокус. При отрицатель-
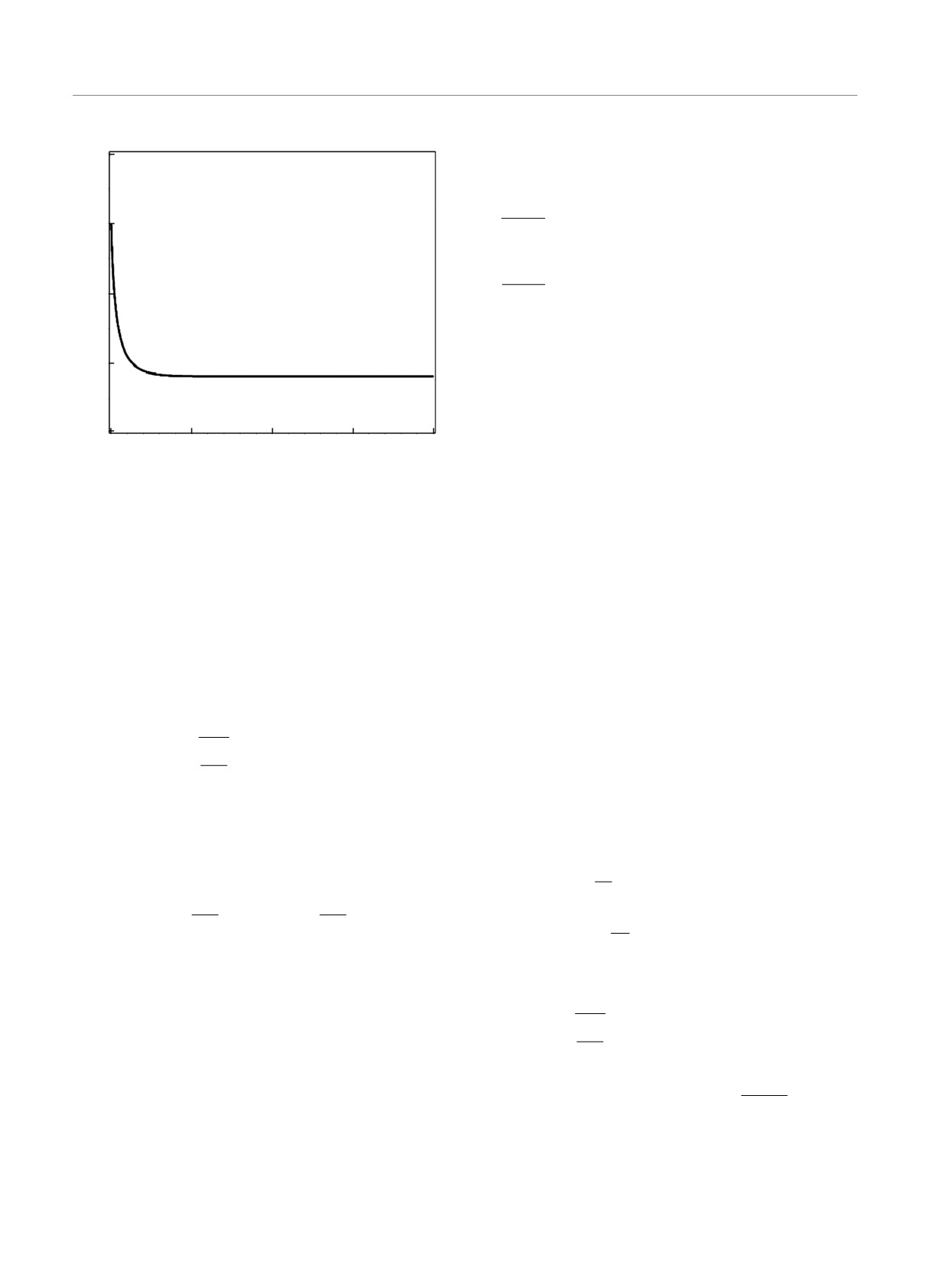
Рис. 6. Зависимость амплитуды |A| от времени τ , постро-
ных значениях (Re λ1,2 < 0) для параметров
r
=
енная по формуле (47) для фиксированных параметров
= -0.1, f(1)i = 3.96, lr = 0.145, li = 0.145 траектории
A0 = 0.8,
r
= 0.57, lr = 0.075. Видно установление
решений (при любых начальных неотрицательных
постоянного уровня амплитуды с ростом τ
условиях) по спирали скручиваются к точке рав-
новесия O(0, 0). Это соответствует затухающим ко-
лебаниям компонент (X, Y ), и фазовый портрет в
окрестности точки O(0, 0) называется устойчивым
Очевидно, что стационарные решения уравнения
фокусом [67, 68]. Изменяя параметры системы, на-
(45) имеют вид
пример при
r
= 0.57, f(1)i = 2.82, lr = 0.075, li =
|A| = 0, для всех значений f(1)r, lr
= 0.335, стационарное состояние O(0, 0) становится
неустойчивым, поскольку появилась замкнутая тра-
и
ектория, на которую изнутри и снаружи накручива-
√
ются по спирали траектории решений. В этом слу-
r
чае точка покоя соответствует неустойчивому фоку-
|A| = ±
для f(1)r > 0, lr > 0.
lr
су.
Для физической интерпретации фазовых траек-
Нестационарное решение уравнения (45) при на-
торий в системе уравнений (48) удобно перейти к
чальном условии |A(τ)|τ=0 = A0 соответственно рав-
полярным координатам X = r cos ϕ, Y = r sin ϕ:
но
(
)
dr
=r f(1)r -lrr2
,
(49)
[
(
)
dτ
lr
lr
|A(τ)|2 = A2
0
A20 +
1-A2
×
dϕ
r
0fr1)
=f(1)i -lir2.
(50)
dτ
]-1
(
)
Частные нетривиальные решения системы (49), (50)
× exp -2f(1)rτ
(47)
имеют вид
√
∫
На рис. 6 показан график зависимости амплитуды
r
r=±
,
ϕ=f(1)τ - li r2dτ + ϕ0.
i
|A(τ)| при фиксированных параметрах A0 = 0.8,
lr
r
= 0.57, lr = 0.075. Видно, что с увеличением
Этим решениям соответствуют траектории, имею-√
времени τ амплитуда становится постоянной.
щие форму окружности радиуса
r
/lr, которые
Проведем более подробный качественный анализ
устойчивости конвективных течений, описываемых
вращаются с частотой f(1)i. Траектории, берущие
уравнением (43) при δ = 0. Для этого, представляя
начало в окрестности неустойчивого фокуса, имеют
914
ЖЭТФ, том 157, вып. 5, 2020 Магнитная конвекция в неоднородно вращающейся электропроводящей среде. . .
√
dX(τ)
начальное значение r <
r
/lr. При этом правая
= f(1)rX(τ) - f(1)iY (τ)-
dτ
часть уравнения (49) положительна, и, следователь-
(
)
но, r будет возрастать. В этом случае траектории
− δ cosZ f(2)rX(τ) + f(2)iY (τ)
-
вращаются по спиралям, стремясь достигнуть ради-√
- (lrX(τ) - liY (τ))(X2(τ) + Y 2(τ)),
уса
r
/lr. Для траекторий, имеющих начало вне
√
dY (τ)
круга с r >
r
/lr, правая часть уравнения (49)
= f(1)iX(τ) + f(1)rY (τ)-
(52)
отрицательна, и поэтому радиус вращения со време-
dτ
(
)
нем должен уменьшаться. Таким образом, возника-
− δ cosZ f(2)iX(τ) - f(2)rY (τ)
-
ющий периодический режим (бифуркация Андроно-
ва - Хопфа) для параметров
r
= 2.57, f(1)i = 0.12,
- (liX(τ) + lrY (τ))(X2(τ) + Y 2(τ)),
lr = 0.42, li = 0.335 связан с присутствием замкну-
той траектории в фазовом пространстве. Все тра-
dZ(τ)
=ωB.
ектории, независимо от начальных условий, будут
dτ
стремиться к этой замкнутой траектории, называе-
Из системы уравнений (51) следует, что положение
мой устойчивым предельным циклом [67, 68].
точки равновесия O(0, 0) сохраняется и при нали-
чии малого возмущения δ = 0. Проведем числен-
ный анализ системы уравнений (51) при фиксиро-
ванных значениях амплитуды и частоты модуляции:
δ = 0.3,ωB = 10. Численное решение системы урав-
5.2. Анализ комплексного уравнения
нений (52) для параметров
r
= -0.1, f(1)i = 3.96,
Гинзбурга - Ландау при δ = 0
lr
= 0.145, li = 0.145,
r
= 0.5, f(2)i = 0.5 пока-
зывает затухание компонент (X, Y ) (рис. 7а). Такое
поведение траекторий на фазовом портрете соответ-
Проведем анализ комплексного уравнения Гинз-
ствует устойчивому фокусу (рис. 7б). При измене-
бурга - Ландау для случая δ = 0. Представляя амп-
нии параметров системы к значениям
r
= 0.57,
литуду как A(τ)
= X(τ) + iY (τ), из уравнения
f(1)i = 2.82, lr
= 0.075, li
= 0.335,
r
= 0.5,
(43) получим систему неавтономных дифференци-
f(2)i = 0.5 стационарное состояние O(0, 0) становит-
альных уравнений
ся неустойчивым. Точка O(0, 0) будет соответство-
вать неустойчивому фокусу. Здесь периодические
dX(τ)
орбиты накручиваются по спирали, исходя из точки
= f(1)rX(τ) - f(1)iY (τ)-
dτ
O(0, 0) (рис. 8). Волнообразное поведение траекто-
(
)
рий вызвано модуляцией внешнего магнитного поля.
− δ cos(ωBτ) f(2)rX(τ) + f(2)iY (τ)
-
В результате численного решения системы уравне-
(1)
ний (52) для параметров f
r
= 2.57, f(1)
= 0.12,
(
)
i
− (lrX(τ) - liY (τ))
X2(τ) + Y2(τ)
,
lr
= 0.42, li = 0.335,
r
= 0.5, f(2)i = 0.5 хорошо
(51)
заметно (рис. 9), что возникает модуляция нелиней-
dY (τ)
= f(1)iX(τ) + f(1)rY (τ)-
ной волны при наличии периодических внешних воз-
dτ
(
)
действий. При этом частота модуляции нелинейной
− δ cos(ωBτ) f(2)iX(τ) - f(2)rY (τ)
-
волны не определяется частотой внешнего воздей-
ствия, а зависит от амплитуды нелинейной волны.
(
)
- (liX(τ) + lrY (τ))
X2(τ) + Y2(τ)
Частота модуляции увеличивается за счет добавки
к частоте нелинейной волны, которая пропорцио-
нальна квадрату ее амплитуды. Другими словами, с
Динамические уравнения (51) описывают движение
ростом амплитуды нелинейной волны период моду-
системы с внешним возмущением (параметр δ мал).
ляции уменьшается. Такое поведение и наблюдает-
Для проведения качественного анализа приведем
ся при численном моделировании с изменением ам-
систему уравнений (51) к автономной за счет увели-
плитуды цикла или амплитуды нелинейной волны.
чения ее размерности. Для этой цели введем обозна-
Внешнее воздействие играет роль только спускового
чение для новой переменной Z = ωBτ. В результате
механизма, при котором возникает модуляционная
система уравнений (51) примет следующий вид:
неустойчивость нелинейной волны.
915
10*
М. И. Копп, А. В. Тур, В. В. Яновский
ЖЭТФ, том 157, вып. 5, 2020
X
X
1.5
3
а
а
1.0
2
1
0.5
0
0
–1
-0.5
-1.0
-2
-1.5
-3
0
10
20
30
40
50
60
0
10
20
30
40
50
60
Y
Y
б
б
1.0
2
1
0.5
0
0
-1
-0.5
-2
-1.0
-1.0
-0.5
0
0.5
1.0
-2
-1
0
1
2
X
X
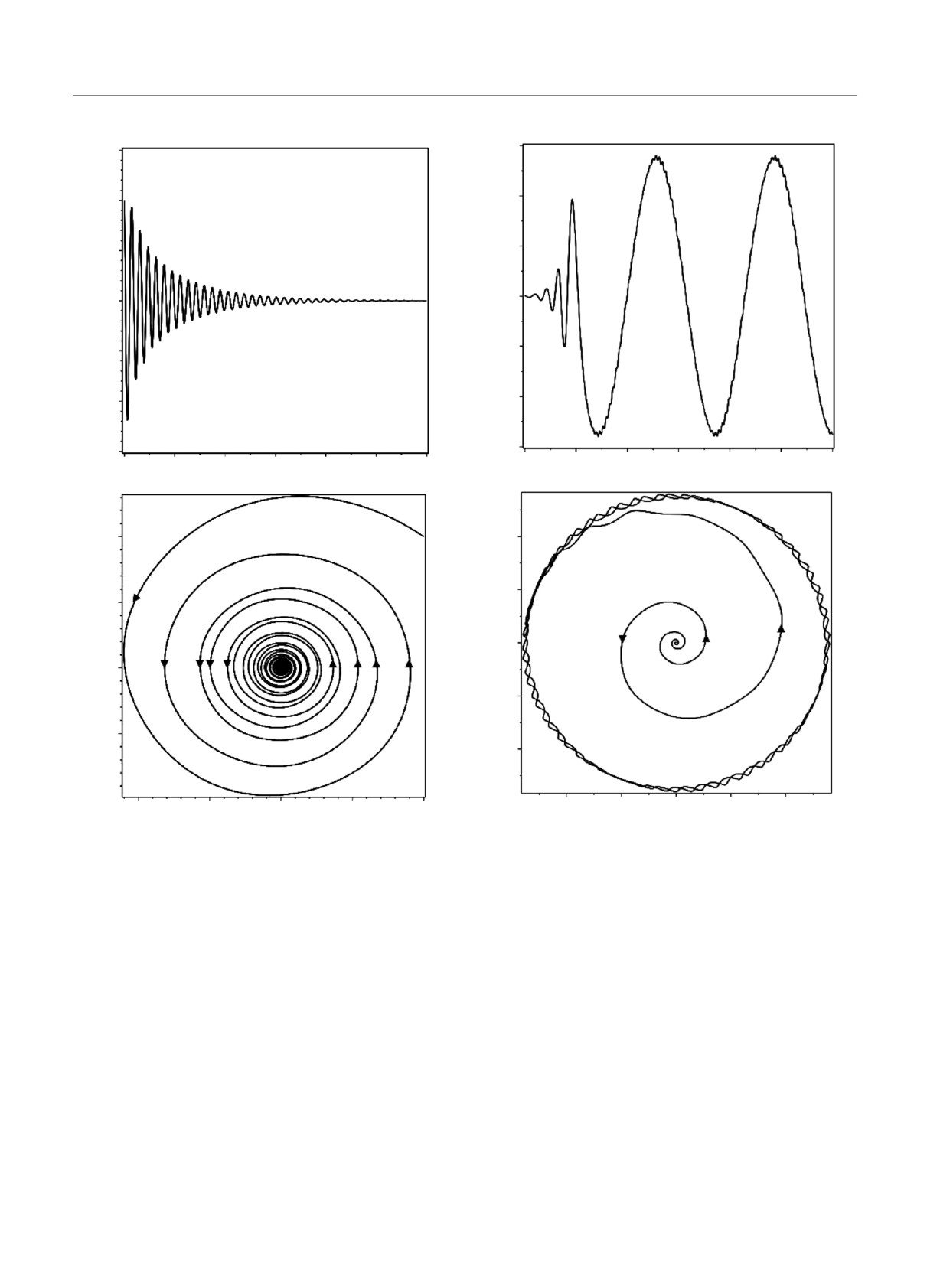
Рис. 7. a) Затухание X(Y )-компоненты в зависимости от
Рис.
8.
a) Установление периодической зависимости
времени τ . б) Фазовый портрет для динамической систе-
X(Y )-компоненты от времени τ. б) Фазовый портрет для
мы уравнений (52) - устойчивый фокус
динамической системы уравнений (52) — неустойчивый
фокус
∑
∑
ψ=
Amn(t)sin(mkx)sin(nπz),
n=1 m=1
6. УРАВНЕНИЯ КОНЕЧНОЙ АМПЛИТУДЫ
∑
∑
В ГАЛЕРКИНСКОЙ АППРОКСИМАЦИИ
v=
Vmn(t)sin(mkx)cos(nπz),
n=1 m=1
∑
∑
φ=
Bmn(t)sin(mkx)cos(nπz),
(53)
Еще одним эффективным способом исследова-
n=1 m=1
ния слабонелинейной стадии развития конвектив-
∑
∑
v=
Wmn(t)sin(mkx)sin(nπz),
ной неустойчивости является метод Галеркина [69].
n=1 m=1
Согласно этому методу, представим все возмущения
∑
∑
в уравнениях (25) в виде рядов Фурье:
θ=
Cmn(t)cos(mkx)sin(nπz).
n=1 m=1
916
ЖЭТФ, том 157, вып. 5, 2020 Магнитная конвекция в неоднородно вращающейся электропроводящей среде. . .
X
ψ(x, z, t) = A11(t) sin(kx) sin(πz),
3
v = V11(t)sin(kx)cos(πz),
а
φ(x, z, t) = B11(t) sin(kx) cos(πz),
(54)
2
v = W11(t)sin(kx)sin(πz),
θ(x, y, t) = C11(t) cos(kx) sin(πz) +
1
+ C02(t)sin(2πz),
где k — безразмерное волновое число, A11, V11, B11,
0
W11, C11, C02 — амплитуды возмущений. В резуль-
тате подстановки разложения (54) в уравнения (25),
-1
используя свойства ортогональности функций
1
{
∫
0,
если m = n,
-2
sin(mπz) sin(nπz)dz =
1/2, если m = n,
0
-3
получим уравнения эволюции для амплитуд возму-
0
10
20
30
40
50
60
щений:
Y
√
б
∂A11
π
Ta
2
= -A11 -
V11 -
∂t
a4
πQPr
(
)
kRa
1 + δϵ2 cos(ΩBt)
B11 +
C11,
(55)
− a2Pm
a4
1
√
∂V11
π
Ta
0
= -V11 +
(1 + Ro)A11 +
∂t
a2
πQPr
(
)
+
1 + δϵ2 cos(ΩBt)
W11,
(56)
a2Pm
–1
∂B11
πPm
(
)
Pm
= -B11+
1+δϵ2 cos(ΩBt)
A11,
(57)
∂t
a2Pr
–2
∂W11
πPm
(
)
-2
-1
0
1
2
Pm
= -W11-
1+δϵ2 cos(ΩBt)
V11 +
X
∂t
a2Pr
√
πPmRo
Ta
Рис.
9.
a) Модуляция автоколебаний X(Y )-компоненты.
+
B11,
(58)
a2
б) Фазовый портрет для динамической системы уравне-
ний (52) — предельный цикл
∂C
11
k
πk
Pr
= -C11 +
A11 +
A11C02,
(59)
∂t
a2
a2
∂C02
4π2
πk
Pr
=-
C02 -
A11C11.
(60)
∂t
a2
2a2
√
Здесь a =
k2 + π2 — общее волновое число, t =
Выражения (53) удовлетворяют граничным услови-
= a2t — редуцированное время, ΩB = ωB/a2 — ре-
ям (24). Ограничимся галеркинской аппроксимаци-
дуцированная частота модуляции магнитного поля.
ей минимального порядка, а именно, для функции
Полученная нами система обыкновенных диффе-
тока ψ рассмотрим моды (1, 1), для y-компоненты
ренциальных уравнений (55)-(60) является спект-
скорости v — моды (1, 1), магнитного потенциала
ральной моделью низкого порядка, но вполне может
φ — (1,1), y-компонентывозмущений магнитного по-
качественно воспроизводить конвективные процес-
ля v — (1, 1) и возмущений температуры θ — (1, 1) +
сы в полной (самосогласованной) нелинейной систе-
+ (0, 2):
ме уравнений (25).
917
М. И. Копп, А. В. Тур, В. В. Яновский
ЖЭТФ, том 157, вып. 5, 2020
Введем для удобства следующие обозначения:
Ta = 2, γ = 1) будем считать фиксированными.
√
Остальные параметры R, δ1, ΩB рассмотрим как
2
k2Ra
π2
Ta
π
QPr
4π2
переменные при исследовании влияния модуляции
R=
,
T=
,
H=
,
γ =
,
a6
a6
a4 Pm
a2
магнитного поля на хаотическое поведение системы
и проведем перемасштабирование амплитуд A11,
(61). Как и ранее, полагаем амплитуду модуляции
V11, B11, W11, C11, C02 в виде
(δ1) достаточно малой.
На рис. 10 и 11 показаны численные решения си-
kπ
kV11(t)
X (t) =
√
A11(t), V (t) =
√
,
стемы уравнений (61) для значений амплитуды δ1 =
a2
2
2
= 0.3 и частоты модуляции ΩB = 10 внешнего маг-
нитного поля при изменении параметра Рэлея R.
kB11(t)
a2k
U (t) =
√
,
W (t) =
√
W11(t),
На рис. 10а для параметра R = 13.8 мы наблюда-
2
π
2
ем извилистые линии траекторий, которые накручи-
πC11(t)
ваются по спирали вокруг неподвижной точки. Эта
Y (t) =
√
,
Z(t) = -πC02(t).
2
точка в отсутствие модуляции соответствует устой-
Тогда уравнения (55)-(60) принимают вид нелиней-
чивому фокусу [48]. Величина возмущенного маг-
ной динамической системы уравнений
нитного поля U(t) (для параметра R = 13.8) умень-
шается по амплитуде, достигая некоторого значения
X
= -X + RY - TV - H(1 + δ1 cos(ΩBt))U,
Um(t), вызванного модуляцией внешнего магнитно-
V
= -V + H(1 + δ1 cos(ΩBt))W +
го поля (см. рис. 11а). На рис. 10б, 11б при пара-
√
метре R = 28.5 показано возникновение гомокли-
+
Ta(1 + Ro)X,
нической петли в фазовом пространстве. Как вид-
U
= -Pm-1U + Pr-1(1 + δ1 cos(ΩBt))X,
но на рис. 10б, извилистость траекторий обуслов-
(61)
W
лена влиянием модуляции. Возмущенное магнитное
= -Pm-1W - Pr-1(1 + δ1 cos(ΩBt))V +
√
поле U(t) здесь также полностью не затухает (см.
+ Ro
TaU,
рис. 11б). При увеличении параметра Рэлея, т. е. при
Y
= Pr-1(-Y + X - XZ),
R = 31.38, наблюдается переход от гомоклинической
Ż
траектории к хаотическому движению (см. рис. 10в,
= Pr-1(-γZ + XY ),
11в). На рис. 11в показаны нерегулярные колебания
где точка сверху обозначает дифференцирование по
с апериодическим изменением амплитуды и направ-
времени t, δ1 = δϵ2. В отсутствие модуляции внеш-
ления (инверсией) возмущенного магнитного поля.
него магнитного поля система уравнений (61) имеет
Результаты численных исследований системы
сходство с уравнениями Лоренца [69], но для шести-
уравнений (61) по влиянию высокочастотной моду-
мерного фазового пространства. Хаотическое пове-
ляции ΩB = 50 на поведение конвекции при раз-
дение системы уравнений (61) без модуляции (δ1 =
ных параметрах Рэлея R = 13.8, 28.5, 31.38 пока-
= 0) было подробно исследовано в работах [48,49].
заны на рис. 12 и 13. Для этого случая величину
Далее мы проведем численное исследование дина-
амплитуды модуляции будем считать без изменения,
мической системы уравнений (61) с периодическими
т. е. δ1 = 0.3. Сравнивая результаты, представлен-
коэффициентами.
ные на рис. 10 и 11, видим, что на высоких ча-
стотах модуляции траектории движения в фазовом
пространстве выглядят более сглаженными. Это яв-
7. РЕЗУЛЬТАТЫ ЧИСЛЕННЫХ РЕШЕНИЙ
ляется следствием того, что с увеличением частоты
НЕАВТОНОМНОЙ СИСТЕМЫ УРАВНЕНИЙ
модуляции теплоперенос (число Нуссельта Nu) в си-
ЛОРЕНЦА (6D)
стеме становится меньше (см. рис. 4).
В этом разделе с помощью стандартных про-
На рис. 14 и 15 показаны результаты численных
грамм в компьютерной среде Mathematica предста-
исследований системы уравнений (61) для большей
вим результаты численных исследований нелиней-
амплитуды модуляции δ1 = 0.5, чем для случая по-
ной системы уравнений (61) с начальными условия-
казанного на рис. 10 и 11. Частота модуляции ΩB
ми X(0) = V (0) = U(0) = W (0) = Y (0) = Z(0) = 1
и параметры Рэлея R остаются без изменения, т. е.
во временной области 0 ≤ t≤ 6000 для кеплеровско-
ΩB = 10, R = 13.8, 28.5, 31.38. На рис. 14 видно, что
го (Ro = -3/4) профиля вращения. Некоторые па-
с увеличением амплитуды модуляции, извилистость
раметры магнитной конвекции в неоднородно вра-
фазовых траекторий становится существенно боль-
щающейся среде (Pm = 1, Pr = 9, H = 5, T = 1,
ше. На рис. 15а,б показаны периодический и «квази-
918
ЖЭТФ, том
157, вып. 5, 2020 Магнитная конвекция в неоднородно вращающейся электропроводящей среде. . .
Y
U
1.0
а
а
0.6
0.8
0.6
0.4
0.4
0.2
0.2
0
0.2
0.4
0.6
0.8
1.0
0
50
100
150
200
250
300
U
~
U
Y
1.0
0.6
б
б
0.4
0.5
0.2
0
0
-0.2
-0.5
-0.4
-0.6
-1.0
-1.0
-0.5
0
0.5
1.0
0
500
1000
1500
U
t
U
Y
0.6
в
в
1.0
0.4
0.5
0.2
0
0
-0.2
-0.5
-0.4
-1.0
-0.6
-1.0
-0.5
0
0.5
1.0
-1.5
0
1000
2000
3000
4000
5000
U
~
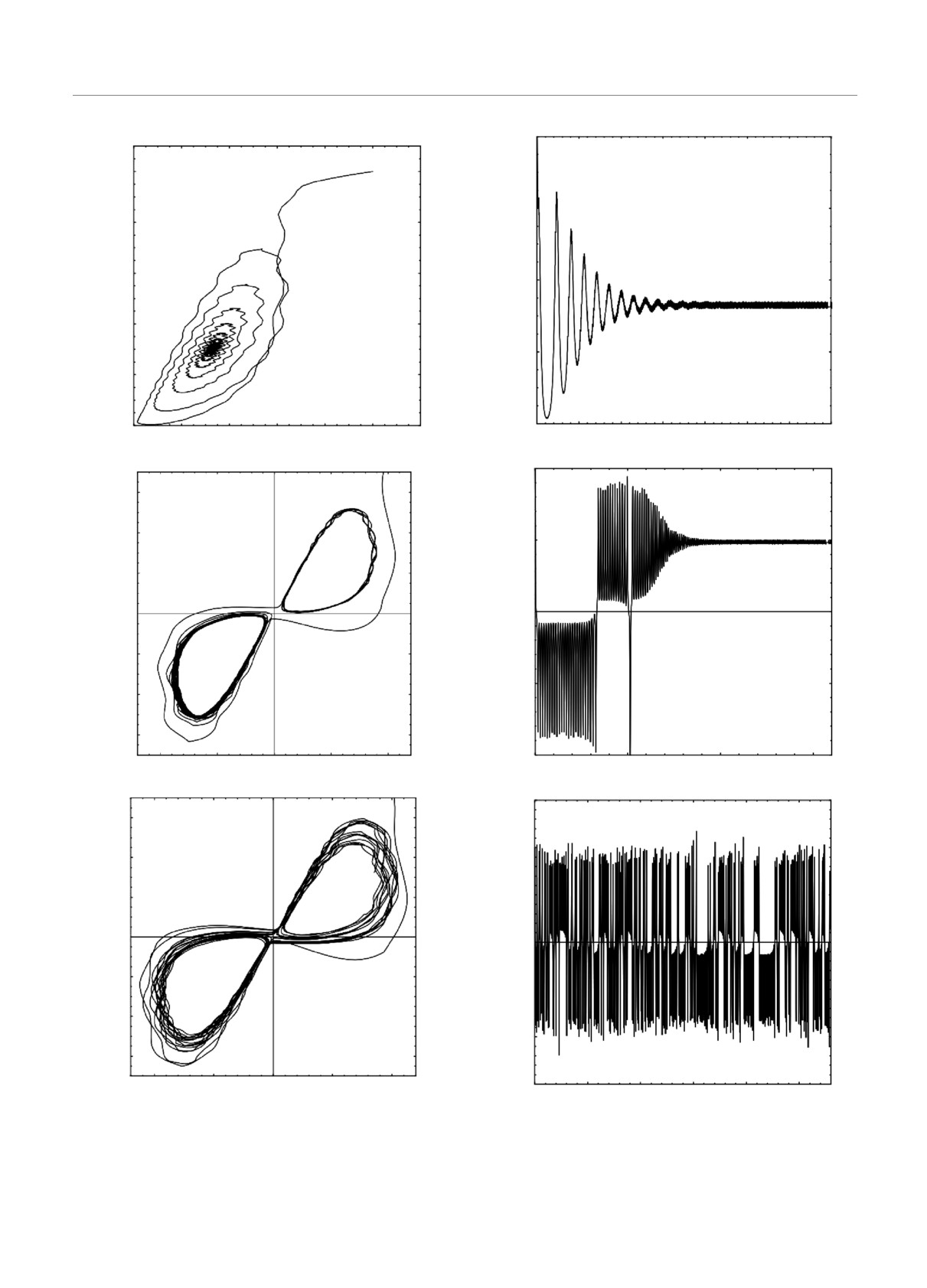
Рис. 10. Проекции фазовых траекторий в плоскости UY
Рис.
11.
Временные зависимости вариаций амплитуды
при изменении параметра R: a — R = 13.8; б — R = 28.5;
магнитной компоненты U(t) при изменении параметра R:
в — R = 31.38, для фиксированной амплитуды δ1 = 0.3 и
a — R = 13.8; б — R = 28.5; в — R = 31.38, для фиксиро-
частоты ΩB = 10
ванной амплитуды δ1 = 0.3 и частоты ΩB = 10
919
М. И. Копп, А. В. Тур, В. В. Яновский
ЖЭТФ, том 157, вып. 5, 2020
Y
U
1.0
а
0.6
а
0.8
0.5
0.6
0.4
0.3
0.4
0.2
0.2
0.1
0
100
200
300
400
0
0.2
0.4
0.6
0.8
1.0
~
U
U
Y
1.0
1.0
б
б
0.5
0.5
0
0
-0.5
-0.5
-1.0
-1.0
0
400
800
1200
~
-1.0
-0.5
0
0.5
1.0
U
U
Y
1.0
в
0.6
в
0.4
0.5
0.2
0
0
-0.2
-0.5
-0.4
-1.0
-0.6
0
1000
2000
3000
4000
5000
–1.0
-0.5
0
0.5
1.0
~
U
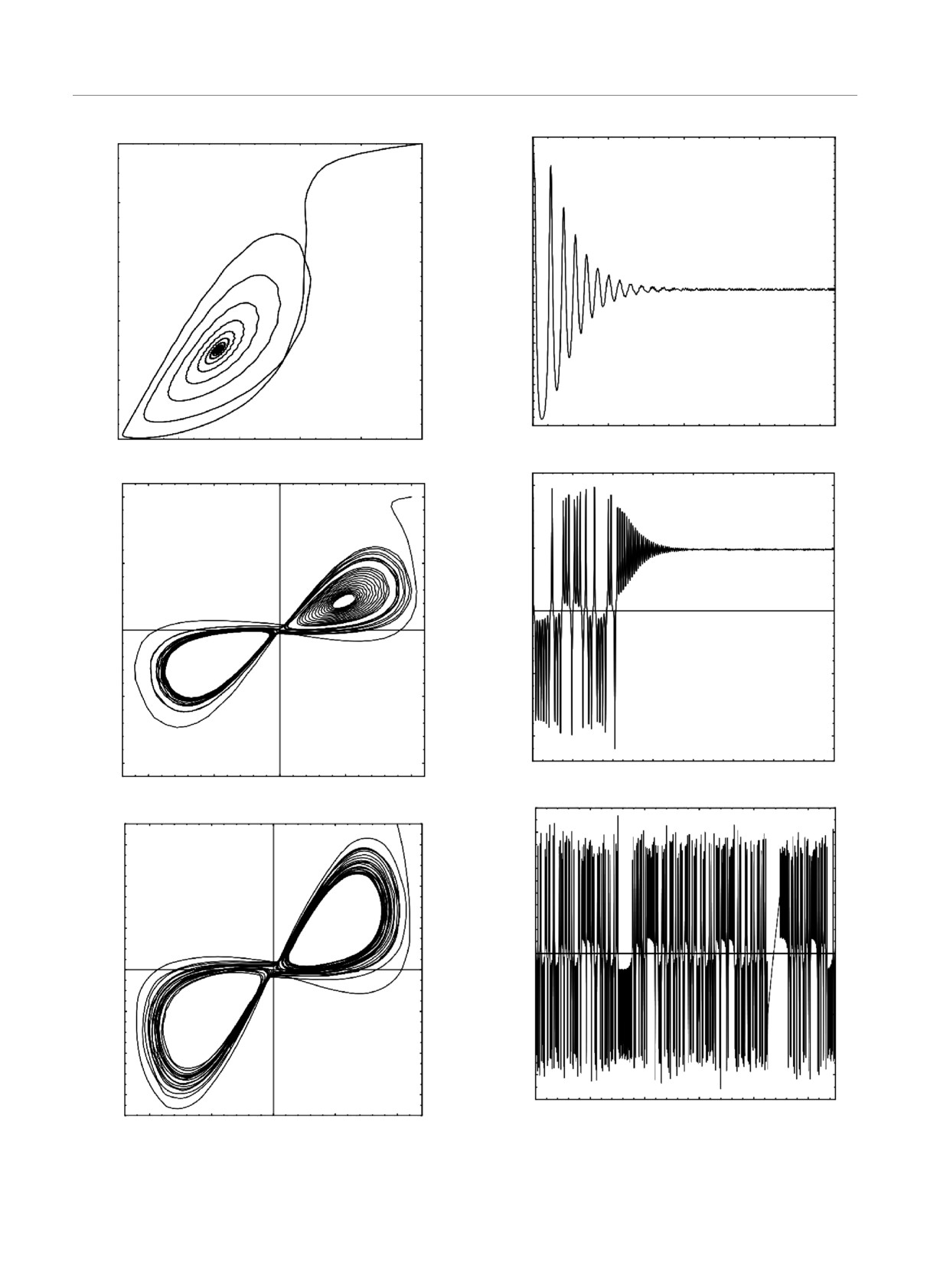
Рис. 13. То же, что на рис. 11, но для ΩB = 50
Рис. 12. То же, что на рис. 10, но для ΩB = 50
920
ЖЭТФ, том
157, вып. 5, 2020 Магнитная конвекция в неоднородно вращающейся электропроводящей среде. . .
U
Y
0.6
а
а
0.6
0.5
0.5
0.4
0.4
0.3
0.3
0.2
0.2
0.1
0.1
0
100
200
300
400
0
0.2
0.4
0.6
0.8
1.0
U
~
U
Y
1.0
0.6
б
б
0.4
0.5
0.2
0
0
-0.2
-0.5
-0.4
-0.6
-1.0
-0.5
0
0.5
1.0
-1.0
0
400
800
1200
U
~
Y
0.6
U
в
в
0.4
1.0
0.2
0.5
0
0
-0.2
-0.5
-0.4
-0.6
-1.0
-1.0
-0.5
0
0.5
1.0
U
-1.5 0
1000
2000
3000
4000
5000
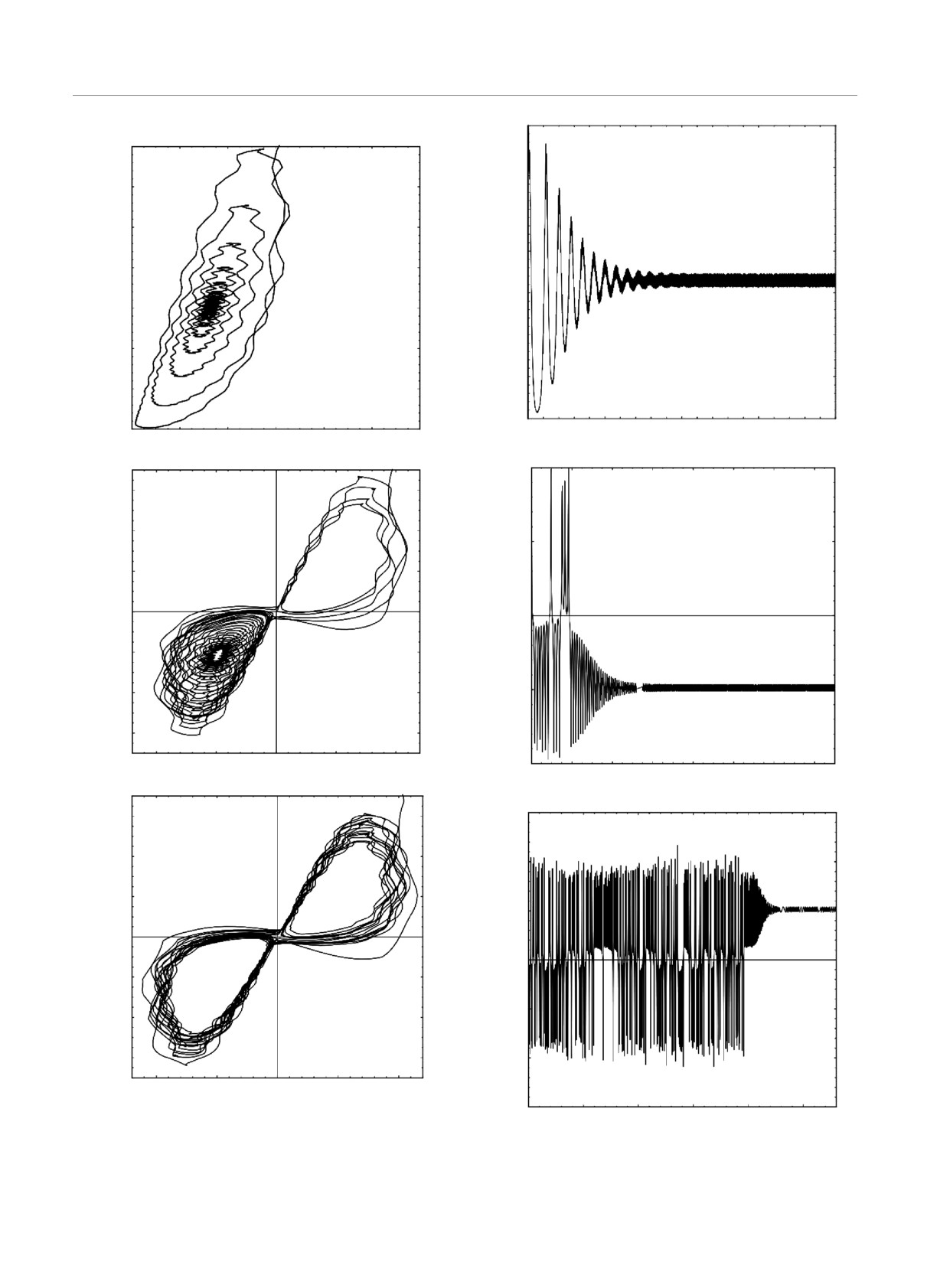
Рис.
14. То же, что на рис. 10, но для ΩB = 10
~
Рис.
15. То же, что на рис. 11, но для ΩB = 10
921
М. И. Копп, А. В. Тур, В. В. Яновский
ЖЭТФ, том 157, вып. 5, 2020
периодический» режимы затухания возмущенного
Численный анализ этой системы уравнений пока-
магнитного поля до некоторого значения Um(t), обу-
зал, что модулированное внешнее магнитное поле
словленного модуляцией внешнего магнитного поля.
оказывает существенное влияние на хаотическое
На рис. 15в показан режим метастабильного хаоса,
поведение возбуждаемого магнитного поля и его
для которого хаотическое поведение на временном
инверсию. В частности, повышение амплитуды
интервале 0 ≤ t≤ 4000 сменяется периодическим за-
модуляции может вызвать переход от хаотического
туханием до определенного уровня осцилляций воз-
к периодическому поведению конвекции.
мущенного магнитного поля Um(t).
Благодарности. Авторы выражают глубокую
благодарность рецензенту за ряд ценных и полез-
ных замечаний.
8. ЗАКЛЮЧЕНИЕ
В работе развита слабонелинейная теория коле-
бательной конвекции в неоднородно вращающейся
ПРИЛОЖЕНИЕ A
электропроводящей жидкости в аксиальном маг-
Коэффициенты f(1)r, f(2)r, f(1)i, f(2)i, lr, li в
нитном поле, которое состоит из суммы регулярной
уравнении (43)
(постоянной) и осциллирующей с малой амплиту-
дой частей. Влияние периодической по времени
Приведем явный вид коэффициентов
r
,
r
,
магнитной модуляции на конвекцию Рэлея - Бе-
f(1)i, f(2)i, lr, li, входящих в уравнение (43):
нара исследовалось при помощи метода теории
возмущений по малому параметру надкритичности
f(1)r = (srFr+ω2siFi)Δ-1, f(2)r = (ω2si
Fi-srFr)Δ-1,
√
числа Рэлея ϵ
=
(Ra - Rac)/Rac. В линейном
приближении, или в первом порядке по ϵ, мы по-
f(1)i = ω(siFr - srFi)Δ-1,
лучили выражение для критического числа Рэлея
Rac в случае колебательной конвекции (ω
= 0).
f(2)i = ω(sr
Fi +siFr)Δ-1, lr = (Rrsr -ω2Risi)Δ-1,
Отрицательный профиль неоднородного вращения
Ro = -3/4 приводит к понижению порога неустой-
li = ω(Rrsi + Risr)Δ-1.
чивости и тем самым оказывает дестабилизирующее
Здесь введены следующие обозначения:
действие на развитие неустойчивости. В третьем
порядке по ϵ мы получили нелинейное комплексное
(
)
a4 - ω2Pr2
уравнение Гинзбурга - Ландау с периодическими по
sr = a2 + k2Rac Pr
-
(a4 + ω2Pr2)2
времени коэффициентами. Численный анализ этого
(
)
a4 - ω2Pm2
уравнения показал, что при неоднородном враще-
- π2a2QPm
- π2Ta · Tr,
нии с положительным числом Россби (Ro
= 2)
(a4 + ω2Pm2)2
теплоперенос в плазме увеличивается. При уве-
личении частоты модуляции ωB вариации числа
(
)
Нуссельта ΔNu уменьшаются, что приводит к
2a2Pr
si = k2Rac Pr
-
подавлению теплопереноса как при положительных
(a4 + ω2Pr2)2
(
)
(Ro = 2), так и при отрицательных (Ro = -3/4)
2a2Pm
- π2a2QPm
- π2Ta · Ti,
профилях вращения. Отсюда можно сделать вывод,
(a4 + ω2Pm2)2
что эффект магнитной модуляции является весьма
существенным и может использоваться для пони-
a2k2Rac
2π2a4Q
Fr =
,
Fr = -
+π4TaQ · Lr,
жения порога возникновения конвекции, т. е. для
a4+ω2Pr2
a4+ω2Pm2
уменьшения теплопередачи. Эффект увеличения
амплитуды модуляции δ приводит к повышению
k2Rac Pr
2π2a2QPm
Fi =
,
Fi =
+ π4TaQ · Li,
теплообмена. Применяя галеркинскую аппрок-
a4 + ω2Pr2
a4 + ω2Pm2
симацию минимального порядка к нелинейной
системе уравнений для неоднородно вращающейся
π2k4Rac
магнитоконвекции, мы получили динамическую
Rr =
×
2
систему уравнений Лоренца (6D) с периодическими
ω2Pr2(π2 - a6 - ω2Pr2(a2 + π2)) + π2a4(1 + a4)
коэффициентами. Эта система уравнений описыва-
×
,
ет нелинейный режим модулированной конвекции.
(ω2Pr2 + a4)(ω2Pr2(a4 + 4π4 + ω2Pr2) + 4π4a4)
922
ЖЭТФ, том 157, вып. 5, 2020 Магнитная конвекция в неоднородно вращающейся электропроводящей среде. . .
2
k4Rac
π2QRoPm
Ri =
×
δi = Pm(2 + Ro) -
,
4
a4 + ω2Pm2
ω2Pr2(ω2Pr2 - 4π2a2 - 1) - a4(a4 + 4π2a2 + 1)
×
κr = (1+Ro)(a6-3ω2a2Pm2)+π2a2QPm(RoPm-1),
(ω2Pr2 + a4)(ω2Pr2(a4 + 4π4 + ω2Pr2) + 4π4a4)
κi = (1 + Ro)(3a4Pm - ω2Pm3) + π2Pm2Q(Ro - 1),
Далее приведем выражения для Tr, Ti, Lr, Li:
π2a2RoQPm2
π2RoQPm3
σr =
,
σi =
Tr = βr(γrκr+ω2γiκi+σr)+ω2βi(γrκi-γiκr-σi),
a4 + ω2Pm2
a4 + ω2Pm2
ПРИЛОЖЕНИЕ B
Ti = βr(γrκi - γiκr - σi) - βi(γrκr + ω2γiκi + σr),
Вывод комплексного уравнения
Lr = βr(γrδr + δiγiω2 - RoPm) + ω2βi(γrδi - γiδr),
Гинзбурга - Ландау из уравнений Лоренца
(6D) с модуляцией внешнего магнитного
Li = βr(γrδi - γiδr) - βi(γrδr + δiγiω2 - RoPm).
поля
Входящие в эти выражения постоянные коэффици-
В этом разделе приведем вывод комплексного
енты βr, βi, γr, γi, γr, γi, δr, δi, κr, κi, σr, σi соот-
уравнения Гинзбурга - Ландау (41) из уравнений
ветственно равны
Лоренца (6D) с модуляцией внешнего магнитного
поля (61). Представим все возмущенные величины
βr =
в уравнениях (61) в виде разложения в ряд по ма-
a2ζ - ω2a2Pm(1 + Pm)
=
,
лому параметру надкритичности ϵ:
ω2(Pmζ+a4(1+Pm))2+(a2ζ-ω2a2Pm(1+Pm))2
X(t) = ϵX1 + ϵ2X2 + ϵ3X3 + . . . ,
X(t) = [X, V, U, W, Y, Z]Tr,
(62)
βi =
R=R0 +ϵ2R2 +...
Pmζ + a4(1 + Pm)
=
,
ω2(Pmζ+a4(1+Pm))2+(a2ζ-ω2a2Pm(1+Pm))2
Амплитуды возмущенных величин зависят как от
быстрого t0, так и от медленного τ = ϵ2t времен.
a4 + π2Q - ω2Pm
γr =
,
Производную по времени в уравнениях (61) пред-
(a4 + π2Q - ω2Pm)2 + ω2a4(1 + Pm)2
ставим в виде [61]
a2(1 + Pm)
γi =
,
∂
∂
∂
(a4 + π2Q - ω2Pm)2 + ω2a4(1 + Pm)2
→
+ϵ2
(63)
∂t
∂t0
∂τ
a2(a4 + π2Q + ω2Pm2)
γr =
,
Для первого порядка по ϵ, после подстановки разло-
(a4 + π2Q - ω2Pm)2 + ω2a4(1 + Pm)2
жений (62), (63) в (61), получим линейную систему
ω2Pm2 + a4 - π2QPm
уравнений
γi =
,
(a4 + π2Q - ω2Pm)2 + ω2a4(1 + Pm)2
L X1 = 0, X1 = [X1,V1,U1,W1,Y1,Z1]Tr,
(64)
π2a2QRoPm
δr = 2a2(1 + Ro) +
- a2RoPm,
2
a4 + ω2Pm
где матрица L имеет вид
⎡
(
)
⎤
∂
-
+1
-T
-H
0
R0
0
⎢
⎥
⎢
∂t0
(
)
⎥
⎢√
∂
⎥
⎢
Ta(1 + Ro)
-
+1
0
H
0
0
⎥
⎢
⎥
⎢
∂t0
(
)
⎥
⎢
∂
⎥
⎢
Pr-1
0
-
+ Pm-1
0
0
0
⎥
⎢
⎥
⎢
∂t0
(
)
⎥
L =
⎢
√
∂
⎥
⎢
0
- Pr-1
Ro
Ta
-
+ Pm-1
0
0
⎥
⎢
⎥
⎢
∂t0
(
)
⎥
⎢
∂
⎥
⎢
⎥
Pr-1
0
0
0
-
+ Pr-1
0
⎢
⎥
⎢
∂t0
(
)⎥
⎣
∂
⎦
0
0
0
0
0
-
+ γPr-1
∂t0
923
М. И. Копп, А. В. Тур, В. В. Яновский
ЖЭТФ, том 157, вып. 5, 2020
⎡
(
)
Решения уравнений (64) относительно перемен-
√
HRoPm2
⎢
Ta
(1 + Ro) Pr +
ной
⎢
(iω′ + 1)2
∂
R32 =
⎢
+
X1 =
X1(τ)eiω′t0 +
X∗(τ)e-iω′t0
HPm
1
⎣
∂τ
Pr(iω′ + 1) +
iω′Pm + 1
соответственно равны
(
(
))⎤
√
Pm(iω′+1)
(
)
√
Pm
Ta
1+Ro
1-
HRoPm2
⎥
iω′Pm+1
Ta
(1+Ro) Pr +
⎥
2
+ δ cos(ΩBτ)
(iω′ + 1)
⎦×
Pr(iω′ + 1)(iω′Pm + 1) + HPm
V1 =
X1(τ)eiω′t0 +c.c.,
HPm
Pr(iω′ + 1) +
iω′Pm + 1
× X1(τ)eiω′t0 + c.c.,
Pm
U1 =
X1(τ)eiω′t0 + c.c.,
Pr(iω′Pm + 1)
[
]
Pm
∂
R33 =
- Pr-1δ cos(ΩB τ)
×
(
(
))
Pr(iω′Pm + 1) ∂τ
√
Pm(iω′ + 1)
Pm
Ta
1 + Ro
1-
× X1(τ)eiω′̃0 + c.c.,
iω′Pm + 1
W1
=-
×
Pr(iω′ + 1)(iω′Pm + 1) + HPm
⎡
(
(
))
× X1(τ)eiω′t0 + c.c.,
√
Pm(iω′ + 1)
⎢
Pm
Ta
1+Ro
1-
⎢
iω′Pm+1
∂
X1(τ)e
iω′t0
R34 =
⎢-
+
Y1 =
+ c.c., Z1 = 0,
⎣
Pr(iω′ + 1)(iω′Pm + 1) + HPm
∂τ
iω′Pr + 1
здесь ω′ = ω/a2 — редуцированная частота.
(
)⎤
√
HRoPm2
Для второго порядка по ϵ имеем следующее урав-
Ta
(1+Ro) Pr +
⎥
(iω′ + 1)2
⎥
нение:
+ Pr-1δ cos(ΩB τ)
⎥
×
HPm
⎦
Pr(iω′ + 1)+
L X2 = [R21,R22,R23,R24,R25,R26]Tr,
iω′Pm + 1
(65)
X2 = [X2, V2, U2, W2, Y2, Z2]Tr,
× X1(τ)eiω′t0 + c.c.,
где нелинейные члены соответственно равны
[
]
R21 = 0, R22 = 0, R23 = 0, R24 = 0,
1
∂X1
R35 =
+Pr-1Z20 X1+Pr-1Z22 X∗
1
×
iω′ Pr+1
∂τ
R25 = Pr-1X1Z1, R26 = -Pr-1X1Y1.
× eiω′t0 + Pr-1Z22 X1e3iω′t
0 + c.c., R36 = 0.
Учет нелинейности только в уравнении температур-
ного баланса приводит к решению уравнений (65)
Условие разрешимости (альтернатива Фредгольма)
следующего вида:
нелинейных уравнений (66) в третьем порядке по ϵ,
согласно определению (26), имеет следующий вид:
Z2 = Z20 + Z22e2iωt0 + Z∗22e-2iω′t0 ,
∑
2
X2
R3jX†1 = 0,
(67)
2|X1|
1
Z20 =
,
Z22 =
j=1
γ(1+ω′2Pr2)
(iω′Pr+1)(2iω′Pr+γ)
здесь
Далее переходим к уравнениям третьего порядка
по ϵ:
R31 =
PPr-1R31, R32 =
PR0R35,
L X3 = [R31,R32,R33,R34,R35,R36]Tr,
(66)
R34 = -
PR33,
X3 = [X3, V3, U3, W3, Y3, Z3]Tr,
√
где нелинейные члены соответственно равны
THRo
TaPm2
R35 =
R33
+
∂
[
]
Pm
+1
∂
R2
HPm
R31 =
-
+δ cos(ΩBτ)
×
∂t0
(
)
∂τ
iω′Pr+1
Pr(iω′Pm+1)
∂
+ T Pm
+1
R32 + THPmR34,
× X1(τ)eiω′t0 + c.c.,
∂t0
924
ЖЭТФ, том 157, вып. 5, 2020 Магнитная конвекция в неоднородно вращающейся электропроводящей среде. . .
(
)
√
√
∂
HRo
TaPm2
Элементы матрицы X†1
=
[X†1, Y†1, Z†1, U†1, V†1]Tr
P =
Ta(1+Ro) Pr Pm
+1
+
∂t0
∂
представляют собой решения линейной самосопря-
Pm
+1
∂t0
женной задачи L†X†1 = 0, где самосопряженная
матрица L† определяется как
⎡
(
)
⎤
∂
Pr-1
P
+1
-R0Pr-1
P
0
HPr-1
P
TPr-1
P
⎢
∂t0
⎥
⎢
(
)
⎥
⎢
∂
⎥
⎢
−R0Pr-1
P
R0Pr-1
P Pr
+1
0
0
0
⎥
⎢
⎥
⎢
∂t0
(
)
⎥
⎢
∂
⎥
L† =
,
⎢
0
0
-
+ γPr-1
0
0
⎥
⎢
⎥
⎢
∂t0
(
)
⎥
⎢
∂
⎥
⎢
HPr-1
P
0
0
-
P
+ Pm-1
0
⎥
⎣
∂t0
⎦
TPr-1
P
0
0
0
-TPr-1 H
где
4.
C. A. Jones, Dynamo Theory, Department of Applied
(
)(
)
Mathematics, University of Leeds, UK (2007).
∂
∂
H = Pr Pm
+1
+1
+ HPm.
∂t0
∂t0
5.
P. H. Roberts and G. A. Glatzmaier, Geophys. Astro-
phys. Fluid Dynam. 94(1), 47 (2001).
Из уравнения (67) получаем нелинейное уравнение
для амплитуды A(τ), которое полностью совпадает
6.
A. Tur and V. Yanovsky, Coherent Vortex Structures
in Fluids and Plasmas, Springer Series in Synergetics,
с комплексным уравнением Гинзбурга - Ландау (41):
Springer, New York (2017).
∂A(τ)
A1
- A2A(τ) + A3|A(τ)|2A(τ) = 0.
(68)
7.
P. G. Drazin and D. H. Reid, Hydrodynamic Stability,
∂τ
Cambridge Univ. Press, Cambridge, UK (2004).
Здесь вид коэффициентов A1,2,3 полностью совпада-
8.
В. В. Алексеев, А. М. Гусев, УФН 141, 311 (1983).
ет с выражениями (42). При выводе уравнения (68)
мы использовали связь перемасштабированной про-
9.
А. В. Гетлинг, УФН 161(9), 1 (1991).
изводной по медленному времени τ:
10.
E. S. Knobloch, Int. J. Eng. Sci. 36, 1421 (1998).
∂
1
∂
=
∂τ
a2 ∂τ
11.
F. H. Busse, in Proceedings of US National Congress
of Applied Mechanics, American Society of Mechani-
Таким образом, применяя асимптотические раз-
cal Engineers (1982), p. 299.
ложения теории возмущений к неавтономным урав-
нениям Лоренца (6D) (61), мы получили комп-
12.
R. Avila and A. Cabello, Math. Problems in Eng.,
лексное уравнение Гинзбурга - Ландау (68), которое
Article ID 236901, 1 (2013).
идентично уравнению (41) для конечной амплиту-
13.
W. V. R. Malkus and G. Veronis, J. Fluid Mech. 4,
ды, полученному в слабонелинейной теории.
225 (1958).
14.
A. C. Newell and J. A. Whitehead, J. Fluid Mech.
ЛИТЕРАТУРА
38, 279 (1969).
1. S. Chandrasekhar, Hydrodynamics and Hydromagne-
15.
E. Knobloch and J. De Luca, Nonlinearity 3, 975
tic Stability, Oxford Univ. Press, London (1961).
(1990).
2. Г. З. Гершуни, Е. М. Жуховицкий, Конвективная
16.
M. Revallo and D. Sevcovic, Physica D 161, 116
устойчивость несжимаемой жидкости, Наука,
(2002).
Москва (1972).
17.
A. Benerji Babu, Ragoju Ravi, and S. G. Tagare, Int.
3. А. В. Гетлинг, Конвекция Рэлея - Бенара. Струк-
J. Geophys. 2011, Article ID 207123, 17 (2011).
тура и динамика, Эдиториал УРСС, Москва
(1999).
18.
J. K. Bhattacharjee, J. Phys. A 22, L1135 (1989).
925
М. И. Копп, А. В. Тур, В. В. Яновский
ЖЭТФ, том 157, вып. 5, 2020
19.
J. K. Bhattacharjee, Phys. Rev. A 41, 5491 (1990).
40.
S. Chandrasekhar, Proc. Nat. Acad. Sci. USA 42, 273
(1956).
20.
B. S. Bhadauria and P. Kiran, Ain Shams Eng. J. 5,
1287 (2015).
41.
Е. П Велихов, ЖЭТФ 36, 1398 (1959).
21.
Ramya Rajagopal, Shelin Elizabeth Jacob, and
42.
S. A. Balbus and J. F. Hawley, Astrophys. J. 376,
Sangeetha George K., Int. J. Math. Trends and Tech-
214 (1991).
nology 54, 477 (2018).
43.
C. Nipoti and L. Posti, arXiv:1206.3890v2.
22.
P. Kiran, Ain Shams Eng. J. 7, 639 (2016).
44.
В. П. Лахин, В. И. Ильгисонис, ЖЭТФ 137, 783
23.
P. G. Siddheshwar, V. Ramchandramurthy, and
(2010).
D. Uma, in Proceedings 37th National and 4th Int.
45.
O. N. Kirillov and F. Stefani, Proc. Int. Astronom.
Conf. Fluid Mechs. Fluid Power, December 16-18,
Union 8, 233 (2012).
2010, IIT Madras, Chennai, FMFP10-AM08 (2010).
46.
O. N. Kirillov, F. Stefani, and Y. Fukumoto, J. Fluid
24.
B. S. Bhadauria, P. G. Siddheshwar, Jogendra Ku-
Mech. 760, 591 (2014).
mar et al., Trans. Porous Med. 92, 633 (2012).
47.
G. Rüdiger, R. Hollerbach, and L. L. Kitchatinov,
25.
P. G. Siddheshwar, B. S. Bhadauria, P. Mishra et al.,
Magnetic Processes in Astrophysics: Theory, Simula-
Int. J. Non-Linear Mech. 47, 418 (2012).
tions, Experiment, Wiley, New York (2013).
26.
B. S. Bhadauria and P. Kiran, Int. J. Eng. Math.
48.
М. И. Копп, А. В. Тур, В. В. Яновский, ЖЭТФ
2014, Article ID 296216 (2014).
154, 1281 (2018).
27.
B. S. Bhadauria and P. Kiran, Transp. Porous Media
49.
М. И. Копп, А. В. Тур, В. В. Яновский, Вопро-
100, 279 (2013).
сы атомной науки и техники (ВАНТ) 4(116), 230
(2018).
28.
B. S. Bhadauria and P. Kiran, Phys. Scr. 89, 095209
(2014).
50.
P. Vadasz and S. Olek, Int. J. Heat Mass Transfer 41,
1417 (1999).
29.
S. Aniss, M. Belhaq, and M. Souhar, ASME J. Heat
Transfer 123, 428 (2001).
51.
V. K. Gupta, B. S. Bhadauria, I. Hasim et al., Ale-
xandria Engin. J. 54, 981 (2015).
30.
А. Н. Мордвинов, Б. Л. Смородин, ЖТФ 81(5), 89
(2011).
52.
V. K. Gupta, R. Prasad, and A. K. Singh, Int. J.
Energy and Technology 5(28), 1 (2013).
31.
А. В. Беляев, Б. Л. Смородин, ПМТФ 50(4), 18
(2009).
53.
V. K. Gupta and A. K. Singh, Int. J. Energy and
Technology 5(27), 1 (2013).
32.
А. В. Беляев, Б. Л. Смородин, ЖТФ 34(5), 79
(2008).
54.
Rajendra Prasad and A. K. Singh, Int. J. Appl. Math.
and Informatics 7(3), 87 (2013).
33.
Б. И. Мызникова, Б. Л. Смородин, ЖЭТФ 128,
1299 (2005).
55.
J. M. Jawdat and I. Hashim, Int. J. Adv. Sci. Eng.
Inform. Technol. 2, 346 (2012).
34.
Б. И. Мызникова, Б. Л. Смородин, ЖЭТФ 139,
597 (2011).
56.
R. Prasad and A. K. Singh, J. Appl. Fluid Mech. 9,
2887 (2016).
35.
B. L. Smorodin and M. Lücke, Phys. Rev. E 79,
026315 (2009).
57.
P. Goldreich and D. Lynden-Bell, Mon. Not. Roy
Astron. Soc. 130, 125 (1965).
36.
B. L. Smorodin, B. I. Myznikova, and J. C. Legros,
Phys. Fluids 20, 094102 (2008).
58.
E. Knobloch and K. Jullien, Phys. Fluids 17, 094106
(2005).
37.
E. R. Priest, Solar Magnetohydrodynamics, Springer,
59.
M. Kopp, A. Tur, and V. Yanovsky, East Eur. J.
Netherland (1984).
Phys. 1, 4 (2019).
38.
C. C. Finlay, Les Houches 88, 403 (2008).
60.
R. Haberman, Elementary Applied Partial Differen-
39.
Palle Kiran and B. S. Bhadauria, J. Heat Transfer
tial Equations with Fourier Series and Boundary
138, 051702 (2016).
Value Problems, Prentice-Hall, Inc. (2004).
926
ЖЭТФ, том 157, вып. 5, 2020 Магнитная конвекция в неоднородно вращающейся электропроводящей среде. . .
61. M. C. Kim, S. B. Lee, S. Kim et al., Int. J. Heat
66. B. S. Bhadauria, M. K. Singh, B. K. Singh et al.,
Mass Transfer 46, 5065 (2003).
Int. J. Appl. Mech. and Engin. 21(4), 785 (2016).
62. P. Kiran, S. H. Manjula, and Y. Narasimhulu, J.
67. Yu. L. Bolotin, A. V. Tur, and V. V. Yanovsky,
Emerging Technol. and Innovative Res. 5(8), 227
Chaos: Concepts, Control and Constructive Use, Se-
(2018).
ries: Understanding Complex Systems, Shpringer
63. P. Kiran, S. H. Manjula, and Y. Narasimhulu, Int. J.
(2016).
Appl. Mech. and Engin. 23, 1 (2018).
68. М. И. Рабинович, Д. И. Трубецков, Введение в
64. P. Kiran, Int. J. Appl. and Comput. Math. 3, 1969
теорию колебаний и волн, Регулярная и хаотичес-
(2017).
кая динамика, Москва (2000).
65. B. S. Bhadauria, A. Singhb, M. K. Singh et al., Asia
Pacific J. Engin. Sci. and Technol. 2(2), 1 (2016).
69. E. N. Lorenz, J. Atmos. Sci. 20, 130 (1963).
927