ЖЭТФ, 2020, том 157, вып. 6, стр. 1002-1019

ЭНТРОПИЯ ВНУТРЕННЕГО ОБЪЕМА ЧЕРНОЙ ДЫРЫ

ШВАРЦШИЛЬДА В ПРЕДПОЛОЖЕНИИ ВОЗРАСТАЮЩЕЙ

СО ВРЕМЕНЕМ МАССЫ

С. Дутта^*, Р. Бисвас^**

Department of Mathematics, The University of Burdwan, Golapbag Academic Complex

713104, Burdwan, West Bengal, India

Поступила в редакцию 25 октября 2019 г.,

после переработки 25 октября 2019 г.

Принята к публикации 15 ноября 2019 г.

(Перевод с английского)

ENTROPY FOR THE INTERIOR OF A SCHWARZSCHILD BLACK

HOLE ASSUMING THE MASS IS INCREASING WITH TIME

S. Dutta, R. Biswas

Термодинамика черных дыр позволяет связать законы термодинамики с существованием горизонта со-

бытий черной дыры. Вычисляется энтропия, соответствующая внутреннему объему черной дыры Шварц-

шильда для безмассовых мод в предположении, что масса черной дыры возрастает со временем. По-

лучено, что энтропия пропорциональна энтропии Бекенштейна - Хокинга. Кроме того, оказалось, что

полученная энтропия удовлетворяет второму закону термодинамики. С использованием законов термо-

динамики получено соотношение между температурой и обратной температурой. Рассмотрены реляти-

вистские поправки к термодинамическим величинам. Проанализированы изменения термодинамических

свойств рассматриваемой системы при скоростях, сравнимых со скоростью света. Учтено влияние ска-

лярного заряда.

DOI: 10.31857/S0044451020060036

Проводившиеся исследования были аналогичны

классическим термодинамическим исследовани-

ям. Энтропия черной дыры рассматривалась как

1. ВВЕДЕНИЕ

величина, пропорциональная постоянно возрас-

тающей площади горизонта событий. Энтропия

Существует много теорий, рассматривающих

Бекенштейна - Хокинга [5] обычно выражается как

компактные объекты, такие как черные дыры.

Недавнее детектирование гравитационных волн

S_BH =

[1] от слияния черных дыр может служить сви-

4ℏG

детельством их существования. Ранее Хокинг

где A — площадь горизонта событий черной дыры.

теоретически показал, что черные дыры могут ис-

Согласно второму закону термодинамики, со време-

паряться и испускать тепловое излучение [2, 3]. На

нем энтропия увеличивается. Еще одно определение

основании этой концепции обсуждались различные

энтропии — это энтропия фон Неймана:

аспекты термодинамики черных дыр [4] и вычис-

лялись различные термодинамические величины.

S[ρ] = - tr(ρ ln ρ),

^* E-mail: duttasandip.mathematics@gmail.com

где ρ — матрица плотности квантовой системы. На

^** E-mail: biswas.ritabrata@gmail.com

классическом уровне известно, что механика черной

1002

ЖЭТФ, том 157, вып. 6, 2020

Энтропия внутреннего объема черной дыры Шварцшильда.. .

дыры подчиняется законам, аналогичным обыкно-

2. МАТЕМАТИЧЕСКОЕ ПОСТРОЕНИЕ

венным законам термодинамики [6]. Хорошо извест-

Рассмотрим координаты Эддингтона - Финкель-

ная формула для энтропии черной дыры в терми-

штейна (v, r, θ, φ). Для простоты выберем светопо-

нах заряда Нетер была получена в конце 90-х гг. [7].

добную сферическую оболочку с энергией, соот-

Однако в классической термодинамике черных дыр

ветствующей массе m, стягивающуюся в направле-

есть вопрос, на который до сих пор не было ответа:

нии поверхности v = 0. Пространство-время перед

что является источником энтропии на классическом

этой поверхностью является плоским. После пересе-

уровне? Или, в более общем виде, каковы класси-

чения поверхности линейный элемент описывается

ческие микросостояния, соответствующие микросо-

стандартной шварцшильдовской геометрией. Чер-

стояниям энтропии? Этому вопросу посвящено мно-

ная дыра Шварцшильда в координатах Эддингто-

го работ, причем недавно он был переформулирован:

на - Финкельштейна описывается как

какую энтропию имеют экстремальные черные ды-

ры — нулевую или ненулевую [8]? Недавно был пред-

ds² = -f dv² + 2dv dr + r²dΩ²,

(1)

ложен новый способ определения внутреннего объ-

ема черной дыры Шварцшильда [17] (объем Крис-

где

тодулу - Ровелли). Эти вычисления были проведены

2M(1 + a₁t + a₂t² + . . . + a_ntⁿ)

для метрики Керра [9]. Введем следующие допуще-

f = f(r,t) = 1 -

ния, которые были сделаны ранее в работе [10] без

0 < a_i ≪ 1,

четкого объяснения.

(а) При учете зависимости от времени в уравне-

а v — опережающее время:

нии Клейна - Гордона скалярное поле выбирается в

∫

виде

v = t+

=t+r+

f (r, t)

+ 2M(1 + a₁t + a₂t² + . . . + a_ntⁿ)×

exp{-iET} exp{iI(λ, θ, φ)},



.

× lnr - 2M(1 + a1t + a2t2 + . . . + antn)

где E — энергия.

Мы используем следующие единицы:

(б) Из свободной энергии можно получить энтро-

G = c = ℏ = κ_B = 1.

пию, вычисляя производную по обратной темпера-

туре.

Такой тип метрики был предложен в работе [11], где

масса черной дыры рассматривалась как функция

ка (выражение Хокинга) [10].

как r, так и t. Испарение черной дыры в некоммута-

тивной заряженной метрике Вайдья исследовалось

Обсудим приведенные выше допущения более

в работе [13] (см. Приложение). Здесь a_i — малые па-

подробно. Выразим внутренний объем в виде ин-

раметры, такие что сумма (1+a₁t+a₂t² +. . . +a_ntⁿ)

теграла [10] и определим эффективную метрику.

близка к 1. Важно отметить, что мы считаем, что

Тогда можно вычислить гамильтониан движущей-

масса черной дыры увеличивается, поскольку с те-

ся частицы. Наконец, используем свободную энер-

чением времени материя аккретирует на черную ды-

гию Гиббса безмассовой частицы и получим, что эн-

ру. Однако средняя плотность материи во Вселен-

тропия зависит от времени, однако ее изменение до-

ной очень мала, поэтому масса черной дыры уве-

вольно медленное.

личивается очень медленно. Вследствие этого мы

Работа построена следующим образом. Сначала

считаем, что, если пренебречь малыми слагаемыми,

приводится краткий обзор результатов, полученных

частная производная f(r, t) по t практически равна

в работе [10]. В следующем разделе вычисляется

нулю, т. е.

энергия безмассовой частицы внутри черной дыры.

∂f

≈ 0,

В разд. 3 вычисляется энтропия, соответствующая

∂t

свободной энергии Гиббса, а в разд. 4 рассматрива-

и поэтому справедливы уравнения Эйнштейна. Кро-

ется система, движущаяся со скоростью, сравнимой

ме того, возрастание радиальной координаты весь-

со скоростью света, и исследуется зависимость соот-

ма незначительно. Поэтому мы предполагаем, что

ветствующей термодинамики от отношения v/c. В

масса черной дыры по прошествии времени t будет

разд. 5 рассматривается эффект присутствия ска-

равна

лярного заряда. Раздел 6 содержит выводы.

M (1 + a₁t + a₂t² + . . . + a_ntⁿ),

1003

С. Дутта, Р. Бисвас

ЖЭТФ, том 157, вып. 6, 2020

при том что в момент времени t = 0 ее масса была

на которой метрика имеет вид

равна m.

{

}

ds² =

-f v² + 2v r

dλ² + r²dΩ²,

Пусть r изменяется от 2M(1+a₁t+a₂t²+. . .+a_ntⁿ)

до нуля. Например, в работе [14] рассматривалось

где r = r(λ) и v = v(λ), а λ — произвольный пара-

обусловленное операторами Линдблада возму-

метр [17].

щение, которое описывает взаимодействие с

Объем можно записать как

марковским термостатом. Для подтверждения

∫

√

предложенного нами изменения массы черной

V_Σ = 4π dλ

r⁴ {-f v² + 2v r}.

(2)

дыры можно использовать зависящие от времени

обобщенные ансамбли Гиббса. Нашу систему можно

Тогда метрика примет вид подынтегрального выра-

рассматривать как открытую квантовую систему.

жения от лагранжиана:

Поиску зависящих от времени решений для чер-

{

}

ных дыр посвящено много работ. В работе [15] ана-

dS2eff = r⁴

-f v² + 2v r

dλ².

(3)

лизируется зависящее от времени решение с исполь-

Этому лагранжиану соответствуют координаты

зованием AdS/CFT-соответствия. Подход, исполь-

∫

(r, v) и импульсы (P_r , P_v). Тогда

dr dv dP_rdP_v

зующий зависящий от времени гамильтониан, пред-

представляет собой объем фазового пространства.

ложен в работе [16].

В настоящей работе мы вычисляем энтропию

Поскольку мы положили, что переменные a₁,

внутри этого объема фазового пространства. Если

a₂, . . . , a_n строго положительны, масса будет толь-

проводить вычисление энтропии, основываясь на

ко возрастать. Это совершенно не нарушает второй

методах квантовой статистики, сначала нужно най-

закон термодинамики¹⁾.

ти гамильтониан частицы, находящейся в данном

Используя преобразования

объеме.

v → v(T,λ), r → r(T,λ),

Пусть m — масса частицы, движущейся в прост-

ранстве-времени с фоновой метрикой

получаем

ds2ansatz = g_abdx^adx^b =

{

}

(

)

⁽∂v⁾

∂v ∂r

= -dt² + r⁴

-f(r, t)dv² + 2dv dr

(4)

ds² =

-f

dT² +

∂T

∂T ∂T

{

}

тогда действие (которое, как мы предполагаем, име-

⁽∂v⁾

∂v ∂r

ет репараметризационную симметрию) будет иметь

-f

dλ² + r²dΩ²,

∂λ

∂λ ∂λ

вид

∫2

∫

при этом кросс-члены будем считать равными нулю.

(

)1/2

Предполагая, что выполняется условие

S = m dS_ansatz = m

g_abdx^adx^b

(5)

)₂

⁽∂v

∂v ∂r

-f

= -1,

Скорости частицы определяются выражением

∂T

∂T ∂T

и рассматривая сферически-симметричную гипер-

u^a =

dτ

поверхность как прямое произведение 2-сферы и

произвольной кривой, параметризованной с помо-

где τ — произвольный параметр, а x^a = x^a(τ). Тогда

щью λ на плоскости v - r, можно найти гиперпо-

путь частицы задается выражением

верхность Σ : T = const, см. [10,17], где

∫

(

)1/2

{

}

dx^b

S = Ldτ = m

g_ab

dτ.

(6)

ds^2Σ = -dT² +

-f v² + 2v r

dλ² + r²dΩ².

dτ dτ

Внутренний объем, ограниченный горизонтом, мож-

Сравнивая обе части, получаем лагранжиан в виде

но описать, используя поверхность

(

)1/2

dx^a dx^b

Σ≡γ×S²,

L=m g_ab

dτ dτ

¹⁾ Если эти переменные выбрать отрицательными, так что

второй закон термодинамики будет нарушен, то рассматри-

Используя уравнение Эйлера - Лагранжа, нетрудно

ваемая система будет нефизической.

найти уравнение движения системы:

1004

ЖЭТФ, том 157, вып. 6, 2020

Энтропия внутреннего объема черной дыры Шварцшильда.. .

d²x^a

dx^b dx^c

du^a

Тогда

+Γ^a

=0⇒

+ Γ^abcu^bu^c = 0,

dτ²

^bc dτ dτ

dτ

ξ=

(14)

где Γ^abc — символы Кристоффеля. Отметим, что при-

Таким образом, полный гамильтониан имеет вид

веденное выше уравнение геодезических верно для

любого пространства-времени. Чтобы получить га-

(

)

H_T =

P² - m²

(15)

мильтониан, полностью описывающий динамику си-

2m²

стемы, сначала нужно вычислить импульсы систе-

До сих пор мы рассматривали только одну связь

мы, которые задаются уравнением

(определяемую уравнением (10)). Это характеризу-

ет систему как систему со связями первого рода, ко-

∂L

dx^b

P_a =

g_ab

(7)

торая поэтому имеет калибровочную свободу [21].

∂x^a

dτ

Накладывая некоторые условия на произвольный

Поэтому канонический гамильтониан имеет вид

параметр τ, который мы будем интерпретировать

как собственное время, можно устранить калибро-

dx^a

H_c = P_a

- L = 0.

(8)

вочную свободу. Калибровку собственного времени

dτ

мы используем позднее. Тогда получаем

Для репараметризационно инвариантной теории ха-

рактерно, что канонический гамильтониан равен ну-

P⁰

ψ₂ =

τ - x⁰ ≈ 0,

(16)

лю; для пространства-времени Минковского наблю-

дается то же самое. В настоящей работе мы бу-

а для первичной связи (11) получаем

дем рассматривать гамильтониан системы, которая

задается метрикой (4). Анализ был проведен для

ψ₁ = P² - m² ≈ 0,

(17)

хронологической калибровки в плоском пространст-

ве-времени [18] и для калибровки собственного вре-

что делает систему системой со связями второго ро-

мени [19]. При вычислении энтропии мы будем ис-

да.

пользовать независимые связи.

Отсюда

Поскольку импульсы не являются независимы-

∂ψ₂

P⁰

{

}

ми,

ψ₂ =

+ {ψ₂, H_T } = 0 ⇒

x⁰, H_T

P² = g^abP_aP_b = m²,

(9)

∂t

{

}

P⁰, H_T

= 0.

(18)

мы получаем первичную связь в виде

Кроме того,

Φ = P² - m² ≈ 0.

(10)

{

}

{

}

Используя алгоритм Дирака [20], получаем, что

x⁰, H_T

x⁰, ξP²

{

}

первичная связь и гамильтониан пропорциональны

= 2ξg^ab

x⁰, P_a

P_b = 2ξP⁰

(19)

друг другу, поэтому

(

)

H_T = ξ(τ)Φ = ξ(τ)

P² - m²

(11)

(

)

∂g0b

∂g

{P⁰, H_T } = ξ

P_b-g0a

P_bP_c

(20)

где ξ — зависящий от τ коэффициент пропорцио-

∂x^a

нальности.

Для метрики (4) получаем

Тогда получаем

{

}

P⁰, H_T

= 0.

xa =

= u^a = {x^a,H_T} = 2ξP^a

(12)

dτ

Тогда уравнения (18) и (19) дают

ξ=

(21)

∂H

∂g

a = {Pa,HT} = -

= -ξ

P_bP_c.

(13)

∂x^a

Из уравнений (14) и (21) можно получить L = m.

Используя (86) и (12), получаем

Также из уравнений (11) и (12) получаем

u^a = 2ξP^a = 2ξ

u^a.

xa =

{x^a, P²} =

(22)

1005

С. Дутта, Р. Бисвас

ЖЭТФ, том 157, вып. 6, 2020

3. ВЫЧИСЛЕНИЕ ЭНТРОПИИ НА

^a =

{P^a, P²} =

ОСНОВАНИИ КЛАССИЧЕСКОЙ

(

)

∂g^ab

∂g^db

СВОБОДНОЙ ЭНЕРГИИ ГИББСА

g^cd -

g^ca P_dP_b,

(23)

∂x^c

Найдем зависимость энтропии от энергии для

безмассовой частицы. Эта энтропия определена

^a =-

Γ^abcP^bP^c.

(24)

внутри черной дыры. Поскольку не имеется слагае-

Здесь мы использовали тождество

мых, соответствующих химическому потенциалу,

свободная энергия Гиббса имеет вид

∂_cg^ab = -g^adg_be∂_cg_de

для двух динамических переменных и вычислили

G₀ = -

ln Z =

Σ_ϵ ln(1 - exp{-βϵ}),

дираковскую скобку [9, 22]

где Z — статсумма большого канонического распре-

{f₁, f₂}^∗ = {f₁, f₂} +

деления, а β — обратная температура. Свободная

2P⁰

(

)

энергия Гиббса релятивистски неинвариантна. Воз-

{f₁, P²}{ψ₂, f₂} - {f₁, ψ₂}{P², f₂}

(25)

растание массы можно рассматривать как медлен-

ный процесс. Поэтому можно сказать, что влияние

Для динамической переменной уравнение движения

свободной энергии Гиббса пренебрежимо мало, т.е.

можно получить, используя следующее соотноше-

свободная энергия Гиббса до и после смены гипер-

ние [20]:

поверхности практически не меняется. На горизон-

1 = {f1,H}^∗.

(26)

те (при максимальном внутреннем объеме) значение

На самом деле полезно воспользоваться соотноше-

радиальной координаты фиксировано, т. е. r = 0,

нием

здесь r можно получить из уравнения (28), откуда

H =P⁰.

следует

Получаем

(P_v + fP_r)

r=r-4

= 0 ⇒ P_v + fP_r = 0.

xa = {x^a, P⁰}^∗ =

P⁰

(

)

Снова r и входящие координаты светового конуса

=ga0 +

P^a +

ga0Γ0bcPbPc

P⁰

зависят от некоторого параметра λ [17], т.е. r = r(λ)

(27)

∂g

и v = v(λ), при этом v = F(r) (функция от r). По-

˙P

^a = {P^a,P⁰}^∗ =

g0cP_b -

Γ^abcP^bP^c +

∂x^c

P⁰

этому свободная энергия Гиббса имеет вид

+g0aΓ0bcP^bP^c.

∫

Фиксируя калибровку a

= 0, получаем уравне-

G₀ =

dP_rdP_vdr dv ×

ние движения для пространственной компоненты

× ln (1 - exp{-βϵ}) × δ (P_v + fP_r) δ(v - F (r)).

a(a = μ):

Используя дельта-функции Дирака, получаем

xμ =

^μ =

Γ^μabP^aP^b.

(28)

[

P⁰

∫

{ (

)1/2}]

fP2r

G₀ =

dP_r dr ln

1- exp

-β

Из этих двух уравнений можно исключить P⁰, тогда

r⁴

мы получим требуемое уравнение геодезической:

(

)₂

где P_r

изменяется от 0 до ∞. Тогда

g^abP_aP_b = -

P⁰

+2r-4P_rP_v-fr-4P2r = m². (29)

∞

[

∫

{ (

)1/2}]

fP2r

Энергия частицы, т. е. гамильтониан, имеет вид

G₀ =

dr ln

1- exp

-β

r⁴

(

)1/2

fP2r

2P_rP_v

ϵ=P⁰ =

-m²

(30)

r⁴

Учитывая равенство

Мы вычисляем энергию для безмассовой частицы

βP_r

√-f

(такой как фотон), поэтому можно положить m → 0.

r²

Тогда уравнение (30) можно записать как

получаем

∫

(

)1/2

π²

r²

fP2r

2P_rP_v

G₀ = -

dr.

(32)

ϵ=

(31)

6β²

√-f

r⁴

1006

ЖЭТФ, том 157, вып. 6, 2020

Энтропия внутреннего объема черной дыры Шварцшильда.. .

Рассмотрим, как увеличивается со временем ра- этом изменяется от 2M(1 + a₁t + a₂t² + . . . + a_ntⁿ) до

диус черной дыры, если радиальная координата при

0. Получаем

∫

r²

G₀ = -

√

dr.

6β²

2M(1 + a₁t + a₂t² + . . . + a_ntⁿ)

2M(1+a1t+a2t²+...+antⁿ)

-1

Учитывая равенство

Согласно второму закону термодинамики, пфаффо-

ва форма δQ₀ зависит только от эмпирической тем-

2M(1 + a₁t + a₂t² + . . . + a_ntⁿ)

пературы. Это приводит к равенству Клаузиуса

получаем

∮

δQ₀

5π

(37)

G₀ =

M³(1 + a₁t + a₂t² + . . . + a_ntⁿ)³.

T₀

12β²

Хокинг показал, что благодаря квантовым эф-

для любого циклического обратимого процесса.

фектам черные дыры испускают электромагнитное

Предположим, что второй закон термодинамики

излучение, аналогичное излучению абсолютно чер-

выполняется также и для релятивистской термоди-

ного тела с температурой, обратно пропорциональ-

намики в любой инерциальной системе отсчета. То-

ной массе черной дыры [2]. Кроме того, наша си-

гда абсолютная температура имеет вид

стема аналогична абсолютно черному телу с заклю-

ченными в нем безмассовыми частицами. Поэтому

T = T(T₀,v), lim

T (T₀, v) = T₀,

(38)

v→0

частицам также соответствует обратная температу-

ра

где термодинамическая система движется с посто-

β = 8πM.

янной скоростью v относительно системы отсчета

Тогда свободная энергия Гиббса имеет вид

K. В системе отсчета K равенство Клаузиуса при-

нимает вид

∮

G₀ =

β(1 + a₁t + a₂t² + . . . + a_ntⁿ)³.

(33)

δQ

6144

= 0.

(39)

Отсюда для энтропии получаем

∂G₀

5β

Релятивистские преобразования теплоемкости, по-

S₀ = β²

(1+a₁t+a₂t² +. . .+a_ntⁿ)³. (34)

∂β

6144

лученные в работе [25] и независимо в работах [26]

и [27, 28], можно записать как

Таким образом, можно сказать, что энтропия мо-

нотонно возрастает со временем, однако это проис-

ходит очень медленно.

δQ = γ(v)δQ₀

(40)

В связи со сказанным выше, мы хотели бы вос-

(см. также [29]).

произвести результат, полученный ранее в работе

[23], где было показано, что планковская энтро-

Подставляя выражения (40) и (38) в выражение

пия является лоренц-инвариантной. Эмпирическая

(39), получаем

температура в релятивистской термодинамике ло-

∮

δQ₀

ренц-инвариантна [24]. Пусть (в собственной систе-

= 0.

(41)

ме отсчета) T₀ — абсолютная температура, δQ₀ —

{γ(v)}-1T(T₀, v)

количество теплоты, входящей в систему, δL₀ — тер-

Сравнивая (41) и (37), получаем

модинамическая работа, произведенная над систе-

мой. Для обратимых процессов

{γ(v)}-1T(T₀, v) = bT₀,

(42)

δQ₀ = T₀ dS₀.

(35)

Вначале, если предположить, что эффективность

где b — произвольная постоянная. Положим v → 0 в

цикла Карно является инвариантом, то энтропия

уравнении (42), тогда, с учетом (38), получаем b = 1.

также будет инвариантом, т. е.

Окончательно находим

δQ

δQ₀

dS =

= dS₀.

(36)

T = γ(v)T₀.

(43)

T₀

1007

С. Дутта, Р. Бисвас

ЖЭТФ, том 157, вып. 6, 2020

Это второй закон релятивистской термодинамики

где A = 16πM² — площадь горизонта событий. Тог-

для обратимых процессов и релятивистское пре-

да S₀ и S_BH связаны следующим образом:

образование абсолютной температуры, что хоро-

5π

шо согласуется с равенством (40). Полученное пра-

S₀ =

(1 + a₁t + a₂t² + . . . + a_ntⁿ)³S_BH .

384

вило преобразования отличается от закона (см.

[23, 30-33])

Таким образом, как можно видеть, энтропия на

горизонте больше энтропии внутри черной дыры,

T(Plank) = {γ(v)}-1T₀,

(44)

т. е. S_BH > S₀. Кроме того, энтропия внутри черной

дыры пропорциональна времени t, т. е. со временем

а следуя правилу преобразования [34-37], имеем

энтропия S₀ внутри черной дыры увеличивается.

На первом законе термодинамики основаны

T(L) = T₀,

(45)

главное определение внутренней энергии и закон

что не противоречит тому, что

сохранения энергии для всех термодинамических

систем. Второй закон термодинамики говорит о

δQ(L) = δQ₀.

(46)

том, что естественные процессы могут проходить

только в одном направлении и не являются обра-

Теперь из уравнений (35), (40) и (43) получаем

тимыми. Кроме того, как следует из сказанного

выше,

δQ = T dS₀,

(47)

dS₀

> 0.

откуда, согласно [23], следует, что энтропия являет-

Поэтому полная энтропия со временем не уменьша-

ся лоренц-инвариантной:

ется и процесс является необратимым.

Согласно первому закону термодинамики,

S =S₀.

(48)

Следует отметить несколько важных моментов.

dM = T₀ dS₀,

(49)

Во-первых, мы считаем, что безмассовым модам

откуда следует

внутри горизонта событий соответствует та же тем-

пература, что и на горизонте. Напомним, что r

768

β=

меняется от 0 до 2M, однако мы рассматриваем

15πT₀ (1 + a₁t + a₂t² + . . . + a_ntⁿ)²

несколько другой случай. Мы предполагаем, что из-

здесь β — обратная термодинамическая температу-

за аккреции материи масса черной дыры возраста-

ра системы [41,42], которая термодинамически, по-

ет со временем. Однако средняя плотность Вселен-

средством энтропии, обусловливает связь между ин-

ной очень мала. Поэтому возрастание массы чер-

формацией и энергией физической системы.

ной дыры происходит очень медленно, так что мы

Случай 1.

считаем, что и рост радиальной координаты так-

Если a_i = 0 при i > 1, то

же очень незначительный. Тогда, если масса черной

дыры M = M(t = t₀ = 0), то по прошествии време-

(1 + a₁t + a₂t² + . . . + a_ntⁿ) ≈ (1 + a₁t),

ни t она будет равна M(1 + a₁t + a₂t² + . . . + a_ntⁿ).

При этом r меняется от 2M(1+a₁t+a₂t² +. . .+a_ntⁿ)

5π

S₀ =

(1 + a₁t)³S_BH ,

до нуля.

384

Кроме того, как показал Хокинг, для черных

768

β=

дыр характерен процесс излучения (излучение

15πT₀ (1 + a₁t)²

Хокинга) [5, 38], которому можно сопоставить неко-

На рис. 1 приведены соотношения между S₀, S_BH

торую температуру (температуру Хокинга) [2, 39].

и t (рис. 1а) и между β, T₀ и t (рис. 1б) при a₁ =

Используя термодинамические соотношения между

= 0.05. На рисунках видно, что зависимость между

энергией, температурой и энтропией, Хокинг смог

β и T₀ является гиперболической, а при изменяю-

подтвердить предположение Бекенштейна и полу-

щемся времени энтропия внутри черной дыры уве-

чить коэффициент пропорциональности, который

личивается быстрее.

оказался равен 1/4 [40]. А именно, на горизонте

Случай 2.

черной дыры энтропия равна

Если a_i = 0 при i > 2, то

S_BH =

(1 + a₁t + a₂t² + . . . + a_ntⁿ) ≈ (1 + a₁t + a₂t²),

1008

ЖЭТФ, том 157, вып. 6, 2020

Энтропия внутреннего объема черной дыры Шварцшильда.. .

a₁ = 0.05

= 0.05,

= 0.04

S₀

1.0

S₀

0.5

S_BH

T₀

Рис. 1. Соотношения между S0, SBH и t (а) и между β,

T0 и t (б) при a1 = 0.05

Рис. 2. Соотношения между S0, SBH и t (а) и между β,

T0 и t (б) при a1 = 0.05, a2 = 0.04

5π

S₀ =

(1 + a₁t + a₂t²)³S_BH ,

384

768

На рис. 3 приведены соотношения между S₀, S_BH и

β=

15πT₀ (1 + a₁t + a₂t²)²

t (рис. 3а) и между β, T₀ и t (рис. 3б) при a₁ = 0.05,

При постоянном времени, если энтропия на гори-

a₂ = 0.04, a₃ = 0.03. При изменяющемся времени

зонте черной дыры возрастает, то энтропия внутри

скорость возрастания энтропии существенно выше,

черной дыры тоже будет увеличиваться. Если время

чем в Случаях 2 и 3.

изменяется, то энтропия внутри черной дыры будет

увеличиваться быстрее. На рис. 2 приведены соот-

4. ФЕНОМЕНОЛОГИЧЕСКАЯ

ношения между S₀, S_BH и t (рис. 2а) и между β, T₀

РЕЛЯТИВИСТСКАЯ ТЕРМОДИНАМИКА

и t (рис. 2б) при a₁ = 0.05, a₂ = 0.04. На рисунках

видно, что энтропия внутри черной дыры увеличи-

В работе [33] приводится распределение Джутт-

вается быстрее, чем в Случае 1.

нера — релятивистский аналог распределения Макс-

Случай 3.

велла для идеального газа в чисто инерциальной

Если a_i = 0 при i > 3, то

системе отсчета (например, K₀). Позднее распре-

деление Джуттнера было принято и использовано

(1+a₁t+a₂t²+ . . . +a_ntⁿ) ≈ (1+a₁t+a₂t²+a₃t³),

многими учеными [32, 43-47]. Если в лабораторном

5π

сосуде, движущемся с постоянной скоростью v от-

S₀ =

(1 + a₁t + a₂t² + a₃t³)³S_BH ,

384

носительно лабораторной системы отсчета K, нахо-

768

дится газ, то можно применять предположения и

β=

рассуждения, аналогичные рассуждениям, исполь-

15πT₀ (1 + a₁t + a₂t² + a₃t3)2

1009

ЖЭТФ, вып. 6

С. Дутта, Р. Бисвас

ЖЭТФ, том 157, вып. 6, 2020

∫

= 0.05,

= 0.04, a

= 0.03

V^N

Z =

exp{-βcu_jP^j} d3N p.

(51)

(2π)3N N!

R3N

60000

При этом мера d³p принимает вид [44]

(

)

40000

v·p₀

d³p = γ(v)

√

d³p₀.

(52)

⁰ 20000

p²⁰ + m²c²

Отсюда

⎛

⎞N

S_BH

∫

V^N

Z =

⎝

exp{-βcu_jp^j}d³p⎠

(2π)3N N!

R3N

⎛

∫

{

√

}

V^N

⎝

exp

-βc p²⁰

+m²c²

(2π)3N N!

R3N

[

(

)]

v·p₀

× γ(v)

√

d³p0

p²⁰ + m²c²

⎛

⎞N

{

}

∫

√

⎝

exp

-βc p²⁰+m2c2

d³p0⎠ =

(2π)3N N!

R3N

=Z₀,

(53)

T₀

где нижний индекс «0» соответствует собственной

системе отсчета K₀. Из приведенного выше уравне-

ния следует, что функция распределения Z является

Рис. 3. Соотношения между S0, SBH и t (а) и между β,

лоренц-инвариантной [44].

T0 и t (б) при a1 = 0.05, a2 = 0.04, a3 = 0.03

Окончательно, релятивистское распределение

Гиббса (50) принимает вид

зованным при выводе распределения Джуттнера.

ω_n =

exp{-βcu_jP^jn}, n = 1, 2, . . .,

(54)

В некоторых работах, основанных на компьютер-

ных симуляциях [48-52], получено частичное под-

где нижний индекс «n» соответствует квантовому

тверждение правильности формулы Джуттнера и ее

состоянию. Кроме того, из первого закона реляти-

обобщения. В этих работах были предложены и дру-

вистской термодинамики (для идеальной жидкости)

гие распределения. Эффективность использования

[24, 54] следует

распределения была показана в работе [53]. Реляти-

вистское распределение Гиббса для идеального газа,

v²

dE = T dS - p dV + {γ(v)}²

V dp.

(55)

находящегося в сосуде, движущемся с постоянной

c²

скоростью v и имеющем 4-скорость

Из уравнения (55) нетрудно найти

(

)

[

]

u^j = γ(v)

,γ(v)

v²

d E - {γ(v)}²

V_p

= T dS - {γ(v)}²pdV.

(56)

имеет вид

Поэтому

dω =

exp{-βcu_jP^j}d3N p d3Nq,

(50)

(

)

(2π)3N N!Z

∂E

v²

⁽∂p⁾

T =

- {γ(v)}²

(57)

∂S_V

c²

∂S_V

где N — число частиц, P^j — полный импульс газа,

)

d3N p d3Nq — элемент объема фазового пространст-

v²

⁽∂p

⁽∂E⁾

p - {γ(v)}

(58)

ва, а Z — функция распределения:

c²

∂V_S

1010

ЖЭТФ, том 157, вып. 6, 2020

Энтропия внутреннего объема черной дыры Шварцшильда.. .

a₁ = 0.05

⁽∂T⁾

⁽∂p⁾

= -{γ(v)}²

(59)

∂V_S

∂S_V

Тогда из уравнений (55) и (56) получаем

)

⁽∂E

T = {γ(v)}²

(60)

1.0

∂S_V,P

0.5

Поскольку давление представляет собой лоренцев

инвариант [24], т. е. p = p₀, если объем V₀ = γ(v)V ,

можно записать

H = E + pV = γ(v)(E₀ + p₀V₀) = γ(v)H₀,

(61)

где H — энтальпия.

Используя определение энтальпии и уравнение

(56), получаем

⁽∂H⁾

T =

(62)

∂S_p

0.6

Отсюда свободная энергия F равна

0.4

F = E - TS - {γ(v)}²

pV = γ(v)F₀,

(63)

c²

0.2

где

F₀ = E₀ - T₀S₀

— свободная энергия системы в собственной системе

S_BH

отсчета K₀.

Подставляя уравнение (63) в уравнение (56), по-

Рис. 4. Соотношения между S0, SBH и t при a1 = 0.05,

лучаем

α = 0.5 (а) и между β, T0 и t при a1 = 0.05, α = 0.9 (б)

dF = -S dT - {γ(v)}² p dV.

(64)

Откуда получаем выражения

Используя уравнения (33) и (67), получаем

)

⁽∂F

⁽∂F⁾

5γ(v)

S =-

{γ(v)}²p = -

β(1 + a₁t + a₂t² + . . . + a_ntⁿ)³.

(69)

∂T_V

∂V_T

6144

(65)

⁽∂F⁾

Тогда энтропия равна

E=F -T

∂T_V

c²

∂V_T

∂G

5γ(v)β

и релятивистское тождество Максвелла

S =β²

(1+a₁t+a₂t² + . . . + a_ntⁿ)³ =

∂β

6144

⁽∂S⁾

⁽∂p⁾

= γ(v)S₀.

(70)

= {γ(v)}²

(66)

∂V_T

∂T_T

Используя уравнение (70), согласно первому закону

Определим функцию Гиббса G стандартным обра-

термодинамики, получаем

зом:

G = E - TS + pV = γ(v)G₀,

(67)

dM = T dS = γ-1T₀γ dS₀ = T₀ dS₀,

(71)

где

поскольку

G₀ = E₀ - T₀S₀ + p₀V₀.

T = γ(v)-1T₀.

Заметим, что некоторые инвариантные термодина-

Приведенное выше уравнение аналогично уравне-

мические величины можно выразить с помощью

нию (49) (см. также [55]).

функции Масье [55]:

Энтропия на горизонте черной дыры равна [40]

G₀

(68)

T₀

S_BH =

1011

С. Дутта, Р. Бисвас

ЖЭТФ, том 157, вып. 6, 2020

= 0.05,

= 0.04

= 0.05,

= 0.04, a

= 0.03

40000

20000

S_BH

20000

10000

S_BH

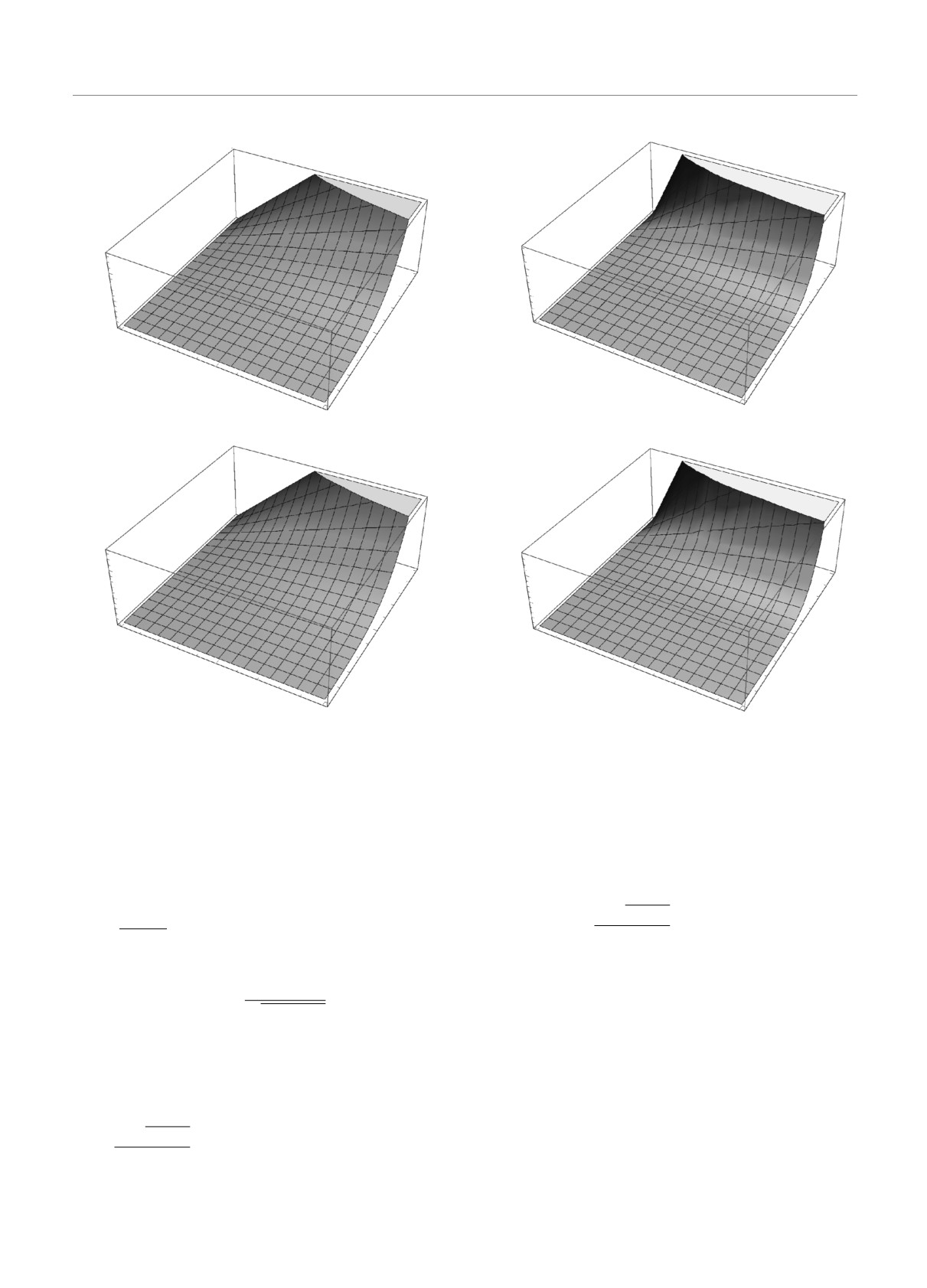
Рис. 5. Соотношения между S, SBH и t при a1 = 0.05,

Рис. 6. Соотношения между S, SBH и t при a1 = 0.05,

a2 = 0.04, α = 0.5 (а) и между β, T0 и t при a1 = 0.05,

a2 = 0.04, a3 = 0.03, α = 0.5 (а) и между β, T0 и t при

a2 = 0.04, α = 0.9 (б)

a1 = 0.05, a2 = 0.04, a3 = 0.03, α = 0.9 (б)

Случай 1.

где A = 16πM² — площадь горизонта событий. От-

Если a_i = 0 при i > 1, то

сюда получаем соотношение между S и S_BH :

(1 + a₁t + a₂t² + . . . + a_ntⁿ) ≈ (1 + a₁t),

√

5πγ(v)

5π

1-α²

S =

(1 + a₁t + a₂t² + . . . + a_ntⁿ)³S_BH ,

(72)

S =

(1 + a₁t)³S_BH .

384

На рис. 4 приведены соотношения между S₀, S_BH и

где

t при a₁ = 0.05, α = 0.5 (рис. 4а) и между β, T₀ и t

при a₁ = 0.05, α = 0.9 (рис. 4б). На рисунках видно,

γ(v) =

√

1 - v²/c²

что когда α увеличивается, энтропия убывает. Это

означает, что система движется со скоростью, близ-

а v — разница скоростей между неподвижной и дви-

кой к скорости света, а энтропия растет медленнее,

жущейся системами отсчета. Будем предполагать,

чем в классическом случае.

что v/c = α, где 0 ≤ α < 1. Тогда из уравнения (72)

Случай 2.

получаем

Если a_i = 0 при i > 2, то

√

5π

1-α

S =

(1+a₁t+a₂t² +. . .+a_ntⁿ)³S_BH . (73)

(1 + a₁t + a₂t² + . . . + a_ntⁿ) ≈ (1 + a₁t + a₂t²),

384

1012

ЖЭТФ, том 157, вып. 6, 2020

Энтропия внутреннего объема черной дыры Шварцшильда.. .

√

5π

1-α

Для среды, движущейся со скоростью, близкой к

S =

(1 + a₁t + a₂t²)³S_BH .

384

скорости света, α = 0.9. На рисунках видно, что

при возрастании скорости среды энтропия убывает

На рис. 5 приведены соотношения между S₀, S_BH

и t при a₁ = 0.05, a₂ = 0.04, α = 0.5 (рис. 5а) и

очень быстро, т. е. если уменьшать значение α, то

между β, T₀ и t при a₁ = 0.05, a₂ = 0.04, α = 0.9

энтропия будет расти.

(рис. 5б). На рисунках видно, что в этих случаях S

растет быстрее, чем в классическом случае.

Случай 3.

5. ЧЕРНЫЕ ДЫРЫ СО СКАЛЯРНЫМ

Если a_i = 0 при i > 3, то

ЗАРЯДОМ

(1+a₁t+a₂t²+ . . . + a_ntⁿ) ≈ (1+a₁t+a₂t²+a₃t³),

Рассмотрим решения для черной дыры другого

типа, а именно, для массивной гравитационной чер-

√

5π

1-α

ной дыры [56]. Анзац для решений для статической

S =

(1 + a₁t + a₂t² + a₃t³)³S_BH .

384

сферически-симметричной черной дыры можно за-

писать в виде

На рис. 6 приведены соотношения между S₀, S_BH и

t при a₁ = 0.05, a₂ = 0.04, a₃ = 0.03, α = 0.5 (рис. 6а)

dr²

(

)

и между β, T₀ и t при a₁ = 0.05, a₂ = 0.04, a₃ = 0.03,

ds² = -g(r, t) dt²+

+r²

dθ² + sin² θdφ²

(74)

g(r, t)

α = 0.9 (рис. 6б). Если a₁, a₂ и a₃ не равны нулю, то

S растет быстрее, чем в предыдущих случаях.

где

На рис. 4a, 5a, 6a и рис. 4б, 5б, 6б приведены со-

2M(1 + a₁t + a₂t² + . . . + a_ntⁿ)

отношения между S, S_BH и t для α = 0.5 и 0.9, соот-

g(r, t) = 1 -

r^λ

ветственно. Отметим, что рисунки для Случаев 1, 2

и 3, для которых α = 0, тождественны соответству-

а λ — параметр модели, зависящий от скалярного

ющим рис. 1a, 2a и 3a (см. разд. 4). Среда движется

заряда Q. Наличие скалярного заряда требует моди-

с постоянной скоростью v относительно инерциаль-

фикации теории гравитации Эйнштейна. В настоя-

ной системы отсчета K. Если скорость v мала по

щей работе мы будем рассматривать случай Q > 0

сравнению со скоростью света, то этому случаю со-

и λ = 1.

ответствует α = 0. Для среды, движущейся со ско-

Из уравнения (32) получаем свободную энергию

ростью v, сравнимой со скоростью света, α = 0.5.

Гиббса:

)₃

⎡

⎛

⎞

⎧

⎛

⎞⎫

⁽aβ

(√

)

⎪

⎨

⎬

4π

⎢

aβ

⎜

⎟

⎜

⎟

G₀ =

⎢

0 sin-1

- 60 sin-1

⎜√

⎟

45 sin

2 sin-1

⎜√

⎟

⎣⁶

⎝

⎠^-

⎝

⎠

576β²

4π

aβ

⎪

aβ

⎪

⎩

⎭

4π

⎧

⎛

⎞⎫

⎧

⎛

⎞⎫

⎪

{

(√

)}

⎨

⎬

⎨

⎬

⎜

⎟

⎜

⎟

aβ

⎜

⎟

⎜

⎟

- 9sin

4 sin-1

√

- sin

6 sin-1

√

+ 45 sin

2 sin-1

⎪

⎝

⎠⎪

⎪

⎝

⎠⎪

aβ

4π

⎩

⎭

⎩

⎭

4π

⎤

{

(√

)}

{

(√

)}

aβ

⎥

+ 9sin

4 sin-1

+ sin

6 sin-1

⎥,

(75)

⎦

4π

где

a = (1 + a₁t + a₂t² + ... + a_ntⁿ).

Тогда энтропия равна

1013

С. Дутта, Р. Бисвас

ЖЭТФ, том 157, вып. 6, 2020

⎡

⎧

⎛

⎞⎫

⎪

⎨

⎬

⎢

⎜

⎟

⎢

⎜

⎟

45aQ cos

2 sin-1

√

⎢

⎝

⎪

⎠⎪

⎢

aβ

)₃

⎩

⎭

⎢

⁽aβ

⎢

15aQ

4π

S₀ =

⎢

)3/2 34

576

4π

⎢

⁽aβ

Q²

⁽aβ

Q²

⎢

⎢2π

√1 -

4π

√1 -

⎢

4π

aβ

4π

aβ

⎣

4π

⎧

⎛

⎞⎫

⎧

⎛

⎞⎫

⎪

⎨

⎬

⎨

⎬

⎜

⎟

⎜

⎟

⎜

⎟

⎜

⎟

9aQ cos

4 sin-1

√

3aQ cos

6 sin-1

√

⎪

⎝

⎠⎪

⎪

⎝

⎠⎪

aβ

⎩

⎭

⎩

⎭

15a

4π

√

)3/2 34

aβ

⁽aβ

Q²

2π

-Q

2π

4π

√1 -

4π

aβ

4π

aβ

4π

⎤

{

(√

)}

{

(√

)}

{

)}⎥

(√

⎥

aβ

⎥

45a cos

2 sin-1

9a cos

4 sin-1

3a cos

6 sin-1

⎥

4π

⎥

√

⎥

aβ

⎥

4π

-Q

2π

-Q

4π

-Q

⎥

4π

⎥

⎦

⎡

⎛

⎞

⎧

⎛

⎞⎫

(√

)

⎪

)₂

⎨

⎬

⁽aβ

⎢

aβ

⎜

⎟

⎜

⎟

⎢

0 sin-1

- 60 sin-1

⎜√

⎟

45 sin

2 sin-1

⎜√

⎟

⎣⁶

⎝

⎠^-

⎝

⎠

768

4π

aβ

⎪

aβ

⎪

⎩

⎭

4π

⎧

⎛

⎞⎫

⎧

⎛

⎞⎫

⎪

{

(√

)}

⎪

⎨

⎬

⎨

⎬

⎜

⎟

aβ

⎜

⎟

⎜

⎟

⎜

⎟

- 9sin

4 sin-1

√

+ 45 sin

2 sin-1

- sin

6 sin-1

√

⎪

⎝

⎠⎪

4π

⎪

⎝

⎠⎪

aβ

⎩

⎭

⎩

⎭

4π

⎤

{

(√

)}

{

(√

)}

aβ

⎥

+ 9sin

4 sin-1

+ sin

6 sin-1

⎥

⎦^-

4π

)₃

⎡

⎛

⎞

⎧

⎛

⎞⎫

⁽aβ

(√

)

⎪

⎨

⎬

4π

⎢

aβ

⎜

⎟

⎜

⎟

⎢

0 sin-1

- 60 sin-1

⎜√

⎟

45 sin

2 sin-1

⎜√

⎟

⎣⁶

⎝

⎠^-

⎝

⎠

288β

4π

aβ

⎪

aβ

⎪

⎩

⎭

4π

⎧

⎛

⎞⎫

⎧

⎛

⎞⎫

⎪

{

(√

)}

⎨

⎬

⎨

⎬

⎜

⎟

⎜

⎟

aβ

⎜

⎟

⎜

⎟

- 9sin

4 sin-1

√

- sin

6 sin-1

√

+ 45 sin

2 sin-1

⎪

⎝

⎠⎪

⎪

⎝

⎠⎪

aβ

4π

⎩

⎭

⎩

⎭

4π

⎤

{

(√

)}

{

(√

)}

aβ

⎥

+ 9sin

4 sin-1

+ sin

6 sin-1

(76)

⎦

4π

Соотношение между S₀, S_BH и t определяется уравнением

1014

ЖЭТФ, том 157, вып. 6, 2020

Энтропия внутреннего объема черной дыры Шварцшильда.. .

⎡

(

√

)₃ ⎢

15aQ

S₀ =

π a

S_BH + Q

⎢

√

⎢

576

(

)3/2

⎣

2π

√S_BH

a√SBH + Q

{

(

)}

-1

45aQ cos

2 sin

√

S_BH + Q

15a

√

(

2π

1-a√SBH - Q√a√SBH + Q

4π

√S_BH + Q⁾ 3/2

a√SBH + Q

{

(

)}

{

(

)}

-1

9aQ cos

4 sin

√

3aQ cos

6 sin-1

√

S_BH + Q

√

(

)

(

)3/2

3/2

Q²

2π

√S_BH

4π

√S_BH

a√SBH + Q

{

(√

)}

{

(√

)}

√

45a cos

2 sin-1

S_BH + Q

9a cos

4 sin-1

S_BH + Q

√

4π

1-a√SBH - Q√a√SBH + Q

2π

1-a√SBH - Q√a√SBH + Q

⎤

{

(√

)}

√

[

⎥

(√

)

3a cos

6 sin-1

S_BH + Q

⎥

(

√

)

√

⎥

√

a a

S_BH + Q

60 sin-1

S_BH + Q

⎥

4π

1-a√SBH - Q√a√SBH + Q⎦

768

(

)

{

(

)}

{

(

)}

- 60 sin-1

√

− 45 sin

2 sin-1

√

− 9sin

4 sin-1

√

a√SBH + Q

S_BH + Q

{

(

)}

{

(√

)}

{

(√

)}

√

− sin

6 sin-1

√

+ 45 sin

2 sin-1

S_BH

+ 9sin

4 sin-1

S_BH + Q

a√SBH + Q

[

{

(√

)}]

(√

)

√

(

√

)

√

+ sin

6 sin-1

S_BH + Q

π a

S_BH + Q

60 sin-1

S_BH + Q

288

(

)

{

(

)}

{

(

)}

- 60 sin-1

√

− 45 sin

2 sin-1

√

− 9sin

4 sin-1

√

a√SBH + Q

S_BH + Q

{

(

)}

{

(√

)}

{

(√

)}

√

− sin

6 sin-1

√

+ 45 sin

2 sin-1

S_BH

+ 9sin

4 sin-1

S_BH + Q

a√SBH + Q

{

(√

)}]

√

+ sin

6 sin-1

S_BH + Q

(77)

Случай 1.

Случай 3.

Если a_i = 0 при i > 1, то

Если a_i = 0 при i > 3, то

(1 + a₁t + a₂t² + . . . + a_ntⁿ) ≈ (1 + a₁t).

(1 + a₁t + a₂t² + . . . + a_ntⁿ) ≈ (1 + a₁t + a₂t² + a₃t³).

Случай 2.

На рис. 7 приведены соотношения между S₀, S_BH и

Если a_i = 0 при i > 2, то

t при a₁ = 0.05, Q = 0.1 (рис. 7а), a₁ = a₂ = 0.05,

Q = 0.1 (рис. 7б), a₁ = a₂ = a₃ = 0.05, Q = 0.1

(1 + a₁t + a₂t² + . . . + a_ntⁿ) ≈ (1 + a₁t + a₂t²).

(рис. 7в), что соответствует Случаям 1, 2 и 3.

1015

С. Дутта, Р. Бисвас

ЖЭТФ, том 157, вып. 6, 2020

Q = 0.1, a

= 0.05

зонта событий. Сторонний наблюдатель только на

основании изменений, сделанных до и после кол-

лапса, не может судить о присутствии какого-либо

физического объекта внутри горизонта событий. В

связи с этим термодинамический сценарий коллап-

0.03

са, который мог бы предсказать сторонний наблюда-

тель, не должен непосредственно зависеть от энтро-

0.02

пии материи и излучения. Это обусловлено именно

S₀

0.01

тем, что они в принципе ненаблюдаемы. Посколь-

ку мы рассматриваем стационарную черную дыру,

2.0

1.5

мы параметризуем ее посредством некоторых изме-

1.0

ряемых термодинамических характеристик, а имен-

0.5

S_BH

но, ее массой, моментом импульса и иногда ее заря-

дом [57]. Различные наборы этих параметров зада-

Q = 0.1, a

0.05

ют различные сценарии формирования черных дыр.

2.0

S_BH

1.5

Каждый такой набор соответствует различным воз-

1.0

0.5

можным состояниям соответствующей черной ды-

ры. Более глубокие исследования термодинамики

0.06

дают аналогичные результаты. Внутренние микро-

0.04

S₀

состояния системы находятся в согласии с наблюда-

емыми макросостояниями. Термодинамическая энт-

0.02

ропия представляет собой аналог кратности мак-

росостояний, и именно поэтому мы рассматриваем

связь между энтропией черной дыры и ее площа-

дью горизонта событий.

Q = 0.1, a

0.05

В настоящей работе вычислена энтропия черной

дыры Шварцшильда в объеме Кристодулу - Ровел-

ли для безмассовых мод. Используемый подход яв-

ляется статистическим. Подынтегральное выраже-

ние для внутреннего объема введено как эффектив-

ная метрика. Получены энергии мод. Поскольку ка-

0.06

нонический гамильтониан обращается в нуль, мож-

0.04

S₀

но использовать метод анализа связей. Ранее точное

0.02

вычисление гамильтониана не проводилось. Исполь-

зуя свободную энергию Гиббса, сначала мы вычис-

2.0

лили энтропию. Результат оказался очень интерес-

1.5

1.0

ным. Масса черной дыры со временем возрастает,

0.5

S_BH

однако средняя плотность Вселенной остается очень

малой. Поэтому масса черной дыры растет очень

Рис. 7. Соотношения между S0, SBH и t при a1 = 0.05,

медленно. Таким образом, масса черной дыры по

Q = 0.1 (а), a1 = a2 = 0.05, Q = 0.1 (б), a1 = a2 = a3 =

прошествии времени t равна

= 0.05, Q = 0.1 (в)

M (1 + a₁t + a₂t² + . . . + a_ntⁿ).

6. ЗАКЛЮЧЕНИЕ

При этом величина r изменяется от 2M(1 + a₁t +

В общем случае формирование компактного объ-

+ a₂t² + . . . + a_ntⁿ) до нуля. Наконец, было получе-

екта типа черной дыры обусловлено катастрофичес-

но, что энтропия со временем монотонно возрастает,

ким коллапсом значительного количества материи

однако скорость ее роста практически не зависит от

или излучения, которые не могут выйти за пределы

времени. Кроме того, мы показали, что энтропия на

гравитационного притяжения. Как материя, так и

горизонте событий больше, чем внутри черной ды-

излучение, порождающие черную дыру, имеют энт-

ры, т. е. S_BH > S. Энтропия внутри черной дыры

ропию, которая сохраняется даже после формиро-

пропорциональна времени t, т. е. со временем энтро-

вания черной дыры, т.е. удерживается внутри гори-

пия S внутри черной дыры возрастает.

1016

ЖЭТФ, том 157, вып. 6, 2020

Энтропия внутреннего объема черной дыры Шварцшильда.. .

Благодарности. С. Д. выражает благодарность

2m(t, r)

e-a(t,r) = 1 -

(86)

Правительству штата Западная Бенгалия за при-

суждение Non-NET Fellowship. Р. Б. выражает бла-

Используя уравнения (79), (81) и (84), получаем

годарность Межуниверситетскому центру астроно-

мии и астрофизики (IUCAA), Пуне, Индия, за при-

1-e^a

a^′ +

+ ˙ae(a-b)/2 = 0.

(87)

глашение.

Финансирование. Работа выполнена при фи-

Окончательно, из уравнений (86) и (87) получаем

нансовой поддержке Правительства штата За-

падная Бенгалия, Факультета высшего образова-

e(b-a)/2 = -

(88)

ния, науки и технологии и биотехнлогии (File

m^′

№ ST/P/S & T/16G-19/2017).

откуда

(

)₂ (

)-1

b(t,r) =

(89)

m^′

ПРИЛОЖЕНИЕ

Таким образом, мы получили решение Вайдья в ви-

Пусть фоновая метрика в области больших вре-

де (78)

мен, записанная в координатах (t, r, θ, φ) [12],

(

)₂ (

)-1

2m(t, r)

ds² = -eb(t,r)dt² + ea(t,r)dr² +

ds² = -

dt² +

(

)

m^′

+r²

dθ² + sin² θ dφ²

(78)

(

)-1

2m(t, r)

(

)

+ 1-

dr²+r²

dθ²+ sin² θ dφ²

(90)

имеет вид метрики Вайдья [13]. Полевые уравнения

Эйнштейна для сферически-симметричной геомет-

где m(t, r)

— медленно-меняющаяся

«массовая

рии лоренцевой сигнатуры вида (78) можно вывести

функция», причем

из полевых уравнений Римана:

∂m

1-e

a^′ = 8πrT_rr +

(79)

∂t

1-e

∂m

b^′ = 8πre^a-bT_tt -

(80)

m^′ =

∂r

a = 8πrT_rr

(81)

ЛИТЕРАТУРА

1-e^-a +

re^-a (a^′ - b^′) -

r²R⁽⁰⁾ =

1. B. P. Abbott et al., Phys. Rev. Lett. 116, 061102

(2016); arXiv:1602.03837v1[gr-qc].

8πT_φφ

= 8πT_θθ =

(82)

sin² θ

2. S. W. Hawking, Commun. Math. Phys. 43,

199

где

(1975).

(

)

3. S. W. Hawking, Phys. Rev. D 14, 2460 (1976).

R⁽⁰⁾ = -

1-e^-a

+e-(a+b)/2×

r²

[

(

)

(

)]

4. J. M. Bardeen, B. Carter, and S. W. Hawking,

× ∂_t

ae(a+b)/2

-∂_r

b^′e(b-a)/2

(83)

Commun. Math. Phys. 31, 161 (1973).

5. J. D. Bekenstein, Phys. Rev. D 7, 2333 (1973).

Штрихи и точки означают дифференцирование по

r и t, соответственно. Тогда из уравнений (82) и (83)

6. R. M. Wald, Living Rev. Relativity 4, 6 (2001); arXiv:

следует, что

9912119[gr-qc].

T_rr = e(a-b)T_tt.

(84)

7. R. M. Wald, Phys. Rev. Relativity D 48, 3427 (1993);

Из уравнений (79) и (80) можно получить

arXiv:9307038v1[gr-qc].

1-e^a

8. S. Carroll, M. C. Jahnson, and L. Randall, JHEP

(a^′ - b^′) =

(85)

0911, 109 (2009); arXiv:0901.0931[hep-th].

Теперь из метрики Вайдья [13] можно определить

9. I. Bengtsson and E. Jakobson, Mod. Phys. Lett. A 30,

функцию m(t, r):

1550103 (2015); arXiv:1502.01907[gr-qc].

1017

С. Дутта, Р. Бисвас

ЖЭТФ, том 157, вып. 6, 2020

10.

B. Zhang, Phys. Rev. D 92, 081501(R) (2015); arXiv:

33.

M. V. Laue, Die Relativitätstheorie, Friedrich Vieweg

1510.02182[gr-qc].

und Sohn, Braunschweig, Germany (1921).

11.

M. Sharif and W. Javed, J. Exp. Theor. Phys. 114,

34.

P. T. Landsberg, Nature 212, 571 (1966).

933 (2012).

35.

P. T. Landsberg, Nature 214, 903 (1967).

12.

A. N. St. J. Farley and P. D. D’Eath, Gen. Relativ.

36.

P. T. Landsberg and K. A. John, Ann. Phys. 56, 299

Gravit. 38, 425 (2006); arXiv:gr-qc/0510040.

(1970).

13.

P. C. Vaidya, Proc. Indian Acad. Sci. A 33, 264

37.

P. T. Landsberg, Europ. J. Phys. 2, 203 (1981).

(1951).

38.

S. W. Hawking, Nature 248, 30 (1974).

14.

F. Lange, Z. Lenarčič, and A. Rosch, Phys. Rev. B 97,

165138 (2018); arXiv:1801.07646[cond-mat.str-el].

39.

S. W. Hawking, The Large Scale Structure of Spa-

ce-Time, Cambridge University Press, New York

15.

D. Bak, M. Gutperle, and M. Karch, JHEP 0712,

(1973).

034 (2007); arXiv:0708.3691[hep-th].

40.

S. W. Hawking, The Nature of Space and Time,

16.

B. R. Majhi and S. Samanta, Phys. Lett. B 770, 314

Princeton University Press (1994); arXiv:9409195

(2017).

[hep-th].

17.

M. Christodoulou and C. Rovelli, Phys. Rev. D 91,

41.

J. Castle, W. Emmenish, R. Henkes, R. Miller, and

064046 (2015); arXiv:1411.2854[gr-qc].

J. Rayne, Science by Degrees: Temperature from Zero

to Zero, Westinghouse Search Book Series, Walker

18.

A. Hanson, T. Reggc, and C. Teitelboim, Constrained

and Company, New York (1965).

Hamiltonian System, Academia Nazionale Dei Lincei

(1976).

42.

C. Garrod, Statistical Mechanics and Thermodyna-

mics, Oxford University Press (1995).

19.

G. Fulop, D. M. Gitman, and I. V. Tyutin, Int. J.

Theor. Phys. 38, 1941 (1999); arXiv:9805040[hep-th].

43.

R. K. Pathria, Proc. Nat. Inst. Sci. India 21, 331

(1955).

20.

P. A. M. Dirac, Lectures on Quantum Mechanics,

Yeshiva University Press, New York (1964).

44.

R. K. Pathria, Proc. Nat. Inst. Sci. India 23, 168

(1957).

21.

H. Kawai and Y. Yokokura, Phys. Rev. D 93, 044011

(2016); arXiv:1509.08472[hep-th].

45.

J. L. Synge, The Relativistic Gas, North-Holland,

Amsterdam (1957).

22.

B. R. Majhi and S. Samanta, Phys. Lett. B 770, 314

(2017); arXiv:1703.00142[gr-qc].

46.

D. T. Haar and H. Wegeland, Phys. Rep. 1, 31 (1971).

23.

M. Planck, Ann. Physik 26, 1 (1908).

47.

S. R. D. Groot, W. W. V. Leeuwen, and

C. G. V. Weert, Relativistic Kinetic Theory: Prin-

24.

M. Przanowski and J. Tosiek, Phys. Scr. 84, 055008

ciples and Applications, North-Holland, Amsterdam

(2011); arXiv:1010.5701[cond-mat.stat-mech].

(1980).

25.

H. Ott, Z. Physik 175, 70 (1963).

48.

D. Cubero, J. C. Pascual, J. Dunkel, P. Talkner, and

26.

H. Arzelies, Nuovo Cim. 35, 792 (1965).

P. Hanggi, Phys. Rev. Lett. 99, 170601 (2007).

27.

C. Moller, Det. Kong. Danske Videnskab. Selskab.

49.

J. Dunkel, P. H´’anggi, and S. Hilbert, Nature Phys. 5,

741 (2009); arXiv:0902.4651v2[cond-mat.stat-mech].

Mat.-Fys. Medd. 36, 1 (1967).

50.

C. Rasinariu, arXiv:0804.3836.

28.

C. Moller, Thermodynamics in the Special and the

General Theory of Relativity, Academic Press (1968).

51.

A. Montakhab, M. Ghodrat, and M. Barati,

Phys. Rev. E 79, 031124 (2009); arXiv:0809.1517v2

29.

C. Moller, The Theory of Relativity, Oxford Univer-

[cond-mat.stat-mech].

sity Press, Oxford (1972).

52.

M. Ghodrat and A. Montakhab, Phys. Rev. E 82,

30.

A. Einstein, Jahrbuch der Radioaktivität und Elekt-

011110 (2010); arXiv:0908.3753[cond-mat.stat-mech].

ronik 4, 411 (1907).

53.

F. Peano, M. Marti, L. O. Silva, and G. Coppa,

31.

K. V. Mosengeil, Ann. Physik 22, 876 (1907).

Phys. Rev. E 79, 025701 (2009); arXiv:0902.1762v1

32.

W. Pauli, Relativitatstheorie, Teubner, Berlin (1921).

[physics.plasm-ph].

1018