ЖЭТФ, 2020, том 157, вып. 6, стр. 1036-1050
© 2020
СУПЕРДИФФУЗИОННЫЙ ПЕРЕНОС «ПРОГУЛКАМИ ЛЕВИ»
В ОДНОРОДНОЙ СРЕДЕ: ОБЩЕЕ И ПРИБЛИЖЕННОЕ
АВТОМОДЕЛЬНОЕ РЕШЕНИЯ
А. А. Куличенкоa*, А. Б. Кукушкинa,b,c**
a Национальный исследовательский центр «Курчатовский институт»
123182, Москва, Россия
b Национальный исследовательский ядерный университет «МИФИ»
115409, Москва, Россия
c Московский физико-технический институт (национальный исследовательский университет)
141700, Долгопрудный, Московская обл., Россия
Поступила в редакцию 13 января 2020 г.,
после переработки 13 января 2020 г.
Принята к публикации 21 января 2020 г.
Получено общее и приближенное автомодельное решения для функции Грина широкого класса интегро-
дифференциальных уравнений двумерного и трехмерного (по пространственным координатам) нестаци-
онарного супердиффузионного переноса возмущения однородной среды для конечной фиксированной
скорости переносчиков. Данная проблема охватывает такие задачи, как перенос резонансного излучения
в астрофизических газах и плазме, миграцию животных, перенос энергии электромагнитными волнами
в плазме. Рассмотрен случай модельной функции распределения по длине свободного пробега (ФРСП),
имеющей степенной спад с ростом расстояния. Численные расчеты проведены для двух конкретных
видов ФРСП, включая случай, соответствующий лоренцевской форме крыльев контура спектральной
линии для излучения фотонов атомами или ионами. Для построения приближенного автомодельного
решения использован метод, развитый нами для бесконечной скорости переносчиков [23]. Учет их ко-
нечной скорости соответствует обобщению переноса «полетами Леви» на перенос «прогулками Леви c
остановками». Полученное нами автомодельное решение для произвольного супердиффузионного одно-
мерного переноса [29] распространено на случай двумерного и трехмерного переноса. Проверена точность
автомодельного решения путем его сравнения с рассчитанным численно общим решением.
DOI: 10.31857/S0044451020060061
на перенос «прогулками Леви c остановками» (см.
рис. 1 в работе [7]) для учета эффектов запаздыва-
ния в полетах Леви.
1. ВВЕДЕНИЕ
Напомним, что в случае нормальной (или обык-
новенной) диффузии, определяемой как броунов-
Интерес к явлениям супердиффузионного пере-
ское движение, описываемое дифференциальным
носа (см., например, [1-4]) и связанной с ними кон-
уравнением фоккер-планковского типа, функция
цепцией «полетов Леви», введенной в работе [5] (см.
Грина является гауссианом, чей аргумент определя-
с. IX в [1]), в последнее время акцентировался на
ет закон распространения фронта rfr(t) ∝ (Dt)β, где
учете конечной скорости переносчиков. В этом слу-
β = 1/2, D — коэффициент диффузии. Этот закон
чае явление супердиффузионного переноса получи-
нарушается в широком классе явлений, где длина
ло название «прогулок Леви» [6] (см. обзор [7]). Точ-
свободного пробега (длина шага) описывается мед-
нее говоря, учет конечной скорости переносчиков со-
ленно, по степенному закону, убывающей функцией
ответствует обобщению переноса «полетами Леви»
распределения переносчиков (ФРСП). Это приводит
* E-mail: andreikulichenko2@mail.ru
к расходимости коэффициента диффузии, формаль-
** E-mail: kukushkin_ab@nrcki.ru
но определяемого из дисперсии ФРСП, и к показа-
1036
ЖЭТФ, том 157, вып. 6, 2020
Супердиффузионный перенос «прогулками Леви» в однородной среде...
телю степени β > 1/2 в законе подобия rfr(t) ∝ tβ,
расстояния супердиффузионного переносчика от
что и называется супердиффузионным переносом.
точки источника) и асимптотических выраже-
В ряде физических задач явление супердиф-
ний для функции Грина далеко позади и далеко
фузии обычно называют нелокальным переносом,
впереди фронта. Справедливость предложенных
который описывается интегральным по простран-
автомодельных решений была показана путем их
ственным переменным уравнением, не сводимым
сравнения с точными численными решениями. В од-
к дифференциальному: например, уравнение Би-
номерном случае — решениями уравнений переноса
бермана - Холстейна [8, 9], которое описывает про-
для простой медленно затухающей ФРСП с раз-
странственно-временную эволюцию плотности воз-
личными степенными показателями, в трехмерном
бужденных атомов/ионов, вызванную переносом из-
случае — решениями уравнений Бибермана - Холс-
лучения в спектральных линиях в плазме и газах
тейна резонансного радиационного переноса для
[10, 11]; перенос возбуждения неравновесными ре-
различных спектральных линий (доплеровской,
зонансными фононами в конденсированных средах,
лоренцевской, фойгтовской и хольцмарковской).
например, в рубине [12], (нестационарный) пере-
Метод [23] приближенных автомодельных реше-
нос тепла продольными (электронными бернштей-
ний для функции Грина, зависящих от времени су-
новскими) плазменными волнами [13], фотоинду-
пердиффузионных (нелокальных) уравнений пере-
цированный перенос минорных переносчиков в по-
носа, был обобщен на случай конечной фиксирован-
лупроводниках (а именно, связанный с поглощени-
ной скорости переносчиков в [29] для задач одномер-
ем фотонов перенос дырок в полупроводниках n-
ного переноса возмущения в однородной среде для
типа) [14]. На примере модели Бибермана - Холстей-
простой ФРСП со степенным спадом на больших
на, в которой резонансное рассеяние фотонов на ато-
расстояниях. Было предложено решение для произ-
ме или ионе происходит с полным перераспределе-
вольной супердиффузионной ФРСП, и с помощью
нием по частоте в акте поглощения и переизлуче-
численного расчета общего решения [29,30] провере-
ния фотона, хорошо прослеживается основное свой-
на точность автомодельного решения для конкрет-
ство супердиффузионного переноса: редкие даль-
ных степенных законов ФРСП, включая случай, со-
ние полеты фотонов («скачки»), которые соответ-
ответствующий лоренцевской форме крыльев кон-
ствуют излучению/поглощению в «крыльях» спек-
тура атомной спектральной линии для излучения
тральной линии, преобладают над вкладом частых
фотонов.
близких перемещений, которые вызывают диффу-
В данной работе получены результаты, являю-
зионное (броуновское) движение возбуждения сре-
щиеся двумерным и трехмерным аналогом резуль-
ды и соответствуют излучению/поглощению в цен-
татов [29]: получены общее и приближенное авто-
тре спектральной линии. В работе [15] было по-
модельное решения для функции Грина широкого
казано, что далекие пролеты, вызванные медлен-
класса интегродифференциальных уравнений дву-
но убывающими (например, степенными) крылья-
мерного и трехмерного (по пространственным коор-
ми интегрального оператора (т. е. ФРСП) в урав-
динатам) нестационарного супердиффузионного пе-
нении переноса, являются полетами Леви. Домини-
реноса возмущения однородной среды для конечной
рующий вклад фотонов с большой длиной свобод-
фиксированной скорости переносчиков. В разд. 2
ного пробега в радиационный перенос в спектраль-
получено общее решение задачи супердиффузион-
ных линиях был показан уже в работах [16, 17].
ного переноса «прогулками Леви с остановками»
Простые модели, основанные на таком доминиро-
на однородной плоскости для случая модельной
вании, были разработаны для квазистационарного
ФРСП, имеющей степенной спад с ростом рассто-
переноса и сегодня известны как методы «escape
яния. Далее представлены результаты численного
probability» [18, 19] или прострельного выхода, или
расчета общего решения для двух конкретных видов
«тау-эффективного» [10, 11, 20-22].
ядра, включая случай, соответствующий лоренцев-
Для супердиффузионного переноса полета-
ской форме крыльев контура спектральной линии
ми Леви, зависящего от времени, недавно было
для излучения фотонов. В разд. 3 дан аналитичес-
показано, что широкий класс явлений переноса
кий вывод асимптотического выражения для ин-
на однородном фоне обладает приближенным
тегральной по пространству характеристики функ-
автомодельным решением
[23-28]. Решения для
ции Грина при больших временах эволюции систе-
функции Грина были построены с использованием
мы. Данная характеристика соответствует количе-
законов скейлинга для фронта распространения
ству возбужденных частиц в среде (стоящих пере-
возмущения (т.е. временной зависимости среднего
носчиков возбуждения). Также в разд. 3 проведе-
1037
А. А. Куличенко, А. Б. Кукушкин
ЖЭТФ, том 157, вып. 6, 2020
но сравнение с результатами численного интегри-
движения переносчиков между точками остановки,
рования общего решения, рассчитанного в разд. 2.
σ — среднее обратное время исчезновения перенос-
В разд. 4 предложено приближенное автомодельное
чиков (для переноса резонансного излучения это
решение для двумерного и трехмерного нелокально-
относится к нерадиационному девозбуждению сре-
го переноса в однородной среде, проверена точность
ды), θ(x) — ступенчатая функция Хевисайда, δ(x) —
такого решения путем сравнения с численно рассчи-
дельта-функция Дирака. В случае, когда переносчи-
танными общими решениями задачи, а также про-
ками возбуждения являются фотоны в плазме, W
веден анализ полученных приближенных решений.
имеет вид (ср. например, разд. 1 в работе [11])
1
dT (ρ)
W (ρ) = -
,
2. ОБЩЕЕ РЕШЕНИЕ УРАВНЕНИЯ
2πρ dρ
∫
(2.3)
НЕСТАЦИОНАРНОГО ДВУМЕРНОГО
T (ρ) = dω eω exp[-κωρ],
СУПЕРДИФФУЗИОННОГО ПЕРЕНОСА
Рассмотрим процессы супердиффузионного пе-
где eω — спектральное распределение вероятности
реноса, которые являются либо переносом возбуж-
испускания фотона с частотой ω; κω — коэффици-
дения неподвижной однородной среды не принадле-
ент поглощения средой фотона с частотой ω (т. е.
жащими среде объектами (например, процессы, опи-
обратная длина свободного пробега такого фотона).
сываемые уравнением для плотности возбужденных
Для получения общего решения уравнения (2.1)
атомов или ионов в плазме при переносе атомного
следует обратиться к системе исходных уравнений в
возбуждения резонансными фотонами), либо дина-
случае переноса возбуждения резонансными фото-
микой объектов или субъектов, которые движутся
нами, а именно, уравнениям для плотности возбуж-
(мигрируют) на однородной плоскости с одной и той
денных частиц f(r, t) в точке r в момент времени t
же скоростью между точками остановки при задан-
и спектральной интенсивности излучения Iω(r, n, t)
ном среднем времени пребывания в точках останов-
в точке r в момент времени t вдоль направления n:
ки. Тогда уравнение для функции Грина плотности
(
)
∫
∂f(r,t)
1
κω
возбуждения среды или плотности стоящих пере-
=-
+ σ f(r,t) + dω
×
∂t
τ
ℏω
носчиков возбуждения, f(r, t), в точке r = {x, y} в
∫
момент времени t имеет вид (это уравнение является
двумерным аналогом уравнения (1) в [29])
× dϕ(n)Iω (r, n, t) + δ(r)δ(t),
(2.4)
0
(
)
∂f(r,t)
1
1 ∂Iω(r,n,t)
=-
+ σ f(r,t)+
+ (n∇)Iω (r, n, t) =
∂t
τ
c
∂t
∫
(
)
1
|r - r1|
ℏω
1
+
d2r1W(|r - r1|)θ t -
×
=
eωf(r, t) - κωIω(r, n, t).
τ
c
τ
2π
S
(
)
В первом уравнении в (2.4) внутреннее интегриро-
|r - r1|
×f r1,t-
+ δ(r)δ(t),
(2.1)
вание ведется по ϕ(n) — углу на плоскости, задава-
c
емому направлением единичного вектора n.
где W (ρ) — вероятность поглощения переносчика
При решении системы уравнений (2.4) будем сле-
(или вероятность остановки переносчика на рассто-
довать методу [31]. Вначале применим к указанным
янии ρ от точки его последнего старта,
уравнениям двумерное преобразование Фурье в ви-
де
∞
∫
∫
W (ρ′)2πρ′dρ′ = 1
(2.2)
1
Iω(r, n, t) =
ω (p, n, t) exp(ip · r),
2π
0
∫
1
f (r, t) =
d2pf (p, t) exp(ip · r),
(в соответствии с указанной нормировкой функ-
2π
∫
(2.5)
ция W (ρ)2πρ является функцией распределения по
1
I
d2r Iω(r, n, t)exp(-ip · r),
длине свободного пробега переносчиков (ФРСП)),
ω(p, n, t) =
2π
τ — среднее время нахождения переносчика в точке
∫
1
остановки (например, среднее время между погло-
f (p, t) =
d2r f(r, t)exp(-ip · r).
2π
щением и последующим испусканием резонансного
фотона атомом или ионом), c — постоянная скорость
Тогда система примет вид
1038
ЖЭТФ, том 157, вып. 6, 2020
Супердиффузионный перенос «прогулками Леви» в однородной среде...
(
)
∫
f (p, t)
1
κω
∫
=-
+σ
f (p, t) + dω
×
1
∂t
τ
ℏω
f (p, t) =
lim
estF(p, s)ds,
2πi
α→+0
∫2π
α-i∞
δ(t)
,
∫
ω (p, n, t) +
2π
1
(2.6)
k(p, t) =
lim
estK(p, s)ds,
0
2πi
α→+0
α-i∞
ω(p, n, t)
(2.12)
ω(p, n, t) =
∫
c
∂t
ℏω
1
F (p, s) =
e-st
f (p, t) dt,
=
eω
ω (p, n, t).
τ
2π
0
∫
Решение второго уравнения в (2.6) с начальным
K(p, s) =
e-stk(p, t)dt.
ω(p, n, 0) = 0 имеет вид (ср. с (17) в [31])
0
ℏω c
I
После указанного преобразования уравнение (2.10)
ω (p, n, t) =
eω ×
τ
2π
примет вид
∫t
(
)
× dt′ exp[-c(t - t′){i(n · p) + κω}
f (p, t′).
(2.7)
1
sF(p, s) = -
+ σ F(p,s)+
0
τ
1
После подстановки (2.7) в первое уравнение в систе-
+ F(p,s)K(p,s) +
(2.13)
2π
ме (2.6) с учетом (2.3) получим
Для супердиффузионного переноса ФРСП,
(
)
f (p, t)
1
задаваемая ядром W(ρ) в интегральном опера-
=-
+σ
f (p, t) +
торе в (2.1), должна быть функцией, убывающей
∂t
τ
медленно, степенным образом, с увеличением
∫
t
c
длины свободного пробега ρ. Выберем ядро (и,
+
dt′
f (p, t′)c(t - t′)W (c(t - t′)) ×
τ
соответственно, ФРСП) в следующем модельном
0
виде:
∫2π
δ(t)
γκ0
× dϕ(n) exp[-ic(t - t′)(n · p)] +
(2.8)
W (ρ) =
,
(2.14)
2π
2πρ(1 + κ0ρ)γ+1
0
где κ0 является характерной длиной и соответству-
Внутренний интеграл по углам можно рассчитать:
ет значению коэффициента поглощения в центре
спектральной линии.
∫
Тогда из (2.11) и (2.12) можно получить следую-
dϕ(n) exp[-ic(t - t′)(n · p)] =
щее выражение для K(p, s):
0
∫
= 2πJ0(cp(t - t′)),
(2.9)
γcκ0
dt′e-st′
K(p, s) =
J0(cpt′).
(2.15)
τ
(1 + cκ0t′)γ+1
где J0 — функция Бесселя нулевого порядка. Тогда
0
(2.8) примет вид
В итоге из (2.13) после интегрирования по углу ϕ с
(
)
учетом (2.15), (2.12) и (2.5) окончательно получим
f (p, t)
1
=-
+σ
f (p, t′) +
общее решение уравнения (2.1) в следующем виде:
∂t
τ
∫t
∫
δ(t)
1
+ dt′
f (p, t′)k(p, t - t′) +
(2.10)
f (r, t) =
dp pJ0(pr) ×
2π
(2π)2i
0
0
∕⎧
∫
⎨
Здесь введена функция
1
×
estds
s+
+σ-
⎩
τ
2
2πc
+0-i∞
k(p, t) =
tW (ct)J0(cpt).
(2.11)
⎫
τ
∫
⎬
γcκ0
dt′e-st′
-
J0(cpt′)
(2.16)
Следуя [31], применим к (2.10) преобразование Лап-
τ
(1 + cκ0
t′)γ+1
⎭
ласа (ср. (2.10) с (23) из работы [31]) в виде
0
1039
А. А. Куличенко, А. Б. Кукушкин
ЖЭТФ, том 157, вып. 6, 2020
Далее перейдем к безразмерным переменным: длину
для асимптотики общего решения вблизи баллисти-
будем измерять в единицах 1/κ0, время — в едини-
ческого конуса в безразмерных переменных имеет
цах τ. Тогда из (2.16) получим общее решение приве-
вид (аналогично (5) из работы [29])
денного к безразмерному виду уравнения (2.1) дву-
мерного нелокального переноса:
fasympt(r, t, Rc) = f(r → Rct - 0, t, Rc) =
(
)
(
)
r
r
∫
= t-
W (r)θ t -
(2.21)
1
Rc
Rc
f2D(r, t, Rc, γ) =
dp pJ0(pr) ×
(2π)2i
0
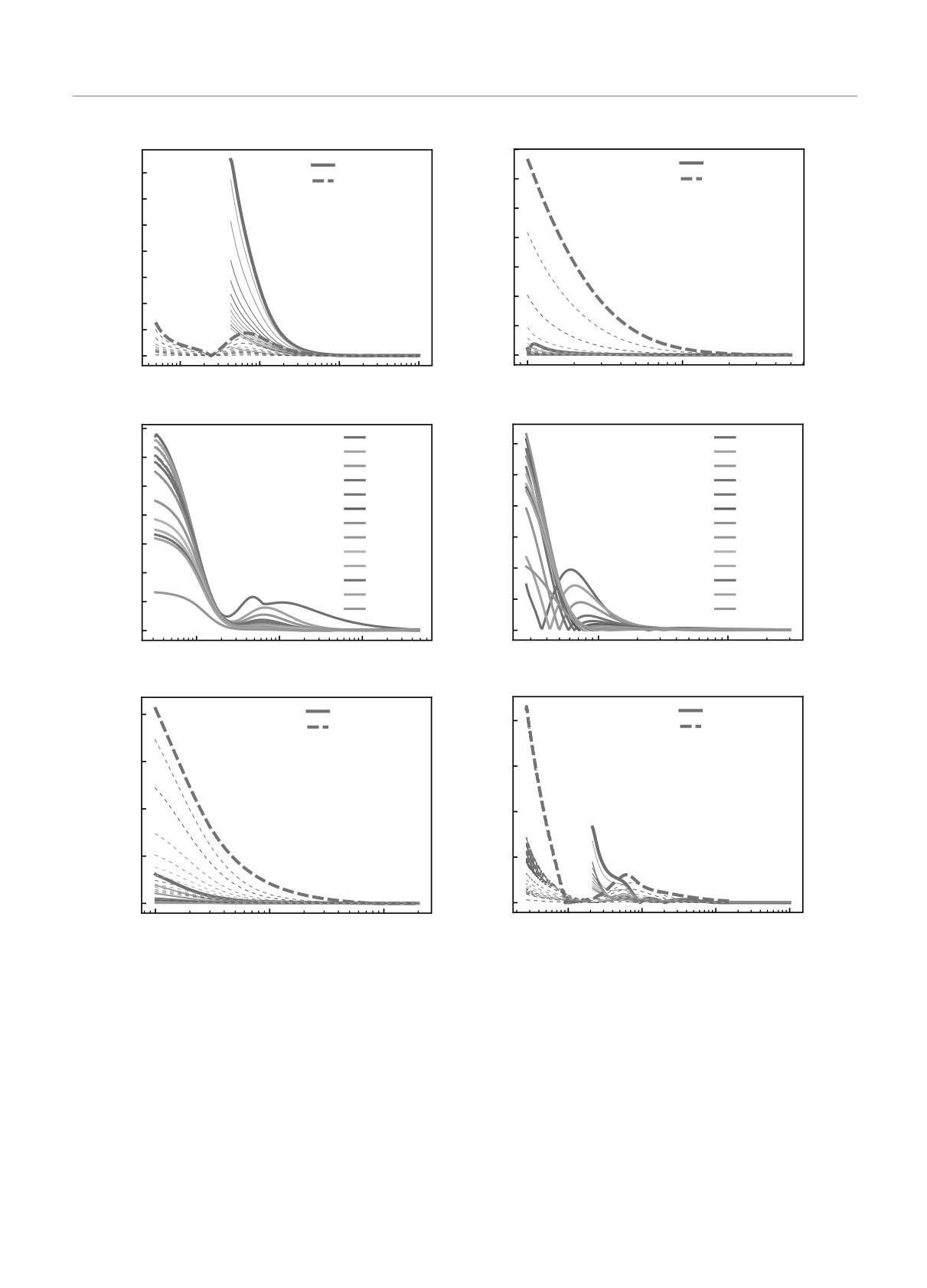
Результаты численного расчета общих реше-
∕⎧
ний (2.19), (2.17) и (2.20) для моментов време-
∫
⎨
ни t
= 30-3000; Rc
= 1, 10; γ
= 0.5, 1.5 при-
×
estds
s+1+στ -
⎩
ведены на рис. 1 соответственно для одномерного
+0-i∞
⎫
(а,б), двумерного (в,г) и трехмерного (д) перено-
+∞
-su/Rc
⎬
du e
сов. Графики представлены в переменных r/(Rct)
− γ
J0(pu)
,
(2.17)
(1 + u)γ+1
⎭
и f(r,t,Rc,γ)/f(r = 0,t,Rc,γ).
0
Отметим, что для трехмерного переноса резуль-
где
таты представлены только для случая γ = 1.5.
Ниже, на рис.
2
показана зависимость
Rc = cτκ0
(2.18)
f (r = 0, t, Rc, γ) от переменной t для различных
и γ и разных мерностей координатного
значений Rc
— отношение среднего времени жизни возбужден-
пространства.
ного состояния к среднему времени свободного про-
лета переносчика (фотона) или отношение средних
времен в состояниях покоя и движения переносчика.
3. ДИНАМИКА ИНТЕГРАЛЬНОЙ ПО
Для сравнения представим общее решение в од-
ПРОСТРАНСТВУ ХАРАКТЕРИСТИКИ
ФУНКЦИИ ГРИНА
номерном случае (см. (4) из работы [29]) при r = |x|:
Обратимся к системе исходных уравнений дву-
∫
1
мерного нелокального переноса (2.4) в случае отсут-
f1D(r, t, Rc, γ) =
dp cos(pr) ×
2π2i
ствия исчезновения переносчиков (σ = 0). Опреде-
0
лим количество возбужденных частиц в среде (сто-
∕⎧
∫
⎨
ящих переносчиков) в момент времени t как N(t):
×
estds
s+1+στ -
∫
⎩
+0-i∞
N (t) = f(r, t) d2r.
(3.1)
⎫
+∞
⎬
-su/Rc
du e
− γ
cos(pu)
(2.19)
Обратим внимание на то, что N(t) не зависит от
(1 + u)γ+1
⎭
0
мерности координатного пространства. Также вве-
дем интегральную по пространству спектральную
Вывод общего решения в трехмерном случае анало-
интенсивность излучения в момент времени t вдоль
гичен получению двумерного решения (2.17):
направления n:
∫
∫
1
Iω(n, t) = Iω(r, n, t)d2r.
(3.2)
f3D(r, t, Rc, γ) =
dp p sin(pr) ×
4π3ri
0
Проинтегрировав систему уравнений (2.4) по эле-
∕⎧
∫
⎨
менту плоскости d2r, получим
×
estds
s+1+στ -
⎩
+0-i∞
∂N(t)
N (t)
⎫
=-
+
∫
∂t
τ
c
⎬
γ
du e-su/R
sin(pu)
∫
∫
-
(2.20)
κω
p
(1 + u)γ+1 u
⎭
+ dω
dϕ(n)Iω(n, t) + δ(t),
(3.3)
0
ℏω
0
Далее рассмотрим только случай без исчезнове-
1 ∂Iω(n,t)
ℏω
1
ния переносчиков возбуждения: σ = 0. Выражение
=
eωN(t) - κωIω(n, t).
c
∂t
τ
2π
1040
ЖЭТФ, том 157, вып. 6, 2020
Супердиффузионный перенос «прогулками Леви» в однородной среде...
f/f(r = 0)
f/f(r = 0)
1.6
1.0
= 0.5, t =30
а
б
0.5,
3000
1.4
1.5,
30
0.8
1.2
1.5,
3000
1.0
0.6
Rc = 10
0.8
0.4
= 0.5, t =30
0.6
R
= 1
0.5,
3000
c
0.4
0.2
1.5,
30
0.2
1.5,
3000
0
0
0
0.2
0.4
0.6
0.8
1.0
0
0.2
0.4
0.6
0.8
1.0
r/(R t)c
r/(R t)c
f/f(r = 0)
f/f(r = 0)
1.0
1.0
в
= 0.5, t =30
г
= 0.5, t =30
0.5,
3000
0.5,
3000
0.8
1.5,
30
0.8
1.5,
30
1.5,
3000
1.5,
3000
0.6
0.6
Rc = 1
Rc = 10
0.4
0.4
0.2
0.2
0
0
0
0.2
0.4
0.6
0.8
1.0
0
0.2
0.4
0.6
0.8
1.0
r/(R t)c
r/(R t)c
f/f(r = 0)
1.0
= 1.5
д
0.8
Рис. 1. (В цвете онлайн) Результаты численного расчета
0.6
общих решений в разные моменты времени t = 30-3000
(крайние значения отмечены штриховыми кривыми) для
разных мерностей пространства и различных значений па-
0.4
раметров Rc = 1, 10 и γ = 0.5, 1.5. Показаны одномерное
Rc
= 1,
t
= 30
1,
30
00
общее решение (2.19) при Rc = 1 (а), Rc = 10 (б); дву-
0.2
10,
30
мерное общее решение (2.17) при Rc = 1 (в), Rc = 10
10,
3000
(г); трехмерное общее решение (2.20) для γ = 1.5 при
0
Rc = 1, 10 (д)
0
10-3
10-2
10-1
10
r/(R t)c
t
Решение второго уравнения в (3.3) при начальном
∫
∂N(t)
N (t)
условии Iω(n, t = 0) = 0 имеет вид
=-
+ dt′N(t′)p(t - t′) + δ(t),
(3.5)
∂t
τ
0
∫
t
где введена функция
ℏω ceω
Iω(n, t) =
dt′N(t′) exp[-κωc(t-t′)].
(3.4)
2πc2t
τ
2π
p(t) =
W (ct).
(3.6)
0
τ
Применим к (3.5) преобразование Лапласа:
Выполнив подстановку (3.4) в первое уравнение в
N (t) :=
N (s), p(t) :=
P (s).
(3.7)
(3.3) с учетом (2.3), получим
1041
6
ЖЭТФ, вып. 6
А. А. Куличенко, А. Б. Кукушкин
ЖЭТФ, том 157, вып. 6, 2020
f
где с учетом (3.7) и (3.6) в случае степенного ядра
а
W (2.14) получаем
10-2
[
](
)γ (
)
γ
s
s
s
P (s) =
exp
Γ
-γ,
,
(3.9)
10-3
τ
cκ0
cκ0
cκ
0
где
= 0.5, R
c
= 1
10-4
∫
∞
0.5,
10
1.5,
1
Γ(a, z) = xa-1 exp(-x) dx
–5
10
1.5,
10
z
— неполная гамма-функция.
10-6
Отсюда имеем предельные случаи зависимости
N (s) при s → 0 для различных γ:
0
500
1000
1500
2000
2500
3000
)γ
t
τ
(cκ0
N (s → 0) =
,
0 < γ < 1,
f
Γ(1 - γ) s
= 0.5, R
= 1
cτκ0
б
c
10-3
N (s → 0) =
γ = 1,
0.5,
10
(cκ0 ),
(3.10)
-4
s Ln
1.5,
1
10
s
1.5,
10
(γ - 1)cτκ0
10-5
N (s → 0) =
,
1 < γ < 2.
s[1 + (γ - 1)cτκ0]
10-6
10-7
При s → ∞ результат не зависит от γ:
10-8
̂(s → ∞) = 1/s.
(3.11)
10-9
Таким образом, из (3.10) и (3.7) с учетом (2.18) мож-
10-10
но получить аналитическое выражение для асимп-
10-11
0
500
1000
1500
2000
2500
3000
тотики интегральной характеристики функции Гри-
t
на — количества возбужденных частиц в среде (сто-
f
ящих переносчиков) при больших временах в без-
Rc = 1
размерных переменных:
в
10
10-4
⎧
Rγc sin(πγ)
⎪
⎨
,
0 < γ ≤ 1,
t1-γ
π
10-5
N (t → ∞) =
(3.12)
⎪
γ-1
= 1.5
⎩
,
1 < γ < 2,
1/Rc
+γ-1
10-6
длина — в единицах 1/κ0, время — в единицах τ.
10-7
Предельный случай (3.11) означает, что в началь-
ный момент времени находилась лишь одна части-
10-8
ца:
0
500
1000
1500
2000
2500
3000
N (t → 0) = 1.
(3.13)
t
Полученный результат (3.12) означает, что в зави-
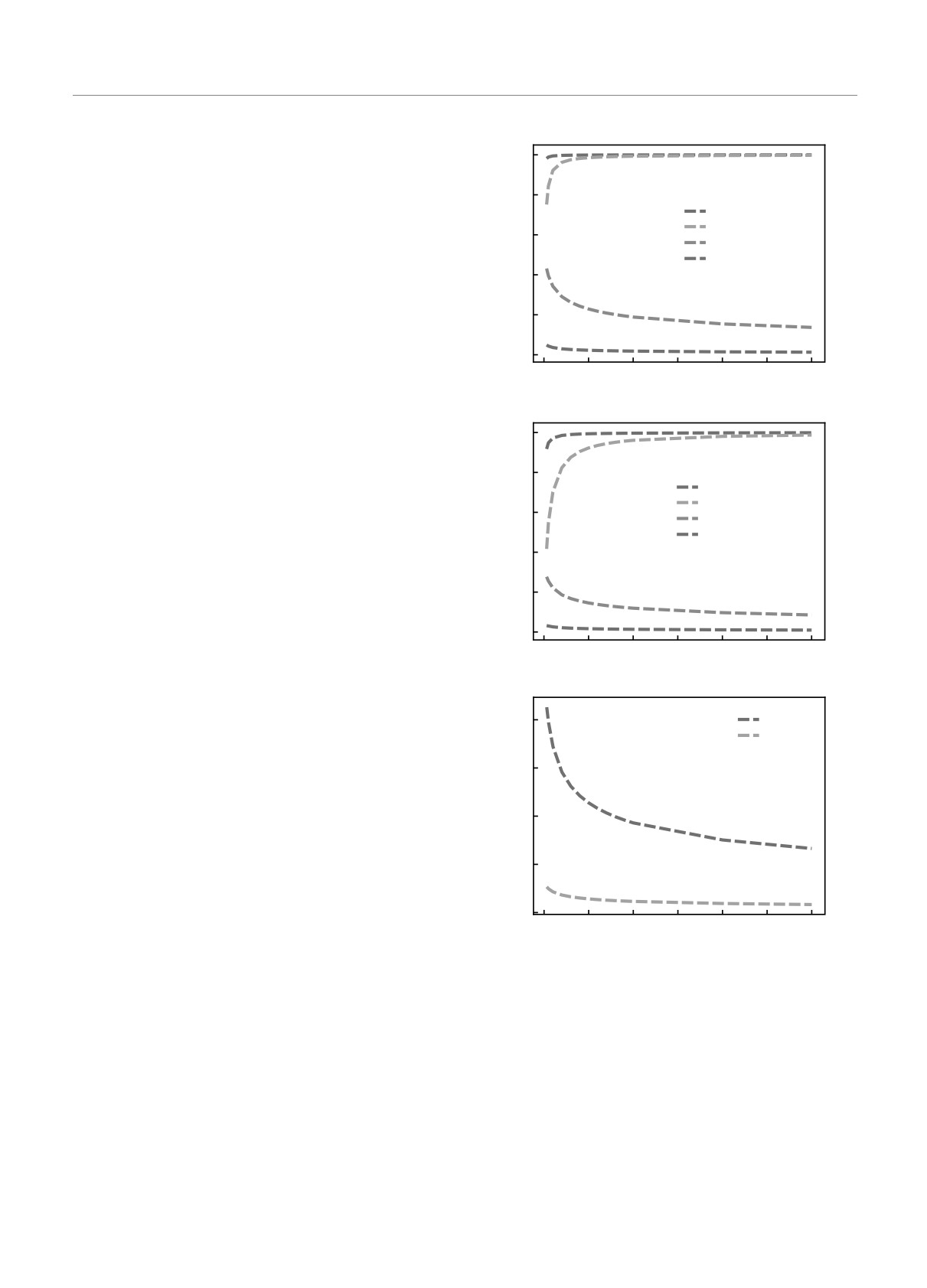
Рис. 2.
(В цвете онлайн) Зависимость f(r = 0, t, Rc, γ)
симости от степени убывания γ модельной ФРСП
от переменной t для различных значений Rc = 1, 10 и
γ = 0.5,1.5 и разных мерностей координатного простран-
количество стоящих переносчиков возбуждения при
ства: одномерного (а), двумерного (б), трехмерного (в)
больших временах может стремиться либо к нулю,
либо к постоянной величине. Формула (3.12), соот-
ветствующая при γ = 0.5 лоренцевской форме кры-
льев контура атомной спектральной линии излуче-
Тогда получим, что
ния фотонов, с точностью до константы согласуется
с законом переключения режимов сохранения пол-
1
N (s) =
,
(3.8)
ного числа частиц на его убывание, см. (18) в работе
s + 1/τ -
P (s)
[32] при β = 1/4.
1042
ЖЭТФ, том 157, вып. 6, 2020
Супердиффузионный перенос «прогулками Леви» в однородной среде...
N.106
в [29], построим приближенное автомодельное реше-
ние в виде
(
а
r
(ρfr(t,Rc,γ)))
fauto(r, t, Rc, γ) = t -
g
×
1d,
= 0.5
Rc
r
105
Rc = 1
(
2d,
= 0.5
(ρfr(t,Rc,γ)))
N t),
= 0.5
×W rg
×
r
1d,
= 1.5
(
r
(ρfr(t,Rc,γ)))
2d,
= 1.5
×θ t-
g
,
(4.1)
Rc
r
N t),
= 1.5
104
где функция автомодельности g имеет следующие
асимптотические пределы:
{
0
500
1000
1500
2000
2500
3000
1, s = smin = ρfr(t, Rc, γ)/(Rc, t),
g(s) =
(4.2)
t
N. 106
s, s ≫ smin,
106
а закон фронта ρfr(t, Rc, γ) определяется аналогич-
но выражению (8) из работы [29], т. е. как резуль-
б
Rc = 10
1d,
= 0.5
тат приравнивания асимптотики точного решения
2d,
= 0.5
вблизи баллистического конуса (2.21) к точному ре-
N t),
= 0.5
шению в начале координат:
1d,
= 1.5
(
)
(
)
105
ρfr
ρfr
2d,
= 1.5
t-
W (ρfr)θ t -
= f(0,t,Rc,γ).
(4.3)
Rc
Rc
N t),
= 1.5
Отметим, что автомодельное решение (4.1) справед-
ливо как для одномерного [29], так и для двумерного
и трехмерного случаев.
0
500
1000
1500
2000
2500
3000
Следуя указанному в [23] и [29] методу для
t
оценки точности предложенного автомодельного
решения (3.1), введем функцию автомодельности
Рис. 3. (В цвете онлайн) Сравнение результатов расче-
Q(r, t, Rc, γ) (ср. с (9) из работы [29]):
та количества возбужденных частиц в среде (стоящих пе-
реносчиков) по аналитическому закону (3.12) (штриховые
(
)
(
)
r
r
кривые) с результатом интегрирования по координате чис-
t-
Q W(rQ)θ t -
Q
=
ленно рассчитанных общих решений для одномерного пе-
Rc
Rc
реноса (2.19) (кружки), двумерного (2.17) (квадраты) и
= f(r,t,Rc,γ).
(4.4)
трехмерного (2.20) (треугольники) в различные моменты
времени при Rc = 1 (а), Rc = 10 (б); γ = 0.5, 1.5 для 106
Для проверки точности указанной автомодельности
частиц в начальный момент времени
следует показать, что функция Q1(s, t, Rc, γ) слабо
зависит от времени:
На рис. 3 представлено сравнение результатов
расчета количества возбужденных частиц в среде
Q1(s, t, Rc, γ) = Q (ρfr(t, Rc)/s, t, Rc, γ) ≈
(стоящих переносчиков) по аналитическому закону
≈ g(s, Rc, γ).
(4.5)
(3.12) с результатом интегрирования по координа-
те численно рассчитанных общих решений (2.19),
Зависимости
функции
автомодельности
(2.17) и (2.20) соответственно для одномерного, дву-
Q1(s, t, Rc, γ) от s для различных моментов вре-
мерного и трехмерного случаев в различные момен-
мени при Rc = 1, 10; γ = 0.5, 1.5 для одномерного,
ты времени при Rc = 1 (а), Rc = 10 (б); γ = 0.5; 1.5
двумерного и трехмерного случаев представлены
для 106 частиц в начальный момент времени.
соответственно на рис. 4а,б,в. Значения по вре-
мени лежат в интервале t
= 30-3000. Крайние
4. ПРИБЛИЖЕННОЕ АВТОМОДЕЛЬНОЕ
моменты отмечены штриховыми кривыми, между
РЕШЕНИЕ И ПРОВЕРКА ЕГО ТОЧНОСТИ
которыми изображены промежуточные времена.
Следуя методу, изложенному в работе [23] и
Из рис. 4 видна точность выполнения (4.2). Иссле-
для конечной скорости переносчиков обобщенному
дуем также относительное отклонение зависимости
1043
6*
А. А. Куличенко, А. Б. Кукушкин
ЖЭТФ, том 157, вып. 6, 2020
Q1
Q1
R
= 1,
t
=30
R
= 1,
t
=30
а
c
б
c
1,
3000
1,
3000
10,
30
10,
30
10,
3000
10,
3000
101
101
= 1.5
= 0.5
100
100
10-2
10-1
100
101
100
101
s
s
Q1
Q1
R
= 1,
t
=30
в
R
= 1,
t
=30
c
c
г
1,
3000
1,
3000
10,
30
10,
30
101
10,
3000
10,
3000
= 1.5
101
= 0.5
100
10-1
100
10-2
10-1
100
101
100
101
s
s
Q1
R
= 1,
t
=30
д
c
1,
3000
101
10,
30
10,
3000
= 1.5
Рис. 4. (В цвете онлайн) Зависимость функции авто-
модельности Q1(s, t, Rc, γ) (4.4) от s при Rc = 1, 10 и
γ = 0.5,1.5 для различных моментов времени (крайние
100
значения отмечены штриховыми кривыми) в одномерном
(а,б), двумерном (в,г) и трехмерном (д) случаях
10-2
10-1
100
101
s
Q1(s, t, Rc, γ) от Q1(s, t = 3000, Rc, γ) при Rc = 1, 10,
пропорциональность и отклонение стремится к
γ = 0.5,1.5 (рис. 5) для одномерного (а), двумер-
нулю. По имеющимся функциям автомодельности
ного (б,в) и трехмерного (г) переносов. Значение
Q1(s, t, Rc, γ) на рис. 6, 7 построены приближенные
функции выбрано в наибольший рассматриваемый
автомодельные решения (3.1) (пунктирные кривые)
момент времени t = 3000, поскольку с ростом t
для значений параметров Rc = 1, 10 соответственно
зависимость функции автомодельности от времени
при γ = 1.5 (рис. 6) и γ = 0.5 (рис. 7) в различные
становится более слабой. Для одномерного случая
моменты времени, а также общие решения (2.19),
максимальное относительное отклонение функции
(2.17) и (2.20) (сплошные кривые), рассчитанные
автомодельности составляет 80 %, для двумерного
численно. В качестве основной функции автомо-
и трехмерного — 70 %. Как видно на рис. 5, макси-
дельности использовалась Q1(s, t
= 3000, Rc, γ),
мальное отклонение соответствует области малых
поскольку она имеет наиболее слабую зависи-
s. С ростом s функция Q1 переходит в прямую
мость от времени. Как и на рис. 1, графики на
1044
ЖЭТФ, том 157, вып. 6, 2020
Супердиффузионный перенос «прогулками Леви» в однородной среде...
|Q /Q (t = 3000)|, %11
|Q /Q (t = 3000)|, %11
17.5
R
= 1,
t
=30
R
= 1,
t
=30
c
c
70
а
10,
30
15.0
б
10,
30
60
12.5
50
10.0
= 1.5
= 0.5
40
7.5
30
5.0
20
10
2.5
0
0
10-1
100
101
102
100
101
s
s
|Q
/Q
(t = 3000)|, %
|Q /Q (t = 3000)|, %11
1
1
70
t = 30
t = 30
30
50
50
60
г
в
100
100
25
200
200
50
300
300
R
= 1
400
20
Rc
= 10
400
40
c
500
500
= 1.5
600
15
= 0.5
600
30
700
700
800
10
800
20
900
900
1000
1000
10
5
2000
2000
0
0
1
10-1
100
10
100
101
s
s
|Q /Q (t = 3000)|, %11
|Q /Q (t = 3000)|, %11
40
R
= 1,
t
=30
R
= 1,
t
=30
c
80
c
10,
30
10,
30
д
е
30
60
= 1.5
= 0.5
20
40
10
20
0
0
100
101
102
10-1
100
101
102
s
s
Рис. 5. (В цвете онлайн) Относительное отклонение функции автомодельности Q1(s, t, Rc, γ) (4.4) в крайние моменты
времени t = 30 и t = 3000 при Rc = 1, 10 и γ = 0.5, 1.5 в одномерном (а,б), двумерном (в,г,д) и трехмерном (е) случаях
рис. 6,
7
представлены в переменных r/(Rct) и
стижения приемлемой точности при γ = 0.5 требу-
f (r, t, Rc, γ)/f(r = 0, t, Rc, γ).
ется дополнительная работа по улучшению дефини-
ции эффективного фронта распространения возму-
Сравнение результатов на рис. 6 и 7 показыва-
щения для функции Грина.
ет, что при γ = 1.5 точность автомодельного реше-
ния существенно выше, чем при γ = 0.5. Для до-
1045
А. А. Куличенко, А. Б. Кукушкин
ЖЭТФ, том 157, вып. 6, 2020
f/f(r = 0)
f/f(r = 0)
1.0
1.0
t = 30
t = 30
100
100
а
500
500
0.8
0.8
б
1000
1000
2000
2000
0.6
0.6
Rc = 1
Rc
= 10
0.4
0.4
0.2
0.2
0
0
-2
10
10-1
100
10-3
10-2
10-1
100
r/(R t)c
r/(R t)c
f/f(r = 0)
f/f(r = 0)
1.0
1.0
t = 30
t = 30
100
100
500
500
г
0.8
в
0.8
1000
1000
2000
2000
0.6
0.6
Rc = 1
Rc = 10
0.4
0.4
0.2
0.2
0
0
-2
10
10-1
100
10-3
10-2
10-1
100
r/(R t)c
r/(R t)c
f/f(r = 0)
f/f(r = 0)
1.0
1.0
t = 30
t = 30
100
100
500
500
0.8
0.8
1000
е
1000
д
2000
2000
0.6
0.6
0.4
0.4
Rc = 1
Rc = 10
0.2
0.2
0
0
10-2
10-1
100
10-3
10-2
10-1
100
r/(R t)c
r/(R t)c
Рис. 6. (В цвете онлайн) Сравнение автомодельных решений (4.1) для одномерного (а,б), двумерного (в,г) и трехмерного
(д,е) случаев, построенных по функции автомодельности в наибольший момент времени Q1(s, t = 3000, Rc, γ) (пунктир-
ные кривые), с общими решениями для переноса 1d (2.19), 2d (2.17) и 3d (2.20) (сплошные кривые) для значений
Rc = 1, 10 и γ = 1.5
1046
ЖЭТФ, том 157, вып. 6, 2020
Супердиффузионный перенос «прогулками Леви» в однородной среде...
f/f(r = 0)
f/f(r = 0)
1.6
1.0
а
1.4
Rc = 1
б
0.8
1.2
1.0
0.6
Rc = 10
0.8
0.4
0.6
t = 30
t = 30
0.4
100
100
500
0.2
500
0.2
1000
1000
2000
2000
0
0
0
0.2
0.4
0.6
0.8
1.0
0
0.2
0.4
0.6
0.8
1.0
r/(R t)c
r/(R t)c
f/f(r = 0)
f/f(r = 0)
1.0
1.0
г
в
0.8
0.8
Rc = 1
0.6
0.6
Rc = 10
0.4
0.4
t = 30
t = 30
100
100
0.2
500
0.2
500
1000
1000
2000
2000
0
0
0
0.2
0.4
0.6
0.8
1.0
0
0.2
0.4
0.6
0.8
1.0
r/(R t)c
r/(R t)c
Рис. 7. (В цвете онлайн) Сравнение автомодельных решений (4.1) для одномерного (а,б) и двумерного (в,г) случаев,
построенных по функции автомодельности в наибольший момент времени Q1(s, t = 3000, Rc, γ) (пунктирные кривые), с
общими решениями для переноса 1d (2.19), 2d (2.17) (сплошные кривые) для значений Rc = 1, 10 и γ = 0.5
Для объяснения обрыва автомодельных кривых
Нам интересно максимальное значение переменной
на рис.
7
обратимся более подробно к построе-
r в автомодельном решении для момента времени t2,
нию автомодельного решения. Рассмотрим исход-
т. е. координата точки обрыва автомодельного реше-
ную функцию автомодельности Q(r, t1, Rc, γ) (4.4) в
ния. Обозначим ее как rmax(t2, Rc, γ). Нетрудно ви-
момент времени t1. Перейдем к автомодельной пе-
деть из (4.7) и (4.6), что
ременной s = ρfr(t1, Rc, γ)/r:
rmax(t2, Rc, γ) = ρfr(t2, Rc, γ)/smin(t1, Rc, γ) =
Q(r, t1, Rc, γ) = Q (ρfr(t1, Rc, γ)/r, t1, Rc, γ) :=
= Rct1ρfr(t2, Rc, γ)/ρfr(t1, Rc, γ).
(4.8)
:= Q1(s, t1, Rc, γ),
Поскольку при γ
= 0.5 асимптотика общего ре-
минимальное значение s:
шения вблизи баллистического конуса (2.21), вхо-
дящая в определение закона фронта ρfr(t, Rc, γ)
smin(t1, Rc, γ) = ρfr(t1, Rc, γ)/(Rct1).
(4.6)
(4.3), справедлива лишь в небольшой области ко-
Далее построим автомодельное решение (4.1) в мо-
ординат вблизи данного баллистического конуса и
мент времени t2 ≪ t1 по функции автомодельности
стремится к вертикальной прямой с ростом времени,
Q1(r, t1, Rc, γ) с переходом к переменной r в виде
ρfr(t, Rc, γ = 0.5) → Rct, при этом smin(t, Rc, γ) =
t) → 1, что хорошо наблюдается
= ρfr(t,Rc,γ)/(Rc
r = ρfr(t2,Rc,γ)/s.
(4.7)
на рис. 4б,г. Отсюда в силу того, что t2 ≪ t1, можем
1047
А. А. Куличенко, А. Б. Кукушкин
ЖЭТФ, том 157, вып. 6, 2020
с хорошей точностью положить ρfr(t1, Rc, γ) ≈ Rct1
r /(R tfr)c
(в работе, например, t1 = 3000). Тогда из (4.8) полу-
1.0
чим
а
0.8
(4.9)
= 0.5, R
= 1
rmax(t2, Rc, γ) = ρfr(t2, Rc, γ).
c
0.5,
10
0.6
1.5,
1
Зависимость закона фронта ρfr(t, Rc, γ) (4.3) от t
1.5,
10
при Rc = 1, 10 и γ = 0.5, 1.5 показана на рис. 8 для
0.4
одномерного (а), двумерного (б) и трехмерного (в)
случаев в переменных t и ρfr(t, Rc, γ)/(Rct). Видно,
0.2
что ρfr(t → ∞, Rc, γ = 0.5) → Rct, т. е. стремится к
баллистическому конусу, задаваемому конечной ско-
0
ростью переносчиков.
0
500
1000
1500
2000
2500
3000
t
r /(R tfr)c
5. ЗАКЛЮЧЕНИЕ
1.0
Перенос с конечной скоростью переносчиков
охватывает широкий круг задач. К таким процессам
0.8
б
= 0.5, R
= 1
c
относятся перенос энергии фотонами в спектраль-
0.5,
10
ных линиях атомов и ионов в плазме и газах в аст-
0.6
1.5,
1
рофизических объектах, нелокальный перенос теп-
1.5,
10
0.4
ла электромагнитными волнами в плазме, миграция
животных (см. обзор [7] и [32, 33]). Данные явле-
0.2
ния носят супердиффузионный характер и должны
описываться интегральным уравнением в простран-
0
ственных координатах, не сводимым к дифференци-
0
500
1000
1500
2000
2500
3000
альному уравнению диффузии, поэтому численное
t
моделирование супердиффузионного переноса явля-
r /(R tfr)c
ется сложной, вычислительно трудоемкой задачей.
В данной работе получено общее решение для
2.0
Rc = 1
в
задачи супердиффузионного переноса «прогулками
Rc = 10
Леви с остановками» на однородной плоскости и в
= 1.5
1.5
однородном трехмерном пространстве для случая
модельной функции распределения по длине сво-
бодного пробега, имеющей степенной спад с ростом
1.0
расстояния. Для таких типов переноса предложено
приближенное автомодельное решение. Также про-
0.5
ведена проверка точности приближенного автомо-
дельного решения путем сравнения с рассчитанны-
0
ми численно общими решениями для конкретных
0
500
1000
1500
2000
2500
3000
степенных законов ядра для переноса в одномерном,
t
двумерном и трехмерном пространствах.
Рис. 8. Зависимость закона фронта ρfr(t, Rc, γ) (4.3) от t
В работе представлен аналитический вывод
при Rc = 1, 10 и γ = 0.5, 1.5 для одномерного (а), двумер-
асимптотического выражения для интегральной по
ного (б) и трехмерного (в) случаев
пространству характеристики функции Грина при
больших временах (данная характеристика соот-
ветствует количеству возбужденных частиц в среде
(стоящих переносчиков)). Также показано, что в
результатов для различных показателей степенного
зависимости от степени убывания модельной ФРСП
спада функции распределения по длине свободного
количество стоящих переносчиков возбуждения
пробега показывает, что для γ
= 1.5 точность
при больших временах может стремиться либо
автомодельного решения существенно выше, чем
к нулю, либо к постоянной величине. Сравнение
для γ = 0.5. Для достижения приемлемой точности
1048
ЖЭТФ, том 157, вып. 6, 2020
Супердиффузионный перенос «прогулками Леви» в однородной среде...
при γ
= 0.5 требуется дополнительная работа
7.
V. Zaburdaev, S. Denisov, and J. Klafter, Rev. Mod.
по улучшению дефиниции эффективного фронта
Phys. 87, 483 (2015).
распространения возмущения для функции Грина.
8.
Л. М. Биберман, ЖЭТФ 17, 416 (1947).
Как показано в работах [27, 28] для случая
переноса полетами Леви, включая задачи переноса
9.
T. Holstein, Phys. Rev. 72, 1212 (1947).
резонансного излучения в спектральных лини-
10.
Л. М. Биберман, В. С. Воробьев, И. Т. Якубов, Ки-
ях атомов и ионов в плазме и газах, получение
нетика неравновесной низкотемпературной плаз-
автомодельных решений во всем пространстве
мы, Наука, Москва (1982).
независимых переменных требует массового чис-
ленного расчета (распределенных вычислений),
11.
В. А. Абрамов, В. И. Коган, В. С. Лисица, в сб.
однако их общий объем значительно снижается
Вопросы теории плазмы, под ред. М. А. Леонто-
за счет автомодельности решения. Разработанный
вича, Б. Б. Кадомцева, Энергоатомиздат, Москва
здесь (как развитие [29]) метод уместно назвать
(1982), вып. 12, c. 114.
методом интерполируемой автомодельности, и он
12.
И. Б. Левинсон, ЖЭТФ 75, 234 (1978).
представляет, на наш взгляд, значительный интерес
для существенного сокращения численных расчетов
13.
А. Б. Кукушкин, В. С. Лисица, Ю. А. Савельев,
в широком круге практических задач супердиф-
Письма в ЖЭТФ 46, 356 (1987).
фузионного переноса в физике и других областях
14.
A. V. Subashiev, O. Semyonov, Z. Chen et al., Phys.
науки.
Lett. A 378, 266 (2014).
Благодарности. Авторы благодарны В. С. Не-
15.
E. Pereira, J. Martinho, and M. Berberan-Santos,
верову за полезные советы по ускорению числен-
Phys. Rev. Lett. 93, 120201 (2004).
ного расчета общего решения, А. В. Соколову —
за обсуждение результатов численных расчетов,
16.
Л. М. Биберман, ДАН 49, 659 (1948).
К. В. Чукбару — за обсуждение работ [32,33].
17.
V. I. Kogan, in Proc. 8th ICPIG, IAEA, Vienna
Финансирование. Работа выполнена при час-
(1968), p. 583.
тичной поддержке Российского фонда фундамен-
тальных исследований (гранты №№ 18-07-01269-а,
18.
Methods in Radiative Transfer, ed. by W. Kalkofen,
19-32-90281), а также в рамках программы повыше-
Cambridge University Press, Cambridge (1984).
ния конкурентоспособности НИЯУ МИФИ.
19.
G. B. Rybicki, in Methods in Radiative Transfer, ed.
Работа выполнена с использованием оборудова-
by W. Kalkofen, Cambridge University Press, Cam-
ния центра коллективного пользования «Комплекс
bridge (1984), ch. 1.
моделирования и обработки данных исследователь-
ских установок мега-класса» НИЦ «Курчатовский
20.
А. П. Напартович, Теплофизика высоких темпера-
тур 9, 26 (1971).
21.
В. И. Коган, Запирание излучения в плазме, Эн-
ЛИТЕРАТУРА
циклопедия низкотемпературной плазмы, под ред.
1. M. Shlesinger, G. M. Zaslavsky, and U. Frisch, Lévy
В. Е. Фортова, Наука, Москва (2000), т. 1, c. 481.
Flights and Related Topics in Physics, Springer, New
22.
А. Н. Старостин, Перенос резонансного излучения.
York (1995).
Энциклопедия низкотемпературной плазмы, под
2. A. A. Dubkov, B. Spagnolo, and V. V. Uchaikin, Int.
ред. В. Е. Фортова, Наука, Москва (2000), т. 1,
J. Bifurcation Chaos 18, 2649 (2008).
c. 471.
3. J. Klafter and I. M. Sokolov, Phys. World 18, 29
23.
A. B. Kukushkin and P. A. Sdvizhenskii, J. Phys. A:
(2005).
Math. Theor. 49, 255002 (2016).
4. I. I. Eliazar and M. F. Shlesinger, Phys. Rep. 527,
24.
A. B. Kukushkin and P. A. Sdvizhenskii, in Proc.
101 (2013).
of 41st EPS Conference on Plasma Physics, Berlin
5. B. B. Mandelbrot, The Fractal Geometry of Nature,
(2014), ECA 38F, P4.133.
Freeman, New York (1982).
25.
A. B. Kukushkin, P. A. Sdvizhenskii, V. V. Voloshi-
6. M. F. Shlesinger, J. Klafter, and J. Wong, J. Stat.
nov et al., Int. Rev. Atom. Molec. Phys. (IRAMP) 6,
Phys. 27, 499 (1982).
31 (2015).
1049
А. А. Куличенко, А. Б. Кукушкин
ЖЭТФ, том 157, вып. 6, 2020
26. A. B. Kukushkin and P. A. Sdvizhenskii, J. Phys.:
30. A. A. Kulichenko and A. B. Kukushkin, in Proc. of
Conf. Series 941, 012050 (2017).
45th EPS Conference on Plasma Physics (Prague,
2018), ECA 42A (2018), P1.4013.
27. A. B. Kukushkin, V. S. Neverov, P. A. Sdvizhenskii,
and V. V. Voloshinov, Int. J. Open Inform. Techno-
31. A. A. Kulichenko and A. B. Kukushkin, Int. Rev.
log. (INJOIT) 6, 38 (2018).
Atom. Molec. Phys. (IRAMP) 8(1), 5 (2017).
28. A. B. Kukushkin, V. S. Neverov, P. A. Sdvizhenskii,
32. В. Ю. Забурдаев, К. В. Чукбар, ЖЭТФ 121, 299
and V. V. Voloshinov, 6, 43 (2018).
(2002).
29. A. B. Kukushkin and A. A. Kulichenko, Phys. Scripta
33. В. Ю. Забурдаев, К. В. Чукбар, Письма в ЖЭТФ
94, 115009 (2019).
77, 654 (2003).
1050