ЖЭТФ, 2020, том 157, вып. 6, стр. 1051-1062
© 2020
ЗАРЯДОВЫЕ КОЛЕБАНИЯ В ПРОСТОЙ МОДЕЛИ
ВЗАИМОДЕЙСТВУЮЩИХ МАГНИТНЫХ ОРБИТ
Ж.-И. Фортэн***
Department of Physics and Astronomy and Center for Theoretical Physics, Seoul National University
08826, Seoul, Korea
Поступила в редакцию 23 августа 2019 г.,
после переработки 22 декабря 2019 г.
Принята к публикации 24 января 2020 г.
(Перевод с английского)
CHARGE OSCILLATIONS IN A SIMPLE MODEL
OF INTERACTING MAGNETIC ORBITS
Jean-Yves Fortin
Исследуются точные собственные состояния для двух или более взаимодействующих электронных орбит
в магнитном поле для класса факторизуемых гамильтонианов с взаимодействующими поверхностями
Ферми. Исследованы условия существования операторов рождения и уничтожения, позволяющие полу-
чить собственные состояния. Для случая двух взаимодействующих циклотронных орбит рассмотрены
зависимости от обратного поля колебаний функции перекрытия и переноса зарядовой плотности меж-
ду орбитами. В квазиклассическом режиме получены выражения для частот Фурье, которые зависят
от геометрической структуры электронной зоны. Получено обобщение этого построения для цепочки из
нескольких взаимодействующих орбит с точными собственными функциями.
DOI: 10.31857/S0044451020060073
может туннелировать. Реализация таких поверхнос-
тей Ферми, напоминающих линейную цепочку свя-
занных орбит, представлена на рис. 1 для орга-
1. ВВЕДЕНИЕ
2
нического проводника (BEDO-TTF)5[CsHg(SCN)4]
(би-этилендиокси-тетратиафульвален) [5]: приходя-
Задача двух состояний в квантовой механике, на-
щий волновой пакет, находящийся на гигантской
пример, двухуровневая модель Розена - Зенера, поз-
орбите β (а), переходит на циклотронную орби-
воляет получать точную информацию о том, как
ту α (b) и отражается на ту же орбиту β (c) в
волновая функция распространяется через контакт,
пределах цепочки. Также существуют поверхнос-
и, кроме того, имеет много важных применений в
ти Ферми с конечным числом взаимодействующих
квантовых системах с зависимостью от времени, см.,
орбит, причем фурье-спектр их магнитных коле-
например работы [1-4], в которых подробно изуча-
баний подробно изучен. Например, компенсирован-
ются резонансные и фазовые сдвиги для тех потен-
ные ферми-структуры, имеющие только три зо-
циалов, для которых имеется точное решение. Эту
ны, состоящие из одной дырочной и двух элек-
общую задачу можно также использовать в случае
тронных зон, можно найти в соединении α-“псев-
магнитного пробоя, когда квазичастица движется по
до-κ-”(ET)4H3O[Fe(C2O4)3]·(C6H4Br2), где слои ти-
поверхности Ферми, состоящей из нескольких ли-
па α и типа “псевдо-κ” соответствуют слоям про-
стов, связанных контактами, через которые частица
водника и изолятора [6]. При магнитопробойном
контакте гамильтониан можно линеаризовать, тогда
* E-mail: jean-yves.fortin@univ-lorraine.fr
** Permanent address: Laboratoire de Physique et Chimie
два листа гибридизуются с некоторой энергией взаи-
Théoriques, CNRS (UMR 7019), Université de Lorraine, BP
модействия g. Такой простейший вид двухуровнево-
70239 F-54506 Vandoeuvre-lès-Nancy Cedex, France
1051
Ж.-И. Фортэн
ЖЭТФ, том 157, вып. 6, 2020
a
c
V1(x) и V2(x) — потенциалы, являющиеся суперсим-
метричными партнерами, они выражаются через
Q(x) и ее производную. Собственные функции и соб-
b
ственные значения гамильтониана H2 тесно связа-
ны с соответствующими собственными функциями и
собственными значениями гамильтониана H1. Если
для H1 можно получить точное выражение, то его
можно получить и для H2 [15,20,21]. Это позволяет
получить точные решения уравнения Шредингера
с нетривиальными потенциалами V2(x), например,
для классов потенциалов с двумя ямами [22].
Еще одна возможность, которую мы использу-
ем в настоящей работе, заключается в рассмот-
рении факторизованного гамильтониана такого же
вида, H
= D†D, когда Q(x) представляет собой
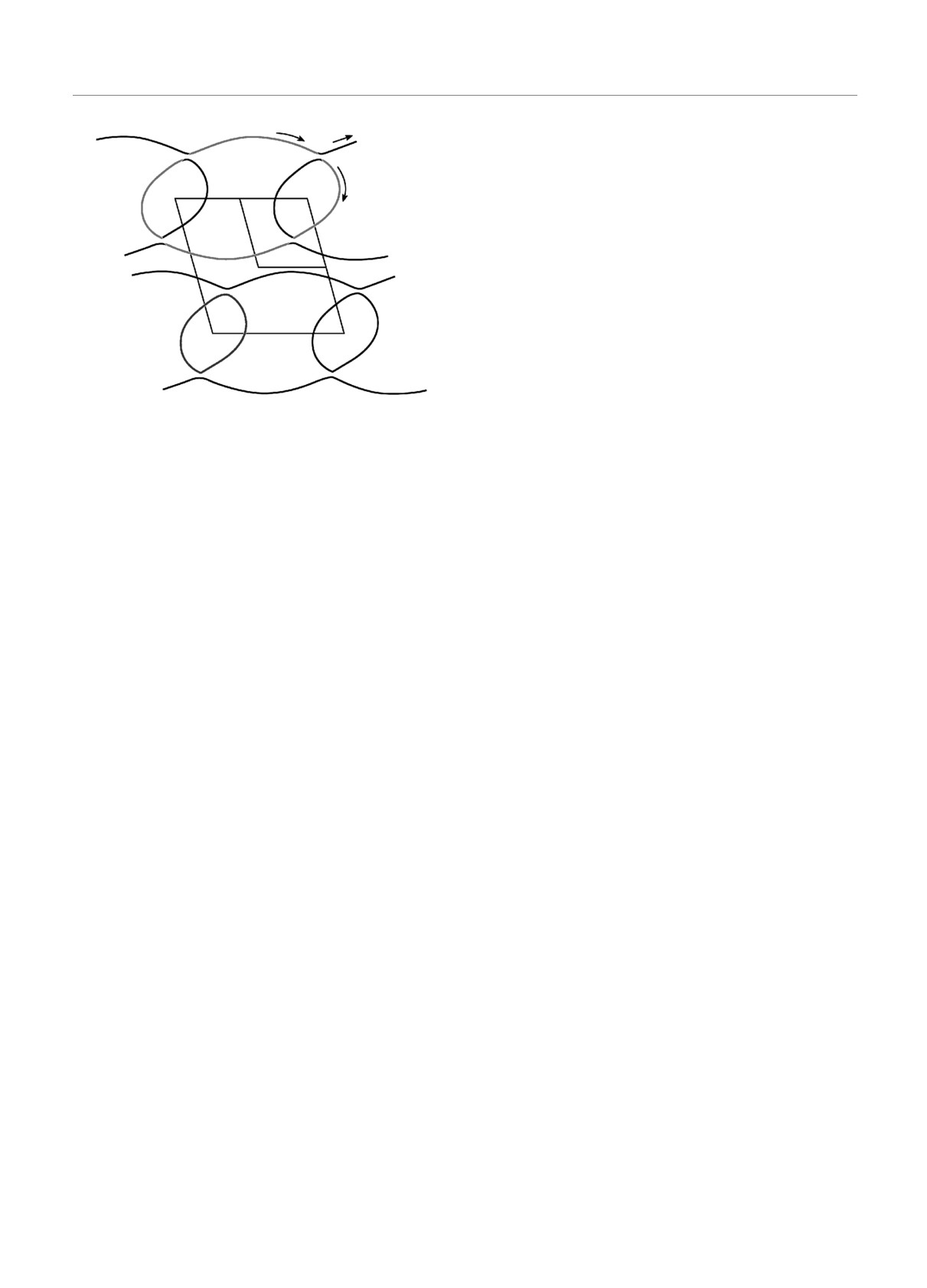
Рис. 1. Поверхность Ферми органического проводника
обобщенную комплексную матрицу, структура ко-
(BEDO-TTF)5[CsHg(SCN)4]2 [5, 23]. Она состоит из це-
торой определяется следующим условием: комму-
почки небольших орбит α и орбит с магнитным пробо-
ем β. Траекториям электронов соответствуют приходящие
татор операторов D и D† удовлетворяет соотноше-
волновые пакеты (а), которые рассеиваются (b) и распро-
нию [D, D†] = 1. В этом случае D и D† называют-
страняются дальше (c)
ся лестничными операторами или операторами уни-
чтожения и рождения, так что, зная основное со-
го гамильтониана был получен для различных слу-
стояние, можно немедленно получить собственные
чаев в работе [7] с использованием аппроксимации
состояния, при этом энергетический спектр явля-
вблизи области туннелирования. Вероятность тун-
ется дискретным. В случае единственной зоны это
нелирования экспоненциально мала, если рассмат-
условие просто означает, что Q(x) является линей-
ривать отношение пробойного поля к магнитному
ной функцией x (гармонический осциллятор), одна-
[8], а также полевую зависимость фазы Онзагера
ко для систем с двумя или многими зонами Q(x)
[9, 10] (в дополнение к тому, что фаза изменяется
может иметь более сложный вид. Кроме того, как
на π/2 каждый раз, когда частица отражается от
мы увидим, матрицу Q(x) можно выбрать так, что
контакта).
два листа поверхности Ферми для данного гамиль-
В настоящей работе получены простые и точные
тониана будут образовывать магнитный зазор. Ре-
выражения для собственных состояний для много-
шение такой задачи является целью настоящей ра-
зонных проводников, для которых имеет место маг-
боты. Мы также покажем, что просто переходя к
нитное туннелирование на таких поверхностях Фер-
многозонному гамильтониану, мы получаем модель
ми, состоящих, например, из цепочки из двух или
приведенной на рис. 1 линейной цепочки связанных
более связанных орбит [11].
орбит, которая обсуждалась выше.
Вообще говоря, для решения гамильтонианов
при комплексных потенциалах, кроме квазикласси-
2. МОДЕЛЬ
ческого подхода, основанного на методе ВКБ [12,13],
где используется матрица рассеяния для взаимодей-
Блоховские электроны в магнитном поле
ствующих орбит, имеются и другие подходы. Напри-
обычно описываются с помощью подстановки
мер, метод факторизации, или метод Дарбу [14-19],
Пайерлса
[24, 25]. При этом блоховский гамильто-
основанный на рассмотрении гамильтониана, кото-
ниан H(k) для дисперсии энергии заменяется на
рый можно факторизовать как
H(-i∇ + eA/ℏ), где -e — заряд электрона. Такое
приближение обычно работает вблизи поверхности
H1 = D†D = -∂2x + V1(x),
Ферми или для гамильтонианов в случае сильной
где
связи
[26]. Оценка квазиимпульса
-i∇ + eA/ℏ
D = ∂x + Q(x), D† = -∂x + Q(x)
в калибровке Ландау A
= (0, Bx1, 0) приводит
— операторы первого порядка. Теперь рассмотрим
к аналогии с движением одномерной частицы в
партнерский гамильтониан H2, построенный путем
потенциале [27], если отождествить безразмерные
перестановки двух операторов D и D†:
операторы
(
)
H2 = DD† = -∂2x + V2(x).
x=a2
-i∂2 + x1/l2B
1052
ЖЭТФ, том 157, вып. 6, 2020
Зарядовые колебания в простой модели...
и
одной и той же функции Q(x). Если Q′(x) — конс-
p= -ia1∂1
танта, то постоянное фермион-бозонное взаимодей-
ствие отсутствует, как для случая бозонного гармо-
с эффективными координатой и импульсом; здесь
нического осциллятора. Классический гамильтони-
(a1, a2) — типичные размеры зоны Бриллюэна еди-
ан Hc в пределе h → 0 получается заменой операто-
ничной ячейки, а l-2B = eB/ℏ — обратный квад-
ра p на импульсную переменную p:
рат магнитной длины. Эти операторы удовлетворя-
ют коммутационным соотношениям
Hc(x, p) = (Q†(x) - iσ0p)(Q(x) + iσ0p) =
[x, p] = ia1a2eB/ℏ ≡ ih,
= σ0p2 + Q†(x)Q(x) + ip[Q†(x) - Q(x)].
(3)
где h = a1a2/l2B — безразмерная эффективная по-
Поверхность Ферми Hx(x, p) = Eσ0 на плоскос-
стоянная Планка. Его также можно определить
ти (x, p) задается собственными значениями Hc при
как отношение магнитного потока через единич-
постоянной энергии E и обычно образована дву-
ную ячейку к квантовому потоку h/e, и часто его
мя замкнутыми поверхностями. Ниже мы рассмот-
рассматривают как малый контрольный параметр
рим примеры матриц Q(x), для которых имеет ме-
в квазиклассических теориях, если размер ячеек в
сто магнитное туннелирование между двумя листа-
зоне Бриллюэна порядка 1Å или если магнитное по-
ми поверхности Ферми. Коммутационное соотноше-
ле порядка 1 Тл. Следует заметить, что в случае
ние для операторов D и D† определяется матри-
положительных зарядов, заряд e, наоборот, отри-
цей P (x):
цательный, поэтому чтобы эффективная постоян-
1
(
)
ная Планка h была положительной, можно поме-
[D, D†] =
∂xQ(x) + ∂xQ†(x)
+
2
нять местами x и p для сохранения коммутацион-
1
ного соотношения.
+
[Q(x), Q†(x)] = P (x).
(4)
2h
Возьмем за основу выражение для гамильтони-
ана для электрона в равномерном магнитном поле
Если P (x) — единичная матрица, то это соотноше-
B, где H(k) квадратичен по импульсу k и описывает
ние представляет собой обычный бозонный комму-
простой гармонический осциллятор вблизи поверх-
татор для операторов рождения и уничтожения D†
ности Ферми, поэтому его можно факторизовать в
и D. При этом собственные состояния
терминах лестничных операторов или операторов
рождения и уничтожения [28]. Введем представле-
Ψn = (φn,φn)⊤
ние
можно построить из основного состояния Ψ0, для ко-
p= -ih∂x
торого DΨ0 = 0, действуя на него лестничным опе-
и рассмотрим класс дифференциальных операторов
ратором D†. Например, это имеет место в случае, ко-
для многозонных систем, которые определяются как
гда система состоит из двух независимых гармони-
ческих осцилляторов, расположенных в точках ±xc:
1
[
]
D† =
√
-hσ0∂x + Q†(x)
,
(
)
2h
x+xc
0
(1)
Q(x) = Q†(x) =
,
1
D =
√
[hσ0∂x + Q(x)] .
0
x-xc
2h
(
)
(5)
1
0
P =
Тогда можно построить факторизованный эрмитов
0
1
гамильтониан
Ĥ:
Исследуем условие, при котором может иметь
Ĥ= 2hD†D = -σ0h2∂2x + [Q†(x) - Q(x)]h∂x -
место туннелирование, а именно, если для матрицы
общего вида Q(x) коммутатор P(x) = 1. Сначала
- hQ′(x) + Q†(x)Q(x),
(2)
разложим матрицу Q(x) в базисе матриц Паули:
где Q(x) — матрица общего вида, зависящая от
∑
x, а σi=0,···,3
— матрицы Паули. Известно, что
Q(x) = αi(x)σi,
с точки зрения суперсимметрии [15] произведение
i=0
Q†(x)Q(x) описывает взаимодействие между бозо-
где αi — комплексные функции, причем для этой
нами, а член hQ′(x) соответствует фермион-бозон-
ному взаимодействию, при этом оба они зависят от
матрицы коммутатор P (x) равен
1053
Ж.-И. Фортэн
ЖЭТФ, том 157, вып. 6, 2020
1
Для других компонент рассмотрим решение
P (x) =
∂x(α0(x) + α0(x))σ0 +
2
1
i
α = (u(x),v(x),iω(x) + xc)⊤,
+
∂x(α + α) · σ +
(α × α) · σ.
(6)
2
h
Выберем функции αi так, что P (x) = σ0. Тогда по-
где u, v и ω — вещественные функции. Константа xc
лучим систему дифференциальных уравнений
определяет, где находятся центры обоих осциллято-
ров, а именно, при x = ±xc. Система уравнений с
∂x Re(α0) = 1,
условием (7) имеет вид
2
∂x Re(α) +
Re(α) × Im(α) = 0,
(7)
h
2
2
u′(x)+
ω(x)v(x) = 0, v′(x)-
ω(x)u(x) = 0.
(8)
∂x Re(α)2 = 0.
h
h
Эта система аналогична уравнению движения час-
Выберем ее решения в виде
тицы, расположенной в точке Re(α), которая вра-
щается вокруг углового вектора Ω = (2/h)Im(α) на
u(x) = g cos θ(x), v(x) = g sin θ(x),
сфере постоянного радиуса ∥ Re(α) ∥, при этом x
играет роль переменной динамического времени. Ре-
где
шение для α0 с точностью до константы имеет вид
∫
x
θ(x) = 2h-1 ω(y) dy,
α0(x) = x + iw(x),
где w(x) — любая вещественная функция x. Огра-
а g — постоянный параметр (постоянная взаимодей-
ничимся решением
ствия). Отсюда
α0(x) = x,
α = (g cosθ(x), g sinθ(x), iω(x) + xc)⊤
(9)
которое в гармоническом случае соответствует сме-
щению осциллятора. Ниже мы покажем, что на-
Тогда матрица Q(x) имеет вид
личие w(x) эквивалентно добавлению к волновой
(
)
функции калибровочного члена
x + xc + iω(x)
ge-iθ(x)
⎧
⎫
Q(x) =
,
(10)
∫
x
geiθ(x)
x - xc - iω(x)
⎨
⎬
exp
ih-1
w(y) dy
⎩
⎭
а классический гамильтониан имеет вид
⎛
⎞
2
(p + ω)2 + (x + xc)2
+g
2ge-iθ(x - iω)
Hc(x, p) =⎝
⎠.
(11)
2geiθ(x + iω)
(p - ω)2 + (x - xc)2 + g2
Поверхность Ферми, образованная двумя листами,
равен нулю. Вообще говоря, если ω(0) = 0, то две
определяется решением уравнения det(Hc - σ0E) =
поверхности не пересекаются и появляется зазор.
= 0:
Следует отметить, что Hc зависит от h через
недиагональные элементы e±iθ(x), которые в клас-
E = p2 + ω(x)2 + x2 + x2c + g2 ±
сическом пределе, когда h → 0, становятся быст-
√
ро осциллирующими, однако уравнение (12) для по-
±2
(pω(x) + xxc)2 + g2(x2 + ω(x)2).
(12)
верхности Ферми в этом пределе не зависит от h,
поскольку две экспоненты в уравнении (11) взаим-
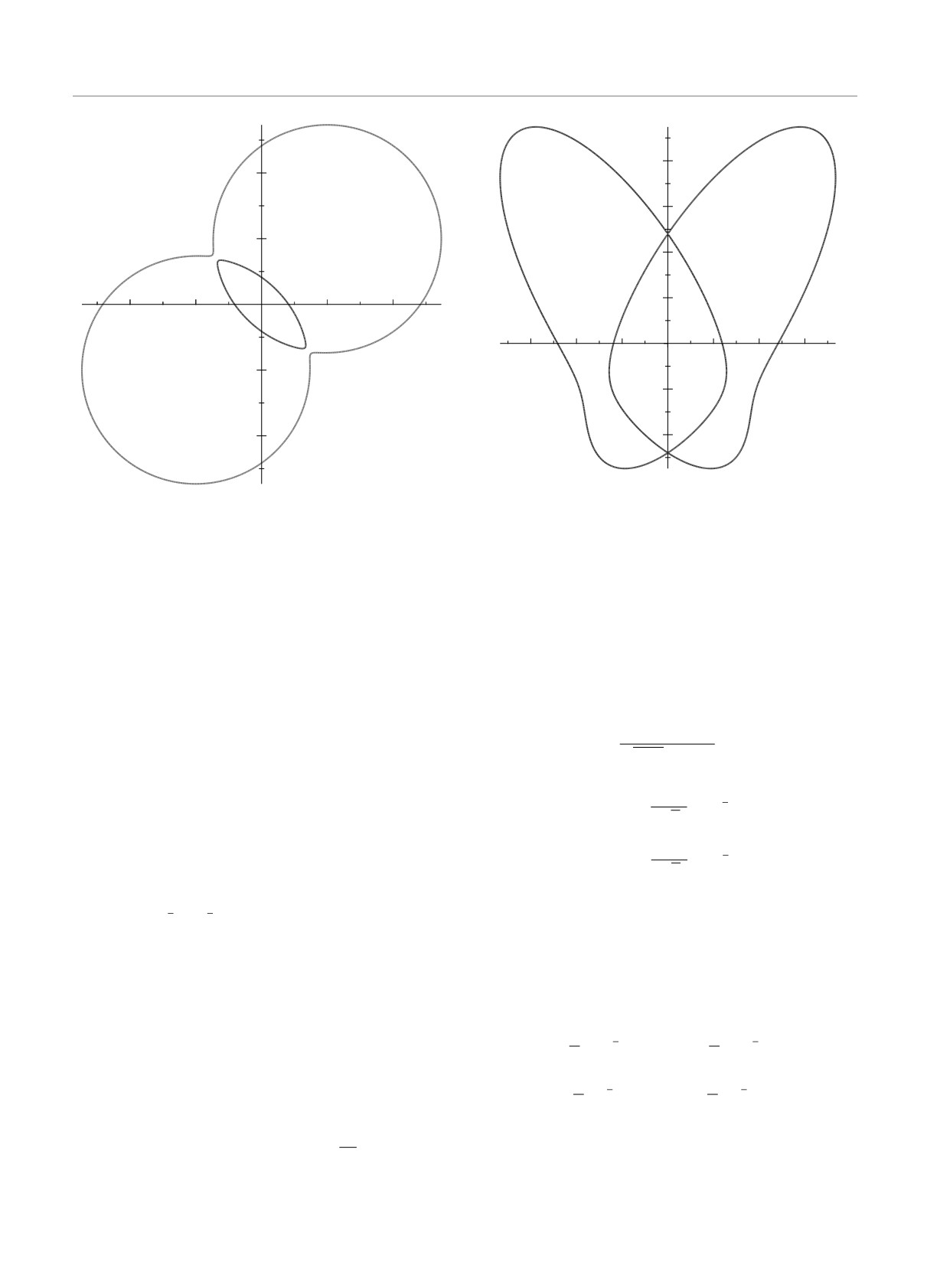
В качестве примера на рис. 2 показана поверх-
ность Ферми, образованная двумя листами при E =
но сокращаются. Вид матрицы Q в уравнении (10)
= 3, xc = 1, g = 0.05 и ω(x) = 1. Две зоны раз-
обеспечивает, что коммутатор P(x) = σ0 и что собст-
делены зазором, размер которого зависит от g. На
венные функции Ψn = (φn,φn)⊤ могут быть постро-
рис. 3 приведен еще один пример поверхности Фер-
ены точно, если подействовать оператором D† на ос-
новное состояние Ψ0:
ми при ω(x) = x, xc = 1, g = 0.5, E = 5. В этом
случае поверхности пересекаются при x = 0, потому
√
что ω(0) = 0 и квадратный корень в уравнении (12)
Ψn = D†nΨ0/
n! ,
1054
ЖЭТФ, том 157, вып. 6, 2020
Зарядовые колебания в простой модели...
p
p
4
2
3
1
2
1
-2
-1
0
1
2
x
-3
-2
-1
0
1
2
3
x
-1
-1
-2
–2
Рис. 3. Поверхность Ферми, определяемая уравнением
Рис. 2. Поверхность Ферми, определяемая уравнением
(12), при E = 5, ω(x) = x, xc = 1 и g = 0.5. В этом
(12), при E = 3, ω(x) = 1, xc = 1 и g = 0.05. Красная
случае между двумя зонами нет зазора, листы пересека-
зона соответствует знаку минус, а синяя — знаку плюс в
ются в точке x = 0
уравнении (12)
при этом энергии уровней Ландау равны En = 2hn.
Поэтому собственные функции связаны с элемен-
Энергия основного состояния равна E0 = 0, в отли-
тарной парой гармонических осцилляторов с поли-
чие от обычного гармонического осциллятора, кото-
номами Эрмита:
рому соответствует спектр En = (2n + 1)h и энергия
в нулевой точке E0 = h. Энергия в нулевой точке
зависит от слагаемого hQ′(x) в уравнении (2), обу-
(
)
φn
1
словливающего взаимодействие между бозонами и
Ψn =
=
√
×
фермионами в суперсимметричных теориях [15].
φn
n!2n(πh)1/4
Чтобы вычислить собственные функции, введем
⎛
)
⎞
(x+δ
преобразование
AHn
√
e-2 (x+δ)2/h
⎜
⎟
h
⎜
⎟
Q(x) = U†(x)Q0(x)U(x) + hU†(x)∂xU(x),
×U†
⎜
)
⎟,
(15)
⎝
⎠
(
)
(x-δ
BHn
√
e-2 (x-δ)2/h
x+δ
0
Q0(x) =
,
(13)
h
0
x-δ
U (x) = e2 ϕσ2 e2 θ(x)σ3 ,
где A и B — комплексные постоянные. U†
принима-
где U(x) — унитарная матрица, а (ϕ, δ ≥ 0) — пара-
ет явный вид:
метры, удовлетворяющие следующим соотношени-
ям:
g = δsin(ϕ), xc = δ cos(ϕ).
(14)
U† =
⎛
⎞
(ϕ)
(ϕ)
Тогда гамильтониан можно выразить как
cos
e-2 θ(x)
- sin
e-2 θ(x)
⎜
2
2
⎟
⎜
⎟
=
,
(16)
H = U†H0U,
⎝
⎠
(ϕ)
i
(ϕ)
θ(x)
sin
e2
cos
e2θ(x)
2
2
где
H0 = 2hD†0D0,
√
D0 = (hσ0∂x + Q0(x))/
2h.
а компоненты Ψn имеют вид
1055
Ж.-И. Фортэн
ЖЭТФ, том 157, вып. 6, 2020
i
θ(x)
e- 2
Наконец, можно выбрать ρ0 и ρ0 как функции A и
φn(x) =
√
×
n!2n(πh)1/4
B, они удовлетворяют системе уравнений
(
)
(ϕ)
(x+δ
(
)
× Acos
Hn
√
×
ϕ
(ϕ)
2
h
|A|2 cos2
+ |B|2 sin2
-
)
2
2
)
(ϕ
(x-δ
(ϕ)
(ϕ)
×e
2h
(x+δ)2 - B sin
Hn
√
×
− cos
sin
(A∗B + AB∗)e-
h
=ρ0,
2
h
2
2
)
(
)
(19)
ϕ
(ϕ)
(x-δ)2
|A|2 sin2
+ |B|2 cos2
+
× e
2h
,
2
2
(
)
ϕ
(ϕ)
i
(17)
+ sin
cos
h
= ρ0.
θ(x)
e2
2
2
φn(x) =
√
×
n!2n(πh)1/4
(
)
Можно параметризовать коэффициенты A и B так,
(ϕ)
(x+δ
× Asin
Hn
√
×
что
2
h
√
)
)
(ϕ
(x-δ
A=
ρ0 + ρ0 cos(φ)eiθA ,
×e
2h
(x+δ)2 + B cos
Hn
√
×
2
(20)
h
√
)
B=
ρ0 + ρ0 sin(φ)eiθB ,
(x-δ)2
× e
2h
где φ удовлетворяет уравнению
Следует заметить, что если учитывать функцию об-
g
щего вида w(x) из решений уравнения (7), то мат-
cos(2φ) -
cos(θA - θB)sin(2φ)e-δ2/h =
xc
рица Q0(x) примет вид
ρ0 - ρ0
δ
(
)
=
(21)
ρ0 + ρ0 x
c
x + iw(x) + δ
0
Q0(x) =
(18)
0
x + iw(x) - δ
Можно выбрать θA и θB так, что
Легко показать, что решения (φn,φn) преобразуют-
cos(θA - θB) = 0,
ся в
⎧
⎫
∫
x
⎨
⎬
тогда φ не будет зависеть от h. Получающееся урав-
(φn,φn)exp
ih-1
w(y) dy
нение для cos(2φ) имеет решения, откуда следует
⎩
⎭
|ρ0 - ρ0|
xc
Определим также токи
<
ρ0 + ρ0
δ
1
Jn(x) =
h Im(φ∗n(x) ∂xφn(x))
Это исключает конфигурации, для которых, напри-
2
мер, ρ0 = 1 и ρ0 = 0, поскольку xc/δ < 1 при g > 0.
и
В этом случае две компоненты волновой функции
1
Jn(x) =
h Im
φ∗n(x)∂x
φn(x)).
«запутываются»: при g > 0 каждая квазичастица
2
в одной зоне имеет ненулевую компоненту в другой
Сумма двух токов удовлетворяет соотношению
зоне, это связано с туннельным эффектом, вызван-
(
)
1
ным унитарным поворотом в уравнении (13), когда
Jn(x) +
Jn(x) =
ω(x)
φn(x)|2 - |φn(x)|2
2
ϕ = 0, даже в отсутствие магнитного поля. При
cos(2φ) = ±1 отношение плотностей равно
Функция ω(x) с физической точки зрения эквива-
лентна внутреннему току, пропорциональному раз-
ρ0
δ±xc
=
ности заселенностей двух орбиталей. A и B выбра-
ρ0
δ∓xc
ны так, что для каждой орбитали ρ0 и ρ0 электроны
находятся в основном состоянии:
Это означает, что при g ≪ 1 небольшая доля плот-
∫
ности ρ0, пропорциональная g2ρ0, переносится с пер-
dx|φ0|2 = ρ0
вой орбитали на вторую. Например, при B = 0 от-
ношение между плотностями имеет простой вид:
и
∫
)
ρ0
(ϕ
g2
dx
φ0|2 = ρ0.
= tg2
=
(22)
ρ0
2
xc + δ
1056
ЖЭТФ, том 157, вып. 6, 2020
Зарядовые колебания в простой модели...
|T
|
Когда ρ0 = |A|2 и ρ0 = 0, переносимая часть ρ0 про-
nn
порциональна g2ρ0, кроме случая g = 0. Пусть ρ0 =
n = 5
0.2
= ρ0. Рассмотрим вещественные решения системы
(20) при θA = θB = 0 и φ, определяемом как
0.1
0
2
10
20
30
xc
tg(2φ) =
eδh .
(23)
0.2
g
n =10
0.1
0
Если ω(x) постоянна, то интеграл от полного ток об-
10
20
30
ращается в нуль. В пределе слабого взаимодействия
0.2
g получаем
n =15
0.1
0
10
20
30
|A|2 ≃ ρ0,
|B|2 ≃ ρ0, φ ≃ π/4.
h-1
Рис. 4. Зависимости модуля функции перекрытия |Tnn|,
При этом функции φ0 и
φ0 разделяются, если каж-
n = 5,10,15, от обратного поля h-1 при g = 0.5 и xc = 1
дый электрон локализован на своей орбитали.
√
n!2m
√
ge-1/h
Tm≥n =
(i
h)n-m
×
m!2n
δ
[(
)
× cos(φ)2e2iδ/h - sin(φ)2e-2iδ/h
×
2.1. Функция перекрытия
)
(2
×Lm-n
n
- e-δ2/h sin(φ)cos(φ)×
В качестве первого приложения рассмотрим слу-
h
чай, приведенный на рис. 2, когда ω(x) = 1, и най-
(
)
g
xx+δ
дем коэффициенты перекрытия и прохождения для
×
(1-iδ)m-n-
(1+iδ)m-n
×
xx+δ
g
двух волновых функций (17). Это нужно для того,
(
)]
(24)
2
чтобы показать, что система осцилляторов зависит
× Lm-n
(1 + δ2)
,
n
h
от обратного магнитного поля. Для этого опреде-
лим внутреннее произведение или функцию перено-
ge-1/h
Tnn =
×
са между состояниями Ландау m и n:
δ
[(
)
× cos(φ)2e2iδ/h - sin(φ)2e-2iδ/h
×
∫∞
)
(
)]
Tmn = dxφm(x
φn(x)dx.
(2
xce-δ2/h
2
× Ln
+
sin(2φ)Ln
(1+δ2)
,
-∞
h
g
h
— полиномы Лагерра. Зависимости моду-
где Ln-mm
Вычисляя произведение с использованием формулы
ля функции перекрытия |Tnn|, n = 5, 10, 15, от об-
для полиномов Эрмита [29], получим
ратного поля h-1 при g = 0.5 и xc = 1 приведены на
рис. 4. Определим функцию пропускания T (h) при
√
n
(
√
заданной энергии E:
m!2
)m-n ge-1/h
Tm≤n =
i
h
×
)
n!2m
δ
∑ (
E
[(
)
T (h) =
δ n-
Tnn(h).
(25)
× cos(φ)2e2iδ/h - sin(φ)2e-2iδ/h
×
2h
n≥0
)
(2
×Ln-m
- e-δ2/h sin(φ)cos(φ)×
Для численных расчетов, результаты которых при-
m h
ведены на рис. 5, мы использовали уширение уров-
(
)
g
xx+δ
ней Ландау с помощью гауссовой функции ширины
×
(1+iδ)n-m-
(1-iδ)n-m
×
xx+δ
g
Γ ≪ 1 вместо дельта-функции,
(
)]
2
× Ln-m
(1 + δ2)
,
δ(x) → e-x2/2Γ2 (2πΓ2)-1/2.
m h
1057
7
ЖЭТФ, вып. 6
Ж.-И. Фортэн
ЖЭТФ, том 157, вып. 6, 2020
Re(T(h))
ет с ростом h. Для двух частот, одной малой и одной
3
|A(F)|
большой, в присутствии поля наблюдается эффект
0.10
биений. Для рассматриваемых значений параметров
и при g = 0 получаем частоту де Гааза-ван Альфе-
2
на F0 = E/2 = 1.5, а также частоты Fα ≃ 0.138,
0.05
Fβ ≃ 2.8621). Также предполагается, что при малых
g площади областей все еще имеют приблизительно
1
0
1.0
2.0
3.0
4.0
те же значения. Тогда можно вычислить амплитуду
F
фурье-преобразования функции T(h) по h-1:
0
∫
∞
A(F ) =
dh-1T (h)e-2iπF/h =
0
-10
5
10
15
20
25
30
1∑
=
Tnn(F0/n)e-2iπnF/F0 .
(27)
h-1
F
0
n≥1
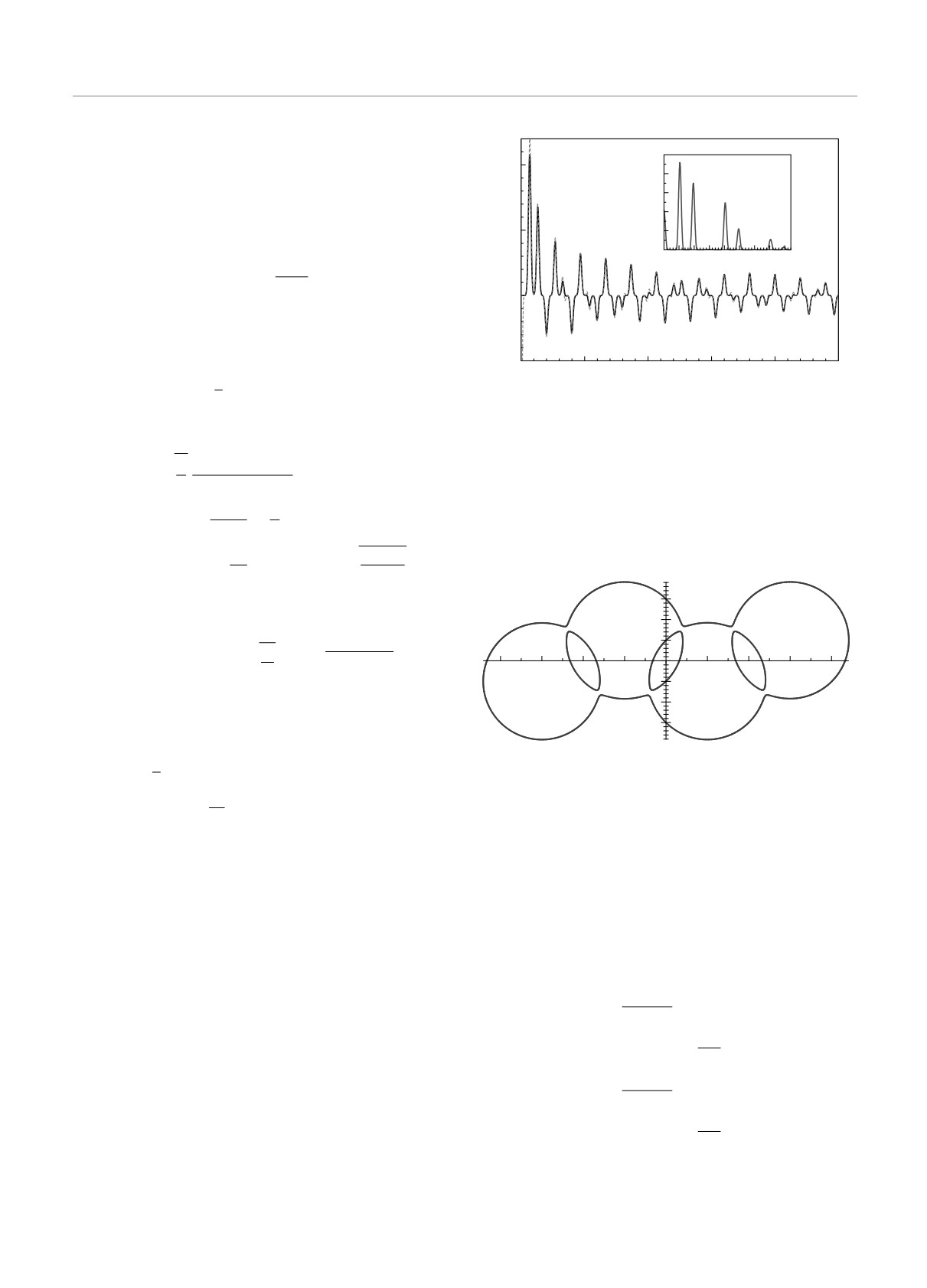
Рис. 5. Зависимости вещественной части функции пере-
На вставке на рис.
5
приведена зависимость
крытия T от обратного поля h-1 при E = 3, g = 0.2,
|A(F )|. Имеются двойные пики, соответствую-
ω(x) = 1 и xc = 1. Параметр уширения Γ = 0.1. Крас-
щие nF0 + (F0 ± Fα)/2, где (F0 - Fα)/2 ≃ 0.68
ная кривая соответствует квазиклассическому выражению
(32). На вставке: фурье-преобразование Re(T (h)). Первый
и (F0 + Fα)/2 ≃ 0.82. Каждая пара пиков разде-
двойной пик находится на частоте F = 0.68, второй — на
лена частотой F0, а частота биений равна Fα. С
частоте F = 0.82
физической точки зрения можно считать, что Fα
соответствует области пересечения двух орбит и
поэтому характеризует функцию Tnn(h) при слабом
Колебания, зависящие от обратного поля, характе-
взаимодействии g, в то время как F0 соответствует
ризуются частотами F фурье-спектра. Например,
периодичности плотности энергии.
в квазиклассической теории де Гааза-ван Альфена
В квазиклассическом режиме h ≪ 1 функцию
фурье-спектр колебаний намагниченности опреде-
T (h) можно найти аналитически методом седловой
ляется набором дискретных основных частот F и их
точки. Для этого будем использовать интегральное
гармоник, пропорциональных площади области A
представление дельта-функции и рассмотрим функ-
всех замкнутых циклотронных орбит на поверхнос-
цию
ти Ферми (x, p) при заданной энергии. Они равны
F = A ℏ/2π. Однако в членах, зависящих от обрат-
∞
∫
ного эффективного поля h-1, они равны F = A /2π.
dx∑
(2w)
G(h, w) = e-w/h
Ln
×
В отсутствие взаимодействия, g = 0, и при посто-
2π
h
-∞
n≥0
янной ω можно получить геометрические выраже-
×eix(n-E/2h)
(28)
ния для площади области Aα, ограниченной синей
кривой, и площади области Aβ > Aα, ограниченной
при w > 0. Используя производящую функцию для
красной кривой (см. рис. 2):
полинома Лагерра, можно преобразовать ряд и фор-
(√
)
E-ω2 -x2c
мально получить2)
Aα = 2E arcsin
-
E
∞
∫
√
(26)
dx e-iϕ(x)/h
-2
(E - ω2 - x2c)(ω2 + x2c),
G(h, w) = e-w/h
,
2π
1-eix
-∞
(29)
Aβ = 2πE - Aα = 2A0 - Aα,
1
2iw
ϕ(x) =
Ex -
где A0 = πE — площадь области, ограниченной
2
e-ix - 1
двумя круговыми циклотронными орбитами радиу-
√
са
E в случае отсутствия взаимодействия.
1) Применение теории де Гааза-ван Альфена для намагни-
На рис. 5 приведены зависимости вещественной
ченности к линейному спектру En = 2hn дает доминирую-
щую частоту F0 = A0/2π
части функции перекрытия T от обратного поля h-1
2) Обычно, чтобы ряд в выражении (28) сходился, требу-
при E = 3, g = 0.2, ω(x) = 1 и xc = 1. Видно, что в
ется использовать малый параметр 0 < ϵ ≪ 1, такой что
квазиклассическом пределе амплитуда T (h) убыва-
ei(x+iϵ) < 1, который затем кладется равным нулю.
1058
ЖЭТФ, том 157, вып. 6, 2020
Зарядовые колебания в простой модели...
Теперь, чтобы найти решения уравнения ϕ′(x) = 0,
(h)
|A(F)|
применим метод седловой точки. Получим, что ре-
0.05
1.0
шения определяются уравнением
0.04
0.03
sin(x/2)2 = w/E
0.02
0.5
0.01
и имеют вид
0
1.0
2.0
3.0
4.0
(√
)
F
x = ±2arcsin w/E
+ 2πk,
0
где k — целое число. Используя выражение для вто-
рой производной
-0.5
0
5
10
15
20
25
1
ϕ′′(x) =
w cos(x/2)/ sin(x/2)3
-1
h
2
и проведя некоторые вычисления, получаем
Рис. 6. Зависимости флуктуаций плотности Δρ(h), см.
уравнение (34), от обратного поля h-1 (черная кривая)
√
h
1
при ρ0 = ρ0 = 1, E = 3, g = 0.2 и xc = 1. Параметр
G(h, w) ≃
×
уширения Γ = 0.1. Красная кривая соответствует квази-
π (w(E - w))1/4
(
)
классическому результату (35). На вставке: фурье-преоб-
F (w)
π
× sin
2π
+
+ γw Ω(h),
(30)
разование, соответствующее черной кривой. Основная час-
h
4
тота F = 0.527, что соответствует F (δ2) (см. текст), гар-
(
)
√
∑
E
w
моникам соответствуют частоты nF0 ± F (δ2), n — целое
Ω(h) =
δ n-
,
tg γw =
2h
E-w
p
n
1.5
Частота F(w) имеет вид
1.0
)
0.5
√
(√ w
2πF(w) = E arcsin
+
w(E - w).
(31)
x
E
-4
-3
-2
-1
0
1
2
3
4
-0.5
Из этого выражения в рассматриваемом пределе
-1.0
для T (h) получаем
-1.5
(
)
[g
Рис. 7. Поверхность Ферми, определяемая уравнением
T (h) ≃
cos(φ)2e2iδ/h-sin(φ)2e-2iδ/h G(h, 1)+
δ
(36), при N = 1, состоящая из четырех связанных орбит,
]
xc
при E = 2, g = 0.1, ω(x) = 1/2 и xc = 1
+
sin(2φ)G(h, 1 + δ2) Ω(h).
(32)
δ
Поэтому из-за периодичности Ω(h) фурье-спектр
и зарядовую плотность
должен представлять собой ряд пиков на частотах,
∫
соответствующих гармоникам частоты F
= F0 и
ρn = dx
φn|2
двух частот биения F (1) и F (1 + δ2) ≃ (F0 - Fα)/2,
причем при малых g последняя является доминиру-
в зависимости от уровня Ландау n. Можно, как и
ющей по амплитуде. Красная кривая на рис. 5 соот-
раньше, проинтегрировать полиномы Эрмита. По-
ветствует выражению (32), которое хорошо согласу-
лучим
ется с решениями, определяемыми уравнением (25)
ρ0 + ρ0
для поля заданного диапазона.
ρn = ρ0 + g
sin(2φ) ×
2δ
(
(2δ2 ))
× 1-Ln
e-δ2/h,
2.2. Колебания переноса заряда
h
(33)
ρ0 + ρ0
В качестве второго приложения вычислим для
sin(2φ) ×
ρn = ρ0 - g
2δ
каждой орбитали электронную плотность
(
(2δ2 ))
∫
× 1-Ln
e-δ2/h.
h
ρn = dx|φn|2
1059
7*
Ж.-И. Фортэн
ЖЭТФ, том 157, вып. 6, 2020
Сумма плотностей является сохраняющейся величи-
Очевидно, Δρ(h) соответствует биению колебаний
ной, однако имеет место перенос заряда, зависящий
с частотой F (δ2). На рис. 6 показаны зависимости
от индекса n. Можно рассмотреть функцию перено-
флуктуаций плотности от обратного поля для слу-
са заряда (далее будем полагать ρ0 = ρ0 = 1)
чая ρ0 = ρ0 = 1 при E = 3, g = 0.2 и xc = 1. Как
)
видно, частота биений F (δ2) ≃ 0.527, что согласует-
∑ (
E
δρ(h) =
δ n-
(ρn - ρn),
(34)
ся с фурье-спектром, приведенным на вставке.
2h
n≥0
как и ранее, в квазиклассическом пределе h ≪ 1
с использованием функции G(h, δ2), см. уравнение
(28). Получим выражение для δρ(h) в этом пределе:
3. ОБЩИЙ СЛУЧАЙ
[
√
2g
h
1
δρ(h) ≃
sin(2φ) e-δ2/h-
√
×
δ
π
δ(E-δ2)1/4
В данном разделе мы обобщим модель двух ос-
цилляторов, рассматривая обобщение матрицы Q(x)
(
)]
F (δ2)
π
из уравнения (10), соответствующее системе 2(N +1)
× sin
2π
+
+γδ2
Ω(h).
(35)
h
4
взаимодействующих орбит, где N ≥ 0, а именно,
⎛
⎞
x + (2N + 1)xc
+ iω(x)
ge-iθ(x)
0
⎜
⎟
⎜
geiθ(x)
x + (2N - 1)xc - iω(x) geiθ(x)
0
⎟
Q(x) =⎜
⎟.
(36)
⎜
⎟
⎝
⎠
0
geiθ(x) x - (2N + 1)xc - iω(x)
Обобщенная матрица удовлетворяет коммутацион-
h∂xΨ0 + Q(x)Ψ0 = 0
ному соотношению P (x) = 1, при условии, как и
ранее, что
можно редуцировать, используя преобразование
∫x
θ(x) = 2h-1 ω(y) dy.
Ψ0 →
Ψ0,
На каждой орбитали имеется знакопеременный
где
внутренний ток, порожденный ±ω(x). На рис. 7
(
Ψ0 =
φ(N)0, . . . ,φ(-N-1)0
)⊤ ,
показана классическая поверхность Ферми, состо-
ящая из линейной цепочки четырех связанных ор-
(
)
2
бит. Решая дифференциальное уравнение DΨ0 = 0,
Ψ0 = e-2h diag e-2θ(x), e2 θ(x), . . ., e2 θ(x)
Ψ0.
можно получить основное состояние. Заметим, что
Это упрощает систему дифференциальных уравне-
(2N + 2)-компонентный вектор
ний
(
)⊤
Ψ0 = φ(N)0, . . . , φ(-N-1)
0
-h∂x Ψ0 =
QΨ0,
систему уравнений
где
Q— постоянная матрица вида
⎛
⎞
(2N + 1)xc
g
0
⎜
⎟
⎜
g
(2N - 1)xc g
0
⎟
Q=
⎜
⎟.
(37)
⎜
⎟
⎝
⎠
0
g
-(2N + 1)xc
Эту матрицу можно диагонализовать, если най-
(2k + 1 - λ)xc
vλk-1 + vλk+1 +
vλk = 0.
(38)
ти соответствующие собственные векторы vλk, k =
g
= -N - 1, . . ., N:
1060
ЖЭТФ, том 157, вып. 6, 2020
Зарядовые колебания в простой модели...
Решения даются функциями Бесселя:
У этого уравнения есть 2(N + 1) решений λk
=
= 2μk +1, поскольку оно представляет собой много-
vλk = aJμ-k(g/xc) + bYμ-k(g/xc),
(39)
член по μ:
где мы положили λ = 2μ + 1. Наложим граничные
μN > . . . > μ-N-1
условия
(при малых g можно использовать аппроксимацию
vλN+1 = vλ-N-2 = 0.
μk ≃ k). Каждое решение x = -λk соответствует по-
Тогда получим уравнение для дискретных собствен-
ложению k-го осциллятора в цепочке. Тогда можно
ных значений μ:
выбрать следующие собственные векторы:
Jμ+N+2(g/xc)Yμ-N-1(g/xc) =
= Yμ+N+2(g/xc)Jμ-N-1(g/xc).
(40)
Yμ-N-1(g/xc)Jμ-k(g/xc) - Jμ-N-1(g/xc)Yμ-k(g/xc)
vλk =
(41)
Yμ-N-1(g/xc)Jμ-N (g/xc) - Jμ-N-1(g/xc)Yμ-N (g/xc)
Например, при N = 1 из уравнения (40) получаем
(13). Простое расширение модели дает матрицу (36),
квадратное уравнение для μ:
которая соответствует поверхности Ферми, состоя-
щей из нескольких связанных орбит, и позволяет
16μ4 + 32μ3 - 4{3(g/xc)2 + 4}μ2 -
найти собственные векторы. В частности, для про-
- 4{3(g/xc)2 + 8}μ + (g/xc)4 = 0.
(42)
стого случая двух связанных орбит мы вычислили
функцию перекрытия (25), колебания которой опи-
Отсюда нетрудно показать, что компоненты Ψ0
сывают геометрические характеристики циклотрон-
можно выразить как
ных траекторий на поверхности Ферми. Кроме того,
мы рассмотрели перенос заряда между двумя орби-
∑
φ(k)0(x) = e±2 θ(x)
2h
,
(43)
талями и показали, что имеют место его колебания
Clvλlke-(x+
l=-N-1
в зависимости от обратного поля, причем для энер-
гетического спектра Ландау колебания происходят
где Ck — константы, определяемые (2N + 2) услови-
не только с доминирующей частотой де Гааза-ван
ями сохранения плотности
Альфена, но и с частотой биений F (δ2).
∫
dx|φ(k)0|2 = ρ(k)0.
Благодарности. Работа выполнена при под-
держке Brain Pool Program, National Research Foun-
Знак фазы волновой функции θ(x) зависит от поло-
dation of Korea (NRF-2018H1D3A2065321).
жения осциллятора, причем первому осциллятору,
расположенному в точке x = -λ-N-1, соответствует
знак минус. Тогда возбужденные состояния φ(k)n≥0(x)
ЛИТЕРАТУРА
с энергией En = 2hn можно построить путем срав-
нения с уравнением (17) с полиномами Эрмита:
1. A. Bambini and P. R. Berman, Phys. Rev. A 23, 2496
(1981).
)
±i2 θ(x)
∑
e
( x+λlxc
φ(k)n(x) =
√
√
×
2. P. Hänggi, Quantum Transport and Dissipation, ed.
ClvλlkHn
n!2n
h
by T. Dittrich, P. Hänggi, G.-L. Ingold, B. Kramer,
l=-N-1
)2
G. Schön, and W. Zwerger, Ch. 5, p. 249, Wiley-VCH,
×e-(x+
2h
(44)
Weiheim (1998).
3. B. T. Torosov and N. V. Vitanov, J. Phys. A: Math.
4. ЗАКЛЮЧЕНИЕ
Theor. 41, 155309 (2008).
4. B. T. Torosov and N. V. Vitanov, Phys. Rev. A 84,
В настоящей работе показано, что можно по-
1 (2011).
строить точные решения для взаимодействующих
зон в магнитном поле, используя факторизованный
5. R. B. Lyubovskii, S. I. Pesotskii, V. I. Nizhankovskii,
гамильтониан и унитарное преобразование, действу-
W. Biberacher, and R. N. Lyubovskaya, JETP 98,
ющее на независимые орбитали зоны, см. уравнение
1037 (2004).
1061
Ж.-И. Фортэн
ЖЭТФ, том 157, вып. 6, 2020
6.
A. Audouard, J. Y. Fortin, V. N. Laukhin, D. Vignol-
19.
J. M. Fellows and R. A. Smith, J. Phys. A: Math.
les, T. G. Prokhorova, E. B. Yagubskii, and E. Cana-
Theor. 42, 335303 (2009).
abs/1408.1331, arXiv:1408.1331.
20.
F. Cannata, G. Junker, and J. Trost, Phys. Lett.
A 246, 219 (1998).
7.
N. Rosen and C. Zener, Phys. Rev. 40, 502 (1932).
21.
B. F. Samsonov, V. V. Shamshutdinova, and
8.
W. Chambers, Phys. Rev. 165, 799 (1968).
A. V. Osipov, Phys. Lett. A 374, 1962 (2010).
9.
A. Slutskin and A. Kadigrobov, Sov. Phys. Sol. State
9 (1967).
22.
C. A. Downing, J. Math. Phys. 54, 072101 (2013),
arXiv:1211.0913
10.
A. Kochkin, Sov. Phys. JETP 27, 324 (1968).
[math-ph].
11.
A. B. Pippard, Proc. Roy. Soc. A: Math. Phys. 270,
23.
J.-Y. Fortin and A. Audouard, Low Temp. Phys. 43,
1 (1962).
173 (2017).
12.
M. Kaganov and A. Slutskin, Phys. Rep. 98, 189
(1983).
24.
R. Peierls, Z. Physik 80, 763 (1933).
13.
A. Kadigrobov, A. Slutskin, and S. Vorontsov, J.
25.
E. I. Blount, Phys. Rev. 126, 1636 (1962).
Phys. Chem. Sol. 53, 387 (1992).
26.
A. Alexandrov and H. Capellmann, Zeitschrift für
14.
L. Infeld and T. E. Hull, Rev. Mod. Phys. 23, 21
Phys. B Condens. Matter 83, 237 (1991).
(1951).
15.
L.
É.Gendenshteın and I. V. Krive, Sov. Phys. Uspe-
27.
L. Landau, E. Lifshitz, and L. Pitaevskij, Statistical
Physics: Part 2: Theory of Condensed State, Perga-
arXiv:0409003 [math-ph].
mon Press (1980).
16.
J. Casahorrán, Physica A 217, 429 (1995).
28.
D. Yoshioka, The Quantum Hall Effect, Springer
Series in Solid-State Sciences 133, Springer-Verlag,
17.
F. Cooper, A. Khare, and U. Sukhatme, Phys. Rep.
Berlin-Heidelberg (2002).
251, 267 (1995).
18.
F. Cooper, A. Khare, and U. Sukhatme, Super-
29.
A. P. Prudnikov, Y. A. Brychkov, and O. I. Marichev,
symmetry and Quantum Mechanics, World Scientific
Integrals and Series, Vol. 2, Special Functions, Gor-
Publishing Company, Singapore (2001).
don and Breach Science Publishers, New York (1992).
1062