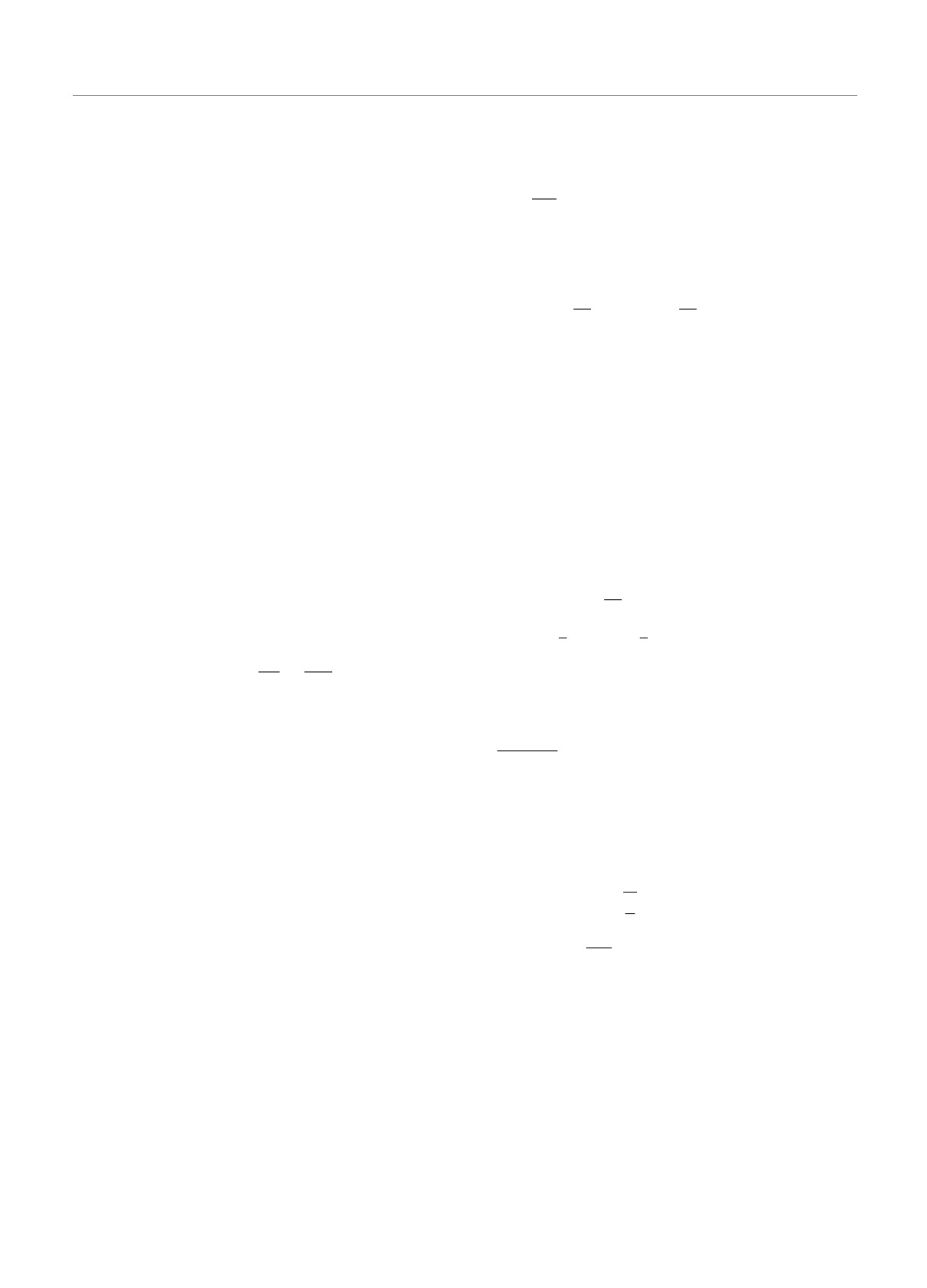ЖЭТФ, 2020, том 157, вып. 6, стр. 1072-1107

РЕШЕНИЕ САМОСОГЛАСОВАННЫХ УРАВНЕНИЙ

КОНА - ШЭМА И ПУАССОНА ДЛЯ КВАЗИДВУМЕРНОГО

ЭЛЕКТРОННОГО ГАЗА В ОБОГАЩЕННОМ СЛОЕ

ПОЛУПРОВОДНИКА С НЕПАРАБОЛИЧЕСКОЙ

ЗОНОЙ ПРОВОДИМОСТИ

А. Я. Шульман^*, Д. В. Посвянский^**

Институт радиотехники и электроники им. В. А. Котельникова Российской академии наук

125009, Москва, Россия

Поступила в редакцию 30 декабря 2019 г.,

после переработки 30 декабря 2019 г.

Принята к публикации 9 января 2020 г.

Предложенный ранее метод самосогласованного решения системы уравнений Кона - Шэма и Пуассо-

на обобщен на случай большой плотности электронов, локализованных вблизи поверхности вследствие

размерного квантования электронного спектра в потенциальной яме области загиба зон. Получено пол-

ностью самосогласованное итеративное решение для квазидвумерного электронного газа в обогащенном

слое на поверхности полупроводника с вырожденным электронным газом в объеме. Рассмотрены случаи

параболического и непараболического энергетического спектра электронов проводимости. Для парабо-

лической зоны проводимости представлены пространственные распределения электронной плотности и

электростатического потенциала, энергии уровней размерного квантования и их зависимость от глуби-

ны приповерхностной потенциальной ямы. Выявлено значительное уменьшение плотности трехмерных

электронов в области обогащенного слоя, занятой квазидвумерным электронным газом. Рассчитаны за-

висимости избыточной поверхностной плотности электронов и емкости структуры от потенциала поверх-

ности. Результаты представлены в безразмерной форме, что позволяет полуколичественно оценивать

параметры обогащенных слоев по известным уровню легирования и величине загиба зон. В случае непа-

раболической зоны проводимости из-за конечной ширины запрещенной зоны спектр квазидвумерного

электронного газа получен в двухзонном приближении Франца - Кейна решением задачи на собственные

значения для нового однозонного уравнения метода эффективной массы. Установлено, что плотность

состояний и эффективная масса электронов в двумерных подзонах линейно растут с энергией. Выве-

дена формула, которая аналитически аппроксимирует рассчитанный энергетический спектр. Найденные

положение, дисперсия энергетического спектра и зависимость эффективной массы от энергии для под-

зон размерного квантования согласуются с опубликованными результатами прямых измерений свойств

квазидвумерных электронов на поверхности n-InAs, полученных методами фотоэлектронной спектроско-

пии с угловым разрешением и магнитотуннельной спектроскопии. Рассмотрены условия, при которых

непараболичность зоны проводимости делает возможным поглощение квазидвумерными электронами

нормально падающего излучения за счет межподзонных переходов.

DOI: 10.31857/S0044451020060097

свойств многоэлектронных систем. В случае неогра-

ниченного электронного газа он сводится к систе-

ме уравнений для одночастичных орбиталей и са-

1. ВВЕДЕНИЕ

мосогласованного поля, которая должна удовлетво-

ряться согласованными распределениями плотности

Метод функционала плотности в приближении

электронов N(r) и электростатического потенциала

Кона - Шэма широко используется при изучении

φ(r). Ввиду существенной нелинейности этой систе-

мы уравнений одним из методов построения само-

^* E-mail: ash@cplire.ru

^** E-mail: dimitrii.posvyanskii@gmail.com

согласованного решения является итеративный спо-

1072

ЖЭТФ, том 157, вып. 6, 2020

Решение самосогласованных уравнений Кона - Шэма и Пуассона. . .

соб, при котором надо поочередно решать уравне-

го на них заряда -eN2D(r) была сравнима с плот-

ние Пуассона для потенциальной энергии электрона

ностью заряда от электронов в состояниях непре-

U (r) = -eφ(r) и уравнение Шредингера для одно-

рывного спектра (см. рис. 2б в работе [2]). В слу-

частичных волновых функций в эффективном по-

чае полупроводника потенциальная яма на границе

тенциале U_eff (r) = U(r) + U_xc(r), где U_xc — обмен-

полупроводник-вакуум и энергетические уровни в

но-корреляционный потенциал.

ней могут стать весьма глубокими при, например,

Возникающие в ряде случаев неустойчивость или

наложении внешнего электрического поля E. Со-

даже расходимость итерационного процесса, когда

ответственно, вблизи поверхности плотность квази-

пространственно-неоднородное распределение N(r)

двумерных электронов может значительно превзой-

электронов, сформированное из решений уравнения

ти плотность электронов непрерывного спектра.

Шредингера, не удовлетворяет условиям совмест-

Такая ситуация реализуется в легированных по-

ности с граничными условиями к уравнению Пуас-

лупроводниковых структурах n-типа с обогащен-

сона, особенно существенно проявляются в случае

ным слоем на поверхности, когда заняты как состоя-

неограниченных систем [1]. Представленные в лите-

ния квазидвумерного электронного газа в размерно-

ратуре методы преодоления этой трудности, по су-

квантованных подзонах, так и состояния непрерыв-

ществу, сводятся к отказу от первоначально сфор-

ного спектра трехмерного электронного газа с за-

мулированного итеративного способа решения и за-

данным значением энергии Ферми в объеме. Поэто-

мене его какой-либо приближенной схемой расчета,

му при самосогласованном расчете энергетического

которая обычно строится полуэмпирически и не поз-

спектра электронов в таких структурах все основ-

воляет оценить степень отклонения от точного ре-

ные трудности, характерные для бесконечных мно-

шения (см. обсуждение в работах [1,2]).

гоэлектронных систем, проявляются в полном объ-

В работе [1] был предложен метод решения урав-

еме: 1) проблема нормировки волновых функций

нений Кона - Шэма, обеспечивающий сходимость

непрерывного спектра; 2) обеспечение совместности

итерационного процесса в рамках исходной поста-

краевых условий к уравнению Пуассона с распреде-

новки задачи. Основная идея этого метода состоит

лением электронной плотности, получаемой на каж-

в том, что полная электронная плотность в урав-

дом итерационном цикле после решения уравнения

нении Пуассона представляется в виде суммы двух

Шредингера [1].

слагаемых,

В связи с этим возникает вопрос, сможет ли ал-

горитм расчета, основанный на квазиклассической

N (r) = N_ind(U_eff (r)) + N_qu(r),

связи между потенциалом и трехмерной плотностью

первое из которых связано с самосогласованным

электронов и не учитывающий квантование энер-

потенциалом U_eff (r) известным квазиклассическим

гетического спектра последних, обеспечить сходи-

выражением, а второе определяется квантовомеха-

мость итерационного процесса в случае, когда доля

нической динамикой электронов. Введение величи-

квантового заряда N_qu в системе становится преоб-

ны N_ind(U_eff (r)) реализует самосогласованное экра-

ладающей в некоторой ограниченной области про-

нирование крупномасштабных неоднородностей за-

странства.

ряда при решении уравнения Пуассона. Это устра-

Поскольку при нашем подходе сходимость ите-

няет кулоновское дальнодействие, которое является

раций означает, что получено точное самосогласо-

причиной жесткой связи между распределением за-

ванное решение, представляло также интерес срав-

ряда и граничными условиями к уравнению Пуассо-

нить найденный энергетический спектр и другие ха-

на.

рактеристики квазидвумерного электронного газа с

В работе [2] предложенный алгоритм был реали-

результатами измерений, чтобы оценить примени-

зован и применен, в частности, для расчета энергии

мость приближения самосогласованного поля для

предсказанных в работе Константинова и Шика [3],

количественного описания таких объектов.

а также независимо чуть позже в работе Аппельбау-

Для ответа на эти вопросы вычисления энер-

ма и Бараффа [4] состояний электронов, которые

гетического спектра и волновых функций, описан-

локализованы вблизи поверхности металл-вакуум

ные в разд. 2, были выполнены с параметрами по-

при нулевом внешнем электрическом поле в само-

лупроводниковых структур, аналогичных n-InAs с

индуцированной потенциальной яме. В этом случае

обогащенным слоем на поверхности полупроводни-

энергетические уровни оказались достаточно мелки-

ка. Этот выбор стимулировался работами Цуи [5-7],

ми по сравнению с энергией Ферми свободных носи-

в которых для большого набора туннельных пе-

телей и, как следствие, плотность локализованно-

реходов Pb/PbO/n-InAs было экспериментально не

1073

ЖЭТФ, вып. 6

А. Я. Шульман, Д. В. Посвянский

ЖЭТФ, том 157, вып. 6, 2020

только обнаружено существование квазидвумерно-

Важно еще, что фотоэлектронная спектроскопия

го электронного газа на поверхности полупровод-

позволяет определить также положение дна зоны

ника, но и методом магнитотуннельной спектро-

проводимости на поверхности полупроводника от-

скопии измерены зависимость эффективной массы

носительно уровня Ферми и, следовательно, глубину

m^∗ квазидвумерных электронов от энергии, а так-

потенциальной ямы. Поэтому сопоставление рассчи-

же вольт-емкостные характеристики. Кроме того, в

танного энергетического спектра с результатами из-

более поздних работах [8,9] энергетический спектр

мерений спектра фотоэлектронов [8, 9] может быть

квазидвумерного электронного газа на поверхнос-

проведено без единого свободного параметра в тео-

ти n-InAs исследовался методом фотоэлектронной

рии, чего нельзя было достичь в случае эксперимен-

спектроскопии. Экспериментальные результаты, по-

тальных данных Цуи [6], когда точная величина па-

лученные последним способом, более удобны для

дения потенциала на обогащенном слое была неиз-

сравнения с расчетными положениями уровней раз-

вестна из-за неопределенности характеристик изо-

мерного квантования, так как в процессе измерения

лирующего слоя окисла свинца на поверхности об-

нет перестройки потенциальной ямы и сопутствую-

разцов.

щего сдвига уровней, что имеет место в методе тун-

Расчеты проводились как в приближении само-

нельной спектроскопии, когда меняется падение на-

согласованного потенциала Хартри, так и с учетом

пряжения на структуре.

обменно-корреляционного потенциала в приближе-

Представленные в разд. 3 результаты вычисле-

нии локальной плотности при значениях эффектив-

ний для параболической зоны проводимости дали

ного радиуса Вигнера - Зейтца R^∗s, типичных для по-

возможность полуколичественно сравнить c данны-

лупроводниковых структур. Это позволило оценить

ми измерений спектр квазидвумерного электронно-

влияние обменно-корреляционного взаимодействия

го газа, а также рассчитать зависимость числа и

на электронный спектр в структурах с обогащенным

положения подзон размерного квантования, поверх-

слоем.

ностной плотности избыточного заряда и емкости

обогащенного слоя от величины загиба зон.

Однако реальные структуры с конечной шири-

2. ПОСТАНОВКА ЗАДАЧИ

ной E_g запрещенной зоны полупроводника часто

имеют на поверхности потенциальную яму, глубина

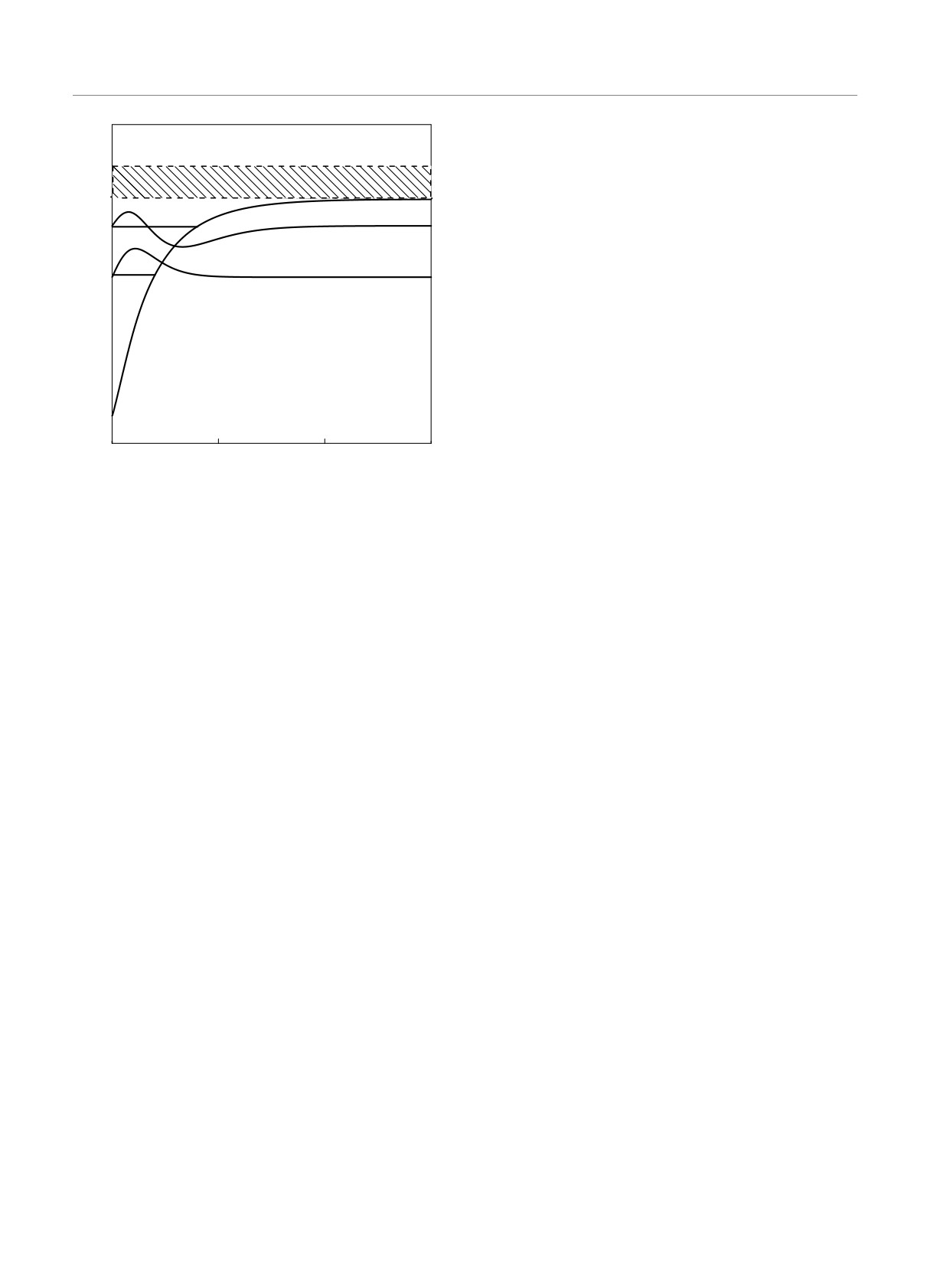
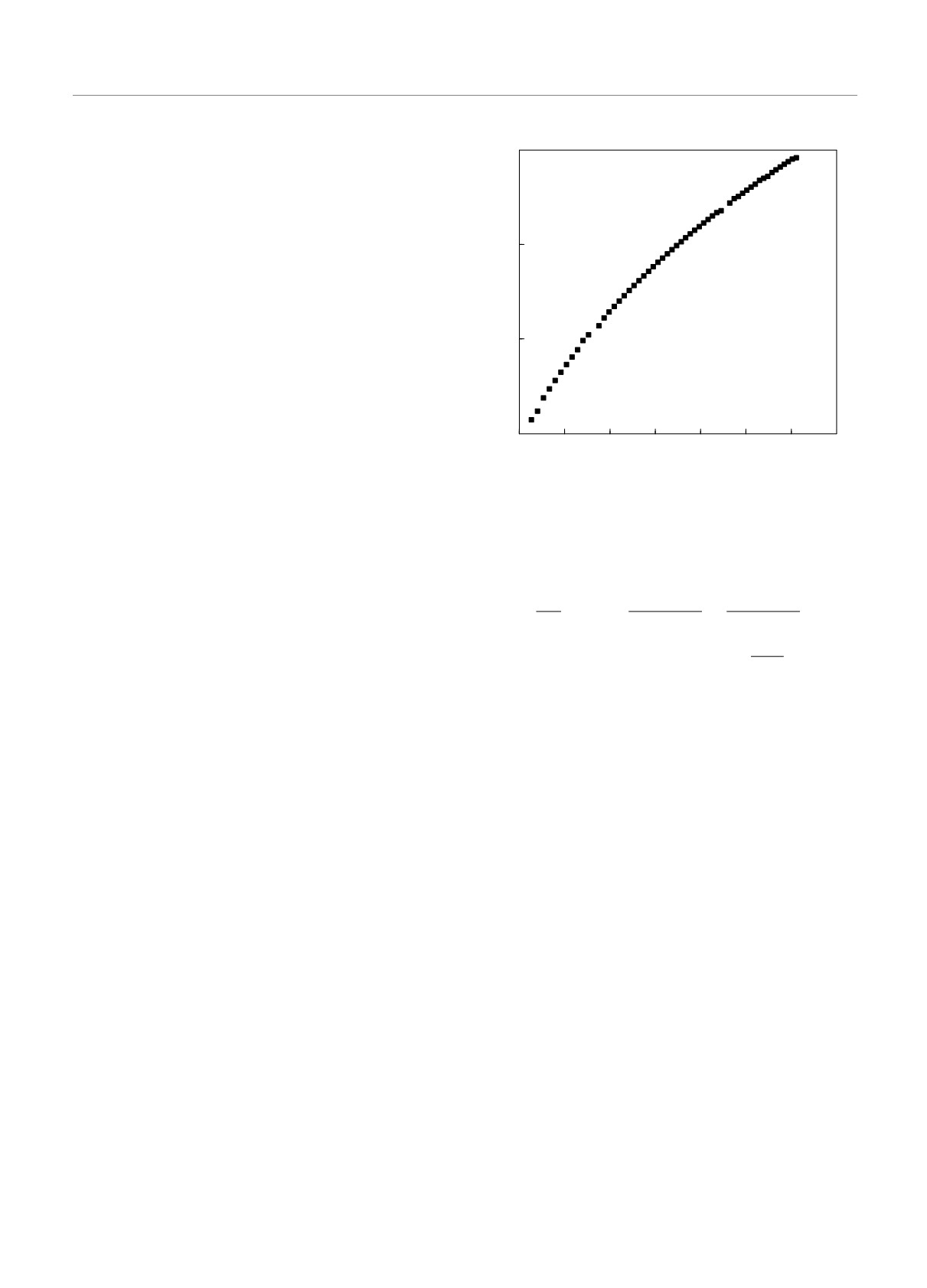
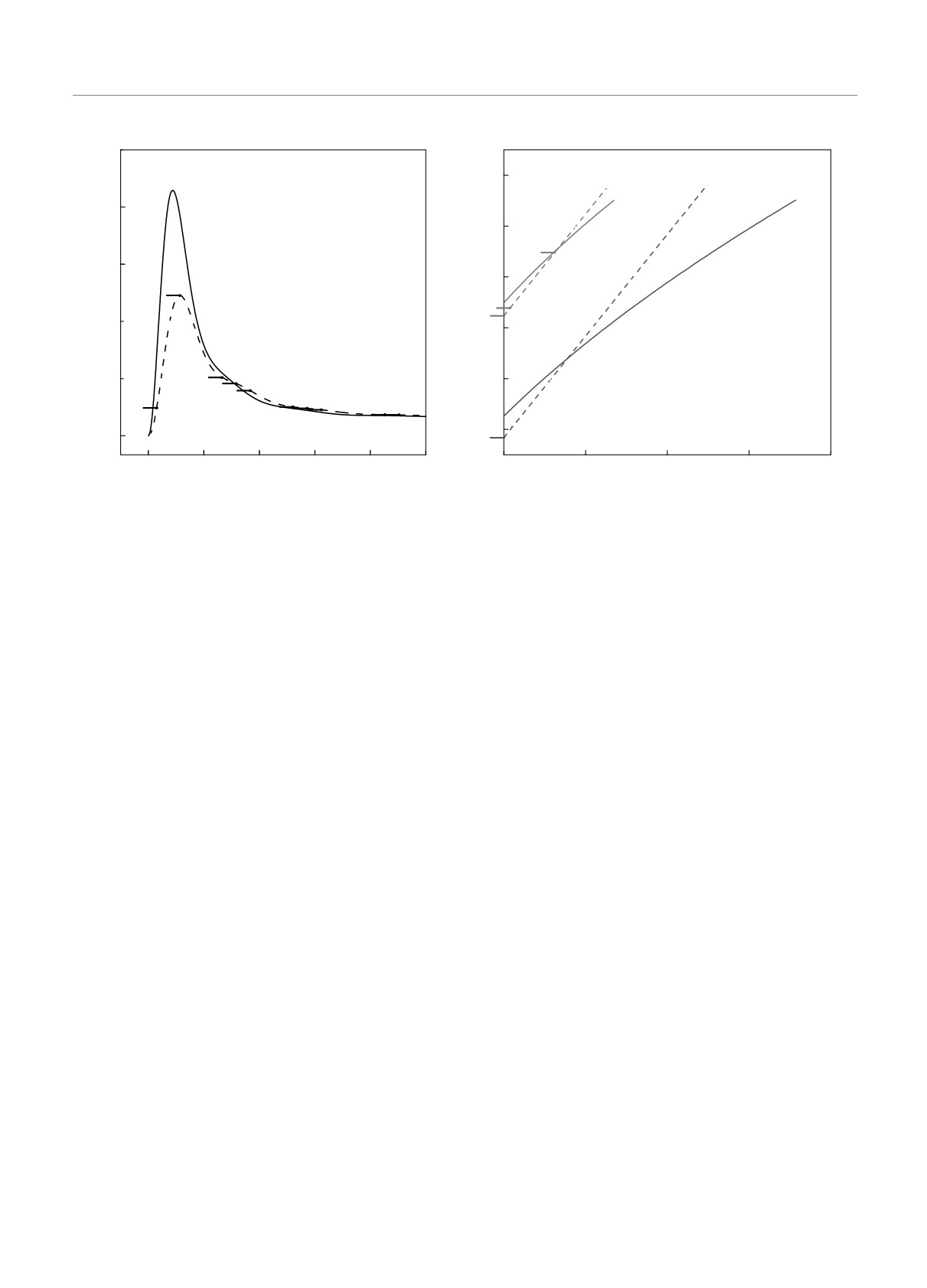
Для иллюстрации на рис. 1 показаны потен-

которой сравнима с E_g. При этом, чтобы получить

циальная яма вблизи поверхности полупроводни-

количественные результаты, пригодные для анали-

ка, энергии минимумов соответствующих размер-

за экспериментальных данных, или рассчитать па-

но-квантованных подзон и волновые функции этих

раметры полупроводниковой структуры с нужны-

состояний, полученные в результате самосогласо-

ми характеристиками квазидвумерного электронно-

ванного расчета. Существенно, что заданный леги-

го газа, необходимо проводить вычисления с учетом

рованием уровень Ферми E_F полупроводника на-

влияния соседних зон. В разд. 4 настоящей работы

ходится выше дна зоны проводимости в объеме,

алгоритм самосогласованных итераций обобщен на

вследствие чего заполненные состояния непрерыв-

случай двухзонного приближения для непараболи-

ного спектра также дают вклад в плотность элект-

ческого изотропного закона дисперсии электронов

ронов в области квантовой ямы. Положение уровня

в зоне проводимости. Проведены необходимые из-

Ферми фиксировано требованием локальной нейт-

менения уравнения эффективной массы и уравне-

ральности объема полупроводника в бесконечно

ния Пуассона. Численным дифференцированием по-

удаленной области, что определяет заполнение под-

лученного энергетического спектра рассчитаны та-

зон размерного квантования и плотность делокали-

кие характеристики квазидвумерного электронного

зованного заряда в каждой итерации.

газа, как зависимость плотности состояний и эф-

В таких полубесконечных системах обычная

фективной массы m^∗ от энергии E. Результаты вы-

схема итеративного решения может приводить

числений количественно сравниваются с экспери-

на каком-то шаге к несовместности полученного

ментальным энергетическим спектром электронов в

распределения электронов с любым типом задан-

размерно-квантованной подзоне, измеренным на об-

ных краевых условий к уравнению Пуассона. Если

разцах n-InAs методом фотоэлектронной спектро-

краевые условия к уравнению Пуассона образова-

скопии с угловым разрешением [8], и c зависимостью

ны заданием величины электрического поля E(0)

m^∗(E), полученной Цуи методом магнитотуннель-

на поверхности полупроводника и требованием

ной спектроскопии [6].

E (z → ∞) = 0, так как на бесконечности всегда

1074

ЖЭТФ, том 157, вып. 6, 2020

Решение самосогласованных уравнений Кона - Шэма и Пуассона. . .

краевые условия к уравнению Пуассона никак учте-

ны быть не могут и не учитываются. Следовательно,

E_F

до получения самосогласованного точного решения

E_c

распределение электронов N(i)(z), найденное на i-м

шаге итераций, только случайно может оказаться

E₁

совместным с граничными условиями к уравнению

Пуассона. Из-за наличия свободных носителей заря-

E₀

да в объеме полупроводника задача об обогащенном

слое представляет большие трудности при обычных

итерационных схемах решения, чем задача с инвер-

сионным слоем. Например, она исключена из обсуж-

дения в известном обзоре электронных свойств дву-

мерных систем [10].

В литературе встречаются две основные схемы

-U₀

борьбы с описанной проблемой при расчете энер-

гетического спектра квазидвумерного электронно-

го газа в квантовых ямах на поверхности полупро-

k z_F

водников. Применительно к структурам с инверси-

онным слоем, где нет подвижных носителей заря-

Рис. 1. Потенциал квантовой ямы, положение минимумов

да в объеме (или ими пренебрегают), схема была

двух подзон и соответствующие им волновые функции.

разработана Стерном [11, 12]. Ключевым моментом

Метка Ec отмечает положение дна зоны проводимости в

объеме, U0 — загиб зон на поверхности

этой схемы служит использование на входе очеред-

ного итеративного цикла вместо полученного к это-

му моменту результата его линейной комбинации с

предполагается локальная нейтральность элект-

несколькими предыдущими. Весовые коэффициен-

ронного газа, то в результате решения уравнения

ты такой линейной комбинации подбираются из со-

Шредингера при очередной итерации в полупро-

ображений баланса между устойчивостью сходимос-

воднике может образоваться полный электронный

ти и длительностью расчета. Под устойчивостью

заряд, который не совместен с заданной разностью

при этом понимают уменьшение разности между

значений электрического поля на поверхности и в

очередным результатом на выходе и заданным зна-

объеме. В обычно используемой схеме итерацион-

чением на входе. Существенно отметить, что, как

ного решения в этот момент применяют различные

правило, последний полученный выход добавляется

приемы, чтобы избежать нарушения теоремы

в линейную комбинацию с коэффициентом, замет-

Гаусса и получить решение уравнения Пуассона.

но меньшим единицы. Иллюзорность надежды обой-

Подправляют руками либо найденную плотность

ти таким образом невозможность решить уравнение

электронов, либо уровень легирования в объеме.

Пуассона при нарушении условий совместности от-

Если задается значение U(0) потенциала на по-

мечалась в работе [1].

верхности относительно выбранного за нуль зна-

Для структур с обогащенным слоем применяет-

чения потенциала на бесконечности, то в этом

ся подход Аппельбаума - Бараффа [4,13], в котором

случае распределение N(i)(z) электронов, получен-

вместо точного решения уравнения Пуассона вво-

ное решением уравнения Шредингера на i-м ша-

дится трехпараметрическое представление для по-

ге итераций, должно удовлетворять теореме о ди-

тенциала и расчет сводится к отысканию этих пара-

польном моменте (см. [1], Sec. 2 Eq. (9), Sec. 4.2

метров. Несмотря на фактический отказ от точно-

Eq. (48)), которая требует, чтобы разность потен-

го решения задачи, этот подход также не обеспечи-

циалов U(0) - U(∞) между поверхностью и беско-

вает автоматического выполнения краевых условий

нечностью равнялась рассчитанному относительно

к уравнению Пуассона в процессе самосогласования

поверхности дипольному моменту полученного рас-

(см. например, текст после формулы (5.9) в рабо-

пределения заряда.

те [13] и замечание после формулы (2.19) в [14]).

Ясно, что в любом из двух случаев при произ-

Вторая трудность в задаче об энергетическом

вольном распределении плотности заряда в прост-

спектре электронов в обогащенном слое связана с

ранстве решение уравнения Пуассона не существует.

необходимостью обеспечить нормировку волновых

В то же время при решении уравнения Шредингера

функций непрерывного спектра на дельта-функцию

1075

А. Я. Шульман, Д. В. Посвянский

ЖЭТФ, том 157, вып. 6, 2020

от квантовых чисел для неоднородной системы, ко-

рых в той или иной форме используется модифика-

гда нельзя накладывать периодические граничные

ция уравнения Пуассона, позволяющая при его ре-

условия Борна - Кармана. Одним из приемов в та-

шении находить одновременно поправки к потенци-

ких случаях служит сведение задачи о полубес-

алу и к распределению электронов [23-26]. Однако

конечном полупроводнике к задаче о достаточно

используемые при этом формулы для индуцирован-

толстой пластине с нулевыми или периодически-

ной плотности электронов получены в упрощающих

ми граничными условиями для волновых функций

предположениях и без оценки вносимой ошибки. Бо-

и квазидискретным энергетическим спектром элек-

лее того, самосогласованно решается только моди-

тронов. Возникающие при этом сложности с явным

фицированное уравнение Томаса - Ферми. Влияние

отысканием спектра и нормировочных констант бы-

заполнения электронами полученного квазидвумер-

ли обойдены, например в работе [13] с помощью

ного спектра на самосогласованность не рассматри-

предположения (3.2) и частного искусственного при-

вается. Поэтому в этих методах нет возможности

ема (3.11) с неясными условиями применимости.

оценивать степень отклонения найденного решения

Это позволило исключить из ответа неопределенные

от точного, если нет независимо полученного точно-

нормировочные константы и плотность уровней ква-

го решения конкретной задачи.

зидискретного спектра неоднородной толстой пла-

В работах [8,9] также проводится сравнение экс-

стины.

периментальных данных для поверхности n-InAs

Однако сходимость простого итерационного про-

с самосогласованными расчетами энергетического

цесса при такой постановке возможна только для

спектра в параболическом приближении. Однако,

нейтральной пластины с симметричными краевы-

как будет показано, в случае n-InAs использова-

ми условиями к уравнению Пуассона, когда равны

ние параболического закона дисперсии для элек-

нулю полный заряд и полный дипольный момент

тронов проводимости дает слишком грубое описа-

структуры (см. Примечание 9 в работе [13]). При

ние спектра квазидвумерных электронов. Кроме то-

периодических граничных условиях и несоблюдении

го, в этих статьях отсутствует существенная инфор-

указанных требований возникают ошибки из-за вза-

мация о способах преодоления перечисленных вы-

имодействия зарядов или дипольных моментов пе-

ше известных трудностей самосогласованного ите-

риодически повторяющихся реплик исходной плас-

ративного расчета.

тины (см., например, работы [15-19]). Другие мину-

Можно лишь предположить, что упоминание в

сы геометрии пластины при расчете спектра поверх-

работе [9] нелинейного уравнения Пуассона означает

ностных состояний отмечаются, например, в рабо-

учет в приближении Томаса - Ферми распределения

те [20]. Обсуждение современного состояния анало-

свободных дырок в потенциальном поле квантовой

гичных проблем, возникающих при замене бесконеч-

ямы [27]. Однако все расчеты в работе [9] сделаны

ного кристалла с заряженным дефектом сверхячей-

для комнатной температуры, потому что при темпе-

кой конечного объема с периодическими граничны-

ратуре 80 К и указанных в этой работе параметрах

ми условиями, а также оценки способов преодоления

полупроводника экранирующее действие дырок ни-

возникающих ошибок можно найти в работе [21].

чтожно и не могло бы обеспечить сходимость ите-

Недостатки известных решений для полубеско-

раций. В работе [8], судя по ссылке, использовал-

нечного электронного газа были обсуждены ранее

ся метод, основанный на представлении рассматри-

[1, 2] вместе с предложенным в работе [1] способом

ваемой системы пластиной конечной толщины, ко-

их устранения за счет введения нелинейного экра-

торый имеет свои известные недостатки [2, 20, 21].

нирования в уравнение Пуассона и конструктивно-

Поэтому представленные в работах [8, 9] результа-

го определения скалярного произведения для вол-

ты теоретических расчетов обсуждаться не будут,

новых функций непрерывного спектра. Математи-

так как отсутствует информация, необходимая для

ческий аппарат введенного таким образом обобщен-

независимого их воспроизведения и оценки надеж-

ного гильбертова пространства также оказался су-

ности (см. обсуждение этого критерия в [28], Sec. 9).

щественно необходим в случае непараболической зо-

Целью настоящей работы было дальнейшее

ны проводимости при выводе однозонного уравне-

развитие метода самосогласованного итерационного

ния эффективной массы и интерпретации его реше-

расчета основного состояния многоэлектронных

ний [22].

систем применительно к особенностям полупровод-

Следует отметить, что за истекшее с 70-х гг. вре-

никовых структур с квазидвумерным электронным

мя для расчета полупроводниковых структур был

газом. В рамках принятой модели полупроводника

предложен ряд вычислительных подходов, в кото-

выполнен точный расчет энергетического спектра

1076

ЖЭТФ, том 157, вып. 6, 2020

Решение самосогласованных уравнений Кона - Шэма и Пуассона. . .

электронов в обогащенном слое на поверхности¹⁾.

Au/n-GaAs [34-38]. В последних работах было пока-

Сравнение с результатами измерений должно пока-

зано, что только при учете непараболичности зоны

зать, насколько хорошо модель описывает реальные

проводимости можно получить количественное опи-

структуры. Обнаруживаемые различия будут сви-

сание туннельных вольт-амперных характеристик.

детельствовать о необходимости либо повысить

Квазиклассическое уравнение Томаса - Ферми

точность измерений, либо уточнить значения пара-

для случая электронного газа с непараболическим

метров полупроводника, либо основывать анализ

спектром вида

(2.1) также использовалось для

на более детальном математическом описании

расчета свойств квазидвумерного электронного

исследуемого явления.

газа в обогащенном слое

[39]. Однако наличие

Учет непараболичности энергетического спектра

дискретного спектра размерно-квантованных по-

для состояний в зоне проводимости, который необ-

верхностных состояний и нулевое граничное условие

ходим для корректного сравнения результатов рас-

для волновых функций, что невозможно учесть

чета с экспериментальными данными в случае полу-

в приближении Томаса - Ферми, требуют полного

проводников с узкой запрещенной зоной, вносит до-

решения квантовомеханической задачи.

полнительные усложнения, которые связаны с изме-

Этому вопросу посвящен разд. 4 настоящей рабо-

нением как уравнения для одночастичных собствен-

ты, в котором рассчитанный энергетический спектр

ных функций, так и формулы для индуцированно-

квазидвумерного электронного газа в обогащенном

го заряда в уравнении Пуассона. В основу расчета,

слое n-InAs сопоставляется с результатами прямых

вместо обычно используемой многозонной системы

измерений спектра методом фотоэлектронной спек-

уравнений для огибающих функций в базисе Латт-

троскопии с угловым разрешением [8] и с экспери-

инжера - Кона, положено уравнение метода эффек-

ментальной зависимостью от энергии эффективной

тивной массы для зоны проводимости, которое по-

массы квазидвумерных электронов [6]. Обоснова-

лучается из двухзонного дисперсионного уравнения

ние однозонного уравнения эффективной массы для

Франца - Кэйна

непараболической зоны проводимости, интерпрета-

(

)

ция решений и условия применимости рассмотрены

ℏ²k²

(2.1)

отдельно в работе [22] на базе kp-теории Кэйна [32]

2m^∗

E_g

и подхода, намеченного Келдышем [40].

путем замены k → -i∇_r, E → E - U_eff . Здесь k —

квазиимпульс, E ≥ 0 — энергия состояния в зоне

3. ПАРАБОЛИЧЕСКИЙ ЭНЕРГЕТИЧЕСКИЙ

проводимости, U_eff — эффективный потенциал, рав-

СПЕКТР ЭЛЕКТРОНОВ ПРОВОДИМОСТИ

ный сумме электростатического U и обменно-кор-

реляционного U_xc потенциалов. Формула (2.1) была

3.1. Основные уравнения

предложена Францем ([31], § 27) из эвристических

В приближении Кона - Шэма газ взаимодейству-

соображений в виде

ющих электронов при температуре T = 0 описыва-

(

)

ℏ²k²

ется системой уравнений для одночастичных волно-

(2.2)

вых функций Ψ_E :

2m^∗

E_g

где T = E - U — кинетическая энергия состояния,

∇²Ψ_E(r) + [E - U_eff (r)]Ψ_E(r) = 0

(3.1)

принадлежащего зоне проводимости при T ≥ 0 и

валентной зоне при T ≤ -Eg. Кэйн [32] получил

с эффективным потенциалом

дисперсионное уравнение (2.1) в рамках kp-теории

U_eff (r) = U(r) + U_xc(r).

(3.2)

зонной структуры.

Квазиклассическое приближение для решения

Здесь собственное значение E — энергия одночас-

волнового уравнения, соответствующего формуле

тичного состояния, U_xc = U_x + U_c — обменно-корре-

(2.2), использовалось при анализе межзонного тун-

ляционный потенциал, U — электростатическая по-

нелирования в задаче о пробое диэлектриков ([31],

тенциальная энергия электрона, для которой урав-

§29), в расчетах вольт-амперных характеристик

нение Пуассона записывается в виде

туннельных p-n-переходов [33] и туннельных пере-

ходов металл-полупроводник с барьером Шоттки

∇²U = 4π [N₊(r) - N(r)] ,

(3.3)

¹⁾ Предварительные результаты были представлены ранее

где N₊(r)

— плотность положительного фона,

[29, 30].

N (r)

— плотность электронов. Начало отсчета

1077

А. Я. Шульман, Д. В. Посвянский

ЖЭТФ, том 157, вып. 6, 2020

шкалы энергий выбирается так, что U(∞)

= 0.

состояниям с энергией E, не превышающей энергию

В случае полупроводников уравнение (3.1) — это

Ферми E_F , включая размерно-квантованные подзо-

уравнение метода эффективной массы для зоны

ны. Энергия Ферми связана с плотностью электро-

проводимости.

нов в нейтральной области на бесконечности фор-

Здесь и далее, пока не оговорено иное, будут ис-

мулой

пользованы эффективные атомные единицы (a.e.^∗)

E_F =

k2F (N₊) + U_xc(N₊),

(3.9)

e^∗ = m^∗e = ℏ = 1. Они связаны со стандартными

единицами соотношениями

где k_F (N₊) = (3π²N₊)1/3 = (9π/4)1/3R∗-1s — ферми-

евский волновой вектор в эффективных атомных

e∗2 =

m^∗e = m^∗cm_e, a^∗

=a_B

единицах (a^∗B = 1).

m^∗

(3.4)

Как отмечалось во Введении, краевые условия

m^∗

Ha^∗ = Ha

к уравнению Пуассона накладывают определенные

κ²

требования на распределение электронной плотно-

где e и m_e — элементарный заряд и масса свободного

сти в пространстве, которым результат интегриро-

электрона, m^∗c — эффективная масса электронов на

вания по формуле (3.8) не обязан удовлетворять, по-

дне зоны проводимости, κ — решеточная диэлектри-

ка не достигнуто самосогласование. В используемом

ческая постоянная полупроводника. При численных

методе решения системы уравнений (3.1) и (3.3) пол-

оценках использованы значения a_B = 0.529Å для

ная электронная плотность в уравнении (3.3) пред-

боровского радиуса и Ha = 27.2 эВ для единицы

ставляется в виде суммы:

энергии Хартри.

Обменный потенциал для электронного газа в

N (r) = N_ind (U_eff (r)) + N_qu(r),

(3.10)

локальном приближении дается известной форму-

лой

где индуцированная плотность N_ind зависит от неиз-

)1/3

вестного потенциала, что снимает проблему несов-

⁽3

местности краевых условий и правой части уравне-

U_x(r) = -

N1/3(r) =

ния Пуассона. В квазиклассическом приближении

(

)2/3

потенциал и N_ind

связаны формулой

(3.5)

2π

r^∗s(r)

23/2

Необходимая для расчета обменно-корреляционного

N_ind(r) =

[E_F - U_eff (r)]3/2 =

3π²

потенциала U_xc корреляционная энергия, как и в ра-

23/2

боте [2], берется в виде

(E_F - U(r) - U_xc(N(r)))3/2 ,

(3.11)

3π²

0.44

E_c = -

(3.6)

где обменно-корреляционный потенциал берется в

r^∗s + 11.5

приближении локальной плотности. Для квантовой

Здесь r^∗s(r) — локальный радиус Вигнера - Зейтца,

плотности электронов N_qu(r), согласно выражениям

определяемый соотношением

(3.8) и (3.10), имеем

∫

4πr∗3s(r)/3 = N-1(r).

(3.7)

N_qu(r) = 2

D {E} |Ψ_E(r)|² - N_ind(r).

(3.12)

Его предельное значение в объеме полупроводника

E≤E

обозначим через

В случае обогащенного слоя помимо плотности ква-

R^∗s ≡ R_s(m^∗c/κ) = r^∗s(∞).

зидвумерного электронного газа в квантовую плот-

Электронная плотность выражается через волновые

ность входит мелкомасштабная часть плотности

электронов непрерывного спектра, которая обуслов-

функции формулой

∫

лена квантовой динамикой электронов.

N (r) = 2

D{E}|Ψ_E(r)|² ,

(3.8)

Уравнение Пуассона теперь записывается в виде

E≤EF

∇²U + 4πN_ind(U) = 4π[N₊(r) - N_qu(r)],

(3.13)

где множитель 2 учитывает спиновое вырождение

одночастичных состояний и интегрирование по диф-

где правая часть в каждом итерационном цикле из-

ференциальной спектральной мере D {E} гамильто-

вестна и уже не связана требованием совместности с

ниана

Ĥ₌ -¹²∇² +U_eff (r) ведется по всем занятым

краевыми условиями. Функция N_ind(U) потенциала

1078

ЖЭТФ, том 157, вып. 6, 2020

Решение самосогласованных уравнений Кона - Шэма и Пуассона. . .

U в левой части нелинейного уравнения (3.13) в про-

В безразмерных переменных уравнение Пуассо-

цессе пошагового решения находится линеаризаци-

на (3.13) запишется в виде

ей ее от шага к шагу с использованием производной

d²u

от обратной функции U(N_ind), которая легко полу-

+ c_nn_ind(u) = c_n[1 - n_qu(ζ)],

(3.16)

dζ²

чается из равенства (3.11). Подробнее детали этого

этапа решения уравнения Пуассона описаны в кон-

где c_n = (8/3π) (4/9π)1/3 R^∗s и 0 ≤ ζ < ∞. Краевые

це разд. 2.1 и в разд. 2.2 работы [2], где аналогич-

условия к уравнению Пуассона брались в виде

ная итеративная схема решения была использова-



на для расчета энергии самоиндуцированных при-

du



= 0.

(3.17)

поверхностных уровней в проводнике в отсутствие



dζ

ζ=0

ζ=∞

внешнего электрического поля.

В настоящей работе тот же алгоритм применяет-

Здесь безразмерное электрическое поле

E = E/E_c

ся для нахождения энергетических уровней, распре-

выражено в единицах характерного поля E_c

деления самосогласованной электронной плотности

= k_FE0F/e. Подставив E0F в эВ, k_F в 1/см и положив

и эффективного потенциала при наличии постоян-

e = 1, получим E_c в В/см. При реальных вычисле-

ного электрического поля, приложенного нормально

ниях граничные условия из бесконечности перено-

к поверхности вырожденного полупроводника, или

сились в точку ζ_max = 150, что обеспечивало доста-

при нанесении положительного поверхностного за-

точную независимость получаемых результатов от

ряда. Геометрия задачи показана выше на рис. 1.

дальнейшего увеличения ζ_max.

Зная распределение плотности N(z, V ) электро-

Положив в уравнении (3.1) r = (z, r_∥), введем

нов в пространстве при заданном падении напряже-

обозначение k = (k_z, k_∥) для волнового вектора и

ния V на структуре, можно вычислить дифферен-

представим решение в виде

циальную электростатическую емкость на единицу

площади системы. Она выражается через полный

Ψ_E(r) =

exp(ik_∥ · r_∥)ψkz (z),

2π

заряд Q в полупроводнике на единицу площади фор-

(3.18)

мулой

k2z = E -

k2∥ - U_xc(∞).

dN_s

C(V ) = -

(3.14)

Получаем отсюда уравнение Шредингера в безраз-

мерных переменных для ψ ˜ (ζ) в виде_k

где V = φ(0) - φ(∞) — разность значений электро-

статического потенциала φ на поверхности и в объ-

[

]

d²ψ˜ (ζ)_k

еме полупроводника, Q = -N_s и

- u_eff(ζ) + u_xc(∞) ψ˜ (ζ) =_k

dζ²

∫∞

(3.19)

N_s(V ) = dz[N(z, V ) - N₊(z)].

(3.15)

c краевыми условиями для собственных состояний

непрерывного спектра

Здесь N_s — избыточная поверхностная плотность

k_z

(0) = 0,

электронов, z — координата по оси, направленной

√

(3.20)

нормально к поверхности в глубь полупроводника.

ψ˜kz (ζ → ∞) →

sin(kz ζ+γ˜k

k_z > 0.

Начало координат z = 0 выбрано на поверхности,

координаты в плоскости поверхности обозначим r_∥.

√

Множитель

2/π при асимптотике решения в бес-

конечности обеспечивает нормировку собственных

функций непрерывного спектра на δ(^k -

k₁). Через

3.2. Детали самосогласованных вычислений

γ˜kz обозначена фаза волновой функции в глубине

Придерживаясь обозначений работы [2], в даль-

полупроводника, где эффективный потенциал ста-

нейшем будем использовать безразмерные величи-

новится постоянным. Достаточные условия на ско-

ны для координаты ζ

= k_Fz, волнового вектора

рость обращения в нуль разности u_eff (ζ) - u_xc(∞),

k = k/k_F, плотности электронов n(ζ) = N(z)/N₊,

при которых асимптотика решений на бесконечно-

энергии ε = E/E0F и потенциала u(ζ) = U(z)/E0F ,

сти имеет вид (3.20), выведены, например, в [41]

где E0F = k2F /2. Плотность N₊ ионизованных доно-

(Гл. III, § 9). Требуемая формулой (3.20) нормиров-

ров в полупроводнике считается не зависящей от z.

ка численно найденного решения

ψ˜ (ζ) однородно-_k

1079

А. Я. Шульман, Д. В. Посвянский

ЖЭТФ, том 157, вып. 6, 2020

го уравнения (3.19) обеспечивается умножением его

ниями уравнения Шредингера (3.19) в безразмер-

на константу A, которая находится из уравнения²⁾

ных координатах (ζ, ρ_∥) = k_F (z, r_∥), связана с ин-

⎡

⎤

тегралом по спектру от |ψ˜ (ζ)|² и удовлетворяет_k

(

)

ψ˜k

требованию сохранения числа электронов в диффе-

⎦₌

A²

ψ^2˜

(ζ) +

ренциальном объеме при замене переменных в виде

dζ

(3.21)

k_z

N (r) dz dr_∥ = ñ(ζ ) dζ dρ_∥, где ζ = k_F r. Другая фор-

ζ ≤ζ_max.

ма, n(r) = N(r)/N₊, введена в уравнении Пуассо-

на, так как условие локальной нейтральности в ви-

При необходимости знать фазу γkz ∈ (-π/2, π/2),

де n(z → ∞) = 1 удобно для численного контроля.

она находится по формуле

С учетом сказанного легко получить соотношение

(

)

]

n = 3π²ñ, которое использовано при выводе выра-

^[˜_k

zψk_z

zζ

γ˜k

= arctg

-kzζ +

π,

жения (3.24).

dψ˜k

/dζ

(3.22)

В тех случаях, когда для сравнения с экспери-

ζ ≤ζ_max,

ментом надо было провести расчет при точно из-

глубины потенциальной ямы

вестном значении U₀

где [a] обозначает целую часть числа a > 0.

для электронов, краевое условие (3.17) к уравнению

Для волновых функций дискретных состояний,

Пуассона при ζ = 0 заменялось на

локализованных в приповерхностной потенциаль-

ной яме, граничные условия и условие нормировки

u₀ = -U₀/E0F ,

имеют вид (k2zj < 0)

ψ˜k2

(0) = 0, ψ˜k2 (∞) = 0,

так как всегда U_xc(0) = 0 в силу условия ψ(0) = 0

∞

для любых решений уравнения Шредингера (3.19).

∫

(3.23)

При обоих типах краевых условий итерационная

dζ|ψ˜k2 (ζ)|² = 1.

процедура сходилась, как правило, за i_max ≈ 10-15

циклов при выполнении условия выхода из цикла в

Плотность электронов дается выражением [2]

виде

⎡

∫¹

max|n(i)Sch(ζ) - n(i)Poi(ζ)| < 10-6.

(3.25)

dkz

n(ζ) = 3π² ⎣

(1 -k2z)|ψ˜ (ζ)|² +_k

2π

⎤

С ростом R^∗s требуется большее число итераций.

∑

Найденные решения уравнений Шредингера и Пуас-

|ψ˜k2

(ζ)|²(μ -k2zj )^⎦ .

(3.24)

сона при обратной подстановке удовлетворяли урав-

2π

<μ

нениям с точностью, лучшей чем 10-5.

Конечно, следует иметь в виду, что эти оценки

Здесь первое слагаемое отвечает электронной плот-

характеризуют точность решения дискретизован-

ности n3D(ζ), сформированной заполненными со-

ной задачи в ограниченной области координат. Ме-

стояниями непрерывного спектра, а второе — плот-

тоды численного интегрирования уравнения Пуас-

ности n2D(ζ) квазидвумерных электронов, заполня-

сона (3.16) и Шредингера (3.19) указаны в работе

ющих размерно-квантованные подзоны с энергией

[2]. Как правило, дискретизация по ζ делалась с ша-

εj (^k∥) =

+k2∥. За начало отсчета энергии принято

гом 0.01, по k — с шагом 0.002. Для интегрирования

значение электростатического потенциала в глубине

по k в области непрерывного спектра в выражении

полупроводника. Через μ = E_F /E0F = 1 + u_xc(∞)

(3.24) использовалась квадратурная формула Симп-

обозначена безразмерная энергия Ферми, которая

сона, за исключением случаев очень больших ζ ≳

учитывает вклад обменно-корреляционного взаимо-

≳ 300, когда для интегрирования быстроосциллиру-

действия электронов в химический потенциал.

ющих функций (см. (3.20)) применялись формулы

Поясним появление в формуле (3.24) множите-

Филона [42]. Абсолютная точность решения зависит

ля 3π². Имеются две формы безразмерной плотно-

от метода и параметров дискретизации, а также, что

сти электронов. Одна из них, ñ, порождается реше-

оказалось наиболее существенным в случае мелких

²⁾ Обратим внимание на описку в аналогичной формуле

уровней, от длины расчетного интервала ζ_max (см.

(2.36) работы [2].

Приложение A).

1080

ЖЭТФ, том 157, вып. 6, 2020

Решение самосогласованных уравнений Кона - Шэма и Пуассона. . .

3.3. Результаты и обсуждение

Наконец, заметим, что все приведенные здесь

Самосогласованное решение системы уравнений

расчетные кривые и значения энергий находились

Кона - Шэма и Пуассона было получено для слу-

с учетом обменно-корреляционного потенциала в

чая, когда обогащенный слой на поверхности полу-

форме, принятой в работе [2]. Отличие их от расчета

проводника n-типа образуется за счет положитель-

в приближении Хартри (без учета u_xc) лежит в пре-

ного заряда атомов щелочного металла, адсорби-

делах 2-5 %, если отсчитывать энергии от соответст-

рованных на поверхности полупроводника. В этих

венно вычисленного уровня Ферми. С учетом ска-

условиях образуется сильный загиб зон у поверх-

занного выше о точности экспериментальных дан-

ности, в котором формируются связанные состоя-

ных и точности задания параметров полупроводни-

ния, что было обнаружено методом фотоэлектрон-

ка можно сделать вывод, что для структур со значе-

ной спектроскопии на образцах p-GaAs с отрица-

нием R^∗s ≤ 0.35 учет обменно-корреляционного взаи-

тельным сродством [43].

модействия при сравнении теории с экспериментом

Глубина потенциальной ямы -U₀ в таких струк-

лежит за пределами точности в большинстве случа-

турах равна электростатической энергии электро-

ев.

на на границе металл-полупроводник (см. рис. 1)

и зависит от химических свойств металла и тол-

3.3.1. Энергетический спектр и распределение

щины осаждаемого слоя. Граничное условие (3.17)

плотности электронов

или (3.23) для уравнения Пуассона на поверхности

при ζ = 0 и величина безразмерного радиуса Виг-

На рис. 2 показаны распределение в простран-

нера - Зейтца R^∗s являются двумя параметрами, ко-

стве плотности свободных электронов, занимающих

торые полностью определяют решение и позволяют

состояния непрерывного спектра, и плотности ква-

найти зависимости числа и положения уровней раз-

зидвумерных электронов, занимающих состояния

мерного квантования от приложенного поля (или

размерно-квантованных подзон и локализованных в

глубины потенциальной ямы) и от R^∗s, т. е. от кон-

потенциальной яме. На этом рисунке хорошо вид-

центрации свободных носителей в объеме. Условия

но, что вблизи поверхности приложение к структуре

(3.20) и (3.23) отбора собственных решений уравне-

притягивающего электрического поля увеличивает

ния Шредингера (3.19) от указанных параметров не

плотность квазидвумерных электронов и уменьша-

зависят.

ет вклад объемных состояний в полную плотность

Для удобства последующего сравнения с экспе-

поверхностного заряда. Тем не менее предложен-

риментом эффективная масса электронов m^∗c и ди-

ный подход позволил получить итеративное реше-

электрическая постоянная κ полупроводника были

ние задачи об энергетическом спектре квазидвумер-

при расчетах взяты близкими к параметрам n-InAs,

ных электронов в обогащенном слое, несмотря на ис-

которые использовались в работах [8, 9]. Тем не ме-

пользование трехмерного квазиклассического выра-

нее следует остановиться на возможном влиянии

жения (3.11) для индуцированной плотности элект-

неточностей в значениях объемных параметров n-

ронов во всем пространстве, включая область вбли-

InAs на результаты расчета. Помимо необходимости

зи поверхности.

учитывать довольно сильную зависимость от тем-

На рис. 3 показаны зависимости энергии связи

пературы ширины запрещенной зоны и связанных

ε_j = -k2zj локализованных состояний от глубины по-

с ней величин, таких как эффективная масса и ди-

тенциальной ямы. Следует отметить, что найти са-

электрическая проницаемость κ, надо отметить, что

мосогласованное решение уравнений в окрестности

значения κ для рассматриваемого полупроводника

значений потенциала на поверхности, при которых в

определены весьма скудно. В справочнике [44] при-

системе появляется новый энергетический уровень,

ведено значение низкочастотной диэлектрической

не удавалось, так как итерации не сходились. Это

постоянной только для 300 К, что должно сильно

связано с тем, что появление нового связанного со-

отличаться от значений при температуре экспери-

стояния начинает заметно влиять на распределе-

мента 30 К. В то же время диэлектрическая прони-

ние электронов в пространстве, когда его энергия

цаемость на низких частотах входит в эффективные

еще очень мала (меньше чем 5 · 10-4E0F ) и, соответ-

атомные единицы длины, энергии и радиус Вигне-

ственно, протяженность волновой функции велика

ра - Зейтца (см. формулы (3.4)). Имеющийся в ли-

по сравнению с ζ_max. Подробнее эта проблема об-

тературе разброс значений κ порядка 20 % также

суждается в Приложении A. Численные результа-

может влиять на степень согласия расчета и экспе-

ты настоящего раздела получены для области 0 ≤

риментальных данных.

≤ k_Fz ≤ 150.

1081

А. Я. Шульман, Д. В. Посвянский

ЖЭТФ, том 157, вып. 6, 2020

N(z)/N₊

1.00

0.75

0.50

0.25

k z_F

Рис. 2. Зависимости составляющих полной электронной плотности от расстояния до поверхности полупроводника. Сплош-

ные кривые — плотность n3D свободных электронов (заполненные состояния непрерывного спектра), штриховые кривые —

плотность n2D квазидвумерных электронов. а) Случай нулевого электрического поля E = 0 на поверхности, когда в само-

индуцированной потенциальной яме имеется одна размерно-квантованная подзона; б) те же зависимости при конечном

E, когда безразмерная глубина ямы u(0) = -4.6 и в энергетическом спектре электронов имеются две двумерные подзоны.

R^∗s = 0.32

Таблица 1. Энергии связи для минимумов подзон размерного квантования, рассчитанные в случае параболической

зоны проводимости с учетом обменно-корреляционного взаимодействия электронов. Значения глубины ямы U0 и

энергий отсчитываются от уровня Ферми EF = 63.7 мэВ и EF = 84.2 мэВ для образцов из работ соответственно

[8] и [9]

exp

Ссылка,

U₀,

Eth0,

E₀

Eth1,

Eexp1,

Eth2,

Eexp2,

Образец

T,К

мэВ

Cs/InAs

[8], 30 K

400

187

184

100

InAs clean

[9], 80 K

230(∗)

115

82(??)

Ag/InAs

[9], 80 K

385

179

185

105

100±5

83(??)

Ag/InAs

[9], 80 K

494

226

228

121

125

Ag/InAs

[9], 80 K

524

239

240

126

128

Примечания. Во второй колонке указана температура образца, при которой проводились измерения. Знаком

(∗) отмечен исходный загиб зон чистой поверхности, найденный нами по измеренной энергии дна основной

подзоны, которая была оценена из графика на Fig. 6 в работе [9] (см. текст). Знаком (??) отмечены приведен-

ные в [9] плохо определяемые положения минимумов третьей подзоны, которые меньше вычисленной энергии

Ферми и формально попадают в непрерывный спектр, что означает невозможность существования третьей

подзоны в параболическом случае.

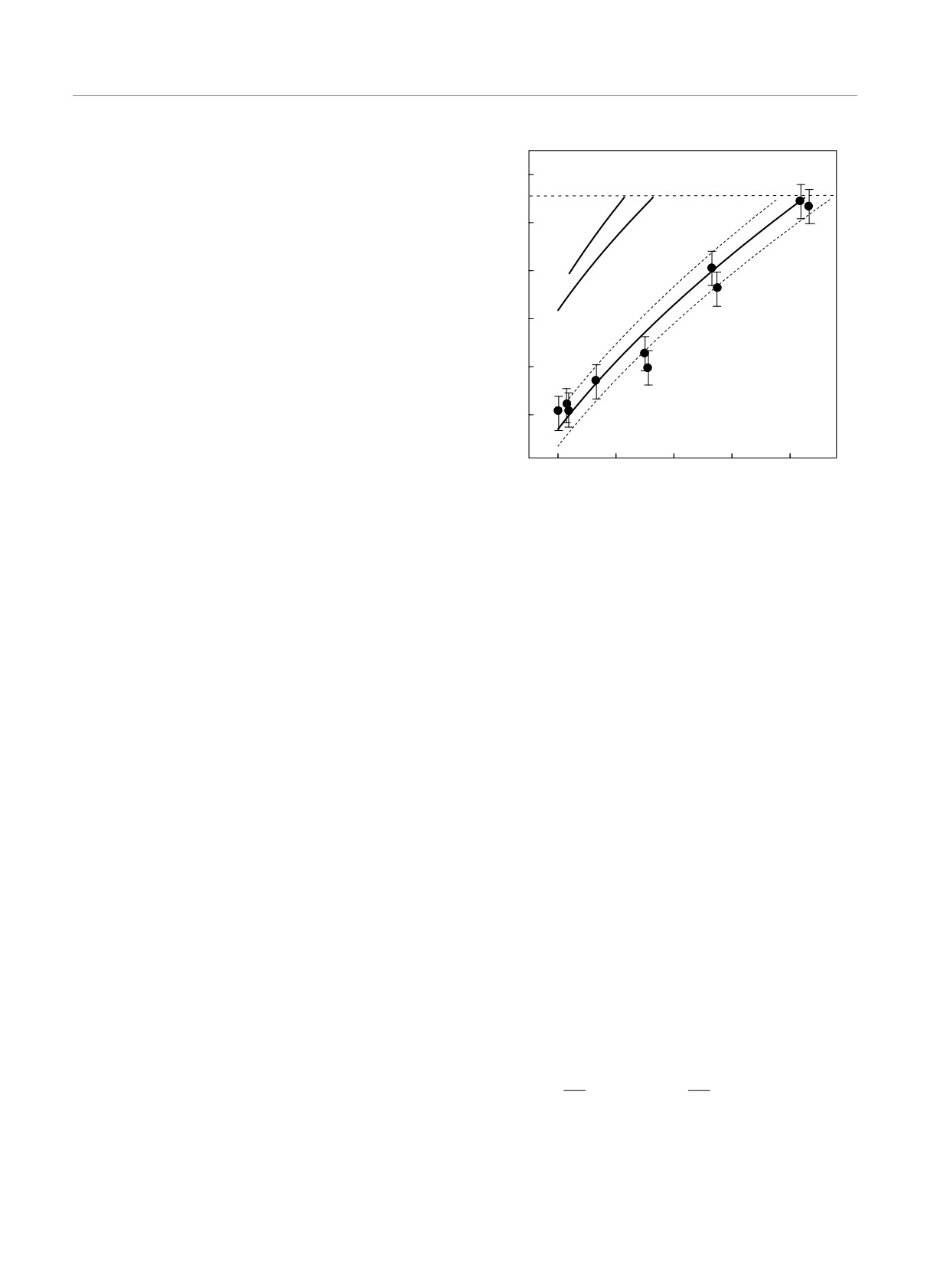
В табл. 1 представлены рассчитанные нами энер-

нов для воспроизведения измеренной зависимости

гии связи для минимумов размерных подзон (верх-

фотоэлектронного тока от напряжения задержки

ний индекс «th») и значения, которые были полу-

(верхний индекс «exp»). При этой подгонке кривых

чены авторами работ [8, 9] подбором параметров

плотность состояний в размерно-квантованных под-

энергетического спектра квазидвумерных электро-

зонах считалась не зависящей от энергии, т.е. пре-

1082

ЖЭТФ, том 157, вып. 6, 2020

Решение самосогласованных уравнений Кона - Шэма и Пуассона. . .

N /N_ssc

-E /EjF0

E₀

10⁰

E₁

10^-1

E₂

10^-2

10^-3

U /E0F

U /E₀

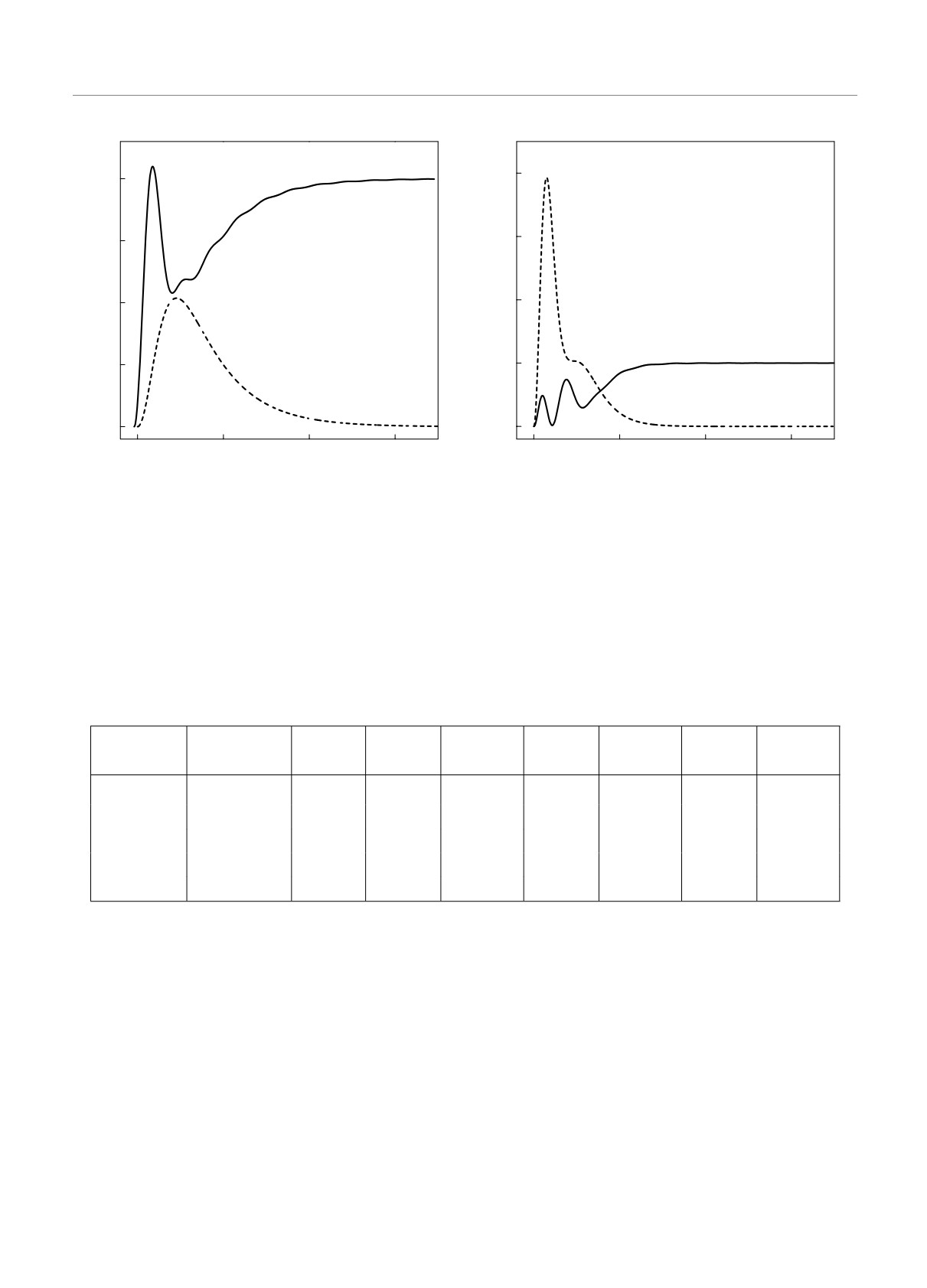
Рис. 3. Зависимости энергии связи для минимумов трех

подзон размерного квантования от глубины потенциальной

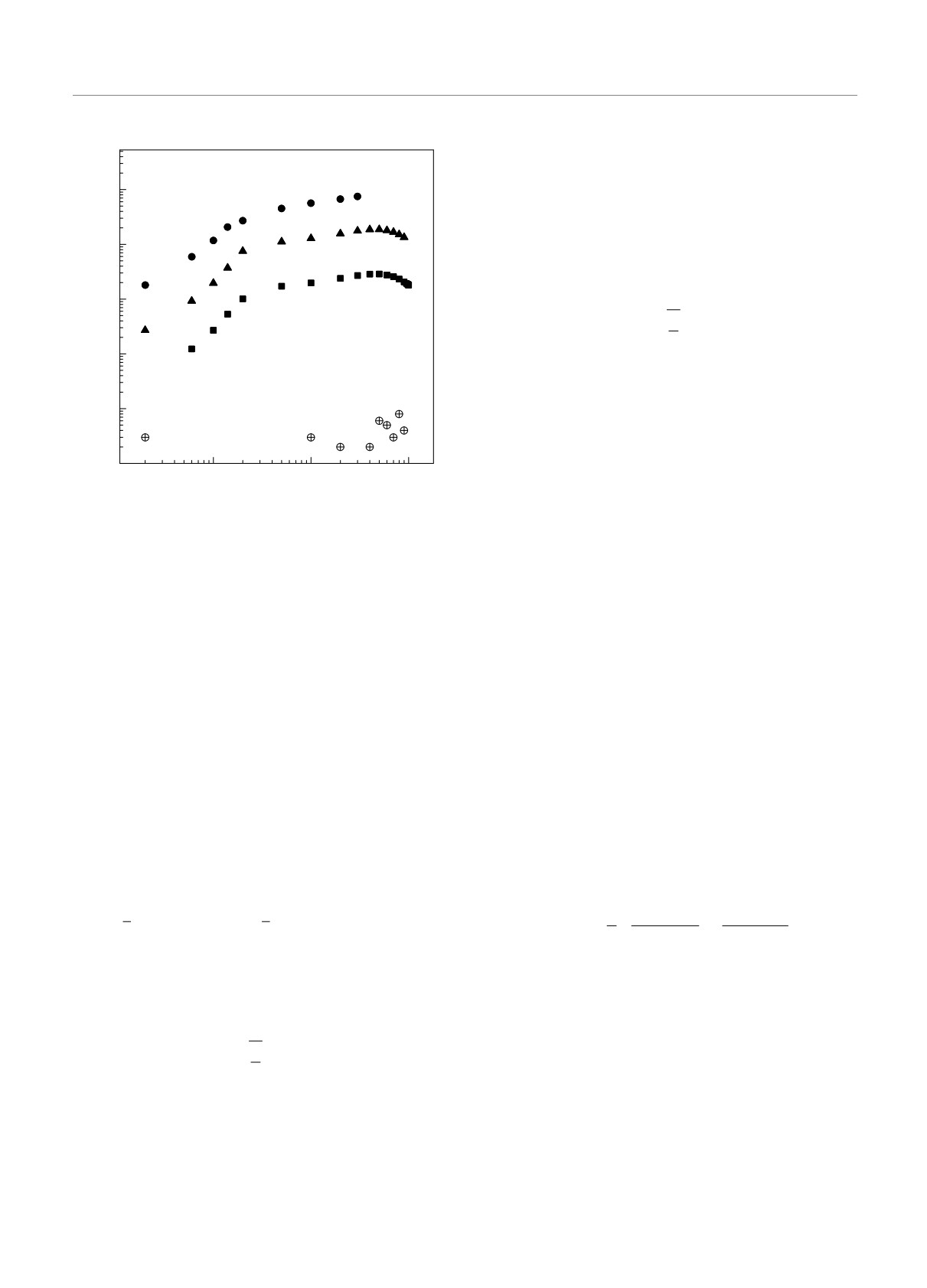
Рис. 4. Безразмерная поверхностная плотность избыточ-

ямы: j = 0 — основная подзона; j = 1, 2 — возбужденные

ных электронов ns = Ns/Nsc в полупроводнике как функ-

подзоны; R^∗s = 0.32

ция глубины потенциальной ямы. Темные кружки показы-

вают полную поверхностную плотность избыточных элек-

тронов, светлые — поверхностную плотность ns2D) элек-

тронов на локализованных состояниях. Характеристиче-

небрегалось непараболичностью закона дисперсии в

ская поверхностная плотность Nsc = N+/kF = k2F/3π2,

подзонах размерного квантования.

R^∗s = 0.32

В разд. 4 показано, что на самом деле двумерная

плотность состояний существенно зависит от энер-

низких температурах. Следует отметить, что в

гии. Тем не менее из табл. 1 видно, что рассчитанные

работе [9] даже на чистой поверхности InAs имелся

нами без свободных параметров положения миниму-

загиб зон. Необходимая для расчета поверхностного

мов двумерных подзон относительно уровня Ферми

потенциала величина начального загиба находилась

оказались в неплохом согласии с эксперименталь-

решением обратной задачи, когда загиб зон на

ными данными, точность которых оценивалась от

чистой поверхности вычисляется по эксперимен-

25 до ±5 мэВ. При k_∥ = 0 рассчитанный в парабо-

тально определенной энергии размерного уровня

лическом приближении энергетический спектр дву-

(см. табл. 1).

мерных подзон будет уже значительно отличаться

от измеренного, как следует из приведенных ниже

3.3.2. Поверхностная плотность электронов

рис. 7б и 8.

На рис. 4 показана зависимость безразмерной из-

В наших вычислениях использованы пара-

быточной плотности n_s электронов на единицу пло-

метры полупроводника, принятые в указанных

щади поверхности от глубины потенциальной ямы

статьях. В работе

[8] исследовались структуры

U₀. Здесь

Cs/n-InAs c объемной концентрацией электронов

N = 3.0 · 10¹⁷ см-3 (R^∗s = 0.321). В работе [9] иссле-

∞

∫

N_s

довались структуры Ag/n-InAs c N = 4.5 · 10¹⁷ см-3

n_s = dζ[n(ζ) - 1] =

(3.26)

(R^∗s

= 0.288). В качестве объемных параметров

N_sc

n-InAs взяты m^∗c = 0.023 для эффективной массы

электронов в минимуме зоны проводимости и

где N_s определяется формулой (3.15) и характерная

= 12.55 для диэлектрической проницаемости

поверхностная плотность N_sc = N₊/k_F = k2F /3π².

решетки. Из-за зависимости параметров полу-

При N₊ = 3 · 10¹⁷ см-3 имеем N_sc = 1.45 · 10¹¹ см-2.

проводника (E_g, m^∗c, κ) от температуры T для

В то время как n_s на рис. 4 непрерывно зави-

сравнения с нашим расчетом (T

= 0) использо-

сит от U₀, поверхностная плотность ns2D) квазидву-

вались только данные, измеренные при наиболее

мерных электронов является разрывной функцией

1083

А. Я. Шульман, Д. В. Посвянский

ЖЭТФ, том 157, вып. 6, 2020

глубины потенциальной ямы. Она имеет скачки по-

C/C_c

4.0

стоянной величины при тех значениях U₀, когда у

уравнения (3.19) при k_∥ = 0 появляется новое дис-

кретное собственное значение

≤ 0. При этом в

системе появляется еще одна подзона E_j (k_∥), кото-

рая сразу заполняется до уровня Ферми конечным

3.5

числом электронов. Одновременно в приповерхност-

ной области плотность трехмерных электронов па-

дает ниже объемной (см. рис. 2). Согласно формуле

(3.26), это делает полную поверхностную плотность

n_s меньше поверхностной плотности двумерных но-

3.0

сителей, что видно на рис. 4 и отмечалось в экс-

периментальных работах (например, Fig. 12 в [45],

рис. 4 и последний абзац разд. 3 в [46]). Получен-

ный результат указывает на необходимость полного

квантового рассмотрения как квазидвумерных, так

2.5

и объемных состояний, поскольку они влияют друг

U /E0F

на друга.

Уменьшение вблизи поверхности плотности

Рис. 5. Зависимость безразмерной электростатической ем-

электронов в состояниях непрерывного спектра

кости на единицу площади от глубины U0 потенциальной

при формировании квазидвумерного электронного

ямы. Характерная емкость Cc на единицу площади опре-

делена в тексте формулой (3.27). R^∗s = 0.32

газа следует учитывать при интерпретации изме-

ренной зависимости фотоэлектронной эмиссии от

энергии возбуждающих фотонов и глубины выхода

2κ

2m^∗c

C_c =

[а.е.^∗] =

фотоэлектронов, которая обсуждается, например,

3π²

3π²a^∗B [см]

3π²a_B [см]

в работе [47] или в работе [8] в связи с Fig. 3 и в

^[ мкФ^]

работе [9] в связи с Fig. 4, 5.

= 0.142m^∗

(3.27)

^c мм²

Сравнение представленного на рис. 4 результата

точного расчета с аналогичными кривыми на Fig. 10

Как и кривая полной поверхностной плотности

работы [13] показывает, что, используя модельный

n_s(u₀) на рис. 4, рассчитанная зависимость полной

потенциал Бараффа - Аппельбаума, можно полуко-

емкости C от глубины потенциальной ямы на рис. 5

личественно оценить связь глубины ямы с плотно-

не показывает никаких особенностей при появлении

стью поверхностного заряда. Однако, что касает-

в яме нового уровня, хотя емкость есть производ-

ся энергии локализованных в такой яме состояний,

ная заряда по потенциалу. Такое поведение экспери-

ошибка может быть значительнее (см. рис. 3а и 3б в

ментальной C-V -кривой в отсутствие нормального

работе [2], где показано аналогичное сравнение для

к поверхности магнитного поля отмечалось Цуи [7].

случая поверхности нейтрального металла).

Непрерывная зависимость от глубины потенци-

альной ямы плотности поверхностного заряда на

3.3.3. Емкость и C-V -характеристика

рис. 4 и ее производной на рис. 5 при одновремен-

обогащенного слоя

ном скачкообразном увеличении плотности двумер-

Полная дифференциальная емкость структуры

ных электронов ns2D) в момент формирования но-

описывается формулой C = C3D +C2D соответствен-

вой двумерной подзоны означает, что вклад в по-

но вкладу от электронов в заполненных состояниях

верхностный заряд электронов в состояниях непре-

непрерывной и дискретной частей спектра (см. фор-

рывного спектра также скачкообразно уменьшается

мулу (3.14) и текст после нее).

на такую же величину.

Зависимость полной электростатической емкос-

Качественно причину синхронности этих измене-

ти C на единицу площади от глубины U₀ потенци-

ний можно усмотреть, сопоставляя пространствен-

альной ямы представлена на рис. 5. Кривая полу-

ные распределения плотности n2D квазидвумерных

чена численным дифференцированием соответству-

и плотности n3D трехмерных электронов, показан-

ющего заряда согласно формуле (3.14), но в безраз-

ные на рис. 2. Видно, что каждому максимуму плот-

мерном виде (см. рис. 4), т. е. C/C_c = dn_s/du₀, где

ности n2D отвечает провал в плотности n3D. Понять

характерная емкость на единицу площади есть

такое поведение можно на основе осцилляционной

1084

ЖЭТФ, том 157, вып. 6, 2020

Решение самосогласованных уравнений Кона - Шэма и Пуассона. . .

теоремы Штурма (см., например, [48, 49]), соглас-

C/C_c

U /E0F

но которой появление связанного состояния в потен-

5.5

циальной яме уравнения (3.19) вызывает появление

5.0

дополнительных нулей в области ямы у всех волно-

вых функций непрерывного спектра со сколь угодно

4.5

малой энергией

> 0. С ростом энергии положение

4.0

этих нулей смещается к поверхности, так как нуль

каждого состояния с большей энергией должен ле-

3.5

жать между нулями состояния с меньшей энергией,

и все решения удовлетворяют граничному условию

3.0

(0) = 0. В силу непрерывности волновых функ-

k_z

ций плотность трехмерных электронов в окрестно-

2.5

сти каждого нуля оказывается подавленной, что ка-

2.0

чественно объясняет уменьшение в этой области ко-

ординат значения интеграла по непрерывному спек-

1.5

тру в (3.24).

0.2

0.4

0.6

0.8

1.0

Непрерывные кривые на рис. 4 и 5 отражают

R_s*

непрерывность зависимости от приложенного элект-

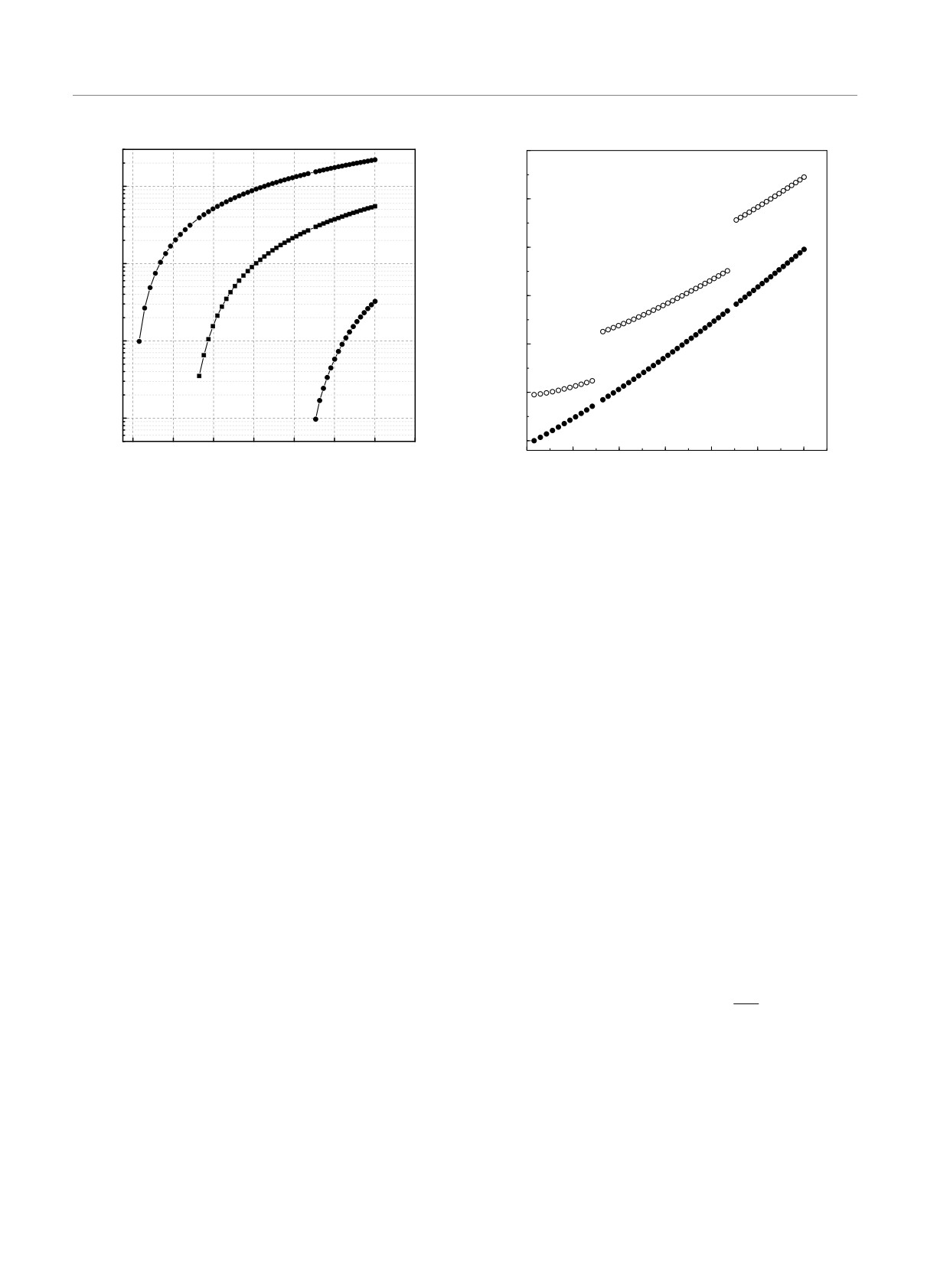
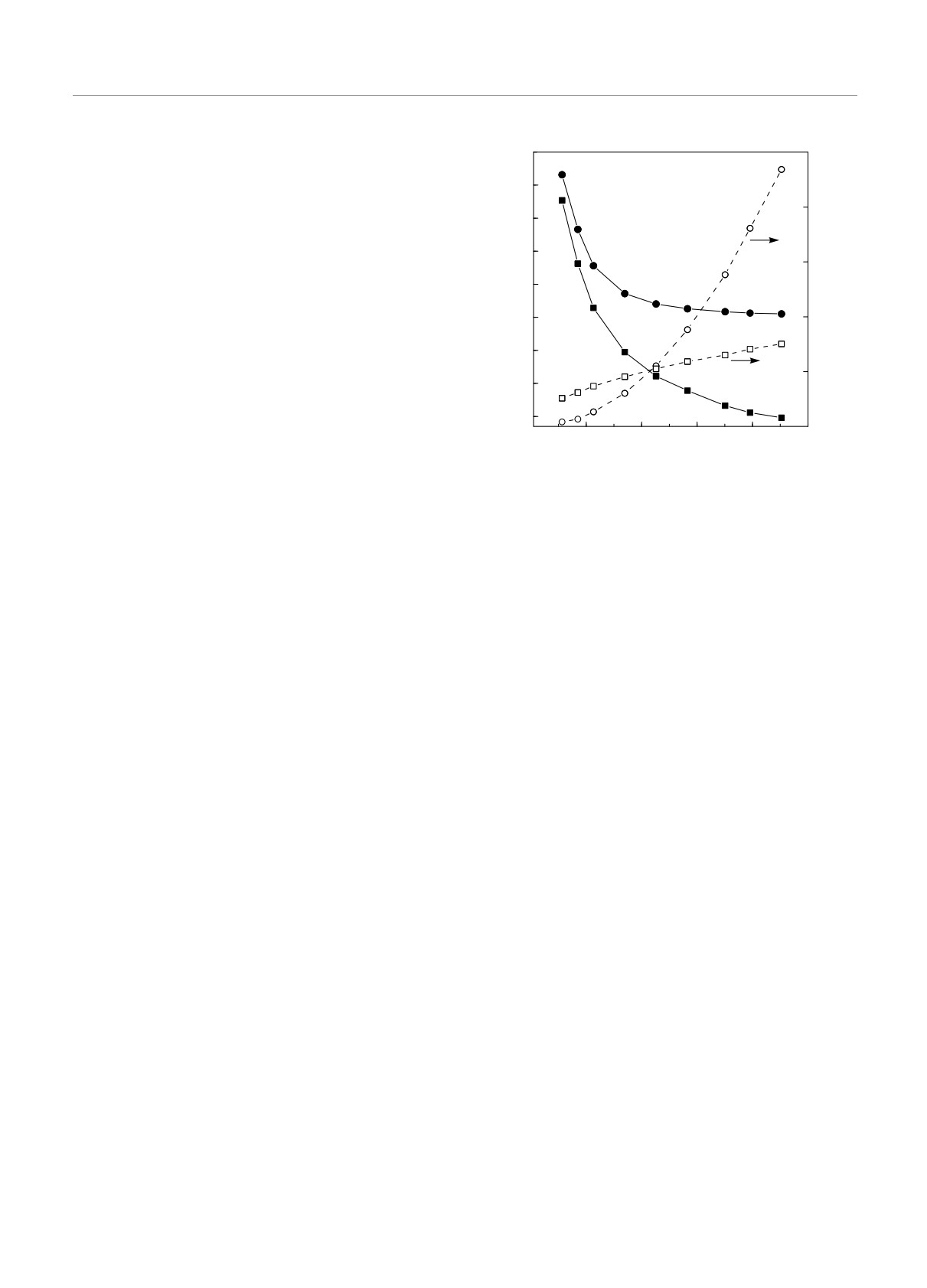
Рис. 6. Зависимости емкости C на единицу площади и

рического поля

E значений u(0) самосогласованно-

глубины потенциальной ямы U0 от концентрации свобод-

го потенциала и его производной du(0)/

E на по-

ных носителей для структуры с обогащенным слоем при

верхности. Отсюда следует, что непрерывно зави-

двух значениях внутреннего электрического поля F на по-

сит от нормальной компоненты электрического поля

верхности. Для кривых 1 и 1^′ поле F = 0, для 2 и 2′

не только полный заряд полупроводника, как пола-

поле F = 1.35 · 10⁵ В/см. В случае F = 0 в приведенном

гается по теореме Гаусса, но и дипольный момент

диапазоне R^∗s имеется только одна размерно-квантованная

пространственного распределения этого заряда, ко-

подзона. В случае F = 1.35 · 10⁵ В/см с ростом R^∗s число

торый равен разности потенциалов V (∞)-V (0). Та-

размерно-квантованных подзон доходит до трех, увеличи-

ким образом, наши вычисления распространяют ре-

ваясь на единицу при R^∗s = 0.22 и R^∗s = 0.7

зультаты работы Кона и Маджумдара [50] на газ

заряженных фермионов с самосогласованным полем

и снимают тем самым сомнения, высказанные в за-

личаются. В последнем случае при больших R^∗s явно

ключительном замечании этой работы.

обозначается выход кривой C(R^∗s) на насыщение.

Рисунок 6 иллюстрирует поведение полной ем-

Сопоставим рассчитанную зависимость емкости

кости на единицу площади от параметра R^∗s при

от глубины потенциальной ямы, представленную

двух заданных значениях нормальной к поверхно-

на рис. 5, с измеренной Цуи в работе [7] (см. в

сти компоненты электрического поля F. При этом

ней рис. 13). При m∗c

= 0.023 по формуле (5)

безразмерное электрическое поле (3.17), которое за-

для характеристической емкости получим C_c

дает граничное условие при решении безразмерного

= 1.74 · 10-3 мкФ/мм². Отсюда, согласно кривой на

уравнения Пуассона (3.16), изменяется, так как оно

рис. 5, получаем изменение емкости от 2.3·10-9 Ф до

зависит от R^∗s (см. определение характерного поля

3.7 · 10-9 Ф для указанной Цуи площади переходов

после формул (3.17)).

5.34 · 10-3 см-2. Измеренная зависимость емкости

Отметим, что в случае кривой 1 в неглубокой са-

образца от напряжения на затворе меняется в пре-

моиндуцированной потенциальной яме (кривая 1^′)

делах от 3 · 10-9 Ф до 4.7 · 10-9 Ф. Таким образом,

имеется только одна размерно-квантованная подзо-

по порядку величины рассчитанные емкость обога-

на с малой энергией связи, тогда как в случае кри-

щенного слоя и масштаб изменения C-V -характе-

вой 2 с ростом R^∗s в квантовой яме (кривая 2^′) чис-

ристики совпадают с данными измерений. Наличие

ло подзон доходит до трех. Тем не менее обе кри-

в образцах Цуи в окисле свинца встроенного поля

вые гладкие, скачков при появлении новых подзон

от контактной разности потенциалов 0.4 В и разли-

на этой зависимости также нет.

чие объемного легирования образцов (3 · 10¹⁷ см-3

Хотя значения емкости с полем и без поля оказа-

в расчете и 1.2 · 10¹⁶ см-3 в работе [7]) не меняют

лись одного порядка, все же зависимости C от объ-

этого вывода согласно показанным на рис. 6 зави-

емной концентрации электронов в отсутствие поля и

симостям емкости от приложенного к поверхности

при фиксированном приложенном поле заметно раз-

поля F и объемного легирования R^∗s.

1085

А. Я. Шульман, Д. В. Посвянский

ЖЭТФ, том 157, вып. 6, 2020

4. НЕПАРАБОЛИЧЕСКИЙ

Однозонное уравнение эффективной массы в

ЭНЕРГЕТИЧЕСКИЙ СПЕКТР

двухзонном приближении для непараболической зо-

ЭЛЕКТРОНОВ ПРОВОДИМОСТИ

ны проводимости можно получить, следуя работе

Келдыша [40], обычным образом используя корень

В предыдущем разделе были представлены ре-

E₁(k) (4.2) как эффективный гамильтониан и делая

зультаты расчета свойств квазидвумерного элект-

замену k → -i∇, E → E - U_eff (r). Тогда для соб-

ронного газа в предположении параболического за-

ственных состояний зоны проводимости в потенци-

кона дисперсии электронов в зоне проводимости

але U_eff (r) получаем уравнение

с параметрами m^∗e, κ, N₊, типичными для образ-

цов n-InAs. Однако InAs обладает сравнительно уз-

[E₁(-i∇) + U_eff (r)] ψ_E (r) = Eψ_E (r),

(4.3)

кой запрещенной зоной, что делает важным учет

где E — энергия собственного состояния. Чтобы из-

непараболичности закона дисперсии при количест-

бавиться от необходимости работать с квадратным

венном сравнении расчета с экспериментальными

корнем из оператора, воспользуемся приемом из ра-

результатами. В настоящем разделе электронный

боты Келдыша [40]. Перепишем уравнение (4.3) в

спектр полупроводника n-типа с обогащенным сло-

виде

ем на поверхности рассчитывается для случая непа-

раболического закона дисперсии электронов в объе-

[E₁(-i∇) - (E - U_eff (r))] ψ_E(r) = 0

(4.4)

ме. Так как при этом эффективная масса зависит от

энергии, будем использовать обычные атомные еди-

и подействуем на него оператором

ницы e = m_e = ℏ = 1 вместо эффективных единиц

E₂(-i∇) - [E - U_eff (r)].

(4.5)

предыдущего раздела.

При этом будем предполагать, что рассматривается

только такая область значений энергии E, в которой

4.1. Основные уравнения для случая

оператор (4.5) не имеет собственных функций.

конечной ширины запрещенной зоны

Для упрощения формул в дальнейшем введем

Конечная ширина запрещенной зоны приводит к

штрихованные переменные

непараболической зоне проводимости. В рамках раз-

E^′ = E - U_xc(∞), U^′(r) = U_eff (r) - U_xc(∞),

рабатываемого алгоритма это влечет за собой изме-

нения в уравнениях эффективной массы и Пуассона,

где U_xc(∞) = U_xc(N₊) в силу нейтральности систе-

образующих в случае неограниченного электронно-

мы на бесконечности. В этих переменных, независи-

го газа систему вариационных уравнений функцио-

мо от учета или пренебрежения U_xc, обеспечивается

нала энергии в приближении Кона - Шэма. Рассмот-

универсальное определение границы непрерывного

рим эти изменения по отдельности.

и дискретного спектров задачи.

Выразив полином второго порядка (4.1) относи-

4.1.1. Уравнение эффективной массы

тельно переменной E через его корни согласно фор-

муле P₂(E) = (E - E₁)(E - E₂), приходим к уравне-

Энергетический спектр электронов в зоне про-

нию

водимости полупроводника с конечной шириной за-

прещенной зоны в двухзонном приближении нахо-

∇²ψ_E′(r) = [E^′ - U^′(r)] ×

дится из решения дисперсионного уравнения, кото-

2m^∗

[

]

рое имеет вид

E^′ - U^′(r)

× 1+

ψ_E′ (r).

(4.6)

(

)

E_g

k²

= 0.

(4.1)

E_g

2m^∗

Нетрудно увидеть, что уравнение (4.6) можно полу-

чить, если сразу в дисперсионном соотношении (4.1)

За начало отсчета энергии выбрано дно зоны про-

заменить E → E^′ - U^′ и k → -i∇. Однако при пере-

водимости, параметр m^∗c — эффективная масса при

ходе от (4.3) к (4.6) нужно было пренебречь комму-

E = 0. Состояниям в зоне проводимости отвечает

татором операторов [U′,

Ê₁]. Эта величина равна ну-

корень E₁(k) — больший из двух корней этого урав-

лю, если U^′ = const. Следовательно, в координатном

нения,

представлении отличие коммутатора от нуля будет

( √

)

пропорционально производным потенциала, из ко-

E_g

торых должен сформироваться малый параметр ме-

E1,2(k) =

−1

(4.2)

E_gm^∗c

тода эффективной массы.

1086

ЖЭТФ, том 157, вып. 6, 2020

Решение самосогласованных уравнений Кона - Шэма и Пуассона. . .

(

)

Последовательный вывод уравнения эффектив-

Ê1,2

= E1,2(k)δ(k - k^′),

(4.11a)

kk^′

ной массы, которое описывает динамику электрона

(

)

в плавном потенциальном поле U^′(r) с учетом непа-

U^′nn′

= Ũ(k - k^′)(unk|u_n′_k′),

kk^′

(4.11b)

раболичности зоны проводимости, проведен в рабо-

n, n^′ = 1, 2.

те [22]. Он основан на разложении решения возму-

щенного уравнения Шредингера по функциям Бло-

Здесь через (unk|u_n′_k′ ) обозначено скалярное произ-

ха зоны проводимости с использованием матема-

ведение по элементарной ячейке кристалла блохов-

тического аппарата обобщенного гильбертова про-

ских амплитуд, ортонормированных при одинако-

странства. Здесь приведем лишь основные моменты

вых k. Через

^Ũ (q) обозначены коэффициенты раз-

этого вывода, которые необходимы для понимания.

ложения потенциала возмущения в интеграл Фурье,

∫

Цель — обосновать однозонное уравнение эффек-

^Ũ (q) =

dr e-iq·rU^′(r).

тивной массы (4.6) в случае непараболической зоны

(2π)³

проводимости и выделить в явном виде малый пара-

Благодаря плавности U^′(r), функция

^Ũ (q) имеет

метр теории — достигается применением регулярной

острый максимум в области малых q. Используя ре-

теории возмущений к уравнению

шения Кэйна ([32], формулы (17)), которые в случае,

[H₀ + U^′(r)] Ψ_E′ (r) = E^′Ψ_E′ (r).

(4.7)

когда вектор k параллелен оси z, выражают unk(r)

через un0(r) в окрестности дна зоны проводимости

Здесь Ψ_E′(r) — точные собственные функции одно-

при k = 0, можно показать, что

частичного гамильтониана кристалла, возмущен-

⁽ (k - k^′)² )

ного потенциалом U^′(r). Кроме того, необходимо

(unk|unk′ ) ≈ 1 + O

(4.12a)

m_cE_g

знать, особенно в задачах с самосогласованным по-

(

)

лем, как связаны точное решение Ψ_E′ (r) и собствен-

|k - k^′|

(unk|u_n′_k′ ) ≈ O

√

n=n^′.

(4.12b)

ные функции задачи (4.6). Приведенный выше вы-

m_cE_g

вод уравнения (4.6) ответа на эти вопросы не дает.

Опустив в уравнениях (4.10) члены, вклад кото-

В рамках двухзонного приближения следует ис-

рых в решение пропорционален малому парамет-

кать решения уравнения (4.7), где H₀ — гамильто-

ру k²/m_cE_g, получим систему из двух несвязанных

ниан невозмущенного кристалла, в виде разложения

уравнений для φ1,2(k):

∫

[

]

∑

E^′δ(k - k^′) -

^Ũ (k - k^′) - E₁(k)δ(k - k^′) ×

Ψ_E(r) =

dk φ_nE (k)ψnk(r)

(4.8)

n=1Ω

∗

× φ1E′(k^′) = 0,

(4.13a)

по функциям Блоха ψ1,2 зоны проводимости и ва-

[

]

лентной зоны,

E^′δ(k - k^′) -

^Ũ (k - k^′) - E₂(k)δ(k - k^′) ×

ψ(1,2)k(r) = (2π)-3/2eik·ru(1,2)k(r).

(4.9)

× φ2E′(k^′) = 0.

(4.13b)

Здесь и далее по повторяющимся штрихованным пе-

Здесь через Ω_∗ обозначена первая зона Бриллюэна,

ременным подразумевается интегрирование по об-

индексы «1» и «2» используются для обозначения

ласти Ω_∗.

величин, относящихся соответственно к зоне прово-

Воспользуемся теперь приемом Келдыша в пред-

димости и к валентной зоне. Для этой цели могут

ставлении с базисом из выбранных функций Блоха

также использоваться буквенные индексы «c» и «v».

(4.9). Для этого подействуем на уравнение (4.13a)

Система уравнений для коэффициентов разло-

оператором, который определяет левую часть урав-

жения φ(1,2)E′ (k) может быть представлена в мат-

нения (4.13b), при условии, что E^′ не является соб-

ричном по зонным индексам виде:

ственным значением задачи (4.13b). После неслож-

(

)

∫

ных преобразований получим

Ê₁ +

U′11

U^′

dk^′

⎧

[

]

U′21

E₂ +

U′22

kk^′

⎨(

)

Ω∗

Ê^′-U′

(

)

(

)

E^′δ(k-k^′′)-Ũ(k-k^′′)

φ1E′ (k^′)

φ1E′ (k)

⎩

k^′′k^′

=E^′

(4.10)

[

]

⎫

φ2E′ (k^′)

φ2E′ (k)

Û,E1

⎬

′

φ1E′ (k^′) =

φ1E′ (k).

(4.14)

Операторные элементы матрицы системы (4.10) с

E_g

⎭

2m_c

учетом k, k^′ ∈ Ω_∗ имеют вид

1087

А. Я. Шульман, Д. В. Посвянский

ЖЭТФ, том 157, вып. 6, 2020

Через [. . .]_kk′ обозначены приближенные матричные

Можно показать, что для вклада от коммутатора

элементы соответствующих операторов, вычислен-

в уравнение эффективной массы получается форму-

ные в базисе из функций Блоха зоны проводимости

ла ([22] разд. 2.1)

согласно (4.12a). В случае коммутатора, например,

[

]

в явном виде имеем

Ê₁

U^′,

Φ(x^′) =

E_g

xx^′

[

]

^[1 ∂²U^′

∂U′ ∂

U^′,E1

= Ũ(k - k^′′)E₁(k^′′)δ(k^′′ - k^′)-

Φ(x),

(4.18)

kk^′

m^∗cE_g

∂x²

∂x ∂x

- E₁(k)δ(k - k^′′)U′(k′′ - k′).

(4.15)

¯2/m∗cEg

которая точна до членов порядка

< 1

включительно.

Уравнение (4.14) представляет собой однозонное

В этой оценке под

k понимается масштаб об-

уравнение эффективной массы для зоны проводи-

ласти волновых векторов, которые дают основной

мости с точностью до межзонных матричных эле-

вклад в искомое решение. Для связанных состояний

ментов потенциала U^′. В работе [22] показано, что

он определяется обратной величиной характерного

множество функций, которые могут быть представ-

масштаба потенциала L_U , для состояний непрерыв-

лены своим разложением по базису из функций Бло-

ного спектра — величиной k_F . Из выражения (4.18)

ха для зоны проводимости, образует ортогональ-

видно, что сравниваться эти масштабы должны, как

ное подпространство H_c в обобщенном гильберто-

и предполагалось в работе [40], с характерной дли-

вом пространстве H. Чтобы перейти к координатной

√

ной L_g ≃ 1/

m^∗cE_g , которая для полупроводника с

форме уравнения эффективной массы, рассмотрим

узкой запрещенной зоной порядка 0.5 эВ превышает

функции φ_cE′(k), определенные выражением (4.8),

типичное значение постоянной решетки примерно в

как проекции некоторого вектора из обобщенного

4-5 раз. Так, при m^∗c ≃ 0.025 и указанной ширине

гильбертова пространства на собственные функции

запрещенной зоны имеем L_g ≃ 2.5 нм.

оператора импульса (2π)-3/2exp(ik · x) в координат-

Очевидно, что условие L2gd²U/dr² < 1 примени-

ном представлении, т. е. введем функции

мости уравнения (4.6) в качестве уравнения метода

∫

эффективной массы несколько жестче, чем в одно-

Φ_E′(x) =

dk φ_cE′ (k)eik·x,

(4.16)

(2π)3/2

зонном случае, когда предполагается плавность воз-

Ω∗

мущающего потенциала и решений уравнения Шре-

дингера на масштабах порядка постоянной решет-

где ограничение области интегрирования первой зо-

ки a ≈ 0.5 нм. Тем не менее оценка параметра ма-

ной Бриллюэна диктуется областью определения

лости теории при k_F LU ≃ 5-10 (см. рис. 1, 2) и

функций φ_cE′.

E_g/E0F ≃ 6 дает вполне удовлетворительный резуль-

Заметим, что множество собственных функций

тат L2g/L2U ≃ 1/75-1/300. Поэтому далее под уравне-

оператора импульса для области значений k ∈ Ω_∗

нием метода эффективной массы в нулевом прибли-

также образует базис в некотором ортогональ-

жении по производным потенциала U^′ будем пони-

ном подпространстве обобщенного гильбертова

мать уравнение (4.17), в котором опущено слагаемое

пространства, которое обозначим через H_∗. Отоб-

с коммутатором.

ражение уравнения (4.14) на это подпространство в

координатном представлении принимает вид

4.1.2. Связь собственных функций уравнения

(

)

эффективной массы с точными собственными

E^′ - U^′(x)

функциями возмущенного кристалла

(E^′ - U^′(x))

Φ_E′(x)+

E_g

[

]

Для того чтобы получить условия отбора собст-

Ê₁

U^′,

Φ_E′(x^′) = -

∇^2xΦ_E′(x).

(4.17)

венных функций уравнения (4.6) из всех возможных

E_g

xx^′

2m_c

решений и формулы для матричных элементов опе-

раторов наблюдаемых в этом представлении, необ-

Без члена с коммутатором это уравнение аналогич-

ходимо установить связь решения Φ_E′ (x) с точной

но (4.6), только теперь определено функциональное

волновой функцией Ψ_E′(r) электронов в зоне про-

пространство, к которому принадлежат решения.

водимости в присутствии внешнего потенциала.

Под U^′(x) в (4.17) можно понимать и обычный куло-

Используя формулы (4.8), (4.9) и (4.16), получим

новский потенциал самосогласованного поля, если

∫

пренебрегать обменно-корреляционным взаимодей-

Ψ_E′(r) = dx^′w_c(r; x^′)Φ_E′ (x^′),

(4.19)

ствием электронов.

1088

ЖЭТФ, том 157, вып. 6, 2020

Решение самосогласованных уравнений Кона - Шэма и Пуассона. . .

где через

так и для условия полноты базиса из соответствую-

∫

щих собственных решений в соответствующем под-

w_c(r; x) =

ψck(r)e-ik·x

(4.20)

пространстве. Отметим, что хотя подпространства

(2π)3/2

Ω∗

H_∗ и H_c эквивалентны в том смысле, что между их

векторами существует взаимнооднозначное соответ-

обозначена обобщенная функция Ваннье для зоны

ствие, они не тождественны, так как состоят из раз-

проводимости.

ных векторов обобщенного гильбертова простран-

Заметим, что функция w_c(r; x) является матрич-

ства. Поэтому вывод условий полноты требует ме-

ным элементом оператора

^Ŵ, который отображает

нее элементарных средств, так что приведем только

подпространство H_∗ в H_c. Его абстрактное пред-

конечный результат:

ставление через векторы обобщенного гильбертова

∫

пространства в обозначениях Дирака имеет вид [22]

∫

δ_c(r - r^′) = DE 〈r|Ψ_E〉〈Ψ_E|r^′〉,

∫

(4.25)

Ŵ_c = dk|k, c 〉〈k| ,

(4.21)

|x^′〉 .

δ_∗(x - x^′) = DE 〈x|Φ_E〉〈Φ_E

Ω∗

где через |k, c 〉 обозначен дельта-нормированный

Здесь DE означает интегрирование по диффе-

собственный вектор гамильтониана H₀ из H, отве-

ренциальной спектральной мере, индексы у дель-

чающий функции Блоха с квазиимпульсом k для зо-

та-функций отмечают, что соответствующие выра-

ны проводимости, и через |k 〉 — собственный вектор

жения обладают всеми свойствами дельта-функции

оператора импульса. Матричные элементы операто-

относительно элементов соответствующих подпро-

ра

Ŵ_c в координатном представлении,

странств.

∫

Для решения вопроса о граничных условиях вос-

Ŵ_c|x = dk 〈r |k, c 〉〈 k| x〉 ,

(4.22)

пользуемся формулой (4.19). В работе [22] доказано,

Ω∗

что с помощью отображения Гельфанда обобщенная

совпадают с формулой (4.20), которая определяет

функция Ваннье w_c(r; x) может быть выражена че-

рез стандартную функцию Ваннье³⁾

обобщенную функцию Ваннье.

В работе [22] показано, что оператор

Ŵ_c унитар-

∫

ный. В данном случае, когда одно подпространст-

w_n(r) =

ψnk(r)

(4.26)

(2π)3/2

во обобщенного гильбертова пространства отобра-

Ω∗

жается на другое, это означает наличие следующих

формулой

свойств:

Ŵ†

Ŵ_c Ŵ†

Ŵ_c = 1_∗,

=1_c,

(4.23)

∑

∫

w_n(r; x) = Ω₀

w_n(r - sa)δ_∗(x - sa),

(4.27)

где введены единичный оператор 1_∗ =

dk|k 〉〈 k|

Ω∗

s=-∞

в подпространстве H_∗ и единичный оператор

1_c =

∫

dk|k, c 〉〈 c, k| в подпространстве H_c. Благо-

где a — постоянная решетки кубического кристалла,

Ω∗

даря унитарности отображения, которое задается

s — вектор трехмерного пространства с целочислен-

оператором

Ŵc, сохраняется скалярное произведе-

ными координатами.

ние векторов. В частности, это справедливо как

Подстановка (4.27) в (4.19) дает

для условия нормировки собственных решений на

∑

δ-функцию от квантовых чисел,

Ψ_E(r) = Ω₀

w_c(r - sa)Φ_E(sa).

(4.28)

∫

s=-∞

δ(E - E^′) = 〈Ψ_E|Ψ_E′〉 = dr 〈Ψ_E |r 〉〈 r|Ψ_E′ 〉 =

∫

Функция Ваннье w_c(r) локализована в окрестности

= dr Ψ^∗E (r)Ψ_E′(r) =

точки r на масштабе порядка нескольких постоян-

∫

ных решетки [52], тогда как Φ_E (x) меняется слабо на

таких расстояниях. Поэтому Φ_E (x) можно вынести

= dr dx dx^′Φ^∗E (x)w^†c(x; r)w_c(r; x^′)Φ_E (x^′) =

из-под знака суммы при sa = r. Оставшаяся сумма

∫

= dx dx^′Φ^∗E (x)δ_∗(x - x^′)Φ_E (x^′) =

³⁾ Функция wn(r) отличается только постоянным множи-

∫

телем Ω∗/(2π)3/2 от обычного определения функции Ваннье

= dx Φ^∗E (x)Φ_E′(x),

(4.24)

через среднее значение ψnk(r) по зоне Бриллюэна (см., на-

пример, [51], формула (10.28)).

1089

ЖЭТФ, вып. 6

А. Я. Шульман, Д. В. Посвянский

ЖЭТФ, том 157, вып. 6, 2020

выражается через функцию Блоха при k = 0 [22]. В

записи отображения, обратного (4.19), и его эрмито-

результате имеем

во-сопряженного:

Ŵ†

Ψ_E(r) = uc0(r)Φ_E(r),

(4.29)

|Φ_E 〉 =

|Ψ_E〉,

〈Φ_E | = 〈Ψ_E|

Ŵ_c.

(4.33)

где uc0(r) — блоховская амплитуда для состояния на

Аналогичные соотношения имеются между вектора-

дне зоны проводимости. Видно, что нулевые гранич-

ми |r_c〉 и |x〉 — отображениями состояния |r〉 на под-

ные условия для обеих функций совпадают. Несмот-

пространства H_c и H_∗:

ря на внешнее сходство приближенной формулы

∫

(4.29) c формулой метода огибающих Латтинже-

|r_c〉 = dk|k, c〉〈c, k|r〉,

ра - Кона [53], функция Φ_E не совпадает с обычной

∗

^Ω∫

(4.34)

огибающей, так как удовлетворяет другому уравне-

|x〉 = dk|k〉〈k|r〉,

|x〉 =

Ŵ†

|r_c〉.

нию (см. разд. II и IV в работе [53]).

Роль блоховской амплитуды при ненулевых гра-

Ω∗

ничных условиях, так же как интерпретация резуль-

Вставив единичный оператор (4.23) в (4.31) с

татов подстановки приближенной формулы (4.29) в

учетом (4.33) и (4.34), получаем

точные формулы данного раздела обсуждаются в

работе [22], разд. 2.2.

∫

Инвариантность скалярного произведения отно-

n_E (r₀) = dr〈Ψ_E|W_cW^†c|r〉δ (r - r₀) ×

сительно отображения H_c → H_∗ влечет за собой

× 〈r|W_cW†c |Ψ_E〉 = 〈Φ_E |x₀〉〈x₀|Φ_E 〉 =

также инвариантность матричных элементов само-

сопряженных операторов наблюдаемых. Убедимся в

= Φ^∗E (x₀)Φ_E (x₀).

(4.35)

этом на примере важного для данной работы (с са-

Ŵ†

мосогласованными расчетами) оператора плотности

Здесь |x₀〉 =

|r₀〉 и было учтено, что Ψ_E ∈ H_c и

электронов n(r₀) = δ(r - r₀).

Φ_E ∈ H_∗.

Средняя плотность электронов в основном состо-

янии системы с точным гамильтонианом (4.7) дается

4.1.3. Уравнение Пуассона

формулой

Энергия Ферми E_F для заданной плотности N =

∫

= k3F/3π² электронов на бесконечности при учете

n (r₀) = DEϱ(E)n_E (r₀) ,

(4.30)

непараболичности спектра и обменно-корреляцион-

ного взаимодействия находится как решение урав-

где через ϱ(E) и n_E (r₀) обозначены диагональ-

нения

ные элементы одночастичной равновесной матри-

(

)

k2F

E_F - U_xc(N)

цы плотности и оператора плотности в базисе соб-

= [E_F - U_xc(N)]

ственных функций |Ψ_E〉 самосопряженного операто-

2m^∗c

E_g

(

)

ра H₀ + U^′. По определению

E^′F

=E^′

(4.36)

E_g

n_E (r₀) = 〈Ψ_E|δ(r - r₀)|Ψ_E〉 =

∫

Входящий в эффективный потенциал обменно-кор-

= dr 〈Ψ_E|r〉 δ (r - r₀) 〈r|Ψ_E 〉 =

реляционный потенциал U_xc по-прежнему будет

приниматься в обычном приближении локальной

= Ψ^∗E (r₀)Ψ_E (r₀),

(4.31)

плотности. Как видно из приведенного выше рис. 2,

пространственные распределения как квазидвумер-

где использовано представление функции от опера-

ных электронов, так и электронов в объемных со-

тора координаты в базисе собственных функций по-

стояниях непрерывного спектра вполне плавно ме-

следнего:

няются на масштабах порядка фермиевской длины

∫

волны. Принимая во внимание, что приближение

n(r₀) = dr|r 〉δ (r - r₀)〈 r|.

(4.32)

локальной плотности позволяет проводить с хоро-

шей точностью расчеты многоэлектронных атомов,

При доказательстве инвариантности формулы

молекул и поверхностных свойств металлов (см. об-

(4.31) для n_E (r₀) относительно отображения H_c →

суждение в [54]), мы в настоящей работе также огра-

→ H_∗ удобно воспользоваться абстрактной формой

ничились стандартным определением U_xc.

1090

ЖЭТФ, том 157, вып. 6, 2020

Решение самосогласованных уравнений Кона - Шэма и Пуассона. . .

В уравнении Пуассона (3.13) учет непараболич-

электронов. Вследствие зависимости квазипотенци-

ности электронного спектра приводит к изменению

ала (4.41) от энергии, для каждого набора значений

квазиклассического выражения для связи индуци-

(k2∥, k2z) получается своя потенциальная яма. Важно

рованной плотности заряда с потенциалом. Вместо

отметить, что при увеличении энергии E^′ глубина

формулы (3.11) имеем

ямы монотонно растет, вследствие чего с ростом k2∥

уровни k2zj монотонно углубляются (см. (4.41)). В

k_F (x)

(2m^∗c)3/2

N_ind(x) =

результате, в отличие от параболического случая,

3π²

двумерный спектр E^′j (k_∥) нетривиальным образом

[

(

)]3/2

E^′F - U^′(x)

зависит от k2∥, а в непрерывном спектре появляется

× [E′F - U^′(x)]

(4.37)

E_g

зависимость от k2∥ собственных функций ψ_E′_k

∥

В безразмерных переменных, аналогичных вве-

4.2. Особенности расчета

денным ранее в разд. 3.2 (с уточнением E0F

= k2F/2m^∗c), уравнение (4.39) для полупроводника

В случае полубесконечного полупроводника с

n-типа с обогащенным слоем на поверхности запи-

обогащенным слоем на поверхности уравнение (4.17)

сывается в виде

допускает разделение переменных r_∥ в плоскости и

[

]

z по нормали к поверхности, так что решение можно

d²

(ζ) =

ψkk (ζ),

(4.42)

+ u_qp(ζ; ε) ψ˜kz˜k

искать в виде

dζ²

∥

Φ_E′(r) =

eik∥·r∥ ψ_E′_k

(z), r = (r_∥, z).

(4.38)

где ζ = k_F z,

k₌ k/k_F , ε = E^′/E0F , u_qp = U_qp/E0F и

∥

2π

[

(

)

]

Подставив это выражение в (4.17) и опустив комму-

= ε

-k2

(4.43)

∥

ε_g

татор, получаем уравнение

[

]

где ε_g = E_g/E0F .

d²

+ U_qp(z; E^′) ψ_E′_k

(z) =

∥

Граничные условия к уравнению (4.42) анало-

2m^∗

гичны случаю параболической зоны проводимости

k2zψ_E′_k

(z),

(4.39)

(см. (3.20) и (3.23)). Для электронных состояний

∥

2m^∗

непрерывной области спектра имеем

где параметр k_z связан с k_∥ и E^′ соотношением

k_z k

(0) = 0,

(

)

∥

E^′

√

(

)

(k2∥ + k2z)=E′

≡ K₂(E^′)

(4.40)

2m^∗c

E_g

lim

sin

(4.44)

ψ˜kz,k_∥ (ζ)=

kz ζ + γ

k_z k

ζ→∞

∥

и введен зависящий от энергии квазипотенциал [22]

kz > 0,

U_qp(z; E^′) = K₂(E^′) - K₂ (E^′ - U^′) =

где γ

k_z k

опять обозначает постоянную фазу волно-

(

)

∥

2E^′

U′2

вой функции в глубине полупроводника. Для нор-

=U^′

(4.41)

E_g

мированных на единицу локализованных состояний

дискретного спектра

который удобен тем, что обращается в нуль на бес-

конечности вместе с U^′(z).

ψj,˜k

(0) = 0, lim

ψj,k (ζ) = 0.

(4.45)

∥

ζ→∞

∥

При решении уравнения (4.39) для каждого зна-

чения параметра k2∥ в диапазоне 0 ≤ k2∥ ≤ k2max

После определения собственных функций уравне-

ищется спектр собственных значений k_z(k2∥). Если

ния эффективной массы вычисляется полная плот-

в квазипотенциальной яме, соответствующей взя-

ность электронов, которая дается выражением

тому значению k2∥, существует дискретный набор

⎡

√

убывающих на бесконечности и нормируемых на

∫

⎢

dkz

единицу решений при некоторых отрицательных

n(ζ) = 3π²

⎢

dk2∥|ψ

(ζ)|² +

⎣

k_z,k∥

2π

значениях k2zj < 0, то соответствующие решения

E^′j(k2∥), j = 0, 1, . . . уравнения (4.40) представляют

⎤

собой размерно-квантованные подзоны энергетичес-

∫

∑

⎥

кого спектра квазидвумерных электронов. Осцилли-

⎥

dk2∥|ψj,˜k

(ζ)|²

(4.46)

∥

⎦

рующие при z → ∞ решения для k2z > 0 отвеча-

2π

(0)≤0

ют состояниям непрерывного спектра трехмерных

1091

А. Я. Шульман, Д. В. Посвянский

ЖЭТФ, том 157, вып. 6, 2020

где

находится из решения уравнения

работы [2]). В отличие от параболического случая,

jmax

когда обычный потенциал в уравнении Шредингера

k2jmax + k2zj(k2jmax) = ε_F (1 + ε_F /ε_g).

зависел только от координаты, в (4.39) квазипотен-

циал (4.41) зависит от координаты и от энергии со-

Структура формулы (4.46) соответствует тако-

стояния E^′. С ростом k2∥ энергия растет, квантовая

вой формулы (3.24), только учитывает явную за-

яма становится глубже. Это приводит к тому, что

висимость решения ψ˜k

z,k∥(ζ)отk∥.Вследствиеэто-

при определенных значениях волнового вектора k_∥

го, интегрирование по k_∥, которое в случае парабо-

начинают проявляться очень мелкие локализован-

лической зоны выполнено в (3.24) аналитически, в

ные состояния.

случае непараболического энергетического спектра

Для нахождения таких уровней методом три-

должно быть реализовано в (4.46) численно наряду

гонометрической прогонки необходимо значитель-

с интегрированием по k_z.

но увеличивать размер моделируемой области, что

Вследствие возможного существования очень

связано с вычислительными трудностями. С другой

мелкого уровня в квазипотенциальной яме может

стороны, пропуск таких мелких уровней в самосо-

возникать необходимость вычислять плотность

гласованных расчетах приводит к «недобору» за-

электронов при очень больших ζ. Из асимптотики

ряда в выражении (4.46) и к расходимости итера-

(4.44) видно, что в этом случае подынтегральное

ционного процесса. Поэтому анализ области энер-

выражение в первом слагаемом в

(4.46) будет

гий связи, близких к границе непрерывного спектра,

очень быстро осциллирующей функцией от k_z .

проводился с использованием свойств решения при

Однако используемый в расчетах набор равно-

k2z = 0.

отстоящих значений k_z будет избыточным для

В работе [22] (Приложение A.1) показано, что

большей части значений ζ, если его выбирать по

асимптотика решения ψkz при k_z = 0 в окрестно-

критерию достаточной точности квадратурной

сти бесконечности, где квазипотенциал стремится к

формулы Симпсона при очень больших значениях

нулю, есть либо константа (и тогда нуль есть соб-

ζ. Периодичность ψ˜kz,k_∥(ζ)отkzприбольшихζ

ственное значение), либо монотонная функция ко-

позволяет аппроксимировать интеграл по k_z более

ординаты, поведение которой может быть исполь-

мощной, чем формула Симпсона, квадратурной

зовано для обнаружения мелких связанных состоя-

формулой Филона (см., например, [42]). Однако

ний. А именно, если в области, где квазипотенциал

предварительное интегрирование в

(4.46) по

∥

становится достаточно близок к нулю, выполняется

разрушает точную периодичность по k_z получаю-

условие

щегося выражения. Для устранения этой трудности

]

при вычислении n(ζ) в случае больших значений

^[ dψ_k2=0 dψk2zc

sign

< 0,

(4.50)

ζ порядок интегрирования в

(4.46) менялся на

dζ

ζmax

обратный.

то принимается, что в квантовой яме имеется мел-

Безразмерное уравнение Пуассона остается неиз-

кий уровень в интервале (k2zc, 0).

менным:

— это минимальная энергия, для

Параметр k2zc

d²u

которой метод тригонометрической прогонки обна-

+ c_nn_ind(u) = c_n[1 - n_qu(ζ)],

(4.47)

dζ²

руживает локализованное состояние в нашем слу-

как и краевые условия к нему:

чае. В расчетах данного раздела при каждом фик-



сированном значении k_∥ граничное условие (4.45)

du



= 0.

(4.48)

из бесконечности переносилось в точку ζ_max = 200



dζ

ζ=0

ζ=∞

в форме dlnψkz,k_∥ /dζ = -|kz|. При этом значение

Формула для индуцированной плотности электро-

k2zc в безразмерных единицах оказывалось порядка

нов следует из (4.37):

-5·10-4. Приближенно энергия замеченного мелко-

го уровня оценивалась как k2zsh = k2zc/2, а в качестве

n_ind(ζ) =

соответствующей волновой функции в области рас-

[

(

)]3/2

четного интервала 0 ≤ ζ ≤ ζ_max бралось решение

ε_F - u^′(ζ)

= [ε_F - u^′(ζ)]

(4.49)

ψkzk_∥ , отвечающее этой энергии. На границе ζmax

ε_g

оно непрерывно продолжалось exp(-|k_z|ζ) и затем

Энергии и волновые функции связанных состоя-

нормировалось. (Подробнее см. Приложение A.)

ний в квантовой яме находились методом тригоно-

Строго говоря, такое решение не является соб-

метрической прогонки (см. детали в конце разд. 2.2

ственной функцией задачи, поскольку в точке ζ_max

1092

ЖЭТФ, том 157, вып. 6, 2020

Решение самосогласованных уравнений Кона - Шэма и Пуассона. . .

N(z)/N

1.0

(p)

E₁

E₀

E(np)

(np)

E₀

0.5

-0.5

-1.0

-1.5

k z_F

k /k||F

Рис. 7. а) Зависимость от координаты самосогласованной электронной плотности электронов. б) Двумерный закон дис-

персии электронов в обогащенном слое. Сплошные кривые рассчитаны для непараболической зоны проводимости, штри-

ховые — для параболической зоны в объеме полупроводника. В плотности электронов на рис. 7а учтен вклад состояний

непрерывного спектра и двух размерно-квантованных подзон, показанных на рис. 7б. Расчет кривых на рис. 7б был

выполнен только для заполненных электронами состояний, энергия которых не превышала энергию Ферми

оно имеет скачок первой производной. Однако в си-

раметрами R^∗s

= 0.32, m^∗c

= 0.023, κ

= 12.55,

лу малости k2zsh неправильное поведение решения на

E_F - U₀ = 400 мэВ и шириной запрещенной зо-

бесконечности мало сказывается на его значениях

ны InAs 430 мэВ, которые соответствуют исследо-

в области 0 < ζ < ζ_max согласно теореме Пуанка-

ванной в работе [8] структуре Cs/InAs (значения

ре о непрерывной зависимости решения уравнения

E_g отвечают температурам T < 80 K). Как видно

от параметра при сохранении граничного условия

на рисунке, учет непараболичности закона диспер-

ψ(0) = 0, dψ/dζ(0) = 1. Такой подход позволил с до-

сии в зоне проводимости может приводить к значи-

статочной точностью учесть заряд мелкого уровня

тельному увеличению электронной плотности в об-

и обеспечил сходимость итерационного процесса по

ласти квантовой ямы. Причина этого — рост дву-

условию max_ζ |n(i) - n(i)Poi| < 2.0 · 10-5.

мерной плотности состояний с энергией (см. ниже

разд. 4.3.4).

4.3. Результаты и обсуждение

Соответствующий спектр двух размерно-кванто-

ванных подзон показан на рис. 7б. Видно, что наи-

4.3.1. Распределение электронов около

большее различие двух законов дисперсии достига-

поверхности и особенности двумерного

ется при больших значениях квазиимпульса. Сле-

энергетического спектра

дует также отметить значительное различие пре-

Самосогласованное решение уравнения Пуассо-

дельных значений квазиимпульсов k_Fj , при которых

на и уравнения эффективной массы с обменно-кор-

энергия подзон равна энергии Ферми. Этот пара-

реляционным потенциалом Кона - Шэма при уче-

метр напрямую определяется по периодам магнито-

те непараболического закона дисперсии электронов

осцилляций Шубникова - де Гааза или C-V -харак-

в зоне проводимости проводилось с параметрами

теристик. На рис. 7б легко увидеть, что если исполь-

структур, которые экспериментально исследовались

зовать измеренные значения k_Fj без учета непара-

в работах [8, 9]. На рис. 7а представлены простран-

боличности двумерного закона дисперсии, это при-

ственные зависимости самосогласованной плотнос-

ведет к заметному углублению или повышению по-

ти электронов, рассчитанные для параболическо-

ложения дна соответствующей подзоны в зависимо-

го и непараболического законов дисперсии с па-

сти от используемого значения эффективной массы,

1093

А. Я. Шульман, Д. В. Посвянский

ЖЭТФ, том 157, вып. 6, 2020

m^∗j(0) или m^∗j(ε_F ).

E_j(k

)/E

Следует также обратить внимание на заметное

различие координат концов соответствующих кри-

1.0

E_F

вых по шкале ординат на рис. 7б и их общее поло-

жение ниже уровня E/E0F = 1. В случае параболиче-

E₀₍₄₀₀₎

0.5

ского спектра (штриховые кривые) в этом проявля-

(470)

ется влияние обменно-корреляционного взаимодей-

E₀

E₂

ствия электронов на энергию Ферми. Несмотря на

его заметную величину, в области R^∗s < 1 оно сла-

E₁

бо влияет на форму потенциальной ямы и поэтому

–0.5

только смещает весь спектр по оси ординат вниз. В

случае сплошных кривых к последнему добавляется

–1.0

еще вклад непараболичности спектра.

Экспериментально положение дна подзоны

-1.5

обычно измеряется относительно уровня Ферми. На

E₀

рис. 7 видно, что соответствующие разности значи-

мо различны в параболическом и непараболическом

случаях.

(k /k||F)2

Рис. 8. Непараболический закон дисперсии подзон раз-

4.3.2. Сравнение рассчитанного и измеренного

мерного квантования для структуры с обогащенным сло-

энергетических спектров

ем на поверхности n-InAs при величине загиба зон

EF - U0 = 435 мэВ (сплошные кривые). Темные круж-

На рис. 8 показаны рассчитанный нами энерге-

ки обозначают измеренные в работе [8] методом ARPES

тический спектр квазидвумерного электронного га-

значения энергии электронов в основной подзоне при раз-

за и экспериментально измеренная в работе [8] ме-

личных

k_∥. Отметим, что третья подзона E2(k2∥) начинает-

тодом фотоэлектронной спектроскопии с угловым

ся при конечном значении квазиимпульса k2∥ = 0.19. Мет-

разрешением (ARPES) зависимость энергии основ-

ки E⁽⁴⁰⁰⁾⁰ и E⁽⁴⁷⁰⁾⁰ около штриховых кривых обозначают,

ной подзоны двумерного спектра от k_∥. Авторы этой

при каком загибе зон на поверхности относительно уровня

работы полагали, что на полученной ими сколом в

Ферми рассчитана соответствующая кривая. R^∗s = 0.32

вакууме чистой поверхности (110) полупроводника

InAs загиб зон не имел места, а после нанесения на

ника задавалось электрическим контактом с мед-

поверхность InAs слоя атомов Cs глубина потенци-

ным держателем образца.

альной ямы на границе соответствовала E_F - U₀ =

Из представленных деталей проведения измере-

= 400 мэВ. Однако мы получили, что расчет лучше

ний ясно, что точное значение величины загиба зон

описывает экспериментальные данные при глубине

после нанесения цезия зависит от значения потенци-

ямы E_F - U₀ = 435 мэВ.

ала, который имеет чистая поверхность. При этом,

Разница в 35 мэВ согласуется с возможной экспе-

как известно, сам факт обращения в нуль волновых

риментальной погрешностью в определении величи-

функций электронов на границе приводит к появле-

ны загиба зон на чистой поверхности методом фото-

нию самосогласованной потенциальной ямы на по-

электронной спектроскопии при указанном в [8] раз-

верхности (см., например, работу [2], разд. 3.1). По-

решении по энергии 35 мэВ. Энергетический спектр

этому было решено рассчитать электронный спектр

фотоэлектронов измерялся в зависимости от угла

поверхности n-InAs без адатомов цезия.

вылета относительно нормали к поверхности в диа-

Чистой поверхности нейтрального в целом полу-

пазоне -3^◦ ≤ Θ ≤ 3^◦ с угловым разрешением 0.5^◦.

проводника отвечают следующие граничные усло-

Для возбуждения фотоэмиссии использовалось син-

вия к уравнению Пуассона (4.47):

хротронное излучение с энергией кванта 8 эВ. Ве-

личина загиба зон на поверхности после нанесения

⁽ du^′ )

= 0,

= 0.

Cs определялась по сдвигу фотоэмиссионного пика

dζζ=0

dζζ=∞

электронов, возбужденных из 4d-оболочки In, отно-

сительно его положения в случае чистой поверхно-

В случае n-InAs при N₊ = 3·10¹⁷ см-3 расчет само-

сти. Положение уровня Ферми в объеме полупровод-

согласованного потенциала для чистой поверхности

1094

ЖЭТФ, том 157, вып. 6, 2020

Решение самосогласованных уравнений Кона - Шэма и Пуассона. . .

полупроводника с учетом обменно-корреляционного

где, таким образом, механизм «кинетического кон-

взаимодействия дает значение E_F - U₀ = 87.1 мэВ,

файнмента» реализуется «естественным путем».

что соответствует загибу зон U₀ = -32.5 мэВ. В та-

Наш опыт таких расчетов с использованием од-

кой потенциальной яме минимум единственной под-

нозонного уравнения эффективной массы для непа-

зоны находится на 0.64 мэВ ниже границы непре-

раболической зоны проводимости не дает оснований

рывного спектра, что не может быть обнаружено в

ни для поддержки гипотезы о существовании дву-

условиях измерений с разрешением 35 мэВ [8].

мерных подзон с минимумом при k_∥ = 0, ни для

Из этих оценок следует, что декларированное

интерпретации эффекта непараболичности как за-

в работе [8] отсутствие загиба зона на чистой по-

висимости эффективной массы от координаты.

верхности InAs после скола в вакууме могло быть

Что касается второго обстоятельства, то выве-

установлено только с такой точностью, которая поз-

денное регулярным образом уравнение эффектив-

воляет допустить существование начального заги-

ной массы (4.39) очевидным образом содержит за-

ба зон порядка 35 мэВ. Соответственно, уменьше-

висимость от энергии состояния в квазипотенциале,

ние потенциала поверхности на 400 мэВ, измерен-

а не в операторе кинетической энергии в коэффици-

ное при нанесении монослоя Cs, означает, что для

енте при второй производной волновой функции.

загиба зон на поверхности в этих условиях мож-

По поводу факта появления в численных расче-

но принять 435 мэВ. Проведенное сопоставление со-

тах двумерной подзоны с k_∥min = 0 следует сказать,

вокупности экспериментальных данных с расчетом

что этот эффект всегда возникает тогда, когда появ-

позволяет также предположить, что найдено пер-

ляются состояния с очень малой энергией связи k2z <

вое экспериментальное доказательство существова-

< 0. Существует ряд объективных причин, которые

ния около поверхности проводника самоорганизу-

затрудняют обнаружение состояний с малой энерги-

ющейся потенциальной ямы Константинова - Ши-

ей связи и увеличивают значение k_∥min, начиная с

ка [3].

которого спектр такой подзоны становится возмож-

ным вычислить (подробнее см. Приложение A).

4.3.3. Особенности расчета спектра

По мере улучшения техники обнаружения со-

возбужденной подзоны, минимум которой

стояний с малой энергией связи в наших расчетах

расположен вблизи границы непрерывного

сначала удалось добиться сходимости итераций при

спектра

некотором k_∥min и тех параметрах потенциальной

На рис. 8 обращает на себя внимание закон дис-

ямы, при которых появлялись подзоны с миниму-

персии третьей подзоны E₂(k2∥), которая появилась

мом вблизи границы непрерывного спектра k2z = 0,

при расчете двумерного спектра для загиба зон в

без чего расчет вообще не может быть закончен, а

435 мэВ. В отличие от спектральных кривых E₀(k2∥)

затем постепенно уменьшать значения k_∥min, хотя и

и E₁(k2∥), минимумы которых находятся в центре

не до нуля. Представленный на рис. 8 спектр тре-

тьей подзоны E₂(k2∥) как раз имеет описанный вид,

двумерной зоны Бриллюэна при

∥

= 0, мини-

но его следует считать скорее артефактом расчета

мальная энергия третьей подзоны E₂ соответству-

с ограниченной точностью, чем подтверждением ги-

ет

= 0.19. При меньших значениях

kz2 = 0, но

∥

потезы кинетического конфайнмента. Дополнитель-

∥ третье локализованное состояние в соответству-

ные аргументы в пользу такого утверждения отне-

ющей потенциальной яме (4.41) не детектировалось.

сены в Приложение A.

Такого типа двумерный энергетический спектр

уже возникал как результат расчетов в случае

непараболической зоны проводимости и стал осно-

4.3.4. Плотность состояний и полуэмпирическая

вой для гипотезы о существовании эффекта, по-

формула для энергетического спектра

лучившего название Motional binding [55], Kinetic

двумерных подзон

confinement [56], или «кинематически связанные»

состояния [57]. Для наглядного его объяснения ис-

Важной характеристикой электронного газа яв-

ляется плотность состояний g(E). Для каждой из

пользуются модели полупроводниковых структур с

эффективной массой, зависящей от пространствен-

размерно-квантованных подзон существует парци-

альная плотность состояний g_j(E). Удобно вместе со

ных координат. При этом зависимость эффектив-

ной массы от энергии в случае непараболической

спектром E_j (k2∥) рассматривать обратную функцию

зоны, как предполагают, в потенциальной яме мож-

k2∥j(E). Номер подзоны соответствует числу конеч-

но трактовать как зависимость массы от координат,

ных нулей функции ψ˜ (ζ), определенной уравне- kk

z ∥

1095

А. Я. Шульман, Д. В. Посвянский

ЖЭТФ, том 157, вып. 6, 2020

g(E)/g p), m* (E)/m_jjc*⁽

ты численного дифференцирования энергетическо-

го спектра двух размерно-квантованных подзон, по-

казанных на рис. 7б.

2.0

Отметим существенные особенности полученных

1.8

графиков. Во-первых, плотность состояний в под-

зонах линейно зависит от энергии, а не постоянна,

1.6

как в параболическом случае, причем коэффициент

наклона не зависит от номера подзоны. Во-вторых,

1.4

j = 0

j = 1

в минимумах подзон эта плотность состояний пре-

1.2

вышает плотность состояний параболического при-

ближения и тем больше, чем глубже расположена

1.0

подзона.

0.8

Пользуясь определением и линейной зависимо-

E₀(0)/EF0

E₁(0)/EF0 E_F/E0

стью плотности состояний от энергии, которую

представим в виде (параметр b не зависит от номера

-1.5

-1.0

-0.5

0.5

1.0

подзоны)

E/E_F

(0)] ,

g_j(ε)/g(p) = a_j + b [ε - ε_j

Рис. 9. Сплошные линии — безразмерная нормирован-

(4.52)

= dk2∥j/dε в основ-

ε_j(0) = ε_j(k2∥)˜k2

ная плотность состояний gj(ε)/g(p)

∥

ной (j

= 0) и первой возбужденной (j

= 1) размер-

но-квантованных подзонах как функции энергии, рассчи-

можно решить соответствующее дифференциальное

танные численным дифференцированием энергетическо-

уравнение первого порядка относительно функции

го спектра, представленного на рис. 7б. Загиб зон равен

dk2∥j(ε)/dε и записать для каждой подзоны получа-

EF -U0 = 400 мэВ, R^s = 0.32. Стрелки отмечают положе-

ющийся полином второй степени от ε в виде, анало-

ния минимумов подзон и энергию Ферми, которая вычис-

гичном закону дисперсии Кэйна:

лена с учетом обменно-корреляционного взаимодействия

(

)

и непараболичности зоны проводимости. Сплошные линии

∥j

(ε) = a_j [ε - ε_j (0)]

(ε - ε_j (0))

(4.53)

также показывают зависимость от энергии нормированной

2a_j

эффективной массы m^∗j(E)/m^∗c в подзонах (см. текст). До-

полнительно построены рассчитанная по формуле (4.56)

Формула (4.53) приобретает еще большее сходст-

зависимость от энергии циклотронной эффективной мас-

во с выражением Кэйна (4.1), если принять во вни-

сы m^∗c(E)/m^∗c для электронов в объеме (штрихпунктир)

мание, что определение (4.51) плотности состояний

и экспериментальная зависимость (кресты) эффективной

квазидвумерного газа с точностью до множителя

массы от энергии, m∗0(E)/m^∗c, в основной подзоне обога-

1/π совпадает с определением циклотронной эффек-

щенного слоя по данным Цуи [6] (магнитотуннельная спек-

тивной массы m^∗cj(E) = k_∥j (E)dk_∥j /dE в j-й под-

троскопия). Все массы нормированы на эффективную мас-

зоне. С учетом сказанного a_j = m^∗j(0)/m^∗c, что поз-

су на дне зоны проводимости

воляет переписать выражение (4.53) в размерном

виде с физически содержательными коэффициента-

ми

нием (4.42). В этих обозначениях с учетом двукрат-

[

]

ного вырождения по спину имеем

k2∥j

E - E_j(0)

= [E - E_j (0)]

(4.54)

∫

2m^∗j(0)

E(eff)

d²k

∥

(

)

g_j(E) = 2

E - E_j(k_∥)

(2π)²

где введена «эффективная» запрещенная зона

∫

dk2∥j

(eff )

E_g

= 2E0F a_j/b.

(4.55)

dE^′

δ (E - E^′) =

(4.51)

2dE^′

2π dE

Согласно оценкам параметров из рис. 9, имеем

В однозонном приближении, E_g → ∞, энергети-

a₀ = 1.25, a₁ = 1.12, b = 0.4. При E0F = 71.5 мэВ по-

ческий спектр в подзонах параболический, E_j (k2∥) =

лучаем E(eff)g0 = 447 мэВ, E(eff)g1 = 400 мэВ. Видно,

= E_j(0) + k2∥/2m^∗c, плотность состояний не зависит

что эти значения близки к объемной ширине запре-

от энергии и будет обозначаться g(p) = m^∗c/π.

щенной зоны E_g = 430 мэВ, но все же не совпадают

На рис. 9 построены нормированные на плот-

с ней, как это иногда предполагают [45], и требует-

ность состояний параболической подзоны результа-

ся их независимое определение. Такая попытка была

1096

ЖЭТФ, том 157, вып. 6, 2020

Решение самосогласованных уравнений Кона - Шэма и Пуассона. . .

предпринята в работе [46] на базе несамосогласован-

mc(3D)(ε)

=1+

2ε.

(4.56)

ного квазиклассического расчета и при некоторых

m^∗c

ε_g

предположениях относительно связи в каждой под-

Соответствующая зависимость построена на рис. 9

зоне между эффективной массой и величиной эф-

штрихпунктиром для принятых нами значений па-

фективной запрещенной зоны. Представленные на

раметров. Видно, что хотя объемная циклотрон-

рис. 6 работы [46] результаты расходятся с наши-

ная масса тоже линейно зависит от энергии, наклон

ми качественно и количественно, что подчеркивает

2E0F /E_g = 0.333 соответствующей прямой заметно

важность полного самосогласованного квантовоме-

меньше наклона b = 0.4 в случае двумерного непа-

ханического рассмотрения.

раболического спектра.

Тождественность в безразмерной форме двумер-

В заключение отметим, что в работе Кэйна [32]

ной плотности состояний и циклотронной эффек-

применимость двухзонного дисперсионного уравне-

тивной массы позволяет сравнить результаты на-

ния связывалась с выполнением неравенств Δ_so ≫

шего расчета с экспериментальной зависимостью от

≫ E_g, E, где Δ_so — энергия спин-орбитального рас-

энергии эффективной массы электронов в основной

щепления валентной зоны. Однако анализ трехзон-

подзоне обогащенного слоя n-InAs, измеренной Цуи

ного дисперсионного уравнения (10) из работы [32]

методом магнитотуннельной спектроскопии [6]. Со-

показывает, что это неравенство можно существен-

ответствующие точки построены на рис. 9 с исполь-

но ослабить. Чтобы доказать это, запишем диспер-

зованием указанных в работе [6] параметров m^∗c =

сионное уравнение Кэйна в окрестности дна зоны

= 0.021, E_g = 410 мэВ, N = 5.4 · 10¹⁷ см-3, E_F =

проводимости в виде

= 95 мэВ.

(

)

На рис. 9 видно, что в безразмерных координа-

k²

E_g + Δ_so

(4.57)

тах данные измерений и расчета близки, несмотря

2m^∗c

E_g

на некоторое отличие параметров реальных образ-

E_g + 2Δ_so/3

цов от использованных нами в расчетах. В измерен-

Множитель в виде дроби не меняет принципиально

ном наборе данных точно так же просматривается

уравнение эффективной массы, и он мало отличен

линейная зависимость эффективной массы от энер-

от единицы в области энергий -E_g/2 < E ≤ E_F .

гии, за исключением начального участка вблизи дна

Конкретно, при E_g = 0.43 эВ и Δ_so = 0.38 эВ [59]

подзоны.

для значений энергии Ферми и энергий связи из

Отметим, что в работе [8] авторы также попы-

табл. 2 отличие этого множителя от единицы не бо-

тались определить эффективную массу на дне ос-

лее 5 %, что лучше точности, с которой известны па-

новной подзоны по измеренной дисперсии E₀(k_∥).

раметры полупроводника и получены эксперимен-

Однако, аппроксимируя экспериментальный набор

тальные данные.

точек параболой, получили m∗0(E₀(0)) = 0.05. Это

значение заметно превышает оценку двумерной эф-

4.3.5. Ортогональность собственных решений

фективной массы на дне основной подзоны, которую

уравнения эффективной массы

можно получить из графика на рис. 9: m∗0(E₀(0)) =

Как уже отмечено в начале разд. 4.2, из-за зави-

= 1.25m∗c = 0.029. Такое различие объясняется,

симости квазипотенциала в уравнении (4.39) от соб-

по-видимому, тем, что параметры аппроксимирую-

ственного значения E каждой собственной функции

щей параболы в значительной мере определялись

отвечает своя потенциальная яма. Поэтому a priori

результатами измерений при больших энергиях, где

нельзя предполагать, что множество собственных

масса больше. Действительно, согласно рис. 9, по-

функций будет ортогональным. Несложные выклад-

лучаем m∗0(E_F )/m^∗c ≃ 2.1.

ки подтверждают, что ортогональности нет. А имен-

Переход от плотности состояний к циклотронной

но [22],

эффективной массе позволяет нам также сравнить

ΦE2k∥2 |ΦE1k∥1

зависимость массы от энергии для двух непарабо-

(

лических законов дисперсии — двумерного и трех-

=δ

k∥2 - k∥1

(4.58)

ψE2k∥2 |ψE1k∥1

мерного в объеме полупроводника. В случае Кэй-

новского закона дисперсии для циклотронной эф-

фективной массы трехмерных электронов имеется

ψE2k_∥ |U|ψE1k∥

ψE2k_∥ |ψE1k∥

(4.59)

выражение [58]

E₁ + E₂ + E_g

1097

А. Я. Шульман, Д. В. Посвянский

ЖЭТФ, том 157, вып. 6, 2020

Таблица 2. Значения загиба зон на поверхности и энергии минимумов подзон размерного квантования, вычислен-

ные с учетом непараболичности зонного спектра и обменно-корреляционного взаимодействия для гетероструктуры

Cs/InAs [8]. Все энергии отсчитаны от уровня Ферми, равного EF = 54.6 мэВ

exp

U₀,

Eth0,

E₀

Eth1,

Eth2,

Образец

T,К

мэВ

InAs clean

87.1^∗

55.2

Cs/InAs

400

160

159^†

Cs/InAs

435^∗

173

Cs/InAs

470

185

88.1

83.7

Примечание. Знак «∗» означает, что загиб зон вычислен нами либо из условия нейтральности образца в случае

чистой поверхности, либо подбором лучшего положения рассчитанного спектра основной подзоны относитель-

но измеренного (см. текст). Знаком «^†» отмечено экспериментальное значение энергии минимума основной

подзоны, определенное из графика фотоэлектронного спектра (вставка на рис. 2 в [8])

Неортогональность собственных функций уравне-

тонормированности точных решений ΨEk∥ уравне-

ния (4.39), казалось бы, влечет за собой наличие

ния (4.7). Только для получения численных резуль-

недиагональных элементов у равновесной одночас-

татов в эти формулы надо подставлять решения

тичной матрицы плотности в этом базисе и усложне-

ΦEk∥ уравнения эффективной массы, взятого в нуж-

ние формул для всех вычисляемых средних, таких,

ном приближении по малому параметру

k²/m^∗cE_g.

например, как формулы (4.30), (4.31) для плотности

Для количественной характеристики степени неор-

электронов.

тогональности решений, полученных в данной рабо-

те, результаты численного расчета интегралов пере-

Однако очевидно, что собственные функции

крытия представлены в Приложении B.

Ψ_E(r) исходной задачи (4.7) образуют ортогональ-

ный набор в силу самосопряженности оператора

Применение сформулированного выше прави-

H₀ + U в обобщенном гильбертовом пространстве.

ла, например, к выражению (4.30) для плотности

В разд. 4.1.2 с использованием унитарного отобра-

электронов позволяет однозначно истолковать его

жения Ψ_E (r) в Φ_E (x) доказано, что из взаимной

как точную формулу, в которую могут быть под-

ортогональности функций Ψ_E должна следовать

ставлены неортогональные решения приближенного

взаимная ортогональность функций Φ_E. Переход от

уравнения эффективной массы. Несоблюдение этого

точной системы уравнений (4.10) к приближенной в

правила может приводить к ошибкам в численных

результате отбрасывания недиагональных межзон-

оценках и физических выводах, как показывает сле-

ных матричных элементов потенциала возмущения

дующий пример.

также не нарушает самосопряженности полученной

В работе [60] аналогичная неортогональность

системы уравнений (4.13). Но при преобразовании

(формула (20)) решений приближенного уравнения

уравнения

(4.17) к окончательному виду

(4.39)

эффективной массы (11) (см. там же (A1)) для по-

был опущен коммутатор невозмущенного гамиль-

лупроводника с непараболической зоной проводимо-

тониана с потенциалом возмущения. В работе [22]

сти послужила основанием для расчета поглощения

доказано, что именно этот шаг порождает неортого-

электронами инверсионного слоя электромагнитно-

нальность собственных решений уравнения (4.39),

го излучения, поляризованного в плоскости слоя,

тогда как собственные решения уравнения (4.17)

за счет переходов 0 → 1 между состояниями ос-

взаимно ортогональны, а последовательный учет

новной подзоны и первой возбужденной (формулы

приближенных выражений для коммутатора во все

(26) и (27) в [60]). Так как уравнение (A1) из [60]

больших порядках по малому параметру

k²/m^∗cE_g

полностью соответствует нашему уравнению (4.6),

приводит ко все меньшим значениям интеграла

а формула (20) из [60] — написанной выше (4.59),

перекрытия 〈ψE1|ψE2 〉.

то в формуле (26) из [60] для вероятности поглоще-

Из сказанного следует, что все формулы, в ко-

ния множитель F_∥ следует положить равным нулю,

торые входят матричные элементы, должны быть

т. е. в принятом приближении поглощение нормаль-

изначально записаны в виде, соответствующем ор-

но падающего электромагнитного излучения долж-

1098

ЖЭТФ, том 157, вып. 6, 2020

Решение самосогласованных уравнений Кона - Шэма и Пуассона. . .

но отсутствовать. И действительно, как отмечено в

ность постановки задачи и упрощенное описание

обзоре [61] (стр. 58, 59), сопоставление с экспери-

обменно-корреляционного взаимодействия электро-

ментом показывает, что расчеты типа проделанных

нов.

в работе [60] переоценивают величину поглощения

В основе метода лежат предложенные в рабо-

при нормальном падении по сравнению с измеряе-

те [1] два изменения обычной теории самосогла-

мым.

сованных уравнений Кона - Шэма: 1) энергия ос-

Можно предположить, что разумная оценка

новного состояния многоэлектронной системы как

электронного поглощения нормально падающего

функционал плотности преобразована в функцио-

излучения за счет межподзонных переходов будет

нал, зависящий не только от плотности электронов,

получена, если выйти за рамки дипольного при-

но и от среднего электростатического потенциала;

ближения для вероятности переходов или учесть

2) в уравнении Пуассона выделен член нелинейного

недиагональные по зонным индексам матричные

экранирования в квазиклассическом приближении.

элементы потенциала в системе уравнений (4.10).

Первое изменение сделало средний потенциал, бла-

Однако в последнем случае это приведет к по-

годаря граничным условиям, независимой от элек-

явлению малых поправок порядка (k2/m^∗cE_g)⁴ в

тронов степенью свободы многоэлектронной систе-

однозонном уравнении эффективной массы

[22]

мы, а уравнение Пуассона — одним из условий ва-

(разд. 3).

риационной задачи на минимум функционала энер-

Доказанный выше запрет межподзонных пере-

гии.

ходов в присутствии электрического поля волны,

Второе изменение обеспечивает сходимость ите-

поляризованной вдоль поверхности гетерострукту-

рационного алгоритма решения совместной систе-

ры, относится к случаю, когда для описания состо-

мы одночастичных уравнений Шредингера и моди-

яний в квантовой яме достаточно представить ис-

фицированного уравнения Пуассона, в котором ста-

комое решение в форме разложения по функциям

тическое экранирование учтено нелинейной квази-

Блоха зоны проводимости. «Многозонность» в раз-

классической формулой (3.11). В результате на каж-

ложении решения по функциям Латтинжера - Ко-

дом шагу итераций в процессе решения уравнения

на не означает реального смешивания состояний зо-

Пуассона с заданными краевыми условиями проис-

ны проводимости и валентной в первом приближе-

ходит самосогласование крупномасштабных неодно-

нии по плавности потенциала ямы. Возможно, что

родностей плотности электронов и потенциала с уче-

в этом причина безуспешных экспериментальных

том наложенных граничных условий. Самосогласо-

попыток реализовать предсказываемое теоретиче-

вание потенциала с мелкомасштабными неоднород-

ски усиление поглощения при нормальном падении

ностями электронной плотности типа фриделевских

за счет непараболичности зоны проводимости [61]

осцилляций или локализации электронов в состо-

(Sec. VIII).

яниях дискретного спектра достигается в рамках

обычной схемы последовательного уточнения реше-

ния.

5. ЗАКЛЮЧЕНИЕ

В разд. 4 продолжена разработка итеративно-

го метода решения самосогласованных уравнений

Результаты разд. 3 показывают, что предложен-

Пуассона и Шредингера для случая, когда учет

ный метод самосогласованного решения системы

непараболического спектра зоны проводимости при-

уравнений Кона - Шэма и Пуассона обеспечивает

водит к уравнению эффективной массы типа урав-

сходимость итерационного цикла даже в тех слу-

нения Шредингера с орбитально-зависимым потен-

чаях, когда вблизи поверхности плотность квази-

циалом и меняет член нелинейного экранирования

двумерных электронов в несколько раз превосходит

в уравнении Пуассона. Выявлены и устранены ос-

плотность электронов в состояниях непрерывного

новные вопросы, которые возникают в процессе ре-

спектра. Вместе с материалом работы [2] это дока-

шения, в частности, неортогональность собствен-

зывает универсальность и дает практически полное

ных решений приближенного уравнения эффектив-

представление об особенностях применения предло-

ной массы и появление размерно-квантованной под-

женного метода к расчету основного состояния по-

зоны с энергией связи вблизи границы непрерывно-

луограниченных многоэлектронных систем. Суще-

го спектра. В последнем случае обнаружен порого-

ственно, что в обоих случаях найденные характери-

вый характер зависимости энергии связи от полной

стики электронного газа оказались близки к опре-

энергии квазидвумерных электронов. Получено, что

деленным экспериментально, несмотря на модель-

учет поправки первого порядка по малому парамет-

1099

А. Я. Шульман, Д. В. Посвянский

ЖЭТФ, том 157, вып. 6, 2020

ру

k²/m^∗cE_g к приближенному уравнению эффек-

жана Российским фондом фундаментальных ис-

тивной массы существенно сдвигает к нулю порого-

следований (проекты №№ 10-02-00869, 13-02-01238 и

вое значение двумерного квазиимпульса, начиная с

16-02-00583).

которого удается рассчитать спектр высоколежащей

Благодарности. Один из авторов (А. Я. Ш.)

подзоны.

благодарен А. Л. Мусатову за разъяснение особен-

Для конкретного случая — обогащенный слой на

ностей экспериментальной техники фотоэлектрон-

поверхности сильнолегированного n-InAs — найден

ной спектроскопии и комментарий к соответствую-

энергетический спектр с линейной зависимостью от

щим разделам работ [8,9], В. А. Волкову за обсужде-

энергии плотности состояний и эффективной мас-

ние деталей метода эффективной массы в многозон-

сы квазидвумерных электронов. Показано количе-

ном случае, проблем с граничными условиями к оги-

ственное согласие с экспериментальными данны-

бающим функциям на поверхности кристалла, воз-

ми. Предложено аналитическое описание двумерно-

можность ознакомиться с соответствующими разде-

го энергетического спектра в виде дисперсионного

лами его диссертации [64] и ссылку на статью Кел-

уравнения типа Кэйна для каждой подзоны, кото-

дыша [40] в связи с проблемой учета непараболич-

рое содержит два параметра — эффективную массу

ности зоны проводимости, а также В. В. Сироткину

на дне подзоны и эффективную ширину запрещен-

за ссылки [24,25].

ной зоны. Этот результат может быть использован в

кинетической теории явлений переноса в квазидву-

мерном электронном газе [62].

ПРИЛОЖЕНИЕ A

Отметим основные отличия количественных ре-

зультатов расчета с учетом конечной ширины за-

Проблема сходимости итераций к

прещенной зоны от часто используемого упрощенно-

самосогласованному решению при наличии

го расчета двумерного спектра для параболической

мелкого уровня

зоны проводимости. Помимо линейной зависимости

A.1. Влияние состояний с малой энергией связи

двумерной плотности состояний от энергии в первом

на сходимость итераций

случае и ее независимости во втором, сопоставле-

ние данных в табл. 1 и 2, а также кривых на рис. 7

Решение системы самосогласованных уравнений

показывает, что расчет в пренебрежении конечной

эффективной массы и Пуассона подразумевает, что

шириной запрещенной зоны завышает энергию свя-

необходимо найти не только спектр собственных

зи для минимумов подзон, занижая при этом зна-

значений задачи для заданной потенциальной ямы,

чения соответствующего граничного квазиимпуль-

но и учитывать, как влияет на потенциал распреде-

са и плотности поверхностного заряда. Перечислен-

ление электронов по состояниям, которые отвечают

ные особенности точного расчета с зависящим от

найденному спектру. Итеративное решение считает-

энергии квазипотенциалом противоречат качествен-

ся полученным, если после очередного цикла ите-

ным выводам о влиянии непараболичности на дву-

раций характеристики системы отличаются от ис-

мерный спектр, которые сформулированы как след-

ходных характеристик перед циклом в пределах до-

ствия расчетов по эмпирической двухзонной модели

пустимых ошибок. Устойчивость полученного реше-

с зависящей от энергии эффективной массой (см.

ния означает, что дальнейшие итерации оставляют

[61], стр. 41 и [63]).

решение неизменным в пределах коридора ошибок.

Обращает также на себя внимание согласие

Для электронного газа в обогащенном слое сфор-

результатов расчета и модельной подгонки фо-

мулированный критерий задает очень жесткие тре-

тоэмиссионных спектров в табл. 1, когда в обоих

бования к выполнению асимптотического условия

случаях используется параболическое прибли-

локальной нейтральности при уходе на бесконеч-

жение для зоны проводимости. Такое согласие

ность по нормали к поверхности. Небольшие откло-

обычно трактуется как оправдание возможности

нения от нейтральности вдали могут приводить к

пренебречь конечной шириной запрещенной зоны.

существенным изменениям решения в области по-

Однако результаты разд. 4 показывают, что эти

тенциальной ямы из-за чувствительности собствен-

совпадающие значения могут значительно отли-

ных функций дискретного спектра к асимптотиче-

чаться от реальных.

ской форме потенциала.

Критически важными становятся указанные об-

Финансирование. Работа выполнена в рам-

стоятельства, если в обогащенном слое имеется ло-

ках государственного задания и частично поддер-

кализованное состояние с малой энергией связи. Та-

1100

ЖЭТФ, том 157, вып. 6, 2020

Решение самосогласованных уравнений Кона - Шэма и Пуассона. . .

ким состояниям соответствует большая протяжен-

После выяснения описанной картины нарушения

ность области, где волновая функция электронов за-

сходимости итераций стало понятно, что необходи-

метно отлична от своего значения на бесконечности.

мо выявлять мелкие уровни и учитывать их вклад,

Поэтому чем мельче уровень, тем на больших рас-

как только для заданного значения k_∥ поведение ре-

стояниях от поверхности надо находить потенциал

шения при k2z = 0 укажет на существование связан-

и электронную плотность, чтобы достичь необходи-

ного состояния с k2zj < 0. Соответствующая часть

мой точности выхода на асимптотическое поведение.

вычислительной процедуры была разработана с ис-

Если в пределах расчетного интервала с доста-

пользованием исследованных в работе [22] свойств

точной точностью не происходит выход потенциала

решения уравнения (4.42) при

= 0 и кратко опи-

на асимптотику и не выполняется условие локаль-

сана в конце разд. 4.2.

ной нейтральности в бесконечности, то итерацион-

Основным инструментом выявления решения

ный процесс перестает сходиться. В случае парабо-

уравнения (4.42) с малой энергией связи

≲ 0, ко-

лической зоны проводимости такая ситуация реали-

торое следовало учесть, был анализ поведения ре-

зуется лишь в малой окрестности определенных зна-

шения ψ0˜k

для

= 0 при заданном значении

∥

чений глубины потенциальной ямы (см. рис. 3 и 4)

Если асимптотика функции ψ0k∥ (ζ) выходит на по-

и может быть проигнорирована, если интересует об-

стоянное значение в области ζ ≲ ζmax (кривая 1

щий ход соответствующих кривых.

на рис. 10а), то принимается, что

= 0 есть соб-

Однако проблема становится острой в непарабо-

ственное значение и соответствующее значение

k∥t

лическом случае, когда мелкие уровни нужно нахо-

является пороговым, начиная с которого становится

дить в целой области значений k_∥ при расчете дву-

возможным вычислять энергетический спектр оче-

мерного спектра для некоторой глубины ямы U₀.

редной подзоны размерного квантования при всех

На первый взгляд, вклад n_sh мелкого состояния в

∥ >

∥t. При этом два узла функции ψ00(ζ) в об-

полную плотность электронов мал, и его не обяза-

ласти ямы (рис. 10а, кривая 1) свидетельствуют о

тельно учитывать, поскольку длина локализации со-

наличии двух нижележащих дискретных уровней в

ответствующей волновой функции ζ_sh ≫ 1 и из-за

квазипотенциальной яме U^′ (рис. 10а, кривая 3),

нормировки связанного состояния на единицу n_sh ∼

что означает существование нормальных основной

∼ 1/ζ_sh ≪ 1.

и первой возбужденной подзон E₀(k_∥) и E₁(k_∥) (см.

Оказалось, что такой подход приводит к рас-

риc. 8) и отсутствие обнаружимого третьего уровня

ходимости всего итерационного процесса по двум

в области 0 ≤ k_∥ < k_∥t .

причинам. Во-первых, появление нового связанного

состояния меняет поведение всех волновых функ-

Если

= 0 не есть собственное значение, то

ций непрерывного спектра вплоть до энергии Фер-

асимптотика решения ψ ˜ (ζ → ∞) представляет со-0k

∥

ми за счет образования у них дополнительного узла

бой монотонно растущую (линейно или логарифми-

в области ямы и соответствующего уменьшения их

чески) функцию (рис. 10а, кривая 2). При выполне-

вклада в плотность электронов.

нии условия ψ0˜k

(ζ_max) · ψ^′ (ζ_max) > 0 считалось,

∥

0k∥

Во-вторых, образуется не одно связанное состо-

что график функции ψ ˜ (ζ) больше не пересека-0k

∥

яние, а двумерная подзона, которая заполнена до

ет ось абсцисс. Следовательно, нет мелкого уровня,

уровня Ферми и содержит конечное число квазидву-

вклад которого надо учитывать, чтобы компенсиро-

мерных электронов. Именно эти электроны должны

вать искажения волновых функций вышележащих

компенсировать уменьшение плотности электронов

состояний непрерывного спектра.

в состояниях непрерывного спектра (см. рис. 2).

В результате без учета вклада мелкой подзоны

Обратное неравенство указывало, что за преде-

в полную плотность вдали от поверхности возни-

лами расчетного интервала [0, ζ_max] находится еще

кал «недобор» заряда электронов, который созда-

один (и только один) узел решения ψ ˜ (ζ), который0k

∥

вал на следующей итерации после решения уравне-

свидетельствует о наличии еще одного дискретного

ния Пуассона самосогласованный потенциал со зна-

уровня с очень малой энергией связи. Выявление та-

чительно уширенной квантовой ямой. В такой яме

ким способом уровня с точкой поворота, лежащей за

возникает уже большое количество мелких дискрет-

границей ζ_max расчетного интервала, задействова-

ных состояний, пренебрежение вкладом которых ве-

ло описанный в разд. 4.2 алгоритм приближенного

дет к дальнейшему увеличению области ямы, в ко-

вычисления решения ψ

(ζ) и его вклада в плот-

k_z k

∥t

торой система не является электронейтральной, и к

ность электронов. Этот прием обеспечил сходимость

расходимости всего итерационного процесса.

итераций с принятой точностью.

1101

А. Я. Шульман, Д. В. Посвянский

ЖЭТФ, том 157, вып. 6, 2020

k /kzF22

(z; k

= 0)

0.4

0.3

-0.001

0.2

0.1

–0.002

-0.1

100

150

200

0.1

0.2

0.3

0.4

k z_F

(E - E ) /(EtF20

)

Рис. 10. а) Свойства решений уравнения эффективной массы вблизи порога рождения новой размерно-квантованной

подзоны E2 на рис. 8а. Волновые функции и квазипотенциал: 1 — нормированная на δ(kz ) собственная функция для

нулевого собственного значения kz = 0 при k∥ = 0.45; 2 — ненормированное решение уравнения эффективной массы

для kz = 0, k∥ = 0 при граничном условии ψ(0) = 0, ψ^′(0) = 1; 3 — квазипотенциал, нормированный на 10Uqp(0). Ось

абсцисс при построении кривых 2 и 3 растянута в 10 раз. б) Проявление порогового эффекта на зависимости энергии

связи k2z от глубины квазипотенциальной ямы, которая пропорциональна полной энергии E^′ двумерного состояния со-

гласно формуле (4.41) для Uqp(z; E^′): кресты — результат самосогласованного решения; сплошная линия построена по

формуле (A.2). Через Et = 0.108E^F обозначено пороговое значение энергии, при котором начинает существовать третья

двумерная подзона E2(^k∥)

Важно отметить, что значение квазипотенциала

вие E^′(k_∥) > -E_g/2. Поэтому с ростом k_∥ энергия

U_qp(ζ_max) < 0 на границе определяет максимальное

растет, глубина квазипотенциальной ямы (4.41) уве-

значение

< 0, для которого решение ψ

бу-

личивается, и при некотором пороговом значении

k_z k

∥

дет иметь реальную точку поворота. При ζ > ζ_max

k_∥

= k_t в ней может появиться новое локализо-

отличием U_qp от нуля пренебрегается, что означа-

ванное состояние. При дальнейшем увеличении k_∥

ет наличие вертикальной потенциальной стенки от

потенциальная яма продолжает углубляться, уве-

U_qp(ζ_max) до нуля в точке ζ_max. Соответственно, все

личивается энергия связи и формируется очередная

решения ψ˜kzk

для U_qp <

< 0 будут иметь точку

двумерная подзона.

∥

поворота на этой стенке, и реальное значение энер-

гии связи не может быть установлено точнее, чем

Такое поведение двумерного спектра отмечалось

ширина полоски (U_qp(ζ_max), 0).

ранее в работе [55] и послужило одним из доводов

в пользу гипотезы о возможной локализации элек-

A.2. Пороговые эффекты в двумерном спектре

трона за счет пространственной неоднородности эф-

электронов обогащенного слоя

фективной массы [55,56,65]. Однако есть основания

Как уже указывалось, квазипотенциал U_qp,

сомневаться, что квазидвумерный электронный газ

входящий в уравнение (4.39), зависит от энергии

в обогащенном слое на поверхности полупроводни-

E^′. Энергетический спектр двумерных собственных

ка с непараболической зоной проводимости может

состояний уравнения эффективной массы (4.17),

быть примером такой системы. Помимо соображе-

сформированных только из функций Блоха зоны

ний в пользу такой точки зрения, приведенных в

проводимости, определяется корнем E₁(k) из (4.2)

разд. 4.3.2, отметим еще ряд чисто вычислительных

для каждой пары значений (k2∥, k2z) формулой

проблем, которые надо учитывать при анализе ре-

E^′(k_∥) = E1(k2∥ + k2z(k2∥)), что накладывает усло-

зультатов численных расчетов.

1102

ЖЭТФ, том 157, вып. 6, 2020

Решение самосогласованных уравнений Кона - Шэма и Пуассона. . .

∫

∞

Прежде всего условимся называть дискретный

ψ_t(ζ)ψ_ε(ζ)

I =

dζ

u^′(ζ)

уровень очень мелким, если нормировочный ко-

ε_g

C_tC_ε

эффициент соответствующей собственной функции

формируется в асимптотической области за пре-

√

и нормировочных констант C_t = 1/

2π, C_ε = 2|kz|.

делами расчетного интервала. Так как при ζ

Через ε_t обозначена энергия состояния с

= 0

> ζ_max полагаем U_qp(ζ) = 0, в этой области ψ

k_z k

∼

∥

при пороговом значении квазиимпульса

∥t. Для ма-

∼ Aexp(-|kz|ζ) и нормировочный интеграл можно

лых энергий вблизи порога выражение в квадрат-

представить в виде

ных скобках близко к единице. Это позволило оце-

[

]-1

нить константу

I² по наклону начального участка

самосогласованного расчета и сравнить пороговую

A² = B² +

exp(-2|kz|ζ_max)

2|kz|

формулу (A.2) для энергии связи с результатом точ-

∫

(A.1)

ного расчета, как показано на рис. 10б. Видно, что,



поведение

вблизи начала подзоны E₂(k∥) носит

B² =

dζ

ψ

k_z k



∥

пороговый характер. Поэтому замедленное углубле-

˜∥ в пороговой области увеличива-

ние

с ростом

ет значение

Очевидно, что при фиксированном значении ζ_max и

∥t, начиная с которого подзона E2(^k∥)

постоянстве начальных условий ψ(0) = 0, ψ^′(0) = 1

проявляется в расчете.

условие мелкого уровня всегда наступит при доста-

Вторым обоснованием гипотезы «кинетическо-

точно малом |kz|. С другой стороны, достаточно ма-

го конфайнмента» послужило экспериментально об-

лые собственные значения

< 0 всегда должны

наруженное замедленное заполнение электронами

иметь место, когда речь идет о глубине потенциаль-

вновь образованной подзоны с ростом напряже-

ной ямы, при которой в спектре появляется новая

ния на затворе МОП-структур на основе n-InAs и

подзона.

HgCdTe ([45] Fig. 10, [46] Рис. 3, [57] Рис. 12).

Учитывая перечисленные выше факторы, кото-

Однако теория порогового эффекта тоже допус-

рые ограничивают снизу возможность обнаруже-

кает такой характер формирования новой подзоны.

ния состояния с малой энергией связи при кон-

И даже предсказывает зависимость от напряжения

кретной реализации численного алгоритма, а также

на затворе вида (V_g - V_t)², где V_t — значение поро-

гового напряжения в момент появления новой под-

рост глубины квазипотенциальной ямы с ростом

∥

вполне естественно ожидать, что состояния вновь

зоны. Квадратичная зависимость от расстройки, а

образовавшейся подзоны начинают обнаруживать-

также наблюдение аналогичного «замедления» при

ся при конечном

= 0. Имеется или нет при этом

образовании новой подзоны в обогащенном слое на

∥t

поверхности полупроводника с широкой запрещен-

для

∥

= 0 более мелкое связанное состояние, ко-

ной зоной и незначительной непараболичностью зо-

торое не удается обнаружить, требует специального

ны проводимости могут позволить выбрать между

анализа.

двумя объяснениями этого эффекта.

Есть еще одна причина, из-за которой величи-

Добавим еще, что уравнения эффективной мас-

на

сдвигается в бóльшую сторону. Сформулиро-

∥t

сы и Пуассона являются экстремалями вариацион-

ванное выше условие малости энергии связи одно-

ной задачи на минимум функционала энергии ос-

временно означает, что зависимость энергии связи

новного состояния ([1] Eq. (62)). Состояние

= 0,

от параметра, определяющего глубину потенциаль-

= 0 обладает меньшей энергией, чем

= 0,

∥

ной ямы, будет носить пороговый характер [66, 67].

> 0. Поэтому следует ожидать такой модификации

В данном случае можно показать, что зависимость

формы самосогласованной потенциальной ямы, при

собственного значения

уравнения (4.39) от пара-

которой минимум любой подзоны, включая близ-

метра E^′ в выражении (4.41) для квазипотенциала

кую к непрерывному спектру, будет находиться при

описывается формулой (в безразмерных величинах)

= 0.

∥

[

]

ε₀ - ε_t

1+2

I²

= -(ε₀ - ε_t)²

I².

(A.2)

A.3. Влияние длины расчетного интервала на

1 + 2ε₀/ε_g

энергию связи мелкого уровня

Здесь введены обозначения для энергий (см. фор-

Как объяснено выше, наличие в спектре мелкого

мулу (4.43)) ε₀ = ε(0,k2∥), ε_t = ε(0,k2t), матричного

уровня может разрушить сходимость итераций, ес-

элемента потенциала

ли не принять меры к его обнаружению и учету. Од-

1103

А. Я. Шульман, Д. В. Посвянский

ЖЭТФ, том 157, вып. 6, 2020

-E₀/EF0

Хотя качественно результаты обоих расчетов со-

0.025

ответствуют примерно одной области концентра-

ции электронов, в которой существует уровень, ко-

личественно величина энергии связи может разли-

0.020

чаться до трех раз, как видно из рис. 11. Поэто-

му одной только сходимости итерационной проце-

дуры недостаточно, необходима проверка устойчи-

вости результатов относительно увеличения ζ_max.

0.015

ПРИЛОЖЕНИЕ B

0.010

Оценка степени неортогональности

собственных функций уравнения

0.005

эффективной массы

Согласно формулам (4.58), (4.59), мерой неор-

тогональности служит скалярное произведение

0.2

0.4

0.6

0.8

1.0

1.2

〈ψE2k_∥ |ψE1k∥〉двухрешенийуравнения(4.39)при

R_s*

совпадающих k_∥, но разных энергиях E. В случае

связанных состояний расчет этого скалярного

Рис. 11. Демонстрация зависимости энергии связи мел-

произведения не представляет трудностей. Для

кого основного состояния от длины расчетного интерва-

собственных функций минимумов основной под-

ла. Построена зависимость от плотности положительного

зоны ψE00 и первой возбужденной подзоны ψE10

фона энергии электрона, локализованного в самосогласо-

ванной потенциальной яме Константинова - Шика вблизи

при U₀ = 400 мэВ получаем 〈ψE10|ψE00〉 = 0.051.

В вероятность поглощения нормально падающего

бесконечно высокой потенциальной стенки. Кривая 1 полу-

на квазидвумерный электронный газ излучения

чена при длине расчетного интервала 200 и остается прак-

тически неизменной при дальнейшем его увеличении. Кри-

войдет квадрат этого скалярного произведения [60]

вая 2 была рассчитана в работе [2] при длине расчетного

(формулы (26), (27)). Этим определяется порядок

интервала 80. Энергия связи отсчитана от положения дна

величины эффекта, полученного в работе

[60],

зоны проводимости с учетом вклада Uxc(∞)

когда использовались неортогональные решения

приближенного уравнения (4.39).

Формула (4.59) позволяет рассчитать степень

неортогональности и в случае состояний непрерыв-

нако даже если сходимость достигнута, важно про-

ного спектра без необходимости вычислять интегра-

верять независимость полученной энергии уровня

лы от функций с осциллирующей на бесконечно-

от длины расчетного интервала. Особенно этот шаг

сти асимптотикой (4.44). Результаты показаны на

необходим в тех случаях, когда в расчете появляется

рис. 12 для разных пар энергий E₁ = E(kz1, k_∥) и

эффект «кинематического конфайнмента». Напри-

E₂ = E(k_z, k_∥) при k_∥ = 0 и k2z > 0. Функция E(k)

мер, в работе [65] существование в обогащенном слое

здесь задана законом дисперсии (4.2) в зоне прово-

InAs подзоны с ненулевым начальным квазиимпуль-

димости. Видно, что во всем квадранте 0 < k_z , kz1 ≤

сом получено при слишком малой длине расчетного

≤ 1 степень неортогональности меньше единицы, а

интервала ζ_max = 16.

ее квадрат не превышает оценки параметра малос-

В подтверждение этой рекомендации на рис. 11

ти, сделанной в конце разд. 4.1.1. Согласно работе

для параболической зоны проводимости построена

[22], если необходима большая точность, однозонное

рассчитанная зависимость энергии связи основно-

уравнение метода эффективной массы может быть

го состояния от плотности положительного фона в

взято с учетом первой поправки (4.18) от коммута-

самосогласованной потенциальной яме Константи-

тора.

нова - Шика при двух длинах расчетного интерва-

Также был проведен расчет скалярных произве-

ла. Заодно этим рисунком исправляется результат,

дений собственных функций непрерывного спектра

недостаточно аккуратно полученный в работе [2] из-

в случае параболической зоны проводимости, рас-

за вычислительных сложностей того времени при

смотренном в разд. 3, чтобы независимо от усло-

большой длине расчетного интервала.

вия (3.25) оценить степень точности критерия оста-

1104

ЖЭТФ, том 157, вып. 6, 2020

Решение самосогласованных уравнений Кона - Шэма и Пуассона. . .

∫∞

〈Ψkz1 |Ψkz 〉 = lim

Ψ^∗k

(z)Ψkz (z) exp^-ϵz dz, (B.3)

ϵ→0

10^-1

через которые выражаются скалярные произве-

дения в обобщенном гильбертовом пространстве

[22] (формула (5.4)), используем прием выделения

10^-2

сингулярной части интегралов, предложенный в

[22] (разд. 5.2.2.IV). Введем остаточную функцию

Θkz(z)

10^-3

√

Θkz(z) = Ψkz(z) -

sin(k_z z + γkz ).

(B.4)

10^-4

Предполагается, что потенциал на бесконечности

стремится к нулю достаточно быстро, чтобы были

выполнены условия для существования асимптоти-

10^-5

ки (B.2) с постоянными амплитудой и фазой [41]

(Гл. III, § 9).

-6

Формулы (B.2)-(B.4) позволяют при численном

0.01

0.1

расчете скалярного произведения найти сингуляр-

k /k_zF

ные вклады аналитически. Представим (B.3) в виде

Рис. 12. Зависимости меры неортогональности самосогла-

∞

∫

(

)_∗

сованных собственных функций непрерывного спектра от

〈Ψkz1 |Ψkz 〉 = lim

Θkz1(z) + Ψ(∞)(z)

kz1

волнового вектора. Номерами 1, 2, 3 обозначены скаляр-

ϵ→0

ные произведения 〈Ψkz1 |Ψkz 〉 собственных функций од-

(

)

нозонного уравнения эффективной массы (4.6) для непа-

× Θkz(z) + Ψ(∞)(z) exp^-ϵz dz. (B.5)_k

раболической зоны проводимости при kz1

= 1.0 (1);

Интеграл от произведения двух асимптотик вычис-

kz1 = 0.01 (2); kz1 = 0.002 (3). Точками 4 показаны зна-

чения скалярных произведений найденных численно соб-

ляется явно и содержит как сингулярные члены

ственных функций уравнения эффективной массы (3.1)

δ(kz1 ± k_z), так и несингулярные.

для параболической зоны проводимости. В последнем слу-

В итоге при k1z = k_z получаем искомую формулу

чае расчет по формуле (B.6) показывает, что эти функции

для отклонения

δ от δ(kz1 - k_z) скалярного произ-

практически ортогональны

ведения собственных функций, найденных численно

на отрезке 0 ≤ z ≤ L:

новки итерационного процесса. Поскольку задача

(3.19), (3.20) самосопряженная, для проверки орто-

∫

гональности надо вычислять скалярные произведе-

δ = dzΘkz1(z)Θkz(z) + dzΘkz1(z)Ψ(∞)(z)+_k

ния непосредственным интегрированием численно

полученных решений.

∫

Для компактности изложения перепишем урав-

+ dzΘkz(z)Ψ(∞)(z) -_k

нение (3.1) в упрощенном виде:

[

]

^[ sin(Δ₁₂γ)

sin(Σ₁₂γ)

Ψ^′′k

(z) + U(z) -

k²

Ψkz(z) = 0.

(B.1)

(B.6)

π Δ₁₂k_z

Σ₁₂k_z

где

Если потенциал U(z → ∞) = 0, то δ-нормированные

собственные функции непрерывного спектра Ψkz(z)

Δ₁₂k_z = kz1 - k_z, Δ₁₂γ = γkz1 - γkz

для задачи на полуоси 0 ≤ z < ∞ имеют асимпто-

Σ₁₂k_z = kz1 + k_z, Σ₁₂γ = γkz1 + γkz .

тику

√

Подстановка в интегралах конечного верхнего

lim

Ψ(∞)k(z) =

sin(k_z z + γkz ),

(B.2)

предела L вместо ∞ оправдана, если подынтеграль-

z→∞

ные выражения содержат как минимум квадратич-

где фаза γkz численного решения определяется фор-

но интегрируемые функции Θkz (z). Нетрудно пока-

мулой (3.22).

зать, составив уравнение для Θkz (z), что достаточ-

Чтобы не искать численно предел регуляризо-

ным условием для этого может служить квадратич-

ванных интегралов

ная интегрируемость потенциала U(z). При kz1 = k_z

1105

ЖЭТФ, вып. 6

А. Я. Шульман, Д. В. Посвянский

ЖЭТФ, том 157, вып. 6, 2020

все члены в (B.6) конечны и могут быть найдены

12.

F. Stern, Phys. Rev. B 5, 4891 (1972).

численно. В случае самосопряженной задачи выра-

13.

G. A. Baraff and J. A. Appelbaum, Phys. Rev. B 5,

жение (B.6) для

^δ равняется нулю при любых сколь

475 (1972).

угодно близких значениях kz1, k_z и может быть до-

определено нулем по непрерывности при kz1 = k_z .

14.

D. H. Ehlers and D. L. Mills, Phys. Rev. B 34, 3939

Для задачи с орбитально-зависимым потенциалом

(1986).

или при подстановке в качестве собственных функ-

15.

G. Makov and M. C. Payne, Phys. Rev. B 51, 4014

ций численно найденных решений величина

δ слу-

(1995).

жит мерой неортогональности собственных функ-

ций непрерывного спектра.

16.

C. W. M. Castleton, A. Höglund, and S. Mirbt, Phys.

Справедливость формулы (B.6) была провере-

Rev. B 73, 035215 (2006).

на на собственных функциях непрерывного спектра

17.

C. A. Rozzi, D. Varsano, A. Marini et al., Phys. Rev.

при непараболической зоне проводимости сравнени-

B 73, 205119 (2006).

ем с формулой (4.59) и прямым вычислением преде-

ла регуляризованных интегралов.

18.

A. F. Wright and N. A. Modine, Phys. Rev. B 74,

235209 (2006).

На рис. 12 точки 4 показывают зависимость ска-

лярного произведения 〈Ψkz1 (ζ)|Ψkz (ζ)〉 состояний

19.

A. Cerioni, L. Genovese, A. Mirone et al., J. Chem.

непрерывного спектра от волнового вектора k_z при

Phys. 137, 134108 (2012).

kz1 = 1, вычисленную для параболического закона

20.

J. A. Appelbaum and D. R. Hamann, Rev. Mod.

дисперсии в зоне проводимости. Видно, что скаляр-

Phys. 48, 479 (1976).

ное произведение равно нулю с точностью до чис-

ленной ошибки порядка 10-6, как и должно быть

21.

T. R. Durrant, S. T. Murphy, M. B. Watkins, and

в этом случае согласно критерию (3.25) остановки

A. L. Shluger, J. Chem. Phys. 149, 024103 (2018).

итераций.

22.

А. Я. Шульман, ЖЭТФ 158 (2020).

23.

Übensee, G. Paasch, and J.-P. Zöllner, Phys. Rev.

ЛИТЕРАТУРА

B 39, 1955 (1989).

1. A. Ya. Shul’man, J. Phys.: Conf. Ser. 35, 163 (2006).

24.

I-H. Tan, G. L. Snider, L. D. Chang, and E. L. Hu,

J. Appl. Phys. 68, 4071 (1990).

2. Д. В. Посвянский, А. Я. Шульман, ЖЭТФ 136,

169 (2009).

25.

A. Trellakis, A. T. Galick, A. Pacelli, and U. Ravaioli,

J. Appl. Phys. 81, 7880 (1997).

3. О. В. Константинов, А. Я. Шик, ЖЭТФ 58, 1662

(1970).

26.

P. D. C. King, T. D. Veal, and C. F. McConville,

Phys. Rev. B 77, 125305 (2008).

4. J. A. Appelbaum and G. A. Baraff, Phys. Rev. Lett.

26, 1432 (1971).

27.

M. G. Betti, V. Corradini, V. De Renzi et al., Sol. St.

Comm. 110, 661 (1999).

5. D. C. Tsui, Phys. Rev. Lett. 24, 303 (1970).

28.

A. E. Mattsson, P. A. Schultz, M. P. Desjarlais et al.,

6. D. C. Tsui, Phys. Rev. B 4, 4438 (1971).

Modelling Simul. Mater. Sci. Eng. 13, R1 (2005).

7. D. C. Tsui, Phys. Rev. B 8, 2657 (1973).

29.

A. Ya. Shul’man and D. V. Posvyanskii, J. Phys.:

Conf. Ser. 510, 012029 (2014).

8. V. Yu. Aristov, G. Le Lay, V. M. Zhilin et al., Phys.

Rev. B 60, 7752 (1999).

30.

Д. В. Посвянский, А. Я. Шульман, в сб. Тези-

сы докл. XII Росс. конф. по физике полупроводни-

9. M. G. Betti, V. Corradini, G. Bertoni et al., Phys.

ков — Полупроводники-2015, Москва, Физический

Rev. B 63, 155315 (2001).

институт им. П. Н. Лебедева РАН (2015), с. 248.

10. T. Ando, A. B. Fowler, and F. Stern, Rev. Mod.

31.

W. Franz, Dielektrische Durchschlag, Handbuch der

Phys. 54, 437 (1982) [Е. Андо, А. Фаулер, Ф. Стерн,

Physik, Band XVII, S. 155, Springer, Berlin (1956)

Электронные свойства двумерных систем, Мир,

[В. Франц, Пробой диэлектриков, Изд-во иностр.

Москва (1985)].

лит., Москва (1961)].

11. F. Stern, J. Comput. Phys. 6, 56 (1970).

32.

E. O. Kane, J. Phys. Chem. Sol. 1, 249 (1957).

1106

ЖЭТФ, том 157, вып. 6, 2020

Решение самосогласованных уравнений Кона - Шэма и Пуассона. . .

33.

P. N. Butcher, J. A. Hulbert, and K. F. Hulme, J.

51.

Н. Ашкрофт, Н. Мермин, Физика твердого тела,

Phys. Chem. Sol. 21, 320 (1961).

т. 1, Мир, Москва (1979).

34.

J. W. Conley and G. D. Mahan, Phys. Rev. 161, 681

52.

N. Marzari, A. A. Mostofi, J. R. Yates et al., Rev.

(1967).

Mod. Phys. 84, 1419 (2012).

35.

A. Ya. Shul’man and V. V. Zaitsev, Sol. St. Comm.

53.

J. M. Luttinger and W. Kohn, Phys. Rev. 97, 869

18, 1623 (1976).

(1955).

36.

И. Н. Котельников, И. Л. Бейнихес, А. Я. Шуль-

54.

W. Kohn, Rev. Mod. Phys. 71, 1253 (1999).

ман, ФТТ 27, 401 (1985).

55.

R. E. Doezema and H. D. Drew, Phys. Rev. Lett. 57,

37.

И. Н. Котельников, Д. К. Чепиков, Е. Г. Чиркова,

762 (1986).

А. Я. Шульман, ФТП 21, 1854 (1987).

56.

M. Kubisa and W. Zawadzki, Semicond. Sci. Technol.

38.

I. N. Kotel’nikov and A. Ya. Shul’man, in Proc.

8, S246 (1993).

19th Int. Conf. on Phys. Semicond., Warsaw (1988),

57.

Г. М. Миньков, О. Э. Рут, А. В. Германенко,

Vol. 1, p. 681.

ЖЭТФ 112, 537 (1997).

39.

T. Ando, J. Phys. Soc. Jpn. 54, 2676 (1985).

58.

И. М. Цидильковский, Зонная структура полу-

40.

Л. В. Келдыш, ЖЭТФ 45, 364 (1963).

проводников, Наука, Москва (1978), § 4.3.

41.

А. Мессиа, Квантовая механика, т. 1, Наука,

59.

I. Vurgaftman, J. R. Meyer, and L. R. Ram-Mohan,

Москва (1978).

J. Appl. Phys. 89, 5815 (2001).

42.

М. Абрамовиц, И. Стигал, Справочник по специ-

60.

W. Zawadzki, J. Phys. C 16, 229 (1983).

альным функциям, Наука, Москва (1975), Гл. 25,

61.

M. Helm, in Intersubband Transitions in Quantum

№№ 25.4.47 и 25.4.54.

Wells: Physics and Device Applications I, ed. by

43.

В. Л. Коротких, А. Л. Мусатов, В. Д. Шадрин,

H. C. Liu and F. Capasso, Acad. Press, London

Письма в ЖЭТФ 27, 652 (1978).

(2000) (Semiconductors and Semimetals, Vol. 62,

Ch. 1).

44.

O. Madelung, Semiconductors: Data Handbook,

Springer, Berlin (2003).

62.

А. Я. Шульман, в сб. Тезисы докл. XIII Росс. конф.

по физике полупроводников (Екатеринбург, 2017),

45.

H. Reisinger, H. Schaber, and R. E. Doezema, Phys.

Институт физики металлов УрО РАН, с. 223.

Rev. B 24, 5960 (1981).

63.

D. F. Nelson, R. C. Miller, and D. A. Kleinman, Phys.

46.

В. Ф. Раданцев, Т. И. Дерябина, Л. П. Зверев и

Rev. B 35, 7770(R) (1987).

др., ЖЭТФ 91, 1016 (1986).

64.

В. А. Волков, Диссертация . . . доктора физ.-ма-

47.

Ö. Olsson, C. B. M. Andersson, M. C. Hakansson

тем. наук, ИРЭ АН СССР, Москва (1987).

et al., Phys. Rev. Lett. 76, 3626 (1996).

65.

A. Zhang, J. Slinkman, and R. E. Doezema, Phys.

48.

Р. Курант, Д. Гильберт, Методы математичес-

Rev. B 44, 10752 (1991).

кой физики, т. 1, Гостехиздат, Москва-Ленинград

(1933), Гл. VI, конец § 6.

66.

А. И. Базь, Я. Б. Зельдович, А. М. Переломов,

Рассеяние, реакции и распады в нерелятивистс-

49.

Б. М. Левитан, И. С. Саргсян, Введение в спект-

кой квантовой механике, Наука, Москва (1971),

ральную теорию, Наука, Москва (1970), Гл. I, § 3.

с. 22.

50.

W. Kohn and C. Majumdar, Phys. Rev. 138, A1617

67.

Л. Д. Ландау, Е. М. Лифшиц, Квантовая механи-

(1965).

ка, Наука, Москва (1989), § 45, задача 1.

1107

10*