ЖЭТФ, 2020, том 157, вып. 6, стр. 1108-1119

МЕЛКОМАСШТАБНЫЙ АНАЛИЗ ПОДАВЛЕНИЯ

ГИДРОДИНАМИЧЕСКОЙ СПИРАЛЬНОСТИ

В ДИНАМО-МОДЕЛИ СРЕДНЕГО ПОЛЯ

Е. В. Юшковa,b*, А. С. Лукин^a,c, Д. Д. Соколов^b,d

^a Институт космических исследований Российской академии наук

117997, Москва, Россия

^b Московский государственный университет им. М. В. Ломоносова

119991, Москва, Россия

^c Национальный исследовательский университет Высшая школа экономики

101100, Москва, Россия

^d Институт земного магнетизма, ионосферы и распространения радиоволн Российской академии наук

108840, Троицк, Москва, Россия

Поступила в редакцию 6 ноября 2019 г.,

после переработки 9 января 2020 г.

Принята к публикации 9 января 2020 г.

Проводится сравнение классической динамо-модели среднего поля, предложенной Штеенбеком, Краузе и

Рэдлером для описания генерации крупномасштабных полей, и модели Казанцева, описывающей работу

мелкомасштабного динамо в неограниченном однородном и изотропном пространстве. Рассматривается

субкритический режим малых магнитных чисел Рейнольдса, при котором отсутствует быстрая генера-

ция. Этот же режим можно понимать и как процесс, в котором мелкомасштабная генерация остановлена

за счет своих внутренних механизмов. В рамках обоих подходов исследуется, чем различаются спектры

линейного и нелинейного процессов при подавлении гидродинамической (кинетической) спиральности,

или другими словами, проводится сравнение альфа-квенчингов. В работе проверяется, ведет ли усред-

нение уравнения индукции по масштабам, большим чем корреляционная длина поля скорости, к потере

каких-либо черт спектра вблизи диссипативного масштаба. Изучаются различные виды стабилизации ди-

намо, использование которых кажется более обоснованным с физической точки зрения, чем стандартное

альфа-подавление, но более затрудненным в рамках крупномасштабных моделей, содержащих ограни-

ченную информацию о случайном поле скорости. В частности, сравнивается интегральное подавление,

при котором сохраняется полная энергия, и спектральное подавление, которое предполагает сохране-

ние энергии и спиральности в каждой спектральной оболочке, не предполагая их перераспределения по

спектру.

DOI: 10.31857/S0044451020060103

Один из них, который принято называть круп-

номасштабным динамо, или динамо среднего поля,

требует зеркальной асимметрии конвекции/турбу-

1. ВВЕДЕНИЕ

лентности и приводит к возникновению магнитно-

Процесс преобразования кинетической энергии

го поля, пространственный масштаб которого сопо-

движений среды в энергию магнитного поля, при-

ставим с размерами самого тела. Одновременно с

водящий, в частности, к формированию магнитных

крупномасштабной генерацией этот механизм созда-

полей Земли, Солнца, звезд и галактик, принято на-

ет и мелкомасштабную компоненту, с характерными

зывать магнитогидродинамическим динамо (см., на-

размерами меньшими, чем размеры тела. Примеча-

пример, обзор [1]). Можно выделить два канала, по

тельно, что уравнения динамо среднего поля мож-

которым происходит это преобразование.

но сформулировать таким образом, чтобы они со-

держали только крупномасштабные переменные и

^* E-mail: yushkov.msu@mail.ru

1108

ЖЭТФ, том 157, вып. 6, 2020

Мелкомасштабный анализ подавления гидродинамической спиральности...

не описывали мелкомасштабные прямо. Поскольку

мелкомасштабного подхода к анализу задачи магни-

крупномасштабное поле на астрофизических мас-

тогидродинамического динамо лежит классическое

штабах интересует исследователей в первую очередь

уравнение магнитной индукции (см., например, [4]):

[2], изучению мелкомасштабных компонент, генери-

B_t = rot[v × B] + η△B .

(1)

руемых этим видом динамо, исторически уделялось

чрезвычайно мало внимания.

Будучи усредненным по случайному однородному

Другой канал генерации, известный как турбу-

полю скорости, оно приводит к широко известной

лентное динамо, производит лишь мелкомасштаб-

модели среднего поля, предложенной Штеенбеком,

ные магнитные поля, характерный размер которых

Краузе и Рэдлером (см., например, описание модели

определяется энергонесущим масштабом турбулент-

в [5], или подробный вывод уравнений в [6]):

ности/конвекции и может быть существенно меньше

размеров всего тела (см., например, [3]). Для работы

B_t = αrotB + η△B.

(2)

этого механизма не нужны ни дифференциальное

вращение, ни зеркальная асимметрия, но, в прин-

В этом подходе величина η характеризует магнит-

ципе, механизм функционирует и во вращающихся

ную вязкость среды, а величина α = τ〈v · rot v/3〉

средах с ненулевой спиральностью. Для описания

определяет зеркально-асимметричные свойства по-

мелкомасштабных процессов естественно приходит-

тока и носит название гидродинамической/кинети-

ся использовать характеристики магнитного поля

ческой спиральности (v — случайная компонента

на малых масштабах, при этом разумной характери-

скорости, а τ — время оборота вихря). Модель Ште-

стикой могут служить энергетические или корреля-

енбека - Краузе - Рэдлера описывает генерацию маг-

ционные функции, так как среднее крупномасштаб-

нитных полей на масштабах много больших, нежели

ное поле при такой генерации может и не изменять-

характерная корреляционная длина случайного по-

ся.

ля, в то же время после усреднения по масштабам

Важно заметить, что уравнение для корреляци-

много меньшим корреляционной длины из уравне-

онного магнитного поля, выписанное в полном объе-

ния индукции можно прийти к уравнению, впервые

ме, содержит информацию о среднем значении поля.

полученному Казанцевым для зеркально-симмет-

Однако такое уравнение очень громоздко и неудоб-

ричных в среднем сред [7] (в иностранной литерату-

но для исследования, поэтому из него путем разно-

ре первое описание турбулентного динамо обычно

образных упрощений выделяют часть, ответствен-

ассоциируется с работой [8], а зеркально-асиммет-

ную за возникновение собственно мелкомасштаб-

ричный случай с работой [9]). В дельта-коррелиро-

ной состовляющей. Кроме того, само разделение на

ванном случайном однородном и изотропном поле

крупно- и мелкомасштабные компоненты магнитно-

скорости усреднение уравнения индукции (1) дает

го поля является приближенным, поскольку дале-

систему двух уравнений второго порядка с фикси-

ко не всегда энергонесущий масштаб и характерные

рованной вязкостью η(r) и спиральностью α(r):

размеры тела отличаются на много порядков, да и

сама форма тела может характеризоваться несколь-

M_t = 2r-4(r⁴ηM_r)_r + 2Mr-4(r⁴η_r)_r - 4αK,

(3)

кими величинами различного масштаба (как, напри-

мер, радиус и толщина тонкого диска галактики, ко-

K_t = r-4(r⁴(αM + 2ηK)_r)_r,

(4)

торые могут отличаться на порядки). В итоге воз-

где

никает два подхода к описанию мелкомасштабных

η(r) =

+ F(0) - F(r),

составляющих магнитного поля, генерируемых ме-

ханизмом динамо. Один из них отталкивается от

α(r) = G(0) - G(r).

уравнения среднего поля (крупномасштабное дина-

мо), а другой — от уравнения для его корреляци-

Неизвестные функции M(r, t) и K(r, t) определяют

онной функции (мелкомасштабное динамо). Вопрос

корреляционный тензор магнитного поля, а извест-

о том, насколько эти два взгляда дополняют друг

ные F (r) и G(r) определяют дельта-коррелирован-

друга или противоречат один другому, вызывает за-

ный тензор поля скорости:

кономерный интерес, поэтому в рамках данной чис-

(

)(

ленной работы мы до некоторой степени стараемся

rM_r

rirj⁾

〈B_i(r, t)B_j (0, 0)〉 = M +

δ_ij -

восполнить этот пробел.

r²

Перейдем к более конкретному рассмотрению

Mr_ir_j

+Kϵ_ijkr_k.

обозначенной проблемы. В основании и крупно, и

r²

1109

Е. В. Юшков, А. С. Лукин, Д. Д. Соколов

ЖЭТФ, том 157, вып. 6, 2020

((

)(

rF_r

rirj⁾

Мы называем эту модель простейшей, так как обыч-

〈V_i(r, t)V_j (0, 0)〉 =

F +

δ_ij -

r²

но рассматривается некоторая ограниченная об-

)

Fr_ir_j

ласть пространства с некоторым распределением по

+ Gϵ_ijkr_k δ(t).

r²

ней параметров α(r) и η(r), а также рассматривает-

ся общее дифференциальное вращение, мы же рас-

Компактность и гибкость модели среднего поля по

сматриваем неограниченную область с постоянными

сравнению с моделью Казанцева обусловливает то,

параметрами. После фурье-преобразования уравне-

что крупномасштабная модель, хотя она и теря-

ние среднего поля для образа B(k, t) принимает вид

ет способность описывать многие мелкомасштабные

алгебраической системы:

черты, так как содержит очень ограниченную ин-

формацию о поле скорости и поле спиральности, ис-

Bt = αi[k, B] - ηk²B, B|t=0 = B0(k).

пользуется гораздо чаще мелкомасштабной.

Заметим теперь, что обе модели, среднего поля

Для линейных уравнений с помощью матриц пово-

и Казанцева, являются линейными, и поэтому из-

рота

⎛

⎞

начально не описывают процесс насыщения и ста-

cosθ

- sinθ

⎜

⎟

билизации роста магнитного поля. Наиболее тра-

Θ=

⎝

⎠,

диционный выход из этой ситуации заключается в

sinθ

cosθ

подавлении гидродинамической/кинетической спи-

⎛

⎞

ральности α, или в так называемом α-квенчинге.

cosϕ sinϕ

Делается это чаще всего феноменологически, пред-

⎜

⎟

Φ=

⎝ -sinϕ cosϕ

⎠

полагая, что за счет сохранения полной энергии па-

раметр α уменьшается с ростом магнитного поля,

например, как

несложно перейти в систему отсчета, в которой вол-

новой вектор направлен вдоль оси z, тогда уравне-

α₀

α(B) =

(5)

ние среднего поля принимает вид следующей систе-

1 + (B/B₀)²

мы трех уравнений

(подробнее см., например, [10-13]). В рамках настоя-

(B^′x)_t = -αikB^′y - ηk²B^′x,

(6)

щей работы, не останавливаясь на обосновании фе-

номенологичности подхода, мы выясняем, работа-

(B^′y )_t = αikB^′x - ηk²B^′y,

(7)

ет ли α-квенчинг в модели Казанцева, на каком

уровне происходит стабилизация процесса, отлича-

(B^′z)_t = -ηk²B^′z .

(8)

ются ли спектры процессов, и можно ли предложить

Очевидно, что решение последнего уравнения

α-стабилизацию, основанную на балансе «зеркаль-

B^′z(k, t)

= 0 в силу условия бездивергентности

ной асимметрии», а не на прикладной идее умень-

(k · B)

= 0, а решение системы (6), (7) мож-

шения параметра α с неограниченным ростом маг-

но получить, найдя корни характеристического

нитного поля. Мы обсуждаем также, можно ли осу-

уравнения

ществить стабилизацию за счет сохранения полной

энергии в модифицированной модели Казанцева и

λ² + 2ηk²λ + η²k⁴ - α²k² = 0.

(9)

как различаются варианты стабилизации при учете

законов сохранения интегрального и спектрального

В этом случае решение имеет вид

типа, когда, например, сохраняется полная энергия

или энергия в каждой спектральной оболочке.

B^′x = -iαkC₁ exp(λ₁t) - iαkC₂ exp(λ₂t),

(10)

2. КРУПНОМАСШТАБНАЯ МОДЕЛЬ

B^′y = (λ₁ + ηk²)C₁ exp(λ₁t) - i(λ₂ + ηk²)×

СРЕДНЕГО ПОЛЯ

× C2 exp(λ₂t),

(11)

Начнем с простейшей модели среднего поля в

λ₁ = -ηk² - αk, λ₂ = -ηk² + αk,

неограниченном пространстве с постоянными коэф-

фициентами, характеризующими диффузию и зер-

где константы определяются из начальных условий:

кальную асимметрию среды:

iB′0x + B′0y

B′0x + iB′0y

B_t = αrotB + η△B, B|t=0 = B₀(x).

C₁ =

C₂ =

2αk

-2iαk

1110

ЖЭТФ, том 157, вып. 6, 2020

Мелкомасштабный анализ подавления гидродинамической спиральности...

Таким образом, в матричной записи решение урав-

3. МЕЛКОМАСШТАБНАЯ МОДЕЛЬ

нение среднего поля можно записать как

КАЗАНЦЕВА

⎛

⎞

Мелкомасштабная модель Казанцева записыва-

B^′x

⎟

ется после усреднения уравнения индукции тради-

B^′(k, t) =^⎝ B^′y

⎠=

ционно не для корреляционных функций M(r, t) и

B^′

K(r, t), а для вспомогательных функций φ(r, t) и

⎛

⎞⎛

⎞

θ(r, t), определяемых выражениями

ch(αkt)

-i sh(αkt)

B′0x

⎟⎜

⎟

= e-ηk2t ^⎝ i sh(αkt) ch(αkt)

⎠⎝ B′0y

⎠,

M (r, t) = r-2η-1/2φ,

(

)

(14)

K(r, t) = 1/2r-4

r⁴

r-2θ

r r

или в исходной системе координат:

Смысл этих замен заключается в том, что они пред-

ставляют в явной форме уравнения модели Казан-

B(k, t) = e-ηk2tΦ-1Θ-1RΘΦB₀,

цева как задачу на собственные функции и собст-

где

венные значения для некоторой системы линейных

⎛

⎞

ch(αkt)

-i sh(αkt)

уравнений (см., например, [15]). Тогда как в исход-

⎜

⎟

⎝ ish(αkt) ch(αkt)

⎠.

ной формулировке линейность задачи не сразу вид-

на — этому мешает условие нормировки, согласно

которому значение корреляционной функции при

Нас, в первую очередь, будет интересовать спектр

совпадении ее пространственных аргументов пред-

энергии:

ставляет собой магнитную энергию. В итоге рас-

сматриваемые замены сводят модель Казанцева для

BB^∗ =

e-2ηk2tBT0 Φ-1Θ-1R^T R^∗ΘΦB∗0.

(12)

ограниченных решений к системе двух дифференци-

альных эволюционных уравнений параболического

Предполагая, что начальное распределение полей в

типа с нулевыми условиями в нуле и на бесконечнос-

пространстве является в среднем сферически сим-

ти:

метричным, и интегрируя по единичной сфере ра-

]

[

]

диуса k, получаем следующее выражение для энер-

φ_t

^[η_rr

2η_r

2η

η2r

2θ

= ηφ_rr+

φ-νη θ_rr-

гии:

r²

4η

r²

[

]

2 ch(2αkt) + 1

θ_t

2θ

α(r)

E(k) =

e-2ηk2tE₀(k) ∼

=η θ_rr -

+ νφ, где ν(r) =

r²

η1/2

(

))

∼ exp

2αt k -

k²

(13)

После нахождения решения системы по вспомога-

тельным функциям могут быть восстановлены кор-

где E₀(k) — начальная форма спектра. Очевидно,

реляционная функция магнитного поля и функция

что на больших временах спектр магнитной энергии

магнитной спиральности (а также спектры энергии

растет на длине волны k = α/2η с максимальной

〈BB〉(k) и спиральности 〈AB〉(k) в результате трех-

скоростью порядка α²/2η. При этом, естественно,

мерного преобразования Фурье):

что в нашем случае никакое уменьшение параметра

)

1 (

α за счет сохранения полной энергии не приведет к

〈BB〉(r) =

η-1/2rφ

〈AB〉(r) = -

(rθ)_r .

подавлению роста поля за конечное время, а лишь

r²

2r²

увеличит характерный корреляционный масштаб и

Заметим, что в исходной модели Казанцева, кроме

уменьшит скорость генерации. В ограниченной же

предположения о временной дельта-коррелирован-

области ситуация изменится, и α-квенчинг приве-

ности потока, предполагается также, что его корре-

дет к подавлению процесса за конечный промежу-

ляционные функции не меняются с течением време-

ток времени, зависящий от размера области (см., на-

ни. Тогда

пример, [14]). Однако, вместо того, чтобы рассмат-

ривать конкретную ограниченную область, мы рас-

〈VV〉(r) = 3F +rF_r ,

〈V rot V〉(r) = -2(3G+rG_r ).

смотрим ту же самую однородную задачу, но не бу-

дем пренебрегать тонкой структурой поля скорости,

Конечно, точный вид корреляционных функций

описывающей масштабы много меньше энергонесу-

обычно известен плохо. Для конкретности мы вы-

щего.

бираем их такими, чтобы они были локализованы

1111

Е. В. Юшков, А. С. Лукин, Д. Д. Соколов

ЖЭТФ, том 157, вып. 6, 2020

на единичном интервале — другими словами за мас-

волновое число k = 1 соответствует корреляцион-

штабную единицу мы берем корреляционную длину

ной длине поля скорости (или, примерно, максиму-

поля скорости. Кроме того, мы выбираем плотность

му кинетического энергетического спектра), поэто-

кинетической энергии равную единице, а плотность

му удобно в дальнейшем считать, что k < 1 соот-

спиральность 0.1 (это стандартная оценка степени

ветствуют крупномасштабной генерации, k > 1 ха-

зеркальной асимметрии в конвекции и турбулентно-

рактеризуют мелкомасштабные процессы. Более по-

сти во вращающихся небесных телах, которую обыч-

дробно о численном анализе можно прочитать в ра-

но связывают с именем Юджина Паркера):

ботах [18-20].

-r²

e-r2

F (r) =

G(r) = -

(15)

4. РЕЗУЛЬТАТЫ ЧИСЛЕННОГО

〈VV〉(k) = 10〈V rot V〉(k) =

√ e-k2/⁴.

ЭКСПЕРИМЕНТА

В силу того, что крупномасштабная структура фор-

4.1. Линейный режим

мируется на масштабах r ≫ 1, а корреляционные

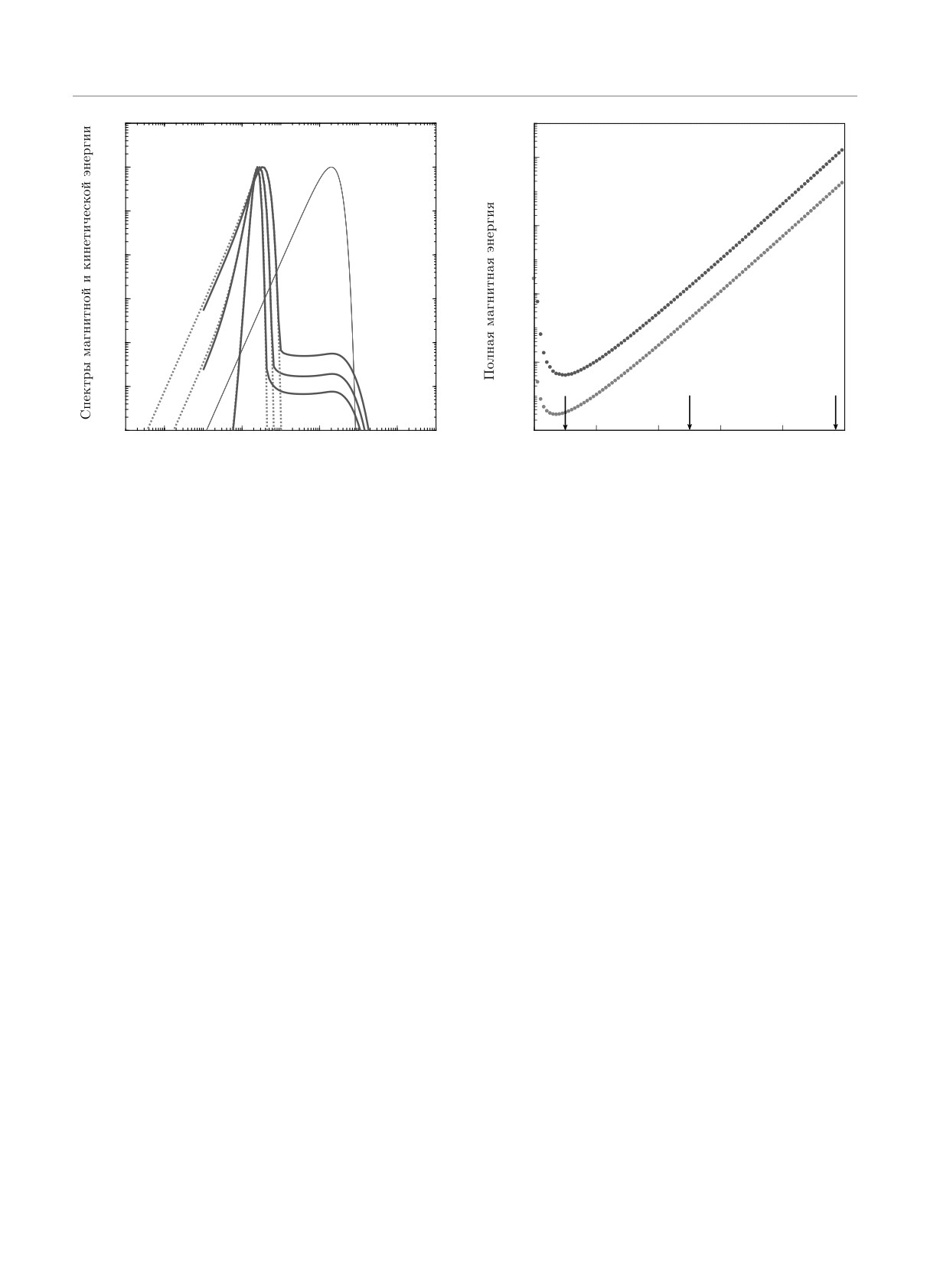
Сравнение результатов моделирования задачи

функции потока локализованы на единичном мас-

среднего поля и мелкомасштабного динамо для ли-

штабе при r < 1, есть возможность грубо проанали-

нейного докритического случая (Rm = 50) пред-

зировать систему Казанцева, считая ν(r) и η(r) кон-

ставлено на рис. 1. На левой панели рисунка пока-

стантами. Действительно, при больших значениях r

заны спектры кинетической и магнитной энергии,

и при экспоненциальной временной зависимости по-

нормированные на свое максимальное значение для

рядка exp(2γt), система принимает достаточно про-

трех моментов времени, отмеченных на правой па-

стой вид

нели. Энергетические спектры показывают хорошее

ηφ_rr = (γ - ν²)φ + γνθ, ηθ_rr = -νφ + γθ.

согласие модели Казанцева (синие линии) и моде-

ли среднего поля (красные штриховые линии) во

Решение такой системы находится в явном виде (см.

всей спектральной области за исключением малых

[16]) и ведет себя как

масштабов, на описание которых уравнение средне-

(

√

)

го поля, конечно, не претендует. Другими словами,

4γ

⁽r⁾

φ ∼ θ ∼ exp

2γt-

-1

cos

2η .

модель Казанцева и модель среднего поля согласу-

ν²

α₀

ются в той области масштабов, где это сравнение

Считая, что амплитуды функций φ(r) и θ(r) ограни-

имеет смысл, при k < 1, в то время как при k ≥ 1

чены при r → ∞, мы получаем максимальную ско-

вклад мелкомасштабного магнитного поля (плато в

рость роста магнитной энергии равную 2γ = ν²/2 =

правой части спектра) медленно затухает со време-

= α²⁰/2η и характерную длину волны α₀/2η. Полу-

нем.

ченные оценки скорости и масштаба полностью сов-

На правой панели рис. 1 изображены зависимос-

падают с характеристиками модели среднего поля,

ти от времени полной магнитной энергии для обе-

что характеризует непротиворечивость моделей и

их моделей. Несмотря на то что по абсолютным ве-

частично верифицирует численные результаты, ко-

личинам полные энергии несколько отличаются (в

торые будут получены при их анализе.

частности, из-за того, что модель среднего поля не

Кратко отметим, что численная реализация мо-

описывает мелких масштабов), скорости роста хо-

дели осуществляется с помощью чисто неявной схе-

рошо согласуются, что подтверждает корректность

мы с нулевыми граничными условиями (идея пред-

как крупномасштабного, так и мелкомасштабного

ложена впервые в работе [17]). Сетка из 5000 узлов

подхода для описания докритического режима (в

выбирается неравномерной и таким образом, чтобы

нашем случае Rm = 50). Конечно, в сверхкрити-

половина узлов попала в интервал r ∈ [0, 1]. Плюсом

ческих режимах (при Rm ≫ 50) наравне с крупно-

такого выбора является то, что качественно удает-

масштабной генерацией должен работать и мелко-

ся реализовать задачу на полупрямой r ∈ [0, ∞) и

масштабный процесс (см. работы [18, 19] и библио-

одновременно восстановить мелкомасштабное поле

графию в них) — его скорости гораздо больше, чем

в областях r ≪ 1. Недостатком является трудность

скорости докритического режима, поэтому в приро-

с восстановлением Фурье-спектров (из-за ячеек раз-

де, по-видимому, существует весьма эффективный

ного размера при больших k возникают ошибки свя-

механизм мелкомасштабной нелинейной стабилиза-

занные с вычислением интегралов). Заметим, что

ции, связанный, например, с трансформацией кине-

1112

ЖЭТФ, том 157, вып. 6, 2020

Мелкомасштабный анализ подавления гидродинамической спиральности...

10⁰

10^-2

10^-4

10^-6

10^-8

10⁰

Время, 10⁴

Рис. 1. (В цвете онлайн) Сравнение линейных режимов. На левой панели спектры фиксированной кинетической энергии

(красная сплошная линия) и магнитной энергии, нормированной на максимальное значение, для трех моментов времени.

На правой панели зависимость магнитной энергии от времени, вертикальными стрелками помечены выбранные моменты

времени. Синие линии соответствуют модели Казанцева, красные линии — энергии модели среднего поля. Выполажива-

ние энергетического спектра Казанцева описывает мелкомасштабные поля, затухающие со временем, поэтому на более

ранних этапах эволюции плато на больших k выше

тического спектра [20], который однако в данной ра-

Результаты численного счета показывают, что в

боте мы обойдем стороной.

этом случае поведения модели среднего поля и мо-

дели Казанцева практически не различаются, см.

рис. 2 (красные и синие точки на правой панели со-

4.2. Традиционный альфа-квенчинг

ответствуют спектрам модели среднего поля и моде-

ли Казанцева). При этом по мере достижения равно-

Простейшее предположение при рассмотрении

распределения экспоненциальный рост прекращает-

нелинейного режима крупномасштабной генерации

ся, но решение продолжает медленно расти. Это свя-

строится на том, что форма уравнений среднего по-

зано с тем, что мы рассматриваем задачу динамо в

ля остается неизменной с течением времени, а из-

неограниченном пространстве. Подобные эффекты

меняется лишь гидродинамическая спиральность,

в других задачах динамо были известны давно (см.,

уменьшаясь с ростом магнитного поля (это пред-

например, обзор [4]). В данной задаче сохранение

положение можно обосновать, по крайней мере, в

медленного роста на нелинейной стадии прямо под-

некоторых моделях, см., например, [21]). Уменьше-

тверждается решением (13), для которого с умень-

ние фактора, обеспечивающего генерацию, приво-

шением α скорость роста замедляется, но не насы-

дит к ее подавлению. Параметризации спирально-

щается, оставаясь пропорциональной α²/2η. Таким

сти в рамках подобного подхода могут различаться,

образом, при стандартном альфа-квенчинге обе мо-

но одна из наиболее распространенных имеет вид

дели ведут себя идентично, а процессы на малых

α(t) = α₀(1 + H²(t))-1 .

(16)

масштабах не играют принципиальной роли, и поз-

воляют пользоваться той моделью, которая удобнее

Здесь предполагается, что магнитная энергия H²(t)

в каждой конкретной задаче.

измеряется в единицах предельной энергии, для ко-

В зависимости от потребности задачи, нетрудно

торой происходит стабилизация работы динамо, а

так модифицировать стандартную параметризацию

α₀ — начальное значение α-эффекта. Эту же пара-

обратного влияния магнитного поля на гидродина-

метризацию можно, конечно, включить и в модель

мику (16), чтобы энергия магнитного поля не пре-

Казанцева. Проверим, насколько согласуется приме-

вышала равнораспределения. Для этого нужно вы-

нение этой параметризации в обеих моделях.

брать подавление зеркальной асимметрии в виде

1113

Е. В. Юшков, А. С. Лукин, Д. Д. Соколов

ЖЭТФ, том 157, вып. 6, 2020

10¹

10⁰

10^-5

10^-1

10^-2

10⁰

10²

Время, 10⁴

Рис. 2. (В цвете онлайн) Сравнение нелинейного подавление в модели среднего поля и в модели Казанцева. На левой

панели спектр магнитной энергии (синяя линия) и спиральности (черная линия), соответствующие нелинейному подав-

лению на основе закона сохранения энергии, красная линия соответствует модели среднего поля. На правой панели

зависимость магнитных энергий от времени (точки соответствуют подавлению (16), крестики — подавлению (17), черная

линия соответствует закону сохранения полной энергии (18)), Rm = 10

α(t) = α₀(1 - H²(t))

(17)

нелинейной эволюции магнитного поля, которые мо-

гут представлять значительный физический инте-

(для малых H²(t) этот способ не отличается от

рес (см., в частности, [23]).

предыдущего). Численный счет показывает, что при

таком подавлении обе модели дают также схожие

результаты, но энергия насыщается быстрее и ста-

4.3. Альфа-квенчинг, основанный на законе

билизируются на уровне меньшем 1 (меньшем рав-

сохранения полной энергии

нораспределения, см. красные и синие крестики на

правой панели рис. 2). Спектры энергии приобрета-

Рассмотрим теперь более качественную модель

ют вид аналогичным спектральным кривым на ле-

нелинейного подавления генерации магнитного по-

вой панели рис. 1, процессы на малых масштабах

ля, в которой прямо предполагается, что рост маг-

по-прежнему не играют существенной роли, хотя и

нитной энергии ограничен кинетической энергией

могут быть зафиксированы по плоскому профилю

случайных движений. В рамках подхода среднего

плотности энергии и степенному профилю плотно-

поля такую параметризацию сформулировать труд-

сти спиральности вблизи энергетического масштаба.

но, поскольку энергия случайных движений, сосре-

Следует заметить, что в реалистических динамо-

доточенная в малых масштабах, прямо не входит в

моделях случаи, когда энергия магнитного поля

эти уравнения, см. (2). Однако это можно сделать в

превышает энергию равнораспределения, встреча-

модели Казанцева. Для этого нужно предположить,

ются и не так уж редко (см., например, [22]). Ко-

что характерная скорость потока V(r, t) убывает та-

нечно, для этого необходимо, чтобы кинетическая

ким образом, что полная магнитная и кинетическая

энергия турбулентности или конвекции восполня-

энергия потока сохраняется:

лась из какого-то источника, которым обычно явля-

ется общее вращение тела, энергия которого на мно-

〈VV〉(0, t) + 〈BB〉(0, t) = 1.

(18)

го порядков превышает магнитную энергию. Таким

образом, обе рассмотренные параметризации нели-

Предполагая, что вид уравнения не изменяется, по-

нейного подавления динамо могут в целом наблю-

лучаем следующую зависимость корреляционных

даться и при этом приводить к различным типам

функций потока от времени:

1114

ЖЭТФ, том 157, вып. 6, 2020

Мелкомасштабный анализ подавления гидродинамической спиральности...

(

)

〈BB〉(0, t)

происходит свое спектральное подавление зеркаль-

〈VV〉(r, t) = 〈VV〉(r, 0) ·

〈VV〉(0, 0)

ной асимметрии, то и форма спектра меняется.

(

)

Мы уже рассмотрели первую возможность (см.

〈BB〉(0, t)

первые три варианта альфа-квенчинга). Перейдем

〈V rot V〉(r, t) = 〈V rot V〉(r, 0) ·

〈VV〉(0, 0)

теперь ко второй. Проблемы, возникающие в этом

В отличие от стандартного альфа-квенчинга при та-

случае, несложно понять, посмотрев на левую па-

ком подавлении с ростом магнитной энергии подав-

нель рис. 1. В потоке с максимумом плотности ки-

ляется не только коэффициент α, но и коэффициент

нетической энергии вблизи энергетического масшта-

турбулентной диффузии η, связанный с продольной

ба k = 1 (тонкая красная линия) магнитное поле

корреляционной функцией. Подавление диффузии

генерируется с максимумом энергии вблизи малых

может эффективно перевести докритический режим

k = α/2η, поэтому достаточно быстро плотность

в критический, при высоких значениях Rm (одна-

магнитной энергии на малых масштабах начинает

ко мы, как было сказано выше, предполагаем на-

превышать плотность кинетической энергии даже

личие эффективного подавления мелкомасштабно-

при сохранении полной энергии. Поэтому приходит-

го динамо и выбираем заведомо малые Rm = 10).

ся допустить либо истощение кинетической энергии,

Тогда, как видно на правой панели рис. 2, маг-

либо ее эффективный транспорт в область малых k,

нитная энергия (черная линия) нарастает быстрее,

что затруднительно описать в рамках сравнительно

чем энергия в стандартных моделях, так как вели-

несложной параметризации.

С другой стороны, можно предположить, что в

чина α²/η становится больше из-за меньшего η, а

ее насыщение происходит на уровне более близком

модели среднего поля (13) параметр α зависит от k,

к равнораспределению. Спектральная картина так-

и в каждой спектральной оболочке он подавляется

же меняется, см. левую панель рис. 2. Максимум

обратно пропорционально энергии в этой оболочке:

плотности энергии (синяя линия), пропорциональ-

α(k) = α₀(1 + (2/π)H²(k) · k²dk)-1,

(19)

ный α/2η, сдвигается в область меньших масштабов

тогда, как при интегральном подавлении, экспонен-

по сравнению с плотностью энергии в задаче сред-

циальный рост прекращается, но решение продол-

него поля (красная штриховая линия). Плотность

жает медленно (линейно по времени) расти, а спектр

спиральности (черная линия) приобретает вблизи

перестает быть локализован в узком диапазоне вол-

энергетического масштаба характерный степенной

новых чисел и приобретает вид распределения со

наклон близкий к -3. Однако если мелкомасштаб-

степенным интервалом порядка k-4 и максимумом,

ная структура не является принципиальной в зада-

смещенным в область больших масштабов (зеленые

че (плотность мелкомасштабной энергии на порядки

линии на рис. 3). В целом, следует признать, что в

меньше плотности энергии среднего поля), то аль-

рамках простейших моделей построение более уни-

фа-квенчинг, основанный на законе сохранения пол-

версальной параметризации, чем классическая, ка-

ной энергии (18), принципиально не отличается от

жется затруднительным.

стандартного альфа-подавления, задаваемого урав-

нениями вида (16) или (17).

4.5. Баланс спиральностей

4.4. Нелинейный режим. Спектральное

Наконец, заметим, что существует и иной путь

подавление

к построению нелинейной спектральной параметри-

зации динамо, который отталкивается не от закона

В рассмотренных выше вариантах параметри-

сохранения энергии, а от закона сохранения полной

зации нелинейного динамо-насыщения мы не учи-

(гидродинамической и магнитной) спиральности. Из

тывали возможного переноса энергии по спектру

анализа задачи Казанцева известно, что при нарас-

(см., например, [24]). Это кажется реалистичным

тании магнитного поля, наравне с генерацией энер-

в том случае, когда перераспределение по спектру,

гии растет мера магнитной асимметрии 〈AB〉(k, t).

осуществляется столь быстро, что форма спектра

Из общих соображений сохранение суммарной сим-

остается неизменной и определяется внемодельны-

метрии может вносить вклад в α-эффект. Такое со-

ми причинами, меняется при этом только амплитуда

хранение уже само по себе приводит к подавлению

спектра. Или, наоборот, если перераспределение по

α. Таким образом, пренебрегая переносом спираль-

спектру столь медленное, что для каждого малого

ности по спектру и полагая, что

интервала волновых чисел отсутствует спектраль-

ный транспорт, т. е. для каждой волновой оболочки

〈V rot V〉(k, t) = 〈V rot V〉(k, 0) - 〈AB〉(k, t)

(20)

1115

Е. В. Юшков, А. С. Лукин, Д. Д. Соколов

ЖЭТФ, том 157, вып. 6, 2020

10⁰

10^-2

10^-4

10^-5

10^-6

10^-3

10^-2

10^-1

10⁰

Время, 10⁴

Рис. 3. (В цвете онлайн) Спектральное подавление. На левой панели изображены энергетические спектры для нелинейной

модели среднего поля с традиционным подавлением ((17), красная линия), спектральным подавлением ((19), зеленая

линия) и спектральным подавлением на балансе полной спиральности ((20), синяя линия). На правой панели изображе-

ны зависимости полной магнитной энергии от времени для традиционного подавления и спектрального квенчинга (19) и

(20) в аналогичных цветах. Плотности энергии на левой панели нормированы на максимальное значение и соответствуют

конечному моменту времени на правой панели

в каждой спектральной оболочке, мы можем ожи-

балансом меры зеркальной асимметрии, фиксирует-

дать динамо-насыщения. Действительно, числен-

ся на уровне, на порядки меньшем, чем для стабили-

ный эксперимент показывает, что при таком подав-

зации, построенной на интегральном законе сохра-

лении в модели Казанцева наблюдается эффектив-

нения (синяя линия на правой панели рис. 3).

ная стабилизация, см. правую панель рис. 3 (крас-

ная линия соответствует модели среднего поля с

5. ОБСУЖДЕНИЕ И ВЫВОДЫ

квенчингом (17), синяя — спектральному альфа-

подавлению вида (20)). На левой панели рис. 3 пока-

Задача о росте магнитного поля в потоке про-

заны соответствующие энергетические спектры маг-

водящей жидкости/плазмы заметно отличается от

нитного поля, а на рис. 4 спектры и корреляци-

многих других задач физики тем, что в ней при-

онные функции кинетической спиральности. Выде-

ходится иметь дело с системами, свойства которых

лим характерные черты такого альфа-квенчинга:

известны весьма приблизительно. Мы очень слабо

во-первых, стабилизация происходит одновременно

знаем те детали внутреннего строения потоков ве-

со стремлением 〈VrotV〉(r, t) к нулю при r = 0 (см.

щества в звездах, галактиках и в других небесных

правую панель рис. 4: сплошная линия соответству-

телах, для которых хочется понять причины наблю-

ет корреляционной функции кинетической спираль-

даемого поведения магнитных полей. Даже при экс-

ности в начальный момент времени, штриховая —

периментальных исследованиях динамо трудно из-

в конечный. Другими словами, это означает смену

мерить все важные величины в условиях реально-

знака плотности спиральности на больших масшта-

го эксперимента. В подобной ситуации ограничены

бах (на левой панели смене знака соответствует пик

и возможности прямого численного моделирования,

на штриховой линии вблизи энергетического мас-

которое само по себе, конечно, очень важно (подроб-

штаба). Во-вторых, спектральная картина для энер-

нее читайте обзор [25]). В итоге приходится пользо-

гии приобретает принципиальные различия с дина-

ваться различными параметризациями свойств тур-

мо среднего поля (увеличивается область локализа-

булентных и конвективных течений. Эти параметри-

ции и максимум смещается на большие масштабы,

зации, конечно, основаны на определенных физиче-

левая панель рис. 3). Наконец, устойчивая стабили-

ских соображениях, однако трудно утверждать, что

зация магнитной энергии, связанная с формальным

они прямо следуют из первопринципов физики.

1116

ЖЭТФ, том 157, вып. 6, 2020

Мелкомасштабный анализ подавления гидродинамической спиральности...

0.15

10⁰

0.10

0.05

10^-5

-0.05

–0.10

10^-10

-0.15

10^-3

10^-2

10^-1

10⁰

10^-2

10⁰

10²

Рис. 4. (В цвете онлайн) Альфа-квенчинг на балансе суммарной спиральности. На левой панели изображены спектры

нормированной магнитной спиральности (черная линия) и кинетической спиральности в начальный момент времени

(красная сплошная линия) и в конечный момент времени (красный пунктир). На правой панели изображены корреляци-

онные функции спиральности в начальный и конечный момент времени. Конечный момент времени соответствует концу

шкалы на правой панели рис. 3

Конечно, по мере усложнения моделей в них вы-

ской спиральности.

деляются специфические элементы, определяющие

Другая важная черта проведенного сравнения

те или иные детали феноменологии, известные из

связана с тем, что на примере альфа-квенчинга в

наблюдений. Однако хотелось бы убедиться, что,

мелкомасштабной модели Казанцева удалось проде-

по крайней мере, в простейших задачах динамо не

монстрировать возможность нелинейной стабилиза-

очень изощренные параметризации действительно

ции другим путем, нежели через интегральное или

приводят к близким результатам. В противном слу-

спектральное уменьшение энергии случайного поля

чае было бы трудно говорить о понимании физиче-

скорости. Численный счет показал, что при генера-

ских процессов генерации магнитных полей.

ции магнитного поля в случайном потоке на боль-

ших масштабах (в сравнении с характерным энер-

В настоящей работе мы продемонстрировали,

гетическим масштабом поля скорости) генерирует-

что такая стабильность описания действительно

ся значительная магнитная спиральность. Феноме-

возникает при сопоставлении двух различных пу-

нологическое предположение о сохранении полной

тей моделирования: одного — на языке динамо сред-

спиральности (суммарной меры асимметрии) при-

них полей, а другого - на языке корреляционной

водит к идее о смене ее знака таким образом, что

динамо-модели Казанцева, которая первоначально

средняя кинетическая спиральность становится ну-

ориентирована на описание мелкомасштабного ди-

левой и генерация прекращается. Именно такой эф-

намо, но (при должном развитии) включает и ди-

фект и наблюдался при численном счете, когда на

намо среднего поля. Мы показали, что в той облас-

масштабах меньших энергетического кинетическая

ти, где эти модели допускают сравнение, их свой-

спиральность приобретает знак противоположный

ства и в самом деле близки. Это касается и спект-

спиральности магнитного поля, в то время как на

ров энергии генерируемого поля, и скоростей роста

масштабах больших — знаки спиральностей совпа-

энергии. Более того, классический альфа-квенчинг

дают. Поэтому совпадение моделей среднего поля и

в данных моделях дает результат близкий к дина-

Казанцева при традиционном альфа-квенчинге еще

мо-стабилизации, основанной на законе сохранения

не означает, что такой способ динамо-подавления

полной энергии, при которой рост магнитного по-

является единственно возможным и безоговорочно

ля приводит к уменьшению кинетической энергии

правильным.

и пропорциональному уменьшению гидродинамиче-

1117

Е. В. Юшков, А. С. Лукин, Д. Д. Соколов

ЖЭТФ, том 157, вып. 6, 2020

Наконец, заметим, что проведенное нами сравне-

же трактовка результатов, осуществляемая всеми

ние имеет еще одну мотивацию. Работа крупномас-

авторами, обеспечивалась грантом фонда БАЗИС

штабного динамо приводит к образованию как круп-

№18-1-1-77-3.

номасштабного (среднего), так и мелкомасштабного

(турбулентного) магнитного поля. Уравнение, опи-

сывающее эволюцию крупномасштабных компонент

ЛИТЕРАТУРА

магнитного поля, строго говоря, является детерми-

Д. Д. Соколов, Р. А. Степанов, П. Г. Фрик, УФН

нированным уравнением для математического ожи-

184, 313 (2014).

дания (среднего значения) магнитного поля и не

должно включать флуктуаций. Для описания же

A. Ruzmaikin, D. Sokoloff, and A. Shukurov,

MNRAS 241(1), 1 (1989).

флуктуаций, строго говоря, необходимо выделить

из уравнения Казанцева уравнение для соответ-

K. Subramanian, MNRAS 294, 718 (1998).

ствующей составляющей магнитного поля. Подоб-

Ya. B. Zeldovich, A. A. Ruzmaikin, and D. D. So-

ная процедура представляет несомненный интерес

koloff, Magnetic Fields in Astrophysics, G&B, NY

с точки зрения разрешения возникающих при этом

(1983).

разнообразных нетривиальных задач математиче-

ской физики, однако с практической точки зрения

F. Krause and K.-H. Rädler, Mean-Field Magneto-

от нее хотелось бы по возможности уклониться и

hydrodynamics and Dynamo Theory, Pergamon

Press, Ltd., Oxford (1980).

рассматривать флуктуации, связанные с работой

крупномасштабного динамо, как составную часть

С. А. Молчанов, А. А. Рузмайкин, Д. Д. Соколов,

решения уравнений среднего поля. Такой прагма-

УФН 145, 307 (1985).

тический подход постоянно применяют в других

А. П. Казанцев, ЖЭТФ 53, 1806 (1967).

областях физики. В частности, уравнения газоди-

намики тоже являются уравнениями среднего поля,

R. Kraichnan and S. Nagarajan, Phys. Fluids 10, 853

но это не мешает метеорологам рассматривать в их

(1967).

рамках, скажем, флуктуации температуры. Анало-

S. Vainshtein and L. Kichatinov, J. Fluid Mech. 168,

гично, специалистам по солнечному циклу хотелось

73 (1986).

бы рассматривать влияние на свойства солнечного

10.

F. Cattaneo and S. I. Vainshtein, Astrophys. J. 376,

цикла флуктуаций альфа-эффекта тоже в рамках

L21 (1991).

уравнений среднего поля [26]. В последнем случае,

однако, правомерность подобного подхода вызыва-

11.

A. V. Gruzinov and P. H. Diamond, Phys. Rev. Lett.

ет больше опасений, поскольку для задачи динамо

72, 1651 (1994).

известно явление перемежаемости, в результате ко-

12.

A. Bhattacharjee and Y. Yuan, Astrophys. J. 449,

торого статистические моменты низших и высших

739 (1995).

порядков могут вести себя существенно различно

13.

A. Brandenburg and K. J. Donner, MNRAS 288(2),

(см. например, [27]). Важно, что проведенное выше

L29 (1997).

сравнение двух подходов показывает, что в данном

случае это опасение оказывается несостоятельным

14.

D. Sokoloff, A. Shukurov, and A. Ruzmaikin, Geo-

и в рамках уравнения динамо среднего поля рас-

phys. Astrophys. Fluid Dyn. 25, 293 (1983).

сматривать задачи с флуктуирующими параметра-

15.

О. Артамонова, Д. Соколов, Вестник МГУ 27, 8

ми динамо можно. Это, конечно, не гарантирует

(1986).

отсутствие каких-то более тонких постановок во-

16.

D. Sokoloff, E. Yushkov, and A. Lukin, GAFD 57,

проса, где подобный подход не полностью отражает

844 (2017).

специфику задачи, однако пока позволяет, скажем,

продолжать учитывать флуктуации параметров ди-

17.

В. Г. Новиков, А. А. Рузмайкин, Д. Д. Соколов,

намо при описании солнечного и звездных циклов.

ЖЭТФ 85, 909 (1983).

18.

E. Yushkov, GAFD 109, 450 (2015).

Финансирование. Работа Д. Д. С. и А. С. Л. по

19.

E. Yushkov, A. Lukin, D. Sokoloff, and P. Frick,

постановке задачи и поиску методов ее решения под-

GAFD 113, 184 (2018).

держивалась Российским фондом фундаменталь-

ных исследований (грант №18-02-0085). Числен-

20.

Е. В. Юшков, А. С. Лукин, Д. Д. Соколов, ЖЭТФ

ный эксперимент, проводимый Е. В. Ю., а так-

155, 1123 (2019).

1118