ЖЭТФ, 2020, том 158, вып. 2 (8), стр. 228-240
© 2020
КОРРЕЛЯЦИОННАЯ СВЯЗЬ КВАНТОВОЙ ЗАПУТАННОСТИ И
КВАНТОВОЙ КОГЕРЕНТНОСТИ В СПИНОВЫХ XY -ЦЕПОЧКАХ
СО ВЗАИМОДЕЙСТВИЕМ ДЗЯЛОШИНСКОГО - МОРИИ
С. Гомбар*, П. Мали, М. Пантич, М. Павков-Хервоевич, С. Радошевич
Department of Physics, Faculty of Sciences, University of Novi Sad
21000, Novi Sad, Serbia
Поступила в редакцию 6 июня 2019 г.,
после переработки 6 июня 2019 г.
Принята к публикации 5 июля 2019 г.
(Перевод с английского)
CORRELATION BETWEEN QUANTUM ENTANGLEMENT
AND QUANTUM COHERENCE IN THE CASE OF XY SPIN CHAINS
WITH THE DZYALOSHINSKII-MORIYA INTERACTION
Sonja Gombar, Petar Mali, Milan Pantić, Milica Pavkov-Hrvojević, Slobodan Radošević
В последнее время повышенный интерес вызывают исследования квантовой запутанности и квантовой
когерентности. Поскольку оба этих явления существуют благодаря принципу квантовой суперпозиции,
представляется полезным определить, являются ли они до некоторой степени коррелированными. Целью
настоящей работы является исследование вида корреляций в нескольких системах, которые характеризу-
ются различными типами анизотропии. Основное внимание уделено спиновым XY -цепочкам со взаимо-
действием Дзялошинского - Мории, и вид упомянутой связи исследуется при помощи метода квантовой
ренормгруппы.
DOI: 10.31857/S0044451020080015
меры транзисторов не могут уменьшаться бесконеч-
но и рост быстродействия чипов заметно замедлил-
ся в последнее время. В некоторых работах предла-
1. ВВЕДЕНИЕ
гается использовать многоядерные чипы, посколь-
ку благодаря параллельному выполнению задач они
По-видимому, один из наиболее специфических
улучшают производительность по сравнению с той,
разделов квантовой механики, квантовая инфор-
которая достигается в моделях с единственным яд-
матика, появился на свет благодаря тому просто-
ром [2].
му факту, что он дает более эффективные спосо-
бы получения результатов, чем те способы, кото-
Однако переход на такие чипы представляется
рые существуют в рамках классического подхода.
не слишком практичным, поскольку использование
В 1965 г. Мур сделал предсказание, касающееся вы-
классических параллельных вычислений оказывает-
числительной мощности компьютеров [1]. Он обра-
ся достаточно дорогим. Поэтому появились работы,
тил внимание на то, что с уменьшением размеров
в которых предлагается использовать возможности
транзисторов их количество в чипе увеличивается,
квантовых вычислений для решения задач в таких
и предположил, что вычислительная мощность бу-
областях, как химия [3]. Отметим, что недавно бы-
дет удваиваться каждые два года при той же цене.
ли выполнены расчеты возбужденного и основного
В этом предположении не учтен тот факт, что раз-
состояний молекулы H2 с использованием процес-
сора на сверхпроводящих кубитах [4]. Причина по-
* E-mail: df.sonja.gombar2@student.pmf.uns.ac.rs
вышенного интереса к этой области заключается в
228
ЖЭТФ, том 158, вып. 2 (8), 2020
Корреляционная связь квантовой запутанности...
том, что производительность параллельных вычис-
этому интерес сфокусировался в области квантовых
лений должна сильно вырасти, поскольку классиче-
вычислений [5]. Было найдено множество систем,
ские биты 0 и 1 заменяются квантовыми кубитами,
которые могут моделировать квантовые компьюте-
которые могут находиться в состоянии квантовой
ры. К ним относятся оптические квантовые компью-
суперпозиции таких состояний. Этот альтернатив-
теры, в которых квантовая информация кодирует-
ный подход возник как следствие последовательного
ся при помощи поляризации, системы, использую-
уточнения формулировки тезиса Чёрча - Тьюринга
щие ядерный магнитный резонанс, в которых ку-
[5] в работах Фейнмана и Дойча [6, 7].
битами служат ядерные спины, ионы в ловушках
В настоящее время ясно, что в случае исполь-
и многие другие [23]. Одна из недавно возникших
зования квантовых компьютеров скорость вычисле-
технологий основана на использовании квантовых
ний сильно возрастет, но это не единственное их пре-
точек и единичных примесей в твердых телах и поз-
имущество. Возрастает и количество разрешимых
воляет создать и охладить большое количество ку-
задач. Шор и Гровер рассмотрели несколько задач,
битов [24]. Однако наиболее распространены кван-
которые можно решить либо только с использова-
товые компьютеры, основанные на использовании
нием квантового компьютера, либо его использова-
спина [25]. Несмотря на то что было разработано
ние сильно уменьшает затраты времени на получе-
несколько систем квантовых вычислений, содержа-
ние ответа [8, 9].
щих по несколько запутанных кубитов, возникла
Крайне полезным в мире квантовой информа-
проблема разрушения когерентности, которая при-
ции является понятие квантовой запутанности. Оно
вела к необходимости разработки методов ее под-
применимо к системам, которые содержат более од-
держания в таких системах [26]. Фактически мож-
ной частицы. Несмотря на то что подчас частицы
но сказать, что разрушение когерентности происхо-
удалены друг от друга на большое расстояние, они
дит благодаря запутанности системы и окружающей
могут находиться в так называемом запутанном со-
среды. Это приводит к необходимости учета окру-
стоянии. В этом состоянии ни одну частицу нель-
жающей среды при расчетах величины когерентнос-
зя рассматривать отдельно от остальных [10]. Пред-
ти изучаемой системы.
ставления о квантовом шифровании, квантовой те-
Целью настоящей работы является рассмотре-
лепортации и плотном кодировании тесно связаны
ние специфической квантовой системы для наблю-
с существованием запутанных состояний [5]. Имеет-
дения за поведением двух очень важных величин
ся критерий для определения наличия запутаннос-
квантовой информатики — квантовой запутанности
ти в системе. Он состоит в проверке выполнимости
и квантовой когерентности, с целью исследовать их
неравенства Белла определенного типа (как прави-
взаимосвязь в данной системе. Модели со спином
ло, CHSH-неравенства) [11].
используются для описания разнообразных физиче-
Однако остается вопрос, каковы возможности
ских явлений, таких как свойства магнитных соеди-
практического применения теоретических предска-
нений [27-31], квантово-холловских систем [32, 33],
заний квантовой информатики. В то время как в
массивов джозефсоновских переходов [34], кванто-
области теории квантовых вычислений существует
вых фазовых переходов [35-39] и т. д., и квантовая
множество разработок, практические решения раз-
информатика не является исключением. В настоя-
рабатываются гораздо медленнее. Тем не менее есть
щее время существенный интерес вызывают спино-
и успехи. Например, уже удалось реализовать кван-
вые XY - и XY Z-цепочки [40, 41], особенно такие,
товое шифрование на разных расстояниях на основе
в которых имеются фрустрации и взаимодействие
различных систем, содержащих кубиты [12,13]. Ана-
Дзялошинского - Мории (ДМ) [42-47]. В этой ра-
логичные результаты были достигнуты и при боль-
боте рассмотрена XY -модель с ДМ-взаимодействи-
ших размерностях квантовых систем с запутанно-
ем в случае системы, содержащей три спина 1/2.
стью (кудитов), в частности, кутритов [14]. Факти-
Важным методом предсказания квантовых фазо-
чески, в течение последних лет многие задачи кван-
вых переходов является метод квантовой ренорм-
товой информатики были исследованы эксперимен-
группы [44-46]. В настоящей работе он используется
тально [15-22].
для проверки результатов, полученных для систем
Задачей чрезвычайной важности является поиск
большего размера (содержащих несколько спиновых
архитектур, которые могут эффективно моделиро-
блоков). Основной целью является выяснение того,
вать квантовые системы. Считается, что ни один
как связаны запутанность и когерентность в систе-
классический компьютер не может выполнить такое
ме, которая оторвана от окружающей среды. Влия-
моделирование с высокой производительностью, по-
нием окружающей среды мы пренебрегаем.
229
С. Гомбар, П. Мали, М. Пантич и др.
ЖЭТФ, том 158, вып. 2 (8), 2020
Особое внимание уделено мерам квантовой за-
следуется теоретически [54, 55]. Это взаимодейст-
путанности и квантовой когерентности, которые ис-
вие было впервые рассмотрено Дзялошинским в
пользуются в настоящее время [48, 49]. В то вре-
1958 г. [56], но его важность, которая вытекает из
мя как про запутанность известно достаточно мно-
практических наблюдений в реальных системах со
гое, квантовая когерентность остается сравнительно
спин-орбитальным взаимодействием, была выясне-
малоисследованной. Следовательно, представляется
на несколько позже, в 1960 г., в работе Мории [57].
полезным выяснить, имеется ли корреляция между
Его также называют антисимметричным обменом
этими двумя величинами. Поскольку обе они воз-
вследствие связи с антисимметричной частью мат-
никают благодаря принципу квантовой суперпози-
рицы взаимодействия.
ции в разных его ипостасях, такое предположение
В первом случае мы рассматриваем гамильтони-
не выглядит неправдоподобным. Ранее авторы ра-
ан спиновой XY -цепочки с анизотропией симмет-
боты [50] пришли к заключению, что относительная
ричного типа и ДМ-взаимодействием, который за-
энтропия когерентности и энтропия фон Неймана
писывается в виде [44]
проявляют противоположное поведение. Кроме то-
(
го, в работе отмечается, что запутанность формиро-
∑
вания состоящей из двух частей системы увеличи-
H =
(1 + γ)σxiσxi+1 + (1 - γ)σyiσyi+1 +
4
вается, если относительная энтропия когерентности
i=1
)
одной из подсистем уменьшается и наоборот. Одной
+ (-1)iD(σxi σyi+1 - σyi σxi+1) ,
(2.1)
из основополагающих работ в этой области являет-
ся работа Стрельцова [51]. В ней рассматривается
где N — количество узлов. Вследствие унитарнос-
способность некогерентных операций приводить к
ти преобразования результаты, представленные в
запутанности некоторого состояния с другим неко-
разд. 3, не меняются, что легко проверить. В слу-
герентным состоянием, но только при условии того,
чае, когда γ = 1 и D = 0, эта модель сводится к
что исходное состояние было когерентным. Целью
модели Изинга, а в случае γ = D = 0 она соответст-
настоящей работы является выяснение того, како-
вует XX-модели [44]. В интервале 0 < γ ≤ 1, моде-
ва корреляция запутанности и когерентности в кон-
ли попадают в изинговский класс универсальности
кретной системе в случае различных типов анизо-
и для N = ∞ при критическом значении параметра
тропии при условии, что никакие операции для рас-
γ происходит фазовый переход [58].
сматриваемой системы не проводятся.
Одна из целей нашей работы состоит в том, что-
После краткого введения в этом разделе,
бы изучить поведение запутанности и когерентно-
несколько используемых для вычислений моделей
сти при увеличении размера системы. Для этого
представлены в разд. 2. Мы рассматриваем три
используется метод квантовой ренормгруппы. По-
ситуации: случаи симметричной анизотропии,
скольку метод подразумевает получение самоподоб-
включающей или не включающей анизотропию
ного гамильтониана в результате необходимого пре-
отдельного иона, а также случай анизотропии асим-
образования, модель должна включать π-поворот
метричного типа. Результаты, полученные для этих
вокруг оси x для всех четных узлов при неизменно-
случаев, приводятся в разд. 3, где определяется
сти нечетных узлов [44]. Следовательно, в случае си-
тип исследуемой корреляции. В разд. 4 приводится
стемы, состоящей из трех узлов, гамильтониан (2.1)
обсуждение полученных результатов.
записывается в виде
J
∑((
)
(
)
2. МОДЕЛЬ
H =
1+γ
σxiσxi+1 -
1-γ
σyiσyi+1 +
4
i=1
)
Связь между запутанностью и когерентностью
(
)
+D
σxiσyi+1 + σyiσxi+1
(2.2)
будет исследоваться с использованием XY -модели
Гейзенберга с двумя типами анизотропии. Оба рас-
сматриваемых гамильтониана включают ДМ-взаи-
(такой же гамильтониан использовался ранее в ра-
модействие, поскольку ранее было доказано, что оно
ботах [44,45,59-61]), где J — константа взаимодейст-
приводит к появлению когерентности [45]. Можно
вия ближайших соседей, γ — параметр анизотропии,
утверждать, что это взаимодействие играет суще-
D — z-компонента силы ДМ-взаимодействия и σαi
ственную роль в различных системах, например в
(α = x, y) — матрицы Паули для i-го узла, которые
CsCuCl3 и FeBO3 [52, 53], и поэтому он много ис-
записываются в виде
230
ЖЭТФ, том 158, вып. 2 (8), 2020
Корреляционная связь квантовой запутанности...
[
]
[
]
3AJ
q|J|
0
1
0
-i
E0 =
-
√
(2.8)
σx =
,
σy =
,
4
2
1
0
i
0
[
]
(2.3)
с комплексными собственными векторами
1
0
σz =
(
0
-1
√
1
q|J|
|Ψ〉 =
√
D2 + 1
-
√
|↑↑↓〉+
Один из основных мотивов использования гамиль-
2q
2J(1 + iD)
тониана (2.2) состоит в том, что в системах куби-
)
γ
q|J|
тов можно экспериментально управлять различны-
+
|↑↓↑〉 -
√
|↓↑↑〉 + |↓↓↓〉
,
(2.9)
1 + iD
2J(1 + iD)
ми типами связи между соседними спинами [62,63].
Как можно видеть, в данном гамильтониане ани-
(
√
зотропия обладает симметричной формой, что так-
1
2J(1 - iD)
|Ψ′〉 =
-
|↑↑↑〉 + |↑↓↓〉-
же сказывается на поведении упомянутых мер. Па-
2
q|J|
раметр D в уравнении (2.2) фактически является
√
)
относительной силой ДМ-взаимодействия, что сле-
2Jγ
-
|↓↑↓〉 + |↓↓↑〉
(2.10)
дует из выражения для гамильтониана, в котором
q|J|
D записывается через параметр взаимодействия J.
Можно заранее считать, что одноионная анизотро-
По этой причине собственные векторы оказываются
пия не влияет на изучаемые нами величины. Этого
не зависимыми от J.
можно было ожидать на интуитивном уровне, по-
Основное состояние гамильтониана (2.2) явля-
скольку в случае спина 1/2 данный тип анизотро-
ется двукратно вырожденным и соответствует соб-
пии является тривиальным, так как он входит в га-
ственному значению (энергия):
мильтониан (2.2) как добавка к единичной матри-
J
E0 = -√ q
(2.4)
це, умноженная на константу. Следовательно, мож-
2
но сделать вывод о том, что одноионная анизотро-
√
пия не влияет ни на запутанность, ни на когерент-
с q =
1 + D2 + γ2, с комплексными собственными
ность, если рассматриваемые спины равны 1/2.
векторами, записанными в стандартном базисе:
Второй случай включает анизотропию асиммет-
(
√
1
q
ричного типа. В этом случае гамильтониан дается
|Ψ〉 =
√
D2 + 1
-
√
|↑↑↓〉+
2q
2(1 + iD)
выражением
)
γ
q
(
+
|↑↓↑〉 -
√
|↓↑↑〉 + |↓↓↓〉
,
(2.5)
∑
J
1 + iD
2(1 + iD)
H =
σxiσxi+1 + Mσyiσyi+1 +
4
i=1
(
√
)
(
)
1
2(1 - iD)
+ D
σxiσyi+1 + σyiσxi+1
,
(2.11)
|Ψ′〉 =
-
|↑↑↑〉 + |↑↓↓〉-
2
q
√
)
2γ
где
J — константа взаимодействия ближайших сосе-
-
|↓↑↓〉 + |↓↓↑〉
,
(2.6)
q
дей, M — параметр анизотропии и
D— z-компонен-
та силы ДМ-взаимодействия. Легко показать, что
где |↑〉 и |↓〉 — базисные векторы матрицы Паули σz
гамильтониан (2.11) переходит в (2.2) посредством
в данном представлении.
простого преобразования:
Включение в рассмотрение одноионной анизот-
ропии, известной также как магнитокристалличе-
D
γ-1
J = (1 + γ)J,
D=
,
M =
(2.12)
ская анизотропия [64,65], дает тривиальный вклад в
1+γ
γ+1
рассмотренный выше случай, когда исследуются си-
Однако можно видеть, что это преобразование не-
стемы со спином 1/2. В этом случае гамильтониан
определено при γ = -1, и нет оснований называть
(2.2) будет иметь добавку
эту модель более общей, чем предыдущая, правиль-
∑
нее называть ее моделью с другим типом анизотро-
JA
HSI =
(σzi )2,
(2.7)
пии. В этом случае получаемое основное состояние
4
i=1
соответствует энергии
где A обозначает силу одноионной анизотропии.
√
1
Найденная выше энергия основного состояния из-
E0 = -
Jm, m =
1+2D2 +M2
(2.13)
2
менится на
231
С. Гомбар, П. Мали, М. Пантич и др.
ЖЭТФ, том 158, вып. 2 (8), 2020
и комплексным собственным состояниям:
случае матрица плотности, полученная из собствен-
ных значений гамильтонианов, должна быть приве-
√
дена к своей бипартитной форме.
4D2 + (-1 + M)2
Квантовая когерентность является сравнительно
|Ψ〉 =
×
2m
новым понятием в квантовой информатике. К ран-
ним исследованиям относится работа Аберга 2006 г.,
(
im
i(1 + M)
в которой был разработан подход для количествен-
×
|↑↑↓〉-
|↑↓↑〉+
2D + i(-1 + M)
2D+i(-1+M)
ного описания суперпозиции ортогональных кванто-
вых состояний [70], а наиболее интересные резуль-
)
im
таты были получены в 2014 г. и состоят в нахож-
+
|↓↑↑〉 + |↓↓↓〉
,
(2.14)
2D+i(-1+M)
дении нескольких условий, которым должна удов-
летворять каждая корректно определенная мера
когерентности [71]. Этим условиям удовлетворяют
несколько мер, среди которых самыми используемы-
1
(-1 + 2i D + M
ми являются норма l1 и относительная энтропия ко-
|Ψ′〉 =
|↑↑↑〉 + |↑↓↓〉-
2
m
герентности. Последняя используется в настоящей
работе и определяется как
)
1+M
-
|↓↑↓〉 + |↓↓↑〉
,
(2.15)
m
Cre(ρ) = S(ρdiag) - S(ρ),
(2.18)
которые существенно отличаются от функций (2.5)
где S(ρ) — энтропия фон Неймана, которая дается
и (2.6), что приводит к ожидаемому различию в по-
выражением
ведении величин квантовой информатики.
Существуют несколько величин, удовлетворяю-
S(ρ) = - Tr ρ log2 ρ.
(2.19)
щих условиям, которые должны выполняться для
любой корректно определенной меры запутанности
Здесь ρdiag является диагональной матрицей, полу-
[48]. К наиболее часто используемым относятся за-
ченной из матрицы ρ путем замены всех недиаго-
путанность формирования, фракционная запутан-
нальных элементов нулями. Поскольку в нашем слу-
ность и относительная энтропия запутанности. Од-
чае рассматриваются чистые состояния (для кото-
нако использование этих мер для конкретной систе-
рых S(ρ) = 0, так как log2(1) = 0), в (2.18) остается
мы может столкнуться с серьезной проблемой. Хотя
только диагональная часть.
несколько мер были определены для многочастич-
ной запутанности [66, 67], мы будем использовать
меру, найденную в работе Вутерса, или согласован-
3. РЕЗУЛЬТАТЫ
ность бипартитной системы [68]:
В этом разделе исследуется поведение квантовой
запутанности и квантовой когерентности в двух упо-
C(ρ) = max{0, λ1 - λ2 - λ3 - λ4},
(2.16)
мянутых выше случаях, а полученные зависимости
двух величин от анизотропии и параметра ДМ-взаи-
где λi (i = 1, . . . , 4) — квадратные корни из собствен-
модействия приведены на рисунках.
ных значений матрицы R = ρρ в порядке убывания,
и матрица ρ задается выражением
3.1. XY -модель с ДМ-взаимодействием и
(
)
(
)
симметричной анизотропией
ρ=
σy ⊗ σy
ρ∗
σy ⊗ σy
,
(2.17)
Для того чтобы вычислить согласованность,
где ρ∗ — результат операции комплексного сопряже-
в соответствии с (2.16) нужно выписать матри-
ния матрицы плотности ρ. Использование матрицы
цу плотности. Поскольку температурные эффекты
плотности уже стало одним из важнейших методов
остаются за рамками нашего рассмотрения, можно
квантовой механики, описания процессов рассеяния,
считать, что система находится в основном состоя-
а также современной атомной физики, лазерной фи-
нии. Следовательно, матрица плотности основного
зики, статистической физики и т. д. [69]. В нашем
состояния записывается в виде
232
ЖЭТФ, том 158, вып. 2 (8), 2020
Корреляционная связь квантовой запутанности...
⎡
⎤
0
0
0
0
0
0
0
0
⎢
⎥
⎢
1
γ
1
-1 + iD
⎥
⎢0
-
√
0
0
0
√
⎥
⎢
⎥
⎢
4
2
2q
4
2
2q
⎥
⎢
⎥
⎢
⎥
γ
γ2
γ
γ(1 - iD)
⎢
⎥
0
-
√
0
-
√
0
0
⎢
⎥
⎢
2
2q
2q2
2
2q
2q2
⎥
⎢
⎥
⎢
⎥
0
0
0
0
0
0
0
0
⎢
⎥
ρ = |Ψ〉〈Ψ| =
⎢
⎥
(3.1)
⎢
⎥
⎢
1
γ
1
-1 + iD
⎥
⎢0
-
√
0
0
0
√
⎥
⎢
4
2
2q
4
2
2q
⎥
⎢
⎥
⎢
⎥
0
0
0
0
0
0
0
0
⎢
⎥
⎢
⎥
⎢0
0
0
0
0
0
0
0
⎥
⎢
⎥
⎢
⎥
⎣
1 + iD
γ(1 + iD)
1 + iD
1+D2
⎦
0
-
√
0
-
√
0
0
2
2q
2q2
2
2q
2q2
В дальнейшем мы будем использовать собственное
случае малых значений параметра ДМ-взаимодей-
состояние (2.5), поскольку можно легко показать,
ствия и достаточно больших значений параметра
что получаемые результаты для двух величин оста-
анизотропии согласованность уменьшается с рос-
нутся неизменными, если рассматривать другой соб-
том параметра D. Это позволяет сделать вывод,
ственный вектор основного состояния (2.6).
что ДМ-взаимодействие способствует подавлению
Однако, как уже упоминалось, для систем с дву-
согласованности, а анизотропия восстанавливает ее.
мя кубитами соответствующей мерой запутанности
Относительная энтропия когерентности вычис-
является согласованность, поэтому нужно задать
ляется из (2.18), и получается следующий резуль-
приведенную матрицу плотности. Имеются два ва-
тат [46]:
рианта задания этой матрицы: вычисление согла-
сованности между узлами 1 и 3 суммированием по
γ2
(γ2 )
Cre = 1 -
log2
-
степеням свободы второго узла и вычисление согла-
2q2
2q2
сованности между средним узлом и любым другим
1+D2
(1+D2)
суммированием по степеням свободы оставшегося
-
log2
(3.4)
2q2
2q2
узла [44]. Мы выбираем первый вариант, но резуль-
тат от этого выбора не меняется:
Зависимости относительной энтропии когерентнос-
ρ13 = Tr2 ρ =
ти от параметров анизотропии γ и ДМ-взаимодей-
⎡
⎤
γ2
γ(1 - iD)
ствия D показаны на рис. 1б. Видно, что это поведе-
0
0
⎢
⎥
2q2
2q2
ние фактически противоположно поведению согла-
⎢
⎥
⎢
1
1
⎥
сованности, описанному выше.
⎢
0
0
⎥
⎢
4
4
⎥
⎢
⎥
Как видно на рис. 1, согласованность и отно-
=
(3.2)
⎢
⎥
1
1
⎢
⎥
сительная энтропия когерентности демонстрируют
⎢
0
0
⎥
⎢
4
4
⎥
противоположное поведение. Положения максиму-
⎦
⎣γ(1 + iD)
1+D2
мов одной из этих величин соответствуют положе-
0
0
2q2
2q2
ниям минимумов другой. Можно сказать, что про-
Согласованность можно легко вычислить, исполь-
цесс, увеличивающий одну из этих величин, умень-
зуя (2.16), и в результате получается [44]
шает при этом другую. В то время как минимум
√
√
согласованности расположен при C13 = 0, относи-
1
(1 + D2)γ
2
C13 =
-
(3.3)
тельная энтропия когерентности имеет в минимуме
4
q4
ненулевое значение Cre = 1.5. Тем не менее поведе-
Зависимость согласованности от параметра анизо-
ние остается противоположным. Зависимости обеих
тропии γ и от параметра ДМ-взаимодействия D по-
величин симметричны относительно оси y, что яв-
казана на рис. 1a. Можно видеть, что в случае ма-
ляется следствием симметричности анизотропии γ.
лых значений параметра анизотропии согласован-
Интересно проверить, выполняется ли это заключе-
ность растет с усилением ДМ-взаимодействия, а в
ние для систем большего размера.
233
С. Гомбар, П. Мали, М. Пантич и др.
ЖЭТФ, том 158, вып. 2 (8), 2020
3.1.1. Обобщение на случай систем большего
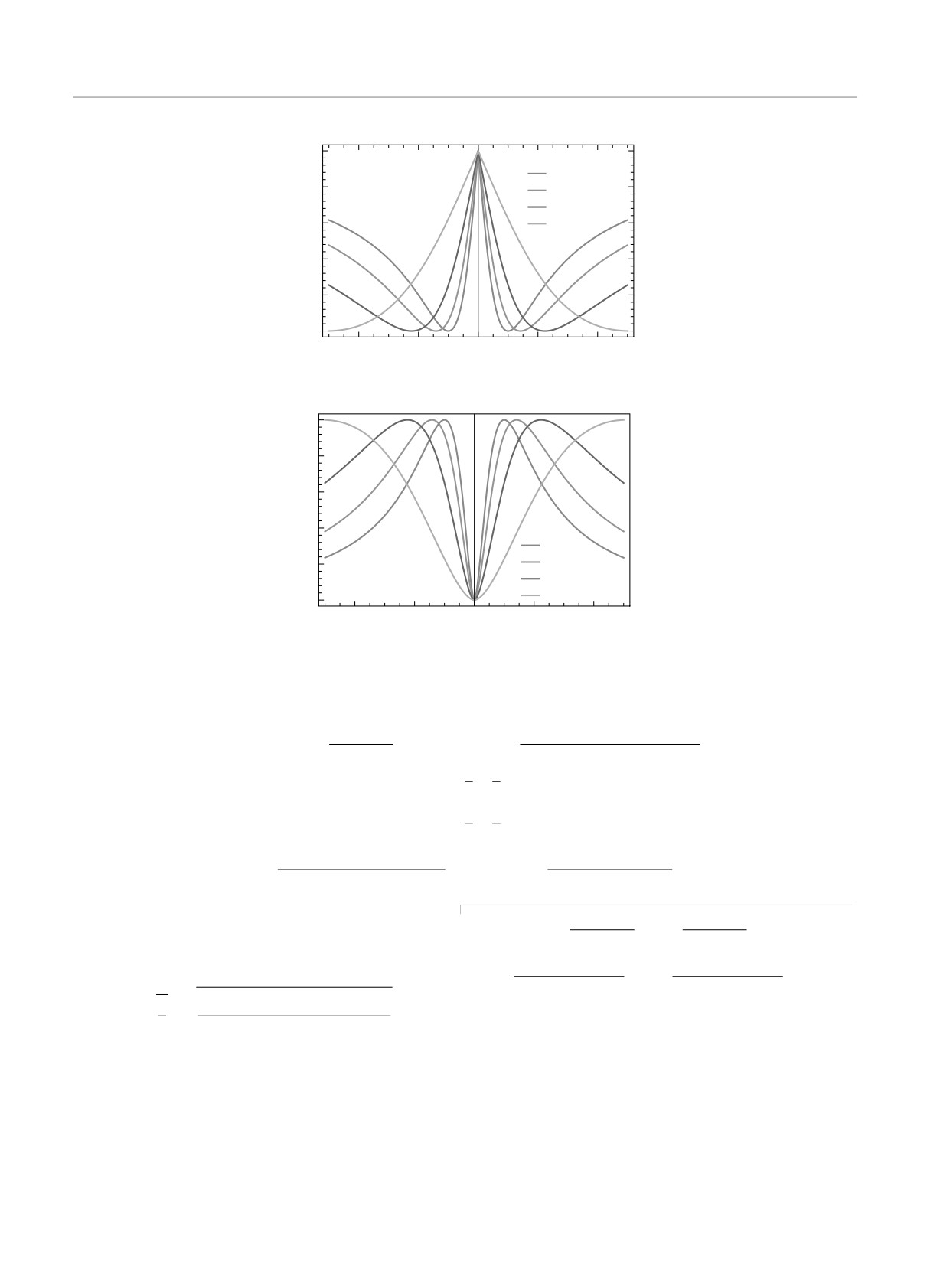
Зависимости согласованности и относительной эн-
размера
тропии когерентности от параметров γ и D в случае
9 и 27 узлов показаны на рис. 2.
В этом разделе мы сделаем обобщение на случай
Снова очевидно противоположное поведение обе-
систем большего размера с помощью метода кван-
их величин квантовой информатики. Минимум од-
товой ренормгруппы (КРГ-метод). Этот метод игра-
ной величины совпадает с максимумом второй и на-
ет большую роль для задач со спиновыми цепочка-
оборот. Кроме того, можно заметить, что с ростом
ми, поскольку их можно свести к рассмотрению си-
размера системы максимумы согласованности ста-
стем более низкой размерности в более удобном про-
новятся острее, а в случае относительной энтропии
странстве [45]. Мы применяем подход, использую-
когерентности острее становятся минимумы. Следо-
щий блочные матрицы, разработанный Кадановым
вательно, когда размер системы N → ∞, когерент-
[72]. Он состоит в разбивке гамильтониана на блоч-
ность имеет минимальное значение только в точ-
ную и межблочную части и нахождении базиса но-
ке γ = 0 и максимальное значение во всех осталь-
вого перенормированного пространства с использо-
ных точках, а согласованность будет иметь ненуле-
ванием основного состояния блочной части гамиль-
вое значение только в этой точке, а во всех осталь-
тониана. Эффективный гамильтониан находится в
ных точках будет равна нулю. Это означает, что в
виде [44]
точке γ = 0 происходит квантовый фазовый пере-
N/3
(
ход и с помощью найденных мер квантовой инфор-
′
∑
J
Heff =
(1+γ′)σxjσxj+1-(1-γ′)σyjσyj+1 +
матики его можно обнаружить. Однако параметр D
4
j=1
никак не влияет на указанное поведение, поэтому
)
изменение этого параметра не приведет к квантово-
+ D′(σxj σyj+1 + σyj σxj+1)
(3.5)
му фазовому переходу системы [44].
с перенормированными параметрами
3.2. XY -модель с ДМ-взаимодействием и
2
асимметричной анизотропией
1 + D2 + 3γ
3γ + 3γD2 + γ3
J′ =
J, γ′ =
,
2q2
1 + D2 + 3γ2
(3.6)
В этом случае матрица плотности основного со-
D′ = -D.
стояния записывается в виде
ρ=
⎡
⎤
0
0
0
0
0
0
0
0
⎢
⎥
⎢
⎥
⎢
1
1+M
1
2iD+(-1+M)
⎥
⎢
0
-
0
0
0
⎥
⎢
4
4m
4
4m
⎥
⎢
⎥
⎢
⎥
⎢
1+M
(1+M)2
1+M
-2iD(1+M)-(M2-1)⎥
⎢
0
-
0
-
0
0
⎥
⎢
4m
4m2
4m
4m2
⎥
⎢
⎥
⎢
⎥
⎢
0
0
0
0
0
0
0
0
⎥
=
⎢
⎥
⎢
1
1+M
1
2iD+(-1+M)
⎥
⎢
0
-
0
0
0
⎥
⎢
4
4m
4
4m
⎥
⎢
⎥
⎢
⎥
⎢
0
0
0
0
0
0
0
0
⎥
⎢
⎥
⎢
⎥
⎢
0
0
0
0
0
0
0
0
⎥
⎢
⎥
⎣
⎦
-2iD+(-1+M)
2iD(1+M)-(M2-1)
-2iD+(-1+M)
4D2+(-1+M)2
0
0
0
0
4m
4m2
4m
4m2
(3.7)
и соответствующая приведенная матрица плотности имеет следующий вид:
234
ЖЭТФ, том 158, вып. 2 (8), 2020
Корреляционная связь квантовой запутанности...
С13
0.5
а
D = 0
0.4
1
2
0.3
5
0.2
0.1
0
-4
-2
0
2
4
Сre
2.0
б
1.9
1.8
1.7
D = 0
1.6
1
2
1.5
5
-4
-2
0
2
4
Рис. 1. Зависимости согласованности (а) и относительной энтропии когерентности (б) от параметра анизотропии γ при
разных параметрах ДМ-взаимодействия в модели с тремя узлами
⎡
⎤
(1 + M)2
-2iD(1 + M) - (M2 - 1)
⎢
0
0
⎥
⎢
4m2
4m2
⎥
⎢
⎥
1
1
⎢
⎥
0
0
⎢
⎥
⎢
4
4
⎥
ρ13 =
⎢
⎥
(3.8)
⎢
1
1
⎥
⎢
0
0
⎥
⎢
4
4
⎥
⎢
⎥
⎣
⎦
2iD(1 + M) - (M2 - 1)
4D2 + (-1 + M)2
0
0
4m2
4m2
)
2
Следовательно, согласованность дается выражени-
(1 + M)2
( (1 + M)
Cre = 1 -
log2
-
ем
4m2
4m2
4D2+(-1+M)2
(4 D2+(-1+M)2)
−
log2
,
(3.10)
√
4m2
4m2
√
1
(1+M)2(1+4D2-2M+M2)
C13 =
-
,
(3.9)
а ее зависимости от параметров M и
D показаны на
4
4m4
рис. 3б.
Снова можно видеть противоположное поведе-
ние обеих величин, рассчитанных для случая ани-
а ее зависимости от параметров M и
D показаны на
зотропии другого типа. Максимумы одной величи-
рис. 3a.
ны соответствуют минимумам другой. Следователь-
Аналогично, относительная энтропия когерент-
но, можно утверждать, что изменение типа анизот-
ности находится в виде
ропии не приводит к изменению описанной выше
235
С. Гомбар, П. Мали, М. Пантич и др.
ЖЭТФ, том 158, вып. 2 (8), 2020
С13
Сre
0.5
2.0
а
D = 0
б
0.4
1.9
1
2
0.3
1.8
5
D = 0
0.2
1.7
1
2
0.1
1.6
5
0
1.5
–4
-2
0
2
4
-4
-2
0
2
4
С13
Сre
0.5
2.0
в
г
0.4
1.9
D = 0
0.3
1.8
1
D = 0
2
1
0.2
1.7
5
2
5
0.1
1.6
0
1.5
-3
-2
-1
0
1
2
3
-3
-2
-1
0
1
2
3
Рис. 2. Зависимости согласованности и относительной энтропии когерентности от параметра анизотропии γ при разных
параметрах ДМ-взаимодействия D для случаев 9 (а, б) и 27 узлов (в, г)
1+
D2(2 + M)
корреляции величин квантовой информатики. В ми-
J′ =
J
,
нимумах когерентность опять принимает ненулевое
m2
значение. Однако в этом случае, несмотря на то, что
D2 + 2D2M + M3
M′ =
,
(3.12)
связь между величинами носит такой же характер,
1+2D2 +
D2M
пики на зависимости согласованности острее, чем
D′ = -D1+D2 +M+M2
пики на зависимости относительной энтропии коге-
1+2D2 +
D2M
рентности. Кроме того, за исключением случая
D=
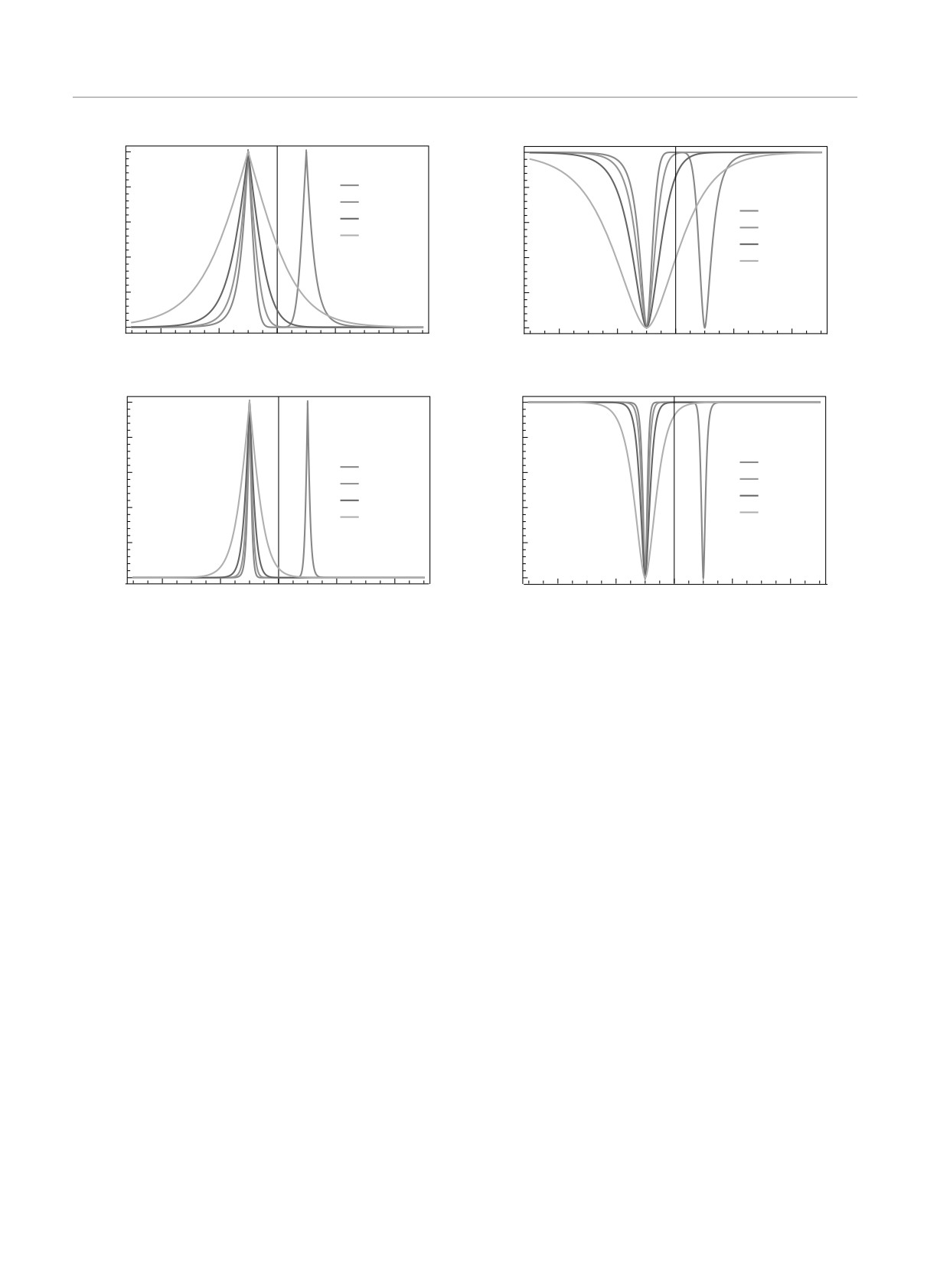
Зависимости согласованности и относительной энт-
= 0, ось y не является осью симметрии. Это следует
ропии когерентности от параметров M и D в случае
из выбора анизотропии.
9 и 27 узлов показаны на рис. 4.
В случае асимметричной анизотропии противо-
3.2.1. Обобщение на случай систем большего
размера
положное поведение зависимостей двух величин для
системы большего размера очевидно и в этом слу-
В качестве метода для исследования корреля-
чае. Следовательно, размер системы не имеет вли-
ции между запутанностью и когерентностью в слу-
яния на корреляцию запутанности и когерентности.
чае систем большего размера мы опять используем
Кроме того видно, что пики становятся острее с рос-
КРГ-метод. Эффективный гамильтониан дается вы-
том размера системы. Это означает, что изменение
ражением
параметра анизотропии M может вызвать кванто-
(
вый фазовый переход, но в этом случае его кри-
′
∑
J
тическое значение M = -1 в силу выбора анизо-
Heff =
σxiσxi+1 + M′σyiσyi+1 +
4
тропии. Фактически существует еще одна крити-
i=1
)
(
)
ческая точка при M
= +1, но только в случае
+ D′
σxiσyi+1 + σyiσxi+1
,
(3.11)
D
= 0, поэтому когда анизотропия асимметрич-
на, квантовый фазовый переход может быть вызван
где перенормированные параметры имеют вид
ДМ-взаимодействием.
236
ЖЭТФ, том 158, вып. 2 (8), 2020
Корреляционная связь квантовой запутанности...
С13
туациях. В этой работе связь между этими двумя
0.5
величинами обнаружена в случае спиновых XY -це-
а
почек со спинами 1/2 и ДМ-взаимодействием. На-
D= 0
0.4
1
ше исследование имело целью установить происхож-
2
дение этой связи. Было исследовано поведение мер
0.3
5
запутанности и когерентности при изменении пара-
метра ДМ-взаимодействия, типа и величины анизо-
0.2
тропии и размера системы.
В настоящей работе мы установили тип связи
0.1
между согласованностью и относительной энтропи-
0.0
ей когерентности в случае симметричного выбора
-4
-2
0
2
4
анизотропии γ. Как оказалось, эта связь носит прос-
M
той характер, демонстрирующий противоположное
Сre
поведение зависимостей двух величин. Мы устано-
2.0
вили, что изменение значений параметров ДМ-взаи-
б
модействия и анизотропии не меняет характера это-
1.9
го противоположного поведения. Мы также под-
твердили, что такая же связь остается и при измене-
1.8
нии размера системы, т. е. корреляция не меняется
1.7
при увеличении количества итераций КРГ-метода.
D= 0
Следовательно, это утверждение остается справед-
1
1.6
ливым и для систем бесконечного размера.
2
5
На следующем этапе была проведена провер-
1.5
ка, останется ли поведение зависимостей противопо-
-4
-2
0
2
4
ложным, если поменять тип анизотропии, для чего
M
мы рассмотрели анизотропию асимметричного ти-
Рис. 3. Зависимости согласованности (а) и относительной
па. Оказалось, что выбор анизотропии другого ти-
энтропии когерентности (б) от параметра анизотропии M
па не привел к изменению характера связи между
при разных параметрах ДМ-взаимодействия
D в модели с
величинами квантовой информатики, зависимости
тремя узлами
которых остались противоположными.
В заключение, парная согласованность и от-
носительная энтропия когерентности демонстриру-
Между тем, в случае анизотропии симметрично-
ют противоположное поведение при изменениях
го типа пик, соответствующий M = +1 и
D = 0,
параметра ДМ-взаимодействия, вида и величины
не появляется. Если выбрать γ = D =
D = 0, то
анизотропии и размера системы. Поскольку ранее
гамильтонианы (2.1) и (2.2) имеют тот же вид, что
уже было указано на важность сохранения коге-
и (2.11), соответственно для M = +1 и M = -1.
рентности в системе, легко видеть, насколько полу-
Выполнение π-вращения, которое связывает (2.1) и
ченные выводы могут быть существенны для разви-
(2.2), позволяет перейти от одного выбора парамет-
тия квантовой информатики. Максимум когерент-
ра M к другому (от +1 к -1 и наоборот). Модель
ности в системе достигается в минимуме парной за-
с анизотропией асимметричного типа включает как
путанности. Следовательно, эту конкретную систе-
(2.1), так и (2.2) для γ = 0. Следовательно, на рис. 1,
му можно ввести в состояние минимальной запутан-
2 можно увидеть лишь критический пик, соответ-
ности и максимальной когерентности, подстраивая
ствующий выбору γ = 0, а на рис. 3, 4 можно видеть
параметры. Возможно, что экстремальные значения
два критических пика при M = -1 и M = +1 для
обеих величин не являются наилучшим выбором,
D= 0.
поскольку обе они играют важную роль в кванто-
вой информатике.
Квантовая когерентность и квантовая запутан-
4. ЗАКЛЮЧЕНИЕ
ность изучались как величины, которые могут сиг-
Авторы работ [50, 51, 73] обсуждали вид связи,
нализировать о наличии квантового фазового пе-
которая существует между квантовой запутанно-
рехода в системе с анизотропией симметрично-
стью и квантовой когерентностью в различных си-
го типа [44, 45]. Авторы работ [44, 45] установи-
237
С. Гомбар, П. Мали, М. Пантич и др.
ЖЭТФ, том 158, вып. 2 (8), 2020
С13
Сre
0.5
2.0
а
D= 0
б
0.4
1.9
1
D= 0
0.3
2
1.8
1
5
2
0.2
1.7
5
0.1
1.6
0
1.5
-4
-2
0
2
4
-4
–2
0
2
4
M
M
С13
Сre
0.5
2.0
в
г
0.4
1.9
D= 0
D= 0
0.3
1.8
1
1
2
2
0.2
1.7
5
5
0.1
1.6
0
1.5
–4
-2
0
2
4
-4
–2
0
2
4
M
M
Рис. 4. Зависимости согласованности и относительной энтропии когерентности от параметра анизотропии M при разных
параметрах ДМ-взаимодействия в случаях 9 (а, б) и 27 узлов (в, г)
ли существование квантового фазового перехода
Финансирование. Работа выполнена при под-
при критическом значении параметра анизотропии
держке Сербского Министерства Науки и Образова-
γC
= 0. Поскольку экстремальные значения ко-
ния (грант № 171009) и Краевого Секретариата Выс-
герентности и согласованности в этой точке оста-
шего Образования и Научных Исследований Воево-
ются неизменными независимо от значения пара-
дины (проект № APV 114-451-2201).
метра ДМ-взаимодействия D, под влиянием ДМ-
взаимодействия в системе не может произойти кван-
товый фазовый переход. В нашей работе показа-
но, что это не так, если рассматривать анизотро-
ЛИТЕРАТУРА
пию асимметричного типа. Во-первых, такой выбор
1. G. E. Moore, Electronics 38, 114 (1965).
анизотропии смещает критическую точку в поло-
жение MC = -1. Более того, эта точка не явля-
2. D. Geer, Computer 38, 11 (2005).
ется единственной критической, поскольку пик при
M = +1 для
D = 0 становится более острым при
3. B. P. Lanyon, J. D. Whitfield, G. G. Gillett,
увеличении количества итераций КРГ-метода. По-
M. E. Goggin, M. P. Almeida, I. Kassal, J. D. Bia-
этому можно указать еще одну критическую точку
monte, M. Mohseni, B. J. Powell, M. Barbieri, A. As-
при MC = +1, DC = 0. Из этого следует, что хотя
puru-Guzik, and A. G. White, Nature Chem. 2, 106
ДМ-взаимодействие не влияет на квантовый фазо-
(2010).
вый переход при анизотропии симметричного типа,
4. J. I. Colless, V. V. Ramasesh, D. Dahlen, M. S. Blok,
оно может влиять для XY -цепочек со спинами 1/2
M. E. Kimchi-Schwartz, J. R. McClean, J. Carter,
в случае, когда анизотропия асимметрична.
W. A. de Jong, and I. Siddiqi, Phys. Rev. X 8, 011021
(2018).
238
ЖЭТФ, том 158, вып. 2 (8), 2020
Корреляционная связь квантовой запутанности...
5.
M. A. Nielsen and I. L. Chuang, Quantum Computa-
24.
T. D. Ladd, F. Jelezko, R. Laflamme, Y. Nakamura,
tion and Quantum Information, Cambridge Universi-
C. Monroe, and J. L. O’Brien, Nature 464, 45 (2010).
ty Press, Cambridge (2000).
25.
P. C. E. Stampa and A. Gaita-Ariсoa, J. Mater.
6.
R. P. Feynman, Int. J. Theor. Phys. 21, 467 (1981).
Chem. 19, 1718 (2009).
7.
D. Deutsch, Proc. R. Soc. Lond. A 400, 97 (1985).
26.
W. G. Unruh, Phys. Rev. A 51, 992 (1995).
8.
P. W. Schor, Proc. 35th Annu. Symp. Found. Com-
27.
M. Matsumoto, B. Normand, T. M. Rice, and M. Sig-
puter Science, IEEE Press 124 (1994).
rist, Phys. Rev. B 69, 054423 (2004).
9.
L. K. Grover, Proc. STOC, 212 (1996).
28.
P. Dai, Rev. Mod. Phys. 87, 855 (2015).
10.
V. Vedral, Introduction to Quantum Information
29.
M. Manojlović, M. Pavkov, M.
Škrinjar, M. Pantić,
Science, Oxford University Press on Demand, Cam-
D. Kapor, and S. Stojanović, Phys. Rev. B 71, 132510
bridge (2006).
(2005).
11.
J. F. Clauser, M. A. Horne, A. Shimony, and
30.
M. Manojlović, M. Pavkov, M.
Škrinjar, M. Pantić,
R. A. Holt, Phys. Rev. Lett. 23, 880 (1969).
D. Kapor, and S. Stojanović, Phys. Rev. B 68, 014435
(2003).
12.
D. Stucki, N. Gisin, O. Guinnard, G. Ribordy, and
H. Zbinden, New J. Phys. 4, 41 (2002).
31.
S. Radošević, M. Pavkov-Hrvojević, M. Pantić,
M. Rutonjski, D. Kapor, and M.
Škrinjar, Europhys.
13.
C. Gobby, Z. L. Yuan, and A. J. Shields, Appl. Phys.
J. B 68, 511 (2009).
Lett. 84, 3762 (2004).
32.
K. Yang, K. Moon, L. Zheng, A. H. MacDonald,
14.
S. Grцblacher, T. Jennewein, A. Vaziri, G. Weihs, and
S. M. Girvin, D. Yoshioka, and Shou-Cheng Zhang,
A. Zeilinger, New J. Phys. 8, 75 (2006).
Phys. Rev. Lett. 72, 732 (1994).
15.
T. Brecht, W. Pfaff, C. Wang, Y. Chu, L. Frunzio,
33.
E. Fradkin, Field Theories of Condensed Matter Phy-
M. H. Devoret, and R. J. Schoelkopf, Quantum Inf.
sics, Cambridge University Press, Cambridge (2013).
2, 16002 (2016).
34.
Rosario Fazio and Herre van der Zant, Phys. Rep.
16.
G. Moody, C. McDonald, A. Feldman, T. Harvey,
355, 235 (2001).
R. P. Mirin, and K. L. Silverman, Phys. Rev. Lett.
116, 037402 (2016).
35.
S. Sachdev, Quantum Phase Transitions, Cambridge
University Press, Cambridge (2011).
17.
P. W. Deelman, L. F. Edge, and C. A. Jackson, MRS
Bulletin 41, 224 (2016).
36.
X. G. Wen, Quantum Field Theory of Many Body
Systems, Oxford University Press, Oxford (2007).
18.
B. Hacker, S. Welte, G. Rempe, and S. Ritter, Nature
536, 193 (2016).
37.
D. J. J. Farnell, O. Gцtze, and J. Richter, Phys. Rev.
B 93, 235123 (2016).
19.
M. Saffman, J. Phys. B: At. Mol. Opt. Phys. 49,
202001 (2016).
38.
P. Mьller, J. Richter, A. Hauser, and D. Ihle, Eur.
Phys. J. B 88, 159 (2015).
20.
Xi-Lin Wang, Luo-Kan Chen, W. Li, H.-L. Huang,
C. Liu, C. Chen, Y.-H. Luo, Z.-E. Su, D. Wu,
39.
M. R. Pantić, D. V. Kapor, S. M. Radošević, and
Z.-D. Li, H. Lu, Y. Hu, X. Jiang, C.-Z. Peng, L. Li,
P. Mali, Sol. State Commun. 182, 55 (2014).
N.-L. Liu, Yu-Ao Chen, Chao-Yang Lu, and Jian-Wei
Pan, Phys. Rev. Lett. 117, 210502 (2016).
40.
A. Auerbach, Interacting electrons and Quantum
Magnetism, Springer, Berlin (1998).
21.
M. Veldhorst, H. G. J. Eenink, C. H. Yang, and
A. S. Dzurak, Nat. Commun. 8, 1766 (2017).
41.
P. Mьller, J. Richter, and D. Ihle, Phys. Rev. B 95,
134407 (2017).
22.
D. M. Zajac, A. J. Sigillito, M. Russ, F. Borjans,
J. M. Taylor, G. Burkard, and J. R. Petta, Science
42.
Q. Meng, X. Sheng-Long, T. Ying-Juan, and
359, 439 (2018).
T. Dong-Ping, Chin. Phys. B 17, 2800 (2008).
23.
I. Kassal, J. D. Whitfield, A. Perdomo-Ortiz,
43.
Y. Y. Yang, W. Y. Sun, W. N. Shi et al., Front. Phys.
Man-Hong Yung, and A. Aspuru-Guzik, Ann. Rev.
(2019)
14:
Phys. Chem. 62, 185 (2011).
018-0880-1.
239
С. Гомбар, П. Мали, М. Пантич и др.
ЖЭТФ, том 158, вып. 2 (8), 2020
44.
Fu-Wu Ma, Sheng-Xin Liu, and Xiang-Mu Kong,
58.
A. Osterloh, L. Amico, G. Falci, and R. Fazio, Nature
Phys. Rev. A 84, 042302 (2011).
416, 608 (2002).
45.
Guo-Qing Zhang and Jing-Bo Xu, J. Phys. A: Math.
59.
X. M. Liu, W. W. Cheng, and J.-M. Liu, Sci. Rep. 6,
Theor. 50, 265303 (2017).
19359 (2016).
60.
B. Q. Liu, B. Shao, J. G. Li, J. Zou, and L. A. Wu,
46.
Jun-Qing Cheng, Wei Wu, and Jing-Bo Xu, Quant.
Phys. Rev. A 83, 052112 (2011).
Inf. Proc. 16, 231 (2017).
61.
M. Kargarian, R. Jafari, and A. Langari, Phys. Rev.
47.
F. Ares, J. G. Esteve, F. Falceto, and A. R. de Quei-
A 79, 042319 (2009).
roz, Phys. Rev. A 92, 042334 (2015).
62.
C. J. Wellard et al., Phys. Rev. B 68, 195209 (2003).
48.
V. Vedral and M. B. Plenio, Phys. Rev. A 57, 1619
(1998).
63.
D. Loss and D. P. DiVincenzo, Phys. Rev. A 57, 120
(1998).
49.
A. Streltsov, G. Adesso, and M. B. Plenio, Rev. Mod.
64.
Y. Ishikawa, N. Miura, Physics and Engineering App-
Phys. 89, 041003 (2017).
lications of Magnetism, Springer, Berlin (1991).
50.
Z. Xi, Y. Li, and H. Fan, Sci. Rep. 5, 10922 (2015).
65.
S. Maekawa, T. Tohyama, S. E. Barnes, S. Ishihara,
W. Koshibae, and G. Khaliullin, Physics of Transi-
51.
A. Streltsov, U. Singh, H. Shekhar Dhar, M. Nath Be-
tion Metal Oxides, Springer, Berlin (2004).
ra, and G. Adesso, Phys. Rev. Lett. 115, 020403
(2015).
66.
A. Wong and N. Christensen, Phys. Rev. A 63,
044301 (2001).
52.
N. Stusser, U. Schotte, A. Hoser, M. Meschke,
M. Meissner, and J. Wosnitza, J. Phys.: Condens.
67.
A. Osterloh and R. Schьtzhold, Phys. Rev. A 96,
Matter 14, 5161 (2002).
012331 (2017).
68.
W. K. Wooters, Phys. Rev. Lett. 80, 2245 (1998).
53.
V. E. Dmitrienko, E. N. Ovchinnikova, S. P. Collins,
G. Nisbet, G. Beutier, Y. O. Kvashnin, V. V. Mazu-
69.
K. Blum, Density Matrix Theory and Applications,
renko, A. I. Lichtenstein, and M. I. Katsnelson, Nat.
Plenum Press, New York (1996).
Phys. 10, 202 (2014).
70.
J. Aberg, arXiv:quant-ph/0612146.
54.
Th. J. Siskens, H. W. Capel, and K. J. F. Gaemers,
Physica A 79, 259 (1975).
71.
T. Baumgratz, M. Cramer, and M. B. Plenio, Phys.
55.
Th. J. Siskens and H. W. Capel, Physica A 79, 296
Rev. Lett. 113, 140401 (2014).
(1975).
72.
J. Rodriguez-Laguna, arXiv:cond-mat/0207340.
56.
I. Dzyaloshinsky, J. Phys. Chem. Sol. 4, 241 (1958).
73.
E. Chitambar and Min-Hsiu Hsieh, Phys. Rev. Lett.
57.
T. Moriya, Phys. Rev. 120, 91 (1960).
117, 020402 (2016).
240