ЖЭТФ, 2020, том 158, вып. 2 (8), стр. 374-394

ВОЛНОВЫЕ ПРОЦЕССЫ В ТРЕХМЕРНЫХ

СТРАТИФИЦИРОВАННЫХ ТЕЧЕНИЯХ ВРАЩАЮЩЕЙСЯ

ПЛАЗМЫ В ПРИБЛИЖЕНИИ БУССИНЕСКА

М. А. Федотоваa*, А. С. Петросян^a,b

^a Институт космических исследований Российской академии наук

117997, Москва, Россия

^b Московский физико-технический институт

141700, Долгопрудный, Московская обл., Россия

Поступила в редакцию 20 декабря 2019 г.,

после переработки 3 февраля 2020 г.

Принята к публикации 4 февраля 2020 г.

Исследуются магнитогидродинамические волны в стратифицированной вращающейся плазме в поле

силы тяжести в приближении Буссинеска. Развита теория течений на f-плоскости, на нестандартной

f-плоскости (с учетом горизонтальной компоненты силы Кориолиса), на β-плоскости и на нестандарт-

ной β-плоскости. В каждом рассматриваемом случае получены линейные решения систем трехмерных

магнитогидродинамических уравнений в приближении Бусcинеска, описывающие магнитные инерцион-

но-гравитационные волны, магнитострофические волны и волны магнито-Россби. С использованием

дисперсионных уравнений найдены все существующие типы трехволновых взаимодействий. Для случая

волн магнито-Россби в приближении β-плоскости показана эквивалентность низкочастотной моды волны

магнито-Россби в приближении Буссинеска и в магнитогидродинамическом приближении мелкой воды.

Методом многомасштабных разложений получена система амплитудных уравнений для взаимодействую-

щих волн и инкременты двух типов неустойчивости, имеющих место в системе: распада и усиления. Для

каждого из найденных типов трехволновых взаимодействий показано различие в коэффициентах и диф-

ференциальных операторах в системе трехволновых взаимодействий.

DOI: 10.31857/S0044451020080155

внутри Солнца [1-4], находящемся под конвектив-

ной зоной (солнечный тахоклин), при аккреции ве-

щества на нейтронные звезды [5-7], а также в дина-

1. ВВЕДЕНИЕ

мике атмосфер нейтронных звезд и магнитоактив-

Большая часть объектов, наблюдаемых во Все-

ных атмосфер экзопланет, захваченных приливами

ленной, находится в состоянии плазмы. Изучением

несущей звезды [8]. Практически, речь идет о раз-

плазменных объектов и сред за пределами земной

витии фундаментальных основ магнитной гидроди-

атмосферы занимается такая наука, как плазменная

намики вращающейся плазмы для понимания ши-

астрофизика. Она включает в себя область астрофи-

рокого класса астрофизических объектов.

зики (при изучении объектов вне солнечной систе-

мы) и область космической физики (при изучении

Одной из ключевых приближенных магнитогид-

процессов на Солнце). Настоящая работа посвяще-

родинамических моделей для описания крупномас-

на изучению волновых процессов в астрофизической

штабных процессов во вращающихся течениях аст-

плазме.

рофизической плазмы, в том числе для перечислен-

Отметим целый ряд новых приложений, возник-

ных выше явлений, является модель мелкой воды.

ших в последние годы, которые делают актуальной

Магнитогидродинамические уравнения в приближе-

задачу изучения крупномасштабных магнитогид-

нии мелкой воды играют такую же важную роль в

космической и астрофизической плазме, как и клас-

родинамических течений, например в тонком слое

сические уравнения мелкой воды в гидродинами-

^* E-mail: fedotova.maria@gmail.com

ке нейтральной жидкости. Большое количество ра-

374

ЖЭТФ, том 158, вып. 2 (8), 2020

Волновые процессы в трехмерных стратифицированных течениях. . .

бот было посвящено изучению волн в магнитогид-

ясь трехмерной, магнитогидродинамическая систе-

родинамическом приближении мелкой воды [9-27],

ма уравнений в приближении мелкой воды не мо-

в особенности волнам магнито-Россби. Такие волны

жет полностью описывать важный для астрофизики

определяют крупномасштабную динамику солнца и

случай устойчиво и непрерывно стратифицирован-

звезд [1, 21, 22], динамику магнитоактивных атмо-

ного слоя плазмы.

сфер экзопланет, захваченных приливами от несу-

В настоящей работе сделан существенный шаг

щей звезды [8], течений в аккреционных дисках ней-

вперед в изучении трехмерных волновых процес-

тронных звезд [5]. Крупномасштабные волны Россби

сов в магнитогидродинамических течениях вра-

в нейтральной жидкости определяют глобальную

щающейся стратифицированной плазмы, являю-

динамику планетных атмосфер и являются пред-

щийся принципиальным для реальных течений с

метом исследований в геофизической гидродинами-

непрерывной стратификацией. Как хорошо извест-

ке [23-25, 28]. Отметим также первые эксперимен-

но, в геофизической гидродинамике стратифициро-

тальные результаты по обнаружению волн Россби

ванных вращающихся течений возникают инерцион-

на Солнце [26, 29, 30].

но-гравитационные волны [40] вследствие двух вос-

Течения в плазменной астрофизике, так же как

станавливающих механизмов — вращения и стра-

и течения в геофизике, как правило, являются стра-

тификации. В рассматриваемом нами случае маг-

тифицированными. Учет стратификации в магни-

нитных течений волновая картина гораздо богаче

тогидродинамических моделях вращающейся плаз-

вследствие наличия дополнительной восстанавлива-

мы важен для анализа множества астрофизических

ющей силы, а именно, силы Лоренца, наряду с си-

объектов и явлений, например процессов в солнеч-

лой Кориолиса и силой плавучести. Кроме того,

ном тахоклине, устойчиво-стратифицированных об-

учет трехмерности позволяет детально исследовать

ластей в недрах звезд (излучающей зоны) и планет

волновые процессы в магнитогидродинамике стра-

(внешний жидкий слой ядра) [31, 32], осцилляций

тифицированной плазмы с учетом горизонтальной

вращающихся звезд и Солнца [33-36], астрофизиче-

составляющей силы Кориолиса, что является осо-

ских дисков [37], экзопланет [38]. Кроме того, учет

бенно принципиальным при изучении экваториаль-

стратификации позволяет существенно расширить

ных течений. Отметим, что волны Россби [34] обна-

возможности для интерпретации имеющихся дан-

ружены именно в экваториальной зоне Солнца.

ных наблюдений крупномасштабных волн Россби на

Мы изучаем устойчиво стратифицированный

Солнце [1, 22, 29]. Полная система уравнений маг-

слой астрофизической плазмы во вращающейся

нитной гидродинамики вращающейся стратифици-

системе координат в приближении Буссинеска

рованной плазмы в поле силы тяжести представляет

с линейным профилем плотности. Приближение

собой практически неразрешимую проблему как для

Буссинеска повсеместно используется для изучения

аналитического исследования, так и для численного

устойчиво-стратифицированных течений как нейт-

моделирования.

ральной жидкости [41-43], так и астрофизической

В работе [39] мы получили магнитогидродина-

плазмы [44-46]. В нашей работе мы используем

мические уравнения мелкой воды во внешнем маг-

трехмерную магнитогидродинамическую систе-

нитном поле, которые учитывают стратификацию

му в приближении Буссинеска с учетом силы

в модели двух слоев плазмы различной, но посто-

Кориолиса в четырех различных приближениях:

янной плотности. На основе данной модели были

на f-плоскости, на нестандартной f-плоскости

получены линейные волны магнито-Россби, найде-

(с учетом горизонтальной составляющей силы

ны поправки к ним, связанные с различием в плот-

Кориолиса), на β-плоскости и на нестандартной

ностях слоев, показано влияние стратификации в

β-плоскости. Получены законы дисперсии различ-

данной модели на групповые и фазовые скорости

ных типов магнитных инерционно-гравитационных

полученных волн, развита слабонелинейная теория

волн, магнитострофических волн, и волн магнито-

волн магнито-Россби и предсказаны параметриче-

Россби, динамика которых определяется силами

ские неустойчивости на основе полученных ампли-

Лоренца, Кориолиса и плавучести. Для уравнений

тудных уравнений трех взаимодействующих волн.

вращающейся стратифицированной плазмы без

Однако магнитогидродинамическая теория мелкой

учета сферичности (в приближении f-плоскости

воды является двумерной, что исключает не только

и нестандартной f-плоскости) найдены дисперси-

вертикальные компоненты скоростей и магнитного

онные соотношения для трехмерных магнитных

поля, но и учет вертикального изменения их гори-

инерционно-гравитационных волн и трехмерных

зонтальных составляющих. Таким образом, не явля-

магнитострофических волн. При распростране-

375

М. А. Федотова, А. С. Петросян

ЖЭТФ, том 158, вып. 2 (8), 2020

нии найденных волн только вдоль вертикальной

для амплитуд взаимодействующих волн и получе-

компоненты волнового вектора их дисперсионные

ны инкременты двух возможных в данной системе

соотношения описывают два типа магнитных волн,

неустойчивостей — распада и усиления. В разд. 3.1

первый из которых является частным случаем

получены дисперсионные соотношения для линей-

магнитных инерционно-гравитационных волн, ра-

ных магнитных инерционно-гравитационных волн и

пространяющихся только по вертикали, а второй —

магнитострофических волн в приближении Бусси-

частным случаем магнитострофических волн,

неска на нестандартной f-плоскости, а в разд. 3.2

распространяющихся только по вертикали.

описаны возможные для найденных типов волн

Кроме того, обнаружено, что аналогичный част-

трехволновые взаимодействия, получены уравнения

ный вид имеют и дисперсионные соотношения, опи-

для амплитуд взаимодействующих волн и инкремен-

сывающие распространение волн с учетом сферич-

ты неустойчивостей.

ности в первом приближении (на β-плоскости и

В разд. 4.1 получены дисперсионные соотноше-

на нестандартной β-плоскости) вдоль вертикальной

ния для горизонтальных магнитогравитационных

компоненты волнового вектора. В частном случае

волн и волн магнито-Россби в приближении Бус-

распространения волн в горизонтальной плоскости

синеска на β-плоскости, а в разд. 4.2 описаны воз-

магнитные инерционно-гравитационные волны пре-

можные для найденных типов волн трехволновые

вращаются в волны Альфвена, а магнитострофичес-

взаимодействия, получены уравнения для амплитуд

кие волны превращаются в магнитогравитацион-

взаимодействующих волн и инкременты неустой-

ные волны. Кроме того, для волн на нестандартной

чивостей. В разд. 5.1 получены дисперсионные со-

f-плоскости показано влияние горизонтальной со-

отношения для горизонтальных магнитогравитаци-

ставляющей силы Кориолиса на существование раз-

онных волн и волн магнито-Россби в приближе-

личных типов трехволновых взаимодействий.

нии Буссинеска на нестандартной β-плоскости, а в

Для уравнений вращающейся стратифицирован-

разд. 5.2 описаны возможные для найденных типов

ной плазмы в приближениях β-плоскости и нестан-

волн трехволновые взаимодействия, получены урав-

дартной β-плоскости найдены дисперсионные со-

нения для амплитуд взаимодействующих волн и ин-

отношения для двумерных волн на горизонталь-

кременты неустойчивостей.

ной плоскости, описывающие магнитогравитацион-

ные волны, аналогичные волнам на f-плоскости, и

различные типы волн магнито-Россби. Кроме то-

2. МАГНИТОГИДРОДИНАМИЧЕСКИЕ

го, показано, что в низкочастотном пределе дис-

ТЕЧЕНИЯ СТРАТИФИЦИРОВАННОЙ

персионное уравнение, описывающее горизонтально

ВРАЩАЮЩЕЙСЯ ПЛАЗМЫ В

распространяющиеся волны в стратифицированных

ПРИБЛИЖЕНИИ БУССИНЕСКА НА

вращающихся течениях в приближении Буссинеска,

f -ПЛОСКОСТИ

имеет решение в виде волны магнито-Россби, ана-

логичное полученному в работах по исследованию

2.1. Магнитные инерционно-гравитационные

магнитогидродинамических течений вращающейся

и магнитострофические волны в

плазмы на β-плоскости в приближении мелкой воды

стратифицированных течениях

[13,39]. Дисперсионные кривые для всех найденных

вращающейся плазмы. Линейная теория

типов волн качественно проанализированы для вы-

явления выполнения условия синхронизма, обеспе-

Будем исследовать плоские течения несжима-

чивающего наличие трехволновых взаимодействий.

емой вращающейся стратифицированной плазмы

Для всех найденных типов трехволновых взаимо-

в рамках трехмерных магнитогидродинамических

действий получены амплитудные уравнения и опи-

уравнений в приближении Буссинеска в геометрии

саны возможные параметрические неустойчивости и

устойчиво стратифицированного слоя с линейным

найдены их инкременты.

профилем плотности:

В разд. 2.1 получены дисперсионные соотно-

шения для линейных магнитных инерционно-гра-

витационных волн и магнитострофических волн

∂u

ρg

+ (u · ∇)u + f × u = -

∇p +

в приближении Буссинеска на f-плоскости, а в

∂t

ρ₀

разд. 2.2 описаны возможные для найденных ти-

пов волн трехволновые взаимодействия, удовлетво-

b × (∇ × b),

4πρ˜₀

ряющие условию синхронизма, выведены уравнения

376

ЖЭТФ, том 158, вып. 2 (8), 2020

Волновые процессы в трехмерных стратифицированных течениях. . .

∂b

нетривиальных решений. Дисперсионное соотноше-

+ (u · ∇)b = (b · ∇)u,

∂t

ние для волн во вращающейся стратифицированной

∂ρ

(1)

плазме в приближении Буссинеска на f-плоскости

+ (u · ∇)_hρ = -

u_z,

∂t

∂z

имеет вид

div u = 0,

(

)

k2z

k2h

ω⁴ - ω²

f²

-N²

+ 2(B₀

· k)²

где u — скорость плазмы, b — напряженность маг-

^V k²

k²

нитного поля в плазме, f — параметр Кориоли-

(

)

k2h

са, ρ — плотность плазмы, ρ0 — плотность при

+ (B₀

· k)²

(B₀ · k)² - N²

= 0,

(5)

k²

равновесной температуре, ρ(z) = N2zρ0/g — на-

чальный линейный профиль плотности, обеспечи-

где k_h = (k_x, k_y) — горизонтальная составляющая

вающий устойчивую стратификацию (N² — часто-

волнового вектора.

та Брента - Вяйсяля), p — давление, g = (0, 0, -g),

Решениями уравнения (5) являются дисперсион-

∂

(u·∇)h = u_x∂

+u_y∂

. Первое уравнение системы —

ные соотношения, описывающие два типа волн, вос-

уравнение изменения импульса, второе — уравнение

станавливающими силами которых являются сила

переноса магнитного поля, третье — уравнение из-

Лоренца, сила Кориолиса и сила плавучести — трех-

менения плотности, четвертое — условие бездивер-

мерные инерционно-гравитационные волны и трех-

гентности поля скоростей. Введем следующие пере-

мерные магнитострофические волны. Рассмотрим

обозначения:

подробнее первый тип волн. Дисперсионное соотно-

шение для трехмерных магнитных инерционно-гра-

ρg

ρ^′ =

P =

√

витационных волн в приближении Буссинеска имеет

ρ₀

4πρ˜₀

следующий вид:

{

Исследуем плоские течения несжимающейся

(

)

k2z

k2h

вращающейся стратифицированной плазмы в при-

ωmig3D = ±

f²

-N²

+ 2(B₀

· k)²

^V k²

k²

ближении Буссинеска на f-плоскости. В данном

[

приближении параметр Кориолиса имеет вид

k2z

f4V k4z + 4(B₀ · k)⁴f²

= (0, 0, f_V ). Запишем стационарное решение,

2k²

^V k²

удовлетворяющее системе (1), в виде

]1/2}1/2

− 2f2V k2zN²k2h + N⁴k⁴

(6)

q₀ = (ux0, uy0, uz0, Bx0, By0, Bz0, P₀, ρ)^T ,

(2)

в котором знак «+» соответствует волне, распро-

где u₀ = 0, B₀ = const, ∂P₀/∂z = -ρ(z). Линеаризо-

страняющейся по направлению волнового вектора

ванная система (1) на фоне стационарного решения

k, а знак «-» — волне, распространяющейся в на-

(2) имеет вид

правлении, противоположном k. В отсутствие маг-

∂u₁

нитного поля в системе (B₀ = 0) полученный тип

+ f × u₁ + ∇P₁ + ρ′1z+

волн описывает трехмерные инерционно-гравитаци-

∂t

+ B₀ × (∇ × B₁) = 0,

онные волны [47], являющиеся точным решением

дисперсионного соотношения (5) при B₀ = 0:

∂B₁

- (B₀ · ∇)u₁ = 0,

(3)

√

∂t

k2z

k2h

ωgr3D = ± f2V

-N²

(7)

∂ρ′1

k²

+ N²uz1 = 0,

∂t

Отметим, что для инерционно-гравитационных

div u₁ = 0,

волн в отсутствие магнитного поля (7) выполняет-

ся условие перпендикулярности групповой скорости

где z — единичный вектор вдоль оси z.

волновому вектору, v_gr · k = 0 [47], в то время как

Ищем решение системы (3) в следующем виде:

присутствие магнитного поля это условие нарушает.

При распространении магнитных инерцион-

q₁e^iϕ = (ux1, uy1, uz1, Bx1, By1, Bz1, P₁, ρ′1)^T ×

но-гравитационных волн только вдоль верти-

× exp[i(ωt - k_xx - k_yy - k_zz)] ,

(4)

кальной компоненты k_z волнового вектора k их

дисперсионное соотношение принимает вид

где ω — частота возмущения, а k — волновой вектор.

√

Условие равенства нулю детерминанта матрицы ли-

f2V

ωz1 = ±

+B20zk2z +f_V

+B20zk2z.

(8)

неаризованной системы (3) обеспечивает наличие

377

М. А. Федотова, А. С. Петросян

ЖЭТФ, том 158, вып. 2 (8), 2020

Знак «+» соответствует волнам, распространяю-

щимся в направлении k_z, а знак «-» — волнам, рас-

пространяющимся в направлении, противополож-

ном k_z. Динамика полученных волн определяется

уже только силой Кориолиса и силой Лоренца. От-

метим, что данный тип волн в отсутствие магнитно-

го поля в системе (B₀ = 0) описывается дисперсион-

ным соотношением ω = ±f₀.

При распространении магнитных инерцион-

но-гравитационных волн в плоскости (k_x, k_y) их

дисперсионное соотношение принимает вид

k=k_x

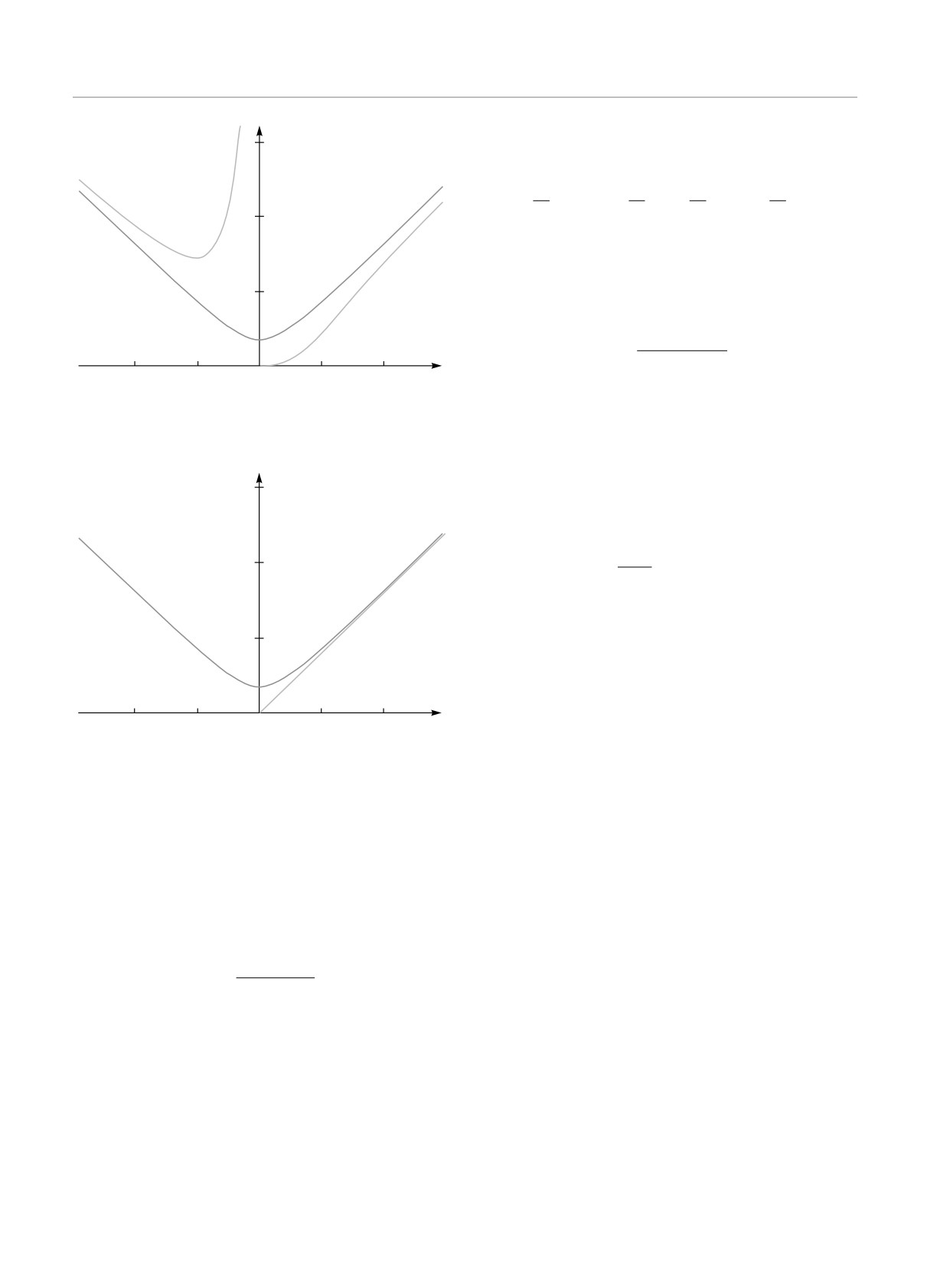
Рис. 1. Дисперсионные кривые: 1 — ωmgr ; 2 — ωA

ω_A = ±(B₀ · k)2h,

(9)

и описывает волны Альфвена, динамика которых

определяется только силой Лоренца. Знак «+» соот-

ветствует волнам Альфвена, распространяющимся

в направлении k_h, а знак «-» — волнам Альфве-

на, распространяющимся в направлении, противо-

положном k_h.

Рассмотрим второй тип волн, удовлетворяющих

дисперсионному уравнению (5) и не имеющих ана-

лога в гидродинамике нейтральной жидкости. Дис-

персионное соотношение для трехмерных магнито-

строфических волн имеет следующий вид:

{

(

)

k2z

k2h

ω_mstr = ±

f²

-N²

+ 2(B₀

· k)²

k=k

^V k²

k²

[

k2z

Рис. 2. Дисперсионные кривые: 1 — ωz1; 2 — ω

f4V k4z + 4(B₀ · k)⁴f²

2k²

^V k²

]1/2}1/2

- 2f2V k2zN²k2h + N⁴k4h

(10)

При распространении магнитострофических

волн в плоскости (k_x, k_y) их дисперсионное соотно-

в котором знак «+» соответствует волне, распрост-

шение принимает вид

раняющейся в направлении k, а знак «-» — волне,

распространяющейся в направлении, противопо-

ложном k. Данный тип волн исчезает в отсутствие

√

магнитного поля.

ω_mgr = ± (B₀ · k)2h - N²,

(12)

При распространении магнитострофических

волн только вдоль вертикальной компоненты k_z

волнового вектора k их дисперсионное соотношение

и описывает магнитогравитационные волны, дина-

принимает вид

мика которых определяется силой Лоренца и силой

√

плавучести. Знак «+» соответствует магнитограви-

√

f2V

тационным волнам, распространяющимся в направ-

ωz2 = ±

+B20zk2z -f_V

+B20zk2z.

(11)

лении k_h, а знак «-» — магнитогравитационным

волнам, распространяющимся в направлении, про-

Знак «+» соответствует волнам, распространяю-

тивоположном k_h.

щимся в направлении k_z, а знак «-» — волнам, рас-

пространяющимся в направлении, противополож-

Общий вид дисперсионных кривых для волн на

ном k_z. Динамика полученных волн определяется

f-плоскости при ω > 0 и k = k_x, k = k_z представлен

уже только силой Кориолиса и силой Лоренца.

на рис. 1 и 2.

378

ЖЭТФ, том 158, вып. 2 (8), 2020

Волновые процессы в трехмерных стратифицированных течениях. . .

k=k_x

Рис. 3. Условие синхронизма для двух магнитогравитаци-

k=k_z

онных волн и одной волны Альфвена: 1 — ω = ωmgr (kx);

2 — ω = ωA(kx - kxc) + ωmgr(kxc)

Рис. 4. Условие синхронизма для двух волн с частотами

ωz1 и одной волны с частотой ωz2: 1 — ω = ωz1(kz); 2 —

ω = ωz2(kz - kzc) + ωz1(kzc)

2.2. Трехволновые взаимодействия и

параметрические неустойчивости в

стратифицированных течениях

вращающейся плазмы

Ниже будем исследовать трехволновые взаимо-

действия волн на f-плоскости. Чтобы оценить воз-

можность существования межволновых взаимодей-

ствий для найденных волн, проанализируем их дис-

персионные соотношения. Наличие трехволновых

взаимодействий определяется выполнением условия

синхронизма [48]

ω(k₁) + ω(k₂) = ω(k₁ + k₂), k₁ + k₂ = k₃.

(13)

k=k

Проверим, существует ли трехволновое взаимо-

Рис. 5. Условие синхронизма для трех волн с частотами

действие между двумя магнитогравитационными

ωz2: 1 — ω = ωz2(kz); 2 — ω = ωz2(kz - kzc ) + ωz2(kzc )

волнами (12) и волной Альфвена (9). Для этого

изобразим дисперсионную кривую для магнитогра-

витационной волны (12) и смещенную относительно

частотой ω_mgr (12) взаимодействуют с волной Альф-

начала координат дисперсионную кривую для вол-

вена с частотой ω_A (9); две магнитные волны с час-

ны Альфвена (9). Если две дисперсионные кривые

тотой ωz1 (8) взаимодействуют с магнитной волной с

пересекаются в некоторой точке (ω(k₃), k₃), то это

частотой ωz2 (11); три магнитные волны с частотой

означает выполнение условия синхронизма (13). На

ωz2 (11) взаимодействуют между собой.

рис. 3 показано пересечение дисперсионных кривых

Для анализа слабонелинейных взаимодействий

двух магнитогравитационных волн (12) и одной вол-

на f-плоскости используем асимптотический ме-

ны Альфвена (9).

тод многомасштабных разложений для системы

Для волн, распространяющихся строго по k_z на

трехмерных магнитогидродинамических уравнений

рис. 4 показано пересечение дисперсионных кривых

вращающейся стратифицированной плазмы в при-

двух волн с частотами ωz1 (8) и одной волны с час-

ближении Буссинеска (1). Данный метод широко

тотой ωz2, а на рис. 5 — трех волн с частотами ωz2

используется для исследования слабонелинейных

(11).

взаимодействий, поэтому ограничимся кратким из-

Таким образом, качественный анализ линейных

ложением вывода амплитудных уравнений и при-

дисперсионных соотношений показывает возмож-

ведем полученные выражения для коэффициентов

ность существования следующих трехволновых вза-

взаимодействия трех волн. Существенные различия

имодействий: две магнитогравитационные волны с

между полученными амплитудными уравнениями

379

М. А. Федотова, А. С. Петросян

ЖЭТФ, том 158, вып. 2 (8), 2020

для взаимодействующих волн содержатся в диф-

где A — линейный оператор системы (3) на f-плос-

ференциальных операторах и коэффициентах, за-

кости, зависящий от q₀, T₀, X₀, Y₀, Z₀; оператор NL₁

висящих от начальных условий и характеристик

из правой части включает в себя производные по

взаимодействующих волн. Таким образом, краткий

медленным переменным, а NL₂

— по быстрым.

вывод уравнений приведен далее только для слу-

Умножая уравнение на собственный вектор z опе-

чая f-плоскости. Детали применения метода мно-

ратора A и последовательно выписывая слагаемые в

гих масштабов в магнитогидродинамических тече-

правой части пропорциональные eiϑ1 , eiϑ2 и eiϑ3 , по-

ниях вращающейся плазмы можно найти в рабо-

лучим систему для трех взаимодействующих волн:

тах [12, 13, 15].

s₁φ = f₁ψ^∗χ,

Получим амплитудные уравнения для всех выяв-

s₂ψ = f₂φ^∗χ,

(16)

ленных нелинейных трехволновых взаимодействий,

используя метод многомасштабных разложений.

s₃χ = f₃φψ,

Подставим в систему (1) на f-плоскости решение

где s_j — дифференциальный оператор по медлен-

в виде асимптотически сходящегося ряда q

ным переменным,

= q₀ + εq₁ + ε²q₂ + ... по малому параметру ε,

∂

характеризующему слабую нелинейность. Здесь

s_j = r_j

+p_j

+q_j

+w_j

(17)

∂T₁

∂X₁

∂Y₁

∂Z₁

q₀

— стационарное решение (2), q₁

— решение

а коэффициенты f_j зависят только от начальных

линейной системы (3), а q₂ — слагаемое, описы-

условий и характеристик взаимодействующих волн.

вающее эффекты квадратичной нелинейности. Во

Именно в выражениях для операторов s_j и коэффи-

втором порядке малости по ε получим уравне-

циентов f_j состоит различие в амплитудных уравне-

ние для q₂, содержащее резонансные слагаемые,

ниях (16) для различных типов взаимодействующих

нарушающие условие сходимости ряда (εq₁

≫

волн.

≫ ε²q₂). Исключим эти слагаемые следующим

Выпишем полученные выражения для диффе-

образом. Введем медленно-меняющуюся амплитуду

ренциальных операторов и коэффициентов взаимо-

q₁(T₁, X₁, Y₁, Z₁) и представим решение в виде

действия волн в магнитной гидродинамике страти-

суммы трех взаимодействующих волн:

фицированной вращающейся плазмы в приближе-

нии Буссинеска на f-плоскости. Коэффициент r_j

q₁(T₁, X₁, Y₁, Z₁)×

при производной по медленному времени имеет вид

× exp(iωT₀ - ik_xX₀ - ik_yY₀ - ik_zZ₀) =

∑

rj =

z_ia_i + z₄a₈ +

z_iai-1.

(18)

= α_ia(k_i)exp(iϑ_i) + c.c.,

(14)

i=1

i=5

i=1

при производной по медленной ко-

Коэффициент p_j

где α₁ ≡ φ, α₂ ≡ ψ, α₃ ≡ χ — амплитуды трех взаи-

ординате X₁ —

модействующих волн, а взаимосвязь «медленных»

переменных (с индексом «1») и «быстрых» (с индек-

p_j = z₁(a₇ + By0a₅ + Bz0a₆)-

(

)

сом «0») определена следующими выражениями:

∑

−Bx0

z_iai+3 +

z_iai-4

+z₈a₁.

(19)

∂

+ε

i=2

i=5

∂t

∂T₀

∂T₁

∂x

∂X₀

∂X₁

(15)

Коэффициент q_j при производной по медленной ко-

∂

+ε

ординате Y₁ —

∂y

∂Y₀

∂Y₁

∂z

∂Z₀

∂Z₁

Подставим решение в виде суммы трех волн (14)

q_j = z₂(a₇ + By0a₅ + Bz0a₆)-

(

)

в систему уравнений (1) на f-плоскости с учетом

∑

−By0

z_iai+3 +

z_iai-4

+z₈a₂.

(20)

(15). Во втором порядке малости получим систему

i=1

i=5

с резонансными слагаемыми, от которых мы мо-

жем избавиться, используя условие совместности,

Коэффициент w_j при производной по медленной ко-

а именно, ортогональность правой части уравнения

ординате Z₁ —

ядру линейного оператора, стоящего в левой части.

w_j = z₃(a₇ + Bx0a₄ + By0a₅) + ρ₀z₄a₃ -

Систему во втором порядке малости по ε для квад-

(

)

ратичной поправки q₂ запишем в следующем виде:

∑

−Bz0

z_iai+3 +

z_iai-4

+z₈a₃.

(21)

Aq₂ = -NL₁(q₀, q₁) - NL₂(q₁, q₁),

i=1

i=5

380

ЖЭТФ, том 158, вып. 2 (8), 2020

Волновые процессы в трехмерных стратифицированных течениях. . .

Коэффициенты f_j, зависящие от начальных условий

В выражениях (23)-(29) использованы следую-

и характеристик взаимодействующих волн, предста-

щие обозначения:

вим в виде

∑

a2i

=a_i

a^′i

a_i,ii

=a_i

a^′ii

+a_ii

a^′

f_j =

z_sκ_sj.

(22)

ikm

s=1

â_i,ii

=a_i

a^′ii

-a_ii

a^′

ikm

Выражение (22) содержит семь слагаемых вме-

сто восьми, поскольку κ₈ = 0. Для слагаемых в сум-

Индексы в коэффициентах f_j связаны следую-

ме (22) в случае волн на f-плоскости имеем

щим образом: когда индекс j = 1, то индекс l = 3,

[

индекс m = 2, индекс n = 1, γ = 1, индекс «^′»

κ1j =

-ik_xn(a²¹

+a²⁵

+a²

6_lm

(штрих) → «*» (комплексное сопряжение); когда ин-

+ iγk_ym(a₂

a′1

-a₅

a^′

4_km

декс j = 2, то индекс l = 3, индекс m = 1, индекс

+ ik_yl(a′5

a₄

-a′2

1_kl

n = 2, γ = 1, индекс «^′» (штрих)→«*» (комплекс-

ное сопряжение); когда индекс j = 3, то индекс l = 1,

+ iγk_zm(a₃

a′1

-a₆

a^′

4_km

]

индекс m = 2, индекс n = 3, γ = -1, а индекс «^′»

+ ik_zl(a′6

a₄

-a′3

1_kl

) ,

(23)

снимается.

[

В приближении f-плоскости при k = k_h взаи-

κ2j = iγk_xm(a₁

a′2

-a4kla^′

5_km

модействуют две магнитогравитационные волны и

волна Альфвена. В таком случае индекс j = 1 соот-

+ ik_xl(a′4

a5kl -a′1

a2kl )-ik_yn(a²²

+a²⁴

+a²

6_lm

ветствует волне Альфвена, а индексы j = 2, j = 3 —

+ iγk_zm(a₃

a′2

-a6kla^′

5_km

магнитогравитационным волнам. При k = k_z взаи-

]

модействуют либо две волны с частотой ωz1 и одна

+ ik_zl(a′6

a5kl - a′3

2_kl

) ,

(24)

волна с частотой ωz2, либо три волны с частотами

[

κ3j = iγk_xm(a₁

a′3

-a4kla^′

ωz2. В первом случае индекс j = 1 соответствует

6_km

волне с частотой ωz2, а индексы j = 2, j = 3 соот-

+ ikxl (a^′k

a6kl - a′1

3_kl

ветствуют волнам с частотой ωz1. Во втором случае,

+ iγk_ym(a₂

a′3

-a5kla^′

очевидно, индексы j = 1, j = 2, j = 3 соответствуют

6_km

волнам с частотой ωz2.

+ ik_yl(a′5

a6kl - a′2

3_kl

Система уравнений (16) является универсальной

]

- ik_zn(a²³

+a²⁴

+a²

) ,

(25)

системой для описания параметрических неустой-

5_lm

[

чивостей трехволновых взаимодействий и для раз-

κ4j = iγa′8

(k_xma1kl + k_yma2kl + k_zma

3_kl

личных случаев различается только коэффициента-

]

ми взаимодействия и дифференциальными опера-

- ia8kl (k_xla′1

+k_yla′2

+k_zla^′

3_km

) ,

(26)

торами. Таким образом, можно говорить о реали-

[

зации двух типов параметрических неустойчивос-

κ5j = i(γk_xm + k_xl)â₁₄

тей [12, 13, 15] в магнитогидродинамических тече-

+ iγk_ym(a₂

a′4

-a5kla^′

ниях стратифицированной вращающейся плазмы в

1_km

]

приближении Буссинеска на f-плоскости. Первый —

+ ik_yl(a′5

a1kl - a′2

4_kl

) ,

(27)

распад волны (магнитогравитационной волны; маг-

[

нитной волны, распространяющейся вертикально с

κ6j = iγk_xm(a₁

a′5

-a4kla^′

2_km

частотой ωz1; магнитной волны, распространяющей-

+ ik_xl(a′4

a2kl -a′1

a5kl )+i(γk_ym+k_yl)â25lm +

ся вертикально с частотой ωz2) с волновым век-

тором k₁ и частотой ω(k₁) на две волны (волна

+ iγk_zm(a₃

a′5

-a6kla^′

2_km

]

Альфвена и магнитогравитационная волна; магнит-

+ ik_zl(a′6

a2kl - a′3

5_kl

) ,

(28)

ная волна, распространяющаяся вертикально с час-

[

тотой ωz2 и магнитная волна, распространяющая-

κ7j = iγk_xm(a₁

a′6

-a4kla^′

3_km

ся вертикально с частотой ωz1; две магнитные вол-

+ ik_xl(a′4

a3kl - a′1

ны, распространяющиеся вертикально с частотами

6_kl

ωz2) с волновыми векторами k₂ и k₃, частотами

+ γk_ym(a₂

a′6

-a5kla^′

3_km

ω(k₂) и ω(k₃) и инкрементом неустойчивости Γ =

√

+ ik_yl(a′5

a3kl - a′2

6_kl

|f₂f₃|/|r₂r₃||φ₀| > 0 реализуется, когда в на-

]

чальный момент времени амплитуда одной из волн

+ i(γk_zm + k_zl)â₃₆

(29)

много больше двух других (φ = φ₀ ≫ ψ, χ).

381

М. А. Федотова, А. С. Петросян

ЖЭТФ, том 158, вып. 2 (8), 2020

Второй тип параметрической неустойчивости —

понентой вектора силы Кориолиса обычно прене-

усиление волны (волна Альфвена и магнитограви-

брегают, однако рост интереса к ее роли в дина-

тационная волна; магнитная волна, распространя-

мике волн на f-плоскости возрос в последнее вре-

ющаяся вертикально с частотой ωz2 и магнитная

мя в силу того, что она играет ключевую роль в

волна, распространяющаяся вертикально с часто-

экваториальных течениях, поскольку вертикальная

той ωz1; две магнитные волны, распространяющиеся

компонента силы Кориолиса на экваторе исчезает

вертикально с частотами ωz2) с волновым вектором

[42]. Если в приближении f-плоскости предполага-

k₁ и частотой ω(k₁) двумя волнами (волной Альф-

ется, что вектор f направлен строго по вертикали

вена и магнитогравитационной волной; магнитной

= (0, 0, f_V )), то в приближении нестандартной

волной, распространяющейся вертикально с часто-

f-плоскости будем полагать небольшое отклонение

той ωz2 и магнитной волной, распространяющейся

вектора f от вертикали. Таким образом, в параметре

вертикально с частотой ωz1; двумя магнитными вол-

Кориолиса появляется горизонтальная составляю-

нами, распространяющимися вертикально с часто-

щая: f = (0, f_H, f_V ), где f_V = 2Ω sinθ, f_H = 2Ω cosθ,

тами ωz2) с волновыми векторами k₂ и k₃, частота-

Ω — угловая скорость вращения, а θ — широта. Ста-

ми ω(k₂) и ω(k₃) и коэффициентом усиления Γ =

ционарное решение (2) удовлетворяет системе (1) в

= (|f₁|/|r₁|)|ψ₀χ₀| > 0 реализуется, когда в началь-

приближении нестандартной f-плоскости. Решени-

ный момент времени амплитуда одной из волн много

ем линеаризованной системы (3) на нестандартной

меньше двух других (φ ≪ ψ = ψ₀, χ = χ₀).

f-плоскости будет дисперсионное соотношение

Таким образом, магнитогидродинамические те-

)

⁽ (f_H k_y+f_V k_z)²

k2h

чения вращающейся плазмы в приближении Бусси-

ω⁴-ω²

-N²

+ 2(B₀

· k)²

неска в устойчиво стратифицированном слое с ли-

k²

(

)

нейным профилем плотности на f-плоскости вклю-

k2h

+ (B₀

· k)²

(B₀ · k)² - N²

= 0,

(30)

чают трехмерные магнитные инерционно-гравита-

k²

ционные волны и трехмерные магнитострофиче-

где k² = k2x + k2y + k2z, k2h = k2x + k2y.

ские волны. Показано, что в частном случае го-

Решениями уравнения (30) являются дисперси-

ризонтальных течений магнитные инерционно-гра-

онные соотношения, которые аналогичны получен-

витационные волны превращаются в волны Альф-

ным в разд. 2 уравнениям (6), (10) и описывают два

вена, а магнитострофические волны превращают-

типа волн: трехмерные инерционно-гравитационные

ся в магнитогравитационные волны. Для них ис-

волны и трехмерные магнитострофические волны.

следовано трехволновое взаимодействие двух маг-

Дисперсионное соотношение для трехмерных маг-

нитогравитационных волн и одной волны Альфвена.

нитных инерционно-гравитационных волн в прибли-

Также найден частный вид магнитных инерционно-

жении Буссинеска на нестандартной f-плоскости

гравитационных и магнитострофических волн в слу-

имеет следующий вид:

чае распространения только по вертикали, для ко-

торых исследованы два типа трехволновых взаимо-

ωmig3D =

действий.

{ (

)

(f_H k_y + f_V k_z )²

k2h

=±

-N²

+ 2(B₀

· k)²

k²

3. МАГНИТОГИДРОДИНАМИЧЕСКИЕ

[

(f_H k_y+f_V k_z)²

ТЕЧЕНИЯ СТРАТИФИЦИРОВАННОЙ

(f_H k_y+f_V k_z)⁴+4(B₀ · k)⁴

2k²

k²

ВРАЩАЮЩЕЙСЯ ПЛАЗМЫ В

ПРИБЛИЖЕНИИ БУССИНЕСКА НА

]1/2}1/2

НЕСТАНДАРТНОЙ f-ПЛОСКОСТИ

− 2(f_Hk_y + f_V k_z)²N²k2h + N⁴k⁴

(31)

3.1. Магнитные инерционно-гравитационные

При распространении магнитных инерцион-

и магнитострофические волны в

но-гравитационных волн только вдоль z-компо-

стратифицированных течениях

ненты волнового вектора (k = k_z ) дисперсионное

вращающейся плазмы. Линейная теория

соотношение

(31) описывает магнитные волны,

Будем исследовать плоские течения в рамках

аналогичные волнам на f-плоскости (8):

линеаризованных уравнений

(3) в приближении

√

нестандартной f-плоскости. В изучении вращаю-

f2V

ωz1 = ±

+B20zk2z +f_V

+B20zk2z.

(32)

щихся течений на f-плоскости горизонтальной ком-

382

ЖЭТФ, том 158, вып. 2 (8), 2020

Волновые процессы в трехмерных стратифицированных течениях. . .

При распространении магнитных инерцион-

но-гравитационных волн в плоскости (k_x, k_y)

дисперсионное соотношение (31) принимает вид

⎧

[

^⎨f2Hk2y

N²

f2Hk2y

ω_mig′ = ±

+ (B₀ · k)2h +

⎩ 2k2h

4k²

(

)

]1/2⎫

1/2

⎬

f²

k2y

N⁴

× H

-2N²+4(B₀ · k)²

(33)

k2h

⎭

и описывает двумерные магнитные инерционно-гра-

витационные волны на нестандартной f-плоскости.

= 0.1

В отсутствие магнитного поля дисперсонное соотно-

шение (33) переходит в

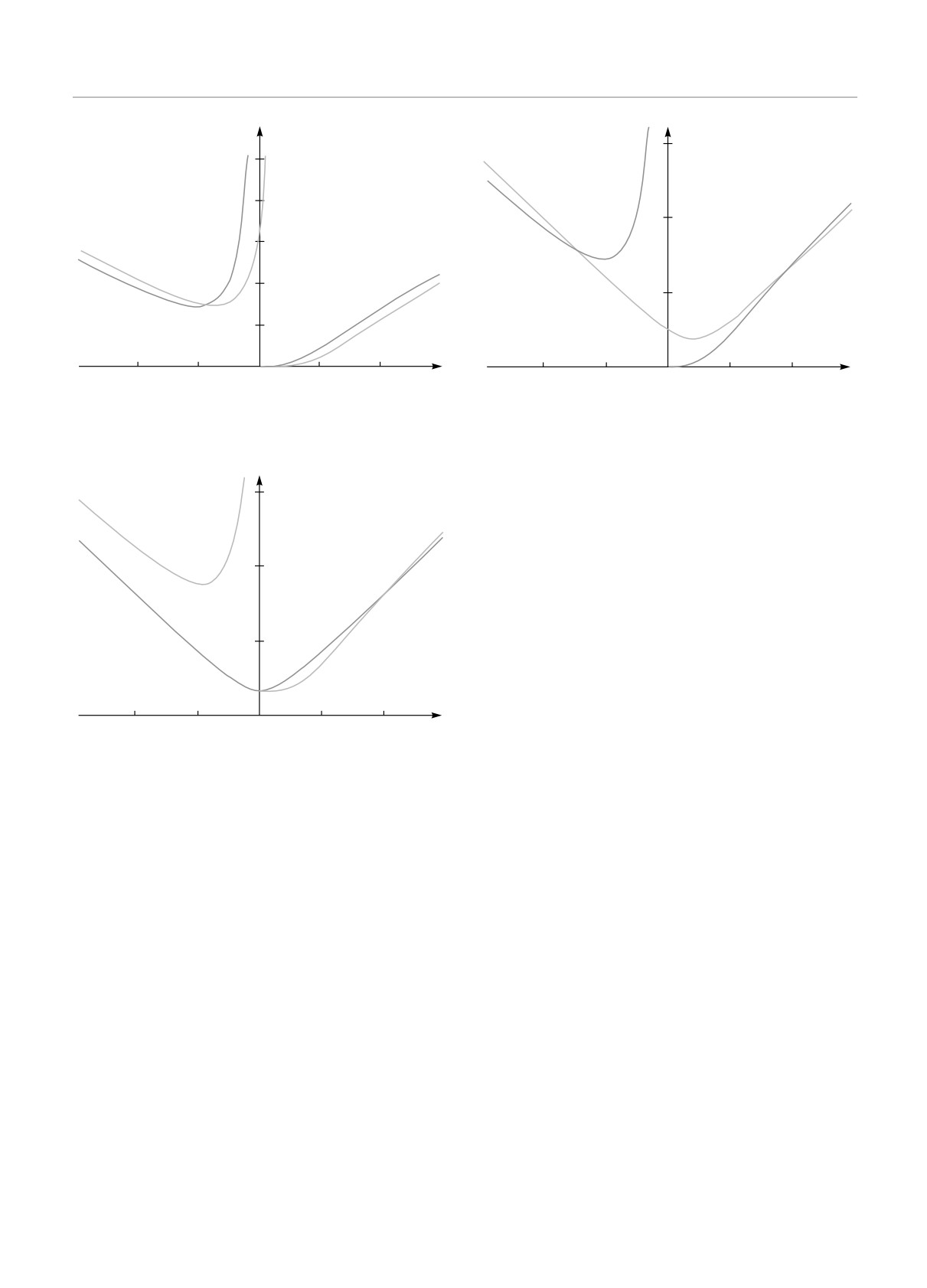
Рис. 6. Дисперсионные кривые: 1 и 3 — магнитная инерци-

√

онно-гравитационная волна с частотой ω_mig′ (kx) и магни-

f2Hk2y

тострофическая волна с частотой ω_mstr′ (kx) при fH < 1; 2

ω=±

-N²

k²

и 4 — магнитная инерционно-гравитационная волна с час-

тотой ω_mig′ (kx) и магнитострофическая волна с частотой

и описывает двумерные инерционно-гравитацион-

ω_mstr′ (kx) при fH ≫ 1

ные волны.

Дисперсионное соотношение для трехмерных

магнитострофических волн на нестандартной

f-плоскости имеет следующий вид:

ω_mstr =

{

)

⁽ (f_H k_y + f_V k_z)

k2h

=±

-N²

+ 2(B₀

· k)²

k²

[

(f_H k_y+f_V k_z)²

(f_H k_y+f_V k_z)⁴+4(B₀ · k)⁴

2k²

k²

]1/2}1/2

- 2(f_Hk_y + f_V k_z)²N²k2h + N⁴k4h

(34)

,k = 0.1

При распространении магнитострофических

волн только вдоль z-компоненты волнового вектора

Рис. 7. Дисперсионные кривые: 1 и 3 — магнитная инерци-

(k = kz) дисперсионное соотношение (34) описы-

онно-гравитационная волна с частотой ω_mig′ (ky) и магни-

вает магнитные волны, аналогичные волнам на

тострофическая волна с частотой ω_mstr′ (ky ) при fH < 1; 2

f-плоскости (11):

и 4 — магнитная инерционно-гравитационная волна с час-

√

тотой ω_mig′ (ky) и магнитострофическая волна с частотой

√

f2V

ω_mstr′ (ky) при fH ≫ 1

ωz2 = ±

+B20zk2z -f_V

+B20zk2z.

(35)

При распространении магнитострофических волн в

и описывает двумерные магнитострофические вол-

плоскости (k_x, k_y) дисперсионное соотношение (34)

ны на нестандартной f-плоскости, не имеющие ана-

принимает вид

лога в гидродинамике нейтральной жидкости.

⎧

[

Дисперсионные кривые имеют различный вид в

^⎨f2Hk2y

N²

f2Hk2y

зависимости от порядка величины горизонтальной

ω_mstr′ = ±

+ (B₀ · k)2h -

⎩ 2k2h

4k²

составляющей f_H параметра Кориолиса. Общий вид

дисперсионных кривых при ω(k_x) > 0, k_y = const и

(

)

]1/2⎫

1/2

⎬

k_x = const представлены на рис. 6 и 7.

f²

k2y

N⁴

× H

-2N²+4(B₀ · k)²

(36)

Найденные различия в дисперсионных кривых,

k2h

⎭

связанные с горизонтальной компонентой f_H в

383

М. А. Федотова, А. С. Петросян

ЖЭТФ, том 158, вып. 2 (8), 2020

= 0.1

Рис. 8. Условие синхронизма для двух магнитострофиче-

Рис. 9. Условие синхронизма для двух магнитных инерци-

ских волн с частотами ω_mstr′ и одной магнитной инерци-

онно-гравитационных волн с частотами ω_mig′ и одной маг-

онно-гравитационной волны с частотой ω_mig′ при fH < 1:

нитострофической волны с частотой ω_mstr′ при fH ≫ 1:

1 — ω = ω_mig′(kx); 2 — ω = ω_mstr′(kx - kxc) + ωmstr′(kxc)

1 — ω = ω_mig′(kx); 2 — ω = ωmstr′(kx - kxc) + ωmig′(kxc)

нестандартном приближении f-плоскости, сущест-

венно влияют на трехволновые взаимодействия, что

будет показано ниже.

3.2. Трехволновые взаимодействия и

параметрические неустойчивости в

стратифицированных течениях

вращающейся плазмы

Исследуем слабонелинейные взаимодействия

волн в стратифицированных течениях вращаю-

щейся плазмы в приближении Буссинеска на

,k = 0.1

нестандартной f-плоскости. Так же как в разд. 2,

Рис. 10. Условие синхронизма для двух магнитных инерци-

проверим выполнение условия синхронизма для

онно-гравитационных волн с частотами ω_mig′ и одной маг-

полученных в разд.

3.1

волн. Поскольку для

нитострофической волны с частотой ω_mstr′ при fH ≫ 1:

нестандартной f-плоскости в частном случае рас-

1 — ω = ω_mig′(ky); 2 — ω = ωmstr′(ky - kyc) + ωmig′(kyc)

пространения магнитных волн вдоль k_z получены

решения, аналогичные решениям на стандартной

f-плоскости, для них будут существовать анало-

гичные трехволновые взаимодействия, а именно,

ствий отображено на рис. 8 при k = k_x (аналогич-

ный вид будет иметь условие синхронизма при k =

взаимодействие двух магнитных волн с частотой

ωz1 (8) и магнитной волны с частотой ωz2 (11),

= k_y).

взаимодействие трех магнитных волн с частотой

Однако при достаточно большом значении f_H

ωz2 (11).

вид дисперсионных кривых сильно изменяется, что

Перейдем далее к анализу дисперсионных кри-

допускает возникновение еще одного типа трехвол-

вых для волн в плоскости (k_x, k_y). При малой гори-

новых взаимодействий помимо найденного выше —

зонтальной составляющей f_H силы Кориолиса суще-

возникновение магнитной инерционно-гравитацион-

ствует один тип трехволновых взаимодействий как

ной волны с частотой ω_mig′ при взаимодействии маг-

при k_y = const, так и при k_x = const — возникнове-

нитной инерционно-гравитационной волны с часто-

ние магнитной инерционно-гравитационной волны с

той ω_mig′ и магнитострофической волны с частотой

частотой ω_mig′ (33) при взаимодействии двух маг-

ω_mstr′ . Выполнение условия синхронизма для этих

нитострофических волн с частотой ω_mstr′ (36). Су-

трех взаимодействующих волн показано на рис. 9

ществование данного типа трехволновых взаимодей-

для k = k_x и на рис. 10 для k = k_y .

384

ЖЭТФ, том 158, вып. 2 (8), 2020

Волновые процессы в трехмерных стратифицированных течениях. . .

Используя метод многомасштабных разложений,

дисперсионных кривых для магнитных инерцион-

описанный в разд. 2, получим систему уравнений

но-гравитационных волн и магнитострофических

для амплитуд взаимодействующих волн на нестан-

волн. Кроме того, помимо описанного трехволново-

дартной f-плоскости:

го взаимодействия двух магнитострофических волн

и одной магнитной инерционно-гравитационной вол-

s′1φ = f′1ψ^∗χ,

ны при достаточно большой горизонтальной состав-

ляющей силы Кориолиса обнаружено и исследовано

s′2ψ = f′2φ^∗χ,

(37)

трехволновое взаимодействие двух магнитных инер-

ционно-гравитационных волн и одной магнитостро-

s′3χ = f′3φψ.

фической волны.

Отметим, что коэффициенты f^′j и дифференциаль-

ные операторы s^′j в полученной системе имеют та-

кой же вид, как и коэффициенты f_j (22) и операто-

4. МАГНИТОГИДРОДИНАМИЧЕСКИЕ

ТЕЧЕНИЯ СТРАТИФИЦИРОВАННОЙ

ры s_j (17) на стандартной f-плоскости и отличаются

ВРАЩАЮЩЕЙСЯ ПЛАЗМЫ В

только собственным вектором z линейного операто-

ПРИБЛИЖЕНИИ БУССИНЕСКА НА

ра системы (3).

β-ПЛОСКОСТИ

Таким образом, в нестандартном приближении

f-плоскости возникает магнитная инерционно-гра-

4.1. Волны магнито-Россби в

витационная волна с частотой ω_mig′ при взаимодей-

стратифицированных течениях

ствии двух магнитострофических волн с частота-

вращающейся плазмы. Линейная теория

ми ω_mstr′ . Кроме того, может возникать магнитная

инерционно-гравитационная волна с частотой ω_mig′

при взаимодействии магнитной инерционно-грави-

Исследуем магнитогидродинамические течения

тационной волны с частотой ω_mig′ и магнитострофи-

стратифицированной вращающейся плазмы с уче-

ческой волны с частотой ω_mstr′ при большом значе-

том эффектов сферичности в приближении β-плос-

нии k_H . В первом случае индекс j = 1 соответствует

кости. Считая, что параметр Кориолиса f слабо ме-

магнитной инерционно-гравитационной волне с час-

няется при малых изменениях широты, разложим

тотой ω_mig′ , а индексы j = 2, j = 3 соответствуют

его в ряд:

магнитострофическим волнам с частотами ω_mstr′.

Во втором случае индексы j = 1, j = 2 соответству-

f = 2Ωsinθ ≈ 2Ωsinθ₀ + 2Ω(θ - ϑ₀)cosθ₀ ≈

ют магнитным инерционно-гравитационным волнам

с частотами ω_mig′ , а индекс j = 3 соответствует маг-

≈f₀ +βy,

(38)

нитострофической волне с частотой ω_mstr′.

В силу универсальности системы уравнений

где f0 = 2Ω sinϑ0 (f0

≡ fV ), β

= ∂f/∂y. При-

(16) в ней реализуются два типа параметрических

ближение β-плоскости, в отличие от приближения

неустойчивостей — распад магнитной инерцион-

f-плоскости, сохраняет первый порядок малости в

но-гравитационной волны с волновым вектором

разложении параметра Кориолиса.

k₁ и частотой ω(k₁) на две волны (либо магнито-

Система магнитогидродинамических уравнений

строфические, либо магнитную инерционно-грави-

вращающейся плазмы с линейным профилем плот-

тационную и магнитострофическую) с волновыми

ности в приближении Буссинеска на β-плоскости

векторами k₂ и k₃, частотами ω(k₂) и ω(k₃) и инкре-

√

имеет вид

ментом неустойчивости Γ =

|f′2f′3|/|r′2r′3||φ₀| > 0;

усиление магнитной инерционно-гравитационной

∂²u_x

∂[(u · ∇)u_x]

∂u_y

∂²P

-f₀

- βu_y +

волны с волновым вектором k₁ и частотой ω(k₁)

∂y∂t

∂y

∂y∂x

двумя волнами (либо магнитострофическими

[

)

либо магнитной инерционно-гравитационной и

∂

⁽∂B

∂B_x

B_y

магнитострофической) с волновыми векторами k₂

∂y

∂x

∂y

и k₃, частотами ω(k₂) и ω(k₃) и коэффициентом

)]

усиления Γ = (|f′1|/|r′1|)|ψ₀χ₀| > 0.

⁽∂B_z

∂B_x

Таким образом, в приближении нестандартной

+ B_z

= 0,

∂x

∂z

f-плоскости показано влияние горизонтальной ком-

поненты вектора силы Кориолиса на общий вид

385

ЖЭТФ, вып. 2 (8)

М. А. Федотова, А. С. Петросян

ЖЭТФ, том 158, вып. 2 (8), 2020

∂u_y

∂P

k²ω⁴+βk_xω³-ω²[f²⁰k2z-N²k2h+2k²(B₀ · k)²] -

+ (u · ∇)u_y + f₀u_x +

∂t

∂y

)

- βk_xω[(B₀ · k)² - N²] + (B₀ · k)²[k²(B₀ · k)2 -

⁽∂B_z

∂B_y

⁽∂B_x

∂B_y

+B_z

+B_x

= 0,

- N²k2h] = 0,

(41)

∂y

∂z

∂y

∂x

)

∂u_z

∂P

⁽∂B_x

∂B_z

где k² = k2x + k2y + k2z, k2h = k2x + k2y.

+(u · ∇)u_z

+ρ^′+Bx

∂t

∂z

∂x

Рассмотрим распространение волн в плоскости

)

⁽∂B_y

∂B_z

(k_x, k_y) при условии k_z ≪ k. Дисперсионное соотно-

+B_y

= 0,

∂z

∂y

шение в данном приближении имеет вид

(39)

∂B_x

- (B · ∇)u_x = 0,

(

)

∂t

ω² - N² + (B₀ · k_h)²

(

)

∂B_y

βk_x

- (B · ∇)u_y = 0,

× ω² +ω

- (B₀ · k_h)2

(42)

∂t

k²

∂B_z

- (B · ∇)u_z = 0,

∂t

и описывает три типа волн. Первый тип волн — маг-

∂ρ^′

нитогравитационные волны, аналогичные волнам на

+ (u · ∇)_hρ^′ + N²u_z = 0,

∂t

f-плоскости (12). Второй тип волн — волны магни-

div u = 0.

то-Россби с дисперсионным соотношением

√

Стационарное решение, удовлетворяющее системе

βk_x

β²k2x

(39), имеет вид (2).

ωmr1 = -

+ 4(B₀ · k)²,

(43)

2k2h

k⁴

Запишем линеаризованную систему (39) на фоне

стационарного решения (2) в следующем виде:

которое в случае отсутствия магнитного поля пере-

ходит в дисперсионное соотношение для стандарт-

∂²ux1

∂uy1

∂²P

-f₀

- βuy1 +

ной гидродинамической волны Россби:

∂y∂t

∂y

∂y∂x

(

∂

∂By1

∂Bz1

βk_x

By0

+Bz0

ω_R = -

(44)

∂y

∂x

)

∂Bx1

- By0

-Bz0

= 0,

Третий тип волн — волны магнито-Россби с диспер-

∂y

∂z

сионным соотношением

∂uy1

∂P

∂Bz1

∂Bx1

+f₀ux1 +

+Bz0

+Bx0

√

∂t

∂y

βk_x

β²k2x

∂By1

ωmr2 = -

+ 4(B₀ · k)²,

(45)

−Bz0

-Bx0

= 0,

2k²

^- 2

k⁴h

∂z

∂x

∂uz1

∂P

∂Bx1

∂By1

которое обращается в нуль в отсутствие магнитного

+ρ^′

+Bx0

+By0

(40)

∂t

∂z

поля в системе.

∂Bz1

−Bx0

-By0

= 0,

Динамика волн магнито-Россби определяется си-

∂x

∂y

лой Кориолиса и силой Лоренца. Оба типа волн маг-

∂Bx1

нито-Россби, (43) и (45), при распространении стро-

- (B₀ · ∇)ux1 = 0,

∂t

вырождаются в альфвеновские волны с дис-

го по k_y

∂By1

- (B₀ · ∇)uy1 = 0,

персионным соотношением

∂t

∂Bz1

ωAy = ±B0yk_y,

(46)

- (B₀ · ∇)uz1 = 0,

∂t

∂ρ′1

аналогичные волнам Альфвена на f-плоскости при

+ N²uz1 = 0,

∂t

k = k_y (9).

div u₁ = 0.

Отметим, что в низкочастотном пределе уравне-

ние (41) имеет решение в виде волны магнито-Рос-

Из условия равенства нулю детерминанта матрицы

сби, динамику которой определяют не только сила

линеаризованной системы (40) получаем следующее

Кориолиса и Лоренца, но и сила плавучести:

дисперсионное соотношение для волн во вращаю-

щейся стратифицированной плазме на β-плоскости

(B₀ · k)²(k²(B₀ · k)² - N²k2h)

ω≈

(47)

в приближении Буссинеска:

βk_x((B₀ · k)² - N²)

386

ЖЭТФ, том 158, вып. 2 (8), 2020

Волновые процессы в трехмерных стратифицированных течениях. . .

щающейся жидкости. В отсутствие магнитного поля

(B₀ = 0) уравнение (41) принимает вид

(

)

k_x

k2z

k2h

k_x

ω³ +β

ω² -ω f²

-N²

+N²β

= 0. (49)

k²

⁰ k²

k²

Заметим, что для решения в низкочастотном преде-

ле можно получить выражение для частоты трех-

мерной гидродинамической волны Россби в прибли-

жении Буссинеска

N²βk_x

ω=

(50)

f²k2z - N2k

k=k_x

которое при условии k_z ≪ k переходит в стандарт-

Рис. 11. Дисперсионные кривые: 1 — магнитогравитаци-

ную гидродинамическую волну Россби (44). Дина-

онная мода; 2 — мода магнито-Россби

мика трехмерной волны Россби (50) определяется

не только силой Кориолиса, но и силой плавучести.

Для двумерных течений в плоскости (k_x, k_y) при

условии k_z ≪ k происходит переход к волнам во

вращающейся нейтральной жидкости. Дисперсион-

ное соотношение магнитогравитационных волн (12)

переходит в соотношение для гравитационных волн

√

-N², а дисперсионное соотноше-

с частотой ω = ±

ние для волн магнито-Россби (43), как было сказано

выше, переходит в дисперсионное соотношение для

гидродинамической волны Россби (44).

4.2. Трехволновые взаимодействия и

параметрические неустойчивости в

k=k_y

стратифицированных течениях

вращающейся плазмы

Рис. 12. Дисперсионные кривые: 1 — магнитогравитаци-

Ниже будем исследовать слабонелинейные взаи-

онная мода; 2 — мода Альфвена

модействия волн в стратифицированных течениях

вращающейся плазмы в приближении Буссинеска

Дисперсионное соотношение

(47) переходит

на β-плоскости. Качественный анализ дисперсион-

в дисперсионное соотношение для волны магни-

ных соотношений для волн вдоль k_x показывает

то-Россби, аналогичное полученному в работах

наличие следующих трехволновых взаимодействий:

по исследованию магнитогидродинамических те-

три волны магнито-Россби с частотами ωmr1 взаимо-

чений вращающейся плазмы на β-плоскости в

действуют между собой (рис. 13), две магнитограви-

приближении мелкой воды [13, 39] при k_z ≪ k:

тационные волны с частотами (12) взаимодействуют

с волной магнито-Россби с частотой (43) (рис. 14);

k2h(B₀ · k)2h

ω=

(48)

две волны магнито-Россби с частотами (43) взаимо-

βk_x

действуют с магнитогравитационной волной с час-

При распространении волн строго по k_z мы получа-

тотой (12) (рис. 15).

ем два типа магнитных волн, аналогичных волнам

Для волн вдоль k_y, аналогично волнам на

на f-плоскости (8), (11).

f-плоскости, реализуется взаимодействие двух

Общий вид дисперсионных кривых для случая

магнитогравитационных волн с частотами (12) и

ω > 0 для k = k_x представлен на рис. 11, а для

одной волны Альфвена с частотой (46). Для волн

k = k_y на рис. 12.

вдоль k_z существуют два типа взаимодействий: три

Рассмотрим переход в дисперсионном соотноше-

магнитные волны с частотами ωz2 (11), взаимодей-

нии (41) к случаю гидродинамики нейтральной вра-

ствующие между собой; две магнитные волны с

387

11*

М. А. Федотова, А. С. Петросян

ЖЭТФ, том 158, вып. 2 (8), 2020

k=k_x

Рис. 13. Условие синхронизма для трех волн магнито-Рос-

Рис. 15. Условие синхронизма для двух волн магнито-Рос-

сби: 1 — ω = ωmr1(kx); 2 — ω = ωmr1(kx -kxc )+ωmr1(kxc )

сби и одной магнитогравитационной волны: 1 — ω

= ωmr1(kx); 2 — ω = ωmg(kx - kxc ) + ωmr1(kxc )

Коэффициент r_j при производной по медленно-

му времени T₁ имеет вид

∑

rj = -iz1kyj a1 +

z_ia_i + z₄a₈ +

z_iai-1.

(52)

i=2

i=5

Коэффициент p_j при производной по медленной ко-

ординате X₁ имеет вид

pj = -iz1kyj (a7 + By0a5 + Bz0a6) -

(

)

∑

-Bx0

z_iai+3 +

z_iai-4

+z₈a₁.

(53)

k=k_x

i=2

i=5

Рис. 14. Условие синхронизма для двух магнитограви-

Коэффициент q_j при производной по медленной ко-

тационных волн и одной волны магнито-Россби:

—

ординате Y₁ имеет вид

ω = ωmgr(kx); 2 — ω = ωmr1(kx - kxc) + ωmgr(kxc)

qj = z1 [iωa1 - f0a2 - ikxj (a7 + By0a5 + Bz0a6) +

+ (2ik_yj By0+ik_zj Bz0)a₄] +z₂(a₇+Bx0a₄+Bz0a₆

частотами ωz1 (8), взаимодействующие с магнитной

(

)

∑

волной с частотой ωz2 (11).

−By0

z₃a₆ +

z_iai-4

+z₈a₂.

(54)

Методом многомасштабных разложений получа-

i=5

ем систему уравнений для амплитуды трех взаимо-

Коэффициент w_j при производной по медленной ко-

действующих волн на β-плоскости, удовлетворяю-

ординате Z₁ имеет вид

щих условию синхронизма (13):

s₁φ =

f₁ψ^∗χ,

w_j = z₃(a₇ + Bx0a₄ + By0a₅) + ρ₀z₄a₃ -

(

)

s₂ψ =

f₂φ^∗χ,

(51)

∑

−Bz0

ik_yjz₁a₄ + z₂a₅ +

z_iai-4

+z₈a₃.

(55)

s₃χ =

f₃φψ,

i=5

где s_j — дифференциальный оператор по медлен-

Коэффициенты

f_j аналогично коэффициентам

ным переменным, аналогичный оператору s_j (17), а

f_j (22) представимы в виде суммы:

коэффициенты

f_j, как и f_j (22), зависят только от

∑

начальных условий и параметров взаимодействую-

f_j =

z_s κ_sj.

(56)

щих волн.

s=1

388

ЖЭТФ, том 158, вып. 2 (8), 2020

Волновые процессы в трехмерных стратифицированных течениях. . .

Первое слагаемое в сумме (56) имеет вид

ющейся плазмы с линейным профилем плотности в

приближении Буссинеска на β-плоскости в низкоча-

κ1j = γ(k_ylk_xm + k_ymk_xl)(a²¹

+a²⁵

+a²

стотном пределе описывают волны магнито-Россби,

6_lm

восстанавливающими силами которых являются не

+ γk_ymk_yl(a₂₁

-a₅₄

только сила Кориолиса и Лоренца, но и сила пла-

+ γk_ymk_zl(a′3

a₁

-a′6

4_kl

вучести. В приближении горизонтальных течений

+ γk_ylk_zm(a₃

a′1

-a₆

a^′

(57)

данный тип волн описывает волны магнито-Рос-

4_km

сби с дисперсионным соотношением в виде, ана-

Остальные слагаемые в сумме (56) не отличаются от

логичном полученному в работах [13, 39] по иссле-

слагаемых в сумме (22).

дованию магнитогидродинамических течений вра-

На β-плоскости при k = ky взаимодействуют

щающейся плазмы на β-плоскости в приближении

волна Альфвена (46) и две магнитогравитационные

мелкой воды. Кроме того, горизонтальные магни-

волны (12). При этом индекс j = 1 соответствует

тогидродинамические течения описывают два типа

волне Альфвена (46), а индексы j = 2, j = 3 соот-

волн магнито-Россби и магнитогравитационные вол-

ветствуют магнитогравитационным волнам (12).

ны. Для найденных типов волн описаны следую-

Для волн, распространяющихся вдоль k_x,

щие трехволновые взаимодействия: три волны маг-

существуют три типа трехволновых взаимодейст-

нито-Россби, две магнитогравитационные волны и

вий. Первый тип определяет возникновение магни-

волна магнито-Россби, две волны магнито-Россби и

тогравитационной волны (12) при взаимодействии

магнитогравитационная волна.

волны магнито-Россби (43) и магнитогравитаци-

онной волны (12). В этом случае индекс j

= 1

соответствует волне магнито-Россби (43), а индексы

5. МАГНИТОГИДРОДИНАМИЧЕСКИЕ

j = 2, j = 3 соответствуют магнитогравитационным

ТЕЧЕНИЯ СТРАТИФИЦИРОВАННОЙ

ВРАЩАЮЩЕЙСЯ ПЛАЗМЫ В

волнам (12). Второй тип описывает возникновение

ПРИБЛИЖЕНИИ БУССИНЕСКА НА

волны магнито-Россби

(43) при взаимодействии

НЕСТАНДАРТНОЙ β-ПЛОСКОСТИ

магнитогравитационной волны (12) и волны маг-

нито-Россби (43). В этом случае индекс j

= 1

5.1. Волны магнито-Россби в

соответствует магнитогравитационной волне (12),

стратифицированных течениях

а индексы j

= 2, j

= 3 соответствуют волнам

вращающейся плазмы. Линейная теория

магнито-Россби (43). Третий тип определяет взаи-

модействие трех волн магнито-Россби (43). В этом

Исследуем сферические течения в нестандарт-

ном приближении β-плоскости [49]. По аналогии с

случае, очевидно, индексы j = 1, j = 2, j = 3

соответствуют волнам магнито-Россби (43).

нестандартным приближением f-плоскости предпо-

Для волн, распространяющихся вдоль k_z , при

лагается наличие горизонтальной компоненты, ко-

торая, как и вертикальная компонента, раскладыва-

взаимодействии трех магнитных волн ωz2 (11) ин-

дексы j = 1, j = 2, j = 3 соответствуют волнам (11);

ется в ряд. Таким образом, в приближении нестан-

дартной β-плоскости параметр Кориолиса выглядит

при взаимодействии двух магнитных волн с часто-

той ωz1 и одной магнитной волны с частотой ωz2

следующим образом:

индекс j = 1 соответствует магнитной волне (11), а

f = (0,f_H + γy,f_V + βy),

(58)

индексы j = 2, j = 3 соответствуют волнам (8).

В силу универсальности системы уравнений (16)

где

можно говорить о реализации двух типов парамет-

рических неустойчивостей: распад волны с волно-

2Ω cosθ

f_V = 2Ω sinθ, β =

f_H = 2Ω cosθ,

вым вектором k₁ и частотой ω(k₁) на две вол-

ны с волновыми векторами k₂ и k₃, частотами

2Ω sinθ

γ=-

ω(k₂) и ω(k₃) и инкрементом неустойчивости Γ =√

f₂f3|/|r2r3||φ0| > 0; усиление волны с волновым

Разложение горизонтальной составляющей

вектором k₁ и частотой ω(k₁) двумя волнами с вол-

компоненты силы Кориолиса добавляет слагае-

новыми векторами k₂ и k₃, частотами ω(k₂) и ω(k₃)

мые f_H ∂_yu_z + γu_z в уравнение для x-компоненты

и коэффициентом усиления Γ = (

f₁|/|r₁|)|ψ₀χ₀| > 0.

импульса и слагаемое

-f_Hu_x в уравнение для

Таким образом, магнитогидродинамические те-

z-компоненты импульса в системе магнитогид-

чения устойчиво стратифицированного слоя враща-

родинамических уравнений на β-плоскости

(39).

389

М. А. Федотова, А. С. Петросян

ЖЭТФ, том 158, вып. 2 (8), 2020

Стационарное решение

(2) удовлетворяет полу-

Точное аналитическое решение (61) мы можем най-

ченной системе. Линеаризованная система на

ти при k = k_x или k = k_y. При k = k_x уравнение

нестандартной β-плоскости имеет вид

(60) описывает три типа волн, аналогичных волнам

на стандартной β-плоскости: магнитогравитацион-

∂²ux1

∂uy1

∂uz1

-f₀

- βuy1 + f_H

ные волны, аналогичные волнам на f-плоскости

∂y∂t

∂y

(

(12) и волны магнито-Россби с дисперсионными со-

∂²P

∂

∂By1

∂Bz1

отношениями (43) и (45). При k = ky получаем

+γuz1+

By0

+Bz0

∂y∂x

∂y

∂x

два типа волн, аналогичных волнам на нестандарт-

)

∂Bx1

ной f-плоскости: одномерные магнитные инерцион-

- By0

-Bz0

= 0,

∂y

∂z

но-гравитационные волны

∂uy1

∂P

∂Bz1

∂Bx1

⎧

+f₀ux1 +

+Bz0

+Bx0

∂t

∂y

^⎨f2H

N²

ωmigy = ±

+B20yk2y

∂By1

⎩ 2

−Bz0

-Bx0

= 0,

∂z

∂x

]1/2⎫

1/2

)₂

∂uz1

∂P

∂Bx1

⎬

[(f2_H

N²

-f_Hux1 +

+ρ^′

+Bx0

(59)

+f2HB20yk²

(62)

∂t

∂z

⎭

∂By1

∂Bz1

+By0

-Bx0

-By0

= 0,

∂z

∂x

∂y

и одномерные магнитострофические волны

∂Bx1

⎧

- (B₀ · ∇)ux1 = 0,

∂t

^⎨f2H

N²

ωmstry = ±

+B20yk2y -

∂By1

⎩ 2

- (B₀ · ∇)uy1 = 0,

∂t

]1/2⎫

1/2

∂Bz1

)₂

⎬

- (B₀ · ∇)uz1 = 0,

[(f2_H

N²

∂t

−

+f2HB20yk²

(63)

⎭

∂ρ′1

+ N²uz1 = 0,

∂t

Важное отличие, связанное с нестандартным

div u₁ = 0.

приближением β-плоскости, которые мы можем по-

Из условия равенства нулю детерминанта матрицы

лучить аналитически, — низкочастотный предел в

уравнении (60), который дает новое выражение для

линеаризованной системы (59) получим следующее

волны магнито-Россби:

дисперсионное соотношение для волн во вращаю-

[

]

щейся стратифицированной плазме на нестандарт-

(B₀ · k)²

k²(B₀ · k)² - N²k²

ω_mr′ ≈

[

(

)

(64)

ной β-плоскости в приближении Буссинеска:

k_z

k_x (B₀ · k)² β - γ

− βN²

(

)

k_y

k_z

[

k²ω⁴ + k_xω³ β - γ

-ω²

(f_V k_z + f_H k_y)² -

Выражение (64), так же как и выражение (47), опи-

k_y

]

сывает волны магнито-Россби, динамика которых

- N²k2h + 2k²(B₀ · k)²

[

(

)

]

определяется не только силами Кориолиса и Лорен-

k_z

ца, но и силой плавучести, а при k_z ≪ k сводится к

- k_xω (B₀

· k)²

β-γ

- βN²

k_y

выражению, аналогичному полученному в работах

[

]

+ (B₀ · k)²

k²(B₀ · k)² - N²k2h

= 0,

(60)

по исследованию магнитогидродинамических тече-

ний вращающейся плазмы на β-плоскости в прибли-

где k² = k2x + k2y + k2z, k2h = k2x + k2y.

жении мелкой воды [13, 39]:

Рассмотрим распространение волн в плоскости

k2h(B₀ · k)2h

(k_x, k_y) при условии k_z ≪ k. Дисперсионное соотно-

ω=

(65)

βk_x

шение в данном приближении имеет вид

[

]

Общий вид дисперсионных кривых волны магни-

βk_x

f²

k2y

то-Россби (64) для различных направлений (k = k_x,

ω⁴ + ω³

-ω²

- N² + 2(B₀ · k)²

k2h

k²

k = k_y, k = k_z) при ω > 0, γ < β приведен на рис. 16.

Рассмотрим переход в дисперсионном соотноше-

βk_x

[

]

-ω

(B₀ · k)2h - N²

+ (B₀ · k)2h ×

нии (60) к случаю вращающейся нейтральной жид-

k²

[

]

кости. В отсутствие магнитного поля (B₀ = 0) урав-

(B₀ · k)2h - N²

= 0.

(61)

нение (60) принимает вид

390

ЖЭТФ, том 158, вып. 2 (8), 2020

Волновые процессы в трехмерных стратифицированных течениях. . .

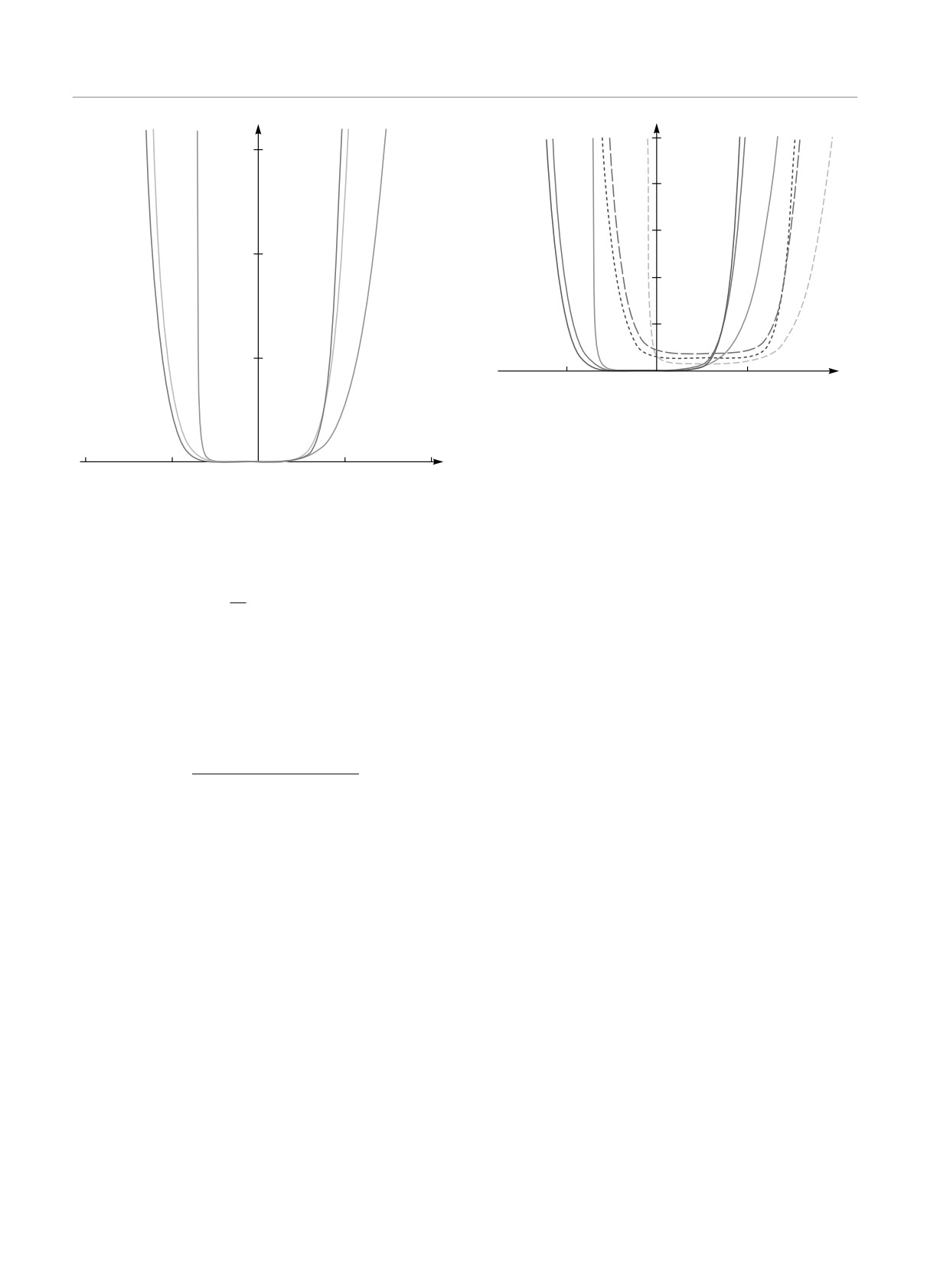
Рис. 17. Условие синхронизма для трех магнито-Россби

волн: 1 — ω = ωmr′(kx); 2 — ω

= ω_mr′(kx - kxc ) +

+ ω_mr′(kxc );

— ω

= ω_mr′(ky);

— ω

= ω_mr′(ky - kyc ) + ωmr′ (kyc ); 5 — ω = ωmr′ (kz); 6 —

ω = ω_mr′(kz - kzc) + ωmr′(kzc

)

Рис. 16. Дисперсионные кривые для волны магнито-Рос-

сби с частотой ω_mr′ : 1 — ω = ω_mr′ (kx), ky = kz = 0.1; 2 —

ω = ω_mr′(ky), kx = kz = 0.1; 3 — ωmr′(kz), kx = ky = 0.1

то-Россби с частотой (43); две волны магнито-Рос-

сби с частотами (43) взаимодействуют с магнитогра-

(

)

витационной волной с частотой (12). Для волн, рас-

k_z

[

k²ω³ + k_xω² β - γ

-ω

(f_V k_y + f_H k_z)² -

пространяющихся вдоль k_y, реализуются взаимо-

k_y

действие двух магнитострофических волн с часто-

]

тами (36) и одной магнитной инерционно-гравитаци-

- N²k2h

+ N²βk_x = 0.

(66)

онной волны с частотой (33) при малом значении f

и взаимодействие двух магнитных инерционно-гра-

В низкочастотном пределе получаем выражение

витационных волн с частотами (33) и одной магни-

для частоты трехмерной гидродинамической волны

тострофической волны с частотой (36) при большом

Россби в приближении Буссинеска:

значении f_H . Кроме того, реализуется взаимодейст-

N²βk_x

вие трех волн магнито-Россби с частотами ω_mr′ (64),

ω=

(67)

(f_V k_y + f_H k_z )² - N²k²

полученных в низкочастотном пределе, что показа-

но на рис. 17.

которое при условии k_z ≪ k переходит в стандарт-

Методом многомасштабных разложений полу-

ную гидродинамическую волну Россби (44).

чим систему уравнений для амплитуд трех взаимо-

действующих волн на нестандартной β-плоскости,

удовлетворяющих условию синхронизма (13):

5.2. Трехволновые взаимодействия и

параметрические неустойчивости в

s′₁φ =

f′1ψ^∗χ,

стратифицированных течениях

вращающейся плазмы

s′₂ψ =

f′2φ^∗χ,

(68)

Ниже исследуем слабонелинейные взаимодейст-

s′₃χ =

f′3φψ,

вия волн в стратифицированных течениях вра-

щающейся плазмы в приближении Буссинеска на

где s′j — дифференциальный оператор по медлен-

нестандартной β-плоскости. Качественный анализ

ным переменным, аналогичный оператору s_j (17), а

дисперсионных кривых для волн, распространяю-

коэффициенты

f^′j, как и f_j (22), зависят только от

щихся вдоль k_x, показывает существование сле-

начальных условий и параметров взаимодействую-

дующих трехволновых взаимодействий: три волны

щих волн.

магнито-Россби с частотами ωmr1 взаимодействуют

Коэффициенты r^′j, p^′j и w^′j не отличаются от ана-

между собой; две магнитогравитационные волны с

логичных коэффициентов на стандартной β-плос-

частотами (12) взаимодействуют с волной магни-

кости, а коэффициент q^′j имеет вид

391

М. А. Федотова, А. С. Петросян

ЖЭТФ, том 158, вып. 2 (8), 2020

q′j = z₁ [iωa₁ - f_V a₂ + f_H a₃ -

дены решения, описывающие трехмерные магнит-

ные инерционно-гравитационные волны (6), кото-

- ik_xj(a₇+By0a₅+Bz0a₆)+(2ik_yjBy0+ik_zjBz0)a₄] +

(

)

рые в отсутствие магнитного поля переходят в трех-

∑

мерные инерционно-гравитационные волны в при-

+ z₂(a₇ + Bx0a₄ + Bz0a₆)-By0 z₃a₆+ z_iai-4

ближении Буссинеска в нейтральной жидкости (7),

i=5

и трехмерные магнитострофические волны (10), не

+z₈a₂.

(69)

имеющие аналога в гидродинамике нейтральной

жидкости. Найдено, что наличие магнитного по-

Коэффициенты

f^′j аналогично коэффициентам f_j

ля нарушает условие перпендикулярности группо-

(22) представимы в виде суммы:

вой скорости инерционно-гравитационных волн вол-

∑

новому вектору. В частном случае распростране-

f^′j =

z_s κ_sj.

(70)

ния трехмерных волн в горизонтальной плоскос-

s=1

ти (k

= (k_x, k_y)) магнитые инерционно-гравита-

ционные волны на f-плоскости превращаются в

Слагаемые в сумме (70) не отличаются от слагаемых

волны Альфвена (9), магнитострофические волны

в сумме (56).

на f-плоскости — в магнитогравитационные волны

На нестандартной β-плоскости в низкочастотном

(12), магнитные инерционно-гравитационные вол-

пределе найден новый тип взаимодействия поми-

ны на нестандартной f-плоскости — в двумерные

мо описанных в предыдущих разделах: трехволно-

магнитные инерционно-гравитационные волны (33),

вое взаимодействие волн магнито-Россби с частота-

а магнитострофические волны на нестандартной

ми ω_mr′. При этом, очевидно, индексы j = 1, j = 2,

f-плоскости — в двумерные магнитострофические

j = 3 соответствуют волнам магнито-Россби (64).

волны (36). При распространении волн на f-плос-

В силу универсальности системы уравнений (68)

кости и на нестандартной f-плоскости только вдоль

можно говорить о реализации двух типов парамет-

вертикальной составляющей волнового вектора (k =

рических неустойчивостей: распад волны с волно-

= k_z) магнитные инерционно-гравитационные вол-

вым вектором k₁ и частотой ω(k₁) на две вол-

ны превращаются в магнитные волны с частотой

ны с волновыми векторами k₂ и k₃, частотами

ωz1 (8), а магнитострофические волны — в волны с

ω(k₂) и ω(k₃) и инкрементом неустойчивости Γ =√

частотой ωz2 (11), динамика которых определяется

f′2f′3|/|r′2r′3||φ0| > 0; усиление волны с волновым

только силой Лоренца и силой Кориолиса.

вектором k₁ и частотой ω(k₁) двумя волнами с вол-

Для сферических течений на β-плоскости и на

новыми векторами k₂ и k₃, частотами ω(k₂) и ω(k₃)

нестандартной β-плоскости также получены диспер-

и коэффициентом усиления Γ = (

f′1|/|r′1|)|ψ₀χ₀| > 0.

сионные уравнения и найдены решения в виде маг-

Таким образом, в нестандартном приближении

нитогравитационных волн (12), одномерных магнит-

β-плоскости найден новый тип волн магнито-Рос-

ных инерционно-гравитационных волн (62) и од-

сби, восстанавливающими силами которых явля-

номерных магнитострофических волн (63), анало-

ются не только сила Кориолиса и Лоренца, но

гичных волнам в плоских течениях, волн магни-

и сила плавучести, а дисперсионное соотношение

то-Россби (43), которые в отсутствие магнитного по-

включает в себя как параметр β, так и параметр

ля превращаются в гидродинамические волны Росс-

γ. Для найденного типа волн магнито-Россби ис-

би (44), и волн магнито-Россби (45), исчезающих в

следовано трехволновое взаимодействие при k =

отсутствие магнитного поля. Отметим, что в низ-

= (k_x, const,const), k

= (const, k_y, const) и k

кочастотном пределе найдены дисперсионные соот-

= (const,const, k_z ).

ношения для трехмерных волн магнито-Россби на

β-плоскости (47) и трехмерных волн магнито-Россби

на нестандартной β-плоскости (64), которые в при-

6. ЗАКЛЮЧЕНИЕ

ближении двумерных потоков (k_z ≪ k) описывают

В работе исследованы магнитогидродинамичес-

волны магнито-Россби (65), аналогичные получен-

кие волны в стратифицированной вращающейся

ным в работах [13, 39] по исследованию магнито-

плазме в поле силы тяжести в приближении Бус-

гидродинамических течений вращающейся плазмы

синеска (в устойчиво стратифицированном слое с

в приближении мелкой воды. Кроме того, в прибли-

линейным профилем плотности). Для плоских те-

жении вертикальных течений (k = k_z ) дисперсион-

чений на f-плоскости и на нестандартной f-плос-

ные соотношения как на β-плоскости (41), так и на

кости получены дисперсионные уравнения и най-

нестандартной β-плоскости (60) описывают магнит-

392

ЖЭТФ, том 158, вып. 2 (8), 2020

Волновые процессы в трехмерных стратифицированных течениях. . .

ные волны, распространяющиеся вдоль вертикаль-

На нестандартной β-плоскости существуют сле-

ной составляющей волнового вектора, аналогичные

дующие типы трехволновых взаимодействий: вза-

магнитным волнам на f-плоскости и на нестандарт-

имодействия волн магнито-Россби (43) и магни-

ной f-плоскости (8), (11).

тогравитационных волн

(12), аналогичные взаи-

Качественный анализ полученных дисперсион-

модействиям на β-плоскости; взаимодействия од-

ных соотношений показывает условие синхронизма

номерных магнитных инерционно-гравитационных

для следующих типов трехволновых взаимодейст-

волн (62) и одномерных магнитострофических волн

вий. Для плоских течений на f-плоскости реализу-

(63), аналогичные взаимодействиям на нестандарт-

ются три типа трехволновых взаимодействий: воз-

ной f-плоскости; взаимодействие трех волн магни-

никновение магнитогравитационной волны с часто-

то-Россби с частотами ω_mr′ (64).

той ω_mgr (12) при взаимодействии альфвеновской

Методом многомасштабных разложений по-

волны с частотой ω_A (9) и магнитогравитационной

лучены амплитудные уравнения для взаимодей-

волны с частотой ω_mgr (12); возникновение магнит-

ствующих волн и инкременты двух типов

ной волны с частотой ωz1 (8) при взаимодействии

неустойчивостей, имеющих место в системе, — рас-

магнитных волн с частотами ωz2 (11) и ωz1 (8); воз-

пад и усиление. Для каждого из найденных типов

никновение магнитной волны с частотой ωz2 (11)

трехволновых взаимодействий показано различие в

при взаимодействии двух магнитных волн с часто-

коэффициентах и дифференциальных операторах в

тами ωz2 (11).

системе трехволновых взаимодействий.

На нестандартной f-плоскости при малой гори-

зонтальной компоненте параметра Кориолиса (k_H <

Благодарности.

Авторы

признательны

< 1) при взаимодействии двух магнитострофичес-

Д. А. Климачкову за полезные обсуждения.

ких волн с частотами ω_mstr′ (36) возникает маг-

Финансирование. Работа поддержана Фондом

нитная инерционно-гравитационная волна с часто-

развития теоретической физики и математики «Ба-

той ω_mig′ (33). Кроме того, при исследовании вли-

зис» и Российским фондом фундаментальных ис-

яния горизонтальной составляющей параметра Ко-

следований (грант № 19-02-00016). Работа выполне-

риолиса на общий вид дисперсионных кривых на

на по проекту КП19-270 «Вопросы происхождения

нестандартной f-плоскости обнаружено, что поми-

и эволюции Вселенной с применением методов на-

мо описанного выше трехволнового взаимодействия,

земных наблюдений и космических исследований»

возможно возникновение магнитной инерционно-

Программы крупных проектов по проведению фун-

гравитационной волны с частотой ω_mig′ (33) при вза-

даментальных научных исследований по приори-

имодействии магнитострофической волны с часто-

тетным направлениям, определяемым Президиумом

той ω_mstr′ (36) и магнитной инерционно-гравитаци-

РАН.

онной волны с частотой ω_mig′ (33) при f_H ≫ 1.

Для сферических течений на β-плоскости реали-

зуются следующие типы трехволновых взаимодей-

ЛИТЕРАТУРА

ствий: два типа взаимодействий магнитных волн,

1. D. W. Hughes, R. Rosner, and N. O. Weiss, The Solar

распространяющихся вдоль вертикальной составля-

Tachocline, Cambridge Univ. Press (2007).

ющей волнового вектора, а также возникновение

магнитогравитационной волны (12) при взаимодей-

2. P. A. Gilman, Astrophys. J. Lett. 544, L79 (2000).

ствии волны Альфвена (46) с магнитогравитаци-

онной волной (12), аналогичные взаимодействиям

3. M. S. Miesch and P. A. Gilman, Solar Phys. 220, 287

(2004).

на f-плоскости; возникновение магнитогравитаци-

онной волны с частотой ω_mgr (12) при взаимодей-

4. M. Dikpati and P. A. Gilman, Astrophys. J. 551, 536

ствии волны магнито-Россби с частотой ωmr1 (43)

(2001).

и магнитогравитационной волны с частотой ω_mgr

(12); возникновение волны магнито-Россби с часто-

5. Н. А. Иногамов, Р. А. Сюняев, Письма в Астрон.

той ωmr1 (43) при взаимодействии магнитогравита-

ж. 36, 896 (2010).

ционной волны с частотой ω_mgr (12) и волны магни-

6. N. A. Inogamov and R. A. Sunyaev, arXiv:astro-ph/

то-Россби с частотой ωmr1 (43); возникновение вол-

9904333 (1999).

ны магнито-Россби с частотой ωmr1 (43) при вза-

имодействии двух волн магнито-Россби с частотой

7. A. Spitkovsky, Y. Levin, and G. Ushomirsky, Astro-

ωmr1 (43).

phys. J. 566, 1018 (2002).

393

М. А. Федотова, А. С. Петросян

ЖЭТФ, том 158, вып. 2 (8), 2020

J. Y. K. Cho, Phil. Trans. Roy. Soc. London A 366,

29.

T. V. Zaqarashvili and E. Gurgenashvili, Front.

4477 (2008).

Astron. Space Sci. 6, 7 (2018).

К. В. Карельский, А. С. Петросян, С. В. Тарасе-

30.

Z.-C. Liang, L. Gizon, A. C. Birch, and T. L. Duvall

вич, ЖЭТФ 140, 606 (2011).

Jr., Astron. Astrophys. 626, A3 (2019).

10.

K. V. Karelsky, A. S. Petrosyan, and S. V. Tarasevich,

31.

J. Braithwaite and H. C. Spruit, Roy. Soc. Open Sci.

Phys. Scripta 155, 014024 (2013).

4, 160271 (2017).

11.

K. V. Karelsky, A. S. Petrosyan, and S. V. Tarasevich,

32.

J. Philidet, C. Gissinger, F. Lignières, and L. Petit-

ЖЭТФ 146, 352 (2014).

demange, Geophys. Astrophys. Fluid Dynam. DOI:

12.

Д. А. Климачков, А. С. Петросян, ЖЭТФ 149, 965

10.1080/03091929.2019.1670827.

(2016).

33.

V. G. A. Böning, H. Hu, and L. Gizon, Astron. Astro-

13.

Д. А. Климачков, А. С. Петросян, ЖЭТФ 152, 705

phys. 629, A26 (2019).

(2017).

34.

B. Loeptien, L. Gizon, A. C. Birch et al., Nature

14.

Д. А. Климачков, А. С. Петросян, ЖЭТФ 150, 602

Astron. 2, 568 (2018).

(2016).

35.

M. Dikpati, P. S. Cally, S. W. McIntosh, and E. Hei-

15.

D. A. Klimachkov and A. S. Petrosyan, Phys. Lett.

fetz, Sci. Rep. 7, 14750 (2017).

A 381, 106 (2017).

36.

M. Dikpati, B. Belucz, P. A. Gilman, and

16.

T. V. Zaqarashvili, R. Oliver, and J. L. Ballester,

S. W. McIntosh, Astrophys. J. 862, 159 (2018).

Astrophys. J. Lett. 691, L41 (2009).

37.

J. M. Stone, J. F. Hawley, C. F. Gammie, and

17.

K. Heng and A. Spitkovsky, Astrophys. J. 703, 1819

S. A. Balbus, Astrophys. J. 463, 656 (1996).

(2009).

38.

K. Batygin, S. Stanley, and D. J. Stevenson, Astro-

18.

M. Dikpati, S. W. McIntosh, and G. Bothunet, Astro-

phys. J. 776, 53 (2013).

phys. J. 853, 144 (2018).

19.

X. Márquez-Artavia, C. A. Jones, and S. M. Tobias,

39.

М. А. Федотова, Д. А. Климачков, А. С. Петросян,

Geophys. Astrophys. Fluid Dynam. 111, 282 (2017).

Физика плазмы 46, 57 (2020).

20.

T. V. Zaqarashvili, Astrophys. J. 856, 32 (2018).

40.

B. Dintrans, M. Rieutord, and L. Valdettaro, J. Fluid

Mech. 398, 271 (1999).

21.

T. V. Zaqarashvili, R. Oliver, J. L. Ballester, and

B. M. Shergelashvili, Astron. Astrophys. 470, 815

41.

P. Billant and J. M. Chomaz, Phys. Fluids 13, 1645

(2007).

(2001).

22.

T. V. Zaqarashvilli, R. Oliver, J. L. Ballester et al.,

42.

J. I. Yano, J. Fluid Mech. 810, 475 (2017).

Astron. Astropys. 532, A139 (2011).

43.

S. Lee and R. Takada, Indiana Univ. Math. J. 66,

23.

В. И. Петвиашвили, О. А. Похотелов, Уединенные

2037 (2017).

волны в плазме и атмосфере, Энергоатомиздат,

Москва (1989).

44.

S. Takehiro, Phys. Earth Planet. Inter. 241,

(2015).

24.

G. K. Vallis, Atmospheric and Oceanic Fluid Dy-

namics: Fundamentals and Large-Scale Circulation,

45.

S. Takehiro and Y. Sasaki, Phys. Earth Planet. Int.

Cambridge Univ. Press (2006).

276, 258 (2018).

25.

V. Zeitlin, Geophysical Fluid Dynamics, Oxford Univ.

46.

T. Nakagawa, Phys. Earth Planet. Int. 187, 342

Press (2018).

(2011).

26.

S. W. McIntosh et al., Nature Astron. 1(4), 0086

47.

D. J. Raymond, http://kestrel.nmt.edu/ raymond/

(2017).

classes/ph589/notes/ssmodes/ssmodes. pdf.

27.

T. D. Kaladze, W. Horton, L. Z. Kahlon et al., Phys.

Scripta 88, 065501 (2013).

48.

G. Falkovich, Fluid Mechanics: a Short Course for

Physicists, Cambridge Univ. Press (2011).

28.

О. Г. Онищенко, О. А. Похотелов, Н. М. Астафье-

ва, УФН 178, 605 (2008).

49.

P. J. Dellar, J. Fluid Mech. 674, 174 (2011).

394