ЖЭТФ, 2020, том 158, вып. 2 (8), стр. 399-412

СПЕКТРАЛЬНЫЕ ХАРАКТЕРИСТИКИ ЗАРЯЖЕННЫХ ЧАСТИЦ

В ОГРАНИЧЕННЫХ ЦЕПОЧЕЧНЫХ СТРУКТУРАХ

О. С. Ваулина^*, Э. А. Саметов, Е. А. Лисин^**

Объединенный институт высоких температур Российской академии наук

125412, Москва, Россия

Московский физико-технический институт (национальный исследовательский университет)

141700, Долгопрудный, Московская обл., Россия

Поступила в редакцию 27 января 2020 г.,

после переработки 12 февраля 2020 г.

Принята к публикации 12 февраля 2020 г.

Представлены результаты исследования спектральных характеристик стохастического движения заря-

женных частиц для цепочечных структур в электрическом поле ловушки. Рассмотрены характерные

частоты частиц и способ их аналитического вычисления. Предложены аналитические соотношения для

спектральной плотности смещений частиц, взаимодействующих с попарным потенциалом, в малораз-

мерных цепочечных структурах. Полученные соотношения проверены путем численного моделирования

задачи.

DOI: 10.31857/S0044451020080179

Подробную информацию об особенностях тепло-

вого движения взаимодействующих частиц можно

1. ВВЕДЕНИЕ

получить путем анализа спектральной плотности их

смещений. Спектральная плотность для случайных

Стохастическое (тепловое) движение заряжен-

(тепловых) смещений частиц является косинус-пре-

ных частиц широко распространено в природе, а его

образованием Фурье для корреляционной функции,

изучение представляет интерес в различных облас-

описывающей зависимость среднего квадрата этих

тях науки и техники [1-6].

смещений от времени [23-25]. В отличие от других

Комплексная (пылевая) плазма является ионизо-

характеристик системы (параметра неидеальности,

ванным газом, содержащим заряженные частицы

коэффициентов массопереноса и т. д.) информация

вещества микронных размеров (пыль) [1-3]. Экс-

о спектральной плотности тепловых смещений час-

периментальные и численные исследования стоха-

тиц позволяет анализировать спектр частот их соб-

стического движения пылевых частиц в газоразряд-

ственных колебаний. Это позволяет оценить реак-

ной плазме представлены в работах [7-13]. Обычно

цию исследуемой системы на различные внешние

в центре газоразрядных камер наблюдается неко-

воздействия, а также дает возможность получить

торое превышение концентрации ионов плазмы над

информацию о потенциале межчастичного взаимо-

концентрацией ее электронной компоненты [14], что

действия [7-9, 26, 27].

приводит к формированию эффективных ловушек

В настоящее время задача о спектральной плот-

для отрицательно заряженных частиц пыли [1, 2].

ности смещений детально рассмотрена только для

Лабораторные эксперименты с небольшим количе-

случая двух взаимодействующих частиц [28, 29]. В

ством пылевых частиц позволяют проводить ис-

данной работе приводятся результаты исследова-

следования спектров их собственных и вынужден-

ния спектральных характеристик для частиц, взаи-

ных колебаний, изучать влияние различных внеш-

модействующих с произвольным попарным потен-

них воздействий, а также разрабатывать новые ме-

циалом, в малоразмерных цепочечных структурах.

тоды диагностики и т. д. [15-22].

Представленные результаты могут быть полезны

для экспериментального анализа характера и типа

^* E-mail: olga.vaulina@bk.ru

потенциала взаимодействия между пылевыми час-

^** E-mail: ealisin@yandex.ru

тицами в плазме.

399

О. С. Ваулина, Э. А. Саметов, Е. А. Лисин

ЖЭТФ, том 158, вып. 2 (8), 2020

Исследование взаимодействий между частицами

в комплексной плазме представляет несомненный

Q₁

интерес [1-3]. За последние годы появилось нема-

ло работ, посвященных этому вопросу. Часть из

них касается разработки экспериментальных мето-

дов определения потенциалов взаимодействия меж-

ду пылевыми частицами в лабораторной плазме

Q₂

E_r

газовых разрядов [30-35]. Наибольшим преимуще-

ством обладают методы, основанные на решении об-

E_z

ратной задачи Ланжевена [34], или на анализе кор-

реляторов смещений и скоростей частиц [35]. В отли-

Рис. 1. Вертикальная (а) и горизонтальная (б) конфигу-

чие от других, упомянутые методы полностью учи-

рации двух взаимодействующих частиц в электрическом

тывают диссипативные и случайные процессы. Тем

поле ловушки E = E(z, r) с цилиндрической симметрией

не менее, и они могут давать некорректные резуль-

таты для частиц, колебания (смещения) которых ис-

Основные гармоники для системы (1) (ее харак-

кажены неучтенными регулярными и/или случай-

терные частоты) можно найти путем решения ха-

ными внешними воздействиями [35].

рактеристического уравнения

2. ОБЩИЙ СЛУЧАЙ

f (λ) = c_nλⁿ + cn-1λn-1 + . . . + c₁λ + c₀,

Рассмотрим равновесную систему, состоящую из

где n определяется числом N взаимодействующих

N частиц массой M_i и зарядами Q_i, взаимодейству-

частиц [36]. Если корни этого уравнения имеют по-

ющих с потенциалом произвольной формы в линей-

ложительную действительную часть, то решение си-

ном электрическом поле E(r, z) цилиндрической ло-

стемы (1) является неустойчивым. Задача об устой-

вушки с радиальной составляющей E_r = β^rr и вер-

чивом положении двух идентичных частиц, взаимо-

тикальной составляющей E_z = E0z + β^z z. Здесь r ≡

действующих с различными типами потенциалов,

≡ (x² + y²)1/2 — радиальная координата, z — вер-

в электрическом поле ловушки рассматривалась в

тикальная координата по оси z в направлении силы

работах [20, 21, 37, 38], где было показано, что вер-

тяжести, β^r и β^z — величины градиентов электри-

тикальная конфигурация частиц наблюдается при

ческого поля, а значение E0z определяется балансом

β^r > β^z, в обратном случае (β^r < β^z) формируется

сил, действующих в системе.

их горизонтальная конфигурация, см. рис. 1. Крите-

В предположении, что смещение ξ_i частиц, где

рии устойчивости для малоразмерных кластерных

i = 1, 2, . . ., N, от их положения равновесия под

систем, включающих до пяти заряженных частиц

действием некоторой случайной силы F_bi ограни-

(2 ≤ N ≤ 5), подробно рассмотрены в работе [38].

чено малыми отклонениями, систему линеаризован-

Спектральные характеристики частиц для систе-

ных уравнений движения в выбранном направлении

мы (1) при F_bi = 0, такие как их характерные часто-

для каждой из степеней свободы можно записать в

ты ω_i и спектральные плотности смещений G_i могут

общем виде:

быть получены численно на основе существующих

dV_i

пакетов математического моделирования. Практи-

M_i

= -ν_iM_iV_i - Q_iβr(z)ξ_i +

чески все современные программные пакеты имеют

∑

встроенные функции символьных вычислений и поз-

b_ji(ξ_i - ξ_j) + F_bi.

(1)

воляют получить конечный результат в виде фор-

j=1,j=i

мул для ω_i и G_i, которые являются математически-

Здесь ν_i — коэффициент трения i-й частицы за счет

ми решениями задачи и не несут какого-либо физи-

ее столкновений с нейтралами окружающего газа,

ческого смысла. Кроме того, такие формулы имеют

V_i = dξ_i/dt — скорость i-й частицы на одну степень

весьма громоздкий вид и занимают со всеми входя-

свободы, F_bi — сила Ланжевена, являющаяся источ-

щими в них коэффициентами от двух (для N = 3) и

ником стохастической кинетической энергии частиц,

более (при N > 3) страниц текста. Таким образом,

а коэффициенты b_ij зависят от физики решаемой

упомянутые соотношения являются малоэффектив-

задачи (для попарного взаимодействия bij ≡ bji)

ными для практического использования, включая

и рассматриваемой степени свободы смещений час-

анализ и/или обращение данных численных и ла-

тиц.

бораторных экспериментов.

400

ЖЭТФ, том 158, вып. 2 (8), 2020

Спектральные характеристики заряженных частиц. ..

Способ простого аналитического решения задачи

по ограниченным траекториям 〈ξ₁V₁〉 = 〈ξ₂V₂〉 ≡ 0,

для малоразмерных цепочек частиц, взаимодейст-

〈V₁₍₂₎Fb1(2)〉 = νT⁰¹⁽²⁾, где T⁰¹⁽²⁾ — температура тепло-

вующих с произвольным попарным потенциалом,

вых источников [28,29]. Тогда уравнения для корре-

описан в следующих разделах работы.

ляторов скоростей и смещений частиц можно пред-

ставить в виде [39, 40]

3. СЛУЧАЙ ДВУХ ЧАСТИЦ

νδT₁₍₂₎

+ a₁₂₍₂₁₎〈V₁₍₂₎ξ₂₍₁₎〉 = 0,

(3a)

В начале раздела отметим, что большинство экс-

T₁₍₂₎

периментов в пылевой плазме проводятся для моно-

a₁₁₍₂₂₎〈(ξ₁₍₂₎)²〉 + a₁₂₍₂₁₎〈ξ₁ξ₂〉 +

= 0,

(3b)

дисперсных частиц, когда различием между их мас-

− ν〈V₁₍₂₎ξ₂₍₁₎〉+a₁₁₍₂₂₎〈ξ₁ξ₂〉+a₁₂₍₂₁₎〈(ξ₂₍₁₎)²〉+

сами и размерами (соответственно, между коэффи-

циентами трения) можно пренебречь: M_i = M, ν_i =

+ 〈V₁V₂〉 = 0,

(3c)

= ν [1-3].

− 2ν〈V₁V₂〉 + (a₁₁ - a₂₂)〈ξ₁V₂〉 = 0,

(3d)

Рассмотрим систему линеаризованных уравне-

ний движения, описывающих отклонения двух заря-

где T1(2) = M〈V21(2)〉 — кинетическая температура

женных частиц (равных масс M и размеров), взаи-

частиц (удвоенная кинетическая энергия их стохас-

модействующих с потенциалом произвольной фор-

тического движения на одну степень свободы) для

мы, от их положения равновесия ξ₁₍₂₎ под действием

равновесного состояния системы, а δT₁₍₂₎ = T⁰¹⁽²⁾ -

случайной силы Fb1(2):

- T₁₍₂₎ — приращение кинетической температуры в

процессе установления равновесия. При численном

d²ξ₁

dξ₁

Fb1

= -ν

+a₁₁ξ₁ + a₁₂ξ₂ +

(2a)

моделировании задачи температура тепловых ис-

dt²

точников, T⁰¹⁽²⁾, соответствует их заданной/началь-

d²ξ₂

dξ₂

Fb2

= -ν

+a₂₂ξ₂ + a₂₁ξ₁ +

(2b)

ной температуре, т. е. температуре термостата.

dt²

Решение системы (3a)-(3d) дает уравнения энер-

Для попарного взаимодействия a₁₂ ≡ a₂₁. Слу-

гетического баланса для двух взаимодействующих

чай a₁₁ = a₂₂ может реализоваться для пылевых

частиц, которые описывают перераспределение сто-

частиц в лабораторной плазме даже для их попарно-

хастической кинетической энергии между этими

го взаимодействия, например, из-за различия их за-

частицами при T⁰¹ = T⁰² [28] или «подкачку» энер-

рядов или отличия градиентов внешнего поля в точ-

гии для случая непопарного взаимодействия час-

ке равновесного положения частиц. Такие условия

тиц [39, 40]:

могут возникать за счет пространственных изме-

нений параметров окружающей плазмы (например,

2a₁₂₍₂₁₎(T⁰¹a₂₁ - T⁰²a₁₂)

концентраций и температур ионов/электронов).

δT₁₍₂₎ = ±

(4a)

(a₁₁-a₂₂)²+4a₁₂a₂₁-2ν²(a₁₁+a₂₂)

Здесь мы рассмотрим вертикальную конфигура-

цию частиц, рис. 1а. (Отметим, что все решения для

где знак «плюс» для δT₂, а знак «минус» для δT₁.

горизонтальной конфигурации частиц при их попар-

Уравнение баланса (4a) согласуется со всеми ранее

ном взаимодействии и Q₁₍₂₎ ≡ Q, см. рис. 1б, будут

полученными результатами для любых взаимодей-

аналогичными [28].)

ствий между двумя частицами системы [28,39,40].

Для поиска корреляторов скоростей и смещений

Решение системы (3a)-(3d) позволяет также по-

частиц в системе (2a), (2b) отметим, что коррелято-

лучить соотношения для корреляторов скоростей и

ры случайной силы Fb1(2) подчиняются уравнениям

смещений частиц, которые необходимы для поиска

〈Fb1〉 = 〈Fb2〉 ≡ 0, 〈Fb1Fb2〉 = 0, 〈Fb1V₂〉 = 〈Fb2V₁〉 ≡

спектральных плотностей:

≡ 0, 〈Fb1ξ₂〉 = 〈Fb2ξ₁〉 ≡ 0, 〈Fb1ξ₁〉 = 〈Fb2ξ₂〉 ≡ 0.

Здесь и далее угловые скобки 〈〉 обозначают усред-

(a₁₁ - a₂₂)(T₁a₂₁ - T₂a₁₂)

〈V₁V₂〉 =

(4b)

нение по времени при t → ∞. При движении частиц

M {(a₁₁ - a₂₂)² - 2ν²(a₁₁ + a₂₂)}

(a^222(11) + a₁₁a₂₂ - a₁₂a₂₁)T₁₍₂₎ + a²¹²T₂₍₁₎ - 2a₁₂₍₂₁₎a₂₂₍₁₁₎M〈V₁V₂

〉

〈ξ²¹⁽²⁾〉 = -

(4c)

(a₁₁ + a₂₂)(a₁₁a₂₂ - a₁₂a₂₁)M

401

ЖЭТФ, вып. 2 (8)

О. С. Ваулина, Э. А. Саметов, Е. А. Лисин

ЖЭТФ, том 158, вып. 2 (8), 2020

Перейдем к определению спектральных характе-

где коэффициенты C_k (k = 0 ÷ 4) вычисляются для

ристик рассматриваемой системы. Еще раз отметим,

условий конкретной задачи. Так, при определении

что 〈ξ²¹⁽²⁾〉 (4c) описывает отклонения частиц от их

〈ξ²¹⁽²⁾〉_t величина C₀ ≡ A₁ = 〈ξ²¹⁽²⁾〉_t→∞ ≡ 2〈ξ²¹⁽²⁾〉,

равновесного положения при t → ∞. При вычис-

а для поиска значений C_k(k

= 1 ÷ 4) использу-

лениях спектральной плотности обычно использу-

ют начальные условия Φ(0) = 0, dΦ(0)/dt = 0,

ют преобразование Фурье для среднеквадратично-

d²Φ(0)/dt2 ≡ A2 = 2T1(2)/M, d3Φ(0)/dt3 ≡ A3 =

го отклонения частиц от их начального положения:

= 2νT⁰¹⁽²⁾/M [6,23]. Таким образом, для коэффици-

(

)₂

〈ξ²¹⁽²⁾〉t = 〈

ξ₁₍₂₎(t) - ξ₁₍₂₎(0)

〉_t, где угловые скоб-

ентов C_k имеет место следующая система уравне-

ки 〈. . .〉_t обозначают усреднение по всем отрезкам

ний [28]:

времени равным t; при t → ∞: 〈ξ²¹⁽²⁾〉_t→∞ ≡ 2〈ξ²¹⁽²⁾〉

[6, 23-25].

A₃ + A₂(λ₂ + λ₃ + λ₄) - A₁λ₂λ₃λ₄

C₁ = -

(7a)

Корни характеристического уравнения для зада-

(λ₁ - λ₂)(λ₁ - λ₃)(λ₁ - λ₄)

чи (2a), (2b) можно записать как [28, 36]

)1/2

A₃ + A₂(λ₁ + λ₃ + λ₄) - A₁λ₁λ₃λ₄

C₂ =

(7b)

⁽ν

λ1,2 = -

-ω²

(5a)

(λ₁ - λ₂)(λ₂ - λ₃)(λ₂ - λ₄)

)1/2

A₃ + A₂(λ₁ + λ₂ + λ₄) - A₁λ₁λ₂λ₄

⁽ν

C₃ = -

(7c)

λ3,4 = -

-ω²

(5b)

(λ₁ - λ₃)(λ₂ - λ₃)(λ₃ - λ₄)

где ω²¹ = -(a₁₁ + a₂₂)/2 - d, ω²² = -(a₁₁ + a₂₂)/2 + d,

A₃ + A₂(λ₁ + λ₂ + λ₃) - A₁λ₁λ₂λ₃

(

)1/2

C₄ =

(7d)

(a₁₁ - a₂₂)²/4 + a₁₂a₂₁

(λ₁ - λ₄)(λ₂ - λ₄)(λ₃ - λ₄)

Любое решение для рассматриваемой здесь зада-

чи (ξ_i(t), ξ_i(t)², 〈ξ2i〉_t; i = 1, 2) можно представить в

С учетом корней характеристического уравнения

виде суперпозиции [28, 36]:

(5a), (5b) и уравнений баланса энергии (4a) в рас-

сматриваемой системе фурье-преобразование функ-

∑

ции Φ(t) дает для спектральной плотности смеще-

Φ(t) = C₀ +

C_k exp(λ_kt),

(6)

ний частиц, G₁₍₂₎ = G₁₍₂₎(ω), соотношение

k=1

{

}

(

)

2ν T⁰¹⁽²⁾

(ω² + a₂₂₍₁₁₎)² + ν²ω²

+T⁰²⁽¹⁾a²

12(21)

G₁₍₂₎ =

(8)

{ω⁴ + (ν² - 2ω²¹)ω² + ω⁴¹} {ω⁴ + (ν² - 2ω²²)ω² + ω⁴²}

2νT/M

Аналогичное соотношение было получено ранее в

G₁₍₂₎ = B₁₍₂₎

работе [29] независимым спектральным методом.

ω⁴ + (ν² - 2ω²¹)ω² + ω⁴

Численное моделирование спектральных плотнос-

2νT/M

+B₂₍₁₎

тей для смещений частиц, выполненное для попар-

ω⁴ + (ν² - 2ω²²)ω² + ω⁴

ных потенциалов (a₁₂ ≡ a₂₁) [28], показывает хоро-

=B₁₍₂₎S₁ + B₂₍₁₎S₂,

(9)

шее согласие с формулой (8).

где B₁ = 0.5 + (a₁ - a₂)/4d, B₂ = 0.5 - (a₁ - a₂)/4d.

Отсюда легко заметить, что G₁ +G₂ ≡ S₁+S₂. Тогда

В случае попарного взаимодействия между час-

для двух идентичных частиц G₁(ω) ≡ G₂(ω) = G(ω)

тицами (a₁₂ ≡ a₂₁ = b, a₁₁ = a₁, a₂₂ = a₂) для

получим [28]

их вертикальных смещений, ξ₁₍₂₎ = δz₁₍₂₎, величины

∑

a₁₍₂₎ = -(Q₁₍₂₎β^z - F^′)/M и b = -F^′/M, где F^′ —

νT/M

G(ω) =

≡

S_i.

(10)

производная силы F взаимодействия между двумя

ω⁴+(ν²-2ω2i)ω2+ω4

i=1

частицами в направлении оси z. Для радиальных

Для одной частицы (N = 1) в ловушке получим

смещений частиц, ξ₁₍₂₎ = δr₁₍₂₎, величины a₁₍₂₎ =

формулу для классического осциллятора в виде

= -(Q₁₍₂₎β^r - F/l)/M и b = F/lM, где l — рассто-

яние между частицами. При этом соотношение (8)

2νT/M

G₁(ω) =

(11)

может быть представлено в виде суперпозиции спек-

ω⁴ + (ν² - 2ω²¹)ω² + ω⁴

тральных плотностей для двух классических осцил-

ляторов S_i = S_i(ω, ν, ω_i):

где ω²¹ = (ωz(r)t)² ≡ Qβz(r)/M.

402

ЖЭТФ, том 158, вып. 2 (8), 2020

Спектральные характеристики заряженных частиц. ..

Нормированные спектральные

плотности

Представленные аналитические соотношения

G^∗(ω) = G(ω)/B, S∗1(ω) = S1(ω)/B и S∗2(ω) =

для спектральной плотности смещений частиц срав-

= S₂(ω)/B смещений в вертикальном и радиальном

нивались с результатами определения спектральной

направлениях для двух идентичных частиц с

плотности, полученными путем преобразования

кулоновским взаимодействием представлены на

Фурье для решений системы (1) при F_bi

= 0 с

рис. 2 при β^r/β^z = 4 и ν = 5 с-1, когда ω^zt/ν = 2,

помощью пакета прикладных программ MATLAB.

ω^rt/ν

= 4. Здесь и далее B

= 2T/(ω2tνM), где

ω_t = ωz(r)t ≡ (Qβz(r)/M)1/2.

4.1. Три частицы

Следует отметить, что при (ω_i/ν)² ≫ 1 максиму-

Обратимся к случаю трех частиц (N = 3), см.

мы спектральных функций G(ω), S₁(ω), S₂(ω) хоро-

рис. 4а. В состоянии равновесия средние расстояния

шо соответствуют аналитическим значениям ω_i. С

между двумя ближайшими частицами равны l₁₂ =

уменьшением отношения ω_i/ν (например, с ростом

= l₂₃ ≡ l_d, а уравнение баланса сил дает Qβ^zl_d =

коэффициента трения ν) максимумы упомянутых

= F₁₂ + F₁₃, где F₁₂ = F₂₃ ≡ F. Исследование дина-

функций смещаются в сторону более низких частот

мики таких частиц в цепочечной структуре сводит-

[23, 28], см. рис. 3.

ся к анализу системы уравнений движения (1) для

i = 1,2,3.

Для поиска спектральных характеристик выпол-

4. СЛУЧАИ ТРЕХ, ЧЕТЫРЕХ И ПЯТИ

ним замену переменных: η₁ = ξ₁ +ξ₂ +ξ₃, η₂ = ξ₁ -ξ₃,

ЧАСТИЦ

η₃ = 2ξ₂ - (ξ₁ + ξ₃). (Здесь и далее для вертикаль-

Рассмотрим спектральные характеристики для

ных смещений частиц в цепочке ξ_i = δz_i, а для их

случаев трех, четырех и пяти идентичных частиц

радиальных смещений ξ_i = δr_i.) С учетом указанной

(Q_i = Q, M_i = M, ν_i = ν), взаимодействующих

замены переменных преобразуем систему уравнений

с произвольной попарной силой F_ij = F_ji ≡ F (l_ij )

движения (1) для случая F_bi = 0 к виду

в линейном электрическом поле E(r, z) ловушки с

d²η₁

dη₁

Qβ

цилиндрической симметрией (см. рис. 4); здесь i =

= -ν

η₁,

(12a)

dt²

= 1, 2, . . ., N, j = 1, 2, . . ., N и i = j. Критерии устой-

)

d²η₂

dη₂

⁽Qβ

чивости таких систем представлены в работе [38]. В

= -ν

- b₁₂ - 2b₁₃ η₂,

(12b)

dt²

силу симметрии задачи относительно центра ловуш-

)

d²η₃

dη₃

⁽Qβ

ки в этих системах функции равны G_j (ω) = G_i(ω)

= -ν

- 3b₁₂

η₃.

(12c)

для частиц j и i, которые расположены на одинако-

dt²

вом расстоянии от центра структуры, см. рис. 4.

Здесь для вертикальных смещений частиц от их по-

Численное моделирование стохастических про-

ложения равновесия β = β^z , b₁₂ = F′12 ≡ F′23 = F^′,

цессов выполнялось методом Ланжевена для иден-

b₁₃ = F′13, где F^′ — первая производная силы взаи-

тичных частиц с равными массами, зарядами и

модействия F в точке l_d и F′13 — первая производ-

температурой. Техника моделирования подробно

ная силы взаимодействия F₁₃ в точке l₁₃ ≡ 2l_d. Для

описана в работах [1-3]. Шаг интегрирования со-

радиальных смещений частиц β = β^r, b₁₂ = F/l_d,

ставлял от Δt

= (40 max[ωz(r)t; ν])-1 до Δt

b13 = F13/2ld. Для систем с кулоновским взаимо-

= (100 max[ωz(r)t; ν])-1 в зависимости от начальных

действием F = Q²/l2d, F₁₃ = Q²/4l2d, F^′ = -2Q²/l3d,

условий задачи. Время расчетов t_c после установле-

F′13 = -Q²/4l3d.

ния равновесия в моделируемых системах варьиро-

Рассматриваемая система (12a)-(12c) имеет по

валось от ∼ 10³/ min[ωz(r)t; ν] до ∼ 10⁴/ min[ωz(r)t; ν];

три характерных частоты в вертикальном и ради-

здесь ωz(r)t = (Qβz(r)/M)1/2 — характерные частоты

альном направлениях: ω²¹ = (Qβ/M), ω²² = (Qβ/M -

ловушки. Температура частиц в процессе моделиро-

-b₁₂-2b₁₃), ω²³ = (Qβ/M-3b₁₂). Ее решение для 〈η2k〉

вания не менялась, т.е. оставалась равной заданной,

(k = 1, 2, 3) с учетом 〈ξ_iξ_j 〉 = 0 при i = j позволя-

T_i = T0i ≡ T.

ет получить для спектральной плотности смещений

отдельных частиц:

Вычисления спектральной плотности по резуль-

татам моделирования проводились на основе чис-

S₁ + 2S₃

G₂(ω) =

(13)

ленных расчетов смещений x(t), y(t) и z(t) для от-

дельных частиц системы при помощи процедуры

«N-D fast Fourier transform» в пакете прикладных

2G₂(ω) - S₃ + S₂

G₁(ω) ≡ G₃(ω) =

(14)

программ MATLAB.

403

12*

О. С. Ваулина, Э. А. Саметов, Е. А. Лисин

ЖЭТФ, том 158, вып. 2 (8), 2020

1.2

1.6

= 2

3.5

= 4

1.2

S*₁

0.8

3.5

0.8

0.4

S*₂

S*₁

0.4

S*₂

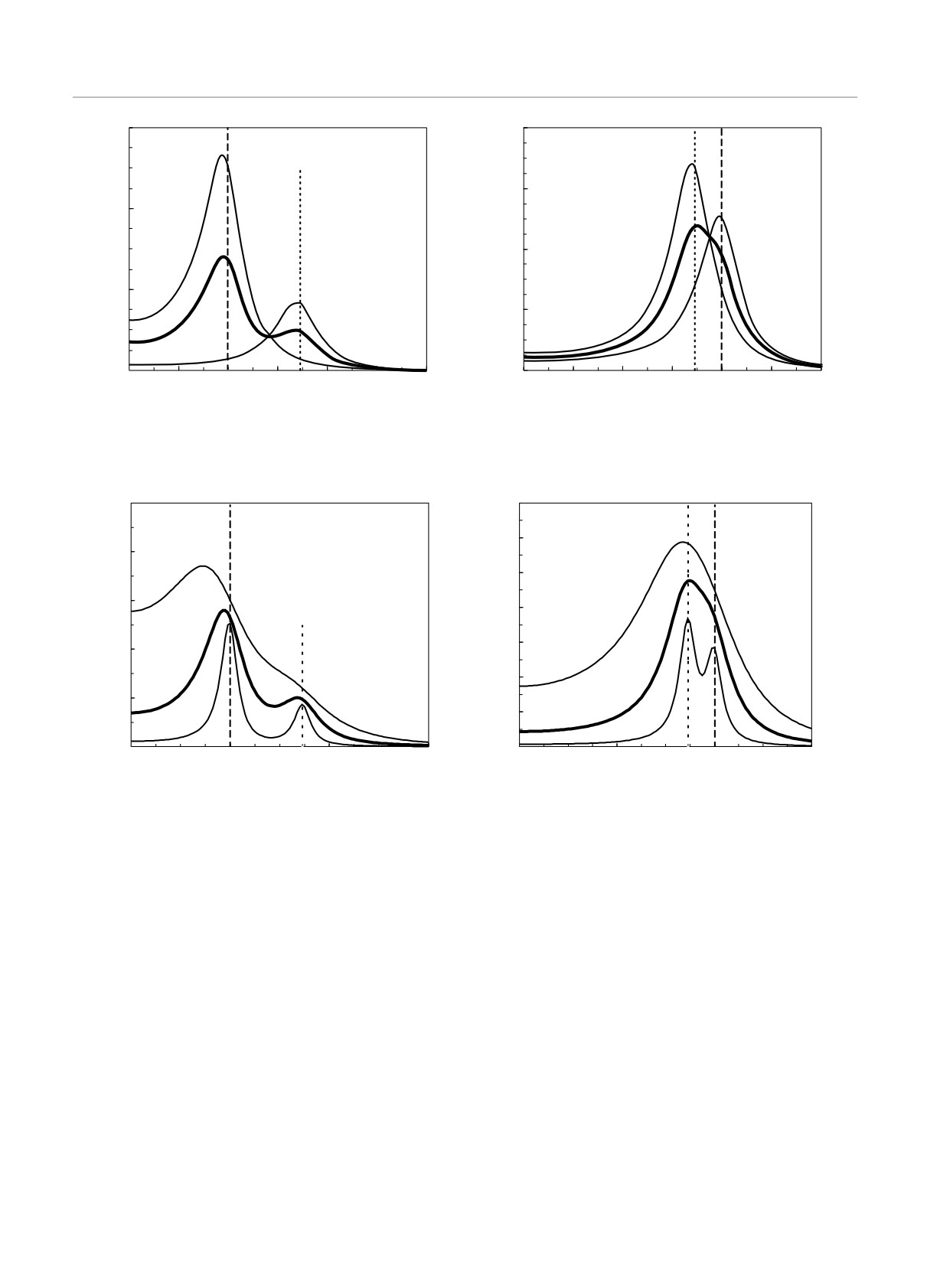
Рис. 2. Функции G^∗(ω), S∗1(ω) и S∗2(ω) для вертикального (а) и радиального (б) направлений смещения частиц при

β^r/β^z = 4, ν = 5 с-1, ω^zt/ν = 2 и ω^rt/ν = 4

1.0

1.4

0.87

1.2

= 1

0.8

= 1

1.0

0.6

0.8

0.6

0.4

1.73

0.4

0.2

0.5

1.0

1.5

/ t

Рис. 3. Функции G^∗(ω) для вертикального (а) и радиального (б) направлений смещения частиц при β^r /β^z = 4, ω

= 10 с-1, ω^rt = 20 с-1 и коэффициентах трения ν = 10 с-1 (1), 5 с-1 (2), 2 с-1 (3)

где S_k — плотность классического осциллятора с

Нормированные спектральные

плотности

частотой ω_k. Отметим, что представленные анали-

S^∗i(ω) = S_i(ω)/B и G^∗i(ω) = G_i(ω)/B для системы

тические кривые полностью совпадают с резуль-

из трех частиц с кулоновским взаимодействием

татами вычислений спектральной плотности путем

представлены соответственно на рис. 5 и рис. 6 при

преобразования Фурье для решений системы (1) при

ν = 2 с-1 и β^r/β^z = 4.

F_bi = 0.

4.2. Четыре частицы

Уравнения баланса сил для вертикальной кон-

Напомним, что спектральная плотность для сме-

щений η_k является фурье-преобразованием функ-

фигурации четырех частиц (N = 4), см. рис. 4б,

можно записать в виде системы двух уравнений:

ций 〈η2k〉_t, а величина S_ηk = D_kS_k, где коэффициент

D_k определяется суммарной температурой частиц,

Qβ^z(2l_o + l_d) = 2Fs2,

(15a)

входящих в данный коррелятор. Так, для η₁ вели-

Qβ^zl_d = 2Fs1,

(15b)

чина D₁ = 3, для η₂ — D₂ = 2, для η₃ — D₃ = 6.

404

ЖЭТФ, том 158, вып. 2 (8), 2020

Спектральные характеристики заряженных частиц. ..

зуем систему уравнений движения (1) для F_bi = 0 к

виду

d²η₁

dη₁

Qβ

= -ν

η₁,

(16a)

l_d

l_o

dt²

(

)

d²η₂

dη₂

Qβ

= -ν

- 2(b₁₂ + b₁₃) η₂,

(16b)

dt²

)

d²η

dη₃

⁽Qβ

= -ν

-2b₁₄-b₁₂-b₁₃ η₃ +

dt²

l_d

+ (b₁₃ - b₁₂)η₄,

(16c)

)

d²η₄

dη₄

⁽Qβ

= -ν

-2b₂₃-b₁₂-b₁₃ η₄ +

dt²

E_r

+ (b₁₃ - b₁₂)η₃.

(16d)

l_o

l_d

Здесь в случае вертикальных смещений частиц от их

E_z

положения равновесия β = β^z , b₁₂ = F′12, b₁₃ = F′13,

b₁₄ = F′14, b₂₃ = F′23, где F^′ — первая производная

соответствующей силы взаимодействия, а в случае

их радиальных смещений β = β^r, b₁₂ = F₁₂/l_o, b₁₃ =

l_o

= F₁₃/(l_d + l_o), b₁₄ = F₁₄/(l_d + 2l_o), b₂₃ = F₂₃/l_d.

Рассматриваемая система имеет по четыре ха-

рактерных частоты в вертикальном и радиальном

направлениях соответственно ω21 = Qβ/M, ω22 =

= Qβ/M -2(b₁₂ +b₁₃), ω²³ = (Qβ/M -b₁₄ -b₂₃ -b₁₂

Рис. 4. Вертикальная конфигурация трех (a), четырех (б)

- b₁₃) - d, ω²⁴ = (Qβ/M - b₁₄ - b₂₃ - b₁₂ - b₁₃) + d,

и пяти (в) взаимодействующих частиц в электрическом

где d = {(b₁₄ - b₂₃)² + (b₁₃ - b₁₂)²}1/2. А ее решение

поле ловушки E = E(z, r) с цилиндрической симметрией

дает для спектральной плотности смещений частиц

где l_d — среднее расстояние между двумя централь-

G₁(ω) ≡ G₄(ω) =

ными частицами, lo — среднее расстояние меж-

)

ду двумя частицами на периферии. Здесь Fs1 ≡

⁽S₁ +S₂

+B₁S₃ + B₂S₄

(17a)

≡ F₂₃ +F₂₄ -F₁₂ ≡ F₂₃ +F₁₃ -F₃₄, Fs2 ≡ F₁₃ +

+F₁₄+F₁₂ ≡ F₃₄+F₁₄+F₂₄, поскольку цепочка сим-

метрична относительно центра системы. Совместное

G₂(ω) ≡ G₃(ω) =

решение уравнений (15a), (15b) позволяет найти и

)

отношение l_o/l_d, и величину градиента β^z электри-

⁽S₁ +S₂

+B₂S₃ + B₁S₄

(17b)

ческого поля ловушки. Для систем с кулоновским

взаимодействием

где S_k — плотность классического осциллятора с

частотой ω_k, а B₁ = 0.5 + (b₂₃ - b₁₄)/4d, B₂ = 0.5 -

Q²

F₁₄ =

F₂₃ =

- (b₂₃ - b₁₄)/4d, см. (9). Полученные аналитические

(l_d + 2l_o)²

l²

кривые полностью совпадают с результатами вычис-

лений спектральной плотности путем преобразова-

Q²

F₂₄ = F₁₃ =

F₁₂ = F₃₄ =

ния Фурье для решений системы (1) при F_bi = 0.

(l_d + l_o)²

l²

Нормированные спектральные

плотности

Исследование динамики четырех частиц в цепо-

G^∗i(ω) = Gi(ω)/B для системы из четырех час-

чечной структуре сводится к анализу системы урав-

тиц с кулоновским взаимодействием представлены

нений (1) для i = 1 ÷ 4. Для поиска спектральных

на рис. 7 при ν = 5 с-1 и β^r/β^z = 9.

характеристик выполним замену переменных: η₁ =

В заключение данного раздела отметим, что с

= ξ₁+ξ₂+ξ₃+ξ₄, η₂ = (ξ₁+ξ₄)-(ξ₂+ξ₃), η₃ = ξ₁-ξ₄,

ростом коэффициента трения ν или радиальной час-

η₄ = ξ₂ - ξ₃. С учетом указанной замены преобра-

тоты ловушки ω^rt экспериментальный анализ спект-

405

О. С. Ваулина, Э. А. Саметов, Е. А. Лисин

ЖЭТФ, том 158, вып. 2 (8), 2020

1.2

2.8

= 1

0.63

2.4

1.0

2.0

0.87

0.8

S*₁

1.6

= 1

1.73

S*₂

0.6

S*₃

1.2

2.41

0.4

0.8

S*₁

0.2

0.4

S*₃

0.5

1.5

2.5

0.25

0.50

0.75

1.00

1.25

/ t

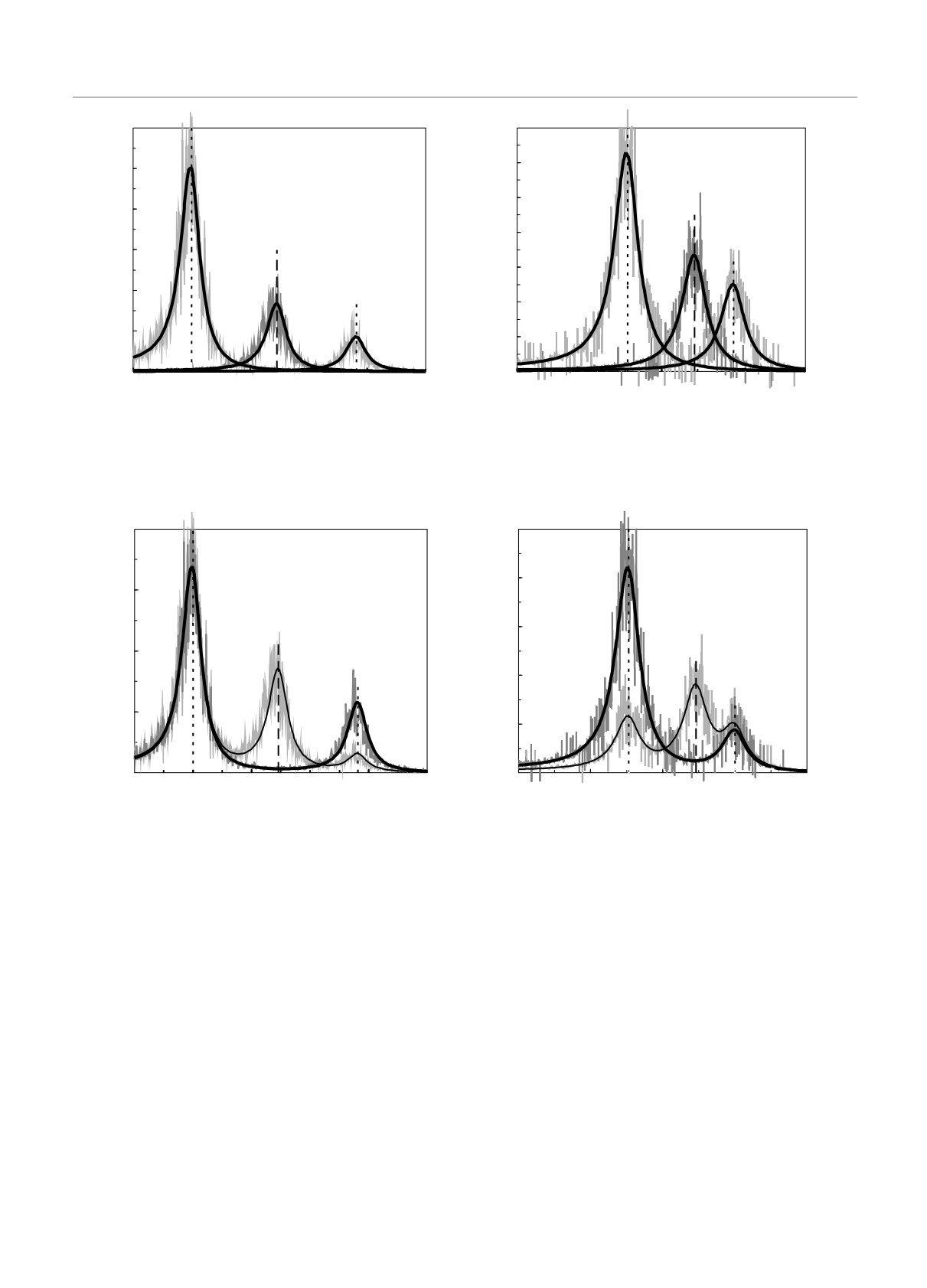
Рис. 5. Функции S^∗i(ω) для вертикальных (а) и радиальных (б) смещений частиц при β^r /β^z = 4, ω^zt = 10 с-1, ω^rt = 20 с-1

и ν = 2 с-1. Здесь S∗1 = S∗η1/3, S∗2 = S∗η2/2, S∗3 = S∗η3/6. Черными линиями показаны аналитические решения задачи,

серыми — результаты численного моделирования

0.4

2.0

= 1

0.63

1.6

0.3

1.73

1.2

G*₂

0.87

0.2

2.41

0.8

G*₁

= 1

G*₁

0.1

G*₂

0.4

0.5

1.5

2.5

0.25

0.50

0.75

1.00

1.25

/ t

Рис. 6. Функции G^∗i(ω) для вертикальных (а) и радиальных (б) смещений частиц при β^r /β^z = 4, ω^zt = 10 с-1, ω^rt = 20 с-1

и ν = 2 с-1. Черными линиями показаны аналитические решения задачи, серыми — результаты численного моделиро-

вания

ральной плотности смещений для отдельных час-

4.3. Пять частиц

тиц с целью определения основных характеристик

Уравнения баланса сил для вертикальной кон-

системы (ω_k, ν) становится затруднительным, см.

фигурации пяти частиц (N = 5), см. рис. 4в, можно

рис. 3, 7. Тем не менее, измерение η_k позволяет без

записать в виде системы двух уравнений:

особого труда определить и коэффициент трения ν,

и основные гармоники системы ω_k. Спектральные

Qβ^z(l_o + l_d) = Fs2,

(18a)

плотности S_ηk(ω) для рассматриваемых смещений

Qβ^zl_d = Fs1,

(18b)

η_k (k = 1 ÷ 4) связаны с функцией S_k(ω) следующи-

ми соотношениями: S_ηk = 4S_k для k = 1, 2; а сумма

где l_d = l₂₃ ≡ l₃₄ — среднее расстояние между цент-

спектральных плотностей Sη3 + Sη4 ≡ 2(S₃ + S₄), см.

ральными частицами системы, а l_o = l₁₂ ≡ l₄₅ —

рис. 8.

среднее расстояние между двумя частицами на пе-

406

ЖЭТФ, том 158, вып. 2 (8), 2020

Спектральные характеристики заряженных частиц. ..

0.73

= 1

0.86

0.3

1.2

0.94

1.73

= 1

0.2

0.8

2.41

3.05

0.1

0.4

G*₂

0.4

0.6

0.8

1.0

1.2

/ t

Рис. 7. Функции G^∗i(ω) для вертикальных (а) и радиальных (б) смещений частиц при β^r /β^z = 9, ω^zt = 10 с-1, ω^rt = 30 с-1

и ν = 5 с-1 . Черными линиями показаны аналитические решения задачи, серыми — результаты численного моделиро-

вания

1.2

2.4

= 1

0.73

0.86

1.0

2.0

0.8

1.6

0.94

1.73

0.6

1.2

= 1

2.41

0.4

0.8

3.05

0.2

0.4

0.6

0.8

1.0

1.2

/ t

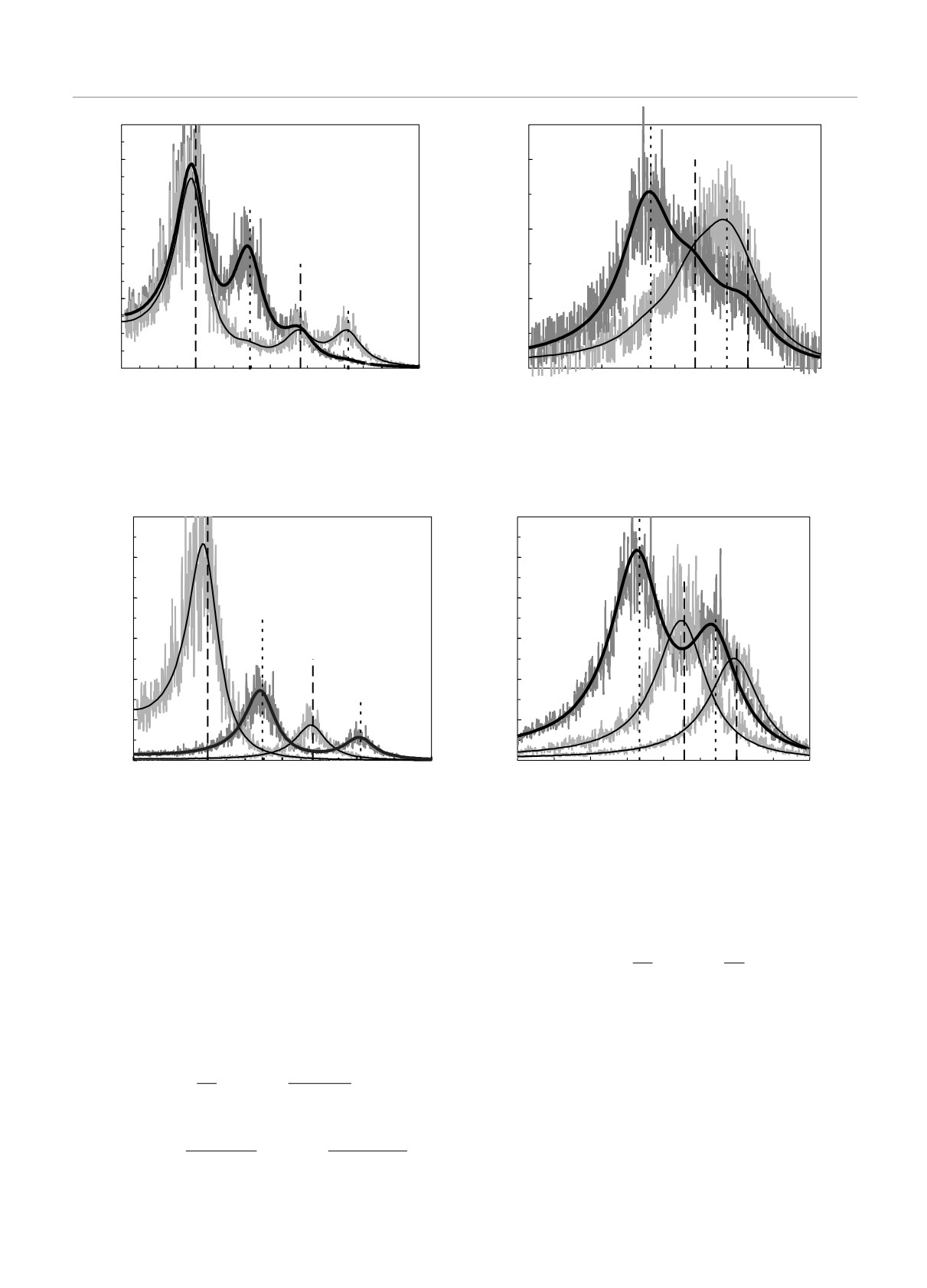
Рис. 8. Функции S^∗ηk(ω) = S_ηk(ω)/B при β^r /β^z = 9, ω^zt = 10 с-1, ω^rt = 30 с-1 и ν = 5 с-1 для вертикальных (а) и

радиальных (б) смещений частиц: 1 — S∗η1/4 = S∗1, 2 — S∗η2/4 = S∗2, 3 — (S∗η3 + S∗η4)/2 ≡ S∗3 + S∗4. Черными линиями

показаны аналитические решения задачи, серыми — результаты численного моделирования

риферии. Здесь Fs1 ≡ F₂₃ + F₂₄ + F₂₅ - F₁₂, Fs2 ≡

Q²

F₂₃ =

F₂₄ =

≡ F12 +F₁₃+F₁₄+F₁₅. Совместное решение уравне-

l2d

4l²

ний (18a), (18b) позволяет найти равновесные значе-

ния l_o, l_d и величину β^z. Для систем с кулоновским

взаимодействием

Исследование динамики системы сводится к ана-

лизу системы уравнений (1) для i = 1÷5. Для поиска

Q²

спектральных характеристик выполним замену пе-

F₁₂ =

F₁₃ =

l2o

(l_d + l_o)²

ременных: η₁ = ξ₁ + ξ₂ + ξ₃ + ξ₄ + ξ₅, η₂ = ξ₁ - ξ₅,

η₃ = ξ₂ - ξ₄, η₄ = 2ξ₃ - (ξ₁ + ξ₅), η₅ = 2ξ₃ - (ξ₂ + ξ₄).

Q²

С учетом указанной замены преобразуем систему

F₁₄ ≡ F₂₅ =

F₁₅ =

уравнений движения (1) при F_bi = 0 к виду

(2l_d + l_o)²

(2l_d + 2l_o)2

407

О. С. Ваулина, Э. А. Саметов, Е. А. Лисин

ЖЭТФ, том 158, вып. 2 (8), 2020

d²η₁

dη₁

Qβ

Здесь мы не приводим аналитических решений

= -ν

η₁,

(19a)

dt²

для G_i(ω), поскольку данные решения совпадают с

)

d²η₂

dη₂

⁽Qβ

результатами определения спектральной плотности

= -ν

-2b₁₅-b₁₂-b₁₃-b₁₄ η₂ +

dt²

для системы (1) при F_bi = 0 и имеют те же недо-

+ (b₁₄ - b₁₂)η₃,

(19b)

статки, которые были перечислены выше.

)

Необходимо отметить, что уравнение (9) не опи-

d²η₃

dη₃

⁽Qβ

= -ν

-2b₂₄-b₁₂-b₁₃-b₁₄ η₃ +

сывает решение системы (19d), (19e) для η₄ и η₅, по-

dt²

скольку в ней отсутствует подкачка энергии (δT_i =

+ (b₁₄ - b₁₂)η₂,

(19c)

= 0, T_i = T0i ≡ T). Тем не менее задачу можно

)

d²η₄

dη₄

⁽Qβ

решить способом, описанным в разд. 3. При этом

= -ν

-3b₁₃-b₁₂-b₁₄ η₄ +

dt²

для системы уравнений (19d), (19e) A₃ = 12νT/M, а

C₀ ≡ A₁ = 2〈η²⁴〉 или C₀ ≡ A₁ = 2〈η²⁵〉 в зависимости

+ (2b₂₃ - b₁₂ - b₁₄)η₅,

(19d)

)

от смещений «квазичастиц». (Здесь под «квазичас-

d²η₅

dη₅

⁽Qβ

= -ν

-3b₂₃-b₁₂-b₁₄ η₅ +

тицей» рассматривается совокупность частиц и их

dt²

взаимных смещений η₄ и η₅.) Значения 〈η²⁴〉 и 〈η²⁵〉

+ (2b₁₃ - b₁₂ - b₁₄)η₄.

(19e)

также подчиняются уравнению (4c) с учетом темпе-

≡ 6T, и корреляци-

ратур «квазичастиц», Tη4 = Tη5

В случае вертикальных смещений частиц β = β^z,

онной функции их скоростей,

b12 = F′12, b13 = F′13, b14 = F′14, b15 = F′15, b23 =

= F′23, b₂₄ = F′24, где F^′ — первая производная со-

6T(a₂₁ - a₁₂)

〈Vη4Vη5〉 = 4T ≡

ответствующей силы взаимодействия, а в случае их

M (a₁₁ - a₂₂)

радиальных смещений β = β^r, b₁₂ = F₁₂/l_o, b₁₃ =

где

= F₁₃/(l_d + l_o), b₁₄ = F₁₄/(2l_d + l_o), b₁₅ = F₁₅/(2l_d +

a₁₁ = Qβ/M - 3b₁₃ - b₁₂ - b₁₄,

+ 2l_o), b₂₃ = F₂₃/l_d, b₂₄ = F₂₄/2l_d.

Рассматриваемая система имеет пять характер-

a₂₂ = Qβ/M-3b₂₃-b₁₂-b₁₄, a₁₂ = 2b₂₃-b₁₂-b₁₄,

ных частот: ω²¹ = Qβ/M, ω²² = c₁ + d₁, ω²³ = c₁ - d₁,

a₂₁ = 2b₁₃ - b₁₂ - b₁₄,

ω²⁴ = c₂ - d₂, ω²⁵ = c₂ + d₂. Здесь

см. (19d), (19e).

Qβ

c₁ =

-b₁₄ -b₁₅ -b₂₄ -b₁₂ -b₁₃,

Спектральные плотности S_ηk(ω) для рассматри-

ваемых смещений η_k (k = 1÷5) связаны с функция-

Qβ

3(b₁₃ + b₂₃)

ми S_k(ω) следующими соотношениями:

c₂ =

-b₁₂ -b₁₄ -

{

}1/2

Sη1 = 5S₁,

(20a)

d₁ =

(b₁₅ - b₂₄)² + (b₁₄ - b₁₂)²

Sη3 + Sη4 = 2(S₃ + S₄),

(20b)

Sη4 + Sη5 = 6(C₁S₄ + C₂S₅),

(20c)

^{9(b₁₃ - b₂₃)

d₂ =

где C₁ = 2/3, C₂

= 4/3 для вертикальных смещений

}1/2

частиц и C₁ = 4/3, C₂ = 2/3 для их радиальных

+ (2b₂₃ - b₁₂ - b₁₄)(2b₁₃ - b₁₂ - b₁₄)

смещений.

Нормированные функции S^∗ηk(ω)

= S_ηk(ω)/B

Нормированные спектральные

плотности

для системы из пяти частиц с кулоновским взаимо-

G^∗i(ω) = G_i(ω)/B, полученные в результате моде-

действием представлены на рис. 10 при ν = 2 с-1 и

лирования системы из пяти частиц с кулоновским

β^r/β^z = 16. Еще раз подчеркнем, что измерение сме-

взаимодействием при их смещениях в вертикаль-

щений η_k в ходе реальных экспериментов с после-

ном и радиальном направлениях, представлены на

дующим вычислением их спектральных плотностей

рис. 9 при ν = 2 с-1 и β^r/β^z = 16. Там же показаны

S_ηk(ω) позволяет определить и коэффициент трения

результаты определения спектральной плотности

частиц ν, и основные гармоники системы ω_k.

для системы (1) при F_bi = 0. Легко увидеть, что

с ростом частоты ловушки ω^rt экспериментальный

4.4. Обсуждение результатов

анализ спектра частот для отдельных частиц с це-

лью определения основных характеристик системы

По результатам настоящей работы можно пред-

(ω_k, ν) становится затруднительным.

положить, что для случая ограниченной цепочки,

408

О. С. Ваулина, Э. А. Саметов, Е. А. Лисин

ЖЭТФ, том 158, вып. 2 (8),

2020

1.2

2.0

= 1

0.86

0.97

1.0

1.6

= 1

0.8

1.73

1.2

0.6

0.8

0.4

3.05

0.4

0.2

00.5

0.7

0.9

1.1

/ t

0.20

2.4

0.86

2.0

0.15

0.92

1.6

0.10

1.2

0.8

0.05

0.4

00.5

0.7

0.9

1.1

/ t

Рис. 10. Функции S^∗ηk(ω) = S_ηk(ω)/B при β^r /β^z = 16, ω

10 с-1, ω^rt = 40 с-1 и ν = 2 с-1 для вертикальных (а, б) и

∗

радиальных (в, г) смещений частиц: 1 — S∗η1/5 = S∗1, 2 — (S

η2

+ S∗η3)/2 ≡ S∗2 + S∗3, 3 — (S∗η4 + S∗η5)/6 ≡ C1S⁴ + C2S⁵.

Черными линиями показаны аналитические решения задачи, серыми — результаты моделирования

состоящей из идентичных частиц с попарным взаи-

≡ (Qβz(r)/M)1/2 (а, соответственно, и величины гра-

модействием, процедуру вычисления спектральной

диентов внешнего поля, β^z и β^r) в реальном экс-

плотности для смещений каждой из частиц G_i(ω)

перименте легко определить из измерений спект-

(i = 1, 2, . . . , N) можно свести к определению супер-

ральной плотности для суммы их смещений, η₁ =

позиции спектральных плотностей S_k = S_k(ω, ν, ω_k)

= ξ₁ + ξ₂ + ... + ξ_N, которая пропорциональна сме-

для отдельных гармоник системы ω_k:

щению центра масс системы. Для определения дру-

гих гармоник системы, ω_k = ω_t, можно использовать

∑

2νT/M

как измерения спектральных плотностей для от-

G_i(ω) =

A_k ω4 + (ν2 - 2ω2k)ω2 + ω⁴ ≡_k

дельных частиц G_i(ω), так и измерения спектраль-

k=1

ных плотностей для их взаимных смещений ξ_i - ξ_j ;

∑

≡ A_kS_k,

(21)

здесь i = 1, 2, . . . , N, j = 1, 2, . . ., N и i = j. По-

k=1

следняя процедура является предпочтительней, по-

скольку с ростом коэффициента трения частиц ν

где A_k — некоторые коэффициенты, N — число час-

или радиальной частоты ловушки ω^rt эксперимен-

тиц.

тальный анализ спектра частот для отдельных час-

При этом для такой системы коэффициент тре-

ния частиц ν и частоту ловушки ω_t

= ωz(r)t

≡ тиц,Gi(ω),становитсязатруднительным.

410

ЖЭТФ, том 158, вып. 2 (8), 2020

Спектральные характеристики заряженных частиц. ..

Добавим также, что измерение вертикальных и

перимент и теория), Физматлит, Москва (2009).

радиальных смещений в цепочке заряженных час-

Complex and Dusty Plasmas, ed. by V. E. Fortov and

тиц дает информацию о силах межчастичного взаи-

G. E. Morfill, CRC Press (2010).

модействия F_ij = F (l_ij ) и их производных F^′ij , что,

A. Ivlev, G. Morfill, H. Lowen, and C. P. Royall,

в свою очередь, позволяет определить характер и

Complex Plasmas and Colloidal Dispersions: Partic-

тип потенциала взаимодействия между частицами

le-Resolved Studies of Classical Liquids and Solids,

системы. Расстояние между частицами как в чис-

World Sci., Singapore (2012).

ленных, так и в реальных экспериментах легко изме-

ряется и в случае численного моделирования полно-

Photon Correlation and Light Beating Spectroscopy,

стью соответствует аналитическим уравнениям ба-

ed. by H. Z. Cummins and E. R. Pike, Plenum, New

York (1974).

ланса сил, см. (15), (18).

Еще раз отметим, что значения характерных

R. Balescu, Equilibrium and Nonequilibrium Statisti-

частот частиц, ω_k, и спектральной плотности их

cal Mechanics, Wiley Interscience, Chichester (1975).

смещений, G_i(ω, ν, ω_k), в системе из любого коли-

А. А. Овчинников, С. Ф. Тимашев, А. А. Белый,

чества N взаимодействующих частиц можно полу-

Кинетика диффузионно-контролируемых хими-

чить численно на основе существующих программ-

ческих процессов, Химия, Москва (1986).

ных пакетов, которые используют различные мето-

О. С. Ваулина, К. Г. Адамович, ЖЭТФ 133, 1091

дики для вычисления указанных спектральных ха-

(2008).

рактеристик для уравнений (1) при F_bi = 0. Одна-

ко использование простых аналитических соотноше-

О. С. Ваулина, К. Г. Адамович, О. Ф. Петров,

ний существенно сокращает время, необходимое для

В. Е. Фортов, ЖЭТФ 134, 367 (2008).

обращения экспериментальных данных.

E. A. Lisin, R. A. Timirkhanov, O. S. Vaulina,

O. F. Petrov, and V. E. Fortov, New J. Phys. 15,

5. ЗАКЛЮЧЕНИЕ

053004 (2013).

Представлены результаты аналитических и чис-

10.

O. S. Vaulina and E. A. Lisin, Phys. Plasmas 16,

ленных исследований спектральных характеристик

113702 (2009).

стохастического движения для малоразмерных це-

11.

В. Е. Фортов, О. Ф. Петров, О. С. Ваулина,

почечных структур (состоящих из нескольких час-

К. Г. Косс, Письма в ЖЭТФ 97, 366 (2013).

тиц, взаимодействующих с произвольным попарным

потенциалом) в анизотропном электрическом поле

12.

G. A. Hebner, M. E. Riley, and K. E. Greenberg,

Phys. Rev. E 66, 046407 (2002).

ловушки. Предложены соотношения для спектраль-

ной плотности смещений частиц в таких системах.

13.

O. S. Vaulina and I. E. Drangevski, Phys. Scripta 73,

Рассмотрены характерные частоты частиц и способ

577 (2006).

их аналитического вычисления.

14.

Ю. П. Райзер, Физика газового разряда, Наука,

Результаты настоящей работы применимы для

Москва (1987).

систем при любом типе попарных взаимодействий,

а также могут быть адаптированы для случая непо-

15.

W.-T. Juan, Z.-H. Huang, J.-W. Hsu, Y.-J. Lai, and

L. I, Phys. Rev. E 58, 6947 (1998).

парных (невзаимных) потенциалов. Полученные ре-

зультаты могут быть полезны для разработки новых

16.

O. Ishihara, T. Kamimura, K. I. Hirose, and N. Sato,

методов диагностики физических свойств пылевой

Phys. Rev. E 66, 046406 (2002).

плазмы.

17.

M. Klindworth, A. Melzer, A. Piel, and V. A. Schwei-

gert, Phys. Rev. B 61, 8404 (2000).

Финансирование. Работа частично поддержа-

18.

A. Melzer, M. Klindworth, and A. Piel, Phys. Rev.

на Российским фондом фундаментальных исследо-

Lett. 87, 115002 (2001).

ваний (грант №18-38-20175), а также Программой

Президиума Российской академии наук.

19.

A. V. Ivlev, J. Bartnick, M. Heinen, C. R. Du, V. No-

senko, and H. Löwen, Phys. Rev. X 5, 011035 (2015).

20.

О. С. Ваулина, И. И. Лисина, К. Г. Косс, Физика

ЛИТЕРАТУРА

плазмы 39, 455 (2013).

1. О. С. Ваулина, О. Ф. Петров, В. Е. Фортов,

21.

I. I. Lisina and O. S. Vaulina, Europhys. Lett. 103,

А. Г. Храпак, С. А. Храпак, Пылевая плазма (экс-

55002 (2013).

411

О. С. Ваулина, Э. А. Саметов, Е. А. Лисин

ЖЭТФ, том 158, вып. 2 (8), 2020

22. A. K. Mukhopadhyay and J. Goree, Phys. Rev. E 90,

32. K. Qiao, Z. Ding, J. Kong, M. Chen, L. S. Matthews,

013102 (2014).

and T. W. Hyde, arXiv:1810.07173 (2018).

23. О. С. Ваулина, Э. А. Саметов, ЖЭТФ 154, 407

33. R. Yousefi, M. Chen, L. S. Matthews, and T. W. Hy-

(2018).

de, arXiv:1607.03177 (2016).

24. Ю. Л. Климонтович, Статистическая физика,

34. О. С. Ваулина, Е. А. Лисин, А. В. Гавриков,

Наука, Москва (1982).

О. Ф. Петров, В. Е. Фортов, ЖЭТФ 137, 751

25. А. А. Воронов, Теория автоматического управле-

(2010).

ния, ч. 2, Высш. школа, Москва (1986).

35. E. A. Lisin, O. S. Vaulina, and O. F. Petrov, Phys.

26. Е. А. Лисин, О. С. Ваулина, ЖЭТФ 142, 1077

Plasmas 25, 013702 (2018).

(2012).

36. И. Н. Бронштейн, К. А. Семендяев, Справочник по

27. Е. А. Лисин, О. С. Ваулина, О. Ф. Петров, ЖЭТФ

математике для инженеров и учащихся втузов,

151, 791 (2017).

Наука, Москва (1986).

28. Э. А. Саметов, Е. А. Лисин, О. С. Ваулина, ЖЭТФ

157, 552 (2020).

37. О. С. Ваулина, К. Г. Адамович, И. Е. Дранжевс-

кий, Физика плазмы 31, 612 (2005).

29. Э. А. Саметов, Е. А. Лисин, О. С. Ваулина, Вест-

ник ОИВТ 2, 33 (2019).

38. О. С. Ваулина, И. И. Лисина, Е. А. Лисин, Физика

плазмы 44, 229 (2018).

30. J. B. Pieper and J. Goree, Phys. Rev. Lett. 77, 3137

(1996).

39. O. S. Vaulina, Phys. Plasmas 24, 023705 (2017).

31. A. Homann, A. Melzer, and A. Piel, Phys. Rev. E 59,

3835 (1996).

40. О. С. Ваулина, ЖЭТФ 151, 982 (2017).

412