ЖЭТФ, 2020, том 158, вып. 3 (9), стр. 504-514

ОБОБЩЕННАЯ МОДЕЛЬ ИЗИНГА В ОТСУТСТВИЕ

МАГНИТНОГО ПОЛЯ

Е. С. Цуваревa*, Ф. А. Кассан-Оглыb**, А. И. Прошкин^b

^a Уральский федеральный университет им. первого Президента России Б. Н. Ельцина

620000, Екатеринбург, Россия

^b Институт физики металлов им. М. Н. Михеева Уральского отделения Российской академии наук

620108, Екатеринбург, Россия

Поступила в редакцию 11 марта 2020 г.,

после переработки 18 марта 2020 г.

Принята к публикации 18 марта 2020 г.

Исследована модель Изинга на одномерной моноатомной эквидистантной решетке с учетом разных об-

менных взаимодействий между атомными спинами на узлах ближайших соседей и разных взаимодей-

ствий между атомными спинами на узлах вторых соседей. Выведена обобщенная трансфер-матрица

Крамерса - Ваннье с переносом на две трансляции решетки. Построены фазовые диаграммы, представля-

ющие все возможные магнитные типы упорядочения в основном состоянии. Найдено множество тройных

точек пересечения фаз и линий парного сосуществования фаз в строгом соответствии с правилом фаз

Гиббса, а также обнаружено свойство, аналогичное известным явлениям переохлаждения или перегрева-

ния. Показано, что в тройных точках фазы не индивидуализированы, а существенно фрустрированы, что

соответствует явлению критической опалесценции. Выведены точные аналитические выражения для сво-

бодной энергии Гиббса, а также для таких термодинамических характеристик системы, как внутренняя

энергия, теплоемкость и энтропия, включая и нуль-температурную энтропию. Проанализированы разно-

образные частные случаи и осуществлено сравнение со всеми известными результатами, в том числе и

на двумерной решетке.

DOI: 10.31857/S0044451020090096

следствии моделью Изинга, привлекла пристальное

и неиссякаемое внимание исследователей. В настоя-

щее время модели Изинга, давно вышедшей за рам-

1. ВВЕДЕНИЕ

ки магнетизма, посвящены тысячи и тысячи статей,

обзоров, монографий, трудов конференций, и число

Первой и одной из самых значимых вех в теории

их непрерывно нарастает [2-4].

магнетизма считается опубликование Изингом сво-

Вторым знаменательным этапом в теории магне-

ей работы [1] в 1925 году, в которой было приведено

тизма было изобретение Крамерсом и Ваннье [5, 6]

точное аналитическое решение задачи о магнитных

весьма эффективного метода так называемой тран-

моментах атомов (спинов), расположенных в узлах

сфер-матрицы. Суть этого метода заключается в

одномерной решетки, связанных короткодействую-

том, что расчет статистической суммы гигантско-

щим обменным взаимодействием и внешним магнит-

го числа (2^N ) магнитных конфигураций сводится к

ным полем. Фактически в этой работе получена пер-

нахождению одного главного (максимального) соб-

вая теоретическая кривая намагниченности как для

ственного значения довольно простой матрицы. В

ферромагнетика, так и антиферромагнетика. И хо-

результате свободная энергия Гиббса и все термоди-

тя главный желаемый результат — температурный

намические и магнитные характеристики системы

фазовый переход из неупорядоченной (парамагнит-

выражаются через это собственное значение прос-

ной) фазы в упорядоченное магнитное состояние —

тым дифференцированием по температуре и маг-

не был получен, эта работа и модель, названная впо-

нитному полю.

^* E-mail: eguny@mail.ru

Именно это изобретение позволило впоследствии

^** E-mail: felix.kassan-ogly@imp.uran.ru

Онзагеру [7] получить выдающийся результат — фа-

504

ЖЭТФ, том 158, вып. 3 (9), 2020

Обобщенная модель Изинга в отсутствие магнитного поля

(

)

зовый переход в модели Изинга на двумерной квад-

VN,1 = exp

s_N s₁ +

(s_N + s₁)

(4)

ратной решетке, что заложило основы бурного раз-

вития исследований физики критических явлений.

Другими словами, осуществляется замыкание

К тому же, решение Онзагера привело к появлению

цепочки в кольцо, и в результате получаем выра-

точных решений на других двумерных решетках: на

жение для статистической суммы в виде

треугольной (Ваннье [8]), на гексагональной (Гутап-

пель [9]) и на решетке кагоме (Кано и Найя [10]).

Z = Sp(V ^N),

(5)

Однако, несмотря на сложность всех ранее рас-

смотренных обобщений, стоит отметить, что до сих

где выражение (3) представлено в виде матрицы V ,

пор трансфер-матрица Крамерса - Ваннье представ-

фактически не зависящей от индексов:

лялась при переносе только на одну трансляцию ре-

(

)

J+H

e T

шетки.

V =

(6)

В данной работе была поставлена цель обобщить

eJTH

метод трансфер-матрицы Крамерса - Ваннье, кото-

Матрица V называется трансфер-матрицей Кра-

рый бы задавал перенос на две трансляции решетки,

мерса - Ваннье, которая может быть определена для

а также исследовать магнитные и термодинамичес-

модели Изинга также и с учетом более сложных вза-

кие свойства этой модели.

имодействий.

Следует отметить, что трансфер-матрица (6) не

2. ТРАНСФЕР-МАТРИЦА

зависит от индексов и, другими словами, одинакова

КРАМЕРСА - ВАННЬЕ

при переносе на одну трансляцию решетки.

След матрицы является одним из инвариантов ее

Первое, что сделали Крамерс и Ваннье, это за-

ортогонального преобразования, и существует такое

ново получили результат Изинга своим методом.

ортогональное преобразование D, которое приводит

Рассмотрим классическую модель Изинга во

ее к диагональной форме

внешнем магнитном поле на одномерной цепочке,

(

)

состоящей из N узлов, в которых расположены спи-

λ₁

ны. Гамильтониан H такой системы описывается вы-

V =D-1VD=

(7)

λ₂

ражением

где λ₁ и λ₂ -— собственные значения матрицы V ,

∑

H(s) = -J s_isi+1 - H s_i,

(1)

которые можно вычислить из секулярного уравне-

i=1

ния, не прибегая к нахождению явного выражения

для диагонализирующей матрицы D:

где индекс i нумерует узлы решетки; J — параметр

обменного взаимодействия между ближайшими со-

(

)

⁽H^)√

⁽H⁾

седними спинами; H — величина внешнего магнит-

λ1,2

= e^J/T ch

± sh²

+e-4J/T

(8)

ного поля; s_i — спиновая переменная, принимающая

в классическом варианте значения ±1.

Таким образом, λ₁ — это максимальное собствен-

Используя гамильтониан (1), получаем выраже-

ное значение трансфер-матрицы (которое всегда су-

ние для статистической суммы в виде

ществует для матрицы с вещественными матричны-

(

)

∑

ми элементами согласно теореме Фробениуса - Пер-

Z =

exp

s_isi+1 +

s_i

(2)

рона [11], будучи также вещественным), и в резуль-

{si=±1}

i=1

тате получаем статистическую сумму в виде

Экспонента в формуле (2) может быть представ-

Z =λN1 +λN2.

(9)

лена в виде произведения сомножителей, каждый

из которых зависит только от одной пары соседних

Свободная энергия Гиббса равна

спинов:

(

)

(

)

f (T, H) = -T ln Z = -T ln

λN₁ + λN2

Vi,i+1 = exp

s_isi+1 +

(s_i + si+1)

(3)

(

))

При наложении так называемых граничных ус-

λN₂

= -T lnλN1 + ln

(10)

ловий Борна - Кармана вводится еще связь послед-

λ^N

него спина с первым:

505

Е. С. Цуварев, Ф. А. Кассан-Оглы, А. И. Прошкин

ЖЭТФ, том 158, вып. 3 (9), 2020

В термодинамическом пределе, т. е. при N → ∞,

котором в гамильтониане учитываются такие об-

второе слагаемое в (10) исчезает и свободная энер-

менные взаимодействия, при которых трансфер-

гия Гиббса зависит лишь от максимального собст-

матрица Крамерса - Ваннье не сохраняется при пе-

венного значения трансфер-матрицы:

реносе на одну трансляцию решетки, а инвариант-

на только относительно переноса на две трансляции

f (T, H) = -T N ln λ₁,

(11)

решетки.

а свободная энергия Гиббса, приходящаяся на один

узел (один спин), имеет вид

3. ОБОБЩЕННАЯ ТРАНСФЕР-МАТРИЦА

F (T, H) = f(T, H)/N = -T ln λ₁.

(12)

КРАМЕРСА - ВАННЬЕ

Как следствие, все термодинамические и магнит-

Рассмотрим гамильтониан с обменными взаимо-

ные величины рассматриваемой модели выражают-

действиями между ближайшими и вторыми соседя-

ся только через максимальное собственное значение

ми в отсутствие магнитного поля, при этом взаи-

трансфер-матрицы λ₁ по обычным формулам тер-

модействия как первых, так и вторых соседей мо-

модинамики, например, энтропия S имеет вид

гут быть не одинаковыми (как по величине, так и

T ∂λ₁

по знаку), но альтернативно чередуются через один.

S(T, H) = ln λ₁ +

(13)

λ1 ∂T

Гамильтониан состоит из двух пар сумм, пробегаю-

щим отдельно по четным и нечетным узлам решет-

В частности, интересующая нас намагничен-

ки. В данном исследовании каждая сумма состоит

ность равна

теперь из N/2 слагаемых:

∂F

T ∂λ₁

M (T, H) = -

(14)

∂H

λ₁ ∂H

∑

H(s) = -J₁

s_isi+1 - J^′

s_isi+2-

Используя явное выражение (8) для λ₁ и форму-

i=1,3,5,...

лу (14), получаем известный результат Изинга:

∑

sh(H/T)

−J₂

si+1si+2 - J^′

si+1si+3,

(16)

M (T, H) =

√

(15)

i=2,4,6,...

sh² (H/T) + e-4J/T

где J₁, J₂ — параметры обменного взаимодействия

В дальнейшем модель Изинга на одномерной

между ближайшими соседями; J′1, J′2 — параметры

цепочке подвергалась разнообразным обобщениям.

обменного взаимодействия между вторыми соседя-

Учитывались обменные взаимодействия между вто-

ми; s_i = ±1.

рыми и третьими соседями, одноионная анизотро-

пия и т. п. Кроме того, модель Изинга рассматри-

Рисунок 1 иллюстрирует одномерную решетку

валась в квантовом варианте для целых и полуце-

спинов, соответствующую предлагаемой обобщен-

лых произвольных значений спина. Необходимо от-

ной модели Изинга, описываемой гамильтонианом

метить, что во всех этих обобщениях, сколь сложны-

(16).

ми бы они ни были, трансфер-матрица сохранялась

Следуя алгоритму вывода трансфер-матрицы

при переносе на одну трансляцию решетки.

Крамерса - Ваннье, представленному выше, получа-

В настоящей работе рассматривается обобще-

ем выражение для трансфер-матрицы рассматрива-

ние совершенно особого рода, а именно, такое, при

емой обобщенной модели (16):

⎛

′

⎞

^J1+J1+J2+J²

^J1+J1+J2-J2

^J1-J1-J2+J²

^J1-J1-J2-J²

⎜

⎟

⎜

′

⎟

⎜

^-J1+J1-J2-J²

^-J1+J1-J2+J²

^-J1-J1+J2-J²

^-J1-J1+J2+J2

⎟

⎜e

⎟

⎜

⎟

W =

(17)

⎜

⎟

^-J1-J1+J2+J²

^-J1-J1+J2-J²

^-J1+J1-J2+J²

^-J1+J1-J2-J²

⎜

⎟

⎜

⎟

⎝

⎠

^J1-J1-J2-J²

^J1-J1-J2+J²

^J1+J1+J2-J²

^J1+J1+J2+J²

506

ЖЭТФ, том 158, вып. 3 (9), 2020

Обобщенная модель Изинга в отсутствие магнитного поля

)

Собственные значения матрицы W вычисляются

⁽2J₁

⁽2J′1 + 2J′2 + 2J₂ )

2 exp

из секулярного уравнения (где E — это единичная

квадратная матрица размером 4 × 4):

det(W - λE) = 0.

(18)

(

)

J′1 + J′2

⁽J₁ +J₂)

c = -16exp

или

λ⁴ + aλ³ + bλ² + cλ + d = 0,

(19)

)

⁽J′1 +J′2

⁽J₁ +J₂)

⁽2J′1 )

⁽2J′2 )

a = -4exp

× sh

)

⁽2J′1 + 2J′2

⁽2J′1 - 2J′2 )

b = 4exp

- 4ch

⁽2J′1 )

⁽2J′2 )

d = 16sh²

sh²

)

⁽-2J₁

⁽2J′1 + 2J′2 - 2J₂ )

+ 2exp

Решая уравнение четвертой степени [12], опреде-

ляем наибольшее собственное значение в виде

)

⁽J′1 +J′2

⁽J₁ +J₂)

⁽-J′1 - J′2 )

⁽J₁ -J₂)

λ_max = exp

+ exp

√

)

⁽2J′₁ - 2J′₂ )

⁽J₁ +J

⁽J₁ -J₂)

⁽J₁ +J₂)

⁽J₁ -J₂)

2 ch

+ 2ch

+ ξ sh²

sh²

(20)

((

)

где ξ = exp

2J′1 + 2J′2

ное значение трансфер-матрицы Крамерса - Ваннье

В рассматриваемом методе трансфер-матрицы

λ_max как

Крамерса - Ваннье все термодинамические и маг-

∂λ_max

T²

∂

∂λ_max

нитные величины исследуемой модели выражаются

C(T ) =

(24)

λ_max

∂T

∂T λ_max

∂T

только через ее максимальное собственное значение

λmax. Для этих целей, в том числе и для изучения

T² ∂λ_max

фрустрационных свойств модели, в данной работе

E(T ) =

(25)

∂T

нам потребуются явные выражения, зависящие от

температуры и четырех обменных параметров, для

Термодинамический параметр порядка по физи-

энтропии S, теплоемкости C, внутренней энергии E

ческому смыслу представляет собой степень упоря-

и термодинамического параметра порядка η, впер-

доченности системы и определяется следующим вы-

вые введенного в статье [13]. Прежде всего, прини-

ражением:

S(T )

мая во внимание то, что в гамильтониане (16) каж-

η(T ) = 1 -

(26)

ln 2

дая сумма пробегает только по половине узлов, а

не по всем узлам решетки, статистическая сумма в

термодинамическом пределе принимает вид

4. ОБОБЩЕННАЯ МОДЕЛЬ ИЗИНГА В

ОТСУТСТВИЕ МАГНИТНОГО ПОЛЯ

Z_N = λN/2max.

(21)

Начнем исследование общих свойств обобщенной

А свободная энергия, приходящаяся на один

модели Изинга на одномерной решетке с построе-

узел, равна

T ln λ_max

ния фазовых диаграмм, представляющих все воз-

F (T ) = -

(22)

можные магнитные типы упорядочения в основном

Энтропия имеет уже другой вид

состоянии. Для этой цели воспользуемся выражени-

ями (19)-(21) для максимального собственного зна-

ln λ_max

∂λ_max

чения трансфер-матрицы и выражением (25) для

S(T ) =

(23)

2λ_max

∂T

определения внутренней энергии при T

→ 0 как

Соответственно, теплоемкость и внутренняя

функции всех четырех обменных параметров моде-

энергия выражаются через максимальное собствен-

ли J₁, J′1, J₂, J′2.

507

Е. С. Цуварев, Ф. А. Кассан-Оглы, А. И. Прошкин

ЖЭТФ, том 158, вып. 3 (9), 2020

J₁

J₂

J₁

J₂

J₁

J₂

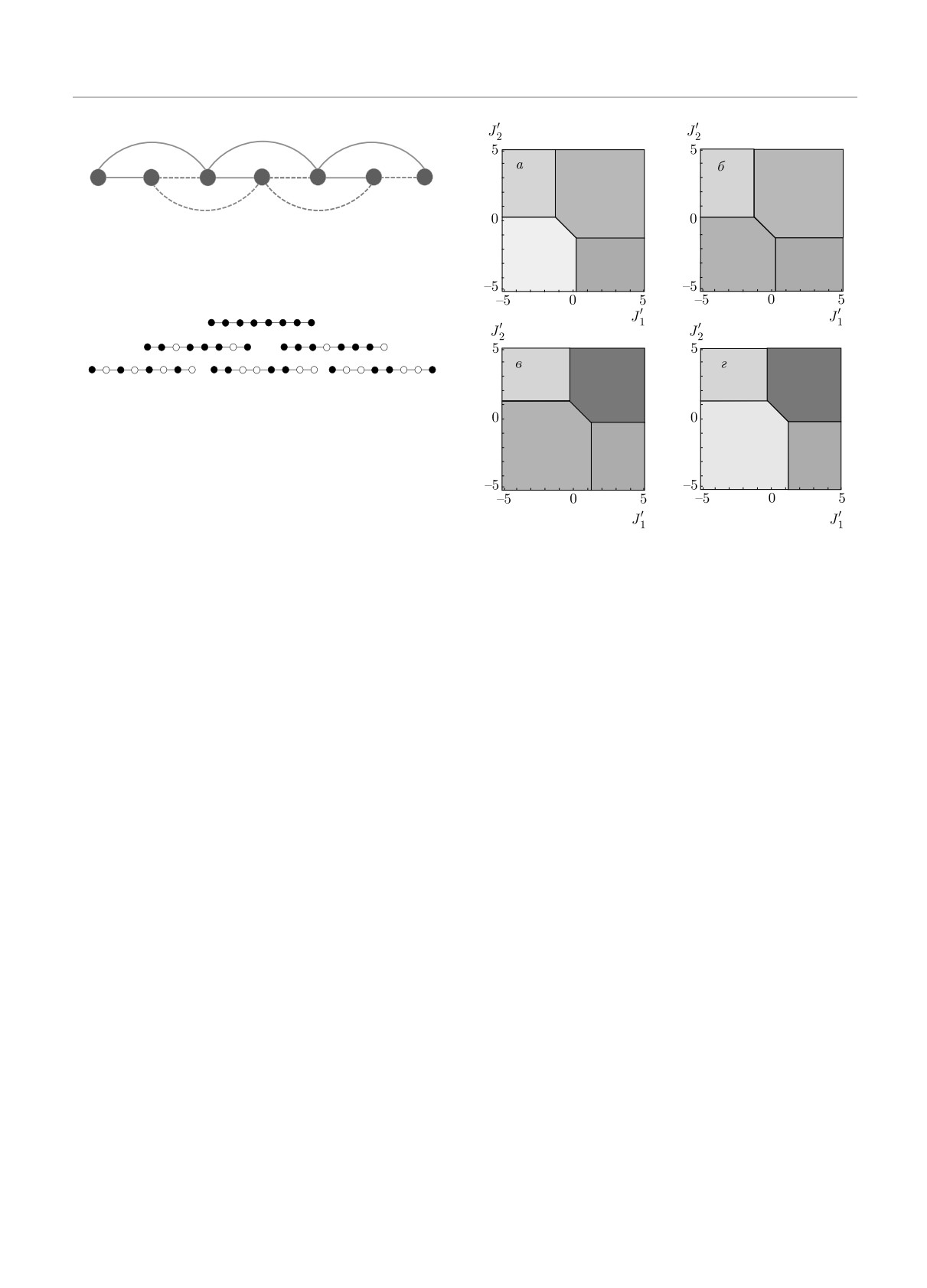
Рис. 1. Одномерная цепочка с учетом различных обмен-

ных взаимодействий между ближайшими (J1, J2) и вторы-

ми соседями (J′1, J′2)

FFAF

FFFA

AAFF

FAAF

Рис. 2. Возможные типы магнитных структур, реализуе-

мые в основном состоянии обобщенной модели Изинга в

отсутствие магнитного поля. Темные кружки соответству-

ют спину, направленному вверх (F ), светлые — вниз (A)

Детальный анализ большого множества всевоз-

можных вариантов числовых величин и знаков че-

Рис. 3. (В цвете онлайн) Фазовые диаграммы основных со-

тырех параметров обменного взаимодействия J₁, J′1,

стояний системы обобщенной модели Изинга в отсутствие

J₂, J′2 приводит к выводу, что в основном состоянии

магнитного поля в координатах (J′1, J′2) при различных об-

реализоваться могут только шесть типов упорядо-

менных взаимодействиях J1, J2: а — J1 = -1.5, J2 = -1,

чения (магнитных структур) (рис. 2). Ферромагнит-

б — J1 = -1, J2 = -1.5, в — J1 = 1.5, J2 = -1, г —

ная структура, соответствующая сохранению пери-

J1 = -1, J2 = 1.5. Каждая закрашенная область соответ-

ода трансляций решетки, внутренняя энергия кото-

ствует конкретной фазе

рой в основном состоянии равна

)/6.

E_FFA = (J₁ + J₂ + J′1 + J′2

E_F = -(J₁ + J₂ + J′1 + J′2)/2.

Поскольку рассматриваемая обобщенная модель

Структура с удвоением периода трансляций решет-

Изинга зависит от четырех независимых парамет-

ки с внутренней энергией

ров J₁, J′1, J₂, J′2, одновременное изображение пол-

ной фазовой диаграммы невозможно из-за того, что

E_AF = (J₁ + J₂ - J′1 - J′2)/2.

для этого требуется четырехмерное пространство.

А также четыре структуры AAF F , F AAF , F F AF

Поэтому на рис. 3 представлены некоторые частные

и FFFA с учетверением периода трансляций ре-

фазовые диаграммы, соответствующие избранным

шетки, внутренние энергии которых равны соответ-

сечениям этого четырехмерного пространства. Тем

ственно

не менее, численное исследование этой задачи оказа-

лось возможным, и как видно на рис. 3, на фазовых

E_AAFF = (J′1 + J′2 - J₁ + J₂)/2,

диаграммах присутствуют точки cхождения фаз, а

также линии пересечения фаз.

E_FAAF = (J′1 + J′2 + J₁ - J₂)/2,

Установлено, что фазовые диаграммы находят-

E_FFAF = (J′1 - J′2)/2, E_FFFA = -(J′1 - J′2)/2.

ся в строгом соответствии с правилом фаз Гиббса,

Внутренние энергии всех остальных типов упо-

которое гласит, что число фаз (A), находящихся в

рядочения при любых величинах и знаках парамет-

одной точке, не может быть больше числа компо-

ров модели J₁, J′1, J₂, J′2 оказываются выше внут-

нентов (K), увеличенного на количество внешних

ренней энергии любой из найденных структур: E_F ,

независимых параметров (N), влияющих на равно-

E_AF , E_AAFF , E_FAAF , E_FFAF или E_FFFA. Напри-

весие. Правило фаз записывается через количество

мер, магнитная структура с утроением периода

степеней свободы (F) равновесной термодинамиче-

трансляций решетки с внутренней энергией в основ-

ской системы, которые необходимы для однозначно-

ном состоянии, равной

го описания системы:

508

ЖЭТФ, том 158, вып. 3 (9), 2020

Обобщенная модель Изинга в отсутствие магнитного поля

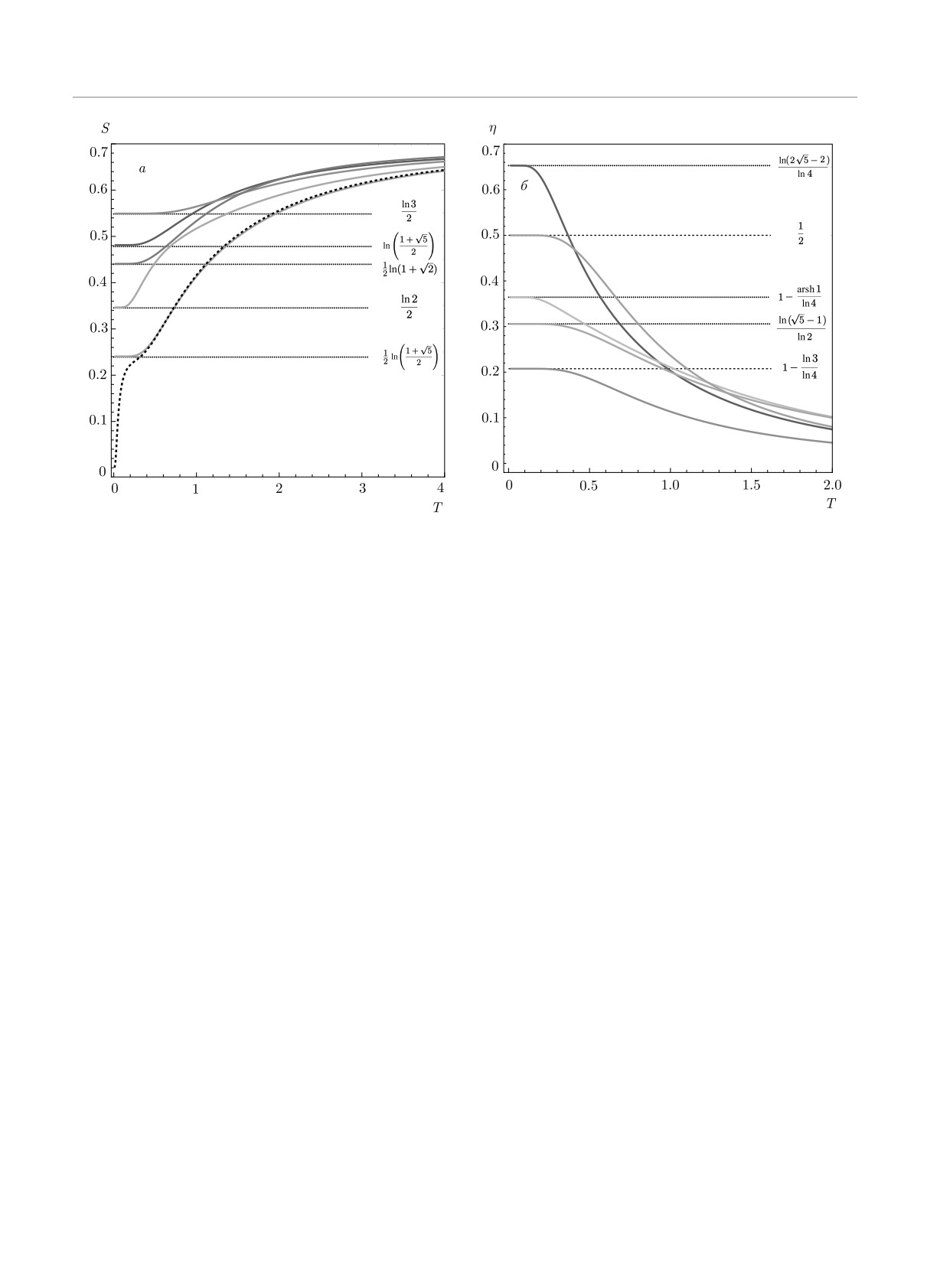
Рис. 4. a) Температурные зависимости энтропий обобщенной модели Изинга в отсутствие магнитного поля, пунктирной

линией показано поведение энтропии вблизи точки фрустрации; б) термодинамический параметр порядка в различных

точках фрустраций

F =K-A+N.

(27)

фазы являются не индивидуализированными, тог-

да можно указать бесконечно много других различ-

Рассматривая фазовые диаграммы (рис. 3), мож-

ных конфигураций с такой же энергией, в том чис-

но убедиться, что выражение (27) действительно

ле и без определенной трансляционной инвариант-

выполняется. По диаграммам видно, как каждая

ности, и чем больше количество сходящихся фаз на-

фаза в рассматриваемых сечениях представлена ча-

блюдается в такой точке, тем выше значение нуль-

стью плоскости, к тому же можно показать, что при

температурной энтропии, отличной от нуля, но ко-

некоторых значениях обменных взаимодействий две

гда нуль-температурная энтропия равна нулю, то

из представленных частей совпадают.

фрустрации не наблюдаются и можно утверждать,

Ферромагнитная фаза F обозначена синим цве-

что в данной точке сосуществуют только сходящие-

том, фаза удвоения периода трансляции (антифер-

ся фазы, т. е. фазы индивидуализированы.

ромагнитная) AF — красная, фазы учетверения пе-

риода трансляции решетки AAF F , F AAF , F F AF и

FFFA — соответственно зеленая, желтая, голубая

Температурные зависимости, изображенные на

и фиолетовая.

рис. 4, демонстрируют наличие ненулевых нуль-тем-

Представленные на рис. 3 диаграммы, хотя и яв-

пературных энтропий в обобщенной модели Изин-

ляются частными, однако, они совместно с прави-

га в отсутствие магнитного поля, а также получен-

лом фаз дают полное представление об обобщенной

ные точные аналитические выражения для каждой

модели в отсутствие магнитного поля. Для обобщен-

из них. При увеличении температуры до бесконеч-

ной модели Изинга максимальное количество фаз,

ности все температурные зависимости стремятся к

сходящихся в одной точке, равно шести.

ln 2, что соответствует тому, что при T → ∞ все

Тщательно проанализировав всевозможные ва-

2^N конфигурации приобретают одинаковый стати-

рианты схождения фаз, можно заключить, что

стический вес, равный 1/2^N . На примере одной за-

нуль-температурная энтропия в некоторых из них

висимости показано, что если изменить величину

принимает ненулевое значение, однако, в остальных

(либо знак) любого параметра обменного взаимодей-

равняется нулю. Данный факт свидетельствует о на-

ствия, нуль-температурная энтропия станет равна

личии фрустраций [14, 15]. Если в какой-то точке

нулю, тем самым явление фрустраций исчезает.

509

Е. С. Цуварев, Ф. А. Кассан-Оглы, А. И. Прошкин

ЖЭТФ, том 158, вып. 3 (9), 2020

T ,T_cm

1.2

1.4

0.8

1.0

1.2

1.0

0.6

0.8

0.6

0.4

0.6

0.4

0.2

0.0

-1.4

-1.2

-1.0

-0.8

-0.6

-1.5

-1.0

-0.5

0.5

-0.4

–0.2

0.2

0.4

T ,T_cm

1.0

0.7

0.6

0.8

0.5

0.6

0.4

0.3

0.4

0.2

0.1

0.2

0.4

0.6

0.8

1.0

0.2

0.4

0.6

0.8

1.0

Рис. 5. Положения пиков теплоемкостей в непосредственной близости к точке фрустрации

Определить степень упорядоченности системы

щепляется на два пика с разным характером пове-

можно, используя термодинамический параметр по-

дения около фрустраций. Если в точке фрустрации

рядка, приведенный на рис. 4. При T → 0 термоди-

существует только один куполообразный пик, то в

намический параметр порядка выходит на некото-

непосредственной близости от фрустрации возника-

рые постоянные значения, для которых также по-

ет дополнительный узкий пик (рис. 6). При дальней-

лучены точные аналитические выражения. Каждое

шем отклонении от точки или линии фрустрации до-

такое выражение связано с нуль-температурной эн-

полнительный пик растет, а исходный уменьшается

тропией по формуле (26).

и исчезает.

Чтобы пронаблюдать за характером изменения

теплоемкостей вблизи точек (линий) фрустраций,

5. ТЕРМОДИНАМИКА ОБОБЩЕННОЙ

построены графики (рис. 5), демонстрирующие по-

МОДЕЛИ ИЗИНГА

ложения пиков теплоемкостей в непосредственной

близости к точкам (линиям) фрустраций.

Точки и линии фрустраций различаются толь-

ко значениями нуль-температурных энтропий (или

Установлено, что пики теплоемкостей двух фаз

термодинамическим параметром порядка). Вблизи

«выходят» за границу фрустрации, однако при

этих точек и линий фрустраций поведение системы

некотором значении J один из пиков исчезает и в

обладает существенными особенностями. Во-пер-

дальнейшем остается одна из фаз упорядочения в

вых, при сколь угодно малом отклонении от них

основном состоянии.

нуль-температурная энтропия становится равной

Другими словами, в нашем случае, как и в тер-

нулю, а нуль-температурный параметр порядка ста-

модинамике, наблюдается явление, когда одна фаза

новится равным единице, что соответствует пол-

существует в области другой фазы и, наоборот, вто-

ному упорядочению. Во-вторых, теплоемкость рас-

рая фаза существует в области первой фазы. Таким

510

ЖЭТФ, том 158, вып. 3 (9), 2020

Обобщенная модель Изинга в отсутствие магнитного поля

0.30

0.20

0.25

0.20

0.15

0.10

0.05

0.5

1.0

1.5

2.0

0.5

1.0

1.5

2.0

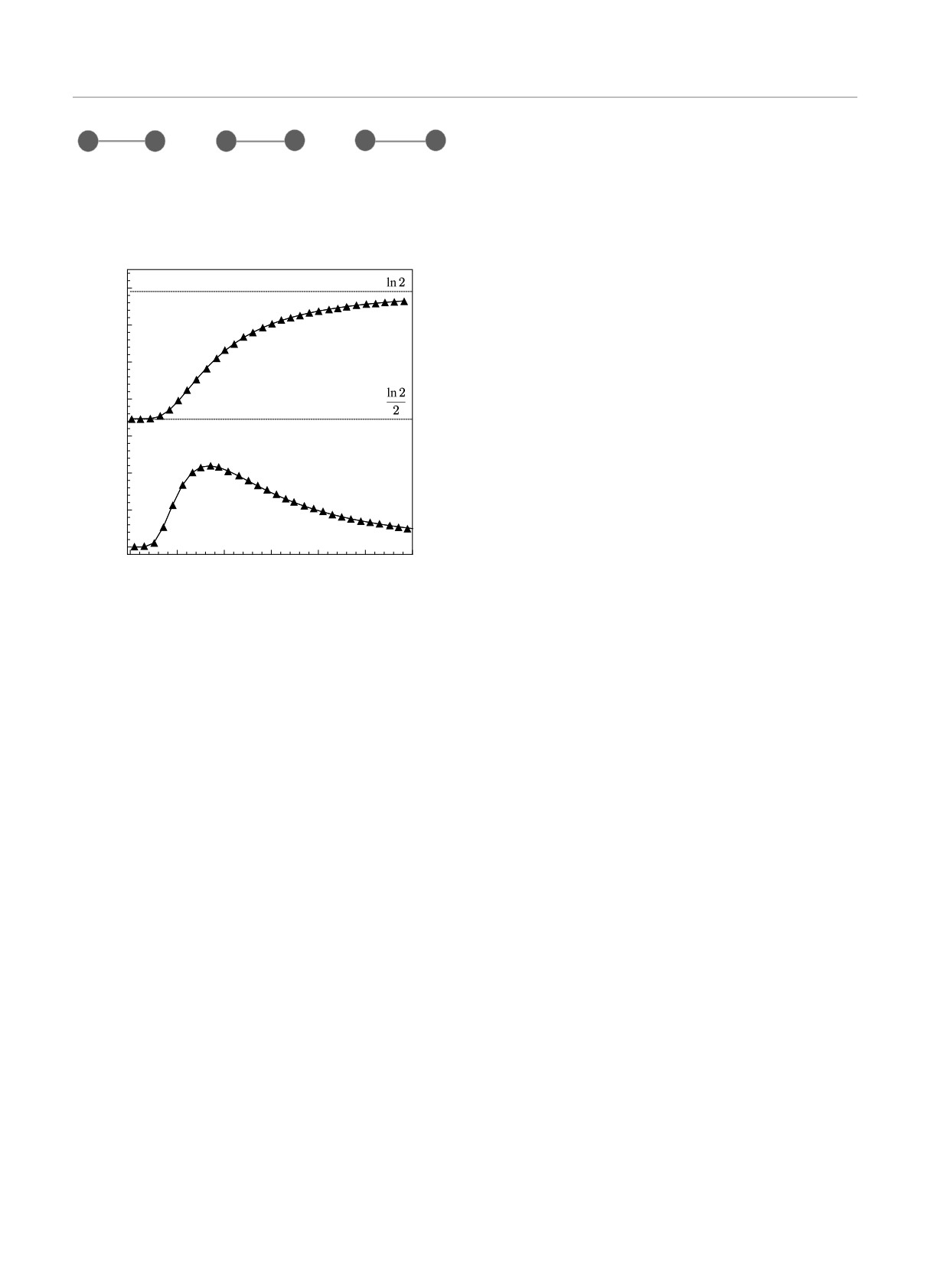
Рис. 6. (В цвете онлайн) Температурные зависимости теплоемкостей в точке фрустрации, а также в непосредственной

близости фрустрации: а — синяя кривая (в точке фрустрации) при J1 = 0.5, J2 = -0.5, J¹ = 0.5, J² = -0.5, красная

кривая при J1 = 0.6 . . ., бирюзовая кривая при J1 = 0.4 . . .; б — синяя кривая (в точке фрустрации) при J1 = -0.5,

J2 = -1, J¹ = 0.25, J² = -0.75, красная кривая при . . . J² = -0.85, бирюзовая кривая при . . . J² = -0.65

J₁

6. ЧАСТНЫЕ СЛУЧАИ ОБОБЩЕННОЙ

МОДЕЛИ ИЗИНГА

J₁

J₂

J₁

J₂

J₁

J₂

Перебором большого количества различных зна-

Рис. 7. Однократно декорированная решетка

чений и знаков обменных взаимодействий между

ближайшими и вторыми соседями можно полу-

чить различные частные случаи обобщенной модели

Изинга.

образом, рассмотренное явление аналогично явле-

Начнем с наиболее очевидного частного случая.

ниям перегрева и переохлаждения.

При выполнении равенств J₁ = J₂, J′1 = J′2 получаем

обычную (не обобщенную) модель Изинга с учетом

Более того, как уже отмечалось выше, в местах

взаимодействий между ближайшими и вторыми со-

схождения сразу нескольких фаз фазы не инди-

седями.

видуализированы, а существенно фрустрированы,

Введение обобщенной модели Изинга позволяет

поскольку помимо сходящихся фаз в этих точках

получать различные виды декорированных реше-

существует бесконечное множество конфигураций

ток. Такую декорированную цепочку получаем, при-

без каких-либо трансляционных инвариантностей, о

равняв нулю одно из взаимодействий между вторы-

чем свидетельствует ненулевая нуль-температурная

ми соседями J′1 = 0 (или, что эквивалентно, J′2 = 0)

энтропия (отличный от единицы параметр порядка).

(рис. 7). При дополнительном равенстве J₁ = J₂ ре-

Это явление вполне аналогично явлению критичес-

шетка является просто декорированной и соответ-

кой опалесценции. Смолуховский [16] был первый,

ствует модели, которая была решена в работе [17].

кто прозорливо предугадал, что явление критичес-

кой опалесценции обусловлено возникновением в

Помимо этого, можно продемонстрировать сход-

тройной точке бесконечного множества термодина-

ство рассматриваемой решетки обобщенной модели

мических флуктуаций. Следует отметить, что фак-

с двумерной гексагональной решеткой в некоторых

тически в тройной точке возникает явление сильных

приближениях. Гексагональная решетка представ-

фрустраций.

лена на рис. 8.

511

Е. С. Цуварев, Ф. А. Кассан-Оглы, А. И. Прошкин

ЖЭТФ, том 158, вып. 3 (9), 2020

Рис. 8. Гексагональная решетка

Рис. 9. Гексагональная решетка с J1 = 0

В 1950 г. Гутаппель получил точное аналитичес-

кое решение для наибольшего собственного значе-

Рис. 10. Решетка обобщенной модели в отсутствие взаи-

ния гексагональной решетки в виде

модействия между вторыми соседями и с различными ве-

⎡

личинами ближайших взаимодействий

∫

^[1⁽

⁽2J₁ )

λ_hex = 2 exp^⎣

16π²

)

⁽2J₂ )

⁽2J

⁽2J₂ )

⁽2J₃ )

× ch

+1- sh

)

⁽2J₃

⁽2J₁ )

× cos(α) - sh

cos(β) -

⎤

)

)]

⁽2J₁

⁽2J₂ )

- sh

cos(α + β) dα dβ^⎦.

(28)

Если положить нулю взаимодействие J₁ меж-

ду узлами гексагональной решетки, получим на-

бор невзаимодействующих подрешеток — цепочек

Рис. 11. Гексагональная решетка при J1 = 0 и J2 = 0

(рис. 9). Выражение для максимального собствен-

ного значения при этом преобразуется к виду

⎡

Наибольшее собственное значение обобщенной

∫

модели Изинга сводится к следующему виду:

^[1⁽

⁽2J₂ )

⁽2J₃ )

λhex = 2 exp⎣1

8π

⁽J₁)

⁽J₂)

λ_max = 4 ch

(30)

⎤

)

)]

⁽2J₂

⁽2J₃ )

+ 1 - sh

cos(α) dα^⎦.

(29)

Видно, что решетки, проиллюстрированные на

рис. 9 и 10 являются одинаковыми топологически.

Графики температурных зависимостей энтропий и

Также, полагая взаимодействия между вторыми

теплоемкостей подтверждают это (рис. 13). Темпе-

соседями J′1 и J′2 равными нулю в обобщенной моде-

ратурные зависимости энтропии и теплоемкости в

ли Изинга, приходим к решетке, представленной на

случае гексагональной решетки полностью совпада-

рис. 10.

ют с зависимостями обобщенной модели Изинга.

512

ЖЭТФ, том 158, вып. 3 (9), 2020

Обобщенная модель Изинга в отсутствие магнитного поля

J₁

диаграммы основного состояния и определено, что

все они строго соответствуют правилу фаз Гиббса.

Рис. 12. Решетка обобщенной модели с отличным от нуля

Определены точки и линии фрустраций, получены

значением только между ближайшими соседями J1

точные аналитические выражения для нуль-темпе-

ратурных энтропий и для температурного парамет-

ра порядка при T → 0. Установлены критерии су-

ществования фрустраций в рассмотренной системе.

S,C

Исследованы некоторые частные случаи обобщен-

0.7

ной модели, в том числе и на гексагональной ре-

шетке.

0.6

Авторами получено точное выражение для

наибольшего собственного значения трансфер-

0.5

матрицы Крамерса - Ваннье обобщенной модели

0.4

Изинга в магнитном поле. Решение, а также анализ

всех частных случаев, включая решетку лестнично-

0.3

го типа (J₂ = 0), предмет отдельного рассмотрения.

0.2

Финансирование. Работа выполнена в

рамках государственного задания Министер-

0.1

ства образования и науки России (тема Квант,

№ АААА-А18-118020190095-4) при частичной

поддержке Уральского отделения РАН (проект

0.5

1.0

1.5

2.0

2.5

3.0

№18-2-2-11).

Рис. 13. Сравнение температурного поведения энтропий

и теплоемкостей для гексагональной решетки и решетки

обобщенной модели Изинга

ЛИТЕРАТУРА

1. E. Ising, Zeit für Physik 21, 253 (1925).

Теперь положим равным нулю взаимодействие

2. S. G. Brush, Rev. Mod. Phys. 39, 883 (1967).

J₂ на гексагональной решетке. Получаемая решетка

3. G. Mussardo, Statistical Field Theory: An Introduc-

показана на рис. 11, и она фактически соответствует

tion to Exactly Solved Models in Statistical Physics,

решетке димеров, так же как и решетка на рис. 12,

(Oxford Graduate Texts), Oxford University Press

в отсутствие взаимодействия J₂.

Inc., New York (2010).

Графики зависимостей энтропий и теплоемкос-

тей при таких значениях взаимодействий для дву-

4. Р. Бэкстер, Точно решаемые модели в статисти-

ческой механике, Мир, Москва (1985).

мерной и одномерной решеток также полностью сов-

падают (рис. 13).

5. H. A. Kramers and G. H. Wannier, Phys. Rev. 60,

252 (1941).

6. H. A. Kramers and G. H. Wannier, Phys. Rev. 60,

7. ЗАКЛЮЧЕНИЕ

263 (1941).

7. L. Onsager, Phys. Rev. 65, 117 (1944).

Главным достижением данной работы являет-

8. G. H. Wannier, Phys. Rev. 79, 357 (1950).

ся обобщение трансфер-матрицы Крамерса - Ваннье

с переносом на две трансляции линейной цепочки.

9. R. M. F. Houtappel, Prog. Theor. Phys. 16, 425

Получено точное аналитическое решение для наи-

(1950).

большего собственного значения обобщенной тран-

10. K. Kanô and S. Naya, Prog. Theor. Phys. 10, 158

сфер-матрицы Крамерса - Ваннье для двух транс-

(1953).

ляций с учетом различных обменных взаимодейст-

вий между ближайшими и вторыми соседями в

11. Ф. Р. Гантмахер, Теория матриц, Наука, Москва

отсутствие магнитного поля. Построены фазовые

(1966).

513

ЖЭТФ, вып. 3 (9)