ЖЭТФ, 2020, том 158, вып. 3 (9), стр. 544-560

ОБ УСТОЙЧИВОСТИ СТРУКТУРЫ НЕЙТРАЛЬНО

УСТОЙЧИВОЙ УДАРНОЙ ВОЛНЫ В ГАЗЕ

И О СПОНТАННОМ ИЗЛУЧЕНИИ ВОЗМУЩЕНИЙ

А. Г. Куликовскийa*, А. Т. Ильичевa,b**, А. П. Чугайноваa***, В. А. Шаргатовc****

^a Математический институт им. В. А. Стеклова Российской академии наук

119991, Москва, Россия

^b Московский государственный технический университет им. Н. Э. Баумана

105005, Москва, Россия

^c Национальный исследовательский ядерный университет «МИФИ»

115409, Москва, Россия

Поступила в редакцию 26 декабря 2019 г.,

после переработки 5 мая 2020 г.

Принята к публикации 7 мая 2020 г.

Исследована устойчивость структуры нейтрально устойчивой ударной волны, называемой также спонтан-

но излучающей. Получены решения, описывающие линейные, синусоидально зависящие от координаты

вдоль изучаемой структуры, возмущения в структуре и ниже по потоку. Показано, что эти возмущения

затухают со временем. Рассмотрен предельный переход при стремящейся к нулю безразмерной ширине

структуры. В пределе получены результаты, совпадающие с классическими, когда ударная волна счита-

лась поверхностью разрыва.

)

DOI: 10.31857/S0044451020090138

1-(v₂/c₂)² - v₁v₂/c²²

⁽ dV₂

<j²

< 1+2

v₂ .

(1)

1-(v₂/c₂)2 + v1v2/c2

dp₂

c₂

1. ВВЕДЕНИЕ

Здесь v — компонента скорости, нормальная к удар-

ной волне, c — скорость звука, V = 1/ρ — удельный

При исследовании линейной устойчивости удар-

объем, j² = (p₂ - p₁)/(V₁ - V₂) — квадрат потока

ных волн в газах [1-5] было обнаружено, что в за-

массы, индексы «1» и «2» относятся к величинам

висимости от уравнения состояния газа и интенсив-

перед и за ударной волной, индекс «H» у производ-

ности ударной волны плоская ударная волна мо-

ной означает, что производная берется вдоль удар-

жет быть асимптотически устойчивой (к устойчи-

ной адиабаты.

вым относятся ударные волны в совершенном газе),

При рассмотрении двумерных возмущений бу-

неустойчивой (когда возмущения поверхности удар-

дем считать ось x направленной по нормали к удар-

ной волны и гидродинамических величин в окрест-

ной волне, невозмущенную скорость — направлен-

ности волны экспоненциально растут со временем)

ной по оси x. Ось y считаем лежащей на невозму-

и нейтрально устойчивой. В последнем случае су-

щенной поверхности ударной волны. Тогда упомяну-

ществуют синусоидальные возмущения поверхности

тое синусоидальное возмущение поверхности удар-

ударной волны и течения за ней, которые не растут

ной волны записывается в виде

и не затухают со временем. Условия, при которых

ударная волна нейтрально устойчива, получены в

x = ξ(y,t), ξ(y,t) = ReAexpi(ky - ωt),

указанных работах и имеют вид

(2)

A = const.

^* E-mail: kulik@mi-ras.ru

Дисперсионное уравнение, являющееся следствием

^** E-mail: ilichev@mi-ras.ru

^*** E-mail: anna_ch@mi-ras.ru

линеаризованных граничных условий на ударной

^**** E-mail: shargatov@mail.ru

волне, определяет отношение

544

ЖЭТФ, том 158, вып. 3 (9), 2020

Об устойчивости структуры нейтрально устойчивой ударной волны...

= ±W.

(3)

В работах [7, 8] был подсчитан коэффициент отра-

жения слабонелинейных волн, который оказался ко-

Для нейтрально устойчивых волн значение W дей-

нечным, но при некоторых условиях стремящимся

ствительно и не зависит от k. Скорость W — «сверх-

к бесконечности, если амплитуда падающей волны

звуковая» в том смысле, что

стремится к нулю.

√

В последующие годы в связи с возможными при-

W > c²² -v²².

(4)

ложениями появился ряд работ, в которых изуча-

лись течения газов большой плотности, когда оказа-

Выражение, стоящее в правой части неравенства

лось возможным существование нейтрально устой-

(4), представляет собой скорость распространения

чивых ударных волн [9-14].

звука вдоль луча, параллельного ударной волне.

Работы [9-11] посвящены численным экспери-

Если по поверхности нейтрально устойчивой

ментам с нейтрально устойчивыми ударными вол-

ударной волны распространяется возмущение вида

нами и их взаимодействию с возмущениями. Выво-

(2) и выполняются условия (3) и (4), то в область

ды из упомянутых численных экспериментов, каса-

за ударной волной уходят акустические, энтропий-

ющиеся спонтанно излучающих ударных волн, сво-

ные и вихревые возмущения, не затухающие при

дятся к тому, что спонтанная (не обусловленная

удалении от ударной волны, поэтому обсуждаемые

внешними воздействиями) генерация акустических

нейтрально устойчивые ударные волны называют-

волн не наблюдалась в численных экспериментах.

ся также спонтанно излучающими ударными волна-

С точки зрения авторов настоящей работы, пред-

ми(СИУВ).

ставленные в [9-11] результаты не дают оснований

Поскольку в выражении (2) для нейтральных

для окончательного вывода из-за несовершенства

возмущений определено только отношение ω/k, а

любых методов численного расчета течений газа с

значение k произвольно, из решений, удовлетворяю-

ударными волнами, а также из-за нелинейности рас-

щих условию (3), можно составить возмущение

считанных примеров. В [9-11] отмечается, что ре-

ξ(y, t) произвольной формы (в том числе возмуще-

зультаты работ [7, 8] носят предположительный и в

ние, имеющее передний фронт), которое будет рас-

известной мере противоречивый характер.

пространяться по ударной волне со скоростью W .

Отметим, что в работе [15], которая идейно и

Эти возмущения как суперпозиция решений вида

методически связана с [9-11], в численном расче-

(2) соответствуют линейному приближению. В нели-

те получены незатухающие многомерные колебания

нейном приближении были получены решения, в ко-

ударной волны с образованием ячеистой структу-

торых по невозмущенной ударной волне двигает-

ры фронта. Существование такой ячеистой струк-

ся точка, за которой ударная волна расщепляется

туры получено в [15] в численном расчете в области

на две ударные волны или ударную волну и волну

неоднозначного представления разрыва и, по мне-

Прандтля - Майера. Если поместить начало коорди-

нию автора [15], является следствием этой неодно-

нат в эту точку, то течение зависит только от по-

значности, т. е. нелинейного эффекта. Там же сдела-

лярного угла [6].

но следующее утверждение: «О существовании ней-

В обзорной статье по устойчивости ударных

трально устойчивых ударных волн можно говорить,

волн [7] сделано следующее замечание: поскольку

лишь принимая во внимание, что вынужденные воз-

скорость распространения возмущений поверхности

мущения их поверхности затухают значительно мед-

ударной волны W сверхзвуковая в смысле выполне-

леннее, чем в случае абсолютно устойчивой ударной

ния неравенства (4), к точке, движущейся со скоро-

волны, а предсказываемое линейной теорией спон-

стью W по ударной волне, не могут прийти никакие

танное излучение звуковых волн фронтом нейтраль-

возмущения из потока за ударной волной, если эти

но устойчивой ударной волны вообще не наблюдает-

возмущения в начальный момент времени были со-

ся».

средоточены в ее окрестности, а не приходят из бес-

Можно отметить, что в статьях [7, 8] вопрос о

конечности. На этом основании в работе [7] возму-

природе процессов развития возмущений с нейт-

щения вида (2), (3) были объявлены несуществую-

рально устойчивой ударной волной остался откры-

щими. Далее в [7] отмечается, что действительность

тым. Нет также указаний на то, как с учетом выска-

величины ω/k означает, что у нейтрально устой-

занных там положений строить решение для линеа-

чивых волн коэффициент отражения акустических

ризованной задачи о поведении возмущений нейт-

возмущений, догоняющих ударную волну, при опре-

рально устойчивых ударных волн. Формальное же

деленном угле падения обращается в бесконечность.

построение решения задачи с начальными данными

545

ЖЭТФ, вып. 3 (9)

А. Г. Куликовский, А. Т. Ильичев, А. П. Чугайнова, В. А. Шаргатов

ЖЭТФ, том 158, вып. 3 (9), 2020

[3] приводит к появлению возмущений, излучаемых

будем в соответствии с неравенством (1) помечать

ударной волной в область за ней, источник которых

индексом «1», а параметры потока за ударной вол-

в виде возмущений формы ударной волны не зату-

ной — индексом «2». Выберем параметры течения и

хает со временем.

ударной волны таким образом, чтобы выполнялись

В связи с изложенным возникает вопрос: ка-

условия (1). Будем считать, что в газе могут про-

кие могут быть механизмы передачи возмущений по

исходить внутренние процессы: химические или ре-

ударной волне и как правильно описывать линейные

лаксационные, скорость протекания которых будет

возмущения нейтрально устойчивых ударных волн.

рассматриваться в следующих разделах как ограни-

В работе

[16] было предложено рассмотреть

ченная. При рассмотрении в этом разделе ударной

структуру СИУВ с целью выяснения возможности

волны как поверхности разрыва считается, что эти

передачи возмущений вдоль нее и далее рассмотреть

процессы происходят мгновенно и за ударной вол-

предельный переход, когда ширина структуры стре-

ной, и перед ней невозмущенное течение представ-

мится к нулю. В работе [17] дана краткая аннотация

ляет собой однородное течение равновесного невяз-

результатов, излагаемых ниже. В предлагаемой ра-

кого нетеплопроводного газа.

боте рассматривается простейшая модель структу-

Для задания свойств газа нужно задать внутрен-

ры СИУВ. Предполагается, что впереди расположе-

нюю энергию единицы массы

на обычная устойчивая ударная волна, такая же как

ε = ε(p,V ).

(5)

в совершенном газе, а за ней наблюдается течение

невязкого нетеплопроводного газа, в котором про-

Соотношения на ударной волне имеют вид [4]

исходят процессы релаксации, приводящие к умень-

шению показателя адиабаты γ. При этом переход

ε(p₂, V₂) - ε(p₁, V₁) -

(V₁ - V₂)(p₁ + p₂) = 0,

(6)

от течения перед ударной волной к течению вдали

за структурой соответствует ударному переходу в

p₂ - p₁

СИУВ.

j² =

(7)

V₁ - V₂

В разд.

выбираются параметры некоторой

СИУВ, структура которой будет далее изучаться.

Уравнение (6) называется ударной адиабатой или

В разд. 3 формулируются предположения, прини-

адиабатой Гюгонио (H). Равенство (7) выражает по-

маемые при описании релаксационного процесса, и

ток массы j = ρ₁v₁ = ρ₂v₂ через единицу площади

представляется решение задачи о структуре СИУВ.

ударной волны. Это равенство — следствие непре-

В разд. 4 приводятся уравнения, описывающие ли-

рывности на ударной волне потоков массы и нор-

нейные возмущения (гармонически зависящие от y)

мальной компоненты импульса.

в структуре СИУВ и ниже по потоку. В разд. 5 фор-

В неравенствах (1), выражающих условие спон-

мулируются условия, обеспечивающие отсутствие

танного излучения ударной волной, следует опреде-

приходящих из бесконечности возмущений, и по-

лить величины c₂ и (dV₂/dp₂)_H . Под c₂ следует по-

строены решения для возмущений, состоящие из

нимать равновесную скорость звука по состоянию за

волн, уходящих от ударной волны вниз по потоку.

зоной релаксации.

Излагается метод численного нахождения собствен-

Найдем значение c₂ как скорость бесконечно сла-

ных частот, приведены результаты этих вычислений

бой ударной волны вблизи состояния 2. Воспользу-

в виде зависимости собственной частоты от k, рас-

емся уравнением ударной адиабаты (6), считая со-

сматривается предельный переход при k → 0 (k —

стояние 1 близким к состоянию 2, так что

волновое число в направлении y) или, что то же, при

стремящейся к нулю безразмерной ширине струк-

dε = dε₂ - dε₁, V₁ - V₂ = -dV.

туры, отнесенной к длине волны возмущения в на-

Тогда при отсутствии вязкости и теплопроводно-

правлении y. В разд. 6 формулируются выводы о

сти получим, что при квазиравновесном процессе в

СИУВ, получающиеся при этом предельном перехо-

окрестности состояния 2

де, и проводится обсуждение результатов.

dε₂+p₂dV₂ = 0, (ε_p)′2dp₂+[(ε_V )′2+p₂]dV₂ = 0,

2. ВЫБОР ПАРАМЕТРОВ ДЛЯ СПОНТАННО

ИЗЛУЧАЮЩИХ УДАРНЫХ ВОЛН

dp₂

V²²[(ε^′V )₂ + p₂]

c²² =

dρ₂

(ε^′p)₂

(8)

В этом разделе ударная волна рассматривается

(

)

как поверхность разрыва, разделяющего два пото-

∂ε

⁽∂ε⁾

ε′V =

ε^′p =

ка газа. Параметры потока перед ударной волной

∂V_p

∂p_V

546

ЖЭТФ, том 158, вып. 3 (9), 2020

Об устойчивости структуры нейтрально устойчивой ударной волны...

Найдем теперь величину (dV₂/dp₂)_H. Для этого

полном объеме, ограничимся следующей областью

возьмем дифференциал от равенства (6), считая со-

значений этих величин:

стояние 1 заданным:

X >

Y >

(17)

(ε^′p)₂ dp₂ + (ε^′V )₂ dV₂ +

(p₂ + p₁) dV₂ -

В этом случае среднее выражение (15) в неравен-

(V₁ - V₂) dp₂ = 0,

(9)

ствах (1) оказывается отрицательным, т. е. отрица-

телен наклон ударной адиабаты (dV₂/dp₂))_H в со-

откуда

стоянии 2. При этом правое неравенство в (1) вы-

⁽ dV₂ )

(ε^′p)₂ - (V₁ - V₂)/2

полняется автоматически, поскольку 1 + 2v₂/c₂ > 0.

(10)

dp₂

(ε^′V )₂ + (p₂ + p₁)/2

Выполнение левого неравенства было сведено к вы-

полнению неравенства (16). При выполнении огра-

Скорость v находится из равенства

ничений (17) неравенство (16) приводится к виду

v=jV,

(11)

[

(

)

]

(Y - X) Y - 1 -

−1

X < 0.

где j определяется согласно (7).

V₂

Воспользуемся равенствами (11), (7), (8) и пре-

Таким образом, для выполнения левого неравенства

образуем комбинацию слагаемых, стоящих в числи-

(1) достаточно выбрать значения X и Y так, что-

теле левой части неравенств (1),

бы они удовлетворяли неравенствам (17) и неравен-

v₂(v₁ + v₂)

⁽V₁

⁾ p₂ -p₁

(ε^′p)₂

ствам

(12)

c²²

V₂

V₁ - V₂ (ε^′V )₂ + p₂

(

)

X <Y <1+

−1

(18)

Обозначим

(ε^′p)₂

(ε^′V )₂ + p₂

= X > 0,

= Y > 0.

(13)

Внутренняя энергия в случае совершенного газа

V₁ - V₂

p₂ - p₁

имеет вид

Неравенство Y

> 0 следует согласно (8) из нера-

венств ε′p2 > 0 и c²² > 0. Равенство (12) примет вид

ε=

, или p = (γ - 1)ρε, γ = const.

(19)

γ-1

v₂(v₁ + v₂)

⁽V₁

⁾X

(14)

c²²

V₂

Как известно, множитель (γ-1) в совершенном газе

зависит от числа степеней свободы молекул газа.

Преобразуем подобным образом знаменатель

Если происходит релаксационный процесс, то до-

дроби в (1). Тогда получим выражение для левой

ля энергии, приходящаяся на поступательные степе-

части неравенств (1):

ни свободы всех частиц (молекул, ионов, электро-

[

]

1 - (v₂/c₂)² + v₁v₂/c²

нов), зависит также от энергии, затраченной (за-

Y - (V₁/V₂ + 1)X

[

] =

пасенной) при диссоциации и ионизации. Поэтому

Y + (V₁/V₂ - 1)X

1 - (v₂/c₂)² - v₁v₂/c²²

можно написать

Среднее выражение в неравенствах (1) с учетом (10)

p = ρεf, или ε = pV /f.

(20)

приводится к виду

Здесь f определяет долю энергии, соответствую-

p₂ - p₁ (ε^p)2 - (V1 - V2)/2

X - 1/2

(15)

щую поступательным степеням свободы, ε — пол-

V₁ - V₂ (ε^′V )₂ + (p₂ + p₁)/2

Y - 1/2

ная энергия единицы массы газа по всем степеням

Таким образом, левое неравенство (1) приобретает

свободы, учитывающая также химическую энергию,

вид

энергию диссоциации и ионизации.

(V₁/V₂ + 1)X - Y

X - 1/2

(16)

Сравнение равенств (19) и (20) показывает, что f

(V₁/V₂ - 1)X + Y

Y - 1/2

и (γ-1) играют одинаковую роль в уравнении состо-

Для выбора ударной волны, возмущения которой

яния, так что далее не делается различия между f

будут изучаться, следует распорядиться величина-

и γ -1. Как известно, в гиперзвуковой аэродинами-

ми X и Y так, чтобы неравенства (1) были выпол-

ке процессы диссоциации и ионизации учитывают-

нены. Не рассматривая решения неравенства (16) в

ся во многих случаях изменением величины γ [18].

547

А. Г. Куликовский, А. Т. Ильичев, А. П. Чугайнова, В. А. Шаргатов

ЖЭТФ, том 158, вып. 3 (9), 2020

При рассмотрении структуры и возможных неста-

течение невязкого нетеплопроводного газа, опреде-

ционарных процессов будут использоваться равен-

ляющееся процессом релаксации, в котором значе-

ства (20), но f будет считаться переменной величи-

ние функции f стремится к своему равновесному

ной, для которой будет постулировано дифференци-

значению f_e.

альное уравнение. Равновесное значение f, соответ-

Процесс релаксации в частице газа должен опи-

ствующее заданным V и p, будем помечать индек-

сываться дифференциальным уравнением, которое

сом e.

зададим простейшим образом:

Выберем значения, обеспечивающие выполнение

= -λ(f - f_e(p, V )), λ > 0.

(26)

неравенств (1),

Величина λ может зависеть от текущего состояния

fe1 = 0.4, fe2 = 0.2, V₂/V₁ = 1/5,

(21)

газа и будет выбрана постоянной из соображений

p₂/p₁ ≈ 4.8, X = 2.5, Y = 9.

удобства.

Далее принимаются следующие обозначения. Ве-

Отношение p₂/p₁ получено с использованием¹⁾ (6).

личины без индекса — текущие значения внутри

Пользуясь равенствами (20) и (13), найдем част-

структуры. Величины с индексом «1» относятся к

ные производные от f_e = pV/ε(p, V ) в состоянии 2:

течению перед лидирующей ударной волной, индек-

[

(

)]

сом «0» будут отмечаться величины непосредствен-

⁽∂f_e)

(f_e)

f-12 - X

-1

≈

но за лидирующей ударной волной, величины с ин-

∂p

p₂

дексом «2» относятся к течению за зоной релакса-

0.200

≈-

(22)

ции. Будем считать, что непосредственно за идущей

p₂

впереди лидирующей ударной волной f₀ ≡ γ₁ - 1 =

= f₁, т. е. считается, что γ в этой ударной волне

не меняется, γ₀ = γ₁. Это равенство основано на

⁽∂f_e)

(f_e)

²[

]

f-12 + 1 - Y (1 - p₁p-12)

≈

представлении, что лидирующая ударная волна уз-

∂V

V₂

кая (порядка нескольких длин свободного пробега)

0.045

и в ней f не изменяется, поскольку изменения f про-

≈-

(23)

V₂

исходят с конечной скоростью.

Рассмотрим течение, в котором все величины за-

Производная вдоль прямой Рэлея - Михельсона в со-

висят от переменной x, а функция f = γ - 1 изме-

стоянии 2 имеет вид

няется согласно уравнению (26) от значения f₀

)

= f₁, до тех пор пока не будет выполнено равенство

⁽ df_e )

⁽∂f

⁽∂f_e)

⁽∂p⁾

f = f_e(p,V ). Если при некотором x известно зна-

dVM2

∂V

∂p

∂VM2

чение функции f, то параметры течения при этом

0.045

0.2(p₂ - p₁)

0.005

≈-

(24)

можно рассчитать из законов сохранения, которые

V₂

p₂(V₁ - V₂)

V₂

выполняются в случае одномерного стационарного

течения.

Выполнение равенства (7) не зависит от процес-

3. СТРУКТУРА СПОНТАННО

ИЗЛУЧАЮЩИХ УДАРНЫХ ВОЛН,

са релаксации. В одномерном стационарном тече-

ОБУСЛОВЛЕННАЯ ПРОЦЕССОМ

нии j = const. Тогда на плоскости V, p равенство

РЕЛАКСАЦИИ

(7) определяет прямую (прямая Рэлея - Михельсо-

на). Значения V (x), p(x) при стационарном течении

Как было сказано, равновесные состояния газа

принадлежат этой прямой.

определяются равенствами (20), в которых

При γ₁ = γ₀ ударная адиабата — гипербола с

асимптотами [4]

f = f_e(p,V ),

(25)

γ₁ - 1

где f_e считается известной функцией, которая будет

V₁

γ₁ + 1

p₁

γ₁ + 1

задана ниже. Предполагается, что вслед за лидиру-

где V₁, p₁ — состояние перед ударной волной.

ющей газодинамической ударной волной происходит

Эта гипербола пересекает прямую (7) в началь-

ной точке и в точке V = V₀, p = p₀, соответствую-

¹⁾ Численные значения приводятся здесь и далее прибли-

женно с малым числом значащих цифр для создания качест-

щей состоянию непосредственно за головной удар-

венных представлений о параметрах.

ной волной. Далее наблюдается одномерное течение

548

ЖЭТФ, том 158, вып. 3 (9), 2020

Об устойчивости структуры нейтрально устойчивой ударной волны...

с уменьшением величины γ, для которого справед-

ливы законы сохранения. При этом значения всех

величин определяются значением γ так же, как в

ударной волне, т. е. в разрыве, в котором меняет-

ся значение γ от значения γ₁ до текущего значения

этой величины.

Уравнение ударной адиабаты (6) в случае изме-

нения в ударной волне значения γ имеет вид [4]

H (γ₁, γ, V₁, p₁, V, p) = 0, H(γ₁, γ, V₁, p₁, V, p) ≡

≡

pV -

p₁V₁ -

(V₁ - V )(p₁ + p).

(27)

γ-1

γ₁ - 1

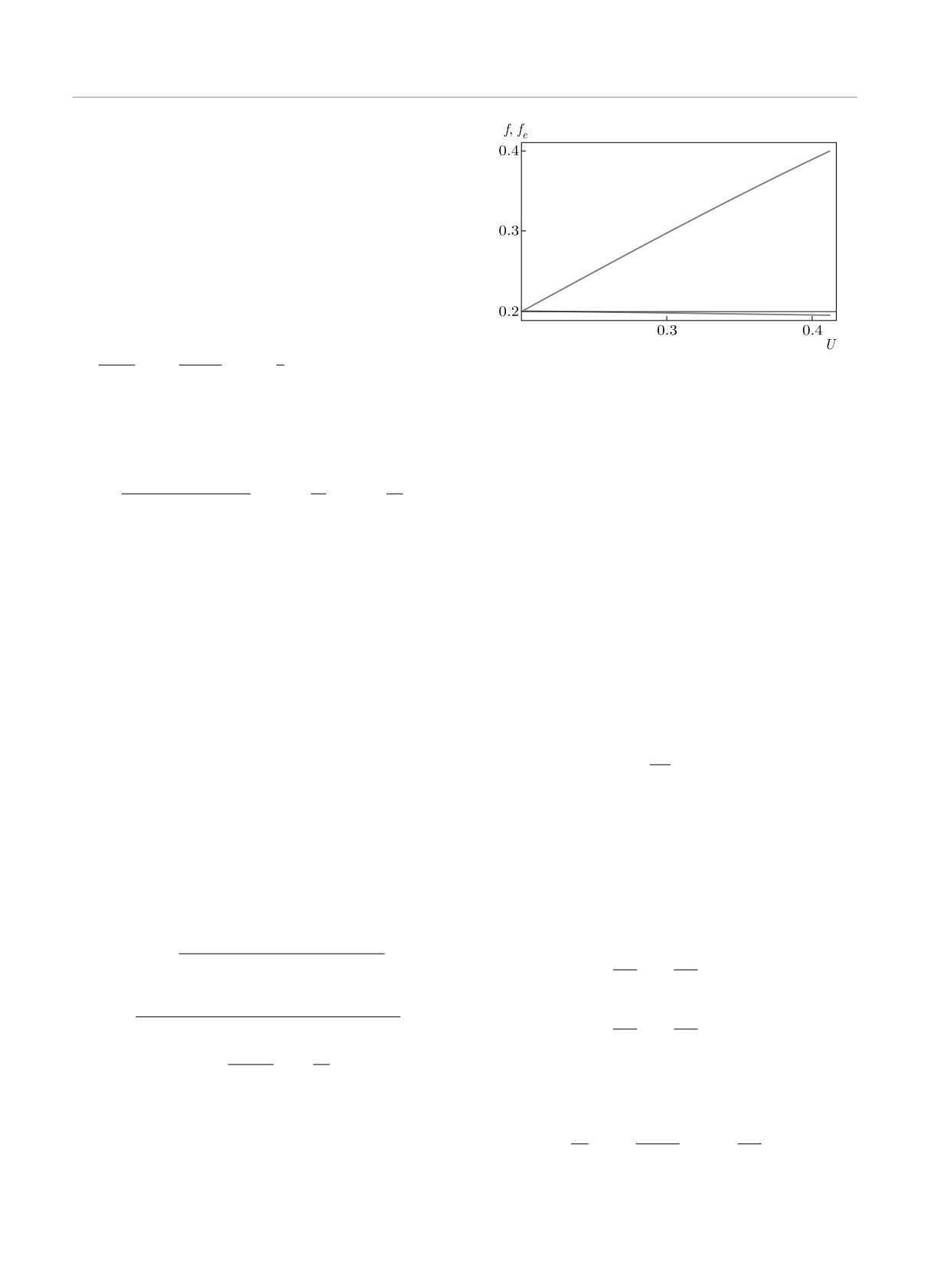
Рис. 1. Графики fe(U) (внизу) и f(U) на прямой Рэ-

лея - Михельсона в интервале (U2, U0), U0 — значение U

В рассматриваемом случае γ (γ < γ₁) — текущее

за головной ударной волной U0 ≈ 0.412

значение в структуре, причем предполагается, что

γ → γ₂ при x → ∞. Из (27) следует

(γ₁+1)/(γ₁-1)-U

Зададим теперь значение функции f_e и ее про-

P =

U =

(28)

(γ+1)/(γ-1)U-1

p₁

V₁

изводных на прямой Рэлея - Михельсона. Функция

Гипербола (28) при γ < γ₁ проходит через точ-

f_e(U) должна удовлетворять условиям

ку U

= 1, P

= (γ - 1)/(γ₁ - 1), расположенную

f_e(1) = 0.4, f_e (0.2) = 0.2.

(31)

на плоскости (V, p) ниже начальной точки U₁ = 1,

P₁ = 1.

При изучении структуры потребуются значения

При различных значениях γ ударные адиабаты,

функции f_e на прямой Рэлея - Михельсона только

заданные уравнением (27), не пересекаются, причем

на отрезке [U₂, U₀], где U₀ — значение U за лидирую-

ударные адиабаты с меньшим значением γ располо-

щей ударной волной U₀ ≈ 0.412, U₂ = 0.2. Функцию

жены ниже ударных адиабат с бóльшим значением

f_e(U) будем далее представлять линейной функцией

величины γ.

от U на отрезке [U₂, U₀] (см. рис. 1) с коэффициен-

На прямой Рэлея - Михельсона (7) имеется точка

том, представленным равенством (24):

V₀, p₀, при γ = γ₁ представляющая значения вели-

чин V, p непосредственно за лидирующей ударной

⁽ df_e )

f_e = 0.2 +

(U - 0.2).

(32)

волной. Состояние, соответствующее текущему зна-

dUM2

чению γ, представляется точкой пересечения удар-

Задание функции f_e вдоль прямой Рэлея - Ми-

ной адиабаты (27) с прямой Рэлея - Михельсона (7).

хельсона в виде линейной функции с коэффициен-

С уменьшением γ эта точка движется по прямой Рэ-

том таким, как в конечной точке структуры U =

лея - Михельсона от точки V₀, p₀ в сторону убыва-

= U₂

= 0.2, позволяет на отрезке прямой Рэ-

ния V .

лея - Михельсона [U₂, U₀] задать частные производ-

Из уравнения (27) получаем f как функцию то-

ные функции f_e(V, p) постоянными, равными их зна-

чек на прямой Рэлея - Михельсона (6):

чениям (22), (23) в состоянии 2:

f ≡γ-1=

∂f_e

⁽∂f_e)

p₁V₁/f₁ + (V₁ - V )(p₁ + p)/2

(33)

∂p

U [1 + J²(1 - U)]

(29)

∂f_e

⁽∂f_e)

1/(γ₁ - 1) + (1 - U)[2 + J²(1 - U)/2]

(34)

∂V

P₂ - 1

J² ≡

=j²

V₁ .

(30)

Таким образом, определены зависимости от U всех

1-U₂

p₁

величин в структуре. Для нахождения U(x) на пря-

Разрешая соотношения (29), (30), получим явные

мой Рэлея - Михельсона запишем уравнение (26) как

выражения для параметров фонового стационарно-

f-f_e

го течения в виде функций, зависящих от f и, со-

= -α

α=

(35)

гласно (29), от функций U.

jV₁

549

А. Г. Куликовский, А. Т. Ильичев, А. П. Чугайнова, В. А. Шаргатов

ЖЭТФ, том 158, вып. 3 (9), 2020

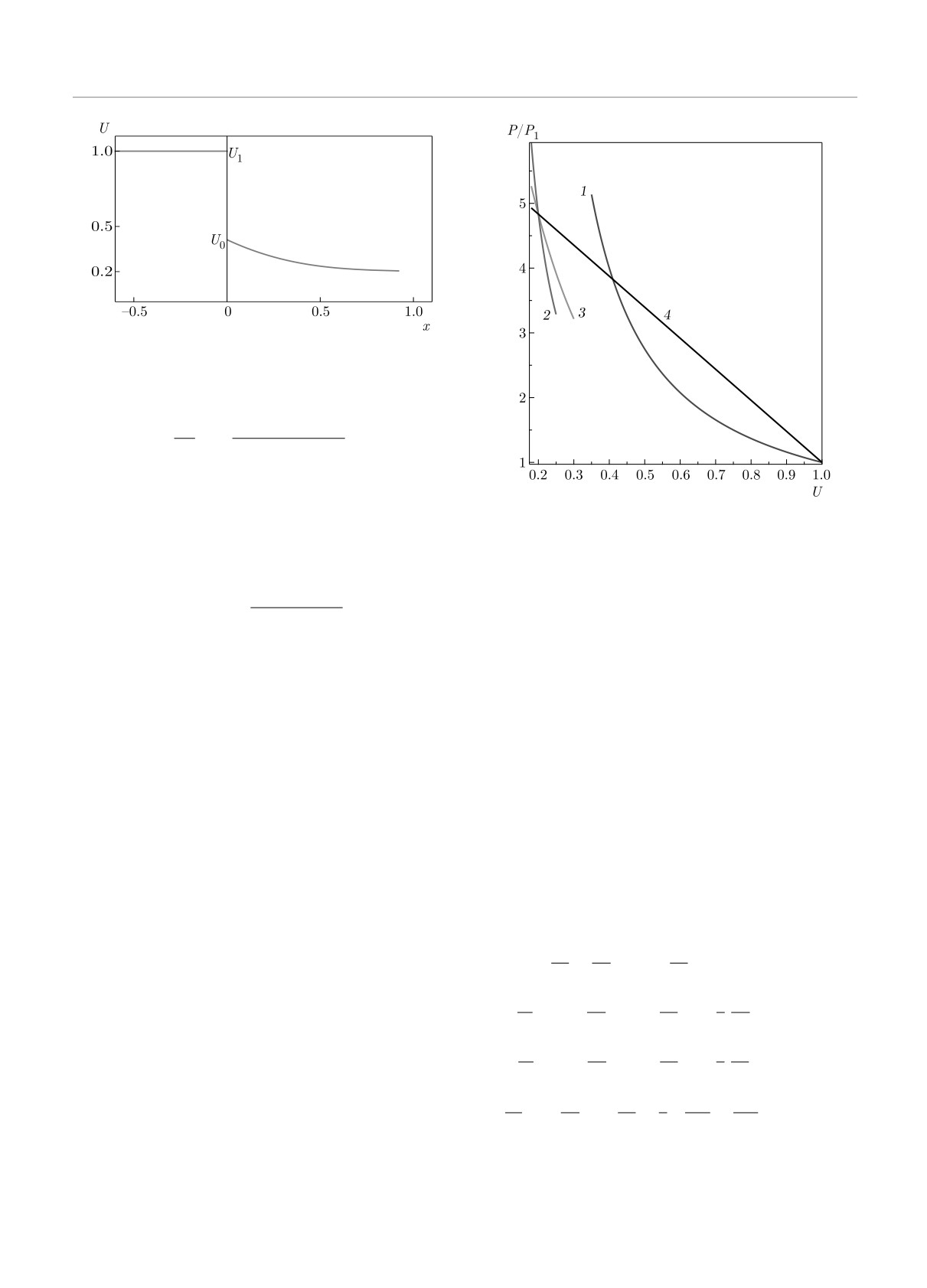
Рис. 2. Форма структуры ударной волны с учетом релак-

сации U = U⁰(x) при α = 1

Уравнение (35) перепишем в виде

Uf(U)^′

(36)

α[f(U) - f_e(U)]

Было использовано, что f и f_e на прямой Рэлея -

Михельсона согласно (30) и (32) выражаются через

U. В структуре U убывает, f - f_e → 0, x → ∞ при

Рис. 3. Ударные адиабаты и прямая Рэлея - Михельсона:

U → U₂ (рис. 1).

1 — γ = γ1 = 1.4, 2 — γ = 1.2, γ1 = 1.4, 3 — γ = 1+fe(p,ρ),

Из (36) при α = const следует

γ1 = 1.4

∫U

sf(s)^′ds

αx = -

(37)

Отметим, что предположения относительно зависи-

[f(s) - f_e(s)]

мости f_e(p, ρ) делают среду как бы более мягкой,

так как при x = 0 непосредственно за лидирующей

что проявляется на рис. 3 в том, что кривая 3 име-

ударной волной U|x=+0 = U₀. Разрешив (37), полу-

ет меньший наклон по сравнению с кривой 2. Ри-

сунок 3 соответствует принятым параметрам удар-

чим, что изменение удельного объема в структуре

ударной волны с релаксацией описывается функ-

ной волны, структура которой далее исследуется на

устойчивость.

цией U = U⁰(x), график которой представлен на

рис. 2. Верхним индексом «0» здесь и далее помеча-

4. ВОЗМУЩЕНИЯ СТРУКТУРЫ

ются функции, характеризующие структуру разры-

СПОНТАННО ИЗЛУЧАЮЩИХ УДАРНЫХ

ва при x > 0.

ВОЛН

На рис. 2 видно, что при α = 1 в качестве эф-

фективной ширины структуры в рассматриваемом

Система уравнений относительно переменных ρ,

случае можно принять δ = 1. Выражения для ско-

v_x, v_y, ε, описывающая плоские течения невязко-

рости и давления в ударной волне определяются из

го нетеплопроводного газа в зоне релаксации, имеет

уравнения прямой Рэлея - Михельсона (30) в пред-

стандартный вид, выражающий законы сохранения

положении, что поток массы задан, а v_x = jV .

массы, двух компонент импульса и энергии:

На рис. 3 ударная адиабата лидирующей ударной

∂ρ

∂

волны представлена линией 1, а прямая Рэлея - Ми-

(ρv_x) +

(ρv_y) = 0,

хельсона — линией 4. Линией 2 показана ударная

∂t

∂x

∂y

адиабата для газа, в котором p₂V₂ = f₂ε, f₂ = fe2 =

∂

v_x + v_x

v_x + v_y

v_x +

p = 0,

= 0.2. Линия 3 — ударная адиабата для случая, ко-

∂t

∂x

∂y

ρ ∂x

гда величина f_e(p, ρ) задается соотношениями (32),

(38)

∂

(33) и (34). Адиабаты 2 и 3 имеют одно и то же зна-

v_y + v_x

v_y + v_y

v_y +

p = 0,

∂t

∂x

∂y

ρ ∂y

чение f = 0.2 в конечной точке. Различие между

)

кривыми 2 и 3 обусловлено тем, что в одном случае

∂ε

⁽∂v_x

∂v_y

+v_x

+v_y

= 0.

f_e = const, а в другом случае величина f_e — пере-

∂t

∂x

∂y

∂x

∂y

менная и в окрестности прямой Рэлея - Михельсо-

на определяется упомянутыми выше равенствами.

550

ЖЭТФ, том 158, вып. 3 (9), 2020

Об устойчивости структуры нейтрально устойчивой ударной волны...

⎛

⎞

⎛

⎞

⎛

⎞

Дополнительное уравнение для f и уравнение состо-

ρ⁰(x)

δρ

⎜

⎟

⎜

⎟

⎜

⎟

яния имеют вид

⎜

v_x

⎟

⎜

u⁰(x)

⎟

⎜

δv_x

⎟

⎜

⎟

⎜

⎟

⎜

⎟

⎜

⎟

⎜

⎟

⎜

⎟

v_y

δv_y

⎜

⎟

⎜

⎟

⎜

⎟

⎜

⎟

⎜

⎟

⎜

⎟

∂f

⎝ ε

⎠

⎝ ε⁰(x)

⎠

⎝ δε

⎠

+v_j

= -λ[f - f_e(p, ρ)], p = ρεf.

(39)

∂t

∂x_j

f⁰(x)

δf

⎛

⎞

⎛

⎞

Пусть имеется стационарное течение релаксиру-

δρ

ρ(x)

ющего газа с лидирующей ударной волной, распо-

⎜

⎟

⎜

⎟

⎜

δv_x

⎟

⎜

vx(x)

⎟

ложенной в плоскости x = 0. Рассмотрим малые ли-

⎜

⎟

⎜

⎟

⎜

⎟

⎜

⎟

^iky e^-iωt,

нейные возмущения течения. Перейдем к безразмер-

⎜

δv_y

⎟

⎜

vy(x)

⎟^e

⎜

⎟

⎜

⎟

ным зависимым и независимым переменным:

⎝ δε

⎠

⎝ ε(x)

⎠

δf

f (x)

где k = k_yL, а k_y — волновое число монохромати-

t→

L t, x → Lx, y → Ly, ρ → ρ₂ρ, V → V₂V,

v₂

ческой волны в направлении вдоль разрыва. Далее

всюду k считается действительным, а ω в общем слу-

чае — комплексным.

Линеаризуя (38) и (39), получим систему урав-

p → p₂p, ε →

p₂ ε, v_x,y → v₂v_x,y

ζ → Lζ,

ρ₂

нений для величин ρ(x), v_x(x), v_y (x), ε(x),

f (x):

где L — характерное значение ширины структуры

By^′ = Ay,

(40)

разрыва, которое можно записать в виде L = 1/α:

^ζ(y, t) — выражение для возмущенного фронта

где штрих означает дифференцирование по x, y =

лидирующей ударной волны. Положим

= {ρ, v_x, v_y, ε,f}⊤,

⎛

⎞

du⁰

dρ⁰

- iω

iρ⁰k

⎜

⎟

⎜

⎟

⎜

⎟

⎜

Qf⁰ε⁰ dρ⁰

Q df⁰ρ⁰

dρ⁰ε⁰

⎟

du⁰

⎜

−

- iω

⎟

⎜

ρ⁰²

ρ⁰

⎟

⎜

⎟

⎜

⎟

⎜

ε⁰f⁰kQ

⎟

⎜

-iω

ikf⁰Q

ikε⁰Q

⎟,

⎜

ρ⁰

⎟

⎜

⎟

⎜

⎟

⎜

dε⁰

du⁰

⎟

⎜

iε⁰f⁰k

f⁰ - iω

ε⁰

⎟

⎜

⎟

⎜

⎟

⎝

⎠

∂f_e

df⁰

∂f_e

f⁰ε⁰ -

f⁰ρ⁰

-ε⁰ρ⁰

- iω + 1

∂p

∂ρ

∂p

y^′ = Cy, C = B-1A

(41)

⎛

⎞

-u₀

-ρ₀

с коэффициентами, зависящими от x.

⎜

⎟

⎜

ε₀f₀Q

⎟

Для линейных возмущений имеем

⎜

-u₀

-f₀Q

-ε₀Q

⎟

⎜

⎟

ρ₀

⎜

⎟

⎜

⎟

n = (1,-ikζ)^⊤, τ = (ikζ,1)^⊤,

⎜

⎟,

⎜

-u₀

⎟

⎜

⎟

^ζ(y, t) = ζe^iky-iωt, D_x = -iωζ,

⎜

⎟

⎜

-ε₀f₀

-u₀

⎟

⎝

⎠

— x-компонента скорости разрыва, n, τ — векторы

-u₀

соответственно нормали и касательной к фронту.

Положим

где

v = (v_x,v_y)^⊤.

V₁ - 1

1-p₁

Граничные условия на лидирующей ударной волне

Таким образом, уравнения (40) принимают вид

x =

^ζ(y, t) имеют следующий вид [4]: равенство ка-

динамической системы

сательных составляющих скорости

551

А. Г. Куликовский, А. Т. Ильичев, А. П. Чугайнова, В. А. Шаргатов

ЖЭТФ, том 158, вып. 3 (9), 2020

(v₁ - v₀) · τ = 0;

(42)

где

скачок нормальных скоростей

β = U₀ = 0.412.

√

(v₁ - v₀) · n =

(p₀ - p₁)(V₁ - V₀).

(43)

Напомним, что безразмерные величины с нижним

Обозначив через D = Dn скорость разрыва, имеем

индексом «0» характеризуют состояние непосред-

соотношение для скорости разрыва как функции p

ственно за лидирующей ударной волной.

и V:

p₀ - p₁

Уравнения (41) c граничными условиями (47)

[(v₁ - D) · n]² = V²

;

(44)

служат для определения поведения возмущений в

V₁ - V₀

соотношение, выражающее сохранение энергии на

области x > 0. Обратим внимание, что соотноше-

ния (47) — это система четырех линейных однород-

разрыве,

ных уравнений, связывающая пять перечисленных

ε₀ - ε₁ -

(V₁ - V₀)(p₁ + p₀) = 0;

(45)

выше величин, и для полного описания возмуще-

ний недостает одного граничного условия. Физичес-

непрерывность f на разрыве

ки это связано с тем, что в области за головной удар-

f₁ = f₀.

(46)

ной волной пять величин, δρ, δv_x, δv_y, δε, δf, в общем

случае могут быть представлены в виде пяти волн,

Из (42)-(46) и выражения p = p(ρ, ε, f) в (38) сле-

четыре из которых уходят от ударной волны, а одна

дует, что для возмущений {ρ, v_x, v_y, ε,f}⊤ при x = 0

приходит из бесконечности сзади. Граничные усло-

после исключения из граничных условий ζ получим

[

]

вия — это условия отражения этой волны, определя-

V₁

ε₀ (1-β)f

(1-β) f₀

V₁β²+

ρ+

ε+v_x -

ющие четыре уходящие волны. Этот вопрос обсуж-

p₀ - p₁

2β (p₀-p₁)

дается ниже.

[(

Аналогично [19-21] введем в рассмотрение со-

f₀ε₀

V₁β

⁾ dρ⁰

f₀

пряженную (41) динамическую систему

2k p₀-p₁

1-β dx

(p₀-p₁) βV₁

]

dε

dv⁰

z′ = -z C.

(48)

vy = 0,

(1 - β)V₁ dx

(

)

Известно, что решения систем уравнений (41), (48)

f₀ε₀

V₁β²

f₀

обладают следующим свойством:

ρ-

ε+

p₀ - p₁

1-β

V₁ (p₀ - p₁)β

[(

(y, z)^′ = 0,

(49)

f₀ε₀

⁾ dρ⁰

k (1-β) V₁ (p₀-p₁)

(1-β) dx

что устанавливается непосредственной проверкой.

]

Здесь (y, z) — скалярное произведение в R5.

f₀

dε

2η

(47)

vy = 0,

С помощью решений уравнений (41) и (49) по-

V₁₂ (p₀ - p₁) β dx

V₁

лучим условие отсутствия приходящих из x = ∞

[

]

β²V₁ (p₀ + p₁) + f₀ε₀ (1 - β)

V₁ ρ+

акустических возмущений.

Асимптотическая система (41) при x → ∞ имеет

(

)

f₀

вид

-f₀-2

ε+

[(f₀ε₀ (-1 + β) -

(1-β) k

y^′ = C_∞y,

(50)

) dρ

- β²V1 (p₀ + p₁)

где

]

((-1 + β) f₀ + 2 β) dε

vy = 0,

C_∞ = lim C

V₁ β

x→∞

— матрица с постоянными коэффициентами при k

vy +

f = 0,

kV₁(1 - β) dx

и ω:

552

ЖЭТФ, том 158, вып. 3 (9), 2020

Об устойчивости структуры нейтрально устойчивой ударной волны...

⎛

⎞

0.758 + 0.00198 iω

0.198 iω

0.198 ik

0.200 - 0.200 iω

9.98 - 4.99 iω

⎜

⎟

⎜

⎟

⎜

-0.758 + 0.998 iω

-0.198 iω

-1.20 ik

-0.200 + 0.200 iω

-9.98 + 4.99 iω

⎟

⎜

⎟

⎜

⎟

⎜

⎟

C_∞ =

−5.04 ik

iω

-1.01 ik

-25.2 ik

⎜

⎟

⎜

⎟

⎜

⎟

⎜

0.758 - 0.998 iω

0.198 iω

0.198 ik

0.200 + 0.800 iω

9.98 - 4.99 iω

⎟

⎝

⎠

-0.152

-0.04

-2.0 + iω

(

)

Было использовано, что ρ₂, p₂, vx2 = 1, ε₂ = f-12 = 5,

∑

lim

G₅(x), lim

ci Fi(x)

V₁ = 5, p₁ = 1/4.83, ∂f_e/∂ρ = 0.045, ∂f_e/∂p = -0.2.

x→∞

i=1

При заданных k и ω, уравнение (50) имеет реше-

(

)

∑

ния

= l5 exp(-μ₅x), ci ri exp(μ_ix)

i=1

y_i = c_ir_i expμ_ix, i = 1, . . . , 5,

∑

= ci (l₅,r_i)exp((μ_i - μ₅)x) = 0.

(54)

где μ_i — собственные значения матрицы C_∞, r_i —

i=1

отвечающие им правые собственные векторы, а c_i —

произвольные постоянные. Пусть волне, приходя-

Тогда из соотношений (49), (51), (53) и (54) сле-

щей из бесконечности сзади, соответствуют индекс

дует (см., например, [22]), что

«5», собственное значение предельной матрицы μ₅,

(

)

(G₅(x), y(x)) = lim

G₅(x), lim y(x)

правый собственный вектор r₅ и левый собственный

x→∞

(

)

вектор (вектор-строка) l₅. Условием отсутствия при-

∑

ходящей волны является c₅ = 0.

= lim

G₅(x), lim

ci Fi(x)

x→∞

Система (48) при x → ∞ имеет решения вида

i=1

(

)

∑

= lim

G₅(x), lim

ciFi(x)+ lim

c₅F₅(x)

zi = czili exp(-μix), i = 1, . . . , 5,

x→∞

i=1

= (l₅ exp(-μ₅x), c₅r₅ exp(μ₅x)) = c₅(l₅, r₅).

(55)

где l_i — левые собственные векторы (векторы-стро-

ки) матрицы C_∞, а c_zi — произвольные постоянные.

Скалярное произведение левого и правого соб-

Запишем решение системы (41) в виде

ственных векторов, отвечающих одному и тому же

собственному значению, отлично от нуля, поэтому

условие отсутствия приходящих возмущений

∑

y = ci F_i(x),

(51)

c₅ = 0

(56)

i=1

можно переписать в виде

где

(G₅(x), y(x)) = 0.

(57)

F_i(x) → r_i expμ_ix

(52)

При этом в силу (49) равенство (57) верно для всех

при x → ∞.

x ≥ 0. Запишем уравнение (57) при x = 0:

Рассмотрим решение системы (48)

(G₅(0), y(0)) = 0.

(58)

Уравнение (58) является недостающим граничным

z = G₅(x),

условием при x = 0, о котором говорилось выше.

Выполнение этого уравнения является необходимым

такое, что

и достаточным условием того, что отсутствует акус-

G₅(x) → l₅ exp(-μ₅x)

(53)

тическое возмущение, приходящее к структуре сза-

ди.

при x → ∞.

Граничные условия (47) вместе с уравнением

Поскольку левый собственный вектор l₅ ортого-

(58) представляют собой однородную систему ли-

нален правым собственным векторам r_i, i = 1, . . . , 4,

нейных уравнений с матрицей H относительно пя-

имеем

ти величин, ρ, v_x, v_y, ε,f, при x = 0. Коэффициенты

553

А. Г. Куликовский, А. Т. Ильичев, А. П. Чугайнова, В. А. Шаргатов

ЖЭТФ, том 158, вып. 3 (9), 2020

матрицы H равны коэффициентам при этих неиз-

мнимой оси, собственное значение μ₅ имеет положи-

вестных в уравнениях (47) и уравнении (58). Эта

тельную действительную часть и решение G₅(x) на

однородная система имеет нетривиальное решение,

начальном этапе интегрирования назад вследствие

если ее детерминант равен нулю:

(53) растет экспоненциально. Чтобы уменьшить вы-

числительные сложности, связанные с быстрым рос-

det H = 0.

(59)

том решения, в [19] предлагается искать решение в

виде

Условие (59) обеспечивает выполнение гранич-

G₅(x) =

G₅(x)exp(-μ₅x),

ных условий на лидирующей ударной волне и отсут-

ствие приходящих из бесконечности возмущений.

где функция

G₅(x) удовлетворяет условию

Оно является уравнением относительно ω при за-

G₅(x_r) = l₅

(60)

данном k.

Задача исследования базового решения на устой-

и является решением системы

чивость состоит в том, чтобы найти такие η = -iω и

dG5(x)

k, при которых detH = 0 и Re η > 0, или показать,

= - ^G5(x)(C - μ₅I).

(61)

что таких значений η и k не существует.

Здесь I — единичная матрица.

Другими словами, задача поиска неустойчивого

Матрица (C - μ₅I) в пределе при x → ∞ имеет

дискретного спектра оператора (41) (собственных

собственный левый вектор l₅, которому соответству-

значений, расположенных в правой полуплоскости

ет собственное значение 0, поэтому функция

G₅(x)

Ω⁺ спектрального параметра η) сводится к опреде-

изменяется значительно медленнее, чем G₅(x).

лению нулей det H(η, k), лежащих в полуплоскости

Аналогично введем новую функцию y(x), такую

Ω⁺ при действительных k. При заданном k количе-

что y(x) = y(x) exp (μ₅x). Эта функция совпадает с

ство нулей det H(η, k), находящихся внутри замкну-

y(x) при x = 0 и удовлетворяет уравнению

того контура на плоскости η, может быть подсчита-

но при помощи принципа аргумента и определяется

dy(x)

= (C - μ₅I) y(x).

(62)

суммарным количеством оборотов образа detH(η, k)

выбранного замкнутого контура вокруг нуля.

При этом в силу выполнения соотношений

(G₅(0), y(0)) = (G5(0), y(0)),

5. АНАЛИЗ УСТОЙЧИВОСТИ СТРУКТУРЫ

(63)

G₅(0) =

G₅(0), y(0) = y(0)

УДАРНОЙ ВОЛНЫ

коэффициенты матрицы H не изменяются.

Для того чтобы определить функцию detH(η, k),

Левый собственный вектор l₅, который исполь-

необходимо найти значения функции G₅(0). Для

зуется при постановке условия (60), определен с

этого при заданных значениях η и k численно ре-

точностью до комплексной константы. Компонен-

шается задача Коши для системы уравнений (48) с

ты вектора-строки

G₅(0) непрерывно зависят от

условием, что

η, если выбирать его так, чтобы одна из компо-

G₅(x_r) = l₅.

нент вектора-строки

G₅(0) оставалась постоянной.

Значение x_r выбирается достаточно большим,

В приведенных ниже расчетах четвертая компонен-

так чтобы параметры основного течения мало изме-

та этого вектора-строки выбиралась постоянной и

нялись при x > x_r , и компоненты столбца G₅(0) вы-

равной 1 (выбор компоненты не имеет принципиаль-

числялись с достаточной точностью. Точность рас-

ного значения). Для вектора-строки

G₅(0), у кото-

чета по отношению к величине x_r проверялась срав-

рого четвертая компонента равна 1, введем обозна-

нением результатов, полученных в случаях, когда

чение

Ĝ₅(0). Очевидно, что

граничное условие задавалось при x = x_r и x = 2 x_r.

Ĝ₅(0) =

G₅(0)/G45(0).

Численное решение системы уравнений (48) вы-

полняется интегрированием назад от x = x_r до x = 0

Алгоритм вычисления det H(η, k) включает в се-

методом Рунге - Кутты второго порядка с постоян-

бя следующие шаги.

ным шагом интегрирования. Точность решения про-

Для заданных значений k и η определим μ₅ (соб-

верялась сравнением результатов, полученных с ша-

ственное значение матрицы C_∞), соответствующее

гом интегрирования, различающимся в два раза.

приходящей звуковой волне, и левый собственный

Для приходящей звуковой волны при значениях

вектор l₅, отвечающий этому собственному значе-

η, расположенных в правой полуплоскости или на

нию и имеющий четвертую компоненту, равную 1.

554

ЖЭТФ, том 158, вып. 3 (9), 2020

Об устойчивости структуры нейтрально устойчивой ударной волны...

Рис. 5. Образ D_h(ω, k) границы сектора, показанного на

рис. 4. Расчет выполнен при λ = 1 и k = 0.0512

Рис. 4. Контур на плоскости (Re(ω), Im(ω))

Решим задачу Коши при заданном значении

G₅(x_r) = l₅ для системы дифференциальных урав-

нений (61) и определим компоненты вектора

G₅(0).

Найдем компоненты вектора

Ĝ₅(0).

При заданных значениях k, η и найденном

Ĝ₅(0)

вычислим матрицу H(η, k) и найдем ее детерминант.

Введем обозначения

D_h(η, k) = det H(η, k),

Рис. 6. Образ D_h(ω, k) границы сектора, показанного на

рис. 4. Расчет выполнен при λ = 1 и k = 1.54

если определитель найден с помощью вектора

Ĝ₅(0).

На рис. 4 представлен замкнутый контур ABC

на плоскости (Re(ω), Im(ω)), который является гра-

и только в том случае, если это справедливо для об-

раза, полученного с помощью функции D_h.

ницей сектора с радиусом 100. Сектор, симметрич-

ный изображенному относительно оси Im(ω), можно

Результаты расчетов приведены на рис. 5, 6 и 7

не рассматривать ввиду очевидной симметрии зада-

соответственно для значений k = 0.0512, k = 1.54,

чи относительно замены y на -y.

k = 5.12. Последнее из трех значений k в 100 раз

|D_h| сильно изменяется при действительных ω

больше первого. На всех этих рисунках видно, что

в пределах 0 < ω < 100. Вследствие этого дета-

образ контура ABC не охватывает начало коорди-

ли образа контура ABC значительно различаются

нат, поэтому функция D_h(ω) не обращается в нуль

по масштабу. Чтобы убедиться, что образ конту-

для значений ω, соответствующих точкам, которые

ра ABC не охватывает начало координат, необхо-

принадлежат сектору ABC. Отметим, что на рис. 7

димо либо изобразить детали этого контура на раз-

представлен график самой функции D_h(ω).

ных графиках в разных масштабах, либо использо-

Контуры на рис. 5, 6 и 7 имеют участок в виде

вать способ, предложенный в работе [19]. Этот спо-

зигзага. Зигзаг между точками D и E на рис. 6 со-

соб состоит в том, чтобы построить график не для

ответствует изменению действительного значения ω

функции D_h, а функции D_h/|D_h|^a, где показатель

от 1.5 до 6. На рис. 8 показаны графики функций

степени a выбирается в зависимости от характера

Re(k_x) и Im(k_x) в зависимости от действительного

изменения функции D_h на контуре. Очевидно, что

значения ω при Im(ω) = 0. Здесь k_x = -iμ₅ — вол-

образ контура ABC, полученный с помощью функ-

новое число, соответствующее приходящей звуковой

ции D_h/|D_h|^a, охватывает начало координат в том

волне при x → ∞. На рис. 8 видно, что Im(k_x) ис-

555

А. Г. Куликовский, А. Т. Ильичев, А. П. Чугайнова, В. А. Шаргатов

ЖЭТФ, том 158, вып. 3 (9), 2020

Рис. 7. Образ D_h(ω, k) границы сектора, показанного на

рис. 4. Расчет выполнен при λ = 1 и k = 5.12

Рис. 9. Контуры на плоскости (Re(ω), Im(ω))

Рис. 8. Re(kx) и Im(kx) при действительных значениях ω.

Расчет выполнен при λ = 1 и k = 1.54

Рис. 10. Образы границы контуров, показанных на рис. 9.

Расчет выполнен при λ = 1 и k = 5.12

пытывает между точками D и E наиболее сильное

изменение и приближается в точке E к асимптоти-

ческому значению. Кроме того, левее точки D и пра-

Поскольку параметр ω также не обращается в

вее точки E наклон графика функции Re(k_x) бли-

нуль вне сектора ABC, нули функции D_M (ω, k) и

зок к постоянным, но разным значениям. Очевидно,

D_h(ω, k) совпадают.

что вместе с k_x при 1.5 < ω < 6 происходит столь

Расчеты показывают, что функция D_M (ω, k)

же сильное изменение l₅, что приводит к изменению

имеет предел i D_∞(k) при |ω| → ∞. Этот предел

компонент вектора-столбца

G₅(0) и D_h.

зависит от k, и D_∞(k) является положительной дей-

Как показано выше, функция D_h(ω, k) не обра-

ствительной функцией. На рис. 9 показаны контуры

щается в нуль при |ω| ≤ 100, Re(ω) ≥ 0 и Im(ω) ≥ 0.

с дугами B₁C₁, B₂C₂, B₃C₃ радиусом |ω|, равным

Покажем теперь, что функция D_h не обращается в

соответственно 104, 524 и 1000. Образы этих линий,

нуль при |ω| > 100, Re(ω) ≥ 0 и Im(ω) ≥ 0, т. е. в пер-

построенные с использованием функции D_M (ω, k),

вом квадранте вне сектора ABC на рис. 4. Введем

приведены на рис. 10. На рис. 10 видно, что при

вспомогательную функцию

|ω| → ∞ образ дуги стягивается в точку C_∞ и при

этом контур B₁C₁C_∞ не охватывает начала коорди-

iD_h(ω, k)

D_M(ω, k) =

нат.

556

ЖЭТФ, том 158, вып. 3 (9), 2020

Об устойчивости структуры нейтрально устойчивой ударной волны...

Рис. 12. Образ окружности, показанной на рис. 11; k =

Рис. 11. Контур на плоскости (Re(ω), Im(ω)); k = 0.0254

= 0.0254, xr = 15.6: 1 — 1200 шагов, 2 — 2400, 3 — 4800,

4 — 9600

Расчеты, выполненные в широком диапазоне из-

менения ω и k, показали отсутствие нулей функции

D_h(ω, k) при Im(ω) ≥ 0. Однако эти нули существу-

ют при Im(ω) < 0 для всех рассмотренных значе-

ний k.

Приближенное значение ω, при котором функ-

ция D_h(ω) имеет нулевое значение, определялось

путем половинного деления. В третьем квадранте

строился прямоугольник со сторонами, параллель-

ными осям координат. Прямоугольник был доста-

точно большим, и его образ, полученный с помощью

функции D_h(ω), охватывал начало координат. Пер-

вая стадия дальнейшей процедуры уточнения поло-

жения корня заключалась в построении таких вло-

Рис. 13. Образ окружности, показанной на рис. 11; k =

женных друг в друга прямоугольников, что образ

= 0.0254, шаг интегрирования Δx = 0.003255: 1 — xr =

каждого прямоугольника содержал начало коорди-

= 7.81, 2 — xr = 15.62, 3 — xr = 31.24

нат. Когда размер каждой стороны прямоугольника

становился достаточно мал, для последующих при-

ближений использовался контур в виде окружности.

Образ окружности малого радиуса был также бли-

в два раза от линии 1 до линии 4. Линии 3 и 4 нахо-

зок к окружности, и координаты двух последова-

дятся близко на графике, поэтому точность расчета

тельных положений центров окружности и ее обра-

с шагом, соответствующим линии 3, можно считать

за использовались для получения нового значения

достаточной. При построении линии 3 использова-

центра окружности на плоскости, соответствующей

лось 4800 шагов интегрирования.

комплексным значениями ω.

Как видно на рис. 11, радиус контура выбирал-

Пример приближенного определения значения

ся таким маленьким, чтобы обеспечить определение

ω, при котором функция D_h(ω) имеет нулевое зна-

как действительной, так и мнимой частей ω до тре-

чение, приведен на рис. 11 и 12. На рис. 11 пред-

тьей значащей цифры.

ставлена окружность на плоскости (Re(ω), Im(ω)).

На точность расчета, как было отмечено вы-

На рис. 12 показан образ этой окружности, внутри

ше, влияет значение параметра x_r. С этого значе-

которого находится начало координат. Расчеты вы-

ния пространственной координаты начинается ин-

полнены с шагом интегрирования, уменьшающимся

тегрирование уравнения (61) назад. Предполагает-

557

А. Г. Куликовский, А. Т. Ильичев, А. П. Чугайнова, В. А. Шаргатов

ЖЭТФ, том 158, вып. 3 (9), 2020

Таблица

Re(ω)/k,

Im(ω)/k²

0.001

1.65

-0.800

0.003

1.65

-0.800

0.01

1.65

-0.800

0.0254

1.65

-0.805

0.1

1.65

-0.833

0.15

1.65

-0.838

Рис. 15. Зависимость Im(ω)/k² от k при условии, что

D_h(ω) = 0

риваемом интервале (см. рис. 14 и 15). В той облас-

ти значений k, в которой можно считать значения

Re(ω)/k = W и Im(ω/k²) = -b постоянными имеет

место равенство

ω = Wk - ibk².

(64)

Рис. 14. Зависимость Re(ω)/k от k при условии, что

Этому равенству соответствует дифференциальное

D_h(ω) = 0

уравнение

∂ξ

∂²ξ

(65)

∂t

∂y

∂y²

ся, что асимптотика (50) обеспечивает необходимую

точность расчета при этом значении координаты. На

рис. 13 показаны результаты расчета при значениях

6. ЗАКЛЮЧЕНИЕ

x_r, различающихся в два раза при постоянном ша-

ге интегрирования, таком же, как для линии 3 на

Построено решение задачи о структуре спон-

рис. 12. Линии 2 и 3 показывают хорошее согласие

танно излучающей ударной волны (СИУВ) в газе,

результатов, полученных при x_r = 15.6 и x_r = 31.2.

и в линейном приближении доказана устойчивость

Подобная процедура оценки точности расчета

этой структуры. Результаты относятся к конкрет-

как по шагу интегрирования, так и по величине x_r

ной ударной волне и конкретной модели ее структу-

выполнялась при проведении всех расчетов. Значе-

ры. Однако эти результаты показывают, что аргу-

ние x_r = 15.6 обеспечивало хорошую точность при

менты против существования СИУВ, высказанные

всех использованных значениях ω, а необходимое ко-

в работе [7] и сомнения в отсутствии спонтанного

личество шагов возрастало с увеличением |ω| и при

излучения, которые могут породить численные экс-

|ω| = 1000 составляло 372000.

перименты [9-11], несправедливы. Авторы данной

В таблице приведены найденные значения ω, при

работы считают, что нет оснований подвергать со-

которых D_h(ω) = 0.

мнению выводы исходных классических работ [1-3],

Приведенные в таблице данные показывают, что

касающиеся СИУВ, и нет оснований сомневаться в

Re(ω)/k и Im(ω)/k² слабо зависят от k на рассмат-

осуществимости нелинейных решений, представлен-

558

ЖЭТФ, том 158, вып. 3 (9), 2020

Об устойчивости структуры нейтрально устойчивой ударной волны...

устойчивость некоторой неподвижной ударной

волны, фронт которой перпендикулярен скоро-

сти набегающего потока. На рис. 16 изображена

неподвижная СИУВ, расположенная на оси y

выше точки A. Пусть возмущение, задаваемое

начальными условиями, таково, что часть ударной

волны, оставаясь плоской, слегка (на малый угол

θ) изменила свое направление (прямая AB на

рис. 16). Это приводит к изменению ее скорости.

Точка пересечения возмущенной и невозмущенной

ударных волн будет двигаться по невозмущенной

ударной волне с некоторой скоростью W . Если

√

c² - v² (c и v —

выполнено условие (4), т. е. W >

скорость звука и нормальная скорость газа за удар-

ной волной), то это означает, что ударная волна —

Рис. 16. Движение возмущений по ударной волне

спонтанно излучающая. Очевидно, что скорость

точки пересечения двух близких по направлениям

ударных волн определяется производной ∂D/∂θ,

где D — скорость ударной волны. Для выполне-

ных в работе [6]. Важно также отметить асимптоти-

ния упомянутого условия (4) производная ∂D/∂θ

ческую устойчивость структуры СИУВ в рассмот-

должна быть достаточно большой. В рамках ли-

ренном в работе конкретном случае. Конечно, вывод

нейного приближения скорость W не зависит от

об устойчивости структуры относится к конкретно-

значения θ, поэтому линейные возмущения любой

му случаю и зависит от модели структуры, но есть

формы распространяются по ударной волне без

некоторые основания думать, что если структура

искажений. Если в уравнении (65) учесть член со

связана с диссипативными процессами, то она ока-

второй производной в правой части, то тупой угол

жется устойчивой.

между возмущенной и невозмущенной ударными

Прокомментируем зависимость (64), полученную

волнами будет сглажен, что изображено на рис. 16

из дисперсионного соотношения (59). Отношение

штриховой линией. Представляя решение уравне-

ω/(v₁k_y) зависит от значений величины k = k_yδ (δ —

ния (65) в форме интеграла Фурье по k_y, имея

эффективная ширина структуры). Как следует из

в виду, что каждому значению k_y соответствует

таблицы, если k ≪ 1, т. е. l/δ ≫ 1 (l — длина вол-

некоторая система волн, излучаемых в область за

ны возмущения в направлении y), то пренебрегая

ударной волной, можно получить в явном виде

членами k² и членами с более высокими степеня-

бегущую по ударной волне волну возмущения ее

ми k_y, получим линейную зависимость ω от k_y, та-

формы с произвольной начальной зависимостью

кую же, как при рассмотрении разрыва без учета

от y и соответствующую систему уходящих от

его структуры. Это ожидаемый результат, посколь-

ударной волны малых возмущений. Сама ударная

ку в этом приближении течение в окрестности каж-

волна при этом служит проводником возмущений

дой точки возмущенной структуры происходит, как

(волноводом), который снабжается извне энергией

в стационарной структуре плоской ударной волны с

протекающего сквозь нее газа.

выполнением законов сохранения. Следующий член

разложения ω по k учитывает кривизну структуры

Финансирование. Работа выполнена при под-

и нестационарность течения в ней. Как показано в

держке Российского фонда фундаментальных ис-

данной работе, наличие структуры разрыва приво-

следований (грант № 17-01-00180).

дит к появлению в дисперсионном уравнении дис-

сипативного члена, пропорционального k², поэтому

возмущение формы достаточно длинной волны, бе-

гущей по СИУВ в положительном (или отрицатель-

ЛИТЕРАТУРА

ном при смене знака W ) направлении y описывается

уравнением (65).

1. С. П. Дьяков, ЖЭТФ 27, 288 (1954).

И, наконец, представим, каким образом переда-

ются возмущения по СИУВ. Пусть рассматривается

2. В. М. Конторович, Акуст. ж. 5, 314 (1959).

559

А. Г. Куликовский, А. Т. Ильичев, А. П. Чугайнова, В. А. Шаргатов

ЖЭТФ, том 158, вып. 3 (9), 2020

3. С. В. Иорданский, Прикл. Мат. Мех. 33, 456

14. V. M. Fomin and V. I. Yakovlev, Shock Waves

(1957).

29,

365

(2019); (https://doi.org./10.1007/s00193-

018-0856-7).

4. Л. Д. Ландау, Е. М. Лившиц, Гидромеханика,

Наука, Москва (1986).

15. А. П. Лихачев, ТВТ 50, 544 (2012).

5. В. Е. Фортов, Мощные ударные волны на земле и

16. А. Г. Куликовский, ДАН 481, 494 (2018).

в космосе, Физматлит, Москва (2018).

17. А. Г. Куликовский, А. Т. Ильичев, А. П. Чугайнова

6. С. А. Егорушкин, Изв. Акад. наук СССР, Механ.

и др., ДАН 487, 27 (2019).

Жидк. Газа (1983).

18. Г. Г. Черный, Газовая динамика, Наука, Москва

7. Н. М. Кузнецов, УФН 159, 493 (1989).

(1988).

8. Н. М. Кузнецов ЖЭТФ 90, 744 (1986).

19. R. L. Pego, P. Smereka, and M. I. Weinstein, Physica

D 67, 45 (1993).

9. А. В. Конюхов, А. П. Лихачев , В. Е. Фортов и

др., Письма в ЖЭТФ 90, 28 (2009).

20. K. Zumbrun, in: Shocks, Singularities and Oscilla-

tions in Nonlinear Optics and Fluid Mechanics ed. by

10. А. В. Конюхов, А. П. Лихачев, В. Е. Фортов и

F. Colombini, D. Del Santo, and D. Lannes, Springer

др., ЖЭТФ 125, 927 (2004).

INdAM Series, Vol. 17. Springer, Cham. (2017).

11. А. В. Конюхов, А. П. Лихачев, В. Е. Фортов и

21. J. Humpherys and K. Zumbrun, Quarterly Appl.

др., Тр. Междунар. конф. IX Забабахинские науч-

Math. 70, 685 (2012).

ные чтения (2007), c. 1.

22. А. Г. Куликовский, Н. В. Погорелов, А. Ю. Семе-

12. J. W. Bates and D. C. Montgomery, Phys. Rev.

нов, Математические вопросы численного реше-

Lett. 84, 1180 (2000).

ния гиперболических систем уравнений, изд. 2-е,

13. J. W. Bates, Phys. Rev. Lett. E 91, 013014 (2015).

Физматлит, Москва (2012).

560