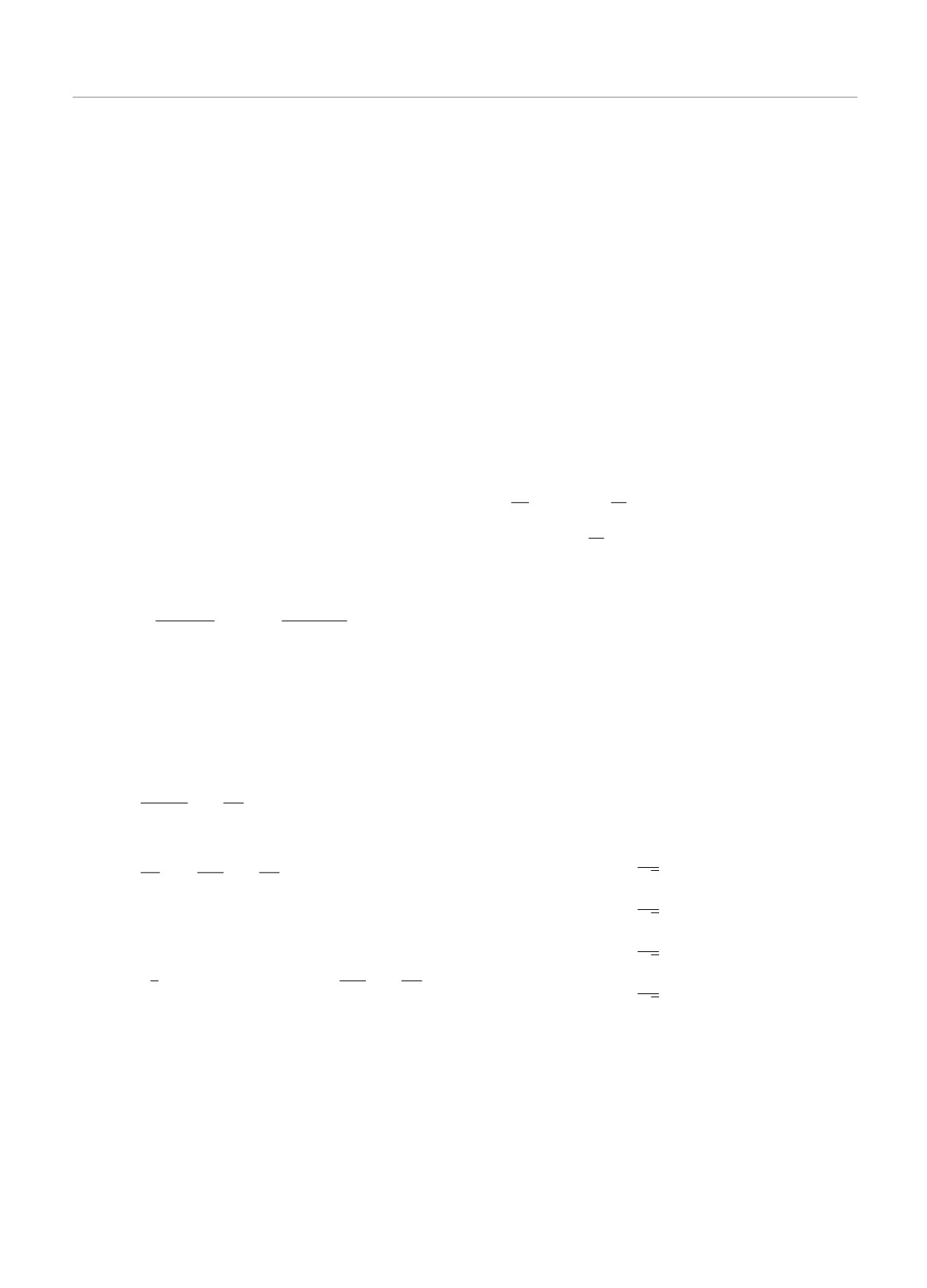ЖЭТФ, 2020, том 158, вып. 4 (10), стр. 579-593

ТОМОГРАФИЯ СОСТОЯНИЙ КУБИТОВ И

РЕАЛИЗАЦИЯ КВАНТОВЫХ АЛГОРИТМОВ

УНИПОЛЯРНЫМИ ИМПУЛЬСАМИ

М. В. Бастраковаa*, Н. В. Клёновb,c**, А. М. Сатанинc,d***

^a Нижегородский исследовательский университет им. Н. И. Лобачевского

603950, Нижний Новгород, Россия

^b Физический факультет, Московский государственный университет им. М. В. Ломоносова

119991, Москва, Россия

^c Всероссийский научно-исследовательский институт автоматики им. Н. Л. Духова

127055, Москва, Россия

^d Национальный исследовательский университет «Высшая школа экономики»

101000, Москва, Россия

Поступила в редакцию 13 января 2020 г.,

после переработки 16 марта 2020 г.

Принята к публикации 30 апреля 2020 г.

Традиционная техника управления состояниями отдельных кубитов и квантовых регистров базируется на

использовании высокочастотных модулированных импульсов, несущая частота которых близка к частоте

перехода между базисными состояниями «искусственных атомов» и «молекул» (техника Раби). В данной

работе развивается альтернативная концепция управления сверхпроводниковыми кубитами, основанная

на идее быстрого возбуждения квантовой системы путем применения уединенных немодулированных

импульсов. На основе численного моделирования продемонстрировано формирование запутанных состо-

яний Белла в двухкубитном сверхпроводниковом регистре под действием импульсов поля, полученных с

использованием устройств быстрой одноквантовой логики. Томография квантовых состояний выполнена

на базе решения уравнения для матрицы плотности. Показано, что с использованием техники «униполяр-

ных импульсов» можно ускорить формирование перепутанных состояний (на пикосекундных временах)

с достоверностью (fidelity) 95-98 %. Продемонстрировано выполнение основных квантовых алгоритмов:

Дойча - Йожи с точностью более 98 % и Гровера с точностью 93 %.

DOI: 10.31857/S0044451020100016

ма, возникающая при работе квантовых компьюте-

ров, обладающих небольшим числом (50-100) куби-

тов, связана с воздействием на квантовую систему

1. ВВЕДЕНИЕ

(на регистры кубитов) окружающей среды, вклю-

В недавней работе [1] было продемонстрировано,

чающей устройства приготовления состояний куби-

что программируемый квантовый компьютер при

тов, управления ими и их измерения, которое по-

решении специально разработанной тестовой зада-

ка не удается устранить или должным образом кон-

чи способен превзойти один из самых мощных су-

тролировать. В связи с этим для описания подоб-

перкомпьютеров мира. Это свидетельствует о суще-

ных систем введено понятие зашумленных кван-

ственном прогрессе в развитии квантовых техноло-

товых устройств (Noisy Intermediate-Scale Quantum

гий, нацеленных на создание квантовых компьюте-

technology) [2], что отражает временную фиксацию

ров, позволяющих решать широкий класс приклад-

доступных масштабов, а также указывает направле-

ных задач. Как известно, принципиальная пробле-

ние поиска путей для создания полностью контроли-

руемых массивов кубитов, например, путем коррек-

^* E-mail: mar.denisenko@gmail.com

ции ошибок с помощью встраивания в чипы допол-

^** E-mail: nvklenov@gmail.com

нительных контролирующих «искусственных ато-

^*** E-mail: asatanin@gmail.com

579

М. В. Бастракова, Н. В. Клёнов, А. М. Сатанин

ЖЭТФ, том 158, вып. 4 (10), 2020

мов». Стабильная манипуляция квантовыми состо-

ления в сверхпроводниковом потоковом двухкубит-

яниями имеет важное значение для квантовой об-

ном регистре (пара слабо взаимодействующих ку-

работки информации. Несмотря на зашумленность

битов) для ускорения квантовых алгоритмов. В от-

доступных устройств (создаваемых, например, ком-

личие от упомянутого выше подхода [15-17], мы

паниями IBM или Rigetti), были предприняты по-

рассматриваем воздействие малого числа импуль-

пытки получения полезной информации при моде-

сов для реализации квантовых операций и алго-

лировании динамики спиновых цепочек с различной

ритмов. Это позволяет уменьшить нежелательное

топологией [3,4].

обратное влияние системы управления на кубит,

Вместе с тем разработка устройств контролируе-

уменьшить характерную длительность операций и

мой квантовой динамики ставит ряд принципиально

реализовать оптимальный контроль за счет подбора

новых вопросов, которые в последнее время активно

параметров управляющего униполярного импуль-

обсуждаются в литературе. Одна из проблем связа-

са. При этом переход к более энергоэффективной

на с методом контроля над состояниями квантовых

адиабатической сверхпроводниковой логике позво-

регистров. В настоящее время для записи и управ-

ляет не только осуществлять однокубитные гейты,

ления применяется техника Раби, которая предпо-

но и создавать перепутанные состояния (entangled

лагает использование высокочастотных модулиро-

states) пар кубитов с высокой точностью.

ванных импульсов, несущая частота которых близка

В работе на классическом компьютере выполне-

к частоте перехода между базисными состояниями

но численное моделирование процесса томографии

контролируемых «искусственных атомов» и «моле-

(восстановления) квантовых запутанных состояний

кул» [5]. Например, для сверхпроводниковых куби-

Белла и реализованы, униполярными пикосекунд-

тов несущая частота составляет несколько гигагерц;

ными импульсами, простейшие квантовые алгорит-

успехи техники Раби для данных кубитов отраже-

мы (Дойча - Йожи и Гровера) на двухкубитном

ны в работах [6, 7], где констатируется, что одно-

сверхпроводниковом регистре. Показано, что пере-

кубитные операции могут осуществляться с досто-

путанные состояния можно реализовать нескольки-

верностью 99.9 % [7,8], тогда как двухкубитные гей-

ми униполярными импульсами на пикосекундных

ты реализуются с достоверностью 99 % [9,10]. Одна-

временах, что в несколько раз быстрее техники Ра-

ко, несмотря на впечатляющие результаты, времена

би на основе протяженных модулированных сигна-

декогеренции в современных регистрах кубитов до-

лов [6]. При этом достоверность создания состояний

стигают порядка сотен микросекунд [6] и проблема

Белла составляет 95-98 %, а исполнения квантовых

ускорения реализации квантовых одно- и двухгей-

алгоритмов 93-98 %.

товых операций по-прежнему является актуальной.

В связи с этим в настоящее время активно раз-

вивается альтернативная схема управления сверх-

2. ОСНОВНЫЕ ПРИНЦИПЫ РЕАЛИЗАЦИИ

проводниковыми кубитами, в основе которой лежит

КВАНТОВЫХ АЛГОРИТМОВ

идея быстрого возбуждения квантовой системы пу-

УНИПОЛЯРНЫМИ ИМПУЛЬСАМИ

тем применения уединенных немодулированных им-

пульсов. Было показано, что для создания таких им-

В случае управления изолированной квантовой

пульсов пикосекундной длительности (что на пару

системой (квантовым регистром), находящейся в

порядков меньше, чем длительность типичных опе-

чистом состоянии, можно говорить об управляемой

раций в технике Раби) могут использоваться схемы

унитарной эволюции. Если же система не замкну-

сверхпроводниковой быстрой одноквантовой логики

та или подвержена воздействию шума, то она опи-

(БОК) [11-13]. Первоначально данная техника раз-

сывается матрицей плотности, в общем случае под-

рабатывалась для создания быстродействующих и

чиняющейся квантовому кинетическому уравнению,

энергоэффективных классических вычислительных

которое, в частности, описывает и процессы потери

комплексов [14]. В последнее время сделаны попыт-

когерентности состояний кубитов.

ки адаптировать варианты БОК-схем для управле-

Пусть в начальный момент времени изолирован-

ния регистрами кубитов с использованием последо-

ная система приготовлена в начальном состоянии,

вательностей пикосекундных униполярных импуль-

|ψ(0)〉, тогда временная эволюция системы, т. е. все

сов, хотя общая длительность таких операций все

операции (гейты), описываются уравнением

равно превышает 1 нс [15-17].

Основная цель данной статьи — разработка но-

∂ |ψ(t)〉

= H(t)|ψ(t)〉, ℏ = 1,

(1)

вых методов имплементации БОК-схем для управ-

∂t

580

ЖЭТФ, том 158, вып. 4 (10), 2020

Томография состояний кубитов и реализация. . .

где H(t) — гамильтониан системы, зависящий от

где Θ(t) — функция Хевисайда, A — амплитуда воз-

времени. В общем виде решение (1) запишется как

действия. Унитарная эволюция кубита на времени

|ψ(t)〉 = U(t) |ψ(0)〉, где введен оператор эволюции

действия импульса τ определяется выражением

⎛

⎞

∫

∑

U⁽¹⁾ =

|ν_k〉 eiλkτ 〈ν_k| =

U (t) =

P exp^⎝-

dt₁H(t₁)^⎠ ,

(2)

ℏ

k=1

⎛

⎞

Ωτ

iΔ

Ωτ

sin

⎜^cos

⎟

где

P — оператор хронологического упорядочения.

⎜

⎟,

(5)

⎝

⎠

Ωτ

iΔ

Ωτ

Сначала введем необходимые для анализа кван-

sin

cos

sin

товых алгоритмов обозначения и понятия на приме-

√

ре однокубитных операций. Динамика «уединенно-

где Ω =

Δ² + A² и H⁽¹⁾(t = 0)|ν_k〉 = λ_k |ν_k〉. В

го» потокового кубита во внешнем поле описывается

этом случае эволюция системы существенно зависит

стандартным гамильтонианом [18] в двухуровневом

от двух параметров импульса: амплитуды A и дли-

приближении:

тельности τ. При этом вероятность перехода между

(

)

базисными состояниями |0〉 → |1〉 равна

H⁽¹⁾(t) = -

Δσ(1)z + ε(t)σ⁽¹⁾

(3)

A²

Ωτ

W|0〉→|1〉 =

sin²

(6)

Ω²

где ε(t) — управляющее внешнее поле, Δ — параметр

туннельного расщепления, что соответствует типич-

что формально совпадает с общеизвестной форму-

ной частоте перехода (для сверхпроводникового по-

лой Раби. Отличие состоит лишь в том, что роль

токового кубита Δ ∼ 100 MГц-10 ГГц, см. [6]) между

частоты Раби в случае униполярного импульса иг-

(₁)

(₀)

базисными уровнями кубита: |0〉 =

и |1〉 =

;

рает его амплитуда, а отстройка по частоте между

σx1), σz1) — матрицы Паули.

резонатором и кубитом заменена туннельным рас-

щеплением, Δ. Используя технику управления со-

Как известно, состояние кубита |ψ(t)〉 = α(t)|0〉+

стояниями кубита униполярным импульсом, мож-

+ β(t)|1〉 (α = cosθ, β = eiφ sinθ) задается векто- }

но осуществить любое вращение на сфере Блоха,

ром R(t) = 〈ψ(t)| σ |ψ(t)〉, σ = σx1), σy1), σz1)

, на

т. е. выполнить любую однокубитную операцию, ес-

сфере Блоха R² = 1, положение которого опреде-

ли выполняются следующие условия для парамет-

ляется полярным θ и азимутальным φ углами. При

ров импульса: A ≫ Δ и Δτ ≪ 1 [19-23].

этом простейшие однокубитные операции можно ин-

Для реализации квантовых алгоритмов требует-

терпретировать как перевод конца вектора из одной

ся выполнение не только однокубитных, но и двух-

точки на сфере Блоха в другую. Данные операции

кубитных квантовых операций. Рассмотрим их на

представляются через три независимых вращения

примере простейшего квантового регистра, состоя-

вокруг осей в спиновом пространстве (на сфере Бло-

щего из двух взаимодействующих кубитов Q₁ и Q₂

ха): x, y, z-вращения. Комбинации вращений Паули

[6, 24]. Гамильтониан такой системы определяется

позволяют создать суперпозицию состояний кубита

как тензорное произведение гамильтонианов подси-

или осуществить операцию Адамара [18]. В техни-

стем (единичных кубитов) H(i) (i = 1, 2), определя-

ке Раби однокубитные операции можно выполнить с

емых выражением (3), и слагаемого H_int, отвечаю-

использованием микроволновых импульсов опреде-

щего за взаимодействие двух подсистем с парамет-

ленной длительности, которые «подаются» на кубит

рически перестраиваемой связью J(t). Полный га-

посредством специального резонатора [7, 8].

мильтониан двухкубитной системы имеет вид

Ранее нами был разработан метод, который поз-

воляет выполнить однокубитные операции с исполь-

H(t) = H⁽¹⁾(t) ⊗ I⁽²⁾ + I⁽¹⁾ ⊗ H⁽²⁾(t) + H_int,

(7)

зованием одиночных униполярных импульсов без

радиочастотной несущей [19-22]. Кратко изложим

где I(i) — единичные матрицы в двумерном гильбер-

основную идею. Пусть на кубит поступает прямо-

товом пространстве, ⊗ — тензорное произведение.

угольный импульс длительности τ, который описы-

Параметрическое взаимодействие между кубитами

вается функцией вида

выбрано в виде H_int = -¹² J(t)σx1) ⊗ σx2), см. [6]. Вы-

ражение (7) для наглядности можно представить в

ε(t) = Af(t), f(t) = Θ(t)Θ(τ - t),

(4)

матричном виде:

581

М. В. Бастракова, Н. В. Клёнов, А. М. Сатанин

ЖЭТФ, том 158, вып. 4 (10), 2020

Когда на систему связанных кубитов поступает

H (t) = -

⎛

⎞

несколько управляющих импульсов, возникают ин-

Δ₁ + Δ₂

ε₂(t)

ε₁(t)

J (t)

терференционные эффекты. Данные явления мож-

⎜

⎟

⎜

ε₂(t)

Δ₁-Δ₂

J (t)

ε₁(t)

⎟

но проиллюстрировать следующим образом: пусть

×^⎜

^⎟.

(8)

⎜

⎟

в начальный момент времени на кубит Q₁ поступа-

⎝ ε1(t)

J (t)

-Δ₁+Δ₂

ε₂(t)

⎠

ет прямоугольный импульс ε₁(t) длительностью τ₁

J (t)

ε₁(t)

ε₂(t)

-Δ₁-Δ₂

(при этом ε₂(t) = 0 и J(t) = 0), в этом случае опе-

ратор эволюции двухкубитной системы

τ1

опре-

Далее предполагаем, что управление состояния-

делен как

τ1

= U⁽¹⁾ ⊗ U⁽²⁾, где U⁽¹⁾ — унитарная

ми кубитов и организация взаимодействия между

матрица кубита Q₁ вида (5), U⁽²⁾ = e-iΔτσz — опе-

ними осуществляется внешними немодулированны-

ратор эволюции второго кубита Q₂ при отсутствии

ми импульсами, которые можно аппроксимировать

возбуждения. Явный вид матрицы

приведен в

прямоугольными импульсами вида

τ1

Приложении А.

ε_i(t) = A_iΘ(t - t_in,i)Θ(t_off,i - t),

Далее будем полагать, что между кубитами

(9)

включается взаимодействие J(t), согласно (9), на

J (t) = JΘ(t - t_in,J )Θ(t_off,J - t),

временном интервале τ_J . При этом область опре-

где A_i — амплитуды униполярных полей, действую-

деления четырехкомпонентной волновой функции

щих на каждый из кубитов в паре с длительностями

двухкубитной системы можно разбить на три под-

τ_i = τ_off,i - τ_in,i; а J — амплитуда перестраиваемо-

области: t < t_in,J, tin,J ≤ t ≤ toff,J и t > toff,J, в

го взаимодействия между кубитами. Отметим, что

каждой из которых компоненты волновой функции

данное взаимодействие может быть реализовано, на-

представляют собой суперпозицию четырех волн,

пример, на основе адиабатического квантового па-

распространяющихся вперед и назад во времени:

раметрона [25,26] в виде шунтированного индуктив-

∑

ностью сверхпроводящего интерферометра [27]. При

χ_j(t) =

c_jkν_ke-iλkt,

(10)

этом происходит передача магнитного потока от ку-

k=1

бита к кубиту лишь под действием управляющего

где λ_k — собственные значения и ν_k — собствен-

импульса.

ные векторы гамильтониана (7). Коэффициенты c

При отсутствии внешнего воздействия и связи

определяются путем сшивки волн на «границах»

(ε_i(t) = 0, J(t) = 0) система кубитов Q1 и Q2

импульса, т. е. в моменты его включения и выклю-

представляет собой четырехуровневую квантовую

чения. Выражение (10) показывает, что после дей-

систему, состояние которой удобно определить в вы-

ствия импульса τ_J каждая компонента функции

числительном базисе [18] как тензорное произведе-

определяется суперпозицией четырех интерфериру-

ние волновых функций отдельных кубитов |ψ_i(0)〉 =

ющих слагаемых, следовательно, населенность каж-

= αi |0_i〉+βi |1_i〉 (индекс i = 1,2 соответствует номе-

дой нормальной моды будет осциллировать. При

ру кубита), а именно: |ψ(0)〉 = |ψ₁(0)〉 ⊗ |ψ₂(0)〉. При

этом оператор эволюции двухкубитной системы пос-

этом состояния взаимодействующих кубитов можно

ле включения взаимодействия можно записать в ви-

представить в виде

де

∑

|ψ(t)〉 = χ₁(t) |0₁0₂〉 + χ₂(t) |0₁1₂〉 +

U⁽¹²⁾ =_τ

|ν_k〉 e-iλkτ^J 〈ν_k| .

(11)

k=1

+ χ₃(t)|1₁0₂〉 + χ₄(t)|1₁1₂〉,

Явный вид оператора (11) приведен в Приложе-

∑₄

где

|χ_j (t)|² = 1.

нии А.

j=1

В случае двух кубитов важной задачей становит-

После выключения взаимодействия между куби-

ся организация короткой последовательности управ-

тами на интервале времени τoff,1 < t < τoff,2 на

ляющих униполярных импульсов (9) для выполне-

кубит Q₂ действует прямоугольный импульс ε₂(t)

ния контролируемых манипуляций в системе. При

(с амплитудой A2 = A). На основе аналогичных

этом важно найти области параметров воздействия

рассуждений, согласно (10), (11), найден явный вид

(амплитуд, длительностей) для реализации требу-

оператора эволюции

τ2

в ходе воздействия на Q₂.

емых двухкубитных операций, в частности, для

Согласно описанной схеме управления под дей-

создания перепутанных (белловских) состояний, а

ствием трех униполярных импульсов — ε₁(τ₁), J(τ_J ),

также для выполнения квантовых алгоритмов Дой-

ε₂(τ₂) — динамика состояния двухкубитной системы

ча - Йожи и Гровера.

может быть определена как

582

ЖЭТФ, том 158, вып. 4 (10), 2020

Томография состояний кубитов и реализация. . .

|ψ(t)〉 = U(12)τU(12)τU(12) |ψ(0)〉 ≡ U(12) |ψ(0)〉.τ

τ₁ = τ₂, позволяют реализовать полный набор двух-

кубитных операций.

Предполагалось, что в начальный момент време-

Для учета эффектов декогеренции, влияющих

ни система приготовлена в основном состоянии

на результаты эволюции в квантовой системе, мож-

|ψ(0)〉 = |0₁0₂〉, а далее рассчитываются вероятно-

но ограничиться рассмотрением простейшей модели

сти переходов между базисными состояниями двух-



шума с гладким спектром. При этом будут сдела-

кубитной системы W_x =

^〈x|U⁽¹²⁾|0₁0₂〉

², где |x〉 —

ны стандартные приближения при выводе уравне-

одно из базисных состояний |0₁0₂〉, |0₁1₂〉, |1₁0₂〉,

ния для матрицы плотности [28]: 1) марковское при-

|1₁1₂〉, а индекс «x», x = 1, 2, 3, 4, нумерует для

ближение: бозонные резервуары настолько большие,

краткости данные состояния. При этом нами бы-

что эффект влияние состояния кубита на состоя-

ли найдены аналитические выражения для веро-

ние резервуара минимален, т. е. время корреляций

ятностей населенностей четырехуровневой системы,

термостата много меньше времен релаксации каж-

которые приведены в Приложении А. Кратко про-

дого из кубитов; 2) борновское приближение: взаи-

анализируем полученные результаты. Как показано

модействие подсистемы (кубита) с термостатом ма-

выше, до включения взаимодействия между куби-

ло (учет во втором порядке по теории возмущений).

тами управляющий импульс ε₁(t), действующий на

При этом получаем уравнение для матрицы плотно-

Q₁, реализует полный набор однокубитных опера-

сти двух кубитов:

ций (населенности |0₁0₂〉 и |1₁0₂〉 осциллируют со-

(

)

гласно формуле (6)). Для реализации двухкубит-

∂ρ

γ₁

iℏ

= [H, ρ] +

σ(1)z ⊗ I⁽²⁾ρσ(1)z ⊗ I⁽²⁾ - ρ

ных операций необходимо осуществлять выбор оп-

∂t

(

)

тимальных амплитуд и длительностей униполяр-

γ₂

I⁽¹⁾ ⊗ σ(2)zρI⁽¹⁾ ⊗ σ(2)z - ρ ,

(13)

ного воздействия. Согласно полученным аналити-

ческим выражениям (см. Приложение А) осцилля-

где ρ — матрица плотности двух связанных кубитов,

ции населенностей уровней кубитов зависят от сле-

γ_i — скорости релаксации i-го кубита, H — гамиль-

дующих комбинаций параметров: τ1,2Ω, τ_J Ω_J , τ_J J

√

тониан системы в форме (8). Уравнение (13) может

(где Ω =

A² + Δ², Ω_J =

J² + 4Δ²). Рассмотрим

быть решено численно, см. подробнее о методе ре-

простой случай двух идентичных импульсов ε1,2(t)

шения в Приложении B.

(A₁ = A₂ = A и τ₁ = τ₂ = τ). Проводя преобразо-

вания выражений (A.1)-(A.3), можно заметить, что

3. ИНИЦИАЛИЗАЦИЯ И ТОМОГРАФИЯ

при данной последовательности импульсов подавле-

СОСТОЯНИЙ БЕЛЛА

ны интерференционные слагаемые, отвечающие за

возбуждения на промежуточные уровни, а вероят-

Для демонстрации возникновения квантовой за-

ности имеют вид

путанности в рассматриваемом двухкубитном кван-

Ωτ

(

)

товом процессоре, управляемом униполярными им-

W2,3 =

sin²

Ω²+Δ²+A² cosΩτ

4Ω⁴Ω_J

пульсами, опишем протокол приготовления состоя-

(

)

J²(1 - cosτ_JΩ_J ) + Ω2J cosτ_JJ

(12)

ния Белла [18]:

τ_JJ

Ωτ

|β₀₀〉 =

√ (|00〉 + |11〉) ,

W₄ =

cos²

sin⁴

Ω⁴

Считая туннельные энергии кубитов малым пара-

|β₀₁〉 =

√ (|01〉 + |10〉) ,

метром (Δ ≪ A, J), выражения (12) можно приве-

(14)

сти к простому виду:

|β₁₀〉 =

√ (|01〉 - |10〉) ,

τ_JJ

Aτ

W2,3 =

sin²(Aτ) и W₄ = cos⁴

sin⁴

|β₁₁〉 =

√ (|00〉 - |11〉) .

Полученные выражения наглядно демонстрируют

тот факт, что максимальное значение населеннос-

Данные состояния образуют ортонормирован-

тей промежуточных состояний кубитов равно 1/4:

ный базис, по которому можно разложить любое

max [W2,3] = 0.25. Это означает, что при идентичных

чистое состояние двух кубитов. Квантовый харак-

импульсах ε1,2(t) невозможно сформировать пере-

тер корреляции имеет важное свойство: при проеци-

путанные состояния Белла. Однако, как будет пока-

ровании одной части системы в одно из двух базис-

зано на базе численного моделирования в разд. 3-5,

ных состояний, другая часть как бы «мгновенно»

униполярные импульсы различной длительности,

приобретает определенное значение, несмотря на то,

583

М. В. Бастракова, Н. В. Клёнов, А. М. Сатанин

ЖЭТФ, том 158, вып. 4 (10), 2020

ное при этом состояние двухкубитной системы |ψ₁〉

(отмечено вертикальной стрелкой на рис. 1) можно

определить как

⎛

⎞

⎜

⎟

⎜

⎟

|ψ₁〉 =

√

(|0₁〉 + |1₁〉) ⊗ |0₂〉 =

√

⎜⁰⎟.

⎜

⎟

⎝1⎠

Далее с помощью двух униполярных импульсов

ε₁(t) и ε₂(t), действующих на кубиты Q₁ и Q₂, и

одного импульса J(t), воздействующего на элемент

связи между кубитами, была реализована двухку-

битная операция «CNOT» с соответствующей мат-

рицей C_CNOT на временах 10 < t < 20 пс, в резуль-

тате чего готовится синглетное состояние Белла:

C_CNOT |ψ₁〉 =

⎛

⎞⎛

⎞

⎛

⎞

⎜

⎟⎜

⎟

⎜

⎟

⎜

0⎟⎜0⎟

⎜0⎟

√

⎜⁰

⎟⎜

⎟

√

⎜

⎟ = |β₀₀〉.

⎜

⎟⎜

⎟

⎜

⎟

⎝0

1⎠⎝1⎠

⎝0⎠

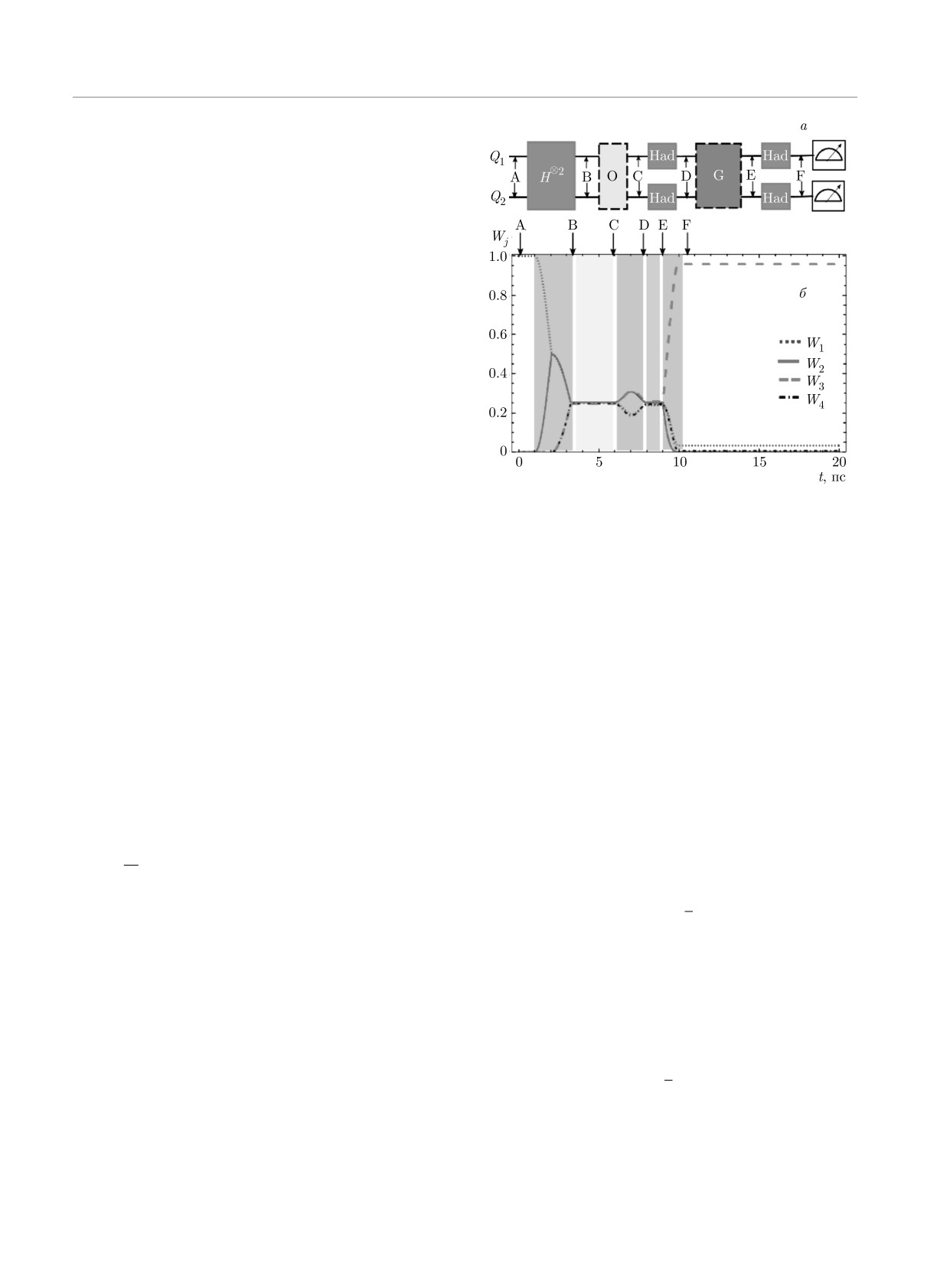
Рис. 1. а) Квантовая схема, создающая состояние Белла.

б) Вероятности населенностей уровней Wj (t) двухкубитной

системы (Δ1 = 0.1 ГГц и Δ2 = 0.12 ГГц) при реализации

Подавая на «вход» кубитов различные комби-

состояния Белла |β00〉. На рисунке выделен временной ин-

тервал для реализации гейта Адамара «Had» униполяр-

нации начальных состояний, можно подготовить

ным импульсом ε1(t) с амплитудой A1 = 0.75 ГГц и дли-

любое требуемое состояние Белла. Так, например,

тельностью τ1 = 2.1 пс, а также выделен временной интер-

|ψ(0)〉 = |0112〉 → |β01〉, |ψ(0)〉 = |1102〉 → |β10〉,

вал для выполнения двухкубитной операции «CNOT», при

|ψ(0)〉 = |1₁1₂〉 → |β₁₁〉. При изучении запутанных

этом параметры униполярных импульсов: A1 = 2.2 ГГц,

состояний важно анализировать не только населен-

A2 = 1.5 ГГц, τ1 = 1.3 пс, τ2 = 4.95 пс, tin,1 = 10 пс,

ности уровней W_j (t), т. е. диагональные элементы

tin,2

= 15 пс, J = 0.1 ГГц, τJ = 10 пс, γ¹¹ = γ²¹ =

матрицы плотности (см. выражение (B.2) в При-

= 100 мкс

ложении B), но и недиагональные элементы, кото-

рые как раз и отвечают за запутанность в систе-

что она могла быть удалена на произвольное рассто-

ме. Для этого в работе была проведена реконструк-

яние.

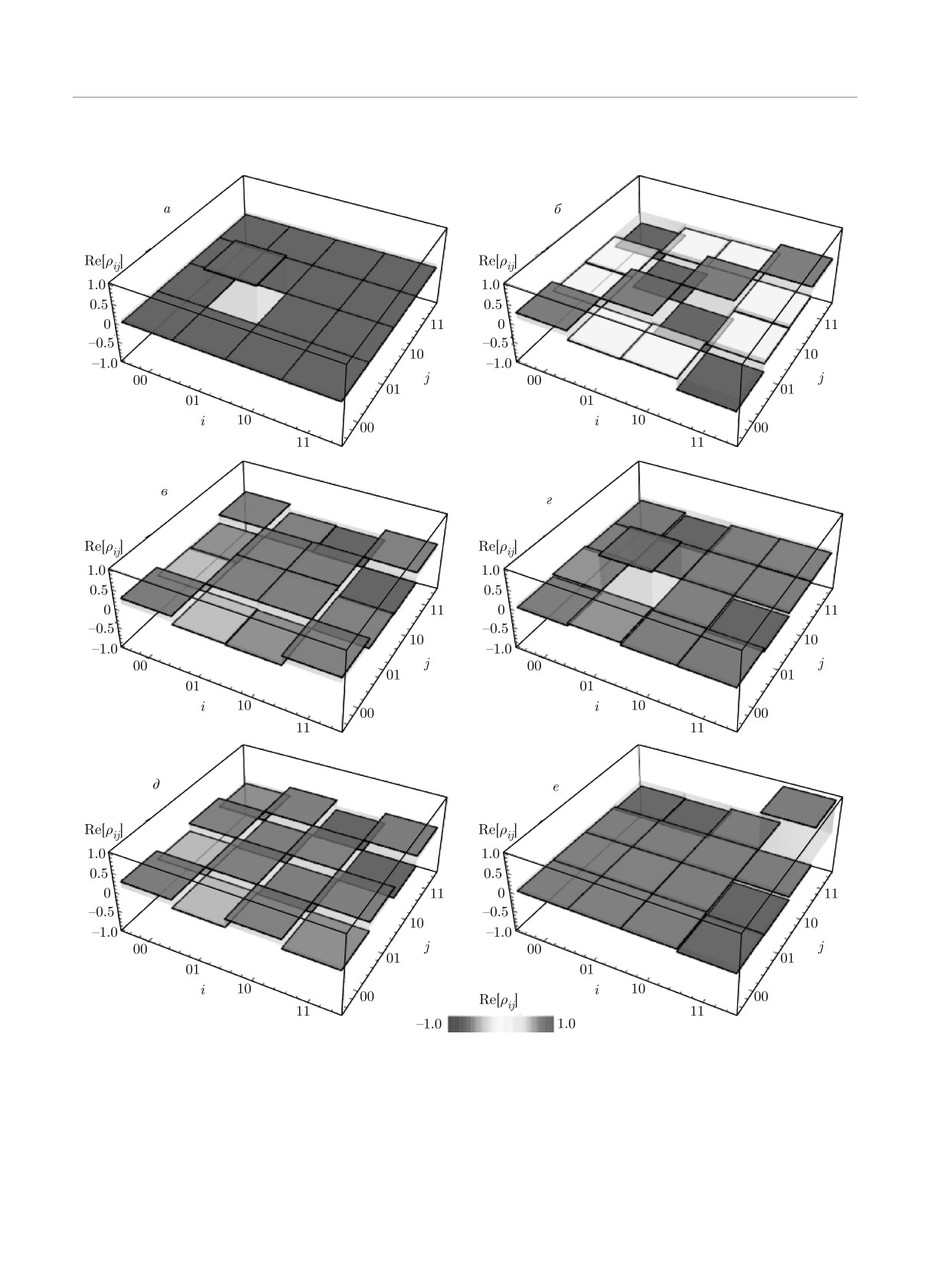
ция (томография) квантовых состояний Белла (14).

Состояния Белла можно подготовить, используя

Матрица плотности восстанавливается путем изме-

комбинацию однокубитного гейта Адамара «Had» и

рения всех «двухспиновых» вероятностей в базисе

двухкубитного гейта «СNOT», что схематично по-

σαi) (i = 1, 2). Действительные компоненты восста-

казано на рис. 1а. Принципы реализации с исполь-

новленных элементов матрицы плотности для четы-

зованием БОК-схем однокубитных гейтов были по-

рех состояний Белла (14) показаны на рис. 2. При

дробно нами изучены в работах [19-21], а двухкубит-

этом достоверность создания состояний Белла F_kl =

ных — в [21,22]. В настоящей работе в качестве при-

= 〈β_kl|ρ|β_kl〉 (k, l = 0, 1) между измеренной матри-

мера подробно продемонстрируем реализацию син-

цей плотности ρ и целевым состоянием Белла |β_kl〉,

глетного состояния Белла (14) |β₀₀〉, используя уни-

согласно (14), варьируется от 95 % до 98 %, что сви-

полярные пикосекундные импульсы.

детельствует о запутанности в системе и хорошей

Пусть в начальный момент времени кубиты

точности создания состояний Белла с помощью уни-

Q₁ и Q₂ инициализированы в основном состоянии:

полярного воздействия.

|ψ(0)〉 = |0102〉 (показано точками на рис. 1б до

включения униполярного воздействия t < 2 пс). Да-

4. КВАНТОВЫЙ АЛГОРИТМ

лее на первый кубит Q₁ подается один униполярный

ДОЙЧА - ЙОЖИ

импульс ε₁(t) на временах 2 ≤ t ≤ 4.1 пс, при этом

J (t) = 0. Данное внешнее воздействие реализует вы-

Рассмотрим процесс реализации квантового ал-

(

)

полнение гейта «Had», C_Had =

√

. Получен-

горитма Дойча - Йожи [18] в сверхпроводниковом

1 -1

584

ЖЭТФ, том 158, вып. 4 (10), 2020

Томография состояний кубитов и реализация. . .

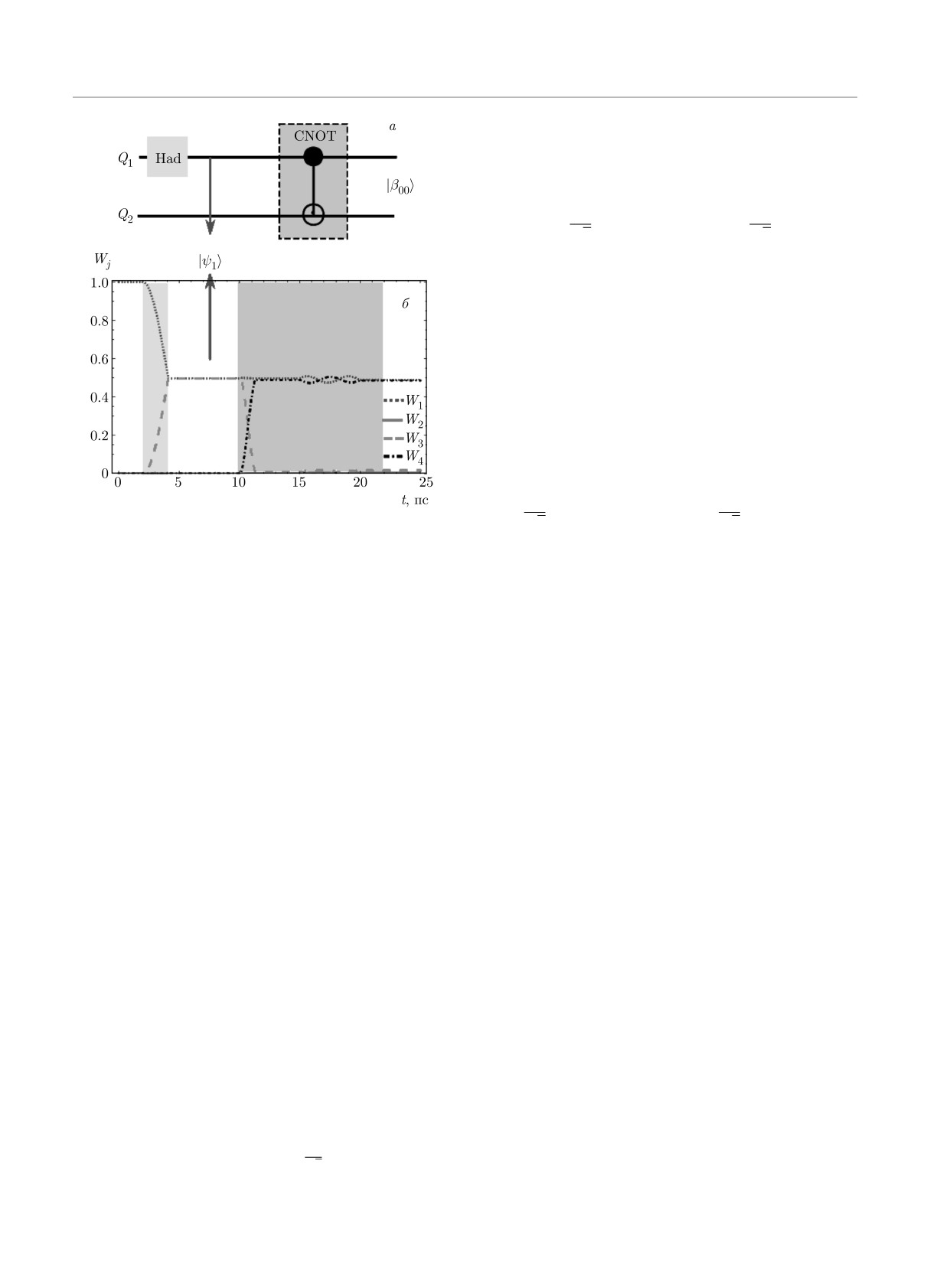
Рис. 2. Квантовая томография состояний Белла (|β00〉 — а, |β10〉 — б, |β11〉 — в, |β01〉 — г) для действительной ком-

поненты матрицы плотности Re[ρij ], формирование которых реализуется униполярным импульсами согласно схеме на

рис. 1а. Точность создания состояний Белла: F00 = 95 %, F10 = 98 %, F01 = 97.5 % и F11 = 96.5 %. Параметры системы

и импульсы идентичны тем, что приведены на рис. 1

двухкубитном регистре (Q₁ и Q₂) по средствам уни-

что, например, первый кубит Q₁ в основном состо-

полярного воздействия. Суть данного алгоритма со-

янии |ψ₁(0)〉 = |0₁〉, а второй Q₂ — в возбужденном

стоит в определении класса булевых функций f_i.

|ψ₂(0)〉 = |12〉. Далее на начальное состояние си-

При этом две функции f₁ и f₂ принимают либо

стемы воздействует последовательность пары уни-

значение 0, либо 1 при любых значениях аргумен-

полярных импульсов ε1,2(t) вида (9), реализующая

та и называются постоянными, а две другие f₃ и

пару гейтов Адамара:

f₄ для половины области определения принимают

⎛

⎞

значение 0, для другой половины 1 и имеют назва-

⎜

⎟

⎜

-1

⎟

ние сбалансированные. Квантовый алгоритм Дой-

C⊗2Had = C_Had ⊗ C_Had =

⎜

⎟.

⎜

⎟

ча - Йожи позволяет решить задачу об определении

-1

⎝ 1

⎠

типа функции за одно действие на двухкубитном

-1

регистре, тогда как классический алгоритм требу-

ет для выполнения два действия.

В результате этого получается равновероятностная

суперпозиция всех возможных значений кубитов.

Для начала инициализируем начальное состоя-

Далее на систему воздействует Оракул Ofi, который

ние |ψ(0)〉 = |ψ1(0)〉 ⊗ |ψ2(0)〉 пары кубитов, так

и отвечает за распознавание типа функции f_i. После

585

М. В. Бастракова, Н. В. Клёнов, А. М. Сатанин

ЖЭТФ, том 158, вып. 4 (10), 2020

воздействия Оракула томография квантового состо-

яния позволит определить тип функции: постоянная

или сбалансированная. Если функция f постоянная,

то Of1 = C_I или Of2 = C_I ⊗ C_NOT , где C_NOT =

(

)

0 -1

— однокубитная операция «NOT», а C_I —

операция, не изменяющая состояния системы. В

случае сбалансированной функции унитарный опе-

ратор преобразования имеет следующий вид: Of3 =

= C_CNOT и Of4 = C_CNOT(C_NOT ⊗ I). Для проек-

тирования результата необходимо снова подейство-

вать гейтом Адамара C⊗2Had. В результате измерения

после внешнего воздействия если населенность си-

стемы не изменилась, то функция постоянная, ина-

че функция — сбалансированная и состояние кубита

Q₁ инвертировалось: |ψ(0)〉 = |0₁1₂〉 → |1₁1₂〉.

На рис. 3 показана динамика поведения населен-

ностей уровней двух взаимодействующих кубитов

при диагностировании типа булевой функции: по-

стоянная (рис. 3б) или сбалансированная (рис. 3в).

Реализация алгоритма Дойча - Йожи была проведе-

на с помощью униполярного воздействия. Выпол-

нение описанного выше алгоритма осуществлялось

за счет возбуждения кубитов Q₁ и Q₂ импульса-

ми ε_i(t) вида (9), а перепутывание состояний про-

водилось за счет действия униполярного импульса

J (t), длительность которого совпадала с длительно-

стью возбуждающих кубитных импульсов, τ_i = τ_J .

В остальное время взаимодействие между кубитами

выключалось, J(t) = 0 (см. схему подачи импульсов

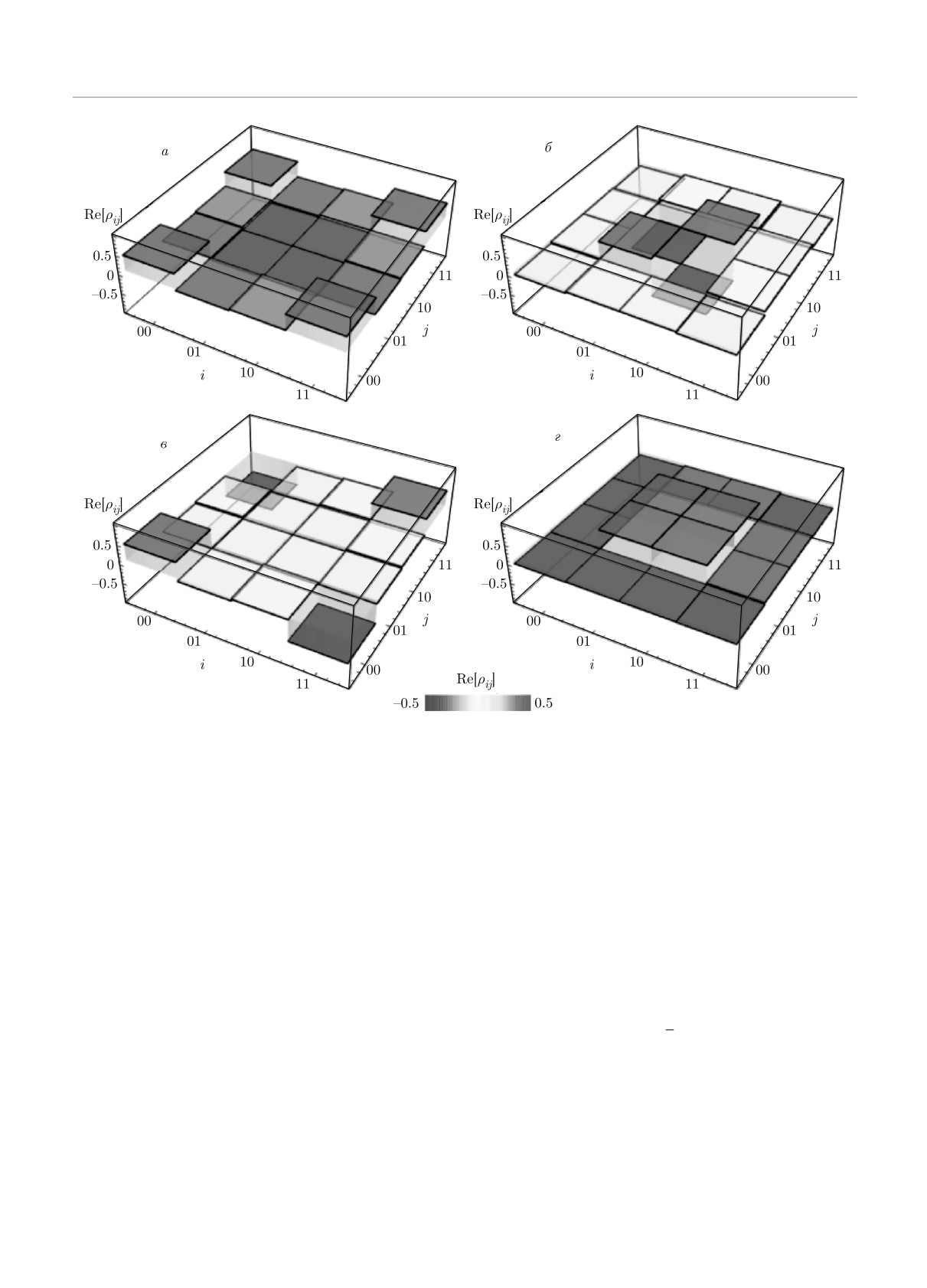
Рис. 3. Квантовая схема подачи униполярных импульсов

на систему на рис. 3а). При этом для проведения

на систему двух взаимодействующих кубитов (а), реали-

двух гейтов Адамара C⊗2Had на систему взаимодей-

зующая алгоритм Дойча - Йожи. Временные зависимости

ствующих кубитов последовательно воздействовали

населенностей уровней двух кубитов под действием уни-

полярных импульсов, реализующих квантовый алгоритм

два униполярных импульса, сдвинутых друг относи-

Дойча - Йожи для постоянной (б) и сбалансированной (в)

тельно друга на оси времени. В результате система

функций. Параметры кубитов и импульсов: Δ1 = 0.1 ГГц,

перешла в запутанное состояние, когда все четыре

Δ2 = 0.12 ГГц, J = 0.01 ГГц, импульс на Q1 — A1 =

уровня заселены с равными вероятностями: W_i(t) =

= 1.2 ГГц (1 пс ≤ t ≤ 5 пс и 8 пс ≤ t ≤ 12 пс) и импульс

= 0.25 (i = 1-4). Далее в результате унитарного воз-

на Q2 — A2 = 1.15 ГГц (2 пс ≤ t ≤ 6 пс и 9 пс ≤ t ≤ 13 пс),

действия, характеризующего постоянную функцию,

γ-11 = γ-12 = 100 мкс

квантовое состояние системы претерпело фазовый

поворот, в результате которого после последующе-

го преобразования Адамара населенность системы

не изменилась (см. рис. 3б). При этом населенность

сами нами была проведена томография (восстанов-

второго состояния системы кубитов после импульс-

ление) квантового состояния двухкубитной систе-

ного воздействия составила W₂ = 0.98. Аналогич-

мы. На рис. 4 показана действительная часть опе-

ные операции были проведены и для сбалансирован-

ратора матрицы плотности в момент инициализации

ной функции, при этом произошло перераспределе-

(а), после гейтов Адамара (б), в конце воздействия

ние населенностей (операция «CNOT»), так что наи-

Оракула для постоянной (в) и сбалансированной (д)

высший уровень заселен с вероятностью W₄ = 0.98

функций. Также представлены результаты модели-

(см. рис. 3в).

рования в момент проектирования (измерения) ко-

В процессе численного решения уравнения для

нечного состояния (г, е). До воздействия Оракула

матрицы плотности (13) для реализации квантово-

поведение системы полностью идентично для обо-

го алгоритма Дойча - Йожи униполярными импуль-

их типов функции (рис. 4а, б). Отметим, что хотя

586

М. В. Бастракова, Н. В. Клёнов, А. М. Сатанин

ЖЭТФ, том 158, вып. 4 (10), 2020

состояние двухкубитной системы и характеризует-

ся равными населенностями уровней (диагональные

элементы оператора матрицы плотности), на рис. 3

это временной интервал от 6 пс до 8 пс. Однако ре-

конструкция квантового состояния показывает их

существенное различие на рис. 4в,д. Именно бла-

годаря вкладам недиагональных элементов, отвеча-

ющих за перепутанные состояния в двухкубитной

системе, повторное униполярное воздействие, реа-

лизующее гейты Адамара, «распутывает» состоя-

ние квантовой системы и диагностирует тип функ-

ции. При этом численное моделирование показа-

ло, что достоверность выполнения квантового ал-

горитма Дойча - Йожи униполярными импульсами

составляет 98 %.

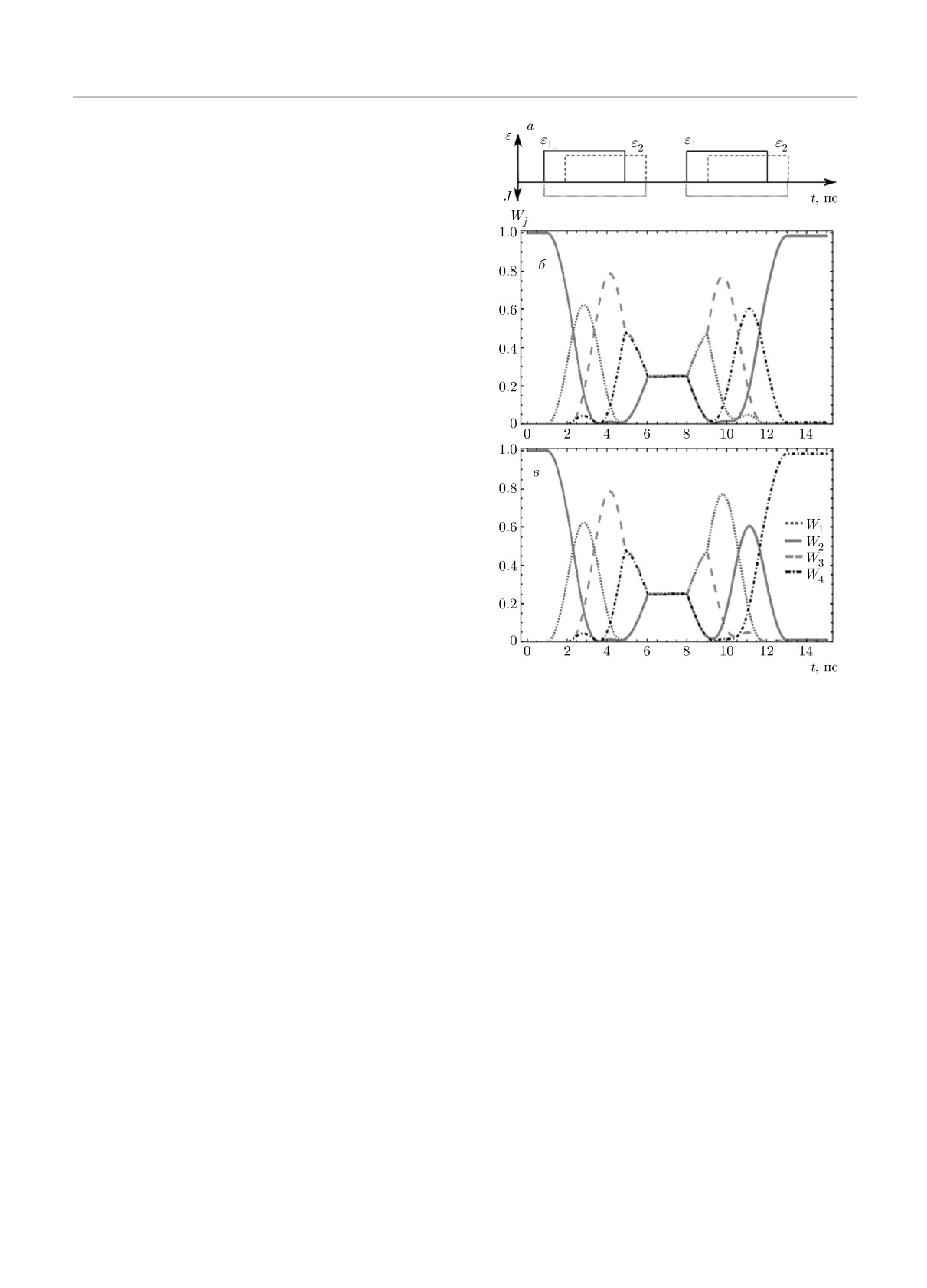
5. КВАНТОВЫЙ АЛГОРИТМ ГРОВЕРА

Рис. 5. а) Квантовая схема двух взаимодействующих ку-

Алгоритм Гровера решает задачу неструктури-

битов, реализующая алгоритм Гровера. б) Зависимость от

рованного поиска, когда есть неупорядоченный на-

времени населенностей уровней двухкубитной системы под

бор данных и требуется найти в нем какой-то один

действием униполярных импульсов, реализующих кванто-

элемент, удовлетворяющий определенному требова-

вый алгоритм Гровера для поиска «помеченного» состо-

нию. Данный алгоритм использует свойство кванто-

яния x0 = |10〉. Параметры кубитов и импульсов: Δ1 =

вой интерференции для того, чтобы найти значения

= 0.1 ГГц, Δ2 = 0.12 ГГц; импульсы, действующие на

некоторого параметра, на котором заданная функ-

Q1: A1 = 1.2 ГГц (1 пс ≤ t ≤ 2.05 пс), A1 = 1.6 ГГц

ция обладает определенными свойствами [18].

(6 пс ≤ t ≤ 7.92 пс и 9 пс ≤ t ≤ 9.92 пс); импульсы, дей-

Кратко опишем суть алгоритма поиска Гровера,

ствующие на Q2: A2 = 1.3 ГГц (2.05 пс ≤ t ≤ 3.25 пс),

который обеспечивает оптимальный метод для на-

A2 = 1.6 ГГц (6 пс ≤ t ≤ 7.92 пс и 9 пс ≤ t ≤ 9.92 пс);

хождения уникального аргумента x₀ булевой функ-

характеристики связи: J = 0.01 ГГц (1 пс ≤ t ≤ 3.25 пс и

7.92 пс ≤ t ≤ 9 пс); параметры шума γ-11 = γ-12 = 100 мкс

ции от n переменных f(x), такого что f(x₀) = 1 и

f (x) = 0 для всех остальных значений x. Класси-

ческие алгоритмы подобного поиска требуют пря-

готовить равновероятностную суперпозицию состо-

мого перебора всех вариантов N = 2n, в то вре-

яний кубитов. Это делается при помощи примене-

мя как использование квантового параллелизма и

ния соответствующего гейта Адамара C⊗2Had [18]. По-

вероятностного характера квантовых вычислений

сле этого состояние квантовой системы можно опре-

сокращает количество перебираемых вариантов до

√

делить как

(π/4)

Для рассматриваемого двухкубитного регистра

|ψ_B〉 = C⊗2Had|ψ_A〉 =

1)^T

(Q₁ и Q₂) есть четыре значения x ∈ {00, 01, 10, 11}

и в результате четыре возможные функции f_ij(x) с

i, j ∈ 0, 1. Реализацию квантового алгоритма Гро-

(символ B на рис. 5 соответствует моменту вре-

вера можно представить как поиск «помеченного»

мени формирования состояния |ψ_B 〉). Блок О на

квантового состояния, причем определение «метки»

рис. 5а определяет действие Оракула, который вы-

проводится Оракулом O|x〉 = (-1)f(x)|x〉, при этом

деляет («помечает») в качестве примера состояние

для помеченного состояния происходит поворот фа-

x₀ = |10〉, что отражается на фазе данного состоя-

зы f_ij(x) = 1.

ния:

Схематично данный алгоритм в виде гейтовых

|ψ_C 〉 = O|ψ_B 〉 =

-1

1)^T .

операций можно представить согласно схеме на

рис. 5a. Сначала проводится инициализация сис-

Далее идет гейт диффузии Гровера, который

темы |ψ_A〉 = |ψ(0)〉 = (1

0)^T (момент отме-

представляет собой соединение трех гейтов, два

чен символом A на рис. 5), далее необходимо под-

из которых

— гейты Адамара, а между ними

588

ЖЭТФ, том 158, вып. 4 (10), 2020

Томография состояний кубитов и реализация. . .

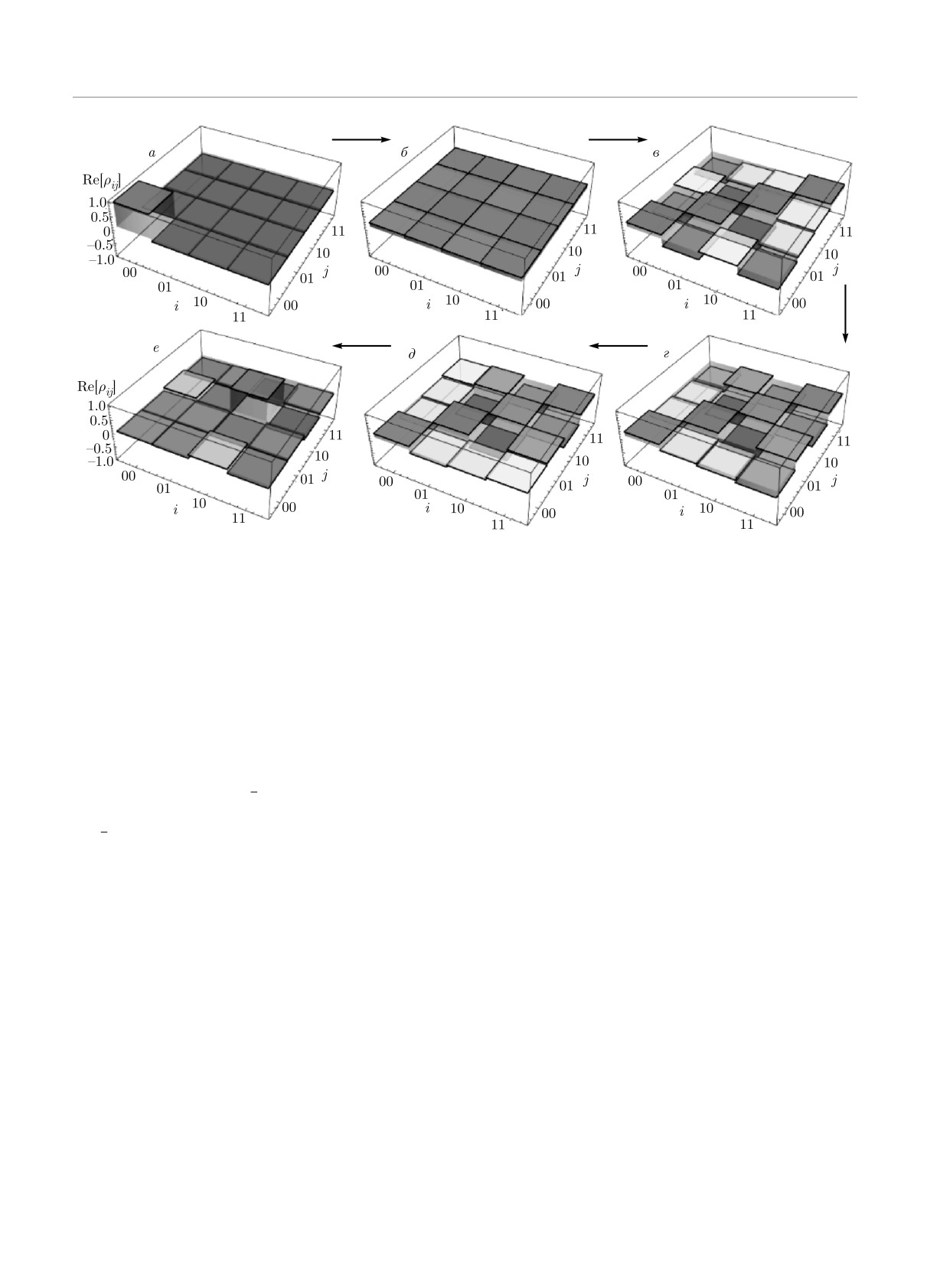
Рис. 6. Квантовая томография состояний для действительной компоненты матрицы плотности Re[ρij ] при выполнении

алгоритма поиска Гровера в моменты времени, указанные стрелками на рис. 5б: А (а), B (б), С (в), D (г), Е (д), F (е).

Параметры кубитов и импульсов аналогичны тем, что приведены на рис. 5а; цветовая шкала Re[ρij ] представлена на

рис. 4

гейт, осуществляющий переворот кубитов относи-

ющимися данными по реализации алгоритма Гро-

тельно среднего значения G

= 2|ψ(0)〉〈ψ(0)| - I

вера в сверхпроводниковых кубитах на основе тех-

(блок между символами D и E на рис. 5а). По-

ники Раби [10]. Как видно из численного анализа

следовательно проследим за преобразованием

одно- и двухкубитных операций, изменение техни-

состояния двухкубитной системы: 1) после бло-

ки управления состояниями на униполярное воздей-

ков Адамара |ψ_D〉

=¹² (1

-1

1)^T , 2) после

ствие позволяет существенно ускорить выполнение

действия оператора Гровера

|ψ_E 〉

= G|ψ_D〉

логических операций, а также выполнить основные

-1

-1)^T , 3) после блоков Адамара

квантовые алгоритмы с высокой точностью.

|ψ_off 〉 = |ψ_F 〉 = (0

0)^T .

6. ЗАКЛЮЧЕНИЕ

На рис. 5б показана динамика поведения насе-

ленностей уровней (диагональных элементов мат-

рицы плотности W_i(t) = ρ_ii) двух взаимодействую-

Проведенное на классическом компьютере мо-

щих кубитов при выполнении квантового алгорит-

делирование функционирования одно- и двухку-

ма Гровера униполярными импульсами для поис-

битных гейтов демонстрирует возможность уско-

ка «помеченного» состояния (для примера «метка»

рения (как минимум на два порядка) выполнения

была на состоянии x₀ = |10〉). Заметим, что точ-

ключевых операций и алгоритмов. Требуемые им-

пульсы поля пикосекундной длительности вполне

ность выполнения алгоритма при этом составила

F = 〈ψ_off|ρ|ψ_off〉 ≈ 93%. Стрелками и символа-

могут быть реализованы с использованием циф-

ми A-F на рис. 5б показаны моменты времени, ко-

ровых устройств сверхпроводниковой электроники,

гда численно была проведена реконструкция кван-

при этом существенно снижаются требования к

тового состояния (томография), изображенная на

сложности и количеству используемых устройств

рис. 6. Полученные зависимости согласуются с име-

СВЧ-электроники для реализации раби-импульсов.

589

М. В. Бастракова, Н. В. Клёнов, А. М. Сатанин

ЖЭТФ, том 158, вып. 4 (10), 2020

Показано, что пикосекундные униполярные импуль-

граммирование двухкубитного квантового процес-

сы позволяют осуществить формирование запутан-

сора.

ных состояний Белла в двухкубитном сверхпровод-

Благодарности.

Авторы

признательны

никовом регистре. Выполнено имитационное моде-

Л. Н. Щуру за внимание к работе.

лирование процедуры томографии квантовых состо-

Финансирование. Работа выполнена при фи-

яний на основе решения уравнения для матрицы

нансовой поддержке Российского фонда фундамен-

плотности. Показано, что с использованием БОК-

тальных исследований (грант № 20-07-00952). Вклад

управления можно осуществить быстрое (на пико-

в работу Н. В. Клёнова выполнен в рамках гранта

секундных временах) формирование перепутанных

Президента МД-186.2020.8.

состояний с достоверностью 95-98 %. На основе чис-

ленного моделирования разработаны протоколы вы-

ПРИЛОЖЕНИЕ А

полнения базовых квантовых алгоритмов: Дойча -

Йожи с точностью более 98 % и Гровера с точностью

Для случая идентичных кубитов (Δ₁ = Δ₂ = Δ)

93 %. Разработанные методы управления с исполь-

операторы эволюции U(τ₁), U(τ_J ), U(τ₂) в матрич-

зованием БОК-цепей позволяют осуществить про-

ном виде определены как

U(12)τ

⎛

⎞

(

)

τ₁Ω

e-i

cos

- i^Δ

sinτ1Ω

-^iAe-i

sinτ1Ω

⎜

⎟

⎜

iΔτ₁

(

)

iΔτ₁

⎟

⎜

τ₁Ω

⎟

⎜

cos

- i^Δ

sinτ1Ω

-^iAe

sinτ1Ω

⎟

⎜

⎟,

⎜

(

)

⎟

⎜

−^iAe-i

sinτ1Ω

e-i

cosτ1Ω

+ i^Δ

sinτ1Ω

⎟

⎜

⎟

⎝

⎠

iΔτ₁

(

)

-^iAe

sinτ1Ω

cosτ1Ω

+ i^Δ

sinτ1Ω

⎛

⎞

2iΔ

cosτJΩJ

sinτJΩJ

-iJ

sinτJΩJ

^ΩJ

⎜

⎟

⎜

⎟

⎜

cosτJΩJ

-i sinτJΩJ

⎟

⎜

⎟

U(12)τ

⎜

⎟,

⎜

⎟

⎜

-i sinτJΩJ

cosτJΩJ

⎟

⎝

⎠

−iJ

sinτJΩJ

cosτJΩJ

+2iΔ

sinτJΩJ

^ΩJ

U(12)τ

⎛

(

)

⎞

τ₂Ω

e-i

cos

- i^Δ

sinτ2Ω

-^iAe-i

sinτ2Ω

⎜

⎟

⎜

(

)

⎟

⎜

⎟

−

e-i

sinτ2Ω

e-i

cosτ2Ω

+ i^Δ

sinτ2Ω

⎜

⎟

⎜

⎟,

⎜

iΔτ₂

(

)

iΔτ₂

⎟

⎜

⎟

cosτ2Ω-iΔ

sinτ2Ω

-^iAe

sinτ2Ω

⎜

⎟

⎝

⎠

iΔτ₂

(

)

-^iAe

sinτ2Ω

cosτ2Ω+iΔ

sinτ2Ω

√

где Ω =

A² + Δ² и Ω_J =

J² + 4Δ².

Вероятности переходов между базисными состояниями двухкубитной системы W_x



12)



〈x|U^τ

|00〉2, где x = 1 соответствует базисному состоянию |x〉 = |0102〉, x = 2 — |x〉 = |0112〉,

τJ

τ1

x = 3 — |x〉 = |1₁0₂〉, x = 4 — |x〉 = |1₁1₂〉, определены как

590

ЖЭТФ, том 158, вып. 4 (10), 2020

Томография состояний кубитов и реализация. . .

(

)

)₂

τ₁Ω

τ_J Ω_J

τ_J J

τ₁Ω

τ_J Ω_J

W₂ =

sin²

2Δ² sin

sin

+ -Δsin

sin

+ Ωcos

cos

Ω_J

Ω⁴Ω2J

)

(

)

)₂

τ₁Ω

τ₂Ω

τ_J Ω_J

τ₁Ω

τ_JΩ_J

τ₂Ω

τ_JJ

2Δcos

sin

Ω + sin

Δcos

sin

+ cos

sin

Ω Ω_J

(A.1)

(

)₂

τ₂Ω

τ₁Ω

τ_JΩ_J

τ_J J

τ₁Ω

W₃ =

sin²

JΩcos

sin

+ ΔΩ_J cos

sin

Ω⁴Ω2J

)

(

)₂

τ₁Ω

τ₂Ω

τ_JΩ_J

τ_J J

τ₂Ω

+ sin²

JΔsin

sin

- ΩΩ_J cos

cos

(A.2)

(

)

((

)

(τ₁ - τ₂)Ω

(τ₁ + τ₂)Ω

(τ₁ - τ₂)Δ

τ_J Ω_J

W₄ =

J²

A² + 2Δ²

cos

+ A2 cos

sin²

4Ω⁴Ω2J

(

)₂)

(τ₁ - τ₂)Δ

τ_J J

τ₁Ω

τ₂Ω

(τ₁ - τ₂)Ω

τ_J Ω_J

+ 4cos²

-A²Ω_J cos

sin

- JΔΩsin

sin

(A.3)

ПРИЛОЖЕНИЕ B

Для численных расчетов матрицу плотности удобно представить в виде разложения по полному набо-

ру матриц группы SU(4), представляющих собой кронекерово (прямое) произведение матриц для группы

(

)

∑

SU(2): ρ =_α,β R_α,β σα1) ⊗ σ(2)β, R_α,β = Tr σα1) ⊗ σ(2)βρ

— компоненты вектора (16 элементов), σαi) =

= {σ(i)0, σxi), σyi), σzi)} — набор матриц, где σ(i)0 = I(i) — единичная матрица 2 × 2 и σx,y,z — матрицы Паули.

Уравнение (13) для матрицы плотности эквивалентно уравнениям для компонент вектора R_α,β (15 ненуле-

вых компонент, R0,0 = 0):

Rx,0 = 4(JR_y,z - Rx,0γ₁ + Ry,0ε₁(t)),

Ry,0 = -4(JR_x,z + Ry,0γ₁ - Rz,0Δ₁ + Rx,0ε₁(t)),

Rz,0 = -4Ry,0Δ₁,

R0,x = 4(JR_z,y - R0,xγ₂ + R0,yε₂(t)),

R0,y = -4(JR_z,x + R0,yγ₂ - R0,zΔ₂ + R0,xε₂(t)),

R0,z = -4R0,yΔ₂,

R_x,x = 4(-R_x,x(γ₁ + γ₂) + R_y,xε₁(t) + R_x,yε₂(t)),

R_x,y = -4(R_x,y(γ₁ + γ₂) - R_x,zΔ₂ - R_y,yε₁(t) + R_x,xε₂(t)),

(B.1)

R_x,z = 4(JRy,0 - R_x,zγ₁ - R_x,yΔ₂ + R_y,zε₁(t)),

R_y,x = -4(R_y,x(γ₁ + γ₂) - R_z,xΔ₁ + R_x,xε₂(t) - R_y,yε₂(t)),

R_y,y = -4(R_y,y(γ₁ + γ₂) - R_z,yΔ₁ - R_y,zΔ₂ + R_x,yε₁(t) + R_y,xε₂(t)),

R_y,z = -4(JRx,0 + R_y,zγ₁ - R_z,zΔ₁ + R_y,yΔ₂ + R_x,zε₁(t)),

R_z,x = 4(JR0,y - R_z,xγ₂ - R_y,xΔ₁ + R_z,yε₂(t)),

R_z,y = -4(JR0,x + R_z,yγ₂ + R_y,yΔ₁ - R_z,zΔ₂ + R_z,xε₂(t)),

R_z,z = -4(R_y,zΔ₁ + R_z,yΔ₂).

В начальный момент времени при t = 0 система двух кубитов находится в основном состоянии, т. е. мат-

рица плотности построена на собственных функциях невозмущенного гамильтониана (7), когда A₁ = A₂ = 0

∑

и J = 0 в (4), и определена выражением ρ(0) =i |ψ_in(0)〉〈ψ_in(0)|. Компоненты вектора R_α,β определены

591

М. В. Бастракова, Н. В. Клёнов, А. М. Сатанин

ЖЭТФ, том 158, вып. 4 (10), 2020

(

)

как R_α,β(0) = Tr σα1) ⊗ σ(2)βρ(0) . Населенности уровней кубитов (диагональные элементы матрицы плот-

ности W_i(t) = ρ_ii) при этом рассчитываются через компоненты вектора R_α,β и имеют вид

1+Rz,0

+R0,z +R_z,z

W₁(t) =

1+Rz,0

-R0,z -R_z,z

W₂(t) =

(B.2)

1+R0,z -Rz,0 -R_z,z

W₃(t) =

1-Rz,0

-R0,z +R_z,z

W₄(t) =

ЛИТЕРАТУРА

J. M. Chow, J. M. Gambetta, L. Tornberg, J. Koch,

L. S. Bishop, A. A. Houck, B. R. Johnson, L. Frunzio,

F. Arute, K. Arya, R. Babbush, D. Bacon,

S. M. Girvin, and R. J. Schoelkopf, Phys. Rev. Lett.

J. C. Bardin, R. Barends, R. Biswas, S. Boixo,

102, 090502 (2009).

F. G. S. L. Brandao, D. A. Buell, B. Burkett,

Yu Chen, Z. Chen, B. Chiaro, R. Collins,

Y. He, S. K. Gorman, D. Keith, L. Kranz, J. G. Kei-

W. Courtney, A. Dunsworth, E. Farhi, B. Foxen,

zer, and M. Y. Simmons, Nature 571, 371 (2019).

A. Fowler, C. Gidney, M. Giustina, R. Graff,

10.

L. DiCarlo, J. M. Chow, J. M. Gambetta, L. S. Bi-

K. Guerin, S. Habegger, M. P. Harrigan,

shop, B. R. Johnson, D. I. Schuster, J. Majer,

M. J. Hartmann, A. Ho , M. Hoffmann, T. Huang,

A. Blais, L. Frunzio, S. M. Girvin, and R. J. Schoel-

T. S. Humble, S. V. Isakov, E. Jeffrey, Z. Jiang,

kopf, Nature 460, 240 (2009).

D. Kafri, K. Kechedzhi, J. Kelly, P. V. Klimov,

S. Knysh, A. Korotkov, F. Kostritsa, D. Landhuis,

11.

D. V. Averin, K. Rabenstein, and V. K. Semenov,

M. Lindmark, E. Lucero, D. Lyakh, S. Mandrà,

Phys. Rev. B 73, 094504 (2006).

J. R. McClean, M. McEwen, A. Megrant, X. Mi,

12.

A. Fedorov, A. Shnirman, G. Schoen, and A. Kidiya-

K. Michielsen, M. Mohseni, J. Mutus, O. Naaman,

rova-Shevchenko, Phys. Rev. B 75, 224504 (2007).

M. Neeley, C. Neill, M. Y. Niu, E. Ostby,

A. Petukhov, J. C. Platt, C. Quintana, E. G. Rieffe,

13.

A. Herr, A. Fedorov, A. Shnirman, E. Ilichev, and

P. Roushan, N. C. Rubin, D. Sank, K. J. Satzinger,

G. Schon, Supercond. Sci. Technol. 20, S450 (2007).

V. Smelyanskiy, K. J. Sung, M. D. Trevithick,

A. Vainsencher, B. Villalonga, T. White, Z. J. Yao,

14.

K. K. Likharev and V. K. Semenov, IEEE Trans.

P. Yeh, A. Zalcman, H. Neven, and J. M. Martinis,

Appl. Supercond. 1, 3 (1991).

Nature 574, 505 (2019).

15.

R. McDermott and M. G. Vavilov, Phys. Rev. Appl.

J. Preskil, Quantum 2, 79 (2018).

2, 014007 (2014).

16.

E. Leonard, M. A. Beck, J. Nelson, B. G. Christensen,

A. A. Zhukov, S. V. Remizov, W. V. Pogosov, and

T. Thorbeck, C. Howington, A. Opremcak, I. V. Pe-

Yu. E. Lozovik, Quant. Inf. Proces. 17, 223 (2018).

chenezhskiy, K. Dodge, N. P. Dupuis, M. D. Hut-

A. A. Zhukov, E. O. Kiktenko, A. A. Elistratov,

chings, J. Ku, F. Schlenker, J. Suttle, C. Wilen,

W. V. Pogosov, and Yu. E. Lozovik, Quant. Inf.

S. Zhu, M. G. Vavilov, B. T. Plourde, and R. McDer-

Proces. 18, 31 (2019).

mott, Phys. Rev. Appl. 11, 014009 (2019).

17.

K. Li, R. McDermott, and M. G. Vavilov, Phys. Rev.

Y. Nakamura, Y. A. Pashkin, and J. S. Tsai, Phys.

Appl. 12, 014044 (2019).

Rev. Lett. 87, 246601 (2001)

18.

М. Нильсен, И. Чанг, Квантовые вычисления и

G. Wendin, Rep. Prog. Phys. 80, 106001 (2017).

квантовая информация, Мир, Санкт-Петербург

R. Barends, J. Kelly, A. Megrant, A. Veitia, D. Sank,

(2006).

E. Jeffrey, T. C. White, J. Mutus, A. G. Fowler,

19.

N. V. Klenov, A. V. Kuznetsov, I. I. Soloviev,

B. Campbell, Y. Chen, Z. Chen, B. Chiaro,

S. V. Bakurskiy, M. V. Denisenko, and A. M. Satanin,

A. Dunsworth, C. Neill, P. O’Malley, P. Roushan,

Low Temp. Phys. 43, 789 (2017).

A. Vainsencher, J. Wenner, A. N. Korotkov,

A. N. Cleland, and J. M. Martinis, Nature 508, 500

20.

M. V. Denisenko, N. V. Klenov, and A. M. Satanin,

(2014).

AIP Conf. Proc. 1936, 020009 (2018).

592