ЖЭТФ, 2020, том 158, вып. 4 (10), стр. 594-604

СОВМЕСТНОЕ ВЛИЯНИЕ ДИПОЛЬ-ДИПОЛЬНОГО

ВЗАИМОДЕЙСТВИЯ И ПОСТОЯННОГО ДИПОЛЬНОГО

МОМЕНТА НА ФОРМУ ИМПУЛЬСА ПОЛЯ БЕЗ ОГИБАЮЩЕЙ

А. А. Заболотский^*

Институт автоматики и электрометрии Сибирского отделения Российской академии наук

690090, Новосибирск, Россия

Поступила в редакцию 15 апреля 2020 г.,

после переработки 21 апреля 2020 г.

Принята к публикации 22 апреля 2020 г.

Предложена интегрируемая модель двухуровневой среды с постоянным дипольным моментом, описываю-

щая эволюцию импульсов электромагнитного поля без огибающей с учетом диполь-дипольного взаимо-

действия. В приближении ближайших соседей это взаимодействие учитывается в виде квадратичной

дисперсии. Найдено, что такое обобщение редуцированных уравнений Максвелла - Блоха сохраняет пол-

ную интегрируемость. На примерах полученных точных солитонных решений показано, что совместное

влияние квадратичной дисперсии и постоянного дипольного момента обладает рядом уникальных осо-

бенностей и дает новые возможности контроля формы импульсов поля. В частности, обнаружено, что

форма и амплитуда импульса поля зависят как от знаков диполь-дипольного взаимодействия, так и знака

постоянного дипольного момента.

DOI: 10.31857/S0044451020100028

[10-13] вне рамок приближения медленно меняю-

щейся огибающей.

Применимость двухуровневой модели к таким

1. ВВЕДЕНИЕ

импульсам требует, чтобы резонансная частота

была хорошо отделена от других частот [23-25].

Нелинейные явления, связанные с эволюцией

Для квазимонохроматических импульсов это

ультракоротких импульсов света в средах, содержа-

условие, как правило, выполняется. Для импуль-

щих резонансные атомы или молекулы, исследуют-

сов с длительностью порядка обратной частоты

ся в рамках уравнений Максвелла - Блоха длитель-

условие применимости таких моделей становится

ное время, см., например, [1-7]. Особенное значение

менее реалистичным. Однако это можно частично

имеют полностью интегрируемые модели [7], в рам-

компенсировать ситуацией, когда дипольный мо-

ках которых можно найти многосолитонные и дру-

мент, соответствующий энергетическому переходу,

гие решения, исследовать взаимодействие импуль-

больше, чем у ближайших переходов [26].

сов поля. Для описания солитонной динамики бы-

ли найдены различные системы волновых и матери-

Для несимметричных молекул и квантовых то-

альных уравнений, интегрируемые методом обрат-

чек и сплошных сред без зеркальной симметрии ха-

ной задачи рассеяния [7], в том числе модели нели-

рактерно наличие постоянного дипольного момента

нейной оптики и акустики [5, 8-19]. Интерес к им-

(ПДМ). В этом случае гамильтониан взаимодейст-

пульсам полей без огибающей стимулировал нахож-

вия оптических электронов, вследствие взаимодей-

дение и изучение интегрируемых редуцированных

ствия с ядрами молекул, неинвариантен относитель-

уравнений Максвелла - Блоха (РУМБ), описываю-

но полной группы вращений. Стационарные состо-

щих явление самоиндуцированной прозрачности в

яния таких молекул не имеют определенной чет-

двухуровневой среде (ДУС) для однокомпонентно-

ности, в результате чего становятся отличными от

го [1, 5, 6, 8-10, 20-22] и двухкомпонентного полей

нуля диагональные элементы оператора дипольного

момента. Для низких частот, например, для микро-

^* E-mail: zabolotskii@iae.nsk.su

волн или терагерцевых частот влияние ПДМ может

594

ЖЭТФ, том 158, вып. 4 (10), 2020

Совместное влияние диполь-дипольного взаимодействия. ..

быть существенным. Наличие ПДМ квантового пе-

В настоящей работе приводится интегрируемое

рехода вызывает при распространении импульса ди-

обобщение редуцированных уравнений Максвел-

намический штарковский сдвиг частоты перехода,

ла - Блоха для ДУС, которое включает ПДМ и

который пропорционален напряженности электри-

нелинейную квадратичную дисперсию при выпол-

ческого поля импульса. Влияние ПДМ на распро-

нении ряда стандартных приближений и условия

странение импульсов достаточно исследовано в слу-

U_p ≲ ℏω₁₂. Несмотря на достаточную очевидность

чае (эффективно) двухуровневых сред [23,24]. Осо-

такого обобщения, эта система не была нами об-

бую роль ПДМ может играть при переносе энергии

наружена в литературе. Целью работы является

между асимметричной квантовой точкой и протя-

получение точных решений и демонстрация с их по-

женной молекулой, например, молекулой ДНК или

мощью синергического эффекта, проявляющегося

белка. Взаимодействие постоянных диполей моле-

в критическом усилении или подавлении импульса

кул и квантовой точки приводит к локализации (де-

поля вследствие совместного действия диполь-

локализации) экситонов и усилению (уменьшению)

дипольного взаимодействия и эффекта Штарка,

эффективности переноса энергии [27-29]. В протя-

вызванного наличием ПДМ в ДУС.

женных молекулярных средах, таких как молеку-

лы ДНК, белка [30] и молекулярные агрегаты кра-

2. ВЫВОД МОДЕЛИ

сителей [31, 32], диполь-дипольное взаимодействие

играет определяющую роль при формировании эк-

Приведем вывод редуцированных уравнений

ситонных импульсов и переносе энергии. Эволюция

Максвела - Блоха для цепочки ДУС с ПДМ и

возбуждений в молекулярных цепочках может быть

диполь-дипольным взаимодействием. Физическое

описана в приближении, в котором каждая моле-

происхождение и вывод аналогичных уравнений

кула представлена ДУС. В приближении ближай-

эволюции импульсов без огибающей в ДУС с ПДМ

ших соседей диполь-дипольное взаимодействие сво-

можно найти, например, в работах [1, 8, 16, 20-22],

дится к пространственной дисперсии второго поряд-

а уравнения Максвелла - Блоха с учетом дисперсии

ка. Для сильного изменения населенностей уровней

второго порядка — в [18,33]. Уравнение Максвелла

эта дисперсия носит нелинейный характер. В работе

для одномерной однородной протяженной среды и

[33] показано, что возможно интегрируемое обобще-

однокомпонентного поля, распространяющегося в

ние уравнений Максвелла - Блоха для ДУС с учетом

ДУС, имеет вид [3]

нелинейной дисперсии.

∂²E_x

4πd_x ∂²P_x

(1)

∂z²

c²∂t²

c²

∂t²

Для сверхсильного поля, т.е. с энергией U_p, мно-

го большей энергии перехода ℏω₁₂, и для эффек-

Здесь компонента поляризации среды P_x имеет вид

{

}

тивного однокомпонентного поля соответствующие

∂H

уравнения Максвелла - Блоха могут быть сведены к

P_x = -n_mTr

(2)

∂E_x

модифицированному уравнению синус-Гордона [34]

и его обобщениям [17, 18]. Однако, это для таких

и n_m

— плотность среды. Считаем, что среда

полей двухуровневое приближение в реальных сре-

состоит из прямой цепочки двухуровневых ато-

дах как правило не применимо. Поэтому более реа-

мов с дипольным моментом в точке z = ln, где

листичным является приближение U_p ≲ ℏω₁₂. Мо-

l — расстояние между ними. В плотной среде на

дель, представляющая собой цепочку ДУС с ПДМ

поляризацию ДУС в точке nl оказывают влияние

и нелинейной квадратичной дисперсией, может при-

поля диполей всех ДУС в точках ml, m

= n.

меняться для эволюции ультракоротких экситон-

Для упрощения задачи используем приближе-

ных возбуждений в длинной молекулярной среде.

ние ближайших соседей, которое применялось

В цитированных выше работах изучалось влияние

для описания подобных сред, например, белко-

ПДМ и нелинейной дисперсии на эволюции импуль-

вые молекулы

[30] или молекулярные агрегаты

сов поля. Однако совместное синергетическое дей-

красителей

[31]. В этом приближении вклад в

ствие этих факторов на формирование возбуждений

поляризацию атома, находящегося в точке z = nl,

в протяженных системах не исследовалось, тем бо-

вносят поляризация в этой точке и поляризации,

лее в условиях U_p ≲ ℏω₁₂. В то же время изучение

вызванные дипольными полями ближайших со-

такого влияния представляется чрезвычайно важ-

седей в точках (n ± 1)l. Этот подход позволил

ным для анализа процессов переноса энергии в виде

описать ряд важных экспериментальных фактов,

коротких импульсов в молекулярных цепочках.

595

А. А. Заболотский

ЖЭТФ, том 158, вып. 4 (10), 2020

в частности, эволюцию слабых возбуждений в моле-

n_d — постоянная диэлектрической восприимчивости

кулах ДНК [30, 32]. С учетом полей диполей толь-

среды. Это означает, что [1]

ко ближайших соседей поляризация в правой части

уравнения (1), где поле берется в точке nl, прини-

∂E_x

≈-

(9)

мает вид

∂z

c∂t

(

)

с требуемой точностью. Соответственно, вкладом

P_x ≈ P(n)x + γ_dd P(n-1)x + P(n+1)

(3)

встречной волны можно пренебречь. Получаемая

в итоге система уравнений описывает эволюцию и

Здесь

— поляризация атома в точке nl, γ_dd —

распространение импульсов с групповой скоростью,

коэффициент диполь-дипольного взаимодействия

близкой с скоростью света в среде [1].

соседних диполей. В континуальном приближении

Для однокомпонентного поля, используя при-

≈ 2P_x(z) + l²∂2zP_x(z), где

→

ближение (9), находим из уравнения (4) и (5) сле-

→ P_x(z), nl → z при l → 0. В итоге из уравнения (3)

дующую систему РУМБ с ПДМ и нелинейной квад-

находим

ратичной дисперсией:

(

)

(1 + 2γ_dde)²

∂2z - c-2∂2t

E_x(z, t) = -4πd_x

∂2t ×

∂S₁

c²

[

]

= -(ω - μE)S₂,

(10)

2γ_ddl²

∂τ

× P_x(z, t) +

G∂2zP_x(z, t)

(4)

∂S₂

1 + 2γ_dd

= (ω - μE) S₁ - ES₃,

(11)

∂τ

Уравнения Блоха имеют вид [3]

∂S₃

=ES₂,

(12)

[

]

∂τ

∂_tρ =

ρ,

(5)

∂E

∂²

iℏ

=S₂ +a

S₂,

(13)

∂χ

∂τ²

со следующим в случае ДУС гамильтонианом:

(

)

(

)

где τ = ω₀t, ω₀ — произвольная частота, ω = ω₁₂/ω₀,

ℏω₁₂

-1

d₁₁

d₁₂

Ĥ₌

μ = (d₁₁ - d₂₂)/(2d₁₂) — приведенный к безразмер-

E_x,

(6)

d₂₁

d₂₂

ному виду постоянный дипольный момент,

где ℏω₁₂ — энергия перехода и d_ij , i, j = 1, 2, — эле-

2d_xE_x

2ω²⁰l²γ_e

менты дипольной матрицы. Поляризации p для од-

E =

(14)

ℏω₀

c²(1 + 2γ_e)

ной ДУС имеет вид

(

)

∂

cℏω

∂

(15)

∂χ

4πd2xn_m (1 + 2γ_e)2

ω₀ ∂z

∂τ

p=tr

(d₁₁ + d₂₂) +

При выводе уравнения (13) учитывалось, что по-

(d₁₁ - d₂₂) (ρ₁₁ - ρ₂₂) + ρ₁₂d₂₁ + ρ₂₁d₁₂,

(7)

ляризация (2) включает как недиагональную про-

порциональную S₁, так и диагональную пропорци-

где ρ_ij — элементы матрицы плотности, ρ₁₁+ρ₂₂ = 1,

ональную S₃ части. Вычисляя первые производные

d₂₁

= d∗12. Динамика ДУС в электрическом по-

по t от этих частей и используя уравнения (10)-(12),

ле описывается вращением вектора Блоха S(t, z) =

находим, что члены, пропорциональные ES₃, сокра-

= {S_x, S_y, S_z} ≡ {S₁, S₂, S₃} с компонентами

щаются и в правой части остается только компонен-

ρ₁₂ + ρ₂₁

ρ₁₂ - ρ₂₁

та S₂. Для случая a = 0 аналогичный вывод системы

S₁ =

S₂ =

уравнений (10)-(13) впервые приведен в работе [8].

(8)

ρ₁₁ - ρ₂₂

S₃ =

Система (10)-(13) является необходимым усло-

вием для коммутативности следующих линейных

Часто плотность активных атомов или молекул

систем:

в реальной среде достаточно мала, что позволяет,

следуя работе [1], ввести малый параметр. Норма-

∂_τ Φ =

лизованная плотность ДУС имеет тот же порядок

[

]

величины, что и производная ∂_z + n_d/c∂_t от ампли-

-iλ

(1-bλ) (F -m)

Φ,

(16)

туды поля. Здесь c/n_d — фазовая скорость света,

− (1+bλ) (F -m)

iλ

596

ЖЭТФ, том 158, вып. 4 (10), 2020

Совместное влияние диполь-дипольного взаимодействия. ..

⎡

(

)

⎤

∑

⎢

if₁S₁ + if₃S₃

h_jS_j + a∂_τ S₂

⎥

⎢

⎥

j=1

⎢

(

)

⎥Φ.

∂_χΦ =

(17)

⎢

⎥

W (λ)

∑

⎣

⎦

h_jS_j + a∂_τ S₂

-if₁S₁ - if₃S₃

j=1

Здесь b = 2√a, a ∈ R,

уравнениям соответствует спектральная проблема

(

)(

)

(СП) Вадати - Конно - Ичикавы [37], которая отли-

f₃ = λ

1+μ²

1-b²λ²

f₁ = μf₃,

(18)

чается от (16) недиагональными членами. Решения

(

)

h₁ = -gω

1-b²λ²

h₃ = -μ h₁,

(19)

этих уравнений были найдены ранее разными спо-

(

)

собами [37-40].

h₁ = -gω

1-b²λ²

h₃ = -μh1,

(20)

(

)

Система уравнений, также описывающая ди-

h₂ = 2igλ

1+μ² -ω²a

(21)

(

)

намику однокомпонентного поля без огибающей с

h₂ = -2igλ

1+μ² -ω²a

(22)

ПДМ, выведена в работе [18]. Авторы работы [18]

(

)

применили приближения, позволяющие свести по-

1+μ²

(1 - bλ)

√

(23)

лученную систему уравнений к тем РУМБ, что и в

1+μ² -ω²a

работах Матсуно [35]. Однако этот подход неприме-

(

)

1+μ²

(1 + bλ)

ним к системе (10)-(13) без исключения безразмер-

g=-

√

(24)

1+μ² -ω²a

ной частоты ω. Поскольку в настоящей работе рас-

(

)

сматривается случай U_d = dE_x ≲ ℏω₁₂, подход Мат-

W (λ) = ω² - 4λ²

1+μ²

(25)

суно неприменим. Поэтому будем находить решение

(

)

1+μ²

другим способом. Следуя работе [33], преобразуем

F =

√

(26)

систему уравнений (16) к СП, которая ранее исполь-

1+μ² -ω²a

ωμ

зовалась при нахождении решений известных моде-

√

(27)

лей, таких как уравнения Ландау - Лифшица, двух-

1+μ² -ω²a

и четырехволнового взаимодействий, см., например,

Для ω = 0 система (10)-(13) приводится к обобще-

работы [41-43] и ссылки в них. Для этого введем но-

√

нию уравнения синус-Гордона [34] вида

вую переменную u и функции R(u) = F/

1+b²F²,

√

H(u) = 1/

1 + b²F² или

∂_τ ∂_χU = (1 + ν∂2t)sin(U).

(28)

R(u)

Решения уравнения (28) найдены в работах [34, 35]

dτ = H(u) du, F (u) =

для разных знаков ν. Матсуно [35] преобразовал

H(u)

(29)

√

уравнение (28) к известной простой версии РУМБ.

H(u) =

1 - b²R(u)².

К такому же уравнению приводятся уравнения Ша-

фера - Вейна [36] и некоторые его обобщения. Этим

Тогда СП (16) принимает вид

[

]

-iλH

(1 - bλ) (R - mH)

∂_uΦ =

Φ.

(30)

− (1 + bλ) (R - mH)

iλH

3. СИММЕТРИИ

L^∗(λ^∗) = M±1L(λ)(M±1)-1.

(31)

Из свойств симметрии линейных систем (16),

Здесь Φ^∗(λ^∗) = M±1Φ(λ),

(

)

(17) или (17), (30) и, соответственно, матричных

f_±(λ)

функций Йоста Φ, приведенных ниже в этом раз-

M±1 =

(32)

деле, следует, что каждый полюс λ_j в верхней или

нижней комплексной полуплоскости преобразуется

b₀λ - 1

f₊(λ) =

a > 0,

(33)

в три следующих: {-λ^∗j, -λ_j, λ^∗j}, с помощью пре-

b₀λ + 1

образований симметрии. Перечислим эти свойства

f_-(λ) = -1, a < 0,

(34)

симметрии для матрицы L. Для второй матрицы A

свойства симметрии те же и мы их не приводим.

b = b₀ ∈ R.

597

А. А. Заболотский

ЖЭТФ, том 158, вып. 4 (10), 2020

II)

по известному решению Φ[0], L[0], A[0] калибровоч-

L^∗(-λ^∗) = M±2L(λ)(M±2)-1.

(35)

ным преобразованием. Новое решение G[1], H[1] на-

ходится из «нулевого» G[0], H[0] посредством урав-

Здесь Φ^∗(-λ^∗) = M±2Φ(λ),

нений

(

)

L[1]P [1] - ∂_τ P [1] = P [1]L[0],

(40)

M±2 =

(36)

-f_±(λ)

A[1]P [1] - ∂_χP [1] = P [1]A[0],

(41)

III)

где L[N], A[N], N = 0, 1, — матрицы (30) и (17) с

L(-λ) = M±3L(λ)(M±3)-1.

(37)

G = G[N], H = H[N] и S_j[N],j = 1,2,3, соответ-

ственно. P в общем виде для произвольного N опре-

Здесь Φ(-λ) = M±3Φ(λ),

деляется из условия, см. [45, 46],

(

)

P (λ_j , τ)Φ(λ_j , τ)q_j = 0,

(42)

M±3 =

(38)

-1

где qj — нетривиальный постоянный вектор, j =

Функция Йоста с учетом свойств симметрии име-

= 0, . . ., 2N. Условие (42) может быть представлено

ет вид

в виде

(

)

(

)

α_j(τ)

P (λ_j , τ)

≡ 0,

(43)

ψj1

f_±(λ^∗j)ψ∗j2

Ψ^±j =

(39)

ψj2

ψ^∗

где

φ₂ - ϱ_jϕ₂

α_j(τ) =

;

(44)

1 - ϱjϕj

4. ПРЕОБРАЗОВАНИЕ ДАРБУ

φ = (φ₁,φ₂)^T, ϕ = (ϕ₁,ϕ₂)^T — два решения линей-

Используем метод построения солитонных реше-

ных систем (17), (30); ϱ_j — произвольная константа.

ний преобразованием Дарбу [44-46]. Новое решение

Свойству симметрии I удовлетворяет следующая

Φ[1] = P Φ[0], отвечающее потенциалу L[1], строится

форма оператора:

⎛

⎞

∑

p₀ +

p_jλ^j

(1 - bλ)

s_jλ

∑

⎜

⎟

⎜

j=1

j=0

⎟

P =

P_j(λ) =

⎜

⎟

(45)

⎝

∑

⎠

j=0

- (1 + bλ)

s^∗jλ^j

p∗0 +

p^∗jλ^j

j=0

j=1

1-b^∗λ^∗a

Из уравнений (43), (44) и выражения (45) нахо-

β_a(-λ^∗a) =

дим линейную систему уравнений

α^∗(λ)

(50)

β_a(-λ_a) = - (bλ_a + 1)α(λ).

∑

p_jλ^j

+β_a

s_jλ^ja = -p₀,

(46)

Таким образом, простейшее невырожденное соли-

j=1

j=0

тонное решение отвечает 4N полюсам в комплекс-

∑

ной плоскости.

p_jλ^j∗a + γ^∗

s_jλ^j∗a = -p₀.

(47)

Из уравнений (30) и выражения (40), сравнивая

j=1

j=0

коэффициенты перед λN+1, найдем связь между ре-

Здесь

шением с N = 0 и N-солитонным решением в мат-

1 - bλ_a

ричной форме:

β_a =

γ_a = -(1 + bλ_a)α_a,

(48)

α_a

-1

L[N] = P_N L[0]P_N

(51)

a = 1,...,N. Используя свойства симметрии I-III,

находим

Из (51) находим

1 - bλ_a

β_a(λ_a) =

[

(

)

]

α(λ)

(49)

G[0]

p2N -b²s2N-1

+2iH[0]p_NsN-1

G[N] =

(52)

β_a(λ^∗a) = - (b^∗λ^∗a + 1)α^∗(λ),

|p_N |² - b²|sN-1|²

598

ЖЭТФ, том 158, вып. 4 (10), 2020

Совместное влияние диполь-дипольного взаимодействия. ..

(

)

(

)

ib²G[0]

p^∗

sN-1 - p_N s∗N-1

+ H[0]

|p_N |² + b²|sN-1|²

H[N] =

(53)

|p_N |²

- b²|sN-1|²

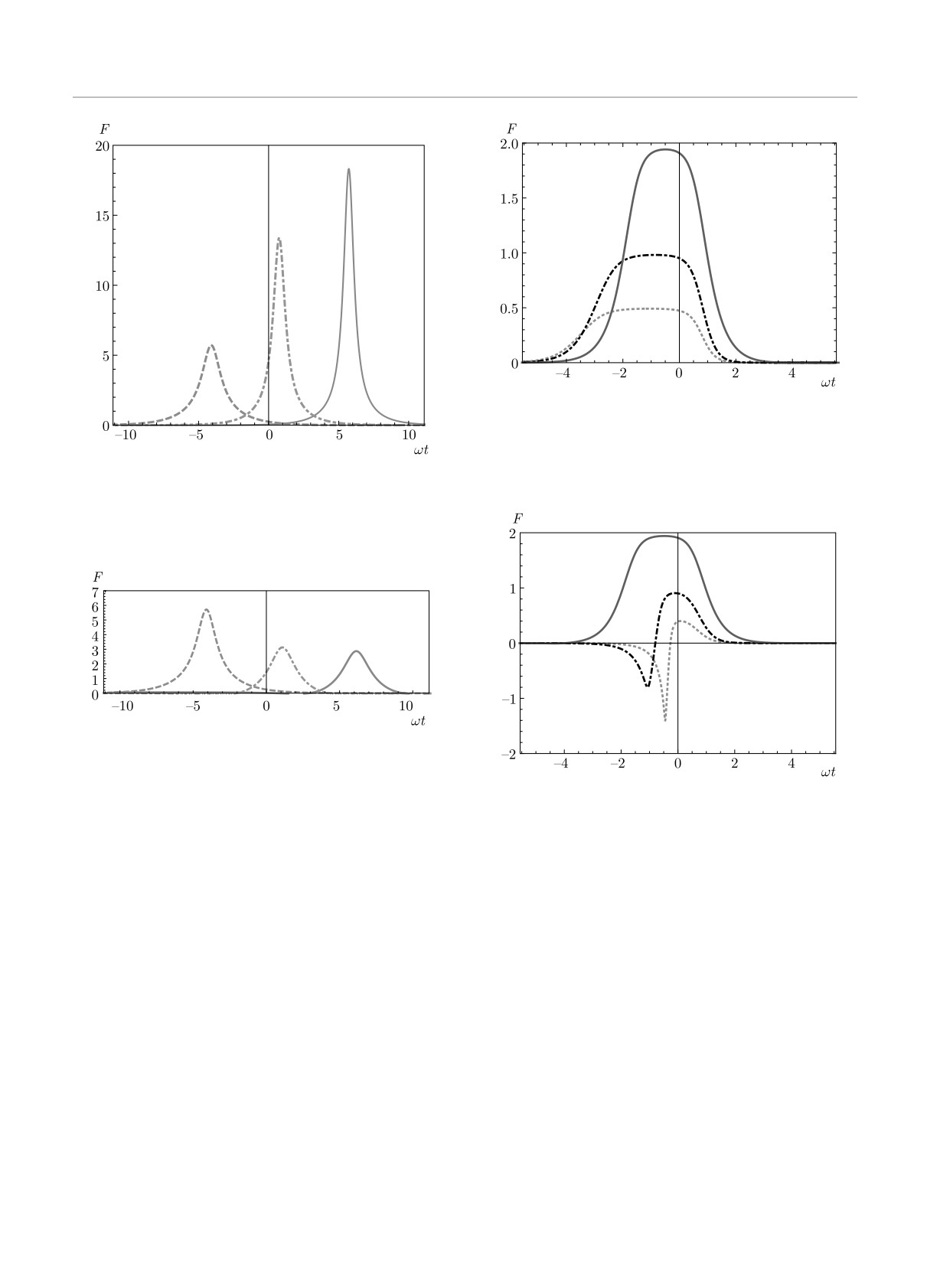
Здесь G[N] = R[N] - mH[N] и G[0] = R[0] - mH[0]

более быстром росте амплитуды импульса, чем в

отвечает исходному решению F(τ) = R(u)/H(u),

случае отсутствия ПДМ. Для параметров η₁ ≈ 0.5,

dτ = H(u)du.

d ≈ 0.5 решение медленно возрастает с ростом m и

Зависимость функции α_j от χ находим из второй

для m ≈ 0.5-1 становится сингулярным. Амплитуда

системы уравнений (17) и соответствующего преоб-

импульса растет как с ростом m для m > 0, так и

разования Дарбу. Система уравнений (17) облада-

с ростом |d|. Для m < 0 с ростом |m| происходит

ет такими же свойствами симметрии, как и система

уменьшение амплитуды импульса, см. рис. 2. Обна-

(30), и для рассматриваемых в работе простых на-

ружено, что форма импульса в присутствии диполь-

чально-краевых условий зависимость от χ проявля-

дипольного взаимодействия критически зависит от

ется в виде сдвига u → u - v_jχ, где v_j — фазовая

знака ПДМ. Это связано с эффектом Штарка и с

скорость.

тем, что выведенная вне рамок приближения мед-

ленных огибающих система уравнений (10)-(13) не

5. РЕШЕНИЯ МОДЕЛИ

симметрична относительно изменения знака поля

5.1. Солитонные решения

E → -E в отличие от уравнений Максвелла-Бло-

ха ДУС [3] для медленных огибающих.

Для асимптотик F (τ) → 0, S₁ → 0, S₂ → 0

Для sign(a) > 0 с ростом a происходит умень-

при τ → ±∞ или R → 0 для u → ±∞ матрицы

шение амплитуды солитона и его уширение. В

в правых частях уравнений (30) и (17) различаются

этом случае с ростом μ также наблюдается уси-

только общим множителем и одновременно приво-

ление действия диполь-дипольного взаимодействия.

дятся к диагональному виду. Найдем два решения

Численное решение системы (10)-(13) для простых

φ, ϕ уравнений (30) и (17) для нулевого фонового

начально-краевых условий, приведенных выше, по-

решения R[0] = 0, H[0] = 1, S₁[0] = S₂[0] = 0 и на-

казывает такую же зависимость от ПДМ, как и по-

чальных условий φ = (1, 0)^T , ϕ = (0, 1)^T . Для ϱ_j =

√

лученные солитонные решения. На рис. 5 приведены

bλ_j - 1/

bλ_j + 1 находим из (44)

результаты численного решения системы (10)-(13)

α_j = -ϱ_je2(u-vjχ)Ωj ≡ e2(u-vjχ)Ωj +gj+ihj .

(54)

для b = 0.5i и разных значений m.

√

Здесь Ω_j = b²λ2jm² - λ2j - m², g_j, h_j — действи-

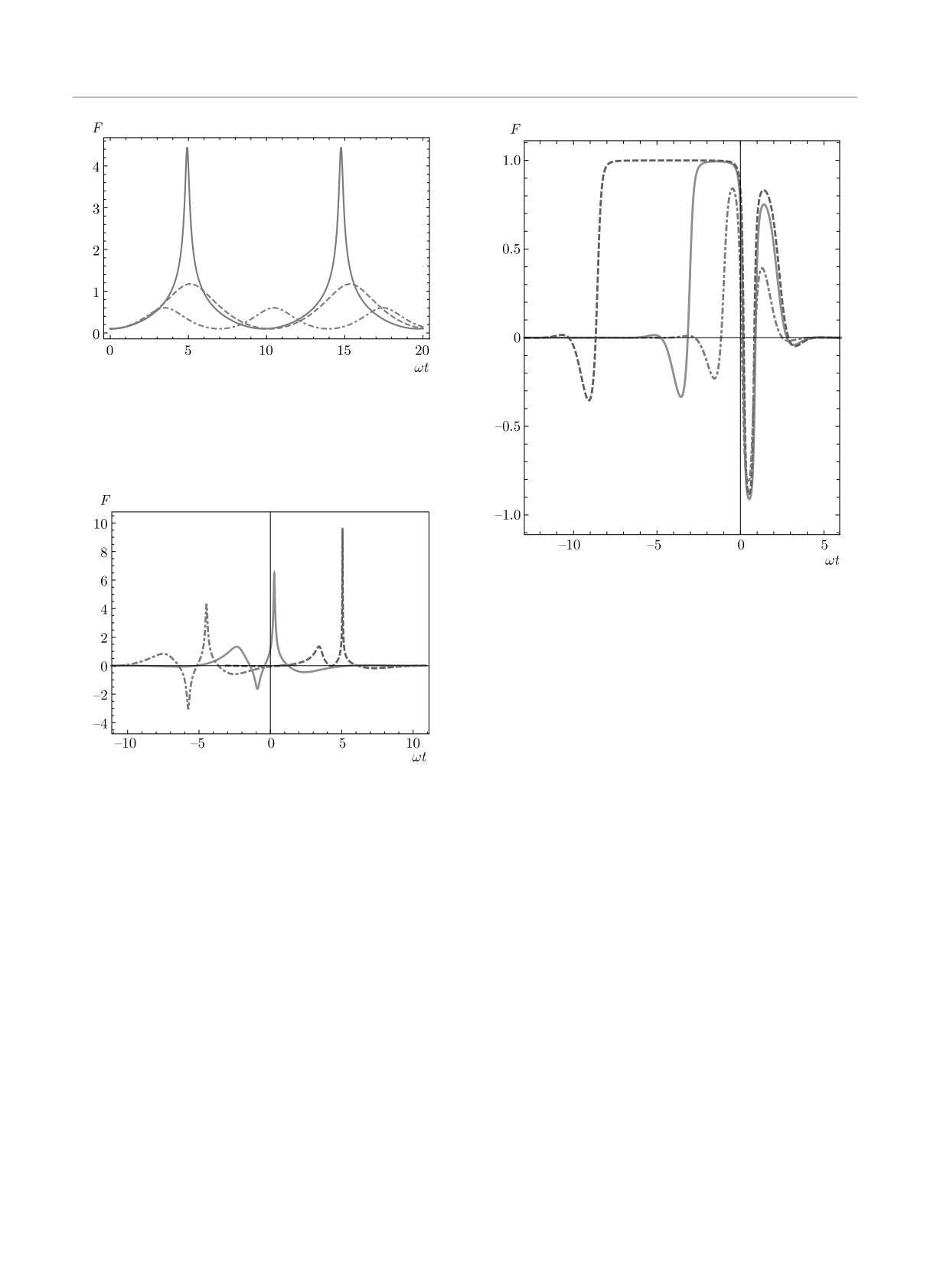
5.2. Бризерные решения

тельные константы и v_j — скорость солитона. Для

b = id, λ_j = iη_j, d,η_j ∈ R имеем

Бризерные решения находим для асимптотики

(

)

(

)(

)

R - mH → 0, т.е. H →

1+b²m²

-1/2. Каждое ре-

μ² + 1

1-d²η²

v_j = - sign(S₃[0])

(55)

шение отвечает четырем полюсам {λ₁, -λ₁, λ^∗, -λ₁}

4η2j (μ² + 1) + ω²

в системе уравнений (46), (47), решения которой

и для b = d, λ_j = iη_j , d, η_j ∈ R —

приведены в Приложении. Полюсу λ₁ отвечает ре-

(

)(

)

шение α₁ = exp(-iλ₁θ(λ₁) + iψ₀ + θ₀), см. подробнее

μ² + 1

d²η2j

v_j = - sign(S₃[0])

(56)

в Приложении. Значения β_j в уравнениях (46), (47)

4η2j (μ² + 1) + ω²

находим из (48) и свойств симметрии (49) и (50).

∫

Интегрируя равенство τ(u) - τ0 =

H (u) du, на-

Совместное влияние диполь-дипольного взаимодей-

ствия и ПДМ для b = id, d ∈ R, приводит к резкому

ходим солитонные решения в виде неявной зависи-

мости F = G/H + m от τ(u). Ввиду громоздкости

усилению более высоких амплитудных пиков бризе-

ра. С ростом параметров m > 0, Im λ₁, |d| решение

эти выражения вынесены в Приложение. Аналити-

ческие вычисления формул (52), (53) могут быть вы-

становится сингулярным. С увеличением m > 0, как

и в случае солитонного решения, приведенного вы-

полнены с помощью пакета Mathematica. Графики

ше, сингулярность возникает для меньших значений

солитонного решения показаны на рис. 1, 2 для зна-

|d|, Im λ₁. Для формирования мощного короткого

ка sign(a) < 0 и на рис. 3, 4 для sign(a) > 0. Анализ

импульса поля требуются меньшие значения коэф-

решений выявил критическое изменение зависимо-

сти формы импульса от b = i d, d ∈ R с ростом m для

фициента диполь-дипольного взаимодействия. Для

m < 0 с ростом |m|, так же как и выше, наблюдает-

m > 0. Совместное действие ПДМ ∝ μ и диполь-ди-

польного взаимодействия проявляется в критически

ся сглаживание и уменьшение амплитуд пульсаций

599

А. А. Заболотский

ЖЭТФ, том 158, вып. 4 (10), 2020

Рис. 3. Солитонное решение для η1 = 1, b = 0.5, m > 0.

Сплошной (синей), штрихпунктирной (черной) и пунктир-

ной (красной) линиям отвечает параметр ПДМ m = 0.01,

1, 1.5 соответственно

Рис. 1. Солитонное решение для η1 = 1, b = 0.6i, m > 0.

Штриховой (синей), штрихпунктирной (зеленой) и сплош-

ной (красной) линиям отвечает параметр ПДМ m = 0, 0.5,

0.6 соответственно

Рис. 2. То же, что на рис. 1, но для m < 0. Штриховой (си-

ней), штрихпунктирной (зеленой) и сплошной (красной)

линиям отвечает параметр ПДМ |m| = 0, 0.5, 0.6 соответ-

ственно

Рис. 4. То же, что на рис. 3, но для m < 0. Сплошной (си-

ней), штрихпунктирной (черной) и пунктирной (красной)

линиям отвечает параметр ПДМ |m| = 0.01, 1, 1.5 соот-

ветственно

бризера. В случае b = d ∈ R увеличение параметра

m, который нелинейно растет с ростом μ, см. выра-

жение (27), приводит к уширению импульса поля без

изменения его амплитуды. На рис. 6 и 7 показано из-

поль-дипольного взаимодействия и эффекта Штар-

менение формы импульса с изменением коэффици-

ка, обусловленного наличием ПДМ в двухуровне-

ента b, характеризующего диполь-дипольное взаи-

вой среде. Обнаружено, что влияние ПДМ в изу-

модействие для m = 0.01. Аналогичная динамика

чаемой системе без учета диполь-дипольного взаи-

наблюдается для фиксированного коэффициента b

модействия несущественно при тех же прочих пара-

и с ростом m.

метрах. В частности, для параметров, отвечающих

рис. 1, те же изменения ПДМ без диполь-дипольного

взаимодействия привели к изменению амплитуды на

менее чем 1 %. Без ПДМ условия формирования уз-

6. ЗАКЛЮЧЕНИЕ

кого мощного импульса требуют значений коэффи-

Решения представленной в работе интегрируе-

циента диполь-дипольного взаимодействия в норми-

мой модели (10)-(13) использованы для анализа эф-

рованном виде ≈ 0.5-1. В присутствии ПДМ, кото-

фектов, вызванных одновременным действием ди-

рый может составлять 1-3 дипольных моментов пе-

600

ЖЭТФ, том 158, вып. 4 (10), 2020

Совместное влияние диполь-дипольного взаимодействия. ..

Рис. 5. Численное решение для F (0) = 0.01, S3(0) = -1,

b = 0.5i для периодических граничных условий. Сплош-

ной, штриховой и штрихпунктирной линиям соответствует

m = 1,0,-1

Рис. 7. Бризерное решение для ζ1 = 0.7, η1 = 0.6. Штрих-

пунктирной (фиолетовой), сплошной (красной) и штрихо-

вой (синей) линиям отвечает параметр b = 0.1, 0.3, 0.47

соответственно

слабого взаимодействия, приводящего к уравнени-

ям типа нелинейного уравнения Шредингера, этот

эффект не удается объяснить, хотя солитонные ре-

шения имеются в случаях, ассоциированных с обе-

Рис. 6. Бризерное решение для ζ1 = 0.7, η1 = 0.6. Штрих-

ими формами агрегатов [31, 47, 48]. В рамках вы-

пунктирной (фиолетовой), сплошной (красной) и штрихо-

веденной системы уравнений (10)-(13) этот резуль-

вой (синей) линиям отвечает параметр b = 0.1i, 0.3i, 0.47i

соответственно

тат можно объяснить различием знаков диполь-ди-

польного взаимодействия для J- и H-агрегатов кра-

сителей [32]. В приближении взаимодействия бли-

рехода [32], формирование короткого импульса воз-

жайших соседей J-агрегат отвечает мнимой конс-

можно и для относительно малых коэффициентов

танте b, а H-агрегат — действительной. Молеку-

диполь-дипольного взаимодействия (≪ 1).

лы цианиновых красителей, составляющие агрегат,

Модель выводилась для описания эволюции им-

как правило, имеют ПДМ, сравнимый с дипольным

пульсов электромагнитного поля. При этом система

моментом энергетического перехода или больший

уравнений (10)-(13) может быть использована для

него [32]. Длительность экситонных импульсов мо-

объяснения особенностей и различия условий фор-

жет быть достаточно мала для оправданности при-

мирования экситонных импульсов в протяженных

ближений, использованных выше. Эти факты ука-

цепочках молекулярных агрегатов разных цианино-

зывают на применимость полученных солитонных

вых красителей. Так, например, в цепочках J-аг-

решений для объяснения наблюдаемых эффектов в

регатов происходит формирование ультракоротких

длинных молекулярных цепочках и динамики воз-

экситонных импульсов [31, 47, 48]. В то же время

буждений в белковых молекулах и в ДНК. Зави-

для H-агрегатов при прочих одинаковых условиях

симость от знаков ПДМ и константы диполь-ди-

такие импульсы не наблюдались. В приближении

польного взаимодействия может быть использова-

601

А. А. Заболотский

ЖЭТФ, том 158, вып. 4 (10), 2020

на для влияния на перенос энергии в системе моле-

= exp(θ + iψ₀) имеем

кулярный агрегат - квантовая точка. Известно, что

i cth θ

несимметричные квантовые точки могут обладать

p₁ =

(A.1)

относительно большим ПДМ. Динамика возбужде-

eiψ0 cschθ

ния в среде, сформированной в виде длинной цепоч-

s₀ =

(A.2)

1 - idη

ки квантовых точек, помещенных вблизи волновода,

может быть описана аналогичной моделью [28, 29].

где θ = θ_sr - θ₀, θ₀, ψ₀ — константы, которые опре-

Изменение направления ПДМ квантовых точек в та-

деляются из равенства

кой системе может быть использовано для контроля

√

bλ₁ - 1

эволюции поля в волноводе.

=eiψ0-θ0,

(A.3)

bλ₁ + 1

Зависимость m(μ) имеет нелинейный вид, как

видно из выражения

(27). Динамика солитона

√

критическим образом

зависит от значений μ.

θ_sr = 2

η² - m² (d²η² + 1)×

[

(

)(

)]

Например, солитонное решение для a < 0, m >

(

)

μ² + 1

d²η² + 1

> m_c, где m2c

d²η² + 1

> η², трансформируется в

× u + ϵχ

(A.4)

4η² (μ² + 1) + ω²

периодическое.

Зависимость амплитуды импульса от ПДМ ∝ μ

Здесь и ниже ϵ = sign(S₃(0)). Для b = id, d ∈ R,

не монотонна для b = d ∈ R и значений ПДМ, таких

λ₁ = iη и α₁(θ) = eθ+iψ0

что 1+μ² ∼ ω²d²/4. Таким образом, приведенные ре-

i(dη sh θ - ch θ)

шения демонстрируют многообразие поведения, за-

p₁ =

(A.5)

η(dη ch θ - sh θ)

висящее от коэффициентов ПДМ и диполь-диполь-

eiψ0

ного взаимодействия.

s₀ = -

(A.6)

dη ch θ - sh θ

В заключение отметим, что модель (10)-(13)

где θ = θ_si - θ₀, θ₀, ψ₀ — константы, которые опре-

допускает обобщение на случай двухкомпонентного

деляются из равенства (A.3),

поля. Интегрируемая модель редуцированных урав-

нений Максвелла - Блоха, описывающая эволюцию

√

θ_si = -2

η² + m² (d²η² - 1)×

поляризации поля в ДУС с ПДМ, но без учета

[

(

)(

)]

диполь-дипольного взаимодействия, представлена в

μ² + 1

d²η² - 1

× u + ϵχ

(A.7)

работе [13]. Критическое влияние поляризационных

4η² (μ² + 1) + ω²

эффектов на формирование импульсов может быть

результатом кручения цепочки [19]. Из этого можно

2. N = 2

сделать вывод, что учет двух компонент поляри-

Для полюсов {λ₁, -λ∗1, λ^∗, -λ₁}, λ₁ = ζ+iη, ζ, η ∈

∈ R и α₁ = exp(iψ + θ) с учетом свойств симметрии

зации может привести к ряду новых интересных

эффектов.

(31) решение системы уравнений (46), (47) в случае

b = id, d ∈ R, имеет вид

{

[

(

)

]

Финансирование. Работа выполнена при

p₂ = -8

-d²ζ⁴ + η² cos(2θ)

d²

ζ² + η²

-1

поддержке Российского фонда фундаментальных

[

(

)

]

+ ζ2 ch(2ψ)

d²

ζ² + η²

исследований (грант

№18-02-00379) и Мини-

}

стерства науки Российской Федерации (грант

+ d²η⁴+2dζ3 sh(2ψ)+2dη3 sin(2θ)+ζ²+η²

(A.8)

№ AAAA-A17-117060810014-9).

{

[

(

)

]

s₁ = 32iζη

ch ψ

ζ cosθ - d

ζ² + η²

sin(θ)

+ η sinθ shψ}. (A.9)

Здесь

ПРИЛОЖЕНИЕ

2η

θ=

√

(u - χc0iv_ti) + θ₀,

(A.10)

1-d²m²

1. N = 1

2ζ

ψ=

√

(u + χc0iv_pi) + ψ₀,

(A.11)

Вследствие свойств симметрии простейшему со-

1-d²m²

(

)₂ √

литонному решению отвечает полюс, лежащий на

c0i = S₃(0)

μ² + 1

1-d²m²,

(A.12)

комплексной оси. Для b = d, d ∈ R, λ₁ = iη и α₁ =

602

ЖЭТФ, том 158, вып. 4 (10), 2020

Совместное влияние диполь-дипольного взаимодействия. ..

(

)(

(

)

(

)

μ² + 1

ζ² + η²

d²

ζ² + η²

-1

+ω²

d²

η² - 3ζ²

-1

v_ti =

(A.13)

16 (μ² + 1)² (ζ² + η²)² - 8 (μ² + 1)ω²(ζ - η)(ζ + η) + ω⁴

(

)(

(

)

(

)

μ² + 1

ζ² + η²

d²

ζ² + η²

-ω²

d²

ζ² - 3η²

v_pi =

(A.14)

16 (μ² + 1)² (ζ² + η²)² - 8 (μ² + 1)ω²(ζ - η)(ζ + η) + ω⁴

θ₀, ψ₀

— действительные константы. Аналогично

Здесь

для b = d находим

2η

{

[

(

)

]

θ=

√

(u - χc0rv_tr) + θ₀,

(A.17)

p₂ = -8

-d²ζ⁴ + η² cos(2θ)

d²

ζ² + η²

-1

1+d²m²

[

(

)

]

+ ζ2 ch(2ψ)

d²

ζ² + η²

+d²η⁴ +

2ζ

}

ψ=

√

(u + χc0rv_pr) + ψ₀,

(A.18)

+ 2dζ³ sh(2ψ) + 2dη³ sin(2θ) + ζ² + η²

(A.15)

1+d²m²

(

)₂ √

{

[

(

)

]

c0r = S₃(0)

μ² + 1

1+d²m²,

(A.19)

s₁ = 32iζη

shψ

ζ² + η²

cosθ + η sinθ

+ ζ cosθchψ}. (A.16)

(

)(

(

)

(

)

μ² + 1

ζ² + η²

d²

ζ² + η²

-1

+ω²

d²

η² - 3ζ²

-1

v_tr =

(A.20)

16 (μ² + 1)² (ζ² + η²)² - 8 (μ² + 1)ω²(ζ - η)(ζ + η) + ω⁴

(

)(

(

)

(

)

μ² + 1

ζ² + η²

d²

ζ² + η²

-ω²

d²

ζ² - 3η²

v_pr =

(A.21)

16 (μ² + 1)² (ζ² + η²)² - 8 (μ² + 1)ω²(ζ - η)(ζ + η) + ω⁴

ЛИТЕРАТУРА

12. A. A. Zabolotskii, Phys. Rev. E 75, 036612 (2007).

J. C. Eilbeck, J. Phys. A: Math. Gen. 5, 1355 (1972).

13. A. A. Zabolotskii, Phys. Rev. E 77, 036603 (2008).

G. L. Lamb, Phys. Rev. A 9, 422 (1974).

14. С. В. Сазонов, Н. В. Устинов, ЖЭТФ 127, 289

(2005).

L. Allen and J. H. Eberly, Optical Resonance and

15. С. В. Сазонов, Н. В. Устинов, ЖЭТФ 142, 842

Two-Level Atoms, Wiley, New York (1975).

(2012).

A. I. Maimistov and A. M. Basharov, Nonlinear Opti-

16. С. В. Сазонов, Н. В. Устинов, ЖЭТФ 151, 249

cal Waves, Kluwer Acad. Publ., Dordrecht (1999).

(2017).

A. A. Zabolotskii, Eur. Phys. J. Spec. Topics 173,

17. S. V. Sazonov and N. V. Ustinov, Physica D 366, 1

193 (2009).

(2018).

А. И. Маймистов, КЭ 40, 756 (2010).

18. S. V. Sazonov and N. V. Ustinov, Phys. Scripta 94,

V. E. Zakharov, S. V. Manakov, S. P. Novikov,

115208 (2019).

and L. P. Pitaevskii, Theory of Solitons: the Inverse

19. А. А. Заболотский, Письма в ЖЭТФ 110, 303

Scattering Method, Nauka, Moscow (1980); Consul-

(2019).

tants Bureau, New York (1984).

20. J.-G. Caputo and A. I. Maimistov, Phys. Lett. A 296,

M. Agrotis, N. M. Ercolani, S. A. Glasgow, and

34 (2002).

J. V. Moloney, Physica D 138, 134 (2000).

21. А. И. Маймистов, Дж.-Ги Капуто, Опт. и спектр.

А. А. Заболотский, Письма в ЖЭТФ 76, 709

94, 275 (2003).

(2002).

22. M. A. Agrotis, Phys. Lett. A 315, 81 (2003).

10.

А. А. Заболотский, Письма в ЖЭТФ 77, 558 (2003)

[A. A. Zabolotskii, JETP Lett. 77, 464 (2003)].

23. L. W. Casperson, Phys. Rev. A 57, 609 (1998).

11.

H. Steudel, A. A. Zabolotskii, and R. Meinel, Phys.

24. A. Brown, W. J. Meath, and P. Tran, Phys. Rev.

Rev. E 72, 056608 (2005).

A 63, 013403 (2000).

603

А. А. Заболотский

ЖЭТФ, том 158, вып. 4 (10), 2020

25.

D. You, D. R. Dykaar, and P. H. Bucksbaum, Opt.

37.

K. Konno, Y. W. Ichikawa, and M. Wadati, J. Phys.

Lett. 18, 290 (1993).

Soc. Jpn 50, 1025 (1981).

26.

M. Wittmann, A. Nazarkin, and G. Korn, Opt. Lett.

38.

J. C. Brunelli, J. Math. Phys. 46, 123507 (2005).

26, 5 (2001).

39.

A. Sakovich and S. Sakovich, J. Phys. A 39, L361

27.

H. Kuhn and C. Kuhn, in J-Aggregates, ed. by T. Ko-

(2006).

bayashi, World Sci., Singapore (1996), Ch. 1.

40.

V. K. Kuetche, T. B. Bouetou, and T. C. Kofane, J.

Phys. Soc. Jpn 76, 024004 (2007).

28.

A. V. Sorokin, A. A. Zabolotskii, N. V. Pereverzev,

S. L. Yefimova, Y. V. Malyukin, and A. I. Plekhanov,

41.

D. J. Kaup, Physica D: Nonlin. Phenom. 6, 143

J. Phys. Chem. C 118, 7599 (2014).

(1983).

29.

А. А. Заболотский, ЖЭТФ

152,

676

(2017)

42.

A. A. Zabolotskii, Physica D: Nonlin. Phenom. 40,

[A. A. Zabolotskii, JETP 125, 572 (2017)].

283 (1989).

30.

J. M. Hyman, D. W. McLaughlin, and A. C. Scott,

43.

R. F. Bikbaev, A. I. Bobenko, and A. R. Its,

Physica D, Nonlin. Phenom. 3, 23 (1981).

Theor. Math. Phys. 178, 143 (2014). https://doi.org/

10.1007/s11232-014-0135-4.

31.

Yu. B. Gaididei, K. Ø. Rasmussen, and P. L. Chris-

tiansen, Phys. Rev. E 52, 2951 (1995).

44.

V. B. Matveev and M. A. Salle, Darboux Transfor-

mations and Solitons, Springer, Berlin (1991).

32.

F. Würthner, T. E. Kaiser, and C. R. Saha-Möller,

Angew. Chem. Int. Ed. 50, 3376 (2011), doi:10.1002/

45.

H. Steudel and R. Meinel, Physica D 87, 127 (1995).

anie.201002307.

46.

H. Steudel, R. Meinel, and G. Neugebauer, J. Math.

33.

A. A. Zabolotskii, Phys. Rev. A 85, 063833 (2012).

Phys. 38, 4692 (1997).

34.

J. Lenells and A. S. Fokas, J. Math. Phys. 51, 023519

47.

Н. В. Высотина, Н. Н. Розанов, В. Е. Семенов, Опт.

(2010).

и спектр. 106, 793 (2009) [N. V. Vysotina, N. N. Ro-

sanov, and V. E. Semenov, Opt. Spectrosc. 106, 713

35.

Y. Matsuno, J. Phys. A: Math. Theor. 43, 105204

(2009)].

(2010); J. Phys. A: Math. Theor. 43, 375201 (2010).

48.

N. N. Rosanov, S. V. Fedorov, L. A. Nesterov,

36.

T. Schäfer and C. E. Wayne, Physica D 196, 90

and N. A. Veretenov, Nanomaterials (Basel) 9, 826

(2004).

(2019).

604