ЖЭТФ, 2020, том 158, вып. 5 (11), стр. 800-811

СПЕКТРЫ ШТАРКА - ЗЕЕМАНА И БЛОХИНЦЕВА

В РИДБЕРГОВСКИХ АТОМАХ

А. Ю. Летунов^*, В. С. Лисица

Национальный исследовательский центр «Курчатовский институт»

123182, Москва, Россия

Национальный исследовательский ядерный университет «МИФИ»

115409, Москва, Россия

Поступила в редакцию 12 мая 2020 г.,

после переработки 12 мая 2020 г.

Принята к публикации 19 июня 2020 г.

Рассматривается проблема ридберговских атомных спектров в скрещенных электрическом F и магнит-

ном B полях (комбинация эффектов Штарка и Зеемана), а также в осциллирующем электрическом

поле. Ключевой проблемой является гигантский массив радиационных переходов между ридберговски-

ми атомными состояниями. Для решения этой задачи были применены различные квазиклассические

подходы. Найдены новые приближенные правила отбора для радиационных переходов и они в дальней-

шем применены для упрощения сложных формул Гордона, содержащих гипергеометрические ряды, до

тривиальных тригонометрических функций. Получены простые аналитические выражения для диполь-

ных матричных элементов в водородоподобном атоме для серии Hnα. Представлены результаты расчетов

для радиационного перехода с уровня n = 10 на n = 9 для случаев параллельных и перпендикулярных

полей F и B. Результат Блохинцева для одной штарковской компоненты обобщен на случай большого

массива радиационных переходов между ридберговскими атомными состояниями. Проведено сравнение

данных спектров в случае больших индексов модуляции со спектрами в статическом случае.

DOI: 10.31857/S0044451020110048

ветствие с классическими результатами [2]. В при-

сутствии электрического поля, переходя к парабо-

лической системе координат, приходится иметь де-

1. ВВЕДЕНИЕ

ло с отсутствием правил отбора для параболических

квантовых чисел n₁, n₂, что приводит к обязатель-

Проблема водородных спектров во внешних по-

ным трудностям в вычислениях, особенно для рид-

лях, рассматриваемая в этой работе, формаль-

берговских атомных состояний, где массив радиа-

но имеет квантовомеханическое решение. Однако

ционных переходов растет очень быстро (пропор-

его применение для определенных радиационных

ционально n⁴). Вопросы переходов между ридбер-

переходов, особенно между высоковозбужденными

говскими атомными состояниями представляют ин-

уровнями (ридберговскими), вынуждает работать

терес как с точки зрения фундаментальной науки,

с большим числом матричных элементов. Случай

так и с позиции приложений в вычислении профи-

постоянного электрического поля глубоко изучен с

лей интенсивности для лабораторной [7-9] и астро-

различных сторон. Общие выражения для сдвига

физической [10] плазмы. Целью настоящей работы

энергии и интенсивности радиационных переходов

является сравнение различных подходов для вычис-

хорошо известны в случаях сферической [1-3] и па-

ления дипольных матричных элементов, получение

раболической [4-6] систем координат. Для сфери-

приближенных правил отбора радиационных пере-

ческого квантования вычисления упрощены суще-

ходов между ридберговскими состояниями в при-

ствованием правила отбора для орбитального кван-

сутствии электрического поля. С учетом этих ре-

тового числа l, которое позволяет делать быстрые

зультатов будет показано, как сложные формулы

расчеты вероятностей перехода и изучать их соот-

для интенсивности в электрическом F и магнитном

B полях могут быть упрощены. В данной работе

^* E-mail: letunovandrey11@yandex.ru

800

ЖЭТФ, том 158, вып. 5 (11), 2020

Спектры Штарка - Зеемана и Блохинцева. ..

рассматриваются сравнительно сильные магнитные

Это становится возможным благодаря наличию

поля. Следовательно, поправками, связанными со

связи в случае кулоновского поля между вектором

спин-орбитальным взаимодействием, можно прене-

Рунге - Ленца и координатой:

бречь.

Общий подход для водородоподобных систем ос-

A=-

(7)

нован на свойствах симметрии кулоновского по-

ля. Эволюция атомных состояний определяется до-

Используя свойства углового момента векторов

полнительными интегралами движения, имеющими

(1), с помощью параболических состояний мы мо-

свойства углового момента J1,2, которые являются

жем выразить волновые функции электрона в пред-

комбинацией векторов обычного углового момента

ставлении чисел n, n^′, n^′′:

L и специфического интеграла движения в кулонов-

∑

ском потенциале — вектора Лапласа - Рунге - Ленца

|n, n^′, n^′′〉 =

d^ji

(α₁)d^ji

(α₂)|ni₁i₂〉,

(8)

1n^′

2n^′′

A [11]:

i1=-j i2=-j

J1,2 =

(L ± A),

(1)

где d^j

(β) — d-функция Вигнера,

m1m2

где «1» относится к знаку +, а «2» к знаку -.

Сдвиг энергии для атома водорода в электричес-

n-1

j =

(9)

ком поле F определяется проекциями векторов (1)

на ось z (ось z совпадает с направлением электри-

В формуле (8) α1,2 — углы между векторами J1,2

ческого поля):

и ω1,2. Формулы записаны в системе координат, в

которой направление магнитного поля совпадает с

ΔE⁽¹⁾ =

nF(i₂ - i₁),

(2)

осью z:

B∓

nF cosθ

где n — главное квантовое число, i1,2 — проекции

cosα1,2 =

(10)

векторов (1) на ось z.

ω1,2

В формуле (2) и во всех выражениях этой статьи

где θ — угол между электрическим F и магнитным

используются атомные единицы. Также нам необхо-

B полями.

дим только первый порядок теории возмущения, так

Выражение для координатного матричного эле-

что верхний индекс «(1)» будет опускаться в фор-

мента в представлении состояний (8) имеет сложную

мулах для сдвига энергии. Между параболическими

структуру. Оно содержит четыре суммы с большим

квантовыми числами и i1,2 существует связь [1]

числом слагаемых (∼ n⁴), четыре функции Вигне-

ра (эти математические объекты выражаются через

i₂ - i₁ = n₁ - n₂,

(3)

полиномы Якоби [12]) и громоздкие матричные эле-

i₂ + i₁ = m,

менты Гордона [4]. Однако использование свойств

симметрии кулоновского поля позволяет упростить

где n₁, n₂ — параболические квантовые числа.

финальные выражения до сравнительно коротких

Сдвиг атомной энергии в скрещенных полях F

формул.

и B определяется направлением векторов (1) на на-

Вычисление матричных элементов дипольного

правления ω1,2:

момента с помощью волновых функций, соответ-

ствующих проекциям векторов (1) на направления

ω1,2 =

B∓

nF.

(4)

(4), является очень громоздким. Тем не менее для

случая Δn ≪ n мы можем использовать новые пра-

Причиной этому служит тот факт, что мы можем

вила отбора для параболических квантовых чисел и

переписать возмущенную часть гамильтониана

приближенные выражения для координатных мат-

ричных элементов и упростить формулы для ин-

H₁ =

B·L+F·r

тенсивности излучения (интенсивность излучения в

в следующем виде:

дипольном приближении пропорциональна квадра-

ту модуля координатного матричного элемента).

H₁ = ω₁J₁ + ω₂J₂,

(5)

Благодаря уникальным свойствам кулоновского

поля, классические результаты начинают работать

E =ω₁n^′ +ω₂n^′′,

(6)

с хорошей точностью, даже когда n ∼ 1. Точные

где n^′ и n^′′ — проекции (1) на векторы (4).

выражения для дипольных матричных элементов

801

ЖЭТФ, вып. 5 (11)

А. Ю. Летунов, В. С. Лисица

ЖЭТФ, том 158, вып. 5 (11), 2020

были получены Гордоном [4-6]. Связь между раз-

при z = p и может оказаться, что удобнее пользо-

личными выражениями для матричного элемента Z

ваться следующим приближением для распределе-

была продемонстрирована в [13,14]. В данных рабо-

ния интенсивности вместо квадрата функции Бес-

тах автор показал, что точный квантовый результат

селя:

может быть выражен с помощью полиномов Якоби.

Используя этот прием, для больших n удается по-

I_s(Δω) =

√

θ((Δω_F )² -

(Δω_F )² - (Δω)²

казать, что формулы Гордона переходят в класси-

ческие борновские выражения для интенсивности.

- (Δω)²),

(14)

Подобные вычисления, оказывается, можно просто

где θ(z) — ступенчатая функция Хевисайда.

проделать для серии nα (Δn = 1) для матричного

Одно из важнейших свойств этого приближе-

элемента X (см. Приложение).

ния — то, что полный интеграл от (14) по всем час-

Вычисление интенсивности излучения водорода

тотам совпадает с интегралом от дельта-функцион-

в осциллирующем электрическом поле — очень ак-

ного распределения:

туальная проблема для атомной физики. Данная си-

туация может быть реализована, например, в турбу-

∫

лентной плазме. Также переменное поле может гене-

δ(ω) dω = 1.

Is(ω) dω =

рироваться лазерным излучением. Впервые данная

−∞

-∞

проблема рассматривалась в работе [15]. Блохинцев

Это демонстрирует соответствие между постоян-

получил выражение для интенсивности в случае од-

ным электрическим полем и случаем Ω → 0.

ной штарковской компоненты. Данная работа дала

толчок как для теоретических [16,17], так и для экс-

периментальных исследований [18, 19]. Подробный

2. ПРАВИЛА ОТБОРА ДЛЯ

анализ данной задачи представлен в [20-23]. Ни-

ПАРАБОЛИЧЕСКИХ КВАНТОВЫХ ЧИСЕЛ

же будет представлена краткая теория, связанная

В РИДБЕРГОВСКОМ АТОМЕ ВОДОРОДА

с этим вопросом.

Как было показано в [15], штарковская компо-

Классическое выражение для координатных

нента распадается на множество сателлитов, нахо-

матричных элементов между параболическими со-

дящихся друг от друга на расстоянии pΩ (p — целое

стояниями в атоме водорода было получено Борном

число, Ω — частота поля).

и Крамерсом [24,25]:

Рассмотрим водородоподобный атом во внешнем

поле:

zn1 n²mn

(σ₂JΔn1 (Δnσ₁)J′Δn

(Δnσ₁) -

1n2m

nΔn

F = F0 cos(Ωt).

(11)

− σ₁JΔn2(Δnσ₁)J′Δn1

(Δnσ₁)),

(15)

Так, приведенная к безразмерному виду интенсив-

ность одной штарковской компоненты будет равна

(

)

(

)

xn1 n² mn

(σ₃JΔn1(Δnσ₁)JΔn2 (Δnσ₁) -

1n2m

Δω

∑

⁽ Δω_F )

Δω

2nΔn

J²

-p

(12)

^p Ω

- σ₄JΔn2+1(Δnσ1)JΔn1+1(Δnσ1)),

(16)

p=-∞

Δn = n - n,

где J_p(z) — функция Бесселя порядка p,

[

]

〈n₁n₂ m|x|n₁n₂m〉 = (-1)Δm〈n₁n₂ m|y|n₁n₂m〉,

(17)

Δω_F =

F₀ n(n₁ - n₂) - n(n₁ - n₂) .

где J_v(x) и J^′v(x) — функция Бесселя и ее производ-

ная соответственно

В действительности индекс «p» пробегает конеч-

1√

ное число значений. Данное обстоятельство опреде-

σ₁ =

n₁(n₁ + m),

ляется условием

1√

∫

σ₂ =

n₂(n₂ + m),

S(z)dz = 1.

(13)

(18)

1√

σ₃ =

(n₁ + m)(n₂ + m),

Проблема числа сателлитов обсуждается в [20].

В случаеΔωFΩ≫1величина

(z) (ΔωFΩ^{называ-}

ется индексом модуляции) имеет резкий максимум

σ₄ =

√n₁n₂.

802

ЖЭТФ, том 158, вып. 5 (11), 2020

Спектры Штарка - Зеемана и Блохинцева. ..

Выражение (17) является общим для всех типов ди-

польных матричных элементов.

Точное выражение для координатных матрич-

ных элементов содержит гипергеометрические ря-

ды:

(

)

-4nn

ψ_m(n_i, n_i) = F

-n_i, -n_i, m + 1,

(19)

(n - n)²

где F (a, b, c, z) — гипергеометрическая функция, n и

n — главные квантовые числа, относящиеся к двум

различным состояниям.

Наличие этих сумм делает вычисление диполь-

ных матричных элементов очень затруднительным

для больших значений n. Для того чтобы решить

Рис. 1. Интенсивность излучения сигма-компоненты (де-

эту проблему, Гуляев получил другую асимптотику

ленная на максимум I) как функция энергетического сдви-

для координатных матричных элементов [26, 27]. В

га (приведенная к безразмерному виду частота — сдвиг

этих работах автор заметил, что последнее слагае-

энергии, деленный на ωF = 3F /2, где F — модуль элект-

мое в (19) много больше остальных (Δn ≪ n). Для

рического поля). Переход с уровня n = 7 на n = 6

серии nα данный подход позволяет получить про-

стые результаты:

данного расчета видно, что приближение ридбер-

√

говского атома применимо для водорода, даже если

Xm-1m =

(n₁ + m)(n₂ + m) ×

[

]

n ∼ 1.

(n₁ + 1)(n₂ + 1)

× 1-

(20)

Одно из важнейших преимуществ сферической

b²

системы координат — это наличие правила отбора

[

]

для орбитального числа l. Как мы увидим ниже, хо-

(n₁ + m)(n₂ + m)

Xm+1m =

√n₁n2 1-

(21)

тя исследование эффекта Штарка гораздо проще в

b²

параболической системе координат, отсутствие пра-

вил отбора для чисел n₁ и n₂ является большой

[√

проблемой для вычисления интенсивности излуче-

Z^mm =

(n₁ + m)n₁δK,+1 +

]

ния во внешних электрических и магнитных полях.

√

(n₂ + m)n₂δK,-1 ,

(22)

Однако для больших n это неудобство может быть

устранено. Для решения этой задачи будет исполь-

где b² = 4nn/(n - n)²,

зован подход из [26,27]. Для начала рассмотрим но-

вое квантовое число K (23).

K = (n₁ - n₂) - (n₁ - n₂).

(23)

Сдвиг энергии может быть переписан в следую-

щем виде:

Здесь величины с чертой относятся к состояниям с

Δω

более низкой энергией.

= Kn + Δnk,

(25)

ω_F

Финальной процедурой, которую необходимо

проделать для анализа приближения, является

где k = n₁ - n₂ — электрическое квантовое число.

сравнение матричных элементов Гуляева и Борна

Для каждого значения Δn квантовое число K

для σ-серии (X). Сдвиг энергии в этом случае равен

может принимать ограниченный ряд значений. Бо-

лее того, в классическом пределе интенсивность из-

Δω

= n(n₁ - n₂) - n(n₁ - n₂),

(24)

лучения сильно зависит от этого числа. Например,

ω_F

для серии nβ [27] абсолютное значение дипольных

где ω_F = 3F /2.

матричных элементов с числами K = ±1 и K = ±2

Во-первых, график, представленный на рис. 1,

на несколько порядков больше, чем остальных. Сле-

демонстрирует, что мы можем использовать любое

довательно, с ростом n нужно вычислять лишь

ранее упомянутое квазиклассическое приближение.

небольшую часть всех матричных элементов. Для

Во-вторых, это сравнение — хорошая иллюстрация

серии nα есть только три возможности: K = +1, -1

принципа соответствия в квантовой механике. Из

и K = 0.

803

А. Ю. Летунов, В. С. Лисица

ЖЭТФ, том 158, вып. 5 (11), 2020

Для K = 0 магнитное квантовое число долж-

Решение (32) представлено в Приложении:

но меняться. Правило отбора в параболических ко-

ординатах для m остается тем же. Формулы для

i₂ =i2 ±

дипольных матричных элементов выражены через

(33)

модуль магнитного квантового числа, так что, если

i₁ =i1 ±

это особо не оговаривается, используется обозначе-

ние |m| = m. Имеем

Здесь знак «+» соответствует m, m ≥ 0 и -m, m ≤

≤ 0. В данном случае m не обозначает модуль маг-

n₁ = n₁, n₂ = n₂,

(26)

нитного квантового числа! Другими словами, верх-

ний знак в (33) соответствует возрастанию магнит-

если Δm = -1,

ного квантового числа, а нижний — убыванию.

n₁ = n₁ + 1, n₂ = n₂ + 1,

(27)

если Δm = +1,

3. ДИПОЛЬНЫЕ МАТРИЧНЫЕ ЭЛЕМЕНТЫ

ДЛЯ ВОДОРОДОПОДОБНОГО АТОМА ВО

n₁ = n₁ + 1, n₂ = n₂

(28)

ВНЕШНИХ ЭЛЕКТРИЧЕСКОМ И

МАГНИТНОМ ПОЛЯХ

для K = +1,

В работе [11] атом водорода в скрещенных элек-

n₁ = n₁, n₂ = n₂ + 1

(29)

трическом и магнитном полях был впервые рассмот-

рен в рамках квантовой механики. Идеи этой работы

для K = -1.

были использованы в [8] для вычисления профилей

Из-за правила отбора для числа m случай K = 0

интенсивности спектральных линий. Согласно фор-

соответствует матричному элементу X, а K = ±1 —

муле (8) координатный матричный элемент может

элементу Z.

быть записан с помощью d-функций Вигнера:

Покажем во всех подробностях процесс получе-

ния правил отбора для дипольных переходов в слу-

∑

∑ j∑

чае серии nα. Начнем с π-компоненты (матричный

ann′ n^′′n =

dj_¯

α₁)×

i1 n^′

элемент Z):

i1=-ji2=-ji1=-ji2=-j

(i₂ - i₁) - (i2 -¯i1) = ±1,

×dj¯

α₂)d^ji

(α₁)d^ji

(α₂)aⁿ

¯i1ⁱ2 ,

(34)

i2 n^′′

1n^′

2n^′′

ni1i2

(30)

i₂ + i₁ =i2 +i1.

где a = X, Y, Z.

Первое уравнение в (30) соответствует определе-

Далее будет продемонстрирован процесс упроще-

нию числа K (см. (23)) и тому обстоятельству, что

ния (34) для случая Δn = 1. Для того чтобы это сде-

число K для дипольных матричных элементов Z в

лать, необходимо использовать результаты Гуляева.

случае серии nα может принимать только два зна-

Покажем выкладки для π-компоненты. Для начала

чения ±1. Второе уравнение описывает правило от-

рассмотрим первый квадратный корень в (22):

бора для магнитного квантового числа. Решение си-

√

(n₁ + m)n₁.

стемы (30) имеет следующий вид:

Существует связь между главным и параболически-

i₂ =i2 ±

ми квантовыми числами:

(31)

i₁ =i1 ∓

n = n₁ + n₂ + |m| + 1.

(35)

Используя (3) и (35), получим

Для σ-компоненты (X) ситуация более сложная.

Причиной служит то обстоятельство, что формулы

n - |i₁ + i₂| + i₂ - i₁ - 1

n₁ =

(20), (21) записаны для модуля Δm, другими сло-

(36)

вами, в этих выражениях Δm = | m - m|. Таким

n - |i₁ + i₂| + i₁ - i₂ - 1

n₂ =

образом, система уравнений, соответствующая ди-

польному матричному элементу X, имеет вид

Здесь Δn ≪ n, так что i₁ + i₂ ≈

i₁ +

i₂ и i₁ - i₂ ≈

(i₂ - i₁) - (i2 -¯i1) = 0,

≈

i₁

i₂. Второе равенство справедливо из-за правил

(32)

|i₂ + i₁| = |i2 +¯i1| ± 1.

отбора для серии nα:

804

ЖЭТФ, том 158, вып. 5 (11), 2020

Спектры Штарка - Зеемана и Блохинцева. ..

a)i1 +¯i2 ≥ 0,

Здесь j = m₁, но мы можем пренебречь этими вкла-

дами в случае n ≫ 1. Для того чтобы можно бы-

n₁ ≈

-i1,

ло использовать (41) и (42), необходимо также по-

n₂ + m ≈

+i2;

менять местами нижние индексы у d-функций. Это

можно осуществить, используя свойства симметрии

б)

i₁ +

i₂ ≤ 0,

функций Вигнера:

n₁ ≈

+i2,

d^jm

(β) = (-1)m1-m2d

(β).

(43)

1,m2

m2,m1

n₂ + m ≈

-i1.

Последним необходимым для упрощения свойст-

вом d-функций является соотношение ортогональ-

В итоге

)

⁽n

⁾⁽n

ности:

(n₁ + m)n₁ =

-i1

+i2

(37)

∑

Проделав аналогичные преобразования для вто-

(-1)m3-m2d^jm

(β)d^jm

2,m3

3,m1

(β) = δm1,m2 . (44)

рого слагаемого в (22), получим

m3=-j

)

⁽n

⁾⁽n

Во всех формулах считаем, что j ≈ n/2. После

(n₂ + m)n₂ =

+i1

-i2

(38)

подстановки (41), (42) в (40) легко увидеть, что мно-

Из формулы (10) нетрудно видеть, что α1,2 ≈

жители в F1,2 совпадают со знаменателями в рекур-

≈ α1,2, когда Δn ≪ n.

рентных формулах и, следовательно, их можно со-

Далее следует использовать правила отбора для

кратить. Поэтому коэффициенты в суммах (40) не

чисел i₁,i₂. Это позволит редуцировать (34) к двой-

зависят от индексов суммирования. Теперь можно

ной сумме. Подстановка (37) и (38) в (34) для a = Z

свободно использовать (44) и получить следующие

разбивает выражение для матричного элемента на

выражения:

две независимые суммы:

Znn′ n^′′n = (-1)Δn′+Δn′′

[

]

Znn′ n^′′n =

1nn^′n^′′

nn^′n^′′

(39)

(1)nn^′ n^′′

b Z_nn′_n′′

+Z(2)nn′n^′′

(45)

nn^′n^′′

∑

,2nn^′n^′′

dj_¯

(α₁) ×

i1 n^′

^(√n

- n′ cos

i1=-ji2=-j

n^′n^′′

δ_n′,n′+1/2 -

)

×dj¯

(α₂)dj¯

(α₁)dj¯

(α₂)F1,2(

i₁,i2),

(40)

i2 n^′′

i1±¹² n^′

i2 ∓¹² n^′′

^√n

−

+ n′ sin

δ_n′,n′-1/2

где

)

√( n

⁾⁽n

^(√ n

F₁ =

-i1

+i2 ,

- n′′ sin

δ_n′′,n′′+1/2 +

)

√( n

⁾⁽n

^√n

α₂

F₂ =

+i1

-i2

+ n′′ cos

δ_n′′,n′′-1/2

Следующим шагом для упрощения является

использование рекуррентных соотношений для

^(√n

α₁

- n′ sin

δ_n′,n′+1/2 +

d-функций [12]:

n^′n^′′

)

√

^√n

α₁

j-m₂

+ n′ cos

δ_n′,n′-1/2

d^jm

(β) =

cos

dj-1/2m

(β) -

1,m2

1+1/2,m2+1/2

j-m₁

√

^(√n

α₂

- n′′ cos

δ_n′′,n′′+1/2 -

j+m₂

sin

dj-1/2m

(β),

(41)

√

)

1+1/2,m2-1/2

j-m₁

α₂

−

+ n′′ sin

δ_n′′,n′′-1/2

√

j-m₂

Делая аналогичные действия для X, получаем

d^jm

(β) =

sin

dj-1/2m

(β) -

1,m2

1-1/2,m2+1/2

j-m₁

′′

√

Xnn′ nnnn′

′

= (-1)Δn′+Δn′′-¹ ×

[

]

j+m₂

cos

dj-1/2m

(β).

(42)

-X(2)nn′n^′′

(46)

j-m₁

1-1/2,m2-1/2

^′n^′′

nn^′n^′′

805

А. Ю. Летунов, В. С. Лисица

ЖЭТФ, том 158, вып. 5 (11), 2020

Рис. 2. Переход с уровня n = 10 на n = 9. Интенсивность, деленная на сумму всех компонент как функция сдвига энергии

(48), (49) с θ = 0: u = 0 (а), 1 (б), 10 (в), 1000 (г); u =^B

3cnE

′′

^(√n

α₁

Как мы можем видеть из формул (45)-(47), для

′′

- n′ sin

δ_n′,n′+1/2 +

больших значений n появляются правила отбора

)

^√n

α₁

для чисел n^′ и n^′′(из-за наличия дельта-символов в

+ n′ cos

δ_n′,n′-1/2

формулах). Это является следствием свойств угло-

вого момента векторов (1).

^(√n

α₂

- n′′ sin

δ_n′′,n′′+1/2 +

Для того чтобы показать связь между выра-

)

жениями (45)-(47) с эффектами Штарка и Паше-

^√n

α₂

на - Бака, вычислим интенсивность как функцию ω

+ n′′ cos

δ_n′′,n′′-1/2

c фиксированным значением угла θ между магнит-

ным B и электрическим F полями с различными

′′

^(√n

α₁

′′

- n′ cos

δ_n′,n′+1/2 -

значениями параметра u:

)

^√n

α₁

(48)

+ n′ sin

δ_n′,n′-1/2

3cnE

^(√n

α₂

ω=

ω₁n^′ +ω¯₂n^′′ - ω₁n^′ - ω₂n^′′)/Ω_FB

(49)

- n′′ cos

δ_n′′,n′′+1/2 -

)

Ω_FB =

B+

nF.

(50)

^√n

α₂

+ n′′ sin

δ_n′′,n′′-1/2

Интенсивность излучения атома водорода как

функция сдвига энергии (49) во внешних параллель-

Согласно (17) и (37),

ных F и B полях представлена на рис. 2. Нуле-

вое значение магнитного поля соответствует u = 0

n^′n^′′

= (-1)Δn′+Δn′′-¹ ×

[

]

(рис. 2a). В этом случае формулы (49)-(51) приво-

′′

дят к обычному эффекту Штарка. Этот результат

′′

+X(2)nn′n^′′

(47)

nn^′n^′′

находится в согласии с [26]. Более того, подстановка

806

ЖЭТФ, том 158, вып. 5 (11), 2020

Спектры Штарка - Зеемана и Блохинцева. ..

Рис. 3. То же, что на рис. 2, но для θ = π/2

θ = 0 и B = 0 в (10) обращает полученные выра-

4. СПЕКТРЫ БЛОХИНЦЕВА В

жения в формулы (20)-(22). С ростом u матричный

РИДБЕРГОВСКОМ АТОМЕ

элемент X остается равным Y (рис. 2). Это заранее

Для того чтобы вычислить интенсивность излу-

очевидно из аккуратного анализа формул (45)-(48).

чения ридберговского атома, находящегося во внеш-

Физическое объяснение этого обстоятельства — на-

нем поле (11), необходимо использовать соотноше-

личие оси симметрии системы, роль которой играет

ния (12), (13) и матричные элементы из [26,27]. Рас-

направление z. В случае B ≫ F полученные вы-

смотрим следующий параметр:

ражения для дипольных матричных элементов вос-

производят эффект Пашена - Бака (рис. 2г).

3 F

(51)

2 Ω

Случай перпендикулярных полей показывает бо-

лее низкую степень симметрии. С ростом парамет-

Практика показывает, что в реальных физичес-

ра u могут возникать попарно неравные серии мат-

ких ситуациях обычно r ≳ 1 или даже r ≫ 1 (см.,

ричных элементов (рис. 3б). Когда магнитное поле

например, [28]). В случае ридберговского атома с

равно нулю, F направлено по оси x. Это теперь при-

большими значениями индекса модуляции возника-

водит к замене X на Z (рис. 3a). Для больших зна-

ет большое число сателлитов. Также, если спект-

чений u мы опять приходим к чисто зеемановским

ральная линия имеет центральную компоненту (на-

компонентам (рис. 3г).

пример, H_nα) и r ≳ 1, то распределение интенсивно-

сти асимптотически приближается к дельта-функ-

На рис. 2 и 3 представлены графики интенсивно-

ции. Боковыми компонентами можно пренебречь по

сти, деленной на сумму всех компонент. Из-за того,

сравнению с центральной. Это обстоятельство по-

что представлены вычисления сразу для трех поля-

дробно обсуждается в [21, 23].

ризаций, в расчетах присутствует несохранение пол-

Для того чтобы выявить новые интересные эф-

ного интеграла интенсивности.

фекты, сфокусируемся на вычислении линий без

807

А. Ю. Летунов, В. С. Лисица

ЖЭТФ, том 158, вып. 5 (11), 2020

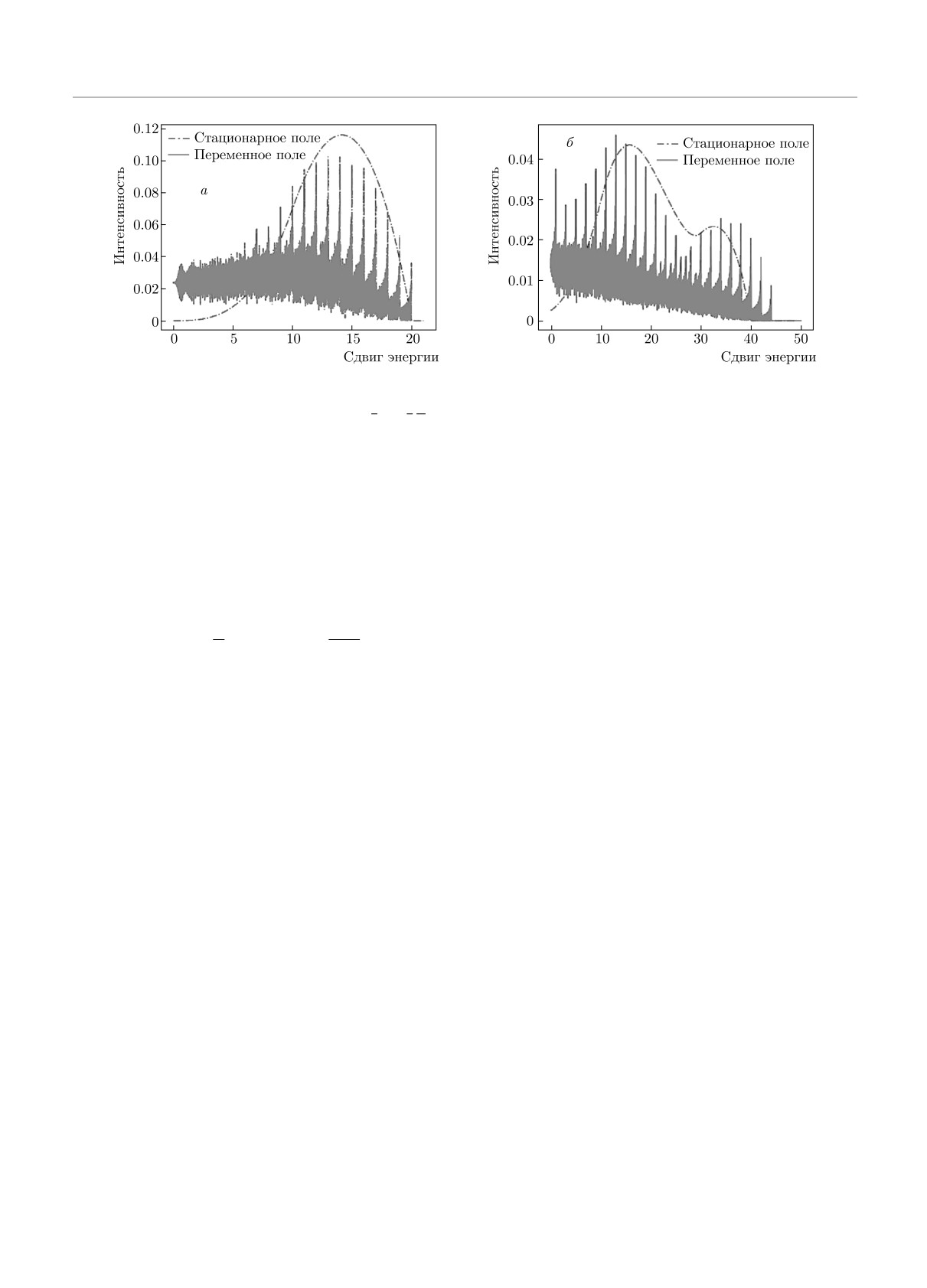
Рис. 4. Интенсивность (деленная на сумму всех компонент) как функция сдвига энергии (приведенная к безразмерному

виду частота — сдвиг энергии, деленный на³F0;3F2Ω = 1000). a) Переход с n = 10 на n = 9 (только π-компонента!).

б) Переход с n = 10 на n = 8

центральной компоненты. Найдем профили интен-

Как было сказано выше, необходимо учитывать

сивности H_nβ и π-компоненты H_nα в случае боль-

только серии элементов с K = ±1 и K = ±2. Интен-

ших значений n. Сравним полученные результаты с

сивностью остальных компонент можно пренебречь.

интенсивностью излучения в постоянном поле.

Используя полученные результаты для матричных

Распределение интенсивности всех штарковских

элементов (для H_nα см. (20)-(23)) и (51), можем вы-

компонент имеет вид

числить распределение интенсивности.

Как можно увидеть из рис. 4, сателлиты, кото-

∑

⁽ Δω_τ )

I(Δω) =

a2τJ²

(52)

рые соответствуют каждой штарковской компонен-

Δω/Ω Ω

те, воспроизводят форму стационарного контура.

Из (14) следует, что при Δω_F → Δω распределение

где τ — полный набор квантовых чисел, a_τ — коор-

интенсивности имеет пик. Это наглядно продемон-

динатный матричный элемент.

стрировано на рис. 4б: сателлиты приходят с «кры-

Используя результаты из [27], соотношения (3),

льев» в точку Δω = 0 и формируют центральную

(9) и положив n ≳ 1, получим матричные элементы

компоненту. Для H_nα это приводит к аномальному

для серии H_nβ :

росту функции распределения в центре (рис. 5a).

Выражение для интенсивности в постоянном поле

(Xm-1m)² + (Xm+1m)² = (j ∓ i₁)(j ± i₂) ×

[

]

можно найти в [26, 27].

× (j - i₁)(j - i₂) + (j + i₁)(j + i₂) .

(53)

Сравнение точных [20] и квазиклассических рас-

четов представлено на рис. 5б. Даже для перехо-

да 4-2 можно наблюдать соответствие между двумя

Здесь K = +1 для верхнего знака и K = -1 — для

подходами. В действительности здесь не соблюдено

нижнего. Это σ±1. Имеем

условие Δn ≲ n. Однако расположение всех пиков

(Z^mm)² = (j ∓ i₁)²(j ± i₂)².

(54)

совпадает. Также существует большая область час-

тот, где классический результат совпадает с кванто-

Здесь K = +2 для верхнего знака и K = -2 — для

вым.

нижнего. Это π±2.

Сдвиг энергии зависит только от двух квантовых

чисел i₁ и i₂ для фиксированного K (в действитель-

5. ЗАКЛЮЧЕНИЕ

ности от

i₁ и

i₂, но это не имеет значения для рид-

берговского атома). Таким образом, в (52) τ = i₁, i₂.

Для различных квазиклассических подходов с

В спектре есть вырождение, поэтому суммирование

использованием параболического представления

по оставшимся квантовым числам приводит только

проведено подробное исследование ридберговских

к общему коэффициенту и не влияет на форму про-

атомных спектров в скрещенных электрическом

филя.

и магнитном полях. С помощью связи полиномов

808

ЖЭТФ, том 158, вып. 5 (11), 2020

Спектры Штарка - Зеемана и Блохинцева. ..

Рис. 5. Сравнение квазиклассического расчета, точных квантовых результатов [20] и стационарного случая. Интенсив-

ность (деленная на сумму всех компонент) как функция сдвига энергии (приведенная к безразмерному виду частота —

сдвиг энергии, деленный на³F0. a) Переход с n = 6 на n = 5,3F2Ω = 8. б) Переход с n = 4 на n = 2,3F2Ω = 3

Якоби и гипергеометрической функции точные

классические выражения для интенсивности упро-

выражения Гордона для матричных элементов све-

стят вычисления. Если в спектральной серии отсут-

дены к классическому результату Борна не только

ствует центральная компонента, контур огибающей

для Z- (как в [13]), но и для X(сигма)-компонент.

линии сателлитов будет повторять кривую стацио-

Сравнение классического выражения Борна для

нарного профиля (рис. 4). Рисунок 5б показывает

интенсивности и квазиклассического [26] для сигма-

классические свойства кулоновского поля. Даже для

компонент продемонстрировано на рис. 1. Это дает

перехода 4-2 имеется хорошее соответствие между

свободу в выборе приближения для дальнейших

классическими и квантовыми результатами. Для бо-

преобразований. Квазиклассическое приближение

лее высоких уровней можно свободно использовать

дает возможность получить приближенные пра-

приближение Гуляева вместо сложных формул Гор-

вила отбора для параболических квантовых чисел

дона.

и затем упростить выражения для вероятностей

радиационных переходов до элементарных функ-

ПРИЛОЖЕНИЕ

ций (тригонометрия и квадратные корни). Так,

сложное выражение

(34) переходит в формулы

Матричный элемент X в представлении

(45)-(48). Этот факт открывает простой путь к

полиномов Якоби

работе с ридберговскими атомными спектрами.

Существует связь между гипергеометрической

Все эти результаты показывают классические и

симметрийные свойства кулоновского поля. Для

функцией и полиномами Якоби:

того чтобы обобщить этот метод на случай Δn > 1,

(

ϕ⁾

k!Γ(1 + β)

необходимо использовать рекуррентные соотно-

-k, -k - α, 1 + β, - ctg²

k+1+β

шения для функций Вигнера (41), (42) несколько

⎛

⎞k

раз.

Результаты, полученные Блохинцевым в [15],

×^⎝-

⎠ P(α,β)k(cosϕ),

(55)

обобщены на случай большого массива радиацион-

sin²

ных переходов. Подобные спектры реализуются в

турбулентной плазме или в поле лазерного излу-

где P(α,β)k(z) — полином Якоби, Γ(z) — гамма-функ-

чения. Квазиклассический подход может быть осо-

ция.

бенно полезен для диагностики водородоподобных

Используя соотношение (55), можно переписать

ионов, так как частота излучения растет как Z²

формулу Гордона с помощью полиномов Якоби:

(Z — заряд ядра). Для того чтобы работать в пре-

Xn1n²,mn

= Π_x[Υ^Jx

- Υ^J ],

(56)

1,n2,m-1

делах видимого диапазона, необходимо исследовать

переходы с большим значением n, так что квази-

где

809

А. Ю. Летунов, В. С. Лисица

ЖЭТФ, том 158, вып. 5 (11), 2020

a₀

Π_x = (-1)n1+n2

В этих выражениях приняты во внимание следу-

4((m - 1)!)²

ющие соотношения:

√

(n₁ + m)!(n₂ + m)!(n₁ + m - 1)!(n₂ + m - 1)!

4nn

n₁!n₂!n₁!n₂!

ctg²

sin

,cos²

Δ²

n+n

(

)m+1 (

)n+¯n

(57)

4nn

n-n

4nn - Δ²

cosϕ =

(n - n)²

n+n

(n + n)²

Теперь не составляет никакого труда показать

⎛

⎞_N

1+N2

для серии nα, что в случае n ≪ Δn выражение

N₁!N₂![(m - 1)!]

Υ^Jx

⎝_-

⎠

(55) совпадает с классическим результатом Борна.

(N₁ + m)!(N₂ + m)!

sin²

Для этого надо использовать асимптотику полино-

мов Якоби:

×P(Δ1,m-1)N

(cos ϕ)P(Δ2,m-1)(cos ϕ),_N

(α,β)

Γ(k + α + 1)

P_k

(cos ϕ) ≈

(

)₂

k!U^α

Δn

N₁!

N₂![(m - 1)!]

√

Υ^Jx

J_α(Uϕ)

n+n

N₁ + m - 1)!(

N₂ + m - 1)!^×

(

(58)

)α (

sinϕ

ϕ⁾β,ϕ≪1,

sin

cos

×P(Δ1,m-1)¯

(cos ϕ)P(Δ2,m-1)(cos ϕ),_¯

где

Δ₁ = |n₁ - n₁|, Δ₂ = |n₂ - n₂|,

Δ₁ = |n₁ - n₁ -1|,

)

Δ₂ = |n₂ - n₂ - 1|, Δ = n - n,

⁽β²

α²

α+β+1

U² = A²⁰ -

A₀ = k +

N₁ = min(n₁, n₁), N₂ = min(n₂, n₂),

N₁ = min(n₁ + 1, n₁),

N₂ = min(n₂ + 1, n₂).

Далее нужно упростить U в случае n ≫ 1:

√(

)₂

Δ₁

(m - 1)²

Δ²¹

U₁ = N₁ +

√(

)(

)

m+Δ₁

m-1

m+Δ₁

m-1

Δ²¹ - 1

= N₁ +

N₁ +

Если мы примем во внимание, что Δ₁ ∼ 1, то

a) i₂ + i₁ ≥ 0,

i₂ +

i₁ ≥ 0:

получим

√

U₁ ≈

N₁(N₁ + m).

i₂ =i2 +

Аналогично для U₁ = U₃, U₂ = U₄.

i₁ =i1 +

;

После подстановки (57) в (55) и простых алгебра-

ических преобразований получаем выражение, кото-

б) i₂ +i₁ ≤ 0,i2 +¯i1 ≥ 0: эти переходы запрещены

рое совпадает с формулой Борна (16).

правилом отбора для m;

в) i₂ +i₁ ≥ 0,i2 +¯i1 ≤ 0: существует только один

переход, который удовлетворяет правилу отбора m:

Правила отбора σ-компоненты для серии

0 → -1; его можно включить в пункт г;

H_nα

г) i₂ + i₁ ≤ 0,

i₂ +¯i1 ≤ 0:

Рассмотрим систему (32) с +1 во втором уравне-

нии:

i₂ =i2 -

(i₂ - i₁) - (i2 -¯i1) = 0,

i₁ =i1 -

|i₂ + i₁| = |i2 +¯i1| + 1.

Проведя аналогичные действия, легко получить

Решение имеет вид

решение системы (32) с -1:

810

ЖЭТФ, том 158, вып. 5 (11), 2020

Спектры Штарка - Зеемана и Блохинцева. ..

i₂ =i2 -

11.

Y. N. Demkov, B. S. Monozon, and V. N. Ostrovsky,

JETP 30, 775 (1970).

i₁ =i1 -

12.

D. A. Varshalovich, A. N. Moskalev, and V. K. Kher-

sonskii, Quantum Theory of Angular Momentum,

когда i₂ + i₁ ≥ 0,

i₂ +¯i1 ≥ 0;

World Sci. (1988).

i₂ =i2 +

13.

D. P. Dewangan, J. Phys. B: Atom. Mol. Opt. Phys.

41, 015002 (2007).

i₁ =i1 +

14.

D. P. Dewangan, J. Phys. B: Atom. Mol. Opt. Phys.

36, 2479 (2003).

когда i₂ + i₁ ≤ 0,

i₂ +¯i1 ≤ 0.

Можно записать решение в виде

15.

D. I. Blochinzew, Phys. Z. Sow. Union 4, 501 (1933).

16.

E. V. Lifshits, Technical Report, Physical-Technical

i₂ =i2 ±

Inst., Kharkov (1967).

(59)

i₁ =i1 ±

17.

E. A. Oks and G. V. Sholin, Zh. Tekhnich. Fiz. 46,

254 (1976).

18.

A. S. Antonov, O. A. Zinovev, V. D. Rusanov, and

ЛИТЕРАТУРА

A. V. Titov, Sov. Phys. JETP 31, 838 (1970).

L. D. Landau and E. M. Lifshitz, Quantum Mecha-

19.

E. K. Zavoyskiy, Yu. G. Kalinin, V. A. Skorupin,

nics: Non-Relativistic Theory, Vol. 3, Elsevier (2013).

V. V. Shapkin, and G. V. Sholin, in Reports of the

N. B. Delone, S. P. Goreslavsky, and V. P. Krainov,

Academy of Sciences, Vol. 194, pp. 55-58, Russian

J. Phys. B: Atom. Mol. Opt. Phys. 27, 4403 (1994).

Academy of Sciences (1970).

I. I. Sobelman, Introduction to the Theory of Atomic

20.

E. A. Oks, Plasma Spectroscopy: The Influence

Spectra: International Series of Monographs in Natu-

of Microwave and Laser Fields, Vol. 9, Springer

ral Philosophy, Vol. 40, Elsevier (2016).

Sci. & Business Media (2012).

Г. Бете, Э. Солпитер, Квантовая механика ато-

21.

А. Б. Березин, Б. В. Люблин, Д. Г. Яковлев,

мов с одним и двумя электронами, Физматлит,

Штарковская спектроскопия водородных линий в

Москва (1960).

плазме, НИИЭФА (1983).

W. Gordon, Ann. Phys. 394, 1031 (1929).

22.

Л. А. Буреева, В. С Лисица, Возмущенный атом,

ИздАТ (1997).

A. B. Underhill, Publ. Dominion Astrophys. Obs. 8,

386 (1951).

23.

V. S. Lisitsa, Atoms in Plasmas, Vol. 14, Springer

Sci. & Business Media (1995).

G. Mathys, Astron. Astrophys. 141, 248 (1984).

24.

M. Born, F. Hund, and P. Jordan, Vorlesungen über

V. G. Novikov, V. S. Vorobyov, L. G. Dyachkov, and

Atommechanik, Vol. 1, Springer (1925).

A. F. Nikiforov, JETP 92, 441 (2001).

25.

H. A. Kramers, Intensities of Spectral Lines, Koben-

J. Rosato, Y. Marandet, and R. Stamm, J. Quant.

havn, A. F. Host (1919).

Spectrosc. Rad. Transfer 187, 333 (2017).

26.

S. A. Gulyaev, Sov. Astron. 20, 573 (1976).

10.

M. A. Gordon and R. L. Sorochenko, Radio Re-

combination Lines: Their Physics and Astronomical

27.

S. A. Gulyaev, Sov. Astron. 22, 572 (1978).

Applications, Vol. 282, Springer Sci. & Business Me-

dia (2009).

28.

E. A. Oks, Atoms 7(1), 25 (2019).

811