ЖЭТФ, 2020, том 158, вып. 5 (11), стр. 812-820

ВИГНЕРОВСКИЕ ВРЕМЕНА ЗАДЕРЖКИ

МЕДЛЕННЫХ ЭЛЕКТРОНОВ ДВУХАТОМНОЙ

МОЛЕКУЛОЙ, МОДЕЛИРУЕМОЙ ПАРОЙ НЕ

ПЕРЕСЕКАЮЩИХСЯ АТОМНЫХ ПОТЕНЦИАЛОВ

М. Я. Амусьяa,b*, А. С. Балтенковc**

^a Racah Institute of Physics, Hebrew University

91904, Jerusalem, Israel

^b Физико-технический институт им. А. Ф. Иоффе Российской академии наук

194021, Санкт-Петербург, Россия

^c Институт ионно-плазменных и лазерных технологий им. У. А. Арифова

100125, Ташкент, Узбекистан

Поступила в редакцию 15 мая 2020 г.,

после переработки 12 июня 2020 г.

Принята к публикации 16 июня 2020 г.

В рамках модели неперекрывающихся атомных потенциалов исследованы времена вигнеровской задерж-

ки в процессах упругого рассеяния медленных электронов двухатомной молекулой. Волновые функции

молекулярного континуума представляются в виде комбинации плоской волны и двух сферических s-

волн, генерируемых центрами атомных сфер. Асимптотика этих функций определяет в замкнутом виде

амплитуду упругого рассеяния электронов. Показано, что на асимптотически больших расстояниях от

молекулы волновые функции в сплошном спектре можно представить в виде разложения в ряд дру-

гих, не сферических, ортонормированных функций. Коэффициенты разложения амплитуды рассеяния

в ряд этих функций определяют фазы рассеяния электронов рассматриваемой молекулярной системой.

С этими молекулярными фазовыми сдвигами рассчитаны вигнеровские времена задержки медленных

электронов двухатомной мишенью. В качестве конкретного примера рассматривается молекула C2.

DOI: 10.31857/S004445102011005X

менной задержке [4-9], зависящей от ориентации

векторов поляризации фотона e и импульса фото-

электрона k относительно осей молекулы {R_i}.

1. ВВЕДЕНИЕ

Вигнеровская задержка времени как квантовая

Эксперименты с фотоионизацией атомов под

динамическая наблюдаемая чрезвычайно чувстви-

действием аттосекундных лазерных импульсов да-

тельна к фазовым сдвигам волновой функции фото-

ют качественно новую информацию о динамике это-

электрона или, точнее, к их производным по энер-

го процесса в реальном времени. Интерпретация

гии. Поэтому анализ правильности методов расчета

этих экспериментальных данных основана на вре-

фазовых сдвигов для несферических мишеней, та-

менных задержках, первоначально введенных в рас-

ких как молекулы, очень важен. При расчете вре-

смотрение Айзенбадом, Вигнером и Смитом [1-3].

мени задержки фотоэлектронов в процессах моле-

По сравнению с атомной фотоионизацией, анализ

кулярной фотоионизации волновые функции конти-

молекулярных временных вигнеровских задержек

нуума и их фазы рассчитываются, как правило, чис-

намного сложнее из-за анизотропности молекуляр-

ленно.

ного потенциала. Временной анализ фотоионизации

Для этих расчетов [6-9] обычно использует-

молекул приводит к так называемой угловой вре-

ся комплекс математических программ ePolyScat

^* E-mail: amusia@vms.huji.ac.il

[10-12]. В рамках этих программ электронные функ-

^** E-mail: arkbalt@mail.ru

ции континуума аналогичны функциям рассеяния

812

ЖЭТФ, том 158, вып. 5 (11), 2020

Вигнеровские времена задержки медленных электронов. . .

электронов на атомах [12]. Асимптотическая форма

ставить в виде разложения в ряд ортонормирован-

волновой функции вдали от молекулы (за предела-

ных функций Z_λ(k)), отличных от обычных сфе-

ми молекулярной сферы) представляет собой сумму

рических функций Y_lm(k). Эти функции зависят, в

плоской волны и сферических волн, излучаемых мо-

частности, от количества атомов, образующих ми-

лекулярным центром. По сути, мы имеем картину

шень, от относительной ориентации центров рассе-

дифракции электронной волны на изолированной

яния в пространстве и т. д. В разд. 3 мы кратко об-

молекулярной сфере¹⁾. Волновая функция контину-

судим основные идеи метода [16] и применим их к

ума представляет собой линейную комбинацию ре-

амплитуде F (k, k^′, R).

гулярных и нерегулярных решений волнового урав-

Разложение амплитуды F (k, k^′, R) в ряд функ-

нения. Коэффициенты этой линейной комбинации

ций Z_λ(k) в разд. 4 определяет набор фаз, назван-

определяют молекулярные фазы рассеяния, а их

ных в [16] «собственно молекулярными фазами».

производные по энергии дают парциальные вигне-

Последние используются для численных расчетов

ровские временные задержки. Этот рецепт построе-

сечений рассеяния медленных электронов молеку-

ния волновой функции молекулярного континуума

лами с различными межатомными расстояниями R.

и расчета молекулярных фазовых сдвигов считается

Радиальные части волновых функций молекулярно-

само собой разумеющимся и, насколько нам извест-

го континуума, асимптотически точные на больших

но, не вызывает сомнений.

расстояниях от мишени, определяют потоки элек-

Другой и более реалистичный подход к описа-

тронов через поверхность сферы с большим ради-

нию рассеяния электронной волны на молекуле рас-

усом, окружающим молекулу. Согласно [3], этими

сматривается в статье [14], где дифракционная кар-

потоками определяются вигнеровские временные за-

тина электронной волны на молекуле представля-

держки медленного электрона мишенью. В разд. 5

ет собой интерференцию сферических волн, генери-

«собственно молекулярные фазы» (далее будем на-

руемых пространственно-разнесенными источника-

зывать их просто «молекулярными фазами») ис-

ми. В этом приближении мишень представляет со-

пользуются для численного расчета двух парциаль-

бой кластер неперекрывающихся атомных сфер, а

ных времен вигнеровских задержек для различных

сферические волны, излучаемые ими, создают ин-

параметров нашей модели. В разд. 6 обсуждаются

терференционную картину, свойства которой пери-

полученные в статье основные результаты исследо-

одически зависят от отношения межъядерного рас-

вания.

стояния к длине волны фотоэлектрона. Данная ста-

тья посвящена ответу на вопрос, существуют ли в

такой картине рассеяния молекулярные фазы и как

их можно рассчитать.

2. МОДЕЛЬНАЯ МОЛЕКУЛА КАК

Для этого целесообразно рассмотреть модель мо-

КЛАСТЕР ИЗ ДВУХ АТОМНЫХ СФЕР

лекулярной системы, которая позволяет получить

точное решение [15]. В настоящей статье мы сде-

лаем это на примере мишени, образованной дву-

Рассмотрим рассеяние медленного электрона на

мя пространственно-разделенными друг от друга на

двух одинаковых непересекающихся атомных потен-

расстоянии R короткодействующими атомными по-

циалах с центрами в точках r = ±R/2. Это простей-

тенциалами. Расчет амплитуды упругого рассеяния

шая многоцентровая система, которая может слу-

F (k, k^′, R) медленных электронов такой мишенью

жить пробным камнем для анализа правильности

(см. разд. 2) является хорошим примером, который

различных методов расчета фазовых сдвигов вол-

имеет аналитическое решение.

новых функций электронов, рассеивающихся на мо-

Задача об упругом рассеянии частицы на несфе-

лекулах.

рической мишени и метод S-матрицы для этого слу-

Представим, как это сделано в статье [17], вол-

чая были исследованы в [16], где было показано, что

новую функцию медленного электрона, рассеянного

асимптотически на больших расстояниях от моле-

этой мишенью, в виде суммы плоской волны и двух

кулы волновую функцию континуума можно пред-

сферических s-волн, излучаемых из центров атом-

ных сфер радиусом ρ²⁾:

¹⁾ Как было показано нами довольно давно [13], введение

воображаемой молекулярной сферы в muffin-tin приводит к

нефизическим особенностям в волновых функциях молеку-

лярного континуума.

²⁾ В этой статье используются атомные единицы.

813

М. Я. Амусья, А. С. Балтенков

ЖЭТФ, том 158, вып. 5 (11), 2020

ik|r+R/2|

ронов на рассматриваемой двухцентровой мишени

ψ+k(r) = eik·r + D₁(k)

|r + R/2|

[17, 18]:

ik|r-R/2|

{

[

]

+ D₂(k)

(1)

|r - R/2|

F (k, k^′, R) =

b cos (k - k^′) ·

a² - b²

[

]}

для |r ± R/2| > ρ. Коэффициенты D₁(k) и D₂(k)

- acos (k + k^′) ·

(3)

здесь определяются после наложения на пробную

волновую функцию (1) следующих граничных усло-

Как и в [17], мы используем здесь следующие обо-

вий в точках R/2 и -R/2:

значения: k и k^′ — импульсы электрона до и по-

[

]

сле рассеяния соответственно, b = k(i - ctg δ₀) =

ψ⁺(r)r→R/2 ≈ C1

+ k ctgδ₀

= -1/f₀(k) и a = exp(ikR)/R. Здесь f₀(k) есть s-

|r - R/2|

[

]

(2)

парциальная амплитуда упругого рассеяния элек-

ψ⁺(r)r→-R/2 ≈ C2

+ k ctgδ₀

трона на изолированном атомном потенциале.

|r + R/2|

Полное сечение рассеяния электрона мишенью

получается из амплитуды (3) с помощью оптической

Здесь δ₀(k) — фазовый сдвиг волновой функции

теоремы [19]:

электрона, испытывающего s-рассеяние на изолиро-

ванном атомном потенциале; C₁ и C₂ — некоторые

∫

dσ

4π

постоянные. Следует иметь в виду, что эта волно-

σ(k, R) =

dΩ_k′ =

Im F (k = k^′, R) =

dΩ_k′

вая функция на самом деле неверна внутри атом-

4π

^[b - acos(k · R)^]

ных сфер, поскольку регулярная волновая функция

(4)

a² - b²

s-типа вблизи центров каждой атомной сферы яв-

ляется постоянной величиной. Однако это не играет

Наличие векторов k и R в аргументе сечения (4)

никакой роли в решении проблемы упругого рассе-

подчеркивает, что мы имеем дело с фиксированной в

яния электронов на мишени. Физически очевидно,

пространстве молекулой. Полное сечение (4), усред-

что полное знание волновой функции молекулярно-

ненное по всем направлениям импульса налетающе-

го континуума во всем пространстве не необходимо

го электрона k относительно вектора R, имеет вид

для удовлетворительного описания амплитуды рас-

∫

сеяния. Достаточно иметь асимптотические волно-

вые функции, непосредственно связанные с фазо-

σ(k) =

σ(k, R) dΩ_k =

4π

вым сдвигом³⁾.

{[

4π

⁽qR + coskR)2]-1

Применяя формулы (2) к функции (1), получа-

ем точное общее решение уравнения Шредингера,

k²

kR + sinkR

[

которое описывает многократное рассеяние элек-

⁽qR - coskR)2]-1 }

трона на двухцентровой мишени [17, 18]. Действи-

+ 1+

(5)

kR - sinkR

тельно, если подставить функцию (1) в волновое

уравнение, в правой части мы получим сумму двух

где волновой вектор q

= -k ctg δ₀(k). Сечение

дельта-функций δ(r± R/2), поскольку второе и тре-

(5) содержит члены (sin kR)/kR, что характеризу-

тье слагаемые в (1) совпадают с точностью до кон-

ет дифракционные явления. Их появление является

стант с функциями Грина волнового уравнения для

следствием интерференции двух s-волн в волновой

свободного движения. Дельта-функции равны нулю

функции континуума (1).

во всем пространстве, кроме точек r = ±R/2. Та-

ким образом, за пределами атомных сфер (где r =

= ±R/2) функция (1) подчиняется волновому урав-

3. МЕТОД ПАРЦИАЛЬНЫХ ВОЛН ДЛЯ

нению для движения свободных частиц.

НЕСФЕРИЧЕСКИХ МИШЕНЕЙ

Амплитуда медленного рассеяния электронов на

мишени находится из асимптотики волновой функ-

Молекулярный потенциал как кластер непере-

ции (1). В результате мы получаем следующую

крывающихся атомных потенциалов не обладает

точную амплитуду многократного рассеяния элект-

сферической симметрией. Решение уравнения Шре-

дингера ψ+k(r) с этим потенциалом невозможно

³⁾ Отметим, что в [18] аналогичная функция использова-

представить в произвольной точке пространства в

лась для описания рассеяния медленных мезонов дейтроном.

виде разложения по сферическим функциям Y_lm(r).

814

ЖЭТФ, том 158, вып. 5 (11), 2020

Вигнеровские времена задержки медленных электронов. . .

Однако асимптотически, на больших расстояниях от

4. РАЗЛОЖЕНИЕ АМПЛИТУДЫ

молекулы, согласно [16], волновая функция может

РАССЕЯНИЯ (3) В РЯД ФУНКЦИЙ Zλ(k)

быть представлена как разложение в ряд других ор-

Согласно формулам разд. 3, амплитуда рассея-

тонормированных функций Z_λ(k):

ния (3) должна быть представлена как разложение

∑

в ряд функций Z_λ(k). Для данной молекулярной си-

ψ+k(r → ∞) ≈ 4π R_kλ(r)Z_λ(r)Z^∗λ(k),

(6)

стемы молекулярные фазовые сдвиги η_λ(k) и функ-

(k) могут быть вычислены явно [17]. Следуя

ции Z_λ

с радиальной частью волновой функции, определя-

статье [17], перепишем амплитуду рассеяния (3) в

емой следующим выражением:

следующем виде:

{ (

)}

R_kλ(r → ∞) ≈ exp i η_λ +

ω_λ

F (k, k^′, R) = -

cos(k · R/2)cos(k^′ · R/2)+

(

)

a+b

sin kr -

ω_λ + η_λ

(7)

sin(k · R/2) sin(k^′ · R/2).

(10)

a-b

Здесь индекс λ нумерует различные парциальные

Согласно [16], амплитуда (10) должна рассматри-

волновые функции, аналогичные квантовым числам

ваться как сумма двух парциальных амплитуд. Пер-

l и m для центрального поля; ω_λ — квантовое число,

вая из них записывается в виде

равное орбитальному моменту l для случая сфери-

ческой симметрии; η_λ(k) — фазовые сдвиги. Явный

4π

(e2iη0 - 1)Z₀(k)Z∗0(k^′) =

вид функций Z_λ(k) ) (в терминологии [16] — «ха-

2ik

рактерные амплитуды») зависит от конкретного по-

cos(k · R/2)cos(k^′ · R/2).

(11)

тенциала мишени, в частности, от числа атомов, ее

a+b

образующих, и от взаимного расположения центров

Вторая амплитуда определяется следующим выра-

рассеяния в пространстве, и т. д. Функции Z_λ(k), по-

жением:

добно сферическим функциям Y_lm(k), создают ор-

тонормированную систему.

4π

(e2iη1 - 1)Z₁(k)Z∗1(k^′) =

Амплитуда упругого рассеяния для несфериче-

2ik

ской мишени, согласно [16], задается следующим вы-

sin(k · R/2) sin(k^′ · R/2).

(12)

ражением:

a-b

∑

2π

После элементарных преобразований формул (11) и

F (k, k^′) =

(e2iηλ - 1)Z^∗λ(k)Z_λ(k^′).

(8)

(12) получаем две молекулярные фазы

qR + coskR

Усредненное по всем направлениям импульса пада-

ctg η₀ = -

kR + sinkR

ющего электрона k сечение упругого рассеяния свя-

(13)

qR - coskR

зано с молекулярными фазами η_λ(k) следующим об-

ctg η₁ = -

kR - sinkR

разом:

4π^∑

(k), и две «характеристические ам-

где q = -k ctg δ₀

σ(k) =

sin² η_λ.

(9)

k²

плитуды»

Парциальные волны (7) и молекулярные фазы

cos(k · R/2)

sin(k · R/2)

Z₀(k) =

√

Z₁(k) =

√

(14)

η_λ(k) классифицируются, согласно [16], по их по-

2πS₊

2πS_-

ведению при низких энергиях электронов, т.е. при

k → 0. В этом пределе длина волны частицы ве-

Здесь S_± = 1 ± (sin kR)/kR. Легко показать, что

лика по сравнению с размером мишени, а функция

функции Z_λ(k), подобно сферическим функциям

Z_λ(k) стремится к некоторой сферической функ-

Y_lm(k), создают ортонормированную систему.

ции Y_lm(k). Фаза рассеяния характеризуется в этом

Очевидно, что функции (14) определяются гео-

пределе следующим асимптотическим поведением:

метрической структурой мишени, т. е. направлением

η_λ(k → 0) ≈ k2λ+1.

молекулярной оси R в произвольной системе коор-

Далее мы применим формулы этого раздела для

динат, в которой векторы импульса электрона до и

расчета упругого рассеяния электронов на мишени,

после рассеяния равны k и k^′ соответственно. Пере-

образованной двумя непересекающимися атомными

ход к пределу k → 0 в формулах (14) дает вместо

потенциалами.

функций Z_λ(k) известные сферические функции:

815

М. Я. Амусья, А. С. Балтенков

ЖЭТФ, том 158, вып. 5 (11), 2020

Z₀(k)k→0 →

√

≡ Y₀₀(k),

Rk0(r → ∞) = exp(iη₀)

sin(kr + η₀),

4π

√

(15)

Rk1(r → ∞) =

(17)

Z₁(k)k→0 →

cosθ ≡ Y₁₀(k).

(

)

π⁾

4π

= exp iη₁ +

sin kr -

+η₁

Здесь θ — угол между вектором k и осью R. Таким

образом, только в пределе k → 0 картина дифрак-

Они определяют потоки частиц через поверхность

ции электронной волны на паре атомных потенциа-

сферы с большим радиусом, окружающим молеку-

лов трансформируется в картину дифракции волны

лу. Согласно [3], эти потоки определяют следующие

на изолированной сфере.

два времени задержки медленных электронов ми-

Молекулярные фазы η_λ(k) можно классифици-

шенью. Первая вигнеровская задержка есть

ровать, рассматривая их поведение при k → 0 [16]. В

dη₀

этом пределе длина волны электрона намного боль-

τ₀(k) = 2

0(k) = -

RF₀(k)×

ше размера мишени, и картина рассеяния прибли-

× [(qR + cos kR)² + (kR + sin kR)²]-1,

(18)

жается к таковой в случае сферической симметрии.

Рассматривая переход к этому пределу в формулах

где функция F₀(k) определяется формулой

(13), получаем η₀(k → 0) ∼ k и η₁(k → 0) ∼ k³.

Таким образом, молекулярные фазы (13) ведут себя

F₀(k) = (1 + coskR)(qR + coskR)-

подобно s- и p-фазам в сферически-симметричном

-(˙q - sinkR)(kR + sinkR).

(19)

потенциале, что объясняет выбор их индексов. Как

Вторая задержка Вигнера есть

и следовало ожидать, сумма парциальных сечений

упругого рассеяния, рассчитанная с молекулярны-

dη₁

τ₁(k) = 2

1(k) = -

RF₁(k)×

ми фазами (13),

4π

× [(qR - cos kR)² + (kR - sin kR)²]-1,

(20)

σ₀(k) =

sin² η₀, σ₁(k) =

sin² η₁,

(16)

k²

(k) записывается в виде

где функция F₁

совпадает с полным сечением (5), следующим из

оптической теоремы. Результаты численных расче-

F₁(k) = (1 - coskR)(qR - coskR)-

тов сечений рассеяния электронов молекулой C₂ по

-(˙q + sinkR)(kR - sinkR).

(21)

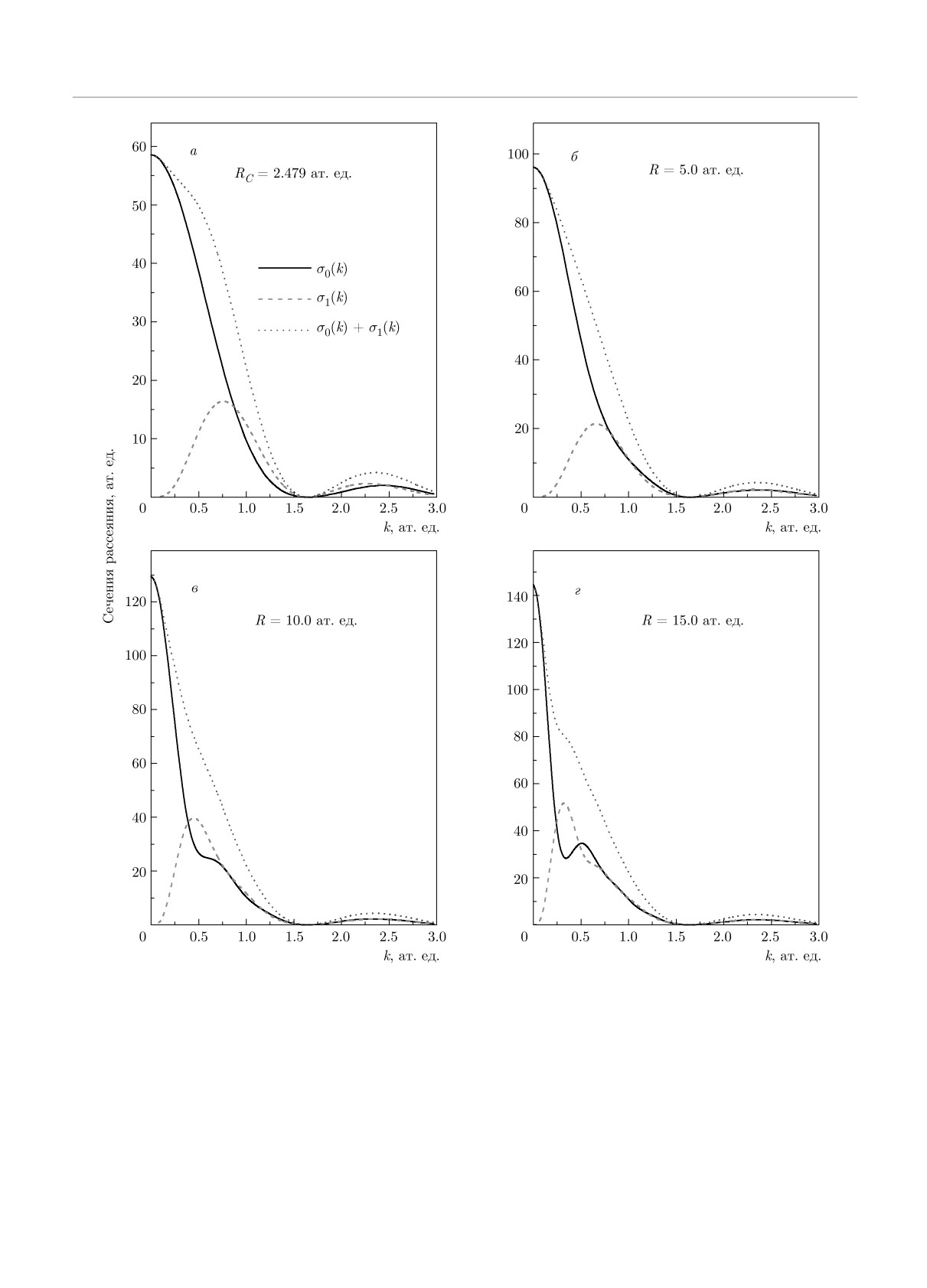
формулам (16) приведены на рис. 1. Наличие чле-

нов (sin kR)/kR в формулах (16) приводит к ос-

В этих формулах функции q(k) и

˙q(k) есть

цилляциям в сечениях. Такие осцилляции связаны

q(k) = -k ctg δ₀(k),

с дифракционными эффектами, возникающими из-

(22)

за интерференции двух сферических s-волн, гене-

sinδ₀ cosδ₀ - k

δ0

˙q(k) = -

рируемых пространственно-разнесенными источни-

sin

δ₀

ками. Подобные дифракционные эффекты, конеч-

Оператор ∂/∂k в формулах (18)-(22) обознача-

но, невозможны, если предположить, что вдали от

ется точкой.

молекулы существует только одна сферическая вол-

На рис. 2 представлены вигнеровские времена

на, как предполагается в подходе, в котором мно-

задержки электронов молекулой C₂ в модели двух

гоцентровая молекула рассматривается как молеку-

непересекающихся атомных сфер для четырех фик-

лярная сфера [10-12].

сированных значений межатомных расстояний R. В

реальной молекуле C₂ это расстояние равно R_C =

= 2.479 ат. ед. [17]. В расчетах по формулам (18)-

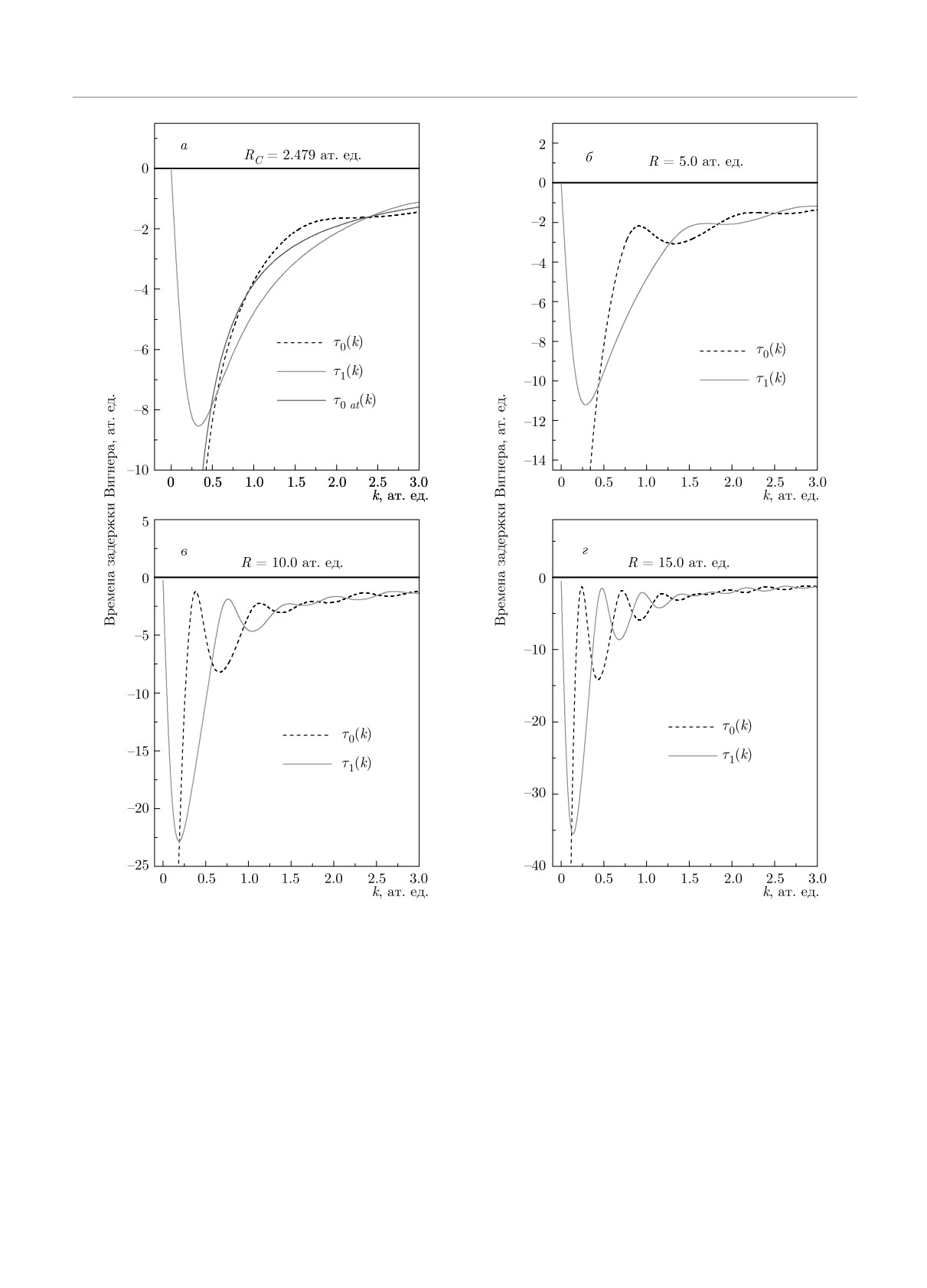
5. ВИГНЕРОВСКИЕ ВРЕМЕНА ЗАДЕРЖКИ

(22) сдвиг s-атомной фазы δ₀(k) описывается анали-

ЭЛЕКТРОНОВ МОЛЕКУЛОЙ

тическим выражением δ₀(k) ≈ 2π - 1.912k [17]. На

Разработанный в разд. 3 метод парциальных

рис. 2а представлена временная задержка Вигнера

волн для несферических мишеней естественным об-

для рассеяния электронов на одном атоме углеро-

разом отделяет кинематику процесса рассеяния, ко-

да τ0at(k) вместе с молекулярными временами τ₀(k)

торая определяется функциями Z_λ(k), от динами-

и τ₁(k). Атомная задержка стремится к минусу бес-

ческой части, которая определяется молекулярны-

конечности, так как волновой вектор электрона k

ми фазами η_λ(k). Парциальные волны с индексами

стремится к нулю:

λ = 0 и 1 описываются следующими асимптотиче-

3.824

скими формулами [17]:

τ0at(k → 0) =

(2π - 1.912k) → -

(23)

k dk

816

М. Я. Амусья, А. С. Балтенков

ЖЭТФ, том 158, вып. 5 (11), 2020

Рис. 2. Времена задержки Вигнера τ0(k) и τ1(k), рассчитанные по формулам (18)-(21) для молекулы C2 и время за-

держки τ0at(k) при рассеянии электрона изолированным атомом C в зависимости от волнового вектора электрона k. R —

межатомные расстояния в молекуле. В реальной молекуле С2 этот радиус RC = 2.479 ат. ед.

увеличением межатомного расстояния R минималь-

фотоэлектрона молекулой H₂ от межатомного рас-

ное значение функции τ₀(k) также увеличивается,

стояния. Задержка становится отрицательной при

т. е. рост межатомного расстояния R молекулы со-

R > 2.6 ат.ед. и ее абсолютная величина возрастает

провождается более интенсивным удалением элек-

с ростом R в молекуле H₂.

трона из внутренней области молекулы.

Обе молекулярные кривые на рис. 2 с ростом R

Аналогичная картина приведена в статье [20] на

быстро осциллируют, что связано с наличием в фа-

рис. 4, где показана зависимость времени задержки

зах рассеяния слагаемых (sin kR)/kR, характерных

818

ЖЭТФ, том 158, вып. 5 (11), 2020

Вигнеровские времена задержки медленных электронов. . .

для интерференции двух s-волн в волновой функ-

потенциалов может быть представлена в виде ряда

ции сплошного спектра (1).

ортонормированных функций Z_λ(k), характерных

для данной системы. Коэффициенты этого раз-

ложения определяют уникальный (опять же для

6. ВЫВОДЫ

данной цели) набор молекулярных фаз рассеяния

η_λ(k). Эти фазы также определяют вигнеровскую

Как правило, в работах по рассеянию электронов

задержку электрона данной N-атомной молекулой.

на молекулах, электрон рассматривается как дви-

Мы уверены в том, что разработанный здесь метод

жущийся в сферически-усредненном молекулярном

расчета молекулярных фаз рассеяния откроет

поле [10-12]. Волновые функции, описывающие рас-

новые горизонты в исследовании процессов упру-

сеяние электрона на многоатомной молекуле вне так

гого рассеяния электронов молекулами, включая

называемой молекулярной сферы, рассматриваются

временную картину этих явлений.

как линейная комбинация регулярных и нерегуляр-

ных решений волнового уравнения. Фазовые сдви-

Благодарности. А. С. Балтенков выражает

ги молекулярной волновой функции определяются

благодарность И. Войцеховскому за полезные об-

из условия сшивки решений волнового уравнения

суждения.

внутри и за пределами этой сферы [21] или в расче-

Финансирование. Работа А. С. Балтенкова

тах радиальных интегралов вплоть до расстояний,

выполнена при финансовой поддержке Узбекского

определяющих диапазон взаимодействия электрона

фонда (грант №ОТ-Ф2-46).

с молекулой (r_max

= 10Å [7]). Соответствующая

этим представлениям картина дифракции электрон-

ной волны на молекуле (рис. 1с в статье [22]) пред-

ЛИТЕРАТУРА

ставляет собой дифракцию волны на изолированной

молекулярной сфере.

L. E. Eisenbud, Ph. D. Thesis, Princeton University

(1948).

Картина рассеяния, при которой вдали от ми-

шени существует набор сферических волн, гене-

E. P. Wigner, Phys. Rev. 98, 145 (1955).

рируемых пространственно-разнесенными центрами

(рис. 1a в [22]), представляется более близким к ре-

F. T. Smith, Phys. Rev. 118, 349 (1960).

альности. В нашей статье было показано, что ме-

P. M. Kraus, A. Rupenyan, and H. J. Wörner, Phys.

тод S-матрицы также может быть разработан и для

Rev. Lett. 109, 233903 (2012).

этой картины рассеяния. Рассмотренный здесь ме-

тод парциальных волн для несферических потенци-

A. Chacon, M. Lein, and C. Ruiz, Phys. Rev. A 89,

алов позволяет отделить кинематику процесса рас-

053427 (2014).

сеяния от динамической части, определяемой моле-

кулярными фазами. Производные по энергии от мо-

P. M. Kraus, D. Baykusheva, and H. J. Wörner,

Phys. Rev. Lett. 113, 023001 (2014).

лекулярных фаз η_λ(k) есть парциальные вигнеров-

ские времена задержки медленного электрона двух-

P. Hockett, E. Frumker, D. M. Villeneuve, and P.

атомной молекулой.

B. Corkum, J. Phys. B 49, 095602 (2016).

Непосредственное применение к несферическим

мишеням обычного метода S-матрицы, основанно-

M. Huppert, I. Jordan, D. Baykusheva, A. von Con-

го на сферических функциях Y_lm(k), приводит к

ta, and H. J. Wörner, Phys. Rev. Lett. 117, 093001

(2016).

неустранимым внутренним противоречиям, и поэто-

му не может считаться удовлетворительным. Мы

D. Baykusheva and H. J. Wörner, J. Chem. Phys.

пришли к такому выводу на основе рассмотре-

146, 1 (2017).

ния модельной системы (1). Было показано в [23]

(разд. 3.1), что набора молекулярных фаз рассе-

10.

F. A. Gianturco, R. R. Lucchese, and N. Sanna, J.

яния, способных воспроизводить сечение упругого

Chem. Phys. 100, 6464 (1994).

рассеяния (5), в рамках классического метода S-

11.

A. P. P. Natalense and R. R. Lucchese, J. Chem.

матрицы не существует.

Phys. 111, 5344 (1999).

Как и в случае рассматриваемой двухатомной

системы, амплитуда упругого рассеяния электро-

12.

F. A. Gianturco and A. Jain, Phys. Rep. 143, 347

нов кластером из N непересекающихся атомных

(1986).

819