ЖЭТФ, 2020, том 158, вып. 5 (11), стр. 884-910

ОСОБЕННОСТИ ВЛИЯНИЯ ДЕФЕКТОВ СТРУКТУРЫ НА

ЭФФЕКТЫ КОРРЕЛЯЦИИ И ВЗАИМОДЕЙСТВИЯ ВИХРЕВЫХ

ВОЗБУЖДЕНИЙ В НЕРАВНОВЕСНОЙ ВКТ-ДИНАМИКЕ

ДВУМЕРНОЙ XY -МОДЕЛИ

В. В. Прудников^*, П. В. Прудников, И. С. Попов

Омский государственный университет им. Ф. М. Достоевского

644077, Омск, Россия

Поступила в редакцию 4 мая 2020 г.,

после переработки 4 мая 2020 г.

Принята к публикации 20 мая 2020 г.

Осуществлено численное исследование методом Монте-Карло неравновесного критического поведения

двумерной структурно-неупорядоченной XY -модели при ее эволюции из начального высокотемператур-

ного состояния. Выявлены особенности влияния структурного беспорядка на временную зависимость кор-

реляционной длины системы ξ(t) и динамический скейлинг спин-спиновой автокорреляционной функции

CSS(t,tw). Осуществлен прямой расчет динамического поведения корреляционной длины ξ(t) двумерной

структурно-неупорядоченной XY -модели и показано, что для нее, как и для чистой модели, выполняет-

ся временная зависимость с логарифмической поправкой ξ(t) ∝ (t/ ln t)1/2, связанная с неравновесной

аннигиляцией вихрей и антивихрей в формирующихся вихревых парах. На основе проведенного анализа

временных зависимостей корреляционной длины ξ(t) и кумулянта намагниченности g2(t) показано, что

двумерная XY -модель со спиновой концентрацией p = 0.7 находится настолько близко к порогу спиновой

перколяции pc, что влияние притяжения перколяционной неподвижной точки становится определяющим

в релаксационных свойствах системы. Однако особенности критической динамики систем со спиновыми

концентрациями p = 0.9 и p = 0.8 определяются притяжением неподвижной точки чистой системы.

Определены температурные и концентрационные зависимости критического индекса Фишера η(p, T) с

использованием скейлинговых свойств рассчитанной двухвременной зависимости спин-спиновой автокор-

реляционной функции CSS(t, tw). Осуществлен расчет скейлинговых функций двухвременной зависимос-

ти спин-спиновой автокорреляционной функции CSS(t, tw) с использованием полученной в результате

моделирования динамической зависимости корреляционной длины ξ(t) и определены значения показа-

телей λC (p, T ) степенного убывания скейлинговых функций в долговременном режиме, находящиеся в

хорошем согласии с соотношением λC (p, T ) = 1 + η(p, T ) и доказывающие выполнение динамического

скейлинга для неравновесных характеристик структурно-неупорядоченных систем.

DOI: 10.31857/S0044451020110139

логического фазового перехода Березинского - Ко-

стерлица - Таулесса при температуре T_BKT

[1-4].

Фазовый переход связан с диссоциацией связанных

1. ВВЕДЕНИЕ

пар вихрь-антивихрь в точке перехода и существо-

ванием данных связанных вихревых возбуждений в

Среди низкоразмерных систем особое место за-

низкотемпературной фазе с T < T_BKT . Особенно-

нимают двумерные системы с непрерывной симмет-

стью данной системы является аномально сильная

рией, в которых дальний магнитный порядок разру-

пространственная и временная корреляция состоя-

шается при всех конечных температурах аномаль-

ний системы во всей низкотемпературной фазе, ха-

но сильными поперечными флуктуациями спино-

рактеризуемая степенным законом убывания и ре-

вой плотности. Однако случай двумерной XY -моде-

ализацией квазидальнего порядка, в то время как

ли характеризуется осуществлением в системе топо-

для термодинамических фазовых переходов второго

рода эффекты сильной корреляции осуществляют-

^* E-mail: prudnikv@univer.omsk.su

884

ЖЭТФ, том 158, вып. 5 (11), 2020

Особенности влияния дефектов структуры. . .

ся лишь вблизи критической точки. Это позволяет

щей динамические зависимости автокорреляцион-

наблюдать медленную динамику двумерной XY -мо-

ной функции и функции отклика системы [7,42,43].

дели не только вблизи критической точки, а во всем

Среди неравновесных релаксационных процес-

низкотемпературном диапазоне при T ≤ T_BKT [5-7].

сов особый интерес вызывает критическое пове-

Двумерная XY -модель является классической

дение двумерной XY -модели, в которой за счет

спиновой моделью статистической механики и ис-

степенного характера пространственной и времен-

пользуется для описания критических и низкотем-

ной корреляции особенности медленной динами-

пературных свойств широкого класса реальных фи-

ки могут наблюдаться не только вблизи крити-

зических систем [8, 9], таких как ультратонкие маг-

ческой точки, но и во всем низкотемпературном

нитные пленки [10]; планарные магнетики с анизот-

диапазоне с T

≤ T_BKT. Присутствие дефектов

ропией типа «легкая плоскость» [11-15]; сингуляр-

структуры приводит к возникновению эффекта пин-

ности в критических свойствах сверхтекучих тон-

нинга вихревых возбуждений на дефектах

[44],

ких пленок [16-19]; решетки джозефсоновских кон-

что существенно замедляет динамические процес-

тактов [8, 20, 21] и SFS-контактов [22-24]; двумер-

сы в системе. Квазидальний порядок в системе

ные кристаллы [2] и смектические жидкие крис-

сохраняется с введением структурного беспоряд-

таллы [25-29]; для описания плавления нескольких

ка [45, 46]. Неравновесное критическое поведение в

слоев сорбированного ксенона в монокристалличес-

структурно-неупорядоченной двумерной XY -моде-

ком графите [30]; процесса сорбции водорода на

ли обусловлено неравновесными процессами в вих-

вольфраме W(011) с реконструкцией поверхности

ревой подсистеме, спин-волновыми процессами и

p(2 × 2) [31]; а также корреляционных свойств дву-

взаимодействием данных подсистем с дефектами

мерной гидродинамической турбулентности [32].

структуры. С учетом того, что двумерная XY -

Хотя равновесные критические свойства двумер-

модель используется для описания поведения и

ной XY -модели достаточно подробно изучены [8],

свойств широкого ряда физических систем [8], ин-

исследование неравновесной критической динамики

терес к исследованию особенностей неравновесного

и влияния структурного беспорядка на ее неравно-

поведения данной модели и влияния на него струк-

весные критические свойства вызывает значитель-

турного беспорядка очень высок.

ный научный интерес [7]. Связано это с явления-

В данной работе мы сосредоточим внимание на

ми аномально медленной релаксации системы из на-

случае эволюции двумерной XY -модели из высоко-

чального неравновесного состояния и возникающи-

температурного начального состояния с температу-

ми в системе эффектами старения, памяти, нару-

рой T₀ ≫ T_BKT , характеризующегося наличием сво-

шения флуктуационно-диссипативной теоремы [5,6,

бодных вихревых возбуждений, с последующем за-

33-39], нарушением канонического динамического

мораживанием при температурах T_s ≤ T_BKT . Как

скейлинга и возникновением явлений сверхстарения

предсказывалось в ряде работ [47, 48], для чистой

и субстарения [36], а также влиянием на них силь-

XY -модели динамическая зависимость корреляци-

ной вихревой неравновесности, огрубления, фраг-

онной длины ξ(t) характеризуется в этом случае до-

ментации квазидальнего порядка и неравновесно-

полнительными логарифмическими поправками ви-

го пиннинга вихрей на дефектах структуры [40, 41].

да ξ(t) ∝ (t/ ln t)1/z за счет эффектов взаимодей-

Старение — это эффект замедления релаксацион-

ствия вихревых возбуждений, в то время как при

ных и корреляционных процессов при увеличении

эволюции из низкотемпературного начального со-

времени, прошедшего с момента приготовления об-

стояния с T₀ = 0, в котором отсутствуют свободные

разца до начала измерения его свойств и называе-

вихревые возбуждения, динамическая зависимость

мого «возрастом» образца или временем ожидания

корреляционной длины ξ(t) удовлетворяет предска-

t_w. Проявление эффектов старения осуществляет-

заниям динамического скейлинга ξ(t) ∝ t1/z , где z =

ся через двухвременные зависимости таких харак-

= 2 — динамический критический индекс для дву-

теристик системы, как автокорреляционная функ-

мерной XY -модели.

ция C(t, t_w), функция отклика R(t, t_w) и динамиче-

Динамическая зависимость корреляционной

ская восприимчивость χ(t, t_w) [7]. В режиме старе-

длины ξ(t) для чистой двумерной XY -модели ранее

ния данные функции зависят не от разности вре-

исследовалась в работах [48-50]. Впоследствии эта

мен t - t_w, а от t и t_w в отдельности, т. е. происхо-

зависимость применялась в исследовании эффектов

дит нарушение однородности процесса релаксации

старения и нарушения флуктуационно-диссипа-

во времени. Старение сопровождается нарушением

тивной теоремы в работах [5, 6, 33-37], в частности,

флуктуационно-диссипативной теоремы, связываю-

для описания структурно-неупорядоченной дву-

885

В. В. Прудников, П. В. Прудников, И. С. Попов

ЖЭТФ, том 158, вып. 5 (11), 2020

мерной XY -модели

[6, 36]. В настоящей работе

не равной температуре T₀. Возникающий в систе-

в результате численного исследования методами

ме процесс установления равновесия характеризу-

Монте-Карло осуществляется прямое определение

ется временем релаксации t_rel(T ), и при t, t_w ≫ t_rel

динамической зависимости корреляционной длины

достигается состояние равновесия, соответствующее

ξ(t) для двумерной чистой и структурно-неупо-

температуре T_s, при этом динамика системы оказы-

рядоченной XY -модели; исследуются особенности

вается стационарной и инвариантной относительно

влияния дефектов структуры на динамические

обращения времени. Однако при t, t_w ≪ t_rel эво-

корреляционные свойства системы; определяются

люция зависит от начального состояния системы.

особенности влияния фазового притяжения перко-

В связи с этим выделяется неравновесное поведе-

ляционной неподвижной точки и неподвижной точ-

ние систем с эволюцией из высокотемпературного

ки чистой системы на динамическую зависимость

(T₀ > T_s) и низкотемпературного (T₀ < T_s) началь-

корреляционной длины от концентрации дефектов;

ных состояний. Эффекты старения и нарушение

осуществляется исследование скейлинговой зависи-

флуктуационно-диссипативной теоремы в чистой и

мости спин-спиновой автокорреляционной функции

структурно-неупорядоченной двумерной XY -моде-

C_SS(t, t_w) от корреляционной длины ξ(t).

ли с эволюцией из высокотемпературного начально-

го состояния детально исследовались в работе [6],

из низкотемпературного начального состояния — в

2. ОСНОВНЫЕ ПОНЯТИЯ И МОДЕЛЬНЫЕ

работе [36].

ПРЕДСТАВЛЕНИЯ

На основании размерного анализа и его обоб-

щения на случай динамики критических явлений

Эффекты старения, проявляющиеся на неравно-

двухвременная зависимость корреляционной функ-

весном этапе релаксации системы с медленной дина-

ции C (t, t_w) при неравновесной критической эволю-

микой, характеризуются существованием двухвре-

ции двумерной XY -модели характеризуется следу-

менной зависимости у автокорреляционной функ-

ющим скейлинговым соотношением [28, 48]:

ции от времени ожидания t_w и времени наблюде-

ния t - t_w. Так, для классической спиновой системы

⁽ξ(t - t_w)⁾

C (t, t_w) =

f_C

(2)

временная корреляционная функция определяется

(t - t_w)η(T)/z

ξ(t_w)

выражением (t > t_w) [6, 35, 36]

где f_C представляет собой скейлинговую функцию,

∫

[

η(T ) — критический индекс Фишера, z — динамичес-

C (t, t_w) =

d^dx

〈S(x, t)S(x, t_w )〉 -

кий критический индекс со значением z = 2 для ре-

]

лаксационной динамики чистой двумерной XY -мо-

- 〈S(x, t)〉〈S(x, t_w )〉

(1)

дели [34, 51], ξ(t) — динамическая зависимость кор-

где угловые скобки 〈. . .〉 соответствуют процедуре

реляционной длины системы в процессе неравновес-

статистического усреднения, а квадратные [. . .] —

ной критической релаксации системы из начального

процедуре усреднения по различным конфигура-

неравновесного состояния.

циям распределения немагнитных атомов приме-

Динамическая зависимость корреляционной

си в структурно-неупорядоченной спиновой систе-

длины ξ(t) для двумерной XY -модели при нерав-

ме; S(x, t) — локальная спиновая плотность. Время

новесной критической релаксации существенно

ожидания t_w определяется временем, прошедшим с

зависит от типа начального состояния системы

момента приготовления образца до начала измере-

и меняет характер своей зависимости от времени

ния его характеристик. В течение t, t_w ≪ t_rel, где

при переходе от случая эволюции из низкотемпе-

t_rel — время релаксации системы, во временном по-

ратурного к высокотемпературному начальному

ведении системы проявляется влияние начальных

состоянию

[48-50]. Так, при релаксации из на-

состояний системы и эффектов старения, характе-

чального полностью упорядоченного состояния с

ризующихся нарушением трансляционной симмет-

T₀

= 0 временная зависимость корреляционной

рии системы во времени и замедлением релаксаци-

длины ξ(t) ∝ t1/z и динамика системы является

онных и корреляционных процессов с увеличением

преимущественно спин-волновой; при релаксации

«возраста» образца t_w.

из высокотемпературного начального состояния

Неравновесное поведение системы реализуется

с T0 ≫ TBKT в равновесное состояние при тем-

путем ее перевода в начальный момент времени t =

пературе T_s ≤ T_BKT временная зависимость кор-

= 0 из равновесного состояния при температуре

реляционной длины приобретает дополнительную

T₀ в состояние при температуре замораживания T_s,

логарифмическую зависимость ξ(t)

∝ (t/ ln t)1/z

886

ЖЭТФ, том 158, вып. 5 (11), 2020

Особенности влияния дефектов структуры. . .

с динамикой, определяемой преимущественно

⁽ξ(t - t_w)⁾

⁽ξ(t - t_w))-λC

f_C

∝

вихревыми возбуждениями и их взаимодействием.

ξ(t_w)

Исторически неравновесная кинетика вихревых

возбуждений в процессе релаксации двумерной

∝

⁽t-t_w)-λC/z ,

(4)

t_w

XY -модели впервые была рассмотрена в рабо-

те

[52]. Показано, что неравновесная вихревая

где λ_C — показатель автокорреляционной функции.

аннигиляция вихрей и антивихрей описывается

Соотношение (4) может быть применено к опи-

кинетическим уравнением бимолекулярной реакции

санию неравновесного критического поведения дву-

аннигиляции со скоростью реакции, определяемой

мерной XY -модели с эволюцией из низкотемпера-

квадратом плотности вихревых возбуждений с

турного полностью упорядоченного начального со-

динамической зависимостью плотности вихрей

стояния, и согласно работам [33, 56, 57] показатель

ρ(t) ∝ 1/R²(t) и R(t) ∝ t1/2 — характеристическим

λ_C автокорреляционной функции в этом случае ра-

пространственным масштабом разделения вихрей

вен λ_C = 1+η(T), а динамический критический ин-

и антивихрей в формирующихся вихревых парах.

декса z = 2. Тем не менее соотношение (4) может

В последующей работе [53] обсуждались вопросы,

быть также применено к описанию скейлингового

связанные с особенностями введения логариф-

поведения автокорреляционной функции двумерной

мических поправок в динамические зависимости

XY -модели с эволюцией из высокотемпературного

плотности вихревых возбуждений, и было показано,

начального состояния с теми же λ_C = 1 + η(T ) и

что пространственный масштаб R(t) соответствует

z = 2, если воспользоваться временной зависимос-

корреляционной длине ξ(t). В серии последую-

тью корреляционной длины ξ(t) ∝ (t/ lnt)1/z. В ре-

щих работ (см. [47-49, 54]) было выявлено, что

зультате, скейлинговая функция f_C (ξ(t - t_w)/ξ(t_w))

R(t) ∝ (t/ ln t)1/2 и, следовательно, динамическая

в долговременном режиме будет характеризовать-

зависимость корреляционной длины ξ(t) также

ся следующей асимптотической степенной зависи-

характеризуется логарифмической поправкой вида

мостью:

ξ(t) ∝ (t/ ln t)1/z, связанной с неравновесными вих-

ревыми процессами. Прямое вычисление временной

⁽ξ(t - t_w)⁾

⁽ξ(t - t_w))-(1+η(T))

f_C

∝

зависимости корреляционной длины ξ для чистой

ξ(t_w)

двумерной XY -модели было осуществлено в работе

⁽ (t - t_w) ln t_w )-(1+η(T))/2

[50]. Однако график зависимости ξ(t)² ln t ∝ t, под-

∝

(5)

t_w ln(t - t_w)

тверждающий наличие логарифмических поправок

в ξ(t), представлен в работе [50] лишь на коротком

Введение структурного беспорядка практичес-

интервале времен с Δt ∼ 10³ шагов Монте-Карло

ки не сказывается на равновесных критических

на спин (MCS/s) с изображением временной зависи-

свойствах двумерной XY -модели в точке фазо-

мости отдельными символами, приходящимися на

вого BKT-перехода при температуре T_BKT , что

временной интервал порядка 100 MCS/s, что резко

удовлетворяет критерию Харриса

[58]. Тем не

снижает доказательную базу приведенных данных.

менее такая неуниверсальная характеристика, как

Возвращаясь к описанию эффектов старения от-

температура фазового перехода T_BKT становится

метим, что данные эффекты проявляются при t -

явной функцией спиновой концентрации p, т. е.

- t_w ∼ t_w и характеризуются замедлением корре-

T_BKT (p), обращаясь в нуль при пороге спино-

ляции и релаксации системы с увеличением ее воз-

вой перколяции T_BKT (p_c)

= 0. Аналитические

раста — времени ожидания t_w. В режиме старения

и численные исследования [45, 46] показали, что

скейлинговая форма (2) принимает вид

структурный беспорядок не влияет на равновесное

)

критическое поведение только при температуре

⁽ξ(t - t_w)

C(t, t_w) ≃ t-η(T)/z

f_C

(3)

фазового перехода T_BKT , а в низкотемпературной

ξ(t_w)

фазе Березинского с T < T_BKT влияние дефектов

Для большинства неравновесных систем, в ко-

структуры становится существенным и приводит к

торых выполняются требования динамического

изменению значений показателя η для равновесной

скейлинга с временной зависимостью корреляци-

корреляционной функции и к его зависимости

онной длины ξ(t) ∝ t1/z, скейлинговая функция

как от температуры, так и спиновой концентра-

f_C(ξ(t - t_w)/ξ(t_w)) в долговременном режиме с

ции η(T, p). Значительно более масштабным и

t - t_w

≫ t_w ≫ 1 характеризуется следующей

разнообразным становится влияние структур-

асимптотической степенной зависимостью [55]:

ного беспорядка на неравновесные критические

887

В. В. Прудников, П. В. Прудников, И. С. Попов

ЖЭТФ, том 158, вып. 5 (11), 2020

∑

свойства двумерной XY -модели

[6, 36, 37, 40, 41].

M(t) = p_iS_i(t),

(9)

Неравновесная критическая релаксация двумер-



ной структурно-неупорядоченной XY -модели при



1∑∑



эволюции из высокотемпературного начального

Φ(t) =



p_iS_i(t)eikn·ri



(10)



состояния сопровождается пиннингом вихревых

возбуждений на дефектах структуры [44, 59]. По-

где k_n [k₁ = (2π/L, 0); k₂ = (0, 2π/L)] — элементар-

тенциал притяжения вихря дефектом структуры

ные векторы обратной решетки (0 ≤ k_n · r_i < 2π);

обладает логарифмической расходимостью

[44],

r_i = (x_i, y_i) — координата i-го узла решетки. Вы-

что соизмеримо с логарифмическим потенциалом

ражение (8) соответствует формуле для корреляци-

межвихревого взаимодействия, вследствие чего

онной длины ξ(t), используемой в работе [50], с реа-

пиннинг вихрей существенно влияет на общую

лизацией более общего усреднения по двум направ-

картину вихревой релаксации системы.

лениям, определяемым векторами k₁ и k₂, в первой

В настоящей работе проведено исследование

зоне Бриллюэна.

влияния дефектов структуры на динамическую

Двухвременная динамическая зависимость спин-

зависимость корреляционной длины ξ(t) и дина-

спиновой автокорреляционной функции задавалась

мический скейлинг автокорреляционной функции

выражением [6, 36]

C (t, t_w) при критической релаксации двумер-

∑

ной структурно-неупорядоченной XY -модели из

C_SS (t, t_w) =

p_iS_i(t)S_i(t_w)

(11)

начального высокотемпературного состояния с

pL²

T0 ≫ TBKT. Гамильтониан системы в настоящей

В процессе критической релаксации системы из вы-

работе выбран в виде

сокотемпературного начального состояния с T₀ ≫

[

]

∑

≫ T_BKT в поведении связанной автокорреляцион-

p, S

p_ip_jS_i · S_j,

(6)

ной функции [36]

〈i,j〉

∑

где J

> 0 — обменный интеграл, S = {S_i(t)} и

C_con (t, t_w) =

p_iS_i(t)S_i(t_w)

p = 〈p_i(t)〉 — решеточные поля спинов и дефектов

pL²

структуры; S_i = (S_i,x, S_i,y) — классический планар-

∑

ный спин, связанный с i-м узлом квадратной решет-

p_iS_i(t)

p_iS_i(t_w)

(12)

ки с линейным размером L; p_i — случайные числа

pL²

заполнения i-го узла: p_i = 1, если i-й узел занят

и спин-спиновой автокорреляционной функции

спином, и p_i = 0, когда в i-м узле расположен де-

C_SS (t, t_w) (11) различий фактически не возникает

фект; суммирование осуществляется по всем парам

[6,36], так как начальное значение намагниченности

ближайших соседей в решетке. Дефекты структуры

M₀ и ее последующие значения M(t) оказываются

распределялись по решетке равномерно в соответ-

малыми [6]. Поэтому исследование поведения авто-

ствии с функцией распределения

корреляционной функции C (t, t_w) при критической

P (p_i) = (1 - p)δ(p_i) + pδ(1 - p_i),

(7)

релаксации двумерной структурно-неупорядо-

ченной XY -модели из высокотемпературного

где p определяет долю узлов на решетке, занятых

начального состояния в настоящей работе проведе-

спинами, и характеризует величину спиновой кон-

но на основе анализа двухвременной зависимости

центрации.

(11) спин-спиновой автокорреляционной функции

Динамическая зависимость корреляционной

C_SS (t, t_w).

длины в настоящей работе задавалась выражением

√

[〈M²(t)〉]

3. РЕЗУЛЬТАТЫ МОДЕЛИРОВАНИЯ И ИХ

ξ(t) =

- 1,

(8)

2 sin(π/L)

[〈Φ(t)〉]

АНАЛИЗ

где угловые 〈. . .〉 и квадратные [. . .] скобки соот-

Мы рассмотрели системы с концентрациями спи-

ветствуют процедурам статистического усреднения

нов p = 1.0 (чистая система), 0.9, 0.8, 0.7 на квадрат-

и усреднения по различным конфигурациям рас-

ной решетке с линейным размером L = 256. Темпе-

пределения примеси в структурно-неупорядоченной

ратуры фазового перехода T_BKT для систем с дан-

системе; M(t) и Φ(t) — соответственно намагничен-

ными спиновыми концентрациями p характеризуют-

ность и структурный фактор системы:

ся следующими значениями:

888

ЖЭТФ, том 158, вып. 5 (11), 2020

Особенности влияния дефектов структуры. . .

T_BKT (p = 1.0) = 0.893(2) [37,45,60],

Расчеты ξ(t) (рис. 1) осуществлялись при следу-

(p):

ющих температурах замораживания системы T_s

T_BKT (p = 0.9) = 0.679(7) [37,45,46],

BKT

в точке фазового BKT-перехода при Ts = T

и в низкотемпературной фазе Березинского при

T_BKT (p = 0.8) = 0.485(4) [37,45,46],

температурах T_s/T_BKT

= 0.75, 0.50, 0.25. Отме-

T_BKT (p = 0.7) = 0.34(2) [45,46].

тим, что с понижением температуры заморажива-

ния при T_s

< T_BKT амплитуда статистических

Температура системы T в настоящей работе выра-

флуктуаций для ξ(t) заметно возрастает, особенно

жается в единицах обменного интеграла J/k_B .

для структурно-неупорядоченных систем. Это свя-

Моделирование осуществлялось с использовани-

зано с усилением влияния взаимодействия вихре-

ем алгоритма Метрополиса, реализующего дисси-

вых возбуждений и замедлением процесса динами-

пативную динамику двумерной XY -модели во всей

ческого самоусреднения при понижении температу-

низкотемпературной фазе при T_s ≤ T_BKT [35, 51].

ры. Статистическая погрешность определения кор-

Время моделирования измеряется в шагах Мон-

реляционной длины ξ(t) для чистой системы со-

те-Карло на спин (MCS/s) с реализацией за этот шаг

ставила величину не превышающую 5 % при t ≥

процедуры из N_s = pL² случайных выборок спинов

≥ 10-50 MCS/s (на меньших временах погрешность

в узлах системы с их пробным переворотом и изме-

больше и данные временные диапазоны в последу-

нением спиновой конфигурации. Проведенные ранее

ющем анализе не используются). Для структурно-

исследования неравновесной критической релакса-

неупорядоченных систем при температурах T_BKT

ции чистой [5, 33] и структурно-неупорядоченной

погрешность определения корреляционной длины

[6, 35-38, 40, 41, 61-64] двумерной XY -модели пока-

ξ(t) не превышает 5 % при t ≥ 50-100 MCS/s. Одна-

зали, что основные неравновесные эффекты, свя-

ко с понижением температуры погрешность дости-

занные с динамическим скейлингом, ростом прост-

гает значений 10 %-15 % для T_s/T_BKT = 0.75, 0.50, а

ранственной корреляции и эффектами старения,

при T_s/T_BKT = 0.25 достигает 20 %-30 %, особенно

проявляются в характерных временных диапазонах

для спиновой концентрации p = 0.7.

20000-50000 MCS/s. Поэтому в настоящей работе с

На рис. 1 приведены полученные временные за-

целью корректно охватить все основные неравно-

висимости корреляционной длины ξ, вычисленной

весные процессы время наблюдения было выбрано

по формуле (8), для двумерной XY -модели с кон-

50000 MCS/s.

центрациями спинов p = 1.0 (чистая система), 0.9,

0.8, 0.7 на квадратной решетке с линейным разме-

3.1. Расчеты временной зависимости

ром L = 256. Для динамической зависимости кор-

корреляционной длины

реляционной длины ξ(t) был выбран масштабный

аргумент (t/ ln t)1/2. Видно, что на выбранных ин-

Предварительные расчеты временной зависи-

тервалах времени наблюдения практически для всех

мости корреляционной длины ξ для двумерной

параметров моделирования ξ(t) демонстрирует ли-

XY -модели показали, что в поведении ξ(t) наблю-

нейный рост в переменных (t/ ln t)1/2. С понижени-

даются значительные статистические флуктуации,

ем температуры замораживания T_s в глубь низко-

и для получения корректных результатов требу-

температурной фазы Березинского с T_s < T_BKT и

ется получение значительного объема статистиче-

увеличением концентрации дефектов (понижением

ской выборки. В результате, статистическая обра-

спиновой концентрации p) наблюдается замедление

ботка динамической зависимости корреляционной

процесса роста корреляционной длины ξ(t).

длины ξ(t) для чистой системы проводилась по

50000 статистически независимым реализациям на-

В случае чистой системы (p = 1.0) при выбран-

чального высокотемпературного состояния с после-

ных временах наблюдения при температуре замора-

дующей прогонкой для каждой спиновой конфигу-

живания в точке фазового перехода T_BKT корреля-

рации до времени наблюдения 50000 MCS/s. Для

ционная длина достигает значений ξ ≈ 85-90 в еди-

структурно-неупорядоченных систем со спиновыми

ницах постоянной решетки, что становится сравни-

концентрациями p = 0.9, 0.8, 0.7 проводилось усред-

мым с линейным размером решетки L = 256. При

нение соответственно по 5000, 10000, 50000 различ-

этом наблюдается заметное отклонение роста ξ(t) ∝

ным конфигурациям распределения немагнитных

∝ (t/ ln t)1/2 от линейной зависимости. Это связано

атомов примеси с реализацией усреднения по 20 про-

с влиянием конечного размера моделируемой сис-

гонкам для каждой примесной конфигурации.

темы, и для устранения влияния конечноразмерных

889

В. В. Прудников, П. В. Прудников, И. С. Попов

ЖЭТФ, том 158, вып. 5 (11), 2020

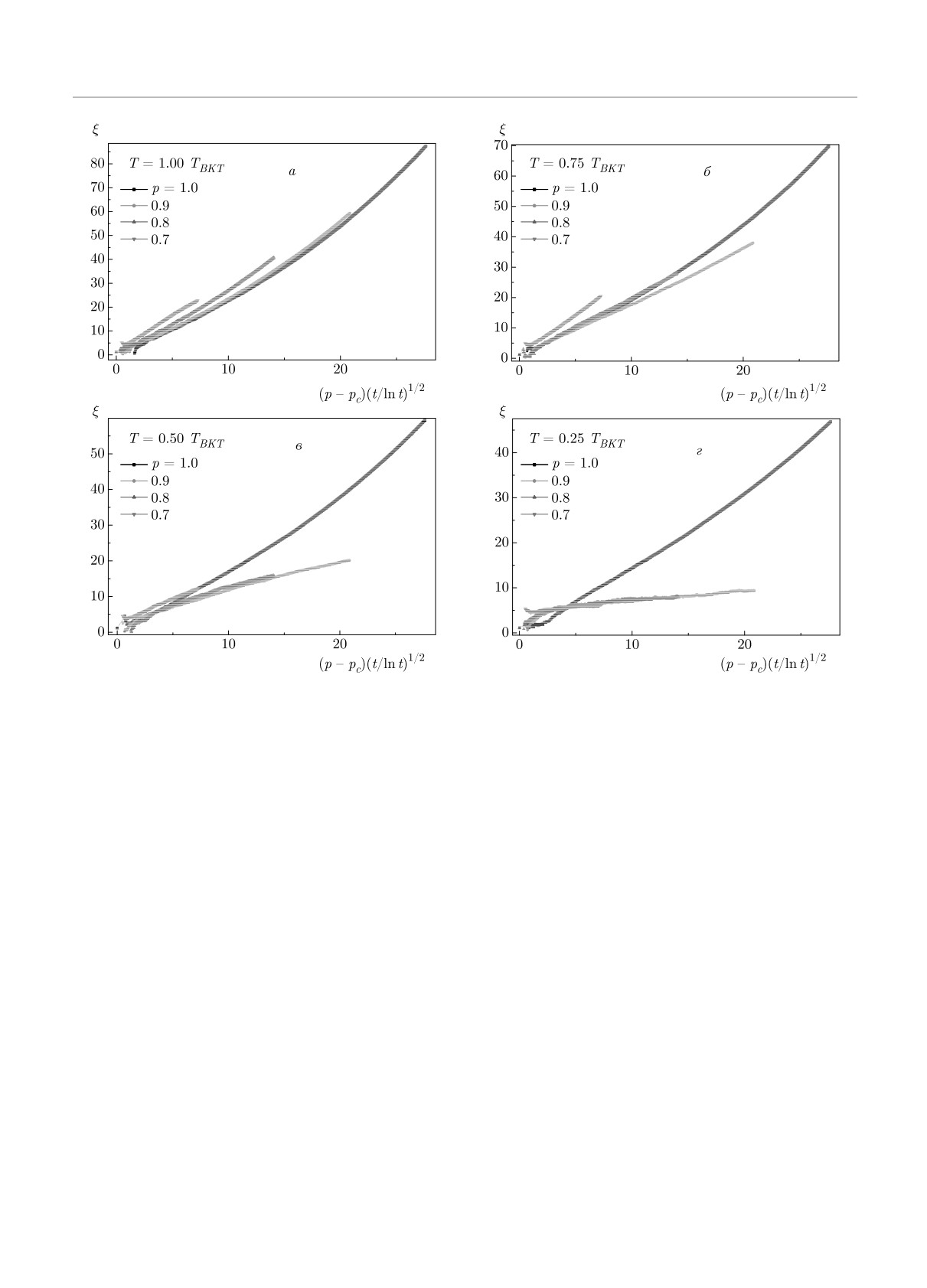
Рис. 1. Динамическая зависимость корреляционной длины ξ от (t/ ln t)1/2 при критической релаксации чистой (p = 1.0)

и структурно-неупорядоченной (p = 0.9, 0.8, 0.7) двумерной XY -модели c линейным размером решетки L = 256; темпе-

ратура замораживания системы Ts/TBKT = 1.0, 0.75, 0.50, 0.25; время наблюдения t = 50000 MCS/s

эффектов на неравновесные динамические характе-

мерной XY -модели на больших временных масшта-

ристики требуется выполнение условия ξ(t) ≪ L.

бах.

Для чистой системы при температурах заморажи-

Для чистой модели с целью уточнения влияния

вания в низкотемпературной фазе при T_s/T_BKT =

конечноразмерных эффектов на соответствие вре-

= 0.75 и 0.50, когда корреляционная длина достига-

менной зависимости корреляционной длины соот-

ет значений ξ ≈ 70 и 60, также наблюдается откло-

ношению ξ(t) ∝ (t/ ln t)1/2 мы провели расчет ξ(t)

нение роста ξ(t) ∝ (t/ ln t)1/2 от линейной зависимо-

для решетки с линейным размером L = 512 (рис. 2).

сти, но меньшее чем при T_s/T_BKT = 1.0. При самой

Статистическая выборка для получения зависимос-

низкой из рассмотренных температур, T_s/T_BKT =

ти ξ(t) в данном случае проводилась по 40000 стати-

= 0.25, величина корреляционной длины не превы-

стическим конфигурациям. Представленные резуль-

шает ξ ≈ 50 и в этом случае отклонение от ожида-

таты показывают, что отклонения от ожидаемой ди-

емой зависимости ξ(t) ∝ (t/ ln t)1/2 практически не

намической зависимости ξ(t) ≈ (t/ lnt)1/2 не возни-

возникает.

кают практически при всех временах наблюдения

Полученные в настоящей работе результаты для

до t = 50000 MCS/s, что наглядно демонстрирует-

чистой системы находятся в хорошем соответствии

ся построенной на рис. 2б зависимостью ξ² ln t от t.

с результатами работы [50], однако в ней авто-

В то же время, для решетки с L = 256 эта зависи-

ры ограничились временами моделирования t

≈

мость выполняется только в некотором начальном

≈ 1000 MCS/s, что не позволило выявить функци-

временном диапазоне (см. рис. 3), который для тем-

ональную временную зависимость корреляционной

пературы замораживания T_s = T_BKT ограничивает-

длины ξ и особенности критической динамики дву-

ся временем наблюдения t ≤ 15000 MCS/s.

890

ЖЭТФ, том 158, вып. 5 (11), 2020

Особенности влияния дефектов структуры. . .

Рис. 2. Динамическая зависимость корреляционной длины

ξ от (t/ ln t)1/2 (а) и величины ξ² ln t от времени наблюде-

Рис. 3. Динамическая зависимость корреляционной длины

ξ от (t/ ln t)1/2 (а) и величины ξ² ln t от времени наблюде-

ния t (б) при критической релаксации чистой (p = 1.0)

двумерной XY -модели c линейным размером решетки

ния t (б) при критической релаксации чистой двумерной

XY -модели c линейным размером решетки L = 256 при

L = 512; время наблюдения t = 50000 MCS/s

t ≤ 15000 MCS/s

Введение в систему структурного беспорядка су-

нение ξ(t) от линейной зависимости в переменных

щественным образом сказывается на динамической

(t/ ln t)1/2 при больших временах наблюдения t ≈

зависимости корреляционной длины ξ(t) — про-

≈ 50000 MCS/s и то только при температуре замо-

исходит существенное замедление динамики кри-

раживания T_s = T_BKT . Для остальных представ-

тической релаксации по сравнению с чистой си-

ленных температур замораживания, T_s < T_BKT (p),

стемой. Так, из результатов, представленных на

и спиновых концентраций, p = 0.8 и p = 0.7, откло-

рис. 1, следует, что к моментам времени наблюде-

нения ξ(t) от ожидаемой динамической зависимости

ния t ≈ 50000 MCS/s корреляционная длина при

(t/ ln t)1/2 практически не возникают. Это позволя-

температуре замораживания T_s = T_BKT достигает

ет сделать вывод, что линейного размера решетки

значений ξ ≈ 85-90 для чистой системы, ξ ≈ 60 —

L = 256 достаточно для достоверной оценки дина-

для структурно-неупорядоченной системы со спи-

мической зависимости корреляционной длины ξ(t)

новой концентрацией p = 0.9, ξ ≈ 40 — для сис-

структурно-неупорядоченной двумерной XY -моде-

темы с p = 0.8 и ξ ≈ 25 — для наиболее разбав-

ли. С понижением температуры замораживания T_s

ленной из рассмотренных систем с p = 0.7. Важно

в область низкотемпературной фазы Березинского,

отметить, что с увеличением концентрации дефек-

т. е. при T_s < T_BKT , в структурно-неупорядоченных

тов (уменьшением спиновой концентрации) влияние

системах наблюдается замедление временного роста

конечноразмерных эффектов существенно снижает-

корреляционной длины ξ с сохранением линейной

ся. Так, для системы со спиновой концентрацией

зависимости от (t/ lnt)1/2 при временах наблюдения

p = 0.9 наблюдается лишь незначительное откло-

вплоть до t ≈ 50000 MCS/s.

891

В. В. Прудников, П. В. Прудников, И. С. Попов

ЖЭТФ, том 158, вып. 5 (11), 2020

Рис. 4. Временная зависимость корреляционной длины ξ, построенная в переменных (1 - g(p)(1 - p)/p)(t/(ln t))1/2,

неравновесной критической релаксации чистой (p = 1.0) и структурно-неупорядоченной (p = 0.9, 0.8, 0.7) двумерной

XY -модели на решетке с L = 256; температура замораживания системы Ts/TBKT = 1.0 (а), 0.75 (б), 0.50 (в), 0.25 (г)

Проведенное в данной работе моделирование ме-

штабов t_L в системе в соответствии с соотношением

тодами Монте-Карло неравновесного критического

ξ(t_L) ≈ L. Из этого следует, что физические предпо-

поведения двумерной XY -модели с эволюцией из

сылки, положенные в основу работ [6, 35-38], явля-

высокотемпературного вихревого начального состо-

ются корректными, и при описании критической ре-

яния показало, что как для чистой, так и струк-

лаксации из высокотемпературного начального со-

турно-неупорядоченных систем при температурах

стояния в двумерной структурно-неупорядоченной

замораживания, соответствующих всей низкотемпе-

XY -модели не возникает качественного изменения

ратурной фазе с T_s ≤ T_BKT , для корреляционной

в проявлениях динамического скейлинга по сравне-

длины выполняется временная зависимость ξ(t) ∝

нию с чистой системой.

∝ (t/ ln t)1/2, связанная с неравновесной аннигиля-

Фазовый переход в двумерной XY -модели пред-

цией вихрей и антивихрей в формирующихся вих-

ставляет непрерывное множество неподвижных то-

ревых парах. Введение в систему структурного бес-

чек ренормгруппового преобразования [1-4,7,8], ког-

порядка приводит к замедлению процессов неравно-

да каждая температура T в низкотемпературной

весной вихревой аннигиляции, но качественно не ме-

фазе Березинского T < TBKT, вплоть до фазово-

няет физических принципов описания неравновес-

го перехода при температуре T_BKT , представляет

ной критической релаксации системы, ограничива-

критическую точку. Введение в систему структур-

ясь замедлением роста корреляционной длины ξ(t) и

ного беспорядка приводит к зависимости темпера-

соответствующим увеличением динамических мас-

туры фазового BKT-перехода от спиновой концент-

892

ЖЭТФ, том 158, вып. 5 (11), 2020

Особенности влияния дефектов структуры. . .

Рис. 5. Временная зависимость корреляционной длины ξ, построенная в переменных (p - pc)(t/ ln t)1/2, неравновесной

критической релаксации чистой (p = 1.0) и структурно-неупорядоченной (p = 0.9, 0.8, 0.7) двумерной XY -модели на

решетке с L = 256; температура замораживания системы Ts/TBKT = 1.0 (а), 0.75 (б), 0.50 (в), 0.25 (г); pc — порог

спиновой перколяции

рации T_BKT (p). С ростом концентрации дефектов

ожидается существенное усиление влияния перко-

спиновая концентрация p понижается, что сопро-

ляционной неподвижной точки в области высокой

вождается уменьшением температуры фазового пе-

концентрации дефектов. Для систем с p

≈ 1.0

рехода T_BKT (p), а при достижении порога спиновой

ожидается проявление притяжения со стороны

перколяции p_c (для рассматриваемой в работе квад-

неподвижной точки чистой системы, в то время как

ратной решетки p_c = 0.592745(2) [65]) температура

для систем с p ≈ p_c должно проявляться влияние

T_BKT (p = p_c) = 0, а фазовый переход в системе пе-

перколяционной неподвижной точки. Интересно

рестает существовать.

выявить влияние данных неподвижных точек на

В структурно-неупорядоченной двумерной

временную зависимость корреляционной длины ξ

XY -модели происходит деформация ренормгруп-

в процессе неравновесной критической релаксации

повых потоков вследствие влияния притяжения со

структурно-неупорядоченной системы. Отметим,

стороны перколяционной неподвижной точки, кото-

что в двумерной XY -модели существует не одна

рое усиливается с ростом концентрации дефектов.

неподвижная точка, а континуум неподвижных

Несмотря на то, что структурный беспорядок в дву-

точек чистой системы, влияние которых может

мерной XY -модели не меняет физической природы

быть выявлено при исследовании неравновесных

релаксационных процессов и сказывается преиму-

критических свойств в низкотемпературной фазе

щественно на динамических масштабах релаксации,

Березинского, а не только в точке BKT-перехода.

893

В. В. Прудников, П. В. Прудников, И. С. Попов

ЖЭТФ, том 158, вып. 5 (11), 2020

В данной работе исследование влияния притя-

жения неподвижной точки чистой системы и пер-

коляционной неподвижной точки было выполнено

на основе анализа динамических скейлинговых за-

висимостей корреляционной длины ξ(t, p) для раз-

личных значений спиновой концентрации p. Из раз-

мерных соображений ясно, что если для чистой сис-

темы имеет место поведение ξ(t) ∝ (t/ lnt)1/2, то со-

ответствующие области притяжения неподвижной

точки чистой системы и перколяционной неподвиж-

ной точки характеризуются скейлинговыми форма-

ми вида

((

)(

)1/2 (

))

1-p

ξ(p; t) = F_P

1-g

(13)

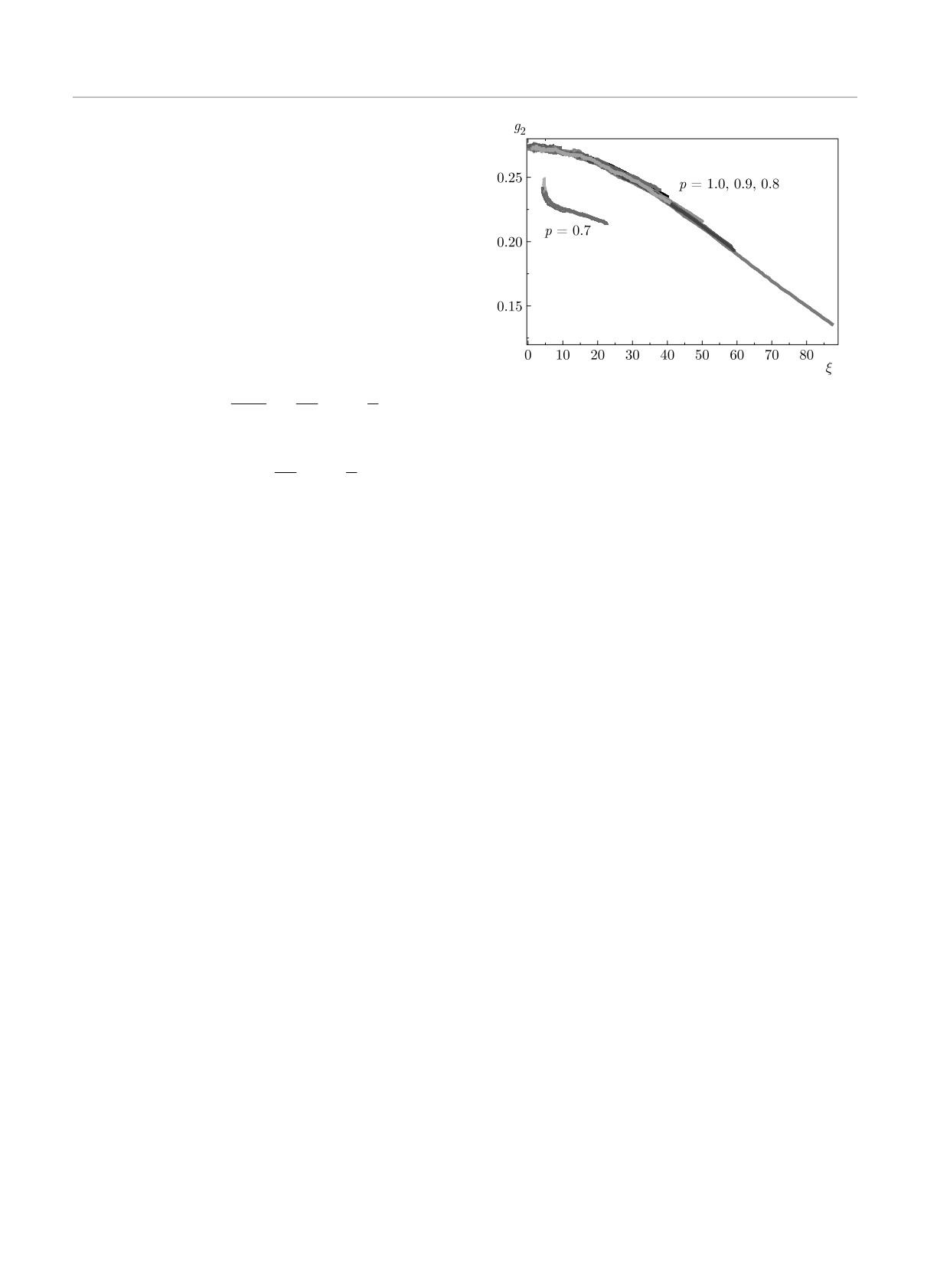
Рис. 6. Параметрическая зависимость кумулянта намагни-

ln t

ченности g2(t) от корреляционной длины ξ(t) для нерав-

новесной критической релаксации двумерной XY -модели

(

)1/2 (

))

с концентрациями спинов p

= 1.0, 0.9, 0.8,

0.7

при

ξ(p; t) = F_D (p - p_c)

(14)

t ≤ 50000 MCS/s; температуры замораживания системы

ln t

Ts/TBKT = 1.00, 0.75, 0.50, 0.25

где F_P и F_D — скейлинговые функции динамичес-

кой зависимости корреляционной длины ξ(t) в об-

кривую чистой системы с p = 1.0. Этот результат по-

ласти действия притяжения неподвижной точки чи-

казывает, что для структурно-неупорядоченных си-

стой системы и перколяционной неподвижной точ-

стем с температурами замораживания в низкотем-

ки; g — константа связи, характеризующая амплиту-

пературной фазе Березинского T_s < T_BKT притяже-

ду взаимодействия флуктуаций в равновесном кри-

ние неподвижной точки чистой системы имеет мес-

тическом состоянии системы. Скейлинговая зависи-

то, но размер ее области притяжения уменьшается

мость вида (13) должна возникать в окрестности p =

с понижением температуры замораживания.

= 1.0, в то время как скейлинговая зависимость ви-

Мы определили значения константы связи g(p)

да (14) должна иметь место для значений спиновой

для рассмотренных спиновых концентраций p, при

концентрации p в окрестности p_c.

которых наблюдается коллапс кривых ξ(t, p) в скей-

Полученные для решетки с линейными размера-

линговой зависимости (13):

ми L = 256 временные зависимости корреляцион-

ной длины ξ(t, p), характеризующие области притя-

g(p = 0.9) = 2.02(4), g(p = 0.8) = 1.68(4),

жения неподвижной точки чистой системы и перко-

g(p = 0.7) = 1.50(5).

ляционной неподвижной точки, приведены соответ-

ственно на рис. 4 и 5. Из представленных на рис. 4

Данные значения константы связи g хорошо ап-

результатов следует, что для температур заморажи-

проксимируются концентрационной зависимостью

вания T_s/T_BKT = 1.0 наблюдается коллапс кривых

g(p)/g₀

= p, при g₀

≡ g(p

= 1.0)

= 2.16(8).

ξ(t, p), полученных для различных спиновых кон-

В результате, скейлинговая форма (13) временной

центраций p, на единой универсальной кривой. В то

зависимости корреляционной длины ξ(t, p) прини-

же время, для других рассмотренных температур

мает вид

замораживания, T_s/T_BKT = 0.75, 0.5, 0.25, наблю-

ξ(t, p) = F_P ((1 - g₀(1 - p))(t/ ln t)1/2),

дается лишь частичный коллапс для некоторых из

рассмотренных спиновых концентраций p, что и го-

означающий, что в области притяжения неподвиж-

ворит о масштабе притяжения неподвижной точки

ной точки чистой системы влияние структурного

чистой системы в каждом конкретном случае. При

беспорядка определяется только малой линейной по

T_s/T_BKT = 1.0 неравновесная критическая динами-

концентрации примеси 1-p поправкой вида g₀(1-p)

ка модели определяется притяжением со стороны

к основной динамической зависимости.

неподвижной точки чистой системы. Для темпера-

Сопоставление графиков на рис. 4, 5 показыва-

тур замораживания T_s/T_BKT = 0.50, 0.25 кривые

ет, что для скейлинговой зависимости (14) коллапс

ξ(t, p) демонстрируют коллапс для спиновых кон-

кривых ξ(t, p) на рис. 5 при температурах замора-

центраций p < 1.0, но при этом не накладываются на

живания T_s/T_BKT = 1.0 осуществляется хуже, чем

894

ЖЭТФ, том 158, вып. 5 (11), 2020

Особенности влияния дефектов структуры. . .

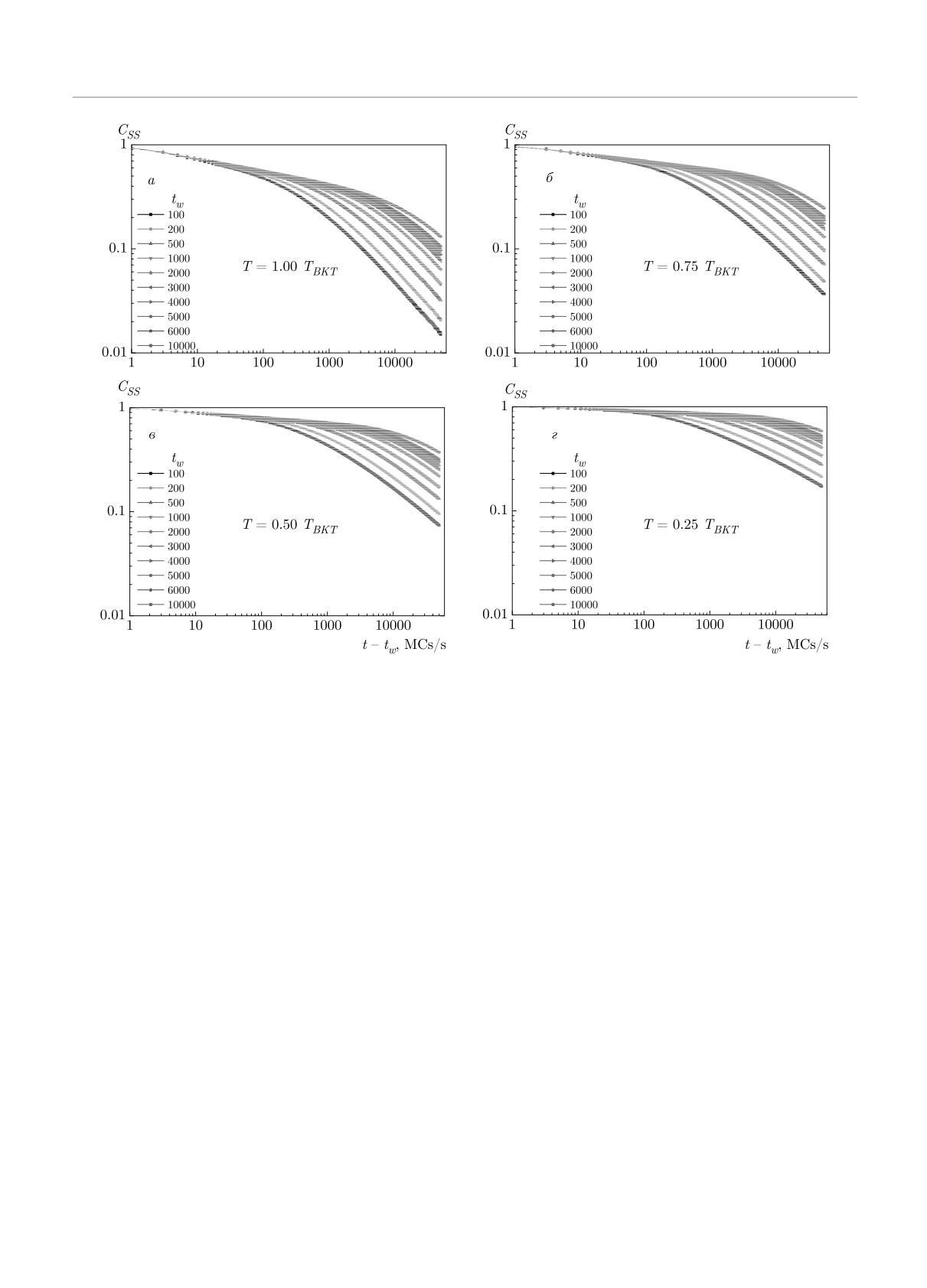
Рис. 7. Двухвременная зависимость спин-спиновой автокорреляционной функции CSS (t, tw) для чистой (p = 1.0) дву-

мерной XY -модели; температуры замораживания Ts/TBKT = 1.0 (а), 0.75 (б), 0.50 (в), 0.25 (г)

на рис. 4 для скейлинговой формы (13). Так, для

дении с кривой ξ(t, p) при p = 1.0. Эти резуль-

спиновых концентраций p = 1.0, 0.9 кривые ξ(t, p)

таты показывают, что в низкотемпературной фа-

демонстрируют хорошее наложение, но с пониже-

зе для структурно-неупорядоченных систем притя-

нием величины p качество коллапса ухудшается.

жение неподвижной точки чистой системы плавно

Эти результаты показывают, что при T_BKT основ-

сменяется притяжением перколяционной неподвиж-

ное притяжение определяется неподвижной точкой

ной точки. При этом влияние перколяционной непо-

чистой системы, а влияние притяжения перколяци-

движной точки на неравновесную критическую ди-

онной неподвижной точки для малых концентраций

намику растет с увеличением концентрации дефек-

дефектов (p = 0.9) оказывается слабым.

тов.

С понижением температуры T_s в низкотемпера-

3.2. Расчеты временной зависимости

турной фазе Березинского T_s < T_BKT общая карти-

кумулянта намагниченности второго порядка

на притяжения перколяционной неподвижной точ-

ки претерпевает существенные изменения, характе-

С целью дополнительного исследования влияния

ризуемые плавным расщеплением коллапса кривых

притяжения перколяционной неподвижной точки и

ξ(t, p) на кривые для структурно-неупорядоченных

неподвижной точки чистой системы нами был про-

систем с p < 1.0 и чистой системы (p = 1.0). Наибо-

веден расчет и анализ динамической зависимости

лее наглядно это проявляется для T_s/T_BKT = 0.25,

кумулянта намагниченности второго порядка

когда кривые ξ(t, p) при p = 0.9, 0.8, 0.7 наклады-

ваются друг на друга при максимальном расхож-

g₂(t) =

M²(t)

/[〈|M(t)|〉]² - 1

(15)

895

В. В. Прудников, П. В. Прудников, И. С. Попов

ЖЭТФ, том 158, вып. 5 (11), 2020

Рис. 8. Двухвременная зависимость спин-спиновой автокорреляционной функции CSS (t, tw) для структурно-неупорядо-

ченной двумерной XY -модели со спиновой концентрацией p = 0.9; температуры замораживания Ts/TBKT = 1.0 (а),

0.75 (б), 0.50 (в), 0.25 (г)

для систем с различными спиновыми концентра-

зе Березинского T_s ≤ T_BKT . Однако для спиновой

циями и температурами замораживания T_s ≤ T_BKT .

концентрации p = 0.7 параметрические зависимости

Для данного кумулянта намагниченности реализу-

g₂(t) от ξ(t), хотя и демонстрируют наложение кри-

ется скейлинговая форма вида

вых для различных температур T_s, но положение

соответствующей кривой сильно отличается от по-

g₂(t) = F_g(ξ(p, T; t)/L).

ложения универсальной кривой для спиновых кон-

Исследование параметрической зависимости куму-

центраций p = 1.0, 0.9, 0.8, образуя два раздель-

лянта намагниченности g₂(t) от корреляционной

ных семейства кривых. Это указывает на то, что

длины ξ(t) позволит выявить скейлинговые свой-

двумерная XY -модель со спиновой концентрацией

ства кумулянта по наложению динамических кри-

p = 0.7 находится достаточно близко к порогу спи-

вых g₂(ξ) для различных значений спиновой концен-

новой перколяции p_c и в результате влияние притя-

трации p и температуры T_s.

жения перколяционной неподвижной точки стано-

Полученные параметрические зависимости ку-

вится определяющим в динамических релаксацион-

мулянта g₂(t) от корреляционной длины ξ(t) пред-

ных свойствах системы. В то же время, системы со

ставлены на рис. 6 для решетки с L = 256. Видно,

спиновыми концентрациями p = 0.9, 0.8 не испы-

что у данных параметрических зависимостей возни-

тывают такого сильного влияния перколяционной

кает коллапс кривых для спиновых концентраций

неподвижной точки, и основные особенности крити-

p = 1.0 (чистая система), 0.9, 0.8 при всех темпера-

ческой динамики обусловлены притяжением непо-

турах замораживания T_s в низкотемпературной фа-

движной точки чистой системы.

896

ЖЭТФ, том 158, вып. 5 (11), 2020

Особенности влияния дефектов структуры. . .

Рис. 9. Двухвременная зависимость спин-спиновой автокорреляционной функции CSS (t, tw) для структурно-неупорядо-

ченной двумерной XY -модели со спиновой концентрацией p = 0.8; температуры замораживания Ts/TBKT = 1.0 (а),

0.75 (б), 0.50 (в), 0.25 (г)

3.3. Расчеты двухвременной зависимости

говременной режим с t-t_w ≫ t_w при временах наб-

автокорреляционной функции

людения до t - t_w = 50000 MCS/s.

Результаты проведенных вычислений двухвре-

Перейдем к рассмотрению полученных резуль-

менных зависимостей спин-спиновой автокорреля-

ционной функции C_SS (t, t_w) для чистой системы

татов для двухвременных зависимостей спин-спи-

новой автокорреляционной функции C_SS(t, t_w) (11)

приведены на рис. 7, для структурно-неупорядочен-

ной двумерной XY -модели со спиновыми концен-

и их динамических скейлинговых свойств в нерав-

новесной критической динамике двумерной чистой

трациями p = 0.9, 0.8, 0.7 представлены соответ-

ственно на рис. 8, 9, 10.

и структурно-неупорядоченной XY -модели при эво-

люции из высокотемпературного начального состо-

Полученные временные зависимости автокорре-

яния. Для корректного определения динамических

ляционной функции C_SS (t, t_w) демонстрируют про-

скейлинговых свойств автокорреляционной функ-

явление неравновесных эффектов старения, харак-

ции C_SS (t, t_w) мы использовали 10 значений вре-

теризующихся замедлением убывания C_SS(t, t_w) с

мени ожидания t_w в широком временном диапа-

ростом времени ожидания t_w. Наиболее наглядно

зоне: 100, 200, 500, 1000, 2000, 3000, 4000, 5000, 6000,

эффекты старения проявляются при t - t_w ∼ t_w

10000 MCS/s. Данный набор значений t_w перекры-

на зависимости автокорреляционной функции от

вает все основные режимы неравновесной эволю-

времени ожидания t_w. В поведении автокорреля-

ции модели: квазиравновесный режим на временах

ционной функции эффекты старения наблюдаются

t - t_w ≪ t_w, режим старения при t - t_w ∼ t_w и дол-

при всех спиновых концентрациях p и температу-

897

ЖЭТФ, вып. 5 (11)

В. В. Прудников, П. В. Прудников, И. С. Попов

ЖЭТФ, том 158, вып. 5 (11), 2020

Рис. 10. Двухвременная зависимость спин-спиновой автокорреляционной функции CSS (t, tw) для структурно-неупоря-

доченной двумерной XY -модели со спиновой концентрацией p = 0.7; температуры замораживания Ts/TBKT = 1.0 (а),

0.75 (б), 0.50 (в), 0.25 (г)

рах замораживания T_s в низкотемпературной фа-

корреляционных эффектов в двумерной XY -модели

зе T_s ≤ T_BKT . Спин-спиновая автокорреляционная

в области низких температур.

функция C_SS(t, t_w) демонстрирует степенной ха-

Введение в двумерную XY -модель структурно-

рактер поведения в квазиравновесном режиме при

го беспорядка (см. рис. 8-10) приводит к ряду из-

t - t_w ≪ t_w в виде

менений в общей картине неравновесных эффектов,

выраженных в двухвременном поведении автокор-

C_SS = C_SS(t - t_w) ∼ (t - t_w)-η(T,p)/2,

реляционной функции. Видно, что при температу-

рах T_s = T_BKT в системах со спиновыми концентра-

а также в долговременном режиме при t - t_w ≫ t_w в

циями p = 0.9 (рис. 8) и 0.8 (рис. 9) не наблюда-

виде C_SS (t, t_w) ∝ (t/t_w)-(1+η(T,p)) с промежуточной

ется существенных изменений в двухвременной за-

областью динамического кроссовера между этими

висимости автокорреляционной функции C_SS(t, t_w)

режимами.

по сравнению с чистой системой. Однако с пони-

Результаты моделирования для чистой системы

жением температуры замораживания T_s и спино-

показывают (рис. 7), что с понижением температу-

вых концентраций p происходит заметное усиление

ры замораживания T_s в низкотемпературной фазе

эффектов корреляции и старения, характеризуемых

происходит замедление убывания автокорреляцион-

еще большим замедлением убывания автокорреля-

ной функции C_SS (t, t_w). Это связано с усилением

ционной функции C_SS (t, t_w) с ростом времени ожи-

898

ЖЭТФ, том 158, вып. 5 (11), 2020

Особенности влияния дефектов структуры. . .

Таблица 1. Значения индекса Фишера η(p, T ) для

дания t_w по сравнением с чистой моделью. Важно

различных температур и спиновых концентраций:

отметить, что для одинаковых приведенных темпе-

значения η(c)(p, T ) получены из условия выполне-

ратур T_s/T_BKT в низкотемпературной фазе с рос-

ния динамического скейлинга для автокорреляци-

том концентрации дефектов кроссоверная область

онной функции; η(m)(p, T ) —

значения из рабо-

смены степенных режимов в поведении автокорре-

ты [6]

ляционной функции C_SS (t, t_w) сдвигается в область

больших значений времени наблюдения.

p = 1.0

Однако для системы со спиновой концентраци-

ей p

= 0.7 представленные на рис. 10 двухвре-

T/T_BKT

η(c)

η(m)

менные зависимости автокорреляционной функции

1.00

0.2500 ± 0.0025

0.2500 ± 0.0014

C_SS(t, t_w) показывают заметные изменения, проис-

0.75

0.1365 ± 0.0075

0.1355 ± 0.0020

ходящие уже при температуре T_s = T_BKT . Видно,

что при одинаковых значениях времени ожидания

0.50

0.1000 ± 0.0100

0.0806 ± 0.0021

t_w и времени наблюдения t - t_w функция C_SS(t, t_w)

0.25

0.0650 ± 0.0125

0.0367 ± 0.0023

характеризуется более низкими значениями для си-

p = 0.9

стемы с p = 0.7, чем для систем с p = 0.8, 0.9,

1.0. Таким образом, эффекты старения в системе

T/T_BKT

η(c)

η(m)

с p = 0.7 оказываются менее ярко выраженными,

1.00

0.2800 ± 0.0025

0.2659 ± 0.0050

т. е. ослабевают, и происходит более быстрое убыва-

0.75

0.1850 ± 0.0075

0.1462 ± 0.0045

ние C_SS (t, t_w) с ростом времени ожидания t_w. Кро-

ме того, степенной характер временного поведения

0.50

0.1650 ± 0.0125

0.0888 ± 0.0039

C_SS(t, t_w) на квазиравновесном этапе при t-t_w ≪ t_w

0.25

0.0650 ± 0.0150

0.0418 ± 0.0042

и в долговременном режиме с t - t_w ≫ t_w оказыва-

p = 0.8

ется выраженным более слабо, что следует из отсут-

ствия на этих интервалах характерных линейных

T/T_BKT

η(c)

η(m)

зависимостей для графиков, построенных в двойном

1.00

0.4900 ± 0.0075

0.2956 ± 0.0028

логарифмическом масштабе. С понижением темпе-

0.75

0.3250 ± 0.0100

0.1731 ± 0.0010

ратуры замораживания в низкотемпературной фазе

выявленные выше различия в двухвременных зави-

0.50

0.2575 ± 0.0125

0.1068 ± 0.0083

симостях автокорреляционной функции для систе-

0.25

0.1200 ± 0.0175

0.0522 ± 0.0102

мы с p = 0.7 сохраняются, а также сохраняются

p = 0.7

и тенденции усиления корреляционных эффектов в

области низких температур. В соответствии с полу-

T/T_BKT

η(c)

η(m)

ченными ранее результатами для корреляционной

1.00

1.0000 ± 0.0075

длины ξ(t, p) и кумулянта намагниченности g₂(t, p)

0.75

0.5065 ± 0.0100

эти особенности для системы с p = 0.7 объясняются

влиянием перколяционной неподвижной точки как

0.50

0.3500 ± 0.0100

на релаксационные, так и корреляционные свойства

0.25

0.1450 ± 0.0075

системы со спиновыми концентрациями близкими к

порогу спиновой перколяции p_c ≈ 0.59.

времени наблюдения ξ(t - t_w) и времени ожида-

ния ξ(t_w) (см. соотношения (2), (3)). Для провер-

3.4. Расчет скейлинговых функций и их

ки выполнения данных скейлинговых соотношений

анализ

у двухвременных зависимостей автокорреляцион-

Важной особенностью двухвременных зависи-

ной функции C_SS (t, t_w) мы сначала воспользуем-

мостей спин-спиновой автокорреляционной функ-

ся подтвержденной временной зависимостью кор-

ции C_SS (t, t_w) в неравновесном критическом по-

реляционной длины ξ(t) ∝ (t/ ln t)1/2 для чистой

ведении двумерной XY -модели является проявле-

и структурно-неупорядоченной двумерной XY -мо-

ние их динамических скейлинговых свойств, ког-

дели и построим графики скейлинговых зависи-

да C_SS (t, t_w) ведет себя как обобщенно однород-

мостей для автокорреляционной функции в ви-

ная функция пространственных масштабов, свя-

де f_C (t, t_w)

= tw(p,T)/2C_SS(t, t_w) от переменных

занных с зависимостью корреляционной длины от

[(t - t_w)/ ln (t - t_w)]1/2/[t_w/ ln t_w]1/2.

899

В. В. Прудников, П. В. Прудников, И. С. Попов

ЖЭТФ, том 158, вып. 5 (11), 2020

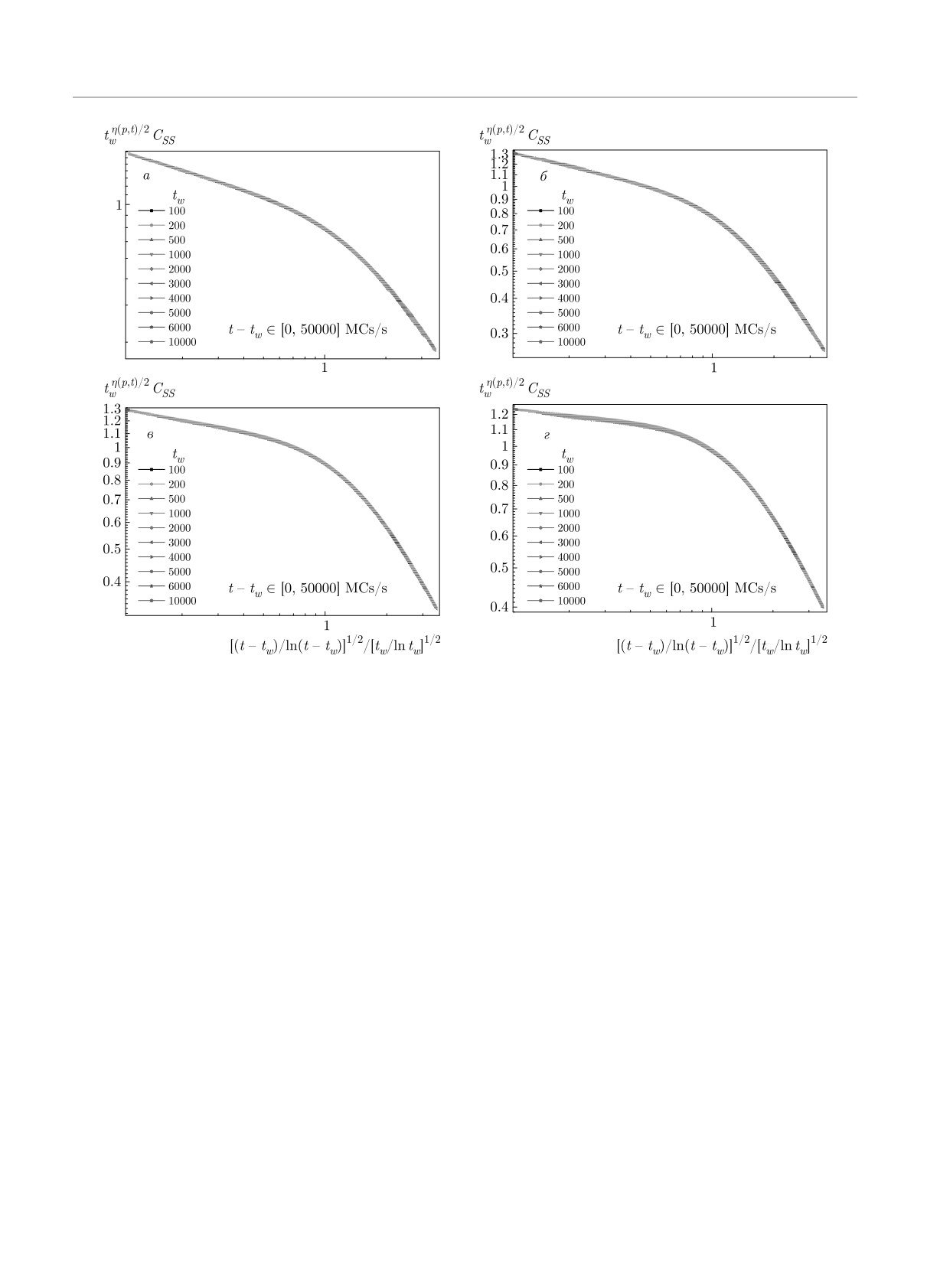
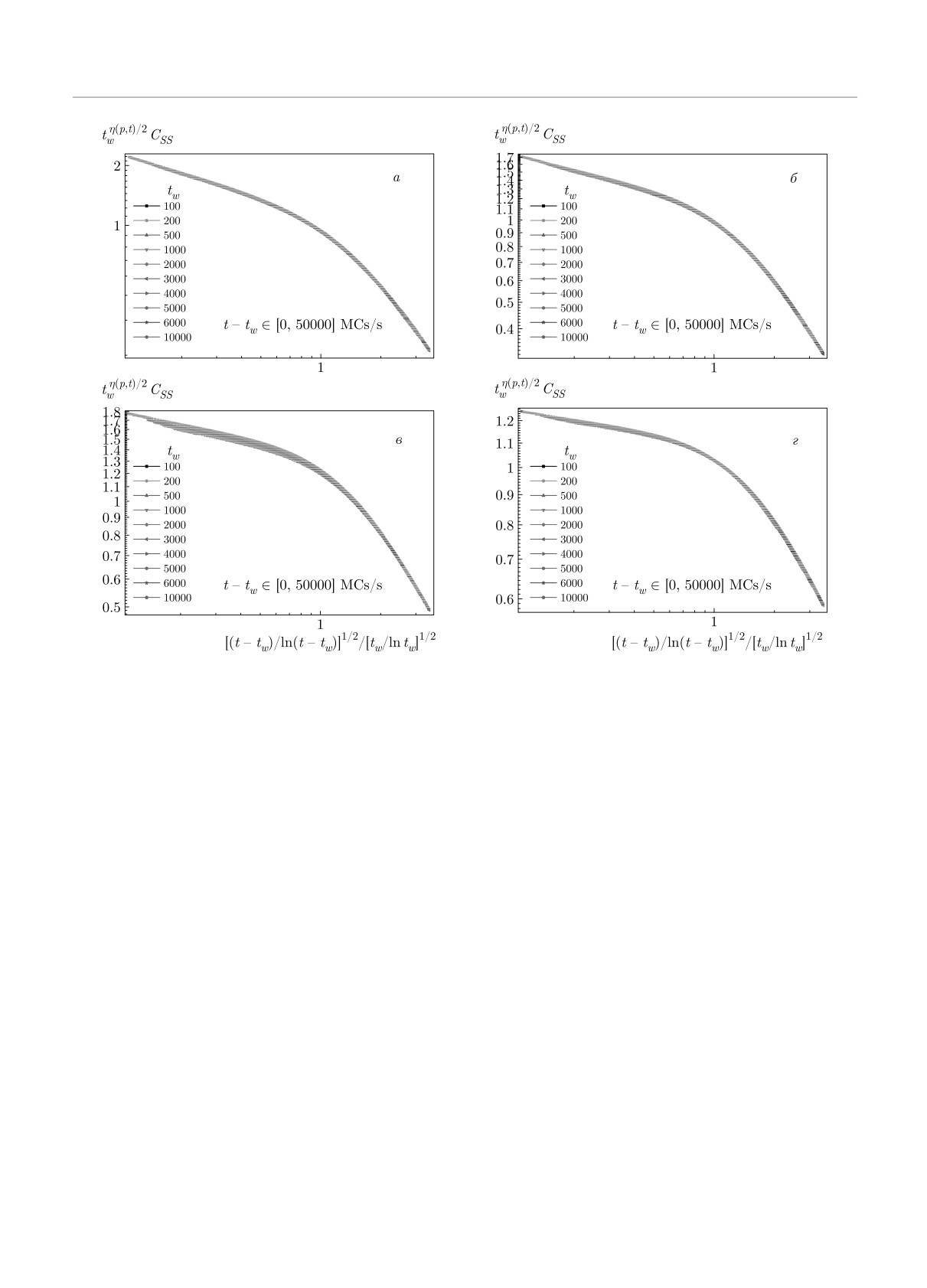
Рис.

11. Скейлинговые зависимости для автокорреляционной функции tw(p,T)/2CSS (t, tw) в переменных

[(t - tw)/ ln (t - tw)]1/2/[tw/ ln tw]1/2 для чистой системы (p = 1.0) с температурами замораживания Ts/TBKT = 1.0 (а),

0.75 (б), 0.50 (в), 0.25 (г)

Подстановка в выражение для скейлинговой

ченных значений η(p, T ) обусловлена по-видимому

функции

малыми линейными размерами решеток L и боль-

шими погрешностями при реализации методики ко-

f_C(t, t_w) = tη(p,T)/2wC_SS(t, t_w)

нечноразмерного скейлинга.

полученных в работе [6] значений критического ин-

В настоящей работе значения индекса Фишера

декса Фишера η(p, T ) для различных температур и

η(p, T ) определялись из процедуры минимизации

спиновых концентраций показала не совсем удовле-

отклонения кривых, соответствующих функции

творительное наложение кривых C_SS(t, t_w) с раз-

tw(p,T)/2C_SS(t, t_w) для различных t_w, от универсаль-

личными временами ожидания t_w и фиксированны-

ной кривой для скейлинговой функции f_C(t, t_w),

ми T_s и p на единую универсальную кривую, соот-

соответствующей соотношению

(5). Полученные

ветствующую скейлинговой функции f_C(t, t_w). В ра-

в результате использования данного метода зна-

боте [6] для получения температурных и концентра-

чения индекса Фишера η(c)(p, T ) представлены

ционных зависимостей η(p, T ) был использован ме-

в табл.

1, где для сравнения приведены так-

тод конечноразмерного скейлинга для равновесных

же значения η(m)(p, T ) из работы [6]. Значение

значений квадрата намагниченности

η(p = 1.0, T = T_BKT ) для чистой двумерной XY -мо-

дели в точке фазового BKT-перехода в пределах

M²(p, T)

∝L-η(p,T),

статистической погрешности хорошо согласуется

реализованного на квадратных решетках с линейны-

с известным аналитическим значением η = 0.25.

ми размерами L = 4, . . . , 128. Низкая точность полу-

Однако полученные значения η(c)(p, T ) совпадают

900

ЖЭТФ, том 158, вып. 5 (11), 2020

Особенности влияния дефектов структуры. . .

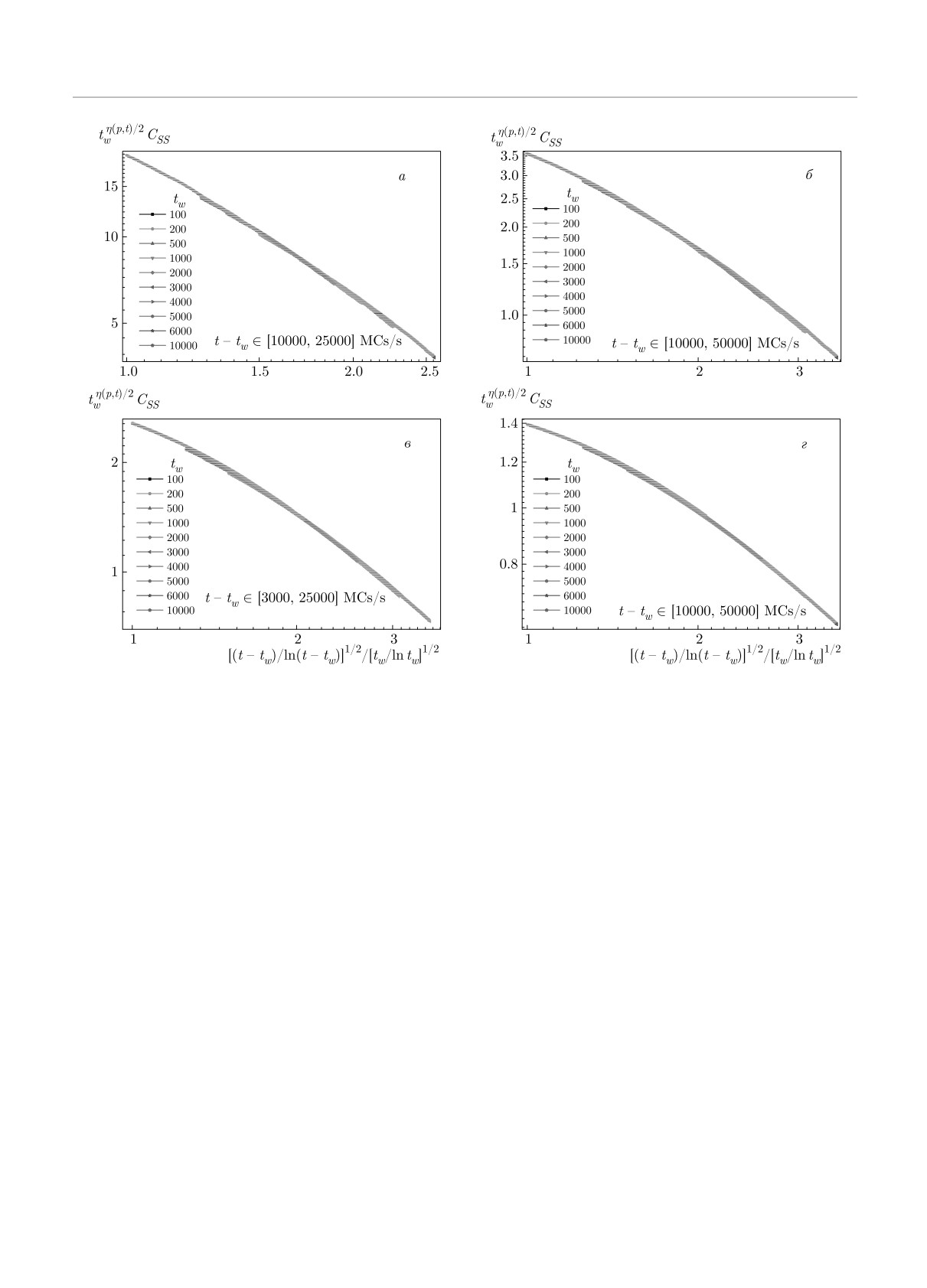
Рис.

12. Скейлинговые зависимости для автокорреляционной функции tw(p,T)/2CSS (t, tw) в переменных

[(t - tw)/ ln (t - tw)]1/2/[tw / ln tw]1/2 для структурно-неупорядоченной системы со спиновой концентрацией p = 0.9 и

температурами замораживания Ts/TBKT = 1.0 (а), 0.75 (б), 0.50 (в), 0.25 (г)

в пределах статистической погрешности с резуль-

веденных в табл. 1, реализуется «коллапс» кри-

татами работы [6] только для чистой системы при

вых tw(p,T)/2C_SS (t, t_w) для различных t_w на уни-

температурах T_s/T_BKT = 1.00, 0.75, а для осталь-

версальной кривой, соответствующей соотношению

ных температур T_s и спиновых концентраций p

(5) для скейлинговой функции f_C (t, t_w). Отметим,

наблюдаются заметные различия. Стоит отметить,

что очень хорошее наложение кривых возникает

что полученные в настоящей работе значения ин-

прежде всего на временах t и t_w, при которых

декса Фишера η(p, T ) для чистой системы (p = 1.0)

ξ(t), ξ(t_w ) ≪ L и поэтому влияние конечноразмер-

хорошо согласуются с результатами работы [33],

ных эффектов на полученные результаты является

где исследовались особенности динамического скей-

несущественным. Стоит отметить, что для системы

линга спин-спиновой автокорреляционной функции

со спиновой концентрацией p = 0.7 при температуре

системы C_SS(t, t_w) в неравновесной критической

T_s = T_BKT (p) было получено максимальное из пред-

релаксации чистой двумерной XY -модели.

ставленных в табл. 1 значений критического индекса

η = 1.0000(75). Мы связываем столь большое зна-

На рис. 11-14 представлены полученные скей-

чение данного критического показателя с сильным

линговые функции f_C (t, t_w) = tw(p,T)/2C_SS (t, t_w) в

влиянием порога спиновой перколяции и притяже-

переменных [(t - t_w )/ ln (t - t_w)]1/2/[t_w/ ln t_w]1/2 для

ния со стороны перколяционной неподвижной точки

спиновых концентраций p = 1.0 (чистая система),

на неравновесные процессы в системе с p = 0.7.

0.9, 0.8,

0.7

и ряда выбранных температур замо-

раживания Ts ≤ TBKT(p). Графики показывают,

Представленные на рис.

11-14

скейлинговые

что при значениях индекса Фишера η(c)(p, T ), при-

функции f_C(t, t_w)

= tw(p,T)/2C_SS(t, t_w) отражают

901

В. В. Прудников, П. В. Прудников, И. С. Попов

ЖЭТФ, том 158, вып. 5 (11), 2020

Рис.

13. Скейлинговые зависимости для автокорреляционной функции tw(p,T)/2CSS (t, tw) в переменных

[(t - tw)/ ln (t - tw)]1/2/[tw/ ln tw]1/2 для структурно-неупорядоченной системы со спиновой концентрацией p = 0.8, и

температурами замораживания Ts/TBKT = 1.0 (а), 0.75 (б), 0.50 (в), 0.25 (г)

картину влияния структурного беспорядка на

сильном изменения наклона кривой при переходе

неравновесные критические свойства двумерной

через кроссоверную область ξ(t - t_w)/ξ(t_w) ≃ 1.

XY -модели. В случае чистой системы (рис.

11)

Данный эффект «замораживания» корреляции в

и систем со спиновыми концентрациями p = 0.9

системе с понижением температуры T_s соответству-

(рис. 12) и p = 0.8 (рис. 13) имеет место классиче-

ет аналогичным неравновесным эффектам роста

ская форма кривой скейлинговой функции f_C (x),

корреляционной длины ξ(t). На примере систем

в которой можно выделить два степенных режима:

со спиновыми концентрациями p = 0.9 (рис. 12)

при x ≪ 1 и x ≫ 1, разделенных областью крос-

и p

= 0.8 (рис. 13) видно, что с увеличением

совера. Данные степенные режимы соответствуют

структурного беспорядка происходит замедление

областям с ξ(t - t_w) ≪ ξ(t_w) и ξ(t - t_w) ≫ ξ(t_w)

корреляционных процессов, отражающееся в уве-

(однако, в обоих случаях выполняется условие

личении значений скейлинговой функции f_C (x)

ξ ≪ L, которое определяет неравновесность крити-

в области с x

≤ 1 при фиксированных значе-

ческой динамики системы), и отражают развитие

ниях температуры замораживания T_s. Случай

неравновесных эффектов старения в системе,

структурно-неупорядоченной системы со спиновой

охватывая времена t - tw ≪ tw и t - tw ≫ tw.

концентрацией p = 0.7 сильно выделяется как по

С понижением температуры замораживания T_s в

сравнению с чистой системой, так и системами с

низкотемпературной фазе происходит замедление

p = 0.9, 0.8: в области ξ(t - t_w) ≪ ξ(t_w) динами-

корреляционных процессов, что отражается в более

ческий скейлинг практически не реализуется (при

902

ЖЭТФ, том 158, вып. 5 (11), 2020

Особенности влияния дефектов структуры. . .

Рис.

14. Скейлинговые зависимости для автокорреляционной функции tw(p,T)/2CSS (t, tw) в переменных

[(t - tw)/ ln (t - tw)]1/2/[tw / ln tw]1/2 для структурно-неупорядоченной системы со спиновой концентрацией p = 0.7 и

температурами замораживания Ts/TBKT = 1.0 (а), 0.75 (б), 0.50 (в), 0.25 (г)

t - t_w, t_w

≤ 3000 MCS/s коллапс скейлинговых

В случае чистой системы (рис. 15) обращает на

кривых практически не наблюдается), а область

себя внимание следующая особенность: по сравне-

динамического кроссовера плавно переходит в

нию с результатами для скейлинговой функции, вы-

режим ξ(t - t_w) ≫ ξ(t_w).

раженной через модельную зависимость (t/ ln t)1/2

(см. рис. 11), скейлинговая функция fC в пере-

Полученные в настоящей работе временные

менных ξ(t - t_w)/ξ(t_w) получается более гладкой,

зависимости корреляционной длины ξ позволили

а перегиб в области динамического кроссовера с

построить динамическую скейлинговую зави-

ξ(t - t_w)/ξ(t_w) ≈ 1 становится более пологим. При

симость автокорреляционной функции системы

этом скейлинговая функция корректно определяет-

C_SS(t, t_w) напрямую от ξ(t - t_w) и ξ(t_w) без

ся в области ξ(t) ≪ L, где влияние эффектов конеч-

использования модельных представлений о ро-

ного размера системы является малым. С пониже-

сте пространственной корреляции ξ с течением

нием температуры замораживания T_s в низкотем-

времени t в системе. Для этого воспользуемся

пературной фазе с T_s < T_BKT происходит замед-

соотношением (3) и проведем анализ скейлинговой

ление релаксационных процессов, что отражается в

функции f_c(t, t_w) = tw(p,T)/2C_SS(t, t_w) в переменных

явном уменьшении наклона скейлинговой функции

ξ(t - t_w)/ξ(t_w), представленной для чистой модели

f_C(x) при x ≪ 1, остающейся по-прежнему в обла-

на рис.

15, а для структурно-неупорядоченных

сти ξ(t) ≪ L. Теперь этот эффект оказывается явно

систем со спиновыми концентрациями p

= 0.9,

связанным с замедлением процесса роста корреля-

p = 0.8, p = 0.7 соответственно на рис. 16, 17, 18.

ционной длины ξ(t) в области низких температур T_s.

903

В. В. Прудников, П. В. Прудников, И. С. Попов

ЖЭТФ, том 158, вып. 5 (11), 2020

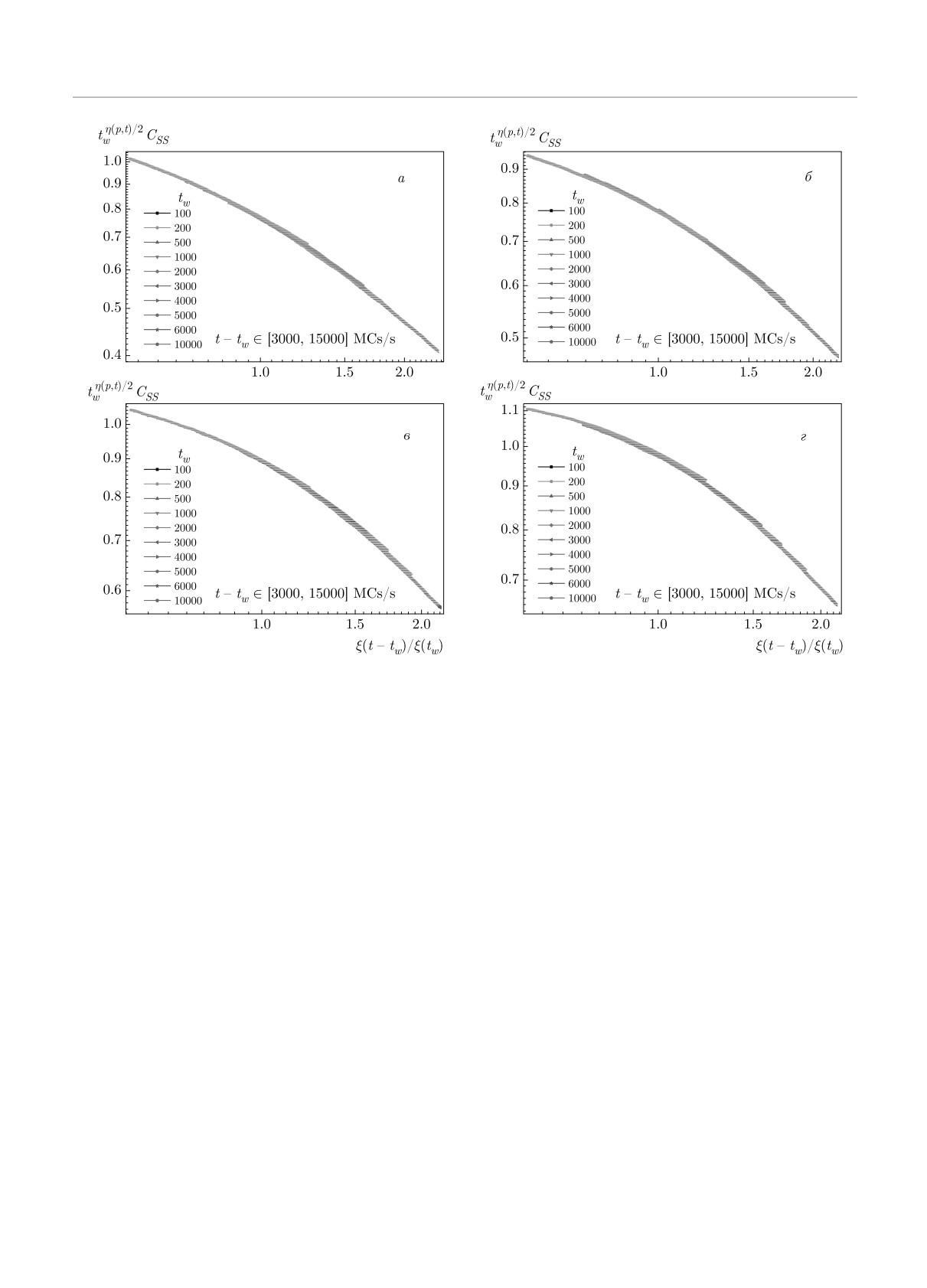
Рис. 15. Скейлинговые зависимости для автокорреляционной функции tw(p,T)/2CSS (t, tw) в переменных ξ(t - tw)/ξ(tw)

для чистой системы (p = 1.0) с температурами замораживания Ts/TBKT = 1.0 (а), 0.75 (б), 0.50 (в), 0.25 (г)

Введение в систему структурного беспорядка

вой перколяции. Отметим, что несмотря на значи-

на примере систем со спиновыми концентрациями

тельный объем использованной статистической вы-

p = 0.9 (рис. 16) и p = 0.8 (рис. 17) показывает, что

борки, в случае T_s/T_BKT = 0.25 относительная ста-

его влияние приводит к заметному замедлению про-

тистическая погрешность вычисления значений ξ(t)

цесса неравновесной критической корреляции. Эф-

достигает величин 20-30 %, особенно для спиновой

фект замедления автокорреляционной функции и ее

концентрации p = 0.7. Поэтому скейлинговые функ-

скейлинговой составляющей проявляется в струк-

ции на рис. 16-18 показывают для T_s/T_BKT = 0.25

турно-неупорядоченных системах для всех темпера-

большие статистические флуктуации.

тур замораживания T_s ≤ T_BKT . Этот результат хо-

Анализ скейлинговой функции f_c в перемен-

рошо соотносится с результатами работы [6], где для

ных ξ(t - t_w)/ξ(t_w) на основе напрямую вычислен-

случаев p = 1.0 (чистая система), 0.9, 0.8 было по-

ной временной зависимости корреляционной длины

казано, что при T_s = T_BKT значение предельного

ξ(t) позволяет в соответствии с соотношением (4)

флуктуационно-диссипативного отношения умень-

определить показатель наклона λ_C , характеризую-

шается с понижением спиновой концентрации p

щий долговременный спад скейлинговой функции

вследствие замедления релаксационных и корреля-

f_C(x) ∝ x-λC при x ≫ 1. Из соображений размерно-

ционных процессов в структурно-неупорядоченной

го анализа [33,56,57] выполняется соотношение (5)

системе. Случай системы с p = 0.7, как и ранее, вы-

с λ_C(p,T) = 1 + η(p,T), которое отражает особен-

деляется по сравнению с системами с p = 0.9, 0.8: в

ности критической релаксационной динамики дву-

области ξ(t - t_w) ≪ ξ(t_w) наложения кривых с раз-

мерной XY -модели. Температурная и концентра-

ными t_w практически не происходит, что мы связы-

ционная зависимости значений показателя наклона

ваем с сильным влиянием эффектов порога спино-

λ_C(p, T) для скейлинговой функции f_C, полученные

904

ЖЭТФ, том 158, вып. 5 (11), 2020

Особенности влияния дефектов структуры. . .

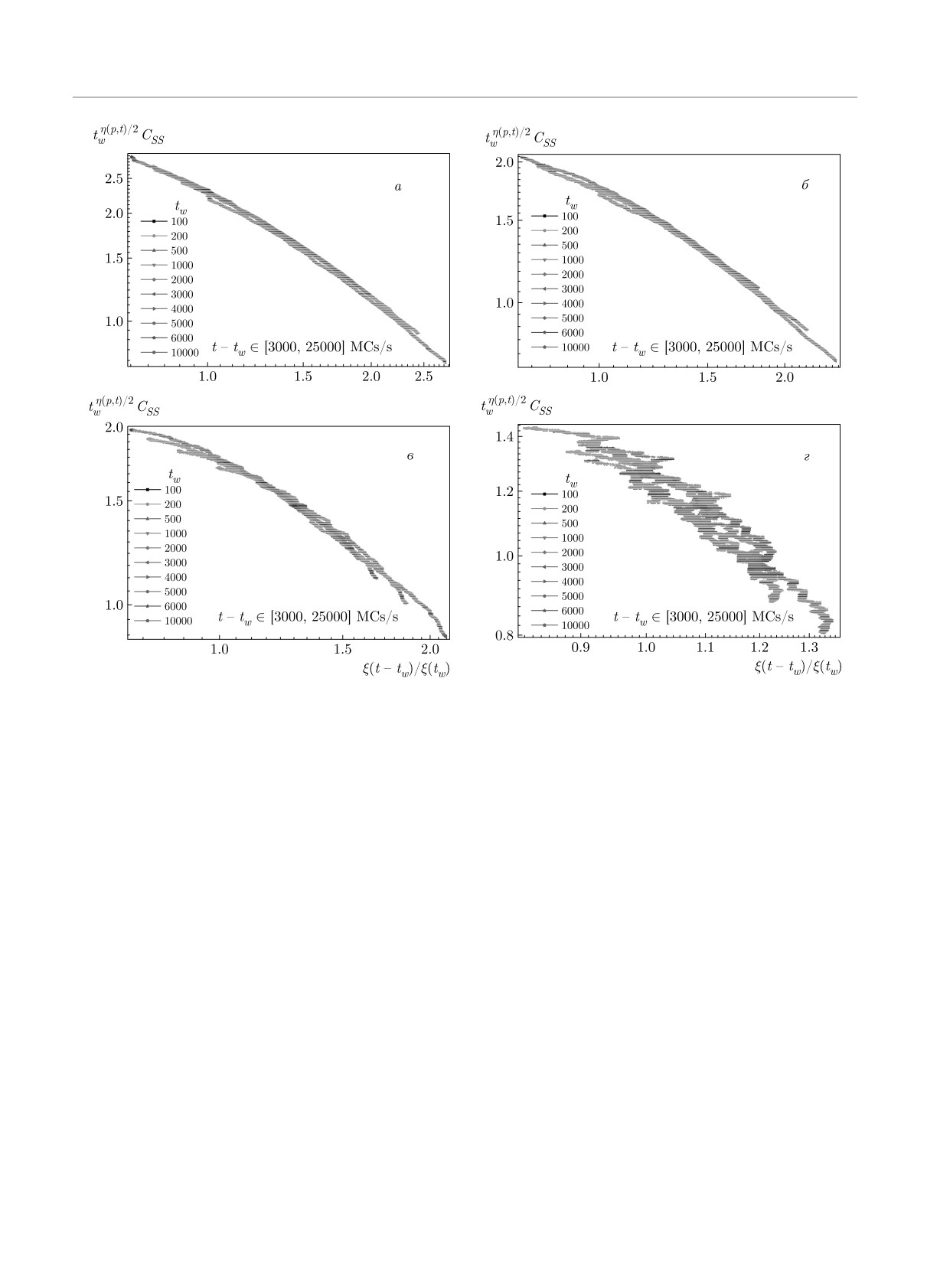
Рис. 16. Скейлинговые зависимости для автокорреляционной функции tw(p,T)/2CSS (t, tw) в переменных ξ(t - tw)/ξ(tw)

для структурно-неупорядоченной системы со спиновой концентрацией p

= 0.9 и температурами замораживания

Ts/TBKT = 1.0 (а), 0.75 (б), 0.50 (в), 0.25 (г)

с использованием напрямую вычисленной корреля-

пользования напрямую вычисленной временной за-

ционной длины ξ(t), представлены в табл. 2. Для

висимости корреляционной длины ξ(t). Отметим,

сопоставления в таблице приведены также значения

что для системы со спиновой концентрацией p = 0.7

величины 1+η(p, T) с полученными в настоящей ра-

при T_s = T_BKT было получено значение индекса

боте значениями показателя η(c)(p, T) (табл. 1). Как

Фишера η = 1.0000(75). Это столь большое значе-

следует из представленных результатов, в пределах

ние индекса Фишера подтверждается вычисленным

статистической погрешности значения λ_C (p, T ) сов-

показателем λ_C (p = 0.7, T_BKT ) = 1.9907(812).

падают с 1 + η(p, T ) для всех рассмотренных тем-

ператур T_s и спиновых концентраций p. Это подт-

верждает корректность полученных в настоящей ра-

4. ЗАКЛЮЧЕНИЕ

боте температурных и концентрационных зависимо-

В результате проведенного в работе Монте-Кар-

стей критического индекса Фишера η(c)(p, T ), вы-

ло-исследования неравновесного критического пове-

численных на основе анализа неравновесных харак-

дения двумерной чистой и структурно-неупорядо-

теристик системы. Полученные результаты показы-

ченной XY -модели с эволюцией из высокотемпера-

вают, что анализ скейлинговой функции f_C для

турного начального состояния были выявлены осо-

двумерной чистой и структурно-неупорядоченной

бенности влияния структурного беспорядка на вре-

XY -модели желательно проводить на основе ис-

менную зависимость корреляционной длины ξ(t) и

905

В. В. Прудников, П. В. Прудников, И. С. Попов

ЖЭТФ, том 158, вып. 5 (11), 2020

Рис. 17. Скейлинговые зависимости для автокорреляционной функции tw(p,T)/2CSS (t, tw) в переменных ξ(t - tw)/ξ(tw)

для структурно-неупорядоченной системы со спиновой концентрацией p

= 0.8 и температурами замораживания

Ts/TBKT = 1.0 (а), 0.75 (б), 0.50 (в), 0.25 (г)

выполнение динамического скейлинга в двухвремен-

ли для широкого диапазона значений спиновой кон-

ной зависимости спин-спиновой автокорреляцион-

центрации p. Полученные в результате моделиро-

ной функции C_SS (t, t_w). При старте системы из вы-

вания зависимости корреляционной длины ξ(t) для

сокотемпературного начального состояния со сво-

чистой и структурно-неупорядоченной двумерной

бодными вихревыми возбуждениями неравновесная

XY -модели показывают, что для температур за-

критическая динамика двумерной XY -модели ха-

мораживания системы во всей низкотемпературной

рактеризуется сильной вихревой неравновесностью,

фазе с T_s ≤ T_BKT наблюдается поведение ξ(t) ∝

процессами аннигиляции вихрей и антивихрей, а

∝ (t/ ln t)1/2, связанное с неравновесной аннигиля-

также огрублением областей квазидальнего поряд-

цией вихрей и антивихрей в формирующихся вих-

ка. Это существенно сказывается на динамической

ревых парах. Полученные результаты показывают,

зависимости корреляционной длины ξ(t), в кото-

что введение в систему структурного беспорядка

рой возникают дополнительные логарифмические

приводит к замедлению процессов неравновесной

поправки. Введение в систему структурного беспо-

вихревой аннигиляции, однако качественно не меня-

рядка приводит к возникновению процесса неравно-

ет физические принципы описания процессов нерав-

весного пиннинга вихрей на дефектах структуры.

новесной критической релаксации системы, ограни-

чиваясь замедлением роста корреляционной длины

В данной работе осуществлен прямой расчет

ξ(t) и соответствующим увеличением динамических

временной зависимости корреляционной длины ξ(t)

масштабов t_L в системе в соответствии с соотноше-

двумерной структурно-неупорядоченной XY -моде-

906

ЖЭТФ, том 158, вып. 5 (11), 2020

Особенности влияния дефектов структуры. . .

Рис. 18. Скейлинговые зависимости для автокорреляционной функции tw(p,T)/2CSS (t, tw) в переменных ξ(t - tw)/ξ(tw)

для структурно-неупорядоченной системы со спиновой концентрацией p

= 0.7 и температурами замораживания

Ts/TBKT = 1.0 (а), 0.75 (б), 0.50 (в), 0.25 (г)

нием ξ(t_L) ≃ L. При неравновесной критической ре-

жения перколяционной неподвижной точки и непо-

лаксации из высокотемпературного начального со-

движной точки чистой системы в настоящей работе

стояния в двумерной структурно-неупорядоченной

было выполнено на основе анализа временной за-

XY -модели не возникает качественного изменения

висимости корреляционной длины ξ(t) для систем

в проявлениях динамического скейлинга по сравне-

с различными спиновыми концентрациями p. На

нию с чистой системой.

основе анализа выполнения скейлинговых свойств

корреляционной длины ξ(t) было показано, что для

Введение в систему структурного беспорядка

температур замораживания в низкотемпературной

приводит к деформации ренормгрупповых потоков

фазе T_s ≤ T_BKT для структурно-неупорядоченных

вследствие влияния притяжения со стороны пер-

систем влияние притяжения неподвижной точки чи-

коляционной неподвижной точки, которое усили-

стой системы плавно сменяется притяжением перко-

вается с ростом концентрации дефектов. Поэтому,

ляционной неподвижной точки. Показано, что си-

несмотря на то, что структурный беспорядок в дву-

стема со спиновой концентрацией p = 0.7 выделяет-

мерной XY -модели не меняет физической природы

ся более медленной релаксацией, связанной с бли-

релаксационных процессов и сказывается преиму-

зостью ее спиновой концентрации к порогу спино-

щественно на динамических масштабах релаксации,

вой перколяции p_C. Данный вывод был подтвер-

возникает существенное усиление влияния перколя-

жден анализом временной зависимости кумулянта

ционной неподвижной точки в области высокой кон-

намагниченности второго порядка g₂(t). Показано,

центрации дефектов. Исследование влияния притя-

907

В. В. Прудников, П. В. Прудников, И. С. Попов

ЖЭТФ, том 158, вып. 5 (11), 2020

Таблица 2. Температурная и концентрационная за-

ческого индекса Фишера η(p, T ) с использовани-

висимости показателя λC (p, T ), полученные в ре-

ем скейлинговых свойств рассчитанной двухвремен-

зультате анализа скейлинговой функции fC в пере-

ной зависимости спин-спиновой автокорреляцион-

менных ξ(t - tw)/ξ(tw)

ной функции C_SS (t, t_w). Полученный коллапс кри-

вых, соответствующих скейлинговым функциям

p = 1.0

)

f_C(t, t_w) = tη(p,T)/2wC_SS(t, t_w

T/T_BKT

λ_C

1+η

для всех рассмотренных значений времени ожи-

1.00

1.2315 ± 0.0312

1.2500 ± 0.0025

, служит подтверждением выполнения

дания t_w

0.75

1.1458 ± 0.0358

1.1365 ± 0.0075

свойств динамического скейлинга в неравновесном

0.50

1.0873 ± 0.0392

1.1000 ± 0.0100

критическом поведении двумерной XY -модели

с различными спиновыми концентрациями при

0.25

1.0556 ± 0.0403

1.0650 ± 0.0125

эволюции из высокотемпературного начального

p = 0.9

состояния. Полученные данным методом значе-

T/T_BKT

λ_C

1+η

ния индекса Фишера η(p, T ) мы считаем более

точными, чем полученные ранее в работе [6] при

1.00

1.2759 ± 0.0523

1.280 ± 0.0025

расчете равновесных характеристик модели. Для

0.75

1.1977 ± 0.0592

1.185 ± 0.0075

системы со спиновой концентрацией p = 0.7 при

0.50

1.1528 ± 0.0628

1.165 ± 0.0125

температуре замораживания T_s = T_BKT было полу-

0.25

1.0672 ± 0.1150

1.065 ± 0.0150

чено необычно высокое значение индекса Фишера

= 1.0000(75). Мы связываем данное необычно

p = 0.8

высокое значение индекса Фишера с сильным вли-

T/T_BKT

λ_C

1+η

янием порога спиновой перколяции и притяжения

1.00

1.5082 ± 0.0624

1.4900 ± 0.0075

со стороны перколяционной неподвижной точки на

неравновесные процессы в системе с p = 0.7.

0.75

1.3263 ± 0.0683

1.3250 ± 0.0100

В данной работе осуществлен расчет скейлинго-

0.50

1.2593 ± 0.0746

1.2575 ± 0.0125

вых функций двухвременной зависимости спин-спи-

0.25

1.1225 ± 0.1223

1.1200 ± 0.0175

новой автокорреляционной функции C_SS(t, t_w), по-

строенной в зависимости от ξ(t - t_w)/ξ(t_w), где

p = 0.7

ξ(t) представляет полученную в результате моде-

T/T_BKT

λ_C

1+η

лирования динамическую зависимость корреляци-

1.00

1.9907 ± 0.0812

2.0000 ± 0.0075

онной длины. Показано, что по сравнению с ре-

зультатами для скейлинговой функции, выражен-

0.75

1.5066 ± 0.0956

1.5065 ± 0.0100

, в слу-

ной через модельную зависимость (t/ ln t)1/2

0.50

1.3503 ± 0.1089

1.3500 ± 0.0100

чае использования напрямую вычисленной дина-

0.25

1.1478 ± 0.1431

1.1450 ± 0.0075

мической зависимости корреляционной длины ξ(t)

скейлинговая функция получается более гладкой,

а ее перегиб в области динамического кроссовера

) ≃ 1 становится более пологим. При

ξ(t - t_w)/ξ(t_w

что двумерная XY -модель со спиновой концентра-

этом скейлинговая функция оказывается коррект-

цией p = 0.7 находится настолько близко к поро-

но определенной в области ξ(t) ≪ L, где влияние

гу спиновой перколяции p_C, что влияние притяже-

эффектов конечного размера системы является ма-

ния перколяционной неподвижной точки становится

лым. В результате анализа полученных скейлинго-

определяющим в релаксационных свойствах систе-

вых зависимостей было показано, что замедление

мы. Однако системы со спиновыми концентрациями

релаксации, связанное с введением в систему струк-

p = 0.9 и 0.8 не испытывают такого сильного влия-

турного беспорядка, проявляется для всех рассмот-

ния эффектов порога спиновой перколяции и основ-

ренных температур замораживания T_s ≤ T_BKT .

ные особенности их критической динамики обеспе-

Осуществлен расчет значений показателей

чиваются притяжением неподвижной точки чистой

λ_C(p, T), характеризующих степенное поведение

системы.

скейлинговых функций f_C (t, t_w) на долговременном

В настоящей работе были определены темпе-

этапе эволюции автокорреляционной функции при

ратурные и концентрационные зависимости крити-

использовании напрямую вычисленной временной

908

ЖЭТФ, том 158, вып. 5 (11), 2020

Особенности влияния дефектов структуры. . .

зависимости корреляционной длины ξ. Показа-

13.

J. Als-Nielsen et al., J. Phys.: Condens. Matter. 5,

но, что в пределах статистической погрешности

7871 (1993).

температурные и концентрационные зависимости

14.

C. Bellitto et al., Inorg. Chem. 26, 191 (1987).

показателя λ_C совпадают со значениями

1 +

+ η(p, T). Полученные результаты подтверждают

15.

A. Paduan-Filho and C. C. Becerra, J. Appl. Phys.

корректность полученных в настоящей работе

91, 8294 (2002).

температурных и концентрационных зависимостей

16.

Ю. С. Каримов, Ю. Н. Новиков, Письма в ЖЭТФ

критического индекса Фишера η, вычисленных на

19, 268 (1974).

основе анализа неравновесных релаксационных

характеристик системы.

17.

D. J. Bishop and J. D. Reppy, Phys. Rev. Lett. 40,

1727 (1978).

Финансирование. Работа выполнена при под-

держке Российского фонда фундаментальных ис-

18.

D. J. Bishop and J. D. Reppy, Phys. Rev. B 22, 5171

следований (проекты №№ 17-02-00279, 18-32-00814,

(1980).

18-42-550003, 20-32-70189), Министерства науки и

19.

S. Misra, L. Urban, M. Kim, G. Sambandamurthy,

высшего образования РФ в рамках государствен-

and A. Yazdani, Phys. Rev. Lett. 110, 037002 (2013).

ного задания (проект № 0741-2020-0002) и грантов

МК-4349.2018.2, МД-2229.2020.2 Президента РФ.

20.

M. R. Beasley, J. E. Mooij, and T. P. Orlando, Phys.

Для проведения расчетов были использованы вы-

Rev. Lett. 41, 1165 (1979).

числительные ресурсы ЦКП «Центр данных ДВО

21.

A. F. Hebard and A. T. Fiory, Phys. Rev. Lett. 44,

РАН» [66], межведомственного суперкомпьютерно-

291 (1980).

го центра РАН, суперкомпьютерного центра МГУ

им. Ломоносова.

22.

Л. Н. Булаевский, В. В. Кузий, A. A. Собянин,

Письма в ЖЭТФ 25, 314 (1977).

ЛИТЕРАТУРА

23.

А. И. Буздин, Л. Н. Булаевский, С. В. Панюков,

Письма в ЖЭТФ 35, 147 (1982).

1. В. Л. Березинский, ЖЭТФ 59, 907 (1970).

24.

А. И. Буздин, Б. Вуйчич, М. Ю. Куприянов,

2. В. Л. Березинский, Низкотемпературные свойст-

ЖЭТФ 101, 231 (1992).

ва двумерных систем, Физматлит, Москва (2007).

25.

A. N. Pargellis, S. Green, and B. Yurke, Phys. Rev.

3. J. M. Kosterlitz and D. J. Thouless, J. Phys. C: Solid

E 49, 4250 (1994).

State Phys. 6, 1181 (1973).

26.

W. Bietenholz, U. Gerber, and F. G. Rejón-Barrera,

4. J. M. Kosterlitz, J. Phys. C 7, 1046 (1974).

J. Stat. Mech. P12009 (2013).

5. L. Berthier, P. C. W. Holdsworth, and M. Sellitto, J.

27.

A. Singh, S. Ahmad, S. Puri, and S. Singh, Eur. Phys.

Phys. A 34, 1805 (2001).

Lett. 100, 36004 (2012).

6. П. В. Прудников, В. В. Прудников, И. С. Попов,

Письма в ЖЭТФ 101, 596 (2015).

28.

A. J. Bray, Adv. Phys. 43, 357 (1994).

7. В. В. Прудников, П. В. Прудников, М. В. Мамоно-

29.

A. J. Bray, Adv. Phys. 51, 481 (2002).

ва, УФН 187, 817 (2017).

30.

W. J. Nuttall, D. Y. Noh, B. O. Wells, and R. J. Bir-

8. С. E. Коршунов, УФН 176, 233 (2006).

geneau, J. Phys.: Condens. Matter. 7, 4337 (1995).

9. A. Taroni, S. T. Bramwell, and P. C. W. Holdsworth,

31.

И. Ф. Люксутов, А. Г. Федорус, ЖЭТФ 80, 2511

J. Phys.: Condens. Matter. 20, 275233 (2008).

(1981).

10. C. A. F. Vaz, J. A. C. Bland, and G. Lauhoff, Rep.

32.

P. Tabeling, Phys. Rep. 362, 1 (2002).

Progr. Phys. 71, 056501 (2008).

11. C. Kawabat and A. R. Bishop, Solid State Commun.

33.

S. Abriet and D. Karevski, Eur. Phys. J. B 37, 47

60, 167 (1986).

(2004).

12. H.-J. Elmers, J. Hauschild, G. H. Liu, and U. Grad-

34.

X. W. Lei and B. Zheng, Phys. Rev. E 75, 040104(R)

mann, J. Appl. Phys. 79, 4984 (1996).

(2007).

909

В. В. Прудников, П. В. Прудников, И. С. Попов

ЖЭТФ, том 158, вып. 5 (11), 2020

35.

V. V. Prudnikov, P. V. Prudnikov, S. V. Alekseev,

51.

A. Asad and B. Zheng, J. Phys. A 40, 9957 (2007).

and I. S. Popov, Phys. Met. Metalogr. 115, 1186

52.

R. Loft and T. A. Deorand, Phys. Rev. B 35, 8528

(2014).

(1987).

36.

В. В. Прудников, П. В. Прудников, И. С. Попов,

53.

B. Yurke, A. N. Pargellis, T. Kovacs, and D. A. Huse,

ЖЭТФ 153, 442 (2018).

Phys. Rev. E 47, 1525 (1993).

37.

P. V. Prudnikov and I. S. Popov, J. Phys.: Conf.

54.

A. J. Bray and A. D. Rutenberg, Phys. Rev. E 49,

Series 510, 012014 (2014).

R27 (1994).

38.

M. V. Mamonova, I. S. Popov, P. V. Prudnikov,

55.

C. Godreche and J. M. Luck, J. Phys. A 33, 1151

V. V. Prudnikov, and A. N. Purtov, Lobachevskii J.

(2000); J. Phys. A 33, 9141 (2000).

Math. 38, 944 (2017).

56.

M. Henkel, Nucl. Phys. B 641, 405 (2002).

39.

F. Krzakala and F. Ricci-Tersenghi, J. Phys.: Conf.

Series 40, 42 (2006).

57.

M. Henkel, M. Paessens, and M. Pleimling, Europhys.

Lett. 62, 664 (2003).

40.

I. S. Popov and P. V. Prudnikov, Sol. St. Phen.

233-234, 8 (2015).

58.

A. B. Harris, J. Phys. C 7, 1671 (1974).

41.

I. S. Popov, P. V. Prudnikov, and V. V. Prudnikov,

59.

A. R. Pereira, J. Magn. Magn. Mater 279,

396

J. Phys.: Conf. Series 681, 012015 (2016).

(2004).6868.2018.2

42.

6868.2018.2 P. V. Prudnikov, V. V. Prudnikov,

60.

H. Weber and P. Minnhagen, Phys. Rev. B 37, 5986

E. A. Pospelov et al., Prog. Theor. Exp. Phys. 2015,

(1988).

053A01 (2015).

61.

I. S. Popov, A. P. Popova, P. V. Prudnikov, and

43.

V. V. Prudnikov, P. V. Prudnikov, and E. A. Pospe-

V. V. Prudnikov, J. Phys.: Conf. Ser. 1163 012042

lov, J. Stat. Mech. 043303 (2016).

(2019).

44.

A. R. Pereira, L. A. S. Mól, S. A. Leonel, P. Z. Coura,

and B. V. Costa, Phys. Rev. B 68, 132409 (2003).

62.

I. S. Popov, A. P. Popova, and P. V. Prudnikov, J.

Phys.: Conf. Ser. 1163, 012039 (2019).

45.

B. Berche, A. I. Farinas-Sanchez, Yu. Holovatch, and

R. Paredes, Eur. Phys. J. B 36, 91 (2003).

63.

I. S. Popov, A. P. Popova, and P. V. Prudnikov, J.

Phys.: Conf. Ser. 1389, 012024 (2019).

46.

O. Kapikranian, B. Berche, and Yu. Holovatch, Eur.

Phys. J. B 56, 93 (2007).

64.

I. S. Popov, A. P. Popova, and P. V. Prudnikov,

47.

A. D. Rutenberg and A. J. Bray, Phys. Rev. E 51,

Europhys. Lett. 128, 26002 (2019).

5499 (1995).

65.

R. M. Ziff and B. Sapoval, J. Phys. A: Math. Gen.

48.

A. J. Bray, A. J. Briant, and D. K. Jervis, Phys. Rev.

19, L1169 (1986).

Lett. 84, 1503 (2000).

49.

F. Rojas and A. D. Rutenberg, Phys. Rev. E 60, 212

66.

А. А. Сорокин, С. В. Макогонов, С. П. Королев,

(1999).

Научно-техническая информация. Серия 1: Орга-

низация и методика информационной работы 12,

50.

A. Jelić and L. F. Cugliandolo, J. Stat. Mech. P02032

14 (2017).

(2011).

910