ЖЭТФ, 2020, том 158, вып. 5 (11), стр. 911-928

СПЕКТРАЛЬНЫЙ АНАЛИЗ УНИВЕРСАЛЬНЫХ

ФЛУКТУАЦИЙ КОНДАКТАНСА

И. М. Суслов^*

Институт физических проблем им. П. Л. Капицы Российской академии наук

119334, Москва, Россия

Поступила в редакцию 29 апреля 2020 г.,

после переработки 29 мая 2020 г.

Принята к публикации 2 июня 2020 г.

Универсальные флуктуации кондактанса обычно наблюдаются в виде апериодических осцилляций в маг-

нитосопротивлении тонких проволочек при изменении магнитного поля B. Фурье-анализ апериодических

осцилляций, наблюдавшихся в классических экспериментах Вебба и Вашбурна, обнаруживает практиче-

ски дискретный спектр — в соответствии со сценарием, следующим из аналогии с одномерными система-

ми, согласно которому флуктуации кондактанса определяются суперпозицией несоизмеримых гармоник.

Более подробный анализ обнаруживает наличие непрерывной компоненты, малость которой объясня-

ется теоретически. Получено множество качественных результатов, подтверждающих представленную

картину: распределение фаз, разностей частот и показателей экспоненциального роста согласуются с

теоретическими предсказаниями; дискретные частоты слабо зависят от процедуры обработки; обнару-

женные сдвиговые осцилляции подтверждают аналогию с одномерными системами. Микроскопические

оценки указывают на соответствие полученных результатов с геометрическими размерами образца.

DOI: 10.31857/S0044451020110140

1. ВВЕДЕНИЕ

Универсальные флуктуации кондактанса [1-4]

обычно наблюдаются в виде апериодических осцил-

ляций в магнитосопротивлении тонких проволочек

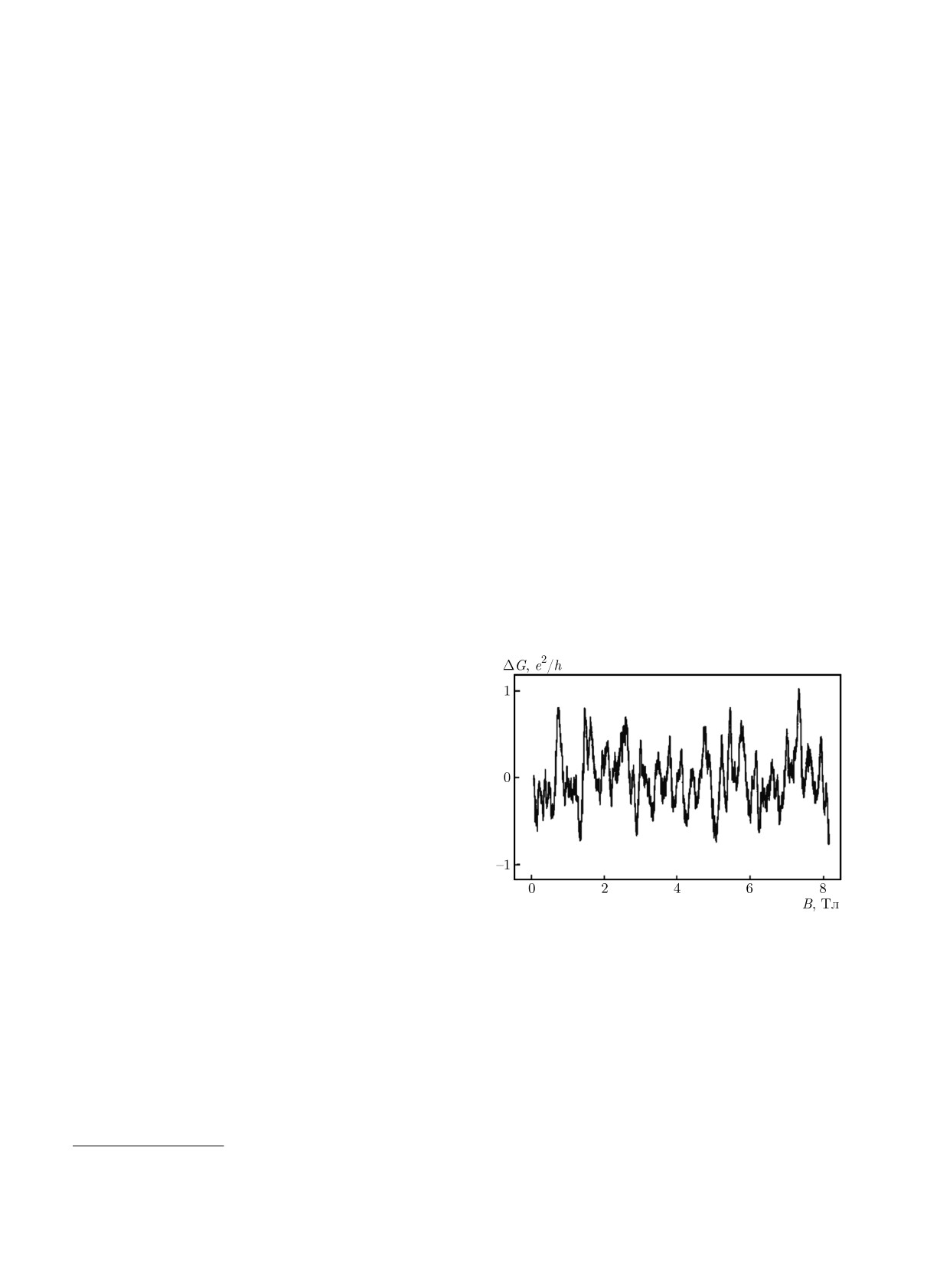
при изменении магнитного поля B [5] (рис. 1) (см.

обзоры [6, 7]). Картина флуктуаций выглядит слу-

чайной, но полностью воспроизводится при повтор-

ных прохождениях по магнитному полю. Она харак-

теризует конкретную реализацию случайного потен-

циала и полностью меняется после отогрева образ-

ца до достаточно высокой температуры, при кото-

Рис. 1. Кондактанс тонкой проволочки из Au как функция

рой примеси получают подвижность, и возникает

магнитного поля [5]

новая примесная конфигурация («магнитные отпе-

чатки пальцев»).

Согласно теории [1-4], кондактанс G(B) при

дать, что на масштабах, больших ξ_B, осцилляции

фиксированном значении поля B испытывает флук-

G(B) на рис. 1 являются полностью случайными;

туации порядка e²/h при изменении примесной кон-

тогда их фурье-анализ должен выявить плоский

фигурации; флуктуации G(B) и G(B + ΔB) ста-

спектр белого шума на частотах, меньших ξ-1B.

тистически независимы, если ΔB превышает неко-

Альтернативная точка зрения возникает при со-

торый характерный масштаб ξ_B. Естественно ожи-

поставлении с результатами для одномерных систем

[8]. Магнитное поле, перпендикулярное к тонкой

^* E-mail: suslov@kapitza.ras.ru

проволочке, создает вдоль нее квадратичный потен-

911

И. М. Суслов

ЖЭТФ, том 158, вып. 5 (11), 2020

циал [9], который эффективно ограничивает длину

это указывает на справедливость второй концепции.

системы L; поэтому изменение магнитного поля ана-

При этом противоречий с диаграммными резуль-

логично изменению L. Сопротивление ρ одномерной

татами [1-4] не возникает, так как в целом фор-

системы является сильно флуктуирующей величи-

ма спектра близка к дискретному белому шуму, ко-

ной, и форма его функции распределения P (ρ) су-

торый по свойствам аналогичен непрерывному. Бо-

щественно зависит от нескольких первых моментов.

лее детальный анализ (разд. 4) обнаруживает нали-

Действительно, фурье-образ P(ρ) определяет харак-

чие непрерывной компоненты, малость которой тео-

теристическую функцию

ретически объясняется в разд. 5. Зависимость ре-

зультатов от процедуры обработки обсуждается в

∑

(it)ⁿ

разд. 3: несмотря на очевидные проблемы, возни-

F (t) =

e^iρt

〈ρⁿ〉 ,

(1)

n=0

кающие при отходе от оптимального режима, дис-

кретные частоты спектральных линий обнаружи-

которая является производящей функцией момен-

вают удивительную стабильность, свидетельствую-

тов 〈ρⁿ〉. Если известны все моменты распределения,

щую об их объективном происхождении. Анализ

то по ним можно построить F(t), после чего P(ρ)

действительной и мнимой частей фурье-образа F (ω)

определяется обратным фурье-преобразованием.

зависимости G(B) (рис. 1) обнаруживает наличие

Если

〈ρⁿ〉 растут с n не слишком быстро, то

быстрых осцилляций, связанных со сдвигом ее аргу-

вклад высших моментов подавлен множителем

мента относительно «естественного» начала отсче-

1/n!, тогда как несколько первых моментов ока-

та, природа которого обсуждается в разд. 6. После

зываются существенными. Эти моменты являются

исключения быстрых осцилляций изучается распре-

осциллирующими функциями L,

деление фазовых сдвигов дискретных гармоник, ко-

〈ρ〉 = a₁(L) + b₁(L) cos(ω₁L + ϕ₁),

торое не противоречит их ожидаемой стохастиза-

ции (разд. 7). Положения экстремумов Re F (ω) и

ρ²

= a₂(L) + b₂(L)cos(ω₂L + ϕ₂)+

(2)

Im F (ω) отличаются от таковых для |F (ω)|, что ука-

+ b₃(L)cos(ω₃L + ϕ₃), и т.д.,

зывает на проявление экспоненциального роста гар-

где a_s(L) и b_s(L) — монотонные функции. Де-

моник, ожидаемого из аналогии с одномерными си-

ло в том, что показатель экспоненциального роста

стемами (разд. 8). Распределение показателей и раз-

для 〈ρⁿ〉 определяется алгебраическим уравнением

ностей частот соответствует теоретическим ожида-

(2n + 1)-го порядка [8], один из корней которого все-

ниям для металлического режима (разд. 9). Мик-

гда действителен, тогда как остальные комплекс-

роскопические оценки подтверждают соответствие

ны для энергий внутри разрешенной зоны; поэто-

результатов с геометрическими размерами образца

му имеются n пар комплексно-сопряженных кор-

(разд. 10). Результаты, полученные в разд. 2, опуб-

ней. Выражение для 〈ρⁿ〉 содержит линейную ком-

ликованы ранее в кратком сообщении [11].

бинацию соответствующих экспонент, и комплекс-

ные корни обеспечивают наличие n осциллирую-

щих членов. В общем случае частоты ω_s являются

2. ФУРЬЕ-СПЕКТР АПЕРИОДИЧЕСКИХ

несоизмеримыми, но их несоизмеримость исчезает в

ОСЦИЛЛЯЦИЙ

глубине разрешенной зоны при слабом беспорядке

(разд. 9). Согласно этой картине, осцилляции G(B)

Фурье-анализ зависимости G(B) (рис. 1) не мо-

на рис. 1 определяются суперпозицией несоизмери-

жет быть проведен непосредственно, так как резкий

мых гармоник и их фурье-спектр должен обнаружи-

обрыв экспериментальных данных приводит к появ-

вать наличие дискретных частот. Косвенным под-

лению медленно спадающих осцилляций в ее спек-

тверждением этой картины являются приведенные

тре и хаотизации последнего¹⁾; для получения чет-

в [8] экспериментальные данные работы [10], соглас-

но которым функция распределения P(ρ) не явля-

¹⁾ На рис. 14 работы [5] фурье-спектр тонкой проволоч-

ки сравнивается со спектром маленького колечка; последний

ется стационарной, а испытывает систематические

обнаруживает дополнительные осцилляции, связанные с эф-

изменения апериодического характера.

фектом Ааронова - Бома. При этом апериодические осцилля-

Из сказанного ясно, что фурье-анализ зависи-

ции не являлись предметом для обсуждения и их спектр (ко-

мости G(B) (рис. 1) позволяет установить, какой

торый в силу резкого обрезания носил хаотический характер)

был огрублен авторами и представлен в виде огибающей по

из двух сценариев является более адекватным. Ни-

осцилляциям. Последнее выявляется путем сопоставления с

же показано, что такой анализ приводит к спект-

рис. 12, 13 работы [5], где хаотические осцилляции присут-

ру, который выглядит чисто дискретным (разд. 2):

ствуют в явном виде.

912

ЖЭТФ, том 158, вып. 5 (11), 2020

Спектральный анализ универсальных флуктуаций кондактанса

ких результатов необходимо использование надле-

так как интеграл от нее по всем частотам равен

жащей сглаживающей функции. Поясним ситуацию

интегралу от |f(x)|² по всем x, поэтому изменение

поподробнее.

спектра f(x) при неизменности среднеквадратичной

Пусть функция f(x) определяется суперпозици-

флуктуации приводит к перераспределению интен-

ей дискретных гармоник и является действитель-

сивностей между различными частотами при сохра-

ной, тогда

нении полной мощности спектра.

∑

Нетрудно видеть, что для получения четкой кар-

1∑ [

]

f (x) =

A_seiωsx =

A_seiωsx+A^∗se-iωsx

(3)

тины в случае дискретного спектра нужно иметь,

по возможности, более узкую форму спектральных

где частоты ω_s без ограничения общности можно

линий g²(ω), что обеспечивается надлежащим вы-

считать положительными. Тогда фурье-образ f(x)

бором функции G(x). Общая стратегия определя-

имеет вид

ется свойствами интегралов от быстро осциллирую-

∑

щих функций [13]. Если f(x) является разрывной, то

F (ω) = π

[A_sδ(ω + ω_s) + A^∗sδ(ω - ω_s)] ,

(4)

ее фурье-образ спадает как 1/ω на больших часто-

тах; если разрыв имеет n-я производная, то соответ-

а его модуль

ственно F(ω) ∼ ω-n-1. В случае гладкой f(x) ее ин-

∑

теграл Фурье вычисляется путем сдвига контура в

|F (ω)| = π

|A_s| [δ(ω + ω_s) + δ(ω - ω_s)]

(5)

комплексную плоскость и определяется ближайшей

сингулярностью или перевальной точкой, что при-

зависит лишь от интенсивностей спектральных ли-

водит к зависимости F (ω) ∼ exp(-αω). Если регу-

ний и не содержит информации о фазовых сдвигах

лярная функция получена путем слабого сглажива-

для соответствующих дискретных гармоник. По-

ния сингулярности, то показатель α является малым

скольку |F (ω)| является четной функцией, можно

и экспонента проявляется лишь при очень больших

ограничиться положительными значениями ω и опу-

ω, тогда как в остальной области сохраняется по-

стить первую дельта-функцию в (5).

ведение, соответствующее сингулярной функции. В

Поскольку функция f(x) может быть экспери-

нашем случае требуется сгладить разрывность G(x),

ментально измерена лишь в некотором конечном ин-

которой соответствует поведение g(ω) ∼ sin ωa/ω.

тервале значений x, то практически мы имеем

При этом слабое сглаживание не эффективно, а

∑[

]

сильное сглаживание приводит к уменьшению G(x)

f (x) =

A_seiωsx + A^∗se-iωsx

G(x),

(6)

вблизи границ рабочего интервала и потере экспери-

ментальной информации, поэтому требуется некото-

где функция G(x) равна единице внутри рабочего

рый разумный компромисс.

интервала и нулю вне его; в дальнейшем она будет

Выберем G(x) в виде симметризованной по x

подвержена сглаживанию. Тогда вместо (4) получим

фермиевской функции

∑

F (ω) =

[A_sg(ω + ω_s) + A^∗sg(ω - ω_s)] ,

(7)

G(x) =

1+e(x-μ)/T +e(-x-μ)/T

где g(ω) — фурье-образ функции G(x), который

(9)

1 + 2e^-μ/Tch(x/T)

является действительным, если G(x) выбрана чет-

ной. Таким образом, ограничение рабочего интерва-

интеграл Фурье для которой вычисляется точно

ла приводит к замене дельта-функций на спектраль-

∞

∫

e^iωx dx

2π sin(ωx₀/β)

ные линии конечной ширины. Если дискретные час-

g(ω) =

тоты являются хорошо разделенными, а g(ω) силь-

b chβx + c

bβshx₀

sh(ωπ/β)

(10)

−∞

но локализована вблизи нуля, то можно пренебречь

x₀ = arch(c/b).

перекрытием функций g(ω ± ω_s)) и записать при по-

ложительных частотах

В нашем случае при выборе x = B - μ₀ эксперимен-

∑

тальные данные соответствуют интервалу |x| ≤ μ₀

|F (ω)|² ≈

|A_s|²g²(ω - ω_s).

(8)

с μ₀

= 4 (при измерении в теслах). Мы приня-

ли μ = μ₀ - 4T , что обеспечивает малое значение

Функция

|F (ω)|²

(так называемая спектральная

G(μ₀) ≈ 0.02 на границе интервала. Как ясно из

плотность мощности [12]) более объективно характе-

рис. 2, при малых T в основном сохраняется пове-

ризует относительный вклад различных гармоник,

дение g(ω) = 2 sin μω/ω, характерное для резкого

913

ЖЭТФ, вып. 5 (11)

И. М. Суслов

ЖЭТФ, том 158, вып. 5 (11), 2020

ным образом состоит из дискретных линий, что под-

тверждает концепцию работы [8]. Однако в интер-

вале ω ≲ 2π/ξ_B (где ξ_B оценивалось как среднее

расстояние между соседними максимумами или ми-

нимумами на рис. 1)²⁾ вид спектра напоминает дис-

кретный белый шум: в грубом приближении линии

эквидистантны, а их интенсивности примерно оди-

наковы. Поскольку сумма по частотам во многих

случаях аппроксимируется интегралом, то дискрет-

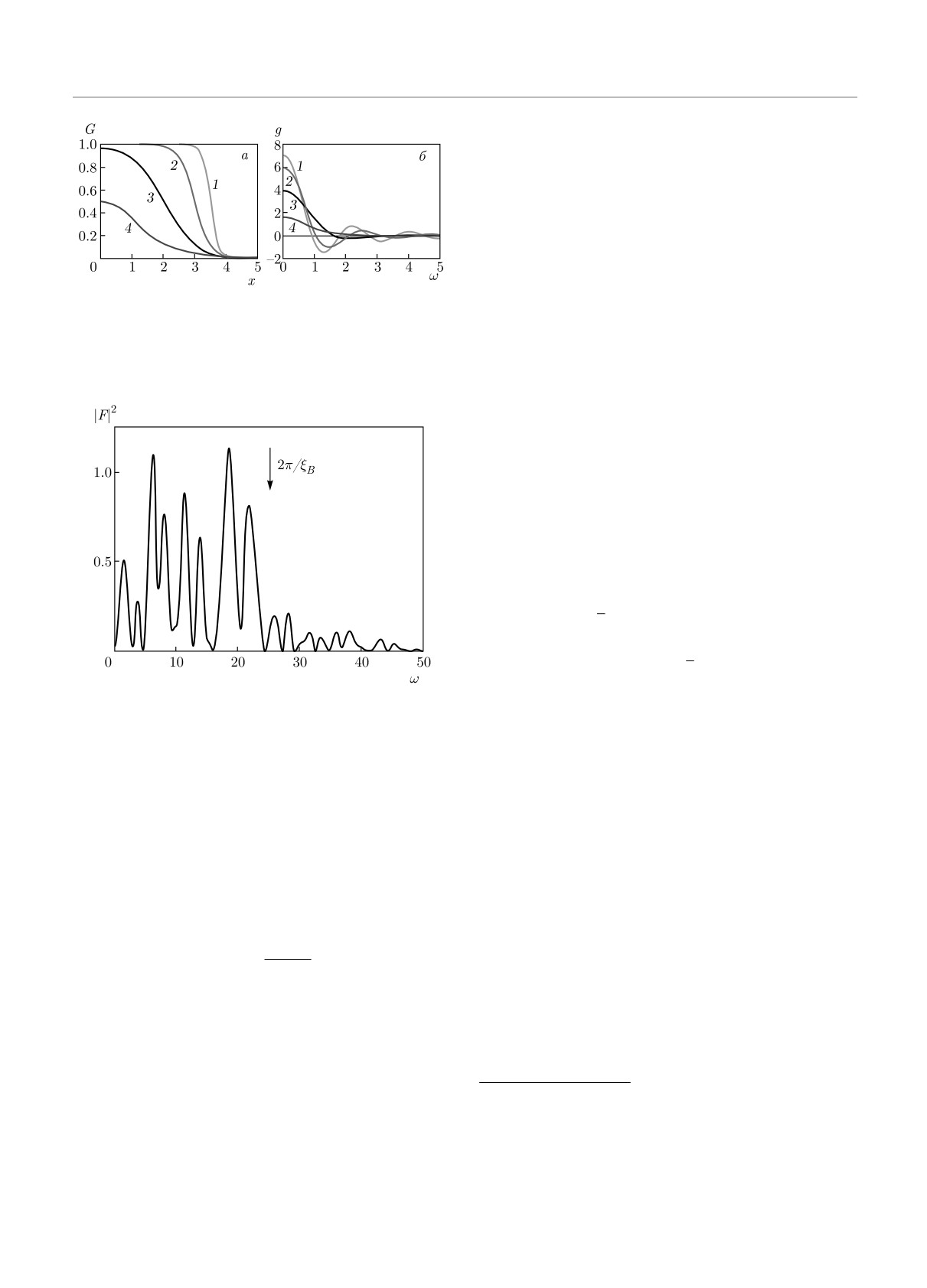
Рис. 2. а) Функция G(x), определенная формулой (9), и

ный белый шум по многим проявлениям не отлича-

б) ее фурье-образ g(ω) при различных значениях μ и T :

ется от непрерывного.

1 — μ = 3.5, T = 0.125; 2 — μ = 3, T = 0.25; 3 — μ = 2,

В качестве примера рассмотрим модель дискрет-

T = 0.5; 4 — μ = T ln2, T = 0.8

ного белого шума, определяемого уравнением [11]

∑

F (ω) = π

[A_sδ(ω+ω_s)+A^∗sδ(ω-ω_s)] H(ω),

(12)

где частоты ω_s эквидистантны (ω_s = sΔ), модули A_s

одинаковы (|A_s| = A), а фазы A_s полностью случай-

ны; функция H(ω) ограничивает спектр интервалом

|ω| ≲ Ω и предполагается четной. Тогда, определяя

f (x) обратным фурье-преобразованием, имеем для

коррелятора

∑

〈f(x)f(x^′)〉 =

A²H²(ω_s)eiωs(x-x′)

≈

A²Δ-1h(x - x^′),

(13)

где h(x) — фурье-образ H²(ω). Если функция H(ω)

Рис. 3. Фурье-анализ экспериментальных данных рис. 1 со

сглаживающей функцией (9) при μ = T ln 2, T = 0.8. На

является гладкой, то h(x) экспоненциально убывает

этом и последующих рисунках значения F (ω) умножены

на масштабе Ω-1, что согласуется с диаграммными

на 10

вычислениями [1-4].

Таким образом, полученные результаты факти-

чески примиряют две альтернативы, указанные в

обрезания. Разумным представляется выбор μ = 2,

начале работы. С одной стороны, спектр дискрет-

T = 0.5, использованный в работе [11]; при этом

ный, что подтверждает концепцию работы [8]. С

эффективно используется 50 % экспериментальных

другой стороны, его форма приблизительно соответ-

данных, а ширина линии примерно такая же, как в

ствует дискретному белому шуму, который по свой-

случае предельного сглаживания, соответствующе-

ствам близок к непрерывному.

го μ = T ln2, x₀ = 0, когда

2πT²ω

g(ω) =

(11)

3. ЗАВИСИМОСТЬ РЕЗУЛЬТАТОВ ОТ

shπT ω

ПРОЦЕДУРЫ ОБРАБОТКИ

и осцилляции полностью исчезают. Для настоящей

работы удобен выбор (11), при котором использует-

Обсудим зависимость результатов от выбора

ся несколько меньше информации, но форма спек-

сглаживающей функции (9), которая при μ = T ln 2

тра практически такая же, как в [11].

приводит к форме линии (11) и зависит от одного

Спектральный анализ экспериментальных дан-

ных (рис. 1) осуществляется путем вычисления ин-

²⁾ При обработке рис. 1 был сильно увеличен и оцифро-

ван вручную. При этом выясняется, что резкие выбросы на

теграла Фурье в области |x| < μ₀ с использовани-

рисунке связаны с вертикальными штрихами, указывающи-

ем указанной сглаживающей функции: полученные

ми экспериментальную погрешность, тогда как фактически

результаты представлены на рис. 3. Спектр очевид-

кондактанс является гладкой функцией магнитного поля.

914

ЖЭТФ, том 158, вып. 5 (11), 2020

Спектральный анализ универсальных флуктуаций кондактанса

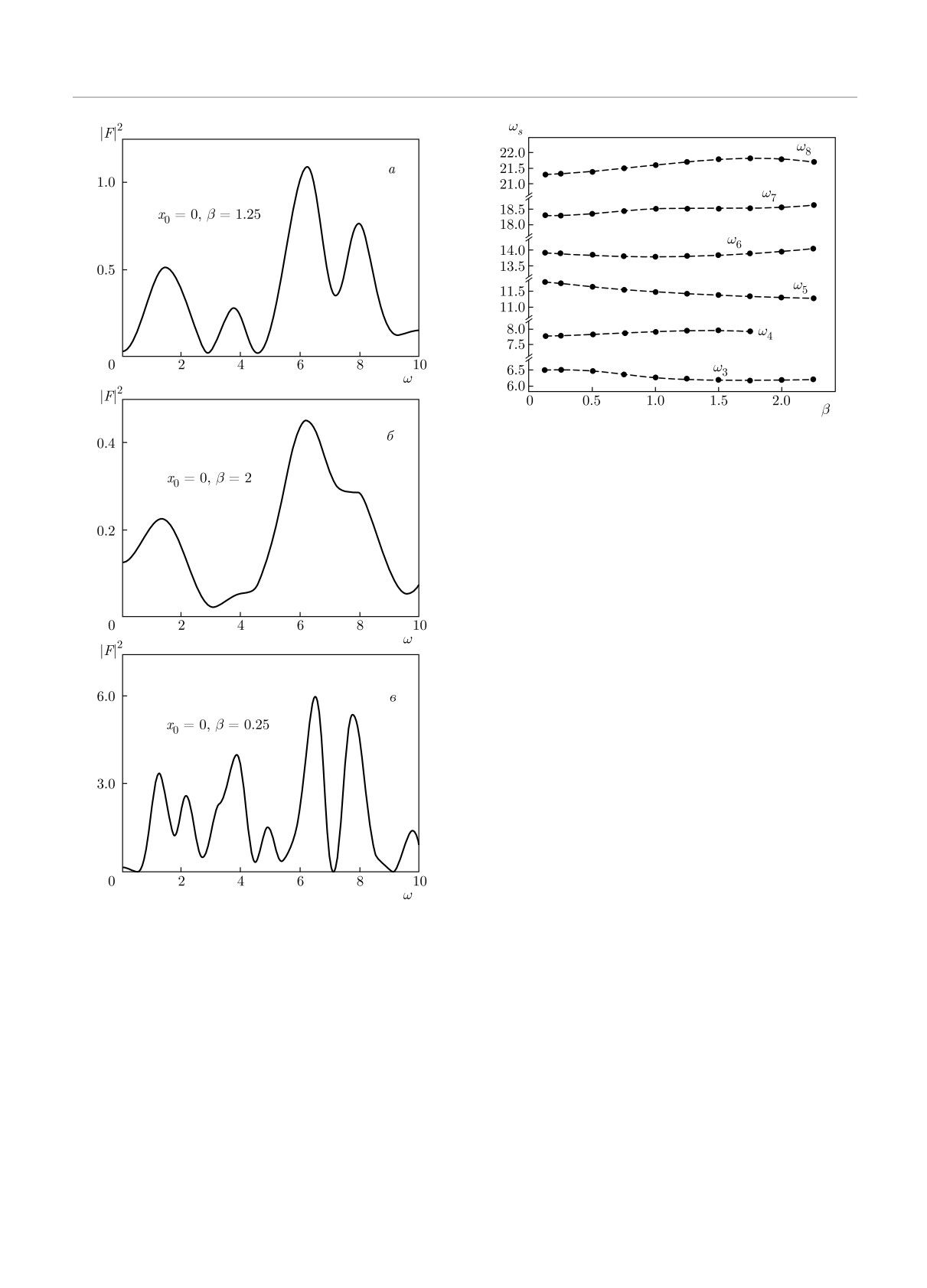
Рис. 5. Зависимость частот наиболее интенсивных гармо-

ник от параметра β = 1/T, определяющего форму сгла-

живающей функции

малым и восстанавливается резкое обрезание, при-

водящее к возникновению паразитных осцилляций

и появлению дополнительных максимумов в |F (ω)|²

(рис. 4в). Смысл введения сглаживающей функции

как раз и состоит в устранении таких осцилляций,

не имеющих отношения к реальному спектру.

Несмотря на очевидные проблемы, возникающие

при отклонении от оптимального режима обработ-

ки, частоты дискретных гармоник обнаруживают

удивительную стабильность при изменении β более,

чем на порядок величины (рис. 5), и нет никаких со-

мнений в их объективном происхождении. Неболь-

шая зависимость от β связана с изменением фор-

мы линий и их взаимным влиянием друг на друга.

Фактически, рис. 5 демонстрирует, насколько хоро-

шо работает приближение независимых гармоник.

Если бы экспериментальный диапазон измене-

ния поля B был меньше, то режим оптимального

разрешения линий (рис. 4а) мог бы отсутствовать

и происходил бы переход от рис. 4б со слившими-

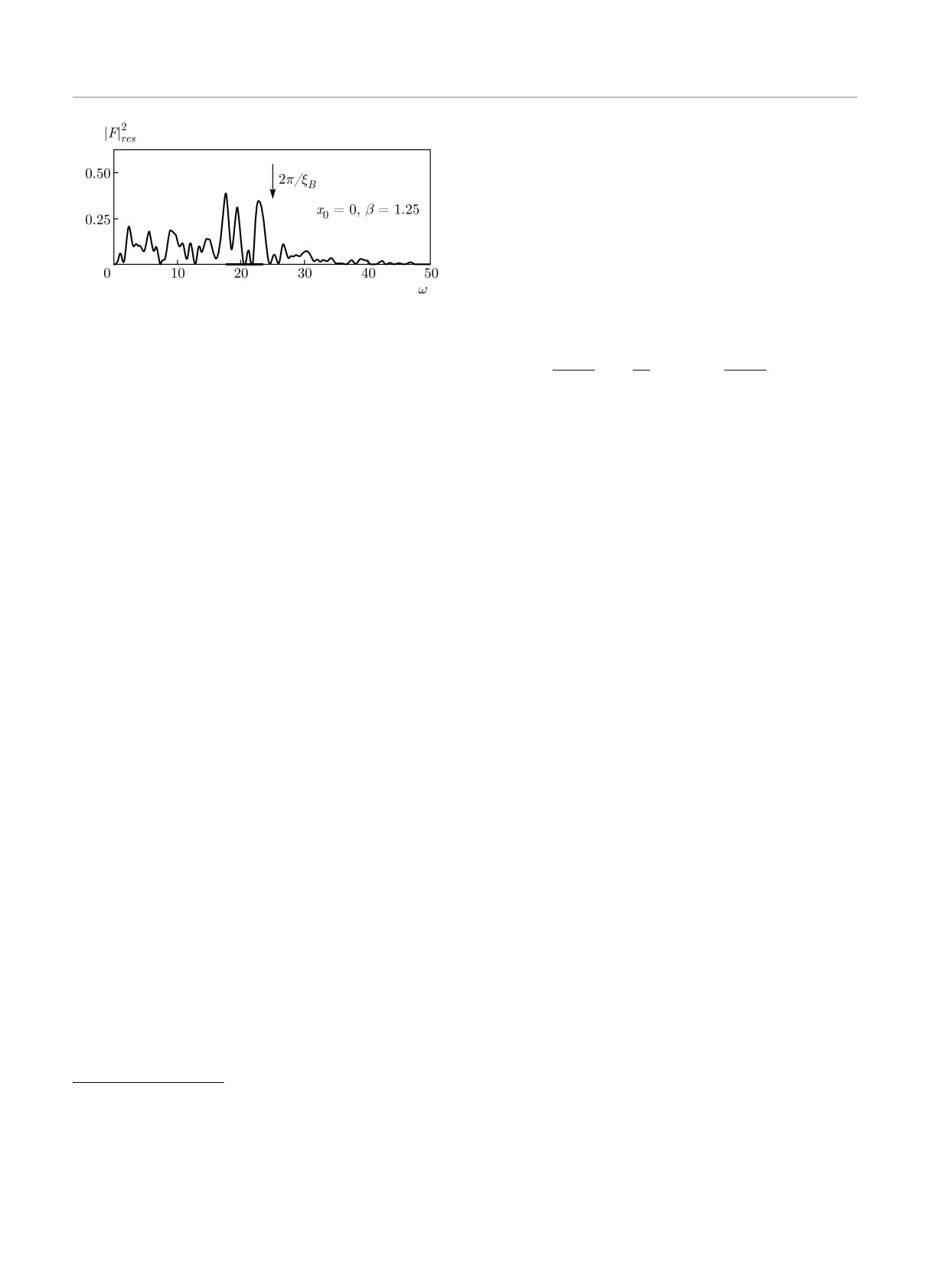
Рис. 4. Зависимость спектра Фурье от выбора сглажива-

ющей функции: а — β = 1.25, б — β = 2.0, в — β = 0.25

ся линиями к рис. 4в с паразитными осцилляциями.

Можно предполагать, что и в настоящих условиях

эксперимента разрешение линий является неполным

и имеет место их частичное слияние.

параметра β = 1/T . При выборе β = 1.25 она обес-

печивает малое значение G(μ₀) ≈ 0.02 на границе

рабочего интервала и спектр |F (ω)|² имеет четкую

4. НЕПРЕРЫВНАЯ КОМПОНЕНТА

дискретную форму (рис. 4а), которая практически

СПЕКТРА

не меняется в интервале β = 1.0-1.5. При увели-

чении β форма линий уширяется в соответствии с

Фурье-спектр на рис. 3 выглядит чисто дискрет-

(11) и происходит их частичное слияние (рис. 4б).

ным, что представляется не вполне естественным.

При уменьшении β значение G(μ₀) перестает быть

Аналогия с одномерными системами приводит к вы-

915

10*

И. М. Суслов

ЖЭТФ, том 158, вып. 5 (11), 2020

последнюю медленно меняющейся и отсчитывая ω

от центра линии, можно положить

F (ω) = Ag(ω) + B

(14)

и считать B постоянным в пределах ширины линии.

Тогда

|F (ω)|² = c₁g²(ω) + c₂g(ω) + c₃,

(15)

где

c₁ = |A|², c₂ = 2|A||B| cosχ, c₃ = |B|²

(16)

и χ определяется разностью фаз A и B. Считая g(ω)

нормированной на единицу при ω = 0, нетрудно по-

нять, что функция g²(ω) соответствует более узкому

максимуму, чем g(ω); поэтому линия уширяется при

c₂ > 0 и сужается при c₂ < 0, оказываясь несиммет-

ричной в случае существенного изменения B вбли-

зи максимума. Согласно (15), |F(ω)|² определяется

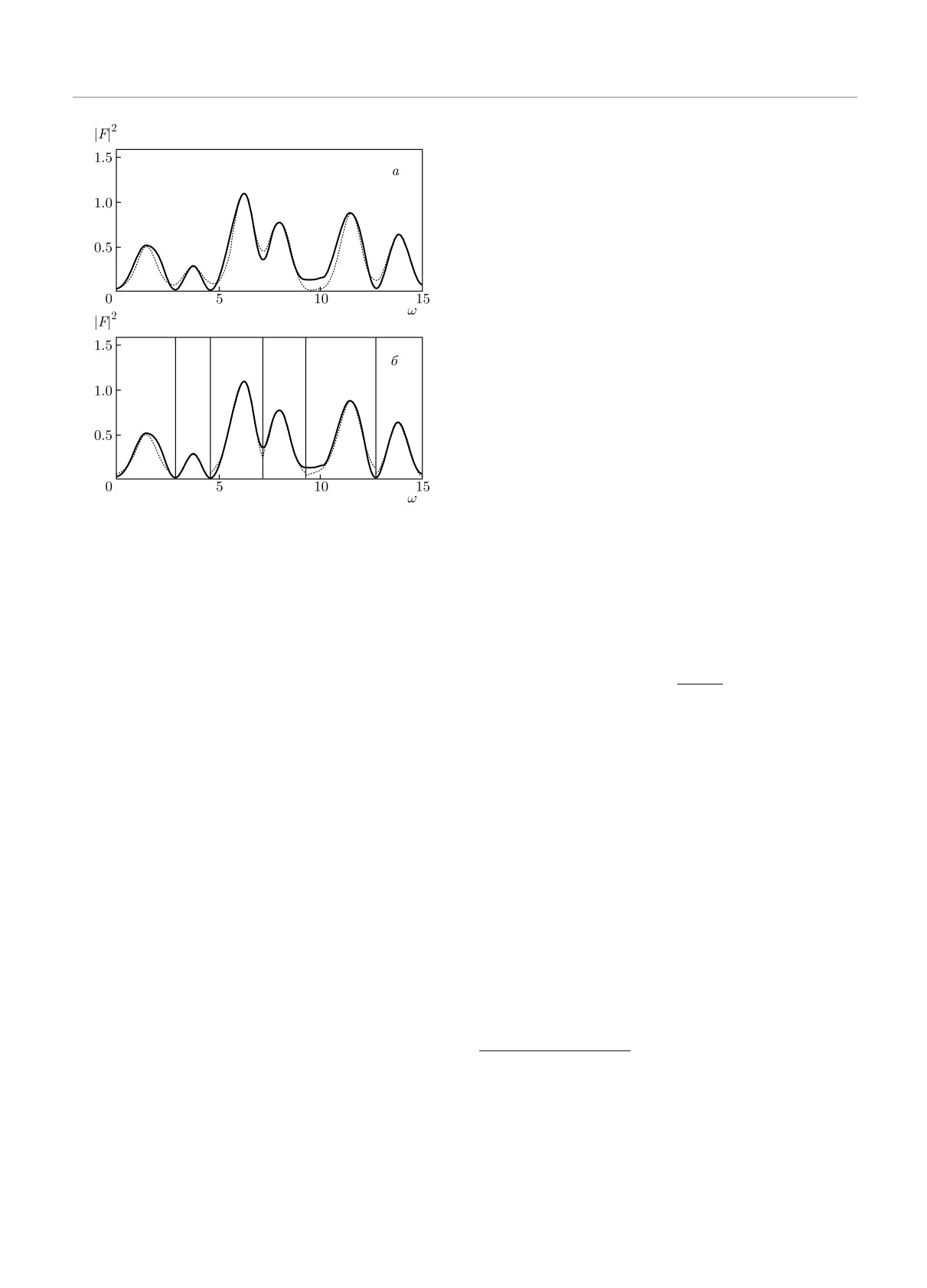
Рис. 6. а) Сравнение экспериментального спектра Фурье

суперпозицией трех базисных функций g²(ω), g(ω)

(сплошная линия) с соотношением (8) (пунктир); частоты

и 1, коэффициенты которой можно установить из

ωs и амплитуды |As| определялись по положению и высо-

условия минимизации среднеквадратичного откло-

те максимумов на рис. 3. б) Подгонка формы отдельных

линий по формуле (18)

нения. Это стандартная процедура обработки [12],

которая является линейной и однозначной. Однако

практически она приводит к нефизическим резуль-

татам ввиду нарушения условия

воду, что функция распределения P (ρ) испытыва-

√

ет систематические изменения детерминированной

|c₂| ≤ 2

|c₁||c₃|,

(17)

природы, приводящие к осцилляциям ρ в конкрет-

ном образце. Но аналогичные осцилляции (случай-

следующего из

(16). По-видимому, оптимальная

ного характера) должны иметь место и при стацио-

подгонка соответствует предельным значениям ±1

нарном распределении P (ρ) ввиду конечности ши-

для cos χ; в этом случае параметры A и B можно

рины последнего. Было бы более естественно, ес-

считать действительными³⁾, полагая

ли бы рис. 3 содержал непрерывную компоненту,

на фоне которой проявлялись дискретные линии.

|F (ω)|² = [(F₀ - B)g(ω) + B]² ,

(18)

Фактически непрерывная компонента действитель-

но присутствует, и ниже мы попытаемся ее оценить.

где F₀ = |F (0)|. Здесь учтено, что используемая про-

цедура оправдана вблизи максимума |F (ω)|², поэто-

Согласно (8), в пренебрежении взаимодействием

му его положение естественно держать фиксирован-

гармоник спектр |F (ω)|² представляется в виде ли-

ным. Подгонка по формуле (18) отдельно для каж-

нейной комбинации функций g²(ω - ω_s), форма ко-

дой линии приводит к рис. 6б: для большинства ли-

торых заранее известна. Проверка соотношения (8)

ний согласие практически идеально, а отсутствие

представлена на рис. 6а, где частоты ω_s определя-

такового для некоторых из них, по-видимому, свя-

лись по положениям максимумов на рис. 3, а ампли-

зано с наличием второстепенных гармоник, которые

туды |A_s| — по высоте этих максимумов; в отноше-

«прячутся» на фоне основных линий.

нии формы g²(ω-ω_s) никакой подгонки не делалось.

Согласие выглядит удовлетворительным, но не яв-

³⁾ Подчеркнем, что действительность параметров A и B

ляется полным: ширина линий отличается от теоре-

является лишь эффективной. Фактически их фазы оказы-

тической то в большую, то в меньшую сторону, а

ваются скоррелированными, либо совпадая друг с другом,

наблюдаемая форма линий не всегда симметрична.

либо отличаясь на π. По-видимому, фазы дискретных гармо-

ник подстраиваются под конкретную реализацию непрерыв-

Естественно предположить, что это связано с на-

ной компоненты; механизм этого явления нам не известен и

личием непрерывной компоненты спектра. Считая

его нужно рассматривать как экспериментальный факт.

916

ЖЭТФ, том 158, вып. 5 (11), 2020

Спектральный анализ универсальных флуктуаций кондактанса

и эффекты интерференции между соседними лини-

ями.

5. ПОЧЕМУ СПЕКТР ПРАКТИЧЕСКИ

ДИСКРЕТНЫЙ?

Обсудим причины малости непрерывной компо-

ненты спектра. Согласно [14-19] эволюция распре-

деления P (ρ) в одномерных системах описывается

Рис. 7. Остаточная часть спектра, полученная путем ис-

уравнением диффузионного типа:

ключения вкладов основных дискретных частот. Резкие

[

]

максимумы, по-видимому, связаны со второстепенными

∂P(ρ)

∂

∂P(ρ)

гармониками, которые «прятались» на фоне основных

=α

ρ(1 + ρ)

(19)

∂L

∂ρ

спектральных линий, тогда как остальное естественно при-

писать непрерывной компоненте спектра

в котором αL играет роль времени. Это уравнение

получено в приближении случайных фаз, которое

хорошо работает в квазиметаллическом режиме, т. е.

После того, как коэффициенты c₁, c₂, c₃ опреде-

в глубине разрешенной зоны при слабом беспоряд-

лены, можно исключить из |F (ω)|² вклады, пропор-

ке [8]. Естественным начальным условием для (19)

циональные g²(ω) и g(ω). Проводя такую процеду-

является

ру для всех линий, получим «остаточный» спектр,

приведенный на рис. 7. Резкие максимумы в этом

P (ρ) = δ(ρ) при L = 0,

(20)

спектре, по-видимому, связаны со второстепенными

дискретными гармониками, тогда как все осталь-

так как при нулевой длине системы ее сопротивле-

ное естественно приписать непрерывной компонен-

ние равно нулю независимо от реализации случай-

те; она составляет 10-15 % от амплитуды основных

ного потенциала. Такое начальное условие приводит

линий, и причина ее малости обсуждается в разд. 5.

к распределению

Спектр непрерывной компоненты приблизительно

P (ρ) = (αL)-1 exp {-ρ/αL}

(21)

соответствует белому шуму для ω ≲ 2π/ξ_B, но пред-

положенная медленность ее изменения не имеет ме-

при малых L (когда типичные ρ малы) и логнор-

ста, поэтому полученный результат следует считать

мальному распределению при больших L (когда ти-

лишь грубой оценкой⁴⁾.

пичные ρ велики). Для распределения (21) среднее

Строго говоря, величина B в (15) представляет

значение 〈ρ〉 совпадает со среднеквадратичным от-

не только непрерывную компоненту, но и вклады

клонением σ, тогда как в логнормальном режиме σ

соседних дискретных линий. Это не влияет на пра-

растет быстрее, чем 〈ρ〉.

вильность определения амплитуды A, что подтвер-

Рассмотрим более общее начальное условие,

ждается аналогичным вычислением для сглажива-

смысл которого обсуждается ниже:

ющей функции с μ = 2, T = 0.5: «хвосты» последней

существенно отличны от таковых для функции (11),

P (ρ) = δ(ρ - ρ₀) при L = L₀.

(22)

но результат не слишком отличается от рис. 7.

Заметим, что спектр |F (ω)|² на рис. 3 выглядит

Решение уравнения (19) с начальным условием (22)

«более дискретным», чем он есть на самом деле: де-

близко к гауссовскому при L, близких к L₀ (см. При-

ло в том, что величина B, оказываясь приблизитель-

ложение A), тогда как при больших L восстанавли-

но постоянной в окрестностях максимумов, меняет

вается распределение (21) или логнормальное рас-

знак в промежутках между некоторыми линиями.

пределение, так как конечность ρ₀ и L₀ становится

Остаточный спектр на рис. 7 не сводится к вели-

несущественной. В условиях близости P (ρ) к гаус-

чине B, но содержит также погрешности обработки

совскому распределению оно адекватно характери-

зуется двумя первыми моментами, эволюцию кото-

⁴⁾ Для несимметричных линий обработка неоднозначна

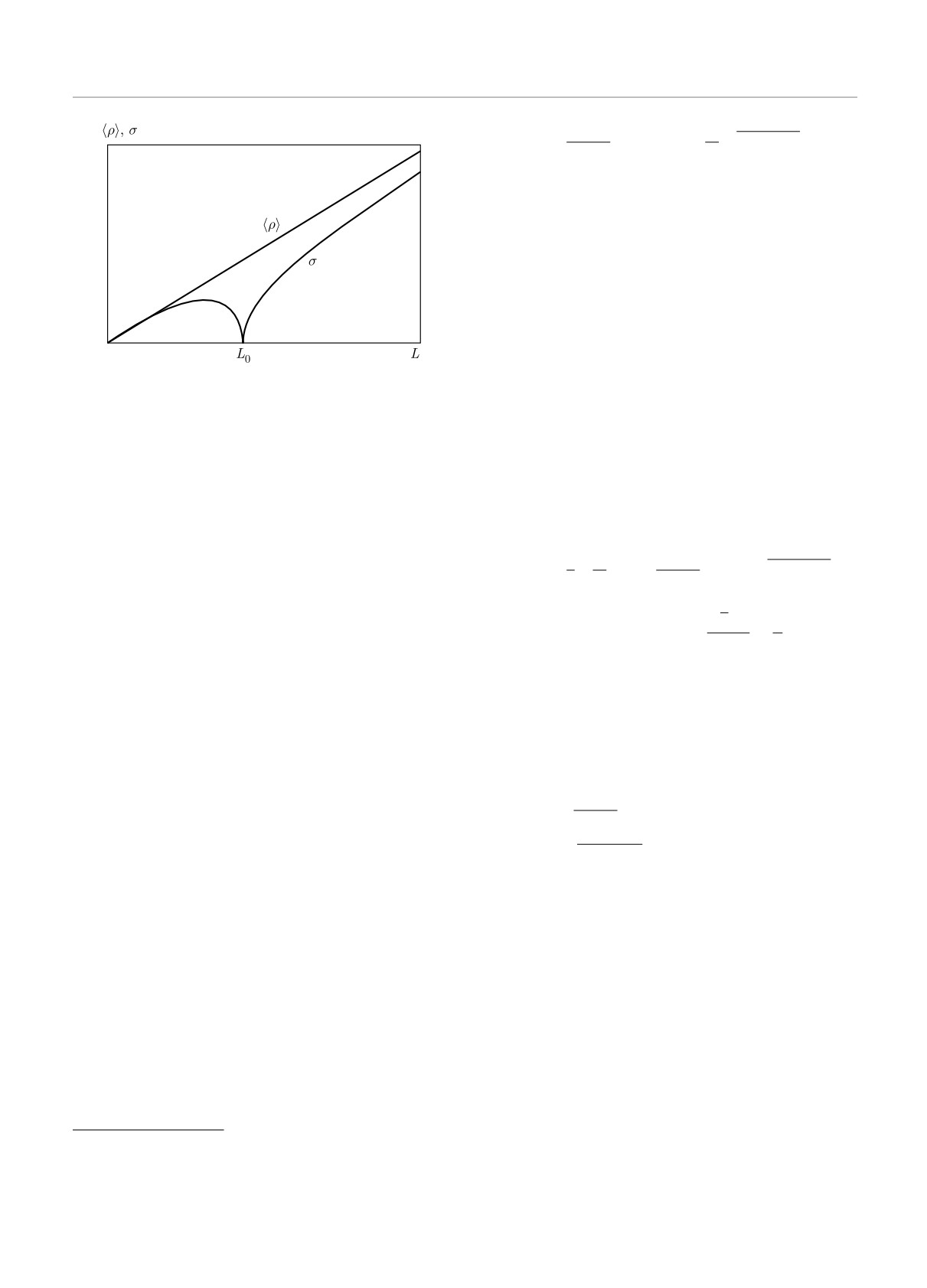
рых легко исследовать (см. Приложение A): типич-

ввиду возможности подгонки их правого или левого скло-

ная ситуация представлена на рис. 8. Нетрудно ви-

на. Эта неоднозначность использована для того, чтобы избе-

жать появления нефизических отрицательных значений для

деть, что 〈ρ〉 существенно превышает σ в окрестно-

|F(ω)|2res.

сти L₀ шириной порядка L₀.

917

И. М. Суслов

ЖЭТФ, том 158, вып. 5 (11), 2020

(

)

√

1+2ρ₀

ϵ²

〈ρ〉 = ρ₀+

e2ϵ2l-1

ρ₀(1+ρ₀)×

[

]

× e2ϵ2l sinψ - e-ϵ2l sin(2δl + ψ) ,

(23)

полученный для дискретной модели Андерсона;

здесь δ = k_F a₀, ϵ² = W²/4δ², l = (L - L₀)/a₀, k_F —

фермиевский импульс, a₀ — постоянная решетки,

W — амплитуда случайного потенциала, ψ опреде-

ляется разностью фаз, входящих в трансфер-мат-

рицу, заданную на масштабе L₀. Нетрудно видеть

существование осцилляций, период которых опреде-

ляется де-бройлевской длиной волны (2δl = 2k_F L

= 0); их амплитуда может быть сравнима с

при L₀

Рис. 8. Поведение 〈ρ〉 и σ в металлическом режиме для

ρ₀ ≪ 1, несмотря на наличие малого параметра ϵ²/δ.

начального условия (22). При выборе ρ0 = 〈ρ〉, принятом

В приближении случайных фаз величина ψ полно-

на рисунке, зависимость 〈ρ〉 от L остается такой же, как

стью стохастизирована и усреднение по ней устраня-

для начального условия (20). Качественная картина не ме-

ет осцилляции, восстанавливая результат, следую-

няется, если для ρ0 выбрано типичное значение из распре-

деления (21)

щий из уравнения (19) (см. (A.6) в Приложении A).

За пределами металлического режима (ϵ² ≳ δ) ам-

плитуда осцилляций заведомо превышает ρ₀,

)

Обсудим смысл начального условия (22). Бу-

⁽ϵ²)2/3 (1+2ρ₀

√

〈ρ〉 = ρ₀+

-cosψ

ρ₀(1+ρ₀)

дем измерять сопротивление ρ системы на длине

L₀, создавая различные примесные конфигурации⁵⁾;

[

(_√

)]

при достаточно большом числе конфигураций мы

3x₁l

воспроизведем распределение (21). Теперь изменим

× ex1l - 2 e-x1l/2 cos

(24)

процедуру и будем отбирать только конфигурации,

для которых ρ попадает в малый интервал вокруг

и они не исчезают при усреднении по ψ ввиду прин-

ρ₀: тем самым искусственно создается ансамбль с

ципиальной неприменимости приближения случай-

(

)1/3

узким распределением типа (22), эволюция которо-

ных фаз [8] (здесь x₁ =

8ϵ²δ²

). Амплитуда ос-

го приводит к картине, представленной на рис. 8.

цилляций в металлическом режиме возрастает при

Теперь возьмем один образец, сопротивление кото-

наличии чужеродных контактов

рого равно ρ₀ на длине L₀. Зависимость ρ(L) для

[

]

такого образца может быть получена теоретически,

1+2ρ₀

〈ρ〉 = ρ₀ +

-1+Δ²²e2ϵ2l-Δ²¹e-ϵ2l cos2δl +

если известны все детали примесной конфигурации.

Обычно такая информация отсутствует, и извест-

√

{

ны лишь общие статистические свойства случайного

+Δ₁

ρ₀(1+ρ₀) e2ϵ2l Δ₂ cosψ - e-ϵ2l ×

потенциала. В этом случае можно установить лишь

[

]}

приблизительный коридор возможностей для зави-

(Δ₂ -1) cos ψ cos 2δl + cos (2δl + ψ)

(25)

симости ρ(L), который и иллюстрируется на рис. 8.

где параметры Δ₁ и Δ₂ определены в Приложении B

Уравнение (19) получено в приближении случай-

и могут быть велики.

ных фаз, которое устраняет все осцилляционные эф-

Таким образом, при достаточно общих услови-

фекты. Однако эволюцию 〈ρ〉 можно исследовать

ях амплитуда осцилляций 〈ρ〉 сравнима с ρ₀ и в

точно, не прибегая ни к каким предположениям (см.

окрестности L₀ заведомо превышает σ. Для высших

Приложение B). В квазиметаллическом режиме для

моментов возможность получения результатов типа

естественных идеальных контактов [8] справедлив

(23)-(25) выглядит практически нереальной из-за

результат

громоздкости вычислений и можно привести лишь

общие соображения. Для второго момента 〈ρ²〉 есте-

ственно ожидать, что амплитуда осцилляций срав-

⁵⁾ Это можно делать практически путем отогрева образца

нима с ρ²⁰ и существенно превышает величину σ².

до достаточно высокой температуры.

Таким образом, изменение ширины распределения

918

ЖЭТФ, том 158, вып. 5 (11), 2020

Спектральный анализ универсальных флуктуаций кондактанса

за счет систематических изменений P (ρ) существен-

но превышает ширину распределения в отсутствие

осцилляций. Поэтому и осцилляции высших момен-

тов также оказываются существенными.

Применимость проведенного анализа к рассмат-

риваемой ситуации определяется тем, что для сгла-

живающей функции с μ = 2, β = 2, использо-

ванной в [11], эффективно задействован интервал

B = 2-6 Тл, соответствующий изменению поля в 3

раза. Ввиду L ∝ B-1/2, это соответствует измене-

нию L в 1.7 раза⁶⁾, а при выборе L₀ в середине интер-

вала отклонения от L₀ оказываются на уровне 30 %.

Дл сглаживающей функции с μ = T ln2, приводя-

щей к (11), это отклонение еще меньше. Заметим,

что ситуация не изменится при увеличении экспе-

риментального диапазона используемых полей, так

как соображения по выбору сглаживающей функ-

ции остаются прежними: изменяется лишь значение

μ₀ при сохранении всех пропорций на рис. 2.

6. СДВИГОВЫЕ ОСЦИЛЛЯЦИИ

Возвращаясь к формулам разд. 2, нетрудно за-

метить, что выражение (7) является более обосно-

ванным, чем (8): если первое является точным след-

ствием (6), то второе предполагает слабое перекры-

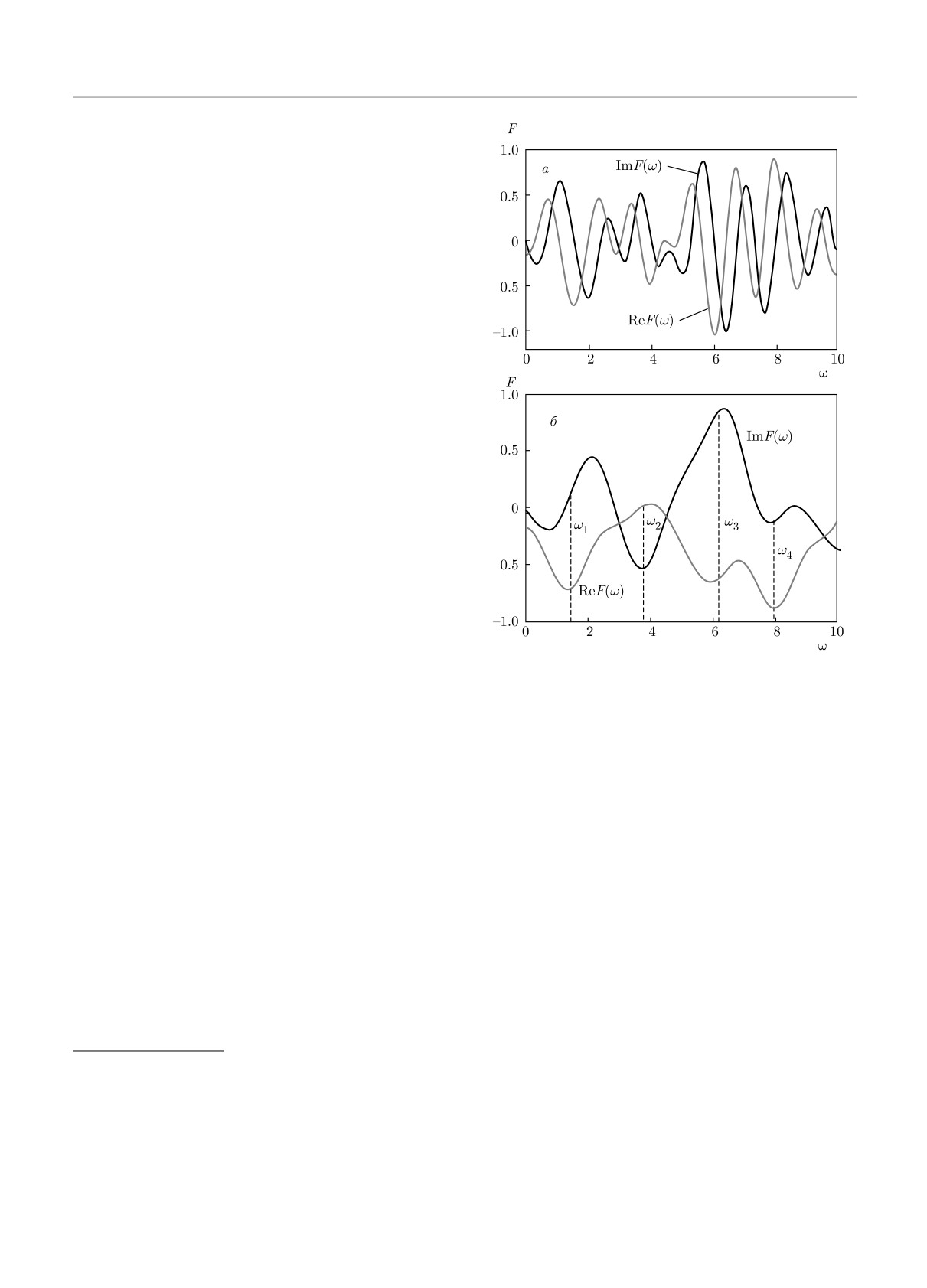
Рис. 9. а) Поведение действительной и мнимой частей

тие спектральных линий. Можно ожидать, что обра-

F(ω) свидетельствует о наличии сдвиговых осцилляций

ботка на основе (7) с использованием представления

e^iωa с a = 4.3. б) Поведение Re F (ω) и Im F (ω) после

(14) и подгонкой по отдельности действительной и

исключения сдвиговых осцилляций; пунктиром отмечены

мнимой частей F (ω) приведет к более плавной зави-

положения максимумов для |F (ω)|²

симости для |F (ω)|2res. К сожалению, эти ожидания

не подтверждаются: получаемая картина не слиш-

ком отличается от рис. 7 и не оправдывает более

и при больших a появляются быстрые осцилляции.

сложной обработки. Однако изучение действитель-

В связи с этим возникает вопрос о «естественном»

ной и мнимой частей F (ω) выявляет много интерес-

выборе начала отсчета, для которого фурье-образ

ного, что определяет содержание этого и последую-

меняется медленно. По среднему периоду осцилля-

щих разделов.

ций на рис. 9а можно установить, что a = 4.3, и ис-

Зависимости Re F(ω) и ImF(ω) оказываются

ключение множителя exp(iωa) приводит к тому, что

быстро осциллирующими (см. рис. 9а). Причину ос-

Re F (ω) и Im F (ω) изменяются на том же масштабе,

цилляций легко понять: если F (ω) есть фурье-образ

что и |F (ω)| (рис. 9б). Естественное начало отсчета

f (x), то сдвиг начала отсчета x приводит к соответ-

определяется условием x = B - μ₀ = a и соответ-

ствию

ствует магнитному полю B₀ = 8.3 Тл, лежащему

за верхней границей экспериментального диапазона

f (x - a) ⇐⇒ e^iωaF (ω)

(26)

полей. Учитывая, что большие поля соответствуют

малым размерам системы, можно предложить сле-

⁶⁾ Масштаб L оценивается как значение координаты x, при

дующую интерпретацию.

котором квадратичный потенциал mω2B x² [9] сравнивается с

энергией Ферми ϵ_F , так что L ∝ B-1. Однако, если энергия

При изучении эволюции P (ρ) по мере изменения

ϵ_F сравнима с первым уровнем Ландау, то ее нужно заменить

длины L одномерной системы естественным нача-

на ℏω_B = ℏeB/mc, что дает зависимость L ∝ B-1/2. Как ясно

из разд. 10, вблизи середины экспериментального интервала

лом отсчета является L = 0. Однако, если эволюция

полей вторая оценка более адекватна.

начинается с конечного масштаба L₀, то при боль-

919

И. М. Суслов

ЖЭТФ, том 158, вып. 5 (11), 2020

ших L возникает такое же распределение, как и в

случае L₀ = 0. Поэтому, изучая ситуацию при боль-

ших L и экстраполируя к начальной стадии эво-

люции, невозможно установить, с какого масшта-

ба она начинается⁷⁾: можно лишь утверждать, что

этот масштаб мал по сравнению с рассматриваемы-

ми. В терминах магнитного поля это означает, что

эволюция начинается с некоторого большого поля

B₀. Однако ввиду нелинейного характера зависимо-

сти L ∝ B-1/2 значение B₀, получаемое в результате

линейной экстраполяции⁸⁾, оказывается не слишком

большим.

Предложенная интерпретация представляется

логичной и является косвенным подтверждением

аналогии с одномерными системами. Формальные

аргументы в отношении выбора начала отсчета

представлены в Приложении C.

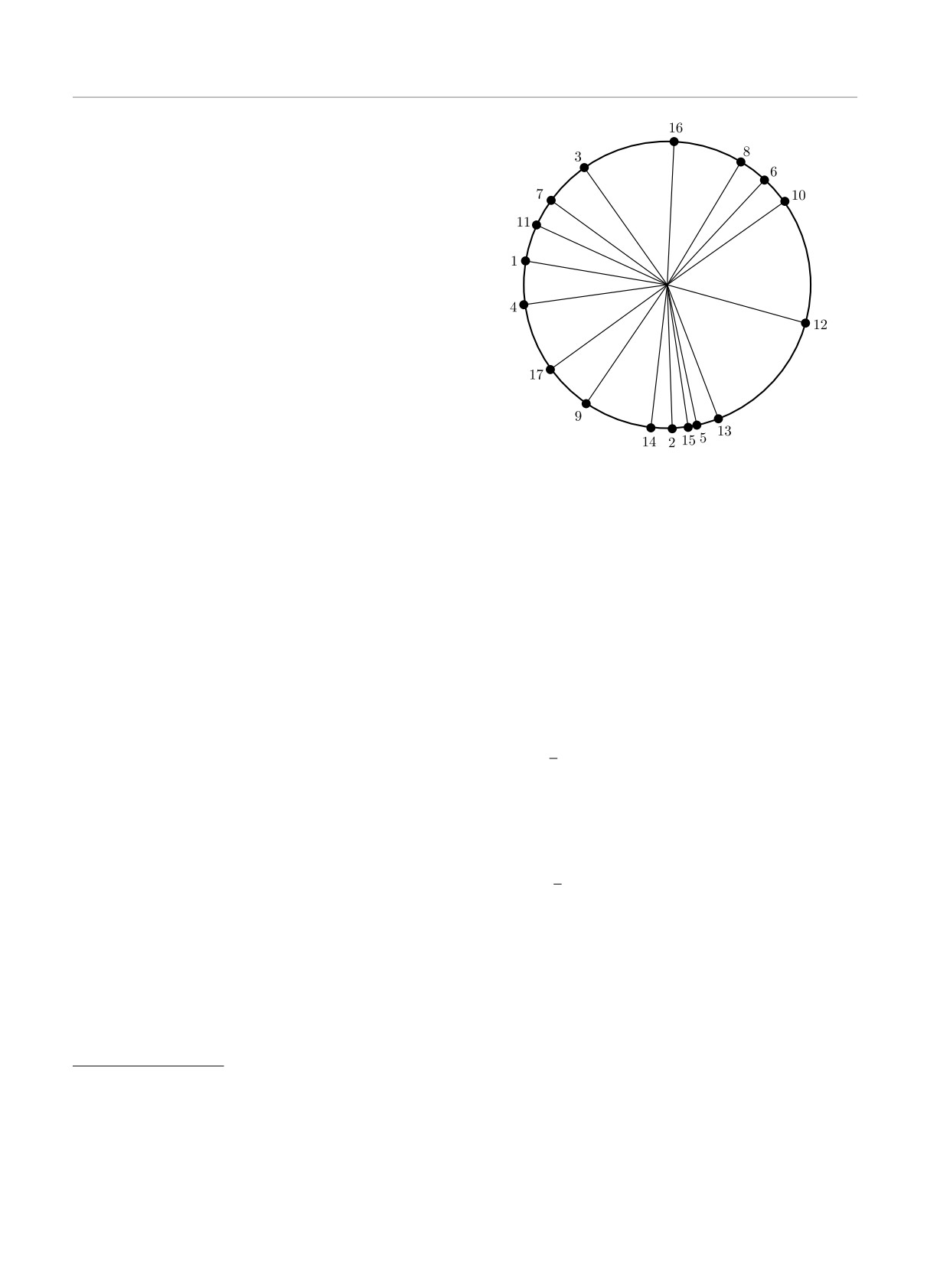
Рис. 10. Распределение фазовых множителей eiϕs на еди-

ничном круге; цифры у точек указывают значение s

7. РАСПРЕДЕЛЕНИЕ ФАЗ

и Im F (ω) находятся в разных точках, не совпада-

После того как установлено естественное нача-

ющих с максимумами |F (ω)|². Это указывает на

ла отсчета аргумента f(x), результаты для действи-

несправедливость формулы (7) и ставит под сомне-

тельной и мнимой частей F(ω) могут быть исполь-

ние исходное выражение (6), следствием которого

зованы для дальнейшего анализа. Оценивая значе-

она является.

ния Re F (ω) и Im F (ω) в точках максимума |F (ω)|²,

Вспомним, что согласно (2) амплитуды осцилля-

можно установить комплексные фазы коэффициен-

ций не являются постоянными, а подвержены экс-

тов A_s в (6)-(8). Их распределение иллюстрируется

поненциальному росту. С учетом последнего вместо

на рис. 10.

(6) нужно использовать выражение

Как обсуждалось в разд. 2, дискретный белый

шум оказывается аналогичным непрерывному, если

1∑ [

фазы A_s полностью случайны. Согласно рис. 10, их

f (x) =

A_seiωsx+αsx +

распределение достаточно равномерно и не противо-

]

речит ожидаемой стохастизации. Было бы интерес-

+ A^∗se-iωsx+αsx

G(x),

(27)

но проверить, как меняется распределение фаз при

переходе к другим примесным конфигурациям.

что вместо (7) приводит к результату

∑

F (ω) =

[A_sg(ω + ω_s - iα_s) +

8. ПРОЯВЛЕНИЯ ЭКСПОНЕНЦИАЛЬНОГО

РОСТА

+ A^∗sg(ω - ω_s - iα_s)] .

(28)

Согласно формуле (7), вклады дискретных гар-

Сосредоточимся на вкладе одной гармоники ω_s и,

моник в F (ω) пропорциональны g(ω - ω_s) и в прене-

изменяя начало отсчета ω, положим

брежении их взаимодействием должны приводить к

экстремумам Re F (ω) и Im F (ω) в точках ω_s. Одна-

A = A^′ + iA^′′ = |A|e^iϕ,

(29)

ко рис. 9б демонстрирует, что экстремумы Re F (ω)

g(ω - iα) = g₁(ω) + ig₂(ω).

⁷⁾ Такая экстраполяция осложняется тем, что существуют

Если ω₁ и ω₂ — положения экстремумов ReF (ω) и

факторы, сдвигающие начало отсчета L (см. разд. 5 в [8]).

ImF (ω), то справедливы соотношения

⁸⁾ Эффективна линейность экстраполяции связана с тем,

что главный вклад в F (ω) происходит от середины экспери-

A^′g′1(ω₁) - A^′′g′2(ω₁) = 0,

ментального интервала полей (см. разд. 5), где связь L и B

(30)

практически линейна.

A^′g′2(ω₂) + A^′′g′1(ω₂) = 0,

920

ЖЭТФ, том 158, вып. 5 (11), 2020

Спектральный анализ универсальных флуктуаций кондактанса

Таблица. Оценки фаз, полученные согласно разд. 7

и фаза ϕ коэффициента A определяется условием

(ϕs) и по формуле (36) (ϕs)

g′1(ω₁)

g′2(ω₂)

tg ϕ =

(31)

g′2(ω₁)

g′1(ω₂)

ϕ_s

Если экспериментальные значения ω₁ и ω₂ извест-

170^◦

161^◦

37^◦

ны, то алгоритм определения ϕ и α состоит в сле-

-88^◦

-84^◦

155^◦

145^◦

дующем. Согласно (29), g₁(ω) и g₂(ω) зависят от α,

125^◦

120^◦

-15^◦

-20^◦

причем g₂(ω) → 0 при α → 0; поэтому при малых

-172^◦

-162^◦

111^◦

121^◦

α первая дробь в (31) велика, а вторая мала по аб-

солютной величине. Увеличивая α, можно добиться

-78^◦

-67^◦

-96^◦

-106^◦

равенства (31), что определяет значения tg ϕ и α.

47^◦

40^◦

-81^◦

-72^◦

Поскольку по известной величине тангенса можно

144^◦

153^◦

87^◦

84^◦

определить ϕ с точностью до аддитивных вкладов,

59^◦

49^◦

-144^◦

-140^◦

кратных π, то выбор правильного квадранта для ϕ

-124^◦

-153^◦

осуществляется с помощью соотношений

A^′g₁(ω₁) - A^′′g₂(ω₁) = F₁,

(32)

квадрант для фазы ϕ, считая, что она находится в

A^′g₂(ω₂) + A^′′g₁(ω₂) = F₂,

интервале (-π, π):

где F₁ и F₂ — значения Re F (ω) и Im F (ω) в точках

α=

√-ω₁ω₂ sign(ω₂F₁F₂),

экстремума.

Если функция g(ω) в (11) нормирована на еди-

ницу при ω = 0, то полагая

ϕ = -arctg(ω₁/α) + π signF₂(1 - signF₁)/2.

(36)

z = πTω, γ = πTα,

(33)

Заметим, что |tgϕ| определяется лишь значениями

ω₁ и ω₂, а F₁ и F₂ требуются лишь для выбора пра-

имеем

вильного квадранта. Эта оценка ϕ принципиально

отличается от использованной в предыдущем раз-

cosγzshz + γ sinγ chz

g₁(ω) =

деле и совпадает с ней лишь в случае, если сдвиги

sh² z + sin² γ

экстремумов Re F (ω) и Im F (ω) действительно явля-

sinγzchz - γ cosγ shz

ются проявлениями экспоненциального роста.

g₂(ω) =

(34)

sh² z + sin² γ

Сравнение двух оценок ϕ (см. таблицу) показы-

z²

+γ

вает их приближенное совпадение для всех гармо-

|g(ω + iα)|² =

sh² z + sin² γ

ник и подтверждает правильность выявления меха-

низма сдвига экстремумов. Небольшие различия мо-

Нетрудно видеть, что экстремумы g₁(ω) и |g(ω+iα)|

гут быть связаны как с приближенностью оценки по

имеют место при ω = 0, т. е. конечность α не влия-

формуле (36), так и с наличием осложняющих фак-

ет на их положение; соответственно частоты ω₁ и ω₂

торов: взаимного влияния гармоник, наличия непре-

естественно отсчитывать от нуля. Функция g₂(ω) яв-

рывного спектра, экспериментальных погрешностей

ляется нечетной, и ее малая добавка к g₁(ω) сдвигает

и пр.

экстремум в ту или другую сторону в зависимости

от знака добавки. Для функций Re F(ω) и ImF(ω)

добавки к g₁(ω), пропорциональные g₂(ω), имеют

9. РАСПРЕДЕЛЕНИЕ ПОКАЗАТЕЛЕЙ И

РАЗНОСТЕЙ ЧАСТОТ

противоположные знаки, что обеспечивает разные

знаки для ω₁ и ω₂. При малых α можно ограничить-

Приведем сводку теоретических результатов для

ся в (34) первым порядком по γ и с учетом малости

эволюции моментов. Принимая для 〈ρⁿ〉 экспонен-

ω₁ и ω₂ получить

циальную зависимость от L, получим для показате-

ω₁

ля экспоненциального роста x алгебраическое урав-

tg ϕ = -

α² = -ω₁ω₂.

(35)

ω₂

нение (2n + 1)-го порядка. Для n = 1 и n = 2 такие

уравнения выписываются в явном виде [8]:

При этом из (32) следует A^′ ≈ F₁, A^′′ ≈ F₂, что

(

)

позволяет установить знак α и выбрать правильный

x² + 4E

= 2W²,

921

И. М. Суслов

ЖЭТФ, том 158, вып. 5 (11), 2020

(

)(

)

x² + 4E

x² + 16E

= 42W²x² + 96W²E,

(37)

где E — энергия, отсчитанная от нижнего края зоны,

W — амплитуда случайного потенциала.

Структура уравнений для произвольного n-го

момента может быть установлена на основе аргу-

ментации разд. 4 работы [8]. В глубине разрешенной

и запрещенной зон можно ограничиться диагональ-

ными элементами в матрицах (42), (47) этой работы

и их аналогами для высших моментов; это приводит

к уравнению

∏[

]

x - 2(n-k)δ - B^knϵ²

= O(ϵ⁴δ2n-1),

(38)

k=0

где ϵ² = W²/4δ², δ² = -E, B^kn = n(2n-1)+3k(k-2n).

Аналогичное уравнение вблизи края зоны,

Рис. 11. Распределение разностей соседних частот Δs =

= ωs+1 -ωs; значение s указано у соответствующих линий.

∑

Разности Δs разбиваются на две группы I и II, локализо-

x2n+1 =

C_kW2kx2n+1-3k,

ванные вблизи

Δ и2Δ

k=0

(39)

^[2n + 1^]

k_max =

точного квантования не должно вызывать беспокой-

ства, так как последнее реализуется лишь в предель-

следует из того, что при x ∼ δ ∼ ϵ² все члены урав-

но металлическом режиме. В реальности металличе-

нения имеют один порядок величины и допустимы

ский режим не является экстремальным, и к нему

лишь комбинации δ2nϵ2m с n ≥ m, из которых ко-

возникают поправки, указанные в (40).

нечными при δ → 0 остаются лишь δ2nϵ2n ∼ W2n.

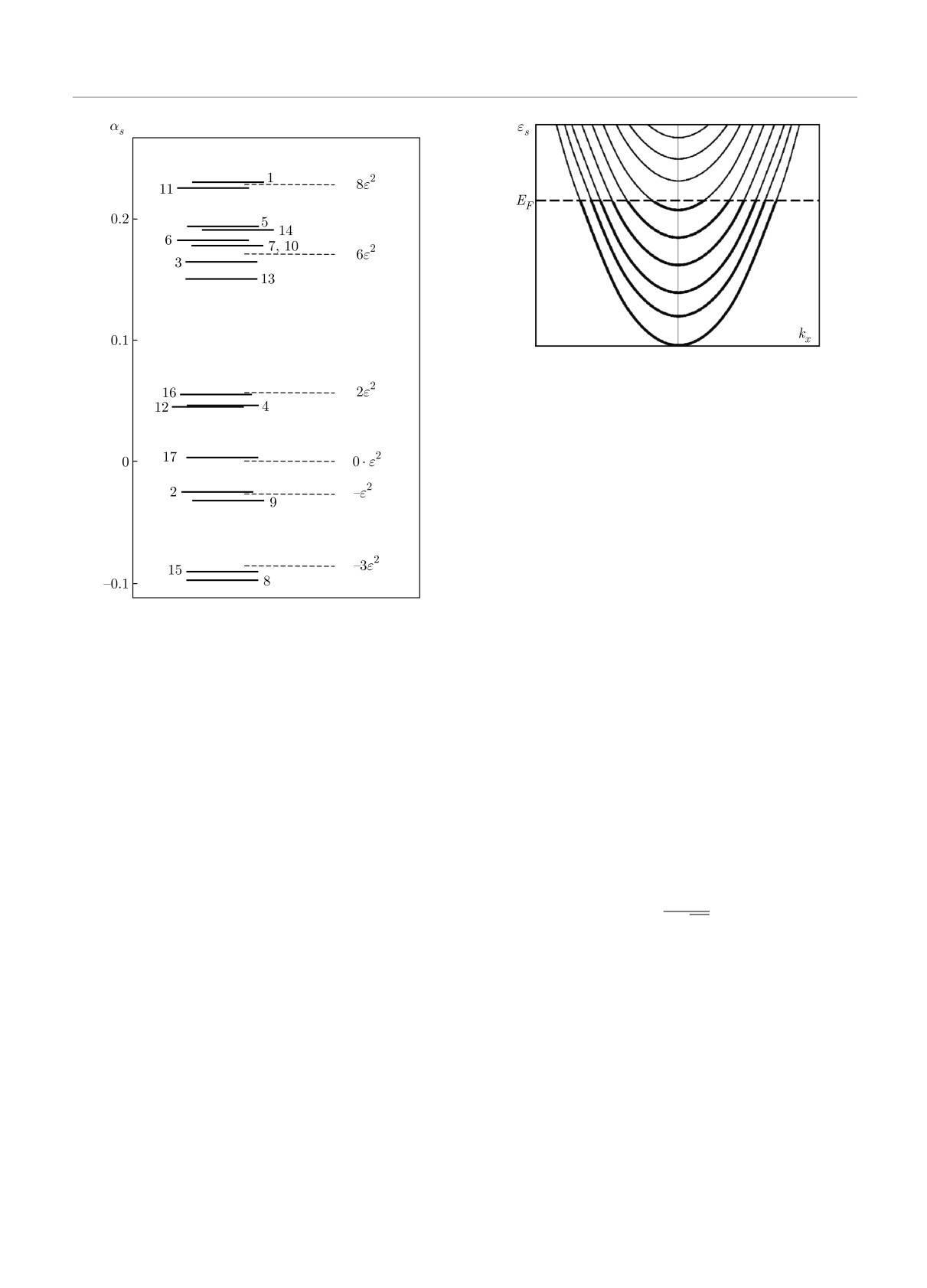
Показатели экспоненциального роста α_s опреде-

Нетривиальные корни уравнения (39) имеют поря-

ляются действительной частью выражения (40) и

док W2/3 и приводят к несоизмеримым частотам в

являются целыми кратными величины ϵ². Переби-

осцилляциях (2).

рая всевозможные значения n и k, получим бес-

В глубине разрешенной зоны параметры δ и ϵ

конечную последовательность показателей, отрезок

комплексные и для перехода к действительным ве-

который вблизи начала координат имеет вид

личинам нужно сделать замену δ → iδ, ϵ → -iϵ. То-

гда уравнение (38) дает полный набор показателей

..., -3ϵ2, -ϵ2, 0, 2ϵ2, 3ϵ2, 6ϵ2, 8ϵ2, . . .

(41)

для предельно металлического режима (ϵ² ≪ δ)

Показатели, полученные в результате обработки

x^kn = 2i(n - k)δ - B^knϵ² + O(ϵ⁴/δ),

экспериментальных данных по формуле (36), пред-

(40)

k = 0,1,...,2n.

ставлены на рис. 12 с противоположным знаком⁹⁾ и

хорошо воспроизводят эту последовательность при

Нетрудно видеть, что все частоты осцилляций в (2)

подходящем выборе ϵ². Единственным исключением

являются целыми кратными величины

Δ= 2δ, т.е.

является отсутствие значения 3ϵ², что, по-видимому,

их несоизмеримость исчезает. В идеальном случае

связано с низкой интенсивностью соответствующих

все разности соседних частот Δ_s = ωs+1 - ω_s долж-

линий. Тот факт, что проявляются только показа-

ны быть равными

Δ, однако, некоторые гармоники

тели в окрестности начала координат, естественно

практически не проявляются из-за слабой интенсив-

объясняется тем, что гармоники с большими (по мо-

ности, так что разности Δ_s «квантуются», т. е. могут

дулю) показателями локализуются вблизи краев ра-

быть равными

Δ, 2Δ, 3Δ и т. д.

Распределение разностей Δ_s для 17 гармоник,

⁹⁾ Показатели αs меняют знак при переходе от магнитного

очевидных из рис.

3, представлено на рис.

11.

поля B к эффективной длине системы L (меняются местами

правое и левое направления). При переходе от кондактанса к

Нетрудно видеть, что они распадаются на две груп-

сопротивлению изменения знаков αs не происходит, так как

пы I и II, локализованные вблизи значений

Δ и

малые флуктуации двух величин пропорциональны друг дру-

2Δ, где

Δ выбрано из лучшего согласия. Отсутствие

гу.

922

ЖЭТФ, том 158, вып. 5 (11), 2020

Спектральный анализ универсальных флуктуаций кондактанса

Рис. 13. Для тонкой проволочки поперечное движение за-

квантовано, что приводит к возникновению N0 дискретных

уровней, которые при учете продольного движения превра-

щаются в одномерные подзоны. Главный вклад в осцилля-

ции кондактанса дает верхняя заполненная подзона

чем для разностей частот Δ_s (рис. 11). Этот факт

имеет простое объяснение.

Тонкая проволочка является квазиодномерной

системой, в которой поперечное движение закванто-

вано, что приводит к возникновению N₀ дискретных

уровней ϵ0s, с учетом продольного движения вдоль

Рис. 12. Распределение показателей экспоненциального

оси x они превращаются в одномерные подзоны со

роста αs и их сопоставление с последовательностью (41)

спектрами

при надлежащем выборе ϵ². Значение s указано у соответ-

ствующих линий

ϵ_s(k_x) = ϵ0s + k2x/2m,

(45)

состояния которых заполнены ниже уровня Ферми

бочего интервала магнитных полей и не видны в его

E_F (рис. 13). Магнитное поле B наиболее сильно

середине.

влияет на верхнюю заполненную подзону с мини-

Заметим, что максимальный показатель для мо-

мальной энергией Ферми ϵ_F , ограничивая движение

мента 〈ρⁿ〉 в запрещенной зоне реализуется при k =

в ней на длине L, определяемой условием

= 2n,

mω2BL² ∼ ϵ_F ∼ E₀/N₀,

(46)

x^maxn = 2nδ + n(2n - 1)ϵ²,

(42)

а в разрешенной зоне — при k = n,

так что

xmaxn = n(n + 1)ϵ².

(43)

B₀

L∼a

√

(47)

N₀

Эти результаты согласуются с функциональной

формой для логнормального режима

где E0 = ℏ2/ma2 и B0 = φ0/a2 — атомные еди-

xmaxn = an + bn²/2

(44)

ницы энергии и магнитного поля (φ₀ = πℏc/e —

квант потока). Кондактанс системы определяется

с параметрами a и b, полученными в [8]: a = 2δ - ϵ²,

суммой кондактансов одномерных подзон, осцилля-

b = 4ϵ² в запрещенной зоне и a = ϵ², b = 2ϵ² в раз-

ции которых экспоненциально затухают при увели-

решенной зоне.

чении L (см. ниже). Поэтому главный вклад в ос-

цилляции дает верхняя подзона, для которой дли-

на L минимальна; однако, и соседние подзоны ока-

10. МИКРОСКОПИЧЕСКАЯ КАРТИНА

зывают некоторое влияние. Для разностей частот

Нетрудно видеть, что для показателей роста α_s

Δ_s это влияние существенно уширяет распределение

(рис. 12) квантование оказывается более четким,

(рис. 11), так как частота осцилляций определяется

923

И. М. Суслов

ЖЭТФ, том 158, вып. 5 (11), 2020

фермиевским импульсом k_F , значение которого раз-

Как ясно из (23), (25), выражение для 〈ρ〉 содер-

лично в разных подзонах. Для показателей роста α_s

жит растущую экспоненту e2ϵ2l и осциллирующие

(рис. 12) ситуация совершенно другая. Фермиевские

члены, убывающие как e-ϵ2l. Аналогичная картина

импульсы для верхних подзон малы, и для рассея-

справедлива для высших моментов: максимальный

ния на примесях справедливо приближение медлен-

показатель (43) в металлическом режиме является

ных частиц¹⁰⁾, так что амплитуда рассеяния не зави-

действительным и не приводит к осцилляциям, то-

сит от импульса. Показатели роста прямо связаны с

гда как осциллирующие члены растут более медлен-

амплитудой рассеяния и не зависят от фермиевских

но и относительно малы даже при положительных

импульсов одномерных подзон. Поэтому влияние со-

α_s. Поэтому для типичного значения ρ ситуация та-

седних подзон не нарушает точного квантования, и

кая же, как для моментов, и при переходе к без-

рис. 12 фактически соответствует строго одномер-

размерному кондактансу g = 1/ρ осцилляции ока-

ной системе. Отклонения от точного квантования

зываются затухающими. При типичных значениях

связаны лишь с неэкстремальностью металлическо-

Δ₁ ∼ Δ₂ ∼ 1 для чужеродных контактов осцилля-

го режима и экспериментальными погрешностями.

ции g в области ϵ²l ≲ 1 оказываются порядка еди-

Минимальная дискретная гармоника на рис. 3

ницы, что дает флуктуации порядка e²/h для раз-

соответствует приблизительно четырем периодам

мерного кондактанса (рис. 1). Согласно этой кар-

осцилляций в интервале полей 1-10 Тл. Ее часто-

тине, универсальным является лишь порядок вели-

та определяется де-бройлевской длиной волны λ ∼

чины флуктуаций, тогда как на их амплитуду мож-

∼a√N0 в верхней подзоне, и число осцилляций при

но существенно влиять, изменяя уровень Ферми или

изменении поля от B_min до 10B_min в силу (47) да-

свойства идеальных контактов.

ется оценкой

N_osc ∼ B₀/N₀B_min,

(48)

11. ЗАКЛЮЧЕНИЕ

что для B₀ ∼ 10⁴ Тл, B_min = 1 Тл, N_osc = 4 дает

N₀ ∼ 2.5 · 10³.

(49)

В работе представлен аккуратный фурье-анализ

апериодических осцилляций кондактанса (рис. 1),

Это примерно в два раза меньше, чем число ато-

обнаруженных в классических экспериментах Веб-

мов в поперечном сечении проволочки диаметром

ба и Вашбурна [5]. Полученные результаты фак-

25 нм [5] и соответствует наполовину заполненной

тически примиряют два альтернативных сценария,

трехмерной зоне. При этом λ ∼ 50a и актуальный

указанных в начале работы. С одной стороны,

диапазон длин

фурье-спектр практически дискретный, подтверж-

L = 20-200a

(50)

дая концепцию работы [8], согласно которой апе-

риодические осцилляции кондактанса определяются

оказывается в пределах длины проволочки

суперпозицией несоизмеримых гармоник. С другой

310 нм [5].

стороны, форма спектра напоминает дискретный бе-

Выше мы предполагали условие ℏω_B ≪ ϵ_F , ко-

лый шум, свойства которого близки к непрерывно-

торое фактически нарушается в середине экспери-

му. Более подробный анализ обнаруживает наличие

ментального интервала полей. При больших полях

непрерывной компоненты, малость которой объяс-

более адекватна оценка L ∼ a(B₀/B)1/2, следующая

няется в разд. 5.

из (46) после замены ϵ_F на ℏω_B. В результате ниж-

В работе приведено множество качественных мо-

няя граница в (50) сдвигается с 20a до 30a, что несу-

ментов, подтверждающих правильность представ-

щественно для приведенных оценок.

ленной интерпретации. Частоты дискретных линий

¹⁰⁾ Здесь существенно отличие реальной системы от моде-

слабо зависят от способа обработки, что доказыва-

ли Андерсона, рассматриваемой в [8]. В модели Андерсона

ет их объективное происхождение. «Естественное»

металлический режим соответствует большой концентрации

начало отсчета f(x), обнаруженное при исключении

слабых примесей, которые можно рассматривать по теории

сдвиговых осцилляций, подтверждает правильность

возмущений. В реальной системе слабый беспорядок созда-

ется малой концентрацией сильных примесей, для которых

аналогии с одномерными системами. О том же сви-

справедливо приближение медленных частиц. Это различие

детельствуют проявления экспоненциального роста

не влияет на результаты для показателей, так как на мас-

амплитуды гармоник. Распределение фаз коэффи-

штабе длины волны конфигурацию случайного потенциала

можно изменять в широких пределах, не влияя на крупно-

циентов A_s согласуется с их предполагаемой слу-

масштабные свойства волновых функций.

чайностью. Распределение показателей роста и раз-

924

ЖЭТФ, том 158, вып. 5 (11), 2020

Спектральный анализ универсальных флуктуаций кондактанса

(

)1/2

{

}

ностей частот согласуются с теоретическими резуль-

(ρ - ρ₀)²

P (ρ, t) =

exp

(A.5)

татами для металлического режима. Микроскопиче-

4πρ₀t

4ρ₀t

ские оценки подтверждают представленную карти-

Близость распределения (A.4) к гауссовскому позво-

ну.

ляет характеризовать его двумя первыми момента-

Универсальные флуктуации кондактанса обсуж-

ми. Умножая (19) на ρⁿ и интегрируя по ρ, получим

даются во многих работах (см., например, [20-40]

уравнения эволюции моментов распределения P (ρ);

и ссылки там), и было бы интересно обработать

их решение для начального условия (22) имеет вид

результаты других экспериментов в духе настоящей

работы.

1 + 2ρ₀

〈ρ〉 = -

e2t,

(A.6)

Благодарности.

Автор

признателен

[

]

1 + 2ρ₀

В. В. Бражкину, по инициативе которого вы-

ρ²

e2t + ρ²⁰ +

e6t.

полнена работа [11].

При малых ρ выражения упрощаются,

〈ρ〉 = ρ₀ + t,

ПРИЛОЖЕНИЕ A

ρ²

= ρ²⁰ + 4ρ₀t + 2t²,

(A.7)

Решение уравнения (19)

σ² = 2ρ₀t + t²,

Ограничимся анализом металлической области,

и соответствуют распределению (A.4). Эти резуль-

когда типичные значения ρ малы. Рассматривая за-

таты справедливы при L > L₀. Описание эволюции

дачу на собственные значения для оператора в пра-

в интервале 0 < L < L₀ затрудняется необходимос-

вой части уравнения (19) и ограничиваясь низшим

тью удовлетворить двум условиям (20) и (22), что

порядком по ρ, имеем уравнение

возможно лишь при наложении ограничений на ре-

ализацию случайного потенциала. Эти ограничения

-λP = P^′ρ + ρP^′′ρρ.

(A.1)

накладываются на интервал (0, L₀) в целом и не су-

Считая, что ρ меняется в интервале от нуля до R,

щественны при малых L и L, близких к L₀. В первом

наложим условие конечности при ρ = 0 и нулевое

случае имеем 〈ρ〉 = σ в соответствии с распределе-

граничное условие при ρ = R. Тогда собственные

нием (21). Во втором случае ситуация определяется

значения и собственные функции имеют вид

тем, что уширение распределения происходит сим-

(

)

метрично¹¹⁾ при отклонении L вправо или влево от

√

λs = μ^s/4R, es(ρ) = J0 μs

ρ/R

(A.2)

L₀. Для величины 〈ρ〉 условия (20) и (22) выполня-

ются автоматически, если ρ₀ выбрано равным сред-

где μ_s — корни функции Бесселя J₀(x). Решая урав-

нему значению для распределения (21) при L = L₀.

нение (19) с начальным условием (22) путем разло-

В результате сказанного приходим к картине, пред-

жения P (ρ) по собственным функциям (A.2), имеем

ставленной на рис. 8.

∫∞

P (ρ, t) =

2μdμ e-μ2tJ₀(2μ√ρ₀)J₀(2μ√ρ ), (A.3)

ПРИЛОЖЕНИЕ B

Эволюция 〈ρ〉 для начального условия (22)

где t = α(L - L₀) и учтено, что при больших R

Вычисление 〈ρ〉 технически сводится к иссле-

спектр собственных значений μ_s становится квази-

дованию эволюции вторых моментов для тран-

непрерывным и суммирование по s можно заме-

сфер-матрицы с комплексными элементами T_ij [8]:

нить интегрированием по μ, используя асимптотику

(



)

;

μ_s = πs + const при больших s. Вычисляя интеграл



z(l)1 =

T⁽



z(l)2 = T(l)11T(l)∗

в (A.3), получим

(



)

(B.1)

{

}

;



ρ+ρ₀

⁽2√ρρ₀ )

z(l)3 = T(l)∗11T(l)

z(l)4 =

T⁽



P (ρ, t) =

exp

I₀

(A.4)

¹¹⁾ Уравнение (19) имеет одинаковый вид, если положить

где I₀(x) = J₀(ix). При ρ ≲ t и t ≫ ρ₀ распределе-

L = L₀ + l или L = L₀ - l и рассматривать эволюцию по l.

ние (A.4) переходит в (21), а при ρ ≈ ρ₀ и t ≪ ρ₀

Это ясно из схемы вывода подобных уравнений (см. Прило-

становится гауссовским

жение A в [41]).

925

И. М. Суслов

ЖЭТФ, том 158, вып. 5 (11), 2020

Они удовлетворяют системе разностных уравнений,

Q₃ = (x₁-x₂)p(x₃),

общее решение которой имеет вид [8]

Q = Q₁-Q₂+Q₃ = x21 (x₂-x₃)-x22 (x₁-x₃)+x23 (x₁-x₂).

⎛

⎞

⎛

⎞

(l)

R₁ = [x₂p(x₃)-x₃p(x₂)] p(x₁),

z₁

-1

⎜

⎟

⎜

⎟

⎜

z(l)2

⎟

⎜

⎟

R₂ = [x₁p(x₃)-x₃p(x₁)] p(x₂),

⎜

⎟

=C₀

⎜

^⎟+

⎜

⎟

⎜

⎟

⎝ z³

⎠

⎝ 0

⎠

R₃ = [x₁p(x₂)-x₂p(x₁)] p(x₃),

z(l)

S₁ = [p(x₃)-p(x₂)] p(x₁), S₂ = [p(x₃)-p(x₁)] p(x₂),

⎛

⎞

S₃ = [p(x₂)-p(x₁)] p(x₃),

⎜

⎟

∑

⎜

⎟

2(xi)

√

C_i

⎜ e

^⎟ exp(x_il), (B.2)

ϵ² sinψ - Δcosψ

⎜

⎟

K₁ =

ρ₀(1 + ρ₀),

i=1

⎝ e3(xi)

⎠

4 [αΔ² + ϵ⁴(α - Δ)]

(B.8)

√

ϵ²(α - Δ)cosψ + αΔsinψ

K₂ =

ρ₀(1 + ρ₀).

2 [αΔ² + ϵ⁴(α - Δ)]

где x₁, x₂, x₃ — корни первого уравнения (37) и

Используя асимптотики для корней x₁, x₂, x₃ в ме-

∗

Ax + B

A^∗x + B

таллической режиме [8], придем к результатам (23)

e₂(x) =

e₃(x) =

p(x)

и (25). Первый из них справедлив для «естествен-

ных» идеальных контактов¹²⁾, которые отличаются

от изучаемой системы лишь отсутствием в них слу-

A = 2ϵ² - 2iΔ, B = 4αΔ + 4iϵ²(α - Δ), (B.3)

чайного потенциала; при этом k =

^k, Δ₁ = 0 и осцил-

ляции возникают в первом порядке по малому пара-

p(x) = x² + 2ϵ²x + 4α².

метру ϵ²/δ. Результат (25) справедлив для чужерод-

Здесь α = -Δ₂δ, Δ = Δ₁δ, δ и ϵ² определены пос-

ных контактов, когда Δ₁ = 0 и осцилляции имеют

ле (23),

место уже в нулевом порядке по ϵ²/δ. Использова-

)

ние асимптотики x₁, x₂, x₃ в «критической» области

k⁾

⁽k

Δ₁ =

Δ₂ =

(B.4)

[8] приводит к результату (24), справедливому вбли-

k⁺

зи края исходной зоны; он приведен для «естествен-

ных» контактов, так как ситуация для чужеродных

где

k и k — фермиевские импульсы в изучаемой сис-

контактов в достаточной мере характеризуется фор-

теме и присоединенных к ней идеальных контактах.

мулами работы [8].

В отличие от [8], в качестве начального условия при-

нимается не единичная матрица, а трансфер-матри-

ца общего вида

ПРИЛОЖЕНИЕ C

)

( √

ρ+1e^iϕ

√ρ e^iθ

О выборе естественного начала отсчета

T =

(B.5)

√ρ e^-iθ

√ρ + 1 e^-iϕ

Согласно соотношениям Онсагера, кондактанс

является четной функцией магнитного поля B и

с ρ = ρ₀ и ψ = θ - ϕ. Величина z(n)4 непосредствен-

при выборе x = B функция f(x) в (3) является

но определяет 〈ρ〉, что дает общее выражение для

четной. Выберем сглаживающую функцию в виде

последней:

G(x- a)+ G(x+ a) с четной G(x), т. е. в симметризо-

ванной по x форме. Тогда фурье-образ является дей-

〈ρ〉 = C₀ + C₁ ex1l + C₂ ex2l + C₃ ex3l,

(B.6)

ствительным и с точностью до знака совпадает со

своим модулем, а потому не содержит сдвиговых ос-

где

цилляций. Теперь устраним функцию G(x + a). Воз-

[

никающий фурье-образ F (ω) функции f(x)G(x - a)

Q_i

C₀ = -

C_i = (-1)i+1 (1 + 2ρ0)

будет комплексным; его действительна часть умень-

]

шается в два раза по сравнению с предыдущим¹³⁾ и

R_i

S_i

+ K₁

+K₂

i = 1,2,3

(B.7)

¹²⁾ В этом случае для x₁, x₂, x₃ требуются разложения по

ϵ2/δ более высокого порядка, чем приведены в [8].

¹³⁾ Легко проверить, что фурье-образы функций

f (x)G(x + a) и f(x)G(x - a) имеют одинаковые дейст-

Q₁ = (x₂ -x₃)p(x₁), Q₂ = (x₁ -x₃)p(x₂),

вительные и противоположные мнимые части.

926

ЖЭТФ, том 158, вып. 5 (11), 2020

Спектральный анализ универсальных флуктуаций кондактанса

не содержит сдвиговых осцилляций. Последние от-

13.

А. Б. Мигдал, Качественные методы в квантовой

сутствуют и в ImF(ω), так как они в равной мере

теории, Наука, Москва (1975).

влияют на действительную и мнимую части. После

14.

В. И. Мельников, ФТТ 23, 782 (1981).

сдвига x → x + a фурье-образ принимает вид

∫

15.

A. A. Abrikosov, Sol. St. Comm. 37, 997 (1981).

F (ω) = e^iωa f(x + a)G(x)e^iωxdx

16.

N. Kumar, Phys. Rev. B 31, 5513 (1985).

и возникающий интеграл при a = μ₀ соответствует

17.

B. Shapiro, Phys. Rev. B 34, 4394 (1986).

тому, который рассматривался в разд. 2, тогда как

18.

P. Mello, Phys. Rev. B 35, 1082 (1987).

множитель e^iωa отвечает за сдвиговые осцилляции.

Однако получаемый при этом знак a не соответству-

19.

B. Shapiro, Phil. Mag. 56, 1031 (1987).

ет найденному эмпирически.

Причина противоречия состоит в том, что сим-

20.

K. M. D. Hals, A. K. Nguyen, X. Waintal, and A. Bra-

метрия Онсагера выделяет не только значение B =

taas, Phys. Rev. Lett. 105, 207204 (2010).

= 0, но и B = ∞; именно последнее соответствует

21.

A. S. Lien, L. Y. Wang, C. S. Chu, and J. J. Lin,

эмпирической ситуации. При выборе x = 1/B мож-

Phys. Rev. B 84, 155432 (2011).

но повторить все предыдущие рассуждения, однако,

приращения B и x имеют противоположные знаки

22.

J. G. G. S. Ramos, D. Bazeia, M. S. Hussein, and

и для качественного соответствия с разд. 2 нужно

C. H. Lewenkopf, Phys. Rev. Lett. 107,

176807

изменить знак ω. Это и приведет к появлению мно-

(2011).

жителя e^iωa с правильным знаком a.

23.

Z. Li, T. Chen, H. Pan et al., Sci. Rep. 2, 595 (2012).

24.

E. Rossi, J. H. Bardarson, M. S. Fuhrer, and

ЛИТЕРАТУРА

S. D. Sarma, Phys. Rev. Lett. 109, 096801 (2012).

Б. Л. Альтшулер, Письма в ЖЭТФ 41, 530 (1985).

25.

P. Y. Yang, L. Y. Wang, Y. W. Hsu, and J. J. Lin,

Phys. Rev. B 85, 085423 (2012).

Б. Л. Альтшулер, Д. Е. Хмельницкий, Письма в

ЖЭТФ 42, 291 (1985).

26.

S. Minke, J. Bundesmann, D. Weiss, and J. Eroms,

Phys. Rev. B 86, 155403 (2012).

P. A. Lee and A. D. Stone, Phys. Rev. Lett. 55, 1622

(1985).

27.

S. Gustavsson, J. Bylander, and W. D. Oliver, Phys.

Rev. Lett. 110, 016603 (2013).

P. A. Lee, A. D. Stone, and Y. Fukuyama, Phys. Rev.

B 35, 1039 (1987).

28.

A. L. R. Barbosa, M. S. Hussein, and J. G. G. S. Ra-

mos, Phys. Rev. E 88, 010901(R) (2013).

S. Washburn and R. A. Webb, Adv. Phys. 35, 375

(1986).

29.

Ph. Jacquod and I. Adagideli, Phys. Rev. B 88,

041305(R) (2013).

Mesoscopic Phenomena in Solids, ed. by B. L. Alt-

shuler, P. A. Lee, and R. A. Webb, North-Holland,

30.

J. Bundesmann, M. H. Liu, I. Adagideli, and K. Rich-

Amsterdam (1991).

ter, Phys. Rev. B 88, 195406 (2013).

C. W. J. Beenakker, Rev. Mod. Phys. 69, 731 (1997).

31.

C. L. Richardson, S. D. Edkins, G. R. Berdiyorov et

al., Phys. Rev. B 91, 245418 (2015).

И. М. Суслов, ЖЭТФ 156, 950 (2019).

32.

T. C. Vasconcelos, J. G. G. S. Ramos, and

Л. Д. Ландау, Е. М. Лифшиц, Квантовая механи-

ка, Наука, Москва (1974).

A. L. R. Barbosa, Phys. Rev. B 93, 115120 (2016).

10.

D. Mailly and M. Sanquer, J. de Phys. I 2, 357 (1992).

33.

C. C. Kalmbach, F. J. Ahlers, J. Schurr et al., Phys.

Rev. B 94, 205430 (2016).

11.

V. V. Brazhkin and I. M. Suslov, accepted to J. Phys.:

Condensed Matter; arXiv:1911.10441.

34.

J. G. G. S. Ramos, A. L. R. Barbosa, B. V. Carlson

et al., Phys. Rev. E 93, 012210 (2016).

12.

W. H. Press, B. P. Flannery, S. A. Teukolsky, and

W. T. Wetterling, Numerical Recipes in Fortran,

35.

Y. Hu, H. Liu, H. Jiang, and X. C. Xie, Phys. Rev.

Cambridge University Press (1992).

B 96, 134201 (2017).

927