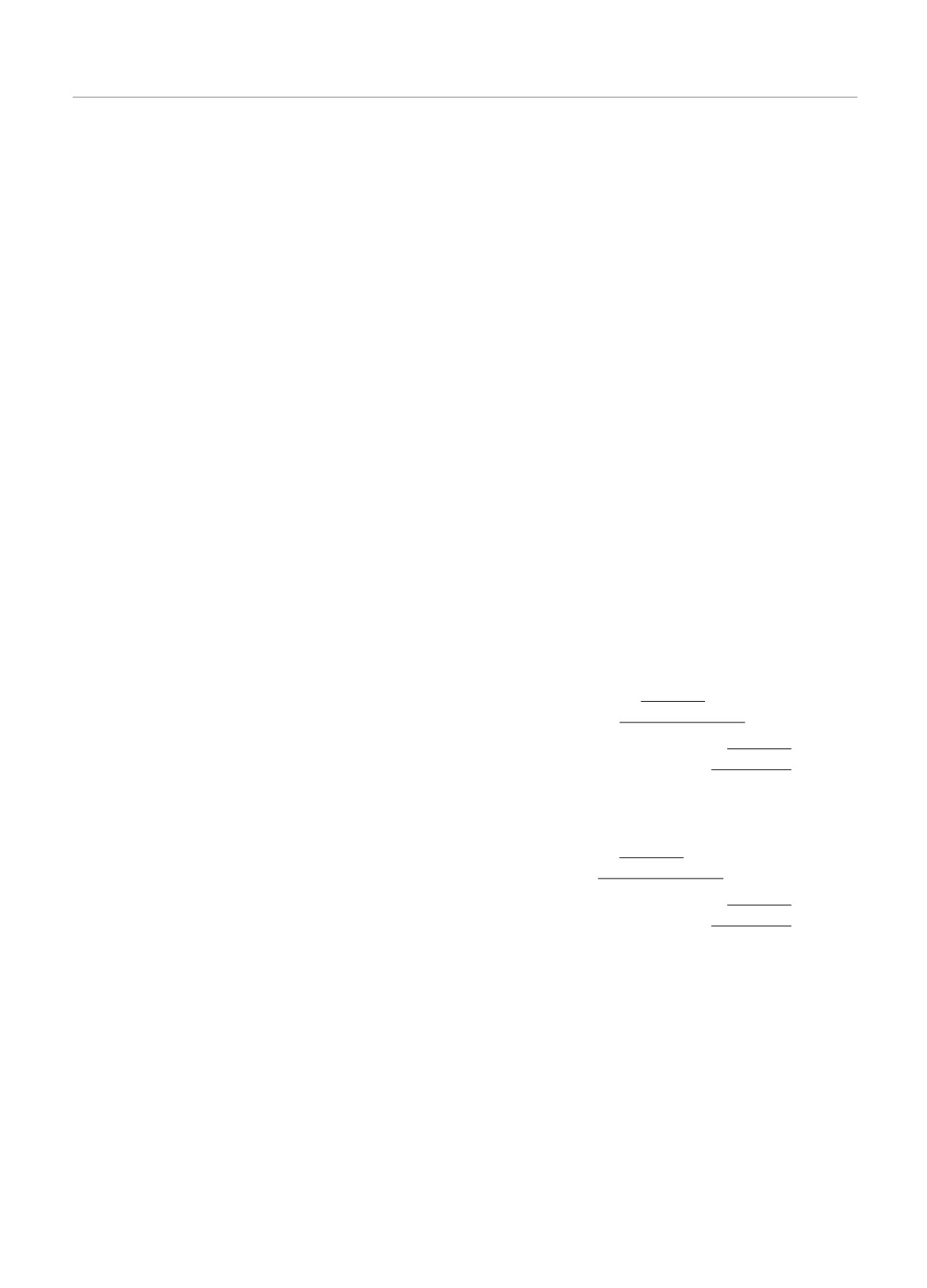ЖЭТФ, 2020, том 158, вып. 5 (11), стр. 929-945

СПИНОВЫЙ РЕЗОНАНС В КВАНТОВОЙ ТОЧКЕ

НА КРАЮ ТОПОЛОГИЧЕСКОГО ИЗОЛЯТОРА

ПРИ УЧЕТЕ СОСТОЯНИЙ КОНТИНУУМА

Д. В. Хомицкий^*, К. С. Кабаев, Е. А. Лаврухина

Национальный исследовательский Нижегородский государственный университет им. Н. И. Лобачевского,

физический факультет

603950, Нижний Новгород, Россия

Поступила в редакцию 6 мая 2020 г.,

после переработки 5 июня 2020 г.

Принята к публикации 5 июня 2020 г.

Исследуется динамика электронных состояний под действием периодического электрического поля, при-

ложенного к квантовой точке, созданной магнитными барьерами на одномерном краю двумерного то-

пологического изолятора на базе квантовой ямы HgTe/CdTe. Рассматривается конфигурация с дву-

мя дискретными уровнями и учитываются переходы в состояния непрерывного спектра над барьерами.

Рассчитывается частота осцилляций заселенностей дискретных уровней для различных амплитуд поля.

Численно и аналитически показано, что учет непрерывного спектра приводит к затуханию суммарной

заселенности дискретных уровней со временем. Определяются характерные времена этого затухания, от-

вечающего переходам в континуум. Рассчитывается динамика средних значений энергии, проекций спина

и координат, а также локальных плотностей вероятности и спиновой плотности. Вычисляется усреднен-

ная во времени локальная плотность тока вероятности, описывающая покидание квантовой точки при

переходах в непрерывный спектр. Результаты работы могут быть полезны при создании новых поколений

устройств наноэлектроники и спинтроники на основе топологических изоляторов.

DOI: 10.31857/S0044451020110152

сти привлекают исследователей как с точки зрения

фундаментальных свойств, так и с позиций перспек-

тивных приложений для создания новых поколе-

1. ВВЕДЕНИЕ

ний устройств для наноэлектроники и спинтроники.

При этом, однако, возникают трудности, связанные

Топологические изоляторы (ТИ) и структуры на

с существенно делокализованным характером про-

их базе привлекают большое внимание в последние

являемых топологических свойств, таких как нечув-

15 лет [1-4]. Основное свойство ТИ — наличие хоро-

ствительность к рассеиванию, и реализуемых преж-

шо проводящих состояний на краю образца, т. е. на

де всего для распространяющихся вдоль края (или

поверхности для трехмерных ТИ и на одномерном

поверхности) состояний вида плоских волн или их

крае для двумерных ТИ. Энергия краевых состоя-

комбинаций. Между тем для практического внед-

ний в основном находится в запрещенной зоне спект-

рения данных структур в экспериментальную или

ра состояний в объемном образце. Такие краевые

приборную базу, в том числе для создания с их по-

состояния устойчивы к рассеиванию на немагнит-

мощью элементарных ячеек для квантовых вычис-

ных примесях в силу требований симметрии по об-

лений (кубитов), желательно создавать на их основе

ращению времени и в ряде моделей характеризуют-

компактные объекты, такие как квантовые точки.

ся линейным, т. е. безмассовым законом дисперсии,

причем проекция спина для каждой ветви диспер-

Известно, однако, что осуществить конфайнмент

сии жестко связана с направлением групповой ско-

электронных состояний в системе с линейным (без-

рости. Такие системы называют фермионами Ди-

массовым) спектром с помощью одних электроста-

рака или фермионами Вейля. Подобные особенно-

тических потенциалов невозможно. Возникающий

при этом эффект прохождения через барьер при

^* E-mail: khomitsky@phys.unn.ru

нормальном падении на него плоской волны назы-

929

ЖЭТФ, вып. 5 (11)

Д. В. Хомицкий, К. С. Кабаев, Е. А. Лаврухина

ЖЭТФ, том 158, вып. 5 (11), 2020

вается клейновским туннелированием, и его суще-

позволяет рассчитывать на когерентную динами-

ствование предсказано в таких популярных систе-

ку состояний во внешнем управляющем поле на

мах с линейным спектром, как графен [5]. Поэто-

временах, меньших указанных.

му для моделей с созданием конфайнмента прихо-

В работе [13] нами подчеркивалось, что в моде-

дится привлекать либо предположения о существо-

ли квантовой точки с барьерами конечной высоты

вании непроницаемых стенок [6], либо вводить маг-

помимо состояний дискретного спектра существу-

нитные барьеры для одномерных [7, 8] или поверх-

ют и состояния непрерывного спектра, располага-

ностных [9] краевых состояний. Наличие намагни-

ющиеся выше и ниже области дискретного спек-

ченности, эквивалентное введению массового чле-

тра. В нормальных условиях при низких темпера-

на в гамильтониан [10], разрушает симметрию по

турах состояния нижней части континуума заняты,

отношению к обращению времени, лишая тем са-

поскольку положение уровня Ферми должно обес-

мым структуру некоторых свойств ТИ. Тем не ме-

печивать занятость и нижнего дискретного уровня,

нее ряд полезных особенностей фермионов Дирака

который располагается выше верхнего края нижней

сохраняется и при наличии локального магнитно-

части континуума. Тем не менее для более высоких

го поля, генерируемого магнитными барьерами. В

температур (порядка 77 К) становятся существен-

первую очередь, это сильная связь спина с волно-

ными и переходы в состояния непрерывного спек-

вым вектором, позволяющая надеяться на прило-

тра с участием фононов. Если же температуры низ-

жения ТИ в спинтронике. Необходимо указать, что

кие, то участие непрерывного спектра возможно, ес-

взаимодействие краевых состояний с магнитными

ли к структуре приложено постоянное или перемен-

неоднородностями структуры, такими как магнит-

ное электрическое поле, что является необходимым

ные барьеры или локализованные неоднородности

условием осуществления с ней операций, требуемых

типа магнитных примесей, требует своего подхода

для функционирования кубита.

для вывода гамильтониана в каждом конкретном

Для системы с парой дискретных уровней, состо-

случае. Так, для задачи о взаимодействии с магнит-

яния которых отличаются знаком какой-либо проек-

ной примесью, которую можно рассматривать как

ции спина, переходы под действием периодического

сильнолокализованный барьер, такой вывод на ос-

и однородного электрического поля обычно называ-

нове модели Bernevig-Hughes-Zhang краевых состо-

ют электрическим дипольным спиновым резонанс-

яний в ТИ HgTe/CdTe [1-4] представлен в Прило-

ном (ЭДСР). Такие переходы начали активно изу-

жении (Supplementary Material) к работе [11].

чать в системах с сильным спин-орбитальным вза-

Следует отметить, что в работах [7, 8] модель

имодействием [14]. Роль состояний континуума при

магнитных барьеров, создаваемых на одномер-

протекании ЭДСР в нанопроволоках с потенциалом

ном крае двумерного ТИ на базе квантовой ямы

квантовой точки изучалась, в частности, в наших

HgTe/CdTe, была построена в приближении бес-

недавних работах [15, 16]. Было показано, что для

конечно тонких (дельта-образных) барьеров. При

осуществления операций по управлению заселенно-

этом для создания конфайнмента требовалось

стью нужного дискретного уровня на временах, су-

переходить к пределу бесконечной амплитуды

щественно меньших времен релаксации, необходи-

потенциальной энергии взаимодействия с таким

мо использовать такие электрические поля, которые

барьером. В наших работах [12, 13] мы обобщили

являются достаточно сильными для индуцирования

данную модель на случай более реалистичных

переходов в непрерывный спектр. Скорость ухода в

барьеров конечной высоты и большой ширины,

континуум и ее влияние на параметры ЭДСР явля-

по сравнению с размером формируемой кванто-

ются нетривиально связанными величинами. Мож-

вой точки. Было обнаружено, что при изменении

но предположить, что учет состояний непрерывного

ширины ямы и высоты барьеров можно добиться

спектра в динамике, вызванной периодическим по-

формирования произвольного числа дискретных

лем, представляет большой интерес и для моделей

уровней в квантовой точке, в том числе получить

квантовой точки в ТИ, где могут проявиться особен-

систему из двух уровней, потенциально пригодную

ности, характерные для дираковского, безмассового

для создания кубитов. В работе [13] нами были

спектра.

найдены параметры энергетической релаксации в

В данной работе мы строим модель динами-

такой системе при участии фононов в HgTe. Было

ки электронных состояний в одномерной квантовой

обнаружено, что при низких температурах (4 К или

точке на базе ТИ HgTe/CdTe с магнитными барье-

ниже) характерное время релаксации составляет

рами, учитывая состояния непрерывного спектра, в

для КТ шириной 40-45 нм величину 10-100 нс, что

которые возможны переходы под действием перио-

930

ЖЭТФ, том 158, вып. 5 (11), 2020

Спиновый резонанс в квантовой точке.. .

дического электрического поля. Мы рассчитываем

эволюцию и заселенности дискретных уровней во

времени при различных напряженностях электриче-

ского поля, находим частоту Раби и устанавливаем

характерные времена ухода в непрерывный спектр.

Явление ухода в континуум рассматривается с точ-

ки зрения динамики заселенностей, средней энер-

гии и средней координаты, причем знание этих ве-

личин дополняет друг друга. Рассчитывается так-

же локальная плотность вероятности и плотность

одной из спиновых проекций в области квантовой

точки, эволюция которых может быть детектирова-

на экспериментально. Вычисляется локальная плот-

ность тока вероятности вблизи квантовой точки,

усредненная по времени, характеризующая интен-

сивность переходов в непрерывный спектр.

Работа построена следующим образом. В разд. 2

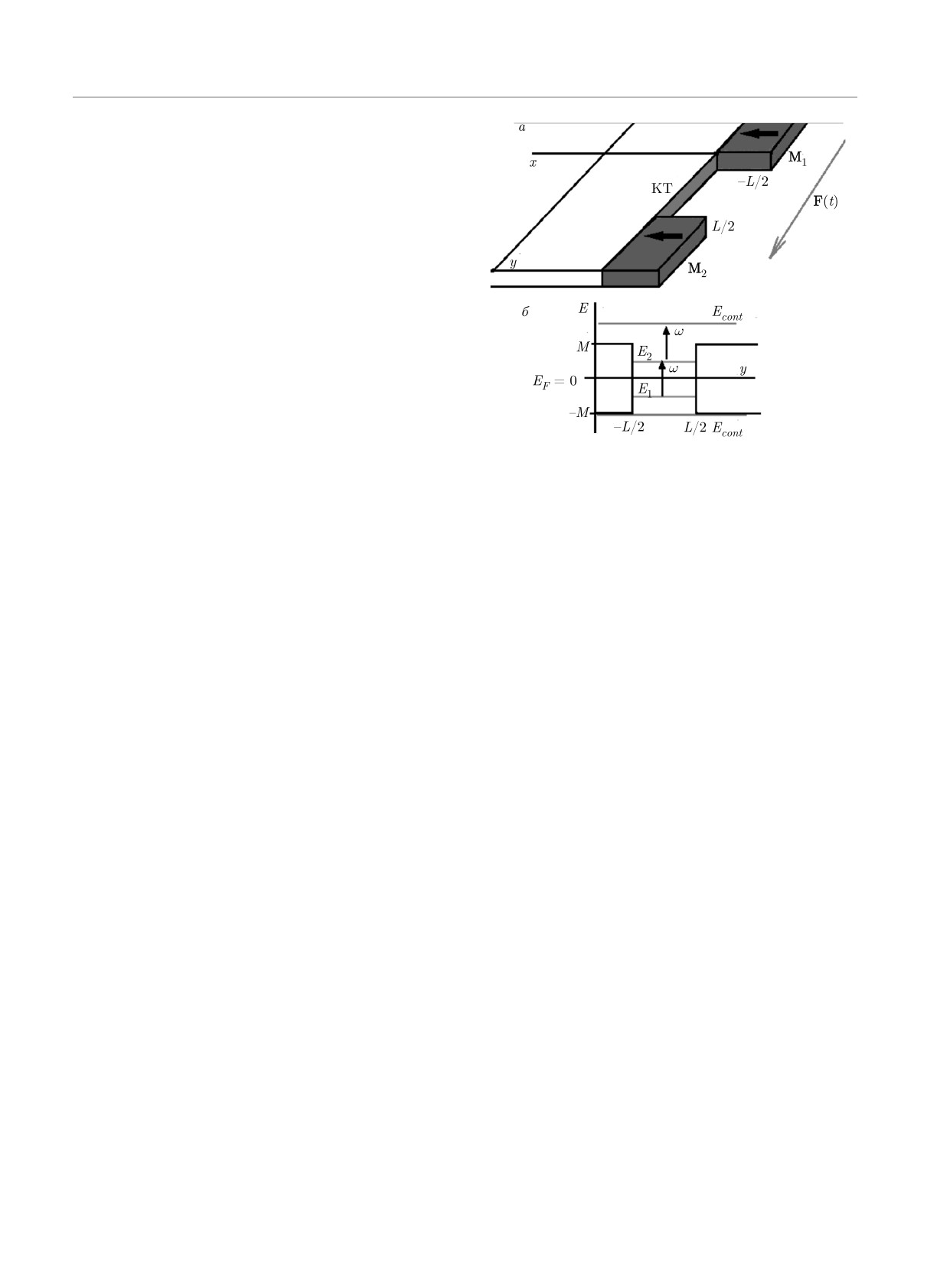
Рис. 1. а) Схема квантовой точки (КТ), сформированной

обсуждаются гамильтониан электронных состояний

магнитными барьерами высоты M1,2 и помещенной в пере-

и его собственные функции для дискретной и непре-

менное электрическое поле (0, F (t), 0). Вариант ориента-

рывной частей спектра, а также схема расчета

ции намагниченности барьеров показан горизонтальными

эволюции в периодическом электрическом поле. В

стрелками. Края структуры вдоль оси y ограничены только

разд. 3 представлены основные результаты для ди-

размерами рисунка. б) Расположение дискретных уровней

намики средних значений наблюдаемых величин,

E1,2 и состояний континуума Econt. Электрическое поле с

полученные при различных амплитудах поля, и при-

частотой ω вызывает переходы между парой уровней E1,2,

а также между уровнем E2 и состояниями континуума с

ведены аналитические оценки вероятности ухода в

энергией Econt > M. Положение уровня Ферми EF = 0

непрерывный спектр. В разд. 4 обсуждаются резуль-

таты расчетов локальной плотности вероятности и

онами Дирака - Вейля, в базисе двухкомпонентных

спиновой плотности, а также плотности тока вероят-

функций краевых состояний модели ТИ Bernevig-

ности. В заключительном разд. 5 представлены вы-

Hughes-Zhang (BHZ), локализованных вдоль коор-

воды по работе. В приложении A обсуждается вывод

динаты x, имеет вид [1-4]

гамильтониана для задачи с магнитными барьера-

ми. В Приложении B рассматриваются различные

H1D = Ak_yσ_z.

(1)

способы включения в гамильтониан нестационарно-

го электрического поля.

Здесь σ_z — матрица Паули, а типичное значение по-

стоянной A, связанной с групповой скоростью кра-

евых состояний v₀

= A/ℏ = 5.5 · 10⁷ см/с, для

2. МОДЕЛЬ

квантовых ям HgTe/CdTe составляет 360 мэВ · нм.

Собственные значения гамильтониана (1) описыва-

2.1. Краевые состояния и спектр

ют две ветви с линейным законом дисперсии E1D =

Мы рассматриваем структуру, схематически по-

= ±Ak_y, пересекающиеся в точке Дирака E = 0,

казанную на рис. 1а. Квантовая яма HgTe/CdTe с

причем проекции спина 〈σ_z 〉 на разных ветвях про-

толщиной, большей критической, при которой про-

тивоположны друг другу. Собственные функции га-

исходит формирование топологически защищенных

мильтониана (1) имеют вид плоских волн, умножен-

краевых состояний, ориентирована в плоскости xy.

ных на двухкомпонентный спинор. Они описывают

Волновая функция краевого состояния локализова-

состояния, распространяющиеся с постоянной ско-

на на краю x = 0 и экспоненциально убывает в глубь

ростью v₀ в противоположных направлениях вдоль

структуры при x > 0. Координата y вдоль края яв-

оси y, в зависимости от проекции спина σ_z = ±1 на

ляется той единственной пространственной степе-

одной из двух ветвей спектра E1D. Среднее значение

нью свободы, которая входит в гамильтониан кра-

проекции спина, пропорциональное среднему значе-

евых состояний. В отсутствие магнитных барьеров

нию от соответствующей матрицы Паули, здесь и

и внешнего электрического поля такой гамильтони-

далее мы откладываем в безразмерных единицах в

ан для одномерных состояний, называемых ферми-

интервале [-1 . . . 1].

931

11*

Д. В. Хомицкий, К. С. Кабаев, Е. А. Лаврухина

ЖЭТФ, том 158, вып. 5 (11), 2020

Для осуществления конфайнмента (локализа-

условий гамильтониан краевых состояний в присут-

ции) краевых состояний и формирования дискрет-

ствии барьеров может быть записан следующим об-

ных уровней вслед за работами [7, 8] нами бы-

разом [12, 13] (см. также Приложение A):

ло предложено вводить в гамильтониан взаимодей-

H₀ = Ak_yσ_z-M₁S(-L/2-y)(σ_x cosθ₁+σ_y sinθ₁) -

ствие с магнитными барьерами. Намагниченность

барьера m, направленная под углом θ к оси x, для

- M₂S(y - L/2)(σx cosθ₂ + σ_y sinθ₂),

(2)

ориентированного в плоскости xy магнитного ба-

где S(y) — ступенчатая функция, аппроксимирую-

рьера имеет компоненты (m cosθ, m sinθ, 0). Взаи-

щая стенку левого и правого магнитного барьеров

модействие магнитного барьера со спином элект-

на границах соответственно y = -L/2 и y = L/2

рона записывается в форме обменного оператора

и отвечающая бесконечно далекой второй стенке

-(M · σ) = -M(σ_x cos θ + σ_y sin θ), определяемо-

каждого барьера. Нами было показано [12, 13], что

го в базисе двух собственных состояний гамильто-

при изменении параметров барьеров и расстояния L

ниана (1) с помощью матриц Паули σ_i второго по-

между ними, т. е. размера квантовой точки, в ней

рядка [1-4, 11, 17-20]. Здесь M обозначает амплиту-

может быть сформировано различное число дис-

ду взаимодействия в энергетических единицах. Та-

кретных уровней с энергиями |E_n| ≤ min(M₁, M₂).

кая запись отвечает представлению в базисе псев-

Собственные функции гамильтониана (2) для состо-

доспина, поскольку собственные состояния гамиль-

яния дискретного спектра с энергией E_n имеют раз-

тониана (1) хотя и имеют противоположные проек-

личный вид в зависимости от пространственной об-

ции спина на ось z, но отвечают комбинациям атом-

ласти: ψ_QD внутри квантовой точки при -L/2 <

ных функций электронной и дырочной зон с раз-

< y < L/2; ψy<-L/2 в левом барьере при y < -L/2 и

личными спинами, из которых строится функция

ψy>L/2 в правом барьере при y > L/2. Для них нами

краевых состояний. Следует отметить, что, несмот-

были получены следующие выражения [12, 13]:

ря на представление гамильтониана (1) в базисе

(

)

псевдоспина, а не истинного спина, можно гово-

C₁ exp(iE_ny/A)

рить о пропорциональности матриц-компонент век-

ψ_QD =

(3)

C₂ exp(-iE_ny/A)

тора σ = (σx, σy, σz ) оператору истинного спина

[21]. Подробный вывод вклада для взаимодействия

⎛

⎞

с магнитной примесью (которую можно рассматри-

вать как сильнолокализованный магнитный барьер)

⎜

√

⎟

ψy<-L/2 = B

⎝

⎠×

M²¹ - E²

+E_n

в рамках модели BHZ краевых состояний выполнен

exp(iθ₁)

в работе [11], а случай нашей конфигурации магнит-

M₁

(√

)

ных барьеров рассмотрен в Приложении A в данной

M²¹ - E²

× exp

(4)

работе.

Рассмотрим барьеры с амплитудой взаимодей-

ствия M1,2 и ориентацией намагниченности, схема-

⎛

⎞

тически показанной на рис. 1а стрелками внутри ба-

⎜

⎟

рьеров. Края структуры вдоль y ограничены только

ψy>L/2 = D

⎠×

^⎝i^√M22 - E2

-E_n

размерами рисунка, истинная структура является

exp(iθ₂)

M₂

протяженной вдоль y. Направление намагниченно-

(

√

)

сти в плоскости xy определяется углами θ₁ и θ₂ соот-

M²² - E²

× exp

(5)

ветственно для левого и правого барьеров. Величина

M1,2 зависит от типа устанавливаемых магнитных

Коэффициенты C₁, C₂, B, D в выражениях (3)-(5)

барьеров и в нашей модели не превосходит 20 мэВ,

определяются из граничных условий при y = ±L/2,

т. е. порядка половины ширины запрещенной зоны в

описывающих непрерывность двухкомпонентной

HgTe [1-4], в которой формируется спектр краевых

волновой функции и представляющих собой четыре

состояний. Пусть барьеры имеют своими границами

скалярных, или два спинорных уравнения:

значения y = -L/2, y = L/2, образующие границы

квантовой точки (область КТ на рис. 1а), и являют-

ψ(-L/2 + 0) = ψ(-L/2 - 0),

(6)

ся толстыми, т. е. простираются достаточно далеко в

ψ(L/2 + 0) = ψ(L/2 - 0).

отрицательном и положительном направлениях оси

y по сравнению с характерной глубиной проникно-

После подстановки функций (3)-(5) в (6) мы

вения волновой функции. С учетом всех описанных

получаем систему четырех линейных однородных

932

ЖЭТФ, том 158, вып. 5 (11), 2020

Спиновый резонанс в квантовой точке.. .

уравнений для коэффициентов C₁, C₂, B, D.

влетворяющих условию [13]

Условие существования нетривиального решения

|E| > max(M₁, M₂).

(7)

Δ(E_n) = 0 определяет дискретный спектр энергий.

Рассмотрим пример системы дискретных уров-

Волновые функции состояний непрерывного

ней для конкретных параметров задачи. Для зна-

спектра могут быть представлены в тех же про-

чения A = 360 мэВ · нм при параллельных магнит-

странственных областях, что и функции (3)-(5)

ных барьерах с θ₁ = θ₂ = 0, имеющих одинаковую

дискретного спектра, в следующей форме:

высоту M₁ = M₂ = M с M = 20 мэВ, отвечающей

(

)

примерно половине запрещенной зоны объемных со-

C₁ exp(iEy/A)

стояний в HgTe, и для ширины квантовой точки L =

ψ_QD =

(8)

C₂ exp(-iEy/A)

= 40 нм, в ней формируется два дискретных уров-

ня с энергиями, симметричными относительно точ-

ки Дирака E = 0, в которой мы далее будем считать

⎛

⎞

расположенным уровень Ферми. Следует отметить,

ψy<-L/2 = B₁ ⎝-E+√E2_-M2

⎠_×

что положение уровня Ферми в конкретном образ-

¹ exp(iθ₁)

M₁

це топологического изолятора может быть различ-

(

)

√

ным [1-4], однако для нашей задачи важным явля-

E² - M²

× exp i

ется лишь такое условие для E_F , при выполнении

которого нижний дискретный уровень E₁ в состоя-

⎛

⎞

нии равновесия занят, а верхний дискретный уро-

+B₂⎝-E-√E2_-M2

⎠_×

вень E₂ свободен, что может быть реализовано в

¹ exp(iθ₁)

достаточно широком интервале положения уровня

M₁

(

√

)

Ферми. Энергии дискретных уровней, полученные

E² - M²

× exp

-i

(9)

численным расчетом, равны E₁ = -9.62 мэВ и E₂ =

= 9.62 мэВ. Схема энергетических уровней при вы-

бранных параметрах задачи показана на рис. 1б.

⎛

⎞

Собственные функции для дискретных уров-

ней обладают интересной особенностью, показан-

ψy>L/2 = D₁ ⎝-E+√E2_-M2

⎠_×

² exp(iθ₂)

ной на рис. 2: распределения плотности вероятно-

M₂

(

√

)

сти (рис. 2а,в) для них одинаковы, а распределения

E² - M²

плотности проекции спина S_x (рис. 2б,г) имеют про-

× exp i

тивоположный знак. Распределения для проекции

⎛

⎞

S_y (не показаны на рис. 2) для этих уровней так-

же одинаковы, а плотность для проекции S_z тож-

⎜

⎟

+D₂

⎠×

дественно равна нулю. Такая особенность спиновой

^⎝-E -^√E2 - M2

² exp(iθ₂)

плотности позволяет рассчитывать на детектирова-

M₂

(

√

)

ние знака спиновой проекции S_x как на метод опре-

E² - M²

× exp

-i

(10)

деления заселенности одного из двух дискретных

уровней в экспериментах. Из рис. 2 можно также

сделать вывод, что приближение бесконечно широ-

Коэффициенты C₁, C₂, B₁, B₂, D₁, D₂ в выражени-

ких барьеров в (2) оправдано, поскольку волновые

ях (8)-(10) определяются следующим образом. Че-

функции убывают в глубь барьеров на расстоянии,

тыре скалярных уравнения определяют непрерыв-

меньшем ширины квантовой точки. Следовательно,

ность волновой функции на границах квантовой

дальняя граница барьера, имеющаяся в реальных

точки, и по форме совпадают с (6). Один из коэф-

магнитах, не оказывает на локализованные состо-

фициентов может быть задан произвольным нену-

яния электрона существенного эффекта, если счи-

левым числом, поскольку волновая функция будет

тать дискретные уровни не уширенными вследствие

нормирована. Для обеспечения численной реализа-

пусть малой, но конечной проницаемости реальной

ции состояний континуума нами предполагается су-

структуры с барьерами конечной ширины.

ществование далеких стенок, или электродов, распо-

Помимо дискретных уровней в нашей модели с

ложенных на большом расстоянии y = ±d, где d ≫

гамильтонианом (2) имеются и состояния непрерыв-

≫ L. В этом случае континуум представляется набо-

ного спектра, существующие при всех энергиях, удо-

ром очень плотного множества дискретных уровней

933

Д. В. Хомицкий, К. С. Кабаев, Е. А. Лаврухина

ЖЭТФ, том 158, вып. 5 (11), 2020

(порядка 10³ на 100 мэВ), сохраняя при этом свои

ти токонесущих краевых состояний, описываемые

физически значимые свойства.

гамильтонианом (1), что позволит рассчитать пол-

Подобная модель континуума с d = 160L была

ный ток через всю структуру. В данной работе наша

успешно применена нами при исследовании дина-

система «квантовая точка + барьеры» находится в

мики в полупроводниковой нанопроволоке в [15,16],

«закрытом» режиме [7, 8], когда полный ток через

поэтому мы рассчитываем на ее адекватность и для

нее отсутствует.

данной задачи, выбирая параметр d = 150L. Такой

размер одномерной краевой области, дающий в на-

2.2. Схема расчета эволюции во внешнем

шем примере величину 2d = 12 мкм, отвечает реа-

поле

листичным условиям экспериментов, где использу-

Нас интересует нестационарная эволюция элек-

ются образцы и меньшей длины. Следует отметить,

тронного состояния, локализованного в начальный

что нами выполнялись расчеты и при других значе-

момент времени на нижнем дискретном уровне E₁,

ниях d в той же области параметров, и все физиче-

находящемся под уровнем Ферми E_F = 0. Эволю-

ски значимые результаты для эволюции при этом от

ция индуцируется переменным электрическим по-

конкретного значения d не зависели. После задания

лем F(t)

= (0, F (t), 0) показанным стрелкой на

значения d мы используем периодическое гранич-

рис. 1а вдоль края x = 0. Здесь F(t) = |e|E(t)

ное условие ψ(-d) = ψ(d), позволяющее адекватно

есть величина электрического поля, измеряемая в

описать модель континуума, и нормируем на еди-

мэВ/нм. Поскольку собственные функции гамиль-

ницу волновые функции (8)-(10) на полной длине

тониана (2) являются двухкомпонентными спино-

краевой области 2d. В результате для любого зна-

рами, у которых, вообще говоря, обе компонен-

чения энергии непрерывного спектра, удовлетворя-

ты отличны от нуля, переходы между состояния-

ющего условию (7), мы получаем шесть уравнений

ми как дискретного, так и непрерывного спектра

для шести коэффициентов для волновых функций

могут быть индуцированы периодическим электри-

(8)-(10), однозначно определяющих собственное со-

ческим полем, подобно тому как это имеет место

стояние, принадлежащее непрерывному спектру.

при ЭДСР в полупроводниковых нанопроволоках с

На рис. 1б красными горизонтальными линиями

квантовой точкой [15,16], в которых имеется сильное

схематически показаны некоторые состояния кон-

спин-орбитальное взаимодействие. Включение пере-

тинуума. Стрелки показывают возможные перехо-

менного электрического поля в гамильтониан может

ды в периодическом электрическом поле, рассмат-

осуществляться различным образом в зависимости

риваемые в следующем разделе. Заметим, что усло-

от выбранной калибровки. Соответствующие разли-

вие (7) говорит о существовании двух симметрич-

чия обсуждаются в Приложении B к данной работе.

ных областей континуума с E > M и E < -M,

В калибровке с использованием скалярного потен-

где M = max(M₁, M₂). Поскольку для рассматрива-

циала и однородного в пространстве электрического

емой нами задачи температура предполагается низ-

поля F(t) = (0, F (t), 0), использованной нами также

кой и нижний дискретный уровень предполагает-

в работах [15, 16], гамильтониан имеет следующий

ся занятым в состоянии равновесия, будут заняты

вид:

и все состояния нижней половины континуума с

H = H₀ + Fysinωt,

(11)

E < -M. Следовательно, влияние состояний непре-

рывного спектра будет реализовываться только в

где F = |e|E₀ — амплитуда электрического поля, из-

переходах в верхнюю часть континуума с E > M,

меряемая в мэВ/нм, а частота удовлетворяет усло-

что отражено вертикальной стрелкой на рис. 1б,

вию резонанса между двумя дискретными уровнями

указывающей на переходы с дискретного уровня E₂

квантовой точки,

в верхнюю половину состояний континуума. Отме-

ℏω = E₂ - E₁.

(12)

тим, что поскольку для гамильтониана (2) принято

приближение бесконечно широких барьеров, состо-

Можно назвать такой резонанс спиновым, посколь-

яния континуума в нем отвечают «пространствен-

ку проекции спина S_x на уровнях E₁ и E₂ имеют

но-надбарьерной» области и нигде не описываются

противоположные знаки, как это видно на рис. 2б,г.

простым выражением (1) для гамильтониана Дира-

Для выбранных параметров задачи ℏω = 19.24 мэВ,

ка - Вейля в отсутствие барьеров. В дальнейших ра-

что отвечает частоте поля ω = 2.93 · 10¹³ 1/c (ли-

ботах мы планируем учесть наличие и второй грани-

нейная частота ν = 4.66 ТГц), при этом период по-

цы для каждого барьера, чтобы в задаче, по крайней

ля T = 0.21 пс. Такие высокие частоты возбужде-

мере далеко от квантовой точки, возникали облас-

ния в терагерцевой области имеют то преимущество,

934

ЖЭТФ, том 158, вып. 5 (11), 2020

Спиновый резонанс в квантовой точке.. .

что явления ЭДСР, связанные со сменой заселенно-

по собственным функциям должен содержать беско-

стей дискретных уровней, занимают малый интер-

нечный набор базисных функций, однако в реаль-

вал времени. В рассмотренных нами случаях они

ности при не слишком больших амплитудах элек-

протекают на временах порядка (16-50)T в зависи-

трического поля в динамику оказывается вовлечена

мости от амплитуды поля, т. е. от 3.4 до 10.5 пс. Это

только часть состояний континуума, непосредствен-

позволяет пренебрегать эффектами релаксации и

но примыкающая к дискретным уровням в нижней

декогерентности, а в случае экспериментальной ре-

части спектра. Наши расчеты показали, что в полях

ализации подобной структуры позволяет рассчиты-

с амплитудой F = 0.03-0.09 мэВ/нм на временах

вать на ее высокое быстродействие и стабильность.

t ≤ 150T, существенных для рассматриваемых эф-

Следует отметить, что хотя источники перемен-

фектов, в динамике активно участвуют состояния

ного поля в терагерцевой области еще не получили

континуума с энергией не выше 30 мэВ. Мы вклю-

очень широкого распространения, необходимость в

чали в численные расчеты все состояния континуу-

их использовании для изучения явлений ЭДСР от-

ма с энергией до 100 мэВ, и применяли при моде-

мечается в недавних работах [16, 22]. Прогресс в их

лировании унитарной эволюции схему Кэли [25,26],

создании заметен на протяжении последних двух

что обеспечивало сохранение нормы волновой функ-

десятилетий [23, 24]. В частности, недавно пред-

ции. После получения решения (13) в данный мо-

ставлены экспериментальные результаты импульс-

мент времени в виде набора коэффициентов C_n(t) с

ной (длительностью до 1 пс) генерации излучения

их помощью могут быть определены все интересую-

со спектром частот, имеющего существенные вкла-

щие нас средние значения и локальные плотности,

ды от гармоник вплоть до 70 ТГц [24]. Приводимые

которые будут рассмотрены в следующих разделах.

ниже результаты, полученные в рамках нашей моде-

ли, показывают, что постоянно действующий источ-

ник с единственной гармоникой на частоте ω не яв-

3. РЕЗУЛЬТАТЫ ДЛЯ ЭВОЛЮЦИИ

ляется необходимым, и основные эффекты для сме-

ЗАСЕЛЕННОСТЕЙ И СРЕДНИХ ЗНАЧЕНИЙ

ны заселенностей уровней могут быть получены на

3.1. Эволюция заселенностей

достаточно малом интервале времени 4-11 пс, что

достаточно близко к длительности импульсов тера-

Мы рассматривали эволюцию в периодическом

герцевых источников, полученной в работе [24].

электрическом поле с гамильтонианом (11) при че-

Необходимо отметить, что для выбранных пара-

тырех значениях напряженности поля: F

= 0.03,

метров задачи для некоторых состояний континуу-

0.05, 0.07, 0.09 мэВ/нм, на временах t ≤ 150T . Такой

ма с E_cont > M оказывается выполненным условие

интервал времени, занимающий около 32 пс, оказы-

резонанса (12) для верхнего дискретного уровня E₂

вается достаточным для наблюдения основных яв-

и состояния континуума с энергией E_cont, что про-

лений, проистекающих от эволюции заселенности

иллюстрировано верхней вертикальной стрелкой с

дискретной и непрерывной частей спектра.

обозначением ω на рис. 1б. Это означает, что состо-

Рассмотрим вначале эволюцию заселенности

яния континуума вовлекаются в резонанс и активно

дискретных уровней, для которых в началь-

участвуют в динамике, что наблюдалось нами ра-

ный момент времени C₁(0) = 1, C₂(0) = 0. На

нее для ЭДСР в полупроводниковой нанопроволоке,

рис. 3а приведен пример эволюции величин |C₁(t)|²

даже когда точное условие резонанса с состояниями

(сплошная линия) и |C2(t)|2 (штриховая линия)

непрерывного спектра не выполнялось [15, 16].

для амплитуды поля F

= 0.05 мэВ/нм. Можно

Полную волновую функцию во внешнем поле бу-

видеть, что заселенности уровней, описываемые

дем искать в виде ряда по всем собственным функ-

значениями |C₁(t)|² и |C₂(t)|², испытывают харак-

циям гамильтониана (2), включая состояния непре-

терные осцилляции, которые для строго двумерной

рывного спектра:

системы называются осцилляциями Раби. Для

(

)

∑

= 0.05 мэВ/нм период таких осцилляций T_R,

iE_nt

Ψ(y, t) =

C_n(t)exp

ψ_n(y).

(13)

определяемый как расстояние между максимумами

ℏ

заселенности, равен примерно 30T , что составляет

После подстановки (13) в нестационарное уравнение

6.3 пс. Кроме того, на рис. 3а заметно затухание ам-

Шредингера с гамильтонианом (11) получим сис-

плитуды осцилляций |C₁(t)|² и |C₂(t)|² со временем,

тему обыкновенных дифференциальных уравнений

что отражает переходы в состояния непрерывного

для коэффициентов C_n(t) с начальным условием

спектра. Из рис. 3а можно сделать вывод, что

C_n(0) = δn1. Следует отметить, что формально ряд

при рассматриваемых параметрах задачи можно

935

Д. В. Хомицкий, К. С. Кабаев, Е. А. Лаврухина

ЖЭТФ, том 158, вып. 5 (11), 2020

Рис. 2. Распределения плотности вероятности (а,в) и Sx-компоненты спиновой плотности (б,г) для дискретных уровней

E1 (а,б) и E2 (в,г), показанные в области квантовой точки -L/2 < y < L/2 и в части области барьеров, примыкающей

к ней

осуществить смену заселенностей на масштабе

т. е. от 10.5 до 3.4 пс. Численные результаты хоро-

нескольких T_R, когда уход в континуум еще не

шо согласуется с линейной зависимостью (14), по-

проявляется заметно.

строенной сплошной линией. Для нее использова-

Зависимость частоты осцилляций заселенностей

но численно определенное значение матричного эле-

уровней |C1,2|², или частоты Раби Ω = 2π/T_R в стро-

мента координаты между двумя дискретными уров-

го двухуровневой модели с состояниями ψ_n и ψ_m, в

нями, модуль которого для наших параметров ра-

приближении вращающейся волны (быстрые осцил-

вен |y₁₂| = 13.19 нм. Достаточно хорошее совпаде-

ляции на удвоенной частоте поля отбрасываются)

ние с линейной зависимостью имеет место, несмот-

имеет простой линейный вид как функция ампли-

ря на участие в динамике многих уровней конти-

туды электрического поля:

нуума. В этом состоит одно из отличий задачи с

безмассовым спектром и однофотонным резонансом

F |r_nm|

Ω=

(14)

(12) с состояниями континуума от задач с кванто-

ℏ

вой точкой в полупроводниковой нанопроволоке, где

где rnm = 〈ψn|r|ψm〉 — матричный элемент опе-

зависимость частоты Ω от амплитуды поля имеет

ратора координаты для оператора возмущения от

существенно нелинейный характер [15, 16]. Анализ

электрического поля, присутствующего в гамильто-

рис. 3б и формулы (14) приводит к очевидному вы-

ниане (11). На рис. 3б кружками изображена чис-

воду, что при увеличении амплитуды поля F про-

ленная зависимость частоты Ω в единицах ω для

цесс смены заселенностей протекает быстрее, однако

смены заселенностей уровней E₁ и E₂, полученная

при этом ускоряется и уход в состояния континуума,

для рассматриваемых амплитуд электрического по-

который будет рассмотрен ниже. Следовательно, в

ля. Значение периода T_R составляет от 50T для

практических приложениях многоуровневой систе-

F = 0.03 мэВ/нм до 16T для F = 0.09 мэВ/нм,

мы с учетом состояний континуума необходимо вы-

936

ЖЭТФ, том 158, вып. 5 (11), 2020

Спиновый резонанс в квантовой точке.. .

бирать некоторый оптимальный интервал электри-

имеет вид w ∝ F², в отличие от экспоненциальных

ческих полей, определение которого составляет одну

зависимостей для нелинейной многофотонной иони-

из целей данной работы.

зации [27,28]. Квадратичный рост вероятности w(F )

по сравнению с линейным ростом частоты Раби (14)

говорит о том, что для удержания электрона в свя-

3.2. Вероятность ухода в континуум

занном состоянии на уровне E₁ или E₂ в течение

Взаимодействие состояний дискретной и непре-

достаточно долгого времени не следует приклады-

рывной частей спектра в присутствии периодиче-

вать к структуре слишком сильного электрическо-

ского электрического поля приводит к росту засе-

го поля. С другой стороны, слишком слабые поля

ленностей состояний континуума и уменьшению за-

также не представляются подходящими, поскольку

селенности немногочисленных дискретных уровней.

частота Раби (14) для смены заселенностей при этом

Другими словами, электрон, первоначально находя-

уменьшается, характерное время «переключения»

щийся в связанном состоянии, под действием пери-

между двумя дискретными уровнями растет и на-

одического поля уходит в континуум, т. е. происхо-

ступившие эффекты релаксации и декогерентности

дит ионизация квантовой точки. Явлению иониза-

приведут к усложнению и подавлению желаемой ди-

ции посвящена обширная литература, где представ-

намики заселенностей.

лено множество аналитических и численных подхо-

Результаты применения выражения (17) для ис-

дов (см., например, [27, 28]). Мы начнем с анализа

пользованного в расчетах набора амплитуд электри-

численных результатов для суммарной заселенно-

ческого поля приведены на рис. 4 в виде штриховых

сти двух дискретных уровней в нашей модели, опре-

линий того же цвета, что и сплошные линии для чис-

деляемой как

ленного расчета. Видно, что соответствие числен-

ных и аналитических результатов весьма хорошее,

P_loc(t) = |C₁(t)|² + |C₂(t)|².

(15)

что позволяет говорить о данном механизме одно-

фотонной ионизации как о доминирующем для на-

На рис. 4 сплошными линиями представлены

шей системы, и не рассматривать режимы нелиней-

временные зависимости (15) для выбранных ампли-

ной многофотонной ионизации. Характерные време-

туд электрического поля, полученные при числен-

на ухода в континуум, определяемые согласно вы-

ным расчете эволюции. Штриховые линии описыва-

ражению (16) как τ = 1/w(F ), составляют от 633T

ют аналитическое приближение для суммарной за-

при F = 0.03 мэВ/нм до 70T при F = 0.09 мэВ/нм,

селенности, которое будет рассмотрено далее. Имен-

т. е. от 133 до 15 пс. Эти времена, хотя и позволя-

но, будем аппроксимировать зависимость (15) на

ют осуществить требуемые операции по смене за-

рис. 4 экспоненциальной кривой

селенностей дискретных уровней, рассмотренные в

P_loc(t) = P(0)e-w(F)t,

(16)

предыдущем разделе, являются все же достаточно

малыми на масштабе быстродействия современные

где P (0) = 1. Для уровня E₂ дискретного спектра

электронных приборов. Поэтому увеличивать ам-

при рассматриваемых параметрах системы выпол-

плитуду электрического поля выше рассмотренных

няется резонансное условие E_cont - E₂ = ℏω с состо-

в наших примерах значений представляется неце-

янием континуума с энергией E_cont ≈ 28.86 мэВ, ле-

лесообразным. Уменьшение амплитуды приведет к

жащим выше барьера. Вероятность перехода в кон-

росту времени ухода в континуум согласно законо-

тинуум в единицу времени, w(F ), фигурирующая в

мерности τ ∝ 1/F². Однако при слишком слабых

выражении (16), может быть оценена по золотому

полях, как уже отмечалось выше, сами операции

правилу Ферми как

по смене заселенностей дискретных уровней (осцил-

ляции Раби) будут протекать медленнее, в соответ-

2π

w(F ) =

|V_if |²δ(E_f - E_i - ℏω),

(17)

ствии с приближением (14), что может привести к

ℏ

активному влиянию эффектов релаксации и декоге-

где Ei = E2 и Ef = Econt. Значение матрично-

рентности, характерный масштаб которых по време-

го элемента V_if

= Fy_if берется нами из числен-

ни начинается для типичных наноструктур от 1 нс и

ных расчетов собственных функций гамильтониа-

выше. Приведенные здесь и в предыдущем разделе

на (2), а дельта-функция в (17) аппроксимируется

оценки показывают, что для нашей структуры воз-

соответствующей плотностью состояний, определя-

можно осуществить операции типа осцилляций Раби

емой по численно найденному спектру гамильтони-

на малом масштабе от 4 до 11 пс. При этом уход в

ана (2). Зависимость w(F ), как это следует из (17),

континуум проявит себя на временах соответствен-

937

Д. В. Хомицкий, К. С. Кабаев, Е. А. Лаврухина

ЖЭТФ, том 158, вып. 5 (11), 2020

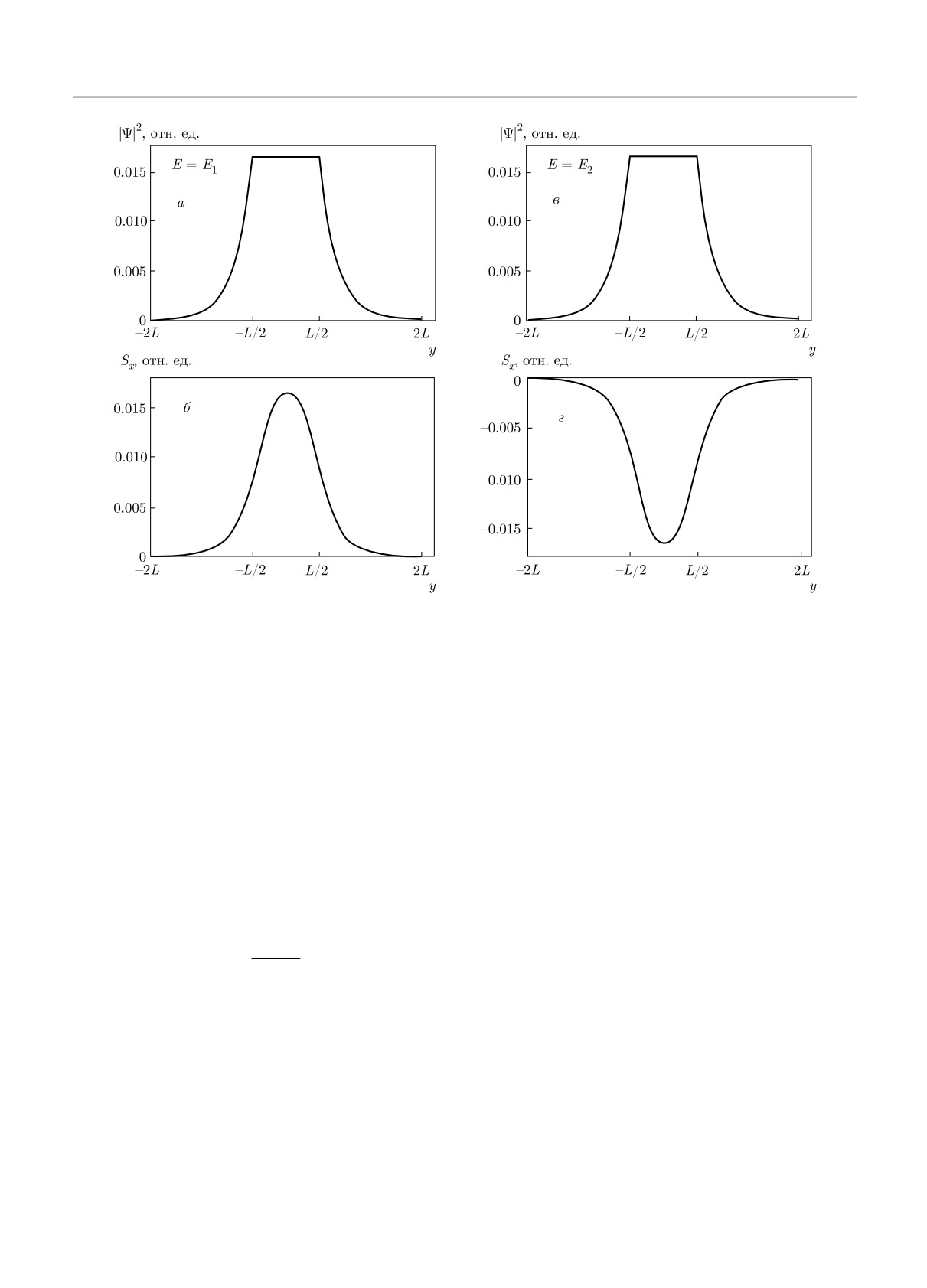
Рис. 3. а) Динамика заселенностей |C1|² (сплошная линия) и |C2|² (штриховая линия) дискретных уровней при резо-

нансе (12) для напряженности поля F = 0.05 мэВ/нм. Видны осцилляции заселенности с периодом около 30T (6.3 пс),

амплитуда которых затухает вследствие развития переходов в непрерывный спектр. б) Зависимость частоты осцилля-

ции заселенностей дискретных уровней Ω (частоты Раби) от амплитуды поля F . Численные результаты, отмеченные

кружками, хорошо соответствуют приближению (14), показанному сплошной линией

но от 15 до 133 пс, что позволит осуществить такие

операции до наступления существенной вероятности

ухода электрона в непрерывный спектр.

3.3. Эволюция средних значений энергии,

спина и координаты

Еще одним инструментом для определения пре-

имущественного вклада в состояние электрона от

дискретной или непрерывной части спектра являет-

ся анализ динамики средних значений физических

величин. Под усреднением величины, описываемой

оператором X, мы понимаем обычное квантовоме-

ханическое усреднение в состоянии (13),

〈X(t)〉 = 〈Ψ(y, t)|X|Ψ(y, t)〉.

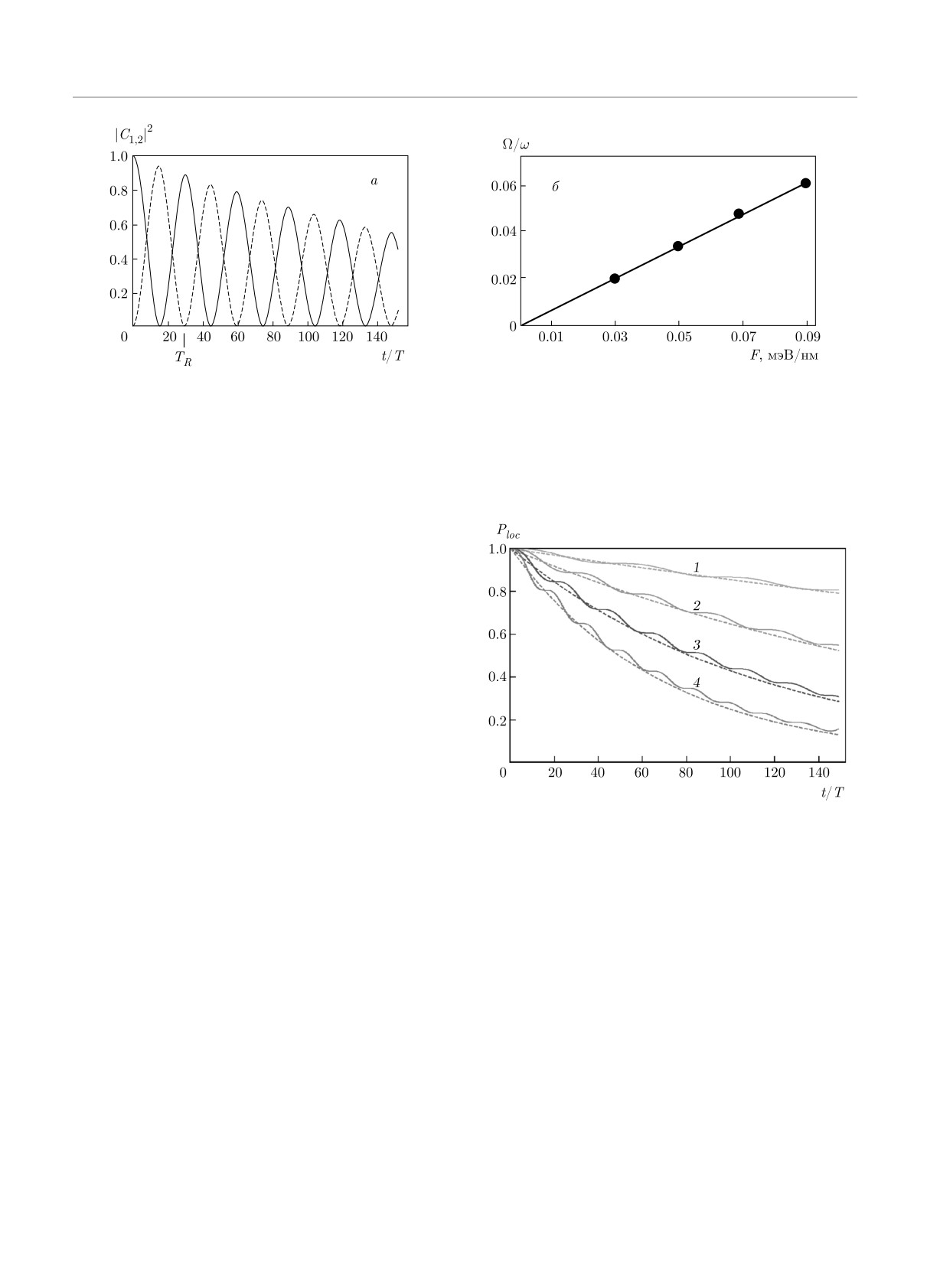
Рис. 4. (В цвете онлайн) Эволюция суммарной заселен-

ности дискретных уровней (15), полученная численным

Рассмотрим вначале поведение средней энергии

расчетом (сплошные линии) и в рамках аналитического

〈E(t)〉 со временем, показанное на рис. 5 для тех

приближения (17) (штриховые линии), построенная для

же амплитуд электрического поля, что на рис. 3б

различных амплитуд электрического поля F [мэВ/нм] =

и 4. В начальный момент времени электрон лока-

= 0.03 (1), 0.05 (2), 0.07 (3), 0.09 (4)

лизован на нижнем дискретном уровне E₁, поэтому

〈E(0)〉 = E₁. В системе только с двумя дискретны-

ми уровнями без учета континуума величина 〈E(t)〉

рактерное время превышения средней энергией по-

менялась бы в интервале E₁ < 〈E(t)〉 < E₂, т. е.

рогового значения, равного высоте барьера M, от-

от -9.62 до 9.62 мэВ, что показано на рис. 5 гори-

вечает времени τ = 1/w(F) затухания суммарной

зонтальными линиями и метками E₁, E₂. Из графи-

заселенности дискретных уровней P_loc(t), показан-

ков эволюции 〈E(t)〉 на рис. 5 видно, что при уче-

ной на рис. 4. Можно сказать, что в эволюцию сред-

те состояний континуума пределы изменения сред-

ней энергии на рассматриваемом интервале времени

ней энергии существенно сдвигаются. Именно, для

дают основной вклад два дискретных уровня, но с

всех амплитуд поля имеет место рост среднего зна-

течением времени состояния континуума начинают

чения 〈E(t)〉, сопровождаемый осцилляциями, соот-

давать все более заметный вклад, в особенности для

ветствующими осцилляциям Раби (см. рис. 3). Ха-

максимальных амплитуд электрического поля.

938

ЖЭТФ, том 158, вып. 5 (11), 2020

Спиновый резонанс в квантовой точке.. .

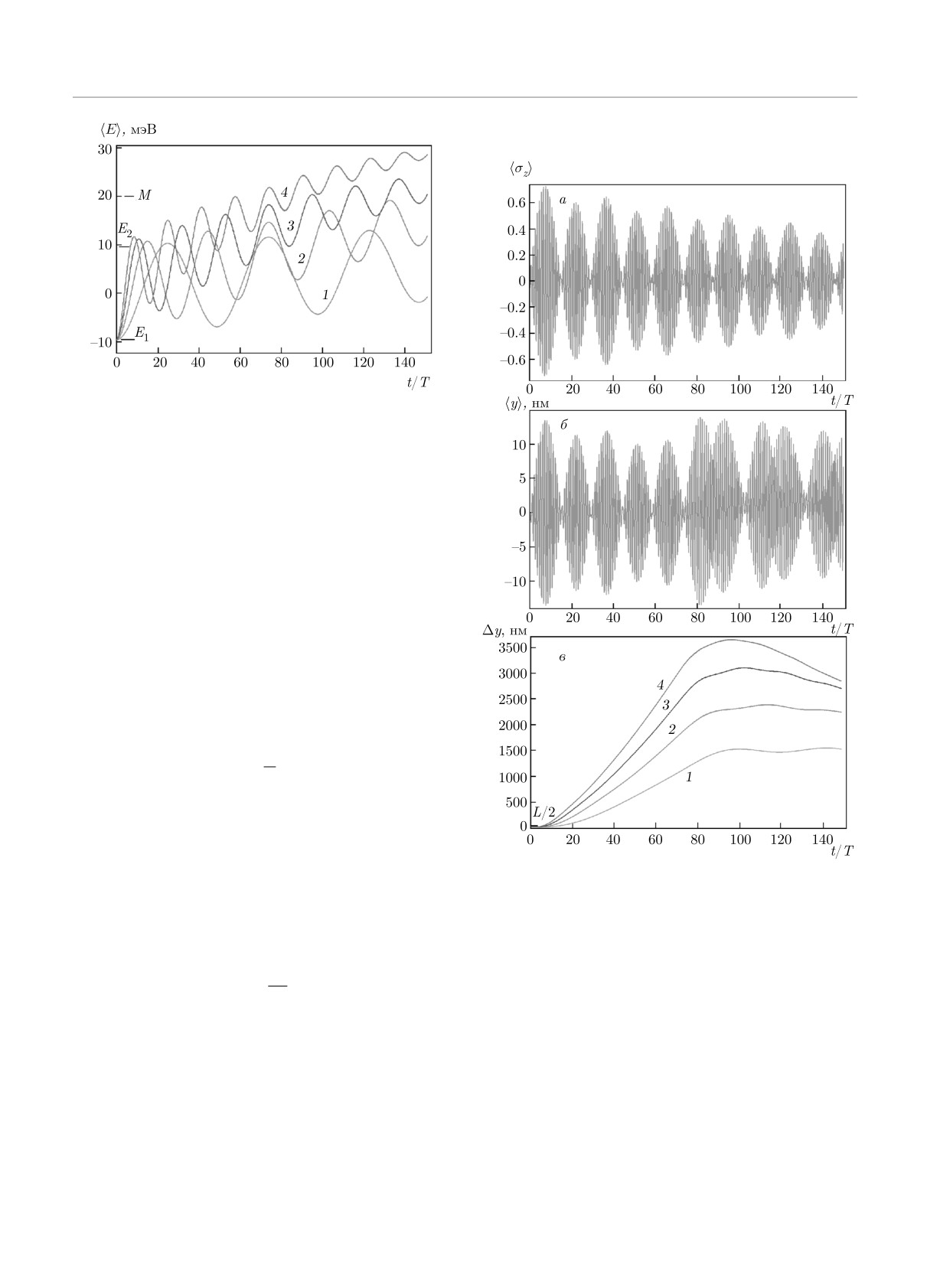
Рис. 5. (В цвете онлайн) Зависимости средней энергии

〈E(t)〉 от времени, построенные для различных ампли-

туд электрического поля F [мэВ/нм] = 0.03 (1), 0.05 (2),

0.07 (3), 0.09 (4). Высота барьера M = 20 мэВ отмечена

горизонтальной линией и отметкой M вместе с энергиями

дискретных уровней E1 и E2

Другую полезную информацию о динамике элек-

тронных состояний можно получить, анализируя

эволюцию среднего значения координаты 〈y(t)〉, что

использовалось нами ранее для задач о динамике в

полупроводниковой нанопроволоке [15,16]. При этом

необходимо отметить важное отличие системы с без-

массовым гамильтонианом (2) от обычной задачи в

приближении эффективной массы. Именно, для га-

мильтониана (2) оператор скорости v_y = ∂H/ℏ∂k_y

имеет вид

v_y =

σz.

(18)

ℏ

Выражение (18) означает, что средняя скорость не

может превышать амплитуду v₀ = A/ℏ и определя-

ется динамикой среднего значения 〈σ_z 〉, завися от

амплитуды электрического поля лишь опосредован-

но. В периодическом поле на частоте ω осцилляции

Рис. 6. (В цвете онлайн) Зависимости от времени средних

〈σ_z 〉 приводят к осцилляциям среднего значения ко-

значений проекции спина 〈σz 〉 (а) и среднего значения ко-

ординаты, амплитуду которых можно оценить как

ординаты 〈y〉 (б) для F = 0.05 мэВ/нм. Амплитуда осцил-

y₀ ∼ v₀/ω, что, согласно выражению (18), дает оцен-

ляций 〈y〉 на панели б находится в согласии с поведением

ку

〈σz 〉 на панели а и оценкой (19). Частота быстрых осцил-

ляций соответствует частоте поля ω, период медленных

y₀ ≤

(19)

ℏω

осцилляций огибающей отвечает половине периода TR/2

осцилляций Раби, показанных на рис. 3а. в) Зависимости

Вначале мы рассмотрим динамику среднего зна-

от времени среднеквадратичного уклонения Δy для ам-

чения 〈σ_z 〉 для какого-то одного значения ампли-

плитуд поля F [мэВ/нм] = 0.03 (1), 0.05 (2), 0.07 (3), 0.09

туды поля F . На рис. 6а показана зависимость от

(4). Рост Δy продолжается от начального значения L/2

времени 〈σ_z〉 для F = 0.05 мэВ/нм. Можно наблю-

до максимального значения, пропорционального амплиту-

дать как быстрые осцилляции на частоте поля ω,

де поля F

так и более медленные осцилляции огибающей, пе-

риод которой отвечает половине периода осцилля-

ций Раби, T_R/2, показанных на рис. 3а, т. е. времени

939

Д. В. Хомицкий, К. С. Кабаев, Е. А. Лаврухина

ЖЭТФ, том 158, вып. 5 (11), 2020

смены заселенностей двух дискретных уровней. На

вне области конфайнмента может иметь отличное от

рис. 6б показан график 〈y(t)〉 для того же значе-

нуля среднее значение на рассматриваемом интерва-

ния F = 0.05 мэВ/нм. Видно, что осцилляции 〈y(t)〉

ле времени, что будет отражать процесс покидания

следуют за осцилляциями 〈σ_z 〉 согласно соотноше-

электроном области квантовой точки. В следующем

нию (18). Амплитуда осцилляций y₀, согласно оцен-

разделе мы рассмотрим зависимость усредненной по

ке (19), не должна превышать для наших парамет-

времени локальной плотности тока в данной точке

ров значения y₀ = 19 нм, что, как видно на рис. 6б,

вне области конфайнмента как функции амплитуды

находится в хорошем согласии с численными резуль-

электрического поля.

татами.

Для описания динамики в координатном про-

Еще одно важное замечание касается взаимо-

странстве наряду с эволюцией среднего значения

отношений между убывающей во времени суммар-

координаты целесообразно рассмотреть и поведение

ной вероятностью заселенности дискретных уровней

среднеквадратичного уклонения

(15) и растущей величиной Δy(t) на рис. 6в. Зна-

√

чительное уширение волновой функции (13) вдоль

Δy(t) =

〈y²(t)〉 - 〈y(t)〉²,

y, что выражается в возрастании Δy(t), обусловле-

определяющего характерную ширину волновой

но растущим со временем вкладом состояний непре-

функции. На рис. 6в показана зависимость Δy(t)

рывного спектра, которые делокализованы на всем

для всех четырех амплитуд поля, рассматриваемых

масштабе нашей структуры, т. е. на области 2d = 12

в данной работе. Можно видеть, что Δy(t) показы-

мкм. Следовательно, даже небольшая примесь со-

вает рост от начального значения L/2, отмеченного

стояний континуума, когда величина (15) в начале

на графике горизонтальной чертой, до значений

эволюции на рис. 4 еще не сильно уменьшилась по

порядка 3000 нм, т. е. происходит расплывание на-

сравнению с единицей, может дать заметный рост

чального состояния вдоль края ТИ. Максимальное

Δy(t) на рис. 6в. При этом максимум электронной

значение Δy(t) на рис. 6в почти линейно зависит от

плотности по-прежнему будет сосредоточен в обла-

амплитуды электрического поля F , что отражает

сти квантовой точки на тех временах t < τ, где вре-

возрастание вклада от состояний континуума в

мя ухода в континуум τ ∝ 1/w(F ), а w(F ) оцени-

волновую функцию (13) с возрастанием амплитуды

вается согласно (17). Кроме того, среднее значение

поля, которая входит линейно в нестационарный

координаты, т. е. «центр тяжести» электронной вол-

гамильтониан (11). Характерное время достижения

новой функции, как это видно на рис. 6б, все время

максимума Δy(t) на рис. 6в можно сопоставить с

эволюции остается в области между барьерами для

пороговым временем пересечения средней энергией

рассматриваемого примера. Это также будет проил-

на рис. 5 границ интервала E₁ < 〈E〉 < E₂, что

люстрировано в следующем разделе при построении

отвечает нарастанию заметного вклада состояний

графика плотности вероятности, на котором будет

континуума в полную волновую функцию.

видно, что основная с точки зрения вклада в норму

Необходимо сделать следующие пояснения отно-

часть волновой функции находится в начале эволю-

сительно результатов, представленных на рис. 6. На-

ции между барьерами. В итоге на временах t < τ да-

личие осцилляций для 〈y(t)〉 и для соответствую-

же при расплывании волновой функции, как мы по-

щей компоненты скорости 〈v_y (t)〉, т. е. проекции спи-

лагаем, можно рассчитывать на осуществление опе-

на 〈σ_z (t)〉, согласно выражению (18), вместо посто-

раций с двухуровневой частью спектра, требуемых

янного тока для краевого состояния, являющегося

для создании кубита.

собственной функцией гамильтониана H1D = Ak_yσ_z

без барьеров, обусловлено двумя обстоятельствами.

Подводя итог данного раздела, мы можем сде-

Во-первых, это принятое нами приближение беско-

лать вывод, что различные методы иследования ди-

нечно широких барьеров, что отвечает функциони-

намики как в гильбертовом пространстве состояний

рованию всей системы «квантовая точка + барье-

для вероятности локализации (15) и средней энер-

ры» в «запертом» режиме. Во-вторых, это периоди-

гии, так и в координатном пространстве для средне-

ческое во времени электрическое поле в гамильтони-

го значения и дисперсии координаты дают согласу-

ане (11), не вызывающее постоянного тока с опреде-

ющиеся друг с другом аппроксимации. Эти аппрок-

ленной направленностью в пространстве, а приводя-

симации позволяют оценить время покидания элек-

щее лишь к осцилляциям скорости и расплыванию

троном зоны локализованных состояний и его по-

начального состояния, как это видно на рис. 6. При

следующего постепенного перехода в непрерывный

этом локальная плотность тока в какой-либо точке

спектр.

940

ЖЭТФ, том 158, вып. 5 (11), 2020

Спиновый резонанс в квантовой точке.. .

4. РАСПРЕДЕЛЕНИЯ ПЛОТНОСТИ В

ПРОСТРАНСТВЕ И ПЛОТНОСТЬ ТОКА

ВЕРОЯТНОСТИ

4.1. Эволюция распределений плотности

Для экспериментального и практического при-

менения обсуждаемых эффектов важное значение

имеет эволюция не только средних значений, но

и локальных плотностей соответствующих физиче-

ских величин. Прежде всего, это плотность заряда,

т. е. плотность вероятности, и плотность спиновой

проекции S_i (в единицах ℏ/2), определяемые в со-

стоянии (13) как

ρ(y, t) = |Ψ(y, t)|²,

(20)

S_i(y, t) = Ψ^†(y, t)σ_iΨ(y, t),

где i = x, y, z. Мы рассмотрим пример эволюции

плотностей (20) для плотности вероятности и ком-

поненты спиновой плотности S_x в области, примы-

кающей к квантовой точке и занимающей простран-

ственный интервал -3L/2 < y < 3L/2, для наиболее

сильного электрического поля F = 0.09 мэВ/нм на

начальном этапе эволюции при 0 < t < 30T .

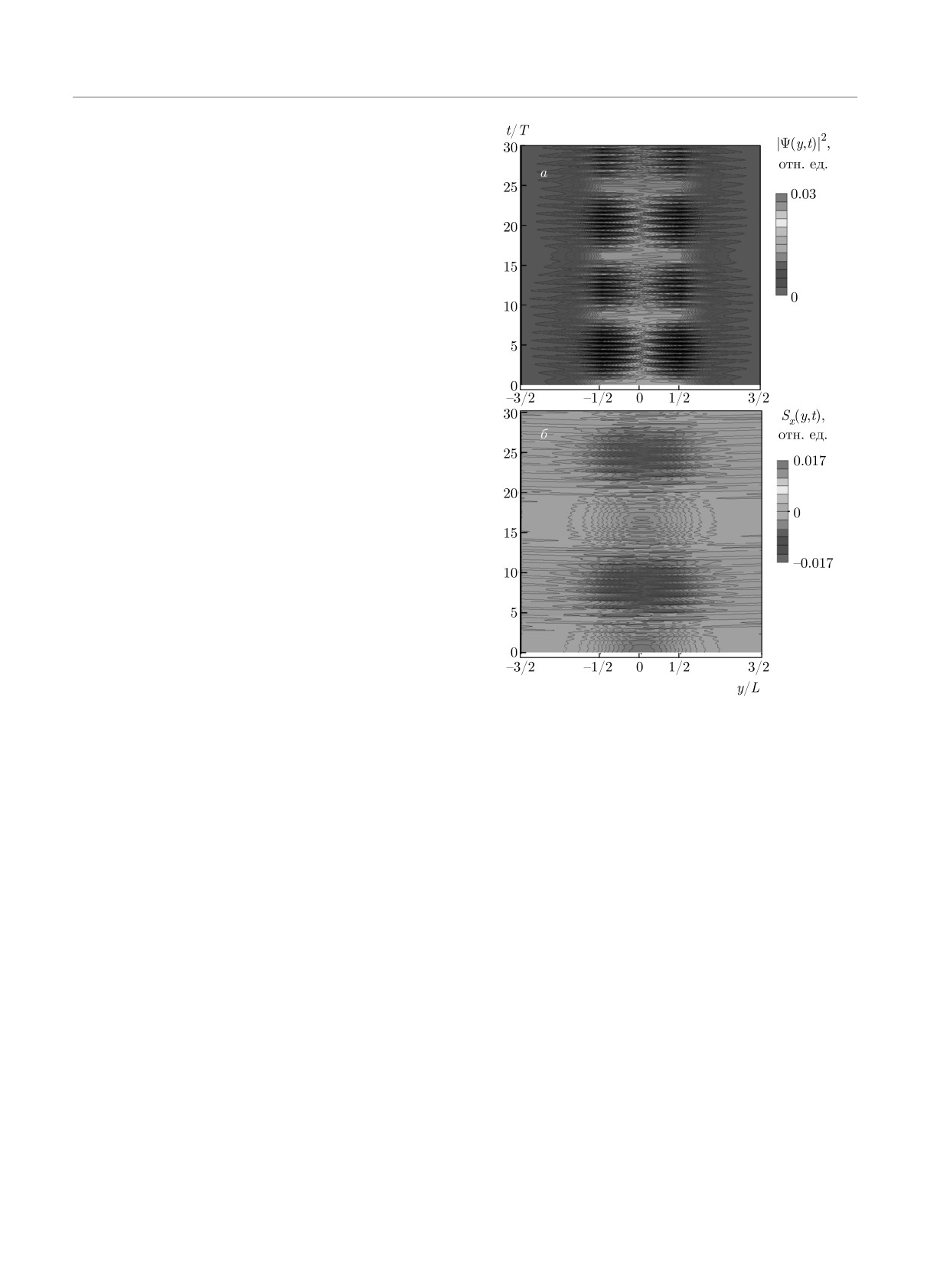
На рис. 7 приведены контурные графики вида

f (y, t) = C для плотности вероятности (рис. 7а) и

компоненты спиновой плотности S_x(y, t) (рис. 7б),

на начальном этапе эволюции 0 < t < 30T . На рис. 7

можно выделить несколько особенностей для эво-

люции плотности, которые качественно присутству-

Рис. 7. (В цвете онлайн) Эволюция распределений (20)

ют и при других значениях амплитуды электриче-

для плотности вероятности (а) и компоненты спиновой

ского поля F . Во-первых, наблюдаются мелкомас-

плотности Sx (б) в периодическом электрическом поле с

штабные быстрые осцилляции на частоте электри-

амплитудой F = 0.09 мэВ/нм, в области -3L/2 < y <

ческого поля ω, подобные осцилляциям для 〈y(t)〉,

< 3L/2 и на интервале 0 < t < 30T . Мелкомасштабные

осцилляции отвечают частоте электрического поля. Ин-

рассмотренным в предыдущем разделе. Во-вторых,

тервал времени, на котором происходит смена знака Sx,

наблюдаются крупномасштабные медленные осцил-

отвечает периоду осцилляций Раби, при котором заселен-

ляции с периодом, соответствующим смене заселен-

ность уровня E1 с Sx > 0 сменяется заселенностью уровня

ностей дискретных уровней E₁ и E₂ с частотой Ра-

E2 с Sx < 0. С течением времени амплитуда обеих плотно-

би. Нам представляется важной следующая особен-

стей в области квантовой точки испытывает затухание, что

ность эволюции плотности S_x, заметная на рис. 7б:

связано с переходами в непрерывный спектр, сопровож-

заселенность уровня E₁ со знаком спиновой плотно-

дающимися нарастающей делокализацией волновой функ-

сти S_x > 0 сменяется на временах порядка T_R = 16T

ции

заселенностью уровня E₂ с S_x < 0. Это связано с

противоположными знаками проекции S_x для сос-

стоит в том, что с течением времени амплитуда обе-

тояний двух дискретных уровней, как показано на

их плотностей в области квантовой точки постепен-

рис. 2б,г. Данная особенность может иметь значе-

но затухает, что на рассматриваемом на рис. 7 мас-

ние для экспериментального детектирования явле-

штабе времени лучше заметно для спиновой плот-

ния осцилляций Раби в данной системе, так как

ности. Это связано с переходами в непрерывный

смена знака проекции спиновой плотности может

спектр, сопровождающимися нарастающей делока-

быть обнаружена магнитным зондом, находящим-

лизацией волновой функции. Мы обсудим интенсив-

ся в непосредственной близости от квантовой точки.

ность такой делокализации в следующем разделе

Наконец, третья особенность графиков на рис. 7 со-

при расчете тока вероятности.

941

Д. В. Хомицкий, К. С. Кабаев, Е. А. Лаврухина

ЖЭТФ, том 158, вып. 5 (11), 2020

что говорит о развитии процесса ухода электрона из

области квантовой точки в континуум. Во-вторых,

из рис. 8 можно сделать вывод, что с ростом амп-

литуды поля F максимальное значение плотности

тока, пропорциональное локальной спиновой плот-

ности S_z(y₀, t), растет в зависимости от F по зако-

ну, близкому к линейному. Это находится в согла-

сии с нашими предыдущими результатами о дина-

мике средних значений проекций спина для лока-

лизованных состояний в подобной квантовой точ-

ке со многими дискретными уровнями, рассмотрен-

ной в работе [12]. Можно надеяться, что полученные

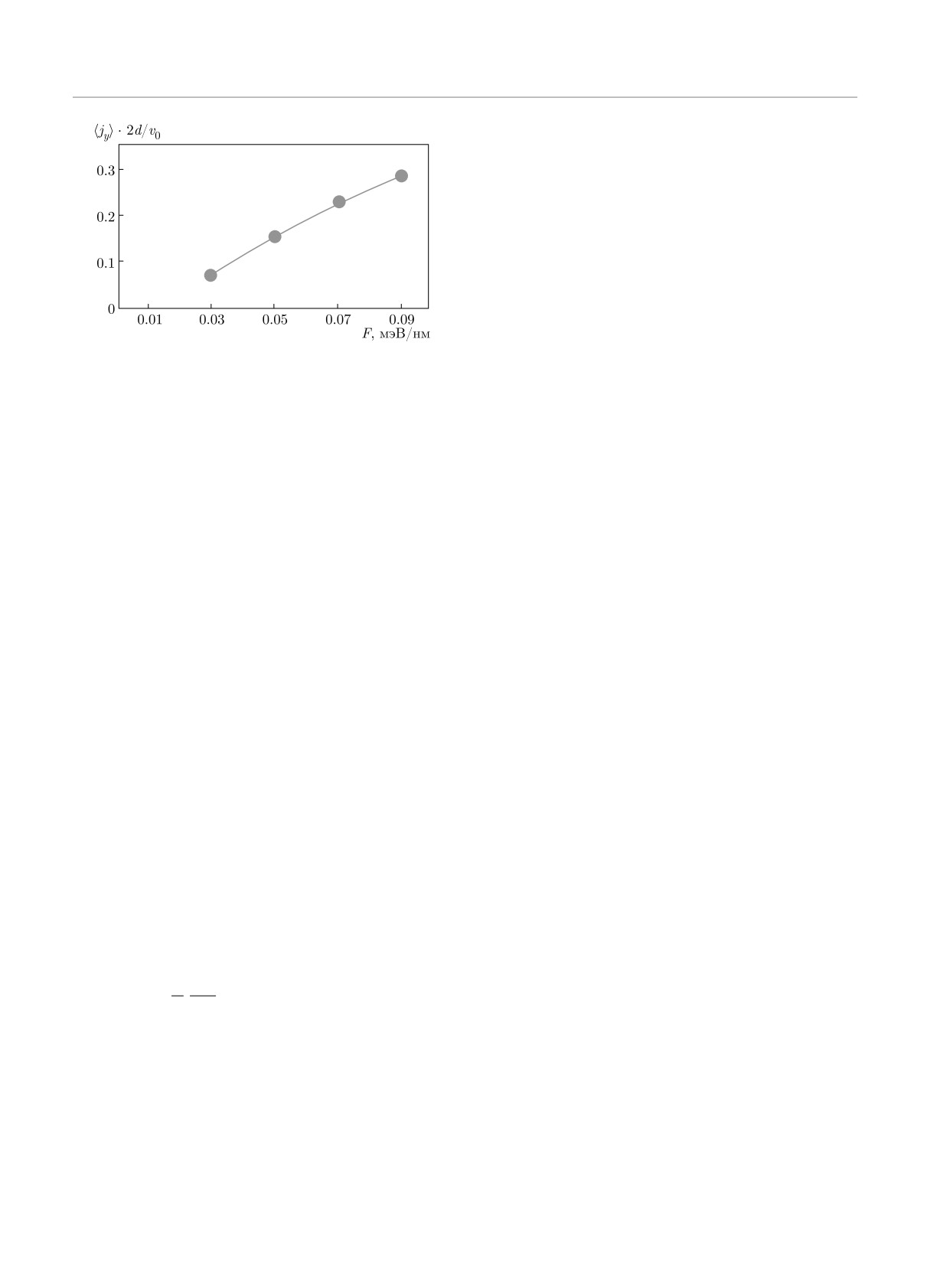
Рис. 8. Зависимость среднего значения локальной плот-

результаты для плотности тока вероятности могут

ности тока вероятности (21) за весь период наблюдения

быть экспериментально проверены при детектиро-

0 < t < NT от амплитуды электрического поля F

вании электрического тока вне области квантовой

4.2. Плотность тока вероятности

точки, что будет служить индикатором перехода в

Для количественного описания интенсивности

состояния непрерывного спектра.

покидания области квантовой точки при переходах

5. ВЫВОДЫ

в континуум помимо эволюции заселенности дис-

Исследована динамика электронных состояний

кретных уровней (15) можно рассчитать плотность

под действием периодического электрического поля,

тока вероятности в некоторой точке вне области

приложенного к квантовой точке, созданной маг-

конфайнмента. Даже если полный ток через струк-

нитными барьерами на краю топологического изо-

туру равен нулю, т. е. система «квантовая точка +

лятора на базе квантовой ямы HgTe/CdTe. Рассмот-

барьеры» находится в «запертом» режиме, ненуле-

рена конфигурация с двумя дискретными уровня-

вой средний ток в конкретной точке вне области

ми с противоположной x-проекцией спина и учте-

конфайнмента служит индикатором ухода в непре-

ны состояния непрерывного спектра над барьера-

рывный спектр [27, 28]. Для нахождения плотно-

ми. Рассчитана частота осцилляций заселенностей

сти тока обратимся к оператору скорости (18), ко-

дискретных уровней для различных амплитуд по-

торый пропорционален оператору проекции спина

ля, а также эволюция суммарной заселенности дис-

σ_z. Мы будем вычислять значение плотности тока в

кретных уровней. Численно и аналитически найде-

выбранной точке y₀ = 3L/2, т. е. вне области кван-

ны времена затухания суммарной заселенности дис-

товой точки. Далее, надо учесть то обстоятельство,

кретных уровней со временем при учете состояний

что в периодическом электрическом поле локальная

континуума. Исследована динамика средних значе-

плотность вероятности испытывает мелкомасштаб-

ний энергии, z-проекции спина и координаты, а так-

ные осцилляции на периоде поля, как это видно на

же локальных плотностей вероятности и x-проекции

рис. 7а, что отразится и на мгновенных значениях

спина, и соответствующей локальной плотности то-

плотности тока. Чтобы определить среднюю плот-

ка вероятности, описывающей покидание квантовой

ность тока за все время наблюдения 0 < t < NT ,

точки. Результаты работы могут быть полезны при

где в наших расчетах N = 150, мы выполним усред-

создании новых поколений устройств наноэлектро-

нение локальной плотности тока по этому интервалу

ники и спинтроники на основе топологических изо-

и после подстановки выражения (18) для оператора

ляторов.

скорости будем вычислять величину

∫

Благодарности. Авторы выражают призна-

〈j_y (y₀)〉 =

Ψ^†(y₀, τ)σ_zΨ(y₀, τ)dτ.

(21)

тельность А. А. Конакову, И. С. Бурмистрову,

ℏ NT

А. Ф. Садрееву, С. В. Морозову, В. Я. Алёшкину и

Результаты расчета усредненного тока (21), нор-

другим участникам XXIV Международного симпо-

мированного на скорость v₀ = A/ℏ и полную дли-

зиума «Нанофизика и наноэлектроника» (Нижний

ну краевой области 2d, показаны на рис. 8. Можно

Новгород, 10-13 марта 2020 г.), а также семинара

выделить следующие особенности полученных ре-

по физике полупроводников Института физики мик-

зультатов. Во-первых, усреднение (21) дает ненуле-

роструктур РАН, за полезные обсуждения. Авторы

вое среднее значение плотности тока вероятности на

благодарны Д. А. Кулакову за техническое содейст-

рассматриваемом интервале времени 0 < t < NT,

вие.

942

ЖЭТФ, том 158, вып. 5 (11), 2020

Спиновый резонанс в квантовой точке.. .

Финансирование. Работа выполнена при под-

стояний, т. е. двухкомпонентных спиноров, являю-

держке гранта в рамках Государственного зада-

щихся собственными функциями гамильтониана (1).

ния Министерства науки и высшего образования

В указанной работе исследовалось взаимодействие

РФ № 0729-2020-0058 и гранта Президента РФ

со спином магнитной примеси, которую можно рас-

МК-1719.2020.2.

сматривать как сильнолокализованный магнитный

барьер. Спиновая часть оператора обменного вза-

имодействия не зависит от пространственного про-

ПРИЛОЖЕНИЕ A

филя потенциала взаимодействия, если он остается

достаточно короткодействующим, что имеет место

В данном Приложении мы обсудим вывод га-

и в нашей модели. Мы воспользуемся выражением

мильтониана (2) для взаимодействия краевых со-

(6) из Supplementary Material работы [11] для опе-

стояний с магнитными барьерами. Будем опирать-

ратора взаимодействия H_ex с магнитной примесью

ся на результаты работы [11], где был получен га-

(барьером):

мильтониан взаимодействия в базисе краевых со-

(

)

J_zS^z + J_anS^- + J^∗anS⁺

J^∗⊥S

H_ex =

f (y).

(22)

J_⊥S⁺

-(J_zS^z + J_anS^- + J^∗anS⁺)

Здесь f(y) есть функция, описывающая пространст-

|J_⊥|S^x = M cos θ, |J_⊥|S^y = M sin θ, с учетом опреде-

венную локализацию магнитного барьера вдоль

ления S^± = S^x ± iS^y мы получаем из (23), что

края, которому параллельна в нашей модели ось y.

(

)

В работе [11], а также в работах [7, 8] функция f(y)

cosθ - i sinθ

H_ex = M

f (y),

(24)

была аппроксимирована дельта-функций. В нашей

cosθ + i sinθ

модели мы предполагаем более плавный профиль

или

намагниченности конечной ширины и высоты, ап-

проксимируемый ступенчатой функцией, что, по на-

( (

)

шему мнению, лучше соответствует реальным маг-

H_ex = Mf(y) cosθ

нитам. При этом характер взаимодействия с магни-

(

))

том имеет по-прежнему обменную, т.е. локальную

-i

и короткодействующую природу. Компоненты на-

+ sinθ

(25)

магниченности барьера обозначены как S^z и S^± =

= S^x ± iS^y. Константы обменного взаимодействия

т. е. выражение

обозначены как J_z, J_⊥ = J^∗⊥ (так как согласно [11]

J_⊥ — вещественная величина), и присутствует до-

H_ex = Mf(y)(σ_x cosθ + σ_y sinθ),

(26)

бавка от анизотропной части обменного взаимодей-

ствия с параметром J_an. В работе [11] принята оцен-

которое определяет взаимодействие краевых состо-

ка |J_an| ≪ |J_⊥| ≪ |J_z|, поэтому анизотропное слага-

яний с каждым из магнитных барьеров в гамильто-

емое в нашей модели может быть опущено, и мы

ниане (2) нашей модели.

положим J_an = 0. Далее, в нашей задаче намагни-

ченность барьера ориентирована в плоскости xy, по-

этому компонента намагниченности S^z = 0. В этих

ПРИЛОЖЕНИЕ B

обстоятельствах гамильтониан взаимодействия (22)

Включение однородного в пространстве, но пере-

с магнитным барьером в базисе двухкомпонентных

менного во времени (т. е. рассматриваемого в квази-

собственных функций гамильтониана краевых со-

стационарном приближении) электрического поля в

стояний (1) примет следующий вид:

гамильтониан может осуществляться при помощи

(

)

скалярного или векторного потенциалов. В приме-

J^∗⊥S

нении к краевым состояниям в ТИ и подобных им

H_ex =

f (y).

(23)

J_⊥S⁺

структурам используются оба подхода. Так, в нашей

работе [12] использовался скалярный потенциал, в

Принимая во внимание вещественность J_⊥ и

работе [29] — только векторный потенциал, а в ра-

обозначая проекции намагниченности барьера как

ботах [30,31] учитывались вклады и от скалярного,

943

Д. В. Хомицкий, К. С. Кабаев, Е. А. Лаврухина

ЖЭТФ, том 158, вып. 5 (11), 2020

и от векторного потенциалов. В данном Приложе-

выражения в (29) нам необходимо значение y₀, рав-

нии мы покажем, что переход от скалярного к век-

ное в нашей задаче 18.71 нм, и значение матрично-

торному потенциалу, приводящий к появлению спи-

го элемента оператора спина σ_z. Численные расче-

нового оператора σ_z в гамильтониане, не изменяет

ты показывают, что для пары дискретных уровней

матричного элемента, отвечающего за частоту Раби

при выбранных параметрах задачи |σ_z|₁₂ = 0.705,

для переходов между двумя дискретными уровнями

что согласно (29) дает значение модуля матрично-

в нашей системе.

го элемента |y⁽¹⁾¹²| = 13.19 нм, т. е. совпадающее с

При использовании векторного потенциала A(t)

полученным из калибровки со скалярным потенци-

включение в гамильтониан переменного электричес-

алом. Совпадение результатов подходов с операто-

кого поля F(t) = -∂A/c∂t осуществляется путем

рами спина и координаты не является случайным,

обычной подстановки k → k - eA/ℏc. Для нашей

поскольку оператор скорости для данной модели,

задачи с гамильтонианом (2) и периодическим элек-

согласно (18), пропорционален оператору спина σ_z ,

трическим полем вдоль оси y с компонентой F sin ωt

т. е. динамика координаты и z-проекции спина тесно

мы получаем после такой подстановки оператор воз-

связаны. Мы полагаем, что найденное хорошее со-

мущения V₁(t) в следующей форме, нормированной

гласие между двумя подходами позволяет использо-

на амплитуду электрического поля F , измеряемую

вать при исследовании осцилляций Раби любой из

у нас в мэВ/нм:

них, что обосновывает применение скалярного по-

тенциала для описания переменного во времени и

V₁(t)

σ_z cosωt,

(27)

однородного в пространстве электрического поля в

ℏω

гамильтониане (11).

где A = 360 мэВ · нм — константа в гамильтониане

(2), а частота электрического поля удовлетворяет

условию резонанса (12). В такой форме возмущение

ЛИТЕРАТУРА

от электрического поля содержит спиновый опера-

B. A. Bernevig, Topological Insulators and Topo-

тор σ_z и не содержит оператора координаты, как в

logical Superconductors, Princeton Univ. Press,

калибровке со скалярным потенциалом, применяв-

Princeton, USA (2013).

шейся в гамильтониане (11), для которой оператор

возмущения V₂(t) имеет вид

Topological Insulators. Fundamentals and Perspecti-

ves, ed. by F. Ortmann, S. Roche, and S. O. Valenzue-

V₂(t)/F = y sinωt.

(28)

la, Wiley-VCH Verlag, Weinheim, Germany (2015).

M. Z. Hasan and C. L. Kane, Rev. Mod. Phys. 82,

В правой части обоих операторов, (27) и (28),

3045 (2010).

стоят величины, имеющие размерность координа-

ты, поэтому матричные элементы данных операто-

X.-L. Qi and S.-C. Zhang, Rev. Mod. Phys. 83, 1057

(2011).

ров без временного множителя можно обозначить

как

M. I. Katsnelson, K. S. Novoselov, and A. K. Geim,

y(1)mn = y₀ · (σ_z)_mn, y(2)mn = y_mn.

(29)

Nature Phys. 2, 620 (2006).

В первом из выражений (29) амплитуда y₀ =

A. Kundu, A. Zazunov, A. L. Yeyati, T. Martin, and

= A/ℏω совпадает с амплитудой, определяемой пра-

R. Egger, Phys. Rev. B 83, 125429 (2011).

вой частью неравенства (19), которое иллюстриру-

C. Timm, Phys. Rev. B 86, 155456 (2012).

ет характерный масштаб осцилляций среднего зна-

чения координаты для динамики в базисе краевых

G. Dolcetto, N. Traverso Ziani, M. Biggio et al., Phys.

Rev. B 87, 235423 (2013).

состояний. Таким образом, оба подхода как со ска-

лярным, так и с векторным потенциалом приводят

G. J. Ferreira and D. Loss, Phys. Rev. Lett. 111,

к одному и тому же набору характерных амплитуд

106802 (2013).

для возмущения от электрического поля.

10.

C. Ertler, M. Raith, and J. Fabian, Phys. Rev. B 89,

Количественное сопоставление двух выражений

075432 (2014).

в (29) для матричных элементов между двумя дис-

кретными уровнями E₁ и E₂ приводит к следую-

11.

L. Kimme, B. Rosenow, and A. Brataas, Phys. Rev.

B 93, 081301(R) (2016).

щему результату. Для матричного элемента коор-

динаты во втором равенстве в (29) мы нашли чис-

12.

D. V. Khomitsky, A. A. Chubanov, and A. A. Kona-

ленно, что |y⁽²⁾¹²| = 13.19 нм. Для оценки первого

kov, ЖЭТФ 150, 1200 (2016).

944

ЖЭТФ, том 158, вып. 5 (11), 2020

Спиновый резонанс в квантовой точке.. .

13. Д. В. Хомицкий, А. А. Чубанов, Е. А. Лаврухина,

23. S. D. Ganichev and W. Prettl, Intense Terahertz

Н. Нжийа, ФТП 51, 1557 (2017).

Excitation of Semiconductors, Series on Semiconduc-

tor Science and Technology 14, Oxford Univ. Press

14. E. I. Rashba and Al. L. Efros, Phys. Rev. Lett. 91,

(2006).

126405 (2003).

24. A. Singh, A. Pashkin, S. Winnerl et al., Light: Sci.

15. D. V. Khomitsky, E. A. Lavrukhina, and E. Ya. Sher-

and Appl. 9, 30 (2020).

man, Phys. Rev. B 99, 014308 (2019).

25. С. Кунин, Вычислительная физика, Мир, Москва

16. D. V. Khomitsky, E. A. Lavrukhina, and E. Ya. Sher-

(1992).

man, Phys. Rev. Applied 14, 014090 (2020).

26. А. М. Сатанин, Динамика электронов в нано-

структурах, Изд-во Нижегородского государст-

17. B. D. Kong, Y. G. Semenov, C. M. Krowne, and

венного университета им. Н. И. Лобачевского,

K. W. Kim, Appl. Phys. Lett. 98, 243112 (2011).

Нижний Новгород (2006).

18. J. P. Zhang and J. H. Yuan, Eur. Phys. J. B 85, 100

27. Н. Б. Делоне, В. П. Крайнов, Атом в сильном све-

(2012).

товом поле, Энергоатомиздат, Москва (1984).

19. Z.-Q. Liu, R.-Q. Wang, M.-X. Deng, and L.-B. Hu,

28. Н. Б. Делоне, В. П. Крайнов, Нелинейная иони-

Comm. Theor. Phys. 63, 777 (2015).

зация атомов лазерным излучением, Физматлит,

Москва (2001).

20. B. Scharf, A. Matos-Abiague, J. E. Han et al., Phys.

Rev. Lett. 117, 166806 (2016).

29. A. Scholz, A. López, and J. Schliemann, Phys. Rev.

B 88, 045118 (2013).

21. C.-X. Liu, X.-L. Qi, H. Zhang et al., Phys. Rev. B 82,

045122 (2010).

30. F. Dolcini, R. C. Iotti, A. Montorsi, and F. Rossi,

Phys. Rev. B 94, 165412 (2016).

22. M. Brooks and G. Burkard, Phys. Rev. B 101, 035204

(2020).

31. F. Dolcini, Phys. Rev. B 95, 085434 (2017).

945

ЖЭТФ, вып. 5 (11)