ЖЭТФ, 2020, том 158, вып. 5 (11), стр. 946-961

ЭЛЕКТРОННАЯ СТРУКТУРА И ЭЛЕКТРОПРОВОДНОСТЬ

НЕУПОРЯДОЧЕННОГО БИНАРНОГО СПЛАВА A1-xB_x

В РАМКАХ КЛАСТЕРНОГО ПОДХОДА

ДЛЯ МОДЕЛИ ХАББАРДА

С. В. Николаевa,b*, Ю. С. Орловa,b**, В. А. Дудников^b

^a Сибирский федеральный университет

660041, Красноярск, Россия

^b Институт физики им. Л. В. Киренского,

Федеральный исследовательский центр «Красноярский научный центр»

Сибирского отделения Российской академии наук

660036, Красноярск, Россия

Поступила в редакцию 14 мая 2020 г.,

после переработки 27 мая 2020 г.

Принята к публикации 27 мая 2020 г.

Предложен метод расчета электронной зонной структуры разупорядоченных систем с сильными элек-

тронными корреляциями. Рассматриваются различные подходы к описанию электропроводности неупо-

рядоченных систем. Расчеты основаны на вычислении усредненной по различным конфигурациям клас-

тера одночастичной функции Грина системы, формализме Больцмана и теории линейного отклика Кубо.

В качестве базовой модели используется модель Хаббарда для бинарного сплава A1-xBx.

DOI: 10.31857/S0044451020110164

литературе посвящено множество работ. Например,

кластерные обобщения приближения когерентного

1. ВВЕДЕНИЕ

потенциала, основанные на рассмотрении единично-

Успехи в исследовании различных свойств

го кластера в эффективной среде [1], приближение

неупорядоченных систем (сплавов, твердых рас-

«блуждающего кластера»

[4]. В работах

[5-7]

творов, аморфных металлов и полупроводников и

развит метод учета статистических корреляций,

т. д.) связаны с развитием их электронной теории.

основанный на кластерном разложении для одно-

Исследованию спектральных характеристик неупо-

и двухчастичной функций Грина, определяющих

рядоченных систем посвящено большое количество

соответственно энергетический спектр электронов

работ

[1-3]. Развиты различные методы вычис-

и электропроводность сплавов. Актуальность такой

ления усредненной по конфигурациям функции

задачи определяется, например, необходимостью

Грина системы. При этом значительные усилия

исследования предсказанной ранее [8, 9] перестрой-

были направлены на обобщение приближения

ки спектра электронов при упорядочении сплавов,

когерентного потенциала, которое является луч-

когда при дальнем упорядочении в спектре электро-

шим одноузельным приближением при описании

нов возникает щель при энергиях, соответствующих

свойств различных сплавов. Однако этот метод не

границе зоны Бриллюэна упорядоченного сплава.

позволяет учесть статистические межатомные кор-

При этом поведение электропроводности сплава

реляции. Чтобы учесть корреляции, обусловленные

при дальнем упорядочении существенно зависит

многократным рассеянием электронов на разных

от положения уровня Ферми по отношению к об-

узлах решетки, или наличие ближнего порядка в

разующейся щели. В работах [8, 9] было высказано

расположении атомов, необходимо выйти за рамки

предположение о возможности существования пере-

одноузельного приближения. Этой проблеме в

хода металл-диэлектрик, который может возникать

в случае, если уровень Ферми попадает в область

^* E-mail: svinikolaev@sfu-kras.ru

^** E-mail: jso.krasn@mail.ru

указанной щели.

946

ЖЭТФ, том 158, вып. 5 (11), 2020

Электронная структура и электропроводность. ..

Кинетические характеристики неупорядоченных

стве базовой модели используется модель Хаббар-

систем интенсивно исследуются в последнее время,

да для бинарного сплава A1-xB_x. Рассматривают-

в том числе в связи с изучением перехода Андер-

ся различные подходы к описанию электропровод-

сона [10]. Здесь наиболее последовательной теори-

ности неупорядоченных систем, основанные на вы-

ей является теория «слабой локализации» [11, 12],

числении усредненной по различным конфигураци-

которая позволяет рассматривать с помощью тео-

ям кластера одночастичной функции Грина систе-

рии возмущений малые эффекты, предшествующие

мы, формализме Больцмана и теории линейного от-

локализации и возникающие в проводящем состоя-

клика Кубо.

нии. Эта теория является теорией линейной реакции

Кубо для электронов, взаимодействующих с приме-

сями, которая строится в терминах одночастичных

2. МИНИМАЛЬНАЯ МОДЕЛЬ И МЕТОД

функций Грина, вычисленных в самосогласованном

В настоящей работе мы ограничились рассмот-

борновском приближении. Малым параметром тео-

рением двумерной простой квадратной решетки би-

рии в случае вырожденного электронного газа (ко-

нарного сплава A1-xB_x. Результаты расчета элек-

торый в основном рассматривается в литературе)

тронной структуры будут представлены для случая

является величина λ = ℏ/E_F τ (E_F — энергия Фер-

x = 0.5, но рассматриваемый подход может быть ис-

ми, τ — время релаксации электрона, обусловленное

пользован для любой концентрации x (0 ≤ x ≤ 1).

упругим рассеянием на примесях). Таким образом,

Вначале рассмотрим полностью разупорядоченный

при λ ≪ 1 рассеяние является слабым и не приво-

случай, когда ионы A и B случайным образом рас-

дит к сильному изменению одночастичных свойств

положены в узлах кристаллической решетки, а за-

(плотности состояний электрона), хотя учет кванто-

тем обсудим возможность учета ближнего порядка

вых поправок по λ к проводимости достаточен для

в расположении ионов типа A и B. Гамильтониан

возникновения эффектов слабой локализации [13].

модели запишем в общем виде:

Представляется необходимым развитие последова-

тельной теории, справедливой и для случая сильно-

∑

Ĥ₌ ε_ia^†i,σa_i,σ -

t_ija^†i,σa_j,σ +

го рассеяния, когда могут существенно изменяться

i,σ

〈i,j〉,σ

одночастичные свойства системы.

∑

U_i

Теория электропроводности неупорядоченных

n_i,σn_i,σ,

(1)

систем с сильными электронными корреляциями

i,σ

находится на стадии развития. Развитие подходов

к описанию электропроводности систем с сильными

где a^†i,σ и a_i,σ — операторы рождения и уничтожения

электронными корреляциями стало особенно акту-

электрона с проекцией спина σ =↑, ↓ на узле i кри-

альным после открытия явления спин-зависимого

сталлической решетки, n_i,σ = a^†i,σa_i,σ — оператор

транспорта, которое имеет широкие перспективы

числа электронов с проекцией спина σ (σ = -σ). Со-

применения в микроэлектронике [14-16].

гласно принципу Паули, на одном узле не может на-

В настоящей работе предложен метод расчета

ходиться больше двух электронов с противополож-

электронной зонной структуры разупорядоченных

ными проекциями спина σ. В гамильтониане (1) ε_i —

систем с сильными электронными корреляциями,

энергия электрона на узле i. ε_i принимает значение

использующий широко распространенный в послед-

ε_A с вероятностью 1 - x и ε_i = ε_A + Δ с вероят-

нее время кластерный подход [17, 18]. Преимуще-

ностью x. Другими словами, ε_i = ε_A, если узел i

ством данного подхода является непосредственный

занят ионом типа A, и ε_i = ε_A + Δ, если узел i при-

учет электронных корреляций, ближнего магнитно-

надлежит иону типа B. В дальнейшем для удобства

го и структурного порядков, которые играют суще-

энергия ε_A выбрана равной нулю. Величина t_ij —

ственную роль при описании низкоразмерных маг-

интеграл перескока с узла j на узел i (t_ij = t_A, ес-

нитных систем и различных сплавов. Схема кла-

ли i, j ∈ A; t_ij = t_B, если i, j ∈ B и t_ij = t_AB, если

стерной теории содержит два основных этапа по-

i ∈ A, j ∈ B или наоборот). Ui — параметр куло-

строения решения: первый — это выбор кластера

новского взаимодействия на узле i (U_i = U_A, если

и нахождение его собственных многоэлектронных

i ∈ A и U_i = U_B, если i ∈ B). Гамильтониан (1) не

состояний методом точной диагонализации; вто-

обладает трансляционной инвариантностью, поэто-

рой — вычисление термодинамических величин и их

му корреляционные функции K (ω, r₁, r₂) зависят от

усреднение по беспорядку — конфигурациям клас-

расположения ионов и, следовательно, от обеих ко-

тера с различным расположением ионов. В каче-

ординат, r₁ и r₂, а не только от их разности. Однако

947

12*

С. В. Николаев, Ю. С. Орлов, В. А. Дудников

ЖЭТФ, том 158, вып. 5 (11), 2020

ными разъяснениями и подробностями к оригиналь-

ным работам [19, 20]. Основная идея заключается в

том, что для матричного представления оператора

K используется базис одноэлектронных состояний

a†1,↑ |0〉, a†2,↑ |0〉, . . ., a^†L,↑ |0〉,

a†1,↓ |0〉, a†2,↓ |0〉, . . ., a^†L,↓ |0〉,

где L = N_c × N_c. При этом генерируются различные

случайные конф:гу;ации кластера со средним чис-

лом электронов

= N_e, удовлетворяющих усло-

вию N_A/N_B ≈ (1 - x)/x (см. выше).

Предложенный метод можно обобщить на общий

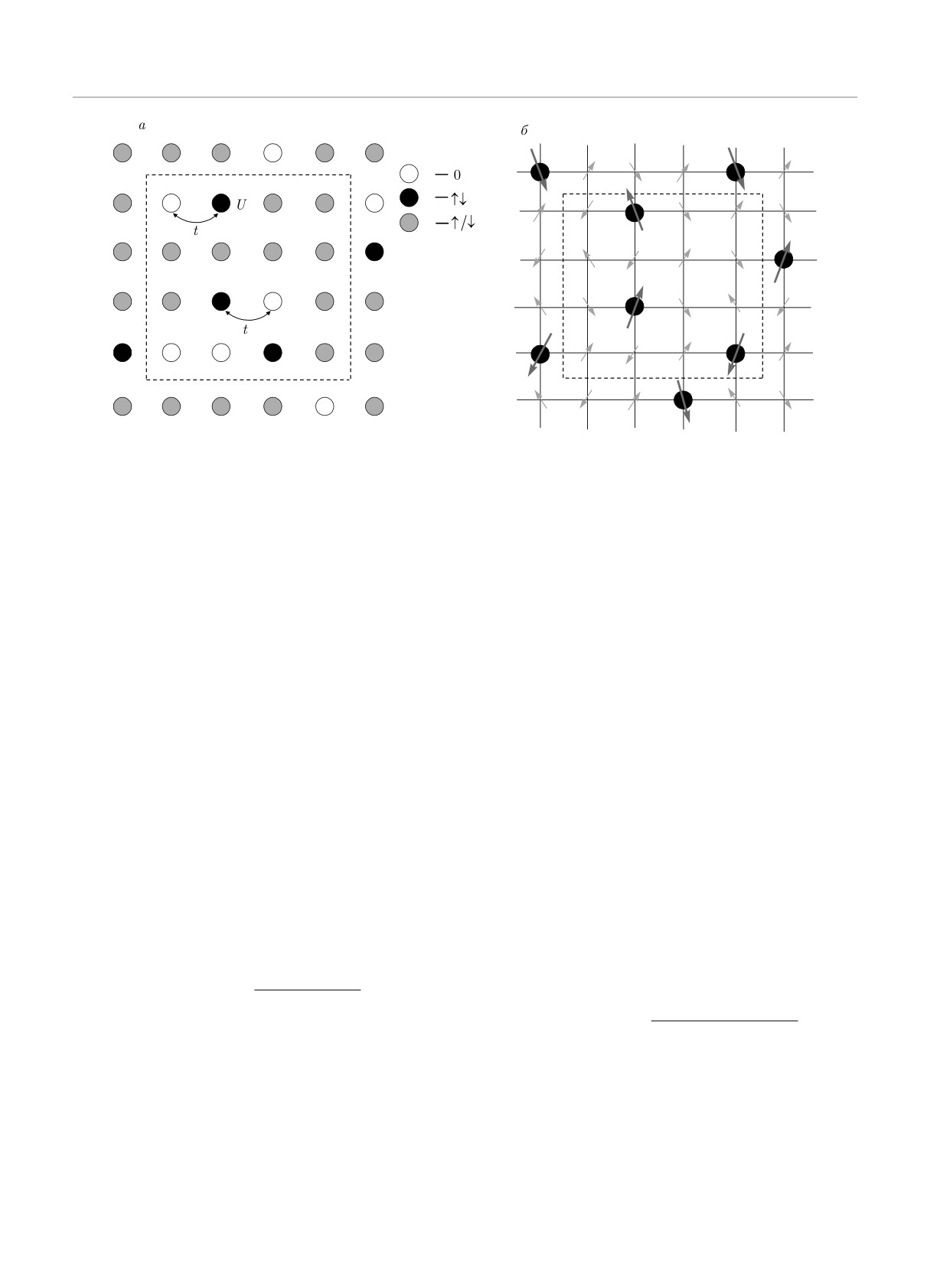
Рис. 1. Фрагмент кристаллической решетки с полностью

случай систем с сильными электронными корреля-

разупорядоченным (случайным) расположением ионов A

циями, и учитывать вместо случайного распреде-

и B. Штриховой линий обозначены границы кластера

ления ионов A и B случайное распределение элек-

тронов с проекцией спина σ =↑, ↓, «нулей» и «дво-

ек» — так называемых состояний с нулем и двумя

система в среднем трансляционно инвариантна, по-

электронами на узел кристаллической решетки. На

этому усредненный по беспорядку коррелятор дол-

рис. 2а в качестве примера представлена одна из воз-

жен зависеть от разности r₁ - r₂:

можных конфигураций распределения электронов с

проекцией спина σ =↑, ↓ внутри кластера для одно-

K (ω, r₁ - r₂) = 〈K (ω, r₁, r₂)〉_disord .

зонной модели Хаббарда в отсутствие ионного бес-

порядка. Рассматриваемый метод может быть так

На рис. 1 представлен фрагмент кристалличе-

же обобщен и использован для описания решеток

ской решетки с полностью разупорядоченным (слу-

Кондо (рис. 2б) с магнитными примесями (или s-

чайным) расположением ионов. Выберем внутри ре-

d-обменной модели Шубина - Вонсовского, где, как

шетки кластер размером N_c × N_c (на рис. 1 кластер

известно, при рассмотрении малого взаимодействия

обозначен штриховой линией) так, чтобы выполня-

электронов проводимости с локализованным момен-

лось примерное отношение N_A/N_B ≈ (1 - x)/x, где

том примеси теория возмущений не применима) и

N_A и N_B — число ионов A и B внутри кластера.

систем с сильным электрон-фононным взаимодейст-

Формируя сверхрешетку из таких кластеров, можно

вием.

моделировать беспорядок в системе; при этом усред-

С помощью унитарного преобразования U мат-

нение по беспорядку будет соответствовать усредне-

рица оператора

K может быть приведена к диаго-

нию по ансамблю таких сверхрешеток с различной

нальному виду:

конфигурацией ионов внутри кластера. Но среднее

число ионов 〈N_A〉 = 1 - x и 〈N_B〉 = x остается по-

⎛

⎞

E₁

···

стоянным.

⎜

⎟

⎜

E₂

···

⎟

Рассмотрим неупорядоченный бинарный сплав в

⎜

U^†KU =

^⎟,

⎜

⎟

отсутствие межэлектронного взаимодействия (U_i =

⎝

⎠

= 0). Процедура расчета включает в себя вычисле-

···

E2L

ние методом точной диагонализации полного набо-

ра собственных значений и состояний гамильтониа-

где E₁, E₂, . . . , E2L — собственные значения опе-

на кластера

Ĥ_c в большом каноническом ансамбле

ратора

^K. Собственный базис оператора

K можно

(Ĥ_c →

K= Ĥ_c -μ

^N) со средним числом электронов

;

записать в виде

= N_e, где

N — оператор числа частиц, и вы-

числение квантово-статистических средних, усред-

u†1 |0〉, u†2 |0〉, . . . , u†2L |0〉.

ненных по беспорядку — различным конфигураци-

Здесь

ям кластера. Для этого удобно использовать подход,

∑∑

u_m =

U^†m,j

a_j,σ,

описанный в работах Даготто [19,20]. Здесь мы толь-

ко вкратце изложим основные идеи применительно

к нашей задаче, отсылая читателя за дополнитель-

j_σ = (j, σ), а m пробегает значения от 1 до 2L.

948

ЖЭТФ, том 158, вып. 5 (11), 2020

Электронная структура и электропроводность. ..

Рис. 2. Фрагменты кристаллической решетки со случайным распределением электронов с проекцией спина σ =↑, ↓, «ну-

лей» и «двоек» для однозонной модели Хаббарда (а) и магнитных примесей в сплавах Кондо (б). Штриховыми линиями

обозначены границы кластера

Квантово-статистическое среднее оператора

Зависящие от времени наблюдаемые величины

для данной электронной и ионной конфигураций

могут быть вычислены с помощью двухвременных

кластера может быть представлено в виде

функций Грина

;

(

)∕

;

= Tr

Ôe^-βK Z_c,

G^>i,j,σ,σ (t) = a_i,σ (t) a^†j,σ (0) ,

где

;

∏

G^<i,j,σ,σ (t) = a^†i,σ (0)a_j,σ (t) ,

Z_c =

(1 + exp(-βE_λ))

λ=1

где

— статистическая сумма для данного кластера, β =

a_i,σ (t) = exp(i

Ĥ_ct)a_i,σexp(-i

Ĥ_ct).

= 1/k_BT. В случае

Ô = a_i,σa^†j,σ′ для статической_:

;

Отметим, что оператор

Ĥ_c имеет диагональный вид

{

}

функции Грина G_i,j,σ,σ′ = a_i,σa^†

j,σ^′

имеем

в том же базисе

u^†m |0〉

, что и оператор

^K, поэтому

(

)∕

можно показать, что

G_i,j,σ,σ′ = Tr a_i,σa^†j,σ′ exp(-β

^K) Z_c.

[

]

∑

Поскольку

a_i,σ (t) =

a_ν,

Uiσ,λexp(-itρλ)U^†

λ,ν

ν λ=1

∑

a^†iσ =

u^†νU^†ν,i

a_iσ =

Uiσ,νuν,

где a_ν = a_ν,↑, если ν ≤ L и a_ν = a_ν-L,↓, если ν > L, а

ν=1

ρ_λ — собственные значения

Ĥ_c, E_λ = ρ_λ-μ. Подстав-

получаем

ляя это выражение в определение временных функ-

ций Грина, получаем

∑

G_i,j,σ,σ′ =

Uiσ,λ

U^†

λ,j

σ^′

1 + exp(-βE_λ)

λ=1

∑

exp(-itρ_λ)

G^>i,j,σ,σ

(t) =

Uiσ,λ

U^†

λ,jσ

С помощью теоремы Вика более сложные двухча-

1 + exp(-β (ρ_λ - μ))

λ=1

стичные корреляторы могут быть выражены через

одночастичные функции Грина:

Запаздывающую функцию Грина можно опреде-

лить как

;

= aj1,σa^j

aj3,σa^j

∞

aj1,σaj2,σaj3,σa^j

,σ

2,σ

4,σ

∫

;

G^Ri,j,σ (ω) =

G^Ri,j,σ,σ (t)e^iωtdt,

+ aj1,σa^j

a^†

aj3,σ

4,σ

,σ

-∞

949

С. В. Николаев, Ю. С. Орлов, В. А. Дудников

ЖЭТФ, том 158, вып. 5 (11), 2020

где

Если теперь рассмотреть сверхрешетку, т. е. ре-

(

)

шетку, составленную из отдельных кластеров, то

G^Ri,j,σ,σ (t) = -iθ (t)

G^>i,j,σ,σ (t) + G^<j,i,σ,σ (t)

можно провести фурье-преобразование и перейти от

кластерных индексов к соответствующему волново-

Используя выражения для G^>i,j,σ,σ (t) и G^<j,i,σ,σ (t),

му вектору в обратном пространстве. Определенная

можно окончательно получить кластерную запаз-

таким образом зона Бриллюэна будет являться ре-

дывающую функцию Грина через собственные зна-

дуцированной (уменьшенной) по отношению к ис-

чения и собственные вектора оператора

Ĥ_c:

ходной зоне Бриллюэна, соответствующей первона-



чальной решетке. Тогда можно записать

∑



( )

G^Ri,j,σ (ω) =



∑

Ujσ,λU^†

λ,i^σ ω - ρ_λ + iδ

T_ij

= t0i,fjexp(ik · r_f),

(3)

λ=1

δ→+0

∑

Ujσ,λU^†

где r_f — радиус-вектор кластера f = 0 относитель-

λ,i^σ (ω - ρ_λ)

λ=1

но основного кластера с индексом 0, а

k— волновой

∑

вектор в редуцированной первой зоне Бриллюэна.

- iπ Ujσ,λU^†λ,i

δ (ω - ρ_λ).

(2)

С учетом этого перепишем уравнение для полной

λ=1

функции Грина как

Здесь буква P перед первой суммой справа означает

(

)

( )

D-1

^k, ω

= Ĝc-1 (ω) -

(4)

вычисление в смысле главного значения.

Расчет электронной структуры проводится в

Искусственное разделение решетки на кластеры

рамках кластерной теории возмущений [17, 18]. Су-

и учет внутрикластерных перескоков отдельно от

ществует много модификаций этой теории, напри-

межкластерных приводит к тому, что нарушается

мер, кластерная теория возмущений в представле-

трансляционная инвариантность. Для ее восстанов-

нии операторов Хаббарда [21,22], но общая идея дан-

ления в рамках кластерной теории возмущений ис-

ного кластерного подхода одна. Она заключается в

пользуется следующая процедура:

том, чтобы разбить решетку на кластеры опреде-

ленного размера, провести точную диагонализацию

∑

в рамках отдельного кластера и учесть межкластер-

G(k, ω) =

D_ij (k, ω)exp[-ik(r_i - r_j)],

(5)

ные взаимодействия по теории возмущений.

i,j=1

Матрицу, отвечающую за межузельные переско-

где r_i — радиус-вектор узлов внутри кластера, а k —

ки, можно записать в виде

волновой вектор в исходной(е)вой зоне Бриллюэна.

Здесь было учтено, что T_ij

= T_ij (k).

t_fi,gj = t^cijδ_fg + T_fi,gj,

Полную функцию Грина

D можно непосред-

где tcij — матрица перескоков внутри кластера, а

ственно вычислить из уравнения (4), но для этого

T_fi,gj — оставшаяся часть, отвечающая за межкла-

надо определить кластерную функцию Грина

Ĝ^c,

стерные перескоки. Здесь i и j являются внутрикла-

что обычно осуществляется по методу Ланцоша, и

стерными индексами узлов, а f и g — кластерные ин-

провести процедуру поиска обратной матрицы. Вся

дексы. В рамках данного кластерного приближения

эта процедура требует достаточно большого време-

полная функция Грина вычисляется из следующего

ни машинных вычислений. Но можно ускорить дан-

матричного уравнения:

ный расчет, если учесть, что кластерная функция

Грина

Ĝ^c не зависит от волнового вектора. Запишем

D-1 =

Ĝc-1 -

уравнение (4) в следующем виде:

(

)

( )

где функция Грина

Ĝ^c описывает движение элек-

D-1

^k, ω

=ω-t^c -

Σ^c -

тронов внутри отдельного кластера. Данное уравне-

ние можно записать и в другой эквивалентной фор-

Отсюда хорошо видно, что полюсы полной функции

ме:

Грина в каждой точке редуцированной первой зоны

Ĝ-1

D-1 =

-Σ^c,

Бриллюэна определяются гамильтонианом отдель-

где

Ĝ-1

= ω -t^c -

T. Здесь

Ĝ₀ — функция Гри-

ного кластера, но с дополнительными слагаемыми,

на системы без взаимодействия, а

Σ^c — кластерная

зависящими от волнового вектора. Если вспомнить

собственно-энергетическая часть.

структуру этих слагаемых (3), то можно заметить,

950

ЖЭТФ, том 158, вып. 5 (11), 2020

Электронная структура и электропроводность. ..

что на изолированный кластер накладываются пе-

Для каждой кластерной конфигурации рассчи-

риодические граничные условия с некоторой фа-

тывается функция Грина в рамках кластерной тео-

зой, определяемой волновым вектором и периодом

рии возмущений (5). Выполнив аналогичный расчет

сверхрешетки. С учетом данного анализа запишем

для N_conf различных конфигураций кластера, про-

гамильтониан отдельного кластера в виде

водим процедуру усреднения:

( )

Ĥ_c

= Ĥ_c +

(6)

^G (k, ω) = 〈G (k, ω)〉_conf .

(7)

Теперь, если воспользоваться выражением (2),

Через полученную таким образом функцию Гри-

можно получить полную функцию Грина

^D, решая

на выражаются спектральная плотность одноча-

в каждой точке редуцированной первой зоны Брил-

стичных возбуждений,

люэна задачу на собственные значения для гамиль-

тониана (6). Одночастичную функцию Грина полу-

A_σ (k, ω) = -

lim

G_σ (k, ω + iδ),

δ→+0

чаем из уравнения (5). Данная процедура эквива-

лента алгоритму расширения редуцированной зоны,

и плотность одночастичных состояний для данной

основанному на теореме Блоха [23].

проекции спина,

Для того чтобы рассматривать неупорядочен-

∑

ный бинарный сплав, необходимо определить про-

N_σ (ω) =

A_σ (k, ω),

цедуру усреднения функции Грина по беспорядку

(конфигурациям кластера с различным расположе-

где N_k — количество точек в первой зоне Брил-

нием ионов). Процедура расчета включает в себя за-

люэна. Следствием а

[

]

дание некоторой конфигурации кластера со случай-

шения для фермионов a_i,σ, a^†

= 1 является со-

i,σ

ным распределением ионов разного типа. В числен-

хранение полного спектрального веса для любого

ном алгоритме все узлы кластера просматриваются

волнового вектора k:

случайным образом и принимают состояние A с ве-

роятностью 1 - x или состояние B с вероятностью x.

∑∫

Таким образом, среднее число ионов типа A и типа

A_σ (k, ω) dω = 2.

B остается постоянным:

Ниже приведены результаты расчетов электрон-

〈N_A〉 = 1 - x, 〈N_B〉 = x.

ной зонной структуры и электропроводности бинар-

В случае неупорядоченной системы гамильтони-

ного сплава с гамильтонианом (1) в отсутствие ме-

ан (1) содержит слагаемые, которые являются неод-

жэлектронного взаимодействия (U_i = 0) для следу-

нородными в пространстве, поэтому фурье-образ

ющих значений параметров модели:

данных слагаемых будет содержать два волновых

вектора, k и k^′, причем недиагональные компоненты

t_A = 1.0 эВ, t_B = 0.85 эВ, t_AB = 0.8 эВ,

при k = k^′ для больших кластеров в силу случай-

Δ = 0.5 эВ.

ности распределения потенциала пропорциональны

√

1/L, где L — число узлов в кластере. Аналогич-

В отсутствие межэлектронного взаимодействия зон-

ное уменьшение вклада от недиагональных слагае-

ная структура не зависит от температуры и числа

мых будет наблюдаться, если проводить усреднение

электронов в системе, т. е. выполняется приближе-

по достаточно большому числу кластерных конфи-

ние «жесткой зоны». На рис. 3 представлены резуль-

гураций со случайным распределением ионов. Та-

таты расчета электронной зонной структуры для

ким образом, функция Грина для неоднородной си-

кластера размером 8×8 с использованием различно-

стемы будет также зависеть от двух волновых век-

го числа случайных конфигураций N_conf = 10-250

торов, G_kk′ (ω), и для больших кластеров или по-

для усреднения по беспорядку. Здесь и ниже цветом

сле усреднения по случайным кластерным конфи-

показано распределение полного спектрального веса

гурациям недиагональные элементы функции Гри-

∑

√

A (k, ω) = A_σ (k, ω),

на при k = k^′ будут пропорциональны

1/L. Полу-

чается, что в пределе большого кластера или после

усреднения по достаточно большому числу случай-

а затравочное уширение спектральных линий δ =

ных конфигураций кластера функция Грина стано-

= 0.01 эВ.

вится диагональной по волновому вектору,

G_k (ω) =

На рис. 4 представлены результаты расчета для

= 〈G_kk′ (ω)〉_conf [23].

кластеров разного размера 8×8-32×32 с N_conf = 10.

951

С. В. Николаев, Ю. С. Орлов, В. А. Дудников

ЖЭТФ, том 158, вып. 5 (11), 2020

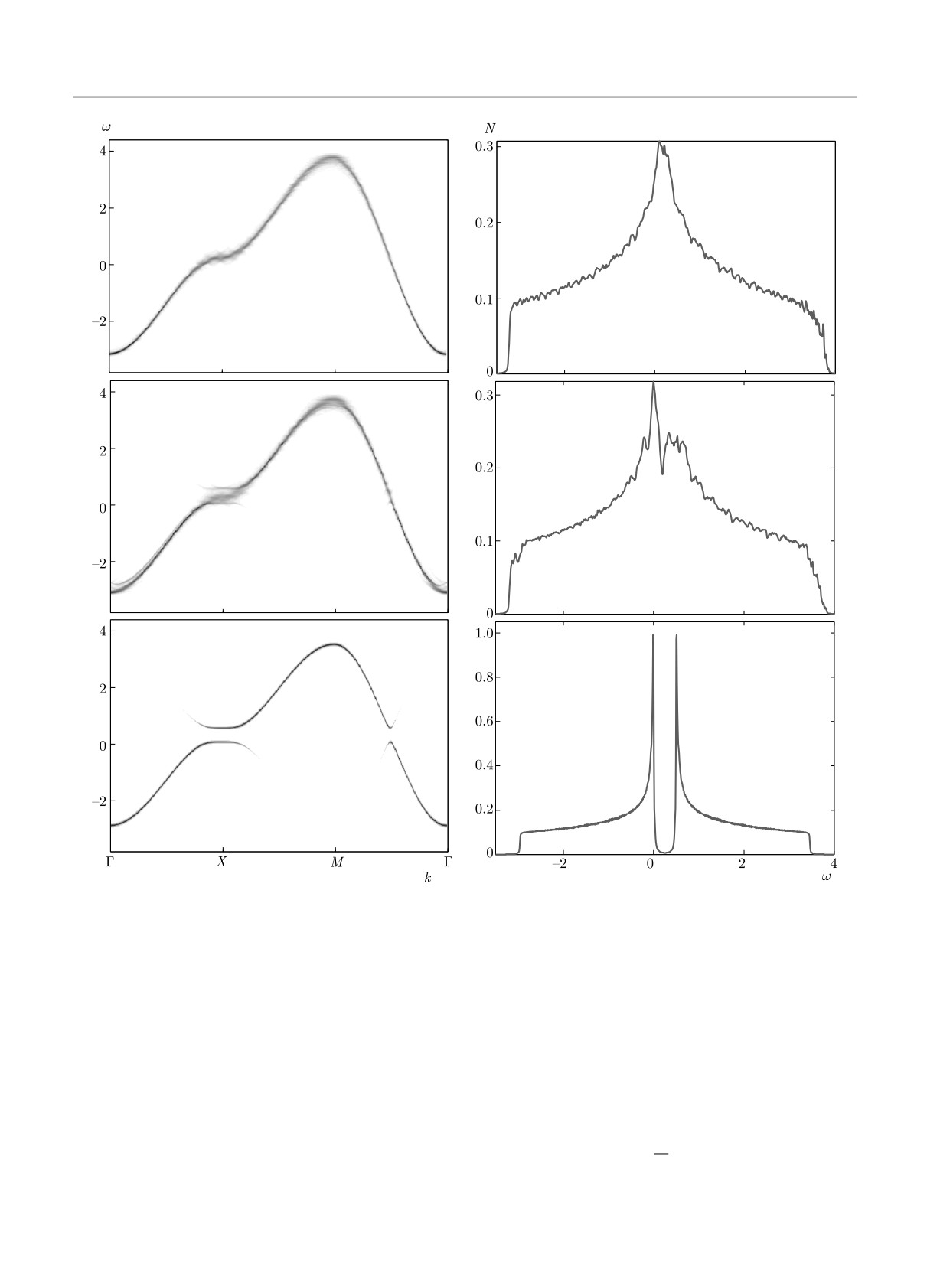
Рис. 3. (В цвете онлайн) Электронная зонная структура бинарного сплава в отсутствие электрон-электронного взаи-

модействия в рамках кластерного приближения. В верхнем ряду представлена дисперсия фермиевских квазичастичных

возбуждений вдоль симметричных направлений зоны Бриллюэна, полученная для кластера размером 8×8, с использова-

нием различного числа случайных конфигураций N_conf = 1-250 для усреднения по беспорядку. В нижнем ряду приведены

соответствующие поверхности Ферми в первой четверти первой зоны Бриллюэна в случае половинного заполнения

Рис. 4. (В цвете онлайн) Электронная зонная структура бинарного сплава в отсутствие электрон-электронного взаи-

возбуждений вдоль симметричных направлений зоны Бриллюэна, полученная для кластеров разного размера 8 × 8-

32 × 32, с использованием фиксированного числа случайных конфигураций N_conf = 10 для усреднения по беспорядку.

В нижнем ряду приведены соответствующие поверхности Ферми в первой четверти первой зоны Бриллюэна в случае

половинного заполнения

952

ЖЭТФ, том 158, вып. 5 (11), 2020

Электронная структура и электропроводность. ..

Видно, что с увеличением размера кластера и

Следует отметить, что данное уширение существен-

числа конфигураций N_conf , по котором происходит

но больше затравочного уширения δ, используемого

усреднение, замываются фиктивные разрывы элек-

в численной схеме расчета. Таким образом, исполь-

тронной дисперсии, обусловленные искусственным

зуемый нами метод позволяет найти время жизни

увеличением периода трансляции кристаллической

τ (k), необходимое для вычисления электропровод-

решетки при образовании сверхрешетки из класте-

ности.

ров.

Чтобы учесть наличие ближнего порядка в рас-

Гамильтониан (1) может быть записан в k-пред-

положении атомов, при усреднении функции Грина

ставлении в виде суммы двух вкладов

по беспорядку внутри кластера можно задавать раз-

∑

Ĥ= Ĥ(0)+ Ĥ(1)₌

личные упорядоченные области меньшего размера.

ε_ka†σ,kaσ,k+

Vk,k′ a†σ,kaσ,k′ .

На рис. 5 в среднем ряду представлены результа-

σ,k

σ,k,k^′

ты расчета электронной зонной структуры и плот-

Если 1-x > x, т. е. решетка больше чем на половину

ности состояний, полученные при усреднении функ-

заполнена ионами типа A, то в качестве

Ĥ (0) удоб-

ции Грина по различным конфигурациям кластера

но выбрать гамильтониан решетки, в узлах которой

размером 16 × 16, содержащем в себе упорядочен-

расположены только ионы типа A и перескоком t_A

ные области различного размера от 2 × 2 до 12 × 12,

между ними, тогда

Ĥ (1) будет описывать возмуще-

причем использовались конфигурации, в которых

ние (рассеяние), обусловленное добавлением ионов

упорядоченные области случайным образом распо-

типа B, и наоборот. Полную функцию Грина

лагались внутри кластера. Для сравнения на рис. 5



в верхнем и нижнем рядах приведены результаты

G_σ (k, k^′, ω) = lim

0

aσ,k′

a†σ,k0

δ→+0



расчета при тех же параметрах в случаях соответ-

ω-

Ĥ₊ iδ/2

ственно полностью разупорядоченного и упорядо-

с помощью уравнения Дайсона можно представить

ченного сплавов. Для удобства сравнения зонная

в виде

структура полностью упорядоченного сплава (рис. 5

нижний ряд) приведена для нередуцированной зо-

G_σ (k, k^′, ω) = G(0)σ (k, ω) +

∑

ны Бриллюэна. На рис. 5 (средний ряд) видно, что

+ G(0)σ(k,ω) H(1)k,k′′G_σ (k^′′,k^′,ω),

с наличием таких упорядоченных областей наблю-

k^′′

дается открытие щели (псевдощели) в спектре при

энергиях, соответствующих границе зоны Бриллю-

где Gσ0) (k, ω) — затравочная функция Грина соот-

эна полностью упорядоченного сплава. Аналогич-

Ĥ (0)_.Или

ветствующая

ная ситуация, связанная с появлением псевдоще-

[

]-1

ли в сильнокоррелированных системах при наличии

G_σ (k, ω) =

-Σ^′σ (k, ω) -iΣ^′′σ (k, ω)

ближнего антиферромагнитного порядка, рассмат-

Gσ0) (k, ω)

ривается, например, в работе [24]. При положении

где G_σ (k, ω) = 〈G_σ (k, k^′, ω)〉_disord — функция Гри-

химического потенциала в истинной диэлектриче-

на, усредненная по беспорядку, а

ской щели (рис. 5, нижний ряд) наблюдается пе-

реход диэлектрик-плохой металл-металл с ростом

Σ_σ (k, ω) = Σ^′σ (k, ω) + iΣ^′′σ (k, ω)

беспорядка (рис. 5).

— массовый оператор, содержащий мнимую и дей-

ствительную части. При наличии ближнего струк-

3. ЭЛЕКТРОПРОВОДНОСТЬ

турного порядка в расположении атомов в качестве

Gσ0) (k, ω) удобно выбрать функцию Грина, отвеча-

Рассмотрим гамильтониан двухмерной модели

ющую полностью упорядоченной решетке, а

Ĥ (1)

Хаббарда во внешнем переменном электромагнит-

тогда будет описывать возмущение, вызванное бес-

ном поле, описываемом векторным потенциалом

порядком в расположении ионов. Мнимая часть мас-

A(r, t):

сового оператора Σ^′′σ (k, ω) определяет время жизни

τ_σ (k) ∼ 1/Σ^′′σ (ω (k)) или затухание квазичастичных

Ĥ₌

T_A +

Û =

возбуждений с проекцией спина σ и уширение дис-

∑

[

= -t

a†r,σar+l,σ exp[ieA_l (r, t)] + a†r+l,σar,σ +

персии (см. рис. 3, 4). На рис. 3 и 4 можно наблюдать

r,l,σ

неоднородное уширение дисперсии, т. е. время жиз-

∑

ни τ (k), обусловленное процессами рассеяния, не

+ exp[-ieA_l (r, t)]] + U

nr↑nr↓,

одинаково для разных k в первой зоне Бриллюэна.

953

С. В. Николаев, Ю. С. Орлов, В. А. Дудников

ЖЭТФ, том 158, вып. 5 (11), 2020

Рис. 5. Электронная зонная структура бинарного сплава в отсутствие электрон-электронного взаимодействия в рамках

кластерного приближения. В среднем ряду слева представлены дисперсия фермиевских квазичастичных возбуждений

вдоль симметричных направлений зоны Бриллюэна и плотность состояний, полученные при усреднении по беспоряд-

ку для кластера размером 16×16, содержащем упорядоченные области различного размера. В верхнем и нижнем ряду

приведены результаты расчета при тех же параметрах в случаях соответственно полностью разупорядоченного и упоря-

доченного сплавов

где r — радиус-вектор узла кристаллической решет-

электрического заряда e:

ки, l — единичный вектор вдоль координатных (кри-

∑

T_A =

T -e

jl (r) Al (r, t) -

сталлических) осей, A_l (r, t) — компонента вектора

r,l

A(r, t) вдоль направления l, ℏ = c = a = 1. Опе-

e² ∑

ратор

T_A может быть разложен в ряд по степеням

K_l (r) A2l (r, t) + . . . ,

r,l

954

ЖЭТФ, том 158, вып. 5 (11), 2020

Электронная структура и электропроводность. ..

где

∑

[

]

T = -t

a†r,σar+l,σ + a^†

ar,σ

:



;₂

r+l,σ



r,l,σ

;

 φ0

j

 φn



πe² ∑

D=πe²

-K_x

-2

— оператор кинетической энергии при отсутствии

E_n - E₀

n=0

электромагнитного поля,

∑(

)

— друдевский вес. При выводе (8) использовалось

jl (r) = it

a†r,σar+l,σ - a^†

ar,σ

r+l,σ

условие полноты

∑

— оператор плотности «парамагнитного» тока в на-

I =

|φ_n〉〈φ_n|,

правлении l, а

∑(

)

Ĥ₀ |φ_n〉 = E_n |φ_n〉. Более подробный вывод уравне-

K_l (r) = -t

a†r,σar+l,σ + a^†

ar,σ

r+l,σ

ния (8) можно найти в работе [25]. Известно, что

;

— оператор плотности «диамагнитного» тока в на-

σ₁ (ω) и

K_x связаны между собой правилом сумм:

правлении l. Таким образом, гамильтониан можно

∞

∫

представить в виде:

Ĥ= Ĥ₀

V . Здесь первое слага-

;

πe²

σ₁ (ω)dω =

-K_x

емое

Ĥ₀ определяет гамильтониан модели Хаббарда

с учетом кулоновского взаимодействия электронов в

отсутствие векторного потенциала, а второе слагае-

Друдевский вес D может быть использован в ка-

мое

V описывает взаимодействие с полем и исчезает

честве параметра порядка для перехода металл-

при A (r, t) = 0.

диэлектрик [25]. Обращение D в нуль свидетель-

В рамках теории линейного отклика выражение

ствует о диэлектрическом основном состоянии сис-

для полного тока имеет вид

темы. Для невзаимодействующих фермионов из (8)

можно получить хорошо известное выражение для

∂Ĥ

J_l (r, t) = -

проводимости Друде:

∂Al (r,t)

n_ee²π

= ejl (r) + e² Kl (r)A2l (r,t) + ...,

σ₁ (ω) =

δ (ω) ,

m_e

где первое слагаемое соответствует парамагнитно-

где n_e = N_e/N — концентрация носителей (свобод-

му, а второе — диамагнитному вкладу. Используя

ных электронов), m_e — масса электрона.

нестационарную теорию возмущений можно пока-

При конечных температурах для большого ка-

зать, что для случая A_l (r, t) = δl,xA_x (r, t)

нонического ансамбля второе слагаемое в (8) имеет

;

вид

J_x (q, ω)

=e²

K_x A_x (q, ω) +

[

(



)



;



(

)

∑

1 πe²



†

+e²

φ₀

jx (-q)

jx (q)

1-e^-βω

eβΩ

e-βEn φ_n

j

 φm



^φ

Ĥ₀-E₀+ω+iδ

ω N

(



)]



;



φ₀

jx (q)

jx (-q)

× φ_m

j

 φn δ (ω + En - Em) ,



^φ

Ĥ₀ - E₀ - ω - iδ

× Ax (q,ω),

где Ω — термодинамический потенциал, -∂Ω/∂μ = )(

= 〈N_e

〉, e-βΩ = Tr e^-β( Ĥ0-μ N) [26]. Поскольку за-

где угловые скобки обозначают квантовомеханиче-

дача на собственные значения

ское среднее по основному состоянию системы |φ₀〉

(

)

с энергией E₀. Здесь рассматривается случай при

Ĥ₀ - μ

|φ_n〉 = E_n |φ_n〉

нулевой температуре. Тогда выражение для частот-

ной зависимости действительной части электропро-

не может быть решена точно, приходится использо-

водности σ₁ (ω) при q = 0 имеет вид

вать различные приближения.

Применим кластерный подход для исследования

σ₁ (ω) = Re σ_xx (ω) = Dδ (ω) +

:



;₂

проводимости неупорядоченного бинарного сплава



∑

 φ0

j

 φn



в рамках формализма Кубо. Выберем достаточно

e²π

δ (ω - (E_n - E₀)),

(8)

большой кластер и проведем точный расчет дина-

E_n - E₀

n=0

мической проводимости при конечной температуре.

955

С. В. Николаев, Ю. С. Орлов, В. А. Дудников

ЖЭТФ, том 158, вып. 5 (11), 2020

Будем рассматривать случай невзаимодействующих

среднего от коммутатора в выражении (10). Можно

фермионов (U_i = 0), но с учетом беспорядочного

показать, что для определения Λ_xx (q, ω) достаточно

расположения ионов (энергии электронов на узле)

вычислить только следующее среднее

и соответствующих интегралов перескоков между

ближайшими соседями (1). Чтобы учесть случай-

〈j_x (l, t)j_x (l^′, 0)〉 =

ный характер распределения ионов в решетке, необ-

5∑

(

)

ходимо проводить процедуру усреднения по разным

tl+lx,l a†l+l

(t) a_l,σ (t) -a^†l,σ (t) al+lx,σ (t)

кластерным конфигурациям.

,σ

В рамках формализма Кубо динамическая элек-

∑

(

тропроводность в длинноволновом пределе (q = 0)

× t_l′+l′

,l^′

a†l′+l′_x,σ′(0)al^′,σ^′ (0)-

σ^′

имеет вид [27]

)



〈-K_x〉 - Λ_xx (0, ω)

,σ^′ (0)



- a†l′,σ′(0)al^′+l^′x

σ_xx (ω) = -e²

(9)



i (ω + iδ)

δ→+0

где

Здесь a_l,σ (t) и a^†l,σ (t) — операторы в гейзенбергов-

ском представлении.

∞

∫

Λ_xx (q, ω) = i

ei(ω+iε)t ×

После раскрытия скобок получатся четыре похо-

жих по структуре слагаемых, в которые будут вхо-

× 〈[j_x (q, t) , j_x (-q, 0)]〉 dt, ε → +0,

(10)

дить средние от четырех фермиевских операторов.

В кластерном подходе эти слагаемые можно выра-

∑

〈-K_x〉 =

〈-K_x (l)〉 ,

зить через собственные значения и собственные век-

торы гамильтониана отдельного кластера

Ĥ_c (см.

∑

предыдущий раздел). В частности, запишем общую

j_x (q, t) =

e-iqrl j_x (l, t).

структуру рассматриваемых средних (для удобства

опустим индекс спина σ):

Здесь

〈. . .〉

— квантово-статистическое сред-

нее, j_x (l, t)

— оператор парамагнитной части

;

x-компоненты плотности тока в точке l в гейзенбер-

a^†i (t)a_j (t)a^†i′ (0)aj′ (0) =

говском представлении,

∑

j_x (l, t) = exp(i

Ĥ_ct)j_x (l)exp(-i

Ĥ_ct),

= U_ηλ′exp(itρ_λ′)U†λ′i^×

ηλ^′

а Kx (l) — оператор плотности кинетической энер-

∑

;

гии движения вдоль оси x. В случае неупорядочен-

× U_jλexp(-itρ_λ)U^†

a^†ηa_νa^†

a_j′

λν

i′

ной системы эти операторы можно записать в виде

νλ

∑

(

)

j_x (l) = i

tl+lx,l a†l+l

a_l,σ - a^†

al+lx,σ

Используя теорему Вика, можно записать

x,σ

l,σ

(

)

;

;)

∑

(

8)(

a_l,σ + a^†

a^†ηa_νa^†

a_j′

δ_ην-

a_νa^†η

δ_i′_j′ - a_j′ a^†

K_x (l) = - tl+lx,l a†l+l

x,σ

l,σ

al+lx,σ

i′

;

(

8):

Учитывая, что Λ_xx (q, ω) — комплексная функ-

δ_ηj′ -

a_j′ a^†η

a_νa^†

i′

ция, из уравнения (9) получим

где

σ₁ (ω) = Re σ_xx (ω) = 2πe²Dδ (ω) +

Im Λ_xx (0, ω) ,

∑

где

a_νa^†η

U_νλ

U^†λη.

1 + exp[-β (ρ_λ - μ)]

〈-K_x〉

Re Λ_xx (0, ω → 0)

Здесь ρ_λ — собственные значения кластерного га-

— друдевский вес.

мильтониана

ˆc, U — матрица унитарного преобра-

При вычислении проводимости основной зада-

зования

Ĥ_c к диагональному виду, μ — химический

чей является определение квантово-статистического

потенциал, β = 1/k_BT — обратная температура.

956

ЖЭТФ, том 158, вып. 5 (11), 2020

Электронная структура и электропроводность. ..

После вычисления всех средних, для фурье-об-

Полученное выражение полностью согласуется с

раза в длинноволновом пределе (q = 0) получаем

определением действительной части проводимости

для нулевой температуры (8). Можно заметить, что

〈j_x (0, t) j_x (0, 0)〉 =

с точностью до температурных множителей роль

∑

exp[it (ρ_λ - ρ_λ′ )]

матричного элемента 〈φ₀ |j_x| φ_n〉 в выражениях (11)

(1 + exp[β (ρ_λ - μ)]) (1 + exp[-β (ρ_λ′ - μ)])

и (12) играет сумма

λ=λ^′



(

)

∑



〈λ|j_x|λ^′〉 =



U_lλ



(

)

tl+lx,l U^†λ′_lUl+lx,λ -

λ^′,l+lx

∑



U_lλ

(13)

= tl+lx,l U^†λ′_lUl+lx,λ - U^λ

^′,l+lx

Используя данное выражение, можно получить

В рамках кластерного подхода так же можно вы-

Λ_xx (q = 0, ω) = Re Λ_xx (0, ω) + i ImΛ_xx (0, ω),

числить и среднюю кинетическую энергию

где

∑

〈K_x〉 =

Re Λ_xx (0, ω) =

1 + exp[-β (ρ_λ - μ)]



∑

(

)



(

)

∑

†



U_lλ

(14)



tl+lx,l U_λ

Ul+lx,λ-U^†λ′,l+l

U_lλ



× tl+lx,l U^†λlUl+lx,λ + U^λ

,l+lx

^′l

∑



(1+exp[β (ρ_λ - μ)])(1+exp[-β (ρ_λ′ - μ)])

В случае конечной температуры можно сформу-

λ=λ^′

лировать следующее правило сумм:

(ρ_λ′ - ρ_λ)

(ρ_λ′ - ρ_λ)² - ω²

∫

^∞σ

1 (ω) dω = e²π 〈-Kx〉 .

-∞

(

)

Im Λ_xx (0, ω) =

1-e^-βω

Можно легко проверить, что полученная нами про-



водимость σ₁ (ω) удовлетворяет данному правилу



(

)

∑

†



сумм, если проинтегрировать по частоте выраже-



tl+lx,l U_λ

Ul+lx,λ - U^†λ′,l+l

U_lλ



^′l

∑



ние (11).

(1 + exp[β (ρ_λ - μ)]) (1 + exp[-β (ρ_λ′ - μ)])

Для вычисления проводимости неупорядочен-

λ=λ^′

ного сплава необходимо еще провести процеду-

× δ (ω - (ρ_λ′ - ρ_λ)).

ру усреднения по различным случайным кластер-

ным конфигурациям. Получить некоторую кластер-

Таким образом, действительная часть электро-

ную конфигурацию можно аналогично описанной в

проводности имеет вид

предыдущем разделе процедуре. Далее для каждой

(

)

-βω

e²π

1-e

кластерной конфигурации вычисляется сумма (13)

σ₁ (ω) = 2πe²Dδ (ω) +

ωL

и проводится усреднение по всем таким конфигура-



(

)

циям:

∑

†



tl+lx,l U_λ

Ul+lx,λ - U^†λ′,l+l

U_lλ



〈λ |j_x| λ^′〉 = 〈〈λ |j_x| λ^′〉〉_conf .

^′l

∑



Аналогичное усреднение необходимо сделать и

(1 + exp[β (ρ_λ - μ)]) (1 + exp[-β (ρ_λ′ - μ)])

λ=λ^′

для средней кинетической энергии 〈K_x〉. В этом

× δ (ω - (ρ_λ′ - ρ_λ)),

(11)

случае усредняется по случайным конфигурациям

кластера сумма, входящая в выражение (14), а

где

именно

〈-K_x〉

〈λ |K_x| λ〉 = 〈〈λ |K_x| λ〉〉_conf,

где



(

)

(

)

∑

†



∑



tl+lx,l U_λ

Ul+lx,λ - U^†λ′,l+l

U_lλ



^′l

〈λ|K_x| λ〉 =

tl+lx,l U^†λlUl+lx,λ + U^λ

U_lλ

∑



,l+lx

(1 + exp[β (ρ_λ - μ)]) (1 + exp[-β (ρ_λ′ - μ)])

λ=λ^′

При этом мы формируем полный спектр всех

случайных кластерных конфигураций {ρ_λ}. Пред-

(12)

(ρ_λ′ - ρ_λ)

ложенную процедуру усреднения по беспорядку

957

С. В. Николаев, Ю. С. Орлов, В. А. Дудников

ЖЭТФ, том 158, вып. 5 (11), 2020

можно рассматривать как усреднение некоторого

В формализме Больцмана (τ-приближение) ди-

сверхкластера, состоящего из невзаимодействую-

намическая проводимость имеет вид

щих кластеров меньшего размера со случайным рас-

∫

∑

пределением ионов разного типа. Это эффектив-

σ_ij

(ω, μ, T ) = e²

но увеличивает размер области, по которой осу-

4π³

(

)

ществляется усреднение, и позволяет получить бо-

∂n_F (ε,μ,T)

лее хорошее приближение в случае неупорядоченно-

υ_λi (k) υ_λj (k)

∂ε

ε=ε_λ (k)

го сплава.

(18)

1/τ_λ (k) - iω

Таким образом, мы получаем средние значения

матричного элемента тока и кинетической энергии

где υ_λi (k) = ℏ-1∂ε_λ (k)/∂k_i — групповая скорость

движения в направлении x, которые подставляются

электронов (квазичастиц), τ_λ (k) ∼ 1/Σ^′′ (ε_λ (k)) —

в выражения (11) и (12). Окончательно для неупо-

время свободного пробега, λ — индекс зоны, n_F —

рядоченного сплава имеем

функция распределения Ферми- Дирака. Выраже-

ние (18) является следствием более общего кван-

(

)

-βω

тово-кинетического уравнения Больцмана для элек-

e²π

1-e

σ₁ (ω) = 2πe²Dδ (ω) +

тропроводности [26]:

ωL



₂



∞

∫

∑

〈λ |jx| λ^′〉

d³p

dω

σμν = e²

υpμυpν ×

(1 + exp[β (ρ_λ - μ)]) (1 + exp[-β (ρ_λ′ - μ)])

(2π)³

2π

λ=λ^′

-∞

(

)

× δ (ω - (ρ_λ′ - ρ_λ)),

(15)

dn_F (ω)

× -

A(p, ω)Λ (p, ω),

dω

(19)

где

n_i

υ_kΛ (k, ω) =

A(k, ω) υ_k +

2Γ (k, ω)

∫

d³p

〈-K_x〉

|T_kp|²A (p, ω) υ_pΛ (p, ω),

(2π)³



₂



∑

〈λ |jx| λ^′〉

где T_kp — матрица рассеяния носителей тока на при-

месях,

(1 + exp[β (ρ_λ - μ)]) (1 + exp[-β (ρ_λ′ - μ)])

λ=λ^′

∫

d³p

(16)

2Γ (k, ω) = n_i

|T_pk|²A (p, ω),

(ρ_λ′ - ρ_λ)

(2π)³

n_i — концентрация примесей, A(p, ω) — спектраль-

∑

ный вес квазичастиц. Матрица рассеяния связана

〈λ |K_x| λ〉

〈K_x〉 =

(17)

с собственно энергетической частью соотношением

(1 + exp[-β (ρ_λ - μ)])

Σ(p, ω_p) = n_iT_pp. Как видно из приведенных выра-

жений, вычисление массового оператора Σ в рамках

В рамках кластерного подхода для расчета элек-

кластерного приближения (см. раз. 2), открывает

тропроводности неупорядоченного бинарного спла-

возможность для использования выражения (18) и

ва в формализме Кубо будем использовать выраже-

более общего выражения (19) для нахождения элек-

ния (15)-(17). Результаты такого расчета для клас-

тропроводности.

тера 50 × 50 в пределе ω → 0 при T = 50 K в зави-

На рис. 6 приведены результаты расчета диспер-

симости от числа частиц в системе или положения

сии (рис. 6а-в), плотности состояний (рис. 6д-ж)

химического потенциала приведены на рис. 6 при

и электропроводности (рис. 6и-л) неупорядоченно-

Δ = -0.5, 0, 0.5 эВ. На рис. 6(м) для сравнения

го бинарного сплава в рамках кластерного подхода

приведены результаты того же расчета для систе-

при Δ = -0.5, 0, 0.5 эВ. На рис. 6ж,з,м для срав-

мы с одним сортом ионов (x = 0). Данные графики

нения приведены результаты расчета для системы с

получены после аппроксимации данных по Гауссу,

одним сортом ионов (x = 0). В этом случае время

что необходимо делать, чтобы устранить эффекты

свободного пробега τ не зависит от волнового век-

от конечности кластера. На всех рисунках проводи-

тора k, так как в системе нет беспорядка. Электро-

мость представлена в единицах σ₀ = e²/ℏ.

проводность от положения химического потенциала

958

ЖЭТФ, том 158, вып. 5 (11), 2020

Электронная структура и электропроводность. ..

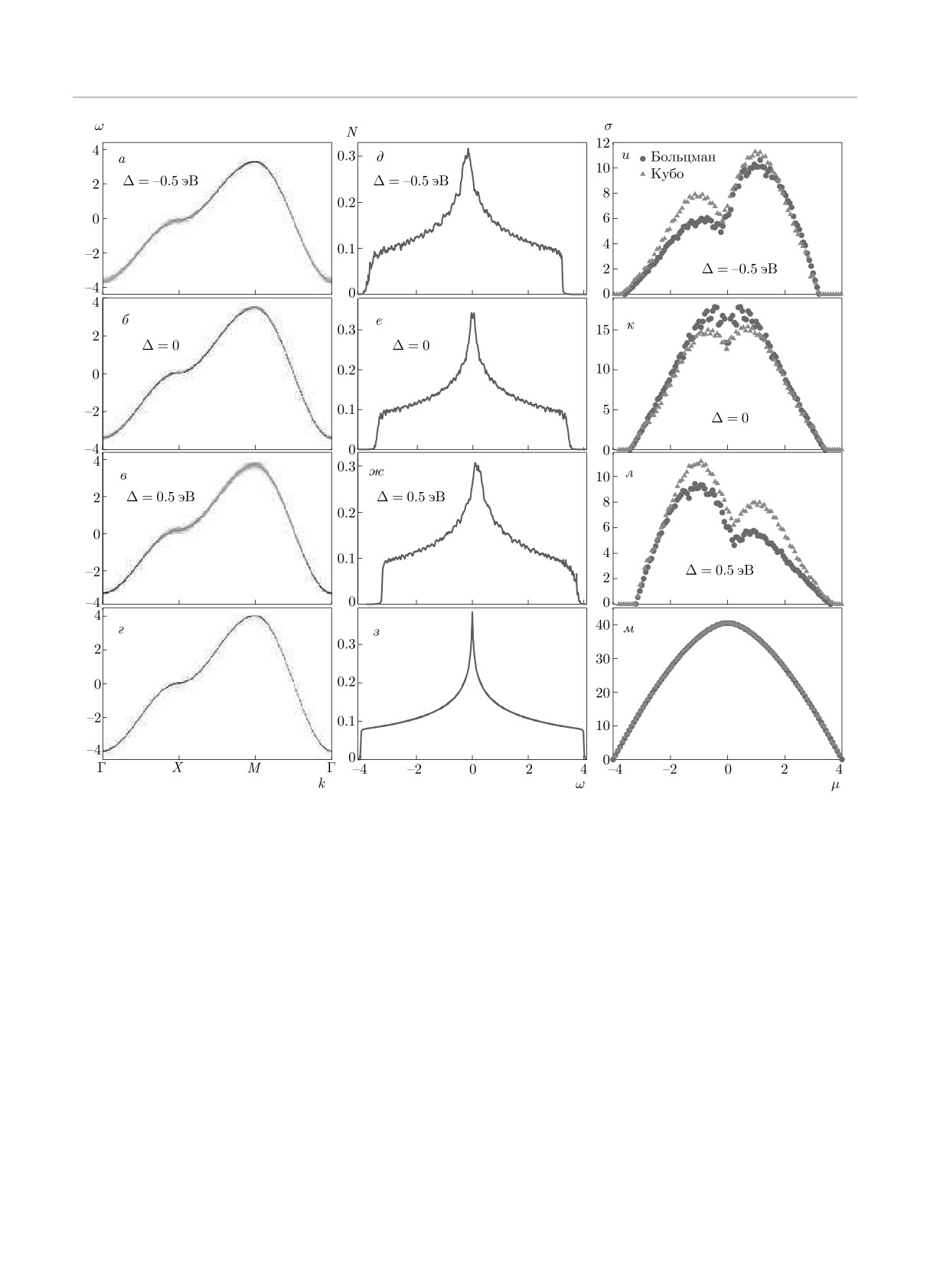
Рис. 6. (В цвете онлайн) Дисперсия, плотность состояний и электропроводность неупорядоченного бинарного сплава в

рамках кластерного подхода при Δ = -0.5, 0, 0.5 эВ. Для сравнения в нижнем ряду приведены результаты расчета для

системы с одним сортом ионов (x = 0). Электропроводность от положения химического потенциала μ (числа частиц в

системе) получена в пределе ω → 0 при T = 50 K в формализме Больцмана для кластера 16 × 16 (синие кружки) и в

формализме Кубо для кластера 50 × 50 (красные треугольники). Усреднение происходило по 20 случайным кластерным

конфигурациям

μ (числа частиц в системе) вычислялась в пределе

На рис. 6а-г хорошо видно, что наличие беспо-

ω → 0 при T = 50 K. На рис. 6и-м синие круж-

рядка в системе приводит к уширению дисперсии,

ки показывают результаты расчета электропровод-

неоднородному по волновому вектору k и зависяще-

ности в рамках кластерной теории возмущений для

му от параметра Δ. При Δ = -0.5 эВ наибольшее

кластера 16 × 16 в формализме Больцмана (18), а

уширение происходит вблизи точки (0, 0) и посте-

красные треугольники — в рамках формализма Ку-

пенно уменьшается к точке (π, π). При Δ = 0.5 эВ

бо (15)-(17) для кластера 50 × 50. Все представлен-

происходит аналогичное поведение только в обрат-

ные кривые являются результатом усреднения по 20

ном направлении — от точки (π, π) к точке (0, 0).

случайным кластерным конфигурациям.

При Δ = 0 также видно небольшое уширение дис-

959

С. В. Николаев, Ю. С. Орлов, В. А. Дудников

ЖЭТФ, том 158, вып. 5 (11), 2020

персии, но уже симметрично относительно ω = 0

вое расслоение (пространственно-неоднородные сис-

(величина уширения вблизи точек (0, 0) и (π, π) оди-

темы). Для последних особенно существенны огра-

наковая). Наши расчеты показывают, что асиммет-

ничения, вызванные размером кластера.

рия в уширении дисперсии (а с ним и времени сво-

В настоящей работе приведены результаты рас-

бодного пробега) определяется параметром Δ, а ве-

четов электронной зонной структуры и электропро-

личина уширения зависит не только от величины

водности бинарного сплава в отсутствие межэлек-

случайного потенциала, но и от неоднородности па-

тронного взаимодействия, когда зонная структура

раметров перескока. При этом в плотности состоя-

не зависит от температуры и числа электронов в си-

ний наблюдается логарифмическая особенность при

стеме, т. е. выполняется приближение «жесткой зо-

любом значении Δ (рис. 6д-ж).

ны». Используемый нами кластерный подход позво-

Из сравнения кривых на рис. 6и-л видно, что

лил проводить расчеты в рамках достаточно боль-

расчеты, выполненные в рамках кластерного подхо-

ших кластеров, что существенно при исследовании

да в двух разных формализмах, приводят к качест-

неупорядоченных систем. В частности, моделирова-

венно одинаковому поведению электропроводности.

ние упорядоченной фазы в неупорядоченном окру-

Количественные различия связаны с достаточно

жении показало появление псевдощели в спектре

небольшим размером кластера (50 × 50), использу-

при энергиях, соответствующих границе зоны Брил-

емого в расчетах в рамках формализма Кубо, по

люэна полностью упорядоченного сплава. Таким об-

сравнению с количеством точек в первой зоне Брил-

разом, при половинном заполнении с ростом беспо-

люэна (600 × 600), используемых в расчетах в рам-

рядка будет наблюдаться переход диэлектрик-пло-

ках формализма Больцмана. В случае однородной

хой металл-металл.

системы при отсутствии беспорядка наблюдается

Сравнение результатов расчета электропровод-

количественное совпадение результатов (рис. 6м).

ности в рамках кластерной теории возмущений в

Влияние параметра Δ на уширение дисперсии хо-

формализме Больцмана и в рамках формализма Ку-

рошо проявляется на зависимостях электропровод-

бо для достаточно больших кластеров показало хо-

ности σ (μ). При Δ = 0 наблюдается симметричная

рошее согласие. Так как расчеты в рамках форма-

кривая относительно середины зоны, а для Δ = 0

лизма Кубо являлись точными (но для конечного

проявляется асимметрия.

кластера), можно утверждать, что использование в

Важным результатом наших расчетов является

формализме Больцмана приближения времени сво-

то, что при наличии беспорядка (примесей) в систе-

бодного пробега, т. е. представления времени релак-

ме сохраняется логарифмическая особенность плот-

сации τ(k) через обратную величину мнимой части

ности состояний (рис. 6), но при этом в электропро-

массового оператора, полученного в рамках исполь-

водности σ (μ) наблюдается провал (даже при Δ =

зуемого кластерного подхода, является достаточно

= 0), обусловленный рассеянием носителей.

хорошим приближением при исследовании неупоря-

доченных систем. Следует отметить, что такое при-

ближение не является очевидным, поскольку время

4. ОБСУЖДЕНИЕ И ВЫВОДЫ

релаксации в уравнении Больцмана является более

сложной величиной [26].

Обобщая полученные результаты, можно выде-

Обнаружено, что при наличии беспорядка

лить основные преимущества и недостатки предла-

(примесей) в системе в зависимости статиче-

гаемого метода. К недостаткам, очевидно, относят-

ской электропроводности σ(μ) в пределе низких

ся: 1) вычислительные ограничения, определяющие

температур наблюдается провал, обусловленный

максимально возможный размер кластера; 2) огра-

рассеянием носителей, но при этом сохраняется ло-

ничения, вызванные использованием метода силь-

гарифмическая особенность плотности состояний.

ной связи. К преимуществам следует отнести воз-

Мы считаем, что данное поведение электропровод-

можность реализации основных идей рассматривае-

ности можно рассматривать как признак появления

мого метода в схеме DFT-расчетов реальных соеди-

локализации в системе.

нений. Кроме того, метод позволяет исследовать до-

вольно разнообразные системы: разупорядоченные

Благодарности. Авторы выражают благодар-

и упорядочивающиеся сплавы, системы с сильными

ность профессору С. Г. Овчинникову за обсуждение

электронными корреляциям и электрон-фононным

результатов и сделанные замечания.

взаимодействием, магнитные сплавы, различные си-

Финансирование. Работа выполнена при фи-

стемы с ближним порядком и испытывающие фазо-

нансовой поддержке Фонда развития теоретиче-

960

ЖЭТФ, том 158, вып. 5 (11), 2020

Электронная структура и электропроводность. ..

ской физики и математики «БАЗИС», Российско-

10.

P. W. Anderson, Phys. Rev. 109, 1492 (1958).

го фонда фундаментальных исследований (грант

11.

Л. П. Горьков, А. И. Ларкин, Д. Е. Хмельницкий,

№19-03-00017), Российского фонда фундаменталь-

Письма в ЖЭТФ 30, 248 (1979).

ных исследований и Правительства Красноярско-

го края, Красноярского краевого фонда науки в

12.

E. Abrahams, P. W. Anderson, D. С. Licciardello,

рамках научного проекта «Эффекты электронных

and Т. V. Ramakrishnan, Phys. Rev. Lett. 42, 673

корреляций и многоорбитальная физика в соедине-

(1979).

ниях железа и купратах» (грант № 19-42-240007) и

13.

G. Bergmann, Phys. Rep. 107, 1-58 (1984).

научного проекта «Особенности электрон-фононной

связи в высокотемпературных сверхпроводниках

14.

R. Flederling, M. Kelm, G. Reuseher, M. Ossau,

с сильными электронными корреляциями» (грант

G. Schmidt, A. Waag, and L. W. Molenkamp, Nature

№18-42-240017).

402, 787 (1999).

15.

G. A. Prinz, Phys. Today 48, 5863 (1995).

ЛИТЕРАТУРА

16.

С. Борухович, УФН 169, 737 (1999).

1. R. J. Elliott, J. A. Krumhansl, and P. L. Leath, Rev.

17.

D. Senechal, D. Perez, and M. Pioro-Ladriere, Phys.

Mod. Phys. 46, 465 (1974).

Rev. Lett. 84, 522 (2000).

2. Дж. Займан, Модели беспорядка, Мир, Москва

18.

D. Senechal, D. Perez, and D. Plouffe, Phys. Rev.

(1982).

B 66, 075129 (2002).

3. И. М. Лифшиц, С. А. Гредескул, Л. А. Пас-

19.

E. Dagotto, T. Hotta, and A. Moreo, Phys. Rep. 344,

тур, Введение в теорию неупорядоченных систем,

1 (2001).

Наука, Москва (1982).

20.

E. Dagotto, Nanoscale Phase Separation and Colossal

4. R. Mills and P. Ratenavaraksa, Phys. Rev. B 18, 5291

Magnetoresistance, Springer, Berlin (2003).

(1978).

21.

С. В. Николаев, С. Г. Овчинников, ЖЭТФ 138,

5. V. F. Los’ and S. P. Repetsky, J. Phys.: Condens.

717 (2010).

Matter 6, 1707 (1994).

22.

С. В. Николаев, С. . Овчинников, ЖЭТФ 141, 135

6. S. P. Repetsky, Ye. G. Len, and N. V. Chubinsky,

(2012).

Met. Phys. Adv. Tech. 17, 867 (1999).

23.

M. W. Haverkort, I. S. Elfimov, and G. A. Sawatzky,

7. С. П. Репецкий, В. Б. Молодкин, И. Г. Вышива-

arXiv:1109.4036v1 [cond-mat.mtrl-sci].

ная, Е. Г. Лень, И. Н. Мельник, О. И. Мусиенко,

24.

М. В. Садовский, УФН 171, 539 (2001).

Б. В. Стащук, Успехи физ. мет. 10, 283 (2009).

25.

E. Dagotto, Rev. Mod. Phys. 66, 763 (1994).

8. М. А. Кривоглаз, А. А. Смирнов, Теория упорядо-

чивающихся сплавов, Физматгиз, Москва (1958).

26.

G. D. Mahan, Many-Particle Physics, Springer, US

(2000).

9. С. М. Бородачев, В. А. Волков, С. И. Машаров,

ФММ 42, 1147 (1976).

27.

D. J. Scalapino, Phys. Rev. B 47, 7995 (1993).

961

ЖЭТФ, вып. 5 (11)