ЖЭТФ, 2020, том 158, вып. 5 (11), стр. 968-977
© 2020
ВОЗМОЖНЫ ЛИ ГИПЕРЗВУКОВЫЕ ЭЛЕКТРОСТАТИЧЕСКИЕ
СОЛИТОНЫ? ОЦЕНКА ПРЕДЕЛЬНЫХ ЧИСЕЛ МАХА
ИОННО-ЗВУКОВЫХ СОЛИТОНОВ В ТЕПЛОЙ ПЛАЗМЕ
А. Е. Дубиновa,b*, О. В. Сусловаb
a Российский федеральный ядерный центр —
Всероссийский научно-исследовательский институт экспериментальной физики
607188, Саров, Нижегородская обл., Россия
b Саровский физико-технический институт —
филиал Национального исследовательского ядерного университета «Московский инженерно-физический институт»
607186, Саров, Нижегородская обл., Россия
Поступила в редакцию 26 марта 2020 г.,
после переработки 19 мая 2020 г.
Принята к публикации 19 мая 2020 г.
Развита нелинейная теория ионно-звуковых волн в бесстолкновительной теплой электрон-ионной плаз-
ме. Теория основана на анализе псевдопотенциала Сагдеева. Рассмотрены две модели ионно-звуковых
волн — изотермическая и адиабатическая. Вычислены зависимости максимального значения числа Ма-
ха для солитонов от приведенной температуры (параметра неравновесности) плазмы для обеих моде-
лей. Показано, что максимальное значение числа Маха не может превышать фундаментального предела
2.54. Решен вопрос о существовании гиперзвуковых ионно-звуковых солитонов: гиперзвуковые солитоны
невозможны.
√
DOI: 10.31857/S0044451020110188
= kBTe/4πe2n0 — электронная длина Дебая, Te —
электронная температура, mi — масса иона, kB —
1. ВВЕДЕНИЕ
постоянная Больцмана. n0 — невозмущенная кон-
центрация плазмы. Закон дисперсии (1) определяет
Ионно-звуковые волны (ИЗВ) в плазме уже мно-
линейную скорость ИЗВ:
го десятилетий привлекают исследователей, специа-
√
лизирующихся в физике плазмы. Общее число опуб-
dω
ω
kBTe
vs0 = lim
= lim
=ωpiλDe =
(2)
ликованных работ, так или иначе связанных с ИЗВ,
k→0 dk
k→0 k
mi
доходит до 10000. В недавней обзоре [1] показано,
Нелинейная теория показала [3], что ИЗВ мо-
что интерес к ИЗВ не иссякает до сих пор и что
гут существовать не только в форме периодичес-
не все проблемы, связанные с физикой ИЗВ, ре-
ких волн, но и в форме солитонов. Было установ-
шены. Кратко напомним главные особенности ИЗВ
лено, что периодические ИЗВ всегда дозвуковые, а
в бесстолкновительной изотропной электрон-ионной
солитоны могут двигаться только со сверхзвуковы-
плазме. Из линейной теории можно получить закон
ми скоростями, причем числа Маха для солитонов
дисперсии для гармонических ИЗВ, который, на-
в плазме с холодными ионами лежат в диапазоне
пример, для электрон-ионной плазмы с холодными
1 < M < M0max ≈ 1.58. В работе [4] получено точное
ионами имеет вид [2]
значение для предельного числа Маха M0max:
ω2piλ2De
k2
√
(
)
ω2 =
,
(1)
1
1+λ2Dek2
M0max =
-1 - 2W-1
-
e-1/2
≈
2
где ω — частота волн, k — волновое число, ωpi =√
≈ 1.5852010065,
(3)
=
4πe2n0/mi — ионная плазменная частота, λDe =
где W-1(x) — действительная отрицательная ветвь
* E-mail: dubinov-ae@yandex.ru
W-функции Ламберта [5].
968
ЖЭТФ, том 158, вып. 5 (11), 2020
Возможны ли гиперзвуковые электростатические солитоны. . .
Существование предельного числа Маха озна-
сти с самого начала нормировать на линейную ско-
чает физически, что при его превышении возни-
рость ИЗВ vsT .
кает отражение ионов потенциальным барьером в
самом солитоне, которое приводит к «опрокидыва-
2. ИЗОТЕРМИЧЕСКИЕ ИОННО-ЗВУКОВЫЕ
нию» ионной составляющей.
СОЛИТОНЫ
Несмотря на огромное количество исследований
по ионно-звуковым солитонам, работ, посвященных
2.1. Закон дисперсии и линейная скорость
оценке предельных чисел Маха Mmax для других
изотермических ИЗВ
моделей плазмы, немного. Можно назвать только
Для вывода закона дисперсии будем исходить
статью [6], а также обзор [1], дублирующий резуль-
из следующей системы газодинамических уравне-
таты работы [6], где рассмотрены величины пре-
ний ионной динамики, считая электроны безынер-
дельного числа Маха для плазмы с холодными иона-
ционными, а ионы — заряженными однократно:
ми и с электронной составляющей, подчиняющей-
ся адиабатическому уравнению состояния. В них
∂ni
∂
+
(niui) = 0,
сообщается, что Mmax может достигать значения
∂t
∂z
(
)
Mmax = 2.54
M2max = 6.46
[6]. Это же значение бы-
∂ui
∂ui
e
∂ϕ
1
∂Pi
ло получено и в [7].
+ui
=
-
,
(4)
∂t
∂z
mi ∂z
mini ∂z
Однако в недавней работе [8] рассматривались
солитоны со значениями чисел Маха Mmax ≈ 3.5
∂2ϕ
= -4πe(ne - ni),
для ИЗВ в четырехкомпонентной плазме, но там бы-
2
∂z
ла допущена весьма распространенная неточность,
где ϕ — электростатический потенциал в ИЗВ, e —
отмеченная в работе [9]: скорость солитона в теплой
элементарный заряд, mi, ni, ui — масса, концентра-
плазме нормировалась на линейную скорость ИЗВ
ция, скорость ионов, Pi — их газодинамическое дав-
для плазмы с холодными ионами, т. е. на скорость
ление, которое удовлетворяет уравнению состояния
звука другой плазмы. Поэтому на вопрос, вынесен-
идеального газа
ный в заголовок данной статьи, о возможности ги-
перзвуковых (по авиационной терминологии) ионно-
Pi = nikBTi
(5)
звуковых солитонов, у которых Mmax ≫ 1, до сих
пор не существует окончательного ответа.
с ионной температурой Ti. Будем считать также, что
электроны подчиняются распределению Больцмана
Цель данной работы — установление зависимо-
(
)
сти предельного числа Маха от температуры ионов,
eϕ
ne = n0 exp
-
(6)
Mmax(Ti), для теплой плазмы с изотермическим
kBTe
и адиабатическим уравнениями состояния ее ион-
ной и электронной составляющих. Как и в рабо-
Придадим переменным системы (4) малое волновое
те [10], предположено, что в бесстолкновительной
гармоническое возмущение с малыми амплитудами,
плазме отсутствуют «лобовые» столкновения час-
отмеченными значком «тильда»:
тиц, а термодинамическое равновесие устанавлива-
ui = ũi exp[i(ωt - kz)],
ется за счет некоррелированных кулоновских взаи-
ni = n0 + ñi exp[i(ωt - kz)],
(7)
модействий посредством согласованного электриче-
ского поля.
ϕ=
ϕi exp[i(ωt - kz)].
Рассмотрение проводилось в рамках двухжид-
Подставим уравнения (7) в систему (4) и после стан-
костной газодинамики [6] методом псевдопотенциа-
дартной процедуры линеаризации получим закон
ла Сагдеева [3]. При этом скорости сначала норми-
дисперсии изотермических ИЗВ:
ровались на удобную для выкладок величину ско-
рости звука в плазме с холодными ионами, vs0 (2),
ω2piλ2Dek2
ω2 =
+ω2piλ2Dik2.
(8)
а затем, на заключительной стадии анализа, все
1+λ2Dek2
скорости перенормировались на линейную скорость
Из уравнения (8) следует выражение для линейной
ИЗВ, полученную из дисперсионного уравнения для
скорости изотермической ИЗВ:
ИЗВ для рассматриваемой модели плазмы (в соот-
√
ветствии с рекомендациями работы [9]). Такой путь
√
kB (Te + Ti)
позволил избежать громоздких математических вы-
vsT = ωpi λ2De + λ2Di =
(9)
mi
кладок, которые неизбежно возникают, если скоро-
969
А. Е. Дубинов, О. В. Суслова
ЖЭТФ, том 158, вып. 5 (11), 2020
2.2. Псевдопотенциал Сагдеева для
изотермических ИЗВ
Будем использовать следующие обозначения и
нормировки для переменных задачи:
z = λ2Dez, t = ω-1pi t, ui = vs0ûi, ne,i = n0ne,i,
kBTe
ϕ=-
ϕ,
τ=
Ti ,
e
Te
при этом в дальнейшем значки «шляпки» над без-
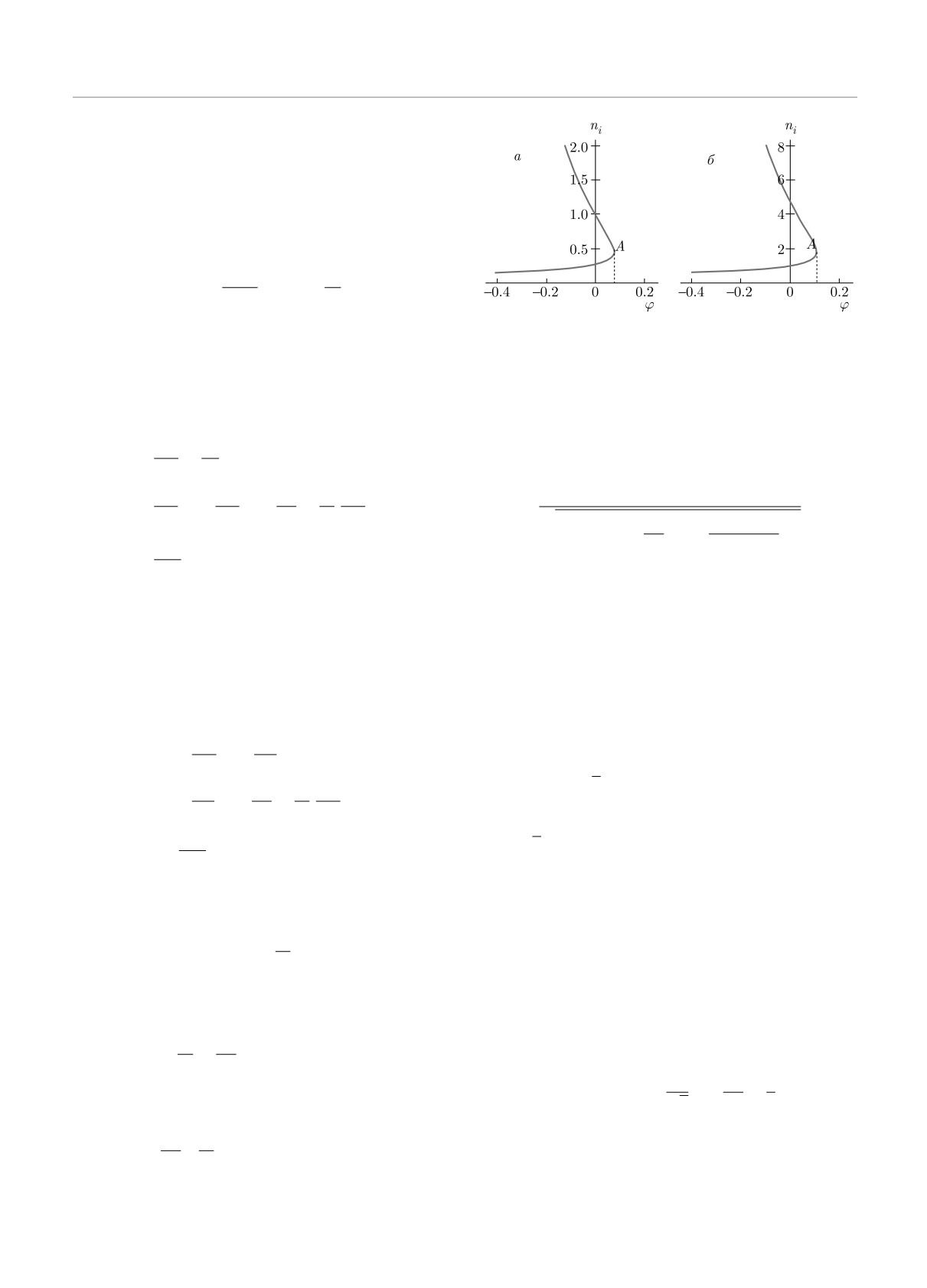
Рис. 1. Зависимости ni(ϕ), определяемые выражением
размерными величинами будем опускать. Попут-
(15), для изотермических ИЗВ при τ = 0.2: а — случай
но отметим, что полезно использовать нормировку
периодических ИЗВ при V = 0.2; б — солитонный случай
электростатического потенциала со знаком минус:
при V = 0.8
тогда знаки ϕ и
ϕ совпадают. Нормированная си-
стема уравнений (4) примет вид
Его необходимо решить относительно ni для подста-
∂ni
∂
новки в уравнение Пуассона. Это удается сделать,
+
(niui) = 0,
∂t
∂z
используя W-функцию Ламберта [4, 5]:
∂ui
∂ui
∂ϕ
τ
∂ni
V
+ui
=-
-
,
(10)
ni =
√
(15)
[
(
)].
∂t
∂z
∂z
ni ∂z
2
-V2 + 2ϕ
-τW0,-1
-Vτ
exp
τ
∂2ϕ
=ne -ni.
2
∂z
Функция ni(ϕ), задаваемая выражением (15), явля-
Рассмотрим стационарную волну, движущуюся
ется двузначной, а ее график имеет две ветви, со-
вдоль оси z со скоростью V . Введем волновую пе-
прягающиеся в точке ветвления A (рис. 1). Одна
ременную ξ = z - V t и перейдем в систему отсчета,
из ветвей нефизична, и ее надо отбросить. Как это
связанную с волной (vi = ui - V ). Тогда с учетом
делается, детально изложено в работе [11]: остаю-
больцмановского распределения электронов (6) по-
щаяся ветвь должна удовлетворять условию квази-
лучим следующую систему обыкновенных диффе-
нейтральности невозмущенной плазмы, т. е. должна
ренциальных уравнений:
проходить через точку ni (ϕ = 0) = 1. Анализ вы-
∂ni
∂vi
ражения (15) показал, что при разных значениях V
vi
+ni
= 0,
∂ξ
∂ξ
остающаяся ветвь может быть нижней или верхней.
Так, при V <
√τ остающаяся ветвь — верхняя, и она
∂vi
∂ϕ
τ
∂ni
vi
=-
-
,
(11)
описывается основной ветвью W-функции Ламберта
∂ξ
∂ξ
ni ∂ξ
W0 (. . .) (случай периодической ИЗВ; рис. 1а, а при
∂2ϕ
V >
√τ остающаяся ветвь — нижняя, она описы-
=eϕ -ni.
2
∂ξ
вается отрицательной ветвью W-функции Ламберта
W-1 (. . .) (солитонный случай, рис. 1б).
Уравнение непрерывности с учетом условия для
Для нахождения максимально возможной скоро-
невозмущенной плазмы, lim
ni = 1, имеет реше-
vi→-V
сти солитона, как мы увидим ниже, важны коор-
ние
V
динаты точки ветвления A, в которой сопрягают-
vi = -
(12)
ni
ся действительные ветви W-функции Ламберта. Из-
Интегрируя уравнение движения с условиями
вестно, что аргумент W-функции в точки ветвления
lim
ni = 1 и lim ϕ = 0, получим
равен -1/ exp (1), а ее значение там -1 [5]. Кроме то-
vi→-V
vi→-V
го, положение точки A определяет и максимально
v2i
V2
возможную амплитуду электростатического потен-
-
= -ϕ - τ ln ni.
(13)
2
2
циала в солитоне:
(
)
V
V2
τ
Подставим выражение (12) в (13) и получим следу-
ϕmax = -τ ln
+
-
(16)
√τ
2
2
ющее трансцендентное уравнение для ni:
)
V2
( 1
При превышении этого значения ионы должны
-1
+ τ lnni = -ϕ.
(14)
отражаться потенциальным барьером солитона, и,
2
ni
970
ЖЭТФ, том 158, вып. 5 (11), 2020
Возможны ли гиперзвуковые электростатические солитоны. . .
Рис. 2. Профили псевдопотенциала Сагдеева Us(ϕ, V, τ ), определяемого выражением (19), для изотермических солитонов
при τ = 0.2 и V = 1.35
(а), 1.38 (б), 1.41 (в)
следовательно, солитон с потенциалом, большим,
При этом константу интегрирования C1 следует вы-
чем (16), стационарно существовать не может.
брать для удобства так, чтобы Us(0, V, τ) = 0.
Далее, подставим в уравнение Пуассона выраже-
ние (15) с отрицательной ветвью W-функции Лам-
2.3. Анализ псевдопотенциала и оценка
берта. Тогда оно примет вид
максимального числа Маха для
∂2ϕ
V
изотермических солитонов
=eϕ-√
[
(
)],(17)
∂ξ2
2
-V2+2ϕ
Перейдем к анализу псевдопотенциала Сагдее-
-τW-1 -Vτ
exp
τ
ва (19). Уравнение (18) математически эквивалент-
но закону сохранения энергии при движении без
где в правой части электронное слагаемое записано
трения некой фиктивной частицы в потенциальном
в форме больцмановской экспоненты согласно фор-
профиле, задаваемой функцией Us(ϕ, V, τ); при этом
муле (6). Умножая правую и левую части уравне-
потенциал ϕ играет роль псевдокоординаты фик-
ния (17) на dϕ/dξ и затем интегрируя, получим вы-
тивной частицы, а переменная ξ — ее псевдовремени.
ражение в форме закона сохранения псевдоэнергии
На рис. 2 представлены три примера формы
некой фиктивной частицы,
псевдотенциала при разных значениях скорости
V >
√τ. Все они имеют максимум в начале коорди-
1
( dϕ)2
+ Us(ϕ, V, τ) = C1,
(18)
нат, монотонно уходят до -∞ в отрицательной обла-
2
dξ
сти и ограничены в положительной области крайней
с псевдопотенциалом Сагдеева в форме
точкой, которая соответствует точке ветвления A на
Us(ϕ, V, τ) = 1 - eϕ +
рис. 1б (поэтому крайняя точка на рис. 2 также по-
⎧
мечена A). При сравнительно небольшом значении
⎪
√
⎨
[
скорости V конечная точка A лежит выше оси абс-
V2
V2
(-V 2+2ϕ)]
-
W-1 -
exp
-
цисс (рис. 2а), что соответствует возможности су-
+τ⎪
τ
τ
τ
⎪
⎩
ществования солитона. Ей соответствует замкнутая
фазовая траектория фиктивной частицы на ее фа-
√
[
(
)]
2
зовом портрете, начинающаяся в начале координат.
V
V2
V2
-
-
W-1 -
exp
-
-
Форма такого солитона с гладкой вершиной пред-
τ
τ
τ
2
ставлена на рис. 3 (кривая 1). При увеличении ско-
3
3
V2
рости V точка A приближается к оси абсцисс. На
-
3-
[
√
2
(-V2 + 2ϕ)]+
рис. 2б показана ситуация, когда крайняя точка ле-
τW-1
-Vτ
exp
τ
жит на оси абсцисс. Она соответствует максималь-
⎫
но возможной амплитуде потенциала в солитоне и
⎪
2
⎬
3
его максимальной скорости для данных параметров
3
V2
+
3-
[
(
(19)
плазмы. Форма такого предельно быстрого солито-
√
V2
V2)] ⎪
⎪
τW-1
-
exp
-
⎭
на с острой вершиной представлена на рис. 3 (кри-
τ
τ
вая 2).
971
А. Е. Дубинов, О. В. Суслова
ЖЭТФ, том 158, вып. 5 (11), 2020
Рис. 4. Зависимость безразмерной максимальной скорости
изотермического солитона от безразмерной температуры
(по формуле (20))
лить безразмерную скорость Vmax из (20) на
√1 + τ,
т. е. максимальное число Маха выразится как
Рис. 3. Профили электростатического потенциала в изо-
термических солитонах при τ = 0.2: 1 — M = 1.04; 2 —
Vmax
Mmax =
√
(21)
M = 1.26
1+τ
При еще большем значении V крайняя точка ле-
Тогда уравнение, определяющее неявную зависи-
жит ниже оси абсцисс (рис. 2в), и никакие солито-
мость Mmax (τ), запишется в виде
ны здесь невозможны, так как замкнутую фазовую
траекторию, начинающуюся в начале координат, по-
[
(
)]
1 - W-1 - M2max exp
-M2
max
строить нельзя.
Mmaxτ2
√
[
(
)]-
Таким образом, для нахождения максимальной
−τW-1 -M2max exp
-M2
скорости солитона при различных значениях приве-
max
денной ионной температуры τ необходимо найти те
(
)τ /2
(
1
τ)
значения Vmax, при которых крайняя точка лежит
M2
-
exp
-
-
max
M2
2
на оси абсцисс, как это показано на рис. 2б. Тогда
max
потенциал ϕ в крайней точке A удовлетворяет урав-
- 2Mmaxτ + 1 = 0,
(22)
нению (16), а значение псевдопотенциала Us(ϕ, V, τ)
в этой точке равно нулю. Записывая это условие,
где
получим зависимость Vmax(τ) в неявной форме:
M2max (1 + τ)
M2
max
=
(23)
[
(
)]
2
τ
V
V2max
max
1-W-1 -
exp
-
График этой зависимости представлен на рис. 5.
τ
τ
Vmaxτ
√
[
(
)]-
Кривая, описывающая зависимость Mmax (τ), как
V2
V2max
max
видно, выходит из точки со значением 1.58 (3) и
-τW-1 -
exp
-
τ
τ
монотонно убывает, устремляясь к единице. Таким
(
)τ/2
(
)
образом, изотермические солитоны не могут иметь
τ
V2max
τ
-
exp
-
-
-
большое число Маха.
V2max
τ
2
− 2V 2max
√τ + 1 = 0.
(20)
3. АДИАБАТИЧЕСКИЕ ИОННО-ЗВУКОВЫЕ
СОЛИТОНЫ
На рис. 4 показан график этой зависимости, кото-
рый по форме совпадает с аналогичным графиком
3.1. Закон дисперсии и линейная скорость
из работы [7]. Видно, что он имеет минимум и тен-
адиабатических ИЗВ
денцию к возрастанию с ростом τ. Для определения
максимального числа Маха необходима перенорми-
Перейдем к рассмотрению ионно-звуковых со-
ровка скорости Vmax. Сравнивая скорости ИЗВ для
литонов в случае, когда фазы сжатия и разреже-
холодной, vs0 (2), и для теплой, vsT (9), плазмы, по-
ния в волне являются адиабатическими процессами
лучим, что для перенормировки достаточно поде-
как для ионов, так и для электронов. Тогда уравне-
972
ЖЭТФ, том 158, вып. 5 (11), 2020
Возможны ли гиперзвуковые электростатические солитоны. . .
Рис. 6. Зависимости ni(ϕ) (29) для адиабатических ИЗВ
Рис. 5. Зависимость максимального числа Маха изотерми-
при θ = 0.2, γe = γi = 2: а — случай периодических ИЗВ
ческого солитона от безразмерной температуры (по фор-
при V = 0.16; б — солитонный случай при V = 1.42
муле (22))
ния (29) следует дополнить уравнением состояния
где
θ— параметр неравновесности плазмы (как и
ионной фракции в виде
выше, «шляпки» над буквами будем опускать). То-
)γi
гда нормированная система уравнений имеет вид
(ni
Pi = n0kBTi
(24)
∂ni
∂
n0
+
(niui) = 0,
∂t
∂z
и распределением электронов
∂ui
∂ui
∂ϕ
(
)1/(γe-1)
+ui
=-
- θnγi-2 ∂nii
,
(28)
γe - 1
eϕ
∂t
∂z
∂z
∂z
ne = n0
1-
,
(25)
γe kBTe
∂2ϕ
= [1 + (γe - 1) ϕ]1/(γe-1) - ni
2
где введены γe и γi — показатели адиабаты соответ-
∂z
ственно для электронов и ионов, остальные обозна-
Снова рассмотрим стационарную волну, движущу-
чения прежние.
юся вдоль оси z со скоростью V . Введем волновую
Подставляя выражение (6) в (29) с учетом (24)
переменную ξ = z - V t и перейдем в систему отсче-
и (25), после несложных выкладок получим закон
та, связанную с волной (vi = ui -V ). Тогда с учетом
дисперсии адиабатических ИЗВ, который формаль-
распределения электронов (25) получим следующую
но записывается так же, как и (8), но с электронной
систему обыкновенных дифференциальных уравне-
и ионной длинами Дебая в виде
ний:
√
√
∂ni
∂vi
γekBTe
γikBTi
vi
+ni
= 0,
λDe =
,
λDi =
(26)
∂ξ
∂ξ
4πe2n0
4πe2n0
∂vi
∂ϕ
∂ni
γi-2
vi
=-
- θn
,
(29)
Из него следует выражение для линейной скорости
i
∂ξ
∂ξ
∂ξ
адиабатической ИЗВ:
∂2ϕ
√
= [1 + (γe - 1) ϕ]1/(γe-1) - ni.
√
2
γikBTi
∂ξ
vsT = ωpi λ2De + λ2Di =
(27)
4πe2n0
Решение уравнения непрерывности из (29) с уче-
ni =
том условия для невозмущенной плазмы lim
vi→-V
3.2. Псевдопотенциал Сагдеева для
= 1 имеет вид (12). Решение уравнения движения
адиабатических ИЗВ
ионов из (29) примет вид
Будем исходить, как и прежде, из уравнений
)
V2
1
θ (
ϕ=
+
1-nγi-1
(30)
(29), но будем использовать соотношения (24) и (25)
i
2
n2i
γi - 1
вместо (5) и (6). Будем использовать следующие
обозначения и нормировки для переменных:
Неявная функция ni(ϕ), задаваемая выражением
(30), как и (15), является двузначной, а ее график
z = λ2Dez, t = ω-1pi t, ne,i = n0ne,i,
имеет две ветви, сопрягающиеся в точке ветвления
γiTi
A (рис. 6). Одна из ветвей также нефизична, и ее на-
ui =
√γevs0 ûi, ϕ = -γekBTeϕ,
θ=
,
до отбрасывать, при этом оставляемая ветвь должна
e
γeTe
973
А. Е. Дубинов, О. В. Суслова
ЖЭТФ, том 158, вып. 5 (11), 2020
[
1
удовлетворять условию квазинейтральности невоз-
Us(ni, V, θ) =
γeγiV2 (1 - ni) + θγenγi+1i -
γeγini
мущенной плазмы, т. е. должна проходить через точ-
]
ку ni(ϕ = 0) = 1.
- θγeni - γini + γiniG0(ni, V, θ) ,
(34)
Анализ показал, что при разных значениях V
оставляемая ветвь может быть нижней или верхней.
где
√
Так, при V <
θ оставляемая ветвь — верхняя (слу-
√
[
]γ
e/(γe-1)
чай периодической ИЗВ, рис. 6а), а при V >
θ —
R0(ni, V, θ)
G0(ni, V, θ) =
-
,
(35)
нижняя (солитонный случай, рис. 6б).
2n2i (γi - 1)
Для нахождения максимально возможной ско-
рости солитона необходимо найти максимум функ-
(
)
ции (30):
R0 (ni, V, θ) = (γe + γi - γeγi - 1)V2
n2i - 1
+
[
2
+ 2ϕ(γe - 1)nγi+1i + 2 (ϕ - γi - ϕγe)n2i.
(36)
V
γi + 1
(V2)-2/(γi+1)]
θ
ϕmax =
-
(31)
2
γi - 1
θ
γi - 1
Формулы (34)-(36) совместно с (30) дают выраже-
ние для функциональной зависимости U(ϕ) в пара-
При превышении этого значения ионы должны от-
метрическом виде, где ионная концентрация ni яв-
ражаться потенциальным барьером солитона, и,
ляется параметром этой функции.
следовательно, солитон с потенциалом, большим,
чем (31), стационарно существовать не может.
Теперь следовало бы решить уравнение (30) от-
3.3. Анализ псевдопотенциала и оценка
носительно ni с последующей подстановкой ni(ϕ) в
максимального числа Маха для
уравнение Пуассона из системы (29), как это бы-
адиабатических солитонов
ло сделано в изотермическом случае с помощью
На рис. 7 представлены три примера формы
W-функции Ламберта. Однако для произвольного
псевдопотенциала при разных значениях скорости
значения показателя адиабаты этого сделать нель-
√
V >
θ. Все они имеют максимум в начале коорди-
зя. Специально для таких сложных случаев были
нат, монотонно уходят до -∞ в отрицательной об-
разработаны два метода, когда аналитическая за-
ласти и ограничены в положительной области край-
пись ni(ϕ) в явном виде невозможна. Первый из
ней точкой, которая соответствует точке ветвления
них основан на сведении уравнения Пуассона к диф-
A на рис. 6б. При сравнительно небольшом значе-
ференциальному уравнению Бернулли и использо-
нии скорости V конечная точка A лежит выше оси
вании так называемого псевдопотенциала Бернул-
абсцисс (рис. 7а), что соответствуетвозможности су-
ли с аргументом ni в качестве псевдокоординаты
ществования солитона. Ей соответствует замкнутая
[9, 12-14]. Другой метод основан на использовании
фазовая траектория фиктивной частицы на ее фа-
интегрирования обратной функции [15]. В настоя-
зовом портрете, начинающаяся в начале координат.
щей работе был выбран именно он как наиболее эф-
При увеличении скорости V точка A приближа-
фективный для данного класса задач.
ется к оси абсцисс. На рис. 7б показана ситуация,
Согласно работам [5,15,16], если имеется ϕ(ni), а
когда крайняя точка лежит на оси абсцисс. Она со-
нужно проинтегрировать ni(ϕ), то справедливо пра-
ответствует максимально возможной амплитуде по-
вило интегрирования обратной функции:
∫
∫
тенциала в солитоне и его максимальной скорости
для данных параметров плазмы.
ni(ϕ)dϕ =
ϕni(ϕ) - ϕ(ni) dni.
(32)
При еще большем значении крайняя точка ле-
ni(ϕ)
жит ниже оси абсцисс (рис. 6в), и никакие солито-
Итак, уравнение Пуассона в (29) после умножения
ны здесь невозможны, так как замкнутую фазовую
его правой и левой частей на dϕ/dξ и интегрирова-
траекторию, начинающуюся в начале координат, по-
ния дает закон сохранения псевдоэнергии:
строить нельзя.
∫
Для нахождения максимальной скорости солито-
1
( dϕ)2
= (ne - ni) dϕ + C2.
(33)
на при различных значениях параметра неравновес-
2
dξ
ности плазмы θ необходимо найти те значения Vmax,
Воспользовавшись правилом (32) и удобным выбо-
при которых крайняя точка лежит на оси абсцисс,
ром константы интегрирования C2, так чтобы гра-
как это показано на рис. 7б. Тогда потенциал ϕ в
фик псевдопотенциала проходил через начало коор-
крайней точке A удовлетворяет соотношению (16),
динат, получим
а значение псевдопотенциала Us(ϕ, V, θ) в этой точке
974
ЖЭТФ, том 158, вып. 5 (11), 2020
Возможны ли гиперзвуковые электростатические солитоны. . .
Рис. 7. Профили псевдопотенциала Сагдеева Us(ϕ, V, τ ), определяемого выражениями (30), (34)-(36), для адиабатиче-
ских солитонов при θ = 0.2, γe = γi = 2 и V = 1.36 (а), 1.42 (б), 1.46 (в)
равно нулю. Записывая это условие, получим зави-
симость Vmax (θ) в неявной форме:
{
[
√
]
γeγiV2
1-
N1 (Vmax, θ)
+ N1 (Vmax,θ) ×
max
}
× [γiG1 (ni, Vmax, θ) - θγe - γi] + γeV2max
×
1
×
√
= 0,
(37)
γeγi
N1 (Vmax, θ)
где
)2/(γi+1)
(V2max
N1 (Vmax, θ) =
,
(38)
θ
G1 (ni, Vmax, θ) =
[
]γe/(γe-1)
R1 (ni, Vmax, θ)
= -
,
(39)
2N1 (Vmax, θ)(γi - 1)
Рис. 8. (В цвете онлайн) Зависимости безразмерной мак-
R1 (ni, Vmax, θ) = (γe + γi - γeγi - 1)V2max ×
симальной скорости адиабатических солитонов от пара-
× [N1 (Vmax, θ) - 1] + 2 (γe - 1) V 2max +
метра неравновесности плазмы (по формуле (37)) для трех
+ 2(θ - γi - θγe)N1 (Vmax,θ).
(40)
значений γe = γi
На рис. 8 показаны зависимости (37) при трех зна-
чениях показателей адиабаты, γe = γi = 5/3, 2, 3,
симальное число Маха выразится в неявном виде
которые, так же как и для изотермического случая,
как
по форме совпадают с аналогичными из работы [8].
{
Видно, что они имеют минимум и тенденцию воз-
[
√
]
растания с ростом параметра неравновесности плаз-
M2max (1+θ) γeγi-γeγi
N2 (Mmax, θ)+γe
+
мы θ. Тем не менее для определения максимального
}
числа Маха опять необходима перенормировка этой
+ N2 (Mmax,θ)[γiG2 (ni, Mmax,θ)-θγe-γi]
×
скорости. Сравнивая скорости ИЗВ для холодной,
vs0 (2), и для теплой, vsT (27), плазмы, получим,
1
что для перенормировки достаточно поделить без-
×
√
= 0,
(41)
√
γeγi
N2 (Mmax, θ)
размерную скорость Vmax из (20) на
1 + θ, т.е. мак-
975
А. Е. Дубинов, О. В. Суслова
ЖЭТФ, том 158, вып. 5 (11), 2020
Следовательно, значения Mmax (0) в нулевых
точках проще определить из анализа более просто-
го, чем (34)-(36), псевдопотенциала Сагдеева для
ИЗВ в плазме с адиабатическими электронами и хо-
лодными ионами (в безразмерном виде):
U (ϕ, Mmax (0)) = [1 + (γe - 1) ϕ]1/(γe-1) -
Mmax (0)
-
√
(45)
M2max (0) - 2ϕ
Приравнивая значения этого псевдопотенциала в
точке ϕmax нулю, получим алгебраические уравне-
ния для нахождения числа Маха в нулевых точках:
]γ
e/(γe-1)
1
[1
1
M2max (0) + 1
= M2max (0) +
(46)
γe
2
γe
Уравнение (46) имеет порядок и число корней, за-
висящие от γe. Поэтому найдем значения Mmax (0)
Рис. 9. (В цвете онлайн) Зависимости максимального чис-
отдельно для каждого из трех значений показателей
ла Маха адиабатических солитонов от параметра нерав-
адиабаты электронов.
новесности плазмы (по формуле (41)) для трех значений
При γe = 5/3 уравнение (46) имеет вид
γe = γi
]5/2
3
[M2
max
(0)
3
+1
= M2max (0) +
(47)
5
3
5
где
и сводится к уравнению пятой степени относительно
]2/(γi+1)
[M2max (1 + θ)
M2max (0). Из всех его корней физический смысл име-
N2 (Mmax, θ) =
,
(42)
θ
ет корень, который может быть найден лишь чис-
ленно: Mmax (0) ≈ 1.85 . . .
При γe=2 уравнение (46) принимает вид
G2 (ni, Mmax, θ) =
]2
[
[M2
(0)
]γe/(γe-1)
max
R2 (ni, Mmax, θ)
-1
= 1 + 2M2max (0)
(48)
= -
,
(43)
2
2N2 (Mmax, θ)(γi - 1)
и сводится к квадратному уравнению относительно
M2max (0). Оно имеет точное положительное решение
R2 (ni, Mmax, θ) =
Mmax (0) = 2.
При γe=3 уравнение (46) имеет вид
= M2max (1 + θ)(γe + γi - γeγi - 1) ×
1
[
]3/2
1
× [N2 (Mmax, θ) - 1] + 2 (γe - 1) (1 + θ) M2max +
M2max (0) + 1
=
+ M2max (0)
(49)
3
3
+ 2(θ - γi - θγe)N2 (Mmax,θ).
(44)
и сводится к кубическому уравнению относительно
Графики зависимости (41) представлены на рис. 9.
M2max (0). Действительный корень этого уравнения
Кривые, описывающие зависимость Mmax (θ), выхо-
есть
дят из разных начальных (нулевых) точек, коорди-
√
√
наты которых зависят от γe, а затем монотонно убы-
Mmax (0) =
3+2
3 ≈ 2.542459757...
(50)
вают, устремляясь к единице. Таким образом, адиа-
батические солитоны также не могут иметь большое
Выражение (50) представляет собой фундаменталь-
число Маха, т. е. гиперзвуковые ионно-звуковые со-
ную величину, которая дает самое максимальное
литоны и здесь невозможны. При этом максималь-
из возможных в плазме значение числа Маха для
но возможное число Маха соответствует холодным
ионно-звуковых солитонов. И амплитуда такого экс-
ионам и электронам с показателем адиабаты γe = 3.
тремального солитона — максимально возможная.
976
ЖЭТФ, том 158, вып. 5 (11), 2020
Возможны ли гиперзвуковые электростатические солитоны. . .
числом Маха может реализовываться в сильноза-
магниченной плазме с холодными ионами и с пока-
зателем адиабаты электронов, равным 3. Вычислен
профиль экстремального солитона. В итоге, вопрос
о существовании гиперзвуковых ионно-звуковых со-
литонов решен: гиперзвуковые солитоны невозмож-
ны.
ЛИТЕРАТУРА
1.
G. M. Webb, R. H. Burrows, X. Ao, and G. P. Zank,
J. Plasma Phys. 80, 147 (2014).
2.
A. E. Dubinov and I. N. Kitayev, Phys. Wave
Phenom. 23, 122 (2015).
3.
A. A. Vedenov, E. P. Velikhov, and R. Z. Sagdeev,
Nuclear Fusion 1, 82 (1961).
Рис. 10. Профиль электростатического потенциала в экс-
4.
A. E. Dubinov and I. D. Dubinova, J. Plasma Phys.
тремальном солитоне при γe = 3, θ = 0, M = 2.5424
71, 715 (2005).
5.
А. Е. Дубинов, И. Д. Дубинова, и С. К. Сайков,
Его профиль показан рис. 10. Экстремальный соли-
W-функция Ламберта и ее применение в матема-
тон может быть сформирован, например, в сильно-
тических задачах физики, РФЯЦ-ВНИИЭФ, Са-
замагниченной плазме с адиабатическими электро-
ров (2006).
нами и холодными ионами для солитонов, распро-
6.
J. F. McKenzie, Phys. Plasmas 9, 800 (2002).
страняющихся вдоль сильного магнитного поля. В
этом случае поперечное движение электронов замо-
7.
А. Е. Дубинов, Прикл. мех. и техн. физ. 48, 3
рожено и они имеют только одну степень свободы
(2007).
i = 1, что дает γe = (i + 2)/i = 3. Так как γe не
8.
S. K. Maharaj and R. Bharuthram, Phys. Plasmas
может быть больше 3, в итоге более быстрые, чем
27, 032306 (2020).
предсказывает формула (50), ионно-звуковые соли-
тоны невозможны, и, следовательно, гиперзвуковые
9.
А. Е. Дубинов, Физика плазмы 35, 1070 (2009).
электростатические солитоны не существуют.
10.
А. Е. Дубинов, А. А. Дубинова, Физика плазмы
33, 935 (2007).
4. ЗАКЛЮЧЕНИЕ
11.
B. А. Гордиенко, И. Д. Дубинова, А. Е. Дубинов,
Физика плазмы 32, 987 (2006).
В работе развита нелинейная теория ИЗВ в
бесстолкновительной теплой электрон-ионной плаз-
12.
А. Е. Дубинов, А. А. Дубинова, М. А. Сазонкин,
ме. Теория основана на анализе псевдопотенциала
Радиотехн. и электрон. 55, 968 (2010).
Сагдеева. Были рассмотрены две модели ИЗВ —
13.
А. Е. Дубинов, Физика плазмы 33, 239 (2007).
изотермическая и адиабатическая. Вычислялись за-
висимости максимального значения числа Маха для
14.
А. Е. Дубинов, М. А. Сазонкин, ЖЭТФ 138, 979
солитонов от приведенной температуры (параметра
(2010).
неравновесности) плазмы для обеих моделей ИЗВ.
15.
В. А. Гордиенко, А. Е. Дубинов, ТВТ 45, 814
Показано, что максимальное значение числа Маха
(2007).
не может превышать фундаментального предела
√
√
3+2
3 (50). Экстремальный солитон с таким
16.
F. D. Parker, Amer. Math. Month. 62, 439 (1955).
977
14
ЖЭТФ, вып. 5 (11)