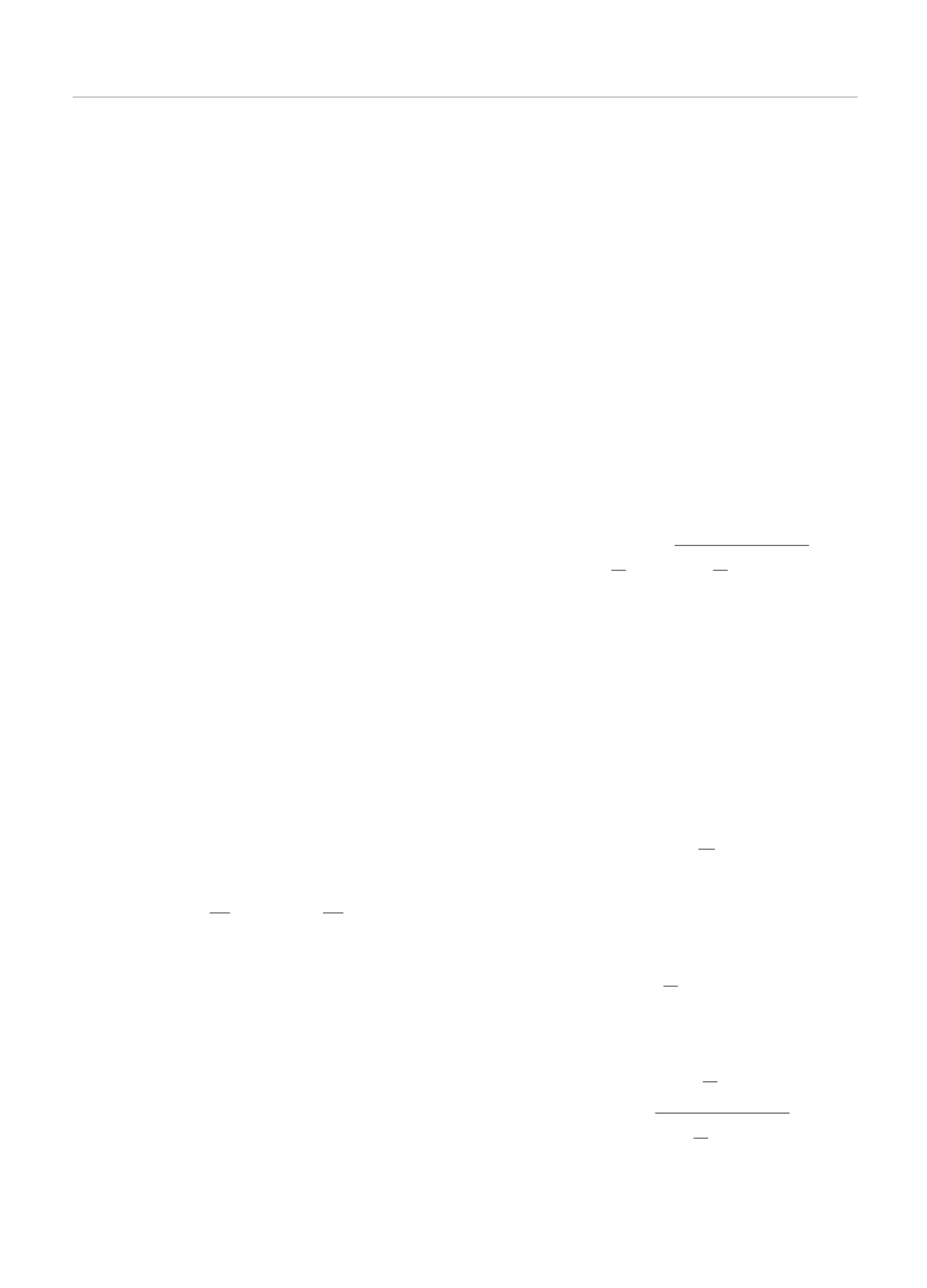ЖЭТФ, 2020, том 158, вып. 6 (12), стр. 1125-1138
© 2020
ДЕКОРИРОВАННАЯ ИЗИНГОВСКАЯ ЦЕПОЧКА
В МАГНИТНОМ ПОЛЕ
Е. С. Цуваревa,b*, Ф. А. Кассан-Оглыb**
a Уральский федеральный университет им. первого Президента России Б. Н. Ельцина
620000, Екатеринбург, Россия
b Институт физики металлов им. М. Н. Михеева Уральского отделения Российской академии наук
620108, Екатеринбург, Россия
Поступила в редакцию 21 июля 2020 г.,
после переработки 16 августа 2020 г.
Принята к публикации 20 августа 2020 г.
Проведено обобщение метода трансфер-матрицы Крамерса - Ваннье на произвольное число декориро-
вания изинговской цепочки. Получено точное аналитическое выражение для наибольшего собственного
значения трансфер-матрицы декорированной изинговской цепочки в присутствии внешнего магнитного
поля. Найдены точки фрустраций и величины фрустрационных магнитных полей, зависящие от величин
и знаков обменных взаимодействий. Получены точные выражения для нуль-температурных энтропий и
нуль-температурных намагниченностей рассматриваемой модели. Построены магнитные фазовые диа-
граммы основного состояния системы для значений декорирования d = 1 и d = 2, в том числе и в
отсутствие магнитного поля. Проведено сравнение с декорированной квадратной решеткой не только в
отсутствие, но и при наличии магнитного поля.
DOI: 10.31857/S0044451020120135
(см., например, [9] с обширно цитируемой литерату-
рой). Это можно объяснить тем, что декорирование
порождает ряд новых, еще не до конца изученных
1. ВВЕДЕНИЕ
эффектов.
Термин декорированная решетка был введен в
Как известно, в модели Изинга, как и во мно-
работе Сиози [10], после чего данная концепция на-
жестве других моделей, на одномерной решетке не
чала стремительно развиваться другими авторами
наблюдается фазовых переходов [1, 2], в отличие от
[11, 12]. Процедура построения декорированной це-
двумерных [3-6] и трехмерных решеток, тем не ме-
почки выглядит следующим образом. Представим
нее одномерная модель Изинга до сих пор привлека-
обычную решетку, в узлы которой помещены оди-
ет внимание исследователей своей простотой и пре-
наковые спины, которые принимают значение либо
имуществом в получении точных аналитических ре-
+1, либо -1. Далее определяются обменные взаимо-
шений в присутствии внешнего магнитного поля [7].
действия между спинами. Спины, между которыми
В данной работе с помощью весьма эффективно-
определено взаимодействие только между вторыми
го метода трансфер-матрицы Крамерса - Ваннье [8]
соседями или только между третьими соседями и
было выведено одно из таких точных решений, ко-
т. д., называются нодальными, а все остальные от-
торое до настоящего момента не было получено. Бо-
носятся к ненодальным (декорированным) спинам с
лее того, метод трансфер-матрицы Крамерса - Ван-
обменным взаимодействием только между ближай-
нье был обобщен на произвольное число трансляций
шими соседями.
изинговской цепочки в сравнении с исходным мето-
дом трансфер-матрицы.
Стоит подчеркнуть, что подавляющее большин-
ство реальных структур являются декорированны-
За последние годы наметилась тенденция в изу-
ми. Более того, некоторые кристаллические соеди-
чении так называемых декорированных решеток
нения можно также назвать декорированными, а
* E-mail: eguny@mail.ru
именно, решетки ГЦК и ОЦК, в отличие от простой
** E-mail: felix.kassan-ogly@imp.uran.ru
кубической, относятся к таким (ОЦК декорирова-
1125
Е. С. Цуварев, Ф. А. Кассан-Оглы
ЖЭТФ, том 158, вып. 6 (12), 2020
на по объему куба, а ГЦК декорирована по шести
Заметим, что экспонента в формуле (2) может
граням куба).
быть представлена как произведение сомножителей,
Основной задачей данной работы стало обобще-
каждый из которых зависит только от одной пары
ние метода трансфер-матрицы Крамерса - Ваннье
соседних спинов:
на произвольное число декорирования изинговской
цепочки с последующим исследованием фрустри-
∑
∏
ZN =
V (si, si+1),
(3)
рующих, термодинамических, а также магнитных
{si} i=1
свойств рассматриваемой модели.
где V (si, si+1) — трансфер-матрица Крамерса - Ван-
нье.
2. МЕТОД ТРАНСФЕР-МАТРИЦЫ
КРАМЕРСА - ВАННЬЕ
Используя матричный формализм, представим
выражение для статистической суммы (3) как след
Из целого ряда способов точного получения ста-
произведения N одинаковых трансфер-матриц, та-
тистических сумм, пожалуй, наиболее предпочти-
ким образом, статистическая сумма может быть пе-
тельным является метод трансфер-матрицы, вве-
реписана в терминах собственных значений введен-
денный Крамерсом и Ваннье.
ной трансфер-матрицы:
В 1941 г. Крамерс и Ваннье в своей работе [8]
показали, что расчет статистической суммы гигант-
ZN = SpVN = λN1 + λN2 .
(4)
ского числа (2N ) магнитных конфигураций сводит-
ся к нахождению одного главного (наибольшего)
где
собственного значения некоторой матрицы конеч-
[
√
]
ной размерности. В результате свободная энергия
(H)
(H)
λ1,2
= eJ/T ch
± sh2
+e-4J/T
,
(5)
и все термодинамические и магнитные характерис-
T
T
тики системы выражаются через это собственное
значение простым дифференцированием по темпе-
полученные корни секулярного уравнения
ратуре и магнитному полю.
Det(V - λI)
= 0. Из непосредственных расче-
Рассмотрим одномерную модель Изинга, состоя-
тов следует, что корень λ1 всегда положителен
щую из N узлов, во внешнем магнитном поле. Га-
и больше корня λ2, т.е. он всегда максимален.
мильтониан этой задачи записывается в следующем
Таким образом, λ1 — это максимальное собственное
виде:
значение трансфер-матрицы (которое всегда суще-
∑
∑
ствует для матрицы с вещественными матричными
H(s) = -J sisi+1 - H si,
(1)
элементами согласно теореме Фробениуса - Перрона
i=1
i=1
[13], будучи также вещественным).
где si = ±1, J — обменное взаимодействие между
Переписав статистическую сумму (4) в виде
ближайшими соседями, H — внешнее магнитное по-
[
]
ле.
)N
(λ2
Статистическая сумма рассматриваемой модели
ZN = λN
1
1+
,
(6)
λ1
будет равна
[
]
∑
∑
∑
и учитывая, что λ1 > λ2, в термодинамическом пре-
ZN =
exp
sisi+1 +
si
(2)
kT
kT
деле (N → ∞) получаем свободную энергию на один
{si}
i=1
i=1
узел решетки (F = f/N) следующим образом:
Отметим, что здесь и в дальнейших преобразова-
[
]
ниях постоянная Больцмана k будет положена рав-
T
F (H, T ) = lim
-
ln ZN
= -T ln λ1,
(7)
ной единице, а величины T и H будут измеряться
N →∞
N
в единицах |J|, как это принято в теории низкораз-
или же
мерных систем.
Кроме того, на задачу накладываются так назы-
{
[
(H)
ваемые периодические условия или еще их называ-
F (H, T ) = -T ln eJ/T ch
+
T
ют граничными условиями Борна - Кармана. Таким
√
]}
образом, узел sN+1 оказывается тождественен уз-
(H)
лу s1. Другими словами, осуществляется замыкание
+ sh2
+e-4J/T
(8)
T
цепочки спинов в кольцо.
1126
ЖЭТФ, том 158, вып. 6 (12), 2020
Декорированная изинговская цепочка в магнитном поле
Такие параметры, как энтропия S, теплоемкость
C и намагниченность M выражаются простым диф-
ференцированием только через максимальное соб-
ственное значение λmax по обычным формулам тер-
модинамики:
∂F
T
∂λmax
S(H, T ) = -
= ln λmax +
,
(9)
Рис. 1. Декорированная цепочка с обменным взаимодейст-
∂T
λmax
∂T
вием ближайших соседей Jd и обменным взаимодействи-
ем J
∂2F
2T
∂λmax
На рис. 1 проиллюстрирована решетка спинов,
C(H, T ) = -T
=
+
∂T2
λmax
∂T
соответствующая декорированной цепочке, описы-
∂
1
∂λmax
ваемой гамильтонианом (12). Красные кружки обо-
+T2
,
(10)
∂T λmax
∂T
значают декорированные спины, синие кружки —
нодальные спины. Каждый спин обладает двумя со-
∂F
sh(H/T )
стояниями s = ±1.
M (H, T ) = -
=
√
(11)
∂H
sh2(H/T) + e-4J/T
В данной работе, в отличие от обычного мето-
да Крамерса - Ваннье, рассмотренного выше, тран-
Выражение для намагниченности (11) в точнос-
сфер-матрица будет обобщена на произвольное чис-
ти такое же, которое получил Изинг при рассмотре-
ло декорирования изинговской цепочки.
нии одномерной решетки [1].
Если рассматривается единожды декорирован-
Отметим, что намагниченность в отсутствие
ная цепочка, т. е. d = 1, то статистическая сумма в
внешнего поля обращается в нуль, т. е. спонтанная
термодинамическом пределе (N → ∞) вычисляется
намагниченность в одномерном случае отсутствует
из выражения ZN = λmax [14]. Для дважды деко-
не только при антиферромагнитном, но и при фер-
рированной цепочки имеем статистическую сумму
ромагнитном взаимодействии!
в виде ZN = λmax, для трижды декорированной це-
почки — ZN = λmax и т. д. В общем случае выра-
жение для статистической суммы с произвольным
числом декорирования цепочки примет вид
3. ТОЧНОЕ РЕШЕНИЕ ДЕКОРИРОВАННОЙ
ИЗИНГОВСКОЙ ЦЕПОЧКИ В МАГНИТНОМ
ZN = λN/(d+1)max.
(13)
ПОЛЕ
Знаменатель в степени наибольшего собственно-
го значения всегда на единицу больше величины де-
Предметом нашего рассмотрения является деко-
корирования цепочки d. Это продиктовано тем, что
рированная изинговская цепочка в магнитном по-
в отсутствие декорированных спинов (d = 0) в це-
ле. Гамильтониан данной решетки представляется в
почке остаются только нодальные спины, таким об-
следующем виде:
разом, получаем обычную (недекорированную) мо-
дель Изинга, статистическая сумма которой вычис-
ляется, как известно, с помощью ZN = λNmax.
∑
∑
H(s) = -Jd sisi+1 - J
sjsj+d+1 -
Любопытно, что если d стремится к бесконечнос-
i=1
j=1,d+2,...
ти, то эта задача вновь сводится к обычной (неде-
корированной) модели Изинга, поскольку с увели-
∑
чением числа «декораций» относительный вклад в
-H si,
(12)
энергию от нодальных спинов становится все более
i=1
и более незначительным.
где Jd
— обменное взаимодействие между бли-
Следуя алгоритму трансфер-матрицы Крамер-
жайшими декорированными спинами и нодальны-
са - Ваннье [8] и применяя предложенное Сиози
ми спинами, а также между декорированными спи-
декорационно-итерационное преобразование (deco-
нами, J — обменное взаимодействие только между
ration-iteration transformation) [12], мы определи-
нодальными спинами, H — величина внешнего маг-
ли точное выражение для наибольшего собственно-
нитного поля. Индекс d обозначает число так назы-
го значения трансфер-матрицы декорированной це-
ваемых декораций цепочки.
почки, находящейся в магнитном поле,
1127
Е. С. Цуварев, Ф. А. Кассан-Оглы
ЖЭТФ, том 158, вып. 6 (12), 2020
[
1
(
)
(
) ]
λmax =
eJ/T
λd+11 + λd+12
+e-J/T
λd+11 - λd+12
ε ,
(14)
2
где
[
√
]
λ1 = exp(Jd/T) ch(H/T) + sh2(H/T) + exp(-4Jd/T)
,
(15a)
[
√
]
λ2 = exp(Jd/T) ch(H/T) - sh2(H/T) + exp(-4Jd/T)
,
(15b)
√
(
)
ε=
1 + sh2(H/T)(exp(4J/T) - 1)/
sh2(H/T) + exp(-4Jd/T)
(15c)
Поскольку термодинамические и магнитные ха-
Такие магнетики Жераром Тулузом в 1977 г. были
рактеристики исследуемой декорированной цепочки
названы фрустрированными [15, 16].
могут быть выражены только через ее максималь-
Экспериментальный материал по фрустрирован-
ное собственное значение λmax, то, принимая во вни-
ным магнитным системам в реальных кристаллах и
мание кратность декорирования цепочки d, анали-
некристаллических веществах весьма богат и изоби-
тические выражения для энтропии, теплоемкости,
лует новыми явлениями и необычными свойства-
намагниченности и параметра порядка запишем в
ми. Однако надлежащая интерпретация и теоре-
виде
тическое объяснение множества экспериментальных
фактов и новых эффектов в настоящее время отсут-
ln λmax
T
∂λmax
S(H, T ) =
+
,
(16)
ствуют, а ряд свойств фрустрированных систем еще
d+1
(d + 1)λmax
∂T
недостаточно понятен [17].
В этом разделе исследуются фрустрационные
2T
∂λmax
свойства декорированной изинговской цепочки во
C(H, T ) =
+
внешнем магнитном поле с учетом обменных взаи-
(d + 1)λmax
∂T
2
модействий между декорированными узлами решет-
T
∂
1
∂λmax
+
,
(17)
ки и между декорированными и нодальными узлами
(d + 1) ∂T λmax
∂T
Jd, а также между нодальными узлами со взаимо-
действием равным J.
T
∂λmax
Несмотря на столь сложную цепочку, нам уда-
M (H, T ) =
,
(18)
(d + 1)λmax
∂H
лось, тем не менее, получить точное решение в тер-
модинамическом пределе, что дает возможность ка-
чественно рассмотреть искомые характеристики, в
ln λmax
η(H, T ) = 1 -
-
том числе и объяснить свойства магнетиков, обу-
(d + 1) ln 2
словленные фрустрациями.
T
∂λmax
-
(19)
При антиферромагнитном обмене спинов деко-
(d + 1)λmax ln 2
∂T
рированной цепочки как между декорированными
спинами, так и между нодальными спинами, а имен-
но, Jd = -1, J = -1 во внешнем магнитном поле
4. ФРУСТРАЦИОННЫЕ СВОЙСТВА
H = 2 при нулевой температуре энтропия системы
ДЕКОРИРОВАННОЙ ИЗИНГОВСКОЙ
(рис. 2а) может быть записана в общем виде для
ЦЕПОЧКИ
любых значений декорирования d:
Явление магнитных фрустраций было обнаруже-
[
]
1
1
(
)
но в середине семидесятых годов двадцатого века в
lim
S =
ln
√
ϕd+1 - (1 - ϕ)d+1
,
(20)
магнетиках, проявляющих необычные свойства, это
T →0
d+1
5
явление объяснялось сильным вырождением основ-
√
ного состояния системы и невозможностью магнит-
где ϕ = (1 +
5)/2 — известное уже в течении тыся-
ного упорядочения даже при нулевой температуре.
челетий золотое сечение.
1128
ЖЭТФ, том 158, вып. 6 (12), 2020
Декорированная изинговская цепочка в магнитном поле
Следовательно, система в данном режиме фруст-
Отметим еще то, что при стремлении температу-
рирована, а внешнее магнитное поле является
ры к бесконечности энтропия равна натуральному
фрустрирующим.
логарифму двух:
На рис. 2а видно, что при стремлении d к беско-
нечности нуль-температурная энтропия сходится к
lim S = ln 2,
(23)
T →∞
логарифму золотого сечения. Можно это показать,
используя выражение (20)
поскольку число состояний на узле равно двум.
Однако при стремлении температуры к нулю ли-
1
lim
lim
S = lim
×
бо к бесконечности удельная теплоемкость системы
d→∞
T →0
d→∞ d + 1
[
]
при любых параметрах обменного взаимодействия
1
(
)
× ln
√
ϕd+1 - (1 - ϕ)d+1
= ln ϕ.
(21)
равна нулю (рис. 3а):
5
Кроме того, наблюдается еще одно фрустрирую-
lim
C = 0, lim C = 0.
(24)
T →0
T →∞
щее поле при H = 4, Jd = -1, J = -1. Нуль-тем-
пературная энтропия при различных значениях де-
Кроме того, в непосредственной близости к точке
корирования (рис. 2б) может быть представлена в
фрустрации теплоемкость расщепляется на два пи-
следующем виде:
ка: острый и куполообразный пики. На рис. 3б изоб-
1
ражена теплоемкость в точке фрустрации (H = 2) —
lim
S =
ln ϕ.
(22)
T →0
d+1
наблюдается один куполообразный пик, тогда как
Обратим внимание на то, что полученные ре-
вблизи фрустрации, а именно, в магнитном поле
зультаты не противоречат третьему началу термо-
равном H = 1.9 и H = 2.1 у теплоемкости возни-
динамики, поскольку энтропия определяется через
кает дополнительный острый пик.
дифференциал dS = δQ/T с точностью до постоян-
Намагниченность системы при антиферромаг-
ной интегрирования S0 ≥ 0, и лишь в формулировке
нитном обменном параметре спинов цепочки для
теоремы Нернста - Планка для равновесных систем
Jd = -1, J = -1 во фрустрирующем поле H = 2 и
с невырожденным основным состоянием данная по-
нулевой температуре имеет конечное значение при
стоянная выбирается нулевой, S0 = 0.
различных параметрах декорирования d (рис. 4а):
(
√
)
(
√
)
d+1
d + 1 - 1/
5
ϕd+1 +
d + 1 + 1/
5
(1 - ϕ)
lim
M =
√
(25)
T →0
5(d + 1) (ϕd+1 - (1 - ϕ)d+1)
Во фрустрирующем поле H = 4 при антифер-
ванными спинами (и между декорированными и но-
ромагнитном обменном параметре спинов цепочки
дальными спинами) Jd сделаем антиферромагнит-
Jd = -1, J = -1 и различных параметрах деко-
ным, а обменное взаимодействие между нодальны-
рирования имеем следующую нуль-температурную
ми спинами J будет ферромагнитным. Соответству-
намагниченность (рис. 4б):
ющие температурные зависимости энтропий в точ-
(
√
)
ках фрустраций для различных значений декориро-
1
1+d
5
lim
M =
√
(26)
вания проиллюстрированы на рис. 5.
T →0
5
d+1
Энтропия системы при таком антиферро-ферро-
Обратим внимание на тот факт, что характер по-
магнитном обмене (рис. 5а) (Jd = -1, J = 1) во
ведения намагниченности в случае антиферромаг-
внешнем магнитном поле H = 2 при стремлении
нитного взаимодействия между спинами при нечет-
температуры к нулю выражается следующим обра-
ных и четных значениях d различен. При нечетных
зом:
значениях d намагниченность около фрустрирующе-
[
]
1
1
(
)
го поля, равного двум, расщепляется на два проме-
lim
S =
ln
√
ϕd+2 - (1 - ϕ)d+2
(27)
T →0
d+1
5
жуточных плато (рис. 4а), а при четных d проис-
ходит образование только одного промежуточного
плато (рис. 4б).
Соответствующие им значения нуль-температур-
Рассмотрим взаимодействие спинов следующего
ных намагниченностей во фрустрирующем поле
типа. Обменное взаимодействие между декориро- H = 2 можно определить в виде
1129
Е. С. Цуварев, Ф. А. Кассан-Оглы
ЖЭТФ, том 158, вып. 6 (12), 2020
(
√
)
(
√
)
d+2
d + 2 - 1/
5
ϕd+2 +
d + 2 + 1/
5
(1 - ϕ)
lim
M =
√
(28)
T →0
5(d + 1) (ϕd+2 - (1 - ϕ)d+2)
Однако для фрустрирующего поля H = 4 уста-
нитном поле с единственным фрустрирующим по-
новлено, что при любом значении декорирования це-
лем равном двум.
почки значения нуль-температурных энтропий рав-
Напоследок необходимо добавить, что при d,
ны нулю, т. е. фрустрирующих состояний не наблю-
стремящемся к бесконечности, нуль-температурное
√
дается, в связи с этим система обладает опреде-
значение намагниченности M равно 1/
5, что соот-
ленной магнитной конфигурацией в основном со-
ветствует тому, что задача снова сводится к недеко-
стоянии. Данный факт отмечен на рис. 5б для ан-
рированной модели Изинга (см. рис. 7).
тиферро-ферромагнитного взаимодействия между
5. ТЕРМОДИНАМИЧЕСКИЕ И
спинами, кроме того, на рис. 6а изображены на-
МАГНИТНЫЕ СВОЙСТВА
магниченности, описываемые выражениями (28) с
ДЕКОРИРОВАННОЙ ИЗИНГОВСКОЙ
фрустрирующим полем H = 2. При четных значе-
ЦЕПОЧКИ
ниях параметра d у намагниченности наблюдается
Для описания термодинамических и магнитных
одно промежуточное плато.
свойств декорированной изинговской цепочки изоб-
В противоположном случае ферро-антиферро-
разим трехмерные графики для теплоемкости и на-
магнитного обмена (Jd = 1, J = -1), называемого
магниченности как функции температуры и магнит-
еще квазиферромагнитным, имеем, что при любых
ного поля.
d при сколь угодно малом магнитном поле намагни-
На рис. 8 проиллюстрирован трехмерный гра-
ченность стремится к полному упорядочению вдоль
фик теплоемкости как функции температуры и маг-
приложенного поля (рис. 6б).
нитного поля для трижды декорированной цепочки
А в случае ферромагнитного обмена (Jd = 1,
при антиферромагнитном взаимодействии (Jd = -1,
J = 1) при любых значениях параметра d наблю-
J = -1). Значения магнитного поля в точках, где
дается аналогичная ситуация, что и в случае квази-
теплоемкость обращается в нуль (при температу-
ферромагнитного обмена.
ре, стремящейся к нулю), соответствуют фрустри-
Отдельно стоит отметить одну особенность по-
рующим полям. Нетрудно увидеть, что имеются три
ведения намагниченности рассматриваемой декори-
фрустрирующих поля, которые равны нулю, двум и
рованной цепочки. Было замечено, что промежу-
четырем. В этих полях намагниченность испытыва-
точные плато намагниченности всегда представля-
ет скачок, в чем можно убедиться, глядя на рис. 9.
ются рациональными дробями. Например, для слу-
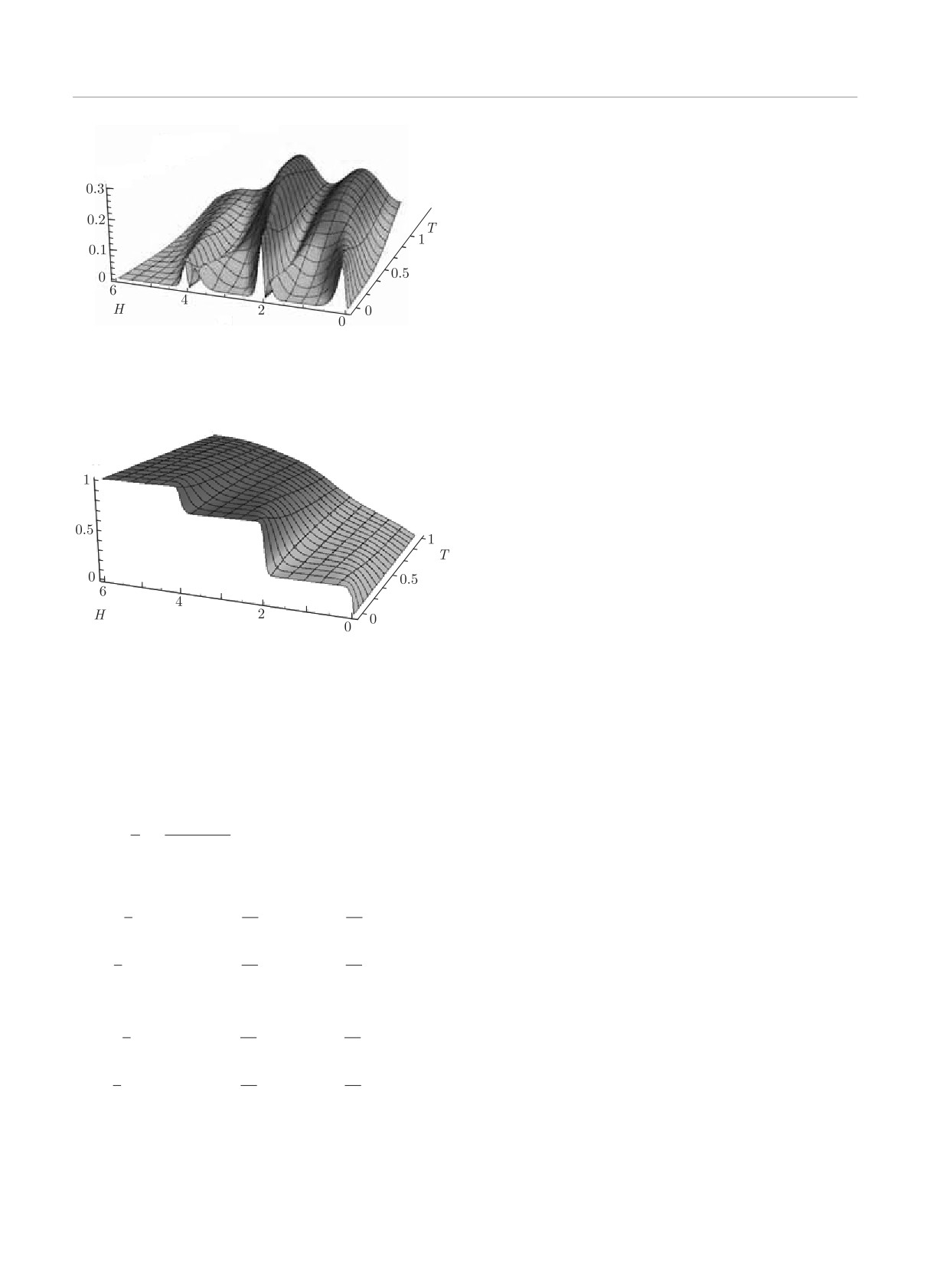
Рисунок 9 демонстрирует трехмерный график
чая единожды декорированной цепочки с антифер-
намагниченности, зависящей от величины магнит-
ромагнитным обменном (Jd = -1, J = -1) имеет-
ного поля и температуры для трижды декорирован-
ся промежуточное плато намагниченности со зна-
ной цепочки при антиферромагнитном взаимодей-
чением 1/2 (рис. 4а), что говорит о том, что поло-
ствии (Jd = -1, J = -1). Видно, что с увеличением
вина спинов развернулась вдоль внешнего магнит-
температуры кривая намагниченности размывается
ного поля, тогда как для трижды декорированной
и промежуточные плато исчезают.
цепочки плато намагниченностей располагаются на
Исследуемая декорированная изинговская це-
уровнях 1/4 и 3/4 и символизируют то, что снача-
почка зависит от четырех независимых параметров,
ла во фрустрирующем поле, равном нулю, повер-
Jd, J, H, d, поэтому не представляется возможным
нулась вдоль внешнего магнитного поля четверть
изобразить полную фазовую диаграмму, поскольку
всех спинов в цепочке, затем во фрустрирующем по-
для этого потребуется четырехмерное пространство.
ле, равном двум, доля повернутых спинов составит
Тем не менее, на рис. 10 представлены некоторые се-
три четверти и уже во фрустрирующем поле, рав-
чения этого четырехмерного пространства.
ном четырем, вдоль магнитного поля развернутся
Построены магнитные фазовые диаграммы в ко-
все спины цепочки. Нетрудно определить, что при
ординатах (H, J) для единожды и дважды декори-
значении декорирования, равном d, получим плато
рованной цепочек, находящихся во внешнем магнит-
намагниченности на уровнях 1/(d + 1) и d/(d + 1).
ном поле (рис. 10). Замечено, что при d = 1 в основ-
И, устремив d к бесконечности, замечаем, что про-
ном состоянии присутствуют три магнитные фазо-
межуточные плато исчезают, а задача сводится к
вые конфигурации, а именно, антиферромагнитная
обычной (недекорированной) модели Изинга в маг-
фаза C2 с удвоением периода трансляции цепочки:
1130
ЖЭТФ, том 158, вып. 6 (12), 2020
Декорированная изинговская цепочка в магнитном поле
}
{...↓ ↑
↓
↑...
может обладать тремя фрустрирующими полями:
C2 =
H = 0, H = 2, H = 4. Поля равные двум и че-
...↑
↓
↑
↓...
тырем мы рассмотрели, исследуем случай нулевого
с энергией Ed=1C
= -J/2+Jd, ферромагнитная фаза
2
фрустрационного поля.
C1 с сохранением периода трансляции:
Полагая в выражениях (14) и (15) H = 0, по-
{
}
лучим, что наибольшее собственное значение тран-
C1 =
...↑
↑
↑
↑...
сфер-матрицы для декорированной изинговской це-
с энергией Ed=1C
= -J/2-Jd -H и упорядочение C4
1
почки в отсутствие магнитного поля имеет вид
с учетверением периода трансляции цепочки:
[
{
}
(Jd)
(J)
C4 =
...↑
↑
↓
↑...
λmax
=2d+1 chd+1
ch
+
T
T
с энергией EC4
= J/2 - H/2 (см. рис. 10а). Все
(Jd)
(J)]
+ shd+1
sh
(29)
остальные фазы имеют более высокую энергию и
T
T
оказываются невыгодными в основном состоянии.
Как известно, одномерная обычная (недекориро-
В случае d = 2 в основном состоянии имеются че-
ванная) модель Изинга в отсутствие магнитного по-
тыре различные конфигурации: антиферромагнит-
ля не содержит нуль-температурных энтропий, не
ная C2 с энергией Ed=2C
= J/3+Jd, ферромагнитная
2
равных нулю. Однако, как можно заметить, в на-
C1 с энергией Ed=2C
= -J/3 - Jd - H, а также кон-
1
шей задаче их возникает целое множество даже в
фигурация C3 c утроением периода трансляции:
}
нулевом магнитном поле.
{...↑ ↑
↓...
Для антиферромагнитного случая как между де-
C3 =
корированными спинами, так и между нодальными
...↑
↓
↑...
спинами (Jd
= -1, J = -1) имеем следующий ряд
с энергией EС3 = -J/3 + Jd/3 - H/3 и фаза C6 с
нуль-температурных энтропий:
ушестерением периода трансляции
⎧
⎧
⎫
⎨ln3
ln 5
ln 7
ln(d + 2)
⎨...↑
↑
↑
↓
↑
↑...⎬
,
,
,...,
,
d — нечетное,
lim
2
4
6
d+1
C6 =
T →0
S=⎩
0,
d — четное.
⎩...↓
↑
↑
↑
↑
↑ ...⎭
Для антиферро-ферромагнитного случая
с энергией EС6 = J/3 - Jd/3 - 2H/3 (см. рис. 10б).
(Jd = -1, J = 1) получился ряд в виде
Также, на приведенных диаграммах можно уви-
⎧
деть, что фазы на рисунках сходятся в точке при
⎨0,
d — нечетное,
Jd = -1, J = 0, H = 2. В этой точке схождения
lim
ln 6
ln 8
ln(d + 2)
T →0
S=⎩ln4,
,
,...,
,
d — четное.
фаз нуль-температурная энтропия равняется лога-
3
5
7
d+1
рифму золотого сечения, т. е. при таких параметрах
В случае ферро-антиферромагнитного взаимо-
задача сводится к обычной (недекорированной) мо-
действия (Jd = 1, J = -1) получаем следующий
дели Изинга в магнитном поле.
ряд:
Кроме того, две фазы могут пересекаться на
линиях схождения фаз. Такие линии схождения
ln 3
ln 4
ln 5
ln(d + 2)
lim
S =
,
,
,...,
двух фаз, представленные на рис. 10, соответству-
T →0
2
3
4
d+1
ют определенному обмену — антиферромагнитно-
при любом d.
му или антиферро-ферромагнитному, которые рас-
Для ферромагнитного случая как между декори-
сматривались в прошлом разделе. Например, линия
рованными спинами, так и между нодальными спи-
схождения фаз C1 - C4 (так же, как и C1 - C6) со-
нами (Jd = 1, J = 1) нуль-температурные энтро-
ответствует антиферромагнитному обмену с нуль-
пии равны нулю, т. е. фрустрированных состояний
температурными энтропиями (22) и нуль-темпера-
не наблюдается.
турными намагниченностями (26).
В отсутствие взаимодействия между ближайши-
ми соседями (Jd = 0) с сохранением антиферро-
магнитного (или ферромагнитного) обменного взаи-
6. СЛУЧАЙ НУЛЕВОГО МАГНИТНОГО
модействия между нодальными спинами J получен
ПОЛЯ
ряд значений для различных d:
Как отмечалось ранее, декорированная изингов-
ln 2
2 ln 2
3 ln 2
d ln 2
ская цепочка при различных обменных параметрах
lim
S =
,
,
,...,
T →0
2
3
4
d+1
1131
Е. С. Цуварев, Ф. А. Кассан-Оглы
ЖЭТФ, том 158, вып. 6 (12), 2020
Рис. 2. Температурные зависимости энтропий в точках фрустраций антиферромагнитной модели Изинга (Jd = -1,
J = -1) для различных значений декорирования цепочки: а — в магнитном поле H = 2; б — в магнитном поле H = 4
Рис. 3. Температурные зависимости теплоемкостей при различных значениях декорирования d: а — теплоемкость всег-
да равна нулю при стремлении температуры к нулю или к бесконечности (H = 2 для всех кривых), б — расщепление
теплоемкости на два пика вблизи фрустрации
Для случая нулевого магнитного поля также бы-
новном состоянии. Из них C2 — антиферромагнит-
ли построены фазовые диаграммы (рис. 11) для зна-
ная фаза, C1 — ферромагнитная фаза, C3 и C6 —
чений декорирования d = 1 и d = 2. Как и в случае
конфигурации соответственно утроения и ушесте-
магнитного поля, фазовые диаграммы, построенные
рения периодов трансляций цепочки, а C4 — фаза
при H = 0, обладают тремя конфигурациями при
учетверения периода трансляции.
d = 1 и четырьмя конфигурациями при d = 2 в ос-
1132
ЖЭТФ, том 158, вып. 6 (12), 2020
Декорированная изинговская цепочка в магнитном поле
Рис. 4. Намагниченность антиферромагнитной модели Изинга (Jd = -1, J = -1) для различных значений декорирования
цепочки: а — нечетные значения d при температуре T = 0.06, б — четные значения d при температуре T = 0.02
Рис. 5. Температурные зависимости энтропий в точках фрустраций антиферро-ферромагнитной модели Изинга (Jd = -1,
J = 1) для различных значений декорирования цепочки: а — в магнитном поле H = 2, б — в магнитном поле H = 4
∫π
∫
π
7. СРАВНЕНИЕ С РЕЗУЛЬТАТАМИ НА
λ
1
ДЕКОРИРОВАННОЙ КВАДРАТНОЙ
ln
=
ln(CxCy - DySx cos φ -
2
2π2Z
РЕШЕТКЕ
0
0
- DxSy cosθ)dφdθ,
(30)
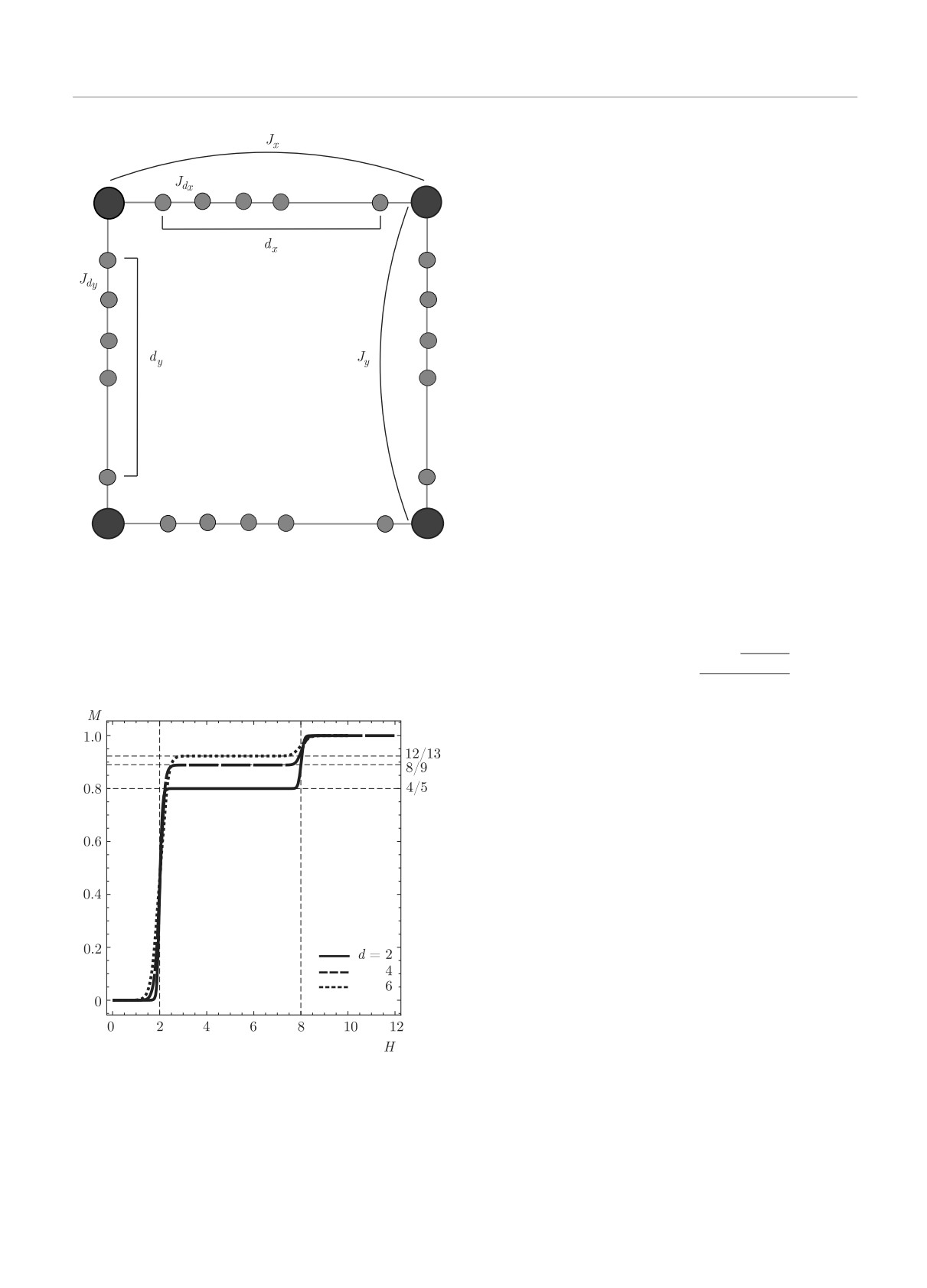
В работах [18, 19] авторами было получено наи-
большее собственное значение для декорированной
где dx и dy — кратности декорирования по направ-
квадратной решетки, представленной на рис. 12, в
лениям x и y, Z = (1 + dx + dy) — число спинов в
отсутствие магнитного поля:
элементарной ячейке,
1133
Е. С. Цуварев, Ф. А. Кассан-Оглы
ЖЭТФ, том 158, вып. 6 (12), 2020
Рис. 6. Намагниченность антиферро-ферромагнитной модели Изинга (Jd = -1, J = 1) при температуре T = 0.06 для чет-
ных значений декорирования цепочки (а), ферро-антиферромагнитной модели Изинга (Jd = 1, J = -1) при температуре
T = 0.06 для различных значений декорирования цепочки (б)
(
)
))2
1
(Jdx
(Jdx
Cx =
e2Jx/T
chdx+1
+ shdx+1
+
2
T
T
(
)
1
(Jdx
+
e-2Jx/T
chdx+1
-
2
T
))2
(Jdx
- shdx+1
,
(31c)
T
(
)
))2
1
(Jdy
(Jdy
Cy =
e2Jy/T
chdy +1
+ shdy+1
+
2
T
T
(
)
1
(Jdy
+
e-2Jy/T
chdy+1
-
2
T
))2
(Jdy
- shdy+1
,
(31d)
T
(
)
))2
1
(Jdx
(Jdx
Sx =
e2Jx/T
chdx+1
+ shdx+1
-
2
T
T
(
)
1
(Jdx
−
e-2Jx/T
chdx+1
-
2
T
))2
Рис. 7. Температурные зависимости намагниченности при
(Jd
x
- shdx+1
,
(31e)
d = 2,4,6,100 (Jd = -1, J = 1) при H = 2. Видно, что
T
при стремлении d к бесконечности, значение нуль-темпе-
(
√
1
(Jdy)
(Jdy))2
ратурной намагниченности становится равно 1/
5
Sy =
e2Jy/T chdy+1
+ shdy+1
-
2
T
T
(
)
)
1
(Jd
y
(Jdx
(Jdx)
−
e-2Jy/T chdy+1
-
Dx = ch2dx+2
- sh2dx+2
,
(31a)
2
T
T
T
))2
)
(Jdy
(Jdy)
(J
dy
- shdy+1
(31f)
Dy = ch2dy+2
- sh2dy+2
,
(31b)
T
T
T
1134
ЖЭТФ, том 158, вып. 6 (12), 2020
Декорированная изинговская цепочка в магнитном поле
1 + d, приходим к выводу, что полученное выраже-
ние в точности совпадет с наибольшим собственным
значением, выведенным для декорированной цепоч-
ки в отсутствие магнитного поля (29).
Таким образом, можно сказать, что выражения
(32) и (33a)-(33b) являются интегральным пред-
ставлением полученного нами точного решения для
декорированной изинговской цепочки в отсутствие
магнитного поля (29).
Помимо этого, наблюдается соответствие линей-
ной декорированной цепочки с квадратной декори-
Рис. 8. Теплоемкость трижды декорированной (d = 3) ан-
рованной решеткой в магнитном поле [20]. Следу-
тиферромагнитной модели Изинга (Jd = -1, J = -1) как
ет отметить, что расчеты намагниченности в на-
функция температуры и магнитного поля
шем случае одномерной цепочки следовали из точ-
ного аналитического решения (14), (15), на квадрат-
ной решетке это было возможно выполнить лишь
трудоемкими численными расчетами, конкретно,
методом Монте-Карло в алгоритме Ванга - Лан-
дау [21, 22]. В качестве примера на рис. 13 про-
демонстрированы намагниченности антиферромаг-
нитной модели Изинга двухкратно-, четырехкратно-
и шестикратно-декорированной квадратной решет-
ки. Видно, что на квадратной декорированной ре-
шетке возникают два фрустрирующих поля при
H = 2 и H = 8, в отличие от линейной деко-
рированной цепочки при H = 2 и H = 4. Кро-
ме того, можно заметить, что возникающие про-
Рис. 9. Намагниченность трижды декорированной (d = 3)
межуточные плато намагниченностей как в одно-
антиферромагнитной модели Изинга (Jd = -1, J = -1)
мерной (плато расположены на уровнях 1/(d + 1) и
как функция температуры и магнитного поля
d/(1 + d)), так и двумерной (плато расположены на
уровне (dx + dy )/(1 + dx + dy)) решетках при стрем-
лении параметра d к бесконечности исчезают, про-
Положим, что Jdy = 0, Jy = 0, dy = 0, а dx = d,
исходит скачок намагниченности из антиферромаг-
тогда интеграл (30) сведется к виду
нитного состояния сразу в ферромагнитное состо-
π
∫
яние во фрустрирующем поле равном двум, таким
λ
1
ln
=
ln(C - S cos φ) dφ,
(32)
образом, задача сводится в этом пределе к обычной
2
2π(1 + d)
0
(недекорированной) модели. Объясняется это совер-
шенно просто. При увеличении количества декори-
(
рованных спинов (d → ∞) влияние нодальных спи-
1
(Jd)
(Jd))2
C =
e2J/T chd+1
+ shd+1
+
нов становится все меньше и меньше, одинаково как
2
T
T
в одномерной цепочке, так и в квадратной решетке,
(
1
(Jd)
(Jd))2
что непосредственно подтверждают рис. 4, 6 и 13.
+
e-2J/T chd+1
- shd+1
,
(33a)
2
T
T
(
8. ЗАКЛЮЧЕНИЕ
1
(Jd)
(Jd))2
S =
e2J/T chd+1
+ shd+1
-
2
T
T
Важнейшим достижением данной работы
(
1
(Jd)
(Jd))2
является обобщение метода трансфер-матрицы
-
e-2J/T chd+1
- shd+1
(33b)
2
T
T
Крамерса - Ваннье на произвольное число де-
корирования изинговской цепочки при наличии
Воспользовавшись специальным тождеством
внешнего магнитного поля. Получено точное
(см. Приложение) и возводя результат в степень
аналитическое выражение для наибольшего соб-
1135
Е. С. Цуварев, Ф. А. Кассан-Оглы
ЖЭТФ, том 158, вып. 6 (12), 2020
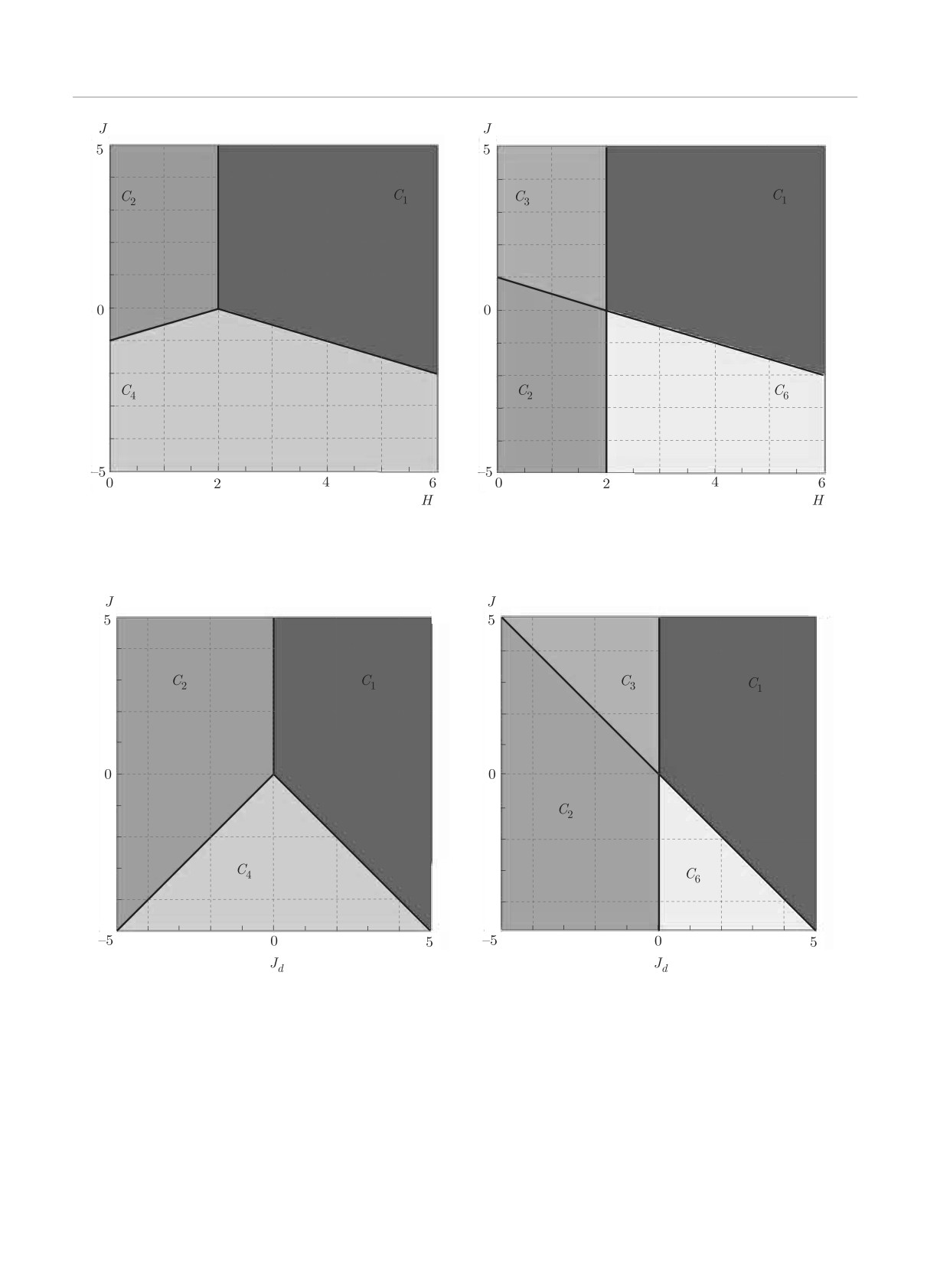
Рис. 10. Фазовые диаграммы основного состояния системы декорированной изинговской цепочки в магнитном поле с
учетом обменного взаимодействия между ближайшими соседями Jd = -1: а — при d = 1, б — при d = 2
Рис. 11. Фазовые диаграммы основного состояния системы декорированной изинговской цепочки в отсутствие магнит-
ного поля: а — при d = 1, б — при d = 2
ственного значения трансфер-матрицы Крамерса -
нуль-температурных намагниченностей. Выявлено,
Ваннье для декорированной цепочки, находящейся
что в непосредственной близости к фрустрации
во внешнем магнитном поле. Выведен ряд точных
теплоемкость расщепляется на два пика. Так же,
выражений для нуль-температурных энтропий и
в зависимости от декорирования изинговской це-
1136
ЖЭТФ, том 158, вып. 6 (12), 2020
Декорированная изинговская цепочка в магнитном поле
почки намагниченность может обладать двумя
промежуточными плато на уровнях 1/(d + 1) и
d/(d + 1). Помимо этого, авторами были построены
и проанализированы фазовые диаграммы основ-
ного состояния только для простейших случаев
декорирования цепочки. Фазовые диаграммы для
более высоких порядков декорирования требуют
отдельного тщательного рассмотрения. Вдобавок,
обнаружено соответствие случая декорированной
цепочки со случаем декорированной квадратной
решетки не только в отсутствие, но и при наличии
магнитного поля.
Финансирование. Работа выполнена в
рамках государственного задания Министер-
ства науки и высшего образования РФ (тема
«Квант»,
№ АААА-А18-118020190095-4) и
«Спла-
вы», № AAAA-A19-119070890020-3 и при частичной
поддержке Уральского отделения Российской
академии наук (проект № 18-2-2-11).
Рис. 12. Декорированная квадратная решетка с обменны-
ПРИЛОЖЕНИЕ
ми взаимодействиями ближайших соседей Jdx и Jdy соот-
ветственно по горизонтальному и вертикальному направ-
Для взятия интеграла в выражении (32) исполь-
лению, а также с обменными взаимодействиями Jx по на-
зуем следующую формулу [23]:
правлению x и с обменными взаимодействиями Jy по на-
∫π
√
правлению y
a+
a2 - b2
ln(a + b cos φ) dφ = π ln
(34)
2
0
ЛИТЕРАТУРА
1. E. Ising, Z. Physik 21, 253 (1925).
2. R. Peierls, Mathematical Proceedings of the
Cambridge Philosophical Society, 32, 477 (1936).
3. L. Onsager, Phys. Rev. 65, 117 (1944).
4. G. H. Wannier, Phys. Rev. 79, 357 (1950).
5. R. M. F. Houtappel, Prog. Theor. Phys. 16, 425
(1950).
6. K. Kanô and S. Naya, Prog. Theor. Phys. 10, 158
(1953).
7. E. S. Tsuvarev, F. A. Kassan-Ogly, and A. I. Prosh-
kin, J. Phys.: Conf. Ser. 1389 012008 (2019).
8. H. A. Kramers and G. H. Wannier, Phys. Rev. 60,
Рис. 13. Намагниченность антиферромагнитной модели
252 (1941).
Изинга двукратно-, четырехкратно- и шестикратно-деко-
рированной квадратной решетки (Jdx = -1, Jdy = -1,
9. M. Jaščur, V.
Štubňa, K. Szalowskib, and T. Bal-
cerzak, J. Magn. Magn. Mater. 417, 92 (2016).
Jx = -1, Jy = -1) при T = 0.005
10. I. Syozi, Prog. Theor. Phys. 35, 306 (1951).
1137
9
ЖЭТФ, вып. 6 (12)
Е. С. Цуварев, Ф. А. Кассан-Оглы
ЖЭТФ, том 158, вып. 6 (12), 2020
11. M. E. Fisher, Phys. Rev. 113, 969 (1958).
18. F. A. Kassan-Ogly and A. I. Proshkin, Physics of
Metals and Metallography Vol. 120 No. 13, 1359
12. I. Syozi, Phase Transitions and Critical Phenomena,
(2019).
Vol. 1, ed. by C. Domb and M. S. Green, Academic,
New York (1972).
19. A. I. Proshkin and F. A. Kassan-Ogly, Physics of
Metals and Metallography, Vol. 120, No. 13, 1366
13. Ф. Р. Гантмахер, Теория матриц, Наука, Москва
(2019).
(1966).
20. Ф. А. Кассан-Оглы, А. И. Прошкин, А. К. Мурта-
14. Е. С. Цуварев, Ф. А. Кассан-Оглы, А. И. Прошкин,
заев, В. А. Мутайламов, ФТТ 5, 683 (2020).
ЖЭТФ 158, 504 (2020).
21. F. Wang and D. P. Landau, Phys. Rev. Lett. 86, 2050
15. G. Toulouse, Comm. Phys. 2, 115 (1977).
(2001).
16. J. Vannimenus and G. Toulouse, J. Phys. C: Solid
22. F. Wang and D. P. Landau, Phys. Rev. E 64, 056101
State Phys. 10, L537 (1977).
(2001).
23. И. С. Градштейн, И. М. Рыжик, Таблицы интегра-
17. А. В. Зарубин, Ф. А. Кассан-Оглы, А. И. Прош-
лов, сумм, рядов и произведений, Наука, Москва
кин, А. Е. Шестаков, ЖЭТФ 155, 914 (2019).
(1971).
1138