ЖЭТФ, 2021, том 159, вып. 1, стр. 35-55

ЭЛЕМЕНТАРНЫЙ ИЗЛУЧАТЕЛЬ НА ГРАНИЦЕ

ПЛОСКОСЛОИСТОЙ СТРУКТУРЫ

А. Б. Петрин^*

Объединенный институт высоких температур Российской академии наук

125412, Москва, Россия

Поступила в редакцию 13 июля 2020 г.,

после переработки 30 июля 2020 г.

Принята к публикации 2 августа 2020 г.

Рассмотрена строгая теория излучения элементарного диполя, расположенного на границе или внутри

плоскослоистой структуры. Для частного случая излучения диполя, расположенного на свободной грани-

це одной пленки, продемонстрирован метод аналитического упрощения решения. Предложенный метод

позволил привести выражения для излучаемых полей к одномерным интегралам, что существенно упро-

стило анализ задачи и ускорило численные расчеты. В качестве конкретного технического приложения

теории были получены диаграммы направленности точечных излучателей (молекул, наноструктур), рас-

положенных на свободной поверхности металлической пленки в схеме Кречмана и имеющих индуциро-

ванный дипольный момент, направленный перпендикулярно поверхности пленки. Обсуждается влияние

поверхностной волны на направленные свойства поверхностных излучателей.

DOI: 10.31857/S004445102101003X

1. ВВЕДЕНИЕ

В настоящее время сохраняется значительный

интерес к физическим явлениям, которые сопро-

вождают возбуждение поверхностной плазмонной

волны на поверхности металлической пленки по схе-

ме Кречмана [1] (см. рис. 1). Поверхностная плаз-

монная волна распространяется вдоль поверхнос-

ти металла и локализуется вблизи его поверхности

Рис. 1. Возбуждение поверхностной плазмонной волны

[2,3], поэтому даже ничтожные изменение показате-

на поверхности металлической пленки 2 по схеме Кречма-

ля преломления в приповерхностной области сильно

на. Падающая поляризованная волна 3 со стороны призмы

влияют на характер ее распространения. На этом

4 порождает на свободной границе поверхностную плаз-

основывается широкое использование схемы Креч-

монную 1 и отраженную 5 волны

мана для создания различного рода высокочувстви-

тельных датчиков, реагирующих на изменение по-

казателя преломления тонкого (олиго- или мономо-

щая на свободную поверхность наночастицы или от-

лекулярного) поверхностного слоя [4].

дельные молекулы, наблюдать именно их излуче-

Исследования показали [5], что амплитуда по-

ние, направленное в сторону свободного полупрост-

верхностной волны на свободной границе пленки в

ранства. Это излучение порождается наведенны-

схеме Кречмана более чем на порядок выше амп-

ми электрическими дипольными моментами наноча-

литуды падающей волны. Поскольку в свободном

стиц, которые индуцируются поверхностной волной.

пространстве над пленкой не возбуждаются распро-

Важно, что только точечные объекты будут излу-

страняющиеся волны, это дает возможность, поме-

чать распространяющиеся волны в свободное про-

странство и исключительно это излучение можно

^* E-mail: a_petrin@mail.ru

будет наблюдать с помощью микроскопа, при этом

А. Б. Петрин

ЖЭТФ, том 159, вып. 1, 2021

можно полностью быть уверенным, что наблюдае-

мый в микроскоп свет исходит именно из точечных

источников на поверхности. В связи с этим возника-

ет фундаментальный вопрос о том, как влияет ме-

таллическая пленка (или в общем случае многопле-

ночная структура) в схеме Кречмана на простран-

ственное излучение в свободное пространство над

пленкой от точечного излучателя, расположенного

на поверхности.

Теоретические методы нахождения излучения от

элементарного точечного электрического диполя,

расположенного на плоской границе двух сред, бы-

ли развиты на заре эры использования электромаг-

нитных волн для передачи сигналов вдоль земной

поверхности [6]. В дальнейшем эти методы получи-

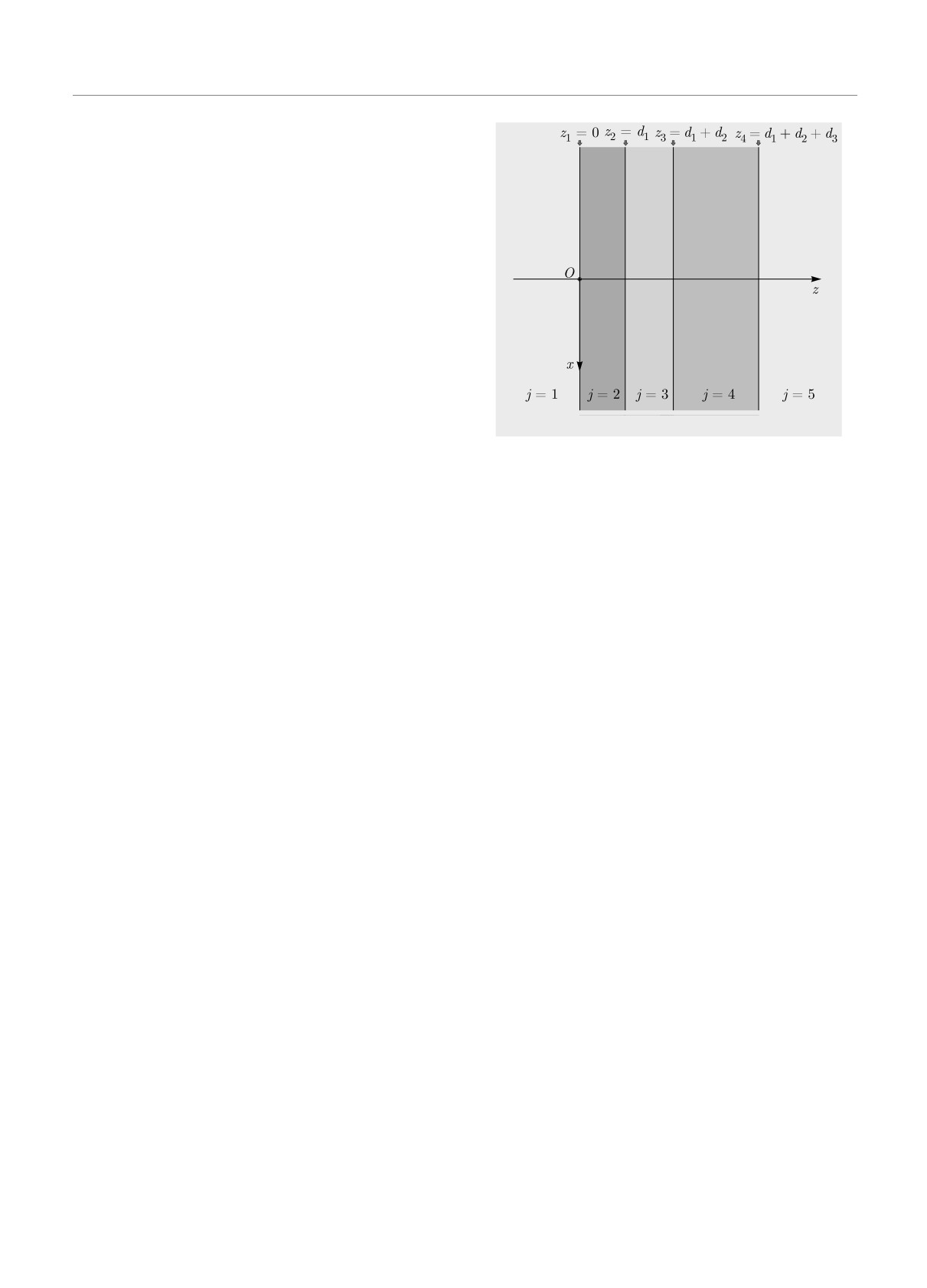
Рис. 2. Геометрия плоскослоистой структуры, состоящей

ли развитие в связи с возникающими новыми зада-

из трех пленок

чами радиосвязи [7, 8]. Развитие антенной техники

привело к развитию теории излучения элементарно-

го диполя, расположенного на границе плоскослои-

2. ПОСТАНОВКА ЗАДАЧИ. ИЗЛУЧЕНИЕ

стой среды, и теории излучения микрополосковых

ЭЛЕМЕНТАРНОГО ИЗЛУЧАТЕЛЯ,

антенн [9-11], которые являются наилучшими кон-

РАСПОЛОЖЕННОГО ВНУТРИ

струкциями с точки зрения их совместимости с мик-

ПЛОСКОСЛОИСТОЙ СТРУКТУРЫ

рополосковыми интегральными схемами. Такие ан-

тенны играют особую роль в современной технике,

Рассмотрим задачу излучения электромагнит-

так как они могут быть изготовлены из фольгиро-

ной волны точечным источником тока единичной

ванных материалов высокопроизводительными ме-

амплитуды, изменяющимся во времени гармониче-

тодами печати и травления.

ски с циклической частотой ω. Пусть этот источник

расположен в плоской слоистой структуре, состоя-

щей из нескольких пленок и из окружающих слоис-

Существующие теоретические методы расчета

тую структуру двух полупространств. Для опреде-

излучения антенн, расположенных на границе сло-

ленности сначала будем считать, что источник рас-

истых структур, сложны и описываются, например,

положен в одной из пленок, а затем обобщим эту

в терминах диадных функций Грина [12]. Кроме то-

задачу на случай, когда источник расположен на их

го, сама теория распространения волн в слоистых

границе.

структурах содержит много тонких моментов, та-

Пусть общее число пленок равно N_f , толщина

ких как необходимость правильного выбора ветвей

m-й пленки равна d_m и полная толщина слоистой

аналитических функций при записи волн в слоях,

∑

структуры d_tot =

d_m. Общее число границ меж-

которые могут приводить к чудесам вроде суперраз-

m=1

решения [13]. Поэтому в данной работе предложен

ду пленками обозначим как N = N_f +1. Пронумеру-

вариант строгой электромагнитной теории излуче-

ем области пространства j = 1, . . ., N + 1 (на рис. 2

ния элементарного диполя, расположенного на гра-

показана для примера задача с N = 4 и N_f = 3).

нице или внутри плоскослоистой структуры. Для

Предположим, что пленки имеют абсолютные ком-

случая излучения диполя, расположенного на сво-

плексные диэлектрические и магнитные проницае-

бодной границе одной пленки, ниже продемонстри-

мости равные ε_j и μ_j на рассматриваемой частоте

рован метод аналитического упрощения решения,

ω, а перед и за слоистой структурой находятся од-

имеющий, как кажется, потенциально общетеоре-

нородные полупространства с проницаемостями ε₁,

тическое значение. Этот метод позволил привести

μ₁ и εN+1, μN+1 (свободное пространство). Обозна-

формулы для излучаемых полей к одномерным ин-

чим также через z_j координаты N границ пленок по

тегралам, что существенно упростило анализ задачи

∑

оси z следующим образом: z₁ = 0, z_j =

d_m при

и ускорило численные расчеты.

m=1

ЖЭТФ, том 159, вып. 1, 2021

Элементарный излучатель на границе. ..

пленке равны соответственно ε_j и μ_j . Тогда, учи-

тывая, что в этой области справедливо уравнение

div D_j = 0, из уравнений (1) и (2) получаем уравне-

ния для электромагнитных полей в виде

rotrotE_j - ω²ε_jμ_jE_j = 0,

(3)

rotrotB_j - ω²ε_jμ_jB_j = 0.

(4)

В рассматриваемой области div E_j = 0 и div B_j =

= 0. Учитывая векторное тождество rotrotF

= graddivF-ΔF, где Δ = ∂2xx+∂2yy +∂2zz — оператор

Лапласа, из (3) и (4) получим

ΔE_j + ω²ε_j μ_j E_j = 0,

(5)

ΔB_j + ω²ε_j μ_j B_j = 0.

(6)

Подставим в полученные выше уравнения ком-

поненты полей в виде фурье-разложений. Напри-

мер, представление для x-компоненты электричес-

кого поля примет вид

E_j,x (x, y, z) =

(2π)²

∫

E_j,x (ξ, η, z) ei(ξx+ηy) dξ dη,

Рис. 3. Пленка с номером j, расположенная между грани-

-∞ -∞

цами zj-1 и zj

где фурье-образы определяются выражением

∫

j = 2,...,N. Уравнения Максвелла для области с

E_j,x (ξ, η, z) =

E_j,x (x, y, z) e-i(ξx+ηy) dxdy.

номером j можно записать в виде

-∞ -∞

rotE_j = iωB_j,

(1)

Для остальных компонент полей будем исполь-

rotB_j = μ_j (-iωε_jE_j + J_j),

(2)

зовать аналогичные представления и соответствую-

где E_j , B_j и J_j — векторы напряженности элек-

щие символы.

трического поля, индукция магнитного поля и плот-

В компонентах полей уравнения (5) и (6) имеют

ность стороннего (известного) тока в области с но-

вид

мером j (если источник тока отсутствует в области

∂2xxE_j,x + ∂2yyE_j,x + ∂2zzE_j,x + ω²μ_jε_jE_j,x = 0,

j, то J_j = 0). Предполагается комплексное времен-

ное представление в виде e^-iωt.

и аналогичные уравнения для E_j,y, E_j,z и состав-

Решая уравнения Максвелла в каждой области с

ляющих магнитного поля, которые выписывать не

учетом граничных условий, найдем электромагнит-

будем. Переходя к фурье-образам, получаем из (5)

ное поле во всех областях. Рассмотрим сначала сле-

уравнения

дующую вспомогательную задачу.

E_j,x

d²

+γ2jEj,x = 0,

dz²

3. РАСПРОСТРАНЕНИЕ

E_j,y

d²

ЭЛЕКТРОМАГНИТНОЙ ВОЛНЫ В СЛОЕ,

+ γ2j E_j,y = 0,

(7)

dz²

СВОБОДНОЙ ОТ СТОРОННИХ ТОКОВ

d²

˜j,z

+ γ2j E_j,z = 0,

Пусть в области с номером j нет сторонних то-

dz²

ков между границами zj-1 и z_j (см. рис. 3). Диэлек-

√

трическая и магнитная проницаемости среды в этой

где γ_j = k2j - ξ² - η², k_j = ω√μj εj.

А. Б. Петрин

ЖЭТФ, том 159, вып. 1, 2021

Решения уравнений (7) для направлений распро-

Если взять вместо (11) другую аналитическую

странения волн вдоль (+) и против (-) оси z, можно

ветвь, с отрицательной мнимой зависимостью, то

записать в виде

волны с большими λ будут экспоненциально возрас-

тать с увеличением z при удалении от источников

E^±j (x, y, z) =

полей, что противоречит принципу причинности.

⎛

⎞

Более строго, в случае поглощающей среды су-

Ê±

∫

j,x

ществует две

точки ветвления функции γ_j (λ): точ-

⎜

⎟

√

⎝

Ê±

⎠e±iγjzei(ξx+ηy) dξ dη.

(8)

j,y

ка kj,1 = ω

|ε_j| |μ_j | exp (i (arg (ε_j) + arg (μ_j ))/2) и

(2π)²

−∞ -∞

Ê±

j,z

точка kj,2 = e^iπkj,1. Аналитическую ветвь функции

(λ), пригодную в том числе для описания мате-

γ_j

В рассматриваемом случае div E_j = 0 и, следова-

риалов с отрицательным преломлением [14] и пере-

Ê±

тельно, ξE±j,x + η

±γ_jE±j,z = 0. Тогда (8) можно

j,y

ходящую в (11) при бесконечно малом поглощении

переписать как

среды, можно определить как

⎛

⎞

∫

√

⁽iarg(kj,1 - λ)⁾

⎜

⎟

γ_j (λ) =

|kj,1 - λ| exp

E^±j (x, y, z) =

⎝

⎠×

(2π)²

−∞ -∞

∓ξ/γ_j

∓η/γ_j

(

)

√

⁽iarg(λ - kj,2)⁾

j,x

|kj,2 - λ| exp

(12)

e±iγjzei(ξx+ηy) dξ dη.

(9)

Ê±

j,y

где функции |ξ| и arg(ξ) — модуль и аргумент комп-

Поэтому общее решение уравнений (7) в области

лексной переменной ξ.

[zj-1, z_j] можно записать в виде

Кроме того, в представлении полей (10) при лю-

бых z и правильном выборе аналитической ветви

⎛

⎞

∫

(12) будет обеспечена сходимость интегралов. При

⎜

⎟

этом не будут возникать экспоненциально усилива-

E_j (x, y, z) =

⎝

⎠×

(2π)²

ющиеся гармоники при больших значениях ξ и η.

-∞ -∞

-ξ/γ_j

-η/γ_j

Из уравнения rotE_j = iωB_j найдем x- и y-ком-

(

)

E+j,x

поненты магнитного поля. Для соответствующих

eiγj(z-zj-1)ei(ξx+ηy) dξ dη +

фурье-компонент имеем

E⁺

j,y

⎛

⎞

∫

)

⁽η

γ_j

⁽ξ

γ_j

⎜

⎟

B+

Ê+

=e_x

-e_y

⎝

⎠×

j,z

j,y

j,z

j,x

(2π)²

−∞ -∞

ξ/γ_j η/γ_j

(

)

Ê-

⁽ξ

Ê+

j,x

+e_z

j,y

j,x

e-iγj(z-zj)ei(ξx+ηy) dξ dη.

(10)

Ê-

j,y

где e_x, e_y и e_z — единичные орты координатных

Ê+

Обратим внимание на отличие в форме запи-

осей. Из выражения div E_j

= 0 следует

j,z

∕

си (9) и (10). Формально эти уравнения перехо-

Ê+

= -ξ

j,x

γ_j - η

j,y

γ_j, тогда

дят одно в другое, они описывают волны, распро-

страняющиеся в противоположных направлениях

(

)

ξη

γ2j + η²

по оси z. Однако формулы содержат функции γ_j =√

B+

Ê+

=e_x

E+j,x -

j,y

= k2j - ξ² - η². Для однозначного определения ви-

ωγ_j

да записи решений необходимо выбрать аналити-

(

)

ческую ветвь функции комплексного переменного

γ2j + ξ²

ξη

+e_y

Ê+

γ_j (λ), где λ² = ξ² + η².

j,x

j,y

ωγ_j

Обычно для сред без поглощения используют

ветвь [8]

)

⎧

√

⁽ξ

Ê+

⎨

+e_z

j,y

j,x

k2j - λ², λ² ≤ k2j,

γ_j (λ) =

√

(11)

⎩ i λ² -k2j, λ² ≥k2j.

или в матричном виде —

ЖЭТФ, том 159, вып. 1, 2021

Элементарный излучатель на границе. ..

⎛

⎞

B+

Тогда общее решение для магнитного поля в рас-

j,x

⎜

⎟

B+

сматриваемой области с номером j (пленке с номе-

⎝

⎠=

j,y

ром j - 1) можно записать в виде

B+

^j,z⎛

(

)∕

⎞

-ξη/ωγ_j

γ2j + η²

ωγ_j

(

)∕

B_j (x, y, z) =

⎜

⎟

⎝

γ2j + ξ²

ωγ_j

ξη/ωγ_j

⎠×

(2π)²

⎛

(

)∕

⎞

-η/ω

ξ/ω

∫

-ξη/ωγ_j

γ2j + η²

ωγ_j

(

)

⎜

(

)∕

⎟

⎝

γ2j + ξ²

ωγ_j

ξη/ωγ_j

⎠×

j,x

−∞ -∞

-η/ω

ξ/ω

E⁺

j,y

(

)

B-

j,x

Аналогично, для

найдем

eiγj(z-zj-1)ei(ξx+ηy) dξ dη +

Ê+

(2π)²

j,y

⎛

⎞

⎛

(

)∕

⎞

B-

j,x

∫

ξη/ωγ_j

γ2j + η²

ωγ_j

⎜

⎟

⎜

(

)∕

⎟

⎝

B-

⎠=

⎝ -

γ2j + ξ²

ωγ_j

-ξη/ωγ_j

⎠×

j,y

B-

−∞ -∞

-η/ω

ξ/ω

^j,z⎛

(

)∕

⎞

(

)

ξη/ωγ_j

γ2j + η²

ωγ_j

Ê-

j,x

⎜

(

)∕

⎟

e-iγj(z-zj)ei(ξx+ηy) dξ dη.

(13)

⎝ -

γ2j + ξ²

ωγ_j

-ξη/ωγ_j

⎠×

Ê-

j,y

−η/ω

ξ/ω

(

)

Из (10) и (13) найдем тангенциальные составля-

Ê-

j,x

ющие фурье-образов полей на границах области j в

Ê-

виде

j,y

⎛

⎞

⎛

⎞

eiγjdj-1

⎛

⎞



E_j,x

⎜

⎟



⎜

eiγjdj-1

⎟

j,x

⎜

⎟

⎜

⎟⎜

⎟

⎜

E_j,y

⎟

Ê+

⎜

γ2j + η²

⎟⎜

⎟

⎜

∕

⎟

ξη

j,y

⎜

⎟⎜

⎜

⎟

− ξηωμ

eiγjdj-1

^⎟,

⎜

⎟⎜

⎟

⎜

B_j,x μ_j

⎟

jγj

ωμ_jγ_j

Ê-

⎜

⎟⎝

j,x

⎠

⎝

∕

⎠

⎜

⎟



⎝ γ2j +ξ²

γ2j + ξ²

⎠

Ê-

B_j,y μ_j



ξη

j,y

z=zj-1

eiγjdj-1

ωμ_jγ_j

⎛

⎞

⎛

⎞

eiγjdj-1



⎛

⎞

⎜

⎟

E_j,x



⎜

eiγjdj-1

⎟

j,x

⎜

⎟

⎜

⎟⎜

⎟

⎜

E_j,y

⎟

⎜

⎟⎜

Ê+

⎟

⎜

∕

⎟

ξη

γ2j + η²

ξη

γ2j + η²

j,y

⎜

⎟⎜

⎜

⎟

−

eiγjdj-1

^⎟,

⎜

⎟⎜

Ê-

⎟

⎜

B_j,x μ_j

⎟

⎜

ωμ_jγ_j

⎟⎝

⎠

⎝

∕

⎠

j,x

⎜

⎟



Ê-

B_j,y μ_j



⎝ γ2j +ξ²

ξη

γ2j + ξ²

ξη

⎠

j,y

z=zj

eiγjdj-1

ωμ_jγ_j

(

)_T

где dj-1 = z_j - zj-1.

Ê+

Ê-

Вводя вектор-столбец

℘_j =

;

; E-j,x;

j,x

j,y

запишем полученные выражения в матричном виде:

⎛

⎞

E_j,x



⎜

⎟

(

)

⎜

E_j,y

⎟

⎜

∕

⎟

eiγjdj-1 I

⎜

⎟

℘_j,

(14)

⎜

B_j,x μ_j

⎟

G_j

-eiγjdj-1 G_j

⎝

∕

⎠



B_j,y μ_j



z=zj-1

А. Б. Петрин

ЖЭТФ, том 159, вып. 1, 2021

⎛

⎞



E_j,x



Записывая граничные условия (17)-(20) с помо-

⎜

⎟

⎜

E_j,y

⎟

щью выражений (14) и (15), получим матричное

⎜

∕

⎟

⎜

⎟

уравнение на границе z = z_j:

⎜

B_j,x μ_j

⎟

⎝

∕

⎠



B_j,y μ_j



z=zj

(

)

⎛

⎞

eiγjdj-1 I

iγj dj-1 I

℘_j,

(15)

⎝

⎠

℘_j =

eiγjdj-1 G_j

-G_j

eiγjdj-1 G_j

-G_j

где I — единичная 2×2-матрица, а матрица G_j пред-

⎛

⎞

ставляется как

eiγj+1d^j I

⎛

⎞

=^⎝

⎠

℘j+1,

(21)

ξη

γ2j + η²

Gj+1

-eiγj+1d^j Gj+1

⎜

⎟

⎜

-ωμ_jγ_j

ωμ_jγ_j

⎟

G_j =

⎜

⎟

(16)

⎝ γ2j +ξ²

ξη

⎠

ωμ_jγ_j

где dj-1 = z_j - zj-1, d_j = zj+1 - z_j .

Уравнение

(21) можно записать для j

4. РАСПРОСТРАНЕНИЕ

= 2, . . ., N - 1, где N + 1 — общее число областей,

ЭЛЕКТРОМАГНИТНОЙ ВОЛНЫ В

N — число границ, т.е. для всех границ, исключая

МНОГОСЛОЙНОЙ СТРУКТУРЕ,

первую (j = 1) и последнюю (j = N) границы. То

СВОБОДНОЙ ОТ СТОРОННИХ ТОКОВ

есть исключаются границы

Рассмотрим теперь многослойную структуру,

внутри которой нет сторонних токов. Рассмотрим

границу z = z_j между областями с номерами j и

∑

z₁ = 0, z_N = d_tot =

d_m,

j+1. Непрерывность тангенциальных компонент на-

m=1

пряженностей электрического и магнитного полей

на этой границе можно записать в виде

E_j,x (x, y, z_j) - Ej+1,x (x, y, z_j) = 0,

где d_tot — общая толщина слоистой структуры (сум-

ма толщин пленок, составляющих рассматриваемую

E_j,y (x, y, z_j) - Ej+1,y (x, y, z_j) = 0,

структуру).

B_j,x (x, y, z_j)

Bj+1,x (x, y, z_j)

= 0,

Общее решение для электрического и магнитно-

μ_j

μj+1

го полей в области j = 1, т. е. в интервале (-∞, z₁],

B_j,y (x, y, z_j)

Bj+1,y (x, y, z_j)

где z₁ = 0, запишем в виде

= 0,

μ_j

μj+1

где электрические и магнитные поля в области j + 1

⎛

⎞

выражаются формулами (10) и (13), в которых про-

∫

ведена замена индексов j → j + 1. Так как уравне-

⎜

⎟

E₁ (x, y, z) =

⎝

⎠×

ния Максвелла являются линейными, то граничные

(2π)²

−∞ -∞

-ξ/γ₁

-η/γ₁

условия должны выполняться для каждого члена

фурье-разложения, т. е. граничные условия выпол-

(

)

няются для фурье-образов полей:

Ê+

1,x

eiγ1zei(ξx+ηy) dξ dη +

Ê+

1,y

E_j,x (ξ, η, z_j) -

Ej+1,x (ξ, η, z_j) = 0,

(17)

⎛

⎞

E_j,y (ξ, η, z_j) -

Ej+1,y (ξ, η, z_j) = 0,

(18)

(

)

∫

Ê-

⎜

⎟

1,x

⎝

⎠

B_j,x (ξ, η, z_j)

Bj+1,x (ξ, η, z_j)

= 0,

(19)

(2π)²

E^-

1,y

μ_j

μj+1

-∞ -∞

ξ/γ₁

η/γ₁

B_j,y (ξ, η, z_j)

j+1,y (ξ, η, zj)

= 0.

(20)

× e-iγ1zei(ξx+ηy) dξ dη,

(22)

μ_j

μj+1

ЖЭТФ, том 159, вып. 1, 2021

Элементарный излучатель на границе. ..

Тогда, записывая условия на границе z₁ = 0, полу-

B₁ (x, y, z) =

(2π)²

чим

⎛

(

)∕

⎞

+∞

∫

-ξη/ωγ₁

γ²¹ + η²

ωγ₁

(

)

⎜

(

)∕

⎟

⎝

γ²¹ + ξ²

ωγ₁

ξη/ωγ₁

⎠×

℘₁ =

G₁

-G₁

−∞ -∞

-η/ω

ξ/ω

(

)

(

)

eiγ2d¹ I

℘₂.

(24)

1,x

eiγ1zei(ξx+ηy) dξ dη +

G₂

-eiγ2d¹ G₂

Ê+

1,y

(2π)²

⎛

(

)∕

⎞

Аналогично, общее решение для электрического

+∞

∫

ξη/ωγ₁

γ²¹ + η²

ωγ₁

⎜

(

)∕

⎟

и магнитного полей в области j = N + 1, т. е. в ин-

⎝ -

γ²¹ + ξ²

ωγ₁

-ξη/ωγ₁

⎠×

тервале [z_N, +∞), запишем в виде

−∞ -∞

-η/ω

ξ/ω

(

)

1,x

e-iγ1zei(ξx+ηy) dξ dη.

(23)

Ê-

1,y

⎛

⎞

∫

(

)

Ê+

⎜

⎟

N +1,x

EN+1 (x, y, z) =

⎝

⎠

eiγN+1(z-zN )ei(ξx+ηy) dξ dη +

(2π)²

E⁺

N +1,y

-∞ -∞

-ξ/γN+1

-η/γN+1

⎛

⎞

(

)

∫

Ê-

⎜

⎟

N +1,x

⎝

⎠

e-iγN+1(z-zN ) ei(ξx+ηy) dξ dη,

(25)

(2π)²

Ê-

N +1,y

-∞ -∞

ξ/γN+1

η/γN+1

BN+1 (x, y, z) =

(2π)²

⎛

(

)∕

⎞

(

)

+^∞

∫

-ξη/ωγN+1

γ2N+1 + η²

ωγN+1

(

)∕

Ê+

⎜

⎟

N +1,x

⎝

γ2N+1 + ξ²

ωγN+1

ξη/ωγN+1

⎠

eiγN+1(z-zN )ei(ξx+ηy)dξdη +

Ê+

N +1,y

−∞ -∞

-η/ω

ξ/ω

⎛

(

)∕

⎞

(

)

∫

ξη/ωγN+1

γ2N+1 + η²

ωγN+1

(

)∕

Ê-

⎜

⎟

N +1,x

⎝ -

γ2N+1 + ξ²

ωγN+1

-ξη/ωγN+1

⎠

Ê-

(2π)²

N +1,y

−∞ -∞

-η/ω

ξ/ω

× e-iγN+1(z-zN)ei(ξx+ηy) dξ dη.

(26)

(

)-1 (

)

Тогда получим граничные условия на границе z_N в

eiγ2d¹ I

℘₁ =

виде

G₁

-G₁

G₂

-eiγ2d¹ G

(

)

(

)-1

eiγN dN-1I

eiγ2d¹ I

℘_N =

×...

eiγN dN-1G_N

-G_N

eiγ2d¹ G₂

-G₂

(

)

(

)

eiγN dN-1 I

℘N+1.

(27)

GN+1

-GN+1

G_N

-eiγN dN-1G_N

(

)-1

eiγN dN-1 I

Граничные условия (21), (24) и (27) позволяют

связать вектор-столбцы электрического поля в пер-

eiγN dN-1G_N

-G_N

(

)

вой и последней областях задачи (т.е. в полупро-

странствах, вне плоскослоистой структуры):

℘N+1,

GN+1

-GN+1

А. Б. Петрин

ЖЭТФ, том 159, вып. 1, 2021

компоненты

Ê+

и Ê+N+1,y вектор-столбца

℘N+1 и

N +1,x

прошедшую волну по формулам (25), (26). Подроб-

ности решения таких задач для пространственно-ог-

раниченных падающих пучков можно найти, напри-

мер, в работах [15-17].

5. РАСПРОСТРАНЕНИЕ

ЭЛЕКТРОМАГНИТНОЙ ВОЛНЫ В

МНОГОСЛОЙНОЙ СТРУКТУРЕ, ОТ

ЭЛЕМЕНТАРНОГО ИСТОЧНИКА

СТОРОННЕГО ТОКА

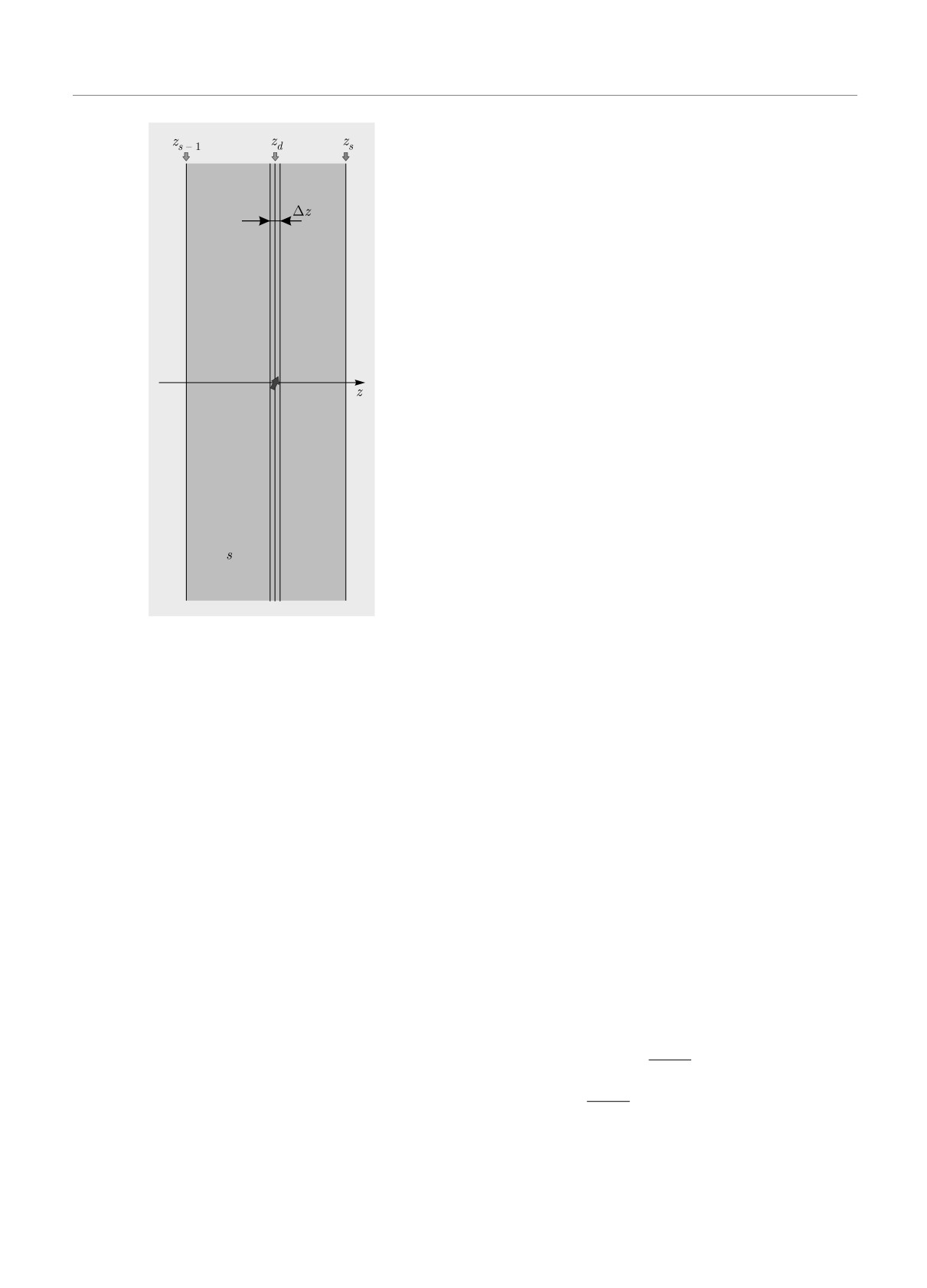
Пусть имеется точечный излучатель, располо-

женный в точке (0, 0, z_d) в области с номером s (см.

рис. 4). Пусть этот излучатель определяется плот-

ностью стороннего тока (в комплексном представле-

нии e^-iωt):

J(x, y, z) = (n_xe_x+n_ye_y+n_ze_z)δ (x) δ (y)δ (z-z_d),

где n_x, n_y, n_z — направляющие косинусы вектора

тока вдоль осей координат, причем n2x +n2y +n2z = 1,

δ (x) — дельта-функция Дирака. Тогда фурье-обра-

зы составляющих этого тока определятся следую-

Рис. 4. Точечный излучатель, расположенный в точке

щими выражениями:

(0, 0, zd) в области с номером s

J_s,x (ξ, η, z) =

или

℘₁ = M ×

℘N+1.

(28)

∫

(

)

=n_x

δ (x) δ (y) δ (z - z_d) e-i(ξx+ηy) dx dy =

∏

Матрица M имеет вид M = T₁ ×

Tm ×TN+1,

-∞ -∞

m=2

где

(

-1

)

= n_xδ (z - z_d),

T₁ =

G₁

-G₁

и аналогично

(

)

J_s,y (ξ, η, z) = n_yδ (z - z_d),

eiγmdm-1 I

T_m =

J_s,z (ξ, η, z) = n_zδ (z - z_d).

G_m

-eiγmdm-1 G_m

(

)-1

Пусть этот элементарный источник тока на-

eiγmdm-1 I

ходится в бесконечно тонком слое (z_d - Δz/2,

eiγmdm-1 G_m

-G_m

z_d +Δz/2). Тогда уравнения Максвелла (1) и (2) для

(

)

фурье-образов полей можно записать (при Δz → 0)

в виде

TN+1 =

⎧

GN+1

-GN+1

⎪

iη

E_s,z -ΔEs,y

= iω

B_s,x,

⎨

Δz

Если нам известна, например, падающая на

E_s,x

(29)

плоскослоистую структуру волна, а значит, компо-

⎪

- iξ

E_s,z = iω

B_s,y,

ненты

Ê+

и Ê+1,y вектор-столбца

℘₁, то из уравне-

⎪

Δz

1,x

⎩

Ê-

iξ

E_s,y - iη

E_s,x = iω

B_s,z,

ния (28) можно найти компоненты

1,x

и Ê-1,y и саму

отраженную волну по формулам (22), (23), а также

ЖЭТФ, том 159, вып. 1, 2021

Элементарный излучатель на границе. ..

⎧

(

)

⎪

iη

B_s,z-ΔBj,y

=μ_s

-iωε_s

E_s,x+n_xδ (z-z_d) ,

⎨

Δz

(

)

ΔBs,x

(30)

⎪

-iξ

B_s,z = μs -iωεs

E_s,y+n_yδ (z-z_d) ,

⎪

Δz

(

)

⎩

iξ

B_s,y-iη

B_s,x = μs -iωεs

E_s,z+n_zδ (z-z_d)

Поскольку z-компоненты полей из уравнений

E_s,z = -

B_s,y +

B_s,x +

J_s,z,

(29) и (30) можно выразить через x- и y-компоненты

ωε_sμ_s

iωε_s

по формулам

для x- и y-компонент напряженностей электричес-

B_s,z =

E_s,y -

E_s,x,

кого и магнитного полей получим

(

)

iξη

ξ²

E_s,x =

B_s,x + i ω -

B_s,y +

n_zδ (z - z_d) Δz,

ωε_sμ_s

ωε_s

(

)

η²

iξη

E_s,y = i

-ω

B_s,x -

B_s,y +

n_zδ (z - z_d) Δz,

ωε_sμ_s

ωε_s

(

)

ΔBs,x

iξη

ξ²

E_s,x + i

− ωε_s

E_s,y + n_yδ (z - z_d) Δz,

μ_s

ωμ_s

( (

)

ΔBs,y

η²

iξη

= i ωε_s -

E_s,x +

E_s,y - n_xδ (z - z_d) Δz.

μ_s

ωμ_s

Тогда в пределе Δz → 0 скачок тангенциальных

Особо отметим, что скачок электрических по-

компонент напряженностей электрического и маг-

лей при переходе через рассматриваемый бесконеч-

нитного полей при переходе через бесконечно тон-

но тонкий слой (при Δz → 0), вообще говоря, зави-

кий слой с током имеет вид

сит от диэлектрической проницаемости среды ε_s, в

которой расположен рассматриваемый источник то-

ка. Но излучение источников, у которых есть толь-

E_s,x → n_zξ/ωε_s,

ко составляющие тока вдоль границы, не зависит в

E_s,y → n_zη/ωε_s,∕

явном виде от диэлектрических свойств среды, в ко-

ΔBs,x μ_s → n_y,

торой они расположены.

∕

ΔBs,y μ_s → -n_x.

Выразим теперь левую часть граничного усло-

вия (31) через вектор-столбцы

℘₁ и

℘N+1 полупро-

странств снаружи плоскослоистой структуры. Для

В матричном виде уравнения, связывающие тан-

этого разобьем область с номером s на две области и

генциальные компоненты полей с двух сторон беско-

обозначим их индексами l и r (левая и правая, если

нечно тонкого слоя с током, можно записать в сле-

смотреть на рис. 4). Введем вектор-столбцы

℘_l и

℘_r

дующем виде:

в этих областях. Тогда тангенциальные компоненты

напряженностей полей в (31) можно выразить как

⎛

⎞

⎛

⎞

E_s,x



E_s,x



⎛

⎞

⎜

⎟

⎜

⎟

⎜

E_s,y

⎟

⎜

⎟

E_s,x



⎜

∕

⎟

⎜

E_s,y∕

⎟

⎜

⎟

⎜

⎟

⎜

⎟

⎜

E_s,y

⎟

⎜

B_s,x μ_s

⎟

⎜

B_s,x μ_s

⎟

⎜

∕

⎟

⎝

∕

⎠

⎝

∕

⎠

⎜

⎟



⎜

B_s,x μ_s

⎟

B_s,y μ_s



B_s,y μ_s



⎝

∕

⎠

z=z_d+0

z=z_d-0



⎛

⎞

B_s,y μ_s



n_zξ/ωε_s

z=z

d-0

(

)

⎜

⎟

⎜

n_zη/ωε_s

⎟

eiγs(zd-zs-1)I

⎜

⎟

(31)

℘_l,

(32)

⎜

⎟

⎝ ny

⎠

eiγs(zd-zs-1)G_s

-G_s

−n_x

А. Б. Петрин

ЖЭТФ, том 159, вып. 1, 2021

⎛

⎞

(

)_T

E_s,x



где V

= n_zξ/ωε_s; n_zη/ωε_s; n_y;

-n_x

—

⎜

⎟

⎜

E_s,y

⎟

⎜

∕

⎟

вектор-столбец, характеризующий возбуждающее

⎜

⎟

⎜

B_s,x μ_s

⎟

воздействие на систему стороннего элементарного

⎝

∕

⎠



тока, а матрицы H_R и H_L характеризуют отклик

B_s,y μ_s



z=z_d+0

на внешнее возбуждение слоистой структуры спра-

(

)

ва и слева излучателя и выражаются следующим

eiγs(zs-zd)I

℘_r.

(33)

образом:

G_s

-eiγs(zs-zd)G_s

(

)

eiγs(zs-zd)I

Кроме того, из (28) следует, что

H_R =

Q_R =

G_s

-eiγs(zs-zd)G_s

(

)

℘₁ = Q_L℘l,

(34)

∏

=T_R ×

×TN+1,

m=s+1

где

(

)

(

)-1 (

)

eiγs(zd-zs-1)I

H_L =

(Q_L)-1

eiγ2d¹ I

eiγs(zd-zs-1)G_s

-G_s

Q_L =

(

)

)-1

G₁

-G₁

G₂

-eiγ2d¹ G₂

∏

(

)-1

= T₁ ×

×T_L

eiγ2d¹ I

m=2

×...

eiγ2d¹ G₂

-G₂

Здесь матрицы T_m при m = s имеют вид

(

)

(

)

eiγs-1ds-2I

eiγmdm-1 I

Tm =

Gs-1

-eiγs-1ds-2 Gs-1

G_m

-eiγmdm-1 G_m

(

)-1

(

)-1

eiγmdm-1 I

eiγs-1ds-2 I

eiγmdm-1 G_m

-G_m

eiγs-1ds-2Gs-1

-Gs-1

(

)

e^iγs(zd-zs-1)I

а матрицы T_L и T_R

—

(

)

G_s

-e^iγs(zd-zs-1)

G_s

eiγs(zd-zs-1)I

TL =

а также

G_s

-eiγs(zd-zs-1)G_s

(

)-1

℘_r = Q_R℘N+1,

(35)

eiγs(zd-zs-1)I

где

eiγs(zd-zs-1)G_s

-G_s

(

)-1

(

)

eiγs(zs-zd)I

Q_R =

TR =

eiγs(zs-zd)G_s

-G_s

G_s

-eiγs(zs-zd)G_s

(

)

(

)-1

eiγs+1d^s I

eiγs(zs-zd)I

Gs+1

-eiγs+1d^s Gs+1

eiγs(zs-zd)G_s

-G_s

(

)-1

В приведенных выше формулах матрицы G_s вы-

eiγs+1d^s I

×...

ражаются по формуле (16).

eiγs+1d^s Gs+1

-Gs+1

Далее, в рассматриваемой задаче источники по-

(

)

eiγN dN-1I

лей находятся исключительно внутри плоскослои-

стой структуры. Поэтому в столбцах

℘₁ и

℘N+1 есть

G_N

-eiγN dN-1G_N

(

)-1 (

)

только компоненты волн, идущие от плоскослоистой

eiγN dN-1 I

структуры. Эти столбцы имеют вид

eiγN dN-1 G_N

-G_N

GN+1

-GN+1.

(

℘₁ =

Ê-

;

Ê-

1,x

1,y

(

)_T

Подставляя (34), (35) в (32), (33) и затем полу-

Ê+

℘N+1 =

N +1,x

;

N +1,y

;

ченные выражения в (31), получаем

Чтобы получить оставшиеся, отличные от нуля,

H_R ×

℘N+1 = H_L ×

℘₁ + V,

(36)

компоненты

℘₁ и

℘N+1, разобьем каждую из матриц

ЖЭТФ, том 159, вып. 1, 2021

Элементарный излучатель на границе. ..

H_R и H_L на четыре 2 × 2-подматрицы H_RA, H_RB,

Полученные уравнения можно снова объединить

H_RC, H_RD и H_LA, H_LB, H_LC, H_LD следующим об-

в одно матричное 4 × 4-уравнение:

разом:

(

)

(

)

H_RA H_RB

-H_LB H_RA

H_R =

℘_out = V,

(38)

H_RC H_RD

−H_LD H_RC

(

)

где введен вектор-столбец

H_LA H_LB

H_L =

(

H_LC H_LD

℘_out =

Ê-

;

Ê-

;

Ê+

;

Ê+

)^T .

1,x

1,y

N +1,x

N +1,y

Тогда уравнение (36) примет вид

Решая это уравнение, найдем

Ê-

E+N+1,x,

⎛

⎞

1,x

1,y

E_N

(

)

+1,x

E+N+1,y, а значит, уходящую из плоскослоистой

⎜

⎟

H_RA H_RB

⎜

E+N+1,y

⎟

структуры влево волну (в направлении z → -∞)

⎜

^⎟=

⎜

⎟

H_RC H_RD

по формулам

⎝

⎠

⎛

⎞

⎛

⎞

∫

⎜

⎟

(

)

E₁ (x, y, z) =

⎝

⎠ ×

⎜

⎟

H_LA H_LB

⎜

⎟

(2π)²

⎜

⎟ + V.

(37)

−∞ -∞

ξ/γ₁

η/γ₁

⎜

⎟

H_LC H_LD

⎝

E-1,x

⎠

(

)

E-1,x

Ê-

1,y

e-iγ1zei(ξx+ηy) dξ dη,

(39)

−

1,y

Если еще разбить вектор

(

V= V₁; V₂; V₃; V₄

B₁ (x, y, z) =

(2π)²

⎛

(

)∕

⎞

на V_A = (V₁, V₂)^T и V_B = (V₃, V₄)^T , то уравне-

∫

ξη/ωγ₁

γ²¹ + η²

ωγ₁

ние (37) можно представить следующей системой из

⎜

(

)∕

⎟

⎝ -

γ²¹ + ξ²

ωγ₁

-ξη/ωγ₁

⎠ ×

двух матричных уравнений:

−∞ -∞

-η/ω

ξ/ω

(

)

(

)

(

)

Ê-

N +1,x

1,x

E-1,x

H_RA

=H_LB

+V_A,

Ê+

Ê-

e-iγ1zei(ξx+ηy) dξ dη

(40)

N +1,y

1,y

E^-

1,y

(

)

(

)

Ê-

N +1,x

1,x

и волну, уходящую вправо от плоскослоистой струк-

H_RC

=H_LD

+V_B.

E+N+1,y

Ê-

туры (в направлении z → +∞):

1,y

⎛

⎞

∫

(

)

Ê+

⎜

⎟

N +1,x

EN+1 (x, y, z) =

⎝

⎠

(2π)²

E⁺

N +1,y

-∞ -∞

-ξ/γN+1

-η/γN+1

× eiγN+1(z-zN)ei(ξx+ηy) dξ dη,

(41)

⎛

(

)∕

⎞

∫

-ξη/ωγN+1

γ2N+1 + η²

ωγN+1

⎜

(

)∕

⎟

BN+1 (x, y, z) =

⎝

γ2N+1 + ξ²

ωγN+1

ξη/ωγN+1

⎠ ×

(2π)²

−∞ -∞

-η/ω

ξ/ω

(

)

N +1,x

eiγN+1(z-zN )ei(ξx+ηy) dξ dη.

(42)

Ê+

N +1,y

А. Б. Петрин

ЖЭТФ, том 159, вып. 1, 2021

(

)

Наконец, при необходимости, зная

℘₁ и

℘N+1,

T₃ =

можно найти вектор-столбцы поля в любой внут-

G₃

-G₃

ренней области

℘_j, так как они однозначно опреде-

а вектор-столбец стороннего тока равен V

ляются граничными условиями. После этого элект-

(

ромагнитные поля в любой из этих областей могут

-1

)^T .

быть найдены по формулам (10), (13). Таким обра-

Учитывая, что (T₁ × T₂)-1 = T-12 × T-11, полу-

зом, электромагнитные поля будут определены во

чим

всем пространстве.

H_L = (T₁ × T₂)-1 = T-12 × T-11 =

6. ИЗЛУЧЕНИЕ ЭЛЕМЕНТАРНОГО

(

)(

)-1

ГОРИЗОНТАЛЬНОГО ДИПОЛЯ,

eiγ2dI

РАСПОЛОЖЕННОГО НА ГРАНИЦЕ

eiγ2dG₂

-G₂

G₂

-eiγ2dG₂

МЕТАЛЛИЧЕСКОЙ ПЛЕНКИ,

(

)

НАНЕСЕННОЙ НА ПОВЕРХНОСТЬ

ПРИЗМЫ

G₁

-G

Рассмотрим теперь задачу излучения элементар-

(

Ê-

Ê+

ного горизонтального источника, расположенного

Вводя вектор-столбец

℘_out

E-1,x;

1,y

;

3,x

;

на свободной границе пленки (см. рис. 5a) в схеме

)_T

E+3,y

, уравнение (38) для данной задачи можно

Кречмана. Поляризация источника — вдоль оси x

записать в виде

(n_x = 1, n_y = 0, n_z = 0). Толщина пленки равна d.

Индекс 1 соответствует полупространству материа-

(

)

-H_LB I

ла призмы, 2 — пленке, 3 — свободному полупро-

℘_out = V.

(44)

странству над пленкой. Тогда N = 2, z_d = z₂ = d,

−H_LD G₃

H_R = T₃, H_L = (T₁ × T₂)-1 и уравнение (36) при-

Ê-

Решая линейное уравнение (44), найдем

мет вид

1,x

E-1,y и

Ê+

, и затем по формулам (39)-(42) при

T₃ ×

℘₃ = (T₁ × T₂)-1 ×

℘₁ + V,

(43)

3,x

3,y

N = 2 получим уходящую волну из плоскослоистой

где матрицы выражаются следующими формулами:

структуры в призму (в область 1) и свободное про-

(

)-1

странство (область 3) над пленкой (в направлениях

z → ±∞ от границ пленки).

T₁ =

G₁

-G₁

Снова будем считать, что среды немагнитные и

(

)(

)-1

μ₁ = μ₂ = μ₃ = μ₀. Тогда, учитывая k2j = ε_jμ₀ω²,

eiγ2dI

выражения для подматриц H_LB и H_LD можно по-

T₂ =

G₂

-eiγ2dG₂

eiγ2dG₂

-G₂

лучить в явном виде:

⎛

⎞

⁽ε₁ -ε

ξ²

⁾ sin(γ₂d)

ε₁ - ε₂ sin(γ₂d)

-γ₁

iξη

⎜ cos(γ2d)+i

⎟

ε₂

γ₁

γ₂

ε₂

γ₁γ₂

⎜

⎟

H_LB =

⎝

⎠

ε₁ - ε₂ sin(γ₂d)

⁽ε₁ -ε₂ η²

⁾ sin(γ₂d)

iξη

cos(γ₂d) + i

-γ₁

ε₂

γ₁γ₂

ε₂

γ₁

γ₂

⎛

)

⎞

ξη

⁽cos(γ₂d)

sin(γ₂d)

γ²¹ + η²

γ²² + η²

-i

cos(γ₂d) - i

sin(γ₂d)

⎜

⎟

μ₀ω

γ₁

γ₂

γ₁μ₀ω

γ₂μ₀ω

H_LD =

⎜

)

⎟

⎝

γ²¹ + ξ²

γ²² + ξ²

ξη

⁽cos(γ₂d)

sin(γ₂d)

⎠

cos(γ₂d) + i

sin(γ₂d)

-i

γ₁μ₀ω

γ₂μ₀ω

μ₀ω

γ₁

γ₂

ξη

Решив уравнение (44), найдем следующие анали-

Ê-

1,y

(a1y cos (γ₂d) + ib1y sin (γ₂d)) ,

(46)

Ê-

ωμ₀D

тические выражения для

1,x

1,y

E-1,z:

a1x + d1xη

Ê-

cos(γ₂d) +

1,x

ωμ₀D

∕

b1x + e1xη

Ê-

=ξE-1,x γ1 + ηE-

γ₁,

(47)

1,z

1,y

sin(γ₂d),

(45)

ωμ₀D

ЖЭТФ, том 159, вып. 1, 2021

Элементарный излучатель на границе. ..

и выражения для

Ê+

Естественно, что полученные выражения

3,x

3,y

3,z

(45)-(50) переходят в соответствующие выражения

a3x + d3xη

для диполя на границе двух полупространств, ко-

Ê+

3,x

cos² (γ₂d) +

ωμ₀D

гда толщина пленки d стремится к нулю, при этом

b3x + e3xη

c3x + f3xη²

полученные выражения можно точно свести к из-

sin² (γ₂d) + i

ωμ₀D

вестным формулам [8].

× cos(γ₂d)sin(γ₂d),

(48)

Аналитические выражения (45)-(50) имеют пер-

востепенное значение, так как позволяют получить

выражения для электрических полей в полупро-

ξη

(

Ê+

a3y cos² (γ₂d) + b3y sin² (γ₂d) +

странствах через одномерные интегралы, что значи-

3,y

ωμ₀D

)

тельно ускоряет счет и повышает точность вычисле-

+ ic3y cos(γ₂d)sin(γ₂d)

(49)

ний. Действительно, если перейти к полярным коор-

∕

динатам в плоскостях (x, y) и (ξ, η) по формулам

Ê+

3,z

= -ξ

3,x

γ₃ - η

3,y

γ₃.

(50)

В формулах (45)-(50) коэффициенты a, b, c, d,

x = ρcosϕ, y = ρsinϕ,

(51)

e, f являются функциями γ₁, γ₂ и γ₃. Выраже-

ξ = λcosϑ, η = λsinϑ

ния для этих коэффициентов представлены в При-

ложении A. Кроме того, функция D (ξ, η) есть де-

√

получим, что величины γ₁

k²¹ - λ², γ₂

терминант матрицы уравнения (44). Оказалось, что

√

k²² - λ², γ₃ =

k²³ - λ², зависящие от них мно-

D (ξ, η) = D (λ) есть функция λ =

ξ² + η² и запи-

жители и детерминант D (λ) = D (λ cos ϑ, λ sin ϑ) яв-

сывается в виде аналитического выражения:

ляются функциями только λ и не зависят от ϑ. По-

этому выражения для соответствующих полей, как

D (λ) = Δ₁ cos² (γ₂d) + Δ₂ sin² (γ₂d) +

будет показано ниже, можно привести к одномер-

+ Δ3 cos(γ₂d)sin(γ₂d),

ным интегралам.

где

Рассмотрим электрические поля в полупростран-

(

)

(γ₁ + γ₃)²

γ₁γ₃ + λ²

ствах (в областях с номерами j = 1 и j = 3). Снача-

Δ₁ =

ω²μ²

γ₁γ₃

ла рассмотрим (см. представление (39)) в полупро-

странстве с j = 1:

(

)₂

γ1γ3 + γ2

Δ₂ = -

ω²μ²

γ₁γ₃γ²²k²

E1,x (x, y, z) =

(

)

(2π)²

γ²² (γ₁ + γ₃)

× λ⁴ +

λ² + γ₁γ²γ3

∫

γ₁γ₃ + γ²

Ê-

e-iγ1zei(ξx+ηy) dξ dη.

1,x

-∞ -∞

i (γ₁+γ₃)

{

(

)(

)

Δ₃ = -

γ₁γ₃+γ²²

γ₁γ₃γ²²+λ⁴

ω²μ²⁰γ₁γ₂γ₃k²

Ê-

Подставим выражение (45) для

1,x

, перейдем к по-

(

)

}

γ²¹γ²³ + γ²¹γ²² + 4γ₁γ₃γ²² + γ²³γ²² + γ⁴²

λ²

лярным координатам (51) и получим

⎛

⎞

∫

(

)

E1,x (ρ, ϕ, z) =

⎝

Q1x (γ) + R1x (γ)λ² sin

²ϑ

e-iγ1zeiρλcos(ϕ-ϑ)dϑ⎠λdλ =

(2π)²

⎛

⎞

∫

(

)

Q1x (γ) + R1x

(γ)λ²

λe-iγ1z ⎝ eiρλcos(ϕ-ϑ)dϑ⎠ dλ -

(2π)²

⎛

⎞

∫

R1x

(γ) λ³e-iγ1z ⎝ cos² ϑeiρλcos(ϕ-ϑ)dϑ⎠ dλ,

(52)

(2π)²

А. Б. Петрин

ЖЭТФ, том 159, вып. 1, 2021

где введены следующие (зависящие только от λ)

Аналогичное рассмотрение проведем для y-ком-

функции:

поненты. Из (39) и (46) получим

∫

Q1x (γ) =

(a1x cos(γ₂d) + ib1x sin(γ₂d)),

ωμ₀D (λ)

E1,y (x, y, z) =

E-1,ye-iγ1zei(ξx+ηy) dξ dη.

(2π)

-∞ -∞

R1x (γ) =

(d1x cos (γ₂d) + ie1x sin (γ₂d)) .

ωμ₀D (λ)

Подставляя выражение (46) для

Ê-

, после перехо-

1,y

да к полярным координатам (51), получим

Интегралы в скобках в (52) могут быть выражены

через функции Бесселя, если использовать их интег-

⎛

∫

ральное представление,

E1,y (ρ, ϕ, z) =

⎝ Q1y (γ)λ2 cosϑsinϑ ×

(2π)

∫

-n

⎞

J_n (ρλ) =

eiρλcosθe^inθdθ.

(53)

2π

× e-iγ1zeiρλcos(ϕ-ϑ)dϑ⎠ λdλ =

В частности, нетрудно показать, что из (53) следует

∫

следующий ряд тождеств:

λ³Q1y (γ)e-iγ1z ×

(2π)

∫

⎛

⎞

∫

eiρλcos(ϕ-ϑ)dϑ = 2πJ₀ (ρλ),

×^⎝ cosϑsinϑeiρλcos(ϕ-ϑ)dϑ⎠dλ,

∫

cosϑeiρλcos(ϕ-ϑ)dϑ = 2πi cosϕJ₁ (ρλ),

где введена функция от λ:

∫

Q1y (γ) =

(a1y cos (γ₂d) + ib1y sin (γ₂d)) .

cos² ϑeiρλcos(ϕ-ϑ)dϑ = π (J₀ (ρλ) -

ωμ₀D (λ)

Учитывая соответствующее интегральное представ-

- J2 (ρλ)cos2ϕ),

(54)

ление (54) интеграла по ϑ, получим для E1,y выра-

∫

жение

sinϑ cosϑeiρλcos(ϕ-ϑ)dϑ =

∫

(

)

sin2ϕ

E1,y (ρ, ϕ, z) =

λ³Q1y (γ) ×

= π sin2ϕ J0 (ρλ) -

J₁ (ρλ)

4π

ρλ

(

)

∫

× J0 (ρλ) -

J₁ (ρλ) e-iγ1zdλ.

(56)

cosϑ sin² ϑeiρλcos(ϕ-ϑ)dϑ = i2π ×

ρλ

(

)

(

) J2 (ρλ)

Оставшуюся компоненту E1,z в первом полупро-

× cosϕ sin² ϕJ₁ (ρλ)+

1-4 sin² ϕ

ρλ

странстве из (39) запишем в виде

Подставляя соответствующие выражения (54) инте-

E1,z (x, y, z) =

гралов по ϑ в (52), получим

(2π)²

)

∫

∫ (

ξÊ-1,x

ηÊ-1,y

∫

(

)

e-iγ1zei(ξx+ηy)dξ dη,

E1,x (ρ, ϕ, z) =

2Q1x (γ) + R1x (γ)λ²

γ₁

4π

-∞ -∞

× λe-iγ1zJ₀ (ρλ) dλ +

Ê-

и, подставляя выражения для

и Ê-1,y по форму-

1,x

∫

лам (45) и (46), после перехода к полярным коорди-

cos2ϕ

R1x (γ)λ³J₂ (ρλ)e-iγ1zdλ.

(55)

натам получим

4π

ЖЭТФ, том 159, вып. 1, 2021

Элементарный излучатель на границе. ..

∫

Q1x (γ)λ²eiγ1z

(R1x (γ) + Q1y (γ)) λ⁴J₁ (ρλ)

E1,z (ρ, ϕ, z) =

e-iγ1zdλ+

(2π)²

γ₁

⎛

⎞

(

)

∫

i cosϕ

1 - 4sin2 ϕ

×^⎝ cosϑeiρλcos(ϕ-ϑ)dϑ⎠ dλ+

2π

∫

(R1x (γ) + Q1y (γ)) λ³J₂ (ρλ)

∫

e-iγ1zdλ.

(57)

(R1x (γ) + Q1y (γ))λ⁴

ργ₁

eiγ1z ×

(2π)²

γ₁

⁰⎛

⎞

Теперь рассмотрим электрическое поле в полу-

∫

пространстве (с номером j = 3). Составляющую по

×^⎝ cosϑ sin² ϑeiρλcos(ϕ-ϑ)dϑ⎠dλ.

оси x получим из (41) в виде

Используя соответствующие интегральные пред-

E3,x (x, y, z) =

ставления (54) для интегралов по ϑ, получим

(2π)²

∫

E+3,xeiγ3(z-d)ei(ξx+ηy)dξ dη.

i cosϕ

Q1x (γ)λ²e-iγ1z

E1,z (ρ, ϕ, z) =

J₁ (ρλ)dλ+

-∞ -∞

2π

γ₁

Преобразуя выражение (48) и переходя к полярным

i cosϕsin²

координатам (51), E3,x можно представить в виде

2π

⎛

⎞

∫

(

)

E3,x (ρ, ϕ, z) =

⎝

Q3x (γ) + R3x (γ)λ² sin² ϑ

eiγ3(z-d)eiρλcos(ϕ-ϑ)dϑ⎠ λdλ =

(2π)²

⎛

⎞

∫

(

)

Q3x (γ) + λ²R3x

(γ)

eiγ3(z-d) ⎝ eiρλcos(ϕ-ϑ)dϑ⎠λdλ-

(2π)²

⎛

⎞

∫

λ²R3x

(γ) eiγ3(z-d) ⎝ cos² ϑeiρλcos(ϕ-ϑ)dϑ⎠ λ dλ,

(2π)²

∫

где введены следующие зависящие только от λ

(

)

функции:

E3,x (ρ, ϕ, z) =

2Q3x (γ) + λ²R3x (γ)

4π

cos2ϕ

(

× J0 (ρλ)eiγ3(z-d)λdλ +

Q3x (γ) =

a3x cos² (γ₂d) + b3x sin² (γ₂d) +

4π

ωμ₀D (λ)

∫

)

× λ³R3x (γ)J2 (ρλ)eiγ3(z-d)dλ.

(58)

+ ic3x cos(γ₂d)sin(γ₂d)

Аналогично, в представлении

(

E3,y (x, y, z) =

R3x (γ) =

d3x cos² (γ₂d) +

ωμ₀D (λ)

∫

)

-2

= (2π)

E+3,yeiγ3(z-d)ei(ξx+ηy)dξ dη

+ e3x sin2 (γ₂d) + if3x cos(γ₂d)sin(γ₂d)

-∞ -∞

Ê+

Используя соответствующие интегральные пред-

запишем

3,y

в виде (49) и перейдем к полярным

ставления (54) для интегралов по ϑ, получим

координатам:

ЖЭТФ, вып. 1

А. Б. Петрин

ЖЭТФ, том 159, вып. 1, 2021

E3,y (ρ, ϕ, z) =

(2π)²

⎛

+^∞

∫

⎝ Q3y (γ)λ2 cosϑsinϑeiγ3(z-d) ×

⎞

× eiρλcos(ϕ-ϑ)dϑ⎠ λdλ =

∫

λ³Q3y (γ)eiγ3(z-d) ×

(2π)²

⎛

⎞

∫

Рис. 5. Геометрия задачи излучения элементарного источ-

×^⎝ cosϑ sinϑeiρλcos(ϕ-ϑ)dϑ⎠ dλ,

ника тока, расположенного на свободной границе пленки в

схеме Кречмана при ориентации дипольного момента па-

где

раллельно (а) и перпендикулярно (б) границе

(

Q3y (γ) =

a3y cos² (γ₂d) +

ωμ₀D (λ)

Учитывая (54), получим

)

+ b3y sin2 (γ₂d) + ic3y cos(γ₂d)sin(γ₂d)

i cosϕ

E3,z (ρ, ϕ, z) = -

Учитывая соответствующее интегральное представ-

2π

ление (54), получим

∫

Q3x (γ)λ²J₁ (ρλ)

eiγ3(z-d)dλ-

∫

γ₃

sin2ϕ

E3,y (ρ, ϕ, z) =

λ³Q3y (γ) ×

4π

i cosϕsin² ϕ

(

)

2π

× J0 (ρλ) -

J₁ (ρλ) eiγ3(z-d)dλ.

(59)

∫

ρλ

(R3x (γ) + Q3y (γ))λ⁴J₁ (ρλ)

eiγ3(z-d)dλ-

γ₃

Наконец, для составляющей E3,z, учитывая (50),

получим аналогично

(

)

i cosϕ

1 - 4sin2 ϕ

−

)

∫

∫ (

2π

E+3,x

ηÊ+3,y

∫

E3,z (x, y, z) = -

(R3x (γ) + Q3y (γ)) λ³J₂ (ρλ)

(2π)²

γ₃

eiγ3(z-d)dλ.

(60)

−∞ -∞

ργ₃

× eiγ3(z-d)ei(ξx+ηy)dξ dη.

Таким образом, мы получили точные аналити-

Переходя к полярным координатам, запишем следу-

ческие выражения для электрических полей в полу-

ющее выражение:

пространствах, окружающих пленку.

∫

Q3x (γ)λ²eiγ3(z-d)

E3,z (ρ, ϕ, z) = -

(2π)²

γ₃

7. ИЗЛУЧЕНИЕ ЭЛЕМЕНТАРНОГО

⎛

⎞

ВЕРТИКАЛЬНОГО ДИПОЛЯ,

∫

РАСПОЛОЖЕННОГО НА ГРАНИЦЕ

×^⎝ cosϑeiρλcos(ϕ-ϑ)dϑ⎠dλ-

МЕТАЛЛИЧЕСКОЙ ПЛЕНКИ,

НАНЕСЕННОЙ НА ПОВЕРХНОСТЬ

∫

ПРИЗМЫ

(R3x (γ) + Q3y (γ))λ⁴

eiγ3(z-d) ×

(2π)²

γ₃

Рассмотрим задачу излучения элементарного

⎛

⎞

вертикального излучателя, расположенного на

∫

свободной границе пленки (см. рис. 5б) в схеме

×^⎝ cosϑ sin² ϑeiρλcos(ϕ-ϑ)dϑ⎠dλ.

Кречмана. Будем считать, что излучатель нахо-

дится в свободном полупространстве, в области 3,

ЖЭТФ, том 159, вып. 1, 2021

Элементарный излучатель на границе. ..

бесконечно близко к границе. Поляризация ис-

В формулах (61)-(66) коэффициенты u, v, w яв-

точника — вдоль оси z (n_x = 0, n_y = 0, n_z = 1).

ляются функциями γ₁, γ₂ и γ₃. Выражения для этих

Применяя те же рассуждения, что и для горизон-

коэффициентов представлены в Приложении B.

тального диполя, получим для фурье-образов полей

Найдем теперь поля в полупространствах.

Ê-

Ê+

E-1,x,

1,y

3,x

E+3,y уравнение (44), в котором

Полупространство j = 1. Составляющая E1,x

вектор-столбец правой части равен

определяется формулой

(

∫

V = ξ/ωε₃; η/ωε₃;

)^T .

E1,x (x, y, z) =

E-1,xe-iγ1zei(ξx+ηy)dξ dη.

(2π)

-∞ -∞

Решая уравнение (44), найдем

Ê-

и Ê+3,x,

1,x

1,y

E+3,y и далее по формулам (39)-(42) при N = 2, z_d =

Ê-

Подставим выражение (61) для

1,x

и перейдем к

= z₂ = d получим уходящую волну из плоскослои-

полярным координатам. Учитывая тождества (54),

стой структуры в призму (в область 1) и свободное

получим

пространство (область 3) над пленкой (в направле-

ниях z → ±∞ от границ пленки).

∫

Снова будем считать, что среды немагнитные и

E1,x (ρ, ϕ, z) =

λS1,x (λ) e-iγ1z ×

(2π)²

μ₁ = μ₂ = μ₃ = μ₀. Выражения для подматриц H_LB

⎛

⎞

и H_LD те же, что и приведенные выше выражения

∫

для горизонтального диполя.

×^⎝ cosϑeiρλcos(ϕ-ϑ)dϑ⎠ λdλ =

Решив уравнение (44) для вертикального дипо-

ля и учитывая, что k²³ = ε₃μ₀ω², найдем следующие

∫

Ê-

аналитические выражения для

E-1,x,

1,y

1,z

i cosϕ

S1,x (λ) J₁ (ρλ) e-iγ1zλ²dλ,

(67)

2π

E-1,x =

(u1x cos (γ₂d) + iv1x sin (γ₂d)) ,

(61)

ωμ₀D

где

Ê-

(u1y cos (γ₂d) + iv1y sin (γ₂d)) ,

(62)

S1,x (λ) =

(u1x cos (γ₂d) + iv1x sin (γ₂d))

1,y

ωμ₀D

ωμ₀D (λ)

— функция только от λ.

E-1,x

ηÊ-1,y

Аналогично для составляющей E1,y, учитывая

Ê-

1,z

γ₁

тождества (54), получим

ξ² + η

(u1z cos (γ₂d) + iv1z sin (γ₂d)) .

(63)

∫

ωμ₀D

E1,y (ρ, ϕ, z) =

λS1,y (λ) e-iγ1z ×

(2π)

Аналогично найдем

Ê+

и Ê+3,z:

3,x

3,y

⎛

⎞

∫

(

Ê+

×^⎝ sinϑeiρλcos(ϕ-ϑ)dϑ⎠λdλ =

3,x

u3x cos² (γ₂d) + v3x sin² (γ₂d) +

ωμ₀D

)

+ iw3x sin(γ₂d) cos(γ₂d)

(64)

∫

i sinϕ

S1,y (λ) J₁ (ρλ) e-iγ1zλ²dλ,

(68)

2π

(

Ê+

u3y cos² (γ₂d) + v3y sin² (γ₂d) +

3,y

где

ωμ₀D

)

+ iw3y sin(γ₂d) cos(γ₂d)

(65)

S1,y (λ) =

(u1y cos (γ₂d) + iv1y sin (γ₂d))

ωμ₀D (λ)

— также функция только от λ.

ξÊ+3,x

E+3,y

ξ² + η

Ê+

3,z

Отметим, что из (67) и (68) следует, что в ци-

γ₃

ωμ₀D

(

линдрических координатах E1,ρ (ρ, z) = E1,x cos ϕ +

u3z cos² (γ₂d) + v3z sin² (γ₂d) +

)

+ E1,y sinϕ не зависит от ϕ, что соответствует сим-

+ iw3z sin(γ₂d) cos(γ₂d)

(66)

метрии задачи. Из симметрии также следует, что

А. Б. Петрин

ЖЭТФ, том 159, вып. 1, 2021

E1,z не зависит от ϕ. Действительно, учитывая (54),

где

получим

(

S3,y (λ) =

u3y cos² (γ₂d) +

∫

ωμ₀D (λ)

)

E1,z (ρ, z) =

λ²S1,z (λ) e-iγ1z ×

+ v3y sin2 (γ₂d) + iw3y sin(γ₂d)cos(γ₂d)

(2π)²

⎛

⎞

∫

Наконец,

×^⎝ eiρλcos(ϕ-ϑ)dϑ⎠ λdλ =

∫

E3,z (ρ, z) =

λ²S3,z (λ) eiγ3(z-d) ×

∫

(2π)²

S1,z (λ) J₀ (ρλ)e-iγ1zλ³dλ,

(69)

2π

⎛

⎞

∫

где

×^⎝ eiρλcos(ϕ-ϑ)dϑ⎠ λdλ =

S1,z (λ) =

(u1z cos (γ₂d) + iv1z sin (γ₂d)) .

ωμ₀D (λ)

∫

Полупространство j = 3. Приведем аналогич-

S3,z (λ)J₀ (ρλ)eiγ3(z-d)λ³dλ,

(72)

ные выражения для составляющих полей. Состав-

2π

ляющая по оси x представляется в виде

где

E3,x (x, y, z) =

(2π)²

(

S3,z (λ) =

u3z cos² (γ₂d) +

+^∞

∫

ωμ₀D (λ)

E+3,xeiγ3(z-d)ei(ξx+ηy)dξ dη.

)

+ v3z sin2 (γ₂d) + iw3z sin(γ₂d)cos(γ₂d)

-∞ -∞

Переходя к полярным координатам и учитывая (54),

Итак, мы получили выражения для электрического

получим

поля вертикального диполя, расположенного на гра-

∫

нице пленки в окружающих пленку полупростран-

E3,x (ρ, ϕ, z) =

λS3,x (λ) eiγ3(z-d) ×

ствах.

(2π)²

⎛

⎞

∫

8. ЭЛЕМЕНТАРНЫЙ ВЕРТИКАЛЬНЫЙ

×^⎝ cosϑeiρλcos(ϕ-ϑ)dϑ⎠ λdλ =

ИЗЛУЧАТЕЛЬ НА СВОБОДНОЙ ГРАНИЦЕ

ПЛЕНКИ ЗОЛОТА В СХЕМЕ КРЕЧМАНА

∫

i cosϕ

S3,x (λ)J₁ (ρλ)eiγ3(z-d)λ²dλ,

(70)

2π

Данная статья задумывалась как продолжение

работы по изучению явлений, связанных с поверх-

где

ностной плазмонной волной, которая возбуждается

(

по схеме Кречмана и распространяется вдоль сво-

S3,x (λ) =

u3x cos² (γ₂d) +

ωμ₀D (λ)

бодной поверхности пленки металла (например, зо-

)

лота) определенной толщины, нанесенной на призму

+ v3x sin2 (γ₂d) + iw3x sin(γ₂d)cos(γ₂d)

[18]. На свободной поверхности пленки возбуждает-

— функция только от λ.

ся волна, которая имеет высокую интенсивность на

Аналогично,

границе раздела и убывает экспоненциально в на-

∫

правлении, нормальном к границе. Если поместить

E3,y (ρ, ϕ, z) =

λS3,y (λ) eiγ3(z-d) ×

на свободной поверхности молекулу или нанострук-

(2π)²

туру, в которой будет индуцироваться поверхност-

⎛

⎞

∫

ной волной дипольный момент, то можно найти из-

×^⎝ sinϑeiρλcos(ϕ-ϑ)dϑ⎠λdλ =

лучение индуцированного диполя, разложив диполь

на параллельную и перпендикулярную границе со-

∫

ставляющие.

i sinϕ

S3,y (λ)J₁ (ρλ)eiγ3(z-d)λ²dλ,

(71)

Излучение диполя, ориентированного парал-

2π

лельно границе, было исследовано в работе [19].

ЖЭТФ, том 159, вып. 1, 2021

Элементарный излучатель на границе. ..

В данной работе мы рассмотрим элементарный

излучатель, с вертикальным дипольным моментом,

направленным перпендикулярно пленке. Интерес

представляет пространственная направленность

излучения этого диполя в двух случаях: при из-

лучении диполя на границе двух полупространств

без пленки (d → 0) и с металлической пленкой, по

свободной границе которой может распространять-

ся поверхностная плазмонная волна. Это сравнение

поможет понять влияние поверхностной волны на

направленные свойства элементарного излучателя.

Итак, выберем частоту излучения диполя ω, со-

ответствующую длине волны в вакууме, равной

λ₀

= 633 нм, показатель преломления полупро-

странства призмы на этой частоте выберем равным

n_p = 1.6 (ε₁ = 2.56ε₀, где ε₀ — диэлектрическая

проницаемость вакуума), показатель преломления

свободного полупространства над пленкой — n₁ =

= 1 (ε₃ = ε₀). Диэлектрическую проницаемость зо-

лотой пленки на заданной частоте примем равной

ε₂

= (-11.6 + i1.2)ε₀ [12], а ее толщину — d =

= 48.6 нм. Как было показано [18], при таких па-

Рис. 6. Нормированные диаграммы направленности по ам-

раметрах в пленке наилучшим образом возбужда-

плитуде поля, вычисленные для элементарного вертикаль-

ется поверхностная плазмонная волна при падении

ного диполя, расположенного на границе двух полупро-

плоской волны p-поляризации со стороны призмы

странств (кривые 1) и на границе золотой пленки опти-

под углом α_opt = 40.98^◦ к нормали. Для того чтобы

мальной толщины, нанесенной на призму (кривые 2), в

сторону призмы (а) и в сторону свободного пространст-

оценить влияние такой пленки на излучение дипо-

ва (б)

ля в полупространство призмы и свободное полу-

пространство, были вычислены диаграммы направ-

ленности вертикального диполя, т. е. в плоскостях,

нормальных границе, проходящих через центр ди-

R_s = 158λ₀, т. е. поля вычислялись в дальней зоне

поля. Диаграммы вычислялись по амплитуде поля

излучения диполя.

и нормировались на максимум излучения.

На рис. 6а показаны диаграммы направленнос-

Из рис. 6a видно, что в отсутствие металличе-

ти элементарного вертикального диполя в полупро-

ской пленки максимум излучения в призму пример-

странство призмы для двух случаев. Первый слу-

но соответствует углу полного внутреннего отраже-

чай — пленка отсутствует (кривая 1 ), при этом ди-

ния призмы (кривая 1), который равен 38.7^◦. Когда

поль расположен на границе двух полупространств

появляется металлическая пленка, возникает резкий

с диэлектрическими проницаемостями ε₁ и ε₃ со сто-

пик излучения (кривая 2) при угле примерно 41^◦,

роны полупространства с ε₃. Второй случай — с

однако однозначно связать этот пик на диаграмме

пленкой (кривая 2 ), когда диполь расположен на

с возбуждением поверхностной волны, как кажет-

свободной границе золотой пленки (см. рис. 5б) (на

ся, нельзя. Интерференционные биения на кривых,

границе областей с проницаемостями ε₂ и ε₃ со сто-

как показали расчеты, определяются конечностью

роны полупространства с ε₃). Диаграммы направ-

радиуса R_s и в пределе бесконечного радиуса ис-

ленности представляют собой графики амплитуды

чезают. На рис. 6б представлены такие же, как на

вектора электрического поля E_a в точках на линии

рис. 6а, диаграммы направленности, но в сторону

пересечения плоскости, проходящей через диполь, и

свободного полупространства (в область с проница-

сферы большого радиуса R_s в зависимости от по-

емостью ε₃). Из рисунка видно, что наличие метал-

лярного угла θ. Центр сферы находился в начале

лической пленки качественно не меняет направлен-

координат. Угол θ отсчитывался от оси z. В чис-

ных свойств излучения диполя в сторону свободного

ленных расчетах радиус сферы принимался равным

полупространства.

А. Б. Петрин

ЖЭТФ, том 159, вып. 1, 2021

γ₃

((

)(

)

9. ЗАКЛЮЧЕНИЕ

c3x =

γ²² + γ²¹

k²³ - γ²³

+ 2γ²¹γ²²

γ₁γ₂k

Итак, предложено теоретическое рассмотрение

(

))

γ⁴² + γ²¹γ²² + 2γ²²

k²² - γ²²

электромагнитного излучения элементарного ди-

γ₂k²

польного источника, расположенного в плоскосло-

истой среде. Предложен аналитический метод све-

(

)

дения электромагнитных полей к одномерным ин-

f3x =

k²³

γ²² + γ²¹

+ 2γ²¹γ²² -

тегралам для задачи излучения точечного диполя,

γ₁γ₂γ₃k²

(

))

(

)

расположенного на границе одной пленки. Показа-

- γ²³

γ²² + γ²¹

2k²² + γ²¹ - γ²²

на общность метода. Рассмотрена прикладная зада-

γ₂k²

ча - нахождение направленных характеристик из-

Коэффициенты в формуле (49):

лучения нанообъектов, находящихся на свободной

поверхности пленки золота оптимальной толщины

γ₁ + γ₃

в схеме Кречмана. Показано, что, при ориентации

a3y =

γ₁γ₃

излучающего диполя перпендикулярно границе, на-

(

)

личие металлической пленки, в которой может воз-

ε₁ - ε₂ γ1

k²³ - γ²³

-γ²²γ₃

γ₁ (γ₁ + γ₃)

b3y =

буждаться поверхностная волна, существенно влия-

ε₂

γ₁γ²²γ₃

γ²²γ₃

ет на диаграмму направленности излучателя в полу-

пространство призмы, а в свободное полупростран-

ε₁ - ε₂ k²³ - γ₃ (γ₁ + γ₃)

2 (γ₁ + γ₃)

c3y =

ство практически не влияет.

ε₂

γ₁γ₂γ₃

γ₂γ₃

ПРИЛОЖЕНИЕ B

ПРИЛОЖЕНИЕ A

Приведем выражения для коэффициентов u, v,

Приведем выражения для коэффициентов a, b, c,

d, e, f.

Коэффициенты в формуле (61):

Коэффициенты в формуле (45):

γ₁ + γ₃

γ₃ + γ₁

γ₁γ₃ + γ²²

a1x = - (γ₁ + γ₃), d1x = -

u1x = -

v1x =

γ₁γ₃

γ₃

γ₂γ₃

Коэффициенты в формуле (62):

γ₁γ₃ + γ²²

b1x =

γ₂

γ₃ + γ₁

γ₁γ₃ + γ²²

u1y = -

v1y =

γ₃

γ₂γ₃

γ₃ + γ₁

(ε₂ - ε₁)k²³

e1x =

γ₂γ₃

ε₂γ₁γ₂γ₃

Коэффициенты в формуле (63):

Коэффициенты в формуле (46):

γ₃ + γ₁

γ₁γ₃ + γ²²

u1z = -

v1z =

γ₁ + γ₃

γ₁γ₃

γ₁γ₂γ₃

a1y =

γ₁γ₃

Коэффициенты в формуле (64):

(

)

(γ₁ + γ₃) k

γ²² + γ₁γ₃

k²²

u3x =

v3x = -

b1y =

⁽ (ε₁ - ε₂) k²³ - γ₁ (γ₁ + γ₃)

γ₁k²³

γ²²k²

γ₁γ₂γ₃

ε₂

Коэффициенты в формуле (48):

w3x =

γ₁ + γ₃

(

)(

)

(

)

a3x = - (γ₁ + γ₃), d3x = -

k²³-γ²³

γ²¹+γ²²+2γ₁γ₃

+γ₁

γ²¹γ₃+γ²²γ₃+2γ₁γ²²

γ₁γ₃

k²³γ₁γ

[

(

)

]

b3x =

γ₁γ₃

k²³ - γ²³

+γ₃γ³¹ + γ²²k²¹

Коэффициенты в формуле (65):

γ₁k²

(

)

[

(

)

]

(γ₁ + γ₃) k²¹

γ²² + γ₁γ₃

k²²

e3x =

γ₃γ²¹

k²² + γ²²

-γ₃γ⁴² + k²¹γ₁γ²²

u3y =

v3y = -

k²²γ₁γ²²γ₃

γ₁k²³

γ²²k²

ЖЭТФ, том 159, вып. 1, 2021

Элементарный излучатель на границе. ..

w3y =

6. A. Sommerfeld, Ann. Physik. (Leipzig) 81,

1135

(

)(

)

(

)

(1926).

k²³-γ²³

γ²¹+γ²²+2γ₁γ₃

+γ₁

γ²¹γ₃+γ²²γ₃+2γ₁γ²²

γ₁γ₂k²

7. J. R. Wait, IEEE Anten. Propag. Magazine 40(5), 7

(1998).

Коэффициенты в формуле (66):

(

)

8. R. W. P. King and G. S. Smith, Antennas in Matters,

(γ₁ + γ₃) k²¹

γ²

+γ₁γ₃

k²²

MA: M.I.T. Press, Cambridge (1981).

u3z = -

v3z =

γ₁γ₃k²³

γ²²γ₃k²

9. T. T. Wu, J. Appl. Phys. 28(3), 299 (1957).

10. R. H. Jansen, IEEE Trans. Microwave Theory Tech.

w3z =

(

)(

)

(

)

33, 1043 (1985).

k²-γ23

γ²¹+γ²²+2γ₁γ₃

+γ₁

γ²¹γ₃+γ²²γ₃+2γ₁γ²

11. R. W. P. King, IEEE Trans. Microwave Theory Tech.

γ₁γ₂γ₃k²

36, 1080 (1988).

12. Л. Новотный, Б. Хехт, Основы нанооптики, под

ЛИТЕРАТУРА

ред. В. В. Самарцева, Физматлит, Москва (2009).

1. E. Kretschmann and H. Z. Raether, Naturforsch.

13. J. B. Pendry, Phys. Rev. Lett. 85, 3966 (2000).

A 23, 2135 (1968).

14. А. Б. Петрин, ЖЭТФ 134, 436 (2008).

2. H. Raether, Surface Plasmons, Springer-Verlag,

Berlin (1988).

15. А. Б. Петрин, Опт. и спектр. 125, 375 (2018).

3. W. L. Barnes, J. Opt. A: Pure Appl. Opt. 8, S87

16. А. Б. Петрин, Опт. и спектр. 126, 350 (2019).

(2006).

17. А. Б. Петрин, Опт. и спектр. 127, 654 (2019).

4. R. Garabedian, C. Gonzalez, J. Richards et al.,

Sensors and Actuators A 43, 202 (1994).

18. А. Б. Петрин, Опт. и спектр. 127, 1051 (2019).

5. А. Б. Петрин, Опт. и спектр. 125, 830 (2018).

19. А. Б. Петрин, Опт. и спектр. 128, 1676 (2020).