ЖЭТФ, 2021, том 159, вып. 1, стр. 150-175

ПРОСТРАНСТВЕННО-ВРЕМЕННЫЕ РЕЖИМЫ

В СИСТЕМЕ НЕИДЕНТИЧНЫХ ОСЦИЛЛЯТОРОВ

КУРАМОТО - БАТТОГТОХА

М. И. Болотовa*, Л. А. Смирновa,b**, Е. С. Бубнова^a,

Г. В. Осиповa***, А. С. Пиковскийc,a****

^a Научно-образовательный математический центр «Математика технологий будущего»,

Институт информационных технологий, математики и механики,

Нижегородский государственный университет им. Н. И. Лобачевского

603950, Нижний Новгород, Россия

^b Институт прикладной физики Российской академии наук

603950, Нижний Новгород, Россия

^c Institute for Physics and Astronomy, University of Potsdam

D-14476, Potsdam-Golm, Germany

Поступила в редакцию 11 августа 2020 г.,

после переработки 11 августа 2020 г.

Принята к публикации 9 сентября 2020 г.

Для ансамбля нелокально связанных неидентичных фазовых осцилляторов рассмотрены пространст-

венно-временные состояния, соответствующие различным режимам долговременной эволюции такого

рода системы. Найдены однородные, градиентные и неоднородные стационарные решения уравнений

Отта - Антонсена, соответствующие ключевым вариантам реализующегося коллективного вращательно-

го движения элементов обсуждаемой среды с ненулевыми мезоскопическими характеристиками, опре-

деляющими степень когерентности динамики расположенных поблизости частиц. Описаны процедуры

поиска класса неоднородных решений как неподвижных точек вспомогательного точечного отображения

и определения устойчивости на основе анализа спектра собственных значений композитного оператора.

Продемонстрированы и описаны статические и бризерные кластерные режимы, а также режимы с нере-

гулярным поведением усредненных комплексных полей, к которым, в частности, относится локальный

параметр порядка.

DOI: 10.31857/S0044451021010120

ве метрономы [3, 4]), но и разнообразные процессы

в электрических (в том числе силовых) сетях [5,6],

1. ВВЕДЕНИЕ

твердотельных структурах [7,8], молекулярных це-

В настоящее время системы связанных осцилля-

почках [9, 10] и т. д. Ссылки на конкретные экспе-

торов являются актуальной темой для теоретичес-

риментальные и теоретические исследования можно

ких и экспериментальных исследований. Обуслов-

найти, например, в книгах [11, 12] и обзоре [13].

лено это, прежде всего, тем, что данные системы

Целый ряд ключевых фундаментальных явле-

представляют собой базовые модели в различных

ний, свойственных нелинейным осцилляторным сре-

областях современной науки и техники. С их по-

дам различной по своей сути природы, нередко и

мощью удается адекватно описывать не только ме-

достаточно успешно удается рассмотреть в рамках

ханические объекты (в частности, взаимодействую-

фазового приближения [12,14,15]. К таким явлени-

щие маятники [1, 2], закрепленные на общей осно-

ям, в частности, относится синхронизация и возник-

новение корреляций в системе [1,11]. Переход от бо-

^* E-mail: maksim.bolotov@itmm.unn.ru

лее точных и конкретных теоретических постановок

^** E-mail: smirnov_lev@appl.sci-nnov.ru

^*** E-mail: osipov@vmk.unn.ru

к универсальному описанию с помощью динамиче-

^**** E-mail: pikovsky@uni-potsdam.de

ских уравнений для фазовых переменных позволя-

150

ЖЭТФ, том 159, вып. 1, 2021

Пространственно-временные режимы в системе. ..

ет выявить единые принципы и общие закономерно-

элементов имеется значительная часть асинхронных

сти в поведении физических, химических, биологи-

осцилляторов.

ческих и социальных систем. При этом для изуче-

Нетривиальные состояния в средах, состоящих

ния поведения популяции осцилляторов, взаимодей-

из фазовых осцилляторов с нелокальной связью,

ствующих через среднее поле, чаще всего исполь-

могут быть описаны как стационарные структуры

зуется широко известная модель Курамото с гло-

с пространственно-неоднородным профилем комп-

бальной связью и ее разнообразные модификации

лексного параметра порядка, который определяется

[11,13,16-22]. Отличительная особенность такого ро-

локально как мера когерентности мезоскопической

да топологии связи состоит в отсутствии какой-ли-

группы соседних элементов. В частности, в данном

бо информация о положении элементов ансамб-

контексте для химерных режимов в распределенных

ля в координатном пространстве. Поэтому в дан-

ансамблях и популяциях с композитной топологией

ном случае, несмотря на то, что возможен процесс

абсолютное значение такого локального комплекс-

объединения осцилляторов в кластеры, нельзя по-

ного параметра порядка обращается тождественно

ставить задачи о формировании пространственных

в единицу там, где соседние осцилляторы синхрон-

структур и распространении волн. Однако карти-

ны, и меньше единицы в областях с асинхронным

на принципиально меняется, если взаимодействие

поведением элементов [24-28, 31-35].

в среде носит не глобальный, а локальный или

нелокальный характер, так как система становит-

Среди проводимых исследований особое место

ся пространственно-упорядоченной. В ней автома-

занимают системы, состоящие из неидентичных ос-

тически пропадает полная симметрия относительно

цилляторов [13, 18, 20-23, 36-43]. В таких систе-

перестановок элементов, и их нумерация начинает

мах каждый осциллятор обладает своей собственной

играть важную роль при изучении динамики осцил-

частотой, значение которой зависит от свойств кон-

ляторных популяций.

кретного элемента. В ансамбле, состоящем из боль-

Нелокальную связь математически можно пред-

шого числа осцилляторов, вполне естественно счи-

ставить, например, в виде оператора свертки. Яд-

тать, что эти частоты выбираются случайным об-

ро этого оператора полностью определяет харак-

разом, и их распределения подчиняется некоторо-

тер взаимодействия внутри такого рода осциллятор-

му закону, который заранее определен из физичес-

ной среды. Несмотря на то, что в литературе рас-

ких соображений. Если рассматриваются популяции

сматривались, в том числе, и дальнодействующие

с нелокальным взаимодействием, то можно сказать,

связи (см., например, [23]), убывающие по степен-

что появляется пространственный беспорядок, спо-

ному закону, в основном значительные и во мно-

собный существенным образом повлиять как на ко-

гом неожиданные результаты были получены для

герентность в группе соседних осцилляторов, так

ядер конечного радиуса, а также с экспоненциально

и на динамику ансамбля в целом. С одной сторо-

убывающими хвостами [24-26]. Прежде всего, среди

ны, его наличие усложняет анализ долговременного

данных результатов стоит выделить образование в

поведения и устанавливающихся в итоге состояний

ансамблях идентичных элементов химерных состо-

среды, так как появляются еще дополнительные па-

яний, которые характеризуются сосуществованием

раметры, ответственные за разброс частот. Можно

синхронных и асинхронных групп осцилляторов. На

ожидать возникновения каких-то новых более слож-

сегодняшний день подобные нетривиальные состоя-

ных режимов, которые отсутствуют в случае иден-

ния остаются одним из привлекательных и интри-

тичных осцилляторов. От степени пространствен-

гующих эффектов для многих исследователей в об-

ного беспорядка зависят бифуркационные значения

ласти нелинейной динамики (см. недавние обзоры

других величин, при которых происходит качествен-

[24-29]). Этот интерес обусловлен тем, что формиро-

ное изменение в возможных сценариях долговремен-

вание химер происходит вследствие фундаменталь-

ной эволюции. С другой стороны, появляется по-

ного явления нарушения симметрии [30], которое в

тенциал для того, чтобы продвинуться в аналитиче-

распределенных популяциях проявляется в том, что

ском описании результатов численного моделирова-

несмотря на то, что однородное полностью синхрон-

ния. Это прежде всего связано с тем, что полностью

ное состояние существует и устойчиво, система (для

когерентный режим не может реализовываться в по-

целого ряда начальных условий) в процессе долго-

добных системах. Поэтому вырожденная ситуация,

временной эволюции может прийти к совершенно

когда модуль локального комплексного параметра

другому (более сложному) режиму своей динами-

порядка тождественно обращается в единицу, ста-

ки, когда наряду с группами взаимно синхронных

новится невозможной.

151

М. И. Болотов, Л. А. Смирнов, Е. С. Бубнова и др.

ЖЭТФ, том 159, вып. 1, 2021

В настоящее время распределенные системы, со-

цировать наблюдаемые турбулентные режимы. А в

стоящие из неидентичных нелокально связанных ос-

недавно вышедшей работе [43] обсуждалось суще-

цилляторов, активно изучаются с различных то-

ствование при наличии разброса собственных час-

чек зрения. Из большого числа статей, вышедших

тот и структурные особенности бризерных квазихи-

за последнее десятилетие по данному направле-

мерных режимов, которые характеризуются, с од-

нию исследования, здесь выделено лишь несколь-

ной стороны, периодическим изменением во време-

ко ключевых работ [37-43]. В частности, в рабо-

ни амплитуд комплексных мезоскопических полей в

тах [37, 38] представлены долгоживущие состояния,

каждой точке пространства, а с другой, сосущест-

которые характеризуются присутствием областей с

вованием областей с повышенной и пониженной ко-

разной степенью когерентности частиц. Такого ро-

герентностью. Отметим, что такие режимы были ра-

да состояния представляют собой аналоги химер и

нее обнаружены для систем идентичных фазовых

трансформируются в них в пределе нулевого раз-

осцилляторов (см., например, [32, 33]). Кроме того,

броса по частотам. Там же впервые продемонстри-

особо подчеркнем, что в большинстве из перечис-

ровано, что для анализа данных режимов можно

ленных публикаций в качестве ядер интегрально-

эффективно использовать редукцию Отта - Антон-

го оператора, описывающего нелокальное взаимо-

сена [20-22], которая позволяет получить самосо-

действие, использовались либо функции с конечным

гласованные динамические уравнения для макро-

числом членов в соответствующем ряде Фурье, либо

скопических комплексных полей, одним из которых

прямоугольные распределения конечной ширины.

оказывается локальный параметр порядка. В ста-

В предлагаемой работе наряду с изложением

тье [39] обсуждается обобщенная фазовая модель,

оригинальных результатов для ядер с экспонен-

которая может быть использована для описания се-

циально убывающими хвостами предпринята так

тей нелокально взаимодействующих между собой

же попытка некоторой систематизации и обобще-

элементов, индивидуальные характеристики кото-

ния ранее полученных данных и встречающих-

рых различаются. Ключевой особенностью рассмат-

ся в литературе сведений. Изучаются синхрон-

риваемой в [39] системы является присутствие в свя-

ные и асинхронные режимы и соответствующие им

зи между двумя парами элементов запаздывания,

пространственно-временные структуры в ансамбле

выбираемого случайным образом и вносящего до-

слабонеидентичных нелокально связанных фазовых

полнительный беспорядок. В частности, было пока-

осцилляторов, равномерно распределенных на коль-

зано, что если значения управляющих параметров

це. При теоретическом исследовании используется

близки к критическим, при которых однородное ча-

подход Отта - Антонсена [20-22]. Характер взаимо-

стично синхронное состояние теряет свою устойчи-

действия (экспоненциального типа) внутри среды

вость, в процессе своей эволюции популяция неиден-

позволяет перейти от интегро-дифференциального

тичных фазовых осцилляторов с временной задерж-

уравнения для параметра порядка к самосогласо-

кой в целом ряде случаев приходит к транзиентным

ванной системе дифференциальных уравнений в

состояниям, которые отличаются наличием несколь-

частных производных для двух комплексных по-

ких (двух и более) экстремумов в распределении

лей аналогично тому, как это было сделано в ра-

усредненных величин, что, в свою очередь, указы-

ботах [31-33]. Неидентичность элементов среды яв-

вает на то, что среда разбивается на регулярные (во

ляется ключевой особенностью, которая позволяет

времени) чередующиеся (в пространстве) участки с

продвинуться прежде всего в изучении разнообра-

повышенной и пониженной когерентностью. В рабо-

зия стационарных неоднородных профилей локаль-

тах [44, 45] (в случае, когда среда состоит из одина-

ного параметра порядка и их устойчивости по срав-

ковых частиц, см., например, публикации [40,41,46])

нению с выполненными нами ранее исследованиями

проанализирован еще один из возможных типичных

систем идентичных осцилляторов [31-33,46], так как

режимов, на который может выйти ансамбль осцил-

интересующие нас комплексные поля представляют

ляторов. Ниже будем называть его градиентным,

собой гладкие функции, которые по модулю мень-

так как он выделяется тем, что в среднем фаза в

ше единицы. Численное моделирование проводится

произвольный момент времени при обходе замкну-

как в рамках исходной модели популяции, состоя-

той в кольцо системы увеличивается на 2πq, где q —

щей из большого количества фазовых осцилляторов

целое число. В статье [42] внимание авторов было

с собственными частотами, выбранными случайно

сосредоточено на состояниях с нерегулярным (хао-

согласно распределению Лоренца, так и на базе за-

тическим) поведением макроскопических полей. В

мкнутых самосогласованных уравнений для макро-

том числе, была предпринята попытка классифи-

скопических (усредненных) величин.

152

ЖЭТФ, том 159, вып. 1, 2021

Пространственно-временные режимы в системе. ..

Математическая постановка изучаемой пробле-

Действующее на осцилляторы поле H_n(t) имеет

мы приводится в разд. 2. Простейшие решения с по-

общий для всех элементов фазовый сдвиг α и опре-

стоянным по модулю значением параметра порядка

деляется через дискретный оператор свертки:

описаны в разд. 3. Здесь речь идет об асинхронных и

(

)

∑

частично синхронных однородных режимах, а так-

H_n(t) = e^-iα

(n - ñ) eiφñ(t).

(3)

же о градиентных состояниях. В разд. 4 приводят-

ñ=1

ся сначала базовые сведения и соотношения, лежа-

Его ядро G(x) характеризует взаимодействие внут-

щие в основе предлагаемого нами метода поиска ста-

ри обсуждаемой среды и удовлетворяет требованию

ционарных (равномерно вращающихся) неоднород-

единичной нормировки. В качестве G(x) выбрана

ных решений уравнения Отта - Антонсена с перио-

функция

дическими граничными условиями. Далее представ-

(

)∕

G(x) = κ ch

κ(|x| - L/2)

2 sh(κL/2),

(4)

лены ключевые аспекты линейного анализа устой-

чивости данных нетривиальных пространственных

хорошо аппроксимирующая случай слабой нело-

структур, которым можно поставить в соответствие

кальной связи [31-33, 46]. Она достаточно адекват-

квазихимерные статические состояния исходной фа-

но описывает эффекты, связанные с влиянием на

зовой модели. Затем обсуждаются основные момен-

произвольно выделенный элемент не только его бли-

ты и преимущества процедуры построения семейств

жайших соседей, но также и других (более далеких)

подобных образований с разным числом областей

осцилляторов. Естественно предположить, что это

повышенной и пониженной когерентности и форму-

влияние относительно быстро уменьшается с уве-

лируются полученные в рамках такого подхода ре-

личением расстояния между частицами. Особо под-

зультаты. Кроме того, сделанные выводы подкреп-

черкнем, что выражение (4) в пределе κL → +∞

ляются прямым численным моделированием дина-

переходит в экспоненциальное ядро

мики распределенных фаз и локального комплекс-

G_KB(x) = κ exp(-κ|x|/2)

ного параметра порядка. Классы возможных наблю-

даемых режимов с более сложным (периодическим

из классической работы Курамото и Баттогтоха [47].

или нерегулярным) поведением (как в пространстве,

Фактически, и G_KB(x), и G(x) в форме (4) являются

так и во времени) мезоскопических (усредненных)

функцией Грина неоднородного уравнения Гельм-

полей обсуждаются в разд. 5. В Заключении подво-

гольца с источником в правой части. Однако в пер-

дятся итоги проведенного исследования.

вом случае система считается распределенной на

всем (бесконечном) интервале от -∞ до +∞, а вто-

рая же ситуация отвечает среде конечной длины,

2. МОДЕЛЬ

замкнутой в кольцо, т. е. для которой выполнены пе-

риодические граничные условия.

Рассмотрим ансамбль из N нелокально связан-

Сделаем еще ряд замечаний, которые позволя-

ных неидентичных осцилляторов (n = 1, 2, . . . , N),

ют сократить число параметров в рассматриваемой

равномерно распределенных на отрезке длины L с

системе. Так, например, совокупность соотноше-

периодическими граничными условиями на концах

ний (3) и (4) инвариантно относительно масштабных

[37-39, 41-43]. Данную систему будем описывать в

преобразований. Благодаря данному обстоятельству

рамках фазового приближения с помощью динами-

без ограничения общности коэффициент κ можно

ческих переменных ϕ_n(t), изменение каждой из ко-

принять равным единице. Поэтому в дальнейшем

торых во времени задается уравнением

будем считать, что κ = 1, а сила связи между эле-

(

)

dφ_n

ментами, фактически, определяется длиной среды

= ω_n + Im H_n

(t)e-iφn(t)

(1)

L. Кроме того, путем перехода во вращающуюся с

где ω_n (n

= 1, 2, . . ., N) — собственные часто-

угловой скоростью ω₀ систему координат несложно

ты осцилляторов. Как и в большинстве работ

исключить ω₀ из обсуждения с точки зрения управ-

[18, 37-39, 41-43], предполагается, что величины ω_n

ляющих параметров. Следовательно, уже на этапе

выбраны случайным образом и имеют функцию

постановки задачи целесообразно положить значе-

распределения Лоренца (или Коши)

ние ω₀ равным нулю, т. е. ниже ω₀ = 0. Таким об-

разом, для характерных режимов долговременной

πg(ω) =

(2)

эволюции обсуждаемого ансамбля нелокально-взаи-

(ω - ω₀)² + γ²

модействующих осцилляторов определяющими яв-

со средним значением ω₀ и полушириной γ.

ляются три величины L, γ и α. Отметим также, что

153

М. И. Болотов, Л. А. Смирнов, Е. С. Бубнова и др.

ЖЭТФ, том 159, вып. 1, 2021

случай идентичных осцилляторов (γ = 0) уже ис-

ется режим частичной синхронизации. В этой ситуа-

следовался нами в работах [31-33, 46].

ции в движении частиц наблюдаются корреляции.

Сформулированная выше модель, состоящая из

Равенство |Z(x, t)| = 0 указывает на то, что элемен-

конечного числа N осцилляторов и описываемая

ты ансамбля вращаются полностью асинхронно. Та-

уравнениями

(1)-(4) имеет достаточно широкий

ким образом, как и для систем с глобальным взаимо-

спектр практических приложений в различных об-

действием, при исследовании систем с нелокальной

ластях науки и техники [11,12,15]. Однако для более

связью комплексный параметр порядка Z(x, t) игра-

глубокого понимания полученных в ходе расчетов

ет важную роль, так как его амплитуда характери-

результатов нередко бывает полезен и даже чаще

зует степень локальной синхронизации в популяции,

всего оказывается необходим анализ динамических

а фаза дает представление о среднем значении, во-

свойств и структурных особенностей изучаемой сис-

круг которого разбросана величина ϕ в окрестности

темы в термодинамическом пределе, когда считает-

точки с координатой x.

ся, что в ней содержится бесконечно большое коли-

С другой стороны, ключевые аспекты эволюции

чество элементов, т. е. N → ∞. В этом случае от

осцилляторной среды в рамках обсуждаемой фа-

выражений (1) и (3) переходят к континуальному

зовой модели в термодинамическом пределе могут

варианту их записи:

быть описаны путем введения плотности вероятнос-

(

)

ти ρ(ϕ, ω, x, t) распределения динамической пере-

∂φ(x, t)

менной ϕ при заданном ω и определенных x, t. В

= ω + Im H(x,t)e-iφ(x,t) ,

(5)

∂t

частности, очевидно, что Z(x, t) определяется непо-

средственно с помощью ρ(ϕ, ω, x, t) как

∫L

∫

H (x, t) = e^-iα G(x - x)eiφ(x,t) dx.

(6)

Z(x, t) =

ρ(ϕ, ω, x, t)eiϕ(x,t) dφ dω.

(7)

−∞ -π

Здесь, согласно нашему предположению, в полном

В свою очередь, действительная функция

соответствии с исходной дискретной моделью вели-

ρ(ϕ, ω, x, t) должна удовлетворять уравнению

чина ω в каждой точке x интервала от 0 до L за-

непрерывности

дается независимо случайным образом с использо-

∂ρ

∂ (

(

) )

ванием вероятностного распределения (2). Обратим

ωρ + Im

He^-iϕ

= 0.

(8)

внимание также на то, что интеграл в представ-

∂t

∂ϕ

лении (6) комплексного поля H(x, t), отвечающего

В работах [20,21] для данного уравнения с H = H(t)

за нелокальное взаимодействие, стоит воспринимать

найдено притягивающее многообразие. Впослед-

как предел интегральных сумм Лебега [48]. Таким

ствии разработанный в [20,21] подход и полученные

образом, в (5) и (6) не требуется гладкости функции

там результаты были обобщены на случай, когда

ϕ(x, t) по пространственной координате x. Данной

действующее на элементы ансамбля поле H зависит

чертой отсутствия гладкости обладают все обсужда-

не только от времени t, но и от пространствен-

емые режимы поведения среды фазовых осциллято-

ной координаты x, т. е. в (8) в такой ситуации

ров, что существенно затрудняет задачу их анализа

H = H(x,t) (см., например, ссылки [22,37], а также

и классификации на микроскопическом уровне рас-

обзор [26]). Здесь лишь кратко остановимся на

смотрения, ограничивающемся только соотношени-

базовой идее этого метода и вытекающих из него

ями (1)-(6). Однако переход к мезоскопическим по-

следствиях.

лям в пределе N → ∞ дает возможность значитель-

Принимая во внимание то, что собственные час-

но продвинуться в решении этой задачи. Основные

тоты фазовых осцилляторов и в (1), и в (5) выбира-

моменты такого перехода состоят в следующем.

ются независимо, а также учитывая условие цик-

С одной стороны, с помощью процедуры усред-

личности ρ(ϕ, ω, x, t) = ρ(ϕ + 2π, ω, x, t), решение

нения (см., например, [19-22, 26]) можно опреде-

уравнения (8) целесообразно искать в виде разло-

лить локальный параметр порядка Z(x, t) =

e^iφ

жения

loc

представляющий собой непрерывную комплексную

g(ω)

функцию координаты x и времени t и удовлетво-

ρ(ϕ, ω, x, t) =

2π

ряющую неравенству |Z(x, t)| ≤ 1. В случае, когда

(

)

|Z(x, t)| = 1, все осцилляторы, находящиеся вблизи

∑[

]

точки x, синхронны по фазе. При выполнении усло-

a_m(ω, x, t)e^imϕ + C.c.

(9)

вия 0 < |Z(x, t)| < 1 принято говорить, что наблюда-

m=1

154

ЖЭТФ, том 159, вып. 1, 2021

Пространственно-временные режимы в системе. ..

являющегося, фактически, рядом Фурье по динами-

деления Коши (2), после интегрирования по ω вы-

ческой переменной ϕ. Для интересующего нас мно-

текает, что в данной ситуации Z(x, t) = a∗1(-iγ, x, t).

гообразия Отта - Антонсена (называемого так по

Отметим, что здесь учтено, что ω₀ = 0. Тогда, исхо-

фамилиям авторов статей [20, 21]) в спектральном

дя из (11), для локального комплексного парамет-

представлении (9) все коэффициенты a_m(ω, x, t) с

ра порядка Z(x, t) получаем эволюционное интег-

индексами m > 1 выражаются через множитель

ро-дифференциальное уравнение

a₁(ω, x, t), стоящий при первой гармонике, путем

∂Z

)

возведения его в соответствующую степень:

= -γZ +

H-H^∗Z²

(12)

∂t

a_m(ω, x, t) = am1(ω, x, t).

(10)

где H(x, t) выражается уже непосредственно через

При этом поведение a₁(ω, x, t) описывается уравне-

Z(x, t) с помощью оператора свертки

нием

)

∂a₁

1⁽

∫

= -iωa₁ +

H^∗ - Ha²

(11)

∂t

H(x, t) = e^-iα

G(x - x)Z(x, t) dx,

(13)

в чем несложно убедиться с помощью прямой под-

становки (9) совместно с (10) в (8).

Далее, следуя предложенной в [20, 21] (см. так-

а интеграл по пространству в (13) следует уже вос-

же [22, 26, 37]) общей концепции и задействовав в

принимать в смысле Римана (в отличии от соот-

равенстве (7) разложение (9), легко устанавливает-

ношения (6)). Кроме того, для многообразия От-

ся связь между a₁(ω, x, t) и Z(x, t), из которой, вос-

та - Антонсена с учетом (2) по Z(x, t) можно восста-

пользовавшись сделанным нами ранее предположе-

новить плотность вероятности f(ϕ, x, t) разброса ϕ

нием о том, что функция g(ω) имеет форму распре-

при определенных x и t [37, 38]:

⎧

(

)

+^∞

⎨δ

ϕ - arg(Z)

|Z|=1,

f (ϕ, x, t) =

ρ(ϕ, ω, x, t) dω =

(14)

-∞

^⎩(1 - |Z|²)/2π⁽1 - 2|Z| cos⁽ϕ - arg(Z)⁾ + |Z|²),

|Z|<1,

применив формулу для суммы тригонометрической

Таким образом, для исходной задачи (1)-(4) в

прогрессии. Это означает, что профилю Z(x, t) мож-

пределе N → ∞, построена редукция, заключающа-

но поставить в соответствие распределение фаз

яся в переходе от рассмотрения негладких профилей

ϕ(x, t) (и наоборот, естественно, тоже) в любой за-

фаз к работе с непрерывными (на характерных мас-

данный момент времени.

штабах среды) распределениями Z(x, t) и H(x, t).

Все перечисленные выше обстоятельства дела-

Как будет показано ниже, при анализе коллектив-

ют методы, базирующиеся на идеях работ [20-22]

ных эффектов в системе (1)-(4), содержащих боль-

и основное внимание уделяющие анализу поведе-

шое число элементов N, для более глубокого пони-

ния мезоскопических полей Z(x, t) и H(x, t), весь-

мания протекающих процессов целесообразно изу-

ма эффективным инструментом изучения и пред-

чать как динамику ансамбля фазовых осциллято-

сказания возможных ключевых режимов поведения

ров, так и эволюцию комплексного локального па-

интересующей нас многочастичной модели (1)-(4).

раметра порядка Z(x, t), задаваемого системой диф-

В представляемом далее материале нами сделан

ференциальных уравнений в частных производных

еще один шаг, позволяющий упростить исследова-

(12), (15) с граничными условиями (16).

ние пространственной структуры Z(x, t) и H(x, t).

Прежде чем переходить к последовательному и

Используя для ядра G(x) конкретный вид (4), от

подробному изложению материала кратко обозна-

соотношения (13) несложно перейти к эквивалент-

чим типичные устанавливающиеся в ходе числен-

ному ему дифференциальному уравнению

ных расчетов режимы поведения замкнутой в коль-

∂²H

цо среды нелокально взаимодействующих элемен-

- H = -Ze^-iα

(15)

тов. Выполненный в рамках модели (1)-(4) и прове-

∂x²

с периодическими граничными условиями на концах

денный на базе моделирования самосогласованных

интервала [0, L), а именно

уравнений (12), (15) анализ показал существование

следующих устойчивых структурно различных сос-

∂H

H (0, t) = H(L, t),

(0, t) =

(L, t) = 0.

(16)

тояний:

∂x

155

М. И. Болотов, Л. А. Смирнов, Е. С. Бубнова и др.

ЖЭТФ, том 159, вып. 1, 2021

4) пространственно-неоднородное кластерное ча-

стично синхронное состояние (рис. 1ж,з), в котором

явным образом выделяются несколько (чаще всего

статичных) участков с большей или меньшей степе-

нью когерентности осцилляторов;

5) бризерный кластерный режим, когда сосуще-

ствуют несколько синхронных кластеров с различ-

ной средней частотой (рис. 1и,к);

6) режим перемежаемости, когда на пространст-

венно-временной диаграмме интервалы с нерегуляр-

ной динамикой усредненных полей сменяются про-

должительными участками с их регулярным поведе-

нием (что можно трактовать как области кластер-

ной синхронизации) (рис. 1л,м);

7) режим турбулентности со сложным нере-

гулярным поведением мезоскопических характери-

стик системы, когда не удается выделить протя-

женные временные интервалы, в течение которых

наблюдается квазистатическая структура простран-

ственных областей с различной степенью когерент-

ности (рис. 1н,о).

Отметим, что второй и третий виды состояний

в пределе бесконечно малого разброса собствен-

ных частот (γ → 0) трансформируются в полнос-

тью синхронные, а образования, описанные в чет-

вертом и пятом пунктах, для идентичных частиц

превращаются в стационарные и бризерные химеры

[26,31-34]. Подчеркнем также то, что рис. 1 не пол-

ностью отражает все особенности последних двух

из перечисленных режимов. Однако несложно за-

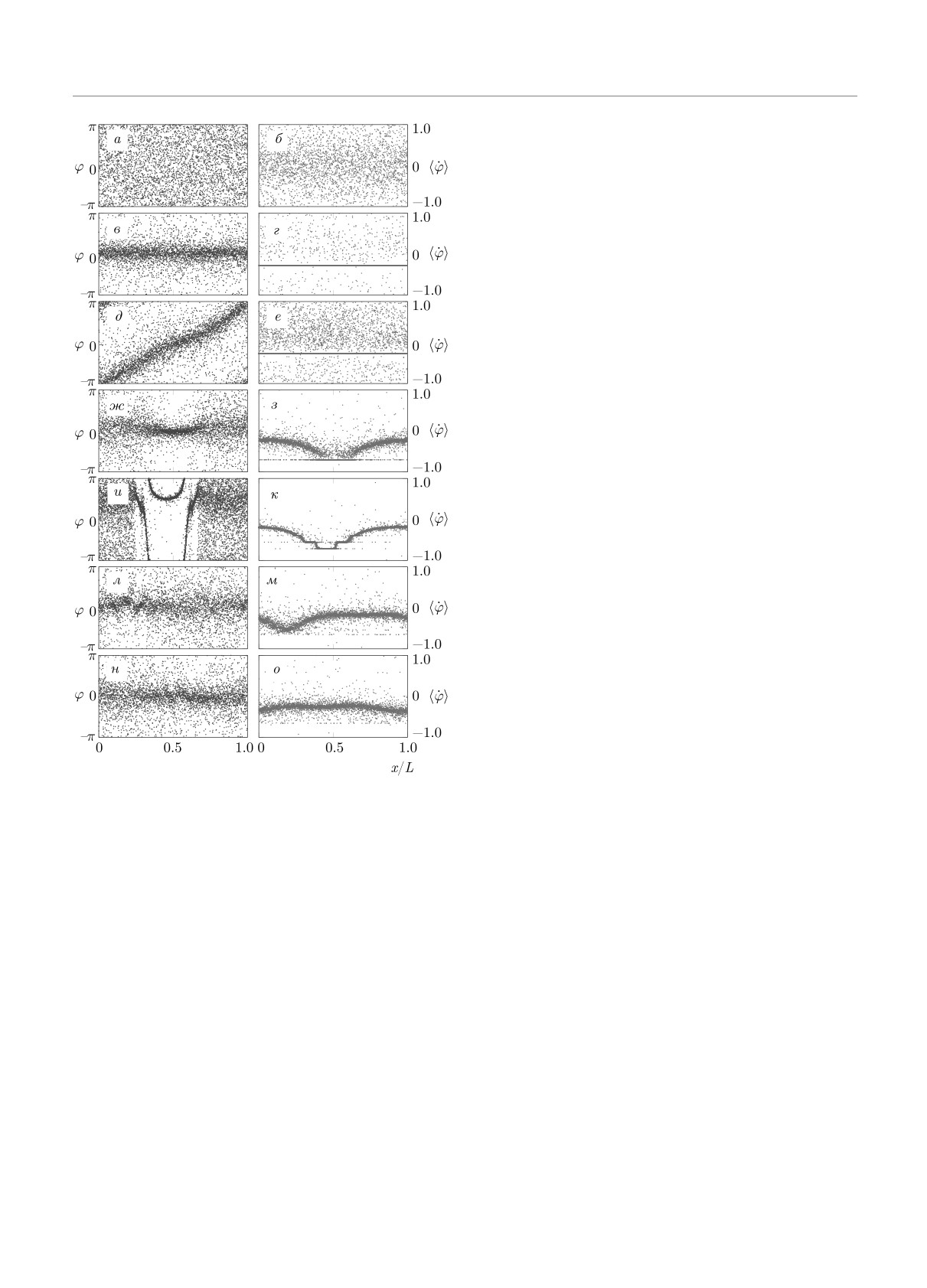
Рис. 1. (В цвете онлайн) Режимы, реализующиеся в си-

метить, что для таких состояний ансамбля с ко-

стеме (1)-(4). Левая колонка — мгновенные снимки фаз

нечным количеством элементов N уровень фазовой

ϕn. Правая колонка — средние частоты осцилляторов

когерентности меняется со временем в окрестности

〈 ϕn〉. а,б) Полностью асинхронное состояние при α = 0.2,

каждой пространственной точки, а в распределении

γ = 0.5, L = 5.0. в,г) Однородный частично синхронный

средних частот не выделяются синхронные класте-

режим при α = 0.4, γ = 0.25, L = 6.0. д,е) Частично

ры, состоящие из макроскопического числа осцил-

синхронный градиентный режим при α = 0.4, γ = 0.25,

ляторов.

L = 25.0. ж,з) Режим кластерной синхронизации при

α = 1.457, γ = 0.02, L = 6.0. и,к Бризерный кластерный

Ниже, для того чтобы понять и объяснить специ-

режим при α = 1.457, γ = 0.002, L = 7.005. л,м) Ре-

фику и условия установления каждого из режимов,

жим перемежаемости при α = 1.457, γ = 0.02, L = 8.837.

наблюдаемых при прямом моделировании системы

н,о) Турбулентный режим при α

= 1.457, γ

= 0.02,

L = 16.655

(1)-(4), будем придерживаться следующей страте-

гии. В первую очередь попытаемся найти в тер-

модинамическом пределе соответствующие решения

1) полностью асинхронное состояние (рис. 1а,б);

уравнения Отта - Антонсена (12), (15) с граничны-

2) однородное частично синхронное состояние

ми условиями (16) и проанализировать их устойчи-

(рис. 1в,г);

вость, а затем проведем проверку полученных ана-

3) частично синхронное состояние с градиент-

литических результатов численно в рамках исход-

ным распределением фаз (рис. 1д,е);

ной модели (1)-(4).

156

ЖЭТФ, том 159, вып. 1, 2021

Пространственно-временные режимы в системе. ..

3. СОСТОЯНИЯ С РАВНОМЕРНО

и γ удовлетворяют условию 2γ < cosα (так как γ

РАСПРЕДЕЛЕННОЙ ПО АНСАМБЛЮ

является полушириной распределения собственных

СТЕПЕНЬЮ ФАЗОВОЙ СИНХРОНИЗАЦИИ

частот, то γ ≥ 0). В этом случае легко убедиться в

СОСЕДНИХ ОСЦИЛЛЯТОРОВ

том, что равенствам (18) можно удовлетворить, если

3.1. Однородные состояния

|z₀|² = r2hps = 1 - 2γ/ cos α,

(19)

Начнем наш анализ с рассмотрения наиболее

Ω_hps = γ tg α - sinα.

простого класса решений самосогласованной систе-

Подчеркнем, что для (19) очевидным образом вы-

мы уравнений (12), (15) с граничными условиями

полняется требование |z₀| ≤ 1, которое вытекает из

(16). Речь идет о стационарных однородных реше-

определения локального параметра порядка. Отме-

ниях, для которых модуль локального комплексно-

тим также, что согласно выражениям (19) длина L

го параметра порядка Z(x, t) представляет собой по-

системы не оказывает влияния на само наличие од-

стоянную величину, а фаза растет линейно со време-

нородных частично когерентных режимов. Несмот-

нем и не зависит от пространственной координаты

ря на то, что результаты численного моделирования

x. При этом в исходной модели (1)-(4) наблюдает-

во многом согласуются со сделанными в ходе прове-

ся в среднем равномерное вращение значительной

денного выше анализа выводами (в частности, уро-

группы осцилляторов, а степень когерентности эле-

вень синхронизации, вычисленный по данным рас-

ментов в каждой точке среды одинакова. В данном

четов в рамках модели (1)-(4), с достаточно хоро-

случае функции Z(x, t) и H(x, t) будем искать в виде

шей степенью точности совпадает с оценкой (19))

Z(x, t) = z₀eiΩt, H(x, t) = h₀eiΩt,

(17)

для целого ряда ситуаций, когда, например, вели-

чина фазовой расстройки α близка к π/2 (α≲π/2),

где с помощью z₀ и h₀ обозначены неизменные (со-

а γ чуть меньше cosα/2 (γ ≲ cosα/2), однород-

гласно нашему предположению) амплитуды усред-

ные частично синхронные состояния перестают на-

ненных полей, Ω (здесь и в других ситуациях далее)

блюдаться, начиная с некоторого значения L. Ниже

играет роль параметра, который задает их общую

будет представлено объяснение и сформулированы

несущую частоту. После подстановки (17) в соотно-

причины такого поведения исходной системы (1)-(4)

шения (12) и (15) получим следующую связь между

на базе линейного анализа устойчивости стационар-

z₀, h₀ и Ω:

ных решений (19) уравнений Отта - Антонсена (12),

2z₀(iΩ + γ) = z₀(h₀ - h∗0z²⁰), h₀ = z₀e^-iα.

(18)

(15). Но перед этим рассмотрим еще один класс ре-

жимов, для которых уровень когерентности осцил-

В первую очередь стоит отметить, что если z₀ =

ляторов оказывается одинаковым вдоль всей среды.

= h₀ = z_as = 0, то очевидно, что алгебраические

равенства (18) выполняются при любых α и γ и неза-

3.2. Градиентные состояния

висимо от длины среды L. Кроме того, величина Ω

остается неопределенной, т.е. существует некий про-

В случае идентичных осцилляторов, когда γ = 0,

извол в ее выборе (в том числе Ω можно положить

обсуждаемые в предыдущем разделе однородные

равной нулю). Такое тривиальное решение уравне-

частично когерентные состояния переходят в пол-

ний Отта - Антонсена (12), (15) отвечает полностью

ностью синхронные, для которых |Z(x, t)| = 1 при

асинхронному поведению элементов в обсуждаемом

каждом x в любой момент времени t, что непосред-

ансамбле, когда фазы осцилляторов распределены

ственно видно из соотношений (19) в пределе γ → 0.

равномерно в интервале от -π до π в каждый мо-

Однако для распределенного в пространстве ансам-

мент времени.

бля, состоящего из нелокально взаимодействующих

Однако нас прежде всего интересуют устано-

частиц с одинаковыми индивидуальными характе-

вившиеся режимы, для которых мезоскопические

ристиками, есть еще один режим с |Z(x, t)| = 1 всю-

характеристики распределенной популяции имеют

ду. Отличительной чертой данного режима являет-

конечные значения, что указывает на присутствие

ся наличие постоянной разности фаз при перехо-

корреляций в движении соседних элементов. Из со-

де от точки к точке (для произвольно выбранного

отношений (18) непосредственно следует, что подоб-

n выполняется равенство ϕn+1(t) - ϕ_n(t) = Δϕ =

ные частично синхронные состояния можно найти в

= const = 0), так что полный набег фазы при про-

рамках рассматриваемого здесь класса стационар-

хождении вдоль всей среды отличен от нуля. По-

ных однородных решений. Существуют данные кол-

добное состояние в англоязычной литературе назы-

лективные моды, когда управляющие параметры α

вают «splay state» [40, 44, 45]. Вполне естественно

157

М. И. Болотов, Л. А. Смирнов, Е. С. Бубнова и др.

ЖЭТФ, том 159, вып. 1, 2021

ожидать присутствия их аналогов при γ =0 для ис-

кольцо ансамбля превышает критическое значение

следуемой нами модели (1)-(4). Случайный разброс

L_gps(q), т. е.

собственных частот осцилляторов, конечно, должен

√

L > L_gps(q) = 2πq

2γ/(cosα - 2γ).

(23)

привести к тому, что распределение фаз тоже станет

нерегулярным. Однако, несмотря на видимый бес-

Заметим, что если формально в (22) положить

порядок, степень которого зависит от γ, поведение

q равным нулю, то выражения (22) совпадут с со-

мезоскопических полей останется тем же, что и при

отношениями (19). Данное обстоятельство лишний

γ = 0, и в среднем общие тенденции (прежде все-

раз подтверждает взаимосвязь частично синхрон-

го наклон) в профиле ϕ(x, t) (или ϕ_n(t)) сохранят-

ных однородных и градиентных состояний. Однако

ся. Поэтому такие состояния далее будем называть

их все-таки стоит выделять в два режима различ-

градиентными. Отметим, что ранее уже предприни-

ных классов. В частности, в пользу подобной точки

мались попытки их изучения, но для ядер G(x) дру-

зрения говорит то, что такая важная в теории син-

гого вида (см., например, [40, 41, 44, 45]).

хронизации характеристика, как глобальный пара-

Учитывая то, что для градиентных режимов,

метр порядка

так же как и для рассмотренных выше однородных



∑



состояний, характерно постоянное значение модуля

1



R(t) =



eiϕn,

(24)

локального параметра порядка Z(x, t) по всей длине

N



n=1

среды, будем искать поля Z(x, t) и H(x, t) в схожем

с (17) виде

который в пределе N → ∞ можно рассчитывать по

формуле



∫



Z(x, t) = z₀eiΩt-iQx, H(x, t) = h₀eiΩt-iQx

(20)

₁



R(t) =

Z(x, t)dx,

(25)



^L



с тем лишь отличием, что в (20) в показателе экспо-

ненты появляется дополнительное слагаемое, про-

для однородных частично синхронных состояний

порциональное пространственной координате x и

принимает конечные значения, а для градиентных

ответственное за общий наклон фазового фронта

режимов всегда равен нулю, в чем несложно убе-

функций Z(x, t) и H(x, t). Коэффициент Q такой ли-

диться, воспользовавшись (20). Подчеркнем также

нейной зависимости в силу периодических гранич-

еще один момент, что для фиксированных α и γ

ных условий должен быть определен как Q = 2πq/L,

в первом случае степень локальной когерентности

где целое (в интересующей нас здесь ситуации от-

всегда выше по сравнению со второй.

личное от нуля) число q (q = ±1, ±2, . . . ) указыва-

Численные расчеты, выполненные в рамках ис-

ет на количество оборотов на 2π, которое совершит

ходной модели (1)-(4), при определенном выборе па-

усредненная фаза при полном обходе системы. Под-

ры значений α и γ демонстрируют хорошее согла-

ставив (20) в уравнения Отта - Антонсена (12), (15),

сие с рассмотренным выше описанием. Во-первых,

получим два алгебраических равенства:

выражается это в том, что частично синхронные

градиентные состояния наблюдаются в течение дли-

2(iΩ + γ)z₀ = h₀ - h∗0z²⁰,

(1 + Q²)h₀ = z₀e^-iα, (21)

тельных промежутков времени и остаются невос-

приимчивыми по отношению к малым возмущени-

для которых легко находится нетривиальное реше-

ям, т. е. представляют собой возможные стабиль-

ние

ные варианты вращения фазовых осцилляторов (см.

2γ(1 + Q²)

|z₀|² = r2gps = 1 -

рис. 1д и рис. 2). Во-вторых, степень локальной

cosα

(22)

когерентности, о которой можно судить по абсо-

sinα

Ω_gps = γ tg α -

лютной величине комплексного параметра порядка,

1+Q²

вычисленного с помощью процедуры мезоскопичес-

отвечающее градиентным состояниям. Непосредст-

кого усреднения результатов прямого моделирова-

венно из выражений (22) следует, что для наличия

ния, достаточно адекватно воспроизводится форму-

такого рода режимов необходимо, чтобы cos α > 2γ.

лой (22). Кроме того, точность оценки (22) становит-

Кроме того, из требования r2gps > 0 вытекает усло-

ся выше с ростом числа N элементов в системе. Од-

вие для протяженности L распределенной популя-

нако в численных расчетах не при всех L > L_gps(q)

ции фазовых осцилляторов. Согласно этому усло-

удается реализовать градиентные режимы. Так, на-

вию градиентные состояния с числом оборотов q

пример, на рис. 2а и 2б показаны две ситуации, ко-

существуют, только когда размер L замкнутого в

торые отвечают одному и тому же выбору α и γ

158

ЖЭТФ, том 159, вып. 1, 2021

Пространственно-временные режимы в системе. ..

тяженных популяциях (L = 28, рис. 2д), и лишь в

некотором интервале длин L градиентные состояния

оказываются устойчивыми. Для того чтобы объяс-

нить теоретически наблюдаемые в численных расче-

тах особенности эволюции обсуждаемых режимов,

требуется линейный анализ их устойчивости.

3.3. Устойчивость частично синхронных

однородных и градиентных состояний

В данном разделе в термодинамическом преде-

ле на базе редукции Отта - Антонсена проведем ли-

нейный анализ устойчивости рассмотренных выше

режимов поведения системы нелокально связанных

неидентичных фазовых осцилляторов. Это позволит

разрешить отмеченные ранее кажущиеся (но не су-

ществующие на самом деле) противоречия между

развитым теоретическим описанием и проведенны-

ми численными расчетами. Указанный анализ вы-

полним в рамках единого формализма, который яв-

ляется общим и может быть применен как для од-

Рис. 2. (В цвете онлайн) Эволюция градиентного частично

нородных, так и для градиентных состояний. От-

синхронного режима (ГС). Результаты прямого численно-

метим, что для удобства и наглядности ниже будет

го моделирования системы (1)-(4) при α = 1.457. Мгно-

использована эквивалентность уравнения (15) с пе-

венные снимки фаз φn для областей, представленных на

рис. 3. Область A: а — неустойчивое ГС, эволюциониру-

риодическими граничными условиями (16) и опера-

ющее к однородному режиму с |z| = r_hps при γ = 0.001,

тора свертки с ядром (13).

L = 4, б — устойчивое ГС при γ = 0.001, L = 14; область

Для того чтобы исследовать аналитически

B: в — неустойчивое ГС, эволюционирующее к неоднород-

устойчивость обсуждаемых распределений осцил-

ному режиму при γ = 0.003, L = 4, г — устойчивое ГС при

ляторов во времени, представим комплексные поля

γ = 0.003, L = 12, д — неустойчивое ГС, эволюциониру-

Z(x, t) и H(x, t) в следующем виде:

ющее к неоднородному режиму при γ = 0.003, L = 28;

(

)

область C: е — неустойчивое ГС, эволюционирующее к

Z(x, t) = z₀ + Z(x, t) eiΩt-iQx,

неоднородному режиму при γ = 0.005, L = 4

(

)

(26)

H(x, t) = h₀ + H(x, t) eiΩt-iQx.

(α = 1.457 и γ = 0.001), но разным L > L_gps ≈ 0.841

Здесь явным образом учтены ключевые особеннос-

(L = 4 (рис. 2а) и L = 14 (рис. 2б)). Видно, что

ти интересующих нас профилей фаз, которым при

при L = 4 (рис. 2а) состояние с q = 1 числом оборо-

фиксированной длине среды L отвечают стационар-

тов средней фазы на 2π относительно быстро распа-

ные решения уравнений Отта - Антонсена (12), (15),

дается и трансформируется в частично синхронный

характеризующиеся параметрами Ω и Q. В выраже-

однородный режим. Когда же L = 14 (рис. 2б) та-

ниях (26) функции Z(x, t) и H(x, t) играют роль сла-

кого процесса не происходит, и характерные особен-

бых (периодических по пространственной координа-

ности пространственного распределения динамиче-

те x) возмущений к однородному состоянию при Q =

ских переменных ϕ_n(t) не претерпевают существен-

= 0 или к градиентному решению с Q = 0. Подста-

ных изменений на протяжении сколь угодно дли-

вив (26) в соотношения (12), (13) и линеаризовав их

тельных временных отрезков. Похожий эффект, за-

вблизи z₀ и h₀ с учетом малости Z(x, t) и H(x, t), по-

ключающийся в разрушении градиентного состоя-

лучим линейное интегро-дифференциальное урав-

ния, несмотря на то, что размер среды L удовлетво-

нение с не зависящими от x и t коэффициентами:

ряет условию существования (23), присутствует для

(

)

α = 1.457 и γ = 0.003 (см. рис. 2в,г,д). Хотя стоит

∂Z

e^iα|z₀|²

)

= - γ+iΩ+

Z+

H-|z₀|²H^∗

(27)

отметить, что здесь в отличие от случая α = 1.457 и

∂t

1+Q²

γ = 0.001 разрушение сформированного в соответ-

∫

ствии с (20), (22) и (14) профиля фаз происходит как

H(x, t) = e^-iα G(x - x)eiQ(x-x)Z(x, t) dx.

(28)

в сравнительно коротких (L = 4, рис. 2в), так и про-

159

М. И. Болотов, Л. А. Смирнов, Е. С. Бубнова и др.

ЖЭТФ, том 159, вып. 1, 2021

Далее, следуя одному из вариантов стандартной

процедуры анализа на устойчивость пространствен-

но-временных структур, будем искать Z(x, t) как су-

перпозицию двух ортогональных компонент, запи-

санных в факторизованной форме:

Z(x, t) = A(x)eΛt + B^∗(x)eΛ∗ t,

(29)

где комплексное число Λ, имеющее в общем случае

как действительную, так и мнимую составляющие,

полностью характеризует динамику каждого из сла-

гаемых в сумме (29). В силу предположения о том,

что рассматриваемая нами система замкнута в коль-

цо, т. е. на концах отрезка [0, L) выполняются пе-

риодические граничные условия, а также благодаря

постоянству множителей во всех членах с Z и H в

соотношении (29), в качестве A(x) и B(x) можно вы-

брать функции, пропорциональные e^iKx:

A(x) = ae^iKx, B(x) = be^iKx,

(30)

где волновые числа K = 2πk/L с k = 0, 1, 2, . . . опре-

деляют пространственный период моды, который не

превышает продольный размер L системы. Тогда

после подстановки (29), (30) в (27), (28) останется

Рис. 3. (В цвете онлайн) а) Области (на плоскости от па-

рассчитать постоянные комплексные амплитуды a

раметров α и γ) существования и устойчивости режимов с

и b, а требование существования нетривиальных ре-

равномерным распределением по ансамблю уровнем син-

шений, для которых хотя бы одна из этих амплитуд

хронизации. Для таких режимов амплитуда локального па-

отлична от нуля, позволит определить соответству-

раметра порядка Z(x, t) одинакова для любой точки сре-

ющие величины Λ. В результате получим задачу на

ды в каждый момент времени. б) Асинхронное состояние

собственные векторы ξ = (a, b)^T и собственные зна-

существует при всех α и γ вне зависимости от длины сре-

чения Λ 2 × 2-матрицы

P_:

ды. Неустойчиво в областях A (часть плоскости α, γ с

(

)

одинарной штриховкой), B (затененная область с двойной

p₁₁

p₁₂

P_ξ,

P₌

штриховкой) и C (светлая область с двойной штриховкой)

Λξ =

(31)

p₂₁

p₂₂

и устойчиво в области D (часть области α, γ без штрихов-

ки). в) Однородное частично синхронное состояние суще-

где

ствует и устойчиво при всех L, если пара величин α и γ

e^iα|z₀|

e^-iα

выбрана из области A. Если же точка α, γ лежит в обла-

p₁₁ = -γ - iΩ -

(

)

1+Q²

1 + (K - Q)²

стях B или C, то существует критическое значение, начи-

ная с которого данный режим становится неустойчивым.

e^iα|z₀|

p₁₂ = -

(

В области D такие состояния отсутствуют. г) Градиентное

1 + (K + Q)²

частично синхронное состояние существует только в обла-

(32)

e^-iα|z₀|

стях A, B и C, когда L > Lgps. Этот режим устойчив в об-

p₂₁ = -

(

ластях A и B, если L > L∗1 и L∗1 < L < L∗2, соответственно.

1 + (K - Q)²

В области C градиентное состояние всюду неустойчиво

e^-iα|z₀|

e^iα

p₂₂ = -γ+iΩ-

(

)

1+Q²

1+(K+Q)

Из (31) непосредственно вытекает, что для нахожде-

Исходя из последнего выражения, несложно сделать

ния Λ требуется решить квадратное уравнение, пара

вывод об устойчивости режимов с однородным рас-

корней которого записывается напрямую через след

пределением модуля комплексного параметра по-

tr^P и детерминант det P только что введенной мат-

рядка. Если действительная часть Λ₁ или Λ₂ оказы-

P_:

рицы

вается положительной, то согласно (29) малые воз-

(

)

√(

)₂

мущения должны экспоненциально нарастать с те-

Λ1,2 =

tr^P ±

tr^P

- 4det ^P

(33)

чением времени.

160

ЖЭТФ, том 159, вып. 1, 2021

Пространственно-временные режимы в системе. ..

Теперь на основе выработанного выше критерия

ных видов ядер, используемых для описания нело-

определим характер поведения отклонений Z(x, t)

кального взаимодействия между элементами попу-

от z₀, отвечающих одному из трех рассмотренных

ляции, что полностью совпадает с выводом работы

ранее режимов, а именно, полностью асинхронно-

[41], где подробно обсуждалась динамика тривиаль-

му, частично синхронному однородному и градиент-

ного режима с |z₀| = z_as = 0 для функции связи

ному состояниям. Резюмирующим отражением опи-

G(x) прямоугольной формы. Отметим также, что

санных выше результатов служит рис. 3.

такого рода неустойчивость достаточно распростра-

Полностью асинхронный режим с |z₀| = z_as при-

нена в нелинейных распределенных моделях и носит

тягивает к себе близлежащие траектории системы,

имя Экхауса в честь автора монографии [49].

если cos α < 2γ, при любой длине среды L, так что в

процессе долговременной эволюции реализуется си-

Для частично когерентных состояний с Q = 0,

туация, при которой отсутствуют какие-либо корре-

|z₀| = r_hps и Ω = Ω_hps (см. формулу (19)), возника-

ляции фаз отдельных элементов. В противном слу-

ющих при тех же условиях, при которых асинхрон-

чае, когда cos α > 2γ, асинхронный режим оказыва-

ный режим теряет свою устойчивость, аналогичным

ется неустойчивым (рис. 3а,б). К развитию данной

образом несложно изучить поведение малых возму-

неустойчивости приводят однородные по простран-

щений Z(x, t) в форме (29), (30). Воспользовавшись

ству линейные моды с K = 0. Отметим, что данный

выражениями (19), (31), (32) и (33), после ряда ал-

результат является универсальным для стандарт-

гебраических преобразований получим

(

)

√(

(

))₂

I(K)

2γ

(

)₂

Λ1,2 = γ - cosα

I(K)

2γ tg α-I(K)sinα

(34)

cosα

где I(K) = (1 + K²)-1 представляет собой коэффи-

На рис. 3а для случая q = ±1 указаны границы об-

циент, к умножению на который сводится оператор

ластей, отвечающих данным трем ситуациям. Если

свертки в (28), если считать, что H(x, t), так же как

α и γ выбирать из той части плоскости, которая име-

и Z(x,t) пропорционально e^iKx. Анализ выраже-

ет одинарную штриховку (область A), то существует

ний (34) показывает, что при γ < (cos α)³ однород-

критическая длина L∗1 такая, что при L < L∗1 гра-

ный частично синхронный режим является устой-

диентный режим неустойчив, а при L > L∗1, наобо-

чивым для любого значения L. В случае, когда γ >

рот, устойчив (рис. 2б). Это подтверждают и прямые

> (cos α)³, для подобного состояния, существующе-

численные расчеты в рамках модели (1)-(4) (см., на-

го лишь при γ < cos α/2, условие Re Λ < 0 оказыва-

пример, рис. 2а,б). Для тонкого слоя B имеются два

ется выполненным, только если K = 2πm/L (m =

критических значения длины L∗1 и L∗2. При этом со-

= 0, 1, 2, . . .) больше некоторого критического значе-

стояние с набегом фазы на 2π устойчиво в интерва-

ния K^∗hps(α, γ). Это означает, что имеется предель-

ле L∗1 < L < L∗2 (рис. 2г) и неустойчиво при L < L∗1

ная длина L^∗hps(α, γ), при превышении которой соот-

(рис. 2в), L > L∗2 (рис. 2д). В области C градиентный

ветствующие пространственно-однородные режимы

режим неустойчив для любого значения L (рис. 2е).

поведения системы неустойчивы:

Отметим, что здесь выписать явные выражения для

√

L∗1, L∗2 не удается и приходится их находить числен-

cos⁴ α - 2γ cos³ α + γ

но.

L^∗hps = 2π

(35)

(cos α - 2γ)(γ - cos³ α)

В заключение данного раздела подчеркнем, что

найденные условия существования и устойчивости

Что касается градиентных состояний, каждое из

режимов с пространственно-однородной степенью

которых определяется своим Q = 2πq/L (q = ±1,

синхронизации фазовых осцилляторов, а также на-

±2, . . .) и формулами (22) для |z₀| = r_gps и Ω_gps, то

личие различных критических значений для длины

исследование их устойчивости и соответствующие

среды теперь хорошо объясняют поведение систе-

результаты выглядят несколько сложнее. Так, де-

мы (1)-(4), демонстрируемое при прямых числен-

тальный анализ собственных значений Λ1,2 показы-

ных расчетах (см. рис. 2). Однако в процессе дол-

вает, что в зависимости от значений параметров α и

говременной эволюции также могут устанавливать-

γ можно выделить различные ситуации, качествен-

ся и менее тривиальные состояния, речь о которых

ное отображение которых представлено на рис. 3г.

пойдет в следующих разделах.

161

ЖЭТФ, вып. 1

М. И. Болотов, Л. А. Смирнов, Е. С. Бубнова и др.

ЖЭТФ, том 159, вып. 1, 2021

4. СОСТОЯНИЯ СО СТАТИЧНЫМ

С целью понять и детально описать в термоди-

ПРОСТРАНСТВЕННО-НЕОДНОРОДНЫМ

намическом пределе ключевые особенности покоя-

РАСПРЕДЕЛЕНИЕМ СТЕПЕНИ ФАЗОВОЙ

щихся пространственных структур с областями с по-

СИНХРОНИЗАЦИИ ЭЛЕМЕНТОВ

вышенной и пониженной степенью локальной фазо-

АНСАМБЛЯ

вой когерентности поведения элементов замкнутой

4.1. Стационарные решения уравнений

в кольцо среды построим и проанализируем стацио-

Отта - Антонсена

нарные (по модулю) решения редуцированной зада-

При подробном изучении сценариев долговре-

чи, полученной с помощью подхода Отта - Антонсе-

менной эволюции модели (1)-(4) в зависимости от

на и сформулированной нами в форме совокупности

величины фазового сдвига α, степени простран-

двух уравнений в частных производных (12), (15) с

ственного беспорядка γ, а также длины среды L с

граничными условиями (16). Для этого представим

помощью прямого численного моделирования уста-

комплексные поля Z(x, t) и H(x, t) в виде

новлено, что особую роль играют кластерные час-

Z(x, t) = z(x)eiΩt, H(x, t) = h(x)eiΩt,

(36)

тично синхронные режимы вращения (как предель-

ные, так и транзиентные), для которых явным обра-

где Ω играет роль неизвестного параметра, кото-

зом выделяются несколько статичных или квазиста-

рый требуется определить. После подстановки вы-

тичных участков с различным уровнем когерентнос-

ражений (36) для мезоскопических величин Z(x, t)

ти осцилляторов. Примеры перехода рассматрива-

и H(x,t) в соотношения (12) и (15) приходим к сле-

емой системы в подобные состояния представлены

дующей системе, состоящей из алгебраического ра-

на рис. 2в,е, где показано, как разрушается гради-

венства и обыкновенного дифференциального урав-

ентное распределение фаз с одинаковым значением

нения второго порядка, в которые входят зависящие

модуля локального параметра порядка в интерва-

только от переменной x комплексные функции z(x)

ле [0, L), и устанавливается неизменная в течение

и h(x):

всего дальнейшего времени расчета картина, харак-

2(-iΩ - γ)z + h - h^∗z² = 0,

(37a)

терные особенности которой отражены на мгновен-

h^′′ - h + ze^-iα = 0.

(37b)

ных снимках при t = 2000. На данных фрагментах

Здесь и далее штрихом обозначена производная по

видно, что имеются две области с большей и мень-

координате x. В ситуации, когда γ = 0, т. е. осцил-

шей степенью скоррелированности движения сосед-

ляторы нетождественны друг другу и различают-

них друг к другу элементов. Указанное обстоятель-

ся по своим индивидуальным характеристикам, при

ство дает основание полагать, что профиль каждо-

N → ∞ в интервале [0,L) не найдется ни одной точ-

го из введенных ранее путем процедуры усреднения

ки, в малой окрестности которой может быть до-

мезоскопических полей становится и затем остает-

стигнута полная синхронизация по фазе, а значит,

ся пространственно-неоднородным. Такие долгожи-

абсолютное значение локального параметра поряд-

вущие режимы поведения распределенных популя-

ка всегда остается меньше единицы, т. е. |z(x)| < 1.

ций вызывают особый интерес прежде всего по двум

Тогда из (37a) несложно выразить h(x) через z(x):

причинам. Во-первых, в обсуждаемых нами ансамб-

(

)

лях нелокально связанных фазовых осцилляторов

iΩ

h=2

(38)

эти нетривиальные режимы наблюдаются даже то-

1 + |z|²

1 - |z|²

гда, когда частично синхронное однородное состоя-

Затем перепишем z(x) как

ние устойчиво. Во-вторых, для идентичных элемен-

тов (т. е. в пределе γ → 0) структурные образования,

z(x) = r(x)eiθ(x),

(39)

аналогичные по своему виду тем, что изображены

введя две действительные функции r(x) и θ(x), ко-

на рис. 2в,е, а также на рис. 1ж,и, трансформиру-

торые естественно называть соответственно ампли-

ются в химеры (в классическом их понимании), от-

тудой и фазой для z(x) с тем лишь отличием от

личительной чертой которых является присутствие

классических определений, что для удобства будем

наряду с участками с частично когерентным движе-

считать r(x) знакопеременной величиной, предпола-

нием элементов макроскопических групп с полно-

гая, в свою очередь, θ(x) непрерывной в том числе

стью синхронным вращением [24-29]. Перечислен-

в тех точках, где r(x) обращается в нуль. При этом

ные факты позволяют сделать вывод об отноше-

выражение (38) для h(x) примет вид

нии состояний, которым посвящен данный раздел, к

(

)

фундаментальному эффекту частичной потери сим-

iΩ

iθ

h = 2re

(40)

метрии [30].

1+r²

1-r²

162

ЖЭТФ, том 159, вып. 1, 2021

Пространственно-временные режимы в системе. ..

Подставив (40) в (37b) и приравняв по отдельности

функция θ(x) определена с точностью до постоян-

нулю действительную и мнимую части получивше-

ного слагаемого, т. е. структура комплексных полей

гося соотношения, перейдем к следующей паре урав-

z(x) и h(x) (а с ними Z(x, t) и H(x, t)) инвариант-

нений:

на относительно совместного сдвига фаз на констан-

ту. По этой же причине без ограничения общности

γ(1 + r²)

Ωr

2Ω(1 - r²)

можно положить θ(0) = 0. Подчеркнем также, что в

r^′′ -

θ^′′ -

r^′θ^′ +

(1 - r²)²

1+r²

(1 + r²)²

силу граничных условий (16) на концах интервала

2γr(r² + 3)

γr

[0, L) нас будут интересовать только периодические

(r^′)² -

(θ^′)² =

(1 - r²)³

1-r²

решения уравнений (42) с периодом, совпадающим

γr

с размером обсуждаемой среды L. Такого рода ре-

cosα,

(41a)

1-r²

шения обладают важной особенностью — трансля-

ционной симметрией, что позволяет удобным спо-

собом (благодаря некоторому произволу) выбирать

Ω(1 - r²)

γr

2γ(1 + r²)

r^′′ +

θ^′′ +

r^′θ^′ +

положение начала отсчета по пространственной ко-

(1 + r²)²

1-r²

(1 - r²)²

ординате x. Кроме того, несложно заметить, что

2Ωr(r² - 3)

Ωr

при замене x → -x, r → r, u → -u, v → -v си-

(r^′)² -

(θ^′)² =

(1 + r²)³

1+r²

стема (42) останется неизменной. Другими словами,

Ωr

для соотношений (42) проходит преобразование ин-

sinα,

(41b)

1+r²

волюции. Перечисленные свойства как зависимос-

тей r(x), u(x) и v(x), так и самих уравнений (42) да-

которую путем введения новой переменной u = r^′ и

ют основание ограничиться поиском лишь симмет-

дополнительной замены v = r²θ^′, после ряда пре-

ричных по отношению к середине интервала [0, L)

образований можно свести к системе обыкновен-

периодических решений r(x), u(x) и v(x), удовлетво-

ных дифференциальных уравнений третьего поряд-

ряющих следующим условиям:

ка для r(x), u(x) и v(x) со свободным параметром Ω

при заданных значениях α, γ:

r(0) = r(L), u(0) = u(L) = 0,

(43)

v(0) = v(L) = 0.

r^′ = u,

(42a)

Данным решениям должны быть поставлены в со-

ответствие пространственные профили z(x) и h(x),

u^′ =

которые вместе с соответствующим значением па-

2(γ²(1 + r²)⁴ + Ω²(1 - r²)⁴)(1 - r⁴)r³

(

раметра Ω определяют вид стационарных структур.

(

)

Подчеркнем также то, что в пользу выбора выде-

× -4r⁴u²

γ²(r²+3)(1+r²)⁴+Ω²(r²-3)(1-r²)⁴

ленного класса функций r(x), u(x) и v(x) как наи-

- 2(8γΩvur³ + γ²(v² + r⁴)(1 + r²)² +

более перспективных в плане описания долгоживу-

)

(

щих состояний со статичным неоднородным распре-

+ Ω²r³(1-r²)

(1-r⁴)²+r⁴

-γ(1+r²)cosα +

)

делением степени фазовой синхронизации элемен-

)

+ Ω(1 - r²) sin α

(1 - r⁴)3 ,

(42b)

тов ансамбля говорят и прямые численные расчеты

в рамках исходной модели (1)-(4) (см., например,

рис. 1ж и фрагменты рис. 2в,е при t = 2000). Сто-

ит однако учитывать, что не все решения системы

v^′ =

(

)

(42), для которых выполнены условия (43), явля-

γ²(1 + r²)⁴ + Ω²(1 - r²)⁴

(1 - r⁴)

(

ются физически реализуемыми. Они имеют смысл

× 8vru²(Ω²(1 - r²)⁵ - 2γ²(1 + r²)⁵)+

только тогда, когда |r(x)| = |z(x)| при всех x на от-

резке [0, L) не превышает единицы. Данное требо-

+ 8γΩ(3r²u² + v² + r⁴)(1 - r⁴)² +

вание вытекает непосредственно из определения ло-

(

)

+r²

Ω(1 - r²)³ cos α + γ(1 + r²)³ sin α

кального комплексного параметра порядка Z(x, t).

)

Таким образом, поставленная нами в начале разде-

× (1 - r⁴)²

(42c)

ла задача о нахождении стационарных решений (36)

системы (12), (15) с граничными условиями (16) мо-

Отметим, что понижение размерности (с четвертой

жет быть сведена к нахождению периодических тра-

у совокупности соотношений (41) до третьей у сис-

екторий системы (42), для которых выполняются

темы (42)) удается осуществить за счет того, что

условия (43).

163

11*

М. И. Болотов, Л. А. Смирнов, Е. С. Бубнова и др.

ЖЭТФ, том 159, вып. 1, 2021

4.2. Процедура поиска статичных

неоднородных состояний и их структурный

анализ

Перейдем теперь к детальному обсуждению клю-

чевых особенностей стационарных режимов с неод-

нородным распределением по пространству локаль-

ного параметра порядка Z(x, t). В данном разделе

прежде всего приведем процедуру поиска всех су-

ществующих периодических решений вспомогатель-

ной системы (42), определяющих вид профилей ком-

плексных полей Z(x, t) и H(x, t) с равномерно вра-

щающейся фазой. Затем выделим основные отличи-

тельные черты семейства подобных решений и со-

отнесем их с той картиной разброса динамических

переменных ϕ_n(t), которая должна, соответствен-

но, реализовываться в исходной модели (1)-(4) ан-

самбля нелокально связанных неидентичных осцил-

ляторных элементов. Далее такого рода состояния

рассматриваемых популяций будут проинтерпрети-

рованы как с позиции мезоскопических (усреднен-

ных) характеристик, так и с точки зрения свойств

движения отдельных осцилляторов.

Начнем с описания разработанного нами мето-

да поиска неоднородных стационарных (по модулю)

состояний вида (36), базирующегося на идее выде-

ления при фиксированных значениях Ω замкнутых

(и тем самым удовлетворяющих условиям (43)) тра-

екторий в фазовом пространстве r, u, v системы

обыкновенных дифференциальных уравнений (42)

третьего порядка. Для нахождения указанных тра-

екторий использовалось сечение Пуанкаре u = 0,

u′ > 0, которое строилось путем численного инте-

грирования системы (42), стартуя при этом с мно-

жества r(0) = r₀, u(0) = 0, v(0) = 0, где r₀ принима-

ет свои значения из интервала (0, 1), и детектируя

каждое событие с u = 0, u^′ > 0, а далее нанося его

для визуализации маркером на плоскость r, v (см.

рис. 4). Наш анализ (прежде всего использующий

представленные в разд. 4.1 факты) показывает, что

неподвижным точкам периода p построенного таким

образом отображения отвечают искомые периодиче-

Рис. 4. (В цвете онлайн) Отображение Пуанкаре для си-

ские решения системы (42) и, следовательно, сим-

стемы (42) при α = 1.457, γ = 0.020. Условия для сечения:

метричные пространственно-неоднородные структу-

u = 0, u^′ > 0. Эллиптические (синие маркеры) и гипербо-

ры с p максимумами модуля локального параметра

лические седловые (красные маркеры) неподвижные точ-

порядка z(x, t). Длина L каждой подобной найден-

ки: а — Ω = -0.8185, б — Ω = -0.78, в — Ω = -0.647.

ной траектории совпадает с размером среды, в ко-

Неподвижная точка (r1, 0) соответствует неоднородному

торой может наблюдаться данное состояние. В ито-

решению (36) с одним максимумом |z(x)|. Черные (фи-

ге, при заданном Ω находим профиль z(x), который

олетовые) точки обозначают траектории, не покидающие

в точности повторяет себя через период L, опреде-

(покидающие) области на плоскости (r,v), отображаемые

на фрагментах а-в

ляемый выбором Ω. При необходимости по форму-

ле (38) легко определяется и зависимость h(x). Но

164

ЖЭТФ, том 159, вып. 1, 2021

Пространственно-временные режимы в системе. ..

более важным является то, что по локальному па-

раметру порядка z(x) с учетом (36) всегда удается

восстановить распределение исходной динамической

переменной ϕ(x, t) или ϕ_n(t). Таким образом, по-

лучается обнаружить разнообразные семейства ста-

тичных неоднородных состояний среды нелокаль-

но связанных неидентичных фазовых осцилляторов.

Каждое такое семейство характеризуется индивиду-

альной зависимостью Ω(L) (см. рис. 5), которая рас-

считывается в неявном виде с помощью описанной

выше процедуры.

Перед тем как перейти к обсуждению конкрет-

ных примеров, отметим, что похожий подход уже

успешно применялся в наших предыдущих работах

[31-33], где с помощью него изучались химеры в сре-

дах, состоящих из одинаковых частиц (т. е. γ = 0).

Однако в изучаемом в статьях [31-33] случае име-

ется ряд сложностей, вызванных наличием участ-

ков с полностью синхронными элементами, затруд-

няющих использование численных процедур, кото-

рые позволяют находить воспроизводящие себя на

конечном отрезке кривые. Когда же γ > 0, удается

избежать проблем, связанных с возможностью тож-

дественного совпадения фаз осцилляторов в окрест-

ности некоторой точки x, так как вырожденная си-

туация |z(x)| = 1 становится недостижимой. Тре-

бование |z(x)| < 1 существенно сужает множество

начальных условий, с которых необходимо старто-

вать для построения сечения Пуанкаре, что упроща-

ет процедуру поиска неподвижных точек отображе-

ния и гарантирует отсутствие потерянных решений.

Однако при γ = 0 нельзя дать аналогичных гаран-

тий, потому что все преобразования и вычисления

проводятся с полем h(x), для амплитуды которого

отсутствует ограничение сверху. С другой стороны,

стоит подчеркнуть, что при стремлении к нулю ве-

личины γ, ответственной за степень пространствен-

ного беспорядка, стационарные неоднородные состо-

яния вида (36), полученные для задачи (12), (15),

способны дать дополнительную информацию о хи-

мерных решениях, образующихся при γ = 0, и их

Рис. 5. (В цвете онлайн) Бифуркационная диаграмма ста-

областях существования.

ционарных решений (36) уравнений Отта - Антонсена (12),

В качестве примера исследуем неподвижные точ-

(13) при α = 1.457: а — γ = 0.002, б — γ = 0.011.

ки отображения Пуанкаре для фиксированных зна-

в — γ = 0.020. Пунктир (A) — однородное частично син-

чений α = 1.457, γ = 0.02 и различных Ω (см. рис. 4).

хронное состояние. Кружки (B1) — неоднородное частично

Для данных значений параметров в системе суще-

синхронное состояние с одним максимумом |z(x)|, крести-

ствует однородное частично синхронное состояние с

ки (C1, C2) — с двумя максимумами, треугольники (D1,

Ω = Ω_hps ≈ -0.81854 и r = r_hps = 0.80482.

D2) — с тремя максимумами |z(x)|. Закрашенные (пустые)

На сечении Пуанкаре (r, v), которое определя-

символы — устойчивые (неустойчивые) режимы. Линии

ется условиями u = 0, u^′ > 0, ему соответствует

B2 и B3 — неоднородное частично-синхронное состояние

неподвижная точка c координатами (r_hps, 0). При

с одним максимумом |z(x)| соответственно с удвоенной и

увеличении параметра Ω данная неподвижная точ-

утроенной длиной среды

165

М. И. Болотов, Л. А. Смирнов, Е. С. Бубнова и др.

ЖЭТФ, том 159, вып. 1, 2021

ка претерпевает бифуркацию, в результате которой

шению к малым возмущениям на устойчивость во

возникают три неподвижные точки: эллиптическая

времени.

(r₁, 0) периода p = 1 и две седловые точки (r₂, v₂)

Далее, следуя общей логике, которой, в част-

и (r₂, -v₂). При этом замкнутым траекториям от-

ности, следовало изложение предыдущего раздела,

вечают квазипериодические решения системы (42)

проведем линейный анализ свойств устойчивости

(рис. 4a). Неподвижная точка (r₁, 0) соответству-

статичных конфигураций с неоднородным профи-

ет неоднородному частично синхронному состоянию

лем локального параметра порядка, что позволит

z = z₁(x) с одним максимумом модуля параметра

достичь более глубокого понимания динамики об-

порядка |z(x)|.

суждаемой среды и кооперативных процессов в ней.

При дальнейшем непрерывном изменении зна-

С данной целью линеаризуем записанное в своей

чения Ω на инвариантных траекториях в результа-

исходной форме интегро-дифференциальное урав-

те резонансов возникают периодические точки раз-

нение Отта - Антонсена (12), (13) вблизи одного из

личных периодов (рис. 4б). Причем в случае пере-

его стационарных решений (36), характеризующих-

крытия резонансов образуются области хаотическо-

ся параметром Ω и длиной L. Согласно стандартной

го блуждания [50]. На отображении Пуанкаре ря-

процедуре, представим Z(x, t) в виде

дом с сепаратрисами седловых точек в такой ситуа-

(

)

ции можно наблюдать так называемые стохастичес-

Z(x, t) = z(x) + Z(x, t) eiΩt,

(44)

кие слои (рис. 4б,в). Далее при Ω ≈ 0.648 из точ-

ки (r₁, 0) рождаются две эллиптические точки, а

где с помощью Z(x, t) обозначены присутствующие

она при этом становится седловой (рис. 4в). Об-

в комплексном поле Z(x, t) периодические по x сла-

ратим внимание, что существует множество непо-

бые отклонения от профиля z(x) [26, 31, 34]. Под-

движных точек отображения Пуанкаре с координа-

ставив (44) в (12), выполнив ряд преобразований с

тами (r, 0), которым соответствуют различные ста-

учетом (37) и сохранив лишь слагаемые первого по-

ционарные решения системы (12) и (15).

рядка малости по Z(x, t), получим

При дальнейшем увеличении параметра Ω все

∂Z

(

)

траектории (кроме устойчивых сепаратрис) вблизи

= -(γ + iΩ + h^∗z)Z +

H-H^∗z²

(45)

∂t

седловой точки (r₁, 0) быстро покидают ее окрест-

ность. Поиск неподвижной точки с помощью опи-

Здесь H(x, t) и Z(x, t) связаны посредством опера-

санного метода усложняется в силу того, что ее мак-

тора свертки с ядром (4), т.е. аналогично тому, как

симальный по модулю мультипликатор значитель-

H(x, t) выражается через Z(x, t) по формуле (13).

но превышает единицу. Аналогичное поведение на-

Выделим действительную и мнимую компоненты у

блюдается в окрестности остальных седловых точек

комплексной функции Z(x, t) = ζ₁(x, t) + iζ₂(x, t)

большего периода, которые расположены на оси v =

и перепишем равенство (45) как систему уравне-

= 0. Такого рода особенность связана с существен-

ний относительно вещественного вектора ζ(x, t) =

(

)_T

ным возрастанием длины возвратных траекторий

ζ₁(x, t), ζ₂(x, t)

непосредственно в трехмерном фазовом простран-

[

]

стве r, u, v.

∂

ζ(x, t) =

^M+

K ζ(x, t),

(46)

∂t

где

^M(x) — мультипликативный оператор:

4.3. Линейный анализ устойчивости

(

)(

)

стационарных неоднородных состояний

μ₁(x)

-μ₂(x)

ζ₁(x, t)

^Mζ(x, t) =

(47)

При изучении (как однородных, так и градиент-

μ₂(x) μ₁(x)

ζ₂(x, t)

ных) режимов с равномерно распределенной сте-

пенью синхронизации вдоль всей популяции (см.

а K(x) — интегральный оператор:

разд. 3) нами было установлено, что информа-

(

)

ции только о существовании состояний оказывается

κ₁₁(x) κ₁₂(x)

Kζ(x, t) =

недостаточно, чтобы предсказывать возможные сце-

κ₂₁(x) κ₂₂(x)

нарии долговременной эволюции ансамблей нело-

(

)

∫

кально связанных фазовых осцилляторов. Для это-

ζ₁(x, t)

G(x - x)

dx.

(48)

го еще дополнительно требуется исследовать соот-

ζ₂(x, t)

ветствующие пространственные структуры по отно-

166

ЖЭТФ, том 159, вып. 1, 2021

Пространственно-временные режимы в системе. ..

Здесь для удобства и краткости записи приведен-

рые оказываются необходимы для выявления истин-

ных выше представлений

^M(x) и

^K(x) были введе-

ных λ_p в случае γ = 0 (см. подробности в работах

ны следующие обозначения:

[31-33]). В итоге, с точки зрения анализа в термоди-

(

)

намическом пределе имеем еще одно преимущество

μ₁(x) = - Re

z(x)h^∗(x)

-γ,

(

)

в задаче с пространственным беспорядком (т. е. при

μ₂(x) = - Im

z(x)h^∗(x)

- Ω,

γ = 0).

(

)

κ₁₁(x) =

cosα - Re(e^iαz²(x))

/2,

(49)

Каждый из выделенных видов неоднородных со-

(

)

стояний отмечен своим типом маркеров. Причем за-

κ₁₂(x) =

sinα - Im(e^iαz²(x))

/2,

крашенные точки отвечают устойчивым режимам,

κ₂₁(x) =κ₁₂ - sinα, κ₂₂(x) = cosα - κ₁₁.

а пустые — неустойчивым. Видно, что ветвь неодно-

Из (46) непосредственно вытекает, что характер

родного частично синхронного режима B₁ рождает-

поведения малых возмущений Z(x, t) определяется

ся из прямой линии, с помощью которой на плоско-

собственными числами λ суммы

^M(x) +

^K(x) не за-

сти L, Ω отражен однородный частично синхронный

висящих от времени операторов

^M(x) и

^K(x). В

режим. Происходит это именно в тот момент, когда

полном спектре обычно в функциональном анали-

последний теряет устойчивость, т. е. в точке с абс-

зе выделяют непрерывную составляющую λ_e, со-

циссой L = L^∗hps там, где сплошная линия меняется

держащую в себе существенную часть всех значе-

на штриховую. Кривые B₂ (B₃) соответствует удво-

ний λ, и дискретную составляющую λ_p, к которой

енным (утроенному) неоднородным состояниям, для

принадлежат обособленные точки спектра λ. Стоит

которых длина среды в два (три) раза превыша-

отметить, что оператор

^K(x) является компактным

ет пространственный размер структур с ветви B₁,

для любого кусочно-гладкого ядра G(x) [34]. В силу

хотя профиль локального комплексного параметра

данного свойства существенная часть λ_e интересу-

порядка полностью совпадает с одним из распреде-

ющего нас набора собственных чисел λ комбинации

лений z(x), полученных при построении семейства

^M(x) +

^K(x) совпадает с соответствующей входя-

B₁. Несложно заметить, что на линии B₁ имеют-

щей в нее компонентой первого слагаемого

^M(x).

ся точки с такими L и Ω, что найденные при этих

Таким образом, получаем, что λ_e = μ₁(x) ± iμ₂(x).

значениях пространственные образования должны

Несложно проверить, что λ_e удовлетворяют усло-

быть устойчивыми, а значит, представляют собой

вию Re (λ_e) < 0. Следовательно, за линейную устой-

возможный наблюдаемый в процессе долговремен-

чивость пространственного профиля z(x) (и связан-

ной эволюции устанавливающийся режим поведе-

ного с ним распределения h(x)) отвечают только

ния системы. Данное обстоятельство подтверждает

значения из точечной части λ_p спектра λ.

и численное моделирование уравнений Отта - Антон-

Полученные с использованием описанных выше

сена. Следует отметить, что в зависимости от ве-

методов результаты поиска стационарных неодно-

личины γ переходы от однородного частично син-

родных решений уравнений Отта - Антонсена и ана-

хронного к кластерному режиму существенно раз-

лиза устойчивости соответствующих структур объ-

личаются. В случае сильных частотных расстроек

единены и показаны на рис. 5. Здесь представле-

(большие γ) (рис. 5б,в) переход происходит мягко.

ны зависимости Ω(L) для однородных частично син-

В случае же слабых частотных расстроек (малые γ)

хронных (ветвь A) и неоднородных с одним (ветвь

переход является жестким, имеет место гистерезис

B₁), двумя (ветви C₁ и C₂) и тремя (ветви D₁ и D₂)

(рис. 5а, см. область сопряжения ветвей A и B₁).

максимумами амплитуды |z(x)| параметра порядка

При увеличении параметра L состояния с одной

стационарных решений для α = 1.457 и нескольких

повышенной и одной пониженной областью коге-

значений γ: γ = 0.002, γ = 0.011 и γ = 0.020 (со-

рентности теряют свою устойчивость. Также рост

ответственно рис. 5а,б,в). В отличие от ситуации,

продольной длины ансамбля приводит к появлению

когда рассматриваются среды из идентичных эле-

режимов с большим числом кластеров с различной

ментов [26, 31-34], при наличии случайного разбро-

степенью фазовой синхронизации. В частности, из

са (беспорядка) в индивидуальных частотах осцил-

ветви B₂ рождается еще дополнительная ветвь ре-

ляторов можно достоверно рассчитать λ_p (по край-

шений, обозначенная нами как C₁. Для структур

ней мере те λ_p, для которых Re λ_p > 0) с примене-

этого типа характерно, что |z(x)| > 0, и, следова-

нием только стандартного метода дискретизации и

тельно, глобальный параметр порядка отличен от

замены операторов

^M(x) и

^K(x) матрицами боль-

нуля. Кривая C₁ заканчивается на семействе C₂, ко-

шой размерности, не задействуя при этом дополни-

торое сформировано также стационарными неодно-

тельных модификаций подобной процедуры, кото-

родными режимами с p = 2. Основное отличие со-

167

М. И. Болотов, Л. А. Смирнов, Е. С. Бубнова и др.

ЖЭТФ, том 159, вып. 1, 2021

стояний с ветви C₂ от образований, параметры кото-

ситуаций, рассмотренных при построении рис. 5, об-

рых лежат на линии C₁, состоит в том, что для них

разования с двумя явно выраженными, практически

|z(x)| в двух точках обращается в нуль, а собранное

не смещающимися, максимумами амплитуды поля

по всей популяции макроскопическое поле R рав-

Z(x, t) дольше всего наблюдаются при γ = 0.011.

няется нулю. С подобной ситуацией нам уже при-

ходилось сталкиваться, когда проводилось сравне-

5. ДИНАМИЧЕСКИЕ РЕЖИМЫ

ние однородных частично синхронных и градиент-

ДОЛГОВРЕМЕННОЙ ЭВОЛЮЦИИ

ных режимов. Если двигаться дальше, то из ветви

СИСТЕМЫ НЕЛОКАЛЬНО СВЯЗАННЫХ

B₃ рождаются семейства D₁ и D₂. Они соответству-

НЕИДЕНТИЧНЫХ ФАЗОВЫХ

ют структурам с p = 3 и переходят друг в друга.

ОСЦИЛЛЯТОРОВ

Так, двигаясь в сторону увеличения L, будем реги-

стрировать возникновение новых решений с после-

В данном разделе сначала еще раз остановимся

довательно возрастающим числом максимумов p.

на режиме со статичной картиной кластерной син-

Несмотря на то, что среди обнаруженных нами

хронизации (рис. 1ж,з), а затем перейдем к подроб-

состояний линейно устойчивыми (в строгом смыс-

ному описанию следующих типов таких динамиче-

ле) оказались лишь режимы с p = 1, для некоторых

ских неоднородных состояний, как бризерный кла-

решений с p > 1 показатели экспоненциального ро-

стерный режим (рис. 1и,к), нерегулярные состояния

ста являются малыми (∼ 10-3, 10-4). Поэтому сто-

с явно выраженной перемежаемостью (рис. 1л,м) и

ит ожидать, что все рассмотренные нами статичес-

без нее (рис. 1н,о). Представленные здесь результа-

кие неоднородные структуры играют важную роль

ты получены в рамках прямого численного моде-

в динамике исходной системы. Подобные ожидания

лирования системы (1)-(4). В качестве начальных

подтверждаются и численными расчетами, прове-

условий задавалось распределение фаз, восстанов-

денными на базе уравнений Отта - Антонсена (12),

ленное по одному из профилей z(x) с соответству-

(15). Моделирование начальной задачи показывает,

ющим значением Ω, которые, как обсуждалось в

что мезоскопические поля Z(x, t) и H(x, t) с высо-

предыдущем разделе, определяются длиной среды

кой долей вероятности переходят в обсуждаемые в

L при фиксированных параметрах α и γ. Выберем

текущем разделе устойчивые или слабо неустойчи-

для определенности в качестве величины параметра

вые состояния, которые наблюдаются в течение дли-

фазового сдвига α = 1.457.

тельных промежутков времени. Ниже (в следующем

разделе) внимание будет уделено результатам чис-

5.1. Статичная кластерная синхронизация

ленных расчетов, выполненных непосредственно в

рамках исходной модели (1)-(4), и исследованию то-

Обсудим прежде всего ситуацию, когда началь-

го, какие еще (уже динамические) режимы могут

ные распределения фаз формируются по стационар-

возникнуть в процессе распада статичных квазихи-

ным неоднородным решениям уравнений Отта - Ан-

мерных структур. В качестве заключительного за-

тонсена (12), (15) с числом максимумов p

= 1.

мечания здесь отметим, что степень беспорядка γ,

Как было указано ранее, на бифуркационных диа-

с одной стороны, приводит к стабилизации стацио-

граммах, представленных на рис. 5, им соответ-

нарных с точки зрения распределения абсолютной

ствуют ветви B₁. Координата каждого максиму-

величины локального параметра порядка образова-

ма амплитуды комплексного поля Z(x, t) задает

ний, но с другой стороны, γ влияет на длину за-

положение середины группы с повышенной степе-

мкнутых траекторий системы (42) (см. рис. 5), а

нью фазовой когерентности и одновременно центра

та, в свою очередь, во многом определяет положе-

кластера с частотной синхронизацией осцилляторов

ние дискретных собственных значений λ_p оператора

(рис. 1ж,з), т. е. набора элементов, которые имеют

^M(x) +

^K(x) на комплексной плоскости Re λ, Im λ.

одинаковые средние частоты 〈ϕ˙_n〉. Чем ближе ве-

Согласно проведенному анализу, чем длиннее среда,

личина max |Z(x, t)| к единице, тем более выраже-

тем выше шансы, что найдутся λ_p с Re λ_p > 0. Та-

на синхронность осцилляторов. Отметим, что для

ким образом, наиболее устойчивыми являются неод-

идентичных частиц (γ = 0) эти две макроскопи-

нородные состояния со статичными кластерами фа-

ческие фракции совпадают и образуют абсолютно

зовой синхронизации в случае промежуточных зна-

скоррелированный участок среды с |Z(x, t)| = 1 и

чений параметра γ, ответственного за разброс в ин-

〈 ϕ〉 = Ω.

дивидуальных характеристиках составляющих сре-

Рассмотрим случай γ = 0.002 (рис. 5а). Тогда

ду осцилляторных элементов. Так, например, среди

ветвь B₁ возникает при Ω = Ω^∗hps = -0.9276 (L^∗hps =

168

ЖЭТФ, том 159, вып. 1, 2021

Пространственно-временные режимы в системе. ..

= 10.5141) из однородного частично синхронного ре-

жима, а отвечающая ей зависимость Ω(L) являет-

ся неоднозначной, что характерно для ситуаций с

бистабильностью и гистерезисом. На данной ветви

существует устойчивый интервал -0.9241 < Ω <

< -0.6851 (3.3882 < L < 7.0). На рис. 6а пред-

ставлены профили |z(x)| и |h(x)|, а на рис. 6б со-

ответствующее им распределение мгновенных фаз

ϕ_n для Ω = -0.7. Рисунок 6в содержит спектр соб-

ственных значений λ_e и λ_p, где в силу инвариант-

ности к сдвигу по пространству x → x + x₀ систе-

мы (12), (15) существует одно дискретное нулевое

собственное значение, при этом для остальных вы-

полняется условие Re λ_p < 0, что говорит об устой-

чивости исследуемого режима. На рис. 6г изобра-

жена пространственно-временная динамика величи-

ны |Z(x, t)|, полученная в результате прямого чис-

ленного моделирования системы (1)-(4) с конечным

числом элементов N = 4096. На рис. 6д представ-

лены средние частоты осцилляторов 〈ϕ˙_n〉. Отчетли-

во виден один кластер синхронных по частоте эле-

ментов, основная группа которых расположена по-

середине интервала [0, L), а также явно выделяется

максимум в профиле модуля локального параметра

порядка Z(x, t). Данный режим при γ = 0 транс-

формируется в устойчивую однокластерную химеру

(см., например, работы [31-33]).

При увеличении γ степень фазовой когерентнос-

ти вдоль всей популяции в целом падает. Также со-

кращается (в процентном соотношении) и количе-

ство осцилляторов, принадлежащих частотно син-

хронному кластеру, т. е. все меньшее число элемен-

тов ансамбля в нем имеют равные средние частоты.

Рис. 6. (В цвете онлайн) а-д) Устойчивое неоднородное со-

Так, например, в случае γ = 0.02 (см. рис. 5в) ста-

стояние при α = 1.457, γ = 0.002, Ω = -0.70, L ≈ 6.4135.

ционарный неоднородный режим с L = 6.5861 и Ω =

е-к) Неустойчивое неоднородное состояние эволюциони-

= -0.68 должен быть устойчивым по отношению к

рует к бризерному режиму при α = 1.457, γ = 0.002,

малым возмущениям, так как выбранное нами зна-

Ω = -0.685, L ≈ 7.0047. Начальные условия соответ-

чение длины среды попадает в интервал устойчивос-

ствуют ветви B1 бифуркационной диаграммы на рис. 5а.

ти L^∗hps < L < L∗1, где L^∗hps = 3.83422, L∗1 = 8.232.

а,е) Профили |z| (синяя сплошная линия), |h| (черная

Результаты анализа в рамках развитых в разд. 4

штриховая линия), определенные методом, описанным в

подходов и прямого численного моделирования си-

разд. 5. б,ж) Начальные распределения фаз ϕn, которые

стемы (1)-(4) приведены на рис. 7а-д. Сравнивая

восстановлены по локальным параметрам порядка Z(x).

данные фрагменты рис. 7 с аналогичными панеля-

в,з) Спектр λ линейных возмущений для соответствующих

стационарных решений Z(x) уравнений Отта - Антонсена.

ми рис. 6, несложно заметить указанные особеннос-

Существенная λe (синие кружки) и точечная λp (красные

ти, обусловленные изменением уровня беспорядка в

ромбы) составляющие спектра λ. г,д,и,к) Результаты пря-

среде.

мого численного моделирования системы (1)-(4). г,и) По-

ведение во времени абсолютной величины комплексного

5.2. Бризерный кластерный режим

поля Z(xn, t). д,к) Средние частоты осцилляторов 〈ϕ˙n〉

Вернемся опять к случаю γ = 0.002. При крити-

ческом значении Ω∗1 ≈ -0.6851 (L∗1 ≈ 7.0) стационар-

ный неоднородный режим теряет устойчивость (см.

169

М. И. Болотов, Л. А. Смирнов, Е. С. Бубнова и др.

ЖЭТФ, том 159, вып. 1, 2021

а также в форме прямоугольника [51]. Для ансам-

блей, состоящих из фазовых осцилляторов с соб-

ственными частотами, распределенными по закону

Коши, подобные решения с периодическим поведе-

нием локальных мезоскопических полей были рас-

смотрены в работах [37, 43]. В работе [43] показано,

что такие бризерные режимы реализуются в наибо-

лее широких диапазонах управляющих параметров,

если ответственная за степень беспорядка величина

параметра разброса γ мала, однако отлична от нуля,

что справедливо и для исследуемой нами ситуации.

Отметим также, что бризерные режимы наблюда-

лись в двумерных решетках связанных фазовых ос-

цилляторов [52, 53].

Когда γ = 0.02, при превышении критической

длины среды L∗1 = 8.232, начиная с которой состоя-

ние со статичной кластерной синхронизацией стано-

вится неустойчивым, бризерный режим регистриру-

ется только в очень узком интервале значений L,

так что его довольно трудно выявить. Однако на-

личие такого режима оказывает ощутимое влияние

на переходные процессы в рассматриваемой систе-

ме. В частности, на рис. 7е-к отчетливо видно, что,

несмотря на существенно более сложный (нерегу-

лярный) характер поведения тех движений, которые

устанавливаются в результате развития неустойчи-

вости структуры, изображенной на рис. 7е, на от-

носительно протяженных временных отрезках име-

ет место квазипериодическая динамика, всеми свои-

ми атрибутами напоминающая бризерный кластер-

ный режим. Подобная динамика прерывается рез-

Рис. 7. (В цвете онлайн) То же, что на рис. 6. а-д) Устой-

ким смещением положений областей повышенной и

чивое неоднородное состояние при α = 1.457, γ = 0.02,

пониженной фазовой когерентности в пространстве,

Ω = -0.68, L ≈ 6.5861. е-к) Неустойчивое неоднород-

после чего снова восстанавливается (рис. 7и). Та-

ное состояние эволюционирует к режиму перемежаемости

кого рода чередование продолжительных колебаний

при α = 1.457, γ = 0.02, Ω = -0.64, L ≈ 8.8373. На-

структуры мезоскопических полей и быстрых (скач-

чальные условия соответствуют ветви B1 бифуркационной

диаграммы на рис. 5в

кообразных) изменений, происходящих за короткие

(в масштабах численных расчетов) промежутки вре-

рис. 6е-к). Два комплексно-сопряженных собствен-

мени, можно интерпретировать как явление пере-

ных значения из спектра λ_p при этом пересекают

межаемости. Данное явление служит одним из ме-

мнимую ось (рис. 6з). Система при этом переходит к

ханизмов перехода к развитой турбулентности, что

бризерному кластерному режиму, когда существуют

фактически и происходит при дальнейшем увеличе-

несколько частотно синхронных кластеров (рис. 6к).

нии длины среды. Система начинает демонстриро-

Причем усредненные величины H(x, t) и Z(x, t) в

вать сложную пространственно-временную динами-

каждой точке пространства испытывают периоди-

ку с нерегулярным поведением усредненных комп-

ческие колебания (рис. 6и). Заметим, что данные

лексных полей Z(x, t) и H(x, t), о чем пойдет речь

состояния в случае сред, состоящих из идентичных

ниже.

элементов, т. е. при γ = 0, переходят в бризерные хи-

меры, которые были обнаружены в системах с раз-

5.3. Нерегулярные режимы

личными типами определяющих нелокальную связь

ядер, заданных как в виде экспоненциально убыва-

Еще раз подчеркнем, что во всех рассмотрен-

ющих [32,33], так и гармонических функций [26,34],

ных нами ситуациях, когда распределение модуля

170

ЖЭТФ, том 159, вып. 1, 2021

Пространственно-временные режимы в системе. ..

комплексного параметра порядка имеет один или

несколько максимумов и нигде не достигает нуля,

процесс разрушения регулярных с точки зрения ме-

зоскопических полей статичных неоднородных со-

стояний протекает всегда по схожему сценарию. При

этом два комплексно-сопряженных значения, при-

надлежащих дискретному спектру λ_p, пересекают

мнимую ось, что указывает на осцилляторный ха-

рактер неустойчивости. Здесь можно провести пря-

мую аналогию с бифуркацией Андронова - Хопфа

[54]. В частности, на справедливость такой интер-

претации указывает то, что при определенных соче-

таниях величин α, γ и L удается достоверно заре-

гистрировать переход к бризерным кластерным ре-

жимам, и только потом при увеличении длины сре-

ды L распад состояний, отвечающих стационарным

квазихимерным решениям уравнения Отта - Антон-

сена (12), (15), заканчивается установлением слож-

ных динамических режимов, отличительными чер-

тами которых являются дрейф и резкие смещения

положений областей с повышенной и пониженной

степенью фазовой когерентности. Стоит обратить

внимание на то, что в большинстве случаев (две

популяции, с одной стороны, достаточно протяжен-

ные, а с другой, обладающие конечным размером)

число локальных экстремумов в пространственных

зависимостях амплитуд усредненных комплексных

полей в каждый момент времени сохранятся (см.

рис. 8г,и).

В данном разделе сначала выделим и обсудим

более детально основные особенности нерегулярных

неоднородных режимов на примере ситуации, ког-

Рис. 8. (В цвете онлайн) То же, что на рис. 6. Неустойчи-

да γ = 0.011, а начальные условия для элементов

вые неоднородные решения с двумя максимумами |z(x)|

ансамбля формируются с использованием стацио-

(для разных значений Ω и L) эволюционируют к режи-

му перемежаемости при α = 1.457, γ = 0.011. Началь-

нарных решений уравнения Отта - Антонсена (12),

ные условия соответствуют ветви C1 при Ω = -0.625,

(15), для которых p = 2, а соответствующие вет-

L ≈ 14.1367 (фрагменты (а-д)) и C2 при Ω = -0.566,

ви на рис. 5б отмечены как C₁ и C₂. С учетом

L ≈ 12.7904 (фрагменты (е-к)) бифуркационной диаграм-

вышесказанного и из приведенного ниже описания

мы на рис. 5б

можно сделать вывод и о других возможных нере-

гулярных режимах (развивающихся из статичных

кластерных состояний с другим числом максимумов

|z(x)|). Примеры типичных профилей |z(x)| локаль-

моделировании демонстрирует переход к сложной

ного параметра порядка и связанных с ними распре-

пространственно-временной динамике (в том числе,

делений фаз ϕ_n представлены на рис. 8а,е и 8б,ж.

комплексных мезоскопических полей). Однако от-

Соответствующие им спектры λ композитного опе-

четливо видно, что на достаточно продолжитель-

ратора

^M(x) +

^K(x) линейной задачи (46) на устой-

ных временных интервалах динамика возвращается

чивость отображены на рис. 8в,з. Нетрудно заме-

к состояниям, в которых выделяются две квазиста-

тить, что среди собственных значений λ имеются

тичные области с высокой степенью когерентности и

такие, для которых Re λ > 0. Хотя отдельно заме-

два (также квазистатичных) участка с практически

тим, что Re λ ∼ 10-2. Таким образом, данные ре-

асинхронным поведением осцилляторов (рис. 8г,и).

жимы являются слабонеустойчивыми, и ансамбль

Причем в конце продолжительных отрезков време-

фазовых осцилляторов (1)-(4) в прямом численном

ни распределение амплитуды Z(x, t) начинает рас-

171

М. И. Болотов, Л. А. Смирнов, Е. С. Бубнова и др.

ЖЭТФ, том 159, вып. 1, 2021

качиваться и уходить от близкой структуры к стаци-

онарной через колебания, что как раз можно объяс-

нить осцилляторным характером развития неустой-

чивости. Таким образом, система демонстрирует пе-

ремежаемость регулярных и хаотических режимов.

Это связано с тем, что среди найденных нами реше-

ний уравнений (12), (15), отвечающим ветвям C₁ и

C₂ на рис. 5, существуют слабонеустойчивые распре-

деления, которым могут быть поставлены в соответ-

ствие относительно простые переходные долгоживу-

щие режимы движения. На профиле средних час-

тот 〈ϕ˙_n〉 (рис. 8д,к) в данном случае не удается вы-

делить кластеры частотно синхронных осциллято-

ров, так как за достаточно продолжительный проме-

жуток времени (интервал усреднения) каждый эле-

мент успевает побывать как в областях с высокой

степенью когерентности фаз, так и в практически

асинхронных участках среды. Это приводит к тому,

что средние частоты имеют практически однород-

но зашумленный профиль, сосредоточенный вблизи

кривой, в форме которой однако прослеживаются

структурные особенности, обусловленные тем, что

популяция достаточно долго находится в окрестнос-

ти одного из слабонеустойчивых образований, об-

суждаемых в разд. 4.

Если профиль |z(x)|, определяющий начальные

значения, является сильнонеустойчивым, то систе-

ма демонстрирует хаотическую пространственную

динамику, которая уже не прерывается выходом на

квазистатичные регулярные структуры. В качестве

примера продемонстрируем случай γ = 0.02 для

Рис. 9. (В цвете онлайн) То же, что на рис. 6. Неустойчи-

неустойчивых неоднородных состояний с тремя мак-

вые неоднородные решения с тремя максимумами |z(x)|

симумами |z(x)|. Рисунки 9а-д соответствуют реше-

(для разных значений Ω и L) эволюционируют к турбу-

нию, расположенному на ветви D₁, а рис. 9е-к —

лентному режиму при α = 1.457, γ

= 0.020. Началь-

решению, расположенному на ветви D₂. Здесь со-

ные условия соответствуют ветви D1 при Ω = -0.66,

стояния, соответствующие режиму с тремя областя-

L ≈ 21.9922 (фрагменты (а-д)) и D2 при Ω = -0.66,

ми повышенной фазовой когерентности, достаточ-

L ≈ 20.7145 (фрагменты (е-к)) бифуркационной диаграм-

но быстро разрушаются, и локальный параметр по-

мы на рис. 5в

рядка начинает демонстрировать нерегулярную ди-

намику (рис. 9г,и). Распределение средних частот

〈 ϕ_n〉 при этом оказывается равномерно зашумлен-

наблюдаться устойчивые неоднородные состояния с

ным (так же, как в случае перемежаемости). Од-

регулярным поведением усредненных полей. Вместо

нако в отличии от рис. 8д,к на рис. 9д,к значения

этого реализуются сложные пространственно-вре-

〈 ϕ_n〉 распределены практически вдоль прямой ли-

менные режимы с хаотической динамикой парамет-

нии с одинаковой по величине степенью разброса,

ра порядка Z(x, t) двух типов. В первом случае име-

что указывает на отсутствие существенных разли-

ет место перемежаемость, при которой чередуются

чий между пространственными точками среды пос-

достаточно протяженные временные отрезки с ква-

ле усреднения по времени.

зистатичным распределением мезоскопических ха-

рактеристик ансамбля и с относительно быстрым

Таким образом, в системе (1)-(4) неидентичных

нелокально-связанных фазовых осцилляторов при

смещением областей с повышенной и пониженной

степенью синхронизации, во втором — чисто турбу-

γ < cosα/2 и γ ≳ cos3 α, начиная с некоторого

критического значения длины среды L, перестают

лентный режим.

172

ЖЭТФ, том 159, вып. 1, 2021

Пространственно-временные режимы в системе. ..

6. ЗАКЛЮЧЕНИЕ

интегро-дифференциальное уравнение Отта - Ан-

тонсена было преобразовано к самосогласованной

системе уравнений в частных производных. Это

Подведем кратко итоги работы и сформулиру-

позволило предложить метод эффективного поис-

ем ее основные результаты. Нами был рассмотрен

ка стационарных (равномерно вращающихся) неод-

ансамбль, состоящий из большого числа нелокаль-

нородных пространственных структур, которые в

но-связанных неидентичных фазовых осциллято-

пределе одинаковых элементов переходят в химер-

ров, которые равномерно распределены на отрезке с

ные состояния. Основная идея данного метода со-

периодическими граничными условиями. При этом

стоит в построении замкнутых траекторий в фазо-

предполагалось, что собственные частоты задают-

вом пространстве вспомогательной системы обыкно-

ся независимо случайным образом согласно распре-

венных дифференциальных уравнений третьего по-

делению Лоренца, а взаимодействие между осцил-

рядка. Отметим, что подобным периодическим ре-

ляторами ослабевает по экспоненциальному закону.

шениям несложно поставить в соответствие непо-

Отметим, что данная конфигурация эквивалентна

движные точки двумерного отображения. После то-

ситуации, когда элементы располагаются на кольце.

го, как были найдены примеры неоднородных про-

Основными параметрами такой системы являются

филей локального комплексного параметра порядка

величина фазового сдвига, определяющая тип свя-

и по ним восстановлены распределения фаз, анали-

зи (притягивающий, нейтральный или отталкиваю-

зировалась устойчивость полученных состояний как

щий), полуширина распределения собственных час-

с помощью расчета спектра линейных возмущений,

тот, задающая степень их неоднородности, а также

так и с использованием прямого численного моде-

длина осцилляторной среды. Основная цель работы

лирования. Для проведения такого рода анализа по-

состояла в том, чтобы в широком диапазоне зна-

требовалось, в частности, разработать и адаптиро-

чений указанных параметров исследовать и клас-

вать процедуру расчета непрерывной и дискретной

сифицировать пространственно-временные структу-

составляющих спектра собственных значений лине-

ры, возникающие в процессе долговременной эволю-

аризованного вокруг одного из стационарных обра-

ции обсуждаемого ансамбля.

зований интегро-дифференциальное уравнение От-

С использованием процедуры усреднения было

та - Антонсена.

получено динамическое уравнение Отта - Антонсе-

на для локального комплексного параметра поряд-

В итоге, установлено, что среди неоднородных

ка, характеризующего степень фазовой скоррели-

состояний со статичным распределением областей с

рованности элементов в малой окрестности произ-

повышенной и пониженной степенью синхронизации

вольной точки рассматриваемой осцилляторной сре-

устойчивыми (в строгом смысле) являются только

ды. В рамках этого уравнения, прежде всего, бы-

те режимы, для которых у профиля локального па-

ли найдены стационарные (равномерно вращающи-

раметра порядка имеется только один максимум.

еся) режимы с постоянным по модулю значением ло-

Однако среди остальных найденных нами структур

кального параметра порядка. Установлено, что сре-

встречаются слабонеустойчивые (транзиентные) об-

ди таких состояний можно выделить два вида: одно-

разования. С помощью прямого численного моде-

родные и градиентные. Далее, была определена их

лирования в рамках исходной системы удалось под-

устойчивость с помощью анализа спектра собствен-

твердить данные выводы и показать, что обсужда-

ных значений соответствующих линеаризованных

емые квазихимерные режимы (как предельные, так

уравнений. Показано, что при больших значениях

и транзиентные) вращения играют важную роль в

полуширины функции распределения собственных

динамике ансамбля из большого числа неиндентич-

частот реализуется только полностью асинхронный

ных нелокально связанных фазовых осцилляторов с

режим с нулевым средним полем. Если же полуши-

экспоненциальным типом взаимодействия, так как

рина случайного разброса становится меньше неко-

одни из них устанавливаются и в последствии не

торой пороговой величины, то данное состояние пе-

разрушаются, а другие возникают в виде переход-

рестает быть устойчивым, а в системе могут наблю-

ных продолжительных процессов между интервала-

даться как однородные, так и градиентные частич-

ми со сложным нерегулярным поведением усреднен-

но синхронные режимы в зависимости от размеров

ных полей. Кроме того, помимо подобной переме-

среды и фазового сдвига.

жаемости регулярных и хаотических коллективных

Воспользовавшись тем, что взаимодействие меж-

движений для протяженных сред численные расче-

ду элементами убывает экспоненциальным образом,

ты позволили выделить и описать такие состояния

173

М. И. Болотов, Л. А. Смирнов, Е. С. Бубнова и др.

ЖЭТФ, том 159, вып. 1, 2021

долговременной эволюции изучаемой системы, как

15.

C. R. Laing, J. Math. Neurosci. 8, 4 (2018).

бризерная кластерная синхронизация и развитый

16.

J. Acebron, L. Bonilla, C. P. Vicente, F. Ritort, and

турбулентный режим.

R. Spigler, Rev. Mod. Phys. 77, 137 (2005).

Финансирование. Работа выполнена при

17.

F. A. Rodrigues, T. K. D. Peron, P. Ji, and J. Kurths,

Phys. Rep. 610, 1 (2016).

поддержке Российского научного фонда (проект

№19-12-00367) (разд. 1 и 2), Министерства науки и

18.

S. Gupta, A. Campa, and S. Ruffo, Statistical Physics

высшего образования РФ (проект № 0729-2020-0036)

of Synchronization, Springer International Publishing

(разд.

3), а также при поддержке Российского

(2018).

фонда фундаментальных исследований (проект

19.

S. Watanabe and S. H. Strogatz, Phys. Rev. Lett. 70,

№19-52-12053) (разд. 4 и 5).

2391 (1993).

20.

E. Ott and T. M. Antonsen, Chaos 18, 037113 (2008).

ЛИТЕРАТУРА

21.

E. Ott and T. M. Antonsen, Chaos 19, 023117 (2009).

G. V. Osipov, J. Kurths, and Ch. Zhou, Synchroniza-

22.

B. Pietras and A. Daffertshofer, Chaos 26, 103101

tion in Oscillatory Networks, Springer Verlag, Berlin

(2016).

(2007).

23.

D. Chowdhury and M. C. Cross, Phys. Rev. E 82,

V. S. Afraimovich, V. I. Nekorkin, G. V. Osipov,

016205 (2010).

and V. D. Shalfeev, Stability, Structures and Cha-

os in Nonlinear Synchronization Networks, World

24.

M. J. Panaggio and D. M. Abrams, Nonlinearity 28,

Scientific, Singapore (1994).

R67 (2015).

25.

N. Yao and Z. Zheng, Int. J. Mod. Phys. B 30,

J. Pantaleone, Amer. J. Phys. 70, 992 (2002).

1630002 (2016).

S. Chhabria, K. A. Blaha, F. D. Rossa, and F. Sor-

26.

O. E. Omel’chenko, Nonlinearity 31, R121 (2018).

rentino, Chaos 28, 111102 (2018).

27.

S. Majhi, B. K. Bera, D. Ghosh, and M. Perc, Phys.

J. Machowski, J. W. Bialek, and J. R. Bumby, Power

Life Rev. 28, 100 (2019).

System Dynamics: Stability and Control, John Wiley

and Sons (2002).

28.

E. Schöll, A. Zakharova, and R. G. Andrzejak,

Chimera States in Complex Networks, Lausanne:

P. J. Menck, J. Heitzig, J. Kurths, and H. J. Schelln-

Frontiers Media SA (2020).

huber, Nature Commun. 5, 3969 (2014).

29.

E. Schöll, Eur. Phys. J. Special Topics 225, 891-919

S. Ryu, W. Yu, and D. Stroud, Phys. Rev. E 53, 2190

(2016).

(1996).

30.

A. E. Motter, Nature Phys. 6, 164 (2010).

Z. Zheng, B. Hu, and G. Hu, Phys. Rev. E 57, 1139

(1998).

31.

L. Smirnov, G. Osipov, and A. Pikovsky, J. Phys. A:

Math. Theor. 50, 08LT01 (2017).

S. Homma and S. Takeno, Progr. Theor. Phys. 72, 4

(1984).

32.

М. И. Болотов, Л. А. Смирнов, Г. В. Осипов,

А. С. Пиковский, Письма в ЖЭТФ 106, 393

10.

S. Takeno and S. Homma, Progr. Theor. Phys. 77, 3

(2017).

(1987).

33.

M. I. Bolotov, L. A. Smirnov, G. V. Osipov, and

11.

A. Pikovsky, M. Rosenblum, and J. Kurths, Synch-

A. Pikovsky, Chaos 28, 045101 (2018).

ronization: a Universal Concept in Nonlinear Scien-

34.

O. E. Omel’chenko, Nonlinearity 26, 9 (2013).

ces, Cambridge University Press, Cambridge (2001).

35.

M. Wolfrum, O. E. Omel’chenko, S. Yanchuk, and

12.

Y. Kuramoto, Chemical Oscillations, Waves, and

Y. L. Maistrenko, Chaos 21, 013112 (2011).

Turbulence, Springer, Berlin, Heidelberg (1984).

36.

G. B. Ermentrout, SIAM J. Appl. Math. 52, 1665

13.

A. Pikovsky and M. Rosenblum, Chaos 25, 097616

(1992).

(2015).

37.

C. R. Laing, Physica D 238, 1569 (2009).

14.

E. Brown, J. Moehlis, and P. Holmes, Neural Comp.

16, 4 (2004).

38.

C. R. Laing, Chaos 52, 013113 (2009).

174