ЖЭТФ, 2021, том 159, вып. 2, стр. 371-380
© 2021
КОНВЕКЦИЯ КОЛЛОИДНОЙ СУСПЕНЗИИ
В ГОРИЗОНТАЛЬНОМ СЛОЕ ПРИ НАГРЕВЕ СНИЗУ
С УЧЕТОМ ВЗАИМОДЕЙСТВИЯ НАНОЧАСТИЦ
И. Н. Черепанов, Б. Л. Смородин*
Пермский государственный национальный исследовательский университет
614990, Пермь, Россия
Поступила в редакцию 17 сентября 2020 г.,
после переработки 7 октября 2020 г.
Принята к публикации 8 октября 2020 г.
В случае горизонтального слоя коллоидной суспензии изучены линейная неустойчивость и двумерные
нелинейные конвективные течения стратифицированной в поле тяжести коллоидной суспензии при учете
взаимодействия частиц. Получены зависимости порога возникновения колебательной конвекции, частоты
нейтральных колебаний и критического волнового числа от среднего значения объемной доли примеси.
Нелинейные слагаемые в диффузионном и седиментационном потоках, отражающие взаимодействие на-
ночастиц, приводят к понижению среднего поперек слоя градиента концентрации и снижению порога
возникновения конвекции и частоты нейтральных колебаний по сравнению с идеальным коллоидным
раствором. Проведено численное моделирование конечно-амплитудного течения в виде бегущей волны.
В отличие от случая молекулярных жидкостей и идеальных коллоидных растворов пространственная
структура поля концентрации хорошо описывается первой гармоникой и имеет слабый пространствен-
ный ангармонизм.
DOI: 10.31857/S0044451021020164
растворах, во многих исследованиях конвекции в
подобных средах они рассматриваются как одно-
родные, поскольку предполагается, что существен-
1. ВВЕДЕНИЕ
ные неоднородности в распределении примеси, обу-
В однородной жидкости, заполняющей горизон-
словленные термодиффузией, магнитофорезом и се-
тальный слой, под влиянием вертикального гради-
диментацией наночастиц примеси возникают толь-
ента температуры возможно состояние механиче-
ко на диффузионных временах, значительно превы-
ского равновесия, когда макроскопическое движе-
шающих тепловое характерное время. Тем не ме-
ние жидкости отсутствует, а передача тепла осу-
нее имеются экспериментальные данные по конвек-
ществляется только за счет молекулярного перено-
тивным течениям коллоидных суспензий, которые
нельзя объяснить с точки зрения модели однород-
са. При нагреве снизу и достаточно большой раз-
ности температуры данное состояние становится
ной жидкости [5-7].
неустойчивым, возникающая неоднородность плот-
Теоретический анализ конвекции в плоском слое
ности благодаря силам плавучести приводит к фор-
коллоида проведен в работах [8,9]. Однако он спра-
мированию конвективного течения [1, 2].
ведлив только для слабоконцентрированных раство-
В случае неоднородных по составу жидкостей
ров. Как показывают исследования, в коллоидах
(молекулярных смесей и коллоидных суспензий) по-
проявляется довольно сильная зависимость вязкос-
является дополнительный механизм формирования
ти от концентрации [10], а также значительное от-
неоднородности плотности за счет перераспреде-
клонение закона диффузии от классического зако-
ления их компонент [1-4]. Благодаря тому, что в
на Фика [11, 12]. Анализ влияния концентрацион-
коллоидных суспензиях коэффициент диффузии на
ной зависимости вязкости на конвекцию коллоид-
несколько порядков меньше, чем в молекулярных
ного раствора в плоском слое при подогреве сни-
зу был проведен в работе [13]. Учет неоднородности
* E-mail: bsmorodin@yandex.ru
вязкости смеси приводит к понижению порога кон-
371
12*
И. Н. Черепанов, Б. Л. Смородин
ЖЭТФ, том 159, вып. 2, 2021
вективной устойчивости. Несмотря на сильную за-
ординат направлена вдоль горизонтальных границ
висимость вязкости от концентрации, влияние дан-
слоя, ось z — перпендикулярно им. В поле тяжес-
ного эффекта на порог устойчивости механическо-
ти возникает поток примеси наночастиц, направ-
го равновесия оказался слабым. Значительные от-
ленный к нижней границе. Поскольку к горизон-
клонения критического числа Рэлея от модели с по-
тальным границам слоя приложен градиент темпе-
стоянной вязкостью наблюдаются только при очень
ратур δΘ/h = (θbottom - θtop)/h > 0, в смеси при
большой неоднородности смеси.
достаточно большом его значении действует и дру-
Теоретическое исследование диффузии твердых
гой (конвективный) механизм транспорта наноча-
частиц представлено в работе [14], в которой полага-
стиц. Плотность коллоидного раствора зависит от
ется, что энергия Гиббса раствора в целом должна
объемной доли ϕ примеси по закону
определяться конфигурационным интегралом час-
ρ = ρf(1 - ϕ) + ρpϕ,
(1)
тиц примеси, который может быть вычислен для
частиц в пустоте. Данная теория была развита в ра-
где ρ — плотность смеси в целом, ρf — плотность
ботах [15,16].
жидкости носителя, ρp — плотность частиц. Урав-
Сравнительный анализ различных моделей га-
нение состояния коллоидной суспензии при слабом
за твердых сфер, проведенный в работе [17], пока-
отклонении температуры θ и объемной концентра-
зал, что в области умеренных значений объемной
ции ϕ от некоторых средних значений θ0, ϕ0 можно
доли частиц ϕ вириальное разложение и приближе-
аппроксимировать линейной зависимостью:
ние Карнагана - Стерлинга дают практически иден-
ρ = ρ0 (1 - α(θ - θ0) + β(ϕ - ϕ0)),
(2)
тичные результаты.
Рассмотрение коллоидов с точки зрения теории
где α и β — положительные коэффициенты тепло-
слабых растворов проведено в работе [12]. Отличие
вого и концентрационного расширения смеси соот-
данной теории от подхода [14] заключается в том,
ветственно:
что проводится разложение энергии Гиббса по сте-
1 ∂ρ
1
∂ρ
ρp - ρf
пеням концентрации частиц примеси без учета рас-
α=-
,
β=
=
(3)
ρ0 ∂T
ρ0 ∂ϕ
ρ0
смотрения конкретных видов межчастичных взаи-
модействий. Последовательное применение теории
В концентрированных коллоидах поток частиц не
слабых растворов [12] с учетом характерных особен-
подчиняется классическому закону Фика, в кото-
ностей твердых частиц приводит к уравнениям, да-
ром полагается линейная зависимость потока час-
ющим распределения концентрации, схожие с при-
тиц от градиента концентрации. Для описания по-
веденными в [14]. Однако стоит отметить ряд отли-
токов частиц используем модель, предложенную в
чий. В теории [12] в химическом потенциале частиц
[12], в которой поток частиц для случая умеренных
примеси добавочное слагаемое зависит от плотности
концентраций (ϕ3 ≪ 1)) имеет вид
смеси как целого, что приводит к появлению допол-
[
]
1
нительного множителя (1 - ϕ).
Jϕ = -D (1 + pϕ)∇ϕ +
ϕ(1 - ϕ)n
,
(4)
lsed
Данная работа посвящена исследованию конвек-
ции коллоидной суспензии в горизонтальном слое с
где D — коэффициент диффузии наночастиц, p —
учетом нелинейного закона диффузионного и седи-
параметр, определяемый свойствами суспензии,
ментационного потоков наночастиц, предложенного
lsed =kbTδρVg
— длина седиментации [18], V — объем
в [12].
частиц, kb — постоянная Больцмана, T — абсолют-
ная температура, δρ = ρp - ρf . Для коллоидных
растворов p ≈ 8.
2. ПОСТАНОВКА ЗАДАЧИ
Система уравнений тепловой конвекции колло-
идной суспензии примет вид
Рассмотрим горизонтальный слой толщиной h,
∂v
1
заполненный коллоидным раствором (коллоидной
+ (v ∇)v = -
∇P + νΔv +
∂t
ρ
суспензией), расположенный в поле тяжести g =
= -gn (n — единичный вектор, направленный
+ (1 - α(θ - θ0) + β(ϕ - ϕ0))g,
(5)
вверх) и подогреваемый снизу. На горизонталь-
∂θ
+ (v · ∇)θ = χΔθ,
(6)
ных идеально теплопроводных и непроницаемых
∂t
для примеси границах слоя выполняется условие
∂ϕ
+ div(ϕv) = -D∇Jϕ,
(7)
прилипания смеси. Ось x декартовой системы ко-
∂t
372
ЖЭТФ, том 159, вып. 2, 2021
Конвекция коллоидной суспензии в горизонтальном слое. ..
где v — скорость течения, P — давление, χ — тем-
времени — h2/χ, скорости — χ/h, температуры —
пературопроводность, D — коэффициент диффузии
δΘ, концентрации — ϕ0, давления — ρχ2/h2. Тогда
наночастиц. Несмотря на неоднородность плотно-
имеем
сти, создаваемую за счет перепадов концентрации,
∂Φ
∂Ψ ∂Φ
∂Ψ ∂Φ
жидкость можно считать несжимаемой. Для под-
+
-
=
∂t
∂x ∂z
∂z ∂x
тверждения этого рассмотрим уравнение неразрыв-
[
]
∂θ
∂ϕ
ности:
= Pr ΔΦ + R
- Bl
,
(12)
∂ρ
∂x
∂x
+ div(ρv) = 0.
(8)
∂t
Φ = ΔΨ,
(13)
Учтем зависимость плотности от температуры и
∂θ
∂Ψ ∂θ
∂Ψ ∂θ
+
-
= Δθ,
(14)
концентрации (2) и, пользуясь уравнениями (6), (7),
∂t
∂x ∂z
∂z ∂x
(16), получим
∂ϕ
∂Ψ ∂ϕ
∂Ψ ∂ϕ
+
-
= -Le∇jϕ.
(15)
∂t
∂x ∂z
∂z ∂x
div v ≃ αχΔθ - βD ×
[
]
[
]
1
1
jϕ = - (1 + pϕ0ϕ)∇ϕ +
ϕ(1 - ϕ0ϕ)n
(16)
× div
(1 + pϕ)∇ϕ +
ϕ(1 - ϕ)n .
(9)
l
lsed
Здесь R = αgh3δΘ/νχ, B = βgh4ϕ0/(νχlsed), Le =
Учитывая, что div v при конвективных течениях
= D/χ, Pr = ν/χ, l = h/lsed — соответственно теп-
имеет значения порядка χ/h2, лапласиан температу-
ловое число Рэлея, число Больцмана, число Льюиса,
ры — значения порядка δΘ/h2, а слагаемые в правой
число Прандтля, безразмерная длина седиментации,
части, отвечающие за пространственное распреде-
а также два дополнительных параметра (по срав-
ление концентрации, — порядка ϕ0/h2 и ϕ0/(hlsed),
нению с задачей [8, 9]): p — коэффициент, характе-
найдем условие применимости модели несжимаемой
ризующий зависимость диффузии от концентрации,
жидкости (div v =0):
ϕ0 — среднее значение концентрации. Отметим, что
βDϕ0
βDϕ0
число Больцмана, используемое при описании кон-
αδΘ ≪ 1,
≪ 1,
≪ 1.
(10)
χ
hlsed
векции коллоидной суспензии, связано с концентра-
ционным числом Рэлея RD = βgh3ϕ0/νχ следую-
Тепловые возмущения не вызывают существенного
щим образом: B = RD/l. Граничные условия к зада-
нарушения условия несжимаемости жидкости даже
че (12)-(16), соответствующие идеально теплопро-
при разности температур в сотню градусов ввиду
водным непроницаемым горизонтальным границам,
малости коэффициента теплового расширения α ∼
на которых отсутствует проскальзывание, запишут-
∼ 10-4-10-3. В случае переноса частиц примеси
ся в виде
концентрационный коэффициент плотности, опре-
деленный по объемной концентрации частиц, может
ψ(0) = 0, ψ(1) = 0,
быть существенно больше: β ≈ 1-5, однако ввиду
(∂ψ)
(∂ψ)=0,
малости коэффициента диффузии для коллоидных
= 0,
∂z
∂z
(17)
суспензий (D ∼ 10-7 см2/с) по сравнению с коэффи-
0
1
циентом температуропроводности (χ ∼ 10-3 см2/с)
θ(0) = 0, θ(1) = 0,
они не способны вызвать значительные отклонения
z = 0,1 : (jϕ)z = 0.
поля скорости от соленоидального вида div v = 0,
даже при сильной концентрации суспензии.
Поскольку задача (5)-(7) изотропна в плоскос-
3. МЕХАНИЧЕСКОЕ РАВНОВЕСИЕ
ти слоя, плоские (двумерные) и пространствен-
ные (трехмерные) возмущения одинаково опасны. В
При подогреве горизонтального слоя жидкости
дальнейшем будем рассматривать двумерные возму-
снизу возможно состояние механического равнове-
щения и эволюцию двумерных течений.
сия, когда макроскопические течения отсутствуют
Введем функцию тока и завихренность жидкос-
(v = 0). При этом распределение температуры яв-
ти соотношениями
ляется линейной функцией вертикальной координа-
ты:
∂Ψ
∂Ψ
=vz,
= -vx, Φ = (rotv)y
(11)
θs = 1 - z.
(18)
∂x
∂z
и запишем уравнения конвекции в безразмерном ви-
Распределение концентрации в горизонтальном слое
де, используя следующие масштабы: длины — h,
в стационарном случае механического равновесия
373
И. Н. Черепанов, Б. Л. Смородин
ЖЭТФ, том 159, вып. 2, 2021
ϕs(z) определяется решением уравнения для эволю-
ции примеси (15) с учетом (16), в котором левая
часть равна нулю:
(
)
∂
∂ϕ
s
ϕs
(1+pϕ0ϕs)
+
(1-ϕ0ϕs)
=0
(19)
∂z
∂z
l
или
)2
∂2ϕs
(∂ϕs
(1 + pϕ0ϕs)
+ pϕ0
+
∂z2
∂z
)
1 - 2ϕ0ϕs
(∂ϕs
+
= 0.
(20)
l
∂z
Решение имеет вид
(
(
G
z))
1-ϕ0
ϕs = 1 +
W Aexp -
-
,
(21)
ϕ0p
r
1 - 2ϕ0
Рис. 1. Зависимости разности концентраций на верхней и
где W — функция Ламберта и введены обозначения
нижней границах слоя от среднего значения концентрации
при l = 10. Штриховая линия соответствует p = 0, сплош-
pϕ20
lG
ная — p = 4, штрихпунктирная — p = 8
G=1+
,
r=
(22)
1 - 2ϕ0
1 - 2ϕ0
Константа A находится из условия постоянства
4. АНАЛИЗ УСТОЙЧИВОСТИ
средней концентрации
Рассмотрим малые возмущения функции тока ψ,
∫
1
температуры θ и концентрации
ϕ от соответствую-
ϕs = 1.
(23)
щих равновесных значений:
0
θ = θs + ϑ,
(26)
Уравнение (23) не имеет аналитического решения
ϕ=ϕs +
ϕ.
для A в общем виде, однако может быть решено
Будем искать решение в виде плоских нормаль-
численно при задании конкретных значений пара-
метров l, p, ϕ0.
ных возмущений:
В случае идеального слабого раствора (p = 0,
ψ(x, z, t) = ψ(z) exp(-λ + ikx),
ϕ0 → 0) распределение концентрации описывается
ϑ(x, z, t) = ϑ(z) exp(-λt + ikx),
(27)
классическим барометрическим распределением
ϕ(x, z, t) =
ϕ(z) exp(-λt + ikx),
1
exp(-z/l)
ϕis =
- 1,
(24)
где k — волновое число, λ — комплексный декремент
l 1 - exp(-1/l)
затухания.
а разность концентраций на верхней и нижней гра-
Тогда уравнения для эволюции малых возмуще-
ницах имеет вид
ний функции тока, температуры и концентрации за-
пишутся в виде
1
δϕis = ϕis(z = 0) - ϕis(z = 1) =
(25)
l
- λΔψ = Pr (ΔΔψ +ikRϑ - ikBl ϕ) ,
(28)
Поведение величины δϕ/δϕis, характеризующей
- λϑ - ikψ = Δϑ,
(29)
(
)
отношение среднего градиента концентрации в слое
∂ϕs
∂jϕz
−
ϕ + ikψ
= Le
-k2(1+pϕ0ϕs
ϕ
,
(30)
к соответствующему значению для идеально слабо-
∂z
∂z
го раствора, в зависимости от средней концентрации
где jϕz — z-компонента потока частиц, связанная с
ϕ0 показано на рис. 1. Учет взаимодействия нано-
возмущениями концентрации
ϕ,
частиц в коллоидной суспензии приводит к умень-
шению разности концентраций δϕ на границах слоя
ϕ
∂ϕs
jϕz = (1 + pϕ0ϕs)
+ pϕ0
ϕ+
по сравнению со случаем идеального раствора. Так,
∂z
∂z
при объемной доле частиц порядка 10 % градиент
ϕ
+
(1 - 2ϕ0ϕs).
(31)
концентрации уменьшается практически вдвое.
l
374
ЖЭТФ, том 159, вып. 2, 2021
Конвекция коллоидной суспензии в горизонтальном слое. ..
Выражение для jϕz заметно упрощается, если ис-
Равенство нулю z-компоненты потока вещества на
пользовать замену
горизонтальных границах, записанного в виде (34),
немедленно дает граничное условие для вспомога-
∂ϕs
ϕ=
φ,
(32)
тельной функции:
∂z
∂φ
как это ранее делалось в более простом случае сла-
=0
при z = 0, 1.
(41)
∂z
бой концентрации коллоидной суспензии [19]. После
Для решения задачи устойчивости (37)-(39) с гра-
подстановки (32) в уравнение (31) и явного вычис-
ничными условиями (40), (41) использовался метод
ления производной получим выражение
Галеркина [2] с разложением полей функции тока,
(
температуры и переменной φ по наборам базисных
∂ϕs ∂φ
jϕz = (1 + pϕ0ϕs)
+
(1 + pϕ0ϕs) ×
функций [19], удовлетворяющих граничным услови-
∂z
∂z
ям (40), (41):
)
)2
∂2ϕs
(∂ϕs
1 - 2ϕ0ϕs ∂ϕs
Nψ
×
+ pϕ0
+
φ,
(33)
∑
∂z2
∂z
l
∂z
ψ=
ψn sin(nπz)sinπz,
n=1
в котором благодаря (20) второе слагаемое обраща-
∑
ется в нуль. Для вертикального потока наночастиц
ϑ = ϑn sin(mπz),
(42)
окончательно получим
m=1
Nφ-1∑
∂ϕs ∂φ
jϕz = (1 + pϕ0ϕs)
(34)
φ=
φq cos(qπz).
∂z
∂z
q=0
Вычисляя далее производную
Подставляя разложения (42) в систему (37)-(39)
и составляя условия ортогональности метода Галер-
∂jϕz
∂ϕs ∂2φ
= (1 + pϕ0ϕs)
+
кина, получим линейную систему уравнений для
∂z
∂z
∂z2
амплитуд ψn, ϑn, φq, содержащую K = Nψ +Nϑ +Nφ
∂2ϕs ∂φ
(∂ϕs)2 ∂φ
уравнений. Условием существования нетривиально-
+ (1 + pϕ0ϕs)
+ pϕ0
(35)
∂z2
∂z
∂z
∂z
го решения полученной системы является равенство
нулю определителя, матрицы A размера K × K,
и еще раз используя соотношение (20), получим
составленной из коэффициентов при соответству-
ющих амплитудах. После преобразования матрицы
∂jϕz
∂ϕs ∂2φ
= (1 + pϕ0ϕs)
-
A к виду, при котором декременты λ расположены
∂z
∂z
∂z2
только на диагонали:
1 - 2ϕ0ϕs ∂ϕs ∂φ
-
(36)
l
∂z
∂z
A = C - λE,
Подставляя
ϕ в виде (32) и ∂jϕz/∂z в систему
где E — единичная матрица, задача определения
(28)-(30) и сокращая множитель ∂ϕs/∂z в уравне-
декрементов возмущений сводится к задаче поиска
нии (30), получим систему уравнений для эволюции
собственных значений матрицы C.
возмущений в окончательном виде:
Декремент λ является функцией параметров за-
(
)
дачи: λ = λ(R, B, l, Pr, Le, p, ϕ0, k), при этом усло-
∂ϕs
− λΔψ = Pr ΔΔψ + ikRϑ - ikBl
φ
,
(37)
вие λr = Re λ = 0 определяет границу конвективной
∂z
устойчивости.
- λϑ - ikψ = Δϑ,
(38)
В расчетах использовалось разложение по 15 ба-
(
зисным функциям для каждого из полей скорости,
- λφ + ikψ = Le
(1 + pϕ0ϕs) ×
температуры и концентрации (Nψ = 15, Nϑ = 15,
)
)
(∂2
φ
1 - 2ϕ0ϕs ∂φ
Nφ = 15). Дальнейшее увеличение количества ба-
×
-k2φ
-
(39)
∂z2
l
∂z
зисных функций приводило к изменению крити-
ческого значения числа Рэлея, не превышающему
Граничные условия для возмущений функции тока
0.05 %.
и температуры имеют вид
Обсудим результаты исследования линейной
устойчивости механического равновесия коллоид-
∂ψ
ψ = 0,
= 0, ϑ = 0 при z = 0, 1.
(40)
ной суспензии, в котором устанавливается линейный
∂z
375
И. Н. Черепанов, Б. Л. Смородин
ЖЭТФ, том 159, вып. 2, 2021
Таблица. Сравнение значений коэффициента a при
некоторых параметрах задачи
a
aef
ϕ0
Pr = 100
Pr = 5.5
Pr = 5.5
Pr = 100
0.01
0.923
0.829
0.904
8.12
0.05
0.684
0.614
0.912
8.19
0.10
0.505
0.456
0.912
8.23
ной доли ϕ0 разность концентраций (а следователь-
но, и градиент внутри слоя) уменьшается.
Зависимости RC(B, Pr) в случае нелинейной за-
Рис. 2. Зависимости порогового числа Рэлея от числа
висимости потока наночастиц от средней концентра-
Больцмана при некоторых значениях средней концентра-
ции так же хорошо описываются соотношением (43).
ции, Pr = 5.5, l = 10, p = 8, Le = 1.5 · 10-4
Значения коэффициентов приведены в таблице.
Отметим, что если в зависимости
(43) ис-
пользовать эффективное число Больцмана Bef
=
профиль температуры и профиль концентрации
= Bδϕs/δϕis:
ϕs(z). При рассмотрении предполагается, что кол-
лоидная суспензия имеет типичное значение числа
Льюиса Le = 1.5 · 10-4, а число Прандтля Pr = 5.5
RC = R0 + aB = R0 + aef Bδϕs/δϕis =
или Pr = 100.
=R0 +aefBef,
(44)
Конвекция возникает в результате возрастания
колебательных возмущений. В работе [9] показано,
то эффективный коэффициент пропорциональности
что без учета зависимости коэффициента диффузии
от концентрации (p = 0, что справедливо для сла-
aef = aδϕis/δϕs
(45)
бых растворов) порог устойчивости механического
равновесия слоя коллоидного раствора RC в области
l ≪ 1 хорошо описывается линейной зависимостью
практически не зависит от средней концентрации
от числа Больцмана:
коллоидного раствора, а определяется только чис-
лом Прандтля (см. таблицу).
RC = R0 + aB,
(43)
Зависимости приведенного критического числа
Рэлея r = RC /(RC (ϕ0 → 0)), волнового числа k,
где R0 = 1708 — порог устойчивости однородной
частоты нейтральных колебаний ω от средней объ-
жидкости, a — некоторая функция от числа Прандт-
емной доли приведены на рис. 3. Увеличение сред-
ля, например, a(Pr = 100) = 1.01, a(Pr = 5.5) = 0.93.
ней объемной доли примеси приводит не только к
Результаты расчетов порога устойчивости для кон-
понижению порога конвективной устойчивости, о
центрированного коллоида (37)-(39) представлены
чем шла речь при обсуждении рис. 2. Уменьше-
на рис. 2.
ние частоты нейтральных колебаний с ростом сред-
Учет квадратичных слагаемых в потоке наноча-
ней концентрации также объясняется уменьшением
стиц приводит к понижению RC с ростом средней
среднего градиента концентрации частиц в слое за
концентрации, что обусловливается, по-видимому,
счет их взаимодействия. В предельном случае од-
уменьшением эффективного градиента концентра-
нородной жидкости конвекция связана с монотон-
ции. Разность концентраций в идеальном коллоид-
ными возмущениями (частота нейтральных колеба-
ном растворе на верхней и нижней границах слоя
ний равна нулю). Отметим, что эффект понижения
в размерном виде определяется отношением δϕis =
порога конвекции проявляется сильнее при боль-
= (ϕ0h)/lsed, а в безразмерных переменных — δϕis =
ших значениях числа Больцмана. Так, при B = 104
= 1/l. Как показано на рис. 1, в концентрированном
при объемной доле примеси 0.15 порог понижается
коллоиде с увеличением среднего значения объем-
практически в два раза.
376
ЖЭТФ, том 159, вып. 2, 2021
Конвекция коллоидной суспензии в горизонтальном слое. ..
Рис. 3. Зависимости приведенного порогового числа Рэ-
лея r (а), волнового числа k (б) и частоты нейтральных
колебаний ω (в) от ϕ0 при различных наборах парамет-
ров B, Pr и l при p = 8 и Le = 1.5 · 10-4. Пунктирные
линии — Pr = 5.5, B = 103, l = 10, штриховые линии —
Pr = 5.5, B = 103, l = 1, сплошные линии — Pr = 5.5,
B = 104, l = 10, штрихпунктирные линии — Pr = 100,
B = 103, l = 10, точки — результаты прямого численного
моделирования при Pr = 5.5, B = 103, l = 1
5. НЕЛИНЕЙНЫЕ ТЕЧЕНИЯ
зовались периодические по горизонтали граничные
условия на длине ячейки L = 2 (или L = 2π/kmin),
Для анализа двумерных конечно-амплитудных
соответствующей минимальному волновому числу
течений система нелинейных уравнений (13)-(15) с
(kmin
∼ π) для следующего набора параметров:
граничными условиями (17) решалась методом ко-
(Pr = 5.5, Le = 1.5 · 10-4, l = 1, p = 8 и ϕ0 = 0.1), а
нечный разностей [20]. При переходе к дискретным
также сетка 129 × 65.
аналогам уравнений движения и теплопроводно-
сти пространственные производные аппроксимиро-
В качестве начальных условий задавалось ли-
вались центральными разностями. Поскольку урав-
нейное распределение температуры и распределение
нение концентрации (15) должно удовлетворять за-
концентрации ϕs(z) при наличии оседания частиц.
кону сохранения массы, оно записывалось в консер-
Решение уравнения (19) для ϕs(z) находилось чис-
вативной форме и аппроксимировалось при помощи
ленно.
метода контрольного объема [20]. Для дискретно-
го представления конвективных слагаемых приме-
Пороги конвективной устойчивости, полученные
нялись центральные разности. Решение уравнения
в ходе линейного анализа (штриховая линия на
Пуассона проводилось c помощью быстрого преоб-
рис. 3а) и в результате расчета с помощью конеч-
разования Фурье. Подробное описание численного
но-разностной схемы (точки на рис. 3а), хорошо со-
алгоритма приведено в [21]. При расчетах исполь-
гласуются.
377
И. Н. Черепанов, Б. Л. Смородин
ЖЭТФ, том 159, вып. 2, 2021
Рис. 4. Зависимости от t a) функции тока в фиксированной точке слоя, б) координаты максимума функции тока при
формировании бегущей волны B = 103, R =
2220, Pr = 5.5, Le = 1.5 · 10-4, ϕ0 = 0.1, p = 8
Зависимости от времени локального значения
Структуры полей функции тока и температуры,
функции тока Ψ = ψloc в точке с координатами (x =
хорошо описывающихся первой пространственной
= 1/4, z = 1/2) и координаты максимального значе-
гармоникой, такие же, как в случае устойчивого
ния функции тока приведены на рис. 4 при фиксиро-
режима сильно нелинейных бегущих волн (strong
ванном наборе параметров. Возникновение неустой-
nonlinear traveling wave, SN TW), наблюдаемых в
чивости начинается ростом колебательных возму-
молекулярных жидкостях [22] и идеальных колло-
щений. На начальном интервале роста возмущений
идных суспензиях [9]. При этом структура поля кон-
(t < 0.5) координата максимума скачком изменяет-
центрации в нашем случае, также хорошо описыва-
ся между значениями xmax = 1.5 и xmax = 0.5, что
ющаяся первой пространственной гармоникой, зна-
соответствует стоячей волне (SW, standing wave),
чительно отличается от структуры в режиме SN
которая с течением времени увеличивает амплиту-
TW, когда распределение примеси характеризует-
ду (рис. 4а). Затем (в интервале 0.5 < t < 15.0)
ся сильным пространственным ангармонизмом, а за-
стоячая волна в результате переходного процесса
висимость распределения концентрации от горизон-
трансформируется в бегущую волну (TW, traveling
тальной координаты на середине высоты слоя имеет
wave). При этом сквозное горизонтальное движе-
трапецеидальную форму: чередование постоянных
ние конвективных валов через всю ячейку появ-
высокой и низкой концентраций в ядрах конвектив-
ляется при t ≈ 1.0 и становится явно заметно на
ных валов и резкие переходы в узких пограничных
графиках xmax(t) (рис. 4б). Фазовая скорость вол-
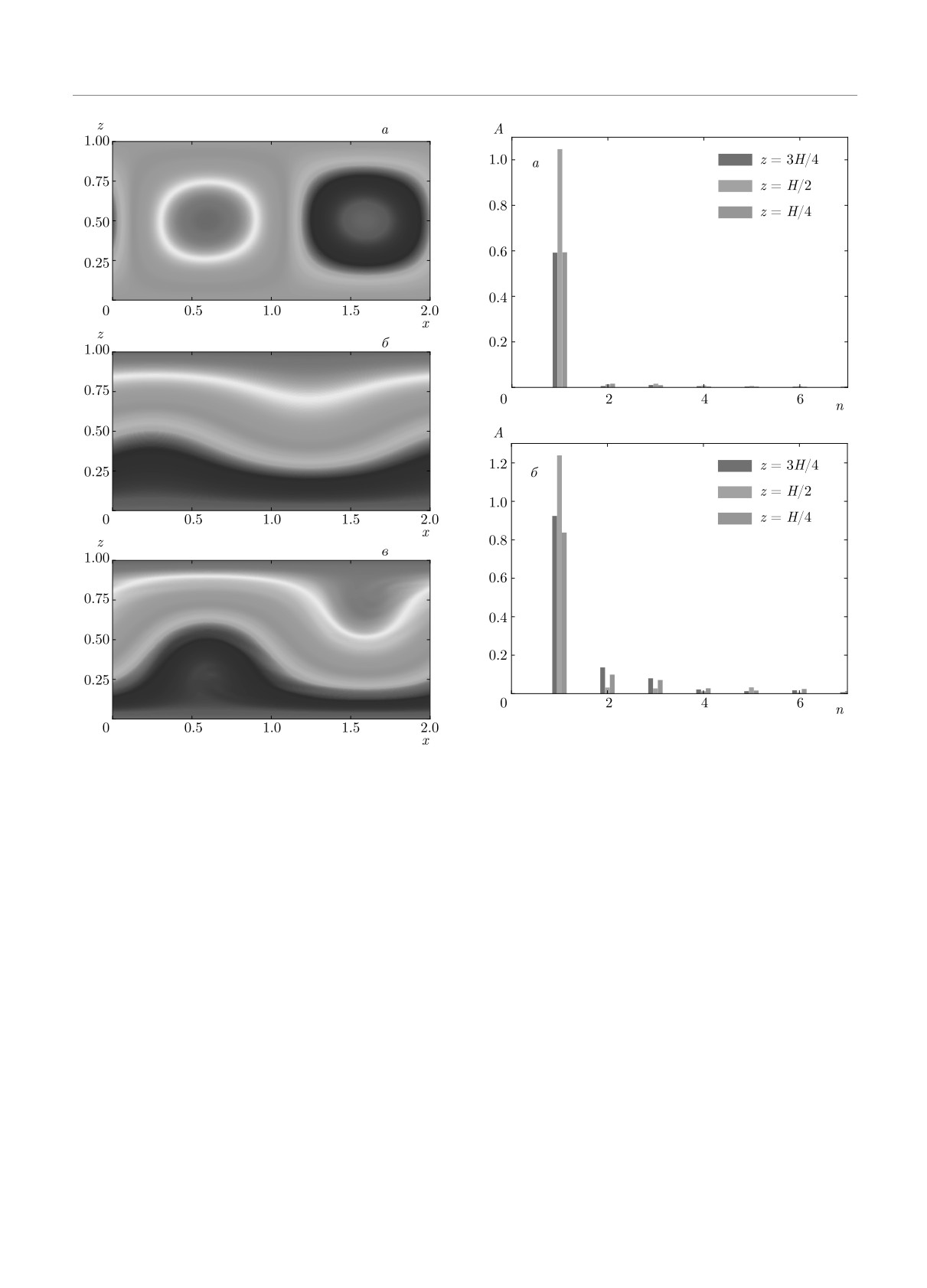
слоях. Относительные величины амплитуд несколь-
ны соответствует тангенсу угла наклона графика
ких первых пространственных гармоник в распреде-
xmax(t). Переход от стоячей волны к бегущей про-
лении полей функции тока и концентрации на раз-
исходит последовательно через 1) смешанное состо-
личных высотах в слое представлены на рис. 6, кото-
яние (1.5 < t < 5.0), в котором присутствуют фазы
рый подтверждает сделанный выше вывод о струк-
бегущей и стоячей волн (горизонтальные части гра-
туре полей функции тока и концентрации. Отметим,
фика xmax(t)), и далее 2) модулированную бегущую
что качественных изменений в эволюции течения от
волну (5.0 < t < 15.0). Изначально сформировавша-
режима стоячей волны к бегущей в нашем случае,
яся бегущая волна (рис. 4б, t ≈ 5.0) сильно моду-
учитывающем взаимодействие частиц, и в режиме
лирована по фазе, затем глубина модуляции умень-
SN TW не наблюдается.
шается до нуля и скорость TW становится постоян-
6. ЗАКЛЮЧЕНИЕ
ной (t > 15.0). Во время всего переходного процес-
са амплитуда функции тока в фиксированной точке
Проведен анализ линейной устойчивости и иссле-
немонотонно растет, достигая постоянного значения
дована нелинейная эволюция стратифицированной
в режиме бегущей волны (Ψ = 1.05).
коллоидной суспензии в плоском горизонтальном
Структуры полей функции тока, температуры и
слое при нагреве снизу при учете зависимости
концентрации в бегущей волне приведены на рис. 5.
диффузии и гравитационного оседания от концент-
378
ЖЭТФ, том 159, вып. 2, 2021
Конвекция коллоидной суспензии в горизонтальном слое. ..
Рис. 6. Относительные амплитуды пространственных гар-
моник в различных горизонтальных разрезах конвектив-
Рис. 5. Поля функции тока (a), температуры (б), концент-
ной ячейки z для полей функции тока (а) и концентра-
рации (в) в режиме бегущей волны. B = 103, R = 2220,
ции (б). B = 103, R = 2220, Pr = 5.5, l = 1, p = 8,
Pr = 5.5, l = 1, p = 8, ϕ0 = 0.1, Le = 1.5 · 10-4
ϕ0 = 0.1, Le = 1.5 · 10-4
рации частиц при условии взаимодействия частиц.
с идеальным раствором. Порог устойчивости,
Показано, что несмотря на значительную неод-
предсказанный теорией в отсутствие учета взаи-
нородность плотности приближение Буссинеска
модействия частиц примеси [8], в случае больших
остается справедливым благодаря медленности
средних объемных концентраций может быть
диффузионных процессов. Получены зависимости
сильно завышен. Методом конечных разностей
порога устойчивости состояния механического
проведено прямое численное моделирование тече-
равновесия, частоты нейтральных колебаний и
ний, формирующихся вблизи порога устойчивости
критического волнового числа от среднего значения
механического равновесия. Показано, что в ре-
концентрации примеси. Наличие взаимодействия
зультате эволюции формируется бегущая волна,
наночастиц и, соответственно, учет нелинейных
со слабонелинейной пространственной структурой
слагаемых в потоке транспорта наночастиц: диф-
поля концентрации.
фузии и седиментации в поле тяжести, приводит
к понижению среднего градиента концентрации
Финансирование. Работа выполнена при фи-
и снижению порога конвективной устойчивости
нансовой поддержке Российского фонда фундамен-
и частоты нейтральных колебаний по сравнению
тальных исследований (проект № 20-01-00491).
379
И. Н. Черепанов, Б. Л. Смородин
ЖЭТФ, том 159, вып. 2, 2021
ЛИТЕРАТУРА
11. S. Buzzaccaro, A. Tripodi, R. Rusconi et al., J. Phys.:
Condens. Matter 20, 494219 (2008).
1. Л. Д. Ландау, Е.М. Лифшиц, Теоретическая фи-
зика, т. 6, Гидродинамика, Наука, Москва (1986).
12. I. N. Cherepanov and P. V. Krauzin, Physica A 540,
123247 (2020).
2. Г. З. Гершуни, Е. М. Жуховицкий, Конвективная
устойчивость несжимаемой жидкости, Наука,
13. И. Н. Черепанов, Б. Л. Смородин, Вестник Пермс-
Москва (1972).
кого университета. Серия: физика 1, 26 (2019).
3. И. Г. Шапошников, ЖЭТФ 21, 1309 (1951).
14. G. K. Batchelor, J. Fluid Mech. 74, 1 (1976).
15. Ю. А. Буевич, А. Ю. Зубарев, А. О. Иванов, Маг-
4. J. K. Platten and J. C. Legros, Convection in Fluids,
нитная гидродинамика 25(2), 39 (1989).
Springer-Verlag, Berlin (1984).
16. A. F. Pshenichnikov and A. S. Ivanov, Phys. Rev.
5. Г. Ф. Путин, в сб. Материалы 11-го Рижско-
E 86, 051401 (2012).
го совещания по магнитной гидродинамике, Рига
(1984), т. 3, с. 15.
17. И. Н. Черепанов, П. В. Краузин, ПМТФ 6, 35
(2019).
6. G. Donzelli, R. Cerbino, and A. Vailati, Phys. Rev.
Lett. 102, 104503 (2009).
18. M. Mason and W. Weaver, Phys. Rev. 2, 412 (1924).
7. F. Winkel, S. Messlinger, W. Schöpfet et al., New J.
19. И. Н. Черепанов, Б. Л. Смородин, ЖЭТФ 152,
Phys. 12, 053003 (2010).
1404 (2017).
8. M. I. Shliomis and B. L. Smorodin, Phys. Rev. E 71,
20. П. Роуч, Вычислительная гидродинамика, Мир,
036312 (2005).
Москва (1980).
9. B. L. Smorodin, I. N. Cherepanov, B. I. Myznikova
21. I. N. Cherepanov, J. Appl. Mech. Techn. Phys. 58,
et al., Phys. Rev. E 84, 026305 (2011).
1181 (2017).
10. И. Н. Черепанов, В. А. Попов, Вестник Пермского
22. M. Lücke, W. Barten, and M. Kamps, Physica D 61,
университета. Серия: физика 2, 26 (2017).
183 (1992).
380