ЖЭТФ, 2021, том 159, вып. 3, стр. 457-472
© 2021
УСТОЙЧИВОСТЬ И ДИНАМИКА РЕГУЛЯРНЫХ
ГРАВАСТАРОВ С ТОНКОЙ ОБОЛОЧКОЙ
М. Шариф*, Ф. Джавед**
Department of Mathematics, University of the Punjab
Lahore-54590, Pakistan
Поступила в редакцию 28 октября 2020 г.,
после переработки 25 ноября 2020 г.
Принята к публикации 25 ноября 2020 г.
(Перевод с английского)
STABILITY AND DYNAMICS
OF REGULAR THIN-SHELL GRAVASTARS
M. Sharif, F. Javed
Исследуются устойчивые и динамические конфигурации гравастаров с тонкой оболочкой на основе сши-
вания внешнего (черные дыры Хейворда и черные дыры Хейворда - анти-де Ситтера) и внутреннего
(черные дыры де Ситтера) пространства-времени. На тонкой оболочке эти два пространства-времени
связываются с помощью “cut and paste” техники Виссера. Плотность поверхностной энергии, материя и
давление описываются уравнениями Ланцоша. Для исследования устойчивости гравастаров рассмотрены
экранированные области, для этого использовалось радиальное возмущение для равновесного радиуса
оболочки. Динамика на тонкой оболочке рассмотрена как для безмассовых, так и для массивных скаляр-
ных полей с использованием уравнений движения и уравнений Клейна - Гордона. В случае скалярного
поля гравастары с тонкой оболочкой могут демонстрировать коллапс и расширение в зависимости от
радиуса оболочки, скорости его изменения и эффективного потенциала. Оказалось, что устойчивые об-
ласти оболочки гравастара уменьшаются, при этом динамические конфигурации (коллапс и расширение)
увеличиваются с ростом космологической постоянной.
DOI: 10.31857/S004445102103007X
ской структуры черных дыр. В работе [1] получе-
но точное решение полевых уравнений, представля-
ющее ЧД с регулярным центром, названное регу-
1. ВВЕДЕНИЕ
лярной ЧД. В работе [2] концепция регулярных ЧД
была расширена введением нелинейного электриче-
Черная дыра (ЧД) образуется в результате гра-
ского поля. Некоторые другие модели регулярных
витационного коллапса массивной звезды под дейст-
ЧД также были предложены в работах [3-6]. Для
вием ее гравитационных сил. Такие области про-
более полного исследования ЧД требуется альтер-
странства-времени нельзя в полной мере наблю-
нативая модель, в которой отсутствовали бы цент-
дать из-за существования горизонта событий и цен-
ральная сингулярность и горизонт событий и была
тральной сингулярности. В центральной сингуляр-
бы получена устойчивая конфигурация для некото-
ности массовая плотность и кривизна пространства-
рого конкретного выбора распределения материи.
времени становятся бесконечными, поэтому общая
теория относительности не описывает геометриче-
В 2001 г. Мазур и Моттола в работе [7] предпо-
ложили, что фазовый переход предотвращает кол-
* E-mail: msharif.math@pu.edu.pk
лапс звезды, а также предложили концепцию звез-
** E-mail: faisalrandawa@hotmail.com
ды гравитационного вакуума (гравастара). Грава-
457
М. Шариф, Ф. Джавед
ЖЭТФ, том 159, вып. 3, 2021
стары являются аналогами ЧД, однако они не име-
геометрии. Было получено, что гравастары с тон-
ют ни сингулярности, ни горизонта событий. Такие
кой оболочкой становятся устойчивыми при под-
звездные объекты можно было бы использовать для
ходящем выборе УС для переходных слоев. В ра-
описания той роли, которую темная энергия играет
боте [18] были построены гравастары для случая
в ускорении расширения вселенной. Кроме того, это
ЧД DS или анти-DS (ADS) в качестве внутренне-
могло бы объяснить, почему некоторые галактики
го пространства-времени и ЧД Шварцшильда-ADS
имеют низкую или высокую концентрацию темной
или Райснера - Нордстрема (РН) в качестве внешне-
материи. Модель гравастара можно описывать с по-
го. В этой работе также исследовались устойчивые
мощью трех различных областей с соответствующи-
решения для гравастаров с использованием УС. В
ми уравнениями состояния (УС), а именно, внешняя
работе [19] были введены два типа теоретических
область (r2 < r) с p = 0 = σ, внутренняя область
гравастаров для пространства-времени РН и иссле-
(0 ≤ r < r1) с σ = -p > 0 и промежуточная область
довалась роль заряда в устойчивости конфигурации
(r1 < r < r2) с p = σ, где σ, p и r1 - r2 — плотность
гравастаров. В работе [20] исследовались граваста-
поверхностной энергии, давление и толщина оболоч-
ры с тонкой оболочкой в присутствии электромаг-
ки, соответственно. Как можно видеть, внутренняя
нитного поля и была определена их энтропия. В ра-
область соответствует геометрии де Ситтера (DS)
боте [21] рассматривался гравастар с использовани-
с материей, имеющей постоянную положительную
ем ЧД в мире на бране в качестве внешнего много-
плотность энергии и отрицательное давление, что
образия.
связано с вакуумым решением Шварцшильда через
В работе [22] была построена динамическая мо-
промежуточную область.
дель прототипа гравастаров, заполненных фантом-
Промежуточная область, толщина которой опре-
ной энергией. В этой работе исследовались грава-
деляется тонким слоем материальной поверхности,
стары с тонкой оболочкой с внешним пространст-
существенно влияет на динамическую конфигура-
вом-временем Вайдьи, заполненные идеальной жид-
цию. Эта область, также известная как тонкая обо-
костью. Было получено, что при различных распре-
лочка, состоит из жестко распределенной материи.
делениях материи на тонкой оболочке такая струк-
Существование материальной поверхности, образу-
тура может представлять собой ЧД, а также устой-
ющей оболочку определенного радиуса, имеет боль-
чивый или неустойчивый гравастар или частичный
шое значение для поддержания устойчивой конфи-
(“bounded excursion”) гравастар. В работе [23] в рам-
гурации тонкой оболочки, при этом возникает силь-
ках подхода Чандрасекара исследовались граваста-
ное давление, достаточное для того, чтобы преодо-
ры с непрерывным давлением, а также было получе-
леть влияние гравитационных сил. Компоненты тен-
но УС для статического случая. В работе [24] было
зора энергии-импульса можно получить, используя
предложено существование гравастара с тонкой обо-
формализм, предложенный в работе [8]. Метод “cut
лочкой в размерности (2 + 1) и исследована его эн-
and paste” Виссера предлагает общий формализм,
тропия, длина, а также различные энергетические
позволяющий соединять внешнюю и внутреннюю
условия. В работе [25] исследовалось влияние раз-
геометрию на тонкой оболочке. Мазур и Мотто-
личных физических характеристик на точные реше-
ла также использовали этот подход для построе-
ния для некоммутативных гравастаров и анализиро-
ния гравастаров с тонкой оболочкой, сшивая внеш-
вались устойчивые конфигурации переходого слоя.
нее пространство-время в виде ЧД Шварцшильда
В этой работе было показано, что тонкая оболоч-
и внутреннее в виде многообразия DS. Этот под-
ка является устойчивой вблизи ожидаемого гори-
ход очень полезен, если нужно избежать возникно-
зонта событий. В работе [26] с использованием ра-
вения горизонта событий и сингулярности в геомет-
диальных возмущений исследовалась устойчивость
рии гравастаров [9]. В работах [10-16] метод “cut and
некоммутативных гравастаров с тонкой оболочкой и
paste” использовался для объяснения кротовых нор
были получены области устойчивости. Недавно ав-
с тонкой оболочкой, образованных из двух эквива-
торами настоящей работы были исследованы грава-
лентных копий ЧД.
стары с тонкой оболочкой, получающиеся при сши-
Новые результаты по исследованию граваста-
вании внутреннего пространства-времени ЧД DS с
ров, полученные с использованием различных под-
внешним пространством-временем ЧД Бардина и
ходов, представлены в целом ряде работ. В рабо-
Бардина-DS [27]. Оказалось, что области устойчи-
те [17] исследовалась динамическая устойчивость
вости увеличиваются при увеличении космологиче-
гравастаров с тонкой оболочкой с использованием
ской постоянной и убывают при возрастании заряда
метода “cut and paste” для внешней и внутренний
во внешнем пространстве-времени.
458
ЖЭТФ, том 159, вып. 3, 2021
Устойчивость и динамика регулярных гравастаров. . .
Скалярное поле играет важную роль при иссле-
дования гравастаров с тонкой оболочкой. В разд. 3
дованиях различных астрофизических явлений, ди-
рассматривается устойчивость тонкой оболочки при
намики кластеров и вообще в теоретической физике.
наличии радиального возмущения. В разд. 4 рас-
В работе [28] была введена концепция электромаг-
сматривается динамическая эволюция тонкой обо-
нитно-гравитационной сущности, названной геоном.
лочки в случае безмассового и массивного скаляр-
В этой работе было предложено частице-подобное
ных полей. В последнем разделе обобщаются полу-
решение на основе взаимодействия гравитационно-
ченные результаты.
го и классического электромагнитного поля, удер-
живаемое в ограниченной области гравитационным
2. ИССЛЕДОВАНИЕ ГРАВАСТАРОВ С
притяжением энергии своего собственного поля. В
ИСПОЛЬЗОВАНИЕМ ГЕОМЕТРИЧЕСКОГО
работе [29] исследовались решения полевых урав-
ФОРМАЛИЗМА
нений для ЧД Шварцшильда в случае скалярного
поля. В работе [30] исследовались геометрические
В данном разделе представлен общий подход к
характеристики комплексного массивного скаляр-
исследованию гравастаров с использованием метода
ного поля. В работе [31] рассматривалась динами-
“cut and paste”. Пусть внешняя геометрия соответ-
ка и устойчивость бозонных звезд и были получены
ствует ЧД Хейворда-ADS, а внутренняя — много-
устойчивые решения для различных значений ска-
образию DS. Используя формализм Израэля и урав-
лярного поля. В работе [32] исследовалась сфери-
нения Ланцоша, получим уравнения движения для
ческая геометрия в случае безмассового скалярного
случая тонкой оболочки. Соответствующий линей-
поля.
ный элемент для внешней (Υ+) и внутренней (Υ-)
В работе [33], с использованием метода “cut and
геометрий имеет вид [5]
paste” для двух эквивалентных копий ЧД Шварц-
шильда, обсуждалась динамика тонких оболочек в
ds2± = -Π±(r±)dt2± + Π-1±(r±)dr2± +
случае безмассового и массивного скалярных полей.
+ r2±(dθ2± + sin2 θ±dφ2±),
(1)
Было получено, что в безмассовом случае тонкая
оболочка демонстрирует коллапс, расширение и сед-
где Π-(r-) = 1 - r2-/α2, α — ненулевая посто-
ловые точки, в то время как в случае массивно-
янная. Явный вид внешней метрической функции
го скалярного поля оболочка демонстрирует толь-
определяет различные регулярные ЧД. Метричес-
ко коллапс. В работе [34] рассматривались тонкие
кая функция ЧД Хейворда-ADS равна [5]
оболочки в случае безмассового и массивного ска-
2r2+m
Λr2+
лярных полей для черных дыр РН и было показано,
Π+(r+) = 1 -
-
,
что коллапс оболочки имеет место только в случае
r3+ + Q3
3
массивного скалярного поля. В работе [35] обсужда-
где m — масса ЧД, а Λ — космологическая постоян-
лись расширение и коллапс тонкой оболочки в слу-
ная. Физический параметр Q связан с полным маг-
чае скалярного поля для регулярных ЧД. Недавно
нитным зарядом ЧД. В отсутствие Λ получаем ЧД
авторы исследовали динамическую эволюцию тон-
Хейворда, метрическая функция которой равна [2]
кой оболочки в случае скалярного поля для раз-
личных вращающихся регулярных ЧД и ЧД BTZ
2r2+m
Π+(r+) = 1 -
,
(Bañados, Teitelboim, Zanelli). Кроме того, рассмат-
r3+ + Q3
ривались тонкие оболочки для d-мерных ЧД в слу-
чае безмассового и массивного скалярых полей [36].
при этом, если и Q, и Λ становятся равными нулю,
В работе [37] в случае скалярного поля рассматри-
мы получаем метрическую функцию ЧД Шварц-
валась динамика тонкой оболочки, сформированной
шильда.
внутренней и внешней копиями черных дыр в мире
Чтобы построить геометрию гравастаров с тон-
на бране.
кой оболочкой, требуется сшить внешнее и внутрен-
В настоящей работе рассмотрены стабильные и
нее пространство-время на гиперповерхности
динамические конфигурации гравастаров с тонкой
∂Υ = r = h = η,
оболочкой для многообразий Хейворда и Хейвор-
да-ADS в качестве внешнего пространства-времени
используя метод “cut and paste”. Таким образом, мы
и многообразия DS в качестве внутреннего прост-
получим новое многообразие
ранства-времени. Работа построена следующим об-
разом. В разд. 2 предлагается общий метод иссле-
Υ=Υ- ∪Υ+
459
М. Шариф, Ф. Джавед
ЖЭТФ, том 159, вып. 3, 2021
с минимальной площадью поверхности ∂Υ. Сшива-
Если
ние внешнего и внутреннего пространства-времени
K+ij - K-ij = 0,
для минимальной площади поверхности соответ-
ствует случаю тонкой оболочки. Радиус оболоч-
то на ∂Υ присутствует тонкий слой материи. Ком-
ки (h = h(τ), где τ — собственное время) дол-
поненты тензора энергии-импульса Sij такой мате-
жен быть больше горизонта событий rh, чтобы рас-
риальной поверхности определяются уравнениями
сматриваемая структура не ушла за горизонт собы-
Ланцоша. Их можно выразить как
тий, а также чтобы не возникло сингулярности в
1
пространстве-времени. Координаты ∂Υ можно опре-
Sij = -
{[Kij] - δij K},
(9)
делить как
8π
ξi = (τ, θ, φ),
где [Kij] = K+ij - K-ij и K = tr[Kij ] = [Kij]. Приве-
тогда соответствующий линейный элемент имеет
денное выше уравнение в терминах распределения
вид
идеальной жидкости принимает вид
ds2 = -dτ2 + h(τ)2dθ2 + h(τ)2 sin2 θdφ2.
Sij = vivj (p + σ) + pδij,
(10)
Векторы nα±, нормальные к Υ±, определяются как
⎛
где vi — компоненты скорости изменения радиу-
⎜
h
са тонкой оболочки, σ — плотность поверхностной
⎜
nμ+ =
,
энергии, а p — поверхностное давление. Радиус-
⎝
2h2m
Λh2
1-
-
вектор на гиперповерхности можно выразить как
h3 + Q3
3
⎞
√
xi = (τ, θ, φ),
2
⎟
2h2m
Λh
⎟
1-
-
+ ˙h2, 0, 0
,
(2)
h3 + Q3
3
⎠
а скорость — как
⎛
⎞
dxi
√
vi =
= (1, 0, 0).
h
dτ
h2
nμ- =⎝
,
1-
+ ˙h2, 0, 0⎠ ,
(3)
h2
α2
Пусть r
= h(τ)
— радиальная координата
1-
α2
пространства-времени ЧД на гиперповерхно-
где
h= dh/dτ.
сти. Тогда радиус оболочки зависит от собственного
Материальная поверхность на оболочке данного
времени τ и можно записать
радиуса обуславливает разрыв внешней кривизны
dh
Ki±j. Математически компоненты внешней кривиз-
h=
dτ
ны для обеих геометрий записываются следующим
образом:
Это — производная радиуса горловины по собствен-
(
)
2mh
h3 - 2Q3
16πΛh
ному времени, которая обычно определяет устойчи-
+
+2h
вые и динамические конфигурации тонкой оболоч-
(Q3 + h3)2
3
Kτ+τ =
√
,
(4)
ки. Не имеется прямого соотношения, связывающе-
2
2h2m
Λh
го между собой vi и
h. Здесь
h— скорость изменения
1-
-
+ ˙h2
h3 + Q3
3
радиуса горловины по отношению к собственному
√
времени, а vi — скорость частицы, движущейся над
1
2h2m
2
Λh
Kθ+θ =
1-
-
+ ˙h2,
(5)
гиперповерхностью.
h
h3 + Q3
3
Из уравнений(3) и (4) получаем выражения для
2h
σ и p:
- α2+2h
Kτ-τ =
√
,
(6)
2
{√
h
1-
+ ˙h2
1
2h2m
Λh2
α2
σ=-
h2 + 1 -
-
-
√
4πh
h3 + Q3
3
2
1
h
√
}
Kθ-θ =
1-
+ ˙h2,
(7)
h
α2
h2
-
h2 + 1 -
,
(11)
Kφ±φ = sin2 θKθ±θ.
(8)
α2
460
ЖЭТФ, том 159, вып. 3, 2021
Устойчивость и динамика регулярных гравастаров. . .
1
3. АНАЛИЗ УСТОЙЧИВОСТИ
p=
×
8πh
⎧
(
)
⎪
4Q3 + h3
32
В данном разделе мы рассмотрим устойчивые
⎪
2h2+2hh-2mh2
+
πΛh2+2
⎨
конфигурации гравастаров с тонкой оболочкой с
(Q3 + h3)2
3
√
-
возмущением вдоль радиального направления отно-
×⎪⎪
⎪
2h2m
Λh2
сительно равновесного радиуса оболочки h = h0. За-
⎩
h2 + 1 -
-
h3 + Q3
3
кон сохранения в терминах σ и p принимает вид
⎫
⎪
4h2
⎪
d
d
2h2 + 2hh + 2 -
⎬
p
(4πh2) +
(M) = 0,
(17)
α2
dτ
dτ
−
√
(12)
2
⎪
h
h2 + 1 -
⎪
где M = 4πh2σ — распределение полной массы
⎭
α2
на тонкой оболочке. Приведенное выше уравнение
можно переписать как
Уравнение движения, описывающее динамиче-
ские и устойчивые конфигурации гравастаров с тон-
2
кой оболочкой, можно получить, перегруппировав
σ′ = -
(p(σ) + σ).
(18)
h
уравнение (5). Его можно записать в виде
Для исследования устойчивых конфигураций с
h2 + Ω(h) = 0,
(13)
возмущением вдоль радиального направления ис-
где Ω(h) — потенциальная функция рассматривае-
пользуем разложение Ω(h) в ряд Тейлора вблизи
мой структуры:
равновесного радиуса оболочки h0:
2
χ(h)
1
Ω(h) = -
+
λ(h) - 4π2h2σ2,
(14)
64π2h2σ2
2
Ω(h) = Ω(h0) + Ω′(h0)(h - h0) +
для простоты мы ввели обозначения χ(h) и λ(h):
1
+
Ω′′(h0)(h - h0)2 + O[(h - h0)3].
2
χ(h) = Π-(h) - Π+(h), λ(h) = Π-(h) + Π+(h).
Получаем
Теперь предположим, что
h и
h обращаются в нуль
Ω(h0) = 0 = Ω′(h0),
для равновесного радиуса оболочки, h0, тогда при
h = h0 движение оболочки в радиальном направле-
тогда приведенное выше уравнение принимает вид
нии прекращается. Соответствующие значения по-
верхностного напряжения при h = h0 принимают
1
Ω(h) =
(h - h0)2Ω′′(h0).
(19)
вид
2
{√
√
}
1
2h20m
Λh2
h20
Соответственно, вторая производная Ω(h) при h =
0
σ0 = -
1-
-
-
1-
,
(15)
= h0 равна
4πh0
h30+Q3
3
α2
⎧
(
)
2M(h0)M′(h0)
h20χ(h0)χ′′(h0)
⎪
2mh20
4Q3 + h3
32
Ω′′(h0) =
-
+
0
⎪-
+
πΛh20 + 2
h30
2M(h0)2
1
(Q3 + h30)2
3
2h20χ(h0)M′(h0)χ′(h0)
M′(h0)2
h20χ′(h0)2
p0 =
√
-
+
-
-
-
8πh0 ⎪
⎪
2h20m
Λh20
M(h0)3
2h20
2M(h0)2
⎩
1-
-
h30 + Q3
3
3h20χ(h0)2M′(h0)2
2h0χ(h0)χ′(h0)
⎫
−
-
+
2M(h0)4
M(h0)2
⎪
4h20
⎪
2-
⎬
λ′′(h0)
3M(h0)2
h20χ(h0)2M′′(h0)
α2
+
-
+
-
-
√
(16)
2
2h40
2M(h0)3
⎪
h20
⎪
1-
⎭
M(h0)M′′(h0)
χ(h0)2
α2
−
-
+
2h20
2M(h0)2
В следующем разделе мы рассмотрим влияние
2h0χ(h0)2M′(h0)
+
(20)
физических параметров на области устойчивости
M(h0)3
оболочки гравастара при линеаризованном радиаль-
ном возмущении. Кроме того, мы рассмотрим влия-
Для исследования областей устойчивости рас-
ние скалярного поля на динамическую конфигура-
сматриваемой структуры мы использовали общее
цию оболочки.
представление для поверхностного давления как
461
М. Шариф, Ф. Джавед
ЖЭТФ, том 159, вып. 3, 2021
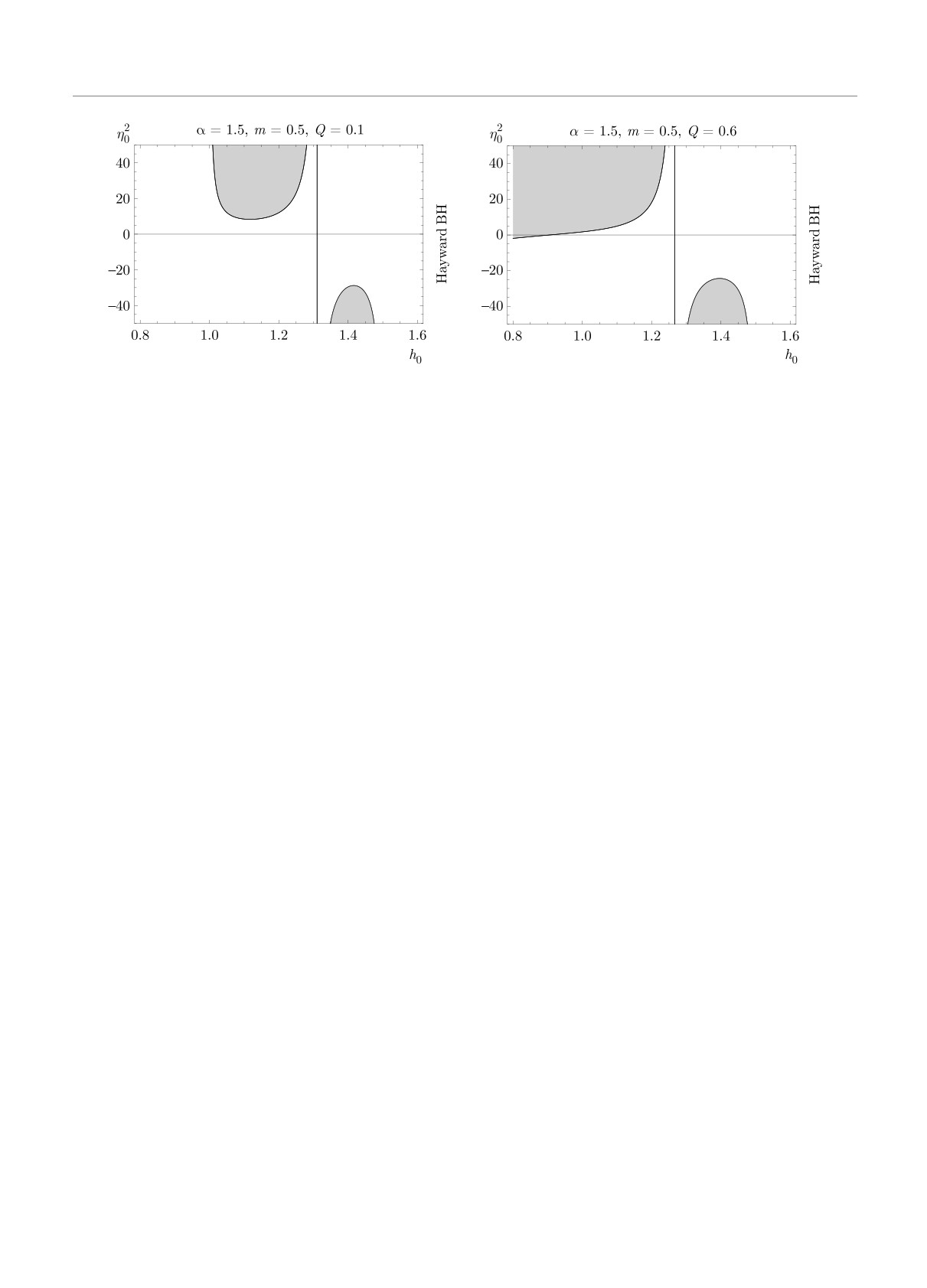
Рис. 1. Области устойчивости для гравастаров с тонкой оболочкой для ЧД Хейворда при различных значениях Q
функции плотности поверхностной энергии, это так-
(i)
Если Υ0 < 0, то η20 < B0/Υ0.
же было рассмотрено в работах [25-27]. Для иссле-
(ii)
Если Υ0 > 0, то η20 > B0/Υ0.
дования устойчивости гравастаров с тонкой оболоч-
Здесь
кой полезно также выбрать конкретный вид УС.
Υ0 = (4σ0p0 + 4σ20)×
Здесь мы рассмотрим зависимость поверхностного
(
)
давления от плотности поверхностной энергии для
×
-256π4h0 + (Π-(h0) - Π+(h0))2)4σ40
,
оболочки гравастара только в общем виде, т. е. p =
(
)
= p(σ). Параметр в уравнении состояния для равно-
B0 = -
4p20 + 6p0σ0 + 3σ20
256π4h40σ40 +
(
(
(
весного радиуса оболочки можно выразить как
+h0σ0
h0σ0
Π-(h0)′′
16π2h20σ20 -
η20 = dp/dσ|h=h0 .
− Π-(h0) + Π+(h0)) + Π+(h0)′′ ×
(
))
×
Π-(h0) + 16π2h20σ20 - Π+(h0)
+
Соответственно, первая и вторая производные пол-
+ 2Π-(h0)′ (h0σ0Π+(h0)′-2(Π-(h0)-Π+(h0)) ×
ной массы по h при h = h0 имеют вид
× (2p0+σ0)) - h0σ0 (Π-(h0)′)2 -h0σ0 (Π+(h0)′)2 +
M′(h0) = -8πh0p0,
+ 4Π+(h0)′(2p0 + σ0)(Π-(h0) - Π+(h0))) -
(
)
M′′(h0) = -8πp0 + 16πη20(σ0 + p0).
-
12p20 + 10p0σ0 + σ20
Π-(h0)2 + 2Π-(h0)×
(
×
12p20 + σ20 + 10p0σ0)Π+(h0) - Π+(h0)2 ×
Поскольку эти выражения зависят от параметра
(
)
УС, вторая производная потенциальной функции по
×
12p20 + 10p0σ0 + σ20
радиусу оболочки также зависит от η20.
Для исследования областей устойчивости рас-
Будем исследовать устойчивость гравастаров с
сматриваемых структур проанализируем графики
тонкой оболочкой, используя вторую производную
зависимостей B0/Υ0 и η20. Области устойчивости для
эффективного потенциала при h = h0. Известно,
гравастаров с тонкой оболочкой при различных зна-
что если Ω′′(h0) < 0, то тонкая оболочка облада-
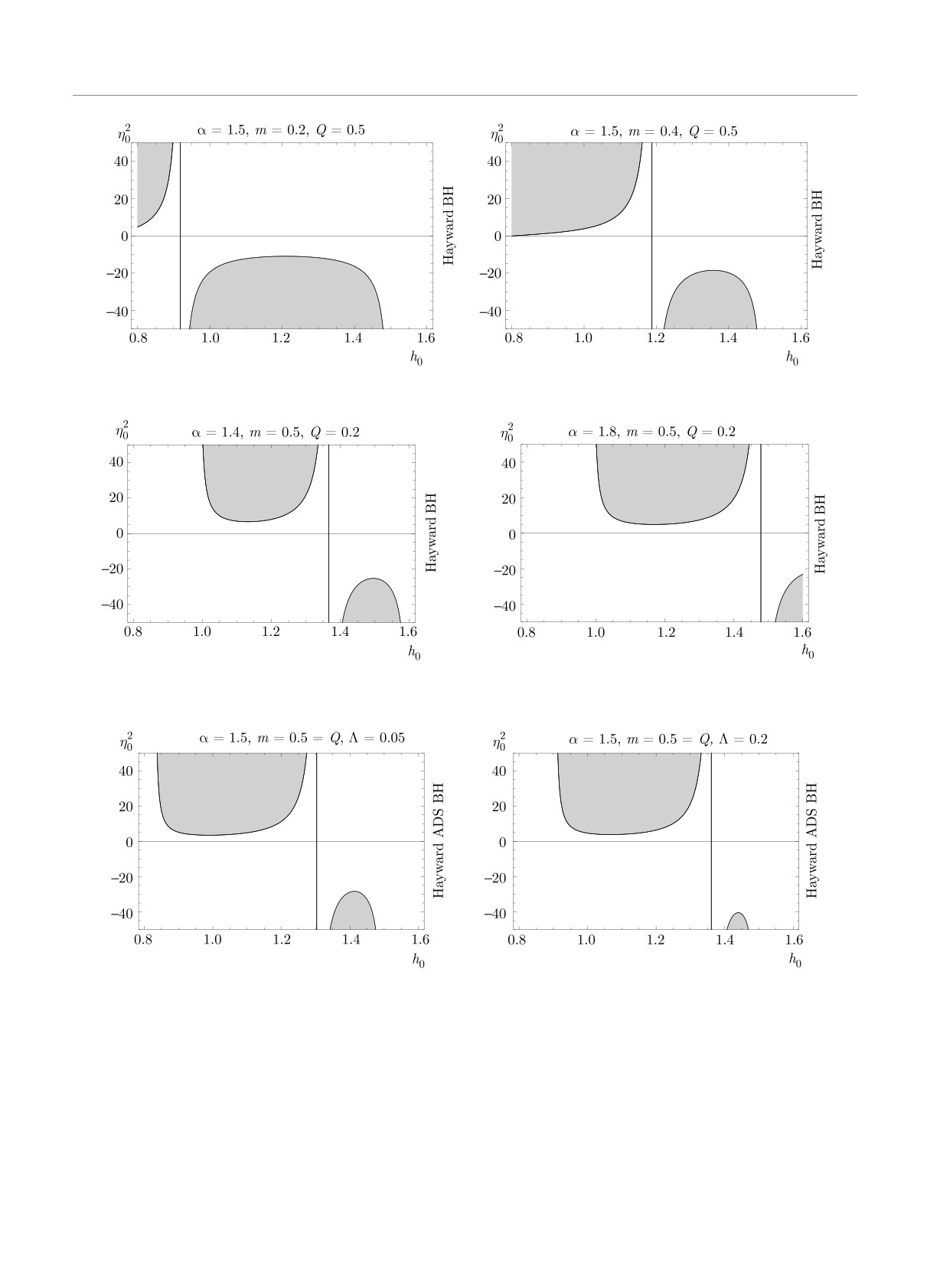
чениях физических параметров показаны на рис. 1
ет неустойчивой конфигурацией, если Ω′′(h0) > 0 —
и 2 темным цветом, при этом светлые области соот-
устойчивой, а если Ω′′(h0) = 0, то об устойчивости
ветствуют неустойчивым конфигурациям. Как вид-
ничего сказать нельзя [38]. Поскольку мы исследуем
но на рис. 1 и 2, размер областей устойчивости для
области устойчивости с помощью второй производ-
гравастаров с тонкой оболочкой в случае ЧД Хей-
ной Ω′′(h0), уравнение (16) можно записать как
ворда увеличивается как с ростом заряда, так и с
ростом массы ЧД. Изменение физических парамет-
Ω′′(h0) > 0
⇒ Υ(h0)η20 - B(h0) > 0.
(21)
ров внутреннего пространства-времени DS оказыва-
Здесь B(h0) = B0 и Υ(h0) = Υ0 обозначают выра-
ет существенное влияние на области устойчивости
жения, в которые не входит параметр УС η20. Что-
гравастаров с тонкой оболочкой. Оказалось, что чем
бы охарактеризовать области устойчивости грава-
больше значение α, тем больше области устойчивос-
старов с тонкой оболочкой, можно записать
ти (см. рис. 3). При этом для гравастаров с тонкой
462
ЖЭТФ, том 159, вып. 3, 2021
Устойчивость и динамика регулярных гравастаров. . .
Рис. 2. Области устойчивости для гравастаров с тонкой оболочкой для ЧД Хейворда при различных значениях m
Рис. 3. Области устойчивости для гравастаров с тонкой оболочкой для ЧД Хейворда при различных значениях α
Рис. 4. Области устойчивости для гравастаров с тонкой оболочкой для ЧД Хейворда при различных значениях Λ
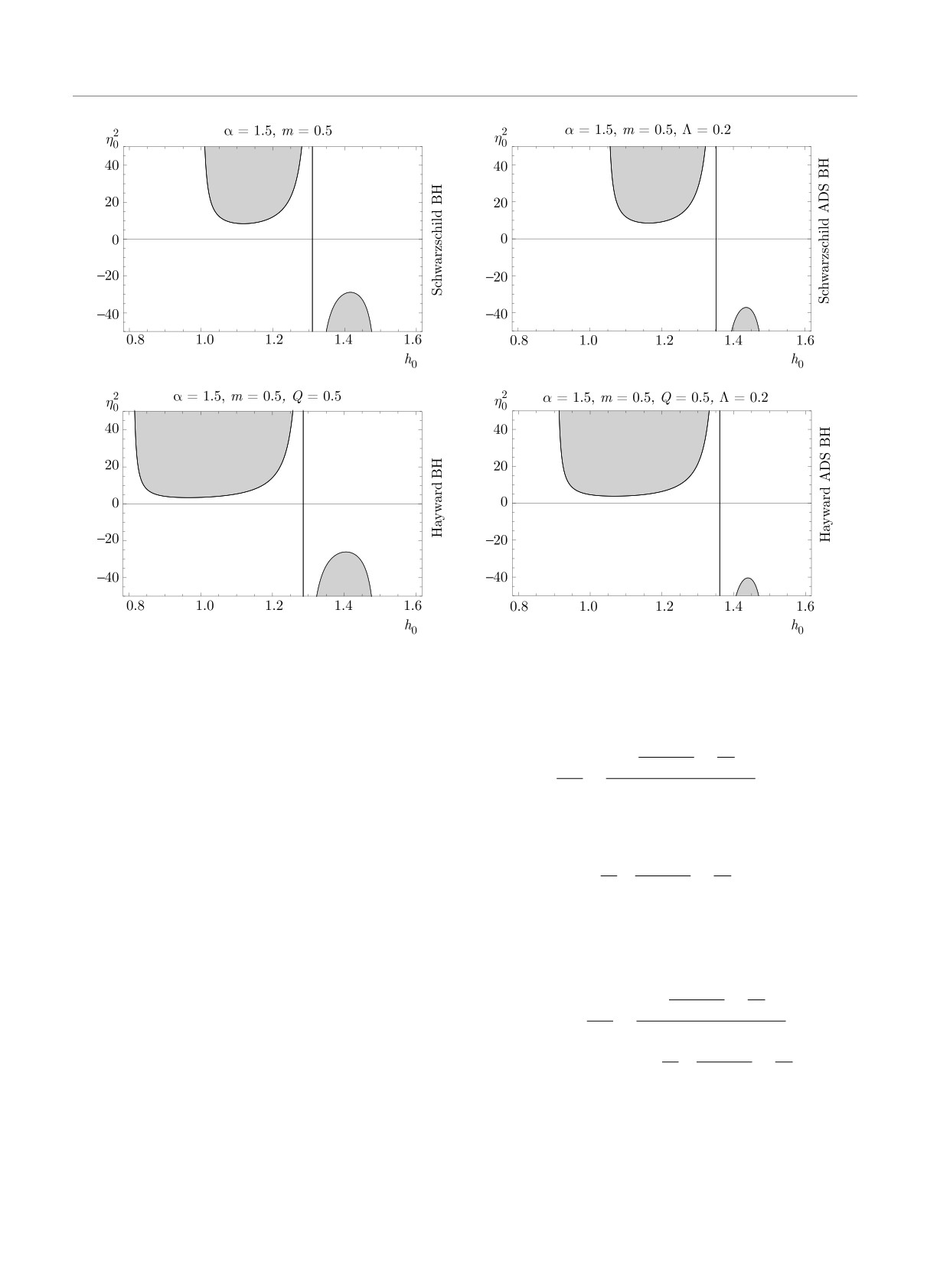
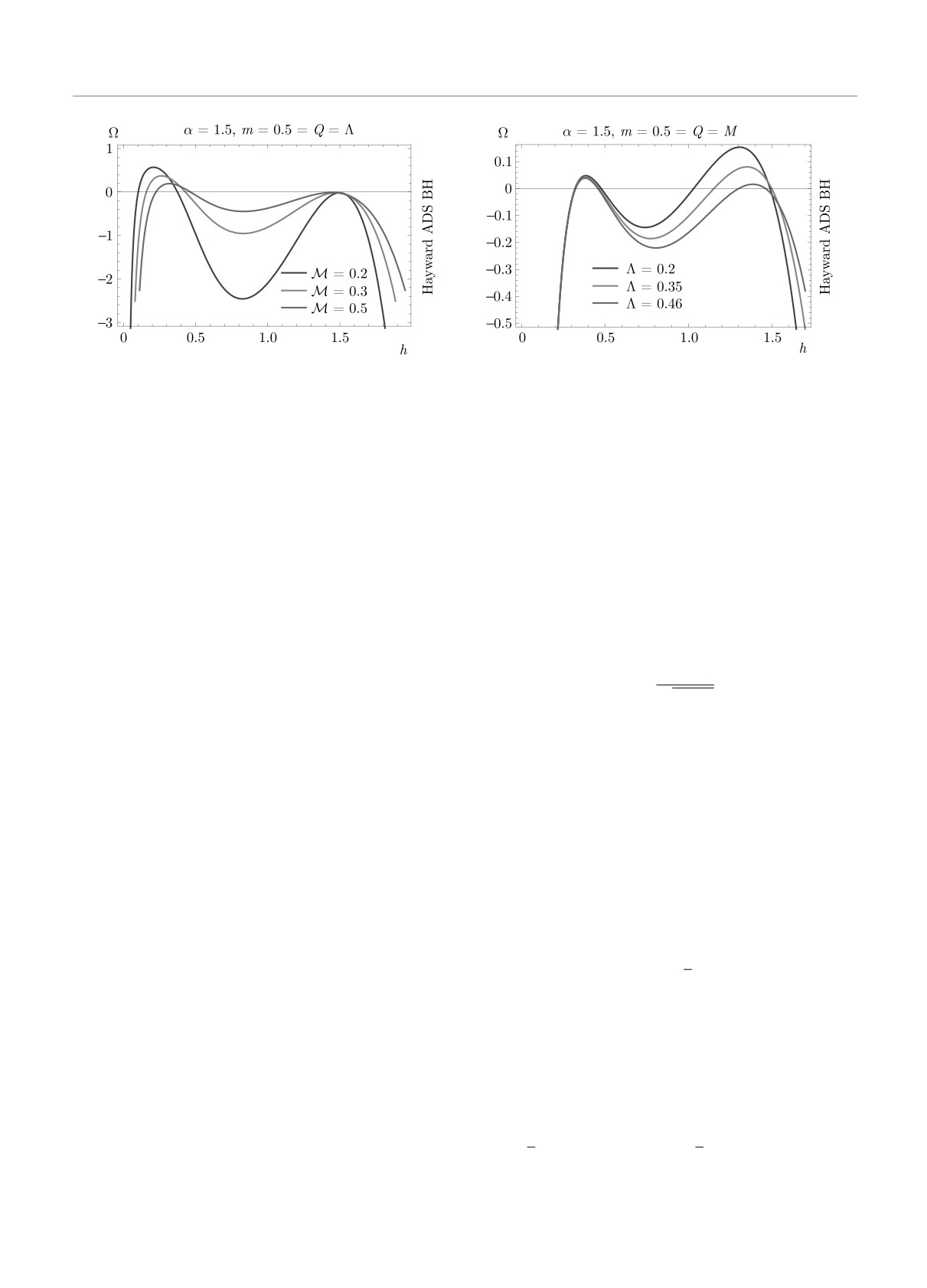
оболочкой для ЧД Хейворда-ADS при возрастании
ти устойчивости для ЧД Шварцшильда больше об-
Λ области устойчивости уменьшаются (см. рис. 4).
ластей устойчивости для ЧД Шварцшильд ADS, а
Можно сказать, что для гравастаров с тонкой обо-
области устойчивости для ЧД Хейворда больше об-
лочкой области устойчивости различны для различ-
ластей устойчивости для ЧД Хейворда ADS (см.
ных случаев внешнего пространства-времени, облас-
рис. 5).
463
М. Шариф, Ф. Джавед
ЖЭТФ, том 159, вып. 3, 2021
Рис. 5. Области устойчивости для гравастаров с тонкой оболочкой при различном выборе внешнего пространства-времени
при m = 0.5
⎧
(
)2
4. ДИНАМИКА ГРАВАСТАРОВ С ТОНКОЙ
⎪
6m
3
⎨
h6
-
ОБОЛОЧКОЙ
M2
h3 + Q3
α2
˙h=±
+
+
⎪4h2
36M2
⎩
⎫
1/2
⎪
(
)
⎬
В данном разделе мы исследуем эффективный
h2
2m
1
+
+
(22)
потенциал и скорость изменения радиуса оболочки
2
h3 + Q3
α2
- 1⎪
⎪
рассматриваемой структуры, которые обеспечивают
⎭
динамику в виде коллапса, расширения и седловых
Соответствующая потенциальная функция матери-
точек. Ниже мы получим соответствующие выраже-
альной поверхности на тонкой оболочке имеет вид
ния для скорости и эффективного потенциала для
(
)2
гравастаров с тонкой оболочкой для случаев ЧД
6m
3
Хейворда и ЧД Хейворда ADS в терминах массы
h6
-
M2
h3 + Q3
α2
оболочки.
Ωh(h) = 1 -
-
-
4h2
36M2
(
)
h2
2m
1
−
-
(23)
A. Черная дыра Хейворда
2
h3 + Q3
α2
B. Черная дыра Хейворда ADS
Скорость изменения радиуса оболочки (уравне-
Скорость изменения радиуса оболочки (уравне-
ние движения) для гравастаров с тонкой оболочкой
ние движения) для гравастаров с тонкой оболочкой
для случая ЧД Хейворда имеет вид
для случая ЧД Хейворда-ADS имеет вид
464
ЖЭТФ, том 159, вып. 3, 2021
Устойчивость и динамика регулярных гравастаров. . .
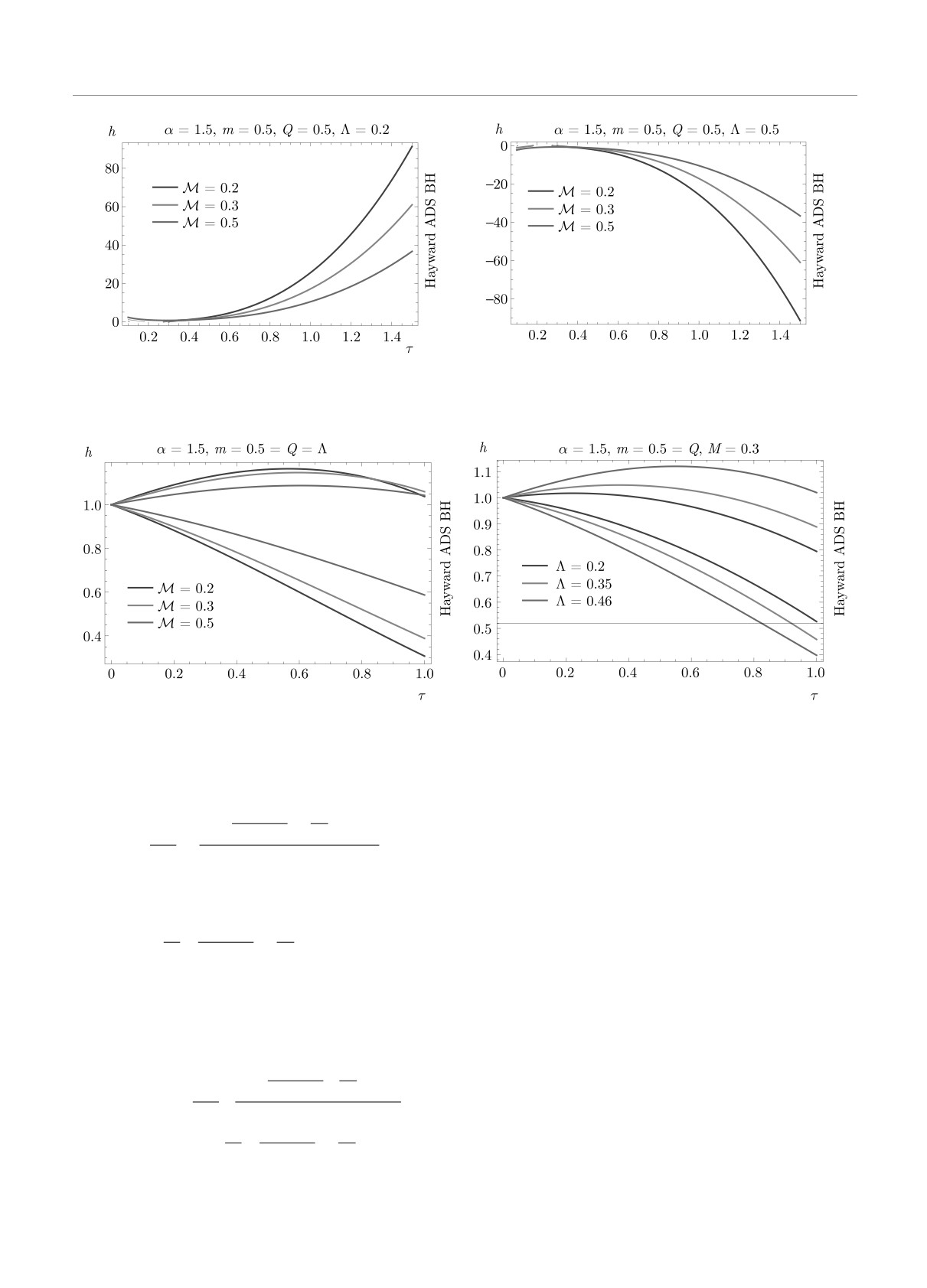
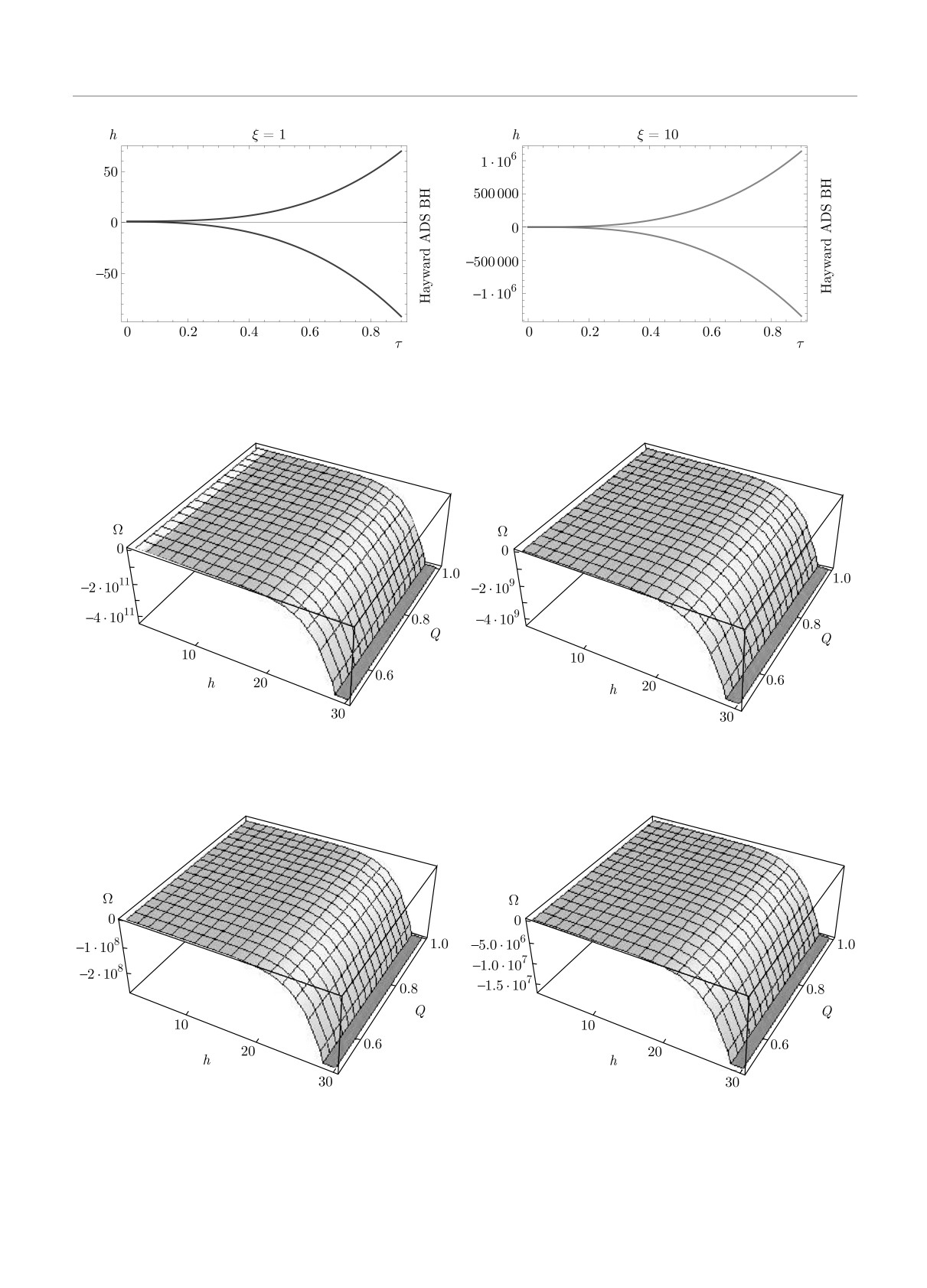
Рис. 6. Динамика гравастаров с тонкой оболочкой, а именно, расширение (левая панель) и коллапс (правая панель) при
различном поведении скорости изменения радиуса оболочки для различных значений M
Рис. 7. Динамика гравастаров с тонкой оболочкой, а именно, зависимости радиуса оболочки h от τ при h(0) = 1 для
различных значений M (левая панель) и Λ (правая панель)
⎧
(
)2
⎪
6m
3
Динамика гравастаров с тонкой оболочкой при
⎨
h6
-
+Λ
M2
h3 + Q3
α2
различных значениях физических параметров, а
h=±
+
+
⎪4h2
36M2
именно, скорости изменения радиуса оболочки, ра-
⎩
диуса оболочки и эффективного потенциала, пока-
⎫
зана на рис. 6, 7 и 8. Если скорость изменения ра-
1/2
⎪
диуса оболочки возрастает, то оболочка гравастара
(
)
⎬
2
h
6m
3
демонстрирует расширение, в противном случае —
+
+
+Λ
(24)
6
h3 + Q3
α2
- 1⎪
коллапс (см. рис. 6). Левый рисунок соответствует
⎪
⎭
расширению, а правый — коллапсу тонкой оболоч-
ки. На рисунке видно, что с ростом массы оболоч-
Соответствующая потенциальная функция матери-
ки динамика замедляется. Оказалось, что при соот-
альной поверхности на тонкой оболочке имеет вид
ветствующем собственном времени тонкая оболочка
может одновременно демонстрировать как расшире-
(
)2
6m
3
6
ние, так и коллапс (см. рис. 7). На рисунке видно,
h
-
+Λ
2
M
h3 + Q3
α2
что скорости как коллапса, так и расширения обо-
Ωhads(h) = 1-
-
-
4h2
36M2
лочки гравастаров больше для больших значений Λ.
(
)
2
h
6m
3
Потенциальная функция демонстрирует осцил-
-
+
+Λ .
(25)
6
h3 + Q3
α2
ляции при изменении радиуса оболочки граваста-
465
6
ЖЭТФ, вып. 3
М. Шариф, Ф. Джавед
ЖЭТФ, том 159, вып. 3, 2021
Рис. 8. Осцилляции потенциальной функции при изменении радиуса оболочки для различных значений M (левая панель)
и Λ (правая панель)
ров при различных значениях физических парамет-
4.1. Гравастары с тонкой оболочкой в случае
ров, см. рис. 8. Значения потенциальной функции
скалярного поля
осциллируют между двумя вещественными корня-
Рассмотрим движение гравастаров с тонкой обо-
ми, h1, h2, при Ω(h1) = 0 = Ω(h2). Локальные ми-
лочкой в случае вещественного скалярного поля.
нимумы или локальные максимумы потенциальной
Они полезны для понимания динамической кон-
функции получены в открытом интервале (h1, h2).
фигурации скалярных тел. Для этого рассмотрим
На рис. 8 показаны различные пары вещественных
преобразование, связывающее уравнения движения
корней потенциальной функции с локальными ми-
тонкой оболочки, состоящей из идеальной жидко-
нимумами и локальными максимумами. Если потен-
сти, в случае скалярного поля. Рассмотрим преоб-
циальная функция имеет локальный минимум меж-
разование
ду своими вещественными корнями, то она демон-
ψ,a
ua =
√
,
стрирует устойчивое поведение, в противном слу-
ψ,bψ,b
чае — неустойчивое. Оболочка демонстрирует кол-
устанавливающее линейную зависимость между
лапс при Ω(h) → -∞ при h → 0 или h → ∞, если
компонентами тензора энергии-импульса идеальной
h > 1.5. Оказалось, что скорость расширения и кол-
лапса оболочки гравастаров зависит от космологи-
жидкости с производной скалярного поля ψ по
собственному времени, а также скалярной потенци-
ческой постоянной и массы оболочки. Приведенным
зависимостям потенциальной функции соответству-
альной функцией Ω(ψ) [33-35]. С помощью этого
преобразования в случае скалярного поля для
ют области устойчивых и неустойчивых осцилляций
гравастаров с тонкой оболочкой можно получить
оболочки гравастаров. Для двух значений радиусов
уравнения движения, которые описывают поведе-
оболочки h1, h2, скорость ее изменения обращается
ние оболочки как аналитически, так и численно. В
в нуль,
h(τ) = 0, что означает, что оболочка пере-
случае скалярного поля соответствующий тензор
стает двигаться и возвращается к прежнему состоя-
энергии-импульса имеет вид [33]
нию. Как можно видеть, при Ω(h) > 0 оболочка гра-
вастара демонстрирует расширение, при Ω(h) > 0 —
(
)
1
коллапс, а Ω(h) = 0 соответствует седловым точкам.
Sij = ∇iψ∇jψ - ηij
(∇ψ)2 - Ω(ψ)
2
Поверхностное давление оболочки максимально при
минимальном значении радиуса оболочки и имеет
Соответствующие компоненты можно выразить как
минимальное значение при его максимальном зна-
[33, 34]
чении. Это означает, что гравитационное притяже-
ние заставляет оболочку сжиматься, что приводит к
2σ = ψ,bψ,b + 2Ω(ψ),
2p = ψ,bψ,b - 2Ω(ψ),
(26)
осцилляциям. Оказалось, что из-за осцилляций обо-
откуда получаем
лочка гравастара может иметь как устойчивые, так
и неустойчивый конфигурации при разных значени-
(
)
(
)
1
1
ях радиуса.
σ=
ψ2 + 2Ω(ψ) ,
p=
ψ2 - 2Ω(ψ)
(27)
2
2
466
ЖЭТФ, том 159, вып. 3, 2021
Устойчивость и динамика регулярных гравастаров. . .
Тогда масса оболочки в случае скалярного поля рав-
Решение этого уравнения имеет вид
на
ξ
ψ=
,
2
h
M = 4πh2σ = 2πh2(
ψ2 + 2Ω(ψ)).
(28)
где ξ
— вещественная константа. Эффективные
потенциалы для гравастаров с тонкой оболоч-
Используя уравнения (24) и (25), из (17) получаем
кой в случае безмассового скалярного поля для
2h
∂Ω
пространства-времени ЧД Хейворда и ЧД Хейвор-
ψ+
ψ+
= 0.
(29)
h
∂ψ
да-ADS принимают вид
(
)2
Приведенное выше уравнение называется уравнени-
6m
3
h10
-
ем Клейна-Гордона (КГ). Для ЧД Хейворда и для
π2ξ4
h3 + Q3
α2
Ωh(h) = 1 -
-
+
ЧД Хейворда-ADS потенциальная функция грава-
h6
144π2ξ4
(
)
старов с тонкой оболочкой в случае скалярного поля
1
6m
3
+
h2
-
-
,
соответственно принимает вид
6
h3 + Q3
α2
(
)2
(
)2
ψ2
Ωh(h) = 1 - π2h2
2Ω(ψ) +
+
6m
3
h10
-
+Λ
(
)
π2ξ4
h3 + Q3
α2
1
6m
3
Ωhads(h) = 1-
-
-
+
h2
-
-
-
h6
144π2ξ4
6
h3 + Q3
α2
(
)
2
(
h
6m
3
2
)2 (
)-2
h
6m
3
-
+
+Λ .
-
-
2Ω(ψ) +
ψ2
,
6
h3 + Q3
α2
144π2
h3 + Q3
α2
Проанализируем расширение и коллапс грава-
старов с тонкой оболочкой в случае безмассового
(
)2
скалярного поля с помощью графиков зависимо-
ψ2
Ωhads(h) = 1 - π2h2
2Ω(ψ) +
+
стей радиуса оболочки и эффективного потенциала
(
)
1
6m
3
при различных конкретных значениях физических
+
h2
-
-
-Λ
-
6
h3 + Q3
α2
параметров. Видно, что зависимости радиуса тон-
2
(
)2 (
)-2
кой оболочки указывают как на расширение, так
h
6m
3
ψ2
-
-
+Λ
2Ω(ψ) +
и на коллапс (рис. 9), причем скорость динамиче-
144π2
h3 + Q3
α2
ских процессов больше для больших значений ξ.
Для исследования тонкой оболочки в случае ска-
Анализируя поведение функции эффективного по-
лярного поля нам необходимо соотношение между
тенциала в случае безмассовой скалярной оболочки,
плотностью поверхностной энергии σ и давлением
можно сделать вывод, что при выборе в качестве
p. Однако нет такого УС, которое связывало бы
внешнего многообразия пространства-времени ЧД
потенциал скалярного поля и кинетические энер-
Хейворда-ADS оболочка демонстрирует менее вы-
гии. Поэтому мы будем использовать частный вид
раженную динамику, чем при выборе пространства-
Ω(ψ) с определенным набором физических парамет-
времени ЧД Хейворда (рис. 10). Зависимости эф-
ров, что позволяет получить выражения для эф-
фективного потенциал указывают на то, что в слу-
фективной массы и напряженности скалярного по-
чае безмассового скалярного поля тонкая оболоч-
ля. Чтобы исследовать динамику гравастаров с тон-
ка демонстрирует только коллапс, причем скорость
кой оболочкой, рассмотрим два типа скалярного по-
коллапса больше для больших значений ξ (рис. 11).
ля, а именно, безмассовое (Ω(ψ) = 0) и массивное
(Ω(ψ) = m2ψ2) скалярные поля.
4.1.2. Массивное скалярное поле
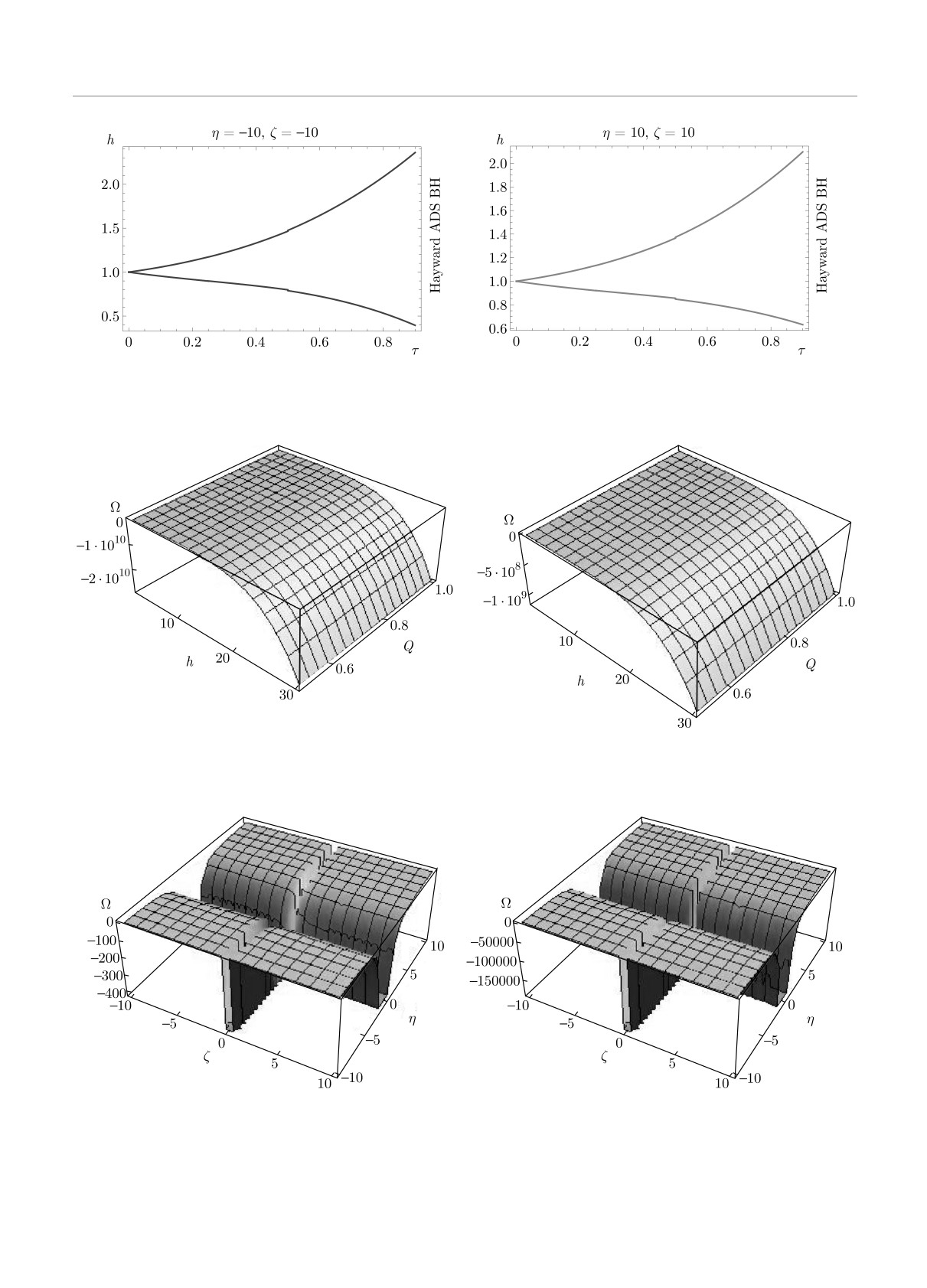
Рассмотрим динамику гравастаров с тонкой обо-
4.1.1. Безмассовое скалярное поле
лочкой в случае массивного скалярного поля,
В этом случае мы получаем прямое соотношение
Ω(ψ) = M2ψ2.
между компонентами тензора энергии-импульса,
В этом случае соответствующие потенциальная
т. е. p = σ при Ω(ψ) = 0. Соответствующее уравне-
функция и производная по собственному времени в
ние КГ можно записать как
выражениях для σ и p имеют вид
2h
ψ+
ψ= 0.
2Ω(ψ) = σ - p,
ψ2 = σ + p.
(30)
h
467
6*
М. Шариф, Ф. Джавед
ЖЭТФ, том 159, вып. 3, 2021
Рис. 9. Динамика гравастаров с тонкой оболочкой в случае безмассового скалярного поля, а именно, зависимости радиуса
оболочки h от τ при h(0) = 1
Рис. 10. Динамические конфигурации гравастаров с тонкой оболочкой, а именно, зависимости эффективного потенциала
от h и Q для Λ = 0 (левая панель) и Λ = 1.2 (правая панель) при ξ = 1, α = 1.5, m = 0.5
Рис. 11. Динамические конфигурации гравастаров с тонкой оболочкой, а именно, зависимости эффективного потенциала
от h и Q для ξ = 5 (левая панель) и ξ = 10 (правая панель) при Λ = 0.5 = m, α = 1.5
468
ЖЭТФ, том 159, вып. 3, 2021
Устойчивость и динамика регулярных гравастаров. . .
Будем считать, что поверхностное давление являет-
Геометрическая структура гравастаров получает-
ся явной функцией от h, т. е.
ся сшиванием внешнего регулярного пространства-
времени (ЧД Хейворда и ЧД Хейворда-ADS) с
p=p0e-ζh,
внутренним многообразием DS с использованием
метода “ cut and paste”. Характеристики образован-
где p0 и ζ — вещественные постоянные. Подставив
ной материей поверхности получены с использова-
это выражение для поверхностного давления в урав-
нием формализм Израэля и уравнений Ланцоша.
нение (18), получим выражение для плотности по-
Получено, что оболочка гравастара может иметь
верхностной энергии:
как устойчивые и неустойчивые конфигурации, а
1
(
)
также демонстрировать динамику. В работе полу-
σ=
2 (1 + ζh) p0e-ζh + ζ2η
,
(31)
чены следующие результаты.
ζ2h2
Во-первых, проанализирована устойчивость рас-
где η — постоянная интегрирования. Подставляя вы-
сматриваемых структур в рамках подхода, исполь-
ражения для σ и p в уравнение (30), получим
зующего регулярные ЧД с радиальным возмуще-
нием на оболочке с равновесным радиусом. Для
1
(
(
))
ψ2 =
ηζ2+p0e-ζh
ζ2h2+2 (1+ζh)
,
(32)
исследования устойчивости тонкой оболочки рас-
h2ζ2
смотрены экранированные области. Оказалось, что
области устойчивости зависят от физических па-
1
(
(
))
раметров, а именно, они увеличиваются с ростом
Ω(ψ) =
ηζ2-p0e-ζh
ζ2h2-2(1+ζh)
(33)
2h2ζ2
Q, m и α и убывают с ростом Λ (см. рис. 1-
4). Гравастары с тонкой оболочкой Хейворда яв-
Заметим, что приведенные выше выражения согла-
ляются более устойчивыми, чем гравастары с тон-
суются с уравнением КГ. Используя уравнения (32)
кой оболочкой Шварцшильда, Шварцшильда-ADS
и (33), для гравастаров с тонкой оболочкой в случае
и Хейворда-ADS (см. рис. 5).
массивного скалярного поля можно получить
Во-вторых, исследована динамика рассматрива-
h2χ(h)
2
M2
λ(h)
емых структур в случае вещественного скалярно-
Ω(h) = -
-
+
,
(34)
4M2
4h2
2
го поля, а именно, для безмассового и массивно-
го скалярных полей. В зависимости от скорости
где
оболочки и ее радиуса гравастары демонстрируют
4π
(
)
как коллапс, так и расширение. Скорость динами-
M=
ηζ2 + 2p0e-ζh (1 + ζh)
(35)
ζ2
ческих процессов уменьшается с ростом массы обо-
лочки. При изменении радиуса оболочки для кон-
Проанализируем динамику гравастарров с тон-
кретных значений физических параметров потен-
кой оболочкой в случае массивного скалярного поля
циальная функция демонстрирует осциллирующее
с помощью графиков зависимостей радиуса оболоч-
поведение (см. рис. 6-8). С использованием урав-
ки и эффективного потенциала. На рисунках видно,
нений КГ получены и проанализированы графиче-
что радиус оболочки может как возрастать (расши-
ски динамические уравнения для тонкой оболочки
рение), так и убывать (коллапс) с изменением соб-
в случае безмассового и массивного скалярных по-
ственного времени (см. рис. 12). На графиках зави-
лей. Для всех значений физических параметров от-
симостей эффективного потенциала видно, что ско-
носительно собственного времени радиус оболочки
рость коллапса уменьшается как с ростом η, так и
демонстрирует как коллапс, так и расширение. В то
с ростом ζ (см. рис. 13). На графиках зависимостей
же время зависимости эффективного потенциала в
радиуса оболочки видно, что скорость коллапса уве-
обоих случаях указывают на то, что оболочка кол-
личивается после перехода через горизонт событий,
лапсирует (см. рис. 9-14).
т. е. при h = 1.48 (левая панель на рис. 14) и h = 4
Исследованию устойчивости и динамики грава-
(правая панель на рис. 14).
старов с тонкой оболочкой в случае скалярного по-
ля посвящено множество работ [33-37]. В настоя-
щей работе рассмотрены расширение и коллапс гра-
5. ЗАКЛЮЧИТЕЛЬНЫЕ ЗАМЕЧАНИЯ
вастаров с тонкой оболочкой, заполненных безмас-
В настоящей работе с использованием уравне-
совыми и массивными скалярными полями. Полу-
ний движения исследованы устойчивые и динамиче-
чено, что тонкая оболочка, построенная из двух
ские конфигурации гравастаров с тонкой оболочкой.
эквивалентых копий ЧД, демонстрирует как рас-
469
М. Шариф, Ф. Джавед
ЖЭТФ, том 159, вып. 3, 2021
Рис. 12. Динамика гравастаров с тонкой оболочкой в случае массивного скалярного поля, а именно, зависимости радиуса
оболочки h от τ при h(0) = 1
Рис. 13. Динамика гравастаров с тонкой оболочкой, а именно, зависимости эффективного потенциала от h и Q для
η = 1 = ζ (левая панель) и η = 5 = ζ (правая панель) при Λ = 0.5 = m, α = 1.5
Рис. 14. Динамика гравастаров с тонкой оболочкой, а именно, зависимости эффективного потенциала от ξ и η для
Λ = 0.05 (левая панель) и Λ = 1.5 (правая панель) при Q = 0.5 = m, α = 1.5
470
ЖЭТФ, том 159, вып. 3, 2021
Устойчивость и динамика регулярных гравастаров. . .
ширение, так и коллапс для обоих случаев ска-
7.
P. Mazur and E. Mottola, arXiv:gr-qc/0109035; Proc.
лярного поля. Для гравастаров с тонкой оболоч-
Nat. Acad. Sci. 101, 9545 (2004).
кой отмечено, что эффективный потенциал рассмат-
8.
W. Israel, Nuovo Cimento B 44, 1 (1966).
риваемой структуры, полученной сшиванием внут-
реннего пространства-времени ЧД DS и внешне-
9.
M. Visser, S. Kar, and N. Dadhich, Phys. Rev. Lett.
го пространства-времени ЧД Хейворда-ADS, для
90, 201102 (2003).
всех значений физических параметров демонстри-
10.
S. H. Mazharimousavi, M. Halilsoy, and Z. Amirabi,
рует только коллапс. Поэтому в зависимости от
Phys. Rev. D 81, 104002 (2010).
выбора пространства-времени ЧД рассматриваемые
структуры ведут себя по-разному. Эти результаты
11.
F. Rahaman, S. Ray, A. K. Jafry, and K. Chakra-
borty, Phys. Rev. D 82, 104055 (2010).
могут оказаться полезными для будущих исследова-
ний динамики гравастаров с тонкой оболочкой при
12.
M. Sharif and M. Azam, Eur. Phys. J. C 73, 2407
различном выборе внутренней и внешней геометрий.
(2013).
Следует отметить, что гравастары должны быть
13.
M. Sharif and F. Javed, Gen. Relativ. Gravit. 48, 158
устойчивыми вблизи ожидаемого горизонта собы-
(2016).
тий [25-27]. Наличие безмассового и массивного
скалярных полей на тонкой оболочке для случая
14.
S. D. Forghani, S. Habib Mazharimousavi, and
эквивалентных копий черных дыр обуславливает
M. Halilsoy, Eur. Phys. J. C 78, 469(2018).
как расширение, так и коллапс для различных зна-
15.
M. Sharif and F. Javed, Astrophys. Space Sci. 364,
чений физических параметров. [33-37]. В настоящей
179 (2019); Chin. J. Phys. 61, 262 (2019); Int. J.
работе на основании зависимостей эффективного
Mod. Phys. D 29, 2050007(2020); Int. J. Mod. Phys.
потенциала мы получили только коллапсирующее
A 35,
2040015
поведение оболочки для всех значений физических
S0217732320503095.
параметров как для безмассового, так и для мас-
сивного поля. Скорость коллапса уменьшается при
16.
M. Sharif, S. Mumtaz, and F. Javed, Int. J. Mod.
увеличении космологической постоянной. Поэтому
Phys. A 35, 2050030 (2020).
теоретическая модель гравастара могла бы быть
17.
M. Visser and D. L. Wiltshire, Class. Quantum Grav.
полезной для лучшего понимания устойчивых и
21, 1135 (2004).
динамических конфигураций астрономических
18.
B. M. N. Carter, Class. Quantum Grav. 22, 4551
компактных объектов.
(2005).
Финансирование. Один из авторов (Ф. Дж.)
19.
D. Horvat, S. Ilijic, and A. Marunovic, Class.
благодарит Высшую Комиссию по образованию Ис-
Quantum Grav. 26, 025003 (2009).
ламабада за финансовую поддержку (6748/Punjab/
20.
Usmani et al., Phys. Lett. B 701, 388 (2011).
NRPU/RD/HEC/2016).
21.
A. Banerjee, A. Rahaman, S. Islam, and M. Goven-
der, Eur. Phys. J. C 76, 34 (2016).
ЛИТЕРАТУРА
22.
P. Rocha, R. Chan, da M. F. A. Silva, and A. Wang, J.
1. J. M. Bardeen, Proc. GR5, Tiflis, USSR (1968),
Cosmol. Astropart. Phys. 2008, 010 (2008); R. Chan,
p. 174.
da M. F. A. Silva, P. Rocha, and A. Wang, J. Cosmol.
Astropart. Phys. 2009, 10 (2009); ibid. 2011, 13
2. E. Ayón-Beato and A. Garc´ia, Phys. Rev. Lett 80,
(2011).
5056 (1998); Gen. Rel. Grav. 629, 31 (1999); Phys.
Lett. B 25, 464 (1999); Phys. Lett. B 149, 493 (2000).
23.
D. Horvat, S. Ilijic, and A. Marunovic, Class.
Quantum Grav. 28, 195008 (2011).
3. S. A. Hayward, Phys. Rev. Lett. 96, 031103 (2006).
24.
F. Rahaman, A.A. Usmani, S. Ray, and S. Islam,
4. M. Wen-Juan, C. Rong-Gen, and S. Ru-Keng, Comm.
Phys. Lett. B 707, 319 (2012); ibid. 717, 1 (2012).
Theor. Phys. 46, 453 (2006).
25.
F. S. N. Lobo and R. Garattini, J. High Energy Phys.
5. Z. Y. Fan and X. Wang, Phys. Rev. D 94, 124027
1312, 065 (2013).
(2016); Z. Y. Fan, Eur. Phys. J. C 77, 266 (2017).
26.
A.
Övgün, A. Banerjee, and K. Jusufi, Eur. Phys. J.
6. S. Fernando, Int. J. Mod. Phys. D 26, 07 (2017).
C 77, 566 (2017).
471
М. Шариф, Ф. Джавед
ЖЭТФ, том 159, вып. 3, 2021
27. M. Sharif and F. Javed, Ann. Phys. 415, 168124
33. D. Núñez, H. Quevedo, and M. Salgado, Phys. Rev.
(2020).
D 58, 083506 (1998).
28. J. A. Wheeler, Phys. Rev. 97, 511 (1955); D. R. Brill,
34. M. Sharif and G. Abbas, Gen. Relativ. Gravit. 44,
and J. A. Wheeler, Phys. Rev. 105, 1662 (1957).
2353 (2012).
29. Q. Bergmann and R. Leipnik, Phys. Rev. 107, 1157
35. M. Sharif and S. Iftikhar, Astrophys. Space Sci. 356,
(1957).
89 (2015).
30. D. J. Kaup, Phys. Rev. 172, 1331 (1968).
36. M. Sharif and F. Javed, Int. J. Mod. Phys. D 28,
1950046 (2019); Ann. Phys. 407, 198 (2019); Mod.
31. E. Seidel and W. Suen, Phys. Rev. D 42, 384 (1990).
Phys. Lett. A 35, 1950350 (2019); Ann. Phys. 416,
168146 (2020).
32. M. W. Choptuik,Phys. Rev. Lett. 706 9 (1993);
C. R. Evans and J. S. Coleman, Phys. Rev. Lett.
37. G. Abbas and M. R. Shahzad, Int. J. Mod. Phys.
72, 1782 (1994); D. Christodoulou, Ann. Math. 140,
A 35, 2050028 (2020).
607 (1994); E. Malec, Class. Quantum Grav. 13,
1849 (1995); C. Gundlach, Phys. Rev. Lett. 75, 3214
38. F. Rahaman, A. Banerjee, and I. Radinschi, Int. J.
(1995); P. R. Bardy, Class. Quantum Grav. 11, 1255
Theor. Phys. 52, 2943 (2013).
(1996).
472