ЖЭТФ, 2021, том 159, вып. 3, стр. 553-562

ПРОВОДИМОСТЬ ДВУМЕРНОЙ МОДЕЛИ РЭЛЕЯ ПРИ

КРИТИЧЕСКОЙ КОНЦЕНТРАЦИИ — ПОРОГЕ ПРОТЕКАНИЯ

Б. Я. Балагуров^*

Институт биохимической физики им. Н. М. Эмануэля Российской академии наук

119334, Москва, Россия

Поступила в редакцию 7 ноября 2020 г.,

после переработки 14 ноября 2020 г.

Принята к публикации 14 ноября 2020 г.

Рассмотрена проводимость двумерной модели Рэлея (изотропной матрицы с периодическим располо-

жением круговых включений) при критической концентрации — пороге протекания. В рамках бинарного

приближения вычислена эффективная проводимость модели с фазовым переходом металл-идеальный

проводник. Для альтернативной модели с фазовым переходом металл-диэлектрик соответствующая эф-

фективная проводимость определена соотношением взаимности Келлера - Дыхне.

DOI: 10.31857/S0044451021030160

ного приближения. В этом приближении исходная

проблема сводится к изучению протекания тока че-

рез пару соседних круговых включений. При этом

1. ВВЕДЕНИЕ

потенциал задачи выражается через электростати-

Двумерная модель композита с регулярным рас-

ческую функцию Грина для «тела», состоящего из

положением включений круговой формы впервые

двух кругов. Для вычисления функции Грина в [5]

рассмотрена Рэлеем в работе [1]. Для эффектив-

определена система собственных функций (см. [6,7])

ной проводимости σ_e этой модели в [1] были вы-

для упомянутого «тела». Использование полученно-

числены первые члены разложения соответствую-

го таким образом потенциала позволило определить

щего вириального ряда по степеням малой концент-

эффективную проводимость рассматриваемой моде-

рации включений. Впоследствии решение, позволя-

ли. Следует отметить, что использованное в рабо-

ющее найти произвольный член этого ряда, было

те [5] бинарное приближение тем точнее описыва-

дано разными методами в работах [2, 3] (см. также

ет проводимость рассмотренной двумерной модели,

[4]). Согласно [2, 3] для вычисления проводимости

чем ближе она к точке фазового перехода.

двумерной модели Рэлея необходимо разрешить бес-

В настоящей работе рассмотрена задача о про-

конечную систему алгебраических уравнений. Как

водимости двумерной модели Рэлея при критичес-

показал численный анализ [3], для определения ве-

кой концентрации (пороге протекания), когда про-

личины σ_e в достаточно широком диапазоне изме-

исходит соприкосновение соседних кругов. В том

нения входящих в задачу параметров достаточно

же бинарном приближении потенциал выражен че-

ограничиться рассмотрением конечной подсистемы

рез функцию Грина, а та, в свою очередь, — че-

уравнений небольшого размера. В то же время для

рез систему собственных функций для пары сопри-

модели с фазовым переходом этот размер может

касающихся включений. Спецификой этого случая

быть неограниченно большим. Это обстоятельство

является непрерывность спектра собственных зна-

серьезно затрудняет исследование обсуждаемой за-

чений и дельта-функционный вид соотношения ор-

дачи численным методом.

тонормированности для поляризационных собствен-

В предыдущей работе [5] обсуждаемая задача о

ных функций. С помощью найденного потенциа-

проводимости двумерной модели Рэлея с фазовым

ла вычислена эффективная проводимость модели

переходом типа металл-идеальный проводник рас-

в точке фазового перехода типа металл-идеальный

смотрена аналитическим методом в рамках бинар-

проводник. Для альтернативной модели с фазовым

переходом типа металл-диэлектрик соответствую-

^* E-mail: balagurov@deom.chph.ras.ru, byabalagurov@mail.ru

щая эффективная проводимость определена из со-

553

Б. Я. Балагуров

ЖЭТФ, том 159, вып. 3, 2021

отношения взаимности Келлера - Дыхне [8,9]. Срав-

В данном случае уравнение сохранения тока при-

нение полученного результата с гипотезой подобия

нимает вид

[10,11] позволяет определить соответствующий кри-

{

}

div j = I

δ(r - ρ₂) - δ(r - ρ₁)

(1)

тический индекс проводимости.

Знание системы собственных функций для како-

Здесь j — плотность тока

го-либо макроскопического тела позволяет не толь-

ко находить соответствующую электростатическую

j = -σ(r)∇ϕ(r),

(2)

функцию Грина, но и давать решение, например,

краевых задач Дирихле и Неймана, а также вычис-

σ(r) — проводимость среды, ϕ(r) — электрический

лять поляризуемость этого тела. В качестве приме-

потенциал. Положим

ра в Приложении найден тензор дипольной поляри-

σ(r) = σ₁[1 - (1 - h)v(r)], h = σ₂/σ₁,

(3)

зуемости двух соприкасающихся кругов (параллель-

ных круговых цилиндров для трехмерной задачи).

где v(r) = 1 внутри включения и v(r) = 0 вне его.

В этом случае уравнение для потенциала принимает

вид

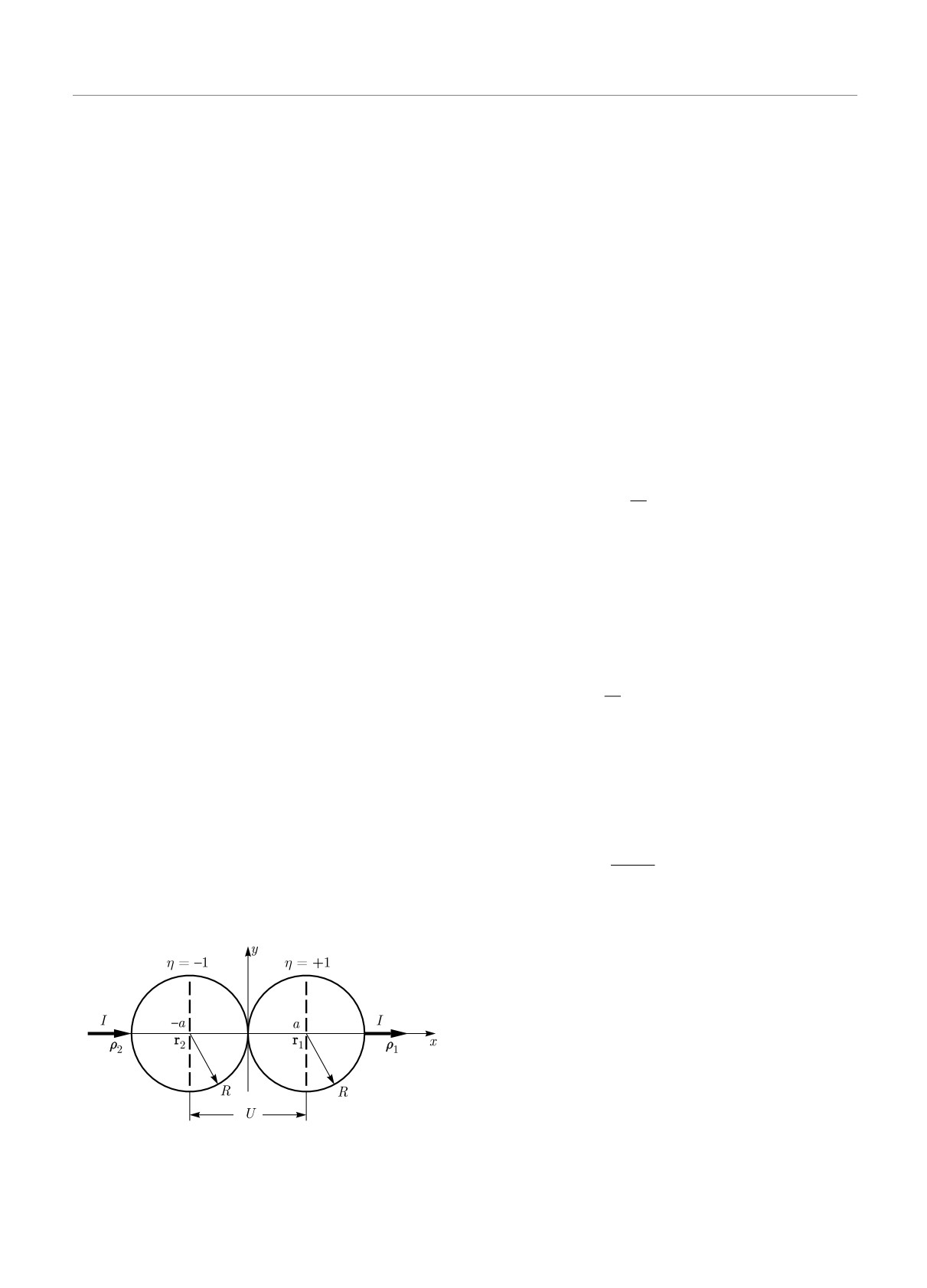
2. БИНАРНОЕ ПРИБЛИЖЕНИЕ

{

]

}

∇

[1 - (1 - h)v(r)

∇ϕ(r)

Двумерная модель Рэлея представляет собой

I {

}

изотропную матрицу проводимости σ₁ c системой

δ(r - ρ₁) - δ(r - ρ₂)

(4)

включений круговой формы радиуса R и проводи-

σ₁

мости σ₂. Центры кругов расположены в узлах квад-

Введем, следуя ссылкам [6, 7], функцию Грина

ратной решетки с периодом 2a. При критической

G(r, r^′), подчиняющуюся уравнению

концентрации a = R — пороге протекания — каж-

{

}

дое из включений касается четырех ближайших со-

∇_r

[1 - (1 - h)v(r)] ∇_r G(r, r^′)

= δ(r - r^′).

(5)

седей. При σ₂ ≫ σ₁ в подобном двумерном компо-

зите происходит фазовый переход типа металл-иде-

С учетом формулы (5) для потенциала ϕ(r) из урав-

альный проводник. В этом случае проводимость мо-

нения (4) получаем следующее выражение:

дели в целом определяется областью контакта сосед-

I {

}

них включений, где ток должен преодолевать низко-

ϕ(r) =

G(r, ρ₁) - G(r, ρ₂)

(6)

σ₁

проводящую прослойку. Следует ожидать при этом,

что ток протекает через эту прослойку в виде узко-

Величина G(r, r^′), подчиняющаяся уравнению

го канала возле точки соприкосновения включений.

(5), определена в [6, 7] с помощью метода собствен-

Для оценки вклада области контакта в эффектив-

ных функций. Для функции Грина G(r, ρ), где ρ

ную проводимость воспользуемся, как и в [5], би-

принадлежит поверхности тела, имеет место следу-

нарным приближением — рассмотрим пару соседних

ющее выражение согласно [6, 7]:

кругов (см. рис. 1), помещенную в неограниченного

∑

размера матрицу. Входящий в эту пару и исходя-

1+ε_ν

G(r, ρ) = -

Ψ_ν(ρ)ψ_ν(r)-

щий из нее токи, расположенные «вдали» от области

h+ε_ν

контакта, представим в виде точечных источника и

∑

Ψ_k(ρ)ψk(r).

(7)

стока.

Здесь вектор r произволен и может принадлежать

как телу, так и пространству вне его.

В выражении (7) ψ_ν(r) и

ψ_k(r) — регулярные

и обращающиеся в нуль при r → ∞ собственные

функции, а Ψ_ν(ρ) и

Ψ_k(ρ) — их значения на по-

верхности тела при r = ρ. Поляризационные функ-

ции ψ_ν (r), обладающие мультипольной асимптоти-

кой, удовлетворяют уравнению Лапласа внутри (i)

и вне (e) тела:

Рис. 1

∇² ψ(i)ν(r) = 0,

∇² ψ(e)ν(r) = 0.

(8)

554

ЖЭТФ, том 159, вып. 3, 2021

Проводимость двумерной модели Рэлея...

На поверхности S тела (при r = ρ) для функции

ψ_ν(r) имеем следующие граничные условия:



∂ψνe)

∂ψνi)

ψ(e)ν

=ψ(i)ν

= -ε_ν

(9)

∂n

Здесь ∂/∂n — нормальная производная, ε_ν > 0 —

собственное значение для поляризационного состо-

яния. Система {ψ_ν (r)} ортонормирована по соотно-

шению

∫

(

)

∇ψ_μ(r) · ∇ψ_ν (r)

dr = δ_μν ,

(10)

Рис. 2

где интегрирование распространяется на все прост-

ранство, или

кругов собственные значения образуют непрерыв-

∫

ный спектр, а соотношение ортонормированности

(

)

ε_ν

∇ψ_μ(r) · ∇ψ_ν (r)

[1 - v(r)] dr =

δ_μν.

(11)

для поляризационных собственных функций имеет

1+ε_ν

дельта-функционный вид. В этом случае сумму в

Здесь интеграл берется по области вне тела.

формуле (7) следует заменить на соответствующий

Функции зарядовых состояний

ψ_k(r) вне тела

интеграл.

также подчиняются уравнению Лапласа и облада-

ют монопольной асимптотикой. Им отвечает одно и

то же собственное значение ε_k = ∞. Для монолит-

3. КООРДИНАТНАЯ СИСТЕМА

ного (неразъемного) тела зарядовая функция

ψ(r)

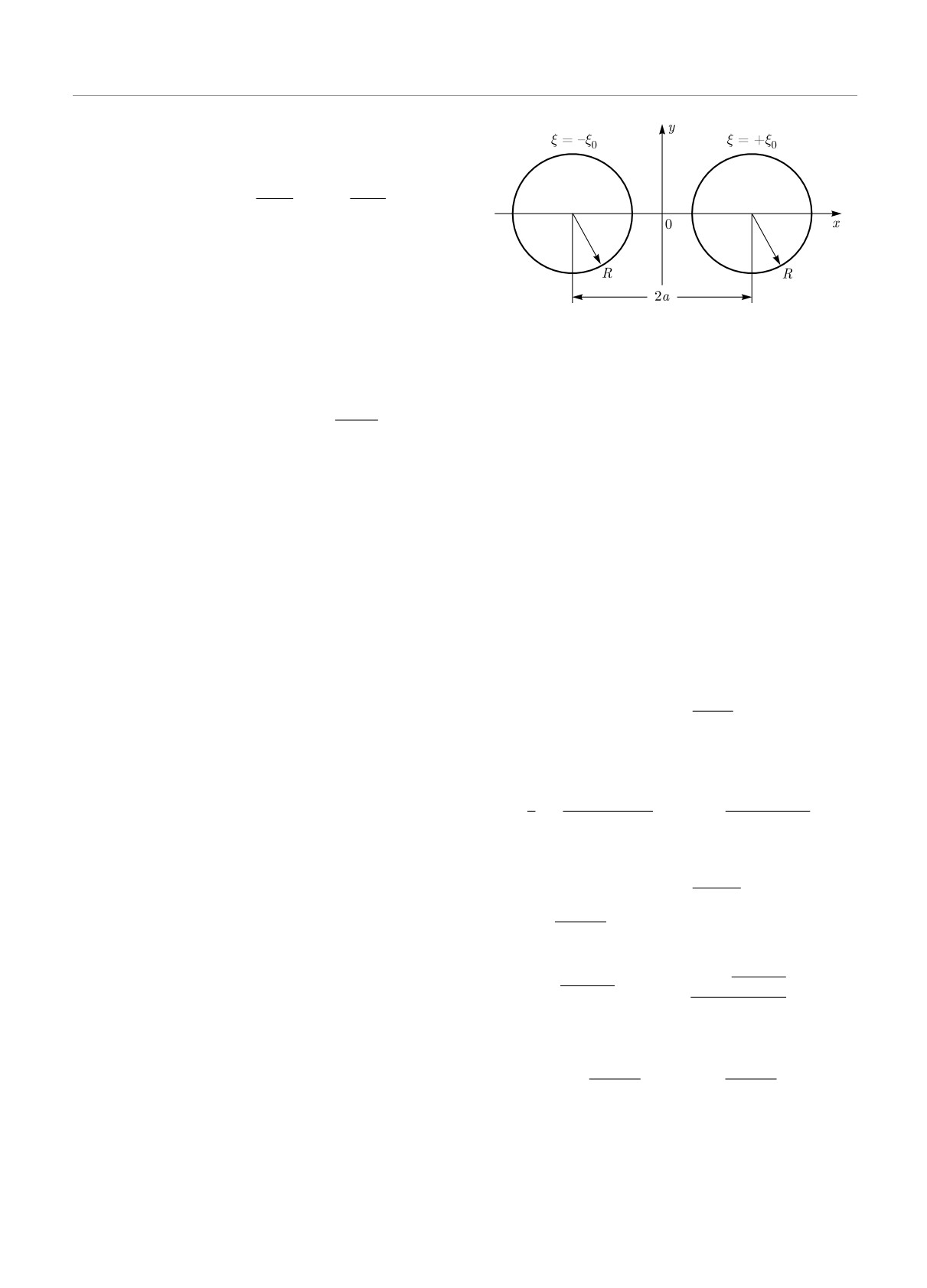
Задачу определения собственных функций для

одна. На поверхности тела она принимает постоян-

«тела» в виде соприкасающихся кругов будем ре-

ное значение

шать в биполярной системе координат, соответству-



ψ(e)(r)

= Ψ = const.

(12)

ющим образом преобразованной. Согласно [12] би-

полярные координаты (ξ, θ) связаны с декартовыми

В то же время

ψ(i)(r) =

Ψ в любой точке внутри

(x, y) с помощью соотношения

тела.

Разъемному «телу», состоящему из n частей, от-

ξ + iθ

x + iy = c th

(15)

вечает n зарядовых функций

ψ_k(r), где k

= 1,

2, . . ., n. Каждая из них принимает постоянные (во-

здесь - ∞ ≤ ξ ≤ + ∞, 0 ≤ θ ≤ 2π. Из (15) следует,

обще говоря, разные) значения на поверхностях час-

что

тей этого тела.

Функции

ψ_k(r) ортонормированы согласно

(x + c)² + y²

2cy

ξ=

tg θ =

(16)

∫

(x - c)² + y²

c² - x² - y²

(

)

ψ_k(r) ·

ψ_k′ (r)

[1 - v(r)] dr = δ_kk′ .

(13)

Подсистемы поляризационных {ψ_ν (r)} и зарядовых

2cy

θ = π - arctg

(17)

ψ_k(r)} функций взаимно ортогональны:

r² - c²

∫

√

(

)

при r =

x² + y² > c. В ситуации, изображенной на

∇ψ_ν (r) ·

ψ_k(r)

[1 - v(r)] dr = 0.

(14)

рис. 2, имеем

Таким образом, совокупность {ψ_ν (r),ψk(r)} пред-

√

a² - R²

ставляет собой ортонормированную систему функ-

a² - R², ξ₀ = ln

(18)

ций. Заметим, однако, что эта совокупность полной

системой не является (см. [6, 7]). Отметим также,

При a → R (c → 0) из (16) и (17) следует

что в рассматриваемой в работе двумерной задаче

2cx

2cy

функции с монопольной асимптотикой логарифми-

θ π-

(19)

x² + y²

чески расходятся при r → ∞. В этом случае на за-

рядовые функции накладывается условие

ψ_k(r) =

= 0 на окружности достаточно большого радиу-

ξ₀

c/R.

(20)

са. Как будет видно ниже, для соприкасающихся

555

Б. Я. Балагуров

ЖЭТФ, том 159, вып. 3, 2021

Координатные линии вырожденной биполярной

системы представляют собой два набора взаимно ор-

тогональных окружностей, соприкасающихся в точ-

ке x = 0, y = 0 (см. рис. 3). Действительно, ис-

ключая из равенств (24) величину β при η = const,

получим уравнение

(

)₂

⁽R)2

+y² =

(26)

Согласно (26) постоянным значениям η = ±η₀ отве-

чает пара соприкасающихся окружностей радиуса

R/η₀ с центрами в точках ±R/η₀ на оси x. Анало-

гичным образом постоянным β = ±β₀ отвечает пара

соприкасающихся окружностей радиуса R/β₀ с цен-

трами в точках ±R/β₀ на оси y.

В вырожденной системе биполярных координат

для градиента потенциала ϕ имеем следующее вы-

ражение:

Рис. 3

eη ∂ϕ

eβ ∂ϕ

∇ϕ=

(27)

H_η ∂η

H_β ∂β

(Здесь и далее символом обозначается асимптоти-

где

ческое выражение.)

H_η = H_β = H(η, β) =

(28)

Положим

η² + β²

— коэффициент Ламе. В (27) e_η и e_β — орты норма-

ξ=ξ₀η, θ=π+ξ₀β,

(21)

лей к координатным линиям η = const и β = const:

тогда из (15) получаем

η² - β²

2ηβ

e_η = - i_x

+i_y

(29)

η² + β²

ξ₀ (η + iβ)

x + iy = c cth

(22)

2ηβ

² -β²

e_β = - i_x

-i_y

(30)

Отсюда в пределе c → 0 находим

η² + β²

Здесь i_x и i_y — орты декартовых осей x и y соответ-

x + iy =

(23)

η + iβ

ственно. Отметим, что e_η является единичным век-

тором внутренней к границе правого круга нормали

так что

и внешней — к границе левого.

Уравнение Лапласа в координатах (η, β) прини-

x = 2R

y = -2R

(24)

η² + β²

мает вид

и, соответственно,

∂²ϕ

= 0.

(31)

∂η²

∂β²

η = 2R

β = -2R

(25)

x² + y²

В данном случае при решении этого уравнения мето-

дом разделения переменных отсутствует, в отличие

Введенные в (23)-(25) величины η и β являются

от работы [5], требование периодичности по одной

координатами вырожденной биполярной системы.

из координат. Поэтому соответствующая константа

Координаты η и β изменяются в пределах от -∞

разделения принимает произвольные значения, об-

до +∞. При этом η → 0, β → 0 при r → ∞ и η →

разуя непрерывный спектр.

→ ±∞, β → ±∞ при r → 0. Значениям η > 0 отве-

Регулярные частные решения уравнения

(31)

чает правая полуплоскость x > 0, а η < 0 — левая

для правого включения, конечные при x → +0 (η →

(x < 0). В то же время значению β > 0 соответству-

→ +∞), имеют следующий вид:

ет нижняя полуплоскость (y < 0), а β < 0 — верхняя

e^-νη sinνβ, e^-νη cosνβ.

(32)

(y > 0).

556

ЖЭТФ, том 159, вып. 3, 2021

Проводимость двумерной модели Рэлея...

Здесь величина ν положительна и меняется в преде-

антисимметричны по x и симметричны по y:

лах от 0 до ∞. Для левого включения аналогичные

ψ(e)2ν(r) = B_ν shνη cosνβ,

|η| ≤ 1,

(41)

решения отличаются от (32) заменой e^-νη на e^νη.

Для исчезающих при r → ∞ (η → 0, β → 0) ре-

гулярных решений с мультипольной асимптотикой

ψ(1)2ν(r) = B_ν shν e-ν(η-1) cosνβ, η ≥ 1,

(42)

имеем соответственно

(2)

ψ₂

(r) = - B_ν sh ν eν(η+1) cos νβ, η ≤ - 1,

(43)

shνη sinνβ, shνη cosνβ,

(33)

ch νη sin νβ, ch νη cos νβ - 1

где

√

с тем же параметром ν.

ε2ν - 1

e^-ν

B_ν =

(44)

Отметим, наконец, что решением уравнения (31)

2πν

2πν shν

с монопольной (логарифмической) асимптотикой

Функции третьего типа ψ3ν (r) с собственными

является функция

значениями ε3ν = ε1ν = th ν симметричны и по x,

ln(η² + β²),

(34)

и по y:

√

(e)

ψ₃

(r) = A_ν (ch νη cos νβ - 1),

|η| ≤ 1,

(45)

или 2 ln(2R/r), где r =

x² + y², в декартовых ко-

ординатах.

[

]

ψ(1)3ν(r) = A_ν

ch ν e-ν(η-1) cos νβ-1

η ≥ 1,

(46)

4. СИСТЕМА СОБСТВЕННЫХ ФУНКЦИЙ

[

]

(2)

ψ₃

(r) = A_ν

ch ν eν(η+1) cos νβ-1

η ≤ -1.

(47)

С рассматриваемым включением в виде пары

соприкасающихся кругов связаны четыре типа по-

Нормировочный коэффициент A_ν определен в фор-

ляризационных собственных функций ψ_λν (r)

муле (39).

= ψ_λν(η,β) (λ = 1,2,3,4), которым отвечают дву-

Функции четвертого типа с собственными значе-

кратно вырожденные собственные значения ε1ν =

ниями ε4ν = ε2ν = cth ν антисимметричны и по x, и

=ε3ν и ε2ν =ε4ν.

по y:

Нормированные функции первого типа ψ1ν(r) с

ψ(e)4ν(r) = B_ν shνη sinνβ,

|η| ≤ 1,

(48)

собственными значениями

ε1ν = th ν

(35)

ψ(1)4ν(r) = B_ν shν e-ν(η-1)

sinνβ, η ≥ 1,

(49)

имеют вид

(2)

ψ₄

(r) = - B_ν sh ν eν(η+1) sin νβ, η ≤ -1.

(50)

ψ(e)1ν(r) = A_ν chνη sinνβ,

|η| ≤ 1,

(36)

Коэффициент B_ν определен в формуле (44).

вне включения и

Зарядовая собственная функция одна:

ψ(1)1ν(r) = A_ν chν e^-νη sinνβ, η ≥ 1,

(37)

⎧

⎨

(

)

ψ(e)(r) =

+ ln

η² + β²

^A⎩^2ln

ψ(2)1ν(r) = A_ν chν e^νη sinνβ, η ≤ - 1,

(38)

⎫

∞

∫

⎬

внутри правого (1) и левого (2) кругов соответствен-

ch νη cos νβ - 1 dν

+ 2

e^-ν

(51)

но. Здесь

ch ν

ν ⎭

√

-ν

1-ε1ν

где

A_ν =

(39)

2πν

2πν chν

[

]-1/2

Функции ψ1ν (r) симметричны по координате x и ан-

√

(52)

2π

тисимметричны по y.

Функции второго типа ψ2ν(r), которым отвечают

∫∞

собственные значения

ch ν - 1 dν

J = e^-ν

(53)

ch ν ν

ε2ν = cthν,

(40)

557

Б. Я. Балагуров

ЖЭТФ, том 159, вып. 3, 2021

∫

Выражение (51) принимает постоянное значение

Ψ_k(ρ)

Φk′ (ρ)dρ = - δ_kk′ .

(62)

при η = ±1, в чем можно убедиться, используя со-

отношение

Здесь dρ = dS — элемент площади, а интегрирова-

∞

∫

η²

+β

dν

ние в (59)-(62) проводится по всей поверхности S

e^-ν|η| (1 - cosνβ )

(54)

η²

тела.

Соотношение полноты для системы поверхност-

при η = ±1. Функция

ψ(r) обращается в нуль при

ных функций имеет вид

r = L, где L ≫ R. Действительно, в случае больших

∑

1+ε_ν

r имеем

Ψ_ν(ρ)Φ_ν(ρ^′) +

Φ_k(ρ)

Φ_k(ρ^′) =

r≫R:

ψ(e)(r)

2 q ln

(55)

= -δ(ρ - ρ^′).

(63)

Здесь

Отметим, что в случае непрерывного спектра соб-

ственных значений ε_ν в правой части равенства (59)

(56)

символ Кронекера δ_νν′ заменяется на дельта-функ-

цию δ(ν - ν^′), а сумма по ν в соотношении (63) — на

— полный заряд рассматриваемого включения.

соответствующий интеграл.

2. Для рассматриваемого в работе включения по-

5. ПОВЕРХНОСТНЫЕ СОБСТВЕННЫЕ

ляризационные поверхностные функции выражают-

ФУНКЦИИ

ся через ψ(e)λν(η, δ) следующим образом:

1. Как отмечено в работах [6, 7], собственные

Ψ(1)λν(β) = ψ(e)λν(+ 1, β), Ψ(2)λν(β) = ψ(e)λν(- 1, β), (64)

функции образуют полную систему на поверхности



S соответствующего тела. Для формулировки соот-

∂ψ(e)λν

Φ(1)λν(β) = -



ношения полноты наряду с поверхностным значени-

H₀

∂η



η=+ 1

ем функций (аналогами потенциалов)



(65)

(e)



(2)

∂ψ_λ



(β) =



λν

Ψ_ν(ρ) = ψ(e)ν(r)

Ψ_k(ρ) =

ψ(e)k(r)

(57)

H₀

∂η



r=ρ

η=-1

где H₀ = H(1, β) — коэффициент Ламе. Выбор зна-

необходимо ввести сопряженные с ними величины

ков в (65) обусловлен тем, что единичный вектор

(

)

Φ_ν(ρ) =

n ∇ψ(e)ν(r)



e_η является ортом внутренней нормали для пра-

r=ρ

вой окружности и внешней для левой. Зарядовые

(58)

(

)

Φ_k(ρ) =

ψ(e)k(r)



поверхностные функции

Ψ⁽¹⁾(β),

Ψ⁽²⁾(β),

Φ⁽¹⁾(β) и

r=ρ

Φ⁽²⁾(β) выражаются через

ψ(e)(η, β) аналогичным

имеющие смысл плотности поверхностного заряда.

образом.

В формуле (58) n — орт внешней к поверхности тела

Используя приведенные в предыдущем разделе

нормали.

выражения для функций ψ(e)λν(η, β) и

ψ(e)(η, β), най-

Введение системы поверхностных функций поз-

дем

воляет, прежде всего, упростить соотношения орто-

Ψ(1)1ν(β) = Ψ(2)1ν(β) = A_ν chν sinνβ,

(66)

нормированности:

∫

ε_ν

Ψ_ν(ρ)Φ_ν′ (ρ)dρ = -

δ_νν′ ,

(59)

Ψ(1)2ν(β) = - Ψ(2)2ν(β) = B_ν shν cosνβ,

(67)

1+ε_ν

(

)

∫

Ψ(1)3ν(β) = Ψ(2)3ν(β) = A_ν

ch ν cos νβ - 1

(68)

Ψ_ν(ρ)

Φ_k(ρ)dρ = 0,

(60)

Ψ(1)4ν(β) = -Ψ(2)4ν(β) = B_ν shν sinνβ ;

(69)

∫

Ψ_k(ρ)Φ_ν(ρ)dρ = 0,

(61)

νA_ν

Φ⁽¹⁾(β) = Φ(2)1ν(β) = -

shν sinνβ,

(70)

1ν

H(1, β)

558

ЖЭТФ, том 159, вып. 3, 2021

Проводимость двумерной модели Рэлея...

νB_ν

Соотношение полноты в данном случае прини-

Φ(1)2ν(β) = -Φ(2)2ν(β) = -

ch ν cos νβ,

(71)

H (1, β)

мает вид

∫

∞

νA_ν

∑

1+ε_λν

Φ(1)3ν(β) = Φ(2)3ν(β) = -

shν cosνβ,

(72)

Ψ(σ)λν(β)Φ(σ′)_λν(β^′)dν +

H(1, β)

λν

λ=1 0

δ(β - β^′)

+ Ψ

(σ)(β)

Φ(σ^′ )(β′)=-δσσ′

(81)

νB_ν

H(1, β)

Φ(1)4ν(β) = -Φ(2)4ν(β) = -

ch ν sin νβ.

(73)

H (1, β)

Нетрудно убедиться, что подстановка выражений

Зарядовые функции равны

(66)-(75) обращает это равенство в тождество.

[

]

Ψ= 2A ln

(74)

6. ПОТЕНЦИАЛ

1. Искомый потенциал ϕ(r) рассматриваемой за-

Φ(β) = -

(75)

дачи находим подстановкой общего выражения для

H(1, β)

πβ

функций Грина G(ρ, r), имеющей в данном случае

вид

с коэффициентом

A из формулы (52) и величиной

∞

∫

J из (53). При выводе выражения (75) использовано

∑

1+ε_λν

G(ρ, r) = -

dν

Ψ_λν(ρ)ψ_λν(r)-

равенство

h+ε

λν

λ=1 0

∫

∞

cosbx

− Ψ(ρ)ψ(r),

(82)

dx =

(76)

ch ax

πb

2a ch

в формулу (6). В результате получаем

Найденная система поверхностных функций

∫

∞

1+ε2ν

(66)-(75) ортонормирована по соотношениям

ϕ(r) = -2

dν

Ψ2ν(ρ₁)ψ2ν(r).

(83)

σ₁

h+ε

2ν

∫

Здесь вектор r — любой, а вектор ρ₁ равен (2R, 0)

Ψ(σ)λν(β)Φ(σ)λ′ν′ (β)H(1, β)dβ =

σ=1_-∞

в декартовых координатах и (1, 0) в вырожденных

ε_λν

биполярных.

δ_λλ′ δ(ν - ν^′),

(77)

1+ε_λν

Для потенциалов вне включений (|η| ≤ 1) и внут-

ри правого круга (η ≥ 1) имеем соответственно

∫

∞

dν

shνη

Ψ(σ) Φ(σ)λν(β) H(1, β) dβ = 0,

(78)

ϕ(e)(r) = -

cosνβ,

(84)

πσ₁

ν h + cthν shν

σ=1_-∞

∫

∞

dν e-ν(η-1)

Ψ(σ)λν(β)

Φ(σ)(β) H(1, β) dβ = 0,

(79)

ϕ⁽¹⁾(r) = -

cosνβ.

(85)

πσ₁

ν h + cthν

σ=1_-∞

Как следует из формул (84), (85), потенциал непре-

∫

рывен на границе (η = + 1) правого круга. Кроме

Ψ(σ) Φ(σ)(β)H(1,β)dβ=-1.

(80)

того, выполняется граничное условие

σ=1_-∞



∂ϕ(e)

∂ϕ⁽¹⁾



- h

δ(β),

(86)



Из равенств (77) и (80) определялись нормировоч-

∂η

σ₁

η=+ 1

ные коэффициенты A_ν , B_ν и

A, приведенные в

предыдущем разделе.

следующее из уравнения (4).

559

Б. Я. Балагуров

ЖЭТФ, том 159, вып. 3, 2021

2. Используя формулу (84), для плотности тока

При малых значениях γ проведем в выражении (95)

на оси y (при η = 0) имеем

интегрирование по частям. В результате получим

⎧

⎫

[

]

∞

⎨

∫

⎬

∂ϕ⁽¹⁾

j(0, y) = -σ₁

(87)

g(γ) = γ²

e^-x ln(x² + γ²)dx

(97)

H(η, β)

∂ηη=0

⎩

⎭

С учетом H(0, β) = 2R/β² из (87) получим выраже-

откуда следует

ние

∞

γ ≪ 1 : g(γ) ≃ ln

- C,

(98)

∫

cth ν

j(0, y) =

β²

dν

cosνβ.

(88)

2πR

h + cthν

где

∫

∞

При h ≫ 1 в интеграле из (88) существенны ν ≪

C = - e^-x lnxdx = 0.577...

(99)

≪ 1:

∫

∞

— постоянная Эйлера.

cosνβ

j(0, y) =

β²

dν

(89)

Согласно (96)-(98) при рассматриваемых значе-

2πR

1 + hν

ниях h ≫ 1 плотность тока имеет острый пик высо-

той j(0, 0) = 〈j〉

h/π ≫ 〈j〉 (в точке контакта вклю-

Представим это выражение в следующем виде:

чений) шириной приблизительно R/h ≪ R.

Этот результат подтверждает справедливость

j(0, y) = 〈j〉

g(γ),

〈j〉 =

(90)

обсуждавшейся в разд. 2 картины протекания то-

где

ка в модели с фазовым переходом типа металл-

идеальный проводник. При этом в пределе h → ∞

∫∞

cosγt

плотность тока j ≈ h → ∞ при y = 0 и j = 0

j(γ) = γ²

dt, γ =

(91)

1+t

при y = 0. Следовательно, величина j в этом пре-

деле принимает дельта-функционный вид: j(0, y) =

Здесь 〈j〉 — средняя плотность тока и учтено, что

= const·δ(y). Определяя обычным образом эту конс-

при η = 0 величина β = - 2R/y.

танту, получим, что

Для упрощения анализа выражения (91) преоб-

j(0, y) = I δ(y)

(100)

разуем величину g(γ) следующим образом. Введем

функцию

в пределе h → ∞. Последний результат означает,

что использованное в работе бинарное приближение

∫∞

cosγt

в пределе h → ∞ становится точным.

F (γ) = γ²

e-x(1+t) dt,

(92)

1+t

так что

7. ЭФФЕКТИВНАЯ ПРОВОДИМОСТЬ

F (0) = g(γ), F (∞) = 0.

(93)

Так как эффективная проводимость σ_e модели в

целом совпадает с проводимостью отдельной ячей-

Для производной F^′(x) соответствующий интеграл

ки, то

может быть вычислен в явном виде:

σe =

(101)

F^′(x) = - γ² e^-x

(94)

x² + γ²

Здесь I — полный ток, текущий через ячейку, U —

откуда с учетом определений (93) находим

приложенная к ней разность потенциалов и учтено,

что a ≈ R. В соответствии с рис. 2 величина U выра-

∫∞

xdx

жается через потенциал ϕ(r) следующим образом:

g(γ) = γ²

e^-x

(95)

x² + γ²

U = ϕ⁽²⁾(r₂) - ϕ⁽¹⁾(r₁) = -2ϕ⁽¹⁾(r₁)

(102)

Отсюда при больших значениях параметра γ полу-

с ϕ⁽¹⁾(r) из формулы (85) при r = r₁ = (R,0). Точке

чаем

x = R, y = 0 соответствуют вырожденные биполяр-

ные координаты (η₁, 0), где, как следует из опреде-

γ ≫ 1 : g(γ)

+...

(96)

x²

лений (25), η₁ = 2.

560

ЖЭТФ, том 159, вып. 3, 2021

Проводимость двумерной модели Рэлея...

Вычисляя с помощью выражения (85) для ϕ⁽¹⁾(r)

Для оценки f(p_c, h) при малых h разобьем инте-

разность потенциалов U, найдем величину σ_e, кото-

грал из (108) на две части, введя величину ν₀ такую,

рую представим в виде

что h ≤ ν₀ ≤ 1:

∞

⎧

∫

ν0

⎨∫

dν e^-ν

dν th ν

(103)

f (p_c, h) =

e^-ν +

σ_e

πσ₁

ν h + cthν

⎩

ν h + thν

⎫

∞

∫

⎬

Выражением

(103) для σ_e, справедливым при

dν th ν

e^-ν

(109)

= σ₂/σ₁

≫ 1, дается эффективная проводи-

ν h + thν

⎭

мость исследуемой модели с фазовым переходом

ν0

металл-идеальный проводник при критической

Для первого интеграла имеем

концентрации — пороге протекания.

∫

ν0

∫ν0

Величину σ_e как функцию ее аргументов запи-

dν th ν

dν

ν₀

шем в виде

e^-ν ≃

≃ ln

(110)

ν h + thν

h+ν

σe = σe(p; σ1, σ2),

(104)

Для второго интеграла получаем

где p — безразмерная концентрация (доля занима-

∞

∫

емой площади) первой компоненты матрицы, σ₁ и

dν th ν

dν

e^-ν ≃ e^-ν

(111)

σ₂ — проводимости матрицы и включений соответ-

ν h + thν

ν0

ственно. Отметим, что в выражении (103) концент-

рация p равна критической p_c = 1 - π/4. Эффек-

Отсюда, интегрируя по частям, находим

тивная проводимость альтернативной модели с фа-

∫

∞

зовым переходом типа металл-диэлектрик может

∞

dν



e^-ν

= e^-ν lnν

быть найдена из полученных выше результатов с

ν0

помощью так называемого соотношения взаимности

ν0

∫

∞

Келлера - Дыхне [8,9]. Как отмечено в этих работах

(см. также книгу [4]), в двумерном случае имеет ме-

+ e^-ν lnν dν ≃ - lnν₀ - C,

(112)

сто соотношение, связывающее эффективные про-

ν0

водимости взаимных, отличающихся друг от друга

где C — постоянная Эйлера, определенная согласно

заменой σ₁ ⇄ σ₂, систем:

(99). В результате получаем окончательно

(

)

σe(p; σ1, σ2) σe(p; σ2, σ1) = σ1σ2.

(105)

f (p_c, h) =

h ln

-C

(113)

Введя безразмерную эффективную проводимость f

согласно

В соответствии со сказанным в предыдущем разде-

ле, следует ожидать, что в пределе h → 0 выраже-

σ_e(p; σ₁, σ₂) = σ₁ f(p, h), h =

σ₂ ,

(106)

σ₁

ние (113) является точным.

В рамках гипотезы подобия [10, 11] величина

приведем равенство (105) к следующему виду:

f (p_c, h) описывается степенной функцией:

f (p, h) f(p, 1/h) = 1.

(107)

f (p_c, h) ∼ h^s,

(114)

Из этого соотношения, используя выражение (103),

где s — второй критический индекс проводимости.

после замены h → 1/h находим безразмерную эф-

В выражении

(114) пренебрегается возможной

фективную проводимость модели с фазовым перехо-

логарифмической зависимостью. Поэтому следует

дом типа металл-диэлектрик при критической кон-

считать, что в (113) s = 1. Отметим, что численные

центрации:

исследования проводимости двумерной модели

Рэлея [3] дает оценку s ≈ 0.95.

∫∞

dν th ν

f (p_c, h) =

e^-ν.

(108)

ν h + thν

Благодарности. Автор выражает благодар-

ность Д. А. Головневой и Н. А. Хлопотуновой за

Выражение (108) справедливо при h ≪ 1.

помощь в подготовке рукописи статьи к печати.

561

ЖЭТФ, вып. 3

Б. Я. Балагуров

ЖЭТФ, том 159, вып. 3, 2021

ПРИЛОЖЕНИЕ

Отметим, что выражения (A.6), (A.7) удовлетворя-

ют равенствам

Знание системы собственных функций для неко-

торого макроскопического тела дает возможность

Λ_xx(ε) = - Λ_yy(1/ε), Λ_yy(ε) = - Λ_xx(1/ε), (A.8)

определить его дипольную поляризуемость.

являющихся следствием соотношения взаимности

В случае тела, помещенного в однородное элект-

(см. [4]).

рическое поле напряженности E₀, соответствую-

В двух частных случаях, используя формулы

щий потенциал ϕ(r) имеет следующую асимптотику

(двумерный случай):

∞

∫

x dx

π²

x dx

π²

(

)

(A.9)

(

)

p·r

e^x - 1

e^x + 1

r → ∞ : ϕ(r)

E₀ · r

+ ... (A.1)

r²

получим

Здесь

π²R²

Λ_xx = -

Λ_yy = -

(A.10)

^ΛE₀

(A.2)

при ε = 0 и

— дипольный момент тела,

Λ— его тензор диполь-

ной поляризуемости. Для составляющих этого тен-

π²R²

Λ_xx =

Λ_yy =

(A.11)

зора согласно [6,7] имеем

∑

при ε = ∞.

d_να d_νβ

Λ_αβ = -4π(1 - ε)

(A.3)

ε+ε_ν

ЛИТЕРАТУРА

где d_ν — аналог дипольного момента в асимптотике

поляризационной собственной функции:

1. Lord Rayleigh, Phil. Mag. S. 34, № 211, 481 (1892).

(

)

r·d_ν

2. W. T. Perrins, D. B. McKenzie, and B. C. McPhed-

r → ∞ : ψ_ν(r)

+...

(A.4)

r²

ran, Proc. Roy. Soc. Lond. A 369, 207 (1979).

В формуле (A.3) ε — диэлектрическая проницае-

3. Б. Я. Балагуров, В. А. Кашин, ЖЭТФ 117, 978

(2000).

мость тела. В случае непрерывного спектра соб-

ственных значений ε_ν в (A.3) вместо суммы должен

4. Б. Я. Балагуров, Электрофизические свойства

стоять интеграл.

композитов. Макроскопическая теория, URSS,

Для пары соприкасающихся кругов дипольным

Москва (2015).

поведением при r → ∞ обладают функции ψ(e)2ν(r) и

5. Б. Я. Балагуров, ЖЭТФ 157, 669 (2020).

ψ(e)1ν(r). Для соответствующих дипольных моментов

имеем

6. Б. Я. Балагуров, ЖЭТФ 94, 95 (1988).

7. Б. Я. Балагуров, Метод собственных функ-

d2ν = ν B_ν Rix, d1ν = ν A_ν Riy.

(A.5)

ций в макроскопической электростатике, URSS,

Москва (2016).

Для составляющих тензора дипольной поляризуе-

мости

Λ получаем

8. J. B. Keller, J. Math. Phys. 5, 548 (1964).

∫

∞

9. А. М. Дыхне, ЖЭТФ 59, 110 (1970).

1-ε e^-ν

Λ_xx = - 2R²

ν dν,

(A.6)

ε + cthν shν

10. A. L. Efros and B. I. Shrlovskii, Phys. Stat. Sol. (b)

76, 475 (1976).

11. J. P. Straley, J. Phys. C 9, 783 (1976).

∞

∫

1-ε e^-ν

Λ_yy = - 2R²

ν dν.

(A.7)

12. Ф. М. Морс, Г. Фешбах, Методы теоретической

ε + thν chν

физики, т. II, Изд-во иностр. лит., Москва (1960).

562