ЖЭТФ, 2021, том 159, вып. 3, стр. 569-572

НУЛИ ДЗЕТА-ФУНКЦИИ РИМАНА НА ЛИНИИ z = 1/2 + it₀ II

Ю. Н. Овчинников^*

Max-Planck Institute for Physics of Complex Systems

01187, Dresden, Germany

Институт теоретической физики им. Л. Д. Ландау Российской академии наук

142432, Черноголовка, Московская обл., Россия

Поступила в редакцию 19 ноября 2020 г.,

после переработки 19 ноября 2020 г.

Принята к публикации 19 ноября 2020 г.

Показано, что все нетривиальные нули дзета-функции Римана расположены на линии z = 1/2 + it0 и

могут быть поделены на две группы: нормальные, номер которых однозначно восстанавливается по вели-

чине корня, и аномальные номера, для однозначного восстановления номера которых требуется знание

величины еще двух соседних корней (левого и правого). Использованные методы анализа могут быть

полезны при исследовании физики явлений, связанных с проскальзыванием фазы.

DOI: 10.31857/S0044451021030184

ем аналитические функции {φ, η}, связанные с дву-

мя функциями: гамма-функцией Эйлера Γ(z) и дзе-

1. ВВЕДЕНИЕ

та-функцией Римана ζ. Положим

z = 1/2 + it = 1/2 + ν + it₀.

(1)

Дзета-функция Римана возникает во многих за-

дачах физики низких температур, связанных с ана-

Аналитическая функция φ в полосе |ν| < 1/2,

литическим продолжением с целочисленных точек

t₀ ≫ 1 имеет следующее асимптотическое разложе-

в температурной технике (техника Мацубары) [1],

ние [3]:

а также при исследовании динамических процес-

(

)

сов, приводящих к проскальзыванию фазы (эффект

φ(t) =

- ln π - 1

(2)

48t

Джозефсона, диссипация тока в квазиодномерных

сверхпроводниках). Поведение дзета-функции в по-

На линии Стокса (ν = 0) выполняется уравне-

лосе 0 < x < 1 весьма сложное и используемые ме-

ние [3]

тоды исследования могут быть полезны во многих

физических задачах. Равно как и при рассмотре-

2e-η2(t0) cos(φ(t₀) + η₁(t₀)) =

нии физических задач могут возникнуть нетриви-

D₁ + iD₂

=eiφ(t0)

√

альные соотношения между функциями Эйлера и

2cos(t₀ ln2) + i

2sin(t₀ ln2)

дзета-функцией Римана [2]. Возможность установ-

D₁ - iD₂

ления точного номера любого нетривиального кор-

+e-iφ(t0)

√

(3)

2 cos(t₀ ln2) - i

2(t₀ ln 2)

ня дзета-функции по его значению означает силь-

где

ную корреляцию нулей на больших расстояниях при

сохранении сравнительно больших отклонений рас-

η = η₁ + iη₂,

стояний между соседними нулями от квазисреднего.

cos(t₀ ln2))+

D₁ = (1 - 2-1/2-ν

)

∑

⁽cos(t₀ ln(2k - 1))

cos(t₀ ln(2k))

2. ОСНОВНЫЕ УРАВНЕНИЯ

(2k - 1)1/2+ν

(2k)1/2+ν

(4)

k=2

Для исследования мы воспользуемся методом,

D₂ = 2-1/2-ν sin(t₀ ln2)-

изложенным в работе [3]. Следуя ему, мы определя-

)

∑

⁽ sin(t₀ ln(2k - 1))

sin(t₀ ln(2k))

E-mail: ovc@itp.ac.ru

(2k - 1)1/2+ν

(2k)1/2+ν

k=2

569

Ю. Н. Овчинников

ЖЭТФ, том 159, вып. 3, 2021

На линии Стокса функция η₁ удовлетворяет

условию

|η₁| < π.

(5)

В нуле дзета-функции с номером N на линии

Стокса выполняются следующие два уравнения:

(φ(t(N)0) + η₁(t(N)0)) = N -

(6)



∂η₁(t₀)



= 0.

(7)



∂t₀

t(N)

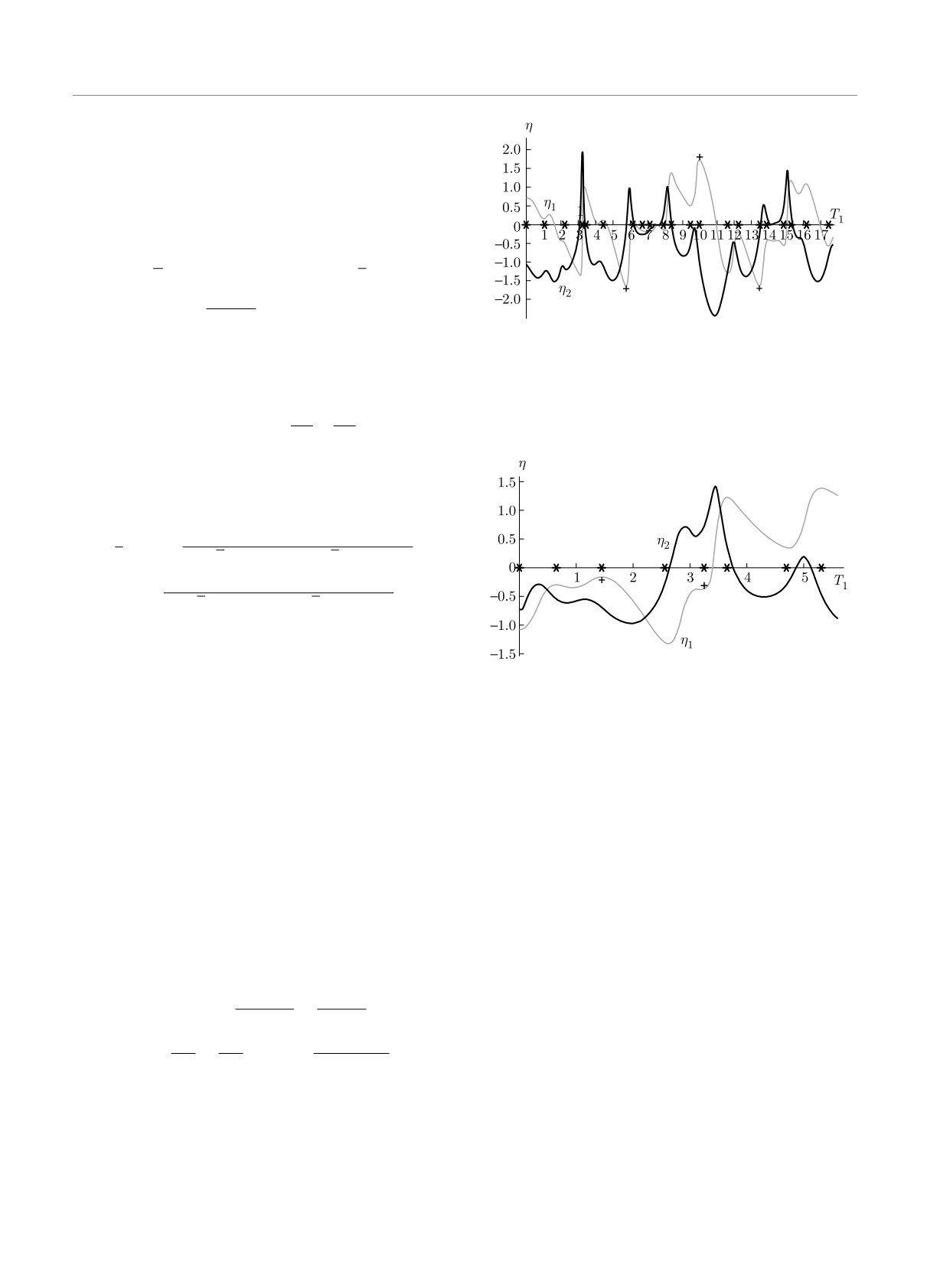
Рис. 1. Функции {η1(t0), η2(t0)} — решения уравнений (3),

Из уравнений (3), (6) находим значение функции

(10) в интервале 0 ≤ T1 ≤ 17.7; t0 = 9860.360205325 + T1.

η₂ в нулях дзета-функции t(N)0:

Точки с одиночными звездочками указывают положение

нулей дзета-функции с номерами N

= {9980-10000}.

(

)

∂μ

^∕∂φ



Крестики указывают положение аномальных нулей

η₂(t(N)0) = - ln

(-1)(N+1)



(8)



∂t₀

t(N)

где

μ(t₀) =

{

D₁ + iD₂

eiφ(t0)

√

2cos(t₀ ln2)+i

2sin(t₀ ln2)

}

D₁ - iD₂

+ e-iφ(t0)

√

(9)

2 cos(t₀ ln2)-i

2 sin(t₀ ln2)

Уравнения (5), (6) существенно улучшают клас-

сический результат, приведенный в [4]. Неравенство

(5) позволяет разделить все нетривиальные нули

Рис. 2. Функции {η1(t0), η2(t0)} в интервале 0 ≤ T1 ≤ 5.6;

дзета-функции на два подмножества: нормальные

t0 = 9882.192215966+T1 . Точки с одиночными звездочка-

нули, если |η₁| < π/2, и аномальные при π/2 < η₁ <

ми указывают положение нулей дзета-функции с номера-

< π. Слева и справа от аномального нуля находят-

ми N = {10005-10012}. Все нули являются нормальными.

ся нормальные нули, поэтому легко установить, яв-

Номера двух нулей N = {10007, 10009} являются просты-

ми числами

ляется ли данный нуль нормальным или нет. Для

этого достаточно найти номера левого (правого) ну-

лей в приближении |η| < π/2. Если номера левого

Существуют точная верхняя и точная нижняя

(правого) нуля окажутся равными {N - 2, N} или

границы функции η₁ на множестве {t(N)0}. Их зна-

{N, N +2}, то данный нуль является аномальным и

чения неизвестны. Неизвестно также, достигаются

имеет номер {N - 1} в первом случае и {N + 1} во

они или нет.

втором. В противном случае данный номер является

На рис.

мы приводим функции

нормальным и имеет номер {N}.

{η₁(t₀), η₂(t₀)} — решения уравнений (3), (10) в

Значения функций (η₁, η₂)|_t

могут быть

0=t(N)

интервале 0 ≤ t₀ - 9860.360205325 ≤ 17.8, получен-

найдены из уравнения

ные по теории возмущений относительно второго

∂μ/∂t₀

члена в правой части уравнения (10). Все номера

tg(φ(t₀) + η₁(t₀)) =

нулей дзета-функции на этом интервале не явля-

μ∂φ/∂t₀

∂φ/∂t₀

]

ются простыми числами. Аномальными являются

^[∂η₂

∂η₁

sin(φ + η₁)

exp(-η₂)

(10)

нули с номерами N = {9986, 9992, 9995}. На рис. 1

∂t₀

они отмечены крестиками.

Используя банк данных для нулей дзета-функ-

На рис.

приведены графики функций

ции Римана, мы приводим в таблице значения функ-

{η₁(t₀), η₂(t₀)} в интервале 0 ≤ t₀ -9882.192215966 ≤

ций η₁, η₂, δ, где δ — расстояние между нулями с но-

≤ 5.6, полученные в том же приближении, что и на

мерами {N - 1, N}.

рис. 1. Все нули дзета-функции в этом интервале

570

ЖЭТФ, том 159, вып. 3, 2021

Нули дзета-функции Римана на линии z = 1/2 + it₀

Таблица. Номера N нулей; значения корней t0 дзета-функции из банка данных; значения функций η1, η2; рассто-

яние δ между нулями с номерами {N - 1, N}. Номера аномальных нулей помечены звездочкой

t₀

η₁

η₂

995

1413.843148788569

-0.3347787

-1.439698

996^∗

1415.585784795495

-1.913157

0.7729658

1.742636

997

1415.781581303283

0.6981624

0.8390399

0.1957965

998

1417.102822933823

0.2604094

-0.7057182

1.32124163

999

1418.696963852452

-0.9173339

-0.2697894

1.5941409

1000

1419.422480945996

0.2581943

-2.734378 · 10-2

0.7255171

9995*

9873.802220903648

-1.622723

-0.2933259

9996

9874.323957629064

-0.4010518

8.274927 · 10-2

0.5217367

9997

9875.218994098847

-0.554381

0.5169054

0.8950364

9998

9875.600956248757

1.182915

0.4075229

0.3819621

9999

9876.479017063784

1.092085

-0.7418838

0.8780608

10000

9877.782654005501

-0.5631968

-0.8569397

1.3036369

99995

74 917.71941582848

-0.8112433

-0.7327937

99996

74 918.37058022667

-0.7321506

0.3116081

0.6511644

99997

74 918.69143345370

0.909442

0.6422741

0.3208532

99998*

74 919.07516112077

2.238535

-0.2387409

0.3837276

99999

74 920.25979325889

-0.1823727

-1.530978

1.1846321

100000

74 920.82749899419

0.30297

-1.534634

0.5677057

999995*

600 267.1935613822

-1.766762

999996

600 267.5137087857

-0.3751698

0.3201474

999 997

600 267.9045547598

0.5164229

0.39084598

999 998

600 268.4774001423

0.4080155

0.5728454

999 999

600 269.0055602490

0.5496082

0.5281601

1000000

600 269.6770124450

-0.3087992

0.6714522

9 999 995

4.992378736958099 · 10

0.1155457

9 999 996

4.992379318476746 · 10⁶

-0.7428616

0.58151865

9 999 997*

4.992380078878498 · 10⁶

-1.601269

0.76040175

9 999 998

4.992380229898413 · 10⁶

-0.4596763

0.1510199

9 999 999

4.992380724410680 · 10⁶

-1.318084

0.49451227

10 000 000

4.992381014003179 · 10⁶

-0.1764911

0.2895925

571

Ю. Н. Овчинников

ЖЭТФ, том 159, вып. 3, 2021

являются нормальными. Номера двух нулей с

мулы восстановления положения хотя бы ближай-

N = {10007,10009} являются простыми числами.

шего нуля к данному неизвестны. Вполне возможно,

Они обозначены крестиками. Рассматривая рис. 1,

что разбиение задачи на две: установление дальне-

2 данной работы и рис. 5 из работы [3], можно

го порядка (нумерация с установлением интервалов

предположить, что существует корреляция между

без перекрытия) при отсутствии ближнего, может

формой функции {η₁, η₂} и наличием близкого нуля

быть эффективным и в других задачах как физичес-

с номером, являющимся простым числом.

ких, так и математических.

3. ЗАКЛЮЧЕНИЕ

ЛИТЕРАТУРА

Распределение нулей дзета-функции представ-

1. А. А. Абрикосов, Л. П. Горьков, И. Е. Дзялошин-

ляет собой хороший пример системы, в которой име-

ский, Методы квантовой теории поля в стати-

ется дальний порядок при отсутствии ближнего по-

стической физике, Физматлит, Москва (1962).

рядка. В результате оказывается возможным уста-

новить номер любого заданного нуля с точностью

2. Yu. N. Ovchinnikov, JETP 123, 838 (2016).

±1. Если известно положение трех нулей подряд,

3. Yu. N. Ovchinnikov, J. Supercond. Novel Magnetism

то их номера восстанавливаются однозначно с ука-

32, 3363 (2019).

занием, к какому подмножеству (нормальному или

аномальному) принадлежит каждый из этих нулей.

4. H. M. Edwards, Riemann’s Zeta Function, Acad.

При этом даже на больших расстояниях общие фор-

Press, New York, London (1974).

572