ЖЭТФ, 2021, том 159, вып. 4, стр. 671-686

ДИНАМИКА ДОМЕННЫХ СТЕНОК

В КИРАЛЬНЫХ МАГНЕТИКАХ

Е. Г. Галкина^a, Б. А. Ивановb,c,d*, Н. Е. Кулагин^e, Л. М. Лерман^f,g, И. А. Ястремский

^a Институт физики Национальной академии наук Украины

03028, Киев, Украина

^b Институт магнетизма Национальной академии наук и Министерства образования и науки Украины

03142, Киев, Украина

^c Киевский национальный университет им. Тараса Шевченко

03127, Киев, Украина

^d Национальный исследовательский технологический университет «МИСиС»

119049, Москва, Россия

^e Институт физической химии и электрохимии им. А. Н. Фрумкина Российской академии наук

119071, Москва, Россия

^f Национальный исследовательский университет «Высшая школа экономики»

603155, Нижний Новгород, Россия

^g Нижегородский национальный исследовательский университет им. Н. И. Лобачевского,

Научный центр «Математика технологий будущего»

603950, Нижний Новгород, Россия

Поступила в редакцию 4 декабря 2020 г.,

после переработки 4 декабря 2020 г.

Принята к публикации 7 декабря 2020 г.

Теоретически исследовано движение доменных стенок в киральных магнетиках, для которых имеет ме-

сто нарушение симметрии относительно пространственной инверсии. Такие стенки называют доменными

стенками Дзялошинского [22], для них экспериментально обнаружены уникальные динамические свой-

ства. Для киральных ферромагнетиков и антиферромагнетиков найдены нелинейные режимы движения

стенки с немалой скоростью, вплоть до предельной. Динамика стенок в антиферромагнетиках допускает

аналитическое описание, в то время как для ферромагнетиков необходимо использовать численный ана-

лиз. Для ферромагнетиков получены простые приближенные формулы, которые с высокой точностью

описывают динамические характеристики стенок во всей области их существования. Определены зако-

ны дисперсии стенок, т. е. зависимости энергии стенки от ее импульса. Для ферромагнетиков с чисто

одноосной анизотропией предельная скорость стенки определяется исключительно киральным взаимо-

действием и обращается в нуль, если это взаимодействие отсутствует. Для антиферромагнетиков роль

кирального взаимодействия не столь очевидна: структура движущейся стенки, как и в стандартных мо-

делях антиферромагнетиков, может быть получена преобразованием Лоренца с избранной скоростью,

равной скорости магнонов на линейном участке спектра, но закон дисперсии более сложный и не описы-

вается лоренц-инвариантными выражениями.

Статья для специального выпуска ЖЭТФ, посвященного 90-летию И. Е. Дзялошинского

DOI: 10.31857/S0044451021040088

1. ВВЕДЕНИЕ

Исследование киральных магнетиков, в которых

нарушена симметрия спиновой системы относитель-

но пространственной инверсии, было начато в клас-

^* E-mail: bor.a.ivanov@gmail.com

сических работах Дзялошинского [1,2]. При феноме-

671

Е. Г. Галкина, Б. А. Иванов, Н. Е. Кулагин и др.

ЖЭТФ, том 159, вып. 4, 2021

нологическом описании таких магнетиков плотность

Даже если подобные вклады в энергию не так

энергии содержит вклады, линейные по градиентам

велики, как для некоторых тяжелых металлов, их

намагниченности вида w_D

= γ_iklM_i(∂M_k/∂x_l). В

роль следует оценить и обсудить. Для киральных

терминах атомных спинов киральные инварианты

магнетиков были обнаружены устойчивые состо-

получаются при учете антисимметричного взаимо-

яния с нетривиальной топологией. Как пример,

действия вида (d1,2[S₁×S₂]), где S₁ и S₂ — спины со-

отметим топологические солитоны — скирмионы

седних атомов, направление вектора d1,2 определя-

и скирмионные решетки [15, 16], киральные маг-

ется симметрией кристалла. В зависимости от рас-

нитные поплавки (chiral magnetic bobbers)

[17],

пределения векторов d1,2 для пар соседних спинов

монополи (ежи) [18,19] и многие другие, см. обзоры

в кристалле такое взаимодействие (взаимодействие

[20, 21].

Дзялошинского) может приводить или к появлению

Важно также, что для тонких пленок с достаточ-

киральных инвариантов, или к неколлинеарности

но сильным взаимодействием Дзялошинского воз-

спинов подрешеток антиферроиагнетиков и появле-

можно движение доменных стенок (их принято на-

нию слабого ферромагнетизма [3-6]. Микроскопиче-

зывать доменными стенками Дзялошинского [22])

ское обоснование существования антисимметрично-

с предельно высокими для ферромагнетиков ско-

го взаимодействия пары спинов предложил Мория

ростями (сотни м/с) [23-25]. Это свойство домен-

[7]; и в настоящее время подобные слагаемые приня-

ных стенок подчеркнуто в названии статьи Арне

то называть взаимодействием Дзялошинского - Мо-

Братааса [26] «Spintronics: chiral domain walls move

рия.

faster» (Спинтроника: киральные доменные стенки

Киральные магнетики долгое время ассоцииро-

движутся быстрее). Возможность реализации дви-

вались с кристаллическими материалами, решет-

жения доменных стенок с немалой скоростью в

ка которых не имеет центра симметрии, например

магнитных пленках толщиной порядка нанометров

MnSi, FeCoSi, FeGe с кристаллической группой B20,

важна для приложений, в частности, систем записи

см., например, недавний обзор [8]. Исследования

информации [27, 28]. Поэтому поиск ферромагнети-

Дзялошинского [1,2] были связаны с анализом спи-

ков с высоким значением предельной скорости до-

ральных структур с длинным периодом, которые

менных стенок представляет собой важную пробле-

были обнаружены в прошлом столетии и исследо-

му, обсуждению которой посвящено большое число

вались многими авторами [9-11].

работ, см. [29-32]. Не менее интересен и чисто теоре-

В текущем столетии обнаружены новые интерес-

тический аспект нелинейной динамики, прежде все-

ные свойства киральных магнетиков, в связи с чем

го, динамики солитонов различного типа.

значительно вырос интерес к этим материалам. Бы-

Настоящая работа посвящена теоретическому

ло обнаружено, что взаимодействие Дзялошинско-

анализу динамики доменных стенок в тонких

го может быть получено практически для всех маг-

пленках киральных магнетиков, ферромагнетиков

нетиков, если приготовить их в виде сверхтонких

и антиферромагнетиков. Для ферромагнетиков

(толщина менее 10 нм) пленок на немагнитной под-

на основе численного анализа построено простое

ложке. Для таких систем понижение симметрии обу-

приближенное решение, позволяющее описать

словлено поверхностными эффектами, анизотропи-

структуру стенки в ферромагнетике и ее дина-

ей контакта магнетик-подложка [12]. В этом случае

мические характеристики, такие как зависимость

плотность энергии взаимодействия Дзялошинского

энергии стенки от ее скорости или импульса. По-

определяется инвариантом

казано, что для антиферромагнетиков наличие

взаимодействия Дзялошинского нарушает стан-

M_z(∇ · M) - (M · ∇)M_z,

дартную лоренц-инвариантность спиновой динами-

где ось z выбрана перпендикулярно поверхности

ки. Однако анализ движения стенки может быть

пленки. Если в качестве подложки выбрать пленку

проведен в достаточно полной мере. Оказалось,

немагнитного металла с сильным спин-орбитальным

что многие свойства доменных стенок для лоренц-

взаимодействием (платина, тантал), то можно полу-

инвариантных моделей антиферромагнетиков

чить достаточно высокие значения константы взаи-

сохраняются и для киральных антиферромагнети-

модействия Дзялошинского [13, 14].

ков. В частности, изменение структуры стенки при

Нарушение киральной симметрии является

движении сводится к лоренцевскому сокращению

неизбежным свойством нанопленок магнетиков, и

ее толщины. Кроме того, как и для стандартных

киральные магнетики могут рассматриваться как

моделей антиферромагнетиков, существуют две

стандартные материалы нанофизики магнетиков.

ветви зависимости энергии доменных стенок от их

672

ЖЭТФ, том 159, вып. 4, 2021

Динамика доменных стенок в киральных магнетиках

импульса, одной из которых отвечают устойчивые

где активация магнонов ω₀ = γH_a, H_a = K/M_s —

√

стенки, а второй — неустойчивые.

поле анизотропии и x₀ =

A/K. Отметим, что на-

магниченность и константу анизотропии для пленок

толщиной порядка нанометров можно эксперимен-

2. МОДЕЛИ КИРАЛЬНЫХ МАГНЕТИКОВ

тально определить с помощью стандартной магни-

тометрии или резонансными методами. Определе-

Динамика намагниченности ферромагнетиков

ние константы неоднородного обмена A и константы

описывается известным уравнением Ландау - Лиф-

Дзялошинского D для таких пленок является более

шица [33] (см. также монографию [34]), которое

сложной задачей. Одной из проблем является то,

обычно записывается для намагниченности:

что зачастую для определения одной из констант

∂M

δW[M]

нужно знать и точное значение другой. Независи-

= -γ[M × H_eff ] + R, H_eff = -

(1)

∂t

δM

мость спектра спиновых волн легкоосного кираль-

где γ = gμB/ℏ — гиромагнитное отношение, g —

ного магнетика от D была использована для опре-

деления A путем анализа температурных зависимо-

фактор Ланде (g-фактор), μ_B — модуль магнетона

Бора, γ ≈ 2.8 МГц/Э при g = 2. Эффективное по-

стей намагниченности сверхтонких киральных фер-

ле H_eff определяется как вариационная производ-

ромагнитных пленок [35].

ная энергии ферромагнетика W = W [M], записан-

Без учета диссипативных процессов уравнение

ной в виде функционала плотности намагниченнос-

Ландау - Лифшица можно записать в лагранжевой

ти M = M(r, t). Слагаемое R описывает диссипа-

форме с лагранжианом вида

цию в системе. Обычно это слагаемое выбирается в

∫

форме Гильберта,

L[m] = G - W, G[m] = A(∂m/∂t) dr,

[

]

α_G

∂M

R=R_G=

M×

где гироскопическое слагаемое записывается через

M_s

∂t

сингулярную векторную функцию, вектор-потенци-

где M_s — намагниченность насыщения. При этом

ал поля монополя Дирака

(M · R) = 0 и длина вектора M сохраняется, M² =

A = A(m), rot_mA ∝ m,

= M2s = const. В этом случае удобно использовать

нормированный (единичный) вектор m = M/M_s,

см. [36,37]. Вектор-потенциал A определен с точно-

m² = 1.

стью до некоторой калибровки, в то время как фик-

Запишем функционал энергии кирального фер-

тивное магнитное поле rot_mA, входящее в уравне-

ромагнетика в простейшем виде, допускающем опи-

ния движения, является калибровочно-инвариант-

сание движения доменной стенки,

ным. Для поля монополя можно выбрать выраже-

∫

^[A

ние

W = dr

(∇m)² +

(m2x + m2y) -

M_s (n × m)

(4)

]

(1 + n · m)

- D [m_z(∇ · m) - (m · ∇)m_z]

(2)

где n — произвольный постоянный единичный век-

тор. Вектор-потенциал поля монополя Дирака име-

Эта энергия включает энергию неоднородного

ет сингулярность, для выражения (4) сингуляр-

обмена с константой A и чисто одноосную анизотро-

ность (струна Дирака) расположена на полупрямой

пию с константой K > 0 и легкой осью, перпенди-

m = -n, см. [36,37].

кулярной к плоскости пленки (плоскости xy); знак

Можно выписать интегралы движения поля на-

минус перед слагаемым с взаимодействием Дзяло-

магниченности ФМ, при этом энергия совпадает со

шинского с константой D выбран для удобства в

значением функционала W [M], рассчитанным для

дальнейшем.

данного распределения намагниченности. Импульс

Отметим интересное свойство легкоосного ки-

поля намагниченности P можно записать в виде

рального магнетика: наличие взаимодействия Дзя-

∫

лошинского не проявляется в спектре спиновых

P_i = - A(∂m/∂x_i).

волн. Закон дисперсии спиновых волн для модели

(2) можно представить в виде

Это выражение не обладает калибровочной инвари-

антностью, и значение импульса зависит от калиб-

ω(k) =

(K + Ak²) = ω₀(1 + x²⁰k²),

(3)

ровки.

M_s

673

ЖЭТФ, вып. 4

Е. Г. Галкина, Б. А. Иванов, Н. Е. Кулагин и др.

ЖЭТФ, том 159, вып. 4, 2021

Проблема определения импульса магнитных со-

направления движения стенки, которое перпенди-

литонов является достаточно сложной, см. работы

кулярно легкой оси e_z. Этот источник движения

[38-43] и обсуждение ниже для конкретных реше-

стенки рассматривали Ландау и Лифшиц в клас-

ний. Поскольку нас интересует движение плоской

сической работе [33], в которой впервые было рас-

доменной стенки, т. е. одномерная задача с m =

смотрено движение доменной стенки, а также Уокер

= m(x, t), отлична от нуля только одна компонента

[44], который исследовал движение стенки с нема-

импульса, P = P e_x. С учетом конкретного выбора

лыми скоростями и нашел ее предельную скорость.

вектор-потенциал A можно записать

Для толстых пленок дипольная энергия эквивалент-

∫ (

)

на энергии магнитной анизотропии с осью в базис-

M_s

(m × n)

∂m

P =S

dx,

(5)

ной плоскости магнетика. Если эти взаимодействия

(1 + n · m)

∂x

слабые, предельная скорость линейно зависит от ха-

рактерного параметра («неодноосного» эффектив-

где S = LL_y — площадь стенки, L и L_y — толщи-

ного поля H_non-uniaxial), v_c/v₀ ∝ H_non-uniaxial/H_a

на пленки и ее размер вдоль оси y. Понятно, что

и мала, здесь и ниже v₀ = ω₀x₀ — характерная ско-

значение импульса зависит от калибровки; в част-

рость магнонов в модели (3). Таким образом, несо-

ности, если выбрать A в виде (4), импульс зависит

от направления струны Дирака n.

хранение

является фактором, способствую-

Кроме энергии и импульса, для анализа магнит-

щим возможности эффективного применения дви-

ных солитонов предельно важно наличие или отсут-

жущихся солитонов типа доменных стенок.

ствие еще одного интеграла движения. Для чисто

В сверхтонких пленках (толщина которых мень-

√

одноосных магнетиков без киральных свойств име-

ше x₀ =

A/K) вклад дипольного взаимодействия

ет место симметрия относительно поворота спинов

подавлен, см. [22, 45]. Создание нанопленок фер-

вокруг оси z, что приводит к сохранению суммарной

ромагнетиков с достаточно сильной кристалличес-

z-проекции намагниченности,

кой двухосной анизотропией, а также использование

∫

сильных магнитных полей в наноприборах является

M(tot)z = M_zdr.

непростой задачей. Однако легко видеть, что взаи-

модействие Дзялошинского не имеет симметрии от-

Наличие такого интеграла принципиально важно

носительно поворотов в спиновом пространстве и не

для физики магнитных солитонов.

сохраняет

. Как отмечалось, взаимодействие

С одной стороны, сохранение

Дзялошинского может присутствовать в достаточно

∫

тонких пленках, при этом значение характерного по-

M(tot)z = M_zdx

ля, обусловленного этим взаимодействием, не мало.

Это определяет возможность достаточно быстрого

несовместимо с существованием одномерных дви-

движения доменных стенок в киральных магнети-

жущихся топологических солитонов, описывающих

ках и открывает перспективы повышения предель-

в бездиссипативном пределе движение доменных

ной скорости стенки в нанопленках магнетиков.

стенок. Действительно, такое движение должно со-

провождаться изменением относительных размеров

Интересно отметить, что сохранение

не

доменов с M_z = M_s и M_z = -M_s. Формально, при

препятствует движению солитонов другого типа, а

условии

= const обращается в нуль величи-

именно, локализованных солитонов, для которых

на предельной скорости стенки v_c, т. е. только непо-

вдали от центра солитона намагниченность имеет

движные стенки. Величина v_c в одноосном ферро-

одно и то же направление, например, M_z → M_s,

магнетике определяется тем взаимодействием, кото-

M_x,y → 0, см. [46-51]. Такому солитону отвечают

рое нарушает сохранение суммарной z-проекции на-

двухпараметрические состояния (движущиеся маг-

магниченности. Такие взаимодействия могут быть

нонные капли) с фиксированным значением

связаны с кристаллической анизотропией в базис-

[46,48-50]. Они описываются решениями, зависящи-

ной плоскости, магнитным дипольным взаимодейст-

ми от двух параметров, скорости солитона v и час-

вием, а также наличием внешнего магнитного поля,

тоты прецессии спинов ω в системе отсчета, движу-

перпендикулярного легкой оси.

щейся вместе с солитоном со скоростью v. Эти со-

Для плоской 180-градусной стенки в достаточ-

литоны можно интерпретировать как связанные со-

но толстой пленке (толщина много больше x0 =

стояния большого числа магнонов N с заданным им-

√

A/K) магнитное дипольное взаимодействие

пульсом P, N =

/gμ_B. Особо важно, что могут

описывается плотностью 2π(Me_x)², e_x — орт вдоль

существовать неодномерные прецессионные солито-

674

ЖЭТФ, том 159, вып. 4, 2021

Динамика доменных стенок в киральных магнетиках

ны такого типа, и эти солитоны устойчивы относи-

В отличие от ферромагнетиков, спиновая дина-

тельно коллапса [47-51]. В данном случае роль еще

мика антиферромагнетика является инерционной.

одного, помимо энергии и импульса, интеграла дви-

Лагранжиан простейшей версии сигма-модели для

жения абсолютно иная, чем для доменных стенок.

антиферромагнетика включает слагаемое, квадра-

Наличие такого интеграла способствует существо-

тичное по временной производной (∂l/∂t)², которое

ванию неодномерных магнитных солитонов.

можно интерпретировать как кинетическую энер-

Отметим, что неодномерные магнитные солито-

гию T и записать в виде

ны могут быть устойчивыми и для одноосного ки-

∫

⁽∂l)2

рального магнетика, для которого не сохраняется

T =

(6)

2c²

∂t

. Дело в том, что энергия (2), несимметрич-

ная относительно поворотов спинов, для двумерно-

где c — фазовая скорость магнонов в той области

го или трехмерного магнетика обладает симметри-

спектра, где их закон дисперсии является линей-

ей относительно одновременного поворота спинов и

ным,

√

координат в плоскости xy на один и тот же угол.

AH_ex

c=γ

(7)

Такой симметрии соответствует сохранение z-проек-

2M₀

ции полного момента импульса магнетика

Здесь H_ex — обменное поле антиферромагнетика,

определенное из условия, что для изотропного ан-

J(tot)z = S(tot)z + L(tot)z,

тиферромагнетика во внешнем поле антиферромаг-

нитный порядок существует (вектор l = 0) толь-

где Lztot) и Sztot) =

/gμ_B — значения соответ-

ко при H₀ < H_ex и разрушается (|M| = 2M₀ и

ственно z-проекций момента импульса поля намаг-

l = 0) при H0 ≥ Hex (об определении обменно-

ниченности (орбитального момента) и полного спи-

го поля см. монографию [53]). Скорость c опреде-

на [52]. Для Lztot) можно выбрать выражение, со-

ляется только обменными взаимодействиями и зна-

гласованное с определением импульса поля намаг-

чительно превышает характерную скорость магно-

ниченности,

нов для ферромагнетика, например, величину v₀ =

√

∫

=ω₀x₀ = γ

AH_a/M_s для модели (2). Действитель-

⁽∂m)dr,

√

L(tot)z = - ε_ijzx_iA

но, значение c/v₀ ∼

H_ex/H_a и содержит отноше-

∂x_j

ние энергии однородного обмена к энергии анизо-

тропии. Это свойство является важным примером

здесь ε_ijk — абсолютный антисимметричный тензор.

обменного усиления динамических параметров ан-

Появление киральных свойств тонких магнит-

тиферромагнетиков.

ных пленок на подложке из тяжелого металла не яв-

Для «чистого» антиферромагнетика лагранжи-

ляется свойством только ферромагнетиков. Дейст-

ан включает только кинетическую энергию (6) и по-

вительно, инварианты типа (2) квадратичны по сте-

тенциальную энергию W, L(AFM)[l] = T - W. За-

пеням намагниченностей, т. е. они допустимы для

метим, что наличие сильного магнитного поля при-

антиферромагнетиков и ферримагнетиков. Наибо-

водит к появлению в лагранжиане антиферромаг-

лее простое и удобное описание динамики антифер-

нетика специфических гироскопических слагаемых,

ромагнетиков базируется на использовании так на-

линейных по компонентам ∂l/∂t. Гироскопические

зываемой сигма-модели (см., например, книги и об-

слагаемые в принципе могут возникать и для неко-

зоры [49, 50, 53, 54]). В рамках этого подхода ос-

торых антиферромагнетиков, допускающих слабый

новной динамической переменной при описании ан-

ферромагнетизм, но они запрещены для киральных

тиферромагнетика является нормированный вектор

магнетиков, см. [53]. Выражение для статической

антиферромагнетизма

энергии W кирального антиферромагнетика в тер-

l = (M₁ - M₂)/|M₁ - M₂|,

минах единичного вектора l имеет такую же струк-

туру, как для ферромагнетика, и может быть полу-

где M₁ и M₂ — намагниченности подрешеток. При

чено из формулы (2) заменой m → l.

этом вектор суммарной намагниченности M = M₁+

Важно заметить, что в обычных (не киральных)

+ M₂ играет роль вспомогательной переменной и

антиферромагнетиках пространственные и времен-

выражается простой формулой через l и ∂l/∂t. Та-

ные производные вектора l входят в лагранжиан в

ким образом, вместо двух уравнений для намаг-

комбинации (∂l/∂t)² - c²(∇l)². Наличие такой фор-

ниченностей подрешеток можно использовать одно

мальной лоренц-инвариантности значительно упро-

уравнение для l.

щает анализ динамики солитонов, см. некоторые

675

Е. Г. Галкина, Б. А. Иванов, Н. Е. Кулагин и др.

ЖЭТФ, том 159, вып. 4, 2021

примеры в работах [55,56] и недавний обзор [54]. В

Здесь и далее штрихом обозначена производная по

частности, если известно решение для неподвижно-

ξ, все величины приводятся на единицу площади

го солитона любого типа, движущееся решение мож-

стенки. Движущаяся 180-градусная плоская домен-

но получить преобразованием Лоренца с характер-

ная стенка описывается решениями типа простой

ной скоростью c. В частности, предельная скорость

волны, для которой

любого солитона совпадает со значением c. Однако

θ = θ(ξ), ϕ = ϕ(ξ), ξ = x - vt,

для киральных магнетиков наличие слагаемых, ли-

нейных по градиентам l, разрушает эту лоренц-ин-

v — скорость стенки. Уравнения для θ и ϕ принима-

вариантность, см. [57]. В частности, это приводит к

ют вид системы обыкновенных дифференциальных

тому, что предельная скорость двумерных топологи-

уравнений. Ось z является легкой осью магнетика,

ческих солитонов (скирмионов) в киральных анти-

т. е. θ = 0 и θ = π по обе стороны от доменной стен-

ферромагнетиках меньше, чем c [57]. С другой сто-

ки. Для определенности, будем считать что θ → π

роны, выражения для интересующих нас интегра-

при ξ → +∞ и θ → 0 при ξ → -∞. Уравнения для

лов движения, энергии и импульса солитона опре-

θ и ϕ принимают вид

деляются производными ∂L/∂(∂l/∂t), и киральные

[

]

инварианты не изменяют их формы.

Aθ^′′ - sin θ cos θ

K + A(ϕ^′)²

Как и в любой лоренц-инвариантностной теории,

− 2Dϕ^′ sin² θ sinϕ + v(M_s/γ)ϕ^′ sinθ = 0,

(11)

энергия поля вектора l для антиферромагнетика яв-

ляется суммой кинетической и потенциальной энер-

гий,

A(ϕ^′ sin² θ)^′ + 2Dθ^′ sin² θ sin ϕ -

E(AFM) = T + W.

- v(M_s/γ)θ^′ sinθ = 0.

(12)

Величина импульса (на единицу площади стенки) не

содержит вклада кирального инварианта и опреде-

Эта система уравнений формально эквивалент-

ляется выражением, характерным для лоренц-инва-

на механической задаче о движении материальной

риантной теории

точки по поверхности сферы при наличии двух ги-

∫ (

)

роскопических слагаемых различной природы, одно

∂l

P(AFM) = -

dx.

(8)

из которых пропорционально параметру кирально-

c²

∂t

∂x

сти D, а другое — скорости стенки v. Здесь перемен-

Заметим, однако, что наличие кирального инвари-

ная ξ играет роль времени, константа A — роль мас-

анта приводит к нарушению стандартных для ло-

сы, а скорость v является параметром, который, в

ренц-инвариантностной теории соотношений между

частности, определяет характер особых точек урав-

импульсом и энергией, см. ниже разд. 4.

нений. Эта задача имеет две степени свободы, для

нее можно построить один первый интеграл

[

]

3. ДИНАМИКА ДОМЕННОЙ СТЕНКИ В

(θ^′)² + (ϕ^′)² sin² θ

sin² θ,

(13)

ФЕРРОМАГНЕТИКЕ

на решении типа стенки значение Q = 0. Домен-

Для конкретного анализа солитонных решений

ной стенке отвечает гетероклиническая сепаратрис-

удобно использовать угловые переменные для еди-

ная траектория, соединяющая два положения рав-

ничного вектора m (или вектора l для антиферро-

новесия, m = e_z, ∂m/∂ξ = 0 и m = -e_z, ∂m/∂ξ = 0.

магнетика), например

Второй интеграл движения, находящийся в инволю-

m_z = cosθ, m_x = sinθ cosϕ,

ции к (13), для системы (11), (12) построить не уда-

(9)

ется. Как будет показано ниже, данная механиче-

m_y = sinθ sinϕ.

ская задача (в отличие, например, от задачи Уоке-

Приведем явный вид функционала энергии ки-

ра, которая описывает движение стенки в двухос-

рального магнетика (2) через эти угловые перемен-

ном ферромагнетике) не является интегрируемой. В

ные для одномерного решения:

этом случае ее общий анализ может быть проведен

∫

только численно.

^[A

[

]

W [θ, ϕ] = dx

(θ^′)²+(ϕ^′)² sin² θ

sin² θ,

Исключением является случай неподвижной до-

]

менной стенки (v = 0). В этом случае легко най-

ти два решения, которым соответствуют постоян-

− D(θ^′ cosϕ - ϕ^′ sinθ cosθ sinϕ)

(10)

ные значения ϕ = 0 и ϕ = π. Для обоих решений

676

ЖЭТФ, том 159, вып. 4, 2021

Динамика доменных стенок в киральных магнетиках

профиль стенки θ(ξ) не зависит от выбора значения

Для уокеровского решения в двухосном ферро-

угла ϕ и определяется стандартной формулой

магнетике Шлеман [58] отметил, что величина v(-)

√

совпадает с предельной скоростью доменной стен-

cosθ(ξ) = - th(ξ/x₀), x₀ =

A/K,

(14)

ки. Это предположение использовалось при анали-

где x₀ определяет толщину доменной стенки. Далее

зе различных магнетиков со сложной магнитной

для определенности считается, что θ(ξ → -∞) → 0,

структурой [59]. Впоследствии было показано, что

θ(ξ → +∞) → π, то есть в стенке θ^′(ξ) ≥ 0.

совпадение v(-) и v_c является в некотором смысле

Легко показать, что энергия неподвижной до-

случайным и обусловлено тем, что система уравне-

менной стенки определяется формулой E(v = 0) =

ний (11), (12) для задачи Уокера является точно ин-

√

= 2E₀ - πD cosϕ₀, где E₀ =

AK и ϕ₀ обозначает

тегрируемой гамильтоновой системой. Для этой за-

два значения угла ϕ в стенке с v = 0, ϕ₀ = 0 или

дачи был построен дополнительный интеграл дви-

жения, находящийся в инволюции к (13) [60-63]. Де-

ϕ₀ = π. Легко видеть, что при D > D_c, где крити-

ческое значение

тальный анализ общих свойств фазового простран-

2√

ства гамильтоновых интегрируемых систем с двумя

D_c =

AK ,

(15)

степенями свободы показал [64-66], что если для та-

энергия стенки с минимальной энергией становится

ких систем особые точки являются седло-фокусами,

отрицательной. Действительно, при D > D_c термо-

что имеет место при v(-) < |v| < v⁽⁺⁾, то все тра-

динамически устойчива спиральная структура. Од-

ектории, выходящие из некоторого седло-фокуса, в

нородное состояние с θ = 0, π, в котором может су-

него же и возвращаются. При этом не существу-

ществовать уединенная стенка, является основным

ет траекторий, идущих из одного седло-фокуса в

состоянием системы только при D < D_c, и далее

другой, т. е. решения типа стенок отсутствуют. Ге-

ограничимся исследованием таких магнетиков. От-

тероклинические сепаратрисные фазовые траекто-

метим, однако, что магнонные частоты вещественны

рии, описывающие стенки, существуют только для

при любом значении D, т. е. при D > D_c однородное

особых точек типа седло, что соответствует условию

состояние устойчиво относительно малых возмуще-

|v| < v(-). Таким образом, для всех интегрируемых

ний, т. е. является метастабильным.

систем предельная скорость стенки совпадает с v(-).

Убывание отклонения намагниченности от рав-

Если же для некоторого магнетика уравнения

новесного значения вдали от солитонов любого типа

для θ(ξ), ϕ(ξ) не обладают свойством точной инте-

(доменных стенок или локализованных солитонов)

грируемости, то величина предельной скорости до-

является экспоненциальным, sin θ ∝ exp(-κ|ξ|) при

менной стенки может не совпадать с v(-), она может

ξ → ±∞. Это поведение проще всего исследовать

быть больше, чем v(-). В частности, такое поведе-

с помощью аналитического продолжения спектра

ние найдено для доменной стенки в ферромагнетике

спиновых волн ω(k) в область комплексных волно-

во внешнем магнитном поле, перпендикулярном оси

вых векторов и частот, k → iκ, ω → iκv [58, 59]. В

легкого намагничивания [67]. Рассмотренный в дан-

общем случае для моделей ферромагнетиков и фер-

ной работе киральный ферромагнетик с одноосной

римагнетиков существуют две характерные скоро-

анизотропией является ярким примером таких си-

сти, v(-) и v⁽⁺⁾, v(-) < v⁽⁺⁾. При скоростях солито-

стем. Для него аналитическое продолжение (3) дает

на 0 ≤ |v| < v(-) величина κ вещественная. В терми-

iκv = ω₀(1 - x²⁰κ²), т.е.

√

нах фазового пространства системы уравнений (11),

2x₀κ = iv/v₀ ±

(v/v₀)² - 4,

(16)

(12) это означает, что положениям равновесия θ = 0

или θ = π отвечают особые точки типа седло. При

где использовано введенное выше значение v₀

v(-) < v < v⁽⁺⁾ величина κ имеет ненулевую мни-

= γx₀K/M_s = γH_ax₀ = ω₀x₀. Таким образом, зна-

мую часть, κ = κ^′ ± iκ^′′, т. е. асимптотика содер-

чения v(-) = 0 и v⁽⁺⁾ = 2v₀, т. е. монотонное пове-

жит затухающие осцилляции и положения равнове-

дение решения, при котором M_x, M_y ∝ exp(-ξ/x₀),

сия представляют собой особые точки типа седло-

см. (14), имеет место только при v = 0.

фокус. Если же |v| > v⁽⁺⁾, то величина κ чисто мни-

Для численного исследования удобно использо-

мая, т. е. волновой вектор вещественный и солито-

вать безразмерные переменные, измеряя ξ в едини-

ны типа простой волны отсутствуют. Скорость v⁽⁺⁾

цах x₀, скорость v в единицах v₀, а константу Дзяло-

√

совпадает с минимальной фазовой скоростью маг-

шинского D в единицах E₀ =

AK. Таким образом,

нонов, т. е. отсутствие солитонных решений со ско-

при данной скорости характер решения определяет-

ростями |v| > v⁽⁺⁾ отвечает естественному условию

ся одним безразмерным параметром D/E₀ (напом-

отсутствия черенковского излучения магнонов.

ним, что критическое значение D_c/E₀ = 2/π).

677

Е. Г. Галкина, Б. А. Иванов, Н. Е. Кулагин и др.

ЖЭТФ, том 159, вып. 4, 2021

Численное построение решений, описывающих

движущуюся доменную стенку, упрощается тем, что

в рамках уравнений (11), (12) они имеют определен-

ную симметрию, а именно, cos θ(ξ) является нечет-

ной, а ϕ(ξ) и sin θ(ξ) являются четными функциями

ξ. Следовательно, фазовые траектории, определяю-

щие доменные стенки, проходят через поверхность

симметрии cos θ = 0, ϕ^′ = 0. У состояния равновесия

θ = 0 имеется двумерное неустойчивое многообра-

зие, т. е. существует однопараметрическое семейство

траекторий, выходящих из него при ξ → -∞. Для

всех этих траекторий существует точка, в которой

cosθ = 0. Эти траектории можно параметризовать

значением величины ϕ_out. Чтобы найти решение ти-

па стенки, надо так подобрать значение величины

ϕ_out, чтобы в той же точке ξ, где cosθ = 0, одновре-

менно обращалась бы в нуль величина ϕ^′ = 0. Для

этого, фактически, надо решить одно уравнение с

Рис. 1. Зависимость энергии доменной стенки (в единицах

одним неизвестным, что легко реализовать числен-

E0) от ее скорости (в единицах v0) при различных значени-

ях D/E0 (указаны около кривых, значение D/E0 = 0.6366

но. Различные примеры решения задач о движении

близко к критическому, Dc/E0 = 2/π). Символы — данные

доменных стенок можно найти в работах [67-69].

численного счета, линии проведены согласно приближен-

В данной работе использовался надежный и про-

ной формуле (21)

стой метод продолжения по параметру (метод про-

должения Келлера [70]). В результате применения

этого метода для каждого значения D/E₀, т. е. для

различных магнетиков в рамках модели (2), можно

построить все многообразие доменных стенок. Если

решение найдено, можно вычислить интегралы дви-

жения, энергию E и импульс P доменной стенки.

Обсудим результаты анализа структуры, энергии и

импульса доменных стенок.

Прежде всего, отметим, что одному значению

скорости соответствуют два типа стенок с различ-

ными энергиями, т. е. зависимость E = E(v) изобра-

жается замкнутой кривой, содержащей две ветви —

верхнюю и нижнюю, см. рис. 1. Это свойство явля-

ется общим для известных нам стенок в различных

ферромагнетиках, в частности, блоховской и неелев-

ской ветвям стенок для уокеровского решения для

двухосного ферромагнетика. Эти ветви начинаются

Рис. 2. Зависимость предельной скорости доменной стен-

с описанных выше доменных стенок с v = 0. Стенка

ки vc (в единицах v0) от константы Дзялошинского D (в

с энергией E(v = 0) = 2E₀ - πD и значением ϕ =

единицах E0). Символы — данные численного счета, штри-

ховая красная прямая линия отвечает линейной зависимо-

= 0 соответствует наименьшему значению энергии

сти (16)

и нижней ветви, а стенка с E(v = 0) = 2E₀ + πD и

ϕ = π — наибольшему значению энергии и верхней

ветви зависимости E = E(v). Напомним, что значе-

ния всех экстенсивных величин, таких как энергия

что решения типа доменных стенок исчезают при

или импульс, приводятся на единицу площади стен-

достаточно больших значениях параметра |v|, т. е.

ки.

возможные значения скоростей стенки v не могут

При увеличении скорости движения стенки энер-

превышать предельного значения v_c, |v| ≤ v_c. При

гия для стенок нижней ветви увеличивается, а для

v = v_c две ветви зависимости E = E(v) сливаются,

стенок верхней ветви уменьшается. Анализ показал,

т. е. доменные стенки с v = v_c идентичны, см. рис. 1.

678

ЖЭТФ, том 159, вып. 4, 2021

Динамика доменных стенок в киральных магнетиках

Оказалось, что во всей допустимой области зна-

чений D ≤ D_c зависимость предельной скорости от

константы Дзялошинского с очень высокой точнос-

тью является линейной, см. рис. 2.

Эту зависимость можно описать формулой

πγD

v_c =

=v₀

(17)

2M_s

D_c

т. е. при D = D_c значение v_c = v₀ и составляет по-

ловину минимальной фазовой скорости магнонов.

При вычислении импульса стенки P имеет место

проблема, связанная с сингулярностью вектор-по-

тенциала A. Положение сингулярной точки для по-

тенциала вида (4) определяется направлением век-

тора n (струны Дирака), m_sing = -n. Доменную

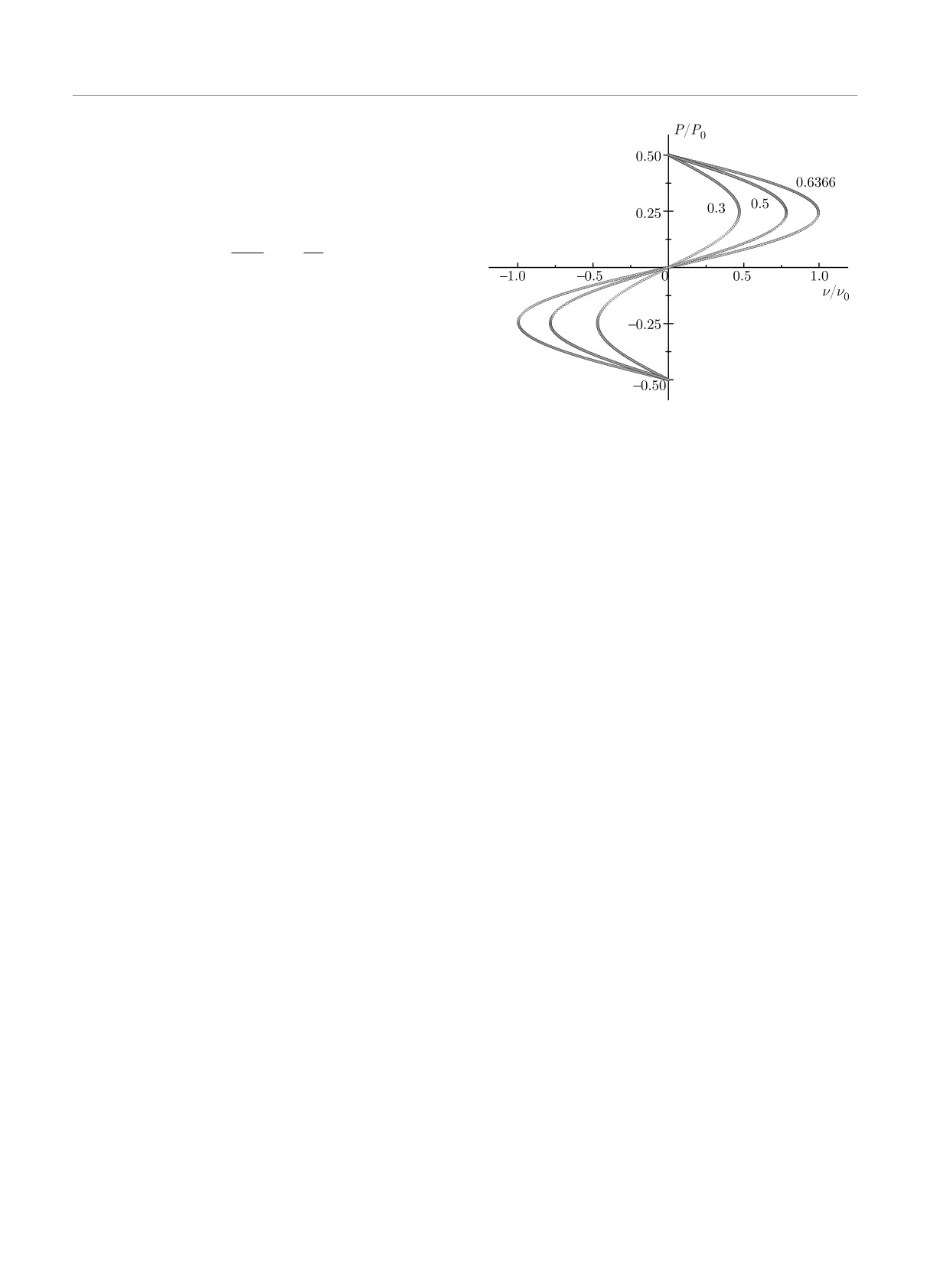
Рис. 3. Полученная численно зависимость импульса до-

стенку можно наглядно представить как траекто-

менной стенки (в единицах P0 ) от ее скорости (в единицах

рию на сфере m² = 1, выходящую из одного полюса

v0) для тех же значений D/E0, что на рис. 1

(скажем, m = -e_z) и входящую в другой (m = e_z).

Величину P можно записать в виде интеграла по

этой траектории:

учетом того, что rot A = mM_s/γ, эта величина опре-

∫∞

деляется интегралом по участку сферы,

∫

P = - A(m)(∂m/∂ξ)dξ =

ΔP = (M_s/γ) sin θ dθ dϕ.

-∞

∫

Интеграл для ΔP, в отличие от содержащего

A(m) dm.

(18)

вектор-потенциал A интеграла для P, является

m=ez

изотропным в плоскости m_x, m_y. В силу этих сооб-

Для данного магнетика при любом выборе n хотя

ражений можно найти разность значений импульса

бы одна из траекторий, отвечающих стенке с неко-

при разных направлениях струны. В частности,

торой скоростью -v_c ≤ v ≤ v_c попадет на такую

для двух использованных выше направлений зна-

сингулярную точку. Кроме того, возникает зависи-

чения импульса для некоторой стенки должны

мость P от выбора калибровки.

различаться на величину πM_s/γ. Это позволяет

Прямое вычисление импульса на основе форму-

восстановить значения импульса для стенок с

лы (5) и численного интегрирования решения пока-

траекториями, проходящими вблизи сингулярности

зало, однако, что для таких траекторий, которые не

для одной из калибровок, за счет использования

попадают в малую окрестность сингулярной точки

данных для другой калибровки. Найденная таким

m_sing (обычно это значения Δv ≤ 0.01v₀), интег-

образом зависимость P(v) представлена на рис. 3.

рал легко находится и импульс является регуляр-

Для наглядности использовано условие, что стенке

ной функцией скорости доменной стенки. Реально

с минимальной энергией (v = 0, ϕ = 0) отвечает

использовались расчеты для двух направлений n, а

значение P = 0.

именно, n = (0, 1, 0) n = (1, 0, 0). Далее для восста-

Разность импульсов неподвижных стенок верх-

новления зависимости импульса от скорости можно

ней и нижней ветвей отвечает половине площади

использовать тот факт, что разность величин P для

сферы и равна величине P = 2πM_s/γ = P₀/2, а за-

двух различных стенок, P₁ и P₂, определяется инте-

висимость энергии доменной стенки от ее импульса

гралом по замкнутому контуру

является периодической,

∮

ΔP = P₂ - P₁ = A(m) dm.

E(P + P₀) = E(P ), P₀ = 4πM_s/γ.

(19)

По теореме Стокса этот интеграл равен потоку век-

Значение периода P₀ для стенки в киральном

торного поля B = rotA через область, ограничен-

магнетике в два раза больше, чем для ферромагне-

ную этими двумя траекториями, т. е. ΔP являет-

тика с двухосной анизотропией. Заметим, что зна-

ся калибровочно-инвариантной величиной [40,41]. С

чения периода по импульсу для стенки в чисто од-

679

Е. Г. Галкина, Б. А. Иванов, Н. Е. Кулагин и др.

ЖЭТФ, том 159, вып. 4, 2021

пульса P , что обуславливает устойчивость всех сте-

нок, в том числе относящихся к верхней ветви дву-

значной зависимости E(v), см. рис. 1.

Численный анализ задачи позволяет устано-

вить основные закономерности динамики домен-

ных стенок в одноосном киральном ферромагнети-

ке для каждого конкретного значения параметра

D/E₀. Однако весьма желательно иметь простые

аналитические формулы, описывающие динамиче-

ские характеристики стенок. Такая возможность

всегда присутствует в том случае, когда взаимо-

действие, разрушающее сохранение

, являет-

ся слабым по сравнению с одноосной анизотропи-

ей, Hnon-uniaxial ≪ Ha. Если Hnon-uniaxial = 0,

то v_c = 0 и стенка не может двигаться, при этом

структура доменной стенки θ(ξ) описывается фор-

мулой для неподвижной стенки, а значение угло-

Рис. 4. Зависимость энергии (в единицах E0) и скорости

вой переменной ϕ(ξ) = const может быть произ-

(в единицах vc) доменной стенки от ее импульса (в едини-

вольным. Если же H_non-uniaxial не равно нулю, но

цах P0), символы — данные численного расчета, сплошная

H_non-uniaxial/H_a

≪ 1, предельная скорость, ко-

красная линия — зависимость E(P ), найденная с помо-

торая линейно зависит от характерного парамет-

щью полученной ниже приближенной формулы (22). Голу-

ра «неодноосности», мала. При малых H_non-uniaxial

бая линия — зависимость v(P ), построенная дифферен-

структура доменной стенки θ(ξ) приближенно опи-

цированием найденной численно функции E(P ) на основе

сывается той же формулой (14), что для неподвиж-

уравнения Гамильтона v = dE(P )/dP

ной стенки. Можно также считать, что угловая пе-

ременная ϕ(ξ) медленно меняется в пределах стен-

ки, и можно заменить ее на постоянное значение

номерном магнетике (спиновой цепочке) можно за-

при расчете энергии и импульса стенки. Естествен-

писать как P0,chain = 4πℏs/a, где s — спин атома

но, при этом энергия стенки слабо зависит от па-

и a — расстояние между спинами в цепочке. Чтобы

раметра H_non-uniaxial/H_a ≪ 1 и от скорости стен-

привести в соответствие данные для объемного маг-

ки. Подробный анализ применимости этих прибли-

нетика и цепочки использовано соотношение M_s =

жений проведен для неинтегрируемой задачи о дви-

= gμ_Bs/aS₀, где объем, приходящийся на один спин,

жении доменной стенки в ферромагнетике при на-

записан как aS₀, S₀ — площадь поперечного сечения

личии внешнего поля H_⊥, перпендикулярного лег-

кристалла, приходящаяся на одну цепочку, а также

кой оси [67]. Как и ожидалось, все эти приближения

учтено, что γ = gμ_B/ℏ. Интересно отметить, что для

хорошо соответствуют данным численного анализа

спина s = 1/2 величина периода совпадает с разме-

при H_⊥ < 0.4H_a.

ром первой зоны Бриллюэна атомной цепочки.

В нашем случае одноосного кирального магнети-

Зависимость E(P) (закон дисперсии стенки)

ка имеет место интересная особенность: описанные

представлена на рис. 4. Для демонстрации пра-

выше приближения справедливы не только при ма-

вильности выбора формы выражения для импульса

лых D, но и для всех актуальных значений D ≤ D_c

и контроля точности счета построена также за-

(напомним, что при D = D_c энергия стенки E об-

висимость v(P), найденная дифференцированием

ращается в нуль, так что это значение никак нельзя

численной зависимости E(P ) и уравнения Гамиль-

считать малым). Это позволило построить прибли-

тона v

= dE(P )/dP . Рисунок 4 демонстрирует

женное решение, найти зависимости энергии и им-

хорошее согласие всех данных.

пульса доменной стенки от ее скорости и записать

Принципиально важно, что зависимость E(P )

закон дисперсии стенки E(P ) в виде простых анали-

для доменных стенок в ферромагнетике в пределах

тических функций. Одним из указаний на эту спе-

одного периода однозначная, т. е. каждому значе-

цифику является линейная зависимость предельной

нию импульса отвечает только одно значение энер-

скорости от D при всех D ≤ D_c, см. рис. 2.

гии. Фактически, верхней и нижней ветвям функ-

Чтобы пояснить эту особенность, обсудим най-

ции E(v) соответствуют различные значения им-

денную численно структуру доменной стенки в наи-

680

ЖЭТФ, том 159, вып. 4, 2021

Динамика доменных стенок в киральных магнетиках

при немалых скоростях. Эта зависимость видна из

численного решения, но области такой асимптотики

находятся далеко от центра доменной стенки. Как

следует из численного решения, условие ϕ = const

выполняется с меньшей точностью, чем x²⁰(θ^′)² =

= sin² θ, особенно для v = vc. Однако перемен-

ная ϕ входит в уравнения только в виде комбина-

ции ϕ^′ sin θ и функции sin ϕ; для последней отклоне-

ние от постоянного значения намного меньшие, чем

для самой ϕ, см. рис. 5. Поэтому можно ожидать,

что при расчете интегральных характеристик стен-

ки условие ϕ = const достаточно адекватно. Такое

свойство доменной стенки достаточно неожиданное;

вероятно, оно возникает потому, что при ϕ = const

в рамках модели (9) энергия взаимодействия Дзя-

лошинского сводится к полной производной и, хотя

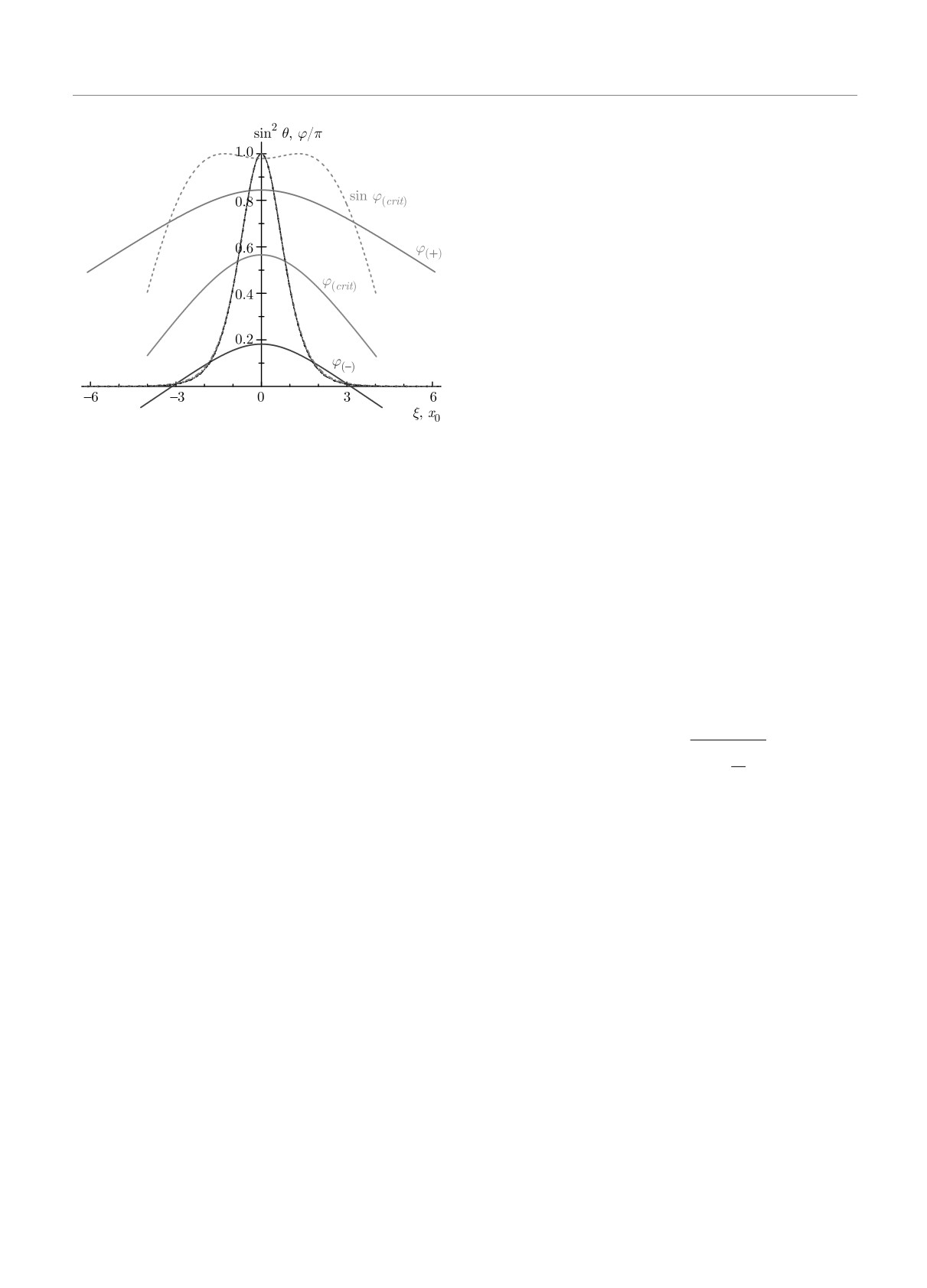
Рис. 5. Распределения намагниченности в доменных стен-

дает вклад в энергию стенки, не проявляется в ва-

ках, движущихся с разными скоростями, а именно, v =

риации энергии.

= 0.5vc для нижней и верхней ветвей и v = vc для ки-

Для получения замкнутых формул в рамках дан-

рального ферромагнетика с максимально возможным зна-

ного приближения проинтегрируем (12) по ξ от -∞

чением D = Dc. Вид функций sin² θ для всех трех стенок,

а также для случая v = 0, представлен разными линия-

до ∞, и получаем πD sin ϕ = 2vM_s/γ, т. е. связь ско-

ми, так что хорошо видно их почти идеальное совпадение;

рости с параметром ϕ можно записать в виде

различия заметны только вдали от центра стенки. Зави-

симости ϕ(ξ) отмечены как ϕ(-) и ϕ₍₊₎ для стенок ниж-

sinϕ = v/v_c,

(20)

ней и верхней ветви с v = 0.5vc и для ϕ(crit) для стенки

v = vc. В последнем случае отклонение ϕ(ξ) от модельно-

где значение предельной скорости определяется

го ϕ = const максимально, однако актуальная величина,

приведенной выше формулой (17). Далее легко вы-

sin ϕ (представлена красной штриховой линией) практиче-

числить энергию доменной стенки как функцию ϕ

ски постоянная в пределах доменной стенки (|ξ| < 3x0,

в виде E = 2E₀ - πD cosϕ. Зависимость энергии от

когда sin² θ < 10-2)

скорости дается формулой

√

(

)₂

E(v) = 2E₀ ± πD

(21)

более критичном случае максимально возможного

v_c

значения D = D_c при различных значениях скорос-

ти v ≤ v_c для стенок верхней и нижней ветвей, см.

где знаки «±» отвечают верхней и нижней ветвям

рис. 5. Видно, что при изменении скорости стенки

этой зависимости. На плоскости v E кривые, пред-

от нуля до предельного значения v = v_c структу-

ставляющие зависимость E(v), являются эллипсами

ра доменной стенки θ(ξ) с высокой точностью такая

с полуосями v_c и E₀ и с центрами в точках v = 0 и

же, как для чисто одноосной модели; она описыва-

E = 2E₀, что с высокой точностью описывает чис-

ется той же формулой (14), см. рис. 5. Используя

ленные данные, см. рис. 1.

выражение для первого интеграла (13), получаем,

Важной характеристикой доменной стенки явля-

что в этом случае значение (ϕ^′)² sin² θ должно быть

ется ее импульс. При расчете энергии стенки в рам-

пренебрежимо мало. По этой причине можно ожи-

ках приближения ϕ = const естественным образом

дать, что решение описывается с очень высокой точ-

получается зависимость E = E(ϕ). В рамках подхо-

ностью в рамках приближения ϕ = const при всех

да коллективных переменных энергия стенки, запи-

допустимых значениях параметров задачи, v ≤ v_c и

санная через ее импульс P, имеет смысл функции

D ≤ D_c. Напомним, что обычно такое условие имеет

Гамильтона. Поэтому импульс P , канонически со-

место только при малых H_non-uniaxial.

пряженный координате стенки X, должен быть свя-

Условие ϕ = const кажется противоречивым для

зан с переменной ϕ, см. подробнее [49, 50]. Связь P

нашей задачи при немалых D, поскольку из асимп-

и ϕ легко установить, используя уравнение Гамиль-

тотик решения (16) следует, что вдали от стенки

тона

значение ϕ ∼ κ^′′ξ, где κ^′′ = v/(2x₀v₀), и не мало

v ≡ dX/dt = dE(P)/dP.

681

Е. Г. Галкина, Б. А. Иванов, Н. Е. Кулагин и др.

ЖЭТФ, том 159, вып. 4, 2021

{

)

Учитывая, что dE/dϕ = πD sin ϕ и применяя фор-

⁽∂²θ

1 ∂²θ

[(∂ϕ)2

-sinθ cosθ K+A

мулу (20) легко записать P = 2M_sϕ/γ = ϕP₀/2π,

∂x²

c² ∂t²

∂x

где величина P₀ = 4πM_s/γ равна периоду зависи-

]}

⁽∂ϕ)2

∂ϕ

мости E(P ), см. (19). Искомая зависимость энергии

−

-2D

sin² θ sinϕ = 0,

(23)

доменной стенки от ее импульса (закон дисперсии

c²

∂t

∂x

стенки E(P )) в рамках этого приближения опреде-

ляется формулой

[

(

)

(

)]

∂

∂ϕ

∂

∂ϕ

)

sin² θ

⁽2πP

∂x

c² ∂t

∂t

E(P ) = 2E₀ - πD cos

(22)

P₀

∂θ

+ 2D

sin²

θ sinϕ = 0.

(24)

∂x

Тот факт, что энергия является периодической

функцией импульса, следует из анализа на осно-

Начнем с исследования структуры движущейся

ве полевого подхода с использованием конкретной

доменной стенки, для которой θ = θ(x - vt), ϕ =

формулы для плотности полевого импульса поля на-

= ϕ(x - vt). Заметим, что уравнение (24) для лю-

магниченности (5). Здесь такой же результат (22)

бой функции θ = θ(x - vt) имеет точное решение

получается в рамках подхода коллективных пере-

sinϕ = 0, т. е. ϕ = const, dϕ/dx = 0. Таким образом,

менных. Полезно сопоставить данные этих подхо-

величина угла ϕ = 0, π, . . . не зависит от скорости

дов. Поскольку расчет в рамках подхода коллек-

стенки. При этом уравнение (23) для θ принимает

тивных переменных проводился в приближении ϕ =

точно такой же вид, как и для статического слу-

= const, это позволяет также оценить точность этого

чая, если заменить A → A(v) = A(1 - v²/c²). Следо-

приближения.

вательно, структура доменной стенки определяется

выражением

Зависимость E(P), построенная с использовани-

ем найденных численно зависимостей E(v) и P (v) с

(

)

x-vt

использованием формул для E (2) и P (5) для сте-

cosθ = - th

√

(25)

нок с различными скоростями, с высокой точностью

x₀

1 - v²/c²

описывается формулой (22), см. рис. 4. Зависимость

√

v(P ), найденная обращением численной функции

где, как и ранее, x₀ =

A/K — толщина неподвиж-

P (v), хорошо согласуется с той, что получается из

ной стенки.

уравнения Гамильтона v = dE(P )/dP . Таким обра-

Таким образом, несмотря на отсутствие ло-

зом, значения энергии и импульса солитона типа до-

ренц-инвариантности для киральных антиферро-

менной стенки, полученные на основе полевого под-

магнетиков, эффект движения доменной стенки сво-

хода с использованием выражений для плотностей

дится только к лоренцевскому сокращению ее ши-

этих величин, хорошо согласуются с данными, полу-

рины, а скорость стенки ограничена сверху толь-

ченными на основе гамильтонового подхода в рам-

ко величиной c. Важно также, что как структура

ках метода коллективных переменных. Ранее такое

доменной стенки, так и предельная скорость не за-

соответствие было установлено только для модели

висят от константы Дзялошинского D. В отличие

Уокера, которая является точно интегрируемой. По-

от стандартных лоренц-инвариантных моделей ан-

скольку последние данные получены в приближении

тиферромагнетиков с произвольным видом энергии

ϕ = const, тем самым проверена высокая точность

анизотропии этот результат не очевиден; в част-

этого приближения для задачи о движении домен-

ности, лоренц-инвариантное поведение отсутствует

ной стенки в киральном магнетике с одноосной ани-

для двумерных топологических солитонов, предель-

зотропией.

ная скорость которых меньше c и зависит от D,

см. [57].

Предельная скорость доменной стенки в анти-

4. ДИНАМИКА ДОМЕННОЙ СТЕНКИ В

ферромагнетике не зависят от константы Дзяло-

КИРАЛЬНОМ АНТИФЕРРОМАГНЕТИКЕ

шинского D, а для ферромагнетика предельная ско-

рость пропорциональна D и обращается в нуль при

Для анализа движения плоской доменной стенки

D → 0. Этот результат можно объяснить, отме-

в антиферромагнетике ограничимся одномерными

тив, что для антиферромагнетика доменная стенка

решениями, l = l(x, t), и запишем уравнения сигма-

разделяет области магнетика с различными направ-

модели в угловых переменных θ и ϕ:

лениями вектора l и нулевой намагниченностью. В

682

ЖЭТФ, том 159, вып. 4, 2021

Динамика доменных стенок в киральных магнетиках

отличие от намагниченности ферромагнетика, сум-

сумму двух слагаемых, первое из которых есть ком-

марная z-проекция вектора l,

понента четырехмерного вектора, а второе — четы-

∫

рехмерный скаляр (инвариант преобразования Ло-

l(tot)z =

l_zdx,

ренца). Таким образом, хотя в киральном антифер-

ромагнетике лоренц-инвариантность разрушена, су-

не сохраняется даже для изотропного или одноосно-

ществуют простые правила получения энергии и им-

го антиферромагнетика. Таким образом, для движе-

пульса движущегося солитона из их значений для

ния доменной стенки никаких специальных условий

неподвижного солитона. Отметим, что такое же по-

типа несохранения z-проекции намагниченности не

ведение имеет место для другой системы с нарушен-

требуется.

ной лоренц-инвариантностью, антиферромагнетика

Несмотря на лоренц-инвариантный характер

во внешнем магнитном поле, направленном вдоль

структуры движущейся доменной стенки, на-

легкой оси [56].

рушение этой инвариантности проявляется при

Наличие двух типов стенок, т. е. двух ветвей за-

вычислении интегралов движения стенки. Исполь-

висимости E(v) или E(P), ставит вопрос об устойчи-

зуя форму энергии антиферромагнетика,

вости одной из них. Для ферромагнетика ситуация

понятная: зависимость E = E(P ) однозначная и обе

E(AFM) = T + W,

стенки устойчивы. Для лоренц-инвариантной мо-

энергию доменной стенки, движущейся со скорос-

дели двухосного антиферромагнетика зависимость

тью v, легко записать в виде

E(P ) содержит две ветви и стенки верхней ветви

неустойчивы для всех значений скорости доменной

2E₀

E(v) =

√

- πD cosϕ₀,

(26)

стенки [55]. Для кирального антиферромагнетика

1 - v²/c²

лоренц-инвариантность нарушена и ответ на этот

где ϕ₀ принимает фиксированные значения, скажем,

вопрос заранее не очевиден.

Для анализа устойчивости движущейся домен-

ϕ₀ = 0 или ϕ₀ = π, так что cosϕ₀ = ±1. Таким

образом, зависимость E(v), как и для ферромагне-

ной стенки рассмотрим малые возмущения на ее

фоне,

тика, содержит две ветви, энергии стенок верхней

и нижней ветвей различаются на величину 2πD.

θ(ξ, τ) = θ(ξ) + ϑ(ξ, τ), ϕ(ξ, τ) = ϕ₀ + ψ(ξ, τ),

Вычисляя импульс доменной стенки по формуле

(8), получаем выражение, характерное для лоренц-

и исследуем поведение малых добавок ϑ(ξ, τ) и

инвариантных моделей

ψ(ξ, τ). Для этого в полных уравнениях для θ(x, t),

ϕ(x, t) (23), (24) сделаем преобразование Лоренца

P = 2E₀

√

(27)

x-vt

t - vx/c²

c² - v²

x→ξ=

√

t→τ =

√

1 - v²/c²

1 - v²/c

в которое, однако, входит только та часть «энер-

гии покоя» стенки, которая не зависит от констан-

Понятно, что форма основных слагаемых с про-

ты Дзялошинского D. Зависимость энергии стенки

изводными не поменяется, например,

от ее импульса P, т.е. закон дисперсии E(P), легко

∂²θ

1 ∂²θ

∂²θ

1 ∂²θ

→

представить в виде

∂x²

c2 ∂t2

∂ξ²

c² ∂τ²

)₂

√

⁽∂ϕ

⁽∂ϕ)2

E(P ) =

(2E₀)² + c²P² - πD cos ϕ₀,

(28)

→

∂x

c²

∂t

∂ξ

c²

∂τ

где, как и в формуле для E(v), cos ϕ₀ = ±1.

но может измениться, вообще говоря, функциональ-

Формулы (26) и (27) определяют искомую зави-

ный вид слагаемых, связанных со взаимодействием

симость энергии E и импульса P от скорости стен-

Дзялошинского. Однако оказывается, что в линей-

ки, т. е. их поведение при преобразованиях Лоренца.

ном приближении по переменным ϑ(ξ, τ) и ψ(ξ, τ)

В лоренц-инвариантной теории (D = 0) достаточ-

эти слагаемые дают вклад только в уравнение для

но ограничиться анализом неподвижных решений и

ψ(ξ, τ), причем остается только слагаемое с dθ(ξ)/dξ

потом получить движущиеся решения из неподвиж-

и не возникает производных ψ(ξ, τ) и ϑ(ξ, τ) по τ.

ных с помощью преобразований Лоренца. При этом

Для конкретного анализа удобно записать

энергия и импульс представляют собой две ком-

ϑ(ξ, τ) = f(ξ) exp(iωτ),

поненты четырехмерного вектора энергии-импульса

P_μ = (E/c, P), точнее, его двумерного аналога. Ес-

ψ(ξ, τ) = [g(ξ)/ sin θ(ξ)] exp(iωτ),

ли же D = 0, то энергию можно представить как

683

Е. Г. Галкина, Б. А. Иванов, Н. Е. Кулагин и др.

ЖЭТФ, том 159, вып. 4, 2021

где θ(ξ) описывают невозмущенную доменную стен-

двумерных топологических солитонов (скирмионов)

ку. Далее будем использовать безразмерную пере-

такое влияние более существенно [57].

менную x = ξ/l₀(v) и измерять скорость и частоту в

√

единицах соответственно c и

c² - v²/x₀. Линеари-

5. ЗАКЛЮЧЕНИЕ

зованные уравнения для f и g образуют пару неза-

висимых уравнений на собственные значения, они

Начатые более шестидесяти лет назад исследова-

имеют вид

ния киральных магнетиков в настоящее время при-

(

)

вели к формированию бурно развивающейся облас-

Ĥf =ω²f,

Ĥ+ 2Dcosϕ0

g=ω²g.

(29)

ch x

ти физики магнетизма, имеющей большое влияние

При записи этих уравнений считалось, что ве-

на развитие прикладной физики. В значительной

личина dθ(ξ)/dξ ∝ 1/ ch ξ > 0 имеет определенный

мере это связано с солитонными аспектами про-

знак, такой же, как выше при записи энергии до-

блемы, а именно, с возможностью реализации дви-

менной стенки.

жения солитонов типа доменных стенок или скир-

Уравнения (29) содержат простой оператор Шре-

мионов с немалыми скоростями. Для киральных

дингера

Ĥ с безотражательным потенциалом,

магнетиков динамика солитонов качественно иная,

чем для изученных ранее случаев стандартных фер-

Ĥ₌ -

+1-

ромагнетиков и антиферромагнетиков. Не менее

dx²

ch² x

интересен и чисто теоретический аспект нелиней-

для которого известен полный набор собственных

ной динамики, прежде всего солитонной динамики,

функций. Этот набор включает одно локализован-

для киральных упорядоченных сред с нарушенной

ное состояние ψ₀,

фундаментальной симметрией относительно про-

странственной инверсии (P-инверсии). Принимая

Ĥψ₀ = 0, ψ₀ ∝

во внимание то, что для любых магнетиков нару-

ch x

шена симметрия относительно отражения времени

и состояния непрерывного спектра,

Ĥψ_k

(T-инверсии), возникает интересная возможность

= (1 + k²)ψ_k, см., например, [55].

исследования, в том числе экспериментальной реа-

Легко видеть, что локализованные возмущения

лизации, динамики солитонов в нелинейных средах

переменной θ(ξ, τ), которые описывают трансляци-

с нарушением симметрии относительно P-инверсии

онную голдстоуновскую моду с ω = 0, не наруша-

и T-инверсии. Авторы надеются, что анализ раз-

ют устойчивости доменной стенки. Эволюцию вто-

личных аспектов этой проблемы для магнетиков

рой переменной ϕ(ξ, τ) определяют решения g ∝ ψ₀,

различного типа поможет понять специфику общей

f = 0; для нее знак ω² определяется знаком Dcosϕ₀.

проблемы и увидеть возможные пути ее реализации

Для стенки с меньшей энергией D cos ϕ₀ > 0 и воз-

и практического применения.

мущения ϕ на фоне стенки определяют собственную

моду колебаний с ненулевой частотой, ω² > 0. Для

Финансирование. Работа выполнена в

стенки верхней ветви D cos ϕ₀ < 0, ω² < 0, т. е. от-

рамках программы НИТУ

«МИСиС» (проект

клонение ϕ от равновесного значения экспоненци-

№К2-2019-006), осуществляемой постановлением

ально нарастают, что определяет нестабильность до-

правительства РФ от 16 марта 2013 г. № 211.

менной стенки верхней ветви. Получается, что стен-

ки нижней ветви зависимости E(P ) или E(v), для

которых D cos ϕ₀ > 0, устойчивы, а стенки верхней

ЛИТЕРАТУРА

ветви — неустойчивы при всех допустимых значе-

ниях скорости доменной стенки. Таким образом, ха-

1. И. Е. Дзялошинский, ЖЭТФ 46, 1420 (1964).

рактер устойчивости доменной стенки такой же, как

2. И. Е. Дзялошинский, ЖЭТФ 47, 992 (1964).

для простейшей лоренц-инвариантной модели [55]:

из двух стенок с тем же значением импульса устой-

3. И. Е. Дзялошинский, ЖЭТФ 32, 1547 (1957).

чива только одна, у которой энергия ниже.

4. И. Е. Дзялошинский, ЖЭТФ 33, 807 (1958).

Таким образом, можно сделать общий вывод, что

нарушение пространственной инверсии влияет на

5. И. Е. Дзялошинский, ЖЭТФ 33, 1454 (1958).

динамику одномерных антиферромагнитных соли-

6. I. Dzyaloshinsky, J. Phys. Chem. Sol. 4, 241 (1958).

тонов в значительно меньшей степени, чем на ди-

намику солитонов в ферромагнетиках. Однако для

7. T. Moriya, Phys. Rev. 120, 91 (1960).

684

ЖЭТФ, том 159, вып. 4, 2021

Динамика доменных стенок в киральных магнетиках

С. М. Стишов, А. Е. Петрова, ЖЭТФ 158, 213

30.

S. Komineas, C. Melcher, and S. Venakides, Nonli-

(2020).

nearity 32, 2392 (2019).

B. Lebech, J. Bernhard, and T. Freltoft, J. Phys.

31.

O. Boulle, S. Rohart, L. D. Buda-Prejbeanu et al.,

Condens. Matter 1, 6105 (1989).

Phys. Rev. Lett. 111, 217203 (2013).

10.

T. Ohyama and A. E. Jacobs, Phys. Rev. B 52, 4389

32.

V. P. Kravchuk, J. Magn. Magn. Mater. 367,

(1995)

(2014).

11.

A. Zheludev, S. Maslov, G. Shirane et al., Phys. Rev.

33.

Л. Д. Ландау, Е. М. Лифшиц, Phys. Zs. Sowjet. 8,

Lett. 78, 4857 (1997).

153 (1935); Л. Д. Ландау, Е. М. Лифшиц, К тео-

рии магнитной проницаемости ферромагнитных

12.

A. Fert, Mater. Sci. Forum 59-60, 439 (1990).

тел, Л. Д. Ландау, Собр. тр. Т. 1, Наука, Москва

13.

C. Moreau-Luchaire, C. Moutafis, N. Reyren et al.,

(1969), с. 128.

Nat. Nanotech. 11, 444 (2016).

34.

А. И. Ахиезер, В. Г. Барьяхтар, С. В. Пелетминс-

14.

O. Boulle, J. Vogel, H. Yang et al., Nat. Nanotech.

кий, Спиновые волны, Наука, Москва (1967).

11, 449 (2016).

35.

I. A. Yastremsky, O. M. Volkov, M. Kopte et al.,

15.

A. Fert, V. Cros, and J. Sampaio, Nat. Nanotech. 8,

Phys. Rev. Appl. 12, 064038 (2019).

152 (2013).

36.

E. Fradkin, Field Theories of Condensed Matter

16.

R. Wiesendanger, Nat. Rev. Mater. 1, 16044 (2016).

Systems, in Frontiers in Physics, Addison-Wesley

(1991).

17.

F. Zheng, F. N. Rybakov, A. B. Borisov et al., Nat.

Nanotech. 13, (2018).

37.

R. Rajaraman, Solitons and Instantons: An Inroduc-

tion to Solitons and Instantons in Quantum Field

18.

G. P. Mueller, F. N. Rybakov, H. Jonsson et al., Phys.

Theory, North-Holland, Amsterdam (1982).

Rev. B 101, 84405 (2020).

38.

A. A. Thiele, Phys. Rev. Lett. 30, 230 (1973).

19.

Y. Fujishiro, N. Kanazawa, and Y. Tokura, Appl.

Phys. Lett. 116, 090501 (2020).

39.

N. Papanicolaou and T. N. Tomaras, Nucl. Phys.

B 360, 425 (1991).

20.

Skyrmions: Topological Structures, Properties, and

Applications, ed. by J. Liu, Z. Zhang, and G. Zhao,

40.

Е. Г. Галкина, Б. А. Иванов, Письма в ЖЭТФ 71,

Series in Materials Science and Engineering, CRC,

372 (2000).

Boca Raton, FL (2016).

41.

E. G. Galkina, B. A. Ivanov, S. Savel’ev, and F. Nori,

21.

D. Sander, S. O. Valenzuela, D. Makarov et al.,

Phys. Rev. B 77, 134425 (2008).

J. Phys. D: Appl. Phys. 50, 363001 (2017).

42.

O. Tchernyshyov, Ann. Phys. (N. Y.) 363, 98 (2015).

22.

A. Thiaville, S. Rohart, E. Jue et al., Europhys. Lett.

100, 57002 (2012).

43.

S. Dasgupta and O. Tchernyshyov, Phys. Rev. B 98,

224401 (2018).

23.

I. M. Miron, T. Moore, H. Szambolics et al., Nat.

Mater. 10, 419 (2011).

44.

L. R. Walker, in: Magnetism, Vol. 3, ed. by G. T. Ra-

do and H. Suhi, Pergamon, New York (1963), p. 451.

24.

L. Thomas, K. S. Ryu, S. H. Yang, and S. S. P. Par-

kin, Nat. Nanotech. 8, 527 (2013).

45.

S. V. Tarasenko, A. Stankiewicz, V. V. Tarasenko,

and J. Ferré, J. Magn. Magn. Mater. 189, 19 (1998).

25.

S. Emori, U. Bauer, S. M. Ahn et al., Nat. Mater. 12,

611 (2013).

46.

А. М. Косевич, Б. А. Иванов, А. С. Ковалев, Пись-

ма в ЖЭТФ 25, 516 (1977).

26.

A. Brataas, Nat. Nanotech. 8, 485 (2013).

27.

S. S. P. Parkin, M. Hayashi, and L. Thomas, Science

47.

В. П. Воронов, Б. А. Иванов, А. М. Косевич,

320, 190 (2008).

ЖЭТФ 84, 2235 (1983).

28.

S. S. P. Parkin and S.-H. Yang, Nat. Nanotech. 10,

48.

A. M. Kosevich, B. A. Ivanov, and A. S. Kovalev,

195 (2015).

Physica D 3, 363 (1981).

29.

V. V. Slastikov, C. B. Muratov, J. M. Robbins and

49.

A. M. Kosevich, B. A. Ivanov, and A. S. Kovalev.

O. A. Tretiakov, Phys. Rev. B 99, 100403(R) (2019).

Phys. Rep. 194, 117 (1990).

685

Е. Г. Галкина, Б. А. Иванов, Н. Е. Кулагин и др.

ЖЭТФ, том 159, вып. 4, 2021

50. А. М. Косевич, Б. А. Иванов, А. С. Ковалев, Нели-

59. В. Г. Барьяхтар, Б. А. Иванов, А. Л. Сукстанский,

нейные волны намагниченности. Динамические и

Письма в ЖЭТФ 27, 226 (1978).

топологические солитоны, Наукова думка, Киев

60. В. М. Елеонский, Н. Н. Кирова, Н. Е. Кулагин,

(1983).

ЖЭТФ 75, 2210 (1978).

51. А. Б. Борисов, В. В. Киселев, Нелинейные волны,

61. В. М. Елеонский, Н. Н. Кирова, Н. Е. Кулагин,

солитоны и локализованные структуры в маг-

ЖЭТФ 77, 409 (1979).

нетиках, в двух томах, УроРАН, Екатеринбург

(2009).

62. В. М. Елеонский, Н. Е. Кулагин, ЖЭТФ 84, 616

(1983).

52. А. А. Жмудский, Б. А. Иванов, ЖЭТФ 115, 1511

(1999).

63. В. М. Елеонский, Н. Е. Кулагин, ЖЭТФ 85, 1437

(1983).

53. Е. А. Туров, А. В. Колчанов, В. В. Меньшенин,

И. Ф. Мирсаев, В. В. Николаев, Симметрия и фи-

64. L. M. Lerman, Selecta Math. Sovietica 12,

333

зические свойства антиферромагнетиков, Физ-

(1993).

матлит, Москва (2001).

65. Л. М. Лерман, Письма в ЖЭТФ 51, 336 (1990).

54. E. G. Galkina and B. A. Ivanov, Low Temp. Phys.

66. Л. М. Лерман, Я. Л. Уманский, Прикл. матем.

44, 618 (2018).

мех. 47, 395 (1983).

55. В. Г. Барьяхтар, Б. А. Иванов, А. Л. Сукстанский,

67. Б. А. Иванов, Н. Е. Кулагин, ЖЭТФ 112, 953

ЖЭТФ 78, 1509 (1980).

(1997).

56. В. Г. Барьяхтар, Б. А. Иванов, ЖЭТФ 85, 328

68. В. М. Елеонский, Н. Н. Кирова, Н. Е. Кулагин,

(1983).

ЖЭТФ 71, 2349 (1976).

57. S. Komineas and N. Papanicolaou, SciPost Phys. 8,

69. В. М. Елеонский, Н. Н. Кирова, Н. Е. Кулагин,

086 (2020).

ЖЭТФ 74, 1814 (1978).

58. E. Schlömann, Appl. Phys. Lett. 19, 274 (1971).

70. T. F. C. Chan and H. B. Keller, SIAM 3, 173 (1982).

686