ЖЭТФ, 2021, том 159, вып. 4, стр. 690-695

CRITICAL FLUCTUATIONS BEYOND THE QUANTUM PHASE

TRANSITION IN DZYALOSHINSKII-MORIYA

HELIMAGNETS Mn1-xFe_xSi

S. V. Grigorieva,b*, O. I. Utesov^a,b, N. M. Chubova^a,

C. D. Dewhurst^c, D. Menzel^d, S. V. Maleyev^a

^a Petersburg Nuclear Physics Institute named by B. P, Konstantinov of National Reserarch Centre “Kurchatov institute”

188300, Saint Petersburg, Gatchina, Russia

^b Saint Petersburg State University

198504, Saint Petersburg, Russia

^c Institut Laue-Langevin

38042, Grenoble, Cedex 9, France

^d Technische Universität Braunschweig

38106, Braunschweig, Germany

Received December 1, 2020,

revised version December 1, 2020

Accepted for publication December 3, 2020

Contribution for the JETP special issue in honor of I. E. Dzyaloshinskii’s 90th birthday

DOI: 10.31857/S0044451021040106

The isostructural solid solutions Mn1-xFe_xSi also

reveal intriguing properties upon Fe concentration

growth. The substitution of manganese by iron sup-

Many years have passed since the first observa-

presses the helical order [11]. Neutron scattering stud-

tion of helical spin structures in cubic B20 com-

ies [12, 13] together with magnetic susceptibility and

pounds FeGe [1] and MnSi [2]. However, helimagnets

specific heat measurements [11, 14-16] discovered a

with Dzyaloshinskii-Moriya (DM) interaction [3,4] are

quantum critical point (QCP) described as a suppres-

among the most studied systems in contemporary con-

sion of the spiral phase with long-range order (LRO)

densed matter physics. In particular, this interest is

in Mn1-xFe_xSi. As it was shown in Refs. [13, 15, 16],

stimulated by rather simple but fancy phase diagram

this QCP located at x_c ≈ 0.11-0.12 is hidden by an

which includes topologically lattice (A-phase) [5]. The

extensive phase of spin helix fluctuations. This fluctu-

theoretical descriptions [6,7] pointed out that the com-

ation regime, sometimes referred to as chiral spin liquid

petition between the ferromagnetic exchange interac-

[17, 18], vanishes at about x ≈ 0.24.

tion and the antisymmetric DM interaction is balanced

in the homochiral helical magnetic structure.

Both magnetic susceptibility measurements

Mixed B20 compounds like Mn1-xFe_xSi or

and neutron scattering experiments demonstrate

Mn1-xFe_xGe are characterized by additional pa-

a short-range order (SRO) and a crossover to the

rameter x which allows fine tuning for the system

helix fluctuating regime [13, 19-21]. The crossover

properties. In Mn1-xFe_xGe its variation leads to

temperature T_DM decreases with x and becomes

change of the sign of magnetic chirality at x_c ≈ 0.75

zero at x_DM ≈ 0.17 [12, 22]. It was shown that the

[8, 9], where the system is in ferromagnetic state due

temperature T_DM is proportional to the spin wave

to cubic anisotropy [10].

stiffness of the compounds Mn1-xFe_xSi [23]. One

concludes that these compounds at x ∼ x_DM ≈ 0.17

represent the only known example of the system,

^* E-mail: grigoryev_sv@pnpi.nrcki.ru

where ferromagnetic exchange approaches zero but

690

ЖЭТФ, том 159, вып. 4, 2021

Critical fluctuations beyond the quantum phase transition. . .

neutrons were detected with a 2D position sensitive

detector. The beam divergence was tuned from 1 to

10 mrad to set the Q-range and Q-resolution optimal

for an individual sample (Q is a momentum transfer).

With these settings, we were able to cover the Q-range

from 2 · 10-2 to 2 nm-1. A weak magnetic field (1 mT)

guiding the polarization P₀ was applied along the Q_x.

The temperature was set in the range from 1.7 to

60 K with accuracy of the order of 0.05 K. As a result,

we obtain the maps of polarized SANS intensities at

various temperatures for three samples with different

x. A background intensity maps were taken for all

samples at high temperature (T

= 60 K) when no

magnetic scattering is observed. These background

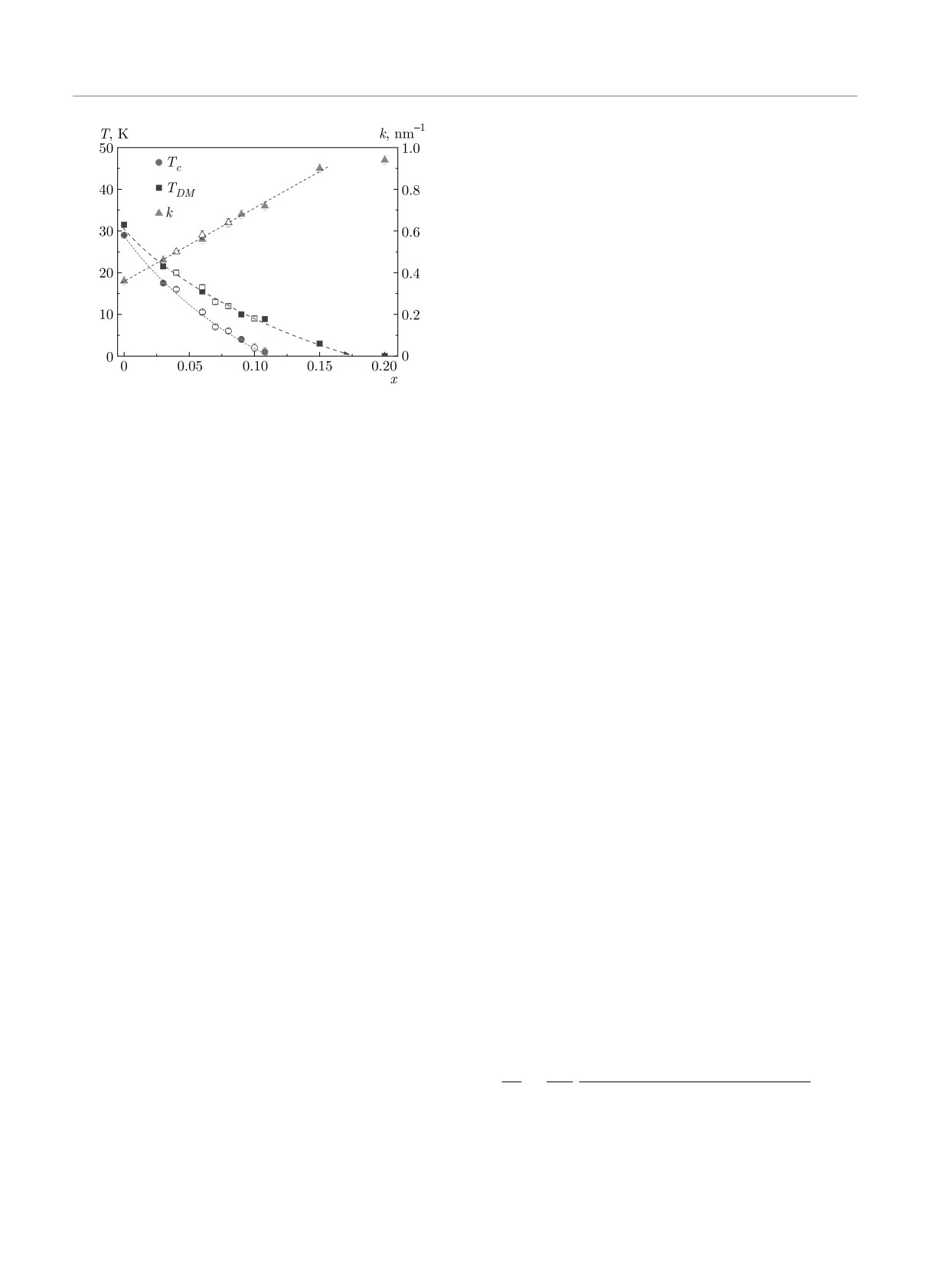
Fig. 1. (Color online) Temperature-concentration (T -x) phase

maps were subtracted from the other scattering maps

diagram of the Mn1-xFexSi compounds and the helix wave

of the given sample. The software GRASP developed

vector k as a function of x. The data taken from several stu-

at the ILL (Grenoble) were used for the primary data

dies [12, 13, 23] are combined with data of the present work.

reduction [24].

The dashed lines are the guides for an eye

Figure 2 shows the maps of the polarized SANS in-

tensities with the polarization along P₀. One can fol-

low the evolution of the scattering patterns with tem-

DM interaction is finite and provides chiral rotation of

perature (vertical axis) and the concentration (horizon-

spins in magnetic fluctuations.

tal axis). The whole diagram can be qualitatively de-

In the present paper, we study the critical fluctua-

scribed in the following way. No scattering is observed

tions in DM helimagnets Mn1-xFe_xSi by means of po-

at the temperature of 15 K for all three concentra-

larized neutron scattering. Three samples with x =

tions. Upon lowering temperature to 9 K, the blurred

= 0.10, x = 0.15, and x = 0.20 are selected so as

but well detectable scattering appears for the sample

to represent three different regimes: namely close to

with x = 0.10, while the samples with x = 0.15 and

the quantum critical point x ∼ x_c, close to the con-

x = 0.20 show no scattering, demonstrating absence

centration with zero ferromagnetic exchange x_DM , and

of short-range magnetic correlations. Further temper-

beyond this concentration, respectively.

ature lowering to 5 K forms a well-defined “half-moon”

The series of Mn1-xFe_xSi single crystals with x =

image (which is typical for chiral helimagnets) for the

= 0.10, 0.15, 0.20 were grown using the Czochralski

sample with x = 0.10. For the ones with x = 0.15 and

technique at the Institute of Condensed Matter Physics

x = 0.20, it results in the appearance of the blurred im-

(Braunschweig, Germany). These samples were pre-

ages. At T = 2 K, the scattering for the sample with

pared as cylinders with a height of 15-20 mm and a

x = 0.10 is almost the same, whereas for the sample

diameter of 5-6 mm.

with x = 0.15, a slightly blurred half-moon image ap-

The temperature-concentration (T -x) phase dia-

pears. For the most disordered sample with x = 0.20,

gram is shown in Fig. 1. One can see (in accord with

the image is still far from being well-defined half-moon.

Refs. [13, 15, 16, 19]) that T_c, which indicates a phase

We note that the scattering is strongly asymmetric in

with LRO, reaches zero at x_c ≈ 0.11-0.12, while the

all cases. The latter is typical for the critical scattering

temperature band of the fluctuating helix regime in-

above T_c in the MnSi system [20,21,25].

creases with x. The decrease in T_c is accompanied by

Similarly to Ref. [26], we treated the obtained data

the linear with x increase in the helix wave vector k, as

using the following mean-field form of the neutron cross

shown in Fig. 1.

section which is appropriate for the disordered fluctu-

The polarized small-angle neutron scattering

ating phase in these compounds (T > T_c) [20, 25]:

(SANS) was performed using the D22 instrument at

dσ

r²T k² + κ² + Q² + 2 sgn(D) kQ · P₀

the Laue-Langevin Institute (Grenoble, France). The

[

][

] .

(1)

dΩ

[110] axis of the single crystal was oriented parallel to

A (Q + k)² + κ² (Q - k)² + κ²

the neutron beam with an accuracy of 5^◦. A polarized

neutron beam with initial polarization P₀ = 0.93 and

Here Q is the scattering vector, r is the classical elect-

mean wavelength λ = 0.60 nm was used. The scattered

ron radius, κ is the inverse correlation length of the

691

ЖЭТФ, том 159, вып. 4, 2021

Critical fluctuations beyond the quantum phase transition. . .

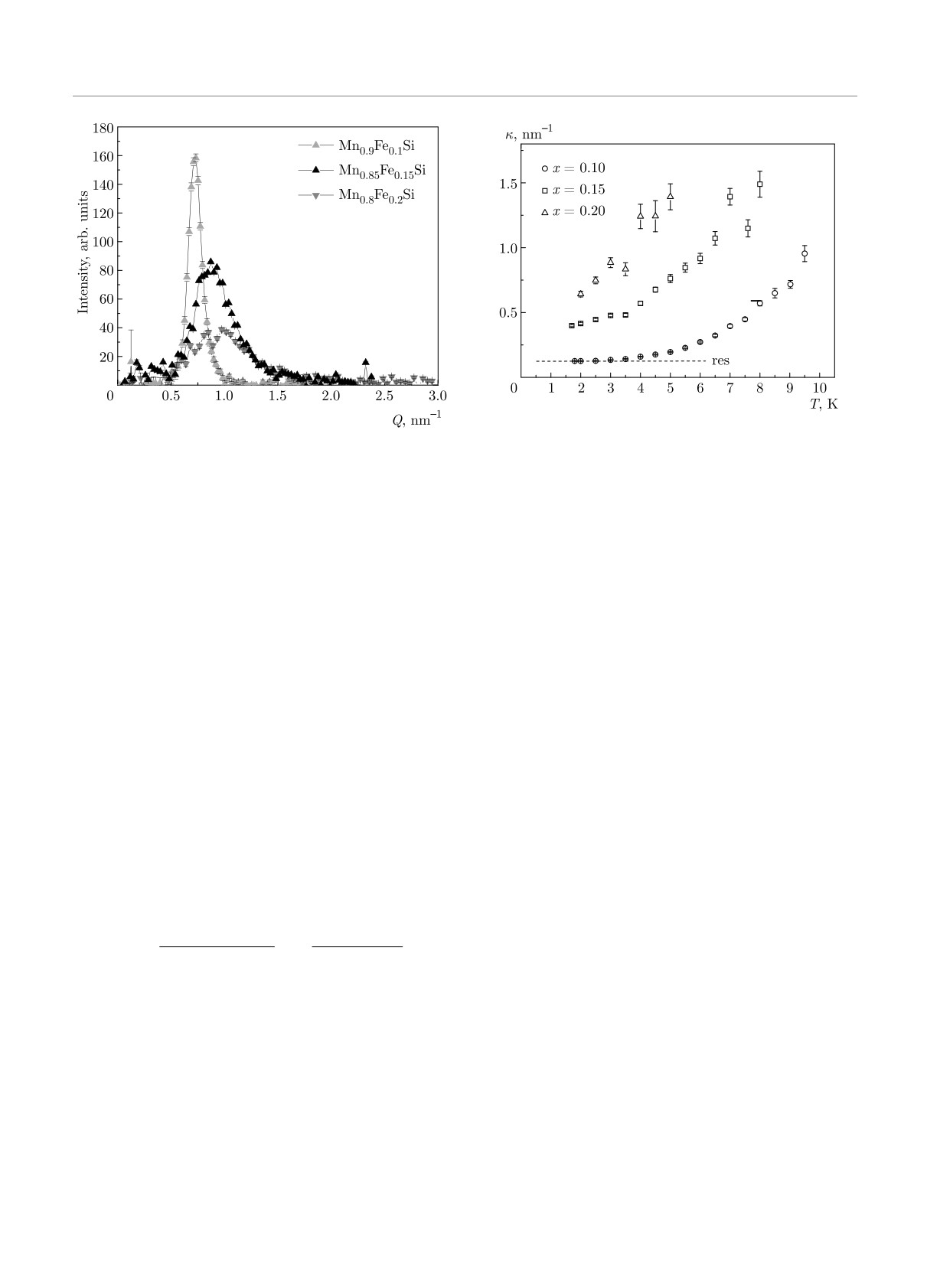
Fig. 4. Temperature dependence of the inverse correlation

Fig. 3. (Color online) Q-dependence of the azimuthally ave-

length of helical fluctuations for the Mn1-xFexSi system with

raged scattering intensity for the Mn1-xFexSi system with

x = 0.10, 0.15, 0.20 in the log-log scale (the line denoted “res”

x = 0.10, 0.15, 0.20 at T = 2.0 K

shows the level of the instrumantal resolution)

critical fluctuation, A is the spin wave stiffness at low

can be ascribed to the scattering on the critical fluc-

temperatures, D is the Dzyaloshinskii constant, and

tuations of the helical structure, whereas at low tem-

P₀ is the incident polarization of neutrons. The cross

peratures, I(Q) is described by the sum of the Gaus-

section (Eq. (1)) has several features provided by DM

sian and Lorentzian for the samples with x = 0.10 and

interaction.

x = 0.15; Gaussian term being attributed to the limi-

(i) Due to the second term of the product in the

tation of the instrument resolution, which exceeds the

denominator, the scattering intensity should form a

value of 0.12 nm-1 (see Fig. 3, curve for x = 0.10).

sphere of radius Q = k with a width of κ. The scalar

variables in (Q - k)² are due to isotropic DM interac-

The whole set of the experimental data obtained

tion.

by polarized SANS was fitted to Eq. (1). The position

(ii) The intensity has the Lorentzian shape typical

of the maximum k (the helix wavevector) and inverse

for critical fluctuations.

correlation length κ of the helix were obtained as a re-

(iii) The scattering intensity is strongly oriented

sult of the fit. The wave vector does not change with

along the incident neutron polarization since the nu-

the temperature within the error bars for the individ-

merator of Eq. (1) is maximal at P₀ parallel to Q and

ual sample. It is equal to 0.72 nm-1, 0.90 nm-1, and

it is minimal at P₀ antiparallel to Q.

0.94 nm-1 for the samples with x = 0.10, 0.15, and

The chirality of the critical fluctuations can be esti-

0.20, respectively. Interesting to note that the wave

mated via measurement of the polarization of the scat-

vector changes linearly with the concentration in the

tering:

range of x = 0-0.15 and saturates at the concentration

x larger that 0.15 (see Fig. 1). It is correlated to the

σ(P₀) - σ(-P₀)

2kQP₀ cosφ

range with the finite crossover temperature T_DM in the

P_s(Q) =

(2)

σ(P₀) + σ(-P₀)

Q² + k² + κ²

Mn1-xFe_xSi compounds.

where φ is the angle between P₀ and Q, and we use

The temperature dependence of the inverse corre-

Eq. (1) to express its value via parameters Q, k and κ.

lation length κ is shown in Fig. 4. As it was noticed

For quantitative analysis, the intensity maps were

above, the value of κ is resolution limited for the com-

azimuthally averaged. Examples of the radial pro-

pound with x = 0.10 for the low temperature range.

files (the Q-dependence of the scattering intensity) are

It saturates with lowering temperature at T_c = 3.0 K

shown in Fig. 3. As it is well seen in Fig. 3, the position

(x = 0.10). In contrast, for the sample with x = 0.15,

and the width of the observed peak differ for the three

κ tends to saturate at larger value, disorder-induced κ_d

samples. The scattering curve I(Q) can be well de-

(see below). For the sample with x = 0.20, κ does not

scribed by the Lorentzian at high temperatures, which

saturate at all.

693

S. V. Grigoriev, O. I. Utesov, N. M. Chubova et al.

ЖЭТФ, том 159, вып. 4, 2021

We observe (it was also noted in Refs. [20,25]) that

In the considered mixed B20 helimagnet, the LRO

the polarization P_s (Q = k) is close to 1 at low tempera-

disappears at xc ≈ 0.11. The correlation length ξd

ture even for the most disordered sample with x = 0.20,

decreases from infinity at x_c to finite values at larger

which shows that DM interaction is still present and

Fe concentrations. We denote disorder-induced inverse

makes short fluctuations chiral. Upon increase of tem-

correlation length as κ_d. When discussing polarized

perature, the polarization P_s was found to decrease

neutron scattering data, κ2d should be added into the

smoothly.

denominator of Eq. (1) and considered as a part of κ²

The behaviour observed experimentally can be

along with temperature-dependent contribution κ2T as

qualitatively understood using the assumption that Fe

the system has effective size ξ_d [32].

ions introduce the defect antiferromagnetic (AF) bonds

Thus, we arrive to the following qualitative picture.

in the system. First of all, strong AF bonds lead to

The sample with x = 0.10 has κ_d = 0 and behaves

significant lowering of the spin wave stiffness, T_c, and

like pure MnSi with lower T_c and T_DM values due to

T_DM . The latter becomes zero at x = x_DM . Moreover,

AF bonds-induced lowering of the spin-wave stiffness.

according to the theory of Ref. [27], strong AF bonds

Half-moon patterns and sharp peaks in the neutron

can lead to large variation of the helical vector even at

scattering (see Figs. 2 and 3), and peaks in magnetic

small concentrations (see Fig. 1).

susceptibility [22] near T_c are well pronounced due to

It is well-known that the strong frustrating defect

mean-field denominator propotional to (Q - k)² + κ2T .

bonds with finite concentration destroy the long-range

For the sample with x = 0.15, the inverse corre-

order in the two-dimensional collinear magnets. In-

lation lenght κ_d is nonzero and it is smaller than k.

stead, the SRO order of the glassy phase emerges in

It leads to the highly chiral fluctuating phase at T <

the system [28, 29]. Strong defects lead to additional

< T_DM, but suppresses the growth of the critical fluc-

rotations of spins, δϕ(r), in the classical ground state

tuations so naturally seen at x < x_c. Moreover, since

of the system. For a single defect bond, they can be

κ has a tendency to saturation upon temperature low-

described as the dipolar field (cf. Refs. [27, 30]),

ering (see Fig. 4), apparently there should be a transi-

d·r

tion to frozen SRO phase (like in usual spin-glasses, see

δϕ(r) =

(3)

r^D

Ref. [33]) with correlation length larger than the spi-

ral period. In the polarized neutron images, such be-

where d is the dipole moment of the defect bond, r

haviour results in blurred half-moon patterns, whereas

is the distance from the defect bond, and D is the di-

in magnetic susceptibility measurements [22] there is a

mension of the system. After averaging over disorder

broad maximum.

configurations, one gets for mean squared transverse

At x = x_DM , spin wave stiffness becomes zero, and

fluctuation of the ordered moment M [31]:

a possible qualitative description of the experimental

∫

data observed at x > x_DM (e. g., blurred SANS maps

〈M2⊥〉 ∼ xM² d^Dr δϕ²(r).

(4)

and negative Curie-Weiss temperature) can be based

on a domination of the AF interaction in the sample.

In two-dimensional systems, this integral diverges as

Concentration x_DM itself is very peculiar, its vicinity

a logarithm on large distances and the cut-off (disor-

in T -x phase diagram should reveal intriguing proper-

der-induced correlation length ξ_d) should be intro-

ties of the fluctuating highly chiral helical state with

duced. Importantly, ξ_d is finite for every nonzero con-

the shortest period possible for such systems. The cor-

centration x. In three-dimensional systems, the same

relation length of these fluctuations are affected by two

scenario can occur at finite concentrations x_c if the dis-

factors not related to temperature: disorder induced

order is strong enough [29]. Correlation length can be

by the AF bonds and DM interaction destabilizing

estimated using the condition

the ferromagnetic order. A detailed description of the

∫ξd

situation in the vicinity of x_DM requires further exper-

1 = x d³r δϕ²(r),

(5)

imental studies.

which at x > x_c yields

Funding. The authors thank for the support the

Russian Science Foundation (grant No. 17-12-01050).

ξ_d ∼ (x - x_c)-1.

(6)

Note, that the correlation length ξ_d is temperature-

The full text of this paper is published in the English

independent since its nature is pure classical.

version of JETP.

694

ЖЭТФ, том 159, вып. 4, 2021

Critical fluctuations beyond the quantum phase transition. . .

REFERENCES

18.

F. Kruger, U. Karahasanovic, and A. G. Green, Phys.

Rev. Lett. 108, 067003 (2012).

L. Lundgren, O. Beckman, V. Attia, S. P. Bhattache-

rjee, and M. Richardson, Phys. Scripta 1, 69 (1970).

19.

V. V. Glushkov, I. I. Lobanova, V. Yu. Ivanov,

V. V. Voronov, V. A. Dyadkin, N. M. Chubova,

Y. Ishikawa, K. Tajima, D. Bloch, and M. Roth, Sol.

S. V. Grigoriev, and S. V. Demishev, Phys. Rev. Lett.

St. Comm. 19, 525 (1976).

115, 256601 (2015).

I. Dzyaloshinskii, J. Phys. Chem. Sol. 4, 241 (1958).

20.

S. V. Grigoriev, S. V. Maleyev, E. V. Moskvin,

T. Moriya, Phys. Rev. 120, 91 (1960).

V. A. Dyadkin, P. Fouquet, and H. Eckerlebe, Phys.

Rev. B 81, 144413 (2010).

S. Muhlbauer, B. Binz, F. Jonietz, C. Pfleiderer,

A. Rosch, A. Neubauer, R. Georgii, and P. Böni, Sci-

21.

M. Janoschek, M. Garst, A. Bauer, P. Krautscheid,

ence 323, 915 (2009).

R. Georgii, P. Böni, and C. Pfleiderer, Phys. Rev.

B 87, 134407 (2013).

O. Nakanishia, A. Yanase, A. Hasegawa, and M. Ka-

taoka, Sol. St. Comm. 35, 995 (1980).

22.

L. J. Bannenberg, F. Weber, A. J. E. Lefering,

T. Wolf, and C. Pappas, Phys. Rev. B 98, 184430

P. Bak and M. H. Jensen, J. Phys. C 13, L881 (1980).

(2018).

S. V. Grigoriev, N. M. Potapova, S.-A. Siegfried,

V. A. Dyadkin, E. V. Moskvin, V. Dmitriev, D. Men-

23.

S. V. Grigoriev, E. V. Altynbaev, S.-A. Siegfried,

K. A. Pschenichnyi, D. Menzel, A. Heinemann, and

zel, C. D. Dewhurst, D. Chernyshov, R. A. Sadykov,

L. N. Fomicheva, and A. V. Tsvyashchenko, Phys.

G. Chaboussant, Phys. Rev. B 97, 024409 (2018).

Rev. Lett. 110, 207201 (2013).

24.

The data reduction software used is Graph-

K. Shibata, X. Z. Yu, T. Hara, D. Morikawa, N. Ka-

ical Reduction and Analysis SANS Program

nazawa, K. Kimoto, S. Ishiwata, Y. Matsui, and

(GRASP), www.ill.eu/instruments-support/instru-

Y. Tokura, Nature Nanotechnology 8, 723 (2013).

ments-groups/groups/lss/grasp/.

10.

S. V. Grigoriev, A. S. Sukhanov, and S. V. Maleyev,

25.

S. V. Grigoriev, S. V. Maleyev, A. I. Okorokov,

Phys. Rev. B 91, 224429 (2015).

Y. O. Chetverikov, R. Georgii, P. Böni, D. Lama-

go, H. Eckerlebe, and K. Pranzas, Phys. Rev. B 72,

11.

Y. Nishihara, S. Waki, and S. Ogawa, Phys. Rev.

134420 (2005).

B 30, 32 (1984).

26.

N. M. Chubova, E. V. Moskvin, V. A. Dyad’kin,

12.

S. V. Grigoriev, V. A. Dyadkin, E. V. Moskvin, D. La-

Ch. Dewhurst, S. V. Maleev, and S. V. Grigor’ev,

mago, Th. Wolf, H. Eckerlebe, and S. V. Maleyev,

JETP 125, 789 (2017).

Phys. Rev. B 79, 144417 (2009).

13.

S. V. Grigoriev, E. V. Moskvin, V. A. Dyadkin,

27.

O. I. Utesov, A. V. Sizanov, and A. V. Syromyat-

nikov, Phys. Rev. B 92, 125110 (2015).

D. Lamago, T. Wolf, H. Eckerlebe, and S. V. Maleyev,

Phys. Rev. B 83, 224411 (2011).

28.

A. Aharony, R. J. Birgeneau, A. Coniglio,

14.

S. V. Demishev, I. I. Lobanova, V. V. Glushkov,

M. A. Kastner, and H. E. Stanley, Phys. Rev. Lett.

T. V. Ischenko, N. E. Sluchanko, V. A. Dyadkin,

60, 1330 (1988).

N. M. Potapova, and S. V. Grigoriev, JETP Lett.

29.

V. Cherepanov, I. Y. Korenblit, A. Aharony, and

98, 829 (2013).

O. Entin-Wohlman, Eur. Phys. J. B 8, 511 (1999).

15.

A. Bauer, A. Neubauer, C. Franz, W. Munzer,

M. Garst, and C. Pfleiderer, Phys. Rev. B 82, 064404

30.

I. Ya. Korenblit, Phys. Rev. B 51, 12551 (1995).

(2010).

31.

S. Dey, E. C. Andrade, and M. Vojta, Phys. Rev.

16.

S. V. Demishev, V. V. Glushkov, S. V. Grigoriev,

B 101, 020411(R) (2020).

M. I. Gilmanov, I. I. Lobanova, A. N. Samarin,

A. V. Semeno, and N. E. Sluchanko, Phys.-Uspekhi

32.

A. Z. Patashinskii and V. L. Pokrovskii, Fluctuation

59, 559 (2016).

Theory of Phase Transitions, Pergamon Press (1979).

17.

S. Tewari, D. Belitz, and T. R. Kirkpatrick, Phys.

33.

S. L. Ginzburg, Irreversible Phenomena of Spin Glas-

Rev. Lett. 96, 047207 (2006).

ses (in Russian), Nauka, Moscow (1989).

695