ЖЭТФ, 2021, том 159, вып. 4, стр. 708-710

PAIRING BY A DYNAMICAL INTERACTION IN A METAL

A. V. Chubukova*, Ar. Abanov^b

^a School of Physics and Astronomy and William I. Fine Theoretical Physics Institute, University of Minnesota

Minneapolis, MN 55455, USA

^b Department of Physics, Texas A&M University

College Station, TX 77843, USA

Received December 17, 2020,

revised version December 17, 2020

Accepted for publication December 17, 2020

Contribution for the JETP special issue in honor of I. E. Dzyaloshinskii’s 90th birthday

DOI: 10.31857/S004445102104012X

stroys the Cooper logarithm and by this reduces the

tendency to pairing, while an opening of a SC gap

eliminates the scattering at low energies and reduces

The pairing near a quantum-critical point (QCP)

in a metal and its interplay with non-Fermi-liquid be-

the tendency to a NFL. To find the winner of this com-

petition (SC or NFL), one needs to analyze the set of

havior in the normal state is a fascinating subject,

which attracted substantial attention in the corre-

integral equations for the fermionic self-energy,

Σ(k, ω),

and the gap function, Δ(k, ω), for fermions with mo-

lated electron community after the discovery of su-

perconductivity (SC) in the cuprates, Fe-based sys-

mentum/frequency (k, ω) and (-k, -ω).

tems, heavy-fermion materials, organic materials, and,

We consider the subset of models, in which col-

most recently, twisted bilayer graphene [1-13]. Itin-

lective bosons are slow modes compared to dressed

erant QC models, analyzed in recent years, include

fermions, for one reason or the other. In this situa-

models of fermions in spatial dimensions D ≤ 3, vari-

tion, which bears parallels with Eliashberg theory for

ous two-dimensional models near zero-momentum spin

electron-phonon interaction [15], the self-energy and

and charge nematic instabilities, and instabilities to-

the pairing vertex can be approximated by their val-

wards spin and charge density-wave order with ei-

ues on the Fermi surface (FS) and computed within

ther real or imaginary (current) order parameter, 2D

the one-loop approximation. The self-energy on the

fermions at a half-filled Landau level, Sachdev - Ye - Ki-

FS,

Σ(k, ω), is invariant under rotations from the point

taev (SYK) and SYK - Yukawa models, strong coupling

group of the underlying lattice. The rotational sym-

limit of electron-phonon superconductivity, and even

metry of the gap function Δ(k_F , ω) and the relation

color superconductivity of quarks, mediated by gluon

between the phases of Δ(k_F , ω) on different FS’s in

exchange. These problems have been studied analyti-

multi-band systems are model specific. E.g., near an

cally and using various numerical techniques [14].

antiferromagnetic QCP in a system with a single FS,

From theory perspective, pairing near a QCP is a

the strongest attraction is in the d-wave channel. In

fundamentally novel phenomenon, because an effective

each particular case, one has to project the pairing in-

dynamic electron-electron interaction, V (q, Ω), medi-

teraction into the irreducible channels V (q, Ω) → V (Ω),

ated by a critical collective boson, which condenses at

find the strongest one, and solve for the pairing vertex

a QCP, provides a strong attraction in one or more

for a given pairing symmetry.

pairing channels and, at the same time, gives rise to a

Away from a QCP, the effective V (Ω) tends to a

non-Fermi liquid (NFL) behavior in the normal state.

finite value at Ω = 0. In this situation, the fermionic

The two tendencies compete with each other: fermionic

self-energy has a FL form at the smallest frequencies,

incoherence, associated with the NFL behavior, de-

and the equation for Δ(ω) is similar to that in a conven-

tional Eliashberg theory for phonon-mediated super-

^* E-mail: achubuko@umn.edu

conductivity. At a QCP, the situation is qualitatively

708

ЖЭТФ, том 159, вып. 4, 2021

Pairing by a dynamical interaction in a metal

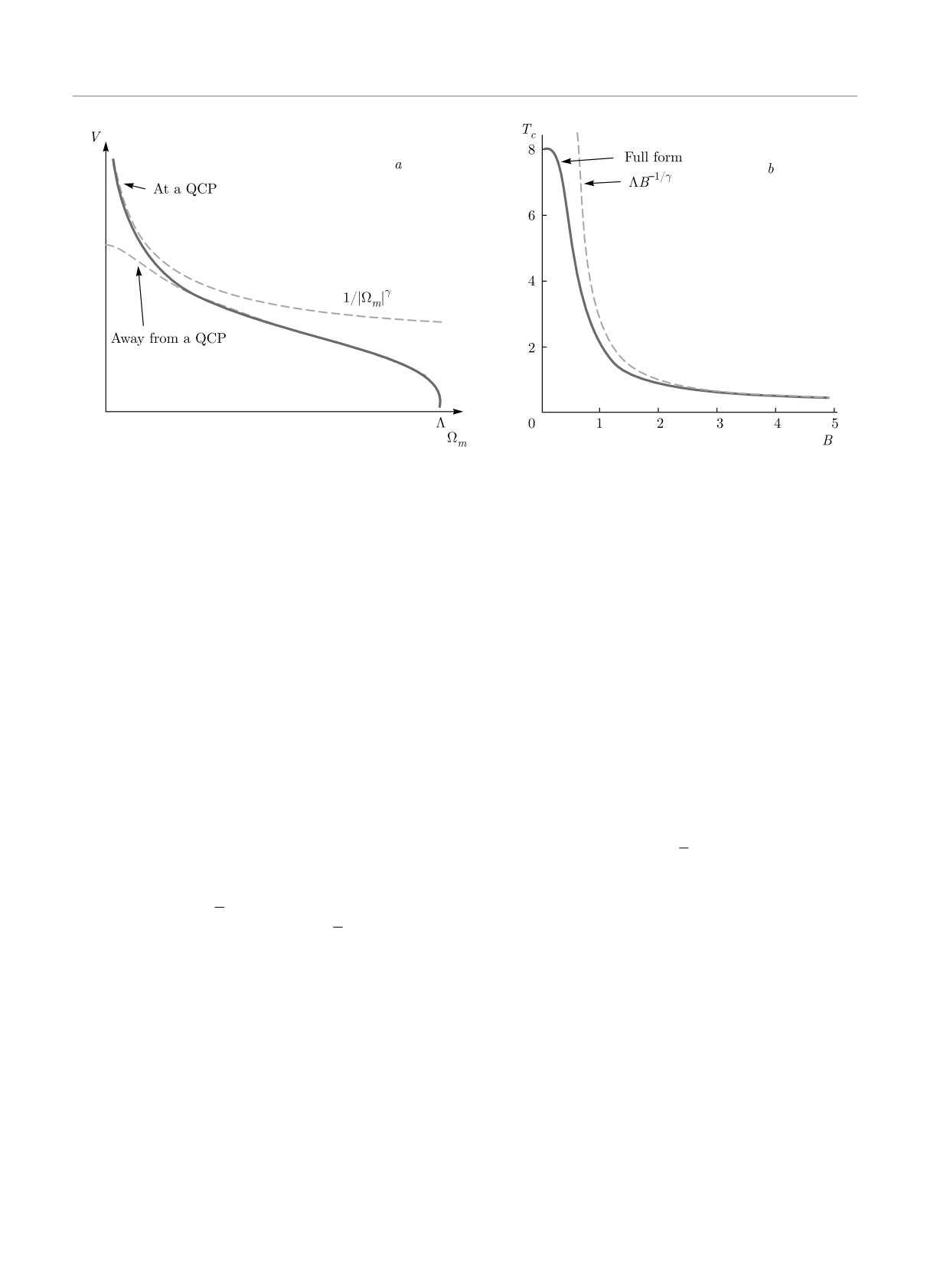
a) The frequency dependence of the effective interaction V (Ωm), mediated by a soft boson, at T = 0. Away from a QCP,

V (Ωm) tends to a finite value at Ωm = 0. Right at a QCP, the boson becomes massless, and at frequencies below the upper

cutoff Λ, the dimensionless V (Ωm) behaves as log Λ/|Ωm| at γ = 0+ and as (g/|Ωm|)^γ at a finite γ. b) Tc as a function of

the parameter B = γ(Λ/g)^γ, which determines the crossover between the behavior at a finite γ (the limit of large B) and at

γ = 0+ (the limit of small B)

different, because the effective interaction V (Ω), medi-

correspond to small and large values of the single pa-

ated by a critical massless boson, is a singular function

rameter B = γ(Λ/g)^γ.

of frequency. Quite generally, the dimensionless inter-

The structure of the paper is the following. Sec-

action behaves at the smallest Ω_m on the Matsubara

tion 1 is a preface for the paper. Section 2 is the

axis as V (Ω_m) = (g/|Ω_m|)^γ, where γ > 0 is some expo-

detailed Introduction. In Sec. 3 we present the set

nent (Figure a). This holds at frequencies below some

of coupled Eliashberg equations for the pairing ver-

upper cutoff Λ. At larger Ω_m > Λ, the interaction

tex Φ(ω_m) and the fermionic self-energy

Σ(ω_m) and

drops even further, and can be safely neglected.

combine them into the equation for the gap function

In this communication, we consider the pairing at

Δ(ω_m). In Sec. 4 we analyze the structure of the log-

small γ. This limit attracted a lot of attention in the

arithmic perturbation theory for γ = 0+ and γ > 0,

last few years from various sub-communities of physi-

keeping a finite high frequency cutoff Λ. We show that

cists [16-31]. We consider this limit analytically for

for γ = 0+, the summation of the leading logarithms

√

V (Ω), which crosses over from (g/|Ω_m|)^γ behavior at a

capture T_c ∼ Λ exp(-π/(2

λ)), although logarithmic

finite γ to the logarithmic behavior at γ = 0+ (the di-

series are not geometric, in distinction from the BCS

mensionless V (Ω) = λ log Λ/|Ω_m|). In the latter case,

theory. However, for a finite γ, summation of the loga-

√

T_c ∼ Λ exp(-π/(2

λ)). This expression is similar to

rithms does not give rise to a pairing instability — the

√

the one in the BCS case, but with

λ instead of λ in

pairing susceptibility does not diverge. In Sec. 5 we go

the exponent, because the “Cooper” logarithm appears

beyond perturbation theory. We re-express the inte-

from the combination of the logarithms in fermion and

gral Eliashberg equation as an approximate differential

boson propagators. At a finite γ, the transition tempe-

equation for the pairing vertex and solve it. We show

rature remains finite even if Λ → ∞ and its dependence

that for γ = 0+, the solution coincides with the result

on γ is T_c ∼ g(1/γ)1/γ. This T_c rapidly increases as γ

of summation of the logarithmic series. For γ > 0, we

decreases.

show that the absence of an instability within the loga-

When both Λ and γ are finite, one expects the

rithmic approximation implies that there is a threshold

crossover between the expressions for T_c at finite γ and

on the strength of the pairing interaction. We find the

Λ → ∞ and at γ = 0+ and a finite Λ. This crossover is

threshold and show explicitly that, once the interac-

the main theme of our paper. We find the full crossover

tion exceeds the threshold, the normal state becomes

function for T_c and show that the two limiting cases

unstable against pairing at some finite T_c. We show

709

A. V. Chubukov, Ar. Abanov

ЖЭТФ, том 159, вып. 4, 2021

that for a finite γ, the calculation of the pairing insta-

14.

A. Abanov and A. V. Chubukov, Phys. Rev. B 102,

bility is ultra-violet convergent, hence T_c remains finite

024524 (2020).

even when the cutoff Λ is set to infinity. We analyze

15.

G. M. Eliashberg, JETP 11, 696 (1960) [ZhETF 38,

the crossover between the forms of T_c at a finite γ and

966 (1960)].

at γ = 0+ and show that the crossover is governed by

16.

D. F. Mross, J. McGreevy, H. Liu, and T. Senthil,

the single parameter B = γ(Λ/g)^γ .

Phys. Rev. B 82, 045121 (2010).

In Sec. 6 we analyze the pairing at small γ from

the renormalization group (RG) perspective — as

17.

M. A. Metlitski, D. F. Mross, S. Sachdev, and T. Sen-

the flow of the 4-fermion pairing vertex at a finite

thil, Phys. Rev. B 91, 115111 (2015).

γ. We show that the solution of the RG equations

18.

S. Raghu, G. Torroba, and H. Wang, Phys. Rev. B 92,

describes the same crossover between T_c at a finite

205104 (2015).

γ and at γ = 0+. We present our conclusions in Sec. 7.

19.

R. Mahajan, D. M. Ramirez, S. Kachru, and

S. Raghu, Phys. Rev. B 88, 115116 (2013); A. L. Fitz-

The full text of this paper is published in the English

patrick, S. Kachru, J. Kaplan, and S. Raghu, Phys.

version of JETP.

Rev. B 88, 125116 A. L. Fitzpatrick, S. Kachru,

J. Kaplan, and S. Raghu, Phys. Rev. B 89, 165114

REFERENCES

(2014); G. Torroba and H. Wang, Phys. Rev. B 90,

165144 (2014); A. L. Fitzpatrick, G. Torroba, and

P. Monthoux, D. Pines, and G. G. Lonzarich, Nature

H. Wang,Phys. Rev. B 91, 195135 (2015), and refer-

450, 1177 (2007).

ences therein.

D. J. Scalapino, Rev. Mod. Phys. 84, 1383 (2012).

20.

H. Wang, S. Raghu, and G. Torroba, Phys. Rev. B 95,

165137 (2017).

NoStop

21.

H. Wang, Y. Wang, and G. Torroba, Phys. Rev. B 97,

M. R. Norman, Novel Superfluids, Oxford Univ.

054502 (2018).

Press, Oxford (2014), Ch. Unconventional Supercon-

ductivity.

22.

A. L. Fitzpatrick, S. Kachru, J. Kaplan, S. Raghu,

G. Torroba, and H. Wang, Phys. Rev. B 92, 045118

S. Maiti and A. V. Chubukov, Novel Superfluids, Ox-

(2015).

ford Univ. Press, Oxford (2014), Ch. Superconduc-

tivity from Repulsive Interaction.

23.

Y.-M. Wu, A. Abanov, and A. V. Chubukov, Phys.

Rev. B 99, 014502 (2019).

B. Keimer, S. A. Kivelson, M. R. Norman, S. Uchida,

and J. Zaanen, Nature 518, 179 (2015).

24.

D. T. Son, Phys. Rev. D 59, 094019 (1999).

T. Shibauchi, A. Carrington, and Y. Matsuda, Ann.

25.

A. V. Chubukov and J. Schmalian, Phys. Rev. B 72,

Rev. Condens. Matter Phys. 5, 113 (2014).

174520 (2005).

R. M. Fernandes and A. V. Chubukov, Rep. Progr.

26.

T. Schäfer and F. Wilczek, Phys. Rev. D 60, 114033

Phys. 80, 014503 (2016).

(1999).

E. Fradkin, S. A. Kivelson, M. J. Lawler, J. P. Eisen-

27.

R. D. Pisarski and D. H. Rischke, Phys. Rev. D 61,

stein, and A. P. Mackenzie, Ann. Rev. Condens. Mat-

051501 (2000).

ter Phys. 1, 153 (2010).

K.-Y. Yang, T. M. Rice, and F.-C. Zhang, Phys. Rev.

28.

Q. Wang and D. H. Rischke, Phys. Rev. D 65, 054005

B 73, 174501 (2006).

(2002).

10.

L. Fratino, P. Sémon, G. Sordi, and A.-M. S. Trem-

29.

J. A. Damia, M. Solís, and G. Torroba, Phys. Rev.

blay, Sci. Rep. 6, 22715 (2016).

B 102, 045147 (2020).

11.

S. Sachdev, Rep. Progr. Phys. 82, 014001 (2018).

30.

D. V. Khveshchenko, J. Phys.: Condens. Matter 21,

075303 (2009).

12.

P. Coleman, Introduction to Many-Body Physics,

Cambridge Univ. Press, Cambridge (2015).

31.

C. M. Varma, P. B. Littlewood, S. Schmitt-Rink,

E. Abrahams, and A. E. Ruckenstein, Phys. Rev.

13.

Y. Cao, V. Fatemi, S. Fang, K. Watanabe, T. Tanigu-

Lett. 63, 1996 (1989); C. M. Varma, Rev. Mod. Phys.

chi, E. Kaxiras, and P. Jarillo-Herrero, Nature 556,

92, 031001 (2020).

43 (2018).

710