ЖЭТФ, 2021, том 159, вып. 4, стр. 755-760

КВАЗИКЛАССИЧЕСКАЯ ДИНАМИКА МОДЕЛИ ДИКЕ

В СВЕРХИЗЛУЧАТЕЛЬНОЙ ДИПОЛЬНОЙ ФАЗЕ

В СОСТОЯНИИ «СВЯЗАННОГО СИЯНИЯ»

С. И. Мухин^*, А. Мукерджи, С. С. Сеидов

Кафедра теоретической физики и квантовых технологий,

Национальный исследовательский технологический университет «МИСиС»

119049, Москва, Россия

Поступила в редакцию 20 ноября 2020 г.,

после переработки 6 декабря 2020 г.

Принята к публикации 6 декабря 2020 г.

Найдено аналитическое решение квазиклассических уравнений движения модели Дике в сверхизлуча-

тельном состоянии. Зависимости от времени колебаний амплитуд сверхизлучательного фотонного кон-

денсата и когерентной заселенности массива двухуровневых атомов в микроволновой полости выражены

через эллиптические функции Якоби и свидетельствуют о существовании адиабатического инварианта в

системе с сильной связью. Периодические биения амплитуд фотонного и когерентного атомного состоя-

ний сдвинуты во времени, представляя собой эффект «связанного сияния», когда энергия, заключенная

в двухуровневых системах, во время «темноты» внезапно переходит в энергию фотонного конденса-

та, «освещающего» полость на время полупериода колебаний перед тем, как она вновь погрузится в

«темноту».

Статья для специального выпуска ЖЭТФ, посвященного 90-летию И. Е. Дзялошинского

DOI: 10.31857/S0044451021040192

ставлении куперовского ящика [7]. Цепочка помеще-

на в резонансную полость с частотой ω — частотой

единственной фотонной моды. Вторично квантован-

1. ВВЕДЕНИЕ

ные операторы фотонной моды есть

Предсказанный ранее сверхизлучательный фазо-

√

ℏω

(

)

ℏ

(

)

вый переход в модели Дике [1] цепочки из N ≫ 1

p=i

â^† - â

â^† + â

(2)

2ω

двухуровневых систем (ДУС), связанных с одной

бозонной модой в резонансной полости [2, 3], был

где [â, â^†] = 1. Полный квадрат псевдоспина

S² со-

представлен как [4] самосогласованный поворот на

храняется, так как он коммутирует с (1):

S², H] = 0.

конечный угол операторов псевдоспина в представ-

Туннелирование куперовских пар представлено чле-

лении Гольштейна - Примакова [5, 6], описывающих

ном -E_JSz. Член gpS

^y описывает дипольную связь

когерентные состояния ДУС. Мы рассматриваем га-

между куперовскими парами и фотонным полем с

мильтониан модели Дике [1] в виде

константой связи g. В работе [2] показано, что кван-

товый фазовый переход переводит систему (1) в два-

(

)

Ĥ₌

p² + ω² q²

S^y - E_J

S^z,

(1)

жды вырожденное дипольно-упорядоченное состоя-

ние. В данной работе мы приводим аналитическое

∑

решение, описывающее динамику джозефсоновских

где введены операторы

S^α =_i ŝ^αi суммарных ком-

понент псевдоспина, описывающих ДУС. Для опре-

контактов в микроволновой полости и демонстри-

рующее существование метастабильного состояния

деленности можно рассмотреть систему из N сверх-

проводящих островков, каждый из которых разде-

«связанного сияния» с когерентными периодически-

ми биениями диполей, которое связано с дважды

лен пополам джозефсоновским контактом, в пред-

вырожденной дипольно-упорядоченной фазой, най-

^* E-mail: i.m.sergei.m@gmail.com

денной ранее. Первые два члена в (1) соответству-

755

12*

С. И. Мухин, А. Мукерджи, С. С. Сеидов

ЖЭТФ, том 159, вып. 4, 2021

ют энергии гармонического осциллятора фотонной

S_z = -g² p²

S_z - gE_J

S_y,

(4)

моды. Расщепление уровней ДУС представлено чле-

S_y = -EJ2

S_y - gE_J

S_z,

(5)

ном -E_JSz, а член g

S^y описывает дипольную энер-

гию связи фотонов с ДУС. В работе [4] было показа-

S_x = -EJ2

S_x - g² p²

S_x,

(6)

но, что самосогласованный поворот представления

{

}

Гольштейна - Примакова операторов

S_x,y,z позволя-

p = -ω²

S_y

(7)

ет достаточно прозрачно описать квантовый фазо-

Для перехода от операторов к их средним значени-

вый переход второго рода в модели Дике (1). А

ям в основном состоянии необходимо сделать следу-

именно, когда константа связи g становится боль-

ющее. Сначала введем амплитуду сверхизлучатель-

ше критического значения g_c, суперспин S = N/2

ного фотонного конденсата λ_R [2] как сдвиг бозон-

постепенно поворачивается от оси z к оси y на

ных операторов в (2):

угол |θ| ≤ π/2, где верхний предел соответству-

ет максимуму дипольного момента

S_y〉 ∝ S sinθ

â^† = ĉ^† - iλ_R,

â = ĉ+ iλ_R,

(8)

ДУС. Одновременно с этим фотонный оператор

p приобретает внедиагональное среднее значение

√

ℏω

(

)

〈p〉 ∝ -gS sinθ, говорящее о возникновении мак-

2ℏωλ_R + i

ĉ† - ĉ

роскопического когерентного («сверхизлучательно-

√

(9)

ℏ

(

)

го») фотонного конденсата, связанного с диполь-

ĉ† + ĉ

ным моментом ДУС с энергией ∝ g

S_y〉〈p〉. Оче-

2ω

видно, что одновременная смена знаков:

S_y〉, 〈p〉 →

Как показано в [4], одновременно с появлением

S_y〉, -〈p〉, приводит систему в новое состояние с

конденсата λ_R происходит поворот псевдоспина на

той же самой энергией спин-фотонной связи, тем

угол θ вокруг оси x. Далее мы совершаем поворот

самым свидетельствуя о существовании дважды

полного спина на угол θ вокруг оси x и на угол

вырожденного основного состояния. Нами найдено

φ - π/2 вокруг оси z, где θ, φ зависят от времени:

аналитическое решение уравнений движения, опи-

сывающих «медленное» блуждание системы меж-

S^z =

J^z cosθ -

J^y sinθ,

ду двумя вырожденными основными состояниями:

S^y =

J^z sinθ sinφ+Jy cosθ sinφ

J^x cosφ,

(10)

хранящаяся в ДУС энергия ∝ 〈S_z〉 периодически за-

S^x =

J^z sinθ cosφ

J^y cosθ cosφ

J^x sinφ,

качивается в фотонный конденсат, в то время как

амплитуда суммарного дипольного момента ДУС

операторы декартовых проекций суммарного спи-

∝ 〈S_y〉 и амплитуда сверхизлучательного конден-

на

J^x,y,z определены через представление Гольштей-

сата ∝ 〈p〉 меняют знак на противоположный, как

на - Примакова:

функции времени. Найдены два первых интеграла

для медленного движения когерентных амплитуд в

J^z = S -b†b,

квазиклассическом пределе.

⎛ √

√

⎞

√

b†b

Квазиклассические уравнения движения сред-

J^y = i

⎝b†

b⎠ ≃

них значений импульса фотона и декартовых проек-

√

ций суммарного псевдоспина в основном состоянии

(

)

≃i

b^† -b ,

могут быть получены согласно [8], начиная с урав-

(11)

нений Гейзенберга, в виде

⎛ √

√

⎞

√

b†b

J^x =

⎝b†

b⎠ ≃

[

]]

√

A=-

Ĥ,

Ĥ,A

(3)

(

)

ℏ²

≃

b^† +b ,

где

A = p,Sα и α = x, y, z. Далее, используем га-

и [b,b†] = 1.

мильтониан модели Дике (1), уравнение (3) и комму-

Поворот объясняется просто: в основном состоя-

тационные отношения между компонентами спина,

нии с малой константой связи g угол поворота θ = 0

координатой и импульсом гармонического осцилля-

и оператор

S_z =

J^z в гамильтониане Дике (1) почти

тора. Получим следующую систему дифференци-

диагонален, следовательно, диагональные элементы

альных уравнений:

S^y〉 = 〈Jy〉 стремятся к нулю. Поэтому «дипольный

756

ЖЭТФ, том 159, вып. 4, 2021

Квазиклассическая динамика модели Дике.. .

момент», пропорциональный

S^y〉, равен нулю и фо-

основное состояние системы возможно, если скре-

тоны квазиклассически расцепляются со спинами. С

щенные электрическое и магнитное поля подчиня-

другой стороны, когда угол поворота θ ненулевой,

ются статическим граничным условиям на границе

возникает конечный «дипольный момент» спиновой

полости, т. е. поверхностный заряд должен быть ста-

подсистемы, пропорциональный

S^y〉

J^z〉sinθ,

тичен и (сверх)ток должен быть постоянен. Мы так-

который связан с когерентным фотонным конден-

же подчеркиваем, что, как следует из правых частей

сатом 〈p〉 = λ_R. Последнее приводит к нестабиль-

уравнений (5) и (7), действительно существуют два

ности основного состояния системы. Мы заменяем

решения, отличающиеся одновременной сменой зна-

операторы в (4)-(7) их средними по основному сос-

ков: θ → -θ и λ_R → -λ_R (ср. с [2]).

тоянию в представлении Гейзенберга:

A → 〈A〉, ис-

пользуя соотношения (9)-(11). Далее рассматриваем

резонансный случай: ℏω = E_J .

3. «СВЯЗАННОЕ СИЯНИЕ»

В отличие от [2] сдвиг бозонных операторов в

СВЕРХИЗЛУЧАТЕЛЬНОГО СОСТОЯНИЯ В

МОДЕЛИ ДИКЕ В ПРЕДЕЛЕ

(11) не проводился, так как его роль на себя взял

АДИАБАТИЧЕСКИХ ДУС

поворот на угол θ. Тогда из (4)-(6) очевидно, что си-

стема уравнений описывает нелинейную эволюцию

В этом разделе получим аналитическое решение

полного спина S в системе отсчета, вращающейся

уравнений (4)-(7), используя подход с двумя вре-

вокруг оси z в фазовом пространстве псевдоспина

менными масштабами [8] в пределе адиабатической

с частотой E_J . Поскольку мы рассматриваем резо-

эволюции ДУС. Мы опускаем уравнение (6), так как

нансный случай ω = E_J , угол φ в (10) меняется во

x не входит в гамильтониан Дике (1) и в уравнения

времени как φ = ωt, следовательно, полный спин S

(4), (5), (7). Также мы разбиваем временную эволю-

вращается с постоянной угловой скоростью ω вокруг

цию на «быструю», пропорциональную exp(iωt), и

оси z, а фотонная переменная p в (7) осциллирует с

«медленную», описываемую функциями g₀(t) и θ(t),

частотой ω и при этом линейно связана со спином

которые определены формулами (12)-(15). Тогда,

через последний член в правой части (7). Удобно

подставляя (12)-(15) в (5) и (7) и усредняя левую и

ввести следующие обозначения для средних значе-

правую части по быстрым осцилляциям ω, получим

ний как функций от времени (ℏ = 1):

следующую систему уравнений для изменяющихся

√

2ωλ_R(t) ≡ -

2ωg₀(t)cos(ωt),

(12)

адиабатически функций:

√

S_z = S cosθ(t),

(13)

2ω

θ(t) =

g₀(t),

(16)

S_y = S sinθ(t)sin(ωt),

(14)

√

S_x = S sinθ(t)cos(ωt).

(15)

sinθ = -

ġ₀(t).

(17)

√ω

Поскольку в сверхизлучательном состоянии [2, 4]

фотонный сдвиг в термодинамическом пределе λ_R ∝

Процедура усреднения по быстрым осцилляциям,

∝ S = N/2 ≫ 1, можно использовать квази-

приводящая к (16) и (17), проста. А именно, необ-

классическое приближение для основного состоя-

ходимо подставить (12)-(15) в (5) и умножить обе

ния: 〈p²〉 ≈ 〈p〉² в (4)-(7).

части уравнения на cos (ωt). Затем надо вычислить

среднее по «быстрым» осцилляциям за короткий пе-

риод времени (∼ ω-1), считая переменные, содер-

2. ДИПОЛЬНЫЙ ФАЗОВЫЙ ПЕРЕХОД В

жащие «медленные» члены, константами (адиаба-

«ЗАМОРОЖЕННЫХ» СКРЕЩЕННЫХ

тическая эволюция ДУС). Интегрируя по коротко-

ЭЛЕКТРИЧЕСКОМ И МАГНИТНОМ ПОЛЯХ

му временному периоду, получим (16). Аналогично,

Примечательно, что в статическом пределе, т. е.

умножая обе части уравнения (7) на sin (ωt) и повто-

при λ_R, θ, φ ≡ const в уравнениях (12)-(15), три

ряя ту же самую процедуру, получим (17). По той

уравнения (4), (5) и (7) становятся алгебраическими

же причине уравнение (4) вновь обращается в тож-

и остаются только два из них, так как уравнение (4)

дество, как в «замороженном» случае, рассмотрен-

обращается в тождество. Это означает, что дважды

ном выше, после пренебрежения второй производ-

вырожденное решение говорит о фазовом переходе

ной по времени от «медленной» функции cos θ в ле-

в спонтанно упорядоченную дипольную фазу ДУС с

вой части (4). Для упрощения обозначений далее бу-

замороженными электрическим и магнитным поля-

дем пользоваться единицами ℏ = 1. Умножая левую

ми в резонансной полости. Очевидно, что подобное

часть (16) на sin θ и используя (17), получим первый

757

С. И. Мухин, А. Мукерджи, С. С. Сеидов

ЖЭТФ, том 159, вып. 4, 2021

адиабатический интеграл динамических уравнений,

Эффективная частота Ω, характеризующая би-

усредненных по быстрым осцилляциям:

ения эллиптических функций Якоби в (20)-(23),

выражается через полный эллиптический интеграл

g²⁰(t)

cosθ(t) -

= const ≡ C ,

(18)

первого рода K(k) [9] (расходится при k = 1) следу-

ющим образом:

где C — полная энергия системы, усредненная по

(

)

быстрым осцилляциям, C ∝ 〈

Ĥ 〉. Далее, дифферен-

2π

π g

цируя (17) единожды по времени и выражая cos θ(t)

g₀

= g₀(t), Ω ≡ ω

K(k) 2g_c

через g₀(t) с использованием (18), получим нелиней-

√

(24)

E_J

ное дифференциальное уравнение второго порядка

g_c ≡

для неизвестной функции g₀(t):

√

(

)

2g₀(t)

g²⁰(t)

Здесь g_c — критическая константа связи, при ко-

g₀(t) C +

= 0.

(19)

√ω⁺

торой сверхизлучательное состояние стабильно [2].

Следовательно, в пределе k → 1 предположение о

Решение данного уравнения точно выражается че-

«медленной» эволюции θ(t), т. е. Ω ≪ ω, которое мы

рез функции Якоби. Если выбрать C = 1 - 2k² с

приняли в начале вычислений, выполняется, если

0 ≤ k ≤ 1 [9], то решение уравнения (19) имеет вид

(

√

)

√

π g

Sω

g₀(t) =

2Sk cn

t,k

Ω≡ω

≪ ω , т.е. K(k) ≫

K(k) 2g_c

2 g

{

}

(25)

(

√

)

(20)

π g

√

следовательно,

1 - 2exp

≤ k ≤ 1.

Sω

2Sk cn

t,k cos(ωt),

2 g_c

λR =

где k — модуль эллиптического интеграла. Исполь-

Таким образом, физическое явление фазы «свя-

зуя решение (20), оставшиеся переменные можно

занного сияния» описывается решениями (20)-(23).

выразить алгебраически из (16), (17) как (ср. с [8])

Выражения для электрического поля и суммарно-

{

(

√

)}

го дипольного момента, создаваемых в камере, ко-

Sω

торые колеблются между двумя вырожденными ос-

S_z

= S cosθ = S

1 - 2k2 sn²

t,k

новными состояниями модели Дике, записываются

как

S_y = -S sinθ sin(ωt) = 2kS ×

(21)

(

) (

)

√

Sω

(

)

× sn

t,k dn

t,k sin(ωt).

Ê= i

â^† - â

ϵ,

(26)

Здесь sn, dn, cn — эллиптические функции Якоби.

С другой стороны, при выборе C = k² - 2, решения

d= -2e l

S_y,

(27)

имеют вид

(

√

)

√

Sω

где ϵ, V, l — вектор поляризации, объем полости и

g₀(t) =

2S dn

t,k

эффективная толщина джозефсоновского контакта

(

√

)

(22)

соответственно, 2e — элементарный заряд куперовс-

√

Sω

λR =

2S dn

t,k cos(ωt),

кой пары. Для двух возможных выборов адиаба-

тического инварианта C, приведенных выше, пред-

ставлены два следующих набора решений для элект-

S_z = S cosθ =

{

(

√

)}

рического поля E и суммарного дипольного момента

Sω

ДУС d.

=Sk²

1-2 sn²

t,k

1. Случай 1. C = 1 - 2k²:

S_y = -S sinθ sin(ωt) =

(

√

)

(23)

(

√

)

Sω

√

2√ω

Sω

= 2k² sn

t,k

E(t) =

√

2Sk cn

t,k

(

√

)

Sω

× cn

t,k sin(ωt).

× cos(ω t),

(28)

758

ЖЭТФ, том 159, вып. 4, 2021

Квазиклассическая динамика модели Дике.. .

(

√

)

Sω

d(t) = 2elSε · 2k sn

t,k

(

√

)

Sω

× dn

t,k sin(ω t),

(29)

[

(

√

)]

Sω

E_J S_z(t) = E_JS

1 - 2k2 sn²

t,k

(30)

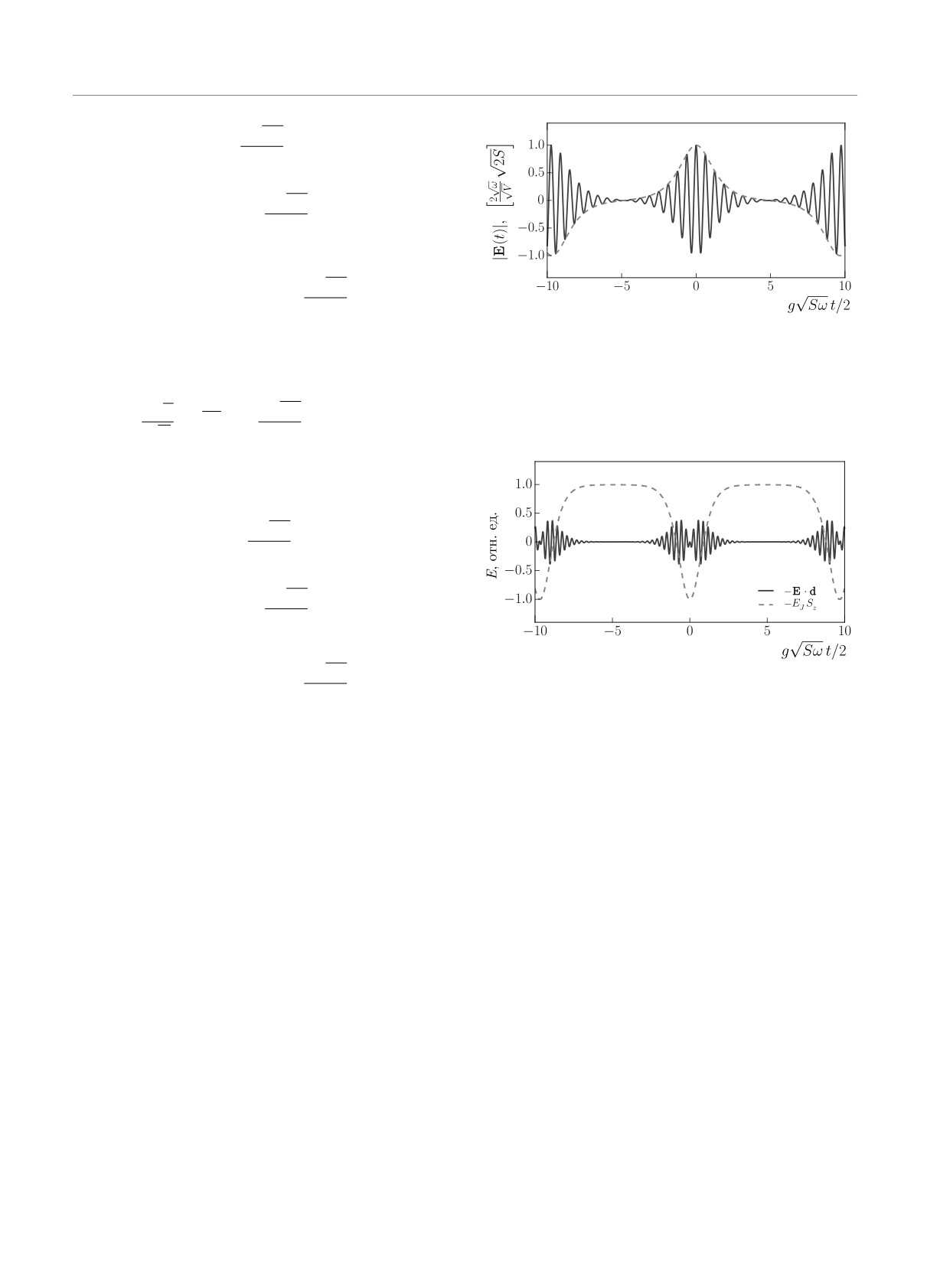
Рис. 1. Зависимость от времени осцилляций когерентно-

го электрического поля фотонного конденсата (сплошная

2. Случай 2. C = k² - 2:

линия) с «медленной» огибающей (штриховая линия), ко-

(

)

торая свидетельствует о периодическом изменении фазы

√

2√ω

√

Sω

осцилляций на π

E(t) =

√

2S dn

t,k

× cos(ω t),

(31)

(

√

)

Sω

d(t) = 2elSε · 2k² sn

t,k

(

√

)

Sω

× cn

t,k sin(ω t),

(32)

[

(

√

)]

Sω

E_J S_z(t) = E_JSk2

1 - 2sn²

t,k

(33)

Рис. 2. Зависимости от времени дипольной энергии в поле

фотонного конденсата, пропорциональной -E · d (сплош-

ная линия), и «зеемановской» энергии, пропорциональной

Следует отметить интересный факт. В обоих слу-

-EJSz (штриховая линия)

чаях выражение для дипольной энергии ДУС, т. е.

-E·d, одинаково. Различие в фотонной части p²/2 и

зеемановской части -E_JS_z. Однако мы рассматри-

состояния снимается динамическим образом. Гра-

вали «медленную эволюцию», что означает k → 1.

фик на рис. 2 ясно демонстрирует, что энергия ос-

В данном пределе выражения для всех энергетичес-

новного состояния проявляет периодическое внезап-

ких вкладов совпадают.

ное превращение «энергии нулевых колебаний» ку-

Используя уравнения, записанные выше для

перовских пар (штриховая линия) в энергию «сия-

двух случаев, построим графики зависимости элек-

ния» фотонного конденсата, связанного с диполями

трического поля фотонного конденсата от време-

ДУС (сплошная линия), правда, модель не включа-

ни E(t), а также распределение энергии системы.

ет диссипацию.

Энергия распределена между энергией связи двух-

уровневых систем электромагнитным полем в по-

лости -E · d и «зеемановской» энергией -E_JSz,

4. ЗАКЛЮЧЕНИЕ

т. е. джозефсоновской энергией туннелирования ку-

перовских пар в гамильтониане (1). Для C = 1 - 2k²

В работе рассмотрена модель Дике с N псевдо-

на рис. 1 показаны зависящие от времени осцил-

спинами 1/2, взаимодействующими с единственной

ляции когерентного электрического поля фотонного

модой фотонного поля в резонаторе в квазикласси-

конденсата (сплошная линия) вместе с «медленной»

ческом сверхизлучательном режиме. С использова-

огибающей кривой (штриховая линия), которая обо-

нием недавно предложенного теоретического метода

значает периодическое изменение фазы быстрых ко-

[4] вращающегося представления Гольштейна - При-

лебаний на π, т. е. двойное вырождение основного

макова декартовых компонент полного спина была

759

С. И. Мухин, А. Мукерджи, С. С. Сеидов

ЖЭТФ, том 159, вып. 4, 2021

рассмотрена квазиклассическая динамика системы

гранту НИТУ «МИСиС» K4-2018-061, выполненной

операторных уравнений Гейзенберга. С помощью

по государственному постановлению от 16 марта

подхода двух временных масштабов («короткий»

2013, №211.

«длинный») впервые получены аналитические

выражения для электрического поля и дипольного

момента (среднего значения компоненты псев-

ЛИТЕРАТУРА

доспина

〈S_y〉) в резонансной полости. Решения

выражаются через эллиптические функции Якоби,

1. R. H. Dicke, Phys. Rev. 93, 99 (1954).

описывая внутреннее сверхизлучательное состояние

«связанного сияния». Множество других задач,

2. C. Emary and T. Brandes, Phys. Rev. E 67, 066203

(2003).

связанных с данной, таких как бифуркации и хаос в

асимптотическом пределе, область интегрируемос-

3. K. Hepp and E. H. Lieb, Ann. Phys. 76, 360 (1973).

ти и т.д., представляет интерес для дальнейшего

исследования.

4. S. I. Mukhin and N. V. Gnezdilov, Phys. Rev. A 97,

053809 (2018).

Благодарности. С. И. М. благодарит Кар-

5. T. Holstein and H. Primakoff, Phys. Rev. 58, 1098

ло Бейнаккера, Константина Ефетова, Бернар-

(1940).

да ван Хека и Николая Гнездилова за полезные

6. В. П. Карасев, ТМФ 95(1), 3 (1993).

дискуссии во время работы над статьей, а также

коллег из Института теоретической физики им. Ло-

7. A. Shnirman, G. Schön, and Z. Hermon, Phys. Rev.

ренца за гостеприимство во время его пребывания

Lett. 79, 2371 (1997).

в Лейдене.

8. S. I. Mukhin and N. V. Gnezdilov, arXiv:1711.00348.

Финансирование. Работа проведена при

финансовой поддержке Министерства науки и выс-

9. E. T. Wittaker and G. N. Watson, A Course of Mo-

шего образования Российской Федерации в рамках

dern Analysis, Cambridge Univ. Press, Cambridge

программы повышения конкурентоспособности по

(1996).

760