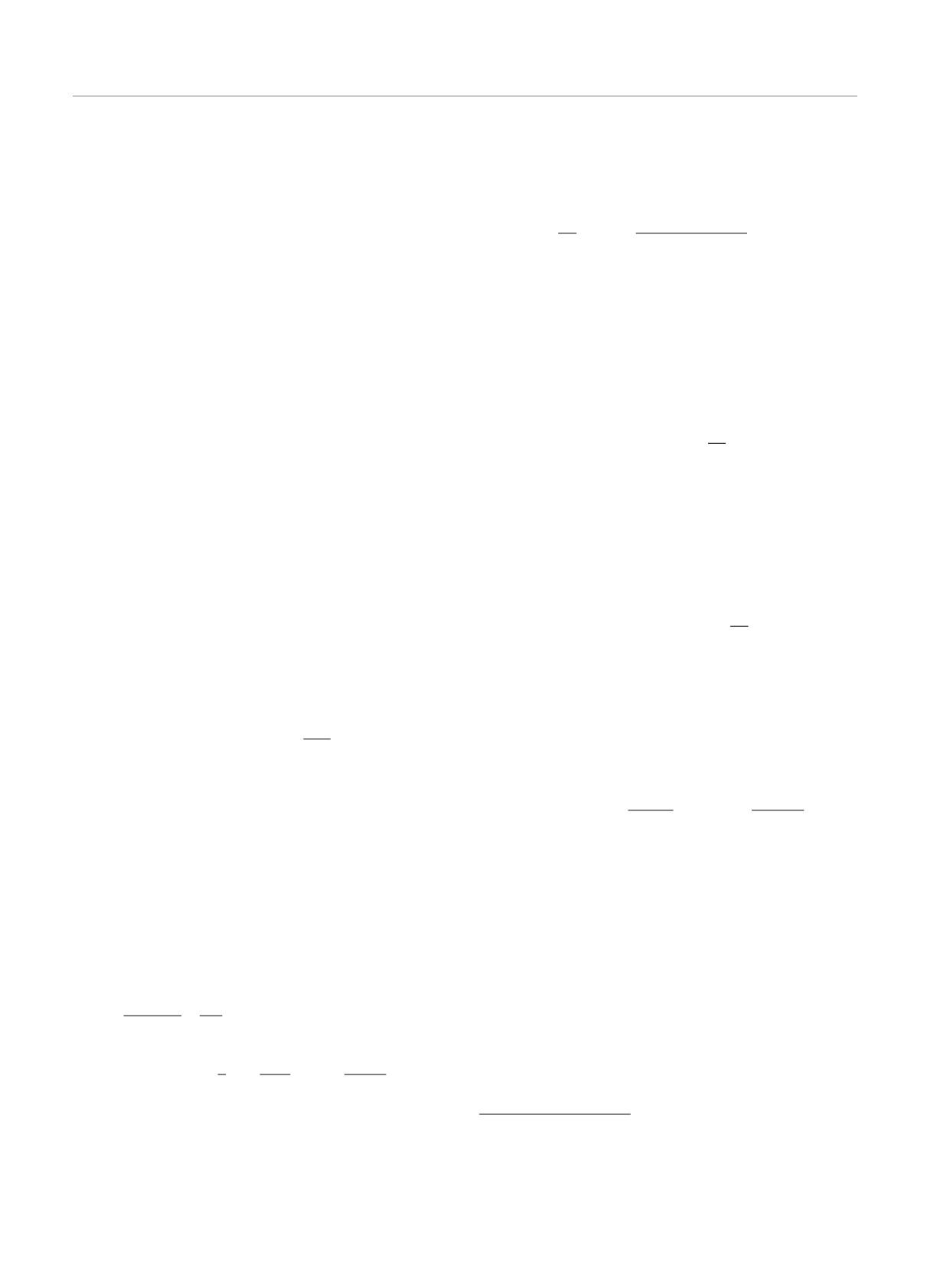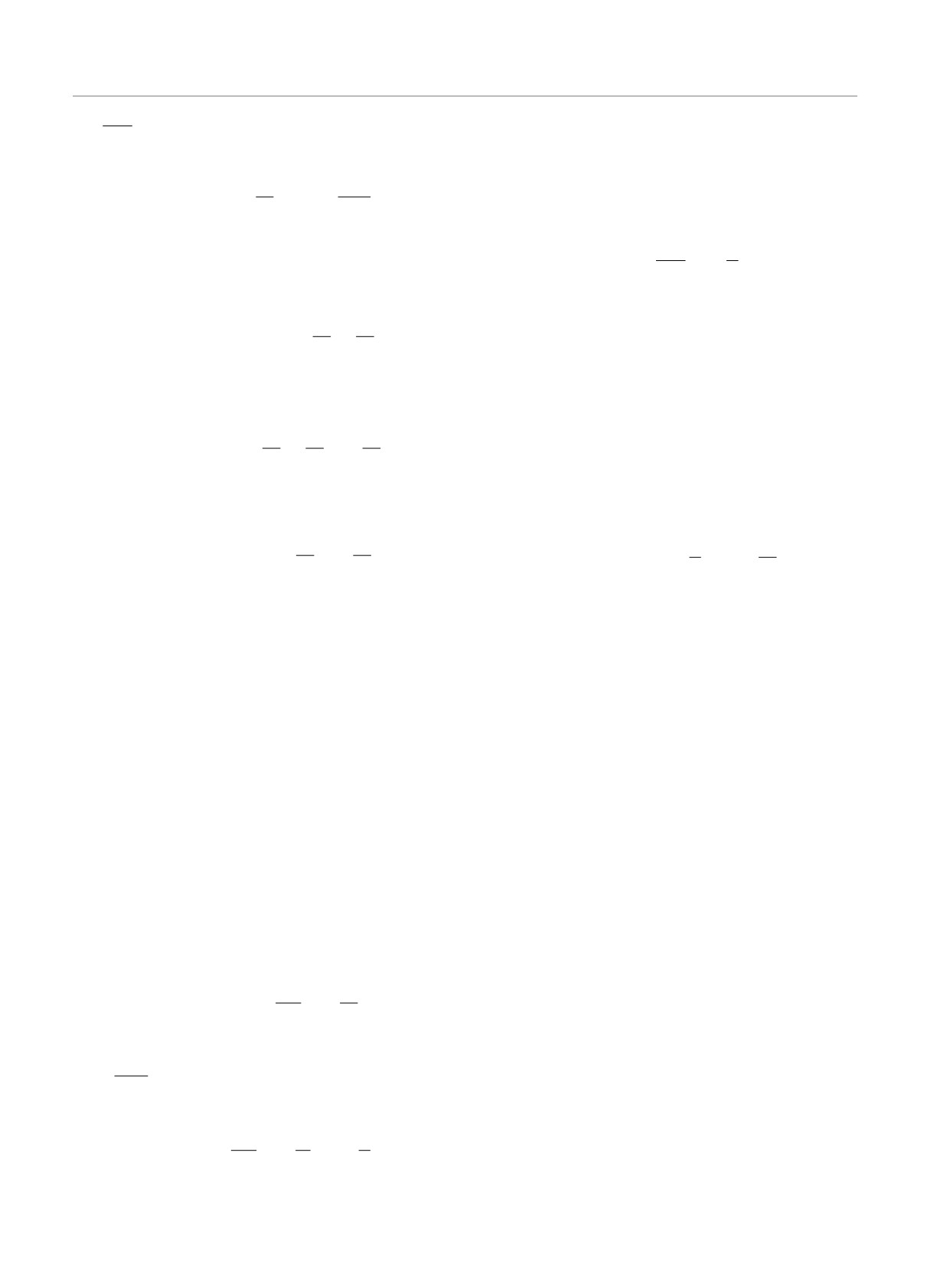ЖЭТФ, 2021, том 159, вып. 4, стр. 776-793
© 2021
KINETIC PROCESSES IN FERMI-LUTTINGER LIQUIDS
A. Levchenkoa*, T. Micklitzb
a Department of Physics, University of Wisconsin-Madison
53706, Madison, Wisconsin, USA
b Centro Brasileiro de Pesquisas Físicas
22290-180, Rio de Janeiro, Brazil
Received January 9, 2021,
revised version January 25, 2021.
Accepted for publication January 25, 2021
Contribution for the JETP special issue in honor of I. E. Dzyaloshinskii’s 90th birthday
DOI: 10.31857/S0044451021040210
of strongly interacting many-body quantum systems
[1, 2]. For instance, in the context of electrons in con-
ductors, one typically views the quasiparticle states as
Abstract. The present work discusses extensions
of the pioneering analysis by Dzyaloshinskii and Larkin
those evolving from the free electron gas to a Fermi
liquid when adiabatically turning on the interaction.
[Sov. Phys. JETP 38, 202 (1974)] of correlation func-
tions for one-dimensional Fermi systems, focusing on
In accordance with Landau theory [3], quasiparticles
inherit some of the basic quantum numbers of bare
the effects of quasiparticle relaxation enabled by non-
linear dispersion. Throughout the work we employ
electrons such as spin, charge, and momentum. Their
respective dispersion relations as well as thermodynam-
both, the weakly interacting Fermi gas picture and non-
ical and kinetic properties may, however, differ signifi-
linear Luttinger liquid model to describe attenuation
of excitations and explore the fermion-boson duality
cantly due to interaction-induced renormalizations. A
crucial advantage of the quasiparticle picture is that
between both approaches. A special attention is de-
voted to the role of spin-exchange processes, effects
residual interactions are assumed to be weak, and can
be systematically and controllably addressed by means
of interaction screening, and integrability. Thermal-
ization rates for electron- and hole-like quasiparticles,
of perturbation theory. The central question related
to the validity of the quasiparticle description concerns
as well as the decay rate of collective plasmon excita-
their lifetime τqp. Indeed, in the process of scattering
tions and the momentum space mobility of spin exci-
quasiparticles decay and their mere notion is meaning-
tations are calculated for various temperature regimes.
ful only if attenuation is weak enough and they can
The phenomenon of spin-charge drag is considered and
the corresponding momentum transfer rate is deter-
be considered as sufficiently long-lived collective exci-
tations. In Fermi systems, the Pauli principle severely
mined. In the context of transport properties, momen-
tum relaxation due to several competing mechanism,
limits the phase space available for quasiparticle col-
lisions. The low temperature decay rate can then be
viz. triple electron collisions, electron-phonon scat-
tering, and long-range inhomogeneities is addressed.
estimated from the Golden rule as
Energy transfer facilitated by plasmons is highlighted
from the perspective of inhomogeneous Luttinger liq-
ε2 + π2T2
uid. The full matrix of thermoelectric coefficients is
τ-1qp(ε, T) ∝ (νV0)2
(1)
εF
found at the quantum critical point of the first conduc-
tance plateau transition.
1. Introduction. The concept of quasiparticles
In this expression, the excitation energy ε = vF (p-pF )
plays a central role in the condensed matter physics
of a quasiparticle with momentum p is counted from
the Fermi energy εF , ν is the density of states and
* E-mail: levchenko@physics.wisc.edu
V0 is the characteristic strength of the short-range re-
776
ЖЭТФ, том 159, вып. 4, 2021
Kinetic processes in Fermi-Luttinger liquids
pulsive interaction1). The dominant microscopic scat-
ficiently high, so that thermally- and disorder-induced
tering channel leading to Eq. (1) involves quasiparti-
transitions to higher sub-bands are suppressed. In ad-
cle decaying into three: another quasiparticle and a
dition, edge modes formed at the boundaries of a 2D
particle-hole excitation. The amplitude for this process
electron gas when placed in a strong magnetic field in
is proportional to V0, hence, the dimensionless factor
the integer or fractional quantum Hall regime [10, 11],
of (νV0)2 in the scattering probability entering Eq. (1).
or edge states of 2D quantum spin Hall topological-in-
The factor ε2 is the phase space volume for scattering
sulators [12], provide other distinct examples of, respec-
of a quasiparticle with energy ε compatible with the
tively, chiral and helical quantum 1D electron liquids.
conservation of total energy and momentum. At finite
In principle, all these systems can be successfully
temperatures the smearing of states in the energy strip
described within the framework of Luttinger liquid
of order ∼ T per particle leads to the corresponding
theory [13-15], which builds out of the Tomonaga-Lut-
T2 dependence of τ-1qp. Higher-order processes involv-
tinger (TL) model [16, 17]. As is known form pioneer-
ing 2n + 1 quasiparticles, namely n > 1 electron-ho-
ing works [18-20], in the asymptotic low-energy limit
le pairs, are usually neglected as their respective rate
ε/εF
≪ 1, the key properties of the TL model are
scales with higher powers of energy. In particular, at
manifestly non-Fermi liquid like. A power-law anomaly
zero-temperature the rate for relaxation processes of
manifests in the suppression of the single particle den-
a quasiparticle with energy ε involving n particle-hole
sity of states
pairs vanishes as τ-1qp ∝ ε2n. One notable property
(
)2g
|ε|
sin(πg)
of Eq. (1) is that it predicts the same relaxation time
ν(ε) = ν0
Γ(1 - 2g),
(2)
vF pΛ
πg
for particle-like and hole-like excitations. Another pro-
perty is that the crossover from zero-temperature to
and collapse of the quasiparticle residue in the distri-
finite-temperature relaxation is governed only by one
bution function. At T → 0 that is
scale, viz. when the excitation energy compares to the
temperature itself ε ∼ T .
Γ(1/2 + g)
n(ε) =
In addition to the quasiparticle relaxation, which
2√πΓ(1 + g)×
[
]
(
)2g
is often viewed as an out-scattering rate from a par-
Γ(1/2 - g)
|ε|
× 1-
sgn(ε)
,
(3)
ticular quantum state, one may address a more gene-
Γ(1/2 + g) vF pΛ
ral question of relaxation of a nonequilibrium quasi-
particle distribution function. In kinetic theory such
where ν0 = 1/(2πvF ), Γ(z) is the Euler’s gamma func-
problem is typically analyzed in the framework of the
tion, and pΛ is the momentum cutoff of the model
linearized Boltzmann equation. The eigenvalues of the
(parametrically pΛ ∼ pF ). In the simplest spinless ver-
corresponding collision operator define relaxation times
sion of the TL-model with short-ranged interaction, a
of different distribution function modes. In three di-
single dimensionless coupling constant,
mensional Fermi liquids this problem is exactly solvab-
[
]
1
1+ν0V0
le [4, 5] and one finds that all these rates are para-
g=
√
-1 ,
(4)
2
1 + 2ν0V0
metrically the same, scaling respectively as ∝ T2. In
contrast, in two-dimensional Fermi liquids, kinematics
can be related to the zero-momentum Fourier compo-
of head-on collisions leads to a parametrically distinct
nent of the bare interaction potential V0. The limit of
relaxation of odd and even momentum harmonics of
weak interaction corresponds to g ≪ 1 and Eqs. (2),
the distribution function, in particular τ-1even ∝ T2/εF
(3) are valid for g < 1/22). However, a direct at-
while τ-1odd ∝ T4/ε3F [6, 7].
tempt to apply Luttinger liquid theory to the question
The role of dimensionality in quasiparticle relaxa-
of quasiparticle lifetime meets formidable challenges.
tion becomes the most dramatic in one-dimension (1D).
In a fermionic representation of the TL-model, elabo-
This special case of electron liquids can be experimen-
rated explicitly by Dzyaloshinskii and Larkin [19], the
tally realized in quantum wires of GaAs/AlGaAs hete-
electron self-energy vanishes on the mass shell in all
rostructure [8] or carbon nanotubes [9] when parti-
orders of perturbation theory and, consequently, corre-
cle density is such that only the lowest sub-band of
lation functions assume power-law tails. These results,
transversal modes is occupied. It further requires that
2) In Ref. [19] the limit of strong interactions, g > 1/2, was
temperature is sufficiently low and sample purity is suf-
also considered, including the scenario when coupling between
fermions of the same chirality is different from coupling bet-
1) Throughout the paper we use units with Planck and Boltz-
ween fermions of different chirality. For additional details on
mann constants set to unity ℏ = kB = 1.
the derivation of Eq. (3) see also Ref. [21].
777
A. Levchenko, T. Micklitz
ЖЭТФ, том 159, вып. 4, 2021
and the absence of relaxation, can be alternatively un-
measurements of quasiparticle properties beyond the
derstood from the Mattis and Lieb [18], and Luther and
parading of linear Luttinger liquid theory. In a parallel
Peschel [20] bosonization construction, which maps in-
line of developments [53-56], cooling of nonequilibrium
teracting 1D fermions to a collection of decoupled har-
quasiparticles in quantum Hall edge fluids was mea-
monic modes of charge-density and spin-density oscil-
sured and corresponding lengths scales of thermaliza-
lations. Notably, in both approaches the exact solution
tion processes were quantified.
relies heavily on the linearization of the fermionic dis-
The focus of this communication is on the descrip-
persion relation.
tion of elementary kinetic processes inducing relax-
One is then left with the natural puzzle whether in-
ation in nonlinear Luttinger liquids and their emergent
corporating curvature of the dispersion relation into the
transport properties. Keeping forward scattering elect-
TL-model would cure the issue and yield a finite life-
ron-electron interactions and accounting for nonlinear
time of excitations, thus possibly restoring Fermi liquid
contributions to the electron dispersion, this theory is
like properties of the system. This line of reasoning can
beyond the Dzyaloshinskii-Larkin theorem. The lat-
be also corroborated within the fermionic picture, not-
ter relax kinematic constraints and open phase space
ing that spectrum nonlinearity softens phase space re-
for multi-loop corrections to the electron self-energy,
strictions for quasiparticle scattering, thus making their
thereby providing a variety of inelastic processes which
relaxation possible.
affect equilibrium as well as nonequilibrium proper-
Similarly, at the level of the bosonic description,
ties of the 1D quantum electron liquids. The rest of
nonlinear terms of the dispersion relation couple charge
this work is structured as follows (see the full text).
and spin modes thus enabling their decay. However, it
Section 2 focuses on the hierarchy of relaxation times
was quickly recognized that curvature cannot be in-
in Fermi-Luttinger liquids. We present results be-
cluded perturbatively, and a naive expansion leads to
yond parametric estimates, including detailed compu-
spurious divergences. These and other related ques-
tations of a number of experimentally relevant interac-
tions to 1D kinetics, including the connection between
tion models3). The complimentary kinetic equation ap-
the two pictures of the fermion-boson duality, attracted
proach, applied to the quasiparticle picture of a weakly
significant recent interest. This has lead to the devel-
interacting Fermi gas, and spin- and charge-excitations
opment of the nonlinear Luttinger liquid theory, also
of a Luttinger liquid, are explored concurrently. We
referred to as Fermi-Luttinger liquid (FLL) theory (see
present numerical estimates for experimentally mea-
Refs. [22, 23] for comprehensive reviews and references
sured relaxation rates and provide detailed comparison
herein). Specifically for the problem of quasiparticle
to previous results. In Sec. 3, the temperature depen-
relaxation in quantum wires, various scattering rates
dence of kinetic coefficients is calculated, accounting
were calculated within different interaction models for
for extrinsic mechanisms of momentum relaxation due
both, spinless [24-33] and spin-1/2 fermions [34-40]. In
to phonons or long-range inhomogeneities. The contri-
parts of the present work we review and extend these
bution to heat transport mediated by plasmons in the
results.
inhomogeneous Luttinger liquid is elucidated. Finally,
On the experimental forefront the hallmark sig-
we devote parts of the discussion to the thermoelectric
natures of Luttinger liquid behavior have been ob-
properties at the first plateau transition of the quan-
served by means of various spectroscopic techniques.
tum conductance. In Sec. 4, we provide a summary of
Namely, power-law anomalies in the density of states,
main findings and open questions, sketching a broader
tunneling conductance, and current-voltage characte-
picture and commenting on related topics relevant for
ristics [9,10,41,42], spin-charge separation [43,44], and
chiral, helical, and spiral versions of 1D quantum fluids.
charge fractionalization [45, 46]. Besides GaAs quan-
Several Appendices accompany our presentation in the
tum wires, carbon nanotubes, and edge modes, clear
main text, providing additional technical details of the
features of Luttinger liquid physics have been identi-
presented analysis and formalism.
fied in many other systems such as bundles of NbSe3
2. Hierarchy of relaxation processes. The
[47] and MoSe [48] nanowires, polymer nanofibers [49]
physics of quasiparticle relaxation in 1D quantum elec-
and conjugated polymers at high carrier densities [50],
tron liquids is perhaps a surprisingly rich and compli-
as well as atomically controlled chains of gold atoms on
cated problem. In part this has to do with the fact
Ge surfaces [51], just to name a few distinct examples.
that, in contrast to their higher dimensional counter-
In the most recent report [52], relaxation processes in
quantum wires were captured and bounds on the cor-
3) In part this material was summarized in Sec. IV of the ex-
responding timescales were determined, thus providing
tensive review in Ref. [23].
778
ЖЭТФ, том 159, вып. 4, 2021
Kinetic processes in Fermi-Luttinger liquids
parts, two-particle collisions, namely scattering pro-
ization to the degenerate quantum limit was presented
cesses with the emission of a single particle-hole ex-
in the work of Ref. [59], and exchange terms were care-
citation, do not result in finite relaxation rates. This
fully examined in Refs. [35, 60]. The resulting ampli-
statement pertains to generic dispersion relations, i. e.
tude takes the form
including curvature, and not only applies to models
with linear dispersion. Indeed, kinematics of two-par-
1∑
A=
sgn(P)sgn(P′)×
ticle scattering in 1D is such that particles either keep
L2
PP′
or swap their momenta, but neither of these options
Vp′a-pa Vp′c -pc
causes relaxation. To allow for the redistribution of
×
Ξσσ′ .
(6)
εp
+εpc -εp
momenta and, at the same time, to comply with re-
b
b+pc -p′
c
strictions of conservations laws one necessarily needs
to consider triple electron collisions, or alternatively,
Here L is the system size and sums are over all possible
assume some extrinsic mechanism.
permutations P of momenta pi with i = 1, 2, 3 star-
ting from the direct scattering process (p1, p2, p3) →
The analysis of 1D kinematics of multi-particle col-
lisions resolving energy and momentum conservations
→ (p′1, p′2, p′3) to all its exchange processes, with
sgn(P) accounting for the sign of the particular per-
reveals a plethora of possible scattering events. They
ultimately lead to a hierarchy of relaxation stages in the
mutation (using the convention that sgn(123) = +1).
system and an emergent asymmetry between the relax-
Each permutation comes with a spin-dependent factor
ation of particle-like and hole-like excitations. All pro-
Ξσσ′ = δσaσ′a δσbσ′
b
δσcσ′ reflecting particle exchange. Inc
cesses can be broken down into several distinct classes.
the spinless case, the amplitude has an identical struc-
First are the forward scattering processes with soft
ture to Eq. (6) with Ξσσ′ ≡ 1. The amplitude con-
momentum transfer that involve either (i) all parti-
sists of 36 distinct terms that can be split into groups
of 6, each representing one direct and five exchange
cles from the same branch, or (ii) particles from both
branches such that all initial and final states are near
scattering processes, respectively. Technically speak-
the Fermi energy. Second are processes involving states
ing Eq. (6) appears from the iteration of the
T-matrix,
Ĝ0
deeper in the band. These latter are relevant for
T =V+V
T, to second order in the bare two-particle
(iii) the drift of quasiholes and (iv) backscattering pro-
interaction potential V . Here
Ĝ0 is the resolvent op-
cesses that change the number of right and left moving
erator (viz. the free particle Green’s function) and εp
excitations before and after the collision. We will refer
denotes the energy-momentum dispersion relation.
to thermalization when discussing relaxation processes
For practical applications to quasiparticle scatter-
that proceed without backscattering. These processes
ing in quantum wires, it is sufficient to assume the sim-
determine the lifetime of quasiparticles associated to
ple dispersion of a parabolic band εp = p2/2m∗ with
the redistribution of excess energy, and affect thermal
effective mass m∗, and use a Coulomb interaction po-
transport properties of the system. In contrast, the no-
tential. Effects of screening due to nearby gates can be
tion of equilibration will be used to refer to relaxation
modeled by a conducting plate placed at a distance d
processes involving the backscattering of quasiparticles,
away from the wire. In this case the interaction poten-
which ultimately govern electrical transport properties.
tial is of the form
2.1. Quasiparticle interaction model. In the
[
]
picture of a weakly nonideal Fermi gas, the probabil-
e2
1
1
V (x) =
-
√
,
(7)
ities of particle collisions can be calculated perturba-
κ
|x|
x2 + 4d2
tively in the interaction, employing the usual
T-matrix
formalism [57]. Within the Golden Rule, the scattering
where κ is the dielectric constant of the host mate-
rate
rial. The diverging short-range behavior of this poten-
W = 2π|A|2δ(E - E′)δP,P′
(5)
tial needs to be regularized in order to evaluate the
entering the
small-momentum Fourier components Vp
is expressed in terms of the scattering amplitude A of
amplitude in Eq. (6). To this end, we introduce the
the corresponding process. Here E(E′) and P (P′) la-
small width w of the quantum wire, w ≪ d, and replace
√
bel total energy and momentum of initial (final) states,
1/|x| → 1/
x2 + 4w2. Upon 1D Fourier transform we
and the delta function δ(E - E′) along with the Kro-
then find
necker delta δP,P ′ enforce energy and momentum con-
servations. In the semiclassical limit, the three-particle
2e2
amplitude A was considered in Ref. [58]. The general-
Vp =
[K0(2w|p|) - K0(2d|p|)] ,
(8)
κ
779
A. Levchenko, T. Micklitz
ЖЭТФ, том 159, вып. 4, 2021
where K0(z) is the modified Bessel function of the
The triple electron scattering rate from Eq. (5) gen-
second kind. Using the asymptotic expression of the
erates the collision integral (Stosszahlansatz) of the cor-
Bessel function at z ≪ 1,
responding Boltzmann equation
(
)
(
)
∑
2
z2
2
St{n} =
W [np′
(1-np1)np′
(1-np2)np′ ×
K0(z) ≈ ln
+
ln
,
1
2
3
zeγE
4
zeγE-1
{p},{σ}
× (1-np3)-np1(1-np′
)np2 (1-np′
)np3 (1-np′ )].
(11)
1
2
3
with γE the Euler constant, one then finds the simpli-
fied form of the interaction potential
Here each pair of Fermi functions, np(1 - np′ ), cap-
tures statistical occupation probabilities, whereas the
[
2
2e
(d)
(e1-γE)]
two terms of the collision integral correspond to in-
Vp ≈
ln
- (pd)2 ln
,
(9)
κ
w
|p|d
coming and outgoing processes. At thermal equilib-
rium these terms nullify each other by virtue of the de-
applicable to the screened limit of Coulomb interac-
tailed balance condition. At weak disequilibrium, one
tion and valid for p ≪ 1/d. In the opposite regime,
can linearize np = fp + δnp in the external perturba-
d-1 ≪ p ≪ w-1, the second term in Eq. (8) can be
tion δnp around the equilibrium Fermi-Dirac distribu-
neglected since K0(z) ∝ e-z/√z at z ≫ 1. One then
tion function fp. The collision term can then be con-
arrives at the simplified form of the unscreened poten-
sidered as a linear integral operator, acting on δnp =
tial
= fp(1 - fp)ψ, and one can formulate the eigenvalue
. The spec-
problem for this operator, St{ψn} = ωnψn
2
2e
trum of eigenvalues ωn may be discrete or continuous,
Vp ≈
×
κ
and captures all the information about the decay of
[
)
E
(e-γ
(e1-γE)]
different distribution function modes. As solving this
× ln
+ (pw)2 ln
(10)
|p|w
|p|w
problem exactly for triple collisions presents a daunting
task [29, 40], we here follow a simpler more pragmatic
A few comments are in order in relation to the in-
approach. Setting, for instance, δnp1 = δp
1,pF +ε/vF de-
teraction model presented in this section. (i) It should
scribes a quasiparticle with excess energy ε. Neglect-
be noted that retaining numerical pre-factors of the
ing then secondary collisions, the Boltzmann equation
order of unity under the logarithm in above expres-
reduces to the simple relaxation time approximation,
sions for Vp would exceed the accuracy of further cal-
(∂t + τ-1qp)δnp = 0, with solution δnp ∝ exp(-t/τqp).
culations, so they will be dropped and simply set to
It is natural to identify the corresponding timescale for
unity. (ii) However, retaining the sub-leading correc-
decay with the quasiparticle life-time
tions containing p2 in the main log-series expansion of
∂St{n}
both Eqs. (9) and (10) is actually crucial. Indeed, in
τ-1qp = -
,
(12)
∂np
the spinless case, the model with contact interaction as
well as the Calogero-Sutherland model, are known to
which follows from Eq. (11) by only retaining the
be completely integrable [61]. This implies that all irre-
out-scattering contribution. Alternatively, one may
ducible multi-particle scattering amplitudes must van-
project the collision operator (11) onto either momen-
ish identically for a constant Vp and Vp ∝ |p|. Fur-
tum or energy modes and thus infer the relaxation time
thermore, the extended model of short-ranged interac-
of interest. This approach is parametrically correct,
tion, Vp ∝ p2, corresponding to the real space poten-
however, may miss numerical factors of order unity
tial V (x) ∝ δ′′(x), is also integrable. This is known
when compared to the exact solution of the eigenvalue
as Cheon-Shigehara model [62]. It is only due to the
problem. We will employ both approaches in the forth-
additional logarithm ∝ p2 ln |p| in Eq. (9), that there
coming sections.
is partial non-cancellation between different terms in
Eq. (6) and the amplitude remains finite. (iii) In the
2.2. Quasiparticle decay rates. Owing to one-
model of long-ranged Coulomb interaction the situa-
dimensionality of the problem, it is convenient to think
tion is more subtle. A priori this model is not known
of particles of different chirality, namely right-movers
to be integrable. Nevertheless, the amplitude in Eq. (6)
(R) and left-movers (L). It can be readily checked
vanishes for pure logarithmic interaction Vp ∝ ln |p|, so
that strictly at zero-temperature quasiparticle relax-
that retaining an additional p2 ln |p| term in Eq. (10) is
ation is only possible if collisions involve both, right-
important to get a finite result.
and left-moving particles since otherwise conservation
780
ЖЭТФ, том 159, вып. 4, 2021
Kinetic processes in Fermi-Luttinger liquids
laws cannot be satisfied. For this reason, consider first
momentum and energy conservations in Eq. (5) can be
a process of relaxation that involves two right-moving
simplified to
particles, with initial momenta p1, p2, and a left-moving
particle labeled by momentum p3. The outgoing mo-
δP,P′ δ(E - E′) ≈
(
)
menta after the collision, p′i = pi +qi, will be labeled by
1
q1(k1 - k2) + q21
momenta transfer qi for each of the particle i = 1, 2, 3.
≈
δ q3 -
(15)
δq1,-q2 .
vF
pF
In these notations, the momentum conservation be-
comes q1 + q2 + q3 = 0, and the energy conservation,
These approximations enable one to complete all five
for a simple parabolic band, can be cast in the form
momentum integrations. Two integrations are removed
by delta functions which fix values of q2 and q3 in terms
2(p1q1 + p2q2 + p3q3) + q21 + q22 + q23 = 0.
of k1,2 and q1. Furthermore, in the zero temperature
limit, T → 0, Fermi occupations become step-func-
These conditions set the phase-space constraints for
tions, fk → θ(-k). The integral over k3 then becomes
collisions.
elementary, contributing by a pure phase space factor
For an initial state with p1 = pF + ε/vF , the quasi-
particle life-time corresponding to an RRL-process is
∑
L
then
f-k3 (1 - f-k2-q3 ) =
|q3|θ(-q3).
2π
k3
τ-1qp =
The product of Fermi factors, fk2 (1 - fk2-q1 ), simply
∑
limits the domain of k2 to the range k2 ∈ [-|q1|, 0],
=
W (1 - fp′
)fp2 (1 - fp′
)fp3 (1 - fp′ ),
(13)
1
2
3
while the remaining 1-fk1+q1 dictates that q1 < k1. Fi-
p2p3
p′1p′2p′
nally, we recall that in this setting k1 = ε/vF . Putting
3
everything together the RRL-process gives the life-time
where we begin analysis from the spinless case. At
(
)4
this point it is convenient to shift momenta of left- and
ε
τ-1qp = c1εF g4λ21(pF w)
,
(16)
right-movers from the respective Fermi points, p1,2 =
εF
= pF + k1,2 and p3 = -pF + k3. In addition, it is
sufficient to linearize the spectrum in the distribution
where g
= e2/κvF is the dimensionless interac-
functions, approximating
tion strength of the model and we introduced
[ (
)
λ1(z) = z2 ln(1/z). The numerical coefficient c1 =
]-1
vF k
= (15 - π2)/32π3 is obtained with help of the following
f±pF +k → f±k = exp
±
+1
,
T
integral
but not in the scattering probability W . Indeed,
∫∫
(
)
an analysis of the kinematic constraints suggests that
x
15 - π2
x2g(x, y)ln2
dx dy =
,
(17)
q1 ≈ -q2 and q3 ≈ (q1/pF )(k1 - k2 + q1), implying
g(x, y)
72
0
that |q3| ≪ |q1,2|. In other words, relaxation occurs in
incremental steps of momentum transfer q3 ∼ ε2/v2F pF
where g(x, y) = 1 - x(1 - y). Notice that the numeri-
from right-movers to left-movers. With these observa-
cal factor in Eq. (16) differs from the one calculated in
tions at hand, we next need the corresponding three-
Refs. [26, 28] as different properties of the interaction
particle scattering amplitude. For the case of long-
potential were assumed4).
ranged Coulomb interaction Eq. (10), one finds from
We see that finite decay rate emerges in forth order
Eq. (6) after a laborious expansion
of the interaction strength. We also notice that the at-
tenuation is inversely proportional to the cube of mass,
2
2(pF w)
(2e2 )2
τ-1
∝ (m∗)-3, and vanishes as the limit m∗ → ∞ is
A≈
×
qp
L2εF
κ
taken at fixed band velocity. This limit corresponds to
[
(
)]
(
)
the situation considered by Dzyaloshinskii and Larkin.
3
1
q21
The energy scaling of the decay rate, ∝ ε4, is consistent
× 1-
ln
ln
(14)
4
pF w
pF |q3|
with expectations based on the Fermi liquid picture for
This result is obtained to leading logarithmic accuracy
4) In Appendix (see full text) we sketch derivation of Eq. (16)
using two small parameters |q1|/pF ∼ |q3|/|q1| ≪ 1 in
from the bosonization framework of an impurity scattering in
the expansion. With the same level of accuracy the
Luttinger liquids.
781
A. Levchenko, T. Micklitz
ЖЭТФ, том 159, вып. 4, 2021
a process involving two particle-hole excitations. How-
They are dominated by 2pF exchange-processes be-
ever, this result is not universal. This becomes evi-
tween branches, in which left-movers are scattered into
dent from repeating the above calculation for the model
right-movers [35]. Even though the strength of 2pF
of screened short-range interaction, i.e. using the po-
exchange interaction is weaker than small momentum
tential given by Eq. (9). Expanding the amplitude in
scattering, V2pF ≪ V0, for Coulomb interaction the rel-
Eq. (6) under the same conditions as above, one then
ative reduction is only logarithmic. The gain in the
finds instead of Eq. (14) the amplitude
amplitude, on the other hand, is more substantial and
q ≫ 1. This
controlled by the large factor ∼ εF /vF
(
)
4
5(pF d)
(2e2 )2
1
statement can be verified explicitly from Eq. (6) where
A≈-
ln
×
3L2εF
κ
pF d
after spin summation one finds for the square of the
[
[
amplitude for the RRL-process
q21
( |q1|)]-
×
1 + 6ln
]
4p2F
pF
∑
3V22p
(V0 - V2pF )2
[q21
4p2F
F
|A|2 =
+
(20)
[
32L4ε2
q23
q2
σ2σ3
F
1
q23
( |q3|)]]
-
1 + 6ln
(18)
σ′1σ′2σ′
3
q21
|q1|
The crucial difference here compared to Eq. (14) is the
To obtain this result we approximated Vp1-p2±qi ≈ V0
appearance of the additional small parameter |q1|/pF ∼
and Vp1,2-p3±qi ≈ V2pF in all the relevant terms since
∼ |q3|/|q1| ∼ ε/εF ≪ 1, which can be related to the fact
p1,2 - p3 ≈ 2pF and qi ≪ |pi|. Again, by repeating
momentum integrations, the decay rate is found to be
that this particular model is nearly integrable. A close
inspection of the amplitude in Eq. (6) reveals that each
of the form
term individually diverges as 1/q at small characteris-
(
)2
ε
(εF )
tic momentum transfer. However, all exchange terms
τ-1qp = c3εF g4λ23(pF w)
ln2
,
(21)
combined together remove the singularity and partially
εF
ε
cancel out all the way to ∼ q2 ln q order. The rest of the
calculation carries through in exactly the same way as
with c3 = 45/32π3 and λ3(z) = ln(1/z). To be consis-
in the previous example, and one finds the decay rate
tent with the approximations that lead to Eq. (20),
(
)8
the difference V0 - V2pF should be understood as a
ε
(εF )
τ-1qp = c2εF g4λ22(pF d)
ln2
(19)
weak logarithmic factor ≃ (2e2/κ) ln(εF /ε) for the
εF
ε
Coulomb interaction potential. This was incorporated
with c2 = 2445/3584π3 and λ2(z) = z4 ln(1/z). The
into Eq. (21). The singularity of the amplitude was
four extra powers in the energy dependence, can be
compensated by phase space factors, and perhaps sur-
traced back to the different asymptotic form of the
prisingly this restores essentially the Fermi liquid form
amplitude in Eq. (18). This demonstrates the high
of the decay rate at T = 0. We note that up to model
sensitivity of decay rates in 1D to details of the in-
dependent pre-factors, the quadratic dependence of the
teraction. The result captured by Eq. (19) is of course
relaxation rate on energy of spin-1/2 particles given by
perturbative. For a generic nonintegrable models with
Eq. (21) is consistent with predictions of previous stu-
short-ranged interaction, it can be generalized to ar-
dies [35, 39].
bitrary interaction strength. It can further be shown
We proceed with discussion of the effects of thermal
that τ-1qp ∝ ε8 remains valid, and the pre-factor can be
broadening on relaxation processes. In the Fermi liquid
expressed in terms of the exact spectrum [31].
picture one expects a simple crossover at excitation en-
As should be anticipated from the discussion above,
ergies of the order of temperature ε ∼ T. For 1D liquids
electron spin plays a crucial role in the transition ma-
this is not the case, as even at T < ε there are inter-
trix element for the three-particle process, and should
mediate regimes and relaxation shows nontrivial tem-
thus significantly affect the quasiparticle decay rate.
perature dependence. Indeed, at finite temperatures
Indeed, in the spinless case antisymmetry of the elect-
each collision results in a typical momentum trans-
ron wave function dictates that its orbital component
fer qi ∼ T/vF allowed by thermal smearing of states
should be odd and therefore relevant exchange ampli-
near the Fermi energy. As RRL relaxation is controlled
tudes are suppressed by Pauli exclusion. Mathemati-
by the momentum transfer between the branches, one
cally, one sees this in a cancellation of various terms
needs to compare phase spaces available to left movers.
that lead to Eq. (18). In contrast, for spinful elect-
Since at zero temperature q3 ∼ ε2/v2F pF , one deduces
rons singular parts of the amplitude do not cancel.
from comparison to q3 ∼ T/vF the crossover scale εT ∼
782
ЖЭТФ, том 159, вып. 4, 2021
Kinetic processes in Fermi-Luttinger liquids
∼
√εF T . Technically, this argument can be also made
where εd = vF /d. In fact, ∝ T7 is a generic property
clear by observing that
for any non-integrable finite-range interaction model
with a sufficient degree of analyticity at small momenta
∑
[
]-1
L
(vFq3)
q3 exp
-1
,
[32, 33]. Lastly, in the case of spin-1/2 chiral electrons
f-k3 (1 - f-k3-q3 ) =
2π
T
k3
one estimates the decay rate to be of the form
and reducing to LT/2πvF as q3 → 0. These consider-
Tε6T
(d)
τ-1qp = c9g4
ln4
(27)
ations suggest that Eqs. (16), (19), and (21) are valid
ε2ε4d
w
for T ≪ ε2/εF . Above this threshold one finds
In addition to relaxation of particles with the same
(
)2
ε
T
chirality, thermal broadening allows for the relaxation
τ-1qp = c4εF g4λ21(pF w)
,
(22)
εF
εF
of hot quasiholes, a process kinematically forbidden at
zero temperature. The derivation of the corresponding
instead of Eq. (16) for the spinless Coulomb case. Si-
decay rate τ-1qh proceeds in close analogy to that for the
milarly,
RRL-process. Crucial modifications are (i) the sign of
(
)6
q3, (ii) a smaller phase space volume, now suppressed
)
ε
T
(εF
τ-1qp = c5εF g4λ22(pF d)
ln2
,
(23)
by an additional factor ∼ T/(ε2/εF ), and (iii) that it
εF
εF
ε
takes ∼ (ε/εT )2 steps to relax the excess energy. As a
result, the quasihole relaxation rate e. g. for the spin-
instead of Eq. (19) for the spinless screened case, and
1/2 model,
finally
)
T
(εF
(T)2
(εF )
τ-1qp = c6εF g4λ23(pF w)
ln2
(24)
τ-1qh = c10εF g4λ23(pF w)
ln2
,
(28)
εF
ε
ε
ε
instead of Eq. (21) for the spin-1/2 Coulomb case. The
is by a factor (εT /ε)4 smaller than τ-1qh defined in
set of coefficients c4,5,6 can be determined from numer-
Eq. (21) when taken at the same energy. This pro-
ical integrations, however, their specific values are of
nounced asymmetry in the relaxation rates of elect-
no particular significance here.
ron-like and hole-like excitations is a direct consequence
At elevated temperatures the above mechanism of
of the 1D kinematics of three-particle scattering with
relaxation competes with another process involving
nonlinear spectrum. This feature marks a sharp dis-
only particles of the same chirality. As indicated ear-
tinction between the quantum 1D Fermi-Luttinger liq-
lier, this RRR- (or equivalently LLL-) process is kine-
uids and higher dimensional Fermi liquids.
matically possible only at finite energies. It follows
We summarize in Table the discussed quasiparticle
from the same amplitude Eq. (6), but admits differ-
relaxation rates in the different regimes.
ent conditions on the involved momenta. In this pro-
cess, a high-energy particle with excess energy ε can
2.3. Distribution imbalance rates. Another
relax on two other comoving particles, which during
common technique in kinetic theory applied to the de-
the collision are scattered in opposite directions in en-
termination of relaxation rates is to project the collision
ergy. Namely, one is drifting slightly upwards in energy,
integral onto specific modes of interest, to infer their
whereas the other float downwards, closer to the Fermi
corresponding decay times. For instance, in the context
energy. A detailed calculation in the spinless Coulomb
of the present problem, one can look at the thermal im-
model shows that the corresponding relaxation rate is
balance relaxation between left- and right-movers. This
given by
amounts to projecting the collision term onto the ener-
, which is even
gy mode of the distribution function np
3
T
(εw)
in momentum.
τ-1qp = c7g4(pF w)4
ln2
,
(25)
εεF
ε
To see the practical implementation of this method,
consider a situation in which right-movers are hotter
where εw = vF /w. This rate exceeds that given in
than left-movers. The goal is then to derive an equa-
Eq. (22), provided that temperature is higher than
√
tion which describes the relaxation of the difference in
∼ ε
ε/εF . In the case of screened Coulomb interac-
temperatures ΔT = TR - TL of left- and right-moving
tion, the same mechanism is more strongly suppressed
electrons. It should be noted that the physical set-
7
T
(εd)
(ε)
ting with imbalanced temperature is justified in 1D:
τ-1qp = c8g4(pF d)8
ln2
ln2
,
(26)
εε5F
ε
T
while three-particle collisions generate both right- and
783
A. Levchenko, T. Micklitz
ЖЭТФ, том 159, вып. 4, 2021
Table. Energy and temperature dependencies of quasi-
The next step is to also linearize the right-hand-si-
particle relaxation rates (only the leading parametric
de of Eq. (29) in ΔT . To accomplish this task we
behavior is indicated and logarithmic terms are omit-
parametrize np = fp+fp(1-fp)ψp, which allows to con-
ted for brevity). First two rows summarize results for
veniently take advantage of the detailed balance con-
spinless electrons interacting via Coulomb and screened
dition in the collision integral St{n}. For the thermal
short-range interaction models, respectively, and the
imbalance ψp = (εp - εF )ΔT/T2, and one finds upon
last row gives the result for the spin-1/2 model. The
expansion in ΔT
first two columns describe processes involving particles
∑
of both chiralities (e. g. the RRL-process), and the
(εp1 - εF )St{n} =
last column describes the relaxation of comoving par-
p1>0
ticles with only same chirality (e. g. the RRR-process).
∑
√
ΔT
=-
(vF k1)(vF q3)W.
(32)
In all cases T1 ∼ ε2/εF , while T2 ∼ ε
ε/εF in the
√
T2
{k,q,σ}
Coulomb model, T2 ∼ ε6
ε/εF in the screened model,
√
and T2 ∼ ε(εd/εF )3
εd/ε in the spinful model
Here
τ-1qp
T <T1
T1 < T < T2 T2 < T < ε
W = Wfk1(1 - fk1+q1)fk2(1 - fk2+q2)×
Coulomb ε4/ε3F
Tε2/ε2F
T3/εεF
× f-k3(1 - f-k3-q3),
(33)
Screened ε8/ε7F
Tε6/ε6F
T7/εε5F
and at intermediate steps we made use of the energy
conservation implicit in W , and approximated εp1 -
Spin-1/2
ε2/εF
T
Tε6T/ε2ε4d
- εF ≈ vFk1 and εp′
- εp3 ≈ -vFq3. It is now evident
3
that Eq. (29) can be cast in form of the usual relaxation
time approximation,
left-moving particle-hole pairs the intrabranch relax-
ation induced by these processes is faster, while inter-
∂tΔT = -ΔT/τth,
(34)
branch is a slow.
We start from the Boltzmann equation, multiply
where we introduced the corresponding thermalization
both sides by εp1 - εF , and sum over p1 > 0
time. For the kinematics of the RRL-process, the latter
∑
∑
evaluates to
(εp1 - εF )∂tnp1 =
(εp1 - εF )St{n},
(29)
)2
p1>0
p1>0
(T
(εF )
-1
τt
= c11εFg4λ23(pFw)
ln2
(35)
h
where, as above, momentum p1 is that of a right-
εF
T
moving particle. We then assume np1 to be of Fer-
In a similar fashion one can find the relaxation rate for
mi-Dirac form with nonequilibrium temperature TR =
the odd part of the imbalanced distribution. For this
= T +ΔT of right-moving excitations, and linearize in
purposes one may consider a boosted frame of referen-
the left-hand-side with respect to ΔT ,
ce, εp - pu, and derive the relaxation equation for u
(εp1 - εF )∂tΔT
by projecting the collision integral onto the momentum
∂tnp1 = ∂T np1 ∂tΔT =
(30)
(εp1 -εF ).
mode. Kinematics of the respective collision is different
4T2 ch2
2T
though, and will be considered in the next section.
To get an idea of the order of magnitude of the
When computing integral over p1 it is convenient to
different timescales, it is instructive to consider the fol-
shift momentum to the respective Fermi point, p1 =
lowing estimates for GaAs quantum wires using exper-
= pF + k1. Linearizing further the dispersion relation
imental parameters of Ref. [52]. For vF ∼ 2 · 105 m/s
in k1, εp1 - εF ≈ vF k1, one may use that the integral
and κ ∼ 10, the interaction parameter is just within
is peaked at pF and rapidly converging. Noting that
the applicability criterion of the perturbative expres-
∫
sions g ∼ 1. For the typical electron density we use
z2dz/ ch2(z) = π2/6,
pF ∼ 108 m-1, w ∼ 10 nm, and εF ∼ 1 meV. Then for
-∞
ε ∼ εF/4, which is a typical excess energy of injected
particles in tunneling experiments, and T ∼ 0.25 K one
one readily finds
is securely in the regime T ≪ ε2/εF . For this set of
∑
πLT
parameters τ-1qp ∼ 1011 s-1, τ-1qh ∼ 109 s-1, and τ-1th ∼
(εp1 - εF )∂tnp1 =
∂tΔT.
(31)
6vF
∼ 106 s-1.
p1>0
784
ЖЭТФ, том 159, вып. 4, 2021
Kinetic processes in Fermi-Luttinger liquids
2.4. Backscattering hole mobility rates. Rela-
change in each scattering event is small, and holes ef-
xation processes of low-energy excitations leading to
fectively drift through the bottom of the band. Thus
the decay of quasiparticles near the Fermi energy do not
relaxation occurs in multiple steps and the underlying
change the numbers of right- and left-moving particles.
dynamics is momentum space diffusion. Under these
Thus they are chirality conserving. It turns out that it
conditions, the mobile impurity falls into the universal
is also possible to have backscattering processes. The
class of problems described by a Fokker-Planck equa-
kinematics of these collisions involves states deep in the
tion [72]. The collision integral Eq. (36) can then be
Fermi sea, and for this reason it is useful to consider
simplified by expanding in the small momentum step
the mobility of holes at the bottom of the band. These
q1 ≪ p1, and maps to the differential operator
processes are commonly considered from the perspec-
1
tive of mobile impurities in a Luttinger liquid [63-69].
St{hp1 } ≈ -∂p1 [A(p1)hp1 ] +
∂2p
[B(p1)hp1 ] .
(38)
1
2
Here we will continue using the kinetic equation ap-
proach for their description. The idea is then to single
Here we introduced
out hole states at the bottom of the band with small
∑
momenta, and to derive an effective kinetic equation
A(p1) = - q1Pq1(p1),
capturing their dynamics and allowing the calculation
q1
∑
(39)
of corresponding backscattering rates [70,71].
B(p1) =
q21Pq1 (p1),
For this purpose, let p1 and p′1 be momenta near the
q1
band bottom, p2 and p′2 lie near the right Fermi point
(+pF ), and p3 and p′3 be taken near the left Fermi point
and used the short-hand notation Pq1 (p1) = P(p′1, p1).
(-pF ). As before, the unprimed momenta correspond
The diffusion coefficient in momentum space B(p1) is a
to incoming states whereas primed ones are associated
function of the hole-momentum p1 varying on a scale
with outgoing states. With these conventions, we intro-
set by pF . For holes at the bottom of the band, one
duce the hole distribution function, hp1 = 1 - np1 , and
may thus approximate B(p1) by its value at p1 = 0,
the collision integral for holes, St{hp1 } = -St{np1 }.
in the following simply denoted by B without argu-
Starting from Eq. (11), the latter can be cast in the
ment. Furthermore, the drift coefficient A(p1) is read-
form
ily obtained from noting that the collision integral (38)
∑[
]
has to vanish for hole distributions of an equilibrium
St{hp1 } =
P (p1, p′1)hp′
- P(p′1,p1)hp1
,
(36)
1
Boltzmann form. This condition leads to the relation
p′
1
A(p) = pB/2m∗T .
where
The rest of the calculation depends on the struc-
∑
∑
P (p1, p′1) = 12
Wfp2(1-fp′
)fp3 (1 - fp′
)
(37)
ture of the amplitude for the given kinematics of the
2
3
{σ}
p2p3
three-particle process. In calculating A from Eq. (6)
p′2p′3
for the momentum configuration under consideration,
is the rate for a transition in which a hole scatters from
and up to small corrections in T/εF ≪ 1, it is sufficient
some state p′1 into p1, while P(p′1, p1) denotes the rate
to approximate p1 ≈ 0, p2 ≈ +pF and p3 ≈ -pF . Mo-
for the inverse process. In the above sums, all momenta
mentum and energy conservations provide additional
have been restricted to the discussed ranges, which ex-
restrictions on the transferred momenta, enforcing that
plains the combinatorial overall factor of 12. Since both
q2 ≈ q3 ≈ -q1/2, again up to small corrections in
p1 and p′1 lie near the bottom of the band, the distri-
T/εF
≪ 1. As a result, the amplitude A can be
bution functions hp1 and hp′ are exponentially small
parametrized only by a single momentum q1. Expan-
1
∝ e-εF/T due to Pauli exclusion, and so is the collision
ding Eq. (6) and summing over spins one then finds
integral of holes St{hp}. It is therefore unnecessary
∑
6
p2F
to account for additional exponentially small contribu-
|A|2 =
V2p
(VpF - V2pF )2
(40)
F
tions in the transition rates P(p1, p′1) and P(p′1, p1),
ε2F L4
q2
1
{σ}
and this is why we replaced fp1 ≃ 1 and fp′
≃ 1 in
1
both. As in the case of the forward scattering process,
The singularity of A at small momenta is cancelled in
the typical scale for momentum change of all three par-
the spinless case. Specifically, for the long-range inter-
ticles in a hole backscattering is set by temperature,
action model with Eq. (10) one finds
qi = p′i - pi ∼ T/vF. At the same time, the typical
√
momentum of a hole is p1 ∼
m∗T so that q1/p1 ∼
9
(2e2 )4
(pF )
√
A≈
λ21(pF w)ln2
,
(41)
∼
T/εF ≪ 1. This means that the net momentum
16ε2FL4
κ
|q1|
785
14
ЖЭТФ, вып. 4
A. Levchenko, T. Micklitz
ЖЭТФ, том 159, вып. 4, 2021
whereas for the screened model
energy. Thus for Δp2 ≃ m∗T the result is (omitting
numerical factor for brevity)
2
9(ln 4 - 1)
(2e2 )4
A≈
λ22(pF d).
(42)
)2
ε2FL4
κ
-1
( T
τd
≃ g4λ23(pFw)
(47)
h
εF
In order to perform remaining momentum integrations
implicit in the definition of B, one can approximate
Finally we recall that the mobility of particles μ is re-
delta functions in the scattering probability by
lated to the diffusion constant by the simple kinetic
formula μ = T/B, and therefore μ ∝ 1/T2.
1
The result is different in the spinless case. From
δP,P′ δ(E - E′) ≈
δ(q2 - q3)δq
2,-q1/2.
vF
Eqs. (41), (42) and (45) one finds B ∝ T5 in both cases,
modulo a logarithmic factor ln2 T in the Coulomb case,
This removes two integrations out of five, and gives
. The results dis-
and thus τ-1dh ∝ T4 and μ ∝ 1/T4
∑
∑
cussed in this section are again perturbative in the in-
12L
B=
q2
|A|2fk
1
2-q1/2(1-fk2)×
teraction. The power laws in the temperature depen-
vF
q1k2k3
{σ}
dence of relaxation rates are, however, generic and also
apply to the strongly interacting regime, as we further
(43)
× fk3+q1/2(1 - fk3),
elaborate below, see also Refs. [67, 68].
2.5. Electron-phonon relaxation rates. Apart
where we shifted momenta p2,3 to the respective Fermi
from the purely electronic mechanisms of relaxation
points, ±pF + k2,3, and linearized the dispersion rela-
electrons may scatter on phonons, disorder, and sam-
tion in all Fermi occupation functions. Finally, using
ple imperfections thus relaxing their energy and mo-
the tabulated integral
mentum. At extremely low temperatures phonons are
∑
L
1
not expected to be efficient at cooling the electronic
fk+q(1 - fk) =
qbq, bq =
,
(44)
sub-system. On the other hand, electron-phonon scat-
2π
evFq/T - 1
k
tering has no such severe phase space restrictions like
where bq is the equilibrium Bose distribution, we arrive
the three-particle collisions considered above. It is thus
at the general expression
instructive to estimate the temperature dependence for
the corresponding relaxation rate. Unlike the previous
)3 ∑
∑
6π
(L
studies of electron-phonon relaxation in multichannel
B=
q4
1
|A|2bq
1/2(1+bq1/2).
(45)
vF
2π
quantum wires [73, 74], and phonon-induced backscat-
q1
{σ}
tering relaxation [75, 76], we focus on the complemen-
A notable feature of this expression is that it is entirely
tary effect of soft collisions in a single-channel geometry
expressed in terms of bosonic modes. In essence, this is
of strictly 1D electrons and 3D phonons.
a manifestation of bosonization at the level of fermionic
The coupling of electrons and phonons is described
kinetic theory, as the occupation of an electron-hole
by the collision integral [77]
pair near one of the Fermi points integrated over the
St{np, Nq} =
center of mass momentum is equivalent to a collective
boson emitted/absorbed in a course of hole diffusion.
∑
It will be shown in the subsequent section that struc-
= W-[np′(1 - np)Nq-np(1-np′)(1+Nq)] +
turally the same expression for B can be obtained from
p′q
a purely bosonic formulation of the problem. Finally,
∑
inserting Eq. (40) into Eq. (45) one finds the momen-
+ W+[np′(1-np)(1+Nq)-np(1-np′)Nq] ,
(48)
tum space diffusion coefficient of spin-1/2 holes
p′q
)3
where the scattering rate
768 ln2(2)
( T
B=
g4λ23(pF w)
p2F εF .
(46)
π
εF
(49)
W±(p, p′, q) = (2π)|A(q)|2δ(εp-εp′ ±ωq)δp=p′ ±qx
The corresponding backscattering relaxation rate can
describes phonon emission and absorption processes
be found from Einstein relation adopted to diffusion in
with an amplitude
momentum space, Δp2 = Bτdh. The notation τdh is
√
meant to emphasize kinetics of a deep hole as opposed
1
A(q) =
(D|q| + iΛ).
to earlier notation τqh
describing quasiholes near Fermi
2ϱVωq
786
ЖЭТФ, том 159, вып. 4, 2021
Kinetic processes in Fermi-Luttinger liquids
Here we took into account that at the level of the lead-
of Fermi and plasmon velocities. In the TL model u =
√
ing Born approximation, the probabilities of scattering
=vF
1 + V0/πvF.
for direct and reverse processes are the same. In the
2.6. Spin-charge scattering rates. The applica-
amplitude we include both deformation (D) and piezo-
bility of the Born approximation, used to construct the
electric (Λ) couplings, ϱ is the mass density, qx the
quantum amplitude for triple particle processes cap-
phonon wave-vector along the wire, and V is the sys-
tured by Eq. (6), requires that incoming spin-1/2 quasi-
tem volume. For simplicity we assume only a single
particles have sufficiently high energy compared to the
acoustic branch ωq = s|q|, with sound velocity s.
typical scale of interparticle interaction ε ≫ m∗vF V0.
For equilibrium Fermi and Bose distribution func-
In the generic interacting environment of a 1D
tions of electrons and phonons respectively, np → fp
quantum fluid, quasiparticle excitations break down
and Nq → bq, the collision integral in Eq. (48) vanishes
into spin and charge modes. At the level of linear Lut-
due to detailed balance condition. As in the above ex-
tinger liquid theory, spin-charge separation is an ex-
ample of the distribution imbalance relaxation, we then
act property of the model [14]. At weak coupling, the
assume that electrons are hot, that is, at an excess tem-
perature T + ΔT with respect to the temperature T of
splitting between velocities of collective spin (vσ) and
charge (vρ) density waves is related to the forward scat-
lattice phonons. Electron-phonon collisions tend to re-
tering component of the interaction vρ -vσ ∼ V0 (recall
lax ΔT , and the corresponding rate for relaxation can
that for repulsive interactions vρ > vσ). Assuming then
be found by projecting the collision integral onto the
thermal excitations with ε ∼ T , the Born condition can
energy mode,
be equivalently formulated as T/(m∗vF ) ≫ vρ - vσ.
∑
∑
ϵp np = -
ϵpSt{np, Nq},
In other words, for fermionic quasiparticles to preserve
p
p
their integrity the excitation energy (or temperature)
should be bigger than the energy scale of spin-charge
with ϵp = εp - εF . To linear order in ΔT one finds
separation.
from the phonon emission processes of hot electrons,
The interplay of spectrum nonlinearities and in-
∂tΔT = -ΔT/τep, where
teractions leads to spin-charge coupling [78, 79]. Al-
though irrelevant in the renormalization group sense,
6vF
τ-1ep = -
×
the newly emerging higher order operators capture
πT3L
the attenuation of quasiparticles. The kinetic prop-
∑
erties of 1D quantum liquids with spin-charge cou-
× Wϵpωqfεp(1 - fεp)(fεp+ωq + bωq).
(50)
pling are not fully understood. There are basically
pp′q
two possible approaches one may pursue. The first is
Upon completion of the remaining momentum integra-
to refermionize the nonlinear bosonic theory to obtain
tions, we then find to leading order in T
an effective description in terms of dressed quasiparti-
cles: holons and spinons. Holon relaxation was conside-
9ζ(3)
τ-1ep =
T (Λ2/s2vF ϱ).
(51)
red in Refs. [36,37] based on non-Abelian bosonization
8π3
[80]. The advantage of this complex theory is that, in
principle, it allows to go beyond the weakly interact-
The scattering rate due to the deformation potential
is parametrically weaker, scaling as τ-1ep ∝ T3. The
ing limit for spinful fermions. Alternatively, one may
backscattering mechanism results in an activated tem-
choose to continue working in bosonic language. In the
perature dependence ∝ e-TA/T with TA = 2spF . It
limit of weak backscattering one can then account for
is straightforward to generalize Eq. (51) to the case
spin-charge interaction perturbatively in the basis of
when electronic relaxation occurs via several acoustic
well-defined spin and charge modes. This second pro-
branches. Notice also that the piezoelectric potential
cedure is limited to weak interactions V2pF ≪ V0 ≪ vF .
may have complicated angular dependence in case of
To complement previous studies, we follow in this sec-
wires oriented arbitrarily with respect to the crystallo-
tion the second path. In part this will enable us to ex-
plore the fermion-boson duality. We delegate technical
graphical axis of the sample. A proper angular aver-
aging would change then numerical factors in Eq. (51)
details of bosonization to the Appendix (see full text)
where we took the simplest geometry. Luttinger liquid
and elucidate here the impact of spin-charge scattering
effects lead to renormalization of the linear-T behavior
on various decay rates.
and transform it into a power-law with interaction de-
The lowest order nonlinearity, compatible with
pendent exponent ∝ TK, where K = vF /u is the ratio
SU(2) symmetry of the problem is cubic. It contains
787
14*
A. Levchenko, T. Micklitz
ЖЭТФ, том 159, вып. 4, 2021
one charge and two spin operators. Treating this term
which after momentum integration gives a factor of
in a perturbative expansion generates a collision ker-
(πLT/6vρ)∂tΔT . The right-hand-side can be linearized
nel that describes the decay of a plasmon into two spin
with the usual substitution Nq = bq + bq(1 + bq)φq,
modes ρ → σσ. It reads
where φq = ωqΔT/T2 for the case of a thermal imbal-
∑
[
ance. After some algebra one finds
St{Nρ, Nσ} = - W
Nρq(1+Nσq
)(1+Nσ ) -q
1
2
∑
q1q2
ωρqSt{Nρ, Nσ} =
]
q>0
- (1 + Nρq)Nσq
Nσ
,
(52)
1
q2
∑
where Nρ/σ are the bosonic occupations of charge (ρ)
= -ΔT (ωρq/T)2W(1 + bρq)bσq
bσ ,
(57)
1
q2
and spin (σ) excitations. The scattering probability
qq1q2
W = 2π|A|2δq=q1+q2δ(ωq - ωq1 - ωq )
(53)
2
where we repeatedly used energy conservation and the
contains an amplitude scaling cubically with momenta
detailed balance condition. Performing the final inte-
of the bosons |A|2 = (π3/8L)|q||q1||q2|Γ2ρσσ. The per-
grations, we then arrive at
turbative result for the coupling constant is Γρσσ =
√
3π
=V′
/
2π2, where the prime denotes the derivative
τ-1ρ =
Γ2ρσσ(T3/v4σ)F(vσ/vρ),
(58)
2pF
16
with respect to pF . Note that it thus vanishes for the
integrable case of constant interaction. At smallest
where the dimensionless function reads
momenta the dispersion relations are linear ωρ/σ =
∞
∫
= vρ/σ|q|. The kinematics of this process uniquely
F (κ) = κ(1 - κ2) dz z5(1 + bz)bz+bz-
(59)
fixes momenta in the final state. Indeed, for concrete-
ness let q > 0, then q1 = q(vρ + vσ)/2vσ and q2 =
0
= -q(vρ - vσ)/2vσ, which means that spin waves are
with bz = (ez - 1)-1 and z± = z(1 ± κ)/2. One can
counterpropagating. From dimensional analysis it be-
readily check that F → 32π4/15 in the limit κ → 1.
comes apparent that St{Nρ, Nσ} defines the decay rate
The same scattering process can be alternatively
of a plasmon, and one can introduce the characteristic
viewed as a mutual spin-charge friction. Physically,
rate
∑
v2ρ - v2σ
this is analogous to the electron-phonon drag effect,
τ-1ρ =
W ≃ q3(V ′2p
)2
F
typically studied in the context of thermoelectricity, or
v3
σ
q1q2
Coulomb drag in double-layers [81] and spin Coulomb
For the sake of an estimate, one may now take V′
∼
2pF
drag [82]. In each of these examples momentum trans-
∼ V2pF/pF and replace vρ/σ ∼ vF, except in their dif-
fer between interactively coupled systems leads to drag-
ference where vρ - vσ ∼ V0, and finds the life-time
ging of one sub-system by the flow of the other. For
)3
instance, in the context of spin physics in Luttinger liq-
V0
(V2pF )2( q
τ-1
∼εF
(54)
ρ
uids, generation of spin current is possible by Coulomb
vF vF
pF
drag [83]. To estimate the spin-charge drag rate, one
Notice the nonanalytic dependence of interaction ∝ V3.
can consider a boosted frame of reference for spin and
For thermal plasmons the relaxation rate can be cal-
charge excitations with mismatched boost velocities
culated from Eq. (52) by a projection onto an energy
uρ/σ. The scattering leads to momentum exchange be-
mode. We observe that as |q2| ≪ q the relaxation
tween spins and charge and, as a result, to relaxation
occurs by small energy transfer from right-movers to
∂tuρ = -(uρ - uσ)/τρσ. To capture this effect, we lin-
left-movers (or vise versa) so that interbrach processes
earize the collision integral for N(ωq - uq) with respect
are slow. Assuming that right-moving excitations are
to u, for both spin and charge occupations, and then
hotter by ΔT , and in complete analogy to the fermionic
project onto the momentum mode to calculate the rate
case, we find
of momentum loss by (e. g.) charge modes
∑
∑
ωρq∂tNρq =
ωρqSt{Nρ, Nσ}.
(55)
∑
q>0
q>0
∂tPρ =
qSt{Nρ, Nσ} =
The left-hand-side is straightforward to evaluate fur-
q
ther, noting that
∑
Δu
ωρq∂t
ΔT
=-
q2W(1 + bρq)bσq
bσ .
(60)
1
q2
∂tNρq = ∂T Nρq∂tΔT =
,
(56)
T
qq1 q2
4T2 sh2(ωq/2T)
788
ЖЭТФ, том 159, вып. 4, 2021
Kinetic processes in Fermi-Luttinger liquids
When we compare this to ∂tPρ = (πLT2/3v3ρ)∂tuρ, we
for momenta q ∼ pF the occupation is small, Nσq ∝
find that thus defined drag relaxation rate τ-1ρσ coin-
∝ e-εσ/T ≪ 1, and correspondingly 1+Nσ ≈ 1, where
cides with Eq. (58) up to a constant factor. It is per-
εσ is the band width of spin excitations. The latter is
haps useful to note that τ-1ρσ ∝ T3 is consistent with
parametrically of the order of the spin exchange cou-
the expectation that Coulomb drag transresistivity be-
pling. Viewing Eq. (61) as the collision integral for
tween double quantum wires due to interwire momen-
spins, we thus write
tum transfer from spin-charge coupling at zero mag-
∑
St{Nσ } =q
[P(q1, q′1)Nσq′
- P(q′1,q1)Nσ ],
(63)
netic field scales as ρD ∝ T5 [37]. Indeed, this rate is
1
1
q1
q′
1
accompanied by two thermal phase space factors ∼ T
per wire, thus leading to T5. In the drag problem,
where
∑
the factor q3 results from the width of the dynamic
P (q′1, q1) =
WNρq′
(1 + Nρ )
(64)
2
q2
charge structure factor and the underlying scattering
′
2
q2q
that gives rise to q3 is precisely the decay of a charge
is the transition rate for spin scattering processes. More
boson into two spin bosons.
specifically, it describes a collision with momentum
The next in complexity is a quartic nonlinearity in
transfer δq, in which a spin is scattered out of the ini-
spin-charge coupling which leads to two-boson scatte-
tial state q1. It can thus be rewritten as P(q′1, q1) =
ring ρσ → ρσ. In particular, we consider backscat-
= Pδq(q1), and following the same prescription, the
tering of spin excitations on plasmons. Such scattering
transition rate for the inverse process reads P(q1, q′1) =
processes correspond to the diffusion of spin excitations
= P-δq(q1 + δq). Performing then a small-momentum
near the spectral edge, and the goal is to calculate the
expansion,
corresponding diffusion constant. As alluded to earlier,
the discussion parallels the previous calculation of the
P (q1, q′1)Nσq′
≈ P-δq(q1)Nσ +q
1
1
backscattering of a deep hole in the fermionic language.
The corresponding collision integral reads
σ
δq2
+ δq∂q1[P-δq(q1)N
]+
∂2q
[P-δq(q1)Nσ ],
(65)
q
1
1
q1
2
St{Nρ, Nσ} =
the collision integral of spin excitations takes the sim-
∑
[
plified form
=-
W Nσq
(1 + Nσq′)Nρq
(1 + Nρq′ ) -
1
1
2
2
q2q1q′
2
St{Nσq
} = -∂q1[Aρσ(q1)Nσ ]+q
1
1
]
- Nσq′
(1 + Nσq
)Nρq′
(1 + Nρ ) .
(61)
1
1
1
2
q2
+
∂2q
[Bρσ(q1)N
σ ],
(66)
1
q1
2
The scattering rate for this process is given by
where
W = 2π|A|2δQ,Q′δ(E - E′)
(62)
∑
∑
Aρσ = -
δqPδq(q1), Bρσ =
δq2Pδq(q1).
(67)
with the amplitude |A|2 = (Γρσ/8L)2|q1q′1q2q′2|, where
δq
δq
the coupling constant at the perturbative level reads
At this stage we focus on the derivation of Pδq(q1). The
Γρσ = V′′
. The notations for momentum and energy
2pF
momentum conservation implicit in W removes the q′2
conservation here are Q = q1 + q2 and E = ωσq
+ωρ .q
1
2
integration. We then notice that distribution functions
Let momenta q1 and q′1 correspond to the initial and fi-
limit the typical momentum transfer and momenta of
nal states of the spin excitation near the spectral edge.
plasmons to q2 ∼ δq ∼ T/vF . At the same time, the
Kinematically each momentum is of the order of the
typical momentum of spins at the spectral edge is q1 ∼
Fermi momentum, q1 ∼ q′1 ∼ pF , while their difference,
∼ pF and it is sufficient to calculate Pδq(pF). With
q′1 - q1 ∼ T/vF , is small. This corresponds to a small
these observations at hand, we can now approximate
momentum change in each collision, which is accom-
energy conservation by
panied by the excitation of plasmons at low momenta
q2 ∼ q′2 ∼ T/vF . For this reason the low-energy de-
1
δ(E - E′) ≈
δ(q2 - δq/2).
scription based on Eq. (61) is sufficient to capture this
vρ
physics. Under the specified conditions and n complete
This removes the q2 integral, and we thus arrive at
analogy with the fermionic case, we can convert the
collision integral into a Fokker-Planck differential op-
V2ρσ
(δq/pF )2
Pδq =
,
(68)
erator, thus describing the diffusion of spins. Indeed,
1024Lvρ sh2(vρδq/4T)
789
A. Levchenko, T. Micklitz
ЖЭТФ, том 159, вып. 4, 2021
with the notation Vρσ = p2F Γρσ. Finally, this defines
of the injected boson is due to scattering with inter-
the diffusion coefficient of spins in momentum space
branch momentum transfer. Indeed, for q1, q2, q′1 > 0
associated to ρσ → ρσ scattering channel
momentum conservation implies that q′2 is order q3,
since energy conservation fixes q′2 ≈ -(3ξ2/2)q1q2q′1
)5
3
π
(Vρσ)2( T
Curiously, even though a finite ξ is crucial to resolve
Bρσ =
p3F vρ.
(69)
30
vρ
pF vρ
the kinematic constraints it drops out from the corre-
√
3
sponding rate provided that q1 ≪
T/vρξ2. In this
In addition to spin-charge scattering, nonlinearities
regime vρ|q′2| ≪ T, implying that Nρq′
≈ T/ωρq′
and q′2
2
2
also allow for spin-spin scattering. Importantly for the
cancels out from W. The decay rate then scales para-
momentum space diffusion, scattering processes with
metrically as τ-1ρ ∝ T q4. This estimate is applicable
√
spin-flips are enhanced. They are thus described by a
as long as T/vρ ≲ q ≪3
T/vρξ2.
different scaling of the probability with momentum as
For thermal plasmons, this rate can be estimated
compared to Eq. (68). That is,
more accurately by projecting the collision integral
onto the energy mode. Assuming that the boson with
V2σσ
1
Pδq =
,
(70)
momentum q1 is “hotter” by a temperature difference
8π2Lvσ sh2(vσδq/4T)
ΔT , one finds upon repeating the steps from the pre-
vious similar calculations
and this crucial detail is technically speaking traced
back to the non-commutativity of spin operators when
∑
6vρ
ωq1 ωq2
calculating the corresponding amplitude. The impor-
τ-1ρ =
×
T2
tance of spin flips is also apparent at the level of
πLTq1q2
q′1q′
2
fermions. Indeed, the ratio of scattering rates between
spinless and spinful cases has exactly the same param-
×WNρq
Nρq
(1 + Nρq′
)(1 + Nρq′ ).
(72)
1
2
1
2
eter (q/pF )2 ≪ 1 as the ratio between probabilities in
For the kinematics of the process specified above, one
Eqs. (68) and (70). The resulting diffusion constant in
sum is removed by momentum conservation setting
the spin-spin channel is then
q′
= q1+q2. Energy conservation removes another inte-
1
)3
4π
(Vσσ)2( T
gral, setting q′2 = -(3ξ2/2)q1q2(q1+q2). The remaining
Bσσ =
p3F vσ.
(71)
integrals can, after rescaling of momentum variables in
15
vσ
pF vσ
units of temperature, be brought to a dimensionless
A microscopic calculation of the respective coupling
double-integral. This results in
constants for the different scattering channels is a chal-
)2
(
)4
lenging task. Known approaches include weak coupling
3c12
(Vρρ
T
τ-1ρ =
T
,
(73)
results obtained via mobile impurity model [69], results
(4π)4
vρ
pF vρ
for Kondo polarons [66], and calculations in the strong
where the coefficient
interaction limit within the non-Abelian bosonization
∞
∫
framework [37], as well as a model departing from the
x2y2(x + y)ex+ydxdy
c12 =
Wigner crystal limit [84].
(ex - 1)(ey - 1)(ex+y - 1)
Two-boson processes also contribute to the thermal-
0
ization rates [33,85,86]. For charge excitations this re-
and Vρρ = p2F Γρρ.
sults in a subleading correction to Eq. (58). In the
The two-spin scattering can be analyzed in the same
spin sector the situation is, however, different since
way, starting out from Eq. (61) by changing Nρ → Nσ.
at the cubic level of nonlinearities spins are kinemati-
The crucial difference is in the momentum dependence
cally forbidden to scatter. In both cases nonlinearity of
of the scattering rate, which is enhanced by spin-flip
the bosonic spectrum plays an important role to open
processes. The resulting spin wave thermalization rate
phase space for such collisions. In order to general-
due to two-boson scattering processes reads
ize the present model, consider first the charge sector
and assume a weakly anharmonic dispersion of plas-
)2
(
)2
(Vσσ
T
mons, ωρq ≈ vρ|q|(1 - (ξq)2). Assume now that a right-
τ-1σ ∼
T
(74)
vσ
pF vσ
moving boson with momentum q1 ≳ T/vρ is injected
into the Luttinger liquid. For this setting the collision
This final estimate exhausts all possible scattering pro-
term from Eq. (61), with replacement Nσ → Nρ, dic-
cesses emerging from the quartic corrections to the lin-
tates that the dominant process limiting the lifetime
ear Luttinger liquid model.
790
ЖЭТФ, том 159, вып. 4, 2021
Kinetic processes in Fermi-Luttinger liquids
Funding. This work was supported by the U. S.
15.
D. L. Maslov, Lecture Notes for the LXXXI Les
Department of Energy (DOE), Office of Science, Ba-
Houches Summer School “Nanoscopic Quantum Tran-
sic Energy Sciences (BES) Program for Materials and
sport” (2004).
Chemistry Research in Quantum Information Science
16.
S. Tomonaga, Prog. Theor. Phys. (Kyoto) 5, 544
under Award No. DE-SC0020313. T. M. acknowl-
(1950).
edges financial support by Brazilian agencies CNPq
17.
J. M. Luttinger, J. Math. Phys. N. Y. 4, 1154 (1963).
and FAPERJ.
18.
D. C. Mattis and E. H. Lieb, J. Math. Phys. 6, 304
The full text of this paper is published in the English
(1965); see also Mathematical Physics in One Dimen-
version of JETP.
sion, Acad. Press, New York (1966).
19.
I. E. Dzyaloshinskii and A. I. Larkin, Sov. Phys.
JETP 38, 202 (1974).
REFERENCES
20.
A. Luther and I. Peschel, Phys. Rev. B 9, 2911 (1974).
1.
A. A. Abrikosov, L. P. Gor’kov, and I. E. Dzyaloshin-
21.
H. Gutfreund and M. Schick, Phys. Rev. 168, 418
skii, Methods of Quantum Field Theory in Statistical
(1968).
Physics, ed. by R. S. Silverman, Dover Publ. (1975).
22.
V. V. Deshpande, M. Bockrath, L. I. Glazman, and
2.
D. Pains, Elementary Excitations in Solids: Lectures
A. Yacoby, Nature 464, 209 (2010).
on Phonons, Electrons, and Plasmons, CRC Press
23.
A. Imambekov, T. L. Schmidt, and L. I. Glazman,
(1999).
Rev. Mod. Phys. 84, 1253 (2012).
3.
L. D. Landau, Sov. Phys. JETP 3, 920 (1957); 5, 101
24.
K. Samokhin, J. Phys.: Condens. Matter 10, 533
(1957); 35, 70 (1959).
(1998).
4.
A. A. Abrikosov and I. M. Khalatnikov, Rep. Prog.
25.
A. V. Rozhkov, Eur. Phys. J. 47, 193 (2005); Phys.
Phys. 22, 329 (1959).
Rev. B 74, 245123 (2006); Phys. Rev. Lett. 112,
106403 (2014).
5.
G. A. Brooker and J. Sykes, Phys. Rev. Lett. 21, 279
(1968).
26.
M. Khodas, M. Pustilnik, A. Kamenev, and L. Glaz-
man, Phys. Rev. 76, 155402 (2007).
6.
R. N. Gurzhi, A. I. Kopeliovich, and S. B. Rutkevich,
Adv. Phys. 36, 221 (1987).
27.
D. A. Bagrets, I. V. Gornyi, A. D. Mirlin, and
D. G. Polyakov, Semiconductors 42, 994 (2008).
7.
P. J. Ledwith, H. Guo, and L. Levitov, Ann. Phys.
411, 167913 (2019).
28.
R. G. Pereira, S. R. White, and I. Affleck, Phys. Rev.
B 79, 165113 (2009).
8.
O. M. Auslaender, A. Yacoby, R. de Picciotto,
29.
T. Micklitz and A. Levchenko, Phys. Rev. Lett. 106,
K. W. Baldwin, L. N. Pfeiffer, and K. W. West, Sci-
196402 (2011).
ence 295, 825 (2002).
30.
S. Teber, Phys. Rev. B 86, 195112 (2012).
9.
M. Bockrath, D. H. Cobden, J. Lu, A. G. Rinzler,
R. E. Smalley, L. Balents, and P. L. McEuen, Nature
31.
K. A. Matveev and A. Furusaki, Phys. Rev. Lett.
397, 598 (1999).
111, 256401 (2013).
32.
Z. Ristivojevic and K. A. Matveev, Phys. Rev. B 87,
10.
A. M. Chang, L. N. Pfeiffer, and K. W. West, Phys.
Rev. Lett. 77, 2538 (1996).
165108 (2013).
33.
I. V. Protopopov, D. B. Gutman, and A. D. Mirlin,
11.
A. M. Chang, Rev. Mod. Phys. 75, 1449 (2003).
Phys. Rev. B 90, 125113 (2014); Phys. Rev. B 91,
12.
T. Li, P. Wang, H. Fu, L. Du, K. A. Schreiber,
195110 (2015).
X. Mu, X. Liu, G. Sullivan, G. A. Csáthy, X. Lin,
34.
L. Balents and R. Egger, Phys. Rev. B 64, 035310
and R.-R. Du, Phys. Rev. Lett. 115, 136804 (2015).
(2001).
13.
F. D. M. Haldane, J. Phys. C: Sol. St. Phys. 14, 2585
35.
T. Karzig, L. I. Glazman, and F. von Oppen, Phys.
(1981); Phys. Rev. Lett. 47, 1840 (1981).
Rev. Lett. 105, 226407 (2010).
14.
T. Giamarchi, Quantum Physics in One Dimension,
36.
T. L. Schmidt, A. Imambekov, and L. I. Glazman,
Clarendon Press (2004).
Phys. Rev. B 82, 245104 (2010).
791
A. Levchenko, T. Micklitz
ЖЭТФ, том 159, вып. 4, 2021
37.
R. G. Pereira and E. Sela, Phys. Rev. B 82, 115324
55.
H. le Sueur, C. Altimiras, U. Gennser, A. Cavanna,
(2010).
D. Mailly, and F. Pierre, Phys. Rev. Lett. 105,
056803 (2010).
38.
A. Levchenko, Phys. Rev. Lett. 113, 196401 (2014).
56.
M. G. Prokudina, S. Ludwig, V. Pellegrini, L. Sorba,
39.
M. Bard, I. V. Protopopov, and A. D. Mirlin, Phys.
G. Biasiol, and V. S. Khrapai, Phys. Rev. Lett. 112,
Rev. B 97, 195147 (2018).
216402 (2014).
40.
K. A. Matveev and Z. Ristivojevic, Phys. Rev. B 102,
57.
J. R. Taylor, Scattering Theory: The Quantum Theo-
045401 (2020).
ry of Nonrelativistic Collisions, Dover Publ. (2006).
58.
Y. M. Sirenko, V. Mitin, and P. Vasilopoulos, Phys.
41.
Z. Yao, H. Postma, L. Balents, and C. Dekker, Nature
Rev. B 50, 4631 (1994).
402, 273 (1999).
59.
A. M. Lunde, K. Flensberg, and L. I. Glazman, Phys.
42.
O. M. Auslaender, A. Yacoby, R. de Picciotto,
Rev. B 75, 245418 (2007).
K. W. Baldwin, L. N. Pfeiffer, and K. W. West Phys.
Rev. Lett. 84, 1764 (2000).
60.
A. Levchenko, Z. Ristivojevic, and T. Micklitz, Phys.
Rev. B 83, 041303(R) (2011).
43.
O. M. Auslaender, H. Steinberg, A. Yacoby, Y. Tser-
kovnyak, B. I. Halperin, K. W. Baldwin, L. N. Pfeif-
61.
B. Sutherland, Beautiful Models, World Sci., Singa-
fer, and K. W. West, Science 308, 88 (2005).
pore (2004).
62.
T. Cheon and T. Shigehara, Phys. Rev. Lett. 82, 2536
44.
Y. Jompol, C. J. B. Ford, J. P. Griffiths, I. Far-
(1999).
rer, G. A. C. Jones, D. Anderson, D. A. Ritchie,
T. W. Silk, and A. J. Schofield, Science 325, 597
63.
T. Ogawa, A. Furusaki, and N. Nagaosa, Phys. Rev.
(2009).
Lett. 68, 3638 (1992).
45.
H. Steinberg, G. Barak, A. Yacoby, L. N. Pfeiffer,
64.
A. H. Castro Neto and M. P. A. Fisher, Phys. Rev.
K. W. West, B. I. Halperin, and K. Le Hur, Nature
B 53, 9713 (1996).
Phys. 4, 116 (2007).
65.
A. Imambekov and L. I. Glazman, Phys. Rev. Lett.
46.
H. Kamata, N. Kumada, M. Hashisaka, K. Muraki,
100, 206805 (2008).
and T. Fujisawa, Nature Nanotechnol. 9, 177 (2014).
66.
A. Lamacraft, Phys. Rev. Lett. 101, 225301 (2008).
47.
E. Slot, M. A. Holst, H. S. J. van der Zant, and
67.
M. Schecter, D. M. Gangardt, and A. Kamenev, Ann.
S. V. Zaitsev-Zotov, Phys. Rev. Lett. 93,
176602
Phys. 327, 639 (2012).
(2004).
68.
K. A. Matveev and A. V. Andreev, Phys. Rev. B 86,
48.
L. Venkataraman, Y. S. Hong, and P. Kim, Phys.
045136 (2012).
Rev. Lett. 96, 076601 (2006).
69.
M.-T. Rieder, A. Levchenko, and T. Micklitz, Phys.
49.
A. N. Aleshin, H. J. Lee, Y. W. Park, and K. Akagi,
Rev. B 90, 245434 (2014).
Phys. Rev. Lett. 93, 196601 (2004).
70.
T. Micklitz, J. Rech, and K. A. Matveev, Phys. Rev.
B 81, 115313 (2010).
50.
J. D. Yuen, R. Menon, N. E. Coates, E. B. Namdas,
S. Cho, S. T. Hannahs, D. Moses, and A. J. Heeger,
71.
M.-T. Rieder, T. Micklitz, A. Levchenko, and
Nature Mater. 8, 572 (2009).
K. A. Matveev, Phys. Rev. B 90, 165405 (2014).
51.
C. Blumenstein, J. Schaefer, S. Mietke, A. Dollinger,
72.
H. Risken, The Fokker-Planck Equation: Methods of
M. Lochner, X. Y. Cui, L. Patthey, R. Matzdorf, and
Solution and Applications, Springer (1996).
R. Claessen, Nature Phys. 7, 776 (2011).
73.
V. L. Gurevich, V. B. Pevzner, and K. Hess, Phys.
52.
G. Barak, H. Steinberg, L. N. Pfeiffer, K. W. West,
Rev. B 51, 5219 (1995).
L. Glazman, F. von Oppen, and A. Yacoby, Nature
74.
A. Sergeev, M. Yu. Reizer, and V. Mitin, Phys. Rev.
Phys. 6, 489 (2010).
Lett. 94, 136602 (2005).
53.
G. Granger, J. P. Eisenstein, and J. L. Reno, Phys.
75.
G. Seelig and K. A. Matveev, Phys. Rev. Lett. 90,
Rev. Lett. 102, 086803 (2009).
176804 (2003).
54.
C. Altimiras, H. le Sueur, U. Gennser, A. Cavanna,
76.
G. Seelig, K. A. Matveev, and A. V. Andreev, Phys.
D. Mailly, and F. Pierre, Nature Phys. 6, 34 (2010).
Rev. Lett. 94, 066802 (2005).
792
ЖЭТФ, том 159, вып. 4, 2021
Kinetic processes in Fermi-Luttinger liquids
77. A. Levchenko and J. Schmalian, Ann. Phys. 419,
82. I. D’Amico and G. Vignale, Phys. Rev. B 62, 4853
168218 (2020).
(2000).
78. S. Brazovskii, F. Matveenko, and P. Nozieres, JETP
83. M. Pustilnik, E. G. Mishchenko, and O. A. Starykh,
Lett. 58, 796 (1993).
Phys. Rev. Lett. 97, 246803 (2006).
79. C. Nayak, K. Shtengel, D. Orgad, M. P. A. Fisher,
84. K. A. Matveev, A. V. Andreev, and A. D. Klirono-
and S. M. Girvin, Phys. Rev. B 64, 235113 (2001).
mos, Phys. Rev. B 90, 035148 (2014).
80. A. O. Gogolin, A. A. Nersesyan, and A. M. Tsvelik,
85. J. Lin, K. A. Matveev, and M. Pustilnik, Phys. Rev.
Bosonization and Strongly Correlated Systems, Cam-
Lett. 110, 016401 (2013).
bridge Univ. Press, Cambridge (1998).
81. B. N. Narozhny and A. Levchenko, Rev. Mod. Phys.
86. S. Apostolov, D. E. Liu, Z. Maizelis, and A. Levchen-
88, 025003 (2016).
ko, Phys. Rev. B 88, 045435 (2013).
793