ЖЭТФ, 2021, том 159, вып. 4, стр. 794-805

СИММЕТРИЙНЫЙ ПОДХОД В ЗАДАЧЕ

О РАСШИРЕНИИ ГАЗОВ В ВАКУУМ

Е. А. Кузнецовa,b,c*, М. Ю. Каган^d,e

^a Физический институт им. П. Н. Лебедева Российской академии наук

119991, Москва, Россия

^b Институт теоретической физики им. Л. Д. Ландау Российской академии наук

142432, Черноголовка, Московская обл., Россия

^c Сколковский Институт науки и технологий

121205, Сколково, Московская обл., Россия

^d Национальный исследовательский университет «Высшая школа экономики»

109028, Москва, Россия

^e Институт физических проблем им. П. Л. Капицы Российской академии наук

119334, Москва, Россия

Поступила в редакцию 7 января 2021 г.,

после переработки 7 января 2021 г.

Принята к публикации 7 января 2021 г.

Представлен краткий обзор результатов о разлете квантовых и классических газов в вакуум на основе

использования симметрий. Для квантовых газов в приближении Гросса - Питаевского дополнительные

симметрии возникают для газов с химическим потенциалом μ, зависящим от плотности n степенным об-

разом с показателем ν = 2/D, где D — размерность пространства. Для газовых конденсатов бозе-атомов

при температурах T → 0 эта симметрия возникает для двумерных систем. При D = 3 и, соответствен-

но, ν = 2/3 такая ситуация реализуется для взаимодействующего ферми-газа при низких температу-

рах в так называемом унитарном пределе [1]. Эта же симметрия для классических газов в трехмерной

геометрии возникает для газов с показателем адиабаты γ = 5/3. Оба эти факта были обнаружены в

1970 году независимо Талановым [2] для двумерного нелинейного Шредингера (совпадающего с уравне-

нием Гросса - Питаевского), описывающего стационарную самофокусировку света в средах с керровской

нелинейностью, а для классических газов — Анисмовым и Лысиковым [3]. В квазиклассическом пределе

уравнения Гросса - Питаевского совпадают с уравнениями гидродинамики идеального газа с показателем

адиабаты γ = 1+2/D. Автомодельные решения в этом приближении описывают на фоне расширяющего-

ся газа угловые деформации газового облака в рамках уравнений типа Ермакова. Такого рода изменения

формы расширяющегося облака наблюдаются в многочисленных экспериментах как при разлете газа

после воздействия мощного лазерного излучения, например, на металл, так и при разлете квантовых

газов в вакуум.

Статья для специального выпуска ЖЭТФ, посвященного 90-летию И. Е. Дзялошинского

DOI: 10.31857/S0044451021040222

речислять много различных физических примеров,

где используются симметрии. Нам кажется доста-

точным сослаться на курс Ландау - Лифшица [4],

1. ВВЕДЕНИЕ: ИСТОРИЯ ВОПРОСА

где их великое множество. В данном кратком об-

зоре мы рассмотрим, как симметрии реализуются

Симметрии в физике всегда играли ключевую

в задаче разлета в вакуум квантовых и классиче-

роль при получении точных соотношений и резуль-

ских газов в рамках соответственно уравнений Грос-

татов, на них основанных. Вряд ли имеет смысл пе-

са - Питаевского (ГП) и уравнений газовой динами-

^* E-mail: kuznetso@itp.ac.ru

ки (уравнения непрерывности и уравнения Эйле-

794

ЖЭТФ, том 159, вып. 4, 2021

Симметрийный подход в задаче о расширении газов в вакуум

ра для одноатомных газов с показателем адиабаты

Наиболее простая симметрия в случае степен-

γ = 5/3). Если говорить о квантовых газах, то мы

ной зависимости химического потенциала от плот-

будем рассматривать такие, для которых химиче-

ности — это симметрия относительно растяжений

ский потенциал μ зависит от плотности n степен-

пространственных координат и времени вида

ным образом с показателем ν = 2/D, где D — раз-

r → αr, t → α²t,

(1)

мерность пространства. Именно только для таких

значений показателя ν возникает дополнительная

где α — скейлинговый параметр. Этот факт легко

симметрия. Отметим, что в приближении ГП при

проверить исходя из уравнения ГП [14] для волно-

температуре T → 0 для конденсата слабонеидеаль-

вой функции бозе-конденсата ψ:

ного бозе-газа главным взаимодействием является

∂ψ

ℏ²

s-рассеяние. Если длина рассеяния a_s положитель-

iℏ

Δψ + μ(n)ψ,

(2)

∂t

на, то между атомами имеется отталкивание и со-

∫

стояние такого газа в магнитооптических ловушках

где n = |ψ|². Сохранение числа частиц N =

|ψ|²dr

оказывается устойчивым. При этом химический по-

и степенная зависимость μ ∝ n2/D обеспечивают

тенциал μ = gn, где g = 4πℏ²a_s/m. Таким образом,

одинаковые зависимости от скейлингового парамет-

только для двумерного бозе-газа появляется сим-

ра α кинетического члена и химического потенциала

метрия, о которой пойдет речь ниже. В случае от-

(определяющего нелинейность в (2)): они пропорци-

рицательной длины рассеяния между бозе-атомами

ональны α-2.

возникает притяжение. В нелинейной оптике тако-

В нелинейной оптике и физике плазмы урав-

го рода притяжение приводит к самофокусировке

нение ГП (2) имеет название нелинейного уравне-

света для сред с керровской нелинейностью. Оттал-

ния Шредингера (НУШ). Стандартный вид НУШ

кивание, в свою очередь, приводит к дефокусировке

возникает после приведения к безразмерному виду

светового пучка, которая приводит к тем же самым

уравнения (2):

эффектам, что и дифракция в поперечном направ-

∂ψ

лении к пучку. В случае a_s < 0 бозе-конденсаты ока-

Δψ - (ν + 1)|ψ|2ν ψ = 0,

(3)

∂t

зываются неустойчивыми, что приводит к формиро-

которое представимо в гамильтоновом виде [5]

ванию сжимающихся областей газа — коллапсу (см.

обзор [5] и ссылки там), наблюдаемому в экспери-

∂ψ

δH

менте [6,7]. Чтобы получить неустойчивое значение

∂t

δψ^∗

длины рассеяния в экспериментах, используют ре-

с гамильтонианом

зонанс Фешбаха [8, 9], позволяющий изменять a_s в

∫ [

]

больших пределах: от очень больших положитель-

H =

|∇ψ|² + |ψ|2(ν+1) dr.

(4)

ных значений до сильно отрицательных. Если для

бозе-атомов в случае отрицательных a_s возникает

Следует отметить, что скейлинговая симметрия (1)

коллапс, то для ферми-газов s-притяжение обеспе-

есть также в уравнении Шредингера для движения

чивает образование куперовских пар, которые при

квантовомеханической частицы в потенциале U =

T → 0 образуют сверхтекучий бозе-конденсат. Ва-

= βr-2 независимо от знака β и при любой размер-

рьируя длину рассеяния с помощью резонанса Феш-

ности D. Эта же симметрия присутствует и для гид-

баха, можно создать бозе-конденсат в так называ-

родинамики идеального газа с показателями адиа-

емом унитарном пределе [1], который реализуется

баты γ = 5/3 для потенциальных трехмерных тече-

при условии (|a_s|k_F )-1 → 0, где p_F = ℏk_F — импульс

ний [3] и γ = 2 в случае двумерных течений. По-

Ферми. В этом режиме положительный химический

следнее, в частности, связано с тем, что уравнение

потенциал μ(n) = 2(1 + β)ε_F , где в соответствии с

ГП (2) в квазиклассическом пределе (приближение

работами [10-13] β = -0.63 есть универсальная кон-

Томаса - Ферми) совпадает с уравнениями гидроди-

станта, а

намики для потенциальных течений газа [15, 16], и

ℏ

(

)2/3

поэтому данная симметрия сохраняется в случае га-

ε_F =

6π²n

зовой динамики с γ = 1+2/D. На это обстоятельство

— локальная энергия Ферми. Величина m представ-

внимание авторов [3] обратил Дзялошинский [17].

ляет собой удвоенную массу ферми-атома. В уни-

Однако скейлиговое преобразование не исчерпы-

тарном пределе, таким образом, химический потен-

вает всех симметрий уравнений (2) и (3). Более об-

циал имеет степенную зависимость от плотности с

щей является симметрия относительно преобразо-

показателем ν = 2/3.

ваний Таланова [2] — преобразований конформного

795

Е. А. Кузнецов, М. Ю. Каган

ЖЭТФ, том 159, вып. 4, 2021

типа, которые включают в себя как скейлинговые

они отличаются от гамильтониана и числа частиц

преобразования амплитуды, так и изменения фазы

наличием явной зависимости от времени t:

волновой функции ψ. Это преобразование было най-

∫

дено для двумерного НУШ, описывающего стацио-

C₁ =

r²|ψ|²dr - 4Ht,

нарную самофокусировку света в среде с керровской

∫

(8)

нелинейностью. Роль времени в уравнении (3) игра-

C₂ = r²|ψ|²dr - 2Ht² - C₁t.

ет координата z вдоль направления распростране-

ния пучка света.

При преобразованиях Таланова общего вида

Такого рода интегралы относятся к неавтономным,

(для всех ν = 2/D) уравнение (3) остается инвари-

что, как будет видно далее, не позволяет установить

антным при замене волновой функции ψ, координат

полную интегрируемость при автомодельной редук-

r и времени t на новую волновую функцию

ψ и но-

ции квазиклассических уравнений. Примером таких

вые координаты r^′ и время t^′ [18]:

неавтономных интегралов движения служит закон

сохранения центра масс, явно содержащий время t.

[

]

В случае газовой динамики впервые, по-види-

ψ(r, t) =

exp

ψ(r^′, t^′),

τ+t

4(τ + t)

мому, эта симметрия была найдена Овсянниковым

(5)

[21], а эффективно была использована Анисимовым

rτ

tτ

r^′ =

t^′ =

и Лысиковым [3] для построения точного осесим-

τ+t

меричного автомодельного решения, описывающе-

В линейной оптике эти соотношения известны как

го нелинейные угловые деформации газового об-

линзовые преобразования.

лака на фоне его расширения в вакуум. Впослед-

Важно отметить, что суперпозиция преобразова-

ствии было выяснено, что такого рода деформа-

ний с λ₁ = τ-11 и λ₂ = τ-12 представляет преобразо-

ции наблюдаются в различных физических зада-

вание (5) c λ₃ = λ₁ + λ₂. Таким образом, преобразо-

чах, например, при воздействии мощного лазерно-

вания (5) образуют абелевую группу [18].

го излучения на твердое вещество, в результате че-

Прямым следствием этой симметрии является

го на фоне расширяющегося газового облака его

теорема вириала, полученная Власовым, Петрище-

первоначальная форма в виде диска преобразует-

ся в сигарообразную форму (см. монографию [22]

вым, Талановым [19] для двумерного НУШ с куби-

ческой нелинейностью:

и содержащиеся там ссылки). Для квантовых га-

зов при их расширении в вакуум такие трансфор-

∫

d²

мации являются типичными как для бозе-газов, так

r²|ψ|²dr = 4H,

(6)

dt²

и для ферми-газов (см. соответственно работы [23] и

[24,25] и ссылки в них). Следует отметить, что пер-

Впервые эта теорема была установлена в работе [19]

вые масштабно-инвариантные, зависящие от време-

для фокусирующей нелинейности. Легко видеть,

ни решения для бозе-конденсатов в гидродинамиче-

что уравнение (6) справедливо и в случая оттал-

ском режиме для анизотропной ловушки были най-

кивания (дефокусирующей нелинейности) [15, 16].

дены Каганом, Сурковым и Шляпниковым [26]; в

Важно, что теорема вириала (6) верна при любом

частности, ими был определен спектр дыхательных

значении ν = 2/D [18, 20]. Отметим, что, с точки

мод осциллирующего типа. Позднее автомодельные

зрения классификации, НУШ с ν = 2/D относится

режимы наблюдались в экспериментах группы То-

к так называемым критическим моделям [5, 18, 20].

маса [24, 25] при анизотропном расширении из оп-

Простое интегрирование уравнения (6) дает, что

∫

тической ловушки в вакуум сильновзаимодействую-

средний квадрат размера облака R² =

r²|ψ|²dr/N

щего вырожденного ферми-газа атомов⁶Li.

меняется во времени квадратично:

Хотелось бы отметить, что в шестидесятых годах

прошлого века эта задача — задача о разлете газа в

NR² = 2Ht² + C₁t + C₂.

(7)

вакуум — была весьма популярна. Первые классиче-

В случае отталкивания (дефокусирующей нелиней-

ские результаты в этом направлении были получе-

ности) гамильтониан H положителен. Поэтому при

ны Овсянниковым (1956 г.) [21] и Дайсоном (1968 г.)

больших временах, t → ∞, средний размер R растет

[27]. Эти работы имели множество различных при-

со временем линейно. Соотношение (7) содержат две

ложений не только в гидродинамике, но также и в

константы, C₁ и C₂, которые являются новыми по

астрофизике (см., например, оригинальную статью

сравнению с H и N интегралами движения. Однако

Зельдовича [28]).

796

ЖЭТФ, том 159, вып. 4, 2021

Симметрийный подход в задаче о расширении газов в вакуум

В данном небольшом обзоре мы в основном огра-

ми имеет место отталкивание, а при a_s < 0 — притя-

ничимся рассмотрением квазиклассического расши-

жение. В последнем случае конденсат неустойчив —

рения квантовых газов в вакуум, что совпадает с

развитие этой неустойчивости ведет к коллапсу (см.,

разлетом идеального газа с показателем адиабаты

например, обзор [5]).

= 1 + 2/D. С помощью автомодельного реше-

Для ферми-атомов отрицательное значение a_s

ния будет показано, каким образом эволюциониру-

при уменьшении температуры, T

→ 0, способ-

ет форма разлетающегося облака для квантовых

ствует сначала формированию куперовского спари-

газов в квазиклассическом пределе и для разлета

вания атомов, впоследствии образующих бозе-кон-

идеального газа. Динамика автомодельного разле-

денсат. Как уже отмечалось во Введении, предел

та в этом случае описывается в рамках системы

(|a_s|k_F )-1 → 0, где p_F = ℏk_F — импульс Ферми, со-

обыкновенных дифференциальных уравнений ерма-

ответствует так называемому унитарному режиму,

ковского типа. Следует отметить, что впервые рас-

для которого

сматриваемая симметрия была использована Ер-

μ(n) = 2(1 + β)ε_F ,

(11)

маковым в 1880 г. [29] при построении решений

для ряда механических систем, включая движение

где β = -0.63, а

классической частицы в потенциале, представляю-

ℏ²

(

)2/3

щем сумму осцилляторного потенциала и потенциа-

ε_F =

6π²n

ла V (r) = β/r². Следует отметить, что эта же сим-

метрия помогает в нахождении спектра в кванто-

— локальная энергия Ферми. В этом случае уравне-

вом случае для систем N частиц, двигающихся в

ние движения для волновой функции конденсата ψ

плоскости и взаимодействующих между собой с по-

(T → 0) представляет собой обобщенное уравнение

тенциалом V (r_ij) = β/r2ij (r_ij — расстояние между

ГП (2) с μ(n) (11).

частицами) в присутствии внешнего осцилляторно-

После простого приведения к безразмерному ви-

го потенциала [30, 31]. Отметим также, что в семи-

ду уравнения ГП при ν = 2/D получаем стандарт-

десятые годы прошлого века результаты Ермакова

ное НУШ (3) с гамильтонианом (4), в котором пер-

были переоткрыты Рейем и Рейдом [32]. Сейчас все

вый член совпадает с полной кинетической энерги-

такого рода уравнения принято называть системами

ей, а второе слагаемое ответственно за отталкивание

Ермакова - Рея - Рейда (см., например, работу [33] и

между бозе-частицами.

ссылки в ней). В Заключении этой статьи мы обсу-

Вводя стандартным образом амплитуду и фазу,

дим, в чем состоит различие между разлетом кван-

ψ = Aexp(iϕ(r,t)) (n = A²), НУШ (3) переписыва-

тового и классического газов, а также эксперимен-

ется в виде двух уравнений — уравнения непрерыв-

тальные данные по разлету квантовых газов в ваку-

ности для n и уравнения эйконала для фазы ϕ:

ум.

∂n

+ (∇ · n∇ϕ) = 0,

(12)

∂t

2. ОСНОВНЫЕ УРАВНЕНИЯ И

КВАЗИКЛАССИКА

∂ϕ

(∇ϕ)²

+ μ(n) + T_QP = 0,

(13)

∂t

Рассмотрим уравнения ГП для волновой функ-

ции ψ бозе-конденсата [14]:

где v =∇ϕ представляет собой скорость (предпола-

гается отсутствие вихрей, ∇ × v = 0). Во втором

∂ψ

ℏ

уравнении слагаемое

iℏ

Δψ + μ(n)ψ.

(9)

∂t

Δ√n

Здесь m — масса бозона. В случае бозе-атомов m —

T_QP = -

(14)

2√n

масса атома, для ферми-атомов m — масса куперов-

ответственно за квантовое давление.

ской пары, т. е. равна удвоенной массе атома. Хими-

Уравнения для плотности n и фазы ϕ сохраняют

ческий потенциал μ для бозе-атомов равен

гамильтонову форму:

μ = gn,

(10)

∂n

δH

∂ϕ

δH

(15)

∂t

δϕ

∂t

δn

где g = 4πℏ²a_s/m — константа взаимодействия, про-

порциональная длине s-рассеяния a_s. Для положи-

где гамильтониан совпадает с (4). В переменных n

тельных значений длины рассеяния между бозона-

и ϕ гамильтониан H имеет вид

797

Е. А. Кузнецов, М. Ю. Каган

ЖЭТФ, том 159, вып. 4, 2021

[

]

∫

n (∇ϕ)

(∇√n)2

Рассмотрим, каким образом происходит разлет

H =

+nν+1

dr.

(16)

квантовых газов в вакуум в квазиклассическом при-

ближении. В этом случае уравнения движения, как

Как уже отмечалось во Введении, НУШ (3) при ν =

отмечалось, совпадают с уравнениями гидродина-

= 2/D обладает дополнительной симметрией отно-

мики для идеального газа с γ = 1 + 2/D. В трехмер-

сительно преобразований Таланова [2]. Преобразо-

ном случае, таким образом, речь идет о разлете в

вания Таланова содержат как скейлинговые преоб-

вакуум одноатомного газа (напомним, что для иде-

разования вида t → α²t и r → αr благодаря сохране-

ального газа γ = (i + 2)/i, где i — число степеней

∫

нию полного числа частиц N =

|ψ|²dr, так и преоб-

свободы).

разования фазы. Обе эти симметрии — нетеровского

В 1970 году Анисимов и Лысиков [3] открыли

типа, они приводят к появлению двух дополнитель-

очень интересное явление, связанное с нелинейными

ных интегралов движения, C₁ и C₂ (7), следующих

деформациями формы газового облака, расширяю-

из интегрирования соотношения вириала (6).

щегося в вакуум. Такое поведение непосредственно

Квазиклассическое приближение (нестационар-

следует из найденного ими решения для газа с γ =

ное приближение Томаса - Ферми) для уравнения

= 5/3 (см. также работы [22,36,37]). В данном разде-

ГП соответствует пренебрежению квантовым давле-

ле мы воспользуется теоремой вириала и построим

нием в уравнении (13):

анизотропное квазиклассическое решение, которое

совпадает с решением Анисимова - Лысикова при

μ(n) ≫ |T_QP |.

(17)

D = 3.

В результате уравнения движения превращаются

Будем искать решение уравнений (12) и (13) в

в уравнения гидродинамики для потенциального

автомодельном виде:

течения идеального газа с показателем адиабаты

f (ξ),

(20)

γ = 1 + 2/D:

V (a)

∂n

где скейлинговые параметры a являются функция-

+ (∇ · n∇ϕ) = 0,

(18)

∂t

ми времени t, ξlD

= x_l/a_l — автомодельные перемен-

ные, а V (a) =

a_l — объем в пространстве скей-

l=1

∂ϕ

(∇ϕ)²

линговых параметров. Отметим, что анзац (20) со-

+ μ(n) = 0.

(19)

∂t

храняет полное число частиц.

Подстановка (20) в уравнение непрерывности

Следует подчеркнуть, что все симметрии в этих

(12) допускает интегрирование, в результате чего

уравнениях сохраняются. Для этой системы оста-

фаза ϕ находится с точностью до произвольной

ется справедливой также и теорема вириала; в

функции ϕ₀(t):

этом случае в гамильтониане (16) необходимо пре-

∑

небречь вторым слагаемым, ответственным за кван-

a˙

lal

ϕ = ϕ₀(t) +

ξ2l.

(21)

товое давление.

В основном далее мы будем пренебрегать кван-

Функция ϕ₀(t) определяется из уравнения эйконала.

товым давлением. Пренебрежение квантовым дав-

Подстановка (21) в (13) дает D уравнений движения

лением предполагает более быстрые пространствен-

для параметров a_l:

ные и временные изменения фазы (большие фазо-

вые градиенты и производные по времени) по срав-

a_la_l =

(22)

нению с пространственно-временными вариациями

V (a)2/D

модуля ψ-функции в уравнении ГП. Подчеркнем,

где λ — произвольная положительная константа,

что все указанные симметрии не зависят от харак-

определяемая из начальных условий. Для f(ξ) в ре-

тера взаимодействия — отталкивания или притяже-

зультате имеем

ния. Это же относится и к теореме вириала (6).

[

]D/2

Для отталкивания из теоремы вириала следует, что

Dλ

f (ξ) =

ξ²

(23)

асимптотически при больших t средний размер об-

2(2 + D)

лака квантового газа, расширяющегося в вакуум,

Таким образом, плотность в переменных ξ зависит

вне зависимости от того, учитывается или не учиты-

только от модуля |ξ|. При

вается квантовое давление, растет линейно со вре-

√

менем, т. е. имеет место выход на баллистический

2(2 + D)

режим [34, 35].

|ξ| > |ξ|_max =

Dλ

798

ЖЭТФ, том 159, вып. 4, 2021

Симметрийный подход в задаче о расширении газов в вакуум

Казалось бы, наличие трех интегралов для системы

(24) — E, C₁ и C₂ — гарантирует ее интегрируемость

для всех физических размерностей, включая D = 3.

Однако это не так в силу того, что интегралы C₁ и

C₂ как функционалы от a_i явно зависят от времени:

∑

C₁ =

a2i - 4Et,

(28)

∑

C₂ =

a2i - 2Et² - C₁t,

(29)

Рис. 1. Поведение f(ξ) для ферми-газа в унитарном пре-

и по этой причине являются неавтономными, хотя

деле (произвольные единицы)

и находятся в инволюции с другими интегралами

движения, ср. с (8).

плотность n следует положить равной нулю (см.

2.1. Разлет двумерного газа

рис. 1 для D = 3). В соответствии с уравнениями

(22) динамика параметров a_i(t) (i = 1, . . . , D) пред-

Вначале рассмотрим более подробно разлет дву-

ставляет собой уравнения Ньютона для движения

мерного газа (см. работу [16]). В цилиндрической

частицы в D-мерном пространстве,

системе координат с a² = a²¹ + a²² и полярным углом

φ интеграл энергии записывается в виде

a_i = -∂U,

(24)

∂a_i

a²

φ2

2λ

в потенциале

a² sin2φ

Dλ

U (a) =

(25)

Домножая далее E на a² = 2Et² + C₁t + C₂, легко

2V (a)2/D

получить, что комбинация

Отметим, что эти уравнения относятся к так назы-

ваемым системам ермаковского типа [29] (см. также

E=Ea² -

a² a² = EC₂ -

C²¹

работу [33] и ссылки там).

Очевидно, что уравнения (24) должны иметь ту

является константой (интеграл Ермакова). В ре-

же симметрию, что и исходное уравнение ГП (2).

зультате мы приходим к закону сохранения новой

Во-первых, уравнения (24) сохраняют энергию

«энергии»

∑

⁽ dφ)2

² + U(a).

(26)

+ U_eff(φ)

(30)

dτ

l=1

с новым временем τ:

Во-вторых, для уравнений (24) прямым вычислени-

ем легко устанавливается вириальное соотношение

∫

dt^′

(6), записанное в терминах a_i. Для

^∑a2i имеем

dτ =

τ =

(31)

]

r²

2E(t^′)² + C₁t^′ + C₂

∑

d² ∑

[(da_i )²

d²a_i

a2i = 2

+a_i

dt²

где

2λ

U_eff (φ) =

(32)

Подстановка (24) в это соотношение дает

sin2φ

играет роль потенциальной энергии. Величина U_eff

d² ∑

∑

⁽ da_i )²

2Dλ

a2i = 2

= 4E,

всегда положительна и стремится к бесконечности

dt²

V (a)2/D

при φ → 0 и φ → π/2. Минимальное значение U_eff =

= 2λ при φ = π/4 соответствует изотропному слу-

что совпадает с (6). Дважды интегрируя, получаем

чаю. В изотропном случае меняется только величи-

два интеграла, C₁ и C₂:

на a², определяемая из соотношения вириала:

∑

= 2Et² + C₁t + C₂.

(27)

a² = 2Et² + C₁t + C₂.

799

Е. А. Кузнецов, М. Ю. Каган

ЖЭТФ, том 159, вып. 4, 2021

Новое время τ (31) может быть легко выражено

и в двумерном случае. При D = 3 энергию (26) сле-

через t:

дует записать, вводя сферическую систему коорди-

√

нат (a, θ, φ):

√

2E(t + t₀)

2E t₀

E τ = arctg

- arctg

⌋

⌊(da)2

⁽ dθ)2

⁽ dφ)2

E =

+a²

+a² sin² θ

где χ² =

E/E и t₀ = C₁/4E, так что τ = 0 при t = 0.

Если начальная скорость газа равна нулю (что ти-

3λ

пично для эксперимента), то константа C₁ = 0 и

(

)2/3

21/3a²

√

sin² θ cosθ sin2φ

√

E τ = arctg

Et.

Соответственно вводим снова энергию

C₂

В этом случае асимптотически при t → ∞

E=Ea² -

a² a² = EC₂ -

τ →τ_∞ =

√

(33)

— ермаковский интеграл, сохранение которого явля-

ется следствием симметрии относительно растяже-

Траектория φ(τ) находится из интегрирования вы-

ражения (30):

ний, и новое время τ с помощью той же формулы

∫

(31). В результате имеем

dφ

τ =

√

[

]^.

⁽ dθ⁾

⁽ dφ)2

E - U_eff(φ)

+ sin² θ

+U_eff,

(34)

Отсюда τ-период в потенциале U_eff (φ) (32) выража-

где эффективный потенциал выражается через сфе-

ется через интеграл

рические углы:

∫

dφ

3λ

T =2

√

U_eff =

(35)

[

(

)2/3

E - U_eff(φ)

21/3

sin² θ cosθ sin2φ

φ(-)

Таким образом, мы приходим к системе с двумя сте-

где φ(±) — корни уравнения

E = U_eff(φ) (точки

пенями свободы, θ и φ.

остановки). При больших значениях

E колебания

Для цилиндрически-симметричных решений, ко-

слабо зависят от деталей потенциала U_eff (φ).

√

гда cos φ = sin φ =

2/2, т.е. при φ = π/4, энергия

Асимптотически угловая

«скорость» dφ/dτ

→

√

E записывается в виде

→ ±

E, а τ-период T

→ π/

E, т. е. в этом

пределе T превосходит в два раза τ_∞ (33). Отметим

⁽ dθ)2

3λ

также, что зависимость T

E) является монотонной

(

)2/3

(36)

21/3

sin² θ cosθ

для U_eff (φ) с максимумом, соответствующим мини-

муму потенциала U_eff (π/4). Это означает, что при

аналогичном (30) для двумерного случая. Разни-

C₁ = 0 вторая точка остановки является недости-

ца состоит только в виде эффективного потенциала

жимой при t → ∞. В частности, если стартовать

U_eff . Интегрирование этого уравнения приводит к

с левой точки остановки, то система не достигает

результату Анисимова - Лысикова [3].

правой точки остановки. И наоборот: если старто-

В общем случае (при учете зависимости от обеих

вая точка правая, то левая недостижима. Такая

углов) одного интеграла

E недостаточно. Как бы-

ситуация, как мы увидим далее, является типичной

ло показано Гафе [38], данная система имеет еще

и для трехмерного цилиндрически-симметричного

один дополнительный интеграл движения (помимо

случая.

̃), который следует из теста Пенлеве. Существо-

вание уже двух интегралов движения гарантирует

2.2. Разлет трехмерного газа

полную интегрируемость этой системы. Важно от-

Для разлета ферми-газа в унитарном пределе,

метить, как и в предыдущем случае, что движение

когда ν = 2/3, уравнения для скейлинговых пара-

в потенциале (35) сохраняет свой нелинейный ква-

метров интегрируются тем же самым способом, что

зиосцилляционный характер.

800

ЖЭТФ, том 159, вып. 4, 2021

Симметрийный подход в задаче о расширении газов в вакуум

2.3. Учет квантового давления

тате приходим к следующему дифференциальному

уравнению для функции g = A/a:

Обсудим теперь, какова роль квантового давле-

ния при расширении квантовых газов в вакуум. От-

√

1 d²g

метим, что в точке ξ = ξ_max для полученных выше

- 2(g² +

λχ)g = 0,

2 dχ²

решений критерий квазиклассичности (17) наруша-

ется — в этой точке вторая производная амплитуды

с гр√ничными условиями g → 0 при χ → ∞ и g →

A по ξ обращается в бесконечность, соответствен-

→

-λ1/2χ при χ → -∞. Это уравнение пред-

но член квантового давления становится бесконечно

ставляет собой уравнение Пенлеве второго типа [40].

большим. Это типичная ситуация для квазикласси-

При больших положительных χ это уравнение пре-

ческих решений в квантовой механике, когда тре-

вращается в уравнение Эйри с экспоненциально за-

буется решить задачу о сшивке решений в точке

тухающим решением. При меньших |χ| решение бу-

остановки [39]. В данном случае роль точки оста-

дет близко к функции Эйри, оно осциллирующего

новки играет ξ = ξ_max. В окрестности точки ξ =

характера. При дальнейшем отходе от границы ξ =

= ξ_max необходимо сшивать построенное решение

= ξ_max во внутреннюю область в решении будут со-

при ξ < ξ_max (внутренняя область) с внешней облас-

храняться осцилляции, но их амплитуда будет убы-

тью ξ > ξ_max. Вдали от ξ_max во внутренней области

вать. Само решение при χ → -∞ будет выходить

решение должно переходить в найденное квазиклас-

на нужную асимптотику.

сическое, а во внешней области ψ должна подчи-

Появление этих осцилляций является главным

няться линейному уравнению Шредингера. Следу-

проявлением квантовой природы бозе-конденсата

ет сказать, что эта задача обсуждалась детально в

при его расширении в вакуум. Эти осцилляции

работе [40] для режима сильного трехмерного кол-

имеют дифракционное происхождение, они подобны

лапса в кубическом НУШ (ν = 1). Задача сшивки в

кольцам Ньютона.

данном случае может быть рассмотрена аналогич-

Хотелось бы отметить, что в одномерной задаче

ным образом.

о разлете бозе-газа в вакуум, как показано в работе

Далее будем предполагать Δξ ≪ ξ_max, т.е. пред-

[41] (см. в ней рис. 3е), вообще нет никаких осцилля-

ставляя переходную область Δξ достаточно узкой.

ций на краю. Причина состоит в том, что плотность

Легко понять, что задача может быть рассмотрена

в этом случае в окрестности крайней точки ведет

как одномерная в направлении, нормальном к по-

себя квадратично, и поэтому никакого нарушения

верхности ξ = ξ_max.

квазиклассики в этой точке не наблюдается. Одна-

Начнем с изотропного разлета двумерного бо-

ко при других условиях [42] осцилляции на краю

зе-газа, когда химический потенциал μ(n) = n. Об-

наблюдаются. Подчеркнем, что задача о сшивке в

ратимся к уравнению (13) для фазы ϕ. Для автомо-

пределе малых Δξ ≪ ξ_max сводится к одномерной

дельного квазиклассического решения фаза, напом-

задаче, но она по построению существенным обра-

ним, находится из интегрирования уравнения непре-

зом отличается от задачи разлета в рамках одно-

рывности, т. е. ϕ не чувствительна к изменению амп-

мерного НУШ, интегрируемого с помощью метода

литуды в области сшивки. Это означает, что всюду

обратной задачи рассеяния [43].

в переходной области можно считать, что

В анизотропном случае, очевидно, осцилляции

сохранятся. Во-первых, в операторе Лапласа наи-

∂ϕ

(∇ϕ)²

большая производная будет по нормали к поверхно-

≈ -2A²⁰,

∂t

сти ξ = ξ_max. Во-вторых, угловая скорость v_Ω = r

при достаточно больших временах t → ∞, когда раз-

где A²⁰ = a-2(1 - λξ²/4) есть решение квазикласси-

мер R газового облака значительно превосходит на-

ческих уравнений. В результате уравнение для ам-

чальный размер R₀, оказывается значительно мень-

плитуды A в области сшивки записывается в виде

ше

^R. Согласно теореме вириала (6),

˙R≈v_∞, а

√

∇²A - 2(A² - A²⁰)A = 0.

|dΩ/dτ|

v_Ω = r|

^Ω| =

≤

√

v_∞t

Поскольку A₀(ξ_max) = 0 (ξmax = 2/

λ), в этом

уравнении в слагаемом A²⁰ нужно удержать линей-

Это означает, что главные изменения будут происхо-

√

ные отклонения по χ = ξ - ξ_max: A²⁰ = -χa-2

λ, a

дить по нормали к границе ξ = ξ_max, а временными

в операторе Лапласа ∇² в силу узости переходного

изменениями по углу можно пренебречь. Если в на-

слоя оставить вторую производную по χ. В резуль-

чальный момент выполнено условие квазаклассич-

801

ЖЭТФ, вып. 4

Е. А. Кузнецов, М. Ю. Каган

ЖЭТФ, том 159, вып. 4, 2021

ности, то оно будет выполнено всюду за исключе-

что в окрестности этой поверхности возникают про-

нием узкой области δξ ≪ |ξ|_max. При этом отноше-

странственные осцилляции плотности дифракцион-

ние δξ и |ξ|_max в силу автомодельности можно счи-

ного характера. Именно этим различаются кванто-

тать неизменным, что справедливо по крайней ме-

вый и классические газы при их разлете.

ре при больших t. Таким образом, асимптотически

В заключение обсудим, в какой мере экспери-

задачу о сшивке следует считать одномерной по |ξ|

ментальные данные соответствуют полученным ана-

с локально-замороженным направлением нормали.

литическим результатам. В экспериментах [24] на-

Отсюда становится ясным, что вокруг поверхности

блюдалось автомодельное расширение сильновзаи-

ξ = ξ_max формируется пояс осцилляций плотности

модействующего ферми-газа из ловушки сигаро-

дифракционного характера.

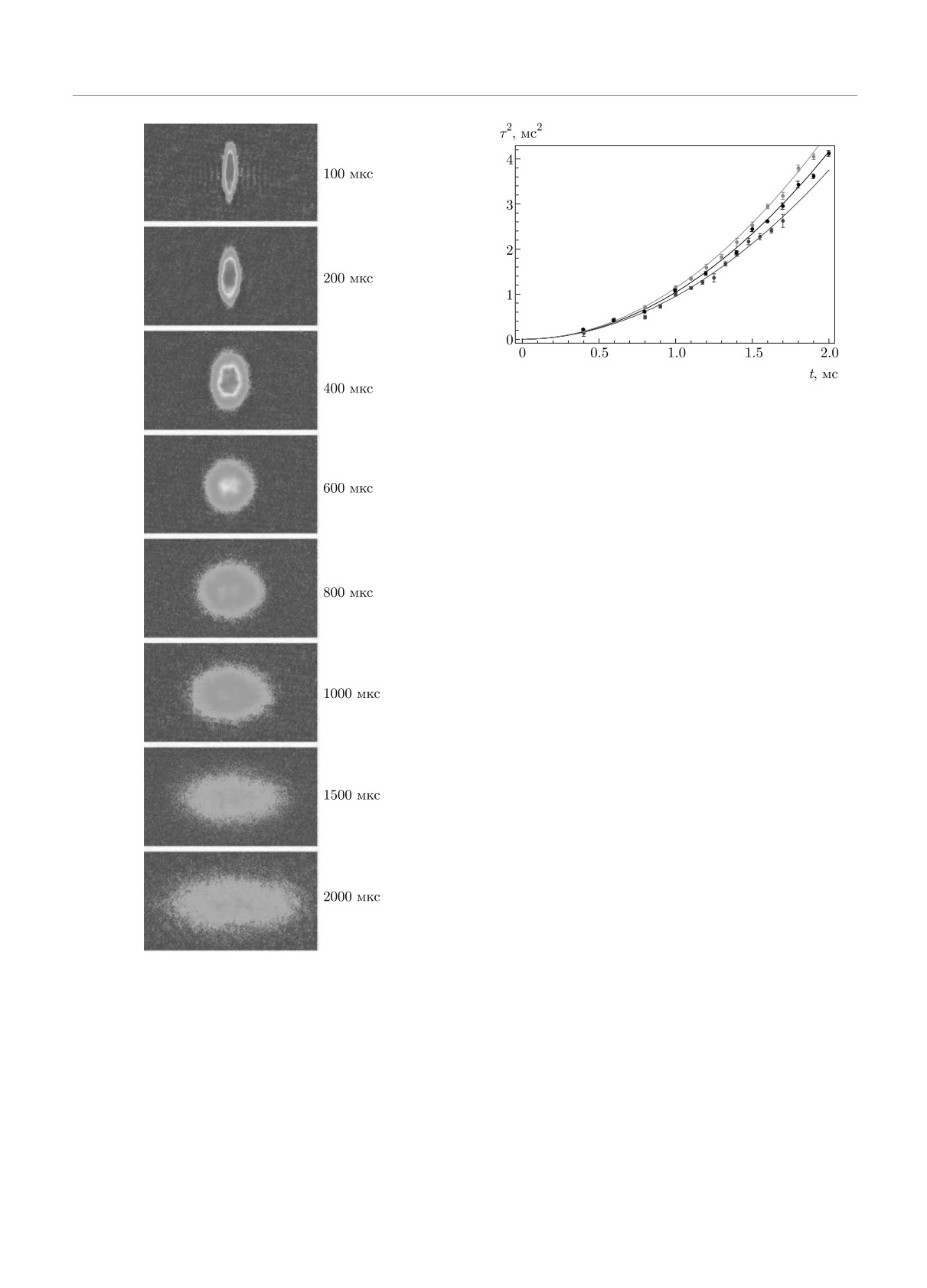
образной формы. На рис. 2, взятом из работы

Аналогичным образом анализируется поведе-

[24], представлены изображения расширяющегося

ние квантового ферми-газа в унитарном пределе в

ферми-газа. В начальный момент времени газовое

окрестности поверхности ξ = ξ_max.

облако имело форму сильно вытянутого эллипсои-

да в виде сигары (время t = 100 мкс), затем при

t = 600 мкс — почти сферическую и на конечной

3. ЗАКЛЮЧЕНИЕ

стадии облако имело форму диска. Общее время на-

блюдения было 2000 мкс, которое можно взять в ка-

Таким образом, мы показали, как симметрии для

честве полупериода (или меньше) угловых осцилля-

уравнения ГП, когда химический потенциал зави-

ций формы газового облака, t ≤ t_osc/2, в соответ-

сит от плотности n степенным образом с показа-

ствии с результатами предыдущего раздела. Таким

телем ν = 2/D и D — размерность пространства,

образом, все эти стадии качественно отвечают авто-

влияют на расширение квантовых газов в вакуум.

модельному решению.

Вследствие теоремы вириала, независимо от соотно-

На рис. 3 представлены результаты измерений

шения между квантовым давлением и химическим

среднего размера облака как функции времени для

потенциалом, средний размер расширяющегося об-

трех значений (k_F a_s)-1 [25]. Все три зависимости

лака растет асимптотически при больших временах

τ²(t) с хорошей точностью представляют собой па-

линейно с t, так что скорость расширения стремится

раболические зависимости в полном соответствии с

к постоянному значению v_∞ = (2H/N)1/2. Наиболее

соотношением (7), следующим из теоремы вириа-

общая симметрия уравнения ГП — симметрия от-

ла (6).

носительно преобразований Таланова, совокупность

Строго в резонансе, (k_F a_s)-1 = 0, средний раз-

которых образует абелеву группу. Эта же симмет-

мер облака 〈r²〉 может быть выражен через началь-

рия имеет место для потенциальных течений газов

ный потенциал ловушки U(r) в виде [25]

с показателем адиабаты γ = 1 + 2/D, описываемых

с помощью уравнений газовой динамики: уравнения

t²

〈r²〉 = 〈r²〉t=0 +

〈r · ∇U(r)〉t=0.

(37)

непрерывности и уравнения Эйлера. Важно, что эта

гидродинамическая система совпадает с уравнением

ГП в квазиклассическом пределе и наследует тем са-

Вычисления, представленные в работе [44], показы-

мым симметрии уравнения ГП.

вают, что закон расширения (37) совпадает с ква-

Мы показали также, что в квазиклассическом

зиклассической зависимостью 〈r²〉 (27) в унитарном

приближении уравнение ГП имеет автомодельные

пределе. Следует отметить, что, согласно выраже-

анизотропные решения, описывающие на фоне раз-

нию (27), величина 〈r²〉 действительно зависит ли-

лета нелинейные угловые квазиосцилляции формы

нейно от энергии, что было проверено в эксперимен-

облака квантового газа. В трехмерном случае эти

тах [25].

решения совпадают с решениями Анисимова - Лы-

Подчеркнем, что эти зависимости опираются на

сикова для расширения в вакуум классического од-

квазиклассическую теорию, которая ничем не отли-

ноатомного газа с показателем адиабаты γ = 5/3

чается от гидродинамики идеального газа с показа-

за исключением области, где в квазиклассике плот-

телем адиабаты γ = 5/3. Как мы показали, отличие

ность обращается в нуль. Это целая поверхность, ко-

квантового газа от классического в задаче о расши-

торая играет ту же самую роль, что и точка оста-

рении в вакуум состоит в учете квантового давле-

новки в квазиклассическом приближении в обыч-

ния, что приводит к появлению осцилляций плот-

ной квантовой механике. Задача сшивки решения

ности на границе расширяющегося облака. Судя по

во внутренней и во внешней областях показывает,

всему, в экспериментах [24,25] наблюдается расши-

802

ЖЭТФ, том 159, вып. 4, 2021

Симметрийный подход в задаче о расширении газов в вакуум

Рис. 3. Зависимость τ2(t): по вертикальной оси отло-

жены экспериментальные значения τ²(t)

≡ m[〈r²〉 -

− 〈r²〉t=0]/〈r · ∇U〉t=0, измеренные при расширении силь-

новзаимодействующего ферми-газа в зависимости от вре-

мени t (U(r)

— начальное значение потенциала ло-

вушки). Черные символы соответствуют газу в резонан-

се, (kF as)-1 = 0, красные и синие — соответственно

(kF as)-1 = 0.59 и (kF as)-1 = -0.61, сплошные кривые —

результаты расчета [25]

и в трехмерной задаче Анисимова-Лысикова. Это

свидетельствует о том, что нормальная компонента

играет в этом эксперименте более существенную

роль, чем сверхтекучая компонента. Напомним, что

одним из ключевых экспериментов по открытию

бозе-эйнштейновских конденсатов газов щелочных

элементов⁷Li,²³Na,⁸⁷Rb [45-47] было определение

функции распределения бозе-атомов при расшире-

нии газа в вакуум после выключения оптической

ловушки. Функция распределения имела бимодаль-

ную форму, которая соответствовала нормальной

и сверхтекучей компонентам. Для нормальной

компоненты распределение по скоростям было

широким — тепловым — максвелловского вида, а

сверхтекучая компонента обладала более узким рас-

пределением с шириной, определяемой параметром

взаимодействия (в смысле ГП). При малых, но ко-

нечных температурах из-за уменьшения плотности

Рис. 2. (В цвете онлайн) Изображения расширяющегося

при разлете температура бозе-конденсации падает,

сильновзаимодействующего ферми-газа во времени. На-

что неминуемо должно приводить к росту числа

чальная форма в виде сигары

атомов нормальной компоненты. По этой причине

форма облака должна определяться нормальной

компонентой, которую можно считать одноатомным

рение скорее нормального ферми-газа, чем сверхте-

газом. Холодная сверхтекучая компонента будет

кучего.

сосредоточена внутри расширяющегося облака.

Что касается разлета бозе-атомов, то в экспе-

Для ферми-газов эта ситуация, по-видимому, также

рименте [23] наблюдалась примерно та же самая

имеет место. В отличие от бозе-газов, переход к нор-

последовательность изменения формы облака, что

мальной компоненте при разлете ферми-газа будет

803

15*

Е. А. Кузнецов, М. Ю. Каган

ЖЭТФ, том 159, вып. 4, 2021

сопровождаться также и разрушением куперовских

11.

M. Bartenstein, A. Altmeyer, S. Riedl, S. Jochim,

пар. Таким образом, разлет квантового газа должен

C. Chin, J. Hecker Denschlag, and R. Grimm, Phys.

приводить к появлению колец Ньютона, что в экс-

Rev. Lett. 92, 120401 (2004).

периментах как [23], так и [24, 25] не наблюдалось.

12.

M. J. H. Ku, A. T. Sommer, L. W. Cheuk, and

Наблюдение таких осцилляций, по крайней мере на

M. W. Zwierlein, Science 335, 563 (2012).

начальной стадии разлета, было бы свидетельством

того, что газ находится в квантовом состоянии.

13.

G. Zürn, T. Lompe, A. N. Wenz, S. Jochim,

P. S. Julienne, and J. M. Hutson, Phys. Rev. Lett.

110, 135301 (2013).

Благодарности. Авторы благодарны А. В. Тур-

лапову и А. М. Камчатнову за ряд полезных обсуж-

14.

E. P. Gross, Nuovo Cim. 20, 454 (1961); L. P Pi-

дений.

taevskii, Sov. Phys. JETP 13, 451 (1961).

Финансирование. Работа одного из авторов

15.

E. A. Kuznetsov, M. Yu. Kagan, and A. V. Turlapov,

(Е. А. К.) выполнялась при поддержке Российского

Phys. Rev. A 101, 043612 (2020).

научного фонда (грант № 19-72-30028). Другой ав-

тор (М. Ю. К.) благодарит за поддержку Програм-

16.

Е. А. Кузнецов, М. Ю. Каган, ТМФ 202, 458

му фундаментальных исследований Национального

(2020).

исследовательского университета «Высшая школа

17.

И. Е. Дзялошинский, частное сообщение (1970).

экономики» и выражает благодарность Российско-

му фонду фундаментальных исследований (грант

18.

E. A. Kuznetsov and S. K. Turitsyn, Phys. Lett.

№20-02-00015). Авторы внесли равные вклады в вы-

A 112, 273 (1985).

полнение этой работы.

19.

С. Н. Власов, В. А. Петрищев, В. И. Таланов, Изв.

вузов, Радиофизика 14, 1353 (1971) [S. N. Vlasov,

V. A. Petrishchev, and V. I. Talanov, Radiophys.

ЛИТЕРАТУРА

Quant. Electr. 14, 1062 (1971)].

Л. П. Питаевский, УФН 178, 633 (2008) [L. P. Pi-

20.

K. Rypdal and J. J. Rasmussen, Phys. Scripta 33,

taevskii, Physics-Uspekhi 51, 603 (2008)].

498 (1986).

В. И. Таланов, Письма в ЖЭТФ 11, 303 (1970)

21.

Л. В. Овсянников, ДАН СССР 111, 47 (1956).

[V. I. Talanov, Sov. Phys. JETP Lett. 11, 199 (1970)].

22.

S. I. Anisimov and V. A. Khokhlov, Instabilities

С. И. Анисимов, Ю. И. Лысиков, ПММ 34, 926

in Laser-Matter Interaction, CRC Press Inc., Boca

(1970) [S. I. Anisimov and Yu. I. Lysikov, J. Appl.

Raton (1995).

Math. Mech. 34, 882 (1970)].

23.

Ю. В. Лиханова, С. Б. Медведев, М. П. Федорук,

Л. Д. Ландау, Е. М. Лифшиц, Теоретическая фи-

П. Л. Чаповский, Письма в ЖЭТФ 103, 452 (2016)

зика в 10 тт., Физматлит, Москва (2002).

[Yu. V. Likhanova, S. B. Medvedev, M. P. Fedoruk,

and P. L. Chapovsky, JETP Lett. 103, 403 (2016)].

В. Е. Захаров, Е. А. Кузнецов, УФН 182, 569

(2012) [V. E. Zakharov and E. A. Kuznetsov, Phy-

24.

K. M. O’Hara, S. L. Hemmer, M. E. Gehm, S. R. Gra-

sics-Uspekhi 55, 535 (2012)].

nade, and J. E. Thomas, Science 298, 2179 (2002).

S. L. Cornish, S. T. Thompson, and C. E. Wieman,

25.

E. Elliott, J. A. Joseph, and J. E. Thomas, Phys. Rev.

Phys. Rev. Lett. 96, 170401 (2006).

Lett. 112, 040405 (2014).

C. Eigen, A. L. Gaunt, A. Suleymanzade, N. Navon,

26.

Yu. Kagan, E. L. Surkov, and G. V. Shlyapnikov,

Z. Hadzibabic, and R. P. Smith, Phys. Rev. X 6,

Phys. Rev. A 55, R18 (1997).

041058 (2016).

27.

F. J. Dyson, J. Math. Mech. 91, 18 (1968).

H. Feshbach, Ann. Phys. 5, 357 (1958).

28.

Я. Б. Зельдович, Астроном. ж. 41, 873 (1964)

C. Chin, R. Grimm, P. Julienne, and E. Tiesinga,

[Ya. B. Zel’dovich, Sov. Astron. J. 8, 700 (1964)].

Rev. Mod. Phys. 82, 1225 (2010).

29.

В. П. Ермаков, Дифференциальные уравнения

10.

J. Joseph, B. Clancy, L. Luo, J. Kinast, A. Turlapov,

второго порядка. Условия интегрируемости в

and J. E. Thomas, Phys. Rev. Lett. 98,

170401

конечном виде: из лекций по интегрированию

(2007).

дифференциальных уравнений

[V. P. Ermakov,

804

ЖЭТФ, том 159, вып. 4, 2021

Симметрийный подход в задаче о расширении газов в вакуум

Differential Equations of the Second Order. Integra-

(1989) [L. D. Landau and E. M. Lifshitz, Quantum

bility Conditions in the Closed Form, University Izv.,

Mechanics: Non-Relativistic Theory, Pergamon Press

Kiev (1880)].

(1965)].

30. F. Calogero, J. Math. Phys. 10, 2191 (1969).

40. В. Е. Захаров, Е. А. Кузнецов, ЖЭТФ 91, 1310

(1986) [V. E. Zakharov and E. A. Kuznetsov, Sov.

31. L. P. Pitaevskii and A. Rosch, Phys. Rev. A 55, R853

Phys. JETP 64, 773 (1986)].

(1997).

41. G. A. El, V. V. Geogjaev, A. V. Gurevich, and

32. J. R. Ray and J. L. Reid, Phys. Lett. A 71, 317

A. L. Krylov, Physica D 87, 186 (1995).

(1979).

42. S. K. Ivanov and A. M. Kamchatnov, Phys. Rev.

33. C. Rogers and W. K. Schief, J. Math. Anal. and Appl.

A 99, 013609 (2019).

198, 194 (1996).

43. В. Е. Захаров, А. Б. Шабат, ЖЭТФ 61, 118 (1971)

34. A. V. Turlapov and M. Yu. Kagan, J. Phys.: Condens.

[V. E. Zakharov and A. B. Shabat, Sov. Phys. JETP

Matter 29, 383004 (2017).

34, 62 (1972)].

35. М. Ю. Каган, А. В. Турлапов, УФН 189, 225 (2019)

[M. Yu. Kagan and A. V. Turlapov, Physics-Uspekhi

44. E. A. Kuznetsov, M. Yu. Kagan, and A. V. Turlapov,

188, 225 (2019)].

arXiv:1903.04245 [cond-mat.quant-gas].

36. O. I. Bogoyavlensky, in Stochastic Behavior in Clas-

45. M. H. Anderson, J. R. Ensher, M. R. Matthews,

sical and Quantum Hamiltonian Systems, Sprin-

C. E. Wieman, and E. A. Cornell, Science 269, 198

ger-Verlag, Berlin (1979), p. 151.

(1995).

37. А. В. Борисов, И. С. Мамаев, А. А. Килин, Нели-

46. Cl. C. Bradley, C. A. Sackett, J. J. Tollett, and

нейная динамика 4, 363 (2008).

R. G. Hulet, Phys. Rev. Lett. 75, 1687 (1995).

38. B. Gaffet, J. Fluid Mech. 325, 113 (1996).

47. K. B. Davis, M.-O. Mewes, M. R. Andrew,

39. Л. Д. Ландау, Е. М. Лифшиц, Квантовая меха-

N. J. van Druten, D. S. Durfee, D. M. Kurn, and

ника. Нерелятивистская теория, Наука, Москва

W. Ketterle, Phys. Rev. Lett. 75, 3969 (1995).

805