ЖЭТФ, 2021, том 159, вып. 4, стр. 806-814

PHASE SLIPS, DISLOCATIONS, HALF-INTEGER VORTICES,

TWO-FLUID HYDRODYNAMICS, AND THE CHIRAL ANOMALY

IN CHARGE AND SPIN DENSITY WAVES

S. Brazovskiia*, N. Kirova^b

^a Université Paris-Saclay, CNRS, Laboratoire de Physique Théorique et Modèles Statistiques

91405, Orsay, France

^b Université Paris-Saclay, CNRS, Laboratoire de Physique des Solides

91405, Orsay, France

Received January 18, 2021,

revised version January 18, 2021

Accepted for publication January 18, 2021

Contribution for the JETP special issue in honor of I. E. Dzyaloshinskii’s 90th birthday

DOI: 10.31857/S0044451021040234

contrarily the conventional TDGL type, the resulting

equations still allow for a numerical modeling of tran-

sient processes related to space- and spatiotemporal

Abstract. This brief review recalls some chapters

vorticity in density waves (DWs).

in theory of density waves in quasi-1D electronic sys-

tems which may have appeared after inspirations from

1. Introduction.

studies of I. E. Dzyaloshinskii and collaborations with

1.1. Inspirations from I. E. Dzyaloshinskii.

him. First we address the spin density waves which

The authors had a chance to publish together with

rich order parameter allows for an unusual object of a

I. E. Dzyaloshinskii (I. E. D. in the following) the article

complex topological nature: a half-integer dislocation

[1] on doubly-quasi-periodic solitonic lattices emerging

combined with a semi-vortex of the staggered magneti-

in a 1D electronic system under simultaneous effects of

zation. It becomes energetically preferable with respect

the charge doping away from the half band filling and

to an ordinary dislocation due to the high Coulomb

of the spin polarization. This publication was in the

energy at low concentration of carriers. Generation of

course of our studies in theory of charge DWs (CDWs)

these objects should form a sequence of π-phase slips in

which had been started in 1976 by one of us (S. B., a

accordance with experimental doubling of phase-slips

thankful disciple of I. E. D.) under the inspiration and

rate. Next, we revise the commonly employed time-de-

initially with participation [2,3] of I. E. D. The trick of

pendent Ginzburg-Landau (TDGL) approach which is

the chiral transformations having been emploied in [2]

shown to suffer from a violation of the charge conser-

(see below), actually suggested by I. E. D., provided a

vation law resulting in nonphysical generation of parti-

handy frame to study adiabatic models of CDWs which

cles which is particularly pronounced for electronic vor-

later would lead S. B. to notice an instability of nor-

tices in the course of their nucleation or motion. The

mal electrons or holes, excited or injected to a CDW,

suggested consistent theory exploits the chiral transfor-

towards formation of solitons with the electron buried

mations taking into account the principle contribution

at the solitons’ midgap state, see [4] for a review. The

of the fermionic chiral anomaly to the effective action.

resulting physics of microscopic solitons and their ar-

The derived equations clarify partitions of charges, cur-

rays [5] can be traced back to I. E. D. invention of the

rents and rigidity among subsystems of the condensate

commensurability locking (published neglectfully only

and normal carriers and the gluing electric field. Be-

in conference proceedings [6]) and forth to his work

ing non-analitical with respect to the order parameter,

on exact solutions of many-body lattice models [7-10].

Much later, an indirect inspiration came to us [11, 12]

^* E-mail: serguei.brazovski@universite-paris-saclay.fr

from the article [13], where I. E. D. had noticed that

806

ЖЭТФ, том 159, вып. 4, 2021

Phase slips, dislocations, half-integer vortices.. .

a presence of a dislocation in a crystal possessing the

should proceed via propulsion of these combined ob-

antiferromagnetic spin order enforces a curious half-in-

jects which provides a natural interpretation for a con-

teger vortex of spins’ rotations.

fusing 2-fold enhancement of a frequency generated by

In this short review, we shall firstly describe com-

moving SDWs in comparison with CDWs.

bined topological defects — half-integer vortices of dis-

Beyond transient dislocations contributing to phase

placements and spin rotations in incommensurate spin

slips, static arrays of dislocations can appear in lat-

DWs (SDWs) which might necessarily appear under ap-

eral geometries when the electric field is applied trans-

plications of the driving electric field. These consider-

versely to the direction x of the CDW sliding. Indeed,

ations are related to I. E. D. study [13] and are co-

the interaction energy eΦ∂_xϕ/π of the deformed CDW

herent with a persistent interest in fractional vortices:

with the electric potential Φ resembles the one for a su-

from helium A ([14, 15] about the same time as [13])

perconductor under a magnetic field described by the

and triplet superconductors (reviews [16,17]) to FFLO

vector potential with the component A_x ≡ Φ. Then

phase [18, 19] and Bose condensate of polaritons [20]

the transverse to the chains electric field E_y = -∂_yΦ

(see also Ref. [21] for a more recent review). This di-

acts upon the CDW phase analogously to the action

rection in general is in line with long standing interests

of the transverse magnetic field in a superconducting

of I. E. D. in topological defects, recall [22] and partic-

film. Hence, an array of static dislocations should ap-

ularly [23].

pear above the electric field threshold as the vortex

lattice above the critical field Hc1 in a superconductor.

Next, we shall quote and augment for modelling

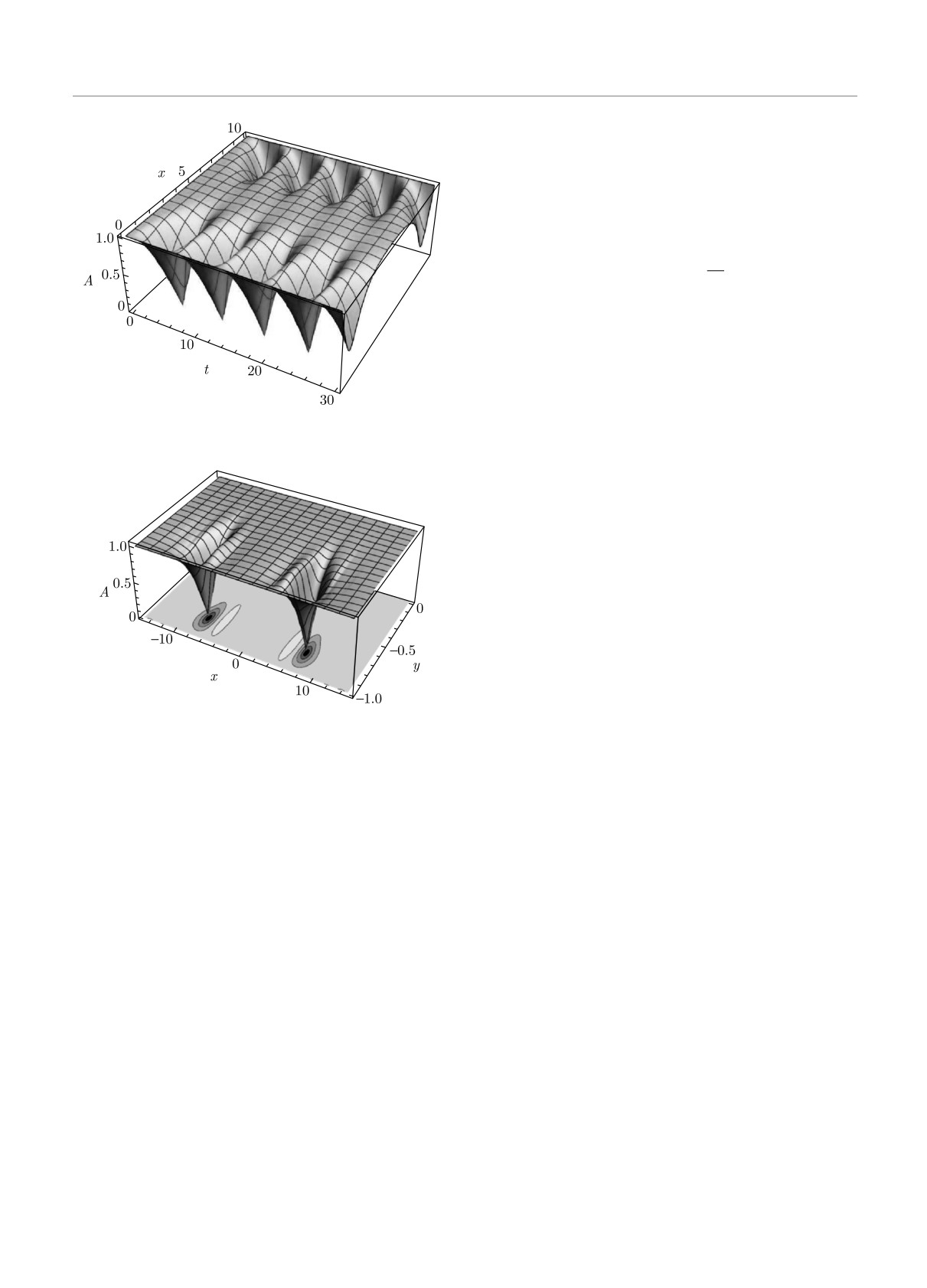
Figures 1 and 2 illustrate the sequences of phase

quite a recent development [24] on construction of the

slips and the static dislocations. The plots were ob-

chirally invariant (recall [2]) description of transient

tained from numerical modelling of a TDGL type equa-

processes in a CDW or SDW in presence of normal

tions as it has been described elsewere [24, 36, 37].

carriers. This formulation is free from a drawback of

the non-conservation of condensed particles which we

2. Combined half-integer dislocation and the

show to be inherent to the traditional TDGL approach.

magnetization vortex in a spin density wave.

CDW and SDW are characterized by scalar and vec-

1.2. Significance of static and transient topo-

tor order parameters: η_cdw(R) = A exp(iϕ) and η_sdw =

logical configurations in incommensurate sliding

= Am exp(iϕ), where m is the unit vector of the stag-

density waves. The DWs, see reviews [25-28], are

gered magnetization and R = (x, r_⊥) with x being the

seen as superstructures, usually weak (with an ampli-

chain direction.

tude A ≪ 1) and hence harmonic (A cos[q₀ ·r+ϕ(r)], q₀

The energy density of spin rotations m(R) in SDWs

and ϕ are the superstructure wave vector and phase).

is not affected by Coulomb forces:

The DWs are produced by modulations of electronic

charges and atomic displacements or of electronic spins

[

for CDWs or SDWs, correspondingly. The spectacular

W_spin{m} =

C_∥ (∂_xm)² +

2N_F

phenomena is the collective Fröhlich conductivity due

]

(

)

to the overall sliding with the collective current pro-

C_⊥

(∂_ym)² + (∂_zm)²

+W_sa .

(1)

portional to the phase velocity, j_c ∝ ∂_tϕ. The DW

sliding is ultimately related to the current conversion

Here N_F = 2/πℏv_F and v_F are the density of states

process which necessarily involves topological defects

and the Fermi velocity of the parent metal,

C_∥ and

[29] like solitons, dislocation lines/loops, and the tran-

C_⊥ are the elastic moduli related to the rotation of

sient processes of phase slips which develop as the edge

the staggered magnetization unit vector m, and W_sa

dislocation line (D-line) proliferating/expanding across

is the spin anisotropy energy. Elastic moduli

C_∥ and

the sample [30,31] or as the plane of the DW amplitude

C_⊥ are similar to bare moduli of phase displacements

vanishing across a narrow sample [32-35].

taken without Coulomb interactions, i. e., C0∥ and C_⊥

The DW deformations generate a local charge den-

in Eq. (2) below.

sity n_c ∝ ∂_xϕ which brings about a high cost of the

The energy for deformations related to phase dis-

Coulomb energy. The Coulomb enhancement of the

placements in both CDW and SDW takes a form

dislocation energy plays an intriguing role in SDWs

[

]

(

)₂

(

)₂

bringing to life a kind of a mixed topological object:

W_chrg{ϕ} =

C⁰

∂_xϕ

+C_⊥

∇_⊥ϕ

a half-integer dislocation combined with a semi-vortex

2N_F

^∥ π

of a staggered magnetization vector. The phase slips,

+W_C +W_str,

(2)

necessary for the current conversion or the depinning,

807

S. Brazovskii, N. Kirova

ЖЭТФ, том 159, вып. 4, 2021

actions and the screening results in hardening of the

effective compessibility [38] which vanishes at T_c and

diverges at low T with freezing out of normal carriers.

The effective compressibility C_∥ hardens with growing

r_⊥ (starting from C0∥ at shortest interchain distances)

as C_∥ ∼ r2⊥/r²⁰ beyond the screening length of the par-

ent metal, r_⊥ > r₀ ∼ 1 Å, until it saturates beyond

√

ρ_n at the value which

the screening length r_scr = r₀/

grows activationally with lowering T. At r_⊥ > r_scr

C0∥ ⇒ C_∥ = ρ_c/ρ_n,

C_∥ ∝ ρ_c ∝ A² ∝ (T_c - T) at T → T_c

and

C_∥ ∝ ρ-1n ∝ exp(Δ/T) at T → 0.

Fig. 1. A time-periodic sequence of phase-slip events seen as

The resulting big energy of dislocations at small

a set of nodes of the DW amplitude A(x, t)

ρ_n does not prevent their creation which just requires

for bigger applied potentials, but the Coulomb energy

changes drastically the energy dependence of the dis-

location on its position Y (with respect to a coun-

terpart or a surface). While the spin-vortex energy

per its unit length is a standard WV ∼ Tc ln(Y/a⊥),

for the dislocation as the charged phase vortex, this

form of the energy is reached only when the Coulomb

interaction is screened at Y

≫ r_scr, where W_D ∼

∼ T_c(r_scr/r₀)ln(Y/r_scr) with the energy scale being

greatly enhanced as r_scr/r₀.

Coulomb interactions become even more important

in an intermediate (wide at low T ) region r₀ < r_⊥ <

< r_scr governed by the nonlocal, due to unscreened

Fig. 2. A static array of dislocations appearing in the electric

Coulomb interactions, elasticity with C_∥ ∼ r2⊥/r²⁰. For

field applied transversely to the direction x of DW displace-

dislocations with rscr ≫ Y ≫ r0, a curious confine-

ments

ment law is established with W_D ∼ T_cY/r₀ meaning a

constant force acting upon the D-line.

(Y ) are similar only

The energies W_V (Y ) and W_D

where dimensionless parameters C0∥ and C_⊥ are the

near T_c at small A (hence, at the vanishing gap Δ)

normalized compression and share moduli; C_⊥

∝

when the abundant free carriers screen Coulomb in-

∝ (AT_cN_F a_⊥)² is a measure of the interchain cou-

teractions already at shortest distances. Otherwise, at

pling related to the transition temperature T_c (a_⊥ is

the developed gap Δ > T, the energy of dislocations is

the interchain distance); W_str is the stress energy from

greatly enhanced with respect to that of vortices which

an applied electric potential and/or from disbalance of

brings about the option of their splitting into combined

normal carriers which promote deformation and/or the

half-integer vortices. In SDWs, the Coulomb enhance-

motion of the DW.

ment of the dislocation energy plays a principal role

The Coulomb part of the energy, W_C , comes from

bringing to life a special combined topological object:

the local charge density related to the DW displace-

the half-integer dislocation ϕ → ϕ + π accompanied

ments: n_c = eρ_c∂_xϕ/πa2⊥, where ρ_c and ρ_n = 1 - ρ_c

by the 180^◦ rotation O_π of the staggered magnetiza-

are the normalized densities of the condensate and of

tion m → -m. Indeed, the SDW order parameter

the normal carriers. The Coulomb interactions dras-

η = mcos(Qx+ϕ) allows for the following three types

tically affect the charged phase deformations of dislo-

of self-mapping η → η associated with vorticities ν_ϕ

cations greatly increasing their energy and stretching

and ν_m.

the shape in the chains’ x-direction, as we shall remind

(i) Normal dislocation D2π: ϕ → ϕ + 2π ≡ ϕ and

below. Vaguely, the combined effect of Coulomb inter-

m → m; ν_ϕ = 1 and ν_m = 0.

808

ЖЭТФ, том 159, вып. 4, 2021

Phase slips, dislocations, half-integer vortices.. .

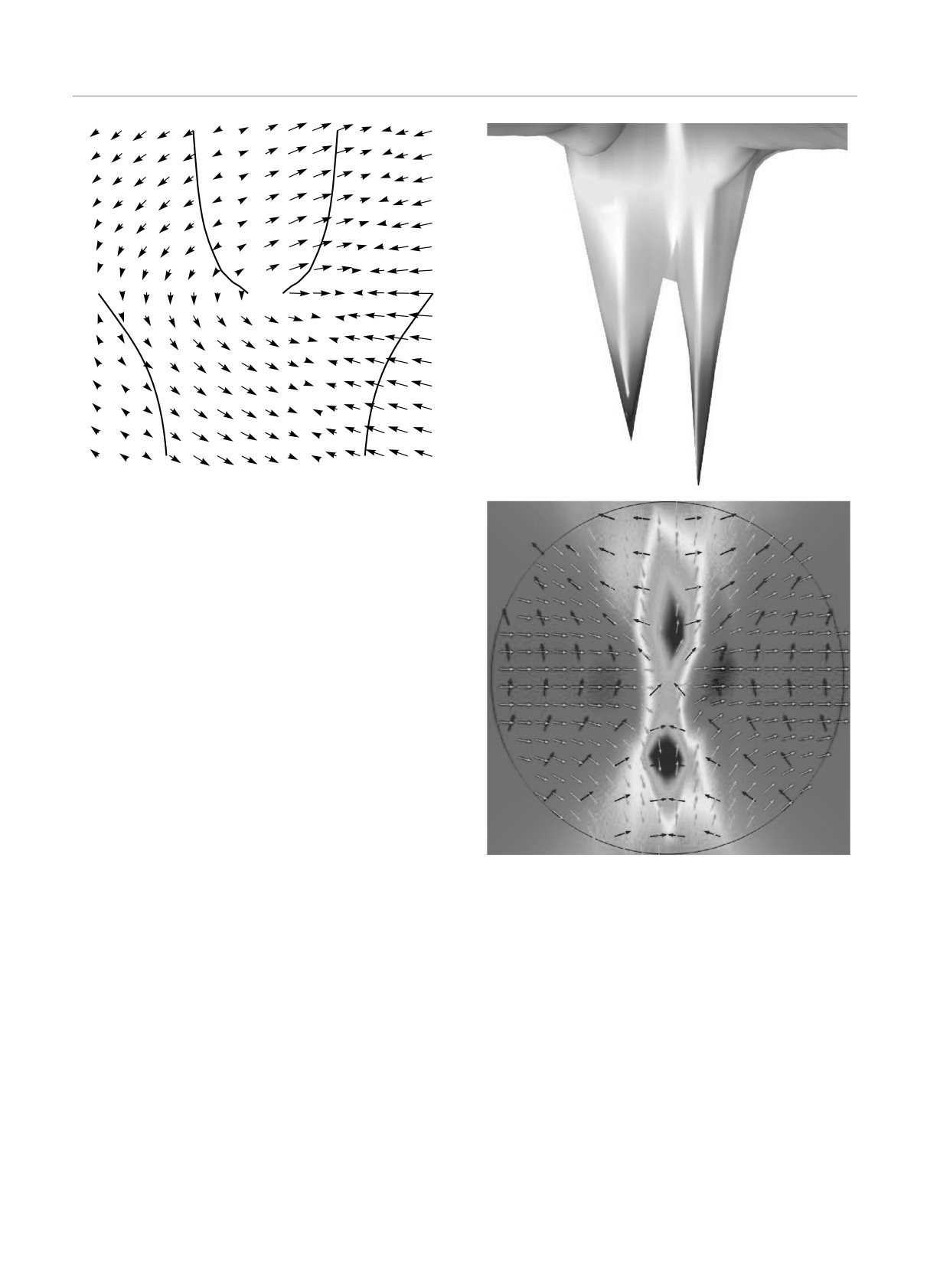
Fig. 3. Vector-field m for the half-integer dislocation combined

with the semi-vortex of the magnetization. Solid lines indicate

constant DW phases. Due to the presence of the half-integer

dislocation, the number of sites changes between the upper

and the lower rows from 2.5 periods (6 + 6 + 3) to 2 periods

(7 + 5)

(ii) Normal m-vortex V2π : m → O2πm ≡ m and

ϕ → ϕ; ν_ϕ = 0 and ν_m = 1.

(iii) Combined object D_πV_π: ϕ → ϕ ± π and

m → O_πm = -m; ν_ϕ = ±1/2 and ν_m = ±1/2.

In the last case, both the orientational factor m and

the translational one cos(Qx + ϕ) change the sign, but

their product in η stays invariant, as it is demonstrated

schematically in Fig. 3. Remind that at a given posi-

tion, the energies of vortices depend on their winding

numbers proportional to ν2ϕ,m

We must compare the energies of objects (i) and (iii)

under the requirement of the charge conservation, i. e.,

Fig. 4. Results of the modeling of the evolution from a sin-

preserving the total phase vorticity

^∑ν_ϕ. For magnetic

gle integer dislocation to the split pair of half-integer com-

vortices the total vorticity

^∑ν_m does not need to be

bined vortices: (upper panel) the order parameter amplitude

conserved but in the bulk it must be kept zero; other-

A(x, y); (lowere panel) vector fields of the CDW phase and of

the spin rotation on the background of the density plot for the

wise, the energy of noncompensated vortices diverges

amplitude

logarithmically at large distances. For phase disloca-

tions, the energy divergence is not a limitation since it

is compensated by driving potentials. Hence, the only

as expected at low T, the magnetic vortex energy can

decomposition path for the conventional dislocation of

be neglected, then the decomposition gains nearly half

of the energy, (ν2π = 1)² ⇒ 2(ν_π = 1/2)² = 1/2, which

the case (i) to the two pairs of half-vortices of the case

(iii) is D2π ⇒ {D_π, V_π} + {D_π, V_-π}. If the energy pa-

makes it inevitable.

Figure 4 demonstrates results of our modeling of the

rameters for both D and V were the same, then the dis-

sociation cost is zero: ν22π = 1 ⇒ 4ν2π = 1, and the re-

evolution from a single phase-only integer vortex (the

dislocation) to the split pair of half-integer combined

sult will depend on a tiny balance of similar coefficients.

But with dominating Coulomb energy of dislocations,

vortices.

809

S. Brazovskii, N. Kirova

ЖЭТФ, том 159, вып. 4, 2021

The known SDW crystals possess low symmetries

the explicitly gauge-invariant theory of superconduc-

which originates the spin anisotropy in all three direc-

tors [39, 40], this approach fails for DWs and other

tions. Being small, the anisotropy will not affect the

electronic crystals. Working at all steps explicitly with

arrangement in a vicinity of the D-line, but at large

interfering order parameter and normal electrons, em-

distances from the D-line, the π-rotation of spins will

ploying the chiral invariance, and taking the account

be concentrated in space within the Neél domain wall,

for the related quantum anomaly have allowed us [24]

as it has been outlined already in [13]. The wall will

to construct the treatable theory without descending

form a string (a plane in 3D) which tempts to confine

to the burdens of microscopic calculations.

the two combined objects.

The equations of motion for the CDW phase cer-

Unusually, there will be no confinement within a

tify the local equilibrium of forces (elastic, Coulomb,

quite wide region r⊥ < rscr, where the linear law,

frictional) with no relation to the charge conservation.

rather than conventional logarithmic one, for the D-line

Instead, the last is usually preserved automatically by

energy takes place as we have sketched above. Here,

construction of the charge and the current densities:

the total energy gain with respect to the normal D-li-

n_c =

ρ_c∂_xϕ, j_c = -

ρ_c∂_tϕ

(3)

ne is -E_C N/2, where E_C ∼ T_ca_⊥/r₀ and N = Y/a_⊥

is the number of chains separating combined vortices.

(to be compared with j_sc ∝ ρ_sc∂_xϑ for the current de-

This repulsive anti-confinement energy directly over-

pendence on the phase ϑ in superconductors).

runs the energy lost due to domain wall formation

The normalized (to T = 0) condensate density or

W^Aspin = w^AN, both having the similar N-dependence.

the phase rigidity ρ_c(A) has a property that ρ_c(0) = 1

Usually w^A ∼ 1 K/chain ≪ E_C ∼ 10¹ K, so the net

and ρ_c(A) ∼ A² → 0 at A → 0. The expressions

interaction between the two semivortices is strongly re-

(3) can ensure the charge conservation automatically

pulsive.

indeed, but only if the CDW amplitude is invariable:

Beyond the screening length r_⊥

> r_scr, the

A(t, x) = const, otherwise

Coulomb energy slows down while the W^Aspin keeps

growing linearly, then the total energy gain of two ob-

dn_c

= ∂_tn_c+∂_xj_c =

(∂_xρ_c∂_tϕ-∂_tρ_c∂_xϕ) = 0.

(4)

jects with respect to one D-line is

rscr

T_c

The charge conservation dn_c/dt = 0 is violated in the

W = -E0 lnN+w^AN, E0 ∼ Tc

√

r₀

ρ_n

current-carrying state (∂_tϕ = 0) if ρ_c is not space ho-

mogeneous (∂_xρ_c = 0) and in the strained (charged)

Hence there is an equilibrium distance between the

state ∂_xϕ = 0 if ρ_c varies in time, ∂_tρ_c = 0. It is ulti-

semi-vortices, N_eq

∼ E₀/w^A ∝ 1/√ρn, which di-

mately necessary to take into account the normal car-

verges with freezing out of the screening when ρ_n → 0.

riers explicitly, without integrating them out prema-

Already at accessibly low temperatures, the string

turely. At first sight, that would require for descend-

length may reach the sample width which is typically

ing to the fully microscopic theory with its notorious

about 1 μm.

complications even in linear or gapless regimes [33,41].

3. Two-fluid hydrodynamics for collective

Still, there is a way [24] to keep the phenomenology

and normal variables in density waves.

which is based on the knowledge of chiral invariance

Related cases of vortices in superconductors and

and transformation, importantly taking into account

dislocations in DWs

[32-34] are described usually

the chiral anomaly.

within GL-like models and their time-dependent

The Lagrangian H - iℏ∂_t for electrons in 1D CDW

(TDGL) generalizations. While being consistent for

has a form

(

)

iϕ

-iℏ∂_t - iℏv_F ∂_x + Φ - v_F A_x

Δe

(5)

Δe^-iϕ

-iℏ∂_t + iℏv_F ∂_x + Φ + v_F A_x

where Φ and A_x are the scalar and the vector poten-

ℏv_F

Φ -→ V = Φ +

∂_xϕ,

tials. The chiral transformation ψ_± -→ ψ_±exp(±iϕ/2)

[2] brings the wave function Ψ to the local frame of a

(6)

distorted CDW phase. It eliminates the phase factors

in non-diagonal elements in L, but in expense of addi-

ℏ

A_x -→ A^∗x = A_x +

∂_tϕ,

tional parts in Φ and A_x:

2v_F

810

ЖЭТФ, том 159, вып. 4, 2021

Phase slips, dislocations, half-integer vortices.. .

E_x -→ E^∗x = -∂_xV + ∂_tA^∗x =

a) The term with ϵ_Δ in Eq. (9) yields to (8) the

(

)

ℏv_F

forth order gradients of the phase (∂2xxϕ)² instead of

=E_x -

∂2x -

∂²t

ϕ.

(7)

v²

the expected second order (∂_xϕ)².

b) The singularity in k in the term with ρ_n seems

The additions to Φ and A_x from x- and t-derivatives

at first to serve fortunately by canceling excess gradi-

of the phase are naturally interpreted as the Fermi en-

ents leading to the contribution proportional to (∂_xϕ)²:

ergy shift δE_F = v_F δP_F following the Fermi momen-

δW_ρn = -ρ_n(ℏv_F /4π)(∂_xϕ + πN_F Φ)². This expres-

tum shift δP_F = ℏ∂_xϕ/2 under the CDW phase defor-

sion brings two confusions with respect to the expected

mations. Under the CDW phase deformation and the

W_ρc = ρ_c(ℏv_F /4π)(∂_xϕ)². The signs in expressions

applied electric field E_x, the electrons experience the

for W_ρn and W_ρc are opposite, and also temperature

chiral invariant potentials V and A^∗x and the longitudi-

dependencies are conflicting among coefficients ρ_n (ex-

nal force E^∗x.

pected to rise from zero at T = 0 up to 1 at T_c) and

At first sight, we have arrived at the transparent

ρ_c (expected to fall to zero at T_c starting from 1 at

picture of a 1D Dirac semiconductor with the gap 2Δ =

T = 0).

= 2AΔ₀ under the effective electric field (7), and it

These contradictions can be traced back to the no-

looks straightforward to exclude the fermions to arrive

∫

tion of the chiral anomaly, and they can be cured by

at an effective action S{Φ, ϕ, A} =

W dx dt. And here

properly taking this anomaly into account. The chiral

we arrive at puzzling contradictions.

anomaly is ubiquitous in the premature linearization of

(i) In view of Eq. (7), the free energy W should

electronic spectra. First, in the course of the lineariza-

contain the potential and the phase only in the in-

tion, the control is lost of the position of the bottom

variant combination V . Having choosen the phase as

of the electronic band, hence of the difference between

(ℏv_F /2)∂_xϕ = -Φ, the effective potential V disappears

actions of the external potential Φ and of the Fermi

from the action, then no density and no polarization are

energy shifting δE_F which wrongly appear to be ad-

perturbed with respect to Φ. This contradicts to ba-

ditive. Moreover, the whole energy cost of the chiral

sic properties of the CDW in both the semiconductor

transformation δW_CT is lost. This energy can be cap-

with respect to electrons and the metal in the collective

tured from the non-linearized spectrum of the normal

behavior.

metal if we consider the chiral transformation pertur-

(ii) We definitely expect W to contain the term pro-

bation δn_CT = ∂_xϕ/π as a redistribution of the total

portional to ρ_c(∂_xϕ)², where ρ_c is a collective density

particle density accompanying this transformation:

responsible for the phase rigidity. But treating the La-

grangian (5) perturbatively with respect to the effective

ℏv_F

electric field (7), we evidently should get

δW_CT =

(∂_xϕ)² +Φ∂xϕ,

(10)

4π

ϵ(k, ω)

δW_n = -

(E^∗x)² =

where the first term is the density perturbation cost

8πe²

(

)₂

(δn_CT )²/2N_F and the second term is its potential en-

ϵ(k, ω)

ℏv_F ∂²ϑ

+E_x

(8)

ergy δn_cΦ. Beyond these physical arguments [43,44],

8πe²

∂x²

the derivation of the chiral anomaly in the spirit of

where ϵ is the dielectric susceptibility as a function of

the field-theory procedure of regularization of fermionic

the wave number k and the frequency ω (the last will

determinants was demonstrated for CDWs [45] and

be neglected here for shortness). At small k,

for SDWs [45, 46], recall also the special field-induced

SDWs [47].

ρ_n

ϵ=ϵ_Δ +

ρ_n =

N-1F.

(9)

Bringing together the nonperturbative contribution

(lk)²

l²

r²⁰

dζ

(10) and the perturbative one (8), we get

Here n is the concentration of free electrons related to

their chemical potential ζ and ρ_n is the normalized den-

W_tot = δW_ρn + δW_CT =

sity of states which also will be found to be the normal

(

)

density. The dielectric constant ϵ_Δ ∝ (r₀ξ₀)-2 collects

ℏv_F

Φ²

=ρ_c

(∂_xϕ)² +Φ∂xϕ

-ρ_n

(11)

the polarization of electrons gapped by the CDW while

4π

πℏv_F

ρ_n comes from conducting carriers thermally excited or

injected [42] above the gap providing the finite screen-

where ρ_c = 1 - ρ_n. The above equation correctly mani-

ing length l = r₀/√ρn. Both contributions to δWn

fests the expected dependencies in T and A yielding

bring drastic contradictions.

also the important relation ρ_c + ρ_n = 1.

811

S. Brazovskii, N. Kirova

ЖЭТФ, том 159, вып. 4, 2021

The total charge density becomes

Here γ_ϕ = γA², γ = const and γ_A = const are the

damping coefficients; γ_ϕ is related to the sliding CDW

∂W_tot

conductivity σ_CDW as γ_ϕσ_CDW = N_F e²/a2⊥ = 1/4πr²⁰.

n_tot =

ρ_c∂_xϕ - ρ_nΦN_F =

∂Φ

In spite of a superficial similarity, Eqs. (14)-(16)

∂_xϕ - ρ_nV N_F .

(12)

show striking differences with respect to commonly

use TDGL ones. Thus, in Eq. (14) the conventional

The above illustrative discussion was valid in lowest

term κ_⊥A(∇_⊥ϕ)² does not find its partner with the

bilinear approximation in gradients and potentials for

x-derivative of ϕ as if the longitudinal gradient of ϕ

the constant amplitude A. Below, we shall suggest a

does not suppress the amplitude — the phase-slip nodes

general nonlinear scheme necessary for modeling con-

would not appear then. In Eqs. (15) and (16), the terms

figurations with vortices.

containing ∂_xϕ, ∂_xxϕ, and (∂_xϕ)² are not multiplied

The above relations written for the limit A = const

by A², so the attempt to present them as derivatives

and for small deviations of n_e and n_h can be generalized

of Ψ will bring singularities proportional to 1/A and

∫

by extending the energy functional as

W dx with

1/A². Contrary to conventional GL-type equations,

now Eqs. (14)-(16) are nonanalytic in the order pa-

[

]

ℏv_F

rameter η = Aexp(iϕ) or, in other words are singular

W =

κ_x(∂_xA)²+κ_⊥(∇_⊥A)²+κ_⊥A²(∇_⊥

ϕ)2 +

4π

in its amplitude. Nevertheless, there are hidden cancel-

{

}

(

)

ℏv_F

lations allowing to compensate for singularities, even if

(∂_xϕ)² +

Φ∂_xϕ

+ Φ+

∂_xϕ n +

4π

implicitly, which is vitally important for allowance of

space- and spaciotemporal vortices.

ϵ_hosta2⊥

+ F(A,n_e,n_h) -

(∇Φ)²,

(13)

There are some technical challenges in numerical

8π

implementations of the quoted above equations which

where ϵ_host is the dielectric permittivity of the host

one commonly does not meet working within conven-

crystal.

tional GL approaches, see, e. g., Refs. [35,48]. The first

Here the parameter κ_⊥ is the CDW share modu-

is the control of compensations at A → 0 in expres-

lus coming from the interchain coupling of CDWs, and

sions for total charges, currents, and the condensate

the on-chain rigidity κx ∼ 1 (to be put κx = 1);

energy bringing to action the hidden function of the

F (A, n_e, n_h) is a free energy as a function of the nor-

condensate density ρ_c. The second is the entanglement

malized gap value A = Δ/Δ₀ and of the concentra-

in dependencies of thermodynamic functions and their

tion of normal carriers: electrons n_e and holes n_h with

derivatives on A and on n or ζ: approaching of n or ζ

n = n_e - n_h. The equilibrium value A_eq is connected

to critical values should eliminate the energy minimum

with n_e and n_h via the minimum of F (A, n_e, n_h) in such

over A at A = 0 opening the metallic state, e. g., in the

a way that A_eq(n_e, n_h) vanishes when n_e,h or, better

vortex core.

say, their chemical potentials ±ζ surpass critical val-

The best, and may be the only analytically trans-

ues, hence the metallic phase with A = 0 is restored.

parent, advancing is possible with the simplest Landau

The terms in brackets {. . .} are originated by the chiral

type expression for F :

anomaly of Eq. (10) coming from background deforma-

[

]

tions of the CDW phase, the next term (proportional

(

)₂

n²

to n) comes from the energy of intrinsic electrons in the

F (n, A) =

-τ +

2N_F

n_cr

combined potential V .

Assuming the dissipative regime for both ϕ and A,

× (AΔ₀)²N_F +

A⁴Δ²⁰N_F ,

(17)

functional derivatives of (13) yield equations for the

time evolution and the Poisson equation for Φ:

where a, b ∼ 1. In Eq. (17), the first term is the con-

∂F

tribution of the normal metal, while two other terms

∂2xA + κ_⊥∇2⊥A + κ_⊥A(∇_⊥ϕ)² -

= γ_A∂_tA,

(14)

give the Landau type expansion in the order parame-

∂A

ter with the proximity τ ∝ (1 - T/T_c) to the transition

temperature being shifted by presence of the normal

∂2xϕ + πN_F ∂_xΦ + π∂_xn +

carriers which critical concentration is n_cr.

(

)

+κ_⊥∇_⊥

A²∇_⊥ϕ

=γ_ϕ∂_t,

(15)

We have performed the numerical modeling employ-

ing the following combination of equations: Eq. (13)

for A with F given by Eq. (17), Eq. (14) for ϕ, and

∂_xϕ + n = -N_F r²⁰∇²Φ.

(16)

the dissipative equation for m generated by the func-

812

ЖЭТФ, том 159, вып. 4, 2021

Phase slips, dislocations, half-integer vortices.. .

tional (1). The vortices can be spontaneously generated

S. Brazovskii and N. Kirova, Soviet Science Revies,

only if equations are written in invariarian variables,

ed. by I. M. Khalatnikov, Harwood Acad. Publ., New

rather than in the economical form for non-unique

York (1984), Vol. A5, p. 99.

phase ϕ and the angle θ. The order parameter η_SDW =

S. Brazovskii, AIP Conf. Proc. 1134, 74 (2009).

= Am exp(iϕ) is written as η_SDW = (u + iv){p, q}.

For the CDW or for frozen alligned spins in SDW,

I. Dzyaloshinskii, Nobel Symposium 24, 143 (1973).

the invariant variables are just u and v. For a SDW

S. A. Brazovskii, I. E. Dzyaloshinskii, and I. M. Kri-

with a spin vorticity, the allowed varibles were taken

chever, Sov. Phys. JETP 56, 212 (1982).

as a set of four bilinear combinations {α, β, γ, δ} =

= {up, uq, vp, vq} imposing the apparent constraint

S. A. Brazovskii, I. E. Dzyaloshinskii, and I. M. Kri-

αδ = βγ. Examples of resulting calculations are shown

chever, Phys. Lett. A 91, 40 (1982).

in Figs. 1, 2, and 4.

I. E. Dzyaloshinskii and I. M. Krichever, Sov. Phys.

4. Conclusions.

JETP 56, 908 (1982).

A necessity of semi-vortices in conventional antifer-

10.

I. E. Dzyaloshinskii and I. M. Krichever, Sov. Phys.

romagnets in presence of frozen-in host lattice dislo-

JETP 58, 1031 (1983).

cations was understood already by I. E. D. [13]. In

the SDW, the semi-vortices become the objects of the

11.

N. Kirova and S. Brazovskii, J. de Phys. IV 9,

lowest energy created in the course of phase slip pro-

Pr10-119 (1999).

cess; the normal dislocation must split into two objects

12.

N. Kirova and S. Brazovskii, J. de Phys. IV 10,

of the combined topology with the repulsion between

Pr3-183 (2000).

them. The combined topological objects, where the

spin rotations are coupled to DW displacements, are

13.

I. E. Dzyaloshinskii, JETP Lett. 25, 98 (1977).

stabilized by lowering the Coulomb energy of disloca-

14.

G. E. Volovik and V. P. Mineev, JETP Lett. 24, 561

tions. This combination effectively reduces the SDW

(1976).

period.

Exploiting the chiral transformation and under-

15.

M. C. Cross and W. F. Brinkman, J. Low Temp.

Phys. 27, 683 (1977).

standing the role of the chiral anomaly allows formu-

lating a phenomenological theory in terms of equations

16.

I. A. Lukyanchuk and M. E. Zhitomirsky, Supercond.

for the DW complex order parameter, the electric po-

Rev. 1, 207 (1995).

tential, and the concentration of normal carriers. This

approach resolves the problem of violation of the con-

17.

G. E. Volovik, PNAS 97, 2431 (2000).

servation law for condensed carriers rising dangerously

18.

L. Radzihovsky and A. Vishwanath, Phys. Rev. Lett.

for nonstationary inhomogeneous regimes; that allows

103, 010404 (2009).

to model consistently such strongly nonlinear effects as

phase slips and nucleation and propagation of phase

19.

S. Brazovskii, Physica B 404, 482 (2009).

vortices.

20.

Y. G. Rubo, Phys. Rev. Lett. 99, 106401 (2007).

The full text of this paper is published in the English

21.

V. P. Mineev, Low Temperature Physics/Fizika Niz-

version of JETP.

kikh Temperatur 39, 1056 (2013).

22.

S. I. Anisimov and I. E. Dzyaloshinskii, Sov. Phys.

JETP 31, 773 (1970).

REFERENCES

23.

I. E. Dzyaloshinskii and G. E. Volovik, Ann. Phys.

125, 67 (1980).

1. S. Brazovskii, I. Dzyaloshinskii, and N. Kirova, Sov.

Phys. JETP 54, 1209 (1981).

24.

S. Brazovskii and N. Kirova, Ann. Phys. 403, 184

(2019).

2. S. Brazovskii and I. Dzyaloshinskii, Sov. Phys. JETP

25.

P. Monceau, Adv. Phys. 61, 325 (2012).

44, 1233 (1976).

26.

G. Grüner, Rev. Mod. Phys. 60, 1129 (1988).

3. S. Brazovskii, I. Dzyaloshinskii, and S. P. Obukhov,

Sov. Phys. JETP 45, 814 (1977).

27.

G. Grüner, Rev. Mod. Phys. 66, 1 (1994).

813

S. Brazovskii, N. Kirova

ЖЭТФ, том 159, вып. 4, 2021

28. Charge Density Waves in Solids, ed. by L. Gor’kov

39. B. I. Ivlev and N. B. Kopnin, Adv. Phys. 33, 47

and G. Grüner, Elsevier Sci. Publ., Amsterdam

(1984).

(1990).

40. N. Kopnin, Theory of Nonequilibrium Superconduc-

29. S. Brazovskii and N. Kirova, JETP 129, 659 (2019).

tivity, Oxford Univ. Press, U.K. (2001).

30. N. P. Ong, G. Varma, and K. Maki, Phys. Rev. Lett.

41. S. Artemenko and A. Volkov, see [28], p. 365.

52, 663 (1984).

42. . S. Brazovskii, N. Kirova, H. Requardt, F. Ya. Nad,

31. N. P. Ong and K. Maki, Phys. Rev. B 32, 6582 (1985).

P. Monceau, R. Currat, J. E. Lorenzo, G. Grbel, and

Ch. Vettier, Phys. Rev. B 61, 10640 (2000).

32. L. P. Gor’kov, JETP Lett. 38, 87 (1983).

43. S. Brazovskii, J. de Phys. I 3, 2417 (1993).

33. L. P. Gor’kov, see [28], p. 403.

44. S. Brazovskii, J. de Phys. IV 3, C2-267 (1993).

34. L. P. Gor’kov, Sov. Phys. JETP 59, 1057 (1984).

35. I. Batistic, A. Bjelis, and L. Gor’kov, J. de Phys. 45,

45. I. V. Krive, A. S. Rozhavsky, and V. A. Rubakov,

JETP Lett. 46, 121 (1987).

1049 (1984).

36. T. Yi, N. Kirova, and S. Brazovskii, Eur. Phys. J.,

46. K. Sengupta and N. Dupuis, Phys. Rev. B 61, 495

Special Topics 222, 1035 (2013).

(2000).

37. T. Yi, A. Rojo Bravo, N. Kirova, and S. Brazovskii,

47. V. M. Yakovenko and H.-S. Goan, Phys. Rev. B 58,

J. Supercond. Nov. Mag. 28, 1343 (2015).

10648 (1998).

38. S. N. Artemenko, A. F. Volkov, and A. N. Kruglov,

48. S. M. Gol’berg, N. B. Kopnin, and M. I. Tribel’skii,

Sov. Phys. JETP 64, 906 (1986).

Sov. Phys. JETP 67, 812 (1988).

814