ЖЭТФ, 2021, том 159, вып. 6, стр. 1003-1012
© 2021
ОТКЛИК ВЫСШИХ ГАРМОНИК ИНТЕНСИВНОГО
КОГЕРЕНТНОГО ЭЛЕКТРОМАГНИТНОГО ПОЛЯ НА
ИЗМЕНЕНИЕ ТОПОЛОГИИ ПОВЕРХНОСТИ ФЕРМИ
В ГРАФЕНОПОДОБНЫХ НАНОСИСТЕМАХ
Б. Р. Авчян, А. Г. Казарян*, К. А. Саргсян, Х. В. Седракян
Центр физики сильных полей, Ереванский государственный университет
0025, Ереван, Армения
Поступила в редакцию 10 января 2021 г.,
после переработки 1 февраля 2021 г.
Принята к публикации 5 февраля 2021 г.
Исследован отклик высших гармоник лазерного поля на изменение топологии поверхности Ферми в гра-
феноподобных наносистемах в процессе генерации. Использована микроскопическая нелинейная кван-
товая теория взаимодействия интенсивного когерентного электромагнитного излучения с такими систе-
мами вблизи критического уровня Ферми. Численно решено уравнение Лиувилля - фон Неймана для
матрицы плотности в режиме многофотонного возбуждения. Полученные результаты показывают, что
высшие гармоники чувствительны к изменению топологии поверхности Ферми, что может быть исполь-
зовано для определения энергии Ферми в таких системах.
DOI: 10.31857/S0044451021060018
материалах, таких как графеноподобные квантовые
точки или замкнуто-выпуклые фуллерены [34].
В связи с этими проблемами представляет инте-
1. ВВЕДЕНИЕ
рес определение энергии Ферми электронов в низ-
коразмерных наноструктурах [35]. Мы будем рас-
В последнее десятилетие большой интерес пред-
сматривать переходы Лифшица с энергией фотона,
ставляет создание интенсивных перестраиваемых
много меньшей, чем так называемая энергия Лиф-
нанолазеров и умножителей частоты в графено-
шица, когда энергия фотона равна энергии Ферми
подобных наносистемах [1-3]. Используются осо-
электрона. Во время перехода Лифшица происходит
бые нелинейно-оптические свойства графеноподоб-
фрагментация односвязной линии Ферми на четы-
ных наноструктур, возникающие в результате нели-
ре отдельные части [36-39]. Используя это свойство,
нейного отклика таких материалов на внешнее элек-
можно теоретически оценить энергию Ферми в гра-
тромагнитное излучение. Задача сводится к иссле-
фене, состоящем из двух сложенных слоев, A и B
дованию процесса нелинейного взаимодействия све-
(далее AB-графен). Это позволяет исследовать вли-
та с наносистемой, в которой происходит много-
яние топологии поверхности Ферми на ГВГ в гра-
фотонное явление — генерация высших гармоник
феноподобной наноструктуре.
(ГВГ) [4-6]. Все больше внимания уделяется рас-
В качестве примера такой структуры можно
смотрению ГВГ в кристаллах [7-13] и двумерных
предложить систему двухслойного графена. Она
(2D) наноструктурах, таких как графен и его про-
представляет особую систему, в которой топология
изводные [7-30], гексагональный нитрид бора [31] и
зонной структуры может быть выбрана и измене-
дихалькогениды переходных металлов [32,33]. В на-
на. Нелинейный когерентный отклик в AB-графене
стоящее время мы наблюдаем рождение новой раз-
под действием интенсивного электромагнитного из-
вивающейся области исследований непертурбатив-
лучения приводит к модификации квазиэнергетиче-
ных оптических явлений в наноструктурированных
ского спектра, индукции поляризованных токов до-
лин [40,41], а также к нелинейно-оптическим эффек-
* E-mail: amarkos@ysu.am
там третьего и пятого порядков [42-45]. Двухслой-
1003
Б. Р. Авчян, А. Г. Казарян, К. А. Саргсян, Х. В. Седракян
ЖЭТФ, том 159, вып. 6, 2021
ный AB-графен — хорошо настраиваемый материал.
Эффективный одночастичный гамильтониан
Можно настроить энергию Ферми с помощью внеш-
[36, 49, 50] низкоэнергетических возбуждений |ε| <
них возмущений, таких как поперечное электриче-
< γ1 ≃ 0.39 эВ в окрестности точек Дирака Kζ, в
ское поле или деформация [46-52].
AB-графене может быть представлен формулой
В настоящей статье с помощью разработанно-
⎛
⎞
го ранее численного моделирования [26-28] и мик-
π2ζ
0
v3ζπζ -
⎜
⎟
роскопической нелинейной квантовой теории взаи-
⎜
2m
⎟
HAB =
,
(3)
⎝
⎠
модействия AB-графена с линейно поляризованной
π2
ζ
v3ζπζ -
0
электромагнитной волной рассматривается процесс
2m
генерации гармоник. Численно решается уравнение
где πζ = px +iζ py, p = {px, py} — оператор импульса
Лиувилля - фон Неймана для ГВГ в режиме много-
фотонного возбуждения вблизи точек Дирака зоны
электрона, ζ = ±1 — квантовое число долины. Член
√
v3 =
3aγ3/2ℏ в гамильтониане (3) связан с межсло-
Бриллюэна. Полученные результаты показывают,
евым переходом γ3 = 0.32 эВ (a ≈ 0.246 нм — рас-
что изменение топологии поверхности Ферми влия-
стояние между ближайшими A-слоями), вызывает
ет на высшие гармоники. Последнее может быть ис-
тригональное искривление в зонной дисперсии. Сле-
пользовано для определения энергии Ферми в таких
дующий член в уравнении (3) дает пару параболи-
системах при ГВГ волны накачки с эффективным
ческих изолиний ε = ±p2/2m, где m = γ1/2v2F — эф-
выходом в терагерцевой (ТГЦ) и субТГц-областях
фективная масса, γ1 ≃ 0.39 эВ, vF — скорость Фер-
спектра при температурах графена выше криоген-
ми в однослойном графене. Функции собственных
ных.
Работа организована следующим образом. В
состояний |n〉 гамильтониана (3) определяются ком-
бинированным квантовым числом n = {σ, p}. Здесь
разд. 2 численно решена система уравнений для
σ — индекс зоны: для зоны проводимости σ = 1, для
одночастичной матрицы плотности в режиме мно-
валентной зоны σ = -1. Таким образом, имеем
гофотонного взаимодействия. В разд. 3 исследуется
влияние изменения топологии поверхности Ферми
(
)
i
на генерацию высших гармоник при низкоэнергети-
|n〉 = |σ, p〉 exp
p·r
,
(4)
ℏ
ческом переходе в графеноподобной наноструктуре.
Выводы приведены в разд. 4.
где
(
)
(
)
2. ОСНОВНАЯ МОДЕЛЬ И ТЕОРИЯ
1
1
i
|σ, p〉 =
√
exp
p·r
(5)
1
Υ (p)
ℏ
Рассмотрим влияние топологии поверхности
2E (n)
E (n)
Ферми при генерации высоких гармоник в графено-
— спиноры, соответствующие энергиям
подобной наноструктуре на примере AB-графена.
В данной статье мы используем результаты мик-
E (n) = σ |Υ (p)| .
(6)
роскопической нелинейной квантовой теории
взаимодействия когерентного электромагнитного
В уравнении (5)
излучения с двухслойным графеном, развитую
в работах
[26-28]. Предположим, что линейно
p2
поляризованная плоская электромагнитная волна
Υ (p) = -
e2iζϑ + ζv3pe-iζϑ,
(7)
2m
с несущей частотой ω и медленно меняющейся
амплитудой E0f(t) электрического поля распро-
и ϑ = arctg(py/px).
страняется в направлении, перпендикулярном
Гамильтониан взаимодействия представим в ви-
плоскости xy слоев графена и имеет вид
де
(
)
E (t) = E0f (t) e cos ωt,
(1)
er · E(t)
0
V=
,
(8)
0
er · E (t)
где e — вектор поляризации. Медленно меняющаяся
огибающая волны накачки равна
где e — элементарный заряд. Для микроскопичес-
{
кой теории нелинейного взаимодействия двухслой-
sin2 (πt/Tp) ,
0≤t≤Tp,
f (t) =
,
(2)
ного графена с сильным полем излучения необходи-
0,
Tp < t < 0,
мо решить основное уравнение для матрицы плот-
где Tp = 40π/ω — длительность импульса.
ности ρmn:
1004
ЖЭТФ, том 159, вып. 6, 2021
Отклик высших гармоник. . .
∂ρmn
ρ-1,1(p, t)
= P∗(p, t), а диагональные элементы
iℏ
= (E (m) - E (n))ρmn +
∂t
представляют собой функции распределения час-
∑[
]
+
〈m|V|l〉ρln - ρml〈l|V|n〉
-
тиц для зоны проводимости, Nc(p, t) = ρ1,1(p, t),
l
и валентной зоны, Nv(p, t) = ρ-1,-1(p, t). Релак-
(
)
сацию определим членом γσ,σ′ (p) = Γ (μ, T ), зави-
- iℏγmn ρmn - ρmn
,
(9)
сящим от химического потенциала и температуры.
Как показано в работах [53, 54], для энергий μ ≪
где ρm0n — матрица плотности в равновесии и γmn —
≪ γ1 = 0.39 эВ доминирующим механизмом ре-
вероятность релаксации. Для ρm0n мы предполагаем
лаксации будет электрон-фононная связь через про-
распределение Ферми - Дирака:
дольные акустические фононы. В низкотемператур-
ρm0n = nF (n)δmn,
ном пределе kBT
≪ 2(cph/vF)
√μγ1, где cph ≃
≃ 2·106 см/с — скорость продольного акустического
где
фонона, скорость релаксации оценивается как [54]
[
(E (n) - μ)]-1
nF (n) ≡ nF (σ, p) =
1+exp
(10)
πD2k2B
T2
√γ1
kBT
Γ (μ, T ) ≃
(15)
8ρmℏ3c3phvF μ
Здесь μ — химический потенциал, kB — постоянная
Здесь D ≃ 20 эВ — постоянная электрон-фононного
Больцмана и T — абсолютная температура.
взаимодействия, ρm
≃ 15 · 10-8 г/см2 — плот-
С учетом гамильтониана (8), основное уравнение
ность массы двухслойного графена. Принимая во
для матрицы плотности (9) сводится к уравнению
внимание уравнение (11), нам необходимо решить
для ρσ,σ′ (p, t):
замкнутую систему дифференциальных уравнений
ρmn (t) ≡ ρ (σ, p;σ′, p′, t) ≡ ρσ,σ′ (p, t)δpp′ ,
для этих величин:
где δpp′ — символ Кронекера.
∂Nc(p, t)
∂Nc(p, t)
iℏ
- iℏeE (t)
=
Таким образом, имеем
∂t
∂p
∂ρσ,σ′ (p, t)
∂ρσ,σ′ (p, t)
= E(t)Dt (p)P∗(p,t) - E(t)D∗t (p)P(p,t)-
iℏ
- iℏeE (t)
= (σ-σ′) ×
∂t
∂p
(
)
- iℏΓ (μ, T)(Nc(p, t) - nF (1, p)),
(16)
× |Υ (p)| - iℏγσ,σ′ (p) ρσ,σ′ (p, t) - ρ(0)σ,σ′ (p)
+
+ E(t)[Dt (σ,p)ρ-σ,σ′(p,t) - Dt (-σ′,p) ×
∂Nv(p,t)
∂Nv(p, t)
iℏ
- iℏeE (t)
=
× ρσ,-σ′(p, t)] ,
(11)
∂t
∂p
где
= -E (t)Dt (p)P∗(p, t) + E (t)D∗t (p)P(p, t)-
Dt (σ, p) = ℏe〈σ, p|i∂p| - σ, p〉
(12)
- iℏΓ (μ, T)(Nv(p, t) - nF (-1, p)),
(17)
— дипольный момент перехода. В соответствии с ра-
ботами [26-28] составляющими дипольного момента
перехода являются
∂P(p, t)
∂P(p,t)
iℏ
- iℏeE (t)
=
∂t
∂p
eℏ
Dtx (p) = -
×
2E2(1, p)
= [2 |Υ (p)| - iℏΓ (μ, T )] P(p, t) +
[(
]
2
p
)ζpy
v3
×
- mv2
+
pxpy
,
(13)
3
+ E(t)Dt (p)[Nv(p,t) - Nc(p,t)].
(18)
2m
m
m
Оптическое возбуждение импульсом когерентного
eℏ
излучения вызывает переходы в море Ферми - Дира-
Dty (p) = -
×
2E2(1, p)
ка, в результате чего возникает поверхностный ток.
[(
]
(
)
Оператор плотности тока задается формулой
p2
)ζpx
v3
×
-
+ mv2
+
p2x - p2y
(14)
3
2m
m
2m
gζ = -2e
Ψ(r, t) |vζ |Ψ(r, t)
(19)
В уравнении (11) недиагональными элемента-
ми являются межзонная поляризация ρ1,-1(p, t) =
Для эффективного 2×2-гамильтониана (3) оператор
= P(p,t) и ее комплексно-сопряженная величина
скорости vζ = ∂
H/∂p имеет вид
1005
Б. Р. Авчян, А. Г. Казарян, К. А. Саргсян, Х. В. Седракян
ЖЭТФ, том 159, вып. 6, 2021
vζx =
⎛
⎞
1
0
-
(ζ px-ipy) +v3
⎜
m
⎟
=ζ
⎝
⎠,
(20)
1
−
(ζpx+ipy) +v3
0
m
vζy =
⎛
⎞
1
0
(ζpx-ipy) +v3
⎜
m
⎟
=i
⎝
⎠,
(21)
1
−
(ζpx+ipy) -v3
0
m
а при ГВГ в AB-графене внутризонная скорость
V (p) дается формулой
(
1
v3p
V (p) =
v3p - 3ζ
pcos3ϑ +
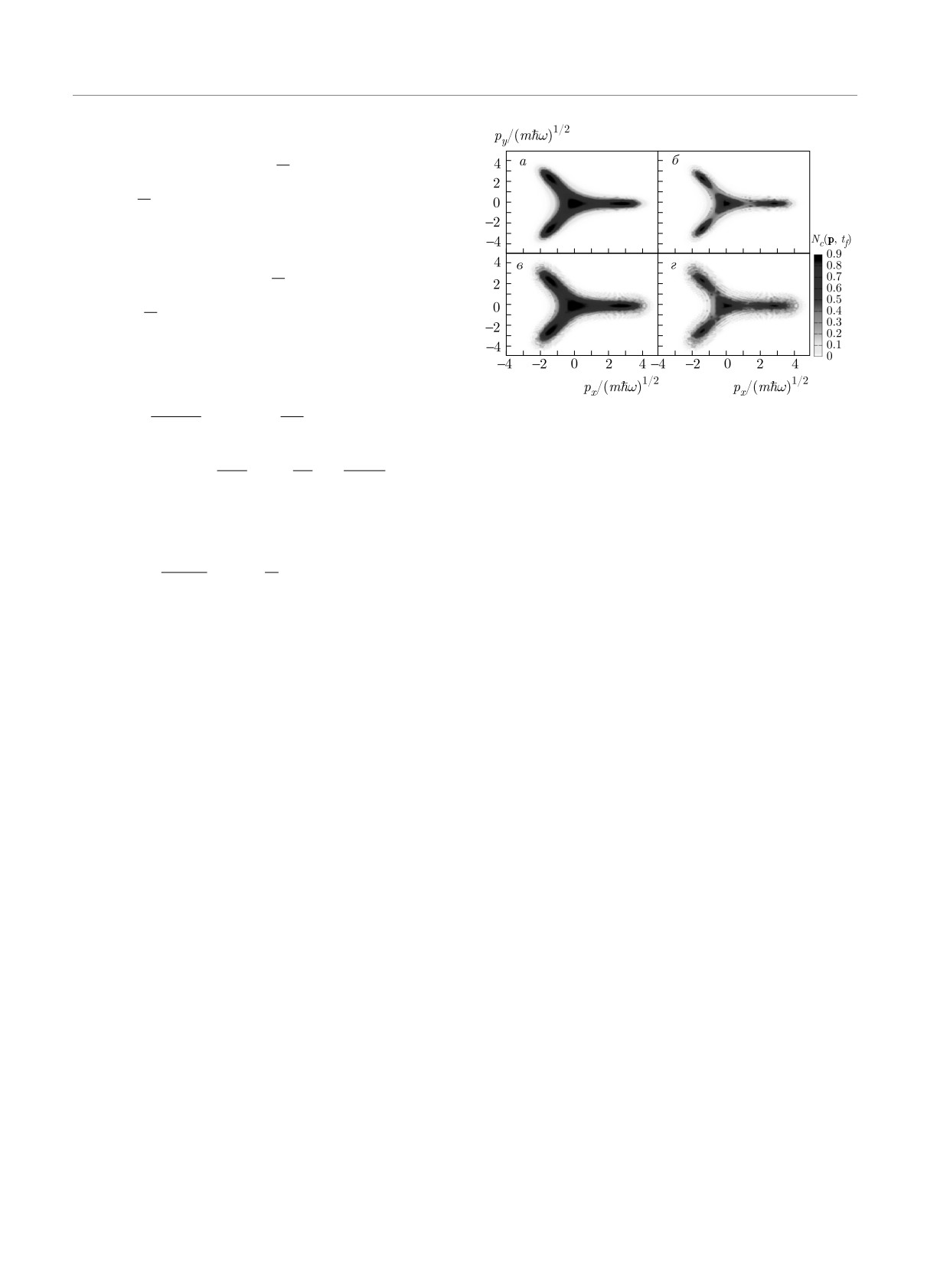
Рис. 1. (В цвете онлайн) Функция распределения частиц
E (1, p)
2m
)
Nc(p, tf ) (в относительных единицах) после взаимодейст-
3
вия в момент t = 40π/ω в зависимости от безразмерных
v3p
∂ϑ
p3
+ 3ζ
sin3ϑ
+2
(22)
компонент импульса. Поле линейно поляризовано вдоль
2m
∂p
(2m)2
оси y. Представлено фотоиспускание при переходе Лиф-
Используя уравнения (5)-(7) и (3), плотность тока
шица (ℏω = 0.9EL) для высокой EF = 1.4EL (а, в) и низкой
для долины ζ мы можем записать в виде
EF = 0.7EL ≃ μ (б, г) энергий. Параметр kBT/ℏω = 0.4,
∫
безразмерный параметр интенсивности χ = 0.5 (а, б) и
2e
{2i
χ = 1 (в,г) для долины с индексом ζ = -1
gζ (t) = -
dp
E (1, p) ×
(2πℏ)2
ℏ
× [Dt (p) P∗(p, t) - D∗t (p) P(p, t)] +
}
гетическом переходе в графеноподобной нанострук-
+ V(p)(Nc(p,t) - Nv(p,t))
(23)
туре. Взаимодействие частицы с когерентной вол-
ной с низкой энергией фотона в ТГц- или субТГц-об-
В уравнении (23) первое слагаемое описывает ГВГ,
ластях (ℏω ≪ EL = 1 мэВ, где EL — энергия Лиф-
возникающую в результате рекомбинации ускорен-
шица), характеризуется безразмерным параметром
ных электронно-дырочных пар. Второй член — это
интенсивности χ [16]:
внутризонный ток, который обусловлен внутризон-
ными высшими гармониками и генерируется в ре-
χ = eE0v3/ℏω2.
(26)
зультате независимого движения частиц в своих со-
ответствующих зонах. Мы изучаем многофотонный
Среднюю интенсивность волны [30] можно предста-
режим, поэтому вклад обоих механизмов существен.
вить как
Полный ток может быть получен суммированием
по ζ:
gx = g1,x + g-1,x,
(24)
Iχ = χ2 · 1.96 · 1013 Вт/см2 (ℏω/эВ)4 .
gy = g1,y + g-1,y.
(25)
Параметр интенсивности χ имеет порядок едини-
Ниже мы исследуем нелинейный отклик двух-
цы для многофотонного процесса ГВГ. В частности,
слойного графена в процессе ГВГ под действием
для фотонов с энергиями 0.4-0.9 мэВ режим много-
лазерного поля в многофотонном режиме с пара-
фотонного взаимодействия может быть реализован
метром интенсивности χ ≳ 1 и субТГц-частотами
при интенсивностях Iχ = 1-102 Вт/см2. Отметим,
ω = 0.4-0.9 мэВ/ℏ.
что современные фотонные ТГц- и субТГц-источни-
ки (с энергиями 0.4-1.24 мэВ) включают квантовые
3. ВЛИЯНИЕ ИЗМЕНЕНИЯ ТОПОЛОГИИ
каскадные лазеры [55, 56].
ПОВЕРХНОСТИ ФЕРМИ НА ГВГ ПРИ
На примере двухслойного графена, рассмотрим
НИЗКОЭНЕРГЕТИЧЕСКОМ ПЕРЕХОДЕ В
нелинейный отклик графеноподобной нанострукту-
ГРАФЕНОПОДОБНОЙ НАНОСТРУКТУРЕ
ры в процессе ГВГ при многофотонном возбуж-
В этом разделе исследуем влияние изменения то-
дении при переходе Лифшица. Система уравнений
пологии поверхности Ферми на ГВГ при низкоэнер-
(16)-(18) аналитически не решается. Для численно-
1006
ЖЭТФ, том 159, вып. 6, 2021
Отклик высших гармоник. . .
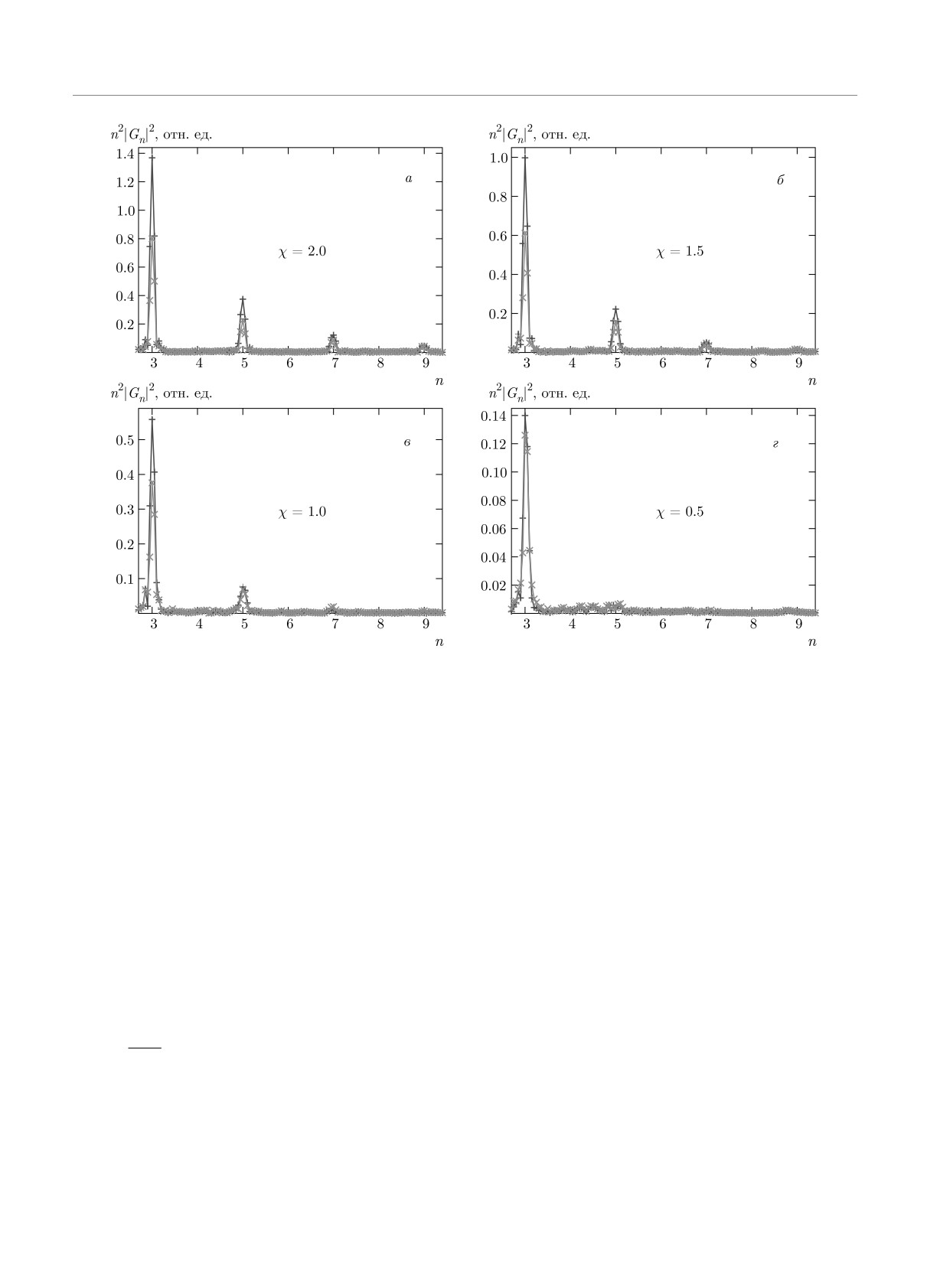
Рис. 2. (В цвете онлайн) Вероятности испускания гармоник в двухслойном графене при переходе Лифшица в зависи-
мости от номера гармоники для разных параметров интенсивности χ и энергий Ферми EF = 0.7EL (косые крестики)
и EF = 1.4EL (прямые крестики). Параметр kBT/ℏω = 0.4. Волна накачки с энергией фотона ℏω = 0.9EL линейно
поляризована
го решения выполнено стандартное преобразование
ствия импульса длительностью Tp ≈ 90 пс показа-
и замена переменных на новые, t и
на при высокой (EF = 1.4EL) и низкой (EF = 0.7EL)
энергиях Ферми. Предполагается, что волна накач-
∫t
ки линейно поляризована вдоль оси y. Как видно
p = p - pE (t), pE (t) = -e E(t′)dt′,
из рис. 1б,г для EF < EL и ℏω < EL две соприкасаю-
0
щиеся параболы преобразуются в четыре отдельных
где pE (t) — классический импульс, переданный вол-
«кармана». Итак, возбужденные искаженные изоли-
новым полем. Преобразуем уравнения с частны-
нии дают возможность оценить значение EF ≃ μ в
ми производными в обыкновенные. Интегрирова-
случае фотона низкой энергии ℏω = 0.7EL.
ние уравнений (16)-(18) выполняется на однород-
Отметим, что при параметре интенсивности χ >
ной сетке из 104 точек (px, py) со стандартным ал-
> 1 количество изолиний увеличивается. Отчет-
горитмом Рунге - Кутта четвертого порядка. В ка-
ливо видно многофотонное и сильноанизотропное
честве максимального импульса принято значение
возбуждение моря Ферми- Дирака вдали от точек
√
pmax/
mℏω = 5. Скорость релаксации Γ (μ, T ) опре-
Дирака. В частности, линии возбуждения искрив-
деляется формулой (15).
лены в направлении вектора поляризации волны.
Нелинейное возбуждение моря Ферми показано
Это указывает на то, что созданные пары частица-
на рис. 1 при переходе Лифшица (ℏω = 0.9EL) при
дырка ускоряются в волновом поле. Таким образом,
параметрах интенсивности χ = 0.5 и χ = 1. Функ-
при исследовании спектра излучения представляют
ция распределения частиц Nc(p, tf ) после воздей-
интерес высшие порядки гармоник. Проясняются
1007
Б. Р. Авчян, А. Г. Казарян, К. А. Саргсян, Х. В. Седракян
ЖЭТФ, том 159, вып. 6, 2021
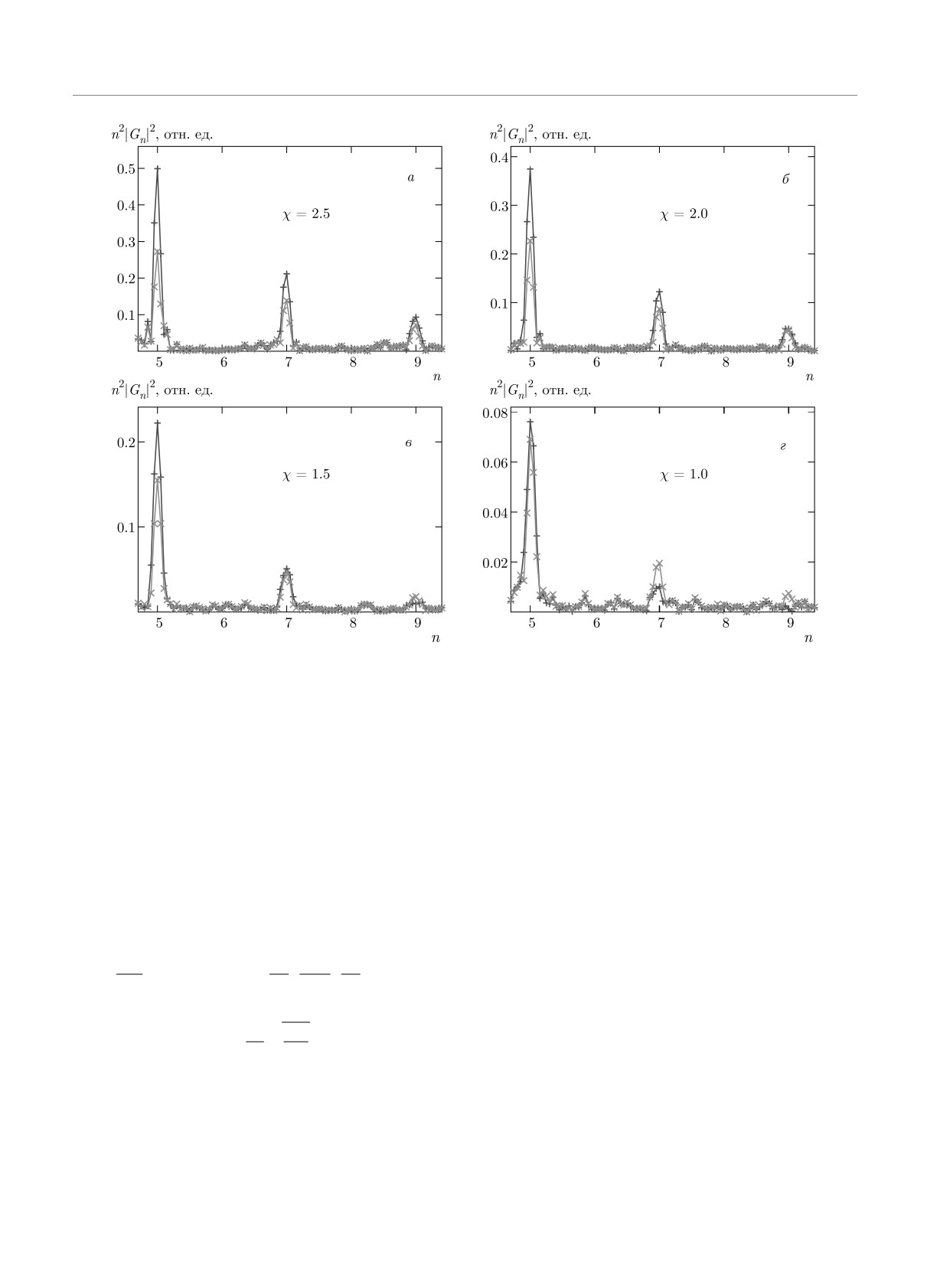
Рис. 3. (В цвете онлайн) Вероятности испускания высших гармоник в двухслойном графене при переходе Лифшица в
зависимости от номера гармоники показана для разных параметров интенсивности χ и энергий Ферми EF = 0.7EL (косые
крестики) и EF = 1.4EL (прямые крестики). Остальные параметры как на рис. 2
предположения о температурной зависимости воз-
шения уравнений (16)-(18) и проведя интегрирова-
буждения моря Ферми- Дирака. Вероятность ГВГ
ние в уравнении (23), можно вычислить спектры из-
для рассмотренных случаев слабо зависит от тем-
лучения гармоник с помощью преобразования Фу-
пературы: возбужденные изолинии слегка размыва-
рье функции Gx,y(t). Вероятность испускания n-й
ются с повышением температуры.
гармоники пропорциональна n2|gn|2, где |gn|2
=
Будем характеризовать вероятность испускания
= |gxn|2 + |gyn|2 и gxn, gyn — компоненты Фурье
n-й гармоники безразмерным нормированными со-
индуцированного полем полного тока. Чтобы найти
ставляющим плотности тока gx,y (24), (25), опреде-
gn, был использован алгоритм быстрого преобразо-
ленным как
вания Фурье. Для всех графиков мы использовали
(
)
нормированную плотность тока (27).
gx,y
EL
kBT
μ
= Gx,y ωt,χ,γ,
,
,
,
(27)
На рис. 2 показаны зависимости вероятности ис-
j0
ℏω
ℏω
ℏω
пускания гармоник от их номера для различных
где
параметров интенсивности. Как видно на этом ри-
eω
√mω
сунке, с увеличением интенсивности волны накачки
j0 =
,
(28)
π2
ℏ
гармоники выше третьего порядка становятся оди-
а Gx и Gy являются безразмерными периодически-
наково существенными.
ми (для монохроматических волн) функциями, ко-
Чтобы показать различия поведения высших
торые зависят от параметра интенсивности χ, энер-
гармоник, на рис. 3 мы построили только высшие
гии Лифшица EL, энергии Ферми EF
≃ μ и тем-
гармоники при параметре интенсивности χ > 1. Как
пературы образца. Таким образом, используя ре-
видно, существуют качественные различия для ве-
1008
ЖЭТФ, том 159, вып. 6, 2021
Отклик высших гармоник. . .
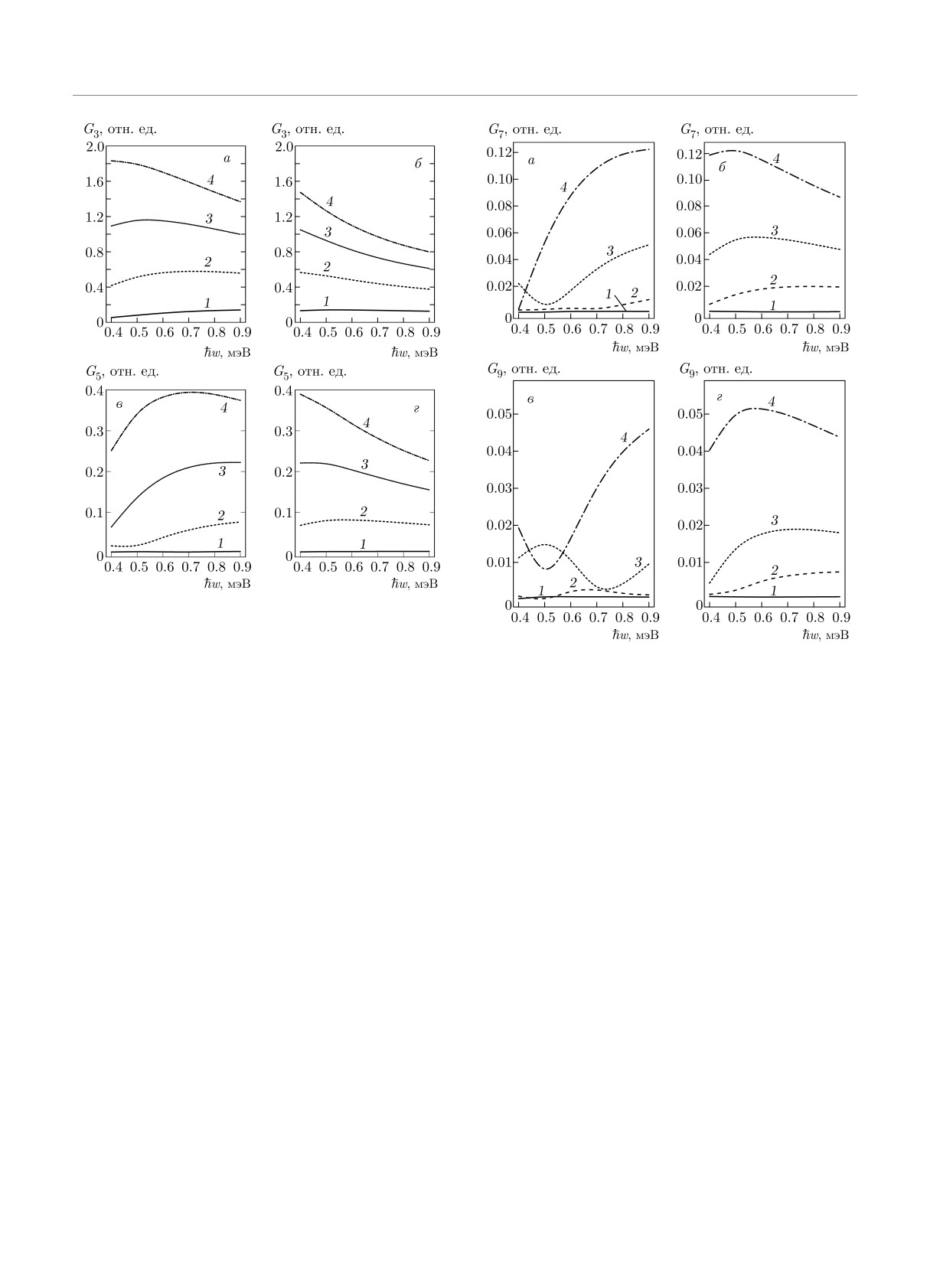
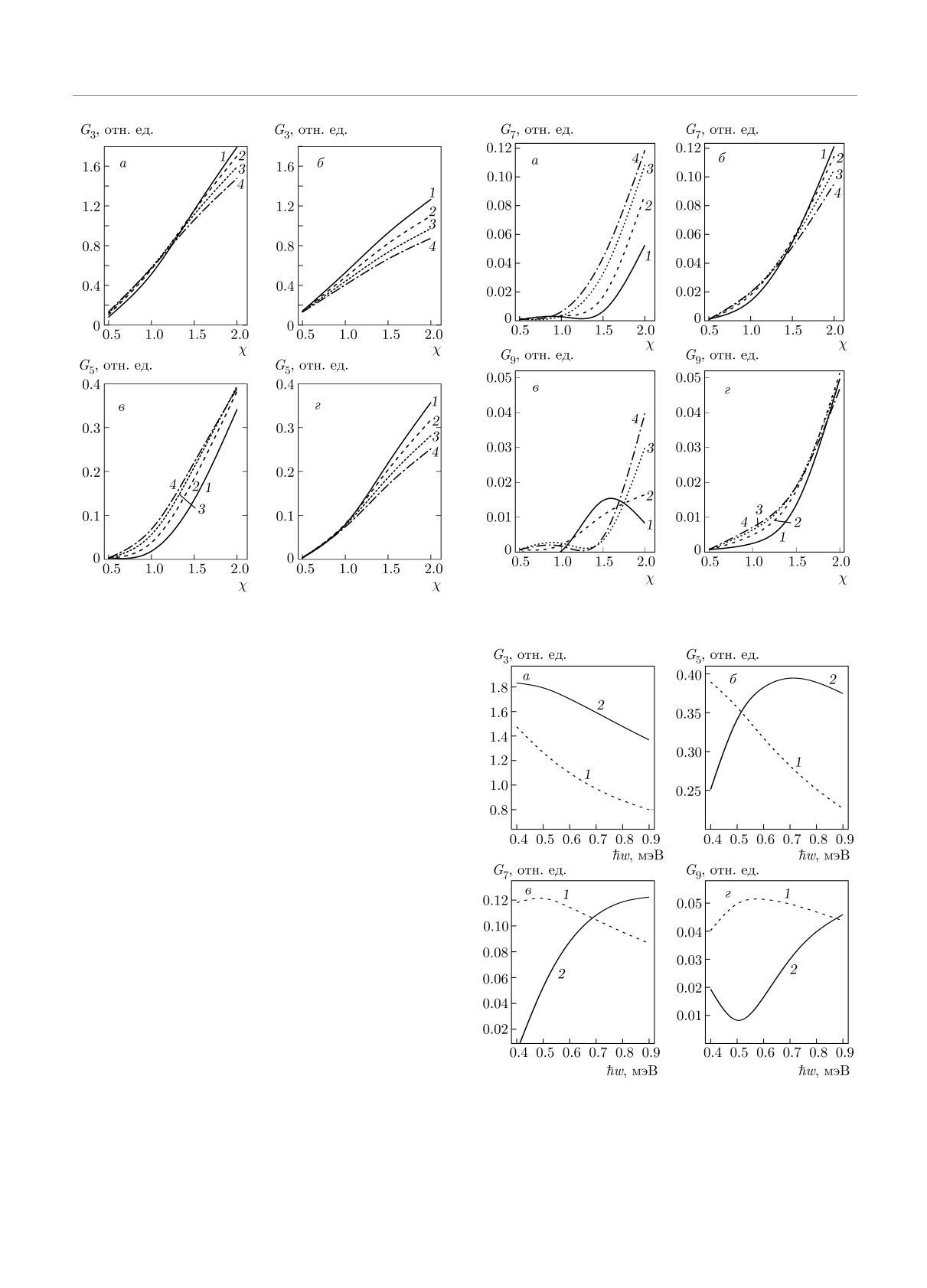
Рис. 4. Вероятности испускания третьей G3 и пятой G5
гармоник в зависимости от энергии фотона ℏω для па-
раметров интенсивности χ = 0.5 (кривые 1), 1.0 (2), 1.5
Рис. 5. То же, что и на рис. 4, для вероятностей испускания
(3), 2.0 (4). Параметр kBT /ℏω = 0.4. Волна накачки ли-
гармоник седьмого G7 и девятого G9 порядков
нейно поляризована. Энергия Ферми EF = 1.4EL (а, в) и
EF = 0.7EL (б, г)
ноструктуре. Надо отметить, что при найденных оп-
роятностей испускания Gn = n2|gn|2 в зависимости
тимальных параметрах вероятность испускания гар-
от порядка n. Функции G7, G9 имеют более выра-
моник значительна при большей интенсивности для
женные нелинейные свойства в сильном поле волны.
рассматриваемой частоты волны.
Вероятность испускания Gn высших гармоник
Чтобы продемонстрировать зависимость скоро-
в зависимости от частоты волны накачки для раз-
сти излучения от энергии Ферми, на рис. 8 пока-
личных интенсивностей волны, определяемых пара-
заны зависимости вероятности испускания третьей
метром χ, продемонстрирована на рис. 4 и 5 для
G3, пятой G5, седьмой G7 и девятой G9 гармоник от
EF > EL и EF < EL. Графики показывают, что для
энергии фотонов при фиксированной интенсивности
обоих случаев в области низкоэнергетических пере-
волны накачки и температуре графена. В соответ-
ходов Лифшица в сильной волне (χ > 1) вероятно-
ствии с результатами рис. 2-8 при ускорении и анни-
сти испускания G3, G5 достигают насыщения с рос-
гиляции частиц или дырок, индуцированных волной
том интенсивности волны накачки. Но более высо-
накачки, в графеноподобной наноструктуре может
кие гармоники 7 и 9 при EF > EL и EF < EL с уве-
быть получено интенсивное излучение высших гар-
личением интенсивности волны ведут себя по-раз-
моник при частоте волны накачки в субТГц-облас-
ному. На рис. 6, 7 показаны зависимости вероятно-
ти. Таким образом, в сильной волне, определяемой
сти испускания гармоник высшего порядка от ин-
параметром интенсивности χ, вероятности испуска-
тенсивности волны накачки в двухслойном графене.
ния высших гармоник различаются по величине для
В результате, как видно на рис. 4-7, меняя тополо-
высоких EF > EL и низких EF < EL энергий Ферми.
гию Ферми и используя ее влияние на ГВГ, можно
Это выявляет влияние топологии поверхности Фер-
определить энергию Ферми в графеноподобной на-
ми на ГВГ в графеноподобной наноструктуре. Как
1009
Б. Р. Авчян, А. Г. Казарян, К. А. Саргсян, Х. В. Седракян
ЖЭТФ, том 159, вып. 6, 2021
Рис. 7. То же, что на рис. 6, для вероятностей испускания
Рис. 6. Вероятности испускания гармоник третьего G3 и
гармоник седьмого G7 и девятого G9 порядков
пятого G5 порядков в зависимости от параметра интенсив-
ности χ показаны для энергий фотонa ℏω = 0.5 мэВ (кри-
вые 1), 0.6 мэВ (кривые 2), 0.7 мэВ (кривые 3), 0.8 мэВ
(кривые 4). Параметр kBT/ℏω = 0.4. Волна накачки ли-
нейно поляризована. Энергия Ферми EF = 1.4EL (а, в) и
EF = 0.7EL (б, г)
и в случае аналогичных расчетов для интенсивной
волны накачки, показано, что вероятность испуска-
ния слабо зависит от температуры при kBT < ℏω.
4. ЗАКЛЮЧЕНИЕ
Мы представили метод исследования вли-
яния топологии поверхности Ферми при ГВГ
в графеноподобной наноструктуре на примере
двухслойного сложенного AB-графена. Во время
перехода Лифшица происходит фрагментация
односвязной линии Ферми на четыре отдельных
участка. При этом энергия Ферми равна энергии
перехода Лифшица. Итак, теоретическое иссле-
дование позволяет оценить энергию Ферми. Мы
используем развитую ранее микроскопическую
Рис. 8. Зависимости вероятностей испускания третьей G3,
теорию нелинейного взаимодействия двухслойного
пятой G5, седьмой G7, девятой G9 гармоник от энергии
графена с сильным полем когерентного излуче-
ℏω фотона для энергий Ферми EF = 0.7EL (кривые 1),
ния для случая низкоэнергетического фотона. EF = 1.4EL (2). Параметр kB T /ℏω = 0.4. Волна накачки с
параметром интенсивности χ = 2 поляризована линейно
1010
ЖЭТФ, том 159, вып. 6, 2021
Отклик высших гармоник. . .
Замкнутая система дифференциальных уравнений
12.
Sh. Ghimire and D. A. Reis, Nature Phys. 15, 10
Лиувилля - фон Неймана для одночастичной мат-
(2019).
рицы плотности решается численно для переходов
13.
Sh. Imai, A. Ono, and S. Ishihara, Phys. Rev. Lett.
Лифшица в двухслойном графене. Для волны
124, 157404 (2020).
накачки взят субТГц-диапазон частот. Показано,
что процесс ГВГ для фотонов субТГц-диапазона
14.
S. A. Mikhailov and K. Ziegler, J. Phys.: Condens.
(длины волн от 0.3 до 1 мм) может наблюдать-
Matter 20, 384204 (2008).
ся уже при интенсивностях Iχ
= 1-102 Вт/см2
15.
H. K. Avetissian, A. K. Avetissian, G. F. Mkrtchian
при температуре образца T
< ℏω. Полученные
et al., Phys. Rev. B 85, 115443 (2012).
результаты показывают, что высшие гармоники
чувствительны к изменению топологии поверхности
16.
H. K. Avetissian, G. F. Mkrtchian, K. G. Batrakov et
Ферми. Последнее может быть использовано для
al., Phys. Rev. B 88, 165411 (2013).
определения энергии Ферми в таких системах.
17.
P. Bowlan, E. Martinez-Moreno, K. Reimann et al.,
Phys. Rev. B 89, 041408(R) (2014).
Благодарности. Выражаем признательность
18.
I. Al-Naib, J. E. Sipe, and M. M. Dignam, Phys. Rev.
Г. К. Аветисяну за многочисленные обсуждения и
B 90, 245423 (2014).
постоянное внимание к работе.
Финансирование. Исследование выполнено
19.
H. K. Avetissian and G. F. Mkrtchian, Phys. Rev.
при финансовой поддержке Комитета по науке
B 94, 045419 (2016).
Республики Армения в рамках научного проекта
20.
H. K. Avetissian, A. G. Ghazaryan, G. F. Mkrtchian
№20TTWS-1C010.
et al., J. Nanophoton. 11, 016004 (2017).
21.
L. A. Chizhova, F. Libisch, and J. Burgdorfer, Phys.
ЛИТЕРАТУРА
Rev. B 95, 085436 (2017).
1.
F. Mackenroth, N. Kumar, A. Di Piazza et al., Proc.
22.
D. Dimitrovski, L. B. Madsen, and T. G. Pedersen,
SPIE 11039, 1103902 (2019).
Phys. Rev. B 95, 035405 (2017).
2.
H. K. Avetissian, Relativistic Nonlinear Electrodyna-
23.
N. Yoshikawa, T. Tamaya, and K. Tanaka, Science
356, 736 (2017).
mics, The QED Vacuum and Matter in Super-Strong
Radiation Fields, Springer (2016).
24.
H. K. Avetissian and G. F. Mkrtchian, Phys. Rev.
B 97, 115454 (2018).
3.
A. Di. Piazza, C. Muller, K. Z. Hatsagortsyan et al.,
Rev. Mod. Phys. 84, 1177 (2012).
25.
H. K. Avetissian, A. K. Avetissian, B. R. Avchyan et
al., Phys. Rev. B 100, 035434 (2019).
4.
K. S. Novoselov, A. K. Geim, S. V. Morozov et al.,
Science 306(5696), 666 (2004).
26.
H. K. Avetissian, A. K. Avetissian, A. G. Ghazaryan
et al., J. Nanophoton. 14, 026004 (2020).
5.
A. K. Geim, Science 324, 1530 (2009).
27.
A. K. Avetissian, A. G. Ghazaryan, and Kh. V. Sed-
6.
A. H. Castro Neto, F. Guinea, N. M. R. Peres et al.,
rakian, J. Nanophoton. 13, 036010 (2019).
Rev. Mod. Phys 81, 109 (2009).
28.
A. G. Ghazaryan, H. H. Matevosyan, and Kh. V. Sed-
7.
F. Langer, M. Hohenleutner, C. P. Schmid et al.,
rakian, J. Nanophoton. 14, 046009 (2020).
Nature 533, 225 (2016).
29.
H. K. Avetissian, B. R. Avchyan, G. F. Mkrtchian,
8.
O. Schubert, M. Hohenleutner, F. Langer et al.,
and K. A. Sargsyan, J. Nanophoton. 14, 026018
Nature Photon. 8, 119 (2014).
(2020).
9.
G. Vampa, C. R. McDonald, G. Orlando et al., Phys.
30.
H. K. Avetissian and G. F. Mkrtchian, Phys. Rev.
Rev. Lett. 113, 073901 (2014).
B 99, 085432 (2019).
10.
G. Vampa, T. J. Hammond, N. Thir et al., Nature
31.
G. L. Breton, A. Rubio, and N. Tancogne-Dejean,
522, 462 (2015).
Phys. Rev. B 98, 165308 (2018).
11.
G. Ndabashimiye, Sh. Ghimire, M. Wu et al., Nature
32.
H. Liu, Y. Li, Y. S. You et al., Nature Phys. 13, 262
534, 520 (2016).
(2017).
1011
Б. Р. Авчян, А. Г. Казарян, К. А. Саргсян, Х. В. Седракян
ЖЭТФ, том 159, вып. 6, 2021
33.
H. K. Avetissian, G. F. Mkrtchian, and K. Z. Hatsa-
45.
N. Kumar, J. Kumar, C. Gerstenkorn et al., Phys.
gortsyan, Phys. Rev. Res. 2, 023072 (2020).
Rev. B 87, 121406 (2013).
34.
A. D. Güçlü, P. Potasz, M. Korkusinski, and P. Ha-
46.
E. V. Castro, K. S. Novoselov, S. V. Morozov et al.,
wrylak, Graphene Quantum Dots, Springer-Verlag
Phys. Rev. Lett. 99, 216802 (2007).
(2014).
47.
J. B. Oostinga, H. B. Heersche, X. Liu et al., Nature
35.
Ch. Torre, Introduction to Quantum Statistical Ther-
Mater. 7, 151 (2008).
modynamics, Springer (2015).
48.
Y. B. Zhang, T.-T. Tang, C. Girit et al., Nature 459,
36.
E. McCann and V. I. Fal’ko, Phys. Rev. Lett. 96,
820 (2009).
086805 (2006).
49.
F. Guinea, A. H. C. Neto, and N. M. R. Peres, Phys.
37.
I. M. Lifshitz, ЖЭТФ 38, 1569 (1960) [Sov. Phys.
Rev. B 73, 245426 (2006).
JETP 11, 1130 (1960)].
50.
M. Koshino and T. Ando, Phys. Rev. B 73, 245403
38.
J. L. Manes, F. Guinea, and M. A. H. Vozmediano,
(2006).
Phys. Rev. B75, 155424 (2007).
51.
M. Lewenstein, Ph. Balcou, M. Yu. Ivanov et al.,
39.
G. P. Mikitik and Yu. V. Sharlai, Phys. Rev. B 77,
Phys. Rev. A 49, 2117 (1994).
113407 (2008).
52.
A.Varleta, M. Mucha-Kruczynski, D. Bischoff et al.,
40.
D. S. L. Abergel and T. Chakraborty, Appl. Phys.
Synth. Met. 210, 19 (2015).
Lett. 95, 062107 (2009).
53.
E. H. Hwang and S. Das Sarma, Phys. Rev. B 77,
41.
E. S. Morell and L. E. F. F. Torres, Phys. Rev. B 86,
115449 (2008).
125449 (2012).
54.
J. K. Viljas and T. T. Heikkila, Phys. Rev. B 81,
42.
J. J. Dean and H. M. van Driel, Phys. Rev. B 82,
245404 (2010).
125411 (2010).
55.
I. F. Akyildiz, J. M. Jornet, and C. Han, Phys.
43.
S. Wu, L. Mao, A. M. Jones et al., Nano Lett. 12,
Comm. 12, 16 (2014).
2032 (2012).
56.
H. Vettikalladi, W. T. Sethi, A. F. Bin Abas et al.,
44.
Y. S. Ang, S. Sultan, and C. Zhang, Appl. Phys. Lett.
Int. J. Anten. Propagat. 2019, 9573647:1 (2019).
97, 243110 (2010).
1012