ЖЭТФ, 2021, том 159, вып. 6, стр. 1013-1017

ВАН-ДЕР-ВААЛЬСОВО ПРИТЯЖЕНИЕ АТОМОВ ВОДОРОДА

А. М. Ишханян^a,b, В. П. Крайновc*

^a Российско-Армянский университет

0051, Ереван, Армения

^b Институт физических исследований Национальной академии наук Армении

0203, Аштарак, Армения

^c Московский физико-технический институт

141700, Долгопрудный, Московская обл., Россия

Поступила в редакцию 7 февраля 2021 г.,

после переработки 10 февраля 2021 г.

Принята к публикации 10 февраля 2021 г.

Найдена потенциальная энергия ван-дер-ваальсова притяжения атомов водорода друг к другу на расстоя-

ниях R порядка aB /α, где aB — боровский радиус, α = e²/ℏc = 1/137 — постоянная тонкой структуры.

Энергия зависит от R согласно закону R-6 на расстояниях aB ≪ R ≪ aB/α и закону R-7 на расстояниях

R ≫ aB/α.

DOI: 10.31857/S0044451021060000

образные приближения с той или иной степенью

точности. Так, в работе [2] для описания переход-

ной области использовалась приближенная модель-

1. ВВЕДЕНИЕ

ная функция в виде арктангенса. В статье [3] для

Ван-дер-ваальсово притяжение между атомами

определения динамической поляризуемости атома

и молекулами на расстояниях, больших по сравне-

водорода бралось приближенное разложение по сте-

нию с размерами атомов и молекул, есть следствие

пеням частоты (до восьмой степени включитель-

различных электромагнитных сил между телами.

но). Аналогично в статье [4] бесконечные сходящие-

Эти силы обусловлены как непосредственным взаи-

ся ряды для динамической поляризуемости обрыва-

модействием зарядов, так и полем электромагнит-

лись на определенном числе слагаемых. Модельные

ного вакуума. Теория ван-дер-ваальсова притяже-

аппроксимации для динамической поляризуемости

ния детально описана в монографии [1]. В насто-

атома гелия рассматривались в работах [5,6].

ящей работе мы вычисляем потенциальную энер-

В случае R ≫ a_B/α притяжение между атома-

гию ван-дер-ваальсова притяжения атомов водорода

ми создается полем электромагнитного вакуума, ко-

друг к другу на расстояниях R порядка a_B/α, где

торое приводит к поляризации атомов. Рассмотрим

a_B — боровский радиус, α = e²/ℏc = 1/137 — посто-

большой резонатор с идеально проводящими стен-

янная тонкой структуры. Энергия зависит от R как

ками. Сначала считаем, что в резонаторе имеется

R-6 на расстояниях a_B ≪ R ≪ a_B/α и как R-7 на

только один атом. Найдем изменение какой-то соб-

расстояниях R ≫ a_B/α.

ственной частоты ω фотона вакуумного электромаг-

Элемент новизны состоит в использовании точ-

нитного поля от внесения этого атома в резонатор.

ного аналитического выражения для динамической

Уравнения Максвелла для напряженностей вакуум-

поляризуемости атома водорода в случае мнимой

ных полей на этой частоте в отсутствие атома имеют

частоты на основе простых выражений (28), (29)

вид

(см. ниже) для сил осциллятора связанно-связанных

iω

rotE =

H, rotH = -

(1)

и связанно-свободных переходов. Прежде всего это

касается формулы (29) для связанно-свободных пе-

При внесении первого атома появляется ток j^′, на

реходов, для которых ранее использовались разно-

малую величину меняется собственная частота ω и

^* E-mail: vpkrainov@mail.ru

уравнения Максвелла приобретают вид

1013

А. М. Ишханян, В. П. Крайнов

ЖЭТФ, том 159, вып. 6, 2021

′

iω

4π

iω^′

фотонов ℏω электромагнитного вакуума, осуществ-

rotE^′ =

H^′, rotH^′ =

j^′ -

E^′.

(2)

ляющих поляризацию, имеют порядок величины

ℏω ∝ ℏc/R ≪ Ry. Здесь Ry = me⁴/ℏ² = 26.2 эВ.

Умножая первое уравнение в (2) на H^∗, а второе

Статическая поляризуемость атома водорода равна

уравнение на -E^∗, получим

′

iω

β=

a3B = 0.66Å.

(9)

H^∗ rotE^′ =

H^∗ · H^′,

(3)

′

4π

iω

Из (7) и (8) получим сдвиг частоты из-за наличия

−E^∗ rotH^′ = -

j^′ · E^∗ +

E^∗ · E^′.

первого атома в резонаторе в точке r₁ [7]:

Умножая сопряженные к (1) уравнения: первое на

δω₁

2π β |E(r₁)|²

=-∫

(10)

H^′, а второе на -E^′, получим

|E(r)|² dV

iω

H^′ rotE^∗ = -

H^′ · H^∗,

(4)

iω

-E^′ rotH^∗ = -

E^′ · E^∗.

2. ВАН-ДЕР-ВААЛЬСОВО ПРИТЯЖЕНИЕ

НА РАССТОЯНИЯХ R ≫ aB/α

Складывая почленно все уравнения (3) и (4), нахо-

Для нахождения ван-дер-ваальсова притяжения

дим (δω₁ = ω^′ - ω ≪ ω)

на расстояниях R ≫ a_B/α добавим в резонатор вто-

{

}

рой атом в точку r₂; r₂ - r₁ = R. В (10) добавится

div

[E^′, H^∗] + [E^∗, H^′]

индуцированная напряженность поля второго атома

δω₁

4π

(H^∗ · H^′ + E^∗ · E^′) -

j^′ · E^∗.

(5)

в точке первого атома: E(r₁) → E(r₁)+E^induced(r₁).

Выделим из (10) сдвиг частоты, связанный только

Интегрируя (5) по всему объему резонатора и ис-

с взаимодействием атомов друг с другом:

пользуя теорему Гаусса, получим, что левая часть

(

)

δω

4π β Re

E^∗(r₁) · E^induced(r₁)

(5) обращается в нуль из-за граничных условий для

∫

(11)

полей на идеально проводящих стенках резонатора.

|E(r)|² dV

Следовательно,

∫

Определим вещественную напряженность поля

iδω₁

(H^∗ · H^′ + E^∗ · E^′) dV = 4π j^′ · E^∗ dV. (6)

свободной стоячей электромагнитной волны в резо-

наторе

В левой части этого уравнения возмущенные поля

можно заменить на невозмущенные, так как возму-

E(r) = E_ω e_λ cos(k · r), k =

e_λ · k = 0,

(12)

щение (атом) занимает ничтожно малую часть объ-

λ = 1,2,

|e_λ| = 1.

ема резонатора. Получаем

∫

Здесь e_λ — единичный вектор поляризации попереч-

2iδω₁

|E|² dV = 4π j^′ · E^∗ dV.

(7)

ного фотона. Второе решение sin(k · r) внесет нуле-

вой вклад в (11), так как для него E(r₁ = 0) = 0.

А в правой части (6) интегрирование проводится по

Индуцированная вещественная напряженность

малому объему, в котором находится атом, и где ва-

электрического поля стоячей волны E^induced(r₁) в

куумное электрическое поле можно вынести за знак

резонаторе, создаваемая индуцированным диполь-

интеграла:

ным моментом второго атома d₂ в точке, где нахо-

дится первый атом, определяется хорошо известным

∫

из теории поля выражением [8]:

j^′ · E^∗ dV = E^∗ j^′ dV = E^∗ ϱ v₁ dV =

∫

{(

)

∂

k²

=E^∗

ϱr1 dV = E^∗

d₁ =

E^induced(r₁) = Re

-i

n(n · d2ω) +

∂t

R²

R³

)

}

= -i ω E^∗ d₁ = -i ω β |E|² .

(8)

⁽k²

d2ω exp(i k R) .

(13)

R²

R³

Здесь β — поляризуемость атома водорода, которую,

как мы увидим ниже, при R ≫ a_B/α можно заме-

Здесь n = R/R. Мы взяли произвольные рассто-

нить на статическую, так как характерные энергии

яния, а не волновую зону; выше уже отмечалось,

1014

ЖЭТФ, том 159, вып. 6, 2021

Ван-дер-ваальсово притяжение атомов водорода

что характерная величина ωR/c порядка единицы,

Подставляя (17) и (19) в (15), находим (интегриро-

несмотря на большие расстояния R. Дипольный мо-

вание идет только по положительным частотам, т.е.

мент равен

k > 0)

d2ω = β E(r₂).

(14)

∫∞

Из (11) находим энергию взаимодействия атомов

ℏβ²

U (R) = -

Re k³ dk exp(i k R) ×

как отрицательный сдвиг энергии основного состо-

2π

яния гармонического осциллятора ℏω/2, просумми-

∫

рованный по всем положительным частотам (пер-

× sinϑdϑcos(k R cosϑ)×

вый атом для определенности помещаем в начало

координат):

{(

)

(

)

k²

∑

-i

sin² ϑ +

2π β ℏ ω

E(0) · E^induced(0)

∫

-R

R²

R³

U (R) = -

)}

k,λ

|E(r)|² dV

⁽k²

+ 2

(20)

(15)

∫

R²

R³

∑

ω > 0.

(2π)³

Вычисляя элементарный интеграл по углу ϑ, полу-

чим

При этом, суммируя по двум поляризациям, можно,

∞

∫

используя (12), вычислить знаменатель в (15):

ℏβ²c

{

∫

U (R) = -

(2 x³ - 6 x) cos(2 x) +

πR⁷

|E(r)|² dV = E2ω V.

(16)

}

+ (x⁴ - 5 x² + 3) sin(2 x)

(21)

Как и должно быть, нормировочный объем резона-

тора V сокращается в наблюдаемой величине потен-

При интегрировании учтем, что осциллирующие

тригонометрические функции на бесконечности при

циальной энергии. Из (15) видно, что величина E_ω

также сокращается в выражении для U(R). Поэто-

усреднении дают нуль. Получаем известный резуль-

тат [9]:

му ее дальше можно опустить.

В сферической системе координат с осью Z

)₇

23 ℏ β² c

1863

⁽a_B

вдоль вектора R обозначим угол между векторами

U (R) = -

Ry.

(22)

4π R⁷

16 π α R

R и k как ϑ. Переходим к вычислению числителя в

(15). Имеем из (15)

3. ВАН-ДЕР-ВААЛЬСОВО ПРИТЯЖЕНИЕ

E(0) · E^induced(0) =

НА РАССТОЯНИЯХ aB ≪ R ≪ aB/α

= β cos(k R cosϑ)Reexp(ikR)×

Теперь обратимся к меньшим расстояниям, a_B ≪

⎧

⎨(

)∑

≪ R ≪ a_B/α. В этом случае нельзя выносить дина-

k²

-i

(n · e^∗λ) (n · e_λ) +

мическую поляризуемость атома за знак интеграла

^×⎩

R²

R³

λ=1,2

и заменять ее на статическую. Перепишем выраже-

⎫

)⎬

ние (21) в тождественном виде:

∑

⁽k²

e^∗

·e_λ

(17)

R²

R³

⎭

∫

∞

λ=1,2

ℏc

U (R) = -

dx β²(x) exp(2 i x) ×

πR⁷

Для суммирования по поляризациям фотона в (17)

используем формулу

{

}

(2 i x³ - 6 i x) + (x⁴ - 5 x² + 3)

(23)

∑

k_i k_j

e_λi e_λj = δ_ij -

(18)

В выражении (23) сдвинем контур интегрирования

k²

λ=1,2

на верхнюю половину мнимой оси, т. е. заменим x =

Тогда

= iz. Получаем

∑

∞

∫

(n · e^∗λ) (n · e_λ) = n_i n_j e^∗λi e_λj =

ℏc

λ=1,2

U (R) = -

dz β²(iz) exp(-2z)×

(

)

πR⁷

k_i k_j

=n_in_j δ_ij -

= 1 - cos2 ϑ = sin2 ϑ .

(19)

{

}

k²

(2 z³ + 6 z) + (z⁴ + 5 z² + 3)

(24)

1015

А. М. Ишханян, В. П. Крайнов

ЖЭТФ, том 159, вып. 6, 2021

При условии R ≪ a_B/α в интеграле (24) суще-

ственны значения z ≪ 1, так как этот интеграл обре-

зается быстрым убыванием поляризуемости β²(i z).

Тогда интеграл существенно упрощается, так как в

нем можно заменить экспоненту на единицу, а из

пяти слагаемых оставить только последнее. Итак,

заменяя z = kR = ωR/c, находим

∞

∫

3ℏc

U (R) = -

dz β²(i z) =

πR⁷

∞

∫

3ℏ

dω β²(i ω).

(25)

πR⁶

4. ДИНАМИЧЕСКАЯ ПОЛЯРИЗУЕМОСТЬ

АТОМА ВОДОРОДА

Динамическая поляризуемость атома водорода

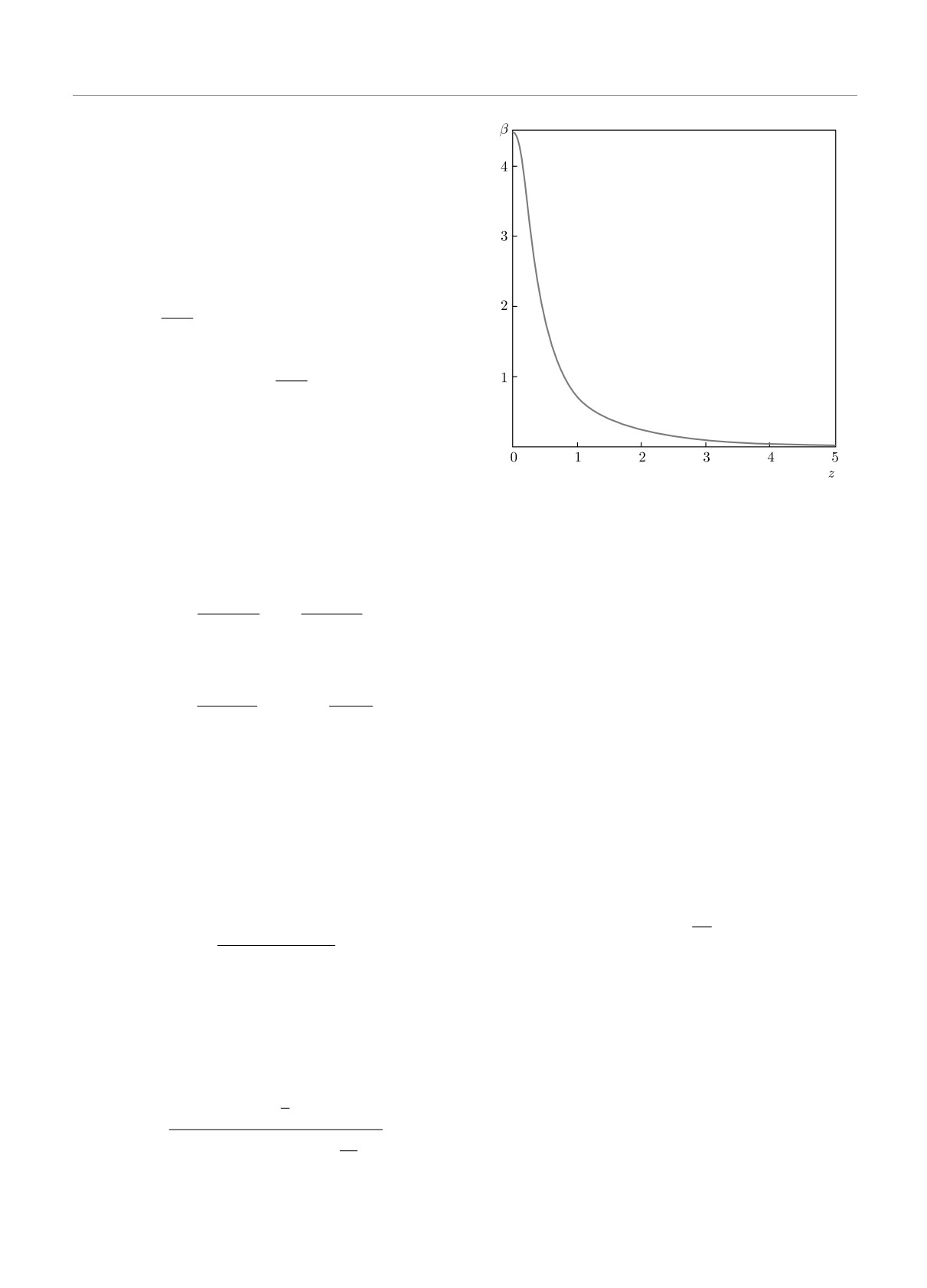
Рис. 1. Динамическая поляризуемость атома водорода

(в единицах a3B ) как функция безразмерной частоты

для мнимых значений частоты быстро убывает с

z = ℏω/Ry

увеличением частоты. Точное выражение для дина-

мической поляризуемости имеет вид

В случае атома водорода первое слагаемое в (27)

∞

∫

∑

равно 0.565, а второе равно 0.435, так что роль пе-

f_n

f_k

β(i ω) =

dk.

(26)

реходов в свободные состояния сравнима с ролью

ω2n1

+ω²

ω2k1 + ω²

n=2

переходов в связанные состояния. Что касается ста-

тической поляризуемости (ω = 0), то первое сла-

Здесь определены частоты переходов

гаемое в (26), соответствующее связанно-связанным

1 - 1/n

1+k²

переходам, дает вклад, равный 3.66, а второе сла-

ωn1 =

ωk1 =

гаемое, соответствующее связанно-свободным пере-

ходам, дает вклад, равный 0.84. В сумме они дают

и силы осцилляторов для связанно-связанных f_n и

известное значение 9/2.

связанно-свободных f_k дипольных переходов. Они

На рис. 1 приведена динамическая поляризуе-

удовлетворяют правилу сумм:

мость атома водорода (в единицах a3B) как функ-

∞

∫

∑

ция безразмерной мнимой частоты z = ℏ ω/Ry, вы-

f_n + f_k dk = 1.

(27)

численная по формуле (26). Подставляя (26) в (25)

n=2

и вычисляя интеграл численно, находим известный

результат [13] для потенциальной энергии на рассто-

Силы осцилляторов для переходов в связанные со-

яниях R ≪ a_B/α:

стояния атома водорода имеют вид [10]

(

)₆

a_B

2n-4

U (R) = -6.50

Ry.

(30)

2⁸ n⁵ (n - 1)

f_n =

(28)

3 (n + 1)2n+4

Численный коэффициент от переходов только в свя-

Силы осцилляторов для переходов в свободные со-

занные состояния при этом составляет 4.0, так что

стояния атома водорода имеют вид, соответствую-

вклад переходов в состояния непрерывного спектра

щий известной формуле Штоббе для сечения фо-

также оказывается значительным.

тоионизации основного состояния атома водорода

[11, 12]:

5. ВАН-ДЕР-ВААЛЬСОВО ПРИТЯЖЕНИЕ

(

)

НА ПРОМЕЖУТОЧНЫХ РАССТОЯНИЯХ

28 k exp

arctg k

R ∝ aB/α

f_k =

(

)) .

(29)

2π

В общем случае R ∝ a_B/α подставляем (26) в

3 (1 + k²)⁴

1 - exp

(24), используя силы осцилляторов (28) и (29). Ре-

1016

ЖЭТФ, том 159, вып. 6, 2021

Ван-дер-ваальсово притяжение атомов водорода

Благодарности. Авторы благодарят В. А. Ас-

тапенко и Ю. С. Бараша за ценные советы по содер-

жанию работы.

Финансирование. Работа выполнена при под-

держке Российского фонда фундаментальных ис-

следований (грант № 20-52-05012), Комитета по нау-

ке Армении (грант № 20RF-171) и Армянского на-

ционального фонда науки и образования (грант

№ PS-5701).

ЛИТЕРАТУРА

Ю.С. Бараш, Силы Ван-дер-Ваальса, Наука, Моск-

ва (1988).

M. O’Carroll and J. Sucher, Phys. Rev. 187, 85

(1969).

P. Getzin and M. Karplus, J. Chem. Phys. 53, 2100

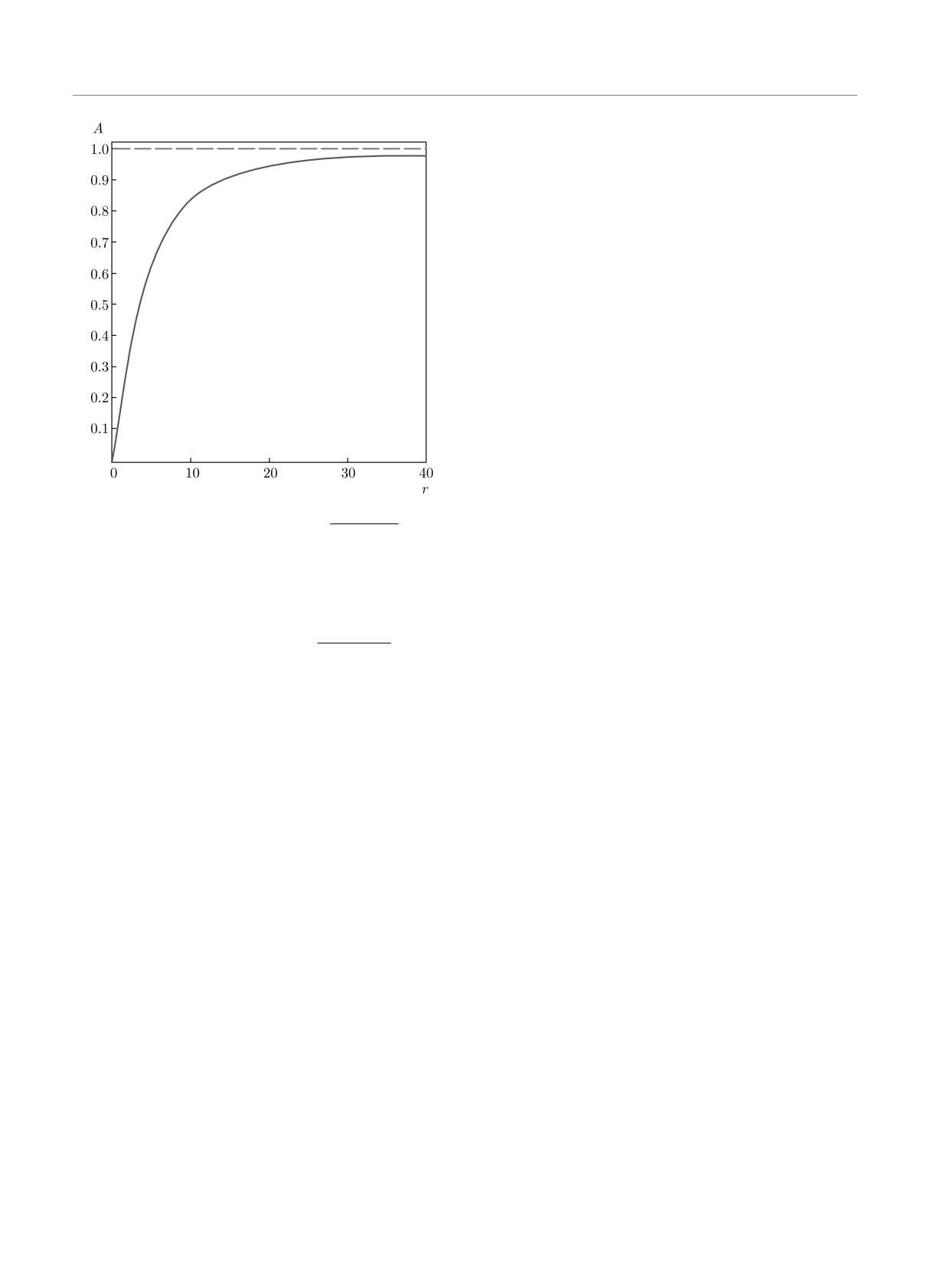
Рис. 2. Зависимость величины A = -16πU(R)R7

от r =

1863 c

(1970).

= R/c согласно (24)

P. W. Langhoff, Chem. Phys. Lett. 12, 223 (1971).

зультаты численного расчета представлены на рис. 2

M. J. Jamieson, G. W. F. Drake, and A. Dalgarno,

Phys. Rev. A 51, 3358 (1995).

(далее используются атомные единицы). Приведен

от R/c.

Ming-Keh Chen and Kwong T. Chung, Phys. Rev.

63 c

При R/c ≫ 1 эта зависимость стремится к посто-

A 53, 1439 (1996).

янному значению, равному единице в соответствии

Л. Д. Ландау, Е. М. Лифшиц, Электродинамика

с (22). В этом случае потенциальная энергия при-

сплошных сред, Физматлит, Москва (2005).

тяжения обратно пропорциональна седьмой степе-

ни расстояния между атомами. А при значениях

Л. Д. Ландау, Е. М. Лифшиц, Теория поля, Физ-

R/c ≪ 1 (но, разумеется, R ≫ 1) получаем ли-

матлит, Москва (2012).

нейную функцию расстояния; она соответствует то-

В. Б. Берестецкий, Е. М. Лифшиц, Л. Л. Питаев-

му, что потенциальная энергия притяжения обратно

ский, Квантовая электродинамика, Физматлит,

пропорциональна шестой степени расстояния между

Москва (2002).

атомами. Из рис. 2 видно, что переход от зависимо-

сти R-6 к зависимости R-7 при увеличении расстоя-

10.

В. А. Астапенко, Взаимодействие излучения с

ния R между атомами водорода оказывается сильно

атомами и наночастицами, Изд-во «Интеллект»,

затянутым.

Долгопрудный (2010).

11.

В. П. Крайнов, Б. М. Смирнов, Излучательные пе-

6. ЗАКЛЮЧЕНИЕ

реходы в атомной физике, Высшая школа, Москва

(1983).

Таким образом, мы получили явное выражение

для потенциальной энергии ван-дер-ваальсова при-

12.

V. Krainov and B. M. Smirnov, Atomic and Molecu-

тяжения атомов водорода друг к другу на расстоя-

lar Radiative Processes with Applications to Modern

ниях R порядка a_B/α. Как и должно быть, эта зави-

Spectroscopy and the Greenhouse Effect, Springer Ser.

симость переходит в известный закон R-6 на рассто-

Atom., Opt. Plasma Phys., Vol. 108, Springer Nature

яниях a_B ≪ R ≪ a_B/α и в известный закон R-7 на

Switzerland AG (2019).

расстояниях R ≫ a_B/α. Отметим, что при увеличе-

13.

Л. Д. Ландау, Е. М. Лифшиц, Квантовая ме-

нии расстояния R между атомами водорода переход

ханика (нерелятивистская теория), Физматлит,

от зависимости R-6 к зависимости R-7 происходит

Москва (2004).

весьма медленно.

1017

ЖЭТФ, вып. 6