ЖЭТФ, 2021, том 159, вып. 6, стр. 1018-1027
© 2021
ПОСТРОЕНИЕ ТЕНЕЙ ЧЕРНЫХ ДЫР.
АНАЛИТИЧЕСКАЯ ТЕОРИЯ
С. В. Чернов*
Астрокосмический центр, Физический институт им. П. Н. Лебедева Российской академии наук
117997, Москва, Россия
Поступила в редакцию 31 декабря 2020 г.,
после переработки 31 декабря 2020 г.
Принята к публикации 26 января 2021 г.
Рассматриваются аналитические методы построения теней черных дыр в метрике Керра - Ньюмена и
возможности их наблюдения с помощью радиоинтерферометрии со сверхдлинными базами (РСДБ).
DOI: 10.31857/S0044451021060031
кого диска. Такой подход более точно сопоставляет
модельные и наблюдательные данные.
1. ВВЕДЕНИЕ
Интерферометрические наблюдения могут до-
статочно точно определить форму фотонного коль-
Благодаря проекту «Телескоп горизонта собы-
ца [13], а это, в свою очередь, позволит более точ-
тий» удалось наблюдать тень черной дыры у ис-
но протестировать общую теорию относительности
точника M87∗ [1-6], но наблюдение фотонных ко-
в сильном поле и определить параметр вращения
лец является более сложной задачей будущего [7].
черной дыры [14]. Существуют различные способы
Для ее решения необходимо, чтобы радиоинтерфе-
моделирования формы фотонных колец. В работе
рометр имел достаточно большую базу (проекцию
[15] форму фотонного кольца моделировали с помо-
баз), которая превышает диаметр Земли (т. е. до-
щью плоской кривой — улитка Паскаля (limaçon), в
статочно высокое угловое разрешение, порядка доли
работе [13] — с помощью выпуклых овалов (phoval).
микросекунд) [7], высокую чувствительность прием-
Форма фотонных колец близко связана с формой
ного комплекса и большую базу численных экспери-
критических кривых в гравитационном поле черной
ментов для моделирования фотонных колец и сопо-
дыры, следовательно, точное моделирование фотон-
ставления данных теории и наблюдений. Одним из
ных колец поможет лучше понять физику вблизи
таких проектов, который способен решить данную
черных дыр.
задачу, является проект «Миллиметрон», который
В разд. 2 выписываются точные аналитические
планируется запустить в 2030-х гг. [8].
решения уравнений изотропных геодезических в
Существует достаточно много свободного про-
метрике Керра - Ньюмена и строятся образы черных
граммного обеспечения, которое способно моделиро-
дыр. В разд. 3 аналитически вычисляются функции
вать фотонные кольца магнитогидродинамических
видности для колец различной формы и интенсив-
моделей. Эти программы решают уравнения изо-
ности. В разд. 4 приводятся выводы.
тропных геодезических численно (например, паке-
В работе используется система единиц, в которой
ты Raptor [9], Ipole [10,11]) или полуаналитически
скорость света и гравитационная постоянная равны
(grtrans [12]). Все эти пакеты имеют как численные
единице, c = G = 1. Размерность длины есть GM/c2,
ошибки, так и неточности, связанные с тем, что на-
размерность времени — GM/c3, где M — масса чер-
блюдатель расположен на конечном, относительно
ной дыры.
близком расстоянии от черной дыры (R ≈ 50Rg).
В данной работе уравнения изотропных геодезиче-
2. УРАВНЕНИЯ ДВИЖЕНИЯ И ТОЧНЫЕ
ских решаются аналитически точно и строятся об-
АНАЛИТИЧЕСКИЕ РЕШЕНИЯ
разы черных дыр для простейшего бесконечно тон-
Метрика вращающейся и заряженной черной ды-
ры Керра - Ньюмена в координатах Бойера - Линдк-
* E-mail: chernov@lpi.ru
виста (t, r, θ,φ) имеет вид [16]
1018
ЖЭТФ, том 159, вып. 6, 2021
Построение теней черных дыр...
(
)
2Mr - Q2
Σ
Σ
√
ds2 = -
1-
dt2 +
dr2 + Σ dθ2 +
pθ = ±θ
Θ,
(1c)
Σ
Δ
E
sin2 θ
(
)
+
(r2 + a2)2 - Δa2 sin2 θ
dφ2 -
Σ
a
λ
Σ
pφ =
(r2 + a2 - aλ) +
- a,
(1d)
2a sin2 θ(2Mr - Q2)
E
Δ
sin2 θ
−
dt dφ,
Σ
где были введены радиальный и угловой потенциа-
где
лы
R = (r2 + a2 - aλ)2 - Δ(η + (a - λ)2),
Σ = r2 + a2 cos2 θ, Δ = r2 - 2Mr + a2 + Q2,
cos2 θ
J = Ma — угловой момент черной дыры. Корни
Θ = η + a2 cos2 θ - λ2
sin2 θ
уравнения
Символы ±r и ±θ означают знаки импульсов фо-
Δ = (r - r1)(r - r2) = 0
тона pr и pθ соответственно. Траектория движения
фотона в плоскости r-θ определяется точками оста-
соответствуют внешнему и внутреннему горизонтам
новки в радиальном и угловом потенциалах. Поэто-
событий
му удобно представить потенциалы в виде
√
r1,2 = M ±
M2 - a2 - Q2.
R = (r - ra)(r - rb)(r - rc)(r - rd),
В данной работе предполагается, что параметр вра-
где корни уравнения расположены в следующем по-
щения и заряд черной дыры ограничены неравен-
рядке: ra > rb > rc > rd, и
ством 0 < a2 + Q2 < M2. Экстремальная черная
дыра соответствует случаю, когда a2 + Q2 → M2.
(u+ - u)(u - u-)
Θ=a2
,
Случаям не вращающейся и не заряженной черной
1-u
дыры отвечают пределы a → 0 и Q → 0 соот-
ветственно. Метрические коэффициенты и символы
где введено обозначение u = cos2 θ и
Кристоффеля выписаны в Приложении A.
√
(
)
(
)2
Траектория фотонов в метрике Керра - Ньюме-
1
η+λ2
1
η+λ2
η
u± =
1-
±
1-
+
на описывается тремя интегралами движения. Это
2
a2
4
a2
a2
полная энергия на бесконечности E = -pt, угловой
Уравнение радиального потенциала является алгеб-
момент вокруг вращающейся оси черной дыры L =
раическим уравнением четвертой степени, решение
= pφ и постоянная Картера
которого можно выписать аналитически (см. Прило-
(
)
p2φ
жение B). Уравнение углового потенциала является
Qc = p2θ - cos2 θ a2p2t -
,
алгебраическим уравнением второго порядка отно-
sin2 θ
сительно u, решение которого имеет вид
где pμ обозначает 4-импульс фотона. Четвертое
(
уравнение получается из условия равенства нулю
u = u±, θ± = arccos
∓√u+ ) ,
массы фотона, gαβ pαpβ = 0. Оказывается, что ин-
где θ+ > θ-.
тегралы движения не зависят от модуля величины
Если ввести аффинный параметр τ,
полной энергии, а зависят только от знака E. Поэто-
му удобно ввести две новые величины, от которых
dxμ
Σ
=
pμ,
зависит траектория движения фотона:
dτ
E
L
Qc
λ=
,
η=
то уравнения (1) перепишутся в дифференциальном
E
E2
виде. Нас будет интересовать интегральная форма
Тогда компоненты 4-импульса фотона записывают-
этих уравнений. Последовательно выражая аффин-
ся в виде
ный параметр из каждого уравнения, легко полу-
чить интегральную форму вида [17, 18]
Σ
r2 + a2
pt =
(r2 + a2 - aλ) - a2 sin2 θ + aλ,
(1a)
E
Δ
(2a)
Ir = Gθ,
φo - φs = Iφ + λGφ,
(2b)
Σ
√
pr = ±r
R,
(1b)
to - ts = It + a2Gt,
(2c)
E
1019
2*
С. В. Чернов
ЖЭТФ, том 159, вып. 6, 2021
[
(
)
где интегралы равны
1
u+
Gφ =
√
2mΠ u+,
-
-a2u-
u-
∫ro
∫
θo
(
)
)
dr
dθ
(cosθs
u+
√
,
Gθ =
√ ,
Ir =
- (±s)Π u+, arcsin
,
+
±r
R
±θ
Θ
√u+
u-
rs
θs
(
)
)]
(cosθo
u+
∫r0
+ (±o)Π u+, arcsin
,
,
(6)
a(2Mr - Q2 - aλ)
√u+
u-
Iφ =
√
dr,
±rΔ
R
rs
[
2u+
(u+)
∫rθ
Gt = -√
2mE′
-
(r2Δ + (2Mr - Q2)(r2 + a2 - aλ)) dr
-a2u-
u-
√
,
It =
(
)
)
±rΔ
R
(cosθs
u+
rs
− (±s)E′ arcsin
,
+
√u+
u-
∫ro
∫
θo
(
)
)]
dθ
cos2 θ dθ
(cosθo
u+
Gφ =
√
,
Gt =
√
,
+ (±o)E′ arcsin
,
,
(7)
±θ sin2 θ
Θ
±θ
Θ
√u+
u-
rs
θs
а обозначения «s» и «o» означают положение источ-
где νo,s = ν(r = ro,s), m — число точек остано-
ника излучения и наблюдателя соответственно. Все
вок в угловом потенциале, (±s) = (±o)(-1)m [17],
эти интегралы легко взять в явном виде. Для этого
(±o = sign(θo)). Значение интеграла It имеет более
представим интеграл I как сумму двух интегралов
сложный вид:
∫ro
∫
ro
∫
rs
α41
It = (4M2 - Q2)Ir + gra
×
I =
[]dr =
[]dr + w
[]dr,
α4
[
]
rs
ra
ra
α2 - α21
(α2 - α21)2
× V0(νo) + 2
V1(νo) +
V2(νo)
+
α21
α4
где w = ±1. Если траектория фотона имеет точку
1
[
]
остановки в радиальном потенциале, то w = 1, если
α41
α2-α21
(α2-α21)2
+wgr2
V0(νs)+2
V1(νs)+
V2(νs)
+
точка остановки совпадает с источником излучения
aα4
α21
α4
1
rs = ra, то w = 0, если точка остановки отсутствует,
∑
gAi
[(
)(
)
то w = -1.
+
1-β2i
Π(νo, γ2i, k)+wΠ(νs, γ2i, k)
+
ra-ri
В Приложении С показаны способы разложения
i=1
]
интегралов I в табличные и представлены значе-
+ β2i (F(νo,k) + wF(νs,k))
+
ния этих табличных интегралов. Здесь выпишем яв-
[
ные решения для интегралов I. Явные решения для
+ 2Mg (ra - rb)(Π(νo, δ, k) + wΠ(νs, δ, k)) +
интегралов G представлены в работе [17]. Решения
]
имеют вид
+ rb (F(νo,k) + wF(νs,k))
(8)
2(F (νo, k) + wF (νs, k))
Ir =
√
,
(3)
(ra - rc)(rb - rd)
Решения (3)-(8) полностью аналитически описыва-
ют траекторию фотона в метрике Керра - Ньюмена.
Iφ =
Для построения тени черной дыры удобно восполь-
зоваться параметрами (α, β), впервые введенными в
∑
[(
)(
)
= ga Γi
1-β2i
Π(νo, γ2i, k) + wΠ(νs, γ2i, k)
+
работе [19]. Считаем, что наблюдатель расположен
i=1
под некоторым углом θo к оси вращения черной ды-
]
ры в диапазоне θo ∈ (0, π/2). Запишем параметры
+ β2i (F(νo,k) + wF(νs,k)) ,
(4)
(α, β) в виде
√
[
λ
cos2 θo
1
(u+)
α=-
,
β = ±o η+a2 cos2 θo-λ2
Gθ =
√
2mK
-
sinθo
sin2
θo
-a2u-
u-
(
)
)
Для построения тени черной дыры нам доста-
(cosθs
u+
- (±s)F arcsin
,
+
точно воспользоваться только решением уравнения
√u+
u-
(
)
)]
(2a). Из этого уравнения можно вывести радиус ис-
(cosθo
u+
точника через радиус наблюдателя ro и углы источ-
+ (±o)F arcsin
,
,
(5)
√u+
u-
ника θs и наблюдателя θo
1020
ЖЭТФ, том 159, вып. 6, 2021
Построение теней черных дыр...
)
(1√
2
ra(rb - rd) - rb(ra - rd)sn
(ra - rc)(rb - rd)Ir - F (νo, q)|k
2
)
,
(9)
rs =
(1√
rb - rd - (ra - rd) sn2
(ra - rc)(rb - rd)Ir - F (νo, q)|k
2
где sn — эллиптический синус Якоби. Для построе-
где u — безразмерная проекция базы интерферомет-
ния образа воспользуемся методом обратной трасси-
ра в единицах длин волн, x — безразмерный размер
ровки лучей. Будем запускать лучи от наблюдателя
образа в радианах. Если ввести полярные координа-
к источнику. Пусть источником излучения является
ты x = (ρ, φρ) и u = (u, φu), то функция видности
бесконечно тонкий диск, расположенный в эквато-
перепишется в виде
риальной плоскости вращения черной дыры с внут-
∫∫
ренним радиусом rin = 6. Тогда θs = π/2. Наблюда-
V (u, φu) =
I(ρ, φρ)e-2πiuρcos(φρ-φu)ρ dρ dφρ.
тель расположен на расстоянии ro = 1010 под углом
θo = 17◦, что приблизительно соответствует источ-
Если интенсивность кольца образа черной дыры
нику M87∗. Для каждого значения параметров α и
описывается бесконечно тонким кольцом с однород-
β вычисляем положение источника rs и сравниваем
ной интенсивностью
с положением внутреннего радиуса диска rs ≷ rin,
таким образом определяем образ диска (черной ды-
(
)
1
d
ры) в картинной плоскости наблюдателя. На рис. 1
I(ρ, φρ) =
δ ρ-
,
πd
2
показан пример образа черной дыры Керра - Нью-
мена, полученный по аналитическим формулам (3)
то функция видности имеет простой вид [7] (в При-
и (5) для параметров черной дыры, равных a = 0.9,
ложении D выписаны табличные интегралы, кото-
Q = 0.3. На рис. 1 показана тень черной дыры, пер-
рые использовались при вычислении интегралов в
вое фотонное кольцо и второе подкольцо (subring).
этом разделе)
Из-за того, что внутренний радиус диска rin = 6
близок к фотонной сфере, происходит наложение об-
V (u, φu) = J0(π du),
(10)
раза диска и первого фотонного кольца.
Для построения распределения угла φ в картин-
где d — диаметр кольца, J0 — функция Бесселя. Ес-
ной плоскости наблюдателя надо воспользоваться
ли фотонное кольцо имеет конечную толщину, то
решениями уравнений (2a) и (2b). Определяя радиус
для конечного кольца c однородной интенсивностью
(9) и подставляя в (4), с помощью (2b) определяем
распределения угла φ. На рис. 2 цветом показан гра-
1
I(ρ, φρ) =
фик распределения угла φ, нормированный на угол
πdw
2π, в картинной плоскости.
Таким же образом можно найти образ распреде-
получаем функцию видности
ления времени t в картинной плоскости. Для это-
го надо воспользоваться решениями уравнений (2a)
∫b
∫
ρ dρ dφρ
и (2c).
V (u) =
e-2πiρucos(φρ-φu)
=
πdw
a
0
∫
b
3. ФУНКЦИЯ ВИДНОСТИ
2
=
ρJ0(2πρu) dρ =
dw
В этом разделе рассмотрим наблюдательное про-
a
(
)
явление колец посредством функции видности и
1
=
bJ1(2πbu) - aJ1(2πau)
,
(11)
представим точные аналитические решения прояв-
π dwu
ления колец с неоднородной плотностью и конечной
толщиной.
где a, b — соответственно внутренний и внешний ра-
Комплексная функция видности V двух элемен-
диус кольца, d = a + b — средний диаметр кольца,
тов интерферометра является фурье-образом рас-
w = b-a — толщина кольца. При a → b решение (11)
пределения интенсивности сигнала на небе I и опре-
сводится к решению (10). Для конечного неоднород-
деляется формулой [20]
ного кольца, интенсивность которого растет линей-
∫
но с увеличением радиуса,
V (u) = I(x)e-2πiu·x d2x,
1021
С. В. Чернов
ЖЭТФ, том 159, вып. 6, 2021
(
)
1
ρ
∫b
∫
I(ρ, φρ) =
-1 ,
ρ dρ dφρ
πdw a
V (u) =
sin φρe-2πiρucos(φρ-φu)
=
2dw
a
0
получаем функцию видности
∫
b
iπ sinφu
=-
ρJ1(2πρu) dρ =
dw
∫b
a
(
)
[
2ρ
ρ
V (u) =
- 1 J0(2πuρ)dρ =
πi sinφu
dw
a
=
a(J1(2πua)H0(2πua) -
a
4udw
[
(
)
− J0(2πua)H1(2πua)) - b(J1(2πub)H0(2πub)-
1
b
]
=
4b
-1
J1(2πub) +
4dwπu
a
- J0(2πub)H1(2πub)) .
(14)
b
+
(J0(2πbu)H1(2πub) - J1(2πub)H0(2πub)) -
au
Данная функция видности является мнимой. Это
a
означает, что фаза функции видности равна π/2.
-
(J0(2πau)H1(2πua) -
au
Амплитуда функции видности равна модулю от вы-
]
ражения (14).
- J1(2πua)H0(2πua)) .
(12)
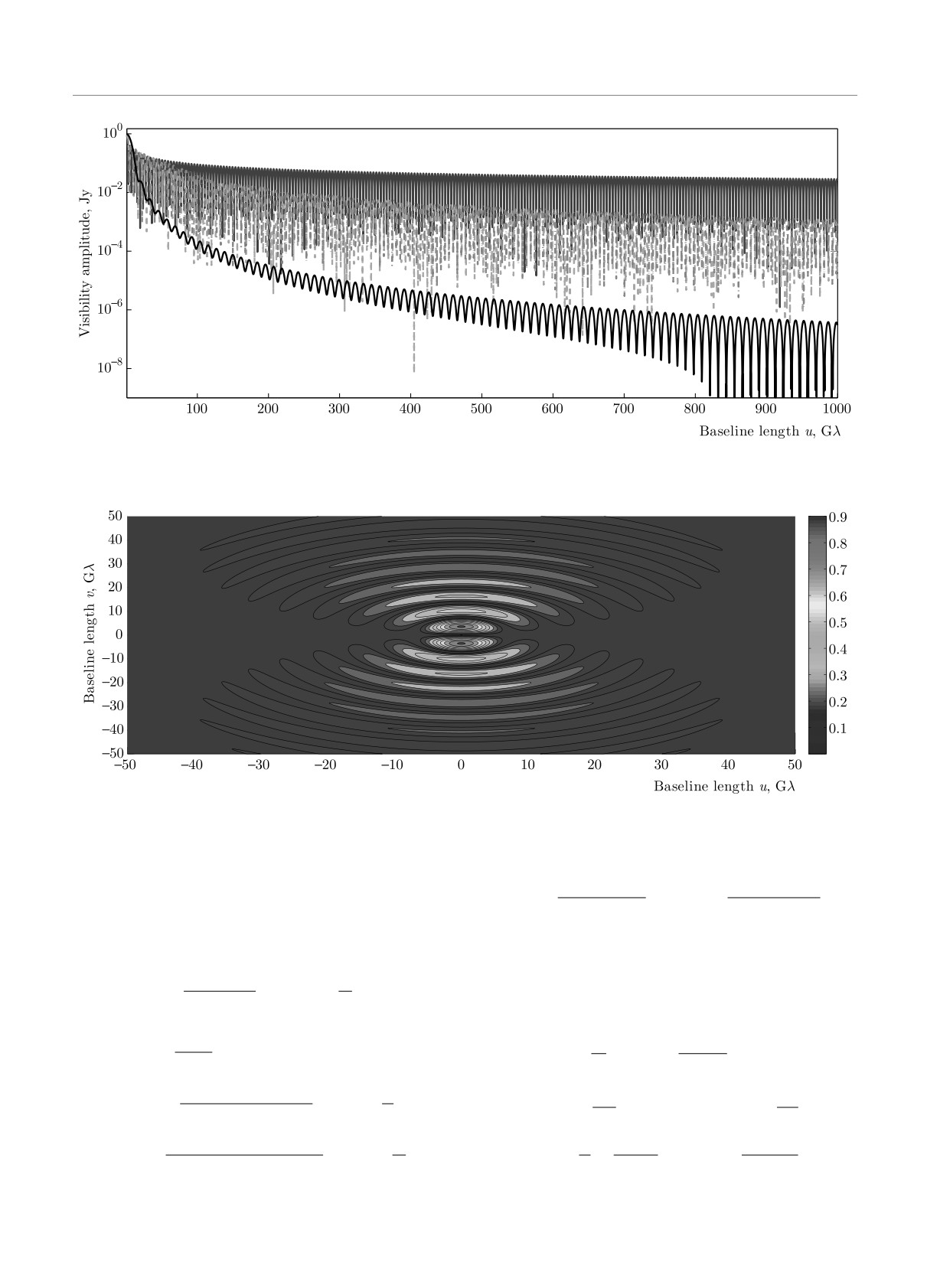
На рис. 3 показаны модуль функции видности
для рассмотренных колец в зависимости от проек-
ции баз интерферометра в единицах миллиард длин
Для конечного неоднородного кольца, интенсив-
волн (Gλ). Синяя кривая соответствует бесконеч-
ность которого зависит параболически от радиуса,
но тонкому кольцу, зеленая кривая — однородно-
(
)
му кольцу с конечной толщиной, красная кривая —
(
)2 (
)
2
1
2
a+b
неоднородному кольцу, интенсивность которого рас-
I(ρ, φρ) =
1-
ρ-
,
πdw
b-a
2
тет линейно с увеличением радиуса, и черная кри-
вая — неоднородному кольцу, интенсивность кото-
рого зависит параболически от радиуса. На данном
получаем более громоздкое решение:
рисунке толщина кольца равна w = 2μas (микросе-
кунд дуги), а диаметр d = 34μas. Все кривые нор-
b
(
)
∫
(
)2 (
)2
2
2
a+b
мированы на единицу функции видности V = 1 при
V (u) =
1-
ρ-
×
dw
b-a
2
нулевых проекциях баз u = 0. Наибольшую скорость
a
уменьшения функции видности в зависимости от
[
проекции баз имеет неоднородное кольцо с парабо-
4
b
× ρJ0(2πρu) dρ =
(-8πbuJ0(2πbu) +
лическим профилем изменения интенсивности. Для
dw3
(2πu)3
того чтобы разрешить однородное кольцо, проекция
+ 8J1(2πbu) - 2dπ2uJ1(2πbu)H0(2πbu)+
баз интерферометра должна быть больше обратной
толщины, u > 1/w [7]. Для толщины w = 2μas это
)
a
+ 2dπ2uJ0(2πbu)H1(2πbu)
-
×
соответствует проекциям базы u > 100Gλ. При усло-
(2πu)3
виях u ≫ 1/w наблюдается периодичность функ-
(-8πauJ0(2πau) + 8J1(2πau) -
ции видности V с периодом 1/w и асимптотикой
V ∼ 1/u3/2. Неоднородное кольцо с линейным рос-
- 2dπ2uJ1(2πau)H0(2πau)+
том интенсивности имеет такую же асимптотику ви-
]
да V ∼ 1/u3/2, но периодичность выражена не так
)
+ 2dπ2uJ0(2πau)H1(2πau)
(13)
ярко. Асимптотика функции видности неоднород-
ного кольца, интенсивность которого зависит пара-
болически от радиуса, имеет вид V ∼ 1/u5/2, т.е.
Для конечного анизотропного кольца, интенсив-
функция видности убывает быстрее, и периодич-
ность которого зависит от угла φρ,
ность не проявляется.
На рис. 4 показана амплитуда двумерной функ-
sinφρ
ции видности в зависимости от координат проекции
I(ρ, φρ) =
,
2dw
баз (u, v) в единицах Gλ. Функция видности не сим-
метрична. Вдоль оси x она имеет нулевое значение
функция видности равна
(sin φu = 0).
1022
ЖЭТФ, том 159, вып. 6, 2021
Построение теней черных дыр...
Рис. 1. Аналитический образ черной дыры, полученный по формулам (3) и (5), в зависимости от α и β
Рис. 2. (В цвете онлайн) Аналитический образ распределения угла φ в зависимости от параметров α, β, полученный по
формулам (3)-(6)
Из сказанного выше можно сделать следующие
решения и в качестве примера построены образы
выводы. Интерферометрическое проявление фотон-
и фотонные кольца бесконечно тонкого диска. Для
ных колец черных дыр зависит от степени неодно-
простейшей формы образа кольца черной дыры
родности распределения интенсивности по ширине
были вычислены аналитически функции видности и
кольца. С увеличением неоднородности требуются
была показана возможность детектирования колец
более чувствительные детекторы, способные фикси-
черной дыры на базах u > 1/w, что соответствует
ровать функцию видности от фотонных колец.
расстоянию порядка расстояния от Земли до Луны
и больше [7].
4. ЗАКЛЮЧЕНИЕ
Финансирование. Работа выполнена при фи-
нансовой поддержке Российского фонда фундамен-
В работе рассматривались аналитические мето-
тальных исследований (грант № 20-02-00469-a) и Го-
ды построения образа черной дыры Керра - Нью-
сударственного задания по научной программе ОКР
мена. Были выписаны точные аналитические
«Миллиметрон».
1023
С. В. Чернов
ЖЭТФ, том 159, вып. 6, 2021
Рис. 3. (В цвете онлайн) Одномерные функции видности в зависимости от u
Рис. 4. (В цвете онлайн) Двумерная функция видности в зависимости от u, v для неоднородного анизотропного кольца
ПРИЛОЖЕНИЕ A
Δ - a2 sin2 θ
(2Mr - Q2)a
gφφ =
,
gtφ = -
ΔΣ sin2 θ
ΣΔ
Метрические коэффициенты метрики Кер-
Определитель метрики равен [16]
ра - Ньюмена равны [16]
(
)
g = -Σ2 sin2 θ.
2Mr - Q2
Σ
gtt = -
1-
,
grr =
,
gθθ = Σ,
Σ
Δ
Символы Кристоффеля равны [16]
sin2 θ
(
)
pb
a sin2 θ
gφφ =
(r2 + a2)2 - Δa2 sin2 θ
,
Γttr = -
,
Γtrφ =
(pb + 2qr),
Σ
Δ
Δ
(2Mr - Q2)a sin2 θ
1
3
qa
Δp
gtφ = -
,
gθθ =
,
Γtθφ = -
sin2 θ sin2θ, Γrtt = -
,
Σ
Σ
Σ
Σ
(r2 + a2)2 - Δa2 sin2
θ
Δ
r
M-r
a2 sin2θ
gtt = -
,
grr =
,
Γrrr =
+
,
Γrrθ = -
,
ΣΔ
Σ
Σ
Δ
2Σ
1024
ЖЭТФ, том 159, вып. 6, 2021
Построение теней черных дыр...
2
a2 sin2θ
a2 sin2θ
A
Γθθθ = -
,
Γθrr =
,
P =-
-C,
2Σ
2ΣΔ
12
[(
)2
]
rΔ
r
A
A
B2
Γrθθ = -
,
Γθrθ =
,
Q=-
-C -
,
Σ
Σ
3
6
8
(
Δsin2 θ
qa2 sin2θ
)
Γrφφ = -
(r + pa2 sin2 θ), Γttθ =
,
)
3
√(P)
(Q)2
Σ
Σ
ω± =3
√-Q
±
+
,
2
3
2
qa2 sin2θ
aΔp sin2 θ
Γθtt =
,
Γrtφ =
,
√
Σ2
Σ
ω+ + ω-
A
z=
-
> 0.
qab sin2θ
2qa cosθ
2
6
Γθtφ = -
,
Γφtθ =
,
Σ2
Σsin θ
[
(
)]
sin2θ
a2 sin2 θ
ПРИЛОЖЕНИЕ C
Γθφφ = -
b - 2a2q sin2 θ
2+
,
2Σ
Σ
Неполные эллиптические интегралы первого,
r
sin2 θ
второго и третьего рода определяются следующим
Γφrφ =
(1 + 2q) + a2p
,
Δ
Δ
образом:
[
]
cosθ
2qa2b sin2 θ
φ
Γφθφ =
(1 + 2q)(b - 2qa2 sin2 θ) -
,
∫
Δsinθ
Σ
dθ
F (φ, k) =
√
,
1 - k sin
2θ
0
Γφtr = -arQ2 +M(Σ-2r2),
ΔΣ2
∫
φ
где
√
E(φ, k) =
1 - k sin2 θdθ,
rQ2+M(Σ-2r2)
Q2-2Mr
0
b = r2+a2, p =
,
q=
Σ2
2Σ
φ
∫
1
dθ
Π(α2, φ, k) =
√
1 - α2 sin2 θ
1 - k sin2 θ
ПРИЛОЖЕНИЕ B
0
Производная эллиптического интеграла второго ро-
Выражение для радиального потенциала являет-
да E по параметру k задается как
ся алгебраическим уравнением четвертого порядка,
которое удобно представить в виде [17]
∂E(φ, k)
E(φ, k) - F (φ, k)
E′ (φ, k) =
=
∂k
2k
R = (r - ra)(r - rb)(r - rc)(r - rd),
Полные эллиптические интегралы определяются
условием φ = π/2 и обозначаются как
где корни уравнения записаны в порядке убывания,
ra > rb > rc > rd. Явный вид решения этого уравне-
K(k) = F (π/2, k), E(k) = E(π/2, k),
ния записывается в виде [17]
√
Π(n, k) = Π(n, π/2, k).
A
B
ra = z +
-
-z2 -
,
Введем обозначения
2
4z
√
√
(rb - rd)(r - ra)
ra - r
d
A
B
ν = arcsin
,
α2 =
,
rb = z -
-
-z2 -
,
(ra - rd)(r - rb)
2
4z
rb - rd
√
2
(rb - rc)(ra - rd)
A
B
g=
√
,
k=
rc = -z +
-
-z2 +
,
(ra - rc)(rb - rd)
(ra - rc)(rb - rd)
2
4z
√
Для вычисления интегралов I в работе использо-
A
B
rd = -z -
-
-z2 +
,
вались следующие табличные значения интегралов
2
4z
для случая, когда r > ra. Данный интеграл вычис-
где
ляется на с. 256 [21]:
A=a2 -η-λ2,
∫r
B = 2M(η + (λ - a)2),
dx
√
= gF(ν, k).
(x - ra)(x - rb)(x - rc)(x - rd)
C = -a2η - Q2(η + (a - λ)2),
ra
1025
С. В. Чернов
ЖЭТФ, том 159, вып. 6, 2021
Этот интеграл вычисляется на с. 257 [21]:
snu, cnu и dnu — эллиптические функции Якоби.
Интеграл Iφ
легко представить в виде табличных
∫r
x dx
интегралов. Для этого разложим Iφ как [23]
√
=
(x - ra)(x - rb)(x - rc)(x - rd)
∫
r
ra
a(2rM - Q2 - aλ)
[
]
Iφ =
√
dr =
(
)
Δ
R
= g (ra - rb)Π
α2, ν, k
+ rbF(ν, k) .
ra
Этот интеграл вычисляется на с. 259 [21]:
∫
Ki dr
=a
√
=
∫
r
(r - ri)
R
i=1
dx
ra
√
=
(p - x)
(x - ra)(x - rb)(x - rc)(x - rd)
]
ra
∑
[(
)
[
(
)
= ga
Γi
1-β2i
Π(ν, γ2i, k) + β2iF (ν, k) ,
g
p-r
b
=
(ra-rb)Π α2
,ν, k
+
i=1
(p-ra)(p-rb)
p-ra
]
где
+ (p - ra)F (ν, k) .
ra - rd ri - rb
ri - ra
γ2i =
,
β2i =
,
rb - rd ri - ra
ri - rb
Этот интеграл вычисляется на с. 130 [22]:
√
Ki
ri = M + (-1)i+1
M2 - a2 - Q2, Γi =
,
∫
r
ra - ri
x2dx
√
=
(x - ra)(x - rb)(x - rc)(x - rd)
M2 - Q2/2 - aλ/2
ra
Ki = M + (-1)i+1
√
,
∫
u1
M2 - a2 - Q2
(1 - α21 sn2 u)2
= gr2a
du,
Аналогично представим интеграл It в виде таблич-
(1 - α2 sn2 u)2
0
ных интегралов как
где
∫r
[
]
A1
A2
dr
√
It =
+
+4M2-Q2+2Mr+r2
√ ,
(rb-rd)(r-ra)
ra-rd rb
r-r1
r-r2
±r
R
amu1 = arcsin
,
α21 =
ra
(ra-rd)(r-rb)
rb-rd ra
где
и am обозначает амплитуду u1.
A1(r1 - r2) = (2Mr1 - Q2)(r21 + a2 - aλ),
Данный интеграл вычисляется на с. 205 [22]:
∫
A2(r1 - r2) = -(2Mr2 - Q2)(r22 + a2 - aλ).
(1 - α21 sn2 u)2
du =
(1 - α2 sn2 u)2
[
]
α41
α2 - α21
(α2 - α21)2
=
V0 + 2
V1 +
V2 ,
α4
α21
α4
1
ПРИЛОЖЕНИЕ D
где (см. с. 201 [22])
∫
Для вычисления функции видности использова-
V0 = du = F(ν, k),
лись следующие табличные значения интегралов.
∫
Для вычисления интеграла (10) использовался таб-
du
V1 =
= Π(α2, ν, k),
личный интеграл
1 - α2 sn2 u
∫
∫
(2πuρ).
e-2πiuρcos(φρ-φu)dφρ = 2πJ0
du
V2 =
=
(1 - α2 sn2 u)2
0
[
1
Для вычисления интеграла (11)-(13), использова-
=
α2E(u) + (k - α2)u +
2(α2 - 1)(k - α2)
лись табличные интегралы (с. 484 [24])
∫z
+ (2α2k + 2α2 - α4 - 3k)Π(α2, ν, k) -
z
]
tJ0(ut) dt =
J1(uz),
α4
snu cnu dnu
u
-
,
0
1 - α2 sn2 u
1026
ЖЭТФ, том 159, вып. 6, 2021
Построение теней черных дыр...
∫z
9.
T. Bronzwaer et al., Astron. Astrophys. 613,
2
t2J0(ut)dt =
(2018).
0
10.
M. Moscibrodzka and C. F. Gammie, Month. Not.
z
=
[2uzJ1(uz)-πJ1(uz)H0(uz)+πJ0(uz)H1(uz)],
Roy. Astron. Soc. 475, 43 (2018).
2u2
11.
S. C. Noble, P. K. Leung, C. F. Gammie, and
∫z
L. G. Book, Class. Quant. Grav. 24, 259 (2007).
z2
t3J0(ut)dt =
(2J2(uz) - uzJ3(uz)) =
u2
12.
J. Dexter, Month. Not. Roy. Astron. Soc. 462, 115
0
(2016).
2
z
=
[uzJ1(uz) - 2J2(uz)] =
13.
S. E. Gralla and A. Lupsasca, arXiv:2007.10336.
u2
2
z
4
14.
S. E. Gralla and A. Lupsasca, arXiv:2008.03879.
=
[uzJ1(uz) -
J1(uz) + 2J0(uz)],
u2
uz
15.
J. R. Farah, D. W. Pesce, M. D. Johnson, and
где H — функция Струве. Для вычисления интегра-
L. L. Blackburn, Astrophys. J. 900, 77 (2020).
ла (14) использовался табличный интеграл
16.
Д. В. Гальцов, Частицы и поля в окрестности
∫
x
черных дыр, МГУ, Москва (1986).
2u
tJ1(ut) dt = x[J1(ux)H0(ux)-J0(ux)H1(ux)].
π
17.
S. E. Gralla and A. Lupsasca, Phys. Rev. D 101,
0
044031 (2020).
18.
S. E. Gralla, A. Lupsasca, Phys. Rev. D 101, 044032
ЛИТЕРАТУРА
(2020).
1. Event Horizon Telescope Collaboration, Astrophys.
19.
C. T. Cunnungham and J. M. Bardeen, Astrophys.
J. Lett. 875, L1 (2019).
J. 173, L137 (1972).
2. Event Horizon Telescope Collaboration, Astrophys.
20.
A. R. Thompson, J. M. Moran, and G. W. J. George,
J. Lett. 875, L2 (2019).
Interferometry and Synthesis in Radio Astronomy,
Springer (2017).
3. Event Horizon Telescope Collaboration, Astrophys.
J. Lett. 875, L3 (2019).
21.
И. С. Градштейн, И. М. Рыжик, Таблицы интег-
ралов, сумм, рядов и произведений, Физматгиз,
4. Event Horizon Telescope Collaboration, Astrophys.
Москва (1963).
J. Lett. 875, L4 (2019).
22.
P. F. Byrd and M. D. Friedman, Handbook of Elliptic
5. Event Horizon Telescope Collaboration, Astrophys.
Integrals for Engineers and Scientists, Springer
J. Lett. 875, L5 (2019).
(1971).
6. Event Horizon Telescope Collaboration, Astrophys.
23.
S. E. Vázquez and E. P. Esteban, Nuovo Cim. B 119,
J. Lett. 875, L6 (2019).
489 (2004).
7. M. D. Johnson et al., Sci. Adv. 6, 1310 (2020).
24.
M. Abramowitz and I. A. Stegun, Handbook of Mathe-
8. Н. С. Кардашёв и др., УФН 184, 1319 (2014).
matical Functions, Nat. Bureau Stand. (1972).
1027