ЖЭТФ, 2021, том 159, вып. 6, стр. 1041-1046

ВЛИЯНИЕ ВМОРОЖЕННЫХ НЕМАГНИТНЫХ ПРИМЕСЕЙ НА

ФАЗОВЫЕ ПЕРЕХОДЫ В ТРЕХМЕРНОЙ МОДЕЛИ ПОТТСА

А. К. Муртазаев^a, А. Б. Бабаевb,c*

^a Институт физики им. Х. И. Амирханова

Дагестанского федерального исследовательского центра Российской академии наук

367003, Махачкала, Россия

^b Дагестанский федеральный исследовательский центр Российской академии наук

367000, Махачкала, Россия

^c Дагестанский государственный педагогический университет

367000, Махачкала, Россия

Поступила в редакцию 31 января 2021 г.,

после переработки 10 февраля 2021 г.

Принята к публикации 10 февраля 2021 г.

С помощью кластерного алгоритма Вольфа метода Монте-Карло исследуется влияние слабого беспоряд-

ка, реализованного в виде вмороженных немагнитных примесей, на фазовые переходы в трехмерной мо-

дели Поттса с числом состояний спина q = 5. Рассмотрены системы с линейными размерами L = 10-120

при концентрациях спинов p = 1.00, 0.80. Используя метод кумулянтов Биндера четвертого порядка и

гистограммный метод анализа данных, мы показали, что внесение в систему слабого вмороженного бес-

порядка (p = 0.80) в виде немагнитных примесей изменяет фазовый переход первого рода на фазовый

переход второго рода.

DOI: 10.31857/S0044451021060055

туры влияют на поведение различных систем при

ФП.

1. ВВЕДЕНИЕ

Критерий Харриса [2] ответил на принципиаль-

ный вопрос о смене критического поведения при вве-

Изучение влияния беспорядка, содержащегося в

дении небольшого количества неподвижных («вмо-

твердом теле в виде примесей или других дефек-

роженных») примесей. Согласно этому критерию,

тов структуры, на фазовые переходы (ФП) и кри-

если dν > 2, где d — размерность систем, а ν — кри-

тические явлений (КЯ) представляет большой тео-

тический индекс (КИ) радиуса корреляции, то при-

ретический и экспериментальный интерес [1]. Это

меси не изменяют критических индексов. Критерий

связано с тем, что большинство реальных твердых

Харриса неприменим к двумерной модели Изинга в

тел всегда содержит примеси и другие дефекты

силу того, что dν = 2. В работе [3] было показа-

структуры, присутствие которых влияет на их фи-

но, что влияние примеси в двумерной модели Изин-

зические свойства и, в частности, может сущест-

га затрагивает только поведение теплоемкости, в то

венно влиять на поведение систем при ФП. По

время как остальные термодинамические и корреля-

этой причине существует серьезная необходимость

ционные функции не изменяют своего критическо-

знать закономерности влияния примесей на те или

го поведения. В случае двумерных моделей Поттса

иные свойства твердых тел. Без предварительных

с числом состояний спина q ≤ 4 примеси могут из-

теоретических и экспериментальных исследований

менить критические индексы и изменить класс уни-

ни один материал не может быть использован для

версальности критического поведения.

практических целей. Поэтому в последнее время

усилия многих исследователей были направлены на

В то же время имеются основания предполагать,

что примеси оказывают совершенно другое влияние

то, чтобы понять, как те или иные дефекты струк-

вплоть до изменения рода ФП в случае спиновых

^* E-mail: b_albert78@mail.ru

систем, испытывающих в однородном состоянии ФП

1041

А. К. Муртазаев, А. Б. Бабаев

ЖЭТФ, том 159, вып. 6, 2021

{

первого рода [4,5]. Такая смена ФП эксперименталь-

1, если S_i = S_j,

ρ_i,j =

но наблюдается в жидких кристаллах в присутствии

0, если S_i = S_j.

аэрогеля [6]. Для низкоразмерных систем (d ≤ 2),

Исследования проводились на основе высоко-

описываемых моделью Поттса с q > q_c(d) (q_c = 4,

эффективного кластерного алгоритма Вольфа [11].

q_c — критическое число состояний спина, d — раз-

мерность), на основе аналитических методов было

Расчеты проводились для систем с периодическими

граничными условиями при концентрациях спинов

показано, что наличие сколь угодно малой величи-

ны беспорядка достаточно, чтобы изменить ФП пер-

p = 1.00,0.80. Исследовались системы с линейными

размерами L × L × L = N, L = 10-120. Начальные

вого рода на ФП второго рода [7]. Для однородных

систем с размерностью d ≥ 3, описываемых моделя-

конфигурации задавались таким образом, чтобы все

спины были упорядочены вдоль оси Z. Для вывода

ми Поттса, для которых наблюдается ФП первого

рода, ситуация может оказаться существенно дру-

системы в равновесное состояние отсекался неравно-

весный участок длиной τ₀ для системы с линейными

гой. В этом случае внесение вмороженного беспо-

рядка может привести к трикритической точке p^∗,

размерами L. Этот неравновесный участок отбра-

сывался. Затем усреднение проводилось по участку

ниже которой будет наблюдаться ФП второго рода,

марковской цепи длиной τ = 200τ₀.

а выше ФП — первого рода [8-10].

В связи с этим целью настоящей работы явля-

Для самой большой системы L

= 120, τ₀

= 2.3·10³ МК-шагов/спин. Кроме того, проводилось

ется исследование на основе однокластерного алго-

ритма Вольфа метода Монте-Карло (МК) влияния

усреднение по различным начальным конфигураци-

слабого беспорядка, реализованного в виде вморо-

ям. В случае p = 1.0 для усреднения использова-

женных немагнитных примесей каноническим спо-

лось 10 начальных конфигураций. Для слабо раз-

собом, на ФП в трехмерных системах, описываемых

бавленных систем с концентрацией спинов p = 0.80

осуществлялось конфигурационное усреднение по

моделью Поттса с числом состояний спина q = 5,

для которой в однородном состоянии наблюдается

1000 различным конфигурациям, причем для каж-

дой примесной конфигурации выполнялось усредне-

ФП первого рода.

ние по длине цепи τ = 200τ₀.

2. МОДЕЛЬ И МЕТОДИКА

ИССЛЕДОВАНИЯ

3. РЕЗУЛЬТАТЫ ЧИСЛЕННОГО

ИССЛЕДОВАНИЯ

В работе рассматривается трехмерная слабо раз-

бавленная модель Поттса с числом состояний спи-

Для наблюдения за температурным ходом пове-

на q = 5. При построении такой модели необходи-

дения теплоемкости и восприимчивости использова-

мо иметь в виду следующие особенности: в узлах

лись флуктуационные соотношения [12]:

кубической решетки расположены спины S_i, кото-

)

рые могут находиться в одном из состояний q ≥ 2, и

C(T ) = (NK²)

U²

- 〈U〉²

(2)

немагнитные примеси (вакансии); немагнитные при-

меси распределены случайно и фиксированы на раз-

)

χ = (NK)(

m2F

- 〈m_F 〉²

(3)

личных узлах решетки (quenched disorder); энергия

связи между двумя узлами равна нулю, если они

где K = |J|/(k_BT ), N = pL³ — число магнитных

находятся в разных состояниях (безразлично, в ка-

узлов, U — внутренняя энергия, m_F — намагничен-

ких именно) или если хотя бы в одном узле находит-

ность системы, угловые скобки обозначают усредне-

ся немагнитный атом, и равна |J|, если взаимодей-

ние по ансамблю. В качестве намагниченности (m_F ),

ствующие узлы находятся в одинаковых состояниях

для ФМ-модели Поттса с числом состояний спина

(опять же, все равно, в каких именно). С учетом

q = 5 использовалось следующее выражение [13]:

этих особенностей микроскопический гамильтониан

такой системы может быть, представлен в виде

q (N_max/N) - 1

m_F =

(4)

∑

q-1

H =-

ρ_iρ_jδ(S_iS_j), S_i = 1, 2, 3, 4, 5,

(1)

i,j

где N_max = max[N₁, N₂, N₃, N₄, N₅], N_i — число спи-

где

{

нов в состоянии с q = i, N = pL³.

1, если S_i = S_j,

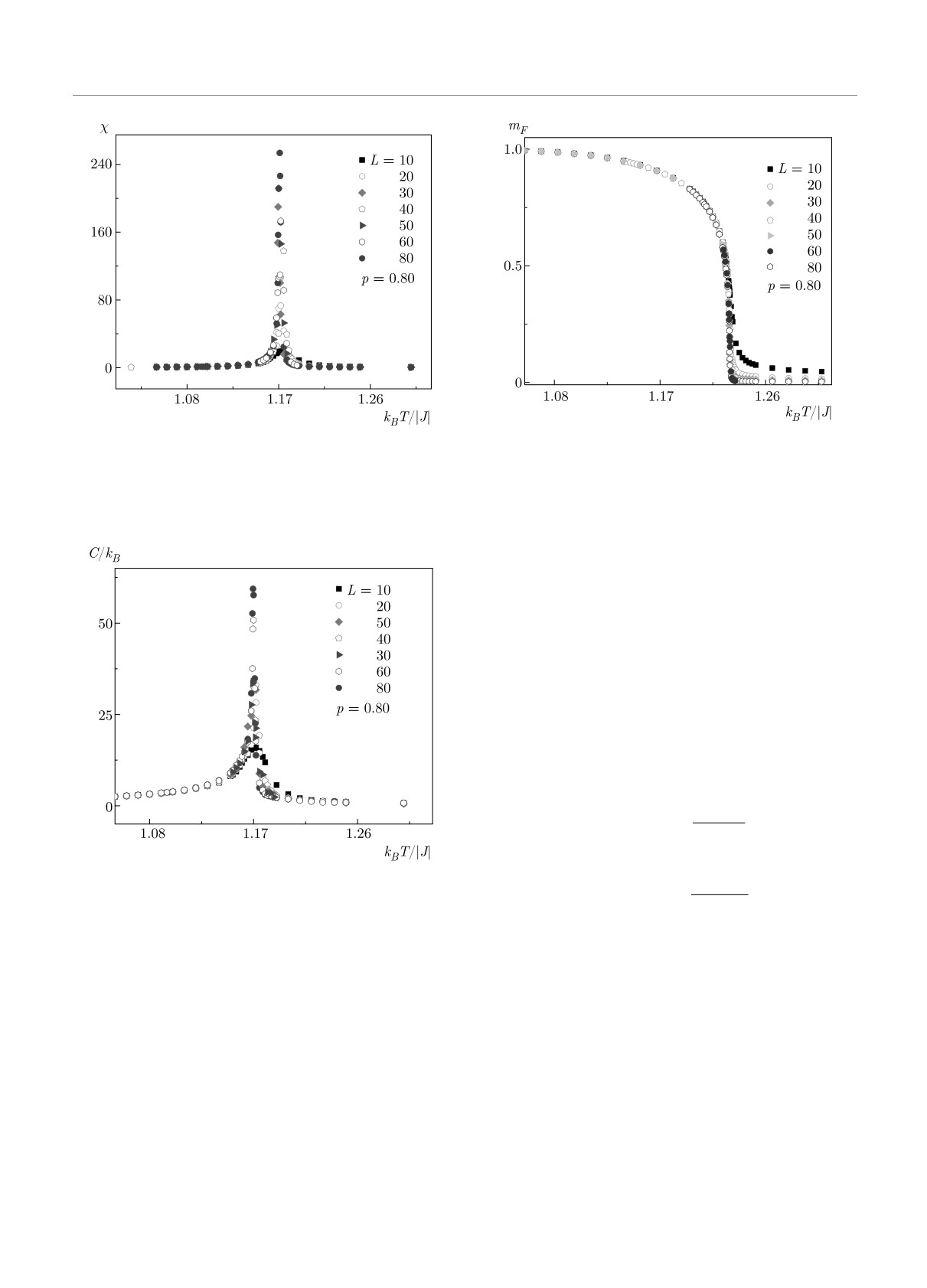
На рис. 1 и 2 представлены характерные зави-

δ(S_i,j ) =

0, если S_i = S_j,

симости для восприимчивости χ и теплоемкости C

1042

ЖЭТФ, том 159, вып. 6, 2021

Влияние вмороженных немагнитных примесей. . .

Рис. 3. Температурная зависимость намагниченности mF

Рис. 1. Температурная зависимость восприимчивости χ

для трехмерной слабо разбавленной модели Поттса с чис-

для трехмерной слабо разбавленной ферромагнитной мо-

лом состояний спина q = 5 на простой кубической решетке

дели Поттса с числом состояний спина q = 5 на простой

кубической решетке

симумы, и эти максимумы в пределах погрешности

соответствуют одной температуре.

На рис. 3 представлены температурные зависи-

мости намагниченности m_F для трехмерной сла-

бо разбавленной модели Поттса с q

= 5 при

p = 0.80. Как видно на рис. 3, наблюдается моно-

тонное уменьшение величины m_F c ростом темпера-

туры и заметное уменьшение высокотемпературных

«хвостов» при увеличении линейного размера L.

Для определения температуры фазового перехо-

да T_l(p) и анализа характера фазового перехода ис-

пользовался метод кумулянтов Биндера четвертого

порядка [14]:

E⁴

VL(T, p) = 1 -

(5)

3 〈E²〉

Рис. 2. Температурная зависимость теплоемкости C для

m4F

U_L(T, p) = 1 -

(6)

трехмерной слабо разбавленной модели Поттса с числом

3 〈m²

〉_L

состояний спина q = 5 на простой кубической решетке

где E — энергия, и m_F — намагниченность систе-

мы с линейным размером L. Выражения (5) и (6)

от температуры T для трехмерной слабо разбавлен-

позволяют определить температуру фазового пере-

ной ФМ-модели Поттса c числом состояний спина

хода T_l(p) с большой точностью в фазовых перехо-

q = 5 на простой кубической решетке для систем

дах соответственно первого и второго рода. Мето-

с линейными размерами L = 10-80 при концентра-

дика определения температуры ФП этим методом

ции спинов p = 0.80. Здесь и далее на всех рисунках

рассмотрена в работах [15-17]. Следует отметить,

погрешность данных не превышает размеров сим-

что применение кумулянтов Биндера позволяет так-

волов, используемых для построения графиков. От-

же хорошо определить род фазового перехода в си-

метим, что в зависимости восприимчивости χ и теп-

стеме. Известно, что фазовые переходы второго ро-

лоемкости C от температуры для всех исследуемых

да характеризуются следующими отличительными

нами систем проявляются четко выраженные мак-

особенностями [18]: усредненная величина V_L(T, p)

1043

А. К. Муртазаев, А. Б. Бабаев

ЖЭТФ, том 159, вып. 6, 2021

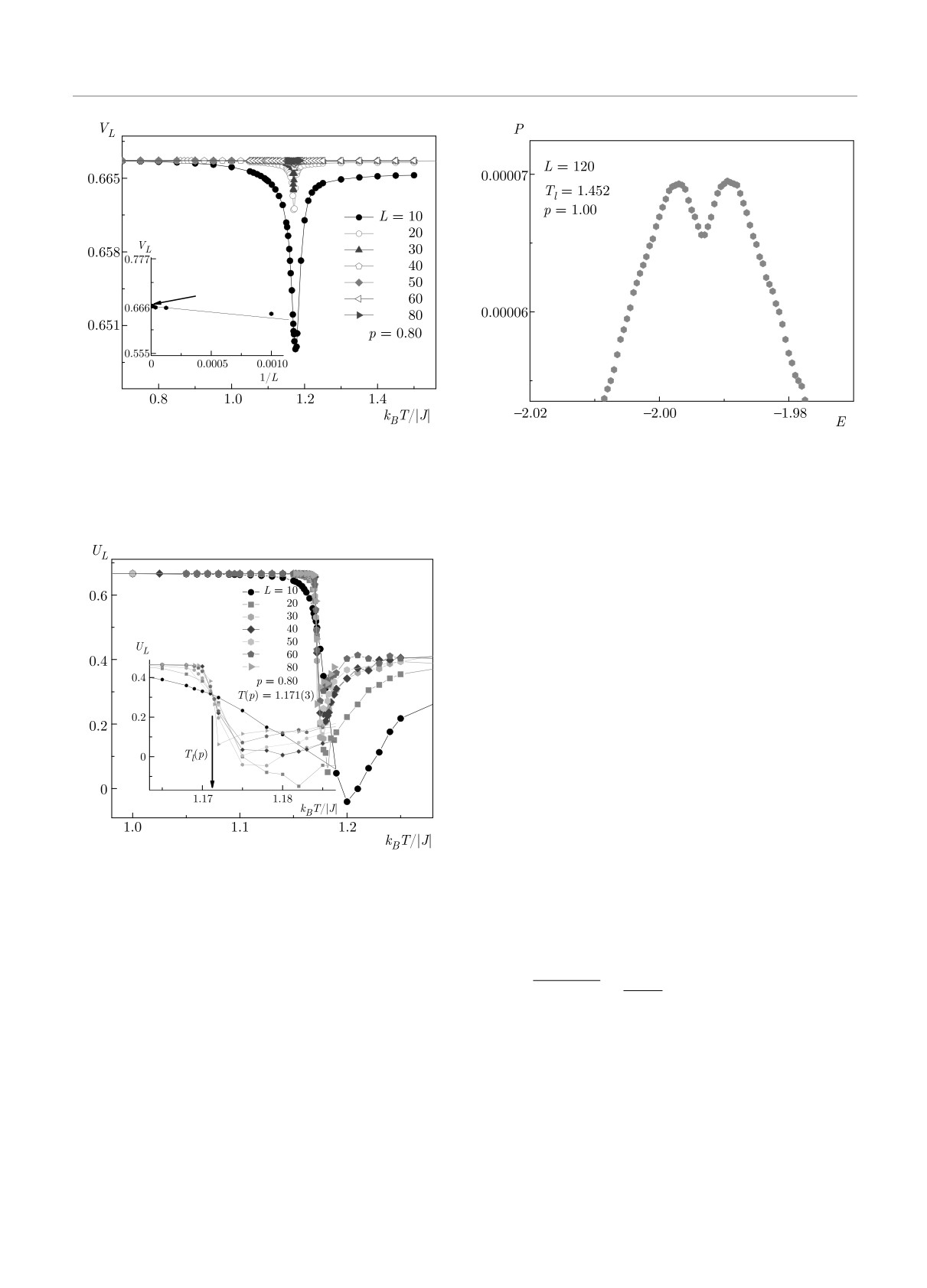
Рис. 4. Температурная зависимость кумулянтов Биндера

Рис. 6. Гистограмма распределении энергии для трехмер-

VL(T) для трехмерной слабо разбавленной модели Поттса

ной чистой модели Поттса с числом состояний спина q = 5

с числом состояний спина q = 5 на простой кубической

на простой кубической решетке при p = 1.0 и T = T_l

решетке

дера V_L(T, p) и U_L(T, p) от температуры для систем с

разными линейными размерами при p = 0.80 приве-

дены соответственно на рис. 4 и 5. Заметим, что на

вставке к рис. 4 наглядно видно, что тривиальная

величина V^∗ → 2/3 в соответствии с выражением

(7) при L → ∞. Такое поведение, как отмечалось

выше, характерно для ФП второго рода. Кроме то-

го, на рис. 5 видно, что в критической области для

U_L(T, p) наблюдается четко выраженная точка пе-

ресечения и U_L(T, p) не проявляет тенденции стрем-

ления к -∞ при L → ∞, что также свидетельству-

ет о ФП второго рода. Определенные методом ку-

мулянтов Биндера температуры фазовых переходов

Т_l(p) в единицах |J|/k_B равны: Т_l(1.0) = 1.452(1),

Т_l(0.80) = 1.171(3).

Кроме кумулянтов Биндера для анализа рода

ФП нами использовался и гистограммный анализ

Рис. 5. Температурная зависимость кумулянтов Биндера

данных метода МК [19,20]. В гистограммном анали-

UL(T ) для трехмерной слабо разбавленной модели Потт-

зе данных вероятность обнаружения системы со зна-

са с числом состояний спина q = 5 на простой кубической

решетке

чением энергии U и параметром порядка m_F опре-

деляется выражением [19]

стремится к тривиальному значению согласно вы-

P (U, m_F ) =

W (U, m_F ) exp[KU],

(8)

ражению

Z(K)

где W (U, m_F ) — число конфигураций с энергией U

V_L(T, p) = V^∗ + bL^-d

(7)

и параметром порядка m_F , Z(K) — функция рас-

при L → ∞ и T = T_l(L), где V^∗ = 2/3.

пределения энергии всей системы и K — обратная

Кроме того, в случае ФП второго рода кри-

температура.

вые температурной зависимости кумулянтов Бинде-

Гистограммный анализ данных проведенный на-

ра U_L(T, p) имеют четко выраженную точку пересе-

ми для чистой неразбавленной трехмерной ферро-

чения. Характерные зависимости кумулянтов Бин-

магнитной модели Поттса с числом состояний спина

1044

ЖЭТФ, том 159, вып. 6, 2021

Влияние вмороженных немагнитных примесей. . .

такая смена ФП наблюдалась и для спиновых си-

стем, в которых беспорядок внесен в виде случай-

ных связей.

Определение точного значения трикритической

точки p_с, отделяющей на фазовой диаграмме об-

ласть ФП первого рода от ФП второго рода для

трехмерной модели Поттса с q = 5 на простой куби-

ческой решетке, — предмет отдельного рассмотре-

ния. Точная величина трикритической точки имеет

большое значение при создании различных новых

магнитных материалов, а также при изучении вли-

яния вмороженного беспорядка на различные тер-

модинамические характеристики.

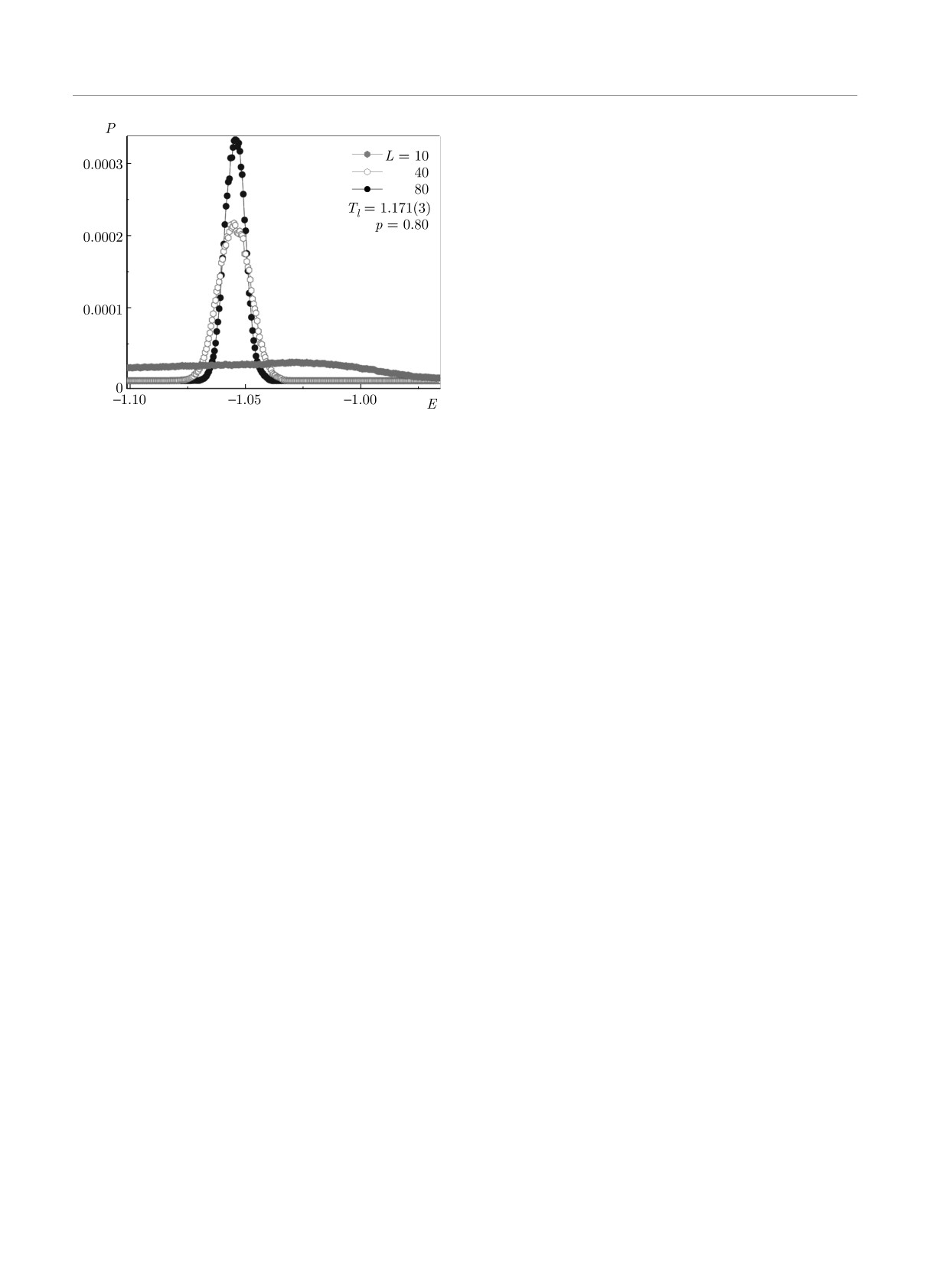
Рис. 7. Гистограмма распределении энергии для трехмер-

4. ЗАКЛЮЧЕНИЕ

ной слабо разбавленной модели Поттса с числом состо-

В данной работе с соблюдением единой методики

яний спина q = 5 на простой кубической решетке при

p = 0.80 и T = T_l

исследовано влияние слабого вмороженного беспо-

рядка, реализованного в виде вмороженных немаг-

нитных примесей на фазовые переходы в трехмер-

ной ферромагнитной модели Поттса с числом состо-

q = 5 на простой кубической решетке также свиде-

яний спина q = 5 на простой кубической решетке.

тельствует о наличии ФП первого рода. Это про-

Данные полученные в результате наших исследова-

демонстрировано на рис. 6. На этом рисунке пред-

ний свидетельствуют о том, что:

ставлена гистограмма распределения энергии вбли-

1. В трехмерной ферромагнитной модели Поттса

зи точки фазового перехода T_l для систем с ли-

с q = 5 на простой кубической решетке наблюдает-

нейным размером L = 120. Как видно на рисунке,

ся фазовый переход первого рода в соответствии с

на зависимости вероятности P от энергии системы

предсказаниями аналитических теорий [21].

U для системы L = 120 наблюдаются два хорошо

2. Внесение слабого беспорядка (p = 0.80) в виде

выраженных максимума. Наличие бимодальности в

вмороженных немагнитных примесей в рассмат-

распределении энергии является достаточным при-

риваемую модель приводит к фазовым переходам

знаком ФП первого рода. Соответствующий гисто-

второго рода.

граммный анализ данных был проведен и для трех-

мерной слабо разбавленной ферромагнитной модели

Финансирование. Исследование выполнено

Поттса на простой кубической решетке при концен-

при поддержке Российского фонда фундамен-

трации спинов p = 0.80, но бимодальность в гисто-

тальных исследований в рамках научного проекта

грамме распределения энергии для этой модели об-

№19-02-00153.

наружить не удалось. В этом случае в зависимости

вероятности P от энергии системы U с достаточно

большим линейным размером L наблюдается один

ЛИТЕРАТУРА

хорошо выраженный максимум (см. рис. 7), что яв-

ляется характерным признаком для ФП второго ро-

1. O. Vasilyev, B. Berche, M. Dudka, and Yu. Holovatch,

да.

Phys. Rev. E 92, 042118 (2015).

Таким образом, наши данные свидетельствуют

2. A. B. Harris, J. Phys. C 7, 1671 (1974).

о том, что в трехмерной ферромагнитной модели

Поттса с q = 5 в отсутствие структурного беспо-

3. Vik. Dotsenko and Vl. Dotsenko, Adv. Phys. 32, 129

рядка происходит ФП первого рода в соответствии

(1983).

с предсказаниями аналитических теории [21]. Вне-

4. A. Bailly-Reyre and H. T. Diep, Physics Procedia 75,

сение слабого вмороженного беспорядка (с = 0.20,

557 (2015).

с = 1 - p) в виде немагнитных примесей каноничес-

ким способом в рассматриваемую модель приводит

5. J. Cardy and J. L. Jacobsen, Phys. Rev. Lett. 79,

к ФП второго рода. Отметим, что в работах [13, 22]

4063 (1997).

1045