ЖЭТФ, 2021, том 159, вып. 6, стр. 1047-1069

ВРАЩАТЕЛЬНАЯ ДИПОЛЬНАЯ ПЛАЗМОННАЯ МОДА В

НАНОРАЗМЕРНЫХ ПОЛУПРОВОДНИКОВЫХ ЧАСТИЦАХ

Л. Г. Герчиковa*, А. Н. Ипатовa,b**

^a Санкт-Петербургский политехнический университет Петра Великого

195251, Санкт-Петербург, Россия

^b Академический университет им. Ж. И. Алфёрова

195220, Санкт-Петербург, Россия

Поступила в редакцию 21 декабря 2020 г.,

после переработки 18 января 2021 г.

Принята к публикации 18 января 2021 г.

Исследован новый тип плазмонной моды в наноразмерных полупроводниковых кристаллах. В оптиче-

ских спектрах фотолегированных нанокристаллов преобладает дипольный плазмонный резонанс враща-

тельного типа, при котором возбуждаются только угловые степени свободы. Такая коллективная мода

принципиально отличается от поверхностных плазмонных резонансов в типичных спектрах фотопогло-

щения металлических нанокластеров и может быть описана как возбужденное состояние в конечной

ферми-системе, так и как вращательное движение квантовой жидкости. Было продемонстрировано, что

подобные дипольные колебания являются гармоническими, что позволяет их определить как плазмонное

резонансное возбуждение.

DOI: 10.31857/S0044451021060067

теров [11-13], лежат в ультрафиолетовой области

спектра для нанокластеров из атомов серебра и зо-

лота [5,8,14-19]. Сильно легированные полупровод-

1. ВВЕДЕНИЕ

никовые нанокристаллы представляют собой новый

многообещающий тип материалов с плазмонным ре-

Интенсивное развитие нанотехнологий в тече-

зонансом в оптическом спектре [4,5,9,14-17,20,21].

ние последних десятилетий требует создания но-

При этом частоты их плазмонных мод, как правило,

вых материалов, физические и химические свой-

лежат намного ниже по сравнению с металлически-

ства которых отличаются от свойств соответству-

ми наночастицами [22]. Главное достоинство полу-

ющих объемных компонентов. Квантовая плазмо-

проводниковых нанокристаллов состоит в том, что

ника в настоящее время является быстро развива-

концентрация носителей в них может варьировать-

ющейся областью исследований, которая включает

ся в широком диапазоне. В то время как концентра-

в себя изучение квантовых свойств света и меха-

ция носителей в металлических проводниках фик-

низмов его взаимодействия с материей на нанораз-

сирована, в полупроводниковых образцах в резуль-

мерном уровне [1-3]. Оптические свойства нанораз-

тате легирования она может изменяться в пределах

мерных проводящих частиц определяются наличи-

10¹⁶-10²² см-3 [22-28]. В результате появляется воз-

ем локализованных поверхностных плазмонных ре-

можность изменять частоты плазмонных резонан-

зонансов (LSPR) в их спектрах возбужденных состо-

сов в оптических спектрах сильно легированных по-

яний [2,4-8]. Для металлических наночастиц харак-

лупроводниковых нанокристаллов в широком диа-

терны высокие плотности носителей заряда, типич-

пазоне частот от терагерцевой до инфракрасной и

ные значения которых могут варьироваться в пре-

видимой части спектра [22, 23, 29-32] путем измене-

делах 10²²-10²³ см-3 [9,10]. Таким образом, частоты

ния параметров как материала самого нанокристал-

плазмонных резонансов, наблюдаемые в оптических

ла, так и окружающей его среды [20, 23, 31, 33-37].

спектрах микроскопических металлических клас-

Для динамических свойств легированных полупро-

водниковых наночастиц характерен переход от ре-

^* E-mail: lgerchikov@mail.ru

^** E-mail: andrei_ipatov@mail.ru

жима размерного квантования к классическому ре-

1047

Л. Г. Герчиков, А. Н. Ипатов

ЖЭТФ, том 159, вып. 6, 2021

жиму плазмонных колебаний [25]. При этом с уве-

ли инжектированы в объем полупроводниковой на-

личением числа свободных носителей заряда в на-

ночастицы донорами/акцепторами, расположенны-

нокластерах в их спектрах возбужденных состоя-

ми на ее поверхности. Пример поверхностного ме-

ний наблюдается переход от чисто квантовомеха-

ханизма легирования подробно обсуждался в рабо-

нических одночастичных возбуждений к классиче-

тах [24, 40], где был экспериментально исследован

ским коллективным плазмонным колебаниям элек-

процесс фотолегирования нанокристаллов ZnO, по-

тронной системы [17, 25]. В случае металлических

мещенных в раствор толуола.

кластеров классическая теория Ми [38] адекватно

При квантовомеханическом подходе описание

описывает оптические свойства наночастиц при зна-

оптических свойств металлических кластеров обыч-

чениях их радиуса превышающих 10 нм [17, 26].

но базируется на сферической модели желе, где по-

При этом выдавливание (spill-out) части электрон-

тенциалы отдельных атомов заменяются потенциа-

ной плотности за пределы ионного остова у клас-

лом равномерно заряженного ионного остова, в ко-

теров, состоящих из атомов щелочных металлов,

тором двигаются делокализованные электроны про-

приводит к смещению резонансной линии в область

водимости [13, 41, 42]. В адиабатическом прибли-

более низких частот по мере уменьшения размера

жении [43, 44] поверхностный дипольный плазмон

частицы, что сопровождается колебаниями ее поло-

может быть описан как гармонические колебания

жения, обусловленными квантовыми оболочечными

центра масс электронного облака в параболическом

эффектами, наблюдаемыми у металлических клас-

потенциале положительно заряженного кора. Учет

теров с числом атомов меньше ста [6]. У микроско-

взаимодействия гармонической коллективной моды

пических кластеров благородных металлов поляри-

с одночастичными возбуждениями электронной си-

зация d-оболочек оказывает дополнительное влия-

стемы приводит к фрагментации резонансной линии

ние на оптические свойства частиц, но при этом ка-

и ее существенному сдвигу в область более низких

чественно картина остается неизменной [7, 8]. Для

частот по отношению к ее положению, определен-

систем достаточно большого размера асимптотиче-

ному согласно классической теории [43]. Аналогич-

ское значение частоты дипольного плазмонного ре-

ная ситуация наблюдается в случае полупроводни-

зонанса может быть оценено в рамках классической

ковых нанокристаллов, легированных по объемному

модели Друде с использованием феноменологиче-

(bulk-like) типу [25, 29, 30, 33], когда распределение

ской диэлектрической функции объемного метал-

плотности легирующих примесей также может быть

ла [19]. Напротив, для наноразмерных металличе-

описано как равномерно заряженный остов. В обоих

ских кластеров эффекты, связанные с размерным

случаях поверхностный плазмон представляет со-

квантованием в системе электронов проводимости,

бой колебания системы делокализованных электро-

оказывают заметное влияние на оптические свой-

нов как единого целого относительно центра поло-

ства частиц. В связи с этим описание оптическо-

жительного кора в направлении нормали к его по-

го отклика полупроводниковых нанокристаллов на

верхности.

основе квантовомеханического и классического под-

В случае нанокристаллов с поверхностным ти-

ходов приводит к существенно различным резуль-

пом легирования ситуация оказывается иной. Сво-

татам [5, 24, 25, 27, 39], но, в отличие от металли-

бодные носители заряда в полупроводниковых нано-

ческих наночастиц, в полупроводниках переход от

частицах формируют структуру электронных обо-

режима размерного квантования к режиму класси-

лочек [45, 46] вне зависимости от типа легирова-

ческих плазмонных колебаний электронной систе-

ния. Однако, как было продемонстрировано в рабо-

мы может быть осуществлен как путем варьиро-

те [47], плазмонный резонанс в фотолегированных

вания числа носителей заряда, так и путем изме-

нанокристаллах принципиально отличается от по-

нения размера нанокристалла. Следует особо отме-

верхностной дипольной моды в металлических клас-

тить, что положение резонансной линии в оптиче-

терах или объемно-легированных полупроводнико-

ских спектрах наночастиц и ее форма определяет-

вых наночастицах, поскольку при поверхностном

ся не только концентрацией носителей, но также

легировании отсутствует эффективная возвращаю-

и типом легирования, который может быть услов-

щая сила, действующая на делокализованные элек-

но определен как объемный (bulk-like) или поверх-

троны со стороны положительно заряженного осто-

ностный (surface-like) [25, 30]. В первом случае за-

ва. В результате кулоновское отталкивание между

ряд свободных носителей распределен по всему объ-

свободными электронами смещает их по направле-

ему кристалла, где нейтрализован зарядом легирую-

нию к поверхности системы, как это было показа-

щих примесей, а во втором случае свободные носите-

но в статье [25] при анализе распределения элек-

1048

ЖЭТФ, том 159, вып. 6, 2021

Вращательная дипольная плазмонная мода. . .

тронной плотности основного состояния нанокри-

полем будут проявлять свойства более характерные

сталлов CdSe. Этот же эффект был наглядно про-

для фуллеренов C₆₀ [48-50], чем для металличес-

демонстрирован авторами работы [47], где представ-

ких кластеров [11-13] или объемно-легированных

лен теоретический анализ экспериментальных спек-

систем

[25, 29, 30, 33]. В нашей работе мы де-

тров фотопоглощения фотолегированных нанокри-

монстрируем, что из-за специфической оболочеч-

сталлов ZnO. Было показано, что особенности элек-

ной структуры основного состояния фотолегирован-

тронной конфигурации, обусловленные поверхност-

ных полупроводниковых наночастиц их оптические

ным механизмом легирования, приводят к тому, что

спектры для систем с числом свободных носите-

при формировании дипольной коллективной моды в

лей N до 100-150 могут быть адекватно описаны

результате взаимодействия с внешним электромаг-

в рамках простой двухуровневой модели. В этой

нитным полем возбуждаются только угловые степе-

модели волновая функция возбужденного состоя-

ни свободы, в то время как движение электронов в

ния дипольной плазмонной моды строится на ос-

радиальном направлении не включается. В отличие

нове только одной электронно-дырочной пары, со-

от поверхностных плазмонных возбуждений в ме-

ответствующей внутризонному переходу между вы-

таллических кластерах и объемно-легированных по-

рожденным высшим занятым электронным уров-

лупроводниковых наночастицах, где колебание сво-

нем (Highest Occupied Molecular Orbital, HOMO)

бодных зарядов носит трансляционный характер,

и низшим свободным уровнем (Lowest Unoccupied

электроны в поверхностно-легированных нанокрис-

Molecular Orbital, LUMO), в то время как многоча-

таллах ZnO осциллируют тангенциально по отноше-

стичные эффекты учитываются как корреляции в

нию к границе системы внутри сравнительно тонко-

основном состоянии. При этом частота плазмонно-

го сферического слоя подобно дипольным плазмон-

го резонанса, полученная на основе двухуровневой

ным колебаниям в фуллеренах [48-50].

модели, оказалась в хорошем согласии с результа-

В данной работе мы представляем подробный

тами вычислений в рамках RPAX с учетом полного

теоретический анализ оптических свойств фото-

базиса одночастичных волновых функций.

легированных полупроводниковых наночастиц, ре-

Анализ радиального распределения плотности

зультаты экспериментальных измерений которых

дипольных переходов, соответствующей различным

приведены в статьях [24, 40]. Основной целью на-

линиям в рассчитанных спектрах фотопоглощения

шего исследования является подтверждение того,

наноклисталлов ZnO подтвердил тот факт, что кол-

что резонансные моды в спектрах фотопоглоще-

лективная плазмонная мода включает только угло-

ния нанокристаллов ZnO с поверхностным меха-

вое движение электронной плотности, в то время

низмом легирования являются поверхностыми плаз-

как радиальные осцилляции возбуждаются при пе-

монными резонансами вращательного типа в от-

реходах между одночастичными состояниями, при-

личие от

«трансляционных» коллективных воз-

чем эти степени свободы практически не смеши-

буждений в металлических кластерах и объем-

ваются между собой. Предсказания разработанной

но-легированных наноразмерных полупроводнико-

теории хорошо согласуются с результатами экспери-

вых системах. Наш подход основан на самосо-

ментальных измерений спектров фотопоглощения

гласованном квантовомеханическом описании мно-

сильно n-легированных нанокристаллов ZnO [24,40],

гочастичных возбуждений в системе электронов

в частности, хорошо описывают зависимость поло-

проводимости в рамках приближения случайных

жения резонансного пика от размера системы. В

фаз (Random Phase Approximation, RPA) c локаль-

данной работе мы показываем, что при малых раз-

ным обменным взаимодействием (RPAX)

[51, 52].

мерах частиц наблюдаемая зависимость обусловле-

Мы показываем, что распределение электронной

на двумя квантовыми эффектами, а именно, оттал-

плотности в поверхностно-легированных полупро-

киванием электронов от границы нанокристалла,

водниковых нанокристаллах при увеличении чис-

что приводит к эффективному уменьшению средне-

ла электронов имеет тенденцию к формированию

го радиуса электронной системы, а также влиянием

узкой сферической электронной оболочки вбли-

квантового давления. С увеличением размера клас-

зи поверхности наночастицы, а не к однородно-

теров роль квантовых эффектов становится незна-

му распределению заряда, характерному для ме-

чительной, и частота резонансного пика плавно сме-

таллических кластеров. С этой точки зрения сле-

щается к классической частоте плазмонного резо-

дует ожидать, что фотолегированные сферически-

нанса в заряженном тонком сферическом слое. Мы

симметричные полупроводниковые нанокристаллы

демонстрируем, что, поскольку вращательное плаз-

при взаимодействии с внешним электромагнитным

монное возбуждение включает только угловые сте-

1049

ЖЭТФ, вып. 6

Л. Г. Герчиков, А. Н. Ипатов

ЖЭТФ, том 159, вып. 6, 2021

пени свободы, сила его осциллятора содержит в се-

гирования которых обсуждалась в работе

[24].

бе только 2/3 от правила сумм в отличие от «тра-

Свободные электроны в зоне проводимости лока-

диционного» плазмона Ми, наблюдаемого в метал-

лизованы внутри объема наночастицы, в то время

лических кластерах [13]. По этой же причине квад-

как дырки, образовавшиеся вместе с электронами

рат частоты вращательного плазмона в классиче-

в процессе фотолегирования захватываются мо-

ском пределе составляет 2/3 от квадрата соответ-

лекулами этанола EtOH в окружающем растворе

ствующей частоты Ми. Оставшаяся часть диполь-

толуола. Далее окисление этанола высвобождает

ных возбуждений, которые включают в себя ради-

протоны H⁺, которые на поверхности нанокристала

альные колебания электронной плотности, практи-

образуют заряженный слой и компенсируют отри-

чески не коррелирует с коллективной модой и может

цательный заряд электронов проводимости в его

быть описана в рамках одночастичного приближе-

объеме. Радиус исследуемых наночастиц, R, варьи-

ния.

руется в диапазоне от 2.4 до 6.0 нм в зависимости

В представляемой статье также предлагается

от числа свободных электронов проводимости, N,

альтернативный подход к описанию вращательных

которое, в свою очередь, меняется в пределах от 10

плазмонных мод в полупроводниковых нанокри-

до 130. При проведении численных расчетов учиты-

сталлах, основанный на гидродинамической моде-

валось значение средней концентрации электронов

ли [6, 53, 54]. Данная модель описывает плазмонное

из работы [24], n_e = 3N/4πR³ = 1.4 · 10²⁰ см-3, т. е.

возбуждение как тангенциальное движение кванто-

бралась максимальная концентрация электронов,

вой жидкости в тонком сферическом слое и нагляд-

которая достигалась при использовании метода

но демонстрирует гармонический характер колеба-

фотолегирования [24]. При этом соответствующий

ния плотности заряда при возбуждении вращатель-

эффективный радиус Вигнера - Зейца, т. е. среднее

ного плазмона. Нами показано, что значение час-

межэлектронное расстояние, оказался равным

тоты плазмонного резонанса, предсказанное на ос-

rs = (3/4πne)1/3 = 1.2 нм. Поскольку целью дан-

нове этой теории, полностью согласуется с резуль-

ной работы является теоретическое исследование

татом, полученным в результате решения матрич-

коллективной динамики электронной системы

ного уравнения RPAX, соответствующего двухуров-

нанокристаллов, мы используем ряд упрощений в

невой квантовомеханической модели. Важно отме-

описании движения отдельных электронов. Так,

тить, что гидродинамическая модель для ферми-

мы используем приближение огибающей функции

жидкости позволяет выйти за рамки приближения

(Envelope Function Approximation, EFA)

[55, 56],

линейного отклика, учитывающего одновременное

применимость которого оправдано большим ра-

возбуждение только одной электрон-дырочной па-

диусом наночастиц по сравнению с постоянной

ры. Исследование динамики электронных осцилля-

решетки ZnO. В этом приближении мы прене-

ций показало, что вращательный плазмон может

брегаем непараболичностью и анизотропией зоны

рассматриваться как гармоническая коллективная

проводимости ZnO

[57] и полагаем дисперсию

колебательная мода при условии, что число участ-

электронов соответствующей изотропной и парабо-

вующих электронов, в частности частиц на уровне

лической зоне с эффективной массой m_e = 0.3m₀

Ферми, достаточно велико. Высокий уровень фото-

[57], где m₀ — масса свободного электрона. По этой

легирования, обеспечивающий большое число носи-

же причине мы описываем нанокристаллы ZnO как

телей в наночастице, гарантирует, что все электро-

сферически-симметричные системы, т. е. наночасти-

ны делокализованы. С другой стороны, необходи-

цы со сферической поверхностью, внутри которой

мые условия для возникновения вращательной ре-

делокализованные электроны в основном состоя-

зонансной моды не зависят от электронной концен-

нии образуют систему сферически-симметричных

трации, а определяются только размерами нанокри-

оболочек. Кроме того, мы заменяем N протонов на

сталла, радиус которого должен превышать эффек-

поверхности нанокристалла однородным положи-

тивный боровский радиус рассматриваемой систе-

тельно заряженным сферическим слоем, который

мы.

не создает напряженности электрического поля

внутри объема системы. В результате полный

гамильтониан представляет собой просто гамильто-

2. ОСНОВНОЕ СОСТОЯНИЕ

ниан N свободных электронов, взаимодействующих

В своем исследовании мы рассматриваем n-

друг с другом посредством кулоновского потенци-

легированные полупроводниковые нанористаллы

ала V , а также с потенциалом V_i положительных

ZnO в окружении толуола, технология фотоле-

зарядов на поверхности,

1050

ЖЭТФ, том 159, вып. 6, 2021

Вращательная дипольная плазмонная мода. . .

∑

p2a

Ĥ₌

V (r_a, r_b) +

V_i(r_a).

(1)

2m_e

a,b

Поскольку электроны жестко ограничены в своем

движении внутри объема наночастицы границей зо-

ны проводимости вблизи поверхности [17], будем

описывать V_i(r) как сферическую потенциальную

яму радиуса R с бесконечно высокими стенками.

При этом условии радиальные электронные волно-

вые функции равны нулю на поверхности для r_a =

= R. Парное кулоновское взаимодействие между

электронами в точках r_a и r_b экранируется в резуль-

тате поляризации как собственно самого материала

ZnO («1»), так и окружающей среды («2»), так что

мультипольное разложение потенциала межчастич-

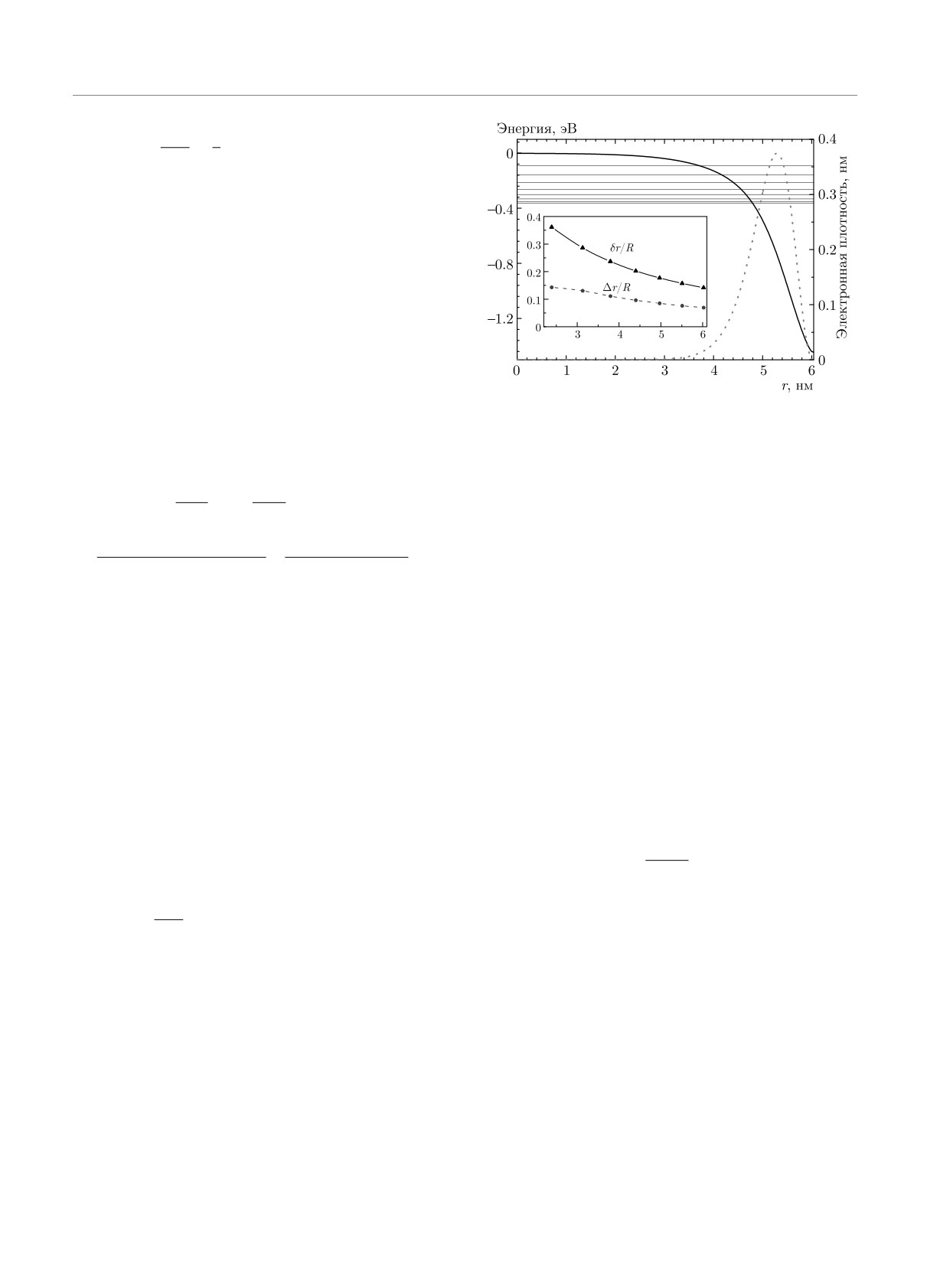
Рис. 1. Радиальный профиль потенциала среднего поля

ного взаимодействия при r_a, r_b < R может быть за-

V_mf (r) сферического нанокристалла ZnO, фотолегирован-

писано в виде [58, 59]

ного 128 электронами — сплошная черная кривая; одно-

(

частичные уровни энергии основного состояния — тонкие

∑

4πe

r^L<

черные горизонтальные линии; радиальная зависимость

V (r_a, r_b) =

электронной плотности основного состояния — красная

rL+1

)

пунктирная кривая. На вставке: зависимости отношения

(ε₁ - ε₂) (L + 1) (r_ar_b)

Y_LM (n_a)Y^∗LM (n_b)

ширины электронного слоя δr (черные треугольники) и

(2)

(Lε₁ + (L + 1)ε₂) R2L+1

2L + 1

смещения среднего электронного радиуса Δr (синие круж-

ки) к радиусу R от размера наночастицы

где r_>,< обозначают соответственно наибольший и

наименьший из радиусов r_a,b. При проведении чис-

∑

и ρ(r)

объемная концентрация

ленных расчетов мы полагали диэлектрические кон-

= a^|ψa(r)|2 —

станты ZnO и толуола равными их значениям для

электронов.

соответствующих объемных материалов, ε₁ = 3.7 и

Для сферически-симметричных систем с замкну-

ε₂ = 2.25 [24]. С этими параметрами эффективный

тыми электронными оболочками и изотропными уг-

боровский радиус, a₀ = ℏ²ε₁/m_ee² = 0.65 нм, ока-

ловыми зависимостями ρ(r) и V_mf (r) совокупный

зывается существенно меньше, чем радиус исследу-

индекс a обозначает a = (n, l, m, σ), где n — ради-

емых наночастиц R.

альное квантовое число, l и m — угловой момент и

Используемое в работе описание основного состо-

его проекция, σ — проекция спина, а сами волновые

яния наночастиц ZnO базируется на приближении

функции записываются как произведение радиаль-

локальной плотности (Local Density Approximation,

ной, угловой и спиновой компонент [61],

LDA), в рамках которого одночастичные волно-

P_nl(r)

вые функции ψ_a(r) удовлетворяют уравнениям Ко-

ψ_nlmσ(r) =

Y_lm(θ, ϕ)χ_σ.

(7)

на - Шема,

(

)

Результаты проведенных численных расчетов

p²

+ V_mf(r) ψ_a(r) = ϵ_aψ_a(r).

(3)

для основного состояния нанокристалла ZnO с ради-

2m_e

усом R = 6 нм и числом электронов проводимиости

Здесь потенциал среднего поля V_mf (r) представляет

N = 128 представлены на рис. 1. Тонкими черны-

собой сумму «прямого» кулоновского потенциала,

ми горизонтальными линиями отмечены положения

V_D(r), и локального обменного потенциала в при-

одночастичных уровней энергии ϵ_a, сплошная чер-

ближении Дирака - Слэтера [60], V_x(r),

ная кривая показывает радиальную зависимость по-

тенциала среднего поля V_mf(r). Электронная плот-

V_mf (r) = V_D(r) + V_x(r),

(4)

ность основного состояния системы ρ(r) изображе-

где

на красной пунктирной линией. Важно отметить,

∫

что электронные конфигурации фотолегированных

V_D(r) = V (r, r^′)ρ(r^′)dr^′,

(5)

наночастиц ZnO отличаются порядком заполнения

электронных оболочек от конфигураций как метал-

Vx(r) = -(e²/ε1)(3ρ(r)/π)1/3

(6)

лических нанокластеров, так и объемно-легирован-

1051

Л. Г. Герчиков, А. Н. Ипатов

ЖЭТФ, том 159, вып. 6, 2021

ных полупроводниковых нанокристаллов. На рис. 1

Эффективное разделение быстрого и жестко

видно, что электронная плотность имеет узкое ради-

квантованного радиального движения и сравни-

альное распределение, смещенное по направлению

тельно медленного углового определяет специфи-

к поверхности из-за кулоновского межэлектронного

ку свойств электронной системы фотолегированных

отталкивания. Таким образом, формируется распре-

наночастиц ZnO, в частности, особенности ее откли-

деление плотности заряда в виде полого сферичес-

ка на внешнее электромагнитное поле. При взаимо-

кого слоя, а не близкого к однородному радиально-

действии с внешним полем жестко квантованная ра-

го распределения делокализованных электронов, ха-

диальная степень свободы остается замороженной и

рактерного для металлических наночастиц [6,10,11].

оптический отклик системы электронов определя-

При этом, в то время как электронная плотность

ется возмущением существенно более «мягкого» уг-

частично выталкивается за пределы ионного остова

лового движения. В результате такого разделения

металлических кластеров, в случае нанокристаллов

радиальной и угловой степеней свободы электрон-

ZnO электроны «вталкиваются» внутрь поверхнос-

ная конфигурация основного состояния формиру-

ти наночастицы. На вставке рис. 1 приведено от-

ется из одночастичных компонент с наименьшими

ношение смещения среднего электронного радиуса

значениями радиальных квантовых чисел n = 1,

Δr = R - 〈r〉 к радиусу нанокристалла R в зави-

соответствующими бескорневым радиальным вол-

симости от его размера. Также представлено отно-

новым функциям P1,l(r). Таким образом, одноча-

шение эффективной ширины распределения элек-

стичные уровни с волновыми функциями, имеющи-

тронной плотности к радиусу наночастицы δr/R, где

ми один или более корень у радиальной компонен-

δr определена как дисперсия электронного радиуса

ты, в основном состоянии остаются не заселенны-

√

δr =

〈r²〉 - 〈r〉². Легко видеть, что δr по порядку

ми. Этот факт был проверен в результате числен-

величины меньше, чем R, и их соотношение умень-

ных расчетов, проведенных для систем, содержащих

шается по мере увеличения размера системы.

число электронов N в пределах от 8 до 128, путем

сравнения энергий всех возможных конфигураций с

Смещение распределения плотности заряда в на-

замкнутыми электронными оболочками. Было под-

правлении поверхности нанокристалла приводит к

тверждено, что низшей энергии основного состояния

важным последствиям для электронной конфигу-

соответствует последовательность заполнения одно-

рации основного состояния. Поскольку электроны

. Эта

оказываются локализованными внутри узкого сфе-

электронная структура соответствует «магическим

рического слоя шириной δr ≪ R, их радиальное

числам» для систем с замкнутыми оболочками,

движение квантуется. Энергия квантования может

N = 2(l_max + 1)²,

(8)

быть оценена как E_r = ℏ²/2m_eδr². Для системы,

содержащей N

= 128 электронов, R

= 6 нм и

где l_max — угловой момент высшей заполненной ор-

δr = 0.4 нм, энергия радиального квантования со-

битали (HOMO). Бескорневые радиальные волно-

ставляет E_r ≃ 0.74 эВ, что по порядку величины

вые функции этих заполненных уровней практиче-

близко к разности энергий 1.08 эВ между низшим

ски идентичны, поскольку центробежная сила, дей-

одночастичным электронным уровнем на рис. 1 и

ствующая на эти состояния, оказывается намного

дном потенциальной ямы среднего поля. Напротив,

меньше силы кулоновского взаимодействия. Силу

движение электронов в тангенциальном направле-

кулоновского отталкивания можно оценить, исхо-

нии вдоль сферического заряженного слоя проис-

дя из значения напряженности электрического поля

ходит существенно медленнее, поскольку его про-

вблизи поверхности нанокристалла,

странственный масштаб 2πR намного больше, чем

eE ≃ e²N/ε₁R².

δr. Кинетическая энергия этого движения равна

ℏ²l(l + 1)/m_e〈r〉², т.е. равна энергии вращательно-

В свою очередь, центробежная сила у поверхности

го движения с постоянным электронным угловым

оценивается как

моментом l, что существенно меньше энергии ради-

F_l ≃ ℏ²l_max(l_max + 1)/(m_eR³).

ального движения E_r. Это хорошо видно на рис. 1,

где разности энергий между электронными уровня-

При этом угловое и радиальное движение не оказы-

ми равны разности энергий их углового движения.

вают влияние друг на друга при условии eE ≫ F_l,

По величине эти интервалы энергии много меньше,

которое выполняется для всех заполненных орбита-

чем расстояние между первым электронным уров-

лей, включая высшее по энергии состояние (HOMO)

нем с l = 0 и дном потенциальной ямы V_mf .

с l = l_max, если

1052

ЖЭТФ, том 159, вып. 6, 2021

Вращательная дипольная плазмонная мода. . .

Flmax

ℏ²l_max(l_max + 1)ε₁

a₀

≃

≪ 1.

(9)

m_ee²NR

Здесь было использовано соотношение (8). Важно

отметить, что условие (9) выполняется независимо

от числа электронов N в системе. Единственное тре-

бование состоит в том, чтобы размер наночастицы

был больше эффективного боровского радиуса a₀,

что выполняется для всех рассматриваемых в рабо-

те наночастиц. Таким образом, радиальная и угло-

вая степени свободы оказываются эффективно раз-

делены, и спектр заполненных одночастичных уров-

ней ϵa (3) может быть приближенно описан как

спектр квантового ротатора,

ℏ²l(l + 1)

ϵ1,l = ϵ1s +

(10)

2m_e〈r〉²

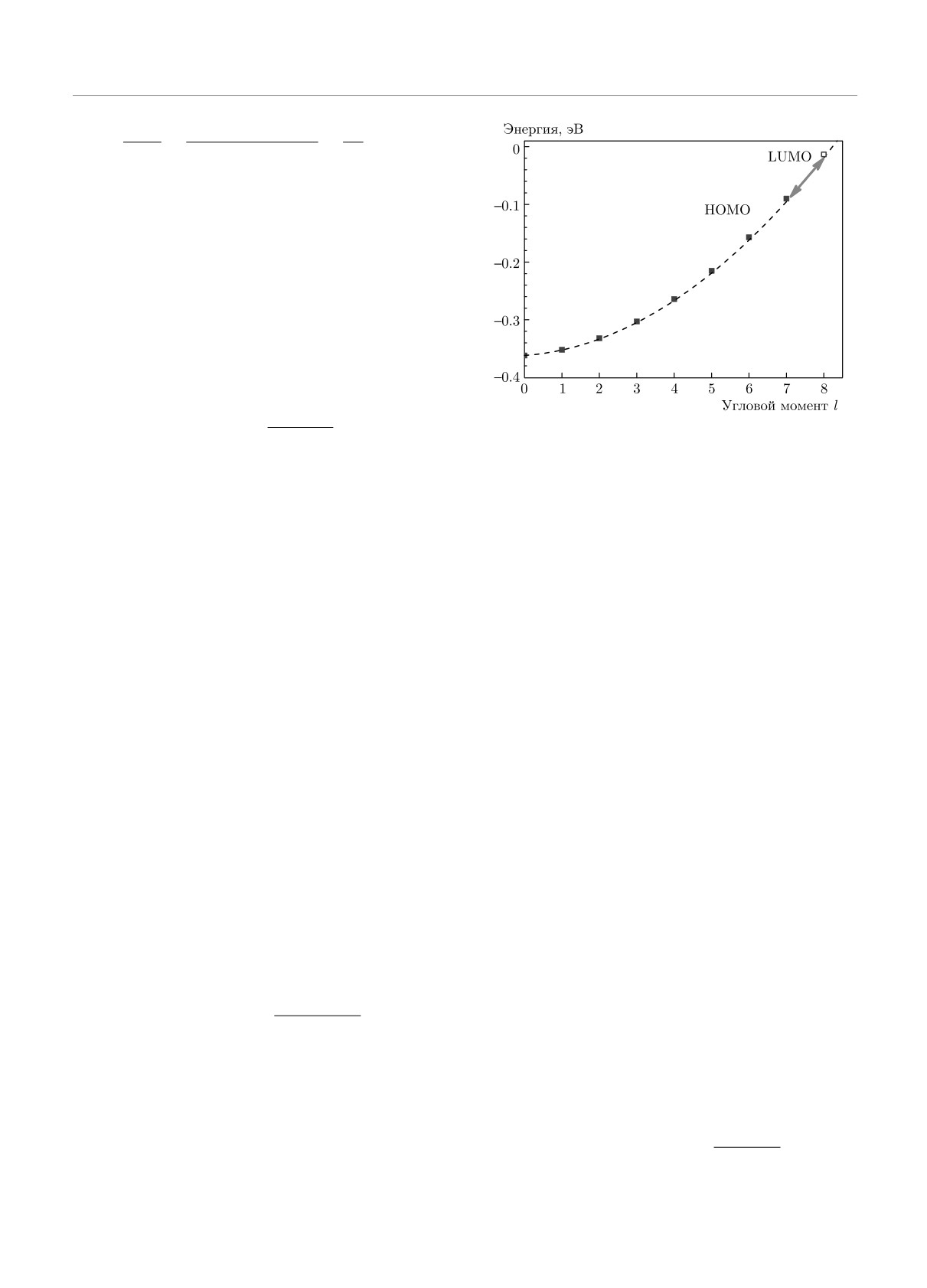
Рис. 2. Одночастичные уровни энергии основного состоя-

ния сферического нанокристалла ZnO cо 128 электронами

При этом, поскольку ширина радиального распреде-

фотолегирования: заполненные уровни — синие квадраты,

ления плотности электронного заряда сравнительно

низшая незаполненная орбиталь (LUMO) — светлый квад-

мала, δr ≪ R, приближение

рат, приближение (10) показано штриховой линией. Меж-

∫

уровневый переход HOMO-LUMO обозначен стрелками

1/r²

= 4π ρ(r)dr/N ≃ 1/〈r²〉 ≃ 1/〈r〉²

был представ-

этого потенциал среднего поля V_mf

выполняется с высокой точностью. Чтобы проде-

лен в виде треугольной потенциальной ямы с углом

монстрировать, насколько точно выполняется осно-

наклона равным напряженности электрического по-

ванная на модели квантового ротатора оценка (10),

ля E = eN/ε₁R² вблизи поверхности нанокристал-

на рис. 2 представлен график зависимости энергий

ла. Как можно увидеть на рис. 1, радиальный про-

ϵ1,l от углового момента l, полученный в соответ-

филь потенциала среднего поля V_mf имеет форму

ствии с приближением (10) исходя из значений 〈r〉

узкой треугольной ямы вблизи поверхности и выхо-

для системы c N = 128. На этом же графике пока-

дит на постоянное значение в центре, где электрон-

заны точные положения заполненных уровней энер-

ная плотность ничтожно мала. При этом вкладом

гии, рассчитанных путем численного решения систе-

обменного взаимодействия можно пренебречь, по-

мы уравнений (3) для N = 128.

скольку его учет только незначительно меняет зна-

Проведенные численные расчеты показали, что

чения δr и Δr, а также энергию квантования в ради-

радиальные компоненты волновых функций низших

альном направлении. В рамках этого приближения

возбужденных состояний также не имеют корней.

радиальная часть волновой функции может быть

Таким образом, при дипольном возбуждении систе-

аппроксимирована функцией Эйри [61], убывающей

мы невзаимодействующих частиц, энергетический

до нуля на границе сферически-симметричной нано-

спектр которых описывается соотношением (10),

частицы,

возникает «дырка» (вакансия) на уровне HOMO и

«частица» на низшей свободной орбитали (LUMO)

P1,l(r) = Ai ((R - r)/r₀ - x₁) , x₁ ≃ 2.34.

с угловым моментом l_p = l_max +1. Энергия соответ-

Здесь r₀ = r_s(a₀/2R)1/3 — радиальный масштаб мо-

ствующего одночастичного перехода равна

дели, малость которого по отношению к радиусу

ℏ²(l_max + 1)

кристалла,

Δ = (ϵ_p - ϵ_h) =

(11)

m_e〈r〉²

r₀/R = (r_s/R)(a₀/2R)1/3 = (a₀/2NR)1/3,

На рис. 2 положение уровня LUMO показано свет-

обеспечивается как большим числом электронов в

лым квадратом, а переход HOMO-LUMO отмечен

системе при рассматриваемом уровне легирования,

стрелками.

так и выполнением условия (9). Из свойств функции

Помимо численных расчетов электронной струк-

Эйри следует, что

туры основного состояния нами был проведен ее ка-

√

чественный анализ в рамках простой модели. Для

Δr = R-〈r〉 ≃ 1.46r₀, δr =

〈r²〉-〈r〉² ≃ 0.73r₀.

1053

Л. Г. Герчиков, А. Н. Ипатов

ЖЭТФ, том 159, вып. 6, 2021

Основываясь на этой оценке, можно предсказать,

ми ε_F (n) определяется локальным значением дву-

что ширина радиального распределения электрон-

мерной электронной плотности, σ(n),

ного заряда δr должна быть в два раза меньше,

ℏ²πσ(n)

чем смещение среднего электронного радиуса Δr

ε_F (n) =

m_e

от границы раздела, что согласуется с результата-

∞

∫

(12)

ми численных расчетов, представленных на рис. 1.

σ(n) = ρ(r) dr.

Что касается абсолютных величин для системы, со-

держащей N = 128 электронов, оценка дает значе-

Для основного состояния электронная плотность

ния δr = 0.33 нм и Δr = 0.66 нм, что также ка-

равна σ(n)

= σ₀

= N/4π〈r〉², и соответствую-

чественно согласуется с результатами вычислений

щая энергия Ферми, ε_F , совпадает с максимальным

δr = 0.42 нм и Δr = 0.86 нм, причем, как и ожи-

далось, оценочные данные оказываются несколько

значением ротационной энергии НОМО-орбитали

в (10).

заниженными по сравнению с их точными значени-

Плазмонные колебания в нанокристаллах ZnO

ями. Энергия размерного квантования радиального

могут быть описаны как волны плотности заряда

движения в рамках этой модели составляет E_r =

в ферми-жидкости, локализованной внутри тонкой

= ℏ²/2m_eδr² ≃ 1.2 эВ. В случае постоянной концен-

сферической оболочки. Данная модель предполага-

трации электронов наблюдается очень слабая зави-

ет, что квантовые состояния всех электронов, во-

симость значений δr и Δr от размера системы, для

влеченных в плазмонные колебания, описываются

всех рассмотренных наночастиц они различаются

одной и той же беcкорневой радиальной волновой

менее, чем на несколько процентов, и всегда ока-

функцией P₁(r), соответствующей низшему уровню

зываются существенно меньше радиуса нанокрис-

радиального движения электронов. Здесь в обозна-

талла R.

чении волновой функции мы опускаем индекс орби-

тального квантового числа, поскольку все радиаль-

ные функции P1,l(r) очень близки. Таким образом,

3. ГИДРОДИНАМИКА ФЕРМИ-ЖИДКОСТИ

радиальное распределение электронной плотности

оказывается «замороженным», ρ(r) ∝ P₁(r)²/r², и

В этом разделе дипольный отклик электрон-

плазмонные колебания электронной плотности ρ(r)

ной системы легированной наночастицы на внешнее

происходят только в тангенциальном направлении.

электромагнитное поле описывается в рамках моде-

Малые отклонения объемной электронной плот-

ли, основанной на разделении радиального и угло-

ности δρ(r) от равновесного распределения и со-

вого движения частиц. Радиальное движение элек-

ответствующие изменения двумерной электронной

тронов квантовано с энергией размерного квантова-

концентрации δσ(n) могут быть записаны в виде

ния E_r ∼ 1 эВ, и взаимодействие с внешним полем

практически не может его возбудить. В то же вре-

δρ(r) = ρ(r) - ρ₀(r) = ρ₀(r)A(t)cos θ,

(13)

мя угловое движение электронов может быть лег-

δσ(n) = σ - σ₀ = σ₀A(t)cos θ,

ко возбуждено, поскольку межуровневый интервал

где

в ротационном спектре (10) много меньше, чем E_r. В

N P₁(r)²

связи с этим, описывая линейный отклик на слабое

ρ₀(r) =

(14)

4π r²

внешнее возмущение, мы рассматриваем только воз-

есть электронная плотность основного состояния, а

буждение угловой степени свободы. При этом ради-

A(t) ∝ e^iωt — безразмерная нормальная координата

альное движение электронов остается невозмущен-

плазмонной степени свободы, в рамках представлен-

ным, т. е. соответствует низшему радиальному кван-

ной модели предполагаемая малой, A ≪ 1.

товому состоянию с n = 1. Напротив, в соответствии

Вектор смещения u ферми-жидкости удовлетво-

с (8), число заполненных ротационных уровней ока-

ряет соотношению

зывается велико, если N ≫ 1, и, следовательно, уг-

δρ(r) = ∇(ρ₀(r)u) = ρ₀(r)∇u.

(15)

ловое движение электронов может быть описано в

рамках полуклассического подхода. Подобные мно-

Последнее равенство верно, поскольку δρ(r) ∝ ρ₀(r).

гочастичные системы с сильным размерным кванто-

Таким образом, вектор u параллелен поверхности

ванием в одном направлении и свободным полуклас-

оболочки, внутри которой движутся электроны, и,

сическим движением в перпендикулярных направ-

в соответствии с (13) и (15), оказывается равным

лениях описываются как двумерная вырожденная

rA(t)

ферми-жидкость [62-65]. Ее локальная энергия Фер-

u=e_θ

sinθ,

(16)

1054

ЖЭТФ, том 159, вып. 6, 2021

Вращательная дипольная плазмонная мода. . .

где e_θ — единичный направляющий вектор в сфери-

δE_C =

(K_D + K_x) A(t)²,

ческой системе координат.

∞

∫

⁽4π)2 e

Соотношения

(13)-(16) показывают, что рас-

K_D =

ρ₀(r)ρ₀(r^′)×

ε₁

сматриваемая ротационная плазмонная мода прин-

)

ципиально отличается от дипольного поверхност-

⁽r_<

2 (ε₁ - ε₂) rr^′

ного плазмона в однородных металлических на-

r²r′2dr dr^′,

r2>

(ε₁ + 2ε₂) R³

(20)

ночастицах, где смещение электронной плотности,

∫

∞

вызванное дипольными плазмонными колебаниями,

4π

δV_x[ρ(r)]

K_x =

ρ²⁰(r)

r²dr =

является чисто трансляционным, u

= Ae_z. Та-

δρ(r)

ким образом, в металлических кластерах изменение

∫

плотности заряда внутри частицы δρ = 0, а возвра-

e²

ρ4/30(r)r²dr.

щающая сила возникает только из-за кулоновского

3ε₁

взаимодействия электронного заряда δρ, индуциро-

ванного на поверхности кластера, с полем положи-

Последний вклад в вариацию полной электрон-

тельного ионного остова. Напротив, согласно (13),

ной энергии плазмонных колебаний связан с увели-

вращательная плазмонная мода имеет компресси-

чением их кинетической энергии, T , за счет коллек-

онную природу. Помимо кулоновского взаимодей-

тивного движения ферми-жидкости, описываемого

ствия появляется дополнительный вклад в возвра-

уравнением (16),

щающую силу, связанный с изменением локальной

∫

электронной энергии Ферми при вариации двумер-

m_eρ₀ u²

MA˙²

T =

dV =

(21)

ной плотности δσ (13), т. е. в результате квантового

давления. Ротационная кинетическая энергия на од-

где M — эффективная масса ротационной плазмон-

ну частицу в двумерной ферми-жидкости в два ра-

ной моды,

за меньше, чем энергия Ферми ε_F (n) (12). Следова-

Nm_e〈r〉²

тельно, вариация полной ротационной электронной

M =

(22)

энергии во втором порядке по отношению к A ≪ 1

В результате суммирования всех вкладов в вари-

равна

ацию полной энергии плазмонных колебаний (21),

(17), (20), эффективный гамильтониан, описываю-

∫

∂ε_F

ℏ²N²A(t)

щий вращательную плазмонную моду, приобретает

δE_rot =

δσ²ds =

(17)

∂σ

24m_e〈r〉²

вид

MA˙

Mω2pA²

При этом вариация первого порядка для E_rot равна

H =

(23)

нулю, поскольку при варьировании должно сохра-

ℏ²N

K_D + K_x

няться полное число электронов N.

ω2p =

(24)

2 (m_e〈r〉²)²

Вариация кулоновской потенциальной энергии

представляет собой сумму «прямой» и обменной со-

где ω_p — частота плазмонного резонанса. Первый

ставляющих,

член в правой части уравнения (24) определяет

вклад квантового давления. С учетом соотношения

∫

(8) для полного числа электронов он в точности сов-

δE_C =

δρ(r)v (r, r^′))δρ(r^′)drdr^′,

(18)

падает с разностью одночастичных энергий Δ (11):

√

ℏ²N

ℏ²(l_max + 1)

где

Δ=ℏ

(25)

2(m_e〈r〉²)²

m_e〈r〉²

δV_x[ρ(r)]

v (r, r^′) = V (r, r^′) +

δ(r - r^′).

(19)

Следует отметить, что ℏl_max/m_e〈r〉

= v_F есть

δρ(r)

скорость Ферми в тангенциальном направлении, а

вклад квантового давления в плазмонную частоту

Здесь V (r, r^′) описывает парное «прямое» кулоновс-

Δ/ℏ ≃ v_F /R по порядку величины близок к часто-

кое взаимодействие (2), а V_x(r) — локальный обмен-

те стоячей акустической волны в однородной сфе-

ный потенциал (6). Вычисление вариации δE_C с ис-

рической капле ферми-жидкости радиуса R. Вто-

пользованием δρ (13) дает

рое слагаемое в правой части (24) описывает вклад

1055

Л. Г. Герчиков, А. Н. Ипатов

ЖЭТФ, том 159, вып. 6, 2021

(

)₂

(

)

кулоновского взаимодействия, причем его «прямая»

a₀

2ε₂

a₀

λ=

≃

(27)

часть K_D/M всегда больше обменной K_x/M, поэто-

ℏω_cl

ε₁

му при проведении качественного анализа мы будем

пренебрегать последней. При фиксированной кон-

центрации электронов n_e влияние квантового дав-

Следует отметить, что полученное значение λ совпа-

ления на величину ω2p уменьшается согласно (11),

дает с параметром, который определяет вращатель-

поскольку (Δ/ℏ)² ∝ 1/R² с увеличением размера

ный характер рассматриваемой плазмонной моды

наночастицы, в то время как кулоновская состав-

согласно условию (9). Таким образом, ротационная

ляющая стремится к некоторому асимптотическо-

плазмонная мода по своей природе близка к класси-

му пределу. Следовательно, в пределе больших R

ческому «кулоновскому» плазмону, в то время как

должно выполняться соотношение Δ ≪ ω_p. Кро-

квантовые эффекты корректируют ее резонансную

ме того, при оценке значения K_D можно принять

частоту, и, как будет показано ниже, отвечают за

r, r^′ = R в (20). В этом приближении асимптотичес-

ее зависимость от размера системы. Важно, что па-

кое значение плазмонной частоты в больших нано-

раметр λ не зависит от концентрации электронов в

частицах, определяемое формулами (20), (24), стре-

нанокристалле, а определяется только его размера-

мится к классической частоте дипольных плазмон-

ми. Поскольку основной целью данной работы явля-

ных колебания в тонком сферическом проводящем

ется исследование вращательного плазмона, в даль-

слое [66, 67],

нейшем анализировать режим размерного кванто-

вания не будем и ограничимся предельным случаем

K_D

2e²N

a₀ ≪ R.

ω2cl =

(26)

(ε₁ + 2ε₂)m_eR³

Чтобы завершить обсуждение в этом разде-

ле, определим условия, при которых вращательная

Важно обратить внимание, что квадрат частоты ро-

плазмонная мода может считаться гармонической.

тационного плазмона ω2cl составляет две трети от

Предложена модель, в рамках которой ротацион-

квадрата классической плазмонной частоты Ми в

ный плазмон описывается гамильтонианом гармони-

однородной проводящей сферической капле радиуса

ческого осциллятора (23) в предположении A ≪ 1,

R, содержащей N электронов. Этот результат явля-

т. е. пренебрегая членами более высоких порядков. В

ется очевидным следствием того, что в рассматри-

классическом случае амплитуда колебаний осцилля-

ваемом случае тонкого сферического слоя одна из

тора A может принимать бесконечно малые значе-

электронных степеней свободы, а именно радиаль-

ния, в то время как в рамках квантового подхода

ное движение, исключена из участия в коллектив-

является оператором и его минимальное собствен-

ных плазмонных колебаниях.

ное значение 〈1|A|0〉 соответствует переходу из ос-

В другом пределе очень маленьких нанокристал-

новного состояния |0〉 в первое возбужденное состо-

лов ожидается, что вклад квантового давления бу-

яние |1〉 гамильтониана

^Ĥ. Плазмонные колебания

дет доминировать по отношению к кулоновскому

являются гармоническими только в том случае, ес-

взаимодействию и, в свою очередь, приводить к

ли эта амплитуда мала,

изменению характера коллективного движения. В

классическом пределе больших систем движущей

силой коллективных колебаний является кулонов-

√

ское взаимодействие, в то время как в пределе сверх-

ℏ

⁽18λ)1/4

〈1|A|0〉 =

≃

≪ 1.

(28)

малых наноразмерных частиц роль движущей силы

2Mω_p

N³

выполняет квантовое давление, связанное с измене-

нием кинетической энергии ферми-жидкости, лока-

лизованной в сферической квантовой яме. Этот пре-

Во всех рассматриваемых системах параметр λ ≪ 1

дельный случай известен также как режим размер-

в соответствии с условием (9). Однако один только

ного квантования [68-70].

этот фактор еще не гарантирует выполнения тре-

С целью контроля перехода от классического

бования (28) по причине наличия степени 1/4. Бо-

плазмонного предела к режиму размерного кван-

лее существенную роль играет множитель N-3/4.

тования введем параметр λ, равный отношению

Следовательно, чтобы плазмонные колебания могли

(Δ/ℏ)² к w2cl. Для простоты сделаем замену значе-

считаться гармоническими, число электронов в ле-

ния среднего радиуса 〈r〉 в выражении для Δ (11)

гированном нанокристалле должно быть достаточно

на R:

велико, N ≫ 1.

1056

ЖЭТФ, том 159, вып. 6, 2021

Вращательная дипольная плазмонная мода. . .

4. СПЕКТР ДИПОЛЬНЫХ ВОЗБУЖДЕНИЙ

Дипольные силы осцилляторов f_ν соответству-

В ПРИБЛИЖЕНИИ СЛУЧАЙНЫХ ФАЗ

ющих возбужденных состояний выражаются через

амплитуды X(ν) и Y(ν), полученные в результате ре-

В приближении случайных фаз [52, 71-73] кол-

шения уравнения (30),

лективные дипольные возбуждения, включая плаз-

монные моды, описываются в виде суперпозиции од-

2m_eD2νΩ_ν

f_ν =

ночастичных возбуждений. Волновая функция ν-го

ℏ

∑

(

)

(33)

возбужденного многочастичного состояния строит-

D_ν =

X(ν)hpd_hp + Y(ν)

d_ph

ся в виде линейной комбинации

h<F,p>F

∑

(

)

где d_im = 〈i|z|m〉 — одночастичные дипольные мат-

|Ψ_ν 〉 =

X(ν)phâ^†pâ_h + Y(ν)phâ^†

â_p

|Ψ₀〉,

(29)

ричные элементы. Определенные таким образом си-

h<F,p>F

лы осцилляторов должны удовлетворять правилу

где â^† и â — одночастичные операторы рождения и

сумм Томаса - Райхе - Куна (TRK) [73],

уничтожения, F обозначает уровни Ферми системы,

∑

f_ν = N,

(34)

|Ψ₀〉 — основное состояние, а |Ψ_ν 〉 — возбужденное

состояние с определенным угловым моментом L и

его проекцией M. В нашей работе мы рассматри-

что позволяет проводить оценку точности проведен-

ваем только дипольные возбуждения (L = 1), и в

ных численных расчетов.

данном разделе приводится квантовомеханическое

В общем случае, например, для наночастиц с

описание оптического спектра исследуемых наноча-

равномерным распределением электронной плотно-

стиц. Индексы h и p обозначают соответственно за-

сти, таких как металлические кластеры или объем-

полненные («дырки») и незаполненные («электро-

но-легированные полупроводниковые нанокристал-

ны») одночастичные уровни и пробегают весь ба-

лы, вклад в коллективное возбужденное состояние

|Ψ_ν 〉 (29) дает большое число электрон-дырочных

зис одночастичных состояний. Коэффициенты X(ν)ph

пар. При этом распределение сил осцилляторов в

(амплитуды «вперед-во-времени») и Y(ν)ph (ампли-

оптическом спектре не может быть описано ана-

туды «назад-во-времени»), характеризующие вклад

литически, а получается только в результате чис-

конкретной электрон-дырочной пары (ph) в много-

ленного решения уравнения (30). В рассматрива-

частичное состояние |Ψ_ν 〉, определяются путем ре-

ем случае с поверхностно-легированными нанокри-

шения матричного уравнения RPAX [51,73,74] с ло-

сталлами ситуация иная. Благодаря разделению ра-

кальным обменным взаимодействием,

диального и углового движения электронов в су-

(

)(

)

(

)

перпозиции (29) появляется доминирующий член

A B

X(ν)

= ℏΩ_ν

(30)

разложения, соответствующий дипольному перехо-

-B^⋆

-A^⋆ Y(ν)

Y(ν)

ду HOMO-LUMO с энергией возбуждения Δ (11).

Действительно, наибольшие дипольные матричные

Положительные собственные числа ℏΩ_ν = E_ν - E₀

элементы имеют переходы между одночастичными

определяют энергии дипольных переходов между

состояниями с одинаковыми радиальными кванто-

коррелированным основным состоянием |Ψ₀〉 и воз-

выми числами n_p = n_h и, следовательно, с мак-

бужденными состояниями |Ψ_ν〉 (29). Элементы мат-

симально перекрывающимися волновыми функци-

риц A и B равны соответственно

ями, в то время, как матричные элементы меж-

A_im,jn = δ_ijδ_mn(ϵ_m - ϵ_i) + 〈ij|v|mn〉,

ду состояниями с n_p = n_h по порядку величины

(31)

оказываются меньше в δr/R ≪ 1 раз. Таким об-

B_im,jn = 〈in|v|mj〉,

разом, только состояния с низшими радиальными

где потенциал парного взаимодействия v (r, r^′) опре-

квантовым числами n_p = n_h = 1 принимают уча-

стие в процессе фотопоглощения, и для дипольных

делен в соответствии с (19), а собственные вектора

возбуждений оказывается эффективно разрешен-

удовлетворяют условию нормировки [71, 73],

ным только переход между HOMO и LUMO элек-

∑

|X(ν)hp|² - |Y(ν)hp|² = 1.

(32)

тронными уровнями с угловыми моментами соответ-

h<F,p>F

ственно l_max и l_max + 1. По этой причине корреля-

ции между одночастичным возбуждением HOMO-

Амплитуды Y(ν)hp учитывают парные электрон-ды-

LUMO и другими электрон-дырочными парами пре-

рочные корреляции в основном состоянии системы.

небрежимо малы. Кулоновские матричные элемен-

1057

Л. Г. Герчиков, А. Н. Ипатов

ЖЭТФ, том 159, вып. 6, 2021

ты V в уравнении RPAX (30) достаточно велики

тив, в режиме размерного квантования, когда R ≪

только для электрон-дырочных пар с сильно пере-

≪ a₀, частота Ω определяется одночастичной энер-

крывающимися волновыми функциями, т. е. в на-

гией Δ (λ ≫ 1). При этом из уравнения (36) сле-

шем случае для состояний n_p = n_h = 1. По сравне-

дует, что учет кулоновских корреляций 2ΔV при-

нию с ними кулоновские матричные элементы для

водит к смещению частоты плазмонного резонанса

пар с n_p

= n_h оказываются меньше в δr/R

≪

в сторону более высоких значений по сравнению с

≪ 1 раз. Этот факт позволяет при описании плаз-

энергией одночастичного возбуждения Δ (11). Важ-

монной моды пренебречь всеми одночастичными

но, что сдвиг энергии возбуждения не сопровож-

p-h-парами за исключением одного единственного

дается какой-либо трансформацией волновой функ-

HOMO-LUMO-возбуждения. В рамках этой двух-

ции |Ψ_ν 〉, поскольку она содержит только электрон-

уровневой модели уравнение RPAX (30) сводится к

дырочные пары HOMO-LUMO, что не противоре-

системе из двух линейных уравнений

чит коллективной природе плазмонного возбужде-

ния. Действительно, суперпозиция (29) содержит

(Δ + V - ℏΩ) X + V Y = 0,

большое количество членов, хотя радиальные кван-

(35)

(Δ + V + ℏΩ) Y + V X = 0,

товые числа n_h = n_p = 1 и угловые моменты l_h =

-1 остаются фиксированными, а суммирование

=l_p

где V одновременно обозначает как кулоновский

происходит по проекциям углового момента. Как

матричный элемент V = 〈ph|v|hp〉 «вперед-во-вре-

было показано в разд. 3, дипольное возбужденное

мени» между двумя одночастичными дипольны-

состояние может рассматриваться как гармониче-

ми возбуждениями p - h, так и V

= 〈pp|v|hh〉

ская плазмонная мода, только если количество сво-

«назад-во-времени» между основным состоянием и

бодных электронов в системе, в частности на по-

возбуждением типа «две-частицы-две-дырки», по-

верхности Ферми, достаточно велико. Это условие,

скольку в случае локального обменного взаимодей-

2l_max + 1 ≫ 1, обеспечивает коллективную при-

ствия (19) эти матричные элементы равны между

роду дипольного возбуждения |Ψ_ν 〉. Особенностью

собой.

рассматриваемого вращательного плазмона являет-

Полученная система уравнений RPAX (35) 2 × 2

ся то, что суперпозиция (29) определятся только

имеет простое аналитическое решение,

сферической симметрией системы и не зависит от

силы кулоновского межчастичного взаимодействия.

ℏ²Ω² = Δ² + 2ΔV,

(36)

Амплитуды X и Y связаны с проекциями углово-

го момента через коэффициенты Клебша - Гордона,

ℏΩ + Δ

ℏΩ - Δ

как показано в Приложении, что обеспечивает со-

X =

√

Y =-

√

(37)

хранение полного углового момента L = 1 многочас-

ℏΩΔ

〉.

тичного состояния |Ψ_ν

Аналитические выражения для матричных элемен-

Другим важным параметром, который позволя-

тов V приведены в Приложении, где продемонстри-

ет оценивать вклад кулоновских корреляций в про-

ровано, что соотношения (24) и (36) совпадают друг

цесс возбуждения дипольной моды, является отно-

с другом. Этого следовало ожидать, поскольку час-

шение RPAX амплитуд,

тота Ω дипольного возбуждения в рамках двухуров-

√

невой модели есть не что иное, как резонансная

ℏΩ - Δ

Δ + 2V -

=-√

√ .

(38)

частота ротационной плазмонной моды. В большин-

ℏΩ + Δ

Δ + 2V +

стве случаев при наличии значительных кулоновс-

В случае самых маленьких нанокристаллов, R ≪ a₀

ких межчастичных корреляций волновые функции

(λ ≫ 1), роль кулоновских корреляций пренебре-

и энергии коллективных возбужденных состояний

жимо мала, X ≃ 1, Y ≪ 1, поскольку энергия ме-

|Ψ_ν 〉 существенно отличаются от одночастичных. В

жэлектронного взаимодействия мала по сравнению

нашем случае индикатором влияния кулоновского

с кинетической энергией электронов, локализован-

взаимодействия является параметр λ (27), который

ных вблизи непроницаемого потенциального барье-

с использованием обозначений (35) записывается в

ра у поверхности частицы. В этом режиме размер-

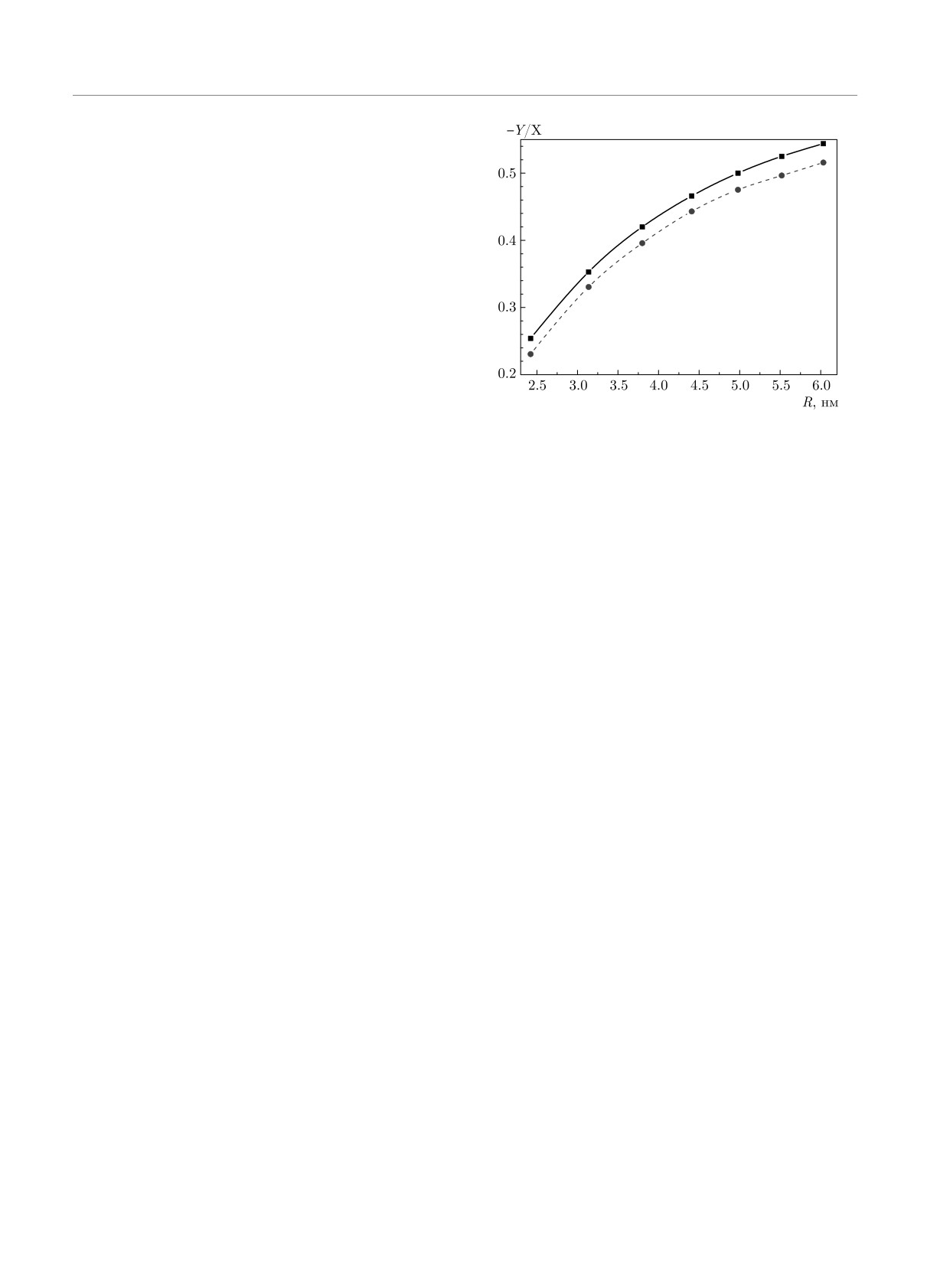
виде

ного квантования приближение независимых одно-

λ = Δ²/2ΔV = Δ/2V.

частичных электронных состояний хорошо описы-

Как уже обсуждалось в разд. 3, в классическом

вает как основное состояние, так и спектр диполь-

пределе больших систем, при R ≫ a0, кулонов-

ных возбуждений. В другом предельном случае, при

ское взаимодействие преобладает и λ ≪ 1. Напро-

R ≫ a₀ (λ ≪ 1), межэлектронное взаимодействие

1058

ЖЭТФ, том 159, вып. 6, 2021

Вращательная дипольная плазмонная мода. . .

играет значительную роль, что подтверждается со-

По этой же причине квадрат частоты ротационно-

отношением X ≃ -Y ≃ 1. Возрастание амплиту-

го плазмона в классическом пределе ω2cl составляет

ды «назад-во-времени» свидетельствует о наличии

2/3 от квадрата частоты Ми. Этот результат также

кулоновских корреляций в основном состоянии |0〉.

может быть получен на основе коммутационных со-

Трансформация некоррелированного основного со-

отношений для правила сумм (34) [73], но с учетом

стояния системы, сформированного из заполненных

только угловых степеней свободы.

одночастичных электронных состояний ниже уров-

ня Ферми, в коррелированное многочастичное ос-

новное состояние происходит путем одновременного

5. ОБСУЖДЕНИЕ РЕЗУЛЬТАТОВ

возникновения возбужденных электрон-дырочных

пар, которые в случае двухуровневой модели соот-

В рамках описанного в разд. 4 подхода бы-

ветствуют переходам между одночастичными состо-

ли проведены расчеты спектров дипольных воз-

яниями HOMO и LUMO. Эта трансформация при-

буждений для всех наночастиц ZnO с замкнуты-

водит как к заметному сдвигу энергии возбужде-

ми электронными оболочками в интервале размеров

ния ℏΩ, так и к изменению дипольного матрично-

2 нм < R < 6 нм, т. е. для N = 8, 18, 32, 50, 72,

го элемента D перехода из основного состояния |0〉

98, 128. Оптические спектры нанокристаллов с раз-

в коллективное возбужденное состояние |1〉. В соот-

ным содержанием электронов проводимости, пред-

ветствии с формулой (36), кулоновские корреляции

ставлены на рис. 3. На графике 3г также сравнива-

приводят существенному увеличению энергии пере-

ется расчетное сечение фотопоглощения с результа-

хода ℏΩ по сравнению с ее одночастичным значени-

тами экспериментальных измерений [24] для нано-

ем Δ. Их соотношение можно оценить как

кристаллов ZnO с R ≃ 6 нм. Распределения сил ос-

цилляторов в процентах от правила сумм (34), полу-

ℏΩ/Δ ≃ 2V/Δ ≃ 1/λ ≫ 1.

ченных путем численного решения уравнений (30)-

В то же время, как следует из (33), сам диполь-

(33), показаны сплошными вертикальными линия-

ный матричный элемент уменьшается. В рамках

ми. Для сравнения штриховыми вертикальными ли-

двухуровневой модели, как показано в Приложе-

ниями также показаны силы осцилляторов, соответ-

нии, значения одночастичных матричных элементов

ствующие двухуровневой модели RPAX (36), (40),

d_im могут быть вычислены аналитически. Посколь-

результаты которой эквивалентны данным, полу-

ку при наличии корреляций выполняется соотноше-

ченным на основе гидродинамического подхода.

ние X ≃ -Y , два слагаемых в правой части уравне-

Для численного решения уравнения (30) тре-

ния (33) компенсируют друг друга, что приводит к

буется полный одночастичный базис |h〉, |p〉, вклю-

уменьшению многочастичного матричного элемента

чающий в себя состояния как дискретного, так и

D по сравнению с его одночастичным значением d.

непрерывного спектра. С практической точки зре-

Согласно формуле (36), сумма амплитуд X и Y рав-

ния, матричное уравнение RPAX удобнее решать,

няется

√

используя только дискретный базис, что позволя-

X+Y =

(39)

ет эффективно уменьшить размер диагонализиру-

ℏΩ

емой матрицы. Проблема трансформации полно-

Таким образом, одновременное уменьшение диполь-

го базиса одночастичных состояний в эквивалент-

ного матричного элемента и увеличение энергии пе-

ный дискретный базис была решена путем исполь-

рехода |0〉 → |1〉 сохраняет неизменным значение си-

зования метода B-сплайнов [75]. Волновые функции

лы осциллятора,

дискретных решений уравнений (3) были получены

2m_eΩ

2m_eΔ

в бесконечно глубокой сферической потенциальной

f =

|D|² =

|d|² =

(40)

ℏ

ℏ²

яме конечного, но достаточно большого радиуса [76]

как это более детально показано в Приложении. При

путем разложения одночастичных волновых функ-

этом сила осциллятора перехода |0〉 → |1〉 состав-

ций в виде линейной комбинации конечного числа B-

ляет 2/3 от правила сумм (34,) что является есте-

сплайнов. Необходимая точность вычислений с ис-

ственным, поскольку с точки зрения двухуровневой

пользованием дискретного базиса достигалась вы-

модели этот переход описывает вклад ротационного

бором числа и порядка B-сплайнов. При проведении

дипольного плазмона в оптический спектр системы.

расчетов были использованы 50 B-сплайнов 7-го по-

Вращательная мода включает в себя только угло-

рядка, что обеспечило достаточную точность вычис-

вое движение электронов, в то время как радиаль-

лений. Для нахождения энергий дипольных перехо-

ные степени свободы остаются невозбужденными.

дов Ω_ν и соответствующих сил осцилляторов (33)

1059

Л. Г. Герчиков, А. Н. Ипатов

ЖЭТФ, том 159, вып. 6, 2021

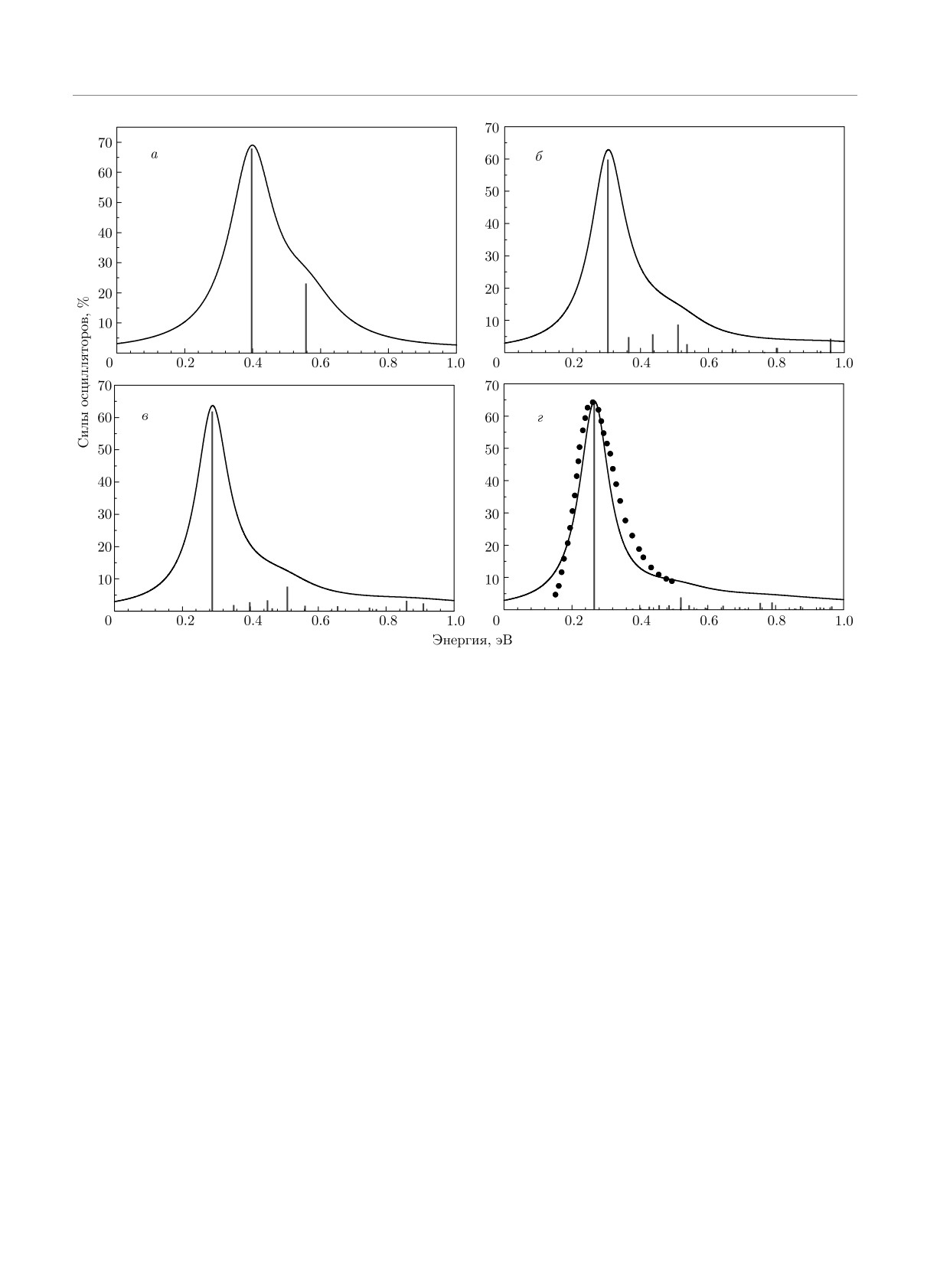
Рис. 3. Распределения сил осцилляторов и соответствующие профили пиков фотопоглощения, рассчитанные в прибли-

жении RPAX для нанокристаллов ZnO, с разным содержанием электронов проводимости: а — N = 8 (R = 2.4 нм),

б — 32 (R = 3.8 нм), в — 50 (R = 4.4 нм), г — 128 (R = 6.0 нм). Вертикальными штриховыми линиями показаны

силы осцилляторов для двухуровневой модели. Для сравнения на рис. г приведена экспериментальная зависимость [24]

сечения фотопоглощения в окрестности резонансного пика для нанокристалла ZnO c R ≈ 6 нм

определялись собственные числа и собственные век-

ний фотопоглощения есть общая особенность в ви-

торы матрицы RPAX (30) с использованием стан-

де резонансного пика, соответствующего одной ярко

дартных процедур из библиотеки EISPACK.

выраженной линии оптического перехода. Его по-

Сечения фотопоглощения были получены путем

ложение и сила осциллятора, полученные как в ре-

уширения спектральных линий, соответствующих

зультате численного решения уравнения RPAX (30),

рассчитанным распределениям сил осцилляторов,

так и в рамках двухуровневой модели, хорошо со-

лоренцевыми профилями с шириной 0.4Ω. Ушире-

гласуются друг с другом и с экспериментальными

ние плазмонного резонансного пика имеет множест-

данными, что позволяет однозначно классифициро-

во причин [77-82], детальный анализ которых не

вать его как вращательный плазмон. Как следует

входит в число задач, стоящих в данной публика-

из графиков, сила осциллятора резонансной моды

ции. Поэтому авторы использовали искусственное

очень близка к 2/3 правила сумм, что полностью

уширение резонансных пиков, чтобы добиться со-

согласуется с теоретическим значением (40). Остав-

гласия с экспериментальными спектрами фотопо-

шаяся 1/3 суммы сил осцилляторов распределена

глощения. Как видно на рис. 3, оптические спектры

между оптическими переходов с более высокими ча-

всех рассматриваемых нами нанокристаллов ZnO

стотами, в которых происходит возбуждение ради-

подобны друг другу. Как и в экспериментально на-

ального движения электронов. Прекрасное согласие

блюдаемых спектрах [24], у всех рассчитанных сече-

между результатами RPAX и двухуровневой моде-

1060

ЖЭТФ, том 159, вып. 6, 2021

Вращательная дипольная плазмонная мода. . .

Рис. 4. Распределения сил осцилляторов нанокристаллов ZnO, содержащих N = 32 (а) и N = 128 (б) электронов: сплош-

ные красные линии — результаты расчетов на основе RPAX (30), черные пунктирные линии — двухуровневая модель,

синие штриховые линии — одночастичное приближение. Радиальные распределения плотности дипольных переходов

для N = 32 (в) и N = 128 (г), соответствующие нескольким спектральным линиям. Для сравнения также показаны

распределения электронной плотности основного состояния

ли подтверждает факт очень слабой связи между

плазмонных мод ℏΩ = ℏω_p, показанных вертикаль-

плазмонной модой и состояниями, в которых воз-

ными пунктирными линиями. Согласно формуле

буждены радиальные степени свободы.

(36), этот сдвиг коллективной моды в сторону более

высоких энергий по отношению к линии одноча-

Чтобы продемонстрировать принципиальное

стичного перехода обусловлен межчастичными

различие между двумя типами оптических перехо-

кулоновскими корреляциями, соответствующими

дов на рис. 4 сплошными черными вертикальными

второму слагаемому в правой части уравнения (36),

линиями показаны распределения сил осцилляторов

и отражает коллективный характер плазмонного

для двух систем с N = 32 и 128 электронами, рас-

возбуждения. Это не противоречит тому факту, что

считанные в рамках RPAX, вместе с их радиальны-

смешивание одночастичных состояний, в которых

ми плотностями переходов и силами осцилляторов

одночастичных возбуждений, которые изображены

происходит возбуждение радиального движения, с

возбуждением перехода HOMO-LUMO в многоча-

синими штриховыми линиями. Одночастичные

стичной волновой функции (29) мало. Несмотря на

возбуждения с низшей энергией, показанные на

то, что мы можем пренебречь вкладом в суперпози-

графиках 4а,б, соответствуют переходам HOMO-

цию (29) от всех состояний, за исключением пары

LUMO между электронными состояниями с бес-

HOMO-LUMO, сумма будет содержать

корневыми радиальными волновыми функциями.

Как видно на графиках, их энергии возбуждения

√

Δ существенно ниже, чем энергии коллективных

2l_max + 1 =

2N + 1 ≫ 1

1061

Л. Г. Герчиков, А. Н. Ипатов

ЖЭТФ, том 159, вып. 6, 2021

Таблица 1. Параметры дипольных возбуждений

электрон-дырочных возбуждений, которые будут

системы, содержащей 32 электрона

отличаться проекциями углового момента. Таким

образом, коллективность плазмонной моды и ее гар-

% от TRK

моничность обеспечивается большим числом элек-

Возбуждение Энергия, эВ

-Y/X

суммы

тронов на поверхности Ферми, как было отмече-

но в разд. 4. Напротив, как видно на графиках,

Плазмон

0.30

62.3

0.40

частотные сдвиги, наблюдаемые у линий, соответ-

1p-2s

0.37

5.3

0.05

ствующих оптическим переходам между состояни-

1d-2p

0.44

6.2

0.08

ями с разными радиальными квантовыми числами,

очень малы. В диапазоне энергий представленных

1f-2d

0.51

8.1

0.09

на рис.4а,б распределений сил осцилляторов показа-

ны линии нескольких оптических переходов между

Таблица 2. Параметры дипольных возбуждений

заполненными состояниями с низшим радиальным

системы, содержащей 128 электронов

квантовым числом n = 1 и возбужденными уров-

нями с n = 2. Все эти линии лежат выше плазмон-

% от TRK

ного пика, причем, как легко видеть, энергии этих

Возбуждение Энергия, эВ

-Y/X

суммы

состояний, рассчитанные в рамках RPAX и в одно-

частичном приближении, лежат очень близко друг к

Плазмон

0.27

64.4

0.52

другу. Это означает, что возбуждения радиального

1p-2s

0.36

0.2

0.01

движения электронов слабо коррелированы и могут

1d-2p

0.38

0.4

0.01

быть описаны как одночастичные состояния в по-

тенциале среднего поля. Этот факт также подтвер-

1f-2d

0.40

0.6

0.01

ждается анализом RPAX амплитуд X и Y , значе-

1s-2p

0.41

0.2

0.01

ния которых для систем, содержащих N = 32 и 128

1g-2f

0.43

0.9

0.01

электронов, представлены соответственно в табл. 1

1g-2f

0.43

0.9

0.01

и 2. Как следует из таблиц, для плазмонных мод

1h-2g

0.46

1.4

0.01

амплитуды близки по порядку величины, X ∼ |Y |,

в то время как для других возбужденных состояний

1i-3h

0.49

1.4

0.01

наблюдается соотношение X ≫ |Y |. Большая ам-

1j-2i

0.52

3.6

0.02

плитуда «назад-во-времени» свидетельствует о зна-

чительном смешивании электрон-дырочных состо-

яний и коллективном характере возбуждения. На-

где ψ(r) — одночастичные волновые функции (7). В

против, малые значения Y соответствуют одноча-

случае, когда электронные оболочки замкнуты и си-

стичным возбужденным состояниям, для которых

стема имеет сферическую симметрию, для диполь-

межчастичные корреляции практически не играют

ного возбуждения выражение (41), как показано в

роли. В табл. 1 и 2 приведены значения сил осцил-

Приложении, может быть приведено к виду

ляторов в процентах от правила сумм (34) для ряда

возбужденных состояний с целью продемонстриро-

ρ(ν)tr(r) = ρ(ν)tr(r)cos θ,

(42)

вать, что плазмонная мода с достаточно большой

точностью аккумулирует 2/3 от всей суммы сил ос-

где

цилляторов, в то время как на долю каждого одно-

√

частичного возбуждения приходится лишь малая ее

∑

Pnh,l_h (r)Pnp,lp (r)

ρ(ν)tr(r) =

(-1)li

часть.

4π

r²

h<F,p>F

Природа каждой конкретной спектральной ли-

(

)√

нии также может быть проанализирована путем ис-

× X(ν)ph +Y(ν)ph

l_h + 1.

(43)

следования плотности переходов, которая определя-

ется как

Для двухуровневой модели радиальная зависи-

(ν)

мость плотности переходов ρ

(r) может быть по-

ρ(ν)tr(r) = 〈Φ_ν|δρ(r)|Φ₀〉 =

лучена аналитически. С учетом того, что при сум-

∑

(

)

мировании в правой части выражения (43) оста-

X(ν)phψ^⋆p(r)ψ_h(r)+Y(ν)phψ_p(r)ψ^⋆h(r) ,

(41)

ется только один член, соответствующий переходу

h<F,p>F

HOMO-LUMO, будем полагать все радиальные вол-

1062

ЖЭТФ, том 159, вып. 6, 2021

Вращательная дипольная плазмонная мода. . .

новые функции идентичными и, в соответствии с

(14), равными

P21,l(r)/r² = 4πρ₀(r)/N.

При этом сумма X + Y определяется соотношени-

ем (39). В этом случае выражение (42) принимает

вид

√

3ℏ

ρ_tr(r) = ρ₀(r)

cosθ =

Nm_eR²Ω

√

ℏ

= ρ₀(r)

cosθ,

(44)

2Mω_p

что в точности совпадает с амплитудой колебаний

электронной плотности в гидродинамической моде-

ли (13), в которой амплитуда плазмонного осцилля-

Рис. 5. Зависимости частоты дипольного резонанса от ра-

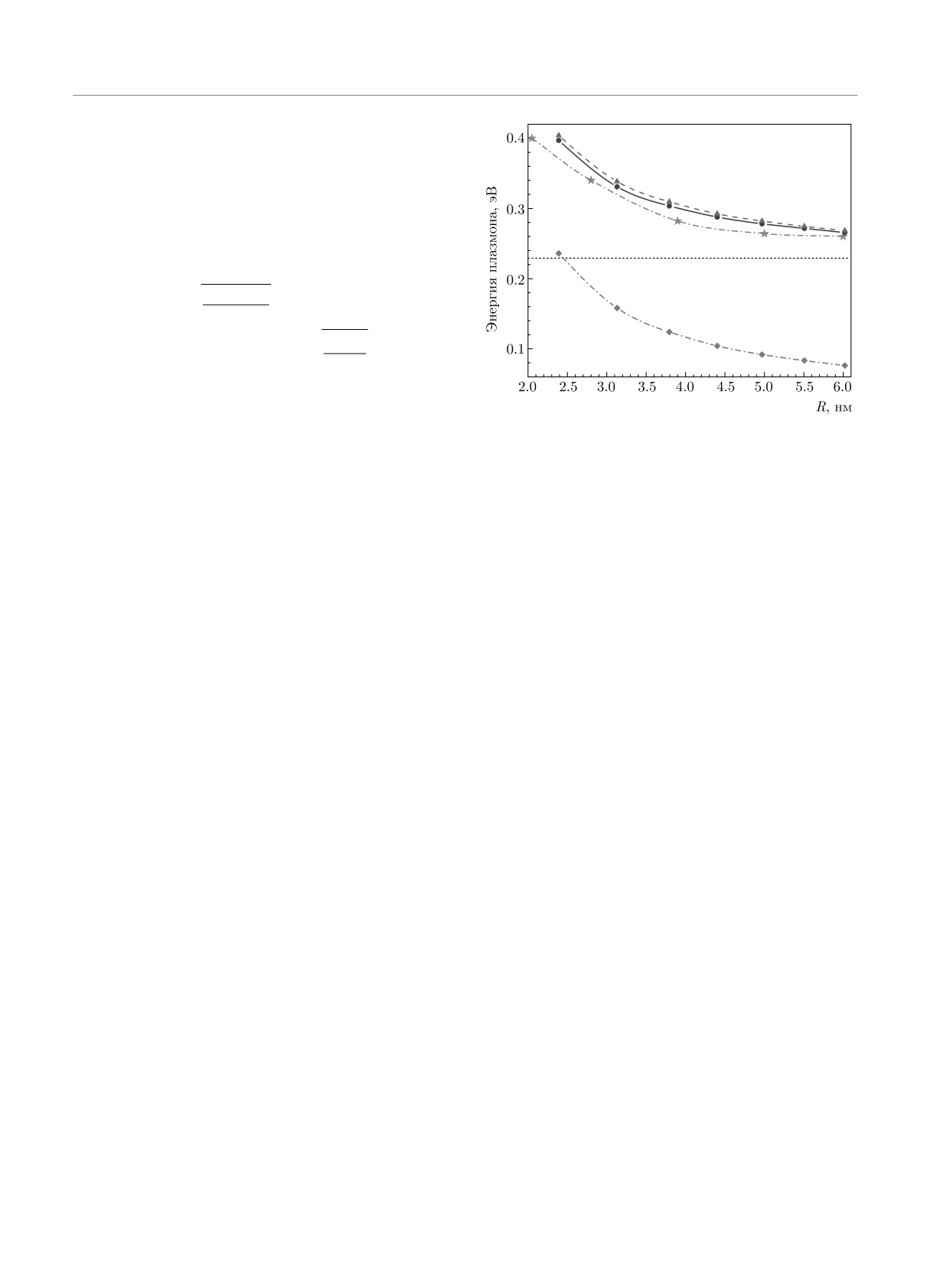
тора 〈1|A|0〉 определяется формулой (28).

диуса наночастицы R. Экспериментальные значения [24] —

На рис. 4в,г представлены радиальные зависимо-

красные звездочки со штрихпунктирными линиями. Двух-

уровневая модель — сиреневые треугольники со штриховы-

сти плотности переходов ρ(ν)tr(r) для спектральных

ми линиями. Полный RPAX расчет (30) — синие кружки

линий, изображенных на графиках рис.

4а,б.

со сплошными синими линиями. Одночастичная модель

Сплошные линии показывают зависимости ρ(ν)tr(r),

невзаимодействующих электронов (11) — зеленые ромбы

полученные на основе RPAX согласно уравне-

со штрихпунктирными линиями. Классическая плазмон-

нию (43). Пунктирными линиями для сравнения

ная частота (26) — горизонтальная черная пунктирная ли-

приведены графики радиального распределения

ния

электронной плотности основного состояния ρ₀(r),

которая, согласно (44), определяет плотность пере-

ходов для гидродинамической и эквивалентной ей

того, что эти переходы не могут быть отнесены к

двухуровневой моделей (44). Прекрасное согласие

коллективным модам.

между результатами, полученными в рамках двух

Применимость предложенной модели, описыва-

подходов к описанию ротационной плазмонной мо-

ющей компрессионный ротационный плазмон, про-

ды, подтверждает сделанное выше предположение,

верена сравнением с экспериментально наблюдае-

что для плазмонной моды с высокой точностью

мыми спектрами фотопоглощения нанокристаллов

выполняется соотношение ρ_tr(r) ∝ ρ₀(r). Следует

ZnO. Наиболее наглядным примером является за-

отметить, что в случае «традиционного» трансляци-

висимость резонансной частоты от размера наноча-

онного поверхностного плазмона Ми распределение

стиц. На рис. 5 приведено сравнение частот резо-

плотности переходов оказывается совершенно дру-

нансных пиков, наблюдаемых в экспериментальных

гим, ρ_tr(r) ∝ dρ₀(r)/dr [13]. В классическом пределе

зависимостях [24] и показанных на графике звез-

чисто трансляционные плазмонные колебания

дочками, с положениями максимумов сечений фо-

однородного электронного облака приводят к вари-

топоглощения, рассчитанных в RPAX (30), которые

ации электронной плотности вблизи границы, где

отмечены синими кружками, для различных ради-

сильна радиальная зависимость ρ₀(r). В терминах

усов исследуемых наночастиц. На графике также

квантового подхода подобная особенность означает,

построены зависимости энергии плазмонного резо-

что ρ_tr(r) складывается из вкладов от множества

нанса ℏω_p от размера частицы, полученные в рам-

одночастичных переходов, при которых меняются

ках гидродинамической модели (24), а также энер-

как угловое, так и радиальное квантовые числа.

гии Δ одночастичных переходов HOMO-LUMO. По-

Плотности одночастичных переходов, также при-

ложение классической энергии плазмона ℏω_cl (26)

веденные на рис. 4б,г, имеют схожие зависимости,

в асимптотическом пределе больших систем пока-

поскольку соответствуют дипольным переходам

зано горизонтальной пунктирной линией. Графи-

между состояниями с разными радиальными кван-

ки, представленные на рис. 5, демонстрируют хо-

товыми числами. Однако их поведение не может

рошее согласие между экспериментальными данны-

быть с хорошей точностью аппроксимировано про-

ми и результатами численных расчетов. При этом

изводной dρ₀(r)/dr, что является подтверждением

квантовомеханические расчеты на основе RPAX и

1063

Л. Г. Герчиков, А. Н. Ипатов

ЖЭТФ, том 159, вып. 6, 2021

полуклассическая гидродинамическая модель дают

почти идентичные значения плазмонной энергии.

Это еще раз подтверждает, что экспериментально

наблюдаемый резонансный пик в спектре фотопо-

глощения нанокристаллов ZnO с поверхностным ле-

гированием связан с возбуждением вращательной

плазмонной моды. Заметная разность между одно-

частичными, Δ, и коллективными, ℏΩ, энергиями

возбуждения показывает, что кулоновские межча-

стичные корреляции играют важную роль при фор-

мировании плазмонной моды. Величина этой разно-

сти меняется с ростом размера нанокристаллов в со-

ответствии с изменением параметра λ ≃ a₀/2R (27).

В случае больших систем кулоновские корреляции

дают основную составляющую энергии плазмонных

колебаний, в то время как вклад квантового давле-

Рис. 6. Зависимость отношения -Y /X дипольной плаз-

ния Δ оказывается минимален, и, таким образом,

монной моды от радиуса системы: численные результаты

RPAX — сплошная кривая; результаты двухуровневой мо-

энергия плазмона стремится к своему классическо-

дели (35) — штриховая линия

му пределу ℏω_cl. Напротив, для самых малоразмер-

ных систем влияние кулоновского взаимодействия

существенно уменьшается, в то время как эффект

от квантового давления возрастает по мере увели-

ской плазмонной частоты ω_cl. Следовательно, одно-

чения параметра λ. Однако в исследованном диа-

временно присутствуют два квантовых механизма,

пазоне размеров наночастиц мы не наблюдаем пе-

приводящих к появлению размерной зависимости

рехода от классического предела, λ ≪ 1, к режиму

ω_p(R), а именно квантовое давление и эффект сме-

размерного квантовая, λ ≫ 1. Действительно, на-

щения электронной плотности. Вклад первого меха-

личие кулоновского взаимодействия, индикатором

низма описывается, соответственно, первым членом

силы которого служит параметр λ, необходимо для

в правой части уравнения (36), в то время как появ-

возникновения вращательного плазмона. Исходя из

ление второго связано с эффективным увеличени-

условия (9), плазмонные колебания могут считать-

ем кулоновского матричного элемента V во втором

ся ротационными, если выполняется соотношение

слагаемом уравнения. Оба механизма обеспечивают

λ ≪ 1. При этом все рассмотренные фотолегирован-

одинаковую зависимость ω_p(R) ∼ 1/R для больших

ные нанокристаллы ZnO, включая самый малень-

R, хотя вклад второго превалирует.

кий, содержащий только 8 электронов, для кото-

Зависимость влияния кулоновских корреляций

рого λ ≃ 0.14, удовлетворяют этому требованию.

на процесс формирования плазмонной моды от раз-

Комбинация кулоновского взаимодействия и кван-

мера наночастицы также может быть проиллюстри-

тового давления приводит к появлению зависимо-

рована на примере сравнительного анализа ампли-

сти плазмонной частоты от размера системы. Одна-

туд X и Y . На рис. 6 построено отношение -Y/X

ко помимо квантового давления присутствует еще

как функция радиуса нанокристалла R, где пред-

один дополнительный вклад в размерную зависи-

ставленные результаты были получены как на ос-

мость ℏω_p(R), а именно эффект смещения электрон-

нове численных расчетов в RPAX (сплошная ли-

ной плотности в результате ее отталкивания от гра-

ния), так и в рамках двухуровневой модели в со-

ницы наночастицы. Как показано на вставке рис.1,

ответствии с (38) (штриховая линия). Для графи-

квантовое отталкивание приводит к сдвигу Δr ∼ a₀

ка RPAX были взяты значения отношения -Y/X

среднего радиуса электронной системы 〈r〉 относи-

для основного перехода в суперпозиции (29), со-

тельно радиуса R. Уменьшение величины 〈r〉 усили-

ответствующего электрон-дырочной паре HOMO-

вает межчастичное кулоновское взаимодействие и, в

LUMO. На рис. 6 видно, что значение отношения

свою очередь, ведет к зависящему от размера систе-

-Y/X, которое является индикатором влияния ку-

мы сдвигу плазмонной частоты ω_p выше ее класси-

лоновских корреляций, возрастает примерно вдвое

ческого значения ω_cl. Этот эффект может быть вос-

при увеличении размера нанокристаллов от наи-

произведен заменой радиуса наночастицы R сред-

меньших до наибольших из рассмотренных. Важ-

ним радиусом 〈r〉 < R в формуле (26) для классиче-

но отметить, что предложенная модель основывает-

1064

ЖЭТФ, том 159, вып. 6, 2021

Вращательная дипольная плазмонная мода. . .

ся на предположении, что электроны проводимости

случае они будут связаны с протонами у поверхнос-

полностью делокализованы в объеме наночастицы.

ти. Для нанокристаллов ZnO с радиусом R = 6 нм

Это, по-видимому, верно в случае высоких концен-

это может произойти при значениях концентрации

траций электронов, когда их волновые функции пе-

n_e как минимум на порядок ниже, чем 1.4·10²⁰ см-3.

рекрываются. Однако при низких электронных кон-

Локализацию электронов с образованием вигнеров-

центрациях ситуация может оказаться другой, и,

ского кристалла [83] в ZnO также можно ожидать

таким образом, необходимо сделать оценку мини-

при существенно более низких уровнях легирова-

мальной концентрации, которая будет обеспечивать

ния.

делокализацию электронов. В обсуждаемом случае

нанокристаллов с поверхностым способом легиро-

вания движение делокализованных электронов про-

6. ЗАКЛЮЧЕНИЕ

исходит практически только в тангенциальном на-

правлении. Радиальное движение строго ограниче-

Наличие дипольных плазмонных резонансных

но в узком слое шириной δr ≪ R из-за кулоновского

мод в спектре фотопоглощения является неотъемле-

отталкивания и потенциального барьера у поверх-

мым свойством наночастиц, содержащих делокали-

ности. Используемая сферически-симметричная мо-

зованные электроны. Легированные полупроводни-

дель пренебрегает наличием угловой зависимости

ковые нанокристаллы представляют собой перспек-

потенциала среднего поля, в силу чего тангенциаль-

тивную основу для новых материалов, используе-

ное движение электронов полагается свободным. В

мых в наноэлектронике, поскольку позволяют ва-

этом приближении мы не учитываем поле, создава-

рьировать положение линии плазмонного резонаса

емое протонами на внешней поверхности нанокри-

в широком диапазоне частот. В представленной ра-

сталла, которые выполняют роль положительно за-

боте теоретически исследован новый тип коллектив-

ряженных доноров [24]. Монопольный член куло-

ного дипольного возбуждения в наноразмерных фо-

новского потенциала протонов наночастицы посто-

толегированных полупроводниковых кристаллах на

янен внутри объема, но его мультипольные компо-

примере кристаллов ZnO в растворе толуола. Дока-

ненты более высоких порядков — нет. Следует ожи-

зано, что доминирующая в их спектрах фотопогло-

дать, что при достаточно низких концентрациях но-

щения резонансная линия соответствует плазмон-

сителей заряда каждый электрон будет связан с со-

ной моде вращательного типа, в которой возбужде-

ответствующим протоном, и электронная система в

ны только угловые степени свободы. Появление та-

целом будет представлять собой систему отдельных

кого плазмона в электронной системе фотолегиро-

нейтральных пар электрон-донор, а не делокали-

ванных нанокристаллов обусловлено особенностью

зованное электронное облако. Радиусы орбит элек-

строения их основного состояния, в котором элек-

тронов, связанных с протонами за пределами нано-

троны проводимости локализованы в узком припо-

кристалла, больше, чем радиус нейтрального доно-

верхностном слое. В результате коллективные ко-

ра в объемном ZnO из-за отталкивания электрона

лебания электронной плотности происходят толь-

от границы. В предположении нулевых граничных

ко в тангенциальном направлении, в то время как

условий для электронной волновой функции на по-

радиальные степени свободы остаются заморожен-

верхности наночастицы можно оценить средний ра-

ными. Эта же особенность распределения электрон-

диус для пары электрон-протон как средний ради-

ной плотности определяет электронную конфигура-

ус электрона в p-состоянии нейтрального донора в

цию исследуемых нанокристаллов, у которых рас-

объемном ZnO: 〈r〉_ep ∼ 5a₀ ≃ 3.25 нм. Таким об-

пределение заполненных уровней энергии с хорошей

разом, электроны становятся делокализованными,

точностью воспроизводит спектр квантового рота-

когда начинают перекрываться волновые функции

тора. Это, в свою очередь, приводит к тому, что

ближайших друг к другу доноров. Это происхо-

в формировании коллективной плазмонной моды

дит при рассматриваемой электронной концентра-

принимают участие практически только электро-

ции n_e = 1.4 · 10²⁰ см-3 [24], соответствующей r_s =

ны из наружной оболочки, что дает возможность

= 1.2 нм, что почти втрое меньше, чем 〈r〉_ep. При

описать резонансный дипольный переход в рамках

этом среднее межэлектронное расстояние внутри уз-

простой двухуровневой модели. При этом проведен-

кой электронной оболочки еще меньше, и его мож-

ный сравнительный анализ амплитуд «вперед»- и

√

но оценить как 2R/

N = 2r_s/N1/6. Если это значе-

«назад-во-времени», а также распределения плотно-

ние оказывается меньше радиуса донора, электроны

сти переходов подтвердил многочастичный харак-

могут считаться делокализованными, в противном

тер этого возбужденного состояния.

1065

ЖЭТФ, вып. 6

Л. Г. Герчиков, А. Н. Ипатов

ЖЭТФ, том 159, вып. 6, 2021

Важно отметить, что плазмонная мода рота-

тей амплитуд Xnplp, nhlhиYnplp, nhlh^{отрадиальных}

ционного типа по своей природе принципиально

квантовых чисел n_p,h и орбитальных моментов l_p,h

отличается от поверхностных Ми-резонансов и

одночастичных состояний определяется в результа-

может быть описана как возбужденное состояние в

те численного решения матричного уравнения (30).

конечной ферми-системе, так и как вращательное

В рамках двухуровневой 2×2 модели RPAX в су-

движение квантовой жидкости. Было продемон-

перпозиции (29) мы учитываем вклад только одного

стрировано, что подобные дипольные колебания

перехода HOMO-LUMO, для которого

являются гармоническими, что позволяет их опре-

n_p = n_h = 1, l_p - 1 = l_h = l_max.

делить как плазмонное резонансное возбуждение.

Результаты проведенных теоретических расчетов в

Следовательно, остается только одна пара приве-

рамках обоих подходов продемонстрировали хоро-

денных амплитуд X и Y , удовлетворяющих урав-

шее совпадение с экспериментальными данными,

нениям (35), а их значения в явном виде записыва-

в которых отчетливо наблюдалась зависимость

ются как (37). Кулоновский матричный элемент V

положения резонансной линии от размера нано-

в уравнениях (35), (36) может быть представлен как

частицы. При изменении радиуса нанокристалла,

∑

V =

(-1)mh+mh C¹⁰

как показано в данной работе, резонансная мо-

l_h-m_h lpmp

m_hmpm^′hm^′

да претерпевает переход от режима размерного

∫

квантования в случае очень маленьких систем к

×C10l

ψ^∗l

h-m^′h lpm^p

hmh

(r)ψlp mp (r)v(r, r^′) ×

режиму «классических» плазмонных колебаний в

пределе больших радиусов. При этом роль пара-

×ψ^∗l

(r^′)ψ_l

(46)

pm^p

hm^′ (r′)drdr^′,

метра, определяющего выбор режима возбуждения

где результат суммирования по спиновым индексам

электронной системы, играет отношение размера

уже учтен в виде множителя 2. Одночастичные вол-

нанокристалла к эффективному боровскому ра-

новые функции определены как произведение (7),

диусу. С увеличением размера кристалла частота

причем мы пренебрегаем зависимостью их радиаль-

плазмона стремится к своему асимптотическому

ных компонент от углового момента

значению, соответствующему классической частоте

плазмонных колебаний в тонкой проводящей сфере,

P1,lmax (r) = P1,lmax+1(r) = P1(r).

что согласуется с результатами экспериментальных

Оператор межчастичного кулоновского взаимодей-

измерений.

ствия v(r, r^′) представлен в виде суммы «прямой»

и обменной компонент (19), что позволяет вычис-

Благодарности. Авторы благодарят профессо-

лить соответствующие слагаемые по раздельности,

ра Claude Guet из Nanyang Technological University

V =V_d +V_x.

за полезные обсуждения.

«Прямая» часть оператора, V (r, r^′), определяет-

ся из мультипольного разложения по сферическим

гармоникам (2). После интегрирования по угловым

ПРИЛОЖЕНИЕ

переменным [59],

Коллективное возбужденное состояние в RPAX

|Φ_ν 〉 (29) имеет определенные значения полного уг-

〈Ylp mp (n)|Ylm(n)|Ylh mh(n)〉=(-1)-mh ×

лового момента L и его проекции M. Это обеспе-

√

чивается зависимостью амплитуд X и Y от проек-

(2l_h + 1)(2l_p + 1)

C^lml

Cl0l

(47)

h-mhlpmp

h0lp0

ций углового момента посредством коэффициентов

4π(2l + 1)

Клебша - Гордана

√

3(l_h + 1)

Xnplpmpσp, nhlhmhσp=(-1)mh Clpm

p, lhM-mh

C10l

= (-1)lh

(48)

h0lp0

(2l_h + 1)(2l_p + 1)

δσpσ_h

√

Xnplp, nhlh^,

и последующего суммирования по m_p,h получаем

(45)

∫

2e²(l_max + 1)

Ynplpmpσp nhlhmhσp=(-1)mp ClpM

-mp lhmh

V_d =

P₁(r)²P₁(r^′)² ×

δσpσ_h

√

Ynplp, nhlh^.

(

)

r^l<

(ε₁ - ε₂)(l + 1)(r₁r₂)

В рассматриваемом случае дипольных возбуждений

dr dr^′.

(49)

ε₁rl+1>

ε₁ (lε₁ + (l + 1)ε₂)R2l+1

L = |l_p - l_h| = 1, а зависимость приведенных час-

1066

ЖЭТФ, том 159, вып. 6, 2021

Вращательная дипольная плазмонная мода. . .

Соответствующий вклад 2ΔV_d/ℏ² в Ω² в правой ча-

Суммирование по m_p, m_h проводится с помощью

сти уравнения (36) с учетом (14), (25), (22), (20) в

(51) и приводит к окончательному результату

точности совпадает со слагаемым K_C/M в форму-

∑

ле (24) для ω2p в гидродинамической модели.

ρ(ν)tr(r) =

√

Pnplp (r)Pnhlh(r)×

6πr²

Аналогичным образом, обменная часть матрич-

np,lp,nh,lh

(

)√

ного элемента записывается в виде

× X^νn

+Y^νn

(2l_h+1)(2l_p+1) ×

plp, nhlh

(

)1/3

×Cl0l

Yl0(n),

(54)

h0 lp0

V_x = -2

9π

ε₁

что с учетом (48) в точности дает (42), (43).

∑

C10l

′

(-1)mh+mh ×

h-mh,lpmp

h-m^′h,lpm

m_hmpm^′hm^′

ЛИТЕРАТУРА

∫ ψ^∗l

hmh

(r)ψlpmp (r)ψlp m′p (r)ψlh m^′ (r)h

dr,

(50)

ρ₀(r))2/3

В. В. Климов, Наноплазмоника, Физматлит, Моск-

ва (2009).

где множитель

вновь появляется в результа-

Quantum Plasmonics, ed. by S. I. Bozhevolniy et al.,

те суммирования по спиновым индексам. Сум-

Springer International Publishing, Switzeland (2016).

ма произведения двух сферических гармоник в

ψ^∗l

Plasmonics. From Basics to Advanced Topics, ed. by

hmh

(r)ψlp mp (r) и коэффициента Клебша - Гордана

может быть преобразована к виду [59]

S. Enoch and N. Bonod, Springer Series in Optical

Sciences 167, Berlin, Springer Verlag (2012).

∑

M. S. Tame, K. R. McEnery, S. K. Ozdemir et al.,

C10l

(n) =

h-mh,lpmp

(-1)mhYlp,mp (n)Yl∗

h,-mh

Nature Phys. 9, 329 (2013).

m_h,mp

√

(2l_p + 1)(2l_h + 1)

J. A. Scholl, A. L. Koh, and J. A. Dionne, Nature

C10l

Y1,0(n).

(51)

h0,lp0

483, 421 (212).

12π

M. Brack, Rev. Mod. Phys. 65, 667 (1993).

После вычисления угловой части (50) получаем

M. Harb, F. Rabilloud, D. Simon et al., J. Chem.

(

)1/3

Phys. 129, 194108 (2008).

2(l_min + 1)

Vx = -

F. Xuan and C. Guet, Phys. Rev. A 94, 043415

9π

ε₁

4π

(2016).

∫∞

P⁴¹(r)

dr.

(52)

U. Kreibig and M. Vollmer, Optical Properties of

r²ρ₀(r)2/3

Metallic Clusters, Springer Series in Materials Science

65, Springer-Verlag, Berlin (1995).

Таким образом, с учетом (14), (25), (22) и (20), об-

10.

Clusters of Atoms and Molecules, ed. by H. Haber-

менный вклад 2ΔV_x/ℏ² в Ω² также в точности сов-

land, Vol. I,II, Springer Series in Chemical Physics,

падает с обменным членом K_x/M в (24).

Vol. 52, 56, Springer, Berlin (1994).

Выражения (45) для амплитуд RPAX также ис-

11.

W. A. de Heer, Rev. Mod. Phys. 65, 611 (1993).

пользовались при вычислении плотности переходов

ρ(ν)tr(r) = 〈Φ_ν|δρ(r)|Φ₀〉 С их помощью после сумми-

12.

C. R. C. Wang, S. Pollack, D. Cameron, and

рования по спиновым индексам формула (41) пре-

M. M. Kappes, J. Chem. Phys. 93, 3787 (1993).

образуется к виду

13.

C. Guet and W. R. Johnson, Phys. Rev. B 45, 11283

√

∑

(1992).

ρ(ν)tr(r) =

(-1)mh

14.

U. Kreibig and P. Zacharias, Z. Physic 231, 128

np,lp,mp,nh,lh,mh

(

(1970).

× X^νn

C10l

ψlhm_h (r)ψ^l m (r) +_pp

plp, nhlh

pmp, lh-mh

)

15.

I. Kriegel, F. Scotognella, and L. Mannaa, Phys. Rep.

+ Y^νn

C10l

ψ^∗l

(53)

674, 1 (2017).

plp, nhlh

p-mp lhmh

hmh

(r)ψlp mp (r)

1067

Л. Г. Герчиков, А. Н. Ипатов

ЖЭТФ, том 159, вып. 6, 2021

16.

Nanocrystal Quantum Dots, ed. by V. I. Klimov, CRC

38.

G. Mie, Ann. Phys. 25, 377 (1908).

Press (2010).

39.

H. Liu, C. K. Brozek, S. Sun et al., J. Phys. Chem.

17.

R. C. Monreal, T. J. Antosiewicz, and S. P. Appel,

C 121, 26066 (2017).

New J. Phys. 15, 083044 (2013).

40.

A. M. Schimpf, C. E. Gunthardt, J. DRinehart et al.,

18.

B. Palpant, B. Prével, J. Lermé et al., Phys. Rev.

J. Amer. Chem. Soc. 135, 16569 (2013).

B 57, 1963 (1998).

41.

W. Ekardt, Phys. Rev. B 31, 6360 (1985).

19.

J. Lermé, B. Palpant, E. Cottancin et al., Phys. Rev.

42.

D. E. Beck, Phys. Rev. B 35, 7325 (1987).

Lett. 80, 5105 (1998).

43.

L. G. Gerchikov, C. Guet, and A. N. Ipatov, Phys.

20.

F. Scotognella, G. Della Valle, A. R. S. Kandada et

Rev. A 66, 053202.1 (2002).

al., Eur. Phys. J. B 86, 154 (2013).

44.

A. N. Ipatov, L. G. Gerchikov, and C. Guet, J. Comp.

21.

Y. Xie, L. Carbone, C. Nobile et al., ACS Nano 7,

Mat. Sci. 35, 347 (2006).

7352 (2013).

45.

U. Banin, Y. Cao, D. Katz, and O. Millo, Nature 400,

22.

A. L. Routzahn, S. L. White, L.-K. Fong et al., Isr.

542 (1999).

J. Chem. 52, 983 (2012).

46.

L. P. Kouwenhoven, D. G. Austing, and S. Tarucha,

23.

J. M. Luther, P. K. Jain, T. Ewers et al., Nature

Rep. Prog. Phys. 64, 701 (2001).

Mater. 10, 361 (2011).

47.

A. N. Ipatov, L. G. Gerchikov, and C. Guet,

24.

A. MSchimpf, N. Thakkar, C. E. Gunthardt et al.,

Nanoscale Res. Lett. 13, 297 (2018).

ACS Nano 8, 1065 (2014).

48.

K. Yabana and G. F. Bertsch, Phys. Scripta 48, 633

25.

H. Zhang, V. Kulkarni, E. Prodan et al., J. Phys.

(1993).

Chem. C 118, 16035 (2014).

49.

N. Ju, A. Bulgac, and J. W. Keller, Phys. Rev. B 48,

26.

E. Townsend and G. W. Bryant, Nano Lett. 12, 429

9071 (1993).

(2012).

50.

¨stling, P. Apell, and A. Rosen, Europhys. Lett.

27.

E. Prodan, P. Nordlander, and N. J. Halas, Nano

21, 539 (1993).

Lett. 3, 1411 (2003).

51.

M. Madjet, G. Guet, and W. R. Johnson, Phys. Rev.

28.

S. Link and M. A. El-Sayed, J. Phys. Chem. B 103,

A 51, 1327 (1995).

4212 (1999).

52.

Applied Many-Body Methods in Spectroscopy and

29.

J. A. Faucheaux, A. L. D. Stanton, and P. K. Jain,

Electronic Structure, ed. by D. Mikharjee, Springer

J. Phys. Chem. Lett. 5, 976 (2014).

Science and Business Media, NY (1992).

30.

S. D. Lounis, E. L. Runnerstrom, A. Bergerud et al.,

53.

H. E. Wilhelm, Phys. Rev. D 1, 2278 (1970).

J. Amer. Chem. Soc. 136, 7110 (2014).

54.

G. Guiliani and G. Vignale, Quantum Theory of

31.

M. A. El-Sayed, Acc. Chem. Res. 37, 326 (2004).

Electron Liquid, Cambridge University Press (2005).

32.

S.-W. Hsu, K. On, and A. T. Rao, J. Amer. Chem.

55.

T. Ihn, Semiconductor Nanostructures: Quantum

Soc. 133, 19072 (2011).

States and Electronic Transport, Oxford University

Press (2010).

33.

X. Liu and M. T. Swihart, Chem. Soc. Rev. 43, 3908

(2014).

56.

F. Rossi, Theory of Semiconductor Quantum Devices:

Microscopic Modeling and Simulation Strategies,

34.

G. Garcia, R. Buonsanti, E. L. Runnerstrom et al.,

Springer Science and Business Media, NY (2011).

Nano Lett. 11, 4415 (2011).

57.

H. Morko and

Ü¨zgür, in Zinc Oxide, WILEY-VCH

35.

M. Kanehara, H. Koike, T. Yoshinaga, and T. Tera-

(2009).

nishi, J. Amer. Chem. Soc. 131, 17736 (2009).

58.

Ll. Serra, F. Garcias, J. Navarro et al., Phys. Rev.

36.

D. J. Rowe, J. S. Jeong, K. A. Mkhoyan, and

B 46, 9369 (1992).

U. R. Kortshage, Nano Lett. 13, 1317 (2013).

59.

D. A. Varshalovich, A. N. Moscalev, V. K. Kherson-

37.

Zh. Sun and B. Zhao, Appl. Phys. Lett. 91, 221106

skii, Quantum Theory of Angular Momentum, World

(2007).

Scientific, Singapore (1988).

1068

ЖЭТФ, том 159, вып. 6, 2021

Вращательная дипольная плазмонная мода. . .

60. R. Dreizler and E. Gross, Density Functional Theory,

72.

D. J. Rowe, Rev. Mod. Phys. 40, 153 (1968).

Plenum Press, New York (1995).

73.

G. F. Bertsch and R. A. Brorlia, Oscillations in Finite

61. L. D. Landau and E. M. Lifshitz Quantum Mechanics,

Quantum Systems, Cambridge University press, UK

Vol. 3, Pergamon Press (1977).

(1994).

62. L. D. Landau, Sov. Phys. JETP 3, 920 (1957).

74.

M. Ya. Amusia and L. V. Chernysheva, Computation

of Atomic Processes, IOP Publishing Ltd (1997).

63. D. P. Grimmer, Physica B+C 106, 9 (1981).

75.

C. de Boor, A Practical Guide to Splines, Springer

64. J. Feldman, H. Knörrer, and E. Trubowitz, Commun.

Verlag, New York (1978).

Math. Phys. 247, 1 (2004).

76.

J. Sapirstein and W. R. Johnson, J. Phys. B: Atomic,

65. B. Fröhlich, M. Feld, E. Vogt et al., Phys. Rev. Lett.

Molec. Opt. Phys. 29, 5213 (1996).

109, 130403 (2012).

77.

W. E. Ormand, J. M. Pacheco, S. Sanguinetti et al.,

66. C. F. Bohren and D. R. Huffman, Absorption

Z. Phys. D 24, 401 (1992).

and Scattering of Light by Small Particles, Wiley

Interscience, New York (1983).

78.

G. F. Bertsch and D. Tomanek, Phys. Rev. B 40,

2749 (1989).

67. F. Alpeggiani, S. D’Agostino, and L. C. Andreani,

Phys. Rev. B 86, 035421 (2012).

79.

J. M. Pacheco and R. A. Broglia, Phys. Rev. Lett.

62, 400 (1989).

68. Quantum Confinement Effects, Observations and In-

sights, ed. by R. Parker, Nova Science Publishers, NY

80.

J. M. Pacheco and W. D. Schöne, Phys. Rev. Lett.

(2017).

79, 4986 (1997).

69. B. Zorman, M. V. Ramakrishna, and R. A. Freisner,

81.

F. Della Salla, R. Rousseau, A. Görling, and D. Marx,

J. Phys. Chem. 99, 7649 (1995).

Phys. Rev. Lett. 92, 183401.1 (2004).

70. S. Neeleshwar, C. L. Chen, C. B. Tsai et al., Phys.

82.

C. Yannouleas and R. A. Broglia, Ann. Phys. (NY)

Rev. B 71, 201307 (2005).

217, 105 (1991).

71. A. Dalgarno and G. A. Victor, Proc. Roy. Soc. A 291,

83.

B. Tanatar and D. Ceperley, Phys. Rev. B 39, 5005

291 (1966).

(1989).

1069