ЖЭТФ, 2021, том 159, вып. 6, стр. 1070-1089
© 2021
БЕЗМАССОВЫЕ ЭЛЕКТРОННЫЕ ВОЗБУЖДЕНИЯ В ГРАФЕНЕ
В ОКРЕСТНОСТИ КУЛОНОВСКИХ ПРИМЕСЕЙ
А. И. Бреевa*, Д. М. Гитманa,b**
a Томский государственный университет
634050, Томск, Россия
b Физический институт им. П. Н. Лебедева Российской академии наук
119991, Москва, Россия
Поступила в редакцию 10 января 2021 г.,
после переработки 2 февраля 2021 г.
Принята к публикации 3 февраля 2021 г.
Исследуются низкоэнергетические безмассовые электронные возбуждения в монослое графена в окрест-
ности точечной кулоновской примеси. Предполагается, что такие возбуждения описываются в рамках
модели Дирака. Построено семейство самосопряженных гамильтонианов, отвечающих этим возбуждени-
ям для любого заряда примеси, и проведен их спектральный анализ. Показано, что в рассматриваемом
случае структура спектров электронных возбуждений качественно другая по сравнению с соответствую-
щими спектрами массивных возбуждений. На основе полученных результатов анализируется локальная
поверхностная плотность электронных состояний в графене и ее зависимость от выбора самосопряжен-
ных гамильтонианов.
DOI: 10.31857/S0044451021060079
сопряженного (в дальнейшем с.с.) оператора в со-
ответствующем гильбертовом пространстве. А для
движения электрона в кулоновском поле проблема
1. ВВЕДЕНИЕ
определения гамильтониана как с.с. оператора яв-
ляется нетривиальной только для ядер с большими
Присутствие примесей и дефектов может зна-
Z (Z > 119), которые не возникают в лабораторных
чительно изменять электронные свойства графена.
условиях, для кулоновских примесей в графене этот
Например, присутствие заряженных примесей, та-
порог значительно меньше из-за свойств дираков-
ких как кулоновские центры, оказывает существен-
ских квазичастиц в дираковской модели графена.
ное влияние на подвижность носителей заряда [1].
Заметим, что в зависимости от структуры под-
В связи с этим исследование свойств графена при
ложки, на которой синтезирован графен, может воз-
наличии взаимодействия носителей с кулоновски-
никнуть (или не возникнуть) щель в электронном
ми центрами важно для понимания электронно-
спектре между валентной зоной и зоной проводимо-
го транспорта в присутствии примесей, см. рабо-
сти. Это определяется свойствами взаимодействия
ты [2-6]. Технически задача облегчается тем обсто-
между слоем графена и подложкой, которое нару-
ятельством, что низкоэнергетические электронные
шает симметрию между подрешетками, но сохраня-
возбуждения в монослое графена во внешнем элек-
ет трансляционную симметрию. Для ненулевой ще-
тромагнитном поле хорошо описываются моделью
ли низкоэнергетические электронные возбуждения
Дирака, где они представляют собой киральные ди-
в модели Дирака являются массивными фермиона-
раковские фермионы в 2 + 1 измерениях [7, 8].
ми, в то время как, если щель между валентной зо-
Корректное описание таких возбуждений (часто
ной и зоной проводимости отсутствует, то эти воз-
называемых ниже квазичастицами) в окрестности
буждения являются безмассовыми фермионами. Ве-
точечной кулоновской примеси требует правильного
личину щели можно менять, варьируя химический
определения дираковского гамильтониана как само-
состав и концентрацию подложки [9].
* E-mail: breev@mail.tsu.ru
В предыдущей работе с участием авторов [10] с
** E-mail: dmitrygitman@hotmail.com
помощью теории с.с. расширений симметрических
1070
ЖЭТФ, том 159, вып. 6, 2021
Безмассовые электронные возбуждения в графене. . .
операторов построено семейство с.с. гамильтониа-
вольным допустимым значением углового момента
нов, описывающих электронные возбуждения в гра-
j. Раздел 6 посвящен описанию особенностей пол-
фене со щелью для любого значения заряда приме-
ного гамильтониана рассматриваемой модели в за-
си. На основе метода направляющих функционалов
висимости от заряда примеси Z. В разд. 7 с помо-
Крейна проведен спектральный анализ таких га-
щью полученных результатов исследуется локаль-
мильтонианов. В частности, найдены их спектры и
ная плотность состояний в графене. Раздел 8 пред-
соответствующие полные наборы (обобщенных) соб-
ставляет собой краткое заключение.
ственных функций. При этом выбор с.с. гамильтони-
ана из всех математически возможных является от-
дельной физической задачей. Отметим, что резуль-
2. УРАВНЕНИЕ ДИРАКА В 2 + 1
ИЗМЕРЕНИЯХ ДЛЯ БЕЗМАССОВОЙ
таты, полученные в работе, не могут быть непосред-
ЗАРЯЖЕННОЙ ЧАСТИЦЫ В
ственным образом использованы в безмассовом слу-
КУЛОНОВСКОМ ПОЛЕ
чае, так как области определения с.с. дираковских
гамильтонианов для графена со щелью обращаются
Мы работаем в рамках модели Дирака в 2 + 1
в нуль в безмассовом пределе (для графена с ну-
измерении для заряженных квазичастиц в окрест-
левой щелью). Поэтому случай графена с нулевой
ности кулоновской примеси. Пусть в начале декар-
щелью требует отдельного исследования, которому
товой системы координат с осями x и y, лежащими в
и посвящена настоящая работа.
плоскости графена, находится кулоновская примесь
В данной работе мы рассматриваем задачу кор-
с зарядом Z. Создаваемый ею потенциал с учетом
ректного определения дираковского гамильтониана
макроскопической диэлектрической проницаемости
как с.с. оператора для квазичастиц в графене без
ϵ имеет вид
щели в присутствии кулоновской примеси с про-
√
извольным зарядом Z. Представлено рассмотрение
Ze2 1
V (ρ) = -
,
ρ = |r| =
x2+y2, r = (x, y).
всех аспектов этой задачи, основанное на теории
ϵ ρ
с.с. расширений симметрических операторов [11-13].
Обозначим через Ks точки Дирака, координаты
Строится семейство всех возможных с.с. гамильто-
которых в зоне Бриллюэна выбраны в виде Ks =
нианов, члены которого различаются параметрами
= (4πs/(3a), 0), где a = 2.46Å — постоянная решет-
соответствующих расширений (таким образом пара-
ки, а s = ±1 — изоспиновое квантовое число.
метризуются ими), и проводится их спектральный
Полное гильбертово пространство Htot кванто-
анализ. Для этого строятся обобщенные собствен-
вых состояний квазичастиц является прямой орто-
ные функции всех таких гамильтонианов, причем
гональной суммой двух гильбертовых пространств
это делается для любых зарядов примеси. Техни-
Hs, s = ±1, каждое из которых связано с соответ-
чески задача сводится к анализу спектров соответ-
ствующей точкой Дирака Ks. Пространства Hs яв-
ствующих с.с. одномерных парциальных радиаль-
ляются гильбертовыми пространствами двумерных
ных гамильтонианов. Показано, что спектры таких
дублетов, так что
гамильтонианов являются непрерывными и занима-
ют всю вещественную ось R, в отличие от массивно-
Htot = H1 ⊕ H-1, H1 = H-1 = H = L2(R2) ⊕ L2(R2).
го случая, где имеется как дискретный, так и непре-
рывный спектр.
В силу дальнодействующей природы кулоновско-
Статья организована следующим образом. В
го поля, междолинные процессы не учитываются
разд. 2 приведены определения базовых понятий
и переходы между гильбертовыми пространствами
и соотношений, объясняющих постановку задачи.
Hs не рассматриваются. Так что полный эффек-
В разд. 3 описана математически строгая процеду-
тивный гамильтониан
Ĥtot квазичастиц является
ра сведения проблемы построения с.с. вращательно-
прямой ортогональной суммой двух гамильтонианов
инвариантного дираковского гамильтониана в пол-
Hs, s = ±1, каждый из которых действует в соответ-
ном гильбертовом пространстве к задаче построе-
ствующем гильбертовом пространстве Hs и может
ния с.с. одномерных парциальных радиальных га-
быть рассмотрен отдельно.
мильтонианов с определенным угловым моментом.
В рамках модели Дирака квазичастицы в окрест-
Затем, в разд. 4, исследуется общее решение ради-
ности каждой точки Дирака Ks описываются эф-
альных уравнений для безмассового уравнения Ди-
фективным безмассовым уравнением Дирака [14]:
рака в 2 + 1 измерении. В разд. 5 строятся с.с.
парциальные радиальные гамильтонианы с произ-
HsΨs = EΨs, s = ±1,
(1)
1071
А. И. Бреев, Д. М. Гитман
ЖЭТФ, том 159, вып. 6, 2021
где волновые функции Ψs являются дублетами, за-
H = L2(R2) ⊕ L2(R2), ассоциированных с соот-
висящими от r, Ψs = Ψs(r) = {ψsα(r), α = 1, 2},
ветствующими дифференциальными выражениями
компоненты ψsα(r) представляют собой огибающие
Hs (3). Поскольку коэффициентные функции диф-
блоховских функций в двух подрешетках графена A
ференциальных выражений
Hs являются гладкими
и B соответственно,
Hs — дифференциальные опе-
вне начала координат, мы выбираем пространство
рации, отвечающие уравнению Дирака в 2 + 1 изме-
гладких дублетов с компактным носителем для об-
Ĥ in
Ĥ in
рениях,
ластей определения D(
s
) операторов
s
(
)
Чтобы обойти проблемы с сингулярностью ку-
g
Hs = ℏvF
-i [sσx∂x + σy∂y] -
,
лоновского потенциала в начале координат, допол-
ρ
нительно потребуем обращения в нуль дублетов
(2)
2
1
Ze
Z
Z
Ĥ in
D(
) в некоторой окрестности начала координат,
g=
=αF
=αFZeff, Zeff =
s
ℏvF
ϵ
ϵ
ϵ
в общем случае различной для каждого дублета. За-
Ĥ in
метим, что области определения D(
) (которые
Здесь vF
≈ 106 см/с — скорость Ферми и αF =
s
совпадают для обоих значений s) плотны в H. Та-
= e2/(ℏvF) — «постоянная тонкой структуры» в гра-
ким образом, операторы
Ĥ in
определяются как
фене, {σx, σy, σz} — матрицы Паули. Вводя обозна-
s
Hs
{
{
}
чения
= (ℏνF )-1
Hs, E = (ℏνF )-1E, запишем
D(
Ĥ in
)=
Ψ(r) : ψα(r) ∈ C∞0(R2 \ {0})
,
Ĥ in
s
уравнение (1) в следующем виде:
=
s
Ĥ in
Ψ(r) =
HsΨ(r).
s
HsΨs(r) = EΨs(r), s = ±1,
яв-
Очевидно, что так определенный оператор
Ĥ in
s
где дифференциальные операции
Hs в полярных ко-
ляется симметрическим.
ординатах ρ, φ, (x = ρ cos φ, y = ρ sin φ) имеют вид
Мы строим с.с. гамильтонианы
Ĥs как с.с. рас-
ширения соответствующих исходных симметричес-
∂
Hs = -i(s cosφσx + sinφσy)
+
ких операторов
Ĥ in
. Мы требуем, чтобы операторы
s
∂ρ
Ĥs были вращательно-инвариантными, так же как
i
∂
g
Ĥ in
+
(s sin φσx - cos φσy )
-
(3)
исходные симметрические операторы
s
. Смысл
ρ
∂φ
ρ
этого требования выяснится ниже.
Для того чтобы придать физический смысл соот-
Существует два различных унитарных представ-
ветствующей квантовомеханической задаче на соб-
ления Us группы вращений Spin(2) в H, которые
ственные значения, мы должны, отправляясь от
связаны с соответствующими операторами
Ĥ in
. Ге-
s
дифференциальных операций
Hs, построить соот-
нератор
Js представления группы Us, называемый
ветствующие гамильтонианы
Ĥs как с.с. операторы
оператором углового момента (их два), является с.с.
с определенными областями определения в гильбер-
оператором в H, определенным на абсолютно непре-
товом пространстве H = L2(R2) ⊕ L2(R2). При ре-
рывных и периодических по φ ∈ [0, 2π] дублетах и
шении этой задачи мы следуем идеям работы [10], в
ассоциированным с дифференциальным выражени-
которой рассмотрена подобная задача для соответ-
ем
∂
σz
ствующих массивных квазичастиц.
Js = -i
+s
∂φ
2
По определению переменная j принимает полу-
целые, положительные и отрицательные, значения,
Для каждого s гильбертово пространство H пред-
j = ±(n+1/2), n ∈ Z+, тогда как переменная Z при-
ставляется в виде прямой ортогональной суммы
нимает неотрицательные целые значения, Z ∈ Z+. В
подпространств Hsj , которые являются собственны-
дальнейшем нам будет удобнее рассматривать пере-
ми пространствами оператора углового момента
Js,
менную Z как величину, принимающую непрерыв-
соответствующими всем его собственным значени-
ные значения и лежащую на неотрицательной вер-
ям j,
∑
∑
тикальной полуоси, Z ∈ R+, а возвращаться к ее
H=
⊕H-1,j =
⊕H+1,j,
естественным целочисленным значениям в случае
j
j
(4)
необходимости.
j = ±1/2,±3/2...
Подпространство Hsj с данными s и j состоит из
дублетов Ψsj вида
3. РЕДУКЦИЯ К РАДИАЛЬНОЙ ЗАДАЧЕ
(
)
Начнем с определения начальных симметричес-
1
e-isφ/2f(ρ)
Ψsj(r) =
∈Hsj,
(5)
ких операторов
Ĥ in
в гильбертовом пространстве
√2πρeijφ
-iseisφ/2g(ρ)
s
1072
ЖЭТФ, том 159, вып. 6, 2021
Безмассовые электронные возбуждения в графене. . .
являющихся собственными функциями операто-
где операторы
Ĥ in
=Psj
Ĥ in
Psj =
Ĥ in
Psj представ-
sj
s
s
ра
Js,
Ĥ in
ляют собой так называемые части оператора
s
,
JsΨsj(r) =
JsΨsj(r) = jΨsj(r).
действующие в Hsj . Их правило действия дается
дифференциальной операцией первого порядка по
Отметим, что спектры операторов
J-1 и
J1 сов-
переменной ρ, которое будет приведено ниже. Итак,
падают. Функции f(ρ) и g(ρ) называются радиаль-
Ĥ in
каждый начальный симметрический оператор
s
ными функциями. На физическом языке разложе-
является прямой ортогональной суммой своих ча-
ния (4) и (5) соответствуют разложению дублетов
стей,
Ψ(r) ∈ H по собственным функциям двух разных
∑
Ĥ in
⊕ Ĥin
операторов углового момента
J-1 и
J1.
s
=
sj
,
j
В дальнейшем для нас является существенным
так что исследование вращательно-инвариантного
следующий факт. Пусть L2(R+) есть гильбертово
Ĥ in
Ĥ in
пространство радиальных дублетов,
оператора
s
сводится к изучению операторов
sj
Ĥ in
(
)
Каждый оператор
sj
является симметричес-
f (ρ)
ким оператором, действующим в подпространстве
F (ρ) =
∈ L2(R+),
g(ρ)
Hsj. Очевидно, он индуцирует симметрический
ĥin
(Z, j, s) в гильбертовом пространстве
оператор
со скалярным произведением
L2(R+), который унитарно эквивалентен операто-
Ĥ in
ру
sj
,
∫∞
(F1, F2) = F+1(ρ)F2 (ρ) dρ =
ĥin(Z, j, s)F = V-1sj ĤinsjΨsj, Ψsj = VsjF.
0
∫∞
[
]
Операторĥin(Z, j, s) определяется следующим обра-
=
f1(ρ) f2(ρ) + g1(ρ) g2(ρ) dρ,
зом:
0
ĥin(Z, j, s) =
так что L2(R+) = L2(R+) ⊕ L2(R+). Тогда (5) и со-
{
отношение
Dhin(Z,j,s) = C0(R+),
=
(7)
∫∞
ĥn(Z, j, s)F(ρ) =
h(Z, j, s)F (ρ),
[
]
∥Ψsj∥2 =
|f(ρ)|2 + |g(ρ)|2
dρ
). Дифференциаль-
где C∞0(R+) = C∞0(R+)⊕C∞0(R+
0
ную операцию
h(Z, j, s),
означают, что пространство Hsj ⊂ H унитарно экви-
d
κ
g
валентно гильбертому пространству L2(R+),
h(Z, j, s) = -iσy
+
σx -
,
dρ
ρ
ρ
(8)
Ψsj(r) = VsjF(ρ), F(ρ) = V-1sjΨsj(r).
(6)
κ = -sj, g = αFϵ-1Z,
Начальные симметрические операторы
Ĥ in
будем называть парциальной радиальной диффе-
s
являются вращательно-инвариантными. А именно,
ренциальной операцией.
каждый оператор
Ĥ in
инвариантен относительно
Построение с.с. вращательно-инвариантных га-
s
представления Us группы вращений. Таким об-
мильтонианов
Ĥs как с.с. расширений начальных
Ĥ in
разом, каждое подпространство Hsj (собственное
симметрических операторов
s
сводится к постро-
пространство генератора
Js с собственным значе-
ению с.с. парциальных радиальных гамильтонианов
нием j) приводит оператор
Ĥ in
. Другими словами,
ĥ(Z, j, s) в L2(R+) как с.с. расширений начальных
s
оператор
Ĥ in
коммутирует с проекторами Psj на
симметрических парциальных радиальных операто-
s
подпространства Hsj , см. [15]. Это, в свою очередь,
ров
ĥin(Z, j, s). А именно, пусть операторы
ĥ(Z, j, s)
означает следующее. Пусть
являются такими расширениями. Они, очевидно,
∑
индуцируют с.с. расширения
Ĥsj = Vsjĥ(Z, j, s)V-1sj
Ĥ in
Ψs(r) =
Ψsj(r) ∈ D(
s
).
Ĥ in
начальных симметрических операторов
sj
в под-
j
пространствах Hsj . Тогда прямая ортогональная
Тогда
сумма парциальных операторов
Ĥsj,
∑
∑
Ψsj = PsjΨs ∈ D(
Ĥ in
),
Ĥ in
Ψs =
Ĥ in
Ψsj,
Ĥs =
⊕ Ĥsj,
(9)
s
s
sj
j
j
1073
А. И. Бреев, Д. М. Гитман
ЖЭТФ, том 159, вып. 6, 2021
представляет собой вращательно-инвариантное рас-
В новых переменных и для новых функций получим
ширение начального симметрического оператора
Ĥ in
d2Q(z)
dQ(z)
. И любое с.с. вращательно-инвариантное рас-
s
z
+ (β - z)
- αQ(z) = 0,
ширение начального симметрического оператора
dz2
dz
(
)
Ĥ in
Ĥs
1
d
(12)
s
имеет структуру (9). Спектр гамильтониана
P (z) = -
z
+ α Q(z),
дается объединением спектров парциальных ради-
κ
dz
альных гамильтонианов,
β = 1 + 2Υ, α = α+, α+ = Υ - ig.
spec
Ĥs = ∪j spec
ĥ(Z, j, s),
Видно, что уравнение (12) для функции Q(z)
представляет собой известное конфлюэнтное гипер-
а соответствующие собственные функции, связан-
геометрическое уравнение. Пусть Υ = -n/2, n ∈ N.
ные с Hsj , получаются из собственных функций опе-
В этом случае общее решение конфлюэнтного гипер-
раторов
ĥ(Z, j, s) в L2(R+) с помощью преобразова-
геометрического уравнения является линейной ком-
ния Vsj , см. (6).
бинацией стандартных гипергеометрических функ-
ций Φ(α, β; z) и Ψ(α, β; z),
Q(z) = AΦ(α, β; z) + BΨ(α, β; z),
4. ОБЩЕЕ РЕШЕНИЕ РАДИАЛЬНЫХ
УРАВНЕНИЙ
где A, B — произвольные постоянные, а
Перейдем к общему решению системы двух ли-
Γ(1 - β)
нейных обыкновенных дифференциальных уравне-
Ψ(α, β; z) =
Φ(α, β; z) +
Γ(α - β + 1)
ний для функций f(ρ) и g(ρ),
Γ(β - 1)
+
z1-βΦ(α - β + 1, 2 - β; z).
Γ(α)
h(Z, j, s)F (ρ) = W F (ρ),
(
)
f (ρ)
(10)
Используя соотношения
F (ρ) =
,
W ∈ C,
g(ρ)
(
)
d
z
+ α Φ(α,β;z) = αΦ(α + 1,β;z),
dz
которое необходимо при исследовании спектра и
(
)
d
собственных функций парциальных радиальных га-
z
+ α Ψ(α,β;z) = α(α - β + 1)Ψ(α + 1,β;z),
dz
мильтонианов. Действительные значения W в даль-
нейшем будут обозначаться буквой E. Для наших
α - β + 1 = -α-, α+α- = κ2,
целей достаточно рассмотреть значения W , принад-
α
α- = Υ + ig, a =
,
лежащие верхней комплексной полуплоскости, W =
κ
= E+iy, y ≥ 0. Также нас будет интересовать предел
найдем общее решение системы (11) в виде
W → E + i0.
Система (10), записанная покомпонентно, имеет
Q(z) =
AΦ(α, β; z) + BΨ(α, β; z),
вид
(
)
P (z) = -AaΦ(α + 1, β; z) + BκΨ(α + 1, β; z).
df
κ
g
+
f (ρ) - W +
g(ρ) = 0,
dρ
ρ
ρ
Как следует из равенств
(
)
(11)
dg
κ
g
-
g(ρ) + W +
f (ρ) = 0.
dρ
ρ
ρ
Φ(α + 1, β; z) = ezΦ(β - α - 1, β; -z),
1+a
κ+Υ
Далее, мы называем уравнения (11) радиальными
i
=
,
1-a
g
уравнениями. Приведем общее решение радиальных
уравнений, следуя стандартной процедуре [12, 16].
общее решение радиальных уравнений можно пред-
Сделаем следующую замену функций и перемен-
ставить в следующей форме:
ных:
F (ρ, Υ, W ) = AX(ρ, Υ, W ) +
f (ρ) = zΥe-z/2 [Q(z) + P (z)] ,
+BzΥe-z/2 [Ψ(α, β; z)ϱ+-κΨ(α + 1, β; z)ϱ-] ,
(13)
g(ρ) = izΥe-z/2 [Q(z) - P (z)] ,
(-2iW )-Υ
ϱ± = (±1, i)T ,
A=
A,
z = -2iWρ, Υ2 = κ2 - g2.
1-a
1074
ЖЭТФ, том 159, вып. 6, 2021
Безмассовые электронные возбуждения в графене. . .
где введен дублет X(ρ, Υ, W ),
Для Υ+ = γ имеем
[
2Γ(2γ)e-πg/2
X (ρ, Υ, W ) = zΥ e-z/2Φ(α, β; z)ϱ+ +
F1(ρ; E) =
×
|Γ(γ - ig)|
]
+ aez/2Φ(α + 1, β; z)ϱ-
=
× |2E|-γ (u+(γ)Fγ-1(-g, |E| ρ) -
1-a
- sgn(sjE)u-(γ)Fγ(-g, |E| ρ)) ,
=
(-2iW ρ)Υ [Φ+(ρ, Υ, W ) +
2
F2(ρ; E) = F1(ρ; E)|γ→-γ ,
(14)
+ Φ-(ρ, Υ, W) Ξ] d+,
⎛
⎞
⎞
⎛Υ - sj
1
u+(Υ) =⎝Υ - sj⎠, u-(Υ) = ⎝ g
⎠,
g
1
Φ+(ρ, Υ, W) = eiWρΦ(α, 1 + 2Υ, -2iWρ)+
g = sgn(E)g .
+ e-iWρΦ(α-, 1 + 2Υ, 2iWρ),
При Υ+ = iσ, σ > 0 имеем другое представление:
1
[
√
Φ-(ρ, Υ, W) =
eiWρΦ(α, 1 + 2Υ, -2iWρ) -
(σ - g) sh(σ - g)
iW
F1(ρ; E) = 2Γ(2iσ)
×
]
π
- e-iWρΦ(α-, 1 + 2Υ, 2iWρ)
,
[
(
)
× e-πg/2 |2E|-iσ u+(iσ)Fiσ-1(-g,|E|ρ) -
(
)
T
0
W
κ±Υ
]
Ξ=
,
d± =
1,
sj
−W
0
g
-
u-(iσ)Fiσ(-g, |E| ρ) ,
g-σ
В дальнейшем будем использовать некоторые
F2(ρ; E) = F1(ρ; E).
частные решения радиальных уравнений, соответ-
ствующие определенному выбору констант A и B и
Еще одно полезное решение F3 дается выраже-
параметра Υ.
нием (13) при A = 0, Υ = Υ+ и специальном выборе
Введем новую величину Υ+ следующим образом:
параметра B = B(W ),
{
√
γ =
κ2 - g2 ≥ 0, g ≤ |κ|,
F3(ρ; W) = B(W)zΥe-z/2
[Ψ(α, β; z)ϱ+ -
Υ+ = Υ+(g, j) =
√
iσ = i
g2 - κ2,
σ > 0.
- b-Ψ(α + 1, β; z)ϱ-] =
gω(W)
Эта величина как функция параметра g имеет ну-
= Γ(-2Υ+)F1(ρ; W) -
F2(ρ; W),
2Υ+
ли в точках g = gc(j) = |κ| = |j|. В случае Υ+ = 0
где
(g = gc(j)) мы имеем два линейно независимых ре-
)-2Υ+
шения F1 и F2, образующих фундаментальную си-
Γ(1 + 2Υ+)Γ(-α-)(
ω(W ) = -i
2e-iπ/2W
=
стему решений системы (11),
aΓ(α)[κ - Υ+]
= -Wr(F1, F3),
F1(ρ; W) = F(ρ, Υ+, W)|A=1,B=0 =
[
](
)-Υ+
1
κ+Υ+
= ρΥ+d+ + O(ρΥ++1), ρ → 0,
B(W ) =
Γ(-α-) 1 +
2e-iπ/2W
2
ig
F2(ρ; W) = F(ρ, -Υ+, W)|A=1,B=0 =
Если Im W > 0, то дублет F3(ρ; W ) убывает экспо-
= ρ-Υ+d- + O(ρ-Υ++1), ρ → 0.
ненциально при ρ → ∞ (с точностью до некоторого
полинома).
Заметим, что оба дублета F1 и F2 являются веще-
ственными целыми функциями от W . Их вронски-
ан легко находится, Wr(F1, F2) = -2Υ+g-1. Если
5. CАМОСОПРЯЖЕННЫЕ РАДИАЛЬНЫЕ
Im W > 0, то оба дублета F1(ρ; W ) и F2(ρ; W ) экспо-
ГАМИЛЬТОНИАНЫ
ненциально растут при ρ → ∞. Для вещественных
значений W = E дублеты F1 и F2 могут быть запи-
Поскольку все возможные с.с. парциальные ра-
саны в терминах кулоновских функций [17],
диальные гамильтонианы
ĥ(Z, j, s) ассоциируются с
общим дифференциальным выражением
h(Z, j, s) в
|Γ(α + 1 + iη)|
Fα(η; r) =
(2r)αr e-πη/2-ir ×
(8), их определение сводится к указанию их облас-
Γ(2α + 2)
ти определения Dh(Z,j,s) ⊂ L2(R+). Каждый опе-
× Φ(α + 1 - iη, 2α + 2, 2ir).
ратор
ĥ(Z, j, s) представляет собой с.с. расширение
1075
А. И. Бреев, Д. М. Гитман
ЖЭТФ, том 159, вып. 6, 2021
начального симметрического оператора
ĥin(Z, j, s) в
Δ∗(F) = [F](∞) - [F](0), [F] (∞) = lim [F] (ρ),
ρ→∞
(7), определенного в пространстве C∞0(R+) гладких
дублетов с компактным носителем на полуоси R+.
[F ] (0) = lim [F ] (ρ),
В то же время каждый оператор
ĥ(Z, j, s) есть с.с.
ρ→0
ĥ+
сужение сопряженного оператора
in
(Z, j, s), кото-
[
]
рый действует на так называемой естественной об-
[F ] (ρ) = -iF+(ρ)σy F (ρ) = - f(ρ)g(ρ) - g(ρ)f(ρ)
ласти определения D∗ˇ
(R+) для
h(Z, j, s), состо-
h(Z,j,s)
Из квадратичной интегрируемости дублета
ящей из дублетов F (ρ) ∈ L2(R+), абсолютно непре-
h(Z, j, s)F для F
∈ D∗ˇ
(R+) следует квад-
h(Z,j,s)
рывных в пространстве R+, и таких, что
ратичная интегрируемость производной F′(ρ) на
бесконечности. Отсюда следует, что любой дуб-
h(Z, j, s)F (ρ) ∈ L2(R+),
лет F
∈ D∗ˇ
(R+) убывает на бесконечности,
h(Z,j,s)
Dh
in(Z,j,s) ⊂Dh(Z,j,s)⊆Dh(Z,j,s)(R+).
[F ] (∞) = 0, и форма асимметрии Δ∗ определяется
поведением данных дублетов в нуле:
Поскольку коэффициентные функции диффе-
ренциальной операции
h(Z, j, s) действительны, ин-
Δ∗(F) = - [F] (0) =
дексы дефекта исходного симметрического опера-
(
)
тора
ĥin(Z, j, s) равны, так что с.с. расширения
= lim
f (ρ)g(ρ) - g(ρ)f(ρ)
(16)
ĥ(Z, j, s) существуют для любых значений парамет-
ρ→0
ров Z и j.
Для вычисления формы асимметрии (16) нам
Согласно работам
[10, 12], с.с. расширения
необходимо иметь явный вид дублетов F из обла-
ĥ(Z, j, s) оператора
ĥin(Z, j, s) будем строить как
сти определения D∗ˇ
(R+). В связи с этим заме-
ĥ+
h(Z,j,s)
с.с. сужения сопряженного оператора
in
(Z, j, s),
тим, что данные дублеты можно рассматривать как
которые определяются некоторыми асимптотиче-
квадратично интегрируемые решения неоднородно-
скими с.с. граничными условиями.
го дифференциального уравнения
h(Z, j, s)F (ρ) =
ĥ+
Оценим асимметрию оператора
in
(Z, j, s) в тер-
= G(ρ) с правой частью G, принадлежащей L2(R+).
минах (асимптотических) граничных значений дуб-
Любое решение данного неоднородного дифферен-
летов из его области определения D∗ˇ
(R+). Для
h(Z,j,s)
циального уравнения может быть представлено в
этого введем квадратичную форму асимметрии Δ∗
виде
ĥ+
для оператора
(Z, j, s) соотношением
in
F (ρ) = c1u1(ρ) + c2u2(ρ) + I1(ρ) + I2(ρ),
Δ∗(F) =
(
)
(
)
(
)
c1, c2 = const,
= F,ĥ+inF
-
ĥ+
F, F
= 2i Im F,ĥ+inF
=
in
∫∞
∫
∞
u1(ρ) = d+ρΥ+,
= F+(ρ)
(hF)(ρ) dρ -
(hF)+ (ρ)F(ρ)dρ.
(15)
⎧
⎨
d-ρ-Υ+, g = gc(j),
0
0
u2(ρ) =
⎩ d0(ρ), g = gc(j),
Форма (15) показывает, в какой мере оператор
ĥ+
in
(Z, j, s) отклоняется от симметрического опера-
ĥ+
h(Z, j, s)uk(ρ) = 0,
(17)
тора. Если Δ∗ ≡ 0, то оператор
(Z, j, s) является
in
симметрическим и поэтому с.с. оператором. Тогда
⎛
⎞
ĥin(Z, j, s) является существенно с.с. оператором и
1
d± =⎝
⎠,
его единственным с.с. расширением является сопря-
ĥ+
(κ ± Υ+)/g
женный ему оператор
(Z, j, s). Если Δ∗ = 0, то
in
с.с. оператор
ĥ(Z, j, s) находится как сужение опера-
⎛
⎞
тора
ĥ+
(Z, j, s) на область Dh(Z,j,s) ⊆ D∗ˇ
(R+),
ln ρ - ζ(j, s)g-1c(j)
in
h(Z,j,s)
d0(ρ) =⎝
⎠,
такую, что сужение формы Δ∗ на Dh(Z,j,s) равно
ζ(j, s) ln ρ
нулю, и область Dh(Z,j,s) нельзя расширить с сохра-
нением условия Δ∗ ≡ 0.
ζ(j, s) = sgn(κ) = -s sgn(j),
При помощи интегрирования по частям в правой
части (15) и с учетом (8) легко увидеть, что форма
где I1(ρ) и I2(ρ) — частные решения неоднородного
асимметрии Δ∗ задается выражением
уравнения,
1076
ЖЭТФ, том 159, вып. 6, 2021
Безмассовые электронные возбуждения в графене. . .
⎧
ρ0
∫
⎪
⎪
g
⎪
[u1(ρ) ⊗ u2(ρ′)] G(ρ′)dρ′, Υ = Υ+ ≥ 1/2, ρ0 > 0,
⎪
2Υ+
⎪
ρ
⎪
ρ
⎨
∫
g
I1(ρ) =
-
[u1(ρ) ⊗ u2(ρ′)] G(ρ′)dρ′, Υ = Υ+ < 1/2, Υ = iσ, σ > 0,
⎪
2Υ+
⎪
0
⎪
ρ
⎪
∫
⎪
⎪
gc(j)
[u1(ρ) ⊗ u2(ρ′)] G(ρ′)dρ′, Υ = 0,
⎩
(18)
0
⎧
∫
0
⎪
⎪
g
⎪
[u2(ρ) ⊗ u1(ρ′)] G(ρ′)dρ′, Υ = 0,
⎨
2Υ+
ρ
I2(ρ) =
ρ
⎪
∫
⎪
⎪
-gc(j)
[u2(ρ) ⊗ u1(ρ′)] G(ρ′)dρ′, Υ = 0.
⎩
0
Выражения (17) и (18) позволяют найти асимптоти-
ĥin(Z, j, s) в каждой из четырех областей изменения
ческое поведение дублетов в нуле и вычислить фор-
заряда примеси Z.
му асимметрии (16). Из (17) и (18) следует, что по-
ведение дублетов F в нуле существенным образом
5.1. Несингулярная область
зависит от значений параметров j и Z.
Удобно разбить верхнюю полуплоскость (j, Z)
Вычислим форму асимметрии (16) для несингу-
на так называемую несингулярную и сингуляр-
лярной области Z ≤ Zs(j), Υ+ = γ ≥ 1/2. Для инте-
ную области, в которых проблема нахождения с.с.
гралов (18) справедлива оценка
расширений
ĥin(Z, j, s) имеет принципиально раз-
ные решения. Эти области разделяются симметрич-
I1(ρ) = O(ρ1/2), I2(ρ) = O(ρ1/2), ρ → 0.
(19)
ной сингулярной кривой Z = Zs(j), где Zs (j) =
√
√
=α-1Fϵ
j2 - 1/4, на которой g = gs(j) =
j2 - 1/4
Из (17) следует, что функция u2(ρ) ∼ ργ квадра-
и Υ+ = γ = 1/2. Несингулярная областьопределяет-
тично интегрируема в начале координат, а функция
ся неравенством Z ≤ Zs(j), что эквивалентно нера-
u2(ρ) ∼ ρ-γ не является квадратично интегрируе-
венству Υ+ = γ ≥ 1/2. Сингулярная область опре-
мой. Дублеты F ∈ D∗ˇ
(R+) определяются вы-
h(Z,j,s)
деляется неравенством Z > Zs(j), что равносильно
ражением (17) c c2 = 0 и ведут себя как O(ρ1/2) при
соотношению 0 ≤ Υ+ = γ < 1/2 или Υ+ = iσ, σ > 0.
ρ → 0. Тогда форма асимметрии равна нулю во всей
Так как сингулярная кривая является верхней гра-
области D∗ˇ
(R+).
h(Z,j,s)
ницей несингулярной области, значение Zs(j) будем
Отсюда следует, что в несингулярной области
называть максимальным несингулярным значением
каждый парциальный радиальный гамильтониан
Z для данного j.
определяется единственным образом,
ĥ1(Z, j, s) =
Мы делим сингулярную область на три под-
= ĥ+in(Z, j, s). Здесь нижний индекс «1» использует-
множества: субкритическую, критическую и сверх-
ся как символ несингулярной области (нижние ин-
критическую. Субкритическая область определяет-
дексы «2», «3», «4» вместе с другими соответствую-
ся неравенствами Zs(j) < Z < Zc(j), что эквива-
щими индексами будут относиться к определенным
лентно 0 < Υ+ = γ < 1/2, где Zc(j) = α-1Fϵ |j|.
подобластям сингулярной области).
Значение Zc(j) будем называть критическим значе-
Другими словами, начальный симметрический
нием Z для данного j. Критическая область пред-
оператор
ĥin(Z, j, s) является существенно с.с. опе-
ставляет собой критическую кривую Z = Zc(j), что
ратором, так как его индексы дефекта равны (0, 0),
равносильно g = gc(j) = |j| или Υ+ = γ = 0.
а область определения оператора
ĥ1(Z, j, s) являет-
Сверхкритическая область определяется неравенст-
ся естественной областью определения для
h(Z, j, s),
вом Z > Zc(j) = α-1ϵ |j|, которое эквивалентно то-
√
Dh1(Z,j,s) = Dˇh(Z,j,s)(R+).
му, что Υ+ = iσ, где σ =
g2 - j2 > 0.
Проведем спектральный анализ с.с. оператора
Далее, будем строить с.с. радиальные гамиль-
ĥ1(Z, j, s). Построим функцию Грина данного опе-
тонианы
ĥ(Z, j, s) как с.с. расширения оператора
ратора:
1077
А. И. Бреев, Д. М. Гитман
ЖЭТФ, том 159, вып. 6, 2021
G(ρ, ρ′; W ) =
Тогда для ℓ - 1 < 2γ < ℓ + 1 имеем
{
F3(ρ; W) ⊗ F1(ρ′; W), ρ > ρ′,
= ω-1(W)
G(c - 0, c + 0, E + i0) =
F1(ρ; W) ⊗ F3(ρ′; W), ρ < ρ′.
= Aℓ(E + i0)F1(c; E) ⊗ F1(c; E)+
В качестве дублета, определяющего направляю-
g
+
F1(c; E) ⊗ Uℓ(c; E).
щий функционал, выберем вещественно-целый дуб-
2γ
лет U1(ρ; W ) = F1(ρ; W ). Так же как и в массивном
случае, можно показать, что данный направляющий
В силу действительности дублетов F1(c; E) и
функционал является простым (см. [12]). Производ-
Uℓ(c; E) производная спектральная функция пред-
ная σ′(E) спектральной функции связана с функци-
ставима следующим образом:
ей Грина и простым направляющим функционалом
U1(ρ; W) соотношением
σ′1(E) = π-1 ImAℓ(E + i0).
U1(c; E)⊗U1(c; E)σ′(E) = π-1 ImG(c-0, c+0; E+i0),
Заметим, что функция Aℓ(E + i0) непрерывна по γ
в точке γ = ℓ/2. Поэтому мы можем положить
где c — произвольная точка в интервале (0; ∞).
Случай полуцелых значений параметра γ = ℓ/2,
σ′1(E)|γ=ℓ/2 = lim
σ′1(E)|γ=ℓ/2 ,
ℓ
∈ N, требует дополнительного исследования,
γ→ℓ/2
так как дублет F2(ρ; W ) имеет сингулярность вида
σ′1(E)|γ=ℓ/2 = π-1Γ(-2γ)Imω-1(E + i0).
Γ(-2γ) в точке γ = ℓ/2,
В тех точках, в которых ω(E + i0) отлична от нуля,
F2(ρ; W)
lim
= -aℓ(W) F1(ρ; W)|γ=ℓ/2 ,
спектральная функция имеет вид
γ→ℓ/2
Γ(-2γ)
[
]-1
aℓ(W) = 2γ g ω(W)|γ=ℓ/2
,
σ′1(E) = π-1Γ(-2γ)Imω-1(E) =
[
]2
γ
|2E|
где функция aℓ(W ) представляет собой полином по
=
×
|Γ(ig - γ)| Γ(2γ + 1)
W с вещественными коэффициентами:
sgn(E)πg
π(κ - γ)e
(
)
×
> 0.
2ℓπγ
ℓ
κ (ch (2πg) - cos (2πγ))
aℓ(W) =
2-
×
g ℓ!
κ
πg
Так как функция ω(E) отлична от нуля для всех E,
e-πg - (-1)ℓe
×
Wℓ.
непрерывна на (-∞, 0) ∪ (0; ∞) и принимает ком-
[(-1)ℓ - ch(2πg)] |Γ (ig - ℓ/2)|2
плексные значения, то значения E ∈ (-∞, ∞) яв-
В окрестности ℓ-1 < 2γ < ℓ+1, ℓ ∈ N, точки γ = ℓ/2
ляются точками непрерывного спектра оператора
дублет F2(ρ; W ) может быть представлен в виде
ĥ1(Z, j, s). В данных точках спектра функция σ′1(E)
положительна, σ′1(E) = Q21(E) > 0, где Q1(E) =
√
F2(ρ; W) = -aℓ(W)Γ(-2γ)F1(ρ; W)+Uℓ(ρ; W), (20)
=
σ′1(E) — нормировочный множитель для со-
ответствующей (обобщенной) собственной функции
где дублет Uℓ(ρ; W ) является вещественно-целым,
U1(ρ; E) непрерывного спектра.
имеет конечный предел при γ → ℓ/2 и удовлетво-
Таким образом, спектр каждого парциального
ряет радиальным уравнениям (11). Из (20) следует,
радиального гамильтонианаĥ1(Z, j, s) в несингуляр-
что
ной области является простым (невырожденным) и
Uℓ(ρ; W) = d-ρ-γ + O(ρ1-γ)
состоит только из непрерывного спектра,
при ρ → 0.
Так как дублеты F1(ρ; W ) и Uℓ(ρ; W ) линейно
spec
ĥ1 (Z, j, s) = (-∞, ∞).
независимы, Wr(F1, Uℓ) = -2γ/g = 0, то в окрестно-
сти ℓ - 1 < 2γ < ℓ + 1 точки γ = ℓ/2 дублет F3(ρ; W)
Ортонормированные (обобщенные) собственные
допускает разложение:
функции U1E(ρ), |E| ≥ 0 непрерывного спектра, от-
[
]
вечающие парциальным радиальным гамильтониа-
g
F3(ρ; W) = ω(W) Aℓ(W)F1(ρ; W) +
Uℓ(ρ; W) ,
нам
ĥ1(Z, j, s), образуют полную ортонормирован-
2γ
[
]
ную систему в пространстве L2(R+) в смысле фор-
Aℓ(W) = Γ(-2γ) ω-1(W) - ω-1(W)
мул обращения (см. [12]) и имеют вид
γ=ℓ/2
1078
ЖЭТФ, том 159, вып. 6, 2021
Безмассовые электронные возбуждения в графене. . .
√
щего простой направляющий функционал, выберем
U1E(ρ) = Q1(E)F1(ρ; E), Q1(E) = σ′1(E) =
вещественно-целый дублет
sgn(E)πg/2
|2E|γ e
=
×
|Γ(ig - γ)| Γ(2γ + 1)
U2,ν(ρ; W) = F1(ρ; W)cosν + F2(ρ; W)sinν.
√
π(κ - γ)
×
(21)
Построим соответствующую функцию Грина:
κ [ch (2πg) - cos (2πγ)]
G(ρ, ρ′; W ) =
{
5.2. Субкритическая область
F3(ρ; W) ⊗ U2,ν(ρ′; W), ρ > ρ′,
= ω-11(W)
В субкритической области изменения заряда,
U2,ν(ρ; W) ⊗ F3(ρ′; W), ρ < ρ′,
Zs(j) < Z < Zc(j), выполняется соотношение 0 <
< Υ+ = γ < 1/2. Здесь для интегралов (18) оста-
ется справедливой оценка (19). Так как функции
ω1(W) = -Wr(F1, F3) =
u1(ρ) ∼ ργ и u2(ρ) ∼ ρ-γ квадратично интегрируе-
= ω(W)cosν + g-1Γ(1 - 2γ)sinν,
мы в начале координат для γ < 1/2, то для дублетов
F ∈D∗ˇ
(R+) имеем
а дублет F3(ρ; W ) запишем в форме
h(Z,j,s)
[
]
F (ρ) = c1ργ + c2ρ-γ + O(ρ1/2), ρ → 0.
(22)
g
F3(ρ; W) =
ω1U2,ν(ρ; W) + ω1 Ũ2,ν(ρ; W) ,
2γ
Отсюда следует, что форма асимметрии является
Ũ2,ν(ρ; W) = -F1(ρ; W)sinν + F2(ρ; W)cosν,
нетривиальной антиэрмитовой квадратичной фор-
ω1(W) = ω(W)sinν - g-1Γ(1 - 2γ)cosν.
мой по коэффициентам асимптотики (22):
2γ
Δ∗(F) =
(c2c1 - c1c2) .
Тогда
g
G(c - 0, c + 0, E + i0) =
Это означает, что индексы дефекта оператора
ĥin(Z, j, s) равны (1, 1) и существует семейство с.с.
= ω-12,ν(E + i0)U2,ν(c;E) ⊗ U2,ν(c;E)+
расширений
ĥ2,ν(Z, j, s) данного оператора, кото-
g
+
U2,ν(c; E) ⊗
Ũ2,ν(c; E),
рые параметризуются параметром ν ∈ [-π/2, π/2],
2γ
-π/2 ∼ π/2, и характеризуются с.с. граничными
условиями в начале координат,
2γω1(W)
F (ρ) = c[ργ d+ cos ν + ρ-γ d- sin ν] + O(ρ1/2),
ω2(W) =
=
(23)
g ω1(W)
ρ → 0,
2γ ω(W)cosν + g-1Γ(1 - 2γ)sinν
=
где c — произвольное комплексное число. Таким об-
g ω(W)sinν - g-1Γ(1 - 2γ)cosν
разом, область определения Dh2,ν (Z,j,s) гамильтони-
Дублеты U2,ν(ρ; E) и
Ũ2,ν(ρ; E) действительны и
ана
ĥ2,ν(Z, j, s) имеет вид
производная σ′2,ν (E) спектральной функции имеет
{
вид
Dh2,ν (Z,j,s) = F(ρ) : F(ρ) ∈ Dˇh(Z,j,s) (R+),
1
1
}
σ′2,ν(E) =
Im
π
ω2,ν(E + i0)
F удовлетворяет (23)
Функция ω2(E) непрерывна, отлична от нуля и
Обратимся к спектральному анализу с.с. опера-
ω2,ν(E + i0) = ω2,ν(E). Тогда для производной спек-
торов
ĥ2,ν(Z, j, s). В качестве дублета, определяю-
тральной функции имеем выражение
A(E) [ctg(πg) + δ sh(πg)] sin(2πγ)
σ′2,ν(E) =
,
[ch(2πg) - cos(2πγ)] cos ν + A2(E)(πγ/g)2(1 - cos(2ν)) + BδA(E) ch(2ν)
κ-γ
A(E) =
|Γ(ig - γ)|2 Γ(1-2γ)
|2E|2γ , δ = sgn(E),
2γκ
Γ(1 + 2γ)
4πγ
[
]
Bδ =
cos2(πγ)sh(πg) - δ sin2(πγ)ch(πg)
g
1079
А. И. Бреев, Д. М. Гитман
ЖЭТФ, том 159, вып. 6, 2021
Функция σ′2,ν (E) непрерывна и, следовательно,
Таким образом, область определения Dh
3,ν (Z,j,s) га-
спектр оператора
ĥ2,ν(Z, j, s) является непрерыв-
мильтониана
ĥ3,ν(Z, j, s) имеет вид
ным и простым,
{
Dh
F (ρ) : F (ρ) ∈ D∗ˇ
(R+) ,
3,ν (Z,j,s) =
h(Z,j,s)
spec
ĥ2,ν (Z, j, s) = (-∞, ∞).
}
F удовлетворяет (25)
В итоге нормированные (обобщенные) собственные
Отметим, что в случае Υ+ = γ = 0 дублеты F1
функции U2,ν(ρ), соответствующие непрерывному
и F2 совпадают. Поэтому в качестве двух линейно
спектру и дающиеся выражениями
независимых решений радиальных уравнений (11)
U2,ν,E(ρ) = Q2,ν(E)U2,ν(ρ; E) =
при γ = 0 выберем два линейно независимых ве-
(0)
щественно-целых решения F1
(ρ; W ), F(0)2(ρ; W ) и
= Q2,ν(E)[F1(ρ;E)cosν + F2(ρ;E)sinν],
(24)
√
. А именно:
их линейную комбинацию F(0)3
Q2,ν(E) = σ′2,ν(E),
F(0)1(ρ; W) = F1(ρ; W)|γ=0 = d+ + O(ρ), ρ → 0,
образуют полную ортонормированную систему в
ζ(j, s)
пространстве L2(R+) в смысле формул обращения.
F(0)2(ρ; W) = ∂γF1(ρ; W)|γ=0 -
F(0)1(ρ; W) =
gc(j)
(ρ) + O(ρ ln ρ), ρ → 0.
=d0
5.3. Критическая область
Соответствующий вронскиан имеет вид
Критическая область определяется критической
кривой Z = Zc(j), на которой g = gc(j) и Υ+ =
Wr(F(0)1, F(0)2) = g-1c(j).
= γ = 0. Отметим, что в данной области физические
В качестве аналога дублета F3(ρ; W ) при γ = 0 возь-
значения пар j (полуцелое число) и Z (целое чис-
мем дублет
ло) лежат на критической кривой для очень специ-
альных значений «постоянной тонкой структуры»
F(0)3(ρ; W) = - lim
F3(ρ; W) =
в графене, αF /ϵ, αF /ϵ = |j|/Z. В частности, если
γ→0
αF /ϵ — иррациональное число, никакая физическая
= F(0)2(ρ; W) + f(W)F(0)1(ρ; W),
пара (j, Z) не лежит на критической кривой.
В этой области асимптотическое поведение дуб-
где
летов F
∈ D∗ˇ
(R+) дается формулами (17) с
f (W ) = gc(j)ω(0)(W ),
h(Z,j,s)
учетом того, что
(0)
ω(0)(W) = -Wr(F2
,F(0)3) =
I1(ρ) = O(ρ1/2 ln ρ), I2(ρ) = O(ρ1/2 ln ρ),
[
(
)
= g-1c(j) ln 2e-iπ/2W
+
при γ = 0, ρ → 0:
]
ζ(j, s) + i
F (ρ) = c1d+ + c2d0(ρ) + O(ρ1/2 ln ρ), ρ → 0.
+
+ ψ(-igc(j)) - 2ψ(1) ,
2gc(j)
Отсюда для формы асимметрии получаем
Γ′(x)
ψ(x) =
Γ(x)
Δ∗(F) = g-1c(j)(c1c2 - c2c1).
Спектральный анализ операторов
ĥ3,ν(Z, j, s)
Следовательно, в этой области также имеется
проводится аналогично случаю субкритической об-
однопараметрическое семейство с.с. расширений
ласти и мы представим здесь только его окончатель-
ĥ3,ν(Z, j, s), ν ∈ [-π/2, π/2], -π/2 ∼ π/2, которые
ные результаты. В качестве дублета, определяющего
задаются асимптотическими с.с. граничными усло-
простой направляющий функционал, выберем вели-
виями
чину
(0)
U3,ν(W) = F1
(ρ, W ) sin ν + F(0)2(ρ, W ) cos ν,
F (ρ) = c[d0(ρ) cos ν + d+ sin ν] +
+ O(ρ1/2 ln ρ), ρ → 0,
(25)
которая является вещественно-целой по W и удовле-
творяет c.с. асимптотическим граничным условиям
где постоянный дублет d+
= d+|γ=0 = (1,ζ)T и
(25). Функция Грина оператора
ĥ3,ν(Z, j, s) дается
дублет d0(ρ), зависящий от ρ, определяется в (17).
выражением
1080
ЖЭТФ, том 159, вып. 6, 2021
Безмассовые электронные возбуждения в графене. . .
G(ρ, ρ′; W ) =
5.4. Сверхкритическая область
{
(0)
F3
(ρ; W ) ⊗ U3,ν (ρ′; W ), ρ > ρ′,
Сверхкритическая область определяется услови-
= ω-13(W)
√
U3,ν(ρ; W) ⊗ F(0)3(ρ′; W), ρ < ρ′,
ями Z > Zc(j) и Υ+ = iσ, где σ =
g2 - j2 > 0. В
этой области асимптотическое поведение дублетов
(
)
F ∈ D∗ˇ
(R+) определяется выражением (17),
ω3(W) = -Wr U3,ν, F(0)
=
h(Z,j,s)
3
где I1(ρ) = O(ρ1/2), I2(ρ) = O(ρ1/2), при ρ → 0:
= g-1c(j)[f(W)cosν - sinν] .
F (ρ) = c1ρiσd+ + c2ρ-iσd- + O(ρ1/2), ρ → 0.
Тогда
G(c - 0, c + 0, E + i0) =
Для формы асимметрии получаем
= ω-13,ν(E + i0)U3,ν(c; E) ⊗ U3,ν(c; E)+
(
)
+ gc(j)U3,ν(c; E) ⊗
Ũ3,ν(c; E),
Δ∗(F ) = 2iσg-1
|c1|2 - |c2|2
f (W ) cos ν - sin ν
ω3,ν(W) = g-1c(j)
,
В этой области мы снова имеем однопараметри-
f (W ) sin ν + cos ν
ческое семейство с.с. расширений
ĥ4ν(Z, j, s), ν ∈
Ũ3,ν(ρ; W) = F(0)1(ρ, W)cosν - F(0)2(ρ, W)sinν.
∈ [-π/2, π/2], -π/2 ∼ π/2, которые задаются асимп-
Производная σ′3,ν (E) этой спектральной функции
тотическими с.с. граничными условиями:
имеет вид
F (ρ) = c[ieiν ρiσd+ - ie-iν ρ-iσd-] + O(ρ1/2),
1
1
σ′3,ν(E) =
Im
(27)
π
ω3,ν(E + i0)
ρ → 0.
Базисная функция ω3,ν (E) отлична от нуля для всех
Отсюда следует, что область определения Dh4,ν(Z,j,s)
E, непрерывна и принимает комплексные значения.
гамильтониана
ĥ4,ν(Z, j, s) имеет вид
Следовательно,
{
1
1
σ′3,ν(E) =
Im
=
Dh4,ν(Z,j,s) = F(ρ) : F(ρ) ∈ Dˇh(Z,j,s) (R+)
π
ω3,ν(E)
}
gc(j)Bδ/π
и F удовлетворяет(27)
=-
,
(A2ζ + В2δ) cos2 ν - Aζ sin(2ν) + sin2 ν
Спектральный анализ операторов
ĥ4,ν(Z, j, s)
Aζ = Re f(W) = -2ψ(1) + ζ(j, s)g-1c(j)/2 +
проводится аналогично предыдущим случаям, пред-
+ ln |2E| + Re ψ (-igc(j)) ,
ставляем здесь только окончательные результаты. В
качестве дублета, определяющего простой направ-
(
ляющий функционал, выберем
)δ
Bδ = Imf(W) =
g-1c(j) - π
+
2
U4,ν(ρ; W) = ieiνF1(ρ, W)sinν - ie-iνF2(ρ, W),
+ Im ψ (-igc(j)) , δ = sgn(E).
Простой спектр гамильтониана
ĥ3,ν(Z, j, s) дает-
который является вещественно-целым по W и удо-
ся выражением
влетворяет c.с. асимптотическим граничным усло-
виям (27). Функция Грина оператора
ĥ4,ν(Z, j, s)
spec
ĥ3,ν (Z, j, s) = (-∞, ∞).
определяется выражением
Нормированные (обобщенные) собственные функ-
ции U3,ν (ρ), отвечающие непрерывному спектру,
G(ρ, ρ′; W ) =
имеют вид
{
F3(ρ; W) ⊗ U4,ν(ρ′; W), ρ > ρ′,
U3,ν,E(ρ) = Q3,ν(E)U3,ν(ρ; E) =
= ω-14(W)
[
]
U4,ν(ρ; W) ⊗ F3(ρ′; W), ρ < ρ′,
= Q3,ν(E) F(0)1(ρ;E)cosν + F(0)2(ρ;E)sinν ,
(26)
√
Q3,ν(E) = σ′3,ν(E),
ω4(W) = -Wr(U4,ν, F3) =
и образуют полную ортонормированную систему в
[
]
Γ(1 - 2iσ)
gω(W)
пространстве L2(R+) в смысле формул обращения.
= -ie-iν
1-
e2iν ,
g
Γ(1 - 2iσ)
1081
6
ЖЭТФ, вып. 6
А. И. Бреев, Д. М. Гитман
ЖЭТФ, том 159, вып. 6, 2021
из которого следует
Было показано, что в сингулярной области из-
менения заряда примеси с.с. парциальные радиаль-
G(c - 0, c + 0, E + i0) =
ные гамильтонианы
ĥ(Z, j, s) как с.с. расширения
= ω-14,ν(E + i0)U4,ν(c;E) ⊗ U4,ν(c;E)-
начальных симметрических операторов
ĥin(Z, j, s)
g
не определены однозначно для каждой тройки па-
-
U4,ν(c; E) ⊗
Ũ4,ν(c; E),
раметров Z, j и s. Поскольку индексы дефекта m+,
4σ
m- каждого симметрического оператора
ĥin(Z, j, s)
1 - e2iνgω(W)/Γ(1 - 2iσ)
ω4,ν(W) = -4iσg-1
,
равны (1, 1) и, следовательно, существует однопа-
1 + e2iνgω(W)/Γ(1 - 2iσ)
раметрическое семейство расширений, такое семей-
Ũ4,ν(ρ; W) = eiνF1(ρ, W) + e-iνF2(ρ, W).
ство параметризуется параметром ν ∈ [-π/2, π/2],
-π/2 ∼ π/2. Парциальные радиальные гамильто-
Производная σ′4,ν (E) спектральной функции имеет
нианы с одинаковыми значениями Z, j и s, но с
вид
разными значениями ν, ассоциированы с одним и
1
1
σ′4,ν(E) =
Im
тем же дифференциальным выражением
h(Z, j, s),
π
ω4,ν(E + i0)
но различаются своими областями определения, ко-
Базисная функция ω4,ν (E) отлична от нуля, непре-
торые являются подмножествами естественной об-
рывна и принимает комплексные значения. Тогда
ласти определения D∗ˇ
(R+) для
h(Z, j, s) и за-
h(Z,j,s)
1
1
δ
A-
даются некоторыми асимптотическими граничными
σ′4,ν(E) =
Im
=-
,
условиями в начале координат, содержащими явно
π
ω4,ν(E)
4σ A+ + Bs(ν; E)
2
параметр ν.
πg
[
]
A± =
sh-1(πσ) - ch-1(πσ)
×
Как и в массивном случае [10] и трехмерной ку-
4σj
{
}
лоновской задаче [12], сингулярная область делит-
×
e2πσ sh-1(π [g - δσ]) ± sh-1(π [g + δσ])
,
ся на три подмножества, которые отличаются ха-
Bs(ν; E) = 2 Re{(j + isσ)Γ (-i(g - σ)) Γ (i(g + σ)) ×
рактером асимптотических с.с. граничных условий
}
× Γ2(-2iσ)exp(2iσ ln |2E| - 2iν)
,
в начале координат. Во всех трех подобластях син-
гулярной области для каждого оператора
ĥk,ν суще-
δ = sgn(E).
ствует простой направляющий функционал. Отсю-
Спектр гамильтониана
ĥ4,ν(Z, j, s) является про-
да следует, что спектр оператора
ĥk,ν является про-
стым (невырожденным в физической терминоло-
стым и задается выражением
гии). В таком случае основным инструментом спек-
spec
ĥ4,ν (Z, j, s) = (-∞, ∞).
трального анализа является спектральная функция
σk,ν (E) и ее (обобщенная) производная σk,ν (E), где
Нормированные (обобщенные) собственные функ-
E, E ∈ R, — вещественная переменная.
ции U4,ν (ρ), отвечающие непрерывному спектру,
Формула (9) позволяет нам восстановить все с.с.
имеют вид
операторы
Ĥs, ассоциированные с дифференциаль-
U4,ν(ρ) = Q4,ν(E)U4,ν(ρ; E) =
ным выражением (3) для любого значения парамет-
[
]
ра g, а также описать решение соответствующих
= iQ4,ν(E)
eiνF1(ρ, W) - e-iνF2(ρ, W)
,
(28)
√
спектральных задач для всех гамильтонианов
Ĥs.
Q4,ν(E) = σ′4,ν(E).
Введем согласно работе [10] множества значений
заряда, для которых спектральная задача описыва-
Они образуют полную ортонормированную систему
ется похожим образом. Эти множества определяют-
в пространстве L2(R+) в смысле формул обращения.
ся при помощи функций gc(k) и gs(k), принимающих
значения в характеристических точках k = l + 1/2,
l∈Z+,
6. CАМОСОПРЯЖЕННЫЕ ПОЛНЫЕ
√
ГАМИЛЬТОНИАНЫ
1
gc(k) = k, gs(k + 1) = (k + 1)2 -
В разд. 5.1-5.4 мы построили все с.с. парциаль-
4
ные радиальные гамильтонианы
ĥ(Z, j, s) для всех
и удовлетворяющих следующим неравенствам:
значений заряда Z как с.с. расширения исходных
симметрических операторов
ĥin(Z, j, s) для любых
gc(k) < gs(k + 1) < gc(k + 1) < gs(k + 2).
(29)
значений j и s и исследовали спектральные задачи
для этих гамильтонианов.
Введем интервалы Δ(k):
1082
ЖЭТФ, том 159, вып. 6, 2021
Безмассовые электронные возбуждения в графене. . .
Δ(0) = (0; 1/2) ,
Δ2(k) = (gs(k + 1), gc(k + 1)),
Δ(k) = (gc(k), gc(k + 1)] = (k, k + 1],
Δ3(k) = {gc(k + 1)}.
)
{
(
)}
1
(⋃
(0, ∞) = Δ(0) ∪ gc
±
∪ Δ(k)
В соответствии с этим разложением, определим три
⋃
2
k
множества Gi =k Δi(k), i = 1, 2, 3, изменения па-
раметров связи g, таких что любому значению g >
Как следует из (29), каждый интервал Δ(k) пред-
> gc(±1/2) = 1/2 можно сопоставить пару двух це-
ставим в виде Δ(k) = ∪i=1,2,3Δi(k), где
лых чисел, k и i = 1, 2, 3: g =⇒ (k, i), такую что
g ∈ Gi. Тогда, как следует из результатов разд. 5.1,
Δ1(k) = (gc(k), gs(k + 1)],
5.2, получим следующую классификацию:
{
U4,ν,E(ρ),
|j| ≤ k,
UE(ρ) =
g ∈ Δ1(k),
U1E(ρ),
|j| ≥ k + 1,
⎧
⎨U4,ν,E(ρ),
|j| ≤ k,
UE(ρ) =
U2,ν,E(ρ),
|j| = k + 1, g ∈ Δ2(k),
⎩
U1E(ρ),
|j| > k + 1,
⎧
⎨U4,ν,E(ρ),
|j| ≤ k,
(30)
UE(ρ) =
U3,ν,E(ρ),
|j| = k + 1, g ∈ Δ3(k),
⎩
U1E(ρ),
|j| > k + 1,
{
U2,ν,E(ρ),
|j| = 1/2,
UE(ρ) =
g ∈ Δ(0),
U1E(ρ),
|j| > 1/2,
{
U3,ν,E(ρ),
|j| = 1/2,
UE(ρ) =
g = gc(±1/2).
U1E(ρ),
|j| > 1/2,
Теперь мы можем описать спектральную про-
7. ЛОКАЛЬНАЯ ПЛОТНОСТЬ СОСТОЯНИЙ
блему для всех с.с. дираковских гамильтонианов
Локальная плотность состояний на единицу по-
для всех значений g. Отметим, что из неравенства
верхности в графене определяется выражением
g > gs(±1/2) = 0 и (9) следует важный факт: пол-
ный с.с. дираковский гамильтониан
Ĥs не определен
∑
N (ρ; E) =
|Ψ(ρ; E′)|2 δ(E - E′) =
однозначно для каждого заряда Z = (ϵg)/αF .
E′
Рассмотрим собственные векторы Ψsj (r) для с.с.
∑
(31)
дираковского гамильтониана
Ĥs, которые удовле-
=
nj(ρ; E),
j=-∞
творяют следующей системе уравнений (см. разд. 3):
nj(ρ; E) = |Ψsj(ρ; E)|2 ,
HsΨsj(r) = E Ψsj(r),
JsΨsj(r) = j Ψsj(r),
см. [8]. Величина N(ρ; E)dE имеет смысл вероятнос-
ти нахождения квазичастицы на элементарной по-
верхности графена в данной точке (φ, ρ) в диапазоне
и имеют вид Ψsj (r) = Vsj UE (ρ), см. (6).
энергий от E до E + dE. Отметим, что существует
Для любых констант связи g энергетический
другое определение локальной плотности состояний
Ĥs
в графене, основанное на вычислении мнимой части
спектр любого с.с. дираковского гамильтониана
функции Грина [18]. Подставляя (5) в (31), получим
состоит из непрерывного спектра, занимающего ось
(-∞, ∞). Все дублеты UE (ρ) зависят от парамет-
1
ров расширения, от квантовых чисел j, параметра
nj(ρ; E) =
|UE (ρ)|2 ,
2πr
s и константы связи g согласно (30). Отметим, что
параметры расширения зависят как от квантовых
где дублеты UE (ρ) для различных значений заряда
чисел j, так и от параметра s.
g и углового момента j определяются выражением
1083
6*
А. И. Бреев, Д. М. Гитман
ЖЭТФ, том 159, вып. 6, 2021
(30). Из равенства
h(Z, j, s) =
h(Z, -j, -s) следует
ческой и субкритической областями изменения за-
nj(ρ; E)|s=+1 = n-j(ρ;E)|s=-1. Отсюда очевидно,
ряда:
что сумма nj (ρ; E) + n-j (ρ; E) не зависит от выбо-
∑
ра параметра s = ±1. Таким образом, имеет место
N (ρ; E) = N0(ρ, ν1; E) =
n1j(ρ; E)+
сохранение симметрии между выбором двух подре-
|j|>1/2
шеток в графене в поведении локальной плотности
состояний (31).
(ρ; E),
(32)
−1/2
1/2
Рассмотрим сначала случай малых значений па-
раметра связи g ∈ Δ(0). В этом случае локальная
где парциальная локальная плотность состояний
плотность состояний определяется только некрити-
n1j(ρ; E) отвечает некритической области,
πgδ
1
(2ρ |E|)2γ |Φγ (ρ)|2 e
n1j(ρ; E) =
|U1E (ρ)|2 = |F1(ρ; E)|2 σ′1(E) =
,
2πρ
ρΓ2 (1 + 2γ) |Γ(ig - γ)|2 [ch(2πg) - cos(2πγ)]
(33)
Φγ(ρ) = Φ(γ - ig, 1 + 2γ, -2iEρ),
ĥ2,ν
(Z, j, s) субкритической области, который па-
а n2,ν1j (ρ; E) соответствует парциальному гамильтониану
1
раметризуется параметром с.с. расширения ν1,
1
1
ϱγ(ρ)cos2 ν1 + ϱ-γ(ρ)sin2 ν1 + Re(ϱ(ρ))sin(2ν1)/g
n2,ν1j(ρ; E) =
|U2ν1,E (ρ)|2
,
2πρ
2π2ρ ϱγ(∞)cos2 ν1 + ϱ-γ(∞)sin2 ν1 + Re(ϱ(∞))sin(2ν1)/g
2
|Φγ (ρ)|
g - iγ
ϱγ(ρ) =
ρ2γ, ϱ(ρ) =
Φγ(ρ)Φ∗-γ(ρ),
j + sγ
j
(34)
-2γ
Γ2(1 + 2γ)e-δπg |2E|
ϱγ(∞) = lim
ϱγ(ρ) =
,
ρ→∞
(j + sγ)Γ(1 - ig + γ)Γ(1 + ig + γ)
2γ sh(π [g - iγ])
ϱ(∞) = lim
ϱ(ρ) =
e-δπ(g+iγ).
ρ→∞
j
sin(2πγ)
В пределе g → 0 величина n1j(ρ; E) выражается че-
и плотность состояний определяется только некри-
рез функции Бесселя:
тической областью,
[
] |E|
lim
n1j(ρ; E) =
J|j|-1/2(Eρ) + J|j|+1/2(Eρ)
,
∑
g→0
4π
N0(ρ, 0; E) =
n1j(ρ; E).
j
а суммирование по j, без учета вклада n2,ν1j(ρ; E)
от субкритической области, приводит к выражению
Если параметр ν1 не равен нулю, то даже для малых
для свободной плотности состояний квазичастиц в
зарядов примеси вклад слагаемых
графене:
∑
|E|
lim
n1j(ρ; E) =
(35)
g→0
2π
(ρ; E)
j=-∞
−1/2
1/2
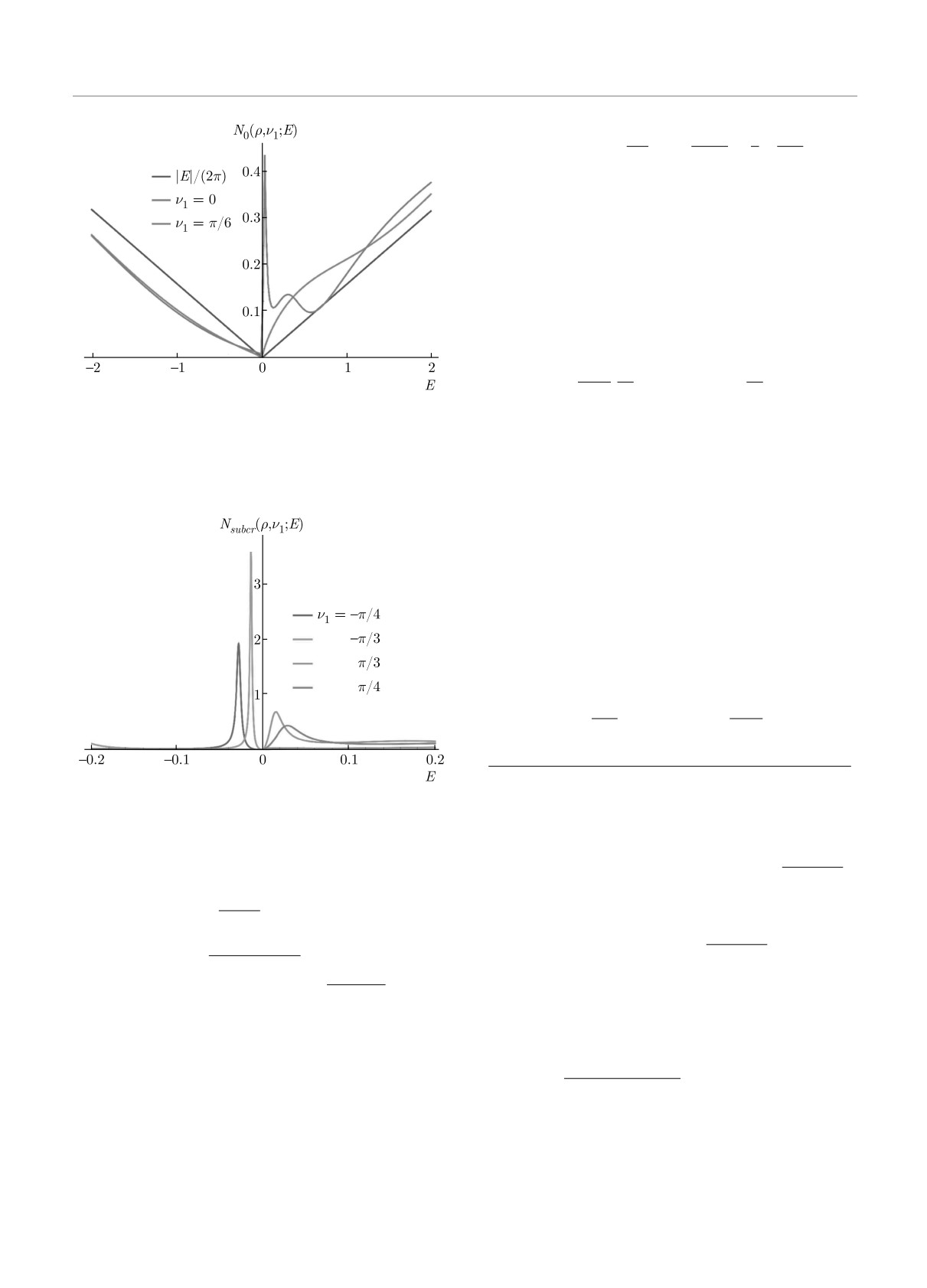
На рис. 1 показаны зависимости плотности состоя-
ний N0(ρ, ν1; E) от энергии квазичастицы для ρ = 1,
в локальную плотность состояний N0(ρ, ν1; E) при-
g = 0.3. Для малых энергий, E → 0, имеем
водит к появлению локальных максимумов (см.
рис. 1, 2). На рис. 2 изображены зависимости вели-
πgδ
(2ρ |E|)2γ e
n1j(ρ; E) ∼
Γ-2 (1+2γ)|Γ(ig-γ)|-2 =
чины Nsubcr(ρ, ν1, E) от энергии для различных зна-
ρ
чений параметра ν1 для ρ = 1, g = 0.3. Мы видим,
= [ch(2πg) - cos(2πγ)]-1 .
что функция Nsubcr(ρ, ν1, E) имеет выраженный ло-
кальный максимум при различных значениях пара-
Заметим, что если параметр c.с. расширения ν1
метра ν1, отличных от нуля.
равен нулю, то вклад от субкритической области
совпадает с вкладом от некритической области,
В окрестности точки E
= 0 величина имеет
асимптотику Nsubcr(ρ, ν1, E),
= n1j(ρ; E)
n2,ν1j(ρ; E)
ν1=0
1084
ЖЭТФ, том 159, вып. 6, 2021
Безмассовые электронные возбуждения в графене. . .
[
)2]
|E|
2 tg ν
1
( tg ν
Nsubcr(ρ, ν1, E) ∼
1+
+
,
2π
ρ
2
gρ
E → 0, g → 0.
Тем не менее для любых значений параметра ν1 ве-
личина Nsubcr(ρ, ν1, E) при E → 0 с точностью до
множителя ведет себя как |E|2γ , что согласуется с
результатом работы [8]. Используя представление
(14), выражение для n1j(ρ; E) можно представить че-
рез кулоновские функции (что также согласуется с
результатами работы [8]):
(
)
1
j2
2g
n1j(ρ; E) =
F2γ-1 + F2γ +
Fγ-1Fγ
,
2π2ρ
γ2
|j|
Рис. 1. (В цвете онлайн) Зависимости локальной плотнос-
Fα = Fα(-g; |E| ρ).
ти состояний N0(ρ, ν1; E) для ρ = 1, g = 0.3 и ν1 = 0, π/6.
Синяя линия описывает локальную плотность состояний в
Для параметров связи g = gc(±1/2) имеем вклад
отсутствие поля
в локальную плотность состояний от критической
области:
∑
N (ρ; E) = N1(ρ, ν2; E) =
n1j(ρ; E)+
|j|>1/2
(ρ; E),
(36)
−1/2
1/2
где n3,ν2j (ρ; E) соответствует парциальному гамиль-
тониану
ĥ3,ν
(Z, j, s) в критической области, ко-
2
торый параметризуется параметром с.с. расшире-
ния ν2,
1
1
|U3,ν2,E (ρ)|2 =
×
n3,ν2j(ρ; E) =
2πρ
2π2ρ
ϱ(0)1(ρ)sin2 ν2+ϱ(0)2(ρ)cos2 ν2+Re ϱ(0)3(ρ)sin(2ν2)
×
,
ϱ(0)(∞) sin2 ν2+ϱ(0)2(∞) cos2 ν2+ Re ϱ(0)3(∞) sin(2ν2)
1
Рис.
2.
(В цвете онлайн) Зависимости вклада
0)
ϱ(0)1(ρ) =
F(
(ρ)2 , ϱ(0)1(∞) = -[gc(j)Imf(W)]-1 ,
Nsubcr(ρ, ν1; E) от энергии E для ρ = 1, g
= 0.3 и
1
различных значений параметра с. с. расширения ν1
(0)
0)
|f(W )|2
ϱ
(ρ) =
F(
(ρ)
2 , ϱ(0)2(∞) = -g-1c(j)
,
2
2
Im f(W )
1
Nsubcr(ρ, ν1, E) ∼
×
ϱ(0)3(ρ) = F(0)1(ρ)F(0)∗2(ρ),
C(g)ρ
[
]
(1-2g2) tg2 ν
Re ϱ(0)3(∞) = g-1c(j)Ref(W)
× 4tgν+2ρ2γ+
ρ-2γ |2E|2γ eδπg +
Im f(W )
g2
(
)
√
Вклад критической области при E → 0 расходится
+ O |2E|2γ+1 ,
γ=
1/4 - g2 < 1/2,
как квадрат логарифма:
(ρ; E) ∼
−1/2
1/2
C(g) = [ch (2πg) - cos (2πγ)] Γ(1 + 2γ)2 |Γ(ig - γ)|2 .
2 + (lnρ + tgν)2
∼
|Im f(W )| ln-2 (2 |E|) .
π2ρ
Отсюда следует, что даже при g → 0 и E → 0 при
ν1 = 0 вклад субкритической области отличается от
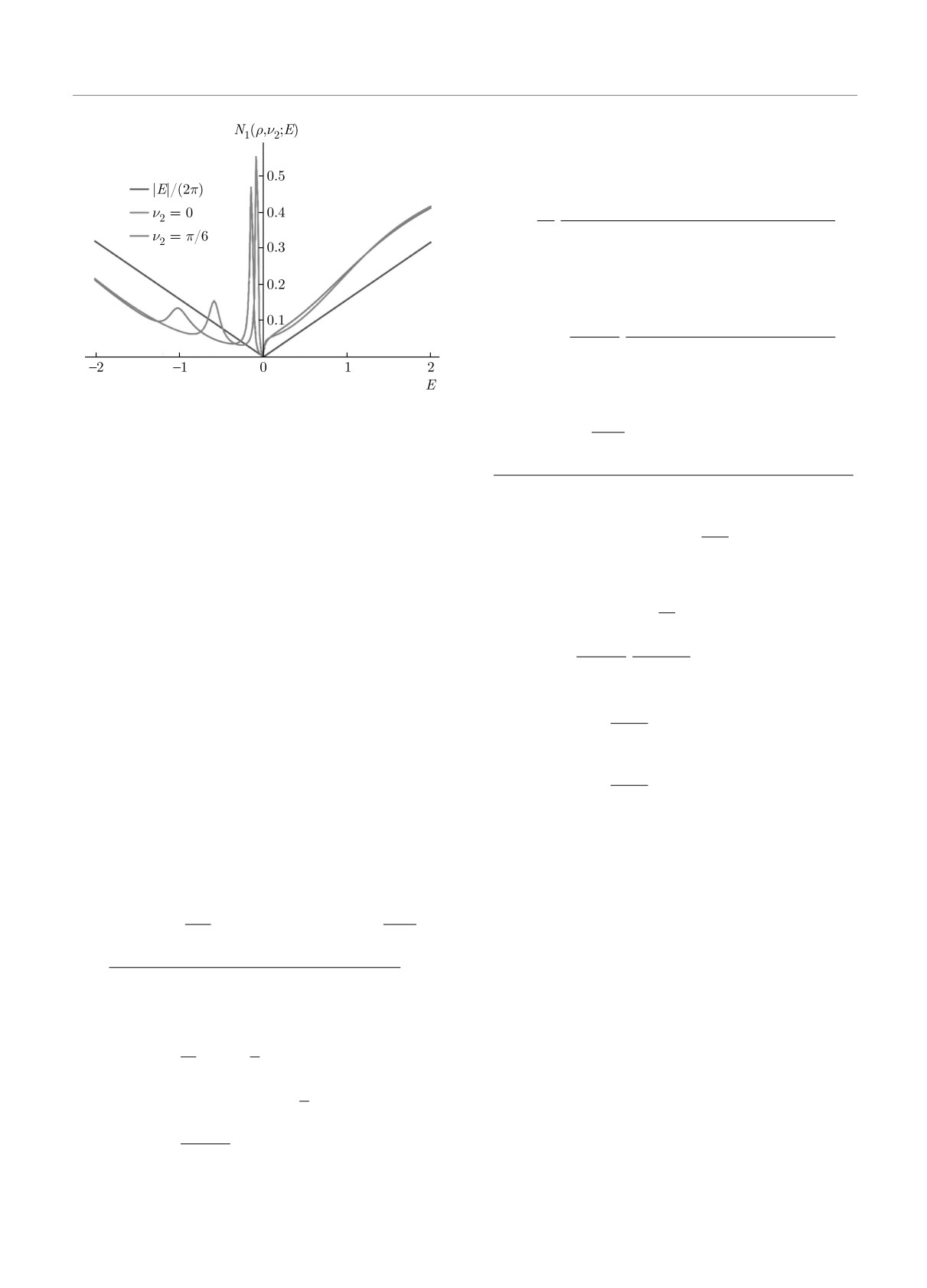
На рис. 3 показаны зависимости плотности со-
выражения (35) для локальной плотности состояний
стояний N1(ρ, ν2; E) от энергии квазичастицы для
свободной частицы наличием расходимости по g:
ρ = 1, g = 0.5.
1085
А. И. Бреев, Д. М. Гитман
ЖЭТФ, том 159, вып. 6, 2021
и
ϱ1(∞) = lim
ϱ1(ρ) =
ρ→∞
δσ
e-πσ sh(π [g - δσ]) + eπσ sh(π [g + δσ])
=-
,
j
e-πσ sh(π [g - δσ]) - eπσ sh(π [g + δσ])
ϱ2(∞) = lim
ϱ2(ρ) =
ρ→∞
j - isσ
Γ2(1 + 2iσ)e-δπg
=
g
Γ(1 - i(g - σ))Γ(1 + i(g + σ))
В терминах кулоновских волновых функций имеем
Рис. 3. (В цвете онлайн) Зависимости локальной плотнос-
1
ти состояний N1(ρ, ν2; E) для ρ = 1, g = 0.5 и ν2 = 0, π/6.
n4,ν3j(ρ; E) =
×
2π2ρ
Синяя линия описывает локальную плотность состояний в
ϱ1(ρ) - s sgn(jE)Re {ϱ2(ρ)exp(2i [ν3 + σ ln(ρ)])}
отсутствие поля
×
,
ϱ1(∞) - s sgn(jE)Re {ϱ2(∞)exp(2i [ν3 + σ ln(ρ)])}
Для полуцелых значений параметра g ∈ Δ3(k),
2 |j|
ϱ1(ρ) = |Fiσ|2 + |Fiσ-1|2 +
Re[F∗iσ-1Fiσ],
g = gc(k), k = 3/2,5/2,..., вклад в локальную плот-
g
ность состояний дает субкритическая и сверхкрити-
ческая области, в связи с чем эта плотность пара-
(
)
|j|
[
]
метризуется двумя параметрами c.с. расширения ν2
ϱ2(ρ) =
2Fiσ-1Fiσ +
F2iσ + F2iσ-1
×
g
и ν3:
sj - iσ
Γ(2iσ)
×
exp[-2iσ ln(2ρ |E|)] ,
N (ρ; E) = N2(ρ, ν2, ν3; E) =
g
Γ(-2iσ)
∑
=
(ρ; E) +
k+1)
+1
(g+σ)1/4
Fiσ =
Fiσ(-g; |E| ρ),
|j|>k+1
g-σ
∑
+
(37)
n4,ν3j(ρ; E),
1/4
|j| ≤ k
(g-σ)
Fiσ-1 =
Fiσ-1(-g; |E| ρ).
g+σ
где n4,ν3j (ρ; E) соответствует парциальному гамиль-
Из
(38) следует, что изменение параметра c.с.
ĥ4,ν
тониану
3
(Z, j, s) в сверхкритической области,
расширения приводит к сдвигу фазы δj (ρ). На
который параметризуется параметром с.с. расшире-
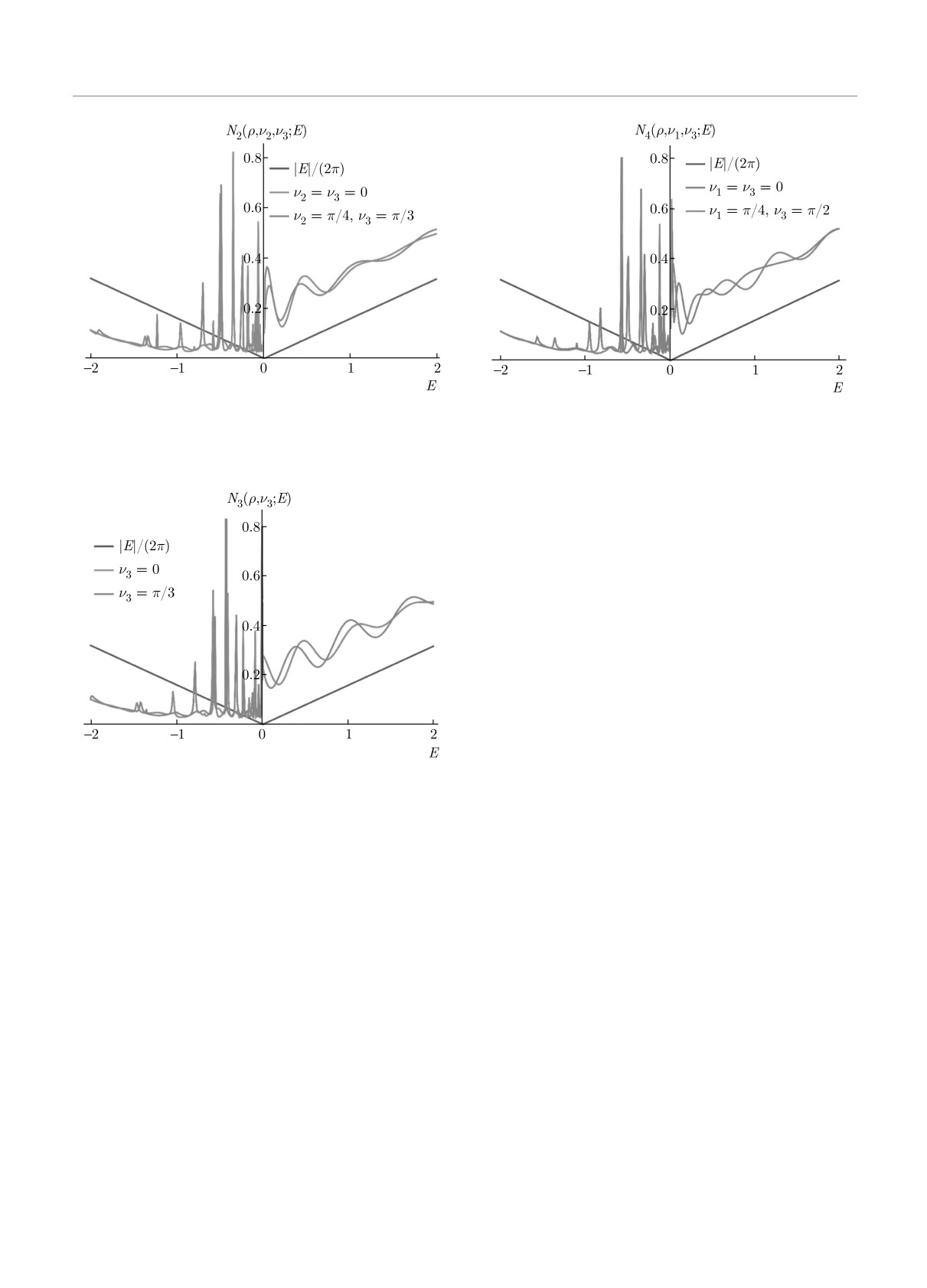
рис. 4 показаны зависимости плотности состояний
ния ν3,
N2(ρ, ν2, ν3; E) от энергии квазичастицы для ρ = 1,
g = 3.5.
1
1
|U4,ν3,E(ρ)|2 σ4,ν3 (E) =
×
n4,ν3j(ρ; E) =
Пусть существует полуцелое число k > 1/2, та-
2πρ
2π2ρ
кое что g ∈ Δ1(k) = (gc(k), gs(k + 1)]. Тогда в ло-
ϱ1(ρ) - Re {ϱ2(ρ)exp(2i [ν3 + σ ln(ρ)])}
×
(38)
кальную плотность состояний вносит вклад только
ϱ1(∞) - Re {ϱ2(∞)exp (2i [ν3 + σ ln(ρ)])}
сверхкритическая область:
Здесь
[(
)
N (ρ; E) = N3(ρ, ν3; E) =
g
σ
∑
∑
ϱ1(ρ) =
1-
|Φ-iσ(ρ)|2 +
=
n1j(ρ; E) +
(39)
2j
g
n4,ν3j(ρ; E).
(
)
]
|j| ≥ k+1
|j| < k
σ
+
1+
|Φiσ(ρ)|2 ,
g
На рис. 5 показаны зависимости плотности со-
j - isσ
стояний N3(ρ, ν3; E) от энергии квазичастицы для
ϱ2(ρ) =
Φiσ(ρ)Φ∗-iσ(ρ)
g
ρ = 3, g = 3.7.
1086
ЖЭТФ, том 159, вып. 6, 2021
Безмассовые электронные возбуждения в графене. . .
Рис. 4. (В цвете онлайн) Зависимости локальной плот-
Рис. 6. (В цвете онлайн) Зависимости локальной плотнос-
ности состояний N2(ρ, ν2, ν3; E) для ρ = 1, g = 3.5 для
ти состояний N4(ρ, ν1, ν3; E) для ρ = 3, g = 3.48 для слу-
ν2 = ν3 = 0 и ν2 = π/6, ν3 = π/3. Синяя линия описывает
чаев ν1 = ν3 = 0 и ν1 = π/4, ν3 = π/2. Синяя линия
локальную плотность состояний в отсутствие поля
описывает локальную плотность состояний в отсутствие
поля
Отметим, что для всех значений заряда примеси
Z имеется нарушение электронно-дырочной симмет-
рии: для положительных и отрицательных значений
энергии локальная плотность состояний ведет себя
различным образом. Притягивающий кулоновский
потенциал примеси приводит к уменьшению локаль-
ной плотности состояний для отрицательных значе-
ний энергии (дырочной) E < 0 относительно состо-
яний с положительной энергией E > 0. Данный эф-
фект наиболее сильно проявляется вблизи примеси.
Отметим, что, ввиду экспоненциального множи-
теля exp(δπg) в выражении (33), вклад несингу-
Рис. 5. (В цвете онлайн) Зависимости локальной плотнос-
лярной области экспоненциально подавлен при от-
ти состояний N3(ρ, ν3; E) для ρ = 3, g = 3.7 и ν3 = 0, π/3.
рицательных значениях энергии и основной вклад
Синяя линия описывает локальную плотность состояний в
отсутствие поля
в локальную плотность состояний N3(ρ, ν3; E) и
N4(ρ, ν1, ν3; E) вносит конечное число слагаемых
∑
|j| < k
n4,ν3j
(ρ; E), отвечающих сверхкритической
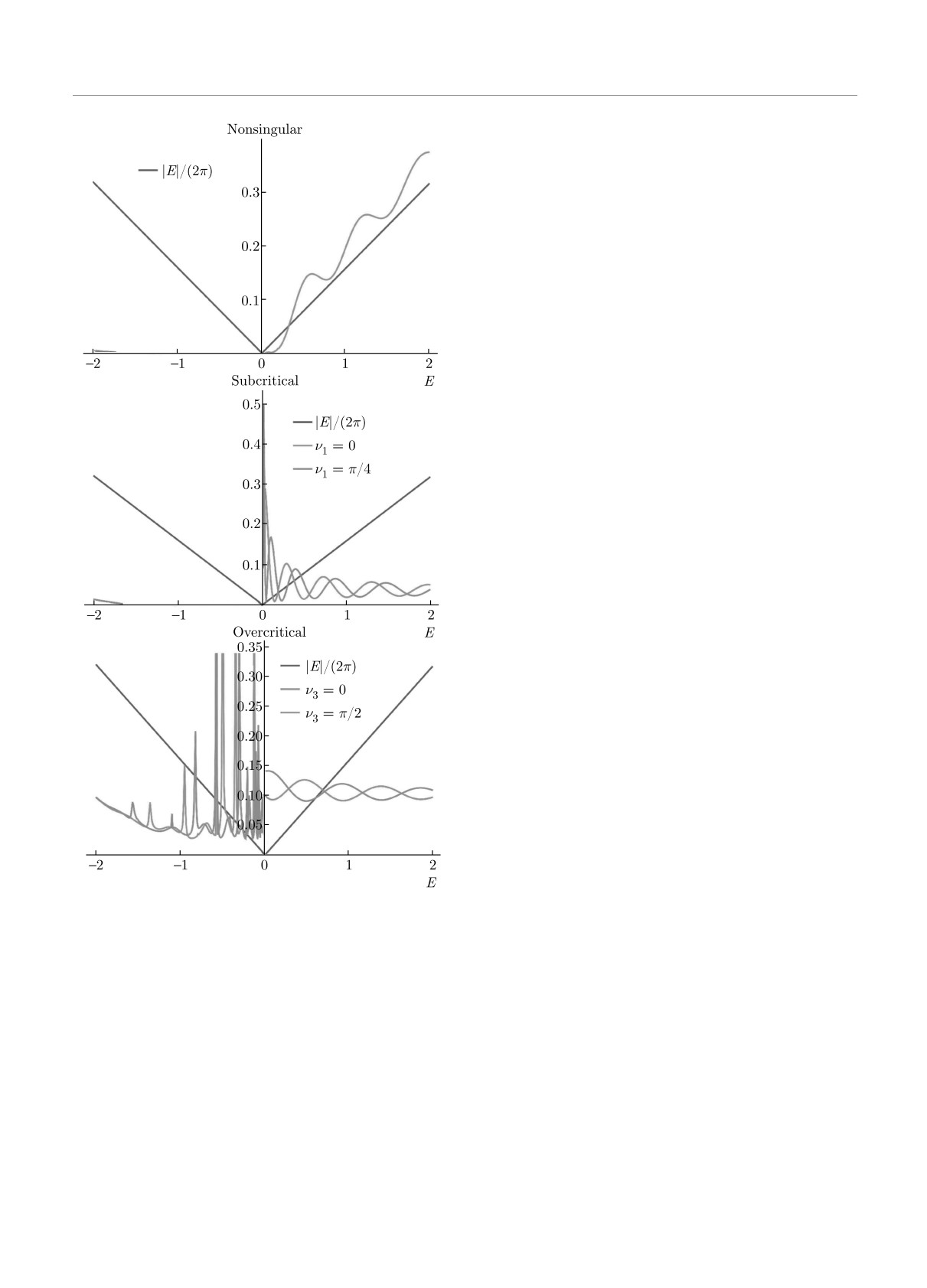
Если же существует полуцелое число k > 1/2,
области. На рис. 7 представлены зависимости вкла-
такое что g ∈ Δ2(k) = (gs(k + 1), gc(k + 1)), то ло-
дов каждой области отдельно для плотности состо-
кальная плотность состояний параметризуется дву-
яний N4(ρ, ν1, ν3; E) от энергии квазичастицы для
мя параметрами c.с. расширения ν1 и ν3:
ρ = 3 и g = 3.48. Из рис. 7 видно, что вклад несингу-
лярной и субкритической областей сильно подавлен
N (ρ; E) = N4(ρ, ν1, ν3; E) =
в отрицательной области энергий.
∑
=
(ρ; E) +
Вклад сверхкритической области в (37), (39) и
k+1)
|j| > k+1
(40) приводит к перестройке плотности состояний
∑
вблизи примеси гораздо сильнее, чем вклад субкри-
(ρ; E) +
(40)
+1
n4,ν3j(ρ; E).
тической области (34) для малых зарядов g ∈ Δ(0).
|j| < k
На рис. 3-5 вклад свехкритической области приво-
На рис. 6 показаны зависимости плотности состо-
дит к наличию резонансов в области отрицательных
яний N4(ρ, ν1, ν3; E) от энергии квазичастицы для
энергий, которые затухают при удалении от при-
ρ = 3 и g = 3.48.
меси. С увеличением заряда примеси Z количество
1087
А. И. Бреев, Д. М. Гитман
ЖЭТФ, том 159, вып. 6, 2021
8. ЗАКЛЮЧЕНИЕ
Отметим, что предыдущая работа с участием ав-
торов [10] была посвящена исследованию спектров
массивных квазичастиц в графене в окрестности ку-
лоновской примеси. Настоящая работа является ее
естественным продолжением. Здесь исследован слу-
чай, когда эффективная масса квазичастиц в гра-
фене равна нулю, и показано, что в этом случае
структура спектров электронных возбуждений ка-
чественно другая. В частности, построено семей-
ство всех возможных с.с. гамильтонианов, отвеча-
ющих безмассовым носителям заряда в графене с
кулоновскими примесями, которые параметризуют-
ся параметрами расширения, и проведен их спек-
тральный анализ. Показано, что спектр с.с. пар-
циальных гамильтонианов является непрерывным,
spec
ĥ (Z, j, s) = (-∞, ∞), в отличие от массивно-
го случая, где имеются дискретный и непрерывный
спектры.
Вычислены обобщенные собственные функции,
отвечающие с.с. парциальным гамильтонианам для
любого заряда примеси (см. (30)). А именно, для
несингулярной области (g ≤ gs(j)) нормированные
(обобщенные) собственные функции даются форму-
лой (21), для субкритической области (gs(j) < g <
< gc(j)) — формулой (24), для критической области
(g = gc(j)) — формулой (26), а для сверхкритичес-
кой области (g > gc(j)) — формулой (28). Получен-
ные собственные функции оказались существенны-
ми для анализа локальной плотности состояний (см.
(32), (36), (37) и (40)), которая зависит от парамет-
ров с.с. расширения.
Следует отметить, что в работе
[20] также
рассматривались с.с. дираковские гамильтониа-
ны, отвечающие безмассовым носителям заряда в
графене с кулоновскими центрами в сочетании с
полем Ааронова - Бома (в 2 + 1 измерении) за ис-
Рис. 7. (В цвете онлайн) Вклады несингулярной (Non-
ключением критической области, когда Z = Zc(j).
singular), субкритической (Subcritical) и срехкритических
Однако не были приняты во внимание существен-
(Overcritical) областей в N4(ρ, ν1, ν3; E)
ные особенности данной задачи в недопированном
графене. Из-за этого радиальные гамильтонианы,
которые рассматривались в [20], параметризованы
резонансов растет и они сдвигаются вниз по энер-
особым образом, что не позволяет отождествить
гии. Точку Дирака можно рассматривать как точ-
их с соответствующими гамильтонианами реальной
ку накопления бесконечного множества резонансов
задачи в графене.
[8,19]. Это объясняется тем, что функции n4,ν3j (ρ; E)
в сверхкритической области осциллируют с лога-
Финансирование. Исследование выполнено за
рифмически расходящейся частотой 2[σ ln |2E| - ν3]
счет гранта Российского научного фонда (проект
при E → 0 для всех значений параметра c.с. расши-
№19-12-00042).
рения ν3.
1088
ЖЭТФ, том 159, вып. 6, 2021
Безмассовые электронные возбуждения в графене. . .
ЛИТЕРАТУРА
12. D. M. Gitman, I. V. Tyutin, and B. L. Voronov,
Self-adjoint Extensions in Quantum Mechanics:
1. K. Nomura and A. H. MacDonald, Phys. Rev. Lett.
General Theory and Applications to Schrödinger and
98, 076602 (2007).
Dirac Equations with Singular Potentials, Birkäuser,
New York (2012).
2. V. N. Kotov, B. Uchoa, V. M. Pereira et al., Rev.
Mod. Phys. 84, 1067 (2012).
13. D. M. Gitman, A. D. Levin, I. V. Tyutin et al., Phys.
3. V. M. Pereira, V. N. Kotov, and A. C. Neto, Phys.
Scripta 87, 038104 (2013).
Rev. B 78, 085101 (2008).
14. Graphene Nanoelectronics. Metrology, Synthesis Pro-
4. E. V. Gorbar, V. P. Gusynin, and O. O. Sobol, Low
perties, and Applications, ed. by H. Raza, Springer,
Temp. Phys. 44, 371 (2018).
New York (2012).
5. O. V. Gamayun, E. V. Gorbar, and V. P. Gusynin,
15. N. I. Akhiezer and I. M. Glazman, Theory of Linear
Phys. Rev. B 80, 165429 (2009).
Operators in Hilbert Space, Pitman, Boston (1981).
6. A. H. Neto, F. Guinea, N. M. R. Peres, K. S. No-
voselov, and A. K. Geim, Rev. Mod. Phys. 81, 109
16. A. I. Akhiezer and V. B. Berestetskii, Elements of
(2009).
Quantum Electrodynamics, Israel Program for Sci.
Tr., London (1962).
7. M. I. Katsnelson, Graphene: Carbon in Two Dimen-
sions, Cambridge Univ. Press, New York (2012).
17. M. Abramovitz and I. A. Stegun, Handbook of Ma-
8. V. M. Pereira, V. M. Nilsson, and A. C. Neto, Phys.
thematical Functions, Nat. Bureau Stand. (1972).
Rev. Lett. 99, 166802 (2007).
18. A. Cortijo and M. A. H. Vozmediano, Europhys. Lett.
9. D. Haberer, D. V. Vyalikh, S. Taioli et al., Nano Lett.
77, 47002 (2007).
10, 3360 (2010).
19. A. V. Shytov, M. I. Katsnelson, and L. S. Levitov,
10. А. И. Бреев, Р. Феррейра, Д. М. Гитман, Б. Л. Во-
Phys. Rev. Lett. 99, 246802 (2007).
ронов, ЖЭТФ 157, 847 (2020).
11. Б. Л. Воронов, Д. М. Гитман, И. В. Тютин, ТМФ
20. V. R. Khalilov and K. E. Lee, Int. J. Mod. Phys.
150, 41 (2007).
A 27, 1250169 (2012).
1089