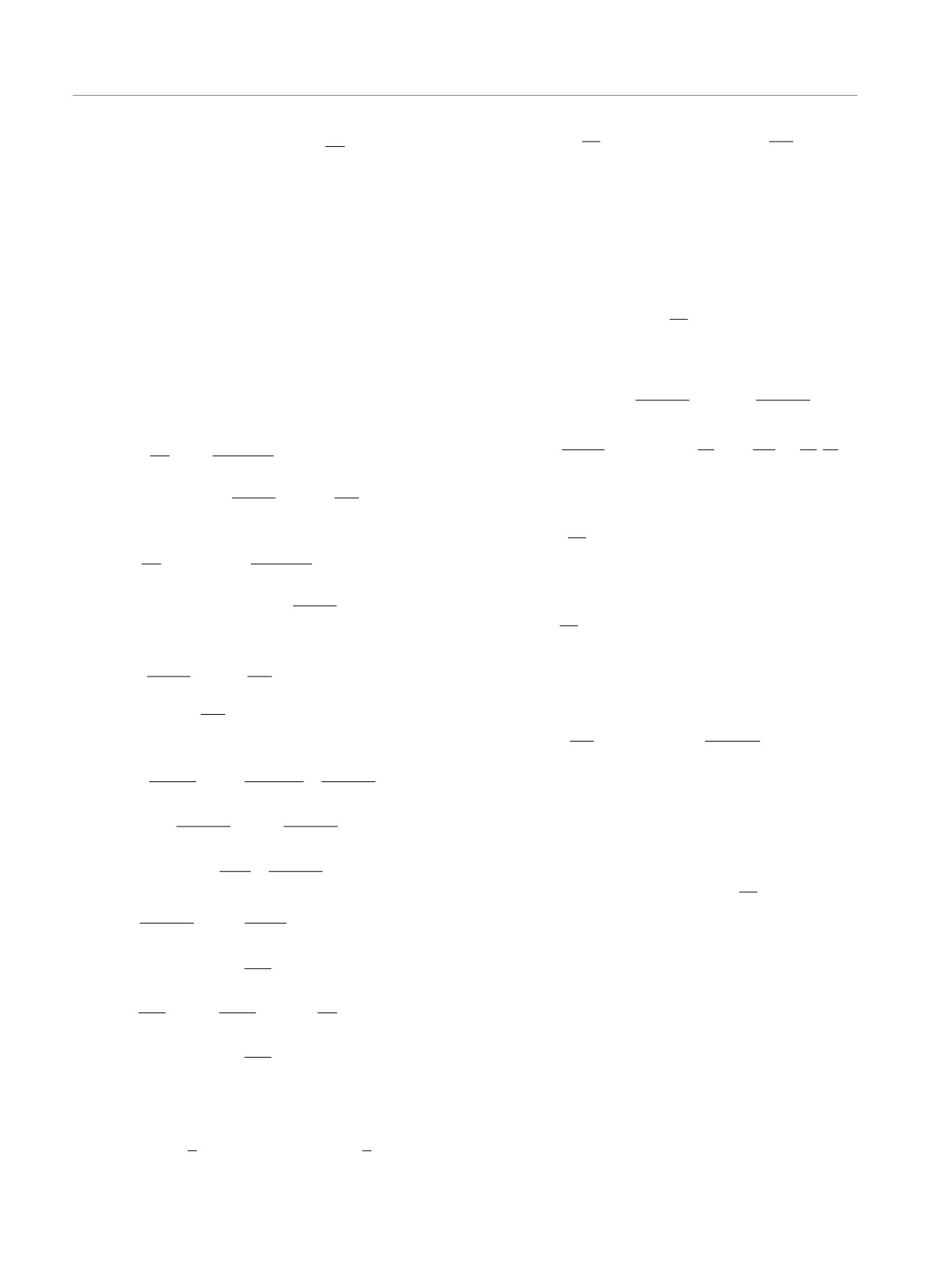ЖЭТФ, 2021, том 159, вып. 6, стр. 1090-1117

ГИДРОМАГНИТНЫЕ НЕУСТОЙЧИВОСТИ

В НЕОДНОРОДНО ВРАЩАЮЩЕМСЯ СЛОЕ

ЭЛЕКТРОПРОВОДЯЩЕЙ НАНОЖИДКОСТИ

М. И. Коппa*, А. В. Турc**, В. В. Яновскийa,b***

^a Институт монокристаллов Национальной академии наук Украины

61001, Харьков, Украина

^b Харьковский национальный университет им. В. Н. Каразина

61000, Харьков, Украина

^c Université de Toulouse [UPS], CNRS, Institut de Recherche en Astrophysique et Planétologie

BP 44346, 31028 Toulouse Cedex 4, France

Поступила в редакцию 15 декабря 2020 г.,

после переработки 15 декабря 2020 г.

Принята к публикации 11 января 2021 г.

Исследуется устойчивость замагниченных потоков неоднородно вращающегося слоя электропроводящей

наножидкости с учетом эффектов броуновской диффузии и термофореза. В отсутствие градиента тем-

пературы рассмотрены новые виды магнитовращательной неустойчивости в аксиальном, азимутальном

и спиральном магнитных полях в тонких слоях наножидкости. Получены инкременты и области разви-

тия этих неустойчивостей в зависимости от профиля угловой скорости вращения (числа Россби Ro) и

радиального волнового числа k. При наличии градиентов температуры и концентрации наночастиц ис-

следуются стационарные режимы неоднородно вращающейся конвекции в аксиальном и спиральном маг-

нитных полях. Получены выражения для критических чисел Рэлея Rast и построены кривые нейтральной

устойчивости в зависимости от профиля угловой скорости вращения, профиля внешнего азимутального

магнитного поля (магнитного числа Россби Rb) и радиального волнового числа k. Определены условия

стабилизации и дестабилизации стационарной конвекции в аксиальном и спиральном магнитных полях.

DOI: 10.31857/S0044451021060080

ки, в качестве базовых жидкостей — вода, этилен-

гликоль, машинное масло. Добавление наночастиц

1. ВВЕДЕНИЕ

приводит к повышению теплопроводности базовой

В последнее время, в связи с ростом произво-

жидкости на десятки процентов, а в случае угле-

дительности электронных устройств и развитием

родных нанотрубок — в несколько раз. Исследова-

высокоэнергетичных технологий, возникает необхо-

ния, проведенные в [2] (см. цитируемую там литера-

димость создания эффективных охлаждающих си-

туру), показали, что коэффициенты переноса нано-

стем. Перспективным направлением интенсифика-

жидкостей зависят не только от концентрации на-

ции теплообмена является повышение теплопровод-

ночастиц, но и от их размера и материала. В ра-

ности жидкости (газа) путем добавления наноча-

боте [3] было показано, что на перенос тепла мо-

стиц с высокой теплопроводностью. Такая смесь

жет оказывать влияние пространственная неодно-

жидкости (газа) с частицами твердой фазы получи-

родность концентрации наночастиц, которая возни-

ла название наножидкости [1]. В качестве наноча-

кает под действием броуновской диффузии и тер-

стиц используются керамические частицы (оксиды

мофореза (возникновения потока частиц под дей-

алюминия, меди, кремния), металлические частицы

ствием градиента температуры). В связи с этим ис-

(алюминий, железо, медь) и углеродные нанотруб-

следование влияния диффузии и термофореза нано-

частиц на вынужденную конвекцию наножидкостей

^* E-mail: michaelkopp0165@gmail.com

в теплообменных устройствах является актуальной

^** E-mail: Anatoly.Tour@irap.omp.eu

задачей.

^*** E-mail: yanovsky@isc.kharkov.ua

1090

ЖЭТФ, том 159, вып. 6, 2021

Гидромагнитные неустойчивости в неоднородно вращающемся слое...

Наряду с вязкостью и теплопроводностью на-

в работе [15] — в спиральном магнитном поле. Ре-

ножидкостей для различных приложений большую

зультаты работ [12-15] показали, что при отсут-

роль играет свойство электропроводности наножид-

ствии градиента температуры Ra = 0, т. е. когда

костей. В недавней работе [4] проведены экспери-

нет подогрева, критерии конвективной неустойчиво-

ментальные исследования электропроводности на-

сти переходят в известные критерии возникновения

ножидкостей на основе воды и этиленгликоля с час-

стандартной магнитовращательной неустойчивости

тицами меди и алюминия. Там же было показано,

(МВН) и спиральной МВН в диссипативной элек-

что электропроводность наножидкостей практиче-

тропроводящей среде (плазме) [16, 17]. Еще одним

ски линейно растет с увеличением концентрации на-

фактором, влияющим на устойчивость неоднородно

ночастиц и, в отличие от теплопроводности, растет

вращающейся электропроводящей жидкости, явля-

с уменьшением размера частиц. С учетом этого был

ется градиент концентрации наночастиц в жидко-

сделан вывод [4], что механизмы электропроводно-

сти. Использование электропроводящих наножид-

сти и теплопроводности наножидкостей существен-

костей, возможно, решит проблемы, возникающие

но различаются.

при использовании жидких металлов для лабора-

торного моделирования МВН. Кратко остановимся

Кроме того, возрастает интерес к исследованиям

на основных проблемах лабораторного моделирова-

механизма теплопередачи электропроводящих на-

ния МВН.

ножидкостей под воздействием магнитного поля с

В лабораторных экспериментах неоднородное

эффектами броуновской диффузии и термофоре-

за [5, 6]. Конвективная неустойчивость в наножид-

(дифференциальное) вращение среды моделируется

течением Куэтта, заключенным между двумя вра-

костном слое с вертикальным магнитным полем для

свободных, жестких-жестких и жестких-свободных

щающимися с разной угловой скоростью цилиндра-

границ изучалась в работе [7]. Там же показано, что

ми. Угловая скорость вращения жидкости в такой

устойчивость наножидкости возрастает с увеличе-

конфигурации описывается соотношением

нием значения магнитного поля, в то время как уве-

личение концентрации наночастиц приводит к уско-

Ω₂R²² - Ω₁R²¹

(Ω₁ - Ω₂)R²¹R²²

Ω(R) =

= a+

рению начала конвекции. Условия возникновения

R²² - R²¹

R²(R²² - R²¹)

R²

конвекции в чистых средах в поле силы тяжести при

где R1,2 и Ω1,2 — соответственно радиус и угло-

наличии однородного вращения и внешнего магнит-

вая скорость вращения внутреннего и внешнего ци-

ного поля изучены достаточно подробно [8-10]. По-

линдров. Устойчивость такого течения для идеаль-

этому представляет интерес исследование конвек-

но проводящей среды в магнитном поле была впер-

тивной неустойчивости во вращающемся слое нано-

вые рассмотрена в работах [19, 20]. Там же пока-

жидкости в присутствии магнитного поля. Впервые

зано, что слабое осевое магнитное поле дестабили-

эта задача была рассмотрена в работе [11], где иссле-

зирует азимутальное дифференциальное вращение

довано совместное влияние вращения и магнитно-

плазмы и при выполнении условия dΩ²/dR < 0 в

го поля на возникновение конвекции в горизонталь-

бездиссипативной плазме возникает МВН, или стан-

ном слое электропроводящей наножидкости с уче-

дартная МВН. Поскольку это условие выполняется

том эффекта броуновского движения наночастиц и

и для кеплеровских течений (Ω ∝ R-3/2), МВН яв-

термофореза. В работе [11] было установлено, что

ляется наиболее вероятным источником турбулент-

критическое число Рэлея Ra_c для наножидкости ни-

ности в аккреционных дисках. Открытие МВН по-

же по сравнению с Ra_c для обычной жидкости при

служило толчком к многочисленным теоретическим

одинаковых значениях числа Чандрасекара Q (ха-

и лабораторным исследованиям по вращению жид-

рактеризует меру влияния силы Лоренца) и числа

ких металлов (натрия, галлия) [21-27]. В этих рабо-

Тейлора Ta (характеризует меру влияния силы Ко-

тах показано, что из-за сильного стабилизирующе-

риолиса). Как было показано [11], увеличение кон-

го эффекта, обусловленного магнитной диффузией

центрации наночастиц оказывает дестабилизирую-

или малыми значениями магнитного числа Прандт-

щее влияние на начало конвекции, а вращение —

ля (Pm ≪ 1) МВН возникает лишь при достаточно

стабилизирующее.

больших угловых скоростях жидкого металла, для

В работах [12-14] впервые рассматривалась кон-

которых число Рейнольдса Re = Ω₁R₁(R₂ - R₁)/ν

вективная неустойчивость неоднородно вращающе-

(ν — коэффициент кинематической вязкости) яв-

гося слоя электропроводящей жидкости в постоян-

ляется величиной порядка 10⁶. При таких больших

ном вертикальном магнитном поле H₀ = const, а

числах Рейнольдса ламинарность течения жидкос-

1091

М. И. Копп, А. В. Тур, В. В. Яновский

ЖЭТФ, том 159, вып. 6, 2021

ти маловероятна, так как оно становится турбулент-

далось в работах [35,36], лабораторные эксперимен-

ным из-за нелинейных неустойчивостей и из-за взаи-

ты с полимерными жидкостями позволяют лучше

модействия с цилиндрами.

понять физический механизм магнитогидродинами-

ческих неустойчивостей.

Теоретический анализ, выполненный в работах

На основании проведенных в настоящей рабо-

[22-24, 26], показал, что среди гидродинамически

те теоретических исследований по реализации стан-

устойчивых профилей вращения самый низкий по-

дартной МВН, азимутальной МВН и спиральной

рог устойчивости имеет место для профиля угловой

МВН в неоднородно вращающемся слое электропро-

скорости вращения a = 0, соответствующего грани-

водящей наножидкости предлагается использование

це гидродинамической устойчивости (линия Рэлея).

электропроводящих наножидкостей для лаборатор-

При этом критическое число Рейнольдса оказывает-

ного моделирования МВН. Содержание работы из-

ся по величине на два порядка меньше, т. е. Re ∼ 10⁴

ложено в следующих разделах. В разд. 2 описана

для жидкого натрия. Однако из-за малости магнит-

постановка задачи и получены уравнения эволюции

ного числа Прандтля Pm порог МВН возрастает на

малых возмущений в приближении Буссинеска во

два порядка с Re ≈ 10⁴ до Re ≈ 10⁶ при малейшем

вращающемся слое несжимаемой электропроводя-

отклонении профиля угловой скорости вращения от

Ω ∝ R-2 в область гидродинамической устойчивос-

щей наножидкости, находящейся в поле силы тяже-

сти с постоянными градиентами температуры и кон-

ти: Ω ∝ R-2 → Ω ∝ R-2+α, α > 0 [27]. В силу

центрации наночастиц. Неоднородно вращающийся

недостижимости поддержания профиля вращения в

слой наножидкости находится во внешнем спираль-

эксперименте с такой точностью в работе [27] бы-

ном магнитном поле. В разд. 3 решается задача Рэ-

ло сделано утверждение о невозможности наблюде-

лея - Бенара для слоя электропроводящей наножид-

ния МВН в эксперименте с профилем угловой ско-

кости, заключенной между двумя вращающимися

рости, соответствующим линии Рэлея Ω = b/R², но

цилиндрами и подогреваемой снизу. Получено об-

эта проблема была решена в работах [28,29]. Там же

щее дисперсионное уравнение для осесимметричных

было показано, что рост величины аксиального маг-

возмущений с учетом эффектов броуновской диф-

нитного поля приводит к тому, что изменение порога

фузии наночастиц и термофореза. В разд. 4-6 рас-

МВН при отклонении профиля вращения от линии

Рэлея перестает быть таким резким, как в случае

сматриваются гидромагнитные неустойчивости при

условии равенства температуры (Ra = 0) на гра-

слабого поля. Вместе с тем, сам порог неустойчивос-

ницах слоя наножидкости. В разд. 4 проведен ана-

ти на линии Рэлея увеличивается пропорционально

лиз дисперсионного уравнения для случая, когда от-

величине магнитного поля.

сутствует азимутальная компонента магнитного по-

В работах [30, 31] было предложено изучать

ля, H0ϕ = 0. Получен критерий развития аналога

неустойчивость азимутального вращения жидкого

стандартной МВН в тонком слое наножидкости. В

галлия в спиральном магнитном поле, т. е. наряду

разд. 5 проведен анализ дисперсионного уравнения

с аксиальным магнитным полем приложено допол-

для случая, когда отсутствует аксиальная компо-

нительное внешнее азимутальное магнитное поле.

нента магнитного поля, H0z = 0, и получен кри-

Численные расчеты, проведенные в этих работах,

терий развития аналога азимутальной МВН в тон-

показали, что критическое число Рейнольдса Re_c в

ком слое наножидкости. В разд. 6 проведен ана-

спиральном магнитном поле уменьшается по вели-

лиз дисперсионного уравнения при наличии внеш-

чине на два порядка. Анализ природы наблюдаемых

него спирального магнитного поля. Также получе-

в эксперименте мод был выполнен в работах [17,32].

ны критерии развития аналога спиральной МВН в

В последней было получено выражение для порога

тонком слое наножидкости. В разд. 7 исследуют-

спиральной МВН.

ся стационарные режимы конвекции в однородном

Однако малость магнитного числа Прандтля

аксиальном и неоднородном спиральном магнитных

(Pm ≪ 1) для жидких металлов является также

полях. Там же получены критические значения чи-

препятствием для дестабилизации кеплеровских по-

сел Рэлея для стационарной конвективной неустой-

токов в экспериментах с азимутальными и спирале-

чивости. Проведен анализ развития этих неустойчи-

видными полями. Поэтому эксперименты с жидки-

востей для различных профилей угловой скорости

ми металлами нуждаются в дальнейшем улучшении

вращения Ω(R) в зависимости от профиля внешнего

[33]. Аналог астрофизической МВН рассматривался

азимутального магнитного поля B0ϕ(R). В Заклю-

в работе [34], где исследовалось течение Куэтта в

чении приводятся основные выводы, полученные в

вязко-упругой полимерной жидкости. Как утверж-

настоящей работе.

1092

ЖЭТФ, том 159, вып. 6, 2021

Гидромагнитные неустойчивости в неоднородно вращающемся слое...

Очевидно, что для исследования данного типа тече-

ния удобно использовать цилиндрическую систему

координат (R, ϕ, z), выбор которой обусловлен воз-

можностью практического применения развиваемой

здесь теории.

Для описания конвективных процессов будем

использовать уравнения гидродинамики Буссинес-

ка - Обербека несжимаемой электропроводящей на-

ножидкости [7], записанные для цилиндрической

системы координат:

(

)

∂V_R

V2ϕ

ρ₀

+ (V · ∇)V_R -

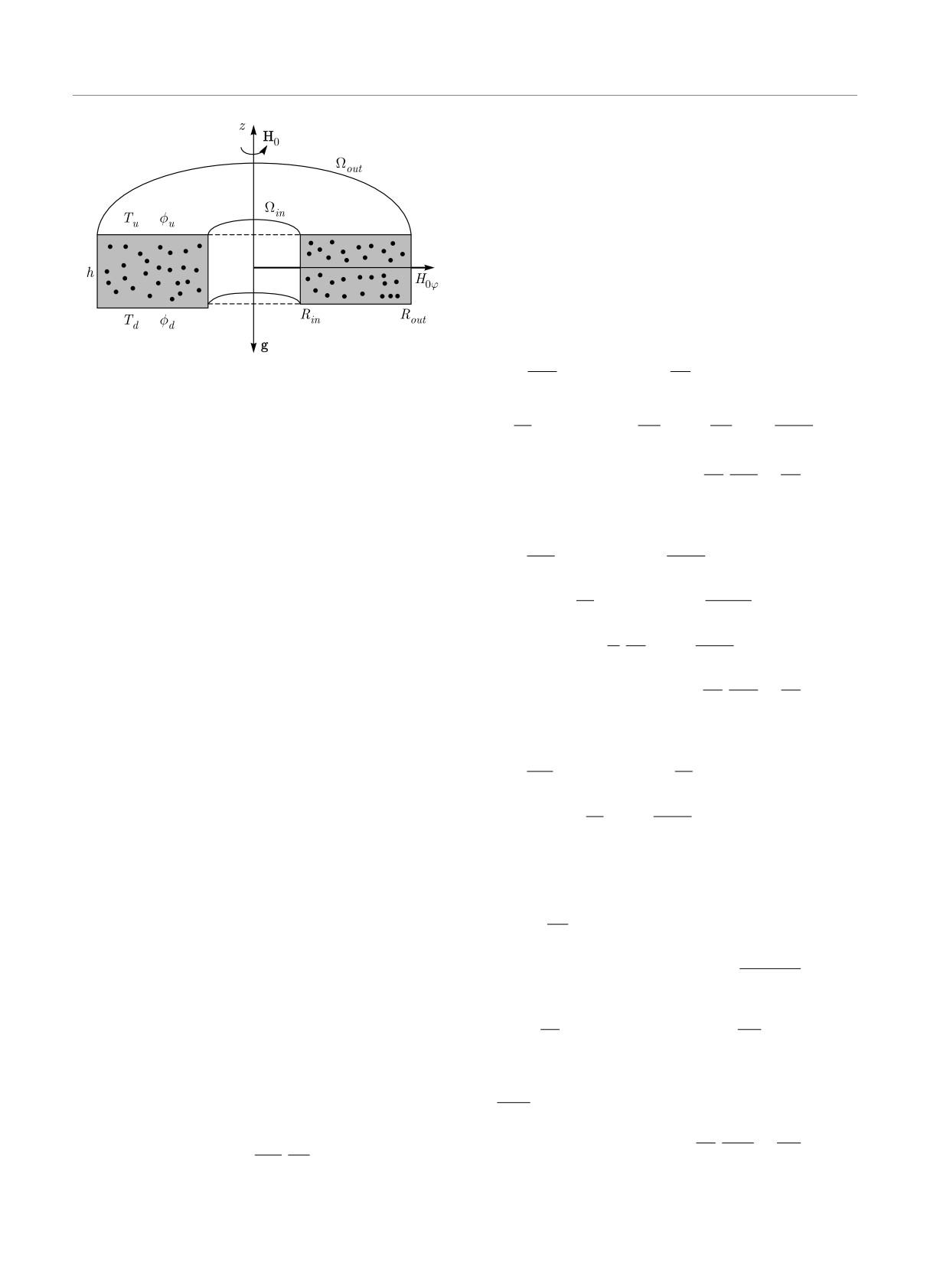
Рис. 1. Электропроводящая наножидкость заполняет слой

∂t

между двумя вращающимися цилиндрами с угловыми ско-

(

)

(

)

ростями Ωin и Ωout и находится в спиральном магнитном

μ_e

H2ϕ

∂

μ_eH²

−

(H · ∇)H_R-

P+

поле H0 = H0ϕ(R)eϕ + H0zez . Нижняя поверхность слоя

4π

∂R

8π

имеет температуру T_d и объемную долю наночастиц φ_d, а

(

)

∂V_ϕ

V_R

верхняя — Tu и φu; Td > Tu, φd < φu

+μ

∇²V_R -

(3)

R² ∂ϕ

R²

2. ПОСТАНОВКА ЗАДАЧИ И УРАВНЕНИЯ

)

ЭВОЛЮЦИИ МАЛЫХ ВОЗМУЩЕНИЙ

⁽∂V

V_ϕV_R

ρ₀

+ (V · ∇)V_ϕ +

∂t

Рассмотрим слой несжимаемой вязкой электро-

(

)

проводящей наножидкости толщины h, которая за-

μ_e

H_ϕH_R

−

(H · ∇)H_ϕ +

ключена между двумя вращающимися цилиндрами

4π

(

)

с внутренним R_in и внешним R_out радиусами, при-

∂

μ_eH²

P +

чем h ≪ (R_out - R_in). Наножидкость заключена

R ∂ϕ

8π

(

)

между двумя параллельными плоскостями z = 0 и

∂V_R

V_ϕ

z = h, где температура T и объемная доля φ на-

+μ

∇²V_ϕ +

(4)

R²

∂ϕ

R²

ночастиц поддерживаются постоянными: T

= T_d,

φ = φ_d при z = 0 и T = T_u, φ = φ_u при z = h,

)

причем T_d > T_u, φ_u > φ_d (рис. 1). Считаем, что

⁽∂V_z

μ_e

жидкость находится в постоянном гравитационном

ρ₀

+ (V · ∇)V_z

(H · ∇)H_z =

∂t

4π

поле g, направленном по оси z вертикально вниз:

(

)

∂

μ_eH²

g = (0,0,-g). Электропроводящая жидкость вра-

P +

+ μ∇²V_z -

∂z

8π

щается с угловой скоростью Ω, направленной верти-

кально вверх по оси z. Вращение жидкости создает

− [φρ_p + (1 - φ)ρ₀(1 - β(T - T_u))]g,

(5)

стационарный поток в азимутальном направлении:

V₀ = e_ϕΩ(R)R, где Ω(R) — угловая скорость вра-

(

)

щения с произвольной зависимостью от координа-

∂T

(ρc)_f

+ (V · ∇)T

=k_f∇²T+

ты R. Кроме того, мы полагаем, что наножидкость

∂t

(

)

находится в спиральном магнитном поле H₀, кото-

∇T · ∇T

+ (ρc)_p D_B∇φ · ∇T + D_T

(6)

рое представимо в виде суммы неоднородного ази-

T_u

мутального H0ϕ(R) и однородного аксиального H0z

полей:

∂φ

+ (V · ∇)φ = D_B∇²φ +

D_T ∇

²T,

(7)

H₀ = H0ϕ(R)e_ϕ + H0ze_z, H0z = const.

(1)

∂t

T_u

Топологической характеристикой силовых линий

∂H_R

спирального магнитного поля (1) является псевдо-

+ (V · ∇)H_R - (H · ∇)V_R =

скалярная величина — магнитная спиральность [37]:

∂t

(

)

∂H_ϕ

H_R

H0z

∂

=η

∇²HR -

(8)

H₀ · rotH₀ =

(RH0ϕ).

(2)

R²

∂ϕ

R²

R ∂R

1093

М. И. Копп, А. В. Тур, В. В. Яновский

ЖЭТФ, том 159, вып. 6, 2021

⎛

⎞

⎛

⎞

⎛

⎞

∂H_ϕ

V_R

u_R

+(V · ∇)H_ϕ - (H · ∇)V_ϕ+

(V_ϕH_R-V_RH_ϕ) =

∂t

⎜

⎟

⎜

⎟

⎜

⎟

(

)

⎝V_ϕ⎠=

⎝Ω(R)R⎠+

⎝u_ϕ⎠,

∂H_R

H_ϕ

=η

∇²H_ϕ +

(9)

V_z

u_z

R²

∂ϕ

R²

⎛

⎞

⎛

⎞

⎛

⎞

H_R

b_R

(12)

∂H_z

⎜

⎟

⎜

⎟

⎜

⎟

+ (V · ∇)H_z - (H · ∇)V_z = η∇²H_z,

(10)

⎝H_ϕ⎠=

⎝H0ϕ⎠+

⎝b_ϕ⎠,

∂t

H_z

H0z

b_z

∂V_R

V_R

1 ∂V_ϕ

∂V_z

= 0,

P = P_b + p, T = T_b + T^′, φ = φ_b + φ^′.

∂R

R ∂ϕ

∂z

(11)

∂H_R

H_R

1 ∂H_ϕ

∂H_z

Равновесие стационарного течения обеспечивается

= 0,

∂R

R ∂ϕ

∂z

балансом сил в радиальном направлении:

где скалярное произведение A · ∇ и лапласиан Δ ≡

dP_b

μ_eH0ϕ d

≡ ∇² соответственно равны

Ω²R =

(RH0ϕ).

(13)

ρ0 dR

4πρ₀R dR

∂

A_ϕ ∂

∂

A·∇=A_R

+A_z

В вертикальном направлении стационарному состо-

∂R

R ∂ϕ

∂z

янию удовлетворяет уравнение гидростатики

∂

∂²

Δ=

dP_b

∂R²

R ∂R

R² ∂ϕ²

∂z²

= -g[φ_b(ρ_p - ρ₀) + ρ₀ - ρ₀β(T_b - T_u)].

(14)

Здесь ρ₀ = φρ_p + (1 - φ)ρ_f — плотность наножид-

кости при контрольной температуре T_u, ρ_p — плот-

Стационарные профили температуры T_b = T_b(z) и

объемной доли наночастиц φ_b = φ_b(z) находятся из

ность наночастиц, ρ_f — плотность базовой жидко-

сти при температуре T_u, φ — объемная доля нано-

решений уравнений

частиц, β — коэффициент теплового расширения,

k_f d²T_b

(ρc)_p

(ρc)_f и (ρc)_p — эффективные теплоемкости базовой

(ρc)_f dz²

(ρc)_f

жидкости и наночастиц, D_B — коэффициент бро-

(

)

)₂

уновской диффузии, D_T — коэффициент термофо-

dφ_b dT_b

D_T

⁽ dT_b

× D_B

(15)

ретической диффузии. Знаки коэффициентов D_B и

dz dz

T_u dz

D_T положительные, а сами коэффициенты равны

d²φ_b

D_T d²T_b

0=D

k_BT

0.26k_f

^B dz² +

T_u

dz²

D_B =

D_T =

3πμd_p

ρ_f 2k_f + k_p

С учетом граничных условий находим линейные за-

где dp — диаметр наночастиц, kB — постоянная

висимости от z для T_b(z) и φ_b(z):

Больцмана, k_f и kp — коэффициенты теплопровод-

ности базовой жидкости и наночастиц, μ — вязкость

T_d - T_u

φ_d - φ_u

T_b(z) = T_d -

z, φ_b(z) = φ_d -

базовой жидкости. Коэффициенты магнитной про-

ницаемости μ_e, магнитной вязкости η и электропро-

Далее нас будет интересовать вопрос об устойчивос-

водности равны

ти малых возмущений физических величин (u =

= (u_R, u_ϕ, u_z), b = (b_R, b_ϕ, b_z), p, T^′, φ^′) на фоне ста-

μ_e = φμ_ep+(1-φ)μ_ef , η =

= φη_p+(1-φ)η_f ,

4πμ_eσ

ционарного состояния. Подставляя уравнения (12) в

(3)-(11), получим уравнения эволюции малых воз-

σ = φσ_p + (1 - φ)σ_f,

мущений в линейном приближении:

где μ_ep и μ_ef — магнитные проницаемости наноча-

∂u_R

μ_e

стиц и базовой жидкости, η_p и η_f — магнитные вяз-

+Ω

- 2Ωu_ϕ -

∂t

∂ϕ

4πρ₀

кости наночастиц и базовой жидкости, σ_p и σ_f — ко-

)

⁽H0ϕ ∂b_R

2H0ϕb_ϕ

∂b_R

∂p

эффициенты электропроводности наночастиц и ба-

+H0z

∂ϕ

∂z

ρ₀ ∂R

зовой жидкости.

(

)

∂u_ϕ

u_R

Представим все величины в уравнениях (3)-(11)

+ν

∇²u_R -

ν =

(16)

в виде суммы стационарной и возмущенной частей:

R² ∂ϕ

R²

ρ₀

1094

ЖЭТФ, том 159, вып. 6, 2021

Гидромагнитные неустойчивости в неоднородно вращающемся слое...

∂u_ϕ

— магнитное число Россби, характеризующее свой-

+Ω

+ 2Ω(1 + Ro)u_R -

∂t

∂ϕ

ства азимутального магнитного поля [17].

)

⁽H0ϕ ∂b_R

2H0ϕ

∂b_ϕ

Отметим, что для твердотельного вращения па-

(1+Rb) +H0z

4πρ₀

∂ϕ

∂z

раметр Россби равен нулю, Ro = 0, в случае кепле-

(

)

∂p

∂u_R

u_ϕ

ровского вращения, Ω(R) ∝ R-3/2, параметр Россби

+ν

∇²u_ϕ +

(17)

ρ₀R ∂ϕ

R²

∂ϕ

R²

равен Ro = -3/4, для рэлеевского профиля угло-

вой скорости Ω(R) ∝ R-2, соответственно, Ro = -1.

)

Если азимутальная составляющая H0ϕ(R) = 2I/R

∂u_z

μ_e

⁽H0ϕ ∂b_z

∂b_z

+Ω

+H0z

магнитного поля H₀ создается внешним аксиаль-

∂t

∂ϕ

4πρ₀

∂ϕ

∂z

ным током I, изолированным от жидкости, то для

∂p

такой зависимости (H0ϕ

∝ R-1) магнитное чис-

+ν∇²u_z -

[φ^′(ρ_p - ρ₀) - ρ₀βT^′],

(18)

ρ₀ ∂z

ρ₀

ло Россби Rb = -1. В этом случае спиральность

магнитного поля равна нулю: H₀ · rot H₀

= 0.

Магнитное число Россби равно нулю, Rb

= 0,

∂T^′

⁽T_d -T_u)

+Ω

-u_z

=χ_f∇²T^′-

при линейной зависимости азимутального магнит-

∂t

∂ϕ

[

ного поля от радиальной координаты, H0ϕ(R) ∝

(ρc)_p

⁽T_d-T_u ) dφ^′

⁽φ_d-φ_u) dT^′

D_B

+D_B

∝ R, но спиральность магнитного поля при этом

(ρc)_f

]

не исчезает: H₀ · rot H₀ = 2H0zH0ϕ/R. Магнитно-

′

2D_T

⁽T_d - T_u) dT

му числу Россби Rb = 1/2 соответствует квадра-

χ_f =

(19)

T_u

(ρc)_f

тичная зависимость азимутального магнитного по-

ля от радиального направления, H0ϕ(R) ∝ R². Для

этого случая спиральность магнитного поля рав-

∂φ^′

⁽φ_u -φ_d)

+Ω

+u_z

на H₀ · rot H₀

= 3H0zH0ϕ/R. Отметим, что для

∂t

∂ϕ

случая однородного азимутального магнитного поля

=D_B∇²φ^′ +

D_T ∇²T^′,

(20)

H0ϕ = const спиральность не исчезает, H₀ · rotH₀ =

T_u

= H0zH0ϕ/R, а магнитное число Россби принимает

значение Rb = -1/2.

∂b_R

H0ϕ ∂u_R

∂u_R

+Ω

-H0z

∂t

∂ϕ

∂z

(

)

∂b_ϕ

b_R

3. ЛОКАЛЬНОЕ ВКБ-ПРИБЛИЖЕНИЕ И

=η

∇²b_R -

(21)

R² ∂ϕ

R²

ДИСПЕРСИОННОЕ УРАВНЕНИЕ

Систему уравнений (16)-(24) будем использовать

∂b_ϕ

H0ϕ ∂u_ϕ

∂u_ϕ

+Ω

-H0z

-2ΩRob_R +

для исследования вопроса устойчивости малых осе-

∂t

∂ϕ

∂z

(

)

симметричных возмущений. Поскольку характер-

2H0ϕ

∂b_R

b_φ

ный масштаб неоднородности среды в горизонталь-

Rbu_R = η

∇²b_ϕ +

(22)

R² ∂ϕ

R²

ной плоскости больше, чем в вертикальном направ-

лении, L_R ≫ L_h, мы можем применить локальный

∂b_z

H0ϕ ∂u_z

∂u_z

+Ω

-H0z

= η∇²b_z,

(23)

метод ВКБ для возмущений, зависящих от радиаль-

∂t

∂ϕ

∂z

ных координат R. Для этой цели разложим все ве-

∂u_R

u_R

1 ∂u_ϕ

∂u_z

= 0,

личины в ряд Тейлора в окрестности фиксирован-

∂R

R ∂ϕ

∂z

(24)

ной точки R₀, оставляя члены нулевого порядка по

∂b_R

b_R

1 ∂b_ϕ

∂b_z

локальным координатам

R = R - R₀. В результа-

= 0,

∂R

R ∂ϕ

∂z

те получим систему дифференциальных уравнений

где p = p + (1/4π) H₀ · b — общее возмущенное дав-

с постоянными коэффициентами с учетом следую-

ление,

щих соотношений:

R ∂Ω

Ro =

2Ω ∂R

∂²

∂

D≡

Ω₀ = Ω(R₀),

∇² →

D²+

— гидродинамическое число Россби, характеризую-

∂R2

R₀ ∂R

∂z

щее неоднородность вращения среды,

(

))

(

)

(

)

u_R

∂

∇²

=∇²

Rb =

(H0ϕR-1)

b_R

R²

b_R

2H0ϕR-1 ∂R

1095

М. И. Копп, А. В. Тур, В. В. Яновский

ЖЭТФ, том 159, вып. 6, 2021

(

))

(

)

(

)

(

)

(

)

u_ϕ

L_χ =

D² -

+k²

L_φ =

D² -

+k²

∇²

=∇

χ_f

D_B

b_ϕ

R²

b_ϕ

Для последующего анализа системы уравнений

Все возмущения в системе уравнений (16)-(24) пред-

(26)-(33) удобно привести ее к безразмерному виду,

ставим в виде плоских волн:

вводя безразмерные величины, которые отметим

⎛

⎞

⎛

⎞

звездочкой:

U(z)

⎜

⎟

⎜

⎟

⎜b⎟

⎜B(z)⎟

⎜

⎟

⎜

⎟

(R∗0, z^∗) = h-1(R₀, z),

⎜

⎟

⎜

⎟

T^′

Θ(z)

xp(γt + ikR).

(25)

⎜

⎟

⎜

⎟^e

⎜

⎟

⎜

⎟

(

)

⎝φ^′⎠

⎝Φ(z)⎠

U^∗R, U^∗ϕ, U^∗z

(U_R, U_ϕ, U_z),

χ_f

P (z)

(

)

B^∗R, B^∗ϕ, B^∗z

= H-10(B_R, B_ϕ, B_z), H₀ = H0z,

Подставляя (25) в систему уравнений (16)-(24), в

коротковолновом приближении k ≫ 1/R₀, пренебре-

ϕ^∗ = ϕ, Θ^∗ =

Φ^∗ =

гая членами ik/R₀ - 1/R²⁰, находим

T_d - T_u

φ_u - φ_d

(

)

h²

( ν

∂

h2 ∂

2Ω

μ_eH0ϕ

P^∗ =

t^∗ = t

L_νU_R +

U_ϕ -

B_ϕ +

ρ₀νχ_f

h²

∂t^∗

ν ∂t

2πρ₀νR₀

μ_eH0z

Опуская звездочку, получим следующую систему

DB_R -

P = 0,

(26)

4πρ₀ν

νρ₀

безразмерных уравнений:

√

L_νU_R +

TaU_ϕ - 2 Pr Pm-1QξB_ϕ +

μ_eH0ϕ

L_νU_ϕ-2Ω(1+Ro)UR+

(1+Rb)B_R +

2πρ₀νR₀

+ PrPm-1QDB_R - i

P = 0,

(34)

μ_eH0z

DB_ϕ = 0,

(27)

4πρ₀ν

√

L_νU_ϕ-

Ta(1+Ro)U_R+2 Pr Pm-1Qξ(1+Rb)B_R +

μ_eH0z

+ PrPm-1Q DB_ϕ = 0,

(35)

L_νU_z +

DH_z -

P-

4πρ₀ν

νρ₀

L_νU_z +PrPm-1QDB_z -

P +RaΘ-R_nΦ = 0, (36)

(Φ(ρ_p - ρ₀) - ρ₀βΘ) = 0,

(28)

ρ₀ν

(

)

N_B

L_χΘ+U_z +

^DΘ -

^DΦ -2NAN^B DΘ = 0, (37)

L_e

)

(

)

⁽T_d-T_u

(ρc)_pD_B

⁽T_d -T_u

L_χΘ+

U_z-

^DΦ -

L_φΦ - L_eU_z + N_A

D² - k2 Θ = 0,

(38)

χ_f h

(ρc)_f χ_f

[

(ρc)_p

⁽φ_d -φ_u)

D_B

L_ηB_R + Pr-1PmDU_R = 0,

(39)

(ρc)_f χ_f

)]

2D_T

⁽T_d -T_u

^DΘ = 0,

(29)

L_ηB_ϕ + Pr-1PmDU_ϕ - 2Pr-1PmξRbU_R +

T_u

√

)

+ PmRo

TaB_R = 0,

(40)

(

)

⁽φ_d -φ_u

D_T

L_φΦ+

U_z +

D² - k2 Θ = 0, (30)

D_Bh

D_BT_u

L_ηB_z + Pr-1PmDU_z = 0,

(41)

L_ηB_R +H0z

DU_R = 0,

(31)

где операторы

L_ν,

L_η,

L_χ,

L_φ в безразмерных пере-

менных имеют вид

2Ω

L_ηB_ϕ +H0z

DU_ϕ -2H0ϕ

RbU_R +

RoB_R = 0, (32)

ηR₀

L_ν =

D² - γ - k²,

L_η =

D² - Pmγ - k²,

L_ηB_z +H0z

DU_z = 0.

(33)

L_χ =

D² - Prγ - k²,

L_φ =

D² - PrL_eγ - k².

Здесь введены следующие обозначения для опера-

В уравнениях (34)-(41) введены безразмерные па-

торов:

раметры Ta = 4Ω²h⁴/ν² — число Тейлора, Pr =

)

⁽γ

= ν/χ_f — число Прандтля, Pm

= ν/η — маг-

L_ν =

D² -

+k²

L_η =

D² -

+k²

нитное число Прандтля, Q

= μ_eH²⁰h²/4πρ₀νη —

1096

ЖЭТФ, том 159, вып. 6, 2021

Гидромагнитные неустойчивости в неоднородно вращающемся слое...

(

)

число Чандрасекара, ξ = H0ϕh/R0H0 — отноше-

√

a₁₂ =

Ta + 2Qξ

ние азимутального магнитного поля к аксиальному,

L_η

D² - k²

Ra = (T_d - T_u)ρ₀gβh³/μχ_f — число Рэлея, R_n =

= (ρ_p - ρ_f )(φ_u - φ_d)gh³/μχ_f — концентрационное

⎡

число Рэлея, L_e = χ_f /D_B — число Льюиса,

L_φ -NB D

ikD

⎢

L_e

(ρc)_p

a₁₃ =

⎢

N_B = (φ_u - φ_d)

⎣^R

D² - k²

(ρc)_f

⎤

— коэффициент, характеризующий прирост плотно-

(

сти наночастиц, и

R_n

)) ⎥

LL_e + N_A(D2 - k²)

L_φ -NB

⎥,

LL_φ

L_e

⎦

D_T (T_d - T_u)

N_A =

D_BT_u(φ_u - φ_d)

— коэффициент модифицированной диффузии.

√

Уравнения (34)-(41) дополняются уравнениями

a₂₁ = -

Ta(1+Ro)+QRoPm

-2Qξ

L_η

соленоидальности полей u и b:

DU_z + ikU_R = 0,

DB_z + ikB_R = 0.

(42)

a₂₂ =

L_ν - Q

D² ,

L_η

Используя условие (42), из уравнений (34) и (36) ис-

ключаем давление

(

)

2Qξik

√

a₃₁ =

2ξRb

TaRoPm

^[√

L_η

P =

TaikU_ϕ -

D² - k²

(

)

(

)

√

DU_ϕ

U_R

- 2Qξik

+2ξRb

+PmRo

U_R

a₃₂ = -

Ta + 2Qξ

L_η

D² - k²

(

)

N_B

L_φ -

L_e

(

)

- Ra

U_z -

k²Ra

a₃₃ =

L_ν - Q

L_φ -NB D +

L_η

L_e

(

)

^L(D2 - k²)

(

))

- R_n

LLe + N_A

D² - k²

k²R_n

LL_φ

LL_e+N_A(D2-k²)

L_φ-NB D

(

))

]

LL_φ(D2-k²)

L_e

L_φ -NB

D Uz ,

(43)

L_e

Уравнение (44) дополняется граничными условиями

где оператор

только в z-направлении:

^L=

L_χ L_φ+NB

(1 - 2N_A)Lφ D+NAN^B ( D²-k²) D.

d²U_z

L_e

U_z =

при z = 0, z = 1.

(45)

dz²

Подставляя выражение (43) в систему линейных

Уравнение (44) описывает конвективные явления

уравнений (34)-(41), в результате несложных, но

в тонком слое неоднородно вращающейся электро-

громоздких преобразований получим одно диффе-

проводящей наножидкости во внешнем спиральном

ренциальное уравнение для U_z:

магнитном поле.

[a₃₃ (a₁₁a₂₂ - a₂₁a₁₂) +

Выберем функцию U_z, удовлетворяющую сво-

бодным граничным условиям (45), в следующем ви-

+ a13 (a₂₁a₃₂ - a₃₁a₂₂)]U_z = 0,

(44)

де:

где

U_z = U0z sinnπz (n = 1, 2, 3, . . .),

(46)

где U0z = const — амплитуда возмущений z-компо-

a₁₁ =

L_ν - Q

−

L_η

ненты скорости. Подставляя (46) в (44) и проводя

(

)

интегрирование по толщине слоя z = (0, 1), получим

√

- 2Qξ

2ξRb +

TaRoPm

дисперсионное уравнение для одномодового прибли-

L_η

L_η(D2 - k²)

жения (n = 1):

1097

ЖЭТФ, вып. 6

М. И. Копп, А. В. Тур, В. В. Яновский

ЖЭТФ, том 159, вып. 6, 2021

[

a₃ = Pr²L_e[2a⁸(1 + Pm) + 2π²a⁴Q(1 + Pm)+

Ra = a²Γ4AΓ_η(a²Γ2AΓ2φΓ_χ - m₀) + a²Γ2AΓ2φΓ_χm₁ -

+ 2π²a²Pm Ta(1 + Ro)] + a²(1 + L_e)×

)

]

⁽N_B

N_AN_B

- π²a²Γ²

Γ_φ

(1-2N_A)Γ_φ+

a²

m₂

× Pr[a⁶(1 + 4Pm + Pm²) + 2a²Pmπ²Q+

L_e

[

]-1

+ π²Pm²Ta(1 + Ro)] + 2a⁸Pm(1 + Pm)-

π²

× k²Γ_ηΓ_φ(a²Γ_ηΓ_φΓ4A+

(N_B-N_A)m₂)

(47)

- k²R_nL_e(PrPma²(2 + Pm) + a²Pm²),

L_e

где введены обозначения

a₄ = a² Pr(1+L_e)[2a⁸(1+Pm)+2π²a⁴Q(1+Pm)+

+ 2π²a²Pm Ta(1 + Ro)] + Pr²L_e[a²(a⁴ + π²Q)² +

Γ2A = (γ + a²)(γPm + a²) + π²Q, Γ_χ = γ Pr+a²,

+ π²a⁴Ta(1 + Ro) + π⁴PmRoTaQ] +

Γ_η = γPm + a², Γ_φ = γPrL_e + a²,

+ a⁴[a⁶(1+4Pm + Pm²) + 2a²Pmπ²Q +

a² = π² + k², m₀ = k²R_nΓ_ηΓ_φ(L_eΓ_χ + a²N_A),

+ π²Pm²Ta(1+Ro)] - k²R_nL_e(Pr(a⁴(1 + 2Pm)+

+ π²QPm) + a⁴Pm(2 + Pm)),

m₁ = π²Ta(1 + Ro)Γ3η + π⁴QTaRoPmΓ_η -

a₅ = a²(1+L_e)Pr[a²(a⁴+π²Q)²+π²a⁴Ta(1+Ro)+

- 4π⁴Q²ξ²Γ_η - 4π²Qξ²Γ2ARbΓ_η,

+ π⁴PmRoTaQ]+a⁴[2a⁸(1+Pm)+2π²a⁴Q(1+Pm)+

√

+ 2π²a²Pm Ta(1+Ro)]-k²R_nL_e(a²Pr(a⁴+π²Q)+

m₂ = 2π²Qξ

Ta[(2 + Ro)Γ2η + PmRo(π²Q - Γ2A)].

+ a⁶(1 + 2Pm) + π²a²QPm),

В отсутствие азимутального магнитного поля (ξ =

= 0) и наночастиц (R_n = N_B = 0) дисперсион-

a₆ = a⁴[a²(a⁴ + π²Q)² + π²a⁴Ta(1 + Ro)+

ное уравнение (47) совпадает с результатами работы

π⁴PmRoTaQ] - k²a⁴(a⁴ + π²Q)R_nL_e.

[12], а при ξ = 0 и R_n = N_B = 0 — с результатами

работы [15].

В предельном случае, когда нет наночастиц, т. е. для

«чистой» электропроводящей жидкости, дисперси-

онное уравнение (48) совпадает с результатами рабо-

4. ДИСПЕРСИОННОЕ УРАВНЕНИЕ ДЛЯ

ты [13]. Аналитическое решение уравнения (48) в об-

СТАНДАРТНОЙ МВН В ТОНКИХ СЛОЯХ

щем случае невозможно. Однако вывод об устойчи-

НАНОЖИДКОСТИ

вости возмущений, описываемых уравнением (48) с

действительными коэффициентами, можно сделать,

Рассмотрим случай, когда температура на грани-

не решая его, а лишь анализируя его коэффициен-

цах слоя наножидкости одинаковая (Ra = N_A = 0)

ты с применением критериев Рауса - Гурвица или

и внешнее азимутальное магнитное поле отсутству-

Льенара - Шипара [38]. В последнем критерии число

ет (ξ = 0). Тогда из уравнения (47) мы получим

детерминантных неравенств примерно вдвое мень-

дисперсионное уравнение для стандартной МВН в

ше, чем в условиях Рауса - Гурвица, поэтому целе-

тонком слое наножидкости в виде полинома шестой

сообразно его использование. Критерий Льенара -

степени по γ:

Шипара асимптотической устойчивости возмуще-

ний, описываемых алгебраическим уравнением (48),

P (γ) ≡ a₀γ⁶ + a₁γ⁵ + a₂γ⁴ + a₃γ³ +

состоит в следующем. Для того чтобы многочлен

+ a₄γ² + a₅γ + a₆ = 0,

(48)

P (γ) имел все корни с отрицательными веществен-

ными частями, необходимо и достаточно, чтобы

где коэффициенты a_j (j = 0, . . . , 6) имеют вид

а) все коэффициенты многочлена P(γ) были по-

ложительны: a_j > 0, j = 0, . . . , 6;

a₀ = Pr²Pm²L_ea²,

б) имели место неравенства для определителей

Гурвица: Δj-1 > 0, Δj-3 > 0, . . ., где Δ_m — обозна-

a₁ = 2Pr²PmL_ea⁴(1 + Pm) + Pr(1 + L_e)a⁴Pm²,

чает определитель Гурвица порядка m:



a₁

a₃

a₅

··



a₂ = Pr²L_e[a⁶(1 + 4Pm + Pm²) + 2a²Pmπ²Q +



a₀

a₂

a₄

··



+ π²Pm²Ta(1+Ro)] + 2a⁶(1+L_e)PrPm(1+Pm)+

Δ_m =



a₁

a₃

··



+ a⁶Pm² - k²R_nL_ePm²,



a_m

1098

ЖЭТФ, том 159, вып. 6, 2021

Гидромагнитные неустойчивости в неоднородно вращающемся слое...

Используя алгоритм Льенара - Шипара, получим

π²

k2z

→ξ² =

необходимые и достаточные условия устойчивости:

a²

k2z + k²

получим

a_j > 0, j = 0, . . ., 6, Δ₃ > 0, Δ₅ > 0.

(49)

ω2A + 2Ω²ξ²(1 + Ro) > 0,

Подставляя значения коэффициентов a_j в условия

√

где ω_A =

μ_ek2zH²⁰/4πρ₀ — альфвеновская частота.

(49), находим следующие неравенства:

4. Неравенства a₄ > 0 и a₅ > 0 не содержат но-

1. (a₀ > 0) ⇒ Pr²Pm²L_ea² > 0,

вых условий стабилизации возмущений.

5. Неравенство a₆ > 0 запишем в виде

(a₁ > 0) ⇒ 2Pr²PmL_ea⁴(1 + Pm) +

+ Pr(1 + L_e)a⁴Pm² > 0.

a²(a⁴ + π²Q)² + π²a⁴Ta

Ro > -

π²Ta(a⁴ + π²QPm)

Эти неравенства выполняются автоматически.

k²(a⁴ + π²Q)R_nL_e

2. (a₂ > 0) ⇒ Pr²L_e[a⁶(1 + 4Pm + Pm²)+

= Ro_cr,

(50)

π²Ta(a⁴ + π²QPm)

+ 2a²Pmπ²Q + π²Pm²Ta(1 + Ro)] +

+ 2a⁶(1 + L_e)PrPm(1 + Pm)+

где параметр Ro_cr — критическое число Россби на

границе устойчивости, соответствующее нейтраль-

+ a⁶Pm² > k²R_nL_ePm².

ному состоянию γ = 0. Выражение (50) в предель-

ном случае «чистой» электропроводящей жидкости

Отсюда видно, что диссипативные процессы есте-

переходит в известное выражение для критического

ственно приводят к стабилизации устойчивости те-

числа Россби Ro [17]:

чений наножидкости. Стабилизирующими фактора-

ми также выступают однородное магнитное поле и

a²(a⁴ + π²Q)² + π²a⁴Ta

неоднородное вращение, если профиль угловой ско-

Ro_cr = -

π²Ta(a⁴ + π²QPm)

рости вращения соответствует положительным чис-

лам Россби (Ro > 0). Напротив, концентрация на-

или, при переходе к размерным переменным

ночастиц приводит к дестабилизации течения нано-

жидкости.

π²Q

ω2A

π²QPm

ω2A

4Ω²

→

a⁴

ω_νω_η

a⁴

ω2η

a⁴

ω2ν

3. (a₃ > 0) ⇒ Pr²L_e[2a⁸(1+Pm)+2π²a⁴Q(1+Pm)+

)₂

+ 2π²a²Pm Ta(1 + Ro)] + a²(1 + L_e)Pr×

π²

⁽k

→α² =

× [a⁶(1 + 4Pm + Pm²) + 2a²Pmπ²Q+

a²

|k|

+ π²Pm²Ta(1+Ro)]+2a⁸Pm(1+Pm) > k²R_nL_e×

находим

× (PrPma²(2 + Pm) + a²Pm²).

(ω2A + ω_ν ω_η)² + 4α²Ω²ω2η

Ro_cr = -

Отсюда мы видим, что однородное магнитное поле

4Ω²α²(ω2A + ω2η)

и неоднородное вращение с положительными чис-

лами Россби (Ro > 0) также оказывают стабилизи-

Здесь ω_ν = ν|k|², ω_η = η|k|² — частоты вязкостной

рующее действие, а концентрация наночастиц (чле-

и омической диссипаций, |k|² = k2R + k2z.

ны с концентрационным числом Рэлея R_n) оказыва-

Перейдем теперь к условиям устойчивости, со-

ет дестабилизирующее влияние. Для «чистой», иде-

стоящим из неравенств с определителями Гурвица

ально электропроводящей, жидкости в однородном

(49). Для определителя Δ₃,

магнитном поле это неравенство совпадает с извест-



ным критерием устойчивости Велихова [20]:



a₁

a₃

a₅



Δ₃ =

a0

a₂

a₄

 = a1a2a3 + a0a1a5 - a¹a4 - a0a³,



2π²QPm-1 +

Ta(1 + Ro) > 0,

₀



a₁

a₃

a²

или, при переходе к размерным переменным

критерий устойчивости имеет вид

π²Q

h⁴

4Ω²h⁴

→

ω2A, Ta(1 + Ro) →

(1 + Ro),

a₁a₂a₃ + a₀a₁a₅ > a²¹a₄ + a₀a²³.

(51)

ν²

1099

М. И. Копп, А. В. Тур, В. В. Яновский

ЖЭТФ, том 159, вып. 6, 2021

Для второго определителя Гурвица из условия (49),



a₁

a₃

a₅



a0

a₂

a₄

a₆



Δ₅ =



a₁

a₃

a₅



= a₁a₂(a₃a₄a₅-a₂a²⁵)-



a₀

a₂

a₄



₀



a₁

a₃

a₅

− a₁a₄(a₁a₄a₅ - a₀a²⁵) + a₁a₆(a₁a₂a₅ - a₀a₃a₅)-

- a₃a₀(a₃a₄a₅ - a₂a²⁵) + a₅a₀(a₁a₄a₅ - a₀a²⁵),

получим следующий критерий устойчивости:

a₄a₅(a₁a₂a₃ + a₀a₁a₅ - a²¹a₄ - a₀a²³)+

+ a²¹a₂a₅a₆ + a₀a²⁵(a₂a₃ + a₁a₄) >

> a₀a₁a₃a₅a₆ + a²⁵(a₁a²² + a²⁰a₅).

(52)

Критерии устойчивости (51) и (52) показывают, что

концентрация наночастиц оказывает дестабилизи-

рующее действие на устойчивость осесимметричных

возмущений.

Используя выражение для критического числа

Россби (50), численным методом определим обла-

сти развития стандартной МВН в «чистой» жидко-

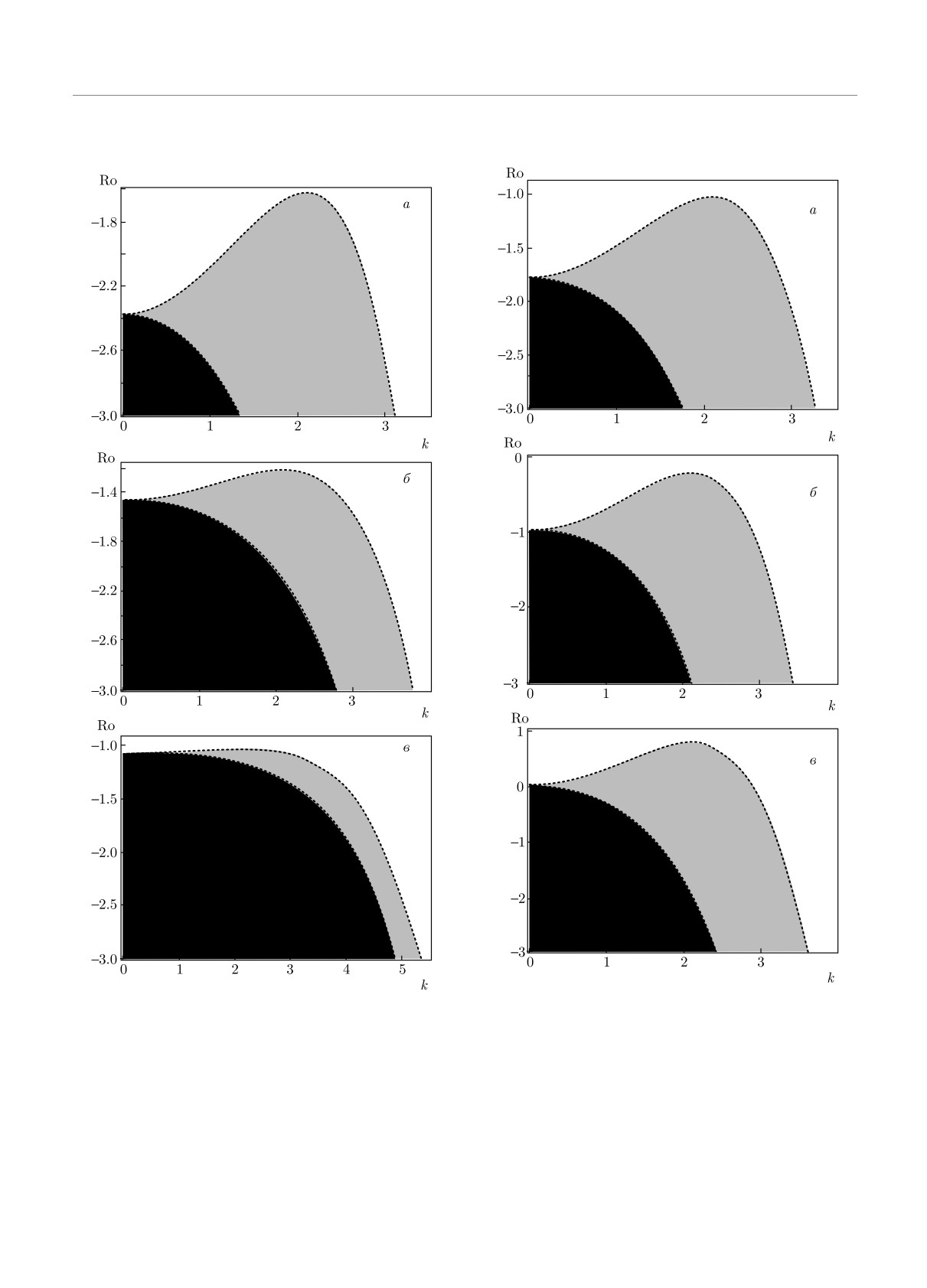
сти и наножидкости. На рис. 2 выделены области

неустойчивости для чисел Россби Ro < Ro_cr при из-

менении параметра вращения Ta (числа Тейлора) в

плоскости (k, Ro), где k — безразмерное радиальное

волновое число. Черным цветом на рис. 2 показа-

ны области неустойчивости в «чистой» жидкости, а

серым цветом — в наножидкости. На рис. 2 видно,

что при небольших числах Тейлора Ta = 100, 300

область развития стандартной МВН в наножидкос-

ти (рис. 2а,б) намного больше области неустойчи-

вости для «чистой» жидкости, R_n

= 0. Напро-

тив, при больших числах Тейлора Ta = 2000 обла-

сти неустойчивости для наножидкости и «чистой»

жидкости уже не так сильно различаются. Значе-

ния параметров R_n = 0.122, L_e = 5000, Pr = 5,

N_A = 5, N_B = 7.5 · 10-4 для наножидкости (напри-

мер Al₂O₃-вода) взяты из работы [11].

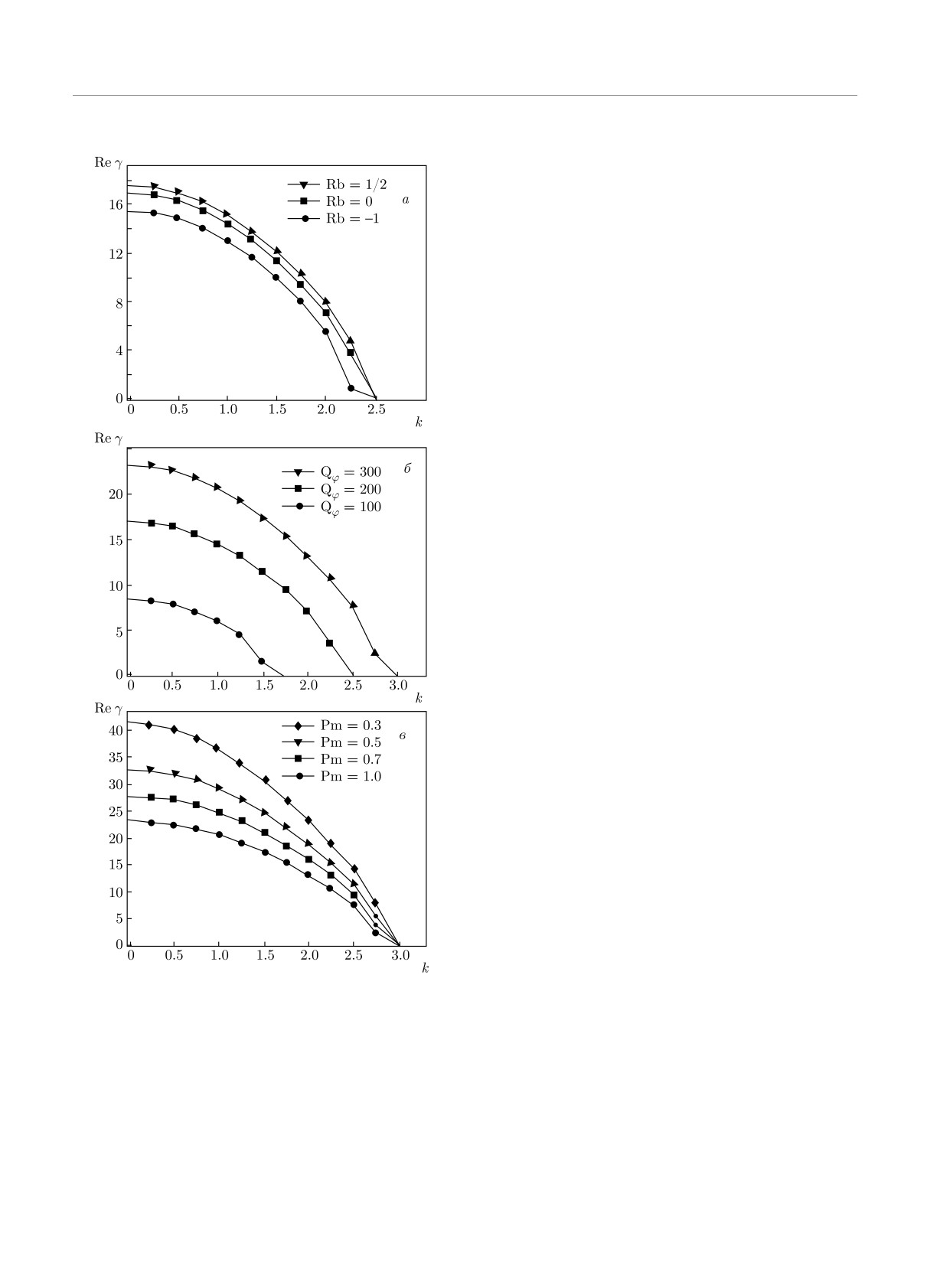
На рис. 3 представлены численные результаты

темпа роста стандартной МВН, т.е. для положи-

тельного вещественного корня (Re γ > 0) дисперси-

Рис. 2. Черным цветом показаны области, в которых воз-

онного уравнения (48), в зависимости от радиаль-

никает стандартная МВН в «чистой» жидкости, и се-

ного волнового числа k. Считая параметры нано-

рым цветом — в наножидкости для параметров Q = 10,

жидкости фиксированными (Pr = 5, R_n = 0.122,

Pm = 1, Rn = 0.122, Le = 5000 и чисел Тейлора Ta =

L_e = 5000, рис. 3a), видим, что темпы роста осесим-

= 100 (а), 300 (б), 2000 (в)

метричных возмущений в случае рэлеевского про-

филя вращения (Ro = -1) выше, чем для случая

кеплеровского (Ro = -3/4) профиля вращения при

1100

ЖЭТФ, том 159, вып. 6, 2021

Гидромагнитные неустойчивости в неоднородно вращающемся слое...

числах Тейлора Ta = 2000. На рис. 3б показаны тем-

пы роста стандартной МВН при различных значени-

ях аксиального магнитного поля Q = 10, 50, 150 для

рэлеевского профиля вращения (Ro = -1) и чис-

ла Тейлора Ta = 2000. Здесь мы видим, что увели-

чение напряженности аксиального магнитного поля

H0z может приводить как к увеличению инкремента

неустойчивости (Q = 10 → Q = 50), так и к умень-

шению инкремента при Q = 50 → Q = 150. Ва-

риации магнитного числа Прандтля Pm также мо-

гут существенно повлиять на развитие стандартной

МВН в наножидкости (рис. 3в). Для фиксирован-

ных параметров Ta = 2000, Q = 10, Ro = -1 мы на-

блюдаем, что темпы роста возмущений значительно

ниже при числах Прандтля Pm ≪ 1.

Отметим, что при изменении физических харак-

теристик наножидкости, например электропровод-

ности σ, теплопроводности χ и вязкости ν, от кото-

рых зависят безразмерные параметры Q, Pr, Pm, Ta,

R_n, при рэлеевском профиле вращения (Ro = -1)

вполне возможно развитие стандартной МВН.

5. ДИСПЕРСИОННОЕ УРАВНЕНИЕ ДЛЯ

АЗИМУТАЛЬНОЙ МВН В ТОНКИХ СЛОЯХ

НАНОЖИДКОСТИ

Рассмотрим неоднородно вращающийся слой на-

ножидкости с постоянной и одинаковой темпера-

турой на границах слоя во внешнем азимутальном

магнитном поле H0ϕ. В этом случае осевое магнит-

ное поле равно нулю, H0z = 0, и Ra = N_A = 0. При

этом стационарный поток наножидкости совпадает

с направлением магнитного поля. Таким образом,

такая геометрия задачи соответствует азимутальной

МВН [17]. Дисперсионное уравнение для азимуталь-

ной МВН в тонких слоях наножидкости получим из

уравнения (47), полагая H0z = 0:

P (γ) ≡ a₀γ⁶ + a₁γ⁵ + a₂γ⁴ + a₃γ³ +

+ a₄γ² + a₅γ + a₆ = 0,

(53)

где коэффициенты a_j (j = 0, . . . , 6) имеют вид

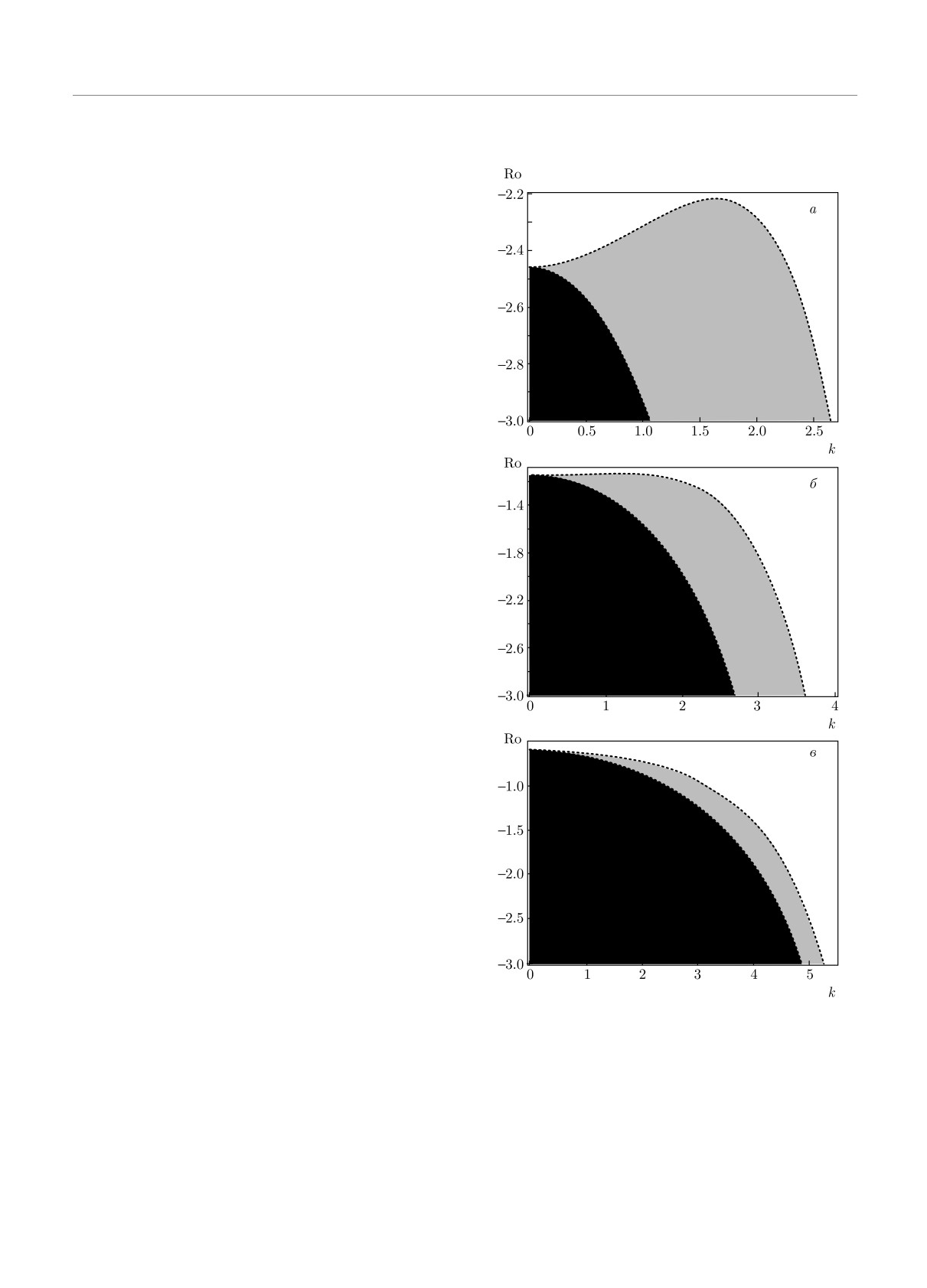
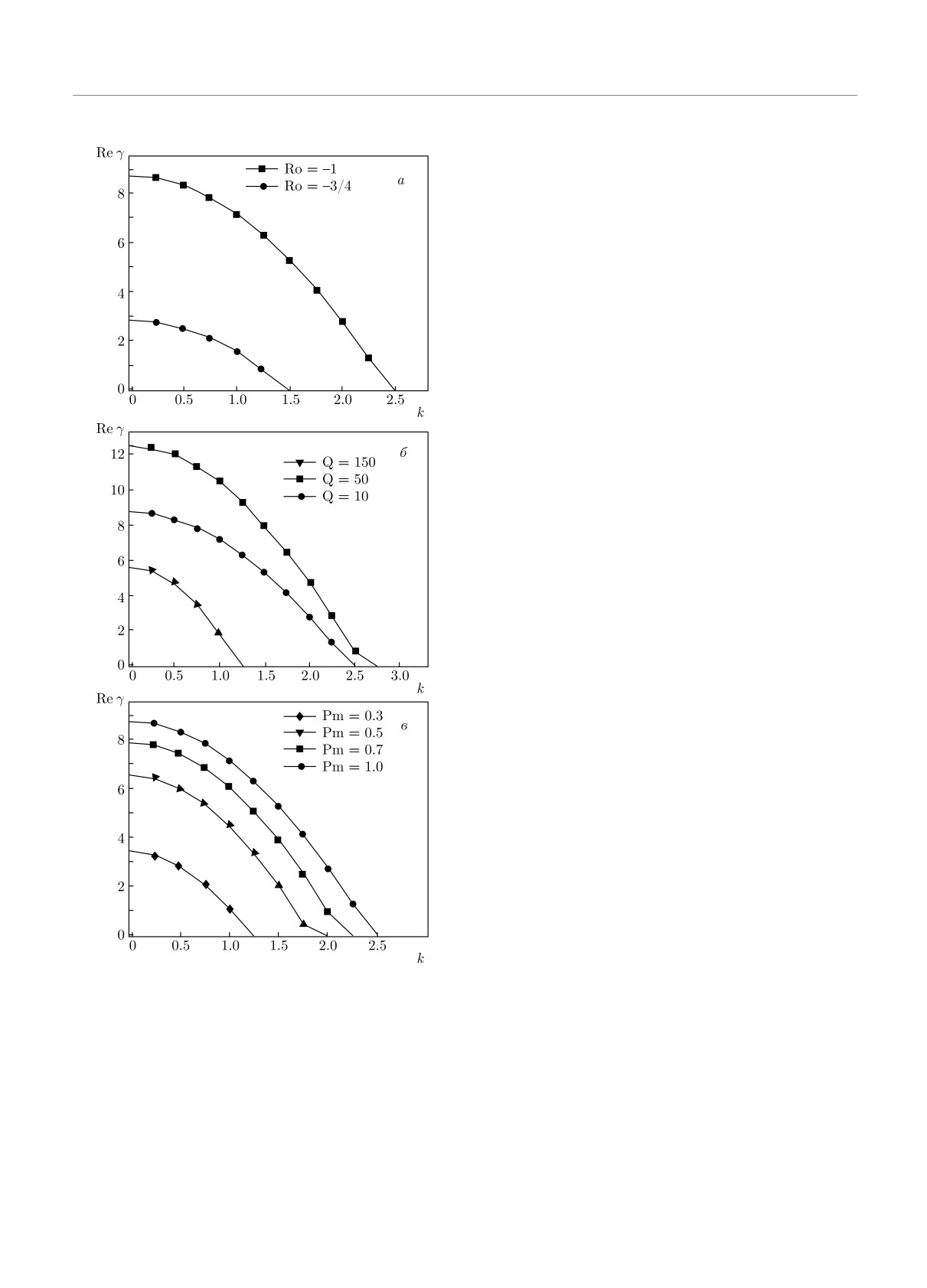
Рис. 3. Зависимости инкремента (Re γ > 0) стандарт-

ной МВН в наножидкости от радиального волнового чис-

a₀ = Pr²Pm²L_ea², a₁ = Pr(1 + L_e)a⁴Pm²,

ла k. Показаны темпы роста возмущений для рэлеевского

(Ro = -1) и кеплеровского (Ro = -3/4) профилей враще-

ния (а), для разных значений величины аксиального маг-

a₂ = a⁶[Pm² + 2Pm(1 + Pm)Pr(1 + L_e)+

нитного поля (числа Чандрасекара) Q = 10, 50, 150 (б)

и для различных значений магнитного числа Прандтля

+ Pr²L_e(1 + Pm²) + 4PmPr²L_e] +

Pm = 0.3, 0.5, 0.7, 1.0 (в)

+ π²Pm²Pr²Ta(1 + Ro)Le -

- k²R_nLe PrPm² - 4π²Q_ϕRbPmPr²L_e,

1101

М. И. Копп, А. В. Тур, В. В. Яновский

ЖЭТФ, том 159, вып. 6, 2021

a₃ = a⁸[2Pm(1+Pm)+Pr(1+L_e)(1+4Pm+Pm²)] +

Течение идеальной «чистой» жидкости было рас-

смотрено в работе [19], в которой кинетическая и

+ π²a²Ta(1 + Ro)(2PmPr²L_e + Pm2 Pr(1 + L_e))-

магнитная энергии равны друг другу:

- k²a²R_nL_e(Pm² + PmPr(2 + Pm))-

ρ₀(ΩR)²

H20ϕ

- 4π²a²Q_ϕRb(Pr²L_e(1 + Pm) + PmPr(1 + L_e)),

4π

a₄ = a¹⁰[2 Pr(1 + Pm)(1 + L_e) + Pr²L_e] +

В [19] было найдено точное стационарное реше-

ние идеальной магнитной гидродинамики: Ω

+ π²a⁴Ta(1+Ro)(Pr²L_e+2PmPr(1+L_e)+Pm²)-

= H0ϕ/R√2πρ0, P = const, называемое чандрасека-

- k²a⁴R_nL_e(Pm(2 + Pm) + Pr(2Pm + 1))-

ровской эквипартицией. Там же было доказано, что

- 4π²a⁴Q_ϕRb(Pr²L_e + Pr(1 + Pm)(1 + L_e) + Pm),

это течение предельно устойчиво. Из эквипартиции

Чандрасекара следует, что [17]

a₅ = a¹²[2(1+Pm)+ Pr(1+L_e)]+π²a⁶Ta(1+Ro)×

μ_eH20ϕ

× (Pr(1+L_e)+2Pm)-k²a⁶R_nL_e(Pr+2Pm+1) -

ω_Aϕ =

= Ω, Ro = Rb = -1.

(56)

4πρ₀R²

- 4π²a⁶Q_ϕRb(Pr(1 + L_e) + 1 + Pm),

Случай чандрасекаровской эквипартиции (56) удо-

a₆ = a¹⁴+π²a⁸Ta(1+Ro)-k²a⁸R_nL_e-4π²a⁸Q_ϕRb.

влетворяет неравенству (55). Следовательно, крите-

Здесь Q_ϕ

= μ_eH20ϕh⁴/4πρ₀R²⁰νη — азимутальное

рии устойчивости для идеальных наножидкостей и

число Чандрасекара. Вещественность коэффициен-

«чистых» жидкостей сопадают с (55).

тов a_j в уравнении (53) позволяет нам использовать

Приступим к исследованию вопроса о развитии

критерий асимптотической устойчивости Льена-

азимутальной МВН в наножидкости для осесиммет-

ра - Шипара, из которого следует положительность

ричных возмущений при числах Россби Ro < Ro_cr.

коэффициентов a_j > 0 и определителей Гурвица Δ₃,

Для этой цели численным способом построим облас-

Δ₅ > 0. Из явного вида коэффициентов a_j следует,

ти развития неустойчивости для различных значе-

что неоднородное вращение с положительными

ний параметров вращения Ta (числа Тейлора), ази-

числами Россби (Ro > 0) оказывает стабилизирую-

мутального магнитного поля Q_ϕ (азимутальное чис-

щее действие, а концентрация наночастиц (члены

ло Чандрасекара) и магнитного числа Россби Rb.

с концентрационным числом Рэлея R_n) — деста-

Для параметров Rb = -1, Q_ϕ = 10, R_n = 0.122,

билизирующее влияние. Азимутальное магнитное

L_e = 5000 на рис. 4 показаны области развития ази-

поле H0ϕ оказывает как стабилизирующее, так

мутальной МВН в плоскости (k, Ro) для различных

и дестабилизирующее влияние в зависимости от

чисел Тейлора Ta = 100, 300, 2000. На рис. 4 видно,

знака магнитного числа Россби Rb. Условие a₆ > 0

что наличие концентрации наночастиц способствует

дает следующий критерий устойчивости:

увеличению области неустойчивости по сравнению с

k²R_nL_e

4Q_ϕRb

«чистой» электропроводящей средой. На рис. 5 по-

Ro > -1 -

= Ro_cr,

(54)

π²Ta

казаны области развития азимутальной МВН с по-

или, в размерных переменных,

ложительным профилем неоднородного магнитного

поля (Rb = 1/2) в плоскости (k, Ro) для различных

ω2ν

ω2Aϕ ω_ν

R_nL_eω2ν

Ro > -1-

+Rb

+(1-α²)

азимутальных чисел Чандрасекара Q_ϕ = 10, 50, 100.

4α²Ω²

Ω²

ω_η

4α²Ω²(|k|h)⁴

Остальные параметры, Ta = 100, R_n = 0.122, L_e =

Для случая «чистой» электропроводящей жид-

= 5000, считались фиксированными. Здесь мы так-

кости критерий устойчивости (54) при R_n = 0 пере-

же видим (см. рис. 5), что наличие концентрации на-

ходит в более простой критерий, полученный в ра-

ночастиц способствует увеличению области неустой-

боте [39]. При ω_Aϕ = 0 и R_n = 0 критерий устой-

чивости по сравнению с «чистой» электропроводя-

чивости (54) согласуется с результатом работы [40].

щей средой. Кроме того, при увеличении величины

Очевидно, что вращающийся поток идеальной нано-

азимутального магнитного поля (числа Q_ϕ) граница

жидкости при ω_ν = ω_η и ω_ν → 0, на который дей-

области неустойчивости смещается в сторону поло-

ствует азимутальное магнитное поле, устойчив от-

жительных чисел Россби (Ro > 0).

носительно осесимметричных возмущений, если вы-

С помощью численного анализа дисперсионного

полняется неравенство

уравнения (53) определим зависимость инкремен-

та (Re γ

> 0) азимутальной МВН от радиально-

ω²

Aϕ

Ro > -1 + Rb

(55)

го волнового числа k для ранее приведенных па-

Ω²

1102

М. И. Копп, А. В. Тур, В. В. Яновский

ЖЭТФ, том 159, вып. 6, 2021

раметров наножидкости. На рис. 6a показано вли-

яние различных профилей неоднородного азиму-

тального магнитного поля (магнитные числа Россби

Rb = -1, 0, 1/2) на инкремент азимутальной МВН

для следующих параметров: Ta = 2000, Ro = -1.2,

Q_ϕ = 10, Pm = 1. Отсюда мы видим, что тем-

пы роста возмущений здесь выше для положитель-

ных магнитных чисел Россби (Rb > 0). Далее, ис-

следуем влияние эффекта усиления азимутального

магнитного поля (азимутальные числа Чандрасека-

ра Q_ϕ = 100, 200, 300) на развитие азимутальной

МВН для фиксированных параметров Ta = 300,

Ro = -1, Rb = 1/2, Pm = 1. Как следует из

результатов, показанных на рис. 6б, темпы роста

возмущений становятся выше с увеличением напря-

женности азимутального магнитного поля H0ϕ. На

рис. 6в приведены численные результаты для ин-

кремента Re γ(k) азимутальной МВН, полученные

для различных значений магнитного числа Прандт-

ля Pm = 0.3, 0.5, 0.7, 1.0 при фиксированной вели-

чине азимутального магнитного поля Q_ϕ = 300 и

Ta = 300, Ro = -1, Rb = 1/2. На рис. 6в видно уве-

личение темпов роста возмущений для магнитных

чисел Прандтля Pm < 1.

Таким образом, азимутальная МВН в наножид-

кости реализуется при увеличении неоднородного

азимутального магнитного поля H0ϕ = CR^α ( α > 1)

с положительным профилем Rb > 0 для магнитных

чисел Прандтля Pm ≤ 1.

6. ДИСПЕРСИОННОЕ УРАВНЕНИЕ ДЛЯ

СПИРАЛЬНОЙ МВН В ТОНКИХ СЛОЯХ

НАНОЖИДКОСТИ

В случае Ra = N_A = 0 из уравнения (47) мы

получим дисперсионное уравнение для спиральной

МВН в тонких слоях наножидкости:

P (γ) ≡ a₀γ⁷ + a₁γ⁶ + a₂γ⁵ + a₃γ⁴ + a₄γ³ +

+ a₅γ² + a₆γ + a₇ = 0,

(57)

где коэффициенты a_j (j = 0, . . . , 7) имеют вид

a₀ = A₀, a₁ = A₁, a₂ = A₂ - k²R_nL_e PrPm³,

Рис. 6. Зависимости инкремента (Re γ > 0) азимутальной

МВН в наножидкости от радиального волнового числа k.

a₃ = A₃ - k²a²R_nL_e(Pm³ + PrPm²(3 + Pm)),

Показаны эффекты влияния неоднородного азимутально-

го магнитного поля при Rb = -1, 0, 1/2 (а), величины ази-

a₄ = A₄ - C₀ - k²R_nL_e(PrPm²(a⁴ + π²Q)+

мутального магнитного поля при Q_ϕ = 100, 200, 300 (б) и

+ a⁴Pm(Pr+Pm)(3 + Pm)),

магнитного числа Прандтля при Pm = 0.3, 0.5, 0.7, 1.0 (в)

на азимутальную МВН

a₅ = A₅ - C₁ - k²R_nL_e(Pr(2a²Pm(a⁴ + π²Q)+

+a⁶(1+Pm))+a²Pm²(a⁴+π²Q)+a⁶Pm(3+Pm)),

1104

ЖЭТФ, том 159, вып. 6, 2021

Гидромагнитные неустойчивости в неоднородно вращающемся слое...

a₆ = A₆ - C₂ - k²R_nL_e(2a⁴Pm(a⁴ + π²Q)+

A₇ = a⁶(a²(a⁴ + π²Q)² + π²a⁴Ta(1 + Ro)+

+ a⁸(1 + Pm) + a⁴(a⁴ + π²Q)Pr),

+π⁴PmRoTaQ - 4π²Qξ²Rb(a4 + π²Q) - 4π⁴Q²ξ²),

√

a₇ = A₇ - C₃ - k²a⁶R_nL_e(a⁴ + π²Q).

C₀ = 4π⁴Qξ

TaN_B Pr Pm²,

Здесь введены следующие обозначения для A_n (n =

√

= 0, . . ., 7) и C_m (m = 0, . . ., 3):

C₁ = 2π⁴a²QPmξ

Ta ×

[

]

2N_B

A₀ = a²Pr²Pm³L_e,

× N_B Pr(4 + Ro(1 - Pm)) +

Pm ,

A₁ = a⁴Pm² Pr[2 PrL_e(1+Pm)+PrL_e +Pm(1+L_e)],

[

√

C₂ = 2π⁴a⁴Qξ

B Pr(2 + Ro(1 - Pm)) +

A₂ = a⁶[Pm²(Pm + Pr(1 + L_e)) + 2Pm(1 + Pm)×

]

× Pr(PrL_e + Pm(1 + L_e))] + (a⁶(1 + 4Pm + Pm²)+

N_B Pm(4 + Ro(1 - Pm)) ,

L_e

+ 2a²Pmπ²Q + π²Pm²Ta(1 + Ro)-

√

- 4π²Qξ²RbPm)PmPr²L_e,

C₃ = 2π⁴a⁶Qξ

N_B (2 + Ro(1 - Pm)).

L_e

В предельных случаях, когда H0ϕ = 0, дисперсион-

A₃ = a⁸[Pm² + 2Pm(1 + Pm)(Pm + Pr(1 + L_e))] +

ное уравнение (57) совпадает с дисперсионным урав-

нением (48) для стандартной МВН, а при H0z = 0 —

+ a2 Pr(a⁶(1 + 4Pm + Pm²) + 2a²Pmπ²Q+

с дисперсионным уравнением (54) для азимутальной

+ π²Pm²Ta(1 + Ro) - 4π²Qξ²RbPm)×

МВН. К дисперсионному уравнению (57) с действи-

× (Pr L_e + Pm(1 + L_e)) + (2a⁴(1 + Pm)(a⁴ + π²Q) +

тельными коэффициентами a_j (j = 0, . . ., 7) при-

+2a²π²Ta(1+Ro)Pm-4π²a²Qξ²Rb(1+Pm))PmPr²L_e,

меним классический критерий устойчивости Льена-

ра - Шипара [38]. Из явного вида коэффициентов

следует, что дестабилизация осесимметричных воз-

A₄ = 2a¹⁰Pm(1 + Pm) + a⁴(a⁶(1 + 4Pm + Pm²)+

мущений может быть вызвана неоднородным вра-

щением с отрицательным профилем (Ro < 0), спи-

+ 2a²Pmπ²Q+π²Pm²Ta(1+Ro)-4π²Qξ²RbPm)×

ральным магнитным полем с положительным про-

× (Pm+Pr(1+L_e))+a² Pr(2a⁴(1+Pm)(a⁴+π²Q) +

филем неоднородного азимутального магнитного

+ 2a²π²Ta(1 + Ro)Pm - 4π²a²Qξ²Rb(1 + Pm))×

поля (Rb > 0), концентрацией наночастиц (R_n = 0),

× (Pr L_e + Pm(1 + L_e)) + (a²(a⁴ + π²Q)² +

а также совместным эффектом спирального магнит-

ного поля и прироста наночастиц (N_B = 0), если

+ π²a⁴Ta(1 + Ro) + π⁴PmRoTaQ-

магнитное число Прандтля Pm = 1. Поскольку пе-

- 4π²Qξ²Rb(a⁴ + π²Q) - 4π⁴Q²ξ²)PmPr²L_e,

реход к неустойчивости происходит через точку γ =

= 0, получаем необходимое и достаточное условие

устойчивости вращающейся наножидкости по отно-

A₅ = a⁶(a⁶(1 + 4Pm + Pm²) + 2a²Pmπ²Q +

шению к осесимметричным возмущениям:

+ π²Pm²Ta(1 + Ro) - 4π²Qξ²RbPm)+

Ro >

+ a⁴(2a⁴(1+Pm)(a⁴+π²Q)+2a²π²Ta(1+Ro)Pm-

-a²(a⁴ + π²Q)² - π²a⁴Ta + k²(a⁴ + π²Q)R_nL_e

- 4π²a²Qξ²Rb(1 + Pm))(Pm + Pr(1 + L_e))+

√

+a² Pr(a²(a⁴+π²Q)²+π²a⁴Ta(1+Ro)+π⁴PmRoTaQ-

π²Ta(a⁴ + π²QPm) - 2π⁴Qξ

N_B (1 - Pm)

L_e

-4π²Qξ²Rb(a⁴+π²Q)-4π⁴Q²ξ²)(Pr L_e+Pm(1+L_e)),

√

N_B

4Qξ²(Rb(a⁴ + π²Q) + π²Q) + 4π²Qξ

L_e

√

A₆ = a⁶(2a⁴(1+Pm)(a⁴+π²Q)+2a²π²Ta(1+Ro)Pm-

Ta(a⁴ + π²QPm) - 2π²Qξ

N_B (1 - Pm)

- 4π²a²Qξ²Rb(1 + Pm)) + a⁴(Pm + Pr(1 + L_e))×

= Ro_cr,

(58)

× (a²(a⁴ + π²Q)² + π²a⁴Ta(1 + Ro) + π⁴PmRoTaQ -

или, в размерных переменных,

− 4π²Qξ²Rb(a⁴ + π²Q) - 4π⁴Q²ξ²),

1105

М. И. Копп, А. В. Тур, В. В. Яновский

ЖЭТФ, том 159, вып. 6, 2021

ω_νω_η

-(ω

+ ω_νω_η)² - 4α²Ω²ω2η + (1 - α²)(ω2A + ω_νω_η)R_nL_e

(|k|h)

Ro >

ω_η

N_B

4α²Ω²(ω2A + ω2η) - 4α³ΩωAωAϕ

(1 - Pm)

(|k|h) L_e

ω_η N_B

(Rb(ω2A + ω_ν ω_η) + ω2A) + 2αΩω_Aω_Aϕ

Aϕ

(|k|h) L_e

= Ro_cr.

ω_η

N_B

Ω²

(ω2A + ω²

) - αΩω_Aω_Aϕ

(1 - Pm)

(|k|h) L_e

Условие устойчивости (58) включает в себя получен-

вития спиральной МВН с положительным профи-

ные в предыдущих разделах критерии устойчивости

лем неоднородного магнитного поля (Rb = 1/2) в

для стандартной МВН при H0ϕ = 0 и азимутальной

плоскости (k, Ro) для различных азимутальных чи-

МВН при H0z = 0. Если Ro = 0 и Ta = 0, то необ-

сел Чандрасекара Q_ϕ = 30, 50, 80 при фиксирован-

ходимое и достаточное условие устойчивости нано-

ных параметрах Q = 10, Ta = 100, Pm = 0.7, Rb =

жидкости по отношению к осесимметричным возму-

= 1/2, R_n = 0.122, L_e = 5000, N_B = 7.5 · 10-4. Здесь

щениям дает ограничение на профиль неоднородно-

мы также видим (см. рис. 8), что наличие концен-

го азимутального магнитного поля:

трации наночастиц способствует увеличению облас-

ти неустойчивости по сравнению с «чистой» элект-

Rb > Rb_cr,

ропроводящей средой. Кроме того, при увеличении

Rb_cr =

величины азимутального магнитного поля (числа

(59)

a²(a⁴+π²Q)²-4π⁴Q²ξ²-k²R_nL_e(a⁴+π²

Q_ϕ), как и в случае азимутальной МВН, граница

4π²Qξ²(a⁴ + π²Q)

области неустойчивости смещается в сторону поло-

жительных чисел Россби (Ro > 0).

или, в размерных переменных,

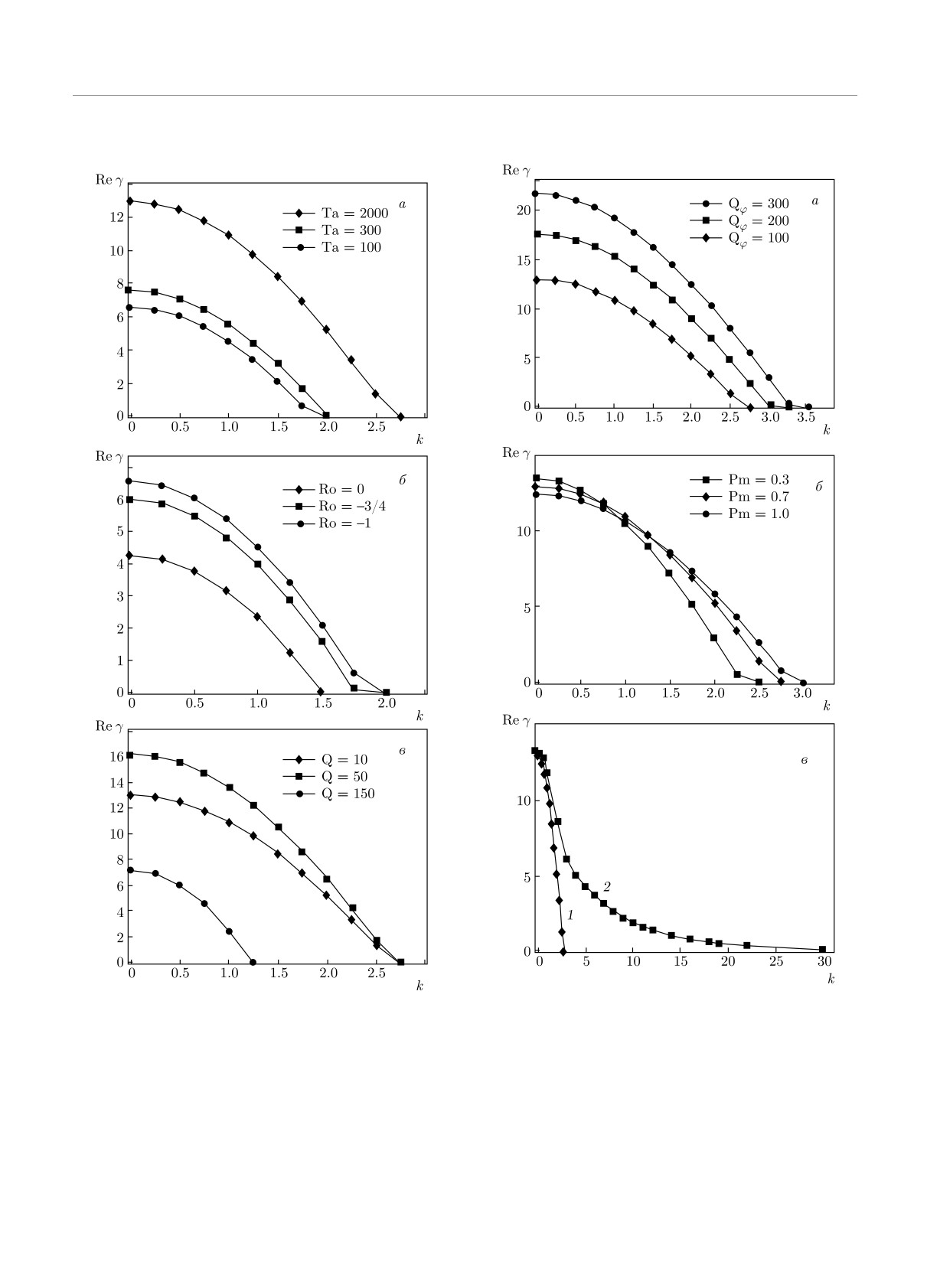
Приступим к численному анализу дисперсион-

(ω2A + ω_ν ω_η)² - 4α²ω2Aω2Aϕ

ного уравнения (57). На рис. 9 показана зависи-

Rb >

4α²ω2Aϕ(ω2A + ω_νω_η)

мость инкремента спиральной МВН от радиаль-

ω_νω_η

ных волновых чисел k для различных вариаций

(1 - α

²)

R_nL_e(ω2A + ω_νω_η)

(|k|h)⁴

физических параметров наножидкости. На рис. 9a

= Rb_cr.

4α²ω2Aϕ(ω2A + ω_νω_η)

видно, что темп роста возмущений повышается с

увеличением эффекта вращения — числа Тейлора

Выражение (59) переходит в передельном случае

Ta = 100, 300, 2000. Остальные параметры наножид-

«чистой» жидкости при R_n = 0 в известное выра-

кости считались фиксированными: Q = 10, Q_ϕ =

жение для критического магнитного числа Россби

= 100, Pm = 0.7, Pr = 5, Rb = 1/2, Ro = -1, R_n =

Rb_cr, которое было получено в работе [41].

= 0.122, L_e = 5000, N_B = 7.5· 10-4. Для этих же па-

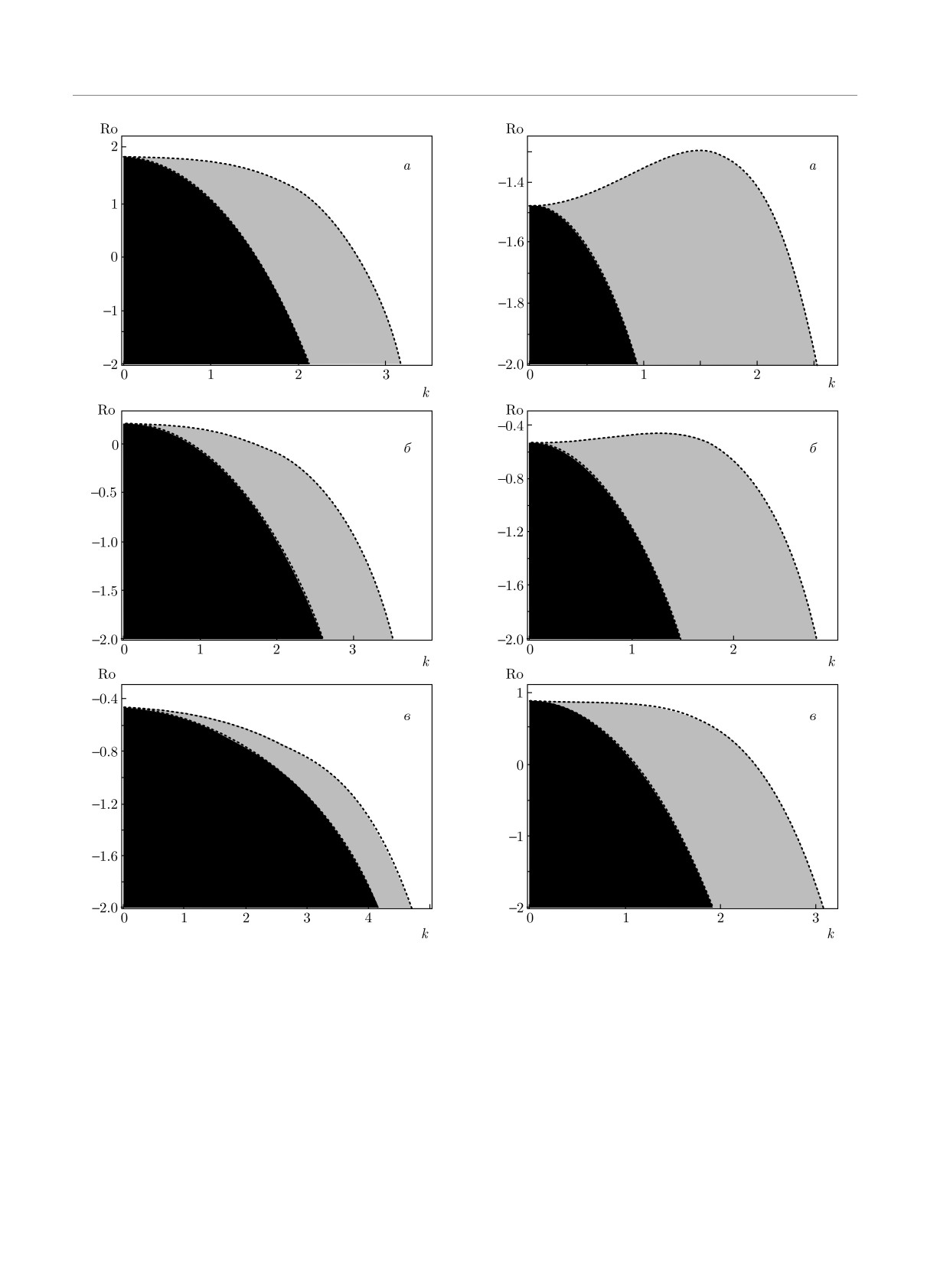
Определим область развития спиральной МВН в

раметров на рис. 9б показаны графики инкремента

тонком слое наножидкости, которая возникает для

спиральной МВН для вращающейся наножидкости

чисел Россби Ro < Ro_cr. С помощью численного

с числом Тейлора Ta = 100 и различными числами

анализа из выражения (58) для критического чис-

Россби Ro = 0, -3/4, -1. Отсюда следует, что тем-

ла Россби определим области развития спиральной

пы роста осесимметричных возмущений выше для

МВН в «чистой» жидкости и наножидкости. На

отрицательных чисел Россби (Ro < 0), чем в случае

рис. 7 серым цветом выделены области неустойчи-

однородного вращения (Ro = 0):

вости наножидкости для чисел Россби Ro < Ro_cr

γ(k)|Ro=-1 > γ(k)|Ro=-3/4 > γ(k)|_Ro=0.

при изменении параметра вращения Ta = 100, 300,

2000 (числа Тейлора) в плоскости (k, Ro). Осталь-

На рис. 9в показаны темпы роста спиральной МВН

ные параметры наножидкости считались фиксиро-

при различных значениях аксиального магнитно-

ванными: Q = 10, Q_ϕ = 100, Pm = 0.7, Rb = 1/2,

го поля Q = 10, 50, 150 для рэлеевского профиля

R_n = 0.122, L_e = 5000, N_B = 7.5·10-4. На рис. 7 вид-

вращения (Ro = -1) и числа Тейлора Ta = 2000.

но, что наличие концентрации наночастиц способ-

Отсюда мы видим, что увеличение напряженно-

ствует увеличению области неустойчивости по срав-

сти аксиального магнитного поля H0z может приво-

нению с «чистой» электропроводящей средой, для

дить как к увеличению инкремента неустойчивости

которой области неустойчивости показаны черным

(Q = 10 → Q = 50), так и к уменьшению инкремента

цветом на рис. 7. На рис. 8 показаны области раз-

при Q = 50 → Q = 150.

1106

ЖЭТФ, том 159, вып. 6, 2021

Гидромагнитные неустойчивости в неоднородно вращающемся слое...

магнитного поля H0ϕ. На рис. 10б показаны графи-

где Ra_r и Ra_i — действительная и мнимая части

ки инкремента спиральной МВН для значений маг-

дисперсионного уравнения для Ra. Так как вели-

нитного числа Прандтля Pm = 0.3, 0.7, 1.0. Из этих

чина Ra является действительной, мнимая часть в

результатов следует, что увеличение темпов роста

(60) должна обращаться в нуль. При этом возмож-

Re γ(k) для магнитных чисел Прандтля Pm < 1 про-

на ситуация ω_i = 0 или Ra_i = 0. Рассмотрим случай

исходит при смещении в длинноволновую (малые k)

ω_i = 0. В результате получаем критическое значение

область спектра возмущений. Результаты влияния

числа Рэлея Ra_c для монотонных или стационарных

на спиральную МВН эффекта концентрации нано-

возмущений: Ra_c = Ra_st.

частиц приведены на рис. 10в. Кривая 1 построена

для следующих параметров наножидкости: Q = 10,

7.1. Стационарный режим конвекции в

Q_ϕ = 100, Ta = 2000, Pm = 0.7, Pr = 5, Rb = 1/2,

аксиальном магнитном поле

Ro = -1, R_n = 0.122, L_e = 5000, N_B = 7.5 · 10-4.

При увеличении концентрации наночастиц, т. е. при

Из дисперсионного уравнения (60) найдем кри-

увеличении объемной доли наночастиц на верхней

тическое значение числа Рэлея Ra_st для стационар-

границе слоя, φ_u, мы принимаем, что изменяются

ной (γ = 0) конвекции в аксиальном магнитном по-

параметры для следующих величин: концентраци-

ле:

онного числа Рэлея R_n = 1200, рождения наноча-

a⁶

π²a²Q

π²a⁴Ta

стиц N_B = 750 и числа Льюиса L_e = 1000, а осталь-

Ra_st =

k²

k²(a⁴ + π²Q)

ные безразмерные числа (Q, Q_ϕ, Ta, Pm, Pr, Rb, Ro)

остаются без изменений. Кривая 2 на рис. 10в со-

π²TaRo(a⁴ + π²QPm)

- R_n(L_e + N_A).

(61)

ответствует результатам повышенной концентрации

k²(a⁴ + π²Q)

наночастиц. Здесь видно, что при повышенной кон-

Минимальное значение критического числа Рэлея

центрации наночастиц инкремент спиральной МВН

находится из условия ∂Ra_st/∂k = 0 и соответствует

выше, γ₂(0) = 13.28 > γ₁(0) = 12.9, и неустойчи-

волновым числам k = k_c, удовлетворяющим уравне-

вость уже начинает развиваться в коротковолновой

нию

(большие k) части спектра возмущений.

В результате повышения концентрации наночас-

2k2c - π²

π⁴Q

тиц увеличиваются темпы роста спиральной МВН

k_c

k_c(π² + k2c)²

из-за совместного эффекта прироста наночастиц,

2π²k_cTa(1 + Ro)

N_B ≫ 1, и спирального магнитного поля для маг-

(π² + k2c) ((π² + k2c)² + π²Q)

нитных чисел Прандтля Pm < 1.

π²Ta((π² + k2c)² + π²Q + 2k2c(π² + k2c))

kc((π2 + kc)2 + π2Q)2

7. СТАЦИОНАРНЫЕ РЕЖИМЫ

π²TaRo((π² + k2c)² + π²QPm)

МАГНИТНОЙ КОНВЕКЦИИ

k_c(π² + k2c)²((π² + k2c)² + π²Q)²

Приступим к исследованию случая, когда есть

× ((π² + k2c)² + π²Q + 2k2c(π² + k2c)) = 0.

(62)

разности температур и концентраций наночастиц на

границах слоя наножидкости (Ra = 0, N_A = 0), ко-

Из уравнения (62) видно, что критическое волно-

вое число не зависит от параметров наножидкостей

торый неоднородно вращается (Ro = 0) в спираль-

ном магнитном поле (ξ = 0). Будем рассматривать

и совпадает с результатом работы [12]. На рис. 11а

минимальному значению критического числа Рэлея

конвективное течение в плоском неоднородно вра-

щающемся слое в виде валов (ячеек). Скорость γ

Ra^minst соответствует точка на нейтральной кривой,

разделяющей области устойчивых и неустойчивых

роста возмущений в общем случае является ком-

плексной, γ = γ_r +iω_i. Очевидно, что система устой-

возмущений. Здесь видно, что для положительного

профиля числа Россби (Ro ≥ 0) минимальное зна-

чива, если γ_r < 0, и неустойчива, если γ_r > 0. Перей-

чение критического числа Рэлея Ra^minst больше, чем

дем к определению границы устойчивости для мо-

нотонных (ω_i = 0) и колебательных (ω_i = 0) возму-

для отрицательных профилей вращения, например

рэлеевского (Ro = -1). Следовательно, для отри-

щений. На границе устойчивости (нейтральные со-

стояния) γ_r = 0, поэтому, сделав в уравнении (47)

цательных профилей вращения мы получаем более

низкий порог развития неустойчивости по сравне-

замену γ = iω_i, находим

нию со случаем однородного (Ro = 0) и неоднород-

Ra = Ra_r + iω_iRa_i,

(60)

ного (Ro = 2) вращения. На рис. 11б показано, что

1109

М. И. Копп, А. В. Тур, В. В. Яновский

ЖЭТФ, том 159, вып. 6, 2021

Для исследования эффектов вращения, числа

Россби, магнитного поля, числа Люиса, модифици-

рованного коэффициента диффузии и концентра-

ции наночастиц вычислим производные

dR₁

dT₁

dRo

dQ₁

dL_e

dN_A

dR_n

в переменных Чандрасекара

Ra_st

k²

R₁ =

T₁ =

Q₁ =

π⁴

π²

Для этих переменных выражение (61) примет вид

(1+x)((1+x)²+Q₁)²+(1+x)²(1+Ro)T₁

R₁ =

x((1+x)²+Q

)

RoPmQ₁T₁

- R_n(L_e + N_A).

(63)

x((1 + x)² + Q

)

Из выражения (63) находим производные

dR₁

(1 + x)²

dT₁

x((1 + x)² + Q₁)

Ro((1 + x)² + Q₁Pm)

(64)

x((1 + x)² + Q

)

dR₁

T₁((1 + x)² + Q₁Pm)

(65)

dRo

x((1 + x)² + Q₁)

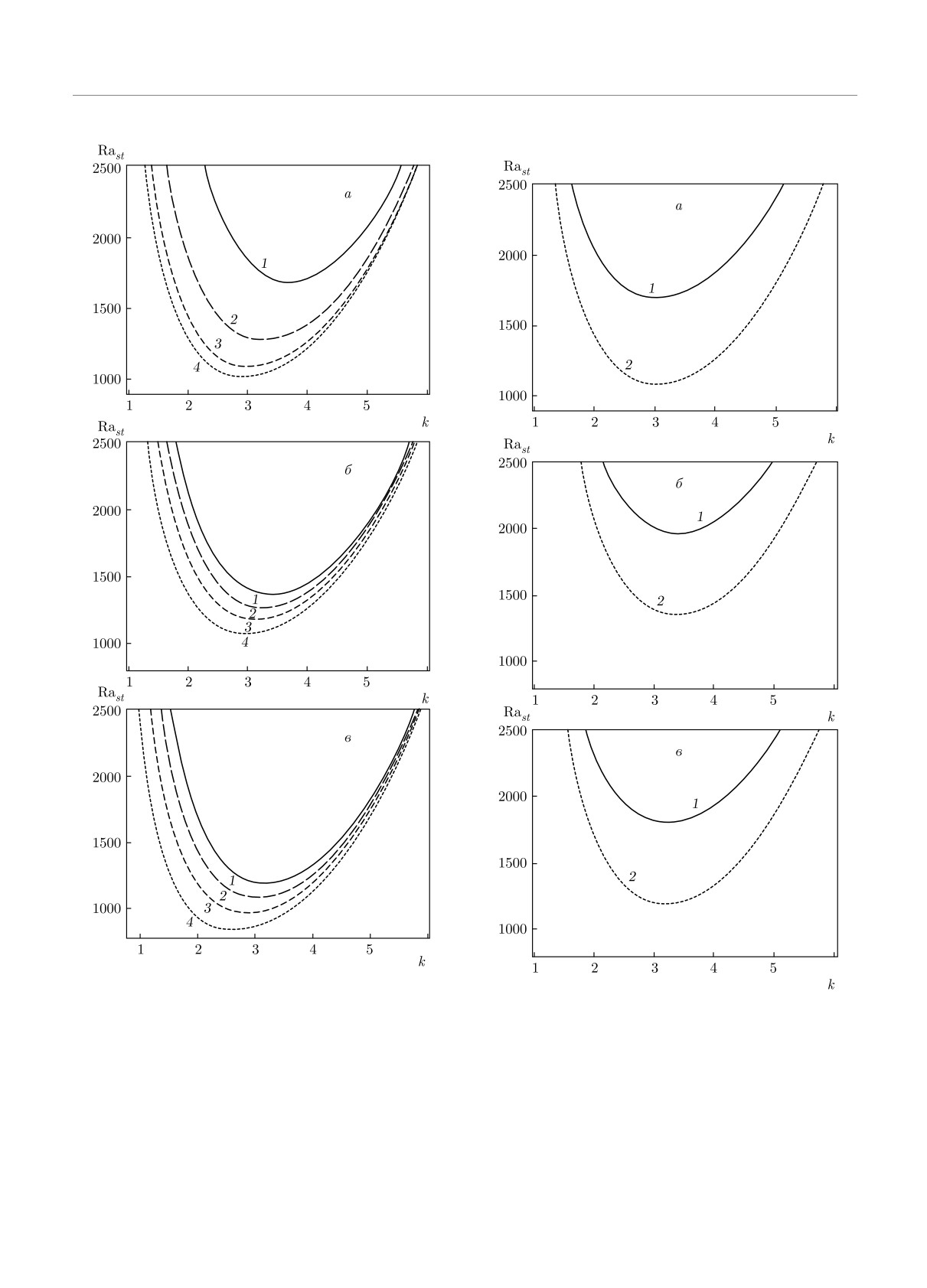
Рис. 11. Зависимости стационарного числа Рэлея Rast от

волновых чисел k для неоднородно вращающейся нано-

dR₁

1+x

(1 + x)²T₁(1 + Ro(1 - Pm))

(66)

жидкости в аксиальном магнитном поле: а — для чисел

dQ₁

x((1 + x)² + Q₁)²

Россби Ro = 2 (кривая 1), 0 (кривая 2), -1 (кривая 3);

б — кривая 1 соответствует «чистой» электропроводящей

dR₁

= -R_n,

(67)

жидкости, кривая 2 — электропроводящей наножидкости

dL_e

dN_A

для числа Россби Ro = 2

dR₁

= -(L_e + N_A).

(68)

dR_n

Из формулы (64) видно, что в случае однород-

концентрация наночастиц способствует понижению

ного вращения (Ro

= 0) сила Кориолиса все-

порога стационарной конвекции. Здесь кривые 1, 2

гда оказывает стабилизирующее действие на кон-

построены для числа Россби Ro = 2, но сделанные

векцию [8, 9]. Однако при неоднородном враще-

выводы остаются в силе при любых числах Ro.

нии (даже в отсутствие внешнего магнитного по-

В некоторых предельных случаях выражение

ля, Q₁ = 0 (см. формулу (64)) сила Кориолиса мо-

(61) содержит уже известные результаты. При от-

жет оказывать дестабилизирующее действие на кон-

сутствии наночастиц (R_n = 0) из (61) получаем кри-

векцию в зависимости от профиля угловой скоро-

тическое число Рэлея для стационарной неоднород-

сти вращения. Для рэлеевского профиля вращения

но вращающейся (Ro = 0) конвекции в постоянном

(Ro = -1) угловая скорость уменьшается с расстоя-

аксиальном магнитном поле [12]. Если в (61) поло-

нием, Ω = const·R-2. Наоборот, при положительных

жить Ro = 0, то мы получим результат работы [11].

Ro > 0, например при Ro = 1, угловая скорость вра-

Для случая Ro = 0 и R_n = 0 мы получаем класси-

щения увеличивается с расстоянием, Ω = const · R².

ческий результат Чандрасекара [8]. При отсутствии

Таким образом, вращение при Ro > 0 стабилизи-

вращения и магнитного поля (Ta = Q = 0) выраже-

рует конвекцию, а при Ro < 0 дестабилизирует. Из-

ние (61) дает результат работы [42].

вестно, что для конечной электропроводности среды

1110

ЖЭТФ, том 159, вып. 6, 2021

Гидромагнитные неустойчивости в неоднородно вращающемся слое...

имеет место частичная «вмороженность» магнитно-

следует, что концентрационное число Рэлея всегда

го поля и неоднородное вращение приводит к иска-

имеет дестабилизирующий эффект. Формулы (67) и

жению силовых линий магнитного поля [37]. В слу-

(68) совпадают с результатами работы [11], где ис-

чае Ro > 0 линии магнитного поля смещаются от

следовалась конвективная неустойчивость однород-

оси вращения, т.е. в сторону увеличения Ω, и на-

но вращающегося слоя наножидкости в постоянном

оборот, при Ro < 0 происходит смещение к оси вра-

вертикальном магнитном поле.

щения. Эффекту влияния неоднородного (диффе-

Таким образом, влияние эффектов вращения,

ренциального) вращения на магнитное поле и, как

числа Россби, магнитного поля на стационарную

следствие, на конвекцию, соответствуют члены, про-

конвекцию в аксиальном магнитном поле происхо-

порциональные RoPm в выражениях (64), (66).

дит независимо от концентрации наночастиц.

Аналогичные выводы следуют из соотношения

(65): при увеличении параметра вращения T₁ на

стационарную конвекцию оказывает влияние про-

филь неоднородного вращения, от которого зависит

7.2. Стационарный режим конвекции в

знак числа Россби. Так, при числах Россби Ro > 0

спиральном магнитном поле

мы также получаем стабилизирующий эффект, по-

скольку производная dR₁/dRo всегда положитель-

Подобным образом из дисперсионного уравнения

на, а при отрицательных числах Россби Ro < 0 —

(60) найдем критическое значение числа Рэлея Ra

дестабилизирующий эффект, так как производная

для стационарной конвекции в спиральном магнит-

dR₁/dRo отрицательная.

ном поле:

Из формулы (66) видно, что величина dR₁/dQ₁

[

может быть положительной или отрицательной, т. е.

аксиальное магнитное поле (число Чандрасекара

Ra_st = Ra(0)st - R_n(L_e + N_A) +

Q₁) оказывает стабилизирующее или дестабилизи-

рующее действие на стационарную конвекцию. По-

√

]

2π⁴Qξ

Ta(2 + Ro(1 - Pm))N_B(N_A - 1)

скольку магнитное поле тормозит движение прово-

k²(a⁴ + π²Q)L_e

дящей жидкости (наножидкости), оно вполне может

оказывать стабилизирующее действие. В свою оче-

[

]-1

√

редь, взаимодействие между полем и токами, инду-

2π⁴Qξ

Ta(2+Ro(1-Pm))(N_A-N_B)

× 1-

цируемыми в движущейся среде, оказывает влия-

a²(a⁴ + π²Q)²L_e

ние на конвективное движение, т. е. на устойчивость

равновесия среды, подогреваемой снизу. Опять же

= D₁(k)D-12(k),

(69)

из-за частичной «вмороженности» магнитного по-

ля неоднородное вращение приводит к искажению

где Ra(0)st — критическое число Рэлея для стацио-

силовых линий магнитного поля, что создает деста-

нарной конвекции «чистой» жидкости в спиральном

билизирующий эффект, когда для профиля неодно-

магнитном поле, совпадающее с результатом [15]

родного вращения (числа Россби Ro) выполняется

условие

Ro(Pm - 1) < 1.

a⁶

π²a²Q

Ra(0)st =

k²

Это неравенство справедливо для положительных

чисел Россби Ro ≥ 0 и магнитных числах Прандтля

π²a⁴Ta

π²TaRo(a⁴+π²QPm)-4π⁴ξ²Q²

Pm < 1 либо Ro < 0 и Pm > 1, а также при Pm = 1

k²(a⁴+π²Q)

k²(a⁴ + π²Q)

для любых чисел Россби Ro.

4π²

Формула (67) показывает, что число Льюиса L_e

ξ²QRb.

и модифицированный коэффициент диффузии N_A

k²

имеют дестабилизирующий эффект, когда число Рэ-

лея наночастиц положительно, R_n > 0. Поскольку

Минимальное значение критического числа Рэлея

для большинства наножидкостей сумма числа Лью-

находится из условия ∂Ra_st/∂k = 0 и соответствует

иса и модифицированного коэффициента диффузии

волновым числам k = k_c, удовлетворяющим следу-

всегда положительна, L_e + N_A > 0 [11], то из (68)

ющему уравнению:

1111

М. И. Копп, А. В. Тур, В. В. Яновский

ЖЭТФ, том 159, вып. 6, 2021

[(

)

∂Ra(0)st

√

(Ro = -1) (кривая 4) наблюдаем уменьшение крити-

- 4π⁴Qξ

Ta(2 + Ro(1 - Pm)) ×

∂k

ческого числа Рэлея, т. е. более низкий порог разви-

k=kc

]

тия неустойчивости по сравнению со случаем одно-

(π² + k2c)² + π²Q + 2k2c(π² + k2c)

родного (Ro = 0) и неоднородного (Ro = 2) враще-

× N_B(N_A - 1)

k3c((π² + k2c)² + π²Q)²L_e

ния. На рис. 13а показано, что концентрация нано-

√

частиц (кривая 2) способствует понижению порога

× D-12(k_c)-D-22(k_c) · 4k_cπ⁴Qξ

Ta(2+Ro(1-Pm)) ×

стационарной конвекции по сравнению с «чистой»

(π² + k2c)² + π²Q + 2(π² + k2c)

жидкостью (кривая 1). Здесь кривые 1, 2 построены

× (N_A - N_B)

(π² + k2c)((π² + k2c)² + π²Q)³L_e

для числа Россби Ro = -3/4, но сделанные выводы

× D₁(k_c) = 0,

(70)

остаются в силе при любых числах Ro.

Проведем анализ влияния азимутального маг-

где

нитного поля на стационарную конвекцию, фикси-

(

)

руя параметр Ro для различных магнитных чисел

∂Ra(0)st

2k2c - π²

π⁴Q

Россби (Rb = -1, -1/2, 0, 1/2) и ξ = 1. На рис. 12б

∂k

k_c

k_c(π² + k2c)²

показаны результаты для случая однородного вра-

k=kc

щения (Ro = 0). Здесь мы видим, что для положи-

2π²k_cTa(1 + Ro)

тельных чисел Rb ≥ 0 (кривая 3 — Rb = 0, кри-

(π² + k2c) ((π² + k2c)² + π²Q)

вая 4 — Rb = 1/2) критические числа Рэлея мень-

π²Ta((π² + k2c)² + π²Q + 2k2c(π² + k2c))

ше, чем для отрицательных чисел Rb < 0 (кривая

k_c((π² + k2c)² + π²Q)²

1 — R b= -1, кривая 2 — Rb = -1/2). Следо-

π²TaRo((π² + k2c)² + π²QPm)

вательно, в зависимости от профиля неоднородно-

−

k_c(π² + k2c)²((π² + k2c)² + π²Q)²

сти азимутального магнитного поля H0ϕ(R) = CR^α

× ((π² + k2c)² + π²Q + 2k2c(π² + k2c)) +

(C = const, α — произвольное вещественное чис-

ло) порог неустойчивости может либо увеличивать-

2((π² + k2c)² + π²Q) + 4k4c(π² + k2c)

+ 4π⁴ξ²Q²

ся (Rb

< 0), либо уменьшаться (Rb

> 0). На

k3c((π² + k2c)² + π²Q)²

рис. 13б кривая 1 соответствует «чистой» электро-

+ 4π²ξ²QRb

проводящей жидкости, кривая 2 — электропрово-

k³

дящей наножидкости. Кривые 1, 2 построены для

Если азимутальное магнитное поле отсутствует (ξ =

чисел Россби Ro = 0, Rb = -1. Здесь мы видим,

= 0), то выражение (70) совпадает с (62) и результа-

что концентрация наночастиц способствует пониже-

том работы [15]. Следовательно, критическое волно-

нию порога стационарной конвекции. Этот вывод

вое число k_c зависит от параметров наножидкости

остается в силе при любых профилях неоднородного

только в спиральном магнитном поле. На рис. 12

азимутального магнитного поля (магнитного числа

показаны зависимости стационарного числа Рэлея

Россби Rb). Аналогичная картина наблюдается для

Ra_st от волновых чисел k для различных профи-

кеплеровского профиля вращения Ro = -3/4 (см.

лей неоднородного вращения (Ro) и магнитного по-

рис. 12в и 13в). Сравнивая результаты на рис. 12б,

ля (Rb). Численные результаты, представленные на

13б и рис. 12в, 13в можно заметить, что для про-

рис. 12, получены при следующих фиксированных

филя вращения Ro = -3/4 пороги неустойчивости

параметрах: Ta = 300, Q = 50, Pm = 0.7, R_n = 0.122,

меньше, чем для случая Ro = 0 при любых профи-

L_e = 5000, N_A = 5, N_B = 7.5 · 10-4. Минимально-

лях неоднородного азимутального магнитного поля.

му числу Ra^minst на рис. 12 соответствует точка на

Приступим к исследованию влияния вращения,

нейтральной кривой, разделяющей области устой-

числа Россби, азимутального магнитного поля, спи-

чивых и неустойчивых возмущений. На рис. 12a по-

рального магнитного поля, числа Льюиса, модифи-

казан случай однородного (Rb = -1/2) азимуталь-

цированного коэффициента диффузии и концентра-

ного магнитного поля с параметром ξ = 1. Здесь

ции наночастиц на стационарную конвекцию. Для

видно, что с возрастанием положительного профи-

этой цели вычислим производные

ля числа Россби Ro (кривая 1 — Ro = 2, кривая

d^R

2 — Ro = 0) минимальное значение стационарно-

d^T

dRo

d^Q

dξ

dRb

dL_e

dN_A

dR_n

го числа Рэлея Ra^minst также возрастает, т. е. повы-

шается порог развития неустойчивости. С другой

Здесь мы ввели переменные Чандрасекара

стороны, для отрицательных профилей вращения:

Ra_st

k²

^ξ=

кеплеровского (Ro = -3/4) (кривая 3) и рэлеевского

π⁴

π²

1112

М. И. Копп, А. В. Тур, В. В. Яновский

ЖЭТФ, том 159, вып. 6, 2021

⎡

В этих переменных выражение для критического

d^R

числа Рэлея (69) принимает вид

=⎣dR(0) +

d^Q

[

√

⎤

2π³ ξ

T(2 + Ro(1 - Pm))N_B (N_A - 1)(1 + x)²

R⁽⁰⁾ - R_n(L_e + N_A) +

⎦_×

x((1 + x)² +

Q)L_e

√

]

2π³ Q^ξ

T(2 + Ro(1 - Pm))NB (NA - 1)

D-2

× D-12 +

D₁ ×

√

x((1 + x)² +

Q)L_e

2^ξ

T(2+Ro(1-Pm))(N_A-N_B)((1+x)²-Q)

[

√

]-1

(75)

2Qξ

T(2 + Ro(1 - Pm))(N_A - N_B)

π(1+x)((1+x)² +

Q)²L_e

× 1-

π(1 + x)((1 + x)² +

Q)²L_e

= D₁(k)D-12(k),

dR(0)

1+x

(1 + x)²

T (1 + Ro(1 - Pm))

d^Q

x((1 + x)² +

где

(

)

4ξ2

Q(2(1 + x)² +

Rb +

(76)

(1+x)((1+x)²+Q)²+T(1+x)²(1+Ro)

(1 + x)² +

R⁽⁰⁾ =

x((1 + x)² +

⎡

TRoPmQ - 4ξ2 Q

4ξ2 Q

d^R

Rb.

=⎣dR(0) +

x((1 + x)² +

dξ

√

]

Используя эти выражения, нетрудно вычислить ис-

2π³ Q

T(2 + Ro(1 - Pm))N_B (N_A - 1)

D-1

комые производные

x((1 + x)² +

Q)L

√

⎡

T(2 + Ro(1 - Pm))(N_A - N_B)

d^R

+ D-2

D₁

(77)

=⎣dR(0) +

π(1 + x)((1 + x)² +

Q)²L_e

d^T

]

(0)

π³ Q^ξ(2+Ro(1-Pm))N_B(N_A-1)

√

D-1

+D-22 D₁ ×

d^R

8^ξQ

Q(1 + Rb) + Rb(1 + x)²

(78)

x((1+x)²+Q)L_e

dξ

(1 + x)² +

Qξ(2+Ro(1-Pm))(NA -N_B)

√ , (71)

d̃

dR(0)

4ξ2 Q

π(1 + x)((1 + x)² +

Q)²L_e

(79)

dRb

[

d^R

dR(0)

(1 + x)²

-R_n -

dL_e

d^T

x((1 + x)² +

√

]

2π³ Q^ξ

T(2+Ro(1-Pm))N_B(N_A-1)

Ro((1 + x)² +

QPm)

D-1

−

(72)

x((1+x)²+Q)L²

x((1 + x)² +

√

T(2+Ro(1-Pm))(N_A-N_B)

2Qξ

D₁

- D-2

(80)

⎡

⎤

π(1+x)((1+x)²+Q)²L²

√

d^R

2π³ Q^ξ

T(1-Pm)N_B(N_A-1)

=⎣dR(0)+

⎦_×

dRo

x((1+x)²+Q)L_e

d^R

√

dN_A

2Qξ

T(1 - Pm)(NA - NB)

√

D-2

D₁

[

]

× D-12 +

(73)

2π³ Q^ξ

T(2+Ro(1-Pm))N_B

π(1 + x)((1 + x)² +

Q)²L_e

D-1

= -R_n+

x((1 + x)² +

Q)L_e

√

2Qξ

T(2 + Ro(1 - Pm))

+ D-2

D₁

(81)

dR(0)

T((1 + x)² +

QPm)

(74)

π(1 + x)((1 + x)² +

Q)²L_e

dRo

x((1 + x)² +

1114

ЖЭТФ, том 159, вып. 6, 2021

Гидромагнитные неустойчивости в неоднородно вращающемся слое...

d^R

(для профиля H0ϕ = CR^α, α > 1) происходит де-

= -(N_A + L_e) D-12.

(82)

dR_n

стабилизация конвекции, а при Rb < 0 (α < 1) —

стабилизация конвекции. Это явление наблюдается

Нетрудно заметить, что в выражениях (71)-(82) со-

в стационарной неустойчивости (см. рис. 11).

держатся члены порядка

QξNB(N_A - 1)/L_e, кото-

Неоднородное азимутальное магнитное поле с

рые связаны совместным действием эффектов при-

профилем неоднородности Rb = -1 оказывает ста-

роста наночастиц (N_B) и спирального магнитно-

билизирующий эффект, поскольку dR/dξ > 0. Для

го поля (Qξ). Оценки этих эффектов при извест-

магнитных чисел Россби Rb ≥ 1 неоднородное ази-

ных параметрах наножидкости (N_A, N_B, L_e) дают

мутальное магнитное поле оказывает дестабилизи-

достаточно малый вклад. Однако произведения ти-

рующий эффект, dR/dξ < 0. Из формулы (78) вид-

па

D₁ QξNB(N_A - 1)/L_e дают вклад в дестабилиза-

но, что однородное азимутальное магнитное поле

цию конвекции, если концентрационное число Рэ-

(Rb = -1/2) может оказывать как стабилизирую-

лея положительно, R_n > 0. Следовательно, во всех

щее, так и дестабилизирующее действие на стаци-

формулах (71)-(82) дестабилизирующим фактором

онарную конвекцию. Формула (79) показывает, что

является концентрация наночастиц (число R_n).

эффекты стабилизации (Rb < 0) и дестабилизации

Из формул (72), (74) следует, что неоднород-

(Rb > 0) зависят от знака магнитного числа Россби,

ное вращение оказывает стабилизирующий эффект

т. е. от профиля неоднородного азимутального маг-

(dR(0)/dT > 0, dR⁽⁰⁾/dRo > 0 ) в случае положи-

нитного поля H0ϕ(R).

тельных чисел Россби, Ro > 0, и в обратном слу-

Из формул (80), (81) видно, что число Льюиса

чае, для Ro < 0, неоднородное вращение может ока-

L_e и модифицированный коэффициент диффузии

зывать дестабилизирующий эффект (dR(0)/dT < 0,

N_A имеют дестабилизирующий эффект, когда число

dR(0)/dRo < 0).

Рэлея наночастиц положительно, R_n > 0. Для боль-

шинства видов наножидкостей сумма числа Льюи-

Из формулы (76) видно, что величина dR(0)/dQ

са и модифицированного коэффициента диффузии

может быть положительной или отрицательной, т. е.

всегда положительна, L_e +N_A > 0 [11], тогда из (82)

аксиальное магнитное поле (число Чандрасекара

следует, что концентрационное число Рэлея всегда

^Q) оказывает стабилизирующее или дестабилизи-

имеет дестабилизирующий эффект.

рующее действие на стационарную конвекцию. Де-

В отличие от стационарной конвекции в аксиаль-

стабилизирующий эффект возникает при выполне-

ном магнитном поле, влияние эффектов вращения,

нии условий для профилей неоднородного вращения

числа Россби, азимутального магнитного поля, спи-

(числа Россби Ro) и неоднородного азимутального

рального магнитного поля на стационарную неод-

магнитного поля (магнитного числа Россби Rb):

нородно вращающуюся конвекцию наножидкости в

Ro(Pm - 1) < 1,

спиральном магнитном поле происходит при деста-

билизирующем вкладе концентрации наночастиц.

Q(2(1 + x)² +

Rb >

(при Rb > 0),

(1 + x)² +

Q)²

8. ЗАКЛЮЧЕНИЕ

Q(2(1 + x)² +

Rb <

(при Rb < 0).

В работе получена линейная система магни-

(1 + x)² +

Q)²

тогидродинамических уравнений для неоднородно

Первое неравенство справедливо для положитель-

вращающейся наножидкости в спиральном магнит-

ных чисел Россби, Ro > 0, и магнитных числах

ном поле с постоянными градиентами температу-

Прандтля Pm < 1, либо Ro < 0 и Pm > 1.

ры и концентрации наночастиц в поле силы тяжес-

Влияние неднородного азимутального магнитно-

ти. Для этой системы уравнений в приближении

го поля на стационарную конвекцию выясним с по-

локального метода ВКБ получено дисперсионное

мощью формул (78) и (79). В силу неоднородности

уравнение для эволюции малых возмущений в тон-

азимутального магнитного поля в силе Лоренца по-

ком слое наножидкости. Рассмотрены различные

является градиент магнитного поля, вызывающий

типы гидромагнитных неустойчивостей, возникаю-

дрейф течения жидкости. В зависимости от знака

щих в отсутствие градиента температуры, но с уче-

градиента магнитного поля (число Rb) изменяется

том градиента концентрации наночастиц. В случае,

направление дрейфа течения, влияющего на устой-

когда неоднородно вращающаяся наножидкость по-

чивость конвективных течений. Так, при Rb > 0

мещена только в аксиальное (H0z = 0) магнитное

1115

М. И. Копп, А. В. Тур, В. В. Яновский

ЖЭТФ, том 159, вып. 6, 2021

поле, возникает стандартная МВН или просто МВН.

В. Я. Рудяк, А. В. Минаков, М. И. Пряжников,

Если наножидкость помещена только в неоднород-

Письма в ЖТФ 45 (9), 36 (2019).

ное азимутальное (H0ϕ(R) = 0) магнитное поле, то

B. Ghasemi and S. M. Aminossadati, Int. J. Therm.

возникает азимутальная МВН. При наличии спи-

Sci. 50, 1748 (2011).

рального магнитного поля H₀ = H0ϕ(R)e_ϕ + H0ze_z

M. A. A. Hamada, I. Pop, and A. I. Md. Ismail,

возникает спиральная МВН. Для каждого типа

Nonlinear Anal. Real World Appl. 12, 1338 (2011).

МВН получены дисперсионные уравнения и про-

веден анализ их асимптотической устойчивости с

D. Yadav, R. Bhargava, and G. S. Agrawal, J. Eng.

помощью критерия Льенара - Шипара. Используя

Math. 80, 147 (2013).

этот критерий, мы определили области развития

S. Chandrasekhar, Hydrodynamics and Hydromagne-

МВН, азимутальной и спиральной МВН в плос-

tic Stability, Oxford Univ. Press, London (1961).

кости (k, Ro) для различных вариаций параметра

вращения Ta и азимутального числа Чандрасека-

Г. З. Гершуни, Е. М. Жуховицкий, Конвективная

ра Q_ϕ. Также получены критические числа Россби

устойчивость несжимаемой жидкости, Наука,

Москва (1972).

(Ro_cr, Rb_cr), характеризующие пороговое значение

для профилей неоднородного вращения (числа Росс-

10.

А. В. Гетлинг, Конвекция Рэлея - Бенара. Струк-

би Ro) и неоднородного азимутального магнитного

тура и динамика, Эдиториал УРСС, Москва

поля (магнитные числа Россби Rb). Области раз-

(1999).

вития МВН, азимутальной и спиральной МВН для

11.

Dhananjay Yadav, R. Bhargava, G. S. Agrawal,

наножидкости имеют большие размеры в плоскости

Gyeong S. Hwang, Jinho Lee, and M. C. Kim, Asia-

(k, Ro), чем для «чистой» жидкости.

Pac. J. Chem. Eng. 9(5), 663 (2014).

При наличии градиентов температуры и концен-

12.

М. И. Копп, А. В. Тур, В. В. Яновский, ЖЭТФ

трации наночастиц рассмотрены стационарные ре-

154, 1281 (2018).

жимы конвекции в аксиальном и спиральном маг-

нитных полях в зависимости от профилей неодно-

13.

M. Kopp, A. Tur, and V. Yanovsky, East Eur. J.

родного вращения (числа Россби Ro) и неоднород-

Phys. 1, 4 (2019).

ного азимутального магнитного поля (магнитные

14.

М. И. Копп, А. В. Тур, В. В. Яновский, ЖЭТФ

числа Россби Rb). Для обоих типов конвективной

157, 901 (2020).

неустойчивости получены выражения для критиче-

ских чисел Рэлея Ra_st и построены кривые ней-

15.

M. I. Kopp, A. V. Tur, and V. V. Yanovsky, Fluid

Dyn. Res. 53, 015509 (2021) .

тральной устойчивости. Показано, что при наличии

концентрации наночастиц пороговое значение ста-

16.

В. П. Лахин, В. И. Ильгисонис, ЖЭТФ 137, 783

ционарного критического числа Рэлея Ra^minst стано-

(2010).

вится меньше как в аксиальной, так и в спиральной

17.

O. N. Kirillov and F. Stefani, Proc. Internat. Astron.

магнитоконвекции.

Union 8, 233 (2012).

Развитая в настоящей работе теория может при-

меняться для проведения лабораторных экспери-

18.

O. N. Kirillov, F. Stefani, and Y. Fukumoto, J. Fluid

ментов с неоднородно вращающейся стратифициро-

Mech. 760, 591 (2014).

ванной электропроводящей наножидкостью в маг-

19.

S. Chandrasekhar, Proc. Nat. Acad. Sci. USA 42, 273

нитном поле.

(1956).

20.

Е. П. Велихов, ЖЭТФ 36, 1398 (1959).

ЛИТЕРАТУРА

21.

А. Б. Михайловский, Дж. Г. Ломинадзе, А. П. Чу-

риков, В. Д. Пустовитов, Физика плазмы 35, 307

1. S. K. Das, S. U. S. Choi , W. Yu, and T. Pra-

(2009).

deep, Nanofluids: Science and Technology, Wiley-In-

22.

H. Ji, J. Goodman and A. Kageyama, Mon. Not. Roy.

terscience, Hoboken, New Jersey (2008).

Astron. Soc. 325, L1 (2001).

2. В. Я. Рудяк, А. В. Минаков, Современные пробле-

23.

K. Noguchi, V. I. Pariev, S. A. Colgate, H. F. Beckley,

мы микро- и нанофлюидики, Наука, Новосибирск

and J. Nordhaus, Astrophys. J. 575, 1151 (2002).

(2016).

24.

G. Rüdiger and Y. Zhang, Astron. Astroph. 378, 302

3. J. Buongiorno, J. Heat Trans. 128, 240 (2006).

(2001).

1116