ЖЭТФ, 2021, том 159, вып. 6, стр. 1118-1133

КВАЗИИЗЭНТРОПИЧЕСКОЕ СЖАТИЕ НЕИДЕАЛЬНОЙ

ПЛАЗМЫ ДЕЙТЕРИЯ И ЕГО СМЕСИ С ГЕЛИЕМ

В ОБЛАСТИ ДАВЛЕНИЙ ДО 250 ГПа

М. А. Мочаловa*, Р. И. Илькаев^a, В. Е. Фортов^b, С. В. Ерунов^a,

В. А. Аринин^a, А. О. Бликов^a, В. А. Огородников^a, А. В. Рыжков^a,

В. А. Комраков^a, В. Г. Куделькин^a, И. П. Максимкин^a, В. К. Грязнов^c,

И. Л. Иосилевский^b, П. Р. Левашов^b, Д. В. Минаков^b, М. А. Парамонов^b

^a Российский федеральный ядерный центр —

Всероссийский научно-исследовательский институт экспериментальной физики

607188, Саров, Нижегородская обл., Россия

^b Объединенный институт высоких температур Российской академии наук

125412, Москва, Россия

^c Институт проблем химической физики Российской академии наук

142432, Черноголовка, Московская обл., Россия

Поступила в редакцию 16 декабря 2020 г.,

после переработки 16 декабря 2020 г.

Принята к публикации 12 февраля 2021 г.

Представлены данные по квазиизэнтропической сжимаемости сильнонеидеальной плазмы смеси дейте-

рия и гелия в области давлений 150-250 ГПа в устройствах цилиндрической геометрии, а также новый

результат, полученный в эксперименте с «чистым» дейтерием при давлении около 200 ГПа. Траекторию

движения металлических оболочек, сжимающих плазму, регистрировали с помощью мощных импульсных

источников рентгеновского излучения с граничной энергией электронов до 60 МэВ. Значения плотнос-

ти плазмы дейтерия и его смеси с гелием определены по измеренным радиусам оболочек в момент их

«остановки». Давление сжатой плазмы получено на основе газодинамических расчетов, учитывающих

реальные характеристики экспериментальных устройств. Полученные данные подтверждают сделанный

ранее во ВНИИЭФ вывод о фазовом переходе в плазме сжатого дейтерия в области давлений 150-160 ГПа

и свидетельствуют о том, что этот фазовый переход сохраняется в смеси дейтерия с гелием.

DOI: 10.31857/S0044451021060092

тической энергии, Γ_D = Ze²n1/3/E_k, много больше

единицы) и частично вырожденной водородной и ге-

1. ВВЕДЕНИЕ

лиевой плазмы [1]. Создание новых способов гене-

рации и диагностики состояния плазмы как водоро-

К изучению свойств водорода и гелия ученые

да и гелия по-отдельности, так и, в особенности, их

всегда проявляли повышенный интерес, так как для

смеси в мегабарном диапазоне давлений дает чрез-

описания строения и эволюции астрофизических

вычайно важную информацию для изучения астро-

объектов необходимо знать их физические свойства

физических объектов [2]. При этом основной нере-

в сжатом и разогретом состояниях. Исследования

шенной до настоящего времени физической пробле-

Юпитера, Сатурна, коричневых карликов и много-

мой и главным источником неопределенности для

численного отряда «внесолнечных» планет требуют

водород-гелиевой плазмы в диапазоне давлений P ∼

информации о теплофизических свойствах сильно-

∼ 10²-10³ ГПа, температур T ∼ 10³-10⁴ K и плот-

неидеальной (когда отношение энергии кулоновско-

ностей ρ ∼ 1-5 г/см³ является проблема возможно-

го взаимодействия заряженных частиц к их кине-

сти фазовых переходов (ФП) и сопутствующих им

^* E-mail: postmaster@ifv.vniief.ru

аномалий термодинамических свойств такой плаз-

1118

ЖЭТФ, том 159, вып. 6, 2021

Квазиизэнтропическое сжатие неидеальной плазмы дейтерия.. .

мы. Следует подчеркнуть, что еще в начале 70-х

• как проявляется и возможно ли зафиксировать

годов в серии экспериментальных работ ВНИИЭФ

в результатах эксперимента существование упомя-

[3] была зафиксирована резкая немонотонность в

нутых выше зон несмесимости, предсказанных тео-

параметрах P -ρ-траектории квазиизэнтропического

ретически?

сжатия водорода с двумя участками этой траекто-

• реализуются ли в этой смеси помимо аномалии

рии, при низких и высоких давлениях, и с заметным

[3-5] иные варианты ФП, предсказывавшиеся в тео-

скачком плотности (около 10 %) при P ∼ 300 ГПа

ретических работах?

при переходе с одной ветви на другую, который то-

гда же интерпретировался как признак фазового пе-

Структура данной статьи следующая. В разд. 2

рехода. Впоследствии результаты работы [3] были

перечислены особенности экспериментальной мето-

критически проанализированы и проведены допол-

дики генерации и диагностики дейтерий-гелиевой

нительные исследования сжимаемости дейтерия на

плазмы. Далее детально описываются эксперимен-

новом уровне генерации и диагностики [4,5]. Экспе-

тальные данные (плотность плазмы), дополнен-

рименты [4,5] подтвердили существование двух вет-

ные параметрами сжатой плазмы, полученными

вей, низкого и высокого давлений, но зона перехода

из газодинамических расчетов экспериментальных

опустилась в район P ∼ 150-160 ГПа.

устройств с исследуемым веществом. Наконец, в

Говоря о проблеме ФП в гелий-водородной сме-

последней части обсуждаются результаты сравни-

си, следует отметить возможное существование двух

тельного расчета параметров изэнтропического сжа-

принципиально различных категорий таких перехо-

тия чистого D₂ и смеси D₂ + He в рамках двух

дов: трансформация в условиях смеси ФП, уже су-

теоретических подходов: «химической модели плаз-

ществующих в чистых веществах, и ФП, сущест-

мы» (код SAHA [10]), традиционно сопровожда-

вующих именно и только в смесях, — появление зон

ющей интерпретацию экспериментальных данных

несмесимости (immiscibility) и расслоение смеси на

ВНИИЭФ по динамическому сжатию дейтерия, ге-

фазы разного химического состава. Следует также

лия и других газов [4, 5, 11-16], и строгого подхо-

подчеркнуть, что обе упомянутые категории ФП в

да ab initio — квантовой молекулярной динамики

соответствии с законами термодинамики обязаны в

(quantum molecular dynamics, QMD), см., например,

общем случае быть неконгруэнтными (или инкон-

работы [17,18], последовательно учитывающей кван-

груэнтными), т. е. допускать равновесие сосуществу-

товые эффекты динамики электронов совместно с

ющих фаз с различающимся химическим составом

эффектами кулоновской неидеальности плазмы. Со-

при сохранении общего брутто-состава (см., напри-

стояния водорода и гелия, близкие к предполагае-

мер, работы [6, 7]). Это очевидно для случая зон

мым в планетах-гигантах Солнечной системы, Юпи-

несмесимости и особенно важно для проблемы суще-

тере и Сатурне, уже достаточно давно воспроизво-

ствования «плазменного» ФП в гелий-водородной

дятся в РФЯЦ-ВНИИЭФ в экспериментах по квази-

смеси планетарных пропорций [8], поскольку при

изэнтропическому сжатию газообразных дейтерия и

трансформации ФП в условия планетарных смесей

гелия [11-16], а достигнутый диапазон параметров

помимо параметров фазовых границ существенно

в настоящее время расширен до уникально высокой

меняется их топология и, следовательно, как распо-

плотности 15 г/см³ при давлениях до P ≈ 20 ТПа. В

ложение, так и свойства критической точки (см., на-

то же время аналогичные экспериментальные дан-

пример, работу [9]). В частности, хорошо известная

ные по сжимаемости смеси водорода (дейтерия) и

одномерная P -T -зависимость межфазной границы

гелия практически отсутствуют.

в «чистых» веществах превращается в случае смеси

в двумерную P -T -зону с дополнительными «конце-

В настоящей работе c использованием рентге-

выми» точками (end-points) — максимумами темпе-

нографического комплекса РФЯЦ-ВНИИЭФ [19]

ратуры, давления и отклонения химического соста-

получены новые данные по квазиизэнтропической

ва у сосуществующих фаз.

сжимаемости смеси дейтерия с гелием, а также про-

Все сказанное выше определяет главные вопро-

веден дополнительный эксперимент по сжимаемос-

сы, поставленные перед экспериментом, использую-

ти «чистого» дейтерия при давлении P ∼ 200 ГПа

щим технику квазиизэнтропического сжатия плот-

с использованием новой цилиндрической конструк-

ной горячей плазмы:

ции. Также в работе проведен критический анализ

• как трансформируется в плотной горячей ге-

некоторых экспериментов с водородом (дейтерием),

лий-водородной смеси аномалия типа ФП, изучав-

выполненных ранее во ВНИИЭФ в области мегабар-

шаяся в работах [3-5]?

ных давлений [3]. Помимо общефизического интере-

1119

М. А. Мочалов, Р. И. Илькаев, В. Е. Фортов и др.

ЖЭТФ, том 159, вып. 6, 2021

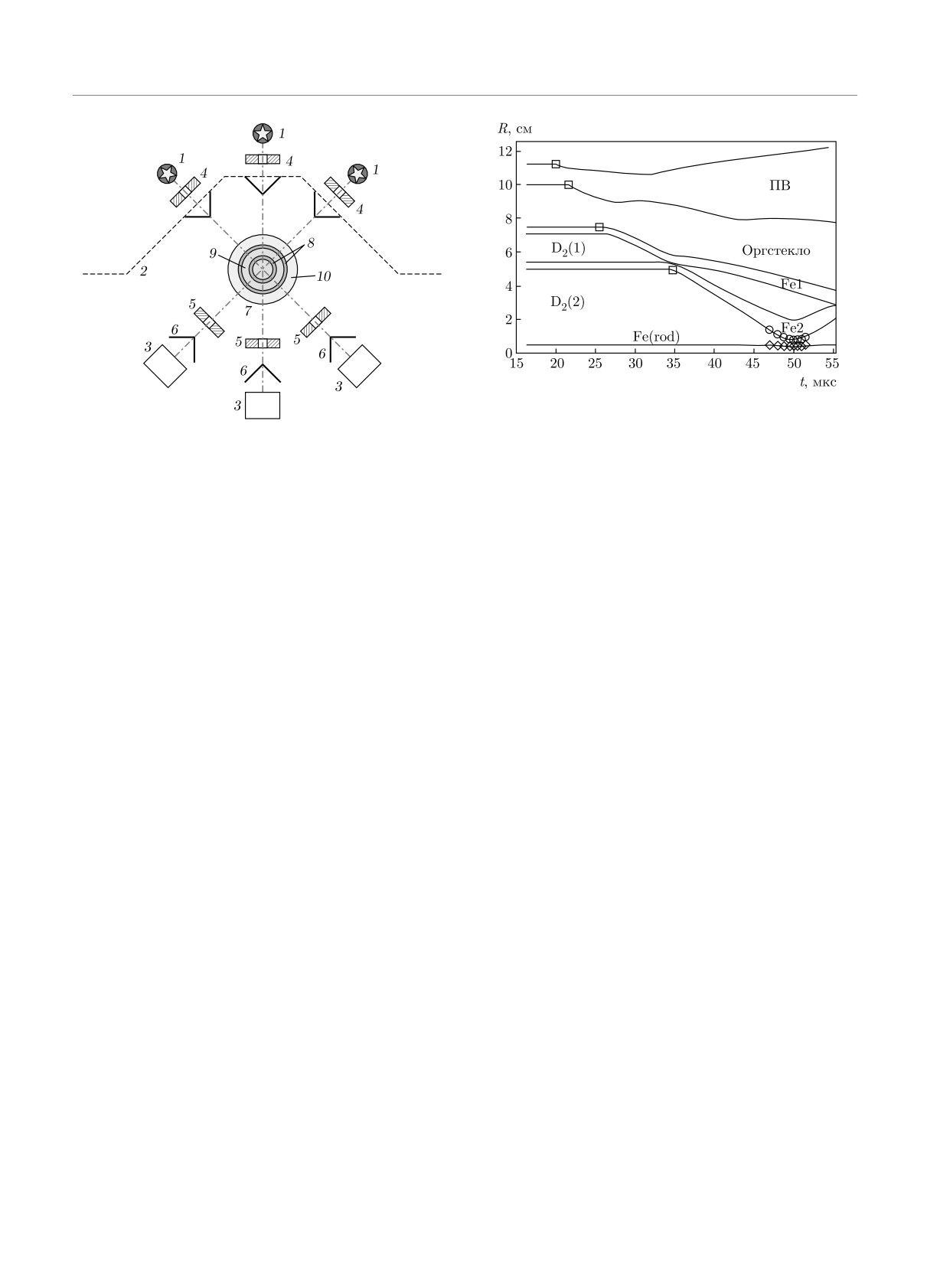
Рис. 2. Геометрия цилиндрического экспериментального

устройства в экспериментах с дейтерием и его смесью с

гелием: R0(rod) — начальный радиус стального стержня,

r01 и R01 — параметры первого каскада, r02 и R02 — пара-

метры второго каскада, Ro.g. — внешний радиус оболочки

из оргстекла

ется распределение давления по радиусу полости

со сжатой плазмой. Металлический стержень с

начальным радиусом R(rod) = 4.5 мм изготовлен

Рис. 1. Цилиндрическое устройство с равномерным про-

из стали.

филем давления в полости сжатой плазмы [20]

Другая особенность двухкаскадной конструкции

заключается в том, что металлогазовая смесь, воз-

никающая при выбросе частиц металлической пы-

са такие данные крайне важны для калибровки су-

ли [21] c внутренней поверхности внешней оболоч-

ществующих моделей уравнений состояния чистых

ки 2, оказывается локализованной в полости A и

газов и их смесей в широкой области фазовых со-

не проникает во внутреннюю полость B, в которой

стояний.

исследуемый газ сжимается серией ударных волн и

плавно сходящейся к центру оболочкой 3. Геомет-

рия экспериментальных устройств для исследова-

2. ПОСТАНОВКА ЭКСПЕРИМЕНТА.

ния сжимаемости дейтерия и его смеси с гелием при-

ЭКСПЕРИМЕНТАЛЬНЫЕ ДАННЫЕ

ведена на рис. 2. Впервые данная конструкция была

В экспериментах настоящей работы использова-

использована при измерении квазиизэнтропической

на конструкция цилиндрического эксперименталь-

сжимаемости дейтерия в работе [5].

ного устройства [20], вдоль оси которого расположен

В настоящей работе в данной постановке про-

цилиндрический металлический стержень (рис. 1).

веден эксперимент М9 по исследованию сжимаемо-

Устройство содержит заряд цилиндрического

сти дейтерия и два эксперимента, М10 и М11, со

взрывчатого вещества (ВВ) 1 (explosive), охваты-

смесью дейтерия (80 %) и гелия (20 %). Заполнение

вающий корпус 2, внутри которого коаксиально

камеры дейтерием проводилось с использованием

размещена дополнительная цилиндрическая обо-

металлогидридного источника [22]. Величина дав-

лочка 3. Таким образом, в устройстве конструктив-

ления в процессе заполнения измерялась датчиком

но образованы две коаксиальные полости, A и B,

S-10 фирмы WIKA (класс точности 0.25). Темпе-

для их заполнения исследуемым газом. Корпус 2

ратура контролировалась хромель-алюмелевой тер-

устройства изготовлен из высокопрочной стали,

мопарой, расположенной внутри трубопровода, ис-

способной выдерживать высокое начальное дав-

пользованного для напуска газов. Давление газа в

ление газа, он деформируется в упругой области

полостях оболочек 1 и 2 (см. рис. 1) было одинако-

без разрушения. Оболочка 3 также изготовлена из

вым. В экспериментах со смесью напуск газа в ка-

стали. Для изменения степени сжатия газа часть

меру проводился последовательно: сначала от тер-

ВВ может заменяться прокладкой из диэлектри-

мокомпрессора подавался гелий с известными пара-

ка 4. Для снижения кумуляции энергии в полости

метрами P₁ и T₁, затем — дейтерий. Конечное со-

B, приводящей к росту давления сжатой плазмы,

стояние для такой смеси известно — параметры P и

в конструкции вдоль оси закреплен металлический

T измеряются, но неизвестна плотность ρ₀. Для ее

цилиндрический стержень 5. При наличии стержня

определения учитывалось, что после напуска второй

отраженная волна формируется не в

«особой»

газовой компоненты (дейтерия) парциальное давле-

области при R

= 0, а на границе R(rod), где

ние первой компоненты изменяется изохорически и

R(rod) — радиус стержня. Тем самым уменьшается

составляет величину

амплитуда отраженной ударной волны, снижается

геометрическая кумуляция энергии и выравнива-

P^∗ = P₁T/T₁.

(1)

1120

ЖЭТФ, том 159, вып. 6, 2021

Квазиизэнтропическое сжатие неидеальной плазмы дейтерия.. .

Рис.

4. Экспериментальные данные и рассчитанные

R(t)-диаграммы. Эксперимент: квадраты — электрокон-

Рис. 3. Схема эксперимента: 1 — источники рентгеновского

тактная методика; кружки — внутренняя граница оболочки

излучения [19]; 2 — защитное сооружение; 3 — регистра-

второго каскада Fe2 (ВГО2); ромбы — граница стального

торы; 4, 5 — коллиматоры (Pb); 6 — конусы (Al); 7 — экс-

стержня Fe(rod), ПВ — продукты взрыва. Сплошные ли-

периментальное устройство; 8 — оболочки; 9 — газ; 10 —

нии — расчет, в области дейтерия использовано УРC из

заряд ВВ

работы [26]

Тогда из закона Дальтона следует, что

го излучения в видимое в данной системе исполь-

P₂ = P-P^∗.

(2)

зовались монокристаллы йодистого натрия и сили-

кат лютеция. Для устранения влияния рассеянно-

Таким образом, для гелия и дейтерия вычислены

го излучения на высокочувствительные детекторы 3

начальное давление и начальная температура: со-

размер поля регистрации в каждой из трех проек-

ответственно (P^∗, T) и (P₂, T). Окончательно плот-

ций ограничивается свинцовыми коллиматорами 4.

ность смеси вычислялась с учетом сжимаемости га-

Для защиты бетатронов 1 и оптико-электронных ре-

зов на основании известных табличных данных: для

гистраторов рентгеновского излучения 3 примене-

гелия — по результатам работы [23] и для дейте-

ны алюминиевые конусы 5. Обработка эксперимен-

рия — [24]. Характеристики устройств и условия

тальных рентгенограмм выполнена функциональ-

проведения опытов приведены в табл. 1.

ным методом [25].

Эксперименты выполнены на рентгенографиче-

Эксперимент М9 (дейтерий). Сравнение экс-

ском комплексе РФЯЦ-ВНИИЭФ с использовани-

периментальных данных и траекторий R(t), рас-

ем оптико-электронной системы регистрации. Схема

считанных с использованием уравнения состояния

экспериментов показана на рис. 3.

(УРС) дейтерия ВНИИЭФ [26], показано на рис. 4.

Теневое изображение границ оболочек, сжимаю-

щих исследуемый газ, получено при одновременном

Подбор параметров расчетной схемы экспери-

использовании тормозного излучения трех мощ-

ментальной конструкции для этого и всех последу-

ных бетатронов 1 с граничной энергией электронов

ющих экспериментов проводился по результатам те-

60 МэВ [19]. Бетатроны расположены под углами

стирования оболочек на их начальной стадии дви-

45^◦ друг к другу в защитном бетонном сооружении

жения (квадраты), когда влиянием исследуемого

2 и работают в режиме последовательной генерации

газа можно пренебречь. Рассчитанные траектории

трех импульсов рентгеновского излучения длитель-

R(t), приведенные на рис. 4, хорошо описывают экс-

ностью 150-180 нс. В опыте использовалась индиви-

периментальные данные, включая фазу разлета обо-

дуальная оптико-электронная система детектирова-

лочки. Отличие рассчитанного радиуса остановки

ния 3, имеющая динамический диапазон регистра-

R_min = 0.808 см от значения R_exp = 0.781 см, по-

ции 10³, которая активируется синхронно с импуль-

лученного из результатов обработки рентгенограмм,

сами бетатрона, что позволяет получать в каждой

составляет примерно 3.5 %. Для большей наглядно-

проекции три независимых рентгеновских изобра-

сти результатов этого эксперимента на рис. 5 показа-

жения. В качестве преобразователей рентгеновско-

ны фрагменты R(t)-диаграмм внутренней границы

1121

М. А. Мочалов, Р. И. Илькаев, В. Е. Фортов и др.

ЖЭТФ, том 159, вып. 6, 2021

Таблица 1. Характеристики устройств и условия проведения опытов (M_expl — масса ВВ, T — температура смеси

газов, P_He — начальное давление гелия, P — суммарное давление смеси, ρ0 — плотность смеси)

Опыт R_o,g, мм M_expl, кг r₀₂, мм R₀₂, мм T ,^◦C P_He, атм P , атм ρ₀, г/см³

М9

100

19.6

255.6

0.0359

М10

122.5

30.2

53.7

267.7

0.0396

М11

100

12.7

50.2

251.1

0.0386

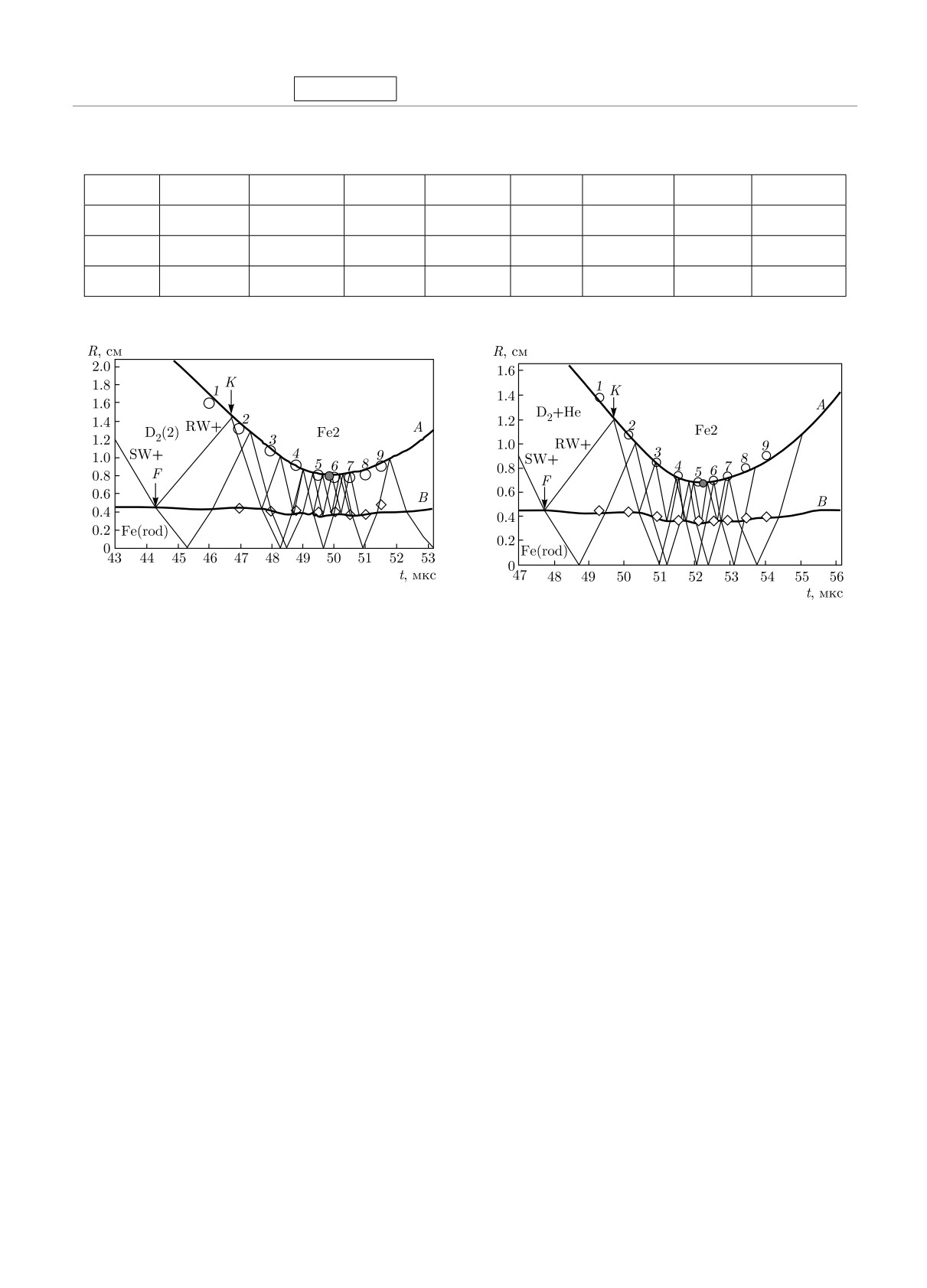
Рис. 5. (В цвете онлайн) Фрагмент R(t)-диаграмм для

эксперимента с дейтерием вблизи момента максимально-

Рис. 6. (В цвете онлайн) Сравнение экспериментальных и

го сжатия. Эксперимент: пустые кружки — ВГО2; ромбы —

рассчитанных R(t)-данных в опыте М10 cо смесью дейте-

граница стального стержня. Расчет: тонкие сплошные ли-

рия и гелия. Обозначения, как на рис. 5

нии — ударные волны, в области газа использовано УРC

дейтерия [26]; SW+ — первая ударная волна; RW+ — пер-

анализ выполненных расчетов, число ударных волн,

вая отраженная ударная волна, F — момент фокусировки

сжимающих плазму дейтерия в устройствах насто-

первой ударной волны, K — момент отражения ударной

ящей работы, достигает 20-25. Таким образом, в се-

волны от движущейся оболочки Fe2; 1-9 — регистрируе-

рии ударных волн, циркулирующих между стерж-

мые фазы сжатия, красная точка — максимальное сжатие,

толстые сплошные линии — расчет для ВГО2 (A) и для

нем Fe(rod) и внутренней границей оболочки Fe2,

внешней границы стального стержня (B)

происходит трансформация ударно-волнового сжа-

тия плазмы дейтерия в квазиизэнтропическое. Ана-

логичные процессы характерны и для сжатия сме-

си дейтерия с гелием в использованных устройствах

оболочки второго каскада (ВГО2) и внешней грани-

(см. ниже).

цы стального стержня Fe(rod) вблизи момента мак-

симального сжатия.

Эксперименты М10 и М11 (D₂ + He). Срав-

Как следует из постановки эксперимента, перво-

нение экспериментальных данных с рассчитанными

траекториями R(t) для эксперимента М10 со смесью

начально дейтерий сжимается в ударной волне. На

рис. 5 приведены рассчитанные для данного устрой-

дейтерия (80 % массы) и гелия (20 % массы) в обла-

сти максимального сжатия показано на рис. 6. Как

ства ударные волны, циркулирующие во внутренней

полости оболочки Fe2. Чтобы не загромождать ри-

видно на рис. 6, экспериментальные и рассчитанные

данные для этого устройства хорошо согласуются

сунок, ударные волны в области оболочки Fe2 не

друг с другом.

показаны. Как видно на рис. 5, первая ударная вол-

на SW+ в момент времени F достигает границы

При исследовании свойств плазмы смеси дейте-

стержня R(rod) и отражается, а в момент контак-

рия (80 %) и гелия (20 %) в области более высоких

та первой отраженной ударной волны RW+ c внут-

давлений в эксперименте М11 для взрывного нагру-

ренней границей оболочки Fe2 в состоянии K плаз-

жения был использован заряд ВВ массой 24 кг в

ма оказывается уже дважды сжатой. Как показал

тротиловом эквиваленте. Экспериментальные дан-

1122

ЖЭТФ, том 159, вып. 6, 2021

Квазиизэнтропическое сжатие неидеальной плазмы дейтерия.. .

∑

P (ρ, T ) =

P_i(ρ_i, T),

(3)

i=1

∑

E(ρ, T ) =

α_iE_i(ρ_i, T),

(4)

i=1

где P — давление, E — удельная внутренняя энер-

гия, T — температура, ρ_i — парциальные плотности,

α_i — массовые концентрации компонентов. Для уче-

та влияния упругопластических свойств стальных

оболочек использована дислокационная модель [30],

учитывающая затухание упругого предвестника и

релаксацию сдвиговых напряжений в волнах нагру-

жения. Дополнительно в газодинамическом расче-

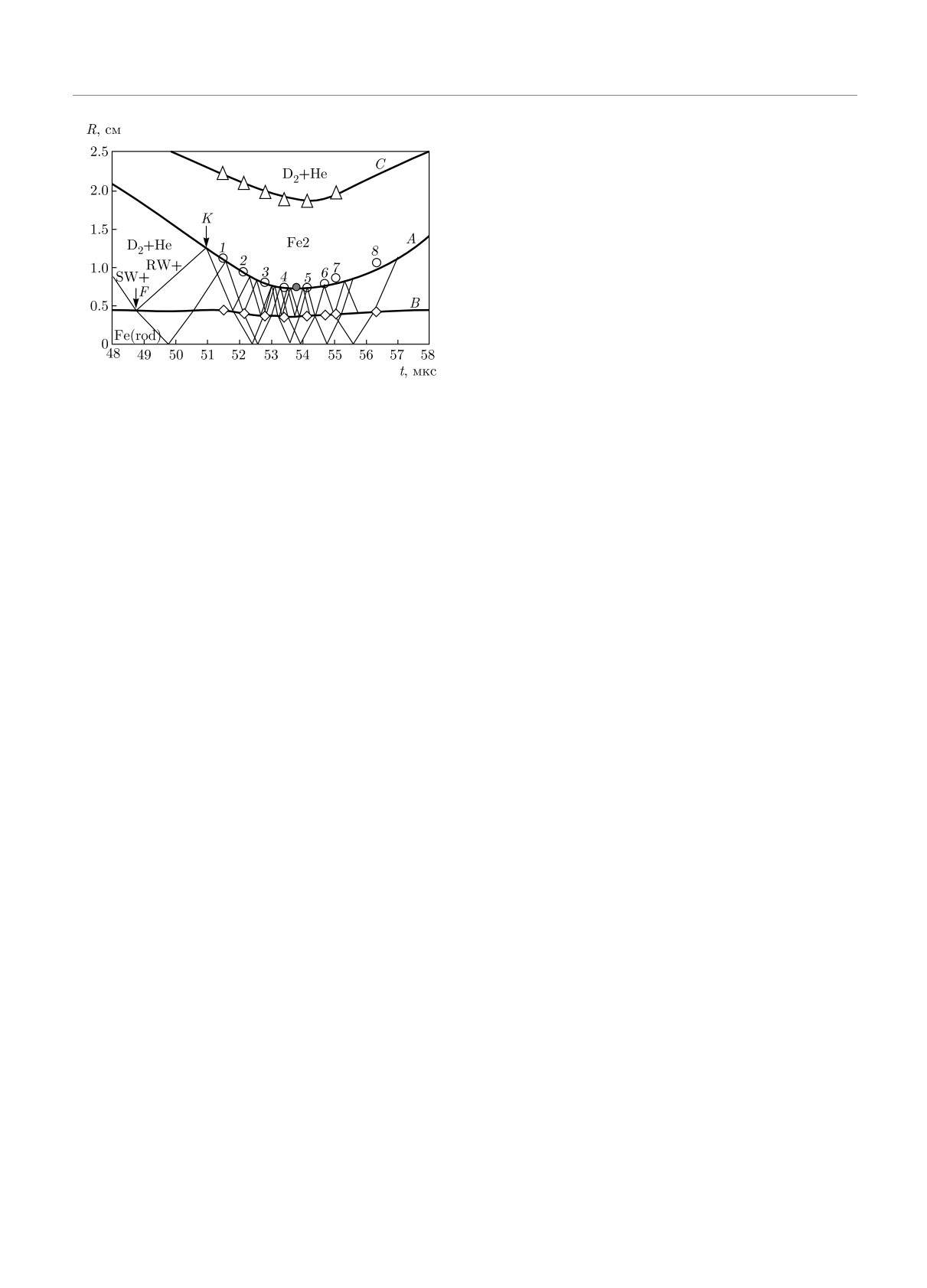
Рис. 7. (В цвете онлайн) Сравнение экспериментальных и

те учитывалась возможность хрупкого разрушения

рассчитанных R(t)-данных в опыте М11 cо смесью дейте-

для оболочек.

рия и гелия. Обозначения, как на рис. 5. Наружная граница

оболочки второго каскада Fe2 (НГО2): △ - эксперимент,

C — расчет

3. ОБСУЖДЕНИЕ ДАННЫХ

Основным критерием истинности получаемого

ные и рассчитанные траектории R(t) с использова-

в расчетах давления является удовлетворительное

нием УРС ВНИИЭФ для гомогенной смеси для это-

описание всей R(t)-траектории движения оболо-

го эксперимента в области максимального сжатия

чек экспериментального устройства. Окончатель-

показаны на рис. 7 и хорошо согласуются друг с дру-

ный подбор параметров расчетной схемы экспери-

гом.

ментальной конструкции проводился по результа-

там рентгенографирования оболочки на ее началь-

Давление в плазме сжатой смеси дейтерия и

ной стадии движения, когда влиянием исследуе-

гелия определялось из газодинамических расчетов

мого газа можно пренебречь. Учитывались дан-

с учетом реальных термодинамических и проч-

ные тестовых экспериментов по регистрации дви-

ностных свойств всех элементов экспериментальных

жения ударных волн по элементам эксперименталь-

устройств и их УРС. Расчет характеристик экспе-

ного устройства. Из расчетов конструкций кроме

риментальных устройств выполнен по одномерной

R(t)-диаграмм получены также распределения дав-

газодинамической программе [27], предназначенной

лений P (R) и температур T (R) в плазме по ради-

для численного моделирования неустановившихся

усу полости. Для оценки основных термодинамиче-

движений сплошной среды и тестированной по экс-

ских параметров сжатой плазмы авторы использо-

периментальным данным, полученным в России и

вали значения давления и температуры в плазме

за рубежом. В расчетах для элементов конструкции

дейтерия и его смеси с гелием в момент ее макси-

и ВВ использованы УРС, введенные в газодинами-

мального сжатия, полученные усреднением расчет-

ческий комплекс ВНИИЭФ. В расчетах компонен-

ных значений P (R) и T (R) по массе.

тов смеси для дейтерия использовалось полуэмпи-

Как следует из анализа полученных данных, в

рическое УРС [26], построенное по эксперименталь-

эксперименте М9 (см. рис. 4 и 5) плазма дейтерия

ным данным [3]. Для гелия УРС ВНИИЭФ в таб-

сжата до плотности ρ_exp = 2.1±0.2 г/см³ давлением

личной форме рассчитано Хрусталевым (ВНИИЭФ)

P = 198 ГПа при температуре T = 4410 K.

по модифицированной модели сжимаемого коволю-

Для экспериментов со смесью дейтерия и гелия,

ма [26, 28].

М10 и М11 (см. рис. 6 и 7), результаты расчетов по

Для расчета термодинамических параметров

УРС РФЯЦ-ВНИИЭФ для гомогенной смеси демон-

смеси газов, для которых наиболее справедливо

стрируют хорошее согласие с данными опытов, что

допущение о перемешивании компонентов на мо-

позволило использовать их для оценки давлений.

лекулярном уровне, использована парциальная

В эксперименте М10 измерена плотность сжатой

модель, в которой для расчета давления и энергии

плазмы гомогенной смеси дейтерия и гелия ρ_exp =

используются следующие соотношения [29]:

= 1.92 ± 0.15 г/см³ при давлении P = 165 ГПа и

1123

М. А. Мочалов, Р. И. Илькаев, В. Е. Фортов и др.

ЖЭТФ, том 159, вып. 6, 2021

Таблица 2. Состояния дейтерия и смеси газов в точке фокусировки F за первой ударной волной и в точке мак-

симального сжатия. В столбцах индексами «foc» и «stop» отмечены параметры, соответствующие моментам

прихода ударной волны на границу стержня R(rod) = 0.45 см и максимального сжатия плазмы

Опыт t_foc, мкс ρ_foc, г/см³ P_foc, ГПа T_foc, К t_stop, мкс ρ_stop, г/см³ P_stop, ГПа T_stop, К

М9

44.25

0.2470

2.643

1815

49.91

2.10 ± 0.20

198

4410

М10

48.70

0.2187

1.153

1400

53.70

1.92 ± 0.15

165

4477

М11

47.70

0.2348

1.424

1577

52.09

2.26 ± 0.15

237

5058

температуре T = 4477 К. В эксперименте М11 гомо-

генная смесь дейтерия и гелия сжата до плотности

ρ_exp = 2.26 ± 0.15 г/см³ давлением P = 237 ГПа при

температуре T = 5058 К. Как видно на рис. 5-7, в

момент времени F первая ударная волна SW+ до-

стигает границы стержня R(rod) и отражается. Рас-

считанные состояния (r_foc, P_foc, T_foc) дейтерия и

смеси дейтерия с гелием на момент времени прихо-

да ударной волны на границу стержня R(rod) при-

ведены в табл. 2. Там же указаны термодинамиче-

ские параметры плазмы в состоянии максимального

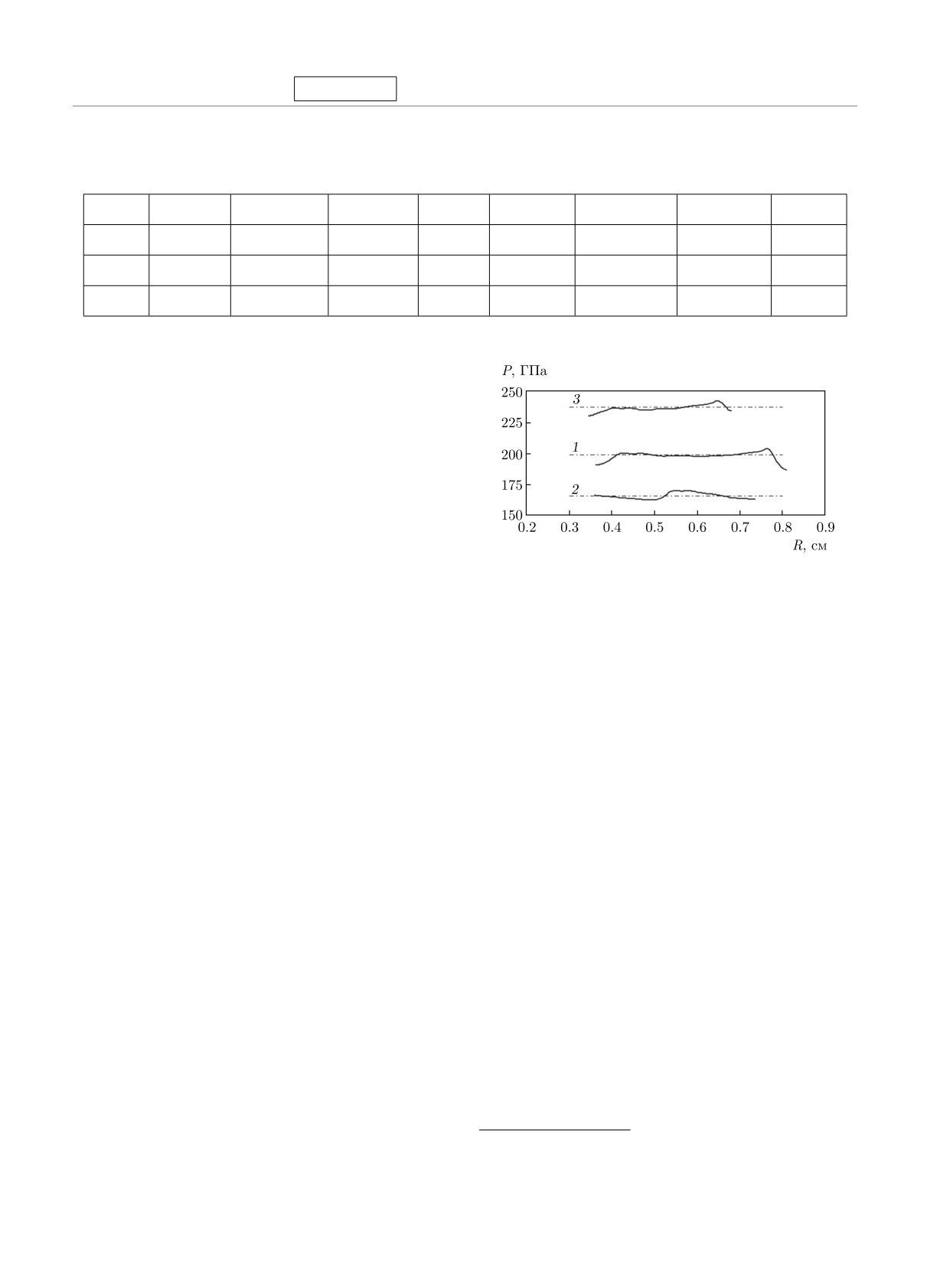
Рис. 8. Распределения давления по радиусу в плазме газов

сжатия.

при максимальном сжатии. Расчет — УРС дейтерия [26]:

Наличие дополнительного адиабатического сжа-

1 — P = 198 ГПа (опыт М9); 2 — P = 165 ГПа (опыт

М10); 3 — P = 237 ГПа (опыт М11)

тия плазмы оболочкой, кумуляции термодинамиче-

ских параметров за фронтом сходящейся ударной

волны и ее поглощения последующими волнами на

этапе движения к центру устройства приводит к

ряде состояний после двукратного сжатия с устано-

тому, что в некоторый момент времени начинает-

вившимся профилем давлений, приведены на рис. 9

ся квазиизэнтропическое сжатие плазмы. По край-

вместе с экспериментальными данными по сжимае-

ней мере начиная с состояния K, когда исследуемая

мости дейтерия из работ [4, 5]. Экспериментальная

плазма оказывается дважды сжатой, и во все после-

плотность из работ [3] при переходе от водорода к

дующие моменты времени получаемые эксперимен-

дейтерию удвоена. Дополнительно на рисунке при-

тальные данные можно отнести к результатам из-

ведена точка по сжимаемости дейтерия (зеленый

мерения квазиизэнтропической сжимаемости плаз-

треугольник), полученная группой С. Б. Кормера,

мы. Наличие стального стержня, расположенного по

и не опубликованная ранее¹⁾. На рис. 9a показаны

оси использованных экспериментальных устройств,

также типичные рентгенограммы проведенных опы-

снижает геометрическую кумуляцию и выравнива-

тов на моменты максимального сжатия.

ет профиль давления в полости сжатой плазмы. Как

Для удобства сравнения с экспериментальными

показывает анализ, только в самом начале процес-

данными ряд расчетов, модельных и ab initio, при-

са сжатия в использованных устройствах имеет ме-

веден отдельно на рис. 9а и 9б. Как видно на рис. 9,

сто кумуляция энергии и отклонение профилей дав-

с учетом экспериментальной ошибки сжимаемость

ления от усредненных по массе значений достига-

смеси дейтерия с небольшой добавкой гелия в экспе-

ет 10 %, а в состояниях, близких к максимально-

риментах М10 и М11 практически не отличается от

му сжатию, не превышает 4 %. Это наглядно видно

сжимаемости чистого дейтерия. Из общей гладкой

на рис. 8, где приведены рассчитанные распределе-

зависимости P(ρ), приведенной на рис. 9, выпадает

ния давлений по радиусу оболочек на момент макси-

одна точка (состояние K3) из работ [3]. При сохра-

мального сжатия для трех описанных конструкций.

нении положения этой точки по плотности сжатой

Параметры плазмы водорода [3], дейтерия и сме-

си газов, полученные в настоящей работе в экспе-

¹⁾ Частное сообщение сотрудника ВНИИЭФ А. П. Толочко

риментах М9-М11 при максимальном сжатии и в

(1926-2009).

1124

ЖЭТФ, том 159, вып. 6, 2021

Квазиизэнтропическое сжатие неидеальной плазмы дейтерия.. .

плазмы водорода ρ_exp = 0.98 ± 0.08 г/см³ в цитиру-

емых работах [3] ее положение по давлению меня-

лось от 263 до 320 ГПа. С учетом неопределенности

состояния K3 мы провели газодинамические расче-

ты состояний водорода для всех устройств из работ

[3] с помощью современных методов на базе моде-

лей УРС РФЯЦ-ВНИИЭФ, которые используем при

анализе результатов и в настоящей работе. Анализ

полученных данных показал, что рассчитанные зна-

чения по плотности для всех устройств хорошо со-

гласуются с данными из работ [3], но в состоянии K3

отличие рассчитанной плотности сжатой плазмы во-

дорода от экспериментального значения составляет

около 12 %. Чтобы понять причину такой разницы,

мы проанализировали согласие рассчитанных и экс-

периментальных R(t)-данных для этого устройства,

взятых из архива ВНИИЭФ. Результаты этого ана-

лиза показаны на рис. 10. Как видно на рис. 10б, рас-

чет с использованием современных подходов хорошо

описывает движение оболочки экспериментального

устройства без газа.

Однако для серии из четырех экспериментов

(точки 1-4 на рис. 10а) по сжимаемости водоро-

да (состояние K3) расчет согласуется только с по-

ложением оболочки в момент первого рентгеногра-

фирования (точка 1 на рис. 10а), который, как

видно на рисунке, не является моментом макси-

мального сжатия. Из расчета по УРС водорода

[26] следует, что в момент максимального сжатия

= 25.39 мкс) минимальное значение радиуса

остановки оболочки составляет величину Rcalc ≈

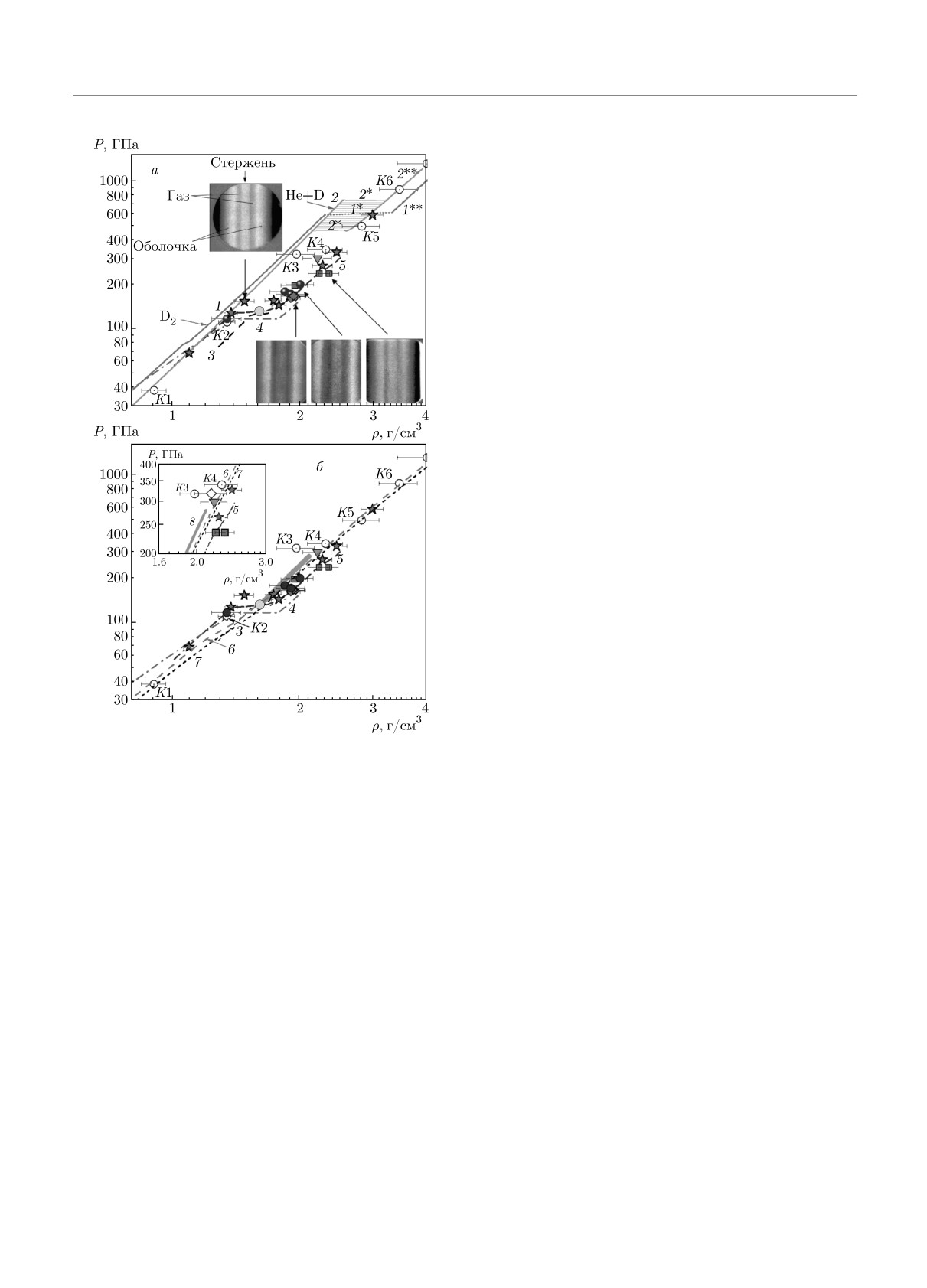
Рис. 9. (В цвете онлайн) Зависимости давления от плот-

≈ 1.908 см, и плазма водорода оказывается сжатой

ности в квазиизэнтропически сжатом дейтерии и его сме-

до плотности ρ = 1.08 г/см³ давлением P = 319 ГПа.

си с гелием. Эксперимент: красные звездочки — [4, 5]; пу-

С учетом проведенного анализа положение точки в

стые кружки — [3]; зеленый треугольник — не опублико-

P-ρ-координатах, соответствующее состоянию K3,

ванная ранее точка по сжимаемости дейтерия, получен-

было скорректировано. Полученные в расчете зна-

ная группой Кормера. Настоящая работа: синие кружки —

чения плотности ρ = 1.08 г/см³ и давления P =

дейтерий (опыт M9); красные ромбы и квадраты — опыты

= 319 ГПа показаны на вставке к рис. 9б и опре-

соответственно М10 и М11 для смеси D2 + He. Расчеты:

деляют новое положение состояния K3 на фазовой

1, 1∗, 1∗∗ — изэнтропа дейтерия (S = 29.5 Дж/г·K) c

диаграмме.

участком фазового перехода 1^∗ (УРС SAHA [5]); 2, 2^∗,

На оценку сжимаемости водорода в состоянии

2^∗∗ — изэнтропа смеси, опыт М11, (S = 23.7 Дж/г·K) c

межфазной зоной (УРС SAHA, настоящая работа); 3 —

K3 [3] могло повлиять качество рентгенографичес-

изотерма водорода T = 1500 K [31]; 4 — изотерма во-

ких изображений сферических полостей, получен-

дорода T = 5000 K [32]; 5 — изэнтропа (REMC-модель)

ных на пределе технических возможностей экспе-

[33]; 6 — изэнтропа дейтерия из точки F (QMD-модель,

риментальной техники в 70-х годах прошлого века.

настоящая работа); 7 — изэнтропа смеси (QMD-модель,

Для сравнения на рис. 10в показаны две оригиналь-

настоящая работа); желтый кружок — критическая точ-

ные рентгенограммы из экспериментов по измере-

ка (Tc = 1400 K, Pc = 130 ГПа, ρc = 1.6 г/см³); 8 —

нию сжимаемости водорода в состоянии K3 [3] и

двухфазная область диссоциативно-плазменного фазового

изображение сжатой плазмы дейтерия с использо-

перехода (QMD-модель [34]). На вставке: пустой ромб —

ванием современной техники. Исходя из проведен-

скорректированное положение состояния K3 из работ [3]

ного анализа, следует признать, что в состоянии K3

[3], по-видимому, не удалось измерить полость обо-

1125

М. А. Мочалов, Р. И. Илькаев, В. Е. Фортов и др.

ЖЭТФ, том 159, вып. 6, 2021

четы изэнтропического сжатия плотного горячего

гелий-дейтериевого флюида по теоретической моде-

ли SAHA, развитой для описания термодинамики

сильнонеидеальной плазмы [35, 36]. Для этой цели

был использован модифицированный вариант мо-

дели SAHA, хорошо зарекомендовавший себя при

описании результатов предыдущей серии экспери-

ментов по динамическому сжатию плазмы дейтерия

до давлений 5000 ГПа [5, 11]. Несомненным досто-

инством модели SAHA применительно к расчетам

плазмы гелий-дейтериевой смеси является то, что

в рамках этого подхода («химическая модель плаз-

мы») непосредственно рассчитываются параметры

именно смеси, а не используются какие-либо полу-

эмпирические «правила смешивания» типа уравне-

ний (3) и (4). В рамках подхода SAHA плотная и

горячая плазма гелий-дейтериевой смеси описыва-

ется как многокомпонентная равновесная сильно-

взаимодействующая («неидеальная») смесь атомов,

молекул, атомных и молекулярных ионов и элект-

ронов. Последние могут быть частично вырожден-

ными. Такой расчет фактически сводится к реше-

нию системы нелинейных уравнений одновременно-

го химического и ионизационного равновесия гелия

и дейтерия с учетом различных «поправок на неиде-

альность», учитывающих как эффект кулоновско-

го взаимодействия ионов и электронов, так и влия-

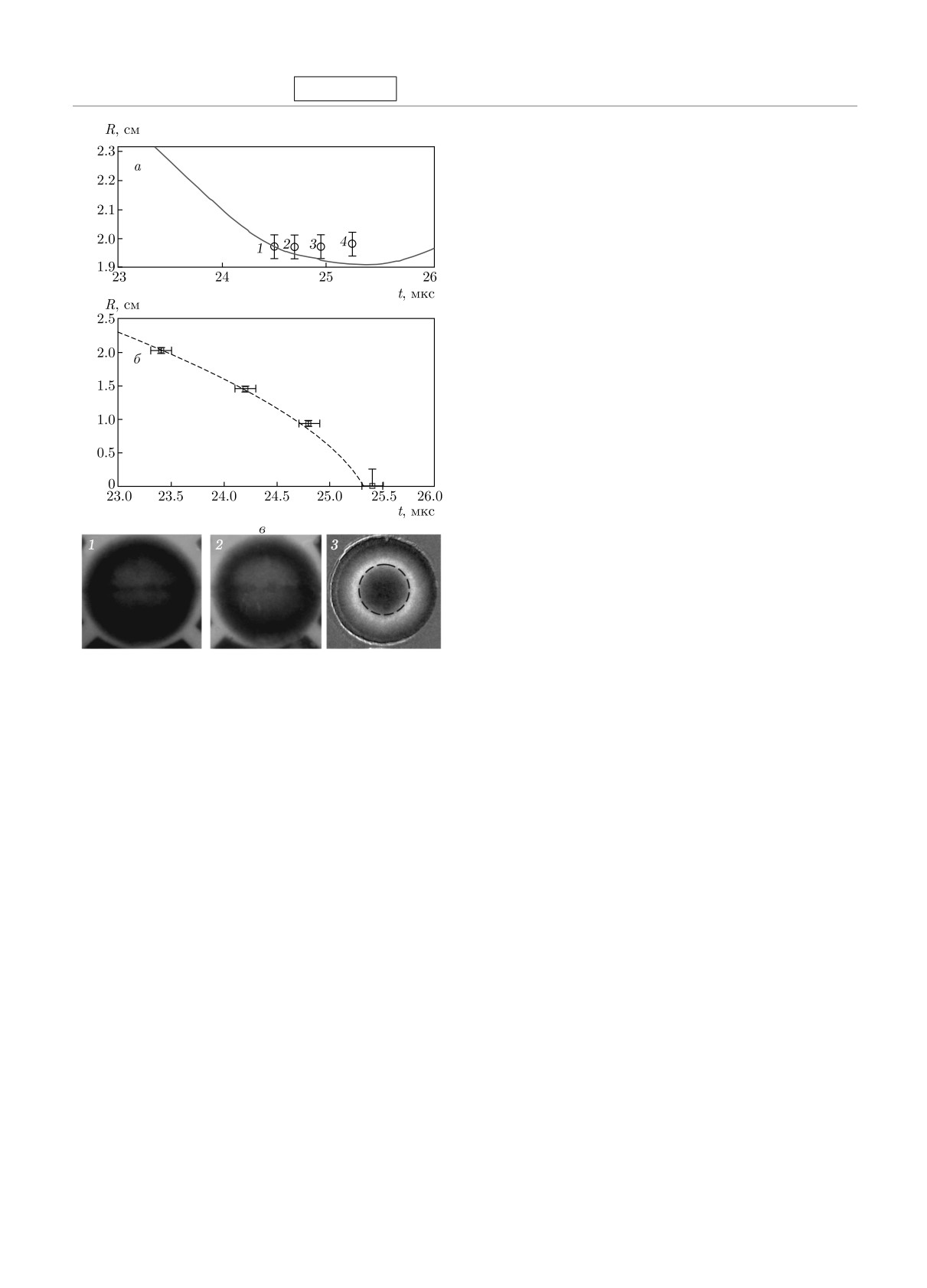
Рис. 10. а) R(t)-диаграммы движения внутренней грани-

ние интенсивного короткодействующего отталкива-

цы оболочки в экспериментальном устройстве для изме-

ния всех участников смеси (эффект «собственного

рения сжимаемости водорода в состоянии K3: значки —

объема»). При этом во всех указанных выше реак-

эксперименты [3]; кривая — расчет по УРС водорода [26].

циях учитывается сдвиг равновесия вследствие час-

б) Движение внутренней границы оболочки без газа: знач-

тичного вырождения электронов.

ки — эксперименты, штрихи — расчет. в) Рентгенограммы

Завершает эту громоздкую процедуру дополни-

1 и 2 из работы [3] соответствуют точкам 1 и 2 на рис. а;

тельный расчет возможности фазовых расслоений

3 — изображение сферической оболочки c использованием

современной техники (штрихи — граница газ-металл)

системы. Следует подчеркнуть, что помимо рас-

чета простых ван-дер-ваальсовых переходов типа

газ-жидкость

[37] (в неконгруэнтном варианте

лочки в момент максимального сжатия, а опублико-

[8]) методология химической модели плазмы и, в

ванное значение плотности сжатой плазмы водоро-

частности, код SAHA приспособлены для описания

да не соответствует максимальному давлению. Под-

необычных

«энтропийных» (делокализацион-

тверждает этот вывод и результат неопубликованно-

ных) фазовых переходов [38] в плотном горячем

го ранее эксперимента по измерению сжимаемости

гелий-водородном флюиде. В частности, это

—

дейтерия, выполненного группой Кормера. Следу-

диссоциативно-плазменный переход в водороде

ет также признать завышенной и точность экспери-

(дейтерии) [35], чисто плазменный переход в во-

ментальной ошибки результатов работ [3] для всех

дороде [31] и двухстадийный плазменный переход

экспериментальных устройств.

в гелии в версии работы [39] или одностадийный,

4. РАСЧЕТЫ ПАРАМЕТРОВ

но сразу с двукратной ионизацией гелия в версии

ИЗЭНТРОПИЧЕСКОГО СЖАТИЯ В

работы [40]. Это особенно важно для изучаемого

РАМКАХ ХИМИЧЕСКОЙ МОДЕЛИ

в настоящей работе фазового перехода в плотном

ПЛАЗМЫ

горячем гелий-дейтериевом флюиде, который, по

Для анализа результатов экcпериментов, вы-

нашим оценкам, должен быть одновременно и

полненных в данной работе, были проведены раc-

энтропийным, и неконгруэнтным.

1126

ЖЭТФ, том 159, вып. 6, 2021

Квазиизэнтропическое сжатие неидеальной плазмы дейтерия.. .

Расчет по модели SAHA настоящей работы был

проведен в режиме изэнтропы с начальными па-

раметрами, соответствующими моменту фокусиров-

ки первой ударной волны на поверхности металли-

ческого стержня цилиндрического генератора на-

стоящей конструкции для всех трех эксперимен-

тов, М9, М10 и М11 (состояния с индексом «foc»

в табл. 2, см. выше). Результаты этих расчетов в

сравнении с экспериментальными данными в коор-

динатах давление-плотность приведены на рис. 9.

При этом указанные изэнтропы, соответствующие

экспериментам на смеси М10 и М11 и стартующие

из соответствующих состояний (ρ_foc, P_foc), оказа-

лись очень близки и по этой причине изображены

на рис. 9б единой зависимостью. Изэнтропа, отве-

чающая эксперименту М9, оказалась близка к соот-

ветствующей изэнтропе, рассчитанной для преды-

дущей серии экспериментов по динамическому сжа-

тию дейтерия [5].

Следует подчеркнуть, что, как и ранее для плаз-

Рис. 11. (В цвете онлайн) а) Зависимости температуры

мы дейтерия [4, 5], настоящие расчеты по модели

от плотности квазиизэнтропически сжатого дейтерия и его

SAHA для плотного и горячего гелий-дейтериевого

смеси с гелием: красные звездочки (D2 [5]); красный кру-

флюида также предсказывают наличие ФП (см.

жок (D2) и квадраты (смесь) — настоящая работа. Рас-

четы (настоящая работа): 1, 1^∗, 1^∗∗ — изэнтропа дей-

рис. 9а), но при давлениях заметно выше соответ-

терия (S = 29.5 Дж/г·K) c участком фазового перехода

ствующего скачка плотности, зафиксированного ра-

1^∗ (УРС SAHA); 2, 2^∗, 2^∗∗ — изэнтропа смеси D2 + He

нее [4, 5] и в настоящей работе (М9) для плазмы

(S = 23.7 Дж/г·K) c межфазной зоной 2^∗ (УРС SAHA);

дейтерия. Таким образом, согласно настоящему рас-

5 — изэнтропа дейтерия из точки F эксперимента М9

чету по модели SAHA, диссоциативно-плазменный

(QMD-метод); 6 и 7 — изэнтропы смеси D2 + He из то-

ФП, предсказанный ранее для плазмы дейтерия, все

чек F экспериментов М10 и М11 (QMD-метод). б) Пара-

еще сохраняется при добавлении к дейтерию око-

метр кулоновской неидеальности Γ_D = (e²/kT )r_D (кривая

ло 20 % гелия, но участок двухфазной зоны (2^∗ на

1) и степень диссоциации дейтерия в смеси вдоль изэнтро-

рис. 9а) заметно смещается в область более высо-

пы, соответствующей эксперименту М11 по модели SAHA

ких давлений, а соответствующий скачок плотно-

(кривая 2)

сти для смеси оказывается меньше, чем для чисто-

го дейтерия. На рис. 9а участок изэнтропы смеси

для дейтерия (опыт М9), рассчитанных по моделям

D₂ + He внутри двухфазной области не приведен

SAHA (кривая 1) и QMD-методом (кривая 5). Про-

точно. Такой расчет еще не реализован ввиду сво-

межуточное положение занимают расчеты темпера-

ей сложности, обусловленной помимо всего прочего

тур для дейтерия по модели ВНИИЭФ из работ [4,5]

неконгруэнтностью этого ФП, который к тому же

и настоящей работы, близкие к температурам смеси

является энтропийным (делокализационным) [38].

в опытах М10 и М11. Отметим удовлетворительное

На рис. 11 показано сравнение результатов расчета

согласие рассчитанных двумя методами температур

температуры динамически сжатых дейтерия и смеси

для смеси в опыте М11 и их отличие от рассчитан-

D₂ + He вдоль изэнтроп, соответствующих экспери-

ных температур для опыта М10. Расчет по модели

ментам настоящей работы.

SAHA для опыта М10 практически совпадает с рас-

Расчеты проведены по модели SAHA и в рамках

четом для опыта М11 и поэтому здесь не приведен.

модификации QMD-метода [17,41]. На рис. 11 также

Кроме того, скачок степени диссоциации в смеси

нанесены значения рассчитанных по УРС ВНИИЭФ

дейтерия и гелия (линии 2, 2^∗, 2^∗∗ на рис. 11) в

температур, использованные при анализе динами-

зоне ФП, рассчитанный по модели SAHA, позволя-

ки элементов экспериментального устройства и в

ет предположить диссоциативную природу фазово-

расчетах термодинамических параметров для иссле-

го превращения, произошедшего в смеси D₂ + He в

дованных веществ в данной работе. Обращает на

диапазоне P ≃ 100-300 ГПа в настоящих экспери-

себя внимание существенное различие температур

ментах.

1127

М. А. Мочалов, Р. И. Илькаев, В. Е. Фортов и др.

ЖЭТФ, том 159, вып. 6, 2021

Все сказанное лишний раз подчеркивает исклю-

T_i контролировалась с помощью термостата Но-

чительную важность реализации в эксперименте до-

зе - Гувера [44]. Равновесные термодинамические ха-

полнительного (прямого или косвенного) измерения

рактеристики вычисляются на равновесном участ-

температуры исследуемого вещества. Следует еще

ке моделирования путем усреднения по конфигура-

раз подчеркнуть, что, согласно законам термоди-

циям. Это определяет статистическую погрешность

намики [2], соотношение термического и калориче-

моделирования. Непосредственными термодинами-

ского УРС веществ таково, что для всех адиабати-

ческими величинами, получаемыми в методе QMD

ческих процессов (включая ударное и изэнтропиче-

в результате описанной выше процедуры атомисти-

ское сжатие и расширение) любое сколь угодно хоро-

ческого моделирования, являются две главные вели-

шее совпадение предлагаемой теории и эксперимен-

чины — давление и внутренняя энергия как функ-

та в измерениях «механических» свойств — давле-

ции плотности и температуры, P (T, ρ) и U(T, ρ). В

ния, плотности и внутренней энергии (P, ρ и U) — не

соответствии с методом Ферми- Зельдовича [2, 46]

означает для этой теории никакой точности в опи-

это позволяет восстановить, во-первых, ход изэнтро-

сании температуры испытуемого материала [6].

пы в плоскости P -V , а во-вторых, темп изменения

температуры вдоль этой изэнтропы. В расчетах на-

стоящей работы использовался способ [41,42], состо-

5. РАСЧЕТЫ ПАРАМЕТРОВ

ящий в интегрировании вдоль указанной выше изэн-

ИЗЭНТРОПИЧЕСКОГО СЖАТИЯ СМЕСИ

тропы известного термодинамического соотношения

ДЕЙТЕРИЯ И ГЕЛИЯ В РАМКАХ

КВАНТОВОЙ МОЛЕКУЛЯРНОЙ

⁽∂lnT⁾

ДИНАМИКИ

⁽∂U(P,V ))-1 =

∂V_S

∂T

Помимо химической модели плазмы в настоя-

⁽∂P(V,T)⁾

щей работе были проведены расчеты параметров

⁽∂U(V,T))-1 .

(5)

∂T

динамического сжатия плазмы дейтерия и гелий-

дейтериевой смеси посредством QMD-метода. Ме-

В расчетах настоящей работы для каждого экспе-

тодика этих расчетов в настоящей работе являет-

римента такая изэнтропа выпускалась в плоскости

ся развитием и продолжением методики, реализо-

P-V из точки F — условного начала изэнтропично-

ванной в работе [41] и практически повторенной

сти траектории динамического сжатия смеси в про-

в [42]. Метод QMD не использует (подобно квази-

цессе реверберации ударных волн, где известна ве-

химической методике SAHA) для расчетов фено-

личина температуры — T_F . Такая изэнтропа для

менологической информации об изучаемом вещест-

эксперимента с чистым дейтерием (опыт М9) пред-

ве, такой как потенциалы ионизации, энергетичес-

ставлена выше на рис. 9б. Что касается смеси, то

кие спектры возбуждений связанных комплексов и

по описанной выше методике были проведены рас-

т. д. Термодинамика квантовых электронов в QMD

четы параметров изэнтроп раздельно для дейтерия

описывается с помощью метода функционала плот-

и гелия, а параметры для давления и энергии гелий-

ности (DFT) [43]. Результатом такого расчета яв-

дейтериевой смеси получены с использованием при-

ляется неоднородное пространственное распределе-

ближенного алгоритма смешения по соотношениям

ние электронов в поле подвижных ионов. Динами-

(3) и (4). Из этих данных по энергии и давлению

ка и термодинамика последних численно модели-

гелий-дейтериевой смеси были вычислены прибли-

руется в рамках молекулярной динамики [44]. Обе

женные параметры P, ρ, T искомых изэнтроп для

указанные процедуры в настоящих QMD-расчетах

экспериментов М10 и М11. Результаты этих расче-

реализованы с использованием известного пакета

тов представлены в координатах P(ρ) на рис. 9 и в

VASP [7] с обменно-корреляционным функционалом

координатах T (ρ) рис. 11.

в обобщенно-градиентном приближение (GGA) с па-

раметризацией PBE [45].

В сравнении с расчетами, реализованными в [41],

6. СРАВНЕНИЕ ПОЛУЧЕННЫХ

в расчетах настоящей работы было заметно увели-

ЭКСПЕРИМЕНТАЛЬНЫХ ДАННЫХ С

чено количество моделируемых частиц (ядер и элек-

РЕЗУЛЬТАТАМИ ТЕОРИИ

тронов), что позволило существенно повысить (вы-

числительную) точность. Сходимость результатов

Проблема существования аномалий типа ФП в

проверялась по числу атомов. Все расчеты проводи-

плотном и горячем флюиде водорода (дейтерия) и

лись в каноническом ансамбле. Температура ионов

гелия имеет давнюю и достаточно противоречивую

1128

ЖЭТФ, том 159, вып. 6, 2021

Квазиизэнтропическое сжатие неидеальной плазмы дейтерия.. .

историю. Целый ряд работ, прежде всего исполь-

ственно, в гелий-водородной смеси были получены

зующих платформу химической модели плазмы, в

в последние десятилетия благодаря стремительному

течение многих лет предсказывали существование

прогрессу вычислительной техники в рамках более

«плазменного» ФП в этих условиях (см. пионерс-

строгих подходов с использованием методов прямо-

кую работу [47] и обзоры [1,2,31,39,48]). Некоторые

го численного моделирования. Так, еще в 2003 г. в

из этих работ [49,50] предсказывают существование

работе [33] с использованием метода функционала

плазменного ФП (в плоскости P -ρ) в непосредствен-

плотности в плазме водорода получались разрыв-

ной близости к месту положения разрыва плотности

ные изотермы. Одна из них (T

= 1500 K) в ка-

квазиизэнтропического сжатия в серии эксперимен-

честве примера приведена на рис. 9а (кривая 3).

тов [4,5], включая и результаты настоящей работы.

Еще более поразительный результат уже непосред-

В качестве примера на рис. 9а приведена изотерма

ственно на изэнтропе, практически совпадающей с

T = 5000 K из работы [31] (кривая 4). Что касает-

P (ρ)-траекторией экспериментов [4, 5], был полу-

ся гелия, то предсказания плазменного ФП в плаз-

чен в прямом моделировании водородного флюида в

ме гелия делались как в варианте единого плазмен-

REMC-ансамбле [32]. Подчеркнем, что помимо раз-

ного ФП с одномоментной двукратной ионизацией

рывоподобной аномалии в ходе изэнтропы, показан-

(He ⇔ He⁺⁺ + 2e) [40], так и в варианте двух по-

ной на рис. 9а (кривая 5), REMC-моделирование [32]

следовательных плазменных ФП раздельно на пер-

предсказывает показательно низкий и к тому же мо-

вой и второй стадиях ионизации [39]. Также, что

нотонно убывающий при сжатии уровень темпера-

важно, еще в работе [51] на базе химической моде-

туры на рассчитанной изэнтропе (T = 800-1200 K).

ли плазмы детально исследовался плазменный ФП

Переходя к теоретическим расчетам настоящей

в гелий-водородной плазме во всем диапазоне про-

работы, отметим, что, как и ранее [4, 5], расчеты по

порций гелия, но, однако, без кого-либо учета де-

модели SAHA предсказывают для изэнтропы дей-

формации параметров этого плазменного ФП из-за

терия, выходящей из точки F (фокусировка первой

его неконгруэнтности [8]. Теоретические оценки ве-

ударной волны на границе центрального стержня),

личины указанной неконгруэнтности на примере по-

наличие двух ветвей, низкого и высокого давления,

пулярной в астрофизических приложениях версии

и ФП между ними, правда, при заметно более высо-

плазменного ФП из работ [52, 53] показывают, что

ком давлении, чем в экспериментах [4,5]. Важно то,

масштаб указанной неконгруэнтности может быть

что при переходе к описанию сжатия в гелий-дейте-

заметным и вполне сравнимым с эмпирической ве-

риевой смеси этот переход сохраняется, но, так же

личиной «гелиевого обеднения» внешних слоев ат-

как и в расчетах работы [51], двухфазная зона пере-

мосферы Юпитера и Сатурна. В контексте экспе-

хода, во-первых, заметно сдвигается в область более

риментов настоящей работы важен главный вывод

высоких давлений, а во-вторых, сжимается, т.е. вет-

из расчетов работы [51] — добавление гелия суще-

ви 2-2^∗∗ на рис. 9а сближаются в сравнении с 1-1^∗∗.

ственно «подавляет» склонность к фазовому рассло-

Что же касается подхода ab initio QMD, то, как

ению водорода, и, в свою очередь, добавление водо-

видно из рис. 9а, изэнтропа, вычисленная в рам-

рода аналогично «подавляет» склонность к фазово-

ках этого подхода как для чистого дейтерия, так

му расслоению гелия.

и для гелий-дейтериевой смеси, не содержит в рай-

Подчеркнем, что результаты настоящего экспе-

оне 100-1000 ГПа никаких разрывов типа ФП. Од-

римента (см. рис. 9) пока не дают явного подтверж-

нако отсюда не следует, что QMD-расчеты про-

дения этого правила. Изэнтропа смеси D₂ + He в

тиворечат экспериментальным данным настоящей

диапазоне P ≃ 100-300 ГПа оказывается практи-

работы. Напротив, многие варианты подходов ab

чески совпадающей с изэнтропой чистого дейтерия.

initio (см. обзор [54]), включая QMD и квантовый

Очевидно, что для прогресса в решении этой про-

метод Монте-Карло (QMС) [34, 55], вплоть до са-

блемы требуются дальнейшие более тщательные ис-

мых последних результатов QMD- и QMC-модели-

следования параметров динамического сжатия сме-

рования [56,57], уверенно предсказывают существо-

сей гелий-дейтерий с более детальной диагностикой,

вание диссоциативно-плазменного ФП.

прежде всего с измерением температуры изэнтропи-

В работе [58] подчеркивалось, что этот ФП рас-

чески сжатой и нагретой плазмы смеси.

положен именно в том диапазоне давлений и плот-

Если вернуться к теории, то помимо упомянутой

ностей, где на протяжении многих лет фиксирует-

выше химической модели плазмы достаточно кате-

ся разрывная аномалия в экспериментах ВНИИЭФ

горичные утверждения о возможности фазовых рас-

при квазиизэнтропическом сжатии водорода (дей-

слоений в водороде (и меньше в гелии) и, соответ-

терия) [3-5]. Это показано на рис. 9, где нанесены

1129

ЖЭТФ, вып. 6

М. А. Мочалов, Р. И. Илькаев, В. Е. Фортов и др.

ЖЭТФ, том 159, вып. 6, 2021

критическая точка обсуждаемого ФП в версии ра-

несмесимости, приведенной в работах [62,64]. Более

боты [34] с параметрами T_c = 1400 K, P_c = 130 ГПа,

того, обсуждаемая зона несмесимости столь обшир-

ρ_c = 1.6 г/см³ и полоса его двухфазной области в

на, что изэнтропа смеси D₂+He, реализованная в на-

диапазоне 1000 K ≤ T

≤ 3000 K в версии рабо-

стоящих экспериментах, входит в эту зону в районе

ты [56]. Примечательно, что эта относительно узкая

P ≃ 100 ГПа и остается в этой зоне двухфазных со-

зона двухфазной области практически совпадает в

стояний до достаточно высоких давлений (по оцен-

P (ρ)-координатах с траекторией квазиизэнтропиче-

кам на основе модели SAHA до P ≥ P^∗ ≃ 1000 ГПа).

ского сжатия дейтерия настоящей работы и предше-

Подчеркнем, что, как известно [2], такой вход

ствующих экспериментов [3-5] с той только прин-

и выход изэнтропы в двухфазную область дол-

ципиальной разницей, что температура вдоль ука-

жен сопровождаться заметным изломом ее накло-

занной полосы двухфазной области с ростом давле-

на в P -V -плоскости, т. е. сжимаемости. Это об-

ния монотонно убывает, в противоположность моно-

стоятельство, как и то, что и в чистом дейте-

тонному росту, ожидаемому вдоль изэнтропы сжа-

рии траектория, описывающая квазиизэнтропиче-

тия в настоящих экспериментах. Как подчеркива-

скую реверберацию ударных волн, пересекает в

лось в работах [37,38,58], это может быть объяснено

этом же диапазоне параметров межфазную границу

аномальным характером термодинамики горячего

диссоциативно-плазменного фазового перехода [3-5]

плотного флюида водорода (дейтерия) в обсуждае-

(см. рис. 11), c особой остротой ставит вопрос о кор-

мой зоне параметров. Эта аномальность [38], реали-

ректности расчета газодинамики сжимаемой смеси

зующаяся, в частности, как отрицательность коэф-

D₂ + He с помощью УРС ВНИИЭФ, которое не со-

фициента Грюнайзена, в общем контексте свойств

держит такого ФП. Важно, что с помощью именно

плотного горячего вещества обсуждалась в [2,59,60].

этих расчетов в экспериментах настоящей работы

Конкретно для водорода в диапазоне давлений 40-

определяется давление и оценивается температура,

75 ГПа и температур 3500-7500 К наличие такой

приведенные в табл. 2. Анализ этой проблемы ввиду

аномалии на основе существующих данных обсуж-

своей сложности выходит за рамки настоящей ста-

далось в работе [61]. Эта сложная проблема требует

тьи. Также кажется очевидной необходимость внед-

отдельного подробного анализа. Пока следует, види-

рения дополнительного альтернативного расчета га-

мо, ограничиться выводом о частичной противоре-

зодинамики сжимаемой смеси D₂ + He с помощью

чивости существующих экспериментальных и теоре-

УРС SAHA с полным учетом диссоциативно-плаз-

тических данных в обсуждаемой области [58].

менного ФП в его корректной версии, полностью

учитывающей неконгруэнтность фазовых превра-

щений в гелий-водородных (дейтериевых) смесях.

7. ЗОНЫ НЕСМЕСИМОСТИ

Как уже подчеркивалось во Введении, при пере-

8. ЗАКЛЮЧЕНИЕ

ходе от чистых дейтерия и гелия к их смеси помимо

деформации и сдвига параметров уже существую-

В настоящей работе с использованием ориги-

щих в них фазовых переходов возможен дополни-

нальных цилиндрических устройств впервые изме-

тельный ФП, присущий именно смеси, — появление

рена квазиизэнтропическая сжимаемость смеси дей-

зон несмесимости. Этот переход, по определению,

терия (80 % по массе) и гелия (20 % по массе) в диа-

является неконгруэнтным, т. е. с различием химиче-

пазоне давлений 150-250 ГПа и «чистого» дейтерия

ских пропорций в сосуществующих фазах. Парамет-

при давлении P

≈ 200 ГПа. Анализ полученных

ры этих зон несмесимости в гелий-водородной сме-

данных показал, что профили термодинамических

си рассчитывались неоднократно с применением, в

величин сжатой плазмы, определенные с использо-

основном, подходов ab initio (см. работы [62-64] и

ванием двухкаскадного цилиндрического экспери-

ссылки там). Эти расчеты все еще содержат боль-

ментального устройства, имеют при максимальном

шую долю неопределенности из-за высокой чувстви-

сжатии разброс не более 4 %, а их рассчитанные

тельности параметров границы зоны расслоения к

средние величины не зависят от вариантов расче-

деталям приближений, принятых при вычислениях

та прочностных процессов конструкции. Экспери-

в указанных вариантах подходов. Но следует под-

ментальные данные по квазиизэнтропической сжи-

черкнуть, что обе точки для смеси в экспериментах

маемости «чистого» дейтерия и его смеси с гели-

М10 и М11, согласно их параметрам, приведенным в

ем, полученные в диапазоне давлений 150-250 ГПа

табл. 2, оказываются глубоко в двухфазной области

на новых прецизионных устройствах, подтверждают

1130

ЖЭТФ, том 159, вып. 6, 2021

Квазиизэнтропическое сжатие неидеальной плазмы дейтерия.. .

сделанный ранее вывод о наличии в квазиизэнтро-

ву, Р. В. Борисову, Е. П. Волкову, Р. В. Тильку-

пически сжатом дейтерии ФП в области давлений

нову, О. А. Есину, В. В. Ковалдову, А. В. Рома-

150-160 ГПа и свидетельствуют о том, что этот ФП

нову, Д. П. Турутину, А. С. Пупкову, Г. С. Янду-

сохраняется в смеси дейтерия с гелием. На основе

баеву, И. A. Блинову, М. В. Логинову, Е. В. Шев-

современных моделей УРС, используемых в насто-

нину, А. И. Гуркину. Авторы выражают благодар-

ящее время в РФЯЦ-ВНИИЭФ, проведены анализ

ность А. В. Шутову за результаты газодинамичес-

и коррекция результатов пионерских экспериментов

ких расчетов с использованием УРС SAHA, а так-

группы Кормера по сжимаемости водорода, выпол-

же А. Б. Медведеву за плодотворные обсуждения

ненных в 70-х годах прошлого века [3]. На основе

проблемы аномальных термодинамических свойств

этого анализа и с учетом неопубликованного ранее

плотного горячего водорода (дейтерия) в зоне мега-

результата еще одного эксперимента группы Кор-

барных давлений.

мера по сжимаемости дейтерия показано хорошее

Финансирование. Настоящая работа выполне-

согласие всей совокупности данных экспериментов,

на при поддержке Российского фонда фундамен-

выполненных ранее во ВНИИЭФ, и настоящей ра-

тальных исследований (проект № 20-02-00287) и Ми-

боты.

нистерства науки и высшего образования России

С использованием двух теоретических моделей

(соглашение с ОИВТ РАН № 075-15-2020-785).

проведены расчеты параметров изэнтропического

сжатия гелий-дейтериевой смеси. Расчеты по хими-

ческой модели плазмы (код SAHA) предсказывают

ЛИТЕРАТУРА

диссоциативно-плазменный ФП со скачком плотно-

сти, близким к экспериментальному, но при более

В. Е. Фортов Экстремальные состояния вещест-

ва на Земле и в космосе, Физматлит, Москва

высоких давлениях. Расчеты ab initio параметров

(2010).

P (ρ) изэнтропы на основе QMD находятся, в це-

лом, в удовлетворительном согласии с эксперимен-

В. Е. Фортов, Tepмодинамика динамических

тальными данными, но не воспроизводят зафикси-

воздействий нa вещество, Физматлит, Москва

рованный в них ФП. Сравнение результатов расче-

(2019).

та, проведенного в рамках двух теоретических под-

ходов, показывает высокую степень неопределенно-

Ф. В. Григорьев, С. Б. Кормер, О. Л. Михайлова,

сти нашего знания температуры квазиизэнтропичес-

А. П. Толочко, В. Д. Урлин, Письма в ЖЭТФ 16,

286 (1972); ЖЭТФ 69, 743 (1975); ЖЭТФ 75, 1683

ки сжатой гелий-дейтериевой смеси, в очередной

(1978).

раз подчеркивая острую необходимость дополнения

существующей методики регистрации сжимаемости

V. E. Fortov, R. I. Il’kaev, V. A. Arinin, V. V. Bur-

плазмы независимыми измерениями ее температу-

tzev, V. A. Golubev, I. L. Iosilevskiy, V. V. Khrus-

ры.

talev, A. L. Mikhailov, M. A. Mochalov, V. Ya. Ter-

Опираясь на проведенные теоретические расче-

novoi, and M. V. Zhernokletov, Phys. Rev. Lett. 99,

ты параметров динамически сжатой плазмы смеси

185001 (2007).

гелия и дейтерия, мы имеем все основания пола-

М. А. Мочалов, Р. И. Илькаев, В. Е. Фортов,

гать, что полученные в эксперименте мегабарные

А. Л. Михайлов, А. О. Бликов, В. А. Огородни-

состояния гелий-дейтериевой плазмы находятся

ков, В. К. Грязнов, И. Л. Иосилевский, ЖЭТФ

глубоко в области несмесимости этих компонент —

152, 1113 (2017).

гелия и дейтерия, — уверенно предсказываемой

сегодня большинством методик ab initio. Изучение

И. Л. Иосилевский, Ю. Г. Красников, Э. Е. Сон,

влияния этого обстоятельства на корректный рас-

В. Е. Фортов, Термодинамика и транспорт

чет газодинамики динамического сжатия является

в неидеальной плазме, Изд-во МФТИ, Москва

первостепенной по важности задачей для даль-

(2000).

нейшего прогресса экспериментального подхода,

И. Л. Иосилевский, В. К. Грязнов, А. М. Семе-

традиционно развиваемого в РФЯЦ-ВНИИЭФ.

нов, Е. С. Якуб, Л. Н. Горохов, В. С. Юнгман,

А. Ю. Башарин, М. В. Брыкин, М. А. Шейндлин,

Благодарности. Авторы признательны сотруд-

В. Е. Фортов, Изв. РАН, Энергетика 5, 115 (2011).

никам, принимавшим участие в организации, прове-

дении экспериментов и обработке полученных дан-

I. Iosilevskiy, V. Gryaznov, E. Yakub, C. Ronchi, and

ных: А. Б. Профе, А. И. Лебедеву, С. Е. Елфимо-

V. Fortov, Contrib. Plasma Phys. 43, 316 (2003).

1131

М. А. Мочалов, Р. И. Илькаев, В. Е. Фортов и др.

ЖЭТФ, том 159, вып. 6, 2021

И. Иосилевский, Физика неидеальных кулоновских

19.

Yu. P. Kuropatkin, V. D. Mironenko, V. N. Suvorov,

систем: Уравнение состояния и фазовые переходы

D. I. Zenkov, and B. F. Tkachenko, in 11th IEEE

(in Russian), Saarbrucken, Germany, Lambert Acad.

Pulsed Power Conf. (29 June-2 July 1997, Baltimore,

Publ. (2011).

Maryland, USA), Digest of Technical Papers, ed. by

G. Cooperstein and I. Vitkovitsky, p. 1669.

10.

В. К. Грязнов, И. Л. Иосилевский, В. Е. Фор-

тов, в сб. Ударные волны и экстремальные со-

20.

А. О. Бликов, М. А. Мочалов, В. А. Огородников,

стояния вещества, под ред. В. Е. Фортова,

В. А. Комраков, Патент (RU) 2471545 C1, Бюлл.

Л. В. Альтшулера, Р. Ф. Трунина, А. И. Фунтико-

изобрет. № 1, 10.01.2013.

ва, Наука, Москва (2000), с. 299 [V. K. Gryaznov,

I. L. Iosilevskiy, and V. E. Fortov, in High-Pressure

21.

В. А. Огородников, А. Г. Иванов, А. Л. Михайлов,

Shock Compression of Solids VII: Shock Waves and

Н. И. Крюков, А. П. Толочко, В. А. Голубев, ФГВ

Extreme States of Matter, ed. by V. E. Fortov,

34, 103 (1998).

L. V. Al’tshuler, R. F. Trunin, and A. I. Funtikov,

22.

A. N. Golubkov, A. A. Kononenko, and A. A. Yu-

Springer-Verlag, New York (2004), p. 437].

khimchuk, Fusion Sci. Technol. 48, 527 (2005).

11.

М. А. Мочалов, Р. И. Илькаев, В. Е. Фортов,

23.

В. В. Сычев, А. А. Вассерман, А. Д. Козлов,

А. Л. Михайлов, Ю. М. Макаров, В. А. Аринин,

Г. А. Спиридонов, В. А. Цымарный, Термодинами-

С. К. Гришечкин, А. О. Бликов, В. А. Огород-

ческие свойства гелия, ГСССД, Изд-во стандар-

ников, А. В. Рыжков, В. К. Грязнов, Письма в

тов, Москва (1984).

ЖЭТФ 92, 336 (2010).

24.

A. Michels, W. De Graaff, T. Wassenaar, J. M. H. Le-

12.

М. А. Мочалов, Р. И. Илькаев, В. Е. Фортов,

velt, and P. Louwerse, Physica 25, 25 (1959).

А. Л. Михайлов, Ю. М. Макаров, В. А. Аринин,

А. О. Бликов, А. Ю. Баурин, В. А. Комраков,

25.

V. A. Arinin and B. I. Tkachenko, Pattern Recogni-

В. А. Огородников, А. В. Рыжков, Е. А. Пронин,

tion and Image Analysis 19, 63 (2009).

А. А. Юхимчук, ЖЭТФ 142, 696 (2012).

26.

В. П. Копышев, В. В. Хрусталев, ПМТФ 21, 122

13.

М. А. Мочалов, Р. И. Илькаев, В. Е. Фортов,

(1980).

А. Л. Михайлов, В. А. Раевский, В. А. Огородни-

ков, А. А. Юхимчук, А. И. Давыдов, Н. Н. Анаш-

27.

Н. Ф. Гаврилов, Г. Г. Иванова, В. И. Селин,

кин, В. А. Аринин, А. О. Бликов, А. Ю. Баурин,

В. Н. Софронов, ВАНТ, сер. Методики и програм-

Н. Б. Давыдов, В. А. Комраков, А. И. Логвинов,

мы числ. решения задач матем. физ. вып. 3, 11

С. Ф. Маначкин, А. В. Рыжков, Б. И. Ткаченко,

(1982).

А. В. Федоров, С. А. Финюшин, Д. А. Калашни-

ков, Е. А. Чудаков, Е. А. Пронин, Е. А. Бакулина,

28.

В. П. Копышев, ПМТФ 12(1), 119 (1971).

ЖЭТФ 146, 169 (2014).

29.

Л. И. Седов, Механика сплошной среды, Наука,

14.

М. А. Мочалов, Р. И. Илькаев, В. Е. Фортов,

Москва (1984).

А. Л. Михайлов, В. А. Аринин, А. О. Бликов,

В. А. Комраков, А. В. Рыжков, В. А. Огородни-

30.

И. Р. Трунин, С. В. Корицкая, В. Арнолд, Пре-

ков, А. А. Юхимчук, Письма в ЖЭТФ 101, 575

принт 75-2000, Саров (2000).

(2015).

31.

S. Scandolo, Proc. Nat. Acad. Sci. 100, 3051 (2003).

15.

М. А. Мочалов, Р. И. Илькаев, В. Е. Фортов,

32.

D. Beule, W. Ebeling, A. Forster, H. Juranek, R. Red-

А. Л. Михайлов, В. А. Аринин, А. О. Бликов,

mer, and G. Ropke, Contrib. Plasma Phys. 39, 21

В. А. Комраков, И. П. Максимкин, В. А. Огород-

(1999).

ников, А. В. Рыжков, Письма в ЖЭТФ 107, 173

(2018).

33.

V. S. Filinov, P. R. Levashov, A. V. Botsan, M. Bo-

16.

М. А. Мочалов, Р. И. Илькаев, В. Е. Фортов,

nitz, and V. E. Fortov, J. Phys. A 42, 214002 (2009);

P. R. Levashov, V. S. Filinov, A. Botan, M. Bonitz,

А. Л. Михайлов, В. А. Аринин, А. О. Бликов,

В. А. Огородников, А. В. Рыжков, В. А. Комра-

and V. E. Fortov, J. Phys. Conf. Ser. 121, 012012

(2008).

ков, И. П. Максимкин, Письма в ЖЭТФ 108, 692

(2018).

34.

W. Lorenzen, B. Holst, and R. Redmer, Phys. Rev.

17.

G. Kresse and J. Hafner, Phys. Rev. B 47, 558 (1993).

B 82, 195107 (2010).

18.

G. Kresse and J. Furthmuller, Phys. Rev. B 54, 11169

35.

V. K. Gryaznov and I. L. Iosilevskiy, J. Phys. A 42,

(1996).

214007 (2009).

1132

ЖЭТФ, том 159, вып. 6, 2021

Квазиизэнтропическое сжатие неидеальной плазмы дейтерия.. .

36.

V. K. Gryaznov, I. L. Iosilevskiy, and V. E. Fortov,

50.

А. А. Пяллинг, ТВТ 48, 181 (2010).

Contrib. Plasma Phys. 50, 77 (2010).

51.

M. Schlanges, M. Bonitz, and A. Tschttschjan,

37.

I. Iosilevskiy, in Physics of Extreme States of Mat-

Contrib. Plasma Phys. 35, 109 (1995).

ter, ed. by V. Fortov et al., IPCP RAS, Russia,

52.

D. Saumon, G. Chabrier, and H. M. Van Horn, Astro-

Chernogolovka (2013), p. 136, arXiv:1403.8053v3.

phys. J. (Suppl) 99, 713 (1995).

38.

I. L. Iosilevskiy, J. Phys. Conf. Series 653, 012077

53.

А. В. Украинец, И. Л. Иосилевский, в сб. Физи-

(2015).

ка экстремальных состояний вещества, под ред.

39.

W. Ebeling, A. Förster, V. E. Fortov, V. K. Gryaz-

В. Е. Фортова, Изд-во ИПХФ РАН, Черноголовка

nov, and A. Ya. Polishuk, Thermophysical Proper-

(2005), с. 181.

ties of Hot Dense Plasmas, B. G. Teubner Ver-

54.

J. M. McMahon, M. A. Morales, C. Pierleoni, and

lagsgesellschaft, Stuttgart-Leipzig

(1991)

[В. Эбе-

D. M. Ceperley, Rev. Mod. Phys. 84, 1607 (2012).

линг, А. Фёрстер, В. Фортов, В. Грязнов, А. По-

лищук, Теплофизические свойства горячей плот-

55.

M. A. Morales, C. Pierleoni, E. Schwegler, and

ной плазмы, НИЦ «Регулярная и хаотическая ди-

D. M. Ceperley, PNAS USA 107, 12799 (2010).

намика», Институт компьютерных исследований,

Москва-Ижевск (2007)].

56.

G. Mazzola, R. Helled, and S. Sorella, Phys. Rev.

Lett. 120, 025701 (2018).

40.

C. Winisdoerffer and G. Chabrier, Phys. Rev. E 71,

026402 (2005).

57.

H. Y. Geng, Q. Wu, M. Marqués, and G. J. Ackland,

Phys. Rev. B 100, 134109 (2019).

41.

A. V. Chentsov and P. R. Levashov, Contrib. Plasma

Phys. 52, 33 (2012).

58.

И. Л. Иосилевский, Аномальная термодинамика

и проблема фазовых переходов в плотном и горя-

42.

A. Becker, N. Nettelmann, B. Holst, and R. Redmer,

чем водороде (дейтерии), Межд. конф. «XXI Ха-

Phys. Rev. B 88, 045122 (2013).

ритоновские тематические научные чтения», Рос-

сия, Саров, 15-19 апреля 2019 г. (пленарный до-

43.

R. M. Martin, Electronic Structure: Basic Theory and

клад).

Practical Methods, Cambridge Univ. (2020).

59.

А. Б. Медведев, Р. Ф. Трунин, УФН 182, 829

44.

S. J. Nosé, J. Chem. Phys. 81, 511 (1984).

(2012).

45.

J. P. Perdew, K. Burke, and M. Ernzerhof, Phys. Rev.

60.

M. P. Desjarlais, M. D. Knudson, and R. Redmer,

Lett. 77, 3865 (1996).

Phys. Rev. B 101, 104101 (2020).

46.

В. Е. Фортов, Физика высоких плотностей энер-

61.

А. Б. Медведев, ФГВ 54(2), 98 (2018).

гии, Физматлит, Москва (2013).

47.

Г. Э. Норман, А. Н. Старостин, ТВТ 6, 410 (1968).

62.

M. A. Morales, S. Hamel, K. Caspersen, and

E. Schwegler, Phys. Rev. B 87, 174105 (2013).

48.

И. Л. Иосилевский, А. Н. Старостин, в сб. Энцик-

лопедия низкотемпературной плазмы, т. 1, под

63.

B. Militzer, Phys. Rev. B 87, 014202 (2013).

ред. В. Е. Фортова, Наука, Москва (2000), с. 327.

64.

M. Schöttler and R. Redmer, Phys. Rev. Lett. 120,

49.

А. Л. Хомкин, А. С. Шумихин, ЖЭТФ 146, 518

115703 (2018).

(2014).

1133