ЖЭТФ, 2021, том 160, вып. 2 (8), стр. 167-174

ИСПОЛЬЗОВАНИЕ МОДЕЛЬНОГО УРАВНЕНИЯ БОЛЬЦМАНА

ДЛЯ АНАЛИЗА ВЛИЯНИЯ ЭНЕРГИИ СВЯЗИ НА РАЗВИТИЕ

КАСКАДА ВЫБИТЫХ АТОМОВ В ТВЕРДОМ ТЕЛЕ

Е. В. Метелкин^*, М. В. Лебедева

Российский химико-технологический университет им. Д. И. Менделеева

124047, Москва, Россия

Поступила в редакцию 9 апреля 2021 г.,

после переработки 9 апреля 2021 г.

Принята к публикации 15 апреля 2021 г.

Рассматривается развитие каскада атомных столкновений в твердом теле, состоящем из одинаковых

атомов с учетом их энергии связи в узлах решетки (ε_d). На основе решения модельного кинетического

уравнения Больцмана получено выражение для функции распределения, описывающей нестационарное

энергетическое распределение движущихся атомов. Предполагается, что рассеяние движущихся атомов

является упругим и сферически-симметричным в системе центра инерции, а сечение взаимодействия яв-

ляется постоянной величиной. В частном случае ε_d = 0 найденное решение хорошо согласуется с точным

решением, полученным ранее.

DOI: 10.31857/S0044451021080022

ства [1-5]. В связи с этим исследование энергетичес-

кого распределения каскада атомных столкновений

и его развития во времени представляет большой

1. ВВЕДЕНИЕ

интерес.

Проектирование и создание ядерных реакторов и

Описание развития каскадов представляет собой

термоядерных установок тесно связано с проблемой

достаточно сложную задачу. В связи с этим для ее

выбора для них радиационно-стойких материалов,

решения с успехом используется компьютерное мо-

поскольку их корпуса и отдельные элементы долж-

делирование [2,6,7]. Однако аналитические решения

ны выдерживать продолжительное воздействие ра-

соответствующей задачи для линейного уравнения

диации. Именно радиационная стойкость материа-

Больцмана, несмотря на то, что они существуют в

ла во многом определяет время жизни установок и

исключительных случаях, также представляют зна-

многие другие их физические характеристики.

чительный интерес. Это связано с тем, что анали-

Облучение твердых тел быстрыми частицами (в

тические решения дают наглядное представление о

частности, нейтронами) приводит к тому, что атомы

протекающем процессе и его особенностях. Кроме

кристаллической решетки, получившие от налетаю-

того, эти результаты могут быть использованы для

щей частицы энергию, большую энергии связи (ε_d),

тестирования достаточно сложных численных рас-

вылетают из своих равновесных положений. В даль-

четов.

нейшем столкновения движущихся атомов с атома-

Исследованию развития каскадов атомных

ми, находящимися в узлах кристаллической решет-

столкновений в твердом теле было посвящено

ки, приводят к появлению новых поколений выби-

достаточно большое количество работ

[8-20]. В

тых атомов. В результате возникает так называемый

работе

[8] с помощью построенной модельной

каскад атомных столкновений. В результате разви-

индикатрисы рассеяния было получено приближен-

тия каскада в твердом теле образуется целый комп-

ное стационарное энергетическое распределение

лекс дефектов (вакансии и междоузельные атомы,

каскада движущихся атомов для произвольных по-

кластеры и т. д.), определяющий степень поврежде-

тенциалов межатомного взаимодействия. В работах

ния материала и его дальнейшие физические свой-

[9, 10] анализировалась возможность образования

^* E-mail: sitech47@mail.ru

субкаскадов

— ряда неперекрывающихся меж-

167

Е. В. Метелкин, М. В. Лебедева

ЖЭТФ, том 160, вып. 2 (8), 2021

ду собой областей в процессе развития каскада

В настоящей работе на основе решения модель-

атомных столкновений. Оценка пороговой энергии

ного кинетического уравнения Больцмана определя-

образования субкаскадов была проведена в работе

ется нестационарное пространственно-энергетичес-

[11]. В работе [12] была разработана теоретическая

кое распределение каскада движущихся атомов с

модель для исследования образования каскадов и

учетом их энергии связи в узлах решетки. Предпо-

субкаскадов атомных столкновений в облучаемых

лагается, что рассеяние движущихся атомов являет-

твердых телах, основанная на использовании ли-

ся упругим и сферически-симметричным в системе

нейного кинетического уравнения Больцмана. На

центра инерции, а сечение рассеяния считается по-

основе расширенного толкования понятия первично

стоянным. Полученное решение при ε_d = 0 хорошо

выбитый атом (ПВА) в [12] был сформулирован

согласуется с точным решением аналогичной задачи

критерий для определения пороговой энергии об-

(см. [18]).

разования субкаскадов в твердом теле и получены

формулы для определения средних размеров и их

числа в зависимости от энергии ПВА. На основе ре-

2. ПОСТАНОВКА ЗАДАЧИ

зультатов, представленных в [12], в работе [13] были

Рассмотрим распространение каскада выбитых

проведены численные расчеты для конкретных

атомов в твердом теле, состоящем из одинаковых

материалов, согласующиеся с экспериментальными

атомов. Кинетическое уравнение Больцмана, описы-

данными.

вающее этот процесс, имеет следующий вид [12,21]:

В работе [14] на основе решения кинетическо-

го уравнения Больцмана была рассчитана функция

1 ∂Φ (E, t)

+ Σ(E)Φ(E,t) =

распределения по энергиям, описывающая стацио-

∂t

нарное энергетическое распределение каскада дви-

∫

жущихся атомов при степенном потенциале взаимо-

= dE^′P (E^′ → E) Σ (E^′) Φ (E^′, t) +

действия (U ∼ 1/rⁿ [15]) с учетом энергии связи ато-

мов в узлах решетки. Кроме того, на основе пред-

∫

ставлений, развитых в [12], в работе [16] были опре-

+ dE^′P (E^′ → E^′ - E - ε_d) ×

делены пространственные и временные характери-

E+ε_d

стики первично выбитых релятивистских электро-

нов, замедляющихся в веществе за счет ионизацион-

× Σ(E^′)Φ(E^′,t) + N₀δ (E - E₀)δ (t),

(1)

ных потерь. В работе [17] эти представления были

где f(E, t)dE — число атомов с энергией E в ин-

использованы для вычисления стационарного энер-

тервале dE в момент времени t в единице объема;

гетического распределения релятивистских элек-

Φ(E, t) = vf(E, t) — поток движущихся атомов; v —

тронов, замедляющихся в веществе за счет иониза-

их скорость;

ционных потерь с учетом их размножения.

В работах [18, 19] было получено точное реше-

P (E^′ → E) = Σ(E^′ → E)/Σ(E^′)

ние кинетического уравнения Больцмана, описыва-

ющее нестационарное энергетическое распределение

— индикатриса рассеяния (вероятность того, что

каскада движущихся атомов с учетом их размноже-

движущийся атом с энергией E^′ в результате рассея-

ния. Предполагалось, что материал состоит из оди-

ния перейдет в единичный интервал энергий вблизи

наковых атомов, рассеяние движущихся атомов яв-

значения E); Σ (E^′ → E) и Σ(E^′) — дифференциаль-

ляется упругим и сферически-симметричным в сис-

ное и полное макроскопические сечения рассеяния

теме центра инерции, а энергия связи атомов в уз-

атомов; δ(x) — дельта-функция Дирака; E₀ — на-

лах решетки не учитывалась (ε_d = 0). В [18] предпо-

чальная энергия движущихся атомов; N₀ — их пол-

лагалось, что сечение рассеяния является постоян-

ное число, испущенное в единицу объема; ε_d — энер-

ной величиной (Σ = const), а в [19] оно полагалось

гия связи атомов в узлах решетки.

обратно пропорциональным скорости (Σ = Σ₀/v;

Первый интеграл, стоящий в правой части ки-

Σ₀ = const). В работе [20] в тех же предположениях

нетического уравнения (1), описывает переход дви-

(ε_d = 0; Σ = const) с использованием P₁ и транс-

жущегося атома с энергией E^′ в состояние с энер-

портного приближений было получено нестационар-

гией E. Второй интеграл описывает образование

ное пространственно-энергетическое распределение

выбитого атома с энергией E, когда движущийся

каскада выбитых атомов.

атом перешел в состояние с энергией (E^′ - E - ε_d).

168

ЖЭТФ, том 160, вып. 2 (8), 2021

Использование модельного уравнения Больцмана...

Точное решение уравнения (1), как отмечалось вы-

обусловлены тем, что часть энергии (p (E)ε_d) дви-

ше, было получено в работах [18, 19] для упруго-

жущийся атом тратит на выбивание атома из узла

го, сферически-симметричного рассеяния в системе

решетки, а часть энергии теряет в столкновениях с

центра масс без учета энергии связи атомов в узлах

передачей энергии покоящемуся атому меньшей ε_d

решетки (ε_d = 0).

(второе слагаемое в (7)), не выбивая его из узла ре-

Из уравнения (1) вытекают следующие законы

шетки.

сохранения полного числа частиц и энергии:

Упростим уравнение (1), представив его в следу-

ющем виде [8]:

∫

= dE p(E)Σ(E)Φ(E, t),

(2)

1 ∂Φ (E, t)

+ ⌈Σ (E) + δΣ₁(E)⌉ Φ (E, t) =

ε_d

∂t

∫

[Σ (E^′) +δΣ₁ (E^′)] P (E^′ → E) Φ (E^′, t) dE^′ +

∫

dE(t)

= - dE Δ0 (E)Σ(E)Φ(E,t),

(3)

∫

[Σ (E^′) + δΣ₂ (E^′)] P (E^′ → E^′ - E) ×

где

∫E0

× Φ(E^′,t) dE^′ + N₀δ (E - E₀)δ (t).

(8)

N (t) = dE f(E, t),

Выражения для δΣ₁(E) и δΣ₂ (E) получим, по-

требовав, чтобы из уравнения (8) вытекали те же

(4)

∫E0

законы сохранения (2), (3), что и из исходного урав-

E (t) = dE E f (E, t),

нения (1). Проинтегрировав уравнение (8) (см. (4)),

найдем

)

⁽Δ0 (E)

δΣ₁ (E) = Σ (E)

+ p(E) - 1

(9)

∫

Δ(E)

p (E) =

P (E → E^′) dE^′,

(5)

δΣ₂(E) = -Σ (E)(1 - p (E)).

(10)

а функция Δ₀ (E) определяется следующими выра-

При E, стремящемся к ε_d , функции δΣ₁ (E)

жениями:

и δΣ₂(E) принимают значения соответственно 0 и

-Σ (E), в уравнении (8) второй интеграл обраща-

∫E

ется в нуль, и оно переходит в обычное уравнение

Δ₀ (E) = Δ(E) = dE^′ (E - E^′)P(E → E^′)

(6)

замедления.

Далее будем считать, что рассеяние движущих-

при E ≤ ε_d,

ся атомов на покоящихся является сферически-сим-

метричным в системе центра инерции и описыва-

∫E

ется индикатрисой рассеяния, имеющей следующий

Δ₀ = p (E)ε_d +

dE^′ (E - E^′) P (E → E^′)

вид [21]:

(7)

E-ε_d

при E ≥ ε_d.

P (E^′ → E) =

(11)

E^′

Величина p(E) представляет собой вероятность

В таком случае при E ≥ ε_d уравнение (8) принимает

того, что движущийся атом с энергией E передает

следующий вид (5)-(7), (9), (10):

атому решетки энергию, большую ε_d. Очевидно, что

[

]

)₂

при E ≤ ε_d величина p(E) обращается в нуль.

∂Ψ(E, t)

ε_d

⁽ε_d

+ 1+

Ψ(E, t) =

Из соотношений (3), (6), (7) вытекает, что поте-

vΣ(E)

∂t

ри энергии движущимися атомами происходят та-

∫

[

]

)₂

ким образом, что при E ≤ ε_d движущийся атом не

dE^′

⁽ε_d

Ψ(E^′, t) +

может выбить атом из узла решетки. В одном таком

E^′

соударении движущийся атом теряет в среднем ко-

+ N₀δ (t)δ (E - E₀),

(12)

личество энергии Δ(E). При E ≥ ε_d потери энергии

169

ЖЭТФ, вып. 2 (8)

Е. В. Метелкин, М. В. Лебедева

ЖЭТФ, том 160, вып. 2 (8), 2021

[

]

)₂

где Ψ (E, t) = Σ(E)Φ(E, t) — плотность соударений.

ε_d

⁽ε_d

+1+

Ψ₀ (E, s) =

vΣ

При E = ε_d уравнение (12) переходит в обычное

уравнение замедления.

∫

[

]

)₂

dE^′

⁽ε_d

Следует отметить, что в работе [22] был проведен

Ψ₀ (E^′, s)+

E^,

менее точный учет влияния энергии связи на раз-

[

]

витие каскада, являющийся частным случаем пред-

N₀ 2 - (ε_d/E₀)2

ставленного выше подхода. В [22] полагалось, что

[

(17)

потери энергии происходят только за счет вырыва-

E₀ s/v₀Σ(E₀) + 1 + ε_d/E₀ - (ε_d/E₀)2

ния атомов из узла решетки:

Далее будем полагать, что сечение рассеяния по-

стоянно (Σ = const). С учетом этого обстоятельства,

E (t) = -ε_d

N (t).

(13)

дифференцируя (17) по энергии, найдем уравнение

для определения функции

Ψ₀ (E, p):

Между (2) и (3) будет существовать связь в виде

[

]

(13), если положить в них p = 1 и Δ₀ = ε_d. Таким

2 - s/2vΣ - ε_d/E + (ε_d/E)2

dΨ0

образом, в [22] не учитывались соударения, сопро-

[

] .

(18)

Ψ₀

1 + s/vΣ + ε_d/E - (ε_d/E)2

вождающиеся передачей энергии, меньшей ε_d, что

привело к завышенному значению каскадной функ-

Граничное условие для

(18) легко получить

ции (см. ниже).

из (17):

Ψ₀ (E₀, s) =

3. РЕШЕНИЕ КИНЕТИЧЕСКОГО

[

]

N₀ 2 - (ε_d/E₀)2

УРАВНЕНИЯ

[

]₂ .

(19)

E₀ s/v₀Σ + 1 + ε_d/E₀ - (ε_d/E₀)²

Рассмотрим решение уравнения (12). Применяя

к обеим частям уравнения преобразование Лапласа

В таком случае решение уравнения (18) легко опре-

по времени [23]

делить:

∫∞

[

]

N₀ 2 - (ε_d/E₀)2

Ψ (E, p) = exp (-st)Ψ (E, t) dt

(14)

Ψ₀ (E, s) =

[

]₂ ×

E₀ s/v₀Σ+1ε_d/E₀- (ε_d/E₀)²

⎧

[

]⎫

получим

∫

2-s/2vΣ-ε_d/E+ (ε_d/E)2

⎬

× exp

[

]

(20)

[

]

)₂

⎩

⎭

ε_d

⁽ε_d

1+s/vΣ+ε_d/E- (ε_d/E)²

+1+

Ψ (E, s) =

vΣ

Вычисление оригинала по формуле (20) является

∫E0

[

]

)₂

dE^′

⁽ε

достаточно сложной задачей. В связи с этим функ-

Ψ (E^′, s) +N₀δ (E-E₀) .

(15)

E^′

цию распределения Ψ₀(E, t) (рассеянное излучение)

будем искать в следующем виде:

Выделим в решении уравнения (15) нерассеянное

Ψ₀ (E, t) = A(E)tb(E) exp[-c (E)t] ,

(21)

излучение

где параметры A (E), b (E), c(E) легко определяют-

Ψ (E, s) =

Ψ₀ (E, s) +

ся через временные моменты (см., например, [21])

N₀δ(E - E₀)

∞

[

(16)

∫

∕

s/vΣ + 1 + ε_d/E - (ε_d/E)2

〈tⁿ(E)〉 = dt tⁿ Ψ₀ (E, t)

В таком случае для определения функции

Ψ₀ (E, p)

∕∫∞

dt Ψ₀(E, t) (n = 1, 2, . . .)

(22)

(рассеянное излучение) получим следующее уравне-

ние:

170

ЖЭТФ, том 160, вып. 2 (8), 2021

Использование модельного уравнения Больцмана...

от функции распределения (20), являющейся точ-

Таким образом, окончательно функцию рас-

ным решением уравнения (15).

пределения f₀(E, t) (рассеянное излучение) можно

Используя (21), (22), найдем

представить в следующем безразмерном виде:

b(E)+1

Ψ₀(E, s = 0)c(E)

f₀(E, t) E₀

A(E) =

f^′ (E, τ) =

Γ [b (E) + 1]

N₀

〈t(E)〉

[c^′ (E)]b(E)+1

b (E) =

- 1,

(23)

= f′0 (E)

τ^b exp[-c^′ (E)τ] ,

(28)

〈t² (E)〉 - 〈t(E)〉²

Γ [b (E) + 1]

〈t(E)〉

c (E) =

где τ

= v₀Σt, c′ (E)

= c(E)/(v₀Σ), f′0 (E)

〈t² (E)〉 - 〈t(E)〉

= Ψ0 (E,s = 0)E₀/(N₀vΣ) (см. (25)).

где Γ(x) — гамма-функция [24].

Соответствующие временные моменты можно

найти с помощью (20) следующим образом:

4. АНАЛИЗ ПОЛУЧЕННОГО РЕШЕНИЯ

Положив в (20) ε_d = 0 и проведя интегрирование,

〈tⁿ(E)〉 =

{[

]

}

получим точное решение соответствующей задачи

∂

= (-1)ⁿ

Ψ₀ (E, s)

/Ψ0(E, s)

(24)

без учета энергии связи (см. в [18] формулу (10)).

∂sⁿ

s=0

Оценим точность использования в качестве ре-

Используя (20), (24), получим

шения уравнения (15) функции распределения в ви-

де (21). На рис. 1 представлены зависимости функ-

(

)

2E²⁰ - ε2d

ции распределения от времени, построенные для

Ψ₀ (E, s = 0) =N0

E₀ E²⁰ + E₀ε_d - ε²

различных значений энергии по формуле (28) без

)

3/2

учета энергии связи (ε_d = 0) и являющиеся точным

⁽E²⁰ +E₀ε_d -ε2d

решением соответствующей задачи (см. (12) в [18]).

E₀

E² + Eε_d - ε²

На рисунке видно, что функция (28) при ε_d = 0 с

[

(

√ )]3/2√

2E₀ + ε_d

(

√ )

2E₀ + ε_d

[

(

√ )]3/2√5

2E + ε_d

(

√ )

(25)

2E + ε_d

2E²⁰

〈t (E)〉v₀Σ =

E²⁰ + E₀ε_d - ε²

∫

√

5E² - Eε_d + ε2d

EE₀

(26)

(E² + Eε_d - ε2d)²

6E²⁰

2E²⁰

〈t² (E)〉v²⁰Σ² =

E²⁰+E₀ε_d-ε2d

E²⁰+E₀ε_d-ε²

∫E0

√

5E² - Eε_d + ε2d

EE₀

(E² + Eε_d - ε2d)²

⎡

⎤₂

∫

1_⎣

√

5E² - Eε_d + ε2d

Рис. 1. Зависимость функции распределения f^′(τ ) от без-

EE₀

⎦ +

размерного времени τ, построенная по формуле (28) при

(E² + Eε_d - ε2d)²

εd = 0 (сплошные кривые) и по формуле (12) из [18]

∫E0

(штриховые кривые) для различных значений безразмер-

5E² - Eε_d + ε2d

ной энергии ε = E/E0: 1 — ε = 10-1, 2 — ε = 10-2, 3 —

dE E₀E²

(27)

(E² + Eε_d - ε2d)

ε = 10-3

171

Е. В. Метелкин, М. В. Лебедева

ЖЭТФ, том 160, вып. 2 (8), 2021

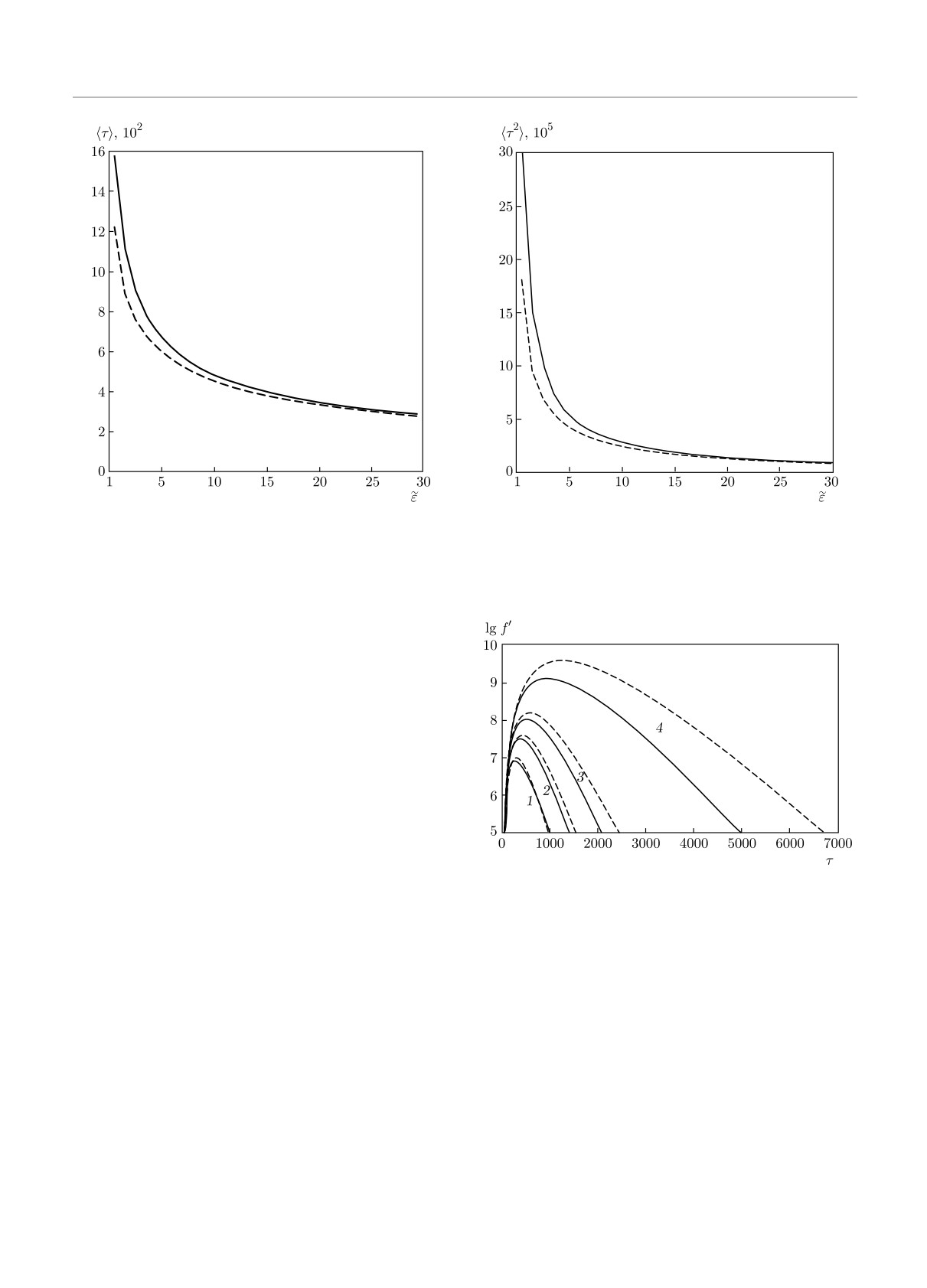
Рис.

2. Зависимости среднего времени замедления

Рис. 3. Зависимости среднего квадрата времени замедле-

(〈τ〉=Σv0〈t〉) от безразмерной энергии ε = E/εd (штрихо-

ния (〈τ²〉=Σ²v²⁰〈t²〉) от безразмерной энергии ε = E/ε_d

вая кривая — с учетом энергии связи; сплошная кривая —

(штриховая кривая — с учетом энергии связи; сплошная

при ε_d = 0), построенные по формуле (26)

кривая — при ε_d = 0), построенные по формуле (27)

хорошей точностью описывает точное решение со-

ответствующей задачи из [18].

Из рис. 2 и 3 следует, что учет энергии связи при-

водит к уменьшению среднего времени замедления и

квадрата этой величины (при расчетах полагалось,

что E₀/ε_d = 10⁵). Отмеченное обстоятельство оче-

видно обусловлено тем, что при учете энергии связи

учитываются потери энергии на выбивание атомов

из узлов решетки.

На рис. 4 представлена зависимость функции

распределения от времени, построенная по форму-

ле (28) для различных значений энергии как с уче-

том, так и без учета энергии связи (полагалось, что

Рис. 4. Зависимость функции распределения от времени,

E₀/ε_d = 10⁵). Из приведенных результатов следу-

построенная по формуле (28) при различных значениях

ет, что при учете энергии связи функция распреде-

безразмерной энергии ε = E/ε_d: 1 — ε = 20, 2 — ε = 10,

ления достигает максимума при меньших значени-

3 — ε= 5, 4 — ε= 1, при учете (сплошные кривые) и без

ях времени (см. рис. 2) и ее значение в максимуме

учета (штриховые кривые) энергии связи

существенно меньше. Очевидно, что последнее об-

стоятельство обусловлено тем, что при учете энер-

гии связи образуется конечное число выбитых ато-

E₀. Из выражения (2) получим, что полное число

мов, а при ε_d = 0 оно неограниченно возрастает (см.

выбитых атомов равно

[18]). Следует отметить, что при увеличении энер-

гии эти различия становятся менее заметными и при

∫

∞

E ≥ 20ε_d они практически исчезают.

N (E₀) = dEp (E) dt Ψ (E, t)

(29)

Найдем каскадную функцию ν(E₀), представля-

ε_d

ющую собой полное число атомов решетки, приходя-

щихся на один первично выбитый атом с энергией

или

172

ЖЭТФ, том 160, вып. 2 (8), 2021

Использование модельного уравнения Больцмана...

N (E₀)

В этом случае временные моменты (см. (22)-(24))

ν (E₀) =

N₀

будут содержать интегралы, требующие численных

∫

расчетов для вычисления и анализа самой функции

dEp (E)

Ψ₀ (E, s = 0),

(30)

распределения.

N₀

ε_d

где

Ψ₀ (E, s = 0) определяется формулой (25).

ЛИТЕРАТУРА

Подставив (25) в (30) и пренебрегая членами по-

К. Лейман, Взаимодействие излучения с твер-

рядка ε_d/E₀ по сравнению с единицей, для каскад-

дым телом и образование элементарных дефек-

ной функции получим следующее выражение (см.

тов, Атомиздат, Москва (1979).

также [8]):

)

С. Вас Гэри, Основы радиационного материало-

⁽E₀

ν (E₀) = ν₀

ведения. Металлы и сплавы, Техносфера, Москва

ε_d

(2014).

(

√

)3/2√5

(31)

И. А. Портных, А. В. Козлов, ФММ 119, 636

ν₀ ≃ 2

√

≃ 0.55.

(2018).

Л. С. Васильев, С. Л. Ломаев, ФММ 120, 771

Численные расчеты, проведенные по формуле

(2019).

(30), показали, что при изменении E₀ от 10⁶ до

10³ эВ значение ν₀ изменяется от 0.55 до 0.53 (при

А. Р. Исинбаев, И. А. Портных, А. В. Козлов,

это полагалось, что ε_d = 10 эВ). Полученное выра-

ФММ 121, 99 (2020).

жение (31) хорошо согласуется с формулой Кинчи-

Р. Е. Воскобойников, ФММ 120, 3 (2019).

на - Пиза ( ν₀ = 0.5 см. [2]).

Р. Е. Воскобойников, ФММ 121, 10 (2020).

5. ВЫВОДЫ

A. I. Ryazanov and E. V. Metelkin, Rad. Effects 52,

15 (1980).

На основе решения модельного кинетического

уравнения Больцмана получена функция распреде-

Y. Sato, S. Kojimo, T. Yoshiie et al., J. Nucl. Mater.

ления, описывающая нестационарное энергетичес-

179-181, 901 (1991).

кое распределение каскада замедляющихся атомов

10.

Y. Sato, T. Yoshiie, and M. Kiritani, J. Nucl. Mater.

в твердом теле с учетом их размножения. Предпола-

191-194, 1101 (1992).

галось, что твердое тело состоит из одинаковых ато-

мов, энергия связи которых равна ε_d. Кроме того,

11.

Е. В. Метелкин, А. И. Рязанов, Атомная энергия

полагалось, что сечение рассеяния движущихся ато-

83, 183 (1997).

мов является упругим и сферически-симметричным

12.

Е. В. Метелкин, А. И. Рязанов, Е. В. Семенов,

в системе центра инерции, а его величина постоян-

ЖЭТФ 134, 469 (2008).

на.

Следует отметить, что интегралы, входящие в

13.

A. I. Ryazanov, E. V. Metelkin, and E. V. Semenov,

(26), (27), выражаются через элементарные функ-

J. Nucl. Mater. 386-388, 132 (2009).

ции (см. [24]). В таком случае сама функция распре-

14.

A. A. Aleksandrov, V. A. Akatev, E. V. Metelkin, and

деления (28) при сделанных предположениях пред-

E. J. Barycheva, Herald of the Bauman Moscow State

ставляет собой относительно простое, хотя и гро-

Technical University, Series Natural Sciences №1, 27

моздкое алгебраическое выражение, которое при

(2019).

ε_d = 0 хорошо согласуется с точным решением соот-

ветствующей задачи (см. рис. 1). На основе получен-

15.

J. Lindhard, V. Nielsen, and M. Scharff, Mat. Fys.

ной функции распределения (28) проанализированы

Medd. Dan. Vid. Selsk. 36, 1 (1968).

особенности развития каскада, связанные с учетом

16.

В. А. Акатьев, Е. В. Метелкин, А. М. Савинов,

энергии связи атомов и имеющие общий характер.

Атомная энергия 122, 295 (2017).

Кроме того, очевидно, что решение уравнения

(17) в виде (21) может быть получено и для произ-

17.

Е. В. Метелкин, М. В. Лебедева, А. В. Черняев,

вольной зависимости сечения рассеяния от энергии.

Атомная энергия 125, 184 (2018).

173