ЖЭТФ, 2021, том 160, вып. 2 (8), стр. 232-248

ОБОБЩЕННАЯ МОДЕЛЬ ИЗИНГА В МАГНИТНОМ ПОЛЕ

Е. С. Цуваревa,b*, Ф. А. Кассан-Оглыb**

^a Уральский федеральный университет им. первого Президента России Б. Н. Ельцина

620000, Екатеринбург, Россия

^b Институт физики металлов им. М. Н. Михеева Уральского отделения Российской академии наук

620108, Екатеринбург, Россия

Поступила в редакцию 11 февраля 2021 г.,

после переработки 22 апреля 2021 г.

Принята к публикации 23 апреля 2021 г.

Представлены результаты по обобщению модели Изинга на произвольное число трансляций линейной

цепочки, находящейся во внешнем магнитном поле, с учетом различных взаимодействий между спи-

нами. Выведено точное аналитическое выражение для наибольшего собственного значения трансфер-

матрицы Крамерса - Ваннье с трансляцией на два периода цепочки во внешнем магнитном поле при

учете ближайших и вторых соседей. Установлены точные выражения для нуль-температурных энтропий

и намагниченностей при различных величинах и знаках обменных взаимодействий и магнитного поля.

Многие найденные нуль-температурные энтропии и нуль-температурные намагниченности представлены

через так называемые математические сечения, издавна известные в удивительном мире математики

чисел (золотое сечение ϕ, серебряное сечение δ, сверхзолотое сечение ψ, пластическое число ρ и новые

(безымянные)). Получен результат, при котором значения фрустрирующих энтропий и намагниченно-

стей могут быть выражены через предел отношения определенных числовых последовательностей без

привлечения формализма трансфер-матрицы Крамерса - Ваннье.

DOI: 10.31857/S0044451021080095

1. ВВЕДЕНИЕ

Первой работой по обобщению модели Изинга на

несколько трансляций решетки была статья Сиози

и Найя [1] (см. также [2, 3]). В этих работах по-

лучено точное аналитическое решение обобщенной

квадратной решетки с трансляцией на два перио-

да в горизонтальном (J₂, J₄) и вертикальном (J₁, J₃)

направлениях (рис. 1) в отсутствие магнитного по-

ля, но исследований каких-либо термодинамических

свойств не проводилось.

Главным преимуществом данной решетки явля-

Рис. 1. Обобщение модели Изинга на квадратной решетке,

ется то, что из структуры такого типа обобщения

предложенное Сиози, с обменными взаимодействиями J1

можно получать различные виды других решеток

и J3 по вертикальному направлению и с обменными взаи-

с помощью предельных переходов. Например, если

модействиями J2 и J4 по горизонтальному направлению

положить J₂ = J₄ и J₁ = J₃, то получим реше-

ние, которое вывел Онзагер [4] для обычной (необоб-

щенной) квадратной решетки в отсутствие магнит-

ного поля. Чтобы осуществить переход к гексаго-

^* E-mail: eguny@mail.ru

нальной решетке, необходимо устремить к нулю од-

^** E-mail: felix.kassan-ogly@imp.uran.ru

но из четырех обменных взаимодействий, например,

232

ЖЭТФ, том 160, вып. 2 (8), 2021

Обобщенная модель Изинга в магнитном поле

Рис. 2. При J3 = 0 обобщенная квадратная решетка пре-

вращается в так называемую кирпичную кладку, которая

топологически эквивалентна гексагональной решетке

Рис. 4. Обобщение модели Изинга, предложенное Утия-

мой, на шахматной решетке

Рис. 3. Переход от обобщенной квадратной решетки к тре-

угольной решетке при J2 → ∞

J₃ → 0. Получаемая таким образом решетка типа

«кирпичной кладки» (brick-wall lattice), показанная

на рис. 2, топологически эквивалентна гексагональ-

ной решетке. В случае же перехода к треугольной

решетке одно из четырех обменных взаимодействий

обобщенной модели устремляется в бесконечность,

например, J₂ → ∞ (см. рис. 3).

Более универсальный вариант обобщения моде-

ли был предложен Утиямой в статье [5] на примере

шахматной решетки, в которой все черные квадраты

замещаются специальными вставками (рис. 4). Ин-

тересно, что в этом случае, помимо полученных ре-

шеток (квадратная необобщенная, треугольная, гек-

сагональная) при n = 0, что означает всего один

Рис. 5. Переход от решетки Утиямы к решетке кагоме:

квадрат в качестве вставки со взаимодействиями

а) решетка Утиямы с одной вертикальной чертой при

J, J₁ и J₀, можно получить также и решетку каго-

J1 → 0, б) решетка кагоме

ме, положив n = 1 (в качестве вставки два квадрата

со взаимодействиями J, J₀, J₁, J₂, J₃) и устремив J₁

к нулю (рис. 5).

угольная [6], гексагональная [7], кагоме [8]). В ре-

Очевидно, что данные варианты обобщения, вве-

зультате, всевозможными вариантами предельных

денные на квадратной решетке Сиози, Найя и Утия-

переходов осуществляется получение множества са-

мой, могут быть применены и к другим планарным

мых разнообразных видов еще не изученных реше-

решеткам с известными точными решениями (тре-

ток.

233

ЖЭТФ, вып. 2 (8)

Е. С. Цуварев, Ф. А. Кассан-Оглы

ЖЭТФ, том 160, вып. 2 (8), 2021

В настоящей работе мы ставим цель обобщить

2. ОБОБЩЕНИЕ МОДЕЛИ ИЗИНГА НА

модель Изинга на произвольное число трансляций

ПРОИЗВОЛЬНОЕ ЧИСЛО ТРАНСЛЯЦИЙ

линейной цепочки, поскольку именно на одномерной

ЛИНЕЙНОЙ ЦЕПОЧКИ

цепочке существует возможность получения точно-

Гамильтониан обобщенной модели Изинга с уче-

го аналитического решения в магнитном поле. От-

том взаимодействий между ближайшими и вторыми

метим, что некоторые предварительные обобщения

соседями с произвольным числом трансляций ли-

модели Изинга на линейной цепочке сделаны в ра-

нейной цепочки, находящейся в магнитном поле, мо-

ботах [9,10].

жет быть записан в следующей форме:

∑

H_n(s) = -J₁

s_isi+1 - J^′

s_isi+2-J₂

si+1si+2-J′2 ×

i=1,n+1,2n+1,...

i=2,n+2,2n+2,...

∑

si+1si+3 - · · · - J_n

si+nsi+n+1 - J^′

si+nsi+n+2 - H

s_i,

(1)

i=2,n+2,2n+2,...

i=n,2n,3n,...

i=1,2,3,...

где J₁, J₂, . . . , J_n

— параметры обменного вза-

Следуя общему алгоритму вывода тран-

имодействия между ближайшими соседями, J′1,

сфер-матрицы Крамерса - Ваннье

[11-13], можно

J′2, . . ., J′n — параметры обменного взаимодействия

получить трансфер-матрицы для одномерной це-

между вторыми соседями, H — внешнее магнитное

почки с двумя, тремя, четырьмя и т. д. трансля-

поле, s = ±1 (см. рис. 6, на котором представлен

циями в виде одной матрицы, например, для двух

частный случай модели для трансляций только на

трансляций:

два периода решетки).

⎛

⎞

eK1+L1+K2+L2+2h eK1+L1+K2-L2+2h eK1-L1-K2+L2+2h eK1-L1-K2-L2+2h

⎜

⎟

⎜

−K1+L1-K2-L2 e-K1+L1-K2+L2 e-K1-L1+K2-L2 e-K1-L1+K2+L2

⎟

W₂ =⎜e

⎟,

(2)

⎜

⎟

⎝ e-K1-L1+K2+L2 e-K1-L1+K2-L2 e-K1+L1-K2+L2 e-K1+L1-K2-L2

⎠

eK1-L1-K2-L2-2h eK1-L1-K2+L2-2h eK1+L1+K2-L2-2h eK1+L1+K2+L2-2h

где K₁ = J₁/T , K₂ = J₂/T , L₁ = J′1/T , L₂ = J′2/T ,

Продолжая построение трансфер-матриц Крамер-

H = h/T.

са - Ваннье для трех, четырех и т. д. трансляций в

С другой стороны, перемножив две матрицы V₁ и

общем алгоритме вывода, будем получать все более

V₂ каждая из которых соответствует одной трансля-

и более громоздкие выражения, аналогичным обра-

ции, получаем в точности исходную матрицу W₂. Та-

зом превращаемые в гораздо более изящном виде в

ким образом, показана эквивалентность W₂ и V₁ ·V₂.

произведения простых матриц:

⎛

⎞

eKi+Li+^h eKi-Li+^h

⎜

⎟

∏

∏⎜

⎟

e-Ki+Li+^h e-Ki-Li+^h

⎜

W_n = V₁ · V₂ · . . . · V_n = V_i =

^⎟,

(3)

⎜

⎟

⎝e-Ki-Li-h e-Ki+Li-h

⎠

i=1

eKi-Li-h eKi+Li-h

где V₁, V₂, . . . , Vn — трансфер-матрицы Крамер-

трансляции линейной цепочки.

са - Ваннье, K_i = J_i/T, L_i = J^′i/T, h = H/T.

Поскольку в гамильтониане (1) каждая сумма

В результате трансфер-матрица Крамерса - Ван-

пробегает только по n узлам, а не по всем узлам ре-

нье W_n представляется как произведение транс-

шетки N, статсумма в термодинамическом пределе

фер-матриц V_i, относящихся к одной определенной

теперь примет вид

234

ЖЭТФ, том 160, вып. 2 (8), 2021

Обобщенная модель Изинга в магнитном поле

∑

′

H₂(s) = -J₁

s_isi+1 - J

s_isi+2 -

i=1,3,5,...

∑

′

-J₂

si+1si+2 - J

si+1si+3 -

Рис. 6. Обобщенная модель Изинга с различными обмен-

i=2,4,6,...

ными взаимодействиями между ближайшими (J1, J2) и

вторыми (J′1, J′2) соседями с трансляцией на два периода

∑

-H

s_i,

(10)

цепочки

i=1,2,3,...

где J₁, J₂ — параметры обменного взаимодействия

Z_N = λ^N/nmax.

(4)

между ближайшими соседями, J′1, J′2 — параметры

Свободная энергия, энтропия, теплоемкость, на-

обменного взаимодействия между вторыми соседя-

магниченность и внутренняя энергия выражают-

ми, H — внешнее магнитное поле, s = ±1.

ся только через наибольшее собственное значение

На рис. 6 проиллюстрирована цепочка, соответ-

трансфер-матрицы Крамерса - Ваннье λ_max

ствующая обобщенной модели Изинга, описываемой

гамильтонианом (10).

T ln λ_max

F (H, T ) = -

(5)

Определяем секулярное уравнение транс-

фер-матрицы W₂ в форме

ln λ_max

∂λ_max

S(H, T ) =

(6)

nλ_max

∂T

det(W₂ - λE) = 0,

(11)

переписав его в виде

∂λ_max

C(H, T ) =

nλ_max

∂T

(

)

λ⁴ + aλ³ + bλ² + cλ + d = 0,

(12)

∂

∂λ_max

(7)

n ∂T λ_max

∂T

решаем его и находим наибольшее собственное зна-

чение, которое принимает вид

∂λ_max

M (H, T ) =

(8)

nλ_max

∂H

√

a² - 4b + 4y - a

∂λ_max

λmax =

E(H, T ) =

(9)

∂T

1(√

)₂

Получение точного аналитического решения для

√

a²-4b+4y-a

2c - ya

наибольшего собственного значения трансфер-мат-

√

(13)

a²-4b+4y

рицы Крамерса - Ваннье с гамильтонианом (1) весь-

ма проблематично. Тем не менее, с конструирова-

где

нием несложной компьютерной программы выраже-

ния для максимальных собственных значений мат-

p³

q²

b²

рицы Крамерса - Ваннье с учетом конкретных взаи-

p=-

+ ac - 4d,

модействий (между третьими, четвертыми и следу-

ющими соседями) могут быть представлены числен-

2b³

bac

8bd

q=-

-a²d - c²,

но, и расчеты термодинамических и магнитных ве-

личин проводятся также по формулам (5)-(9). В на-

√

стоящей статье ввиду громоздкости общего решения

√√

√

y=³

Q-

+³ -

Q-

мы его не приводим, а ограничимся рассмотрением

обобщенной модели Изинга с учетом ближайших и

вторых соседей в присутствии магнитного поля.

⁽J′1 +J′2)(

⁽2H⁾

⁽J₁ +J₂)

a = -2exp

exp

Тогда гамильтониан обобщенной модели Изинга

с трансляцией трансфер-матрицы только на два уз-

⁽-J₁ - J₂ ))

ла линейной цепочки в магнитном поле представит-

+ exp

ся в виде

235

Е. С. Цуварев, Ф. А. Кассан-Оглы

ЖЭТФ, том 160, вып. 2 (8), 2021

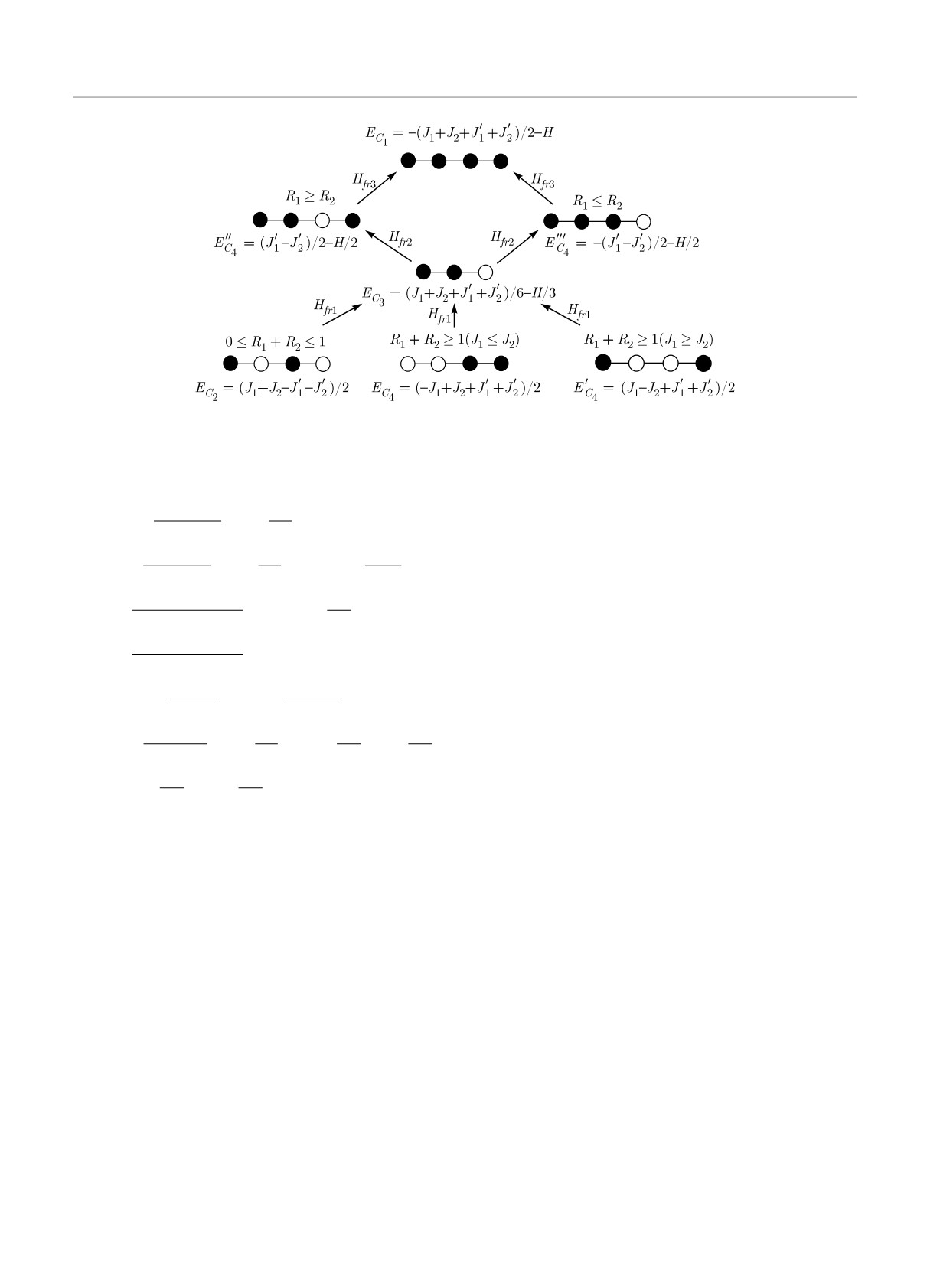
Рис. 7. Схема переходов в варианте конкурирующих взаимодействий при J1 < 0, J¹ < 0, J2 < 0, J² < 0. Темные кружки —

спин направлен вверх, светлые — вниз

)

}

⁽2J′1 + 2J′2

⁽2H⁾

^{...↓ ↑

↓

↑...

b = 4exp

C₂ =

)

...↑

↓

↑

↓...

⁽2J′1 - 2J′2

⁽2H⁾

⁽-2J₁ )

- 4ch

+ 2exp

с внутренней энергией EC2 = (J₁+J₂)/2-(J′1+J′2)/2,

)

ферромагнитное упорядочение

⁽2J′1 + 2J′2 - 2J₂

⁽2J₁ )

× sh

+ 2exp

{

}

C₁ =

...↑

↑

↑...

)

⁽2J′1 + 2J′2 + 2J₂

× sh

с внутренней энергией EC1 = -(J₁+J₂)/2-(J′1+J′2)/2-

)(

с учетверением

⁽J′1 +J′2

⁽J₁ +J₂)

c = -8exp

exp

периода трансляции решетки

)

}

⁽-J₁ - J₂

⁽2H⁾⁾

⁽2J′1 )

⁽2J′2 )

^{. . . ↓ ↓

↑

↑...

^{. . . ↑ ↓

↓

↑...

+ exp

C₄ =

C′4 =

)

...↑

↑

↓

↓...

...↓

↑

↓...

⁽2J′1

⁽2J′2 )

d = 16sh²

sh²

{

}

{

}

C^′′4 =

...↑

↑

↓

↑...

C^′′′4 =

...↑

↑

↓...

внутренними

энергиями

соответственно

Поскольку вновь рассматривается перенос толь-

EC4

-(J₁ - J₂)/2 + (J′1 + J′2)/2, E_C′

ко на два периода трансляции цепочки, для на-

= (J₁ - J₂)/2 + (J′1 + J′2)/2, E_C′′

= (J′1 - J′2)/2 - H/2,

хождения термодинамических и магнитных величин

системы можно воспользоваться формулами, пред-

E_C′′′

= -(J′1 - J′2)/2 - H/2 и конфигурация C₃ с

ставленными в статье [9].

утроением периода трансляции

{

}

C₃ =

...↑

↑

↓...

3. ТЕРМОДИНАМИЧЕСКИЕ, МАГНИТНЫЕ

с внутренней энергией EC3 = (J₁ + J₂ + J′1 + J′2)/6 -

И ФРУСТРИРУЮЩИЕ СВОЙСТВА

- H/3.

ОБОБЩЕННОЙ МОДЕЛИ ИЗИНГА

Рассматриваемая обобщенная модель Изинга в

Детальный анализ большого количества всевоз-

магнитном поле обладает восемью вариантами кон-

можных вариантов величин и знаков обменных вза-

курирующих взаимодействий между ближайшими и

имодействий показал, что при учете как ближай-

вторыми соседями. Обсудим каждый из них отдель-

ших, так и вторых соседей в магнитном поле, систе-

но. Но для начала введем коэффициенты взаимо-

ма обладает семью магнитными конфигурациями в

действий: R₁ = |J′1/J₁| и R₂ = |J′2/J₂|. Коэффициент

основном состоянии: антиферромагнитная структу-

R₁ отвечает за отношение взаимодействий на нечет-

ра

ных узлах решетки, а R₂ на четных узлах.

236

ЖЭТФ, том 160, вып. 2 (8), 2021

Обобщенная модель Изинга в магнитном поле

1. Антиферромагнитные взаимодействия меж-

Значение нуль-температурной намагниченности,

ду ближайшими и вторыми соседями (J₁

< 0,

в свою очередь, может быть выражено через плас-

J′1 < 0, J₂ < 0, J′2 < 0)

тическое число

Сравнивая энергии конфигураций (рис. 7), уста-

новленных выше, определим фрустрационные поля,

MT→0 =

= 0.1770 . . .

(15)

3ρ³ - ρ

в которых происходят переходы между соответству-

ющими упорядочениями:

Первое фрустрирующее поле при R₁ + R₂ > 1 и

J₁ < J₂ или при R₁ + R₂ > 1 и J₁ > J₂. В этом

Hfr1 =

фрустрирующем поле возникает переход между фа-

⎧

⎨-J1 + 2J′1 - J2 + 2J′2,

0 ≤ R₁ + R₂ ≤ 1,

зами учетверения периода трансляций решетки и

между фазой утроения периода трансляций, а имен-

2J₁-J′1-J₂-J′2,

R₁ + R₂ ≥ 1 и J₁ ≤ J₂,

⁼⎪⎩

но, между фазами C₄ и C₃ либо между фазами C′4

−J₁-J′1+2J₂-J′2,

R₁ + R₂ ≥ 1 и J₁ ≥ J₂;

и C₃, в зависимости от величин J₁ и J₂. Значение

{

энтропии при стремлении температуры к нулю рав-

-J₁ + 2J′1 - J₂ - 4J′2, R₁ ≥ R₂,

но натуральному логарифму квадратного корня из

Hfr2 =

-J₁ - 4J′1 - J₂ + 2J′2, R₁ ≤ R₂;

пластического числа

{

ST→0 = ln

√ρ = 0.1406 . . .

(16)

-J₁ - 2J′1 - J₂, R₁ ≥ R₂,

Hfr3 =

-J₁ - J₂ - 2J′2, R₁ ≤ R₂.

Соответствующая намагниченность равна выраже-

нию (15).

Первое фрустрирующее поле при R₁ + R₂

Первое фрустрирующее поле при R₁ + R₂ > 1 и

< 1. Данное фрустрирующее поле получается при

J₁ = J₂. В случае, когда J₁ = J₂, энергии конфи-

рассмотрении перехода между антиферромагнитной

гураций с учетверением периода трансляций C₄ и

конфигурацией C₂ и конфигурацией C₃ с утроением

C′4 станут равны, тем самым, фрустрирующие поля

периода трансляций решетки [14]. Значение нуль-

также совпадут [12]. Нуль-температурная энтропия

температурной энтропии находится как натураль-

находится как натуральный логарифм наибольшего

ный логарифм единственного вещественного корня

вещественного корня уравнения x⁴ - x - 1 = 0

уравнения x³ - x - 1 = 0, известного как пластичес-

ST→0 = ln ξ = 0.1995 . . .,

(17)

кое число

а нуль-температурная намагниченность

ST→0 = ln ρ = 0.2812 . . .,

(14)

MT→0 =

= 0.1593 . . .,

(18)

√(

√

)

√(

√

)

ξ + 4ξ³ - ξ⁴

где ρ =³

/18 +³

/18 — плас-

тическое число.

где

{

}1/2

√(_√

)

√(_√

)

ξ=

849 + 9

/1152 -³

849 - 9

/1152

⎧

⎛ √

⎞

⎫

√

⎨

(_√

)

√(_√

)

√(_√

)

√(_√

)

⎬1/2

849 + 9

/1152 -³

849 - 9

/1152^⎠ -³

849 + 9

/1152 +³

849 - 9

/1152

⁺⎩1/⎝4

⎭

Это математическое сечение пока безымянное.

Первое фрустрирующее поле при R₁ + R₂

Второе фрустрирующее поле при R₁

> R₂ или

1. При таком условии система вырождает-

R₁ < R₂. Если R₁ > R₂, то система претерпевает

ся в обычную (необобщенную) модель Изинга с

переход в конфигурацию учетверения C^′′4 из фазы

взаимодействиями между ближайшими и вторы-

утроения периода трансляций C₃, а если R₁ < R₂,

ми соседями [14]. Фрустрирующее поле равно ну-

тогда система перейдет в конфигурацию C^′′′4 из фа-

лю, а энтропия равна логарифму золотого сечения

зы C₃. Тем не менее, значения нуль-температурных

энтропий для этих двух переходов будут одинаковы

ST→0 = ln ϕ = 0.4812 . . .,

(19)

(

√

)

(16), как и намагниченности

где ϕ =

/2 — золотое сечение.

237

Е. С. Цуварев, Ф. А. Кассан-Оглы

ЖЭТФ, том 160, вып. 2 (8), 2021

ρ2

MT→0 =

= 0.4115 . . .,

(20)

MT→0 =

= 0.2417 . . .,

(26)

3ρ² - 1

3ν² - 2ν - 2

где

√

(

√

)

ρ =³ (9 +

69)/18 +³ (9 -

69)/18

√

ν =

1 + ³ 98/(3

3i - 1) +³ (21

3i - 7)/2

/3.

— пластическое число.

Второе фрустрирующее поле при R₁ = R₂. При

Это математическое сечение пока безымянное.

равенстве коэффициентов взаимодействий R₁ и R₂

Перечисленные фрустрационные значения энт-

получаем обычную (необобщенную) модель Изин-

ропий и намагниченностей отражены на рис. 8.

га с взаимодействиями между первыми и вторы-

2. Антиферро-антиферромагнитное взаимодей-

ми соседями в магнитном поле. Происходит переход

ствие между ближайшими соседями, антифер-

из конфигурации с утроением периода трансляций

ро-ферромагнитное взаимодействие между вторы-

C₃ сразу в ферромагнитную конфигурацию C₁ [14].

ми соседями (J₁ < 0, J′1 < 0, J₂ < 0, J′2 > 0)

Нуль-температурная энтропия в данном фрустри-

рующем поле выражается как натуральный лога-

Hfr1 = -J₁ + 2J′1 - J₂,

рифм единственного вещественного корня уравне-

Hfr2 = -J₁ - 2J′1 - J₂.

ния x³ - x² - 1 = 0, известного как сверхзолотое

сечение

3. Антиферро-антиферромагнитное взаимодей-

ST→0 = ln ψ = 0.3822 . . .,

(21)

ствие между ближайшими соседями, ферро-анти-

ферромагнитное взаимодействие между вторыми

а нуль-температурная намагниченность равна

соседями (J₁ < 0, J′1 > 0, J₂ < 0, J′2 < 0)

MT→0 =

= 0.6115 . . .,

(22)

Hfr1 = -J₁ - J₂ + 2J′2,

ψ² + 3

Hfr2 = -J₁ - J₂ - 2J′2.

где

(

√

)

√

Варианты конкурирующих взаимодействий 2 и 3

ψ = 1 + ³ (29 + 3

93)/2 +³ (29 - 3

93)/2

схожи. Достаточно привести только одну схему пе-

реходов, например, J₁ < 0, J′1 > 0, J₂ < 0, J′2 < 0

— сверхзолотое сечение.

(рис. 9). Отличительной чертой этих двух вариантов

Третье фрустрирующее поле при R₁ < R₂ или

является только разница в промежуточном состоя-

R₁ > R₂. В данном фрустрирующем поле происхо-

) между антиферромагнитной (C₂)

дит переход из конфигураций с учетверением пери-

и ферромагнитной (C₁) конфигурациями.

) в ферромагнитное со-

Первое фрустрирующее поле. В данном фруст-

стояние C₁. Значение нуль-температурной энтропии

рирующем поле происходит переход из антифер-

равно натуральному логарифму квадратного корня

ромагнитного упорядочения C₂ в конфигурацию с

из золотого сечения

′′′

учетверением периода трансляции C

. Энтропия

ST→0 = ln

√ϕ = 0.2406 . . . ,

(23)

равна натуральному логарифму корня из золотого

сечения (23) с соответствующим значением намаг-

а нуль-температурная намагниченность

ниченности

MT→0 =

= 0.7236 . . .,

(24)

2ϕ - 1

MT→0 =

= 0.2763 . . .

(27)

2ϕ² - ϕ

(

√

)

где ϕ =

/2 — золотое сечение.

Второе фрустрирующее поле. Энтропия соот-

Однако, если положить |R₁ - R₂| = 1, первое

ветствует выражению (23), а намагниченность

и второе фрустрирующие поля совпадут (Hfr1 =

= Hfr2), при этом произойдет переход из конфи-

MT→0 =

= 0.4472 . . .,

(28)

гураций с нулевой намагниченностью (C₂, C₄ или

2ϕ - 1

C′4) непосредственно в фазу с учетверением перио-

(

√

)

где ϕ =

/2 — золотое сечение.

), энтропия в

При R₁ = R₂ = 0 приходим к случаю необобщен-

этом случае находится как натуральный логарифм

ной модели Изинга с взаимодействием ближайших

квадратного корня наибольшего решения уравнения

соседей в магнитном поле [13,14] с хорошо известны-

x³ - x² - 2x + 1 = 0

ми значениями для нуль-температурных энтропий

√

ST→0 = ln

ν = 0.2944...,

(25)

(19) и намагниченностей (28).

238

ЖЭТФ, том 160, вып. 2 (8), 2021

Обобщенная модель Изинга в магнитном поле

Рис.

9. Вариант конкурирующих взаимодействий при

J1 < 0, J¹ > 0, J2 < 0, J² < 0. Темные кружки — спин

направлен вверх, светлые — вниз

4. Антиферро-ферромагнитное взаимодействие

между ближайшими соседями, ферро-антиферро-

магнитное взаимодействие между вторыми сосе-

дями (J₁ < 0, J′1 > 0, J₂ > 0, J′2 < 0)

{

-J₁ - J′1 - J′2,

0 ≤ R₁ + R₂ ≤ 1,

Hfr1 =

-J1 - 2J1 + J2, R1 + R2 ≥ 1;

Hfr2 = -J₁ - J₂ - 2J′2.

При R₁ ≥ (|J₁| + |J₂|)/2, (|J₁| ≥ 1, |J₂| ≥ 1) и любом

R₂: основное состояние C^′′′4.

5. Антиферро-ферромагнитное взаимодействие

между ближайшими и вторыми соседями (J₁ < 0,

J′1 < 0, J₂ > 0, J′2 > 0)

{

-J₁ - J′1 - J′2,

0 ≤ R₁ + R₂ ≤ 1,

Hfr1 =

-J1 - 2J1 + J2, R1 + R2 ≥ 1;

Hfr2 = -J₁ - 2J′1 - J₂.

При R₂ ≥ (|J₁| + |J₂|)/2, (|J₁| ≥ 1, |J₂| ≥ 1) и любом

′′

R₁: основное состояние C₄ .

Рис. 8. Температурные зависимости энтропий (а) и намаг-

6. Ферро-антиферромагнитное взаимодействие

ниченностей (б). Зеленые кривые — J1 = -1, J¹ = -0.5,

между ближайшими и вторыми соседями (J₁ > 0,

= -1, J′2 = -0.2, H = 1.8, красные — J1 = -1,

J′1 > 0, J₂ < 0, J′2 < 0)

J′1 = -0.5, J2 = -1, J² = -0.2, H = 0.6, синие — J1 = -1,

{

J′1 = -2, J2 = -1, J² = -1, H = 2, черные — J1 = -1,

-J′1 - J₂ - J′2,

0 ≤ R₁ + R₂ ≤ 1,

J′1 = -0.5, J2 = -1, J² = -0.5, H = 3, фиолетовые —

Hfr1 =

J₁ - 2J′1 - J₂, R₁ + R₂ ≥ 1;

J1 = -1, J¹ = -0.5, J2 = -1, J² = -0.5, H = 0, оранже-

вые — J1 = -0.2, J¹ = -0.4, J2 = -1, J² = -0.2, H = 2,

Hfr2 = -J₁ - J₂ - 2J′2.

бирюзовые — J1 = -1, J¹ = -1.5, J2 = -1, J² = -1.6,

H = 2.1

При R₁ ≥ (|J₁| + |J₂|)/2, (|J₁| ≥ 1, |J₂| ≥ 1) и любом

R₂: основное состояние C^′′′4.

7. Ферро-антиферромагнитное взаимодействие

между ближайшими соседями, антиферро-ферро-

239

Е. С. Цуварев, Ф. А. Кассан-Оглы

ЖЭТФ, том 160, вып. 2 (8), 2021

Рис. 10. Возможные варианты переходов между конфи-

гурациями в магнитном поле при J1 < 0, J¹ > 0, J2 > 0,

Рис. 11. Конкурирующие взаимодействия J1 > 0, J¹ < 0,

J′2 < 0. Темные кружки — спин направлен вверх, светлые —

J2 > 0, J² < 0 при условии J1 = J2. Темные кружки —

вниз

спин направлен вверх, светлые — вниз

магнитное взаимодействие между вторыми сосе-

дями (J₁ > 0, J′1 < 0, J₂ < 0, J′2 > 0)

Второе фрустрирующее поле. Энтропия равна

{

выражению (23), намагниченность выражению (24).

-J′1 - J₂ - J′2,

0 ≤ R₁ + R₂ ≤ 1,

Hfr1 =

При R₁ + R₂ = 1 получается переход из фазы

J₁ - J₂ - 2J′2, R₁ + R₂ ≥ 1;

с учетверением периода трансляций C^′′′4 в ферро-

Hfr2 = -J₁ - 2J′1 - J₂.

магнитную фазу C₁, при этом энтропия равна нату-

ральному логарифму квадратного корня из двух

При R₂ ≥ (|J₁| + |J₂|)/2, (|J₁| ≥ 1, |J₂| ≥ 1) и любом

√

R₁: основное состояние C^′′4.

S_fr = ln

(31)

Характерной чертой четырех рассматриваемых

вариантов является то, что один из коэффициен-

а соответствующая намагниченность будет равна

тов взаимодействия может быть сколь угодно боль-

шим по модулю. Главное, чтобы знак этого взаимо-

MT→0 =

(32)

действия сохранялся. Кроме того, если второй ко-

эффициент достигает величины (|J₁| + |J₂|)/2 при

Такое значение намагниченности символизирует

(|J₁| ≥ 1, |J₂| ≥ 1), то фаза с учетверением перио-

то, что вдоль поля направлена половина всех спинов

) становится начальным

в цепочке.

состоянием системы. На рис. 10 приведена схема пе-

8. Ферромагнитное взаимодействие между бли-

реходов при J₁ < 0, J′1 > 0, J₂ > 0, J′2 < 0.

жайшими соседями, антиферромагнитное взаимо-

Первое фрустрирующее поле при 0 ≤ R₁ + R₂ ≤

действие между вторыми соседями (J₁ > 0, J′1 < 0,

≤ 1. Энтропия находится из выражения (23), а на-

J₂ > 0, J′2 < 0)

магниченность из выражения (28).

Данный вариант является обобщением конкури-

Первое фрустрирующее поле при R₁ + R₂ ≥ 1.

рующих взаимодействий между ближайшими сосе-

Данное фрустрирующее поле описывает переход

дями в обычной модели Изинга [16]. Положим, что

между фазами с учетверением периода трансляций,

J₁ = J₂, таким образом, энергии конфигураций с

конкретнее, переход осуществляется из фазы C^′′4 в

учетверениями периода трансляций с нулевой на-

фазу C^′′′4. Нуль-температурная энтропия равна на-

магниченностью совпадут. При увеличении магнит-

туральному логарифму корня четвертой степени из

ного поля будут происходить переходы в состоя-

двух

√

ния с намагниченностью 1/2, более того, при неко-

ST→0 = ln⁴

2 = 0.1733...,

(29)

торых значениях обменных взаимодействий возмо-

нуль-температурная намагниченность равна

жен переход сразу в ферромагнитную конфигура-

цию (рис. 11).

MT→0 =

(30)

240

ЖЭТФ, том 160, вып. 2 (8), 2021

Обобщенная модель Изинга в магнитном поле

⎧

(

√

)

⎨J1 - J2 - 2J′2, R1 - R2 ≥ 1,

где ϕ =

/2 — золотое сечение.

Hfr1 =

-J′1-J₂-J′2,

-1 ≤ R₁-R₂ ≤ 1,

Первое фрустрирующее поле при -1 ≤ R₁-R₂ ≤

⎩

≤ 1. В этом случае наблюдается переход из фазы

J₁ - 2J′1 - J₂, R₁ - R₂ ≤ -1;

{

учетверения периода трансляции C₄ в ферромагнит-

-J₁ - 2J′1 - J₂, R₁ - R₂ ≥ 1,

ную конфигурацию C₁ [14] с энтропией, равной на-

Hfr2 =

-J₁ - J₂ - 2J′2, R₁ - R₂ ≤ -1.

туральному логарифму наибольшего вещественного

корня уравнения x⁴ - x³ - 1 = 0

Первое фрустрирующее поле при R₁ - R₂ ≥ 1

(или R₁ - R₂ ≤ -1). Происходит переход из фазы

ST→0 = ln μ = 0.3223 . . .,

(34)

учетверения периода трансляции C₄ (или C′4) в дру-

) с энтропией (23)

μ⁴

и намагниченностью

MT→0 =

= 0.3967 . . .,

(35)

μ³ + 4μ + 1

MT→0 =

= 0.2236 . . .,

(33)

где

4ϕ - 2

{

(

)}1/2

√(_√

)

√(_√

)

∕

μ = 1/4 +

1 - 16

849 + 9

/1152 -³

849 - 9

/1152

⎧⎛

⎞

(

))1/2

⎨

√(_√

)

√(_√

)

∕

⎝3+2/

1 - 16

849 + 9

/1152 -³

849 - 9

/1152

⎠

16 -

⁺⎩

(

)

)⎫

1/2

√(_√

)

√(_√

)

⎬

∕

−

1 - 16

849 + 9

/1152 -³

849 - 9

/1152

⎭

Это математическое сечение пока безымянное.

3.1. Частные случаи обобщенной модели

Первое фрустрирующее поле при R₁-R₂ = 1 или

Изинга в присутствии магнитного поля

R₁ - R₂ = -1. Происходит переход из фаз с учетве-

Ранее мы говорили, что главным преимуществом

рением периода трансляции C₄ или C′4 в ферромаг-

обобщенной квадратной решетки с трансляциями в

нитное упорядочение C₁. Энтропия принимает зна-

горизонтальном и вертикальном направлениях яв-

чение натурального логарифма квадратного корня

ляется возможность получения известных видов ре-

наибольшего решения уравнения x³ -2x² -x+1 = 0:

шеток (таких как гексагональная, треугольная и

квадратная решетки) через предельные переходы.

ST→0 = ln

^√κ = 0.4048 . . .,

(36)

Таким образом, обобщением на произвольное число

трансляций можно получить такую решетку, кото-

рая будет включать, помимо известных нам реше-

MT→0 =

= 0.43556 . . .,

(37)

2κ² + 2κ - 3

ток, совершенно новые типы структур в двумерном

где

пространстве. Очевидно, что все те же манипуляции

справедливы и в одномерии.

(

√

)

√

Ниже приведены некоторые частные случаи

κ=

2 + ³ 98/(3

3i + 1) +³ (21

3i + 7)/2

/3.

обобщенной модели Изинга с учетом различных об-

менных взаимодействий между ближайшими и вто-

Это математическое сечение пока безымянное.

рыми соседями, находящихся в магнитном поле.

Второе фрустрирующее поле. Энтропия опреде-

1. Единожды декорированная цепочка

ляется из выражения (23), а соответствующая на-

Полагая нулю одно из взаимодействий между

магниченность будет равна выражению (24).

вторыми соседями (например, J′2 = 0), представим

Рисунок 12 демонстрирует обнаруженные фруст-

обобщенную цепочку в виде, показанном на рис. 13.

рационные значения энтропий и намагниченностей

При J₁ = J₂ получим простейший случай декориро-

в данном варианте конкурирующих взаимодейст-

ванной цепочки, а именно, единожды декорирован-

вий.

ную цепочку [10] с двумя фрустрирующими полями:

241

Е. С. Цуварев, Ф. А. Кассан-Оглы

ЖЭТФ, том 160, вып. 2 (8), 2021

Рис. 13. Цепочка без взаимодействия J′2. В случае J1 = J2

реализуется случай единожды декорированной цепочки

Рис. 14. Узлы в данной цепочке связаны взаимодействия-

ми только между вторыми соседями, образуя две незави-

симые друг от друга цепочки

двух (31) с намагниченностью (30).

Первое фрустрирующее поле при J′1 = J₂ и J′2 =

= 0 (J′2 = J₂ и J′1 = 0 аналогично). Приравни-

вая взаимодействие между ближайшими соседями

к взаимодействию между вторыми соседями, полу-

чаем ситуацию при H_fr = 0 и с нуль-температурной

энтропией равной натуральному логарифму корня

из трех:

√

S_fr = ln

(38)

Второе фрустрирующее поле. Энтропия (23) с

намагниченностью (24).

2. Набор двух независимых подрешеток

Довольно любопытный случай получается, если

убрать из рассмотрения взаимодействия между бли-

жайшими соседями. Тогда цепочка примет вид, по-

Рис. 12. Температурные зависимости энтропий (а) и на-

казанный на рис. 14.

магниченностей (б). Зеленые кривые — J1 = 1, J¹ = -2,

⎧

J2 = 1, J² = -1, H = 2, красные — J1 = 1, J¹ = -2,

⎨-2J′1, J′1 ≤ J′2,

J2 = -0.5, J² = -0.5, H = 1, синие — J1 = 1, J¹ = -1,

Hfr1 =

J2 = 1, J² = -1, H = 1, фиолетовые — J1 = 1, J¹ = -2,

^⎩-2J′2, J′1 ≥ J′2;

J2 = 1, J² = -0.5, H = 2

⎧

⎨-2J′2, J′1 ≤ J′2,

{

Hfr2 =

-J₁ - J₂,

J′1 = 0,

^⎩-2J′1, J′1 ≥ J′2.

Hfr1 =

−J₁ + 2J′1 - J₂,

0≥J′1 ≥J₂;

Hfr2 = -J₁ - 2J′1 - J₂.

Первое фрустрирующее поле при J′1 ≤ J′2 или

при J′1

≥ J′2. Энтропия (23) с намагниченнос-

Первое фрустрирующее поле при J′1 = 0. Энтро-

тью (33).

пия (19) с намагниченностью (24).

Первое фрустрирующее поле при 0 ≥ J′1 ≥ J₂.

Первое фрустрирующее поле при J′1 = J′2. Лю-

Энтропия равна натуральному логарифму корня из бопытно, что при равенстве взаимодействий мож-

242

ЖЭТФ, том 160, вып. 2 (8), 2021

Обобщенная модель Изинга в магнитном поле

нуль-температурная намагниченность, равная золо-

тому сечению, деленному на два золотого сечения

минус единица (24), а также фрустационное поле,

равное двум.

Таким образом, создается впечатление, что по-

ведение системы (по крайней мере, в основном со-

Рис. 15. Цепочка лестничного типа

стоянии) одинаково при обменных взаимодействиях,

разных как по величине, так и по знаку. Ложность

этого впечатления доказывается при дополнитель-

но прийти к результатам, полученным для обычной

ном исследовании других наблюдаемых, а именно

(необобщенной) решетки с ближайшими соседями с

теплоемкости и особенно внутренней энергии, су-

энтропией (19) и намагниченностью (24).

щественно разной даже в основном состоянии (см.

Второе фрустрирующее поле. Энтропия (23) с

рис. 16). Отсюда следует важный вывод о том,

намагниченностью (24).

что получение истинного поведения системы может

3. Цепочка лестничного типа

быть достигнуто только при комплексном исследо-

И, наконец, рассмотрим лестничную цепочку

вании, а исследование ограниченного числа наблю-

(рис. 15).

даемых приводит к ошибочным результатам.

{

-J₂ - 2J′2, R₂ ≤ J′1,

Hfr1 =

-2J′1 - J₂, R₂ ≥ J′1;

4. МАТЕМАТИЧЕСКИЕ СЕЧЕНИЯ И

{

ПОСЛЕДОВАТЕЛЬНОСТИ В МОДЕЛИ

-J₂ - 2J′1, R₂ ≤ J′1,

ИЗИНГА

Hfr2 =

-2J′2 - J₂, R₂ ≥ J′1.

Как уже отмечено, некоторые значения

Первое фрустрирующее поле при R₂ ≤ J′1 или

нуль-температурных энтропий и нуль-темпера-

при R₂

≥ J′1. Энтропия (29) с намагниченнос-

турных намагниченностей выражаются через

тью (30).

сечения, хорошо известные в математике чисел,

Первое фрустрирующее поле при J₁ = 0 и R₂ =

а именно, через золотое сечение ϕ, серебряное

= J′1 (J₂ = 0 и R₁ = J′2 аналогично). Энтропия

сечение δ, сверхзолотое сечение ψ, пластическое

равна логарифму квадратного корня наибольшего

число ρ и другие. Чтобы объяснить такое удиви-

решения уравнения x² - x - 1 = 0, известного как

тельное появление весьма большого количества

серебряное сечение

математических констант при рассмотрении модели

√

Изинга, стоит обратиться к важной теореме Фро-

ST→0 = ln

δ = 0.4407...,

(39)

бениуса - Перрона. Эта теорема утверждает, что

√

квадратная матрица со строго положительными

где δ = 1 +

2 — серебряное сечение, а намагничен-

вещественными элементами имеет одно наиболь-

ность равна 1/2.

шее собственное значение, которое обязательно

Второе фрустрирующее поле. Энтропия (23) с

является вещественным и строго положительным.

намагниченностью (24).

Кроме того, известно, что это наибольшее собствен-

При исследовании фрустрационных свойств рас-

ное значение является так называемым числом

сматриваемой в статье модели обнаружилась лю-

Перрона. Это означает, что искомое собственное

бопытная особенность, а именно, при некоторых

значение уравнения является вещественным и

наборах обменных взаимодействий и некоторых

больше единицы, при этом все сопряженные корни

(иногда совпадающих) фрустационных полях нуль-

уравнения меньше искомого собственного значения

температурные энтропии и намагниченности мо-

по абсолютной величине.

гут совпадать. В частности, это имеет место при

J₁ = 1.0, J′1 = -2.0, J₂ = 1.0, J′2 = -0.5, H = 2,

Поскольку аргумент натурального логарифма в

а также при J1 = -0.2, J′1 = -0.4, J2 = -1.0,

выражениях для нуль-температурной энтропии яв-

J′2 = -0.2, H = 2.

ляется статистическим весом системы Ω, эта величи-

В этом случае совпадают три наблюдаемых:

на может принимать значение только в промежутке

нуль-температурная энтропия, равная логариф-

1 ≤ Ω ≤ 2. Откуда следует, что S = lnΩ = ln1 = 0

му квадратного корня из золотого сечения (23);

(при T → 0), что в результате соответствует ситу-

243

Е. С. Цуварев, Ф. А. Кассан-Оглы

ЖЭТФ, том 160, вып. 2 (8), 2021

Рис. 16. Температурные зависимости энтропий (а), намагниченностей (б), внутренних энергий (в) и теплоемкостей (г).

Фиолетовые кривые — J1 = 1.0, J¹ = -2.0, J2 = 1.0, J² = -0.5, H = 2, оранжевые — J1 = -0.2, J¹ = -0.4, J2 = -1.0,

J′2 = -0.2, H = 2

ациям, при которых система обладает лишь одной

в том числе и без какой-либо трансляционной инва-

конфигурацией (фрустрации отсутствуют). Поэто-

риантности. Следует отметить, что в модели Изин-

му все остальные найденные значения статистичес-

га энтропия достигает своего максимального значе-

√

кого веса (при T → 0), выраженные через ϕ, ρ, ψ,

ния ln 2 в двух случаях: 1) При стремлении темпера-

и другие математические сечения, в том числе и но-

туры к бесконечности, при которой статистические

вые (безымянные), приходящегося на один узел це-

веса всех 2^N конфигураций при любых значениях

почки, помимо того что они являются числами Пер-

обменных интегралов совпадают. 2) В парамагнети-

рона [17-19], соответствуют определенным фрустри-

ке, в котором все обменные интегралы равны нулю,

рующим состояниям системы, т. е. в основном состо-

статистические веса всех 2^N конфигураций совпада-

янии наблюдается бесконечно много конфигураций,

ют при любой температуре, так что энтропия равна

244

ЖЭТФ, том 160, вып. 2 (8), 2021

Обобщенная модель Изинга в магнитном поле

ln 2 при всех температурах, и фактически парамаг-

нетик является абсолютно фрустрированный систе-

мой, что впервые отмечено в работе [14].

Можно показать, что фрустрирующее значе-

ние нуль-температурной энтропии определяется как

предел некоторой последовательности в следующем

виде:

[

]

N +1

S_fr = lim

(40)

N →∞

Z_N

где

ZN+1 — число допустимых конфигураций в ос-

новном состоянии для (N +1) узлов,

Z_N — число до-

пустимых конфигураций в основном состоянии для

N узлов.

Фрустрационную нуль-температурную намагни-

ченность также можно найти как предел последова-

тельности

M_fr = lim

M_Σ,

(41)

N →∞

Z_N

где M_Σ — общая (суммарная) намагниченность всех

допустимых конфигураций в основном состоянии.

После подсчета возможных конфигураций

Z_N

для конкретного числа узлов N для случая толь-

ко ближайших соседей во внешнем магнитном поле

была определена последовательность

Z^ϕN = 2, 1, 3, 4, 7, 11, 18, 29, 47, 76, . . .

Полученная последовательность чисел известна

как последовательность Люка, которая задается ре-

куррентным соотношением a_n = an-1 + an-2 с на-

чальными значениями a₀ = 2 и a₁ = 1.

Как известно [20-22], отношение

ZϕN+1

Z^ϕN стре-

мится к золотому сечению ϕ, а следовательно,

ZϕN+1

Z^ϕN ) стремится к натуральному логарифму

золотого сечения ln ϕ.

В свою очередь, можно показать, что общая на-

магниченность для всех допустимых конфигураций

Рис. 17. Наглядное представление сходимости последова-

в основном состоянии M_Σ для случая только бли-

тельности ln

ZϕN+1

Z^ϕN ) к нуль-температурному значению

жайших соседей во внешнем магнитном поле пред-

энтропии равной ln ϕ (а) и последовательности MϕΣ

Z^ϕN

ставлена последовательностью чисел Фибоначчи c

к нуль-температурному значению намагниченности равной

таким же рекуррентным соотношением, как и у чи-

1/(2ϕ - 1) (б)

сел Люка, a_n = an-1 + an-2, но с начальными усло-

виями a₀ = 0 и a₁ = 1

MϕΣ = 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, .. .

В правильности полученных выше результатов

можно убедиться, глядя на рис. 17. Видно, что по-

Взяв отношение последовательности Фибонач-

следовательности

чи к последовательности Люка MϕΣ

Z^ϕN в термоди-

намическом пределе (N → ∞), получим значение

фрустрационной намагниченности равное 1/(2ϕ-1).

ZϕN+1

Z^ϕN) и MϕΣ

Z^ϕN

245

Е. С. Цуварев, Ф. А. Кассан-Оглы

ЖЭТФ, том 160, вып. 2 (8), 2021

быстро сходятся соответственно к нуль-температур-

ной энтропии равной ln ϕ и нуль-температурной на-

магниченности равной 1/(2ϕ - 1).

При учете взаимодействия не только между бли-

жайшими, но и между вторыми соседями в магнит-

ном поле при антиферромагнитных взаимодейст-

виях и тех и других возникают два фрустрирую-

щих поля. Значение нуль-температурной намагни-

ченности в первом фрустрирующем поле выражает-

ся отношением некоторых последовательностей чи-

сел, первая из которых определяется по правилу

a_n = an-3 + an-4 с начальными значениями a₀ = 1

и a₁ = a₂ = a₃ = 1:

MξΣ = 0, 0, 0, 1, 0, 0, 1, 1, 0, 1, 2, 1, 1, 3,. . .

Вторая последовательность определяется по тому

же правилу a_n = an-3 + an-4, но с начальными зна-

чениями a₀ = 4, a₁ = a₂ = 0, a₃ = 3

Z^ξN = 4, 0, 0, 3, 4, 0, 3, 7, 4, 3, 10, 11, 7, 13, .. .

Взяв отношение первой последовательности ко

второй при N

→ ∞, получим значение нуль-

температурной намагниченности 1/(ξ + 4ξ³ - ξ⁴) с

соответствующей энтропией равной ln ξ.

Значение намагниченности во втором фрустри-

рующем поле представлено отношением последова-

тельности коров Нараяны [23, 24] c рекуррентным

уравнением a_n = an-1 + an-3 и начальными значе-

ниями a₀ = a₁ = a₂ = 1:

MψΣ = 1, 1, 1, 2, 3, 4, 6, 9, 13, 19, 28, . . .

к последовательности c тем же рекуррентным урав-

нением, что и последовательность Нараяны, но с на-

чальными значениями a₀ = 3, a₁ = a₂ = 1:

Z^ψN = 3, 1, 1, 4, 5, 6, 10, 15, 21,. . .

Отметим, что приведенная последовательность

Z^ψN

до сих пор не изучена. Отношение данных после-

Рис. 18. Наглядное представление сходимости последова-

тельности ln

ZψN+1

Z^ψN ) к нуль-температурному значению

довательностей при N → ∞ дает значение нуль-

температурной намагниченности ψ³/(ψ² + 3), а со-

энтропии равной ln ψ (а) и последовательности MψΣ

Z^ψN

к нуль-температурному значению намагниченности равной

ответствующая энтропия равна натуральному лога-

ψ³/(ψ² + 3) (б)

рифму сверхзолотого сечения ln ψ. Сходимости по-

следовательностей проиллюстрированы на рис. 18.

При ферромагнитных взаимодействиях ближай-

к последовательности c тем же рекуррентным урав-

ших соседей и антиферромагнитных взаимодействи-

нением a_n = an-1 + an-4, но с начальными значени-

ях вторых соседей намагниченность равна отноше-

ями a₀ = 4, a₁ = a₂ = a₃ = 1:

нию последовательности, задаваемой рекуррентным

уравнением a_n = an-1 + an-4 с начальными значе-

Z^μN = 4, 1, 1, 1, 5, 6, 7, 8, 13, . . .

ниями a₀ = 0, a₁ = a₂ = a₃ = 1:

Обратим внимание на то, что последовательность

MμΣ = 0, 1, 1, 1, 1, 2, 3, 4, 5, 7, 10, 14, 19, 26, . . .,

Z^μN также до настоящего момента не была исследо-

246

ЖЭТФ, том 160, вып. 2 (8), 2021

Обобщенная модель Изинга в магнитном поле

вана. При N → ∞ отношение последовательностей

Финансирование. Работа выполнена в

дает значение нуль-температурной намагниченнос-

рамках государственного задания Министер-

ти μ⁴/(μ³ + 4μ + 1) с энтропией равной ln μ.

ства науки и высшего образования РФ (тема

Другие значения нуль-температурных энтропий

«Квант»,

№ АААА-А18-118020190095-4) и

«Спла-

и нуль-температурных намагниченностей, представ-

вы» (№ AAAA-A19-119070890020-3) и при частичной

ленные в данной работе, могут быть записаны че-

поддержке Уральского отделения Российской ака-

рез пределы последовательностей (также известных

демии наук (проект № 18-2-2-11).

из математики целочисленных последовательностей

[20,21,25-27]) только с помощью формул (40) и (41)

без привлечения формализма трансфер-матрицы

ЛИТЕРАТУРА

Крамерса - Ваннье. Однако многие из встречаемых

последовательностей являются неизученными.

I. Syozi and S. Naya, Prog. Theor. Phys. 23, 374

Таким образом, установлено, что фрустрацион-

(1960).

ные свойства модели Изинга тесным образом связа-

ны с достижениями в математике чисел, известными

I. Syozi and S. Naya, Prog. Theor. Phys. 24, 829

уже на протяжении столетий.

(1960).

I. Syozi, Phase Transitions and Critical Phenomena,

Vol. 1, ed. by C. Domb and M. S. Green, Academic,

New York (1972).

5. ЗАКЛЮЧЕНИЕ

L. Onsager, Phys. Rev. 65, 117 (1944).

В данном исследовании проведено обобщение мо-

T. Utiyama, Prog. Theor. Phys. 6, 907 (1951).

дели Изинга на произвольное число трансляций ли-

G. H. Wannier, Phys. Rev. 79, 357 (1950).

нейной цепочки в присутствии магнитного поля. Ме-

тодом трансфер-матрицы Крамерса - Ваннье полу-

R. M. F. Houtappel, Prog. Theor. Phys. 16, 425

чено точное аналитическое решение обобщенной мо-

(1950).

дели Изинга при учете различных взаимодействий

K. Kanô and S. Naya, Prog. Theor. Phys. 10, 158

между ближайшими и вторыми соседями, находя-

(1953).

щихся в магнитном поле. Найдены фрустрирующие

поля не только при наличии ближайших, но и вто-

Е. С. Цуварев, Ф. А. Кассан-Оглы, А. И. Прошкин,

рых соседей. Исследованы некоторые частные слу-

ЖЭТФ 3, 504 (2020).

чаи обобщенной модели Изинга при учете ближай-

10.

Е. С. Цуварев, Ф. А. Кассан-Оглы, ЖЭТФ 6, 1125

ших и вторых соседей во внешнем магнитном по-

(2020).

ле. Следует особо отметить, что статистический вес

(при T → 0), приходящийся на один узел цепоч-

11.

Р. Бэкстер, Точно решаемые модели в статисти-

ки, является числом Перрона. Значения нуль-темпе-

ческой механике, Мир, Москва (1985).

ратурных энтропий и намагниченностей выражены

12.

H. A. Kramers and G. H. Wannier, Phys. Rev. 60,

исключительно через известные и новые (безымян-

252 (1941).

ные) математические сечения.

13.

H. A. Kramers and G. H. Wannier, Phys. Rev. 60,

Установлено, что значения нуль-температурных

263 (1941).

энтропий, так же как и нуль-температурных намаг-

ниченностей, могут быть выражены соответствен-

14.

А. В. Зарубин, Ф. А. Кассан-Оглы, А. И. Прош-

но через предел натурального логарифма отноше-

кин, А. Е. Шестаков, ЖЭТФ 155, 914 (2019).

ния определенных последовательностей (40) и пре-

15.

F. A. Kassan-Ogly, Phase Transitions 74, 353 (2001).

дел отношения последовательностей (41). И, что

немаловажно, для этого не требуется знание транс-

16.

E. Ising, Zeitschrift für Physik 21, 253 (1925).

фер-матрицы Крамерса - Ваннье! Достаточно лишь

сосчитать число допустимых конфигураций и на-

17.

Q. Wu, Mathem. Comput. 79, 2387 (2010).

магниченностей в основном состоянии для конкрет-

18.

D. Lind, J. Number Theory 40, 211 (1992).

ного числа узлов цепочки в термодинамическом пре-

деле.

19.

D. W. Boyd, Mathem. Comput. 45, 243 (1985).

247