ЖЭТФ, 2021, том 160, вып. 2 (8), стр. 155-166

ДИНАМИКА ВРЕМЕННОЙ ЭВОЛЮЦИИ ВОЗБУЖДЕНИЯ

КВАНТОВОГО ОСЦИЛЛЯТОРА

ЭЛЕКТРОМАГНИТНЫМИ ИМПУЛЬСАМИ

В. А. Астапенкоa*, Ф. Б. Розмиa,b,c**, Е. В. Сахно^a

^a Московский физико-технический институт (национальный исследовательский университет)

141701, Долгопрудный, Московская обл., Россия

^b Sorbonne University, Faculty of Sciences and Engineering

75252, Paris, France

^c Ecole Polytechnique, LULI Laboratory

91128, Palaiseau, France

Поступила в редакцию 11 марта 2021 г.,

после переработки 19 марта 2021 г.

Принята к публикации 22 марта 2021 г.

Теоретически исследуется динамика временной эволюции возбуждения квантового осциллятора элек-

тромагнитными импульсами при произвольном значении амплитуды поля в импульсе. Рассматривается

гармонический осциллятор без затухания и возбуждение между стационарными состояниями. Общая

формула для возбуждения квантовых состояний как функции времени выведена в терминах мгновенной

энергии ассоциированного классического осциллятора в поле электромагнитного импульса. С помощью

полученного выражения детально исследована зависимость вероятности возбуждения квантового осцил-

лятора от времени вне рамок теории возмущений для различных параметров импульса, включая полное

возбуждение из основного состояния, возбуждение из возбужденных состояний и спектры возбуждения.

DOI: 10.31857/S0044451021080010

ленно были проанализированы эволюция спектров

возбуждения и зависимость его вероятности от дли-

1. ВВЕДЕНИЕ

тельности импульса при увеличении амплитуды по-

ля.

Квантовый гармонический осциллятор является

В последнее время успешно развиваются экспе-

уникальной физической системой, поскольку дина-

риментальные методы наблюдения фотопроцессов,

мику его временной эволюции можно аналитически

индуцируемых УКИ, в реальном времени [13, 14].

описать при взаимодействии с возмущением произ-

Данному вопросу посвящены, например, работы

вольной величины вне рамок теории возмущений

[15, 16], в которых наблюдались возбуждение резо-

[1, 2]. Развитие методов генерации ультракоротких

нанса Фано в атоме гелия и рождение фотоэлект-

лазерных импульсов (УКИ) [3, 4] делает актуаль-

рона с субфемтосекундным разрешением. В связи с

ным рассмотрение взаимодействия таких импульсов

этим становится актуальным адекватное теоретиче-

с различными мишенями [5-10], включая колеба-

ское описание таких явлений.

тельные системы [11,12]. Так, в предыдущей работе

Настоящая работа посвящена детальному теоре-

авторов [12] рассматривалось возбуждение кванто-

тическому анализу возбуждения квантового осцил-

вого осциллятора за все время действия УКИ в за-

лятора под действием УКИ в зависимости от време-

висимости от длительности импульса и частотной

ни для различных параметров возбуждающего им-

отстройки его несущей частоты от собственной час-

пульса вне рамок теории возмущений.

тоты осциллятора при произвольном значении ам-

плитуды электрического поля. Аналитически и чис-

2. ОСНОВНЫЕ ФОРМУЛЫ

^* E-mail: astval@mail.ru

Зависящая от времени вероятность W_mn(t) воз-

^** F. B. Rosmej

буждения квантового гармонического осциллятора

155

В. А. Астапенко, Ф. Б. Розми, Е. В. Сахно

ЖЭТФ, том 160, вып. 2 (8), 2021

(КО) под действием электромагнитного импульса

где ω, τ — несущая частота и длительность импуль-

(ЭМИ) для перехода n → m, m > n, определяет-

са, E₀ — амплитуда напряженности электрического

ся формулой (см. Приложение A)

поля импульса.

Для гауссова импульса (4) НПФ можно предста-



W_mn(t) =

ν(t)^m-n exp(-ν(t))

^L^m-nn(ν(t))

² .

(1)

вить в виде [17]

Здесь L^kn(ν(t)) — обобщенный полином Лагерра.

F G(t, ω^′, ω, τ) = F Gw(t, ω^′ + ω, τ) +

Выражение (1) было получено Швингером [1] в

+ FGw(t,ω^′ - ω,τ),

(5)

теории квантованных полей для вероятностей пере-

ходов между состояниями с различным числом фо-

тонов, индуцированных заданным электронным то-

^√π

F Gw(t, w, τ) =

τE₀×

ком. С помощью метода канонического преобразо-

(

){

(

)

}

вания Хусими получил выражение для вероятности

w²τ²

wτ

× exp

erf

√

-i√

(6)

возбуждения квантового осциллятора через полино-

2τ

мы Шарля [2].

В настоящей статье мы рассматриваем осцилля-

Здесь erf(z) — функция ошибки, ω^′ — текущая час-

тор без затухания. Из (1) видно, что зависимость

тота неполного преобразования Фурье.

вероятности возбуждения от времени определяется

Отметим, что в пределе больших времен t → ∞

безразмерной функцией ν(t). Как показано в При-

фурье-образ гауссова импульса дается выражением

ложении A, функция ν(t) равна

√

{

(

)

(ω^′ - ω)²τ²

ε_clas(t)

E(ω, ω^′, τ) =

E₀τ exp

ν(t) =

(2)

ℏω₀

(

)}

(ω^′ + ω)²τ²

+ exp

(7)

где ε_clas(t) — энергия, поглощаемая классическим

осциллятором, ассоциированным с квантовым, под

Для околорезонансных частот |ω - ω₀| ≪ ω₀ и

действием ЭМИ в момент времени t. Под ассоци-

времен t ≫ τ формула (3) в рассматриваемом слу-

ированным классическим осциллятором подразуме-

чае принимает вид

вается осциллятор с одинаковыми значениями пара-

метров: собственной частотой ω₀, массой M и заря-

{

}

дом q.

ε_clas(t ≫ τ)=πq2E⁰τ²

exp -(ω - ω0

)²τ²

(8)

Отметим, что параметр ν можно интерпретиро-

вать как среднее число квантов КО, возбужденных

Подставляя (8) в (2) и (1), приходим к выраже-

под действием ЭМИ.

нию для асимптотической (для t ≫ τ) вероятности

Выражение для ε_clas(t) имеет следующий вид

возбуждения КО, которая подробно исследована в

(см. Приложение B):

статье [12].



На рис. 1 показаны временные зависимости энер-



∫



гии, поглощенной классическим осциллятором (2),



ε_clas(t) =

E(t^′) exp(iω₀t^′)

(3)



нормированной на квант энергии (ℏω₀), для раз-



-∞

личных относительных отстроек несущей частоты

импульса от собственной частоты осциллятора δ =

Здесь E(t) — напряженность электрического поля в

= (ω - ω₀)/ω₀. Видно, что с увеличением отстройки

ЭМИ как функция времени. В данной статье поло-

δ появляется максимум в зависимости ν(t), а вели-

жено, что E(t → ±∞) → 0.

чина этой функции уменьшается.

Из формулы (3) следует, что мгновенная энергия

Еще одна особенность — наличие осцилляций

классического осциллятора определяется неполным

в зависимости поглощенной энергии от времени.

преобразованием Фурье (НПФ) от напряженности

Частота этих колебаний равна собственной часто-

электрического поля в импульсе на собственной час-

те квантового осциллятора. Математически нали-

тоте осциллятора.

чие данных осцилляций следует из формул (5), (6),

Далее для определенности рассматривается

определяющих неполное преобразование Фурье на-

ЭМИ с гауссовой огибающей:

пряженности электрического поля в импульсе. Как

(

)

t²

видно из этих формул, осцилляции возникают из-за

E(t, ω, τ) = E₀ exp

cos(ωt),

(4)

интерференции вкладов в НПФ от положительной и

2τ²

156

ЖЭТФ, том 160, вып. 2 (8), 2021

Динамика временной эволюции возбуждения. . .

Рис.

1. Временные зависимости нормированной энер-

Рис. 2. Временные зависимости вероятности возбуждения

гии ассоциированного классического осциллятора (2) для

КО из основного состояния для E0 = 2·10-2 и разных воз-

различных спектральных отстроек: сплошная кривая —

бужденных состояний: жирная сплошная кривая — m = 1,

δ = 0.05, пунктирная кривая — δ = 0.1, штриховая кри-

пунктирная кривая — m = 2, штрихпунктирная кривая —

вая — δ = 0.15, штрихпунктирная кривая — δ = 0.2;

m = 3, тонкие сплошные линии соответствуют асимпто-

= 10³ ат. ед., E0 = 10-2 ат. ед., q = 1 ат. ед., M =

тическим значениям вероятности, вычисленным с исполь-

= 10⁴ ат. ед., ω0 = 0.01 ат. ед.

зованием (8), (9); относительная спектральная отстройка

δ = 0.1

отрицательной частотных составляющих напряжен-

ности поля в ЭМИ. Таким образом, они имеют дру-

гую природу, нежели колебания Раби.

Для возбуждения КО из основного состояния

(n = 0 → m) выражение (1) упрощается к виду

ν(t)

Wm0(t) =

exp(-ν(t)).

(9)

Легко получить из (9) формулу для полной ве-

роятности возбуждения КО из основного состояния:

∑

W_tot(t) =

Wm0(t) = 1 - exp(-ν(t)).

(10)

m=1

Как следует из рис. 1, функция W_tot(t) по-раз-

ному зависит от времени при различных значениях

параметра δ.

3. РЕЗУЛЬТАТЫ И ОБСУЖДЕНИЕ

Рис. 3. Временные зависимости вероятности возбуждения

КО из основного состояния для E0 = 3·10-2 и разных воз-

Результаты расчетов временной зависимости ве-

бужденных состояний: жирная сплошная кривая — m = 1,

роятности возбуждения КО по полученным форму-

пунктирная кривая — m = 2, штрихпунктирная кривая —

лам представлены на рисунках ниже для ω₀ = 0.01,

m = 3, тонкие сплошные линии соответствуют асимпто-

q = 1, M = 10⁴ и различных значений E₀, τ и δ.

тическим значениям вероятности, вычисленным с исполь-

Здесь и ниже используются атомные единицы e =

зованием (8), (9); относительная спектральная отстройка

= m_e = ℏ = 1.

δ = 0.1

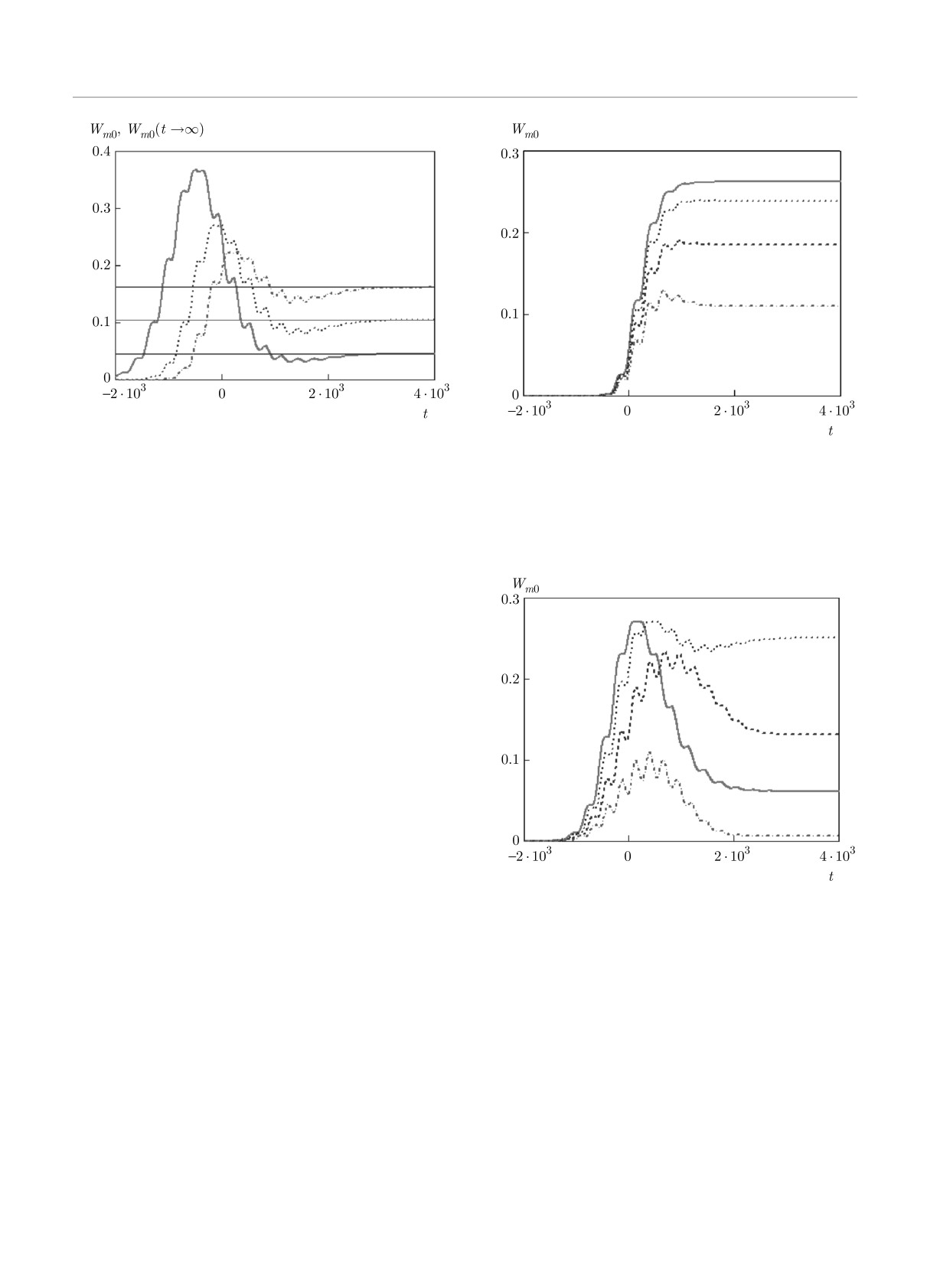
На рис. 2-4 показаны зависимости вероятности

возбуждения КО от времени из основного состояния

157

В. А. Астапенко, Ф. Б. Розми, Е. В. Сахно

ЖЭТФ, том 160, вып. 2 (8), 2021

Рис. 4. Временные зависимости вероятности возбуждения

КО из основного состояния для E0 = 4·10-2 и разных воз-

Рис. 5. Временные зависимости вероятности возбуждения

бужденных состояний: жирная сплошная кривая — m = 1,

КО на переходе 0 → 2 для τ = 500 и различных отстро-

пунктирная кривая — m = 2, штрихпунктирная кривая —

ек: сплошная кривая — δ = 0.05, пунктирная кривая —

m = 3, тонкие сплошные линии соответствуют асимпто-

δ = 0.1, штриховая кривая — δ = 0.15, штрихпунктирная

тическим значениям вероятности, вычисленным с исполь-

кривая — δ = 0.2; E0 = 3 · 10-2

зованием (8), (9); относительная спектральная отстройка

δ = 0.1

в ближайшие возбужденные состояния (m = 1, 2, 3)

для различных значений амплитуды электрическо-

го поля в ЭМИ. Асимптотические значения вероят-

ности возбуждения на больших временах, рассчи-

танные по формулам (2), (8), (B.6), здесь показаны

тонкими сплошными линиями.

Из рис. 2-4 следует, что с увеличением ампли-

туды напряженности электрического поля зависи-

мость Wm0(t) из монотонно возрастающей функции

превращается в функцию с максимумом, амплиту-

да которого практически не меняется с увеличением

E₀, а положение слабо смещается в область малых

времен.

Осцилляции кривых, изображенных на рис. 2-4,

Рис. 6. Временные зависимости вероятности возбуждения

возникают из-за осцилляций во временной зависи-

КО на переходе 0 → 2 для τ = 1000 и различных отстро-

мости поглощенной энергии (см. рис. 1) вследствие

ек: сплошная кривая — δ = 0.05, пунктирная кривая —

указанного выше интерференционного эффекта.

δ = 0.1, штриховая кривая — δ = 0.15, штрихпунктирная

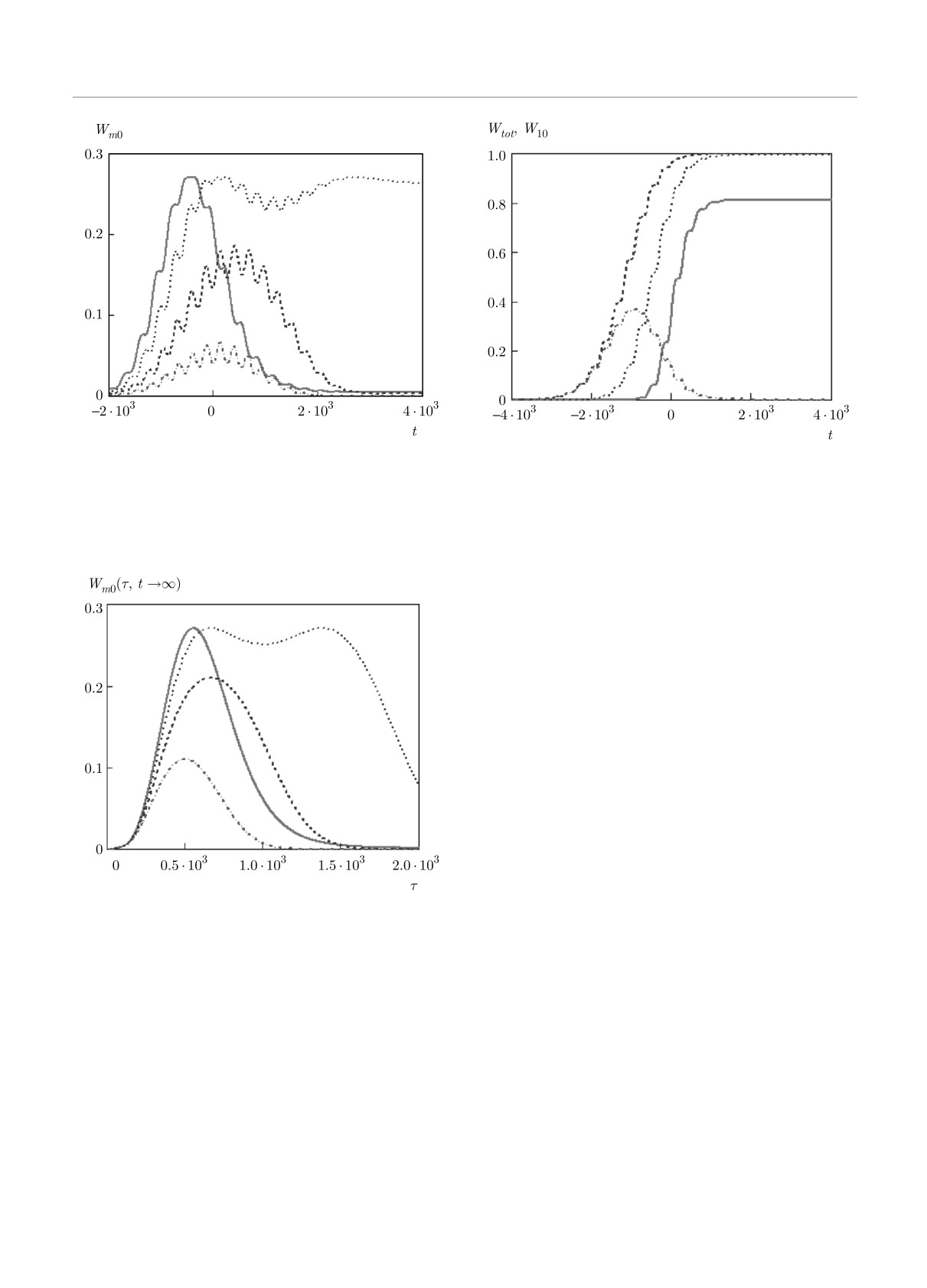
На рис. 5-7 представлены зависимости вероятно-

кривая — δ = 0.2; E0 = 3 · 10-2

сти возбуждения перехода 0 → 2 от времени для раз-

личных длительностей импульса и различных спек-

тральных отстроек δ.

ситуация характерна для относительно небольших

Из рис. 5 видно, что при малой длительности

величин ν, когда exp(-ν) ≈ 1, и можно пользовать-

импульса вероятность возбуждения увеличивается

ся теорией возмущений. С увеличением длительно-

практически монотонно, достигая значения насыще-

сти импульса роль нелинейности во взаимодействии

ния при временах t ≥ 2τ. В этом случае значение

ЭМИ с КО возрастает и зависимость вероятности

стационарной вероятности возбуждения уменьшает-

возбуждения от времени становится более сложной,

ся с увеличением спектральной отстройки δ. Такая

как видно из рис. 6, 7. Одной из характерных особен-

158

ЖЭТФ, том 160, вып. 2 (8), 2021

Динамика временной эволюции возбуждения. . .

Рис. 7. Временные зависимости вероятности возбуждения

Рис. 9. Полная вероятность возбуждения КО из основного

КО на переходе 0 → 2 для τ = 1500 и различных отстро-

состояния как функция времени для δ = 0.05 и различ-

ек: сплошная кривая — δ = 0.05, пунктирная кривая —

ных длительностей импульса: сплошная кривая — τ = 500,

δ = 0.1, штриховая кривая — δ = 0.15, штрихпунктирная

пунктирная кривая — τ

= 1000, штриховая кривая —

кривая — δ = 0.2; E0 = 3 · 10-2

τ = 1500; штрихпунктирная кривая описывает возбужде-

ние перехода 0 → 1; E0 = 3 · 10-2

Асимптотические значения вероятности возбуж-

дения также существенно зависят от величины от-

стройки и длительности импульса. Так, например,

в случае, показанном на рис. 5-7, максимальное

асимптотическое значение вероятности возбужде-

ния соответствует спектральной отстройке δ = 0.1.

Это согласуется с графиками, представленными на

рис. 8, где показаны зависимости асимптотической

вероятности возбуждения от длительности импуль-

са для различных спектральных отстроек, рассчи-

танные по формулам (2), (8), (B.6). Отметим, что

асимптотическая вероятность возбуждения подроб-

но исследовалась в работе [12], где, в частности, ана-

литически была рассмотрена зависимость вероятно-

сти возбуждения от длительности импульса для раз-

Рис. 8. Асимптотическая вероятность возбуждения КО пе-

личных значений других параметров импульса (см.

рехода 0 → 2 как функция длительности импульса для

рис. 4 из цитируемой статьи).

различных значений относительной отстройки: сплошная

Полная вероятность возбуждения КО из основ-

кривая — δ = 0.05, пунктирная кривая — δ = 0.1, штрихо-

ного состояния как функция времени показана на

вая кривая — δ = 0.15, штрихпунктирная кривая — δ = 0.2;

рис. 9-11 для различных значений δ и τ; E0

E0 = 3 · 10-2

= 3 · 10-2. На этих же рисунках представлены вре-

менные зависимости вероятности возбуждения пе-

рехода 0 → 1 для длительности импульса τ = 1500

ностей временной зависимости в случае более длин-

и различных значений отстройки δ.

ных импульсов является то, что со временем вероят-

Из рисунков следует, что в случае короткого им-

ность возбуждения импульсами с большей отстрой-

пульса временная зависимость полной вероятности

кой частоты становится больше, чем для импульсов

возбуждения КО практически не меняется с уве-

с меньшим δ.

личением спектральной отстройки. Напротив, для

159

В. А. Астапенко, Ф. Б. Розми, Е. В. Сахно

ЖЭТФ, том 160, вып. 2 (8), 2021

Рис. 12. Временная эволюция спектра вероятностей воз-

Рис. 10. Полная вероятность возбуждения КО из основно-

буждения для перехода 0 → 1: сплошная кривая — t = 10,

го состояния как функция времени для δ = 0.1 и различ-

пунктирная кривая — t = 500, штриховая кривая — t =

ных длительностей импульса: сплошная кривая — τ = 500,

пунктирная кривая — τ

= 1000, штриховая кривая —

= 10³; E0 = 3 · 10-2, τ = 1000; штрихпунктирная кривая

показывает асимптотический спектр для t → ∞

τ = 1500; штрихпунктирная кривая описывает возбужде-

ние перехода 0 → 1; E0 = 3 · 10-2

Рис. 13. Временная эволюция спектра вероятностей воз-

буждения для полного возбуждения КО из основного со-

Рис. 11. Полная вероятность возбуждения КО из основ-

стояния: сплошная кривая — t = 10, пунктирная кривая —

ного состояния как функция времени для δ

= 0.15 и

= 500, штриховая кривая — t = 10³; E0 = 3 · 10-2,

различных длительностей импульса: сплошная кривая —

τ = 1000

τ = 500, пунктирная кривая — τ = 1000, штриховая кри-

вая — τ = 1500; штрихпунктирная кривая описывает воз-

буждение перехода 0 → 1; E0 = 3 · 10-2

аналогу для возбуждения перехода 0 → 1 с увели-

чением спектральной отстройки δ.

Временная эволюция спектра возбуждения КО

длинного импульса форма кривой существенно ме-

для перехода

→ 1 показана на рис. 12, на

няется, что хорошо видно на рис. 11.

рис. 13 — для полного возбуждения из основного со-

Еще один вывод, следующий из рис. 9-11, заклю-

стояния. Под спектром возбуждения понимается за-

чается в том, что зависимость полной вероятности

висимость вероятности возбуждения от относитель-

возбуждения КО от времени приближается к своему

ной отстройки частоты δ = (ω - ω₀)/ω₀.

160

ЖЭТФ, том 160, вып. 2 (8), 2021

Динамика временной эволюции возбуждения. . .

Как следует из рис. 12, спектр возбуждения пе-

рехода 0 → 1 для данной амплитуды поля имеет

провал в центре при δ = 0. Кроме того, спектр име-

ет слабо выраженную асимметрию, которая исчеза-

ет в пределе больших времен. Расчет показывает,

что при меньших значениях амплитуды поля ука-

занный провал отсутствует. Спектр возбуждения в

этом случае представляет собой колоколообразную

кривую с максимумом при δ = 0. Спектр вероятно-

стей полного возбуждения КО имеет один максимум

при δ = 0 для всех значений напряженности поля в

импульсе. С увеличением времени форма этого мак-

симума изменяется от колоколообразной до столооб-

разной, как это видно на рис. 13.

Описанные особенности связаны с наличием

множителя exp(-ν) в выражении для вероятности

Рис. 14. Зависимости вероятности возбуждения КО под

возбуждения КО. Физически появление спектраль-

действием ЭМИ от времени с амплитудой поля E0 =

ного провала при переходе между стационарными

= 2·10-2 для переходов n → 3: сплошная кривая — 0 → 3,

состояниями соответствует насыщению этого

пунктирная кривая — 1 → 3, штриховая кривая — 2 → 3;

δ = 0.1; τ = 10³

перехода под действием ЭМИ.

Рассмотрим теперь переходы из возбужденных

состояний КО по формулам (A.26), (A.30), которые

следуют из выражения (1):

Wmn(t) = n!m!ν(t)m+n exp(-ν(t)) ×



∑

(-1)^kν(t)^k



(11)



k!(m - k)!(n - k)!

 k=0



Следует отметить, что в отличие от (1) выраже-

ние (11) представляет результат в явном виде как

функцию параметра ν и квантовых чисел стацио-

нарных состояний (m, n).

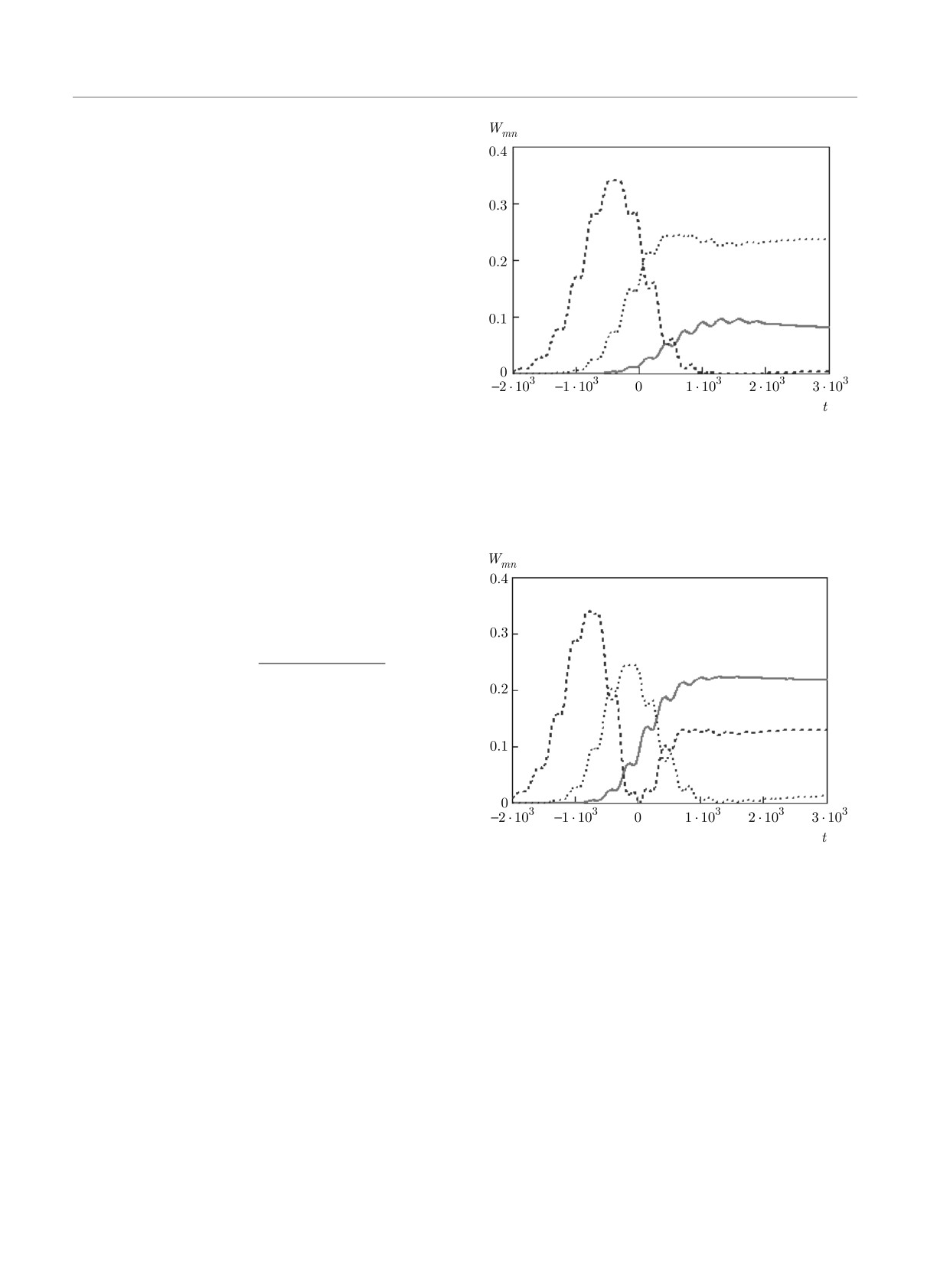
Результаты расчетов вероятности возбуждения

переходов n → 3 (n = 0, 1, 2) для разных значений

амплитуды ЭМИ E₀ представлены на рис. 14-16.

Видно, что зависимость вероятности возбужде-

Рис. 15. Зависимости вероятности возбуждения КО под

ния от времени наиболее сильно изменяется при пе-

действием ЭМИ от времени с амплитудой поля E0 =

реходе между ближайшими энергетическими уров-

= 3·10-2 для переходов n → 3: сплошная кривая — 0 → 3,

нями (переход 2 → 3), так что появляется новый

пунктирная кривая — 1 → 3, штриховая кривая — 2 → 3;

максимум, а зависимость вероятности возбуждения

δ = 0.1; τ = 10³

перехода от времени 0 → 3 изменяется относитель-

но слабо. Отметим, что для переходов из основного

состояния КО при достаточно сильных полях суще-

значениях амплитуды (рис. 17) появляются два мак-

ствует только один максимум вероятности возбуж-

симума с провалом в центре (рис. 18), который при

дения как функции времени (см. рис. 3, 4).

дальнейшем увеличении амплитуды превращается в

Временная эволюция спектра возбуждения пере-

максимум (рис. 19). Таким образом, с увеличением

хода 1 → 3 для разных значений амплитуды ЭМИ

поля спектр возбуждения расширяется, а количе-

показана на рис. 17-19.

ство максимумов и минимумов увеличивается. Су-

Из рисунков видно, что с увеличением ампли-

щественно, что при больших амплитудах поля зави-

туды поля спектр возбуждения становится все бо-

симость спектра возбуждения со временем меняется

лее сложным. Вместо одного максимума при малых

сильнее.

161

В. А. Астапенко, Ф. Б. Розми, Е. В. Сахно

ЖЭТФ, том 160, вып. 2 (8), 2021

Рис. 16. Зависимости вероятности возбуждения КО под

Рис. 18. Временная эволюция спектра возбуждения пере-

действием ЭМИ от времени с амплитудой поля E0 =

хода 1 → 3 в КО для амплитуды поля E0 = 2·10-2: сплош-

= 4·10-2 для переходов n → 3: сплошная кривая — 0 → 3,

ная кривая — t = 10, пунктирная кривая — t = 10², штри-

пунктирная кривая — 1 → 3, штриховая кривая — 2 → 3;

ховая кривая — t = 10³; длительность импульса τ = 10³

δ = 0.1; τ = 10³

Рис. 19. Временная эволюция спектра возбуждения пере-

хода 1 → 3 в КО для амплитуды поля E0 = 3·10-2: сплош-

ная кривая — t = 10, пунктирная кривая — t = 10², штри-

Рис. 17. Временная эволюция спектра возбуждения пере-

ховая кривая — t = 10³; длительность импульса τ = 10³

хода 1 → 3 в КО для амплитуды поля E0 = 10-2: сплош-

ная кривая — t = 10, пунктирная кривая — t = 10², штри-

ховая кривая — t = 10³; длительность импульса τ = 10³

4. ЗАКЛЮЧЕНИЕ

В статье динамика временной эволюции возбуж-

дения КО под действием ЭМИ детально численно

исследована вне рамок теории возмущений. Уста-

Примечательно, что значение вероятности воз-

новлено, что эта зависимость определяется энергией

буждения в максимумах остается неизменным при

ассоциированного классического осциллятора в дан-

достаточно большой амплитуде поля и равно для

ный момент времени.

данного перехода одному и тому же значению:

Показано, что поведение функции W_mn(t) силь-

W_max(1 → 3) ≈ 0.245.

но зависит от параметров ЭМИ: отстройки несущей

162

ЖЭТФ, том 160, вып. 2 (8), 2021

Динамика временной эволюции возбуждения. . .

частоты от собственной частоты КО, длительности

времен [19]. Заметим также, что в последние годы

импульса и амплитуды напряженности электриче-

появились предложения по генерации одиночных

ского поля. Так, с увеличением значений указан-

импульсов лазера на свободных электронах [20], а

ных параметров вероятность возбуждения КО, мо-

также аттосекундных одноцикловых импульсов [21].

нотонно возрастающая со временем, превращается

в функцию, имеющую огибающую с максимумом и

осцилляции с частотой, равной собственной часто-

Финансирование. Работа выполнена при фи-

те КО. Амплитуда этих осцилляций увеличивается

нансовой поддержке Московского физико-техничес-

с увеличением длительности импульса τ и частот-

кого института в рамках Программы 5-топ-100.

ной отстройки несущей частоты от собственной час-

тоты δ. Данные осцилляции имеют иную природу,

чем осцилляции Раби. Они возникают в результате

5. ПРИЛОЖЕНИЕ А

интерференции вкладов в процесс положительной и

Полагаем, что до возбуждения (t → -∞) осцил-

отрицательной частотных составляющих напряжен-

лятор находился в n-м стационарном состоянии с

ности электрического поля в импульсе.

волновой функцией (без временного фактора) [22]

Полная вероятность возбуждения КО в случае

коротких импульсов остается монотонно возрастаю-

)1/4

⁽Mω

щей функцией времени при увеличении отстройки δ,

ψ(0)n(x) =

√

а для длинных импульсов вероятность возбуждения

πℏ

2ⁿn!

(

√

)

(

)

достигает максимума с ростом δ.

Mω

× exp

x²

H_n x

(A.1)

Исследована временная эволюция спектров воз-

2ℏ

ℏ

буждения КО для различных амплитуд электриче-

ского поля ЭМИ. В частности, показано, что с уве-

где H_n — полиномы Эрмита. Введем безразмерную

личением амплитуды поля у спектральной кривой

переменную

√

вместо одного максимума при δ = 0 появляются

Mω

боковые максимумы, положение и форма которых

x=x

(A.2)

ℏ

со временем меняются. В случае возбуждения из

и безразмерную функцию

возбужденного состояния центральный спектраль-

ный минимум со временем превращается в макси-

(

)1/4

ℏ

мум (рис. 19). Спектр полного возбуждения КО из

ψ=

ψ.

(A.3)

Mω

основного состояния в пределе сильных полей опи-

сывается столообразной кривой, ширина которой со

Под действием ЭМИ исходная функция преоб-

временем уменьшается.

разуется как

ψn0)(x) →

ψ_n(x, t). Тогда для вероят-

Получено выражение возбуждения КО перехода

ности перехода между стационарными состояниями

n → m (11) с явной зависимостью от квантовых чи-

квантового осциллятора n → m получаем (в момент

сел стационарных состояний (m, n). В частности, из

времени t)

этого выражения следует, что вероятности взаимно



обратных переходов в квантовом осцилляторе под



∫

∞



действием ЭМИ равны между собой в приближении

W_mn(t) =



dxψn(x, t

ψ(0)m(x)

m > n, (A.4)



заданного поля.



-∞

В заключение отметим, что в данной статье рас-

четы проведены для гауссовой огибающей импульса

здесь вводится функция (см. [2])

и параметров КО, характерных для молекулярных

колебаний. В рентгеновском диапазоне длин волн

ψ_n(x, t) = exp(iϕt

ψ(0)n(x - η(t))exp(

ηx), (A.5)

обычно используются лазеры на свободных элек-

которая является аналитическим решением времен-

тронах, импульсы которых состоят из субимпульсов

ного уравнения Шредингера для одномерного гар-

[18]. Тогда нужно пользоваться общей формулой (3)

монического осциллятора, на который действует

для расчета энергии, поглощаемой классическим

внешняя сила, зависящая от времени. Определим

осциллятором, ассоциированным с КО. В случае

безразмерную функцию:

применимости теории возмущений и гауссовых

субимпульсов можно получить аналитическое

Mω

η(t) =

η(t),

(A.6)

выражение для вероятности в пределе больших

ℏ

163

В. А. Астапенко, Ф. Б. Розми, Е. В. Сахно

ЖЭТФ, том 160, вып. 2 (8), 2021

∞

∫

где η(t) является решением уравнения для вынуж-

e-x2 H_m(x + w)H_n(x + z)dx =

денных колебаний классического осциллятора под

действием внешней силы:

-∞

√

=2^m

π n!z^m-nL^m-nn(-2wz), m > n, (A.15)

f (t)

η+ω²η=

(A.7)

где L^m-nn — обобщенный полином Лагерра.

(η, y) к табличному интегралу

Для приведения I₂

с начальными условиями η(-∞) = η(-∞) = 0, а

(A.15) необходимо сделать замену

также соответствующие производные:

w=y,

dη

(A.16)

η=

dη,

(A.8)

z = y - η.

ωdt

Тогда получаем

√

η=

η.

(A.9)

I₂(η, y) =

ℏω

=2^m√π n!(y - η)m-nLm-nn(-2y(y - η)). (A.17)

С учетом сказанного получаем



Введем обозначение: arg = -2y(y-η). Используя



∫

(

)



(A.16), находим

(x - η)²



W_mn(t) =

dxexp



)(

)

π2ⁿn!2^mm!



⁽i

−∞

arg = -2

η+

η-η

× H_n(x - η(t))exp(

ηx) ×

)(

)



⁽i

η2 +η

(

)

= -2

η+

η-

(A.18)

x²



× H_m(x)exp

(A.10)



или в размерных переменных

M η² +ω²Mη²

ε(t)

A(t)

Далее необходимо вычислить интеграл:

arg =

≡

= ν(t), (A.19)

2ℏω

ℏω

∫∞

[

]

A(t)

η²

ν(t) =

(A.20)

I₁ =

du exp -u2 + uη-

ηu

ℏω

здесь A(t) — работа над классическим осциллятором

−∞

η(t) под действием ЭМИ. Учитывая, что

× H_m(u)H_n(u - η). (A.11)

² +η²

M(η² +ω²η²)

Введем переменную

|y - η|² =

(A.21)

4ℏω

находим

η+

η,

(A.12)

ν^m-n



|I₂|² = 22mπ(n!)

^L^m-nn(ν)

² =

тогда

2^m-n

(

)



= 2n+mπ(n!)²ν^m-n

^L^m-nn(ν)

² . (A.22)

I₁ = exp

ηη-

I₂(η, y),

(A.13)

Так как

|I₁|² = exp(-ν) |I₂|² ,

(A.23)

где

получаем

∫∞

I₂(η, y) ≡

due-(u-y)2 H_m(u)H_n(u - η) =

W_mn(t) =

|I₁|² .

(A.24)

-∞

π2ⁿn!2^mm!

∫∞

Окончательно находим вероятность возбуждения

(u=x+y)

dx e-x2 H_m(x + y) ×

КО на переходе n → m, m > n:

-∞

W_mn(t) =Wmn[ν(t)] =

× H_n(x + y - η). (A.14)



Воспользуемся табличным интегралом

(7.378)

ν(t)^m-n exp(-ν(t))

^L^m-nn(ν(t))

² . (A.25)

из [23]:

164

ЖЭТФ, том 160, вып. 2 (8), 2021

Динамика временной эволюции возбуждения. . .

Для вывода формулы (11) используется следующее

Подставляя формулу (B.3) в (B.1), получаем

представление обобщенного полинома Лагерра [23]:

∫

q²

L^αn(x) =

e^xx^-α

(e^-xxn+α).

(A.26)

ε_clas(t) =

dt^′E(t^′) ×

dxⁿ

-∞

Подстановка (A.26) в (A.25) дает

∫

′

dω

iω^′ exp(-iω^′t)



E(ω^′)

(B.4)

 dⁿ

²

2π

ω′2 - ω²⁰ + 2iγω^′



Wmn(ν) =

e^νν^n-m

e^-νν^m)

(A.27)

-∞



n!m!

^ dνⁿ (

Частотный интеграл в правой части уравнения

Учитывая, что

(B.4) можно вычислить с помощью теоремы о выче-



тах. В пределе γ → 0 этот интеграл равен

 dⁿ

²



ν^n-m 

(e^-ν ν^m)



dνⁿ

∫



dω^′ iω^′ exp(-iω^′(t^′ - t^′′))



∑



n!m!(-1)^kν^-k



2π ω′2 - ω²⁰ - 2iγω^′

=νm+ne-2ν

(A.28)



-∞

k!(m - k)!(n - k)!

 k=0



= θ(t^′ - t^′′)cos[ω₀(t^′ - t^′′)], (B.5)

получаем

где θ(τ) — тета-функция Хевисайда. Подставляя

Wmn(ν) = n!m!νm+ne^-ν ×

правую часть уравнения (B.5) в формулу (B.4), на-



2

ходим



∑

(-1)^kν^-k



(A.29)



t^′

k!(m - k)!(n - k)!

∫

 k=0



q²

ε_clas(t) =

dt^′E(t^′)

dt^′′E(t^′′) cos[ω₀(t^′-t^′′)] =

Из (A.29), в частности, следует, что

−∞

-∞

∫

Wmn(ν) =^Wnm(ν).

(A.30)

q²

dt^′E(t^′)

dt^′′E(t^′′) cos[ω₀(t^′ - t^′′)] =

Таким образом, временная зависимость вероят-

−∞

-∞



ности перехода n → m, m > n, совпадает с таковой



∫t



q²



на обратном переходе m → n.



dt^′E(t^′) exp(iω₀t^′)

(B.6)



-∞

6. ПРИЛОЖЕНИЕ B

При переходе ко второму равенству в (B.6) исполь-

зован тот факт, что подынтегральная функция сим-

Для энергии ЭМИ, поглощенной заряженным

метрична относительно перестановки переменных

классическим осциллятором к моменту времени t,

интегрирования: t^′ ↔ t^′′.

имеем

∫^t

ε_clas(t) = q

x(t^′)E(t^′) dt^′.

(B.1)

−∞

ЛИТЕРАТУРА

Решение уравнения для гармонического осцил-

1. J. Schwinger, Phys. Rev. 91, 728 (1953).

лятора выглядит следующим образом (например,

см. [24]):

2. K. Husimi, Prog. Theor. Phys. 9, 381 (1953).

∫

3. M. T. Hassan, A. Wirth, I. Grguras et al., Rev. Sci.

E(ω^′) exp(-iω^′t)

dω^′

Instrum. 83, 111301 (2012).

x(t) =

(B.2)

ω²⁰

- ω′2 - 2iγω^′ 2π

-∞

4. M. Chini, K. Zhao, and Z. Chang, Nat. Photon. 8,

178 (2014).

где γ — константа релаксации. Из формулы (B.1)

следует выражение

5. D. N. Makarov, M. R. Eseev, and K. A. Makarova,

Opt. Lett. 44, 3042 (2019).

∫

ω^′E(ω^′)exp(-iω^′t)

dω^′

x(t) = -i

(B.3)

6. D. N. Makarov, Opt. Express 27, 31989 (2019).

ω²⁰

- ω′2 - 2iγω^′

2π

-∞

165

В. А. Астапенко, Ф. Б. Розми, Е. В. Сахно

ЖЭТФ, том 160, вып. 2 (8), 2021

7. D. N. Makarov, Sci. Rep. 8, 8204 (2018).

17. В. А. Астапенко, ЖЭТФ 157, 67 (2020).

8. V. A. Astapenko, Appl. Phys. B 126, 110 (2020).

18. E. Saldin, E. V. Schneidmiller, and M. V. Yurkov,

The Physics of Free Electron Lasers, Springer, Berlin

9. F. B. Rosmej, V. A. Astapenko, and V. S. Lisitsa, J.

(1999).

Phys. B 50, 235601 (2017).

10. F. B. Rosmej, V. A. Astapenko, and V. S. Lisitsa,

19. F. B. Rosmej, V. A. Astapenko, and E. S. Khramov,

Phys. Rev. A 90, 043421 (2014).

Matter Rad. Extrem. Lett. 6, 034001 (2021).

11. Z. Fu and M. Yamaguchi, Sci. Rep. 6, 38264 (2016).

20. T. Tanaka, Phys. Rev. Lett. 114, 044801 (2015).

12. V. A. Astapenko and E. V. Sakhno, Appl. Phys.

21. A. Mak, G. Shamuilov, P. Salen et al., Rep. Prog.

B 126, 23 (2020).

Phys. 82, 025901 (2019).

13. S. Beaulieu, A. Comby, A. Clergerie et al., Science

358, 1288 (2017).

22. Л. Д. Ландау, Е. М. Лифшиц, Квантовая механи-

ка, Физматлит, Москва (2004).

14. M. Isinger, R. J. Squibb, D. Busto et al., Science 358,

893 (2017).

23. И. С. Градштейн, И. М. Рыжик, Таблицы интег-

ралов, сумм, рядов и произведений, Физматгиз,

15. A. Kaldun, A. Blättermann, S. Donsa, V. Stooß et

Москва (1963).

al., Science 354, 738 (2016).

16. V. Gruson, L. Barreau, A. Jiménez-Galan et al.,

24. F. B. Rosmej, V. A. Astapenko, and V. S. Lisitsa,

Science 354, 734 (2016).

Plasma Atomic Physics, Springer Ser. 104 (2021).

166