ЖЭТФ, 2021, том 160, вып. 3 (9), стр. 327-365
© 2021
ПОБОЧНЫЕ КАНАЛЫ УТЕЧКИ ИНФОРМАЦИИ В КВАНТОВОЙ
КРИПТОГРАФИИ: НЕ СТРОГО ОДНОФОТОННЫЕ
СОСТОЯНИЯ, РАЗНЫЕ КВАНТОВЫЕ ЭФФЕКТИВНОСТИ
ДЕТЕКТОРОВ, КОНЕЧНЫЕ ПЕРЕДАВАЕМЫЕ
ПОСЛЕДОВАТЕЛЬНОСТИ
С. Н. Молотков*
Институт физики твердого тела Российской академии наук
142432, Черноголовка, Московская обл., Россия
Академия криптографии Российской Федерации
121552, Москва, Россия
Центр квантовых технологий, Московский государственный университет им. М. В. Ломоносова
119899, Москва, Россия
Поступила в редакцию 20 апреля 2021 г.,
после переработки 20 апреля 2021 г.
Принята к публикации 25 апреля 2021 г.
Реализации систем квантовой криптографии существенно отличаются от идеализированных моделей,
которые используются для доказательства секретности распределяемых ключей. Без учета неидеаль-
ностей реальных систем невозможно всерьез говорить о криптографической стойкости. Для практиче-
ского использования систем квантовой криптографии необходимо учитывать все реальные факторы,
влияющие на секретность распределяемых ключей. В работе предложен, по сути, аналитический метод,
учитывающий нестрогую однофотонность информационных состояний, различные квантовые эффектив-
ности детекторов, флуктуации параметров за счет конечных передаваемых последовательностей, утечку
информации через побочные каналы как при пассивном детектировании побочного излучения, так и
при активном зондировании элементов системы. Состояния в побочных каналах могут иметь предельно
низкую интенсивность, поэтому рассматриваются квантовым образом. Максимально возможная полная
утечка информации к подслушивателю по всем каналам достигается на совместных коллективных из-
мерениях как квантовых информационных состояний, так и квантовых состояний в побочных каналах.
Метод применим при любом спектральном распределении числа фотонов в побочных каналах.
DOI: 10.31857/S0044451021090029
связи. При этом квантовый канал связи доступен
не только для прослушивания, но и для произ-
вольных модификаций третьей нелегитимной сторо-
1. ВВЕДЕНИЕ
ной. Для согласования результатов измерений, кор-
рекции ошибок в первичных ключах на приемной
Квантовая криптография [1] — квантовое рас-
стороне и сжатия очищенных ключей использует-
пределение ключей — один из разделов квантовых
ся вспомогательный классический открытый аутен-
технологий, который доведен до практических при-
тичный канал связи.
менений. Квантовая криптография, по сути, являет-
ся процедурой согласования двух независимых слу-
Секретность ключей в квантовой криптографии
чайных последовательностей на передающей и при-
базируется на фундаментальном свойстве кванто-
емной сторонах путем передачи и регистрации кван-
вых состояний — вторжение в квантовый канал свя-
товых состояний через открытый квантовый канал
зи неизбежно приводит к возмущению передавае-
мых квантовых состояний и ошибкам измерений на
* E-mail: sergei.molotkov@gmail.com
приемной стороне.
327
С. Н. Молотков
ЖЭТФ, том 160, вып. 3 (9), 2021
Анализ криптостойкости квантовой криптогра-
альными — детекторы имеют идеальную и одинако-
фии прошел длинный путь. Первоначально рассмат-
вую квантовую эффективность, что также не отве-
ривались «идеальные» системы квантовой крипто-
чает реальной ситуации. Метод не позволяет пере-
графии и отдельные атаки на передаваемые кван-
нести доказательство на случай неидеальных детек-
товые состояния. На первом этапе предполагалось,
торов с разными квантовыми эффективностями.
что квантовые состояния являются строго однофо-
Обычно в системах квантовой криптографии ис-
тонными, что не отвечает реальной ситуации.
пользуется пара детекторов. В одном из базисов от-
В реальной ситуации в качестве информаци-
счеты в одном детекторе D1 отвечают за регистра-
онных квантовых состояний используются сильно
цию 0, в другом детекторе D2 — за регистрацию 1. В
ослабленные когерентные состояния, которые явля-
сопряженном базисе, наоборот, отсчеты в детекторе
ются квазиоднофотонными — имеют пуассоновскую
D2 отвечают за регистрацию 0, в детекторе D1 —
статистику по числу фотонов, что приводит к воз-
за регистрацию 1. Базисы передающей и приемной
никновению новых атак, которые отсутствуют в слу-
сторон раскрываются через открытый аутентичный
чае строго однофотонных состояний.
канал связи. Информация о том, в каком базисе бы-
Предполагалось, что передающая и приемная
ла регистрация, известна подслушивателю.
станции изолированы от внешнего мира, т. е. под-
Интуитивно ясно, что в случае, когда квантовая
слушиватель не имеет ни прямого, ни косвенного
эффективность одного из детекторов стремится к
доступа к аппаратуре. В реальности системы кван-
нулю (отсчеты имеют место только в одном из де-
товой криптографии являются открытыми система-
текторов), невозможно гарантировать секретность
ми в том смысле, что подслушиватель может иметь
ключей. Базис подслушивателю известен, и сраба-
опосредованный доступ через линию связи к прием-
тывает только один детектор. В такой ситуации под-
ной и передающей аппаратуре. Кроме того, подслу-
слушиватель знает весь ключ даже без вторжения в
шиватель может детектировать побочное излучение
квантовый канал связи. При этом подслушиватель
самой аппаратуры [2, 3].
не производит ошибок на приемной стороне и не об-
Для практического использования систем кван-
наруживается, а система квантовой криптографии
товой криптографии необходимо учитывать все ре-
оказывается несекретной.
альные факторы, влияющие на секретность распре-
Как видно из приведенного простого примера,
деляемых ключей, а именно:
учет различных квантовых эффективностей детек-
1) разную и неидеальную квантовую эффектив-
торов играет принципиальную роль в обеспечении
ность однофотонных детекторов;
секретности ключей в квантовой криптографии да-
2) нестрогую однофотонность информационных
же в случае строго однофотонных состояний. В
состояний;
этом направлении имеются лишь частичные резуль-
3) побочные каналы утечки информации;
таты [6].
4) атаки активного зондирования;
В рамках энтропийных соотношений неопреде-
5) конечную длину передаваемых последователь-
ленностей также невозможно учесть утечку ин-
ностей.
формации к подслушивателю по побочным кана-
Доказательство секретности ключей должно учиты-
лам. Интуитивно данный факт имеет простое объ-
вать все упомянутые выше факторы. До сих пор
яснение. Энтропийные соотношения неопределенно-
комплексный учет всех факторов, влияющих на сек-
стей связывают утечку информации с возмущени-
ретность распределяемых ключей, не сделан.
ем квантовых состояний — ошибкой на приемной
В случае строго однофотонных информацион-
стороне. Утечка информации по побочным кана-
ных состояний и идеальных детекторов фундамен-
лам, например детектирование побочного излуче-
тальные энтропийные соотношения неопределенно-
ния передающей и приемной аппаратуры, не при-
стей позволяют связать утечку информации к под-
водит к возмущению подслушивателем информаци-
слушивателю с наблюдаемой ошибкой на приемной
онных состояний и ошибкам на приемной стороне.
стороне. Энтропийные соотношения неопределенно-
По этой причине утечка информации по побочным
стей позволяют не перебирать и не строить явно все-
каналам лежит за рамками энтропийных соотноше-
возможные атаки, а выразить утечку только через
ний неопределенностей.
наблюдаемую ошибку на приемной стороне. Данный
Неоднофотонность информационных состояний
метод применим также и для конечных передавае-
приводит к атаке с расщеплением по числу фотонов
мых последовательностей [4,5]. При этом считалось,
(PNS-атака, Photon Number Splitting). В канале с
что измерения на приемной стороне являются иде-
потерями, при уровне потерь больше некоторой кри-
328
ЖЭТФ, том 160, вып. 3 (9), 2021
Побочные каналы утечки информации в квантовой криптографии.. .
тической величины, данная атака приводит к тому,
терминах, и доказательства секретности являются
что подслушиватель знает весь передаваемый ключ
«многоходовыми» [4]. Для самодостаточности изло-
и не производит ошибок на приемной стороне — не
жения приведем определения величин, которые ис-
детектируется. Для детектирования PNS-атаки ис-
пользуются в доказательстве секретности.
пользуется Decoy State-метод. Данный метод в ис-
Секретность ключей в квантовой криптографии
ходном виде перестает работать при атаках актив-
дается в терминах следовой метрики — расстояния
ного зондирования — атаках с зондированием моду-
между двумя квантовыми состояниями, описываю-
лятора интенсивности, и требует обобщения. Такое
щими реальную ситуацию после квантового распре-
обобщение было сделано в работах [7,8].
деления ключей и идеальную ситуацию, когда клю-
Анализ криптостойкости систем квантовой крип-
чи строго равновероятны и полностью некоррелиро-
тографии с полным учетом неидеальностей 1)-5) до
ваны с квантовыми состояниями подслушивателя.
сих пор не сделан.
Данный критерий вызывал споры даже среди
Цель данной работы — учесть упомянутые вы-
специалистов [9, 10]. Абстрактность критерия сек-
ше неидеальности систем квантовой криптографии
ретности ключей на основе следовой метрики не со-
в доказательстве секретности ключей.
держит интуитивно прозрачных соображений, ко-
Логика доказательства будет состоять в следую-
торые были выработаны применительно к исполь-
зованию ключей в классической криптографии, на-
щем. Секретный ключ формируется из однофотон-
ной компоненты информационных состояний, до-
пример, таких как переборная сложность по поис-
ку истинного ключа, число шифр-сообщений до их
стигающей приемной стороны. Информация, содер-
жащаяся в многофотонных компонентах состояний
первого дешифрования при условии, что шифрова-
ние происходит на ключах, полученных в результате
в пользу подслушивателя, считается ему известной
и не фигурирует в секретном ключе. Оценка до-
квантового распределения.
ли однофотонной компоненты проводится обобщен-
Явная связь следового критерия секретности
ключей в квантовой криптографии с переборными
ным Decoy State-методом. Учет побочных каналов
утечки информации требует построения явной ата-
критериями секретности в классической криптогра-
фии была установлена в работе [11].
ки на состояния в квантовом канале связи. Кро-
ме того, учет разной и неидеальной квантовой эф-
В задачах квантовой криптографии после пере-
дачи и измерения квантовых состояний возникает
фективности детекторов также требует явного вида
однофотонной компоненты информационных состо-
матрица плотности ρXE Алиса-Ева, которая име-
ет классически-квантовую структуру. Алиса имеет
яний. Состояния в побочных каналах также необ-
ходимо рассматривать квантовым образом. Нефор-
в своем распоряжении случайную эталонную бито-
вую строку, к которой Ева не имеет доступа. Ева
мально говоря, данные квантовые состояния «под-
имеет в своем распоряжении квантовое состояние,
цепляются» явно к однофотонной компоненте состо-
яний.
которое возникает из-за вторжения в квантовый ка-
нал связи. Матрица плотности имеет вид
Предложен также простой метод учета флуктуа-
∑
ций наблюдаемых параметров, которые имеют ме-
ρ(n)XE =
|x〉XX 〈x| ⊗ ρxE ,
сто при конечных длинах передаваемых последова-
x∈{0,1}
n
(1)
тельностей.
|x〉X = |x1〉X ⊗ |x2〉X ⊗ . . . ⊗ |xn〉X .
Ниже будем последовательно включать в рас-
смотрение неидеальности системы, чтобы продемон-
Удобно классической битовой строке x длиной n
стрировать, как зависит оценка длины секретного
сопоставить регистр ортогональных квантовых
ключа от каждого из факторов.
состояний
|x〉X , отвечающих состоянию класси-
ческого регистра с последовательностью битов
(x1, x2, . . . , xn), ρxE
— квантовое состояние Евы,
2. СЛЕДОВОЕ РАССТОЯНИЕ,
коррелированное с битовой строкой Алисы.
СГЛАЖЕННЫЕ min- И max-ЭНТРОПИИ
Для дальнейшего потребуются сглаженные min-
и max-квантовые энтропии, которые мажорируют
Выше была описана на неформальном уровне
следовое расстояние. По определению имеем (см. де-
причина секретности ключей, которая гарантирует-
тали в [4])
ся фундаментальными законами Природы. На фор-
мальном уровне секретность ключей в квантовой
Hεmin(ρ(n)XE|ρ(n)E) =
sup
Hmin(ρ(n)XE|ρ(n)E),
(2)
криптографии выражается в довольно абстрактных
ρ(n)XE ∈Bε(ρ(n)XE )
329
С. Н. Молотков
ЖЭТФ, том 160, вып. 3 (9), 2021
Hεmax(ρ(n)XE|ρ(n)E) =
inf
Hmax(ρ(n)XE|ρ(n)E),
(3)
3. СЛЕДОВОЕ РАССТОЯНИЕ И КРИТЕРИЙ
ρ(n)XE ∈Bε(ρ(n)XE)
СЕКРЕТНОСТИ КЛЮЧЕЙ
далее, пусть λ — минимальное число, такое что
Секретность ключей в квантовой криптографии
λIX ⊗ ρ(n)E - ρ(n)XE ≥ 0,
формулируется в терминах следового расстояния
[4]. После передачи и регистрации квантовых состо-
тогда по определению
яний, но до коррекции ошибок у Боба, квантовое
Hmin(ρ(n)XE|ρ(n)E) = - log(λ),
(4)
состояние Алиса-Ева описывается матрицей плот-
(n)
ности ρX
(1), которая содержит корреляции меж-
E
где log
≡ log2. Матрицы плотности, по кото-
ду эталонной битовой строкой Алисы и квантовой
рым определяются inf и sup, лежат внутри шара
системой Евы. После коррекции ошибок через от-
Bε(ρXE),
крытый аутентичный канал связи Ева получает до-
полнительную информацию о битовой строке Али-
Tr{|ρ(n)XE - ρ(n)XE |} = ||ρ(n)XE - ρ(n)XE ||1 ≤ ε.
(5)
сы. При коррекции ошибок через открытый канал
Для дальнейшего будет полезно эквивалентное
между Алисой и Бобом передается множество бито-
определение, которое следует из (4):
вых строк C.
После коррекции ошибок Алиса и Боб проводят
Hmin(ρ(n)XE|ρ(n)E) = - log(λmax((IX ⊗ (ρ(n)E)-1/2)×
усиление секретности очищенного ключа при по-
мощи универсальных хеш-функций второго поряд-
× ρ(n)XE(IX ⊗ (ρ(n)E)-1/2))),
(6)
ка, которое сводится к сжатию очищенной битовой
где
строки f : x = {0, 1}n → ℓ = {0, 1}ℓ. Хеш-функция
сама является случайной величиной, которая рав-
λmax((IX ⊗ (ρ(n)E)-1/2)ρ(n)XE(IX ⊗ (ρ(n)E)-1/2))
новероятно выбирается из множества хеш-функций
— максимальное собственное число оператора в
F. Выбор хеш-функции проводится через открытый
скобках (6). Далее
канал связи и известен Еве.
Универсальные хеш-функции второго порядка
Hmax(ρ(n)XE|ρ(n)E) = log(Tr{IX ⊗ ρ(n)EP(ρ(n)XE)}),
(7)
обладают свойством [12]
где P(ρ(n)XE ) — проектор на носитель матрицы плот-
1
Prf∈F {f(x) = f(x′)} <
∀ x=x′.
(8)
ности ρ(n)XE .
2ℓ
Данные определения предполагают минимиза-
После усиления секретности матрица плотности
цию/максимизацию по матрицам плотности, ле-
Алиса-Ева и матрица плотности Евы, коррелиро-
жащим в некоторой области пространства состоя-
ванная с битовой строкой x, переходит в новую мат-
ний. При конкретных практических вычислениях
рицу плотности ρ(n)XE → ρ(ℓ)F(X)F(E).
такая минимизация/максимизация вряд ли возмож-
После сжатия следовое расстояние мажорирует-
на. Кроме того, данные определения предполагают,
ся условной min-энтропией (см. детали в [4]):
что матрица плотности ρ(n)XE (центр шара) извест-
на точно. В реальной ситуации матрица плотности
||ρ(ℓ)F(X)F(E) - ρF(U
X) ⊗ρFℓ(E)||1<
ρ(n)XE точно не известна по двум причинам. Первая —
передаваемые последовательности имеют конечную
<2-(1/2)(Hmin(ρXnEC|ρEnC)-ℓ) =
длину, поэтому можно получить лишь оценку самой
(n)
n)
= 2-(1/2)(Hmin(ρXE|ρ(
E
)-log |C|-ℓ).
(9)
ρ(n)XE. Вторая причина состоит в том, что даже если
матрица плотности всей последовательности точно
Отметим, что в правой части (9) фигурируют мат-
известна и имеет структуру тензорного произведе-
рицы плотности после передачи и регистрации кван-
ния, ρ(n)XE = ρ⊗nXE , то вычислить сглаженные энтро-
товых состояний в согласованных базисах, но до
пии точно не удается, можно лишь получить верх-
усиления секретности и коррекции ошибок. В (9),
нюю/нижнюю оценку для сглаженных энтропий.
(11) U = F(UX ), C — множество битовых строк (син-
По этим причинам приходится делать двойное
дрома ошибок и др.), передаваемых через открытый
усечение матрицы плотности — вычисление сгла-
канал между Алисой и Бобом при коррекции оши-
женных энтропий в два этапа (см. подробности ни-
бок, log |C| — количество информации в битах, со-
же). На первом этапе оценивается матрица плотно-
держащееся в этих строках,
сти ρ(n)XE — центр шара. На втором этапе получается
верхняя/нижняя оценка для сглаженных энтропий.
log |C| = leak.
(10)
330
ЖЭТФ, том 160, вып. 3 (9), 2021
Побочные каналы утечки информации в квантовой криптографии.. .
Далее, ρF(X)F(E) — матрица плотности после сжа-
Напомним, что в правую часть (12) входит мат-
тия битовой строки f : x = {0, 1}n → ℓ = {0, 1}ℓ,
рица плотности до стадии усиления секретности.
∑
Если величина сжатия (длина секретного ключа
1
ρUX =
|x〉XX 〈x|,
ℓ) выбрана такой, что
2n
x∈{0,1}n
∑
1
ρU =
|x〉XX 〈x|,
(11)
2ε + 2-(1/2)(Hmin(ρXnE |ρEn))-log|C|-ℓ) ≤ ε′,
(13)
2ℓ
x∈{0,1}ℓ
то ключ называется ε′-секретным в смысле следово-
ρ(ℓ)F(E) = TrF(X){ρ(ℓ)F(X)F(E)}.
го расстояния (9), (12). После усиления секретности
следовое расстояние оказывается меньше ε′ — пара-
Матрица плотности ρ(ℓ)F(X)F(E) описывает реаль-
метра секретности ключей, который выбирается ле-
ную ситуацию после усиления секретности — оста-
гитимными пользователями и достигается соответ-
точные корреляции между новой битовой строкой
ствующим сжатием (выбором хеш-функций) очи-
Алисы и новой квантовой системой Евы.
щенных ключей.
Матрица плотности ρF(U
ρ(ℓ)F(E) описывает
X) ⊗
Таким образом, доказательство секретности сво-
идеальную ситуацию, когда ключи равновероятно
распределены и никак не коррелированы с кванто-
дится к вычислению условной сглаженной min-энт-
ропии после передачи и измерения квантовых состо-
выми состояниями Евы ρ(ℓ)F(E).
яний до коррекции ошибок и усиления секретности.
Для конструктивного вычисления сглаженной
4. ПЕРЕХОД К min-ЭНТРОПИИ
min-энтропии требуется получить оценку для мат-
(n)
рицы плотности ρX
— центра шара.
По «техническим математическим» причинам
E
удобно перейти от условной min-энтропии в (9) к
сглаженной условной min-энтропии. Почему возни-
кает min-энтропия?
5. КВАНТОВАЯ КРИПТОГРАФИЯ КАК
Умозрительно можно было бы вычислить услов-
РАСПРЕДЕЛЕННЫЙ СТАТИСТИЧЕСКИЙ
ную min-энтропию в (2)-(4), (9), если матрица плот-
ЭКСПЕРИМЕНТ СО
ЗЛОУМЫШЛЕННИКОМ
ности ρ(n)XE в (2)-(4) была бы точно известна и ее
можно было бы вычислить. Однако это невозмож-
но. В лучшем случае можно получить оценку мат-
Квантовое распределение ключей представля-
ет собой статистический эксперимент в следующем
рицы плотности. Определения (2)-(7) с математиче-
смысле. Легитимные пользователи Алиса и Боб свя-
ской точки зрения очень удобны при доказательстве
заны между собой через «черный ящик» — кванто-
различных неравенств. Однако при практических
вый канал связи, в который вторгается Ева. Алиса
вычислениях ими невозможно напрямую воcпользо-
контролирует информационные состояния на входе,
ваться.
Боб на приемной стороне видит результаты изме-
Пусть матрица плотности ρ(n)XE лежит в шаре
рений при условии, что были посланы конкретные
ρ(n)XE ∈ Bε(ρ(n)XE), тогда
квантовые состояния. Это осуществляется на стадии
оценки параметров путем раскрытия части переда-
||ρ(ℓ)F(X)F(E) - ρ(ℓ)F(U
⊗ ρ(ℓ)F(E)||1 ≤
X)
ваемой последовательности.
≤ ||ρ(ℓ)F(X)F(E) - ρ(ℓ)F(X)F(E)||1 +
Целью этой стадии протокола является оценка
(n)
частичной матрицы плотности ρX
= TrB{ρ(n)XBE }
E
+ ||ρ(ℓ)F(X)F(E) - ρU ⊗ ρ(ℓ)F(E)||1 + ||ρ(ℓ)F(E)-ρ(ℓ)F(E)||1 ≤
при условии, что Боб получает результаты изме-
(n)
рений на частичной матрице плотности ρX
=
B
≤ 2ε + 2-(1/2)(Hmin(ρXnE |ρEn))-log|C|-ℓ) ≤
= TrE {ρ(n)XBE
}.
≤ 2ε + 2-(1/2)(Hm in(ρXnE |ρEn))-log|C|-ℓ).
(12)
Если бы матрица плотности ρ(n)XE была бы точно
известна, то задача вычисления длины секретного
В (12) дважды использовано неравенство треуголь-
ключа сводилась бы к вычислению Hmin(ρ(n)XE |ρ(n)E)
ника для следового расстояния, а также тот факт,
в (2).
что следовое расстояние не возрастает при взятии
частичного следа. Последнее неравенство следует из
В реальной ситуации матрица плотности ρ(n)XE
определения (2) условной min-энтропии.
точно не известна. Вопрос об оценке матрицы плот-
331
С. Н. Молотков
ЖЭТФ, том 160, вып. 3 (9), 2021
ности должен решаться в терминах теории веро-
ρ(n)XEQ =
∑
∑
ятностей и математической статистики. Матрица
=
PX(x)|x〉XX〈x| ⊗
PQ(Q)|Q〉〈Q| ⊗ ρx(n)E|Q =
плотности Алиса-Ева зависит от действий Евы —
x∈(X)
Q∈Q
от параметров (ошибки на приемной стороне, доли
∑
однофотонной компоненты и пр.), которые управля-
=
PX(x)|x〉XX〈x| ⊗ ρx(n)EQ,
(14)
ются Евой и которые в явном виде недоступны ле-
x∈(X)
гитимным пользователям. Легитимные пользовате-
здесь PX (x) — вероятность распределения битовых
ли имеют косвенную информацию об этих парамет-
строк у Алисы,
рах из результатов измерений. Точнее говоря, они
∑
имеют лишь оценку параметров (например, оценку
PX(x) = 1.
(15)
вероятности ошибки), которая зависит от длины по-
x∈(X)
следовательности и истинной вероятности ошибки.
В (14) введено обозначение
Обозначим набор параметров, от которых зави-
∑
сит матрица плотности, как {Q}. Данные парамет-
ρx(n)EQ =
PQ(Q)|Q〉〈Q| ⊗ ρx(n)XE|Q,
ры известны Еве точно, поскольку ей и определя-
Q∈Q
(16)
ются. Для легитимных пользователей данные пара-
TrE {ρx(n)E|Q} = 1.
метры «скрыты».
Каждому набору параметров Q удобно сопо-
Ниже увидим, что имеются два типа скрытых
ставить соответствующие ортогональные (различи-
параметров: 1) наблюдаемые скрытые параметры,
мые) квантовые состояния |Q〉Q. Набор параметров
которые могут быть определены из измерений на
Q имеет распределение вероятностей PQ(Q), кото-
приемной стороне Боба, иначе говоря, вероятности
рое известно Еве, более того, Еве известен в каж-
фотоотсчетов на приемной стороне напрямую зави-
дом акте распределения ключей сам набор парамет-
сят от данных параметров; 2) ненаблюдаемые скры-
ров. Неформально ситуацию можно интерпретиро-
тые параметры, от которых не зависят вероятности
вать следующим образом. Ева «случайно генериру-
результатов измерений на приемной стороне, но от
ет» в соответствии с распределением PQ(Q) набор
них зависит утечка информации к подслушивателю.
параметров атаки Q. После «генерации» парамет-
ры самой Еве точно известны, но не известны Али-
Нет другого способа, кроме как рассматривать
се и Бобу. В результате атаки Ева имеет условную
скрытый набор параметров для легитимных поль-
матрицу плотности ρx(n)E|Q, зависящую от атаки, кото-
зователей как случайные величины, которые име-
рая параметризуется набором сгенерированных па-
ют свое распределение вероятностей, определяе-
раметров.
мое Евой, но явно неизвестное легитимным поль-
Матрица плотности параметров и функция рас-
зователям. В этом смысле квантовое распределение
пределения параметров имеют вид
ключей представляет собой статистический экспе-
римент, когда истинное совместное распределение
∑
ρQ(Q) = PQ(Q)|Q〉QQ〈Q|,
PQ(Q) = 1.
(17)
параметров и величин легитимных пользователей
Q∈Q
неизвестно, но требуется получить оценку данного
совместного распределения (оценку совместной мат-
Поскольку сами параметры и их распределение
рицы плотности) по маргинальному распределению
Алисе неизвестны, статистический ансамбль по все-
(частичной матрице плотности). Оценка частичной
возможным наборам параметров дается матрицей
матрицы плотности в реальной ситуации должна
плотности Алиса-Ева:
быть получена по конечному, а не асимптотическо-
∑
му (бесконечному) набору наблюдаемых данных.
ρ(n)XE =
PQ(Q)ρ(n)XE|Q,
Q∈Q
∑
(18)
Сказанное означает, что недоступные параметры
ρ(n)XE|Q =
PX(x)|x〉XX〈x| ⊗ ρx(n)E|Q.
должны рассматриваться легитимными пользовате-
x∈(X)
лями как случайные величины, которые подчиняют-
ся некоторому, также неизвестному для них, распре-
Набор скрытых от легитимных пользователей пара-
делению вероятностей. Данные параметры должны
метров параметризует атаку Евы и определяет ве-
быть включены в матрицу плотности, которая мо-
роятности результатов измерений на приемной сто-
жет быть записана в виде
роне Боба. Например, таким параметром в строго
332
ЖЭТФ, том 160, вып. 3 (9), 2021
Побочные каналы утечки информации в квантовой криптографии.. .
однофотонном случае и при идеальных детекторах
Введем события.
является один параметр Q — вероятность ошибоч-
Первое событие Ω1 — параметры матрицы плот-
ных отсчетов на приемной стороне.
ности попадают в доверительный интервал (23).
По этой причине, если имеется оценка параметра
Второе событие Ω2 — собственные числа матрицы
Q по результатам измерений, то можно оценить мат-
плотности попадают в типичное множество после-
рицу плотности ρx(n)XE|Q, которая приводит к таким
довательностей при условии, что ее параметры уже
результатам измерений. Более точно, попадание па-
лежат в доверительном интервале (23). Совместная
раметров в доверительный интервал с определенной
вероятность двух событий есть
вероятностью позволяет оценить следовое расстоя-
ние.
Pr{Ω1 ∩ Ω2} = Pr{Ω2|Ω1}Pr{Ω1},
(25)
Разобьем все множество параметров на две обла-
сти:
здесь Pr{Ω2|Ω1} — условная вероятность того, что
∑
∑
матрица плотности попадает в типичное простран-
ρ(n)XE =
PQ(Q)ρ(n)XE|Q +
PQ(Q)ρ(n)XE|Q,
(19)
ство при условии, что параметры матрицы плотно-
Q∈δQ
Q∈δQ
сти лежат в доверительном интервале.
где
TrXE {ρ(n)XE|Q} = 1.
(20)
Введем символические обозначения
6.1. Первое усечение матриц плотности
Q ∈ δQ = Q ∈ δQ, Q ∈ δQ = Q ∈ δQ,
(21)
Пусть событие Ω1
такое, что параметры попа-
параметры попадают в доверительнный интервал
дают в доверительный интервал, пусть вероятность
или лежат вне его. Далее, используя (14)-(21), по-
данного события
лучаем
Pr{Ω1} = Pr{Q ∈ δQ} > 1 - ε1.
(26)
∑
PQ(Q)ρ(n)XE|Q
ρ(n)XE = Pr{Q ∈ δQ}
+
Pr{Q ∈ δQ}
Q∈δQ
Матрица плотности после первого усечения истин-
ной матрицы плотности, с учетом (18), (19), имеет
∑
PQ(Q)ρ(n)XE|Q
+ Pr{Q ∈ δQ}
=
вид
Pr{Q ∈ δQ}
∑
Q∈δQ
ρ(n)XE =
PQ(Q)ρ(n)XE|Q.
(27)
= Pr{Q ∈ δQ}ρ(n)
+
Q∈δQ
XE|Q∈δQ
+ Pr{Q ∈ δQ}ρ(n)
,
(22)
Усеченная матрица плотности ρ(n)XE является ε1-
XE|Q∈δQ
близкой в смысле следового расстояния к истинной
где
∑
матрице плотности ρ(n)XE . Действительно,
Pr{Q ∈ δQ} =
PQ(Q),
Q∈δQ
∑
∑
(23)
||ρ(n)XE - ρ(n)XE ||1 = ||
PQ(Q)ρ(n)XE|Q||1 ≤
Pr{Q ∈ δQ} =
PQ(Q).
Q∈δ
Q
Q∈δQ
∑
∑
≤
PQ(Q)||ρ(n)XE|Q||1 ≤
PQ(Q) ≤ ε1.
(28)
При этом условные матрицы плотности в (22) нор-
мированы:
Q∈δQ
Q∈δQ
TrXE {ρ(n)XE|Q∈δ
} = 1, TrXE{ρ(n)
} = 1. (24)
Q
XE|Q∈δQ
В (28) использовано неравенство треугольника для
следового расстояния.
Тот факт, что параметры усеченной матрицы
6. ДВОЙНОЕ УСЕЧЕНИЕ МАТРИЦ
плотности (событие Ω1) лежат в доверительном ин-
ПЛОТНОСТИ
тервале с вероятностью
Матрица плотности ρ(n)XE является истинной и за-
висит от скрытых параметров. В дальнейшем при-
Pr{Ω1} = Pr{Q ∈ δQ} > 1 - ε1,
дется иметь дело с усеченными матрицами плотно-
сти, которые близки к истинной матрице плотно-
гарантирует, что наблюдаемые параметры на при-
сти в смысле следового расстояния. Усечение мат-
емной стороне (например, ошибка Q) также лежат
риц плотности приходится делать дважды.
в доверительном интервале с той же вероятностью.
333
С. Н. Молотков
ЖЭТФ, том 160, вып. 3 (9), 2021
6.2. Второе усечение матриц плотности
венные числа попадают в множество ε2-типичных
последовательностей, равна
Второе усечение матрицы плотности ρ(n)XE в (27),
в отличие от первого усечения, связано, скорее, с
Pr{Ω1 ∩ Ω2} ≥ (1 - ε1)(1 - ε2) ≥ 1 - ε1 - ε2.
(31)
техническими вычислительными причинами, чем с
принципиальными причинами, диктуемыми стати-
Матрица плотности ρ⊗nXE после двойного усечения
стикой.
является ε1 + ε2-близкой, в смысле следового рас-
Пусть параметры матрицы плотности уже лежат
стояния, к истинной матрице плотности:
в доверительном интервале.
∑
При вычислении min-энтропии необходимо выби-
||ρ⊗nXE - ρ⊗nXE ||1 = ||ρ⊗nXE -
PQ(Q)ρ⊗nXE|Q +
рать значения параметров на нужной границе (пра-
Q∈δ
∑
вой или левой) доверительного интервала, которые
+ PQ(Q)(ρ⊗nXE|Q - ρ⊗nXE|Q)||1 ≤
в пользу подслушивателя приводят к минимально-
Q∈δ
му значению условной min-энтропии. Минимальное
∑
значение условной min-энтропии для параметров на
≤ ε1 + PQ(Q)||ρ⊗nXE|Q - ρ⊗nXE|Q||1 ≤
Q∈δ
нужной границе доверительного интервала означа-
ет (в пользу подслушивателя) выбор минимальной
≤ ε1 + (1 - ε1)ε2 ≤ ε1 + ε2,
(32)
нехватки информации подслушивателя о битовой
здесь
ρ⊗nXE|Q
— усеченная матрица плотности
строке Алисы.
Обозначим символически это значение как Qmax.
(Q ∈ δ), которая отличается от не усеченной ρ⊗nXE|Q
Обсудим теперь технические подробности вычис-
тем, что в ней присутствуют слагаемые с собствен-
ления min-энтропии на усеченной матрице плотно-
ными числами, которые попадают в ε2-типичное
сти ρ(n)XE.
множество (см. следующий раздел).
Реально вычислить сглаженную энтропию мож-
но, если матрица плотности имеет структуру тен-
6.3. Иллюстративный пример вычисления
зорного произведения ρ(n)XE|Q = ρ⊗nXE|Q. Второе усе-
условной сглаженной min-энтропии
чение связано с тем, что даже, если матрица плот-
Для интуитивного подкрепления сказанного в
ности имеет структуру тензорного произведения, то
предыдущем разделе приведем краткое эвристичес-
для конечной последовательности большой длины
кое вычисление условной энтропии на усеченной
и при заданном значении параметров Qmax не уда-
матрице плотности. Более аккуратный вывод см. в
ется точно вычислить условную сглаженную min-
[4]. Результат вычислений, естественно, будет одина-
энтропию. Можно лишь получить оценку верхней
ковым при нашем выводе и точном выводе [4]. При
границы для нее.
вычислении воспользуемся определением (6). При-
Матрица плотности после второго усечения
ведем матрицу плотности ρXE|Qmax к диагонально-
ρ⊗n
это матрица плотности, полученная из
XE|Qmax
му виду, имеем
ρ⊗n
оставлением только тех слагаемых, чьи
XE|Qmax
собственные числа реализуются с вероятностью не
)⊗n
(∑
менее 1 - ε2 — попадают в множество ε2-типичных
(ρXE|Qmax )⊗n =
Λi|Λi〉〈Λi|
=
последовательностей,
i
)
∑∑ ∑
{ (( (
)-1/2
⊗n
=
Λi1 Λi2 . . . Λin |Λi1 〉〈Λi1 | ⊗
Ω2 = λ IX ⊗ ρ
×
E|Qmax
i1
i2
in
(
))
}
(
)-1/2
⊗ |Λi2 〉〈Λi2 | ⊗ . . . |Λin 〉〈Λin |,
(33)
× ρ⊗nXE|Q
IX ⊗ ρ⊗nE|Q
∈Typ
,
(29)
max
max
ε2
здесь Λi — собственные числа, |Λi〉 — собственные
при условии, что параметры уже лежат в довери-
векторы, отвечающие собственным числам, матри-
тельном интервале.
цы плотности ρXE|Qmax.
Вероятность попадания собственных чисел в
Усеченная матрица плотности содержит слагае-
множество ε2-типичных последовательностей
мые, которые попадают в множество ε2-типичных
последовательностей. Это такие последовательнос-
Pr{Ω2|Ω1} ≥ 1 - ε2.
(30)
ти, вероятности которых удовлетворяют неравенст-
В итоге вероятность события, при котором пара-
вам
метры лежат в доверительном интервале и собст-
P (i1, i2, . . . , in) = Λi1 Λi2 . . . Λin ,
(34)
334
ЖЭТФ, том 160, вып. 3 (9), 2021
Побочные каналы утечки информации в квантовой криптографии.. .
2-n(H(ρXE|Qmax)+δ(ε2)) ≤ P(i1, i2, . . ., in) ≤
Смысл данного неравенства интуитивно понятен.
Неформально, условная энтропия есть нехватка ин-
≤ 2-n(H(ρXE|Qmax)-δ(ε2)).
(35)
формации Евы о битовой строке Алисы при усло-
вии, что ошибка на приемной стороне из-за вторже-
Аналогично предыдущему приведем к диаго-
ния в квантовый канал есть Qmax. Соответственно,
нальному виду матрицу плотности ρE|Q
, находим
max
чем меньше ошибка, тем больше нехватка информа-
)⊗n
ции Евы.
(∑
(ρE|Q
)⊗n =
λi|λi〉〈λi|
=
С учетом (6), (29) получаем
max
i
∑∑ ∑
in
(ρ(n)XE|Q
|ρ(n)
)=
max
E|Qmax
=
λi1 λi2 . . .λin |λi1 〉×
( ((
)
(
)-1/2
i1
i2
in
⊗n
= -log λ IX ⊗ ρ
×
E|Qmax
× 〈λi1 | ⊗ |λi2 〉〈λi2 | ⊗ . . . |λin 〉〈λin |,
(36)
(
)))
(
)-1/2
⊗n
где λi — собственные числа, |λi〉 — отвечающие им
× ρ⊗nXE|Q
IX ⊗ ρ
=
max
E|Qmax
собственные векторы матрицы плотности ρE|Qmax.
Усеченная матрица плотности содержит слагаемые,
= n(H(ρXE|Qmax|ρE|Q
) - δ(ε2)),
(41)
max
вероятности которых попадают в множество ε2-ти-
пичных последовательностей. Это такие слагаемые,
здесь H(ρ) = -Tr{ρ log(ρ)} — энтропия фон Нейма-
вероятности которых удовлетворяют условиям
на. Таким образом, вычисление условной сглажен-
ной min-энтропии при неизвестных скрытых пара-
p(i1, i2, . . . , in) = λi1 λi2 . . . λin ,
(37)
метрах сводится к вычислению условной (не сгла-
женной) энтропии для параметров — вероятности
2-n(H(ρE|Qmax)+δ(ε2)) ≤ p(i1, i2, . . . , in) ≤
ошибки Q, лежащей на правой границе доверитель-
ного интервала Q = Qmax.
≤ 2-n(H(ρE|Qmax)-δ(ε2)).
(38)
Оценка вероятности Pr{Ω2|Ω1} того, что собствен-
7. ПОСТРОЕНИЕ ЯВНОЙ АТАКИ НА
ные числа лежат в интервале при условии, что па-
ОДНОФОТОННУЮ КОМПОНЕНТУ
раметры атаки Евы Q лежат в доверительном ин-
СОСТОЯНИЙ
тервале, есть
Для вычисления условной min-энтропии в (9), а
также учета побочных каналов утечки информации,
2-n(H(ρXE|Qmax|ρE|Qmax)+δ(ε2)) ≤
разных квантовых эффективностей детекторов, как
((
)
(
)-1/2
⊗n
было отмечено выше, требуется явное построение
≤λ IX ⊗ ρ
×
E|Qmax
атаки на однофотонную компоненту состояний.
(
))
При побочных каналах утечки фундаментальная
(
)-1/2
⊗n
× ρ⊗nXE|Q
=
связь между ошибкой и утечкой к Еве расцепляет-
max
IX ⊗ ρ
E|Qmax
ся. По этой причине, чтобы «подцепить» побочные
квантовые состояния к информационным состояни-
P (i1, i2, . . . , in)
=
≤
ям, требуется явное знание состояний и, соответ-
p(i1, i2, . . . , in)
ственно, явное построение атаки.
≤ 2-n(H(ρXE|Qmax|ρE|Qmax)-δ(ε2)),
(39)
В следующих разделах будет построена явная
атака на однофотонные состояния, затем будут при-
где собственные числа лежат в множестве
ведены оценки для длины секретного ключа.
Typ
(29).
ε2
Атака Евы на однофотонные информационные
Вычисление min-энтропии через максимальное
состояния в квантовом канале связи определяется
собственное число матрицы плотности после второ-
унитарным оператором, который определяется и па-
го усечения, с учетом (6) и (29), дает
раметризуется набором параметров, контролируе-
мых Евой. Атака Евы приводит к преобразованию
(ρ(n)XE|Q∈δ
|ρ(n)
)≥
in
Q
E|Q∈δQ
входных квантовых состояний в новые квантовые
состояния. Самое общее преобразование квантовых
(ρ(n)XE|Q
|ρ(n)E|Q
).
(40)
in
max
max
состояний (матриц плотности) в матрицы плотности
335
С. Н. Молотков
ЖЭТФ, том 160, вып. 3 (9), 2021
задается линейным вполне положительным отобра-
вспомогательное состояние Евы — ancilla, |Φ0+ 〉Q и
жением — супероператором [13]. Любой суперопера-
|Θ0+ 〉Q — искаженные состояния, возникающие из
тор согласно [14] унитарно представим. Неформаль-
вспомогательного состояния Евы.
но, супероператор может быть реализован как сов-
Формулы (42), (43) представляют собой разло-
местная унитарная эволюция исходного состояния
жение Шмидта, параметр Q+ пока является свобод-
вместе со вспомогательным состоянием. В результа-
ным. Ниже увидим, что Q+ является наблюдаемой
те возникает совместное запутанное состояние. Взя-
ошибкой на приемной стороне, к которой приводит
тие частичного следа по вспомогательной системе
атака на квантовые состояния в канале связи.
дает преобразованную матрицу плотности исходно-
Индекс «Q» для состояний Евы символизиру-
го состояния.
ет атаку на квантовые информационные состояния.
Построение супероператора сводится к построе-
Аналогичные (42), (43) выражения имеют место, ко-
нию унитарного оператора, который параметризует-
гда в канал посылаются состояния в базисе ×, |0×〉Y ,
ся набором параметров, которые находятся в руках
|1×〉Y . Имеем
подслушивателя.
|0×〉X ⊗ |0×〉Y → |0×〉X ⊗ UBE (|0×〉Y ⊗ |E〉Q) =
Естественно, подслушиватель должен выбирать
унитарный оператор оптимальным образом. Опти-
√
= |0×〉X ⊗ [
1 - Q×|0+〉Y ⊗ |Φ0×〉Q +
мальность понимается в смысле максимизации ин-
√
формации подслушивателя о передаваемых битах
+
Q×|1+〉Y ⊗ |Θ0×〉Q],
(44)
ключа при заданной наблюдаемой ошибке на при-
емной стороне.
|1×〉X ⊗ |1×〉Y → |1×〉X ⊗ UBE (|1×〉Y ⊗ |E〉Q) =
При идеальных детекторах и без учета побочных
√
каналов утечки информации можно явно не строить
= |1×〉X ⊗ [
1 - Q×|1×〉Y ⊗ |Φ1×〉Q +
атаку, а воспользоваться энтропийными соотноше-
√
ниями неопределенностей. Оптимальная унитарная
+
Q×|0×〉Y ⊗ |Θ1×〉Q].
(45)
атака, достигающая нижнюю границу энтропийных
Связь между информационными состояниями в раз-
соотношений неопределенностей [5], может быть по-
ных базисах дается соотношениями
строена явно [15].
(
)
Для дальнейшего потребуется построение явной
1
|0×〉 =
√
|0+〉 + |1+〉
,
атаки с учетом разных и неидеальных квантовых
2
(46)
эффективностей детекторов. Для определенности
1
(
)
будем иметь в виду протокол BB84, который явля-
|1×〉 =
√
|0+〉 - |1+〉
2
ется базовым. Предлагаемый метод применим и к
другим протоколам.
Связь между состояниями Евы в разных базисах
Унитарная атака на информационные состояния
следует из линейности унитарного оператора. С уче-
в базисе + имеет вид
том (42)-(46) получаем
|Φ±〉E = |Φ0+〉E ± |Φ1+〉E,
|0+〉X ⊗ |0+〉Y → |0+〉X ⊗ UBE (|0+〉Y ⊗ |E〉Q) =
(47)
√
|Θ±〉E = |Θ0+〉E ± |Θ1+〉E ,
= |0+〉X ⊗ [
1 - Q+|0+〉Y ⊗ |Φ0+〉Q +
где
√
= 1,
E 〈Φ0× |Φ0×〉E + E 〈Θ0× |Θ0×〉E
+
Q+|1+〉Y ⊗ |Θ0+〉Q],
(42)
E 〈Φ1× |Φ1×〉E + E 〈Θ1× |Θ1×〉E = 1,
|1+〉X ⊗ |1+〉Y → |1+〉X ⊗ UBE (|1+〉Y ⊗ |E〉Q) =
|Φ+〉E + |Θ+〉E
|Φ0× 〉E =
,
√
2
= |1+〉X ⊗ [
1 - Q+|1+〉Y ⊗ |Φ1+〉Q +
(48)
|Φ-〉E - |Θ-〉E
√
|Θ0× 〉E =
,
+
Q+|0+〉Y ⊗ |Θ1+〉Q],
(43)
2
|Φ+〉E - |Θ+〉E
|Φ1× 〉E =
,
где |0+〉X — эталонное состояние на стороне Али-
2
сы, доступное только ей, |0+〉Y — состояние, кото-
(49)
|Φ-〉E + |Θ-〉E
рое посылается к Бобу через квантовый канал связи,
|Θ1× 〉E =
2
UBE — унитарный оператор Евы, |E〉Q — исходное
336
ЖЭТФ, том 160, вып. 3 (9), 2021
Побочные каналы утечки информации в квантовой криптографии.. .
Таким образом, атака Евы параметризуется величи-
детекторах можно считать отсчетом в фиктивном
нами Q+, Q×, имеющими смысл вероятностей оши-
состоянии ⊥. В этом случае измерения в базисах +
бок в базисах + и ×.
и × даются разложением единицы:
Отметим, что, как было показано в [16], векторы
{|Φ0+ 〉Q, |Φ1+ 〉Q} и {|Θ0+ 〉Q, |Θ1+ 〉Q} лежат в ортого-
IY =
нальных подпространствах. Аналогично для состоя-
= η0|0+〉Y Y 〈0+|+η1|1+〉Y Y 〈1+|+η+⊥|⊥+〉⊥⊥〈⊥+| =
ний {|Φ0×〉Q, |Φ1× 〉Q} и {|Θ0× 〉Q, |Θ1× 〉Q}. Этот факт
будет использован в дальнейшем.
= η1|0×〉Y Y 〈0×| + η0|1×〉Y Y 〈1×| +
Ниже будет видно, что не все параметры, кото-
рыми параметризуется унитарная атака, являются
+ η×⊥|⊥×〉⊥⊥〈⊥×|.
(51)
наблюдаемыми при измерениях на приемной сто-
роне. Существуют параметры, от которых зависит
Исходы измерений, при которых отсутствуют отсче-
утечка информации к Еве, но которые явно не про-
ты в детекторах, отбрасываются.
являются в измерениях Боба. Такими параметрами
Необходимо отметить важный факт (см. расста-
являются скалярные произведения между различ-
новку квантовых эффективностей в формуле (51)).
ными состояниями Евы.
Поскольку квантовые эффективности детекторов
различаются, число регистрируемых 0 и 1 внутри
каждого базиса не равно друг другу. Для выравни-
7.1. Идеальные и реальные измерения
вания суммарного количества регистрируемых 0 и
Для дальнейшего нам потребуются описания из-
1 в двух базисах, на приемной стороне при фазо-
мерений для случаев идеальных и реальных детек-
вом кодировании разность фаз в плечах интерферо-
торов. С формальной точки зрения любое измерение
метра в разных базисах выбирается таким образом,
задается разложением единицы.
чтобы 0 в одном базисе регистрировался в детекто-
Идеальные измерения Боба в базисах + и × да-
ре D0, а единица — в детекторе D1. В сопряженном
ются разложением единицы IY (IY
— единичный
базисе, наоборот, 0 регистрируется в детекторе D1,
оператор в пространстве состояний Боба):
а 1 — в детекторе D0.
IY = |0+〉Y Y 〈0+| + |1+〉Y Y 〈1+| =
7.2. Матрицы плотности после идеальных
= |0×〉Y Y 〈0×| + |1×〉Y Y 〈1×|.
(50)
измерений
Ситуацию с не равной единице квантовой эф-
Измерения (50) фактически сводятся к проекти-
фективностью детекторов можно описывать следу-
рованию на набор ортогональных состояний. С уче-
ющим образом. Пусть квантовые эффективности де-
том (42)-(46), после идеальных измерений Боба мат-
текторов равны η0 и η1. Отсутствие отсчета в обоих
рица плотности Алиса-Боб-Ева принимает вид
1
ρ+XYE =
|0+〉XX 〈0+| ⊗ [(1 - Q+)|0+〉YY 〈0+| ⊗ |Φ0+ 〉QQ〈Φ0+ | + Q+|1+〉Y ×
2
1
×Y 〈1+| ⊗ |Θ0+〉QQ〈Θ0+|] +
|1+〉XX 〈1+| ⊗ [(1 - Q+)|1+〉YY 〈1+| ⊗ |Φ1+ 〉Q ×
2
×Q〈Φ1+| + Q+|0+〉YY 〈0+| ⊗ |Θ1+〉QQ〈Θ1+|].
(52)
Частичная матрица плотности Алиса-Ева
1
1
ρ+XE =
|0+〉XX 〈0+| ⊗ [(1 - Q+)|Φ0+ 〉QQ〈Φ0+| + Q+|Θ0+〉QQ〈Θ0+|] +
|1+〉XX 〈1+| ⊗
2
2
⊗[(1 - Q+)|Φ1+〉QQ〈Φ1+ |+Q+|Θ1+〉QQ〈Θ1+|].
(53)
Частичная матрица плотности Евы
1
1
ρ+E =
(1 - Q+)[|Φ0+〉QQ〈Φ0+ | + |Φ1+〉QQ〈Φ1+ |] + Q+
[|Θ0+ 〉QQ〈Θ0+ | + |Θ1+ 〉QQ〈Θ1+|].
(54)
2
2
337
ЖЭТФ, вып. 3 (9)
3
С. Н. Молотков
ЖЭТФ, том 160, вып. 3 (9), 2021
В базисе × с учетом (42)-(46) и (50) находим
1
ρ×XYE =
|0×〉XX 〈0×| ⊗ [(1 - Q×)|0×〉YY 〈0×| ⊗ |Φ0× 〉QQ〈Φ0× | + Q×|1×〉YY 〈1×| ⊗ |Θ0×〉QQ〈Θ0×|] +
2
1
+
|1×〉XX 〈1×| ⊗ [(1-Q×)|1×〉YY 〈1×| ⊗ |Φ1×〉QQ〈Φ1× | + Q×|0×〉YY 〈0×| ⊗ |Θ1×〉QQ〈Θ1× |].
(55)
2
Частичная матрица плотности Алиса-Ева
1
1
ρ×XE =
|0×〉XX 〈0×| ⊗ [(1 - Q×)|Φ0×〉QQ〈Φ0×| + Q×|Θ0×〉QQ〈Θ0×|] +
|1×〉XX 〈1×| ⊗
2
2
⊗ [(1-Q×)|Φ1× 〉QQ〈Φ1×| + Q×|Θ1×〉QQ〈Θ1×|].
(56)
Частичная матрица плотности Евы
1
1
ρ×E =
(1 - Q×)[|Φ0× 〉QQ〈Φ0×|+|Φ1×〉QQ〈Φ1×|] + Q×
[|Θ0× 〉QQ〈Θ0× | + |Θ1× 〉QQ〈Θ1×|].
(57)
2
2
7.3. Матрицы плотности после реальных измерений
После реальных измерений и отбрасывания холостных исходов матрица плотности Алиса-Боб-Ева в
базисе +, нормированная на полную вероятность отсчетов η0 + η1 в детекторах, принимает вид
ρ+XYE = |0+〉XX〈0+| ⊗ [ξ0(1 - Q+)|0+〉YY 〈0+| ⊗ |Φ0+〉QQ〈Φ0+| + ξ1Q+|1+〉Y ×
×Y 〈1+| ⊗ |Θ0+〉QQ〈Θ0+|] + |1+〉XX〈1+| ⊗ [ξ1(1 - Q+)|1+〉YY 〈1+| ⊗ |Φ1+〉Q ×
×Q〈Φ1+| + ξ0Q+|0+〉YY 〈0+| ⊗ |Θ1+〉QQ〈Θ1+|].
(58)
Частичная матрица плотности Алиса-Ева
ρ+XE = |0+〉XX〈0+| ⊗ [ξ0(1 - Q+)|Φ0+〉QQ〈Φ0+| + ξ1Q+|Θ0+〉QQ〈Θ0+|] + |1+〉XX〈1+| ⊗
⊗[ξ1(1 - Q+)|Φ1+ 〉QQ〈Φ1+| + ξ0Q+|Θ1+〉QQ〈Θ1+|].
(59)
Частичная матрица плотности Евы
ρ+E = (1-Q+)[ξ0|Φ0+〉QQ〈Φ0+|+ξ1|Φ1+〉QQ〈Φ1+|] + Q+[ξ1|Θ0+〉QQ〈Θ0+| + ξ0|Θ1+〉QQ〈Θ1+|].
(60)
В базисе × получаем
ρ×XYE = |0×〉XX〈0×| ⊗ [ξ1(1-Q×)|0×〉YY 〈0×| ⊗ |Φ0×〉QQ〈Φ0×| + ξ0Q×|1×〉YY 〈1×| ⊗ |Θ0×〉Q ×
×Q〈Θ0×|] + |1×〉XX〈1×| ⊗ [ξ0(1 - Q×)|1×〉YY 〈1×| ⊗ |Φ1×〉QQ〈Φ1×| + ξ1Q×|0×〉YY 〈0×| ⊗ |Θ1×〉QQ〈Θ1×|].
(61)
Частичная матрица плотности Алиса-Ева
ρ×XE = |0×〉XX〈0×| ⊗ [ξ1(1 - Q×)|Φ0×〉QQ〈Φ0×| + ξ0Q×|Θ0×〉QQ〈Θ0×|] + |1×〉XX〈1×| ⊗ [ξ0(1-Q×)×
×|Φ1×〉QQ〈Φ1×| + ξ1Q×|Θ1×〉QQ〈Θ1× |].
(62)
Частичная матрица плотности Евы
1
ρ×E = (1 - Q×)[ξ1|Φ0×〉QQ〈Φ0×| + ξ0|Φ1×〉QQ〈Φ1×|] + Q×
[ξ0|Θ0× 〉QQ〈Θ0× | + ξ1|Θ1× 〉QQ〈Θ1× |].
(63)
2
В (58)-(63) для удобства введены обозначения
η0
η1
ξ0 =
,
ξ1 =
(64)
η0 + η1
η0 + η1
338
ЖЭТФ, том 160, вып. 3 (9), 2021
Побочные каналы утечки информации в квантовой криптографии.. .
7.4. Скрытые ненаблюдаемые параметры —
висят от скалярных произведений (65)-(68), но от
скалярные произведения между
них зависит утечка информации к Еве.
состояниями подслушивателя
По этой причине при определенных из измере-
ний параметрах Q+ и Q×, по ненаблюдаемым скры-
Измерения на приемной стороне не являются ин-
тым параметрам необходимо проводить максимиза-
формационно полными, поскольку не позволяют од-
цию утечки информации к Еве при данных наблю-
нозначно восстановить искаженное информацион-
даемых Q+ и Q×.
ное квантовое состояние на входе в приемную стан-
цию. Этот факт приводит к тому, что утечка инфор-
мации, которая выражается через условную энтро-
7.5. Область допустимых значений
пию, зависит от ненаблюдаемых скрытых для леги-
ненаблюдаемых скрытых параметров
тимных пользователей параметров атаки Евы. Точ-
Покажем, что независимым является только
нее говоря, при одних и тех же вероятностях исходов
один параметр ε+(Φ), остальные выражаются через
измерений на приемной стороне значения ненаблю-
него. Кроме того, поскольку состояния |Φ0+,×,0+,× 〉
даемых скрытых параметров будут разными. Исхо-
и |Θ0+,×,0+,× 〉 ортогональны, в утечку информации,
ды измерений не чувствительны к данным парамет-
которая выражается через собственные числа мат-
рам, но в то же время условная энтропия — утечка
рицы плотности Евы (см. ниже), входят только мо-
информации к Еве — зависит от данных парамет-
дули скалярных произведений. Это означает, что
ров.
утечка информации к Еве не зависит от фаз, вообще
Такими ненаблюдаемыми скрытыми для Алисы
говоря, комплексных скалярных произведений. Из-
и Боба параметрами являются скалярные про-
за такой нечувствительности к фазе можно считать
изведения между состояниями подслушивателя,
скалярные произведения вещественными.
〈Φ0+ |Φ1+ 〉 и 〈Θ0+ |Θ1+ 〉.
Из наблюдаемых величин (вероятностей исхо-
Фундаментальное требование унитарности опе-
дов измерений) можно определить не все скалярные
ратора в (42)-(49) приводит к тому, что скалярные
произведения, от которых зависит утечка инфор-
произведения между квантовыми состояниями под-
мации к подслушивателю. Из четырех скалярных
слушивателя в разных базисах связаны определен-
произведений ε+(Φ), ε+(Θ), ε×(Φ) и ε×(Θ) остается
ными соотношениями.
неопределенным ε+(Φ). Остальные три могут быть
С учетом выражений (42)-(49), следующих из
выражены через него.
унитарности оператора Евы, получаем соотношения
С учетом уравнений (65)-(68) получаем следую-
между скалярными произведениями в разных бази-
щие соотношения:
сах:
(1 - Q+)ε(Φ+) = |〈Φ0+|Φ1+〉|,
1 - 2Q× - (1 - Q+)ε+(Φ)
ε+(Θ) =
,
(69)
(65)
Q+
Q+ε(Θ+) = |〈Θ0+|Θ1+〉|,
1
(1 - Q×)ε(Φ×) = |〈Φ0× |Φ1×〉|,
ε×(Φ) =
×
2(1 - Q×)
(66)
(
)
Q×ε(Θ×) = |〈Θ0×|Θ1×〉|,
×
(1-2Q+)-(1-2Q×)+2(1 - Q+)ε+(Φ)
,
(70)
1
1
(1 - Q+)ε(Φ+) =
[1 - 2Q+ +
ε×(Θ) =
×
2
2Q×
(
)
+ (1-Q+) Re(ε(Φ+))-Q+ Re(ε(Θ+))],
(67)
×
(1-2Q+)+(1-2Q×)-2(1 - Q+)ε+(Φ)
(71)
Скалярные произведения между квантовыми состо-
1
яниями по модулю не должны превышать единицы,
Q×ε(Θ×) =
[1 - 2Q+ -
2
с учетом (65)-(71) это приводит к следующим нера-
венствам:
- (1 - Q+) Re(ε(Φ+)) + Q+ Re(ε(Θ+))].
(68)
1 - 2Q× - Q+
L1(Q+, Q×) =
≤ ε+(Φ) ≤
Параметры Q+ и Q× являются экспериментально
1-Q+
наблюдаемыми параметрами и имеют смысл веро-
1 - 2Q× + Q+
ятностей ошибок в прямом + и сопряженном × ба-
≤
= R1(Q+, Q×),
(72)
зисах. Результаты измерений на стороне Боба не за-
1-Q+
339
3*
С. Н. Молотков
ЖЭТФ, том 160, вып. 3 (9), 2021
1
Аналогично для матрицы плотности ρ×XE :
L2(Q+, Q×) =
×
2(1 - Q+)
(
)
ξ1(1 - Q×), ξ0Q×, ξ0(1 - Q×), ξ1Q×.
(80)
×
-2(1 - Q×) - [(1 - 2Q+) - (1 - 2Q×)]
≤
Собственные числа матрицы плотности ρ+E в бази-
1
(
се + равны
≤ ε+(Φ) ≤
2(1 - Q×) -
2(1 - Q+)
Λ±(Φ+) = (1 - Q+)λ±(Φ+),
)
- [(1 - 2Q+) - (1 - 2Q+)]
= R2(Q+, Q×),
(73)
(81)
Λ±(Θ+) = Q+λ±(Θ+),
где
1
L3(Q+, Q×) =
×
2(1 - Q+)
λ±(Φ+) =
(
)
{
√
}
×
(1 - 2Q+) + (1 - 2Q×) - 2Q×
≤ ε+(Φ) ≤
1
4(A(Φ+)B(Φ+) - |ε(Φ+)|2)
=
1±
1-
,
(82)
1
(
)
2
1 - |ε(Φ+)|2
≤
(1 - 2Q+) + (1 - 2Q×) + 2Q×
=
2(1 - Q+)
A(Φ+) = ξ0 + ξ1|ε(Φ+)|2,
= R3(Q+, Q×).
(74)
(83)
B(Φ+) = ξ0|ε(Φ+)|2
+ξ1,
Таким образом, максимизацию утечки информации
к подслушивателю достаточно проводить по одному
λ±(Θ+) =
параметру ε+(Φ), который с учетом (72)-(74) меня-
{
√
}
ется на отрезке
1
4(A(Θ+)B(Θ+)-|ε(Θ+)|2)
=
1±
1-
,
(84)
2
1-|ε(Θ+)|2
{
R(Q+, Q×) = min
R1(Q+, Q×),
}
A(Θ+) = ξ0 + ξ1|ε(Θ+)|2,
R2(Q+, Q×), R3(Q+, Q×)
,
(75)
(85)
B(Θ+) = ξ0|ε(Θ+)|2 + ξ1,
{
Аналогично (79)-(85) для собственных чисел матри-
L(Q+, Q×) = max
L1(Q+, Q×),
цы плотности ρ×E в базисе × получаем
}
L2(Q+, Q×), L3(Q+, Q×)
,
(76)
Λ±(Φ×) = (1 - Q×)λ±(Φ×),
(86)
V (Q+, Q×) = R(Q+, Q×) - L(Q+, Q×).
(77)
Λ±(Θ×) = Q×λ±(Θ×),
Удобно параметризовать ε+(Φ) следующим обра-
где
зом:
λ±(Φ×) =
ε+(Φ) = L(Q+, Q×) + xV (Q+, Q×), x ∈ [0, 1]. (78)
{
√
}
1
4(A(Φ×)B(Φ×)-|ε(Φ×)|2)
=
1±
1-
,
(87)
Остальные параметры выражаются по формулам
2
1 - |ε(Φ×)|2
(62)-(71).
В итоге максимизацию утечки информации к
A(Φ×) = ξ1 + ξ0|ε(Φ×)|2,
(88)
Еве при данных наблюдаемых параметрах Q+ и Q×
B(Φ×) = ξ1|ε(Φ×)|2 + ξ0,
можно проводить только по одной переменной x.
λ±(Θ×) =
7.6. Собственные числа матрицы плотности
{
√
}
подслушивателя
1
4(A(Θ×)B(Θ×)-|ε(Θ×)|2)
=
1±
1-
,
(89)
Для вычисления условных энтропий нужны соб-
2
1 - |ε(Θ×)|2
ственные числа матриц плотности. Для собственных
чисел матрицы плотности ρ+XE в базисе + находим
A(Θ×) = ξ0 + ξ1|ε(Θ×)|2,
(90)
B(Θ×) = ξ0|ε(Θ×)|2 + ξ1.
ξ0(1 - Q+), ξ1Q+, ξ1(1 - Q+), ξ0Q+.
(79)
340
ЖЭТФ, том 160, вып. 3 (9), 2021
Побочные каналы утечки информации в квантовой криптографии.. .
8. ОЦЕНКА ДЛИНЫ СЕКРЕТНОГО КЛЮЧА:
Утечка информации при коррекции ошибок в
ОДНОФОТОННЫЙ СЛУЧАЙ, ИДЕАЛЬНЫЕ
асимптотическом шенноновском пределе с учетом
ДЕТЕКТОРЫ, АСИМПТОТИЧЕСКИЙ
(52)-(71) имеет вид
ПРЕДЕЛ
⊗n
Hεmax(ρ
|ρ⊗nY) = H(ρ⊗nXY ) - H(ρ⊗nY) + δ(ε) =
Для того чтобы показать, как изменяется оцен-
XY
(
√
ка длины секретного ключа по мере включения в
1
(1))
рассмотрение различных реальных каналов утечки
= n h(Q) + const
log
(92)
n
ε
информации, сначала приведем такие оценки для
строго однофотонного источника, когда парамет-
Оценка длины ε-секретного ключа принимает вид
ры атаки Евы известны точно. Затем учтем тот
факт, что имеется только оценка параметров ата-
ℓε = Hεmin(ρ⊗nXE|ρ⊗nE) - Hεmax(ρ⊗nXY |ρ⊗nY) =
ки — ошибки на приемной стороне при конечной
(
√
длине переданных последовательностей.
1
(1))
Сначала рассмотрим асимптотический случай
=n
1 - 2h(Q) - 2const
log
(93)
n
ε
длинных последовательностей. При стремлении
длины передаваемой последовательности к беско-
В асимптотическом пределе n → ∞, ε → 0 последнее
нечности оценка вероятности ошибки становится
слагаемое в (93) стремится к нулю, и мы приходим к
самой вероятностью, т.е. параметр ошибки известен
знаменитой формуле для длины секретного ключа
точно.
протокола BB84 [4, 17] ℓε→0 = n(1 - 2h(Q)). Дли-
В случае идеальных детекторов нижняя граница
на секретного ключа обращается в нуль при ошибке
энтропийных соотношений неопределенностей до-
выше критической Qc ≈ 11 %.
стигается на симметричной атаке [15], Q+ = Q× =
= Q. Ненаблюдаемые скрытые параметры — ска-
лярные произведения в этом случае равны
9. ОЦЕНКА ПАРАМЕТРОВ ПО
РЕЗУЛЬТАТАМ ИЗМЕРЕНИЙ
ε(Φ+,×) = ε(Θ+,×) = 1 - 2Q.
В реальной ситуации истинная вероятность
Оценки параметров и первого усечения матриц
ошибки Q точно не известна, имеется лишь оценка
плотности, связанного с оценкой наблюдаемых па-
данной вероятности. Есть различные способы оцен-
раметров, не требуется. Достаточно только второго
ки данной вероятности. Первый способ состоит в
усечения при вычислении условной сглаженной эн-
раскрытии и сравнении части последовательности,
тропии матрицы плотности в виде тензорного произ-
посланной Алисой, и последовательности, измерен-
ведения ρ(n)XE = ρ⊗nXE. Сглаженная условная min-энт-
ной Бобом. Пусть оценка вероятности ошибки —
ропия, вычисленная на усеченной матрице плотнос-
доля неправильных отсчетов nincorr, зарегистри-
ти ρ⊗nXE, удовлетворяющей условию ε-близости в
рованных Бобом из последовательности длины
смысле следового расстояния, имеет вид
n1, есть Q
= nincorr/n1. Из-за конечной длины
последовательности число (частота) неправильных
Hεmin(ρ⊗nXE|ρ⊗nE) =
отсчетов флуктуирует.
= max Hmin(ρ⊗nXE |ρ⊗nE) =
Второй способ оценки вероятности состоит в
||ρ⊗nXE-ρ⊗nXE||1≤ε
следующем. Существующие процедуры коррекции
= H(ρ⊗nXE) - H(ρ⊗nE) - δ(ε) =
ошибок позволяют сразу проводить коррекцию оши-
(
√
бок без предварительной оценки вероятности ошиб-
1
(1))
ки. Пусть проведена чистка ошибок, после коррек-
= n 1-h(Q)-(2Hmax(ρX)+1)
log
,
(91)
n
ε
ции известна оценка вероятности ошибки — извест-
но число исправленных битов. Однако это не озна-
где Q — истинная вероятность ошибки, матрица
чает, что такое число и есть истинное число ошибок
плотности в (91) берется из соотношений (52)-(57),
в последовательности n1. Для определенности будем
const = 2Hmax(ρX) + 1,
иметь в виду первый способ. При этом для экономии
обозначений будем считать, что длина n1
раскры-
Hmax(ρX) = rank(ρX) = 2
ваемой последовательности для оценки вероятности
[4], n — длина зарегистрированной последователь-
ошибки совпадает с длиной не раскрываемой после-
ности.
довательности n для получения ключа.
341
С. Н. Молотков
ЖЭТФ, том 160, вып. 3 (9), 2021
При оценке вероятности ошибки фактически мы
В итоге вычисление условной сглаженной энтро-
имеем дело с бернуллиевской схемой испытаний.
пии проводится на матрицах плотности ε = ε1 + ε2,
Для бернуллиевской схемы испытаний вероятность
близких в смысле следового расстояния к истинной
того, что частота ошибок Q в последовательности
матрице плотности, находим
длины n отличается от вероятности Q, есть (см., на-
пример, [18])
in
(ρ(n)XE|Q∈δ
|ρ(n)
)≥
Q
E|Q∈δQ
(
√
))
Pr{Ω1} = Pr{|Q - Q| ≤ δ(ε1)} ≥
1
(1
≥n
1-h(Q+δ(ε1))-const
log
(96)
n
ε2
≥ 1 - 2exp{-2δ(ε1)2n1} = 1 - ε1.
(94)
Для оценки длины секретного ключа нужно учесть
Важно отметить, что данная оценка является одно-
информацию, выдаваемую при коррекции ошибок.
родной в том смысле, что вероятность отклонения
В шенноновском пределе аналогично (91)-(93) по-
частоты Q от истинной вероятности Q не зависит
лучаем
от величины вероятности Q. По этой причине фор-
мулу (94) можно интерпретировать следующим об-
ax
(ρ(n)XE|Q∈δ
|ρ(n)
)≤
Q
E|Q∈δQ
разом: вероятность события, что наблюдаемая ве-
(
√
личина ошибки попадает в δ-окрестность истинной
1
(1))
≤ n h(Q + δ(ε1)) + const
log
(97)
вероятности Q (Q - δ(ε1), Q + δ(ε1)), реализуется с
n
ε2
вероятностью не менее 1 - ε1.
После этого проверяется факт исправления оши-
бок. Алиса генерирует открыто случайную битовую
10. ОЦЕНКА ДЛИНЫ СЕКРЕТНОГО
строку длиной n и вычисляет бит четности данной
КЛЮЧА: ОДНОФОТОННЫЙ СЛУЧАЙ,
строки со своим ключом. Боб поступает аналогично.
ИДЕАЛЬНЫЕ ДЕТЕКТОРЫ, КОНЕЧНЫЕ
Биты четности Алисы и Боба открыто сравнивают-
ПОСЛЕДОВАТЕЛЬНОСТИ
ся. Процедура проводится M раз. Если все M срав-
При конечной длине последовательности, когда
нений успешны, то вероятность того, что все ошибки
вероятность ошибки точно не известна, для вычис-
действительно исправлены и очищенный ключ Боба
ления сглаженной min-энтропии нужно использо-
XB совпадает с ключом Алисы XA, есть
вать формулы (52)-(57) для матриц плотности, в ко-
Pr[XA = XB] ≥ 1 - εcorr, εcorr = 1/2M .
(98)
торых вместо Q должно быть подставлено Qmax =
= Q + δ(ε1) — чем больше ошибка, тем меньше
Поскольку при такой проверке через открытый ка-
условная энтропия, тем меньше нехватка информа-
нал связи выдается M = log(1/εcorr) битов инфор-
ции Евы о ключе. Значение берется на правой гра-
мации, длина финального секретного ключа долж-
нице доверительного интервала в (94). При этом ве-
на быть уменьшена на M битов. Окончательно для
роятность события Ω1 не менее 1 - ε1. С учетом ска-
оценки длины ε = ε1 + ε2-секретного ключа получа-
занного для тензорного произведения
ем
ρ(n)XE|Q
=ρ⊗nXE|Q
max
max
ℓε = n (1 - 2h (Q + δ(ε1))) -
для сглаженной энтропии с учетом (52)-(57) полу-
√
)
(
)
чаем
( 1
1
- 2const n log
- log
(99)
ε2
εcorr
(ρ(n)XE|Q∈δ
|ρ(n)
)≥
in
Q
E|Q∈δQ
Связь между δ(ε1) и ε1 дается формулой (94).
(
Формула (99) означает, что если n-битовая стро-
≥ n H(ρXE|Qmax|ρE|Q
)-
max
ка первичного ключа до коррекции ошибок сжима-
ется при помощи универсальных хеш-функций вто-
√
рого порядка до длины, определяемой (99), то сжа-
1
(1))
- const
log
,
Qmax = Q + δ(ε1),
(95)
тая строка — финальный ключ — будет ε-секретным
n
ε2
в смысле следового расстояния.
где Q — наблюдаемая ошибка на приемной стороне,
Из сравнения (93) и (99) видно, что при конечной
Qmax — оценка вероятности ошибки — значение на
длине передаваемой последовательности эффектив-
правой границе доверительного интервала.
ная ошибка Qmax, входящая в формулу для длины
342
ЖЭТФ, том 160, вып. 3 (9), 2021
Побочные каналы утечки информации в квантовой криптографии.. .
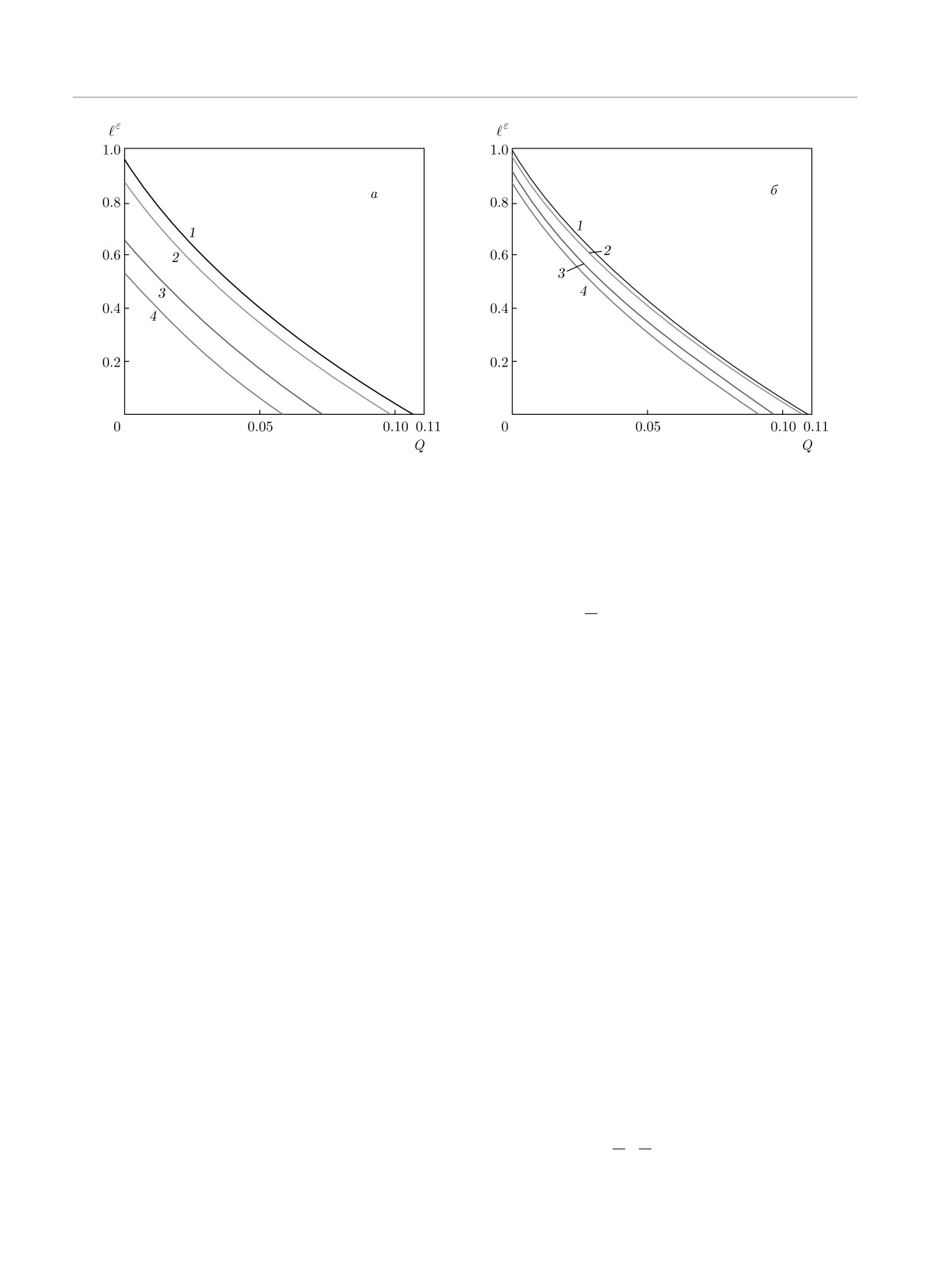
Рис. 1. Зависимости длины секретного ключа в пересчете на одну посылку от наблюдаемой величины ошибки Q: a) предел
конечных последовательностей, имеется оценка вероятности ошибки, б) вероятность ошибки точно известна. Параметр
секретности ε1 = ε2 = 10-9 для всех кривых. Длина последовательности n для оценки параметров и длина последова-
тельности для получения ключа приняты одинаковыми и равными n = 107 (1), 106 (2), 105 (3), 104 (4)
секретного ключа, оказывается большей, чем реаль-
нок 1б относится к случаю, когда истинная вероят-
ная ошибка Q.
ность ошибки Q точно известна.
Результат, аналогичный выражению (99), был
Как видно из рис. 1, с ростом длины последо-
получен ранее в [5] с использованием энтропий-
вательности n, используемой для оценки величины
ных соотношений неопределенностей. В нашем слу-
ошибки, критическая наблюдаемая ошибка Q, до ко-
чае результат получается явным построением ата-
торой возможно секретное распределение ключей,
ки Евы на передаваемый ключ, что требуется для
увеличивается и принимает асимптотическое значе-
последующего вычисления длины ключа в случае
ние Q ≈ 11 %. Таким образом, при заданном пара-
неидеальных детекторов с различными квантовыми
метре секретности ε1,2 для достижения большей ве-
эффективностями, а также для учета побочных ка-
личины критической ошибки требуется более длин-
налов утечки информации к Еве.
ная последовательность для оценки истинной веро-
ятности ошибки.
Однофотонный случай, разные квантовые
11. РЕЗУЛЬТАТЫ РАСЧЕТОВ В
эффективности детекторов, конечные последова-
ОДНОФОТОННОМ СЛУЧАЕ
тельности.
Для иллюстрации эволюции длины секретного
Отметим, что поиск минимума по одной перемен-
ключа по мере последовательного включения в рас-
ной x проводился с учетом флуктуаций параметра
смотрение различных факторов приведем результа-
ошибки (см. формулу (78)). Как видно на рис. 2,
ты численных расчетов.
длина ключа обнаруживает минимум как функция
Однофотонный случай, предел конечных после-
параметра минимизации x. Кроме того, скалярные
довательностей, равные квантовые эффективнос-
произведения между состояниями Евы в симмет-
ти детекторов.
ричном случае — одинаковые наблюдаемые ошибки
На рис. 1 приведены зависимости от Q длины
в прямом и сопряженном базисах, ξ0 = ξ1 = 0.5 —
секретного ключа для строго однофотонных инфор-
равные квантовые эффективности детекторов, ока-
мационных состояний в пределе конечных последо-
зываются одинаковыми в минимуме длины секрет-
вательностей (рис. 1a) в случае, когда истинная ве-
ного ключа. В симметричном случае скалярные про-
роятность ошибки неизвестна, а делается ее оцен-
изведения ε+(Φ) и ε×(Φ), ε+(Θ) и ε×(Θ) оказывают-
ка через наблюдаемую величину ошибки Q. Рису-
ся равными 1 - 2Q (Q — ошибка с учетом флук-
343
С. Н. Молотков
ЖЭТФ, том 160, вып. 3 (9), 2021
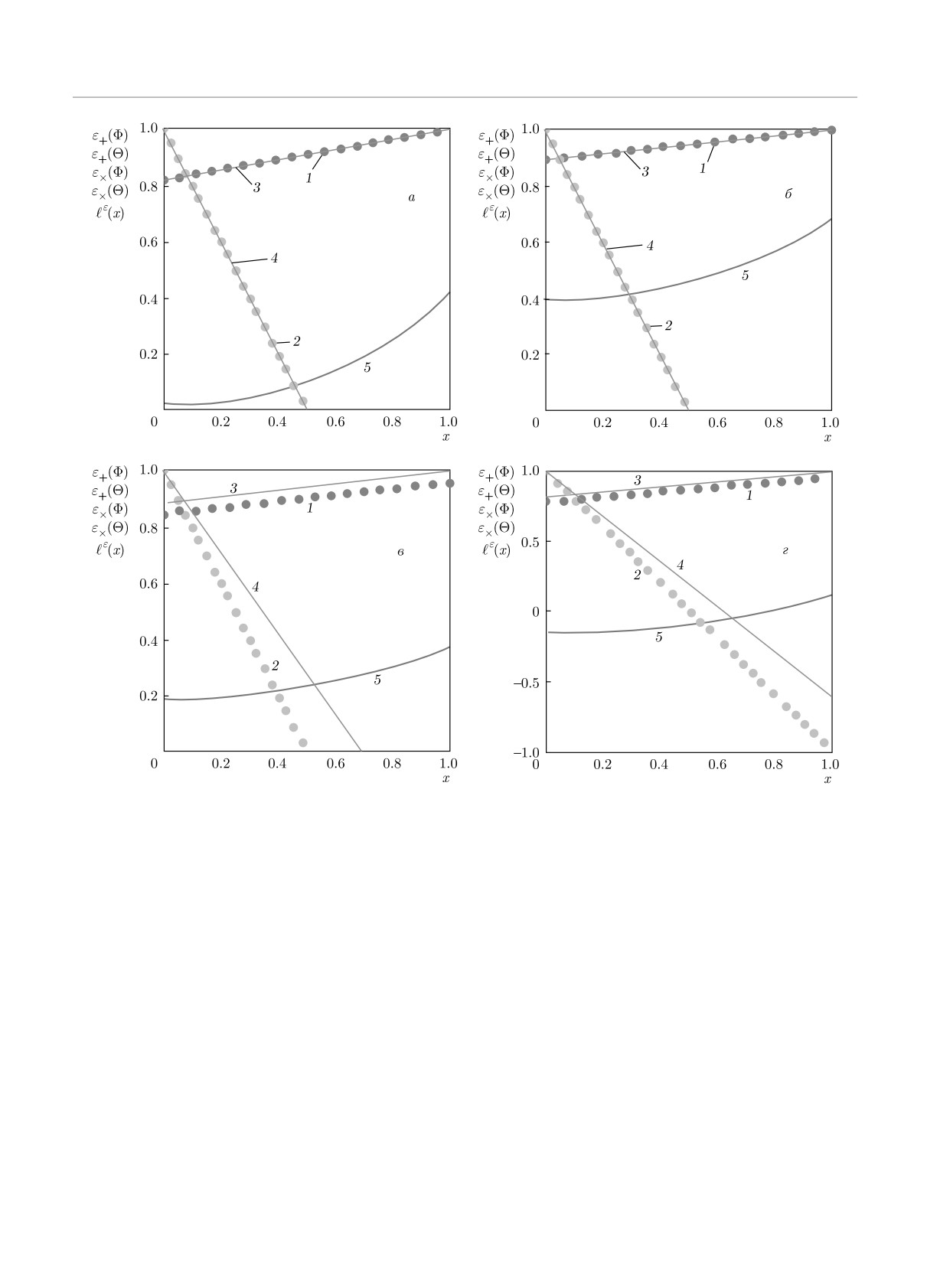
Рис. 2. Зависимости ненаблюдаемых скрытых параметров — скалярных произведений между состояниями Евы в раз-
ных базисах (кривые 1-4), кривые 5 — зависимости длины секретного ключа от параметра оптимизации x (формула
(78)). Кривым 1 отвечает зависимость ε+(Φ), 2 — ε+(Θ), 3 — ε×(Φ), 4 — ε×(Θ) как функция параметра x. Значения
параметров: ξ0 = 0.5, ξ1 = 0.5 для всех кривых рис. а,б. Вероятность наблюдаемой ошибки Q+ = Q× = 0.05 для всех
кривых рис. а,б. Длина последовательности n = 104 для кривых рис. a, n = 106 для кривых рис. б. Значения параметров:
ξ0 = 0.25, ξ1 = 0.75 для всех кривых рис. в,г. Вероятность наблюдаемой ошибки Q+ = 0.05, Q× = 0.07 для всех кривых
рис. в, г. Длина последовательности n = 104 для кривых рис. г, n = 106 для кривых рис. в. Параметр секретности для
всех кривых ε1 = ε2 = 10-9
туаций) в разных базисах. Как видно из сравне-
ностей детекторов длина секретного ключа умень-
ния рис. 2а и б, а также рис. 2г и в, с уменьшени-
шается. Например, из рис. 2г видно, что при до-
ем длины последовательности n, используемой для
статочно большой разности квантовых эффективно-
оценки параметров, длина секретного ключа умень-
стей детекторов (ξ0 = 0.25, ξ1 = 0.75) длина ключа
шается из-за большего доверительного интервала
в минимуме оказывается отрицательной, что озна-
при заданном параметре секретности ε. Кроме то-
чает невозможность получить секретный ключ при
го, с увеличением разницы квантовых эффектив-
таких параметрах. При длине последовательности
344
ЖЭТФ, том 160, вып. 3 (9), 2021
Побочные каналы утечки информации в квантовой криптографии.. .
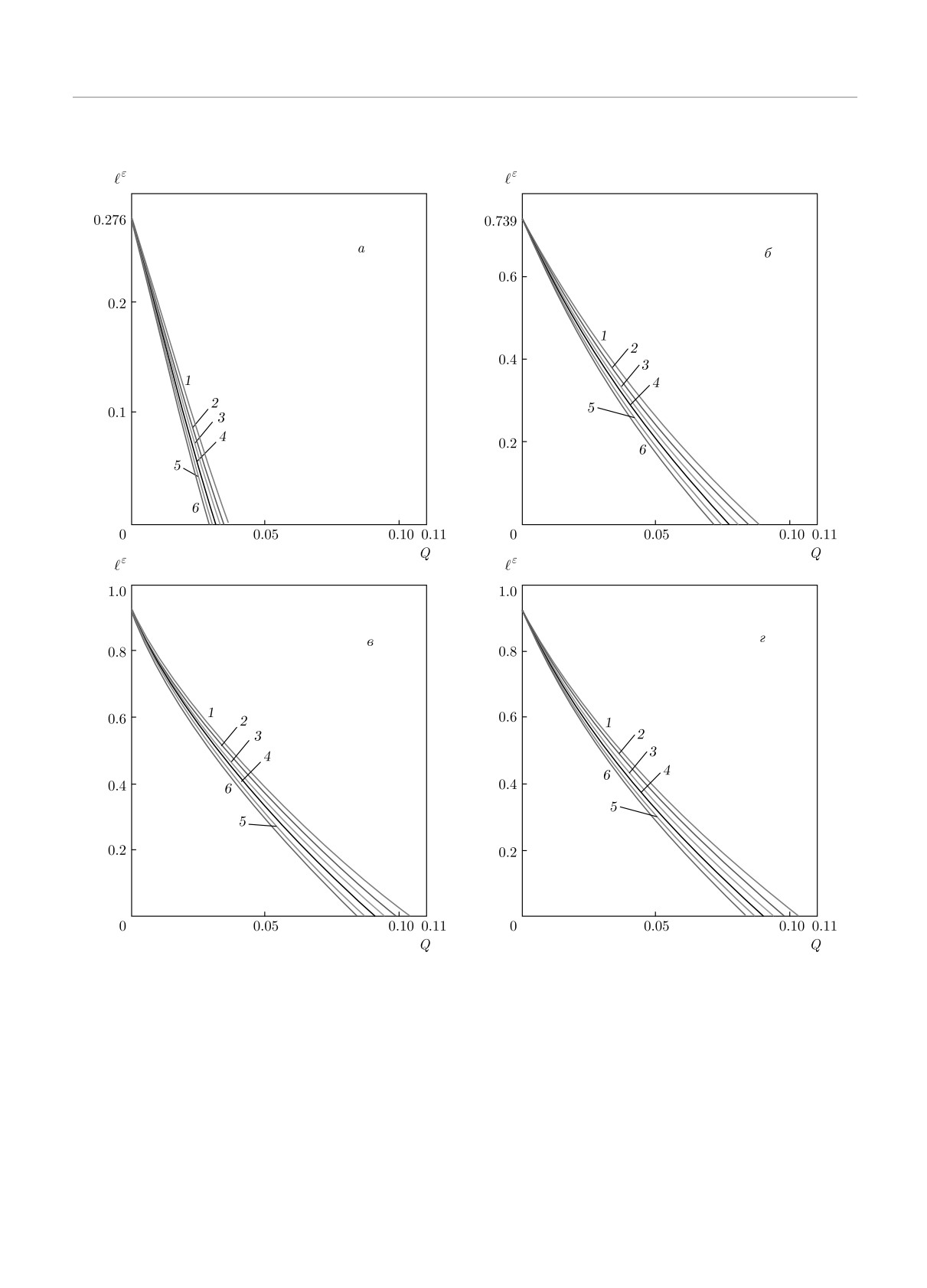
Рис. 3. Зависимости длины секретного ключа от наблюдаемой ошибки Q в базисе + в случае конечной длины после-
довательности. Параметры для рис. а, б: квантовые эффективности детекторов ξ0 = 0.25, ξ1 = 0.75 для всех кривых;
наблюдаемая ошибка в базисе Q× = Q, 1.1Q, 1.2Q, 1.3Q, 1.4Q, 1.5Q соответственно для кривых 1-6; длина последо-
вательности для оценки параметров n = 104 (а), n = 106 (б). Параметры для рис. в,г: в) квантовые эффективности
детекторов ξ0 = 0.5, ξ1 = 0.5 для всех кривых; г) квантовые эффективности детекторов ξ0 = 0.45, ξ1 = 0.55 для всех
кривых; наблюдаемая ошибка в базисе Q× = Q, 1.1Q, 1.2Q, 1.3Q, 1.4Q, 1.5Q соответственно для кривых 1-6; длина
последовательности для оценки параметров рис. в, г n = 106. Параметр секретности для всех рисунков ε1 = ε2 = 10-9
345
С. Н. Молотков
ЖЭТФ, том 160, вып. 3 (9), 2021
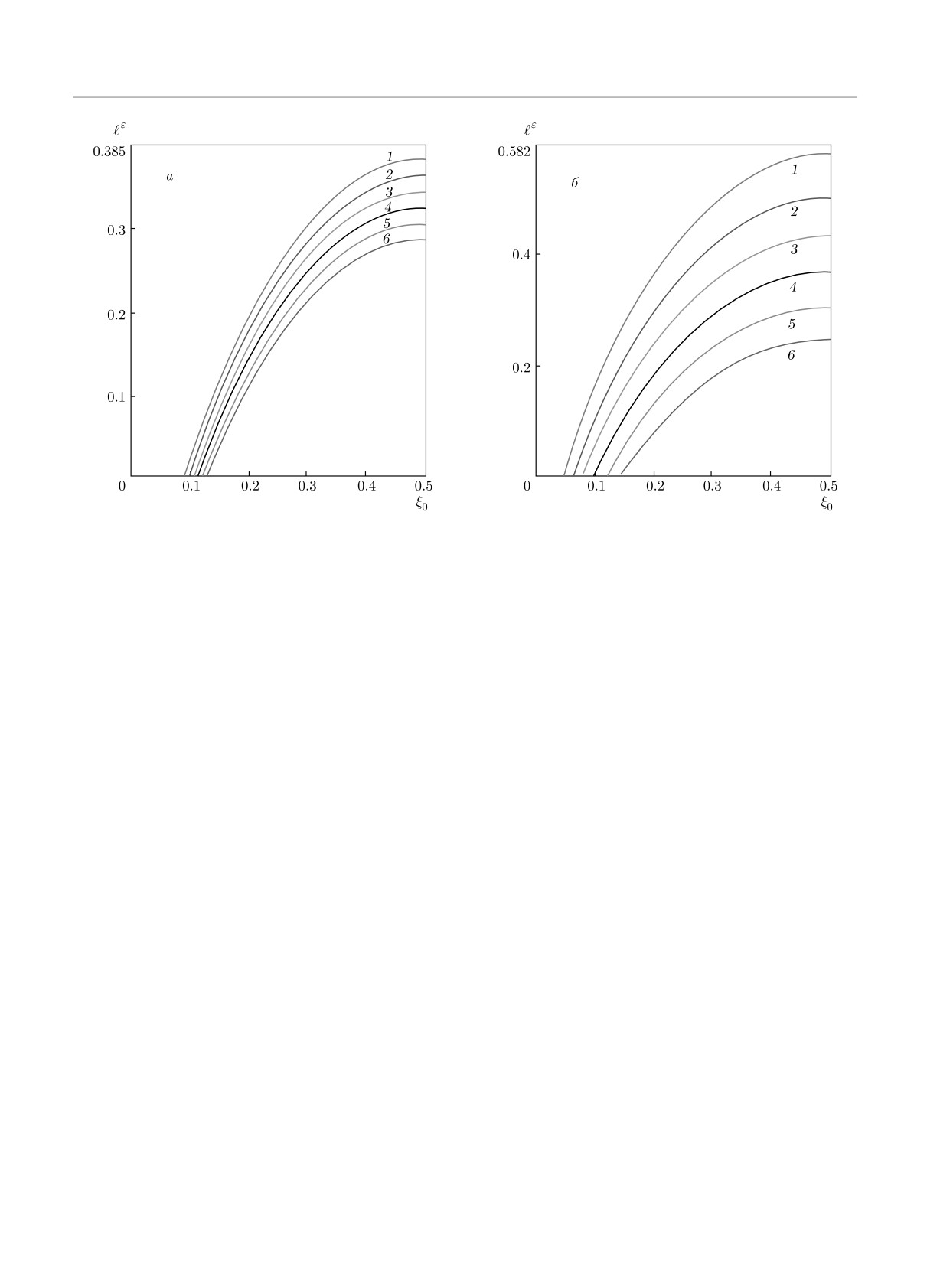
Рис. 4. Зависимости длины секретного ключа от квантовой эффективности детекторов ξ0 = η0/(η0 + η1) при различных
значениях наблюдаемой ошибки в разных базисах. Значения используемых параметров: а) Q+ = 0.05 для всех кривых,
Q× = 0.05, 1.1 · 0.05, 1.2 · 0.05, 1.3 · 0.05, 1.4 · 0.05, 1.5 · 0.05 соответственно для кривых 1-6; б) Q+ = 0.01, 0.02, 0.03,
0.04, 0.05, 0.06, Q× = 0.05, 1.1 · 0.05, 1.2 · 0.05, 1.3 · 0.05, 1.4 · 0.05, 1.5 · 0.05 соответственно для кривых 1-6. Длина
последовательности для всех кривых n = 106, параметр секретности ε1 = ε2 = 10-9
n = 104 для оценки параметров доверительный ин-
Как следует из рис. 4, при данной наблюдаемой
тервал оказывается широким и оценка истинной ве-
вероятности ошибки существует критическое значе-
роятности ошибки завышенной (ср. рис. 2в и 2г).
ние разности квантовых эффективностей, при ко-
торой еще возможно распределение секретных клю-
Зависимости длины секретного ключа от наблю-
чей. При стремлении квантовой эффективности од-
даемой ошибки в однофотонном случае при ко-
ного из детекторов к нулю длина секретного ключа
нечных длинах последовательностей приведены на
обращается в нуль при сколь угодно малой ошибке.
рис. 3. Однородная оценка параметров по наблюда-
емой ошибке проводилась по формуле (94). После
этого проводилась минимизация длины ключа по
12. УЧЕТ НЕОДНОФОТОННОСТИ
параметру x. Основной вывод из рис. 3 сводится к
ИНФОРМАЦИОННЫХ СОСТОЯНИЙ,
тому, что критическая наблюдаемая ошибка и длина
DECOY STATE-МЕТОД ПРИ РАЗНЫХ
секретного ключа уменьшаются по мере несиммет-
КВАНТОВЫХ ЭФФЕКТИВНОСТЯХ
ричности по наблюдаемой ошибке в разных базисах
ДЕТЕКТОРОВ
и при разных квантовых эффективностях детекто-
ров. Выход длины секретного ключа на асимптоти-
Как упоминалось выше, секретный ключ наби-
ческий режим происходит при длинах n, используе-
рается из однофотонной компоненты состояний, до-
мых для оценки истинной вероятности ошибки, т. е.
стигающей приемной стороны. В этом разделе по-
при значениях n ≈ 106 (см. рис. 3а,б и рис. 3в,г).
лучим оценки для вероятности однофотонной ком-
поненты состояний, когда параметры атаки Евы из-
Представляет интерес поведение длины секрет-
ного ключа в широком диапазоне квантовых эффек-
вестны точно. В следующем разделе учтем тот факт,
тивностей детекторов. На рис. 4 приведены зависи-
что параметры точно не известны, а имеется лишь
мости от ξ0 длины секретного ключа в строго одно-
оценка параметров. Затем будут учтены поправки,
фотонном случае при конечных длинах последова-
связанные с конечной длиной передаваемых после-
тельностей.
довательностей.
346
ЖЭТФ, том 160, вып. 3 (9), 2021
Побочные каналы утечки информации в квантовой криптографии.. .
Исходный Decoy State-метод исходит из следу-
Стандартная квантовомеханическая интерпрета-
ющих посылок [19-22]. Информационными состоя-
ция матрицы плотности — квантового ансамбля,
ниями являются когерентные состояния. Использу-
сводится к тому, что в канале присутствуют состо-
ется несколько когерентных состояний с разными
яния |Ψxk〉BB〈Ψxk| с разными числами фотонов с ве-
средними числами фотонов. Часть состояний явля-
роятностями
ются информационными, часть — состояниями «ло-
(2ξ)k
вушками», которые используются для оценки доли
Pk(ξ) = e-2ξ
k!
однофотонной компоненты регистрируемых состоя-
Основная идея метода состоит в том, что под-
ний и вероятности ошибки в однофотонной компо-
ненте информационных состояний. Фаза когерент-
слушиватель, не имея дополнительной информации
и обнаружив в канале связи компоненту состоя-
ных состояний считается полностью рандомизиро-
ванной — равнораспределенной на отрезке [0, 2π].
ний с данным числом фотонов k, не знает, из ка-
кого состояния и с каким средним числом фотонов
Поскольку фаза когерентных состояний в каждой
данная компонента возникла. Основное предполо-
посылке подслушивателю неизвестна, подслушива-
жение стандартного Decoy State-метода основано на
тель «видит» в канале не чистые когерентные состо-
том, что, обнаружив число фотонов k, подслушива-
яния, а статистическую смесь фоковских состояний
с разным числом фотонов. Статистика состояний по
тель действует каждый раз одинаково, т. е. дейст-
вия подслушивателя зависят только от обнаружен-
числу фотонов является пуассоновской.
Далее для определенности будем рассматривать
ного числа фотонов в состоянии. На формальном
уровне действия подслушивателя после обнаруже-
Decoy State-метод с тремя состояниями (одно ин-
формационное, два состояния «ловушки») соответ-
ния состояния с данным числом фотонов описыва-
ются действием супероператора — вполне положи-
ственно со средним числом фотонов ξ
∈ I
=
тельного отображения — наиболее общего преобра-
= {μ, ν1, ν2}. Для матрицы плотности состояний в
зования квантовых состояний в квантовые состоя-
канале имеем
ния. Вид супероператора зависит только от обнару-
∑
(2ξ)k
ρx(ξ) = e-2ξ
|Ψxk〉BB〈Ψxk| =
женного числа фотонов в канале.
k!
k=0
Супероператор в самом общем виде может быть
представлен как
∑
= P(k)(μ)|Ψxk〉BB〈Ψxk|,
(100)
TBE[|Ψxk〉BB〈Ψxk|] = ρxk,BE.
(102)
k=0
В результате возникает запутанное состояние
k
(2ξ)
Боб-Ева ρxk,BE. Явный вид состояния в (102) в стан-
Pk(ξ) = e-2ξ
,
k!
дартном Decoy State-методе не требуется. Для оцен-
√
ки доли однофотонной компоненты и вероятности
∑
k!
|m〉1 ⊗ |k - m〉2
|Ψxk〉B =
eiϕxm
√
,
(101)
ошибки в ней достаточно только наблюдаемого тем-
2k
m!(k - m)!
па отсчетов в посылках, отвечающих состояниям с
m=0
где ϕx — относительная фаза состояний, локали-
различными средними числами фотонов.
В итоге Боб на приемной стороне измеряет не
зованных во временных окнах 1 и 2, в которую
кодируется информация о битах ключа, состояния
исходные состояния, а состояния (102).
|m〉1 ⊗ |k - m〉2 — фоковские состояния при фазо-
Измерения Боба на приемной стороне описыва-
вом кодировании во временных окнах 1 и 2 (нижние
ются разложением единицы, обычно ортогональным
индексы).
(50), (51). В результате измерений у Боба возникает
Нужно отметить следующее. Состояния в (100),
отсчет, который интерпретируется как логический
(101) после рандомизации фаз в среднем имеют та-
бит y = 0 или y = 1.
кой вид в канале связи. При фазовом кодирова-
Пусть Алисой было послано состояние, отвеча-
нии число фотонов в двух временных окнах равно
ющее логическому значению бита x = 0, 1, тогда
условная вероятность того, что Боб зарегистриру-
2ξ. Перед регистрацией данные (см., например, [8])
состояния преобразуются на интерферометре Ма-
ет значение y, есть
ха - Цандера, затем регистрируются в определенном
(103)
P(k)Y|X(y|X = x) = TrBE{Myρxk,BE}.
временном окне, поэтому вероятность регистрации
пропорциональна ξ, а не 2ξ. Этот факт учитывается
Для Decoy State-метода принципиально важно, что
при численных расчетах ниже.
условная вероятность не зависит от ξ — среднего
347
С. Н. Молотков
ЖЭТФ, том 160, вып. 3 (9), 2021
∑
числа фотонов в квантовом состоянии, а только от
(2ξ)k
Ptotξ(1α|X = 1α) = e-2ξ
Yαk(11),
(111)
обнаруженного числа фотонов в данной посылке.
k!
k=0
Полный темп отсчетов (условная вероятность пока
не нормирована) для посылок, когда посылалось со-
∑
(2ξ)k
Ptotξ(0α|X = 1α) = e-2ξ
Yαk(01),
(112)
стояние со средним числом фотонов ξ, отвечающее
k!
k=0
логическому значению бита Алисы x, и когда Боб
зарегистрировал логическое значение бита y, с уче-
том (100), (103) равен
Ptot,αξ = Ptotξ(0α|X = 0α) + Ptotξ(1α|X = 0α)+
Pξ(yα|X = xα) =
+ Ptotξ(1α|X = 1α) + Ptotξ(0α|X =α).
(113)
∑
Дадим интерпретацию вероятностей в
(105)-
= P(k)(ξ)P(k)Y|X(yα|X = xα).
(104)
(113). Состояния, отвечающие 0 и 1, в каждом бази-
k=0
се посылаются равновероятно. Величина
Темп отсчетов (104) зависит от базиса α = +, × из-за
(2ξ)k
разных квантовых эффективностей детекторов, но
e-2ξ
k!
не зависит от ξ.
Для дальнейшего рассмотрения будут нужны
есть вероятность того, что в канале будет присут-
парциальные темпы отсчетов, а именно, посылались
ствовать компонента состояний с фоковским числом
0 и 1, отсчеты были 0, аналогично, посылались 1 и
фотонов k при условии, что в канал было посла-
0, отсчеты были 1 (как правильные, так и непра-
но когерентное состояние со средним числом фото-
вильные). Соответствующие условные вероятности
нов ξ. Yαk(ji) есть вероятность того, что Бобом будет
в базисе + имеют вид
зарегистрирован отсчет j = 0, 1 при условии, что в
канал была послана компонента состояний с числом
Yαk(00) = P(k)Y|X(0+|X = 0+),
(105)
фотонов k, отвечающая логическому биту Алисы i.
Данная вероятность не зависит от ξ.
Используем устоявшиеся в Decoy State-методе
Yαk(10) = P(k)Y|X(1+|X = 0+),
(106)
обозначения для данных вероятностей.
Подчеркнем, что парциальные темпы отсчетов
Yαk(11) = P(k)Y|X(1+|X = 1+),
(107)
Yk (в англоязычной версии Yields) не зависят от
среднего числа фотонов ξ в состоянии.
Yαk(01) = P(k)Y|X(0+|X = 1+).
(108)
Определим парциальный темп ошибочных отсче-
тов для k-фотонной компоненты состояний, находим
Полный условный темп отсчетов есть
(k)
Errαk = PY
(1α|0α) + P(k)Y|X (0α|1α) =
∑
|X
(2ξ)k
Ptotξ(0α|X = 0α) = e-2ξ
Yαk(00),
(109)
k!
k=0
= Y αk (10) + Y αk (01).
(114)
∑
(2ξ)k
Вероятность ошибки в k-фотонной компоненте со-
Ptotξ(1α|X = 0α) = e-2ξ
Yαk(10),
(110)
k!
стояний
k=0
(k)
PY
(1α|0
α) + P(k)Y|X(0α|1α)
|X
Qαk =
(115)
P(k)Y|X(1α|0α) + P(k)Y|X(0α|0α) + P(k)Y|X(0α|1α) + P(k)Y|X(1α|1α)
Полный темп ошибочных отсчетов
∑
(2ξ)k
12.1. Оценки вероятности однофотонной
Errαξ = e-2ξ
Errαk,
k!
компоненты состояний и ошибки по Decoy
k=0
State-методу
(116)
Errαξ
Для дальнейшего удобно ввести обозначения (да-
Qtot,α =
Ptot,αξ
лее α = +, × — индекс базиса)
348
ЖЭТФ, том 160, вып. 3 (9), 2021
Побочные каналы утечки информации в квантовой криптографии.. .
Ptotξ(yα|X = xα) = e2ξPtotξ(yα|X = xα),
Из (109)-(113), (117) получаем оценку вероятности
(117)
вакуумной компоненты состояний на приемной сто-
роне:
Errαξ = e2ξ Errαξ .
{
}
2ν1Ptotν
(yα|X = xα) - 2ν2Ptot(yα|X = xα)ν
2
1
Y0(yα|X = xα) ≤ max
,0
(118)
2(ν1 - ν2)
Для оценки вероятности однофотонной компоненты
Аналогично для других компонент однофотон-
с учетом (109)-(113), (117), (118) находим
ных состояний. Далее, принимая во внимание фор-
мулу (119) для вероятности однофотонной компо-
Y1(yα|X = xα) ≥
ненты Y1, находим
1
∑
≥
×
2
(2ν1)2 - (2ν2)
(η0 + η1)Y1 =
Y1(j+|X = i+).
(122)
2(ν1 - ν2) -
2μ
i,j=0,1
{[
]
× Ptotν(yα|X = xα) - Ptot(yα|X = xα)
-
В базисе × имеем
1
ν2
2
[
Y1(0×|X = 0×) = η1Y1(1 - Q×1),
(2ν1)2 - (2ν2)
-
Ptotμ(yα|X = xα) -
(123)
(2μ)2
Y1(1×|X = 0×) = η0Y1Q+1,
]}
- Y0(yα|X = xα)
(119)
×
),
Y1(1×|X = 1×) = η0Y1(1 - Q
1
Полная вероятность детектирования однофотонной
(124)
компоненты Y1(yα|X
= xα) зависит от детекто-
Y1(0×|X = 1×) = η1Y1Q×1,
ра. Удобно представить вероятности однофотонной
∑
компоненты состояний в следующем виде:
(η0 + η1)Y1 =
Y1(jα|X = iα).
(125)
i,j=0,1
Y1(0+|X = 0+) = η0Y1(1 - Q+),
(120)
Представление (122)-(125) вероятности однофо-
Y1(1+|X = 0+) = η1Y1Q+,
тонной компоненты имеет простой смысл. После
Y1(1+|X = 1+) = η1Y1(1 - Q+),
обнаружения однофотонной компоненты состояний
(121)
в канале (данная вероятность зависит от среднего
Y1(0+|X = 1+) = η0Y1Q+.
числа фотонов в состоянии и равна e-2ξ2ξ) под-
Смысл такой параметризации вероятностей сле-
слушиватель принимает решение, с какой вероят-
дует из унитарной атаки на однофотонную ком-
ностью блокировать данную компоненту, а с какой
поненту состояний. Подслушиватель может блоки-
вероятностью доставить ее на приемную сторону по-
ровать часть однофотонных посылок, оставшуюся
сле унитарной атаки. Величина Y1 есть вероятность
часть неблокируемых посылок, атакует унитарно.
перепосыла искаженной однофотонной компоненты
Вероятность неблокируемых посылок есть Y1. Ес-
состояний, соответственно величина Y1η0 есть пол-
ли, например, в канале присутствовала однофотон-
ная вероятность регистрации однофотонной ком-
ная компонента состояния |0+〉 в базисе +, то по-
поненты детектором с квантовой эффективностью
сле унитарной атаки данное состояние превратится
η0 с учетом правильных и неправильных отсчетов.
в искаженное состояние (42)-(45), в котором присут-
Вероятность правильных отсчетов среди них будет
ствуют компоненты |0+〉 и |1+〉 (см. формулы (42)-
Y1η0(1-Q+,×), соответственно вероятность ошибоч-
(45)). Компонента |0+〉 будет давать отсчет в детек-
ных отсчетов в данном детекторе есть Y1η0Q+,×.
торе D0 с вероятностью η0(1 - Q+), а компонента
Для оценки вероятности ошибки в однофотон-
|1+〉 — отсчет в детекторе D1 с вероятностью η1Q+.
ной компоненте в базисе +, используя (114)-(119),
Полное число отсчетов, правильных и ошибочных,
находим
от однофотонной компоненты состояний будет рав-
но
(η0 + η1)Y1Q+1 = Y+1(10) + Y+1(01) =
Y1[η0(1 - Q+) + η1Q+]
полной вероятности регистрации однофотонной
Err+ν
- Err+ν
1
2
= Err+1 ≤
(126)
компоненты (с точностью до множителя e-2ξ2ξ/1!).
2(ν1 - ν2)
349
С. Н. Молотков
ЖЭТФ, том 160, вып. 3 (9), 2021
Аналогично для оценки вероятности ошибки в
α = +,× со средним числом фотонов ξ. Боб про-
однофотонной компоненте в базисе × с учетом
водит измерения в согласованном базисе и получает
(114)-(119) получаем
Nregξ(jα|X = iα) отсчетов для j = 0, 1. Частота от-
счетов равна
(η0 + η1)Y1Q×1 = Y×1(10) + Y×1(01) =
Nregξ(jα|X = iα)
Ptotξ(jα|X = iα) =
(131)
Err×ν
- Err×ν
Nsentξ(jα|X = iα)
1
2
= Err×1 ≤
(127)
2(ν1 - ν2)
Частота отсчетов является случайной величиной и
подвержена флуктуациям.
Комбинируя (126), (127) и (119), для вероятностей
Существует две постановки задачи.
Q+,×1 получаем
1. Точные вероятности известны и требуется
определить вероятность того, что при конечной се-
Err+1
Err×1
Q+1 ≤
,
Q×1 ≤
,
(128)
рии испытаний произойдет число отсчетов, количе-
(η0 + η1)Y1
(η0 + η1)Y1
ство которых лежит в заданном интервале.
В такой постановке задача относится к области
Yα1(00) + Yα1(10) + Yα1(01) + Yα1(11) =
теории вероятностей.
2. Точные значения вероятностей неизвестны и
1
= (η0 + η1)Y1 ≥
×
требуется определить вероятность того, что истин-
2
(2ν1)2 - (2ν2)
2(ν1 - ν2) -
ная вероятность отсчетов лежит в заданном интер-
2μ
вале значений.
{[
]
Именно такая ситуация имеет место в квантовой
×
ν1
-Pνot,α
2
-
криптографии (см. разделы выше). Такая постанов-
ка относится к области математической статистики.
2
[
]}
(2ν1)2 - (2ν2)
Нас интересует вторая постановка задачи, а
-
μ
-Yα
0
(129)
(2μ)2
именно, вычисление вероятности Pr{Ω1} события
Ω1, что истинная вероятность лежит в заданном
В (129) для краткости введены обозначения
диапазоне значений.
∑∑
Для решения задачи в такой постановке исполь-
Ptot,αξ =
Ptotξ(yα|X = xα),
зуются так называемые концентрационные неравен-
yα xα
(130)
ства. Существует обширная литература по данному
∑∑
Yα0 =
Y0(yα|X = xα).
вопросу и различные типы концентрационных нера-
yα xα
венств (см., например, [18] и большое число ссылок
в работе).
Вероятности парциальных и полных вероятностей
Удобна следующая формулировка применитель-
отсчетов в разных базисах определяются из экспе-
но к нашему случаю: пусть ζi (i = 1, . . . , n) — неза-
риментальных данных. Формулы (126)-(128) дают
висимые случайные величины, 0 ≤ ζi ≤ 1. Пусть
вероятность регистрации однофотонной компонен-
эмпирическое математическое ожидание
ты и вероятность ошибки в ней.
(
)
∑
1
ζ =
ζi
,
(132)
12.2. Определение вероятностей из
n
i=1
экспериментальных данных,
тогда имеет место соотношение
концентрационные неравенства
(
)
Pr
|ζ - E(ζ)| ≤ δ
≥ 1 - 2e-2δ2n,
(133)
Для определения вероятности однофотонной
где E(ζ) — математическое ожидание.
компоненты состояний и вероятности ошибки в
Применительно к нашей ситуации оценка веро-
ней необходимо знать вероятности отсчетов. В
ятности выглядит следующим образом:
реальности данные вероятности неизвестны, из
эксперимента определяются частоты отсчетов для
соответствующих вероятностей.
Pr{|Ptotξ(jα|X = iα)-Ptotξ(jα|X = iα)| ≤ δ(ε1)} ≥
Оценка условных вероятностей в (109)-(113) по-
(
)
≥ 1 - 2exp
-2δ2(ε1)Nsentξ(jα|X = iα)
=
лучается путем раскрытия части переданной по-
следовательности состояний. Пусть Алиса посыла-
=1-ε1.
(134)
ет Nsentξ(jα|X = iα) состояний i = 0, 1 в базисе
350
ЖЭТФ, том 160, вып. 3 (9), 2021
Побочные каналы утечки информации в квантовой криптографии.. .
Для получения ε-секретного ключа фиксируется
лиевское распределение (ζi = ∗ — есть фотоотсчет
значение ε1, по этому значению определяется ве-
с вероятностью p, ζi = ⊔ — нет фотоотсчета с ве-
личина δ(ε1) — ширина доверительного интервала,
роятностью 1 - p). В этом случае вероятность того,
который используется при вычислении ошибки и
что при n испытаниях число отсчетов p = ñp бу-
условной сглаженной min-энтропии.
дет уклоняться от математического ожидания np не
Важно отметить, что, строго говоря, оценки ве-
более, чем на δ, есть (см., например, [18])
роятности должны быть однородными — правые
(
)
части (94), (133) не должны зависеть от самой неиз-
δ2n
Pr{|p - p| ≤ δ} ≥ 1 - 2 exp
-
(135)
вестной вероятности, которую нужно оценить.
2p(1 - p)
Для того чтобы проиллюстрировать существен-
ную разницу в оценках при первой постановке за-
В (135) используем стандартную оценку в пра-
дачи (вероятности известны) и второй (вероятности
вой части, существует множество вариантов с раз-
неизвестны, см. выше), приведем оценку вероятнос-
личными функциями вероятностей в правой части
ти при первой постановке. Наиболее ясно это можно
[18], но для наших целей достаточно такой оценки.
сделать на примере бернуллиевской схемы испыта-
В нашем случае оценка с известным распределением
ний. Пусть случайные величины ζi имеют бернул-
вероятностей выглядит как
Pr{|Ptotξ(jα|X = iα) - Ptotξ(jα|X = iα)| ≤ δ(ε1)} ≥
(
)
δ2(ε1)Nsentξ
(jα|X = iα)
≥ 1-2 exp
-
= 1-ε1.
(136)
Ptot(jα|X = iα)(1-Ptotξ(jα|X = iα))
ξ
Сравнение (134) и (136) показывает, что для то-
буется оценивать не единственный параметр, неточ-
го, чтобы получить оценку числа отсчетов за се-
ности оценок по отдельным параметрам складыва-
рию испытаний с одинаковой точностью (δ) при из-
ются и длина требуемой серии может возрастать на
вестной и неизвестной вероятности, длины серий ис-
6 порядков.
пытаний должны быть существенно разными. Дей-
Нам не известны работы, в которых бы огова-
ствительно, при неизвестной вероятности длина се-
ривалось данное обстоятельство. Обычно использу-
рии должна быть
ют оценки (136) или подобные, при этом молчаливо
предполагая, что вероятности известны, т. е. исполь-
Nunknown,sentξ(jα|X = iα) =
зуют неоднородную оценку.
Однородность оценки истинной вероятности по
= Nknown,sentξ(jα|X = iα)×
наблюдаемой частоте означает вероятность того,
1
×
,
(137)
что наблюдаемая частота уклоняется от истинной
4Ptotξ(jα|X = iα)(1 - Ptotξ(jα|X = iα))
вероятности не более, чем на δ(ε1), не зависит от са-
где
мой истинной вероятности. Однородная оценка га-
рантирует, что вероятность Pr{Ω1} того, что истин-
Nunknown,sentξ(jα|X = iα), Nknown,sentξ(jα|X = iα)
ные значения параметров, которые определяют сек-
ретность ключа, не выходят из заданного интерва-
— длина серии испытаний при неизвестной и
ла, не менее 1 - ε1.
известной вероятности. Вероятность фотоотсчета
Ptotξ(jα|X = iα) имеет порядок μηT(L = 100 км) ≈
≈ 10-4-10-5 (при типичном среднем числе фото-
нов в информационном состоянии 0.1-0.5, T (L) =
12.3. Учет флуктуаций параметров
= 10-dL/10, d ≈ 0.2 дБ/км, L — длина линии, η ≈
≈ 0.1 — квантовая эффективность детекторов). Ска-
В этом разделе получим оценки вероятности од-
занное означает, что длина серии, используемой для
нофотонной компоненты и вероятности ошибки в
оценки параметров атаки, должна быть в 104-105
ней, которые затем будут использованы при оценке
раз больше для достижения одинаковой точности δ,
длины секретного ключа. Считаем, что вероятности
соответственно, параметра ε1, определяющего сек-
априорно неизвестны (см. обсуждение в предыду-
ретность ключей. Как увидим ниже, поскольку тре-
щем разделе).
351
С. Н. Молотков
ЖЭТФ, том 160, вып. 3 (9), 2021
Вероятность того, что частота отсчетов
̂
тинной вероятности
Ptotξ(yα|X = xα) на величину не
Ptotξ(yα|X = xα) (умноженная на коэффициент e2ξ)
более δαx,y,ξ, оказывается не менее
в последовательности длины Nξ отличается от ис-
{
}
{
}
̂
Pr
|Ptotξ(yα|X = xα)-Ptotξ(yα|X = xα)| ≤ δα
≥ 1 - 2exp
-2(δαx,y,ξ)2Nξ
=1-εαx,yξ,
(138)
x,y,ξ
δαx,y,ξ = eξδαx,y,ξ.
(η0 + η1)Y-1 ≥
Аналогично вероятность того, что частота ошибок
1
≥
×
Errαξ в последовательности длины NErr,ξ отличается
(2ν1)2 - (2ν2)2
2(ν1 - ν2) -
̂
от истинной вероятности ошибок
Errα
на величину
2μ
ξ
не более δαErr,ξ, не менее, чем
{[
]
(2ν1)2 - (2ν2)2
×
ν1
- -Ptot,αν2
+ -
×
{
}
(2μ)2
̂
Pr
|Errαξ -
Errα|≤δα
≥
[
]}
ξ
Err,ξ
tot,α
× P
+ - (Y α
)-
(143)
{
}
μ
0
≥ 1 - 2exp
-2(δαErr,ξ)2NErr,ξ
=1-εαErr,ξ,
(139)
δαErr,ξ = eξδαErr,ξ.
12.4. Матрицы плотности и оценка длины
Для дальнейшего нам понадобятся значения па-
секретного ключа с учетом флуктуаций
раметров на левой и правой границах доверительно-
параметров
го интервала. Значения на границах доверительного
Набором наблюдаемых флуктуирующих пара-
интервала обозначим как
метров являются
{
}
Ptotξ(yα|X = xα)± = Ptotξ(yα|X = xα) ± δαx,y,ξ, (140)
,
Q = Ptotξ(yα|X = xα),Errα
ξ
(144)
Errαξ± = Errαξ ± δαErr,ξ.
(141)
α = +,×, x,y = 0,1.
Для вероятности ошибки нужна консервативная
Вероятность события Ω1 — все параметры лежат в
оценка в пользу подслушивателя, т. е. необходимо
доверительном интервале — есть
выбирать значение на правой границе, для (Q+,×1)+
получаем
∑
+
Pr{Ω1} ≥ 1 -
εαErr,ξ -
Err+1
α=+,×
(Q+1)+ ≤
,
∑
∑
(η0 + η1)Y-
1
(142)
-
εαx,yξ = 1 - εΩ1 .
(145)
+
α=+,× x,y=0,1
Err×1
(Q×1)+ ≤
-
(η0 + η1)Y
1
Однофотонная компонента частичной матрицы
Индекс «+» в (140)-(142) отвечает значениям на
плотности Алиса-Ева, из которой формируется сек-
правой границе доверительного интервала, а индекс
ретный ключ, после первого усечения, с использова-
«-» — на левой.
нием оценок параметров (138)-(143), имеет вид
При вычислении Err+1
+ и Err×1+ в (142) исполь-
зуются формулы (128), в которых оценки вероятно-
ραXE = |0α〉XX〈0α| ⊗ [ξα0(1 - (Qα)+)|Φ0α〉Q ×
стей, входящие со знаком «+», берутся на правой
×Q〈Φ0α| + ξα1(Qα)+|Θ0α〉QQ〈Θ0α|] +
границе доверительного интервала, а входящие со
знаком «-» берутся на левой границе доверитель-
+ |1α〉XX 〈1α| ⊗ [ξα1 (1 - (Qα)+)|Φ1α 〉QQ〈Φ1α | +
ного интервала.
Аналогично при вычислении оценки вероятности
(146)
+ ξα0 (Qα)+|Θ1α〉QQ〈Θ1α|].
однофотонной компоненты нужно брать ее значение
на левой границе доверительного интервала, с уче-
Частичная матрица плотности Евы после первого
том (129) находим
усечения
352
ЖЭТФ, том 160, вып. 3 (9), 2021
Побочные каналы утечки информации в квантовой криптографии.. .
{
ραE =
(1 - (Qα1)+)[ξα0|Φ0α 〉EE 〈Φ0α | +
где
+ ξα1 |Φ1α〉EE〈Φ1α|] + (Qα1)+[ξα1 |Θ0α〉E ×
h(ξ0) = -ξ0 log(ξ0) - ξ1 log(ξ1), ξ1 = 1 - ξ0,
(153)
× E〈Θ0α| + ξ1|Θ1α〉EE〈Θ1α|]} .
(147)
h(Θα) = -λ+(Θα) log(λ+(Θα)) +
Оценка числа информационных однофотонных по-
сылок nαμ с учетом (138)-(143) дает
+ λ-(Θα)log(λ-(Θα)),
(154)
nαμ = e-2μ(2μ)(η0 + η1)Y-1Nαμ,
(148)
где Nαμ — полное число зарегистрированных инфор-
h(Φα) = -λ+(Φα) log(λ+(Φα)) +
мационных посылок в базисе α = +, ×.
Условная сглаженная энтропия вычисляется на
+ λ-(Φα)log(λ-(Φα)).
(155)
матрице плотности для однофотонных посылок. В
(148) nαμ — число однофотонных посылок. Второе
Собственные числа вычисляются по формулам
усечение матрицы плотности возникает при вычис-
(81)-(90), где в качестве вероятностей ошибок Qα
лении условной сглаженной min-энтропии от тен-
в базисе α используются их оценки из (138)-(143)
зорного произведения матриц плотности, с учетом
(Qα)+.
(146), (147) получаем
Финальная длина секретного ключа по двум ба-
(
)
зисам определяется минимизацией по ненаблюдае-
(ραXE )⊗nμ | (ραE )⊗nμ
≥
in
мых скрытым параметрам, получаем
√
(
)
{
}
1
ℓΣε
= min
ℓ+ε
+ℓ×
(156)
≥ nαμH (ραXE|ραE) - const nαμ log
,
(149)
Ω
Ω
εΩ
x∈[0,1]
εΩ2
где
εΩ = εΩ1∩Ω2 = εΩ1 + εΩ2.
(150)
13. КВАНТОВЫЕ ПОБОЧНЫЕ КАНАЛЫ
УТЕЧКИ ИНФОРМАЦИИ
Для утечки информации при коррекции ошибок по-
лучаем
Системы квантовой криптографии являются от-
крытыми системами. Кроме вторжения в квантовый
leakα ≤ Nαμh((Qtot,αμ)+) +
√
канал связи при передаче информационных состоя-
(
)
1
ний подслушиватель может детектировать побочное
+ const Nαμ log
(151)
εΩ2
излучение передающей и приемной аппаратуры, а
также активно зондировать состояние элементов ап-
Считаем для экономии обозначений, что длина се-
паратуры через волоконную линию связи. В данном
рии для оценки различных параметров одинакова и
направлении имеются только отдельные разрознен-
равна Nμ. Правая граница доверительного интерва-
ные результаты [23-25], которые не учитывают все
ла — величина (Qtot,αμ)+ в (151) вычисляется с ис-
критические факторы, в том числе различную кван-
пользованием δ(Nμ, ε2), а оценки величин в (149)
товую эффективность.
вычисляются с использованием δ(nμ, ε2) (см. фор-
Критическими побочными каналами утечки ин-
мулы (138), (139)).
формации являются следующие: электромагнитное
Наконец, для длины εΩ-секретного ключа в ба-
излучение приемной и передающей аппаратуры, ак-
зисе α получаем
тивное зондирование фазового модулятора и моду-
ℓα
≥
лятора интенсивности, обратное переизлучение ла-
εΩ
(
)
винных детекторов (back-flash radiadion) при реги-
(ραXE )⊗nμ | (ραE )⊗nμ
- leakα ≥
страции информационных состояний. Состояния во
in
{
[
]}
всех перечисленных побочных каналах несут инфор-
≥nαμ
h(ξ0)-
(1-(Qα1)+)h(Φα)+(Q+1)+h(Θα)
-
мацию о передаваемом ключе. Генерация случайных
√
(
)
чисел, наложение импульсов напряжения на фазо-
1
- Nαμ h(Qtot,α,+μ) - const nαμ log
-
вый модулятор, приложение стробирующих импуль-
εΩ2
сов на лавинные детекторы приводит к излучению,
√
(
)
состояния излучения различаются при генерации 0
1
- const Nαμ log
,
(152)
и 1. Поэтому регистрация состояний в побочных ка-
εΩ2
налах дает дополнительную информацию о битах
353
4
ЖЭТФ, вып. 3 (9)
С. Н. Молотков
ЖЭТФ, том 160, вып. 3 (9), 2021
передаваемого ключа. Аналогично активное зонди-
экранированием аппаратуры. По этой причине мож-
рование фазового модулятора с последующим изме-
но считать, что спектральная функция распределе-
рением отраженного зондирующего излучения так-
ния числа излученных фотонов известна.
же дает информацию о состоянии фазового моду-
Ситуация с состояниями в побочных каналах при
лятора, а значит, о битах ключа. При регистрации
активном зондировании более деликатная. Состоя-
информационных состояний на приемной стороне
ния при активном зондировании элементов системы
происходит образование лавины носителей, которая
полностью определяются подслушивателем, поэто-
при рекомбинации приводит к обратному переизлу-
му напрямую никак не контролируются легитимны-
чению в линию связи. Обычно в системах квантовой
ми пользователями.
криптографии используется пара лавинных детек-
Возникает вопрос: как учитывать побочные ка-
торов, отсчет в одном детекторе интерпретируется
налы утечки информации?
как логический 0, во втором — как логическая 1. По-
Для каналов с активным зондированием возмож-
скольку характеристики детекторов всегда несколь-
но только контролировать верхнюю границу интен-
ко различаются, обратное переизлучение также раз-
сивности отраженных зондирующих состояний, в
личается при регистрации детектором 0 и 1. Реги-
идеале в разных спектральных диапазонах. Уточ-
страция back-flash-излучения также дает дополни-
ним, что имеется в виду. Для волоконных систем
тельную информацию о битах ключа.
квантовой криптографии существует верхняя гра-
Важно отметить, что в отличие от вторжения в
ница интенсивности (или мощности) излучения, при
квантовый канал связи, которое приводит к возму-
которой волокно еще не начинает плавиться. По-
щению информационных состояний и ошибкам на
этому верхнюю границу по интенсивности входного
приемной стороне, детектирование (пассивное или
зондирующего излучения можно считать известной
активное) в побочных каналах не приводит к возму-
для конкретного типа волокна (см., например, [26]).
щению информационных состояний и, соответствен-
Зная максимальную интенсивность входного излу-
но, к ошибкам на приемной стороне. Побочные кана-
чения, используя асимметричные оптические изоля-
лы утечки информации являются дополнительным
торы, можно указать верхнюю границу по интен-
информационным «бонусом» для подслушивателя.
сивности (числу фотонов) выходного зондирующего
При наличии побочных каналов утечки информа-
излучения, которое будет доступно подслушитателю
ции фундаментальная связь между возмущением
для детектирования. По этой причине далее будем
состояний и извлечением информации из них разры-
считать эту границу заданной.
вается. По этой причине фундаментальные энтро-
Таким образом, кроме информационных состо-
пийные соотношения неопределенностей [5], кото-
яний подслушиватель имеет в своем распоряжении
рые связывают возмущение состояний с утечкой ин-
квантовые состояния в побочных каналах, которые
формации к подслушивателю, оказываются непри-
могут совместно измеряться с информационными
менимыми.
состояниями. Максимально допустимая информа-
Имеется принципиальное отличие состояний в
ция, которую может получить подслушиватель, до-
побочных каналах от информационных состояний
стигается на совместных коллективных измерениях
в квантовом канале. Перед посылкой информаци-
информационных состояний и состояний в побоч-
онных квантовых состояний, последние контроли-
ных каналах.
руемым образом приготавливаются на передающей
Перейдем к детальному описанию состояний в
станции. Иначе говоря, известно, какие состояния
побочных каналах.
посылаются в канал связи, которые будут атако-
ваться подслушивателем. Поскольку состояния из-
13.1. Побочный канал — зондирование
вестны, это позволяет связать возмущение исход-
фазового модулятора
но известных состояний с утечкой информации из
них. Состояния в побочных каналах, вообще гово-
При активном зондировании фазового модулято-
ря, неизвестны. Действительно, побочное излучение
ра подслушиватель будет иметь в своем распоряже-
передающей и приемной аппаратуры представляет
нии кроме информационных состояний еще и отра-
собой источник с макроскопически большим числом
женные зондирующие состояния, которые зависят
степеней свободы, состояния которых точно неиз-
от того, в каком состоянии находится фазовый мо-
вестно. Все, что можно контролировать, так это ин-
дулятор — какой логический бит кодируется, 0 или
тенсивность побочного излучения в разных спек-
1. В пользу подслушивателя можно считать отра-
тральных диапазонах. Это достигается аккуратным
женные состояния чистыми, поскольку чистые со-
354
ЖЭТФ, том 160, вып. 3 (9), 2021
Побочные каналы утечки информации в квантовой криптографии.. .
Удобно выбрать базисные функции максимально ло-
кализованными во временном окне [0, T ]. Условие
максимальной локализации состояний во временном
окне [0, T ], фактически базисных функций φn(t, c),
имеющих ширину спектра Ω,
T
∫
max
|φn(t, c)|2(t) dt,
(158)
ω∈[0,Ω]
0
Рис. 5. Схематичное представление состояний в побочном
приводит к известному интегральному уравнению
канале, связанном с излучением аппаратуры, в каждом
[27-29]
такте передачи квантовых состояний. |ψ0,1{n}〉 — квантовые
состояния, возникающие в побочном канале при передаче
∫
T
0 и 1
1
sin[Ω(t - t′)]
λn(c)φn(t, c) =
×
π
t-t′
0
стояния более различимы, чем смешанные состоя-
× φn(t′, c)dt′, c = ΩT.
(159)
ния. В дальнейшем будет видно, что непосредствен-
ная структура отраженных от фазового модулятора
Решением являются функции вытянутого сферои-
состояний непринципиальна. В формулу для длины
да [27-29]. При разных n и n′ функции ортогональ-
секретного ключа будет входит лишь скалярное про-
ны как на конечном [0, T ], так и на бесконечном
изведение (перекрытие) отраженных зондирующих
(-∞, ∞) интервалах,
квантовых состояний, отвечающих 0 и 1. Запишем
T
∫
отраженные зондирующие состояния в виде
φn(t, c)φn′ (t, c)dt = λn(c)δn,n′ ,
= |ψ0α,1α 〉PMPM 〈ψ0α,1α |,
(157)
0
M
(160)
∞
∫
здесь |ψ0α,1α 〉PM — отраженные зондирующие состо-
φn(t, c)φn′ (t, c)dt = δn,n′ .
яния для 0 и 1 в разных базисах α = +, ×. Индекс
-∞
«P M» символизирует зондирование фазового моду-
Степень локализации во временном окне [0, T ] соб-
лятора (Phase Modulator).
ственной функции с номером n, являющейся реше-
В окончательный ответ для длины секретного
нием уравнения (159), дается ее собственным чис-
ключа будет входить лишь модуль перекрытия со-
лом:
стояний |PM 〈ψ0α,1α |ψ0α,1α 〉PM |.
T
∫
φ2n(t, c) dt = λn(c).
(161)
13.2. Побочный канал — излучение
0
аппаратуры
Для дальнейшего удобно перейти к нормирован-
Излучение аппаратуры приводит к излучению в
ным на отрезке функциям
некотором частотном диапазоне Ω. Ширина спектра
√
λn(c)ϕn(t) = φn(t, c),
излучения Ω определяется наименьшей длительно-
стью импульсов τ при работе управляющей электро-
параметр c фиксирован. Уникальным свойством
ники. Подслушиватель для различения состояний
волновых функций вытянутого сфероида является
излучения в побочном канале проводит измерения
их поведение в зависимости от величины парамет-
в каждом такте длительностью T посылки инфор-
ра ΩT . При значении параметра ΩT ≫ 1 имеется
мационных состояний (см. рис. 5). Максимальная
N = ΩT функций, которые локализованы во вре-
различимость состояний возникает, если состояния
менном окне с экспоненциальной точностью [29] по
в побочном канале в разных тактах не перекрыва-
параметру ΩT :
ются между собой.
4
√π8ncn+1/2
Для описания квантовых состояний в побочном
λn(c) ∼ 1 -
e-c, c = ΩT.
(162)
n!
канале необходимо выбрать набор базисных функ-
ций, по которым будет раскладываться квантовое
Имеются также примерно log(ΩT ) функций в пе-
состояние. Таким естественным набором базисных
реходной области номеров собственных чисел, ко-
функций являются функции вытянутого сфероида.
торые стремятся к нулю. Для остальных номеров
355
4*
С. Н. Молотков
ЖЭТФ, том 160, вып. 3 (9), 2021
собственные числа почти равны нулю в окне [0, T].
M =n1 +n2 +...+nN)
Принципиальным фактом при использовании в ка-
∫
честве базисных функций вытянутого сфероида яв-
|ψ{n}〉 = . . . ×
ляется следующий результат [27]. Для любого ε > 0
Ω
имеет место
∫
×
dω1dω2 . . . dωn1 dωn1+1dωn1+2 . . . dωn2 . . . ×
lim
λΩT(1-ε) = 1,
lim
λΩT(1+ε) = 0.
(163)
Ω
ΩT →∞
ΩT →∞
× dωnN-1+1dωnN-1+2 . . . dωnN ×
Неформально это означает, что имеется ΩT номеров
× ϕ1(ω1)ϕ1(ω2). . . ϕ1(ωn1)ϕ2(ωn1+1)×
функций, которые почти целиком локализованы во
× ϕ2(ωn1+2). . . ϕ2(ωn2). . . ϕN(ωnN-1+1)×
временном окне T . Для остальных номеров функции
× ϕN(ωnN-1+2). . . ϕN(ωnN)×
равны нулю (при этом они остаются нормирован-
× |ω1, ω2, . . . ωn1 , ωn1+1, ωn1+2, . . . ωn2 , . . . ωnN -1+1,
ными, нормировка набирается на всем бесконечном
ωnN-1+2, . . .ωnN 〉.
(165)
интервале). Переходная область по номерам имеет
масштаб ∼ ln(2πΩT ), т. е. является крайне узкой —
Максимальное количество информации, которое
логарифмически узкой по сравнению с ΩT .
можно извлечь при измерениях квантового состоя-
Перейдем к построению квантового состояния.
ния, достигается, если ортогональные компоненты
Логика построения квантового состояния с но-
состояний с разными разбиениями числа фотонов
сителем в частотной полосе Ω будет сводиться к
M присутствуют с одинаковой вероятностью. С
следующему. В пользу подслушивателя будем стро-
учетом сказанного в пользу подслушивателя счита-
ить состояние так, чтобы из него можно было из-
ем, что состояние в побочном канале, связанном с
влечь максимум информации. Пусть полное число
излучением аппаратуры, имеет вид
фотонов в состоянии равно M. Данное полное чис-
ло фотонов нужно таким образом распределить по
∑
1
= P0α,1α
×
N = ΩT одночастичным состояниям, чтобы из него
X,GY
GX,GY N
M =0
можно было получить максимум информации. Мак-
∑
×
|ψ{n}〉〈ψ{n}|,
(166)
симум извлекаемой информации достигается на со-
стоянии, в котором различные ортогональные (до-
{n}=n1+n2+...=M
стоверно различимые) компоненты присутствуют с
— функция распределения по числу
равной вероятностью. Энтропия такого состояния
X,GY
фотонов в побочном канале при генерации аппара-
будет максимальной, соответственно, максимальной
турой 0α или 1α в базисе α. Данные функции рас-
будет информация.
пределения, по сути, описывают распределение фо-
В качестве базисных одночастичных состояний
тонов по спектру. Индексы «GX» и «GY » относятся
будем использовать функции (158) φn(ω) — фу-
к передающей и приемной аппаратуре соответствен-
рье-образ от функций в (158). Рассмотрим кванто-
но.
вое состояние поля, которое содержит M фотонов.
Как будет видно ниже, полное число одночастич-
Число многочастичных ортогональных векторов со-
ных ортогональных состояний N, имеющих спектр в
стояний с M фотонами, локализованных во времен-
частотной полосе Ω и максимально локализованных
ном окне T (таких функций N = ΩT ), равно числу
во временном окне T, в окончательный ответ для
способов размещения M фотонов по N одночастич-
длины секретного ключа не входит. Длина ключа
ным состояниям. Число размещений бозе-частиц по
зависит лишь от функции распределения по числу
N состояниям равно [30]
, последняя должна определяться
X,GY
экспериментально для каждой конкретной техниче-
(N - 1 + M)!
ской реализации системы.
CMN-1+M =
(164)
(N - 1)!M!
13.3. Побочный канал — back flash
Вектор состояния, отвечающий размещению M
однофотонных детекторов
тождественных частиц по N одночастичным со-
стояниям, имеет вид (ниже введено символическое
При построении состояний в побочном канале,
обозначение
{n} для разбиения числа фотонов
связанном с обратным переизлучением детекторов,
356
ЖЭТФ, том 160, вып. 3 (9), 2021
Побочные каналы утечки информации в квантовой криптографии.. .
применима та же логика, что и в предыдущем раз-
каналах только к однофотонной компоненте инфор-
деле. Излучение детектируется подслушивателем в
мационных состояний.
каждом временном такте посылки/регистрации со-
Матрица плотности с учетом побочных каналов
стояний. Аналогично рассуждениям в предыдущем
может быть записана в виде
разделе, для квантовых состояний в этом побочном
{
канале утечки информации получаем
ραXEG
XGY
PMD
= |0α〉XX 〈0α| ⊗ ρ0αGX⊗ρPαM⊗
[
∑
P0α,1α 1D
×
⊗ ξ0α(1 - Qα)ρ0αGY⊗ρDα ⊗
|Φ0〉EE 〈Φ0α | +
ρ0α,1αD =
N
]
M =0∑
+
+ ξ1αQαρ1αGY
⊗ ρ1αD ⊗ |Θ0α〉E E 〈Θ0α|
×
|ψ{n}〉〈ψ{n}|,
(167)
{n}=n1+n2+...=M
+ |1〉XX 〈1| ⊗ ρ1αGX ⊗ ρPαM ⊗
[
(N + M - 1)!
α
N =
⊗ ξ1α(1 - Qα)ρ1G
Y
⊗ ρ1αD ⊗ |Φ1α〉E E 〈Φ1α | +
(N - 1)!M!
]}
α
+ ξ0αQαρ0G
⊗ ρ0αD ⊗ |Θ1α〉E E 〈Θ1α|
(168)
Индекс «D» обозначает побочный канал переизлу-
Y
чения детекторов. Здесь P0α,1αD — функции распре-
Интерпретация (168) имеет простой смысл. Пусть
деления числа фотонов при переизлучении детекто-
аппаратура Алисы приготавливает состояние 0α, это
ров при регистрации 0α и 1α в базисах α = +, ×. Вид
функций распределения по числу фотонов должен
приводит к появлению квантового состояния ρ0αGX
в побочном канале излучения аппаратуры Алисы.
определяться экспериментально для данного типа
Кроме того, подслушиватель может активно зонди-
детекторов и конкретной реализации системы.
ровать состояние фазового модулятора, и это при-
водит к тому, что подслушиватель дополнительно
13.4. Матрицы плотности с учетом побочных
имеет в своем распоряжении состояние ρ0αPM .
каналов
Далее, если на приемной стороне станции проис-
ходит стробирование детектора, например, 0 в ба-
При реализации Decoy State-метода использует-
зисе α, то это приводит к излучению аппаратуры,
ся модуляция интенсивности состояний при помо-
что описывается состоянием в побочном канале ρ0α .G
щи модулятора интенсивности. Существуют реали-
Y
Правильное детектирование информационного со-
зации систем квантовой криптографии, в которых
стояния с вероятностью (1 - Qα) приводит к об-
модуляция интенсивности проводится фазовым мо-
ратному переизлучению данного детектора в линию
дулятором. Далее будем иметь в виду такую реа-
лизацию системы. Если модуляция интенсивности
связи, которое дается состоянием ρ0αD.
Частичный след (168) по состояниям Алисы да-
информационных состояний проводится модулято-
ет матрицу плотности Евы с учетом всех каналов
ром интенсивности, то нужно добавить побочный
утечки информации, находим
канал утечки, связанный с модулятором интенсив-
ности, что можно сделать методом, приведенным в
{
[
α
ραEG
= (1 - Qα) ξ0αρ0G
работе [7].
XGY
PMD
X
⊗ ρ0αPM ⊗
Как отмечалось выше, секретный ключ форми-
|Φ0α 〉EE 〈Φ0α |+
руется только из однофотонной компоненты состо-
⊗ ρ0αGY⊗ ρDα ⊗
]
яний, достигающей приемной стороны. Информа-
+ ξ1αρ1αGX⊗ρPαM⊗ρGαY
⊗ ρ1αD ⊗ |Φ1α〉E E 〈Φ1α | +
ция, заключенная в многофотонных компонентах
[
информационных состояний, в пользу подслушива-
|Θ0α 〉EE 〈Θ0α |+
+Qα ξ1αρ0αGX⊗ρPαM⊗ρGαY⊗ρDα ⊗
теля считается ему известной.
Разумеется, что побочное излучение аппарату-
+ ξ0αρ1αGX ⊗ ρPαM ⊗ ρGαY⊗ ρDα ⊗
ры, зондирование фазового модулятора, измерение
]}
обратного переизлучения детекторов имеют место
⊗ |Θ1α〉EE 〈Θ1α|
(169)
независимо от того, какая компонента информаци-
онных состояний приготавливается или регистри-
13.5. Собственные числа матриц плотности
руется. Но поскольку информация многофотонных
компонент и так считается известной подслушивате-
Для вычисления сглаженной условной энтропии,
лю, достаточно «подцепить» состояния в побочных
фигурирующей в оценке для длины ключа, потре-
357
С. Н. Молотков
ЖЭТФ, том 160, вып. 3 (9), 2021
буются собственные числа матриц плотности Али-
переменные MGX , MGY , MD отвечают за число фо-
сы-Евы и Евы (168), (169), находим две группы соб-
тонов в функциях распределения вероятностей в по-
ственных чисел матрицы плотности ραXEG
:
бочных каналах. Также введены обозначения
XGY PMD
EΦα = |PM 〈ψ0α|ψ1α〉PM | · |E〈Φ0α |Φ1α 〉E|,
(178)
α
]
[P0G
X
[P0αGY]
[P0αD]
[(1 - Qα)ξ0α ] ·
·
·
,
N
N
N
(170)
EΘα = |PM 〈ψ0α|ψ1α〉PM | · |E〈Θ0α |Θ1α 〉E|.
(179)
α
]
[P1G
X
[P1αGY]
[P1αD]
[(1 - Qα)ξ1α ] ·
·
·
,
Величины в правой части (170)-(177) зависят от на-
N
N
N
блюдаемых параметров Qα и скрытых для легитим-
α
]
ных пользователей параметров — скалярных произ-
[P0G
X
[P1αGY]
[P1αD]
ведений (65)-(68) векторов состояний подслушива-
[Qαξ1α ] ·
·
·
,
N
N
N
теля. Учет конечной длины передаваемых последо-
(171)
α
]
вательностей сводится к тому, что в формулах (168),
[P1G
X
[P0αGY]
[P0αD]
(169) вместо значений Qα и при вычислении скаляр-
[Qαξ0α ] ·
·
·
N
N
N
ных произведений в (65)-(68) нужно использовать
оценки вероятности ошибок. Фактически нужно за-
Собственные
числа
матрицы
плотности
менить Qα на (Qα)+.
ραEG
имеют вид
XGY PMD
После подстановки соответствующих значений
параметров, при вычислении длины секретного
1
1
1
1
1
1
(1 - Qα)
Λ±Φα, Qα
Λ±Θα,
(172)
ключа необходимо сделать поиск минимума по
N N N
N N N
одной переменной x ∈ [0, 1] (см. формулу (78)).
где
{
√
}
1
4(AΦα BΦα - E2Φα)
14. УСЛОВНАЯ СГЛАЖЕННАЯ ЭНТРОПИЯ
Λ±Φα =
1±
1-
,
2
1-E2
ОДНОФОТОННОЙ КОМПОНЕНТЫ
Φα
(173)
СОСТОЯНИЙ, ОЦЕНКА ДЛИНЫ
{
√
}
СЕКРЕТНОГО КЛЮЧА
1
4(AΘαBΘα - E2Θα)
Λ±Θα =
1±
1-
2
1-E2
Θα
При вычислении условной энтропии с учетом по-
бочных каналов утечки информации будем считать,
Как видно из (170)-(172), собственные числа явля-
что параметры, описывающие состояния в побочных
ются N3-кратно вырожденными. Далее,
каналах, известны подслушивателю точно. Консер-
вативно в пользу подслушивателя можно считать,
AΦα = ξ0αP0αGX(MGX)
GY
(MGY )P0αD (MD) +
что подслушиватель может иметь точную копию ап-
паратуры, используемой Алисой и Бобом. Имея точ-
+ξ1αP1αGX (MGX )
GY
(MGY )P1αD (MD)EΦα,
(174)
ную копию аппаратуры, подслушиватель не ограни-
чен во времени, чтобы, проводя длительные измере-
ния, точно определить параметры состояний в по-
BΦα = ξ0αP0αGX(MGX)
GY
(MGY )P0αD (MD)EΦα +
бочных каналах. Разумеется, в реальной ситуации у
подслушивателя такой возможности нет, и парамет-
(175)
+ξ1α P1αGX (MGX )
GY
(MGY )P1αD (MD),
ры состояний в побочных каналах также подверже-
ны флуктуациям за счет конечной длины последо-
вательностей. Такие флуктуации также могут быть
AΘα = ξ1αP0αGX(MGX)
GY
(MGY )P1αD (MD) +
учтены способом, который использовался для оцен-
ки параметров выше. Для того чтобы не загромож-
+ξ0α P1αGX (MGX )
GY
(MGY )P0αD (MD)EΘα,
(176)
дать изложение излишними выкладками, будем счи-
тать, что параметры состояний в побочных каналах
известны точно.
BΘα = ξ1αP0αGX(MGX)
GY
(MGY )P1αD (MD)EΘα +
Вычисление условной сглаженной min-энтропии
для однофотонной компоненты состояний после пер-
+ξ0α P1αGX (MGX )
GY
(MGY )P0αD (MD),
(177)
вого и второго усечений дает
358
ЖЭТФ, том 160, вып. 3 (9), 2021
Побочные каналы утечки информации в квантовой криптографии.. .
(
)
(ρXE )⊗nμ | (ρE )⊗nμ
≥
Далее,
in
∑
∑
∑[
{
(
)
≥nαμ
h(ξ0) + [H(PαGX ) + H(PαGY ) + H(PαD)] -
h(Φα) = -
Λ+Φα log
Λ+Φα
+
[
]}
MGX MGY MD
-
(1 - (Qα1)+)h(Φα) + (Qα1)+h(Θα)
-
(
)]
-
+ Λ
log
Λ-Φα
,
(183)
√
Φα
(
)
1
- const nαμ log
,
(180)
εΩ2
∑
∑∑[
(
)
h(Θα) = -
Λ+Θα log
Λ+Θα
+
где
MGX MGY M
D
∑[
(
)]
H(PαGX ) = -
+ Λ-Θα log
Λ-Θα
(184)
[ξα0(1-Qα)+ξα1Qα]P0αGX (M) ×
M
(
)
и в (180)-(184) используются оценки параметров из
(140)-(143).
× log P0αGX (M)
+ [ξα1 (1-Qα)+ξα0 Qα]P1αGX (M) ×
Для утечки информации при коррекции ошибок
(
)]
в шенноновском пределе получаем
,
(181)
× log P1αGX (M)
leakα ≤ Nαμh((Qtot,αμ)+) +
H(PαGY,D) =
√
(
)
1
∑[
(
)
+ const Nαμ log
(185)
=-
ξα0P0αGY,D(M)log
GY,D
(M)
+
εΩ2
M
(
)]
Наконец, для оценки длины εΩ-секретного ключа в
+ ξα1P1αGY,D(M)log
GY,D
(M)
(182)
двух базисах получаем
{
}
{
√
(
)}
∑
(
)
∑
1
HεΩ1+εΩ2
(ρXE )⊗nμ | (ρE )⊗nμ
-
Nαμh((Qtot,αμ)+)-const Nαμ log
-
ℓεΩΣ≥min
min
x∈[0,1]
εΩ2
α=+,×
α=+,×
{
(
)
1
∑{
- log
= nαμ min
h(ξ0)+ [H(PαGX )+H(PαGY ) +
εcorr
x∈[0,1]
α=+,×
}
{
√
(
)}
[
]}
∑
1
+ H(PαD)]-
(1-(Qα1)+)h(Φα)+(Qα1)+h(Θα)
-
Nαμh((Qtot,αμ)+)-const Nαμ log
-
εΩ2
α=+,×
(
)
1
- log
,
(186)
εcorr
где Nαμ — общее число зарегистрированных посылок
каналов утечки и конечной длины последователь-
в базисе α, nαμ — число однофотонных посылок в ба-
ности. Для того чтобы не загромождать изложение,
зисе α, εcorr = 1/2M — параметр корректности при
примем в расчет только утечку информации при
исправлении ошибок, M — число раундов провер-
детектировании излучения передающей аппаратуры
ки по идентичности очищенных ключей. В форму-
Алисы. Для примера будем считать, что побочное
ле (186) считается, что проверка корректности клю-
излучение подчиняется пуассоновской статистике по
чей — равенства очищенных ключей Алисы и Боба
числу фотонов k, т. е. функция распределения при
после исправления ошибок проводится совместно в
приготовлении 0 и 1 на передающей стороне имеет
двух базисах.
вид
Для иллюстрации разработанного метода приве-
Mk0
Mk1
дем зависимости длины секретного ключа от дли-
P0GX(k) = e-M0
,
P1GX(k) = e-M1
(187)
k!
k!
ны линии связи с учетом всех факторов: неоднофо-
тонности информационных состояний, различных
Для простоты считаем, что функции распределения
квантовых эффективностей детекторов, побочных
в (187) не зависят от базиса.
359
С. Н. Молотков
ЖЭТФ, том 160, вып. 3 (9), 2021
Рис. 7. Зависимости длины секретного ключа от длины
Рис. 6. Зависимости длины секретного ключа от длины
линии связи. Параметры для кривых: кривая 1 — кванто-
линии связи. Параметры для кривых (общие): квантовые
вые эффективности детекторов η0 = η1 = 0.15, M0 = 0.2,
эффективности детекторов ξ0 = ξ1 (η0 = η1 = 0.15), сред-
нее число в информационных состояниях μ = 0.5, в со-
M1 = 0.4; кривая 2 — η0 = 0.1, η1 = 0.15, M0 = 0.2,
M1 = 0.4; кривая 3 — η0 = η1 = 0.15, M0 = 0.2, M1 = 0.6.
стояниях ловушках ν1 = 0.32, ν2 = 0, вероятность темно-
Вероятность темновых шумов одинакова для двух детек-
вых шумов для обоих детекторов pd = 10-6 отсч./строб.
Для кривой 1 оценка параметров по наблюдаемым прово-
торов pd = 10-6, μ = 0.5, ν1 = 0.32, ν2 = 0. Удельные
потери в волоконной линии 0.2 дБ/км. Длина последо-
дилась с помощью однородной оценки (134), для кривой
вательности при оценке вероятностей n = 106 для всех
2 — с помощью неоднородной оценки (136). Длина после-
кривых, использовалась неоднородная оценка вероятнос-
довательности n, используемой для оценок параметров,
тей (136). При вычислениях использовалась минимизация
n = 1010 (1), 106 (2), параметры секретности ε1 = ε2 =
длины секретного ключа с учетом конечных последова-
= 10-9 общие для обеих кривых. Среднее число фотонов
тельностей и побочных каналов утечки информации
в состояниях (см. формулу (187)) в побочном канале вы-
брано равным M0 = M1 = 0.2
дя из этого, можно получить степень экранирова-
Как видно из сравнения кривых 1 и 2 на рис. 6,
ния аппаратуры, при которой гарантируется такой
дальность секретного распределения ключей суще-
уровень интенсивности побочного излучения. Кро-
ственно зависит от точности оценки истинных ве-
ме того, при длинах последовательностей n ≈ 106,
роятностей. При однородной оценке вероятностей
используемых для оценки вероятностей, длина сек-
длина последовательности n, по которой проводит-
ретного ключа практически выходит на асимптоти-
ся оценка, на несколько порядков превосходит длину
ческую зависимость (n → ∞). Различие квантовых
последовательности при неоднородной оценке.
эффективностей детекторов на 10-15 % также не яв-
Строго говоря, при оценке вероятностей по на-
ляется критичным для длины секретного ключа.
блюдаемым частотам отсчетов требуется однород-
ная оценка, однако на практике почти все системы
используют нестрогую неоднородную оценку веро-
15. ПРЕДЕЛЬНЫЕ СЛУЧАИ
ятностей.
На рис. 7 приведены зависимости длины секрет-
Интересно рассмотреть некоторые предельные
ного ключа от длины линии связи. Минимизация
случаи, которые позволят оценить характерные ве-
длины секретного ключа проводилась с использова-
личины параметров состояний в побочных каналах,
нием неоднородной оценки вероятностей по наблю-
при которых еще возможно секретное распределе-
даемым частотам. При среднем числе фотонов в по-
ние ключей. Такие оценки необходимы при экспери-
бочном канале, связанным с излучением передаю-
ментальной реализации систем, например, они поз-
щей аппаратуры, не превышающем нескольких де-
воляют оценить требуемые потери в оптических изо-
сятых, влияние утечки по данному каналу на длину
ляторах, ограничивающих мощность выходного зон-
секретного ключа является несущественным. Исхо-
дирующего излучения.
360
ЖЭТФ, том 160, вып. 3 (9), 2021
Побочные каналы утечки информации в квантовой криптографии.. .
15.1. Зондирование фазового модулятора
Максимально достижимая классическая информа-
Алисы
ция (192) совпадает с пропускной способностью
идеального классически-квантового канала связи с
Первый пример — активное зондирование фазо-
входными состояниями (193) и достигается на кол-
вого модулятора. Пусть выходное зондирующее из-
лективных измерениях [31].
лучение представляет собой когерентное состояние.
В (192) введено обозначение для перекрытия от-
Кодирование битов ключа происходит приложени-
раженных состояний:
ем импульсов напряжения на фазовый модулятор.
При приложении напряжения на фазовый модуля-
ε = |PM〈ψ0|ψ1〉PM| = |〈αS| - αS〉| = e-2μS.
тор происходит изменение фазы отраженного зон-
дирующего состояния. В пользу подслушивателя бу-
Оценка длины секретного ключа в пересчете на од-
дем считать, что фаза зондирующего когерентного
ну зарегистрированную посылку дает
состояния при двух состояниях фазового модулято-
ра, отвечающих кодированию 0 и 1, изменяется на
ℓPM = 1 - χ(EPM ).
(194)
максимально возможную величину π, что соответ-
ствует максимальной различимости отраженных со-
Для выяснения критической мощности отраженно-
стояний.
го зондирующего состояниями от фазового модуля-
В целях иллюстрации считаем, что отраженные
тора приведем зависимости длины секретного клю-
состояния, отвечающие 0 и 1, одинаковы в разных
ча от среднего числа фотонов в отраженном коге-
базисах. В этом случае подслушиватель будет иметь
рентном состоянии (рис. 8a). Как следует из рис. 8a,
в своем распоряжении одно из двух состояний (ин-
при среднем числе фотонов μS ≈ 1 секретное рас-
декс базиса опускаем):
пределение ключей оказывается уже невозможным,
длина секретного ключа ℓPM → 0 без вторжений в
|ψ0〉PM = |αS 〉PM ,
|ψ1〉PM = | - αS 〉PM ,
(188)
квантовый канал связи. Таким образом, для обеспе-
μS = |αS|2,
чения секретности ключа требуется уровень отра-
где μS — среднее число фотонов в отраженном зон-
женного зондирующего излучения μS ≪ 0.1 фото-
дирующем когерентном состоянии, индекс «S» от-
на. Это достигается асимметричными оптическими
вечает за побочный канал утечки информации (Side
изоляторами.
Channel).
Матрица плотности с учетом зондирования толь-
ко фазового модулятора Алисы имеет вид
15.2. Регистрация back-flash-излучения
детекторов
1
ρXPM =
{|0〉XX 〈0| ⊗ |ψ0〉PMPM 〈ψ0| +
2
Рассмотрим предельный случай, когда подслу-
+ |1〉XX 〈1| ⊗ |ψ1〉PMPM 〈ψ1|} ,
(189)
шиватель измеряет только побочное back-flash-из-
соответственно, матрица плотности Евы имеет вид
лучение лавинных детекторов. Для простоты будем
считать, что обратное переизлучение не зависит от
1
ρPM =
{|ψ0〉PMPM 〈ψ0| + |ψ1〉PMPM 〈ψ1|} .
(190)
базиса.
2
Матрица плотности Алиса-Ева с учетом толь-
Условная энтропия, отнесенная к одной посылке,
ко переизлучения детекторов на приемной станции
принимает вид
имеет вид
H(ρXPM |ρPM ) = 1 - χ(EPM ),
(191)
1
{
}
ρXED =
|0〉XX 〈0| ⊗ ρ0D + |1〉XX 〈1| ⊗ ρ1D
(195)
где
2
)
1-ϵ
(1-ϵ
Частичная матрица плотности
χ(EPM ) = -
log
-
2
2
)
1
{
}
1+ϵ
(1+ϵ
ρED =
ρ0D + ρ1D
(196)
-
log
(192)
2
2
2
Подслушиватель имеет дело с квантовым ансамблем
— величина Холево для квантового ансамбля
{
}
}
1
1
{1
1
EPM =
|ψ0〉PM ,
|ψ1〉PM
(193)
ED =
,ρ0D;
,ρ1
D
2
2
2
2
361
С. Н. Молотков
ЖЭТФ, том 160, вып. 3 (9), 2021
Рис. 8. Зависимости длины секретного ключа: а) от среднего числа фотонов μS в отраженном от фазового модулято-
ра зондирующем излучении; б) от среднего числа фотонов при детектировании переизлучения детекторов на приемной
стороне; в) от среднего числа фотонов при детектировании излучения передающей и приемной аппаратуры. Параметр
σ = 2 (1), 5 (2), 10 (3), 20 (4). Дисперсии состояний в (204) для всех кривых рис. б,в выбраны одинаковыми при
регистрации 0 и 1
Для подслушивателя возникает ситуация идеально-
Учитывая, что
го квантово-классического канала побочного кана-
ла. Цель подслушивателя, имея в своем распоряже-
H(ρXED|ρED) = 1 - χ(ED),
(201)
нии квантовые состояния в побочном канале, ассо-
окончательно для величины Холево получаем
циированные с классическими значениями битов 0
и 1, узнать классические биты посредством измере-
{
(
)
∑
1
2P0D(M)
ний квантовых состояний, т.е. получить классиче-
χ(ED) =
P0D(M)log
+
2
P0D(M)+P1D(M)
скую информацию из квантовых состояний. Макси-
M =0
мум классической информации, которую можно по-
(
)}
2P1D(M)
лучить из квантового ансамбля ED, дается фунда-
+ P1D(M)log
,
(202)
P0D(M) + P1D(M)
ментальной величиной Холево [31-33]. Для инфор-
мации Холево (см. [33]) получаем
здесь P0D(M), P1D(M) — функции распределения
1
1
числа фотонов обратного переизлучения лавинных
χ(ED) = H (ρD) -
H(ρ0D) -
H (ρ1D),
(197)
2
2
детекторов при регистрации соответственно 0 и 1.
Напомним, что подслушиватель при детектиро-
где матрицы плотности берутся из (195), (196),
вании обратного побочного переизлучения детекто-
ρ0D + ρ1D
ров в линию связи не производит ошибок на прием-
ρD =
(198)
2
ной стороне, leak = 0.
Для оценки длины секретного ключа находим
Вычисляя энтропии в (197), получаем
ℓD = 1 - χ(ED).
(203)
∑
P0D(M) + P1D(M)
H (ρD) = -
×
2
Отметим, что число состояний, локализованных во
M =0
)
временном окне T каждого такта посылки информа-
(P0D(M) + P1D(M)
(1)
ционных состояний N (слагаемое log (1/N) в (199),
× log
- log
,
(199)
2
N
(200)), при вычислении условной энтропии сокра-
щается. На рис. 8б представлены зависимости дли-
ны секретного ключа, если подслушиватель измеря-
∑
H(ρ0,1D) = -
P0,1D(M)log(P0,1D(M))-
ет переизлучение лавинных детекторов. Для иллю-
M =0
страции считаем, что распределение по числу фото-
(1)
нов при регистрации детектором 0 и 1 имеет гаус-
- log
(200)
N
совский вид:
362
ЖЭТФ, том 160, вып. 3 (9), 2021
Побочные каналы утечки информации в квантовой криптографии.. .
(
)
1
(M - M0)2
Матрица плотности только с учетом побочного
P0D(M) =
√
exp
-
,
2πσ0
2σ2
излучения от аппаратуры Алисы и Боба имеет вид
0
(
)
(204)
2
1
(M - M1)
(считаем для простоты, что излучение не зависит от
P1D(M) =
√
exp
-
2σ2
базиса, поэтому индекс базиса опускаем)
2πσ1
1
Различимость состояний ρ0D и ρ1D в побочном ка-
1
{
|0〉XX 〈0| ⊗ ρ0G
⊗ρ0
+
нале зависит от среднего числа фотонов M0,1 и дис-
ρXEGXGY =
X
GY
2
}
персий σ0,1, определяющих перекрытие состояний.
+ |1〉XX 〈1| ⊗ ρ1G
⊗ρ1
(205)
X
GY
На рис. 8б приведены зависимости длины секретно-
го ключа при различных средних числах фотонов и
Частичная матрица плотности Евы
перекрытиях состояний.
1
{
}
Как следует из рис. 8б, даже при достаточно
ρ0G
⊗ρ0G
+ρ1G
⊗ρ1
(206)
ρEGXGY =
X
Y
X
GY
2
большом среднем числе фотонов в переизлученном
состоянии при перекрытии (дисперсии) состояний,
Для оценки длины секретного ключа получаем
различимость состояний оказывается малой. Как
(207)
ℓG = H(ρXGXGY ) - H(ρGXGY ) = 1 - χ(EG),
показывает опыт, если характеристики спектра пе-
реизлучения лавинных детекторов из одной серии
мало отличаются друг от друга, то данный побоч-
χ(EG) = H(ρ
)-
XGXGY
ный канал не является столь критичным.
1
[
]
0
-
H(ρ
⊗ρ0G
) + H(ρ1G
⊗ρ1
)
,
(208)
G
X
Y
X
GY
2
15.3. Детектирование побочного излучения
где величина Холево для ансамбля EG
от передающей и приемной аппаратуры
1
{
}
Рассмотрим последний частный пример, когда
ρ0G
⊗ρ0G
+ρ1G
⊗ρ1
(209)
ρGXGY=
X
Y
X
G
Y
2
подслушиватель может одновременно детектиро-
вать побочное излучение аппаратуры Алисы и Боба. Вычисление энтропий дает
∑
∑P0G
(Mx)P0G
(My) + P1G
(Mx)P1G
(My)
X
Y
X
Y
χ(EG) = -
×
2
Mx=0 My=0
)
(P0
(Mx)P0G
(My) + P1G
(Mx)P1G
(My)
1
∑
[(
Y
X
Y
× logGX
+
P0G
(M) log(P0 (M)) +G
X
X
2
2
M =0
)
(
)]
+ P1G
(M) log(P1G
(M))
+
P0G
(M) log(P0G
(M)) + P1G
(M) log(P1 (M))
(210)
X
X
Y
Y
Y
GY
Для длины ключа получаем (напомним, что под-
На рис.
8в для иллюстрации приведены ре-
слушиватель в этом случае не производит ошибок,
зультаты расчетов длины секретного ключа (211)
leak = 0)
при совместных коллективных измерениях побочно-
го излучения передающей и приемной аппаратуры.
ℓG = 1 - χ(EG).
(211)
Функции распределения по числу фотонов (210) вы-
браны гауссовскими, аналогично (204). Как видно
Максимум величины (210) достигается на сов-
из сравнения рис. 8б и 8в, появление еще одного по-
местных коллективных измерениях побочного излу-
бочного канала уменьшает длину секретного ключа.
чения передающей и приемной аппаратуры, что на-
Длина ключа зависит от среднего числа фотонов
ходится за пределами современных технологий. Од-
в состояниях, отвечающих приготовлению и реги-
страции 0 и 1, и дисперсии состояний. Длина ключа
нако знание данной границы является принципиаль-
но важным для понимания, поскольку данная гра-
обращается в нуль, когда среднее число фотонов и
дисперсия оказываются одного порядка величины.
ница является фундаментальной верхней границей
информации, которую позволяет получить Приро-
В отсутствие других каналов утечки данный факт
интуитивно понятен. Однако в общем случае, когда
да при измерении квантовых состояний в побочном
канале утечки информации.
имеется несколько побочных каналов утечки, а так-
363
С. Н. Молотков
ЖЭТФ, том 160, вып. 3 (9), 2021
же вторжение в квантовый канал, и подслушиватель
асимметричных оптических изоляторов и т. д. При
использует совместные коллективные измерения во
известной верхней границе интенсивности состоя-
всех каналах, ситуация не столь очевидна.
ний существует фундаментальная верхняя граница
информации, которая может быть получена при са-
мых общих измерениях над квантовым ансамблем
16. ОБСУЖДЕНИЕ РЕЗУЛЬТАТОВ
состояний в побочных каналах. Как было видно из
рассмотрения предельных случаев детектирования
Резюмируем полученные результаты. Разрабо-
только побочного излучения, данная фундаменталь-
тан метод, который позволяет учесть конструк-
ная граница является границей Холево [31-33].
тивным образом все неидеальности реальных си-
стем квантовой криптографии: нестрогую однофо-
Благодарности. Выражаем благодарность кол-
тонность информационных состояний, неидеальную
легам по Академии криптографии Российской Фе-
и разную квантовую эффективность детекторов,
дерации за обсуждения и поддержку, а также
различные побочные каналы утечки информации и
И. М. Арбекову и С. П. Кулику за многочисленные
конечные передаваемые последовательности.
интересные обсуждения и замечания, позволившие
Результат, который получен в работе, в отли-
улучшить изложение.
чие от многочисленных работ, где рассматривались
отдельные разрозненные каналы утечки информа-
ции, состоит в том, что c использованием предло-
ЛИТЕРАТУРА
женного метода дано доказательство секретности
1.
C. H. Bennett and G. Brassard, in Proc. IEEE Int.
ключей, которое позволяет определить максималь-
Conf. on Comp., Sys. and Signal Process., Bangalore,
но возможную длину секретного ключа при задан-
India (1984), pp. 175-179.
ных экспериментально наблюдаемых на приемной
стороне величинах, а также состояниях в побочных
2.
P. Smulders, Computers & Security 9, 53 (1990).
каналах утечки информации. Определение макси-
3.
M. G. Kuhn, Technical Report, Cambridge Univ.,
мально возможной длины секретного ключа прово-
UCAM-CL-TR-577, ISSN 1476-2986, Number 577
дится минимизацией всего лишь по одному пара-
(2003).
метру, при этом совместно учитываются все каналы
4.
R. Renner, PhD thesis, ETH Zürich (2005); arXiv/
утечки информации.
quant-ph:0512258.
В заключение во избежание недоразумений от-
метим следующее. Не нужно думать, что учет по-
5.
M. Tomamichel, Ch. Ci Wen Lim, N. Gisin, and
бочных каналов утечки информации переводит сис-
R. Renner, arXiv:1103.4130 v2; Nature Commun. 3,
темы квантовой криптографии из разряда крипто-
1 (2012).
графических систем, где секретность ключей гаран-
6.
C.-H. F. Fung, K. Tamaki, B. Qi, H.-K.Lo, and
тируется фундаментальными законами квантовой
X. Ma, Quant. Inf. Comput. 9, 131 (2009).
механики, в разряд систем, где секретность гаран-
7.
С. Н. Молотков, ЖЭТФ 157, 963 (2020).
тируется техническими ограничениями. Даже при
наличии побочных каналов утечки информации сек-
8.
С. Н. Молотков, ЖЭТФ 158, 1011 (2020).
ретность ключей по-прежнему гарантируется фун-
9.
H. P. Yuen, Phys. Rev. A
82,
062304
(2010);
даментальными ограничениями квантовой механи-
H. P. Yuen, arXiv:1109.1051 [quant-ph]; H. P. Yuen,
ки на различимость состояний.
arXiv:1109.2675 [quant-ph]; H. P. Yuen, arXiv:1109.
Среднее число фотонов в информационных ква-
1066 [quant-ph].
зиоднофотонных состояниях, выходящих из пере-
дающей станции, также достигается техническими
10.
R. Renner, arXiv:1209.2423 [quant-ph].
средствами — ослаблением до нужного уровня ис-
11.
И. М. Арбеков, С. Н. Молотков, ЖЭТФ 152, 62
ходного сигнала. При заданном уровне сигналов их
(2017).
максимально допустимая различимость диктуется
12.
J. L. Carter and M. N. Wegman, J. Comp. System
квантовой механикой. Точно так же и для состояний
Sci. 18, 143 (1979).
в побочных каналах. Верхняя граница интенсив-
ности состояний в побочных каналах достигается
13.
K. Kraus, States, Effects and Operations: Funda-
техническими средствами при реализации систе-
mental Notions of Quantum Theory, Springer Verlag
мы — экранированием аппаратуры, использованием
(1983).
364
ЖЭТФ, том 160, вып. 3 (9), 2021
Побочные каналы утечки информации в квантовой криптографии.. .
14. W. F. Stinespring, Proc. Amer. Math. Soc. (1955),
24. M. Pereira, M. Curty, and K. Tamaki, Nature Parther
pp. 211-216.
Journals, Quant. Inf. 62, 1 (2019).
15. С. Н. Молотков, ЖЭТФ 153, 895 (2018).
25. W. Wang, K. Tamaki, and M. Curty, New J. Phys.
20, 083027 (2018).
16. S. N. Molotkov, Laser Phys. Lett. 18, 045202 (2021).
26. R. M. Wood, Laser-Induced Damage of Optical Ma-
17. P. Shor and J. Preskill, Phys. Rev. Lett. 85, 441
terials, Taylor & Francis (2003).
(2000).
27. H. J. Landau and H. O. Pollak, Bell Syst. Techn. J.
18. S. Bouceron, G. Lugosi, and P. Massart, Con-
40, 65 (1961).
centration Inequalities. A Nonasymptotic Theory of
Independence, Clarendon Press, Oxford (2012).
28. D. Slepian and H. O. Pollak, Bell Syst. Techn. J. 40,
43 (1961).
19. Won-Young Hwang, arXiv[quant-ph]:0211153.
29. W. H. J. Fuchs, J. Math. Anal. Appl. 9, 317 (1964).
20. Xiang-Bin Wang, Phys. Rev. Lett. 94, 230503 (2005).
30. Л. Д. Ландау, Е. М. Лифшиц, Статистическая
21. Hoi-Kwong Lo, Xiongfeng Ma, and Kai Chen, Phys.
физика, т. V, ч. I, Наука, Москва (1995).
Rev. Lett. 94, 230504 (2005).
31. A. S. Holevo, Probl. Inf. Transm. 9, 177 (1973).
22. Xiongfeng Ma, Bing Qi, Yi Zhao, and Hoi-Kwong Lo,
arXiv[quant-ph]:0503005.
32. А. С. Холево, УМН 53, 193 (1998).
23. K. Tamaki, M. Curty, and M. Lucamarini, New J.
33. А. С. Холево, Квантовые системы, каналы, ин-
Phys. 18, 065008 (2016).
формация, МЦНМО, Москва (2010).
365