ЖЭТФ, 2021, том 160, вып. 3 (9), стр. 372-392
© 2021
О РЕАКЦИИ РАЗВАЛА В ТРЕХЧАСТИЧНЫХ КУЛОНОВСКИХ
СИСТЕМАХ С ПРИЛОЖЕНИЕМ К ОПИСАНИЮ ПРОЦЕССОВ
ДИССОЦИАТИВНОЙ РЕКОМБИНАЦИИ И ПЕРЕЗАРЯДКИ
В АНТИПРОТОННОЙ ФИЗИКЕ
А. М. Будылинa, Я. Ю. Коптеловa,b, С. Б. Левинa*
a Физический факультет, Санкт-Петербургский государственный университет
199034, Санкт-Петербург, Россия
b Санкт-Петербургский электротехнический университет «ЛЭТИ» им. В. И. Ленина
197376, Санкт-Петербург, Россия
Поступила в редакцию 23 марта 2021 г.,
после переработки 23 мая 2021 г.
Принята к публикации 30 мая 2021 г.
Предлагается новый подход к описанию реакции развала в системах трех заряженных квантовых частиц
при наличии кулоновских парных потенциалов притяжения. Предполагается, что аналитическая форма
асимптотики волновой функции на бесконечности в конфигурационном пространстве является извест-
ной. При этом впервые предлагается упрощенная форма асимптотики, связанная с выделением основных
вкладов, порождаемых бесконечной совокупностью парных асимптотических каналов рассеяния. Предло-
женный подход представляется нам принципиальным для описания реакции развала в многочастичных
системах. Рассматривается возможность приложения развитого подхода для описания процессов диссо-
циативной рекомбинации и перезарядки в экспериментах по накоплению антиатомов.
DOI: 10.31857/S0044451021090042
полезен и в более общей ситуации рассеяния в си-
стеме нескольких частиц (больше трех), по крайней
мере, для двухкластерного рассеяния.
1. ВВЕДЕНИЕ
Задача трехчастичного квантового рассеяния яв-
Мы рассматриваем задачу рассеяния трех трех-
ляется одной из фундаментальных физических за-
мерных квантовых заряженных частиц при наличии
дач. Ее решение, как решение модельной задачи,
парных кулоновских потенциалов притяжения. Для
определяет протекание многих макроскопических
определенности полагаем, что парные короткодей-
процессов в физике и химии. В случае быстро убы-
ствующие потенциалы отсутствуют, хотя их акку-
вающих парных потенциалов эта задача была реше-
ратный учет не является принципиальной пробле-
на в знаменитой работе Фаддеева [1] более полуве-
мой в рамках предлагаемой нами схемы. Кроме то-
ка назад. В случае медленно (кулоновским образом)
го, мы предполагаем, что массы частиц равны, что
убывающих парных потенциалов многие существен-
также не является принципиальным ограничением
ные вопросы стационарной постановки были реше-
предлагаемого метода, а лишь позволяет избежать
ны или обсуждались в последующих работах Фад-
более громоздких вычислений. На примере такой
деева, Меркурьева [2-4] и их учеников, а также в
упрощенной задачи мы хотим продемонстрировать
огромном количестве работ, инициированных пер-
новый подход к задаче рассеяния трех заряженных
выми результатами.
квантовых частиц при энергиях выше порога раз-
Тем не менее, несмотря на существенные продви-
вала. Предлагаемый подход позволяет контролиро-
жения, достигнутые за прошедшее с тех пор время,
вать точность описания реакции развала в задаче
квантовая задача рассеяния трех заряженных час-
трех тел. Мы надеемся также, что подход окажется
тиц до сих пор оставляет ряд не решенных до конца
вопросов. Основная проблема связана с отсутстви-
* E-mail: s.levin@spbu.ru
ем так называемой асимптотической свободы час-
372
ЖЭТФ, том 160, вып. 3 (9), 2021
О реакции развала в трехчастичных кулоновских системах. ..
тиц на бесконечности. Это делает неприменимым
сматривается влияние рассеяния бесконечного чис-
(по крайней мере в исходной классической форме)
ла парных кулоновских уровней возбуждения на
подход Фаддеева, основанный на асимптотическом
структуру асимптотики решения задачи. Соответ-
разделении волновой функции на компоненты. При
ственно, остается без ответа вопрос о количестве
этом существенно усложняется структура асимпто-
парных состояний дискретного спектра, которые
тики волновой функции на бесконечности.
нужно учесть явно для достижения определенной
Другая проблема, специфичная для реакции раз-
точности вычислений.
вала кластера, находящегося в связанном кулонов-
В настоящей работе мы отвечаем на поставлен-
ском состоянии, налетающей заряженной частицей
ные выше вопросы. Мы показываем, что для описа-
связана с наличием бесконечного числа уровней воз-
ния с контролируемой точностью процессов разва-
буждения кластера и уровней перекластеризации.
ла в трехчастичной кулоновской системе невозмож-
Каждый уровень возбуждения (или перекластери-
но ограничиться лишь конечным числом парных
зации) порождает свой канал рассеяния. Чем ниже
кулоновских возбуждений. Дополнительный беско-
полная положительная энергия системы, тем более
нечный набор не учтенных явно процессов дол-
существенной при описании характеристик рассея-
жен учитываться с помощью введения некоторо-
ния становится роль парных возбуждений с высоки-
го «эффективного состояния», которое удается по-
ми значениями парного главного квантового числа.
строить явно. Детали построения описаны, напри-
Отметим, что размерность матрицы рассеяния ста-
мер, в работе [9]. Здесь отметим лишь, что эф-
новится фактически бесконечной, что существенно
фективное состояние определяется методом перева-
усложняет оценки точности при вычислении харак-
ла при анализе спектрального разложения асимп-
теристик рассеяния.
тотики собственных функций непрерывного спек-
Необходимо отметить работы [5-7], в которых
тра трехчастичного оператора в асимптотической
проблема бесконечного числа парных кулоновских
области «почти разделения переменных». Это эф-
каналов рассеяния в процессах трехчастичного раз-
фективное состояние и является обоснованной аль-
вала решается путем «дискретизации континуума»,
тернативой упомянутому выше штурмовскому бази-
т. е. введения конечного базиса для описания асимп-
су. Точность предложенных построений регулирует-
тотики решения задачи рассеяния. Несмотря на хо-
ся параметром, описывающим количество учтенных
рошее совпадение некоторых численных построений
явно уровней возбуждения парной подсистемы, и со-
с экспериментом, существенные вопросы, связанные
ответствующей областью применимости эффектив-
с таким подходом, остаются. Эти вопросы касают-
ного состояния. Мы следуем идеям дифракционного
ся оценок погрешности описания динамики заведо-
подхода в задаче рассеяния, предложенного в рабо-
мо бесконечномерной системы с помощью конечного
тах [10-12] для случая короткодействующих парных
«штурмовского базиса». Отметим, что при описании
потенциалов и одномерных частиц. На основе прин-
низкоэнергетического рассеяния такие оценки ста-
ципа локального поля, сформулированного Фоком
новятся принципиальными. Они отвечают на вопрос
в асимптотической теории дифракции [13], идеи ди-
о том, сколько уровней парных возбуждений долж-
фракционного подхода были развиты позднее для
но быть учтено явно для описания процесса развала
случая кулоновских парных потенциалов отталки-
с фиксированной точностью. Более того, возникает
вания для одномерных и трехмерных частиц в ра-
вопрос о том, можно ли в принципе ограничиться
ботах [14-17].
рассмотрением конечного числа уровней возбужде-
Отметим также, что развиваемые в работе идеи,
ния при описании процессов развала с контролируе-
на наш взгляд, сохраняют актуальность и для мно-
мой точностью в рамках квантовомеханической мо-
гочастичных (больше трех) квантовых реакций вза-
дели. А если нет, то как именно в рамках конечно-
имодействия. А именно, предложенный еще Фоком
мерной конструкции описать не учитываемое явно
метод локального поля и развитый в более позд-
бесконечное число степеней свободы системы. Фак-
них работах дифракционный подход позволяют при
тически вопрос сводится к доказательству справед-
взаимодействии сложных многочастичных кванто-
ливости штурмовского базиса или к построению его
вых систем выделять наборы эффективных состоя-
обоснованной альтернативы.
ний, заменяющих в локальных областях конфигура-
Отметим работу [8], посвященную построению
ционного пространства сложную динамику с беско-
асимптотики решения задачи рассеяния трех заря-
нечным числом степеней свободы. Выделение таких
женных кулоновских частиц, а также построению
состояний эквивалентно выделению в сложной си-
кулоновской функции Грина. Здесь также не рас-
стеме простой конечномерной модели, сохраняющей
373
А. М. Будылин, Я. Ю. Коптелов, С. Б. Левин
ЖЭТФ, том 160, вып. 3 (9), 2021
основные черты исходной системы и допускающей
кой функцией точки на пятимерной сфере единич-
стандартное решение.
ного радиуса. Уравнение будет построено на основе
В заключение мы рассматриваем приложение
многомерной формулы Грина. Идея этих построе-
развитого в работе метода к описанию процес-
ний близка, например, работе [7], однако имеет и
сов диссоциативной рекомбинации и перезарядки
свои отличительные черты. Мы обсудим разреши-
в экспериментах по проверке CPT-симметрии (за-
мость построенного уравнения.
ряд-четность-время), проводившихся в CERN в те-
Основываясь на предыдущем шаге, на следую-
чение последних нескольких лет [18].
щем этапе мы построим и решим неоднородную гра-
ничную задачу для амплитуды рассеяния 2 → 3 в
шестимерном шаре большого радиуса ρ с граничным
2. ПОСТАНОВКА ЗАДАЧИ
условием типа модифицированного условия излуче-
ния.
Будем рассматривать процессы рассеяния 2 → 2
Наконец, на третьем этапе мы восстановим все
и 2 → 3, предполагая для определенности, что в
амплитуды рассеяния 2 → 2, воспользовавшись ре-
начальном состоянии имеются заряженная частица
зультатами решения граничной задачи (амплитуда
и двухчастичный кластер в кулоновском связанном
рассеяния 2 → 3). Этот результат позволяет мо-
состоянии. Будем предполагать, что полная энергия
дифицировать свободный член в неоднородной гра-
системы допускает развал, т. е. допустимы процессы
ничной задаче, решаемой на втором шаге, и повто-
2 → 3. Будем искать решение уравнения Шрединге-
рить этапы два и три. Таким образом, мы прихо-
ра для такой трехчастичной системы, полагая, что
дим к итеративной процедуре, позволяющей уточ-
это решение обладает на бесконечности в конфигу-
нить решение с контролируемой точностью за опре-
рационном пространстве определенной асимптоти-
деленное число шагов.
кой. Нам известна структура (анзац) асимптотики,
Упомянутая выше процедура сводится к нахож-
каждый член которой отвечает некоторому процес-
дению парных амплитуд рассеяния 2 → 2, отвечаю-
су рассеяния, 2 → 2 или 2 → 3. Нам не известны
щих дискретному спектру в подсистемах, по извест-
амплитуды рассеяния (коэффициенты в этих асимп-
ным данным рассеяния на непрерывном спектре. В
тотических членах), определяемые интегральными
некотором роде такая процедура известна в теории
операторами. При этом каждая амплитуда рассе-
рассеяния как процедура «одевания».
яния однозначно определяется некоторой весовой
функцией (плотностью в структуре этих интеграль-
3. ОПИСАНИЕ МОДЕЛИ
ных операторов). Интегральные операторы по по-
строению учитывают вырождение парных связан-
3.1. Уравнение и граничные условия
ных состояний с фиксированной энергией [19], а так-
Пусть в начальном состоянии частицы в паре σ
же вырождение состояний непрерывного спектра.
находятся в связанном состоянии с главным кван-
Нашей целью является нахождение полного на-
товым числом l. Пусть H — оператор Гамильтона
бора амплитуд рассеяния, отвечающих различным
системы трех заряженных частиц:
процессам. Отметим, что для математически кор-
ректного учета бесконечного числа парных кулонов-
∑
cα
ских возбуждений в процессах 2 → 2 будет опре-
H = -Δx - Δy +
vα(xα), vα(xα) =
,
xα
делено упомянутое выше эффективное состояние,
α=1
что позволит сделать задачу рассеяния эффетив-
xα = |xα|, cα ∈ R.
но-конечномерной. Это эффективное состояние мо-
√
Пусть ρ =
x2α + y2α — гиперрадиус системы трех
жет рассматриваться как замена конструкций, опре-
частиц, (xα, yα), α = 1, 2, 3 — пары якобиевых ко-
деленных с помощью штурмовского базиса в рабо-
ординат, (kα, pα) — соответствующие им пары им-
тах [5-7]. При этом будет найдено и решение трех-
пульсов, xα, yα ∈ R3, kα, yα ∈ R3.
частичного уравнения Шредингера. Задача может
Будем искать решение уравнения Шредингера
быть решена в три этапа.
(
)
На первом этапе мы построим матричное инте-
xβ
HΨ(X, P) = EΨ(X, P), X =
,
гральное уравнение, которое свяжет полный набор
yβ
упомянутых выше плотностей, отвечающих процес-
(
)
(1)
сам 2 → 2, с амплитудой рассеяния 2 → 3. Отме-
kβ
P=
,
X, P ∈ R6
тим, что амплитуда рассеяния 2 → 3 является глад-
pβ
374
ЖЭТФ, том 160, вып. 3 (9), 2021
О реакции развала в трехчастичных кулоновских системах. ..
с асимптотикой
упрощения. В данном случае таким упрощением яв-
ляется почти разделение переменных. Подробнее об
Ψ(X, P)
∼ Ψ(0) + Ψ(02) + Ψ(03),
(2)
этом будет сказано ниже. Сейчас мы лишь отме-
X→∞
тим, что выделение различных асимптотических об-
где
ластей в конфигурационном пространстве с после-
∫
дующим упрощением решения в этих областях при-
Ψ(0) =
dP′ exp[i〈p′lσ, yσ〉 + iwlσ(yσ, plσ)] ×
ведет к возможности свести набор упрощенных ре-
S2×S2
шений в единое решение во всем пространстве. Эти
рассуждения, как уже было сказано выше, основаны
× ϕlσ(xσ, k′lσ)a0lσ(P,
P′),
на принципе локального поля, сформулированном
∑
и использованном Фоком в асимптотической теории
Ψ(02) =
Ψ(02)α, Ψ(02)α =
дифракции [13].
α=1
В данной задаче мы принимаем во внимание, что
∫
∑
(3)
лишь две парные подсистемы в произвольной систе-
=
dP′ exp[i〈p′jα, yα〉+iwjα(yα, pjα)] ×
ме трех заряженных частиц могут порождать двух-
j=1
S2×S2
частичные связанные состояния. Вклад в асимп-
×ϕjα(xα,k′jα)ajα(P,
P′),
тотику вносит также расходящаяся шестимерная
√
сферическая волна с гладкой амплитудой (процесс
EX + iW0(X, P)]
Ψ(03) →A(X, P)exp[i
2 → 3, третье слагаемое Ψ(03) в (2)), а, кроме того,
w
X5/2
и начальное состояние, вклад которого отражен в
Здесь введены обозначения
первом слагаемом Ψ(0) в формуле (2).
Приведем использованные обозначения. Функ-
k
p
k≡
dP ≡ dkdp,
,
p≡
ция
k
p
(
)
В дальнейшем символ «шляпка» также будет ис-
|cα|
ϕnα(xα,k′
) = exp
-xα
×
nα
пользоваться для обозначения единичного вектора.
2n
(
)
Асимптотика (2) в слабом смысле определяет
|cα|xα
×Ln-1
(1 - 〈k′nα, xα〉)
,
структуру решения задачи рассеяния. Необходимо
2n
отметить, что структура расходящейся волны Ψ(03)
должна быть модифицирована в областях, опреде-
где Ln — полиномы Лагерра, а 〈k′nα, x〉 обозначает
k′
ляемых условиями xα < yνα, 0 < ν < 1, α = 1, 2, 3.
скалярное произведение векторов
nα
и x, описыва-
Структура искаженных плоских волн (частью сла-
ет двухчастичное кулоновское связанное состояние
бой асимптотики которых является выражение для
с главным квантовым числом n в паре α с энергией
Ψ(03)) с учетом модификации подробно описана в
κn = -c2n/4n2 в следующем смысле.
работах [15,17,20]. В работе [17] показано, что такая
Как показано в Приложении, такая функция иг-
модификация сводится к аналитической замене
рает роль производящей функции в разложении ви-
да Ψ(02), а само разложение может рассматривать-
∇kαψc(xα, kα)
xα → -i
,
(4)
ся как набор производящих интегралов. Согласно
ψc(xα, kα)
уравнению (74) Приложения, интегрирование функ-
ции ϕnα(xα,k′nα) по dk′nα c некоторой гладкой функ-
где функция ψc(xα, kα) является решением уравне-
цией an, заданной на единичной сфере S2ˆ
, пред-
ния Шредингера в парной подсистеме. Такую моди-
k′nα
фикацию в дальнейшем мы и будем иметь в виду.
ставляет собой суперпозицию всех возможных двух-
частичных кулоновских состояний с квантовыми
числами (n, l, m) при фиксированном главном кван-
3.2. Обсуждение структуры анзаца
товом числе n. Структура коэффициентов в такой
Отметим, что асимптотика (2) содержит разло-
суперпозиции n2 слагаемых полностью определяет-
жение по всевозможным парным состояниям, до-
ся структурой функции an.
пустимым в данной реакции рассеяния (процессы
Именно в этом смысле Ψ(02) является спек-
2 → 2, второе слагаемое Ψ(02) в (2)). Такие разло-
тральным разложением трехчастичных собствен-
жения допустимы в тех асимптотических областях
ных функций непрерывного спектра по полному на-
конфигурационного пространства, в которых исход-
бору состояний двухчастичных подсистем. Асимп-
ный оператор Шредингера допускает определенные
тотические области конфигурационного простран-
375
А. М. Будылин, Я. Ю. Коптелов, С. Б. Левин
ЖЭТФ, том 160, вып. 3 (9), 2021
ства, в которых такие разложения применимы, по-
Мы используем также следующие обозначения.
дробно обсуждались в работе [19]. Ранее они исполь-
Импульс p′nα
=
√E - κn p′nα, интегрирование
зовались в [2].
ведется по dP′
= dk′nαdp′nα. Фазовые функции
Более точно, каждое кулоновское парное свя-
wnα(yα, pnα) и W0(X, P) определены следующим
занное состояние с главным квантовым числом n
образом:
имеет вырождение кратности n2, каждый асимпто-
ceffα
тический канал рассеяния вырожден также по на-
wnα(yα, pnα) = -
ln yα,
2pnα
правлению импульса pnα. Это совокупное вырож-
(
)
дение отражено в интегрировании по dP′ по «че-
∑
X
cα
тырехмерной сфере» S2 × S2 с неизвестной плотно-
W0(X, P) = -
√
ln X.
2
xα
E α=1
стью anα(P,
P′). Отметим, что нахождение полного
набора плотностей anα в совокупности с амплиту-
Еще раз отметим, что функция W0 в асимптотичес-
дой трехчастичного развала системы определяет, в
ких областях, в которых одна из парных координат
смысле сказанного выше, полный набор амплитуд
Якоби xα становится существенно меньше других,
рассеяния и, тем самым, решает задачу. Еще раз
должна быть модифицирована в соответствии с ре-
подчеркнем, что нахождение такого полного набора
зультатами работ [17, 20]. Выражение для ceffα в об-
амплитуд или, точнее, эквивалентного ему набора и
щей ситуации имеет вид
является целью данной работы.
cβ
cγ
ceffα =
+
Предложенный нами анзац не является вполне
|ωβα|
|ωγα|
стандартным в следующем смысле. Во-первых, па-
Здесь {α, β, γ} — четная перестановка номеров пар-
дающая волна Ψ(0) задается плотностью a0lσ. В
ных подсистем. Коэффициенты ωαβ являются ко-
смысле обсуждавшегося выше эта функция зада-
эффициентами матрицы преобразования координат
ет начальное состояние кластера с главным кван-
Якоби,
товым числом l в паре σ. С нашей точки зрения,
xβ = σαβxα + ωαβyα.
такой «вероятностный» способ задания начального
состояния (не требующий задания фиксированного
Например, в рассматриваемом нами случае частиц
набора квантовых чисел) является наиболее есте-
равных масс при α = 1 имеем
ственным в квантовомеханической постановке зада-
√
√
1
3
1
3
чи. Очевидно, что можно подобрать и такую плот-
x2 = -
x1 +
y1, x3 = -
x1 -
y1,
2
2
2
2
ность b0lσ, которая отвечала бы именно одному фик-
сированному набору квантовых чисел.
2
ceff1 =
√
(c2 + c3).
Во-вторых, как уже обсуждалось выше, спек-
3
тральное разложение трехчастичного состояния
Отметим, что вследствие экспоненциально-
системы по набору парных состояний (слагаемое
го убывания функции ϕnα по переменной xα
Ψ(02)) содержит не только расходящиеся волны по
асимптотика решения при ρ → ∞ оказывается эк-
переменной yα (как это принято в стандартных
вивалентной асимптотике при yα → ∞ для любого
разложениях), но и сходящиеся волны. Иначе
конечного значения n.
говоря, разложение строится по набору плоских
Выражение для A(X, P) является гладкой функ-
волн, который включает в себя как расходящиеся,
цией, описывает амплитуду шестимерной расходя-
так и сходящиеся волны. Отметим, что такой выбор
щейся волны и подлежит определению. Неизвестные
разложения обусловлен, с математической точки
плотности anα(P,
P′) также подлежат определению.
зрения, полнотой набора собственных функций пар-
ного оператора Шредингера. С физической точки
3.3. Схема решения
зрения, включение в разложение сходящихся волн
обусловлено дальнодействием парных кулоновских
Ниже, воспользовавшись многомерной форму-
потенциалов. Иными словами, таким образом мы
лой Грина, определим уравнения, которые связы-
учитываем ненулевую вероятность процессов пере-
вают плотности anα(P,
P′) и трехчастичную ампли-
стройки в кулоновской системе трех тел даже на
туду A(X, P). Учитывая эти связи, мы предложим
больших расстояниях. В то же время распределе-
процедуру нахождения амплитуды A(X, P) путем
ние амплитуд в сходящихся и расходящихся волнах
решения граничной задачи в шаре большого ради-
определяется структурой плотностей anα и должно
уса ρ с граничными условиями типа модифициро-
быть найдено в процессе решения задачи.
ванного условия излучения. Решив поставленную
376
ЖЭТФ, том 160, вып. 3 (9), 2021
О реакции развала в трехчастичных кулоновских системах. ..
граничную задачу для функции A(X, P) в первом
Данное разложение представляет собой спект-
приближении, мы сможем восстановить плотности
ральное разложение решения по собственным функ-
anα(P,
P′) и, как было отмечено выше, определим
циям парной подсистемы в соответствующей об-
амплитуды также во всех парных каналах рассея-
ласти. При этом можно сказать, что выделенное
ния. Найденные амплитуды позволят скорректиро-
эффективное состояние соответствует спектральной
вать начальные данные для граничной задачи и по-
окрестности точки накопления дискретного спек-
вторить описанную процедуру. Число коррекций ре-
тра оператора Шредингера соответствующей пар-
шения определяется необходимой точностью реше-
ной подсистемы.
ния поставленной задачи.
Механизм выделения асимптотического члена
Параллельно мы определим волновую функцию
в выражении (5) связан со сложной структурой
трехчастичной системы во всем пространстве.
асимптотики функций ϕnα(xα,k′nα) (а фактиче-
Данный подход в некотором смысле связан с из-
ски — полиномов Лагерра) по совокупности боль-
вестным R-матричным подходом [21], однако несо-
ших значений переменных n и xα [22]. Более точно:
мненно имеет и свои отличительные черты. Преиму-
при увеличении xα основной вклад в полное выра-
щество данного метода заключается в том, что мы
жение (5) вносят слагаемые, отвечающие все боль-
учитываем бесконечное число парных каналов рас-
шим значениям индекса «n». Таким образом, выде-
сеяния с помощью явного выделения их совокупного
ление асимптотики функциональной суммы (5) по
вклада в асимптотику (2).
переменной xα приводит к выделению совокупного
вклада слагаемых, отвечающих большим значениям
индекса «n».
3.4. Выделение асимптотических вкладов в
Значение параметра Nα определяется структу-
структуре спектральных разложений
рой асимптотической области конфигурационного
Начнем с того, что запишем выражение (3) для
пространства, в которой используется асимптоти-
Ψα02), отвечающее набору всевозможных связанных
ка (5).
состояний в парной подсистеме α с кулоновским по-
тенциалом притяжения, следующим образом:
4. ВСПОМОГАТЕЛЬНАЯ ЗАДАЧА И
Ψ(02)α =
ПОСТРОЕНИЕ «ЭФФЕКТИВНОГО»
∫
∑
КАНАЛА РАССЕЯНИЯ
=
dP′ exp[i〈p′jα, yα〉 + iwjα(yα, pjα)] ×
j=1
S2×S2
4.1. Постановка вспомогательной задачи
× ϕjα(xα, k′jα)ajα(P,
P′) ∼
Рассмотрим теперь вспомогательную задачу о
∫
∑
распространении решения уравнения Шредингера
∼
dP′ exp[i〈p′jα, yα〉 + iwjα(yα, pjα)] ×
(1) типа искаженной шестимерной плоской волны,
j=1
S2×S2
являющейся приближенным решением в области
× ϕjα(xα, k′jα)ajα(P,
P′) +
конфигурационного пространства, где все частицы
∫
√
хорошо разделены (забегая вперед, назовем эту об-
+
dP′Ψaccc,α(X,
EP′)aaccα(P,
P′).
(5)
ласть ΩBBK ), в область, где частицы выбранной па-
S2×S2
ры α с парным кулоновским потенциалом притяже-
ния сближаются, а третья частица по-прежнему на-
На этом шаге происходит выделение из бесконеч-
ходится далеко (назовем эту область Ω+α).
ной суммы слагаемых, в которую раскладывается
На первый взгляд, такая вспомогательная зада-
решение уравнения Шредингера в соответствующей
ча (задача 3 → 3(2)) не связана с задачей рассеяния
области конфигурационного пространства1), одного
2 → 2(3), которую мы исследуем. Однако это не так
эффективного состояния, определяющего совокуп-
в следующем смысле.
ный вклад в разложение всех высоковозбужденных
Ниже показано, что в области Ω+α оператор Шре-
состояний в выделенной паре частиц с индексом α.
дингера асимптотически упрощается и допускает
Точность такого разбиения определяется величиной
почти разделение переменных. Напомним, что реше-
параметра Nα. Оценка значения этого параметра
ние типа искаженной плоской волны, так называе-
дана ниже.
мое BBK-приближение, ΨBBKc (X, P), было исследо-
1) Полный набор областей описан в следующем разделе.
вано в работе [23] (см. также [2]), хотя использова-
377
А. М. Будылин, Я. Ю. Коптелов, С. Б. Левин
ЖЭТФ, том 160, вып. 3 (9), 2021
лось и ранее. С точностью до нормировки оно имеет
теории дифракции. Этот же принцип был исполь-
вид
зован [15, 17] для системы трех трехмерных одно-
именно заряженных частиц.
ΨBBKc(X, P) ∼
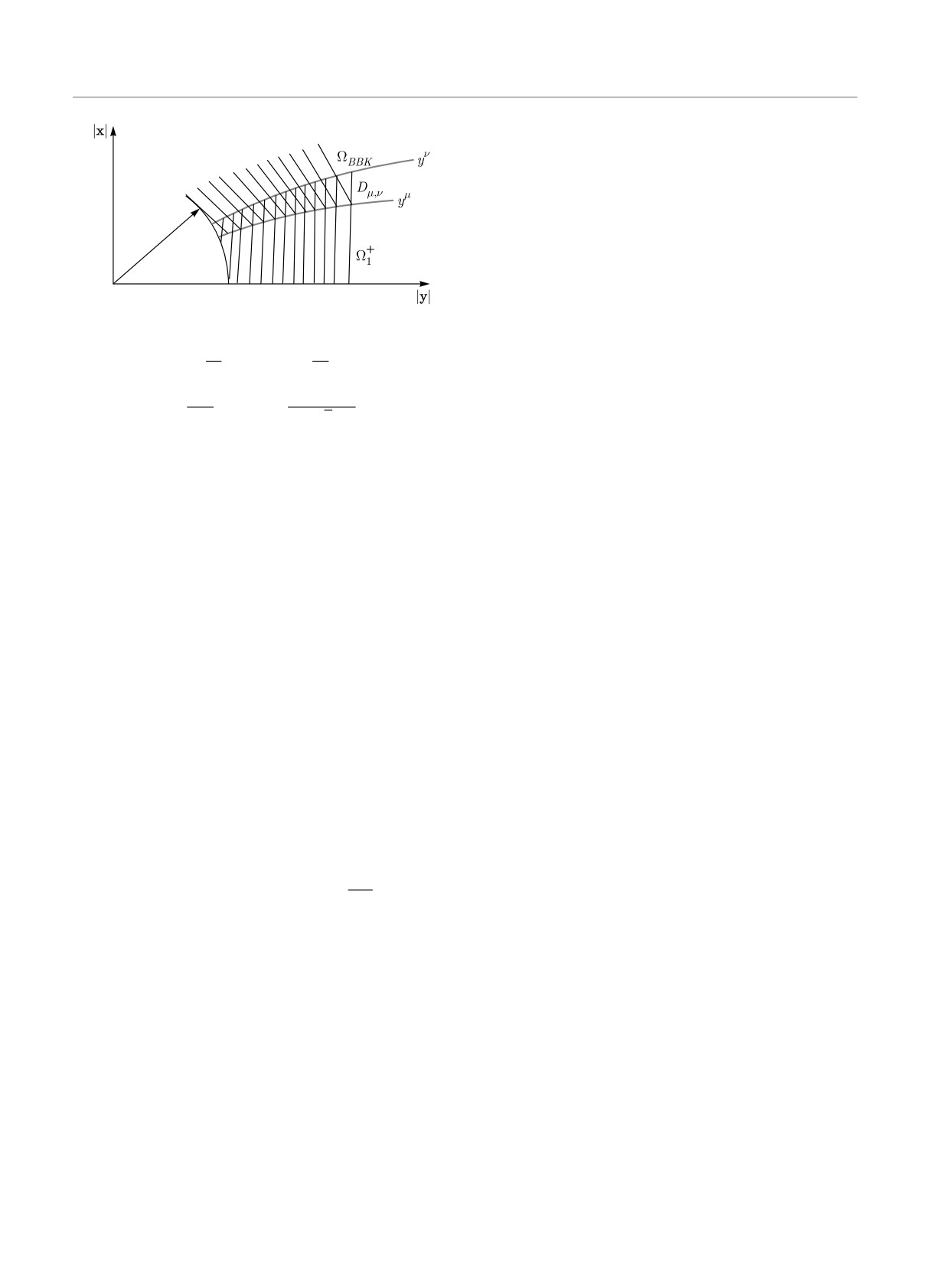
Следуя работе [15], введем набор асимптотиче-
ских областей конфигурационного пространства в
∼ ei〈X,P〉D(x1, k1)D(x2, k2)D(x3, k3).
(6)
терминах введенных выше пар координат Якоби
(xα, yα) (как и выше, индекс α = 1, 2, 3 нумерует
Здесь
парные подсистемы):
D(x, k) = Φ(-iη, 1, ixk - i〈x, k〉),
{
c
(7)
Ωα = (xα, yα), yμα < xα < yα,
x, k ∈ R3, η =
,
2k
}
1
Φ
— вырожденная гипергеометрическая функ-
< μ < 1, yα → ∞
,
(9)
2
ция [24].
В смысле сказанного выше, решение типа
3
ΩBBK =
∪
Ωα,
(10)
ΨBBKc(X, P) в пересечении областей ΩBBK и Ω+α
α=1
может быть разложено по базису собственных
функций оператора Шредингера парной подсисте-
Ω+α = {(xα, yα), xα ≤ yνα,
мы α. Главный вклад разложения по совокупности
парных высоковозбужденных (отвечающих боль-
(11)
0 < ν < 1, yα → ∞},
шим значениям главного квантового числа n)
состояний может быть отсуммирован в некоторое
{
эффективное состояние, допускающее следующее
Dαμ,ν = (xα, yα), yμα < xα < yνα,
представление:
}
1
< μ < ν < 1, yα → ∞
(12)
Ψacc
∼ U(yα,P,-xα)Λ(|cα|xα).
(8)
2
c
Функции U(yα, P, -xα) и Λ(|cα|xα) будут явно опре-
Отметим, что область ΩBBK (10) отвечает ситуации,
делены ниже.
когда все три заряженные частицы хорошо разделе-
Это эффективное состояние заменяет разложе-
ны. В этой области применимо приближенное реше-
ние искаженной шестимерной плоской волны по бес-
ние уравнения Шредингера ΨBBK , описанное, на-
конечному (n > Nα ≫ 1) вырожденному набору со-
пример, в работе [23], где, в частности, предложена
стояний двухчастичного дискретного спектра.
рекуррентная процедура улучшения точности это-
Воспользовавшись принципом локального поля,
го приближения. При этом границы параболических
мы покажем, что разложение решения задачи рассе-
областей Ωα (9) выбраны так, чтобы невязка при-
яния 3 → 3(2) типа шестимерной расходящейся вол-
ближенного решения ΨBBK в этих областях убыва-
ны с произвольной амплитудой в области Ω+α по пол-
ла быстрее кулоновского потенциала.
ному набору собственных функций парного опера-
Параболические области Ω+α (11) соответствуют
тора Шредингера также допускает выделение неко-
асимптотическим конфигурациям, в которых сум-
торого эффективного состояния. А само это состо-
ма трех парных кулоновских потенциалов допускает
яние (8) связано со структурой определенного вы-
разделение переменных с точностью до короткодей-
ше в (5) (для исходной задачи рассеяния 2 → 2(3))
ствующей поправки. При этом короткодействующая
асимптотического выражения для Ψaccc,α с помощью
поправка всюду является поправкой следующего по-
интегрального оператора. В этом и заключается ос-
рядка малости по величине 1/yα (yα ≫ 1, yα ≫ xα)
новной результат данного раздела.
к основной части потенциала, допускающей разде-
ление переменных. Область Dαμ,ν является пересече-
нием области ΩBBK и области Ω+α. Упрощенная схе-
4.2. Основные результаты, полученные ранее
ма выделения асимптотических областей при α = 1
на пути решения вспомогательной задачи
приведена на рисунке. В дальнейшем мы будем, где
Вернемся теперь к решению вспомогательной за-
это возможно, опускать индекс «α», полагая α = 1.
дачи. Для этого воспользуемся принципом локаль-
Рассмотрим теперь область Ω+1. В ней полный по-
ного поля, установленным Фоком в 1947 году и ис-
тенциал в уравнении Шредингера в старшем поряд-
пользованным им при развитии асимптотической
ке допускает следующее упрощение:
378
ЖЭТФ, том 160, вып. 3 (9), 2021
О реакции развала в трехчастичных кулоновских системах. ..
При этом весовая функция R = Rc, а k2 > 0.
Функция ψc(x, k) = ϕn(x,k) — функция дис-
кретного спектра оператора hx, определенная в
Приложении. Здесь весовая функция R = Rn, а
двухчастичный спектральный параметр k2 при-
нимает бесконечный набор дискретных значений
-c2/4n2, n = 1, 2, . . . Таким образом, условие k2 +
+p2 = E отражает закон сохранения энергии, а им-
пульсы k и p принимают все возможные допустимые
значения, определяемые структурой спектра опера-
торов hx и hy (16), (17).
)
(x
c1
Иными словами, как уже отмечалось выше, при-
V =Vsep +O
,
Vsep =
+ veff(y),
y2
x1
ближенное представление для искомого решения
(13)
eff
c
2(c2 + c3)
Ψsep уравнения Шредингера исходной задачи трех
veff =
,
ceff =
√
y
3
тел в области Ω+1 является фактически разложени-
(
)
ем по собственным функциям (спектральным разло-
При этом поправка O
x/y2
в данной области убы-
жением) оператора Шредингера парной подсистемы
вает быстрее кулоновского потенциала при y → ∞.
с индексом «1». Коэффициентами этого разложения
Скорость убывания поправки регулируется грани-
являются некоторые весовые функции Rc и Rn, не
цами области в определении (11). Таким образом, в
зависящие от координат x и y. Весовая функция
области Ω+1 уравнение Шредингера в старшем по-
Rc отвечает непрерывному спектру оператора hx, а
рядке имеет вид[
]
весовая функция Rn — дискретному спектру опе-
-Δx - Δy + v1(x) + veff (y)
Ψsep = EΨsep
(14)
ратора hx. Вырождение двухчастичного кулонов-
ского связанного состояния с фиксированным глав-
и тем самым допускает разделение переменных. Мы
обсудим ниже границы применимости такого при-
ным квантовым числом учитывается, как показано
в Приложении, с помощью интегрирования по еди-
ближения.
Представление Ψsep для решения уравнения (14)
ничной сфере S2ˆ. Детали построения функции Ψsep
k
могут быть найдены в работе [19]. Весовые функ-
с разделением переменных строится как произве-
дение решений ψc(x, k) и ψeffc (y, p) при условии
ции Rn, n ≫ 1 определяются единственным обра-
зом из условия согласования приближенного реше-
k2 + p2 = E, умноженное на произвольную весовую
ния Ψsep и приближенного решения ΨBBKc в области
функцию R импульсных переменных:
∫
∫
Dμ,ν (12), в которой оба эти приближенные решения
Ψsep(X, P) ∼ dk′ dp′ψ(x, k′)ψeffc (y, p′)×
справедливы.
R3
R3
∫
∑
4.3. Структура функции
Ψacc
× δ(k′2 + p′2 - E)Rc(P, P′) +
dk′ ×
c
n=1
S2
Как отмечалось выше, чтобы построить выраже-
∫
(
)
Ψacc
c2
ние для
, нам нужно провести процедуру согла-
1
c
× dp′ϕn(x,k′)ψeffc (y, p′)δ p′2-
-E
×
4n2
сования решения типа спектрального разложения
R3
Ψsep (5) и решения типа ΨBBKc в асимптотической
× Rn(P, p′, k′), (x, y) ∈ Ω+1 .
(15)
области Dμ,ν (при больших значениях переменной
x). Отметим, что этот шаг аналогичен процедуре на-
Здесь функции ψc(x, k) = ψ(x, k) и ψeffc (y, p) абсо-
хождения амплитуд рассеяния в спектральном раз-
лютно непрерывного спектра удовлетворяют двух-
ложении решения полной задачи рассеяния, однако
частичным кулоновским уравнениям соответствен-
не эквивалентен этой процедуре. Различие заклю-
но
чается в том, что на данном (элементарном) этапе
hxψc(x, k) = (-Δx + v1(x)) ψc(x, k) =
мы строим не полное решение задачи рассеяния, ко-
торое мы не знаем, а лишь, с определенной точно-
= k2ψc(x, k),
(16)
стью, собственную функцию непрерывного спектра
(
)
трехчастичного оператора, продолжая внутрь пара-
hyψeffc (y, p) =
-Δy + veff (y)
ψeffc (y, p) =
искаженную плоскую волну
болической области Ω+1
= p2ψeffc(y, p).
(17)
ΨBBKc. Для нахождения коэффициентов разложе-
379
А. М. Будылин, Я. Ю. Коптелов, С. Б. Левин
ЖЭТФ, том 160, вып. 3 (9), 2021
(
)ib
ния Rn в выражении для Ψsep мы приравниваем в
ϖ(in)(P)0
p
Rn(P, t, ϕ,k′) =
t-
√
×
области Dμ,ν представления ΨBBKc и Ψsep:
n3(B2 lnn + B1)
E +
(out)
ϖ0
(P)
Ψsep|Dμ,ν ∼ ΨBBKc|Dμ,ν .
(18)
× ce2l(ϕ, s)Zin(P, k′) +
×
n3(B2 lnn + B1)
(
)ib
Фактически мы согласовываем их слабые асимпто-
p
× t-
√
ce2l(ϕ, s)Zout(P,k′).
(20)
тики, существенно уменьшая число степеней сво-
E +
боды в исследуемых выражениях. В этом смыс-
ле мы повторяем идеологию, изложенную в работе
Знак «тильда» в выражении для
Rn отражает пере-
[15]. Пользуясь ортогональностью функций, образу-
ход к сферическим координатам для векторной пе-
ющих спектральное разложение Ψsep, мы домножа-
ременной p′n. Здесь использованы также обозначе-
ем уравнение (18) на одну из базисных функций ви-
ния
да Ψ∗n,
c Γ(3 + iη)
Zin(out)(P,k′) = -
×
k4+iη
Ψn(X, P′) = exp[i〈p′n, y〉 + iwn(y, pn)]ϕn(x,k′n),
[
(
)
|c1|
× eπη/2〈k, Lin(out)(P)〉Φ
3+iη, 1, i
(1+〈k′,k〉)
-
2k
n > N ≫ 1,
]
и интегрируем по пространственной переменной.
- e-πη/2Hin(out)(P, k′) ,
Продолжая функцию ΨBBKc регулярным образом
где
внутрь параболической области Ω+1 как функцию
∫
ΨBBK
, мы находим коэффициенты разложения Rn
c
Hin(out)(P,k′) ≡ dx〈x, Lin,(out)(P)〉×
ΨBBK
в терминах скалярных произведений 〈Ψn,
c
〉R6 .
2
S
Как показано в работе [19], в старшем порядке спра-
(
)
|c1|
ведливо равенство
× Φ 3 + iη,1,-i
(1 - 〈k′, x〉) sc(x, k).
2k
〈Ψn,
ΨBBK
〉R6 ∼ 〈Ψn,
ΨBBK
〉Dμ,ν = 〈Ψn, ΨBBKc〉Dμ,ν .
В выражении (20) t = 〈p, p′n〉, переменная ϕ — угол
c
c
между векторами [p×k] и [p× p′n], отсчитываемый в
Таким образом, структура спектрального разло-
положительном направлении при условии, что трой-
жения в параболической области Ω+1 позволяет, со-
ка векторов [p ×
k], [p × p′n] и p является положи-
гласно результатам работы [19], получить для функ-
тельно ориентированной,
Ψacc
ции
c
(8) следующее выражение:
in(out)
|c1|3E1+ib/2eπb/2
ϖ0
(P) = Bin(out)0(P)
∫
25π2A(2l)0Γ(1 + ib)
∑
1
Ψacc
(X, P) ∼
dk′ ×
c
2p′
Здесь b — параметр, b = ηeff - ω, ω = η2 + η3,
n=N+1
n
S2
ηj (j = 1, 2, 3) и ηeff — соответствующие парамет-
∫
(
√ )ib
× dp′nϕn(x,k′)ψeffc(y,p′n)Rn(P,p′n,k′),
(19)
ры Зоммерфельда. Обозначение t - p/
E вве-
+
S2
дено для обобщенной функции χλ+ [25]. Функция
√
ce2l(ϕ, s) — функция Матье [26]:
c21
(x, y) ∈ Ω+1, p′n = E +
∑
4n2
ce2l(ϕ, s) =
A(2l)2r cos(2rϕ),
(21)
Напомним, что функция ϕn имеет вид
r=0
(
)
)
коэффициенты разложения A(2l)2r определяются ре-
|c1|
( |c1|
θ
ϕn(x,k) = exp -
x Ln-1
xsin2
,
куррентным образом согласно выражению (8.60) в
2n
n
2
[24], s — некоторый вещественный параметр.
Использованы также обозначения
θ
1 - 〈k, x〉
sin2
=
2
2
Bin0(P) = A0Γ(-iη2)Γ(-iη3)e-πω/2
×
Выражение для ядра Rn(P, p′n,k′) в смысле ска-
× (1 - e2πη2)(1 - e2πη3 ) ×
[√
]iη2 [√
]iη3
занного выше определено в работе [19]. Для полноты
(
)
(
)
3
3
изложения приведем полученные в [19] результаты
×
k2
1 - 〈p, k2〉
k3
1 + 〈p, k3〉
,
2
2
и список использованных обозначений:
380
ЖЭТФ, том 160, вып. 3 (9), 2021
О реакции развала в трехчастичных кулоновских системах. ..
(
)
1
k2 - p
k3 + p
4.4. Выделение асимптотики функции
Ψacc
c
Lin(P) =
√
η2
+η
,
3
1 - 〈p, k2〉
31 + 〈p, k3〉
Сформулируем следующее утверждение: исполь-
зуя метод Пуассона, можно переписать выражение
Bout0(P) = A0Γ(-iη2)Γ(-iη3)e-πω/2 ×
(22) в виде
× (1 - e2πη2 )(1 - e2πη3 ) ×
1
[√
]iη
[√
]iη
Ψacc
2
3
c
(X, P) ∼ U(y, P, -x)
(
)
(
)
3
3
2
√πR3/2×
×
k2
1 + 〈p, k2〉
k3
1 - 〈p, k3〉
,
2
2
∫
d
∑
1
exp[iRΦ+l(s)] + exp[iRΦ-l(s)]
(
)
×
ds
(
)
×
2
R
1
k2 + p
k3 - p
l=-∞
0
B1 + B2 ln
Lout(P) =
√
η2
+η
,
2√s
3
1+〈p,k2〉
31-〈p,k3〉
χδd(s)
√
|c1|x, x ≫ 1.
(23)
где A0 = -N(23)0/4π2. Постоянная N(23)0 =
c
c
× (1 - s)1/4,R≡
выражается через составляющие
Мы используем здесь обозначения
N(j)c = (2π)-3/2e-πηj/2Γ(1 + iηj).
(
)
π
1
Подставляя выражение (20) с соответствующи-
Φ±l(s) ≡
l+
±
√s
2
ми обозначениями в представление (19) и выделяя
(
)
1
основной вклад, согласно работам [9,19] получаем
±
arccos
(√s) -√s(1 - s)
,
(24)
√s
Ψacc
c
(X, P) ∼ U(y, P, -x) ×
функция χδd(s) является срезающей функцией в кру-
∑
(-1)n
ге радиуса δ с центром в точке s = d в комплексной
×
(8πn|c1|tn)-1/2 ×
n4(B2 ln n + B1)
плоскости s. Выход с вещественной оси в комплекс-
n=N+1
)-1/4 (
)-1/4
ную плоскость s окажется эффективным в дальней-
( |c1|tn
|c1|tn
ших вычислениях. Вещественные постоянные B1, B2
×
1-
×
4
4
были определены в работе [9] при решении модель-
(
[
√
√
|c1|tn
|c1|tn
ной задачи:
× cos
2n arccos
-
×
4
4
B1 = -0.31, B2 = -0.67.
√
])
|c1|tn
×
1-
(22)
Уводя контур интегрирования по переменной s
4
в верхнюю или нижнюю полуплоскость, нетрудно
показать, что только слагаемые с l = 0 и l = -1
в терминах обозначения tn = x/n2. Здесь B1 и B2 —
порождают ненулевой вклад в исходное выражение.
вещественные постоянные. Функция U(y, P, -x) —
Вклад остальных слагаемых оказывается экспонен-
гладкая функция своих аргументов. Мы не приво-
циально малым. Это означает, что основной вклад
дим здесь ее явное представление вследствие гро-
в выражение (23) имеет вид
моздкости выражения. Для изложения дальнейших
результатов нам будет достаточно упомянутых вы-
1
ше свойств функции U. При построении выражения
Ψacc
(X, P) ∼ U(y, P, -x)
c
4√πR5/2Υ(R)+
(22) нам нужна асимптотика полиномов Лагерра по
1
переменной x при больших значениях индекса «n».
+ U(y,P,-x)
(25)
4√πR5/2Υ∗(R),
Как было показано в работе [22], вклад в асимпто-
тику такого типа вносят четыре области изменения
где
переменной x (в зависимости от соотношения вели-
∞
∫
(
чин x и n): окрестности нуля, область колебаний,
dte-t/3
(1))
Υ(R) ≡ -ie2iR
1+O
(26)
переходная область и область монотонности. Отме-
C(R)-D ln t
R
0
тим, что основной вклад в выражение (22) вносит
область колебаний. В работе [9] было показано, что
Здесь использовано обозначение
вклады областей окрестности нуля, переходной и
3
π
монотонности являются лишь поправочными.
C(R) = B1 +
B2 ln R - B2 ln2 + iB2
,
2
4
Выделим теперь, следуя результатам работы [9],
(27)
1
асимптотику этого выражения.
D= 2B2.
381
А. М. Будылин, Я. Ю. Коптелов, С. Б. Левин
ЖЭТФ, том 160, вып. 3 (9), 2021
Таким образом, мы приходим к выводу, что в об-
области Ω+1 описывается независимо (вследствие ор-
ластях типа (11) конфигурационного пространства,
тогональности вкладов дискретного и непрерывного
в которых справедливо почти разделение перемен-
спектров в спектральном разложении) методами ра-
ных в окрестностях экранов σ при y ≫ x (где y
бот [17,20].
и x — якобиевы переменные, отвечающие выделен-
Отметим также осцилляторный характер и мед-
ной парной подсистеме с потенциалом кулоновско-
ленное степенное убывание на бесконечности полу-
го притяжения), полный вклад парных состояний
ченного выражения, что делает необходимым учет
дискретного спектра в трехчастичную собственную
данного асимптотического вклада на фоне экспо-
функцию непрерывного спектра имеет вид
ненциально убывающих явно учтенных членов сум-
мы (5).
sin(2R)
Ψacc
(X, P) = U(y, P, -x)
c
2
√πR5/2×
Ψacc
4.5. Положение
в иерархии
c
∫∞
(
асимптотических вкладов
dte-t/3
(1))
×
1+O
(28)
C(R) - D ln t
R
Необходимо сказать несколько слов о месте по-
0
Ψacc
лученного выражения
c
в иерархии вкладов раз-
Проводя дальнейшие упрощения, получим
личной природы, представляющих асимптотику ре-
шения типа искаженной плоской волны в области
3
Ψacc
c
(X, P) =
Ω+1, а точнее — в переходной области D1μ,ν (12). На-
2√πU(y,P,-x)×
√
(
(
))
помним, что область D1μ,ν характеризуется следую-
sin(2
|c1|x)
1
×
)
1+O
(29)
щим соотношением координат Якоби:
(√
ln(|c1|x)
C
|c1|x
(|c1|x)5/4
y ≫ 1,
1≪x≪y, yμ <x<yν,
1
(32)
в области, ограниченной соотношением
< μ < ν < 1.
2
2
4(N + 1)
1≪x≤
,
N ≫ 1, yμ < x < yν,
Асимптотика решения в этой области описывается
|c1|
(30)
выражением (15). Вклад непрерывного спектра опе-
1
< μ < ν < 1.
ратора Шредингера (16) парной подсистемы (пер-
2
вое слагаемое в выражении (15)) является старшим.
Соотношение (30) позволяет установить ограниче-
Как уже было упомянуто выше, этот вклад опи-
ния на величину параметра N. Заменяя величину x
сан, например, в работах [17,20]. Для его выделения
на yν и помня, что гиперрадиус системы
рассматривалась слабая асимптотика приближенно-
(
( x2 ))
го решения по большой переменной y. При этом для
ρ=y
1+O
,
2y2
согласования слабых асимптотик решений ΨBBKc и
получаем искомое ограничение
Ψsep оказывалось достаточным фиксировать коэф-
√
фициенты порядка 1/y и порядка x/y2, пренебрегая
|c|
N ≥
ρν/2.
(31)
членом следующего порядка малости 1/y2.
2
Ψacc
Полученные нами выражения (28), (29) для
c
Отметим, что чем больше парных состояний бу-
также записываются в виде слабой асимптотики по
дет учтено явно в сумме (5) (т. е. с ростом параметра
большой переменной y. Одновременно это выраже-
N ), тем более широкой будет область применимости
ние отвечает асимптотике по второй, подчиненной,
выражения (29). При этом само выражение (29) ока-
координате Якоби x второго слагаемого в выраже-
жется старшим порядком асимптотики при больших
нии (15). Тем самым оно отражает вклад в асимп-
значениях координаты x, а область применимости
тотику трехчастичного состояния типа искаженной
асимптотики с ростом N будет смещаться в область
плоской волны спектральной окрестности точки на-
больших значений x. С другой стороны, структура
копления дискретного спектра выделенной парной
асимптотики (29) не зависит явно от параметра об-
подсистемы. Определим переходную область D1μ,ν
резания ряда N и является, таким образом, коорди-
более точно:
1
4
натной асимптотикой по переменной x (отвечающей
<ν <
полному кулоновскому дискретному спектру опера-
2
5
тора Шредингера подсистемы α = 1) в асимптоти-
В этом случае, согласно выражению (29), мы фикси-
ческой области Ω+1. Отметим, что вклад непрерыв-
руем коэффициент в слабой асимптотике по y, убы-
ного спектра парной подсистемы с индексом α = 1 в
вающей как
382
ЖЭТФ, том 160, вып. 3 (9), 2021
О реакции развала в трехчастичных кулоновских системах. ..
∫
∫
∫
1
1
1
<
<
dτΨc(X, P′)aacc1
(P,
P′) = dk′ dp′ ×
y2
yx5/4
y13/8
S5
S2
S2
π
∫
2
Таким образом, найденный нами асимптотический
Ψacc
× dψΨc(X, P′)aacc1(P,
P′), X → ∞.
(33)
вклад
c
является всюду в области D1μ,ν поправоч-
ным по отношению ко вкладу непрерывного спектра
0
оператора Шредингера парной подсистемы, но стар-
Мы использовали здесь обозначение ψ
=
шим по отношению к членам, которыми мы прене-
= arctg(k′/p′). Выражение (33) содержит интеграл
брегли в процедуре согласования асимптотик.
по всем допустимым состояниям шестимерного
импульса P′, P′2 = k′2 + p′2 = E, отвечающим иска-
Отметим, что при выходе из области D1μ,ν в об-
Ψacc
женной плоской волне в асимптотической области
ласть ΩBBK вклад выражения
c
становится пре-
ΩBBK, где Ψc ∼ ΨBBKc. Такой интеграл порождает
небрежимо малым.
в асимптотической области ΩBBK в старшем по-
рядке суперпозицию расходящейся и сходящейся
шестимерных волн с гладкими амплитудами, вид
которых определяется видом функции aacc1(P,
P′):
4.6. Формулировка результата
∫
Мы выделили асимптотику по переменной x раз-
dτΨBBKc (X, P′)aacc1(P,
P′)|ΩBBK ∼
ложения решения (ведущего себя в области ΩBBK ,
S5
[
√
]
как искаженная шестимерная плоская волна ΨBBKc )
exp i
EX + iW0(X, P)
по состояниям дискретного спектра парной подси-
∼A˜+(X,P)
+
X5/2
стемы в области Ω+1.
[
]
√
exp -i
EX - iW0(X, P)
Таким образом, полное представление решения
+A˜-(X, P)
(34)
типа ΨBBKc , продолженного из области ΩBBK в об-
X5/2
ласть Ω+1, состоит из трех вкладов. Первый вклад
Мы используем при интегрировании метод стацио-
отвечает непрерывному спектру парной подсисте-
нарной фазы. Асимптотика вырожденных гипергео-
мы α = 1 (первое интегральное слагаемое в пред-
метрических функций в выражении для ΨBBKc по-
ставлении (15)). Второй вклад представляет собой
рождает лишь логарифмическую поправку к глав-
конечный набор интегральных слагаемых, отвечаю-
ному линейному члену 〈P′, X〉 с большим парамет-
щих разложению по состояниям дискретного спек-
ром X. Поэтому основной вклад в интеграл (34) дает
тра подсистемы с главными квантовыми числами
стационарная точка ψ0 = arcsin (x/X).
n = 1,2,...,N1 (суммирование по конечному набо-
В промежуточной области D1μ,ν , определенной в
ру значений главного квантового числа n во вто-
выражении (12), справедливо (со сколь угодно хо-
ром слагаемом в представлении (15)). Третий вклад
рошей точностью) приближенное равенство
(суммирование по оставшемуся бесконечному набо-
∫
∫
ру значений главного квантового числа n во втором
ΨBBKc(X, P) ∼ dk′ dp′ψ(x, k′)ψeffc (y, p′) ×
слагаемом в представлении (15)) отвечает разложе-
R3
R3
нию по бесконечному набору состояний дискретно-
∫
∑
го спектра подсистемы с главными квантовыми чис-
× δ(k′2 + p′2 - E)Rc(P, P′) +
dk′ ×
лами n > N1 (описан в выражении (29)). Как уже
n=1
S2
говорилось выше, структура первого вклада (непре-
∫
(
)
рывный спектр парной подсистемы) была подробно
1
c2
× dp′ϕn(x,k′)ψeffc (y, p′)δ p′2 -
-E
×
исследована в работах [15, 17].
4n2
R3
Рассмотрим слабую асимптотику решения урав-
Ψacc
× Rn(P, p′, k′) +
c
(X, P),
(35)
нения Шредингера (1) типа искаженной шестимер-
Ψacc
ной плоской волны Ψc, определенного в области
где функция
c
(X, P) определена в выраже-
ΩBBK как ΨBBKc и продолженного в область Ω+1 как
нии (29).
Ψsep. Для этого проинтегрируем функцию Ψc с неко-
Подставим теперь правую часть равенства (35)
торой гладкой функцией aacc1(P,
P′) по пятимерной
в представление (34), сохраняя в полученной сла-
сфере. В области ΩBBK получим следующее выра-
бой асимптотике лишь расходящуюся волну. Полу-
жение:
чим равенство
383
А. М. Будылин, Я. Ю. Коптелов, С. Б. Левин
ЖЭТФ, том 160, вып. 3 (9), 2021
[
√
]
∫
абсолютно непрерывного спектра типа искаженных
exp i
EX + iW0(X, P)
A+(X, P)
= dk′ ×
плоских волн (а также их слабые асимптотики) из
X5/2
асимптотической области конфигурационного про-
R3
∫
странства ΩBBK (10) в асимптотические области ви-
× dp′ψ(x, k′)ψeffc (y, p′)δ(k′2 + p′2 - E)B+c(P, P′) +
да Ω+α (11).
R3
В случае, когда в паре с индексом «α» куло-
∫
∫
∑
новский потенциал является притягивающим, выше
+
dk′ dp′ϕn(x,k′)ψeffc (y, p′)×
изложена процедура описания вклада дискретного
n=1
S2
R3
(
)
кулоновского спектра парной подсистемы в асимп-
c2
1
тотику продолжения искаженных плоских волн
×δ p′2 -
- E B+n (P,p′, k′)+
4n2
(шестимерных расходящихся искаженных волн) в
√
3
sin(2
|c1|x )
область Ω+α. Процедура описания вклада непре-
+
×
2√πC(√|c1|x )(|c1|x)5/4
рывного кулоновского спектра парной подсистемы
∫
в асимптотику продолжения искаженных плоских
× dτUout(y, P
P′′, -x)aacc1(P,
P′′).
(36)
волн (искаженных расходящихся волн) в область Ω+α
S5
была дана в работах [15, 17]. В случае, когда ин-
декс «α» соответствует паре одноименно заряжен-
Мы используем обозначения
ных частиц (случай кулоновского отталкивания),
∫
очевидно, нужно воспользоваться лишь процедурой
B+c(P, P′) = dτRoutc(P
P′′, P′)aacc1(P,
P′′),
описания вклада непрерывного спектра.
S5
∫
Наиболее важным сейчас для нас является тот
факт, что при описании процедуры построения
B+n(P, p′,k′) = dτRoutn(P
P′′, p′,k′)aacc1(P,
P′′).
вклада дискретного спектра парной подсистемы
S5
в асимптотику продолжения искаженных расходя-
Таким образом, согласно выражению (36), рас-
щихся волн в области Ω+α выделяется совокупный
ходящаяся искаженная шестимерная волна с про-
вклад парных высоковозбужденных состояний (эф-
извольной гладкой амплитудой представима в об-
фективное состояние) и тем самым полный базис со-
ласти D1μ,ν в виде разложения по конечному бази-
стояний оказывается конечным. Размерность такого
су со сколь угодно хорошей точностью. Посколь-
эффективного базиса также обсуждалась выше.
ку структура базиса не меняется при переходе к
Ниже излагается пример возможного приложе-
слабым асимптотикам, продолжение внутрь области
ния описанной выше процедуры к численным рас-
Ω+1 осуществляется автоматически.
четам характеристик физической системы.
На основании сказанного можно сделать вывод,
что состояние
Ψacc
(29) по структуре совпадает с
c,1
определенным выше в (5) выражением для Ψaccc,1.
Таким образом, основной результат вспомога-
тельной задачи получен.
5. ПРИЛОЖЕНИЯ МЕТОДА ДЛЯ
ПОСТРОЕНИЯ ВЫЧИСЛИТЕЛЬНОЙ
СХЕМЫ
4.7. Обсуждение
Акцентируем внимание на особенностях полу-
Для приложения метода к численным расчетам
ченного результата. Частично эти особенности уже
мы вернемся к асимптотическим граничным усло-
обсуждались выше. Выражение (28) возникло в про-
виям (2), понимая их в смысле изложенного вы-
цессе согласования двух приближенных решений
ше. Приведем еще одно замечание, которое касается
уравнения Шредингера. Однако одно из этих ре-
первого слагаемого в выражении (2), отвечающего
шений (ΨBBKc — решение типа искаженной плос-
начальному состоянию. Будем в дальнейшем счи-
кой волны) может уточняться, например, согласно
тать, что плотность a0lσ(P,
P′) является известной
процедуре, предложенной в работе [23]. Короткодей-
функцией и тем самым начальное состояние систе-
ствующая поправка к потенциалу в асимптотиче-
мы определено.
ских областях Ω+α может быть сделана сколь угод-
но малой. Таким образом, описанная выше проце-
Перейдем к построению системы связей между
дура позволяет продолжить собственные функции
плотностями anα(P,
P′) и амплитудой A(X, P).
384
ЖЭТФ, том 160, вып. 3 (9), 2021
О реакции развала в трехчастичных кулоновских системах. ..
5.1. Построение уравнений для неизвестных
этом смысле мы можем заменить оператор ∂/∂n опе-
плотностей anα
ратором ∂/∂X.
Положим вначале α = σ. Подставляя представ-
Из соображений удобства введем следующую си-
ление (2) в уравнение (39), получаем
стему обозначений:
∫
ψnα(Xα, Pα) = exp[i〈pnα, yα〉+iwnα(yα, pnα)] ×
∑ ∫
dP′ajα(P,
P′)
dτ ×
× ϕnα(xα, knα),
S2×S2
∂D
j=1[
√
∂
ψnα(Xα, Pα) = ψnα(Xα, Pα)ζ(ρ), ρ =
x2 + y2.
×
ψ∗mα(Xα, Pα)
ψjα(Xα, P′α) - ψjα(Xα, P′α) ×
∂n
Здесь функция ζ(ρ) ∈ C2[0,∞) является так называе-
]
∫
∂
мой срезающей функцией гиперрадиуса ρ и опреде-
×
ψ∗mα(Xα, Pα)
+ dτA(X, P) ×
∂n
ляется следующим образом:
∂D
⎧
(
√
)
⎧
⎨
EX + iW0
⎪
0 при 0 ≤ ρ ≤ ρ1-ε,
∂ expi
⎪
ψ∗mα(Xα, Pα)
-
⎨
×
∂n
X5/2
монотонно возрастает при
ζ(ρ) =
(37)
(
)
⎫
⎪
ρ1 - ε ≤ ρ ≤ ρ2 + ε,
√
⎪
exp i
EX + iW0
⎬
∂
⎩ 1 при ρ2 + ε ≤ ρ ≤ ∞.
−
ψ∗mα(Xα, Pα)
=
X5/2
∂n
⎭
Здесь 1 ≪ ρ1 < ρ2 < ∞, 0 < ε < 1.
(
)
√
∫
Рассмотрим систему уравнений
exp i
EX + iW0
=-
dX A(X, P)
Qmα(X, P)-
X5/2
(H - E)Ψ = 0,
D
(38)
(H - E
ψ∗mα = -Qmα,
∑ ∫
-
dP′ajα(P,
P′) ×
где Qmα — невязка функции
ψ∗mα, определенной вы-
j=1
S2×S2
∫
ше. Домножим первое уравнение системы (38) на
× dXQmα(X, P)ψjα(Xα, P′α).
(40)
функцию
ψ∗mα, а второе — на функцию Ψ и вычтем
первое уравнение из второго. Проинтегрируем по-
D
лученное равенство в шестимерном шаре большого
Напомним, что расходящаяся шестимерная иска-
радиуса ρ (область D). Воспользовавшись формулой
женная волна должна быть модифицирована с по-
Грина, придем к уравнению
мощью замены (4) в областях Ω+α, как уже было от-
∫ (
)
мечено выше.
∂
∂
ψ∗
Ψ-Ψ
ψ∗
mα
dτ =
Полагая m = 1, 2, . . ., Nα + 1, получим систему
mα ∂n
∂n
∂D
Nα + 1 тождеств вида (40). Будем рассматривать
∫
систему тождеств (40) как систему уравнений отно-
= - QmαΨdX.
(39)
), j = 1, 2, . . . , Nα + 1.
сительно плотностей ajα(P,
P′
D
Отметим, что полученная система уравнений может
Повторив проведенную процедуру в случае m = 1,
рассматриваться как матричное уравнение Фред-
2, . . ., Nα +1, получим систему Nα +1 уравнений ви-
гольма второго рода с компактным ядром, что поз-
да (39). Отметим, что в смысле сказанного мы рас-
воляет доказать существование и единственность
сматриваем в качестве базисной функции с индек-
решения.
сом Nα + 1 эффективное состояние, определенное
Простые вычисления показывают, что элемен-
выше:
тарная площадь поверхности пятимерной сферы ра-
диуса ρ имеет вид
ψNα+1 α(Xα, Pα) ≡ Ψcαc(Xα, Pα).
Отметим также, что интеграл по ∂D является
dτ = ρ5 cos2 ω sin2 ω sin θx ×
интегралом по границе области D, т. е. интегралом
× sinθydωdθxdϕxdθydϕy.
(41)
по поверхности пятимерной сферы радиуса ρ. Опе-
ратор ∂/∂n является оператором дифференцирова-
Здесь пары переменных θx, ϕx и θy, ϕy являются уг-
ния по нормали к поверхности интегрирования. В
ловыми переменными, определяющими положение
385
6
ЖЭТФ, вып. 3 (9)
А. М. Будылин, Я. Ю. Коптелов, С. Б. Левин
ЖЭТФ, том 160, вып. 3 (9), 2021
точки на двумерных сферах радиусов соответствен-
После замены переменной t = ρω и удобного в дан-
но xα и yα. Здесь введены также обозначения
ном случае переобозначения
t≡ x выражение (44)
факторизуется следующим образом:
π
xα = ρ sinω, yα = ρ cosω,
0≤ω≤
2
Σ∼ρ2Σ(1)Σ(2).
(45)
Отметим, что все слагаемые в первой сумме
Здесь
уравнения (40) экспоненциально убывают по пере-
менной xα, переменная ρ ≫ 1. Это ведет к суще-
∫
∞
∫
(
)
ственным упрощениям в старшем порядке выраже-
t
Σ(1)
≡ t2dt dtexp
-
|cα|
×
ний:
2j
0
S2
∂
(
)
(
)
0 ≤ ω ≤ ε ≪ 1,
(. . .) ∼ 〈∇(. . .), ŷ〉.
(42)
t
t|cα|
∂n
× exp
-
|cα| Lj-1
(1 - 〈k′jα, t〉)
×
2m
2j
(
)
Проинтегрируем первые два слагаемых в левой
t|cα|
части уравнения (40) по dp′α, принимая в расчет ска-
×Lm-1
(1 - 〈kmα, t〉)
,
(46)
2m
занное выше:
∫
∫
∫
∑
Ξ=
dP′ajα(P,
P′)
dτ ×
Σ(2)
≡ dŷajα(P,k′jα, ŷα)×
j=1
S2×S2
∂D
S2
[
[
]
∂
× exp
i(ρp′jα - ρ〈pmα, ŷα〉)
×
×
ψ∗mα(Xα, Pα)
ψjα(Xα, P′α) -
{
}
∂n
× exp
i[wjα(ρ, p′jα) - wmα(ρ, pmα)]
(47)
]
∂
- ψjα(Xα, P′α)
ψ∗mα(Xα, Pα)
∼
Заметим, что интегралы Σ(1) (46) являются соот-
∂n
(
)
ношением ортогональности по индексам «j» и «m»
∫
∑
2π
pmα
как интегралы от произведения собственных функ-
∼
dk′
1+
×
jα ρ
p′
ций дискретного спектра парного кулоновского опе-
j=1
jα
S2
∫
ратора Шредингера, отвечающих различным глав-
× dτ ϕjα(xα,k′jα) ϕmα(xα,kmα)ajα( P,k′jα, ŷα) ×
ным квантовым числам. Это свойство подробно об-
суждалось в работе [19]. Как было показано в рабо-
∂D
{
}
тах [9,19], при больших значениях индекса «m» (или
× exp
i(p′jαyα - 〈pmα, yα〉)
×
{
}
«j») ортогональность асимптотически выполняет-
× exp
i[wjα(yα, p′jα) - wmα(yα, pmα)]
(43)
ся и по направлению. Таким образом, при m ≫ 1
или(и) j ≫ 1
Анализ интеграла по dτ в S5 проведем с помо-
щью представления (41), заменяя в старшем поряд-
Σ(1) ∼ Cmδmjδ(k′mα -
kmα),
(48)
ке sin ω ∼ ω, cos ω ∼ 1, при условии ερ ≫ 1 (42).
Таким образом,
где Cm — некоторая постоянная, зависящая от глав-
∫
ного квантового числа и приведенная в работе [19].
Σ ≡ dτ ϕjα(xα, k′jα) ϕmα(xα, kmα)×
Интеграл (47) описывается методом стационарной
фазы следующим образом:
∂D
[
]
∫
× ajα(P, k′jα, ŷα) exp
i(p′jαyα - 〈pmα, yα〉)
×
[
]
{
}
Σ(2) ∼
dŷ exp
i(ρp′jα - ρ〈pmα, ŷα〉)
×
× exp
i[wjα(yα, p′jα) - wmα(yα, pmα)]
∼
S2
∫ε
∫
{
}
× exp
i[wjα(ρ, p′jα) - wmα(ρ, pmα)]
×
∼ρ5
ω2dω dφx sinθxdθx ×
× ajα(P, k′jα, ŷα)|j=m ∼
0
S2
∫
2πi
× dφy sin θydθyϕjα(ρωx,k′jα) ×
∼
amα(P,k′mα, pmα).
(49)
pmαρ
S2
Подставляя выражения (48) и (49) в выражение (43)
× ϕmα(ρωx, kmα)ajα(P, k′jα, ŷα)×
(
]
для Ξ, получаем
× exp
i(ρp′jα - ρ〈pmα, ŷα〉)
×
{
}
8π2
× exp
i[wjα(ρ, p′jα) - wmα(ρ, pmα)]
(44)
Ξ∼
√
iCmamα(Pα,
Pα),
(50)
E
386
ЖЭТФ, том 160, вып. 3 (9), 2021
О реакции развала в трехчастичных кулоновских системах. ..
что определяет асимптотически (по номеру главно-
6. ПОСТРОЕНИЕ ГРАНИЧНОЙ ЗАДАЧИ
го квантового числа) диагональную структуру опе-
ДЛЯ АМПЛИТУДЫ A(X, P)
ратора в уравнении (40), если рассматривать это
Проведем итеративную самосогласованную про-
равенство как уравнение относительно плотностей
цедуру построения решения задачи рассеяния. Эта
amα(Pα,
Pα), m = 1, 2, . . ., Nα +1, Nα ≫ 1. Нетрудно
процедура содержит несколько шагов.
показать, например, аналогично тому, как это было
продемонстрировано в (41)-(50) для первого слага-
емого в левой части (40), что при ρ → ∞ остальные
6.1. Первое приближение
слагаемые уравнения (40) в старшем порядке также
В качестве первого приближения зададим полное
не зависят от ρ.
распределение плотностей ajα(P, P′) и ajσ (P, P′)
Возвращаясь к системе уравнений (40) для век-
следующим образом:
торной функции
ajα = 0, α = σ,
1 ≤ j ≤ Nα + 1,
(54)
⎛
⎞
a1α
⎜
⎟
ajσ = 0,
1 ≤ j ≤ Nβ + 1, j = l; alσ = a0lσ,
(55)
⎜
a2α
⎟
âα =⎜
⎟,
(51)
⎟
где плотность a0lσ соответствует фиксированной
⎝ ...
⎠
плотности падающей волны, описанной в уравне-
aNα+1 α
нии (2).
Определив полный набор плотностей, мы, таким
получим уравнение следующего вида:
образом, фиксируем в первом приближении полный
набор амплитуд рассеяния процессов 2 → 2 в выра-
âα + Bαâα = Sα.
(52)
жениях для Ψ(0) (2) и Ψ(02)
(5).
Будем искать решение уравнения (1) в виде
Здесь Bα
— ограниченный матрично-значный
интегральный оператор с размерностью матрицы
Ψ = χ + ϕ.
(56)
(Nα + 1) × (Nα + 1). Матричные элементы этого
оператора являются интегральными операторами
Здесь первое слагаемое χ содержит асимптотику
с ядрами, заданными на пятимерной сфере (на
всех возможных парных каналов рассеяния на бес-
компактном носителе), а Sα — неоднородный член.
конечности в конфигурационном пространстве:
Полученное уравнение является интегральным
(
)
уравнением Фредгольма второго рода. Описанные
χ = ζ(ρ) Ψ(0) + Ψ(02)
(57)
выше свойства ядер гарантируют существование и
Срезающая функция ζ(ρ) описана в уравнении (37).
единственность решения этого уравнения.
Функция ϕ, как следует из уравнения (56), являет-
Отметим, что при α = σ уравнение (40), а следо-
ся дополнением определенной выше функции χ до
вательно, и уравнение (52) будут содержать допол-
точного решения Ψ задачи рассеяния. Согласно при-
нительные члены, отвечающие вкладу начального
веденному в (2) анзацу, асимптотика ϕ на бесконеч-
состояния. Однако принципиально структура урав-
ности совпадает с асимптотикой расходящейся ше-
нения типа (52) меняться не будет.
стимерной сферической волны и тем самым с выра-
Совокупность интегральных уравнений вида
жением для Ψ(03) (2). Поскольку параметры ρ1, ρ2
(52) при α = σ и α = β = σ позволяет установить
срезающей функции ζ велики, выражение для Ψ(02)
связь между вектор-функцией âα(β) (51) и амплиту-
закономерно является асимптотическим (2). Следо-
дой A(X, P) рассеяния 2 → 3. Здесь индексы «σ» и
вательно, выражение для χ (57) полностью опреде-
«β» нумеруют две возможные парные подсистемы
лено.
с кулоновскими потенциалами притяжения.
Построим теперь граничную задачу в шестимер-
Запишем решение уравнения (52) как
ном шаре большого радиуса ρ:
âα =
ΛαA,
(53)
(H - E)ϕ = -Q, X ≤ ρ,
(
[
])
√
∑
∂ϕ
1
cα
где оператор
Λα действует как матрично-значный
-i E-
√
ϕ|X=ρ =
∂n
2
xα
(58)
интегральный оператор на единичной сфере S5X.
E α=1
При этом, как было упомянуто выше, мы различаем
(
)
(
)
случаи α = σ и α = β = σ.
=O ρ-7/2
,
X ∈
S5ρ ∩ Ω+γ
,
γ = 1,2,3.
387
6*
А. М. Будылин, Я. Ю. Коптелов, С. Б. Левин
ЖЭТФ, том 160, вып. 3 (9), 2021
Здесь функция Q — невязка выражения χ,
гов итерактивной процедуры определяет также точ-
ность полученного результата.
Q ≡ (H - E)χ.
Граничное условие типа условия излучения, задан-
7. ОБСУЖДЕНИЕ И РЕЗУЛЬТАТЫ
ное на пятимерной сфере радиуса ρ, должно мо-
дифицироваться внутри каждой из параболических
Предложенные в работе методы позволяют све-
областей Ω+γ (11), т.е. на поверхностях
сти задачу рассеяния трех заряженных квантовых
частиц (при наличии парных кулоновских потенци-
S5ρ ∩ Ω+γ, γ = 1, 2, 3,
алов притяжения) при энергии выше порога раз-
в соответствии с результатами работ [15,17].
вала для процессов 2 → 2(3) к модельной задаче
Техника решения граничной задачи такого ти-
с конечным числом асимптотических каналов рас-
па успешно использовалась, хотя и в более простом
сеяния. При этом в каждой парной подсистеме α,
случае задачи рассеяния трех одномерных кванто-
отвечающей кулоновскому потенциалу притяжения,
вых частиц с финитными парными потенциалами, в
состояния с главным квантовым числом меньше
работах [27, 28].
Nα ≫ 1 учитываются явно. Вклад остальных высо-
Решение граничной задачи (58) порождает сле-
ковозбужденных состояний заменяется некоторым
дующий шаг итеративной процедуры, поскольку
эффективным состоянием. Это эффективное состо-
позволяет выделить амплитуду развала
2
→ 3
яние строится на основе выражений (28)-(30), полу-
A(X, P) в соответствии с соотношением
ченных в ходе решения вспомогательной задачи рас-
сеяния 3 → 2(3), с учетом преобразования (36). Ве-
Ψ(03)(X, P) = ϕ(X, P), X ≫ 1.
(59)
личина параметра Nα определяется условием (31).
Такая редукция заведомо бесконечномерной задачи
Выражение для Ψ(03) было определено ранее в урав-
к конечномерной модели является новой и позволя-
нении (2).
ет естественным образом контролировать точность
вычислений.
6.2. Коррекция решения
Предложенный метод, идейно близкий мето-
Вернемся теперь к описанной выше процедуре,
ду локального поля Фока, основан на согласова-
основанной на многомерной формуле Грина и ве-
нии приближенных решений уравнения Шрединге-
дущей к построению системы уравнений (52). От-
ра ΨBBKc и Ψsep в области Dμ,ν , в которой оба эти
метим, что в соответствии с решением граничной
решения справедливы. Особо отметим, что оба при-
задачи (58) и уравнением (59) свободный член Sα,
ближенных решения допускают процедуру уточне-
(α = σ, α = σ) системы уравнений (52) на данном
ния. Для решения типа ΨBBKc такая процедура по-
шаге меняется. Решая систему уравнений (52) для
дробно описана в работе [23]. Для решения типа Ψsep
процедура уточнения связана с учетом поправочно-
скорректированного свободного члена Sα1) (α = σ,
го потенциала вида
α = σ), мы получим новый набор плотностей âα
(α = σ, α = σ). Этот шаг позволяет скорректиро-
x
вать слагаемое Ψ02 в уравнении (2) в соответствии
Vcorr = C
y2
с уравнением (5). Это, в свою очередь, позволяет
определить новое приближение для функции χ =
С одной стороны, наличие такого потенциала в
= χ(1) в соответствии с уравнением (57).
представлении (13) разрушает процедуру деления
Вновь повторяя процедуру решения граничной
переменных в редуцированном операторе Шредин-
задачи (58), мы приходим к новому приближению
гера. Однако данный потенциал является в области
для расходящейся волны ϕ(1).
Ω+α лишь поправочным к главной части оператора,
Отметим, что в основе изложенной выше про-
допускающей деление переменных. Таким образом,
цедуры лежит вариационный подход, связанный с
учет потенциала Vcorr приводит лишь к возникнове-
перераспределением плотности вероятности обнару-
нию медленно меняющегося дополнительного слага-
жения системы частиц в некотором состоянии меж-
емого в фазовой функции. Такое слагаемое оказы-
ду всеми возможными процессами рассеяния, учи-
вается решением некоторого аналога градиентного
тываемыми с контролируемой точностью. Эта ве-
уравнения и может быть найдено обычным методом
роятностная трактовка задачи и определяет схо-
характеристик в асимптотической области конфи-
димость изложенной выше процедуры. Число ша-
гурационного пространства Ω+α. Добавим, что учет
388
ЖЭТФ, том 160, вып. 3 (9), 2021
О реакции развала в трехчастичных кулоновских системах. ..
потенциала Vcorr в структуре, например, эффектив-
измерения. Они, однако, формируются в большин-
ного состояния должен строиться на основе двух-
стве случаев в высоковозбужденных состояниях.
масштабных разложений (x ≫ 1, y ≫ 1, y ≫ x).
В самом деле, основные механизмы формиро-
Отметим также, что учет спиновых степеней сво-
вания антипротоннных атомов — так называемая
боды и, например, аннигиляционного канала рассе-
трехчастичная рекомбинация, в процессе которой
яния не влияет на полученные в работе результа-
принимают участие два позитрона и антипротон
ты, касающиеся структуры состояния Ψassc. Причи-
(дополнительный позитрон уносит излишек энер-
на этого заключается именно в том, что речь в этом
гии), и так называемая перезарядка, в процессе ко-
случае идет о дополнительных степенях свободы си-
торой позитроний Ps (связанное состояние электро-
стемы, усложнении матричной структуры полного
на и позитрона) в возбужденном состоянии переда-
решения, но не сказывается на структуре асимпто-
ет свой положительный заряд антипротону, а остав-
тики пространственных степеней свободы решения.
шийся электрон уносит излишек энергии. Первый
Отметим также, что предложенный нами метод
механизм является почти непрерывным процессом,
может быть непосредственно применен для вычис-
который имеет место, пока позитронная и антипро-
ления наблюдаемых в задачах квантового рассеяния
тонная плазмы поддерживаются в процессе взаи-
в системах нескольких частиц при энергиях выше
модействия (обычно несколько сотен миллисекунд
порога развала. Нам представляется, что метод был
[31]), и порождает широкое распределение высоко-
бы особенно эффективен при низких и ультранизких
возбужденных ридберговских атомов на всех под-
энергиях. Возможно, например, изучение задачи
уровнях [32]. Механизм перезарядки может приво-
рассеяния электрона на электрон-позитронной па-
дить к импульсному формированию атомов позит-
ре. Рассмотрение систем частиц разных масс долж-
рония, контролируемому временем лазерного воз-
но повлечь несущественные технические изменения
буждения. При механизме перезарядки распределе-
в уравнениях.
ние главного квантового числа n формируемых ато-
Рассмотрим одну из возможных областей приме-
мов антиводорода частично определяется распреде-
нения предложенного метода.
лением главного квантового числа атомов позитро-
ния. Типичные экспериментальные величины n ∼
∼ 30 [33,34], но с широким распределением подуров-
ней.
8. ПРИЛОЖЕНИЕ МЕТОДА В
АНТИПРОТОННОЙ ФИЗИКЕ
В итоге оба процесса формируют высоковоз-
бужденные антиатомы с широким распределением
Техника антипротонных экспериментов активно
всех (l, m) угловых моментов. Наиболее заселенны-
развивается уже несколько десятнков лет. В настоя-
ми при этом являются состояния с высокими значе-
щее время антиводородные атомы достаточно лег-
ниями главного квантового числа n. Более точные
ко формируются на Антипротонном деселератор-
характеристики распределения оказываются важ-
ном комплексе в CERN [29]. Деселераторный ком-
ными для предсказания дальнейшего хода экспери-
плекс проводил в последнее время несколько экс-
мента, в частности, для оценок времени жизни ан-
периментов, направленных на высокоточные изме-
тиатомов до перехода в основное состояние в зависи-
рения физических свойств антиводородного атома
мости (в случае процессов перезарядки) от значения
для проверки комбинированной CPT-симметрии и
главного квантового числа, отвечающего исходному
первого прямого измерения эффекта действия гра-
состоянию позитрония Ps.
витационных сил на антиматерию.
Отметим, что развитые в данной работе мето-
Тем не менее описание результатов эксперимента
ды расчета характеристик трехчастичного рассея-
не всегда однозначно. Построение адекватных моде-
ния заряженных частиц позволяют точно (в рамках
лей, охватывающих все стороны проводимых иссле-
описанной точности модели) предсказать заселен-
дований, также остается незавершенным, что без-
ность уровней антиатомов, в том числе с высокими
условно связано со сложностью протекающих про-
значениями главных квантовых чисел в зависимос-
цессов. В ходе эксперимента антиатомы или же за-
ти от номера главного квантового числа, отвечаю-
хватываются в магнитных полях [30], или формиру-
щего исходному состоянию заряженного кластера
ют пучок, который извлекается из области форми-
(Ps) до взаимодействия. В самом деле вычисление
рования в почти свободную среду [31]. В обоих слу-
амплитуды рассеяния выделенного асимптотическо-
чаях требуются антиводородные атомы в основном
го состояния Ψassc позволяет, проведя его парциаль-
состоянии для того, чтобы выполнить необходимые
ный анализ, вычислить распределение состояний с
389
А. М. Будылин, Я. Ю. Коптелов, С. Б. Левин
ЖЭТФ, том 160, вып. 3 (9), 2021
квантовыми числами (l, m). Вычисление корреляци-
функции. Проведем ее разложение в ряд по орто-
онной функции
гональным полиномам Лежандра Pl. Согласно, на-
пример, (8.904) [24], это разложение принимает вид
〈Ψassc, ϕn〉
позволяет найти заселенности уровней с любым
Φ(1 + iγ, 1, -ikx(1 - t)) =
(сколь угодно большим) главным квантовым числом
∑
n антиатома с последующим вычислением распреде-
=
(2l + 1)Φl(k, x)Pl(t).
(62)
ления заселенности состояний с квантовыми числа-
l=0
ми (l, m).
Здесь Φl(k, x) — парциальные компоненты функции
Указанная методика может существенно повы-
Φ(1 + iγ, 1, -ikx(1 - t)), которые, согласно условиям
сить точность предсказания характеристик экспе-
ортогональности полиномов Лежандра, вычисляют-
римента по увеличению продуктивности процессов
ся следующим образом:
создания антиатомов в высоковозбужденных состо-
∫
1
яниях с последующим их радиационным переходом
1
в основное состояние.
Φl(k, x) =
dt Φ(1 + iγ, 1, -ikx(1 - t))Pl(t).
(63)
2
В этом смысле предлагаемая методика расчетов
−1
применима к описанию любых процессов трехча-
Для вычисления интеграла в (63) воспользуемся ги-
стичной рекомбинации и трехчастичной перезаряд-
пергеометрическим разложением
ки при энергиях эксперимента выше порога развала.
∑
(a)j
Φ(a, 1, b(1 - t)) =
bj(1 - t)j,
(j!)2
j=0
(64)
ПРИЛОЖЕНИЕ
Γ(a + j)
a = 1 + iγ, b = -ikx, (a)j =
,
Определение ядра ϕn(x,k) производящего
Γ(a)
интеграла
в терминах которого
Рассмотрим собственную функцию абсолютно
∫1
∑
(a)j
непрерывного спектра
ψc(x, k) кулоновского двух-
Φl(k, x) =
bj
dt(1 - t)j Pl(t).
(65)
2
(j!)2
частичного оператора Шредингера, определенную
j=0
-1
стандартным образом с точностью до нормиров-
Делая в интеграле замену переменной s2 = (1-t)/2,
ки (нормировочный коэффициент положен равным
вычислим его явно и получим новое гипергеометри-
единице),
ческое разложение, ведущее к следующему предель-
ному соотношению для парциальной компоненты:
ψc(x, k) = ei〈k,x〉Φ(-iγ, 1, ikx(1 - 〈k, x〉)),
(60)
(-1)l
1
и проведем ее парциальный анализ (разложение по
Φl(k, x) =
lim
×
Γ(l + 2)
u→-m Γ(u)
сферическим функциям). В ситуации, когда функ-
ция является инвариантной относительно поворота
×2F2(a, 1; u, l + 2; 2b), m = l - 1,
(66)
системы координат (в данном случае угловая зави-
где2F2 — гипергеометрическая функция. Восполь-
симость содержится лишь в скалярном произведе-
зуемся теперь выражением
нии 〈k, x〉), такой анализ эквивалентен разложению
по полиномам Лежандра [35].
1
Для того чтобы провести такое разложение, вос-
lim
2(A, B; u, D; z) =
u→-m Γ(u)2F
пользуемся преобразованием Куммера (9.212.1) [24]
(A)m+1(B)
m+1
zm+1
=
×
(D)m+1
(m + 1)!
Φ(a, c, z) = ezΦ(c - a, c, -z),
×2F2(A+m+1, B+m+1; m + 2, D + m + 1; z),
(67)
что позволяет переписать выражение (60) в виде
где
ψc(x, k) = eikxΦ(1 + iγ, 1, -ikx(1 - t)),
(61)
A = a, B = 1, m = l - 1, D = l + 2, z = 2b.
где t = 〈k, x〉. Теперь угловая зависимость сосредо-
Подставляя выражение (67) в (66), получим оконча-
точена только в вырожденной гипергеометрической
тельное выражение для парциальной компоненты:
390
ЖЭТФ, том 160, вып. 3 (9), 2021
О реакции развала в трехчастичных кулоновских системах. ..
Γ(iγ + l + 1)
ние (70) оказывается конечной суммой слагаемых и
Φl(k, x) =
(2ikx)l ×
Γ(iγ + 1)Γ(2l + 2)
может быть записано в виде
(
)
× Φ(iγ + l + 1, 2l + 2, -2ikx).
(68)
|α|
ψc(x, kn) = exp
-
x
×
2n
Подставляя полученное соотношение в разложение
(
)
|α|
(61), (62) для собственной функции непрерывно-
× Φ 1 - n,1,
x(1 - 〈k, x〉)
=
2n
го спектра кулоновского двухчастичного оператора
Шредингера, получаем
(
)n-1∑
∑
|α|
1
= 4π exp
-
x
βnl
×
2n
(2l + 1)!
l=0 m=-l
∑
Γ(iγ + l+1)
ψc(x, k) = eikx
(2l + 1)
(2ikx)l ×
(
)l
(
)
Γ(iγ+1)Γ(2l+2)
|α|
|α|
l=0
× -
xlΦ
-n + l + 1, 2l + 2,
x
×
n
n
× Φ(iγ+l+1, 2l+2, -2ikx)Pl(t).
(69)
× Y ml(x)Y ml∗(k),
(72)
Рассмотрим теперь аналитическое продолжение
где Yml — соответствующие сферические функции.
построенной нами функции в верхнюю полуплос-
Последнее равенство справедливо в силу теоремы
кость комплексной плоскости k при
сложения сферических гармоник (5.17.9) [35],
(
)
∑
2l + 1
|α|
Pl
〈k, x〉 =
Yml(x)Yml∗(k).
k=kn =i
,
α < 0,
4π
2n
m=-l
Наконец, введем функцию
α
α
iγ = i
=i
= -n, n = 1, 2, 3, . . .
ϕn(x,k) ≡
ψc(x, kn)
(73)
2k
k=kn
2kn
согласно выражению (72). Мы предъявили функ-
Здесь k2n = -|α|/4n2 — энергия двухчастичного свя-
цию, парциальные компоненты которой с точностью
занного состояния, отвечающего главному кванто-
до нормировки совпадают с кулоновскими радиаль-
вому числу n. В этом случае выражение (69) прини-
ными функциями дискретного спектра [36]
мает вид
Rnl = ρle-ρ/2Φ(-n + l + 1, 2l + 2, ρ),
(
)
l = 0,1,2,...,n - 1
|α|
ψc(x, kn) = exp
-
x
×
2n
при фиксированном главном квантовом числе n.
Интегрируя функцию ϕn по dk на единичной
(
)l
∑
2l + 1
|α|
сфере с некоторой гладкой функцией â(k), получим
× βnl
-
x
×
Γ(2l + 2)
n
стандартное разложение вида
l=0
∫
(
)
|α|
ϕn(x,k)â(k)dk =
× Φ -n+l+1,2l+2,
x Pl(t).
(70)
n
S2
∑
∑
Мы понимаем здесь вектор kn как вектор с на-
=
DnlmRnl(x)Yml(x)
(74)
правлением, совпадающим с направлением исходно-
l=0 m=-l
го вектора k (kn =
k), и длиной, принимающей чи-
по полному набору кулоновских парных состояний
сто мнимое значение в верхней полуплоскости ком-
дискретного спектра, отвечающих фиксированному
плексной плоскости k (kn = i|α|/2n). Здесь коэф-
главному квантовому числу n. При этом набор
фициент βnl определяется следующим образом:
амплитуд Dnlm будет полностью определяться
аналитическим видом функции â(k).
βnl = (1 - n)(2 - n). . . (l - n).
(71)
Финансирование. Работа выполнена при под-
Отметим, что, согласно (71), коэффициент βnl обра-
держке Российского научного фонда в рамках гран-
щается в нуль при l ≥ n. Таким образом, выраже-
та РНФ 17-11-01003-П.
391
А. М. Будылин, Я. Ю. Коптелов, С. Б. Левин
ЖЭТФ, том 160, вып. 3 (9), 2021
ЛИТЕРАТУРА
18.
T. Wolz, C. Malbrunot, M. Vieille-Grosjean, and
D. Comparat, Phys. Rev. A 101, 043412 (2020).
1.
L. D. Faddeev, Mathematical Aspects of the
Three-Body Problem of the Quantum Scattering
19.
A. M. Budylin, Ya. Yu. Koptelov, and S. B. Levin,
Theory, Daniel Davey and Co., Jerusalem (1965),
J. Math. Sci. 238, 601 (2019).
p. 114.
20.
E. O. Alt and A. M. Mukhamedzhanov, Phys. Rev.
2.
С. П. Меркурьев, Л. Д. Фаддеев, Квантовая тео-
A 47, 2004 (1993).
рия рассеяния для систем нескольких частиц,
21.
J. Tennyson, Phys. Rep. 491, 29 (2010).
Наука, Москва (1985).
22.
F. Tricomi, Ann. Mat. Pura Appl. 28, 263 (1949).
3.
С. П. Меркурьев, ЯФ 24, 289 (1976).
23.
M. Brauner, J. S. Briggs, and H. Klar, J. Phys. B 22,
4.
С. П. Меркурьев, ТМФ 32, 187 (1977).
2265 (1989).
5.
I. Bray and A. T. Stelbovics, Phys. Rev. Lett. 69, 53
24.
И. С. Градштейн, И. М. Рыжик, Таблицы интег-
(1992).
ралов, сумм, рядов и произведений, Физматгиз,
Москва (1963).
6.
I. Bray and A. T. Stelbovics, Phys. Rev. A 48, 4787
(1993).
25.
И. М. Гельфанд, Г. Е. Шилов, Обобщенные функ-
ции и действия над ними, Физматгиз, Москва
7.
A. S. Kadyrov, I. Bray, A. M. Mukhamedzhanov, and
(1959).
A. T. Stelbovics, Ann. Phys. 324, 1516 (2009).
26.
Н. Мак-Лахлан, Теория и приложения функций
8.
A. S. Kadyrov, A. M. Mukhamedzhanov, A. T. Stel-
Матье, Изд. иностр. лит-ры, Москва (1953).
bovics et al., Phys. Rev. A 68, 022703 (2003).
27.
V. S. Buslaev, S. B. Levin, P. Neittaannmäki, and
9.
A. M. Budylin, Ya. Yu. Koptelov, S. B. Levin, and
T. Ojala, J. Phys. A 43, 285205 (2010).
S. V. Sokolov, arXiv:1810.06056 [quant-ph] (2018).
28.
В. С. Буслаев, Я. Ю. Коптелов, С. Б. Левин,
10.
M. Gaudin and B. Derrida, J. de Phys. 36, 1183
Д. А. Стрыгина, ЯФ 76, 236 (2013).
(1975).
29.
W. A. Bertsche, E. Butler, M. Charlton, and N. Mad-
11.
В. С. Буслаев, С. П. Меркурьев, С. П. Саликов,
sen, J. Phys. B 48, 232001 (2015).
в сб. Проблемы математической физики, т. 9,
30.
M. Ahmadi, B. X. R. Alves, C. J. Baker et al., Nature
Изд-во ЛГУ, Ленинград (1979), с. 14.
Comm. 8, 681 (2017).
12.
В. С. Буслаев, С. П. Меркурьев, С. П. Саликов,
31.
N. Kuroda, S. Ulmer, D. J. Murtagh et al., Nature
Зап. научн. сем. ЛОМИ 84, 16 (1979).
Comm. 5, 3089 (2014).
13.
В. А. Фок, Новые методы в теории диффракции,
32.
G. Gabrielse, N. S. Bowden, P. Oxley et al., Phys.
Вестник Ленингр. ун-та 4, 5 (1947); Проблемы ди-
Rev. Lett. 89, 233401 (2002).
фракции и распространения электромагнитных
волн, Сов. радио, Москва (1970).
33.
D. Krasnicky, G. Testera, and N. Zurlo, J. Phys. B 52,
115202 (2019).
14.
В. С. Буслаев, С. Б. Левин, Алгебра и анализ
22(3), 60 (2010).
34.
D. Krasnicky, R. Caravita, C. Canali, and G. Testera,
Phys. Rev. A 94, 022714 (2016).
15.
В. С. Буслаев, С. Б. Левин, Функц. анализ и его
прилож. 46(2), 83 (2012).
35.
Д. А. Варшалович, А. Н. Москалев, В. К. Херсонс-
кий, Квантовая теория углового момента, Нау-
16.
С. Б. Левин, Математ. заметки 108, 469 (2020).
ка, Ленинград (1975).
17.
С. Б. Левин, Зап. научн. сем. ПОМИ 451, 79
36.
Л. Д. Ландау, Е. М. Лифшиц, Квантовая механи-
(2016).
ка, Наука, Москва (1989).
392