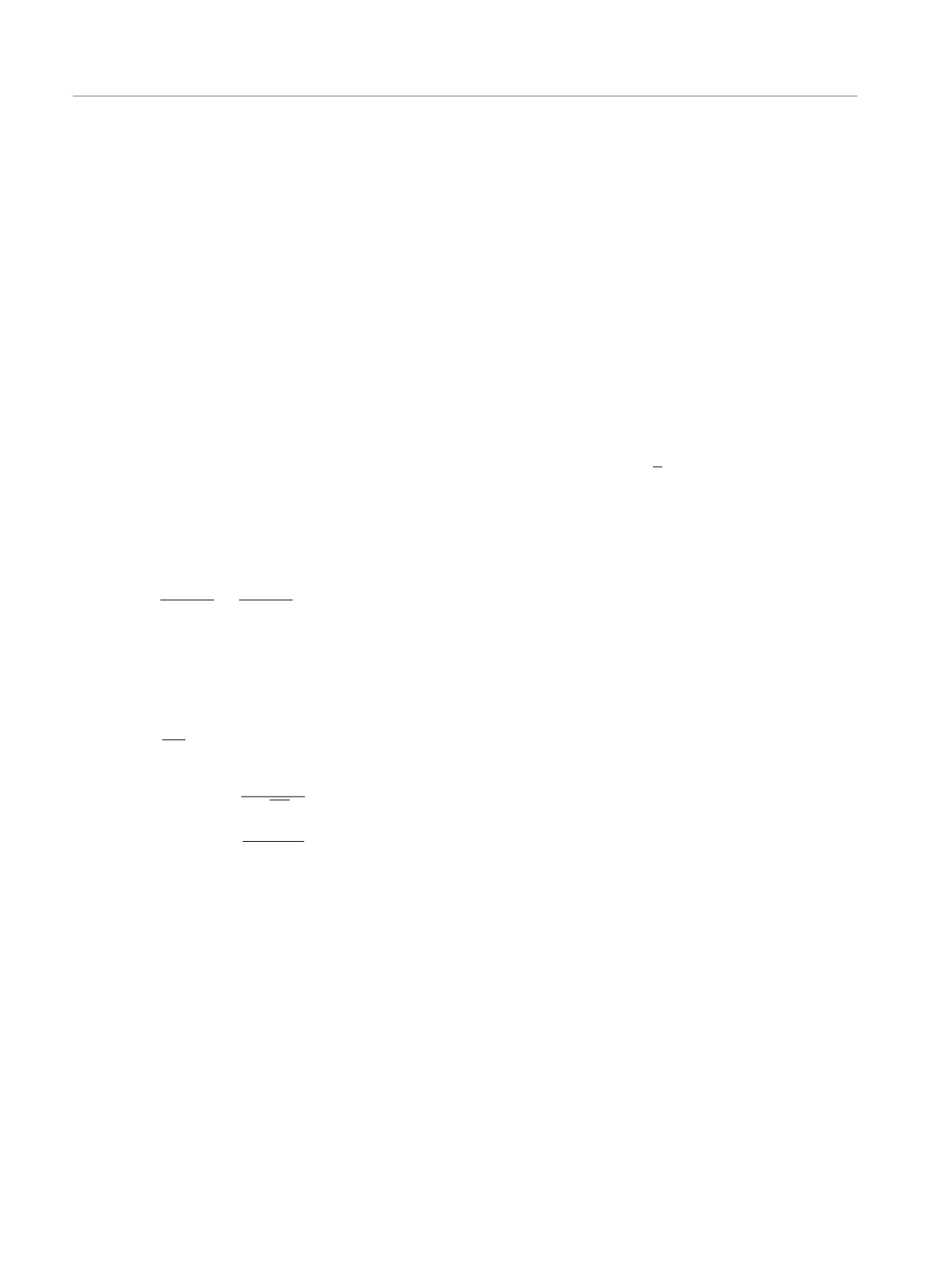ЖЭТФ, 2022, том 161, вып. 2, стр. 189-205

СИНГУЛЯРНЫЕ ФУНКЦИИ СПИНОРНОГО ПОЛЯ В КЭД

С СИЛЬНЫМ ВНЕШНИМ ПОЛЕМ

А. И. Бреевa*, С. П. Гавриловa,b**, Д. М. Гитманa,c,d***

^a Томский государственный университет

634050, Томск, Россия

^b Российский государственный педагогический университет им. А. И. Герцена

191186, Санкт-Петербург, Россия

^c Физический институт им. П. Н. Лебедева Российской академии наук

119991, Москва, Россия

^d Институт физики, Университет Сан-Паулу

05508-090, Сан-Паулу, Бразилия

Поступила в редакцию 29 сентября 2021 г.,

после переработки 29 сентября 2021 г.

Принята к публикации 18 октября 2021 г.

Построены и исследованы сингулярные функции в КЭД сильного поля с двумя типами внешних электро-

магнитных полей, которые принципиально различны. Первый тип относится к классу так называемых

t-потенциальных электрических ступеней (электрические поля включаются и выключаются в начальный

и конечный моменты времени), а второй — к классу так называемых x-потенциальных электрических

ступеней (не зависящие от времени электрические поля постоянного направления, которые сосредоточе-

ны в ограниченном пространстве). Первый тип (T-постоянное электрическое поле) представляет собой

однородное электрическое поле, которое действует в течение конечного промежутка времени T , а второй

(L-постоянное электрическое поле) — постоянное электрическое поле, ограниченное двумя обкладками

конденсатора, разделенными большим расстоянием L. Для обоих случаев найдены in- и out-решения

уравнения Дирака в терминах переменных светового конуса. При помощи этих решений строятся ин-

тегральные представления Фока - Швингера по собственному времени для всех сингулярных функций,

которые обеспечивают непертурбативные (по отношению к внешнему полю) вычисления любых ампли-

туд переходов и средних значений всех физических величин. Рассматривая T -постоянное и L-постоянное

поля как различные регуляризации постоянного однородного электрическом поля, можно показать их эк-

вивалентность для достаточно больших T и L.

DOI: 10.31857/S0044451022020055

которых при определенных обстоятельствах может

быть описана полуклассически [1] и выглядит в мо-

дели как внешнее поле. Таким образом, в данной мо-

1. ВВЕДЕНИЕ

дели электромагнитное поле проявляется как внеш-

нее классическое поле и фотоны, которые описыва-

Квантовая электродинамика (КЭД) идеально

ются чисто квантовым образом. Такая модель обыч-

описывает процессы с взаимодействующими заря-

но называется КЭД сильного поля.

женными частицами и фотонами. КЭД с внешним

Внешнее поле в КЭД сильного поля не может

электромагнитным полем представляет собой удоб-

трактоваться пертурбативно и должно учитывать-

ную модель для рассмотрения процессов с неболь-

ся точно, тогда как для процессов с заряженны-

шим количеством данных частиц на фоне, создава-

ми частицами и фотонами можно построить тео-

емом огромным количеством фотонов, совокупность

рию возмущений. В такой теории возмущений воз-

никают процессы нулевого порядка без фотонов и

^* E-mail: breev@mail.tsu.ru

^** E-mail: gavrilovsergeyp@yahoo.com

процессы более высокого порядка с фотонами. Су-

^*** E-mail: dmitrygitman@hotmail.com

щественная и нетривиальная часть КЭД сильного

189

А. И. Бреев, С. П. Гаврилов, Д. М. Гитман

ЖЭТФ, том 161, вып. 2, 2022

поля связана с процессами нулевого порядка. Рож-

ния теорий возмущений в КЭД сильного поля, как

дение частиц из вакуума сильными электрическими

в t-ступеньках, так и в x-ступеньках. При этом

внешними полями (эффект Швингера [2], привлека-

амплитуды перехода и средние значения физичес-

ющий внимание уже давно, или, другими словами,

ких величин выражаются через причинный пропа-

нестабильность вакуума), по сути, является прояв-

гатор (in-out-пропагатор) S^c(X, X^′), так называе-

лением процессов нулевого порядка. Для зависящих

мый in-in-пропагатор Scin(X, X^′) и out-out-пропага-

от времени внешних электрических полей, которые

тор Scout(X, X^′). В свою очередь, данные сингуляр-

включаются и выключаются в начальный и конеч-

ные функции связаны с in- и out-вакуумом следую-

ный моменты времени, теория возмущений с учетом

щим образом:

радиационных поправок и с точным учетом взаи-

S^c(X, X^′) = i 〈0, out|T Ψ(X) ×

модействия с сильным внешним полем была разви-

∕

та в работах [3]. Данные внешние поля постоянно-

× Ψ^†(X^′)γ0 |0, in〉

〈0, out|0, in〉 ,

(1)

го направления называются t-электрическими сту-

Scin(X, X^′) = i 〈0, in|T Ψ(X)Ψ†(X′)γ0 |0, in〉,

пеньками (далее — t-ступеньками). А теория возму-

щений использует существенно специальные набо-

Scout(X, X^′) = i 〈0, out|T Ψ(X)Ψ†(X′)γ0 |0, out〉 .

ры точных решений уравнения Дирака для соответ-

Здесь

Ψ (X) — оператор поля в представлении Гей-

ствующих t-ступенек (примеры, когда такие реше-

зенберга, удовлетворяющий уравнению Дирака в со-

ния могут быть найдены и все вычисления могут

ответствующем внешнем поле,

быть выполнены аналитически, мы называем точно

решаемыми случаями). Она включает в себя техни-

X = (X^μ) = (t,r), t = X⁰, r = (X^k),

ку расчета процессов нулевого порядка, модифици-

x = X¹, μ = 0,1,...D, k = 1,...,D,

рованные правила Фейнмана для расчета амплитуд

рассеяния с заряженными частицами и фотонами и

T обозначает операцию хронологического упорядо-

теорию возмущений для расчета средних значений.

чения; |0, in〉 и |0, out〉 — начальный и конечный ва-

Для простоты эффекты рождения частиц обычно

куум, соответственно.

рассматриваются в однородных внешних электри-

Отметим, что, несмотря на то, что формальные

ческих полях, зависящих от времени.

представления (1) верны в КЭД сильного поля как

Подходы к рассмотрению квантовых эффектов

в t-ступеньках, так и в x-ступеньках, in- и out-реше-

ния строятся по-разному, так же, как и операторы

в КЭД сильного поля в t-ступеньках не применимы

напрямую к КЭД сильного поля в не зависящих от

рождения и уничтожения и соответствующие ваку-

умные состояния.

времени электрических внешних полях постоянного

направления, которые сосредоточены в ограничен-

Уравнение Дирака во внешнем электромагнит-

ном поле заданным потенциалом A_μ(X) в d-мерном

ной пространственной области, в так называемых

пространстве-времени имеет вид (ℏ = c = 1)

x-ступеньках электрического потенциала (далее —

x-ступеньках). В работе [4] был построен непер-

(γ^μP_μ - m)ψ(X) = 0,

турбативный подход для расчета процессов нулево-

го порядка в КЭД сильного поля в x-ступеньках.

P_μ = i∂_μ - qA_μ(X),

Соответствующая техника основана на использова-

где ψ(X) — 2[d/2]-компонентный спинор, γ^μ — мат-

нии специальных наборов точных решений уравне-

рицы Дирака,

ния Дирака в x-ступеньке. Эти решения представ-

[γ^μ, γ^ν ]₊ = 2η^μν , η^μν = diag(1, -1, . . . , -1),

ляют собой стационарные плоские волны с заданны-

ми продольными импульсами p^L и p^R в макроскопи-

ческих областях слева и справа от x-ступеньки, со-

d=D+1,

ответственно (см. [4-6]). По аналогии с КЭД силь-

q = -e, e > 0 — заряд электрона, m — его масса.

ного поля в t-ступеньках можно построить теорию

Заметим, что в случае, когда вакуум нестаби-

возмущений для КЭД сильного поля в критических

лен, все сингулярные функции (1) различны. Раз-

x-ступеньках по радиационным поправкам и с точ-

личия между функциями Scin(X, X^′), Scout(X, X^′) и

ным учетом взаимодействия с сильным полем.

причинным пропагатором S^c(X, X^′) обозначаются

Сингулярные функции спинорного поля в соот-

через S^p(X, X^′) и S^p(X, X^′),

ветствующих внешних полях (обобщающие извест-

ные сингулярные функции в стандартной КЭД, см.

S^p(X, X^′) = Scin(X, X^′) - S^c(X, X^′),

(2)

[7]) являются ключевыми элементами для построе-

S^p(X, X^′) = Scout(X, X^′) - S^c(X, X^′).

190

ЖЭТФ, том 161, вып. 2, 2022

Сингулярные функции спинорного поля в КЭД.. .

Перестановочная функция

му полю) вычисления любых амплитуд переходов и

средних значений любых физических величин. Эти

S(X, X^′) = i[Ψ (X) ,

Ψ^†(X^′)γ⁰]₊,

(3)

представления получены для произвольной ориен-

S(X, X^′)|t=t′ = iγ⁰δ(r - r^′) ,

тации внешнего электрического поля, что нетриви-

является важной характеристикой спинорного поля.

альным образом обобщает результаты работ [18,19].

Ее вид существенно зависит от структуры внешне-

В разд. 3 мы находим соответствующие наборы in-

го поля. В работах [3] сформулированы правила по-

и out-решений уравнения Дирака в L-постоянном

строения всех необходимых сингулярных функций

электрическом полем в переменных светового кону-

в виде сумм по соответствующим точным решени-

са. При помощи данных наборов мы строим инте-

ям уравнения Дирака для t-ступенек. Те же идеи

гральные представления Фока - Швингера для со-

можно использовать для построения сингулярных

ответствующих спинорных сингулярных функций.

функций в КЭД сильного поля в x-ступеньках.

Полученные результаты обсуждаются в разд. 4. Рас-

В случае постоянного однородного электромаг-

сматривая вычисления в T -постоянном поле и L-по-

нитного поля причинный пропагатор электрона

стоянном поле как различные регуляризации соот-

S^c(X, X^′) был найден в явном виде как интеграл по

ветствующих вычислений в постоянном однородном

собственному времени Фока - Швингера много лет

электрическом поле, мы показываем их эквивалент-

назад [2]. Этот вид основывается на методе эффек-

ность для достаточно больших значений T и L.

тивного действия, см. [8]. Очевидно, что постоян-

ное однородное электромагнитное поле — это идеа-

2. СИНГУЛЯРНЫЕ ФУНКЦИИ В КЭД

лизация, которая полезна для описания эффектов в

СИЛЬНОГО ПОЛЯ В T -ПОСТОЯННОМ

медленно меняющихся и слабо неоднородных полях.

ЭЛЕКТРИЧЕСКОМ ПОЛЕ

Случай постоянного однородного электромагнитно-

го поля рассматривается как приближение в веду-

2.1. In- и out-решения

щем порядке теоретико-полевых расчетов [9,10], т. е.

В данном разделе мы рассмотрим случай t-сту-

приближения локально постоянного поля (см., на-

пеньки, которая представляет собой T -постоянное

пример, работы [11-17] и ссылки в них).

электрическое поле, действующее в течение боль-

Постоянное однородное электрическое поле мож-

шого промежутка времени. T -постоянное поле яв-

но рассматривать как предел T -постоянного элект-

ляется одной из возможных регуляризаций посто-

рического поля (однородное электрическое поле, ко-

янного однородного электрического поля в пределе

торое действует в течение временного интервала T)

T → ∞. Для построения спинорных сингулярных

большой длительности или как предел L-постоян-

функций нам понадобятся два полных набора ре-

ного электрического поля (постоянного электричес-

шений уравнения Дирака, in-решения {_ζ ψ_n (x)} и

кого поля, заключенного между двумя обкладками

{

}

out-решения

^ζψn (x)

со специальной асимптоти-

конденсатора, разделенными расстоянием L) боль-

кой при t → -∞ и t → +∞, соответственно. Ниж-

шого пространственного масштаба. КЭД сильно-

ний индекс ζ = + асимптотически соответствует

го поля для T -постоянного электрического поля и

электронам, а ζ = - асимптотически соответствует

L-постоянного электрического поля описывает фи-

позитронам. Поскольку явный вид искомых реше-

зически разные задачи. В этой работе мы получим

ний нетривиально зависит от ориентации электри-

явный вид для всех указанных выше сингулярных

ческого поля относительно оси x, ниже мы рассмот-

функций и покажем, что в пределе T, L → ∞ оба

рим оба случая по отдельности.

подхода приводят к одним и тем же результатам.

Рассмотрим постоянное электрическое поле, ко-

В данной работе мы строим и исследуем спинор-

торое имеет только одну ненулевую компоненту E_x

ные сингулярные функции в КЭД сильного поля в

вдоль оси x. Поле задается зависящим от времени

T-постоянном электрическом поле и в КЭД сильно-

электромагнитным потенциалом A_μ(X),

го поля в L-постоянном электрическом поле. С этой

целью в разд. 2 мы находим in- и out-решения урав-

A_μ(X) = E_xtδ1μ, E_x = κE, κ = ±1, E > 0 .

(4)

нения Дирака в T -постоянном электрическом по-

ле, используя переменные светового конуса. С помо-

Случай κ = -1 был рассмотрен в работах [18, 19].

щью этих решений мы строим интегральные пред-

Отметим, что в случае κ = +1 направление поля

ставления Фока - Швингера по собственному време-

совпадает с направлением поля в общей формули-

ни для всех сингулярных функций, которые обеспе-

ровке КЭД сильного поля в x-ступеньках, приведен-

чивают непертурбативные (по отношению к внешне-

ной в [4].

191

А. И. Бреев, С. П. Гаврилов, Д. М. Гитман

ЖЭТФ, том 161, вып. 2, 2022

Введем полный набор решений уравнения Дира-

Асимптотики решений (7) для κ = -1 и κ = +1

ка, имеющих следующий вид:

при t → ±∞ были исследованы в работах [19] и [20],

соответственно. Решения

ψ (X) = (γP + m)Φ(X), X = (t, x, r_⊥) ,

φ_n (t, x) = C_neipxxD_-ρ [±(1 + i )ξ] , κ = +1,

−

Φ (X) = φ (t, x) ϕ_p

(r_⊥) v_χ,σ ,

φ_n (t, x) =

C_neipxxDρ-1 [±(1 - i )ξ] , κ = +1,

⊥

(8)

−

ϕ_p

(r_⊥) = (2π)-(d-2)/2 exp (ip_⊥r_⊥) ,

(5)

φ_n (t, x) = C_neipxxDρ-1 [±(1 - i )ξ] , κ = -1,

⊥

(

)

(

)

r_⊥ =

X², . . . , X^D

p_⊥ =

p², . . ., p^D

φ_n (t, x) =

C_neipxxDρ-1 [±(1 + i )ξ] , κ = -1,

(

)

γ_⊥ =

γ², . . . , γ^D

C_n = (4πeE)-1/2 e-πλ/8,

C_n

= (2πλeE)-1/2 e-πλ/8 ,

где v_χ,σ

— набор постоянных ортонорированных

κ+1

спиноров,

ρ=

λ+

eEt - κp_x

ξ=

√

χ = ±1, σ = (σ₁,σ₂,...,σ[d/2]-1), σ_j = ±1.

p⊥2 + m²

λ=

Спиноры v_χ,σ удовлетворяют соотношениям

уравнения (6) использованы для построения in-ре-

γ⁰γ¹v_χ,σ = χv_χ,σ, v^†χ,σv_χ′_,σ′ = δ_χ,χ′ δ_σ,σ′ .

шений и out-решений. Будем говорить, что функ-

ции_ζ φ_n(t, x) соответствуют in-решениям {_ζ ψ_n (X)},

Фактически, функции (5) соответствуют состояни-

а функции^ζφ_n (t, x) соответствуют out-решениям

{

}

^ζψn (X)

. В (8) функции D_ν(x) — функции парабо-

ям с заданными импульсами p_⊥ в направлении, пер-

пендикулярном оси x. Квантовые числа χ и σ_j опи-

лического цилиндра. In- и out-решения ортонорми-

рованы относительно стандартного скалярного про-

сывают поляризацию спина и обеспечивают удоб-

ную параметризацию решений. Поскольку в изме-

изведения,

(_ζ

)

рениях (1 + 1) и (2 + 1) (d = 2, 3) нет спиновых сте-

(_ζψ_n,_ζ ψ_n′ ) =

ψ_n,^ζ ψ_n′

= δ(p_⊥ - p^′⊥)δ(p_x - p^′x)δ_σ,σ′,

пеней свободы, квантовые числа σ отсутствуют. За-

∫

метим, что в размерностях (2 + 1) существуют два

(ψ, ψ^′) = ψ^† (x) ψ^′ (x)dr,

неэквивалентных представления для γ-матриц, ко-

dr = dx¹ . . . dx^D .

торые соответствуют разным сортам фермионов, ко-

торые параметризуются параметром χ = ±1. В d-из-

Удобнее работать с решениями уравнения (6), ко-

мерениях для любых заданных импульсов существу-

торые зависят от координат на световом конусе

ет только J(d) = 2[d/2]-1 различных состояний спи-

x_± = t ± x.

на. Причем решения (5), которые различаются толь-

ко значениями χ, линейно зависимы. Без ограниче-

Данные решения параметризуются набором кванто-

ния общности положим χ = 1 и введем обозначение

вых чисел n_- = (p_-, p_⊥, σ) и имеют следующий вид:

v_σ = v1,σ.

+κ

φn- (t, x) = Cn- ×

-κ

{

)

Скалярные функции φ(t, x) удовлетворяют урав-

κE

⁽1

нению

× exp

-ie

x2-

-x²

p_-x₊ -

(

)]}

{

^[∓π_-

iπ

−

[κλ - 2i] ln

√

exp

θ(κ)

∂2t - ∂2x + 2ieκEt∂_x +

[

]}

(9)

+ (eEt)² - ieκE + p2⊥

+m²

φ(t, x) = 0 .

(6)

Cn- = (4πeE)-1/2 ×

{

}

× exp

[(2λ log 2 + π) κ + π(1 + iλ)]

Рассмотрим решения уравнения Дирака с опре-

p2⊥ + m²

деленными значениями импульсов,

λ=

, π_- = p_- + eκEx_- .

Для удобства мы ввели следующее обозначение:

ψ_n (X) = (γP + m) φ_n (t, x)ϕ_p

⊥

(r_⊥)v_σ,

{

φ_n (t, x) = eipxxφ_n(t), n = (p_x, p_⊥, σ),

(7)

φ, κ = +1,

+κ

-κ

φ=

−

p_x = p¹,

pxψn (X) = pxψn (X) ,

px = -i∂x .

φ, κ = -1,

192

ЖЭТФ, том 161, вып. 2, 2022

Сингулярные функции спинорного поля в КЭД.. .

где^ζ φ и_ζ φ — различные наборы функций. Здесь

∫

p_- — импульс, принимающий непрерывные значе-

(2πeE)-1/2

M^∗(p_x, p_-)-κ+κφn- (t, x)dp_- =

ния и являющийся собственным значением опера-

-∞

тора 2i(∂/∂x₊). Знак ±κ, отвечающий функциям

= -κ+κφn (t, x) .

+κ

-κ

φn- (t, x), совпадает со знаком кинетического им-

пульса π_- при x_- → ±∞. Далее мы покажем, что

Функциям^-κφ_n (t, x) соответствуют out-реше-

состояния (9) необходимы для построения специаль-

ния^-κψ_n (X), тогда как функциям+κφ_n(t, x) со-

ных асимптотик при t → ±∞.

ответствуют in-решения+κψ_n (X). Преобразования

Наборы решений (9) и (8) связаны между собой

(11) позволяют нам построить in- и out-решения

интегральным преобразованием

+κψn- (X) и^-κψn- (X) с квантовыми числами n-:

+κ

-κ

φ_n (t, x) =

ψn- (X) = (γP + m)-κ+κφn- (t, x)ϕ_p

(r_⊥) v_σ .

+κ

⊥

+∞

Таким образом, мы построили in- и out-решения

= (2πeE)-1/2 M^∗(p_x, p_-)+κ-κφn- (t, x) dp_-,

для двух различных направлений электрического

-∞

(10)

поля, κ = ±1. Причем имеют место преобразования

M (p_x, p_-) =

данных решений друг через друга:

{

}

iκ

[

]

(



)

(



)

= exp

(p_- + 2p_x)² - 2(p_x)²

ζ

4eE

^ζψn-(X) =₊ψn- (X)g₊

+ -ψn- (X)g -

(₊

)

(_-

)

|_ζ

+ -ψn- (X)g

|_ζ

ζ ψn- (X) =⁺ψn- (X) g

Обратное преобразование имеет вид

Здесь g-коэффициенты определяются соотношения-

+κ

-κ

φn- (t, x) =

ми

+^∞

√

(_ζ

)

πλexp(-πλ/4)

= (2πeE)-1/2 M(p_x, p_-)+κ-κφ_n (t, x) dp_x .

(11)

|_ζ

Γ (1 - iζλ/2)

(13)

-∞

(_-

)

(₊

)

|₊

= -g

|_-

= κ exp(-πλ/2).

Заметим, что в случае постоянного однородно-

го электрического поля преобразования (10) и (11)

2.2. Представления собственного времени

были рассмотрены в работе [21].

Как мы упоминали выше, функциям+κφ_n (t, x)

Используя представления сингулярных функций

соответствуют out-решения

+κψ_n (X), тогда как

в виде некоторых сумм решений уравнения Дирака,

функциям

-κφn(t, x) соответствуют in-решения

построенных в работах [3,19], можно найти их пред-

-κψn (X). Преобразования (11) позволяют нам по-

ставления по собственному времени. Таким образом,

строить in- и out-решения_-κψn- (X) и+κψn- (X) с

представления по собственному времени для сингу-

квантовыми числами n_-, соответственно:

лярных функций S^p(X, X^′) и S^p(X, X^′) следуют из

выражений

+κ

-κ

ψn- (X) = (γP + m)+κ-κφn- (t, x)ϕ_p

⊥

(r_⊥)v_σ .

∞

∫

На данном шаге мы введем два различных набо-

S^p(X, X^′) = i dp_- ×

ра решений:

∫

^-∞ ∑

κ = +1 :

× dp_⊥

-ψn- (X) ×

{

σ=±1

Rd-2

+φn- (t, x) = θ(+π-)⁺φn- (t, x)g (⁺ |+ ) ,

[

(



) (



)-1]†

-

^-φn- (t, x) = θ(-π_-)_-φn- (t, x)g (- |^-),

× g₊

ψn- (X^′) ,

(12)

(14)

κ = -1 :

∫

∞

{

S^p(X, X^′) = -i dp_- ×

⁺φn- (t, x) = θ(+π_-)₊φn-(t, x)g (+ |⁺),

-∞

-φn- (t, x) = θ(-π-)^-φn- (t, x)g (^- |- ) ,

∫

∑

dp_⊥

⁺ψn-(X)×

где θ (x) — ступенчатая функция Хевисайда. Мы мо-

σ=±1

Rd-2

жем проверить что выполняются следующие соот-

[ (



)

(



)]

+

-

ношения:

× g₊

-1 g

ψn-(X^′).

193

А. И. Бреев, С. П. Гаврилов, Д. М. Гитман

ЖЭТФ, том 161, вып. 2, 2022

Заметим, что сингулярные функции (14) в рабо-

Функция f(X, X^′; s) удовлетворяет следующему

те [19] были обозначены по-другому, а именно, как

дифференциальному уравнению с начальным

-S^a(X, X^′) и -S^p(X, X^′), соответственно. Учиты-

условием:

вая (13) и (12), получим

(

)

-i

f (X, X^′; s) =

P² - m² + ieEγ⁰γ¹

f (X, X^′; s) ,

S^p(X, X^′) =

∫∞

lim f(X, X^′; s) = ±i δ(X - X^′) .

s→±0

= -κ dp_-θ(+κπ^′-)₊Y (X, X^′; p_-),

-∞

Заметим что только член Λ в (18) является калиб-

ровочно-зависимой величиной, которая может быть

S^p(X, X^′) =

представлена в виде интеграла вдоль кривой, про-

∫∞

ходящей через точки X и X^′,

= +κ dp_-θ(-κπ^′-)+κY (X, X^′; p_-),

-∞

(15)

∫

Λ=- A_μ(

^X)d

X^μ .

(19)

+Y (X, X^′; p-) =

∫

∑

X^′

dp_⊥

+ψn- (X)

ψn- (X^′),

В рассматриваемой калибровке электромагнитный

Rd-2

потенциал A_μ(X) задается формулой (4), так что

+κY (X, X^′; p_-) =

∫

мы имеем

∑

dp_⊥

+κψn-(X)+κ

ψn-(X^′).

Λ = κEy₁(t + t^′)/2.

Rd-2

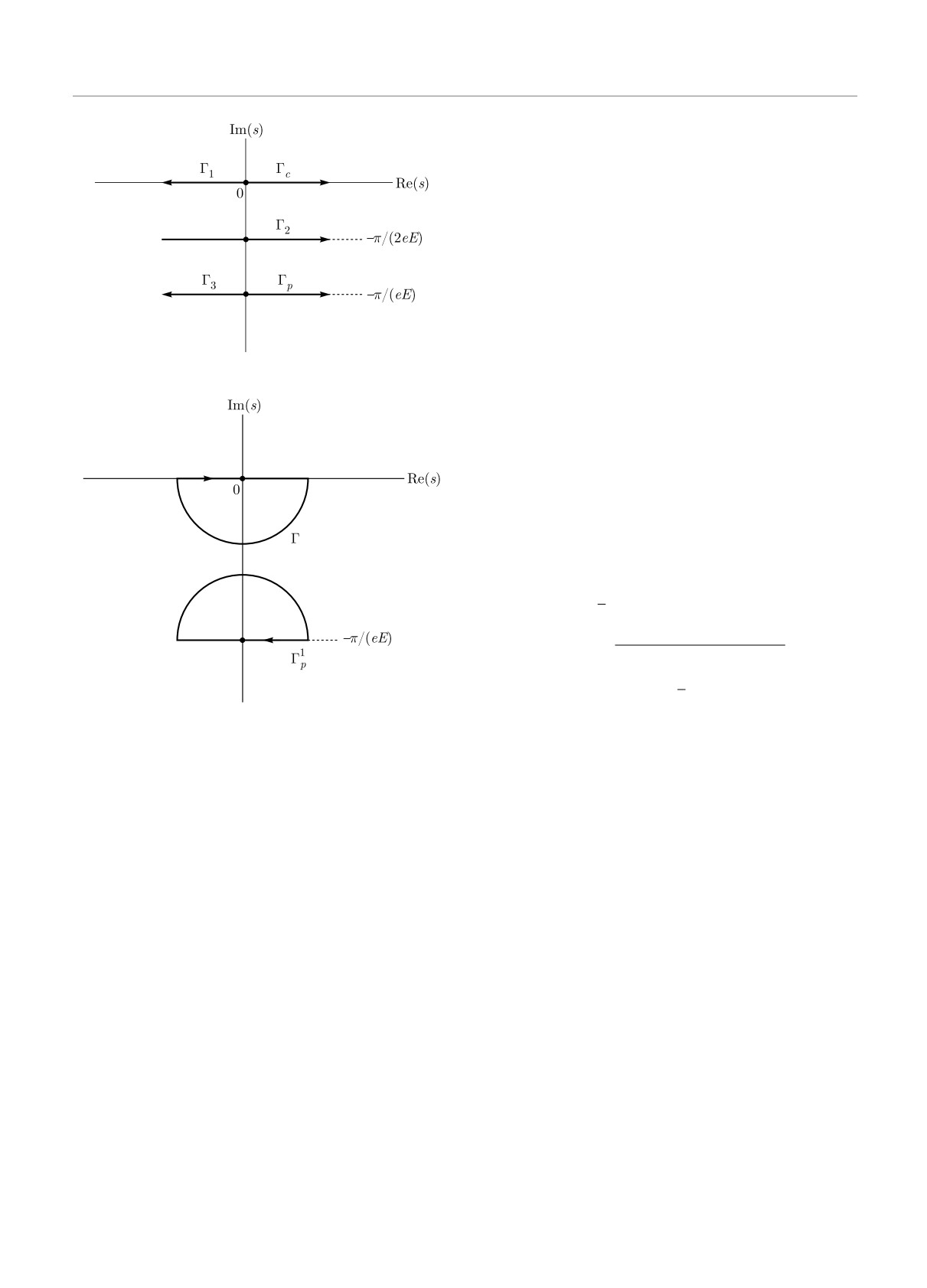
Контуры интегрирования показаны на рис. 1 и

рис. 2. Контуры Γ_c и Γ₁ обходят снизу все особые

В соответствии с работой [19], причинный пропа-

точки на вещественной оси, кроме начала коорди-

гатор и перестановочная функция могут быть пред-

нат. Функция f⁽⁰⁾(X, X^′; s) имеет две особые точки

ставлены в виде

s₀ = 0 и eEs₁ = -iπ на комплексной плоскости меж-

S^c(X, X^′) = (γP + m)Δ^c(X, X^′),

ду контурами Γ_c - Γ₁ и Γ_p - Γ₃.

∫

Контур Γ расположен в нижней части комплекс-

(16)

Δ^c(X, X^′) = f(X, X^′; s)ds,

ной плоскости s в достаточно малой окрестности

Γc

точки s = 0, а также соединяет точки s = +0 и s =

= e^-iπ0. Заметим, что интеграл по контуру Γ в (17)

S(X, X^′) = (γP + m)Δ(X, X^′),

∫

может быть представлен как интеграл по контуру

(17)

Δ(X, X^′) = sgn(t - t^′) f(X, X^′; s) ds,

Γ_c - Γ₂ - Γ₁. Так как ядро f(X, X^′; s) не имеет дру-

гих особенностей в достаточно малой окрестности

точки s = 0, то замыкание контура интегрирования

где

sgn(t - t^′) = θ (t - t^′) - θ (t^′ - t),

Γ_c - Γ₂ - Γ₁ при Re s → ±∞, дает контур интегри-

рования Γ.

и функция

Заметим что представление (16) имеет форму

(

)

представления Швингера [2]. Представление (17) об-

f (X, X^′; s) = exp

-eκEγ⁰γ¹s

f⁽⁰⁾(X, X^′; s),

)d/2

ладает универсальной структурой присущей пред-

⁽-i

ставлению собственного времени для перестановоч-

f⁽⁰⁾(X, X^′; s) = -

4π

ной функции, см. [18]. Отсюда следует, что интеграл

(17) удовлетворяет уравнению Дирака и начальному

s(d-2)/2 sinh(eEs)

(18)

условию

[

× exp -ism² + ieΛ +

|r_⊥ - r^′⊥|² -

S(X, X^′)|t=t′ = iγ⁰δ(r - r^′).

]

(

)

eE coth(eEs)

y²⁰ - y²

В свою очередь, это показывает полноту двух набо- } { }

ров

^±ψn-(x)

на гиперповерхности

±ψn-(x)

t = const.

представляет собой ядро Фока - Швингера [2, 22].

Следуя процедуре, указанной в работе [19], и

Здесь и далее мы вводим четыре-вектор

учитывая что

y_μ = X_μ - X^′μ, y₀ = t - t^′, y₁ = x^′ - x.

Ey = κEy¹,

194

ЖЭТФ, том 161, вып. 2, 2022

Сингулярные функции спинорного поля в КЭД.. .

Контур интегрирования Γ1p (радиус которого стре-

мится к нулю) соединяет точки

s = e^-iπ0 - iπ/(eE)

s = +0 - iπ/(eE).

Заметим, что интеграл по контуру Γ1p в (20) сво-

дится к интегралу по контуру Γ₂ + Γ₃ - Γ_p, так как,

замыкая контур интегрирования Γ₂ + Γ₃ - Γ_p при

Re s → ±∞, мы можем преобразовать его в кон-

тур Γ1p.

Используя

(20), получаем представление по

Рис. 1. Контуры интегрирования Γ1, Γ2, Γ3, Γc, Γp

собственному времени для сингулярных функций

Scin/out(X, X^′):

Scin/out(X, X^′) = S^p/p(X, X^′) + S^c(X, X^′).

(21)

Представления (16), (17) и (20) могут быть за-

писаны в ковариантной форме при помощи тензора

электромагнитного поля F_μν , см. работы [18,19]. На-

пример, для d = 4 получим

f (X, X^′; s) =

(

)

= exp

[γ^μ, γ^ν ]F_μν s

f⁽⁰⁾(X, X^′; s),

e²EB exp(-ieΛ^′)

f⁽⁰⁾(X, X^′; s) =

(4π)² sinh(eEs) sin(eBs)

[

]

(22)

× exp

-im²s - i

yqF coth(qFs)y

∫

Рис. 2. Контуры интегрирования

(

)

Λ^′ = -

A^Eμ(

^X)+A^Bμ(

^X) d

X^μ,

X^′

мы можем представить сингулярные функции (15)

где E и B — электрические и магнитные поля в F_μν ,

в виде интегралов по собственному времени:

A^Eμ + A^Bμ — потенциалы электрических (E) и маг-

нитных (B) компонент тензора F_μν , соответственно.

Интеграл в (22) берется вдоль кривой соединяющей

S^p(X, X^′) = (γP + m)Δ^p(X, X^′),

точки X и X^′.

S^p(X, X^′) = (γP + m)Δ^p(X, X^′),

∫

Как следует из

(18) и

(20), для функций

(20)

− Δ^p(X, X^′) = f(X, X^′; s)ds +

S^p,p(X, X^′) (а также для Scin/out(X, X^′)), замена

= -E эквивалентна замене

E_x = E → E_x

Γp

x → -x, x^′ → -x^′, γ¹ → -γ¹.

∫

Причем проекция

+ θ(Ey)

f (X, X^′; s) ds ,

Ey/E = (E_x/E)y¹

Γ¹

∫

вектора смещения

- Δ^p(X, X^′) = f(X, X^′; s) ds +

Γp

y = (y²,...,y^D)

∫

+ θ(-Ey)

f (X, X^′; s) ds .

на направление поля и функция f(X, X^′; s) не ме-

Γ¹

няются. Это означает, что средний ток созданных

195

А. И. Бреев, С. П. Гаврилов, Д. М. Гитман

ЖЭТФ, том 161, вып. 2, 2022

частиц остается направленным вдоль электрическо-

Выберем электромагнитные потенциалы, описы-

го поля.

вающие постоянное однородное электрическое поле

Заметим, что контуры интегрирования в пред-

E, направленное вдоль оси x, следующим образом:

ставлениях собственного времени для причинно-

A₀(X) = -Ex, A_k(X) = 0 .

(23)

го пропагатора и перестановочной функции нечув-

ствительны к направлению электрического поля.

Рассмотрим полный набор стационарных реше-

Однако контуры интегрирования в представлени-

ний уравнения Дирака в электромагнитном поле

ях собственного времени для сингулярных функций

(23) вида

S^p,p(X, X^′) зависят от проекции Ey. Это естествен-

но, поскольку именно эти сингулярные функции

ψn0 (X) = (γP + m)Φn0 (X),

определяют влияние внешнего электрического поля

Φn0 (X) = ϕn0 (t, x) ϕ_p

(r_⊥) v_χ,σ,

⊥

на электрические токи создаваемых частиц. Такое

(24)

n₀ = (p₀, p_⊥, σ),

наблюдение невозможно было сделать из представ-

лений, полученных в работах [18,19] для конкретно-

ϕn0 (t, x) = (2π)-1/2 exp(-ip₀t)ϕn0 (x) ,

го выбора системы координат.

где ϕp⊥ (r_⊥) и v_χ,σ даны в (5). В силу причин, опи-

санных выше в разд. 2, выберем χ = 1. Скалярные

3. СИНГУЛЯРНЫЕ ФУНКЦИИ В КЭД В

функции ϕn0 (x) удовлетворяют дифференциально-

L-ПОСТОЯННОМ ЭЛЕКТРИЧЕСКОМ ПОЛЕ

му уравнению второго порядка

{

}

3.1. In- и out-решения

p2x - iU^′ (x) - [p₀ - U (x)]² + p2⊥

+m²

В этом разделе мы построим спинорные сингу-

× ϕn0 (x) = 0,

лярные функции в КЭД в L-постоянном электричес-

(25)

U (x) = -eA₀(x) .

ком поле. Данное поле имеет только одну ненулевую

компоненту E_x вдоль оси x,

Решения уравнения Дирака с хорошо определен-

{

ными левыми и правыми асимптотиками обозначим

0, x ∈ (-∞, -L/2] ∪ [L/2, ∞),

как_ζ ψn0 (X) и^ζ ψn0 (X),

E_x (x) =

L > 0.

E, x ∈ S_int = (-L/2, L/2),

ζ ψn

px ζ ψn0 (X) = p

(X) , x → -∞, ζ = sgn(p^L),

Будем предполагать, что соответствующая по-

^ζψn0 (X) = p^Rζψn0 (X), x → +∞ , ζ = sgn(p^R).

тенциальная ступенька имеет достаточно большую

высоту, eEL

≫ 2m (такая ступенька назывется

Решения_ζ ψn0 (X) и^ζ ψn0 (X) описывают асимпто-

критической). В этом случае поле E_x (x) и веду-

тически частицы с определенными импульсами p^L

щие вклады в вакуумные средние можно рассмат-

при x → -∞ и p^R при x → +∞, соответственно.

ривать как макроскопические физические величи-

Мы видим, что решения_ζ ψn0 (X) и^ζ ψn0 (X) име-

ны. В этом смысле L-постоянное электрическое по-

ют вид (24), при этом функции ϕn0 (x) обозначены

ле является слабо неоднородным, и характеристики

как_ζ ϕn0 (x) и^ζ ϕn0 (x), соответственно. Они имеют

вакуумной нестабильности имеют некоторые уни-

следующие асимптотики:

версальные особенности, см. [15]. Эффект рождения

[

]

пар связан с наличием зоны Клейна. Подчеркнем,

ip^Lx

x → -∞,

ζ ϕn0 (x) = ζ C exp

[

]

что в пределе L → ∞ L-постоянное электрическое

^ζϕn0 (x) =^ζC exp

ip^Rx

x → +∞.

поле является одной из возможных регуляризаций

постоянного однородного электрического поля.

Здесь_ζC и^ζC — нормировочные множители.

Некоторые характеристики вакуумной неста-

Решения_ζ ψn0 (X) и^ζ ψn0 (X) удовлетворяют сле-

бильности, в частности, деформации спинорных

дующим соотношениям ортогональности на гипер-

сингулярных функций в КЭД в L-постоянном

поверхности x = const:

электрическом полем при больших L, могут быть

(

)

приближенно вычислены в КЭД с постоянным

ζ ψn0 , ζ^′ ψn^′

= ζδ_ζ,ζ′δn0,n′₀,

(

)

однородным электрическим полем. Последняя

^ζψn0,ζ′ψ_n′

= -ζδ_ζ,ζ′ δn0,n′ ,₀

задача важна сама по себе, и ее решение в рамках

∫

(26)

последовательной формулировки КЭД [4] дается

(ψ, ψ^′)_x = ψ^† (X)γ⁰γ¹ψ^′ (X) dt dr_⊥ ,

ниже, см. также результаты, полученные в работе

[5] для L-постоянного электрического поля.

= δ_σ,σ′ δ (p₀ - p′0)δ (p_⊥ - p^′⊥) .

δn0,n′0

196

ЖЭТФ, том 161, вып. 2, 2022

Сингулярные функции спинорного поля в КЭД.. .

Они выражаются друг через друга следующим об-

результате получим четыре набора решений уравне-

разом:

ния (29):

^ζψn0 (X) =

+ϕn0 (x) =

(



)

(



)

ζ

= +ψn0(X)g +

- -ψn0(X)g -

= +CD-1-ρ[-(1+i)ξ] ∝ e-iξ2/², ξ → -∞ ,

(27)

(30)

ζ ψn0 (X) =

-ϕn0 (x) =

(_-

)

(₊

)

= -ψn0 (X) g

|_ζ

- +ψn0 (X) g

|_ζ

= -C Dρ[-(1 - i)ξ] ∝ eiξ2/², ξ → -∞;

где коэффициенты разложения определяются из со-

⁺ϕn0 (x) =

отношений

(

)

(



)

= +C D_ρ[(1 - i)ξ] ∝ eiξ2/², ξ → ∞ ,



=g_ζ

ζ^′

δ_n

ζ ψn0 ,ζ′ ψn^′ (X)₀

0,n^′ ,₀

^-ϕn0 (x) =

(

)

(



)_∗



ζ^′ |_ζ

=g_ζ

ζ′

= -C D-1-ρ[(1 + i)ξ] ∝ e-iξ2/², ξ → ∞,

(31)

^-ζC =_ζC = (eE)-1/2 eπλ/8 ×

Заметим, что коэффициенты g отличаются от ко-

[

]-1/2

эффициентов g, которые имеют место в КЭД в t-сту-

(1 + ζ) + 1 - ζ

пеньках, см. разд. 2. Коэффициенты g удовлетворя-

ют следующим соотношениям:

Что позволяет нам построить соответствующие ди-

 (



)

 (



)

раковские спиноры, которые являются in- и out-ре-

+

-

^g

² =

^g

² ,

 (



)

 (



)

шениями:

+

-

^g

² =

^g

² ,

(28)

in-solutions:

-ψn0 (X),^-ψn0 (X) ,

g(₊|^-)

g(⁺|_-)

(32)

out-solutions:

g(_-|^-)

g(⁺|₊)

+ψn0 (X),⁺ψn0 (X) .

 (



)

 (



)

^g

-

² -

^g

+

² = 1 .

Коэффициенты g имеют вид

(



)

(



)

Вернемся к решению уравнения (25), которое мы

+

-

g -

=g₊

=eπλ/2.

(33)

можем записать в виде

[

]

Согласно общей теории [4], дифференциальные

d²

+ ξ² + i - λ ϕn0 (x) = 0,

(29)

средние числа рожденных пар определяются соот-

dξ²

ношением

 (



)

eEx - p₀

-

ξ=

√

Ncrn

^g

-2 = e^-πλ .

p2⊥ + m

Действуя тем же образом, как и в разд. 2 при

λ=

вычислении спинорных сингулярных функций (1)

Общее решение уравнения (29) полностью опре-

и (2), построим полные наборы решений уравнения

деляется подходящей парой линейно независимых

Дирака с корректно определенными левыми и пра-

выми асимптотиками в терминах переменных свето-

функций параболического цилиндра. А именно, па-

рой

вого конуса x_± = t±x. С этой целью мы рассмотрим

спиноры

ψn- (X), параметризованные квантовыми

D_ρ[(1 - i)ξ], D-1-ρ[(1 + i)ξ]

числами n_- = (p_-, p_⊥, σ):

или парой

ψ_n

(X) = (γP + m) Φn- (X) ,

(34)

D_ρ[-(1 - i)ξ], D-1-ρ[-(1 + i)ξ],

Φn- (X) = ϕn- (t, x)ϕ_p

(r_⊥)v_σ ,

⊥

где

где функции ϕn- (t, x) удовлетворяют уравнению

ρ = -iλ/2 - 1.

{

}

Учитывая асимптотические разложения функ-

p2x - iU^′ (x) - [p₀ - U (x)]² + p2⊥

+m²

ций параболического цилиндра, мы можем класси-

× ϕn- (t,x) = 0.

(35)

фицировать решения по знаку импульсов p^L и p^R. В

197

А. И. Бреев, С. П. Гаврилов, Д. М. Гитман

ЖЭТФ, том 161, вып. 2, 2022

Построим нестационарные решения уравнения

π_- = p_- + eEx_- .

(35). Заметим, что данное уравнение допускает ин-

Квантовое число p_- является собственным значени-

тегралы движения

Y_α , α = 0, 1, 2, 3, в классе линей-

ем оператора симметрии i

Y₁ +

Y₂):

ных дифференциальных операторов первого поряд-

ка:

Y₁ +

Y₂)+-ϕn- (t, x) = p-+-ϕn- (t, x) .

Y₀ = ie,

Y₁ = ∂_t,

Y₂ = ∂_x + ieEt ,

В этом случае решения уравнения Дирака имеют

ieE

Y₃ = x∂_t + t∂_x +

(t² + x²) .

вид (34) с функциями (36):

Операторы

Y_α образуют четырехмерную алгебру

ψn- (X) = (γP + m)+-Φn- (X) ,

(37)

Ли L, заданную ненулевыми коммутационными со-

Φn- (X) =+-ϕn-(t, x)ϕ_p

(r_⊥) v_σ ,

⊥

отношениями:

Построим прямое и обратное интегральные пре-

Y₁,Y2] = E

Y₀,

Y₁,Y3] =

Y₂,

Y₂,Y3] =

Y₁ .

образования, которые связывают функции (36) с

Уравнение (35) представляет собой уравнение на

функциями (30) и (31). Посмотрим на решения урав-

собственные функции оператора Казимира

нения (25) вида

K= 2E

Y₀

Y₃ -

Y²¹ +

Y²²,

ϕn0 (t, x) = (2πeE)-1/2 ×

а именно,

∫

(

)

Kϕn- (t,x) =

p2⊥ + m²

ϕn-(t, x),

[K,Ya] = 0 .

M^∗(p₀, p_-)+-ϕn- (t, x) dp_-,

(38)

−∞

Для построения полных наборов решений тако-

го рода уравнений эффективно применение метода

которые удовлетворяют уравнению

некоммутативного интегрирования [23-25], основан-

p0+-ϕn0(t, x) = p0+-ϕn0 (t, x).

(39)

ного на алгебре симметрии уравнения Дирака. Сна-

чала определим неприводимое λ-представление ал-

Подставляя (38) в (39) с учетом условия

гебры Ли в пространстве функций от переменной

[

]

p_- ∈ (-∞, +∞) при помощи операторов

∂_t - eE∂p- +

p_- ϕn- (t, x) = 0 ,

ℓ_a(p_-, ∂p- , j), α = 0, 1, 2, 3; j ∈ (0, ∞),

получим

видим, что функция

^M (p₀, p_-) определяется как ре-

шение уравнения

ℓ₀(p_-, ∂p- , j) = ie ,

(

)

ℓ₁(p_-, ∂p- , j) = -eE∂p- +

p_- ,

-i

-eE∂p- +

p_-

^M (p₀, p_-) = p₀ M˜ (p₀, p_-) .

ℓ₂(p_-, ∂p- , j) = eE∂p- +

p_- ,

Выберем частное решение

ℓ₃(p_-, ∂p- , j) = -p_-∂p- + ij - 1 ,

(

)

^M (p₀, p_-) = exp

p2- - 4p_-p₀ + 2p²⁰

ℓ²¹(p_-, ∂p- , j) - ℓ²²(p_-, ∂p- , j)-

4eE

- 2Eℓ₀(p_-, ∂p-, j)ℓ₃(p_-, ∂p- , j) = (2eE)j .

которое удовлетворяет условию ортогональности

Интегрируя систему уравнений

∫

[

]

Y_a + ℓ_a(p_-, ∂p- , j) ϕn- (t, x) = 0

M^∗(p₀, p_-)

^M (p₀, p^′-) dp0

−∞

вместе с уравнением (35), получим алгебраическое

(40)

уравнение j = -λ/2 и два его полных набора реше-

= 2πeE δ(p_- - p^′-).

ний_-ϕn- и⁺ϕn-. Данные решения параметризуют-

Запишем обратное преобразование

ся набором квантовых чисел n_-:

[

)

⁽1

ϕn-(t, x) = (2πeE)-1/2 ×

ϕn- (t, x) = C^′ exp ie

x2-

-t²

∫

]

±iπ_-

^M (p₀, p_-)+-ϕn0 (t, x) dp₀ .

(41)

(λ - 2i) ln

√

−

p_-x₊

(36)

−∞

198

ЖЭТФ, том 161, вып. 2, 2022

Сингулярные функции спинорного поля в КЭД.. .

Для совместности преобразований (38) и (41), в

Применяя интегральное преобразование типа

выражениях (30), (31) положим

(38) к решениям (45), получим

C^′ = 2iλ/4eπλ/4 (4πeE)-1/2 .

∫

-1/2

(2πeE)

M^∗(p₀, p_-)^-ϕn- (t, x) dp_-

Обратное преобразование (41) показывает, что

функции+-ϕn-(t, x) выражаются через функции

−∞

ϕn0 (t, x) с хорошо определенными левыми и пра-

= -ϕn0(t, x),

выми асимптотиками.

Из преобразований (38) и (41) следуют соответ-

∫

ствующие соотношения между решениями уравне-

(2πeE)-1/2

M^∗(p₀, p_-)₊ϕn- (t, x) dp_-

ния Дирака:

−∞

ψn0 (X) = (2πeE)-1/2 ×

= +ϕn0(t, x).

+∞

M^∗(p₀, p_-)+-

ψn- (X)dp_- ,

Тогда

−∞

(42)

ψn0 (X) =

ψn- (X) = (2πeE)-1/2 ×

∫

+∞

= (2πeE)-1/2

M^∗(p₀, p_-)-+

ψn- (X) dp_- ,

^M (p₀, p_-)+-ψn0 (X) dp₀ ,

-∞

(46)

-∞

ψn- (X) =

где+-ψn0 (X) даны в (24) с функциями ϕn0 (x), обо-

∫

значенными как+-ϕn0(x), функции+-

ψn- (X) даются

= (2πeE)-1/2

^M (p₀, p_-)-+ψn0 (X) dp₀ ,

выражением (37). Из второго преобразования в (42)

-∞

и соотношения (40) следует, что спиноры+-

ψn- (X)

удовлетворяют условию ортогональности на гипер-

где-+ψn0 (X) даны в (24), а функции ϕn0 (x) обозна-

поверхности x = const:

чены как-+ϕn0 (X). Функции-+

ψn- (X) даны в (44).

(

)

Используя второе преобразование в (46) и соот-

ψn-,+-

ψ_n′

= -δn-,n^′ ._-

ношения (26), мы видим что выполняются соотно-

^- x

шения ортогональности:

В соответствии с (32), функции⁺ψn- (X) описыва-

(

)

ют out-решения, а функции_-ψn- (X) — in-решения.

ψn-,_-

ψ_n′

= 0,

^- x

Коэффициенты g(_- |⁺ ) даны в (33) и не зависят от

(

)

p₀ и p_-, а также связывают между собой наборы

ψn-,⁺

ψ_n′

=0.

решений+-

ψn-.

^- x

Очевидно, что

}

и ортогональных набора решений

ψn-(x) и

{

}

ψn-(X) = 0, π_- > 0,

ψn-(x)) уравнения Дирака; дополнительные на-

−

ψn-(X) = 0, π_- < 0 .

боры решений выберем следующим образом:

(



)

Используя (42) и (46) и учитывая, что коэффи-

-ψn- (X) = -θ (π-)-ψn- (X) g-

-

циенты g^′ не зависят от p₀, из (27), находим

(₊

)

(43)

ψn- (X) = -θ (-π_-)⁺

ψn- (X) g

|₊

(



)

ψn- (X) = g₊

-

-1 ×

Они могут быть представлены в виде

[

]

(



)

ψn- (X) g_-

-

ψn- (X)

= 0, π_- > 0 ,

ψn- (X) = (γP + m)-+Φn- (X) ,

(_-

)-1

−

ψn- (X) = g

|₊

Φn- (X) =-+ϕn-(t, x)ϕ_p

(r_⊥)v_χ,σ ,

(44)

⊥

[

]

(₊

)

−

ϕn-(t, x) = (2π)-1/2 exp(-ip₀t)

ϕn-(x),

ψn- (X) g

|₊

ψn- (X)

= 0, π_- < 0 .

где

Таким образом, соотношения (43) справедливы для

(



)

^-ϕn- (t, x) = -θ (π_-)_-ϕn-(t, x)g_-

-

всех g(_- |^- ) и g(⁺ |₊ ), удовлетворяющих услови-

(₊

)

(45)

|₊

ям (28).

+ϕn- (t, x) = -θ (-π-)⁺ϕn-(t, x)g

199

А. И. Бреев, С. П. Гаврилов, Д. М. Гитман

ЖЭТФ, том 161, вып. 2, 2022

Заметим, что подобные наборы решений урав-

Используя соотношения (27), представим сингу-

нения Клейна - Гордона для скалярных частиц, на-

лярные функции S^p(X, X^′) и S^p(X, X^′) в (2) следу-

ходящихся между двумя обкладками конденсатора,

ющим образом:

получены в работе [26]. Эти решения связаны между

собой при помощи интегральных преобразований,

S^p(X, X^′) =

аналогичных преобразованиям (42) и (46).

∑

(_-

)-1-

-1

|_-

ψn0 (X^′) ,

-ψn0 (X) g

3.2. Представления собственного времени

(50)

Спинорные сингулярные функции в КЭД в

S^p(X, X^′) =

x-ступеньках определяются уравнениями (1), (2) и

∑

(



)-1

(3). В случае L-постоянного электрического поля

= -i M-1n

⁺ψn0 (X) g₊

+

ψn0 (X^′) .

их можно найти как суммы по построенным выше

решениям, см. [4]. Отметим, что для L → ∞ доста-

точно рассматривать суммы только в зоне Клейна.

Подчеркнем, что если вакуум стабилен, то обе функ-

В этой зоне решения (30) и (31) удовлетворяют

ции обращаются в нуль.

следующим соотношениям ортонормированности

на гиперплоскости t = const:

Используя (42), (46) и (43), получим следующие

интегральные представления:

(

)

ζ ψn0 , ζ ψn′0

(^ζψn0,^ζψ_n′ ) =

∫

= δ_σ,σ′ δ(p₀ - p′0)δ(p_⊥ - p^′⊥)Mn0 ,

∑

(

)

S^-(X, X^′) = -i

dp_-dp_⊥ ×

=0,

ζ ψn0 ,^ζ ψn^′

∫⁰

(

)

(ψ, ψ^′) = ψ^† (X) ψ^′ (X) dr ,

×θ

+π^′-

e-πλ/2+

ψn- (X)_-ψ

(X^′) ,

 (



)

(51)

_g

-

Mn0 =

² = e^πλ .

∑∫

S⁺(X, X^′) = -i

dp_-dp_⊥ ×

Тогда сингулярные функции можно представить в

виде

(

)

×θ

-π^′-

e-πλ/2-

ψn- (X)

+ ˜ψ (X^′) ,_n

S^c(X, X^′) =

= θ(t - t^′)S^- (X, X^′) - θ(t^′ - t)S⁺ (X, X^′) ,

∑

∫

S^-(X, X^′) = i M-1 ×_n

∑

S^p(X, X^′) = -i

dp_-dp_⊥ ×

(₊

)

(_-

)-1-

× +ψn0 (X) g

|_-

ψn0 (X^′) ,

(47)

(

)

×θ

+π^′-

e^-πλ-

ψn- (X)_-

ψ (X^′) ,_n

∑

∫

(52)

S⁺(X, X^′) = i M-1 ×_n

∑

S^p(X, X^′) = i

dp_-dp_⊥ ×

n⁰(



)

(



)-1

+

ψn0 (X^′) ;

× -ψn0 (X) g -

g +

(

)

S(X, X^′) = S^- (X, X^′) + S⁺ (X, X^′) ;

(48)

×θ

-π^′-

e-πλ+

ψn- (X)⁺

ψ (X^′) ._n

Scin/out(X, X^′) =

Учитывая (37) и (43) и выполнив суммирование

= θ(t - t^′)S-in/out (X, X^′)-θ(t^′-t)S+in/out (X, X^′),

по квантовым числам σ,

S-in/out(X, X^′) =

∑

(

)

=i M-1n

^∓ψn0 (X)^∓

ψn0 (X^′) ,

(49)

v1,σv†1,σ =

(v1,σ ⊗ v†1,σ) = Ξ₊ =

1+γ⁰γ¹

∑

S+in/out(X, X^′) = i

M-1n

ψn0 (X^′) ,

∓ψn0 (X)

перепишем представление (51) следующим образом:

ψ=ψ^†γ⁰.

200

ЖЭТФ, том 161, вып. 2, 2022

Сингулярные функции спинорного поля в КЭД.. .

∫

(

)

Полагая y_- = 0, выполним замену переменной

S^±(X, X^′) = θ

∓π^′-

Y (±)(X, X^′; p_-)dp- ,

s = ^-a в интеграле Δ⁺(X, X^′) и замену переменной

[

]

(m - γ_⊥p_⊥)

s =₊a в интеграле Δ^-(X, X^′):

Y (±)(X, X^′; p_-) =

γ⁰ +

Ξ₊ ×

4π

π_-

[

]

∫

(m + γ_⊥p^′∗⊥)

(

× γ⁰ +

γ0-+F ,

Δ⁺(X, X^′) = θ

-π^′-

) ^-f(X,X^′;p_-)dp_- =

π^′

[

)

−∞

∫

^{i

⁽x2- -x′2-

eE ds

F =

I₁ exp

-t²+t′2

f (X, X^′; s)

(2π)d-2

sinh(eEs)

]

}

Γc

∫

− p_-(x₊ - x′+)

- im²-+a

eE ds

- θ(+y_-)

f (X, X^′; s)

∫

sinh(eEs)

[

]

Γc -Γ2-Γ1

I₁ = exp

-i-+ap2⊥ + i(r_⊥ - r^′⊥)p_⊥

dp_⊥ ,

∫

{

}

(

)

[

(

)]_∗

Δ^-(X, X^′) = θ

+π^′

ln (∓iπ_-) -

±iπ^′-

+f(X, X^′; p-)dp- =

2eE

√

-∞

∫

π_- = π_-/

eE,

π^′- = π^′-/

eE .

eE ds

f (X, X^′; s)

sinh(eEs)

Для комплексной переменной-+a выберем главную

Γc

∫

ветвь логарифма:

eE ds

- θ(-y_-)

f (X, X^′; s)



sinh(eEs)

π- 

Γc -Γ2-Γ1

Re(-+a) =



,

2eE

^π^′

−

Im(-+a) = ∓

sgn(π_-)θ(-π_-π^′-).

f (X, X^′; s) =

2eE

)d/2

[

⁽ -i

exp

- eEγ⁰γ¹ s+ieΛ-ism² +

Вычисляя гауссовый интеграл I₁, получим

4πs

]

(

)

(

)(d-2)/2

|r_⊥ - r^′⊥|² -

eE coth(eEs)

y²⁰ - y²¹

-i

F (X, X^′; p_-) = i

4π-+a

Все контуры интегрирования показаны на рис. 1.

{

π_- + π^′-

Замыкая контур интегрирования Γ_c - Γ₂ - Γ₁ на

× exp

-i

y₊ +

(53)

Re s → ±∞, преобразуем его в контур Γ (см. рис. 2).

}

В итоге получим

+ ieΛ - i-+am² +

|r_⊥ - r^′⊥|²

4-₊a

S^±(X, X^′) = (γP + m)Δ^±(X, X^′),

∫

Λ = -Ey₀(x + x^′)/2 , y_± = x_± - x^′±.

(55)

∓ Δ^±(X, X^′) = f(X, X^′; s)ds -

Γc

Учитывая данный результат, можно записать

∫

функции S^±(X, X^′) в виде

-θ(±y_-) f(X, X^′; s)ds .

S^±(X, X^′) = ∓(γP + m)Δ^±(X, X^′),

∫

Ядро Фока - Швингера f(X, X^′; s) дано выражени-

(

Δ^±(X, X^′) = dp_- θ

∓π^′-

f (X, X^′; p_-) ,

ем (18) с калибровочно-зависимым членом Λ в (53).

(

Заметим, что этот член может быть представлен как

) -

(54)

f (X, X^′; p_-) = exp

-eEγ⁰γ1-+a

f⁽⁰⁾ ,

интеграл по кривой (19), где в нашем случае потен-

)d/2

⁽-i

(_-

)

циал A_μ(X) определяется выражением (23).

(2-d)/2

f⁽⁰⁾ = -

В работе [18], было показано что

4π

∫

{

F (X, X^′; s) ds = 0, y_μy^μ < 0 ,

× exp

-i-+am² +

|r_⊥-r^′⊥|² -iπ-+π−

y₊ +

4-₊a

{

}}

[

(

)]

∗

откуда следует, что интегралы Δ^±(X, X^′) в (55) мо-

+ ieΛ -

ln (∓iπ_-) +

∓iπ^′-

гут быть записаны следующим образом:

201

ЖЭТФ, вып. 2

А. И. Бреев, С. П. Гаврилов, Д. М. Гитман

ЖЭТФ, том 161, вып. 2, 2022

∫

так что

∓ Δ^±(X, X^′) = f(X, X^′; s)ds -



π-

Γc



∫

Re(s) =

log

,

2eE

^π^′

−

- θ(±y₀) f(X, X^′; s)ds .

(56)

Im(s) = -

[θ(+π_-) + θ(-π_-)] ,

Таким образом, мы вывели интегральное пред-

2eE

ставление Швингера (16) для причинного пропага-

а в интеграле S^p(X,X^′) — замену переменных

тора (47) и продемонстрировали, что перестановоч-

ная функция (48) имеет универсальную структу-

s = b₊ - iπ/(2eE),

ру (17):

так что



S^c(X, X^′) = (γP + m)Δ^c(X, X^′),

π-

∫

Re(s) =

log



,

2eE

^π^′

−

Δ^c(X, X^′) = f(X, X^′; s)ds ,

[

]

Γc

Im(s) = -

θ(-π_-) + θ(-π^′-)

2eE

S(X, X^′) = (γP + m)Δ(X, X^′),

∫

Тогда

Δ(X, X^′) = sgn(t - t^′) f(X, X^′; s) ds .

∫

S^p(X, X^′) = - f(X, X^′; s)ds -

Фактически, приведенный выше результат пред-

Γp

ставляет собой косвенное доказательство полноты

∫

построенных выше наборов решений на гиперплос-

- θ(-y_-)

f (X, X^′; s) ds ,

кости t-const. Представление (56) верно для произ-

Γ2+Γ3-Γ

вольных X и X^′, несмотря на то, что замена пере-

∫

(57)

менных в интеграле (54) проводилась при условии

S^p(X, X^′) = - f(X, X^′; s)ds -

y_- = 0. Все это подтверждает, что представление

Γp

(56) эквивалентно представлению (47).

∫

Действуя аналогично, представим сингулярные

− θ(+y_-)

f (X, X^′; s) ds .

функции S^p(X, X^′) и S^p(X, X^′) в (52) следующим

образом:

Γ2+Γ3-Γp

∫

(

)

Замыкая контур интегрирования Γ₂ + Γ₃ - Γ_p при

S^p(X, X^′) = dp_- θ

+π^′-

Y (-)(X, X^′; p_-),

Re s → ±∞ трансформируем его в контур Γ1p (см.

∫

(

)

рис. 2) с радиусом, стремящимся к нулю:

S^p(X, X^′) = dp_- θ

-π^′-

Y (+)(X, X^′; p_-),

[

]

S^p(X, X^′) = (γP + m)Δ^p(X, X^′),

(m - γ_⊥ p_⊥)

Y (±)(X, X^′; p_-) =

γ⁰ +

Ξ₊×

∫

4π

π_-

Δ^p(X, X^′) = - f(X, X^′; s)ds -

[

]

(m + γ_⊥p^′∗⊥)

× γ⁰ +

γ⁰ F˜(±) ,

π^′

∫

[

)

±iI₂

^{i

⁽x2--x′2-

- θ(-y_-)

f (X, X^′; s) ds ;

F(±) =

exp

-t²+t′2

(2π)d-2

Γ¹

]

(

)

}

iπ

(58)

− p_-(x₊ - x′+) -i b± -

m²

S^p(X, X^′) = (γP + m)Δ^p(X, X^′),

2eE

∫

[ (

)

]

∫

iπ

I₂ = exp -i b±-

p2⊥+i(r_⊥-r^′

)p_⊥ dp_⊥ ,

⊥

Δ^p(X, X^′) = - f(X, X^′; s)ds -

2eE

(

)

[

(

)]_∗

Γp

b_± = ln(±i π_-) -

±iπ^′-

/(2eE) .

∫

- θ(+y_-)

f (X, X^′; s) ds .

Полагая y_- = 0, выполним в интеграле S^p(X, X^′)

замену переменных

Γ¹p

s = b_- - iπ/(2eE),

Заметим, что в пределе s → ±0-iπ/eE мы имеем

202

ЖЭТФ, том 161, вып. 2, 2022

Сингулярные функции спинорного поля в КЭД.. .

lim

f (X, X^′; s) =

Можно проверить, что представления (60) (и

s→±0-iπ/eE

следовательно, представления

(61)) справедливы

= ±f_⊥(X, X^′)δ(y⁰)δ(y¹),

для произвольных X и X^′. Для этого мы нужно

)(d-2)/2

⁽ eE

(59)

показать, что для всех X и X^′ представления (60)

f_⊥(X, X^′) = -i

4π²

удовлетворяют тому же самому уравнению Дирака,

(

)

πm²

что и представления (50). Сначала мы должны про-

× exp iπγ⁰γ¹ -

|r_⊥ - r^′⊥|2

верить, что интегралы (60) удовлетворяют уравне-

4π

нию Дирака для всех X и X^′. Затем остается убе-

Принимая во внимание (59), можно выделить все

диться, что при t = t^′ условия Коши для обобщен-

особенности в интеграле (58):

ных функций (50) совпадают с условиями для вы-

∫

ражений (60).

f (X, X^′; s) ds = θ(y²¹ - y²⁰)Δ^pR(X, X^′) ,

Заметим, что соответствующие скалярные син-

Γ1p

гулярные функции могут быть получены из пред-

∫

ставлений для спинорных функций Δ^±(X, X^′),

Δ^pR(X, X^′) =

f (X, X^′; s) ds .

Δ^c(X, X^′), Δ(x, x^′) и Δ^p/p(X, X^′), если формально

Γ^p

положить все γ-матрицы равными нулю.

Здесь Γ^pR — контур интегрирования проходящий по

Мы рассмотрели случай, когда L-постоянное

часовой стрелке в виде круга с центром s = -iπ/eE

электрическое поле направлено вдоль оси x, E_x = E.

и достаточно малого радиуса R, так что внутри дан-

Ясно, что выбор противоположного направления со-

ного контура функция f(x, x^′, s) не имеет других

ответствует отражению x → -x, x^′ → -x^′ и замене

особенностей.

γ¹ → -γ¹. Поэтому достаточно рассмотреть случай

Приведем окончательный вид сингулярных

одного направления электрического поля. Мы ви-

функций S^p/p:

дим, что представления (60) и (61) с точностью до

калибровочного слагаемого совпадают с представ-

S^p/p(X, X^′) = (γP + m)Δ^p/p(X, X^′),

лениями (20) и (21). Их легко записать в ковари-

∫

(60)

антном виде с помощью тензора электромагнитного

- Δ^p(X, X^′) = f(X, X^′; s)ds +

поля F_μν , см. (22). Напомним, что выражение (22)

Γ^p∫

было найдено для постоянного электрического поля,

задаваемого нестационарным потенциалом в рамках

+ θ(y¹)

f (X, X^′; s) ds ,

общей формулировки КЭД для такого случая [3].

Γ¹

∫

− Δ^p(X, X^′) = f(X, X^′; s) ds +

Γp

4. ОБСУЖДЕНИЕ

∫

+ θ(-y¹)

f (X, X^′; s) ds .

В данной работе построены и исследованы син-

Γ¹p

гулярные функции в КЭД сильного поля в T -посто-

Заметим, что контур Γ1p трансформируется в контур

янном электрическом поле и в КЭД сильного по-

Γ₂ + Γ₃ - Γ_p. Ступенчатая функция θ(±y¹) может

ля в L-постоянном электрическом поле. Для обоих

быть представлена как функция θ(yE/E) от проек-

случаев найдены in- и out-решения уравнения Дира-

ции yE/E вектора смещения y на направление элек-

ка специального вида в переменных светового кону-

трического поля.

са. С помощью этих решений построены интеграль-

Учитывая (60), мы получаем представление по

ные представления Фока - Швингера по собственно-

собственному времени для сингулярных функций

му времени для всех видов сингулярных функций,

Scin/out(X, X^′) и S∓in/out(X, X^′):

необходимых для вычисления амплитуд вероятно-

стей процессов и средних значений физических ве-

Scin/out(X, X^′) = S^p/p(X, X^′) + S^c(X, X^′),

личин. Впервые получены интегральные представ-

(61)

ления Фока - Швингера для сингулярных функций

S∓in/out(X, X^′) = ∓S^p/p(X, X^′) + S^±(X, X^′).

в КЭД сильного поля в L-постоянном электриче-

Заметим, что замена переменных в интеграле

ском поле. Получены представления сингулярных

(57) была выполнена при условии y_- = 0. Однако

функций в КЭД сильного поля в T-постоянном элек-

представления (52) справедливы для всех y_-.

трическом поле для произвольной ориентации внеш-

203

А. И. Бреев, С. П. Гаврилов, Д. М. Гитман

ЖЭТФ, том 161, вып. 2, 2022

него электрического поля, что нетривиальным обра-

Тем не менее, в случаях, когда соответствующие

зом обобщает результаты работ [18,19].

вклады в диаграммы Фейнмана конечны, можно ис-

После стандартной ультрафиолетовой регуляри-

пользовать полученные собственно-временные пред-

зации и перенормировки все физические величины,

ставления сингулярных функций S^p/p(X, X^′). Тогда

которые могут быть получены при помощи при-

регуляризация постоянного однородного электриче-

чинного пропагатора S^c(X, X^′), конечны в преде-

ского поля L-постоянным полем эквивалентна регу-

ле L → ∞ и T → ∞. К примеру, это видно для

ляризации T -постоянным полем при T, L → ∞.

вакуумных матричных элементов тензора энергии-

импульса:

Финансирование. Исследование выполнено

при финансовой поддержке Российского научного

〈T_μν 〉^c = 〈0, out| T_μν |0, in〉 c-1v ,

фонда (проект № 19-12-00042).

(

)

T_μν =

Tcanμν + Tcanνμ

{[

]

ЛИТЕРАТУРА

Tcanμν =

Ψ^†(X)γ⁰, γ_μP_ν Ψ(X) +

[

]}

W. Greiner, B. Müller, and J. Rafelski, Quantum

+ P∗ν Ψ^†(X)γ⁰,γ_μΨ(X)

Electrodynamics of Strong Fields, Springer-Verlag,

Berlin (1985).

которые могут быть представлены в виде

J. Schwinger, Phys. Rev. 82, 664 (1951).

〈T_μν〉^c = i tr [A_μνS^c(X, X^′)]|X=X′ ,

D. M. Gitman, J. Phys. A

10,

2007

(1977);

[

]

E. S. Fradkin and D. M. Gitman, Fortschr. Phys.

A_μν =

γ_μ(P_ν + P^′∗ν) + γ_ν(P_μ + P^′∗μ)

29, 381 (1981); E. S. Fradkin, D. M. Gitman, and

S. M. Shvartsman, Quantum Electrodynamics with

Естественно, что проблемы нестабильности ва-

Unstable Vacuum, Springer-Verlag, Berlin (1991).

куума и ее проявления совершенно различны в L-по-

S. P. Gavrilov and D. M. Gitman, Phys. Rev. D 93,

стоянном поле и T-постоянном поле для конечных

045002 (2016).

интервалов T и L. Однако в пределе T, L → ∞ со-

ответствующие характеристики нестабильности ва-

S. P. Gavrilov and D. M. Gitman,Phys. Rev. D 93,

куума оказываются одинаковыми. В частности, этот

045033 (2016).

факт можно интерпретировать следующим образом:

S. P. Gavrilov, D. M. Gitman, and A. A. Shishmarev,

оба случая представляют собой разные регуляри-

Phys. Rev. D 96, 096020 (2017).

зации в идеализированном случае постоянного од-

нородного электрического поля. Однако эта экви-

N. N. Bogoliubov and D. V. Shirkov, Introduction to

валентность может отсутствовать для средних зна-

the Theory of Quantized Fields, John Willey & Sons.

чений физических величин, которые могут быть

Inc., New York (1980).

получены с использованием сингулярных функций

G. V. Dunne (eds.), From Fields to Strings: Cir-

Scin/out(X, X^′). Например, вакуумные средние тензо-

cumnavigating Theoretical Physics, World Scientific,

ра энергии-импульса,

Singapore (2005).

〈T_μν 〉in/out = 〈0, in/out| T_μν |0, in/out〉 ,

G. V. Dunne and T. Hall, Phys. Rev. D 58, 10502

(1998).

могут быть представлены в виде

10.

V. P. Gusynin and I. A. Shovkovy, Can. J. Phys.

[

]

74, 282 (1996); V. P. Gusynin and I. A. Shovkovy,



〈T_μν 〉in/out = i tr A_μν Scin/out(X, X^′)



J. Math. Phys. 40, 5406 (1999).

X=X^′

11.

H. Gies and F. Karbstein, J. High Energy Phys.

где учтены вклады от S^p/p(X, X^′). Такие вклады

2017(3), 108 (2017).

неограниченно растут в пределах T → ∞ и L → ∞,

см. работы [5, 20]. Этот факт связан с неограничен-

12.

F. Karbstein, Phys. Rev. D 95, 076015 (2017).

ным ростом плотности рождающихся пар электро-

13.

F. Karbstein, Phys. Rev. Lett. 122, 211602 (2019).

нов и позитронов. Отсюда следует, что в таких слу-

чаях существует существенная физическая разница

14.

S. P. Gavrilov and D. M. Gitman, Phys. Rev. D 95,

между T -постоянным и L-постоянным полем.

076013 (2017).

204