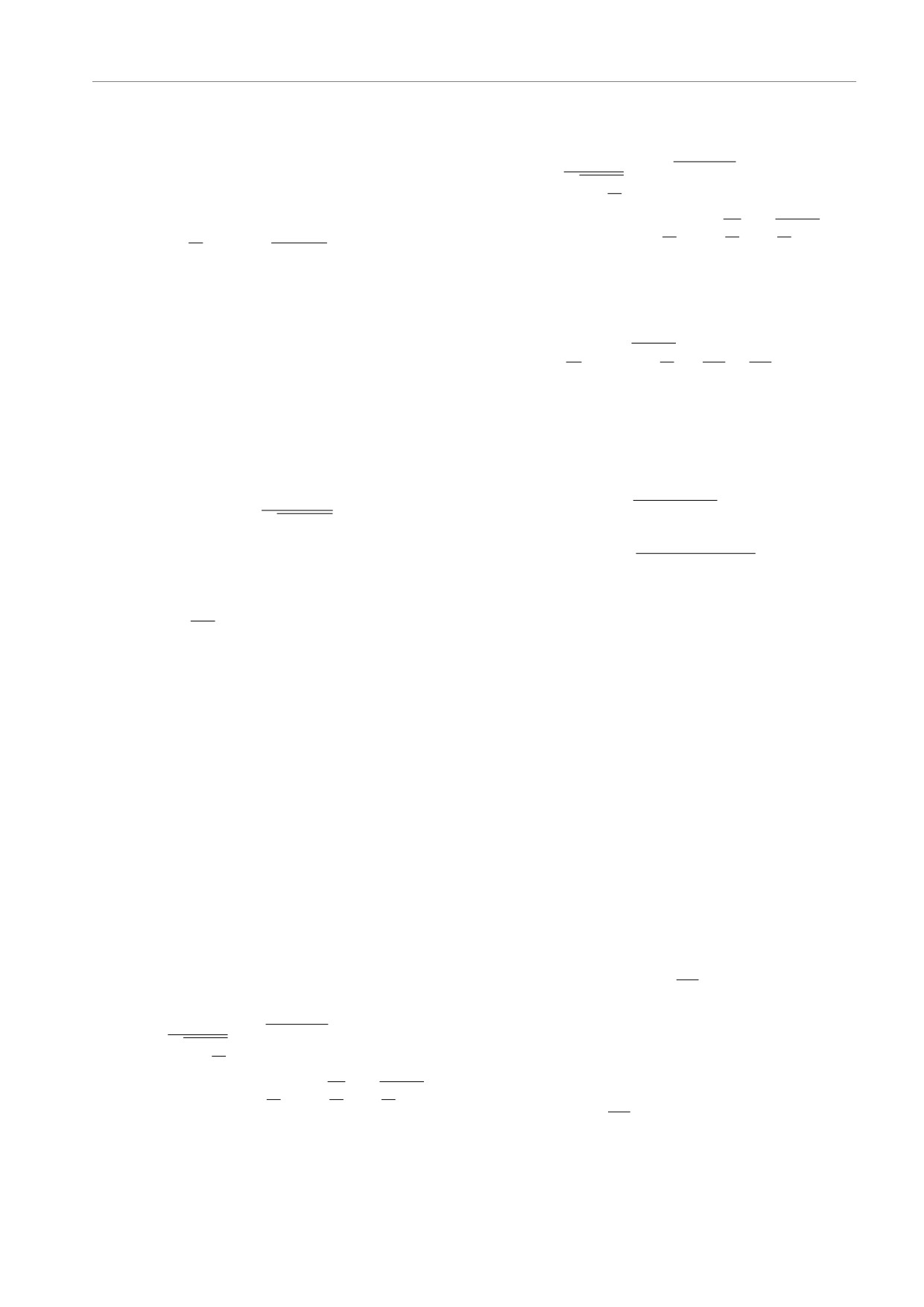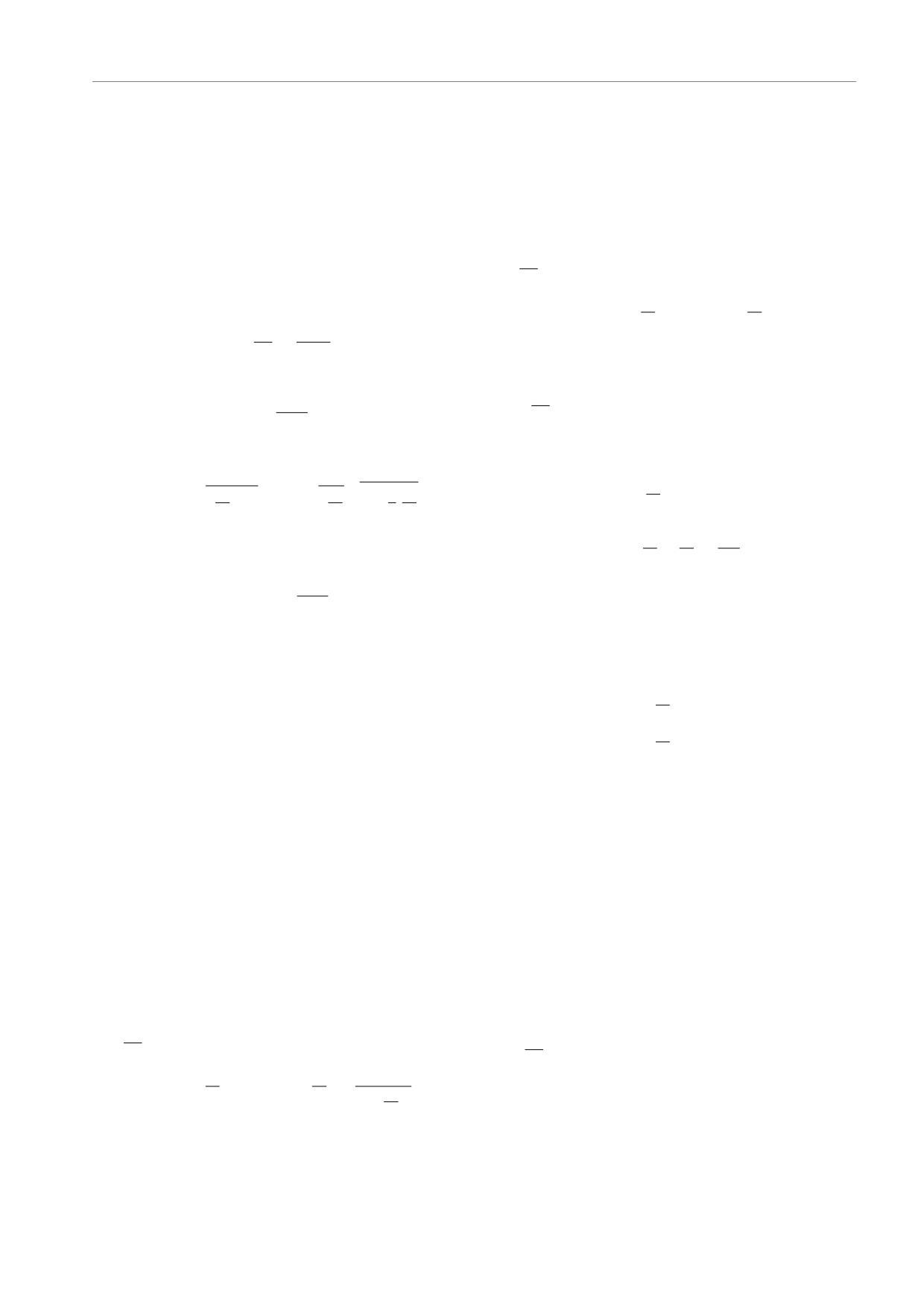ЖЭТФ, 2022, том 162, вып. 1 (7), стр. 96-107

ГЕОДЕЗИЧЕСКИЕ В ГРАВИТАЦИОННОМ ПОЛЕ

КРОТОВОЙ НОРЫ

М. В. Сажин, О. С. Сажина^*, А. А. Шацкий

Государственный астрономический институт им. П. К. Штернберга,

Московский государственный университет им. М. В. Ломоносова

119234, Москва, Россия

Поступила в редакцию 10 февраля 2022 г.,

после переработки 10 февраля 2022 г.

Принята к публикации 16 февраля 2022 г.

Теоретически исследуются структура пространства-времени вблизи кротовой норы (КН) и возможные

наблюдательные следствия. В связи с растущей точностью наблюдений и перспективностью нового гра-

витационно-волнового канала задача различения астрофизических проявлений черных дыр и гипотети-

ческих КН приобретает актуальность. КН, наряду с черными дырами, естественно возникают в рамках

ОТО. Для наблюдательных поисков КН необходимо знание характерных траекторий тел в ее окрест-

ности, в том числе траекторий, заходящих в ее горловину. Выведены уравнения движения пробной

частицы в метрике КН, а также рассмотрены наиболее интересные свойства этих движений. Выведено

общее уравнение геодезических в метрике КН и рассмотрены некоторые свойства этих геодезических.

Проанализированы точное решение для круговых орбит пробных частиц вокруг КН, а также приближен-

ное аналитическое решение уравнений геодезических. Рассмотрено смещение перицентра орбиты проб-

ной частицы в поле КН и обсуждаются возможные наблюдательные следствия. Представлены примеры

траекторий пробных частиц у КН, полученные путем численного моделирования.

DOI: 10.31857/S0044451022070100

Для описания наблюдательных проявлений

EDN: EEGIMJ

вблизи КН необходимо знать закон движения проб-

ных частиц, другими словами, форму геодезических

вблизи КН. В предлагаемой работе будут выведены

1. ВВЕДЕНИЕ

уравнения движения пробной частицы в метрике

КН, а также рассмотрены наиболее интересные

В общей теории относительности (ОТО) появля-

свойства этих движений.

ется несколько решений, которые описывают реля-

тивистские объекты, скорость пробных частиц вбли-

зи которых сравнима со скоростью света. Это преж-

де всего ¾черные дыры¿ (далее ЧД)

решения

уравнений ОТО, найденные Шварцшильдом и Кер-

В разд. 2 мы рассматриваем метрику КН и неко-

ром. ЧД открыты как в электромагнитном канале

торые общие свойства этой метрики. В разд. 3 мы

наблюдений [1], так и в гравитационно-волновом ка-

выводим общее уравнение геодезических в метрике

нале [2]. Открытие ЧД внушает уверенность, что и

КН и рассматриваем некоторые свойства этих гео-

другие решения ОТО (на сегодняшний день толь-

дезических. В разд. 4 анализируем точное решение

ко теоретические) могут существовать в космосе.

для круговых орбит пробных частиц вокруг КН. В

Одним из таких гипотетических решений являют-

разд. 5 мы рассматриваем приближенное аналити-

ся кротовые норы (далее КН). Сейчас существует

ческое решение уравнений геодезических и некото-

несколько решений типа КН [3, 4], см. обзор [5]. В

рые его свойства. Наконец, в разд. 6 мы рассматри-

литературе рассматривают как решения ОТО, так

ваем смещение перицентра орбиты пробной частицы

и наблюдательные проявления КН [6-8].

в поле КН и обсуждаем возможные наблюдатель-

ные следствия. В Приложении представлены при-

меры траекторий движения пробных частиц у КН,

^* E-mail: cosmologia@yandex.ru

полученные путем численного моделирования.

ЖЭТФ, том 162, вып. 1 (7), 2022

Геодезические в гравитационном поле кротовой норы

2. МЕТРИКА КРОТОВОЙ НОРЫ И ЕЕ

а для нижней полы пространства КН

СВОЙСТВА

∫

√

l=-

√

r (r - r₀) -

Метрику КН примем в простейшем виде:

r₀

√

}

(

r₀

{√ r

rg⁾

dr²

-1

ds² =

c²dt² -

r₀

1 - r₀/r

(

)

-r²

dθ² + sin² θ dϕ²

(1)

Метрика (2), а также первые и вторые производ-

ные радиальной координаты по l регулярны во всей

Здесь ct, r, θ, ϕ

соответственно координаты x⁰,

области определения (-∞ < l < +∞):

x¹, x², x³. Величина r_g

гравитационный ради-

√

r₀

d²r

r₀

ус КН, а r₀ радиус ее горловины. В отличие от

=±

(3)

dl²

2r²

шварцшильдовской метрики, метрика (1) является

двухпараметрической и определяется параметрами

Метрике (2) соответствует тензор энергии-импульса

rg и r0.

T^ik, нарушающий нулевое энергетическое условие

Можно преобразовать радиальную координату

(NEC) для радиальных фотонов.

следующим образом:

Ненулевые компоненты этого тензора имеют вид

r₀ - r_g

T^rr =

> 0,

dl = ±√

8πr²(r - r_g)

1 - r₀/r

(r_g - r₀)(2r - r_g)

T^θθ = T^ϕϕ =

< 0.

Тогда метрика КН (1) запишется в виде

32πr²(r - r_g)²

Ниже мы обсудим вид траекторий пробных частиц

(

)

как в r-координатной системе, так и в l-координат-

ds² =

c²dt² - dl² -

r(l)

ной системе.

(

)

- r(l)²

dθ² + sin² θdϕ²

(2)

3. УРАВНЕНИЯ ДВИЖЕНИЯ ПРОБНОЙ

Для того чтобы у КН не было горизонтов ЧД, необ-

ЧАСТИЦЫ ВОКРУГ КРОТОВОЙ НОРЫ

ходимо на функцию g₀₀(l) наложить условие, со-

3.1. Анализ геодезических в

гласно которому она во всей области определения

пространстве-времени кротовой норы

(-∞ < l < ∞) должна быть больше нуля. При

выполнении условия r₀ > r_g величина g₀₀(l) будет

Проанализируем уравнение геодезических в про-

больше нуля во всей области определения. При этом

странстве-времени КН. Метрику возьмем в виде (1)

функция r²(l) (квадрат радиуса) должна достигать

(радиальная координата есть r). Геодезические так-

своего минимума на горловине КН, которая опреде-

же будут уравнениями движения пробных частиц.

ляется точками l = 0 и r = r₀. Преобразование от

Будем также считать, что полученные нами уравне-

радиальной координаты r, которая является неодно-

ния движения относятся к движению пробной час-

значной (одно и то же значение r может принадле-

тицы по верхней поле пространства.

жать разным полам полного пространства), к ради-

Обыкновенная производная от траектории час-

альной координате l, которая уже однозначно опре-

тицы по собственному времени s выражается через

деляет положение каждой точки в полном простран-

компоненты

стве, для верхней полы пространства КН есть

dxⁱ

uⁱ ≡

∫r

Эту величину в ОТО называют также контравари-

√

l=+

√

r (r - r₀)+

антной 4-скоростью. Уравнение геодезической опре-

r₀

деляется для касательного вектора вдоль траекто-

рии частицы uⁱ

√

}

r₀

{√ r

-1

duⁱ

r₀

+ Γ^ijku^ju^k = 0.

ЖЭТФ, вып. 1 (7)

М. В. Сажин, О. С. Сажина, А. А. Шацкий

ЖЭТФ, том 162, вып. 1 (7), 2022

)

(

Для ковариантных компонент касательного век-

r₀ )( ǫ²

h²

(u^r)² =

-1-

(8)

тора u_i соответствующее уравнение имеет вид

1 - r_g/r

r²

du_i

1 ∂g_jk

Далее сделаем подстановку

u^ju^k.

∂xⁱ

Поскольку метрика (1) является статической и

сферически-симметричной, можно сразу написать

которая окончательно приведет к уравнению

два интеграла движения [9]:

( du)2

ǫ² - 1 + r_gu 1 - r₀u

+ (1 - r₀u) u² =

(9)

u₀ ≡ ǫ = const,

(4)

dϕ

h²

1-r_gu

u₃ ≡ h = const.

(5)

При анализе уравнений движения в метрике ЧД

существует аналогичное уравнение, которое выгля-

Первый интеграл есть сохранение полной энер-

дит как

гии системы, а второй сохранение момента коли-

чества движения. Кроме того, можно показать, что

( du)2

ǫ² - 1

+ (1 - r_gu) u² =

пробная частица движется в плоскости, а это озна-

dϕ

h²

чает, что θ(s) = const. Можно выбрать θ(s) = π/2.

Можно также сравнить (13) с нерелятивистским

Тогда интегралы можно переписать в виде

уравнением движения. Оно получается, если прене-

(

бречь величинами r₀u, r_gu по сравнению с единицей:

rg) dt

= ǫ,

r ds

(6)

( du)2

ǫ² - 1 + r_gu

dϕ

+u² =

r²

= h.

dϕ

h²

Выпишем еще несколько полезных уравнений.

Итак, у нас есть уравнения для трех координат.

Для КН (в отличие от ЧД) радиальную коорди-

Выведем уравнение для эволюции радиальной ко-

нату r можно рассматривать как компоненту мет-

ординаты r. Это уравнение будем выводить так же,

рики (1). Можно сказать, что величина r являет-

как это делается при анализе движения в метрике

ся поперечной радиальной координатой, а продоль-

ЧД. Для нахождения уравнений движения по ради-

ной радиальной координатой является величина l из

усу используем уравнение метрики:

метрики (2).

(

Поэтому равенство нулю производной r не озна-

rg) dt²

dr²

r₀

чает прекращения движения по продольной ради-

r ds²

ds²

альной координате l. По этой причине на горловине

)

( dθ

dϕ²

КН всегда будет выполняться условие r = 0, но в

-r²

+ sin² θ

ds²

общем случае величина

l = 0 на горловине КН.

Будем рассматривать случай массивной пробной

3.2. Условие достижимости горловины

частицы (двигающейся со скоростью, меньшей ско-

кротовой норы свободно падающей частицей

рости света).

Подставим в уравнение метрик величину θ = π/2

Запишем величину

l на горловине КН. С учетом

и получим уравнение

выражений (3) и (8) получаем в произвольной точ-

(

ке:

√

rg) dt²

dr²

dϕ²

-r²

h²

r ds²

1 - r₀/r ds²

ds²

=u^l =±

-1-

1 - r_g/r

r²

Это уравнение можно преобразовать как

В точке горловины, r = r₀,

(

)

(

rg) dt²

dϕ²

dr²

(

)₂

ǫ²

h²

+r²

= 1.

u^l0

-1-

(10)

r ds²

ds²

1 - r₀/r dϕ²

1 - r_g/r₀

Подставим интегралы движения и получим

причем для чисто радиального падения имеем h =

уравнения

= 0, поэтому

(

)

ǫ²

h²

dr²

(

)₂

ǫ²

+r²

= 1,

(7)

u^l00

- 1.

(11)

1 - r_g/r

r⁴

1 - r₀/r dϕ²

1 - r_g/r₀

ЖЭТФ, том 162, вып. 1 (7), 2022

Геодезические в гравитационном поле кротовой норы

Из этого выражения видно, что при радиальном

Обозначая точкой производную по собственному

падении подавляющее число траекторий достигают

времени ds, получаем

горловины КН с ненулевой продольной скоростью.

И наоборот: для того чтобы частица не достигла

r₀/r²

r² =

горловины КН, необходимо, чтобы правая часть вы-

1 - r₀/r

(1 - r₀/r)²

]

ражений (10) или (11) была отрицательной.

[r_g

ǫ²

r₀/r²

r²

(12)

При этом никаких ограничений на величину ин-

r² (1 - r_g/r)²

(1 - r₀/r)²

теграла движения для удельной полной энергии ǫ,

Здесь r ≡ u^r определяется выражением (20) (см. ни-

кроме того, что ǫ > 0, не существует. Величина ǫ = 1

же).

соответствует тому, что частица на бесконечности

имеет нулевую скорость. Диапазон значений ǫ > 1

Переносим в выражении (12) все члены в правую

часть и умножаем их на (1 - r₀/r)²:

соответствует тому, что траектория частицы будет

инфинитной, и наоборот: диапазон значений ǫ < 1

(

r₀ )

r₀

rgǫ²(1 - r0/r)²

соответствует тому, что частица гравитационно за-

r² +

= 0.

2r²

2r²⁰(1 - r_g/r)²

хвачена, и ее траектория будет финитной.

Анализ траекторий можно проводить в r-коор-

Или, обозначая δr ≡ r - r₀, получаем

динатах (уравнения движения выглядят проще), а

δr δr

r₀(δ r)²

rgǫ²(δr)²

можно в l-координатах. Во втором случае уравне-

= 0.

(13)

2r²

2r²⁰(r - r_g)²

ния содержат не только квадрат производных, но

также и нелинейные функции l, которые являют-

Вблизи горловины величину r можно разложить в

ся также неявными функциями этой переменной.

ряд по малым значениям l. Используем для этого

Тем не менее будем анализировать уравнения дви-

выражения (3):

жения также и в l-координатах. Причина заключа-

ется в том, что в r-координатах на уравнения дви-

l²

r(l) ≈ r₀ +

δr ≈

δr≈

жения накладываются связи вида r ≥ r₀, что приво-

4r₀

2r₀

(14)

дит рассматриваемую задачу к задаче о движении

l)²

с уравнениями с неголономными неудерживающими

δr≈

2r₀

связями [10,11]. Такие уравнения требуют специаль-

ного рассмотрения, которого в нашем случае мож-

Делим выражение (13) на δr/r и подставляем в него

но избежать, рассматривая задачу о движении в l-

значения производных из (14), в квадратичном при-

координатах. Особенно удобно рассмотрение задачи

ближении по l получаем

о движении пробных частиц в l-координатах вблизи

горловины КН. В этом случае r ≈ r₀ и можно ана-

l)²

r₀ l²(˙l)2/(4r20)

лизировать уравнения движения в пределе малых l,

2r₀

l²/(4r₀)

т. е. l ≪ r₀.

rgǫ²l²

= 0.

(15)

8r²⁰(r₀ - r_g)²

3.3. Собственная частота малых колебаний

В квадратичном приближении по l второй и третий

через горловину кротовой норы

члены в (15) взаимно сокращаются:

Найдем частоту колебаний пробной частицы че-

rgǫ²l²

= 0.

рез горловину КН в предположении малости ампли-

2r₀

8r²⁰(r₀ - r_g)²

туды колебаний.

Отсюда получаем уравнение гармонических колеба-

Уравнение движения частицы запишем в виде

ний по l:

du_k

1 ∂g_ij

ǫ²r_g

uⁱu^j.

l+ ω²l = 0 , ω² ≡

2 ∂x^k

4r₀(r₀ - r_g)²

Тогда для k = r имеем

Величина ω и определяет собственную частоту ма-

]

лых колебаний вблизи горловины КН для зависимо-

d (u^rg_rr)

[∂g_tt

(

)₂

∂g_rr

сти продольной физической координаты l от собст-

u^t

(u^r)²

∂r

венного времени s.

М. В. Сажин, О. С. Сажина, А. А. Шацкий

ЖЭТФ, том 162, вып. 1 (7), 2022

4. АНАЛИЗ ТОЧНОГО РЕШЕНИЯ В

Эти два уравнения определяют связь удельного уг-

МЕТРИКЕ КРОТОВОЙ НОРЫ ДЛЯ

лового момента h и удельной полной энергии ǫ с ра-

СЛУЧАЯ КРУГОВОЙ ОРБИТЫ

диусом r устойчивой круговой орбиты частицы.

Обратим особое внимание на то, что выражения

4.1. Круговые орбиты и их устойчивость

(7) и (19) не зависят от величины r₀. Это связано

Рассмотрим важный случай круговых орбит во-

с тем, что величины ǫ и h не зависят от компо-

круг КН. Анализировать будем точное уравнение

ненты g_rr метрики (1). В нерелятивистском пределе

движения (13). Круговые орбиты определяются со-

rg/r → 0 второе выражение (19) переходит в извест-

отношением

ную ньютоновскую формулу для ¾постоянной энер-

гии¿ частицы на круговой орбите вокруг массивного

u^r

= 0.

(16)

центра с массой M:

u^t

Кроме этого, есть еще одно соотношение, кото-

ǫ → 1 - M/(2r).

рое определяет устойчивые и неустойчивые орбиты.

Минимальный радиус неустойчивой орбиты есть

Для того чтобы получить критерий устойчивости,

r = (3/2)r_g, при этом h → ∞, ǫ → ∞.

надо через (16) выписать уравнение для производ-

Поскольку в метрике КН орбиты с r < r₀ невоз-

ной радиуса по времени:

можны, наличие последней устойчивой орбиты, а

(

)(

тем более последней неустойчивой орбиты опреде-

( dr)2

rg⁾

= 1-

ǫ^-2 ×

ляется соотношением между гравитационным ради-

[

)]

усом КН и радиусом горловины. При r₀ > 3r_g все

(

rg⁾⁽

h²

круговые орбиты являются устойчивыми.

× ǫ² -

(17)

r²

Для случая r₀ = r_g появляется последняя устой-

чивая орбита. В случае метрики Шварцшильда

Экстремумы функции

пробная частица, минуя r = (3/2)r_g, совершает ме-

)

√(

нее одного оборота вокруг ЧД. Вычислим полное из-

rg⁾⁽

h²

U (r) =

менение угла при сходе частицы с последней устой-

r²

чивой орбиты в случае КН. Выпишем уравнение

для u^r:

определяют устойчивость орбиты. Минимумы

функции отвечают устойчивым орбитам, максиму-

(

)

r₀ )( ǫ²

h²

мы неустойчивым. Из вида функции следует, что

(u^r)² =

-1-

(20)

1 - r_g/r

r²

она совпадает с функцией энергии, определяющей

круговые орбиты в метрике Шварцшильда с грави-

С другой стороны, имеем

тационным радиусом r_g. Поэтому так же, как и для

dϕ

u^ϕ

u_ϕg^ϕϕ

ЧД Шварцшильда, в метрике КН (1) последняя

u^r

r²u^r

устойчивая круговая орбита находится при r = 3r_g

√

и имеет параметры: h =

3r_g, ǫ =

8/9 (см. [9],

Подставляя сюда (20), получаем

§102).

Из сказанного выше следует, что устойчивая

dϕ

круговая орбита соответствует совместному реше-

√

нию двух уравнений:

1 - r_g/r

√

(21)

)

r²

[ǫ² - (1 + h²/r²)(1 - r_g/r)] (1 - r₀/r)

(

rg⁾⁽

h²

ǫ² -

=0,

r²

(18)

Полное изменение угла ϕ находится из этой форму-

U^′(r) = 0 .

лы интегрированием по радиусу.

интегрируем выражение (21)

Для случая r₀ = r_g

Здесь и далее штрих означает производную по r. Ре-

и получаем полное изменение угла от момента схода

шая совместно систему (18), получаем

с минимально устойчивой орбиты до гравитацион-

rgr

ного радиуса:

h² =

2 - 3r_g/r

∫

(19)

9h dr

(1 - r_g/r)

∆ϕ =

ǫ² =

1 - (3/2)r_g/r

r² (3r_g/r - 1)^3/2

3rg

100

ЖЭТФ, том 162, вып. 1 (7), 2022

Геодезические в гравитационном поле кротовой норы

Этот интеграл расходится в точке r = 3r_g, что со-

Новая переменная x лежит в интервале 0 ≤ x ≤

ответствует бесконечному количеству оборотов при

≤ 1. В принятом нами приближении величиной

сходе с минимально устойчивой орбиты для ЧД.

(r_g /r₀)x можно пренебречь по сравнению с едини-

цей, но нельзя пренебрегать по сравнению с величи-

ной ǫ² - 1, которая сама является малой. Поэтому

4.2. Собственное время витка обращения по

уравнение (16) упрощается и имеет вид

круговой орбите

Рассчитаем собственное время обращения проб-

( dx)2

ной частицы вокруг КН (или ЧД). Учтем, что эле-

+ (1 - x)x² =

dϕ

мент собственного времени это просто инвариант-

(

)

)₂

(r₀

ный элемент интервала ds:

ǫ² - 1 +

r^g x (1 - x) .

r₀

dϕ

ds ≡

u^ϕ

hg^ϕϕ

Это уравнение можно преобразовать к виду

Отсюда для полного оборота δϕ = 2π получаем

( dx)

(

)

2πr

= f(u) = (1 - x)

A+Bx-x²

(23)

δs =

dϕ

Подставляя сюда для h первое выражение (19), по-

Введем обозначения

лучаем

√

)₂ (

)

√

(r₀

3 r_g

A≡

ǫ² - 1

δs = 2πr

- 3 = 2πr

2 r

Отсюда видно, что выражение для собственного

(r₀)2 r_g

2r₀

B≡

времени витка оборота вокруг КН δs на бесконеч-

h r₀

ности совпадает с его ньютоновским пределом δτ:

Форма геодезических определяется корнями

√

δτ = 2πr

r/M .

функции f(u). Она представляет собой полином

третьей степени и, соответственно, имеет три корня.

Кроме того, величина собственного времени δs не

Первый корень, очевидно, есть x₁ = 1, два других

зависит от параметра r₀ для КН, т.е. она одинакова

корня

и для КН, и для ЧД.

r₀

x₂ =

(1 + e) ,

5. ПРИБЛИЖЕННЫЙ АНАЛИЗ

(24)

r₀

УРАВНЕНИЙ ДВИЖЕНИЯ

x₃ =

(1 - e) .

5.1. Уравнение траектории пробной частицы

Первый корень полинома третьей степени (x₁) пред-

Аналитический вид решения уравнения (13) нам

ставляет собой орбиту, находящуюся на горловине

найти не удалось, поэтому будем анализировать

КН, второй корень (x₂) является расстоянием в апо-

приближенное уравнение. Надо отметить, что это не

центре орбиты в ньютоновском приближении, а тре-

просто постньютоновское приближение, принятое в

тий корень (x₃) расстоянием в перицентре. Соот-

ОТО. Поскольку существует условие r_g < r₀, можно

ношение между корнями представляется в зависи-

также рассматривать приближение по малому пара-

мости от параметра орбиты p. В случае, когда p >

метру r_g/r₀. В зависимости от величины этого отно-

> 2r₀, соотношение между корнями имеет вид x₁ >

шения, разложение может быть достаточно точным.

> x₂ > x₃. В случае, когда r₀ ≤ p ≤ 2r₀, соотноше-

В данном разделе мы примем, что r_g ≪ r₀.

ние между корнями имеет вид x₂ > x₁ > x₃.

Для этого сделаем замену x = r₀u, тогда уравне-

Разложив многочлен третьей степени в произве-

ние (13) примет вид

дение линейных членов, получим уравнение

(

)₂

( dx)2

+ (1 - x)x² =

= f(x) = (1 - x)(x₂ - x)(x - x₃).

(25)

dϕ

)

)₂ (

(r₀

1-x

ǫ² - 1 +

(22)

r₀

Решением этого уравнения является эллиптичес-

r₀

кий интеграл первого рода.

101

М. В. Сажин, О. С. Сажина, А. А. Шацкий

ЖЭТФ, том 162, вып. 1 (7), 2022

Рассмотрим решение для орбиты пробной части-

где ∆ϕ(α) изменение угловой координаты ϕ при

цы вокруг КН. Для этого в уравнении (18) сделаем

изменении ¾релятивистской аномалии¿ от π - 2α

подстановку [12]:

до π.

Эти решения можно записать в виде функций

r₀

(1 + e cos χ) .

Якоби:

)

(

)

sin α = sn

∆ϕ(α)

cosα = cn

∆ϕ(α)

Здесь χ новая переменная, которую можно на-

звать ¾релятивистской аномалией¿. Производная от

Соответственно выражение для

¾релятивистской

функции x по переменной χ есть

аномалии¿ есть

r₀

(qϕ)

= -e

sin χ.

cos(χ) = cn²

- sn²

dχ

Здесь cn и sn эллиптические косинус и синус со-

Введем новый параметр задачи ρ = r₀/p. Тогда

ответственно.

можно написать уравнения для линейных членов и

Таким образом, уравнение траектории пробной

производной в виде

частицы на орбите вокруг КН имеет вид

1 - x = 1 - ρ - eρcosχ,

(

x₂ - x = eρ (1 - cosχ),

(qϕ)

(qϕ)).

1 + e cn²

- sn²

x - x₃ = eρ(1 + cosχ),

( dx)2

( dχ)2

5.2. Энергия пробной частицы

= (eρ)² sin² χ

dϕ

Выведем теперь формулу для постоянной энер-

Теперь для релятивистской аномалии получаем

гии в случае пробной частицы на орбите вокруг КН.

уравнение

Используем первые интегралы задачи о движе-

нии:

( dχ)2

= (1 - ρ - eρ cos χ) .

dr²

dϕ²

dϕ

-r²

1 - r_g/r

1 - r₀/r ds²

ds²

Отсюда следует, что параметр орбиты p в слу-

Преобразуем это уравнение как

чае эксцентричных орбит не может быть меньше,

(

чем (1 + e cos χ)r₀. Это неравенство соответствует

rg⁾⁽

r₀ )

ǫ² - 1 +

тому, что в случае эксцентричных орбит расстояние

(

от центра не может быть менее, чем r₀:

rg) dr²

rg⁾⁽

r₀ )

dϕ²

= 1-

- 1-

r²

r ds²

ds²

1+e

r(ϕ) >

r₀.

1 + ecosχ

В этом уравнении мы можем пренебречь множи-

телем (1 - r_g/r) в правой части, получаем уравнение

Переобозначим α = π/2 - χ/2 и запишем окон-

(

чательно уравнение для величины α:

rg⁾⁽

r₀ )

dr²

r₀ )

dϕ²

ǫ² - 1 +

- 1-

r²

ds²

dα

q√

=±

1 - k2 sin2 α,

теперь сделаем подстановку

dϕ

где

r²

= h.

2eρ

k² =

1 + eρ - ρ

Воспользуемся также подстановкой для траектории,

которую, как и в [12], в случае e < 1 будем называть

q² = 1 + eρ - ρ.

¾релятивистским эллипсом¿,

Решением этого уравнения является эллиптичес-

кий интеграл первого рода:

(1 + e cos χ)

∫

dτ

√

=±

∆ϕ(α),

e sinχ dχ

=r²

1-k2 sin2 τ

p ds

102

ЖЭТФ, том 162, вып. 1 (7), 2022

Геодезические в гравитационном поле кротовой норы

а также

финитных траектории они имеют вид ¾релятивист-

ского¿ эллипса, другими словами, почти эллиптиче-

( dχ)2

( dϕ)2

ской траектории со смещением перицентра орбиты.

= (1 - ρ - eρ cos χ)

Выпишем неравенства, которым должны удов-

летворять параметры геодезической. Прежде всего

= (1 - ρ - eρ cosχ)

напишем значения апоцентра и перицентра траек-

r⁴

тории:

окончательно получим

ra =

1-e

ǫ² - 1 +

(1 + e cosχ) =

rp =

1+e

(

)

2eh²

1+e²

cosχ.

Из неравенства r ≥ r₀ следует, что

p²

p≥r₀

(1 + e cos χ) .

(28)

Приравнивая члены при функции cos χ получаем

выражение для h(p):

Также получаем

1 - ρ - eρcosχ ≥ 0.

(29)

h² =

rgp,

(26)

Отметим, что неравенства (28) и (29) эквива-

а также для ǫ(e, p):

лентны.

Отсюда получаем неравенство, которое опреде-

(

)

ǫ² = 1 -

1-e²

=1-

(27)

ляет интервал изменения χ:

p-r₀

Здесь a

большая полуось ¾релятивистского эл-

≥ cosχ ≥ -1.

er₀

липса¿. Мы приняли, что

В случае

(

)

p=a

1-e²

p = r0 (1 + e)

угол χ содержится в интервале π ≥ χ ≥ 0. Для

В классической небесной механике [13] величина

меньших значений p интервал значений угла χ мень-

ше, чем π. Возникает ¾дефицит угла¿, аналогичный

W =-

геометрии пространства с космической струной [14].

Например, при

называется постоянной энергии. При этом W < 0 и

(

)

e < 1

эллиптическая орбита, W = 0 и e = 1

p=r₀

параболическая орбита, W > 0 и e > 1 гипербо-

лическая орбита.

интервал значений χ есть π ≥ χ ≥ 60^◦.

Будем также считать, что имеют место две все-

5.3. Анализ вида финитных траекторий

ленные: ¾первая вселенная¿ (или верхняя пола про-

странства, или верхняя вселенная) и ¾вторая все-

Рассмотрим вид траекторий при различных зна-

ленная¿ (или нижняя пола пространства, или ниж-

чениях параметров орбиты (или ǫ, h, или e и p) для

няя вселенная). Будем также полагать, что апо-

приближенного решения. Ограничимся рассмотре-

центр рассматриваемой системы (траектории или

нием финитных траекторий. Независимо от свойств

геодезической) находится в ¾первой вселенной¿. По-

горловины КН (она может быть ¾проходимой¿ или

ложение траектории может быть только в ¾первой

¾непроходимой¿), геодезические в этом случае всег-

вселенной¿ или может находиться частично в ¾пер-

да можно построить.

вой вселенной¿, частично во ¾второй вселенной¿.

Наиболее простой вид траектории имеют в слу-

Рассмотрим эти случаи в зависимости от соот-

чае

ношения между параметрами, которые определяют

p ≥ r0 (1 + e).

траектории движения. Положение траектории зави-

В этом случае траектория полностью находится на

сит от трех параметров: p, r₀ и e. Если p ≥ r₀(1 + e),

одной поле пространства, касаясь горловины КН в

то траектория полностью лежит в ¾первой вселен-

одной точке, когда параметр p = r₀ (1 + e). В случае

ной¿, причем траектория касается горловины КН в

103

М. В. Сажин, О. С. Сажина, А. А. Шацкий

ЖЭТФ, том 162, вып. 1 (7), 2022

одной точке только при p = r₀(1 + e). Далее, если

(здесь мы отсчитываем ¾релятивистскую анома-

p < r₀(1 + e), то траектория переходит во ¾вторую

лию¿ от апоцентра) составит

вселенную¿. Когда траектория располагается в обе-

их вселенных (¾первой¿ и ¾второй¿), угол χ меня-

πr₀

∆ϕ = 2π +

ется в интервале

p-r₀

≥ cosχ ≥ -1,

er₀

Отметим, что связь между периодом пробной

или

частицы на орбите вокруг КН и ее большой полу-

p-r₀

π ≥ χ ≥ arccos

осью определяется гравитационным радиусом КН, в

er₀

то время как смещение перицетра орбиты определя-

В случае, когда p < r₀, интервал есть

ется радиусом горловины КН. В рассматриваемом

случае, когда r₀ ≫ r_g, смещение перицентра может

π≥χ≥

значительно превосходить величину, предсказывае-

мую ОТО для ЧД. Это может служить критери-

В случае, когда r₀(1 + e) ≥ p ≥ r₀ интервал есть

ем для различения КН от ЧД при астрономических

наблюдениях.

≥ χ ≥ 0.

В случае, когда радиус головины превосходит

три гравитационных радиуса (r₀ > 3r_g) и все круго-

Полученные численно примеры характерных

вые орбиты вокруг КН являются устойчивыми, ве-

траекторий движения пробной частицы вблизи КН

личина смещения перицентра пробной частицы на

приведены в Приложении.

орбите вокруг КН превосходит смещение перицен-

тра этой частицы на орбите ЧД с таким же грави-

6. ОЦЕНКИ СМЕЩЕНИЯ ПЕРИЦЕНТРА

тационным радиусом.

Как известно, смещение перигелия планеты Мер-

курий явилось первым тестом ОТО. Существует

значимое расхождение между предсказаниями нью-

тоновской теории гравитации и наблюдаемым сме-

7. ЗАКЛЮЧЕНИЕ

щением перигелия. Оно составляет примерно 43^′′ за

100 лет.

В связи с растущей точностью наблюдений и

С тех пор смещение перицентра различных ре-

новым наблюдательным каналом

гравитацион-

лятивистских объектов в двойных системах превра-

но-волновой астрономией отличия движения ве-

тилось в один из самых мощных тестов исследова-

щества вблизи ЧД и КН могут стать различимыми.

ния двойных звездных систем. В частности, после

Для будущих поисков наблюдательных эффек-

открытия первого двойного пульсара PSR 1913+16

этот тест позволил точно измерить массы компонент

тов, отличающих именно КН, необходимо знать

формы характерных траекторий тел (пробных час-

двойной системы.

Для вычисления смещения перицентра проинте-

тиц) вблизи КН. В предлагаемой работе выведе-

грируем уравнение (17):

ны уравнения движения пробной частицы в метри-

ке КН, а также рассмотрены наиболее интересные

∫

свойства этих движений. Выведено общее уравнение

dχ

= ∆ϕ.

геодезических в метрике КН и рассмотрены неко-

√1 - ρ - eρ cos χ

−π

торые свойства этих геодезических. Проанализиро-

ваны точное решение для круговых орбит пробных

В случае ρ ≪ 1 интеграл имеет простой вид:

частиц вокруг КН, а также приближенное аналити-

∫

ческое решение уравнений геодезических. Рассмот-

(

)

eρ

рены смещение перицентра орбиты пробной части-

dχ

cosχ

= ∆ϕ.

цы в поле КН и обсуждены возможные наблюда-

−π

тельные следствия. Представлены примеры траек-

Смещение угловой координаты ϕ при полном

торий движения пробных частиц у КН, полученные

обороте по ¾релятивистской аномалии¿ -π ≤ χ ≤ π

путем численного моделирования.

104

ЖЭТФ, том 162, вып. 1 (7), 2022

Геодезические в гравитационном поле кротовой норы

Рис. 3. (В цвете онлайн) Данная траектория представля-

Рис. 1. (В цвете онлайн) Геодезическая начинается в зеле-

ет наибольший интерес. Она начинается, как и прежде, в

ной точке, доходит до горловины КН, переходит на вторую

зеленой точке, доходит до горловины, входит во ¾вторую

полу пространства (¾вторую вселенную¿) и кончается в

вселенную¿, совершает половину одного оборота, возвра-

черной точке. Для такой траектории момент количества

щается к горловине, проходит через нее и заканчивается

движения h = 0, т. е. пробная частица движется толь-

в черной точке. Небольшой разрыв в траектории соответ-

ко по радиусу. Полная энергия ǫ ≈ 0.949. Минимальное

ствует смещению апоцентра. Момент количества движе-

расстояние от центра КН rmin = r0. Траектория в ¾пер-

ния h = rg. Полная энергия ǫ ≈ 0.953. Минимальное рас-

вой вселенной¿ накладывается на траекторию во ¾второй

стояние от центра КН rmin = r0

вселенной¿, поэтому в проекции r, φ две части траектории

сливаются

Рис. 2. (В цвете онлайн) Геодезическая выходит из зеле-

ной точки, движется по ¾первой вселенной¿. Этот уча-

сток геодезической обозначается красной линией. Дости-

гает горловины, проходит ее. Далее геодезическая дви-

жется по ¾второй вселенной¿, которая обозначена синей

линией. Затем геодезическая возвращается к горловине,

Рис. 4. (В цвете онлайн) Траектория, представленная на

вновь пересекает ее и возвращается в ¾первую вселенную¿

рис. 3, изображенная в искусственной виртуальной проек-

(красная линия). Геодезическая останавливается в черной

ции, которая графически разделяет верхнюю и нижнюю

точке. Момент количества движения h = 0.1rg . Полная

полы пространства

энергия ǫ ≈ 0.949. Минимальное расстояние от центра КН

rmin = r0

Наиболее простой вид траектории имеют в слу-

ПРИЛОЖЕНИЕ

чае

Моделирование финитных траекторий

p≥r₀.

Рассмотрим теперь вид траекторий при различ-

В этом случае траектория полностью находится на

ных значениях параметров орбиты ǫ, h или e, p (см.

одной поле пространства, касаясь горловины КН в

(26), (27)).

одной точке, в случае, когда параметр p = r₀ см.

105

М. В. Сажин, О. С. Сажина, А. А. Шацкий

ЖЭТФ, том 162, вып. 1 (7), 2022

Рис. 5. (В цвете онлайн) Траектория, аналогичная изоб-

раженным на рис. 1, 2. Момент количества движения h =

= 1.9rg . Полная энергия ǫ ≈ 0.966. Минимальное рассто-

яние от центра КН rmin = r0

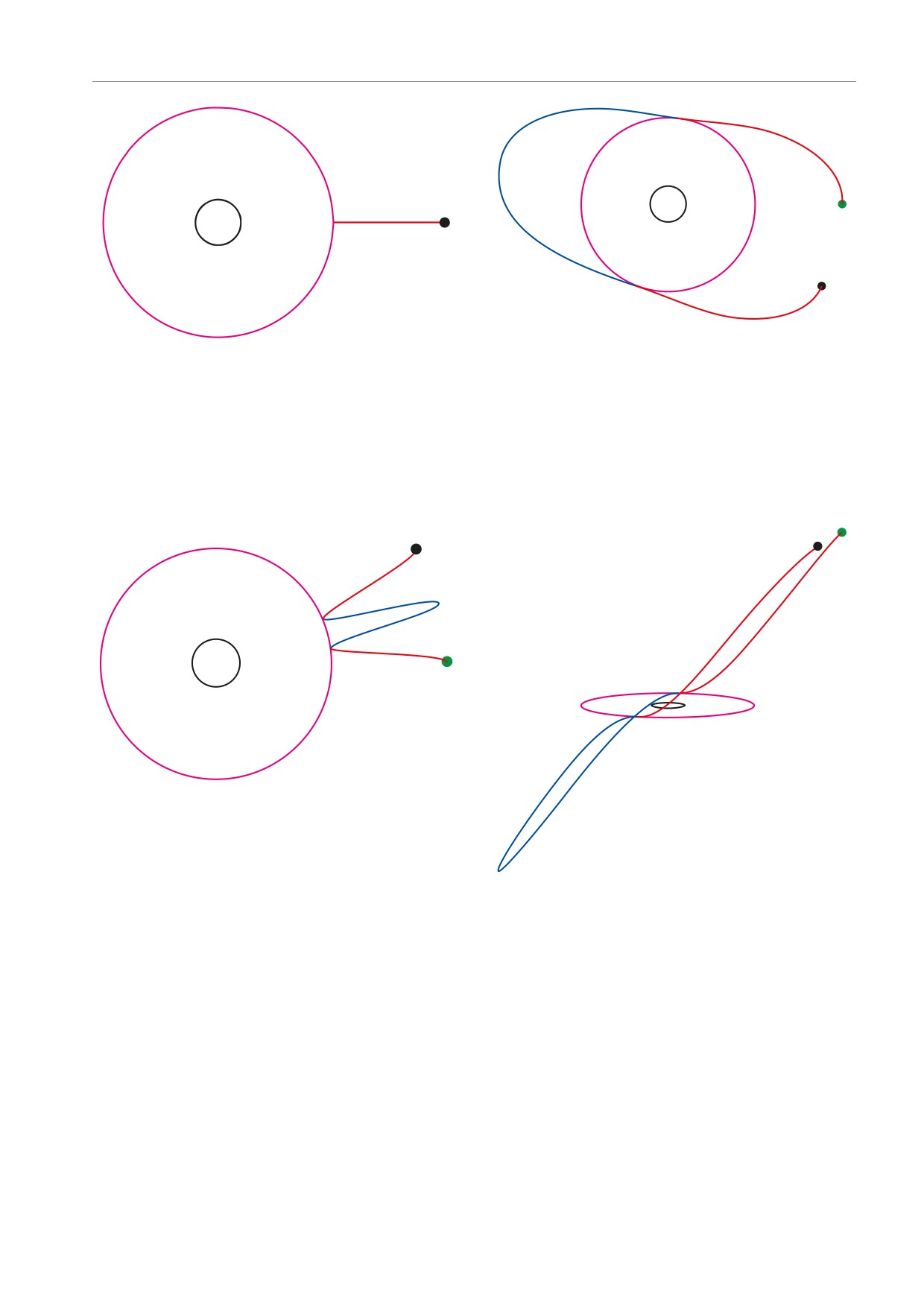
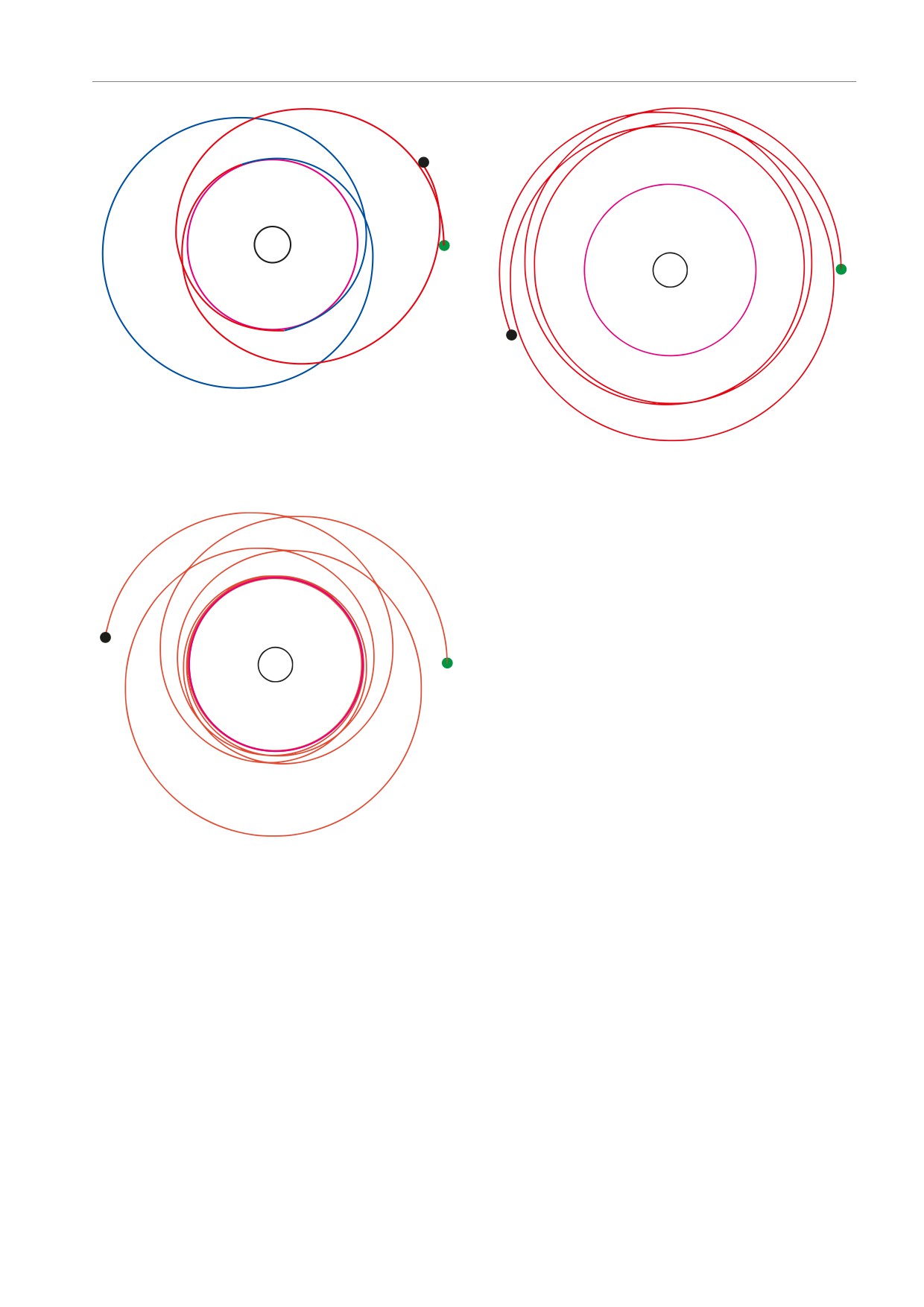
Рис. 7. (В цвете онлайн) Траектория, аналогичная изоб-

раженным на рис. 1, 2. Момент количества движения h =

= 2.3rg . Полная энергия ǫ ≈ 0.973. Минимальное рассто-

яние от центра КН rmin = r0

представляет качественный вид траектории, когда

луч зрения лежит в плоскости горловины КН. Па-

раметры траектории представлены в единицах гра-

витационного радиуса (r_g) КН. Максимальное уда-

ление (апоцентр) траектории от центра КН для всех

траекторий есть r_max = 10r_g. Черные линии го-

ризонт ЧД. Фиолетовые линии положение горло-

вины КН. Зеленая точка точка старта геодезиче-

ской, черная точка точка окончания геодезиче-

ской. Зеленая точка находится при φ = 0.

ЛИТЕРАТУРА

Рис. 6. (В цвете онлайн) Траектория, аналогичная изоб-

1. А. М. Черепащук, Тесные двойные звезды, Физ-

раженным на рис. 1, 2. Момент количества движения h =

матлит, Москва (2013).

= 2rg. Полная энергия ǫ ≈ 0.973. Минимальное расстояние

от центра КН rmin = r0

2. B. P. Abbott et al., Phys. Rev. Lett. 116, 061102

(2016).

3. K. Bronnikov, Acta Phys. Polon. B 4, 251 (1973).

рис. 1. В случае финитных траекторий они имеют

вид ¾релятивистского¿ эллипса, другими словами,

4. M. Morris and K. Thorn, Amer. J. Phys. 56, 395

почти эллиптической траектории со смещением пе-

(1988).

рицентра орбиты.

5. C. Bambi and D. Stojkovic, arXiv:2105.00881v2.

Приведем несколько примеров финитных траек-

торий вблизи КН (рис. 2-7). Все рисунки сделаны в

6. Н. С. Кардашев, Л. Н. Липатова, И. Д. Новиков,

координатах r, φ, за исключением рис. 4, который

А. А. Шацкий, ЖЭТФ 146, 75 (2014).

106