ЖЭТФ, 2022, том 162, вып. 1 (7), стр. 143-160

НЕУСТОЙЧИВОСТЬ СОЛИТОНОВ И КОЛЛАПС ЗВУКОВЫХ

ВОЛН В СРЕДАХ С ПОЛОЖИТЕЛЬНОЙ ДИСПЕРСИЕЙ

Е. А. Кузнецов^*

Физический институт им. П. Н. Лебедева Российской академии наук

119991, Москва, Россия

Институт теоретической физики им. Л. Д. Ландау Российской академии наук

142432, Черноголовка, Московская обл., Россия

Сколковский институт науки и технологии

143026, Сколково, Москва, Россия

Институт космических исследований Российской академии наук

117997, Москва, Россия

Поступила в редакцию 28 февраля 2022 г.,

после переработки 28 февраля 2022 г.

Принята к публикации 28 февраля 2022 г.

Представлен краткий обзор результатов исследования коллапса звуковых волн в средах с положительной

дисперсией, который описывается в рамках трехмерного уравнения Кадомцева - Петвиашвили (КП) [1].

Рассмотрена неустойчивость КП одномерных солитонов в длинноволновом пределе с помощью разло-

жения для соответствующей спектральной задачи. Продемонстрировано, что неустойчивость КП имеет

место также для двумерных солитонов в рамках трехмерного уравнения КП с положительной диспер-

сией. Согласно [2] эта неустойчивость относится к самофокусировочному типу. Нелинейная стадия этой

неустойчивости представляет собой коллапс. Одним из критериев коллапса является неограниченность

гамильтониана снизу при фиксированной проекции импульса, совпадающей с L2-нормой. Этот факт

следует из масштабных преобразований, сохраняющих эту норму постоянной. Коллапс по этой причине

можно представлять как процесс падения частицы в самосогласованном неограниченном потенциале.

Показано, что излучение волн из области с отрицательным гамильтонианом, благодаря его неограничен-

ности снизу, способствует коллапсу волн. Этот сценарий был подтвержден численными экспериментами

[3,4]. Представлены два аналитических подхода исследования коллапса: с помощью вариационного мето-

да и квазиклассического приближения. В отличие от нелинейного уравнения Шредингера с фокусирую-

щей нелинейностью особенность квазиклассического подхода для описания звукового коллапса состоит

в том, что этот метод предложен для трехмерного уравнения КП как системы с гидродинамической

нелинейностью. В рамках квазиклассического описания найдено семейство автомодельных коллапсов.

Верхняя граница этого семейства соответствует сильному коллапсу, при котором энергия, захваченная в

особенность, конечна. Существование такого режима подтверждается также с помощью вариационного

подхода. Другая граница коллапсирующей иерархии совпадает с автомодельным решением трехмерного

уравнения КП, описывающим наиболее быстрый слабый коллапс.

DOI: 10.31857/S004445102207015X

образования особенности за конечное время (см., на-

EDN: EFCRQF

пример, обзор [5]). Если уединенные волны соли-

тоны характерны для низкоразмерных нелиней-

ных волновых систем, то коллапсы, в отличие от со-

1. ВВЕДЕНИЕ

литонов, типичны для многомерных систем. Причи-

на такого поведения, как известно, связана с усиле-

В настоящее время хорошо известно, какую роль

нием нелинейности с ростом размерности простран-

в нелинейной физике играет коллапс волн процесс

ства. Например, для одномерных нелинейных вол-

новых систем, таких как уравнения Кортевега - де

^* E-mail: kuznetso@itp.ac.ru

143

Е. А. Кузнецов

ЖЭТФ, том 162, вып. 1 (7), 2022

Вриза (КДВ) или нелинейные уравнения Шредин-

сти, которые распространяются со скоростью, мень-

гера, солитоны играют существенную роль в их ди-

шей скорости звука c_s. Ситуация для отрицательной

намике. С гамильтоновой точки зрения, солитоны

дисперсии обратная: солитоны представляют собой

в этих моделях, являясь стационарными точками

горбы плотности, движущиеся со скоростью, боль-

гамильтониана H при фиксации соответствующих

шей c_s (в частности, для гравитационных волн в

младших положительно определенных интегралов

пределе мелкой воды такие солитоны представля-

движения, реализуют минимум H и тем самым ока-

ют собой движущиеся с постоянной скоростью воз-

зываются устойчивыми по Ляпунову. Как правило,

вышения водной поверхности). Именно это физи-

гамильтонианы для этих моделей имеют два вклада,

ческое свойство корреляция между отклонением

соответствующих волновой дисперсии (положитель-

плотности от равновесной и знаком дисперсии яв-

но определенной) и нелинейности. Баланс этих двух

ляется ключевым моментом для понимания проис-

факторов приводит к существованию солитонов в

хождения неустойчивости КП одномерных солито-

таких моделях. В отличие от устойчивых по Ляпу-

нов по отношению к поперечным возмущениям [1].

нову солитонов коллапс возникает в волновых сис-

Солитоны в средах с отрицательной дисперсией ока-

темах с неограниченными гамильтонианами. Ког-

зываются устойчивыми, а при положительной дис-

да гамильтониан является неограниченным функ-

персии неустойчивыми. Как было указано Кадом-

ционалом (снизу или сверху), коллапс волн, приво-

цевым [2], эта неустойчивость имеет самофокусиро-

дящий к образованию особенности, представляется

вочную природу.

наиболее вероятным сценарием поведения нелиней-

Уравнение КП учитывает не только дисперсию,

ной волновой системы. В этом случае коллапс подо-

но и дифракцию звуковых пучков в направлении,

бен процессу падения частицы в самосогласованном

поперечном к их распространению. Уравнение КП

потенциале (см., например, [4-6]).

может быть получено по той же схеме, что и урав-

Основная цель настоящей статьи дать крат-

нение КДВ, с учетом нелинейной перенормировки

кий обзор результатов, полученных при изучении

скорости звука, линейной дисперсии и дифракции;

коллапса звуковых волн в средах со слабой поло-

все эти факторы считаются слабыми по сравнению

жительной дисперсией. Такой коллапс можно опи-

с основным распространением (скажем, вдоль x)

сать в рамках уравнения Кадомцева - Петвиашвили

акустических пучков со средней скоростью звука

(КП) [1, 2]. Как известно (см., например, [7]), вол-

c_s и по этой причине они могут быть учтены пер-

ны акустического типа в жидком гелии He⁴ при

турбативно. Очевидно, что распространение пуч-

температурах ниже лямбда-точки для некоторой об-

ка со скоростью c_s можно исключить с помощью

ласти давлений имеют положительную дисперсию.

преобразования Галилея. Остальные малые члены,

Положительной дисперсией обладает также спектр

однако, могут быть одного порядка. Гамильтонова

Боголюбова для волн малой амплитуды в газовых

структура уравнения КП с учетом дифракционно-

бозе-эйнштейновских конденсатах с отталкиванием

го члена остается такой же, как и в случае уравне-

между атомами в рамках уравнения Гросса - Пи-

ния КДВ. Гамильтониан H уравнения КП из-за ди-

таевского [8, 9]. В сильно замагниченной плазме с

фракции получает дополнительный квадратичный

β = 8πp/B² ≪ 1 быстрые магнитоакустические вол-

вклад. В случае положительной дисперсии квадра-

ны представляют собой другой пример волн акусти-

тичная часть H оказывается положительно опре-

ческого типа с положительной дисперсией, реализу-

деленной (в случае отрицательной дисперсии квад-

ющийся практически для всех углов распростране-

ратичный вклад не является знакоопределенным).

ния (см. [4], где этот вопрос подробно обсуждается).

Как и уравнение КДВ, уравнение КП кроме H со-

Уравнение КП, как известно, представляет собой

храняет x-проекцию импульса P , которая является

многомерное обобщение уравнения КДВ. Напом-

положительно определенной величиной. Динамика

ним, что уравнение КДВ для акустических волн со

звуковых волн с положительной дисперсией, опи-

слабой дисперсией может быть выведено исходя из

сываемая уравнением КП, существенно зависит от

систем гидродинамического типа с помощью много-

размерности пространства d.

масштабного разложения (см., например, [10]). Дис-

Как было показано в работе [11], двумерное урав-

персия разного типа (положительная или отрица-

нение КП принадлежит к интегрируемым моделям,

тельная) для уравнения КДВ проявляется в том,

обладающим представлением Лакса, что дает воз-

что для солитонов КДВ знак отклонения плотности

можность эффективно исследовать эту модель с по-

от среднего значения противоположен знаку диспер-

мощью метода обратной задачи рассеяния. Приме-

сии. При положительной дисперсии это ямы плотно-

нение этого подхода позволило аналитически найти

144

ЖЭТФ, том 162, вып. 1 (7), 2022

Неустойчивость солитонов и коллапс звуковых волн...

локализованное двумерное солитонное решение, так

лапса для трехмерного НУШ соответствует квази-

называемый ламп [12]. Отметим, что впервые такие

классическому сжатию волнового пакета как цело-

решения были обнаружены численно Петвиашви-

го. Кроме того, было указано на существование це-

ли [13]. В виде солитона ламп, двигающийся вдоль

лого семейства квазиклассических слабых коллап-

оси x с постоянной скоростью, представляет собой

сов. Верхняя граница этого семейства совпадает с

стационарную точку гамильтониана при фиксиро-

автомодельным решением НУШ, которое описывает

ванном импульсе P. Как было показано [14], при

наиболее быстрый процесс формирования особенно-

фиксированном P гамильтониан оказывается огра-

сти в режиме слабого коллапса.

ниченным снизу функционалом, достигая своего ми-

В настоящем обзоре представлена квазикласси-

нимума, соответствующего солитонному решению.

ческая теория акустического коллапса на основе ра-

По этой причине двумерное солитонное решение

боты [15]. Такого рода описание коллапсов примени-

ламп оказывается устойчивым по Ляпунову при

тельно к звуковым волнам с положительной диспер-

d = 2.

сией имеет ряд особенностей, связанных с нелиней-

Однако в трехмерной геометрии ситуация кар-

ностью гидродинамического типа, отличной от той,

динально меняется: гамильтониан КП оказывается

которая есть в НУШ. Несмотря на это, удается раз-

неограниченным снизу функционалом (см. [3,4,14]),

вить вариационный подход для трехмерного урав-

что легко проверяется путем применения двух неза-

нения КП. Как известно, такой подход может пре-

висимых масштабных преобразований вдоль оси x и

тендовать лишь на некоторое качественное описание

в поперечной плоскости, для каждого из которых P

коллапса. Важно отметить, что решение в рамках

остается инвариантным. Именно это свойство стало

вариационного подхода к НУШ дало ту же автомо-

отправной точкой для проведения численных экс-

дельность, что и точное квазиклассическое решение,

периментов по наблюдению коллапса [3] (см. так-

найденное в [6]. Такое же поведение прослеживает-

же [4]).

ся и относительно акустического коллапса в квази-

Результаты этих численных экспериментов по-

классическом пределе. Для трехмерного уравнения

казали тенденцию к формированию сингулярности

КП, как и для трехмерного НУШ, находятся авто-

за конечное время. В этих расчетах было изучено

модельности для целого семейства квазиклассиче-

влияние излучения волн малой амплитуды на про-

ских коллапсирующих распределений.

цесс схлопывания. Было показано, что излучение

Следует отметить, что в рамках трехмерного

способствует коллапсу, приводящему к образованию

уравнения КП можно увидеть много общего в зада-

особенностей слабого типа, когда волновая энергия,

че о коллапсе в уравнении КДВ со степенной нели-

захваченная в особенность, формально стремится

нейностью (∼ u^p-2u_x), другом примере системы с

к нулю, но в действительности из-за малой дисси-

гидродинамической нелинейностью [16]. Это уравне-

пации оказывается конечной, но достаточно малой

ние демонстрирует критическое поведение при сте-

величиной. Как было показано в [4], для сильно

пени p = 6. При меньшем значении p гамильтони-

замагниченной плазмы коллапс быстрых магнито-

ан оказывается ограниченным снизу при фиксиро-

звуковых волн играет весьма существенную роль в

ванном импульсе P. В этом случае солитоны реали-

динамике косых (относительно среднего магнитно-

зуют минимум H и, соответственно, устойчивы по

го поля) ударных волн, определяя тонкую струк-

Ляпунову [17] (см. также [5]). При p ≥ 6 гамильто-

туру фронта и его ширину. Коллапс в этом случае

ниан становится неограниченным функционалом, и

представляет собой эффективный механизм переда-

поэтому в таком случае возникает коллапс, что чис-

чи энергии волн ионам.

ленно наблюдалось в [16]. Отметим, что для коллап-

Необходимо отметить, что примерно в то же

са в уравнении КДВ со степенной нелинейностью

время, когда проводились численные эксперименты

так же, как и для трехмерного уравнения КП, нахо-

по наблюдению коллапса звуковых волн, т. е. около

дятся автомодельности для целого семейства квази-

1985 г., в рамках нелинейного уравнения Шрединге-

классических коллапсирующих распределений, име-

ра (НУШ) разрабатывалась трехмерная квазиклас-

ется соответствие между квазиклассическим авто-

сическая теория волнового коллапса [6]. В рамках

модельным решением и предсказаниями вариацион-

этой теории дана классификация волновых коллап-

ного подхода.

сов, начиная с сильного коллапса, когда захвачен-

Статья организована следующим образом. В

ная в особенность энергия конечна, и заканчивая

разд. 2 обсуждаются общие свойства уравнения КП

слабыми коллапсами. В [6] (см. также обзор [5]) бы-

для сред с положительной дисперсией. Вначале в ка-

ло установлено, что решение в виде сильного кол-

честве примера приводится вывод уравнения КП с

145

ЖЭТФ, вып. 1 (7)

Е. А. Кузнецов

ЖЭТФ, том 162, вып. 1 (7), 2022

помощью дефокусирующего НУШ на основе приме-

превращается в вихревую пару для двумерной гид-

нения многомасштабного разложения (об этом ме-

родинамики Эйлера. Как показано в [23], все это

тоде см., например, [10]). В этом случае одномер-

семейство двумерных солитонов неустойчиво отно-

ный солитон (солитонное решение уравнения КДВ)

сительно поперечных возмущений (вдоль третьей

представляет собой яму плотности, распространяю-

оси z). Для малой амплитуды солитона эта неустой-

щуюся со скоростью, меньшей средней скорости зву-

чивость представляет собой аналог неустойчивости

ка. Именно это свойство является ключевым в пони-

КП для лампа; для солитонов, распространяющих-

мании природы неустойчивости КП [1,2]. Далее мы

ся со скоростями меньше критической, эта неустой-

обсуждаем гамильтонову структуру уравнения КП

чивость переходит в неустойчивость Кроу, которая

и общие свойства солитонов как стационарных то-

впервые была открыта для дипольной вихревой па-

чек гамильтониана при фиксированном импульсе P .

ры в рамках несжимаемых уравнений Эйлера [24].

Найдено, как значение гамильтониана на солитон-

ных решениях при произвольной размерности d вы-

ражается через импульс солитонов. Эти соотноше-

ния получаются с помощью масштабных преобразо-

В разд. 4 рассматривается вопрос о коллапсе для

ваний, сохраняющих P. Раздел 3 посвящен неустой-

трехмерного уравнения КП. Показана неограничен-

чивости КП солитонов относительно длинноволно-

ность гамильтониана H снизу, следующая из скей-

вых поперечных возмущений. Вначале рассмотрена

линговых преобразований, сохраняющих P . Вслед-

задача об устойчивости одномерных (КДВ) солито-

ствие неограниченности гамильтониана излучение

нов, ключевая по нашему мнению, с помощью мето-

волн малой амплитуды из области с отрицательным

да, предложенного в работе [14]. Далее этот подход

значением H способствует коллапсу, благодаря че-

используется при анализе неустойчивости двумер-

му происходит формирование особенностей слабого

ных солитонов КП относительно трехмерных возму-

типа. Далее представлены два аналитических под-

щений (аналог трехмерной неустойчивости КП). На

хода исследования коллапса: с помощью вариаци-

основе этого метода была предсказана неустойчи-

онного метода и квазиклассического приближения.

вость типа КП для серых/темных солитонов в рам-

Выяснено, что решение квазиклассических уравне-

ках дефокусирующего НУШ [18]. Факт существо-

ний Уизема для сильного коллапса и анзац в рамках

вания этой неустойчивости был подтвержден экс-

вариационного подхода имеют вблизи особенности

периментально, а также численно в работах [19, 20]

одинаковую автомодельную асимптотику. В рамках

при стационарном распространении электромагнит-

квазиклассического описания найдено семейство ав-

ных волн в дефокусирующих керровских средах. В

томодельных коллапсов. Верхняя граница этого се-

этих работах было выяснено, что нелинейная ста-

мейства соответствует сильному коллапсу, при ко-

дия этой неустойчивости приводит к образованию

тором энергия, захваченная в особенность, конечна.

периодической цепочки точечных вихрей (см. так-

Существование такого режима подтверждается так-

же [21]).

же исходя из вариационного подхода. Другая гра-

В этом же разделе рассмотрена задача об устой-

ница коллапсирующей иерархии совпадает с авто-

чивости двумерных солитонов для дефокусирующе-

модельным решением трехмерного уравнения КП,

го НУШ. Солитоны такого типа имеют ряд особен-

описывающим наиболее быстрый слабый коллапс.

ностей. Когда глубина ям плотности солитона до-

статочно мала, такие солитоны асимптотически сов-

падают с лампами. С увеличением глубины в со-

литоне и соответственно уменьшением его скорости

В Заключении перечислены основные результа-

V , как было впервые численно показано в [22], су-

та данного обзора и обсуждены проблемы, которые

ществует некоторое критическое значение V_cr, при

остаются до сих пор нерешенными. Среди этих про-

котором плотность в центре солитона обращается в

блем важнейшая относится к нахождению достаточ-

нуль. Ниже этого критического значения солитон-

ного условия коллапса. Напомним, что для фоку-

ное решение претерпевает бифуркацию, связанную

сирующего НУШ впервые такой критерий был по-

с появлением двух нулей в плотности, соответству-

лучен в двумерном случае Власовым, Петрищевым

ющих двум вихрям с противоположными циркуля-

и Талановым [25], а затем обобщен Захаровым на

циями. Это дипольная пара, распространяющаяся в

трехмерное НУШ [26]. Как для d = 2, так и для

направлении, перпендикулярном диполю. При даль-

d = 3 достаточным условием коллапса является от-

нейшем уменьшении скорости солитонов эта пара

рицательность гамильтониана H.

146

ЖЭТФ, том 162, вып. 1 (7), 2022

Неустойчивость солитонов и коллапс звуковых волн...

2. ОБЩИЕ СВОЙСТВА УРАВНЕНИЯ

Данный закон дисперсии учитывает как слабую по-

КАДОМЦЕВА - ПЕТВИАШВИЛИ И

ложительную дисперсию, так и дифракцию в попе-

СОЛИТОННЫЕ РЕШЕНИЯ

речном направлении. Оба эти члена в (5) становятся

одного порядка, если k^4x ∝ k^2⊥. Именно это простое

Рассмотрим вначале общие свойства уравнения

наблюдение является одним из ключевых при выво-

КП с положительной дисперсией, часто называемо-

де уравнения КП.

го уравнением КП-I. Прежде всего покажем, как это

Для вывода уравнения КП перепишем НУШ в

уравнение выводится исходя из уравнения движе-

виде системы гидродинамического типа для плот-

ния для сред с гидродинамической нелинейностью.

ности n и фазы ϕ (ψ =

√ne^iϕ):

В качестве примера рассмотрим дефокусирующее

нелинейное уравнение Шредингера:

∂n

+ ∇(n∇ϕ) = 0,

∂ψ

∂t

∆ψ + (1 - |ψ|²)ψ = 0.

(1)

∂ϕ

∆√n

∂t

(∇ϕ)² + n - 1 =

∂t

2√n

Это уравнение записано в безразмерном виде. При-

менительно к газовым бозе-эйнштейновским кон-

Далее к этой системе будем применять многомас-

денсатам (БЭК) при температуре T → 0 величи-

штабное разложение, следуя работе [10] (см. так-

на ψ имеет смысл волновой функции конденсата

же [18]).

(в этом контексте уравнение (1) называется уравне-

Введем медленное время и медленные координа-

нием Гросса - Питаевского), |ψ|² представляет собой

ты,

плотность конденсата n. В нелинейной оптике ψ

t^′ = ε³t, x^′ = ε(x - t), r^′⊥ = ε²r_⊥,

огибающая волнового пакета электрического поля

и будем искать решение этой системы в виде ряда

в средах с дефокусирующей керровской нелинейно-

по степеням малого параметра ε,

стью.

Будем предполагать, что волновая функция

∑

стремится к 1 при r → ∞, а соответственно плот-

n = 1 + ε^2kn_k(x^′,r^′⊥,t^′).

ность n → 1. В этом случае, как хорошо известно,

k=1

волны малой амплитуды имеют закон дисперсии

Первые два порядка легко находятся (см., напри-

√

ω=k

1 + k²/4,

(2)

мер, [10, 18]). Уравнение КП-I получается в рамках

этой теории возмущений как условие разрешимости

это так называемый спектр Боголюбова. При k → 0

третьего порядка (∼ ε³):

этот спектр преобразуется в закон дисперсии аку-

(

)

стического типа с положительной дисперсией

∂

n_1t +

n₁n_1x -

n_1xxx

∆_⊥n₁,

(6)

∂x

ω = k(1 + k²/8 + ...),

(3)

где скорость звука c_s = 1. Чтобы вывести отсюда

где ∆_⊥ = ∂^2y + ∂^2z поперечный оператор Лапласа

уравнение КП из (1), рассмотрим пучок звуковых

(штрихи ниже опущены).

волн малой (но конечной) амплитуды, распростра-

Как известно, уравнение КП (6) представляет со-

няющийся в основном в одном направлении (ска-

бой многомерное обобщение одномерного уравнения

жем, вдоль x) с малым угловым распределением

КДВ (∆_⊥ = 0). В последнем случае солитонное ре-

(k_⊥/k_x ≪ 1). Последнее означает, что для таких вол-

шение имеет вид

новых пучков дисперсионное соотношение (3) запи-

ν²

сывается в виде

n₁ = -

(7)

[

]

ch² ν(x + ν²t/2 - x₀)

)

k^2x

(k_⊥

ω=k_x

(4)

оно представляет собой ямки плотности (n₁ < 0),

k_x

/2, меньшей ско-

двигающиеся со скоростью c_s - ν²

В этом случае первый член в скобке может быть ис-

рости звука. Отметим, что это условие имеет место

ключен с помощью галилеевского преобразования в

также и для многомерных солитонов. Это требо-

систему координат, двигающуюся со скоростью зву-

вание эквивалентно отсутствию черенковского ре-

ка вдоль оси x, так что (4) имеет стандартный для

зонанса между солитоном и линейными волнами

КП вид закона дисперсии:

(см., например, [27]). Таким образом, в одномерном

[

]

случае скорость солитона уменьшается с увеличе-

Ω = k_x k^2x/8 +

(k_⊥/k_x)2

(5)

нием амплитуды солитона. Это свойство является

147

10*

Е. А. Кузнецов

ЖЭТФ, том 162, вып. 1 (7), 2022

ключевым для понимания происхождения неустой-

Данное решение представляет собой стационарную

чивости КП [1] относительно возмущений, попереч-

точку гамильтониана H при фиксированном P,

ных солитону КДВ. Как показал Кадомцев [2], эта

δ(H + V P ) = 0.

(11)

неустойчивость имеет самофокусировочный харак-

тер. Пусть солитон промодулирован в поперечном

Эта вариационная задача эквивалентна стационар-

направлении. Тогда согласно (7) области солитона с

ному уравнению КДВ

большей амплитудой будут двигаться медленнее тех

-V u_x + 6uu_x + u_xxx = 0

(12)

участков, которые имеют меньшую амплитуду. В ре-

зультате области с меньшей амплитудой будут обго-

с решением (10) в виде солитона, двигающегося со

нять области с повышенной амплитудой, что при-

скоростью V = 4κ². В многомерном случае, а имен-

ведет к фокусировке фронта солитона и аккумуля-

но в рамках уравнения КП (8), солитонные реше-

ции его энергии. Легко понять, что эти аргументы

ния, распространяющиеся вдоль оси x с постоян-

применимы также на нелинейной стадии неустойчи-

ными скоростями V , также являются стационарны-

вости, т.е. на стадии формирования коллапса, опи-

ми точками H при фиксированном P . В двумерном

сываемого в рамках трехмерного уравнения КП (7)

случае это локализованные по всем направлениям

(см. следующие разделы).

так называемые решения в виде лампа со степенной

асимптотикой при r → ∞. Впервые такие решения

были обнаружены численно Петвиашвили [13]. За-

2.1. Гамильтонова структура и солитоны

тем в работе [12] лампы были найдены как точные

Прежде чем обсуждать гамильтонову структу-

решения уравнения КП на основе применения мето-

ру уравнения КП, солитоны и их устойчивость, пе-

да обратной задачи рассеяния.

репишем (6) в стандартной форме, которую можно

В трехмерном случае солитоны такого типа мо-

получить с помощью простых замен и перемасшта-

гут быть найдены численно, возможно и аналити-

бированием:

чески, с привлечением схемы Хироты [28]. Пред-

ставление Хироты, как было выяснено сравнитель-

∂

(u_t + 6uu_x + u_xxx) = ∆_⊥u.

(8)

но недавно в ряде работ (см. [29-34]), применимо к

∂x

уравнению КП при произвольной размерности. Од-

В одномерном случае это уравнение принимает

нако этот вопрос вопрос об аналитическом нахож-

стандартный вид, принятый для уравнения КДВ.

дении солитонного решения в трехмерном случае

Как и уравнение КДВ, уравнение (8) относится к

пока остается открытым.

гамильтоновским уравнениям

Несмотря на это, для солитонов уравнения КП

(8) при произвольной размерности пространства d

∂ δH

u_t =

можно установить ряд соотношений, в частности

∂x δu

связь между значениями гамильтонина и импуль-

с гамильтонианом

[

]

са P на солитонном решении. Эти соотношения яв-

∫

u^2x

(∇_⊥w)

ляются следствиями вариационной задачи (9), ко-

-u³

dr ≡

I₁+

I₂-I₃, (9)

торая справедлива при произвольной размерности

d. Впервые этот факт был установлен в работе [14]

где w_x = u. Здесь первый член ответствен за диспер-

(см. также [3, 4]). Для этого требуется найти связи

сию волн, второй учитывает дифракцию акустичес-

между интегралами, входящими в H. Первое такое

кого пучка в поперечном направлении, последний

соотношение между интегралами получается, если

член описывает нелинейность акустических волн.

уравнение для солитона

Помимо H, уравнение КП сохраняет полный им-

-V u_x + 6uu_x + u_xxx = ∆_⊥w

пульс, x-компонента которого является положитель-

но определенной величиной,

сначала умножить на w, а затем проинтегрировать

∫

по r. Это дает

P =

u²dr.

2V P + I₁ + I₂ - 3I₃ = 0.

(13)

Уравнение КДВ отсюда следует при w = 0. В пере-

Два других соотношения следуют из вариационной

менных u солитон КДВ (7) переписывается как

задачи (11) после применения масштабных преобра-

зований, сохраняющих P,

2κ

u_s =

(10)

u(x, r_⊥) → a^-1/2b^(1-d)/2u(x/a, r_⊥/b).

ch² κ (x - 4κ²t - x₀)

148

ЖЭТФ, том 162, вып. 1 (7), 2022

Неустойчивость солитонов и коллапс звуковых волн...

При этих преобразованиях H становится функцией

в длинноволновом пределе. Здесь мы применим ме-

масштабных параметров a и b:

тод, несколько отличающийся от того, который ис-

пользовали Кадомцев и Петвиашвили. Будет по-

H(a, b)=

a^-2I₁+

a²b^-2I₂-a^-1/2b^(1-d)/2I₃.

(14)

казано, как можно исследовать КП-неустойчивость

одномерного солитона в длинноволновом пределе с

В соответствии с вариационной задачей (12) на со-

помощью теории возмущений, следуя [14] (см. также

литонном решении производные от H(a, b) относи-

[35, 36]). Отметим, что изначально этот метод был

тельно a, b должны обратиться в нуль при a = b = 1,

применен при исследовании устойчивости двумер-

что приводит к двум дополнительным соотношени-

ных солитонов по отношению к трехмерным возму-

ям:

щениям. Позже он успешно использовался для задач

устойчивости одномерных темных/серых солитонов

-I₁ + I₂ +

I₃ = 0,

(15)

относительно поперечных возмущений в рамках де-

1-d

фокусирующего НУШ [18], а также двумерных со-

−I₂ -

I₃ = 0.

(16)

литонов относительно трехмерных возмущений [23].

Выражая далее I₁, I₂ и I₃ из соотношений (13), (15),

Впоследствии этот подход показал свою эффек-

(16) через P_s на солитонном решении, для H_s нахо-

тивность при исследовании устойчивости одномер-

дим

ных солитонов, распространяющихся в погранич-

2d - 5

ном слое [37], в рамках уравнения Шриры [38] (дву-

H_s =

VP_s.

7 - 2d

мерное обобщение уравнения Бенджамина - Оно).

В одномерном и двумерном случаях гамильтониан

на солитонном решении отрицателен, равный соот-

3.1. Неустойчивость солитонов

ветственно -(3/5)V P_s и -(1/3)V P_s. Более того, в

Кортевега - де Вриза

обоих случаях гамильтониан оказывается ограни-

ченным снизу при фиксированном P [14] (см. также

Начнем наш анализ с устойчивости одномерных

[5]) не только относительно масштабных преобразо-

солитонов.

ваний, но и относительно возмущений общего вида.

Решение в уравнении КП (8) будем искать в виде

При этом H достигает своего минимума на солитон-

u = u_s(x - V t) + ψ(x - V t,r_⊥,t),

ном решении в одномерном и двумерном случаях.

Это означает, что солитоны при d = 1 и 2 устой-

где ψ предполагается малым возмущением по срав-

чивы по Ляпунову. В трехмерном случае ситуация

нению с солитоном КДВ u_s (10).

обратная: гамильтониан на солитоне H_s = V P_s по-

Переходя далее в систему координат, двигающу-

ложителен, а соответствующая стационарная точка

юся со скоростью V , и линеаризуя уравнение (8) на

представляет собой седло (по этой причине трех-

фоне u_s, для возмущения

мерный солитон неустойчив, см. разд. 4) и, кроме

того, H оказывается неограниченным снизу функ-

ψ(x, r_⊥, t) = ϕ(x) exp (-iωt + ikr_⊥)

ционалом. Чтобы проверить последнее, достаточно

рассмотреть линии наискорейшего спуска функции

приходим к следующей спектральной задаче:

H(a, b) a²/b = const. Неограниченный характер га-

(

)

∂

∂²

мильтониана, обусловленный нелинейным членом,

-iω

ϕ+k²ϕ = -

-V + 6u_s+

ϕ ≡ Lϕ.

∂x

∂x²

приводит к тому, что его роль с уменьшением мас-

штабов a, b становится доминирующей по сравнению

Ищем решение этого уравнения в длинноволновом

как с дисперсионным, так и с дифракционным чле-

пределе, разлагая ϕ и ω в ряды по малому k:

нами, при этом H → -∞. Как мы увидим в сле-

дующих разделах, неограниченность гамильтониана

ϕ=ϕ₀ +ϕ₁ +ϕ₂ +...,

снизу играет весьма существенную роль в формиро-

ω=ω₁ +ω₂ +...

вании сингулярности, т.е. при коллапсе.

В главном порядке

(

)

3. НЕУСТОЙЧИВОСТЬ

∂²

-V + 6u_s +

ϕ₀ ≡ Lϕ₀ = 0.

КАДОМЦЕВА - ПЕТВИАШВИЛИ

∂x²

Неустойчивость КП для солитонов КДВ была

Сравнивая с (12), легко увидеть, что это уравне-

впервые получена Кадомцевым и Петвиашвили [1,2]

ние выполняется для ϕ₀ = ∂u_s/∂x. Эта нейтрально

149

Е. А. Кузнецов

ЖЭТФ, том 162, вып. 1 (7), 2022

устойчивая мода соответствует малому сдвигу соли-

Следует отметить, что точное выражение для ин-

тона как целого.

кремента этой неустойчивости было найдено Заха-

В следующем порядке имеем

ровым [40] с помощью метода обратной задачи рас-

сеяния (МОЗР), примененного к уравнению КП (8).

∂

-iω₁

ϕ₀ = Lϕ₁.

Причина этой неустойчивости, как объяснил Ка-

∂x

домцев в своей книге [2], связана с тем, что соли-

Чтобы найти ϕ₁, рассмотрим уравнение (12), произ-

тоны звуковых волн с положительной дисперсией

водная по V которого записывается в виде

представляют собой ямы плотности, скорость кото-

(

рых уменьшается с увеличением амплитуды соли-

∂u_s

∂

∂²

)∂u_s

тона (см., например, уравнение (7)). Как следствие,

-V + 6u_s +

∂x

∂x²

∂V

если такой солитон модулируется в поперечном на-

правлении, то области с большей амплитудой бу-

Отсюда из сравнения двух последних уравнений за-

дут отставать от областей с меньшей амплитудой.

ключаем, что

∂u_s

Это приводит к неустойчивости самофокусировоч-

ϕ₁ = iω₁

ного типа, развитие которой ведет к фокусировке

∂V

фронта солитона и аккумуляции волновой энергии.

В результате второй порядок записывается как

Эти аргументы справедливы для всех упомя-

∂

нутых выше неустойчивостей типа КП, а именно,

-iω₁

ϕ₁ + k²ϕ₀ = Lϕ₂.

(17)

∂x

неустойчивостей одномерных темных/серых солито-

нов в рамках дефокусирующего НУШ относитель-

Условие разрешимости этого уравнения (для ϕ₂) со-

но поперечных возмущений [18], двумерных солито-

стоит в ортогональности левой части этого уравне-

нов на фоне трехмерных возмущений [23], а также

ния собственной функции χ с нулевым собственным

для одномерных солитонов, распространяющихся в

значением оператора, сопряженного к L,

пограничном слое [37], в рамках так называемого

(

)

∂²

уравнения Шриры [38]. Поскольку неустойчивость

-V + 6u_s +

χ = 0.

∂x²

КП относится к самофокусировочному типу, такая

аргументация может быть использована и на нели-

Легко видеть, что

нейной стадии этой неустойчивости в рамках трех-

мерного уравнения КП с положительной дисперси-

∂

χ=u_s,

ей. Следует отметить, что в двумерном случае на-

∂x

личие устойчивых двумерных солитонов лампов

т. е. χ есть гидродинамический потенциал w_s соли-

существенно влияет на развитие неустойчивости

тона. Отсюда, подставляя

КП. Как показано в [39], неустойчивость на нели-

нейной стадии приводит к отщеплению от солито-

∂

∂u_s

ϕ₀ =

u_s, ϕ₁ = iω₁

на цепочки лампов, которые, в свою очередь, также

∂x

∂V

испытывают неустойчивость относительно попереч-

в (17) и затем скалярно умножая на χ, получаем

ных возмущений.

∫

∂

∂u_s

∂

ω²¹

dx + k²

u_s = 0.

∂x ∂V

∂x

3.2. Неустойчивость двумерных КП

солитонов

Интегрирование по частям в стоящих здесь двух ин-

тегралах дает

Рассмотрим теперь, следуя [14], задачу о линей-

ной устойчивости лампа относительно возмущений

по третьей координате z. Решение в виде лампа u =

ω² = -k²

∂P/∂V

= u_s(x - V t, y), распространяющегося со скоростью

V вдоль оси x, удовлетворяет стационарному урав-

Для солитона КДВ импульс P ∝ V^3/2, откуда окон-

нению КП,

чательно имеем

[

]

∂²

∂⁴

∂²

ω² = -

k² < 0.

(18)

-V

u_s + 3

u^2s = 0.

(19)

∂x²

∂x⁴

∂y²

∂x²

Таким образом, мы приходим к неустойчивости. Это

Как отмечалось выше, двумерное солитонное реше-

и есть неустойчивость Кадомцева - Петвиашвили.

ние этого уравнения впервые численно было полу-

150

ЖЭТФ, том 162, вып. 1 (7), 2022

Неустойчивость солитонов и коллапс звуковых волн...

чено Петвиашвили [13]. Позднее точное решение в

Чтобы найти ω(k) из этого уравнения, нужно вос-

виде лампа было найдено в [12] с помощью метода

пользоваться условием разрешимости

ортого-

обратной задачи рассеяния.

нальностью правой части этого уравнения к соб-

Для решения линейной задачи устойчивости

ственной функции φ₀ с нулевым собственным значе-

лампа будем считать возмущение малым, завися-

нием для оператора, сопряженного к A. Легко най-

щим от времени и координаты z экспоненциально:

ти, что φ₀ = w_s. Отсюда имеем

∫

∂²u_s

∂u_s

ψ = ψ(x - V t,y)exp(-iωt + ikz).

ω²

dx dy = -k²

w_s

dx dy.

w_s ∂x∂V

∂x

Тогда линеаризация (8) на фоне стационарного ре-

Интегрирование по частям дает

шения уравнения (8) приводит к следующей спект-

ральной задаче:

∂P

ω²

= -2k²P.

∂V

∂ψ

Aψ - iω

= -k²ψ,

(20)

Для решения в виде лампа P ∼ V^1/2. В результате

∂x

мы получаем неустойчивость:

где оператор

V < 0.

ω² = -4k²

∂

∂⁴

∂²

[-V + 6u_s] +

(21)

Для нейтрально устойчивой моды ∂u_s/∂y такого ро-

∂x²

∂x⁴

∂y²

да процедура приводит к устойчивости.

Как и в предыдущем примере, решение этой задачи

на собственные значения будем искать в длинновол-

3.3. Неустойчивость

новом пределе, k → 0, в виде ряда

Кадомцева - Петвиашвили серых/темных

солитонов

ψ=ψ₀ +ψ₁ +ψ₂ +...

Для НУШ (1) решение в виде серого/темного со-

Здесь ψ₀ определяется из уравнения

литона ψ₀(x-κt) находится в виде уединенной одно-

мерной волны, двигающейся со скоростью κ. В этом

Aψ₀ = 0,

случае ψ₀(x - κt) удовлетворяет следующему обык-

новенному дифференциальному уравнению:

т. е. ψ₀ есть нейтрально устойчивая мода, которую

∂ψ₀

1 ∂²ψ₀

можно представить как суперпозицию двух беско-

-iκ

+ (1 - |ψ₀|²)ψ₀ = 0,

∂x

∂x²

нечно малых сдвигов солитона как целого вдоль на-

(22)

правлений x и y,

|ψ₀|² → 1 при |x| → ∞.

∂u_s

Его решение записывается как

ψ₀ = C₁

+C₂

∂x

∂y

ψ₀ = ν thν(x - κt - x₀) + iκ, κ² + ν² = 1.

(23)

Оба сдвига, очевидно, независимые и могут быть

рассмотрены по отдельности.

Когда κ = 0, это решение представляет собой тем-

В следующем порядке для первой моды имеем

ный солитон (или доменную стенку). Если κ = 0, мы

имеем серые солитоны. Когда κ стремится к скоро-

∂

сти звука (равной в наших переменных 1), эти ре-

Aψ₀₁ - iω

u_sx = 0.

∂x

шения трансформируются в солитоны КДВ (7).

Для решения задачи устойчивости таких солито-

Как и в одномерном случае, дифференцирование

нов будем следовать работе [18]. Предполагая малые

стационарного уравнения (19) по V позволяет най-

возмущения φ₁ = δψ, φ₂ = δψ^∗, распространяющие-

ти ψ₁₁:

ся со скоростью κ и зависящие от времени и коорди-

∂u_s

ψ₁₁ = iω

наты y экспоненциально, ∝ exp(-iωt + iky), прихо-

∂V

дим к следующей спектральной задаче для матрич-

Следующий порядок записывается как

ного дифференциального оператора:

∂²us

∂u_s

Aψ₂ = -ω²

-k²

ωσ₃u -

k²u + Lu = 0,

(24)

∂x∂V

∂x

151

Е. А. Кузнецов

ЖЭТФ, том 162, вып. 1 (7), 2022

где

и по этой причине принадлежит связанному состо-

[

]

янию.

σ₃ =

Второй порядок записывается как

-1

матрица Паули,

ωσ₃u₁ -

k²u₀ = -Lu₂.

(

)

φ₁

Разрешимость этого уравнения приводит к следую-

φ₂

щей зависимости ω(k):

k²

(

)

ω〈u₀|σ₃|u₁〉 =

〈u₀|u₀〉,

∂

∂²

2|ψ₀|² - 1

ψ²⁰

L = -iκσ₃

∂x

2 ∂x²

что дает неустойчивость

ψ^∗20

2|ψ₀|² - 1

k²ν

эрмитовский оператор.

ω² = -

< 0.

Решение этой задачи на собственные значения

будем искать, как и прежде, в длинноволновом пре-

Отметим, что при малых ν² = 1 - κ² ≪ 1 инкре-

деле (k → 0) в виде степенных рядов относитель-

мент этой неустойчивости совпадает с найденным

но k,

для солитона КДВ (ср. с (18)). Данная неустойчи-

вость представляет собой естественное продолже-

u=u₀ +u₁ +u₂ +..., ω=ω₁ +ω₂ +...

ние неустойчивости КП для серых (темных) соли-

тонов. В заключение этого раздела необходимо от-

Здесь u₀

нейтрально устойчивая мода, Lu₀ = 0,

метить, что неустойчивость темных солитонов была

соответствующая бесконечно малым сдвигам соли-

подтверждена экспериментально, а также численно

тона как целое,

[19, 20]. В этих работах, в частности, показано, что

(

)

нелинейная стадия неустойчивости солитона приво-

∂

ψ₀

u₀ =

дит к образованию дорожки точечных вихрей, ана-

∂x ψ^∗

логичных вихревой дорожке фон Кармана в жидко-

стях.

В следующем порядке имеем

ωσ₃u₀ + Lu₁ = 0.

3.4. Двумерные солитоны НУШ и их

устойчивость

Что касается u₁, то оно находится с помощью того

же трюка, который мы использовали в предыдущем

В заключение этого раздела рассмотрим двумер-

разделе. Дифференцируя уравнение (22) по скорос-

ные солитоны НУШ в рамках уравнения (1). Эти

ти κ, получаем

солитоны имеют много общих свойств с решением в

(

)

виде лампов.

∂

ψ₀

Мы ограничимся рассмотрением только осесим-

u₁ = iω

(25)

∂κ ψ^∗

метричных солитонов

ψ₀(x^′, y) = ψ₀(x^′, -y), x^′ = x - V t,

Если подставить (23) в это выражение, то получит-

ся, что u₁ стремится к постоянному значению при

которые представляют собой стационарные точки

|x| → ∞. На первый взгляд поэтому кажется, что

гамильтониана H при фиксированном полном им-

u₁ принадлежит непрерывному спектру и не может

пульсе P (очевидно, имеющим только одну ненуле-

обеспечить неустойчивость, поскольку возмущения

вую x-проекцию):

из непрерывного спектра, очевидно, устойчивы. На

самом деле, как было продемонстрировано в [18], в

δ(H - V P ) = 0,

(26)

этом случае необходимо учитывать более аккуратно

асимптотическое поведение этой функции на беско-

где

∫

[

]

нечности на основе точного линеаризованного урав-

H =

|∇ψ|² + (|ψ|² - 1)²

dx dy,

(27)

нения (24) путем решения задачи сшивки асимпто-

∫ [

]

тик. Проведенный анализ [18] дает, что u₁ при |x| →

∂ψ^∗

∂ψ

P =

-ψ^∗

dx dy.

(28)

→ ∞ затухает экспоненциально с показателем ∼ k

∂x

152

ЖЭТФ, том 162, вып. 1 (7), 2022

Неустойчивость солитонов и коллапс звуковых волн...

Пусть ε есть энергия солитона значение гамиль-

Когда ямы плотности (интенсивности) малы, но

тониана на солитонном решении, и P его импульс.

c_s - V > 0, решение этого уравнения будет прибли-

Тогда, согласно (26), скорость солитона V записы-

жаться к двумерному солитону КП (лампу) и соот-

вается через ε и P в следующем виде:

ветственно уравнение (30) переходить в стационар-

ное уравнение КП (19). Отсюда сразу можно сде-

∂ε

лать вывод, что эти двумерные солитоны в преде-

V =

(29)

∂P

ле мелких ям будут подвержены КП-неустойчивости

относительно модуляций вдоль направления z. Для

Вариационная задача (26) позволяет так же, как

большей амплитуды солитона данный вопрос требу-

для лампов, выразить все интегралы в (27) на соли-

ет дополнительного анализа.

тонном решении через ε и P (28).

Увеличение глубины этих ям и соответственно

Для этого выполним два независимых масштаб-

уменьшение скорости солитона V , как впервые было

ных преобразования вдоль осей x и y:

численно показано в работе [22], происходит вплоть

до некоторого критического значения V_cr. Для это-

ψ₀(x, y) → ψ₀(ax, y), ψ₀(x, y) → ψ₀(x, by),

го значения скорости плотность в центре солитона

обращается в нуль. Ниже этого критического значе-

где a и b скейлинговые параметры. Отсюда бла-

ния солитонное решение претерпевает бифуркацию,

годаря (26) легко получить два соотношения:

связанную с появлением двух нулей плотности, со-

∂

ответствующих двум вихрям с противоположными

(H - V P )|_a=1 =

(H - V P )|_b=1 = 0,

∂a

∂b

циркуляциями. Это дипольная пара, распространя-

ющаяся в направлении, перпендикулярном диполю.

из которых следуют значения интегралов на соли-

При дальнейшем увеличении скорости солитона эта

тонном решении:

пара нулей превращается в вихревую пару для дву-

∫ 



мерной гидродинамики Эйлера.

∂ψ2



Покажем теперь, следуя [23], что все семейство

x dy = ε,

 d

∂x

двумерных солитонов неустойчиво по отношению

∫ 



∂ψ2

к поперечным (относительно оси z) возмущениям.



x dy = ε - V P,

 d

Очевидно, что при малой амплитуде солитона эта

∂y

∫

неустойчивость совпадает с КП-неустойчивостью

(|ψ|² - 1)²dx dy = V P.

лампа в полном согласии с результатами предыду-

щих разделов. Для солитонов, распространяющих-

Сравнивая с (29), отсюда мы получаем неравенство

ся со скоростями ниже критической, эта неустойчи-

вость с ростом расстояния между вихрями перехо-

∂ε

дит в неустойчивость, открытую впервые Кроу для

∂P

диполей двух точечных вихрей в случае идеальных

несжимаемых жидкостей [24].

которое для линейных волн в соответствии со спек-

В длинноволновом пределе инкремент для все-

тром Боголюбова (2) имеет противоположный знак,

го семейства солитонных решений находится по той

∂ω

же схеме, что и выше. Для малых возмущений, рас-

∂k

пространяющихся со скоростью V , которые в этой

системе отсчета зависят от z и t экспоненциально,

Отметим еще раз, что скорость солитона должна

∼ exp(-iωt + ikz), мы приходим к следующей зада-

быть меньше минимальной фазовой скорости ли-

че на собственные значения:

нейных волн, в нашем случае это скорость звука

(c_s = 1). Напомним, что это требование эквивалент-

ωσ₃u -

k²u + Lu = 0,

(31)

но отсутствию черенковского резонанса между со-

литоном и линейными волнами.

где вместо второй производной по x в операторе L

Легко видеть, что вариационная задача (26) сво-

для спектральной задачи (24) стоит оператор Ла-

дится к нахождению решения стационарного урав-

пласа относительно x и y:

нения для солитонов

(

)

∂

2|ψ₀|² - 1

ψ²⁰

∂ψ₀

L = -iκσ₃

∆-

-iV

∇²ψ₀ + (1 - |ψ₀|²)ψ₀ = 0.

(30)

∂x

ψ^∗20

2|ψ₀|² - 1

∂x

153

Е. А. Кузнецов

ЖЭТФ, том 162, вып. 1 (7), 2022

В этом случае, как и раньше, ищем решение (31) в

В общем случае, согласно численным результа-

виде степенных рядов относительно малых k:

там [22], производная ∂P/∂V отрицательна для все-

го семейства двумерных солитонов.

u=u₀ +u₁ +u₂ +..., ω=ω₁ +ω₂ +...

Таким образом, две неустойчивости, т. е. неустой-

чивости КП и Кроу, в некотором смысле аналогич-

В нулевом приближении, Lu₀ = 0, мы имеем две без-

ны друг другу. Неустойчивость КП при уменьше-

различно устойчивых моды, соответствующих двум

нии скорости солитона переходит в неустойчивость

независимым малым сдвигам солитона,

Кроу, и поэтому эти неустойчивости следует объеди-

нить. Обе эти неустойчивости относятся к самофо-

u₀ = C₁u₀₁ + C₂u₀₂,

кусировочному типу.

где

В заключение этого раздела хотелось бы отме-

тить, что неустойчивость типа КП может быть по-

(

)

(

)

∂

ψ₀

∂

ψ₀

лучена также для одномерных солитонов [37] в рам-

u₀₁ =

u₀₂ =

ках так называемого уравнения Шриры [38], описы-

∂x ψ^∗0

∂y ψ^∗

вающего длинноволновые нелинейные возмущения

C₁ и C₂

константы.

в пограничном слое.

Уравнение следующего порядка для первой мо-

ды, соответствующей малому сдвигу u₀₁,

4. КОЛЛАПС

ωσ₃u₀₁ + Lu₁₁ = 0,

Как было показано в разд. 2, гамильтониан (9)

имеет решение, аналогичное (25),

для трехмерного уравнения КП с положительной

(

)

дисперсией при фиксированном P представляет со-

∂

ψ₀

бой неограниченный снизу функционал, что следует

u₁ = iω

∂V ψ^∗

из скейлинговых преобразований для H(a, b) (14).

Неограниченность H возникает на малых масшта-

Последующая процедура нахождения инкремента,

бах благодаря нелинейному члену. Хорошо известно

аналогичная предыдущей, дает следующее выраже-

(см., например, обзор [5]), что неограниченность га-

ние для ω²:

мильтониана для нелинейных волновых систем яв-

ω² =

k².

ляется одним из основных критериев возникновения

∂P/∂V

коллапса. Коллапс в этом случае можно понимать

Как было показано аналитически в работе [23], про-

как процесс падения частицы в самосогласованном

изводная ∂P/∂V отрицательна в двух предельных

неограниченном потенциале.

случаях: для лампа и для солитонов с малыми ско-

Обратим внимание на то, что при масштабных

ростями V ≪ c_s = 1. В первом случае

преобразованиях вдоль парабол b ∝ a² первые два

члена в (14) ведут себя как a^-2, а кубический член,

γ² = 2(1 - V )k² > 0,

ответственный за нелинейность, меняется пропор-

ционально a^-5/2. По этой причине возможный кол-

что совпадает с квадратом инкремента неустойчи-

лапс не является критическим он должен быть

вости для лампа. Для малых скоростей V → 0 рас-

слабым, как мы увидим ниже, соответствует авто-

стояние L между вихрями растет пропорционально

модельному коллапсу. В таких режимах излучение

V^-1, а энергия ε ≈ 2π log(1/V ). Тогда из опреде-

волн малой амплитуды из области коллапса способ-

ления скорости (29) следует отрицательность иско-

ствует коллапсу, что опять-таки связано с неограни-

мой производной: ∂P/∂V = -2πV^-2. В результате в

ченностью H.

этом пределе мы получаем неустойчивость с инкре-

Чтобы это показать, рассмотрим некоторую об-

ментом γ, квадрат которого

ласть Ω с отрицательным гамильтонианом, H_Ω < 0.

γ² = 2(kV )² log(1/V ) > 0.

Используя теорему о среднем значении, мы можем

записать оценку для максимального значения |u|_max

Этот инкремент совпадает с выражением для ин-

в этой области:

кремента неустойчивости Кроу [24] для двух ан-

∫

типараллельных точечных вихрей для идеальных

u³dr ≤ |u|max u2dr.

несжимаемых жидкостей.

Ω

154

ЖЭТФ, том 162, вып. 1 (7), 2022

Неустойчивость солитонов и коллапс звуковых волн...

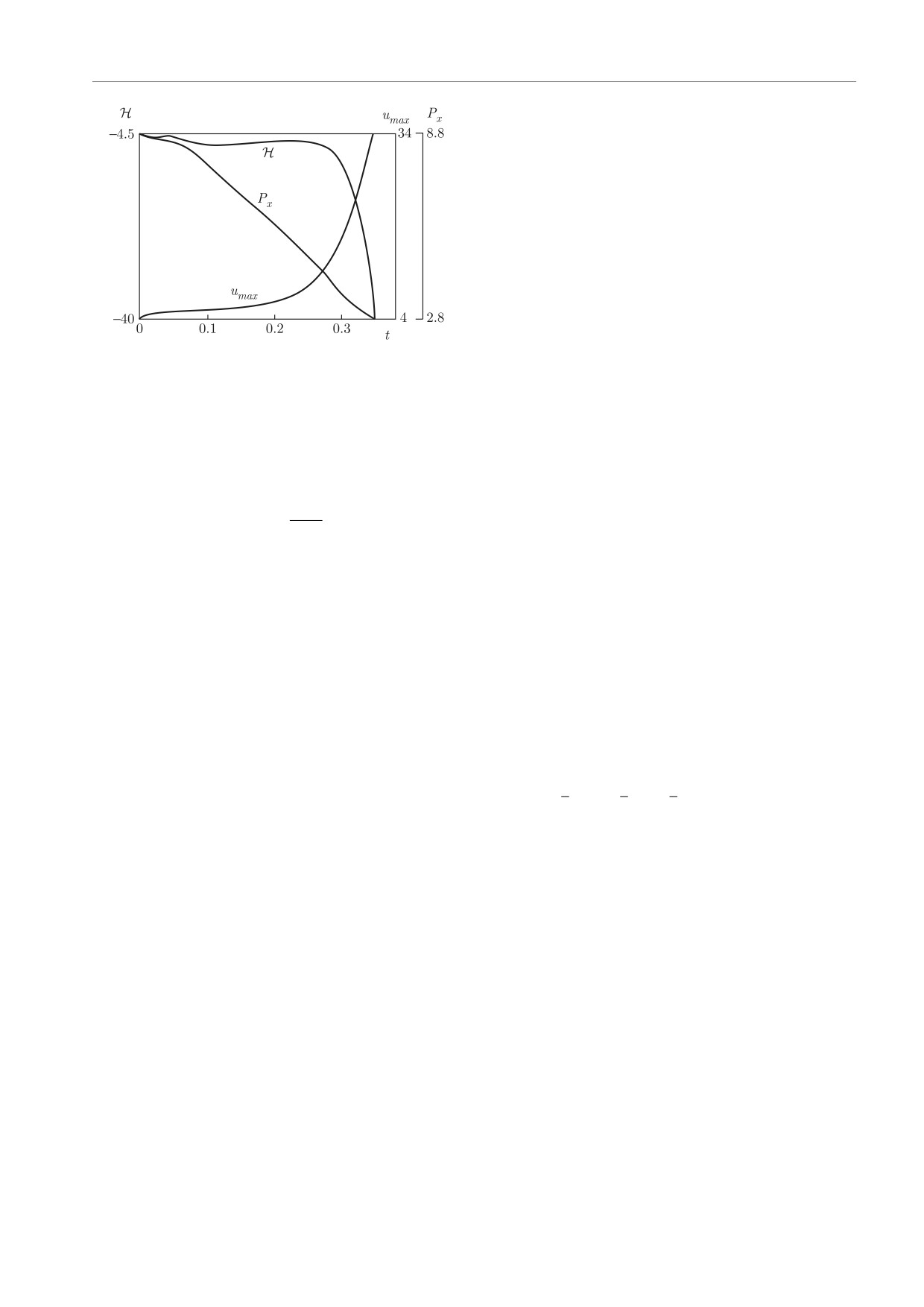
На рисунке представлены зависимости гамиль-

тониана H и P_x, вычисленные по области интегри-

рования, и максимальной амплитуды от времени.

Видно, что со временем происходит уменьшение им-

пульса P_x и увеличение |H| при одновременном ро-

сте max_r u, это как раз свидетельствует о том, что

коллапс является слабым.

Таким образом, можно сказать, что излучение

волн из области коллапса способствует коллапсу,

ускоряет его, что приводит к образованию слабых

особенностей.

4.1. Вариационный анзац

Зависимости гамильтониана H, Px и максимальной амп-

литуды от времени

Все изложенные выше соображения, однако, не

дают ответа на главный вопрос о конечности време-

ни формирования особенности. Мы приведем неко-

Используя это неравенство при выполнении условия

торые аргументы в пользу конечности этого време-

H_Ω < 0, можно получить следующую оценку для

ни, используя так называемый вариационный метод.

|u|_max [4]:

Следует отметить, что этот подход является доста-

точно грубым. Например, в задаче о релаксации со-

|H_Ω |

|u|_max ≥

(32)

литонов в одномерном НУШ с фокусирующей нели-

2P_Ω

нейностью, допускающим интегрирование методом

Отсюда видно, что за счет излучения волн из этой

обратной задач рассеяния, применение вариацион-

области отношение в правой части этого неравен-

ного подхода дает неправильный ответ. Вместо ко-

ства со временем будет только расти. Во-первых,

лебаний солитона, предсказываемых при примене-

излученные волны уносят положительную часть га-

нии этого метода, точное решение дает затухающие

мильтониана, поскольку вдали от этой области они

со временем колебания релаксационного типа [41].

становятся линейными, для которых нелинейность

Однако в задаче коллапса для трехмерного НУШ

стремится к нулю. Это приводит к уменьшению H_Ω

оказалось, что применение вариационного подхода

(т. е. гамильтониан становится более отрицательным

продемонстрировало качественно правильное пове-

из-за неограниченности H) и, соответственно, увели-

дение для описания режима сильного коллапса [6].

чению |H_Ω |. Во-вторых, в то же время P_Ω как поло-

Как известно, действие для уравнения КП (8)

жительная величина уменьшается. Отсюда следует,

может записываться как

∫ [

]

что отношение в (32) растет, а значит, увеличива-

S =

w_tw_x-

w^2xx-

(∇_⊥w)² +w³

dt dr,

(33)

ется |u|_max. Этот процесс, подобный испарению ка-

пель воды, приводит к формированию слабых син-

гулярностей, когда энергия захваченных в особен-

так что δS = 0 эквивалентно уравнению (8). Тесто-

ность звуковых волн E (с точностью до постоянного

вую функцию выберем в автомодельном виде:

множителя совпадающая с P ) формально в момент

коллапса обращается в нуль.

w = a^1/2b^-1f(ξ_∥,ξ_⊥), u = a^-1/2b^-1U(ξ_∥,ξ_⊥),

(34)

Численный эксперимент [3,4] по моделированию

где предполагается, что скейлинговые параметры a

звукового коллапса полностью подтвердил, что из-

и b являются неизвестными функциями времени t,

лучение из области каверны способствует коллап-

ξ∥ = x/a и ξ⊥ = r⊥/b автомодельные перемен-

су. В этих численных экспериментах для цилиндри-

ные. Функция U(ξ_∥, ξ_⊥) = ∂f/∂ξ_∥ есть решение (8)

чески-симметричных распределений (P_⊥ = 0) ста-

для трехмерного солитона с известными значениями

вились нулевые граничные условия для u по r и x,

интегралов I₁, I₂ и I₃, определяемых (13), (15), (16):

которые в силу нелокальности уравнения КП не со-

храняют ни H, ни P_x. Это позволило выяснить, как

I₁ = 6V P, I₂ = I₃ = 4V P.

излучение из области коллапса влияет на измене-

ния гамильтониана, импульса и максимального зна-

Подставляя тестовую функцию (34) в (33) и усред-

чения u.

няя по пространственным переменным, получаем

155

Е. А. Кузнецов

ЖЭТФ, том 162, вып. 1 (7), 2022

следующее выражение для лагранжиана в перемен-

и далее после исключения b определить зависи-

ных a и b:

мость a(t) вблизи особенности для обоих корней.

b_t

При a → 0

L=a

M - H(a,b).

I₂

2I₃

Здесь константа

b₁ =

a^5/2, b₂ =

a^3/2.

2I₃

I₁

∫

Отсюда для первого корня имеем

M =

fξ_⊥∇_ξ

⊥

Ud³ξ,

2I²³

Ma_t =

а H(a, b) уже известная функция, задаваемая (14)

I₂a³

при d = 3, исходя из скейлинговых преобразований.

Это приводит к сингулярному решению

Для данного лагранжиана уравнения Эйле-

a → (t₀ - t)1/4 ,

(37)

ра - Лагранжа записываются в виде

если константа M < 0. В этом случае вблизи мо-

∂H

Ma_t = -b

=a²b^-2I₂ - a^-1/2b^-1I₃,

(35)

мента коллапса t = t₀ в H(a, b) дисперсионный и

∂b

нелинейный члены компенсируют друг друга. Для

положительных M решение с особенностью отсут-

∂H

ствует.

Mb_t =b

Для другого корня b = b₂ при a → 0 уравнение

∂a

[

]

(35) асимптотически преобразуется к следующему:

= β -a^-3I₁ + ab^-2I₂ +

a^-3/2b^-1

I₃

(36)

I₁

Ma_t =-

2a²

Эти уравнения по построению имеют стационарное

которое при M > 0 имеет решение коллапсирующе-

решение в виде трехмерного солитона при a = b = 1.

го вида

Линейная устойчивость этого решения определяется

a → (t₀ - t)1/3 .

из линеаризованных уравнений (35), (36) для малых

возмущений α, β (a = 1 + α, b = 1 + β):

Для этой асимптотики нелинейный член в H (a, b) и

дифракционный член сокращаются.

Mα_t = V P (10α - 4β),

Ниже будет показано, что режим (37) реализует-

Mβ_t = V P (19α - 10β).

ся для квазиклассических начальных условий.

Отсюда следует, независимо от знака M, неустойчи-

4.2. Квазиклассический коллапс

вость этого решения с инкрементом

Рассмотрим начальные распределения u, при ко-

√

торых можно пренебречь как дисперсией, так и ди-

γ = ±2

фракцией. Тогда, по крайней мере вначале, времен-

ное поведение u будет определяться уравнением

Собственный вектор неустойчивой моды имеет один

и тот же знак для обоих компонентов α и β. Та-

u_t + 6uu_x = 0,

ким образом, солитонное решение представляет со-

где u зависит от r_⊥ как от параметра. Как извест-

бой седловую точку.

но, это уравнение описывает опрокидывание волны

Рассмотрим теперь, что происходит на нелиней-

или градиентную катастрофу, возникающую в неко-

ной стадии этой неустойчивости. Как упоминалось

торой точке r = r₀. Вблизи точки опрокидывания

выше, при фиксированном импульсе P гамильтони-

наше предположение относительно дисперсии и ди-

ан трехмерного уравнения КП представляет собой

фракции становится несправедливым, и мы должны

неограниченный снизу функционал. В данном слу-

учитывать как дифракционные, так и дисперсион-

чае мы имеем дело с неограниченной снизу функци-

ные члены. В результате за счет таких линейных

ей H(a, b).

эффектов вблизи этой точки будет развиваться ос-

Ввиду гамильтоновости система (35), (36) сохра-

циллирующая пространственная структура. Напом-

няет энергию E = H(a, b), что позволяет выразить b

ним, что в одномерном случае такого рода структу-

через a:

ра имеет вид расплывающегося со временем соли-

[

√

]

тонного цуга [42], характерного для бесстолкнови-

b^-1 =

a^-1/2I3 ± a-1I23 - I1I2 + 2a2EI2

тельных ударных волн.

I₂a2

156

ЖЭТФ, том 162, вып. 1 (7), 2022

Неустойчивость солитонов и коллапс звуковых волн...

В трехмерном случае, как мы выяснили, все ти-

В результате вместо (40) и (39) для n = 0 получаем

пы солитонов неустойчивы. Одномерные солитоны

∂A_n

∂

неустойчивы по отношению к поперечным модуля-

div(A²ⁿv_n) + 3

s_n = 0,

(41)

∂t

2A_n

∂x

циям благодаря неустойчивости КП. То же утверж-

дение верно для двумерных и трехмерных солито-

нов [14]. Нелинейной стадией этой неустойчивости

s_n

Φ_nt + ω(∇Φ_n) + 3Φ_nx

= 0,

(42)

должен быть коллапс. Это означает, что вместо цу-

A_n

га солитонов в одномерной геометрии следует ожи-

где

∑

дать образования осциллирующих структур, содер-

Φ_n = nΦ, s_n =

An1An2.

жащих коллапсирующие солитоны.

n=n1+n2

Для описания структур такого типа нужно обра-

титься к квазиклассической теории. Решение в этом

Для нулевой гармоники возникает отдельное урав-

случае следует представлять в виде

нение,

∂A₀

∂

〈u²〉 = 0.

(43)

u = u(r,t,Φ(r,t)),

∂t

∂x

где u как функция фазы Φ является 2π-периоди-

Здесь

ческой, а относительно двух первых аргументов r и

∑

〈u²〉 =

A²ⁿ = s₀.

медленно меняющейся функцией. Зависимость

n=-∞

Φ(r, t) предполагается такой, что ее производные

Φ_t и ∇Φ являются также медленно меняющимися

Следует отметить, что эта бесконечная система яв-

функциями от r и t.

ляется переопределенной: из (41), (42) для каждых

Вначале рассмотрим линейный случай, когда u

n, m = 0 следуют соотношения

подчиняется линейному уравнению КП:

π_n(r, t) = π_m(r, t),

(44)

∂

(u_t + u_xxx) = ∆_⊥u.

(38)

∂x

где

В этой ситуации можно ограничиться зависимостью

s_n

π_n(r, t) = n²Φ^2x -

в виде одной гармоники:

A_n

На первый взгляд кажется, что эти уравнения весь-

u = Ae^iΦ + c.c.

ма сложны и вряд ли могут быть проанализиро-

Тогда первый порядок в квазиклассическом прибли-

ваны. В действительности данная система уравне-

жении дает уравнение Гамильтона - Якоби,

ний полностью эквивалентна уравнениям, которые

следуют из процедуры Уизема [42, 44] для случая

Φ_t + ω(∇Φ) = 0,

(39)

КДВ. Прежде всего, легко найти число независи-

где

мых функций с учетом всех ограничений (44). Это

k^2⊥

ω = ω(k) = -k^3x -

всего лишь три функции, в качестве которых мы мо-

k_x

жем, например, выбрать 〈u〉, 〈u²〉 и Φ. Более того,

есть закон дисперсии (38), а k = ∇Φ соответствен-

условия (44) можно разрешить, если представить u

но волновой вектор.

с помощью эллиптической функции Вейерштрасса

В следующем порядке получаем уравнение

в виде кноидальной волны (см., например, [45]). В

непрерывности для A² (здесь для простоты ампли-

результате можно получить обычную форму урав-

туда A предполагается действительной величиной),

нений Уизема. Однако, по нашему мнению, уравне-

∂A

ния (41), (43) для исследования квазиклассическо-

div(A²v) = 0,

(40)

∂t

го коллапса представляются более удобными, чем

где v

= ∂ω(k)/∂k

групповая скорость (ср. с

уравнения Уизема.

[6, 43]).

Из-за нелинейности исходного уравнения

(8)

4.3. Иерархия коллапсов

необходимо учитывать все гармоники,

Будем искать решение системы (41)-(43) в авто-

∑

A_ne^inΦ,

модельном виде:

n=-∞

(

)

r⊥

A_n = A_-n = A^∗n.

A_n(r, t) = (t₀ - t)^-αf_n

(45)

(t₀ - t)^β

(t₀ - t)^γ

157

Е. А. Кузнецов

ЖЭТФ, том 162, вып. 1 (7), 2022

∫

нижнюю границу этого семейства, где критерий ква-

Φ(r, t) = λ²

зиклассичности нарушается. Значение α = 2/3 отве-

(t₀ - t)^κ+1

(

)

чает автомодельному решению трехмерного уравне-

r⊥

+ (t₀ - t)^-κϕ

(46)

ния КП, описывающему наиболее быстрый слабый

(t₀ - t)^β

(t₀ - t)^γ

коллапс.

где t₀

время коллапса, константа λ² > 0, α, β, γ и

κ неизвестные показатели.

После подстановки (45), (46) в систему (41)-(43)

5. ЗАКЛЮЧЕНИЕ

легко найти, что только один показатель является

свободным (скажем, пусть это будет α), в этом слу-

Таким образом, мы продемонстрировали воз-

чае все остальные индексы выражаются через него:

можность коллапса звуковых волн в средах с

положительной дисперсией на основе трехмерного

β = 1 - α, γ = 1 - α/2, κ = 3α/2 - 1.

уравнения Кадомцева - Петвиашвили. Этот процесс

можно рассматривать как нелинейную стадию

Таким образом, мы имеем целое семейство автомо-

КП-неустойчивости солитонов КДВ в поперечном

дельных решений (более точно

автомодельных

направлении. Эта неустойчивость имеет простое

подстановок). Только некоторые из этих решений

объяснение, данное впервые Кадомцевым [2]. Соли-

имеют физический смысл. Согласно (45), (46), про-

тоны при положительной дисперсии представляют

дольный размер коллапсирующей области (кавер-

собой области с пониженной плотностью, скорость

ны) и ее поперечный размер пропорциональны со-

которых убывает с увеличением амплитуды соли-

ответственно (t₀ - t)^β и (t₀ - t)^γ. Физическое требо-

тона. По этой причине при модуляции солитона в

вание состоит в том, что полный импульс каверны

поперечном направлении к его распространению

P (фактически это энергия звуковых волн с точно-

области с пониженной амплитудой обгоняют об-

стью до постоянного множителя) во время коллапса

ласти с большей амплитудой. В результате фронт

благодаря излучению может только уменьшаться:

солитона испытывает неустойчивость самофоку-

∫

сирочного типа, которая приводит к аккумуляции

P_cav =

u²d³r ∝ (t₀ - t)^3-4α,

солитонного распределения. Этот факт является

cav

ключевым моментом для понимания природы

неустойчивости КП. Важно, что характер неустой-

т. е. α ≤ 3/4. Отсюда видно, что режиму сильно-

чивости сохраняется и на ее нелинейной стадии,

го коллапса будет соответствовать α = 3/4. Следу-

которая в трехмерном случае ведет к коллапсу.

ет отметить, что автомодельность для данного типа

При меньших размерностях, например в двумер-

коллапсов та же самая, что и для асимптотики (37)

в случае вариационного анзаца. Это дает основание

ном случае, солитон уравнения КП

ламп

реализует минимум гамильтониана при фиксиро-

считать, что такой режим может существовать. Все

остальные коллапсы являются слабыми.

ванном импульсе P и по этой причине оказывается

устойчивым по Ляпунову. В трехмерной геометрии

Для автомодельного семейства (45), (46) ниж-

няя граница определяется исходя из квазиклассиче-

солитоны представляют собой седловые точки

гамильтониана и по этой причине оказываются

ского критерия. Последнее означает, что отношение

неустойчивыми. Развитие этой неустойчивости

между характерным периодом, ∼ ω^-1 = (∂_tΦ)^-1,

и характерным временем изменения амплитуды

приводит к коллапсу, одним из критериев кото-

рого является неограниченность гамильтониана H

∼ (t₀ - t), или отношение длины волны k^-1x

= (∂_xΦ)^-1 к характерному пространственному раз-

снизу при фиксированном импульсе P . Коллапс в

этом случае можно понимать как процесс падения

меру амплитуды, должны быть большими (≫ 1).

Оба эти отношения приводят к одному и тому же

частицы в самосогласованном неограниченном

снизу потенциале. Благодаря неограниченности

критерию:

гамильтониана образование особенности оказыва-

ω(t₀ - t) ∝ (t₀ - t)^1-3α/2,

ется возможным за счет излучения волн малой

амплитуды из областей, имеющих отрицательные

k_x(t₀ - t)^1-α ∝ (t₀ - t)^1-3α/2.

значения H, что способствует коллапсу. При этом

Отсюда видно, что при α > 2/3 критерий квазиклас-

излучение способствует формированию слабого

сичности улучшается по мере приближения к точ-

коллапса, когда захватываемая в особенность энер-

ке коллапса. Значение α = 2/3 представляет собой

гия волн (совпадающая с точностью до множителя

158

ЖЭТФ, том 162, вып. 1 (7), 2022

Неустойчивость солитонов и коллапс звуковых волн...

с L₂-нормой) формально стремится к нулю по мере

грируемых моделей. Сравнительно недавно было

приближения к точке особенности. Показано, что

продемонстрировано, что трехмерное уравнение

при квазиклассическом описании коллапса звуко-

КП также допускает представление Хироты [29,30].

вых волн с положительной дисперсией возможно

Однако до сих пор все построенные решения для

целое семейство автомодельных коллапсирующих

трехмерного КП, основанные на этом подходе, ока-

режимов, начиная с сильного, когда захваченная в

зываются только двумерными, см. также [31-34].

сингулярность энергия конечна, вплоть до слабых

Поэтому одна из главных задач

это задача

коллапсов, сопровождаемых волновым излучением.

построения точных трехмерных решений, имеющих

Нижняя граница этого семейства соответствует

физический смысл. Необходимо подчеркнуть, что,

автомодельному решению трехмерного уравнения

строго говоря, существование представления Хи-

КП, которое описывает наиболее быстрый из сла-

роты не гарантирует наличие представления Лакса.

бых коллапсов. Тенденция к уменьшению H при

коллапсе за счет излучения было впервые проде-

Благодарности. Автор благодарит А. М. Кам-

монстрировано в численном моделировании [3, 4]. В

чатного и Ю. А. Степанянца за полезные обсужде-

этих численных экспериментах было показано, что

ния и замечания.

гамильтониан каверны становится со временем все

Финансирование. Работа выполнена при фи-

более и более отрицательным, одновременно с этим

нансовой поддержке Российского научного фонда

значение P уменьшается, что способствует росту

(грант № 17-01-00622).

амплитуды в коллапсирующей области.

Несмотря на предсказания иерархии квазиклас-

сических коллапсов, роли излучения в этих процес-

ЛИТЕРАТУРА

сах и пр., в этой проблеме существует множество

Б. Б. Кадомцев, В. И. Петвиашвили, ДАН СССР

открытых вопросов. С нашей точки зрения, наибо-

192, 753 (1970) [Sov. Phys. Dokl. 15, 539 (1970)].

лее важным является вопрос относительно точно-

го критерия коллапса для трехмерного уравнения

Б. Б. Кадомцев, Коллективные явления в плазме,

КП (8), причем такого же уровня строгости, как и

Физматгиз, Москва (1976).

критерий Власова - Петрищева - Таланова для дву-

Е. А. Кузнецов, С. Л. Мушер, А. В. Шафаренко,

мерного фокусирующего НУШ [25] или его обобще-

Письма ЖЭТФ 37, 204 (1983) [JETP Lett. 37, 241

ние для трехмерного случая, найденное Захаровым

(1983)].

[26] (о других обобщениях см. [46]). Эти критерии

дают достаточное условие возникновения коллапса

Е. А. Кузнецов, С. Л. Мушер, ЖЭТФ 64, 947

для начальных распределений с отрицательным га-

(1986) [Sov. Phys. JETP 64, 947 (1986)].

мильтонианом. Следует особо отметить, что крите-

В. Е. Захаров, Е. А. Кузнецов, УФН 182, 569

рий для трехмерного уравнения КП, но с кубиче-

(2012) [Phys. Usp. 55, 535 (2012)].

ской нелинейностью фокусирующего типа, был по-

лучен в работе Турицына и Фальковича [47]. Соглас-

В. Е. Захаров, Е. А. Кузнецов, ЖЭТФ 91, 1310

но этой работе, достаточным условием для коллапса

(1986) [Sov. Phys. JETP 64, 773 (1986)].

также является отрицательность гамильтониана.

В. Л. Гуревич, Кинетика фононных систем, Нау-

Другой открытый вопрос касается построения

ка, Москва (1980).

аналитического решения для трехмерного уравне-

ния КП. Напомним, что, как было показано в [11],

E. P. Gross, Nuovo Cim. 20, 454 (1961).

двумерное уравнение КП допускает представление

Л. П. Питаевский, ЖЭТФ 40, 646 (1961) [Sov.

Лакса и соответственно применение метода об-

Phys. JETP 13, 451 (1961)].

ратной задачи рассеяния, использование которого

показало большую эффективность в аналитических

10.

V. E. Zakharov and E. A. Kuznetsov, Physica D 8,

исследованиях двумерного уравнения КП. Доста-

455 (1986).

точно здесь упомянуть работу [12], в которой было

11.

В. С. Дрюма, Письма в ЖЭТФ 19, 753 (1974)

построено решение в виде лампа и исследована зада-

[JETP Lett. 19, 387 (1974)].

ча о рассеянии двумерных солитонов. Как известно,

существует другой подход, так называемый метод

12.

S. V. Manakov, V. E. Zakharov, L. A. Bordag,

Хироты [28], который позволяет строить некоторые

A. R. Its, and V. A. Matveev, Phys. Lett. A 63, 205

аналитические решения для большого числа инте-

(1977).

159

Е. А. Кузнецов

ЖЭТФ, том 162, вып. 1 (7), 2022

13.

В. И. Петвиашвили, Физика плазмы 2, 469 (1976)

33.

Dan-Dan Zhang, Lei Wang, Lei Liu, Tai-Xing Liu,

[Sov. J. Plasma Phys. 2, 257 (1976)].

and Wen-Rong Sun, Commun. Theor. Phys. 73,

095001 (2021).

14.

Е. А. Кузнецов, С. К. Турицын, ЖЭТФ 82, 1457

(1982) [Sov. Phys. JETP 55, 844 (1982)].

34.

О. В. Капцов, Д. О. Капцов, Прикл. мех. тех. физ.

62, 142 (2021) [J. Appl. Mech. Tech. Phys. 62, 649

15.

R. Blaha, E. A. Kuznetsov, E. W. Laedke, and

(2021)].

K. H. Spatschek, in Nonlinear World, Proc. of IV

Workshop Nonlinear and Turbulent Processes in Phy-

35.

E. A. Kuznetsov, A. M. Rubenchik, and V. E. Zakha-

sics, ed. by V. G. Bar’yakhtar et al., World Sci., Sin-

rov, Phys. Rep. 142, 103 (1986).

gapore (1990), Vol. 1, pp. 25-36.

36.

Yu. S. Kivshar and D. E. Pelinovsky, Phys. Rep. 331,

16.

R. Blaha, E. W. Laedke, and K. H. Spatschek,

117 (2000).

Physica D 40, 249 (1989).

37.

A. I. Dyachenko and E. A. Kuznetsov, Physica D 87,

17.

E. A. Kuznetsov, Phys. Lett. A 101, 314 (1984).

301 (1995).

18.

Е. А. Кузнецов, С. К. Турицын, ЖЭТФ 94, 119

38.

В. И. Шрира, ДАН СССР 308, 732 (1989) [Trans.

(1988) [Sov. Phys. JETP 67, 1583 (1988)].

USSR Acad. Sci., Earth Sci. Sec. 308, 276 (1989)].

19.

G. A. Swartzlander and C. T. Law, Phys. Rev. Lett.

39.

Д.Е. Пелиновский, Ю.А. Степанянц, ЖЭТФ 104,

69, 2503 (1992).

3387 (1993) [D.E. Pelinovsky and Yu.A. Stepanyats

JETP 77, 602 (1993)].

20.

C. T. Law and G. A. Swartzlander, Opt. Lett. 18,

586 (1993).

40.

В. Е. Захаров, Письма в ЖЭТФ 22, 364 (1975)

[JETP Lett. 22, 172 (1975)].

21.

D.E. Pelinovsky, Yu.A. Stepanyants, and Yu.S.

41.

E. A. Kuznetsov, A. V. Mikhailov, and I. A. Shimo-

Kivshar, Phys. Rev. E 51, 5016 (1995).

khin, Physica D 87, 201 (1995).

22.

C. A. Jones and P. H. Roberts, J. Phys. A 15, 2599

42.

А. В. Гуревич, Л. П. Питаевский, Письма в ЖЭТФ

(1982).

17, 268 (1973); ЖЭТФ 65, 590 (1973) [Sov. Phys.

23.

E. A. Kuznetsov and J. J. Rasmussen, Phys. Rev.

JETP 38, 291 (1974)].

E 51, 4479 (1995).

43.

Е. А. Кузнецов, С. К. Турицын, Физика плазмы

24.

S. C. Crow, AIAA J. 8, 2172 (1970).

16, 901 (1990) [Sov. J. Plasma Phys. 16, 524 (1990)].

25.

С. Н. Власов, В. А. Петрищев, В. И. Таланов, Изв.

44.

G. B. Whitham, Linear and Nonlinear Waves, John

вузов. Радиофизика 14, 1453 (1971) [Radiophys.

Wiley & Sons (2011).

Quant. Electron. 14, 1062 (1971)].

45.

Е. А. Кузнецов, А. В. Михайлов, ЖЭТФ 40, 855

26.

В. Е. Захаров, ЖЭТФ 62, 1745 (1972) [Sov. Phys.

(1974) [Sov. Phys. JETP 40, 855 (1975)].

JETP 35, 908 (1972)].

46.

E. A. Kuznetsov, S. K. Turitsyn, J. J. Rasmussen,

27.

В. Е. Захаров, Е. А. Кузнецов, ЖЭТФ 113, 1892

and K. Rypdal, Physica D 87, 273 (1995).

(1998) [Sov. Phys. JETP 86, 1035 (1998)].

47.

С. К. Турицын, Г. Е. Фалькович, ЖЭТФ 89, 258

(1985) [Sov. Phys. JETP 62, 146 (1985)].

28.

R. Hirota, The Direct Method in Soliton Theory,

Cambridge Univ. Press, Cambridge (2004).

29.

Wen-Xiu Ma, Comm. Nonlin. Sci. Numer. Simul. 16,

2663 (2011).

30.

Chao Qian, Ji-Guang Rao, and Jing-Song He,

Chinese Phys. Lett. 33, 110201 (2016).

31.

X. B. Wang, S. F. Tian, C. Y. Qin, and T. T. Zhang,

Appl. Math. Lett. 72, 58 (2017).

32.

J. J. Mao, S. F. Tian, X. J. Yan, and T. T. Zhang,

Int. J. Numer. Methods Heat Fluid Flow 29, 3417

(2019).

160